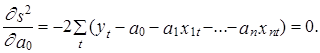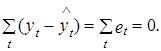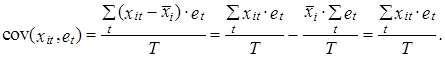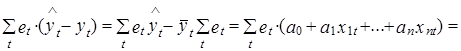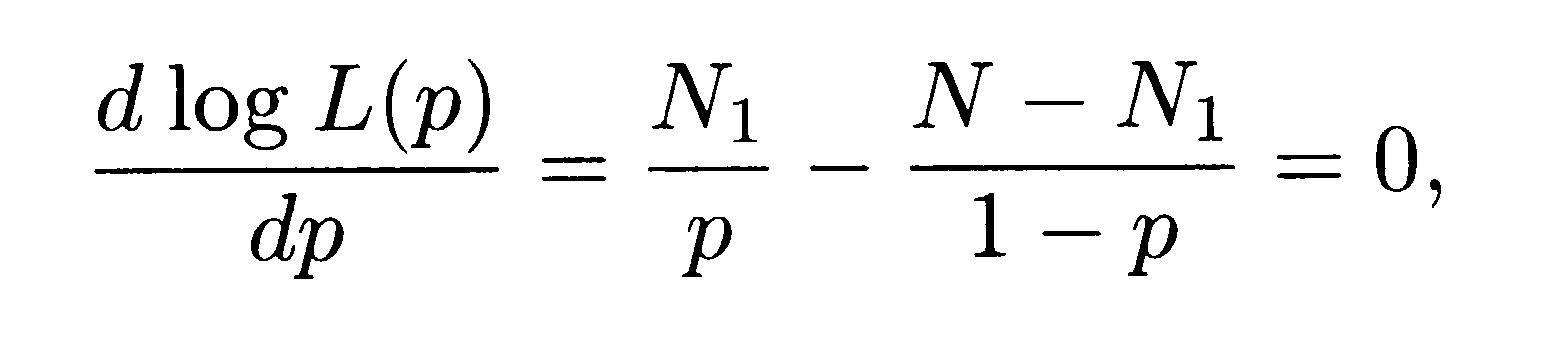Желательные свойства теоретической ошибки эконометрика - Решение и исправление самых разных ошибок на TopOshibok.ru

В данном разделе рассматриваются некоторые подходы к проверке наличия стандартных свойств (2.20)–(2.23) у “истинной” ошибки эконометрической модели et на основе анализа соответствующих свойств фактической ошибки еt.

В этой связи сразу следует отметить, что наличие у ошибки еt каждого из этих свойств не всегда является доказательством присутствия соответствующего свойства и у ошибки et. Иными словами, наличие определенных свойств у ошибки еt не является необходимым условием существования этих свойств и у истинной ошибки et. Дело в том, что некоторые свойства фактической ошибки еt являются своего рода ограничениями на ее значения, которые вытекают из критерия МНК как метода оценки параметров модели, т. е. выполняются практически всегда. В то же время свойства “истинной” ошибки определены теоретическими предпосылками, положенными в основу этой модели. Поэтому вывод о правомочности использования МНК на основе существования таких “априорных” свойств фактической ошибки модели не может считаться обоснованным.

Вместе с тем, если фактическая ошибка et не обладает некоторым свойством, то можно говорить о том, что теоретические предпосылки эконометрической модели не подтверждены полученными эмпирическими данными и “качество” ее уравнения не достаточно высоко.

В этой связи отметим, что к “априорным” свойствам фактической ошибки еt, которые выполняются при использовании МНК всегда, относятся свойства (2.20) и (2.23). Приведем доказательства этого утверждения.

1. Сумма значений фактической ошибки равна нулю

Условие (2.43) является аналогом свойства (2.20), поскольку рассматривается как оценка математического ожидания фактической ошибки.

Использование МНК обеспечивает выполнение условия (2.43) автоматически. В самом деле, дифференцируя сумму квадратов ошибки еt s2 (см. выражение (2.31)) по параметру a0 , получим

Из этого выражения автоматически вытекает, что

2. Произведение транспонированной матрицы Х¢ на вектор фактической ошибки е равно нулевому вектору.

Х¢е=0. (2.44)

Условие (2.44) является аналогом условия (2.23), поскольку произведение каждой строки матрицы Х¢ на вектор e представляет собой скалярное произведение вектора значений соответствующих факторов хit на вектор ошибки.

Внимание!

Если вам нужна помощь в написании работы, то рекомендуем обратиться к
профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные
корректировки и доработки. Узнайте стоимость своей работы.

Тогда векторно-матричное выражение (2.44) можно представить в виде следующей системы скалярных произведений:

где х0t º1 для t=1, 2,…, Т.

Для доказательства справедливости выражения (2.44) представим вектор ошибки е в виде разности фактических и расчетных значений независимой переменной yt

е=у –=у–Х×a.

Получим

Х¢×e=Х¢×(у–Х×a)=Х¢×у–Х¢×Х×a=(Х¢×Х)–1×Х¢×у–(Х¢×Х)–1 ×(Х¢×Х)×a=0.

Из (2.44) и (2.45) автоматически следует, что

Еще раз отметим, что выполнение условий (2.45) и (2.46) не может считаться доказательством отсутствия корреляционных взаимосвязей между значениями независимых переменных хit и “истинной” ошибкой et. В данном случае эти условия сами являются следствием результатов применения МНК для оценки коэффициентов эконометрической модели, т. е. они как бы выполняются автоматически. Для некоторых классов эконометрических моделей, как это будет показано в главах V и VIII, уже априорно, т. е. до построения модели, можно доказать существование ковариационной связи между некоторыми независимыми переменными и истинной ошибкой модели et. Выполнение условия (2.45) в таком случае не является свидетельством корректности применения “классического” МНК для оценки ее параметров.

3. Из условий (2.43) и (2.45) также вытекает, что сумма произведений отклонений расчетных значений независимых переменных от ее среднего значения и расчетных значений ошибки равна нулю.

Раскрывая скобки в выражении (2.47), непосредственно получим

Выражение (2.47) включает в себя также и следующее условие:

означающее, что сумма произведений расчетных значений зависимой переменной и ошибки еt равна нулю.

Здесь еще раз подчеркнем, что условия (2.43)–(2.48) для фактической ошибки еt эконометрической модели автоматически вытекают из метода оценки ее параметров – МНК, и поэтому их непосредственно нельзя переносить на условия (2.20)–(2.23), характеризующие свойства истинной ошибки e t.

Вместе с тем, условия (2.21) и (2.22) для фактической ошибки еt не являются “априорными”. Они выполняются лишь в том случае, если исходные предпосылки МНК оказались справедливыми для данной модели, что является свидетельством обоснованного выбора формы ее уравнения, состава учтенных факторов и т. п.

Получить выполненную работу или консультацию специалиста по вашему
учебному проекту

Узнать стоимость

Как отмечалось в п.2.1, по ограниченным
данным выборки объема n можно
построить модель лишь с некоторой
точностью. её параметры a и b
являются оценками истинных значений α
и β, которые определяются генеральной
совокупностью объема N >> n.
Последней приписываются вероятностные
свойства с применением аксиом теории
вероятности, определений случайной
величины, вероятности, плотности
вероятности, оператора усреднения и
т.д. В рамках свойств генеральной
совокупности объема N рассматривается
спецификация модели линейной
регрессии

в
которой α, β, x_i–
детерминированные (фиксированные или
известные) величины, а значения показателя
y_i и ошибки модели _i– случайные величины (СВ) с
заданным распределением (например,
плотности вероятности). Часто y_i,
_iсчитаются
нормальными СВ (НСВ), тогда модель
называют нормальной.

Ограниченные данные выборки объема n
<< N позволяют вместо точной
модели (2.1) с параметрами α и β
построить приближенную модель (2.2)

Здесь е_і – остатки
регрессии, вероятностные свойства
которых считаются аналогичными ошибкам
_i, а
a, b – некоторые оценки (приближенные
значения) параметров модели.

Мы
будем оценивать дисперсии и
среднеквадратичные ошибки (СКО) для
оценок параметров модели и величины :

;

где M[X], D[X] – математическое
ожидание и дисперсия случайной величины
Х.

Для непрерывной случайной величины Х
с плотностью вероятности р(х)
они определяются как

Следовательно, для точного определения
того или иного параметра случайной
величины достаточно знать (или задать)
её распределение плотности вероятности.

2.4.1. Основные условия (гипотезы) анализа ошибок

Поскольку в корреляционно-регрессионном
анализе мы опираемся на методы
математической статистики и теории
вероятности, любые оценки ошибок
моделирования являются корректными
лишь при выполнении исходно принятых
условий (гипотез) в отношении величин
и переменных, входящих в модель. Примем
следующие гипотезы:

1. В спецификации модели (2.1) фактор х
и параметры модели α, β – детерминированные
величины, а показатель у_i
и ошибки моделирования _i
– случайные величины.

2. Ошибки моделирования имеют нулевое
среднее значение и некоррелированны:

Невыполнение второго условия называют
автокорреляцией ошибок модели.

3. Дисперсия ошибок моделирования _i
показателя не зависят от номера i
(гомоскедастичность):

Невыполнение этого условия называют
гетероскедастичностью.

Дополнительным условием, которое может
не выполняться в ряде случаев, является
свойство нормальной модели:

4. Ошибки _i
являются нормальными СВ:  N(0,
²) c нулевым
математическим ожиданием m_ε
= 0 и дисперсией ².

2.4.2. Ошибки оценок параметров модели

Покажем сначала, что оценки МНК параметров
линейной модели являются несмещенными,
т.е. математические ожидания оценок
совпадают с истинными значениями
параметров:

M[b] = β, M[a] = α.

Действительно, согласно (2.12) и (2.7) имеем:

. (2.27)

С учетом (2.1), детерминированности v_iи условия

M[_i]
= 0 гипотезы 2 получим в результате
усреднения оценки b в рамках
генеральной совокупности

Здесь использовано одно из свойств для
коэффициентов v_i

(2.28)

которые
следуют из (2.27).

Аналогично, для параметра a с учетом
(2.6) и несмещенности b получим

Таким
образом, обе оценки МНК параметров
линейной модели являются несмещенными,
то есть сходятся при неограниченном
увеличении объема выборки к точным
значениям параметров α и β. Поэтому при
определении их дисперсий усредняются
квадраты разностей оценок и истинных
значений параметров.

Определим дисперсию коэффициента
регрессии. Известными свойствами
дисперсии СВ Х, умножаемой или
складываемой с константой с, являются:

. (2.29)

Тогда
с использованием (2.27) – (2.29)

.(2.30)

Здесь принято во внимание, что дисперсии
D[y_i] =D[_i],
так как показатель и ошибка модели
как случайные величины отличаются на
детерминированное слагаемое a+ bx_i.

Дисперсию
постоянной составляющей модели определим
как

. (2.31)

Так как

. (2.32)

, (2.33)

то с
учетом (2.32), (2.33) дисперсия (2.31) становится
равной

. (2.34)

Более
сложным является определение оценки
дисперсии ошибок модели. Опуская вывод,
приведем окончательную формулу для
несмещенной оценки дисперсии ошибок
моделирования

, (2.35)

выраженную
через остатки регрессии (2.2).

Выражения (2.30), (2.34) дают точные значения
дисперсий оценок параметров модели,
однако практически воспользоваться
ими нельзя, так как точное значение
дисперсии ошибок ²
неизвестно (оно определяется из
генеральной совокупности, а не из
выборки). На основе выборочных данных
можно лишь оценить с помощью (2.35) эту
дисперсию. Поэтому на практике в формулы
(2.31), (2.35) вместо ²
подставляют её оценку (2.35) и получают
оценки дисперсий параметров b и a:

, (2.36)

. (2.37)

Эти
оценки используют лишь выборочные
данные. СКО этих оценок равны положительным
значениям квадратного корня из дисперсий.

лияние
СКО оценок параметров на точность модели
отражается на рис.2.5, а, б. Сдвиг
постоянной составляющей в пределах а
 _а
не является существенным при моделировании,
так как он не изменяется при всех
значениях фактора х и его можно
легко скорректировать. Более существенные
последствия имеет ошибка в определении
коэффициента регрессии b. Как видно
из рис.2.5, б, ошибки в прогнозах
показателя у^* становятся тем
больше, чем больше отклонение от среднего
значения фактора х. Стандартное отклонение
у^*  _b
имеет место при

.
В общем случае граничная ошибка регрессии
(с доверительной вероятностью 68%)
пропорциональна величине

.
Иначе говоря, чем больше отличается
значение фактора х при прогнозе от
среднего, тем больше можно ошибиться в
результате прогнозирования. Ясно также,
что СКО _b
уменьшается с ростом объема выборки n,
так как растет число положительных
слагаемых в знаменателе (2.36).

а б

Рис.2.5

Пример 2.2. Оценим
СКО и доверительные интервалы оценок
параметров модели примера 2.1 для малой
выборки объема n
= 5, приняв доверительную вероятность Р
= 0,954.

Оценка дисперсии
ошибок модели согласно (2.36) и расчетов,
приведенных в таблице 2.1, равна

Тогда СКО оценок
b
= 0,588 a
= – 0,529 параметров модели в соответствии
с (2.37), (2.38) равны

Ошибки оказались
сравнительно большими в связи с малым
объемом выборки (n
= 5). Найденные значения СКО являются
точечными ошибками оценок параметров.
Определим далее доверительные интервалы
этих оценок. Для нормальной модели
граничная ошибка равна

Δ = tσ,

где
параметр доверия t
= 1 при доверительной вероятности Р
= 0,68,

t = 2
при Р
= 0,954,

t =
3 при Р
= 0,997.

В нашем примере

t = 2
(Р
= 0,954), Δ_b
= 0,256, Δ_a
= 1,678,

тогда
доверительные интервалы для истинных
значений параметров 
и α с границами b

Δ_b,
a

Δ_a
определяются как 

[0,332; 0,844],

α 
[ – 2,207; 1,149].

Это значит, что
при доверительной вероятности 95,4%
коэффициент регрессии
b (и,
соответственно, наклон прямой линии
модели) может измениться более чем в
2,5 раза, а девиация (отклонение) постоянной
составляющей а
близка к 
1,7 у.е. Очевидно, подобные ошибки малой
выборки неприемлемы для практических
целей, поэтому реальные объемы выборки
должны составлять десятки, сотни и более
элементов.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Условия Гаусса-Маркова
Свойства коэффициентов регрессии
проверка гипотез
Источники
1. Доугерти, К. Введение в эконометрику : учеб. для экон.
специальностей вузов / К. Доугерти; пер. с англ. Е. Н. Лукаш
[и др.]. – М. : ИНФРА-М, 1997. [Глава 3].
2. Магнус, Я. Р. Эконометрика. Начальный курс : учеб. /
Я. Р. Магнус, П. К. Катышев, А. А. Пересецкий. – 3-е изд.,
перераб. и доп. – М. : Дело, 2000. [Глава 2, разделы 2.3-2.4]
Теоретическая регрессия
u4
u1
u2
u3
случайного члена
yi = α + βxi + ui
где i=1,…,n ;
xi — неслучайная (детерминированная) величина, yi и ui — случайные величины.
yi – зависимая переменная, состоит из (1) неслучайной составляющей α + βxi,
где xi – объясняющая (независимая) переменная, а постоянные α и β
параметры уравнения;
(2) случайного члена (ошибки) ui .
xi и yi — координаты точек Р1 , Р2 , Р3, Р4, это фактические значения (реально
собранные данные/наблюдения).
Используя метод МНК получаем
^
расчетную регрессию (y = a + b x )
i
i
где a и b – оценки параметров теоретической регрессии, т.е. α и β.
Обращаем внимание, что a и b зависят от исходных значений y!
А y зависит от случайного члена/ошибок, yi = α + βxi + ui
значит и оценки a и b зависят от случайного члена/ошибок ui
Основная наша задача определить значения истинных
параметров α и β.
Методом МНК мы находим их оценки – a и b,
и они оказываются зависимы от случайной
составляющей — от случайного члена/ошибок ui .
Для того чтобы судить насколько a и b являются
точными/хорошими оценками истинных
параметров α и β нам необходимо знать свойства
случайной составляющей — ui .
=> Пришлось ввести предположения о случайном
члене ui
Предположения о случайном члене ui
(Условия Гаусса-Маркова)
Пусть у нас есть модель парной линейной регрессии yi = α + βxi + ui
I. Регрессионная модель линейна по параметрам (коэффициентам), корректно
специфицирована (т.е. выбрана правильная функциональная форма, включены
необходимые факторы и нет лишних), и содержит аддитивный случайный член (ui);
II. Случайный член имеет нулевое математическое ожидание E(ui) = 0;
III. Случайный член имеет постоянную дисперсию для всех наблюдений,
Var(ui)=D(ui)= σu2 , i= 1,…,n (гомоскедастичность)
Замечание: величина σu неизвестна (основана на данных генеральной совокупности),
одна из задач регрессионного анализа состоит в том чтобы оценить σu (найти оценку
для этого параметра).
IV. Случайные члены с разными номерами не коррелируют друг с другом,
Cov(ui, uj) = 0 (для i ǂ j);
V. Объясняющая переменная не коррелированна со случайным членом, Cov(ui,
xi ) = 0 ;
Тогда оценки МНК (а и b) являются наиболее эффективными и несмещенными
оценками коэффициентов регрессии [BLUE (Best Linear Unbiased Estimator)].
Классическая линейная регрессия
VI. Предположение о нормальности распределения случайного
члена/ошибок/возмущений
ui ~ N (0,  ),
2
u
тог да
коэффициенты регресии также будут иметь нормальное распределение:
Что дает нам возможность проверять гипотезы о значимости коэффициента
регресии и строить доверительные интервалы
7
Несмещенные оценки коэффициентов регрессии
Есть теоретическая модель парной линейной регрессии
yi = α + βxi + ui
^
Есть расчетная регрессия yi = a + b xi
где a и b это оценки истинных значений α и β
Тогда несмещенность означает следующее
Мат. ожидание E(a) = α
Мат. ожидание E(b) = β
Эффективные оценки коэффициентов регрессии
Т.е. среди всех несмещенных оценок оценки a и b обладают
наименьшей дисперсией
Одно из предположений о случайном члене ui
(условие Гаусса-Маркова)
III. Случайный член имеет постоянную дисперсию
для всех наблюдений, Var(ui)=D(ui)= σu2 , i= 1,…,n
(гомоскедастичность)
Замечание: величина σu неизвестна (основана на данных
генеральной совокупности), одна из задач регрессионного
анализа состоит в том чтобы оценить σu (найти оценку для
этого параметра).
Оценкой для дисперсии случайного члена (σu2 )является
величина:
Т.е. оценкой для дисперсии случайного члена/ошибок ui
является сумма квадратов остатков / на (n-2).
Остатки (ei)
Упростили обозначения, опускаем в обозначениях индекс «i».
a и b – оценки параметров теоретической регрессии (методом МНК),
т.е. оценки параметров α и β.
Расчетные значения
это ординаты точек R1, R2, R3, R4 ,лежащих на
линии регрессии = a + bx.
т.е. каждое получаем подставив в уравнение регрессии для
каждого x значения а и b.
Вспомним, что
для каждой выборки своя
^
расчетная регрессия (yi = a + b xi )
Пусть первая выборка включает наблюдения P1, P2, P4
^
Pасcчетная регрессия (yi = a + b xi ) для выборки (P1, P2, P4)
Пусть первая выборка включает наблюдения P1, P2, P4
^
Расcчетная регрессия (yi = a + b xi ) для выборки (P1, P3, P4)
А вторая выборка включает наблюдения P1, P3, P4
Для каждой выборки своя
^
расчетная регрессия (yi = a + b xi )
Для каждой выборки получили свою линии расчетной регрессии;
как результат, для каждой выборки оценки параметров (a, b) будут
отличатся => a, b – оценки регрессии это случайные величины!
• Так как оценки a, b –это случайные
величины и они изменяются от выборки к
выборке, то нам необходимо задаться
мерой «надежности» нашей оценки.
Для этих целей используют стандартные
ошибки.
Вспомним, что наши оценки – нормально
распределенные величины
Тогда стандартные ошибки для оценок a, b
принимают вид:
— оценкой для дисперсии (σu2 )случайного члена ui .
Значимость коэффициентов регрессии
На прошлой лекции мы рассмотрели как проверить
значимость коэффициентов по P-значению (P-value), в
данной лекции посмотрим как проверить значимость
коэффициентов по их стандартным ошибкам.
Сравнивая значение коэффициента с его стандартной
ошибкой, можно судить о значимости коэффициента;
Коэффициент называется значимым, если есть
достаточно высокая вероятность того, что его
истинное значение отлично от нуля;
Для стандартных ошибок нет таблиц критических
уровней – для точного суждения о значимости
коэффициентов используется t-статистика.
t-статистика для проверки значимости
коэффициентов регрессии
t-статистика соизмеряет значения
коэффициента с его стандартной ошибкой
(s.e., еще используется обозначение c.o.)
См. word/pdf файл
Коэффициент детерминации R2
Напомним
Рассмотрели вариацию (разброс) зависимой переменной yi вокруг ее среднего , т.е.
Которую можно разложить на
.
Обозначили
общую/всю вариацию
= TSS (total sum of squares)
не объясненную регрессией вариацию
= ESS (error sum of squares),
объясненную регрессией вариацию
= RSS (regression sum of squares).
Получили выражение для R2
коэффициента детерминации, или доли
объясненной дисперсии:
F тест на качество оценивания/значимости
уравнения регрессии в целом
Для парной регрессии F-тест, нулевая и альтернативная
гипотезы примут вид:
yi = α + βxi + ui
Ho: β = 0, H1: β ǂ 0
к – количество оцененных
в регрессии параметров
n – количество
наблюдений
Заметим, что для парной линейной регрессии нулевая и альтернативная
гипотеза F-теста соответствуют двухстороннему t-тесту (тестирование гипотезы о
значимости коэффициента регрессии при объясняющей переменной).
Может ли так случиться, что F-тест и t-тест приведут к различным выводам?
20
F тест на качество оценивания/значимости
уравнения регрессии в целом
Для парной регрессии F-тест, нулевая и альтернативная
гипотезы примут вид:
yi = α + βxi + ui
Ho: β = 0, H1: β ǂ 0
к – количество оцененных
в регрессии параметров
n – количество
наблюдений
Ответ: конечно нет.
И мы продемонстрируем, что F-тест (на качество оценивания/значимости
уравнения регрессии в целом), в случае парной линейной регрессии равен
квадрату t- статистики соответствующего коэффициента при объясняющей
переменной.
20
F тест на качество оценивания/значимости уравнения регрессии в целом
Начнем с того, что запишем формулу F-теста для случая
k=2 (т.е. парной линейной регрессии) и запишем ESS и RSS
через yi и ei .
22
F тест на качество оценивания/значимости уравнения регрессии в целом
— оценка дисперсии случайного члена ui
В знаменателе у нас «оценка дисперсии случайного члена» (см.
слайд 10). Числитель распишем через оценки коэффициентов
регрессии (т.е. a и b).
22
F тест на качество оценивания/значимости уравнения регрессии в целом
В знаменателе у нас «оценка дисперсии случайного члена».
Числитель распишем через оценки регрессии (т.е. a и b).
23
F тест на качество оценивания/значимости уравнения регрессии в целом
Упростим, сократив в числителе a и вынеся за скобку b.
24
F тест на качество оценивания/значимости уравнения регрессии в целом
Вынесем b2 из под знака суммы.
25
F тест на качество оценивания/значимости уравнения регрессии в целом
Преобразуем выражение.
26
F тест на качество оценивания/значимости уравнения регрессии в целом
Вспомним выражение стандартной ошибки коэффициента
при объясняющей переменной (т.е. коэффициента b) (см.
слайд 17).
F тест на качество оценивания/значимости уравнения регрессии в целом
Т. е. в знаменателе у нас квадрат стандартной ошибки b.
27
F тест на качество оценивания/значимости уравнения регрессии в целом
Вспомним выражение t-статистики для коэффициента
регрессии.
F тест на качество оценивания/значимости уравнения регрессии в целом
Таким образом мы получили t-статистику в квадрате (t2 ).
28
F тест на качество оценивания/значимости уравнения регрессии в целом
Так как F-тест эквивалентен двухстороннему t-тесту, то в случае парной
регрессии нет необходимости проводить оба теста (т.е. тестировать
значимость уравнения в целом, если уже протестировали значимость
коэффициента при объясняющей переменной).
30
F тест на качество оценивания/значимости уравнения регрессии в целом
В случае множественной регрессии F-тест тестирует гипотезу о значимости
/отличия от нуля нескольких коэффициентов при объясняющих переменных;
в этом случае t-тест и F-тест не эквивалентны.
30
F тест на качество оценивания
Данные/анализ данных/регрессия
Регрессионная статистика
Множественный R
0,7865947
R-квадрат
0,6187313
Нормированный R-квадрат
0,5710727
Стандартная ошибка
402,8516
Наблюдения
10
Дисперсионный анализ
df
1
8
9
Регрессия
Остаток
Итого
SS
2106934,736
1298315,264
3405250
MS
2106934,736
162289,408
F
12,982577
Значимость F
0,006950592
Коэффициен Стандартная
tНижние Верхние Нижние Верхние
P-Значение
ты
ошибка
статистика
95%
95%
95,0% 95,0%
Y-пересечение
-82,32524964
732,0218651
-0,112462829
0,9132272 -1770,37 1605,72 -1770,37 1605,72
Переменная X 1
77,532097
21,51795906
3,603134331
0,0069506 27,91159 127,1526 27,91159 127,1526
Дана оценка регрессионного уравнения зависимости «y -цена
квартиры, тыс. руб.» от «x — размера жилой площади». Количество
наблюдений = 10.
Необходимо поверить гипотезу о значимости уравнения в целом;
32
F тест на качество оценивания
Данные/анализ данных/регрессия
Регрессионная статистика
Множественный R
0,7865947
R-квадрат
0,6187313
Нормированный R-квадрат
0,5710727
Стандартная ошибка
402,8516
Наблюдения
10
Дисперсионный анализ
df
1
8
9
Регрессия
Остаток
Итого
SS
2106934,736
1298315,264
3405250
MS
2106934,736
162289,408
F
12,982577
Значимость F
0,006950592
Коэффициен Стандартная
tНижние Верхние Нижние Верхние
P-Значение
ты
ошибка
статистика
95%
95%
95,0% 95,0%
Y-пересечение
-82,32524964
732,0218651
-0,112462829
0,9132272 -1770,37 1605,72 -1770,37 1605,72
Переменная X 1
77,532097
21,51795906
3,603134331
0,0069506 27,91159 127,1526 27,91159 127,1526
Значение RSS = 2106934,736
32
F тест на качество оценивания
Данные/анализ данных/регрессия
Регрессионная статистика
Множественный R
0,7865947
R-квадрат
0,6187313
Нормированный R-квадрат
0,5710727
Стандартная ошибка
402,8516
Наблюдения
10
Дисперсионный анализ
df
1
8
9
Регрессия
Остаток
Итого
SS
2106934,736
1298315,264
3405250
MS
2106934,736
162289,408
F
12,982577
Значимость F
0,006950592
Коэффициен Стандартная
tНижние Верхние Нижние Верхние
P-Значение
ты
ошибка
статистика
95%
95%
95,0% 95,0%
Y-пересечение
-82,32524964
732,0218651
-0,112462829
0,9132272 -1770,37 1605,72 -1770,37 1605,72
Переменная X 1
77,532097
21,51795906
3,603134331
0,0069506 27,91159 127,1526 27,91159 127,1526
Значение ESS = 1298315,264
32
F тест на качество оценивания
Данные/анализ данных/регрессия
Регрессионная статистика
Множественный R
0,7865947
R-квадрат
0,6187313
Нормированный R-квадрат
0,5710727
Стандартная ошибка
402,8516
Наблюдения
10
Дисперсионный анализ
df
1
8
9
Регрессия
Остаток
Итого
SS
2106934,736
1298315,264
3405250
MS
2106934,736
162289,408
F
12,982577
Значимость F
0,006950592
Коэффициен Стандартная
tНижние Верхние Нижние Верхние
P-Значение
ты
ошибка
статистика
95%
95%
95,0% 95,0%
Y-пересечение
-82,32524964
732,0218651
-0,112462829
0,9132272 -1770,37 1605,72 -1770,37 1605,72
Переменная X 1
77,532097
21,51795906
3,603134331
0,0069506 27,91159 127,1526 27,91159 127,1526
Запишем формулу для расчета F-статистики
32
F тест на качество оценивания
Данные/анализ данных/регрессия
Регрессионная статистика
Множественный R
0,7865947
R-квадрат
0,6187313
Нормированный R-квадрат
0,5710727
Стандартная ошибка
402,8516
Наблюдения
10
Дисперсионный анализ
df
1
8
9
Регрессия
Остаток
Итого
SS
2106934,736
1298315,264
3405250
MS
2106934,736
162289,408
F
12,982577
Значимость F
0,006950592
Коэффициен Стандартная
tНижние Верхние Нижние Верхние
P-Значение
ты
ошибка
статистика
95%
95%
95,0% 95,0%
Y-пересечение
-82,32524964
732,0218651
-0,112462829
0,9132272 -1770,37 1605,72 -1770,37 1605,72
Переменная X 1
77,532097
21,51795906
3,603134331
0,0069506 27,91159 127,1526 27,91159 127,1526
Запишем формулу для расчета F-статистики, проверим степени
свободы.
32
F тест на качество оценивания
Данные/анализ данных/регрессия
Регрессионная статистика
Множественный R
0,7865947
R-квадрат
0,6187313
Нормированный R-квадрат
0,5710727
Стандартная ошибка
402,8516
Наблюдения
10
Дисперсионный анализ
df
1
8
9
Регрессия
Остаток
Итого
SS
2106934,736
1298315,264
3405250
MS
2106934,736
162289,408
F
12,982577
Значимость F
0,006950592
Коэффициен Стандартная
tНижние Верхние Нижние Верхние
P-Значение
ты
ошибка
статистика
95%
95%
95,0% 95,0%
Y-пересечение
-82,32524964
732,0218651
-0,112462829
0,9132272 -1770,37 1605,72 -1770,37 1605,72
Переменная X 1
77,532097
21,51795906
3,603134331
0,0069506 27,91159 127,1526 27,91159 127,1526
Наш результат F-статистики = 12,982577
32
F тест на качество оценивания
Данные/анализ данных/регрессия
Регрессионная статистика
Множественный R
0,7865947
R-квадрат
0,6187313
Нормированный R-квадрат
0,5710727
Стандартная ошибка
402,8516
Наблюдения
10
Дисперсионный анализ
df
1
8
9
Регрессия
Остаток
Итого
SS
2106934,736
1298315,264
3405250
MS
2106934,736
162289,408
F
12,982577
Значимость F
0,006950592
Коэффициен Стандартная
tНижние Верхние Нижние Верхние
P-Значение
ты
ошибка
статистика
95%
95%
95,0% 95,0%
Y-пересечение
-82,32524964
732,0218651
-0,112462829
0,9132272
Переменная X 1
77,532097
21,51795906
3,603134331
0,0069506 27,91159 127,1526 27,91159 127,1526
-1770,37 1605,72 -1770,37 1605,72
(или) Рассчитаем F-статистику через R2
32
F тест на качество оценивания
Данные/анализ данных/регрессия
Регрессионная статистика
Множественный R
0,7865947
R-квадрат
0,6187313
Нормированный R-квадрат
0,5710727
Стандартная ошибка
402,8516
Наблюдения
10
Дисперсионный анализ
df
1
8
9
Регрессия
Остаток
Итого
SS
2106934,736
1298315,264
3405250
MS
2106934,736
162289,408
F
12,982577
Значимость F
0,006950592
Коэффициен Стандартная
tНижние Верхние Нижние Верхние
P-Значение
ты
ошибка
статистика
95%
95%
95,0% 95,0%
Y-пересечение
-82,32524964
732,0218651
-0,112462829
0,9132272 -1770,37 1605,72 -1770,37 1605,72
Переменная X 1
77,532097
21,51795906
3,603134331
0,0069506 27,91159 127,1526 27,91159 127,1526
Сравним наш результат с расчетом Excel F-статистики = 12,982577
32
F тест на качество оценивания
Данные/анализ данных/регрессия
Регрессионная статистика
Множественный R
0,7865947
R-квадрат
0,6187313
Нормированный R-квадрат
0,5710727
Стандартная ошибка
402,8516
Наблюдения
10
Дисперсионный анализ
df
1
8
9
Регрессия
Остаток
Итого
SS
2106934,736
1298315,264
3405250
MS
2106934,736
162289,408
F
12,982577
Значимость F
0,006950592
Коэффициен Стандартная
tНижние Верхние Нижние Верхние
P-Значение
ты
ошибка
статистика
95%
95%
95,0% 95,0%
Y-пересечение
-82,32524964
732,0218651
-0,112462829
0,9132272 -1770,37 1605,72 -1770,37 1605,72
Переменная X 1
77,532097
21,51795906
3,603134331
0,0069506 27,91159 127,1526 27,91159 127,1526
Проверим также, что F-статистика = t2
32
F тест на качество оценивания
Данные/анализ данных/регрессия
Регрессионная статистика
Множественный R
0,7865947
R-квадрат
0,6187313
Нормированный R-квадрат
0,5710727
Стандартная ошибка
402,8516
Наблюдения
10
Дисперсионный анализ
df
1
8
9
Регрессия
Остаток
Итого
SS
2106934,736
1298315,264
3405250
MS
2106934,736
162289,408
F
12,982577
Значимость F
0,006950592
Коэффициен Стандартная
tНижние Верхние Нижние Верхние
P-Значение
ты
ошибка
статистика
95%
95%
95,0% 95,0%
Y-пересечение
-82,32524964
732,0218651
-0,112462829
0,9132272
Переменная X 1
77,532097
21,51795906
3,603134331
0,0069506 27,91159 127,1526 27,91159 127,1526
-1770,37 1605,72 -1770,37 1605,72
Проверим также, что F-статистика = t2
12,982577 = 3,6031343312 = 12,982577
Все верно.
32
F тест на качество оценивания
Теоретическая модель множественной линейной
регрессии имеет вид:
yi = α + β1x1i + β2x2i + …+ βmxmi + ui, i = 1,…, n
где n – число наблюдений, x1i,…, xmi – объясняющие
переменные, yi – зависимая переменная, ui –
случайный член, α, β1, β2, …βm — параметры
теоретической модели.
И расчетная регрессия:
a+ b1x1i + b2x2i + …+ bmxmi , где a, b 1, b2, …bm
— оценки параметров α, β1, β2, …βm
теоретической модели.
F тест на качество оценивания
Проверка гипотезы о значимости уравнения в
целом сводится к проверке гипотезы
H0: β1 = β2 = ..= βm = 0 (все параметры при
объясняющих переменных одновременно = 0)
против альтернативной
HА: не все коэффициенты при объясняющих
переменных одновременно = 0
(или формализовано,
F тест на качество оценивания
Вычисляется расчетная статистика:
Затем рассчитанная статистика F (т.е. сравнивается с
табличным критическим значением при выбранном
уровне значимости α, т.е.
Если Fрасчетн. превышает критическое (
)
то гипотеза H0: β1 = β2 = ..=βm =0 отклоняется в пользу
альтернативной (HА) при выбранном уровне значимости
α, и мы заключаем, что регрессия является значимой (или
адекватной).
Иначе, регрессия считается незначимой (неадекватной).
F тест на качество оценивания
Данные/анализ данных/регрессия
Регрессионная статистика
Множественный R
0,7865947
R-квадрат
0,6187313
Нормированный R-квадрат
0,5710727
Стандартная ошибка
402,8516
Наблюдения
10
В случае парной регрессии
Ho: β = 0,
HА: β ǂ 0
Дисперсионный анализ
df
1
8
9
Регрессия
Остаток
Итого
SS
2106934,736
1298315,264
3405250
MS
2106934,736
162289,408
F
12,982577
Значимость F
0,006950592
Коэффициен Стандартная
tНижние Верхние Нижние Верхние
P-Значение
ты
ошибка
статистика
95%
95%
95,0% 95,0%
Y-пересечение
-82,32524964
732,0218651
-0,112462829
0,9132272 -1770,37 1605,72 -1770,37 1605,72
Переменная X 1
77,532097
21,51795906
3,603134331
0,0069506 27,91159 127,1526 27,91159 127,1526
Вывод!
Наша уравнение статистически значимо на 5%-ом уровне значимости т.к.
(1) Это парная регрессия и значим коэффициент при единственной объясняющей переменной X1,
t_расчетное = 3,60313 > t_крит (α = 0.05, n – k = 10 – 2) = 2,306.
(2) Или по результатам F-теста
F_расчетное = 12,983 > F_критическое (α = 0.05; k-1, n – k = 1;8) = 5,32
47

Источник

Ограничения
в классической линейной модели регрессии.
Свойства оценок коэффициентов при
регрессорах, получаемых методом
наименьших квадратов. Теорема
Гаусса-Маркова.

Корреляция
и регрессия взаимосвязаны между собой
– корреляция исследует силу(тесноту)
связи, регрессия исследует её форму. И
та и другая служат для установления
соотношения между явлениями, для
определения наличия или отсутствия
связи. По форме зависимости различают
линейную регрессию (уравнение прямой
Ῡ_x
= a0
+ a1x)
и нелинейную ( парабола Ῡ_x=a0
+ a1
* x
+ a2*x^2,
гипербола и т.д.). Направление связи –
прямая, обратная.

Целью
регрессионного анализа является оценка
функциональной зависимости математического
ожидания результативного признака У
от факторных (х1, х2,…).

Метод
наименьших квадратов (МНК,
OLS, Ordinary Least Squares) —
один из базовых методов регрессионного
анализа для оценки неизвестных параметров
регрессионных моделей по выборочным
данным. Метод основан на минимизации
суммы квадратов остатков регрессии.

Оценки,
полученные по МНК, обладают следующими
свойствами:

Оценки
параметров являются несмещенными,
т. е. M(b₁)
= β₁,
M(b₀)
= β₀
(математические ожидания оценок
параметров равны их теоретическим
значениям). Это вытекает из того, что
M(ε_i)
= 0, и говорит об отсутствии систематической
ошибки в определении положения линии
регрессии. Оценка, для которой смещение
– разность между значением параметра
и его оценкой – стремится к нулю при
возрастании выборки – является
асимптотически
несмещенной.
Оценки
параметров состоятельны,
если при
увеличении объема выборки надежность
оценок увеличивается
(b₁
наверняка близко к β₁,
b₀
— близко к β₀),
т.е. D(b₀)
→ 0, D(b₁)
→ 0 при n → ∞ .
Оценки
параметров эффективны,
т. е. они имеют наименьшую дисперсию по
сравнению с другими оценками данных
параметров, линейными относительно
величин y_i.

Т.е.
МНК-оценки
являются несмещенными линейными оценками
с минимальной дисперсией, имеющими
нормальное распределение.

В
полученном уравнении регрессии параметр
а0 показывает усредненное влияние на
результативный признак неучтенных
факторов; параметр а1, а2 и т.д. показывает,
насколько в среднем изменяется значение
результативного признака при увеличении
факторного на единицу собственного
измерения.

Теорема Гаусса-Маркова.

Известно,
что для получения по МНК наилучших
результатов требуется, чтобы выполнялся
ряд предпосылок относительно случайного
отклонения. Их также называют предпосылками
Гаусса-Маркова. Теорема Гаусса-Маркова
гласит, что наилучшие оценки параметров
уравнения регрессии могут быть получены
при обязательном соблюдении следующих
предпосылок:

Математическое
ожидание случайного отклонения е_i
равно нулю: M(е_i)
= 0 для всех наблюдений.

Данное
условие означает, что случайное отклонение
в среднем не оказывает влияния на
зависимую переменную, случайный член
может быть положительным или отрицательным,
но он не должен иметь систематического
смещения.

Дисперсия
случайных отклонений постоянна: D(ε_ij)
= σ²
= const для любых наблюдений i и j.

Условие
независимости дисперсии ошибки от
номера наблюдения называется
гомоскедастичностью (homoscedasticity).
Невыполнимость этой предпосылки
называется гетероскедастичностью
(heteroscedasticity).

Поскольку
D(ε)=M((εj — Mεj))²
= M(ε²),
то эту предпосылку можно переписать в
форме: M(е²_i)
= σ².

Случайные
отклонения εi и εj являются независимыми
друг от друга для i ≠ j. Выполнимость
этой предпосылки предполагает, что
отсутствует систематическая связь
между любыми случайными отклонениями.
Величина и определенный знак любого
случайного отклонения не должны быть
причинами величины и знака любого
другого отклонения.

Выполнимость
данной предпосылки влечет следующее
соотношение:

Если
данное условие выполняется, то можно
говорить об отсутствии автокорреляции.

Случайное
отклонение должно быть независимо от
объясняющих переменных.

Данное
условие предполагает выполнимость
следующего соотношения:

Заметим,
что выполнимость этой предпосылки не
столь критична для эконометрических
моделей.

Модель
является линейной относительно
параметров. Для случая множественной
линейной регрессии существенными
являются еще две предпосылки.
Отсутствие
мультиколлинеарности. Между объясняющими
переменными отсутствует сильная
линейная зависимость.
Случайные
отклонения εi, i = 1, 2, … , n, имеют нормальное
распределение.

Выполнимость
данной предпосылки важна для проверки
статистических гипотез и построения
интервальных оценок.

Наряду
с этим, есть еще некоторые предположения.
Например:

объясняющие
переменные не являются случайными
величинами;
число
наблюдений намного больше числа
объясняющих переменных (числа факторов
уравнения);
отсутствуют
ошибки спецификации, т. е. правильно
выбран вид уравнения и в него включены
все необходимые переменные.

Билет № 2. Оценка параметров классической линейной модели регрессии методом максимального правдоподобия.

Пример
из учебника Доугерти про матожидание
между 4 и 6.

Этот
метод требует знания общего вида
распределения анализируемых случайных
величин. Для оценивания неизвестных
параметров используется следующий
факт: распределение переменной y_i,условное
по совокупности переменных xi, известно
вплоть до небольшого количества
неизвестных параметров, и следует
подбирать эти параметры таким образом,
чтобы получающееся распределение
«насколько возможно лучше соответствовало
наблюдаемым данным».

Допустим,
мы имеем урну, наполненную красными и
желтыми шарами. Нас интересует доля p
красных
шаров. Чтобы получить информацию о p,
мы извлекаем случайную выборку из N
шаров, yi = 1 если шар красный, и yi = 0 если
желтых, P (yi=1) = 1. Предположим, что выборка
содержит
красных шаров иN
– N1
желтых. Вероятность получения такой
выборки в заданном виде является

P(N1,
N-N1)
= p^N¹(1-p)^N^—^N¹.
Это выражение, интерпретируемое как
функция от неизвестного параметра p,
называется функцией правдоподобия.
Оценивание методом максимального
правдоподобия неизвестного параметра
p
означает, что мы выбираем такое значение
p,
что вероятность является максимальной.
Это значение является оценкой методом
максимального правдоподобия (ММП-оценкой).
В вычислительных целях удобно
максимизировать натуральный логарифм
вероятности. Это приводит к логарифмической
ф-ии правдоподобия

log
L(p)
= N1
log(p)
+ (N—N1)
log
(1-p)

Максимизация
этой функции даёт условие первого
порядка

из
которого получается решение для
неизвестного параметра p,
являющееся оценкой методом максимального
правдоподобия

Т.о.
ММП-оценка соответствует выборочной
доле красных шаров, и, вероятно,
соответствует наилучшей догадке о
параметре p, основанной на извлеченной
выборке.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

где матрица Q определена выражением (2.25).

Обобщая полученные результаты, отметим, что оценки коэффициентов эконометрической модели со стохастическими независимыми переменными,

полученные на основе МНК, являются асимптотически состоятельными и эффективными, если выполняются следующие условия:

lim M [( )|Х]= 2 E;

lim	[	1	( X ‘	)]=0;
T

T
lim	1	( X ‘ X )	1


T T					Q.

(2.42)

Заметим, что условия (2.42) являются “предельными” аналогами предположений (2.20)–(2.24), имевших место в случае конечной выборки.

Таким образом, выражение (2.8), являющееся результатом МНК, позволяет получить значения оценок коэффициентов линейной эконометрической модели “хорошего качества” и при детерминированных, и при стохастических значениях независимых переменных, если выполняются определенные предпосылки относительно соответствующих свойств ошибки этой модели и наблюдаемых исходных данных.

Однако априорно проверить справедливость этих предпосылок, как правило, не представляется возможным. Обычно это можно сделать, лишь получив информацию о фактической ошибке модели, после того как она была построена. Фактическая ошибка модели еt в данном случае может быть рассмотрена как оценка ее истинной ошибки t. Тогда совпадение свойств фактической ошибки с предположениями, выдвигаемыми относительно свойств истинной ошибки, может являться достаточно “веской гарантией”

обоснованности использования “классического” МНК в качестве метода оценки параметров модели.

Для определения свойств фактической ошибки еt могут быть использованы специальные тесты и процедуры, рассмотренные, как в разделе

(1.4) (см. тест Дарбина-Уотсона), так и в следующем параграфе данной главы.

2.2. Особенности проверки качества оценок МНК

Проверка условий, выполнение которых свидетельствует о “высоком” качестве полученных оценок параметров эконометрической модели (а,

следовательно, в значительной степени и самой модели), на практике обычно осуществляется с использованием ряда процедур и критериев, на основе исходной и новой, полученной после построения модели, информации. К

исходной информации относятся наблюдаемые (измеренные) значения

зависимой и независимых переменных	yt и хit	соответственно. Новую

информацию составляют значения	y	t ,	найденные	оценки параметров ai,

соответствующие им фактические значения ошибки еt, а также ковариационные матрицы оценок и ошибок (в последнем случае возможно только дисперсии), i=0, 1,…, п; t=1, 2,…, Т. Иными словами, значение Т при проверке предполагается конечным.

При этом следует иметь в виду, что новая информация обычно рассматривается как некоторая оценка (заменитель) истинных (но неизвестных) значений соответствующих характеристик. В этой связи совпадение свойств оценок с предполагаемыми теорией априорными свойствами соответствующих характеристик (часто, но не всегда) является определенной гарантией качества модели (оценок ее параметров). Особенно важную роль в определении качества модели играют значения ее фактической ошибки еt, t=1, 2,…, Т; соответствующие полученным оценкам ее параметров.

2.2.1.Свойства фактической ошибки эконометрической модели

Вданном разделе рассматриваются некоторые подходы к проверке наличия стандартных свойств (2.20)–(2.23) у “истинной” ошибки эконометрической модели t на основе анализа соответствующих свойств фактической ошибки еt.

Вэтой связи сразу следует отметить, что наличие у ошибки еt каждого из этих свойств не всегда является доказательством присутствия соответствующего свойства и у ошибки t. Иными словами, наличие определенных свойств у ошибки еt не является необходимым условием существования этих свойств и у истинной ошибки t. Дело в том, что

некоторые свойства фактической ошибки еt являются своего рода ограничениями на ее значения, которые вытекают из критерия МНК как метода оценки параметров модели, т. е. выполняются практически всегда. В

то же время свойства “истинной” ошибки определены теоретическими

предпосылками, положенными в основу этой модели. Поэтому вывод о

правомочности использования МНК на основе существования таких

“априорных” свойств фактической ошибки модели не может считаться обоснованным.

Вместе с тем, если фактическая ошибка t не обладает некоторым свойством, то можно говорить о том, что теоретические предпосылки эконометрической модели не подтверждены полученными эмпирическими данными и “качество” ее уравнения не достаточно высоко.

В этой связи отметим, что к “априорным” свойствам фактической ошибки

еt, которые выполняются при использовании МНК всегда, относятся свойства

(2.20) и (2.23). Приведем доказательства этого утверждения.

1. Сумма значений фактической ошибки равна нулю

Условие (2.43) является аналогом свойства (2.20), поскольку

еt t

рассматривается как оценка математического ожидания фактической ошибки.

Использование МНК обеспечивает выполнение условия (2.43)

автоматически. В самом деле, дифференцируя сумму квадратов ошибки еt s2

(см. выражение (2.31)) по параметру a0 , получим

2 ( y

… a

) 0.

Из этого выражения автоматически вытекает, что


( y	y	) е	0.
t	t	t
t		t

2. Произведение транспонированной матрицы Х на вектор фактической ошибки е равно нулевому вектору.

Х е=0. (2.44)

Условие (2.44) является аналогом условия (2.23), поскольку произведение каждой строки матрицы Х на вектор представляет собой скалярное произведение вектора значений соответствующих факторов хit на вектор ошибки.

	(xit xi ) еt		xit еt	xi еt	xit еt
cov(xit ,еt )	t		t	t	t	.
T	T	T	T

Тогда векторно-матричное выражение (2.44) можно представить в виде следующей системы скалярных произведений:

xit еt 0,i 0,1,…,n,	(2.45)
t

где х0t 1 для t=1, 2,…, Т.

е=у – y =у–Х a.

Получим

Х e=Х(у–Х a)=Х у–Х Х a=(Х Х)–1 Х у–(Х Х)–1 (Х Х) a=0.

Из (2.44) и (2.45) автоматически следует, что

Еще раз отметим, что выполнение условий (2.45) и (2.46) не может считаться доказательством отсутствия корреляционных взаимосвязей между значениями независимых переменных хit и “истинной” ошибкой t. В данном случае эти условия сами являются следствием результатов применения МНК для оценки коэффициентов эконометрической модели, т. е. они как бы выполняются автоматически. Для некоторых классов эконометрических моделей, как это будет показано в главах V и VIII, уже априорно, т. е. до построения модели, можно доказать существование ковариационной связи между некоторыми независимыми переменными и истинной ошибкой модели t. Выполнение условия (2.45) в таком случае не является

свидетельством корректности применения “классического” МНК для оценки

еепараметров.

3.Из условий (2.43) и (2.45) также вытекает, что сумма произведений отклонений расчетных значений независимых переменных от ее среднего значения и расчетных значений ошибки равна нулю.


е	t	( y	y	) 0.	(2.47)
t	t	t

Раскрывая скобки в выражении (2.47), непосредственно получим

( y

) е

… a

)

a0 еt a1 x1t

еt … an xnt еt

Выражение (2.47) включает в себя также и следующее условие:

	е		0,
y	t	(2.48)
t
t

означающее,			что сумма	произведений расчетных значений зависимой

переменной	y	t	и ошибки еt	равна нулю.

что является свидетельством обоснованного выбора формы ее уравнения,

состава учтенных факторов и т. п.

2.2.2. Тестирование свойств фактической ошибки эконометрической

модели

На практике справедливость предпосылок (2.21) и (2.22) можно подтвердить или опровергнуть только путем анализа свойств фактической ошибки еt, после оценки ее значений. В таком случае фактическая ошибка рассматривается как оценка истинной ошибки и выполнение для нее этих предпосылок может рассматриваться в качестве доказательства их обоснованности, а, следовательно, и достаточно высокого качества оценок параметров эконометрической модели.

Заметим, что условие (2.21) 2 = const нельзя интерпретировать как постоянство значений t для t=1, 2,…, Т. Оно лишь означает, что дисперсия истинной ошибки t является постоянной величиной на любом из отрезков рассматриваемого временного интервала (1,Т). В этой связи проверка условия (2.21) может быть идентична проверке гипотезы о постоянстве дисперсии фактической ошибки еt на различных отрезках интервала (1,Т). Такая проверка обычно проводится с использованием соответствующих тестов.

1. Тестирование условия постоянства дисперсии ошибки модели.

Проверку гипотезы 2=const (выражение (2.21)) можно провести с использованием расчетных значений ошибки еt на основе, например,

двустороннего критерия Фишера. Общая схема реализации процедуры такой проверки состоит в следующем. Интервал (1,Т) разбивается на три интервала

(1,Т1), (Т1+1, Т2), (Т2+1, Т). При этом первый и третий интервалы обычно выбираются одинаковой длины. В моделях со статической информацией соответственно на три группы разбивается исходная совокупность объектов,

которые в данном случае должны быть расположены в порядке возрастания

(или убывания) результирующей переменной yt. Для данных,

соответствующих первому и третьем интервалам, строятся эконометрические модели, аналогичные исходному варианту. Для каждой из них определяются

последовательности ошибки еt	– е1, е2,…,	еT1	и	еT2 1	,	еT2 2	,…,	еТ

соответственно.

Для первого и третьего интервалов на основании известных значений ошибки, рассчитываются дисперсии

3e2 =

	T
			2	/ (T T2 (n 1)),
	et
t	T	2	1

где n – число параметров модели.
Отношение 3e2 / 1e2 сопоставляется	с граничными	значениями
двухстороннего критерия Фишера F* и F* с заданным уровнем доверительной
вероятности р* и числом степеней свободы	1=T–(n+1) и 2=T–T2–(n+1).
Если оказывается, что выполняется соотношение
F* 3e2 / 1e2	F*,	(2.49)

где, то гипотеза о постоянстве дисперсии на интервале (1,Т) принимается. В

противном случае – эта гипотеза отвергается.

Напомним, что F* =1/F*( 2, 1).

В целом, надежность проверки гипотезы (2.21) по рассмотренной процедуре зависит от правильности выбора числа измерений на каждом из интервалов. С одной стороны, уменьшение их длины приводит к потере точности в оценках 1e2 и 3e2 , с другой – ее увеличение может сделать данные оценки статистически неразличимыми, поскольку колебания

квадратов ошибок будут уравновешиваться на расширенных интервалах, и

значения их дисперсий с ростом Т сблизятся.

Если количество измерений Т достаточно велико, то для проверки гипотезы о постоянстве дисперсии может быть использован критерий Бартлетта. В этом случае интервал (1,Т) разбивается на k участков. По данным каждого из них формируется собственный вариант эконометрической модели, по форме (т. е. по используемым переменным и характеру их взаимосвязей) тождественный вариантам других участков. Для каждого варианта определяется значение дисперсии ошибки 12, 22,…, k2.

Гипотеза постоянства дисперсии предполагает, что 12= 22=…= k2= 2. Если эта гипотеза верна, то усредненная оценка дисперсий i 2, i=1,2,…, k,

рассчитываемая как

2	k	2	k
	/ ni	(2.50)
ni i
	i 1		i 1

распределена как выборочная дисперсия, т. е. по нормальному закону со

средним значением 2 и Т степенями свободы, где Т= ni, ni – количество

i 1

измерений на i-м участке.

Бартлетт показал, что величина

		1	k				2
	ni ln	i	,		(2.51)
		2
		c i 1

где
c 1		1		k		1			1
								(2.52)
3(k 1)				k
	i 1ni
		ni

										i 1

распределена примерно по закону 2 с k–1 степенями свободы.

Для частного случая, когда количество измерений на всех участках равны,

т. е. n1=n2=…=nk

1	k ni (ln	2	1	k	2	),	(2.53)
		i
c			k i 1

где с=1+[(k+1)/3k ni].

Таким образом, проверка гипотезы о постоянстве дисперсии эконометрической модели на интервале (1,Т) состоит в сопоставлении расчетного значения 2, определяемого по формуле (2.51) или (2.53), с

табличным значением этого критерия 2*, взятым при заданной доверительной вероятности р* и k–1 степенях свободы. Если оказывается ,

что 2= 2*, то гипотеза о постоянстве дисперсии принимается, если 2*,

то рассматриваемую гипотезу следует отвергнуть.

2. Тестирование автокорреляционной зависимости ошибки.

Проверка выполнимости условия (2.22), свидетельствующего об отсутствии автокорреляционных взаимосвязей в ряду “истинной” ошибки модели t, на практике осуществляется путем тестирования ряда значений фактической ошибки et.

При этом предполагается, как и в случае тестирования условия (2.21), что свойства фактической ошибки в значительной степени соответствуют свойствам ее теоретического аналога. В данном случае имеется в виду характер автокорреляционных взаимосвязей между значениями ошибок в моменты времени t и t–1, t и t–2 и т. д.

Обычно у случайного процесса (если отсутствуют сезонные эффекты)

наиболее существенны взаимосвязи между соседними значениями. Это выражается в том, что абсолютное значение его первого коэффициента автокорреляции превосходит аналогичные значения его коэффициентов автокорреляции более высоких порядков. Вследствие этого проверка выполнимости условия (2.22) часто рассматривается как проверка гипотезы о

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

1. Сумма значений фактической ошибки равна нулю

Из этого выражения автоматически вытекает, что

2. Произведение транспонированной матрицы Х¢ на вектор фактической ошибки е равно нулевому вектору.

Х¢е=0. (2.44)

Внимание!

Тогда векторно-матричное выражение (2.44) можно представить в виде следующей системы скалярных произведений:

где х0t º1 для t=1, 2,…, Т.

е=у –=у–Х×a.

Получим

Х¢×e=Х¢×(у–Х×a)=Х¢×у–Х¢×Х×a=(Х¢×Х)–1×Х¢×у–(Х¢×Х)–1 ×(Х¢×Х)×a=0.

Из (2.44) и (2.45) автоматически следует, что

Раскрывая скобки в выражении (2.47), непосредственно получим

Выражение (2.47) включает в себя также и следующее условие:

означающее, что сумма произведений расчетных значений зависимой переменной и ошибки еt равна нулю.

Получить выполненную работу или консультацию специалиста по вашему
учебному проекту

Узнать стоимость

1. Актуальность эконометрических исследований, пути совершенствования эконометрических знаний.

2. Основы эконометрического моделирования: этапы, типы эконометрических моделей, типы данных.

3. Природа возникновения ошибки в регрессионной модели. Статистические свойства теоретической и фактической ошибки.

4. МНК для множественной регрессии.

5. Теорема Гаусса-Маркова для множественной регрессии. Определение ковариационно-дисперсионной матрицы вектора коэффициентов регрессии.

6. Критериальная проверка качества множественной регрессии.

7. Коэффициенты эластичности.

8. Проблема мультиколлинеарности. Примеры. Геометрическая интерпретация. Практические пути ее решения.

9. Проблема гетероскедастичности. Примеры. Геометрическая интерпретация. Практические пути ее решения.

10. Обобщение МНК на случай непостоянства ковариационно-дисперсионной матрицы ошибки. Статистические методы тестирования дисперсии ошибки.

11. Доступные методы реализации МНК при непостоянстве дисперсии ошибки.

12. Метод главных компонент. Его преимущества и недостатки при построении моделей. Компоненты и факторы, их взаимосвязи.

13. Модели с лаговыми независимыми переменными. Основные подходы и процедуры оценки их параметров. Метод Ш. Алмон.

14. Модели с лаговыми зависимыми переменными. Проблемы оценки их параметров. Схема Койка.

15. Двухшаговый МНК и особенности его применения в моделях с лаговыми зависимыми переменными. Инструментальные переменные, их содержание и особенности формирования.

16. Системы взаимозависимых эконометрических моделей. Свойства моделей и их влияние на качество оценок параметров. Структурная и приведенная формы системы моделей.

17. Основные подходы к оценке параметров взаимозависимых уравнений. Косвенный и двухшаговый МНК.

18. Методы выявления переменной структуры эконометрической модели.

19. Эконометрические модели с переключениями.

20. Эконометрические модели с эволюционирующими коэффициентами.

21. Точечные и интервальные прогнозы.

Источник