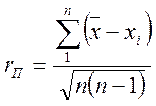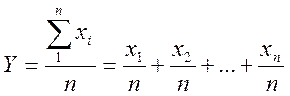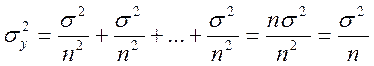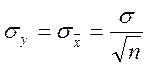Закон сложения ошибок

Важнейшей задачей статистики является разработка методов, позволяющих по результатам исследования выборки сделать выводы о параметрах распределения всей совокупности.

На практике исследователь обладает лишь ограниченным объемом значений случайной величины, представляющим собой некоторую выборку из генеральной совокупности. Под генеральной совокупностью понимаем все допустимые значения случайной величины. При анализе непрерывной случайной величины (например, температура, давление) под наблюдаемыми значениями случайной величины понимают такие дискретные значения, разделенные определенным интервалом времени, при котором произведенные замеры можно считать независимыми.

Выборка называется репрезентативной, если она дает достаточно полное представление о генеральной совокупности.

В математической статистике доказано (теорема Гливенко), что при достаточно большой выборке функцию распределения вероятностей генеральной совокупности можно заменять функцией распределения выборки.

Числовые характеристики, определенные при ограниченном объеме информации, называются оценками.

Другими словами, на практике мы всегда имеем дело с~·оценками числовых характеристик случайных величин. Пусть является оценкой параметра a.

К оценкам числовых характеристик предъявляются следующие требования:

1. Состоятельность – при увеличении числа опытов оценка сходится по вероятности к оцениваемому параметру, т.е. выполняется условие F Œ~·q = ~Œ L + G при увеличении объема выборки n.

2. Несмещенность – математическое ожидание оценки равно

оцениваемому параметру, т.е. при увеличении объема выборки ее Qматематическое~· ~ ожидание стремится к оцениваемому параметру:

q при увеличении n.

3. Эффективность – несмещенная оценка должна обладать

¸ ~· ¸

минимальной дисперсией по сравнению с другими оценками, т.е.

q X%q.

5.7.2. Точечные оценки параметров нормального

распределения

Как известно, параметрами нормального распределения являются математическое ожидание и дисперсия. В качестве оценки для математического ожидания естественно предположить среднее арифметическое наблюденных значений (выборочное среднее), т.е.

x = 1n∑n xi ,

i=1

которое получается из ранее приведенной зависимости для математического ожидания, если положить

pi = p =1/ n.

В математической статистике доказано, что выборочное среднее является наилучшей (состоятельной, несмещенной и эффективной) оценкой математического ожидания случайной величины, подчиняющейся нормальному закону распределения.

На

первый

взгляд

естественной

оценкой для дисперсии

Но эта оценка

ªT «

= «lº

D[X]будет

для

получается несколько смещенной:

YV¹

^V W

Поэтому

оценки

дисперсии

используется несмещенная

Уменьшение

» = «l º =

оценка:

знаменателя

на единицуT

непосредственно связано с

тем, что величина

, относительно которой берутся отклонения, сама

зависит

от

объема выборки. Каждая величина, зависящая от

«l

элементов выборки и входящая в формулу, называется связью. В статистике доказывается, что знаменатель выборочной дисперсии всегда равен разности между объемом выборки и числом связей l, наложенных на эту выборку. Эта разность

называется числом	степеней свободы выборки. В практических
	/ = 9
вычислениях для		оценки	дисперсии	часто	используется более
удобная формула:						ªT »
	¹		= »RT «	=		¼

Преимущество этой формулы в том, что в ней нет операций вычитания близких чисел, приводящих к потере точности.

5.7.3.Классификация ошибок измерения

Каждый результат измерения – случайная величина. Отклонение реального результата от истинного называется ошибкой наблюдения. Ошибка наблюдения также является случайной величиной. Она является результатом воздействия неучтенных факторов1 . Если обозначить истинный результат через a, ошибку – через , результат измерения =X,2то 1

Различают ошибки трех видов:

1. Грубые ошибки, которые возникают вследствие нарушения основных условий измерения. Результат, содержащий грубую ошибку, резко отличается по величине от остальных измерений. На этом основаны некоторые критерии по исключению грубых ошибок.

2.Систематические ошибки постоянны во всей серии измерений или изменяются по определенному закону. Выявление их требует специальных исследований, но как только систематические ошибки обнаружены, они могут быть устранены путем введения соответствующих поправок в результаты измерения.

3.Случайные ошибки – это те ошибки измерения, которые остаются после устранения всех выявленных грубых и систематических ошибок. Они вызываются большим количеством факторов, эффекты воздействия которых столь незначительны, что их нельзя выделить в отдельности ( на данном уровне используемой техники измерения). При этом распределение случайных ошибок симметрично относительно нуля: ошибки, противоположные по знаку, но равные по абсолютной величине, встречаются одинаково часто. Из симметрии распределения ошибок следует, что истинный

результат

наблюдения

есть

математическое

ожидание

соответствующей случайной величины.	Т.к.		YV1W <	при
		, и
YV W 2	ошибок			то
отсутствии грубых и систематических		2 1

В дальнейшем будем рассматривать только случайные ошибки измерений.

5.7.4.Закон сложения ошибок

Для независимых случайных величин свойством аддитивности

дисперсии,

не

среднеквадратические

2 2 2

обладают

ошибки. Если

—

независимые

случайные

величины;

—

неслучайные величины и

То выборочная

ƒ 2 2 ™ 2

дисперсия величины Z определяется следующим

образом:

то

Если положить«½

2 «

, ™ 2 «

™

В этом случае

™ «

«l

«˜

где

ª Àš ¾¿u

наблюдений

интерпретировать

как n

независимых

Еслиl

™ « « , тогда получим

¾¿u.

« š « u

одной и той же случайной величины X, то

«˜

Из полученного выражения следует один очень важный практический вывод: при оценке точности двух методов измерений следует учитывать длительность анализа. Применяя менее точные методы можно сделать большее число опытов и получить более точные результаты, чем при использовании трудоемкого точного метода. Можно сделать вывод о возможности уменьшить погрешность окончательного результата при увеличении количества n отдельных измерений. Однако также следует помнить, что повышение точности никогда не дается бесплатно. Так, чтобы узнать

Источник

1. ОСНОВЫ ТЕОРИИ ОШИБОК ИЗМЕРЕНИЙ

Виды измерений и погрешностей
• Измерением какой-либо физической величины наз-ся
операция, в результате которой мы узнаем, во сколько
раз измеряемая величина больше (или меньше)
соответствующей величины, принятой за единицу
Виды измерений классифицируются:
– по способу получения результата (прямые и косвенные);
– по методу измерений (абсолютные, относительные и
пороговые);
– по условиям измерений (равноточные, неравноточные);
– по степени достаточности измерений (необходимые,
избыточные)

2.

При прямых измерениях измеряется непосредственно
исследуемая величина
При косвенных измерениях исследуемая величина
измеряется как функция по результатам измерения других
величин
Например, ускорение автомобиля при разгоне определяется
по результатам измерения расстояния и времени разгона;
вычисление плотности – по массе и объему
Абсолютные измерения – это прямые измерения в
единицах измеряемой величины
Относительные измерения представляют собой
отношения измеряемой величины к величине играющей роль
единицы или к величине, принимаемой за исходную
При пороговых измерениях фиксируется только факт
нахождения величины в одностороннем или двухстороннем
допуске (по принципу «да/нет»)

3.

• Равноточные измерения проводятся в одинаковых
условиях одними и теми же измерительными приборами и
с одинаковой степенью тщательности. При этом в ряду
измерений нельзя отдать предпочтение какому-либо
одному или нескольким значениям
Неравноточные измерения не отвечают указанным выше
требованиям
Избыточные измерения имеют по сравнению с
необходимыми большее число измерений либо большую
точность, содержат среди измерений зависимые, т. е. дают
избыточную информацию
Надежность результатов исследования в значительной
степени зависит от точности измерений
Под точностью измерений понимают степень
соответствия результата измерения
действительному значению измеряемой величины

4.

Снять показания с прибора – не значит только измерить.
Необходимо еще оценить ошибки (погрешности) измерений
Погрешность измерения – это отклонение результата
измерения от истинного значения измеряемой величины
Под истинным значением измеряемой величины принято считать
– среднюю арифметическую величину ряда измерений;
– известное эталонное значение;
– величину, полученную в результате более точных (не менее
чем на порядок) измерений

5.

Основные источники ошибок
Первый источник заключен в датчике, который
неправильно реагирует на измеряемую величину.
Например, если тензосопротивление плохо наклеено на
упругий элемент, то деформация его решетки не будет
соответствовать деформации упругого элемента
Второй источник – измерительное устройство, в котором
возможны погрешности из-за неправильного
функционирования его механических или электрических
элементов
Третий источник – сам наблюдатель, который из-за
неопытности или усталости неправильно считывает
показания прибора
Ошибки могут возникнуть из-за влияния измерительного
устройства на объект измерения (например, при
разрушающем методе контроля), влияния окружающей
среды (температура, загазованность и т. п.), методических
погрешностей, допущенных экспериментатором

6.

Эти источники ошибок приводят к появлению трех типов
ошибок: случайных, систематических и грубых
Случайная погрешность – это погрешность, которая в
отдельных измерениях может принимать случайные, заранее
конкретно неизвестные значения.
Случайные погрешности обязаны своим происхождением ряду
как объективных, так и субъективных факторов, действие
которых неодинаково в каждом опыте и не может быть учтено.
Случайные погрешности различаются в отдельных измерениях,
сделанных в одинаковых условиях одними и теми же
измерительными приборами. Исключить случайные
погрешности нельзя. Можно только оценить их значение
Случайные погрешности определяются по законам теории
ошибок, основанной на теории вероятностей

7.

Систематическая погрешность – это погрешность,
вызванная факторами, действующими одинаковым образом
при многократном повторении одних и тех же измерений с
помощью одних и тех же измерительных приборов
В качестве примера систематической ошибки рассмотрим
случай взвешивания на чашечных весах с помощью
неточных гирь. Если взятая нами гиря имеет ошибку, скажем
0,1 г, то вес тела (пусть 1000 г) будет завышенным (или
заниженным) на эту величину, и чтобы получить верное
значение, необходимо учесть эту ошибку, прибавив к
полученному весу (или вычтя из него) 0,1 г, P=(1000±0,1) г
Грубая погрешность или промах вызывается просчетом
экспериментатора или неисправностью средств измерения,
или резко изменившимися внешними условиями
Грубые погрешности приводят к явному искажению рез-та,
поэтому их надо исключить из общего числа измерений

8.

По форме числового представления погрешности
делятся на абсолютные и относительные
Абсолютная погрешность – это разность между
результатом измерения и его истинным значением:
x x a
где x – результат измерения; a – истинное значение
Относительная погрешность – это погрешность,
приходящаяся на единицу измеренной величины;
она обычно выражается в процентах
x
100%.
a

9.

Случайные погрешности и их распределение
Чтобы выявить случайную погрешность измерений,
необходимо повторить измерение несколько раз
Если каждое измерение дает заметные от других
результаты, мы имеем дело с ситуацией, когда случайная
погрешность играет существенную роль
Наиболее вероятным значением измеряемой величины из
серии измерений является ее среднее значение
Разброс измеряемой величины относительно ее среднего
значения определяется величиной средней квадратической
погрешности отдельного измерения

10.

Пусть в эксперименте в результате независимых и
равноточных измерений постоянной величины а получены
значения х1, х2, …, хn
Абсолютные погрешности xi xi a рассматривают как
случайные величины
Независимость измерений понимается как взаимная
независимость случайных величин xi, а равноточность –
как подчинение величин xi одному и тому же закону
распределения (кроме того измерения сделаны одним и тем
же методом и с одинаковой степенью тщательности)
В качестве оценки неизвестной величины а по данным
измерений обычно берут среднее арифметическое x
результатов измерений
1 n
x
xi .
n
i 1
Дисперсия отдельных измерений 2
n
2
(
x
a
)
i
i 1
n 1
обычно неизвестна, и для ее оценки используется величина

11.

n
( xi x )2
Sn2 i 1
n 1
.
Среднюю квадратическую (стандартную) погрешность (СКО)
находятся по формуле 2 ,
2
для ее оценки вычисляется величина Sn Sn
lim Sn .
n
Величина
Sn
w
100 %
x
называется коэффициентом вариации
Обычно принимается, что погрешности подчиняются
нормальному закону распределения случайных величин

12.

При этом предполагается:
1) погрешности измерений могут принимать непрерывный
ряд значений;
2) при большом числе наблюдений погрешности равных
значений, но разных знаков встречаются одинаково часто;
3) частота появления погрешностей уменьшается с
увеличением величин погрешностей
Эти предположения приводят к закону распределения
погрешностей, описываемому формулой Гаусса:
y
1
2
e
( x ) 2
2 2
.

13.

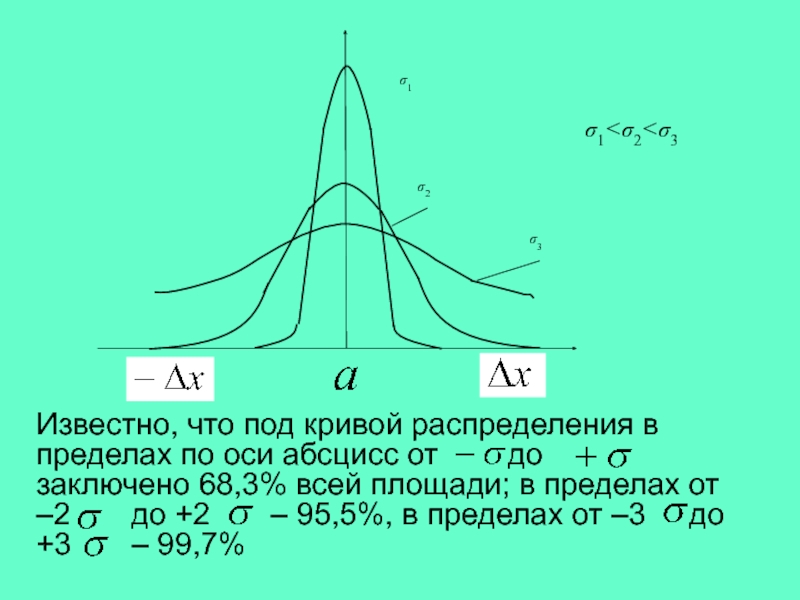
Форма кривых Гаусса зависит от величин . Чем больше
тем больше рассеивание случайной погрешности
σ1
σ1<σ2<σ3
σ2
σ3
x
a
x
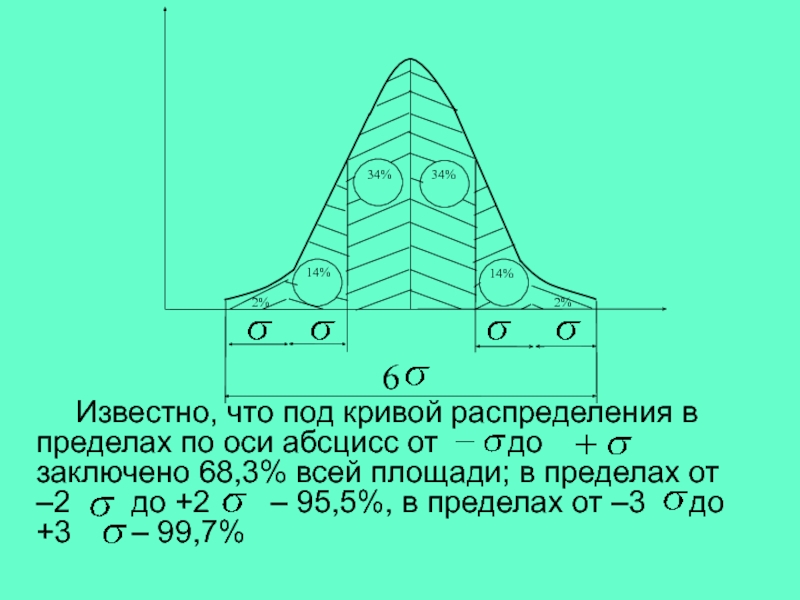
Известно, что под кривой распределения в пределах по оси
абсцисс от до заключено 68,3% всей площади; в
пределах от –2 до +2 – 95,5%, в пределах от –3 до
+3 – 99,7%
,

14.

Замечание. В ряде случаев экспериментальные данные лучше
описываются другими законами распределения случайных
величин, например, законом Пуассона:
y
2 x 2
e
x!
.

15. Закон сложения случайных ошибок

Пусть измеряемая величина Z является суммой (или разностью)
двух величин X и Y, результаты измерений которых независимы.
2
2
2
Тогда, если S X , S Y , S Z – дисперсии величин X, Y и Z, то можно
доказать, что
S Z S X2 SY2
S Z2 S X2 S Y2
или
Если Z является суммой не двух, а большего числа
слагаемых, то закон сложения ошибок будет таким же, т. е.
средняя квадратичная ошибка суммы или разности двух (или
нескольких) независимых величин равна корню квадратному
из суммы дисперсий отдельных слагаемых
Для нахождения суммарной ошибки нужно складывать
не сами ошибки, а их квадраты

16.

Из закона сложения ошибок следуют два чрезвычайно важных
вывода
1: роль каждой из ошибок в общей ошибке результата.
Значение отдельных ошибок очень быстро падает по мере их
уменьшения
Пример: пусть X и Y – два слагаемых, определенных со
средними квадратичными ошибками S X и S Y , причем,
известно, что S Y В два раза меньше, чем S X . Тогда ошибка
суммы Z X Y будет
SZ2
S X2
SY2
S X2
S Z 1,1S X .
Sx 2 5 2
( ) SX .
2
4
В первую очередь надо уменьшать ошибку, имеющую
наибольшую величину

17.

Если нужная величина Z является разностью двух независимо
измеряемых величин X и Y, то из выражения для среднего
значения следует, что ее относительная погрешность
Sz
Z
S x2 S y2
X Y
будет тем больше, чем меньше X Y , и относительная
погрешность возрастает до бесконечности, если X Y
Невозможно добиться хорошей точности измерений какойлибо величины, строя измерения так, что она находится как
небольшая разность результатов независимых измерений
двух величин, существенно превышающих искомую. В
противоположность этому относительная погрешность суммы
Sz
Z
S x2 S y2
X Y
очевидно, не зависит от соотношения величин X и Y

18.

2: средняя квадратическая погрешность среднего
арифметического равна средней квадратической
погрешности отдельного результата, деленная на
Sn
корень квадратный из числа измерений
Sx
n
,
S n – средняя квадратичная погрешность отдельного измерения
Cреднеарифметическое ряда измерений
1 n
x1 x2
xn
x xi
n i 1
n n
n
согласно закону сложения случайных погрешностей
2
2
2
Sn2
Sn
Sn
2 Sn
Sx
,
n
n n
n
Это рассуждение относится лишь к измерениям, при которых
точность результата полностью определяется случайной
ошибкой

19.

При практической работе очень важно строго разграничивать
применение средней квадратичной ошибки отдельного
измерения S n и средней квадратичной среднего
арифметического S x
В тех случаях, когда требуется характеризовать точность
применяемого способа измерений, следует
характеризовать его ошибкой S n .
S x применяется всегда, когда нужно оценить погрешность
того числа, которое получили в результате всех
произведенных измерений

20.

Доверительный интервал и доверительная
вероятность
Обозначим истинное значение измеряемой величины через x,
погрешность измерения этой величины – x . Среднее
арифметическое значение, полученное в результате
измерений, будет x . Пусть означает вероятность того, что
результат измерений отличается от истинного значения на
величину, не большую, чем x .
или
P( x x x x)
P( x x x x x)
Вероятность называется доверительной вероятностью,
или коэффициентом надежности. Интервал значений от x x
до x x называется доверительным интервалом

21.

Для характеристики величины случайной ошибки
необходимо задать два числа, а именно: величину
самой ошибки (или доверительного интервала) и
величину доверительной вероятности
При обычных измерениях можно ограничиться
доверительной вероятностью 0,9 или 0,95
Для измерений, по условиям которых требуется
чрезвычайно высокая степень надежности, иногда задают
доверительную вероятность 0,997
Удобство применения стандартной ошибки в качестве
основного численного выражения погрешности наблюдений
заключается в том, что этой величине соответствует вполне
определенная доверительная вероятность, равная 0,68.
(Здесь и дальше полагаем, что ошибки распределены по
нормальному закону)

22.

Средней квадратичной ошибке
соответствует
доверительная вероятность 0,68, удвоенной средней
квадратичной ошибке (2
) – доверительная
вероятность 0,95, утроенной (3
) – 0,997
Определение доверительного интервала и доверительной
вероятности
При определении среднеквадратичной ошибки из малого
числа наблюдений находим последнюю с малой точностью
Заменяя S n на , мы уменьшаем надежность нашей оценки.
Чтобы учесть это обстоятельство, будем записывать
x n
вероятность через коэф. Стьюдента, найденные по t ,n
P( x t ,n
Sn
Sn
x x t ,n
) .
n
n
Sn

23.

Группы систематических погрешностей и методы их
компенсации
При измерениях необходимо учитывать и исключать
систематические ошибки, которые иногда могут быть так
велики, что совершенно исказят результаты измерений
Их можно разделить на четыре группы:
1. Погрешности, природа которых нам известна, и их
величина может быть достаточно точно определена
Такие ошибки могут быть устранены введением соотв-щих
поправок. Источники таких ошибок нужно тщательно
анализировать, величины поправок определять и учитывать в
окончательном результате
ПРАВИЛО: если поправка не превышает 0,005 от средней
квадратической ошибки результата измерений , то ею следует
пренебречь

24.

2. Погрешности известного происхождения, но неизвестной
величины
К числу таких погрешностей относится погрешность
измерительных приборов, которая определяется иногда
классом точности прибора. Если на приборе указан класс
точности 0,5, то это означает, что показания прибора
правильны с точностью до 0,5% от всей действующей шкалы
прибора
Электроизмерительные приборы характеризуются обычно
классом точности в пределах от 0,05 до 4. Менее точные
приборы обозначения класса не имеют
Максимальные погрешности, даваемые измерительными линейками,
микрометрами и некоторыми другими приборами, иногда наносят на самом
приборе, иногда указывают в прилагаемом к нему паспорте. Обычно дается
наибольшая абсолютная погрешность, которую вынуждены считать
постоянной по всей шкале прибора, если последний не сопровождается
специальной таблицей поправок для каждого деления шкалы. Последняя
прилагается только к наиболее точным измерительным приборам

25.

3. Ошибки, природа которых неизвестна, но которые могут
иметь существенное значение
Эта группа систематических ошибок самая опасная. Это
ошибки, о существовании которых мы не подозреваем, но
их величина может быть значительной. Они чаще всего
проявляются при сложных измерениях, и иногда бывает, что
какая-нибудь величина, которая считается определенной с
точностью, например, до 2 3%, в действительности
оказывается в 2 раза больше измеренного значения
Один из наиболее надежных способов убедиться в отсутствии
таких погрешностей – провести измерения интересующей
величины совсем другим методом и в других условиях.
Совпадение полученных результатов служит известной, хотя, к
сожалению, не абсолютной, гарантией их правильности. Бывает,
что и при измерении разными методами в результатах
присутствует ускользнувшая от наблюдателя систематическая
ошибка, и в этом случае оба совпавшие друг с другом результата
окажутся одинаково неверными

26.

4. Ошибки, обусловленные свойствами измеряемого объекта
Эта группа ошибок, хотя и не связана непосредственно с
измерительными операциями, может существенным
образом искажать результат измерений
Систематическая ошибка, связанная со свойствами
измеряемого объекта, часто может быть переведена в
случайную. Перевод систематических ошибок в случайные
часто оказывается полезным, так как позволяет улучшить
точность получаемых результатов
Можно перевести систематическую ошибку в случайную,
организовав измерения таким образом, что постоянный
фактор, влияющий на результат измерений, в каждом из них
действует разным образом, т.е. результат его действий носит
случайный характер. Этот прием называется рандомизацией.
Он позволяет практически исключить многие неизвестные
систематические ошибки

27.

Определение грубых погрешностей
Можно считать какое-то измерение промахом, если
вероятность случайного появления такого значения в данном
ряду измерений является достаточно малой
Если известно точное значение
, то вероятность
появления значения, уклоняющегося от среднего
арифметического x более чем на 3
, равна 0,003; и все
измерения, отличающиеся от на эту (или большую) величину,
могут быть отброшены как очень маловероятные
Алгоритм определения грубых погрешностей
Пусть известен ряд измерений случайных величин:
x1 , x 2 ,…, x r , x n .
Установим, есть ли среди этих значений измерения,
проведенные с грубыми погрешностями (промахами)

28.

Пусть
x k – первое подозреваемое на грубую погрешность
Вычисляем среднеарифметическое с учетом подозреваемой
величины xk и оценку СКО S n .. Определяем величину
максимального отклонения в долях среднеквадратической
ошибки:
Vmax
xk x
.
Sn
По таблице оценки выскакивающих измерений, зная число
измерений n и Vmax, находим вероятность β того, что
данное измерение содержит случайную погрешность
Оставить
Отбросить
0
0,01
0,10
β

29.

Определение числа измерений
Допустим, что все систематические ошибки учтены, т.е.
поправки, которые следовало определить, вычислены, класс
точности прибора известен и есть уверенность, что
отсутствуют какие-либо существенные и неизвестные
источники систематических ошибок
Если случайная ошибка окажется меньше систематической,
то очевидно, что нет смысла пытаться еще уменьшить
величину случайной ошибки: все равно результаты
измерений не станут от этого заметно точнее, и, желая
получить большую точность, нужно искать пути к
уменьшению систематической ошибки. Наоборот, если
случайная ошибка больше систематической, то именно
случайную ошибку нужно уменьшать в первую очередь
Для уменьшения случайной ошибки следует произвести ряд измерений,
тем больший, чем меньшую величину случайной ошибки хотим получить.
Но нет смысла производить измерений больше, чем это необходимо,
чтобы систематическая ошибка существенно превышала случайную

30.

ПРАВИЛА
1. Если систематическая ошибка является определяющей,
т.е. ее величина существенно больше величины случайной
ошибки, присущей данному методу, то достаточно выполнить
измерение один раз
2. Если случайная ошибка является определяющей, то
измерения следует производить несколько раз. Число
измерений целесообразно выбирать таким, чтобы случайная
ошибка среднего арифметического была меньше
систематической ошибки с тем, чтобы последняя опять
определяла окончательную ошибку результата
Для уменьшения случайной ошибки результата могут быть
использованы два пути: улучшение точности измерений, т.е.
уменьшение величины σ, и увеличение числа измерений, т.е.
использование соотношения
.
x
n

31.

Считаем, что все возможности совершенствования техники
измерений уже использованы
Пусть систематическая ошибка измерений, определяемая
классом точности прибора или другими аналогичными
обстоятельствами, будет δ
Уменьшать случайную ошибку целесообразно только до тех
пор, пока общая погрешность измерений не будет полностью
определяться систематической ошибкой. Для этого
необходимо, чтобы доверительный интервал, определенный
с выбранной степенью надежности, был бы существенно
меньше величины систематической ошибки. Иначе говоря,
x .
Нет необходимости определять общую ошибку с точностью
большей 10%.
x / 10
x / 3
x / 2

32.

Надежность α с какой хотим установить доверительный
интервал, в большинстве случаев не должна превышать
0,95, хотя иногда требуются и более высокие значения α
Суммарная погрешность
Если систематическая и случайная погрешности измерений
близки друг к другу, они обе в одинаковой степени определяют
точность результата. Значение суммарных ошибок можно
оценить так: обозначим величину систематической ошибки δ,
дисперсию измерений – σ2, тогда в качестве верхней границы
суммарной ошибки можно принять 2 .
Вопрос о сложении систематических и случайных ошибок
актуален только тогда, когда одна из них не более чем в
несколько раз превышает другую. В противном случае в
качестве меры погрешности измерения следует указывать
только большую ошибку

33. Ошибки первого и второго рода

В тех случаях, когда измеряются какие-то свойства готовой
продукции (диаметр подшипника, состав металла, и т.п.),
задача измерений обычно состоит не в получении точного
значения измеряемой величины, а в необходимости
уложиться в определенные допуски, установленные для
данной продукции. Те изделия, которые не укладываются в
эти допуски, будем называть браком. Но следствием ошибок
измерений могут быть два обстоятельства: 1) хорошее
изделие бракуется и 2) брак пропускается
В той или иной мере ошибки Ι и ΙΙ рода всегда наблюдаются
Ввиду того, что ошибки Ι и ΙΙ рода всегда обусловлены
многочисленными факторами, их количественные
характеристики могут носить только статистический характер
и задаваться как вероятности РI и РII

34. ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА

Методы графического изображения результатов
измерений
Графическое изображение дает наиболее наглядное
представление о результатах экспериментов, позволяет
лучше понять физическую сущность исследуемого
процесса, выявить общий характер функциональных
зависимостей изучаемых переменных величин,
установить наличие максимума или минимума функции
y
x5y5
x4y4
x3y3
x1y1
x6y6
x2y2
1
2
x

35.

При графическом изображении результатов экспериментов
большую роль играет выбор систем координат или
координатной сетки. Координатные сетки бывают
равномерными и неравномерными
Из неравномерных координатных сеток наиболее
распространены полулогарифмические, логарифмические,
вероятностные.
Назначение неравномерных сеток различное. В большинстве
случаев их применяют для более наглядного изображения
функций. Функция имеет различную форму на различных
сетках. Так, многие криволинейные функции спрямляют на
логарифмических сетках.
Правильно подобранный масштаб позволяет существенно
повысить точность результатов исследований.
Расчетные графики, имеющие максимум (минимум) функции
или какой-либо сложный вид, особо тщательно необходимо
вычерчивать в зонах изгиба. Количество точек на таких
участках должно быть значительно больше, чем на плавных

36. Методы подбора эмпирических формул

На основе экспериментальных данных можно подобрать
алгебраические выражения, которые называют
эмпирическими формулами. Такие формулы подбирают
лишь в пределах измерений значений аргумента x1,…,xn.
Эмпирические формулы имеют тем большую ценность, чем
больше они соответствуют результатам эксперимента
y f (x)
Эмпирические формулы часто незаменимы для анализа
измеренных величин. К эмпирическим формулам
предъявляют два основных требования:
по возможности они должны быть наиболее простыми и
точно соответствовать экспериментальным данным в
пределах изменения аргумента

37.

Эмпирические формулы являются приближенными
выражениями аналитических формул. Замену точных
аналитических выражений приближенными, более простыми
называют аппроксимацией, а функции –аппроксимирующими
Процесс подбора эмпирических формул состоит из двух этапов
•данные измерений наносят на сетку прямоугольных координат,
соединяют экспериментальные точки плавной кривой и
выбирают ориентировочно вид формулы
•вычисляют параметры формул, которые наилучшим образом
соответствовали бы принятой формуле
Метод выравнивания заключается в том, что кривую,
построенную по экспериментальным точкам, представляют
линейной функцией
Y a bX
Линеаризацию кривых можно легко осуществить на полу- или
логарифмических координатных сетках, которые применяют
при графическом методе подбора эмпирических формул

38.

Графический метод выравнивания может быть применен
в различных случаях, когда экспериментальная кривая на
сетке прямоугольных координат имеет вид плавной кривой
1.
y ax b
— степенная функция
Заменяя X = lgx и Y = lgy, имеем Y = lga + bX.
При этом экспериментальная кривая превращается в
прямую линию на логарифмической сетке
2.
y ae bx
Заменяя
— показательная функция
Y lg y
, имеем
Y lg a xb lg e
.

Источник

Все мы ошибаемся. Мы люди. Но иногда мы совершаем глупые мелкие оплошности просто от недостатка внимания — и дорого расплачиваемся за них в дальнейшем. Первая ошибка влечет за собой вторую, затем следующую… а пять ошибок подряд могут сбить с пути истинного, и вернуться на него уже не удастся. Гении знают о Законе сложения ошибок и много работают над тем, чтобы избежать этой ловушки.

Мы, возможно, никогда не узнаем в точности, что делает гения гением, откуда берутся в человеке необычайная творческая мощь и изобретательность, почему одни люди используют свои творческие возможности чаще, чем другие, или почему некоторые люди в определенный период своей жизни проявляют особую творческую активность. Моцарт написал свои лучшие вещи в юности, тогда как другой музыкальный гений — Людвиг ван Бетховен — создал главные свои шедевры ближе к концу жизни. Кроме того, существуют гении, которые в течение всей жизни демонстрируют исключительные результаты, подобно Стиву Джобсу или Стивену Спилбергу. Никакой системы здесь не просматривается. Но даже если ответы на эти вопросы навсегда останутся для нас загадкой, одно очень важное утверждение мы смело можем сделать: нельзя назвать точный набор ингредиентов гения. Гений имеет сложный состав, хотя следует, конечно, обратить внимание на некоторые тенденции. Так, спагетти можно приготовить бесконечным числом способов путем комбинирования обычных ингредиентов; все равно получатся спагетти. (Надо сказать, что не все спагетти одинаковы на вкус, точно так же как вклад Моцарта в копилку общества — то, что вышло из его «кухни» — совершенно не похож на вклад Эйнштейна.) Так что рецепт гениальности весьма неточен, но это и хорошо: дверь открыта для каждого, кто готов работать над общими характеристиками (обычными ингредиентами) гения. Это сортировка и анализ данных, желание экспериментировать и нестандартно смотреть на вещи, работа воображения и творческий подход, хранение в памяти большого количества хорошо организованной информации, отвага, необходимая, чтобы выступать с новыми идеями, отвергающими здравый смысл, готовность ломать устоявшиеся каноны и срывать покровы. Мы перечислили те самые шесть умений, которые вы сможете приобрести при помощи этой книги. Еще раз: можно ли научить свой мозг работать подобно мозгу гения? Да!

Я должен также добавить, что каждый из нас обладает способностями, позволяющими достичь вершин во всех перечисленных областях. Это не врожденные способности немногих избранных. Может быть, вы считаете, что ваше воображение не особенно богато, а творческое начало слабо развито. А может быть, уверены, что слова «изобретатель» и «первопроходец» не годятся для описания вас и ваших способностей. Моя задача при написании этой книги состояла отчасти в том, чтобы доказать вам: эти навыки можно развить, независимо от того, велики или малы соответствующие врожденные таланты. Не принимайте ничего за чистую монету и ни в коем случае не ограничивайте себя жесткими рамками. Будьте всегда открыты новым возможностям.

Источник

Для применения закона сложения ошибок надо знать формулы, связывающие отдельные измеряемые величины и частные ошибки различных стадий процесса измерения. В дальнейшем мы будем исходить из предположения, что все измерения взаимно независимы (см. с. 42). [c.64]

Закон сложения ошибок [c.64]

Ошибку определения получают из уравнения (4.12) по закону сложения ошибок [уравнение (4.36)] [c.69]

Закон сложения ошибок. Для независимых случайных величин свойством аддитивности обладают дисперсии, а не среднеквадратичные ошибки. Если 1, Х2….. Хп — независимые случайные величины а, й2,. .., йп — неслучайные величины и [c.31]

Случайная ошибка метода анализа чаще всего складывается из нескольких частных ошибок. Для минимизации общей ошибки анализа надо найти оптимальные условия измерения. Этому способствуют законы сложения ошибок. Рассмотрение ошибок такого рода прежде всего сосредоточивается на возникающих ошибках измерений. Поэтому рассмотрение таких ошибок лишь в исключительных случаях может дать некоторые представления о точности аналитического метода, так как ошибки измерений обычно гораздо меньше, чем случайные колебания, например хода химических реакций. Тем не менее метод анализа может полностью проявить свои возможности только в том случае, когда ошибки измерений сведены к минимуму. [c.64]

Ниже описывается действие закона сложения ошибок при поиске наилучших условий измерения для нескольких типичных методов аналитической химии. [c.64]

Глава 4. Закон сложения ошибок [c.68]

Из уравнения (4.34) по закону сложения ошибок [уравнение (4.3а)] и с учетом (7 яа [уравнение (3.14)] получаем [c.78]

Пусть даны два средних Хх и Х2, которые получены из двух независимых друг от друга серий с Пх и пг измерениями. Средние слегка различаются. Надо проверить, можно ли объяснить это различие только случайной ошибкой, т. е. принадлежат ли оба средних нормально распределенной генеральной совокупности с одним и тем же средним р. Значит, проверяется гипотеза для данного параметрического критерия р = рз = Р- Перед ее проверкой надо выяснить, нет ли разницы между стандартными отклонениями обеих серий 1 и г (по Г-критерию, см. разд. 7.2). Если значимое различие между 1 и 2 не обнаруживается, то сначала по закону сложения ошибок находят стандартное отклонение для разности двух средних из пх и П2 измерений. Уравнения (4.3а) и (3.4) дают [c.121]

Общая ошибка метода анализа чаще всего складывается из ряда отдельных частных ошибок. Они суммируются по закону сложения ошибок (см. гл. 4). Знание этих частных ошибок важно, например, при разработке нового метода анализа, так как стоит улучшать ход анализа на наиболее ответственной стадии — там, где наибольшая ошибка. [c.140]

Если из двух взаимосвязанных (коррелированных) случайных величин х и у вычисляют третью 2 = [/(х у)], то в законе сложения ошибок надо дополнительно учесть еще и степень корреляции между хну. Для четырех основных действий арифметики — как обобщение уравнения (4.3) — получим следующие закономерности [c.162]

Дисперсии для констант а тл Ь можно искать с помощью закона сложения ошибок тогда получим [c.168]

Закон сложения ошибок. Для независимых случайных величин свойством аддитивности обладают дисперсии, а не среднеквадратичные [c.35]

Закон сложения ошибок. В химическом эксперименте искомая величина часто не может быть измерена непосредственно. Для ее определения используются различные математические выражения, в которых эта искомая величина является функцией других измеряемых в эксперименте величин. Таким образом, возникает вопрос о нахождении среднего значения функции и ее средней квадратичной ошибки, если известны средние значения и средние квадратичные ошибки аргументов. [c.229]

Формулы (17) и (18) известны в математической статистике под названием закона сложения ошибок. Они позволяют рассчитать ошибку функции, если известны ошибки аргументов при различных видах функциональной зависимости. [c.230]

I 4] ЗАКОН СЛОЖЕНИЯ ОШИБОК 53 [c.53]

ЗАКОН СЛОЖЕНИЯ ОШИБОК [c.55]

Закон сложения ошибок можно интерпретировать геометрически при помощи векторов, так как. это показано на рис. 7. В первом примере на рис. 7 между величинами X ш у нет линейной корреляционной связи (г у = 0). Из геометрического построения ясно видно, что в этом случае нет необходимости затрачивать усилия на з меньше-ние меньшей из двух компонентов, так как уменьшение [c.55]

Пользуясь законом сложения ошибок, можно получить формулу для подсчета ошибок воспроизводимости по текущим измерениям, состоящим из двух параллельных определений [101, 117, 121]. Допустим, что анализу подвергалось п различных по своему составу проб. Обозначим через d разность между двумя параллельными определениями тогда мы можем написать [c.56]

ЗАКОН СЛОЖЕНИЯ ОШИБОК 57 [c.57]

ЗАКОН СЛОЖЕНИЯ ОШИБОК 59 [c.59]

Здесь м общ — результирующая ошибка, и 1 — ошибки отдельных операций. При этом безразлично, какие из случайных ошибок суммируются формула (118) написана для коэффициента вариации йУ, совершенно так н<е суммируются средние квадратичные ошибки а пли средние арифметические ошибки г. Из закона сложения ошибок следует важное правило существенный вклад вносят только те ошибки, которые близки к наибольшей из ошибок. Поясним сказанное численным примером. Допустим, что ошибка измерения интенсивности составляет 1%, ошибка, вносимая источником возбуждения, 3% и ошибка, вносимая неоднородностью проб, 0,5%. Тогда суммарная ошибка будет н, общ = V 9 1 0,25 = = 3,2%. Практически эта величина не отличается от 3%. Поэтому нет никакого смысла для повышения точности стараться уменьшить ошибку измерения интенсивности или неоднородности проб, пока не уменьшена ошибка, вносимая генератором. В разных случаях анализа ошибки различных звеньев процесса играют определяющую роль. При анализе руд обычно так велики неоднородности проб, что нет смысла прибегать к точным методам регистрации спектров. При анализе сплавов именно измерительное звено часто играет решающую роль. Воспроизводимость и точность тех или иных методов анализа будут приведены в соответствующих разделах. Здесь ограничимся только указанием, что лучшие методы количественного анализа позволяют делать определения с коэффициентом вариации до 0,1%. Обычно нри количественных анализах его значение лежит в пределах 1—10%. При определениях вблизи границы чувствительности метода ю быстро возрастает. [c.164]

Из закона сложения ошибок следует, что существенное влияние на величину Отобщ оказывают наибольшие из ошибок. [c.195]

По закону сложения ошибок средняя квадратичная ошибка суммы независимых величин равна корню квадратному из суммы дисперсий отдельных слагаемых, т. е. ошибка определения содержания Н3РО4 в пробе — Sxi равна [c.85]

Статистика в аналитической химии (1994) — [

c.64

]

Применение математической статистики при анализе вещества (1960) — [

c.53

c.60

]

Источник

Среднее квадратическое
отклонение

случайной величины
(сокращенно
с. к. о.). Это положительное значение
квадратного корня из ее дисперсии

где D
— дисперсия,
т. е. второй центральный момент случайной
величины, а р(х)
— плотность
распределения, X_ц
– координата центра распределения..
Для определения оценки дисперсии по
экспериментальным данным пользуются
соотношением

где x_i—значения
отдельных отсчетов; п—объем
выборки.

Отсюда оценка с.
к. о. определяется как

Основным достоинством
оценки разброса случайных величин
средним квадратическим значением

является возможность определения
дисперсии суммы статистически независимых
величин независимо от разнообразия
законов распределения каждой из
суммируемых величин и деформации законов
распределения при образовании композиций.

Таким образом для
того, чтобы отдельные составляющие
погрешности средств измерений можно
было суммировать расчётным путём, они
должны быть предварительно представлены
своими средними квадратическими
значениями ,
а не максимальными _m
или доверительными _д
значениями. При этом открывается
возможность расчётным путём не только
складывать любое число составляющих
погрешности, что необходимо при анализе
точности косвенных измерений или сложных
измерительных устройств, но и достаточно
точно вычитать погрешности, что необходимо
при синтезе методов измерений или
сложных устройств с заданной результирующей
погрешностью. Действительно, если
,
то.
Это правомерно для независимых случайных
величин.

Из предыдущего
следует, что
.
В случае сложения не двух, а большего
числа дисперсий или с.к.о. независимых
случайных величин закон сложения будет
таким же. Следует обратить внимание на
то, что как вы уже убедились, для нахождения
суммарной погрешности следует складывать
не сами погрешности, а их квадраты. В
том случае. Если мы складываем вероятности,
то закон сложения будет тем же..

Из закона сложения
погрешностей следуют два очень важных
вывода. Первый относится к роли каждой
из погрешностей в общей погрешности
результата. Он состоит в том, что значение
отдельных погрешностей очень быстро
падает по мере
их уменьшения.
Поясним сказанное примером: пусть X
и Y
— два слагаемых, определенных со средними
квадратическими погрешностями _x
и _y
, причем
известно, что _y.
в два раза меньше, чем _x.
Тогда погрешность суммы Z=X+Y
будет

Откуда
.
Следовательно, если одна из погрешностей
в два раз меньше другой, то общая
погрешность возросла за счет этой
меньшей погрешности всего на 10%, что
обычно играет очень малую роль. Это
означает, что если мы хотим повысить
точность измерений величины Z,
то нам нужно в первую очередь стремиться
уменьшить ту погрешность измерения,
которая больше, т.е. погрешность измерения
величины X.
Если оставим точность измерения Х
неизменной, то, как бы мы ни повышали
точность измерения слагаемого Y,
нам не удастся уменьшить погрешность
конечного результата измерений величины
Z
более чем
на 10%.

Этот вывод всегда
нужно иметь в виду, и для повышения
точности измерений в первую очередь
уменьшать погрешность, имеющую наибольшее
значение. Конечно, если слагаемых много,
а не два, как в нашем примере, то и малые
погрешности могут внести заметный вклад
в суммарную погрешность.

Если нужная нам
величина Z;
является разностью двух независимо
измеряемых величин Х
и Y,
то из выражения для суммы с.к.о. следует,
что ее относительная погрешность

где X,
Y,
Z
– погрешности измерений величин X,
Y,
Z.

Очевидно, что она
будет тем больше, чем меньше
,
и относительная погрешность возрастает
до бесконечности, еслиX
стремиться к Y.

Это означает, что
невозможно добиться хорошей точности
определения какой-либо величины, строя
измерения так, что она находится как
небольшая разность результатов
независимых измерений двух величин,
существенно превышающих искомую. В
противоположность этому относительная
погрешность суммы

очевидно не зависит
от соотношения величин X
и Y.

Следующий вывод,
вытекающий из закона сложения погрешностей,
относится к определению погрешности
среднего арифметического. Следует
отметить, что среднее арифметическое
из ряда измерений числом n
отягощено меньшей погрешностью, чем
результат каждого отдельного измерения.
Запишем этот вывод в количественной
форме. Пусть x₁,
x₂,
x_n
результаты отдельных измерений, причем
каждое из них характеризуется одной и
той же дисперсией D
. Образуем
величину Y
, равную

Дисперсии этой
величины D_y
определяются в соответствии с формулой
сложения дисперсий

как

Но у
, по определению, это — среднее арифметическое
из всех величин x_i
и мы можем написать

(13)

Средняя квадратическая
погрешность среднего арифметического
равна средней квадратической погрешности
отдельного результата измерений,
деленной на корень квадратный из числа
измерений. Это — фундаментальный закон
возрастания точности при росте числа
наблюдений. Мы его уже обсуждали в
разделе 5.1. Из него следует, что, желая
повысить точность измерений в 2 раза,
мы должны сделать вместо одного — четыре
измерения; чтобы повысить точность в 3
раза, нужно увеличить число измерений
в 9 раз, и, наконец, увеличение числа
наблюдений в 100 раз приведет к десятикратному
увеличению точности измерений.

Разумеется, это
рассуждение относится лишь к измерениям,
при которых точность результата полностью
определяется случайной погрешностью.
В этих условиях, как уже указывалось,
выбрав n
достаточно большим, мы можем существенно
уменьшить погрешность результата. Такой
метод повышения точности широко
используется. Отметим, что повышение
точности измерений целесообразно
производить таким способом в том случае,
если погрешность измерительного средства
намного превышает цену деления шкалы
отсчёта. В этом случае погрешность можно
свести к значению цены деления. Очевидно,
что получить точность выше цены деления
не представляется возможным т.к. при
отсчёте показаний округления производятся
до целых делений шкалы. С помощью такого
приёма легко снизить погрешность от
вариации показаний.

При практической
работе очень важно строго разграничивать
применение средней квадратической
погрешности отдельного измерения _i
и средней квадратической погрешности
среднего арифметического

Последняя применяется
всегда, когда нам нужно оценить погрешность
того значения, которое мы получили в
результате всех произведенных измерений.

В тех случаях,
когда мы
хотим
характеризовать точность применяемого
способа измерений, следует использовать
погрешность _i
, если n,
достаточно велико.

Приведем примеры пользования результатами
таблицы. Пусть для некоторого ряда измерений получили =20,
σ =2. Какова вероятность того, что результат отдельного измерения не выйдет за
пределы, определяемые равенством 17 < х_i < 23?
Доверительные границы равны ± 3, что составляет в долях σ -1,5. Из таблицы 3.1
находим, что доверительная вероятность для ε = 1,5 равна 0,87. Иначе говоря,
87% всех измерений уложится в интервал погрешности ± 3 .

Сформулируем вторую задачу, какой
доверительный интервал нужно выбрать для тех же измерений, чтобы 99% результатов
попала в него? По таблице 3.1 находим, что значению α =0,99 соответствует значение
ε =2.6, следовательно, доверительный искомый интервал равен Δх = ε*σ = 2,6*
2=5,2.

Таким образом, для нахождения случайной
погрешности нужно определи два числа — доверительный интервал /величину
погрешности/ и доверительную вероятность. Средней квадратичной погрешности σ
соответствует доверительная вероятность 0.68, удвоенной средней квадратичной
погрешности 2σ — доверительная вероятность 0.95; утроенной /Зσ/ — 0.997.

Приведенные три значения α полезно
запомнить, так как обычно в литературе дается значение средней квадратичной
погрешности и не указывается соответствующая ей доверительная вероятность.

Наряду со среднеквадратичной погрешностью
иногда используется погрешность среднеарифметическая, вычисляемая по формуле

;

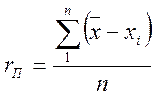
При большом числе наблюдений r_п
и S_П существуют простые соотношения

S_П =1.25 r_П;
r_П = 0.80 S_П

Известным преимуществом средней
арифметической погрешности является сравнительно простой способ ее вычисления. Если
пользоваться средней арифметической погрешностью и при малой n, то правильнее
ее вычислять по соотношению

СЛОЖЕНИЕ
СЛУЧАЙНЫХ ПОГРЕШНОСТЕЙ

Предположим, что измеряемая величина Z
является суммой /или разностью/ двух величин Х и Y, результаты измерений
которых независимы. Тогда, если , —
дисперсия величин Х и Ү, то дисперсия измеряемой величины будет равна

=+ или =

Если Z является суммой не двух, а
большего числа слагаемых — закон сложения погрешностей будет таким же.

Таким образом, средняя квадратичная
погрешность суммы /ила разности/ нескольких независимых величин равна корню квадратному,
из суммы дисперсий отдельных слагаемых. Необходимо твердо помнить, что для
нахождения суммарной погрешности нужно складывать не сами погрешности, а их квадраты
и извлечь квадратный корень.

Из закона сложения погрешностей следует
два важных вывода. Первый из них относится к роли каждой из погрешностей в
общей погрешности результата. Поясним сказанное на примере: пусть Х и Y два
слагаемых, определенных со средней квадратичной погрешностью и , причем
в два раза меньше.
Тогда ошибка суммы будет

=+=+;

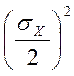
Иначе говоря, если одна из ошибок в два
раза меньше другой, то общая погрешность возросла за счет меньшей из
погрешностей всего на 10%. Это означает, что если необходимо повысить точность
измерения величины Z, то нужно в первую очередь стремиться уменьшить ту
погрешность измерения, которая больше. Если оставить точность измерения Х
неизменной, то, как бы мы не повышали точность измерения Y, погрешность
конечного результата не удастся уменьшить более чем на 10%. Этот вывод нужно
иметь в виду и при повышении измерений в первую очередь уменьшать погрешность,
имеющую наибольшую величину.

Второй вывод, вытекающий из закона
сложения погрешностей, относится к определению погрешности среднего
арифметического. Среднее арифметическое оточено меньшей ошибкой, чем результат
каждого отдельного измерения. Покажем это. Пусть х₁,х₂,…,х_n
— результаты отдельных измерений, каждое из которых характеризуется дисперсией
σ². Среднее арифметическое всех измерений можно представить в виде

В соответствии с законом сложения
погрешностей дисперсию величины Y можно найти как

Но Y и есть среднее арифметическое из всех величин х_i,
поэтому

Уважаемый посетитель!

Чтобы распечатать файл, скачайте его (в формате Word).

Ссылка на скачивание — внизу страницы.

Закон сложения ошибок [c.64]

Ошибку определения получают из уравнения (4.12) по закону сложения ошибок [уравнение (4.36)] [c.69]

Глава 4. Закон сложения ошибок [c.68]

Из уравнения (4.34) по закону сложения ошибок [уравнение (4.3а)] и с учетом (7 яа [уравнение (3.14)] получаем [c.78]

Дисперсии для констант а тл Ь можно искать с помощью закона сложения ошибок тогда получим [c.168]

I 4] ЗАКОН СЛОЖЕНИЯ ОШИБОК 53 [c.53]

ЗАКОН СЛОЖЕНИЯ ОШИБОК [c.55]

ЗАКОН СЛОЖЕНИЯ ОШИБОК 57 [c.57]

ЗАКОН СЛОЖЕНИЯ ОШИБОК 59 [c.59]

Статистика в аналитической химии (1994) — [

c.64

]

Применение математической статистики при анализе вещества (1960) — [

c.53

c.60

]

Слайд 1ОСНОВЫ ТЕОРИИ ОШИБОК ИЗМЕРЕНИЙ
Измерением какой-либо физической величины называется операция, в

результате которой мы узнаем, во сколько раз измеряемая величина больше (или меньше) соответствующей величины, принятой за единицу

Виды измерений и погрешностей

Слайд 2Виды измерений классифицируются:
– по способу получения результата (прямые и косвенные);
– по

методу измерений (абсолютные, относительные и пороговые);
– по условиям измерений (равноточные, неравноточные);
– по степени достаточности измерений (необходимые, избыточные)

Слайд 3 При прямых измерениях измеряется непосредственно исследуемая величина
При косвенных измерениях

исследуемая величина измеряется как функция по результатам измерения других величин

Например, ускорение автомобиля при разгоне определяется по результатам измерения расстояния и времени разгона; вычисление плотности – по массе и объему

Слайд 4 Абсолютные измерения – это прямые измерения в единицах измеряемой величины

Относительные измерения представляют собой отношения измеряемой величины к величине играющей роль единицы или к величине, принимаемой за исходную

При пороговых измерениях фиксируется только факт нахождения величины в одностороннем или двухстороннем допуске
(по принципу «да/нет»)

Слайд 5Равноточные измерения проводятся в одинаковых условиях одними и теми же измерительными

приборами и с одинаковой степенью тщательности.
При этом в ряду измерений нельзя отдать предпочтение какому-либо одному или нескольким значениям

Неравноточные измерения не отвечают указанным выше требованиям

Слайд 6Избыточные измерения имеют по сравнению с необходимыми большее число измерений либо

большую точность, содержат среди измерений зависимые, т. е. дают избыточную информацию

Надежность результатов исследования в значительной степени зависит от точности измерений
Под точностью измерений понимают степень соответствия результата измерения действительному значению измеряемой величины

Слайд 7Снять показания с прибора – не значит только измерить. Необходимо еще

оценить ошибки (погрешности) измерений

Погрешность измерения – это отклонение результата измерения от истинного значения измеряемой величины

Слайд 8Под истинным значением измеряемой величины принято считать
– среднюю арифметическую величину

ряда измерений;
– известное эталонное значение;
– величину, полученную в результате более точных (не менее чем на порядок) измерений

Слайд 9Основные источники ошибок
Первый источник заключен в датчике, который неправильно реагирует

на измеряемую величину.
Например, если тензосопротивление плохо наклеено на упругий элемент, то деформация его решетки не будет соответствовать деформации упругого элемента

Второй источник – измерительное устройство, в котором возможны погрешности из-за неправильного функционирования его механических или электрических элементов

Слайд 10Третий источник – сам наблюдатель, который из-за неопытности или усталости неправильно

считывает показания прибора

Ошибки могут возникнуть из-за влияния измерительного устройства на объект измерения (например, при разрушающем методе контроля), влияния окружающей среды (температура, загазованность и т. п.), методических погрешностей, допущенных экспериментатором

Слайд 11Случайная погрешность – это погрешность, которая в отдельных измерениях может принимать

случайные, заранее конкретно неизвестные значения.
Случайные погрешности обязаны своим происхождением ряду как объективных, так и субъективных факторов, действие которых неодинаково в каждом опыте и не может быть учтено.

Эти источники ошибок приводят к появлению трех типов ошибок: случайных, систематических и грубых

Слайд 12Случайные погрешности различаются в отдельных измерениях, сделанных в одинаковых условиях одними

и теми же измерительными приборами. Исключить случайные погрешности нельзя. Можно только оценить их значение

Случайные погрешности определяются по законам теории ошибок, основанной на теории вероятностей

Слайд 13Систематическая погрешность – это погрешность, вызванная факторами, действующими одинаковым образом при

многократном повторении одних и тех же измерений с помощью одних и тех же измерительных приборов

В качестве примера систематической ошибки рассмотрим случай взвешивания на чашечных весах с помощью неточных гирь. Если взятая нами гиря имеет ошибку, скажем 0,1 г, то вес тела (пусть 1000 г) будет завышенным (или заниженным) на эту величину, и чтобы получить верное значение, необходимо учесть эту ошибку, прибавив к полученному весу (или вычтя из него) 0,1 г, P=(1000±0,1) г

Слайд 14Грубая погрешность или промах вызывается просчетом экспериментатора или неисправностью средств измерения,

или резко изменившимися внешними условиями

Грубые погрешности приводят к явному искажению результата, поэтому их надо исключить из общего числа измерений

Слайд 15Абсолютная погрешность – это разность между результатом измерения и его истинным

значением:

где x – результат измерения; a – истинное значение

По форме числового представления погрешности делятся на абсолютные и относительные

Относительная погрешность – это погрешность, приходящаяся на единицу измеренной величины; обычно выражается в процентах

Слайд 16 Чтобы выявить случайную погрешность измерений, необходимо повторить измерение несколько

раз

Случайные погрешности и их распределение

Если каждое измерение дает заметные от других результаты, мы имеем дело с ситуацией, когда случайная погрешность играет существенную роль

Слайд 17 Наиболее вероятным значением измеряемой величины из серии измерений является

ее среднее значение

Разброс измеряемой величины относительно ее среднего значения определяется величиной средней квадратической погрешности отдельного измерения

Слайд 18Абсолютные погрешности

рассматривают как случайные величины

Пусть в эксперименте в результате независимых и равноточных измерений постоянной величины получены значения х1, х2, …, хn

Независимость измерений понимается как взаимная независимость случайных величин , а равноточность – как подчинение величин одному и тому же закону распределения (кроме того измерения сделаны одним и тем же методом и с одинаковой степенью тщательности)

Слайд 19 В качестве оценки неизвестной величины по данным

измерений обычно берут среднее арифметическое результатов измерений

Дисперсия отдельных измерений

обычно неизвестна, и для ее оценки используется величина

Слайд 20
Среднюю квадратическую (стандартную) погрешность (СКО) находятся по формуле
Величина
для ее

оценки вычисляется величина

называется коэффициентом вариации

Обычно принимается, что погрешности подчиняются нормальному закону распределения случайных величин

Слайд 21При этом предполагается:
2) при большом числе наблюдений погрешности равных значений,

но разных знаков встречаются одинаково часто;

1) погрешности измерений могут принимать непрерывный ряд значений;

3) частота появления погрешностей уменьшается с увеличением величин погрешностей

Слайд 22Эти предположения приводят к закону распределения погрешностей, описываемому формулой Гаусса:
Форма

кривых Гаусса зависит от величин .
Чем больше , тем больше рассеивание случайной погрешности

Слайд 23Известно, что под кривой распределения в пределах по оси абсцисс от

до заключено 68,3% всей площади; в пределах от
–2 до +2 – 95,5%, в пределах от –3 до +3 – 99,7%

Слайд 24Известно, что под кривой распределения в пределах по оси абсцисс от

до заключено 68,3% всей площади; в пределах от
–2 до +2 – 95,5%, в пределах от –3 до +3 – 99,7%

Слайд 25Замечание. В ряде случаев экспериментальные данные лучше описываются другими законами распределения

случайных величин, например, законом Пуассона:

Слайд 26 Пусть измеряемая величина Z является суммой (или разностью) двух

величин X и Y, результаты измерений которых независимы.

Закон сложения случайных ошибок

Тогда можно доказать, что
если , , – дисперсии величин, или

Слайд 27
Если Z является суммой не двух, а большего числа слагаемых, то

закон сложения ошибок будет таким же, т. е. средняя квадратичная ошибка суммы или разности двух (или нескольких) независимых величин равна корню квадратному из суммы дисперсий отдельных слагаемых

Для нахождения суммарной ошибки нужно складывать не сами ошибки, а их квадраты

Слайд 28Средняя квадратичная ошибка суммы или разности двух (или нескольких) независимых величин

равна корню квадратному из суммы дисперсий отдельных слагаемых

Слайд 29Необходимо учитывать роль каждой из ошибок в общей ошибке результата.

Значение отдельных ошибок очень быстро падает по мере их уменьшения.

Выводы:

В первую очередь стоит уменьшать ошибку, имеющую наибольшую величину

Относительная погрешность суммы

Слайд 30
Пример: пусть X и Y – два слагаемых, определенных со средними

квадратичными ошибками и , причем, известно, что В два раза меньше, чем . Тогда ошибка суммы будет

Слайд 312. Средняя квадратическая погрешность среднего арифметического равна средней квадратической погрешности отдельного

результата, деленная на корень квадратный из числа измерений:

– средняя квадратичная погрешность отдельного измерения

Слайд 32 Пусть измеряемая величина Z является разностью двух величин X

и Y, результаты измерений которых независимы.

Тогда ее относительная погрешность

Слайд 33Невозможно добиться хорошей точности измерений какой-либо величины, строя измерения так, что

она находится как небольшая разность результатов независимых измерений двух величин, существенно превышающих искомую

Слайд 36Необходимо учитывать роль каждой из ошибок в общей ошибке результата.

Значение отдельных ошибок очень быстро падает по мере их уменьшения.

Доверительный интервал и доверительная вероятность

Тогда можно доказать, что
если , , – дисперсии величин, или

Средняя квадратичная ошибка суммы или разности двух (или нескольких) независимых величин равна корню квадратному из суммы дисперсий отдельных слагаемых

Слайд 37Необходимо учитывать роль каждой из ошибок в общей ошибке результата.

Значение отдельных ошибок очень быстро падает по мере их уменьшения.

Доверительный интервал и доверительная вероятность

Тогда можно доказать, что
если , , – дисперсии величин, или

Слайд 38где 2n – количество опытов, образующих полный факторный эксперимент; 2n –

число так называемых «звездных» точек в факторном пространстве, имеющих координаты (±α, 0, 0, …, 0);
(0, ±α, 0, …, 0), …, (0, 0, …, ±α). Здесь величина α называется «звездным» плечом; 1 – опыт в центре планирования, т. е. в точке факторного пространства с координатами (0, 0, …, 0)

Значения «звездного» плеча α для ЦКП с различным числом факторов n следующие:

Количество опытов при ортогональном ЦКП определяется по формуле

Эти значения α выбраны из условия ортогональности матрицы планирования

Слайд 41 Если поверхность отклика не может быть описана многочленом вида

Закон сложения случайных ошибок

для адекватного математического описания используется многочлен более высокой степени, например, отрезок ряда Тейлора, содержащий члены с квадратами переменных. Тогда используют центральное композиционное планирование (ЦКП) эксперимента.
Различают два вида ЦКП:

ортогональное и
ротатабельное

Слайд 42где 2n – количество опытов, образующих полный факторный эксперимент; 2n –

Значения «звездного» плеча α для ЦКП с различным числом факторов n следующие:

Количество опытов при ортогональном ЦКП определяется по формуле

Эти значения α выбраны из условия ортогональности матрицы планирования

Слайд 43Переменные величины

здесь j – номер опыта; i – номер фактора,

введены для того, чтобы матрица планирования была ортогональна и коэффициенты регрессии определялись независимо друг от друга по результатам опытов. Чтобы получить уравнение регрессии в обычной форме

Уравнение регрессии при ортогональном ЦКП ищут в следующем виде

находят величину

Слайд 44Это план 2-ого порядка после преобразований (*)

Эти преобразования позволяют усреднить случайные

погрешности

Ортогональный план

Ортогональный план 2-ого порядка

Тогда уравнение регрессии

В итоге уравнение регрессии преобразуется к виду

Слайд 45где i ≠ 0

Коэффициенты регрессии при ортогональном ЦКП считают по

следующим формулам

где i ≠ k

Слайд 46где i ≠ 0

Для расчета оценок дисперсий в определении коэфф-тов

регрессии используют следующие выражения

Коэффициент bi, считается значимым, если . Аналогично проверяется значимость остальных коэфф-тов регрессии. Проверка адекватности уравнения регрессии осуществляется с помощью критерия Фишера

где i ≠ k

Слайд 47 Метод ротатабельного планирования эксперимента позволяет получать более точное математическое

описание поверхности отклика по сравнению с ортогональным ЦКП, что достигается благодаря увеличению числа опытов в центре плана и специальному выбору величины «звездного» плеча α.

Метод ротатабельного центрального композиционного планирования

Это план, у которого точки плана располагаются на окружностях (сферах, гиперсферах)

Точность оценивания функции отклика по любому направлению факторного пространства (для всех точек плана) одинаковая, что позволяет наилучшим образом извлечь максимальное количество (несмещенной) информации из плана

Слайд 48Ротабельный план 2-ого порядка
Для того, что бы привести план

2-ого порядка к ротатабельному, величину плеча выбирают из условия

Слайд 49 При ротатабельном ЦКП для вычисления коэффициентов регрессии и соответствующих

оценок дисперсий находят следующие константы

где n – число факторов; N – общее число опытов ротатабельного ЦКП; N0 – число опытов в центре плана

На основании результатов эксперимента вычисляют след. суммы

(где i=1,2,…,n),

(где i ≠ k),

(где i=1,…, n)

Слайд 50
Формулы для расчета коэффициентов регрессии имеют следующий вид

где i ≠

Слайд 51
Оценки дисперсий в определении коэфф-тов регрессии вычисляют по следующим формулам

Коэффициент

bi, считается значимым, если . Аналогично проверяется значимость остальных коэфф-тов регрессии

(где i=1,2,…,n)

(где i≠k)

Слайд 52
Оценку дисперсии адекватности рассчитывают по формуле

С ней связано число степеней

свободы

Проверку адекватности уравнения регрессии осуществляют с помощью критерия Фишера

Слайд 53
Пример. Рассмотреть ротатабельное ЦКП для двух факторов. Матрица планирования и результаты

эксперимента приведены в таблице

Матрица планирования и результаты эксперимента

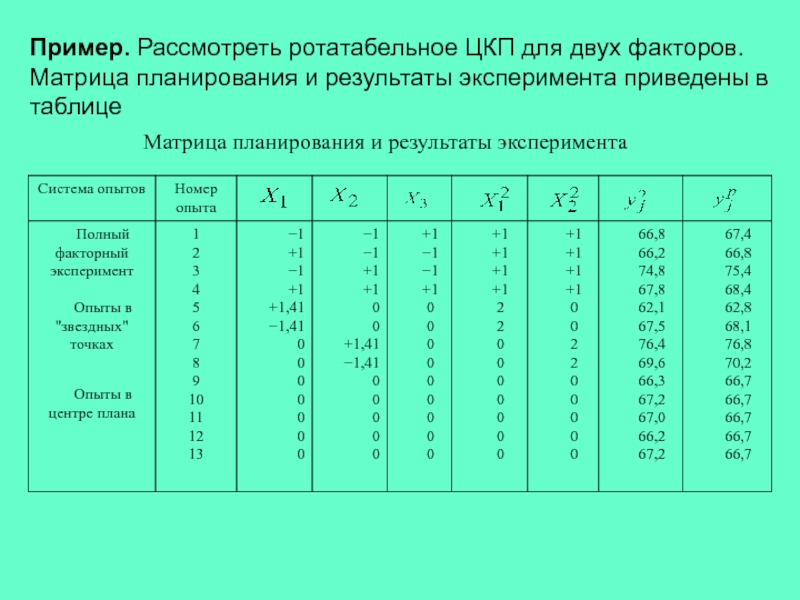
Слайд 54Для нахождения коэффициентов регрессии вычислим следующие вспомогательные коэффициенты

На основании результатов

опытов вычислим вспомогательные суммы

Коэффициенты регрессии рассчитываем по формулам

Слайд 56Оценку дисперсии воспроизводимости можно найти на основании результатов опытов, проведенных в

центре плана

Эта величина найдена при числе степеней свободы

Оценки дисперсий в определении коэфф. регрессии

Слайд 57Пользуясь таблицей значений критерия Стьюдента, находим
для

Для проверки значимости коэффициентов регрессии рассмотрим соотнош.

Все коэффициенты регрессии значимы. Вычисляем оценку дисперсии адекватности

Слайд 58Число степеней свободы, связанных с этой оценкой дисперсии

Расчетное значение критерия

Фишера

Из таблицы значений критерия Фишера соответствующее значение критерия . Условие выполнено, следовательно, уравнение регрессии

адекватно представленным результатам эксперимента

Перейдем в уравнение регрессии от кодированных переменных к физическим

Пусть в нашем примере кодированные переменные X1 и X2 представляют собой температуру и концентрацию, причем координаты центра плана
x01= 60°С и x02= 30%, а шаги варьирования Δx1= 5°С и Δх2= 1% . Тогда

Слайд 59Подставляя их в полученное в этом примере уравнение регрессии, преобразуем его

к виду

Пользуясь таким уравнением, исследователь избавляется от необходимости переводить всякий раз условия опыта в кодированные переменные

Слайд 60Планирование активного эксперимента
При планировании экспериментов чаще всего применяются планы 1-ого и

2-ого порядков. Планы более высоких порядков применяются редко из-за их большой вычислительной сложности

Планы 1-ого порядка – это планы, которые позволяют провести эксперимент для отыскания уравнения регрессии, содержащее только первые степени факторов и их произведения

Планы 2-ого порядка – это планы, которые позволяют провести эксперимент для отыскания уравнения регрессии, содержащие вторые степени факторов

Слайд 61Планирование первого порядка
В качестве факторов выбираются только контролируемые и управляемые факторы

(переменные)
Обеспечивается возможность независимого изменения каждого из факторов и поддержание его на определенном уровне
Для каждого фактора указывается интервал (+/-), в пределах которого ставится исследование

Слайд 62Представления плана эксперимента
(на примере эксперимента с 3-мя независимыми факторами)
Табличное (матричное) представление
Геометрическое

представление

Уравнением регрессии

b0, b1, b2, b3 – коэффициенты регрессии
xi*xu – члены двойного взаимодействия
x1*x2*x3 – члены тройного взаимодействия

Слайд 63Свойства матрицы представления эксперимента
1. Свойство симметричности – алгебраическая сумма элементов вектор-столбца

каждого фактора равна нулю (за исключением столбца, соответствующего свободному члену)

2. Свойство нормирования – сумма квадратов каждого столбца равна числу опытов

3. Свойство ортогональности – скалярное произведение всех вектор-столбцов (сумма почленных произведений элементов любых вектор столбцов) равно нулю

i = номер фактора, j – номер опыта

Слайд 64Определение коэффициентов b уравнения регрессии
По свойствам матрицы планирования
Методом наименьших квадратов находятся

оценки b коэффициентов

Получаем

Слайд 65Планирование второго порядка
Применяется если описание функции отклика первым порядком получается недостаточным

(например, процесс носит нелинейный характер)
Каждый фактор варьируется не менее чем на трех уровнях – полный эксперимент содержит 3^k (k – количество факторов) опытов.

План 2-ого порядка при k=2 n=1

Опыты проводятся
В «крайних точках» — как в планировании 1-ого порядка
В «звездных точках» — xi=(+/-)a, xj=0, 1,…,n; 1,…,n; i!=j
В «центре» — xi=0, j=1,2,3,…,n

Уравнение регрессии для эксперимента с 2-мя факторами

Источник

5.7.3.Классификация ошибок измерения

5.7.4.Закон сложения ошибок

1. ОСНОВЫ ТЕОРИИ ОШИБОК ИЗМЕРЕНИЙ

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15. Закон сложения случайных ошибок

16.

17.

18.

19.

20.

21.

22.

23.

24.

25.

26.

27.

28.

29.

30.

31.

32.

33. Ошибки первого и второго рода

34. ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА

35.

36. Методы подбора эмпирических формул

37.

38.