Виды ошибок математика - Решение и исправление самых разных ошибок на TopOshibok.ru

From Wikipedia, the free encyclopedia

«Invalid proof» redirects here. For any type of invalid proof besides mathematics, see Fallacy.

«0 = 1» redirects here. For the algebraic structure where this equality holds, see Null ring.

In mathematics, certain kinds of mistaken proof are often exhibited, and sometimes collected, as illustrations of a concept called mathematical fallacy. There is a distinction between a simple mistake and a mathematical fallacy in a proof, in that a mistake in a proof leads to an invalid proof while in the best-known examples of mathematical fallacies there is some element of concealment or deception in the presentation of the proof.

For example, the reason why validity fails may be attributed to a division by zero that is hidden by algebraic notation. There is a certain quality of the mathematical fallacy: as typically presented, it leads not only to an absurd result, but does so in a crafty or clever way.^[1] Therefore, these fallacies, for pedagogic reasons, usually take the form of spurious proofs of obvious contradictions. Although the proofs are flawed, the errors, usually by design, are comparatively subtle, or designed to show that certain steps are conditional, and are not applicable in the cases that are the exceptions to the rules.

The traditional way of presenting a mathematical fallacy is to give an invalid step of deduction mixed in with valid steps, so that the meaning of fallacy is here slightly different from the logical fallacy. The latter usually applies to a form of argument that does not comply with the valid inference rules of logic, whereas the problematic mathematical step is typically a correct rule applied with a tacit wrong assumption. Beyond pedagogy, the resolution of a fallacy can lead to deeper insights into a subject (e.g., the introduction of Pasch’s axiom of Euclidean geometry,^[2] the five colour theorem of graph theory). Pseudaria, an ancient lost book of false proofs, is attributed to Euclid.^[3]

Mathematical fallacies exist in many branches of mathematics. In elementary algebra, typical examples may involve a step where division by zero is performed, where a root is incorrectly extracted or, more generally, where different values of a multiple valued function are equated. Well-known fallacies also exist in elementary Euclidean geometry and calculus.^[4]^[5]

Howlers[edit]

${\begin{array}{l}\;\;\;{\dfrac {d}{dx}}{\dfrac {1}{x}}\\={\dfrac {d}{d}}{\dfrac {1}{x^{2}}}\\={\dfrac {d\!\!\!\backslash }{d\!\!\!\backslash }}{\dfrac {1}{x^{2}}}\\=-{\dfrac {1}{x^{2}}}\end{array}}$

Anomalous cancellation in calculus

Examples exist of mathematically correct results derived by incorrect lines of reasoning. Such an argument, however true the conclusion appears to be, is mathematically invalid and is commonly known as a howler. The following is an example of a howler involving anomalous cancellation:

${\frac {16}{64}}={\frac {16\!\!\!/}{6\!\!\!/4}}={\frac {1}{4}}.$

Here, although the conclusion 16/64 = 1/4 is correct, there is a fallacious, invalid cancellation in the middle step.^{[note 1]} Another classical example of a howler is proving the Cayley–Hamilton theorem by simply substituting the scalar variables of the characteristic polynomial by the matrix.

Bogus proofs, calculations, or derivations constructed to produce a correct result in spite of incorrect logic or operations were termed «howlers» by Maxwell.^[2] Outside the field of mathematics the term howler has various meanings, generally less specific.

Division by zero[edit]

The division-by-zero fallacy has many variants. The following example uses a disguised division by zero to «prove» that 2 = 1, but can be modified to prove that any number equals any other number.

Let a and b be equal, nonzero quantities
Multiply by a

$a^{2}=ab$
Subtract b²

$a^{2}-b^{2}=ab-b^{2}$
Factor both sides: the left factors as a difference of squares, the right is factored by extracting b from both terms
Divide out (a − b)
Use the fact that a = b
Combine like terms on the left
Divide by the non-zero b

Q.E.D.^[6]

The fallacy is in line 5: the progression from line 4 to line 5 involves division by a − b, which is zero since a = b. Since division by zero is undefined, the argument is invalid.

Analysis[edit]

Mathematical analysis as the mathematical study of change and limits can lead to mathematical fallacies — if the properties of integrals and differentials are ignored. For instance, a naive use of integration by parts can be used to give a false proof that 0 = 1.^[7] Letting u = 1/log x and dv = dx/x, we may write:

$\int {\frac {1}{x\,\log x}}\,dx=1+\int {\frac {1}{x\,\log x}}\,dx$

after which the antiderivatives may be cancelled yielding 0 = 1. The problem is that antiderivatives are only defined up to a constant and shifting them by 1 or indeed any number is allowed. The error really comes to light when we introduce arbitrary integration limits a and b.

$\int _{a}^{b}{\frac {1}{x\,\log x}}\,dx=1|_{a}^{b}+\int _{a}^{b}{\frac {1}{x\,\log x}}\,dx=0+\int _{a}^{b}{\frac {1}{x\log x}}\,dx=\int _{a}^{b}{\frac {1}{x\log x}}\,dx$

Since the difference between two values of a constant function vanishes, the same definite integral appears on both sides of the equation.

Multivalued functions[edit]

Many functions do not have a unique inverse. For instance, while squaring a number gives a unique value, there are two possible square roots of a positive number. The square root is multivalued. One value can be chosen by convention as the principal value; in the case of the square root the non-negative value is the principal value, but there is no guarantee that the square root given as the principal value of the square of a number will be equal to the original number (e.g. the principal square root of the square of −2 is 2). This remains true for nth roots.

Positive and negative roots[edit]

Care must be taken when taking the square root of both sides of an equality. Failing to do so results in a «proof» of^[8] 5 = 4.

Proof:

Start from

Write this as

Rewrite as

$5^{2}-5\times 9=4^{2}-4\times 9$

Add 81/4 on both sides:

$5^{2}-5\times 9+{\frac {81}{4}}=4^{2}-4\times 9+{\frac {81}{4}}$

These are perfect squares:

$\left(5-{\frac {9}{2}}\right)^{2}=\left(4-{\frac {9}{2}}\right)^{2}$

Take the square root of both sides:

$5-{\frac {9}{2}}=4-{\frac {9}{2}}$

Add 9/2 on both sides:

Q.E.D.

The fallacy is in the second to last line, where the square root of both sides is taken: a² = b² only implies a = b if a and b have the same sign, which is not the case here. In this case, it implies that a = –b, so the equation should read

$5-{\frac {9}{2}}=-\left(4-{\frac {9}{2}}\right)$

which, by adding 9/2 on both sides, correctly reduces to 5 = 5.

Another example illustrating the danger of taking the square root of both sides of an equation involves the following fundamental identity^[9]

$\cos ^{2}x=1-\sin ^{2}x$

which holds as a consequence of the Pythagorean theorem. Then, by taking a square root,

$\cos x={\sqrt {1-\sin ^{2}x}}$

Evaluating this when x = π , we get that

$-1={\sqrt {1-0}}$

$-1=1$

which is incorrect.

The error in each of these examples fundamentally lies in the fact that any equation of the form

$x^{2}=a^{2}$

where $a\neq 0$ , has two solutions:

$x=\pm a$

and it is essential to check which of these solutions is relevant to the problem at hand.^[10] In the above fallacy, the square root that allowed the second equation to be deduced from the first is valid only when cos x is positive. In particular, when x is set to π, the second equation is rendered invalid.

Square roots of negative numbers[edit]

Invalid proofs utilizing powers and roots are often of the following kind:

$1={\sqrt {1}}={\sqrt {(-1)(-1)}}={\sqrt {-1}}{\sqrt {-1}}=i\cdot i=-1.$

The fallacy is that the rule ${\sqrt {xy}}={\sqrt {x}}{\sqrt {y}}$ is generally valid only if at least one of and is non-negative (when dealing with real numbers), which is not the case here.^[11]

Alternatively, imaginary roots are obfuscated in the following:

$i={\sqrt {-1}}=\left(-1\right)^{\frac {2}{4}}=\left(\left(-1\right)^{2}\right)^{\frac {1}{4}}=1^{\frac {1}{4}}=1$

The error here lies in the third equality, as the rule $a^{bc}=(a^{b})^{c}$ only holds for positive real a and real b, c.

Complex exponents[edit]

When a number is raised to a complex power, the result is not uniquely defined (see Exponentiation § Failure of power and logarithm identities). If this property is not recognized, then errors such as the following can result:

${\begin{aligned}e^{2\pi i}&=1\\\left(e^{2\pi i}\right)^{i}&=1^{i}\\e^{-2\pi }&=1\\\end{aligned}}$

The error here is that the rule of multiplying exponents as when going to the third line does not apply unmodified with complex exponents, even if when putting both sides to the power i only the principal value is chosen. When treated as multivalued functions, both sides produce the same set of values, being {e^2πn | n ∈ ℤ}.

Geometry[edit]

Many mathematical fallacies in geometry arise from using an additive equality involving oriented quantities (such as adding vectors along a given line or adding oriented angles in the plane) to a valid identity, but which fixes only the absolute value of (one of) these quantities. This quantity is then incorporated into the equation with the wrong orientation, so as to produce an absurd conclusion. This wrong orientation is usually suggested implicitly by supplying an imprecise diagram of the situation, where relative positions of points or lines are chosen in a way that is actually impossible under the hypotheses of the argument, but non-obviously so.

In general, such a fallacy is easy to expose by drawing a precise picture of the situation, in which some relative positions will be different from those in the provided diagram. In order to avoid such fallacies, a correct geometric argument using addition or subtraction of distances or angles should always prove that quantities are being incorporated with their correct orientation.

Fallacy of the isosceles triangle[edit]

The fallacy of the isosceles triangle, from (Maxwell 1959, Chapter II, § 1), purports to show that every triangle is isosceles, meaning that two sides of the triangle are congruent. This fallacy was known to Lewis Carroll and may have been discovered by him. It was published in 1899.^[12]^[13]

Given a triangle △ABC, prove that AB = AC:

Draw a line bisecting ∠A.
Draw the perpendicular bisector of segment BC, which bisects BC at a point D.
Let these two lines meet at a point O.
Draw line OR perpendicular to AB, line OQ perpendicular to AC.
Draw lines OB and OC.
By AAS, △RAO ≅ △QAO (∠ORA = ∠OQA = 90°; ∠RAO = ∠QAO; AO = AO (common side)).
By RHS,^{[note 2]} △ROB ≅ △QOC (∠BRO = ∠CQO = 90°; BO = OC (hypotenuse); RO = OQ (leg)).
Thus, AR = AQ, RB = QC, and AB = AR + RB = AQ + QC = AC.

Q.E.D.

As a corollary, one can show that all triangles are equilateral, by showing that AB = BC and AC = BC in the same way.

The error in the proof is the assumption in the diagram that the point O is inside the triangle. In fact, O always lies on the circumcircle of the △ABC (except for isosceles and equilateral triangles where AO and OD coincide). Furthermore, it can be shown that, if AB is longer than AC, then R will lie within AB, while Q will lie outside of AC, and vice versa (in fact, any diagram drawn with sufficiently accurate instruments will verify the above two facts). Because of this, AB is still AR + RB, but AC is actually AQ − QC; and thus the lengths are not necessarily the same.

Proof by induction[edit]

There exist several fallacious proofs by induction in which one of the components, basis case or inductive step, is incorrect. Intuitively, proofs by induction work by arguing that if a statement is true in one case, it is true in the next case, and hence by repeatedly applying this, it can be shown to be true for all cases. The following «proof» shows that all horses are the same colour.^[14]^{[note 3]}

Let us say that any group of N horses is all of the same colour.
If we remove a horse from the group, we have a group of N − 1 horses of the same colour. If we add another horse, we have another group of N horses. By our previous assumption, all the horses are of the same colour in this new group, since it is a group of N horses.
Thus we have constructed two groups of N horses all of the same colour, with N − 1 horses in common. Since these two groups have some horses in common, the two groups must be of the same colour as each other.
Therefore, combining all the horses used, we have a group of N + 1 horses of the same colour.
Thus if any N horses are all the same colour, any N + 1 horses are the same colour.
This is clearly true for N = 1 (i.e., one horse is a group where all the horses are the same colour). Thus, by induction, N horses are the same colour for any positive integer N, and so all horses are the same colour.

The fallacy in this proof arises in line 3. For N = 1, the two groups of horses have N − 1 = 0 horses in common, and thus are not necessarily the same colour as each other, so the group of N + 1 = 2 horses is not necessarily all of the same colour. The implication «every N horses are of the same colour, then N + 1 horses are of the same colour» works for any N > 1, but fails to be true when N = 1. The basis case is correct, but the induction step has a fundamental flaw.

Notes[edit]

^ The same fallacy also applies to the following:

${\begin{aligned}{\frac {19}{95}}={\frac {19\!\!\!/}{9\!\!\!/5}}&={\frac {1}{5}}\\{\frac {26}{65}}={\frac {26\!\!\!/}{6\!\!\!/5}}&={\frac {2}{5}}\\{\frac {49}{98}}={\frac {49\!\!\!/}{9\!\!\!/8}}&={\frac {4}{8}}={\frac {1}{2}}\end{aligned}}$
^ Hypotenuse–leg congruence
^ George Pólya’s original «proof» was that any n girls have the same colour eyes.

References[edit]

^ Maxwell 1959, p. 9
^ ^a ^b Maxwell 1959
^ Heath & Heiberg 1908, Chapter II, §I
^ Barbeau, Ed (1991). «Fallacies, Flaws, and Flimflam» (PDF). The College Mathematics Journal. 22 (5). ISSN 0746-8342.
^ «soft question – Best Fake Proofs? (A M.SE April Fools Day collection)». Mathematics Stack Exchange. Retrieved 2019-10-24.
^ Heuser, Harro (1989), Lehrbuch der Analysis – Teil 1 (6th ed.), Teubner, p. 51, ISBN 978-3-8351-0131-9
^ Barbeau, Ed (1990), «Fallacies, Flaws and Flimflam #19: Dolt’s Theorem», The College Mathematics Journal, 21 (3): 216–218, doi:10.1080/07468342.1990.11973308
^ Frohlichstein, Jack (1967). Mathematical Fun, Games and Puzzles (illustrated ed.). Courier Corporation. p. 207. ISBN 0-486-20789-7. Extract of page 207
^ Maxwell 1959, Chapter VI, §I.1
^ Maxwell 1959, Chapter VI, §II
^ Nahin, Paul J. (2010). An Imaginary Tale: The Story of «i«. Princeton University Press. p. 12. ISBN 978-1-4008-3029-9. Extract of page 12
^ S.D.Collingwood, ed. (1899), The Lewis Carroll Picture Book, Collins, pp. 190–191
^ Robin Wilson (2008), Lewis Carroll in Numberland, Penguin Books, pp. 169–170, ISBN 978-0-14-101610-8
^ Pólya, George (1954). Induction and Analogy in Mathematics. Mathematics and plausible reasoning. Vol. 1. Princeton. p. 120.

Barbeau, Edward J. (2000), Mathematical fallacies, flaws, and flimflam, MAA Spectrum, Mathematical Association of America, ISBN 978-0-88385-529-4, MR 1725831.
Bunch, Bryan (1997), Mathematical fallacies and paradoxes, New York: Dover Publications, ISBN 978-0-486-29664-7, MR 1461270.
Heath, Sir Thomas Little; Heiberg, Johan Ludvig (1908), The thirteen books of Euclid’s Elements, Volume 1, The University Press.
Maxwell, E. A. (1959), Fallacies in mathematics, Cambridge University Press, ISBN 0-521-05700-0, MR 0099907.

External links[edit]

Invalid proofs at Cut-the-knot (including literature references)
Classic fallacies with some discussion
More invalid proofs from AhaJokes.com
Math jokes including an invalid proof

Источник

Ошибки учащихся при изучении математики,

их предупреждение и объяснение

Автор работы:

Дука Наталья Ивановна

учитель математики МОУ «СОШ №4 г. Ртищево Саратовской обл.» ____________________________

Аннотация

В данной работе рассматриваются типичные ошибки, которые допускают учащиеся при выполнении математических заданий. Здесь разобраны причины, способы исправления и предупреждения ошибок, разобраны конкретные ошибки из курса алгебры и начал анализа и способы их объяснения и устранения, указаны ошибки в работах государственной итоговой аттестации учащихся 9 и 11 классов. Рассмотрены ошибки по математике в учебниках и методической литературе. Материал, представленный в работе, может заинтересовать учителей математики.

Тезисы

В математике приходится учиться, в основном, на собственных ошибках. Если ученик не ошибается, то он не учится. Ошибка – вещь необходимая и полезная.

Цель исследования: рассмотреть методику предупреждения типичных ошибок учащихся в процессе обучения математике.

Объект исследования: процесс обучения математике в основной общеобразовательной школе.

Предмет исследования: процесс возникновения типичных ошибок и средства их предупреждения.

Гипотеза исследования заключается в следующем: если в процессе обучения математике целенаправленно и систематически организовывать работу учащихся над типичными ошибками, то это будет способствовать повышению качества математической подготовки учащихся.

Необходимо осуществлять процесс обучения правилам с помощью специальной модели с использованием приема, активизирующего рефлексивную деятельность учащихся по предупреждению и исправлению ошибок, которые возникают в результате формального усвоения правил.

Самостоятельная работа учащихся над ошибками обеспечивает более осознанный их анализ и анализ собственных действий по решению конкретной задачи, что оказывает благоприятное влияние на качество получаемых знаний и стимулирует развитие логического мышления.

Пример неосознанного применения алгоритма: получив уравнение sin x = 1,2, ученик автоматически ищет его корни по хорошо известной формуле, не обращая внимания на недопустимые значения sin x.

Для исправления и предупреждения многих ошибок важно сформировать у школьников навыки самоконтроля. Выработке навыков самоконтроля помогает и приём приближённой оценки ожидаемого результата.

Каждый учитель знает, что планомерное и систематическое повторение и есть основной помощник в ликвидации пробелов, а, следовательно, и ошибок.

Некоторые учащиеся считают, что arcsin(sink)= k при любом k и дают такой ответ: arcsin(sin) =. Это очень грубая ошибка. Аналогичное задание «вычислить arctg(tg130о)» вызывает у учащихся неверный ответ 130о.

Иногда ученики используют неверную формулу, не задумываясь над ней.

Например, определяя, является ли число рациональным, ученик пишет: = и получает неверный ответ,

При работе с «многоэтажными дробями» ученики делают много ошибок. Например: . Должна появиться верная запись .

При выполнении преобразований со степенями учащиеся не только допускают ошибки, но просто забывают формулы, например формулу

an am = an+m.

Пример ошибки на свойство степени: . Если при этом объяснить ученику, что дробь только в показателе степени, он это объяснение забудет и следующий раз опять ошибется. Необходимо в результате записать формулу .

Встречаются ошибки от непонимания. Большинство учащихся, решая впервые неравенство х24, приводят неверное решение х2.

Выполняя тригонометрические задания, ученик часто «изобретает формулы», например: «sin 2 х = 2 sin x».

Систематические проверки чужих записей формируют у ученика привычку критически относиться к своему решению. Для этого подходят задания типа «найди ошибку в решении». Процесс отыскания и исправления ошибок самими учащимися под руководством учителя можно сделать поучительным для учащихся.

Учебный год в 9-х и 11-х классах должен заканчиваться повторением и систематизацией учебного материала. повторение нужно нацелить на закрепление опорных знаний.

В учебнике Л. С. Атанасяна и других «Геометрия 7-9» была приведена некорректно составленная задача № 536: «Отрезок BD является биссектрисой треугольника АВС. Найдите DС, если АВ = 30, АD = 20, ВD = 16 и ∠ВDС = ∠С». Треугольник, описанный в условии задачи, не существует.

Объяснение деления с остатком круглых чисел в теме «Деление круглых чисел» ( урок 66) учебника математики для 4 –ого класса (Т. Е. Демидова, С. А. Козлова, А. П. Тонких) дается с ошибкой.

В газете «Математика» предлагается уравнение и к нему ответ:1. Приведенное решение неверное, так как приводит к потере корней.

Вступление

Вспоминается расхожая истина – умные люди учатся на чужих ошибках. В математике приходится учиться, в основном, на собственных ошибках. Если ученик не ошибается, то он не учится. Ошибка – вещь необходимая и полезная. Нужно лишь правильно относиться к ошибке, правильно ее использовать.

Обидно получать плохие оценки из-за ошибок «на ровном месте». Глупые ошибки – проблема многих учеников: случайная потеря знака, скобки, необоснованное изменение чисел, пропуски переменных и всевозможные ляпы. Сами ученики не могут объяснить, чем вызваны эти ошибки.

Причины ошибок, допускаемых учащимися при изучении математики

Проблема исследования состоит в теоретическом обосновании и разработке такой методики обучения математике, которая создавала бы условия для развития рефлексивной деятельности учащихся, способствующей предупреждению типичных ошибок.

Объект исследования: процесс обучения математике в основной общеобразовательной школе.

Предмет исследования: процесс возникновения типичных ошибок и средства их предупреждения.

Большинство ошибок напрямую не связаны с наличием или отсутствием знаний, хотя доведение некоторых вычислительных операций до автоматизма несколько снижает вероятность их появления. Снижает, но не исключает. Можно ли избавиться от таких ошибок? Ученик знает, что нужно решать внимательно, но ничего не может с собой поделать.

Известно, что осознание правила или определяет действия, или, по крайней мере, их контролирует. Знание правила необходимо и для того, чтобы осуществить проверку решения и дать его обоснование. Но большинство учащихся воспринимают курс алгебры как набор несвязанных между собой правил, которые заучиваются (иногда формально) для применения их к решению задач. Поэтому необходимо осуществлять процесс обучения правилам с помощью специальной модели с использованием приема, активизирующего рефлексивную деятельность учащихся по предупреждению и исправлению ошибок, которые возникают в результате формального усвоения правил.

Процесс отыскания и исправления ошибок самими учащимися под руководством учителя можно сделать поучительным для учащихся, в результате чего изучение и анализ ошибок становится эффективным средством в развитии познавательного интереса к изучению математики.

Выполняя математические задания, учащиеся допускают типичные ошибки:

Незнание правил, определений, формул.
Непонимание правил, определений, формул.
Неумение применять правила, определения, формулы.
Неверное применение формул.
Невнимательное чтение условия и вопроса задания.
Вычислительные ошибки.
Не использование свойств фигур при решении геометрических задач.
Логические ошибки при решении текстовых задач.
Раскрытие скобок и применение формул сокращенного умножения.

Какие причины ошибок по математике?

Пропуски занятий приводят к незнанию материала, пробелам в знаниях.
Поверхностное, невдумчивое восприятие нового материала приводят к непониманию его.
Недостаточная мозговая деятельность приводит к неумению применять правила, определения и формулы .
Неряшливый, неаккуратный почерк ученика приводит к досадным ошибкам. Учащиеся не всегда сами понимают, что именно они написали.
Усталость. Чрезмерная нагрузка и недостаточный сон приводит к снижению внимания, скорости мышления и, как следствие, к многочисленным ошибкам.
Кратковременное или полное переключение внимания с одной деятельности на другую (учебную или внеучебную) приводит к утрате только что воспринятого материала, приходится все начинать сначала.
Скорость работы. Низкая скорость выполнения мыслительных операций часто мешает ученику контролировать себя и это может стать еще одной причиной ошибки. «Зависание» с какой-нибудь одной частью задания удаляет из «оперативной памяти» информацию о другой, в которой допускается не вынужденная ошибка. Скорость работы определяется физиологией конкретного школьника и навыками выполнения тех или иных операций.
Мотивация. Следствие низкой мотивации – потеря внимания и ошибка.

Работа над ошибками

В приемах работы над ошибками отсутствует диагностика причин ошибок. Не уделяется должного внимания работе по формированию рефлексивной деятельности учащихся и ее использованию в работе по предупреждению и исправлению математических ошибок. При отсутствии должной доли самостоятельности при работе над ошибками, совершаемые учеником действия никак не контролируются, допущенные ошибки не замечаются, причины их появления остаются невыясненными, что приводит к их повторению. Напротив, самостоятельная работа учащихся над ошибками обеспечивает более осознанный их анализ и анализ собственных действий по решению конкретной задачи, что оказывает благоприятное влияние на качество получаемых знаний и стимулирует развитие логического мышления. При этом у школьников постепенно развиваются стремление и умение разобраться в задаче, планировать ее решение, продумывать возможные варианты действий и прогнозировать их результаты. Например, ученик многократно применяет к преобразованию алгебраических выражений формулы квадрата суммы и разности двух чисел, но получив задание представить в виде многочлена

(–х–5)2, теряется. Следует предложить учащемуся ответить на вопрос что вызывает затруднение? И как преобразовать выражение, чтобы можно было применить одну из формул в том виде, в каком они предложены в учебнике. Другой пример неосознанного применения алгоритма: получив уравнение

sin x = 1,2, ученик автоматически ищет его корни по хорошо известной формуле, не обращая внимания на недопустимые значения sin x. Полезно предложить ученику представить наглядное решение на тригонометрическом круге.

Самоконтроль

Для исправления и предупреждения многих ошибок важно сформировать у школьников навыки самоконтроля. Эти навыки состоят из двух частей: а) умения обнаружить ошибку; б) умения её объяснить и исправить. В процессе обучения применяются несколько приёмов самоконтроля, которые помогают обнаружить допущенные ошибки и своевременно их исправить. К ним относятся:

проверка вычисления и тождественного преобразования путём выполнения обратного действия или преобразования;
проверка правильности решения задач путём составления и решения задач, обратных к данной;
оценка результата решения задачи с точки зрения здравого смысла;
проверка аналитического решения графическим способом.

Выработке навыков самоконтроля помогает и приём приближённой оценки ожидаемого результата. Установление возможных пределов ожидаемого ответа предупреждает недочёты типа описок, пропуска цифр.

Например, рассмотрим задачу: “За неделю завод выпустил 130 холодильников, выполнив месячный план на 25%. Сколько холодильников должен выпустить завод за месяц по плану”.

Ученик написал = 52, ошибка становится очевидной, если перед решением ученик прикинет в уме: “За неделю завод выпустил 130 холодильников. Следовательно, за месяц он выпустит больше. Значит, ответ должен быть больше, чем 130” .

Объяснение и предупреждение ошибок

Свести ошибки к минимуму способствуют следующие профилактические меры.

Тексты письменных заданий должны быть удобными для восприятия: грамотно сформулированными, хорошо читаемыми.
Активная устная отработка основных ЗУН, регулярный разбор типичных ошибок.
При объяснении нового материала предугадать ошибку и подобрать систему заданий на отработку правильного усвоения понятия. Акцентировать внимание на каждом элементе формулы, выполнение разнотипных заданий позволит свести ошибочность к минимуму.
Подбирать задания, вызывающие интерес, формирующие устойчивое внимание.
Прочному усвоению (а значит, отсутствию ошибок) способствуют правила, удобные для запоминания, четкие алгоритмы, следуя которым заведомо придешь к намеченной цели.

Каждый учитель знает, что планомерное и систематическое повторение и есть основной помощник в ликвидации пробелов, а, следовательно, и ошибок. В математике, как ни в какой другой науке, особенно сильна взаимосвязь материала. Изучение и понимание последующего невозможно без знания предыдущего, отсюда неизбежность повторения на каждом уроке. При объяснении нового материала следует использовать ряд определений и теорем, которые были изучены ранее.

Например, перед изучением темы «Теоремы сложения» следует повторить следующие теоретические вопросы:

1. Четные и нечетные функции.
2. Изменение тригонометрических функций при возрастании и убывании аргумента.
3. Знаки тригонометрических функций.
4. Таблицы значений тригонометрических функций.

А также выполнить задания:

1. Определите четность и нечетность тригонометрической функции:

а) y = – cos x + x2; б) y = sin2 x; в) y = .
2. Найдите область определения функции y = x2 – 6x + 10.

3. При каких значениях x функции y = sin x и y = cos x принимают одинаковые значения?

Перед прохождением темы «Первообразная и интеграл» повторяем все формулы дифференцирования. Затем предлагается самостоятельная работа (на 10–15 мин), на которой ученики получают карточки-задания, в которых «опущены» один–два компонента из формулы дифференцирования и приведены две функции, производные которых необходимо найти. После проверки самостоятельной работы анализируем допущенные ошибки, определяем пробелы в знаниях и проводим работу по их устранению.

Рассмотрим ошибки, допускаемые в курсе алгебры и начал анализа. Задание. Найти точное значение arcsin (sin).

Некоторые учащиеся считают, что arcsin(sink)= k при любом k и дают такой ответ: arcsin(sin) =. Это очень грубая ошибка. По определению . Следовательно, число arcsin(sin) должно принадлежать промежутку , число этому промежутку не принадлежит. Имеем: arcsin (sin) = arcsin (sin)) = arcsin (sin ) = arcsin =

Аналогичное задание «вычислить arctg(tg130о)» вызывает у учащихся неверный ответ 130о. Можно исправить ошибку следующим образом: учитывая, что 90о 90о для любого и arctg (tgх) = х при

х arctg (tg130о) = arctg (tg180о 50о) = arctg (tg( 50о)) = 50о. Существует второй способ решения. Пусть arctg (tg130о) = х, получаем tg х = tg (arctg (tg130о)), откуда tg х = tg 130о. По условию равенства тангенсов имеем х = 130о + k, где kZ. Учитывая область определения функции у = arctg х, где х(90О; 90О), при k = 1 х = 130о 180о = 50о.

Рассмотрим еще один пример правильного решения аналогичного задания вычислить arcsin(sin2) при неверном ответе учащихся «2». Решение: arcsin (sink) = k, если , arcsin (sin2) = arcsin (sin() = 2, т. к. 2.

Иногда ученики используют неверную формулу, не задумываясь над ней. Например, определяя, является ли число рациональным, ученик пишет: = и получает неверный ответ, выполняя преобразование иррационального выражения, учащийся получил = х+2. Во-первых, учащиеся забывают, что , во-вторых, опять ошибочная аналогия с формулой = , где Применение «формулы =» в классе обязательно происходит независимо от того, повторяются свойства радикалов на уроках или нет. Ученик проводит аналогию с формулой = , где и не понимает, почему он неправ. Если заставить ученика написать правильно по свойству, то долговременного эффекта не получится. Необходимо, чтобы ученик понял и осознал свою ошибку. Для этой цели пригоден совет: вычислите по тому алгоритму, который только что применили, имеем = и по действиям 2 = 1 и определите, какое решение верное. Ученик задумывается и находит ошибку.

Можно предложить учащимся проверить себя, взяв, например, значение х = 2 но ;

при х = –2 но .

Делаем вывод: преобразование выполнено неверно, формула «=» не существует и

При работе с «многоэтажными дробями» ученики делают много ошибок. Например: . Нужно посоветовать ученику проверить написанное при конкретных значениях переменных. Так, при a = b = 1, c = 2, получим , с другой стороны , тогда 2= В результате ученик должен сделать вывод, что при работе с «трехэтажными дробями» лучше ставить скобки, чем сравнивать длины дробных «черточек»: . И, разумеется, должна появиться верная запись .

an am = an+m. Полезно учащимся показать, как они могут вспомнить формулу, пользуясь определением степени, например a3a4=aaa=a 7=a 3+4. Применяя определение степени в подобных ситуациях, учащиеся могут вывести любую формулу действий со степенями. Аналогично можно показать ошибки в действиях со степенями.

Ещё пример ошибки: . Если при этом объяснить ученику, что дробь только в показателе степени, он это объяснение забудет и следующий раз опять ошибется. Следует привести конкретный пример с удобным вычислением

=. Здесь же можно предложить другой способ

Необходимо в результате записать формулу .

Встречаются ошибки от непонимания. Большинство учащихся, решая впервые неравенство х24, приводят неверное решение х2. Полезно в этом случае предложить учащимся проверить число, например. -3, при этом учащиеся убеждаются в неверности ответа. Можно показать три способа решения этого неравенства. 1 способ тот, которым и пользовались учащиеся «», но допустили следующую ошибку «=х». Верное решение Этот способ решения содержит опасный момент – необходимо обратить внимание на возрастание функции у = при х0, иначе в дальнейшем будут еще ошибки при решении неравенств. Второй способ основан на методе интервалов х24, х2,

(х-2)(х+2)0, . Третий способ графический.

х24 при .

Выполняя тригонометрические задания, ученик часто «изобретает формулы», например: «sin 2 х = 2 sin x». В этом случае можно поступить двумя способами: подставить х =/6 и получить неверное равенство sin 2sin , /2 = 21/2 или вспомнить определение sin х на тригонометрическом круге. Наглядно хорошо видно, что sin 2х 2sinх. Обращение к тригонометрическому кругу всегда полезно повторением определения тригонометрических функций и наглядностью определений.

Не нужно специально исправлять каждое ошибочное утверждение ученика и предупреждать его об ошибках. Лучше поставить это утверждение на обсуждение всего класса и добиться осознанного исправления ошибки. Практика показывает, что систематические проверки чужих записей формируют у ученика привычку критически относиться к своему решению. Для этого подходят задания типа «найди ошибку в решении»:

Анализ работ ГИА и ЕГЭ

Анализ работ государственной итоговой аттестации учащихся 11-х классов показал, что типичные ошибки допущены при:

преобразовании дробно-рациональных выражений, содержащих корень

n-ой степени

исследовании функций на наибольшее и наименьшее значения;
решении показательных и логарифмических неравенств (отсутствует ссылка на соответствующие свойства функций);
вычислении площади криволинейной трапеции;
построении графика функции с модулем;
изображении тел вращения в геометрической задаче;
теоретическом обосновании используемых формул и фактов при решении задачи по стереометрии;
построении множества точек плоскости, удовлетворяющего заданному условию;
решении задач с параметром.

Для повышения уровня учебных достижений учащихся на ГИА за курс старшей школы рекомендуется обратить внимание на следующие темы и разделы курса алгебры и начал анализа и геометрии:

комбинация тел;
углы в пространстве;
производная и её применение к исследованию функции на отрезке;
построение ГМТ, удовлетворяющего заданным условиям;
логарифмические и показательные неравенства;
тригонометрические функции и их свойства;
тождественные преобразования дробно-рациональных выражений, содержащих корень n-ой степени.

Учебный год в 9-х и 11-х классах должен заканчиваться повторением и систематизацией учебного материала. повторение нужно нацелить на закрепление опорных знаний, построение и развитие межпредметных связей и осознание взаимосвязи с ранее выученными темами, на подготовку к итоговому оцениванию знаний, установлению формально-логических подходов к построению курса школьной математики, закрепление необходимости обосновывать и доказывать математические факты.

Ошибки в учебниках и методической литературе

В учебнике Л. С. Атанасяна и других «Геометрия 7-9» была приведена задача № 536: «Отрезок BD является биссектрисой треугольника АВС. Найдите DС, если АВ = 30, АD = 20, ВD = 16 и ∠ВDС = ∠С».

Решение.

ВD – биссектриса АВС =

∠ВDС = ∠С ВDС равнобедренный ВD = DС =

Отсюда СD =

Ответ:

Решим задачу вторым способом.

ВЕ – высота АВС. Пусть DЕ = х. Из прямоугольных треугольников АВЕ и DВЕ получаем:

АВ2 – АЕ2 = ВD2 – DЕ2,

302 – (20 + х)2 = 162 – х2,

900 – 400 – 40х – х2 = 256 – х2,

40х = 244,

х = 6,1.

ВЕ высота и медиана DЕ = СЕ СD = 2х = 12,2. Получили несоответствие с ответом первого способа решения.

Проверим, существует ли треугольник, у которого выполнены условия: ∠ВDС = ∠С и ∠АВD = ∠DВС. Найдем величины ∠DВС, ∠ВDС, ∠С.

АD2 = АВ2 + ВD2 – 2 cos ∠AВD

cos ∠AВD =

Тогда ∠АВD 38,5о. ∠DВС = ∠АВD 38,5о.

Аналогично cos ∠ADВ =

Тогда ∠АDВ = 180о – 67,59о ∠ВDС 67,59о. Из ВDС

∠С = 180о – 38,05о – 67,59о = 74,36о,

Отсюда следует, что ∠ВDС ∠С и треугольник DВС неравнобедренный.

Значит, задача составлена некорректно: треугольник, описанный в условии задачи, не существует.

Возможны два корректных варианта задачи:

Дан треугольник АВС, точка D лежит на стороне ВС. Найдите DС, если АВ = 30, АD = 20, ВD = 16 и ∠ВDС = ∠С.

В этом случае ВD не является медианой. По второму способу получаем СD = 12,2.

Отрезок BD является биссектрисой треугольника АВС. Найдите DС, если АВ = 30. АD = 20, ВD = 16.

∠ВDС ∠С, в этом случае из треугольника DВС по теореме синусов получаем

В действующем учебнике задача № 536 имеет вид:

Отрезок BD является биссектрисой треугольника АВС. а) Найдите АВ, если ВС = 9 см, АD = 7,5 см, DС = 4,5 см. б) Найдите DС, если АВ = 30. АD = 20, ВD = 16.

Посмотрим объяснение деления с остатком круглых чисел в теме «Деление круглых чисел» ( урок 66) учебника математики для 4 –ого класса (Т. Е. Демидова, С. А. Козлова, А. П. Тонких).

Цитируем: «Прочитай, объясни и проверь записи.

190 : 20 = 190 : 10 : 2 = 9 ( 1 остаток)

190 : 20 = 19 д. : 2 д. = 9 ( 1 остаток)

4700 : 500 = 4700 : 100 : 5 = 9 ( 2 остаток)

4700 : 500 = 47 с. : 5 с. = 9 ( 2 остаток)»

Проверяем 20 ∙ 9 + 1 = 190 – равенство неверное, делаем вывод: ошибка при выполнении деления с остатком. В чем ошибка? Анализируем 1-ое равенство 190 : 20 = 190 : 10 : 2 = 19 : 2, получаем деление числа 19 на число 2 и соответственно остаток от деления 19 на 2, но не от деления 190 на 20, действительно 19 : 2 = 9 ( 1 остаток). В этом случае 19 показывает, сколько десятков содержится в числе 190, поэтому остаток так же получаем в десятках, но не в единицах.

Анализируем 2-ое равенство 190 : 20 = 19 д. : 2 д. здесь мы делим десятки, поэтому остаток также будет в десятках 9 о чем сказано ранее), т, е. получаем 19 д. : 2 д. = 9 (1 д. остаток), проверкой убеждаемся в истинности деления 9 ∙ 2 д. + 1 д. = 19 д. = 190.

Предлагаем верные записи:

190 : 20 = 190 : 10 : 2 = 9 ( 1 д. остаток)

190 : 20 = 19 д. : 2 д. = 9 ( 1 д. остаток)

4700 : 500 = 4700 : 100 : 5 = 9 ( 2 с. остаток)

4700 : 500 = 47 с. : 5 с. = 9 ( 2 с. остаток).

В газете «Математика» предлагается уравнение и к нему ответ:1. Предложено решение уравнения по следующей схеме:

af(x)bg(x) = apbp

Приведенное решение неверное, так как приводит к потере корней. данное уравнение следует решать по схеме:

a f(x) b g(x) = a p b p a f(x)– р b q – g(x)

Вернемся к данном уравнению.

= 40 2 3

Заключение

Хотя проблемы формирования и развития рефлексивной деятельности в процессе обучения и поиск новых форм работы над математическими ошибками школьников и не являются абсолютно новыми, изучение такого аспекта, как использование рефлексивной деятельности учащихся при работе над типичными ошибками всегда актуальны. В данной работе рассмотрены некоторые типичные ошибки, допускаемые учащимися при изучении математики, их объяснение, меры их предупреждения. Хорошо организованная учителем работа учащихся над типичными ошибками посредством исследовательского приема приводит к улучшению результата обучению математики и развитию рядя показателей логического мышления. К тому же предмет «математика» настолько сложен, что даже методисты допускают ошибки.

Литература

Далингер В. А. «Анализ типичных ошибок, допускаемых в курсе алгебры и начала анализа» «Математика в школе» 6-98
2-98 Ярский А. С, «Что делать с ошибками»
Хэкало С. П. «Корни терять нельзя» 5-98
Игнатенко В. З. «Сюрпризы биссектрисы» 5-98

Интернет-ресурсы

http://mat.1september.ru/view_article.php?ID=200900304
http://www.distedu.ru/mirror/_fiz/archive.1september.ru/mat/1998/no38.htm
http://www.ankolpakov.ru/2011/10/03/repetitor-po-matematike-o-durackix-oshibkax/
http://www.referun.com/n/preduprezhdenie-tipichnyh-oshibok-uchaschihsya-v-protsesse-obucheniya-algebre-posredstvom-formirovaniya-i-ispolzovaniya-r#ixzz2PJHLl9cJ
http://www.referun.com/n/preduprezhdenie-tipichnyh-oshibok-uchaschihsya-v-protsesse-obucheniya-algebre-posredstvom-formirovaniya-i-ispolzovaniya-r

Источник

Авторы
Файлы
Литература

Далингер В.А.

1 Омский государственный педагогический университет

1. Асанов Р.А. Работа над ошибками при обучении математике // Из опыта преподавания математики в школе. – М.: Просвещение, 1978. – С. 23-48.

2. Бескин Н.М. Роль задач в преподавании математики // Математика в школе. – 1992. – № 4-5. – С. 3-4.

3. Высоцкий И.Р., Ященко И.В. Типичные ошибки в преподавании теории вероятностей и статистики // Математика в школе. – 2014. – № 5. – С. 32-43.

4. Далингер В.А. Анализ типичных ошибок, допускаемых в курсе алгебры и начал анализа // Математика в школе. – 1998. – № 6. – С. 13-18.

5. Далингер В.А. Типичные ошибки по математике на вступительных экзаменах и как их не допускать. – Омск: Изд-во Омского ИУУ, 1991. – 129 с.

6. Далингер В.А. Начала математического анализа. Типичные ошибки, их причины и пути предупреждения: учебное пособие. – Омск: Изд-во ООО «Издатель-Полиграфист», 2002. – 158 с.

7. Далингер В.А. Совершенствование процесса обучения математике на основе целенаправленной реализации внутрипредметных связей: монография. – Омск: Изд-во ОИПКРО, 1993 г. – 323 с.

8. Далингер В.А., Тарасова О.А. Причины типичных ошибок, допускаемых учащимися в процессе изучения математики и самоконтроль как средство организации рефлексии по предупреждению ошибок // Научные исследования: информация, анализ, прогноз: монография / под общ. ред. проф. О.И. Кирикова. – Книга 2. – Воронеж: Изд-во ВГПУ, 2004. – С. 216-143.

9. Зеленский А.С., Панфилов И.И. Различные способы решения задач С 5 ЕГЭ: сравнительный анализ, ошибки и недочеты, оценивание // Математика в школе. – 2013. – № 8. – С. 15-23.

10. Зеленский А.С., Панфилов И.И. Задачи с параметром на ЕГЭ – 2014: способы решения, ученические ошибки и недочеты // Математика в школе. – 2014. – № 7. – С. 17-24.

11. Зеленский А.С. Формирование навыков самоконтроля у старшеклассников // Математика в школе. – 2014. – № 9. – С. 26-30.

12. Лында А.С. Самостоятельная работа и самоконтроль учебной деятельности старших школьников. – М.: Изд-во МОПИ, 1972. – 198 с.

13. Матизен В. Найдем ошибку // Квант. – 1980. – № 10. – С. 43-46.

14. Рыжик В.И. Формирование потребностей в самоконтроле при обучение математике // Математика в школе. – 1980. – № 3. – С. 7-11.

15. Самсонов П.И. Анализ ошибок выпускников школ на ЕГЭ по математике в 2014 году: от анализа к предупреждению // Математика в школе. – 2014. – №8. – С. 3-7; Математика в школе. – 2014. – № 9. – С. 3-10.

16. Шашкина М.Б., Якименко М.Ш. Типичные ошибки при решении заданий С 3 на ЕГЭ в 2010-2011 гг. // Математика в школе. – 2011. – № 9. – С. 11-17.

17. Ягунова Е.Б. Ошибки по невнимательности. Работа над ошибками // Компьютерные инструменты в школе. – 2012. – № 1. – С. 9-16.

Ошибки делятся на случайные и систематические, то есть устойчивые. Случайными ошибками следует считать те, которые появляются однократно, не систематически у одного-двух обучающихся. К устойчивым (типичным) ошибкам относятся те, которые появляются у одного и того же обучающегося (или у нескольких) неоднократно, или те, которые появляются хотя и однократно, но у многих обучающихся. Типичные ошибки имеют массовый характер, высокую частоту «встречаемости» в работах обучающихся.

К типичным ошибкам по математике можно, например, отнести: ассоциативный перенос методов решения уравнений на неравенства, неверное применение метода декомпозиции неравенства, потеря решений при выполнении заданий на решение уравнений и неравенств, неверное определение вида геометрической фигуры, тавтология в рассуждениях и т.д.

Особо рассмотрим такой пример типичной ошибки по математике. При решении логарифмических уравнений и неравенств учащиеся используют свойства логарифмов:

;

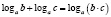
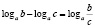
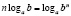
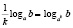
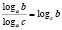
Но анализ практики показывает, что большинство учащихся не знают или не до конца осознают условия применения этих формул.

Если мы читаем формулы слева направо, то обязательно подразумеваем, что все аргументы логарифмов и все основания положительны, основания логарифмов не равны единице.

Но если мы запишем, например, формулу 1 справа налево: 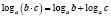, то положительным должно быть произведение (то есть числа и должны быть одного знака). Значит, учащиеся должны иметь в виду формулу: , .

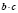
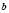
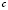
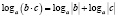
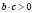
Следовательно, мы имеем дело не с одной формулой, а с двумя, причем каждая из них имеет свою область определения, что и важно учитывать при решении.

Эти рассуждения имеют место и для многих других формул.

Приведем еще примеры типичных ошибок учащихся:

на вопрос «Чему равны точные значения 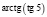и arcsin(sin10)?», учащиеся дают неверный ответ: , arcsin(sin10)=10, ссылаясь на то, что мы имеем дело со взаимно обратными функциями (верные ответы будут соответственно такими: ; );

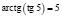
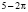
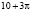
учащиеся ошибочно считают, что при решении иррациональных уравнений надо опасаться возведения обеих частей уравнения в четную степень, − могут появиться посторонние корни, и не стоит опасаться возведения в нечетную степень; если появляются посторонние корни, то они обязательно окажутся в той области, которая, после преобразований исходного уравнения, добавится к его области определения;

учащиеся ошибочно считают, что при решении систем уравнений методом деления одного уравнения системы на другое, не происходит потери решений (хотя это не так; например, при решении этим методом системы

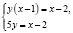
получаем решение 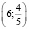, в то время как и пара также является решением);

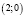
учащиеся неверно записывают ответ в случае решения систем тригонометрических уравнений (в записи ответов к двум уравнениям системы используется одна и та же буква);

учащиеся ошибочно считают, что если числа и являются корнями квадратного уравнения, то они исчерпывают все множество корней этого уравнения (ошибочность этого утверждения демонстрируют решения двух таких задач: 1. Найдите числа и такие, что корни уравнения есть числа и (Ответ: или ) и 2. При каких и числа и являются корнями уравнения ? (Ответ: или или ));

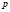
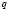
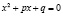
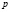
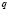
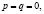
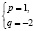
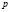
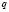
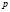
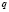
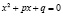
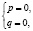
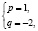
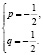
при решении логарифмических уравнений путем перехода к новому основанию, учащиеся, как правило, забывают наложить ограничения на это новое основание, а если и осуществили это действие, то забывают проверить те значения неизвестной, которые входили в прежнюю область ограничения, но оказались выброшенным из области определения нового основания;

при решении дробно-рациональных неравенств (со знаком нестрогого неравенства) учащиеся в ответ забывают записать изолированные решения (те, которые обращают в ноль числитель дроби);

при решении уравнений вида 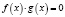учащиеся всегда пользуются утверждением: «произведение двух сомножителей равно нулю, когда хотя бы один из них равен нулю», хотя есть уравнения, при решении которых следует пользоваться утверждением: «произведение двух сомножителей равно нулю, когда хотя бы один из них равен нулю, а другой при этом имеет смысл».

Большинство ошибок связаны, как правило, с формализмом в знаниях учащихся, которые внешне проявляется следующим образом: отрыв формы от содержания; неумение применять теорию на практике; преобладание памяти над пониманием; господство трафарета, шаблона.

Заметим, что во второй половине XIX века господствовала ошибочная теория «недопущения ошибок» (Н. Кульман, Ф. Флеров), согласно которой акцентирование внимания на ошибке повлечет за собой упрочение ошибки в сознании обучающихся. Лозунгами этой теории были следующие: «Ни одной ошибки для глаз!», «Ни одной ошибки для рук!».

Современная дидактика и частные методики доказывают, что работа над ошибками не просто полезна, но и необходима, причем над типичными ошибками должна проводиться фронтальная работа, а над случайными – индивидуальная. Скорее всего, вначале «На ошибках учат», а затем уже «На ошибках учатся». Любая ошибка должна быть использована для более детального и глубокого проникновения в суть каждого правила, понятия, теоремы и т.д.

В каждой ошибке следует различать содержание и причину ее возникновения. В содержание ошибки входит то, что объективно неверно, неадекватно выполнено в действиях обучающихся.

Причина же появления ошибки – это некоторое обстоятельство (или их совокупность), которое повлекло за собой выполнение неадекватного действия обучающимся.

Содержание ошибки легко установить по внешнему выражению действия обучающихся (сужает или расширяет объем понятия, неправильно произносит или пишет, неверно выполняет какое-то действие и т.д.). Причина же ошибка, как правило, внешне себя не проявляет. Задача учителя определить исходные корни допущенной ошибки, что даст ему возможность верно строить работу по ликвидации и предупреждению различного рода ошибок.

П.И. Самсонов замечает, что, судя по допускаемым учащимися ошибкам на ЕГЭ по математике, можно «с уверенностью говорить о недостаточной методической работе в школе, о недостаточной дидактической гибкости учителя. А ведь за этими недоработками стоит будущее ученика!» [15, с. 3-4].

Высказанной мысли созвучны слова Н.М. Бескина: «Как это ни странно звучит, ошибки в процессе изучения не вредны, а полезны. Они аналогичны симптомам болезни. По этим симптомам врач ставит диагноз. Точно так же ошибки учащихся сигнализируют учителю, чего именно школьник не понимает. Учитель мог этого и не знать, а ошибка дает ему нужную информацию. От учителя требуется умение понять неправильный ход мыслей ученика, который не может объяснить, почему он пришел к такому результату. … Учитель должен не просто поправить ошибку, а выкорчевать ее. Для этого он должен понять неправильный ход мыслей и заблуждений ученика, который сам ученик не может сформулировать» [2, с. 3].

Укажем причины типичных математических ошибок учащихся (да они имеют место и по другим учебным дисциплинам):

• причины, связанные с психологическими факторами (ослабление психических функций у обучающихся: внимания, памяти, мышления);

• причины, обусловленные недостатками учебных программ и учебников;

• причины, обусловленные несовершенством организации учебного процесса;

• причины, обусловленные невладением обучающимися на требуемом уровне синтаксисом и семантикой математического языка.

В наших учебных пособиях [5, 6], монографии [7] и статьях [4, 8] приведены примеры типичных ошибок обучающихся по математике и указаны их причины.

В данной статье укажем какие типичные ошибки учащиеся допустили в ЕГЭ по математике в 2014 году при выполнении заданий раздела С.

При решении задачи С 1 (тригонометрическое уравнение) типичными ошибками были:

• ошибки в применении формул приведения;

• ошибки из-за незнания формул тригонометрии;

• ошибка, допущенные в записи корней тригонометрического уравнения;

• ошибки в преобразовании выражений со степенью;

• выполнение преобразования уравнения, ведущее к потере корней.

При решении задания С 2 (стереометрическая задача на нахождение угла между плоскостью основания треугольной пирамиды и плоскостью, проходящей через три заданные точки) типичными были следующие ошибки:

• неверное определение искомого угла;

• неверное определение вида фигуры;

• использовались необоснованные выводы.

При решении задания С 3 (решение системы неравенств, одно из которых показательной, а другое логарифмическое) были допущены такие типичные ошибки:

• потеря части решения неравенства;

• неверное преобразование неравенств;

• не учитывались условия существования решения неравенств;

• ошибки в записи числового промежутка;

• нет четкого понимания сути понятий «система» и «совокупность»;

• неверное применение метода декомпозиции;

• ошибки в преобразовании показательного и логарифмического неравенств;

• ошибки при выполнении тождественных преобразований степенных и логарифмических выражений.

При выполнении задания С 4 (планиметрическая задача с элементами доказательства) были допущены такие типичные ошибки:

• неверное определение центра описанной окружности;

• ошибки в формулировании утверждения;

• неверное определение вида четырехугольника;

• из рассмотрения частных случаев делается общее заключение.

• При выполнении задания С 5 (логарифмическое уравнение с параметром) типичными ошибками были:

• неверно формулируется условие после замены переменной;

• ошибки в нахождении корней квадратного уравнения;

• не учтен возможный случай равенства корней 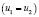, что привело к потере условия ;

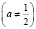
• использованы неравносильные преобразования при переходе от одного уравнения к другому;

• неверно решены рациональные неравенства;

• неполное исследование свойств новой переменной.

При решения задания С 6 (задача целочисленной арифметики) учащиеся допустили следующие типичные ошибки:

• сужен круг поиска необходимых значений;

• ошибка в формулировании свойства чисел;

• проводится неверное обобщение.

Следует заметить, что при выполнении всех шести задач раздела С были допущены речевые ошибки. Например, «угол между плоскостями есть угол между двумя перпендикулярами, проведенными к линии их пересечения», «наложим ОДЗ», «разобьем неравенство на интервалы», «число 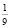− число нечетное», «число − число четное», «меньше чисел нет, поэтому быть не может» и др.

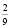
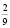
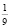
Практика показывает, что очень важно воспитывать и развивать у школьников навыки самоконтроля для того, чтобы каждый из них мог бы проводить диагностику своего решения задач.

Стихийно, сам по себе самоконтроль у ученика не рождается. Самоконтролю следует обучать специально.

Анализ причин типичных ошибок по математике показывает, что это как раз и есть ошибки, связанные с недостаточным или полным отсутствием самоконтроля.

Для проведения учащимися самоконтроля правильности проведенного решения задачи им можно дать на вооружение весьма простые средства, которые позволят установить неправильность решения задачи. Примеры таких средств читатель найдет в работах [11, 12, 13, 14].

Библиографическая ссылка

Далингер В.А. ТИПИЧНЫЕ ОШИБКИ УЧАЩИХСЯ ПО МАТЕМАТИКЕ И ИХ ПРИЧИНЫ // Современные наукоемкие технологии. – 2014. – № 12-1.
– С. 94-97;

URL: https://top-technologies.ru/ru/article/view?id=34851 (дата обращения: 21.09.2023).

Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»

(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)

Источник

ОГЭ -2021 по математике: типичные ошибки и пути их
преодоления

Воротницкая А.И.,
учитель математики

МБОУ «Мужевская
СОШ имени Н.В.Архангельского

Специфика математики как школьного предмета
состоит в том, что ее изучение в значительной степени строится на системе
опорных знаний, без овладения которыми невозможно дальнейшее продвижение по
курсу. В ходе ОГЭ учащийся должен продемонстрировать наличие у него
опорных знаний, позволяющих изучать математику в старшей школе.

Результаты ОГЭ по математике в этом году не
очень хорошие. Эти результаты уже привлекли внимание общественности всей
страны. Поэтому предлагаю поговорить о типичных ошибках учащихся и путях их
преодоления.

ОГЭ представляет собой форму государственной
итоговой аттестации, цель которой определить соответствие результатов освоения
ООП ООО соответствующим требованиям ФГОС

Результатом
освоения ООП ООО должна стать математическая компетентность выпускников.
Выпускники
должны:

·
овладеть
специфическими для математики знаниями и видами деятельности;

·
научиться
преобразованию знания и его применению в учебных и внеучебных ситуациях;

·
сформировать
качества, присущие математическому мышлению;

·
овладеть
математической терминологией, ключевыми понятиями, методами и приёмами.

Работа по математике состоит
из двух частей.

Часть 1, нацеленная на проверку овладения курсом на базовом уровне, содержит 19 заданий, в совокупности охватывающих все разделы курса и предусматривающих три формы ответа: задания с выбором ответа из четырех предложенных вариантов, задания с кратким ответом, задание на соотнесение

Часть 2 состоит из заданий повышенного и высокого
уровней сложности и
включает 6 заданий с развернутым ответом. Их назначение – дифференцировать хорошо успевающих обучающихся по уровням подготовки, выявить наиболее подготовленную часть выпускников. Все задания требуют записи решений и ответа. Задания расположены по нарастанию трудности.

При проверке базовой
математической компетентности обучающиеся должны продемонстрировать:

— владение основными алгоритмами, знание и понимание ключевых элементов содержания (математических
понятий, их свойств, приемов
решения задач и прочее);

— умение пользоваться математической записью;

— умение
применять знания в решении
математических задач, не сводящихся к прямому применению алгоритма;

— умение применять математические
знания в простейших практических ситуациях.

ОГЭ
проверяет не только знания по предмету, но и умение читать и понимать
прочитанное, внимательность и аккуратность в оформлении решений (запись ответов
в бланк), умение проверять свои решения.

Виды
типичных ошибок обучающихся на ОГЭ по математике:

1)
языковые
;

2) технические;

3) содержательные.

Для
преодоления языковых ошибок я применяю групповую, парную формы работы на
уроке, постоянно прошу обучающихся аргументировать свои ответы, часто провожу
устные диктанты и тематические зачеты (особенно по геометрии).

Для преодоления технических ошибок я систематически (ежемесячно) провожу
диагностические работы, которые помогают обучающимся вырабатывать
внимательность и приучают детей делать проверку в каждом задании.

Вероятные
причины затруднений и типичных ошибок в 2021 году:

·
Сложная
эпидемиологическая обстановка в 2019-2021 уч.годах: переход на дистанционное
обучение, что привело к сокращению времени на отработку материала.

·
Низкие
проценты выполнения заданий 3-5, 11-14 можно объяснить тем, что они
соответствуют трудно формируемым умениям у многих школьников: выполнять
преобразования со степенями, решение квадратных и линейных неравенств и их
систем, применение знаний в практических ситуациях, построение математической
модели, вычисление числовых характеристик прогрессии.

·
Геометрические
задачи также традиционно вызывают трудности у обучающихся.

·
Отсутствие
у обучающихся должного уровня развития логического мышления – одна из основных
причин затруднений в выполнении геометрических заданий.

Традиционно
основными направлениями подготовки обучающихся к ГИА по математике
являются:

1) Информационная
работа;

2) Психологическая
поддержка;

3) Предметная
работа.

Важно заранее
познакомить обучающихся с особенностями структуры КИМ и технологией проведения
экзамена. Используя образовательные сайты ФИПИ или ОБРНАДЗОР ознакомиться
самому и ознакомить родителей с нормативной базой ГИА. Настроить
ребят на то, что экзамен-это
возможность показать свои знания, поэтому не следует бояться и переживать.
Выработке психологической готовности помогает апробирование и отработка
формы проведения экзамена в формате и по материалам ОГЭ.

В
организации предметной подготовки необходимо обращать внимание на опорные
алгоритмы (формирование вычислительных навыков), на теоретическую подготовку
по геометрии (зачеты), учить составлять план решения задачи, решать геометрические
задач разного вида на применение теоретических знаний. Необходимо готовить
учащихся к использованию справочных материалов, усилить работу по формированию
языковых умений ( учить четко и лаконично выражать свои мысли при развернутом ответе),
«нарешивать» задачи с практическим содержанием, использовать различные формы (устный
счет, математический диктант) формирования алгоритмов и вычислительных навыков.

Итак,
считаю эффективными следующие пути преодоления типичных ошибок:

— необходимо
достаточно часто проводить диагностические работы, направленные на выявление
уровня подготовки обучающихся по отдельным темам, что позволит спланировать
индивидуальную и групповую работу обучающихся;

— при изучении
нового материала и его отработке необходимо сочетать различные методы обучения:
традиционные и интерактивные, направленные на организацию самостоятельной
работы каждого ученика, что также позволит устранить пробелы в знаниях и
умениях, и поможет проводить подготовку к аттестации дифференцированно для
слабых и сильных учеников;

— особое внимание
следует уделять формированию навыков самоконтроля и самопроверки выполненных
заданий;

— необходимо повышать
уровень вычислительных навыков, развивать умение пользоваться справочными
материалами, читать условие и вопрос задачи, записывать математически верно
решение задачи, применять знания в нестандартных ситуациях;

— со слабо
успевающими обучающимися необходимо выделить круг доступных ему заданий,
помочь освоить основные математические факты, позволяющие их решать и
сформировать уверенные навыки их решения;

— для «средних»
учеников необходимо использовать методику, при которой они смогут перейти
от теоретических знаний к практическим навыкам, от решения стандартных
алгоритмических задач к решению задач похожего содержания, но иной формулировки
и применению уже отработанных навыков в новой ситуации;

— для сильных
учеников требуется
создание условия для продвижения: дифференцированные по уровню сложности
задания, возможность саморазвития, помощь в решении заданий второй части;

— «нарешивание» заданий
открытого банка ОГЭ необходимо для формирования устойчивых навыков решения, но
его нужно сочетать с фундаментальной подготовкой, позволяющей сформировать у
учащихся общие учебные действия, способствующие более эффективному усвоению
изучаемых вопросов, а также дифференциации обучающихся по уровню подготовки;

— учителю следует ставить
перед каждым учащимся ту цель, которую он может реализовать в соответствии с
уровнем его подготовки, при этом опираясь на самооценку и устремления каждого
учащегося

— наряду с более
тщательным изучением тем «Уравнения, неравенства и их системы» (более сложные
виды), «Решение текстовых задач», «Решение планиметрических задач, содержащих
комбинацию фигур», «Решение задач на доказательство» (причем как по геометрии,
так и по алгебре) необходимо уделять внимание и остальным темам с тем, чтобы
поддерживать и повышать достигнутый уровень их освоения;

— для успешного
выполнения заданий второй части необходимо овладение отдельными элементами
знаний и умений переводить на овладение навыками решения комплексных,
многошаговых заданий;

— в процессе
подготовки к ОГЭ должны участвовать все стороны: обучающийся, школа и родители,
поэтому необходимо своевременно знакомить родителей с нормативными документами
по подготовке к экзаменам, информировать их о процедуре итоговой аттестации,
особенностях подготовки к тестовой форме сдачи экзаменов, о всевозможных
методических рекомендациях и ресурсах, о результатах пробных испытаний и
текущей успеваемости;

— необходимо
использовать имеющиеся в достаточном количестве дополнительные материалы,
уделять внимание различным способам решения задач, их сопоставлению и выбору
лучшего; учить использовать логические цепочки не только при доказательстве, но
и при решении задач, стараться достичь осознанности знаний учащихся,
сформированности умения применять полученные знания в практической
деятельности, умения анализировать, сопоставлять, делать выводы в нестандартных
ситуациях.

Таким
образом, необходимым условием успешной подготовки обучающихся к сдаче ГИА
является освоение учителем материалов, публикуемых ФИПИ:
демонстрационного варианта, кодификатора элементов содержания и кодификатора
требований к уровню подготовки, спецификации КИМ по математике, учебно-методических
материалов для председателей и членов региональных предметных комиссий по
проверке выполнения заданий с развернутым ответом экзаменационных работ ОГЭ и,
конечно, изучение заданий открытого банка, их систематизация, выделение
основных способов решения различных классов заданий. А также, изучить
разнообразные методические пособия, учебно-тренировочные материалы,
представленные на сайтах и различными издательствами.

Для
успешного выполнения заданий второй части КИМ необходим особый подход в работе
с наиболее подготовленными учащимися.

В целом,
для успешного прохождения ГИА необходима дифференцированная работа с учащимися
класса и на уроке, и при составлении домашних заданий и заданий, предлагающихся
обучающимся на контрольных, проверочных, диагностических работах. Необходимо
обратить серьёзное внимание на решение прикладных и ситуационных задач, а также
на формирование уверенных вычислительных навыков

Список
используемой литературы:

1.
Документы,
определяющие структуру и содержание КИМ ) ОГЭ 2021 г.;

2.
Учебно-методические
материалы для председателей и членов региональных предметных комиссий по
проверке выполнения заданий с развёрнутым ответом экзаменационных работ ОГЭ;

3.
Методические
рекомендации на основе анализа типичных ошибок участников ОГЭ прошлых лет
(2019, 2020 гг.);

4.
Методические
рекомендации для учителей школ с высокой долей обучающихся с рисками учебной
неуспешности (fipi.ru);

5.
журнал
«Педагогические измерения»;

6.
Youtube-канал
Рособрнадзора.

Приложение
1

Анализ
типичных ошибок обучающихся на ОГЭ 2021

по
математике в МБОУ «Мужевская МОШ имени Н.В. Архангельского»

Таблица1

№	Содержание задания в КИМ ОГЭ	Содержательные ошибки
№ 1.	Выделять из текста нужную информацию, преобразование информации из одного вида в другой, сопоставлять информацию, представленную в таблице с текстовой, отвечать на поставленный вопрос.	Задание выполнено на ожидаемом уровне.
№ 2.	Решить задачу на нахождение расстояния по шоссе между селами, используя информацию из текста, картинки, масштаб	не обращают внимание на единицы измерения, не учитывают масштаб, вычислительные ошибки.
№ 3.	Решить задачу на нахождение расстояния по прямой с помощью теоремы Пифагора, используя информацию из текста, таблицы.	невнимательное прочтение текста, работа с формулой, вычисления.
№ 4.	Решить задачу на нахождение времени движения, используя информацию из текста и данные задачи 2.	невнимательное прочтение текста, неверное построение математической модели, вычислительная ошибка, не знание формул
№ 5.	Задание на определение наиболее дешевого набора продуктов, используя информацию из таблицы	вычислительные, невнимательное прочтение вопроса к заданию, в построении математической модели.
№ 6.	Задание направлено на проверку умения выполнять арифметические действия с десятичными дробями.	в применении правил выполнения арифметических действий с десятичными дробями.
№ 7.	Задание направлено на проверку умений выполнять вычисления и преобразования на координатной прямой.	Задание выполнено на ожидаемом уровне.
№ 8.	Задание на умение выполнять преобразования алгебраических выражений, содержащих степень или корень, и находить значение данного выражения при заданном неизвестном.	в применении свойств степени или корня, вычислительная ошибка.
№ 9.	Задание проверяет умения решать линейные уравнения или неполное квадратное уравнение	в алгоритме решения уравнений, вычислительная.
№ 10.	Задание проверяет умения решать практическую расчетную задачу на вычисление вероятности события. Для решения таких задач необходимо знать определение вероятности события и, что общая вероятность несовместных событий равна 1; достаточно уметь находить отношение числа благоприятных для наступления некоторого события исходов к числу всех равновозможных исходов. Иногда это требует определённых вычислительных навыков.	невнимательное чтение условия, неумение определять число благоприятных исходов, кроме того, часть учеников вероятности события записали в процентах.
№ 11.	Задание направлено на проверку умений чтения графиков функций, содержащие задания, в которых требуется установить соответствие между знаками коэффициентов квадратичной функции	Неверное установление соответствия между знаками коэффициентов, неумение читать графики.
№ 12.	Задание представляет собой задачу на умение осуществлять практические расчёты по формулам; составлять несложные формулы, выражающие зависимости между величинами. В условиях таких задач даются формулы из разных областей знаний, причём значения всех величин за исключением одной в этих формулах известны. Требуется найти значение именно этой величины.	Данное задание некоторые учащиеся пропускают, это говорит о том, что девятиклассники не умеют работать с математической моделью. Вычислительные ошибки
№13	Задание представляет собой квадратное неравенство или линейное неравенство. Необходимо было решить неполное квадратное неравенство	Ошибки связаны с незнанием свойств неравенств и алгоритма решения квадратных неравенств, неумением определить знак соответствующей функции (или многочлена) на интервале.
№ 14.	Задание с практическим содержанием, направленное на проверку умения применять знания об арифметической и геометрической прогрессиях в прикладных задачах.	неверное установление вида прогрессии, вычислительные ошибки, непонимание прочитанного текста
№ 15.	Несложная планиметрическая задача в одно действие, проверяющая владение базовыми знаниями по теме «Треугольники». Для успешного решения задачи достаточно знать теорему о сумме углов треугольника	Неверное нахождение острого угла прямоугольного треугольника и вычислительные ошибки. Незнание теоремы о сумме углов тр-ка
№ 16.	Представляет собой задачу, связанную с окружностью . Для решения данной задачи необходимо знать теорему об угле между хордой и касательной к окружности	вычислительная, незнание нужной теоремы, определения касательной
№ 17.	Представляет собой задачу по теме «Четырехугольники». Решение задачи сводилось к применению формулы площади параллелограмма.	вычислительная, по причине невнимательности учащихся, незнание формулы площади
№ 18.	Представляет собой задачу по планиметрии на вычисление геометрических величин по готовому чертежу, изображённому на клетчатой бумаге. В таких задачах данные представлены в виде чертежа на бумаге в клетку, причём размеры клеток одинаковы и заданы условием. В данном случае на клетчатой бумаге была изображена фигура, необходимо было найти площадь, посчитав к-во клеток треугольник или трапеция, требовалось найти их площади.	невнимательность при подсчете клеток, незнание способа нахождения площади по клеткам
№19	Задание на умение оценивать логическую правильность рассуждений, распознавать ошибочные заключения, требующее выбрать одно или несколько верных утверждений из множества данных (в настоящее время – из трёх данных). В большинстве случаев правильный ответ на вопрос задачи связан со знанием простейших геометрических фактов и утверждений.	не владеют достаточными знаниями точных определений и формулировок теорем, свойств геометрических фигур.
№ 20	требовалось решить иррационального алгебраическое уравнение, применив один из основных методов решения: 1) преобразование уравнения к виду квадратного уравнения, 2)Найти область определения ; 3)Определить посторонний корень	ошибки в действиях: 1) Вычеркивание квадратного корня из обеих частей уравнения без учёта условий выполнимости данного действия и равносильности преобразования (рассматривание одного случая из возможных); 2) перенос слагаемых из одной части уравнения в другую; 3) решение квадратного уравнения. Данное обстоятельство свидетельствует о недостаточном уровне освоения методов решения алгебраических уравнений, формальном, не осмысленном выполнении шагов алгоритмов решения уравнений тем или иным методом. 4) не содержит записи ответа, хотя данный шаг является обязательным при решении уравнений, кроме того, перед заданиями второй части в прямоугольной рамке фиксируется инструкция: «…запишите его решение и ответ». В связи с чем, учителям следует обратить внимание на обеспечение условий для качественной реализации этапов осмысления и применения методов решения алгебраических уравнений на уроках математики в школе.
№ 21	требовалось решить текстовую задачу на нахождение количества свежих фруктов из определенного количества высушенных. Для верного и полного решения обучающимися должны быть выполнены следующие этапы работы с задачей: составление математической модели, преобразование составленной модели, интерпретация полученных результатов и запись ответа. Все этапы должны быть зафиксированы в представленном решении.	Самая распространённая ошибка при решении задачи на нахождение количества свежих фруктов из определенного количества высушенных. В неумении составить модель задачи. у большинства обучающихся возникают серьезные затруднения при решении этих задач. Это свидетельствует о необходимости изменения подходов к обучению по решению текстовых задач, в частности, обучению деятельности по реализации основных этапов решения задачи: анализу условия задачи, составлению математической модели, преобразованию составленной модели, интерпретации полученных результатов и записи ответа.
№ 22	В задании предусмотрено построение графика функции, содержащей переменную в знаменателе дроби, Задания, предполагающие построение графиков функций и их анализ, всегда вызывают у обучающихся трудности. Такие задачи рассчитаны на более серьёзную, выходящую за рамки пятичасового курса алгебры, математическую подготовку выпускников.	1) неправильное преобразование формулы, задающей функцию; 2) отсутствие обоснований построения графика функции; 3) вычислительные ошибки при определении координат точек; 4) несоблюдение масштаба при построении системы координат, графика; 5) отсутствие вычислений координат точек «стыка», и как следствие, – неверное построение графика; 6) не определено значение параметра в соответствие с требованиями задачи или нет пояснений, как этот параметр определен; 7) ограничение графика (кривой или прямой) точкой, когда рассматриваемая функция не является ограниченной. Самой распространённой ошибкой при решении задания № 22 является неграмотное обоснование построения графика функции. Достаточно большое количество работ, в которых представлено решение задания 22, ежегодно не содержит описание построения графика функции, хотя развернутый ответ, который требуется в этом задании, предполагает описание рассуждений.
№ 23	В задании предложена планиметрическая задача на нахождение высоты прямоугольного треугольника, если известны длины двух катетов	обучающийся должен показать все шаги решения, хотя его объяснения могут быть неполными или может быть допущена одна вычислительная ошибка. Встречаются ошибки, связанные с некорректным использованием чертежа, приводящим к решению другой задачи. В этом случае задача не считается решенной. Требуется знание теоремы о высоте прямоугольного треугольника
№24	При выполнении задания требовалось доказать подобие треугольников, применив два признака подобия. Для того чтобы получить 1 балл за решение этой задачи достаточно было составить верно пропорцию без обоснования подобия треугольников. Задания на применение признаков подобия треугольников по-прежнему являются для большинства девятиклассников сложным Решение проблемы освоения темы «Подобные треугольники» возможно при условии целенаправленной подготовительной работы к изучению данной темы, связанной с развитием понятийного, логического мышления обучающихся в процессе обучения математике с 5 по 8 класс и выполнением условия: опора на личный опыт ученика при введении в тему, изучении темы.	К сожалению, оказалось, что обучающиеся недостаточно глубоко владеют темой «Признаки подобия треугольников». Несмотря на стандартную формулировку задачи, наличие в учебниках геометрии большого количества подобных задач, незначителен процент участников экзамена, верно ее решивших. При выполнении задания № 24 обучающиеся допускали неверное использование терминов, При обосновании подобия треугольников использовались неверные формулировки признаков, неверные посылки для суждения о подобии треугольников, например, подобие следует из равенства углов и параллельности сторон. Данные факты говорят о недостаточном уровне сформированности понятийного и логического мышления, действия «построение логических рассуждений». Встречаются ошибки, связанные с некорректным использованием чертежа, приводящим к решению другой задачи, не соответствующей заданному условию, в таком случае задание нельзя считать выполненным верно. . Это серьезная проблема в целом, источником которой может быть: несформированность понятий «пропорциональность» (5 – 6 классы), «соответствие» (5 – 9 классы), «пропорциональные отрезки», «сходственные стороны» (8 класс), недостаточный уровень развития понятийного мышления, несформированность умений составлять и преобразовывать пропорцию (6 класс), несформированность познавательного действия «построение логических рассуждений» (5 – 9 классы), недостаточность опыта доказательства подобия треугольников с помощью признаков подобия, недостаточность опыта составления пропорции из сходственных сторон подобных треугольников (8 класс), и др.
№25	Выполнение задания традиционно остается низким, так как это геометрическая задача высокого уровня.	— обучающимся не известны стратегии поиска решения задач (принципы отбора математических предложений (теорем, аксиом, др. из большого набора теоретических фактов) методов решения (из перечня методов); — недостаточно опыта применения разных методов решения одной задачи; — недостаточно опыта конструирования задач (опыт переформулирования задачи, конструирования задачи, решаемой с помощью заданного математического предложения (теорем, аксиом, др.)), заданным методом); — недостаточно опыта самостоятельного поиска решения задачи (опыт, основанный на планировании решения, использовании различных способов решения одной задачи, анализа и сравнения этих способов решения, опыт самостоятельного поиска решения трудных задач).

Источник

Типичные ошибки на ОГЭ по математике и методические приемы их устранения

Специфика математики как школьного предмета состоит в том, что ее изучение в значительной степени строится на системе опорных знаний, без овладения которыми невозможно дальнейшее продвижение по курсу. В ходе ОГЭ учащийся должен продемонстрировать наличие у него опорных знаний, позволяющих изучать математику в старшей школе.

Результаты ОГЭ по математике в этом году не очень хорошие. Эти результаты уже привлекли внимание общественности всей страны. Поэтому предлагаю поговорить о типичных ошибках учащихся и путях их преодоления.

ОГЭ представляет собой форму государственной итоговой аттестации, цель которой определить соответствие результатов освоения ООП ООО соответствующим требованиям ФГОС

Результатом освоения ООП ООО должна стать математическая компетентность выпускников. Выпускники должны:

овладеть специфическими для математики знаниями и видами деятельности;
научиться преобразованию знания и его применению в учебных и внеучебных ситуациях;
сформировать качества, присущие математическому мышлению;
овладеть математической терминологией, ключевыми понятиями, методами и приёмами.

Работа по математике состоит из двух частей.

Часть 2 состоит из заданий повышенного и высокого уровней сложности и включает 6 заданий с развернутым ответом. Их назначение – дифференцировать хорошо успевающих обучающихся по уровням подготовки, выявить наиболее подготовленную часть выпускников. Все задания требуют записи решений и ответа. Задания расположены по нарастанию трудности.

При проверке базовой математической компетентности обучающиеся должны продемонстрировать:

владение основными алгоритмами, знание и понимание ключевых элементов содержания (математических понятий, их свойств, приемов решения задач и прочее);
умение пользоваться математической записью;
умение применять знания в решении математических задач, не сводящихся к прямому применению алгоритма;
умение применять математические знания в простейших практических ситуациях.

ОГЭ проверяет не только знания по предмету, но и умение читать и понимать прочитанное, внимательность и аккуратность в оформлении решений (запись ответов в бланк), умение проверять свои решения.

Виды типичных ошибок обучающихся на ОГЭ по математике:
1) языковые ;
2) технические;
3) содержательные.

Для преодоления языковых ошибок я применяю групповую, парную формы работы на уроке, постоянно прошу обучающихся аргументировать свои ответы, часто провожу устные диктанты и тематические зачеты (особенно по геометрии).

Для преодоления технических ошибок я систематически (ежемесячно) провожу диагностические работы, которые помогают обучающимся вырабатывать внимательность и приучают детей делать проверку в каждом задании.

Вероятные причины затруднений и типичных ошибок в 2021 году:

Сложная эпидемиологическая обстановка в 2019-2021 уч.годах: переход на дистанционное обучение, что привело к сокращению времени на отработку материала.
Низкие проценты выполнения заданий 3-5, 11-14 можно объяснить тем, что они соответствуют трудно формируемым умениям у многих школьников: выполнять преобразования со степенями, решение квадратных и линейных неравенств и их систем, применение знаний в практических ситуациях, построение математической модели, вычисление числовых характеристик прогрессии.
Геометрические задачи также традиционно вызывают трудности у обучающихся.
Отсутствие у обучающихся должного уровня развития логического мышления – одна из основных причин затруднений в выполнении геометрических заданий.

Традиционно основными направлениями подготовки обучающихся к ГИА по математике являются:

Информационная работа;
Психологическая поддержка;
Предметная работа.

Важно заранее познакомить обучающихся с особенностями структуры КИМ и технологией проведения экзамена. Используя образовательные сайты ФИПИ или ОБРНАДЗОР ознакомиться самому и ознакомить родителей с нормативной базой ГИА. Настроить ребят на то, что экзамен-это возможность показать свои знания, поэтому не следует бояться и переживать. Выработке психологической готовности помогает апробирование и отработка формы проведения экзамена в формате и по материалам ОГЭ.

В организации предметной подготовки необходимо обращать внимание на опорные алгоритмы (формирование вычислительных навыков), на теоретическую подготовку по геометрии (зачеты), учить составлять план решения задачи, решать геометрические задач разного вида на применение теоретических знаний. Необходимо готовить учащихся к использованию справочных материалов, усилить работу по формированию языковых умений ( учить четко и лаконично выражать свои мысли при развернутом ответе), «нарешивать» задачи с практическим содержанием, использовать различные формы (устный счет, математический диктант) формирования алгоритмов и вычислительных навыков.

Итак, считаю эффективными следующие пути преодоления типичных ошибок:

необходимо достаточно часто проводить диагностические работы, направленные на выявление уровня подготовки обучающихся по отдельным темам, что позволит спланировать индивидуальную и групповую работу обучающихся;
при изучении нового материала и его отработке необходимо сочетать различные методы обучения: традиционные и интерактивные, направленные на организацию самостоятельной работы каждого ученика, что также позволит устранить пробелы в знаниях и умениях, и поможет проводить подготовку к аттестации дифференцированно для слабых и сильных учеников;
особое внимание следует уделять формированию навыков самоконтроля и самопроверки выполненных заданий;
необходимо повышать уровень вычислительных навыков, развивать умение пользоваться справочными материалами, читать условие и вопрос задачи, записывать математически верно решение задачи, применять знания в нестандартных ситуациях;
со слабо успевающими обучающимися необходимо выделить круг доступных ему заданий, помочь освоить основные математические факты, позволяющие их решать и сформировать уверенные навыки их решения;
для «средних» учеников необходимо использовать методику, при которой они смогут перейти от теоретических знаний к практическим навыкам, от решения стандартных алгоритмических задач к решению задач похожего содержания, но иной формулировки и применению уже отработанных навыков в новой ситуации;
для сильных учеников требуется создание условия для продвижения: дифференцированные по уровню сложности задания, возможность саморазвития, помощь в решении заданий второй части;
«нарешивание» заданий открытого банка ОГЭ необходимо для формирования устойчивых навыков решения, но его нужно сочетать с фундаментальной подготовкой, позволяющей сформировать у учащихся общие учебные действия, способствующие более эффективному усвоению изучаемых вопросов, а также дифференциации обучающихся по уровню подготовки;
учителю следует ставить перед каждым учащимся ту цель, которую он может реализовать в соответствии с уровнем его подготовки, при этом опираясь на самооценку и устремления каждого учащегося
наряду с более тщательным изучением тем «Уравнения, неравенства и их системы» (более сложные виды), «Решение текстовых задач», «Решение планиметрических задач, содержащих комбинацию фигур», «Решение задач на доказательство» (причем как по геометрии, так и по алгебре) необходимо уделять внимание и остальным темам с тем, чтобы поддерживать и повышать достигнутый уровень их освоения;
для успешного выполнения заданий второй части необходимо овладение отдельными элементами знаний и умений переводить на овладение навыками решения комплексных, многошаговых заданий;
в процессе подготовки к ОГЭ должны участвовать все стороны: обучающийся, школа и родители, поэтому необходимо своевременно знакомить родителей с нормативными документами по подготовке к экзаменам, информировать их о процедуре итоговой аттестации, особенностях подготовки к тестовой форме сдачи экзаменов, о всевозможных методических рекомендациях и ресурсах, о результатах пробных испытаний и текущей успеваемости;
необходимо использовать имеющиеся в достаточном количестве дополнительные материалы, уделять внимание различным способам решения задач, их сопоставлению и выбору лучшего; учить использовать логические цепочки не только при доказательстве, но и при решении задач, стараться достичь осознанности знаний учащихся, сформированности умения применять полученные знания в практической деятельности, умения анализировать, сопоставлять, делать выводы в нестандартных ситуациях.

Таким образом, необходимым условием успешной подготовки обучающихся к сдаче ГИА является освоение учителем материалов, публикуемых ФИПИ: демонстрационного варианта, кодификатора элементов содержания и кодификатора требований к уровню подготовки, спецификации КИМ по математике, учебно-методических материалов для председателей и членов региональных предметных комиссий по проверке выполнения заданий с развернутым ответом экзаменационных работ ОГЭ и, конечно, изучение заданий открытого банка, их систематизация, выделение основных способов решения различных классов заданий. А также, изучить разнообразные методические пособия, учебно-тренировочные материалы, представленные на сайтах и различными издательствами.

Для успешного выполнения заданий второй части КИМ необходим особый подход в работе с наиболее подготовленными учащимися.

В целом, для успешного прохождения ГИА необходима дифференцированная работа с учащимися класса и на уроке, и при составлении домашних заданий и заданий, предлагающихся обучающимся на контрольных, проверочных, диагностических работах. Необходимо обратить серьёзное внимание на решение прикладных и ситуационных задач, а также на формирование уверенных вычислительных навыков

Список используемой литературы:

Документы, определяющие структуру и содержание КИМ ) ОГЭ 2021 г.;
Учебно-методические материалы для председателей и членов региональных предметных комиссий по проверке выполнения заданий с развёрнутым ответом экзаменационных работ ОГЭ;
Методические рекомендации на основе анализа типичных ошибок участников ОГЭ прошлых лет (2019, 2020 гг.);
Методические рекомендации для учителей школ с высокой долей обучающихся с рисками учебной неуспешности (fipi.ru);
журнал «Педагогические измерения»;
Youtube-канал Рособрнадзора.

В помощь учителю

Уважаемые коллеги! Опубликуйте свою педагогическую статью или сценарий мероприятия на Учительском портале и получите свидетельство о публикации методического материала в международном СМИ.

Для добавления статьи на портал необходимо зарегистрироваться.

Конкурсы

Диплом и справка о публикации каждому участнику!

© 2007 — 2023 Сообщество учителей-предметников «Учительский портал»
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель / главный редактор: Никитенко Е.И.

Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание этих материалов и разрешение любых спорных вопросов с третьими лицами.
При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.

Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.

Фотографии предоставлены

Источник

Howlers[edit]

Division by zero[edit]

Analysis[edit]

Multivalued functions[edit]

Positive and negative roots[edit]

Square roots of negative numbers[edit]

Complex exponents[edit]

Geometry[edit]

Fallacy of the isosceles triangle[edit]

Proof by induction[edit]

See also[edit]

Notes[edit]

References[edit]

External links[edit]

Библиографическая ссылка

Типичные ошибки на ОГЭ по математике и методические приемы их устранения