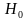На
разных стадиях статистического
исследования и моделирования возникает
необходимость в формулировке и
экспериментальной проверке некоторых
предположений (гипотез) относительно
природы и величины неизвестных параметров
анализируемой генеральной совокупности
(совокупностей). Например, исследователь
высказывает предположение: «выборка
извлечена из нормальной генеральной
совокупности» или «генеральная
средняя анализируемой совокупности
равна пяти». Такие предположения
называются статистическими
гипотезами.
Сопоставление
высказанной гипотезы относительно
генеральной совокупности с имеющимися
выборочными данными, сопровождаемое
количественной оценкой степени
достоверности получаемого вывода,
осуществляется с помощью того или иного
статистического критерия и называется
проверкой
статистических гипотез.
Выдвинутая
гипотеза называется нулевой
(основной).
Ее принято обозначать Н0.
По
отношению к высказанной (основной)
гипотезе всегда можно сформулировать
альтернативную
(конкурирующую),
противоречащую ей. Альтернативную
(конкурирующую) гипотезу принято
обозначать Н1.
Цель
статистической проверки гипотез
состоит в том, чтобы на основании
выборочных данных принять решение о
справедливости основной гипотезы Н0.
Если
выдвигаемая гипотеза сводится к
утверждению о том, что значение некоторого
неизвестного параметра генеральной
совокупности в
точности равно
заданной величине, то эта гипотеза
называется простой,
например: «среднедушевой совокупный
доход населения России составляет 650
рублей в месяц»; «уровень безработицы
(доля безработных в численности
экономически активного населения) в
России равна 9%» . В других случаях
гипотеза называется сложной.
В
качестве нулевой гипотезы Н0
принято выдвигать простую гипотезу,
т.к. обычно бывает удобнее проверять
более строгое утверждение.
По
своему содержанию статистические
гипотезы можно подразделить на несколько
основных типов6:
— гипотезы о виде
закона распределения исследуемой
случайной величины;
—
гипотезы о числовых значениях параметров
исследуемой генеральной совокупности7;
—
гипотезы об однородности двух или
нескольких выборок или некоторых
характеристик анализируемых совокупностей;
— гипотезы об общем
виде модели, описывающей статистическую
зависимость между признаками и др.
Так
как проверка статистических гипотез
осуществляется на основании выборочных
данных, т.е. ограниченного ряда наблюдений,
решения относительно нулевой гипотезы
Н0
имеют
вероятностный характер. Другими словами,
такое решение неизбежно сопровождается
некоторой, хотя возможно и очень малой,
вероятностью ошибочного заключения
как в ту, так и в другую сторону.
Так,
в какой-то небольшой доле случаев α
нулевая гипотеза Н0
может оказаться отвергнутой, в то время
как в действительности в генеральной
совокупности она является справедливой.
Такую ошибку называют ошибкой
первого рода.
А ее вероятность
принято называть
уровнем
значимости
и обозначать α.
Наоборот,
в какой-то небольшой доле случаев β
нулевая
гипотеза Н0
принимается, в то время как на самом
деле в генеральной совокупности она
ошибочна, а справедлива альтернативная
гипотеза Н1.
Такую ошибку называют ошибкой
второго рода.
Вероятность ошибки второго рода принято
обозначать β.
Вероятность 1
— β называют
мощностью
критерия.
При
фиксированном объеме выборки можно
выбрать по своему усмотрению величину
вероятности только одной из ошибок α
или β.
Увеличение вероятности одной из них
приводит к снижению другой. Принято
задавать вероятность ошибки первого
рода α
— уровень
значимости. Как правило, пользуются
некоторыми стандартными значениями
уровня значимости α:
0,1; 0,05; 0,025; 0,01; 0,005; 0,001. Тогда, очевидно,
из двух критериев, характеризующихся
одной и той же вероятностью α
отклонить
правильную в действительности гипотезу
Н0,
следует принять тот, который сопровождается
меньшей ошибкой второго рода β,
т.е. большей мощностью. Снижения
вероятностей обеих ошибок α
и β
можно добиться путем увеличения объема
выборки.
Правильное
решение относительно нулевой гипотезы
Н0
также может быть двух видов:
—
будет принята нулевая гипотеза Н0,
тогда как и на самом деле в генеральной
совокупности верна нулевая гипотеза
Н0
; вероятность
такого решения 1
— α;
—
нулевая гипотеза
Н0
будет отклонена в пользу альтернативной
Н1,
тогда как и на самом деле в генеральной
совокупности нулевая гипотеза
Н0
отклоняется в пользу альтернативной
Н1;
вероятность такого решения 1
— β — мощность критерия.
Результаты
решения относительно нулевой гипотезы
можно проиллюстрировать с помощью
таблицы 8.1.
Таблица 8.1
-
Нулевая
гипотеза Н0Результаты
решения относительнонулевой
гипотезы Н0отклонена
принята
верна
ошибка
первого рода,ее вероятность
Р(Н1/Н0)
= αправильное
решение,его вероятность
Р(Н0/Н0)
= 1 — αне верна
правильное
решение,его вероятность
Р(Н1/Н1)
= 1 — βошибка
второго рода,ее вероятность
Р(Н0/Н1)
= β
Проверка
статистических гипотез осуществляется
с помощью статистического
критерия
(назовем его в общем виде К),
являющего
функцией от результатов наблюдения.
Статистический
критерий — это правило (формула), по
которому определяется мера расхождения
результатов выборочного наблюдения с
высказанной гипотезой Н0.
Статистический
критерий, как и всякая функция от
результатов наблюдения, является
случайной величиной и в предположении
справедливости нулевой гипотезы Н0
подчинена
некоторому хорошо изученному (и
затабулированному) теоретическому
закону распределения с плотностью
распределения f(k).
Выбор
критерия для проверки статистических
гипотез может быть осуществлен на
основании различных принципов. Чаще
всего для этого пользуются принципом
отношения правдоподобия,
который позволяет построить критерий
наиболее мощный среди всех возможных
критериев. Суть его сводится к выбору
такого критерия К
с известной функцией плотности f(k)
при условии справедливости гипотезы
Н0,
чтобы при заданном уровнем значимости
α
можно было бы найти критическую точку
Ккр.
распределения
f(k), которая
разделила бы область значений критерия
на две части: область допустимых значений,
в которой результаты выборочного
наблюдения выглядят наиболее
правдоподобными, и критическую область,
в которой результаты выборочного
наблюдения выглядят менее правдоподобными
в отношении нулевой гипотезы Н0.
Если
такой критерий К
выбран, и известна плотность его
распределения, то задача проверки
статистической гипотезы сводится к
тому, чтобы при заданном уровне значимости
α
рассчитать по выборочным данным
наблюдаемое значение критерия Кнабл.
и определить
является ли оно наиболее или менее
правдоподобным в отношении нулевой
гипотезы Н0.
Проверка
каждого типа статистических гипотез
осуществляется с помощью соответствующего
критерия, являющегося наиболее мощным
в каждом конкретном случае. Например,
проверка гипотезы о виде закона
распределения случайной величины может
быть осуществлена с помощью критерия
согласия Пирсона χ2;
проверка гипотезы о равенстве неизвестных
значений дисперсий двух генеральных
совокупностей — с помощью критерия F
— Фишера; ряд
гипотез о неизвестных значениях
параметров генеральных совокупностей
проверяется с помощью критерия Z
— нормальной распределенной случайной
величины и критерия T—
Стьюдента и т.д.
Значение
критерия, рассчитываемое по специальным
правилам на основании выборочных данных,
называется наблюдаемым
значением критерия
(Кнабл.).
Значения
критерия, разделяющие совокупность
значений критерия на область
допустимых значений
(наиболее правдоподобных в отношении
нулевой гипотезы
Н0)
и критическую
область
(область значений, менее правдоподобных
в отношении таблицам распределения
случайной величины К,
выбранной в качестве критерия, называются
критическими
точками(Ккр.).
Областью
допустимых значений (областью принятия
нулевой гипотезы Н0)
называют совокупность значений критерия
К,
при которых нулевая гипотеза
Н0
не отклоняется.
Критической
областью
называют совокупность значений критерия
К,
при которых нулевая гипотеза Н0
отклоняется
в пользу конкурирующей Н1.
Различают
одностороннюю
(правостороннюю или левостороннюю) и
двустороннюю
критические области.
Если
конкурирующая гипотеза — правосторонняя,
например, Н1:
а > а0,
то и критическая область — правосторонняя
(рис 1). При правосторонней конкурирующей
гипотезе критическая точка (Ккр.
правосторонняя)принимает
положительные значения.
Если
конкурирующая гипотеза — левосторонняя,
например, Н1:
а < а0,
то и критическая область — левосторонняя
(рис 2). При левосторонней конкурирующей
гипотезе критическая точка принимает
отрицательные значения (Ккр.
левосторонняя).
Если
конкурирующая гипотеза — двусторонняя,
например, Н1:
а
а0,
то и критическая область — двусторонняя
(рис 3). При двусторонней конкурирующей
гипотезе определяются две критические
точки (Ккр.
левосторонняя и
Ккр.
правосторонняя).
Область
допустимых Критическая
значений
область
К
0
Ккр.
Рис
8.1. Правосторонняя критическая область.
Критическая
Область допустимых
область
значений
К
-Ккр.
0
Рис 8.2. Левосторонняя
критическая область.
Критическая
Область допустимых
Критическая
область
значений
область
К
-Ккр.
0
Ккр.
Рис
8.3. Двусторонняя критическая область.
Основной
принцип проверки статистических гипотез
состоит в следующем:
—
если наблюдаемое значение критерия
(Кнабл.)
принадлежит критической области, то
нулевая гипотеза Н0
отклоняется в пользу конкурирующей Н1;
—
если наблюдаемое значение критерия
(Кнабл.)
принадлежит области допустимых значений,
то нулевую гипотезу Н0
нельзя отклонить.
Можно
принять решение относительно нулевой
гипотезы Н0
путем
сравнения наблюдаемого (Кнабл.)
и критического
значений критерия (Ккр.).
При правосторонней
конкурирующей гипотезе:
Если
Кнабл.
Ккр.,
то нулевую гипотезу Н0
нельзя отклонить;
если
Кнабл.
> Ккр.,
то нулевая гипотеза Н0
отклоняется в пользу конкурирующей Н1.
При левосторонней
конкурирующей гипотезе:
Если
Кнабл.
— Ккр.,
то нулевую гипотезу Н0
нельзя отклонить;
если
Кнабл.
— Ккр.,
то нулевая гипотеза Н0
отклоняется в пользу конкурирующей Н1.
При двусторонней
конкурирующей гипотезе:
Если
— Ккр.
Кнабл.
Ккр.,
то нулевую гипотезу Н0
нельзя отклонить;
если
Кнабл.
> Ккр.
или Кнабл.
< —
Ккр.,
то нулевая гипотеза Н0
отклоняется в пользу конкурирующей Н1.
Алгоритм
проверки статистических гипотез
сводится к
следующему:
1.
Сформулировать нулевую Н0
и альтернативную Н1
гипотезы;
2.
Выбрать уровень значимости ;
3.
В соответствии с видом выдвигаемой
нулевой гипотезы Н0
выбрать статистический критерий для
ее проверки, т.е. — специально подобранную
случайную величину К,
точное или приближенное распределение
которой заранее известно;
4.
По таблицам распределения случайной
величины К,
выбранной в качестве статистического
критерия, найти его критическое значение
Ккр.
(критическую точку или точки);
5.
На основании выборочных данных по
специальному алгоритму вычислить
наблюдаемое
значение критерия Кнабл.;
6.
По виду конкурирующей гипотезы Н1
определить тип критической области;
7.
Определить, в какую область (допустимых
значений или критическую) попадает
наблюдаемое значение критерия Кнабл.,
и в зависимости от этого — принять решение
относительно нулевой гипотезы Н0.
Следует
заметить, что даже в том случае, если
нулевую гипотезу Н0
нельзя
отклонить, это не означает, что высказанное
предположение о генеральной совокупности
является единственно подходящим: просто
ему не противоречат имеющиеся выборочные
данные, однако таким же свойством наряду
с высказанной могут обладать и другие
гипотезы.
Можно
интерпретировать результаты проверки
нулевой гипотезы следующим образом:
—
если в результате проверки нулевую
гипотезу Н0
нельзя отклонить, то это означает, что
имеющиеся выборочные данные не позволяют
с достаточной уверенностью отклонить
нулевую гипотезу Н0,
вероятность нулевой гипотезы Н0
больше α,
а конкурирующей Н1
— меньше 1 —
α;
—
если в результате проверки нулевая
гипотеза Н0
отклоняется в пользу конкурирующей Н1,
то это означает, что имеющиеся выборочные
данные не позволяют с достаточной
уверенностью принять нулевую гипотезу
Н0,
вероятность нулевой гипотезы Н0
меньше α,
а конкурирующей Н1
— больше 1 —
α.
Пример
8.1 В
семи случаях из десяти фирма-конкурент
компании «А» действовала на рынке
так, как будто ей заранее были известны
решения, принимаемые фирмой «А».
На уровне значимости 0,05 определите,
случайно ли это, или в фирме «А»
работает осведомитель фирмы-конкурента?
Решение.
Для того
чтобы ответить на вопрос данной задачи,
необходимо проверить статистическую
гипотезу о том, совпадает ли данное
эмпирическое распределение числа
действий фирмы-конкурента с равномерным
теоретическим распределением?
Если
ходы, предпринимаемые конкурентом,
выбираются случайно, т.е. в фирме «А»
— нет осведомителя (инсайдера), то число
«правильных» и «неправильных»
ее действий должно распределиться
поровну, т.е. по 5 (10/2). А это и есть
отличительная особенность равномерного
распределения.
Этот
вид статистических гипотез относится
к гипотезам о виде закона распределения
генеральной совокупности.
Сформулируем
нулевую и конкурирующую гипотезы
согласно условию задачи.
Н0:
Х~R(a;
b)
— случайная величина Х подчиняется
равномерному распределению с параметрами
(a;
b)
(в контексте задачи — «в фирме «А»
— нет осведомителя (инсайдера)»;
«распределение числа удачных ходов
фирмы-конкурента — случайно»).
Н1:
Случайная величина Х не подчиняется
равномерному распределению (в контексте
задачи — «в фирме «А» — есть
осведомитель (инсайдер)»; «распределение
числа удачных ходов фирмы-конкурента
— не случайно»).
В
качестве критерия для проверки
статистических гипотез о неизвестном
законе распределения генеральной
совокупности используется случайная
величина 2
. Этот критерий называют критерием
Пирсона.
Его
наблюдаемое значение ()
рассчитывается по формуле:
,
(8.1)
где
m(эмп.)i
— эмпирическая
частота i-той
группы выборки;
m(теор.)i
— теоретическая
частота i-той
группы выборки.
Составим
таблицу распределения эмпирических и
теоретических частот:
-
m(эмп.)i
7
3
m(теор.)i
5
5
Найдем
наблюдаемое значение
:
Критическое
значение ()
следует определять по таблице распределения2
(см. приложение 4) по уровню значимости
и числу степеней свободы k.
По
условию
= 0,05, а число степеней свободы рассчитывается
по формуле:
k
= n
— l
—1,
где
k
— число степеней свободы;
n
— число групп выборки;
l
— число неизвестных параметров
предполагаемой модели, оцениваемых по
данным выборки (если все параметры
предполагаемого закона известны точно,
то l
= 0).
По
условию задачи число групп выборки (n)
равно 2, т.к. могут быть только два варианта
действий фирмы-конкурента: «удачные»
и «неудачные», а число неизвестных
параметров равномерного распределения
(l)
равно 0.
Отсюда,
k
= 2 — 0 — 1 = 1.
Найдем
по
уровню значимости
= 0,05 и числу степеней свободы k=1.
,
следовательно, на данном уровне значимости
нулевую гипотезу нельзя отклонить,
расхождения эмпирических и теоретических
частот — незначимые. Данные наблюдений
согласуются с гипотезой о равномерном
распределении генеральной совокупности.
Это
означает, что для утверждения о том, что
действия фирмы-конкурента на рынке
неслучайны; на уровне значимости
= 0,05 можно утверждать, что в фирме «А»
нет платного осведомителя фирмы-конкурента.
Ответ.
на уровне значимости
= 0,05 можно утверждать, что в фирме «А»
нет платного осведомителя фирмы-конкурента.
Пример
8.2 На
уровне значимости
= 0,025 проверить гипотезу о нормальном
распределении генеральной совокупности,
если известны эмпирические и теоретические
частоты:
-
m(эмп.)i
5
10
20
25
14
3
m(теор.)i
6
14
28
18
8
3
Решение.
Сформулируем
нулевую и конкурирующую гипотезы
согласно условию задачи.
Н0:
Х~N(a;
2)
— случайная величина Х подчиняется
нормальному закону распределения с
параметрами а и 2.
Н1:
Случайная величина Х не подчиняется
нормальному закону распределения с
параметрами а и 2.
В
качестве критерия для проверки нулевой
гипотезы используем критерий Пирсона
2
.
Найдем
наблюдаемое значение ():
Найдем
критическое значение критерия ()
по таблице распределения2
(приложение 4) по уровню значимости
и числу степеней свободы k.
По
условию
= 0,025; число степеней свободы найдем по
формуле:
k
= n
— l
—1,
где
k
— число степеней свободы;
n
— число групп выборки;
l
— число неизвестных параметров
предполагаемой модели, оцениваемых по
данным выборки.
По
условию задачи число групп выборки (n)
равно 6, а число неизвестных параметров
нормального распределения (l)
равно 2.
Отсюда,
k
= 6 — 2 — 1 = 3.
Найдем
по
уровню значимости
= 0,025 и числу степеней свободы k=3.
,
следовательно, на данном уровне значимости
нулевая гипотеза отвергается в пользу
конкурирующей, расхождения эмпирических
и теоретических частот — значимые. Данные
наблюдений не согласуются с гипотезой
о нормальном распределении генеральной
совокупности.
Ответ.
На уровне значимости
= 0,025 данные наблюдений не согласуются
с гипотезой о нормальном распределении
генеральной совокупности.
Пример
8.3 Техническая
норма предусматривает в среднем 40 сек.
на выполнение определенной технологической
операции на конвейере по производству
часов. От работниц, работающих на этой
операции, поступили жалобы, что они в
действительности затрачивают на эту
операцию больше времени. Для проверки
данной жалобы произведены хронометрические
измерения времени выполнения этой
технологической операции у 16 работниц,
занятых на этой операции, и получено
среднее время выполнения операции
=
42 сек. Можно ли по имеющимся хронометрическим
данным на уровне значимости
= 0,01 отклонить гипотезу о том, что среднее
время выполнения этой операции
соответствует норме, если:
а)
исправленное выборочное среднее
квадратическое отклонение s
составило 3,5 сек.;
б)
выборочное среднее квадратическое
отклонение
составило 3,5 сек.?
Решение.
а) Для решения
данной задачи необходимо проверить
гипотезу о том, что неизвестная генеральная
средняя нормальной совокупности точно
равна определенному числу, когда
дисперсия
генеральной совокупности неизвестна
(выборка
мала, т.к. n
= 16, меньше 30).
Сформулируем
нулевую и конкурирующую гипотезы
согласно условию задачи.
Н0:
a
= а0
= 40 — неизвестное математическое ожидание
а
(нормально распределенной генеральной
совокупности с неизвестной дисперсией)
равно гипотетическому предполагаемому
числовому значению а0
(применительно к условию данной задачи
— время выполнения технологической
операции соответствует норме).
Н1:
a
> 40 — неизвестное математическое
ожидание а
(нормально распределенной генеральной
совокупности с неизвестной дисперсией)
больше числовому значению а0
(применительно к условию данной задачи
— время выполнения технологической
операции больше установленной нормы).
Так как конкурирующая
гипотеза — правосторонняя, то и критическая
область — правосторонняя.
В
качестве критерия для сравнения
неизвестного математического ожидание
а
(нормально распределенной генеральной
совокупности с неизвестной дисперсией)
с гипотетическим числовым значением
а0,
используется случайная величина t
— критерий Стьюдента:
Его
наблюдаемое значение (tнабл.)
рассчитывается по формуле:
.
(8.2)
где
—
выборочная средняя;
а0
— числовое значение генеральной средней;
s
— исправленное среднее квадратическое
отклонение;
n
— объем выборки.
Найдем
наблюдаемое значение tнабл.:
Критическое
значение (tкр.)
следует
находить
по таблице
распределения Стьюдента (приложение
5) по уровню значимости
и числу степеней свободы k.
По
условию
= 0,01; число степеней свободы найдем по
формуле:
k
= n
— 1,
где
k
— число степеней свободы;
n
— объем выборки.
k
= 16 — 1 = 15.
Найдем
tкр.
по уровню значимости
= 0,01 (для односторонней критической
области) и числу степеней свободы k
= 15:
Заметим,
что при левосторонней конкурирующей
гипотезе Н1:
a
40 tкр.
следует находить по таблицам распределения
Стьюдента (приложение 5) по уровню
значимости
(для односторонней критической области)
и числу степеней свободы k
= n
— 1 и присваивать ему «минус»;
При
двусторонней конкурирующей гипотезе
Н1:
a
40 tкр.
следует находить по таблицам распределения
Стьюдента (приложение 5) по уровню
значимости
(для двусторонней критической области)
и числу степеней свободы k
= n
— 1).
tнабл.
< tкр,
следовательно, на данном уровне значимости
нет оснований отклонить нулевую гипотезу.
Ответ.
По имеющимся хронометрическим данным
на уровне значимости
= 0,01 нельзя отклонить гипотезу о том,
что среднее время выполнения этой
операции соответствует норме.
Следовательно, жалобы работниц —
необоснованны.
Область
допустимых
Критическая
значений
область
t
0
tнабл.=
2,21 tкр.=
2,6
Рис 8.4.
Наблюдаемое
значение критерия попадает в область
допустимых значений, следовательно,
нет оснований отклонить нулевую гипотезу.
б)
Для решения данной задачи необходимо
проверить гипотезу о том, что неизвестная
генеральная средняя нормальной
совокупности точно равна определенному
числу, когда дисперсия
генеральной совокупности неизвестна.
Алгоритм
решения задачи будет тот же, что и в
первом случае. Однако наблюдаемое
значение tнабл.
будет рассчитывается по формуле:
.
(8.3)
где
—
выборочная средняя;
а0
— числовое значение генеральной средней;
—
выборочное среднее квадратическое
отклонение;
n
— объем выборки.
Найдем
наблюдаемое значение (tнабл.):
Критическое
значение (tкр.)
следует
находить
по таблице
распределения Стьюдента (приложение
5) по уровню значимости
и числу степеней свободы k.
tнабл.
< tкр,
следовательно, на данном уровне значимости
нет оснований отвергнуть нулевую
гипотезу, жалобы работниц — необоснованны.
Ответ.
По имеющимся хронометрическим данным
на уровне значимости
= 0,01 нельзя отклонить гипотезу о том,
что среднее время выполнения этой
операции соответствует норме, жалобы
работниц — необоснованны.
Пример
8.4 Изменим
условие предидущей задачи. Техническая
норма предусматривает в среднем 40 сек.
на выполнение определенной технологической
операции на конвейере по производству
часов. От работниц, работающих на этой
операции, поступили жалобы, что они в
действительности затрачивают на эту
операцию больше времени. Для проверки
данной жалобы произведены хронометрические
измерения времени выполнения этой
технологической операции у 36 работниц,
занятых на этой операции, и получено
среднее время выполнения операции
=
42 сек. Можно ли (предполагая время
выполнения технологической операции
случайной величиной, подчиняющейся
нормальному закону) по имеющимся
хронометрическим данным на уровне
значимости
= 0,01 отклонить гипотезу о том, что среднее
время выполнения этой операции
соответствует норме, если известно, что
среднее квадратическое отклонение
генеральной совокупности
составляет 3,5 сек.?
Решение.
Для решения
данной задачи необходимо проверить
гипотезу о том, что неизвестная генеральная
средняя нормальной совокупности точно
равна числовому значению, когда дисперсия
генеральной совокупности известна
(большая выборка, т.к. n
= 36, больше 30).
Сформулируем
нулевую и конкурирующую гипотезы
согласно условию задачи.
Н0:
a
= а0
= 40 — неизвестная генеральная средняя
нормально распределенной совокупности
с известной дисперсией равна числовому
значению (применительно к условию данной
задачи — время выполнения технологической
операции соответствует норме).
Н1:
a
> 40 — неизвестная генеральная средняя
нормально распределенной совокупности
с известной дисперсией больше числового
значения (применительно к условию данной
задачи — время выполнения технологической
операции больше установленной нормы).
Так как конкурирующая
гипотеза — правосторонняя, то и критическая
область — правосторонняя.
В
качестве критерия для сравнения
выборочной средней с гипотетической
генеральной средней нормальной
совокупности, когда дисперсия генеральной
совокупности известна, используется
случайная величина U:
Его
наблюдаемое значение (uнабл.)
рассчитывается по формуле:
.
(8.4)
где
—
выборочная средняя;
а0
— числовое значение генеральной средней;
—
выборочное среднее квадратическое
отклонение;
n
— объем выборки.
Найдем
наблюдаемое значение (uнабл.):
Так
как конкурирующая гипотеза — правосторонняя,
критическое значение uкр.
следует
находить
по таблице
функции Лапласа (приложение 2) из
равенства:
Ф0(uкр
) = (1 — 2)
/ 2.
По
условию
= 0,01.
Отсюда:
Ф0(uкр
) = (1 — 2·0,01) / 2 = 0,49.
По
таблице функции Лапласа (приложение 2)
найдем при каком uкр.
Ф0(uкр
) = 0,49.
0(2,33)
= 0,49.
Следовательно:
uкр.
= 2,33.
Заметим,
что при левосторонней конкурирующей
гипотезе Н1:
a
40 uкр.
следует находить по таблице функции
Лапласа (приложение 2) из равенства
Ф0(uкр)
= (1 — 2)
/ 2 и присваивать ему «минус».
При
двусторонней конкурирующей гипотезе
Н1:
a
40 uкр.
следует находить по таблице функции
Лапласа (приложение 2) из равенства
Ф0(uкр
) = (1 — )
/ 2).
uнабл.
> uкр,
следовательно, на данном уровне значимости
нулевая гипотеза отвергается в пользу
конкурирующей. По имеющимся хронометрическим
данным с более чем 99%-ной надежностью
можно утверждать, что среднее время
выполнения этой операции превышает
норму. Следовательно, жалобы работниц
— обоснованны.
Область
допустимых Критическая
значений
область
U
0
uкр.=
2,33 uнабл.=
3,43
Рис. 8.5.
Наблюдаемое
значение критерия попадает в критическую
область, следовательно, нулевая гипотеза
отвергается в пользу конкурирующей.
Ответ.
По имеющимся хронометрическим данным
на уровне значимости
= 0,01 можно утверждать, что среднее время
выполнения этой операции превышает
норму, жалобы работниц — обоснованны.
Пример
8.5 Экономический
анализ производительности труда
предприятий отрасли позволил выдвинуть
гипотезу о наличии двух типов предприятий
с различной средней величиной показателя
производительности труда. Выборочное
обследование 42-х предприятий первой
группы дало следующие результаты:
средняя производительность труда
составила 119 деталей. По данным выборочного
обследования 35-и предприятий второй
группы средняя производительность
трудасоставила 107 деталей. Генеральные
дисперсии известны:D(X)
= 126,91 (дет.2);
D(Y)
= 136,1 (дет.2).
Считая, что выборки извлечены из нормально
распределенных генеральных совокупностей
Х и Y,
на уровне значимости 0,05 проверьте,
случайно ли полученное различие средних
показателей производительности труда
в группах или же имеются два типа
предприятий с различной средней величиной
производительности труда.
Решение.
Для решения
данной задачи необходимо сравнить две
средние нормально распределенных
генеральных совокупностей, генеральные
дисперсии которых известны
(большие независимые выборки). В данной
задаче речь идет о больших выборках,
так как nx
= 42 и ny
= 35 больше 30. Выборки — независимые, так
как из контекста задачи видно, что они
извлечены из непересекающихся генеральных
совокупностей.
Сформулируем
нулевую и конкурирующую гипотезы
согласно условию задачи.
Н0:
=
— генеральные средние двух нормально
распределенных совокупностей с известными
дисперсиями равны (применительно к
условию данной задачи — предприятия
двух групп относятся к одному типу
предприятий, — средняя производительность
труда в двух группах — одинакова).
Н1:
— генеральные средние двух нормально
распределенных совокупностей с известными
дисперсиями не равны (применительно к
условию данной задачи — предприятия
двух групп относятся к разному типу
предприятий, — средняя производительность
труда в двух группах — неодинакова).
Выдвигаем
двустороннюю конкурирующую гипотезу,
так как из условия задачи не следует,
что необходимо выяснить больше или
меньше производительность труда в одной
из групп предприятий по сравнению с
другой.
Так
как конкурирующая гипотеза — двусторонняя,
то и критическая область — двусторонняя.
В
качестве критерия для сравнения двух
средних генеральных совокупностей,
дисперсии которых известны (большие
независимые выборки), используется
случайная величина Z.
Его
наблюдаемое значение (zнабл.)
рассчитывается по формуле:

(8.5)
где
— выборочная средняя дляX;
—
выборочная средняя для Y;
D(X)
— генеральная дисперсия для X;
D(Y)
— генеральная дисперсия для Y;
nx
— объем выборки для X;
ny
— объем выборки для Y.
Найдем
наблюдаемое значение (zнабл.):
Так
как конкурирующая гипотеза — двусторонняя,
критическое значение (zкр.)
следует
находить
по таблице
функции Лапласа (приложение 2) из
равенства:
Ф0(zкр
) = (1 — )
/ 2.
По
условию
= 0,05.
Отсюда:
Ф0(zкр
) = (1 — 0,05) / 2 = 0,475.
По
таблице функции Лапласа (приложение 2)
найдем при каком zкр.
Ф0(zкр
) = 0,475.
0(1,96)
= 0,475.
Учитывая, что
конкурирующая гипотеза — двусторонняя,
находим две критические точки:
zкр.(прав.)
= 1,96;
zкр.(лев.)
= — 1,96.
Заметим,
что при левосторонней конкурирующей
гипотезе Н1:
zкр.
следует находить по таблице функции
Лапласа (приложение 2) из равенства
Ф0(zкр
) = (1 — 2)
/ 2 и присваивать ему «минус».
При
правосторонней конкурирующей гипотезе
Н1:
>
zкр.
следует находить по таблице функции
Лапласа (приложение 2) из равенства
Ф0(zкр
) = (1 — 2)
/ 2).
zнабл.
> zкр,
следовательно, на данном уровне значимости
нулевая гипотеза отвергается в пользу
конкурирующей. На уровне значимости
= 0,05 можно утверждать, что полученное
различие средних показателей
производительности труда в группах —
неслучайно, имеются два типа предприятий
с различной средней величиной
производительности труда.
Критическая
Область допустимых
Критическая
область
значений
область
Z
—zкр.
=
-1,96
0
zкр.=
1,96 zнабл.=
4,565
Рис. 8.6.
Наблюдаемое
значение критерия попадает в критическую
область, следовательно, нулевая гипотеза
отвергается в пользу конкурирующей.
Ответ.
На уровне
значимости
= 0,05 можно утверждать, что полученное
различие средних показателей
производительности труда в группах —
неслучайно, имеются два типа предприятий
с различной средней величиной
производительности труда.
Пример
8.6 Предполагается,
что применение нового типа резца сократит
время обработки некоторой детали.
Хронометраж времени обработки 9 деталей,
обработанных старым типом резцов, дал
следующие результаты: среднее время
обработки детали
составило 57 мин., исправленная выборочная
дисперсия=
186,2 (мин.2).
Среднее время обработки 15 деталей,
обработанных новым типом резца,
по данным хронометражных измерений
составило 52 мин., а исправленная выборочная
дисперсия=
166,4 (мин.2).
На уровне значимости
= 0,01 ответьте на вопрос, позволило ли
использование нового типа резцов
сократить время обработки детали?
Решение.
Для решения
данной задачи необходимо сравнить две
средние нормально распределенных
генеральных совокупностей, генеральные
дисперсии которых неизвестны,
но предполагаются одинаковыми (малые
независимые выборки). В данной задаче
речь идет о малых выборках, так как nx
= 9 и ny
= 15 меньше 30. Выборки — независимые, так
как из контекста задачи видно, что они
извлечены из непересекающихся генеральных
совокупностей.
Сформулируем
нулевую и конкурирующую гипотезы
согласно условию задачи.
Н0:
=
— генеральные средние двух нормально
распределенных совокупностей с
неизвестными дисперсиями (но предполагаемыми
одинаковыми) равны (применительно к
условию данной задачи — среднее время,
затрачиваемое на обработку детали
резцами нового и старого типа — одинаково,
т.е. использование нового типа резца не
позволяет снизить время на обработку
детали).
Н1:
>
— генеральная средняя для Х больше, чем
генеральная средняя для Y
(применительно к условию данной задачи
— среднее время, затрачиваемое на
обработку детали резцами старого типа
больше, чем — нового, т.е. использование
нового типа резца позволяет снизить
время на обработку детали).
Так как конкурирующая
гипотеза — правосторонняя, то и критическая
область — правосторонняя.
Приступать
к проверке гипотезы о равенстве
генеральных средних двух нормально
распределенных совокупностей с
неизвестными дисперсиями можно лишь в
том случае, если генеральные дисперсии
равны. В противном случае, данная задача
в теории неразрешима.
Поэтому,
прежде чем проверять эту гипотезу,
проверим гипотезу о равенстве генеральных
дисперсий нормальных совокупностей.
Сформулируем
нулевую и конкурирующую гипотезы
согласно условию задачи.
Н0:
D(X)
= D(Y)
— генеральные дисперсии двух нормально
распределенных совокупностей равны.
Н1:
D(X)
D(Y)
— генеральная дисперсия для X
больше генеральной дисперсии для Y.
Выдвигаем правостороннюю конкурирующую
гипотезу, так как исправленная выборочная
дисперсия для Х значительно больше, чем
исправленная выборочная дисперсия для
Y.
Так как конкурирующая
гипотеза — правосторонняя, то и критическая
область — правосторонняя.
В
качестве критерия для сравнения двух
дисперсий нормальных генеральных
совокупностей используется случайная
величина F
— критерий Фишера-Снедекора.
Его
наблюдаемое значение (fнабл.)
рассчитывается по формуле:

(8.6)
где
— большая (по величине) исправленная
выборочная дисперсия;
—
меньшая (по величине) исправленная
выборочная дисперсия.
Найдем
fнабл.:
.
Критическое
значение (fкр.)
следует
находить
по таблице
распределения Фишера-Снедекора
(приложение 6) по уровню значимости
и числу степеней свободы k1
и k2.
По
условию
= 0,01; число степеней свободы найдем по
формуле:
k1
= n1
— 1; k2
= n2
— 1,
где
k1
— число степеней свободы большей (по
величине) исправленной дисперсии;
k2
— число степеней свободы меньшей (по
величине) исправленной дисперсии;
n1
— объем выборки большей (по величине)
исправленной дисперсии;
n2
— объем выборки меньшей (по величине)
исправленной дисперсии.
Найдем
k1
и k2:
k1
= 10 — 1 = 8;
k2
= 15 — 1 = 14.
Определяем
fкр.
по уровню значимости
= 0,01 и числу степеней свободы k1=9
и k2=14:
fнабл.
< fкр,
следовательно, на данном уровне значимости
нет оснований отвергнуть нулевую
гипотезу о равенстве генеральных
дисперсий нормальных совокупностей.
Следовательно,
можно приступить к проверке гипотезы
о равенстве генеральных средних двух
нормально распределенных совокупностей.
В
качестве критерия для проверки этой
гипотезы, используется случайная
величина t
— критерий Стьюдента:
Его
наблюдаемое значение (tнабл.)
рассчитывается по формуле:
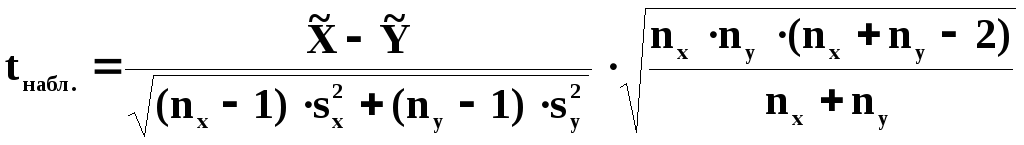
(8.7)
где
— выборочная средняя дляX;
—
выборочная средняя для Y;
D(X)
— генеральная дисперсия для X;
D(Y)
— генеральная дисперсия для Y;
nx
— объем выборки для X;
ny
— объем выборки для Y.
Найдем
tнабл.:
.
Критическое
значение (tкр.)
следует
находить
по таблице
распределения Стьюдента (приложение
5) по уровню значимости
и числу степеней свободы k.
По
условию
= 0,01; число степеней свободы найдем по
формуле:
k
= nx
+ ny
— 2,
где
k
— число степеней свободы;
nx
— объем выборки для X;
ny
— объем выборки для Y.
k
= 9 + 15 — 2 = 22.
Найдем
tкр.
по уровню значимости
= 0,01 (для односторонней критической
области) и числу степеней свободы k
= 22:
Заметим,
что при левосторонней конкурирующей
гипотезе
tкр.
следует находить по таблицам распределения
Стьюдента (приложение 5) по уровню
значимости
(для односторонней критической области)
и числу степеней свободы k
= nx
+ ny
— 2 и присваивать ему «минус»;
При
двусторонней конкурирующей гипотезе
tкр
следует находить по таблицам распределения
Стьюдента (приложение 5) по уровню
значимости
(для двусторонней критической области)
и числу степеней свободы k
= nx
+ ny
— 2).
tнабл.
< tкр,
следовательно, на данном уровне значимости
нет оснований отвергнуть нулевую
гипотезу. По имеющимся хронометрическим
данным на уровне значимости
= 0,01 нельзя отклонить гипотезу о том,
что генеральные средние равны, т.е.
среднее время, затрачиваемое на обработку
детали старым и новым типом резцов
отличается незначимо, расхождения между
средними — случайны, использование
нового типа резцов не позволяет снизить
время обработки детали.
Область
допустимых
Критическая
значений
область
T
0
tнабл.=
0,9 tкр.=
2,51
Рис
8.7.
Наблюдаемое
значение критерия попадает в область
допустимых значений, следовательно,
нулевую гипотезу нельзя отвергнуть.
Ответ.
На уровне значимости
= 0,01 нельзя утверждать, что использование
нового типа резцов позволило сократить
время обработки детали.
Пример
8.7 Партия
изделий принимается в том случае, если
вероятность того, что изделие окажется
соответствующим стандарту, составляет
не менее 0,97. Среди случайно отобранных
200 изделий проверяемой партии оказалось
193 соответствующих стандарту. Можно ли
на уровне значимости
= 0,02 принять партию?
Решение.
Для решения
данной задачи необходимо проверить
гипотезу о том, что неизвестная генеральная
доля точно равна определенному числу.
Сформулируем
нулевую и конкурирующую гипотезы
согласно условию задачи.
Н0:
р = р0
= 0,97 — неизвестная генеральная доля р
равна р0
(применительно к условию данной задачи
— вероятность того, что деталь из
проверяемой партии окажется соответствующей
стандарту, равна 0,97; то есть партию
изделий можно принять).
Н1:
р < 0,97 — неизвестная вероятность р
меньше гипотетической вероятности р0
(применительно к условию данной задачи
— вероятность того, что деталь из
проверяемой партии окажется соответствующей
стандарту, меньше 0,97; то есть партию
изделий нельзя принять).
Так
как конкурирующая гипотеза — левосторонняя,
то и критическая область — левосторонняя.
В
качестве критерия для сравнения
наблюдаемой относительной частоты с
гипотетической вероятностью появления
события используется случайная величина
U:
Его
наблюдаемое значение (uнабл.)
рассчитывается по формуле:

(8.8)
где
m
/ n
— относительная частота (частость)
появления события;
р0
— гипотетическая вероятность появления
события;
q0
— гипотетическая вероятность непоявления
события;
n
— объем выборки.
По
условию: m
= 193; n
= 200; p0
= 0,97; q0
= 1 — p0
= 0,03;
= 0,02.
Найдем
наблюдаемое значение (uнабл.):
Так
как конкурирующая гипотеза — левосторонняя,
то критическое значение (uкр.)
следует
находить
по таблице
функции Лапласа (приложение 2) из
равенства:
Ф0(uкр
) = (1 — 2)
/ 2.
По
условию
= 0,02.
Отсюда:
Ф0(uкр
) = (1 — 2 · 0,02) / 2 = 0,48.
По
таблице функции Лапласа (приложение 2)
найдем при каком uкр.
Ф0(uкр
) = 0,48.
0(2,05)
= 0,48.
Учитывая,
что конкурирующая гипотеза — левосторонняя,
критическому значению необходимо
присвоить знак «минус».
Следовательно:
uкр.
= — 2,05.
Заметим,
что при правосторонней конкурирующей
гипотезе Н1:
р > 0,97 uкр.
следует находить по таблице функции
Лапласа (приложение 2) из равенства
Ф0(uкр
) = (1 — 2)
/ 2.
При
двусторонней конкурирующей гипотезе
Н1:
p
0,97 uкр.
следует находить по таблице функции
Лапласа (приложение 2) из равенства
Ф0(uкр
) = (1 — )
/ 2).
uнабл.
> uкр,
следовательно, на данном уровне значимости
нет оснований отвергнуть нулевую
гипотезу. По имеющимся данным на уровне
значимости
= 0,02 нельзя отклонить гипотезу о том,
что вероятность того, что изделие
окажется соответствующим стандарту,
составляет 0,97. Следовательно, партию
изделий принять можно.
Критическая
Область допустимых
область
значений
U
—uкр.=
— 2,05
uнабл.
= — 0,28 0
Рис.8.8.
Наблюдаемое
значение критерия попадает в область
допустимых значений, следовательно,
нет оснований отклонить нулевую гипотезу.
Ответ.
На уровне значимости
= 0,02 партию изделий принять можно.
Пример
8.8 Два завода
изготавливают однотипные детали. Для
оценки их качества извлечены выборки
из продукции этих заводов и получены
следующие результаты:
-
Завод №1
Завод №2
Объем выборки
n1
n2
Число бракованных
деталейm1
m2
На
уровне значимости
= 0,025 определите, имеется ли существенное
различие в качестве изготавливаемых
этими заводами деталей?
Решение.
Для решения
данной задачи необходимо сравнить две
вероятности биномиальных распределений.
Сформулируем
нулевую и конкурирующую гипотезы
согласно условию задачи.
Н0:
р1
= р2
— вероятности появления события в двух
генеральных совокупностях, имеющих
биномиальное распределение, равны
(применительно к условию данной задачи
— вероятность того, что деталь изготовленная
на первом заводе, окажется бракованной,
равна вероятности того, что деталь
изготовленная на втором заводе, окажется
бракованной).
Н1:
р1
р2 —
вероятности появления события в двух
генеральных совокупностях, имеющих
биномиальное распределение, не равны
(применительно к условию данной задачи
— вероятность того, что деталь изготовленная
на первом заводе, окажется бракованной,
не равна вероятности того, что деталь
изготовленная на втором заводе, окажется
бракованной; заводы изготавливают
детали разного качества). Так как по
условию задачи не требуется проверить,
на каком заводе качество изготавливаемых
деталей выше, выдвигаем двустороннюю
конкурирующую гипотезу.
Так
как конкурирующая гипотеза — двусторонняя,
то и критическая область — двусторонняя.
В
качестве критерия для сравнения двух
вероятностей биномиальных распределений
используется случайная величина U:
Его
наблюдаемое значение uнабл.
рассчитывается по формуле:
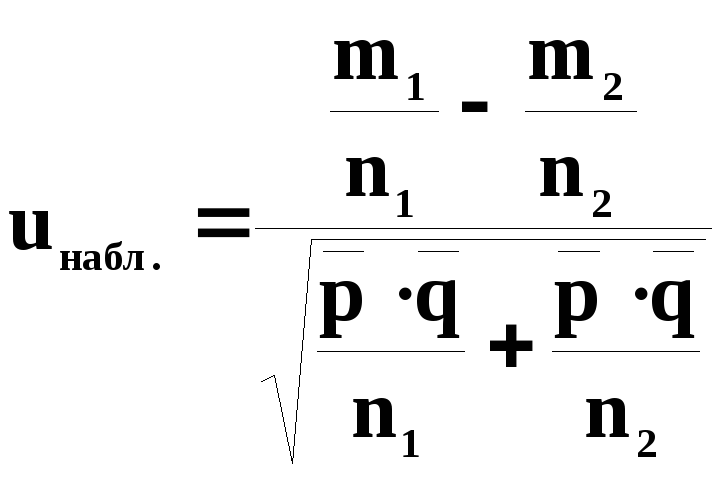
(8.9)
где
m1
/ n1
— относительная частота (частость)
появления события в первой выборке;
m2
/ n2
— относительная
частота (частость) появления события
во второй выборке;
—
средняя частость появления события;
—
средняя частость непоявления события;
;
n1
— объем первой выборки;
n2
— объем второй выборки.
По
условию: m1
= 20; n1
= 200; m2
= 15; n2
= 300;
= 0,025.
Найдем
— среднюю частость появления события:
.
Найдем
— среднюю частость непоявления события:
=
1 — 0,07 = 0,93.
Найдем
uнабл.:
Так
как конкурирующая гипотеза — двусторонняя,
критическое значение (uкр.)
следует
находить
по таблице
функции Лапласа (приложение 2) из
равенства:
Ф0(uкр
) = (1 — )
/ 2.
По
условию
= 0,025.
Отсюда:
Ф0(uкр
) = (1 — 0,025) / 2 = 0,4875.
По
таблице функции Лапласа (приложение 2)
найдем при каком uкр.
Ф0(uкр
) = 0,4875.
0(2,24)
= 0,4875.
Учитывая, что
конкурирующая гипотеза — двусторонняя,
находим две критические точки:
uкр.(прав.)
= 2,24;
uкр.(лев.)
= — 2,24.
Заметим,
что при правосторонней конкурирующей
гипотезе Н1:
р1
> р2 uкр.
следует находить по таблице функции
Лапласа (приложение 2) из равенства
Ф0(uкр
) = (1 — 2)
/ 2.
При
левосторонней конкурирующей гипотезе
Н1:
р1
< р2
uкр.
следует находить по таблице функции
Лапласа (приложение 2) из равенства
Ф0(uкр
) = (1 — 2)
/ 2 и присваивать ему знак «минус»).
-uкр.
< uнабл.
< uкр,
следовательно, на данном уровне значимости
нет оснований отвергнуть нулевую
гипотезу. По имеющимся данным на уровне
значимости
= 0,025 нет оснований отклонить нулевую
гипотезу. Следовательно, заводы
изготавливают детали одинакового
качества.
Критическая
Область допустимых
Критическая
область
значений
область
U
—uкр.
=
-2,24
uнабл.=
2,15 uкр.=
2,24
Рис.8.9.
Наблюдаемое
значение критерия попадает в область
допустимых значений, следовательно,
нет оснований отклонить нулевую гипотезу.
Ответ.
Нет оснований отклонить нулевую гипотезу,
то есть имеющееся различие в качестве
изготавливаемых этими заводами деталей
— случайно, незначимо.
Задачи
к теме 8
1.
Компания, производящая средства для
потери веса, утверждает, что прием
таблеток в сочетании со специальной
диетой позволяет сбросить в среднем в
неделю 800 граммов веса. Случайным образом
отобраны 25 человек, использующих эту
терапию, и обнаружено, что в среднем
еженедельная потеря в весе составила
830 граммов со средним квадратическим
отклонением 250 граммов. Ответьте, правда
ли, что потеря в весе составляет 800
граммов? Уровень значимости
= 0,05.
2.
Компания утверждает, что новый вид
зубной пасты для детей лучше предохраняет
зубы от кариеса, чем зубные пасты,
производимые другими фирмами. Для
проверки эффекта в случайном порядке
была отобрана группа из 500 детей, которые
пользовались новым видом зубной пасты.
Другая группа из 600 детей, также случайно
выбранных, в это же время пользовалась
другими видами зубной пасты. После
окончания эксперимента было выяснено,
что у 30 детей, использующих новую пасту,
и 35 детей из контрольной группы появились
новые признаки кариеса. Имеются ли у
компании достаточные основания для
утверждения о том, что новый сорт зубной
пасты эффективнее предотвращает кариес,
чем другие виды зубной пасты? Принять
уровень значимости
= 0,05.
3.
По оценкам оператора сотовой связи
средняя длительность ежедневных звонков
составляет 24 минуты на одного абонента.
Выборочное обследование 100 абонентов
показало, что среднедневная длительность
звонков составляет 30 минут. На уровне
значимости
= 0,05 оцените статистическую значимость
различий выборочного обследования,
если известно, что стандартное отклонение
длительности звонков в генеральной
совокупности составляет 3 минуты.
4.
По оценкам финансовых аналитиков риск
потери денежных средств для инвесторов
арт — бизнеса составляет 17% в течение
пяти лет. Среди 400 постоянных клиентов
аукционного дома был проведен опрос, в
ходе которого выяснилось, что 65 из них
потеряли средства на вложениях в предметы
искусства за последние пять лет. Можно
ли утверждать, что оценки финансовых
аналитиков совпадают с действительностью
на уровне значимости
= 0,01?
5.
Крупный коммерческий банк заказал
маркетинговое исследование по выявлению
эффекта «премирования» (калькулятор,
набор ручек и др.), как стимула для
открытия счета в банке. Для проверки
случайным образом было отобрано 230
«премированных» посетителей и 200 «не
премированных». В результате выяснилось,
что 80% посетителей, которым предлагалась
премия и 75% посетителей, которым не
предлагалась премия, открыли счет в
банке в течение 6 месяцев. Используя эти
данные, проверьте гипотезу о том, что
доля «премированных» посетителей,
открывших счет в банке, статистически
существенно отличается от удельного
веса «не премированных» посетителей,
открывших счет в банке. Принять уровень
значимости
= 0,01.
6.
По данным российской аналитической
компании средняя розничная цена покупки
мобильного телефона в 2006 году составила
5000 рублей. Выборочная оценка 25 случайно
выбранных телефонов, купленных в одном
из салонов города показала, что средняя
цена купленного телефона составляет
5200 рублей с исправленным средним
квадратическим отклонением 250 рублей.
На уровне значимости
= 0,01 проверьте гипотезу о том, что средняя
розничная цена мобильного телефона,
купленного в 2006 году равна 5200 рублей.
7.
Компания, выпускающая в продажу новый
сорт сока, проводит оценку вкусов
покупателей по случайной выборке из
500 человек, и оказалось, что 310 из них
предпочли новый сорт всем остальным.
Проверьте на уровне значимости
= 0,01 гипотезу о том, что новый сорт сока
предпочитают 65 % потребителей.
8.
Страховая компания изучает вероятность
дорожных происшествий для подростков,
имеющих мотоциклы. За прошедший год
проведена случайная выборка 1000 страховых
полисов подростков-мотоциклистов и
выявлено, что 11 из них попадали в дорожные
происшествия и предъявили компании
требование о компенсации за ущерб. Может
ли аналитик компании отклонить гипотезу,
о том, что менее одного процента всех
подростков-мотоциклистов, имеющих
страховые полисы, попадали в дорожные
происшествия в прошлом году? Принять
уровень значимости
= 0,05.
9.
Новое лекарство, изобретенное для
лечения атеросклероза, должно пройти
экспериментальную проверку для выяснения
возможных побочных эффектов. В ходе
эксперимента лекарство принимали 7000
мужчин и 6000 женщин. Результаты выявили,
что 100 мужчин и 100 женщин испытывали
побочные эффекты при приеме нового
медикамента. Можем ли мы на основании
эксперимента утверждать, что побочные
эффекты нового лекарства у женщин
проявляются в большей степени, чем у
мужчин? Принять уровень значимости
= 0,01.
10.
Руководство фирмы — провайдера полагает,
что проведение рекламной акции приведет
к увеличению числа новых клиентов. За
30 рабочих дней после проведения рекламной
акции число новых клиентов составило
120 чел., тогда как до нее в среднем за
день к услугам Internet
впервые подключились 2 чел. Считая
среднее квадратическое отклонение
равным 3, на уровне значимости 0,01
определите принесла ли успех рекламная
акция?
11.
Владелец фирмы
считает, что добиться более высоких
финансовых результатов ему помешала
неравномерность поставок комплектующих
по месяцам года, несмотря на то, что
поставщик в полном объеме выполнил свои
обязательства за год. Поставщик
утверждает, что поставки были не так уж
неравномерны. Распределение поставок
по месяцам года имеет следующий вид:
|
Месяцы |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Объем единиц |
19 |
23 |
26 |
18 |
20 |
20 |
20 |
20 |
32 |
27 |
35 |
40 |
На
уровне значимости
= 0,05 определите кто прав: владелец фирмы
или поставщик? Изменится ли ответ на
поставленный вопрос, если уровень
значимости принять равным 0,01? Объясните
результаты.
12.
Годовой оборот 8 супермаркетов некоторой
федеральной сети в Ростовской области
составил 16 млн. у.е. с исправленным
средним квадратическим отклонением
0,25 млн. у.е., а годовой оборот 5 супермаркетов
этой же сети в Краснодарском крае
составил 9,5 млн. у.е. с исправленным
средним квадратическим отклонением
0,4 млн. у.е. Можно ли на уровне значимости
= 0,05 утверждать, что в Ростовской области
сеть супермаркетов работает более
эффективно?
13.
Компания по производству безалкогольных
напитков предполагает выпустить на
рынок новую модификацию популярного
напитка, в котором сахар заменен
сукразитом. Компания хотела бы быть
уверенной в том, что не менее 60% её
потребителей предпочтут новую модификацию
напитка. Новый напиток был предложен
на пробу 1500 человек, и 850 из них сказали,
что он вкуснее старого. Может ли компания
отклонить предположение о том, что 60%
всех её потребителей предпочтут новую
модификацию напитка старой? Принять
уровень значимости
= 0,01.
14.
Кондитерская компания решила выяснить,
действительно ли новая упаковка
увеличивает объем продаж дорогих конфет.
Исследования были проведены в 35 магазинах
и супермаркетах, продающих конфеты в
старой упаковке и в 42 магазинах, в которых
продавались конфеты в новой упаковке.
Среднедневной объем продаж конфет в
старой упаковке составил 27,4 коробки с
дисперсией 6,8, а объем продаж конфет в
новой упаковке составил 35,6 с дисперсией
4,2. Можно ли на уровне значимости
= 0,01 утверждать, что новая упаковка
увеличила объем продаж конфет?
15.
Производители нового типа аспирина
утверждают, что он снимает головную
боль за 30 минут. Случайная выборка 100
человек, страдающих головными болями,
показала, что новый тип аспирина снимает
головную боль за 33,6 минуты при среднем
квадратическом отклонении 4,2 минуты.
Проверьте на уровне значимости
= 0,05 справедливость утверждения
производителей аспирина о том, что это
лекарство излечивает головную боль за
30 минут.
16.
Для определения среднего размера
валютного вклада клиентов коммерческого
банка осуществлена случайная выборка
200 вкладчиков банка. В результате были
получены следующие данные:
|
Размер вклада |
До 500 |
500-1000 |
1000-1500 |
1500-2000 |
2000-2500 |
2500-3000 |
Более 3000 |
|
Число вкладов |
8 |
16 |
40 |
72 |
36 |
18 |
10 |
|
Теоретические |
6 |
18 |
36 |
76 |
39 |
18 |
7 |
На основании этих
данных проверить на 5% уровне значимости
гипотезу о нормальном законе распределения
размера валютного вклада.
17.
На двух станках с программным управлением
обрабатываются одинаковые детали. Для
оценки точности станков отобраны 10
деталей с первого станка и 12 деталей со
второго станка. По этим выборкам найдены
исправленные выборочные дисперсии,
равные соответственно 30 кв.ед. и 10 кв.ед.
Можно ли на основании этих данных
утверждать на 5% уровне значимости, что
точность станков существенно различается?
18.
По данным
Росстата средний возраст безработного
по РФ составляет 40 лет. Выборочное
обследование демографических характеристик
безработных в регионе выявило, что
средний возраст безработного составил
38 лет, со стандартным отклонением 4 года.
Выяснить, существенны ли результаты
выборочного исследования, если в выборку
попало 25 человек? Ответ дать на 5% уровне
значимости
19.
Главный бухгалтер большой корпорации
провел обследование по данным прошедшего
года с целью выяснения доли некорректных
счетов. Из 2000 выбранных счетов в 25
оказались некорректные проводки. Для
уменьшения доли ошибок он внедрил новую
систему. Год спустя он решил проверить,
как работает новая система, и выбрал
для проверки в порядке случайного отбора
3000 счетов компании. Среди них оказалось
30 некорректных. Можно ли утверждать,
что новая система позволила уменьшить
долю некорректных проводок в счетах?
Принять уровень значимости
= 0,05.
20.
На предприятии исследовалось изменение
расхода сырья на производство продукции
в условиях применения новой и старой
технологий изготовления изделий.
Дисперсия расхода сырья на изделие по
новой технологии составила 124 кв.ед., а
по старой – 189 кв.ед. Считая, что расход
сырья на изделие по старой и новой
технологии имеет нормальный закон
распределения с одинаковыми дисперсиями,
выяснить, существенны ли различия в
вариации расхода сырья на изделие при
использовании старой и новой технологий.
Ответ дать на 1% уровне значимости,
применив двухстороннюю альтернативную
гипотезу.
Л
И Т Е Р А Т У Р А
1.
Абезгауз Г.Г., Тронь А.П., Коненкин Ю.Н.,
Коровина И.А. Справочник по вероятностным
расчетам. М. 1970.
2. Белинский В.А.,
Калихман И.А., Майстров Л.Я., Митькин А.М.
Высшая математика с основами математической
статистики. -М.: Высшая школа, 1965.
3. Вентцель Е.С.
Теория вероятностей. — М.: Наука, 1964.
4. Ван-дер-Варден
Б.Л. Математическая статистика. М.: Изд-во
иностр. лит-ра, 1960.
5. Вайнберг Дж.,
Шумекер Дж. Статистика. — М.: Статистика,
1979.
6.
Вентцель Е.С., Овчаров Л.А. Теория
вероятностей (задачи и упражнения). —
М.: Наука, 1969.
7.
Венецкий И.Г., Кильдишев Г.С. Теория
вероятностей и математическая статистика.
М., 1975.
8.
Венецкий И.Г., Венецкая В.И. Основные
математико-статистические понятия и
формулы в экономическом анализе. — М.:
Статистика, 1974.
9. Гнеденко Б.Г.
Курс теории вероятностей. — 6-е изд. — М.:
Наука, 1988.
10.
Гнеденко Б.В., Хинчин А.Я. Элементарное
введение в теорию вероятностей. — М.:
Наука, 1970.
11. Гершгорн А.С.
Элементы теории вероятностей и
математической статистики. Львов, 1961 .
12. Гмурман В.Е.
Теория вероятностей и математическая
статистика. М., 1975.
13.
Гмурман В.Е. Руководство к решению задач
по теории вероятностей и математической
статистике. — М.: Высшая школа, 1975, 1979,
1997.
14. Гурский Е.И.
Теория вероятностей с элементами
математической статистики. М.: Высшая
школа, 1971.
15. Дружинин Н.К.
Математическая статистика в экономике.
М., 1971.
16. Емельянов Г.В.,
Скитович В.П. Задачник по теории
вероятностей и математической статистике.
— Л.: Изд-во ЛГУ, 1967.
17. Ивашев-Мусатов
О.С. Теория вероятностей и математическая
статистика. — М.: Наука, 1979.
18. Иванова В.М.,
Калинина В.Н., Нешумова Л.А., Решетникова
И.О. Математическая статистика. — М.:
Высшая школа, 1981.
19.
Коваленко И.Н., Вилиппова А.А. Теория
вероятностей и математическая статистика.
— 2-е изд. — М.: Высшая школа, 1982.
20.
Карасев А.И., Аксютина З.М., Савельева
Т.И. Курс высшей математики для
экономических вузов. ч.II.
Теория вероятностей и математическая
статистика. — М.: Высшая школа, 1982.
21.
Колемаев В.А., Староверов О.В., Турундаевский
В.Б. Теория вероятностей и математическая
статистика. — М.: Высшая школа, 1991.
22.
Колемаев В.А., Калинина В.Н. Теория
вероятностей и математическая статистика.
— М.: ИНФРА-М, 1997.
23. Карасев А.И.
Теория вероятностей и математическая
статистика. М., 1971.
24. Колде Я.К.
Практикум по теории вероятностей и
математической статистике. М.: Высшая
школа, 1991.
25. Козлова З.А.
Методические указания по изучению темы
«Закон больших чисел» — Ростов-на-Дону,
1979.
26.
Кремер Н.Ш. Теория вероятностей и
математическая статистика.-М.:
Юнити-Дана,2000.
27. Мостллер Ф.,
Рурке Р., Томас Дж. Вероятность. — М.:
Изд-во «Мир», 1969.
28.
Маринеску И., Мойнягу Ч., Никулеску Р.,
Ранку Н., Урсяну В. Основы математической
статистики и ее применение. — М.: Статистика,
1970.
29.
Павловский З. Введение в математическую
статистику. — М.: Статистика, 1967.
30. Румшинский Л.З.
Элементы теории вероятностей. М., 1970.
31.
Сборник задач по теории вероятностей,
математической статистике и теории
случайных функций/ под ред. Свешникова
А.А.- М.: Наука, 1965.
32. Феллер. В. Введение
в теорию вероятностей и ее приложения.
— М.: ИЛ, 1952.
33. Чистяков В.П.
Курс теории вероятностей.-3-е изд. — М.:
Наука, 1987.
34. Четыркин Е.И.,
Калихман И.Л. Вероятность и статистика.
— М.: Финансы и статистика, 1982.
35. Mendenhall W., Wackerly
D., Scheaffer R. Mathematical statistics with Applications.- PWS-KENT
Publishing Company, USA, 1990.
36. Canavos G. Applied
Probability and Statistical Methods. — Little, Brown… Company, USA,
1984.
37.
Aczel A. Complete Business Statistics. — 2nd
ed., Richard D. Irwin, INC., 1993.
Приложение
1
Таблица
функции
Ошибки первого рода (англ. type I errors, α errors, false positives) и ошибки второго рода (англ. type II errors, β errors, false negatives) в математической статистике — это ключевые понятия задач проверки статистических гипотез. Тем не менее, данные понятия часто используются и в других областях, когда речь идёт о принятии «бинарного» решения (да/нет) на основе некоего критерия (теста, проверки, измерения), который с некоторой вероятностью может давать ложный результат.
Содержание
- 1 Определения
- 2 О смысле ошибок первого и второго рода
- 3 Вероятности ошибок (уровень значимости и мощность)
- 4 Примеры использования
- 4.1 Радиолокация
- 4.2 Компьютеры
- 4.2.1 Компьютерная безопасность
- 4.2.2 Фильтрация спама
- 4.2.3 Вредоносное программное обеспечение
- 4.2.4 Поиск в компьютерных базах данных
- 4.2.5 Оптическое распознавание текстов (OCR)
- 4.2.6 Досмотр пассажиров и багажа
- 4.2.7 Биометрия
- 4.3 Массовая медицинская диагностика (скрининг)
- 4.4 Медицинское тестирование
- 4.5 Исследования сверхъестественных явлений
- 5 См. также
- 6 Примечания
Определения[править | править исходный текст]
Пусть дана выборка 

где 

,
сопоставляющий каждой реализации выборки 
- Распределение
выборки
соответствует гипотезе
, и она точно определена статистическим критерием, то есть
.
- Распределение
выборки
соответствует гипотезе
, но она неверно отвергнута статистическим критерием, то есть
.
- Распределение
выборки
соответствует гипотезе
, и она точно определена статистическим критерием, то есть
.
- Распределение
выборки
соответствует гипотезе
, но она неверно отвергнута статистическим критерием, то есть
.
Во втором и четвертом случае говорят, что произошла статистическая ошибка, и её называют ошибкой первого и второго рода соответственно. [1][2]
| Верная гипотеза | |||
|---|---|---|---|
 |
 |
||
| Результат применения критерия |
 |
 верно принята верно принята |
 неверно принята неверно принята (Ошибка второго рода) |
 |
 неверно отвергнута неверно отвергнута (Ошибка первого рода) |
 верно отвергнута верно отвергнута |
О смысле ошибок первого и второго рода[править | править исходный текст]
Как видно из вышеприведённого определения, ошибки первого и второго рода являются взаимно-симметричными, то есть если поменять местами гипотезы 



С учётом этого ошибку первого рода часто называют ложной тревогой, ложным срабатыванием или ложноположительным срабатыванием — например, анализ крови показал наличие заболевания, хотя на самом деле человек здоров, или металлодетектор выдал сигнал тревоги, сработав на металлическую пряжку ремня. Слово «положительный» в данном случае не имеет отношения к желательности или нежелательности самого события.
Термин широко используется в медицине. Например, тесты, предназначенные для диагностики заболеваний, иногда дают положительный результат (т.е. показывают наличие заболевания у пациента), когда на самом деле пациент этим заболеванием не страдает. Такой результат называется ложноположительным.
В других областях обычно используют словосочетания со схожим смыслом, например, «ложное срабатывание», «ложная тревога» и т.п. В информационных технологиях часто используют английский термин false positive без перевода.
Из-за возможности ложных срабатываний не удаётся полностью автоматизировать борьбу со многими видами угроз. Как правило, вероятность ложного срабатывания коррелирует с вероятностью пропуска события (ошибки второго рода). То есть: чем более чувствительна система, тем больше опасных событий она детектирует и, следовательно, предотвращает. Но при повышении чувствительности неизбежно вырастает и вероятность ложных срабатываний. Поэтому чересчур чувствительно (параноидально) настроенная система защиты может выродиться в свою противоположность и привести к тому, что побочный вред от неё будет превышать пользу.
Соответственно, ошибку второго рода иногда называют пропуском события или ложноотрицательным срабатыванием — человек болен, но анализ крови этого не показал, или у пассажира имеется холодное оружие, но рамка металлодетектора его не обнаружила (например, из-за того, что чувствительность рамки отрегулирована на обнаружение только очень массивных металлических предметов).
Слово «отрицательный» в данном случае не имеет отношения к желательности или нежелательности самого события.
Термин широко используется в медицине. Например, тесты, предназначенные для диагностики заболеваний, иногда дают отрицательный результат (т.е. показывают отсутствие заболевания у пациента), когда на самом деле пациент страдает этим заболеванием. Такой результат называется ложноотрицательным.
В других областях обычно используют словосочетания со схожим смыслом, например, «пропуск события», и т.п. В информационных технологиях часто используют английский термин false negative без перевода.
Степень чувствительности системы защиты должна представлять собой компромисс между вероятностью ошибок первого и второго рода. Где именно находится точка баланса, зависит от оценки рисков обоих видов ошибок.
Вероятности ошибок (уровень значимости и мощность)[править | править исходный текст]
Вероятность ошибки первого рода при проверке статистических гипотез называют уровнем значимости и обычно обозначают греческой буквой 

Вероятность ошибки второго рода не имеет какого-то особого общепринятого названия, на письме обозначается греческой буквой 


Обе эти характеристики обычно вычисляются с помощью так называемой функции мощности критерия. В частности, вероятность ошибки первого рода есть функция мощности, вычисленная при нулевой гипотезе. Для критериев, основанных на выборке фиксированного объема, вероятность ошибки второго рода есть единица минус функция мощности, вычисленная в предположении, что распределение наблюдений соответствует альтернативной гипотезе. Для последовательных критериев это также верно, если критерий останавливается с вероятностью единица (при данном распределении из альтернативы).
В статистических тестах обычно приходится идти на компромисс между приемлемым уровнем ошибок первого и второго рода. Зачастую для принятия решения используется пороговое значение, которое может варьироваться с целью сделать тест более строгим или, наоборот, более мягким. Этим пороговым значением является уровень значимости, которым задаются при проверке статистических гипотез. Например, в случае металлодетектора повышение чувствительности прибора приведёт к увеличению риска ошибки первого рода (ложная тревога), а понижение чувствительности — к увеличению риска ошибки второго рода (пропуск запрещённого предмета).
Примеры использования[править | править исходный текст]
Радиолокация[править | править исходный текст]
В задаче радиолокационного обнаружения воздушных целей, прежде всего, в системе ПВО ошибки первого и второго рода, с формулировкой «пропуск цели» и «ложная тревога» являются одним из основных элементов как теории, так и практики построения радиолокационных станций. Вероятно, это первый пример последовательного применения статистических методов в целой технической области.
Компьютеры[править | править исходный текст]
Понятия ошибок первого и второго рода широко используются в области компьютеров и программного обеспечения.
Компьютерная безопасность[править | править исходный текст]
Наличие уязвимостей в вычислительных системах приводит к тому, что приходится, с одной стороны, решать задачу сохранения целостности компьютерных данных, а с другой стороны — обеспечивать нормальный доступ легальных пользователей к этим данным (см. компьютерная безопасность). Moulton (1983, с.125) отмечает, что в данном контексте возможны следующие нежелательные ситуации:
- когда авторизованные пользователи классифицируются как нарушители (ошибки первого рода)
- когда нарушители классифицируются как авторизованные пользователи (ошибки второго рода)
Фильтрация спама[править | править исходный текст]
Ошибка первого рода происходит, когда механизм блокировки/фильтрации спама ошибочно классифицирует легитимное email-сообщение как спам и препятствует его нормальной доставке. В то время как большинство «антиспам»-алгоритмов способны блокировать/фильтровать большой процент нежелательных email-сообщений, гораздо более важной задачей является минимизировать число «ложных тревог» (ошибочных блокировок нужных сообщений).
Ошибка второго рода происходит, когда антиспам-система ошибочно пропускает нежелательное сообщение, классифицируя его как «не спам». Низкий уровень таких ошибок является индикатором эффективности антиспам-алгоритма.
Пока не удалось создать антиспамовую систему без корреляции между вероятностью ошибок первого и второго рода. Вероятность пропустить спам у современных систем колеблется в пределах от 1% до 30%. Вероятность ошибочно отвергнуть валидное сообщение — от 0,001 % до 3 %. Выбор системы и её настроек зависит от условий конкретного получателя: для одних получателей риск потерять 1% хорошей почты оценивается как незначительный, для других же потеря даже 0,1% является недопустимой.
Вредоносное программное обеспечение[править | править исходный текст]
Понятие ошибки первого рода также используется, когда антивирусное программное обеспечение ошибочно классифицирует безвредный файл как вирус. Неверное обнаружение может быть вызвано особенностями эвристики, либо неправильной сигнатурой вируса в базе данных. Подобные проблемы могут происходить также и с антитроянскими и антишпионскими программами.
Поиск в компьютерных базах данных[править | править исходный текст]
При поиске в базе данных к ошибкам второго рода можно отнести документы, которые выдаются поиском, несмотря на их иррелевантность (несоответствие) поисковому запросу. Ошибочные срабатывания характерны для полнотекстового поиска, когда поисковый алгоритм анализирует полные тексты всех хранимых в базе данных документов и пытается найти соответствия одному или нескольким терминам, заданным пользователем в запросе.
Большинство ложных срабатываний обусловлены сложностью естественных языков, многозначностью слов: например, «home» может обозначать как «место проживания человека», так и «корневую страницу веб-сайта». Число подобных ошибок может быть снижено за счёт использования специального словаря. Однако это решение относительно дорогое, поскольку подобный словарь и разметка документов (индексирование) должны создаваться экспертом.
Оптическое распознавание текстов (OCR)[править | править исходный текст]
Разнообразные детектирующие алгоритмы нередко выдают ошибки первого рода. Программное обеспечение оптического распознавания текстов может распознать букву «a» в ситуации, когда на самом деле изображены несколько точек, которые используемый алгоритм расценил как «a».
Досмотр пассажиров и багажа[править | править исходный текст]
Ошибки первого рода регулярно встречаются каждый день в компьютерных системах предварительного досмотра пассажиров в аэропортах. Установленные в них детекторы предназначены для предотвращения проноса оружия на борт самолёта; тем не менее, уровень чувствительности в них зачастую настраивается настолько высоко, что много раз за день они срабатывают на незначительные предметы, такие как ключи, пряжки ремней, монеты, мобильные телефоны, гвозди в подошвах обуви и т.п. (см. обнаружение взрывчатых веществ, металлодетекторы).
Таким образом, соотношение числа ложных тревог (идентифицикация благопристойного пассажира как правонарушителя) к числу правильных срабатываний (обнаружение действительно запрещённых предметов) очень велико.
Биометрия[править | править исходный текст]
Ошибки первого и второго рода являются большой проблемой в системах биометрического сканирования, использующих распознавание радужной оболочки или сетчатки глаза, черт лица и т.д. Такие сканирующие системы могут ошибочно отождествить кого-то с другим, «известным» системе человеком, информация о котором хранится в базе данных (к примеру, это может быть лицо, имеющее право входа в систему, или подозреваемый преступник и т.п.). Противоположной ошибкой будет неспособность системы распознать легитимного зарегистрированного пользователя, или опознать подозреваемого в преступлении.[3]
Массовая медицинская диагностика (скрининг)[править | править исходный текст]
В медицинской практике есть существенное различие между скринингом и тестированием:
- Скрининг включает в себя относительно дешёвые тесты, которые проводятся для большой группы людей при отсутствии каких-либо клинических признаков болезни (например, мазок Папаниколау).
- Тестирование подразумевает гораздо более дорогие, зачастую инвазивные, процедуры, которые проводятся только для тех, у кого проявляются клинические признаки заболевания, и которые, в основном, применяются для подтверждения предполагаемого диагноза.
К примеру, в большинстве штатов в США обязательно прохождение новорожденными процедуры скрининга на оксифенилкетонурию и гипотиреоз, помимо других врождённых аномалий. Несмотря на высокий уровень ошибок первого рода, эти процедуры скрининга считаются целесообразными, поскольку они существенно увеличивают вероятность обнаружения этих расстройств на самой ранней стадии.[4]
Простые анализы крови, используемые для скрининга потенциальных доноров на ВИЧ и гепатит, имеют существенный уровень ошибок первого рода; однако в арсенале врачей есть гораздо более точные (и, соответственно, дорогие) тесты для проверки, действительно ли человек инфицирован каким-либо из этих вирусов.
Возможно, наиболее широкие дискуссии вызывают ошибки первого рода в процедурах скрининга на рак груди (маммография). В США уровень ошибок первого рода в маммограммах достигает 15%, это самый высокий показатель в мире.[5] Самый низкий уровень наблюдается в Нидерландах, 1%.[6]
Медицинское тестирование[править | править исходный текст]
Ошибки второго рода являются существенной проблемой в медицинском тестировании. Они дают пациенту и врачу ложное убеждение, что заболевание отсутствует, в то время как в действительности оно есть. Это зачастую приводит к неуместному или неадекватному лечению. Типичным примером является доверие результатам кардиотестирования при выявлении коронарного атеросклероза, хотя известно, что кардиотестирование выявляет только те затруднения кровотока в коронарной артерии, которые вызваны стенозом.
Ошибки второго рода вызывают серьёзные и трудные для понимания проблемы, особенно когда искомое условие является широкораспространённым. Если тест с 10%-ным уровнем ошибок второго рода используется для обследования группы, где вероятность «истинно-положительных» случаев составляет 70%, то многие отрицательные результаты теста окажутся ложными. (См. Теорему Байеса).
Ошибки первого рода также могут вызывать серьёзные и трудные для понимания проблемы. Это происходит, когда искомое условие является редким. Если уровень ошибок первого рода у теста составляет один случай на десять тысяч, но в тестируемой группе образцов (или людей) вероятность «истинно-положительных» случаев составляет в среднем один случай на миллион, то большинство положительных результатов этого теста будут ложными.[7]
Исследования сверхъестественных явлений[править | править исходный текст]
Термин ошибка первого рода был взят на вооружение исследователями в области паранормальных явлений и привидений для описания фотографии или записи или какого-либо другого свидетельства, которое ошибочно трактуется как имеющее паранормальное происхождение — в данном контексте ошибка первого рода — это какое-либо несостоятельное «медиасвидетельство» (изображение, видеозапись, аудиозапись и т.д.), которое имеет обычное объяснение.[8]
См. также[править | править исходный текст]
- Статистическая значимость
- Атака второго рода
- Случаи ложного срабатывания систем предупреждения о ракетном нападении
- Receiver_operating_characteristic
Примечания[править | править исходный текст]
- ↑ ГОСТ Р 50779.10-2000. «Статистические методы. Вероятность и основы статистики. Термины и определения.». Стр. 26
- ↑ Valerie J. Easton, John H. McColl. Statistics Glossary: Hypothesis Testing.
- ↑ Данный пример как раз характеризует случай, когда классификация ошибок будет зависеть от назначения системы: если биометрическое сканирование используется для допуска сотрудников (нулевая гипотеза: «проходящий сканирование человек действительно является сотрудником»), то ошибочное отождествление будет ошибкой второго рода, а «неузнавание» — ошибкой первого рода; если же сканирование используется для опознания преступников (нулевая гипотеза: «проходящий сканирование человек не является преступником»), то ошибочное отождествление будет ошибкой первого рода, а «неузнавание» — ошибкой второго рода.
- ↑ Относительно скрининга новорожденных, последние исследования показали, что количество ошибок первого рода в 12 раз больше, чем количество верных обнаружений (Gambrill, 2006. [1])
- ↑ Одним из последствий такого высокого уровня ошибок первого рода в США является то, что за произвольный 10-летний период половина обследуемых американских женщин получают как минимум одну ложноположительную маммограмму. Такие ошибочные маммограммы обходятся дорого, приводя к ежегодным расходам в 100 миллионов долларов на последующее (ненужное) лечение. Кроме того, они вызывают излишнюю тревогу у женщин. В результате высокого уровня подобных ошибок первого рода в США, примерно у 90-95% женщин, получивших хотя бы раз в жизни положительную маммограмму, на самом деле заболевание отсутствует.
- ↑ Наиболее низкие уровни этих ошибок наблюдаются в северной Европе, где маммографические плёнки считываются дважды, и для дополнительного тестирования устанавливается повышенное пороговое значение (высокий порог снижает статистическую эффективность теста).
- ↑ Вероятность того, что выдаваемый тестом результат окажется ошибкой первого рода, может быть вычислена при помощи Теоремы Байеса.
- ↑ На некоторых сайтах приведены примеры ошибок первого рода, например: Атлантическое Сообщество Паранормальных явлений (The Atlantic Paranormal Society, TAPS) (недоступная ссылка с 13-05-2013 (398 дней)) и Морстаунская организация по Исследованию Привидений (Moorestown Ghost Research) (недоступная ссылка с 13-05-2013 (398 дней) — история).
5.3. Ошибки первого и второго рода
Ошибка первого рода состоит в том, что гипотеза будет отвергнута, хотя на самом деле она правильная. Вероятность
допустить такую ошибку называют уровнем значимости и обозначают буквой («альфа»).
Ошибка второго рода состоит в том, что гипотеза будет принята, но на самом деле она неправильная. Вероятность
совершить эту ошибку обозначают буквой («бета»). Значение
называют мощностью критерия – это вероятность отвержения неправильной
гипотезы.
В практических задачах, как правило, задают уровень значимости, наиболее часто выбирают значения .
И тут возникает мысль, что чем меньше «альфа», тем вроде бы лучше. Но это только вроде: при уменьшении
вероятности —
отвергнуть правильную гипотезу растёт вероятность — принять неверную гипотезу (при прочих равных условиях).
Поэтому перед исследователем стоит задача грамотно подобрать соотношение вероятностей и
, при этом учитывается тяжесть последствий, которые
повлекут за собой та и другая ошибки.
Понятие ошибок 1-го и 2-го рода используется не только в статистике, и для лучшего понимания я приведу пару
нестатистических примеров.
Петя зарегистрировался в почтовике. По умолчанию, – он считается добропорядочным пользователем. Так считает антиспам
фильтр. И вот Петя отправляет письмо. В большинстве случаев всё произойдёт, как должно произойти – нормальное письмо дойдёт до
адресата (правильное принятие нулевой гипотезы), а спамное – попадёт в спам (правильное отвержение). Однако фильтр может
совершить ошибку двух типов:
1) с вероятностью ошибочно отклонить нулевую гипотезу (счесть нормальное письмо
за спам и Петю за спаммера) или
2) с вероятностью ошибочно принять нулевую гипотезу (хотя Петя редиска).
Какая ошибка более «тяжелая»? Петино письмо может быть ОЧЕНЬ важным для адресата, и поэтому при настройке фильтра
целесообразно уменьшить уровень значимости , «пожертвовав» вероятностью
(увеличив её). В результате в основной ящик будут попадать все
«подозрительные» письма, в том числе особо талантливых спаммеров. …Такое и почитать даже можно, ведь сделано с любовью
Существует примеры, где наоборот – более тяжкие последствия влечёт ошибка 2-го рода, и вероятность следует увеличить (в пользу уменьшения
вероятности ). Не хотел я
приводить подобные примеры, и даже отшутился на сайте, но по какой-то мистике через пару месяцев сам столкнулся с непростой
дилеммой. Видимо, таки, надо рассказать:
У человека появилась серьёзная болячка. В медицинской практике её принято лечить (основное «нулевое» решение). Лечение
достаточно эффективно, однако не гарантирует результата и более того опасно (иногда приводит к серьёзному пожизненному
увечью). С другой стороны, если не лечить, то возможны осложнения и долговременные функциональные нарушения.
Вопрос: что делать? И ответ не так-то прост – в разных ситуациях разные люди могут принять разные
решения (упаси вас).
Если болезнь не особо «мешает жить», то более тяжёлые последствия повлечёт ошибка 2-го рода – когда человек соглашается
на лечение, но получает фатальный результат (принимает, как оказалось, неверное «нулевое» решение). Если же…, нет, пожалуй,
достаточно, возвращаемся к теме:


| Оглавление |
Ошибки первого и второго рода
Выдвинутая гипотеза
может быть правильной или неправильной,
поэтому возникает необходимость её
проверки. Поскольку проверку производят
статистическими методами, её называют
статистической. В итоге статистической
проверки гипотезы в двух случаях может
быть принято неправильное решение, т.
е. могут быть допущены ошибки двух родов.
Ошибка первого
рода состоит в том, что будет отвергнута
правильная гипотеза.
Ошибка второго
рода состоит в том, что будет принята
неправильная гипотеза.
Подчеркнём, что
последствия этих ошибок могут оказаться
весьма различными. Например, если
отвергнуто правильное решение «продолжать
строительство жилого дома», то эта
ошибка первого рода повлечёт материальный
ущерб: если же принято неправильное
решение «продолжать строительство»,
несмотря на опасность обвала стройки,
то эта ошибка второго рода может повлечь
гибель людей. Можно привести примеры,
когда ошибка первого рода влечёт более
тяжёлые последствия, чем ошибка второго
рода.
Замечание 1.
Правильное решение может быть принято
также в двух случаях:
-
гипотеза принимается,
причём и в действительности она
правильная; -
гипотеза отвергается,
причём и в действительности она неверна.
Замечание 2.
Вероятность совершить ошибку первого
рода принято обозначать через
;
её называют уровнем значимости. Наиболее
часто уровень значимости принимают
равным 0,05 или 0,01. Если, например, принят
уровень значимости, равный 0,05, то это
означает, что в пяти случаях из ста
имеется риск допустить ошибку первого
рода (отвергнуть правильную гипотезу).
Статистический
критерий проверки нулевой гипотезы.
Наблюдаемое значение критерия
Для проверки
нулевой гипотезы используют специально
подобранную случайную величину, точное
или приближённое распределение которой
известно. Обозначим эту величину в целях
общности через
.
Статистическим
критерием
(или просто критерием) называют случайную
величину
,
которая служит для проверки нулевой
гипотезы.
Например, если
проверяют гипотезу о равенстве дисперсий
двух нормальных генеральных совокупностей,
то в качестве критерия
принимают отношение исправленных
выборочных дисперсий:
Эта величина
случайная, потому что в различных опытах
дисперсии принимают различные, наперёд
неизвестные значения, и распределена
по закону Фишера – Снедекора.
Для проверки
гипотезы по данным выборок вычисляют
частные значения входящих в критерий
величин и таким образом получают частное
(наблюдаемое) значение критерия.
Наблюдаемым
значением
называют значение критерия, вычисленное
по выборкам. Например, если по двум
выборкам найдены исправленные выборочные
дисперсиии
,
то наблюдаемое значение критерия
Критическая
область. Область принятия гипотезы.
Критические точки
После выбора
определённого критерия множество всех
его возможных значений разбивают на
два непересекающихся подмножества:
одно из них содержит значения критерия,
при которых нулевая гипотеза отвергается,
а другая – при которых она принимается.
Критической
областью называют совокупность значений
критерия, при которых нулевую гипотезу
отвергают.
Областью принятия
гипотезы (областью допустимых значений)
называют совокупность значений критерия,
при которых гипотезу принимают.
Основной принцип
проверки статистических гипотез можно
сформулировать так: если наблюдаемое
значение критерия принадлежит критической
области – гипотезу отвергают, если
наблюдаемое значение критерия принадлежит
области принятия гипотезы – гипотезу
принимают.
Поскольку критерий
— одномерная случайная величина, все её
возможные значения принадлежат некоторому
интервалу. Поэтому критическая область
и область принятия гипотезы также
являются интервалами и, следовательно,
существуют точки, которые их разделяют.
Критическими
точками (границами)
называют точки, отделяющие критическую
область от области принятия гипотезы.
Различают
одностороннюю (правостороннюю или
левостороннюю) и двустороннюю критические
области.
Правосторонней
называют критическую область, определяемую
неравенством
>
,
где— положительное число.
Левосторонней
называют критическую область, определяемую
неравенством
<
,
где— отрицательное число.
Односторонней
называют правостороннюю или левостороннюю
критическую область.
Двусторонней
называют критическую область, определяемую
неравенствами
где
.
В частности, если
критические точки симметричны относительно
нуля, двусторонняя критическая область
определяется неравенствами ( в
предположении, что
>0):
,
или равносильным неравенством
.
Отыскание
правосторонней критической области
Как найти критическую
область? Обоснованный ответ на этот
вопрос требует привлечения довольно
сложной теории. Ограничимся её элементами.
Для определённости начнём с нахождения
правосторонней критической области,
которая определяется неравенством
>
,
где>0.
Видим, что для отыскания правосторонней
критической области достаточно найти
критическую точку. Следовательно,
возникает новый вопрос: как её найти?
Для её нахождения
задаются достаточной малой вероятностью
– уровнем значимости
.
Затем ищут критическую точку,
исходя из требования, чтобы при условии
справедливости нулевой гипотезы
вероятность того, критерийпримет значение, большее
,
была равна принятому уровню значимости:
Р(>
)=
.
Для каждого критерия
имеются соответствующие таблицы, по
которым и находят критическую точку,
удовлетворяющую этому требованию.
Замечание 1.
Когда
критическая точка уже найдена, вычисляют
по данным выборок наблюдаемое значение
критерия и, если окажется, что
>
,
то нулевую гипотезу отвергают; если же<
,
то нет оснований, чтобы отвергнуть
нулевую гипотезу.
Пояснение. Почему
правосторонняя критическая область
была определена, исходя из требования,
чтобы при справедливости нулевой
гипотезы выполнялось соотношение
Р(>
)=
?
(*)
Поскольку вероятность
события
>
мала (
— малая вероятность), такое событие при
справедливости нулевой гипотезы, в силу
принципа практической невозможности
маловероятных событий, в единичном
испытании не должно наступить. Если всё
же оно произошло, т.е. наблюдаемое
значение критерия оказалось больше,
то это можно объяснить тем, что нулевая
гипотеза ложна и, следовательно, должна
быть отвергнута. Таким образом, требование
(*) определяет такие значения критерия,
при которых нулевая гипотеза отвергается,
а они и составляют правостороннюю
критическую область.
Замечание 2.
Наблюдаемое значение критерия может
оказаться большим
не потому, что нулевая гипотеза ложна,
а по другим причинам (малый объём выборки,
недостатки методики эксперимента и
др.). В этом случае, отвергнув правильную
нулевую гипотезу, совершают ошибку
первого рода. Вероятность этой ошибки
равна уровню значимости.
Итак, пользуясь требованием (*), мы с
вероятностьюрискуем совершить ошибку первого рода.
Замечание 3. Пусть
нулевая гипотеза принята; ошибочно
думать, что тем самым она доказана.
Действительно, известно, что один пример,
подтверждающий справедливость некоторого
общего утверждения, ещё не доказывает
его. Поэтому более правильно говорить,
«данные наблюдений согласуются с нулевой
гипотезой и, следовательно, не дают
оснований её отвергнуть».
На практике для
большей уверенности принятия гипотезы
её проверяют другими способами или
повторяют эксперимент, увеличив объём
выборки.
Отвергают гипотезу
более категорично, чем принимают.
Действительно, известно, что достаточно
привести один пример, противоречащий
некоторому общему утверждению, чтобы
это утверждение отвергнуть. Если
оказалось, что наблюдаемое значение
критерия принадлежит критической
области, то этот факт и служит примером,
противоречащим нулевой гипотезе, что
позволяет её отклонить.
Отыскание
левосторонней и двусторонней критических
областей***
Отыскание
левосторонней и двусторонней критических
областей сводится (так же, как и для
правосторонней) к нахождению соответствующих
критических точек. Левосторонняя
критическая область определяется
неравенством
<
(
<0).
Критическую точку находят, исходя из
требования, чтобы при справедливости
нулевой гипотезы вероятность того, что
критерий примет значение, меньшее,
была равна принятому уровню значимости:
Р(<
)=
.
Двусторонняя
критическая область определяется
неравенствами
Критические
точки находят, исходя из требования,
чтобы при справедливости нулевой
гипотезы сумма вероятностей того, что
критерий примет значение, меньшееили большее
,
была равна принятому уровню значимости:
.
(*)
Ясно, что критические
точки могут быть выбраны бесчисленным
множеством способов. Если же распределение
критерия симметрично относительно нуля
и имеются основания (например, для
увеличения мощности) выбрать симметричные
относительно нуля точки (-
)и
(
>0),
то
Учитывая (*), получим
.
Это соотношение
и служит для отыскания критических
точек двусторонней критической области.
Критические точки находят по соответствующим
таблицам.
Дополнительные
сведения о выборе критической области.
Мощность критерия
Мы строили
критическую область, исходя из требования,
чтобы вероятность попадания в неё
критерия была равна
при условии, что нулевая гипотеза
справедлива. Оказывается целесообразным
ввести в рассмотрение вероятность
попадания критерия в критическую область
при условии, что нулевая гипотеза неверна
и, следовательно, справедлива конкурирующая.
Мощностью критерия
называют вероятность попадания критерия
в критическую область при условии, что
справедлива конкурирующая гипотеза.
Другими словами, мощность критерия есть
вероятность того, что нулевая гипотеза
будет отвергнута, если верна конкурирующая
гипотеза.
Пусть для проверки
гипотезы принят определённый уровень
значимости и выборка имеет фиксированный
объём. Остаётся произвол в выборе
критической области. Покажем, что её
целесообразно построить так, чтобы
мощность критерия была максимальной.
Предварительно убедимся, что если
вероятность ошибки второго рода (принять
неправильную гипотезу) равна
,
то мощность равна 1-.
Действительно, если— вероятность ошибки второго рода, т.е.
события «принята нулевая гипотеза,
причём справедливо конкурирующая», то
мощность критерия равна 1 —.
Пусть мощность 1
—
возрастает; следовательно, уменьшается
вероятностьсовершить ошибку второго рода. Таким
образом, чем мощность больше, тем
вероятность ошибки второго рода меньше.
Итак, если уровень
значимости уже выбран, то критическую
область следует строить так, чтобы
мощность критерия была максимальной.
Выполнение этого требования должно
обеспечить минимальную ошибку второго
рода, что, конечно, желательно.
Замечание 1.
Поскольку вероятность события «ошибка
второго рода допущена» равна
,
то вероятность противоположного события
«ошибка второго рода не допущена» равна
1 —,
т.е. мощности критерия. Отсюда следует,
что мощность критерия есть вероятность
того, что не будет допущена ошибка
второго рода.
Замечание 2. Ясно,
что чем меньше вероятности ошибок
первого и второго рода, тем критическая
область «лучше». Однако при заданном
объёме выборки уменьшить одновременно
и
невозможно; если уменьшить
,
тобудет возрастать. Например, если принять
=0,
то будут приниматься все гипотезы, в
том числе и неправильные, т.е. возрастает
вероятностьошибки второго рода.
Как же выбрать
наиболее целесообразно? Ответ на этот
вопрос зависит от «тяжести последствий»
ошибок для каждой конкретной задачи.
Например, если ошибка первого рода
повлечёт большие потери, а второго рода
– малые, то следует принять возможно
меньшее.
Если
уже выбрано, то, пользуясь теоремой Ю.
Неймана и Э.Пирсона, можно построить
критическую область, для которойбудет минимальным и, следовательно,
мощность критерия максимальной.
Замечание 3.
Единственный способ одновременного
уменьшения вероятностей ошибок первого
и второго рода состоит в увеличении
объёма выборок.
Соседние файлы в папке Лекции 2 семестр
- #
- #
- #
- #
Ошибки первого рода (англ. type I errors, α errors, false positives) и ошибки второго рода (англ. type II errors, β errors, false negatives) в математической статистике — это ключевые понятия задач проверки статистических гипотез. Тем не менее, данные понятия часто используются и в других областях, когда речь идёт о принятии «бинарного» решения (да/нет) на основе некоего критерия (теста, проверки, измерения), который с некоторой вероятностью может давать ложный результат.
Содержание
- 1 Определения
- 2 О смысле ошибок первого и второго рода
- 3 Вероятности ошибок (уровень значимости и мощность)
- 4 Примеры использования
- 4.1 Радиолокация
- 4.2 Компьютеры
- 4.2.1 Компьютерная безопасность
- 4.2.2 Фильтрация спама
- 4.2.3 Вредоносное программное обеспечение
- 4.2.4 Поиск в компьютерных базах данных
- 4.2.5 Оптическое распознавание текстов (OCR)
- 4.2.6 Досмотр пассажиров и багажа
- 4.2.7 Биометрия
- 4.3 Массовая медицинская диагностика (скрининг)
- 4.4 Медицинское тестирование
- 4.5 Исследования сверхъестественных явлений
- 5 См. также
- 6 Примечания
Определения
Пусть дана выборка 

где 

,
сопоставляющий каждой реализации выборки 
- Распределение
выборки
соответствует гипотезе
, и она точно определена статистическим критерием, то есть
.
- Распределение
выборки
соответствует гипотезе
, но она неверно отвергнута статистическим критерием, то есть
.
- Распределение
выборки
соответствует гипотезе
, и она точно определена статистическим критерием, то есть
.
- Распределение
выборки
соответствует гипотезе
, но она неверно отвергнута статистическим критерием, то есть
.
Во втором и четвертом случае говорят, что произошла статистическая ошибка, и её называют ошибкой первого и второго рода соответственно. [1][2]
| Верная гипотеза | |||
|---|---|---|---|
 |
 |
||
| Результат применения критерия |
 |
 верно принята верно принята |
 неверно принята неверно принята (Ошибка второго рода) |
 |
 неверно отвергнута неверно отвергнута (Ошибка первого рода) |
 верно отвергнута верно отвергнута |
О смысле ошибок первого и второго рода
Как видно из вышеприведённого определения, ошибки первого и второго рода являются взаимно-симметричными, то есть если поменять местами гипотезы 



С учётом этого ошибку первого рода часто называют ложной тревогой, ложным срабатыванием или ложноположительным срабатыванием — например, анализ крови показал наличие заболевания, хотя на самом деле человек здоров, или металлодетектор выдал сигнал тревоги, сработав на металлическую пряжку ремня. Слово «положительный» в данном случае не имеет отношения к желательности или нежелательности самого события.
Термин широко используется в медицине. Например, тесты, предназначенные для диагностики заболеваний, иногда дают положительный результат (т.е. показывают наличие заболевания у пациента), когда на самом деле пациент этим заболеванием не страдает. Такой результат называется ложноположительным.
В других областях обычно используют словосочетания со схожим смыслом, например, «ложное срабатывание», «ложная тревога» и т.п. В информационных технологиях часто используют английский термин false positive без перевода.
Из-за возможности ложных срабатываний не удаётся полностью автоматизировать борьбу со многими видами угроз. Как правило, вероятность ложного срабатывания коррелирует с вероятностью пропуска события (ошибки второго рода). То есть: чем более чувствительна система, тем больше опасных событий она детектирует и, следовательно, предотвращает. Но при повышении чувствительности неизбежно вырастает и вероятность ложных срабатываний. Поэтому чересчур чувствительно (параноидально) настроенная система защиты может выродиться в свою противоположность и привести к тому, что побочный вред от неё будет превышать пользу.
Соответственно, ошибку второго рода иногда называют пропуском события или ложноотрицательным срабатыванием — человек болен, но анализ крови этого не показал, или у пассажира имеется холодное оружие, но рамка металлодетектора его не обнаружила (например, из-за того, что чувствительность рамки отрегулирована на обнаружение только очень массивных металлических предметов).
Слово «отрицательный» в данном случае не имеет отношения к желательности или нежелательности самого события.
Термин широко используется в медицине. Например, тесты, предназначенные для диагностики заболеваний, иногда дают отрицательный результат (т.е. показывают отсутствие заболевания у пациента), когда на самом деле пациент страдает этим заболеванием. Такой результат называется ложноотрицательным.
В других областях обычно используют словосочетания со схожим смыслом, например, «пропуск события», и т.п. В информационных технологиях часто используют английский термин false negative без перевода.
Степень чувствительности системы защиты должна представлять собой компромисс между вероятностью ошибок первого и второго рода. Где именно находится точка баланса, зависит от оценки рисков обоих видов ошибок.
Вероятности ошибок (уровень значимости и мощность)
Вероятность ошибки первого рода при проверке статистических гипотез называют уровнем значимости и обычно обозначают греческой буквой 

Вероятность ошибки второго рода не имеет какого-то особого общепринятого названия, на письме обозначается греческой буквой 


Обе эти характеристики обычно вычисляются с помощью так называемой функции мощности критерия. В частности, вероятность ошибки первого рода есть функция мощности, вычисленная при нулевой гипотезе. Для критериев, основанных на выборке фиксированного объема, вероятность ошибки второго рода есть единица минус функция мощности, вычисленная в предположении, что распределение наблюдений соответствует альтернативной гипотезе. Для последовательных критериев это также верно, если критерий останавливается с вероятностью единица (при данном распределении из альтернативы).
В статистических тестах обычно приходится идти на компромисс между приемлемым уровнем ошибок первого и второго рода. Зачастую для принятия решения используется пороговое значение, которое может варьироваться с целью сделать тест более строгим или, наоборот, более мягким. Этим пороговым значением является уровень значимости, которым задаются при проверке статистических гипотез. Например, в случае металлодетектора повышение чувствительности прибора приведёт к увеличению риска ошибки первого рода (ложная тревога), а понижение чувствительности — к увеличению риска ошибки второго рода (пропуск запрещённого предмета).
Примеры использования
Радиолокация
В задаче радиолокационного обнаружения воздушных целей, прежде всего, в системе ПВО ошибки первого и второго рода, с формулировкой «ложная тревога» и «пропуск цели» являются одним из основных элементов как теории, так и практики построения радиолокационных станций. Вероятно, это первый пример последовательного применения статистических методов в целой технической области.
Компьютеры
Понятия ошибок первого и второго рода широко используются в области компьютеров и программного обеспечения.
Компьютерная безопасность
Наличие уязвимостей в вычислительных системах приводит к тому, что приходится, с одной стороны, решать задачу сохранения целостности компьютерных данных, а с другой стороны — обеспечивать нормальный доступ легальных пользователей к этим данным (см. компьютерная безопасность). Moulton (1983, с.125) отмечает, что в данном контексте возможны следующие нежелательные ситуации:
- когда нарушители классифицируются как авторизованные пользователи (ошибки первого рода)
- когда авторизованные пользователи классифицируются как нарушители (ошибки второго рода)
Фильтрация спама
Ошибка первого рода происходит, когда механизм блокировки/фильтрации спама ошибочно классифицирует легитимное email-сообщение как спам и препятствует его нормальной доставке. В то время как большинство «антиспам»-алгоритмов способны блокировать/фильтровать большой процент нежелательных email-сообщений, гораздо более важной задачей является минимизировать число «ложных тревог» (ошибочных блокировок нужных сообщений).
Ошибка второго рода происходит, когда антиспам-система ошибочно пропускает нежелательное сообщение, классифицируя его как «не спам». Низкий уровень таких ошибок является индикатором эффективности антиспам-алгоритма.
Пока не удалось создать антиспамовую систему без корреляции между вероятностью ошибок первого и второго рода. Вероятность пропустить спам у современных систем колеблется в пределах от 1% до 30%. Вероятность ошибочно отвергнуть валидное сообщение — от 0,001 % до 3 %. Выбор системы и её настроек зависит от условий конкретного получателя: для одних получателей риск потерять 1% хорошей почты оценивается как незначительный, для других же потеря даже 0,1% является недопустимой.
Вредоносное программное обеспечение
Понятие ошибки первого рода также используется, когда антивирусное программное обеспечение ошибочно классифицирует безвредный файл как вирус. Неверное обнаружение может быть вызвано особенностями эвристики, либо неправильной сигнатурой вируса в базе данных. Подобные проблемы могут происходить также и с антитроянскими и антишпионскими программами.
Поиск в компьютерных базах данных
При поиске в базе данных к ошибкам первого рода можно отнести документы, которые выдаются поиском, несмотря на их иррелевантность (несоответствие) поисковому запросу. Ошибочные срабатывания характерны для полнотекстового поиска, когда поисковый алгоритм анализирует полные тексты всех хранимых в базе данных документов и пытается найти соответствия одному или нескольким терминам, заданным пользователем в запросе.
Большинство ложных срабатываний обусловлены сложностью естественных языков, многозначностью слов: например, «home» может обозначать как «место проживания человека», так и «корневую страницу веб-сайта». Число подобных ошибок может быть снижено за счёт использования специального словаря. Однако это решение относительно дорогое, поскольку подобный словарь и разметка документов (индексирование) должны создаваться экспертом.
Оптическое распознавание текстов (OCR)
Разнообразные детектирующие алгоритмы нередко выдают ошибки первого рода. Программное обеспечение оптического распознавания текстов может распознать букву «a» в ситуации, когда на самом деле изображены несколько точек, которые используемый алгоритм расценил как «a».
Досмотр пассажиров и багажа
Ошибки первого рода регулярно встречаются каждый день в компьютерных системах предварительного досмотра пассажиров в аэропортах. Установленные в них детекторы предназначены для предотвращения проноса оружия на борт самолёта; тем не менее, уровень чувствительности в них зачастую настраивается настолько высоко, что много раз за день они срабатывают на незначительные предметы, такие как ключи, пряжки ремней, монеты, мобильные телефоны, гвозди в подошвах обуви и т.п. (см. обнаружение взрывчатых веществ, металлодетекторы).
Таким образом, соотношение числа ложных тревог (идентифицикация благопристойного пассажира как правонарушителя) к числу правильных срабатываний (обнаружение действительно запрещённых предметов) очень велико.
Биометрия
Ошибки первого и второго рода являются большой проблемой в системах биометрического сканирования, использующих распознавание радужной оболочки или сетчатки глаза, черт лица и т.д. Такие сканирующие системы могут ошибочно отождествить кого-то с другим, «известным» системе человеком, информация о котором хранится в базе данных (к примеру, это может быть лицо, имеющее право входа в систему, или подозреваемый преступник и т.п.). Противоположной ошибкой будет неспособность системы распознать легитимного зарегистрированного пользователя, или опознать подозреваемого в преступлении.[3]
Массовая медицинская диагностика (скрининг)
В медицинской практике есть существенное различие между скринингом и тестированием:
- Скрининг включает в себя относительно дешёвые тесты, которые проводятся для большой группы людей при отсутствии каких-либо клинических признаков болезни (например, мазок Папаниколау).
- Тестирование подразумевает гораздо более дорогие, зачастую инвазивные, процедуры, которые проводятся только для тех, у кого проявляются клинические признаки заболевания, и которые, в основном, применяются для подтверждения предполагаемого диагноза.
К примеру, в большинстве штатов в США обязательно прохождение новорожденными процедуры скрининга на оксифенилкетонурию и гипотиреоз, помимо других врождённых аномалий. Несмотря на высокий уровень ошибок первого рода, эти процедуры скрининга считаются целесообразными, поскольку они существенно увеличивают вероятность обнаружения этих расстройств на самой ранней стадии.[4]
Простые анализы крови, используемые для скрининга потенциальных доноров на ВИЧ и гепатит, имеют существенный уровень ошибок первого рода; однако в арсенале врачей есть гораздо более точные (и, соответственно, дорогие) тесты для проверки, действительно ли человек инфицирован каким-либо из этих вирусов.
Возможно, наиболее широкие дискуссии вызывают ошибки первого рода в процедурах скрининга на рак груди (маммография). В США уровень ошибок первого рода в маммограммах достигает 15%, это самый высокий показатель в мире.[5] Самый низкий уровень наблюдается в Нидерландах, 1%.[6]
Медицинское тестирование
Ошибки второго рода являются существенной проблемой в медицинском тестировании. Они дают пациенту и врачу ложное убеждение, что заболевание отсутствует, в то время как в действительности оно есть. Это зачастую приводит к неуместному или неадекватному лечению. Типичным примером является доверие результатам кардиотестирования при выявлении коронарного атеросклероза, хотя известно, что кардиотестирование выявляет только те затруднения кровотока в коронарной артерии, которые вызваны стенозом.
Ошибки второго рода вызывают серьёзные и трудные для понимания проблемы, особенно когда искомое условие является широкораспространённым. Если тест с 10%-ным уровнем ошибок второго рода используется для обследования группы, где вероятность «истинно-положительных» случаев составляет 70%, то многие отрицательные результаты теста окажутся ложными. (См. Теорему Байеса).
Ошибки первого рода также могут вызывать серьёзные и трудные для понимания проблемы. Это происходит, когда искомое условие является редким. Если уровень ошибок первого рода у теста составляет один случай на десять тысяч, но в тестируемой группе образцов (или людей) вероятность «истинно-положительных» случаев составляет в среднем один случай на миллион, то большинство положительных результатов этого теста будут ложными.[7]
Исследования сверхъестественных явлений
Термин ошибка первого рода был взят на вооружение исследователями в области паранормальных явлений и привидений для описания фотографии или записи или какого-либо другого свидетельства, которое ошибочно трактуется как имеющее паранормальное происхождение — в данном контексте ошибка первого рода — это какое-либо несостоятельное «медиасвидетельство» (изображение, видеозапись, аудиозапись и т.д.), которое имеет обычное объяснение.[8]
См. также
- Статистическая значимость
- Ложноположительный
- Атака второго рода
- Случаи ложного срабатывания систем предупреждения о ракетном нападении
- Receiver_operating_characteristic
Примечания
- ↑ ГОСТ Р 50779.10-2000. «Статистические методы. Вероятность и основы статистики. Термины и определения.». Стр. 26
- ↑ Valerie J. Easton, John H. McColl. Statistics Glossary: Hypothesis Testing.
- ↑ Данный пример как раз характеризует случай, когда классификация ошибок будет зависеть от назначения системы: если биометрическое сканирование используется для допуска сотрудников (нулевая гипотеза: «проходящий сканирование человек действительно является сотрудником»), то ошибочное отождествление будет ошибкой второго рода, а «неузнавание» — ошибкой первого рода; если же сканирование используется для опознания преступников (нулевая гипотеза: «проходящий сканирование человек не является преступником»), то ошибочное отождествление будет ошибкой первого рода, а «неузнавание» — ошибкой второго рода.
- ↑ Относительно скрининга новорожденных, последние исследования показали, что количество ошибок первого рода в 12 раз больше, чем количество верных обнаружений (Gambrill, 2006. [1])
- ↑ Одним из последствий такого высокого уровня ошибок первого рода в США является то, что за произвольный 10-летний период половина обследуемых американских женщин получают как минимум одну ложноположительную маммограмму. Такие ошибочные маммограммы обходятся дорого, приводя к ежегодным расходам в 100 миллионов долларов на последующее (ненужное) лечение. Кроме того, они вызывают излишнюю тревогу у женщин. В результате высокого уровня подобных ошибок первого рода в США, примерно у 90-95% женщин, получивших хотя бы раз в жизни положительную маммограмму, на самом деле заболевание отсутствует.
- ↑ Наиболее низкие уровни этих ошибок наблюдаются в северной Европе, где маммографические плёнки считываются дважды, и для дополнительного тестирования устанавливается повышенное пороговое значение (высокий порог снижает статистическую эффективность теста).
- ↑ Вероятность того, что выдаваемый тестом результат окажется ошибкой первого рода, может быть вычислена при помощи Теоремы Байеса.
- ↑ На некоторых сайтах приведены примеры ошибок первого рода, например: Атлантическое Сообщество Паранормальных явлений (The Atlantic Paranormal Society, TAPS) и Морстаунская организация по Исследованию Привидений (Moorestown Ghost Research).
Введение в проверку гипотез
17 авг. 2022 г.
читать 2 мин
Статистическая гипотеза – это предположение о параметре совокупности .
Например, мы можем предположить, что средний рост мужчины в США составляет 70 дюймов.
Предположение о росте является статистической гипотезой , а истинный средний рост мужчины в США является популяционным параметром .
Проверка гипотезы — это формальный статистический тест, который мы используем, чтобы отвергнуть или не опровергнуть статистическую гипотезу.
Два типа статистических гипотез
Чтобы проверить, верна ли статистическая гипотеза о параметре совокупности, мы получаем случайную выборку из совокупности и выполняем проверку гипотезы на выборочных данных.
Существует два типа статистических гипотез:
Нулевая гипотеза , обозначаемая как H 0 , представляет собой гипотезу о том, что выборка данных происходит чисто случайно.
Альтернативная гипотеза , обозначаемая как H 1 или H a , представляет собой гипотезу о том, что на выборочные данные влияет какая-то неслучайная причина.
Проверка гипотез
Проверка гипотезы состоит из пяти шагов:
1. Сформулируйте гипотезы.
Сформулируйте нулевую и альтернативную гипотезы. Эти две гипотезы должны быть взаимоисключающими, поэтому, если одна верна, другая должна быть ложной.
2. Определите уровень значимости для гипотезы.
Определите уровень значимости. Распространенные варианты: .01, .05 и .1.
3. Найдите тестовую статистику.
Найдите тестовую статистику и соответствующее значение p. Часто мы анализируем среднее значение или долю населения, и общая формула для нахождения тестовой статистики выглядит следующим образом: (выборочная статистика — параметр совокупности) / (стандартное отклонение статистики)
4. Отклонить или не отклонить нулевую гипотезу.
Используя тестовую статистику или p-значение, определите, можете ли вы отклонить или не отклонить нулевую гипотезу на основе уровня значимости.
Значение p говорит нам о силе доказательств в поддержку нулевой гипотезы. Если p-значение меньше уровня значимости, мы отклоняем нулевую гипотезу.
5. Интерпретируйте результаты.
Интерпретируйте результаты проверки гипотезы в контексте заданного вопроса.
Два типа ошибок принятия решений
Есть два типа ошибок принятия решений, которые можно сделать при проверке гипотезы:
Ошибка I типа: вы отвергаете нулевую гипотезу, когда она на самом деле верна. Вероятность совершения ошибки первого рода равна уровню значимости, часто называемому альфа и обозначаемому как α.
Ошибка типа II: вы не можете отвергнуть нулевую гипотезу, когда она на самом деле ложна. Вероятность совершения ошибки типа II называется мощностью теста или бета и обозначается как β.
Односторонний и двусторонний тесты
Статистическая гипотеза может быть односторонней или двусторонней.
Односторонняя гипотеза предполагает утверждение «больше» или «меньше».
Например, предположим, что средний рост мужчины в США больше или равен 70 дюймам. Нулевой гипотезой будет H0: µ ≥ 70 дюймов, а альтернативной гипотезой будет Ha: µ < 70 дюймов.
Двусторонняя гипотеза предполагает утверждение «равно» или «не равно».
Например, предположим, что мы предполагаем, что средний рост мужчины в США равен 70 дюймам. Нулевой гипотезой будет H0: µ = 70 дюймов, а альтернативной гипотезой будет Ha: µ ≠ 70 дюймов.
Примечание. Знак «равно» всегда включается в нулевую гипотезу, будь то =, ≥ или ≤.
По теме: Что такое гипотеза направления?
Типы проверки гипотез
Существует множество различных типов проверки гипотез, которые вы можете выполнять в зависимости от типа данных, с которыми вы работаете, и цели вашего анализа.
Следующие руководства содержат объяснение наиболее распространенных типов проверки гипотез:
Введение в одновыборочный t-критерий
Введение в двухвыборочный t-критерий
Введение в t-критерий парных выборок
Введение в Z-тест одной пропорции
Введение в двухпропорционный Z-тест
Ошибки I и II рода при проверке гипотез, мощность
Общий обзор
Принятие неправильного решения
Мощность и связанные факторы
Проверка множественных гипотез
Общий обзор
Большинство проверяемых гипотез сравнивают между собой группы объектов, которые испытывают влияние различных факторов.
Например, можно сравнить эффективность двух видов лечения, чтобы сократить 5-летнюю смертность от рака молочной железы. Для данного исхода (например, смерть) сравнение, представляющее интерес (например, различные показатели смертности через 5 лет), называют эффектом или, если уместно, эффектом лечения.
Нулевую гипотезу выражают как отсутствие эффекта (например 5-летняя смертность от рака молочной железы одинаковая в двух группах, получающих разное лечение); двусторонняя альтернативная гипотеза будет означать, что различие эффектов не равно нулю.
Критериальная проверка гипотезы дает возможность определить, достаточно ли аргументов, чтобы отвергнуть нулевую гипотезу. Можно принять только одно из двух решений:
- отвергнуть нулевую гипотезу и принять альтернативную гипотезу
- остаться в рамках нулевой гипотезы
Важно: В литературе достаточно часто встречается понятие «принять нулевую гипотезу». Хотелось бы внести ясность, что со статистической точки зрения принять нулевую гипотезу невозможно, т.к. нулевая гипотеза представляет собой достаточно строгое утверждение (например, средние значения в сравниваемых группах равны ).
Поэтому фразу о принятии нулевой гипотезы следует понимать как то, что мы просто остаемся в рамках гипотезы.
Принятие неправильного решения
Возможно неправильное решение, когда отвергают/не отвергают нулевую гипотезу, потому что есть только выборочная информация.
| Верная гипотеза | |||
|---|---|---|---|
| H0 | H1 | ||
| Результат
применения критерия |
H0 | H0 верно принята | H0 неверно принята
(Ошибка второго рода) |
| H1 | H0 неверно отвергнута
(Ошибка первого рода) |
H0 верно отвергнута |
Ошибка 1-го рода: нулевую гипотезу отвергают, когда она истинна, и делают вывод, что имеется эффект, когда в действительности его нет. Максимальный шанс (вероятность) допустить ошибку 1-го рода обозначается α (альфа). Это уровень значимости критерия; нулевую гипотезу отвергают, если наше значение p ниже уровня значимости, т. е., если p < α.
Следует принять решение относительно значения а прежде, чем будут собраны данные; обычно назначают условное значение 0,05, хотя можно выбрать более ограничивающее значение, например 0,01.
Шанс допустить ошибку 1-го рода никогда не превысит выбранного уровня значимости, скажем α = 0,05, так как нулевую гипотезу отвергают только тогда, когда p< 0,05. Если обнаружено, что p > 0,05, то нулевую гипотезу не отвергнут и, следовательно, не допустят ошибки 1-го рода.
Ошибка 2-го рода: не отвергают нулевую гипотезу, когда она ложна, и делают вывод, что нет эффекта, тогда как в действительности он существует. Шанс возникновения ошибки 2-го рода обозначается β (бета); а величина (1-β) называется мощностью критерия.
Следовательно, мощность — это вероятность отклонения нулевой гипотезы, когда она ложна, т.е. это шанс (обычно выраженный в процентах) обнаружить реальный эффект лечения в выборке данного объема как статистически значимый.
В идеале хотелось бы, чтобы мощность критерия составляла 100%; однако это невозможно, так как всегда остается шанс, хотя и незначительный, допустить ошибку 2-го рода.
К счастью, известно, какие факторы влияют на мощность и, таким образом, можно контролировать мощность критерия, рассматривая их.
Мощность и связанные факторы
Планируя исследование, необходимо знать мощность предложенного критерия. Очевидно, можно начинать исследование, если есть «хороший» шанс обнаружить уместный эффект, если таковой существует (под «хорошим» мы подразумеваем, что мощность должна быть по крайней мере 70-80%).
Этически безответственно начинать исследование, у которого, скажем, только 40% вероятности обнаружить реальный эффект лечения; это бесполезная трата времени и денежных средств.
Ряд факторов имеют прямое отношение к мощности критерия.
Объем выборки: мощность критерия увеличивается по мере увеличения объема выборки. Это означает, что у большей выборки больше возможностей, чем у незначительной, обнаружить важный эффект, если он существует.
Когда объем выборки небольшой, у критерия может быть недостаточно мощности, чтобы обнаружить отдельный эффект. Эти методы также можно использовать для оценки мощности критерия для точно установленного объема выборки.
Вариабельность наблюдений: мощность увеличивается по мере того, как вариабельность наблюдений уменьшается.
Интересующий исследователя эффект: мощность критерия больше для более высоких эффектов. Критерий проверки гипотез имеет больше шансов обнаружить значительный реальный эффект, чем незначительный.
Уровень значимости: мощность будет больше, если уровень значимости выше (это эквивалентно увеличению допущения ошибки 1-го рода, α, а допущение ошибки 2-го рода, β, уменьшается).
Таким образом, вероятнее всего, исследователь обнаружит реальный эффект, если на стадии планирования решит, что будет рассматривать значение р как значимое, если оно скорее будет меньше 0,05, чем меньше 0,01.
Обратите внимание, что проверка ДИ для интересующего эффекта указывает на то, была ли мощность адекватной. Большой доверительный интервал следует из небольшой выборки и/или набора данных с существенной вариабельностью и указывает на недостаточную мощность.
Проверка множественных гипотез
Часто нужно выполнить критериальную проверку значимости множественных гипотез на наборе данных с многими переменными или существует более двух видов лечения.
Ошибка 1-го рода драматически увеличивается по мере увеличения числа сравнений, что приводит к ложным выводам относительно гипотез. Следовательно, следует проверить только небольшое число гипотез, выбранных для достижения первоначальной цели исследования и точно установленных априорно.
Можно использовать какую-нибудь форму апостериорного уточнения значения р, принимая во внимание число выполненных проверок гипотез.
Например, при подходе Бонферрони (его часто считают довольно консервативным) умножают каждое значение р на число выполненных проверок; тогда любые решения относительно значимости будут основываться на этом уточненном значении р.
Связанные определения:
p-уровень
Альтернативная гипотеза, альтернатива
Альфа-уровень
Бета-уровень
Гипотеза
Двусторонний критерий
Критерий для проверки гипотезы
Критическая область проверки гипотезы
Мощность
Мощность исследования
Мощность статистического критерия
Нулевая гипотеза
Односторонний критерий
Ошибка I рода
Ошибка II рода
Статистика критерия
Эквивалентные статистические критерии
В начало
Содержание портала
Ошибки первого и второго рода
Выдвинутая гипотеза
может быть правильной или неправильной,
поэтому возникает необходимость её
проверки. Поскольку проверку производят
статистическими методами, её называют
статистической. В итоге статистической
проверки гипотезы в двух случаях может
быть принято неправильное решение, т.
е. могут быть допущены ошибки двух родов.
Ошибка первого
рода состоит в том, что будет отвергнута
правильная гипотеза.
Ошибка второго
рода состоит в том, что будет принята
неправильная гипотеза.
Подчеркнём, что
последствия этих ошибок могут оказаться
весьма различными. Например, если
отвергнуто правильное решение «продолжать
строительство жилого дома», то эта
ошибка первого рода повлечёт материальный
ущерб: если же принято неправильное
решение «продолжать строительство»,
несмотря на опасность обвала стройки,
то эта ошибка второго рода может повлечь
гибель людей. Можно привести примеры,
когда ошибка первого рода влечёт более
тяжёлые последствия, чем ошибка второго
рода.
Замечание 1.
Правильное решение может быть принято
также в двух случаях:
-
гипотеза принимается,
причём и в действительности она
правильная; -
гипотеза отвергается,
причём и в действительности она неверна.
Замечание 2.
Вероятность совершить ошибку первого
рода принято обозначать через
;
её называют уровнем значимости. Наиболее
часто уровень значимости принимают
равным 0,05 или 0,01. Если, например, принят
уровень значимости, равный 0,05, то это
означает, что в пяти случаях из ста
имеется риск допустить ошибку первого
рода (отвергнуть правильную гипотезу).
Статистический
критерий проверки нулевой гипотезы.
Наблюдаемое значение критерия
Для проверки
нулевой гипотезы используют специально
подобранную случайную величину, точное
или приближённое распределение которой
известно. Обозначим эту величину в целях
общности через
.
Статистическим
критерием
(или просто критерием) называют случайную
величину
,
которая служит для проверки нулевой
гипотезы.
Например, если
проверяют гипотезу о равенстве дисперсий
двух нормальных генеральных совокупностей,
то в качестве критерия
принимают отношение исправленных
выборочных дисперсий:
Эта величина
случайная, потому что в различных опытах
дисперсии принимают различные, наперёд
неизвестные значения, и распределена
по закону Фишера – Снедекора.
Для проверки
гипотезы по данным выборок вычисляют
частные значения входящих в критерий
величин и таким образом получают частное
(наблюдаемое) значение критерия.
Наблюдаемым
значением
называют значение критерия, вычисленное
по выборкам. Например, если по двум
выборкам найдены исправленные выборочные
дисперсиии
,
то наблюдаемое значение критерия
Критическая
область. Область принятия гипотезы.
Критические точки
После выбора
определённого критерия множество всех
его возможных значений разбивают на
два непересекающихся подмножества:
одно из них содержит значения критерия,
при которых нулевая гипотеза отвергается,
а другая – при которых она принимается.
Критической
областью называют совокупность значений
критерия, при которых нулевую гипотезу
отвергают.
Областью принятия
гипотезы (областью допустимых значений)
называют совокупность значений критерия,
при которых гипотезу принимают.
Основной принцип
проверки статистических гипотез можно
сформулировать так: если наблюдаемое
значение критерия принадлежит критической
области – гипотезу отвергают, если
наблюдаемое значение критерия принадлежит
области принятия гипотезы – гипотезу
принимают.
Поскольку критерий
— одномерная случайная величина, все её
возможные значения принадлежат некоторому
интервалу. Поэтому критическая область
и область принятия гипотезы также
являются интервалами и, следовательно,
существуют точки, которые их разделяют.
Критическими
точками (границами)
называют точки, отделяющие критическую
область от области принятия гипотезы.
Различают
одностороннюю (правостороннюю или
левостороннюю) и двустороннюю критические
области.
Правосторонней
называют критическую область, определяемую
неравенством
>
,
где— положительное число.
Левосторонней
называют критическую область, определяемую
неравенством
<
,
где— отрицательное число.
Односторонней
называют правостороннюю или левостороннюю
критическую область.
Двусторонней
называют критическую область, определяемую
неравенствами
где
.
В частности, если
критические точки симметричны относительно
нуля, двусторонняя критическая область
определяется неравенствами ( в
предположении, что
>0):
,
или равносильным неравенством
.
Отыскание
правосторонней критической области
Как найти критическую
область? Обоснованный ответ на этот
вопрос требует привлечения довольно
сложной теории. Ограничимся её элементами.
Для определённости начнём с нахождения
правосторонней критической области,
которая определяется неравенством
>
,
где>0.
Видим, что для отыскания правосторонней
критической области достаточно найти
критическую точку. Следовательно,
возникает новый вопрос: как её найти?
Для её нахождения
задаются достаточной малой вероятностью
– уровнем значимости
.
Затем ищут критическую точку,
исходя из требования, чтобы при условии
справедливости нулевой гипотезы
вероятность того, критерийпримет значение, большее
,
была равна принятому уровню значимости:
Р(>
)=
.
Для каждого критерия
имеются соответствующие таблицы, по
которым и находят критическую точку,
удовлетворяющую этому требованию.
Замечание 1.
Когда
критическая точка уже найдена, вычисляют
по данным выборок наблюдаемое значение
критерия и, если окажется, что
>
,
то нулевую гипотезу отвергают; если же<
,
то нет оснований, чтобы отвергнуть
нулевую гипотезу.
Пояснение. Почему
правосторонняя критическая область
была определена, исходя из требования,
чтобы при справедливости нулевой
гипотезы выполнялось соотношение
Р(>
)=
?
(*)
Поскольку вероятность
события
>
мала (
— малая вероятность), такое событие при
справедливости нулевой гипотезы, в силу
принципа практической невозможности
маловероятных событий, в единичном
испытании не должно наступить. Если всё
же оно произошло, т.е. наблюдаемое
значение критерия оказалось больше,
то это можно объяснить тем, что нулевая
гипотеза ложна и, следовательно, должна
быть отвергнута. Таким образом, требование
(*) определяет такие значения критерия,
при которых нулевая гипотеза отвергается,
а они и составляют правостороннюю
критическую область.
Замечание 2.
Наблюдаемое значение критерия может
оказаться большим
не потому, что нулевая гипотеза ложна,
а по другим причинам (малый объём выборки,
недостатки методики эксперимента и
др.). В этом случае, отвергнув правильную
нулевую гипотезу, совершают ошибку
первого рода. Вероятность этой ошибки
равна уровню значимости.
Итак, пользуясь требованием (*), мы с
вероятностьюрискуем совершить ошибку первого рода.
Замечание 3. Пусть
нулевая гипотеза принята; ошибочно
думать, что тем самым она доказана.
Действительно, известно, что один пример,
подтверждающий справедливость некоторого
общего утверждения, ещё не доказывает
его. Поэтому более правильно говорить,
«данные наблюдений согласуются с нулевой
гипотезой и, следовательно, не дают
оснований её отвергнуть».
На практике для
большей уверенности принятия гипотезы
её проверяют другими способами или
повторяют эксперимент, увеличив объём
выборки.
Отвергают гипотезу
более категорично, чем принимают.
Действительно, известно, что достаточно
привести один пример, противоречащий
некоторому общему утверждению, чтобы
это утверждение отвергнуть. Если
оказалось, что наблюдаемое значение
критерия принадлежит критической
области, то этот факт и служит примером,
противоречащим нулевой гипотезе, что
позволяет её отклонить.
Отыскание
левосторонней и двусторонней критических
областей***
Отыскание
левосторонней и двусторонней критических
областей сводится (так же, как и для
правосторонней) к нахождению соответствующих
критических точек. Левосторонняя
критическая область определяется
неравенством
<
(
<0).
Критическую точку находят, исходя из
требования, чтобы при справедливости
нулевой гипотезы вероятность того, что
критерий примет значение, меньшее,
была равна принятому уровню значимости:
Р(<
)=
.
Двусторонняя
критическая область определяется
неравенствами
Критические
точки находят, исходя из требования,
чтобы при справедливости нулевой
гипотезы сумма вероятностей того, что
критерий примет значение, меньшееили большее
,
была равна принятому уровню значимости:
.
(*)
Ясно, что критические
точки могут быть выбраны бесчисленным
множеством способов. Если же распределение
критерия симметрично относительно нуля
и имеются основания (например, для
увеличения мощности) выбрать симметричные
относительно нуля точки (-
)и
(
>0),
то
Учитывая (*), получим
.
Это соотношение
и служит для отыскания критических
точек двусторонней критической области.
Критические точки находят по соответствующим
таблицам.
Дополнительные
сведения о выборе критической области.
Мощность критерия
Мы строили
критическую область, исходя из требования,
чтобы вероятность попадания в неё
критерия была равна
при условии, что нулевая гипотеза
справедлива. Оказывается целесообразным
ввести в рассмотрение вероятность
попадания критерия в критическую область
при условии, что нулевая гипотеза неверна
и, следовательно, справедлива конкурирующая.
Мощностью критерия
называют вероятность попадания критерия
в критическую область при условии, что
справедлива конкурирующая гипотеза.
Другими словами, мощность критерия есть
вероятность того, что нулевая гипотеза
будет отвергнута, если верна конкурирующая
гипотеза.
Пусть для проверки
гипотезы принят определённый уровень
значимости и выборка имеет фиксированный
объём. Остаётся произвол в выборе
критической области. Покажем, что её
целесообразно построить так, чтобы
мощность критерия была максимальной.
Предварительно убедимся, что если
вероятность ошибки второго рода (принять
неправильную гипотезу) равна
,
то мощность равна 1-.
Действительно, если— вероятность ошибки второго рода, т.е.
события «принята нулевая гипотеза,
причём справедливо конкурирующая», то
мощность критерия равна 1 —.
Пусть мощность 1
—
возрастает; следовательно, уменьшается
вероятностьсовершить ошибку второго рода. Таким
образом, чем мощность больше, тем
вероятность ошибки второго рода меньше.
Итак, если уровень
значимости уже выбран, то критическую
область следует строить так, чтобы
мощность критерия была максимальной.
Выполнение этого требования должно
обеспечить минимальную ошибку второго
рода, что, конечно, желательно.
Замечание 1.
Поскольку вероятность события «ошибка
второго рода допущена» равна
,
то вероятность противоположного события
«ошибка второго рода не допущена» равна
1 —,
т.е. мощности критерия. Отсюда следует,
что мощность критерия есть вероятность
того, что не будет допущена ошибка
второго рода.
Замечание 2. Ясно,
что чем меньше вероятности ошибок
первого и второго рода, тем критическая
область «лучше». Однако при заданном
объёме выборки уменьшить одновременно
и
невозможно; если уменьшить
,
тобудет возрастать. Например, если принять
=0,
то будут приниматься все гипотезы, в
том числе и неправильные, т.е. возрастает
вероятностьошибки второго рода.
Как же выбрать
наиболее целесообразно? Ответ на этот
вопрос зависит от «тяжести последствий»
ошибок для каждой конкретной задачи.
Например, если ошибка первого рода
повлечёт большие потери, а второго рода
– малые, то следует принять возможно
меньшее.
Если
уже выбрано, то, пользуясь теоремой Ю.
Неймана и Э.Пирсона, можно построить
критическую область, для которойбудет минимальным и, следовательно,
мощность критерия максимальной.
Замечание 3.
Единственный способ одновременного
уменьшения вероятностей ошибок первого
и второго рода состоит в увеличении
объёма выборок.
Соседние файлы в папке Лекции 2 семестр
- #
- #
- #
- #
Проверка корректности А/Б тестов
Хабр, привет! Сегодня поговорим о том, что такое корректность статистических критериев в контексте А/Б тестирования. Узнаем, как проверить, является критерий корректным или нет. Разберём пример, в котором тест Стьюдента не работает.
Меня зовут Коля, я работаю аналитиком данных в X5 Tech. Мы с Сашей продолжаем писать серию статей по А/Б тестированию, это наша третья статья. Первые две можно посмотреть тут:
-
Стратификация. Как разбиение выборки повышает чувствительность A/Б теста
-
Бутстреп и А/Б тестирование
Корректный статистический критерий
В А/Б тестировании при проверке гипотез с помощью статистических критериев можно совершить одну из двух ошибок:
-
ошибку первого рода – отклонить нулевую гипотезу, когда на самом деле она верна. То есть сказать, что эффект есть, хотя на самом деле его нет;
-
ошибку второго рода – не отклонить нулевую гипотезу, когда на самом деле она неверна. То есть сказать, что эффекта нет, хотя на самом деле он есть.
Совсем не ошибаться нельзя. Чтобы получить на 100% достоверные результаты, нужно бесконечно много данных. На практике получить столько данных затруднительно. Если совсем не ошибаться нельзя, то хотелось бы ошибаться не слишком часто и контролировать вероятности ошибок.
В статистике ошибка первого рода считается более важной. Поэтому обычно фиксируют допустимую вероятность ошибки первого рода, а затем пытаются минимизировать вероятность ошибки второго рода.
Предположим, мы решили, что допустимые вероятности ошибок первого и второго рода равны 0.1 и 0.2 соответственно. Будем называть статистический критерий корректным, если его вероятности ошибок первого и второго рода равны допустимым вероятностям ошибок первого и второго рода соответственно.
Как сделать критерий, в котором вероятности ошибок будут равны допустимым вероятностям ошибок?
Вероятность ошибки первого рода по определению равна уровню значимости критерия. Если уровень значимости положить равным допустимой вероятности ошибки первого рода, то вероятность ошибки первого рода должна стать равной допустимой вероятности ошибки первого рода.
Вероятность ошибки второго рода можно подогнать под желаемое значение, меняя размер групп или снижая дисперсию в данных. Чем больше размер групп и чем ниже дисперсия, тем меньше вероятность ошибки второго рода. Для некоторых гипотез есть готовые формулы оценки размера групп, при которых достигаются заданные вероятности ошибок.
Например, формула оценки необходимого размера групп для гипотезы о равенстве средних:
где и
– допустимые вероятности ошибок первого и второго рода,
– ожидаемый эффект (на сколько изменится среднее),
и
– стандартные отклонения случайных величин в контрольной и экспериментальной группах.
Проверка корректности
Допустим, мы работаем в онлайн-магазине с доставкой. Хотим исследовать, как новый алгоритм ранжирования товаров на сайте влияет на среднюю выручку с покупателя за неделю. Продолжительность эксперимента – одна неделя. Ожидаемый эффект равен +100 рублей. Допустимая вероятность ошибки первого рода равна 0.1, второго рода – 0.2.
Оценим необходимый размер групп по формуле:
import numpy as np
from scipy import stats
alpha = 0.1 # допустимая вероятность ошибки I рода
beta = 0.2 # допустимая вероятность ошибки II рода
mu_control = 2500 # средняя выручка с пользователя в контрольной группе
effect = 100 # ожидаемый размер эффекта
mu_pilot = mu_control + effect # средняя выручка с пользователя в экспериментальной группе
std = 800 # стандартное отклонение
# исторические данные выручки для 10000 клиентов
values = np.random.normal(mu_control, std, 10000)
def estimate_sample_size(effect, std, alpha, beta):
"""Оценка необходимого размер групп."""
t_alpha = stats.norm.ppf(1 - alpha / 2, loc=0, scale=1)
t_beta = stats.norm.ppf(1 - beta, loc=0, scale=1)
var = 2 * std ** 2
sample_size = int((t_alpha + t_beta) ** 2 * var / (effect ** 2))
return sample_size
estimated_std = np.std(values)
sample_size = estimate_sample_size(effect, estimated_std, alpha, beta)
print(f'оценка необходимого размера групп = {sample_size}')оценка необходимого размера групп = 784Чтобы проверить корректность, нужно знать природу случайных величин, с которыми мы работаем. В этом нам помогут исторические данные. Представьте, что мы перенеслись в прошлое на несколько недель назад и запустили эксперимент с таким же дизайном, как мы планировали запустить его сейчас. Дизайн – это совокупность параметров эксперимента, таких как: целевая метрика, допустимые вероятности ошибок первого и второго рода, размеры групп и продолжительность эксперимента, техники снижения дисперсии и т.д.
Так как это было в прошлом, мы знаем, какие покупки совершили пользователи, можем вычислить метрики и оценить значимость отличий. Кроме того, мы знаем, что эффекта на самом деле не было, так как в то время эксперимент на самом деле не запускался. Если значимые отличия были найдены, то мы совершили ошибку первого рода. Иначе получили правильный результат.
Далее нужно повторить эту процедуру с мысленным запуском эксперимента в прошлом на разных группах и временных интервалах много раз, например, 1000.
После этого можно посчитать долю экспериментов, в которых была совершена ошибка. Это будет точечная оценка вероятности ошибки первого рода.
Оценку вероятности ошибки второго рода можно получить аналогичным способом. Единственное отличие состоит в том, что каждый раз нужно искусственно добавлять ожидаемый эффект в данные экспериментальной группы. В этих экспериментах эффект на самом деле есть, так как мы сами его добавили. Если значимых отличий не будет найдено – это ошибка второго рода. Проведя 1000 экспериментов и посчитав долю ошибок второго рода, получим точечную оценку вероятности ошибки второго рода.
Посмотрим, как оценить вероятности ошибок в коде. С помощью численных синтетических А/А и А/Б экспериментов оценим вероятности ошибок и построим доверительные интервалы:
def run_synthetic_experiments(values, sample_size, effect=0, n_iter=10000):
"""Проводим синтетические эксперименты, возвращаем список p-value."""
pvalues = []
for _ in range(n_iter):
a, b = np.random.choice(values, size=(2, sample_size,), replace=False)
b += effect
pvalue = stats.ttest_ind(a, b).pvalue
pvalues.append(pvalue)
return np.array(pvalues)
def print_estimated_errors(pvalues_aa, pvalues_ab, alpha):
"""Оценивает вероятности ошибок."""
estimated_first_type_error = np.mean(pvalues_aa < alpha)
estimated_second_type_error = np.mean(pvalues_ab >= alpha)
ci_first = estimate_ci_bernoulli(estimated_first_type_error, len(pvalues_aa))
ci_second = estimate_ci_bernoulli(estimated_second_type_error, len(pvalues_ab))
print(f'оценка вероятности ошибки I рода = {estimated_first_type_error:0.4f}')
print(f' доверительный интервал = [{ci_first[0]:0.4f}, {ci_first[1]:0.4f}]')
print(f'оценка вероятности ошибки II рода = {estimated_second_type_error:0.4f}')
print(f' доверительный интервал = [{ci_second[0]:0.4f}, {ci_second[1]:0.4f}]')
def estimate_ci_bernoulli(p, n, alpha=0.05):
"""Доверительный интервал для Бернуллиевской случайной величины."""
t = stats.norm.ppf(1 - alpha / 2, loc=0, scale=1)
std_n = np.sqrt(p * (1 - p) / n)
return p - t * std_n, p + t * std_n
pvalues_aa = run_synthetic_experiments(values, sample_size, effect=0)
pvalues_ab = run_synthetic_experiments(values, sample_size, effect=effect)
print_estimated_errors(pvalues_aa, pvalues_ab, alpha)оценка вероятности ошибки I рода = 0.0991
доверительный интервал = [0.0932, 0.1050]
оценка вероятности ошибки II рода = 0.1978
доверительный интервал = [0.1900, 0.2056]Оценки вероятностей ошибок примерно равны 0.1 и 0.2, как и должно быть. Всё верно, тест Стьюдента на этих данных работает корректно.
Распределение p-value
Выше рассмотрели случай, когда тест контролирует вероятность ошибки первого рода при фиксированном уровне значимости. Если решим изменить уровень значимости с 0.1 на 0.01, будет ли тест контролировать вероятность ошибки первого рода? Было бы хорошо, если тест контролировал вероятность ошибки первого рода при любом заданном уровне значимости. Формально это можно записать так:
Для любого выполняется
.
Заметим, что в левой части равенства записано выражение для функции распределения p-value. Из равенства следует, что функция распределения p-value в точке X равна X для любого X от 0 до 1. Эта функция распределения является функцией распределения равномерного распределения от 0 до 1. Мы только что показали, что статистический критерий контролирует вероятность ошибки первого рода на заданном уровне для любого уровня значимости тогда и только тогда, когда при верности нулевой гипотезы p-value распределено равномерно от 0 до 1.
При верности нулевой гипотезы p-value должно быть распределено равномерно. А как должно быть распределено p-value при верности альтернативной гипотезы? Из условия для вероятности ошибки второго рода следует, что
.
Получается, график функции распределения p-value при верности альтернативной гипотезы должен проходить через точку , где
и
– допустимые вероятности ошибок конкретного эксперимента.
Проверим, как распределено p-value в численном эксперименте. Построим эмпирические функции распределения p-value:
import matplotlib.pyplot as plt
def plot_pvalue_distribution(pvalues_aa, pvalues_ab, alpha, beta):
"""Рисует графики распределения p-value."""
estimated_first_type_error = np.mean(pvalues_aa < alpha)
estimated_second_type_error = np.mean(pvalues_ab >= alpha)
y_one = estimated_first_type_error
y_two = 1 - estimated_second_type_error
X = np.linspace(0, 1, 1000)
Y_aa = [np.mean(pvalues_aa < x) for x in X]
Y_ab = [np.mean(pvalues_ab < x) for x in X]
plt.plot(X, Y_aa, label='A/A')
plt.plot(X, Y_ab, label='A/B')
plt.plot([alpha, alpha], [0, 1], '--k', alpha=0.8)
plt.plot([0, alpha], [y_one, y_one], '--k', alpha=0.8)
plt.plot([0, alpha], [y_two, y_two], '--k', alpha=0.8)
plt.plot([0, 1], [0, 1], '--k', alpha=0.8)
plt.title('Оценка распределения p-value', size=16)
plt.xlabel('p-value', size=12)
plt.legend(fontsize=12)
plt.grid()
plt.show()
plot_pvalue_distribution(pvalues_aa, pvalues_ab, alpha, beta)P-value для синтетических А/А тестах действительно оказалось распределено равномерно от 0 до 1, а для синтетических А/Б тестов проходит через точку .
Кроме оценок распределений на графике дополнительно построены четыре пунктирные линии:
-
диагональная из точки [0, 0] в точку [1, 1] – это функция распределения равномерного распределения на отрезке от 0 до 1, по ней можно визуально оценивать равномерность распределения p-value;
-
вертикальная линия с
– пороговое значение p-value, по которому определяем отвергать нулевую гипотезу или нет. Проекция на ось ординат точки пересечения вертикальной линии с функцией распределения p-value для А/А тестов – это вероятность ошибки первого рода. Проекция точки пересечения вертикальной линии с функцией распределения p-value для А/Б тестов – это мощность теста (мощность = 1 —
).
-
две горизонтальные линии – проекции на ось ординат точки пересечения вертикальной линии с функцией распределения p-value для А/А и А/Б тестов.
График с оценками распределения p-value для синтетических А/А и А/Б тестов позволяет проверить корректность теста для любого значения уровня значимости.
Некорректный критерий
Выше рассмотрели пример, когда тест Стьюдента оказался корректным критерием для случайных данных из нормального распределения. Может быть, все критерии всегда работаю корректно, и нет смысла каждый раз проверять вероятности ошибок?
Покажем, что это не так. Немного изменим рассмотренный ранее пример, чтобы продемонстрировать некорректную работу критерия. Допустим, мы решили увеличить продолжительность эксперимента до 2-х недель. Для каждого пользователя будем вычислять стоимость покупок за первую неделю и стоимость покупок за второю неделю. Полученные стоимости будем передавать в тест Стьюдента для проверки значимости отличий. Положим, что поведение пользователей повторяется от недели к неделе, и стоимости покупок одного пользователя совпадают.
def run_synthetic_experiments_two(values, sample_size, effect=0, n_iter=10000):
"""Проводим синтетические эксперименты на двух неделях."""
pvalues = []
for _ in range(n_iter):
a, b = np.random.choice(values, size=(2, sample_size,), replace=False)
b += effect
# дублируем данные
a = np.hstack((a, a,))
b = np.hstack((b, b,))
pvalue = stats.ttest_ind(a, b).pvalue
pvalues.append(pvalue)
return np.array(pvalues)
pvalues_aa = run_synthetic_experiments_two(values, sample_size)
pvalues_ab = run_synthetic_experiments_two(values, sample_size, effect=effect)
print_estimated_errors(pvalues_aa, pvalues_ab, alpha)
plot_pvalue_distribution(pvalues_aa, pvalues_ab, alpha, beta)оценка вероятности ошибки I рода = 0.2451
доверительный интервал = [0.2367, 0.2535]
оценка вероятности ошибки II рода = 0.0894
доверительный интервал = [0.0838, 0.0950]Получили оценку вероятности ошибки первого рода около 0.25, что сильно больше уровня значимости 0.1. На графике видно, что распределение p-value для синтетических А/А тестов не равномерно, оно отклоняется от диагонали. В этом примере тест Стьюдента работает некорректно, так как данные зависимые (стоимости покупок одного человека зависимы). Если бы мы сразу не догадались про зависимость данных, то оценка вероятностей ошибок помогла бы нам понять, что такой тест некорректен.
Итоги
Мы обсудили, что такое корректность статистического теста, посмотрели, как оценить вероятности ошибок на исторических данных и привели пример некорректной работы критерия.
Таким образом:
-
корректный критерий – это критерий, у которого вероятности ошибок первого и второго рода равны допустимым вероятностям ошибок первого и второго рода соответственно;
-
чтобы критерий контролировал вероятность ошибки первого рода для любого уровня значимости, необходимо и достаточно, чтобы p-value при верности нулевой гипотезы было распределено равномерно от 0 до 1.
5.6. Вероятность ошибки р
Если следовать подразделению статистики на описательную и аналитическую, то задача аналитической статистики — предоставить методы, с помощью которых можно было бы объективно выяснить,
например, является ли наблюдаемая разница в средних значениях или взаимосвязь (корреляция) выборок случайной или нет.
Например, если сравниваются два средних значения выборок, то можно сформулировать две предварительных гипотезы:
-
Гипотеза 0 (нулевая): Наблюдаемые различия между средними значениями выборок находятся в пределах случайных отклонений.
-
Гипотеза 1 (альтернативная): Наблюдаемые различия между средними значениями нельзя объяснить случайными отклонениями.
В аналитической статистике разработаны методы вычисления так называемых тестовых (контрольных) величин, которые рассчитываются по определенным формулам на основе данных,
содержащихся в выборках или полученных из них характеристик. Эти тестовые величины соответствуют определенным теоретическим распределениям
(t-pacnpeлелению, F-распределению, распределению X2 и т.д.), которые позволяют вычислить так называемую вероятность ошибки. Это вероятность равна проценту ошибки,
которую можно допустить отвергнув нулевую гипотезу и приняв альтернативную.
Вероятность определяется в математике, как величина, находящаяся в диапазоне от 0 до 1. В практической статистике она также часто выражаются в процентах. Обычно вероятность обозначаются буквой р:
0 < р < 1
Вероятности ошибки, при которой допустимо отвергнуть нулевую гипотезу и принять альтернативную гипотезу, зависит от каждого конкретного случая.
В значительной степени эта вероятность определяется характером исследуемой ситуации. Чем больше требуемая вероятность, с которой надо избежать ошибочного решения,
тем более узкими выбираются границы вероятности ошибки, при которой отвергается нулевая гипотеза, так называемый доверительный интервал вероятности.
Обычно в исследованиях используют 5% вероятность ошибки.
Существует общепринятая терминология, которая относится к доверительным интервалам вероятности:
- Высказывания, имеющие вероятность ошибки р <= 0,05 — называются значимыми.
- Высказывания с вероятностью ошибки р <= 0,01 — очень значимыми,
- А высказывания с вероятностью ошибки р <= 0,001 — максимально значимыми.
В литературе такие ситуации иногда обозначают одной, двумя или тремя звездочками.
| Вероятность ошибки | Значимость | Обозначение |
| р > 0.05 | Не значимая | ns |
| р <= 0.05 | Значимая | * |
| р <= 0.01 | Очень значимая | ** |
| р <= 0.001 | Максимально значимая | *** |
В SPSS вероятность ошибки р имеет различные обозначения; звездочки для указания степени значимости применяются лишь в немногих случаях. Обычно в SPSS значение р обозначается Sig. (Significant).
Времена, когда не было компьютеров, пригодных для статистического анализа, давали практикам по крайней мере одно преимущество. Так как все вычисления надо было выполнять вручную,
статистик должен был сначала тщательно обдумать, какие вопросы можно решить с помощью того или иного теста. Кроме того, особое значение придавалось точной формулировке нулевой гипотезы.
Но с помощью компьютера и такой мощной программы, как SPSS, очень легко можно провести множество тестов за очень короткое время. К примеру, если в таблицу сопряженности свести 50 переменных
с другими 20 переменными и выполнить тест X2, то получится 1000 результатов проверки значимости или 1000 значений р. Некритический подбор значимых величин может
дать бессмысленный результат, так как уже при граничном уровне значимости р = 0,05 в пяти процентах наблюдений, то есть в 50 возможных наблюдениях, можно ожидать значимые результаты.
Этим ошибкам первого рода (когда нулевая гипотеза отвергается, хотя она верна) следует уделять достаточно внимания. Ошибкой второго рода называется ситуация,
когда нулевая гипотеза принимается, хотя она ложна. Вероятность допустить ошибку первого рода равна вероятности ошибки р. Вероятность ошибки второго рода тем меньше, чем больше вероятность ошибки р.
Статистические гипотезы
Определение статистической гипотезы. Нулевая и альтернативная, простая и сложная гипотезы. Ошибки первого и второго рода. Статистический критерий, наблюдаемое значение критерия. Критическая область. Область принятия нулевой гипотезы; критическая точка. Общая методика построения право-, лево- и двухсторонней критических областей
Понятие и определение статистической гипотезы
Проверка статистических гипотез тесно связана с теорией оценивания параметров. В естествознании, технике, экономике для выяснения того или иного случайного факта часто прибегают к высказыванию гипотез, которые можно проверить статистически, т. е. опираясь на результаты наблюдений в случайной выборке. Под статистическими подразумеваются такие гипотезы, которые относятся или к виду, или к отдельным параметрам распределения случайной величины. Например, статистической является гипотеза о том, что распределение производительности труда рабочих, выполняющих одинаковую работу в одинаковых условиях, имеет нормальный закон распределения. Статистической будет также гипотеза о том, что средние размеры деталей, производимые на однотипных, параллельно работающих станках, не различаются.
Статистическая гипотеза называется простой, если она однозначно определяет распределение случайной величины , в противном случае гипотеза называется сложной. Например, простой гипотезой является предположение о том, что случайная величина распределена по нормальному закону с математическим ожиданием, равным нулю, и дисперсией, равной единице. Если высказывается предположение, что случайная величина имеет нормальное распределение с дисперсией, равной единице, а математическое ожидание — число из отрезка , то это сложная гипотеза. Другим примером сложной гипотезы является предположение о том, что непрерывная случайная величина с вероятностью принимает значение из интервала , в этом случае распределение случайной величины может быть любым из класса непрерывных распределений.
Часто распределение величины известно, и по выборке наблюдений необходимо проверить предположения о значении параметров этого распределения. Такие гипотезы называются параметрическими.
Проверяемая гипотеза называется нулевой и обозначается . Наряду с гипотезой рассматривают одну из альтернативных (конкурирующих) гипотез . Например, если проверяется гипотеза о равенстве параметра некоторому заданному значению , то есть , то в качестве альтернативной гипотезы можно рассмотреть одну из следующих гипотез: где — заданное значение, . Выбор альтернативной гипотезы определяется конкретной формулировкой задачи.
Правило, по которому принимается решение принять или отклонить гипотезу , называется критерием . Так как решение принимается на основе выборки наблюдений случайной величины , необходимо выбрать подходящую статистику, называемую в этом случае статистикой критерия . При проверке простой параметрической гипотезы в качестве статистики критерия выбирают ту же статистику, что и для оценки параметра .
Проверка статистической гипотезы основывается на принципе, в соответствии с которым маловероятные события считаются невозможными, а события, имеющие большую вероятность, — достоверными; Этот принцип можно реализовать следующим образом. Перед анализом выборки фиксируется некоторая малая вероятность , называемая уровнем значимости. Пусть — множество значений статистики , а — такое подмножество, что при условии истинности гипотезы вероятность попадания статистики критерия в равна , то есть .
Обозначим выборочное значение статистики , вычисленное по выборке наблюдений. Критерий формулируется так: отклонить гипотезу , если ; принять гипотезу , если . Критерий, основанный на использовании заранее заданного уровня значимости, называют критерием значимости. Множество всех значений статистики критерия , при которых принимается решение отклонить гипотезу , называется критической областью; область называется областью принятия гипотезы .
Уровень значимости определяет размер критической области . Положение критической области на множестве значений статистики зависит от формулировки альтернативной гипотезы . Например, если проверяется гипотеза , а альтернативная гипотеза формулируется как , то критическая область размещается на правом (левом) «хвосте» распределения статистики , т. е. имеет вид неравенства , где — значения статистики , которые принимаются с вероятностями соответственно и при условии, что верна гипотеза . В этом случае критерий называется односторонним (соответственно правосторонним и левосторонним). Если альтернативная гипотеза формулируется как , то критическая область размещается на обоих «хвостах» распределения , то есть определяется совокупностью неравенств и в этом случае критерий называется двухсторонним.
Расположение критической области для различных альтернативных гипотез показано на рис. 30, где — плотность распределения статистики критерия при условии, что верна гипотеза , — область принятия гипотезы, .
Проверку параметрической статистической гипотезы с помощью критерия значимости можно разбить на этапы:
1) сформулировать проверяемую и альтернативную гипотезы;
2) назначить уровень значимости ;
3) выбрать статистику критерия для проверки гипотезы ;
4) определить выборочное распределение статистики при условии, что верна гипотеза ;
5) в зависимости от формулировки альтернативной гипотезы определить критическую область одним из неравенств или совокупностью неравенств и ;
6) получить выборку наблюдений и вычислить выборочные значения статистики критерия;
7) принять статистическое решение: если , то отклонить гипотезу как не согласующуюся с результатами наблюдений; если , то принять гипотезу , т. е. считать, что гипотеза не противоречит результатам наблюдений.
Обычно при выполнении пп. 4-7 используют статистику с нормальным распределением, статистику Стьюдента, Фишера.
Пример 3. По паспортным данным автомобильного двигателя расход топлива на 100 км пробега составляет 10 л. В результате изменения конструкции двигателя ожидается, что расход топлива уменьшится. Для проверки проводятся испытания 25 случайно отобранных автомобилей с модернизированным двигателем, причем выборочное среднее расходов топлива на 100 км пробега по результатам испытаний составило 9,3 л. Предположим, что выборка расходов топлива получена из нормально распределенной генеральной совокупности со средним и дисперсией л². Используя критерий значимости, проверить гипотезу, утверждающую, что изменение конструкции двигателя не повлияло на расход топлива.
Решение. Проверим гипотезу о среднем нормально распределенной генеральной совокупности. Проверку проведем по этапам:
1) проверяемая гипотеза ; альтернативная гипотеза ;
2) уровень значимости ;
3) в качестве статистики критерия используем статистику математического ожидания — выборочное среднее;
4) так как выборка получена из нормально распределенной генеральной совокупности, выборочное среднее также имеет нормальное распределение с дисперсией . При условии, что верна гипотеза , математическое ожидание этого распределения равно 10. Нормированная статистика имеет нормальное распределение;
5) альтернативная гипотеза предполагает уменьшение расхода топлива, следовательно, нужно использовать односторонний критерий. Критическая область определяется неравенством . По прил. 5 находим ;
б) выборочное значение нормированной статистики критерия
7) статистическое решение: так как выборочное значение статистики критерия принадлежит критической области, гипотеза отклоняется: следует считать, что изменение конструкции двигателя привело к уменьшению расхода топлива. Границу критической области для исходной статистики критерия можно получить из соотношения , откуда , т. е. критическая область для статистики определяется неравенством .
Ошибки первого и второго рода
Решение, принимаемое на основе критерия значимости, может быть ошибочным. Пусть выборочное значение статистики критерия попадает в критическую область, и гипотеза , отклоняется в соответствии с критерием. Если, тем не менее, гипотеза верна, то принимаемое решение неверно. Ошибка, совершаемая при отклонении правильной гипотезы if о, называется ошибкой первого рода. Вероятность ошибки первого рода равна вероятности попадания статистики критерия в критическую область при условии, что верна гипотеза , т. е. равна уровню значимости
Ошибка второго рода происходит тогда, когда гипотеза принимается, но в действительности верна гипотеза . Вероятность ошибки второго рода вычисляется по формуле
Пример 4. В условиях примера 3 предположим, что наряду с гипотезой л рассматривается альтернативная гипотеза л. В качестве статистики критерия снова возьмем выборочное среднее . Предположим, что критическая область задана неравенством л. Найти вероятности ошибок первого и второго рода для критерия с такой критической областью.
Решение. Найдем вероятность ошибки первого рода. Статистика критерия при условии, что верна гипотеза л, имеет нормальное распределение с математическим ожиданием, равным 10, и дисперсией, равной . Используя прил. 5, по формуле (11.1) находим
Это означает, что принятый критерий классифицирует примерно 8% автомобилей, имеющих расход 10 л на 100 км пробега, как автомобили, имеющие меньший расход топлива. При условии, что верна гипотеза л, статистика имеет нормальное распределение с математическим ожиданием, равным 9, и дисперсией, равной . Вероятность ошибки второго рода найдем по формуле (11.2):
Следовательно, в соответствии с принятым критерием 13,6% автомобилей, имеющих расход топлива 9 л на 100 км пробега, классифицируются как автомобили, имеющие расход топлива 10 л.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Ошибки первого и второго рода. Понятие о статистических критериях
Проверить статистическую гипотезу – значит проверить, согласуются ли данные, полученные из выборки с этой гипотезой. При этом проверяемая гипотеза может подтвердиться, а может и не подтвердиться. Проверка статистических гипотез сопряжена с возможностью допустить ошибку.
Ошибка первого рода состоит в том, что будет отвергнута верная гипотеза.
Ошибка второго рода состоит в том, что будет принята ложная гипотеза.
Вероятность совершения ошибки первого рода обозначается 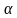
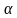
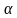
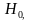
Вероятность не отклонить ложную гипотезу обозначается 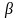
При проверке нулевой гипотезы могут возникнуть следующие ситуации (табл.):
|
|
верная |
ложная |
|
отклоняется |
Ошибка второго рода |
Решение верное |
|
не отклоняется |
Решение верное |
Ошибка второго рода |
Проверка любой статистической гипотезы осуществляется с помощью статистического критерия.
Статистический критерий – это случайная величина [статистика], которая используется с целью проверки нулевой гипотезы.
В дальнейшем статистический критерий непараметрических гипотез будем обозначать, как правило, буквой
Статистические критерии носят название соответственно распределению: 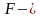
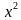
Наблюдаемое значение статистического критерия – это значение критерия, которое рассчитано по выборке с определенным законом распределения.
Множество всех возможных значений выбранного статистического критерия разделяется на два непересекающихся подмножества. Первое из этих подмножеств включает в себя значения критерия, при которых нулевая гипотеза отвергается, а второе – те значения критерия, при которых нулевая гипотеза принимается.
Критическая область – это множество возможных значений статистического критерия, при которых нулевая гипотеза отвергается.
Область принятия гипотезы [область допустимых значений] – это множество возможных значений статистического критерия, при которых нулевая гипотеза принимается.
В том случае, если наблюдаемое значение статистического критерия (рассчитанное по выборочной совокупности) принадлежит критической области, нулевую гипотезу отвергают. Если же наблюдаемое значение статистического критерия принадлежит области принятия гипотезы, то нулевая гипотеза принимается.
Критические точки [квантили] – это точки, которые разграничивают критическую область и область принятия гипотезы.
Выделяют одностороннюю и двустороннюю критические области. Дадим определения данных критических областей на примере условного статистического критерия 
Правосторонняя критическая область определяется неравенством 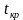
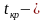
Левосторонняя критическая область определяется неравенством 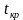
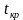
Двусторонняя критическая область определяется неравенствами 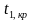
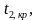
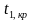
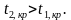








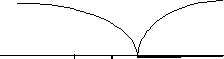






 ,
, соответствует гипотезе
соответствует гипотезе  .
. .
.
 ,
, соответствует гипотезе
соответствует гипотезе  .
. .
.