Вероятностная ошибка это

Вероятностная ошибка

Cтраница 1

Вероятностная ошибка равна 0 6745 а. Эта ошибка такова, что большие ошибки встречаются столь же часто, как и меньшие. Обычно можно принять за стандартную ошибку УМ, где М — общее число отсчетов независимо от интервала времени. Если измеряется препарат с низкой активностью, вносимая фоном ошибка становится значительной.
 [1]

Определим вероятностную ошибку положения механизма.
 [2]

Необходимо придерживаться трех простых правил, которые позволяют получить графики с минимальной неопределенностью: 1) вероятностная ошибка в данной точке должна быть примерно равна половине наименьшего деления шкалы графика; 2) по возможности для любых данных следует пытаться строить линейный график; 3) длина шкалы должна выбираться из условия максимального использования формата графической бумаги.
 [4]

В том случае, когда в сообщении о совершении предсказуемого события повторяются все сведения, которые содержались в сообщении о прогнозе, они используются для обработки МОД и ДИН МАСС, и вероятностные ошибки не переходят на эти массивы. Эта схема не всегда оказывается технологически удобной. Сообщение о совершении событий может быть коротким ( возможно, что оно вырабатывается в автоматическом датчике), и все подробности этого события ( например, перечень прибывших материалов с данным транспортом) будут записаны в предыдущем сообщении о прогнозе. В этом случае после получения сообщений о фактическом совершении событий при использовании данных сообщений о прогнозе для обработки МОД и ДИН МАСС некоторые вероятностные искажения могут переходить в эти массивы.
 [5]

Так называются квадратуры с одинаковыми весами — коэффициентами At, В &, Ck, Dk, имеющие также, как и квадратуры Гаусса — Маркова, наивысшую возможную степень точности относительно алгебраических многочленов. Применение равных весов минимизирует вероятностную ошибку, если значения / ( s) подвержены нормально распределенным вероятностным ошибкам.
 [7]

Так называются квадратуры с одинаковыми весами — коэффициентами At, В &, Ck, Dk, имеющие также, как и квадратуры Гаусса — Маркова, наивысшую возможную степень точности относительно алгебраических многочленов. Применение равных весов минимизирует вероятностную ошибку, если значения / ( s) подвержены нормально распределенным вероятностным ошибкам.
 [9]

Внешние воздействия могут быть детерминированными или случайными функциями времени. В данной главе рассматривается качество систем только при детерминированных внешних воздействиях. Для оценки качества систем при возмущениях, представляющих собой случайные функции времени, служит вероятностная ошибка; этот показатель качества рассмотрен в гл.
 [10]

Программные меры защиты, осуществляемые на ЭВМ ( 10 — 17), являются последними и решающими. Возможны остаточные искажения, возникающие в результате случайных сбоев на ЭВМ после осуществления соответствующих программных мер защиты и поступающие в МОД и ДИН МАСС. Эти редкие искажения показаны на рис. 45 в виде тончайших струй потока ошибок, входящего в МОД и ДИН МАСС. Поток вероятностных ошибок может быть очень большой, а описанные меры защиты не могут его выявить. Природа этих ошибок заключается в том, что не предугаданы помехи, которые не совпадают с прогнозируемыми, связанными с предстоящими воздействиями среды ( поставки, подход транспорта и др.) на объект.
 [11]

То есть существует такая с, что если амплитуды в унитарной матрице, описывающей квантовый гейт, возмущаются не более, чем на c / t, то у квантового компьютера остается вполне реальный шанс дать желаемый ответ. Точно также необходимо, чтобы декогеренция была полиномиально мала по t, для того, чтобы иметь после t шагов вычислений разумную вероятность успеха. Однако, построение квантового компьютера с высоким уровнем точности и низким уровнем декогерентности, предназначенного для реализации длинных вычислений, может являть собой фундаментальную проблему для экспериментальной физики. В классических компьютерах вероятностные ошибки преодолеваются не только за счет средств оборудования, но и за счет программного обеспечения, введения избыточности и кодов, корректирующих ошибки. По всей видимости, метод избыточности для квантовых вычислений не годится в силу существования теоремы о невозможности клонирования битов [ Peres, 1993, § 9 — 4 ], но этот аргумент не отрицает возможности применения более сложных программных методов повышения точности и уменьшения декогеренции.
 [12]

Программные меры защиты, осуществляемые на ЭВМ ( 10 — 17), являются последними и решающими. Возможны остаточные искажения, возникающие в результате случайных сбоев на ЭВМ после осуществления соответствующих программных мер защиты и поступающие в МОД и ДИН МАСС. Эти редкие искажения показаны на рис. 45 в виде тончайших струй потока ошибок, входящего в МОД и ДИН МАСС. Поток вероятностных ошибок может быть очень большой, а описанные меры защиты не могут его выявить. Природа этих ошибок заключается в том, что не предугаданы помехи, которые не совпадают с прогнозируемыми, связанными с предстоящими воздействиями среды ( поставки, подход транспорта и др.) на объект. Однако часть вероятностных ошибок может и при этом оставаться.
 [13]

Страницы:  

   1

From Wikipedia, the free encyclopedia

In statistics, the term «error» arises in two ways. Firstly, it arises in the context of decision making, where the probability of error may be considered as being the probability of making a wrong decision and which would have a different value for each type of error. Secondly, it arises in the context of statistical modelling (for example regression) where the model’s predicted value may be in error regarding the observed outcome and where the term probability of error may refer to the probabilities of various amounts of error occurring.

Hypothesis testing[edit]

In hypothesis testing in statistics, two types of error are distinguished.

• Type I errors which consist of rejecting a null hypothesis that is true; this amounts to a false positive result.
• Type II errors which consist of failing to reject a null hypothesis that is false; this amounts to a false negative result.

The probability of error is similarly distinguished.

• For a Type I error, it is shown as α (alpha) and is known as the size of the test and is 1 minus the specificity of the test. This quantity is sometimes referred to as the confidence of the test, or the level of significance (LOS) of the test.
• For a Type II error, it is shown as β (beta) and is 1 minus the power or 1 minus the sensitivity of the test.

Statistical and econometric modelling[edit]

The fitting of many models in statistics and econometrics usually seeks to minimise the difference between observed and predicted or theoretical values. This difference is known as an error, though when observed it would be better described as a residual.

The error is taken to be a random variable and as such has a probability distribution. Thus distribution can be used to calculate the probabilities of errors with values within any given range.

ошибка вероятностная

probability bias. — Фактор организационного плана, влияющий на проведение эксперимента или наблюдения. например, синдром азартного игрока (gambler’s fallacy). — предположение, что на случайные конкретные события оказывают влияние предыдущие случайные события; иллюзорная корреляция (illusory correlation). — ошибочное предположение о взаимоотношениях определенных действий и результата и др. См. метод включенного наблюдения, метод прямого наблюдения.

Источник: Словарь терминов межкультурной коммуникации 2013.

вероятность ошибки

Полезное

Ошибки, встроенные в систему: их роль в статистике

В прошлой статье я указал, как распространена проблема неправильного использования t-критерия в научных публикациях (и это возможно сделать только благодаря их открытости, а какой трэш творится при его использовании во всяких курсовых, отчетах, обучающих задачах и т.д. — неизвестно). Чтобы обсудить это, я рассказал об основах дисперсионного анализа и задаваемом самим исследователем уровне значимости α. Но для полного понимания всей картины статистического анализа необходимо подчеркнуть ряд важных вещей. И самая основная из них — понятие ошибки.

Ошибка и некорректное применение: в чем разница?

В любой физической системе содержится какая-либо ошибка, неточность. В самой разнообразной форме: так называемый допуск — отличие в размерах разных однотипных изделий; нелинейная характеристика — когда прибор или метод измеряют что-то по строго известному закону в определенных пределах, а дальше становятся неприменимыми; дискретность — когда мы чисто технически не можем обеспечить плавность выходной характеристики.

И в то же время существует чисто человеческая ошибка — некорректное использование устройств, приборов, математических законов. Между ошибкой, присущей системе, и ошибкой применения этой системы есть принципиальная разница. Важно различать и не путать между собой эти два понятия, называемые одним и тем же словом «ошибка». Я в данной статье предпочитаю использовать слово «ошибка» для обозначения свойства системы, а «некорректное применение» — для ошибочного ее использования.

То есть, ошибка линейки равна допуску оборудования, наносящего штрихи на ее полотно. А ошибкой в смысле некорректного применения было бы использовать ее при измерении деталей наручных часов. Ошибка безмена написана на нем и составляет что-то около 50 граммов, а неправильным использованием безмена было бы взвешивание на нем мешка в 25 кг, который растягивает пружину из области закона Гука в область пластических деформаций. Ошибка атомно-силового микроскопа происходит из его дискретности — нельзя «пощупать» его зондом предметы мельче, чем диаметром в один атом. Но способов неправильно использовать его или неправильно интерпретировать данные существует множество. И так далее.

Так, а что же за ошибка имеет место в статистических методах? А этой ошибкой как раз и является пресловутый уровень значимости α.

Ошибки первого и второго рода

Ошибкой в математическом аппарате статистики является сама ее Байесовская вероятностная сущность. В прошлой статье я уже упоминал, на чем стоят статистические методы: определение уровня значимости α как наибольшей допустимой вероятности неправомерно отвергнуть нулевую гипотезу, и самостоятельное задание исследователем этой величины перед исследователем.
Вы уже видите эту условность? На самом деле, в критериальных методах нету привычной математической строгости. Математика здесь оперирует вероятностными характеристиками.
И тут наступает еще один момент, где возможна неправильная трактовка одного слова в разном контексте. Необходимо различать само понятие вероятности и фактическую реализацию события, выражающуюся в распределении вероятности. Например, перед началом любого нашего эксперимента мы не знаем, какую именно величину мы получим в результате. Есть два возможных исхода: загадав некоторое значение результата, мы либо действительно его получим, либо не получим. Логично, что вероятность и того, и другого события равна 1/2. Но показанная в предыдущей статье Гауссова кривая показывает распределение вероятности того, что мы правильно угадаем совпадение.

Наглядно можно проиллюстрировать это примером. Пусть мы 600 раз бросаем два игральных кубика — обычный и шулерский. Получим следующие результаты:

До эксперимента для обоих кубиков выпадение любой грани будет равновероятно — 1/6. Однако после эксперимента проявляется сущность шулерского кубика, и мы можем сказать, что плотность вероятности выпадения на нем шестерки — 90%.

Другой пример, который знают химики, физики и все, кто интересуется квантовыми эффектами — атомные орбитали. Теоретически электрон может быть «размазан» в пространстве и находиться практически где угодно. Но на практике есть области, где он будет находиться в 90 и более процентах случаев. Эти области пространства, образованные поверхностью с плотностью вероятности нахождения там электрона 90%, и есть классические атомные орбитали, в виде сфер, гантелей и т.д.

Так вот, самостоятельно задавая уровень значимости, мы заведомо соглашаемся на описанную в его названии ошибку. Из-за этого ни один результат нельзя считать «стопроцентно достоверным» — всегда наши статистические выводы будут содержать некоторую вероятность сбоя.

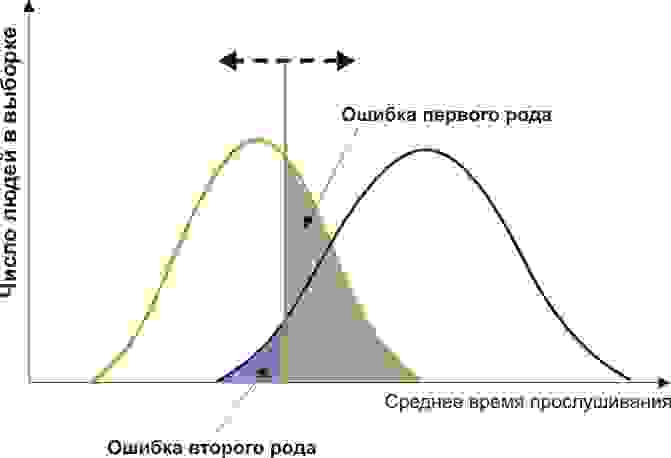
Ошибка, формулируемая определением уровня значимости α, называется ошибкой первого рода. Ее можно определить, как «ложная тревога», или, более корректно, ложноположительный результат. В самом деле, что означают слова «ошибочно отвергнуть нулевую гипотезу»? Это значит, по ошибке принять наблюдаемые данные за значимые различия двух групп. Поставить ложный диагноз о наличии болезни, поспешить явить миру новое открытие, которого на самом деле нет — вот примеры ошибок первого рода.

Но ведь тогда должны быть и ложноотрицательные результаты? Совершенно верно, и они называются ошибками второго рода. Примеры — не поставленный вовремя диагноз или же разочарование в результате исследования, хотя на самом деле в нем есть важные данные. Ошибки второго рода обозначаются буквой, как ни странно, β. Но само это понятие не так важно для статистики, как число 1-β. Число 1-β называется мощностью критерия, и как нетрудно догадаться, оно характеризует способность критерия не упустить значимое событие.
Однако содержание в статистических методах ошибок первого и второго рода не является только лишь их ограничением. Само понятие этих ошибок может использоваться непосредственным образом в статистическом анализе. Как?

ROC-анализ

ROC-анализ (от receiver operating characteristic, рабочая характеристика приёмника) — это метод количественного определения применимости некоторого признака к бинарной классификации объектов. Говоря проще, мы можем придумать некоторый способ, как отличить больных людей от здоровых, кошек от собак, черное от белого, а затем проверить правомерность такого способа. Давайте снова обратимся к примеру.

Пусть вы — подающий надежды криминалист, и разрабатываете новый способ скрытно и однозначно определять, является ли человек преступником. Вы придумали количественный признак: оценивать преступные наклонности людей по частоте прослушивания ими Михаила Круга. Но будет ли давать адекватные результаты ваш признак? Давайте разбираться.
Вам понадобится две группы людей для валидации вашего критерия: обычные граждане и преступники. Положим, действительно, среднегодовое время прослушивания ими Михаила Круга различается (см. рисунок):

Здесь мы видим, что по количественному признаку времени прослушивания наши выборки пересекаются. Кто-то слушает Круга спонтанно по радио, не совершая преступлений, а кто-то нарушает закон, слушая другую музыку или даже будучи глухим. Какие у нас есть граничные условия? ROC-анализ вводит понятия селективности (чувствительности) и специфичности. Чувствительность определяется как способность выявлять все-все интересующие нас точки (в данном примере — преступников), а специфичность — не захватывать ничего ложноположительного (не ставить под подозрение простых обывателей). Мы можем задать некоторую критическую количественную черту, отделяющую одних от других (оранжевая), в пределах от максимальной чувствительности (зеленая) до максимальной специфичности (красная).
Посмотрим на следующую схему:

Смещая значение нашего признака, мы меняем соотношения ложноположительного и ложноотрицательного результатов (площади под кривыми). Точно так же мы можем дать определения Чувствительность = Полож. рез-т/(Полож. рез-т + ложноотриц. рез-т) и Специфичность = Отриц. рез-т/(Отриц. рез-т + ложноположит. рез-т).

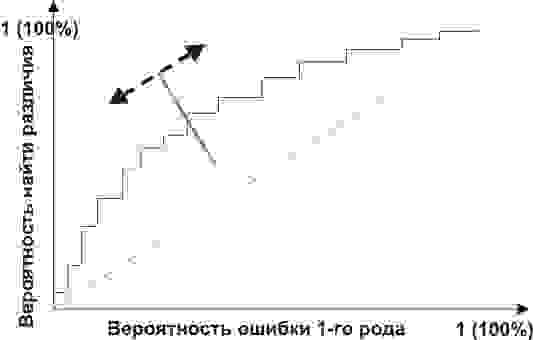
Но главное, мы можем оценить соотношение положительных результатов к ложноположительным на всем отрезке значений нашего количественного признака, что и есть наша искомая ROC-кривая (см. рисунок):

А как нам понять из этого графика, насколько хорош наш признак? Очень просто, посчитать площадь под кривой (AUC, area under curve). Пунктирная линия (0,0; 1,1) означает полное совпадение двух выборок и совершенно бессмысленный критерий (площадь под кривой равна 0,5 от всего квадрата). А вот выпуклость ROC кривой как раз и говорит о совершенстве критерия. Если же нам удастся найти такой критерий, что выборки вообще не будут пересекаться, то площадь под кривой займет весь график. В целом же признак считается хорошим, позволяющим надежно отделить одну выборку от другой, если AUC > 0,75-0,8.

С помощью такого анализа вы можете решать самые разные задачи. Решив, что слишком много домохозяек оказались под подозрением из-за Михаила Круга, а кроме того упущены опасные рецидивисты, слушающие Ноггано, вы можете отвергнуть этот критерий и разработать другой.

Возникнув, как способ обработки радиосигналов и идентификации «свой-чужой» после атаки на Перл-Харбор (отсюда и пошло такое странное название про характеристику приемника), ROC-анализ нашел широкое применение в биомедицинской статистике для анализа, валидации, создания и характеристики панелей биомаркеров и т.д. Он гибок в использовании, если оно основано на грамотной логике. Например, вы можете разработать показания для медицинской диспансеризации пенсионеров-сердечников, применив высокоспецифичный критерий, повысив эффективность выявления болезней сердца и не перегружая врачей лишними пациентами. А во время опасной эпидемии ранее неизвестного вируса вы наоборот, можете придумать высокоселективный критерий, чтобы от вакцинации в прямом смысле не ускользнул ни один чих.

С ошибками обоих родов и их наглядностью в описании валидируемых критериев мы познакомились. Теперь же, двигаясь от этих логических основ, можно разрушить ряд ложных стереотипных описаний результатов. Некоторые неправильные формулировки захватывают наши умы, часто путаясь своими схожими словами и понятиями, а также из-за очень малого внимания, уделяемого неверной интерпретации. Об этом, пожалуй, нужно будет написать отдельно.