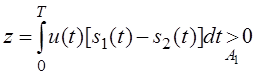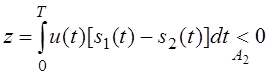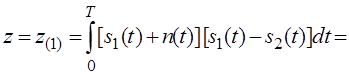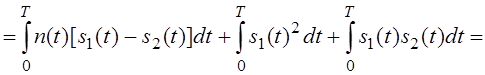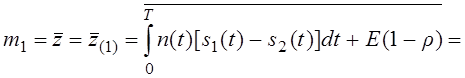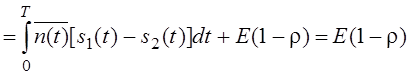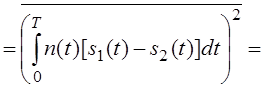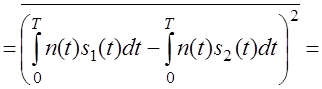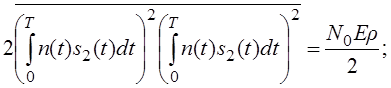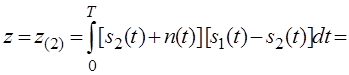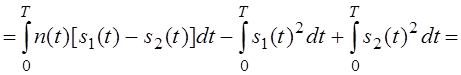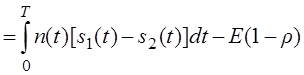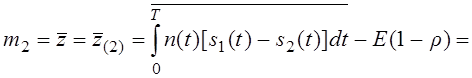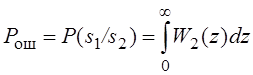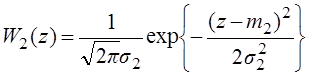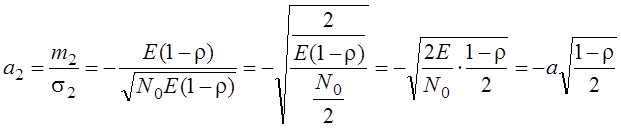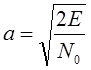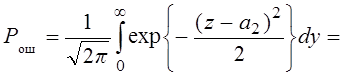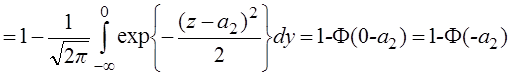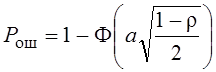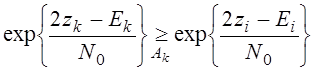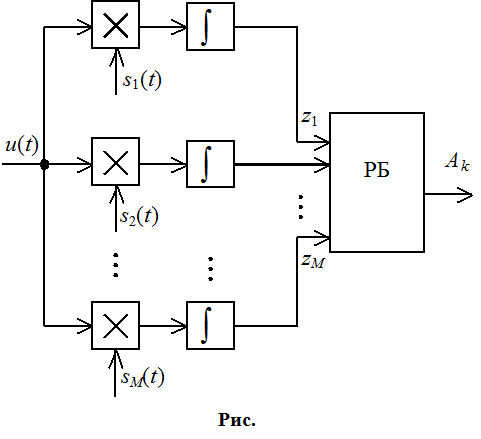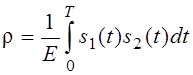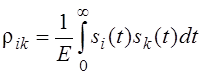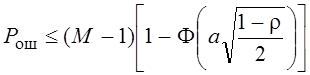Вероятность ошибки различения - Решение и исправление самых разных ошибок на TopOshibok.ru

Полная вероятность ошибки при различении двух сигналов

Страницы работы

Содержание работы

1.5. Полная вероятность ошибки при различении двух сигналов

Рассмотрим
симметричную систему передачи двух сигналов: p₁=p₂=p,
E₁=E₂=E . Пусть начальная фаза известна то есть сигнал
детерминированный.

Где u(t)=s_i(t)+n(t),
i=1,2. Поэтому W(z) – нормальная плотность распределения вероятности.
Каждый сигнал имеет свои характеристики – это

математическое ожидание – m, дисперсия — .
Пусть передан сигнал s₁(t). Тогда:

Учтём, что
коэффициент взаимной корреляции:

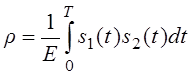
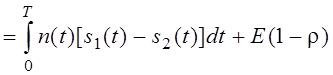
Найдём
математическое ожидание – m₁ (первого
сигнала):

Так как ,
то

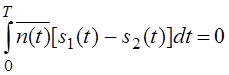
То видно, что найдём
дисперию – (первого
сигнала):

; ;

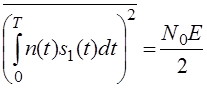
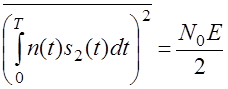
Аналогичную
операцию проделаем для сигнала s₂(t). Пусть передан сигнал s₂(t). Тогда:

Найдём
математическое ожидание – m₂
(второго сигнала):

Проведя
рассуждения аналогично как и с первым сигналом получим:

Найдём
дисперию – (второго
сигнала):

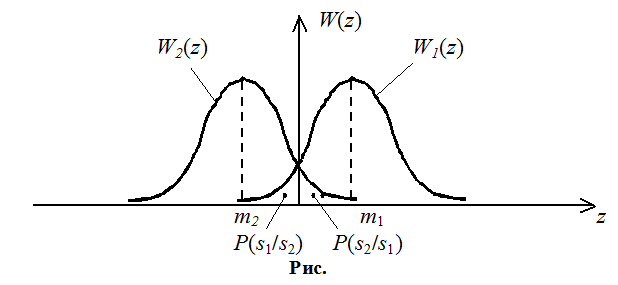
Вероятность решения А₁,
что передан сигнал s₁(t),

при условии что передан сигнал s₂(t).

Вероятность решения А₂,
что передан сигнал s₂(t),

при условии что передан сигнал s₁(t).

p₁=p₂=1/2

Где параметр
:

Пусть r=1 s₁(t)=s₂(t) Р_ош= 1- Ф(0) = 1- 0,5 = 0,5
Одинаковые сигналы различить невозможно. m₁=m₂ =E(1-r)

Пусть r=-1 s₁(t)=-s₂(t) Р_ош= 1- Ф(а)
значит сигналы
оптимальные, сдвиг по фазе между сигналами составляет .

Пусть r=0 тогда сигналы будут ортогональны 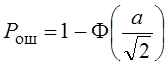. Чтобы добиться
того же эффекта как и у r=-1
то необходимо: , а энергия
сигналов должна быть в два раза больше =3 dB. Эти
сигналы широко распространённые:

— Их сдвиг по фазе

— Фазоманипулитованные сигналы

— Сигналы непрерывные по времени
и по спектру

1.6. Различение М сигналов

С данной
проблемой сталкиваются в радиотелеметрии. В каком-то интервале 0<t<T может быть передан
один из М сигналов: s_i(t).где i=1,2,…,M.

u(t)= s_i(t)+n(t)
i=1,2,…,M.

Будем
искать по критерию: ,
априорные вероятностиp_i=1/М,

где i=1,2,…,M. Данному критерию характерно различае по максимальному
правдоподобию.

Гипотезе Н_i соответствует сигнал s_i(t). Примем решение об различении такого сигнала для
которого функция правдоподобия будет максимальной.

при решении А_к
. Е_i=Е, где i=1,2,…,M.

,где i=1,2,…,M

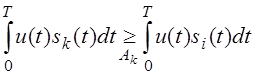
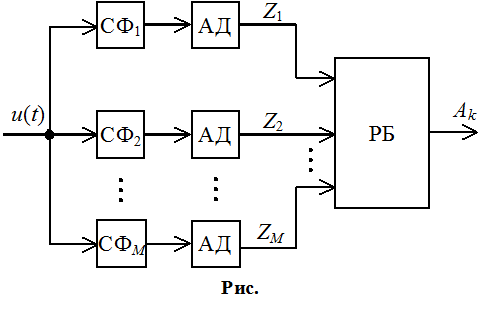
Различие
сигналов проводится с помощью многоканальной схемы:

Различитель:

В каждом из i
– сигналов определяется корреляция s_i(t) в виде корреляционного интеграла. Решение принимается
решающим блоком, в котором корреляционный интеграл наибольший. Схему можно
реализовать на основе СФ:

В каждом канале СФ (его
импульсная характеристика s_i( T-t )
). Число каналов можно сократить на один, если в качестве опорного использовать
разность синалов: s_i(t)—s₁(t) i=2,3,..,M . Тогда будет разность корреляционных интегралов: Если z_i-z₁<0
то передавался сигнал s₁(t) [z_i>z₁].

Если

, где i=2,3,..,M

При передачи
происходит перепутывание. Нужно найти Р_ош:

, где :

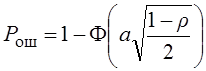
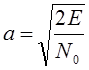
ЕслиM>2, то

считаем, что все сигналы
равнокоррелированные Е_i=Е
и .

Если передаётся сигнал s(t), то его можно
перепутать с остальными (М-1) сигналами. Тогда полная Р_ош может
возрасти в (М-1) раз, но не более.

1.7. Обнаружение М сигналов с неизвестной начальной фазой

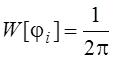
; — cлучайная
величина

Функция провдоподобия
находится усреднением по :

,где i=1,2,..,M

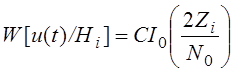
; , гдеквадратурные
составляющиекорреляционного интеграла, которые образуются на выходе
СФ. Правило
максимального правдоподобия требует нахождения максимального значения
функционала правдоподобия при различных i. I₀— функция Бесселя (монотонная
функция, по этому для различения можно использовать огибающую корреляционного
интеграла).

, где i,k=1,2,..,M

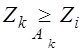
Необходимо
СФ и АД для вычисления огибающей:

Решение
принимается по параметру канала к о передачи сигнала s_k(t), в
котором значение корреляционного интеграла максимально. Характеристика АД –
может быть любой, но одинаковой для всех каналов. Сократить каналы нельзя так
как используются нелинейные преобразователи – АД.

Информация о работе

Уважаемый посетитель!

Чтобы распечатать файл, скачайте его (в формате Word).

Ссылка на скачивание — внизу страницы.

Источник

		88
наименьшей – амплитудная манипуляция с пассивной паузой. Приведённые
зависимости	характеризуют потенциальную	помехоустойчивость. В
реальных	системах	осуществить	идеальный	когерентный	приём
сигналов	не удаётся	из-за влияния	случайных	дестабилизирующих

факторов на фазу и амплитуду радиосигнала. Поэтому реальная помехоустойчивость при рассмотренных условиях (помеха – гауссовский шум) всегда ниже потенциальной.

Рассмотрим радиосигналы со случайными начальными фазами. Такие сигналы можно представить квазигармоническими колебаниями в виде[см. выражение (1.19)]

si (t) = S0i (t) cos(wit +yi (t) +ji ), i =1, 2 ,

где Soi (t ) , yi (t) — функции, определяющие закон модуляции; wi — несущая частота; ji начальная фаза i -го сигнала. Считаем начальные фазы сигналов неизвестными случайными величинами, равномерно распределёнными на интервале [—p ,p ] .

Оптимальное решающее правило различения сигналов характеризуется соотношением (2.81). Чтобы определить отношение правдоподобияl1 (r(t)) , воспользуемся методикой, применённой при решении задачи обнаружения сигнала со случайной начальной фазой(п. 2.3.3). Введём обозначения для корреляционных интегралов:

	T
zic	= òr(t)S0i (t) cos(wit +yi (t))dt ;
	0
	T
zis	= òr(t)S0i (t) sin(wit +yi (t))dt ;
	0
				, i =1, 2 ,	(2.93)
z	= z2	+ z2
i		ic	is

после преобразований, аналогичных описанным в п. 2.3.3, получим

æ E	— E	ö I	(2Z	N	)	.	(2.94)
l1 (r(t)) = exp ç	2	1	÷	0	1	0
N0	I0 (2Z2	N0 )
è	ø

Логарифмируя

выражение (2.94),

можно

оптимальное

различения привести к виду

ln I

(2Z N

) — ln I (2Z

— E

+ ln

P(s )

= h .

)

P(s2 )

< N0

Здесь

E1 ,

E2 —

энергия

сигнала;

I0 (x)

— модифицированная

Бесселя нулевого порядка; h — порог.

Структурные схемы оптимальных различителей сигналов, имеющих случайные начальные фазы, можно реализовать на базе квадратурных корреляционных каналов (рисунок 2.41) или на базе согласованных фильтров с детекторами огибающих(рисунок 2.42). В приведённых схемах различителей используются те же элементы, что и в обнаружителях сигналов со случайными начальными фазами(см. рисунки 2.14, 2.15). Кроме указанных методов построения различителей, используется корреляционнофильтровой, который основан на преобразовании сигнала, фильтрации и детектировании. Входная смесь умножается на сигналы s1‘ (t) и s2‘ (t) , частоты которых сдвинуты относительно входных частот на величину w‘ .

Рисунок 2.42.

Рисунок 2.43.

Рисунок 2.44.

После перемножителей включаются идеальные(с малым затуханием)

колебательные контуры (К),	настроенные	на	частотыw —w‘ ,	i =1, 2	и
						i
выполняющие роль интеграторов, и детекторы огибающих(ДО) (рисунок
2.43).	ДО имеют	нелинейные	характеристики, определяемые	функцией
ln I0 (x) .	Следует	отметить,	что	из	всех	рассмотренных	вариантов

корреляционно-фильтровой приёмник наиболее прост в реализации. Определим вероятность Pe ошибочного приёма. Для этого необходимо

вычислить условные вероятности ошибок Pe1 и Pe 2 . С этой целью определяют совместную плотность вероятности случайных величин zic , zis i =1, 2 , а затем,

по

известному

правилу

переходят

новым

,величинамиспользуя

соотношение

(2.93).

общем

случае

выражение

дляP

оказывается

громоздким. Для

симметричной

системы,

использующей

ортогональные

сигналы ( rs = 0 ),

Pe = 0,5 exp(— q 4) .

(2.96)

В случае АМ с пассивной

паузой показатель

экспоненты

берётся

равным

—q 8 .

Рассчитанные кривые

помехоустойчивости

для

некоторых

систем передачи двоичных сигналов приведены на рисунке2.44. Штриховые

кривые относятся к некогерентному приёму(сигналы со случайными

начальными фазами) и рассчитаны по формуле(2.96), сплошные кривые – к

когерентному

приёму, определяемому

выражением (2.91).

Как

видно

из

сопоставления

кривых,

наибольшей

помехоустойчивостью

обладают

когерентные приёмники ФМ сигналов. При некогерентном приёме

наименьшую

вероятность

ошибки

обеспечивают

системы

ЧМ

сигналами, которые являются практически ортогональными. Благодаря

простоте реализации системы с ЧМ сигналами наиболее часто применяются

на практике.

2.5.3 Различение ансамблей сигналов

В РТС ПИ для передачи информации нередко используют несколько

различных сигналов si (t),

i =1,…, m . При этом на каждом временном интервале

длительностью T

может передаваться один

изm сигналов.

Рассмотрим

оптимальный различитель (по критерию минимума вероятности полной

ошибки)

m детерминированных сигналов si (t) ,

принимаемых на фоне белого

шума n(t) . Входное колебание имеет вид r(t) = si (t) + n(t), t Î[0,T ], i =1,…, m .

Предполагаем, что сигналы имеют одинаковые энергии и равные

априорные вероятности появления P(si ) =1 m . Считаем, что в реализации r(t)

присутствует тот из сигналов, апостериорная вероятность для которого

наибольшая, т.е. принимается решение

о наличии сигналаsi , если для всех

j ¹ i

Pps (si ) ³ Pps (s j ) .

(2.97)

Апостериорная вероятность определяется выражением

Pps (si ) = kP(si )w(r(t) | si ) ,

(2.98)

которое характеризует условную вероятность присутствияi -го сигнала при

наблюдении реализации

смеси r(t)

на

интервале [0,T ] . В Выражение (2.98)

входит

P(si )

—

априорная

вероятность

присутствияi -го

сигнала;

w(r(t) | si ) º wс.пi (r(t))

—

функционал

плотности

вероятности

реализации,

вычисленный

при

условии

наличия

смесиr(t)

сигнала si (t) ; k

—

нормирующий коэффициент.

Рисунок 2.45.

Выполнение условия (2.97) обеспечивает наибольшую вероятность правильного решения для каждой реализации и, следовательно, минимальную полную вероятность ошибки. С помощью уже известной методики можно записать выражение для условной плотности вероятности wс.пi (r) по аналогии

с формулой (2.14),	а	затем перейти к непрерывному наблюдению. В
результате условие (2.97) примет вид
æ		E	2		T	ö
P(si ) exp ç —		i	+			r(t)si (t)dt ÷	³
			N0
è		N0	ò0		ø	(2.99)
			E j
æ				2 T		ö
³ P(s j ) exp ç	—			+				r(t)s j (t)dt ÷.
N0	N0 ò0
è				ø

Это соотношение определяет оптимальный алгоритм различенияm сигналов. При априорно равновероятных сигналах, имеющих равные энергии, алгоритм (2.99) приводится к более простому путём логарифмирования обеих частей неравенства. В результате имеем

T	T
ui = òr(t)si (t)dt ³ òr(t)s j (t)dt = u j .
0	0			схемаm —
Приведённому	алгоритму	соответствует	структурная
канального корреляционного различителя, показанная	на рисунке2.45.

Различитель включает устройство принятия решения(УПР), которое определяет канал с наибольшим значением корреляционного интеграла.

Вместо коррелятора каждый канал можно включать согласованный фильтр, настроенный на соответствующий сигнал из ожидаемого ансамбля. Решение вырабатывается в момент окончания действия . Схемасигнала, представленная на рисунке 2.45, является обобщением рассмотренных схем различения двоичных сигналов. Отметим, что принцип многоканального построения различителя сохраняется и при различенииm сигналов, содержащих случайные параметры.

Вероятность полной ошибки можно вычислить достаточно просто для

ансамбля	равновероятных	ортогональных	сигналов	с	одинаковым
энергиями. Условие ортогональности сигналов записывается в виде

T		ìE,	если	i = j;
òsi	(t)s j
(t)dt = í	если	i ¹ j.
0		î0,

Определим

вначале

условную

совместную плотность

вероятности

w(u1,…, um | si )

гауссовских

случайных величинui , i =1,…, m .

Характеристики

этих случайных величин определяются выражениями:

ìE, если i = j;

< u j >= òsi (t)s j (t)dt = í

î0, если i ¹ j;

< u2j > — < u j >2 = EN0 2 ;

ìEN0 2 , если

i = j;

< (ui — < ui >)(u j — < u j >) >= í

i ¹ j.

î0, если

Зная

условную

плотность

вероятностиw(u1,…, um | si ) , можно

найти

вероятность правильного решения:

Pii

= ò dui ò…-¥òw(u1,…,um | si )du1…dui—1dui+1…dum .

-¥

результате

интегрирования

и заменыu

на x

можно

получить

следующее выражение для Pii :

Pii

ò exp çæ —

(x —

÷öФm—1 (x)dx ,

(2.100)

-¥

где Ф(x) — интеграл вероятности (2.29). Для равновероятных сигналов вероятность правильного приёма каждого из сигналов одинакова.

Полная вероятность ошибки при различении равновероятных сигналов определяется соотношением

Pe = å(1— Pii )P (si =) 1— Pii , P (si )=1m ,

i=1

где вероятность Pii вычисляется по формуле (2.100).

Кривые помехоустойчивости когерентного приёма ортогональных сигналов для значений m , равных 2, 4, 16, 256, приведены на рисунке 2.46.

Рисунок 2.46.

	94
Как видно из рисунка, увеличение числа	каналов m	приводит к
росту вероятности Pe .	Это можно объяснить	увеличением	вероятности
превышения напряжением канала, где действует в момент t = T	только шум,
напряжения канала, в котором действует ожидаемый сигнал и шум.
Каналы приёма в	различителеm ортогональных сигналов,	имеющих

случайные начальные фазы, строятся аналогично рисунку2.42. Выход детектора каждого канала подключается к УПР, где вырабатывается решение.

Оценка

помехоустойчивости

некогерентного

различителя показывает, что

при log2 m > 7

разница между когерентными и некогерентными приёмниками

становится

пренебрежительно

малой. В

пределе

приm ® ¥

полные

вероятности

ошибки Pe для

когерентного

некогерентного

приёмников

совпадают. Верхняя граница для вероятности Pe

определяется соотношением

£ (m —1)(1—Ф

(2.101)

q 2

или с учётом асимптотики функции Ф(

) получается

q 2

£ (m

—1

) exp (—q 4)

(2.102)

p q

где q = 2E N0 — отношение сигнал/шум.

2.5.4 Обнаружение	и	различение	сигналов	с	неизвестными
параметрами
В рассмотренных выше задачах обнаружения и различения сигналов
предполагались	известными	статистические	характеристики	помехи	и
случайных параметров сигнала. Во многих случаях априорные плотности
вероятности	параметров		могут	существенно	отличаться	от	реальн
существующих. При этом качественные показатели приёма ухудшаются по
сравнению с ожидаемыми. Отсутствие или неполнота априорных сведений о
параметрах сигналов и помех приводит к необходимости постановки задачи
приёма сигнала в условиях априорной неопределённости.
Возможны различные подходы к решению указанной задачи. Первый
подход заключается в использовании приближенных априорных плотностей
вероятности, например, равномерной	в ожидаемом	интервале	изменения
параметра. Вид априорного распределения оказывает влияние на переходный
(нестационарный) режим	работы	устройств. В	стационарном	режиме

результаты почти не зависят от вида априорной плотности вероятности неизвестных параметров. Второй подход основан на применении оценок неизвестных параметров, полученных с использованием результатов на всём интервале наблюдения.

С практической точки зрения наиболее интересен третий ,подход предполагающий использование текущих оценок неизвестных параметров и осреднения с учётом текущей апостериорной плотности вероятности. Обобщённая схема оценочно-корреляционного обнаружителя приведена на

рисунке 2.47. Оценка сигнала формируется в блоке оценки сигнала(БОС) на

основе апостериорной плотности вероятности параметров l :

s* (t, l) = ò s(t, l)w(t, l)dl .

-¥

Рисунок 2.47.

Формирование такой оценки сигнала в общем случае сопряжено с большими трудностями, связанными с необходимостью получения текущей

апостериорной

плотности

вероятности

параметров

сигн. Заламетное

упрощение алгоритма

схемы

приема

может

быть

получено

при

замене

оценки

на

* ),

оценка

сигнала s* (t, l )

функциюs (t, l

которой l* —

неизвестных

параметров.

условиях,

когда

отношение

сигнал/шум q >>1,

такая

замена

практически

не

снижает

качества

приёма. Формирование

осуществляется с

помощью генератора сигнала, параметры

функции s (t, l* )

которого изменяются в соответствии с текущими оценками l* (t ) . Эти оценки

вырабатываются с помощью специальных устройств фильтрации.

Особое

место

занимают

задачи

обнаружения

сигналов

нефиксированном времени анализа. В таких задачах используется критерий

последовательного

наблюдения.

При

последовательном

наблюдении

производится

непрерывный

анализ отношения правдоподобия и сравнение

его с двумя порогами: низким

h1 = (1— D)

(1— F )

высоким h2

= D F . Если

отношение

правдоподобия

больше

порогаh ,

принимается

решение

наличии сигнала (цели). Если отношение правдоподобия меньше порогаh1 , принимается решение об отсутствии сигнала(цели). Если отношение правдоподобия находится между высоким и низким порогами, наблюдение продолжается до тех пор, пока не будет принято определенное решение. Последовательный анализ, разработанный А. Вальдом, позволяет независимо

задавать	вероятность ложной	тревогиF и правильного обнаруженияD ,
экономит	среднее время, требуемое для принятия решения, т.е. время
анализа.	Теория показывает,	что процедура последовательного анализа

обеспечивает минимизацию среднего времени, необходимого для принятия решения при заданных вероятностях D и F .

			96
2.6 Обнаружение и	различение	сигналов	при дискретной	и
цифровой обработке
Некоторые особенности цифровой обработки были отмечены при
рассмотрении	накопителей	импульсных		сигналов(см.	п. 2.4.3). В
обеспечении стабильной и точной реализации алгоритмов оптимальной
обработки сигналов цифровые методы являются основным направлением.
Следует отметить, что по мере роста сложности алгоритмов обработки
аппаратурные	затраты	при	использовании	аналоговых	мет
увеличиваются гораздо быстрее, чем при использовании цифровых методов.
Наименьший	рост	затрат	обеспечивается	при	применении	цифровой
аппаратуры на основе программируемой логики (микропроцессоров).

Рисунок 2.48.

Рассмотрим некоторые особенности дискретной и цифровой обработки

на

примере

обнаружения

детерминированного

сигнала. Принимаемая

реализация r(t)

подвергается дискретизации по времени,

результате на

интервале

[0,T ]

наблюдается

конечное

число значений

реализацииr = r(t

)

(рисунок 2.48).

Такое преобразование реализации связано с возможным

использованием

дискретных

устройств. Если

дискретные

выборки

подвергаются квантованию по уровню и преобразованию в цифровую форму,

то

после

аналого-цифрового

преобразователя

включается

цифровое

устройство обработки.

Предположим, что

сигнал s(t)

полностью известен,

неизвестен лишь

факт

его

наличия

в смесиr(t)

шумомn(t) . Этот

шум полагаем

стационарным гауссовским процессом с нулевым средним значением и корреляционной функцией Rп (t,t +t ) = sп2 exp (—a t ), где a — коэффициент,

характеризующий время корреляции (ширину спектра помехи). Наблюдаются значения r(ti ) = ri при ti = iDt, i =1,…, m , причём m = T(Dt ) — число подинтервалов

дискретизации.

Алгоритм оптимального обнаружения можно записать на основании соотношений (2.16), (2.17) в следующем виде:

		wс.п (r0 ,…, rm )	q* =1
ln l (r0	,…, rm ) = ln	>
	ln l0 .	(2.103)
wп (r0 ,…, rm )
		<

q* = 0

Чтобы определить совместные плотности вероятности, входящие в выражение (2.103), введём вспомогательные случайные величины для отсчёта шума n0 ,…, nm : x0 = n0 ; x1 = n1 —g n0 ; …; x i = ni —g ni —1 ;…; xm = nm —g nm—1 , где g = exp (—aDt ) , найдём совместную плотность вероятности этих m гауссовских

случайных величин с нулевыми средними значениями. Введенные случайные величины xi взаимно некоррелированны и имеют дисперсии< ni2 >= sп2 (1—g 2 ) .

С учётом указанного запишем плотность вероятности:

w (x0 ,…,xm ) = (2psп2 )—(m+1) 2 (1—g 2 )—m 2 ´
æ			1		æ	2 2	2	öö
					ç(1—g	)x0	m
exp ç	—				+ åxi	÷÷.
2		2
ç		2sп	(1—g )è			÷
è			i=1	øø

Якобиан преобразования при переходе к переменнымn ,…, n	m	равен
0
единице, поэтому

Рисунок 2.49.

w (n0 ,…, nm ) = (2psп2 )—(m+1) 2 (1—g 2 )—m 2 ´
æ			1		çæ(1—g 2 )n02	m	÷ö	ö	(2.104)
´exp ç	—			+ å(ni —g ni—1 )2	÷.
2		2
ç		2sп (1—g )è		ø	÷
è		i=1	ø

На	основе	выражения(2.104)	запишем	условные	плотности
вероятности,	входящие	в отношение правдоподобия(2.103). В результате
придём к следующему алгоритму обнаружения:
zd = 2	1	2 çæ(1—g		q* =1	h .
2 )r0 s0 + å(ri —g ri—1 )(si —g si—1 )÷ö >
					m
	sп (1—g	)	è	i =1	ø <
						q * = 0

Вероятность ложной тревоги и правильного обнаружения определяются на основе условных плотностей вероятности величиныzd при отсутствии и наличии сигнала в смеси. С учётом того, что величина zd является

результатом линейной комбинации совокупности гауссовских случайных

величин,	в	итоге получим: F = 1—Ф (h d ); D =1—Ф (h d — d ), где	h — порог;
d 2 = m2	s	2	— отношение мощности сигнала на выходе	обнаружителя к
1		0

Источник

3. 3. Оптимальное различение полностью известных сигналов Принятая смесь сигнала и шума Апостериорная вероятность параметра 46

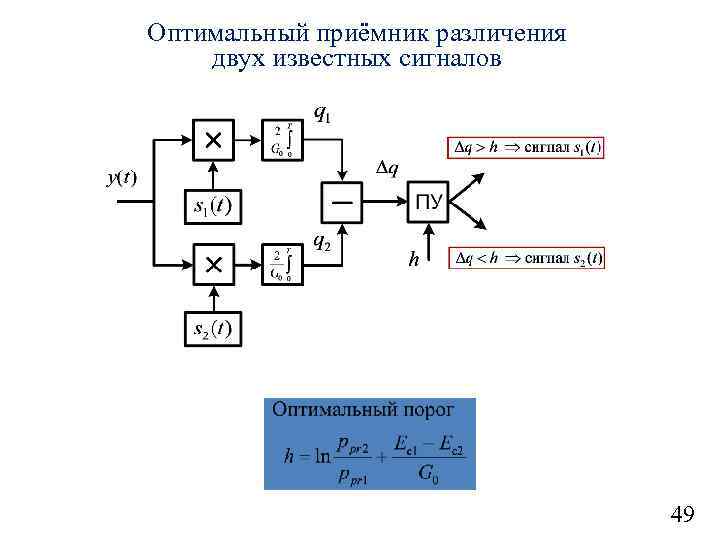
Оптимальное различение двух полностью известных сигналов (1) 47

Оптимальное различение двух полностью известных сигналов (2) Оценка параметра Алгоритм оптимального различения 48

Оптимальный приёмник различения двух известных сигналов 49

Вероятность ошибки при оптимальном различении двух известных сигналов (1) Равновероятные сигналы с одинаковой энергией Вероятность ошибки различения условные вероятности ошибок приёме сигналов 50

Вероятность ошибки при оптимальном различении двух известных сигналов (2) Статистические характеристики напряжения на входе ПУ 51

Вероятность ошибки при оптимальном различении двух известных сигналов (3) Условные плотности вероятности Условное математическое ожидание 52

Вероятность ошибки при оптимальном различении двух известных сигналов (4) 53

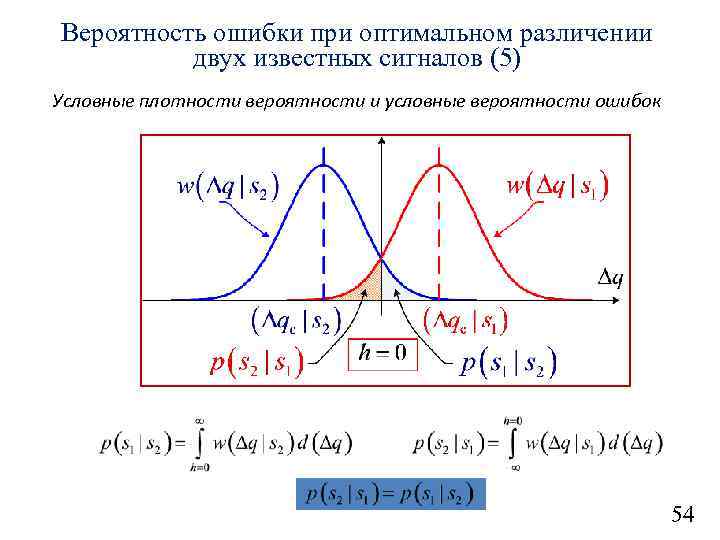
Вероятность ошибки при оптимальном различении двух известных сигналов (5) Условные плотности вероятности и условные вероятности ошибок 54

Вероятность ошибки при оптимальном различении двух известных сигналов (6) Вероятность ошибки различения 55

Вероятность ошибки при оптимальном различении двух известных сигналов (7) Противоположные сигналы: Ортогональные сигналы: Неразличимые сигналы: 56

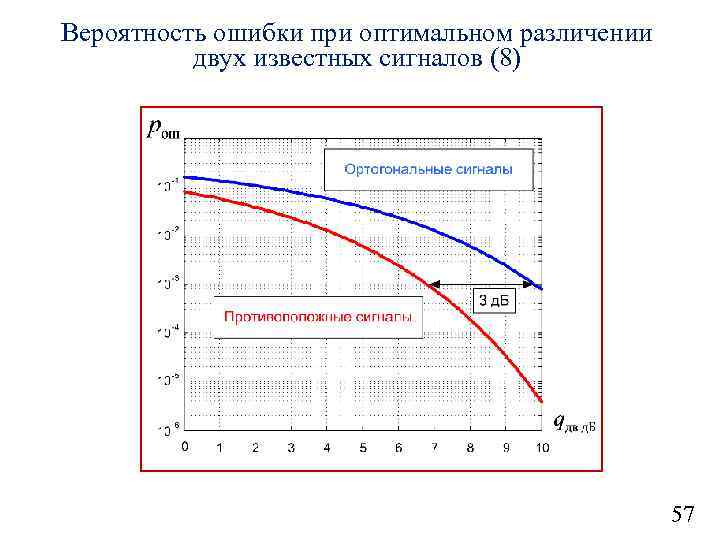
Вероятность ошибки при оптимальном различении двух известных сигналов (8) 57

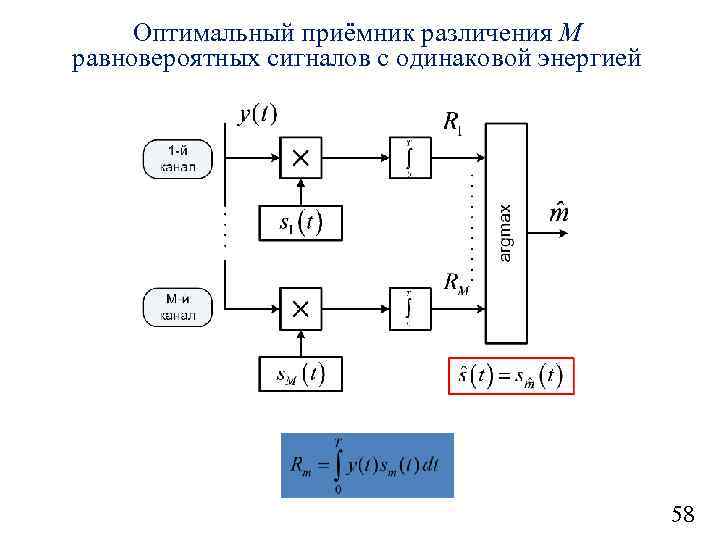
Оптимальный приёмник различения M равновероятных сигналов с одинаковой энергией 58

3. 4. Оптимальная обработка сигналов с использованием согласованных фильтров Импульсная характеристика Передаточная функция АЧХ ФЧХ 59

Характеристики согласованного фильтра (1) Отклик СФ Корреляционный интеграл Отклик СФ на сигнал Пиковое значение отклика 60

Характеристики согласованного фильтра (2) Отношение сигнал-шум на выходе СФ Теорема Парсеваля: Максимальное отношение сигнал-шум на выходе СФ не зависит от вида сигнала и определяется только отношением его энергии к спектральной плотности шума 61

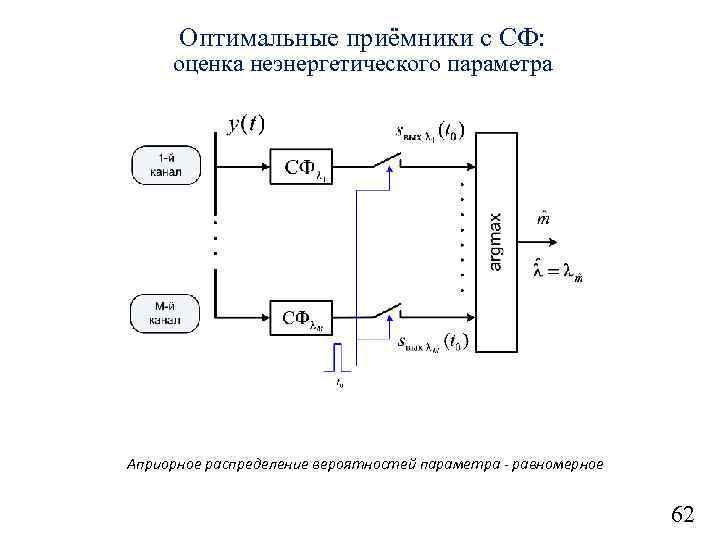
Оптимальные приёмники с СФ: оценка неэнергетического параметра Априорное распределение вероятностей параметра — равномерное 62

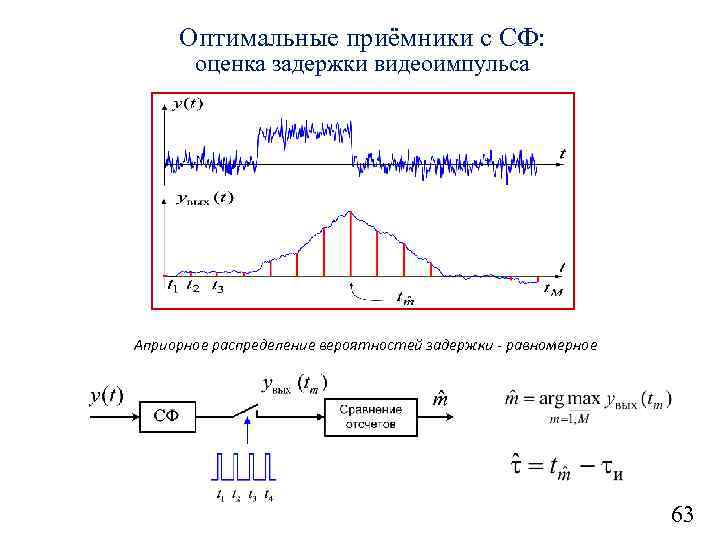
Оптимальные приёмники с СФ: оценка задержки видеоимпульса Априорное распределение вероятностей задержки — равномерное 63

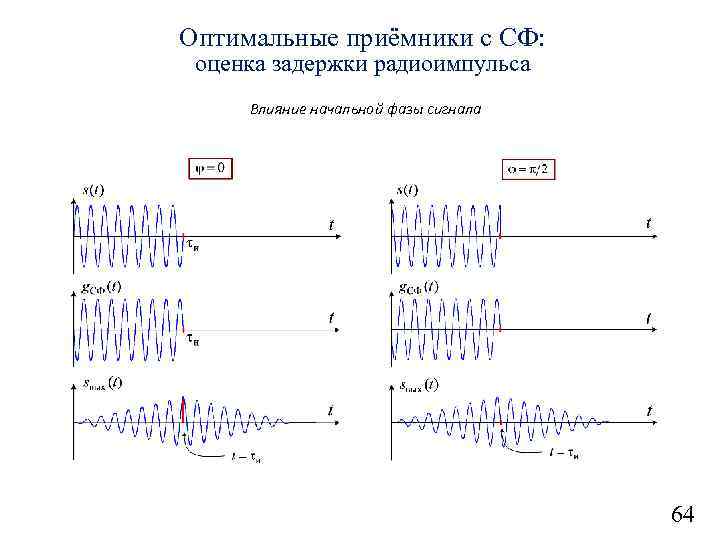
Оптимальные приёмники с СФ: оценка задержки радиоимпульса Влияние начальной фазы сигнала 64

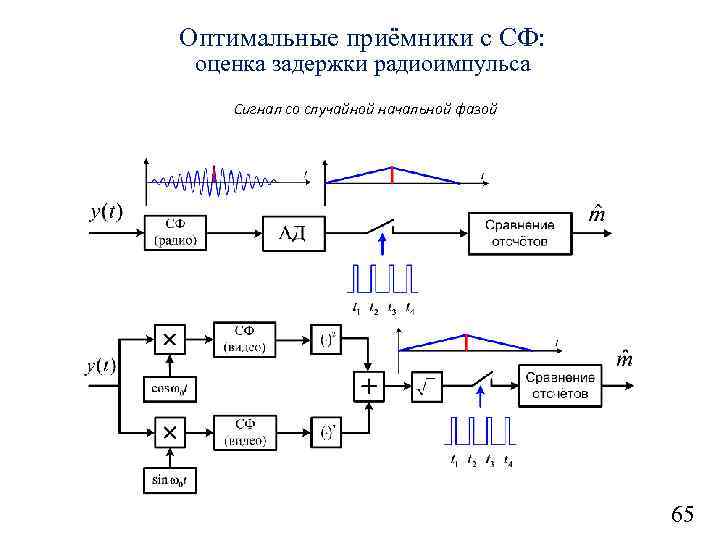
Оптимальные приёмники с СФ: оценка задержки радиоимпульса Сигнал со случайной начальной фазой 65

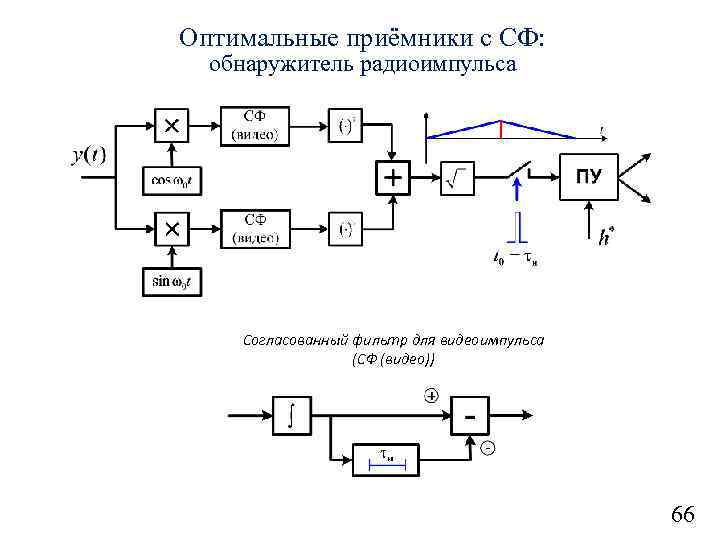
Оптимальные приёмники с СФ: обнаружитель радиоимпульса Согласованный фильтр для видеоимпульса (СФ (видео)) 66

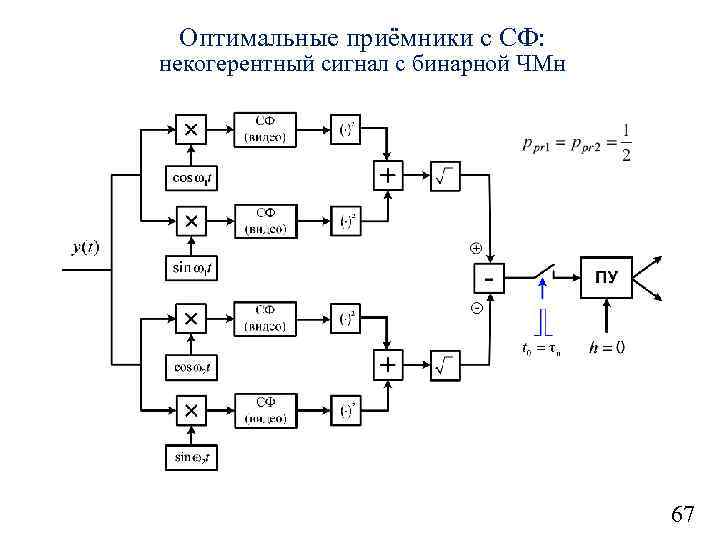
Оптимальные приёмники с СФ: некогерентный сигнал с бинарной ЧМн 67

Источник

Полная вероятность ошибки при различении двух сигналов

Страницы работы

Содержание работы

1.5. Полная вероятность ошибки при различении двух сигналов

1.6. Различение М сигналов

1.7. Обнаружение М сигналов с неизвестной начальной фазой

Похожие материалы

Информация о работе

2.5.3 Различение ансамблей сигналов