Распределение
весов W(С)
= {Ai
,0 ≤ i
≤ n}
кода С, исправляющего
ошибки, определено как совокупность п
+ 1
целых Ai
где
Ai
— количество
кодовых слов Хеммингова веса i.
В следующем ниже
разделе выводится оценка вероятности
необнаруженной
ошибки линейного кода в ДСК. Заметим,
прежде
всего, что вес wt(v)
слова
v
равен Хеммингову расстоянию
до нулевого слова, т.е. wt(v)
=
dH(v,0).
Напомним также, что
Хеммингово расстояние между кодовыми
словами v1
и v2
равно
весу их разности,
где из линейности
кода следует, что v3
С
Вероятность
необнаруженной ошибки PU(C)
равна
вероятности
того, что принятое из канала связи слово
отличается от переданного, но имеет
нулевой синдром, т.е.
Таким образом,
вероятность того, что синдром принятого
ненулевого слова равен нулю, есть
вероятность того, что вектор ошибок
совпадает с одним из ненулевых кодовых
слов.
В ДСК вектор ошибок
веса i
возникает с вероятностью, равной
вероятности того, что i
символов приняты с ошибкой, а
остальные n—i
приняты
правильно. Обозначим вероятность этого
события через Р(е,i).
Тогда
Для
того чтобы возникла необнаруженная
ошибка, вектор ошибок
должен быть ненулевым кодовым словом.
Имеется Аi
кодовых
слов веса i
в кодовом множестве С. Следовательно,
(1.26)
Формула (1.26) дает
точное значение Ри(С)
в ДСК. К
сожалению, для
большинства кодов, имеющих практическое
значение, распределение
весов неизвестно. В таких случаях, можно
использовать тот факт, что число кодовых
слов веса i
меньше (или равно) общего
числа слов веса i
в двоичном векторном пространстве V2.
Следовательно,
справедлива следующая верхняя граница:
(1.27)
Примечание На
самом деле допустима и более сильная
оценка:
В
уравнении еНт
= 0 матрица Н имеет ранг p=dmin-1
и, по меньшей
мере, р неизвестных элементов любого
вектора ошибок е
определяются
однозначно. Следовательно, средняя
вероятность того,
что произвольный вектор ошибок совпадает
с некоторым кодовым словом, не превосходит
2—p.
Формулы
(1.26) и (1.27) полезны в системах, использующих
помехоустойчивое кодирование только
для обнаружения ошибок
таких, как системы связи с обратной
связью и автоматическим
Рис. 6. Точное
значение и верхняя граница вероятности
необнаруженной ошибки для двоичного
линейного (4,2,2) кода в ДСК.
запросом
(ARQ)
на повторную передачу сообщения с
обнаруженными ошибками. Оценки
помехоустойчивости для
случая, когда кодирование используется
для исправления ошибок, выводятся в
следующем ниже разделе.
Пример 8. Для
двоичного линейного (4,2,2) кода из Примера
4 W(C)=(
1,0,1,2,0).
С помощью (1.26) находим
На Рисунке 6 показана
зависимость Ри(С)
вместе с
правой частью границы (1.27).
1.4.2. Границы вероятности ошибки в дск, каналах с абгш и с замираниями
Целью этого раздела
является введение в базовые модели
каналов
связи, которые будут рассматриваться
в пособии, и вывод формул
для оценки помехоустойчивости линейных
кодов. Первым
рассматривается ДСК.
Модель ДСК
Для двоичного
линейного кода процедура декодирования
с помощью стандартной таблицы состоит
в выборе кодового слова, ближайшего
к принятому слову. Ошибка декодирования
возникает всякий раз, когда принятое
слово оказывается вне правильной
области декодирования.
Обозначим Li
число лидеров
смежных классов веса i
в стандартной таблице линейного кода
С. Вероятность
правильного декодирования равна
вероятности того, что вектор ошибок
совпадает с одним из лидеров смежных
классов,
(1.28)
где
это максимальный вес лидера смежного
класса е. Для совершенных кодов
=
t,
и из границы
Хемминга (1.24) следует, что
В общем случае для
двоичных кодов выражение (1.28) дает нижнюю
границу PC(C),
так как существует хотя бы один лидер
смежного класса веса более t.
Вероятность
неправильного декодирования
или вероятность
ошибки декодирования равна
вероятности того, что вектор
ошибок принадлежит дополнению множества
исправляемых
ошибок, т.е. Pe(C)
=
1 — PC(C).
Из
(1.28) получаем,
(1-29)
Наконец, учитывая
обсуждение оценки (1.28), получаем верхнюю
границу
(1.30)
которую можно
записать и в следующем виде
(1.31)
Рис. 7.
Вероятность ошибки декодирования для
двоичного (3,1,3) кода.
Эти границы
удовлетворяются с равенством только
для совершенных кодов (когда и граница
Хемминга удовлетворяется с равенством).
Пример 9. На
Рисунке 7 показана зависимость Ре(С)
по оценке
(1.31) от переходной вероятности ДСК p
для двоичного (совершенного) кода-повторения
(3,1,3).
Модель канала с
АБГШ Пожалуй,
наиболее важной моделью для систем
цифровой связи является модель канала
с аддитивным белым гауссовым шумом
(АБГШ — additive
white
Gaussian
noise
(AWGN)).
В этом разделе выводятся оценки
вероятности ошибки декодирования и
вероятности ошибки на бит для линейных
кодов в канале с АБГШ. Хотя аналогичные
выражения оказываются справедливыми
и для сверточных кодов, они будут выведены
в последующих разделах, вместе с
обсуждением декодирования с «мягким
решением» по алгоритму Витерби. Следующие
ниже результаты содержат необходимые
инструменты для оценки помехоустойчивости
двоичных систем кодирования в гауссовом
канале.
Рассмотрим двоичную
систему передачи сигналов, в которой
кодовые символы {0,1} отображаются в
действительные числа {+1,-1}, соответственно,
как показано на Рисунке 8. В дальнейшем,
вектора имеют размерность п
и обозначение
х
= (x0,
x1,
…, xn-1).
Условная функция плотности вероятности
(ф.п.в.) последовательности у на выходе
канала при условии, что на его входе
передавалась последовательность х,
равна
(1-32)
где
рп(п)
есть ф.п.в.
п статистически
независимых и одинаково распределенных
(i.i.d.)
отсчетов шума, каждый из которых имеет
Гауссово распределение с нулевым средним
и дисперсией, равной N0/2.
Величина
N0
называется
односторонней спектральной плотностью
мощности шума. Легко показать, что
декодирование
по максимуму правдоподобия (м.п.)
линейного кода в таком канале соответствует
выбору последовательности х’, минимизирующей
квадрат
Евклидова расстояния между
принятой последовательностью у
и х’,
т.е.
(1.33)
Следует заметить,
что декодер, использующий (1.33) как
метрику,
называется
декодером с
мягким решением не
зависимо от того, используется или нет
принцип максимума правдоподобия.
Рис. 8.
Система двоичной передачи с кодированием
по каналу с АБГШ.
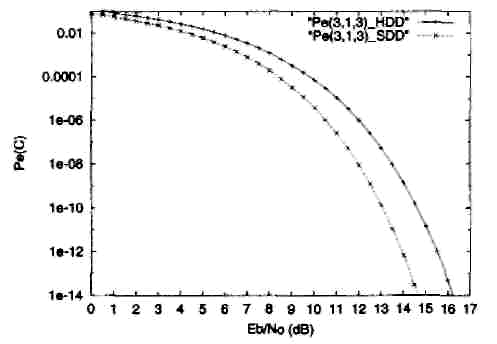
Рис.
9.
Вероятность
ошибки декодирования для жесткого
декодирования (Pt(3,l,3)_HDD) и мягкого
декодирования (Pe(3,l,3)_SDD) двоичного (3,1,3)
кода при передаче двоичных сигналов в
канале с АБГШ.
Вероятность ошибки
для МП декодирования, Ре(С),
равна
вероятности того, что при передаче
последовательности х вектор шума
оказался таким, что принятая
последовательность у = х + n
ближе к другой кодовой последовательности
х»
С, х» ≠ х.
Для линейного кода можно предположить,
что передается нулевое кодовое слово.
Тогда вероятность Ре(С)
может быть
ограничена сверху с помощью границы
объединения и
распределения весов W(C)
следующим
образом:
(1-34)
где R
= k/n
скорость кода, Еь/N0
отношение энергии сигнала на бит к
мощности шума или (SNR
на бит) и Q(x)
определено в (1.2).
На Рисунке 9 показаны
оценки вероятности ошибки для жесткого
декодирования (1.30) и для мягкого
декодирования (1.34) для двоичного (3,1,3)
кода. Декодирование
с жестким решением (или
жесткое
декодирование) означает,
что декодер для ДСК использует выход
двоичного демодулятора. Эквивалентный
ДСК имеет переходную вероятность равную
Заметим, что в
данном частном случае, обе оценки
вероятности ошибки являются точными,
т.е. не оценками сверху, так как используется
совершенный код, содержащий только два
кодовых слова. Рисунок 9 показывает
также, что мягкое декодирование
обеспечивает большую эффективность,
чем жесткое декодирование, в том смысле,
что одинаковое значение Pe(C)
при меньшей
мощности передачи сигналов. Разность
(в дБ) между соответствующими отношениями
SNR
на бит обычно
называют выигрышем
от кодирования.
Показано, что для
вероятности
ошибки на бит,
обозначаемой
Pb(C)
двоичного
систематического
кода при
передаче двоичных сигналов по каналу
с АБГШ, справедлива следующая верхняя
граница:
(1.35)
Эта граница
справедлива только для систематического
кода. Кроме того, систематическое
кодирование минимизирует вероятность
ошибки на бит. Это
означает, что систематическое кодирование
не только желательно, но и оптимально
в рассматриваемом выше смысле.
Пример 10. Рассмотрим
двоичный линейный (6,3,3) код с порождающей
и проверочной матрицами
Рис. 10. Моделирование
и границы объединения для двоичного
(6,3,3) кода при передаче двоичных сигналов
в канале с АБГШ.
соответственно.
Распределение весов этого кода равно
W(C)
= {1,0,0,4,3,0,0},
которое может быть проверено
непосредственным вычислением для всех
кодовых слов v
= (u,vp):
|
u |
vp |
|
000 |
000 |
|
001 |
101 |
|
010 |
011 |
|
011 |
110 |
|
100 |
110 |
|
101 |
011 |
|
110 |
101 |
|
111 |
000 |
В этом частном
случае, МП декодирование состоит в
вычислении квадрата Евклидова расстояния
по формуле (1.33) между принятым словом и
каждым из восьми возможных кодовых
слов. В качестве решения выбирается
слово с наименьшим расстоянием. На
Рисунке 10 показаны результаты моделирования
и границы объединения для жесткого и
мягкого декодирования по максимуму
правдоподобия для передачи двоичных
сигналов в канале с АБГШ.
Модель канала с
общими Релеевскими замираниями.
Другой важной
моделью канала является модель с общими
Релеевскими замираниями. Замирания
сигналов происходят в системах
беспроводной связи в виде меняющихся
во времени искажений передаваемых
сигналов. В этом пособии рассматриваются
только общие
замирания (flat
fading).
Термин
«общие» (или «гладкие») означает, что
канал не является частотно-селективным,
т.е. передаточная функция канала в полосе
пропускания равна константе.
Модель канала с
покомпонентными мультипликативными
искажениями показана на Рисунке 11.
Мультипликативные искажения представлены
случайным вектором α размерности п,
компоненты
которого являются независимыми, одинаково
распределенными случайными величинами
(i.i.d.),
имеющими
плотность вероятности Релея,
(1.36)
При такой плотности
вероятностей множителей среднее значение
отношения сигнал-шум (SNR)
на бит равно
Eb/N0
(как и для
АБГШ без замираний), так как второй
момент коэффициентов замирания равен
E{a2i}
= 1.

Рис. 11 Передача
двоичных кодированных сообщений в
канале с гладкими Релеевскими замираниями
Рис. 12. Двоичная
передача по Релеевскому каналу. Результаты
моделирования
(SIM),
оценка границы объединения методом
Монте-Карло
(Ре(3,1,3)_МС)
и граница Чернова (Ре(3,1,3)_ЕХР)
для двоичного (3,1,3) кода.
Оценки
эффективности двоичных линейных кодов
в канале
с общими Релеевскими замираниями
находятся из оценок условной вероятности
ошибки декодирования, Ре(С\α),
или
условной вероятности ошибки на бит,
Рь(С\α).
Безусловные
вероятности ошибки находятся
интегрированием условных вероятностей
с весами αi,
имеющими плотность вероятности
(1.36).
Условные
вероятности ошибки идентичны безусловным
в канале
с АБГШ. Существенное различие имеется
только в аргументах функции Q(x),
которые
теперь взвешены на коэффициенты
замирания αi,.
Рассматривая передачу двоичных
кодированных сообщений при отсутствии
(внешней) информации
о состоянии
канала, находим,
что
(1.37)
где
(1.38)
Окончательно,
вероятность ошибки декодирования при
передаче
двоичных сигналов в канале с Релеевскими
замираниями
получается как математическое ожидание
относительно
случайной величины ∆w,
(1.39)
Известны несколько
методов оценивания выражения (1.39). Один
из них состоит в применении метода
Монте-Карло
численного интегрирования с
использованием следующей аппроксимации:
(1.40)
где
равно сумме квадратов w
независимых
одинаково распределенных
(i.i.d.)
случайных величин с Релеевской плотностью
вероятностей (1.38), выданных на
-ом
обращении к
компьютерной программе генерации, и N
достаточно большое целое число, зависящее
от ожидаемого диапазона значений
Ре(С).
Хорошим
правилом, которое следует запомнить,
является
следующее: величина N должна быть, по
меньшей мере, в 100 раз больше обратной
величины Pe(C).
Другим
методом является экспоненциальная
аппроксимация
сверху функции Q,
которая позволяет проинтегрировать
выражение или воспользоваться границей
Чернова.
Этот
подход хоть и несколько ухудшает
результат, зато
дает замкнутое выражение:
(1.41)
Рис. 13.
Двоичная передача по Релеевскому каналу.
Результаты моделирования (SIM_(6,3,3)),°neHKa
границы объединения методом
Монте-Карло (Ре(6,3,3)_МС)
и граница Чернова (Ре(6,3,3)_ЕХР)
для двоичного (6,3,3) кода.
Граница (1.41) полезна
в случаях, когда достаточно знать первое
приближение в оценке помехоустойчивости
кода.
Пример
11. На
Рисунке 12 показаны результаты компьютерного
моделирования двоичного (3,1,3) кода в
канале с
общими Релеевскими замираниями. Заметим,
что интегрирование методом Монте-Карло
дает точное значение помехоустойчивости
кода, так как граница (1.40) содержит только
один член. Заметим также, что граница
Чернова дает результат,
смещенный почти на 2дБ, относительно
результата
моделирования при отношении сигнал-шум
на бит Еь/N0>18
дБ,
Пример 12. На
Рисунке 13 показаны результаты компьютерного
моделирования двоичного (6,3,3) кода из
примера 10 в
Релеевском канале. В этом случае граница
объединения теряет точность при малых
значениях Eb/N0
из-за
присутствия дополнительных
членов в формуле (1.40). Как и раньше,
граница Чернова
проигрывает около 2 дБ в отношении сигнал
— шум на бит при Eb/N0>
18
дБ.
Рис. 14. Общая
структура жесткого декодера для линейных
блоковых кодов для ДСК.
Вопросы для
самоконтроля:
Если бы можно было применить идеальный код, обеспечивающий заданную высокук> верность при скорости передачи, равной пропускной способности канала, то никакого выигрыша по скорости передачи по сравнению с примитивным кодированием мы бы не получили. Но даже отсутствие проигрыша в скорости возможно голько в асимптотическом смысле, ко~да длина кодируемого блока стремится к бесконечности, как видно, например, для случайного кодирования из (2.47). Что же касается реально применимых кодов, то для них всегда о 1аИ >Че — — ‘(С,т. е. скорость передачи меньше пропускной л способности и, следовательно, меньше скорости, достижимой при примитивном кодировании, без исправления или обнаружения ошибок.
Таким образом, повышение верности связано с некоторой потерей скорости передачи информации не только по сравнению с технической скоростью, но и по сравнению с информационной скоростью при примитивном кодировании. Как правило,эта потеря тем больше, чем выше требования к верности. Здесь можно провести несколько вольную, но поучительную анало ию с добычей ценного металла из руды. Никакой технологический процесс пе позволит получить больше металла, чем его первоначальное содержание в руде — любой реальный процесс приводит к некоторым потерям, которые обычно тем значительнсе, чем выше требования к чистоте металла.
Точно так же корректирующий код ие увеличивает количества ннформа- 126 цпн, содержащегося в принятом сигнале, а только по- зволяет «очистить ее от примесей» ценой некоторых по- терь, Для того чтобы оценить качество кода с точки зре- ния скорости передачи информации, можно воспользо- ваться его избыточностью. Действительно, скорость пе- редачи можно определить (пренебрегая неисправленны- ми при декодировании ошибками) как Г (х, х’) = о — ‘, И яе л или согласно (2.23) 7′(х, х’) =.о(1 — г„) 1о9>п. Таким образом, при заданном дискретном канале (т.
е. при заданном о) преимущество и скорости передачи информации имеют коды с меньшей избыточностью. Поэтому выбор корректирующего кода целесообразно производить следующим образом. Прежде всего отбираются коды, позволяющие в заданном канале обеспечить требуемую верность передачи, а также удовлетворяющие другим технико-экономическим требованиям, в частности коды с допустимой сложностью кодирования н декодирования.
Затем из них отбирается код с наименьшей избыточностью. При таком подходе необходимо уметь оценивать верность передачи информации и формулировать требования к ней. К сожалению, в этом вопросе нет установившейся точки зрения и различные авторы пользуются разными параметрами для оценки верности. Довольно часто, особенно в теоретических работах, при рассмотрении блочных кодов мерой верности считают вероятность правн.льного декодирования блока (кодовой комбинации). Мы также пользовались этой мерой в 9 2.5 при отыскании асимптотических значений прн увеличении длины блока. Однако для сравнения различных кодов с различной длиной кодовой комбинации и различной избыточностью такая мера не адекватна, не говоря уж о том, что она не применима для непрерывных кодов.
Так, например, если в одном коде блок содержит 5> информационных символов и правильно декодируется с вероятностью 0,999, а в другом коде блок содержит 200 информационных символов и пра- 127 вильно декодпруется (в том же канале) с вероятностью 0,99, то было бы опрометчиво считать, что первый код обеспечивает более высокую верность, нежели второй. Действительно, если нужно передать сообщение, состоящее, скажем, нз 400 информационных символов, то при использовании первого кода это сообщение заимет 80 кодовых комбинаций и вероятность того, что сообщение будет принято правильно: равна 0,999 Если жс применить второй код, то все сообщение уложится в 2 кодовые комбинации и будет принято верно с вероятностью 0,99’= 0,98.
Таким образом, вероятность правильно припять сообщение при втором оде к бал ыпс, чем при первом, хотя вероятность правильного декодирования кодовой комбинации для первого кода выше, чем для второго. Более разумной мерой верности, с которой часто п иходится встречаться (например, (24)), является вероятность правильного приема символа после р пр пения ошибок (или после представления декодирован- ного сообщения примитивным кодом). Обычно удобнее пользоваться не вероятностью правильного приема после исправления, а ее дополнением до единицы — вероятностью неисправленной ошибки. Такая мера позволяет сравнивать коды с различной длиной кодовых комбинаций и даже непрерывные коды. Она достаточно объективна и вполне пригодна для таких систем связи, в которых некоторое количество неисправленных ошибок в принятом сообщении допустимо, но желательно, чтобы их было меньше.
Чаще всего это происходит, когда само сообщение имеет нскоторую избыточность и отдельные ошибки не искажают его смысла и могут быть исправлены получателем. Примером служит телеграфная связь при передаче осмысленного текста. Тем не менее вероятность неисправленной ошибки не является пригодной мерой верности в тех случаях, когда ошибки в принятом сообщении вовсе недопустимы, т.
е. когд . к гда одна ошибка в такой же мере делает сооб- полощсние непригодным, как и тысяча ошибок. Такое о жение имеет место в некоторых системах передачи данных для пифровых вычислительных машин. * Для простоты предполагается, что канал постоянный я ошибке при декодирования отдельных ходовых комбинаций валяются независимыми сабытаяма. 123 Для иллюстрации сказанного вернемся к рассмотренному выше примеру и вычислим вероятность неисправленной ошибки для двух конкурирующих кодов.
Предположим при этом, что по структуре кодов в случае ошибочного декодирования кодовой комбинации в среднем половина информационных символов оказывается искаженной «:. Прн первом коде в среднем на 1000 комбинаций (т. е, на 5000 информационных символов) ошибочно декодируется одна комбинация. Это значит, что в сродном на 5000 информационных символов приходится 2,5 неисправленной ошибки, т.
е. вероятность неисправленной ошибки равна 5 ° !О’. Для второго кода ошибочно декодпруется одна комбинация нз стг, т. е. на 20000 информационных символов приходится 100 неисправленных, или вероятность нсисправленной ошибки равна 5 10-‘. Таким образом, вероятность неисправленной ошибки для второго кода в 10 раз больше, чем для первого, тогда как вероятность ошибочного приема сообщения из 400 информационнь>х символов, как было показано выше, для первого кода почти втрое больше, чем для второго. Это кажущееся противоречие объясняется тем, что при использовании второго кода неисправленные ошибки группируются более тесно, чем для первого.
Поэтому, хотя во втором коде вероятность неисправленной ошибки больше, чем в первом, все же имеется больше шансов избе>кать образования пачки ошибок при передаче одного сообщения. Заметим еще, если наше сообщение, содер>кащее 400 информационных символов, декодировано неверно, то прп использовании псрвого кода оно будет, вероятнее всего, содержать 2 — 3 ошибоч>ш принятых символа, тогда как при втором коде количество ошибочно принятых символов будет близко к 100. Отсюда можно заключить, что при телеграфной передаче осмысленного текста лучше применять первый код, тогда как в тех системах связи, где любые ошибки одинаково недопустимы, второй код имеет явное преимущество.
ь Эта действительна имеет место для двоичных заеадастантных кодов, т. е. таких, а которых хеммингоео расстояяае между ла>бой парой комбинаций одинаково. Приближенно зто верно и для маетах других колов. 9 — 2447 129 Заметим, что именно в тех системах, где любые ошибки декодирования одинаково недопустимы, чаще всего используются корректирующие коды. Поэтому именно для них важно иметь меру верности. Но ни вероятность правильного декодирования кодовой комбинации, ни вероятность неисправленной ошибки в информационных символах для таких систем, как мы видели, не могут слузкить такой мерой.
В предыдущем примере была использована вероятность правильного декодирования сообщения, содержащего 400 информационных символов. Но цифра 400 была выбрана совершенно произвольно. Если передавать более длинное сообщение, то вероятность принять его безошибочно, очевидно, уменьшится. Легко понять, что при любом блочном коде в канале с шумами с увеличением длины передаваемого сообщения вероятность его безошибочного декодирования стремится к нулю. Так, если вероятность правильного декодирования кодовой комбинации равна (;1(п), а сообщение содержит г кодовых комбинаций, то вероятность принять все сообщение без ошибок Равна (2.62) (;1,(Г() =[(,1(П))г.
В этом обозначении ! — количество информации (в двоичных единицах), содержащееся в кодовой комбинации (1=!паз!Уо), а и’ вЂ” количество информации в сообщении. Предполагается, что избыточность источника устранена при кодировании. Тзн кан орн любом конечном л Я(н) <1, то е увеличением г Я,(л) стремится н нул|о. Тем не менее орн любых конечных и н г существует положительная вероятность безошибочного нрнемз сообщения.
Применительно н любой системе связи можно указать такие значения л’ н Юй(гй, я которых систему можно считать нрзктнчеекн безупречной. Тзн, нзнрнмер, если зелнчннн л’ определяется колнчеетзом информация, передаваемой в теченне суток, з Яе(г(1 = 1 — 10 ‘, то зто значит, что н среднем однц рзз зз 300 лет настудят такой день, когда сообщение неледстяне действия помех будет принято ненрзяяльно. Лйожно смело утверждать, что почта для любых применений такая система связи может считаться безупречной. Ззметнм, что врннцнпнзльных препятствий для достнженяя указанной верности (еслн пропускнзя способность канала достзточнз) нет, з техончеснне трудноезн отнюдь не больше, чем трудность получения зпнзрнтурной нздежноетн, обеспечивающей время наработкн нз один отказ порядке 300 лет.
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5
Я хочу сравнить надежность различных RAID-систем с накопителями (URE/bit = 1e-14) или корпоративными (URE/bit = 1e-15). Формула для определения вероятности успеха восстановления (без учета механических проблем, которые я буду принимать во внимание позже) проста:
error_probability = 1 — (1-per_bit_error_rate)^ bit_read
Важно помнить, что это вероятность получить по крайней мере один URE, а не только один.
Предположим, мы хотим использовать 6 ТБ свободного места. Мы можем получить это с:
-
RAID1 с 1+1 дисками по 6 ТБ каждый. Во время восстановления мы читаем 1 диск по 6 ТБ, и риск составляет: 1-(1-1e-14) ^(6e12 *
= 38% для потребителя или 4,7% для корпоративных накопителей.
-
RAID10 с 2+2 дисками по 3 ТБ каждый. Во время восстановления мы читаем только 1 диск объемом 3 ТБ (тот, который связан с неисправным!) и риск ниже: 1-(1-1e-14) ^(3e12 *
= 21% для потребителя или 2,4% для корпоративных накопителей.
-
RAID5/RAID Z1 с 2+1 дисками по 3 ТБ каждый. Во время восстановления мы читаем 2 диска по 3 ТБ каждый, и риск составляет: 1-(1-1e-14) ^(2 * 3e12 *
= 38% для потребительских или 4,7% или корпоративных дисков.
-
RAID5/RAID Z1 с 3+1 дисками по 2 ТБ каждый (часто используется пользователями продуктов SOHO, таких как Synologys). Во время восстановления мы читаем 3 диска по 2 ТБ каждый, и риск составляет: 1-(1-1e-14) ^(3 * 2e12 *
= 38% для потребительских или 4,7% или корпоративных дисков.
Вычислить погрешность для допуска на один диск легко, сложнее рассчитать вероятность для систем, допускающих отказы нескольких дисков (RAID6/Z2, RAIDZ3).
Если для восстановления используется только первый диск, а второй считывается снова с начала в случае или URE, то вероятность ошибки равна той, которая рассчитана с квадратным корнем (14,5% для потребителя RAID5 2+1, 4,5% для потребителя RAID1 1+2). Тем не менее, я полагаю (по крайней мере, в ZFS, которая имеет полные контрольные суммы!) что второй диск четности / доступный диск доступен только для чтения там, где это необходимо, а это означает, что требуется всего несколько секторов: сколько URE может произойти на первом диске? не так много, в противном случае вероятность ошибки для систем с допуском одного диска взлетела бы даже больше, чем я рассчитывал
Если я прав, второй диск четности практически снизит риск до крайне низких значений.
Помимо этого, важно иметь в виду, что производители увеличивают вероятность URE для накопителей потребительского класса по маркетинговым причинам (продают больше накопителей корпоративного класса), поэтому ожидается, что даже жесткие диски потребительского класса достигнут 1E-15 URE/ бит считывания ,
Некоторые данные: http://www.high-rely.com/hr_66/blog/why-raid-5-stops-working-in-2009-not/
Поэтому значения, которые я указал в скобках (диски предприятия), реально применимы и к дискам потребителя. А у реальных корпоративных накопителей надежность еще выше (URE/ бит = 1e-16).
Что касается вероятности механических сбоев, они пропорциональны количеству дисков и пропорционально времени, необходимому для восстановления.




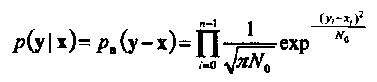











 = 38% для потребителя или 4,7% для корпоративных накопителей.
= 38% для потребителя или 4,7% для корпоративных накопителей.