
13
период выходной последовательности всегда8 в два раза больше периода входной!
Расчет вероятности битовой ошибки
Перейдем теперь к расчету вероятности ошибки на выходе дифференциального декодера. Вероятность ошибки на входе декодера считается заданной, и определяется каналом передачи информации.
Пусть ошибки в канале независимые и происходят с вероятностью p . Тогда дифференциальный кодер, канал и декодер в эквиваленте дадут канал с памятью, т. е. такой канал, ошибки в котором — зависимые. Канал с памятью может быть описан с помощью следующей модели, рис. 2.
Рис. 2 Модель канала с памятью
Такой канал полностью вероятностей
Здесь буквой «П» обозначено событие «правильный прием», буквой «О» — «ошибочный прием». Обозначение PП/О означает «вероятность правильного приема при условии, что предыдущий прием был ошибочным». Эта вероятность является условной. Зависимость вероятности от условия является признаком наличия памяти в канале. определяется матрицей условных (переходных)
|
P= |
PП/П |
PП/О |
. |
(9) |
|
PО/О) |
||||
|
(PО/П |
Обратите внимание, что буквам «П» и «О» слева соответствует момент времени tn−1 , а таким же буквам справа — tn . Время — это неотъемлемая черта каналов с памятью. Говорят, «канал помнит несколько предыдущих состояний», и эти состояния влияют на вероятность текущего состояния.
Систему «дифференциальный кодер, канал и декодер» удобно рассматривать как некоторый цифровой автомат, на выходе которого в каждый момент времени либо правильный прием, либо — ошибочный; жизнь такого автомата описывается некоторой последовательностью букв
8 За исключением случая когда числитель Y (z) сокращает знаменатель K (z ) , — в этом случае период не меняется
(матрице переходных вероятностей)
(т. е. в канале с независимыми
14
… О П П П П П О О П П П …
Цель нашего повествования — вычислить вероятность ошибки на выходе дифференциального декодера, которая в рамках принятых обозначений
|
соответствует событию «О» и обозначается |
как PО |
. Эта вероятность будет |
|
зависеть от вероятностей перехода PX/X , |
которых, |
по сути, всего две, т. к. |
|
оставшиеся две являются дополнениями до единицы. |
Всякая вероятность есть предельная величина, определяемая по бесконечному количеству событий, поэтому чтобы определить PО требуется выписать всю «линию жизни» автомата и подсчитать долю букв «О» относительно общего количества букв; практически это сделать невозможно, а вот в уме — возможно, чем мы и займемся.
Предположим, что автомат начал жить, и его жизнь кратна дням, т. е. каждый день выпадает буква, «О» или «П». Какова вероятность того, что в первый день жизни произойдет ошибочный прием «О»? Эту вероятность логично приравнять к вероятности ошибки в канале без памяти
ошибками), PО 1 =p . Во второй день могут выпасть буквы либо «О», либо «П». Соответствующие вероятности вычисляются вполне однозначно по матрице канала
(PPПО)2 =(PPП/ПО/П PPП/ОО/О)(PPПО)1 ,
и так далее. Логика данного уравнения основана на формуле умножения и сложения вероятностей.
Упражнение: распишите матричное уравнение в виде системы линейных алгебраических уравнений, и поразмыслите над смыслом умножения и сложения вероятностей.
Пусть теперь уже прошло очень много дней жизни автомата… В этом случае вероятности PО n и PП n должны сходиться к искомым безусловным вероятностям PО и PП
|
PП n+1 ≈ PП n |
, |
lim |
PП n = PП |
. |
(10) |
|
|
(PО) |
(PО) |
n→∞ |
(PО) (PО) |
Тогда справедливо предельное равенство

15
(PPПО)=(PPП/ПО/П PPП/ОО/О)(PPПО) ,
из которого однозначно определяются искомые вероятности
|
PО= |
PО/П |
, |
PП=1−PО= |
PП/О |
. |
(11) |
|
|
PП/О +PО/П |
PО/П+PП/О |
||||||
|
Остается понять как |
переходные вероятности |
зависят |
от вероятности |
ошибки p в канале без памяти, и цель данного повествования будет достигнута.
Предположим для наглядности, что передаются одни нули, тогда единицы будут указывать на ошибки Рассмотрим все возможные комбинации канальных ошибок на входе дифференциального декодера. Разделим рассмотрение на четыре части, согласно матрице переходных вероятностей (9).
I. Правильный прием в предыдущем и текущем битах, PП/П :
1 1 1, декодируем как 0 0,
0 0 0, декодируем как 0 0,
(1 + 1 = 0, 1 + 1 = 0),
(0 + 0 = 0, 0 + 0 = 0).
Вероятность этого события равна PП/П=p2 +(1−p)2 .
Замечание: здесь и далее первый бит (вспомогательный), который не выделен жирным шрифтом, не влияет на вероятность, потому что перебираются все его возможные значения, 0 и 1; следующие два бита полностью определяются значением вспомогательного и поставленным ограничивающим условием.
II. Ошибочный прием в предыдущем бите и правильный — в текущем, PП/О : 0 1 1, декодируем как 1 0, (0 + 1 = 1, 1 + 1 = 0), 1 0 0, декодируем как 1 0, (1 + 0 = 1, 0 + 0 = 0).
Вероятность этого события равна PП/О=p2 +(1−p)2 . III.Ошибочный прием в предыдущем и текущем битах, PО/О :
0 1 0, декодируем как 1 1, (0 + 1 = 1, 1 + 0 = 1), 1 0 1, декодируем как 1 1, (1 + 0 = 1, 0 + 1 = 1).
Вероятность этого события равна PО/О= p(1−p)+(1−p) p=2 p(1− p) .
16
IV.Правильный прием в предыдущем и ошибочный — в текущем, PО/П : 0 0 1, декодируем как 0 1, (0 + 0 = 0, 0 + 1 = 1), 1 1 0, декодируем как 0 1, (1 + 1 = 0, 1 + 0 = 1).
|
Вероятность этого события равна |
PО/П=p(1−p)+(1− p) p=2 p(1−p) . |
||
|
Подставим найденные переходные вероятности в (11) и получим |
|||
|
окончательный результат |
|||
|
PО=2 p(1−p) , |
PП= p2 +(1−p)2 . |
(12) |
|
|
Таким образом, вероятность ошибки на выходе дифференциального |
|||
|
декодера почти в два раза превышает канальную вероятность ошибки p |
; этот |
||
|
результат тем точнее, чем лучше |
канал, |
т. е. чем меньше p . Данный |
факт |
объясняется достаточно просто: при малых p ошибки происходят изредка и, в основном, по одиночке, а из логики дифференциального декодирования следует, что одна одиночная ошибка после декодирования трансформируется в две.
Любопытно также отметить, что если в канале вероятность ошибки равна ½, то после дифференциального декодирования вероятность ошибки остается той же!
4.7.1. Вероятность появления ошибочного бита при когерентном обнаружении сигнала BPSK
4.7.2. Вероятность появления ошибочного бита при когерентном обнаружении сигнала в дифференциальной модуляции BPSK
4.7.3. Вероятность появления ошибочного бита при когерентном обнаружении сигнала в бинарной ортогональной модуляции FSK
4.7.4. Вероятность появления ошибочного бита при некогерентном обнаружении сигнала в бинарной ортогональной модуляции FSK
4.7.5. Вероятность появления ошибочного бита для бинарной модуляции DPSK
4.7.6. Вероятность ошибки для различных модуляций
4.7.1. Вероятность появления ошибочного бита при когерентном обнаружении сигнала BPSK
Важной мерой производительности, используемой для сравнения цифровых схем модуляции, является вероятность ошибки, РЕ Для коррелятора или согласованного фильтра вычисление РЕ можно представить геометрически (см. рис. 4.6). Расчет РЕ включает нахождение вероятности того, что при данном векторе переданного сигнала, скажем si вектор шума n выведет сигнал из области 1. Вероятность принятия детектором неверного решения называется вероятностью символьной ошибки, рE. Несмотря на то что решения принимаются на символьном уровне, производительность системы часто удобнее задавать через вероятность битовой ошибки (Ps). Связь РВ и РЕ рассмотрена в разделе 4.9.3 для ортогональной передачи сигналов и в разделе 4.9.4 для многофазной передачи сигналов.
Для удобства изложения в данном разделе мы ограничимся когерентным обнаружением сигналов BPSK. В этом случае вероятность символьной ошибки — это то же самое, что и вероятность битовой ошибки. Предположим, что сигналы равновероятны. Допустим также, что при передаче сигнала принятый сигнал r(t) равен
, где n(t) — процесс AWGN; кроме того, мы пренебрегаем ухудшением качества вследствие введенной каналом или схемой межсимвольной интерференции. Как показывалось в разделе 4.4.1, антиподные сигналы
и
можно описать в одномерном сигнальном пространстве, где
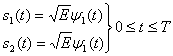
Детектор выбирает с наибольшим выходом коррелятора
; или, в нашем случае антиподных сигналов с равными энергиями, детектор, используя формулу (4.20), принимает решение следующего вида.
(4.74)
Как видно из рис. 4.9, возможны ошибки двух типов: шум так искажает переданный сигнал , что измерения в детекторе дают отрицательную величину z(T), и детектор выбирает гипотезу H2, что был послан сигнал s2(t). Возможна также обратная ситуация: шум искажает переданный сигнал
, измерения в детекторе дают положительную величину z(T), и детектор выбирает гипотезу Н1, соответствующую предположению о передаче сигнала
.
В разделе 3.2.1.1 была выведена формула (3.42), описывающая вероятность битовой ошибки РB для детектора, работающего по принципу минимальной вероятности ошибки.
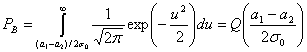
Здесь σ0 — среднеквадратическое отклонение шума вне коррелятора. Функция Q(x), называемая гауссовым интегралом ошибок, определяется следующим образом.
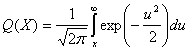
Эта функция подробно описывается в разделах 3.2 и Б.3.2.
Для передачи антиподных сигналов с равными энергиями, таких как сигналы в формате BPSK, приведенные в выражении (4.74), на выход приемника поступают следующие компоненты: , при переданном сигнале
, и
, при переданном сигнале s2(t), где Еь — энергия сигнала, приходящаяся на двоичный символ. Для процесса AWGN дисперсию шума
вне коррелятора можно заменить N0/2 (см. приложение В), так что формулу (4.76) можно переписать следующим образом.
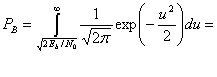
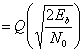
Данный результат для полосовой передачи антиподных сигналов BPSK совпадает с полученными ранее формулами для обнаружения антиподных сигналов с использованием согласованного фильтра (формула (3.70)) и обнаружения узкополосных антиподных сигналов с применением согласованного фильтра (формула (3.76)). Это является примером описанной ранее теоремы эквивалентности. Для линейных систем теорема эквивалентности утверждает, что на математическое описание процесса обнаружения не влияет сдвиг частоты. Как следствие, использование согласованных фильтров или корреляторов для обнаружения полосовых сигналов (рассмотренное в данной главе) дает те же соотношения, что были выведены ранее для сопоставимых узкополосных сигналов.
4.7.2. Вероятность появления ошибочного бита при когерентном обнаружении сигнала в дифференциальной модуляции BPSK
Сигналы в канале иногда инвертируются; например, при использовании когерентного опорного сигнала, генерируемого контуром ФАПЧ, фаза может быть неоднозначной. Если фаза несущей была инвертирована при использовании схемы DPSK, как это скажется на сообщении? Поскольку информация сообщения кодируется подобием или отличием соседних символов, единственным следствием может быть ошибка в бите, который инвертируется, или в бите, непосредственно следующим за инвертированным. Точность определения подобия или отличия символов не меняется при инвертировании несущей. Иногда сообщения (и кодирующие их сигналы) дифференциально кодируются и когерентно обнаруживаются, чтобы просто избежать неопределенности в определении фазы.
Вероятность появления ошибочного бита при когерентном обнаружении сигналов в дифференциальной модуляции PSK (DPSK) дается выражением [5].
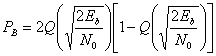
Это соотношение изображено на рис. 4.25. Отметим, что существует незначительное ухудшение достоверности обнаружения по сравнению с когерентным обнаружением сигналов в модуляции PSK. Это вызвано дифференциальным кодированием, поскольку любая отдельная ошибка обнаружения обычно приводит к принятию двух ошибочных решений. Подробно вероятность ошибки при использовании наиболее популярной схемы — когерентного обнаружения сигналов в модуляции DPSK — рассмотрена в разделе 4.7.5.
Рис. 4.25. Вероятность появления ошибочного бита для бинарных систем нескольких типов
4.7.3. Вероятность появления ошибочного бита при когерентном обнаружении сигнала в бинарной ортогональной модуляции FSK
Формулы (4.78) и (4.79) описывают вероятность появления ошибочного бита для когерентного обнаружения антиподных сигналов. Более общую трактовку для когерентного обнаружения бинарных сигналов (не ограничивающихся антиподными сигналами) дает следующее выражение для РВ [6].
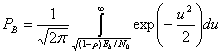
Из формулы (3.64,б) — временной коэффициент взаимной корреляций между
и
, где θ — угол между векторами сигналов
и s2 (см. рис. 4.6). Для антиподных сигналов, таких как сигналы BPSK, θ = π, поэтому ρ = -1.
Для ортогональных сигналов, таких как сигналы бинарной FSK (BFSK), θ = π/2, поскольку векторы и s2 перпендикулярны; следовательно, ρ = 0, что можно доказать с помощью формулы (3.64,а), поэтому выражение (4.81) можно переписать следующим образом.
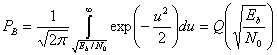
Здесь Q(x) — дополнительная функция ошибок, подробно описанная в разделах 3.2 и Б.3.2. Зависимость (4.82) для когерентного обнаружения ортогональных сигналов BFSK, показанная на рис. 4.25, аналогична зависимости, полученной для обнаружения ортогональных сигналов с помощью согласованного фильтра (формула (3.71)) и узкополосных ортогональных сигналов (униполярных импульсов) с использованием согласованного фильтра (формула (3.73)). В данной книге мы не рассматриваем амплитудную манипуляцию ООК (on-off keying), но соотношение (4.82 применимо к обнаружению с помощью согласованного фильтра сигналов ООК, так же как и к когерентному обнаружению любых ортогональных сигналов.
Справедливость соотношения (4.82) подтверждает и то, что разность энергий между ортогональными векторами сигналов и s2 с амплитудой
, как показано на рис. 3.10, б, равна квадрату расстояния между концами ортогональных векторов Ed = 2Eb. Подстановка этого результата в формулу (3.63) также дает формулу (4.82). Сравнивая формулы (4.82) и (4.79), видим, что, по сравнению со схемой BPSK, схема BFSK требует на 3 дБ большего отношения E/N0 для обеспечения аналогичной достоверности передачи. Этот результат не должен быть неожиданным, поскольку при данной мощности сигнала квадрат расстояния между ортогональными векторами вдвое (на 3 дБ) больше квадрата расстояния между антиподными векторами.
4.7.4. Вероятность появления ошибочного бита при некогерентном обнаружении сигнала в бинарной ортогональной модуляции FSK
Рассмотрим бинарное ортогональное множество равновероятных сигналов FSK , определенное формулой (4.8).
Фаза φ неизвестна и предполагается постоянной. Детектор описывается М = 2 каналами, состоящими, как показано на рис. 4.19, из полосовых фильтров и детекторов огибающей. На вход детектора поступает принятый сигнал r(t) = si(t) + n(t), где n(i) — гауссов шум с двусторонней спектральной плотностью мощности No/2. Предположим, что и
достаточно разнесены по частоте, чтобы их перекрытием можно было пренебречь. Вычисление вероятности появления ошибочного бита для равновероятных сигналов
и
начнем, как и в случае узкополосной передачи, с уравнения (3.38).
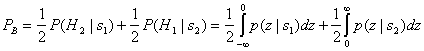
Для бинарного случая тестовая статистика z(T) определена как . Предположим, что полоса фильтра Wf равна 1/T, так что огибающая сигнала FSK (приблизительно) сохраняется на выходе фильтра. При отсутствии шума в приемнике значение z(T) равно
при передаче s1(t) и —
— при передаче s2(t). Вследствие такой симметрии оптимальный порог γ0=0. Плотность вероятности
подобна плотности вероятности
.
(4.84)
Таким образом, можем записать
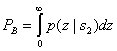
или
(4.86)
где z1 и z2 обозначают выходы z1(T) и z2(T) детекторов огибающей, показанных на рис.4.19. При передаче тона , т.е. когда r(t) = s2(t) + n(t), выход z1(T) состоит исключительно из случайной переменной гауссового шума; он не содержит сигнального компонента. Распределение Гаусса в нелинейном детекторе огибающей дает распределение Релея на выходе [6], так что
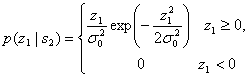
где — шум на выходе фильтра. С другой стороны, z2(T) имеет распределение Раиса, поскольку на вход нижнего детектора огибающей подается синусоида плюс шум [6]. Плотность вероятности p(z2\s2) записывается как
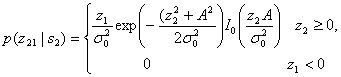
где и, как и ранее,
— шум на выходе фильтра. Функция 10(х), известная как модифицированная функция Бесселя первого рода нулевого порядка [7], определяется следующим образом.
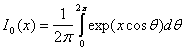
Ошибка при передаче s2(t) происходит, если выборка огибающей z1(T), полученная из верхнего канала (по которому проходит шум), больше выборки огибающей z2(T), полученной из нижнего канала (по которому проходит сигнал и шум). Таким образом, вероятность этой ошибки можно получить, проинтегрировав до бесконечности с последующим усреднением результата по всем возможным z2.
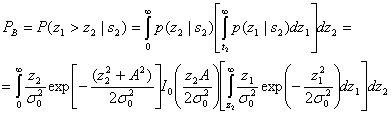
Здесь , внутренний интеграл — условная вероятность ошибки, при фиксированном значении z2, если был передан сигнал s2(1), а внешний интеграл усредняет условную вероятность по всем возможным значениям z2. Данный интеграл можно вычислить аналитически [8], и его значение равно следующему.
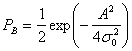
С помощью формулы (1.19) шум на выходе фильтра можно выразить как
(4.93)
где a Wf — ширина полосы фильтра. Таким образом, формула (4.92) приобретает следующий вид.
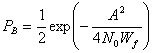
Выражение (4.94) показывает, что вероятность ошибки зависит от ширины полосы полосового фильтра и РB уменьшается при снижении Wf. Результат справедлив только при пренебрежении межсимвольной интерференцией (intersymbol interference — ISI). Минимальная разрешенная Wf (т.е. не дающая межсимвольной интерференции) получается из уравнения (3.81) при коэффициенте сглаживания г = 0. Следовательно, Wf= R бит/с =1/T, и выражение (4.94) можно переписать следующим образом.
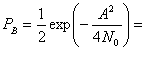
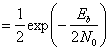
Здесь Еь= (1/2)А2Т — энергия одного бита. Если сравнить вероятность ошибки схем некогерентной и когерентной FSK (см. рис. 4.25), можно заметить, что при равных РB некогерентная FSK требует приблизительно на 1 дБ большего отношения Eb/N0, чем когерентная FSK (для РB < 10-4). При этом некогерентный приемник легче реализуется, поскольку не требуется генерировать когерентные опорные сигналы. По этой причине практически все приемники FSK используют некогерентное обнаружение. В следующем разделе будет показано, что при сравнении когерентной ортогональной схемы FSK с нёкогерентной схемой DPSK имеет место та же разница в 3 дБ, что и при сравнении когерентной ортогональной FSK и когерентной PSK. Как указывалось ранее, в данной книге не рассматривается амплитудная манипуляция ООК (on-off keying). Все же отметим, что вероятность появления ошибочного бита РB, выраженная в формуле (4.96), идентична РB для некогерентного обнаружения сигналов ООК.
4.7.5. Вероятность появления ошибочного бита для бинарной модуляции DPSK
Определим набор сигналов BPSK следующим образом.
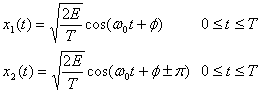
Особенностью схемы DPSK является отсутствие в сигнальном пространстве четко определенных областей решений. В данном случае решение основывается на разности фаз между принятыми сигналами. Таким образом, при передаче сигналов DPSK каждый бит в действительности передается парой двоичных сигналов.
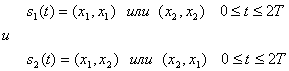
Здесь обозначает сигнал
, за которым следует сигнал
. Первые Т секунд каждого сигнала — это в действительности последние Т секунд предыдущего. Отметим, что оба сигнала s1(t) и s2(t) могут принимать любую из возможных форм и что
и
— это антиподные сигналы. Таким образом, корреляцию между
и s2(t) для любой комбинации сигналов можно записать следующим образом.
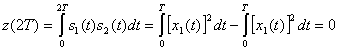
Следовательно, каждую пару сигналов DPSK можно представить как ортогональный сигнал длительностью 2Т секунд. Обнаружение может соответствовать некогерентному обнаружению огибающей с помощью четырех каналов, согласованных с каждым возможным выходом огибающей, как показано на рис. 4.26. Поскольку два детектора огибающей, представляющих каждый символ, обратны друг другу, выборки их огибающих будут совпадать. Значит, мы можем реализовать детектор как один канал для , согласовывающегося с
или
, и один канал для
, согласовывающегося с
или
, как показано на рис. 4.26. Следовательно, детектор DPSK сокращается до стандартного двухканального некогерентного детектора. В действительности фильтр может согласовываться с разностным сигналом; так что необходимым является всего один канал. На рис. 4.26 показаны фильтры, которые согласовываются с огибающими сигнала (в течение двух периодов передачи символа). Что это означает, если вспомнить, что DPSK — это схема передачи сигналов с постоянной огибающей? Это означает, что нам требуется реализовать детектор энергии, подобный квадратурному приемнику на рис. 4.18, где каждый сигнал в течение периода
представляется синфазным и квадратурным опорными сигналами.
синфазный опорный сигнал квадратурный опорный сигнал
синфазный опорный сигнал
квадратурный опорный сигнал
Поскольку пары сигналов DPSK ортогональны, вероятность ошибки при подобном некогерентном обнаружении дается выражением (4.96). Впрочем, поскольку сигналы DPSK длятся 2Т секунд, энергия сигналов , определенных в формуле (4.98), равна удвоенной энергии сигнала, определенного в течение одного периода передачи символа.
а)
б)
Рис. 4.26. Обнаружение в схеме DPSK: а) четырехканальное дифференциально-когерентное обнаружение сигналов в бинарной модуляции DPSK; б) эквивалентный двухканальный детектор сигналов в бинарной модуляции DPSK
Таким образом, РВможно записать в следующем виде.
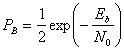
Зависимость (4.100), изображенная на рис. 4.25, представляет собой дифференциальное когерентное обнаружение сигналов в дифференциальной модуляции PSK, или просто DPSK. Выражение справедливо для оптимального детектора DPSK (рис. 4.17, в). Для детектора, показанного на рис. 4.17, б, вероятность ошибки будет несколько выше приведенной в выражении (4.100) [3]. Если сравнить вероятность ошибки, приведенную в формуле (4.100), с вероятностью ошибки когерентной схемы PSK (см. рис. 4.25), видно, что при равных РB схема DPSK требует приблизительно на 1 дБ большего отношения E^N0, чем схема BPSK (для ). Систему DPSK реализовать легче, чем систему PSK, поскольку приемник DPSK не требует фазовой синхронизации. По этой причине иногда предпочтительнее использовать менее эффективную схему DPSK, чем более сложную схему PSK.
4.7.6. Вероятность ошибки для различных модуляций
В табл. 4.1 и на рис. 4.25 приведены аналитические выражения и графики РB для наиболее распространенных схем модуляции, описанных выше. Для РB = 10-4 можно видеть, что разница между лучшей (когерентной PSK) и худшей (некогерентной ортогональной FSK) из рассмотренных схем равна приблизительно 4 дБ. В некоторых случаях 4 дБ — это небольшая цена за простоту реализации, увеличивающуюся от когерентной схемы PSK до некогерентной FSK (рис. 4.25); впрочем, в других случаях ценным является даже выигрыш в 1 дБ. Помимо сложности реализации и вероятности РB существуют и другие факторы, влияющие на выбор модуляции; например, в некоторых случаях (в каналах со случайным затуханием) желательными являются некогерентные системы, поскольку иногда когерентные опорные сигналы затруднительно определять и использовать. В военных и космических приложениях весьма желательны сигналы, которые могут противостоять значительному ухудшению качества, сохраняя возможность обнаружения.
Таблица 4.1. Вероятность ошибки для различных бинарных модуляций
|
Модуляция |
PB |
|
PSK (когерентное обнаружение) |
|
|
DPSK (дифференциальное когерентное обнаружение) |
|
|
Ортогональная FSK (когерентное обнаружение) |
|
|
Ортогональная FSK (некогерентное обнаружение) |
|
From Wikipedia, the free encyclopedia
In digital transmission, the number of bit errors is the numbers of received bits of a data stream over a communication channel that have been altered due to noise, interference, distortion or bit synchronization errors.
The bit error rate (BER) is the number of bit errors per unit time. The bit error ratio (also BER) is the number of bit errors divided by the total number of transferred bits during a studied time interval. Bit error ratio is a unitless performance measure, often expressed as a percentage.[1]
The bit error probability pe is the expected value of the bit error ratio. The bit error ratio can be considered as an approximate estimate of the bit error probability. This estimate is accurate for a long time interval and a high number of bit errors.
Example[edit]
As an example, assume this transmitted bit sequence:
1 1 0 0 0 1 0 1 1
and the following received bit sequence:
0 1 0 1 0 1 0 0 1,
The number of bit errors (the underlined bits) is, in this case, 3. The BER is 3 incorrect bits divided by 9 transferred bits, resulting in a BER of 0.333 or 33.3%.
Packet error ratio[edit]
The packet error ratio (PER) is the number of incorrectly received data packets divided by the total number of received packets. A packet is declared incorrect if at least one bit is erroneous. The expectation value of the PER is denoted packet error probability pp, which for a data packet length of N bits can be expressed as
,
assuming that the bit errors are independent of each other. For small bit error probabilities and large data packets, this is approximately
Similar measurements can be carried out for the transmission of frames, blocks, or symbols.
The above expression can be rearranged to express the corresponding BER (pe) as a function of the PER (pp) and the data packet length N in bits:
Factors affecting the BER[edit]
In a communication system, the receiver side BER may be affected by transmission channel noise, interference, distortion, bit synchronization problems, attenuation, wireless multipath fading, etc.
The BER may be improved by choosing a strong signal strength (unless this causes cross-talk and more bit errors), by choosing a slow and robust modulation scheme or line coding scheme, and by applying channel coding schemes such as redundant forward error correction codes.
The transmission BER is the number of detected bits that are incorrect before error correction, divided by the total number of transferred bits (including redundant error codes). The information BER, approximately equal to the decoding error probability, is the number of decoded bits that remain incorrect after the error correction, divided by the total number of decoded bits (the useful information). Normally the transmission BER is larger than the information BER. The information BER is affected by the strength of the forward error correction code.
Analysis of the BER[edit]
The BER may be evaluated using stochastic (Monte Carlo) computer simulations. If a simple transmission channel model and data source model is assumed, the BER may also be calculated analytically. An example of such a data source model is the Bernoulli source.
Examples of simple channel models used in information theory are:
- Binary symmetric channel (used in analysis of decoding error probability in case of non-bursty bit errors on the transmission channel)
- Additive white Gaussian noise (AWGN) channel without fading.
A worst-case scenario is a completely random channel, where noise totally dominates over the useful signal. This results in a transmission BER of 50% (provided that a Bernoulli binary data source and a binary symmetrical channel are assumed, see below).
In a noisy channel, the BER is often expressed as a function of the normalized carrier-to-noise ratio measure denoted Eb/N0, (energy per bit to noise power spectral density ratio), or Es/N0 (energy per modulation symbol to noise spectral density).
For example, in the case of QPSK modulation and AWGN channel, the BER as function of the Eb/N0 is given by:

People usually plot the BER curves to describe the performance of a digital communication system. In optical communication, BER(dB) vs. Received Power(dBm) is usually used; while in wireless communication, BER(dB) vs. SNR(dB) is used.
Measuring the bit error ratio helps people choose the appropriate forward error correction codes. Since most such codes correct only bit-flips, but not bit-insertions or bit-deletions, the Hamming distance metric is the appropriate way to measure the number of bit errors. Many FEC coders also continuously measure the current BER.
A more general way of measuring the number of bit errors is the Levenshtein distance.
The Levenshtein distance measurement is more appropriate for measuring raw channel performance before frame synchronization, and when using error correction codes designed to correct bit-insertions and bit-deletions, such as Marker Codes and Watermark Codes.[3]
Mathematical draft[edit]
The BER is the likelihood of a bit misinterpretation due to electrical noise 





Knowing that the noise has a bilateral spectral density 


and 

Returning to BER, we have the likelihood of a bit misinterpretation 


where 

We can use the average energy of the signal 
±§
Bit error rate test[edit]
BERT or bit error rate test is a testing method for digital communication circuits that uses predetermined stress patterns consisting of a sequence of logical ones and zeros generated by a test pattern generator.
A BERT typically consists of a test pattern generator and a receiver that can be set to the same pattern. They can be used in pairs, with one at either end of a transmission link, or singularly at one end with a loopback at the remote end. BERTs are typically stand-alone specialised instruments, but can be personal computer–based. In use, the number of errors, if any, are counted and presented as a ratio such as 1 in 1,000,000, or 1 in 1e06.
Common types of BERT stress patterns[edit]
- PRBS (pseudorandom binary sequence) – A pseudorandom binary sequencer of N Bits. These pattern sequences are used to measure jitter and eye mask of TX-Data in electrical and optical data links.
- QRSS (quasi random signal source) – A pseudorandom binary sequencer which generates every combination of a 20-bit word, repeats every 1,048,575 words, and suppresses consecutive zeros to no more than 14. It contains high-density sequences, low-density sequences, and sequences that change from low to high and vice versa. This pattern is also the standard pattern used to measure jitter.
- 3 in 24 – Pattern contains the longest string of consecutive zeros (15) with the lowest ones density (12.5%). This pattern simultaneously stresses minimum ones density and the maximum number of consecutive zeros. The D4 frame format of 3 in 24 may cause a D4 yellow alarm for frame circuits depending on the alignment of one bits to a frame.
- 1:7 – Also referred to as 1 in 8. It has only a single one in an eight-bit repeating sequence. This pattern stresses the minimum ones density of 12.5% and should be used when testing facilities set for B8ZS coding as the 3 in 24 pattern increases to 29.5% when converted to B8ZS.
- Min/max – Pattern rapid sequence changes from low density to high density. Most useful when stressing the repeater’s ALBO feature.
- All ones (or mark) – A pattern composed of ones only. This pattern causes the repeater to consume the maximum amount of power. If DC to the repeater is regulated properly, the repeater will have no trouble transmitting the long ones sequence. This pattern should be used when measuring span power regulation. An unframed all ones pattern is used to indicate an AIS (also known as a blue alarm).
- All zeros – A pattern composed of zeros only. It is effective in finding equipment misoptioned for AMI, such as fiber/radio multiplex low-speed inputs.
- Alternating 0s and 1s — A pattern composed of alternating ones and zeroes.
- 2 in 8 – Pattern contains a maximum of four consecutive zeros. It will not invoke a B8ZS sequence because eight consecutive zeros are required to cause a B8ZS substitution. The pattern is effective in finding equipment misoptioned for B8ZS.
- Bridgetap — Bridge taps within a span can be detected by employing a number of test patterns with a variety of ones and zeros densities. This test generates 21 test patterns and runs for 15 minutes. If a signal error occurs, the span may have one or more bridge taps. This pattern is only effective for T1 spans that transmit the signal raw. Modulation used in HDSL spans negates the bridgetap patterns’ ability to uncover bridge taps.
- Multipat — This test generates five commonly used test patterns to allow DS1 span testing without having to select each test pattern individually. Patterns are: all ones, 1:7, 2 in 8, 3 in 24, and QRSS.
- T1-DALY and 55 OCTET — Each of these patterns contain fifty-five (55), eight bit octets of data in a sequence that changes rapidly between low and high density. These patterns are used primarily to stress the ALBO and equalizer circuitry but they will also stress timing recovery. 55 OCTET has fifteen (15) consecutive zeroes and can only be used unframed without violating one’s density requirements. For framed signals, the T1-DALY pattern should be used. Both patterns will force a B8ZS code in circuits optioned for B8ZS.
Bit error rate tester[edit]
A bit error rate tester (BERT), also known as a «bit error ratio tester»[4] or bit error rate test solution (BERTs) is electronic test equipment used to test the quality of signal transmission of single components or complete systems.
The main building blocks of a BERT are:
- Pattern generator, which transmits a defined test pattern to the DUT or test system
- Error detector connected to the DUT or test system, to count the errors generated by the DUT or test system
- Clock signal generator to synchronize the pattern generator and the error detector
- Digital communication analyser is optional to display the transmitted or received signal
- Electrical-optical converter and optical-electrical converter for testing optical communication signals
See also[edit]
- Burst error
- Error correction code
- Errored second
- Pseudo bit error ratio
- Viterbi Error Rate
References[edit]
- ^ Jit Lim (14 December 2010). «Is BER the bit error ratio or the bit error rate?». EDN. Retrieved 2015-02-16.
- ^
Digital Communications, John Proakis, Massoud Salehi, McGraw-Hill Education, Nov 6, 2007 - ^
«Keyboards and Covert Channels»
by Gaurav Shah, Andres Molina, and Matt Blaze (2006?) - ^ «Bit Error Rate Testing: BER Test BERT » Electronics Notes». www.electronics-notes.com. Retrieved 2020-04-11.
This article incorporates public domain material from Federal Standard 1037C. General Services Administration. (in support of MIL-STD-188).
External links[edit]
- QPSK BER for AWGN channel – online experiment
Основные теоремы
Некоторые результаты теории вероятностей
- Среднее
- для действительной случайной переменной \(x\) из ансамбля \(X\), среднее значение определяется как \(\overline x = \sum_x P(x) x\)
- Дисперсия
- для действительной случайной переменной \(x\) из ансамбля \(X\), дисперсия определяется как \(\sigma_x^2 = \sum_x P(x) (x-\overline x)^2\)
- Первое Неравенство Чебышева
-
Пусть \(t\) неотрицательная действительная случайная переменная, а \(\alpha\) – положительное действительное число. Тогда, \[P(t\ge \alpha) \le \frac{\overline t}{\alpha}\]
Доказательство: \(P(t\ge\alpha)=\sum_{t\ge\alpha}P(t)\). Умножая каждый член правой части на \(\frac{t}{\alpha}\ge 1\): \(P(t\ge\alpha)\le\sum_{t\ge\alpha}P(t)\frac{t}{\alpha}\). Добавляя недостающие (заведомо положительные) члены в сумму: \(P(t\ge\alpha)\le \frac{1}{\alpha}\sum_{t}P(t)t = \frac{\overline t}{\alpha}\)
- Второе Неравенство Чебышева
-
Пусть \(x\) неотрицательная действительная случайная переменная, а \(\alpha\) – положительное действительное число. Тогда, \[P((x — \overline x)^2 \ge \alpha) \le \frac{\sigma_x^2}{\alpha}\]
Доказательство: Из первого неравенства Чебышева, пусть \(t=(x-\overline x)^2\): \(P((x-\overline x)^2\ge\alpha) \le \frac{\overline{(x — \overline x)^2}}{\alpha} =\frac{\sum_x P(x)(x-\overline x)^2}{\alpha} = \frac{\sigma_x^2}{\alpha}\)
- Слабый закон больших чисел (закон Хинчина)
-
Пусть \(x\) есть среднее от \(N\) независимых случайных переменных \(h_i\) (\(i\in\{1,\ldots,N\}\)), имеющих одинаковые средние \(\overline h\) и одинаковые дисперсии \(\sigma_h^2\): \(x=\frac{1}{N}\sum_i h_i\). Тогда, \[P((x-\overline h)^2 \ge \alpha)\le \frac{\sigma_h^2}{\alpha N}\]
Доказательство: Применяя 2 неравенство Чебышева к \(x\), \[P((x-\overline x)^2 \ge \alpha) \le \frac{\sigma_x^2}{\alpha},\] но из линейности математического ожидания, \(\overline x = \frac{1}{N}\sum_i \overline h = \overline h,\) а \(\sigma_x^2 = \frac{1}{N^2}\sum_i \sigma_h^2 = \frac{\sigma_h^2}{N}\) в силу независимости \(h_i\).
Выражаясь неформально, слабый закон больших чисел говорит нам, что среднее \(N\) опытов вероятно произвольно близко к статистическому среднему, для достаточно больших \(N\).
Теорема о кодировании источника
Теорема Шеннона о кодировании источника определяет пределы возможного сжатия данных при передаче, и определяет энтропию Шеннона для источника как оперативную характеристику.
- Пропускная способность канала
- Пропускная способность \(C\) дискретного канала определяется как \[C = \lim_{T\to\infty}\frac{\log N(T)}{T},\] где \(N(T)\) – число допустимых сигналов продолжительности \(T\).
- Теорема (оригинальная формулировка)
- Пусть источник имеет энтропию \(H\) (бит на символ), а канал обладает пропускной способностью \(C\) (бит в секунду). Тогда возможно подобрать схему кодирования, такую, что средняя скорость передачи будет составлять \(\frac{C}{H}-\epsilon\) символов в секунду, где \(\epsilon\) произвольно мало. Невозможна передача со средней скоростью выше, чем \(\frac{C}{H}\).
- Альтернативная формулировка
- Пусть \(X\) – ансамбль с энтропией \(H(X)\). Тогда, для любого данного \(\epsilon>0\), \(\exists\, N_0 \in \mathbb N: \forall N > N_0,\) \[\left|\frac{1}{N}H(X^N)-H(X)\right|<\epsilon,\] где \(X^N\) – последовательность \(N\) значений из ансамбля \(X\).
Доказательство
Рассмотрим случайную переменную \(\frac{1}{N}\log_2\frac{1}{P(\mathbf x)}\), где \(\mathbf x \in X^N\).
Определим множество “типичных” значений из \(X^N\) как \[T_{N\beta} = \left\{\mathbf x \in X^N : \left|\frac{1}{N}\log_2\frac{1}{P(\mathbf x)} — H(X)\right| < \beta \right\},\] т.е. таких “слов” (последовательностей символов) длины \(N\) из \(X^N\), среднее информационное содержание которых отличается от \(H(X)\) не более, чем на \(\beta\).
Для \(\mathbf x \in T_{N\beta}\), \[2^{-N(H(X)+\beta)} < P(\mathbf x) < 2^{-N(H(X)-\beta)}.\]
По закону больших чисел, \[P(\mathbf x\notin T_{N\beta}) \le \frac{\sigma^2}{\beta^2 N}\]
Покажем, что \[\frac{1}{N}H(X^N) < H(X)+\epsilon\]
Сумма вероятностей элементов, входящих в \(T_{N\beta}\) не выше 1. Тогда \[|T_{N\beta}| 2^{-N(H(X)+\beta)} < 1,\] \[|T_{N\beta}| < 2^{N(H(X)+\beta)}.\]
Тогда для кодирования любого \(\mathbf x \in T_{N\beta}\) нам достаточно \[log_2|T_{N\beta}| < N(H(X)+\beta)\] бит.
Пусть теперь мы кодируем символы из \(T_{N\beta}\) последовательностями длины \(\log_2|T_{N\beta}|+1\) бит, и первый бит всех кодов для \(\mathbf x \in T_{N\beta}\) равен \(0\). Тогда мы можем закодировать все последовательности из \(U_{N\beta} = X^N — T_{N\beta}\) кодами, первый бит которых равен \(1\), а число бит в коде не больше \(\log_2|U_{N\beta}|+1\). Тогда средний информационный объём последовательности, кодирующей \(\mathbf x \in X^N\)
\[\begin{align}H(X^N)
& < P(\mathbf x \in T_{N\beta})(1+log_2|T_{N\beta}|) + P(\mathbf x \notin T_{N\beta})(1+\log_2|U_{N\beta}|)
\\ & < 1 + N(H(X)+\beta)+\frac{\sigma^2}{\beta^2 N}(1+\log_2|U_{N\beta}|)
\\ & < 1 + N(H(X)+\beta)+\frac{\sigma^2}{\beta^2 N}(1+\log_2|X|^N)
\\ & = N(H(X)+\beta+\frac{1}{N}+\frac{\sigma^2}{\beta^2 N}\log_2|X|+\frac{\sigma^2}{\beta^2 N^2})
\end{align}\]
Выбрав \(\beta = N^{-1/4}\) \[\frac{1}{N} H(X^N) < H(X)+\frac{1}{N^{1/4}}+\frac{1}{N}+\frac{\sigma^2}{N^{1/2} }\log_2|X|+\frac{\sigma^2}{N^{3/2}}\]
Для любого наперёд заданного сколь угодно малого \(\epsilon > 0\), можно выбрать такое \(N_0\), что для любых \(N>N_0\), \[\frac{1}{N^{1/4}}+\frac{1}{N}+\frac{\sigma^2}{N^{1/2} }\log_2|X|+\frac{\sigma^2}{N^{3/2}} < \epsilon,\] и \[\frac{1}{N} H(X^N) < H(x) + \epsilon.\]
Покажем теперь, что \[\frac{1}{N}H(X^N) > H(X)-\epsilon\]
Предположим, что это не так. Тогда, существует некоторое подмножество \(S \subset X^N\), такое, что \(|S| \le 2^{N(H(X)-\epsilon)}\) и при этом \(P(\mathbf x \notin S) \to 0\) при \(N\to\infty\).
\[P(\mathbf x \in S) = P(\mathbf x \in S \cap T_{N\beta}) + P(\mathbf x \in S \cap (X^N — T_{N\beta})).\]
Положим \(\beta = \epsilon/2\). Первый член достигает максимального значения, если \(S \cap T_{N\beta}\) содержит \(2^{N(H(X)-2\beta)}\) элементов, каждый с максимальной вероятностью \(2^{-N(H(X)-\beta)}\). Максимальное значение второго члена \(P(\mathbf x \notin T_{N\beta})\). Тогда \[P(\mathbf x \in S) \le 2^{N(H(X)-2\beta)} 2^{-N(H(X)-\beta)} + \frac{\sigma^2}{\beta^2 N}.\] \[P(\mathbf x \in S) \le 2^{-N\beta} + \frac{\sigma^2}{\beta^2 N}.\]
\[P(\mathbf x \notin S) \ge 1 — 2^{-N\beta} — \frac{\sigma^2}{\beta^2 N}.\]
Таким образом, для любых подмножеств размерности меньше, чем \(2^{N(H(X)-\epsilon)}\), при \(N\to\infty,\) \(P(\mathbf x \notin S) \to 1\).
Теорема Шеннона для канала с шумами
- Пропускная способность канала с шумом
- Пропускная способность \(C\) дискретного канала с шумом определяется как \[C = \max_{\mathcal{P}_M} I(M R),\] где \(M\) – случайная дискретная переменная источника, \(R\) – случайная дискретная переменная приёмника, \(I(M R) = H(M)-H(M|R)\) – взаимная информация, \(\mathcal{P}_M\) – множество вероятностей \(\{P(m): m \in M\}\) каждого значения источника.
Иными словами, пропускная способность \(C\) – это теоретически максимально возможное количество взаимной информации между приёмником и источником, т.е. количество информации, переданной через канал, для некого “оптимального” источника.
- Теорема (оригинальная формулировка)
- Пусть дискретный канал имеет пропускную способность \(C\) и дискретный источник с энтропией \(H=H(M)\). Если \(H\le C\), то существует схема кодирования, такая, что сигнал источника может быть передан через канал с произвольно малой частотой ошибок (произвольно малой \(H(M|R)\)). Если \(H > C\), то \(H(M|R) = H — C + \epsilon\), где \(\epsilon\) произвольно мало. Не существует метода кодирования, такого, чтобы \(H(M|R) < H-C\).
Некоторые определения
- \((N, K)\) блочный код
- Множество \(2^K\) кодовых слов длины \(N\), кодирующих некий источник с алфавитом мощности \(2^K\).
- Плотность кодирования \((N, K)\) блочного кода
- \(ρ = K/N\).
- Декодер \((N, K)\)-блочного кода
- Отображение множества всех последовательностей длины \(N\) сигналов на выходе из канала на множество \(2^K+1\) меток кодовых слов, где “лишняя” метка означает неудачу.
- Вероятность ошибки блочного кода
- \[p_B = \sum_{m\in M}P(m)P(r\neq m|m),\] где \(M\) множество сообщений на входе канала, \(R\) множество сигналов на выходе канала, \(r \in R\)
- Максимальная вероятность ошибки блочного кода
- \[p_{BM} = \max_{m\in M}{P(r\neq m|m)}\]
- Оптимальный декодер
- декодер, минимизирующий вероятность ошибки блочного кода.
- Вероятность битовой ошибки
- Пусть номер кодового слова \(s\) в \((N, K)\)-блочном коде представлен двоичным числом \(\vect{s}\) длиной \(K\) бит. Вероятность битовой ошибки \(p_b\) составляет среднюю вероятность того, что один бит в представлении \(\vect{s}\) изменился после передачи соответствующего кода через канал.
Доказательство
Используем альтернативную формулировку теоремы.
- Теорема (альтернативная формулировка)
-
- Для любого дискретного канала без памяти с пропускной способностью \(C\), \(\forall \epsilon > 0, \forall ρ < C\), \(\exists N > 0,\) такое, что для кода длины \(N\), плотности кодирования \(\ge ρ < C\) и данного алгоритма декодирования, максимальная вероятность ошибки блочного кода \(\le \epsilon.\)
- Если вероятность битовой ошибки \(p_b\) приемлема, то достижима плотность кодирования до \[ρ(p_b) = \frac{C}{1-H_2(p_b)},\] где \(H_2(p_b) = — p_b \log_2 p_b — (1-p_b) \log_2 (1-p_b)\) – формула энтропии Шеннона для двоичного алфавита.
- Плотность кодирования выше \(ρ(p_b)\) недостижима.
Совместно-типичные последовательности
Пара случайных последовательностей \(\vect{x}\), \(\vect{y}\), элементы которых принадлежат ансамблям, соответственно, \(X\) и \(Y\), называются совместно-типичными (с точностью \(\beta\)), если:
- \(\vect{x}\) типичный относительно \(P(\vect{x})\), т.е. \[\left|-\frac{1}{N}\log P(\vect{x}) — H(X)\right| < \beta\]
- \(\vect{y}\) типичный относительно \(P(\vect{y})\), т.е. \[\left|-\frac{1}{N}\log P(\vect{y}) — H(Y)\right|< \beta\]
- \(\vect{x}\), \(\vect{y}\) типичны относительно \(P(\vect{x},\vect{y})\), т.е. \[\left|-\frac{1}{N}\log P(\vect{x},\vect{y}) — H(XY)\right|< \beta\]
Достижимость кодирования с произвольно малой вероятностью ошибки
Рассмотрим следующую систему кодирования-декодирования с плотностью \(ρ’\):
- Пусть \(K = N ρ’\), тогда случайным образом составим блочный код \((N, Nρ’)\), в соответствии с \[P(\vect x) = \prod_{n=1}^N P(x_n),\] где \(\vect x\) – кодовые слова. Обозначим этот код \(\mathcal{C}\).
- Код известен отправителю и получателю.
- Сообщение \(s\) выбирается из множества \(\{1, 2, \ldots, 2^{Nρ’}\},\) после чего посылается код \(\vect x^{(s)}\). Получаемый (кодированный) сигнал \(\vect y\) имеет вероятность \[P(\vect y | \vect x^{(s)}) = \prod_{n=1}^N P(y_n|x_n^{(s)})\]
- \(\vect y\) декодируется как \(\hat s\), если \((\vect x^{(\hat s)}, \vect y)\) взаимно типичные, и \(\nexists s’: (\vect x^{(s’)}, \vect y)\) взаимно типичные. В противном случае, сообщить об ошибке, \(\hat s = 0\).
- Ошибка декодирования соответствует ситуации \(\hat s \neq s\).
Мы можем выделить следующие вероятности ошибки декодирования:
- Средняя вероятность ошибки для конкретного кода \(\mathcal C\): \[p_B(\mathcal C) \equiv 2^{-N\rho’}\sum_s P(\hat s \neq s | s, \mathcal C).\]
- Средняя вероятность ошибки по всем (случайно составленным) кодам: \[\langle p_B \rangle = \sum_\mathcal{C} p_B(\mathcal C) P(\mathcal C)\]
- Максимальная условная вероятность ошибки: \[p_{BM}(\mathcal C) = \max_s P(\hat s \ne s|s,\mathcal C).\]
Обозначим множество взаимно-типичных \(\vect x, \vect y\) (с точностью \(\beta\)) как \(J_{N\beta}\).
Оценим среднюю вероятность ошибки. Существует два потенциальных источника ошибки:
- \((\vect x^{(s)},\vect y) \notin J_{N\beta}\)
- \(\exists s’ \neq s, \vect x^{(s’)} \in \mathcal C: (\vect x^{(s’)},\vect y) \in J_{N\beta}\)
В силу симметрии построения кодов, \(\langle p_B\rangle\) не зависит от конкретного \(s\), поэтому без ограничения общности можем рассмотреть \(s=1\): \[\angle{p_B} = \sum_{\mathcal C} P(\mathcal C) P(\hat s \ne 1|s = 1,\mathcal C)\]
По закону больших чисел, \[P\left[\left(-\frac{1}{N}\log P(\vect{x}) — H(X)\right)^2 \ge \beta^2\right] \le \frac{\sigma_X^2}{\beta^2 N},\] \[P\left[\left(-\frac{1}{N}\log P(\vect{y}) — H(Y)\right)^2 \ge \beta^2\right] \le \frac{\sigma_Y^2}{\beta^2 N},\] \[P\left[\left(-\frac{1}{N}\log P(\vect{x}\vect{y}) — H(XY)\right)^2 \ge \beta^2\right] \le \frac{\sigma_{XY}^2}{\beta^2 N}.\]
Тогда вероятность, что \(\vect x, \vect y\) не взаимно типичны \[p_{NJT} \le \frac{\sigma_X^2+\sigma_Y^2+\sigma_{XY}^2}{\beta^2N} = \delta.\] Тогда вероятность ошибки из-за (a) не превшывает \(\delta\).
Сумма вероятностей \(P(\vect x \vect y)\) для \((\vect x, \vect y) \in J_{N\beta}\) не выше 1, а сами вероятности по построению удовлетворяют условию \[2^{-N(H(XY) + \beta)} < P(\vect{x}\vect{y}) < 2^{-N(H(XY) — \beta)}.\] Тогда \[|J_{N\beta}| 2^{-N(H(XY) + \beta)} \le 1,\] \[|J_{N\beta}| \le 2^{N(H(XY) + \beta)}.\]
Для двух независимых \(\vect x’ \in X^N\) и \(\vect y’ \in Y^N\), вероятность того, что они совместно типичны \[\begin{align}
P((\vect x’, \vect y’) \in J_{N\beta}) & =
\sum_{(\vect x, \vect y) \in J_{N\beta}} P(\vect x)P(\vect y)
\\& \le |J_{N\beta}|2^{-N(H(X)-\beta)}2^{-N(H(Y)-\beta)}
\\& \le 2^{N(H(XY) + \beta)}2^{-N(H(X)-\beta)}2^{-N(H(Y)-\beta)}
\\& = 2^{N(H(XY)-H(X)-H(Y)+3\beta)}
\\& = 2^{-N(I(XY)-3\beta)}
\end{align}\]
Всего имеем \(2^{N\rho’}\) возможных значений \(x’\neq x^{(1)}\). Тогда вероятность ошибки из-за (b) не превышает \[2^{Nρ’}2^{-N(I(XY)-3\beta)} = 2^{-N(I(XY)-ρ’-3\beta)}.\]
Тогда средняя вероятность ошибки \[\langle p_B\rangle \le \delta + 2^{-N(I(XY)-ρ’-3\beta)},\] причём равенство достигается только если (a) и (b) никогда не происходят одновременно.
Тогда, если \(ρ’ < I(XY)-3 \beta\), \((I(XY)-ρ’-3\beta) > 0\) и можно выбрать достаточно большой \(N\), такой, что \(\langle p_B \rangle < 2\delta\) (т.к. \(\delta \sim \frac{1}{N}\), а экспонента убывает быстрее гиперболы)
Пусть теперь источник – оптимальный источник для данного канала, тогда \(I(XY)=C\), и тогда \(ρ’ < C-3 \beta\). Поскольку средняя вероятность ошибки по всем случайно составленным кодам \(<2\delta\), то существует хотя бы один код \(\mathcal C\), такой, что средняя вероятность ошибки по всем сигналам у этого кода \(p_B(\mathcal C) < 2\delta\).
Составим на основе этого кода новый код, в котором исключим половину кодовых слов, имеющих наиболее высокие вероятности ошибки. Вероятность ошибки у каждого из оставшихся кодовых слов менее \(4 \delta\). Таким образом, мы получили новый код с плотностью \(\rho» = \rho’-\frac{1}{N}\) и получили максимальную вероятность ошибки \(p_{BM} < 4 \delta\). Положим \(ρ’ = (ρ+C)/2\), \(\delta = \epsilon/4\), \(\beta < (C-ρ’)/3\) и получим формулировку первой части теоремы.
Ошибка при передаче сверх пропускной способности
Из первой части теоремы, мы по сути знаем, что любой канал с шумом можно превратить в практически бесшумный с меньшей плотностью кодирования (т.е. в итоге меньшей пропускной способностью). Теперь, зададимся вопросом, с какой скоростью мы можем передавать данные через идеальный (бесшумный) канал, если допустима ошибка передачи?
Рассмотрим канал без шума с пропускной способностью \(C\). Теперь представим, что мы передаём (ну или по крайней мере пытаемся передать) количество информации \(H>C\). Простая стратегия заключается в том, чтобы передавать только количество информации, равное \(C\), и отбрасывать остальное. Приёмник тогда должен угадать \(H-C\) бит сообщения. Потери информации в канале очевидно \(H(M|R) = H-C\) (при \(N\to\infty\)). Доля сообщения, которое приёмник должен угадать \(\frac{H-C}{H} = 1-\frac{C}{H}\), тогда вероятность битовой ошибки \[p_b = \frac{1}{2}(1-\frac{C}{H}).\]
Можно получить несколько лучший результат (в смысле уменьшения \(p_b\)), если распределить вероятность битовой ошибки равномерно по всем битам.
- Неравенство Фано
-
Пусть \(X\), \(Y\) – случайные переменные, а \(p_e\) – вероятность ошибки “угадывания” \(X\) по \(Y\) (при известных вероятностях \(P(X|Y)\)). Тогда, \[H_2(p_e)+p_e\log(N-1) \ge H(X|Y),\] где \(N\) – размерность алфавита \(X\).
\(Δ:\)
Пусть \(E\) – двоичная случайная переменная, возвращающая 1, если возникла ошибка “угадывания”, 0 в противном случае. Заметим, что \(P(E=1) = p_e\), и \(H(E) = H_2(p_e).\)
По правилу цепочки, \[\begin{align}
H(EXY) & = H(E|XY) + H(XY)
\\& = H(E|XY) + H(X|Y) + H(Y)
\end{align}\] с другой стороны, \[\begin{align}
H(EXY) & = H(X|EY)+H(EY)
\\& = H(X|EY) + H(E|Y) + H(Y)
\end{align}\]Тогда, \[H(E|XY) + H(X|Y) = H(X|EY) + H(E|Y)\]
\(H(E|XY) = 0\), поскольку \(E\) однозначно определена, если определены \(X\) и \(Y\). \(H(E|Y) \le H(E)\), поскольку условие не увеличивает энтропию. Наконец, \[\begin{align}H(X|EY) & = P(E=0)H(X|Y, E=0) \\& + P(E=1)H(X|Y,E=1) \\& \le p_e \log(N-1),\end{align}\] где неравенство следует из \(H(X|Y, E=0) = 0\) и \(H(X|Y,E=1) \le \log(N-1)\). \(N-1\), поскольку при \(E=1\), \(X\) точно не “правильный”, т.е. одно значение исключается.
Собирая вместе, получаем: \[\begin{align}
H(X|Y) & = H(X|EY) + H(E|Y)
\\& \le p_e \log(N-1) + H(E)
\end{align}\]Для двоичного алфавита, \(N=2\) и \[H(X|Y) \le H(E) = H_2(p_e)\]
- Неравенство Йенсена (дискретный случай)
-
Пусть \(f(x)\) выпуклая вниз на некотором отрезке \(\mathcal X\), и пусть числа \(q_i\) (\(i=1,\ldots, n\)) представляют веса (\(q_i > 0\), \(\sum_i q_i = 1\)). Тогда \(\forall x_i \in \mathcal X\) \[f(\sum_i q_i x_i) \le \sum_i q_i f(x_i).\]
Для выпуклой вверх функции неравенство обращается.
\(Δ\): Для \(n=2\) прямо следует из определения выпуклой функции. Далее индукция по n.
Пусть \(R^N\) – кодовое слово на выходе из канала, использующее \((N, K)\)-блочный код, имеющий вероятность битовой ошибки \(p_b\), \(S\) – отправленное сообщение, \(M^N\) – кодовое слово на входе в канал.
\[\begin{align}
H(M^N R^N S) & = H(M^{N-1} R^{N-1} S)
\\& + H(M_N|M^{N-1} R^{N-1} S) & (= 0)
\\& + H(R_N|M^{N-1} R^{N-1} S) & (= H(R^N|M^N))
\\& = H(M^{N-1} R^{N-1} S) + H(R_N|M_N)
\\& = \ldots
\\& = H(S) + \sum_{i=1}^N H(R_i|M_i)
\end{align}\]
Первое равенство следует из того, что один символ кодового на входе в канал точно известен, если известны остальные символы кодового слова и исходное сообщение.
С другой стороны, \[\begin{align}
H(M^N R^N S) & = H(R^N S)
\\& + H(M_N|R^N S) & (= 0)
\\& = H(R^N S)
\end{align}\]
Тогда взаимная информация между исходным сообщением и кодовым словом на выходе из канала:
\[\begin{align}
I(S R^N) & = H(S)+H(R^N)-H(R^N S)
\\& = H(R^N)-\sum_{i=1}^N H(R_i|M_i)
\\& \le \sum_{i=1}^N (H(R_i) — H(R_i|M_i))
\\& = \sum_{i=1}^N I(R_i M_i)
\\& \le C N = C \frac{K}{ρ}
\end{align}\]
Тогда: \[\begin{align}
H_2(p_b) & = H_2(\frac{\sum_{i=1}^K P(\text{ошибка в }i\text{-том бите})}{K})
\\& \ge \frac{\sum_{i=1}^K H_2(P(\text{ошибка в }i\text{-том бите}))}{K} & \text{н-во Й.}
\\& \ge \frac{\sum_{i=1}^K H(i\text{-й бит сообщения}|R^N)}{K} & \text{н-во Ф.}
\\& \ge \frac{H(S|R^N)}{K} & \text{св-во }H
\\& = \frac{H(S) — I(S R^N)}{K} & \text{опр. }I
\\& \ge \frac{K — K\frac{C}{ρ}}{K} & \text{при } P(s_i)=P(s_j)
\\& = 1 — \frac{C}{ρ}
\end{align}\]
\[\begin{align}
ρ \le \frac{C}{1 — H_2(p_b)}
\end{align}\]
Теорема Шеннона-Хартли
Определяет пропускную способность канала с аддитивным гауссовским шумом.
\[C = B \log_2(1+\frac{S}{N}),\]
где C – пропускная способность канала, бит/с, \(B\) – полоса пропускания (частотная ширина канала), Гц, \(S\) – средняя мощность сигнала над полосой пропускания, Вт, \(N\) – средняя мощность шума над полосой пропускания, Вт.
Аксиоматическое определение энтропии
Не всегда энтропия вводится как у Шеннона. Её так же можно непосредственно ввести аксиоматически. Понятно, что любые полезные системы аксиом будут эквивалентны друг другу. Рассмотрим две системы аксиом.
Аксиомы Хинчина
А.Я. Хинчин показал, что энтропия конечной вероятностной схемы может быть однозначно определена с точностью до постоянного множителя при задании следующей системы аксиом:
- \(H(p_1,\ldots,p_n)\) – непрерывная относительно аргументов функция в области определения \(0\le p_i \le 1\), \(\sum_i p_i = 1\)
- \(H(p_1, \ldots, p_n)\) не меняется от перестановок аргументов.
- \(H(p_1, \ldots, p_n, 0) = H(p_1,\ldots,p_n)\)
- \(H(XY)=H(X)+H(Y|X)\), где \(H(Y|X) = \sum_{x\in X} P(x) H(\frac{P(x_i y_1)}{P(x_i)},\ldots,\frac{P(x_i y_m)}{P(x_i)}).\)
- \(H(p_1, \ldots, p_n)\leq H(\frac{1}{n},\ldots,\frac{1}{n})\)
Этот набор аксиом однозначно приводит к энтропии Шеннона. Аксиома 4 кажется несколько неестественной: действительно, в аксиомах, определяющих энтропию, появляется условная энтропия. Более естественно могла бы выглядеть аксиома такого вида:
- Энтропия двух независимых систем аддитивна, \(H(XY) = H(X)+H(Y)\).
Однако оказывается, что такая модифицированная 4-ая аксиома приводит к более общей функции энтропии, чем энтропия Шеннона, известной как энтропия Реньи или α-энтропия: \[H_\alpha(X)={\frac{1}{1-\alpha}}\log \sum _{x\in X} (P_{i}(x))^{\alpha},\] которая эквивалентна энтропии Шеннона только в пределе \(\alpha\to 1\): \[\begin{align}
\lim_{\alpha\to 1} \frac{\log \sum_{x\in X} (P_{i}(x))^{\alpha}}{1-\alpha}
& = — \lim_{\alpha\to 1} \frac{\sum_{x\in X}(P_{i}(x))^{\alpha} \log (P_{i}(x))}{\sum_{x\in X}(P_{i}(x))^{\alpha}}
\\ & = — \sum_{x\in X} P_{i}(x) \log (P_{i}(x))
\end{align}\]
Аксиомы Фаддеева
Эквивалентная системе Хинчина аксиоматика.
- \(H(p, 1-p)\) непрерывна при \(p\in[0,1]\) и положительна хотя бы в одной точке.
- \(H(p_1, \ldots, p_n)\) не меняется от перестановок аргументов
- При \(n\ge 2\), \(H(p_1,\ldots, p_{n-1}; q_1, q_2) = H(p_1, \ldots, p_n) + p_n H\left(\frac{q_1}{p_n}, \frac{q_2}{p_n}\right)\), где \(p_n=q_1+q_2\).
Отличия от аксиом Хинчина в том, что аксиома 5 заменяется на требование положительности \(H\) хотя бы в одной точке, а аксиомы Хинчина 3, 4 заменяются одной аксиомой Фаддеева 3.
Аксиома Фаддеева 3 оказывается более естественной, если интерпретировать энтропию как меру неопределённости. Тогда неопределённость, возникающая от деления события с вероятностью \(p_n\) на два события с условными вероятностями \(\frac{q_1}{p_n}\), \(\frac{q_2}{p_n}\), должна возникать только если собственно происходит событие с вероятностью \(p_n\) – чему, собственно, и соответствует член \(p_n H\left(\frac{q_1}{p_n}, \frac{q_2}{p_n}\right)\).
Содержание лабораторной работы
В ходе выполнения данной лабораторной работы будет:
- создан новый проект;
- продемонстрирован процесс установки блоков на схему и их соединения между
собой; - продемонстрирован процесс задания свойств блоков;
- проведено моделирование передачи данных через канал связи.
Создание нового проекта
Необходимо создать новый проект, для этого:
- В главном окне SimInTech нажать кнопку «Файл» и выбрать пункт «Новый
проект». - В выпадающем меню выбрать пункт «Схема модели общего вида» (Рисунок 4).
Рисунок 4. Главное окно SimInTech c выделенным меню создания нового проекта.
Откроется новое окно проекта «Схема модели общего вида», в котором производится
разработка моделей (Рисунок 5).
Рисунок 5. Окно проекта «Схема модели общего вида».
Требуется сохранить созданный проект. Для этого:
- В главном окне SimInTech нажать кнопку «Файл» и выбрать пункт «Сохранить
проект как…». - В появившемся окне выбрать или при необходимости создать папку, в которую будет
сохранен данный проект. - В поле «Имя файла» указать желаемое имя проекта либо оставить имя проекта по
умолчанию и нажать на кнопку «Сохранить».
Разработка модели канала связи
В ходе выполнения лабораторной работы будет проведено сравнение вероятности ошибки при
передаче данных с использованием кодирования и без него. Для этого необходимо разработать
две идентичные модели передачи данных и оценки вероятности ошибки, затем в одну из них
будут добавлены модели кодера и декодера.
Добавление блоков на схему
Требуется добавить на схему блок «Цифровая связь – Генератор псевдослучайной битовой
последовательности» из подменю «Источники» вкладки «Цифровая связь».
Данный блок будет формировать последовательность информационных бит, передаваемых через
канал связи. Для добавления блока на схему необходимо выполнить следующие действия:
- В главном окне SimInTech в палитре блоков выбрать вкладку «Цифровая связь»
(Рисунок 6).Рисунок 6. Главное окно SimInTech с выбранной вкладкой «Цифровая связь» в палитре
блоков. - Нажать левой кнопкой мыши по подменю «Источники», в результате чего появится
список блоков, находящихся в данном подменю (Рисунок 7).Рисунок 7. Главное окно SimInTech с выбранным подменю «Источники» вкладки «Цифровая
связь». - Одинарным нажатием левой кнопкой мыши выбрать блок «Цифровая связь – Генератор
псевдослучайной битовой последовательности». - Перевести курсор мыши на рабочую область проекта. В рабочей области появится
графическое изображение блока «Цифровая связь – Генератор псевдослучайной битовой
последовательности», которое будет следовать за указателем мыши. - В рабочей области окна проекта выбрать место для установки блока и установить блок
одинарным нажатием левой кнопкой мыши (Рисунок 8).Рисунок 8. Окно проекта с добавленным блоком «Цифровая связь – Генератор псевдослучайной
битовой последовательности».
После установки блока его можно переместить. Для перемещения блока внутри рабочей области
окна проекта необходимо нажать на блок левой кнопкой мыши и, удерживая, переместить.
Аналогичным образом необходимо добавить на схему следующие блоки:
- 1 блок «Цифровая связь – BPSK модулятор» и 1 блок «Цифровая связь – BPSK
демодулятор» из подменю «Модуляция» вкладки «Цифровая связь». Данные
блоки необходимы для моделирования алгоритма BPSK модуляции. - 1 блок «Цифровая связь – Канал с АБГШ» из подменю «Каналы связи» вкладки
«Цифровая связь». Данный блок необходим для моделирования канала передачи
данных с помехами. - 1 блок «Цифровая связь – Измеритель WER» и 1 блок «Цифровая связь –
Измеритель BER» из подменю «Измерители» вкладки «Цифровая связь». С
помощью данных блоков будет вычисляться вероятность ошибки передачи кодового слова и
бита соответственно.
Блоки необходимо расположить согласно рисунку (Рисунок 9).
Рисунок 9. Окно проекта с добавленными блоками.
Перед тем, как приступать к выполнению следующего пункта лабораторной работы, необходимо
сохранить проект.
Задание свойств блоков
Одно кодовое слово разработанного кода содержит 4 информационных бита. Для формирования
4-х информационных бит на каждом шаге моделирования необходимо изменить свойства блока
«Цифровая связь – Генератор псевдослучайной битовой последовательности». Для
этого:
- Одинарным нажатием левой кнопкой мыши выделить блок «Цифровая связь – Генератор
псевдослучайной битовой последовательности» - Одинарным нажатием правой кнопкой мыши по выделенному блоку вызвать контекстное меню
блока и в нем выбрать пункт «Свойства объекта» (Рисунок 10).Рисунок 10. Окно проекта с пунктом «Свойства объекта», выбранным в контекстном меню
блока. - Откроется окно «Свойства», в котором задаются свойства блока (Рисунок 11).
Рисунок 11. Окно «Свойства» блока «Цифровая связь – Генератор псевдослучайной битовой
последовательности» со свойствами по умолчанию. - Необходимо задать значение свойства «Размер выхода» в поле «Формула»
равным «4».
Требуется изменить настройки передачи данных через канал связи, для этого необходимо
задать значения свойств блока «Цифровая связь – Канал с АБГШ» согласно рисунку
(Рисунок 12). Значение свойства
«Величина отношения сигнал-шум, дБ» соответствует значению, полученному в
результате аналитических расчетов.
Рисунок 12. Окно «Свойства» блока «Цифровая связь – Канал с АБГШ» с измененными значениями
свойств.
Демодулятору необходимо задать режим «жесткой оценки», для этого в окне свойств блока
«Цифровая связь — BPSK демодулятор» для свойства «Тип оценки» в поле
«Значение» требуется выбрать «Биты».
Блоки «Цифровая связь — BPSK демодулятор», «Цифровая связь – Канал с АБГШ»
и «Цифровая связь — BPSK демодулятор» предназначены для моделирования передачи
данных по каналу связи без кодирования. Для формирования второго канала передачи данных
(для моделирования помехозащищенной передачи данных с кодированием) требуется скопировать
ряд блоков на схеме. Для этого при зажатой клавише «Shift» необходимо выделить на
схеме блоки:
- «Цифровая связь – BPSK модулятор».
- «Цифровая связь – Канал с АБГШ».
- «Цифровая связь – BPSK демодулятор».
- «Цифровая связь – Измеритель WER».
- «Цифровая связь – Измеритель BER».
Требуется скопировать выбранные блоки, для этого необходимо вызвать контекстное меню
блоков нажатием правой кнопкой мыши по рабочей области окна проекта. В открывшемся
контекстном меню необходимо выбрать пункт «Копировать» (Рисунок 13).
Рисунок 13. Окно проекта с пунктом «Копировать», выбранным в контекстном меню блоков.
Необходимо вставить скопированные блоки на схему, для этого требуется вызвать контекстное
меню нажатием правой кнопкой мыши и выбрать пункт «Вставить». В рабочей области
окна проекта появятся графические изображения вставляемых блоков, которые будут следовать
за указателем мыши. Необходимо выбрать место в рабочей области окна проекта, разместить
блоки согласно рисунку (Рисунок 14) и
нажать левую кнопку мыши. После установки блоков на схему для снятия выделения блоков
следует нажать левой кнопкой мыши по свободному пространству рабочей области окна
проекта.
Рисунок 14. Окно проекта с вставленными блоками.
При использовании кодирования через канал связи будет передаваться кодовое слово,
состоящее из 7 бит, вместо 4. По этой причине для вставленного блока «Цифровая связь –
Канал с АБГШ» для свойства «Кодовая скорость» в поле «Формула»
требуется задать формулу расчета «4/7». После задания формулы произойдет
автоматический расчет значения свойства в поле «Значение».
Для упрощения идентификации канала связи без кодирования и канала связи с кодированием
следует добавить на схему подписи. Требуется нажать на кнопку «Панель примитивов» в
главном окне программы (Рисунок 15),
в открывшемся меню выбрать и разместить на схеме примитив «Текст».
Рисунок 15. Главное окно SimInTech с выделенной кнопкой «Панель примитивов».
Двойным нажатием левой кнопки мыши по изображению примитива на схеме необходимо открыть
окно редактирования отображаемого текста примитива. В открывшемся окне требуется задать
текст «Без кодирования» и нажать кнопку «Применить и закрыть» (Рисунок 16).
Рисунок 16. Окно «Редактирование текста» с выделенной кнопкой «Применить и закрыть».
После выполнения этих действий отображаемый текст примитива изменится. Аналогичным
образом необходимо добавить на схему еще один примитив «Текст», задать отображаемый
текст примитива и разместить примитивы на схеме согласно рисунку (Рисунок 17).
Рисунок 17. Окно проекта с добавленными примитивами «Текст».
Перед тем, как приступать к выполнению следующего пункта лабораторной работы, необходимо
сохранить проект.
Разработка модели кодера
Блочный кодер должен сформировать кодовое слово U путем перемножения вектора
сообщения I и порождающей матрицы G:
Необходимо создать текстовый файл, в котором будет сохранена порождающая матрица блочного
кода, в одной директории с файлом проекта. Для этого необходимо открыть окно
«Проводник», перейти в директорию сохранения текущего проекта и создать текстовый
файл с именем «G.txt». Необходимо открыть файл, заполнить его согласно рисунку
(Рисунок 18) и сохранить.
Рисунок 18. Окно текстового файла с заполненными данными.
Добавление блоков на схему
Необходимо разработать модель блочного кодера в виде одного блока. Для этого требуется
добавить на схему блок «Субмодель» из вкладки «Субструктуры» и разместить
его согласно рисунку (Рисунок 19).
Рисунок 19. Окно проекта с добавленным блоком «Субмодель».
Необходимо задать подпись блоку «Субмодель», для этого:
- Выделить на схеме блок «Субмодель» одинарным нажатием левой кнопкой мыши по
нему (Рисунок 20).Рисунок 20. Окно проекта с выделенным блоком «Субмодель».
- Открыть область подписи блока двойным нажатием левой кнопкой мыши на прямоугольную
область, расположенную рядом с выделенным блоком, и задать подпись
«Кодер». - Для того, чтобы переместить поле подписи блока, необходимо нажать левой кнопкой мыши
на красный прямоугольник в верхней части этого поля и переместить его, не отпуская
левую кнопку мыши.Двойным нажатием по блоку «Субмодель» необходимо зайти в
субмодель. В окне проекта откроется рабочая область блока «Субмодель» (Рисунок 21).Рисунок 21. Рабочая область блока «Субмодель».
Необходимо добавить в рабочую область субмодели и разместить, согласно рисунку (Рисунок 22), следующие блоки:
- 1 блок «Константа» и 1 блок «Таблица данных из файла» из вкладки
«Источники». Данные блоки будут формировать сигналы, необходимые для
функционирования блочного кодера. - 1 блок «Запаковка матрицы» и 1 блок «Матричные – Умножение матриц» из
вкладки «Векторные». Данные блоки необходимы для реализации алгоритма работы
блочного кодера. - 1 блок «Порт входа» и 1 блок «Порт выхода» из вкладки
«Субструктуры». Данные блоки необходимы для приема и передачи данных через
порты блока «Субмодель». - 1 блок «Целочисленные операции» из вкладки «Логические». Данный блок
необходим для реализации алгоритма работы блочного кодера.
Рисунок 22. Окно проекта с добавленными блоками.
Вектор сообщения будет передаваться в субмодель при помощи блока «Порт входа».
Блок «Таблица данных из файла» будет считывать из текстового файла столбцы
порождающей матрицы блочного кода, а блок «Запаковка матрицы» будет формировать из
них матрицу.
Перед тем, как приступать к выполнению следующего пункта лабораторной работы, необходимо
сохранить проект.
Задание свойств блоков
Для корректного считывания данных из текстового файла необходимо настроить свойства блока
«Таблица данных из файла». Необходимо открыть окно свойств блока и выполнить
следующие действия:
- В поле «Формула» задать значение свойства «Число столбцов» равным
«7». - В поле «Значение» свойства «Имя файла данных» указать имя файла
«G.txt».
Для корректного формирования матрицы из ее столбцов необходимо задать значения свойств
блока «Запаковка матрицы» согласно рисунку (Рисунок 23).
Рисунок 23. Окно свойств блока «Запаковка матрицы» с измененными значениями свойств.
Для блока «Умножение матриц» требуется задать:
- Значение свойства «Количество строк матрицы 1» равным «1».
- Значение свойства «Количество столбцов матрицы 1» равным «4».
- Значение свойства «Количество строк матрицы 2» равным «4».
- Значение свойства «Количество столбцов матрицы 2» равным «7».
Результирующий вектор, полученный в результате умножения вектора сообщения на порождающую
матрицу, в общем случае может содержать элементы, отличные от 0 и 1. Для получения
двоичного кодового слова при умножении вектора сообщения на порождающую матрицу вместо
обычной операции сложения (для определения значения каждого элемента результирующего
вектора) следует использовать операцию сложения по модулю 2. Для того, чтобы получить
корректный результат работы кодера без внесения изменений в алгоритм умножения вектора на
матрицу, необходимо найти остаток от деления каждого элемента результирующего вектора на 2
(математически это будут две тождественные операции).
Для блока «Целочисленные операции» требуется открыть окно свойств, в поле
«Значение» свойства «Тип операции» открыть список доступных операций и
выбрать «% (Остаток от деления)».
Для блока «Константа» требуется задать значение свойства «Значение» равным
«2».
Для упрощения внешнего вида модели следует изменить размер блока «Запаковка
матрицы». Для этого необходимо:
- Открыть окно свойств блока «Запаковка матрицы» и перейти на вкладку
«Общие». - Задать значение свойства «Высота» равным «112».
Перед тем, как приступать к выполнению следующего пункта лабораторной работы, необходимо
сохранить проект.
Соединение блоков на схеме
Необходимо соединить блоки линиями связи, для этого:
- Навести курсор мыши на выходной порт блока «Порт входа» (курсор мыши изменится
на вертикальную стрелку) и нажать левую кнопку мыши. - Появившуюся линию соединить с верхним входным портом блока «Умножение матриц» и
нажать левую кнопку мыши.
После выполнения этих действий появится линия связи. Необходимо соединить блоки на схеме
согласно рисунку (Рисунок 24).
Рисунок 24. Окно проекта с соединенными блоками.
Разработка модели кодера завершена. Следует выйти из рабочей области субмодели одинарным
нажатием левой кнопкой мыши по кнопке «Возврат из субмодели» на панели кнопок окна
проекта (Рисунок 25).
Рисунок 25. Окно проекта с выделенной кнопкой «Возврат из субмодели».
Перед тем, как приступать к выполнению следующего пункта лабораторной работы, необходимо
сохранить проект.
Разработка модели декодера
Необходимо разработать модель синдромного декодера в виде одного блока. Для этого
требуется добавить на схему блок «Субмодель» из вкладки «Субструктуры» и
разместить его согласно рисунку (Рисунок 26).
Рисунок 26. Окно проекта с добавленным блоком «Субмодель».
Добавленному блоку «Субмодель» необходимо задать подпись «Декодер».
Синдромный декодер должен принять искаженное кодовое слово и восстановить исходный вектор
информационных бит. Для этого он должен решить следующие задачи:
- Вычислить синдром кодового слова.
- Вычислить вектор ошибки.
- Устранить ошибку.
Вычисление синдрома кодового слова
Вычисление синдрома S принятого кодового слова r производится побитно по
следующему алгоритму:
Для реализации данного соотношения требуется зайти в субмодель, добавить в рабочую
область субмодели и разместить, согласно рисунку (Рисунок 27), следующие блоки:
- 1 блок «Демультиплексор» из вкладки «Векторные». Данный блок необходим
для работы с отдельными элементами вектора данных. - 1 блок «Порт входа» из вкладки «Субструктуры». Данный блок необходим
для приема данных через порт блока «Субмодель». - 3 блока «XOR» из вкладки «Логические». Данные блоки необходимы для
реализации алгоритма работы синдромного декодера.
Рисунок 27. Окно проекта с добавленными блоками.
Необходимо увеличить число портов блока «Демультиплексор». Для данного блока
требуется в поле «Формула» свойства «Массив размерностей выходов» задать
формулу «7#1». Данная формула задает массив из семи единиц. После задания формулы
произойдет автоматический расчет значения свойства в поле «Значение» и изменится
количество портов блока. В ходе моделирования на выходных портах блока будут формироваться
соответствующие биты кодового слова, нумерация битов идет сверху вниз.
Каждый бит синдрома определяется как сумма четырех битов по модулю 2. Необходимо
увеличить количество портов всех блоков «XOR». Для каждого блока «XOR»
требуется задать значение свойства «Количество портов» равным «4».
Для упрощения внешнего вида модели следует изменить размер и ориентацию ряда блоков.
Необходимо изменить размер блока «Демультиплексор». Для этого необходимо:
- Открыть окно свойств блока «Демультиплексор» и перейти на вкладку
«Общие». - Задать значение свойства «Высота» равным «224».
Требуется изменить ориентацию всех блоков «XOR». Для этого необходимо:
- Выделить все блоки «XOR» на схеме и вызвать контекстное меню блоков.
- В контекстном меню выбрать пункт «Повернуть»
- В раскрывшемся меню выбрать пункт «90 градусов по часовой стрелке».
Требуется расположить блоки на схеме и соединить их линиями связи согласно рисунку (Рисунок 28).
Рисунок 28. Окно проекта с соединенными блоками.
В ходе моделирования в блоках «XOR» будут вычисляться значения трех битов синдрома
кодового слова. Нумерация битов идет слева направо.
Перед тем, как приступать к выполнению следующего пункта лабораторной работы, необходимо
сохранить проект.
Вычисление вектора ошибки
Вычисление ошибки e производится побитно по следующему алгоритму:
Для реализации данного алгоритма необходимо добавить в рабочую область субмодели 4 блока
«Оператор И» и 3 блока «Оператор НЕ» из вкладки «Логические» и
разместить их согласно рисунку (Рисунок 29).
Рисунок 29. Окно проекта с добавленными блоками.
Необходимо увеличить число портов всех блоков «Оператор И», для каждого блока
«Оператор И» требуется задать значение свойства «Количество портов» равным
«3».
Для упрощения внешнего вида модели необходимо изменить размер всех блоков «Оператор
НЕ». Для каждого блока «Оператор НЕ» на вкладке «Общие» окна свойств
требуется задать:
- значение свойства «Высота» равным «16»;
- значение свойства «Ширина» равным «16».
Требуется расположить блоки на схеме и соединить их линиями связи согласно рисунку (Рисунок 30).
Рисунок 30. Окно проекта с соединенными блоками.
В ходе моделирования в блоках «Оператор И» будут вычисляться значения четырех
битов ошибки. Нумерация битов идет сверху вниз.
Перед тем, как приступать к выполнению следующего пункта лабораторной работы, необходимо
сохранить проект.
Устранение ошибки
Устранение ошибки производится путем сложения по
модулю 2 первых 4-х бит кодового слова и вектора ошибки. Для реализации данного алгоритма
необходимо добавить в рабочую область субмодели и разместить, согласно рисунку (Рисунок 31), следующие блоки:
- 1 блок «Мультиплексор» из вкладки «Векторные». Данный блок необходим
для формирования вектора данных из отдельных битов. - 1 блок «Порт выхода» из вкладки «Субструктуры». Данный блок необходим
для передачи данных через порт блока «Субмодель». - 4 блока «Логические операции» из вкладки «Логические». Данные блоки
необходимы для реализации алгоритма устранения ошибки.
Рисунок 31. Окно проекта с добавленными блоками.
Для формирования вектора сообщения из четырех его битов для блока
«Мультиплексор» требуется задать значение свойства «Количество портов»
равным «4».
Для каждого блока «Логические операции» требуется открыть
окно свойств, в поле «Значение» свойства «Тип операнда» открыть список
доступных операций и выбрать «(ИСКЛЮЧАЮЩЕЕ ИЛИ, XOR)».
Для упрощения
внешнего вида модели необходимо изменить размер блока «Мультиплексор». Для данного
блока на вкладке «Общие» окна свойств требуется задать значение свойства
«Высота» равным «128».
Необходимо расположить и соединить блоки
линиями связи согласно рисунку (Рисунок 32).
Рисунок 32. Окно проекта с соединенными блоками.
Разработка модели синдромного декодера завершена. Следует выйти из рабочей
области субмодели одинарным нажатием левой кнопкой мыши по кнопке «Возврат из
субмодели», расположенной на панели кнопок окна проекта.
Необходимо соединить
блоки на схеме согласно рисунку (Рисунок 33).
Рисунок 33. Окно проекта с соединенными блоками.
Перед тем, как приступать к выполнению следующего пункта лабораторной работы,
необходимо сохранить проект.
Настройка параметров расчета
Перед запуском моделирования необходимо настроить параметры расчета. Для этого в окне
проекта на панели кнопок следует нажать на кнопку «Параметры расчета» (Рисунок 34).
Рисунок 34. Окно проекта с выделенной кнопкой «Параметры расчета».
В появившемся окне параметров проекта на вкладке «Параметры расчета» установить
новые значения свойств «Минимальный шаг», «Максимальный шаг» и «Конечное
время расчета» (Рисунок 35):
- «Минимальный шаг» – «1».
- «Максимальный шаг» – «1».
- «Конечное время расчета» – «1000000».
Рисунок 35. Вкладка «Параметры расчета» окна «Параметры проекта».
Закрыть окно «Параметры расчета», при этом внесенные изменения будут сохранены
автоматически.
Перед тем, как приступать к выполнению следующего пункта лабораторной работы, необходимо
сохранить проект.
Моделирование передачи данных
Необходимо запустить моделирование одинарным нажатием левой кнопкой мыши по кнопке
«Пуск», расположенной на панели кнопок окна проекта (Рисунок 36).
Рисунок 36. Окно проекта с выделенной кнопкой «Пуск».
После завершения процесса моделирования необходимо сравнить значения вероятностей битовых
и символьных ошибок, полученные в результате моделирования (Рисунок 37), со значениями, вычисленными
аналитически.
Рисунок 37. Окно проекта с отображаемыми результатами моделирования.
Вероятность приема ошибочного бита (BER) при передаче данных без кодирования отображается
на схеме в графическом изображении блока «Цифровая связь – Измеритель BER»,
расположенного в канале связи с подписью «Без кодирования» (Рисунок 38). После окончания процесса
моделирования вероятность должна быть равна примерно «1E-5», аналитически
вычисленное значение равняется «1.02E-5».
Рисунок 38. Окно проекта с выделенным блоком «Цифровая связь – Измеритель BER», расположенным
в канале связи с подписью «Без кодирования».
Вероятность приема ошибочного кодового слова (WER) при передаче данных без кодирования
отображается на схеме в графическом изображении блока «Цифровая связь – Измеритель
WER», расположенного в канале связи с подписью «Без кодирования». После
окончания процесса моделирования вероятность должна быть равна примерно «4E-5»,
аналитически вычисленное значение равняется «4.08E-5».
Вероятность приема ошибочного бита при передаче данных с кодированием отображается на
схеме в графическом изображении блока «Цифровая связь – Измеритель BER»,
расположенного в канале связи с подписью «С кодированием». После окончания процесса
моделирования вероятность должна быть равна примерно «6.5E-4», аналитически
вычисленное значение равняется «6.75E-4».
Вероятность приема ошибочного кодового слова при передаче данных с кодированием
отображается на схеме в графическом изображении блока «Цифровая связь – Измеритель
WER», расположенного в канале связи с подписью «С кодированием». После
окончания процесса моделирования вероятность должна быть равна примерно «1.2E-5»,
аналитически вычисленное значение равняется «1.59E-5».
Результаты моделирования с достаточной точностью совпадают с результатами аналитических
расчетов. Из-за применения кодирования вероятность битовой ошибки значительно увеличилась,
но благодаря алгоритму коррекции ошибок вероятность символьной ошибки уменьшилась примерно
в 3 раза.
Перед завершением выполнения лабораторной работы необходимо сохранить проект.

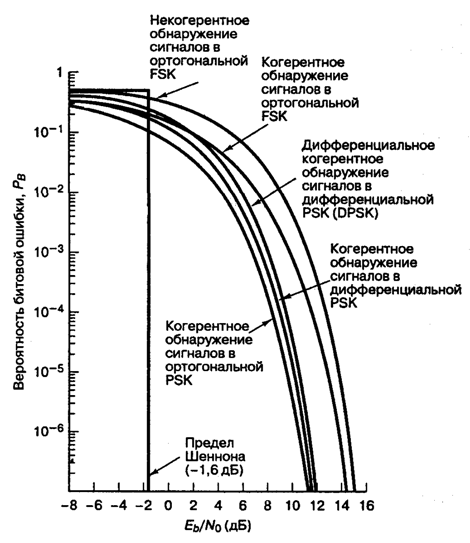
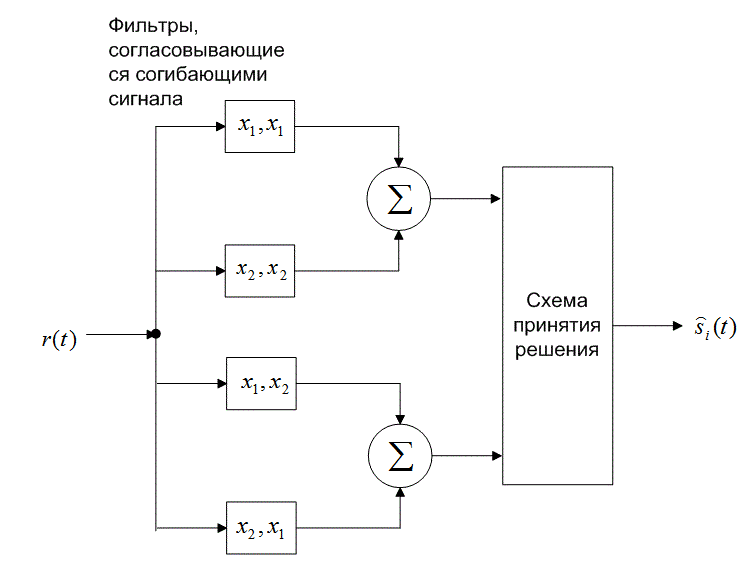
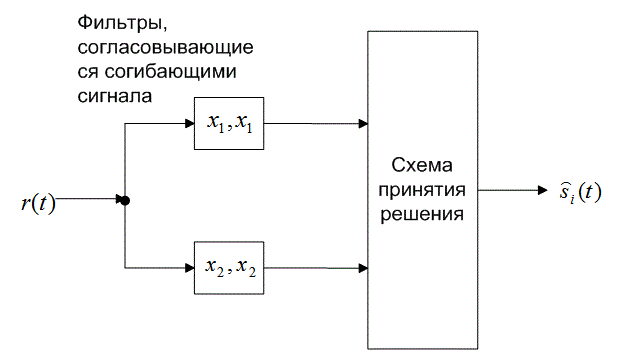
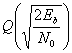
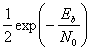
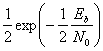


![{\displaystyle p_{e}=1-{\sqrt[{N}]{(1-p_{p})}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5d380e45b0451c45265e199221fae5bd5b84bf9)








































