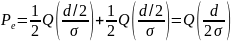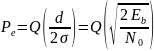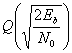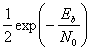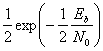Вероятность битовой и символьной ошибки способы измерения

4.9.1. Вероятность символьной ошибки для модуляции MPSK

4.9.2. Вероятность символьной ошибки для модуляции MFSK

4.9.3. Зависимость вероятности битовой ошибки от вероятности символьной ошибки для ортогональных сигналов

4.9.4. Зависимость вероятности битовой ошибки от вероятности символьной ошибки для многофазных сигналов

4.9.5. Влияние межсимвольной интерференции

4.9.1. Вероятность символьной ошибки для модуляции MPSK

Для больших отношений сигнал/шум вероятность символьной ошибки для равновероятных сигналов в M-арной модуляции PSK с когерентным обнаружением можно выразить как [7]

(4.105)

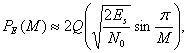
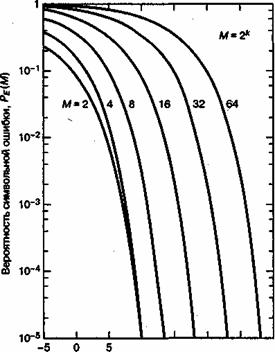
где — вероятность символьной ошибки, — энергия, приходящаяся на символ, а М = 2k — размер множества символов. Зависимость от для передачи сигналов MPSK с когерентным обнаружением показана на рис. 4.35.

Рис. 4.35. Вероятность символьной ошибки для многофазной передачи сигналов с когерентным обнаружением. (Перепечатано с разрешения авторов из W. С. Lindsey and M. К. Simon. Telecommunication Systems Engineering. Prentice-Hall, Inc., Engle-wood Cliffs, N. J., 1973.)

Вероятность символьной ошибки для дифференциального когерентного обнаружения М-арной схемы DPSK (для больших значений ) выражается подобно тому, как это было приведено выше [7].

(4.106)

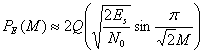
4.9.2. Вероятность символьной ошибки для модуляции MFSK

Вероятность символьной ошибки для равновероятных ортогональных сигналов с когерентным обнаружением можно выразить как [5]

(4.107)

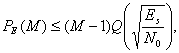
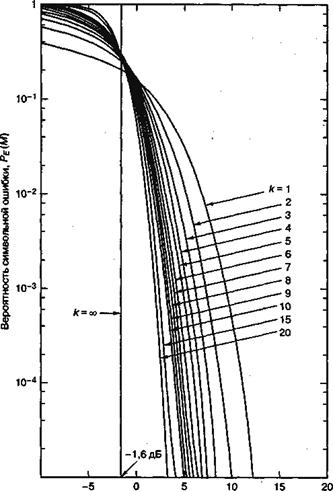
где — энергия, приходящаяся на символ, а M — размер множества символов. Зависимость от для М-арных ортогональных сигналов с когерентным обнаружением показана на рис. 4.36.

Вероятность символьной ошибки для равновероятных М-арных ортогональных сигналов с некогерентным обнаружением дается следующим выражением [9].

(4.108)

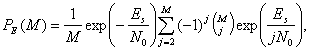
где

(4.109)

является стандартным биномиальным коэффициентом, выражающим число способов выбора j ошибочных символов из М возможных. Отметим, что для бинарного случая формула (4. 108) сокращается до

(4.110)

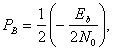
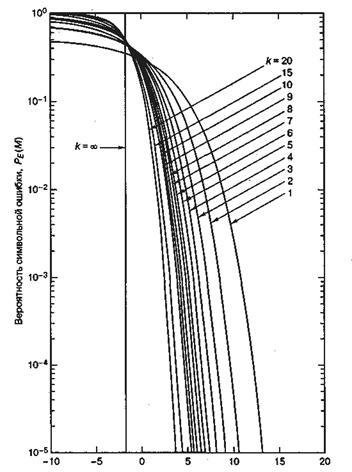
что совпадает с результатом, полученным в выражении (4.96). Кривая зависимости от для M-арной передачи сигналов с некогерентным обнаружением изображена на рис. 4.37. При сравнении данных графиков с приведенными на рис. 4.6 и соответствующими когерентному обнаружению можно заметить, что для k > 7 различием уже можно пренебрегать. В заключение отметим, что для когерентного и некогерентного приема ортогональных сигналов верхний предел вероятности ошибки дается выражением [9].

(4.111)

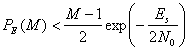
Здесь Es — энергия на символ, а М — размер алфавита символов.

Рис. 4.36. Вероятность символьной ошибки для М-арной ортогональной передачи сигналов с когерентным обнаружением. (Перепечатано с разрешения авторов из W. С. Lindsey and M. К. Simon. Telecommunication Systems Engineering. Prentice-Hall, Inc., Englewood Cliffs, N. J., 1973.)

4.9.3. Зависимость вероятности битовой ошибки от вероятности символьной ошибки для ортогональных сигналов

Можно показать [9], что соотношение между вероятностью битовой ошибки (РВ) и вероятностью символьной ошибки (РЕ) для ортогональных M-арных сигналов дается следующим выражением.

(4.112)

Рис. 4.37. Вероятность символьной ошибки для М-арной ортогональной передачи сигналов с некогерентным обнаружением. (Перепечатано с разрешения авторов из W. С. Lindsey and М. К. Simon, Telecommunication Systems Engineering. Prentice-Hall, Inc., Engtewood Cliffs, N. J., 1973.)

В пределе при увеличении k получаем следующее.

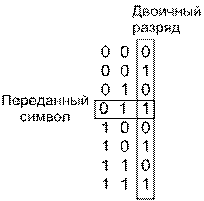
Понять формулу (4.112) позволяет простой пример. На рис. 4.38 показан восьмеричный набор символов сообщения. Эти символы (предполагаемые равновероятными) передаются с помощью ортогональных сигналов, таких как сигналы FSK. При использовании ортогональной передачи ошибка принятия решения равновероятно преобразует верный сигнал в один из (М — 1) неверных. Пример на рисунке демонстрирует передачу символа, состоящего из битов 011. Ошибка с равной вероятностью может перевести данный символ в любой из оставшихся 2k— 1 = 7 символов. Отметим, что наличие ошибки еще не означает, что все биты символа являются ошибочными. Если (рис. 4.38) приемник решит, что переданным символом является нижний из указанных, состоящий из битов 111, два из трех переданных битов будут верными. Должно быть очевидно, что для недвоичной передачи РВвсегда будет меньше РЕ (РB и РЕ — средние частоты появления ошибок).

Рис. 4.38. Пример зависимости рв от ре

Рассмотрим любой из столбцов битов на рис. 4.38. Каждая битовая позиция на 50% заполнена нулями и на 50% — единицами. Рассмотрим первый бит переданного символа (правый столбец). Сколько существует возможностей появления ошибочного бита 1? Всего существует 2k— 1 =4 возможности (нули в столбце появляются в четырех местах) появления битовой ошибки; то же значение получаем для каждого столбца. Окончательное соотношение рв/ре Для ортогональной передачи сигналов в формуле (4.112) получается следующим образом: число возможностей появления битовой ошибки (2k-1) делится на число возможностей появления символьной ошибки (2k— 1). Для случая, изображенного на рис. 4.38, .

4.9.4. Зависимость вероятности битовой ошибки от вероятности символьной ошибки для многофазных сигналов

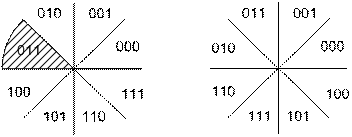
При передаче сигналов MPSK значение РВменьше или равно РЕ, так же как и при передаче сигналов MFSK. В то же время имеется и существенное отличие. Для ортогональной передачи сигналов выбор одного из (М- 1) ошибочных символов равновероятен. При передаче в модуляции MPSK каждый сигнальный вектор не является равноудаленным от всех остальных. На рис. 4.39, а показано восьмеричное пространство решений, где области решений обозначены 8-ричными символами в двоичной записи. При передаче символа (011) и появлении в нем ошибки наиболее вероятными являются ближайшие соседние символы, (010) и (100). Вероятность превращения символа (011) вследствие ошибки в символ (111) относительно мала. Если биты распределяются по символам согласно двоичной последовательности, показанной на рис. 4.39, а, то некоторые символьные ошибки всегда будут давать две (или более) битовые ошибки, даже при значительном отношении сигнал/шум.

а) б)

Рис. 4.39. Области решения в сигнальном пространстве MPSK: а) в бинарной кодировке; 6) в кодировке Грея

Для неортогональных схем, таких как MPSK, часто используется код преобразования бинарных символов в M-арные, такие, что двоичные последовательности, соответствующие соседним символам (сдвигам фаз), отличаются единственной битовой позицией; таким образом, при появлении ошибки в М-арном символе высока вероятность того, что ошибочным является только один из k прибывших битов. Кодом, обеспечивающим подобное свойство, является код Грея (Gray code) [7]; на рис/4.39, б для восьмеричной схемы PSK показано распределение битов по символам с использованием кода Грея. Можно видеть, что соседние символы отличаются одним двоичным разрядом. Следовательно, вероятность появления многобитовой ошибки при данной символьной ошибке значительно меньше по сравнению с некодированным распределением битов, показанным на рис. 4.39, а. Реализация подобного кода Грея представляет один из редких случаев в цифровой связи, когда определенная выгода может быть получена без сопутствующих недостатков. Код Грея — это просто присвоение, не требующее специальных или дополнительных схем. Можно показать [5], что при использовании кода Грея вероятность ошибки будет следующей.

(4.113)

Напомним из раздела 4.8.4, что передача сигналов BPSK и QPSK имеет одинаковую вероятность битовой ошибки. Формула (4.113) доказывает, что вероятности символьных ошибок этих схем отличаются. Для модуляции BPSK РЕ = РВ, а для QPSK РЕ 2РВ. Точное аналитическое выражение вероятности битовой ошибки РB в восьмеричной схеме PSK, а также довольно точные аппроксимации верхнего и нижнего пределов РB для M-арной PSK при больших М можно найти в работе [10].

4.9.5. Влияние межсимвольной интерференции

Обнаружение сигналов рассматривалось при наличии шума AWGN в предположении, что межсимвольная интерференция (intersymbol interference — ISI) отсутствует. Это упростило анализ, поскольку процесс AWGN с нулевым средним описывается единственным параметром — дисперсией. На практике обычно оказывается, что межсимвольная интерференция — это второй (после теплового шума) источник помех, которому необходимо уделять пристальное внимание. ISI может возникать вследствие использования узкополосных фильтров на выходе передатчика, в канале или на входе приемника. Результатом этой дополнительной интерференции является ухудшение достоверности передачи как для когерентного, так и некогерентного приема. Вычисление вероятности ошибки при ISI (помимо AWGN) является значительно более сложной задачей, поскольку в вычислениях будет фигурировать импульсная характеристика канала. Этот вопрос мы не рассматриваем; впрочем, для читателей, интересующихся данной темой, можно порекомендовать работы [11-16].

Источник

  • Среды

  • Согласованная
    фильтрация и

  • фильтрация
    по Найквисту

  • Полная
    система передачи данных

  • Вероятности
    символьной и битовой

  • ошибки
    для модуляционных схем

  • Синхронизация
    элементов сети

Согласованная
фильтрация и фильтрация по Найквисту. 

фильтрация
по Найквисту

  • Временной
    критерий Найквиста:

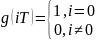
  • Частотный
    критерий Найквиста:

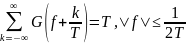
  • Для
    простоты реализации, в качестве ФН
    применяют т.н. фильтр «с приподнятым

косинусом»
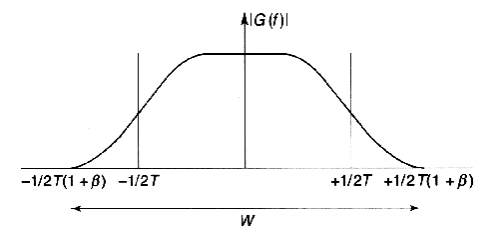
(англ. raised cosine), имеющий полосу пропускания,
полосу задержки и спад между ними по 1
+ cos(f) (отсюда название)

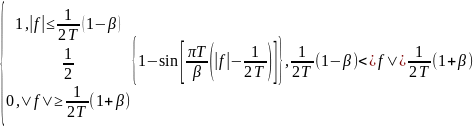
  • Коэффициент
    β в диапазоне 0..1 определяет крутизну
    перехода от полосы пропускания к полосе
    задержки. Для
    телефонных
    модемов обычно β = 0.75

  • Занимаемая
    сигналом полоса определяется β и

    :

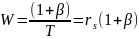
Согласованная
фильтрация

  • Для
    верного обнаружения переданного
    символа, на приемной стороне необходимо
    максимизировать отношение сигнал/шум
    для моментов измерения параметров
    сигнала t
    = i*T
    (используем равенство Парсевал)

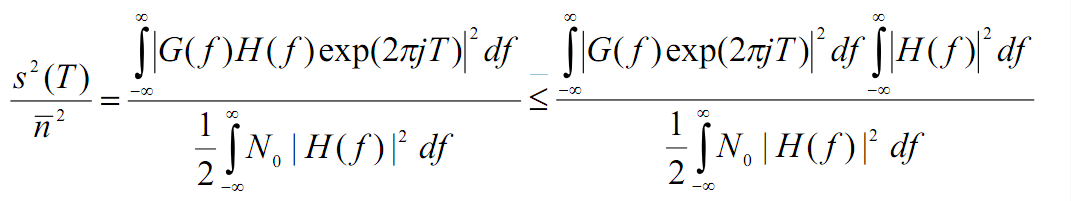
  • Здесь
    используется неравенство Коши-Шварца,
    которое в нашем случае становится
    равенством при условии:

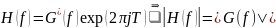
Согласованный
фильтр (СФ)

  • Фильтр
    с частотной характеристикой, совпадающей
    (согласованной) со спектром входного
    сигнала называется СФ. Отношение
    сигнал/шум на выходе СФ:

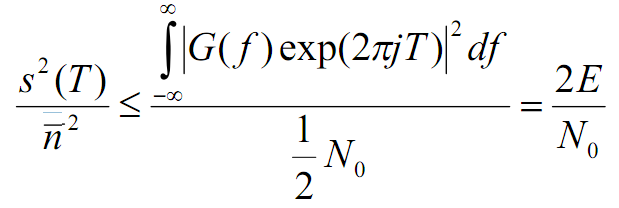
  • Импульсная
    характеристика СФ обратна повремени
    импульсу сигнала

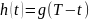
Полная
система передачи

  • Система
    передачи данных, состоящая из приемника,
    передатчика и линии связи, должна в
    целом удовлетворять обоим критериям:
    Найквиста и согласованной фильтрации

  • Обозначая
    частотные характеристики передатчика
    и приемника T(f), R(f), и используя фильтр
    «с приподнятым косинусом», получим
    T(f) и R(f):

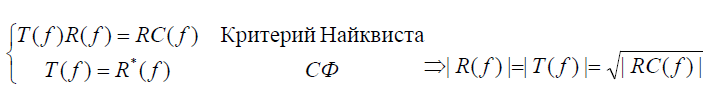
  • Полная
    мощность принятого шума при использовании
    такого фильтра для rb = 1/T:

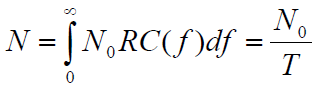
9) Расчет вероятностей символьной и битовой ошибки для модуляционных схем (bpsk, mpsk, qam). Основной подход, примеры.

Вероятность
битовой ошибки для BPSK
модуляции

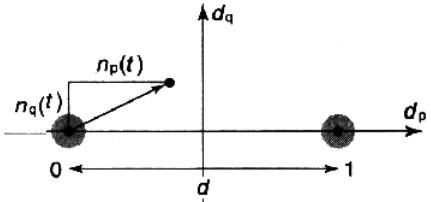
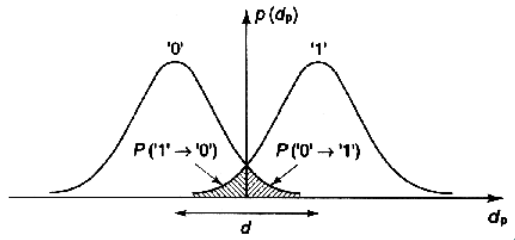
Ошибка
возникает, когда np
> d/2
(см.созвездие). Тогда вероятность ошибки
определяется как:

n(t)
— гаус. сл. процесс: µ=0, P{n(t)>d/2}=Q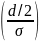



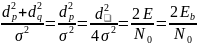
Вероятность
битовой ошибки для QPSK
модуляции

  • Энергетическая
    эффективность QPSK аналогична BPSK, а
    спектральная эффективность в 2 раза
    выше.

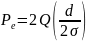
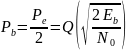
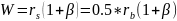
Вероятность
битовой ошибки для МPSK
модуляци

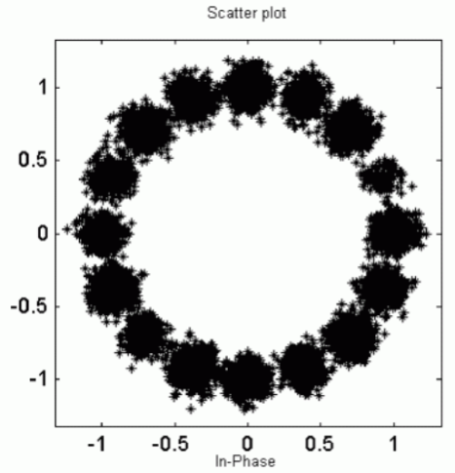
  • MPSK
    модуляция определяет более 4-х фазовых
    состояний (см. рис).

  • Количество
    состояний– степени 2, следовательно
    символьная скорость в

k=log2M
меньше битовой

  • Определите
    Pe
    и Pb
    для M=16, а также W для маркировки состояний
    по Грею

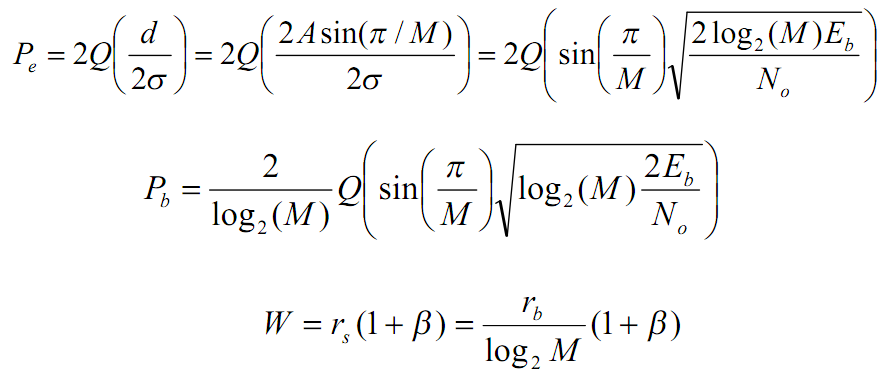
  • Энергетическая
    эффективность MPSK
    меньше BPSK,QPSK,
    а спектральная эффективность выше.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

4.7.1. Вероятность появления ошибочного бита при когерентном обнаружении сигнала BPSK

4.7.2. Вероятность появления ошибочного бита при когерентном обнаружении сигнала в дифференциальной модуляции BPSK

4.7.3. Вероятность появления ошибочного бита при когерентном обнаружении сигнала в бинарной ортогональной модуляции FSK

4.7.4. Вероятность появления ошибочного бита при некогерентном обнаружении сигнала в бинарной ортогональной модуляции FSK

4.7.5. Вероятность появления ошибочного бита для бинарной модуляции DPSK

4.7.6. Вероятность ошибки для различных модуляций

4.7.1. Вероятность появления ошибочного бита при когерентном обнаружении сигнала BPSK

Важной мерой производительности, используемой для сравнения цифровых схем модуляции, является вероятность ошибки, РЕ Для коррелятора или согласованного фильтра вычисление РЕ можно представить геометрически (см. рис. 4.6). Расчет РЕ включает нахождение вероятности того, что при данном векторе переданного сигнала, скажем si вектор шума n выведет сигнал из области 1. Вероятность принятия детектором неверного решения называется вероятностью символьной ошибки, рE. Несмотря на то что решения принимаются на символьном уровне, производительность системы часто удобнее задавать через вероятность битовой ошибки (Ps). Связь РВ и РЕ рассмотрена в разделе 4.9.3 для ортогональной передачи сигналов и в разделе 4.9.4 для многофазной передачи сигналов.

Для удобства изложения в данном разделе мы ограничимся когерентным обнаружением сигналов BPSK. В этом случае вероятность символьной ошибки — это то же самое, что и вероятность битовой ошибки. Предположим, что сигналы равновероятны. Допустим также, что при передаче сигнала принятый сигнал r(t) равен , где n(t) — процесс AWGN; кроме того, мы пренебрегаем ухудшением качества вследствие введенной каналом или схемой межсимвольной интерференции. Как показывалось в разделе 4.4.1, антиподные сигналы и можно описать в одномерном сигнальном пространстве, где

(4.74)

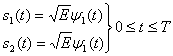
Детектор выбирает с наибольшим выходом коррелятора ; или, в нашем случае антиподных сигналов с равными энергиями, детектор, используя формулу (4.20), принимает решение следующего вида.

(4.74)

Как видно из рис. 4.9, возможны ошибки двух типов: шум так искажает переданный сигнал , что измерения в детекторе дают отрицательную величину z(T), и детектор выбирает гипотезу H2, что был послан сигнал s2(t). Возможна также обратная ситуация: шум искажает переданный сигнал , измерения в детекторе дают положительную величину z(T), и детектор выбирает гипотезу Н1, соответствующую предположению о передаче сигнала .

В разделе 3.2.1.1 была выведена формула (3.42), описывающая вероятность битовой ошибки РB для детектора, работающего по принципу минимальной вероятности ошибки.

(4.76)

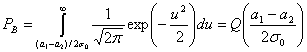
Здесь σ0 — среднеквадратическое отклонение шума вне коррелятора. Функция Q(x), называемая гауссовым интегралом ошибок, определяется следующим образом.

(4.77)

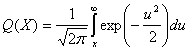
Эта функция подробно описывается в разделах 3.2 и Б.3.2.

Для передачи антиподных сигналов с равными энергиями, таких как сигналы в формате BPSK, приведенные в выражении (4.74), на выход приемника поступают следующие компоненты: , при переданном сигнале , и , при переданном сигнале s2(t), где Еь — энергия сигнала, приходящаяся на двоичный символ. Для процесса AWGN дисперсию шума вне коррелятора можно заменить N0/2 (см. приложение В), так что формулу (4.76) можно переписать следующим образом.

(4.78)

(4.79)

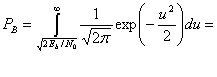
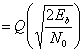
Данный результат для полосовой передачи антиподных сигналов BPSK совпадает с полученными ранее формулами для обнаружения антиподных сигналов с использованием согласованного фильтра (формула (3.70)) и обнаружения узкополосных антиподных сигналов с применением согласованного фильтра (формула (3.76)). Это является примером описанной ранее теоремы эквивалентности. Для линейных систем теорема эквивалентности утверждает, что на математическое описание процесса обнаружения не влияет сдвиг частоты. Как следствие, использование согласованных фильтров или корреляторов для обнаружения полосовых сигналов (рассмотренное в данной главе) дает те же соотношения, что были выведены ранее для сопоставимых узкополосных сигналов.

4.7.2. Вероятность появления ошибочного бита при когерентном обнаружении сигнала в дифференциальной модуляции BPSK

Сигналы в канале иногда инвертируются; например, при использовании когерентного опорного сигнала, генерируемого контуром ФАПЧ, фаза может быть неоднозначной. Если фаза несущей была инвертирована при использовании схемы DPSK, как это скажется на сообщении? Поскольку информация сообщения кодируется подобием или отличием соседних символов, единственным следствием может быть ошибка в бите, который инвертируется, или в бите, непосредственно следующим за инвертированным. Точность определения подобия или отличия символов не меняется при инвертировании несущей. Иногда сообщения (и кодирующие их сигналы) дифференциально кодируются и когерентно обнаруживаются, чтобы просто избежать неопределенности в определении фазы.

Вероятность появления ошибочного бита при когерентном обнаружении сигналов в дифференциальной модуляции PSK (DPSK) дается выражением [5].

(4.80)

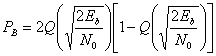
Это соотношение изображено на рис. 4.25. Отметим, что существует незначительное ухудшение достоверности обнаружения по сравнению с когерентным обнаружением сигналов в модуляции PSK. Это вызвано дифференциальным кодированием, поскольку любая отдельная ошибка обнаружения обычно приводит к принятию двух ошибочных решений. Подробно вероятность ошибки при использовании наиболее популярной схемы — когерентного обнаружения сигналов в модуляции DPSK — рассмотрена в разделе 4.7.5.

Рис. 4.25. Вероятность появления ошибочного бита для бинарных систем нескольких типов

4.7.3. Вероятность появления ошибочного бита при когерентном обнаружении сигнала в бинарной ортогональной модуляции FSK

Формулы (4.78) и (4.79) описывают вероятность появления ошибочного бита для когерентного обнаружения антиподных сигналов. Более общую трактовку для когерентного обнаружения бинарных сигналов (не ограничивающихся антиподными сигналами) дает следующее выражение для РВ [6].

(4.81)

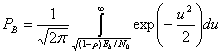
Из формулы (3.64,б) — временной коэффициент взаимной корреляций между и , где θ — угол между векторами сигналов и s2 (см. рис. 4.6). Для антиподных сигналов, таких как сигналы BPSK, θ = π, поэтому ρ = -1.

Для ортогональных сигналов, таких как сигналы бинарной FSK (BFSK), θ = π/2, поскольку векторы и s2 перпендикулярны; следовательно, ρ = 0, что можно доказать с помощью формулы (3.64,а), поэтому выражение (4.81) можно переписать следующим образом.

(4.82)

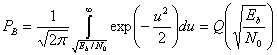
Здесь Q(x) — дополнительная функция ошибок, подробно описанная в разделах 3.2 и Б.3.2. Зависимость (4.82) для когерентного обнаружения ортогональных сигналов BFSK, показанная на рис. 4.25, аналогична зависимости, полученной для обнаружения ортогональных сигналов с помощью согласованного фильтра (формула (3.71)) и узкополосных ортогональных сигналов (униполярных импульсов) с использованием согласованного фильтра (формула (3.73)). В данной книге мы не рассматриваем амплитудную манипуляцию ООК (on-off keying), но соотношение (4.82 применимо к обнаружению с помощью согласованного фильтра сигналов ООК, так же как и к когерентному обнаружению любых ортогональных сигналов.

Справедливость соотношения (4.82) подтверждает и то, что разность энергий между ортогональными векторами сигналов и s2 с амплитудой , как показано на рис. 3.10, б, равна квадрату расстояния между концами ортогональных векторов Ed = 2Eb. Подстановка этого результата в формулу (3.63) также дает формулу (4.82). Сравнивая формулы (4.82) и (4.79), видим, что, по сравнению со схемой BPSK, схема BFSK требует на 3 дБ большего отношения E/N0 для обеспечения аналогичной достоверности передачи. Этот результат не должен быть неожиданным, поскольку при данной мощности сигнала квадрат расстояния между ортогональными векторами вдвое (на 3 дБ) больше квадрата расстояния между антиподными векторами.

4.7.4. Вероятность появления ошибочного бита при некогерентном обнаружении сигнала в бинарной ортогональной модуляции FSK

Рассмотрим бинарное ортогональное множество равновероятных сигналов FSK , определенное формулой (4.8).

Фаза φ неизвестна и предполагается постоянной. Детектор описывается М = 2 каналами, состоящими, как показано на рис. 4.19, из полосовых фильтров и детекторов огибающей. На вход детектора поступает принятый сигнал r(t) = si(t) + n(t), где n(i) — гауссов шум с двусторонней спектральной плотностью мощности No/2. Предположим, что и достаточно разнесены по частоте, чтобы их перекрытием можно было пренебречь. Вычисление вероятности появления ошибочного бита для равновероятных сигналов и начнем, как и в случае узкополосной передачи, с уравнения (3.38).

(4.83)

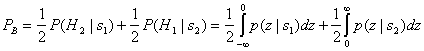
Для бинарного случая тестовая статистика z(T) определена как . Предположим, что полоса фильтра Wf равна 1/T, так что огибающая сигнала FSK (приблизительно) сохраняется на выходе фильтра. При отсутствии шума в приемнике значение z(T) равно при передаче s1(t) и — — при передаче s2(t). Вследствие такой симметрии оптимальный порог γ0=0. Плотность вероятности подобна плотности вероятности .

(4.84)

Таким образом, можем записать

(4.85)

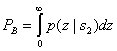
или

(4.86)

где z1 и z2 обозначают выходы z1(T) и z2(T) детекторов огибающей, показанных на рис.4.19. При передаче тона , т.е. когда r(t) = s2(t) + n(t), выход z1(T) состоит исключительно из случайной переменной гауссового шума; он не содержит сигнального компонента. Распределение Гаусса в нелинейном детекторе огибающей дает распределение Релея на выходе [6], так что

(4.87)

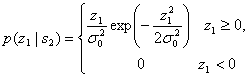
где — шум на выходе фильтра. С другой стороны, z2(T) имеет распределение Раиса, поскольку на вход нижнего детектора огибающей подается синусоида плюс шум [6]. Плотность вероятности p(z2s2) записывается как

(4.88)

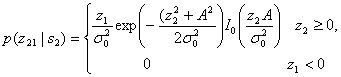
где и, как и ранее, — шум на выходе фильтра. Функция 10(х), известная как модифицированная функция Бесселя первого рода нулевого порядка [7], определяется следующим образом.

(4.89)

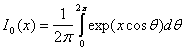
Ошибка при передаче s2(t) происходит, если выборка огибающей z1(T), полученная из верхнего канала (по которому проходит шум), больше выборки огибающей z2(T), полученной из нижнего канала (по которому проходит сигнал и шум). Таким образом, вероятность этой ошибки можно получить, проинтегрировав до бесконечности с последующим усреднением результата по всем возможным z2.

(4.91)

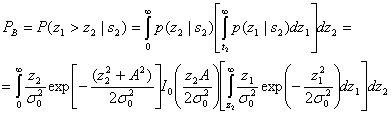
Здесь , внутренний интеграл — условная вероятность ошибки, при фиксированном значении z2, если был передан сигнал s2(1), а внешний интеграл усредняет условную вероятность по всем возможным значениям z2. Данный интеграл можно вычислить аналитически [8], и его значение равно следующему.

(4.92)

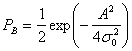
С помощью формулы (1.19) шум на выходе фильтра можно выразить как

(4.93)

где a Wf — ширина полосы фильтра. Таким образом, формула (4.92) приобретает следующий вид.

(4.94)

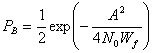
Выражение (4.94) показывает, что вероятность ошибки зависит от ширины полосы полосового фильтра и РB уменьшается при снижении Wf. Результат справедлив только при пренебрежении межсимвольной интерференцией (intersymbol interference — ISI). Минимальная разрешенная Wf (т.е. не дающая межсимвольной интерференции) получается из уравнения (3.81) при коэффициенте сглаживания г = 0. Следовательно, Wf= R бит/с =1/T, и выражение (4.94) можно переписать следующим образом.

(4.95)

(4.96)

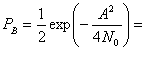
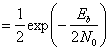
Здесь Еь= (1/2)А2Т — энергия одного бита. Если сравнить вероятность ошибки схем некогерентной и когерентной FSK (см. рис. 4.25), можно заметить, что при равных РB некогерентная FSK требует приблизительно на 1 дБ большего отношения Eb/N0, чем когерентная FSK (для РB < 10-4). При этом некогерентный приемник легче реализуется, поскольку не требуется генерировать когерентные опорные сигналы. По этой причине практически все приемники FSK используют некогерентное обнаружение. В следующем разделе будет показано, что при сравнении когерентной ортогональной схемы FSK с нёкогерентной схемой DPSK имеет место та же разница в 3 дБ, что и при сравнении когерентной ортогональной FSK и когерентной PSK. Как указывалось ранее, в данной книге не рассматривается амплитудная манипуляция ООК (on-off keying). Все же отметим, что вероятность появления ошибочного бита РB, выраженная в формуле (4.96), идентична РB для некогерентного обнаружения сигналов ООК.

4.7.5. Вероятность появления ошибочного бита для бинарной модуляции DPSK

Определим набор сигналов BPSK следующим образом.

(4.97)

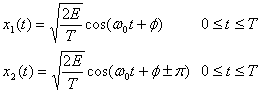
Особенностью схемы DPSK является отсутствие в сигнальном пространстве четко определенных областей решений. В данном случае решение основывается на разности фаз между принятыми сигналами. Таким образом, при передаче сигналов DPSK каждый бит в действительности передается парой двоичных сигналов.

(4.98)

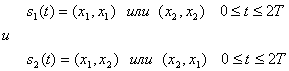
Здесь обозначает сигнал , за которым следует сигнал . Первые Т секунд каждого сигнала — это в действительности последние Т секунд предыдущего. Отметим, что оба сигнала s1(t) и s2(t) могут принимать любую из возможных форм и что и — это антиподные сигналы. Таким образом, корреляцию между и s2(t) для любой комбинации сигналов можно записать следующим образом.

(4.99)

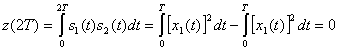
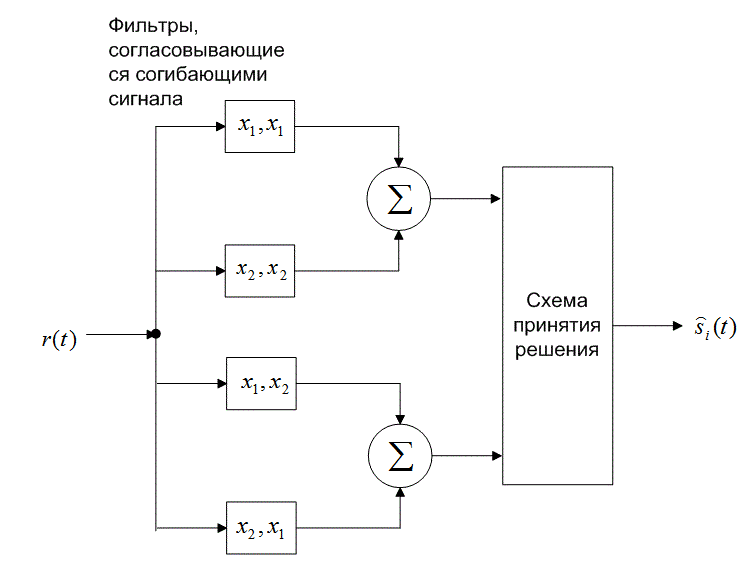
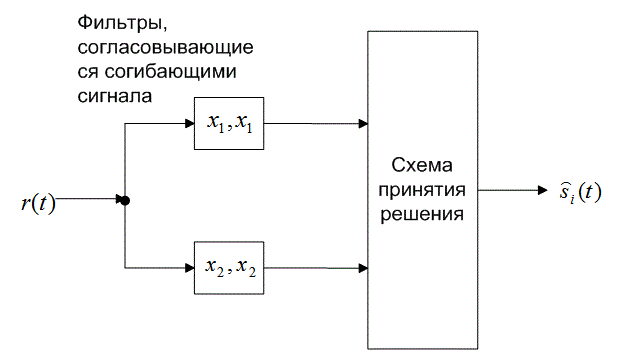
Следовательно, каждую пару сигналов DPSK можно представить как ортогональный сигнал длительностью 2Т секунд. Обнаружение может соответствовать некогерентному обнаружению огибающей с помощью четырех каналов, согласованных с каждым возможным выходом огибающей, как показано на рис. 4.26. Поскольку два детектора огибающей, представляющих каждый символ, обратны друг другу, выборки их огибающих будут совпадать. Значит, мы можем реализовать детектор как один канал для , согласовывающегося с или , и один канал для , согласовывающегося с или , как показано на рис. 4.26. Следовательно, детектор DPSK сокращается до стандартного двухканального некогерентного детектора. В действительности фильтр может согласовываться с разностным сигналом; так что необходимым является всего один канал. На рис. 4.26 показаны фильтры, которые согласовываются с огибающими сигнала (в течение двух периодов передачи символа). Что это означает, если вспомнить, что DPSK — это схема передачи сигналов с постоянной огибающей? Это означает, что нам требуется реализовать детектор энергии, подобный квадратурному приемнику на рис. 4.18, где каждый сигнал в течение периода представляется синфазным и квадратурным опорными сигналами.

синфазный опорный сигнал квадратурный опорный сигнал синфазный опорный сигнал квадратурный опорный сигнал

Поскольку пары сигналов DPSK ортогональны, вероятность ошибки при подобном некогерентном обнаружении дается выражением (4.96). Впрочем, поскольку сигналы DPSK длятся 2Т секунд, энергия сигналов , определенных в формуле (4.98), равна удвоенной энергии сигнала, определенного в течение одного периода передачи символа.

а)

б)

Рис. 4.26. Обнаружение в схеме DPSK: а) четырехканальное дифференциально-когерентное обнаружение сигналов в бинарной модуляции DPSK; б) эквивалентный двухканальный детектор сигналов в бинарной модуляции DPSK

Таким образом, РВможно записать в следующем виде.

(4.100)

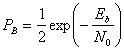
Зависимость (4.100), изображенная на рис. 4.25, представляет собой дифференциальное когерентное обнаружение сигналов в дифференциальной модуляции PSK, или просто DPSK. Выражение справедливо для оптимального детектора DPSK (рис. 4.17, в). Для детектора, показанного на рис. 4.17, б, вероятность ошибки будет несколько выше приведенной в выражении (4.100) [3]. Если сравнить вероятность ошибки, приведенную в формуле (4.100), с вероятностью ошибки когерентной схемы PSK (см. рис. 4.25), видно, что при равных РB схема DPSK требует приблизительно на 1 дБ большего отношения E^N0, чем схема BPSK (для ). Систему DPSK реализовать легче, чем систему PSK, поскольку приемник DPSK не требует фазовой синхронизации. По этой причине иногда предпочтительнее использовать менее эффективную схему DPSK, чем более сложную схему PSK.

4.7.6. Вероятность ошибки для различных модуляций

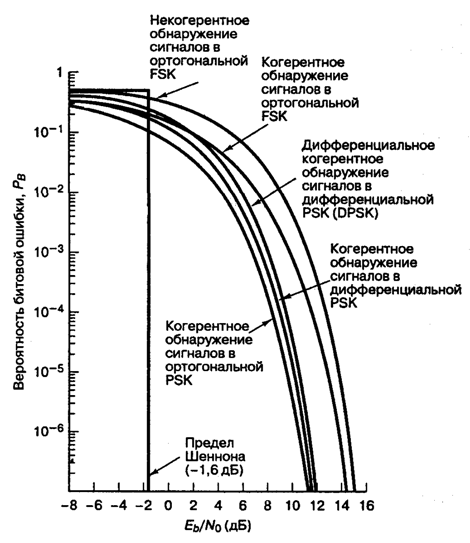
В табл. 4.1 и на рис. 4.25 приведены аналитические выражения и графики РB для наиболее распространенных схем модуляции, описанных выше. Для РB = 10-4 можно видеть, что разница между лучшей (когерентной PSK) и худшей (некогерентной ортогональной FSK) из рассмотренных схем равна приблизительно 4 дБ. В некоторых случаях 4 дБ — это небольшая цена за простоту реализации, увеличивающуюся от когерентной схемы PSK до некогерентной FSK (рис. 4.25); впрочем, в других случаях ценным является даже выигрыш в 1 дБ. Помимо сложности реализации и вероятности РB существуют и другие факторы, влияющие на выбор модуляции; например, в некоторых случаях (в каналах со случайным затуханием) желательными являются некогерентные системы, поскольку иногда когерентные опорные сигналы затруднительно определять и использовать. В военных и космических приложениях весьма желательны сигналы, которые могут противостоять значительному ухудшению качества, сохраняя возможность обнаружения.

Таблица 4.1. Вероятность ошибки для различных бинарных модуляций

Модуляция

PB

PSK (когерентное обнаружение)

DPSK (дифференциальное когерентное обнаружение)

Ортогональная FSK (когерентное обнаружение)

Ортогональная FSK (некогерентное обнаружение)

Pв
– вероятность ошибки зависит от
соотношения «сигнал/шум».
Pв=f(ОСШ)

Для
бинарного случая

ОСШ=Eb/No

Eb
– энергия
бита

No
– спектральная
плотность мощности шума

ОСШ=Eb/No=(PS/PN)*(ΔF/C)

PS
– мощность
сигнала

No
– мощность
шума

PS/PN
= 2С/ΔF-1

C=log2(PS/PN+1)
– формула Шеннона.

Для m-мерной

ES=Eblog2M
M-
разрядность системы (сколько уровней
может принимать единичный импульс). ES
– энергия
символа.

В большинстве
формул для определения вероятности
используется функция Крампа

18 Кодирование

Суть
линейного кодирования заключается в
преобразовании последовательности
передаваемых импульсов с целью
уменьшения мощности передатчика и
сужения требуемой полосы частот.

1)
Потенциальный код без возращения к 0

«+»
– простота реализации; хорошая
распознаваемость ошибок (благодоря
наличию 2-х однозначно отличающихся
потенциалов); сравнительно узкий спектр

«-»
– метод не обладает свойством
самосинхронизации; при высоких скоростях
обмена данными или длинных последовательностей
1 или 0 не большое рассогласование
тактовых частот может привести к
некоторому считыванию битов; наличие
низкочастотной составляющей, кот.
приближается к постоянному сигналу
при передачи длинных последовательностей
нулей или единиц.

2)
Биполярное кодирование. бипол-й код
явл. модификацией потенциального с
альтернат-й инверсией. В этом методе
использ-ся 3 уровня потенциала: «0» лог
кодируется 0, «1 лог» код-ся либо
положительным потенц-ом либо отрицат-м
в зависимости от предыдущего значения
1, т.е. каждый послед. потенциал 1
противополож. предыдущему. Этот код
частично решает проблему постоян-й
составл-ей. Длинные последов-ти нулей
характ-ся наличием постоян-й составляющей.
При равномерном потоке 0 и 1 спектр
сигнала более узкий по сравнению с
потенц-м кодом.

3)
Потенциальный код с инверсией используется
2 уровня сигнала при передаче нуля
перед-ся потенциал установ-й в педыдущем
такте. При передаче 1 сигнал инверт-ся
на противоположный. Этот код удобен в
случае если наличие 3-го уровня сигнала
нежел-но. Например в оптич-х системах.
Для улучшения потенц-х кодов испол-ся
2 метода: 1. Основан на добавл-нии в исход-й
код исбыточ-х битов, содерж-х лог. «1». В
этом случае длинные послед-ти 0 прерываются,
исчезает постоя-я составляющ-я, сужает-ся
спектр, однако снижается полезная
пропуск-я способ-ть. 2-й метод основан
на предварительном перемешивании
битового потока, след-но вероят-ть
появл-я 0 и 1 стан-ся практич-ки одинаковой.

4) Биполярный
импульсный код. Данные представлены
фронтом сигнала. «1» — импульс одной
полярности; «0» — другой. «+» — хорошая
самосинхронизирующая способность; «-»
– широкий спектр; наличие постоянной
составляющей при передаче длительной
последовательности импульсов 0 и 1.

19 Сравнение кодов, используемых в каналообразующих устройствах

Основными кодами,
используемыми в коу, являются: NRZ,
AMI,
NRZI,
биполярный импульсный, манчестерский,
2B1Q.

Код NRZ
обладает узким спектром, хорошей
распознаваемостью ошибок и простотой
реализации.

AMI-код
обладает хорошими синхронизирующими
свойствами при передаче серий единиц
и сравнительно прост в реализации.
Недостатком кода является ограничение
на плотность нулей в потоке данных,
поскольку длинные последовательности
нулей ведут к потере синхронизации.

Код NRZI
удобен в тех случаях, когда наличие
третьего уровня сигнала весьма
нежелательно, например в оптических
кабелях, где устройство распознаются
только два сигнала – свет и темнота.

Биполярный
импульсный код обладает отличными
самосинхронизирующими свойствами, но
постоянная составляющая, может
присутствовать, например, при передаче
длинной последовательности единиц или
нулей. Кроме того, спектр у него шире,
чем у потенциальных кодов.

Полоса пропускания
манчестерского
кода уже,
чем у биполярного импульсного. У него
также нет постоянной составляющей, а
основная гармоника в худшем случае (при
передаче последовательности единиц
или нулей) имеет частоту N Гц, а в лучшем
(при передаче чередующихся единиц и
нулей) она равна N/2 Гц, как и у кодов AMI
или NRZ. В среднем ширина полосы
манчестерского кода в полтора раза уже,
чем у биполярного импульсного кода, а
основная гармоника колеблется вблизи
значения 3N/4. Манчестерский код имеет
еще одно преимущество перед биполярным
импульсным кодом. В последнем для
передачи данных используются три уровня
сигнала, а в манчестерском — два.

Сигнальная скорость
у кода 2B1Q
в два раза ниже, чем у кодов NRZ
и AMI,
а спектр сигнала в два раза уже.
Следовательно с помощью 2B1Q-кода
можно по одной и той же линии передавать
данные в два раза быстрее, однако для
его реализации мощность передатчика
должна быть выше, чтобы четыре уровня
четко различались приемником на фоне
помех.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Обязательными элементами современных сетей связи являются системы сетевого управления, с помощью которых решаются такие задачи, как реконфигурация сети, непрерывный мониторинг параметров системы связи (например, SIP GSM шлюзов), фиксация аварийных состояний, защитные переключения, хранение и обработка результатов мониторинга и т. д. Все указанные операции выполняются, как правило, автоматически, с помощью встроенных аппаратных и программных средств.

В то же время зачастую при обслуживании сетей связи не удается обойтись без ручных операций с применением портативных измерительных приборов. Классический пример – устранение сложных повреждений металлических кабелей связи, случившихся по причине намокания.

АНАЛИЗ ОШИБОК В ЦИФРОВЫХ СИСТЕМАХ ПЕРЕДАЧИ

Основное преимущество цифровой передачи по сравнению с аналоговой заключается в отсутствии накопления помех вдоль линии. Это достигается за счет восстановления формы передаваемого сигнала на каждом регенерационном участке.

Все факторы, от которых зависит длина участка, можно разделить на внутренние и внешние.

Наиболее важными внутренними считают затухание линии, межсимвольные помехи, нестабильность тактовой частоты системы, вариацию задержки, возрастание уровня шумов вследствие старения системы.

К существенным внешним факторам обычно относят переходные и импульсные помехи, внешние электромагнитные влияния, механические повреждения контактов при вибрации или ударах, ухудшение свойств передающей среды вследствие перепадов температуры.

Все они обычно предопределяют ухудшение самого чувствительного к ошибкам параметра цифровой передачи — соотношения сигнал/шум. Действительно, снижение величины данного соотношения всего на 1 дБ приводит к увеличению обобщенного параметра качества цифровых систем передачи, которым является коэффициент битовых ошибок (Bit Error Rate, BER), по крайней мере на порядок.

Согласно определению, BER представляет собой отношение числа ошибочно принятых битов к общему числу принятых битов. Его величина статистически колеблется около значения среднего коэффициента ошибок за длительный промежуток времени. Разница между непосредственно измеренным коэффициентом ошибок и долговременным средним значением зависит от числа контролируемых бит и тем самым от длительности измерения.

База времени формируется при помощи двух основных методов.

В соответствии с первым из них, на принимающем конце задается фиксированное число наблюдаемых бит и регистрируется соответствующее число бит с ошибками.

Например, если число ошибочно принятых бит оказалось равным 20, а заданное общее число принимаемых бит – 106, то коэффициент ошибок составит 20/106 = 20 x 10-6 = 2 x 10-5 .

Достоинством такого подхода является точно известное время измерения, а недостатком – невысокая надежность измерения при малом числе ошибок.

Согласно второму методу, время измерений определяется заданным числом ошибок. Измерение длится до тех пор, пока, например, не будет зафиксировано 100 ошибок. Затем на основании соответствующего числа битов данных вычисляется коэффициент ошибок.

Его недостаток заключается в том, что неизвестно время измерений, которое при малых коэффициентах ошибок может оказаться очень большим. Кроме того, вполне возможно, что счетчик бит данных заполнится полностью, и измерения прекратятся. Поэтому такой способ используется редко.

На начальном этапе развития цифровых систем передачи они применялись главным образом для передачи аналогового телефонного сигнала, и потому требования к качеству цифровых систем передачи определялись характеристиками этого сигнала.

Ошибка в цифровом сигнале приводит к быстрому изменению величины сигнала АИМ на входе канального демодулятора, и абонент слышит неприятный щелчок на выходе канала ИКМ. Экспериментально установлено, что заметные щелчки возникают только при ошибках в одном из первых двух наибольших по весу символов кодовой группы, что соответствует максимальному (положительному или отрицательному) изменению сигнала АИМ. Качество связи считается удовлетворительным, если в каждом канале наблюдается не более одного щелчка в минуту. При частоте дискретизации, равной 8 кГц, по каналу передается 8000 x 60 = 480 тыс. кодовых групп в минуту, причем опасными в отношении щелчков являются 960 тыс. старших разрядов. Если считать, что вероятность ошибки для любого разряда кодовой группы одинакова, то при допущении одного щелчка в минуту вероятность ошибки в линейном тракте не должна быть более 1/960 000 = 10-6.

С учетом передачи данных, которая более чувствительна к ошибкам передачи, для эталонного международного соединения протяженностью 27 500 км величина BER не должна превышать 10-7.

Ошибки можно обнаружить двумя основными методами.

Во-первых, во время приемки и настройки линий связи, поиске неисправностей и ремонте выполняются измерения с перерывом связи, которые реализуются по трем схемам подключения: точка-точка, шлейф и транзит.

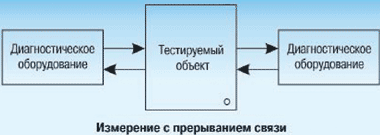
Во-вторых, для мониторинга сети и качественной оценки ее состояния, обнаружения и устранения повреждений используются измерения без перерыва связи.

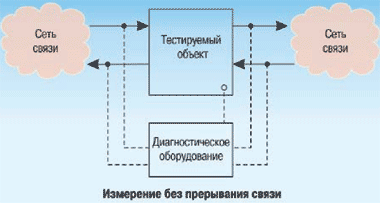
Измерение BER без перерыва связи требует точного знания структуры цифрового сигнала. Таким сигналом в составе цикла, например первичного цифрового сигнала Е-1, является цикловой синхросигнал, занимающий 7 бит нулевого канального интервала (КИ) сигнала E-1.

Цикловой сигнал передается в каждом втором цикле сигнала E-1, причем каждый цикл E-1 содержит 32 КИ и, следовательно, 32 х 8 = 256 бит. Таким образом, относительная доля циклового синхросигнала в сигнале E-1 составляет 7/(256 x 2) < 1,4%. Поэтому достоверность оценки BER с помощью циклового синхросигнала очень низка.

Еще один известный метод оценки качества цифровой передачи основан на обнаружении ошибок кода. Он используется, например, в цифровых трактах T-1/E-1, где применяются коды с чередованием полярности единиц AMI и HDB-3. Однако с помощью измерителя ошибок кода нельзя выявить истинное значение коэффициента битовых ошибок. Отклонения между результатами измерения ошибок кода и обычного измерения ошибок методом побитового сравнения становятся особенно заметными при коэффициентах ошибок более 10-3. Кроме того, нарушение правил кодирования часто распространяется и на нескольких бит, находящихся после бита с ошибкой. Вследствие этого зависящее от содержания сигнала смещение и погрешность при больших коэффициентах ошибок делают невозможным точный анализ распределения ошибок.

Итак, практическая оценка BER возможна только в режиме измерений с перерывом связи и посылкой эталонных испытательных сигналов. При измерении BER испытательный сигнал должен как можно лучше имитировать реальный, т. е. иметь случайный характер. В качестве такого испытательного сигнала обычно используют псевдослучайную последовательность битов (ПСП) с заданной структурой, близкой к настоящему информационному сигналу. Такие последовательности формируются тактируемыми регистрами сдвига с обратной связью.

Цифровой испытательный сигнал заменяет обычно передаваемый информационный сигнал и оценивается на приемном конце измерителем ошибок.

Таким образом, необходимый в условиях нормальной эксплуатации непрерывный мониторинг ошибок цифровой передачи методом BER без перерыва связи практически невозможен.

В настоящее время для оценки качества цифровых систем передачи в эксплуатационных условиях применяется метод измерения блочных ошибок. Как нетрудно догадаться, главное его достоинство состоит в том, что он основан на использовании самого информационного сигнала и выполняется без прерывания связи.

Все методы измерения блочных ошибок предполагают введение избыточности в информационный сигнал, обработку этого вспомогательного сигнала по определенному алгоритму и передачу результата обработки на принимающую сторону, где принятый сигнал обрабатывается по тому же алгоритму, что и при передаче, а итог сравнивается с результатом обработки, полученным от передающей стороны. При их разнице переданный блок считается ошибочным.

Известно несколько способов обнаружения блочных ошибок. Способы поблочного контроля четности и контрольной суммы не позволяют распознать все типы ошибок, тем самым ограничивая их практическую применимость. Пожалуй, единственным универсальным способом измерения ошибок без перерыва связи является контроль при помощи циклического избыточного кода (Cyclical Redundancy Check, CRC).

�

Таблица 1. Измерения в цифровых системах связи и соответствующие им процедуры могут применяться для решения целого ряда задач.

Область применения измерений Измерительные процедуры
Разработка оборудования Испытания с применением высокоточного контрольно-измерительного оборудования, отработка и проверка программного обеспечения, анализ результатов
Производство оборудования Оперативные измерения параметров оборудования и сравнение их с эталонными, проверка дистанционного управления, контроль комплектующих изделий
Инсталляция и линейные испытания оборудования Измерения с перерывом связи, долговременный анализ, сохранение результатов, использование высокоточных и стандартных приборов
Нормальная эксплуатация и техническое обслуживание при поиске и устранении неисправностей Измерения с перерывом и без перерыва связи, включая непрерывный мониторинг с помощью встроенных систем тестирования и измерения с помощью стандартных приборов, имитация ошибок и аварийных сигналов, контроль качества каналов
Ремонт и калибровка — локализация дефектов монтажа и печатных плат, имитация условий эксплуатации Лабораторное оборудование для проверки на соответствие нормативной документации, испытательные стенды
Источник

This topic describes how to compute error statistics for various communications
systems.

Computation of Theoretical Error Statistics

The biterr function, discussed in the
Compute SERs and BERs Using Simulated Data section, can help you gather empirical error
statistics, but validating your results by comparing them to the theoretical error
statistics is good practice. For certain types of communications systems,
closed-form expressions exist for the computation of the bit error rate (BER) or an
approximate bound on the BER. The functions listed in this table compute the
closed-form expressions for the BER or a bound on it for the specified types of
communications systems.

Type of Communications System Function
Uncoded AWGN channel berawgn
Uncoded Rayleigh and Rician fading channel berfading
Coded AWGN channel bercoding
Uncoded AWGN channel with imperfect synchronization bersync

The analytical expressions used in these functions are discussed in
Analytical Expressions Used in BER Analysis. The reference pages of these functions also list
references to one or more books containing the closed-form expressions implemented
by the function.

Theoretical Performance Results

  • Plot Theoretical Error Rates

  • Compare Theoretical and Empirical Error Rates

Plot Theoretical Error Rates

This example uses the bercoding function to compute upper bounds on BERs for convolutional coding with a soft-decision decoder.

coderate = 1/4; % Code rate

Create a structure, dspec, with information about the distance spectrum. Define the energy per bit to noise power spectral density ratio (Eb/N0) sweep range and generate the theoretical bound results.

dspec.dfree = 10; % Minimum free distance of code
dspec.weight = [1 0 4 0 12 0 32 0 80 0 192 0 448 0 1024 ...
    0 2304 0 5120 0]; % Distance spectrum of code
EbNo = 3:0.5:8;
berbound = bercoding(EbNo,'conv','soft',coderate,dspec);

Plot the theoretical bound results.

semilogy(EbNo,berbound)
xlabel('E_b/N_0 (dB)'); 
ylabel('Upper Bound on BER');
title('Theoretical Bound on BER for Convolutional Coding');
grid on;

Figure contains an axes object. The axes object with title Theoretical Bound on BER for Convolutional Coding, xlabel E indexOf b/N 0 baseline blank (dB), ylabel Upper Bound on BER contains an object of type line.

Compare Theoretical and Empirical Error Rates

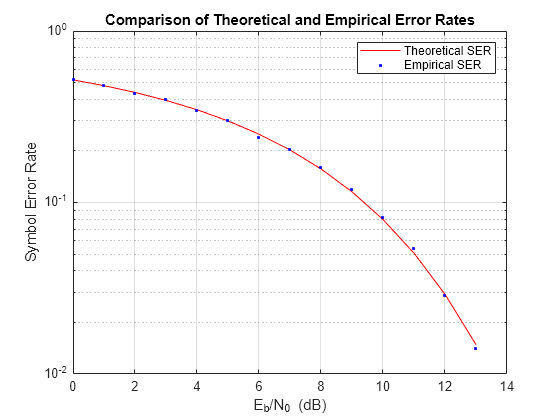
Using the berawgn function, compute the theoretical symbol error rates (SERs) for pulse amplitude modulation (PAM) over a range of Eb/N0 values. Simulate 8 PAM with an AWGN channel, and compute the empirical SERs. Compare the theoretical and then empirical SERs by plotting them on the same set of axes.

Compute and plot the theoretical SER using berawgn.

rng('default') % Set random number seed for repeatability
M = 8;
EbNo = 0:13;
[ber,ser] = berawgn(EbNo,'pam',M);

semilogy(EbNo,ser,'r');
legend('Theoretical SER');
title('Theoretical Error Rate');
xlabel('E_b/N_0 (dB)');
ylabel('Symbol Error Rate');
grid on;

Figure contains an axes object. The axes object with title Theoretical Error Rate, xlabel E indexOf b/N 0 baseline blank (dB), ylabel Symbol Error Rate contains an object of type line. This object represents Theoretical SER.

Compute the empirical SER by simulating an 8 PAM communications system link. Define simulation parameters and preallocate variables needed for the results. As described in [1], because N0=2×(NVariance)2, add 3 dB to the Eb/N0 value when converting Eb/N0 values to SNR values.

n = 10000; % Number of symbols to process
k = log2(M); % Number of bits per symbol
snr = EbNo+3+10*log10(k); % In dB
ynoisy = zeros(n,length(snr));
z = zeros(n,length(snr));
errVec = zeros(3,length(EbNo));

Create an error rate calculator System object™ to compare decoded symbols to the original transmitted symbols.

errcalc = comm.ErrorRate;

Generate a random data message and apply PAM. Normalize the channel to the signal power. Loop the simulation to generate error rates over the range of SNR values.

x = randi([0 M-1],n,1); % Create message signal
y = pammod(x,M); % Modulate
signalpower = (real(y)'*real(y))/length(real(y));

for jj = 1:length(snr)
    reset(errcalc)
    ynoisy(:,jj) = awgn(real(y),snr(jj),'measured'); % Add AWGN
    z(:,jj) = pamdemod(complex(ynoisy(:,jj)),M); % Demodulate
    errVec(:,jj) = errcalc(x,z(:,jj)); % Compute SER from simulation
end

Compare the theoretical and empirical results.

hold on;
semilogy(EbNo,errVec(1,:),'b.');
legend('Theoretical SER','Empirical SER');
title('Comparison of Theoretical and Empirical Error Rates');
hold off;

Figure contains an axes object. The axes object with title Comparison of Theoretical and Empirical Error Rates, xlabel E indexOf b/N 0 baseline blank (dB), ylabel Symbol Error Rate contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent Theoretical SER, Empirical SER.

Performance Results via Simulation

  • Section Overview

  • Compute SERs and BERs Using Simulated Data

Section Overview

This section describes how to compare the data messages that enter and leave
a communications system simulation and how to compute error statistics using the
Monte Carlo technique. Simulations can measure system performance by using the
data messages before transmission and after reception to compute the BER or SER
for a communications system. To explore physical layer components used to model
and simulate communications systems, see PHY Components.

Curve fitting can be useful when you have a small or imperfect data set but
want to plot a smooth curve for presentation purposes. To explore the use of
curve fitting when computing performance results via simulation, see the Curve Fitting for Error Rate Plots section.

Compute SERs and BERs Using Simulated Data

The example shows how to compute SERs and BERs using the biterr and symerr functions, respectively. The symerr function compares two sets of data and computes the number of symbol errors and the SER. The biterr function compares two sets of data and computes the number of bit errors and the BER. An error is a discrepancy between corresponding points in the two sets of data.

The two sets of data typically represent messages entering a transmitter and recovered messages leaving a receiver. You can also compare data entering and leaving other parts of your communications system (for example, data entering an encoder and data leaving a decoder).

If your communications system uses several bits to represent one symbol, counting symbol errors is different from counting bit errors. In either the symbol- or bit-counting case, the error rate is the number of errors divided by the total number of transmitted symbols or bits, respectively.

Typically, simulating enough data to produce at least 100 errors provides accurate error rate results. If the error rate is very small (for example, 10-6 or less), using the semianalytic technique might compute the result more quickly than using a simulation-only approach. For more information, see the Performance Results via Semianalytic Technique section.

Compute Error Rates

Use the symerr function to compute the SERs for a noisy linear block code. Apply no digital modulation, so that each symbol contains a single bit. When each symbol is a single bit, the symbol errors and bit errors are the same.

After artificially adding noise to the encoded message, compare the resulting noisy code to the original code. Then, decode and compare the decoded message to the original message. 

m = 3; % Set parameters for Hamming code
n = 2^m-1;
k = n-m;
msg = randi([0 1],k*200,1); % Specify 200 messages of k bits each
code = encode(msg,n,k,'hamming');
codenoisy = bsc(code,0.95); % Add noise
newmsg = decode(codenoisy,n,k,'hamming'); % Decode and correct errors

Compute the SERs.

[~,noisyVec] = symerr(code,codenoisy);
[~,decodedVec] = symerr(msg,newmsg);

The error rate decreases after decoding because the Hamming decoder correct errors based on the error-correcting capability of the decoder configuration. Because random number generators produce the message and noise is added, results vary from run to run. Display the SERs.

disp(['SER in the received code: ',num2str(noisyVec(1))])
SER in the received code: 0.94571

disp(['SER after decoding: ',num2str(decodedVec(1))])
SER after decoding: 0.9675

Comparing SER and BER

These commands show the difference between symbol errors and bit errors in various situations.

Create two three-element decimal vectors and show the binary representation. The vector a contains three 2-bit symbols, and the vector b contains three 3-bit symbols.

bpi = 3; % Bits per integer
a = [1 2 3]; 
b = [1 4 4];
int2bit(a,bpi)
ans = 3×3

     0     0     0
     0     1     1
     1     0     1


ans = 3×3

     0     1     1
     0     0     0
     1     0     0

Compare the binary values of the two vectors and compute the number of errors and the error rate by using the biterr and symerr functions.

format rat % Display fractions instead of decimals
[snum,srate] = symerr(a,b)

snum is 2 because the second and third entries have bit differences. srate is 2/3 because the total number of symbols is 3. 

[bnum,brate] = biterr(a,b)

bnum is 5 because the second entries differ in two bits, and the third entries differ in three bits. brate is 5/9 because the total number of bits is 9. By definition, the total number of bits is the number of entries in a for symbol error computations or b for bit error computations times the maximum number of bits among all entries of a and b, respectively.

Performance Results via Semianalytic Technique

The technique described in the Performance Results via Simulation
section can work for a large variety of communications systems but can be
prohibitively time-consuming for small error rates (for example,
10-6 or less). The semianalytic technique is an
alternative way to compute error rates. The semianalytic technique can produce
results faster than a nonanalytic method that uses simulated data.

For more information on implementing the semianalytic technique using a
combination of simulation and analysis to determine the error rate of a
communications system, see the semianalytic function.

Error Rate Plots

  • Section Overview

  • Creation of Error Rate Plots Using semilogy
    Function

  • Curve Fitting for Error Rate Plots

  • Use Curve Fitting on Error Rate Plot

Section Overview

Error rate plots can be useful when examining the performance of a
communications system and are often included in publications. This section
discusses and demonstrates tools you can use to create error rate plots, modify
them to suit your needs, and perform curve fitting on the error rate data and
the plots.

Creation of Error Rate Plots Using semilogy Function

In many error rate plots, the horizontal axis indicates
Eb/N0
values in dB, and the vertical axis indicates the error rate using a logarithmic
(base 10) scale. For examples that create such a plot using the semilogy function, see Compare Theoretical and Empirical Error Rates and Plot Theoretical Error Rates.

Curve Fitting for Error Rate Plots

Curve fitting can be useful when you have a small or imperfect data set but
want to plot a smooth curve for presentation purposes. The berfit function includes
curve-fitting capabilities that help your analysis when the empirical data
describes error rates at different
Eb/N0
values. This function enables you to:

  • Customize various relevant aspects of the curve-fitting process, such
    as a list of selections for the type of closed-form function used to
    generate the fit.

  • Plot empirical data along with a curve that berfit fits to the
    data.

  • Interpolate points on the fitted curve between
    Eb/N0
    values in your empirical data set to smooth the plot.

  • Collect relevant information about the fit, such as the numerical
    values of points along the fitted curve and the coefficients of the fit
    expression.

Note

The berfit function is
intended for curve fitting or interpolation, not extrapolation.
Extrapolating BER data beyond an order of magnitude below the smallest
empirical BER value is inherently unreliable.

Use Curve Fitting on Error Rate Plot

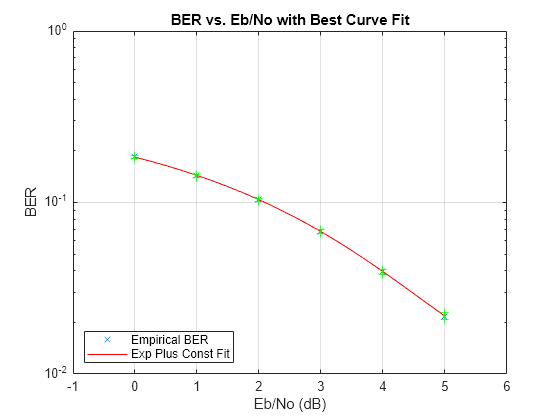
This example simulates a simple differential binary phase shift keying (DBPSK) communications system and plots error rate data for a series of Eb/N0 values. It uses the berfit and berconfint functions to fit a curve to a set of empirical error rates.

Initialize Simulation Parameters

Specify the input signal message length, modulation order, range of Eb/N0 values to simulate, and the minimum number of errors that must occur before the simulation computes an error rate for a given Eb/N0 value. Preallocate variables for final results and interim results.

Typically, for statistically accurate error rate results, the minimum number of errors must be on the order of 100. This simulation uses a small number of errors to shorten the run time and to illustrate how curve fitting can smooth a set of results.

siglen = 100000; % Number of bits in each trial
M = 2; % DBPSK is binary
EbN0vec = 0:5; % Vector of EbN0 values
minnumerr = 5; % Compute BER after only 5 errors occur
numEbN0 = length(EbN0vec); % Number of EbN0 values

ber = zeros(1,numEbN0); % Final BER values
berVec = zeros(3,numEbN0); % Updated BER values
intv = cell(1,numEbN0); % Cell array of confidence intervals

Create an error rate calculator System object™.

errorCalc = comm.ErrorRate;

Loop the Simulation

Simulate the DBPSK-modulated communications system and compute the BER using a for loop to vary the Eb/N0 value. The inner while loop ensures that a minimum number of bit errors occur for each Eb/N0 value. Error rate statistics are saved for each Eb/N0 value and used later in this example when curve fitting and plotting.

for jj = 1:numEbN0
    EbN0 = EbN0vec(jj);
    snr = EbN0; % For binary modulation SNR = EbN0
    reset(errorCalc)
    
    while (berVec(2,jj) < minnumerr)
        msg = randi([0,M-1],siglen,1); % Generate message sequence
        txsig = dpskmod(msg,M); % Modulate
        rxsig = awgn(txsig,snr,'measured'); % Add noise
        decodmsg = dpskdemod(rxsig,M); % Demodulate
        berVec(:,jj) = errorCalc(msg,decodmsg); % Calculate BER
    end

Use the berconfint function to compute the error rate at a 98% confidence interval for the Eb/N0 values.

    [ber(jj),intv1] = berconfint(berVec(2,jj),berVec(3,jj),0.98);
    intv{jj} = intv1;
    disp(['EbN0 = ' num2str(EbN0) ' dB, ' num2str(berVec(2,jj)) ...
        ' errors, BER = ' num2str(ber(jj))])
end
EbN0 = 0 dB, 18427 errors, BER = 0.18427
EbN0 = 1 dB, 14322 errors, BER = 0.14322
EbN0 = 2 dB, 10384 errors, BER = 0.10384
EbN0 = 3 dB, 6789 errors, BER = 0.06789
EbN0 = 4 dB, 3945 errors, BER = 0.03945
EbN0 = 5 dB, 2175 errors, BER = 0.02175

Use the berfit function to plot the best fitted curve, interpolating between BER points to get a smooth plot. Add confidence intervals to the plot.

fitEbN0 = EbN0vec(1):0.25:EbN0vec(end); % Interpolation values
berfit(EbN0vec,ber,fitEbN0);
hold on;
for jj=1:numEbN0
    semilogy([EbN0vec(jj) EbN0vec(jj)],intv{jj},'g-+');
end
hold off;

Figure contains an axes object. The axes object with title BER vs. Eb/No with Best Curve Fit, xlabel Eb/No (dB), ylabel BER contains 8 objects of type line. One or more of the lines displays its values using only markers These objects represent Empirical BER, Exp Plus Const Fit.

See Also

Apps

  • Bit Error Rate Analysis

Functions

  • berawgn | bercoding | berconfint | berfading | berfit | bersync

Related Topics

  • Analyze Performance with Bit Error Rate Analysis App
  • Analytical Expressions Used in BER Analysis
Источник

Понравилась статья? Поделить с друзьями:

Интересное по теме:

  • Вероятностное моделирование ошибок
  • Вероятностная ошибка это
  • Вероятности ошибки блочных кодов
  • Вероника любила и гордилась старшей сестрой где ошибка
  • Вероятно произошла ошибка

    • 0 0 голоса
    Рейтинг статьи
    Подписаться
    Уведомить о
    guest

    0 комментариев
    Старые
    Новые Популярные
    Межтекстовые Отзывы
    Посмотреть все комментарии