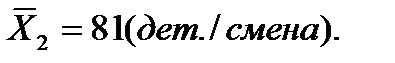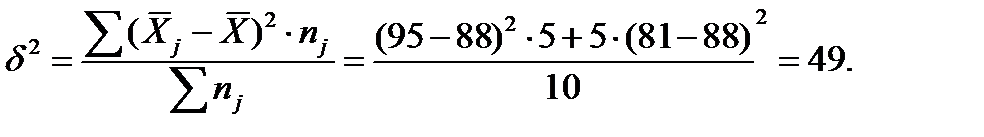11.2. Оценка результатов выборочного наблюдения
11.2.1. Средняя и предельная ошибки выборки. Построение доверительных границ для средней и доли
Средняя ошибка выборки показывает, насколько отклоняется в среднем параметр выборочной совокупности от соответствующего параметра генеральной. Если рассчитать среднюю из ошибок всех возможных выборок определенного вида заданного объема (n), извлеченных из одной и той же генеральной совокупности, то получим их обобщающую характеристику — среднюю ошибку выборки (
В теории выборочного наблюдения выведены формулы для определения 
Например, если применяется повторная собственно случайная выборка, то 


При бесповторном собственно случайном отборе в формулы вносится поправка (1 — n/N):


Вероятность получения именно такой величины ошибки всегда равна 0,683. На практике же предпочитают получать данные с большей вероятностью, но это приводит к возрастанию величины ошибки выборки.
Предельная ошибка выборки (

Если ошибку выборки увеличить в два раза (t = 2), то получим гораздо большую вероятность того, что она не превысит определенного предела (в нашем случае — двойной средней ошибки) — 0,954. Если взять t = 3, то доверительная вероятность составит 0,997 — практически достоверность.
Уровень предельной ошибки выборки зависит от следующих факторов:
- степени вариации единиц генеральной совокупности;
- объема выборки;
- выбранных схем отбора (бесповторный отбор дает меньшую величину ошибки);
- уровня доверительной вероятности.
Если объем выборки больше 30, то значение t определяется по таблице нормального распределения, если меньше — по таблице распределения Стьюдента.
Приведем некоторые значения коэффициента доверия из таблицы нормального распределения.
| Значение доверительной вероятности P | 0,683 | 0,954 | 0,997 |
|---|---|---|---|
| Значение коэффициента доверия t | 1,0 | 2,0 | 3,0 |
Доверительный интервал для среднего значения признака и для доли в генеральной совокупности устанавливается следующим образом:
Итак, определение границ генеральной средней и доли состоит из следующих этапов:
Ошибки выборки при различных видах отбора
- Собственно случайная и механическая выборка. Средняя ошибка собственно случайной и механической выборки находятся по формулам, представленным в табл. 11.3.
 |
|
где |
Пример 11.2. Для изучения уровня фондоотдачи было проведено выборочное обследование 90 предприятий из 225 методом случайной повторной выборки, в результате которого получены данные, представленные в таблице.
| Уровень фондоотдачи, руб. | До 1,4 | 1,4-1,6 | 1,6-1,8 | 1,8-2,0 | 2,0-2,2 | 2,2 и выше | Итого |
|---|---|---|---|---|---|---|---|
| Количество предприятий | 13 | 15 | 17 | 15 | 16 | 14 | 90 |
В рассматриваемом примере имеем 40%-ную выборку (90 : 225 = 0,4, или 40%). Определим ее предельную ошибку и границы для среднего значения признака в генеральной совокупности по шагам алгоритма:
- По результатам выборочного обследования рассчитаем среднее значение и дисперсию в выборочной совокупности:
| Результаты наблюдения | Расчетные значения | |||
|---|---|---|---|---|
| уровень фондоотдачи, руб., xi | количество предприятий, fi | середина интервала, xi\xb4 | xi\xb4fi | xi\xb42fi |
| До 1,4 | 13 | 1,3 | 16,9 | 21,97 |
| 1,4-1,6 | 15 | 1,5 | 22,5 | 33,75 |
| 1,6-1,8 | 17 | 1,7 | 28,9 | 49,13 |
| 1,8-2,0 | 15 | 1,9 | 28,5 | 54,15 |
| 2,0-2,2 | 16 | 2,1 | 33,6 | 70,56 |
| 2,2 и выше | 14 | 2,3 | 32,2 | 74,06 |
| Итого | 90 | — | 162,6 | 303,62 |
Выборочная средняя
Выборочная дисперсия изучаемого признака
- Определяем среднюю ошибку повторной случайной выборки
- Зададим вероятность, на уровне которой будем говорить о величине предельной ошибки выборки. Чаще всего она принимается равной 0,999; 0,997; 0,954.
Для наших данных определим предельную ошибку выборки, например, с вероятностью 0,954. По таблице значений вероятности функции нормального распределения (см. выдержку из нее, приведенную в Приложении 1) находим величину коэффициента доверия t, соответствующего вероятности 0,954. При вероятности 0,954 коэффициент t равен 2.
- Предельная ошибка выборки с вероятностью 0,954 равна
- Найдем доверительные границы для среднего значения уровня фондоотдачи в генеральной совокупности
Таким образом, в 954 случаях из 1000 среднее значение фондоотдачи будет не выше 1,88 руб. и не ниже 1,74 руб.
Выше была использована повторная схема случайного отбора. Посмотрим, изменятся ли результаты обследования, если предположить, что отбор осуществлялся по схеме бесповторного отбора. В этом случае расчет средней ошибки проводится по формуле
Тогда при вероятности равной 0,954 величина предельной ошибки выборки составит:
Доверительные границы для среднего значения признака при бесповторном случайном отборе будут иметь следующие значения:
Сравнив результаты двух схем отбора, можно сделать вывод о том, что применение бесповторной случайной выборки дает более точные результаты по сравнению с применением повторного отбора при одной и той же доверительной вероятности. При этом, чем больше объем выборки, тем существеннее сужаются границы значений средней при переходе от одной схемы отбора к другой.
По данным примера определим, в каких границах находится доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., в генеральной совокупности:
- рассчитаем выборочную долю.
Количество предприятий в выборке с уровнем фондоотдачи, не превышающим значения 2,0 руб., составляет 60 единиц. Тогда
m = 60, n = 90, w = m/n = 60 : 90 = 0,667;
- рассчитаем дисперсию доли в выборочной совокупности

- средняя ошибка выборки при использовании повторной схемы отбора составит
Если предположить, что была использована бесповторная схема отбора, то средняя ошибка выборки с учетом поправки на конечность совокупности составит
- зададим доверительную вероятность и определим предельную ошибку выборки.
При значении вероятности Р = 0,997 по таблице нормального распределения получаем значение для коэффициента доверия t = 3 (см. выдержку из нее, приведенную в Приложении 1):
- установим границы для генеральной доли с вероятностью 0,997:
Таким образом, с вероятностью 0,997 можно утверждать, что в генеральной совокупности доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., не меньше, чем 54,7%, и не больше 78,7%.
- Типическая выборка. При типической выборке генеральная совокупность объектов разбита на k групп, тогда
N1 + N2 + … + Ni + … + Nk = N.
Объем извлекаемых из каждой типической группы единиц зависит от принятого способа отбора; их общее количество образует необходимый объем выборки
n1 + n2 + … + ni + … + nk = n.
Существуют следующие два способа организации отбора внутри типической группы: пропорциональной объему типических групп и пропорциональной степени колеблемости значений признака у единиц наблюдения в группах. Рассмотрим первый из них, как наиболее часто используемый.
Отбор, пропорциональный объему типических групп, предполагает, что в каждой из них будет отобрано следующее число единиц совокупности:
n = ni · Ni/N
где ni — количество извлекаемых единиц для выборки из i-й типической группы;
n — общий объем выборки;
Ni — количество единиц генеральной совокупности, составивших i-ю типическую группу;
N — общее количество единиц генеральной совокупности.
Отбор единиц внутри групп происходит в виде случайной или механической выборки.
Формулы для оценивания средней ошибки выборки для среднего и доли представлены в табл. 11.6.

|
Здесь 
Пример 11.3. В одном из московских вузов проведено выборочное обследование студентов с целью определения показателя средней посещаемости вузовской библиотеки одним студентом за семестр. Для этого была использована 5%-ная бесповторная типическая выборка, типические группы которой соответствуют номеру курса. При отборе, пропорциональном объему типических групп, получены следующие данные:
| Номер курса | Всего студентов, чел., Ni | Обследовано в результате выборочного наблюдения, чел., ni | Среднее число посещений библиотеки одним студентом за семестр, xi | Внутригрупповая выборочная дисперсия, 
|
|---|---|---|---|---|
| 1 | 650 | 33 | 11 | 6 |
| 2 | 610 | 31 | 8 | 15 |
| 3 | 580 | 29 | 5 | 18 |
| 4 | 360 | 18 | 6 | 24 |
| 5 | 350 | 17 | 10 | 12 |
| Итого | 2 550 | 128 | 8 | — |
Число студентов, которое необходимо обследовать на каждом курсе, рассчитаем следующим образом:
- общий объем выборочной совокупности:
n = 2550/130*5 =128 (чел.);
- количество единиц, отобранных из каждой типической группы:
аналогично для других групп:
n2 = 31 (чел.);
n3 = 29 (чел.);
n4 = 18 (чел.);
n5 = 17 (чел.).
Проведем необходимые расчеты.
- Выборочная средняя, исходя из значений средних типических групп, составит:
- Средняя из внутригрупповых дисперсий
- Средняя ошибка выборки:
С вероятностью 0,954 находим предельную ошибку выборки:
- Доверительные границы для среднего значения признака в генеральной совокупности:
Таким образом, с вероятностью 0,954 можно утверждать, что один студент за семестр посещает вузовскую библиотеку в среднем от семи до девяти раз.
- Малая выборка. В связи с небольшим объемом выборочной совокупности те формулы для определения ошибок выборки, которые использовались нами ранее при «больших» выборках, становятся неподходящими и требуют корректировки.
Среднюю ошибку малой выборки определяют по формуле
Предельная ошибка малой выборки:
Распределение значений выборочных средних всегда имеет нормальный закон распределения (или приближается к нему) при п > 100, независимо от характера распределения генеральной совокупности. Однако в случае малых выборок действует иной закон распределения — распределение Стьюдента. В этом случае коэффициент доверия находится по таблице t-распределения Стьюдента в зависимости от величины доверительной вероятности Р и объема выборки п. В Приложении 1 приводится фрагмент таблицы t-распределения Стьюдента, представленной в виде зависимости доверительной вероятности от объема выборки и коэффициента доверия t.
Пример 11.4. Предположим, что выборочное обследование восьми студентов академии показало, что на подготовку к контрольной работе по статистике они затратили следующее количество часов: 8,5; 8,0; 7,8; 9,0; 7,2; 6,2; 8,4; 6,6.
Оценим выборочные средние затраты времени и построим доверительный интервал для среднего значения признака в генеральной совокупности, приняв доверительную вероятность равной 0,95.
- Среднее значение признака в выборке равно
- Значение среднего квадратического отклонения составляет
- Средняя ошибка выборки:
- Значение коэффициента доверия t = 2,365 для п = 8 и Р = 0,95 .
- Предельная ошибка выборки:
- Доверительный интервал для среднего значения признака в генеральной совокупности:
То есть с вероятностью 0,95 можно утверждать, что затраты времени студента на подготовку к контрольной работе находятся в пределах от 6,9 до 8,5 ч.
11.2.2. Определение численности выборочной совокупности
Перед непосредственным проведением выборочного наблюдения всегда решается вопрос, сколько единиц исследуемой совокупности необходимо отобрать для обследования. Формулы для определения численности выборки выводят из формул предельных ошибок выборки в соответствии со следующими исходными положениями (табл. 11.7):
- вид предполагаемой выборки;
- способ отбора (повторный или бесповторный);
- выбор оцениваемого параметра (среднего значения признака или доли).
Кроме того, следует заранее определиться со значением доверительной вероятности, устраивающей потребителя информации, и с размером допустимой предельной ошибки выборки.
 |
Примечание: при использовании приведенных в таблице формул рекомендуется получаемую численность выборки округлять в большую сторону для обеспечения некоторого запаса в точности.
Пример 11.5. Рассчитаем, сколько из 507 промышленных предприятий следует проверить налоговой инспекции, чтобы с вероятностью 0,997 определить долю предприятий с нарушениями в уплате налогов. По данным прошлого аналогичного обследования величина среднего квадратического отклонения составила 0,15; размер ошибки выборки предполагается получить не выше, чем 0,05.
При использовании повторного случайного отбора следует проверить
При бесповторном случайном отборе потребуется проверить
Как видим, использование бесповторного отбора позволяет проводить обследование гораздо меньшего числа объектов.
Пример 11.6. Планируется провести обследование заработной платы на предприятиях отрасли методом случайного бесповторного отбора. Какова должна быть численность выборочной совокупности, если на момент обследования в отрасли число занятых составляло 100 000 чел.? Предельная ошибка выборки не должна превышать 100 руб. с вероятностью 0,954. По результатам предыдущих обследований заработной платы в отрасли известно, что среднее квадратическое отклонение составляет 500 руб.
Следовательно, для решения поставленной задачи необходимо включить в выборку не менее 100 человек.
-
Ошибка выборки
2.1. Понятие и виды ошибок выборки
Поскольку изучаемая статистическая
совокупность состоит из единиц с
варьирующими признаками, то состав
выборочной совокупности может в той
или иной мере отличаться от состава
генеральной совокупности.
Расхождение
между характеристиками выборки и
генеральной совокупности составляет
ошибку
выборки.
Виды ошибок выборки
|
Ошибки выборки |
Систематические |
Случайные |
|
Ошибки регистрации |
Обусловлены |
Проявляются |
|
Ошибки репрезентативности |
Неправильный, |
Несмотря |
Основная
задача выборочного метода – изучение
случайных ошибок репрезентативности.
2.2. Средняя ошибка выборки
Случайная ошибка
репрезентативности зависит от следующих
фактов (при этом считается, что ошибок
регистрации нет):
-
Чем
больше численность выборки при прочих
равных условиях, тем меньше величина
ошибки выборки, т.е. ошибка выборки
обратно пропорциональна ее численности. -
Чем
меньше варьирование признака, тем
меньше ошибка выборки. Если признак
совсем не варьирует, а, следовательно,
величина дисперсии равна нулю, то ошибки
выборки не будет, т.к. любая единица
совокупности будет совершенно точно
характеризовать всю совокупность по
этому признаку. Таким образом, ошибка
выборки прямо пропорциональна величине
дисперсии.
В
математической статистике доказывается,
что величина средней ошибки случайной
повторной выборки может быть определена
по формуле
(6.1)
Однако
следует иметь в виду, что величина
дисперсии в генеральной совокупности
2
нам не известна, т.к. наблюдение выборочное.
Мы можем рассчитать лишь дисперсию в
выборочной совокупности S2.
Соотношение между дисперсиями генеральной
и выборочной совокупности выражается
формулой:
(6.2)
Если
n
велико, следовательно
Таким
образом, можно приблизительно считать,
что выборочная дисперсия равна генеральной
дисперсии.
2 =
S2
И формула средней ошибки повторной
выборки (6.1.) примет вид:
(6.3)
Но
здесь мы рассмотрели только ошибку
выборки для средней величины интересующего
признака. Существует также показатель
доли единиц с интересующим признаком.
Расчет ошибки этого показателя имеет
свои особенности.
Дисперсия
для показателя доли признака определяется
по формуле:
S2=(1-)
(6.4)
Тогда средняя ошибка повтора выборки
для показателя доли признака будет
равна:
(6.5)
Доказательство
формул (6.3) и (6.5) исходит из схемы повторной
выборки. Обычно же выборку организуют
бесповторным способом. Т.к. при бесповторном
отборе численность генеральной
совокупности N
в коде выборки сокращается, то в формулы
ошибки выборки включают дополнительный
множитель
,
и формулы
принимают вид:
(6.6)
(6.7)
Пример
1. Определим, на сколько отличаются
выборочные и генеральные показатели
по данным 10%-ной бесповторной выборки
успеваемости студентов.
|
Оценка, |
Число |
|
2 |
9 |
|
3 |
27 |
|
4 |
54 |
|
5 |
10 |
|
Итого |
100 |
Расчет ошибки бесповторной выборки для
средней величины:
n
= 100 N
= 1000
Найдем выборочную
дисперсию по формуле:
Здесь
не известна величина
,
которую можно найти как обычную среднюю
взвешенную величину:
Таким
образом,
Т.е.
можно сказать, что средний балл всех
студентов ()
равен 3,650,07
Теперь
рассчитаем долю студентов в генеральной
совокупности, обучающихся на «4» и «5».
Найдем по выборке
долю студентов, получивших оценки «4»
и «5».
(или
64%)
Расчет
ошибки бесповторной выборки для доли
производится по формуле:
(или
4,5%)
Таким образом, доля студентов, обучающихся
на «4» и «5» по генеральной совокупности
(P) составляет
0,640,045 (или 64%4,5%).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
При проведении любого статистического наблюдения возникают ошибки наблюдения, которые могут быть случайными и преднамеренными. При высоком уровне организации наблюдения их можно избежать.
При проведении выборочных наблюдений возникают ошибки репрезентативности, которые связаны не с организацией наблюдения, а с самой сутью выборочного исследования, которая заключается в том, что по части (по выборочной совокупности) приходится судить о целом (о генеральной совокупности). Ошибка выборки неизбежна и состоит в том, что значения характеристик выборочной совокупности (показатели, рассчитанные по выборке), в той или иной степени, не совпадают со значениями аналогичных параметров генеральной совокупности. Задача исследователя состоит в том, чтобы сформировать репрезентативную выборку, позволяющую получить несмещенные оценки параметров генеральной совокупности и минимальную ошибку выборки. Основной принцип формирования выборки – случайность отбора, т.е. каждой единице в генеральной совокупности должна быть обеспечена равная вероятность попадания в выборку.
Теоретической основой определения ошибки выборки являются теоремы Чебышева, Ляпунова и Бернулли.
§ Суть теоремы Чебышевасостоит в том, что при неограниченном увеличении числа наблюдений в генеральной совокупности с ограниченной дисперсией (вариацией), с вероятностью, близкой к единице, можно утверждать, что величина ошибки выборки не превысит сколь угодно малой положительной величины 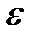
n→∞, 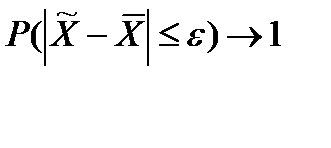
где 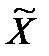

На эти вопросы отвечает теорема Ляпунова,которая одновременно доказывает, что распределение ошибок выборки при больших объемах выборки подчинено нормальному закону распределения.Суть теоремы состоит в том, что при неограниченном увеличении числа наблюдений в генеральной совокупности с ограниченной дисперсией, вероятность того, что ошибка выборки не превысит величины tμ (предельная ошибка), равна нормированной функции Лапласа (Ф (t)):
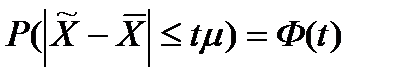
где μ – средняя ошибка выборки, μ= 


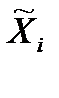
Данная формула средней ошибки выборки не может быть использована на практике, так как при организации выборочного наблюдения формируется лишь одна выборка и исследователю не известна величина генеральной средней.
Математической статистикой доказано, что величина μ2 прямо пропорциональна дисперсии генеральной совокупности (


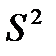



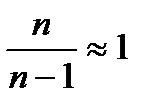

Т.о., величина средней ошибки выборки прямо пропорциональна вариации признака в генеральной совокупности (хотя в практических расчетах вынужденно используется выборочная дисперсия (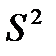
В теореме Ляпунова речь идет о предельной ошибке, которую принято обозначать 

Известно, что 


На практике нет необходимости рассчитывать величину t. Ее находят по таблице нормального распределения, исходя из установленного исследователем уровня вероятности. Социально-экономические исследования проводятся, как правило, с вероятностью Р=0,95. Согласно таблице нормального распределения, если Р=0,954, то t=1,96 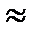
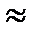
Т.о., если исследователь устанавливает вероятность оценок 95%, то 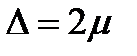
Представленная выше формула расчета ошибки выборки применима при проведении выборки методом повторного отбора. В статистике понятия «повторного» и «бесповторного» отбора соответствуют понятиям «возвратного» и «безвозвратного» шара в теории вероятности. При осуществлении повторного отбора, единицы совокупности, изъятые в выборку, возвращаются назад в генеральную совокупность и могут быть повторно выбраны в выборочную совокупность. При осуществлении бесповторной выборки единицы совокупности, изъятые в выборку, не возвращаются назад в генеральную совокупность и не могут быть повторно выбраны в выборочную совокупность.
При повторном отборе от начала до конца вероятность попадания единиц в выборку сохраняется неизменной, т.е. 
При бесповторном отборе вероятность изменяется от 

Формула средней ошибки выборки для бесповторного отбора, который используется чаще, имеет вид:

Величина ошибки выборки зависит и от вида выборки. В формулах средней ошибки при реализации различных видов выборки используются разные дисперсии, для чего необходимо знание и понимание правило сложения дисперсий.
Правило сложения дисперсий заключается в том, что общая дисперсия изучаемого признака есть сумма межгрупповой и внутригрупповой дисперсий.
Пример: проведена группировка рабочих по признаку «наличие специального технического образования» и зафиксирован уровень производительности труда, результаты приведены в таблице 4.1.
Таблица 4.1.
Зависимость производительности труда рабочих (число деталей в смену) от наличия специального образования
| Группы рабочих | Число рабочих, чел. | Производительность труда, дет./смена | Средняя производительность труда, дет./смена | Дисперсия |
| Имеющие специальное техническое образование | 84, 93, 95, 101, 102 |
|||
| Не имеющие специального технического образования | 62, 68, 82, 88, 105 |
231,2 |
||
| Всего | — | 185,6 |
Средний уровень производительности труда в целом по совокупности рабочих: 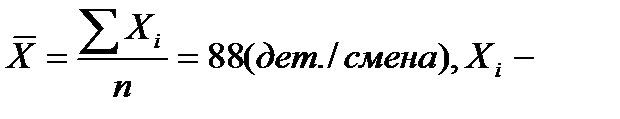
Средний уровень производительности труда рабочих первой группы: 
Средний уровень производительности труда рабочих второй группы:
Общая дисперсия:

Дисперсия каждой группы:
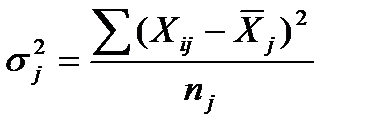
где 
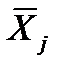


дисперсия второй группы:
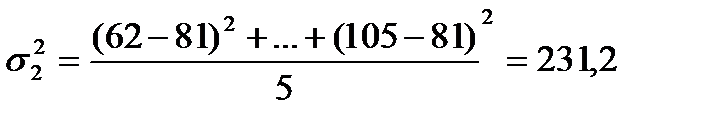
На основе внутригрупповых дисперсий рассчитывается среднее значение внутригрупповой дисперсии:
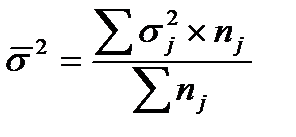
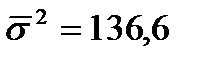
Межгрупповая дисперсия:
(41)
Правило сложения дисперсии: общая дисперсия равна сумма внутригрупповой и межгрупповой дисперсий: 185,6=49+13,6:

Общая дисперсия – это дисперсия, характеризующая вариацию результативного признака под влиянием всех факторов. В данном случае она отражает степень варьирования уровня производительности труда рабочих под влиянием всех факторов, ее определяющих в конкретных условиях.
Межгрупповая дисперсия характеризует вариацию признака (производительности труда), обусловленную вариацией группировочного признака (есть специальное техническое образование или нет).
Внутригрупповая дисперсия оценивает вариацию признака, обусловленную всеми факторами, за исключением группировочного, поскольку внутри групп этот фактор не варьирует.
В условиях собственно случайной выборки в формуле средней ошибки выборки используется общая дисперсия, поскольку в генеральной совокупности не выделяются группы (страты):
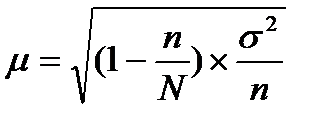
При стратифицированной выборке для расчета ошибки репрезентативности используется внутригрупповая дисперсия:
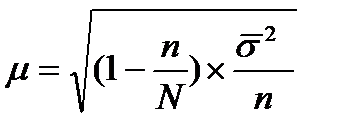
При серийной выборке в формуле средней ошибки выборки используется межгрупповая дисперсия, поскольку внутри отобранных серий проводится сплошное обследование, то вариация не носит характер случайной составляющей:

где r-число серий в выборочной совокупности; R- число серий в генеральной совокупности.
Наибольшая величина ошибки возникает в условиях собственно случайной выборки.
Стратифицированная и серийная выборки, позволяющие сформировать выборочную совокупность по структуре, закономерности распределения более близкую к генеральной совокупности, дают наименьшую величину ошибки (это демонстрируют и формулы расчета величины ошибки).
Ошибка выборки для показателя доли единиц, обладающих тем или иным признаком.
В практических исследованиях часто используется такая характеристика, как доля, доля единиц совокупности, обладающих тем или иным признаком, например: не абсолютное число рабочих, имеющих техническое образование, а их доля в общей численности; доля пенсионеров в общей численности населения города; доля инновационных предприятий в общем числе предприятий отрасли и т.п.
Теоретической основой расчета ошибки выборки для доли служит теорема Бернулли, являющаяся частным случаем теоремы Чебышева (хотя исторически доказана раньше).
При расчете средней ошибки доли используется формула, аналогичная формуле ошибки выборки для средней величины, но при этом учитывается дисперсия доли.
Долю единиц, обладающих тем или иным значением признака (например, доля женщин среди работающего населения) в выборочной совокупности принято обозначать 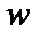
Средняя ошибка показателя доли рассчитывается:
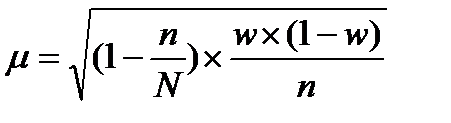
где 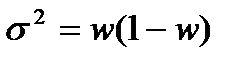














 ) при использовании типического отбора, пропорционального объему типических групп
) при использовании типического отбора, пропорционального объему типических групп