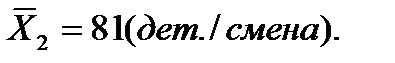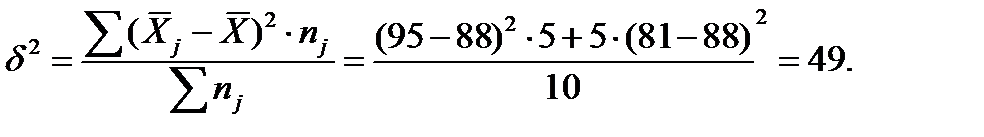-
Ошибка выборки
2.1. Понятие и виды ошибок выборки
Поскольку изучаемая статистическая
совокупность состоит из единиц с
варьирующими признаками, то состав
выборочной совокупности может в той
или иной мере отличаться от состава
генеральной совокупности.
Расхождение
между характеристиками выборки и
генеральной совокупности составляет
ошибку
выборки.
Виды ошибок выборки
|
Ошибки выборки |
Систематические |
Случайные |
|
Ошибки регистрации |
Обусловлены |
Проявляются |
|
Ошибки репрезентативности |
Неправильный, |
Несмотря |
Основная
задача выборочного метода – изучение
случайных ошибок репрезентативности.
2.2. Средняя ошибка выборки
Случайная ошибка
репрезентативности зависит от следующих
фактов (при этом считается, что ошибок
регистрации нет):
-
Чем
больше численность выборки при прочих
равных условиях, тем меньше величина
ошибки выборки, т.е. ошибка выборки
обратно пропорциональна ее численности. -
Чем
меньше варьирование признака, тем
меньше ошибка выборки. Если признак
совсем не варьирует, а, следовательно,
величина дисперсии равна нулю, то ошибки
выборки не будет, т.к. любая единица
совокупности будет совершенно точно
характеризовать всю совокупность по
этому признаку. Таким образом, ошибка
выборки прямо пропорциональна величине
дисперсии.
В
математической статистике доказывается,
что величина средней ошибки случайной
повторной выборки может быть определена
по формуле
(6.1)
Однако
следует иметь в виду, что величина
дисперсии в генеральной совокупности
2
нам не известна, т.к. наблюдение выборочное.
Мы можем рассчитать лишь дисперсию в
выборочной совокупности S2.
Соотношение между дисперсиями генеральной
и выборочной совокупности выражается
формулой:
(6.2)
Если
n
велико, следовательно
Таким
образом, можно приблизительно считать,
что выборочная дисперсия равна генеральной
дисперсии.
2 =
S2
И формула средней ошибки повторной
выборки (6.1.) примет вид:
(6.3)
Но
здесь мы рассмотрели только ошибку
выборки для средней величины интересующего
признака. Существует также показатель
доли единиц с интересующим признаком.
Расчет ошибки этого показателя имеет
свои особенности.
Дисперсия
для показателя доли признака определяется
по формуле:
S2=(1-)
(6.4)
Тогда средняя ошибка повтора выборки
для показателя доли признака будет
равна:
(6.5)
Доказательство
формул (6.3) и (6.5) исходит из схемы повторной
выборки. Обычно же выборку организуют
бесповторным способом. Т.к. при бесповторном
отборе численность генеральной
совокупности N
в коде выборки сокращается, то в формулы
ошибки выборки включают дополнительный
множитель
,
и формулы
принимают вид:
(6.6)
(6.7)
Пример
1. Определим, на сколько отличаются
выборочные и генеральные показатели
по данным 10%-ной бесповторной выборки
успеваемости студентов.
|
Оценка, |
Число |
|
2 |
9 |
|
3 |
27 |
|
4 |
54 |
|
5 |
10 |
|
Итого |
100 |
Расчет ошибки бесповторной выборки для
средней величины:
n
= 100 N
= 1000
Найдем выборочную
дисперсию по формуле:
Здесь
не известна величина
,
которую можно найти как обычную среднюю
взвешенную величину:
Таким
образом,
Т.е.
можно сказать, что средний балл всех
студентов ()
равен 3,650,07
Теперь
рассчитаем долю студентов в генеральной
совокупности, обучающихся на «4» и «5».
Найдем по выборке
долю студентов, получивших оценки «4»
и «5».
(или
64%)
Расчет
ошибки бесповторной выборки для доли
производится по формуле:
(или
4,5%)
Таким образом, доля студентов, обучающихся
на «4» и «5» по генеральной совокупности
(P) составляет
0,640,045 (или 64%4,5%).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
При проведении любого статистического наблюдения возникают ошибки наблюдения, которые могут быть случайными и преднамеренными. При высоком уровне организации наблюдения их можно избежать.
При проведении выборочных наблюдений возникают ошибки репрезентативности, которые связаны не с организацией наблюдения, а с самой сутью выборочного исследования, которая заключается в том, что по части (по выборочной совокупности) приходится судить о целом (о генеральной совокупности). Ошибка выборки неизбежна и состоит в том, что значения характеристик выборочной совокупности (показатели, рассчитанные по выборке), в той или иной степени, не совпадают со значениями аналогичных параметров генеральной совокупности. Задача исследователя состоит в том, чтобы сформировать репрезентативную выборку, позволяющую получить несмещенные оценки параметров генеральной совокупности и минимальную ошибку выборки. Основной принцип формирования выборки – случайность отбора, т.е. каждой единице в генеральной совокупности должна быть обеспечена равная вероятность попадания в выборку.
Теоретической основой определения ошибки выборки являются теоремы Чебышева, Ляпунова и Бернулли.
§ Суть теоремы Чебышевасостоит в том, что при неограниченном увеличении числа наблюдений в генеральной совокупности с ограниченной дисперсией (вариацией), с вероятностью, близкой к единице, можно утверждать, что величина ошибки выборки не превысит сколь угодно малой положительной величины 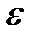
n→∞, 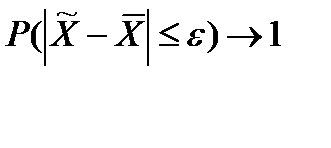
где 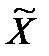

На эти вопросы отвечает теорема Ляпунова,которая одновременно доказывает, что распределение ошибок выборки при больших объемах выборки подчинено нормальному закону распределения.Суть теоремы состоит в том, что при неограниченном увеличении числа наблюдений в генеральной совокупности с ограниченной дисперсией, вероятность того, что ошибка выборки не превысит величины tμ (предельная ошибка), равна нормированной функции Лапласа (Ф (t)):
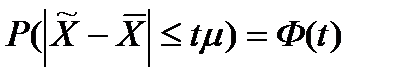
где μ – средняя ошибка выборки, μ= 


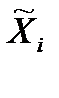
Данная формула средней ошибки выборки не может быть использована на практике, так как при организации выборочного наблюдения формируется лишь одна выборка и исследователю не известна величина генеральной средней.
Математической статистикой доказано, что величина μ2 прямо пропорциональна дисперсии генеральной совокупности (


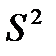



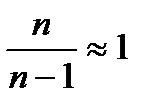

Т.о., величина средней ошибки выборки прямо пропорциональна вариации признака в генеральной совокупности (хотя в практических расчетах вынужденно используется выборочная дисперсия (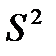
В теореме Ляпунова речь идет о предельной ошибке, которую принято обозначать 

Известно, что 


На практике нет необходимости рассчитывать величину t. Ее находят по таблице нормального распределения, исходя из установленного исследователем уровня вероятности. Социально-экономические исследования проводятся, как правило, с вероятностью Р=0,95. Согласно таблице нормального распределения, если Р=0,954, то t=1,96 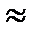
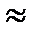
Т.о., если исследователь устанавливает вероятность оценок 95%, то 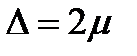
Представленная выше формула расчета ошибки выборки применима при проведении выборки методом повторного отбора. В статистике понятия «повторного» и «бесповторного» отбора соответствуют понятиям «возвратного» и «безвозвратного» шара в теории вероятности. При осуществлении повторного отбора, единицы совокупности, изъятые в выборку, возвращаются назад в генеральную совокупность и могут быть повторно выбраны в выборочную совокупность. При осуществлении бесповторной выборки единицы совокупности, изъятые в выборку, не возвращаются назад в генеральную совокупность и не могут быть повторно выбраны в выборочную совокупность.
При повторном отборе от начала до конца вероятность попадания единиц в выборку сохраняется неизменной, т.е. 
При бесповторном отборе вероятность изменяется от 

Формула средней ошибки выборки для бесповторного отбора, который используется чаще, имеет вид:

Величина ошибки выборки зависит и от вида выборки. В формулах средней ошибки при реализации различных видов выборки используются разные дисперсии, для чего необходимо знание и понимание правило сложения дисперсий.
Правило сложения дисперсий заключается в том, что общая дисперсия изучаемого признака есть сумма межгрупповой и внутригрупповой дисперсий.
Пример: проведена группировка рабочих по признаку «наличие специального технического образования» и зафиксирован уровень производительности труда, результаты приведены в таблице 4.1.
Таблица 4.1.
Зависимость производительности труда рабочих (число деталей в смену) от наличия специального образования
| Группы рабочих | Число рабочих, чел. | Производительность труда, дет./смена | Средняя производительность труда, дет./смена | Дисперсия |
| Имеющие специальное техническое образование | 84, 93, 95, 101, 102 |
|||
| Не имеющие специального технического образования | 62, 68, 82, 88, 105 |
231,2 |
||
| Всего | — | 185,6 |
Средний уровень производительности труда в целом по совокупности рабочих: 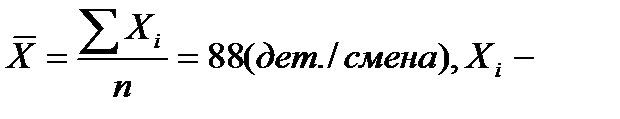
Средний уровень производительности труда рабочих первой группы: 
Средний уровень производительности труда рабочих второй группы:
Общая дисперсия:

Дисперсия каждой группы:
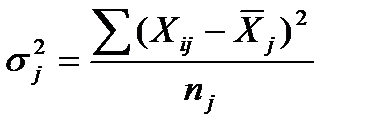
где 
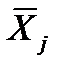


дисперсия второй группы:
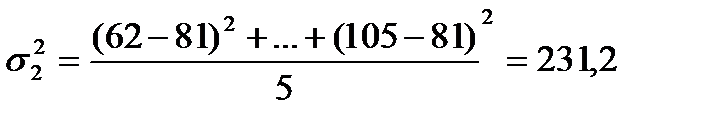
На основе внутригрупповых дисперсий рассчитывается среднее значение внутригрупповой дисперсии:
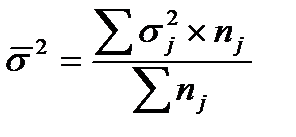
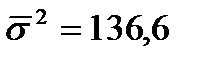
Межгрупповая дисперсия:
(41)
Правило сложения дисперсии: общая дисперсия равна сумма внутригрупповой и межгрупповой дисперсий: 185,6=49+13,6:

Общая дисперсия – это дисперсия, характеризующая вариацию результативного признака под влиянием всех факторов. В данном случае она отражает степень варьирования уровня производительности труда рабочих под влиянием всех факторов, ее определяющих в конкретных условиях.
Межгрупповая дисперсия характеризует вариацию признака (производительности труда), обусловленную вариацией группировочного признака (есть специальное техническое образование или нет).
Внутригрупповая дисперсия оценивает вариацию признака, обусловленную всеми факторами, за исключением группировочного, поскольку внутри групп этот фактор не варьирует.
В условиях собственно случайной выборки в формуле средней ошибки выборки используется общая дисперсия, поскольку в генеральной совокупности не выделяются группы (страты):
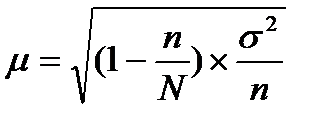
При стратифицированной выборке для расчета ошибки репрезентативности используется внутригрупповая дисперсия:
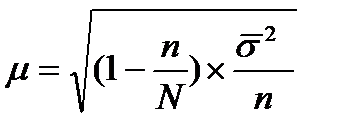
При серийной выборке в формуле средней ошибки выборки используется межгрупповая дисперсия, поскольку внутри отобранных серий проводится сплошное обследование, то вариация не носит характер случайной составляющей:

где r-число серий в выборочной совокупности; R- число серий в генеральной совокупности.
Наибольшая величина ошибки возникает в условиях собственно случайной выборки.
Стратифицированная и серийная выборки, позволяющие сформировать выборочную совокупность по структуре, закономерности распределения более близкую к генеральной совокупности, дают наименьшую величину ошибки (это демонстрируют и формулы расчета величины ошибки).
Ошибка выборки для показателя доли единиц, обладающих тем или иным признаком.
В практических исследованиях часто используется такая характеристика, как доля, доля единиц совокупности, обладающих тем или иным признаком, например: не абсолютное число рабочих, имеющих техническое образование, а их доля в общей численности; доля пенсионеров в общей численности населения города; доля инновационных предприятий в общем числе предприятий отрасли и т.п.
Теоретической основой расчета ошибки выборки для доли служит теорема Бернулли, являющаяся частным случаем теоремы Чебышева (хотя исторически доказана раньше).
При расчете средней ошибки доли используется формула, аналогичная формуле ошибки выборки для средней величины, но при этом учитывается дисперсия доли.
Долю единиц, обладающих тем или иным значением признака (например, доля женщин среди работающего населения) в выборочной совокупности принято обозначать 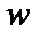
Средняя ошибка показателя доли рассчитывается:
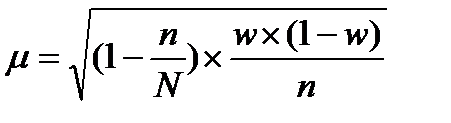
где 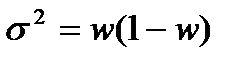
What Is the Standard Error?
The standard error (SE) of a statistic is the approximate standard deviation of a statistical sample population.
The standard error is a statistical term that measures the accuracy with which a sample distribution represents a population by using standard deviation. In statistics, a sample mean deviates from the actual mean of a population; this deviation is the standard error of the mean.
Key Takeaways
- The standard error (SE) is the approximate standard deviation of a statistical sample population.
- The standard error describes the variation between the calculated mean of the population and one which is considered known, or accepted as accurate.
- The more data points involved in the calculations of the mean, the smaller the standard error tends to be.
Standard Error
Understanding Standard Error
The term «standard error» is used to refer to the standard deviation of various sample statistics, such as the mean or median. For example, the «standard error of the mean» refers to the standard deviation of the distribution of sample means taken from a population. The smaller the standard error, the more representative the sample will be of the overall population.
The relationship between the standard error and the standard deviation is such that, for a given sample size, the standard error equals the standard deviation divided by the square root of the sample size. The standard error is also inversely proportional to the sample size; the larger the sample size, the smaller the standard error because the statistic will approach the actual value.
The standard error is considered part of inferential statistics. It represents the standard deviation of the mean within a dataset. This serves as a measure of variation for random variables, providing a measurement for the spread. The smaller the spread, the more accurate the dataset.
Standard error and standard deviation are measures of variability, while central tendency measures include mean, median, etc.
Formula and Calculation of Standard Error
Used in algorithmic trading, the standard error of an estimate can be calculated as the standard deviation divided by the square root of the sample size:
SE = σ / √n
where
- σ = the population standard deviation
- √n = the square root of the sample size
If the population standard deviation is not known, you can substitute the sample standard deviation, s, in the numerator to approximate the standard error.
Requirements for Standard Error
When a population is sampled, the mean, or average, is generally calculated. The standard error can include the variation between the calculated mean of the population and one which is considered known, or accepted as accurate. This helps compensate for any incidental inaccuracies related to the gathering of the sample.
In cases where multiple samples are collected, the mean of each sample may vary slightly from the others, creating a spread among the variables. This spread is most often measured as the standard error, accounting for the differences between the means across the datasets.
The more data points involved in the calculations of the mean, the smaller the standard error tends to be. When the standard error is small, the data is said to be more representative of the true mean. In cases where the standard error is large, the data may have some notable irregularities.
The standard deviation is a representation of the spread of each of the data points. The standard deviation is used to help determine the validity of the data based on the number of data points displayed at each level of standard deviation. Standard errors function more as a way to determine the accuracy of the sample or the accuracy of multiple samples by analyzing deviation within the means.
Standard Error vs. Standard Deviation
The standard error normalizes the standard deviation relative to the sample size used in an analysis. Standard deviation measures the amount of variance or dispersion of the data spread around the mean. The standard error can be thought of as the dispersion of the sample mean estimations around the true population mean. As the sample size becomes larger, the standard error will become smaller, indicating that the estimated sample mean value better approximates the population mean.
Example of Standard Error
Say that an analyst has looked at a random sample of 50 companies in the S&P 500 to understand the association between a stock’s P/E ratio and subsequent 12-month performance in the market. Assume that the resulting estimate is -0.20, indicating that for every 1.0 point in the P/E ratio, stocks return 0.2% poorer relative performance. In the sample of 50, the standard deviation was found to be 1.0.
The standard error is thus:
SE = 1.0/√50 = 1/7.07 = 0.141
Therefore, we would report the estimate as -0.20% ± 0.14, giving us a confidence interval of (-0.34 — -0.06). The true mean value of the association of the P/E on returns of the S&P 500 would therefore fall within that range with a high degree of probability.
Say now that we increase the sample of stocks to 100 and find that the estimate changes slightly from -0.20 to -0.25, and the standard deviation falls to 0.90. The new standard error would thus be:
SE = 0.90/√100 = 0.90/10 = 0.09.
The resulting confidence interval becomes -0.25 ± 0.09 = (-0.34 — -0.16), which is a tighter range of values.
What Is Meant by Standard Error?
Standard error is intuitively the standard deviation of the sampling distribution. In other words, it depicts how much disparity there is likely to be in a point estimate obtained from a sample relative to the true population mean.
What Is a Good Standard Error?
Standard error measures the amount of discrepancy that can be expected in a sample estimate compared to the true value in the population. Therefore, the smaller the standard error the better. In fact, a standard error of zero (or close to it) would indicate that the estimated value is exactly the true value.
How Do You Find the Standard Error?
The standard error takes the standard deviation and divides it by the square root of the sample size. Many statistical software packages automatically compute standard errors.
The Bottom Line
The standard error (SE) measures the dispersion of estimated values obtained from a sample around the true value to be found in the population. Statistical analysis and inference often involves drawing samples and running statistical tests to determine associations and correlations between variables. The standard error thus tells us with what degree of confidence we can expect the estimated value to approximate the population value.
Среднее арифметическое, как известно, используется для получения обобщающей характеристики некоторого набора данных. Если данные более-менее однородны и в них нет аномальных наблюдений (выбросов), то среднее хорошо обобщает данные, сведя к минимуму влияние случайных факторов (они взаимопогашаются при сложении).
Когда анализируемые данные представляют собой выборку (которая состоит из случайных значений), то среднее арифметическое часто (но не всегда) выступает в роли приближенной оценки математического ожидания. Почему приближенной? Потому что среднее арифметическое – это величина, которая зависит от набора случайных чисел, и, следовательно, сама является случайной величиной. При повторных экспериментах (даже в одних и тех же условиях) средние будут отличаться друг от друга.
Для того, чтобы на основе статистического анализа данных делать корректные выводы, необходимо оценить возможный разброс полученного результата. Для этого рассчитываются различные показатели вариации. Но то исходные данные. И как мы только что установили, среднее арифметическое также обладает разбросом, который необходимо оценить и учитывать в дальнейшем (в выводах, в выборе метода анализа и т.д.).
Интуитивно понятно, что разброс средней должен быть как-то связан с разбросом исходных данных. Основной характеристикой разброса средней выступает та же дисперсия.
Дисперсия выборочных данных – это средний квадрат отклонения от средней, и рассчитать ее по исходным данным не составляет труда, например, в Excel предусмотрены специальные функции. Однако, как же рассчитать дисперсию средней, если в распоряжении есть только одна выборка и одно среднее арифметическое?
Расчет дисперсии и стандартной ошибки средней арифметической
Чтобы получить дисперсию средней арифметической нет необходимости проводить множество экспериментов, достаточно иметь только одну выборку. Это легко доказать. Для начала вспомним, что средняя арифметическая (простая) рассчитывается по формуле:
где xi – значения переменной,
n – количество значений.
Теперь учтем два свойства дисперсии, согласно которым, 1) — постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат и 2) — дисперсия суммы независимых случайных величин равняется сумме соответствующих дисперсий. Предполагается, что каждое случайное значение xi обладает одинаковым разбросом, поэтому несложно вывести формулу дисперсии средней арифметической:
Используя более привычные обозначения, формулу записывают как:
где σ2 – это дисперсия, случайной величины, причем генеральная.
На практике же, генеральная дисперсия известна далеко не всегда, точнее совсем редко, поэтому в качестве оной используют выборочную дисперсию:
Стандартное отклонение средней арифметической называется стандартной ошибкой средней и рассчитывается, как квадратный корень из дисперсии.
Формула стандартной ошибки средней при использовании генеральной дисперсии
Формула стандартной ошибки средней при использовании выборочной дисперсии
Последняя формула на практике используется чаще всего, т.к. генеральная дисперсия обычно не известна. Чтобы не вводить новые обозначения, стандартную ошибку средней обычно записывают в виде соотношения стандартного отклонения выборки и корня объема выборки.
Назначение и свойство стандартной ошибки средней арифметической
Стандартная ошибка средней много, где используется. И очень полезно понимать ее свойства. Посмотрим еще раз на формулу стандартной ошибки средней:
Числитель – это стандартное отклонение выборки и здесь все понятно. Чем больше разброс данных, тем больше стандартная ошибка средней – прямо пропорциональная зависимость.
Посмотрим на знаменатель. Здесь находится квадратный корень из объема выборки. Соответственно, чем больше объем выборки, тем меньше стандартная ошибка средней. Для наглядности изобразим на одной диаграмме график нормально распределенной переменной со средней равной 10, сигмой – 3, и второй график – распределение средней арифметической этой же переменной, полученной по 16-ти наблюдениям (которое также будет нормальным).
Судя по формуле, разброс стандартной ошибки средней должен быть в 4 раза (корень из 16) меньше, чем разброс исходных данных, что и видно на рисунке выше. Чем больше наблюдений, тем меньше разброс средней.
Казалось бы, что для получения наиболее точной средней достаточно использовать максимально большую выборку и тогда стандартная ошибка средней будет стремиться к нулю, а сама средняя, соответственно, к математическому ожиданию. Однако квадратный корень объема выборки в знаменателе говорит о том, что связь между точностью выборочной средней и размером выборки не является линейной. Например, увеличение выборки с 20-ти до 50-ти наблюдений, то есть на 30 значений или в 2,5 раза, уменьшает стандартную ошибку средней только на 36%, а со 100-а до 130-ти наблюдений (на те же 30 значений), снижает разброс данных лишь на 12%.
Лучше всего изобразить эту мысль в виде графика зависимости стандартной ошибки средней от размера выборки. Пусть стандартное отклонение равно 10 (на форму графика это не влияет).
Видно, что примерно после 50-ти значений, уменьшение стандартной ошибки средней резко замедляется, после 100-а – наклон постепенно становится почти нулевым.
Таким образом, при достижении некоторого размера выборки ее дальнейшее увеличение уже почти не сказывается на точности средней. Этот факт имеет далеко идущие последствия. Например, при проведении выборочного обследования населения (опроса) чрезмерное увеличение выборки ведет к неоправданным затратам, т.к. точность почти не меняется. Именно поэтому количество опрошенных редко превышает 1,5 тысячи человек. Точность при таком размере выборки часто является достаточной, а дальнейшее увеличение выборки – нецелесообразным.
Подведем итог. Расчет дисперсии и стандартной ошибки средней имеет довольно простую формулу и обладает полезным свойством, связанным с тем, что относительно хорошая точность средней достигается уже при 100 наблюдениях (в этом случае стандартная ошибка средней становится в 10 раз меньше, чем стандартное отклонение выборки). Больше, конечно, лучше, но бесконечно увеличивать объем выборки не имеет практического смысла. Хотя, все зависит от поставленных задач и цены ошибки. В некоторых опросах участие принимают десятки тысяч людей.
Дисперсия и стандартная ошибка средней имеют большое практическое значение. Они используются в проверке гипотез и расчете доверительных интервалов.
Поделиться в социальных сетях:
Что такое Стандартная формула ошибки?
Стандартная ошибка — это ошибка, которая возникает в распределении выборки при выполнении статистического анализа. Это вариант стандартного отклонения, так как оба понятия соответствуют мерам спреда. Высокая стандартная ошибка соответствует более высокому разбросу данных для взятой выборки. Вычисление формулы стандартной ошибки выполняется для выборки. В то же время стандартное отклонение определяет генеральную совокупность.
Оглавление
- Что такое Стандартная формула ошибки?
- Объяснение
- Пример формулы стандартной ошибки
- Калькулятор стандартной ошибки
- Актуальность и использование
- Стандартная формула ошибки в Excel
- Рекомендуемые статьи
Следовательно, стандартная ошибка среднего значения будет выражаться и определяться в соответствии с соотношением, описанным следующим образом:
σ͞x = σ/√n
Здесь,
- Стандартная ошибка, выраженная как σ͞x.
- Стандартное отклонение совокупности выражается как σ.
- Количество переменных в выборке, выраженное как n.
В статистическом анализе среднее значение, медиана и мода являются центральной тенденцией. Центральная тенденция Центральная тенденция — это статистическая мера, которая отображает центральную точку всего распределения данных, и вы можете найти ее с помощью 3 различных мер, т. е. среднего, медианы и моды.Подробнее меры. Стандартное отклонение, дисперсия и стандартная ошибка среднего классифицируются как меры изменчивости. Стандартная ошибка среднего для выборочных данных напрямую связана со стандартным отклонением большей совокупности и обратно пропорциональна или связана с квадратным корнем. число. Чтобы использовать эту функцию, введите термин =SQRT и нажмите клавишу табуляции, которая вызовет функцию SQRT. Более того, эта функция принимает один аргумент из нескольких переменных, используемых для создания выборки. Следовательно, если размер выборки Размер выборкиФормула размера выборки отображает соответствующий диапазон генеральной совокупности, в которой проводится эксперимент или опрос. Он измеряется с использованием размера генеральной совокупности, критического значения нормального распределения при требуемом доверительном уровне, доли выборки и предела погрешности. Если больше, то может быть равная вероятность того, что стандартная ошибка также будет большой.
Объяснение
Можно объяснить формулу для стандартной ошибки среднего, используя следующие шаги:
- Определите и организуйте выборку и определите количество переменных.
- Затем среднее значение выборки соответствует количеству переменных, присутствующих в выборке.
- Затем определите стандартное отклонение выборки.
- Затем определите квадратный корень из числа переменных, включенных в выборку.
- Теперь разделите стандартное отклонение, вычисленное на шаге 3, на полученное значение на шаге 4, чтобы получить стандартную ошибку.
Пример формулы стандартной ошибки
Ниже приведены примеры формул для расчета стандартной ошибки.
.free_excel_div{фон:#d9d9d9;размер шрифта:16px;радиус границы:7px;позиция:относительная;margin:30px;padding:25px 25px 25px 45px}.free_excel_div:before{content:»»;фон:url(центр центр без повтора #207245;ширина:70px;высота:70px;позиция:абсолютная;верх:50%;margin-top:-35px;слева:-35px;граница:5px сплошная #fff;граница-радиус:50%} Вы можете скачать этот шаблон стандартной формулы ошибки Excel здесь — Стандартная формула ошибки Шаблон Excel
Пример №1
Возьмем в качестве примера акции ABC. В течение 30 лет акции приносили средний долларовый доход в размере 45 долларов. Кроме того, было замечено, что акции приносят прибыль со стандартным отклонением в 2 доллара. Помогите инвестору рассчитать общую стандартную ошибку средней доходности, предлагаемой акцией ABC.
Решение:
- Стандартное отклонение (σ) = $2
- Количество лет (n) = 30
- Средняя доходность в долларах = 45 долларов.
Расчет стандартной ошибки выглядит следующим образом:
- σ͞x = σ/√n
- = 2 доллара США/√30
- = 2 доллара США / 5,4773
Стандартная ошибка,
- σx = 0,3651 доллара США
Таким образом, инвестиция предлагает инвестору стандартную долларовую ошибку в среднем 0,36515 доллара при удерживании позиции ABC в течение 30 лет. Однако, если бы акции сохранялись для более высокого инвестиционного горизонта, то стандартная ошибка среднего значения в долларах значительно уменьшилась бы.
Пример #2
Возьмем в качестве примера инвестора, который получил следующую доходность акций XYZ:
Год инвестиций Предлагаемая доходность120%225%35%410%
Помогите инвестору рассчитать общую стандартную ошибку средней доходности акций XYZ.
Решение:
Сначала определите среднее значение доходности, как показано ниже: –
- ͞X = (x1+x2+x3+x4)/количество лет
- = (20+25+5+10)/4
- =15%
Теперь определите стандартное отклонение доходности, как показано ниже: –
- σ = √ ((x1-͞X)2 + (x2-͞X)2 + (x3-͞X)2 + (x4-͞X)2) / √ (количество лет -1)
- = √ ((20-15) 2 + (25-15) 2 + (5-15) 2 + (10-15) 2) / √ (4-1)
- = (√ (5) 2 + (10) 2 + (-10) 2 + (-5) 2 ) / √ (3)
- = (√25+100+100+25)/ √ (3)
- =√250/√3
- =√83,3333
- «=» 9,1287%
Теперь вычисление стандартной ошибки выглядит следующим образом:
- σ͞x = σ/√n
- = 9,128709/√4
- = 9,128709/2
Стандартная ошибка,
- σx = 4,56%
Таким образом, инвестиции предлагают инвестору стандартную ошибку в долларах в среднем 4,56% при удержании позиции XYZ в течение 4 лет.
Калькулятор стандартной ошибки
Вы можете использовать следующий калькулятор.
.cal-tbl td{ верхняя граница: 0 !важно; }.cal-tbl tr{ высота строки: 0.5em; } Только экран @media и (минимальная ширина устройства: 320 пикселей) и (максимальная ширина устройства: 480 пикселей) { .cal-tbl tr{ line-height: 1em !important; } } σnСтандартная формула ошибки
Формула стандартной ошибки =σ =√n 0 = 0√0
Актуальность и использование
Стандартная ошибка имеет тенденцию быть высокой, если размер выборки для анализа мал. Следовательно, выборка всегда берется из большей совокупности, которая включает больший размер переменных. Это всегда помогает статистику определить достоверность среднего значения выборки относительно среднего значения генеральной совокупности.
Большая стандартная ошибка говорит статистику, что выборка неоднородна в отношении среднего значения генеральной совокупности. Относительно населения наблюдается большой разброс в выборке. Точно так же небольшая стандартная ошибка говорит статистику, что выборка однородна относительно среднего значения генеральной совокупности. Отсутствуют или незначительные различия в выборке относительно населения.
Не следует смешивать его со стандартным отклонением. Вместо этого следует рассчитать стандартное отклонение для всей совокупности. Стандартная ошибкаСтандартная ошибкаСтандартная ошибка (SE) — это метрика, которая измеряет точность выборочного распределения, обозначающего совокупность, с использованием стандартного отклонения. Другими словами, это мера дисперсии среднего значения выборки, связанная со средним значением генеральной совокупности, а не стандартное отклонение. С другой стороны, оно определяется для среднего значения выборки.
Стандартная формула ошибки в Excel
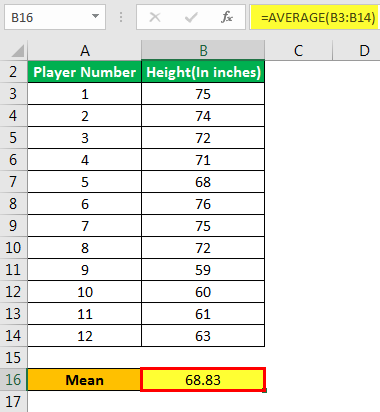
Теперь давайте возьмем пример Excel, чтобы проиллюстрировать концепцию стандартной формулы ошибки в шаблоне Excel ниже. Предположим, администрация школы хочет определить стандартную ошибку среднего значения роста футболистов.
Выборка состоит из следующих значений: –
Помогите администрации оценить стандартную ошибку среднего значения.
Шаг 1: Определите среднее значение, как показано ниже: –
Шаг 2: Определите стандартное отклонение, как показано ниже: –
Шаг 3: Определите стандартную ошибку среднего значения, как показано ниже: –
Следовательно, стандартная ошибка среднего значения для футболистов составляет 1,846 дюйма. Руководство должно заметить, что оно значительно велико. Таким образом, выборочные данные, взятые для анализа, неоднородны и имеют большую дисперсию.
Руководству следует либо исключить более мелких игроков, либо добавить игроков значительно выше, чтобы сбалансировать средний рост футбольной команды, заменив их людьми с меньшим ростом по сравнению с их сверстниками.
Рекомендуемые статьи
Эта статья была руководством по формуле стандартной ошибки. Здесь мы обсуждаем формулу для расчета среднего значения, стандартную ошибку, примеры и загружаемый лист Excel. Вы можете узнать больше из следующих статей: –
- Формула рентабельности EBITDA
- Формула валовой прибыли
- Формула относительного стандартного отклонения
- Формула погрешности
Ошибки выборочного наблюдения
Информация, получаемая в результате
любого статистического наблюдения,
имеет расхождение с реальной
действительностью. Такое расхождение
получило название ошибок статистического
наблюдения. При массовом наблюдении
ошибки неизбежны, но возникают они
в результате действия различных причин
(см. гл. 4).
В данной главе рассматривается только
ошибка репрезентативности и причины
ее возникновения. Под ошибкой
репрезентативности (представительства)
понимают расхождение между выборочной
характеристикой и предполагаемой
характеристикой генеральной
совокупности. Причиной образования
этой ошибки является то обстоятельство,
что обследуются не все единицы генеральной
совокупности, а лишь их некоторая часть,
и различия между единицами, попавшими
в выборку, не соответствуют различиям
единиц, не попавших в выборку. Вследствие
этого выборочная совокупность становится
непредставительной по отношению к
генеральной совокупности. Ошибка
репрезентативности может возникнуть
по двум причинам: из-за нарушения научных
принципов отбора —систематическая
ошибка — и в результате случайности
отбора —случайная ошибка. В результате
первой причины выборка легко может
оказаться смещенной, так как при отборе
каждой единицы допускается ошибка,
всегда направленная в одну и ту же
сторону. Эта ошибка получила названиеошибки смещения. Ее размер может
превышать величину случайной ошибки.
Особенность ошибки смещения состоит
в том, что, представляя собой постоянную
часть ошибки репрезентативности, она
увеличивается с увеличением объема
выборки. Случайная же ошибка с увеличением
объема выборки уменьшается. Кроме того,
величину случайной ошибки можно
определить (см. ниже), тогда как размер
ошибки смещения непосредственно
практически определить очень сложно,
а иногда — невозможно. Поэтому необходимо
знать причины, вызывающие ошибку смещения
и меры, способствующие её устранению.
Ошибки смещения бывают преднамеренные
и непреднамеренные. Причиной
возникновения преднамеренной ошибки
является тенденциозный подход к
выбору единиц из генеральной совокупности.
Мерой устранения этой ошибки может быть
только исключение тенденциозности.
Выявить эту ошибку можно только путем
проведения повторного отбора с
обязательным соблюдением принципа
случайности.
Непреднамеренные ошибки могут
возникать на стадии подготовки
выборочного наблюдения, формирования
выборочной совокупности и анализа ее
данных. Чаще всего создаются условия
для возникновения ошибок смещения на
стадии подготовки выборочного наблюдения.
Недостаточно хорошо продуманные и четко
сформулированные взаимоувязанные
вопросы плана организации и проведения
выборочного обследования могут дать
информацию, не соответствующую цели
исследования или, что еще хуже, вводящую
в заблуждение. Если при сплошном
наблюдении это возможно только при
преднамеренном искажении фактов, то
при выборочном это связано с
непреднамеренными ошибками смещения.
При разработке плана организации и
проведения выборочного наблюдения
особое внимание следует уделятьединице
отбора, т. е. такой единице изучаемой
совокупности, которая является
основанием самого процесса отбора.
Единицей отбора могут служить естественные
единицы изучаемого явления, например
предприятие, рабочий, покупатель, семья
и т. д. В некоторых случаях необходимо
создать искусственные единицы, не
соответствующие естественному делению
изучаемой совокупности. Удачное
установление единицы отбора уменьшает
вероятность получить смещенную выборку.
Сокращению опасности возникновения
ошибок смещения во многом способствует
хорошая основа выборки, т. е. та
генеральная совокупность, из которой
предполагается производить отбор,
например список единиц отбора. Поэтому
при подготовке выборочного наблюдения
необходимо особенно тщательно
ознакомиться с тем, какова основа
выборки, пригодна ли она для производства
отбора, позволит ли она образовать
несмещенную выборку. Если готовой основы
выборки нет, то ее необходимо построить.
Основа выборки должна быть достоверной,
полной и соответствовать цели
исследования, а единицы отбора и их
характеристики должны соответствовать
действительному их состоянию на
момент подготовки выборочного наблюдения.
Если основа выборки не отвечает
перечисленным требованиям, ее
необходимо либо существенно улучшить,
внеся соответствующие изменения,
уточнения, дополнения, либо создать
заново.
На стадиях формирования выборочной
совокупности и производства наблюдения
ошибки смещения особенно опасны, так
как их трудно заметить и исправить. При
формировании выборочной совокупности
ошибку смещения чаще всего дает неточное
соблюдение установленного порядка
отбора, предусматривающего отбор
вполне определенных единиц. Иногда
может показаться, что выборочная
совокупность «не пострадает», если,
например, вместо предусмотренной десятой
единицы по списку взять одиннадцатую
или двенадцатую; в действительности же
такое нарушение установленного порядка
отбора нередко приводит к смещенной
выборке. Ошибки смещения при анализе
данных могут возникнуть из-за неправильных
приемов распространения выборочных
характеристик на генеральную
совокупность (см. 11.4).
Случайная ошибка выборки возникает
в результате случайных различий
между единицами, попавшими в выборку,
и единицами генеральной совокупности,
т. е. она связана со случайным отбором.
Теоретическим обоснованием появления
случайных ошибок выборки является
теория вероятностей и ее предельные
теоремы.
Сущность предельных теорем состоит в
том, что в массовых явлениях совокупное
влияние различных случайных причин на
формирование закономерностей и обобщающих
характеристик будет сколь угодно малой
величиной или практически не зависит
от случая. Так как случайная ошибка
выборки возникает в результате случайных
различий между единицами выборочной
и генеральной совокупностей, то при
достаточно большом объеме выборки она
будет сколь угодно мала. Этот вывод,
опирающийся на доказательства предельных
теорем, позволяет предполагать, что
характеристики выборочного наблюдения
могут достаточно хорошо представлять
характеристики генеральной
совокупности.
Предельные теоремы исходят из закона
нормального распределения, согласно
которому большая часть выборочных
средних сосредоточивается около
генеральной средней
.
Следовательно, закон нормального
распределения теоретически позволяет
установить, в какой мере изменяется
размер случайной ошибки выборки с
изменением вероятности ее появления.
Так как многие массовые явления
подчиняются закону нормального
распределения, то он служит основой при
оценке вероятности тех или иных
результатов выборочного наблюдения.
Предельные теоремы теории вероятностей
позволяют определять размер случайных
ошибок выборки. Различают среднюю
(стандартную) и предельную ошибку
выборки. Под средней (стандартной)
ошибкой выборки понимают расхождение
между средней выборочной и генеральной
совокупностей,не
превышающее.
Предельной ошибкой выборки принято
считать максимально возможное расхождение,
т. е. максимум ошибки при заданной
вероятности ее появления. На основании
теоремы, доказанной П. Л. Чебышевым,
величину стандартной ошибки так
называемого собственно-случайного
отбора при достаточно большом объёме
выборки можно определить по формуле:
,
где
— стандартная ошибка.
Величина стандартной ошибки прямо
пропорциональна колеблемости признака
в генеральной совокупности и обратно
пропорциональна квадратному корню
объёма выборки. Величина
зависит также от способа и вида отбора.
Академик А.М.Ляпунов, продолжив разработки
П.Л.Чебышева, доказал, что вероятность
появления случайной ошибки выборки при
её достаточно большом объёме подчиняется
закону нормального распределения. Эта
вероятность определяется по формуле:
Значения функции
табулированы
при различных значенияхt.
Предельная ошибка выборки определяется
по формуле
,
где
-предельная
ошибка,t– заданный
коэффициент доверия.
Так, при t=1 величина
предельной ошибки составит,
гарантированную с вероятностью 0,683. Это
означает, что в 683 выборках из тысячи
подобных максимальная ошибка выборки
(предельная) не превысит.
Приt=2 с вероятностью
0,954 она не выйдет за пределыи
т.д. В практике выборочных наблюдений
массовых общественных явлений максимальный
предел ошибок, как правило, вполне
достаточен в пределах.
Однако приведённые формулы нахождения
ошибок выборки практически непригодны,
т.к. в них σ – это показатель колеблемости
признака в генеральной совокупности,
который неизвестен, как неизвестна и
генеральная средняя. Но в теории
вероятностей доказывается, что
.
Так как
при
достаточно большомn– величина, близкая к единице, то условно
принимается, что.
На основании этого утверждения в
вышеприведённых формулах вместо
генеральной дисперсии принимают значение
выборочной дисперсии.
Предельная ошибка выборки позволяет
определять предельные значения
характеристик генеральной совокупности
при заданной вероятности и их доверительные
интервалы:
.
Это означает следующее: с заданной
вероятностью можно утверждать, что
значение генеральной средней ожидается
в пределах от
до
.
Наряду с абсолютной величиной предельной
ошибки выборки рассчитывают и относительную
ошибку, определяемую как процентное
отношение предельной ошибки выборки к
соответствующей характеристике
выборочной совокупности:
,
,
Если при выборочном наблюдении изучению
подлежит альтернативный признак, то
случайная ошибка выборки для доли
определяется в соответствии с теоремой
Я.Бернулли. так
как вероятность расхождения между
частостью и долей тоже подчиняется
закону нормального распределения, то
стандартная ошибка выборки альтернативного
признака определяется по формуле:
,
где pq– дисперсия
доли альтернативного признака в
генеральной совокупности.
Так как pqнеизвестно,
то на практике её заменяют дисперсией
выборочной совокупностиw(1-w)
и формула принимает вид:
Соседние файлы в папке 14-05-2013_10-41-11
- #
- #
- #
- #
- #
- #
- #
Стандартная ошибка показывает, насколько разбросаны измерения в пределах выборки данных. Это стандартное отклонение, деленное на квадратный корень из размера выборки данных. Выборка может включать данные научных измерений, результаты тестов, температуру или серию случайных чисел. Стандартное отклонение указывает на отклонение значений выборки от среднего значения выборки. Стандартная ошибка обратно пропорциональна размеру выборки — чем больше выборка, тем меньше стандартная ошибка.
Вычислите среднее значение вашей выборки данных. Среднее — это среднее значение выборки. Например, если наблюдения за погодой в четырехдневный период в течение года составляют 52, 60, 55 и 65 градусов по Фаренгейту, то среднее значение будет 58 градусов по Фаренгейту: (52 + 60 + 55 + 65) / 4.
Вычислите сумму квадратов отклонений (или разностей) каждого значения выборки от среднего. Обратите внимание, что умножение отрицательных чисел на себя (или возведение чисел в квадрат) дает положительные числа. В примере квадраты отклонений равны (58-52) ^ 2, (58-60) ^ 2, (58-55) ^ 2 и (58-65) ^ 2 или 36, 4, 9 и 49 соответственно.. Следовательно, сумма квадратов отклонений составляет 98 (36 + 4 + 9 + 49).
Найдите стандартное отклонение. Разделите сумму квадратов отклонений на размер выборки минус один; затем извлеките квадратный корень из результата. В этом примере размер выборки равен четырем. Следовательно, стандартное отклонение — это квадратный корень из [98 / (4 — 1)], который составляет около 5,72.
Вычислите стандартную ошибку, которая представляет собой стандартное отклонение, деленное на квадратный корень из размера выборки. Чтобы завершить пример, стандартная ошибка составляет 5,72, деленное на квадратный корень из 4, или 5,72, деленное на 2, или 2,86.
Teachs.ru