Вектор ошибки синдром ошибки

Корректирующие коды «на пальцах»

Время на прочтение
11 мин

Количество просмотров 64K

Корректирующие (или помехоустойчивые) коды — это коды, которые могут обнаружить и, если повезёт, исправить ошибки, возникшие при передаче данных. Даже если вы ничего не слышали о них, то наверняка встречали аббревиатуру CRC в списке файлов в ZIP-архиве или даже надпись ECC на планке памяти. А кто-то, может быть, задумывался, как так получается, что если поцарапать DVD-диск, то данные всё равно считываются без ошибок. Конечно, если царапина не в сантиметр толщиной и не разрезала диск пополам.

Как нетрудно догадаться, ко всему этому причастны корректирующие коды. Собственно, ECC так и расшифровывается — «error-correcting code», то есть «код, исправляющий ошибки». А CRC — это один из алгоритмов, обнаруживающих ошибки в данных. Исправить он их не может, но часто это и не требуется.

Давайте же разберёмся, что это такое.

Для понимания статьи не нужны никакие специальные знания. Достаточно лишь понимать, что такое вектор и матрица, как они перемножаются и как с их помощью записать систему линейных уравнений.

Внимание! Много текста и мало картинок. Я постарался всё объяснить, но без карандаша и бумаги текст может показаться немного запутанным.

Каналы с ошибкой

Разберёмся сперва, откуда вообще берутся ошибки, которые мы собираемся исправлять. Перед нами стоит следующая задача. Нужно передать несколько блоков данных, каждый из которых кодируется цепочкой двоичных цифр. Получившаяся последовательность нулей и единиц передаётся через канал связи. Но так сложилось, что реальные каналы связи часто подвержены ошибкам. Вообще говоря, ошибки могут быть разных видов — может появиться лишняя цифра или какая-то пропасть. Но мы будем рассматривать только ситуации, когда в канале возможны лишь замены нуля на единицу и наоборот. Причём опять же для простоты будем считать такие замены равновероятными.

Ошибка — это маловероятное событие (а иначе зачем нам такой канал вообще, где одни ошибки?), а значит, вероятность двух ошибок меньше, а трёх уже совсем мала. Мы можем выбрать для себя некоторую приемлемую величину вероятности, очертив границу «это уж точно невозможно». Это позволит нам сказать, что в канале возможно не более, чем $k$ ошибок. Это будет характеристикой канала связи.

Для простоты введём следующие обозначения. Пусть данные, которые мы хотим передавать, — это двоичные последовательности фиксированной длины. Чтобы не запутаться в нулях и единицах, будем иногда обозначать их заглавными латинскими буквами ($A$, $B$, $C$, …). Что именно передавать, в общем-то неважно, просто с буквами в первое время будет проще работать.

Кодирование и декодирование будем обозначать прямой стрелкой ($\rightarrow$), а передачу по каналу связи — волнистой стрелкой ($\rightsquigarrow$). Ошибки при передаче будем подчёркивать.

Например, пусть мы хотим передавать только сообщения $A=0$ и $B=1$. В простейшем случае их можно закодировать нулём и единицей (сюрприз!):

$ \begin{aligned} A &\to 0,\\ B &\to 1. \end{aligned} $

Передача по каналу, в котором возникла ошибка будет записана так:

$ A \to 0 \rightsquigarrow \underline{1} \to B. $

Цепочки нулей и единиц, которыми мы кодируем буквы, будем называть кодовыми словами. В данном простом случае кодовые слова — это $0$ и $1$.

Код с утроением

Давайте попробуем построить какой-то корректирующий код. Что мы обычно делаем, когда кто-то нас не расслышал? Повторяем дважды:

$ \begin{aligned} A &\to 00,\\ B &\to 11. \end{aligned} $

Правда, это нам не очень поможет. В самом деле, рассмотрим канал с одной возможной ошибкой:

$ A \to 00 \rightsquigarrow 0\underline{1} \to ?. $

Какие выводы мы можем сделать, когда получили $01$? Понятно, что раз у нас не две одинаковые цифры, то была ошибка, но вот в каком разряде? Может, в первом, и была передана буква $B$. А может, во втором, и была передана $A$.

То есть, получившийся код обнаруживает, но не исправляет ошибки. Ну, тоже неплохо, в общем-то. Но мы пойдём дальше и будем теперь утраивать цифры.

$ \begin{aligned} A &\to 000,\\ B &\to 111. \end{aligned} $

Проверим в деле:

$ A \to 000 \rightsquigarrow 0\underline{1}0 \to A?. $

Получили $010$. Тут у нас есть две возможности: либо это $B$ и было две ошибки (в крайних цифрах), либо это $A$ и была одна ошибка. Вообще, вероятность одной ошибки выше вероятности двух ошибок, так что самым правдоподобным будет предположение о том, что передавалась именно буква $A$. Хотя правдоподобное — не значит истинное, поэтому рядом и стоит вопросительный знак.

Если в канале связи возможна максимум одна ошибка, то первое предположение о двух ошибках становится невозможным и остаётся только один вариант — передавалась буква $A$.

Про такой код говорят, что он исправляет одну ошибку. Две он тоже обнаружит, но исправит уже неверно.

Это, конечно, самый простой код. Кодировать легко, да и декодировать тоже. Ноликов больше — значит передавался ноль, единичек — значит единица.

Если немного подумать, то можно предложить код исправляющий две ошибки. Это будет код, в котором мы повторяем одиночный бит 5 раз.

Расстояния между кодами

Рассмотрим поподробнее код с утроением. Итак, мы получили работающий код, который исправляет одиночную ошибку. Но за всё хорошее надо платить: он кодирует один бит тремя. Не очень-то и эффективно.

И вообще, почему этот код работает? Почему нужно именно утраивать для устранения одной ошибки? Наверняка это всё неспроста.

Давайте подумаем, как этот код работает. Интуитивно всё понятно. Нолики и единички — это две непохожие последовательности. Так как они достаточно длинные, то одиночная ошибка не сильно портит их вид.

Пусть мы передавали $000$, а получили $001$. Видно, что эта цепочка больше похожа на исходные $000$, чем на $111$. А так как других кодовых слов у нас нет, то и выбор очевиден.

Но что значит «больше похоже»? А всё просто! Чем больше символов у двух цепочек совпадает, тем больше их схожесть. Если почти все символы отличаются, то цепочки «далеки» друг от друга.

Можно ввести некоторую величину $d(\alpha, \beta)$, равную количеству различающихся цифр в соответствующих разрядах цепочек $\alpha$ и $\beta$. Эту величину называют расстоянием Хэмминга. Чем больше это расстояние, тем меньше похожи две цепочки.

Например, $d(010, 010) = 0$, так как все цифры в соответствующих позициях равны, а вот $d(010101, 011011) = 3$.

Расстояние Хэмминга называют расстоянием неспроста. Ведь в самом деле, что такое расстояние? Это какая-то характеристика, указывающая на близость двух точек, и для которой верны утверждения:

  1. Расстояние между точками неотрицательно и равно нулю только, если точки совпадают.
  2. Расстояние в обе стороны одинаково.
  3. Путь через третью точку не короче, чем прямой путь.

Достаточно разумные требования.

Математически это можно записать так (нам это не пригодится, просто ради интереса посмотрим):

  1. $d(x, y) \geqslant 0,\quad d(x, y) = 0 \Leftrightarrow x = y;$
  2. $d(x, y) = d(y, x);$
  3. $d(x, z) + d(z, y) \geqslant d(x, y)$.

Предлагаю читателю самому убедиться, что для расстояния Хэмминга эти свойства выполняются.

Окрестности

Таким образом, разные цепочки мы считаем точками в каком-то воображаемом пространстве, и теперь мы умеем находить расстояния между ними. Правда, если попытаться сколько нибудь длинные цепочки расставить на листе бумаги так, чтобы расстояния Хэмминга совпадали с расстояниями на плоскости, мы можем потерпеть неудачу. Но не нужно переживать. Всё же это особое пространство со своими законами. А слова вроде «расстояния» лишь помогают нам рассуждать.

Пойдём дальше. Раз мы заговорили о расстоянии, то можно ввести такое понятие как окрестность. Как известно, окрестность какой-то точки — это шар определённого радиуса с центром в ней. Шар? Какие ещё шары! Мы же о кодах говорим.

Но всё просто. Ведь что такое шар? Это множество всех точек, которые находятся от данной не дальше, чем некоторое расстояние, называемое радиусом. Точки у нас есть, расстояние у нас есть, теперь есть и шары.

Так, скажем, окрестность кодового слова $000$ радиуса 1 — это все коды, находящиеся на расстоянии не больше, чем 1 от него, то есть отличающиеся не больше, чем в одном разряде. То есть это коды:

$ \{000, 100, 010, 001\}. $

Да, вот так странно выглядят шары в пространстве кодов.

А теперь посмотрите. Это же все возможные коды, которые мы получим в канале в одной ошибкой, если отправим $000$! Это следует прямо из определения окрестности. Ведь каждая ошибка заставляет цепочку измениться только в одном разряде, а значит удаляет её на расстояние 1 от исходного сообщения.

Аналогично, если в канале возможны две ошибки, то отправив некоторое сообщение $x$, мы получим один из кодов, который принадлежит окрестности $x$ радиусом 2.

Тогда всю нашу систему декодирования можно построить так. Мы получаем какую-то цепочку нулей и единиц (точку в нашей новой терминологии) и смотрим, в окрестность какого кодового слова она попадает.

Сколько ошибок может исправить код?

Чтобы код мог исправлять больше ошибок, окрестности должны быть как можно шире. С другой стороны, они не должны пересекаться. Иначе если точка попадёт в область пересечения, непонятно будет, к какой окрестности её отнести.

В коде с удвоением между кодовыми словами $00$ и $11$ расстояние равно 2 (оба разряда различаются). А значит, если мы построим вокруг них шары радиуса 1, то они будут касаться. Это значит, точка касания будет принадлежать обоим шарам и непонятно будет, к какому из них её отнести.

Именно это мы и получали. Мы видели, что есть ошибка, но не могли её исправить.

Что интересно, точек касания в нашем странном пространстве у шаров две — это коды $01$ и $10$. Расстояния от них до центров равны единице. Конечно же, в обычно геометрии такое невозможно, поэтому рисунки — это просто условность для более удобного рассуждения.

В случае кода с утроением, между шарами будет зазор.

Минимальный зазор между шарами равен 1, так как у нас расстояния всегда целые (ну не могут же две цепочки отличаться в полутора разрядах).

В общем случае получаем следующее.

Этот очевидный результат на самом деле очень важен. Он означает, что код с минимальным кодовым расстоянием $d_{\min}$ будет успешно работать в канале с $k$ ошибками, если выполняется соотношение

$ d_{\min} \geqslant 2k+1. $

Полученное равенство позволяет легко определить, сколько ошибок будет исправлять тот или иной код. А сколько код ошибок может обнаружить? Рассуждения такие же. Код обнаруживает $k$ ошибок, если в результате не получится другое кодовое слово. То есть, кодовые слова не должны находиться в окрестностях радиуса $k$ других кодовых слов. Математически это записывается так:

$d_{\min}\geqslant k + 1.$

Рассмотрим пример. Пусть мы кодируем 4 буквы следующим образом.

$ \begin{aligned} A \to 10100,\\ B \to 01000,\\ C \to 00111,\\ D \to 11011.\\ \end{aligned} $

Чтобы найти минимальное расстояние между различными кодовыми словами, построим таблицу попарных расстояний.

A B C D
A — 3 3 4
B 3 — 4 3
C 3 4 — 3
D 4 3 3 —

Минимальное расстояние $d_{\min}=3$, а значит $3\geqslant2k+1$, откуда получаем, что такой код может исправить до $k=1$ ошибок. Обнаруживает же он две ошибки.

Рассмотрим пример:

$ A \to 10100 \rightsquigarrow 101\underline{1}0. $

Чтобы декодировать полученное сообщение, посмотрим, к какому символу оно ближе всего.

$ \begin{aligned} A:\, d(10110, 10100) &= 1,\\ B:\, d(10110, 01000) &= 4,\\ C:\, d(10110, 00111) &= 2,\\ D:\, d(10110, 11011) &= 3. \end{aligned} $

Минимальное расстояние получилось для символа $A$, значит вероятнее всего передавался именно он:

$ A \to 10100 \rightsquigarrow 101\underline{1}0 \to A?. $

Итак, этот код исправляет одну ошибку, как и код с утроением. Но он более эффективен, так как в отличие от кода с утроением здесь кодируется уже 4 символа.

Таким образом, основная проблема при построении такого рода кодов — так расположить кодовые слова, чтобы они были как можно дальше друг от друга, и их было побольше.

Для декодирования можно было бы использовать таблицу, в которой указывались бы все возможные принимаемые сообщения, и кодовые слова, которым они соответствуют. Но такая таблица получилась бы очень большой. Даже для нашего маленького кода, который выдаёт 5 двоичных цифр, получилось бы $2^5 = 32$ варианта возможных принимаемых сообщений. Для более сложных кодов таблица будет значительно больше.

Попробуем придумать способ коррекции сообщения без таблиц. Мы всегда сможем найти полезное применение освободившейся памяти.

Интерлюдия: поле GF(2)

Для изложения дальнейшего материала нам потребуются матрицы. А при умножении матриц, как известно мы складываем и перемножаем числа. И тут есть проблема. Если с умножением всё более-менее хорошо, то как быть со сложением? Из-за того, что мы работаем только с одиночными двоичными цифрами, непонятно, как сложить 1 и 1, чтобы снова получилась одна двоичная цифра. Значит вместо классического сложения нужно использовать какое-то другое.

Введём операцию сложения как сложение по модулю 2 (хорошо известный программистам XOR):

$ \begin{aligned} 0 + 0 &= 0,\\ 0 + 1 &= 1,\\ 1 + 0 &= 1,\\ 1 + 1 &= 0. \end{aligned} $

Умножение будем выполнять как обычно. Эти операции на самом деле введены не абы как, а чтобы получилась система, которая в математике называется полем. Поле — это просто множество (в нашем случае из 0 и 1), на котором так определены сложение и умножение, чтобы основные алгебраические законы сохранялись. Например, чтобы основные идеи, касающиеся матриц и систем уравнений по-прежнему были верны. А вычитание и деление мы можем ввести как обратные операции.

Множество из двух элементов $\{0, 1\}$ с операциями, введёнными так, как мы это сделали, называется полем Галуа GF(2). GF — это Galois field, а 2 — количество элементов.

У сложения есть несколько очень полезных свойств, которыми мы будем пользоваться в дальнейшем.

$ x + x = 0. $

Это свойство прямо следует из определения.

$ x + y = x - y. $

А в этом можно убедиться, прибавив $y$ к обеим частям равенства. Это свойство, в частности означает, что мы можем переносить в уравнении слагаемые в другую сторону без смены знака.

Проверяем корректность

Вернёмся к коду с утроением.

$ \begin{aligned} A &\to 000,\\ B &\to 111. \end{aligned} $

Для начала просто решим задачу проверки, были ли вообще ошибки при передаче. Как видно, из самого кода, принятое сообщение будет кодовым словом только тогда, когда все три цифры равны между собой.

Пусть мы приняли вектор-строку $x$ из трёх цифр. (Стрелочки над векторами рисовать не будем, так как у нас почти всё — это вектора или матрицы.)

$\dots \rightsquigarrow x = (x_1, x_2, x_3). $

Математически равенство всех трёх цифр можно записать как систему:

$ \left\{ \begin{aligned} x_1 &= x_2,\\ x_2 &= x_3. \end{aligned} \right. $

Или, если воспользоваться свойствами сложения в GF(2), получаем

$ \left\{ \begin{aligned} x_1 + x_2 &= 0,\\ x_2 + x_3 &= 0. \end{aligned} \right. $

Или

$ \left\{ \begin{aligned} 1\cdot x_1 + 1\cdot x_2 + 0\cdot x_3 &= 0,\\ 0\cdot x_1 + 1\cdot x_2 + 1\cdot x_3 &= 0. \end{aligned} \right. $

В матричном виде эта система будет иметь вид

$ Hx^T = 0, $

где

$ H = \begin{pmatrix} 1 & 1 & 0\\ 0 & 1 & 1 \end{pmatrix}. $

Транспонирование здесь нужно потому, что $x$ — это вектор-строка, а не вектор-столбец. Иначе мы не могли бы умножать его справа на матрицу.

Будем называть матрицу $H$ проверочной матрицей. Если полученное сообщение — это корректное кодовое слово (то есть, ошибки при передаче не было), то произведение проверочной матрицы на это сообщение будет равно нулевому вектору.

Умножение на матрицу — это гораздо более эффективно, чем поиск в таблице, но у нас на самом деле есть ещё одна таблица — это таблица кодирования. Попробуем от неё избавиться.

Кодирование

Итак, у нас есть система для проверки

$ \left\{ \begin{aligned} x_1 + x_2 &= 0,\\ x_2 + x_3 &= 0. \end{aligned} \right. $

Её решения — это кодовые слова. Собственно, мы систему и строили на основе кодовых слов. Попробуем теперь решить обратную задачу. По системе (или, что то же самое, по матрице $H$) найдём кодовые слова.

Правда, для нашей системы мы уже знаем ответ, поэтому, чтобы было интересно, возьмём другую матрицу:

$ H = \begin{pmatrix} 1 & 0 & 1 & 0 & 0 \\ 0 & 1 & 1 & 0 & 1\\ 0 & 0 & 0 & 1 & 1 \end{pmatrix}. $

Соответствующая система имеет вид:

$ \left\{ \begin{aligned} x_1 + x_3 &= 0,\\ x_2 + x_3 + x_5 &= 0,\\ x_4 + x_5 &= 0. \end{aligned} \right. $

Чтобы найти кодовые слова соответствующего кода нужно её решить.

В силу линейности сумма двух решений системы тоже будет решением системы. Это легко доказать. Если $a$ и $b$ — решения системы, то для их суммы верно

$H(a+b)^T=Ha^T+Hb^T=0+0=0,$

что означает, что она тоже — решение.

Поэтому если мы найдём все линейно независимые решения, то с их помощью можно получить вообще все решения системы. Для этого просто нужно найти их всевозможные суммы.

Выразим сперва все зависимые слагаемые. Их столько же, сколько и уравнений. Выражать надо так, чтобы справа были только независимые. Проще всего выразить $x_1, x_2, x_4$.

Если бы нам не так повезло с системой, то нужно было бы складывая уравнения между собой получить такую систему, чтобы какие-то три переменные встречались по одному разу. Ну, или воспользоваться методом Гаусса. Для GF(2) он тоже работает.

Итак, получаем:

$ \left\{ \begin{aligned} x_1 &= x_3,\\ x_2 &= x_3 + x_5,\\ x_4 &= x_5. \end{aligned} \right. $

Чтобы получить все линейно независимые решения, приравниваем каждую из зависимых переменных к единице по очереди.

$ \begin{aligned} x_3=1, x_5=0:\quad x_1=1, x_2=1, x_4=0 \Rightarrow x^{(1)} = (1, 1, 1, 0, 0),\\ x_3=0, x_5=1:\quad x_1=0, x_2=1, x_4=1 \Rightarrow x^{(2)} = (0, 1, 0, 1, 1). \end{aligned} $

Всевозможные суммы этих независимых решений (а именно они и будут кодовыми векторами) можно получить так:

$ a_1 x^{(1)}+a_2 x^{(2)}, $

где $a_1, a_2$ равны либо нулю или единице. Так как таких коэффициентов два, то всего возможно $2^2=4$ сочетания.

Но посмотрите! Формула, которую мы только что получили — это же снова умножение матрицы на вектор.

$ (a_1, a_2)\cdot \begin{pmatrix} 1 & 1 & 1 & 0 & 0 \\ 0 & 1 & 0 & 1 & 1 \end{pmatrix} = aG. $

Строчки здесь — линейно независимые решения, которые мы получили. Матрица $G$ называется порождающей. Теперь вместо того, чтобы сами составлять таблицу кодирования, мы можем получать кодовые слова простым умножением на матрицу:

$ a \to aG. $

Найдём кодовые слова для этого кода. (Не забываем, что длина исходных сообщений должна быть равна 2 — это количество найденных решений.)

$ \begin{aligned} 00 &\to 00000,\\ 01 &\to 01011,\\ 10 &\to 11100,\\ 11 &\to 10111. \end{aligned} $

Итак, у нас есть готовый код, обнаруживающий ошибки. Проверим его в деле. Пусть мы хотим отправить 01 и у нас произошла ошибка при передаче. Обнаружит ли её код?

$ a=01 \to aG=01011 \rightsquigarrow x=01\underline{1}11 \to Hx^T = (110)^T \neq 0. $

А раз в результате не нулевой вектор, значит код заподозрил неладное. Провести его не удалось. Ура, код работает!

Для кода с утроением, кстати, порождающая матрица выглядит очень просто:

$G=\begin{pmatrix}1&1&1\end{pmatrix}.$

Подобные коды, которые можно порождать и проверять матрицей называются линейными (бывают и нелинейные), и они очень широко применяются на практике. Реализовать их довольно легко, так как тут требуется только умножение на константную матрицу.

Ошибка по синдрому

Ну хорошо, мы построили код обнаруживающий ошибки. Но мы же хотим их исправлять!

Для начала введём такое понятие, как вектор ошибки. Это вектор, на который отличается принятое сообщение от кодового слова. Пусть мы получили сообщение $x$, а было отправлено кодовое слово $v$. Тогда вектор ошибки по определению

$ e = x - v. $

Но в странном мире GF(2), где сложение и вычитание одинаковы, будут верны и соотношения:

$ \begin{aligned} v &= x + e,\\ x &= v + e. \end{aligned} $

В силу особенностей сложения, как читатель сам может легко убедиться, в векторе ошибки на позициях, где произошла ошибка будет единица, а на остальных ноль.

Как мы уже говорили раньше, если мы получили сообщение $x$ с ошибкой, то $Hx^T\neq 0$. Но ведь векторов, не равных нулю много! Быть может то, какой именно ненулевой вектор мы получили, подскажет нам характер ошибки?

Назовём результат умножения на проверочную матрицу синдромом:

$ s(x)=Hx^T.$

И заметим следующее

$ s(x) = Hx^T = H(v+e)^T = He^T = s(e). $

Это означает, что для ошибки синдром будет таким же, как и для полученного сообщения.

Разложим все возможные сообщения, которые мы можем получить из канала связи, по кучкам в зависимости от синдрома. Тогда из последнего соотношения следует, что в каждой кучке будут вектора с одной и той же ошибкой. Причём вектор этой ошибки тоже будет в кучке. Вот только как его узнать?

А очень просто! Помните, мы говорили, что у нескольких ошибок вероятность ниже, чем у одной ошибки? Руководствуясь этим соображением, наиболее правдоподобным будет считать вектором ошибки тот вектор, у которого меньше всего единиц. Будем называть его лидером.

Давайте посмотрим, какие синдромы дают всевозможные 5-элементные векторы. Сразу сгруппируем их и подчеркнём лидеров — векторы с наименьшим числом единиц.

$s(x)$ $x$
$000$ $\underline{00000}, 11100, 01011, 10111$
$001$ $\underline{00010}, 11110, 01001, 10101$
$010$ $\underline{01000}, 10100, 00011, 11111$
$011$ $01010, 10110, \underline{00001}, 11101$
$100$ $\underline{10000}, 01100, 11011, 00111$
$101$ $\underline{10010}, 01110, 11001, \underline{00101}$
$110$ $11000, \underline{00100}, 10011, 01111$
$111$ $11010, \underline{00110}, \underline{10001}, 01101$

В принципе, для корректирования ошибки достаточно было бы хранить таблицу соответствия синдрома лидеру.

Обратите внимание, что в некоторых строчках два лидера. Это значит для для данного синдрома два паттерна ошибки равновероятны. Иными словами, код обнаружил две ошибки, но исправить их не может.

Лидеры для всех возможных одиночных ошибок находятся в отдельных строках, а значит код может исправить любую одиночную ошибку. Ну, что же… Попробуем в этом убедиться.

$ a=01 \to aG=01011 \rightsquigarrow x=01\underline{1}11 \to s(x)=Hx^T = (110)^T \to e=(00100). $

Вектор ошибки равен $(00100)$, а значит ошибка в третьем разряде. Как мы и загадали.

Ура, всё работает!

Что же дальше?

Чтобы попрактиковаться, попробуйте повторить рассуждения для разных проверочных матриц. Например, для кода с утроением.

Логическим продолжением изложенного был бы рассказ о циклических кодах — чрезвычайно интересном подклассе линейных кодов, обладающим замечательными свойствами. Но тогда, боюсь, статья уж очень бы разрослась.

Если вас заинтересовали подробности, то можете почитать замечательную книжку Аршинова и Садовского «Коды и математика». Там изложено гораздо больше, чем представлено в этой статье. Если интересует математика кодирования — то поищите «Теория и практика кодов, контролирующих ошибки» Блейхута. А вообще, материалов по этой теме довольно много.

Надеюсь, когда снова будет свободное время, напишу продолжение, в котором расскажу про циклические коды и покажу пример программы для кодирования и декодирования. Если, конечно, почтенной публике это интересно.

Источник

Занятие № 4. “Помехоустойчивое кодирование” 1. Принципы помехоустойчивого кодирования

Помехоустойчивое или избыточное кодирование применяется для обнаружения и (или) исправления ошибок, возникающих при передаче по дискретному каналу. Отличительное свойство помехоустойчивого кодирования состоит в том, что избыточность источника, образованного выходом кодера, больше, чем избыточность источника на входе кодера. Помехоустойчивое кодирование используется в различных системах связи, при хранении и передаче данных в сетях ЭВМ, в бытовой и профессиональной аудио- и видеотехнике, основанной на цифровой записи.

Классификация помехоустойчивого кодирования показана на рис.1 (возможен другой вариант).

Двоичные коды

Равномерные

Простые

Отраженные

Двоично-десятичные

Неравномерные

Равномерные

Неравномерные

Блочные

Непрерывные

Шеннона-Фано

Хаффмена

Разделимые

Неразделимые

Цепной

Сверточный

Систематические

Несистематические

Циклические

Простейший

Хэмминга

Боуза-Чоудхури-

Рида-Соломона

Хоквингема

Рис. 1. Классификация помехоустойчивого кодирования

Помехоустойчивые коды называют корректирующими. Помехоустойчивость кода основана на введении избыточности в передаваемый сигнал. Помехоустойчивый код отличается от обычного тем, что в канал передаются не все кодовые комбинации, которые можно сформировать. Из всего множества комбинаций выделяются так называемые разрешенные комбинации, которые выделяются по наличию определенных свойств. Только разрешенные кодовые комбинации передаются в канал связи. Остальные неиспользуемые кодовые комбинации называются запрещенными. Передаче по каналу связи они не подлежат.

Для двоичного кода все множество кодовых комбинаций равно N=2n, где n – число разрядов в кодовой комбинации. Это множество разбивается на два подмножества: разрешенных кодовых комбинаций и запрещенных. Эти подмножества известны как на передающей, так и на приемной сторонах.

Если в результате искажений передаваемых кодов комбинация перейдет в подмножество запрещенных комбинаций, то ошибка будет обнаружена. Коды, позволяющие только определить наличие ошибок, но не указывающие номер искаженных разрядов называют кодами с обнаружением ошибок.

При необходимости исправления некоторых возникающих искажений поступают следующим образом. Все множество кодовых комбинаций N разбивают на N0<N непересекающихся подмножеств. Каждое из этих подмножеств, приписывается к одной из N0 разрешенных комбинаций. Принцип исправления ошибок иллюстрируется на рис.2.

Если принятая комбинация Аj входит в подмножество N0j (Aj N0j), то принимается решение, что передана комбинация Aj. То есть, если принятая кодовая комбинация осталась в том же подмножестве, что и передаваемая, то прием будет без ошибки. Если

1

кодовая комбинация в результате искажений переходит в другое подмножество, то прием будет с ошибкой.

A j

N0 j

Рис. 2. Принцип исправления возникающих ошибок

Коды, которые не только обнаруживают ошибку, но и указывают номер искаженной позиции, называются кодами с исправлением ошибок. При использовании помехоустойчивого кода в канале связи передаются только разрешенные кодовые комбинации. Если бы не было помех, то для передачи этих кодовых комбинаций

потребовалось бы меньшее число разрядов n0: n0 log 2 N0 n .

Таким образом, обнаружение и исправление возникающих в каналах связи ошибок достигается за счет введения в передаваемые кодовые комбинации избыточных разрядов.

2. Обнаруживающая и исправляющая способность кодов

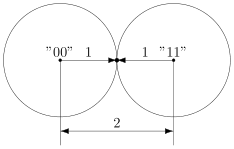
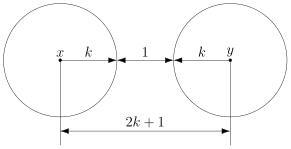
Рассмотрим возможность обнаружения и исправления ошибок на простейшем примере. Предположим, что информация передается одноразрядным двоичным кодом. То есть передается информация 0 или 1. Число возможных кодовых комбинаций N0=2n0, где n0=1, N0=21=2. В каждой кодовой комбинации добавим еще один разряд: n= n0+1=1+1=2. Число кодовых комбинаций N=2n=22=4. Эти комбинации составляют множество, состоящее из 00, 01, 10, 11. Это множество разделим на два подмножества разрешенных и запрещенных комбинаций. К числу разрешенных отнесем те комбинации, у которых сумма единиц всегда четная. Разрешенными выберем такие комбинации, которые отличаются друг от друга двумя разрядами – это 00 и 11. При таком выделении разрешенных комбинаций любая одиночная (или нечетная) ошибка будет изменять число единиц на нечетное. Принятая кодовая комбинация в этом случае переходит в подмножество запрещенных и ошибка будет обнаружена.

Если в кодовую комбинацию ввести количество дополнительных разрядов, то можно не только обнаруживать, но и исправлять ошибки. Если разрешенные комбинации определить таким образом, что любые из них отличаются друг от друга не менее чем тремя разрядами, то одиночная ошибка может быть исправлена. Возможность исправления одиночной ошибки в этом случае связана с тем, что ошибочная комбинация будет отличаться от истинной только одним разрядом и останется в области, относящейся к передаваемой разрешенной комбинации.

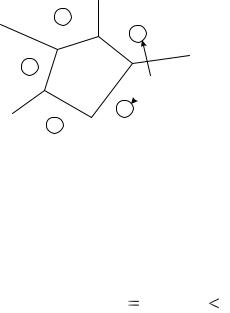
Рассмотрим сказанное на геометрической модели трехразрядного двоичного кода при помощи которого можно получить 23=8 комбинаций. А именно: 000, 001, 010, 011, 100, 101, 110, 111. Каждую новую комбинацию можно представить точкой в трехмерном пространстве (рис. 3).

Для исправления одиночной ошибки разобьем все множества комбинаций на две области, и будем передавать только две кодовые комбинации 111 и 000. Эти комбинации отличаются друг от друга тремя разрядами. Любая одиночная ошибка оставляет кодовую комбинацию в области, относящейся к передаваемой комбинации. Так, при искажении одного разряда в комбинации 000 она превратится в 001, или в 100, или в 010. Все эти

2

2t s 1.

комбинации находятся в той же области, что и комбинация 000.

101

100

111

110

001

000

011

010

Рис. 3. Геометрическая модель помехоустойчивого кода

Рассмотренные примеры показывают, что для обнаружения одиночных ошибок кодовые комбинации должны различаться не менее чем двумя разрядами. Для исправления одиночной ошибки кодовые комбинации должны различаться не менее чем тремя разрядами. Это различие именуют кодовым (Хэминговым) расстоянием. Под кодовым расстоянием понимают минимальное число позиций, на которых символы данной кодовой комбинации отличаются от символов другой кодовой комбинации. Например, для показанных на рис. 4 комбинаций кодовое расстояние d равно 3.

0

0

1

0

1

0

1

0

1

1

Рис. 4. Кодовое расстояние между двумя кодовыми комбинациями

В общем случае кодовое расстояние между комбинациями выражается формулой:

n

d(a,b)

(аi bi ) ,

(1)

i 0

где

– операция сложения по модулю два;

а=(а0,a1,…,an-1); b=(b0,b1,…,bn-1).

Пользуясь расстоянием Хэмминга как метрикой в множестве кодовых слов можно выделить зоны исправления и обнаружения ошибок.

Утверждение. Если код используется только для обнаружения ошибок, то, чтобы обнаружить в кодовом слове произвольную комбинацию из s ошибок, необходимо и достаточно, чтобы расстояние Хэмминга для любых двух разрешенных кодовых слов было на 1 больше, чем s (количество обнаруживаемых ошибок): dmin a,b s 1

В соответствии с утверждением в данном примере могут быть обнаружены ошибки кратные s=1 и s=2. При s=3 передаваемая кодовая комбинация переходит в другую разрешенную комбинацию. Ошибка не обнаруживается.

Утверждение. Если код используется только для исправления ошибок, то, чтобы исправить t ошибок необходимо и достаточно, чтобы dmin a,b 2t 1.

Утверждение. Для того, чтобы исправить t и обнаружить s ошибок в кодовом слове, необходимо и достаточно, чтобы dmin a,b

Таким образом, правильный выбор разрешенных и запрещенных кодовых комбинаций передаваемого сообщения позволяет сформировать помехоустойчивый код с обнаружением и исправлением ошибок.

3

3. Блочные помехоустойчивые коды

Разделимые коды обычно обозначают как (n, k) — коды. Здесь n – количество элементов в кодовой комбинации, k – число информационных элементов.

Общепринятым методом задания (n, k) кодов является представление набора используемых кодовых комбинаций в виде матрицы, имеющей n столбцов и k строк. Такую матрицу называют порождающей матрицей. Обозначается порождающая матрица – Gn k .

Путем элементарных преобразований (перестановкой строк; заменой строки суммой данной строки с любой другой строкой, перестановкой столбцов) порождающая матрица может быть преобразована к канонической форме:

Gn k

Ik k _ hr k

,

(2)

где

Ik k

– единичная матрица размерностью k k ;

hr k

– матрица размерностью r

k ;

r n

k – число проверочных элементов.

Важным подмножеством групповых кодов являются коды Хэмминга.

Коды Хэмминга – это n, k

коды, длина которых равна n 2r

1.

Примеры кодов Хэмминга: (7,4); (15,11) и т.д. Для данных кодов dmin 3 .

Код Хэмминга (7,4) как правило задается порождающей матрицей, причем эта

матрица может быть приведена к каноническому виду:

1000 _ 011

0100 _101

.

G7 4

0010 _110

(3)

0001_111

I4 4 __ h3 4

Построение подматрицы

hr k

производится следующим

образом: в столбик

записывается двоичное представление чисел от 0 до n разрядами r , после этого вычеркиваются строки с количеством единиц меньше двух, из оставшихся строк

составляется подматрица hr k .

Алгоритм кодирования кодом Хэмминга

Пусть задано информационное слово С b0b1b2b3 1010 , которое нужно

закодировать кодом Хэмминга (7,4). Код Хэмминга (7,4) задан порождающей матрицей вида (3).

Комбинация на выходе кодера получается из соотношения:

1000 _ 011

С С G

b b b b

0100 _101

b b b b _ a a a .

4

7

0

1

2

3

0010 _110

0

1

2

3

0

1

2

0001_111

Проверочные символы для кода Хэмминга (7,4) формируются в соответствии с приведенными выражениями:

a0

b1

b2

b3

0 1 0 1,

a1

b0

b2

b3

1

1 0 0 ,

a2

b0

b1

b3

1

0 0 1.

При записи кодовой комбинации на выходе кодера первые k символов кода

называются информационными, остальные r

n k – проверочными.

На выходе кодера получим кодовую комбинацию:

С b0b1b2b3 _ a0a1a2

1010 _101 .

4

Структурная схема кодера для кода Хэмминга (7,4)

bo

bo

приведена на рис. 2.

b1

b1

Задача

декодирования

состоит

в

том,

чтобы

принятому

кодовому

слову поставить

в

соответствие

b2

b2

кодовое слово из числа разрешѐнных. Используя принцип

b3

b3

максимального правдоподобия, в соответствие

ставится

такое разрешѐнное слово, которое минимально отличается

от принятого.

M2

Алгоритмы

декодирования

можно

задавать

ao

№1

таблично. Однако гораздо удобнее знание математической

M2

структуры

кода,

что

может

облегчить

реализацию

№2

a1

операций кодирования и декодирования.

M2

№3

a2

Необходимо

отметить,

что

операция

Рис. 2. Схема кодера

декодирования,

не

есть операция,

обратная операции

кодирования. Это операция оценки принятого сообщения и

Хэмминга (7,4)

принятия наиболее достоверного решения относительно

того, какое из возможных сообщений было передано.

Различают синдромное и мажоритарное декодирование.

Синдромом называется

кодовая

комбинация

размерностью

r

n

k ,

равная

произведению принятого кодового слова на транспонированную проверочную матрицу. Если кодовое слово будет принято без искажений, то синдром будет равен нулю,

т.е. S 000. Если же какой-либо символ будет принят с искажением, то синдром совпадает со столбцом проверочной матрицы и укажет на номер разряда (символа в кодовом слове), который принят с ошибкой.

Для исправления ошибки нужно к символу разряда в котором произошла ошибка прибавить единицу по модулю два.

Под мажоритарными групповыми кодами принято понимать такие групповыми коды, которые позволяют при декодировании использовать принцип решения по большинству (мажоритарный принцип).

При декодировании кодом Хэмминга используется синдромное декодирование.

Для порождающей матрицы вида (3),

проверочная матрица имеет канонический

вид:

0111_100

H

1011_ 010

.

(4)

1101_ 001

h k r __ Ir

r

Проверочная матрица H состоит из 2-х подматриц:

h k

r – транспонированной матрицы, определяемой из порождающей матрицы;

I r r

– единичной матрицы размерностью r

r .

Свойство проверочной матрицы: произведение закодированного слова (разрешенной кодовой комбинации) на транспонированную проверочную матрицу равно нуль-вектору:

b0 ,b1,b2 ,…,bk 1, a0 , a1,…,ar 1 H T 0,0,…,0r 1 .

Проверочная и порождающая матрицы связаны выражением:

В обобщенном виде, алгоритм исправления ошибок включает в себя три этапа: вычисление синдрома; синтез вектора ошибок; исправление ошибки.

Рассмотрим этапы более подробно.

5

Вычисление синдрома.

Для кода Хэмминга (7,4) синдромом будет 3-х разрядная кодовая комбинация:

011

101

110

S С H T b b b b _ a a a

2

111

S

0

S S

2

,

0

1

2

3

0

1

1

100

010

001

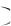
где Сb0b1b2b3 _ a0a1a2 – принятое сообщение;

H T – транспонированная проверочная матрица.

Согласно правилу умножения вектора на матрицу элементы синдрома будут определяться выражениями:

S0 b1 b2 b3 a0 , S1 b0 b2 b3 a1 , S2 b0 b1 b3 a2 .

Если кодовое слово будет принято без искажений, то синдром будет равен нулю,

т.е. S 000 .

Если же какой-либо символ будет принят с искажением, то синдром укажет на номер элемента в кодовом слове, который принят ошибочно.

Вектор ошибок это кодовая комбинация, которая ставится в соответствие синдрому и содержит единицу в том разряде, где произошла ошибка, и нули во всех остальных разрядах. Составим таблицу соответствия синдрома и вектора ошибок:

Таблица 1

Таблица соответствия вектора ошибки синдрому сообщения

S0

S1

S2

e0

e1

e2

e3

0

0

0

0

0

0

0

0

1

1

1

0

0

0

1

0

1

0

1

0

0

1

1

0

0

0

1

0

1

1

1

0

0

0

1

На основании данной таблицы получим элементы вектора ошибок: e0 S0S1S2 , e1 S0 S1S2 , e2 S0S1S2 , e3 S0 S1S2 .

Например, с ошибкой был принят символ b2 , в этом случае синдром будет равен

S 110 , а это третий столбец в проверочной матрице, которому соответствует вектор ошибок e 0010 .

Исправить ошибку довольно легко, для этого нужно произвести поразрядное сложение по модулю два принятого кодового слова и синтезированного вектора ошибок.

Пример.

Пусть принята кодовая комбинация C 1010 _101 без ошибки. Произведем вычисление синдрома:

S0

b1

b2

b3

a0

0 1 0

1

0 ,

S1

b0

b2

b3

a1

1 1 0 0 0 ,

S2

b0

b1

b3

a2

1 0 0

1

0 .

Т.к. полученный синдром является нулевым, то ошибки нет и можно сразу записать

итоговую кодовую комбинацию: C

1010 .

6

Пример.

Введем в принятую кодовую комбинацию, ошибку во втором разряде, т.е.

C 1110 _101.

Произведем вычисление синдрома:

S0

b1

b2

b3

a0

1

1

0

1

1,

S1

b0

b2

b3

a1

1 1 0 0 0 ,

S2

b0

b1

b3

a2

1

1

0

1

1.

Полученному синдрому

S

101,

соответствует

второй столбец проверочной

матрицы, в таблице соответствия (табл. 2.1) это третья строка следовательно вектор ошибок примет вид e 0100 .

Запишем процесс исправления ошибки:

С 1110 – информационные символы принятой кодовой комбинации,

e0100 – вектор ошибок,

С1010 – исправленная информационная кодовая комбинация.

Схема декодера для выбранного кода Хэмминга (рис. 3) строится по известной проверочной матрице H с использованием метода синдромного декодирования.

В состав структурной схемы декодера кода Хэмминга (7,4) входят: блок вычисления синдрома; формирователь вектора ошибок;

выходные сумматоры по модулю два, в которых происходит процесс исправления ошибок.

bo

M2

bo

№4

b1

M2

b1

№5

b2

M2

b2

№6

b3

M2

b3

№7

e0

e1

e2

e3

&

&

&

&

ao

M2

S0

1

S0

№1

a1

M2

S1

1

S1

№2

a2

M2

S2

1

S2

№3

Блок вычисления синдрома

Формирователь вектора ошибок

Рис. 3. Схема декодера Хэмминга (7,4)

Таким образом, как следует из материалов занятия:

1.Помехоустойчивость корректирующих кодов основана на введении избыточности в передаваемый сигнал. Из множества всех кодовых комбинаций в канал связи передаются только некоторые – разрешенные комбинации. Ошибка обнаруживается, если принятая комбинация кода отличается от разрешенных. Помехоустойчивые коды могут не только обнаруживать ошибки, но и исправлять их.

2.Кроме длины кодовой комбинации n, для характеристики помехоустойчивых кодов пользуются кодовым расстоянием d. Кодовое расстояние определяет насколько различаются кодовые комбинации между собой. С увеличением кодового расстояния корректирующие возможности помехоустойчивого кода расширяются. Однако, для этого необходимо увеличивать число избыточных разрядов кода.

7

Соседние файлы в папке ТСиТ

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Вообще говоря, практически все блочные помехоустойчивые коды “достаточно хорошие”, но практически все они требуют построения таблиц размера, экспоненциально зависящего от длины блока. А по теореме о канале с шумом, длина блока должна быть большой. Понятно, что построение и поиск в очень больших таблицах с практической точки зрения нежелательны. Соответственно в основном рассматриваются коды, которые можно построить более просто – под “более просто” в данном случае означает за полиномиальное время от длины блока – желательно, линейное время от длины блока.

На практике, построение практически применимых кодов, настолько хороших, как обещает теорема о канале с шумом, на текущий момент является нерешённой проблемой. Т.е. предел, установленный Шенноном на практике не достигается. Тем не менее, существуют “достаточно хорошие” практически применимые коды.

Очень хорошие коды
Семейство блочных кодов, которые для данного зашумлённого канала дают произвольно малую вероятность ошибки при любой скорости передачи вплоть до пропускной способности канала.
Хорошие коды
Семейство блочных кодов, которые для данного зашумлённого канала дают произвольно малую вероятность ошибки при любой скорости передачи вплоть до некоторого максимума, который может быть меньше пропускной способности канала.
Плохие коды
Семейства блочных кодов, которые не могут обеспечить произвольно малую вероятность ошибки, либо (номинально) могут только при нулевой скорости передачи.
Практические коды
Коды, кодирование-декодирование которых имеет полиномиальную сложность1 при кодировании и декодировании.

Большинство известных кодов являются линейными блочным кодами. Напомним,

\((N, K)\) блочный код
Множество \(2^K\) кодовых слов длины \(N\), кодирующих некий источник с алфавитом мощности \(2^K\).
\((N, K)\) блочный линейный код
Блочный код, в котором кодовые слова \(\brace{\vect x^{(s)}}\) образуют \(K\)-мерное линейное векторное пространство, являющееся подпространством \(\mathcal A_X^N\) всех возможных кодовых слов длины \(N\), т.е. линейная операция над любыми двумя разрешёнными кодовыми словами даёт разрешённое кодовое слово.

Напомним несколько определений из линейной алгебры.

Магма
Множество \(M\) и бинарная операция \(\bullet: M\times M \to M\) называются вместе магмой, если \(\forall a, b \in M: a\bullet b \in G\), т.е. \(M\) замкнуто относительно \(\bullet\).
Полугруппа
Магма, \((S, \bullet)\), такая, что \(\forall a, b, c \in S: (a\bullet b)\bullet c = a\bullet (b\bullet c),\) т.е. операция \(\bullet\) ассоциативна.
Моноид
Полугруппа \((S, \bullet)\), такая, что \(\exists e \in S: \forall a \in S: a\bullet e = e \bullet a = a\), т.е. существует элемент, нейтральный относительно \(\bullet\).
Группа
Моноид \((G, \bullet)\): \(\forall a \in G, \exists b \in G: a\bullet b = b\bullet a = e\), т.е. для каждого элемента существует обратный ему относительно \(\bullet\).
Абелева группа (Коммутативная группа)
Группа, в которой бинарная операция коммутативна, т.е. \(\forall a, b \in G: a\bullet b = b\bullet a\).
Кольцо

Множество \(R\) и две бинарных операции \(+\) и \(\cdot\) называются вместе кольцом, если:

  1. \((R, +)\) является абелевой группой
  2. \((R, \cdot)\) является моноидом
  3. Операция \(\cdot\) дистрибутивна по отношению к \(+\), т.е. \(\forall a,b,c \in R:\) \(a\cdot(b+c) = a\cdot b + a\cdot c,\) \((b+c)\cdot a = b\cdot a + c\cdot a.\)
Поле
Кольцо \((R, +, \cdot)\), в котором операция \((R\setminus\brace{e}, \cdot)\) образует абелеву группу, где \(e\) – нейтральный элемент операции \(+\).
Поле Галуа (конечное поле)
Поле \(GF = (F, +, \cdot),\) где \(F\) – конечное множество.

Нетривиальное поле, очевидно, не может содержать менее двух элементов.

Векторное пространство над полем \(F\)

Поле \((F, +_F, \cdot_F)\), множество \(V\) и операции \(+: V\times V\to V,\) \(\cdot: F\times V \to V,\) такие, что:

  1. \((V, +)\) образуют абелеву группу
  2. \(\forall a,b \in F, v\in V: a\cdot(b\cdot v) = (a\cdot_F b) \cdot v\)
  3. \(\forall v \in V: u\cdot v = v\), где \(u\in F\) – нейтральный элемент относительно \(\cdot_F\).
  4. \(\forall a\in F, u,v \in V: a\cdot (u+v) = a\cdot u + a\cdot v\)
  5. \(\forall a, b\in F, v \in V: (a+_F b)\cdot v = a\cdot v + b\cdot v\)

Если любой линейный код образует векторное пространство, то процесс построения кода должен естественным образом описываться в терминах линейной алгебры. Это действительно так.

Операция кодирования может быть представлена в виде матрицы \(\vect G\), такой, что при кодировании сообщения \(\vect s\), кодированный сигнал \(\vect t = \vect G^\mathrm T \vect s\).

Множество всех кодовых слов \(\brace{\vect t}\) может быть определено как множество, удовлетворяющее уравнению \(\vect H \vect t = 0,\) где \(0\) – нейтральный элемент операции \(+\).

Матрица \(\vect G\) называется порождающей матрицей, матрица \(\vect H\) – проверочной матрицей. Они, ясно, должны удовлетворять условию \(\vect H \vect G^\mathrm T = \vect 0\), где \(\vect 0\) – нулевая матрица.

Синдром
Произведение проверочной матрицы и принятого сигнала \(\vect s = \vect H \vect r\) называется синдромом. Для разрешённых кодовых слов, синдром равен нулю.

Поскольку \(\vect H \vect t = 0\), для принятого сигнала \(\vect r\), \(\vect s = \vect H \vect r = \vect H t + \vect H \vect e = \vect H \vect e\), где \(t\) – разрешённое кодовое слово и \(e\) – ошибка. Таким образом, между синдромом и вектором ошибки можно поставить взаимно однозначное соответствие. Если быть точным, то это возможно, если, по крайней мере, \(q^{(n-k)} \ge \sum_{j=0}^t C_n^j (q-1)^j\), где \(t\) – максимальная кратность ошибки, что совпадает с границей Хэмминга.

Пусть \(\mathbb F_q^n\) – линейное \(n\)-мерное пространство над полем Галуа мощности \(q\). Тогда линейный код \(C\), являющийся подпространством \(\mathbb F_q^n\) можно представить в виде некоторого минимального базиса \(k \le n\) векторов. Векторы этого базиса образуют строки порождающей \(k\times n\) матрицы \(\vect G\). Если матрица \(\vect G\) имеет блочную форму \(\vect G = \brack{\vect I_k | \vect P},\) где \(I_k\) – единичная матрица \(k\times k\), \(P\) – некоторая матрица \(k \times (n-k)\), мы говорим, что \(\vect G\) находится в стандартной форме.

Если \(\vect G = \brack{\vect I_k | \vect P},\) то \(\vect H = \brack{-\vect P^{\mathrm T} | \vect I_{n-k}}\) – одно из решений уравнения \(\vect H \vect G^\mathrm T = \vect 0\). Проверочная матрица имеет размер \((n-k)\times n\).

Следует отметить, что \(n\) – число символов в коде, \(k\) – число информационных символов и \(n-k\) – число проверочных символов.

Линейность гарантирует, что минимальное расстояние Хэмминга между кодовым словом \(c_0\) и любым другим кодовым словом \(c\neq c_0\) не зависит от \(c_0\). Действительно, свойство линейности даёт \(c-c_0 \in C\), а из определения расстояния Хэмминга, \(d(c_0, c) = d(c-c_0, 0)\), тогда \[\underset{c\neq 0}\min d(c_0, c) = \underset{c\neq 0}\min d(c-c_0, 0) = \underset{c\neq 0}\min d(c, 0).\]

Два кода называются эквивалентными, если их порождающие матрицы отличаются только перестановкой столбцов и элементарными линейными операциями над строками. Такие коды по сути отличаются только положением проверочных символов в кодовых словах.

В менее общих, более практических терминах, коды в основном строятся над двоичными алфавитами. Тогда поле \(F\) представляет собой двоичное поле Галуа, где операции \(+_F\) и \(\cdot_F\) соответственно представляют собой сложение \(\mod 2\) и умножение. Элементы векторного пространства, в свою очередь, представляют собой элементы пространства \(F^N\), сложение является поэлементным сложением \(\mod 2\), умножение – поэлементное умножение.

Коды Хэмминга

Коды Хэмминга – один из наиболее широко известных классов линейных кодов.

Коды Хэмминга конструируются следующим образом: биты, находящиеся в кодовом слове в разрядах с номером, являющимся степенью 2, являются проверочными, остальные – информационные. Значение \(i\)-го проверочного бита определяется суммой по модулю 2 всех информационных бит с номерами \(j\), таких, что \(i \& j \neq 0,\) где \(\&\) – побитовая конъюнкция двоичных представлений чисел \(i\) и \(j\). В каноническом варианте биты нумеруются слева направо.

Число проверочных бит выбирается исходя из возможности исправить 1 ошибку в соответствии с границей Хэмминга: \(r = \ceil{\log_2 (n+1)}\). Собственно, обычно поступают наоборот – исходя из числа проверочных бит, определяют максимально возможное число информационных: \(2^r — 1 = n\). Тогда, кодов Хэмминга с 1 проверочным битом не существует, код Хэмминга с 2 проверочными битами содержит 1 информационный бит и т.д.

Коды Хэмминга обозначаются парой чисел: количеством бит в кодовом слове и количеством информационных бит.

С точки зрения систематического подхода, проверочная матрица кодов Хэмминга \(H\) состоит из \(r\) строк и \(n\) столбцов, причём столбцы различны и не равны нулю. А поскольку \(n = 2^r — 1\), столбцы этой матрицы неизбежно включают все ненулевые комбинации из \(r\) бит.

Например, код Хэмминга (7, 4) имеет проверочную матрицу (упорядоченную по возрастанию столбцов) \[\vect H = \begin{pmatrix}
1 & 0 & 1 & 0 & 1 & 0 & 1 \\
0 & 1 & 1 & 0 & 0 & 1 & 1 \\
0 & 0 & 0 & 1 & 1 & 1 & 1 \\
\end{pmatrix}\]

Или в каноническом варианте (получается перестановкой 1, 2 и 4 столбцов на 5, 6, 7 позиции соответственно):

\[\vect H = \paren{\begin{array}{cccc|ccc}
1 & 1 & 0 & 1 & 1 & 0 & 0 \\
1 & 0 & 1 & 1 & 0 & 1 & 0 \\
0 & 1 & 1 & 1 & 0 & 0 & 1 \\
\end{array}}\]

Каноническая порождающая матрица тогда: \[\vect G^\mathrm T = \begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
\hline
1 & 1 & 0 & 1 \\
1 & 0 & 1 & 1 \\
0 & 1 & 1 & 1 \\
\end{pmatrix}\]

Порождающая матрица, соответствующая исходной проверочной (получается перестановкой 5,6,7 строк на 1, 2, 4 позиции соответственно): \[\vect G^\mathrm T = \begin{pmatrix}
1 & 1 & 0 & 1 \\
1 & 0 & 1 & 1 \\
1 & 0 & 0 & 0 \\
0 & 1 & 1 & 1 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
\end{pmatrix}\]

Тогда коды для соответствующих сообщений:

Сообщение \(\vect m\) Код \(\vect G^\mathrm T \vect m\)
0000 0000000
0001 0001111
0010 0010011
0011 0011100
0100 0100101
0101 0101010
0110 0110110
0111 0111001
1000 1000110
1001 1001001
1010 1010101
1011 1011010
1100 1100011
1101 1101100
1110 1110000
1111 1111111

Таблица синдромов:

Синдром Вектор ошибки
110 0000001
101 0000010
011 0000100
111 0001000
100 0010000
010 0100000
001 1000000

Например, получив сообщение r=1101010, вычислим синдром Hr = 110, что соответствует вектору ошибки 1000000. Тогда исходное сообщение c=0101010, m=0101.

Канонический вариант кода Хэмминга получается перестановкой проверочных бит на соответствующие позиции кодового слова:

Сообщение \(\vect m\) Код \(\vect G^\mathrm T \vect m\)
0000 0000000
0001 1101001
0010 0101010
0011 1000011
0100 1001100
0101 0100101
0110 1100110
0111 0001111
1000 1110000
1001 0011001
1010 1011010
1011 0110011
1100 0111100
1101 1010101
1110 0010110
1111 1111111

Циклические коды

Циклический код – это линейный блоковый код, обладающий свойством цикличности: циклический сдвиг разрешённого кодового слова влево или вправо на 1 бит даёт разрешённое кодовое слово.

При построении циклических кодов, используют формализм операций над многочленами: множество кодовых слов длины \(n\) представляется как множество многочленов степени \(n-1\), делящихся без остатка на некоторый многочлен \(g(x)\) степени \(r = n-k\), являющийся делителем \(x^n-1\). Все операции над многочленами производятся по модулю \(x^n-1\), таким образом, множество таких многочленов образует кольцо, а умножение на \(x\) соответствует циклическому сдвигу. Проверочный многочлен \(h(x) = (x^n-1)/g(x)\), для любого разрешённого кодового слова \(f(x)\), \(f(x) h(x) = 0\).

Для произвольного сообщения \(m(x)\) в соответствующем кольце, разрешённое кодовое слово немедленно получается умножением \(m(x)\) на \(g(x)\). В таком случае, при \(g(x) = \sum_{i=0}^{r} g_i x^i\), соответствующая порождающая матрица имеет вид \[\vect G =
\begin{pmatrix}
g \\
x g \\
x^2 g \\
\vdots \\
x^k g \\
\end{pmatrix} =
\begin{pmatrix}
0 & \cdots & 0 & 0 & g_r & \cdots & g_0 \\
0 & \cdots & 0 & g_r & \cdots & g_0 & 0 \\
\vdots & & & \ddots & & & \vdots \\
g_r & g_{r-1} & \cdots & g_0 & 0 & \cdots & 0 \\
\end{pmatrix}\tag{1}\] (либо отражённая по горизонтали при обратном порядке бит – мы однако будем исходить из того, что младший бит соответствует нулевой степени)

Однако на практике используется систематический подход, разделяющий информационные и проверочные символы.

Для данного сообщения \(m(x)\), оно умножается на \(x^r\) и делится на \(g(x)\), так, что \[m(x) x^r = q(x) g(x) + r(x),\] где \(q(x)\) – частное, \(r(x)\) – остаток. Тогда кодовое слово \[c(x) = q(x)g(x) = m(x)x^r — r(x).\]

Тогда кодовые слова представляют из себя конкатенацию исходного сообщения \(m(x)\) и отрицания остатка от деления \(m(x)x^r\) на \(g(x)\), и тогда порождающая матрица имеет вид

\[\vect G =
\begin{bmatrix}
\vect I_k | — \vect R \\
\end{bmatrix},\] где \[\vect R = \begin{pmatrix}
\mathrm{rem}(x^n, g(x))\\
\mathrm{rem}(x^{n-1}, g(x))\\
\vdots\\
\mathrm{rem}(x^r, g(x))\\
\end{pmatrix}\] (либо отражённая по вертикали при обратном порядке бит – мы однако будем исходить из того, что младший бит соответствует нулевой степени)

Синдром \(s(x)\) определяется как остаток от деления полученного кодового слова на \(g(x)\). Соответствующий вектор ошибки определяется из \(\mathrm{rem}(e(x),g(x)) = s(x).\) Ясно, что, поскольку кодовые слова имеют делителем \(g(x)\) по построению, для них синдром равен нулю.

Немаловажным нюансом является то, что выбор порождающего многочлена, вообще говоря, не произволен – это ясно, если внимательно посмотреть на порождающую матрицу.

Действительно, рассмотрим первые две строчки матрицы \(\vect G\) из \((1).\) Эти строчки являются разрешёнными кодовыми словами. Нулевой вектор так же является разрешённым кодовым словом. Находя расстояние Хэмминга от нулевого кодового слова до первой строчки \(\vect G\), получаем, что кодовое расстояние циклического кода не может превышать число ненулевых членов в порождающем многочлене. Находя расстояние Хэмминга между первой и второй строчками, получаем, что, если все коэффициенты порождающего многочлена отличны от нуля, то кодовое расстояние не может быть больше 2, а вообще не превышает \(2+\floor{\frac{r-1}{2}}\). Соответственно, не более половины “средних” (т.е. кроме старшего и младшего) членов \(g(x)\) будут ненулевыми, причём младший и старший всегда ненулевые.

Некоторые коды Хэмминга, а именно, коды \((n, k)\), в которых \(n\) и \(k-1\) являются взаимно простыми (или \(k=2\)), являются так же циклическими (с точностью до перестановок)

Например, код, эквивалентный коду Хэмминга (7,4) можно представить как циклический код с порождающим многочленом \(g(x) = x^3+x+1\). Действительно, \(n=7\), \(k=4\), \(r=3\).

m \(m(x)\) \(r(x)\) Код
0000 \(0\) \(0\) 0000 000
0001 \(1\) \(x+1\) 0001 011
0010 \(x\) \(x^2+x\) 0010 110
0011 \(x+1\) \(x^2+1\) 0011 101
0100 \(x^2\) \(x^2+x+1\) 0100 111
0101 \(x^2+1\) \(x^2\) 0101 100
0110 \(x^2+x\) \(1\) 0110 001
0111 \(x^2+x+1\) \(x\) 0111 010
1000 \(x^3+0\) \(x^2+1\) 1000 101
1001 \(x^3+1\) \(x^2+x\) 1001 110
1010 \(x^3+x\) \(x+1\) 1010 011
1011 \(x^3+x+1\) \(0\) 1011 000
1100 \(x^3+x^2\) \(x\) 1100 010
1101 \(x^3+x^2+1\) \(1\) 1101 001
1110 \(x^3+x^2+x\) \(x^2\) 1110 100
1111 \(x^3+x^2+x+1\) \(x^2+x+1\) 1111 111

Допустим, мы получили код \(0011 000\), что соответствует многочлену \(x^3+x^4\). Остаток от деления на \(g(x)\) \(x^2+1\), что соответствует ошибке передачи. \(x^6/g(x) = x^2+1\), тогда синдром соответствует ошибке в 7-м бите. Кодовое слово тогда \(1011 000\) и исходное сообщение \(1011\). Таблица синдромов имеет вид:

Синдром Вектор ошибки
1 0000001
x 0000010
x^2 0000100
x+1 0001000
x^2+x 0010000
x^2+x+1 0100000
x^2+1 1000000

О возможности существования очень хороших совершенных кодов

Рассмотрим двоичный симметричный канал с вероятностью перехода \(f\).

Ёмкость двоичного симметричного канала \(C(f) = 1 — H_2(f)\) (см. семинар 1, пример 6). По теореме Шеннона о канале с шумом, для достаточно большой длины кода \(N\), существуют блочные коды, имеющие плотность кодирования \(\rho\), сколь угодно близкую к \(C(f)\) и исчезающе малую вероятность ошибки. Для больших \(N\), число битовых ошибок в блоке примерно \(fN\), следовательно, такие блочные коды можно назвать исправляющими fN ошибок (почти наверняка).

Рассмотрим теперь ДСК, где \(f > 1/3\). Пусть существует совершенный исправляющий fN ошибок код. Рассмотрим три кодовых слова из этого кода (у такого кода должно быть \(2^{N\rho} \approx 2^{NC(f)}\) кодовых слов, поэтому при больших N найдётся хотя бы три). Без ограничения общности, пусть один из этих кодов будет нулевым (т.е. состоящим из нулей), второй имеет \((u+v)N\) первых единиц, прочие нули, третий – \(uN\) нулей, \((v+w)N\) единиц, остальные нули. Все коды (из рассматриваемых трёх) имеют \(x = (1-u-v-w)N\) нулей в конце. Если это совершенный исправляющий fN ошибок код, то кодовое расстояние должно быть больше \(2fN\), тогда \[u+v > 2 f,\] \[v+w > 2 f,\] \[u+w > 2 f,\]

Суммируя, получаем: \[u+v+w > 3 f.\]

Но \(f>1/3\), и \(u+v+w > 1\), тогда \(x < 0\), что невозможно.

То есть, совершенный исправляющий \(fN\) ошибок код не может иметь даже трёх кодовых слов, не говоря уже о \(2^{N\rho}\).

О возможности существования очень хороших линейных кодов

Несмотря на невозможность существования очень хороших совершенных кодов, очень хорошие линейные коды существуют. В первую очередь это связано с тем, что на самом деле при длине кодовых слов \(N\to\infty\), вероятность того, что в результате изменения \(fN\) бит в кодовом слове, результат будет неоднозначен, стремится к нулю.

Рассмотрим линейный код с двоичной проверочной матрицей \(\vect H\), имеющей \(M\) строк и \(N\) столбцов. Считаем, что \(M \sim N\). Плотность кодирования такого кода по крайней мере \[\rho \ge 1 — \frac{M}{N}.\] Далее полагаем худший случай, т.е. \(\rho = 1 — \frac{M}{N}.\)

Выбирается кодовое слово \(\vect t\), такое, что \[\vect H \vect t = 0 \mod 2.\]

ДСК добавляет вектор шума \(\vect x\), так, что \[\vect r = \vect t+\vect x \mod 2.\]

Получатель должен восстановить \(t\) и \(x\) из \(r\). Используя подход декодирования по синдрому. Получатель вычисляет синдром \[\vect z = \vect H \vect r \mod 2 = \vect H \vect x \mod 2.\]

Поскольку синдром \(\vect z\) зависит только от вектора шума \(\vect x\), задача декодирования состоит в нахождении наиболее вероятного \(\vect {\hat x}\), удовлетворяющего условию \[\vect H \vect {\hat x} = \vect z \mod 2,\] который затем можно вычесть из \(\vect r\) чтобы получить наиболее вероятное исходное кодовое слово \(\vect {\hat t}\).

Мы хотим показать, что вероятность ошибки стремится к нулю с ростом \(N\) для случайной матрицы \(\vect H\).

Рассмотрим субоптимальную стратегию. Пусть субоптимальный декодер (назовём его декодером типичных множеств) рассматривает множество типичных векторов шума \[T = \brace{\vect x \in X^N : \left|\log_2\frac{1}{P(\mathbf x)} — N H(X)\right| < \beta},\] где для ДСК \(H(X) = H_2(f)\), проверяя, какие из них удовлетворяют найденному синдрому. Если ни один элемент типичного множества не удовлетворяет вычисленному синдрому, или если ему удовлетворяют более одного, то декодер сообщает об ошибке.

Для данной матрицы \(\vect H\), вероятность ошибки можно записать как \[P = P_1 + P_2,\] где \(P_1\) – вероятность того, что \(\vect x\) не типичный, а \(P_2\) – что \(\vect x\) типичный, и по крайней мере ещё один вектор \(\vect x’\) имеет такой же синдром. \(P_1\) уменьшается с ростом \(N\), как показано при доказательстве теоремы Шеннона о кодировании источника (см. лекцию 5). \(P_2\) по сути есть вероятность наличия двух типичных векторов \(\vect x\) и \(\vect x’\), таких, что \[\vect H(\vect x’ — \vect x) = 0.\]

Введём функцию \[f(\vect x, \vect x’) = \left\{\begin{align}
1, && \vect H (\vect x’ -\vect x) = 0 \\
0, && \vect H (\vect x’ -\vect x) \neq 0
\end{align}\right.\]

Количество ошибок \(N_e\) для данного типичного вектора \(\vect x\) тогда \[N_e(\vect x) \le \sum_{\begin{align}\vect x’\in T\\\vect x’\neq \vect x\end{align}} f(\vect x, \vect x’)\]

\(N_e(\vect x) \in \brace{0,1}\), правая часть может быть больше 1.

Тогда усредняя по \(\vect x\), \[P_2 = \sum_{x\in T} P(\vect x) N_e(\vect x) \le \sum_{x\in T} P(\vect x) \sum_{\begin{align}\vect x’\in T\\\vect x’\neq \vect x\end{align}} f(\vect x, \vect x’).\]

Усредняя по всем матрицам \(\vect H\), \[\bar P_2 \le \sum_{\vect H} P(\vect H) \sum_{x\in T} P(\vect x) \sum_{\begin{align}\vect x’\in T\\\vect x’\neq \vect x\end{align}} f(\vect x, \vect x’)\]

\(P(\vect x)\) не зависит от \(\vect H\), поэтому

\[\bar P_2 \le \sum_{x\in T} P(\vect x) \sum_{\begin{align}\vect x’\in T\\\vect x’\neq \vect x\end{align}} \sum_{\vect H} P(\vect H) f(\vect x, \vect x’)\]

Выражение \(\sum_{\vect H} P(\vect H) f(\vect x, \vect x’)\) это по сути вероятность равенства вектора синдрома нулю по всем возможным случайным матрицам \(\vect H\). Она не превышает вероятности равенства нулю случайного вектора, т.е., поскольку вектор синдрома имеет размер \(M\), \[\sum_{\vect H} P(\vect H) f(\vect x, \vect x’) \le 2^{-M}.\]

Тогда, \[\bar P_2 \le (\sum_{x\in T} P(\vect x)) \paren{\abs T -1} 2^{-M} \le \abs T 2^{-M}.\]

При доказательстве теоремы о кодировании источника, было показано, что в типичном множестве примерно \(2^{NH(X)}\) элементов, тогда \[\bar P_2 \le 2^{NH(X)-M}.\]

Если \(NH(X)-M < 0\), т.е. \(H(X) < M/N,\) то вероятность средняя вероятность ошибки экспоненциально убывает с ростом \(N\). Тогда, если в среднем по всем возможным проверочным матрицам вероятность ошибки убывает, то неизбежно существуют такие линейные коды, для которых она так же убывает. Более того, таких кодов большинство.

Отметим, что подставляя условие на энтропию в \(\rho = 1 — M/N,\) получаем \[1 — \rho = M/N,\] \[1 — \rho > H(X),\] \[\rho < 1 — H(X) = 1-H_2(f),\] что совпадает с условием теоремы Шеннона для ДСК.

Отдельно следует отметить, что по сути мы заодно доказали теорему о кодировании источника. Действительно, поскольку мы “угадываем” вектор шума \(\vect x\) длины \(N\) по вектору синдрома \(\vect z\) длины \(M\), с исчезающе малой вероятностью ошибки, если \(H(X) < M/N\), то это означает, что, при достаточно больших \(N\), существует схема кодирования, позволяющая “почти безошибочно” передать \(N\) бит сообщения в коде длины \(M\), так, что \(M = N H(X) + \varepsilon\).

  1. Вообще говоря, имеется ввиду временная или пространственная сложность. Однако в теории сложности алгоритмов доказывается, что \(P(n) \subseteq PSPACE(n)\), т.е. семейство алгоритмов, полиномиальных по времени есть нестрогое подмножество семейства алгоритмов, полиномиальных по памяти, поэтому требование \(P\) и/или \(PSPACE\) по сути эквивалентно требованию \(P\).↩︎

Источник

Обнаружение ошибок в технике связи — действие, направленное на контроль целостности данных при записи/воспроизведении информации или при её передаче по линиям связи. Исправление ошибок (коррекция ошибок) — процедура восстановления информации после чтения её из устройства хранения или канала связи.

Для обнаружения ошибок используют коды обнаружения ошибок, для исправления — корректирующие коды (коды, исправляющие ошибки, коды с коррекцией ошибок, помехоустойчивые коды).

Способы борьбы с ошибками[]

В процессе хранения данных и передачи информации по сетям связи неизбежно возникают ошибки. Контроль целостности данных и исправление ошибок — важные задачи на многих уровнях работы с информацией (в частности, физическом, канальном, транспортном уровнях модели OSI).

В системах связи возможны несколько стратегий борьбы с ошибками:

  • обнаружение ошибок в блоках данных и автоматический запрос повторной передачи повреждённых блоков — этот подход применяется в основном на канальном и транспортном уровнях;
  • обнаружение ошибок в блоках данных и отбрасывание повреждённых блоков — такой подход иногда применяется в системах потокового мультимедиа, где важна задержка передачи и нет времени на повторную передачу;
  • исправление ошибок (forward error correction) применяется на физическом уровне.

Коды обнаружения и исправления ошибок[]

Корректирующие коды — коды, служащие для обнаружения или исправления ошибок, возникающих при передаче информации под влиянием помех, а также при её хранении.

Для этого при записи (передаче) в полезные данные добавляют специальным образом структурированную избыточную информацию (контрольное число), а при чтении (приёме) её используют для того, чтобы обнаружить или исправить ошибки. Естественно, что число ошибок, которое можно исправить, ограничено и зависит от конкретного применяемого кода.

С кодами, исправляющими ошибки, тесно связаны коды обнаружения ошибок. В отличие от первых, последние могут только установить факт наличия ошибки в переданных данных, но не исправить её.

В действительности, используемые коды обнаружения ошибок принадлежат к тем же классам кодов, что и коды, исправляющие ошибки. Фактически, любой код, исправляющий ошибки, может быть также использован для обнаружения ошибок (при этом он будет способен обнаружить большее число ошибок, чем был способен исправить).

По способу работы с данными коды, исправляющие ошибки делятся на блоковые, делящие информацию на фрагменты постоянной длины и обрабатывающие каждый из них в отдельности, и свёрточные, работающие с данными как с непрерывным потоком.

Блоковые коды[]

Пусть кодируемая информация делится на фрагменты длиной {\displaystyle k} бит, которые преобразуются в кодовые слова длиной {\displaystyle n} бит. Тогда соответствующий блоковый код обычно обозначают {\displaystyle (n,\;k)}. При этом число {\displaystyle R={\frac {k}{n}}} называется скоростью кода.

Если исходные {\displaystyle k} бит код оставляет неизменными, и добавляет {\displaystyle n-k} проверочных, такой код называется систематическим, иначе несистематическим.

Задать блоковый код можно по-разному, в том числе таблицей, где каждой совокупности из {\displaystyle k} информационных бит сопоставляется {\displaystyle n} бит кодового слова. Однако, хороший код должен удовлетворять, как минимум, следующим критериям:

  • способность исправлять как можно большее число ошибок,
  • как можно меньшая избыточность,
  • простота кодирования и декодирования.

Нетрудно видеть, что приведённые требования противоречат друг другу. Именно поэтому существует большое количество кодов, каждый из которых пригоден для своего круга задач.

Практически все используемые коды являются линейными. Это связано с тем, что нелинейные коды значительно сложнее исследовать, и для них трудно обеспечить приемлемую лёгкость кодирования и декодирования.

Линейные коды общего вида[]

Линейный блоковый код — такой код, что множество его кодовых слов образует {\displaystyle k}-мерное линейное подпространство (назовём его {\displaystyle C}) в {\displaystyle n}-мерном линейном пространстве, изоморфное пространству {\displaystyle k}-битных векторов.

Это значит, что операция кодирования соответствует умножению исходного {\displaystyle k}-битного вектора на невырожденную матрицу {\displaystyle G}, называемую порождающей матрицей.

Пусть {\displaystyle C^{\perp }} — ортогональное подпространство по отношению к {\displaystyle C}, а {\displaystyle H} — матрица, задающая базис этого подпространства. Тогда для любого вектора {\displaystyle {\overrightarrow {v}}\in C} справедливо:

{\displaystyle {\overrightarrow {v}}H^{T}={\overrightarrow {0}}.}
Минимальное расстояние и корректирующая способность[]

Основная статья: Расстояние Хемминга

Расстоянием Хемминга (метрикой Хемминга) между двумя кодовыми словами {\displaystyle {\overrightarrow {u}}} и {\displaystyle {\overrightarrow {v}}} называется количество отличных бит на соответствующих позициях, {\displaystyle d_{H}({\overrightarrow {u}},\;{\overrightarrow {v}})=\sum _{s}{|u^{(s)}-v^{(s)}|}}, что равно числу «единиц» в векторе {\displaystyle {\overrightarrow {u}}\oplus {\overrightarrow {v}}}.

Минимальное расстояние Хемминга {\displaystyle d_{\min }=\min _{u\neq v}d_{H}({\overrightarrow {u}},\;{\overrightarrow {v}})} является важной характеристикой линейного блокового кода. Она показывает насколько «далеко» расположены коды друг от друга. Она определяет другую, не менее важную характеристику — корректирующую способность:

{\displaystyle t=\left\lfloor {\frac {d_{\min }-1}{2}}\right\rfloor }, округляем «вниз», так чтобы {\displaystyle 2t<d_{\min }}.

Корректирующая способность определяет, сколько ошибок передачи кода (типа {\displaystyle 1\leftrightarrow 0}) можно гарантированно исправить. То есть вокруг каждого кода {\displaystyle A} имеем {\displaystyle t}-окрестность {\displaystyle A_{t}}, которая состоит из всех возможных вариантов передачи кода {\displaystyle A} с числом ошибок ({\displaystyle 1\leftrightarrow 0}) не более {\displaystyle t}. Никакие две окрестности двух любых кодов не пересекаются друг с другом, так как расстояние между кодами (то есть центрами этих окрестностей) всегда больше двух их радиусов {\displaystyle d_{H}(A,\;B)\geqslant d_{\min }>2t}.

Таким образом получив искажённый код из {\displaystyle A_{t}} декодер принимает решение, что был исходный код {\displaystyle A}, исправляя тем самым не более {\displaystyle t} ошибок.

Поясним на примере. Предположим, что есть два кодовых слова {\displaystyle A} и {\displaystyle B}, расстояние Хемминга между ними равно 3. Если было передано слово {\displaystyle A}, и канал внёс ошибку в одном бите, она может быть исправлена, так как даже в этом случае принятое слово ближе к кодовому слову {\displaystyle A}, чем к любому другому, и в частности к {\displaystyle B}. Но если каналом были внесены ошибки в двух битах (в которых {\displaystyle A} отличалось от {\displaystyle B}) то результат ошибочной передачи {\displaystyle A} окажется ближе к {\displaystyle B}, чем {\displaystyle A}, и декодер примет решение что передавалось слово {\displaystyle B}.

Коды Хемминга[]

Коды Хемминга — простейшие линейные коды с минимальным расстоянием 3, то есть способные исправить одну ошибку. Код Хемминга может быть представлен в таком виде, что синдром

{\displaystyle {\overrightarrow {s}}={\overrightarrow {r}}H^{T}}, где {\displaystyle {\overrightarrow {r}}} — принятый вектор, будет равен номеру позиции, в которой произошла ошибка. Это свойство позволяет сделать декодирование очень простым.
Общий метод декодирования линейных кодов[]

Любой код (в том числе нелинейный) можно декодировать с помощью обычной таблицы, где каждому значению принятого слова {\displaystyle {\overrightarrow {r}}_{i}} соответствует наиболее вероятное переданное слово {\displaystyle {\overrightarrow {u}}_{i}}. Однако, данный метод требует применения огромных таблиц уже для кодовых слов сравнительно небольшой длины.

Для линейных кодов этот метод можно существенно упростить. При этом для каждого принятого вектора {\displaystyle {\overrightarrow {r}}_{i}} вычисляется синдром {\displaystyle {\overrightarrow {s}}_{i}={\overrightarrow {r}}_{i}H^{T}}. Поскольку {\displaystyle {\overrightarrow {r}}_{i}={\overrightarrow {v}}_{i}+{\overrightarrow {e}}_{i}}, где {\displaystyle {\overrightarrow {v}}_{i}} — кодовое слово, а {\displaystyle {\overrightarrow {e}}_{i}} — вектор ошибки, то {\displaystyle {\overrightarrow {s}}_{i}={\overrightarrow {e}}_{i}H^{T}}. Затем с помощью таблицы по синдрому определяется вектор ошибки, с помощью которого определяется переданное кодовое слово. При этом таблица получается гораздо меньше, чем при использовании предыдущего метода.

Линейные циклические коды[]

Несмотря на то, что декодирование линейных кодов уже значительно проще декодирования большинства нелинейных, для большинства кодов этот процесс всё ещё достаточно сложен. Циклические коды, кроме более простого декодирования, обладают и другими важными свойствами.

Циклическим кодом является линейный код, обладающий следующим свойством: если {\displaystyle {\overrightarrow {v}}} является кодовым словом, то его циклическая перестановка также является кодовым словом.

Слова циклического кода удобно представлять в виде многочленов. Например, кодовое слово {\displaystyle {\overrightarrow {v}}=(v_{0},\;v_{1},\;\ldots ,\;v_{n-1})} представляется в виде полинома {\displaystyle v(x)=v_{0}+v_{1}x+\ldots +v_{n-1}x^{n-1}}. При этом циклический сдвиг кодового слова эквивалентен умножению многочлена на {\displaystyle x} по модулю {\displaystyle x^{n}-1}.

В дальнейшем, если не указано иное, мы будем считать, что циклический код является двоичным, то есть {\displaystyle v_{0},\;v_{1},\;\ldots } могут принимать значения 0 или 1.

Порождающий (генераторный) полином[]

Можно показать, что все кодовые слова конкретного циклического кода кратны определённому порождающему полиному {\displaystyle g(x)}. Порождающий полином является делителем {\displaystyle x^{n}-1}.

С помощью порождающего полинома осуществляется кодирование циклическим кодом. В частности:

Коды CRC[]

Коды CRC (cyclic redundancy check — циклическая избыточная проверка) являются систематическими кодами, предназначенными не для исправления ошибок, а для их обнаружения. Они используют способ систематического кодирования, изложенный выше: «контрольная сумма» вычисляется путем деления {\displaystyle x^{n-k}u(x)} на {\displaystyle g(x)}. Ввиду того, что исправление ошибок не требуется, проверка правильности передачи может производиться точно так же.

Таким образом, вид полинома {\displaystyle g(x)} задаёт конкретный код CRC. Примеры наиболее популярных полиномов:

название кода степень полином
CRC-12 12 {\displaystyle x^{12}+x^{11}+x^{3}+x^{2}+x+1}
CRC-16 16 {\displaystyle x^{16}+x^{15}+x^{2}+1}
CRC-CCITT 16 {\displaystyle x^{16}+x^{12}+x^{5}+1}
CRC-32 32 {\displaystyle x^{32}+x^{26}+x^{23}+x^{22}+x^{16}+x^{12}+x^{11}+x^{10}+x^{8}+x^{7}+x^{5}+x^{4}+x^{2}+x+1}
Коды БЧХ[]

Коды Боуза — Чоудхури — Хоквингема (БЧХ) являются подклассом циклических кодов. Их отличительное свойство — возможность построения кода БЧХ с минимальным расстоянием не меньше заданного. Это важно, потому что, вообще говоря, определение минимального расстояния кода есть очень сложная задача.

Математически полинома {\displaystyle g(x)} на множители в поле Галуа.

Коды коррекции ошибок Рида — Соломона[]

Коды Рида — Соломона — недвоичные циклические коды, позволяющие исправлять ошибки в блоках данных. Элементами кодового вектора являются не биты, а группы битов (блоки). Очень распространены коды Рида-Соломона, работающие с байтами (октетами).

Математически коды Рида — Соломона являются кодами БЧХ.

Преимущества и недостатки блоковых кодов[]

Хотя блоковые коды, как правило, хорошо справляются с редкими, но большими пачками ошибок, их эффективность при частых, но небольших ошибках (например, в канале с АБГШ), менее высока.

Свёрточные коды[]

Файл:ECC NASA standard coder.png

Свёрточный кодер ({\displaystyle k=7,\;R=1/2})

Свёрточные коды, в отличие от блоковых, не делят информацию на фрагменты и работают с ней как со сплошным потоком данных.

Свёрточные коды, как правило, порождаются дискретной линейной инвариантной во времени системой. Поэтому, в отличие от большинства блоковых кодов, свёрточное кодирование — очень простая операция, чего нельзя сказать о декодировании.

Кодирование свёрточным кодом производится с помощью регистра сдвига, отводы от которого суммируются по модулю два. Таких сумм может быть две (чаще всего) или больше.

Декодирование свёрточных кодов, как правило, производится по алгоритму Витерби, который пытается восстановить переданную последовательность согласно критерию максимального правдоподобия.

Преимущества и недостатки свёрточных кодов[]

Свёрточные коды эффективно работают в канале с белым шумом, но плохо справляются с пакетами ошибок. Более того, если декодер ошибается, на его выходе всегда возникает пакет ошибок.

Каскадное кодирование. Итеративное декодирование[]

Преимущества разных способов кодирования можно объединить, применив каскадное кодирование. При этом информация сначала кодируется одним кодом, а затем другим, в результате получается код-произведение.

Например, популярной является следующая конструкция: данные кодируются кодом Рида-Соломона, затем перемежаются (при этом символы, расположенные близко, помещаются далеко друг от друга) и кодируются свёрточным кодом. На приёмнике сначала декодируется свёрточный код, затем осуществляется обратное перемежение (при этом пачки ошибок на выходе свёрточного декодера попадают в разные кодовые слова кода Рида — Соломона), и затем осуществляется декодирование кода Рида — Соломона.

Некоторые коды-произведения специально сконструированы для итеративного декодирования, при котором декодирование осуществляется в несколько проходов, каждый из которых использует информацию от предыдущего. Это позволяет добиться большой эффективности, однако, декодирование требует больших ресурсов. К таким кодам относят турбо-коды и LDPC-коды (коды Галлагера).

Оценка эффективности кодов[]

Эффективность кодов определяется количеством ошибок, которые тот может исправить, количеством избыточной информации, добавление которой требуется, а также сложностью реализации кодирования и декодирования (как аппаратной, так и в виде программы для ЭВМ).

Граница Хемминга и совершенные коды[]

Основная статья: Граница Хэмминга

Пусть имеется двоичный блоковый {\displaystyle (n,k)} код с корректирующей способностью {\displaystyle t}. Тогда справедливо неравенство (называемое границей Хемминга):

{\displaystyle \sum _{i=0}^{t}{n \choose i}\leqslant 2^{n-k}.}

Коды, удовлетворяющие этой границе с равенством, называются совершенными. К совершенным кодам относятся, например, коды Хемминга. Часто применяемые на практике коды с большой корректирующей способностью (такие, как коды Рида — Соломона) не являются совершенными.

Энергетический выигрыш[]

При передаче информации по каналу связи вероятность ошибки зависит от отношения сигнал/шум на входе демодулятора, таким образом при постоянном уровне шума решающее значение имеет мощность передатчика. В системах спутниковой и мобильной, а также других типов связи остро стоит вопрос экономии энергии. Кроме того, в определённых системах связи (например, телефонной) неограниченно повышать мощность сигнала не дают технические ограничения.

Поскольку помехоустойчивое кодирование позволяет исправлять ошибки, при его применении мощность передатчика можно снизить, оставляя скорость передачи информации неизменной. Энергетический выигрыш определяется как разница отношений с/ш при наличии и отсутствии кодирования.

Применение кодов, исправляющих ошибки[]

Коды, исправляющие ошибки, применяются:

  • в системах цифровой связи, в том числе: спутниковой, радиорелейной, сотовой, передаче данных по телефонным каналам.
  • в системах хранения информации, в том числе магнитных и оптических.

Коды, обнаруживающие ошибки, применяются в сетевых протоколах различных уровней.

Автоматический запрос повторной передачи[]

Системы с автоматическим запросом повторной передачи (ARQ — Automatic Repeat reQuest) основаны на технологии обнаружения ошибок. Распространены следующие методы автоматического запроса:

Запрос ARQ с остановками (stop-and-wait ARQ)[]

Идея этого метода заключается в том, что передатчик ожидает от приемника подтверждения успешного приема предыдущего блока данных перед тем как начать передачу следующего. В случае, если блок данных был принят с ошибкой, приемник передает отрицательное подтверждение (negative acknowledgement, NAK), и передатчик повторяет передачу блока. Данный метод подходит для полудуплексного канала связи. Его недостатком является низкая скорость из-за высоких накладных расходов на ожидание.

Непрерывный запрос ARQ с возвратом (continuous ARQ with pullback)[]

Для этого метода необходим полнодуплексный канал. Передача данных от передатчика к приемнику производится одновременно. В случае ошибки передача возобновляется, начиная с ошибочного блока (то есть, передается ошибочный блок и все последующие).

Непрерывный запрос ARQ с выборочным повторением (continuous ARQ with selective repeat)[]

При этом подходе осуществляется передача только ошибочно принятых блоков данных.

См. также[]

  • Цифровая связь
  • Линейный код
  • Циклический код
  • Код Боуза — Чоудхури — Хоквингема
  • Код Рида — Соломона
  • LDPC
  • Свёрточный код
  • Турбо-код

Литература[]

  • Мак-Вильямс Ф. Дж., Слоэн Н. Дж. А. Теория кодов, исправляющих ошибки. М.: Радио и связь, 1979.
  • Блейхут Р. Теория и практика кодов, контролирующих ошибки. М.: Мир, 1986.
  • Морелос-Сарагоса Р. Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение. М.: Техносфера, 2005. — ISBN 5-94836-035-0

Ссылки[]

Имеется викиучебник по теме:
Обнаружение и исправление ошибок

  • Помехоустойчивое кодирование (11 ноября 2001). — реферат по проблеме кодирования сообщений с исправлением ошибок. Проверено 25 декабря 2006.

Эта страница использует содержимое раздела Википедии на русском языке. Оригинальная статья находится по адресу: Обнаружение и исправление ошибок. Список первоначальных авторов статьи можно посмотреть в истории правок. Эта статья так же, как и статья, размещённая в Википедии, доступна на условиях CC-BY-SA .

Источник
Определение:
Линейный код (англ. Linear code) — код фиксированной длины (блоковый код), исправляющий ошибки, для которого любая линейная комбинация кодовых слов также является кодовым словом.

Линейные коды обычно делят на блоковые коды и свёрточные коды. Также можно рассматривать турбо-коды, как гибрид двух предыдущих.[1]

По сравнению с другими кодами, линейные коды позволяют реализовывать более эффективные алгоритмы кодирования и декодирования информации (см. синдромы ошибок).

Содержание

  • 1 Формальное определение
  • 2 Порождающая матрица
  • 3 Проверочная матрица
  • 4 Кодирование и декодирование, примеры
    • 4.1 Пример
  • 5 Минимальное расстояние и корректирующая способность
  • 6 Синдромы и метод обнаружения ошибок в линейном коде
  • 7 Преимущества и недостатки линейных кодов
  • 8 Примечания
  • 9 Источники информации

Формальное определение

Определение:
Линейный код длины и ранга является линейным подпространством размерности векторного пространства , где — конечное поле (поле Галуа) из элементов. Такой код с параметром называется -арным кодом (напр. если  — то это 5-арный код). Если или , то код представляет собой двоичный код, или тернарный соответственно.

Векторы в называют кодовыми словами. Размер кода — это количество кодовых слов, т.е. .

Весом кодового слова называют число его ненулевых элементов. Расстояние между двумя кодовыми словами определяется как расстояние Хэмминга. Расстояние линейного кода — это минимальный вес его ненулевых кодовых слов или равным образом минимальное расстояние между всеми парами различных кодовых слов.

Линейный код длины , ранга и с расстоянием называют -кодом (англ. [n,k,d] code). Параметр d в обозначении кода часто опускается, потому что через него не задается структура кода. В таком случае пишут просто -код. В литературе встречается обозначение как в квадратных, так и в круглых скобках.[2][3]

Порождающая матрица

Определение:
Порождающая матрица — это матрица, столбцы которой задают базис линейного кода.

Так как линейный код является линейным подпространством , целиком код (может быть очень большим) может быть представлен как линейная оболочка набора из кодовых слов (т.е. базис). Этот базис часто объединяют в столбцы матрицы и называют такую матрицу порождающей матрицей кода .

В случае, если , где — это единичная матрица размера , а — это матрица размера говорят, что матрица находится в каноническом виде.

Имея матрицу можно получить из некоторого входного вектора кодовое слово линейного кода

,

где и — векторы-строки. Порождающая матрица линейного -кода имеет вид . Число избыточных бит тогда определяется как .

Проверочная матрица

Определение:
Проверочная матрица линейного кода — это порождающая матрица ортогонального дополнения . Другими словами, это матрица, которая описывает правила, которым должны удовлетворять части кодового слова.

Используется, чтобы определить, является ли некий вектор кодовым словом, а также в алгоритмах декодирования (напр. syndrome decoding).

Кодовое слово принадлежит коду тогда и только тогда, когда или, что то же самое, .

Проверочную матрицу можно получить из порождающей и наоборот: пусть дана порождающая матрица в каноническом виде , тогда проверочную матрицу можно получить по формуле

,

так как .

Кодирование и декодирование, примеры

Предположим, что имеется линия связи, по которой мы можем пересылать и принимать биты. В среднем какой-то известный процент переданных битов будет поврежден, ошибочен. Такая модель называется двоичным симметричным каналом.

Блок из символов сообщения будет кодироваться в кодовое слово , где ; эти кодовые слова образуют код.

Первая часть кодового слова состоит из информационных битов сообщения:

,

за которым следуют проверочных битов . Проверочные биты выбраны так, чтобы кодовые слова удовлетворяли уравнению

,

где — проверочная матрица.

Пример

Проверочная матрица

определяет код с и . Для этого кода

.

Сообщение кодируется в кодовое слово , которое начинается с самого сообщения:

,

а последующих три проверочных символа выбираются так, чтобы выполнялось уравнение .

Если сообщение , то , и проверочные биты легко определяются: , так что кодовое слово .

Минимальное расстояние и корректирующая способность

Линейность гарантирует, что расстояние Хэмминга между кодовым словом и любым другим кодовым словом не зависит от . Так как — тоже кодовое слово, а , то

Иными словами, чтобы найти минимальное расстояние между кодовыми словами линейного кода, необходимо рассмотреть ненулевые кодовые слова. Тогда ненулевое кодовое слово с минимальным весом будет иметь минимальное расстояние до нулевого кодового слова, таким образом показывая минимальное расстояние линейного кода.

Минимальное расстояние кода однозначно определяет количество ошибок, которое способен обнаружить () и исправить () данный код.

Синдромы и метод обнаружения ошибок в линейном коде

Любой код (в том числе нелинейный) можно декодировать с помощью обычной таблицы, где каждому значению принятого слова соответствует наиболее вероятное переданное слово . Однако, данный метод требует применения огромных таблиц уже для кодовых слов сравнительно небольшой длины.

Для линейных кодов этот метод можно существенно упростить. При этом для каждого принятого вектора вычисляется синдром . Поскольку , где  — кодовое слово, а  — вектор ошибки, то . Затем с помощью таблицы по синдрому определяется вектор ошибки, с помощью которого определяется переданное кодовое слово. При этом таблица получается гораздо меньше, чем при использовании предыдущего метода.

Преимущества и недостатки линейных кодов

+ Благодаря линейности для запоминания или перечисления всех кодовых слов достаточно хранить в памяти кодера или декодера существенно меньшую их часть, а именно только те слова, которые образуют базис соответствующего линейного пространства. Это существенно упрощает реализацию устройств кодирования и декодирования и делает линейные коды весьма привлекательными с точки зрения практических приложений.

— Хотя линейные коды, как правило, хорошо справляются с редкими, но большими пачками ошибок, их эффективность при частых, но небольших ошибках (например, в канале с АБГШ), менее высока.

Примечания

  1. ↑ William E. Ryan and Shu Lin (2009). Channel Codes: Classical and Modern. Cambridge University Press. p. 4. ISBN 978-0-521-84868-8.
  2. ↑ В. А. Липницкий, Н. В. Чесалин — Линейные коды и кодовые последовательности: учеб.-метод. пособие для студентов мех.-мат. фак. БГУ. Минск: БГУ, 2008. — 41 с., стр. 6
  3. ↑ Мак-Вильямс Ф. Дж., Слоэн Н. Дж. А. Теория кодов, исправляющих ошибки: Пер. с англ. — М: Связь, 1979. — 744 с., стр. 17

Источники информации

  • wikipedia.org — Линейный код
  • wikipedia.org — Linear code
  • Мак-Вильямс Ф. Дж., Слоэн Н. Дж. А. Теория кодов, исправляющих ошибки: Пер. с англ. — М: Связь, 1979. — 744 с., стр. 12-33
  • Ф.И. Соловьева — Введение в теорию кодирования
  • В. А. Липницкий, Н. В. Чесалин — Линейные коды и кодовые последовательности: учеб.-метод. пособие для студентов мех.-мат. фак. БГУ. Минск: БГУ, 2008. — 41 с.
Источник

Понравилась статья? Поделить с друзьями:
  • Вектор ошибки рассчитывается как
  • Вероника степанова ошибки психотерапевта
  • Вербальные ошибки это
  • Вероника иванова право учить работа над ошибками читать
  • Верный пугачев своему обещанию приближался к оренбургу ошибка