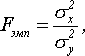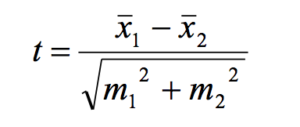T критерий стьюдента стандартная ошибка

Критерий
позволяет найти вероятность того, что
оба средних значения в выборке относятся
к одной и той же совокупности. Данный
критерий наиболее часто используется
для проверки гипотезы: «Средние двух
выборок относятся к одной и той же
совокупности».

При
использовании критерия можно выделить
два случая. В первом случае его применяют
для проверки гипотезы о равенстве
генеральных средних двух независимых,
несвязанных выборок (так называемый
двухвыборочный t-критерий). В этом случае
есть контрольная группа и экспериментальная
(опытная) группа, количество испытуемых
в группах может быть различно.

Во
втором случае, когда одна и та же группа
объектов порождает числовой материал
для проверки гипотез о средних,
используется так называемый парный
t-критерий. Выборки при этом называют
зависимыми, связанными.

а)
случай независимых выборок

Статистика
критерия для случая несвязанных,
независимых выборок равна:

(1)

где

— средние арифметические в
экспериментальной и контрольной группах,

—
стандартная ошибка разности средних
арифметических. Находится из формулы:

(2)

где
n1 и n2 -соответственно величины первой
и второй выборки.

Если
n1=n2, то стандартная ошибка разности
средних арифметических будет считаться
по формуле:

(3)

где
n -величина
выборки.

Подсчет
числа степеней свободы осуществляется
по формуле:

k
= n1 + n2 – 2.
(4)

При
численном равенстве выборок k = 2n — 2.

Далее
необходимо сравнить полученное значение
tэмп с теоретическим значением
t—распределения Стьюдента (см. приложение
к учебникам статистики). Если tэмп<tкрит,
то гипотеза H0 принимается, в противном
случае нулевая гипотеза отвергается и
принимается альтернативная гипотеза.

Рассмотрим
пример использования t-критерия Стьюдента
для несвязных и неравных по численности
выборок.

Пример
1.
В двух группах учащихся — экспериментальной
и контрольной — получены следующие
результаты по учебному предмету (тестовые
баллы; см. табл. 1)

Таблица
1. Результаты эксперимента

Первая
группа (экспериментальная) N1=11 человек

Вторая
группа (контрольная)

N2=9
человек

12
14 13 16 11 9 13 15 15 18 14

13
9 11 10 7 6 8 10 11

Общее
количество членов выборки: n1=11, n2=9.

Расчет
средних арифметических: Хср=13,636; Yср=9,444

Стандартное
отклонение: sx=2,460; sy=2,186

По
формуле (2) рассчитываем стандартную
ошибку разности арифметических средних:

Считаем
статистику критерия:

Сравниваем
полученное в эксперименте значение t с
табличным значением с учетом степеней
свободы, равных по формуле (4) числу
испытуемых минус два (18).

Табличное
значение tкрит равняется 2,1 при допущении
возможности риска сделать ошибочное
суждение в пяти случаях из ста (уровень
значимости=5 % или 0,05).

Если
полученное в эксперименте эмпирическое
значение t превышает табличное, то есть
основания принять альтернативную
гипотезу (H1) о том, что учащиеся
экспериментальной группы показывают
в среднем более высокий уровень знаний.
В эксперименте t=3,981, табличное t=2,10,
3,981>2,10, откуда следует вывод о преимуществе
экспериментального обучения.

Здесь
могут возникнуть такие вопросы:

1.
Что если полученное в опыте значение t
окажется меньше табличного? Тогда надо
принять нулевую гипотезу.

2.
Доказано ли преимущество экспериментального
метода? Не столько доказано, сколько
показано, потому что с самого начала
допускается риск ошибиться в пяти
случаях из ста (р=0,05). Наш эксперимент
мог быть одним из этих пяти случаев. Но
95% возможных случаев говорит в пользу
альтернативной гипотезы, а это достаточно
убедительный аргумент в статистическом
доказательстве.

3.
Что если в контрольной группе результаты
окажутся выше, чем в экспериментальной?
Поменяем, например, местами, сделав

средней арифметической экспериментальной
группы, a

— контрольной:

Отсюда
следует вывод, что новый метод пока не
проявил себя с хорошей стороны по разным,
возможно, причинам. Поскольку абсолютное
значение 3,9811>2,1, принимается вторая
альтернативная гипотеза (Н2) о преимуществе
традиционного метода.

б)
случай связанных (парных) выборок

В
случае связанных выборок с равным числом
измерений в каждой можно использовать
более простую формулу t-критерия
Стьюдента.

Вычисление
значения t осуществляется по формуле:

(5)

где

—
разности между соответствующими
значениями переменной X и переменной
У, а d — среднее этих разностей;

Sd
вычисляется по следующей формуле:

(6)

Число
степеней свободы k определяется по
формуле k=n-1. Рассмотрим пример использования
t-критерия Стьюдента для связных и,
очевидно, равных по численности выборок.

Если
tэмп<tкрит, то нулевая гипотеза
принимается, в противном случае
принимается альтернативная.

6.1.3
F — критерий Фишера

Критерий
Фишера позволяет сравнивать величины
выборочных дисперсий двух независимых
выборок. Для вычисления Fэмп нужно найти
отношение дисперсий двух выборок, причем
так, чтобы большая по величине дисперсия
находилась бы в числителе, а меньшая –
в знаменателе. Формула вычисления
критерия Фишера такова:

(8)

где

—
дисперсии первой и второй выборки
соответственно.

Так
как, согласно условию критерия, величина
числителя должна быть больше или равна
величине знаменателя, то значение Fэмп
всегда будет больше или равно единице.

Число
степеней свободы определяется также
просто:

k1=nl
— 1 для первой выборки (т.е. для той выборки,
величина дисперсии которой больше) и
k2=n2 — 1 для второй выборки.

Если
tэмп>tкрит, то нулевая гипотеза
принимается, в противном случае
принимается альтернативная.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

A t-test is a type of statistical analysis used to compare the averages of two groups and determine if the differences between them are more likely to arise from random chance. It is any statistical hypothesis test in which the test statistic follows a Student’s t-distribution under the null hypothesis. It is most commonly applied when the test statistic would follow a normal distribution if the value of a scaling term in the test statistic were known (typically, the scaling term is unknown and is therefore a nuisance parameter). When the scaling term is estimated based on the data, the test statistic—under certain conditions—follows a Student’s t distribution. The t-test’s most common application is to test whether the means of two populations are different.

History[edit]

William Sealy Gosset, who developed the «t-statistic» and published it under the pseudonym of «Student»

The term «t-statistic» is abbreviated from «hypothesis test statistic».^[1] In statistics, the t-distribution was first derived as a posterior distribution in 1876 by Helmert^[2]^[3]^[4] and Lüroth.^[5]^[6]^[7] The t-distribution also appeared in a more general form as Pearson Type IV distribution in Karl Pearson’s 1895 paper.^[8] However, the T-Distribution, also known as Student’s t-distribution, gets its name from William Sealy Gosset who first published it in English in 1908 in the scientific journal Biometrika using the pseudonym «Student»^[9]^[10] because his employer preferred staff to use pen names when publishing scientific papers.^[11] Gosset worked at the Guinness Brewery in Dublin, Ireland, and was interested in the problems of small samples – for example, the chemical properties of barley with small sample sizes. Hence a second version of the etymology of the term Student is that Guinness did not want their competitors to know that they were using the t-test to determine the quality of raw material. Although it was William Gosset after whom the term «Student» is penned, it was actually through the work of Ronald Fisher that the distribution became well known as «Student’s distribution»^[12] and «Student’s t-test».

Gosset had been hired owing to Claude Guinness’s policy of recruiting the best graduates from Oxford and Cambridge to apply biochemistry and statistics to Guinness’s industrial processes.^[13] Gosset devised the t-test as an economical way to monitor the quality of stout. The t-test work was submitted to and accepted in the journal Biometrika and published in 1908.^[9]

Guinness had a policy of allowing technical staff leave for study (so-called «study leave»), which Gosset used during the first two terms of the 1906–1907 academic year in Professor Karl Pearson’s Biometric Laboratory at University College London.^[14] Gosset’s identity was then known to fellow statisticians and to editor-in-chief Karl Pearson.^[15]

Uses[edit]

The most frequently used t-tests are one-sample and two-sample tests:

A one-sample location test of whether the mean of a population has a value specified in a null hypothesis.
A two-sample location test of the null hypothesis such that the means of two populations are equal. All such tests are usually called Student’s t-tests, though strictly speaking that name should only be used if the variances of the two populations are also assumed to be equal; the form of the test used when this assumption is dropped is sometimes called Welch’s t-test. These tests are often referred to as unpaired or independent samples t-tests, as they are typically applied when the statistical units underlying the two samples being compared are non-overlapping.^[16]

Assumptions[edit]

^{[dubious – discuss]}

Most test statistics have the form t = Z/s, where Z and s are functions of the data.

Z may be sensitive to the alternative hypothesis (i.e., its magnitude tends to be larger when the alternative hypothesis is true), whereas s is a scaling parameter that allows the distribution of t to be determined.

As an example, in the one-sample t-test

$t={\frac {Z}{s}}={\frac {{\bar {X}}-\mu }{{\widehat {\sigma }}/{\sqrt {n}}}}$

where X is the sample mean from a sample X₁, X₂, …, X_n, of size n, s is the standard error of the mean, ${\textstyle {\widehat {\sigma }}}$ is the estimate of the standard deviation of the population, and μ is the population mean.

The assumptions underlying a t-test in the simplest form above are that:

X follows a normal distribution with mean μ and variance σ²/n
s²(n − 1)/σ² follows a χ² distribution with n − 1 degrees of freedom. This assumption is met when the observations used for estimating s² come from a normal distribution (and i.i.d for each group).
Z and s are independent.

In the t-test comparing the means of two independent samples, the following assumptions should be met:

The means of the two populations being compared should follow normal distributions. Under weak assumptions, this follows in large samples from the central limit theorem, even when the distribution of observations in each group is non-normal.^[17]
If using Student’s original definition of the t-test, the two populations being compared should have the same variance (testable using F-test, Levene’s test, Bartlett’s test, or the Brown–Forsythe test; or assessable graphically using a Q–Q plot). If the sample sizes in the two groups being compared are equal, Student’s original t-test is highly robust to the presence of unequal variances.^[18] Welch’s t-test is insensitive to equality of the variances regardless of whether the sample sizes are similar.
The data used to carry out the test should either be sampled independently from the two populations being compared or be fully paired. This is in general not testable from the data, but if the data are known to be dependent (e.g. paired by test design), a dependent test has to be applied. For partially paired data, the classical independent t-tests may give invalid results as the test statistic might not follow a t distribution, while the dependent t-test is sub-optimal as it discards the unpaired data.^[19]

Most two-sample t-tests are robust to all but large deviations from the assumptions.^[20]

For exactness, the t-test and Z-test require normality of the sample means, and the t-test additionally requires that the sample variance follows a scaled χ² distribution, and that the sample mean and sample variance be statistically independent. Normality of the individual data values is not required if these conditions are met. By the central limit theorem, sample means of moderately large samples are often well-approximated by a normal distribution even if the data are not normally distributed. For non-normal data, the distribution of the sample variance may deviate substantially from a χ² distribution.

However, if the sample size is large, Slutsky’s theorem implies that the distribution of the sample variance has little effect on the distribution of the test statistic. That is as sample size increases:

Unpaired and paired two-sample t-tests[edit]

Type I error of unpaired and paired two-sample t-tests as a function of the correlation. The simulated random numbers originate from a bivariate normal distribution with a variance of 1. The significance level is 5% and the number of cases is 60.

Power of unpaired and paired two-sample t-tests as a function of the correlation. The simulated random numbers originate from a bivariate normal distribution with a variance of 1 and a deviation of the expected value of 0.4. The significance level is 5% and the number of cases is 60.

Two-sample t-tests for a difference in means involve independent samples (unpaired samples) or paired samples. Paired t-tests are a form of blocking, and have greater power (probability of avoiding a type II error, also known as a false negative) than unpaired tests when the paired units are similar with respect to «noise factors» (see confounder) that are independent of membership in the two groups being compared.^[21] In a different context, paired t-tests can be used to reduce the effects of confounding factors in an observational study.

Independent (unpaired) samples[edit]

The independent samples t-test is used when two separate sets of independent and identically distributed samples are obtained, and one variable from each of the two populations is compared. For example, suppose we are evaluating the effect of a medical treatment, and we enroll 100 subjects into our study, then randomly assign 50 subjects to the treatment group and 50 subjects to the control group. In this case, we have two independent samples and would use the unpaired form of the t-test.

Paired samples[edit]

Paired samples t-tests typically consist of a sample of matched pairs of similar units, or one group of units that has been tested twice (a «repeated measures» t-test).

A typical example of the repeated measures t-test would be where subjects are tested prior to a treatment, say for high blood pressure, and the same subjects are tested again after treatment with a blood-pressure-lowering medication. By comparing the same patient’s numbers before and after treatment, we are effectively using each patient as their own control. That way the correct rejection of the null hypothesis (here: of no difference made by the treatment) can become much more likely, with statistical power increasing simply because the random interpatient variation has now been eliminated. However, an increase of statistical power comes at a price: more tests are required, each subject having to be tested twice. Because half of the sample now depends on the other half, the paired version of Student’s t-test has only n/2 − 1 degrees of freedom (with n being the total number of observations). Pairs become individual test units, and the sample has to be doubled to achieve the same number of degrees of freedom. Normally, there are n − 1 degrees of freedom (with n being the total number of observations).^[22]

A paired samples t-test based on a «matched-pairs sample» results from an unpaired sample that is subsequently used to form a paired sample, by using additional variables that were measured along with the variable of interest.^[23] The matching is carried out by identifying pairs of values consisting of one observation from each of the two samples, where the pair is similar in terms of other measured variables. This approach is sometimes used in observational studies to reduce or eliminate the effects of confounding factors.

Paired samples t-tests are often referred to as «dependent samples t-tests».

Calculations[edit]

Explicit expressions that can be used to carry out various t-tests are given below. In each case, the formula for a test statistic that either exactly follows or closely approximates a t-distribution under the null hypothesis is given. Also, the appropriate degrees of freedom are given in each case. Each of these statistics can be used to carry out either a one-tailed or two-tailed test.

Once the t value and degrees of freedom are determined, a p-value can be found using a table of values from Student’s t-distribution. If the calculated p-value is below the threshold chosen for statistical significance (usually the 0.10, the 0.05, or 0.01 level), then the null hypothesis is rejected in favor of the alternative hypothesis.

One-sample t-test[edit]

In testing the null hypothesis that the population mean is equal to a specified value μ₀, one uses the statistic

$t={\frac {{\bar {x}}-\mu _{0}}{s/{\sqrt {n}}}}$

where ${\bar {x}}$ is the sample mean, s is the sample standard deviation and n is the sample size. The degrees of freedom used in this test are n − 1.
Although the parent population does not need to be normally distributed, the distribution of the population of sample means ${\bar {x}}$ is assumed to be normal.

By the central limit theorem, if the observations are independent and the second moment exists, then will be approximately normal N(0;1).

Slope of a regression line[edit]

Suppose one is fitting the model

$Y=\alpha +\beta x+\varepsilon$

where x is known, α and β are unknown, ε is a normally distributed random variable with mean 0 and unknown variance σ², and Y is the outcome of interest. We want to test the null hypothesis that the slope β is equal to some specified value β₀ (often taken to be 0, in which case the null hypothesis is that x and y are uncorrelated).

Let

$\begin{align} \widehat\alpha, \widehat\beta & = \text{least-squares estimators}, \\ SE_{\widehat\alpha}, SE_{\widehat\beta} & = \text{the standard errors of least-squares estimators}. \end{align}$

Then

$t_\text{score} = \frac{\widehat\beta - \beta_0}{ SE_{\widehat\beta} }\sim\mathcal{T}_{n-2}$

has a t-distribution with n − 2 degrees of freedom if the null hypothesis is true. The standard error of the slope coefficient:

$SE_{\widehat {\beta }}={\frac {\sqrt {{\dfrac {1}{n-2}}\displaystyle \sum _{i=1}^{n}\left(y_{i}-{\widehat {y}}_{i}\right)^{2}}}{\sqrt {\displaystyle \sum _{i=1}^{n}\left(x_{i}-{\bar {x}}\right)^{2}}}}$

can be written in terms of the residuals. Let

${\begin{aligned}{\widehat {\varepsilon }}_{i}&=y_{i}-{\widehat {y}}_{i}=y_{i}-\left({\widehat {\alpha }}+{\widehat {\beta }}x_{i}\right)={\text{residuals}}={\text{estimated errors}},\\{\text{SSR}}&=\sum _{i=1}^{n}{{\widehat {\varepsilon }}_{i}}^{2}={\text{sum of squares of residuals}}.\end{aligned}}$

Then t_score is given by:

$t_{\text{score}}={\frac {\left({\widehat {\beta }}-\beta _{0}\right){\sqrt {n-2}}}{\sqrt {\frac {SSR}{\sum _{i=1}^{n}\left(x_{i}-{\bar {x}}\right)^{2}}}}}.$

Another way to determine the t_score is:

$t_{\text{score}}={\frac {r{\sqrt {n-2}}}{\sqrt {1-r^{2}}}},$

where r is the Pearson correlation coefficient.

The t_{score, intercept} can be determined from the t_{score, slope}:

$t_{\text{score,intercept}}={\frac {\alpha }{\beta }}{\frac {t_{\text{score,slope}}}{\sqrt {s_{\text{x}}^{2}+{\bar {x}}^{2}}}}$

where s_x² is the sample variance.

Independent two-sample t-test[edit]

Equal sample sizes and variance[edit]

Given two groups (1, 2), this test is only applicable when:

the two sample sizes are equal;
it can be assumed that the two distributions have the same variance;

Violations of these assumptions are discussed below.

The t statistic to test whether the means are different can be calculated as follows:

$t={\frac {{\bar {X}}_{1}-{\bar {X}}_{2}}{s_{p}{\sqrt {\frac {2}{n}}}}}$

where

$s_{p}={\sqrt {\frac {s_{X_{1}}^{2}+s_{X_{2}}^{2}}{2}}}.$

Here s_p is the pooled standard deviation for n = n₁ = n₂ and s²
_X₁ and s²
_X₂ are the unbiased estimators of the population variance. The denominator of t is the standard error of the difference between two means.

For significance testing, the degrees of freedom for this test is 2n − 2 where n is sample size.

Equal or unequal sample sizes, similar variances (1/2 < s_X₁/s_X₂ < 2)[edit]

This test is used only when it can be assumed that the two distributions have the same variance. (When this assumption is violated, see below.)
The previous formulae are a special case of the formulae below, one recovers them when both samples are equal in size: n = n₁ = n₂.

The t statistic to test whether the means are different can be calculated as follows:

$t={\frac {{\bar {X}}_{1}-{\bar {X}}_{2}}{s_{p}\cdot {\sqrt {{\frac {1}{n_{1}}}+{\frac {1}{n_{2}}}}}}}$

where

$s_{p}={\sqrt {\frac {\left(n_{1}-1\right)s_{X_{1}}^{2}+\left(n_{2}-1\right)s_{X_{2}}^{2}}{n_{1}+n_{2}-2}}}$

is the pooled standard deviation of the two samples: it is defined in this way so that its square is an unbiased estimator of the common variance whether or not the population means are the same. In these formulae, n_i − 1 is the number of degrees of freedom for each group, and the total sample size minus two (that is, n₁ + n₂ − 2) is the total number of degrees of freedom, which is used in significance testing.

Equal or unequal sample sizes, unequal variances (s_X₁ > 2s_X₂ or s_X₂ > 2s_X₁)[edit]

This test, also known as Welch’s t-test, is used only when the two population variances are not assumed to be equal (the two sample sizes may or may not be equal) and hence must be estimated separately. The t statistic to test whether the population means are different is calculated as:

$t={\frac {{\bar {X}}_{1}-{\bar {X}}_{2}}{s_{\bar {\Delta }}}}$

where

$s_{\bar {\Delta }}={\sqrt {{\frac {s_{1}^{2}}{n_{1}}}+{\frac {s_{2}^{2}}{n_{2}}}}}.$

Here s_i² is the unbiased estimator of the variance of each of the two samples with n_i = number of participants in group i (i = 1 or 2). In this case
${\textstyle (s_{\bar {\Delta }})^{2}}$
is not a pooled variance. For use in significance testing, the distribution of the test statistic is approximated as an ordinary Student’s t-distribution with the degrees of freedom calculated using

$\mathrm {d.f.} ={\frac {\left({\frac {s_{1}^{2}}{n_{1}}}+{\frac {s_{2}^{2}}{n_{2}}}\right)^{2}}{{\frac {\left(s_{1}^{2}/n_{1}\right)^{2}}{n_{1}-1}}+{\frac {\left(s_{2}^{2}/n_{2}\right)^{2}}{n_{2}-1}}}}.$

This is known as the Welch–Satterthwaite equation. The true distribution of the test statistic actually depends (slightly) on the two unknown population variances (see Behrens–Fisher problem).

Exact method for unequal variances and sample sizes[edit]

The test^[24] deals with the famous Behrens–Fisher problem, i.e., comparing the difference between the means of two normally distributed populations when the variances of the two populations are not assumed to be equal, based on two independent samples.

The test is developed as an exact test that allows for unequal sample sizes and unequal variances of two populations. The exact property still holds even with small extremely small and unbalanced sample sizes (e.g. $n_{1}=5,n_{2}=50$ ).

The statistic to test whether the means are different can be calculated as follows:

Let $X=[X_{1},X_{2},\ldots ,X_{m}]^{T}$ and $Y=[Y_{1},Y_{2},\ldots ,Y_{n}]^{T}$ be the i.i.d. sample vectors ( m>n ) from $N(\mu _{1},\sigma _{1}^{2})$ and $N(\mu _{2},\sigma _{2}^{2})$ separately.

Let $(P^{T})_{n\times n}$ be an $n\times n$ orthogonal matrix whose elements of the first row are all $1/{\sqrt {n}}$ , similarly, let $(Q^{T})_{n\times m}$ be the first n rows of an $m\times m$ orthogonal matrix (whose elements of the first row are all $1/{\sqrt {m}}$ ).

Then $Z:=(Q^{T})_{n\times m}X/{\sqrt {m}}-(P^{T})_{n\times n}Y/{\sqrt {n}}$ is an n-dimensional normal random vector.

$Z\sim N((\mu _{1}-\mu _{2},0,...,0)^{T},({\frac {\sigma _{1}^{2}}{m}}+{\frac {\sigma _{2}^{2}}{n}})I_{n}).$

From the above distribution we see that

$Z_{1}-(\mu _{1}-\mu _{2})\sim N(0,{\frac {\sigma _{1}^{2}}{m}}+{\frac {\sigma _{2}^{2}}{n}}),$

${\frac {\sum _{i=2}^{n}Z_{i}^{2}}{n-1}}\sim {\frac {\chi _{n-1}^{2}}{n-1}}\times ({\frac {\sigma _{1}^{2}}{m}}+{\frac {\sigma _{2}^{2}}{n}})$

$Z_{1}-(\mu _{1}-\mu _{2})\perp \sum _{i=2}^{n}Z_{i}^{2}.$

$T_{e}:={\frac {Z_{1}-(\mu _{1}-\mu _{2})}{\sqrt {(\sum _{i=2}^{n}Z_{i}^{2})/(n-1)}}}\sim t_{n-1}.$

Dependent t-test for paired samples[edit]

This test is used when the samples are dependent; that is, when there is only one sample that has been tested twice (repeated measures) or when there are two samples that have been matched or «paired». This is an example of a paired difference test. The t statistic is calculated as

$t={\frac {{\bar {X}}_{D}-\mu _{0}}{s_{D}/{\sqrt {n}}}}$

where ${\bar {X}}_{D}$ and $s_{D}$ are the average and standard deviation of the differences between all pairs. The pairs are e.g. either one person’s pre-test and post-test scores or between-pairs of persons matched into meaningful groups (for instance drawn from the same family or age group: see table). The constant μ₀ is zero if we want to test whether the average of the difference is significantly different. The degree of freedom used is n − 1, where n represents the number of pairs.

Example of repeated measures

Number	Name	Test 1	Test 2
1	Mike	35%	67%
2	Melanie	50%	46%
3	Melissa	90%	86%
4	Mitchell	78%	91%

Example of matched pairs

Pair	Name	Age	Test
1	John	35	250
1	Jane	36	340
2	Jimmy	22	460
2	Jessy	21	200

Worked examples[edit]

Let A₁ denote a set obtained by drawing a random sample of six measurements:

$A_1=\{30.02,\ 29.99,\ 30.11,\ 29.97,\ 30.01,\ 29.99\}$

and let A₂ denote a second set obtained similarly:

$A_2=\{29.89,\ 29.93,\ 29.72,\ 29.98,\ 30.02,\ 29.98\}$

These could be, for example, the weights of screws that were chosen out of a bucket.

We will carry out tests of the null hypothesis that the means of the populations from which the two samples were taken are equal.

The difference between the two sample means, each denoted by X_i, which appears in the numerator for all the two-sample testing approaches discussed above, is

${\bar {X}}_{1}-{\bar {X}}_{2}=0.095.$

The sample standard deviations for the two samples are approximately 0.05 and 0.11, respectively. For such small samples, a test of equality between the two population variances would not be very powerful. Since the sample sizes are equal, the two forms of the two-sample t-test will perform similarly in this example.

Unequal variances[edit]

If the approach for unequal variances (discussed above) is followed, the results are

${\sqrt {{\frac {s_{1}^{2}}{n_{1}}}+{\frac {s_{2}^{2}}{n_{2}}}}}\approx 0.04849$

and the degrees of freedom

${\text{d.f.}}\approx 7.031.$

The test statistic is approximately 1.959, which gives a two-tailed test p-value of 0.09077.

Equal variances[edit]

If the approach for equal variances (discussed above) is followed, the results are

$s_{p}\approx 0.08396$

and the degrees of freedom

${\text{d.f.}}=10.$

The test statistic is approximately equal to 1.959, which gives a two-tailed p-value of 0.07857.

[edit]

Alternatives to the t-test for location problems[edit]

The t-test provides an exact test for the equality of the means of two i.i.d. normal populations with unknown, but equal, variances. (Welch’s t-test is a nearly exact test for the case where the data are normal but the variances may differ.) For moderately large samples and a one tailed test, the t-test is relatively robust to moderate violations of the normality assumption.^[25] In large enough samples, the t-test asymptotically approaches the z-test, and becomes robust even to large deviations from normality.^[17]

If the data are substantially non-normal and the sample size is small, the t-test can give misleading results. See Location test for Gaussian scale mixture distributions for some theory related to one particular family of non-normal distributions.

When the normality assumption does not hold, a non-parametric alternative to the t-test may have better statistical power. However, when data are non-normal with differing variances between groups, a t-test may have better type-1 error control than some non-parametric alternatives.^[26] Furthermore, non-parametric methods, such as the Mann-Whitney U test discussed below, typically do not test for a difference of means, so should be used carefully if a difference of means is of primary scientific interest.^[17] For example, Mann-Whitney U test will keep the type 1 error at the desired level alpha if both groups have the same distribution. It will also have power in detecting an alternative by which group B has the same distribution as A but after some shift by a constant (in which case there would indeed be a difference in the means of the two groups). However, there could be cases where group A and B will have different distributions but with the same means (such as two distributions, one with positive skewness and the other with a negative one, but shifted so to have the same means). In such cases, MW could have more than alpha level power in rejecting the Null hypothesis but attributing the interpretation of difference in means to such a result would be incorrect.

In the presence of an outlier, the t-test is not robust. For example, for two independent samples when the data distributions are asymmetric (that is, the distributions are skewed) or the distributions have large tails, then the Wilcoxon rank-sum test (also known as the Mann–Whitney U test) can have three to four times higher power than the t-test.^[25]^[27]^[28] The nonparametric counterpart to the paired samples t-test is the Wilcoxon signed-rank test for paired samples. For a discussion on choosing between the t-test and nonparametric alternatives, see Lumley, et al. (2002).^[17]

One-way analysis of variance (ANOVA) generalizes the two-sample t-test when the data belong to more than two groups.

A design which includes both paired observations and independent observations[edit]

When both paired observations and independent observations are present in the two sample design, assuming data are missing completely at random (MCAR), the paired observations or independent observations may be discarded in order to proceed with the standard tests above. Alternatively making use of all of the available data, assuming normality and MCAR, the generalized partially overlapping samples t-test could be used.^[29]

Multivariate testing[edit]

A generalization of Student’s t statistic, called Hotelling’s t-squared statistic, allows for the testing of hypotheses on multiple (often correlated) measures within the same sample. For instance, a researcher might submit a number of subjects to a personality test consisting of multiple personality scales (e.g. the Minnesota Multiphasic Personality Inventory). Because measures of this type are usually positively correlated, it is not advisable to conduct separate univariate t-tests to test hypotheses, as these would neglect the covariance among measures and inflate the chance of falsely rejecting at least one hypothesis (Type I error). In this case a single multivariate test is preferable for hypothesis testing. Fisher’s Method for combining multiple tests with alpha reduced for positive correlation among tests is one. Another is Hotelling’s T² statistic follows a T² distribution. However, in practice the distribution is rarely used, since tabulated values for T² are hard to find. Usually, T² is converted instead to an F statistic.

For a one-sample multivariate test, the hypothesis is that the mean vector (μ) is equal to a given vector (μ₀). The test statistic is Hotelling’s t²:

$t^{2}=n({\bar {\mathbf {x} }}-{{\boldsymbol {\mu }}_{0}})'{\mathbf {S} }^{-1}({\bar {\mathbf {x} }}-{{\boldsymbol {\mu }}_{0}})$

where n is the sample size, x is the vector of column means and S is an m × m sample covariance matrix.

For a two-sample multivariate test, the hypothesis is that the mean vectors (μ₁, μ₂) of two samples are equal. The test statistic is Hotelling’s two-sample t²:

$t^{2}={\frac {n_{1}n_{2}}{n_{1}+n_{2}}}\left({\bar {\mathbf {x} }}_{1}-{\bar {\mathbf {x} }}_{2}\right)'{\mathbf {S} _{\text{pooled}}}^{-1}\left({\bar {\mathbf {x} }}_{1}-{\bar {\mathbf {x} }}_{2}\right).$

The two-sample t-test is a special case of simple linear regression[edit]

The two-sample t-test is a special case of simple linear regression as illustrated by the following example.

A clinical trial examines 6 patients given drug or placebo. 3 patients get 0 units of drug (the placebo group). 3 patients get 1 unit of drug (the active treatment group). At the end of treatment, the researchers measure the change from baseline in the number of words that each patient can recall in a memory test.

Data and code are given for the analysis using the R programming language with the t.test and lmfunctions for the t-test and linear regression. Here are the (fictitious) data generated in R.

> word.recall.data=data.frame(drug.dose=c(0,0,0,1,1,1), word.recall=c(1,2,3,5,6,7))

Patient	drug.dose	word.recall
1	0	1
2	0	2
3	0	3
4	1	5
5	1	6
6	1	7

Perform the t-test. Notice that the assumption of equal variance, var.equal=T, is required to make the analysis exactly equivalent to simple linear regression.

> with(word.recall.data, t.test(word.recall~drug.dose, var.equal=T))

Running the R code gives the following results.

The mean word.recall in the 0 drug.dose group is 2.
The mean word.recall in the 1 drug.dose group is 6.
The difference between treatment groups in the mean word.recall is 6 – 2 = 4.
The difference in word.recall between drug doses is significant (p=0.00805).

Perform a linear regression of the same data. Calculations may be performed using the R function lm() for a linear model.

> word.recall.data.lm =  lm(word.recall~drug.dose, data=word.recall.data)
> summary(word.recall.data.lm)

The linear regression provides a table of coefficients and p-values.

Coefficient	Estimate	Std. Error	t value	P-value
Intercept	2	0.5774	3.464	0.02572
drug.dose	4	0.8165	4.899	0.000805

The table of coefficients gives the following results.

The estimate value of 2 for the intercept is the mean value of the word recall when the drug dose is 0.
The estimate value of 4 for the drug dose indicates that for a 1-unit change in drug dose (from 0 to 1) there is a 4-unit change in mean word recall (from 2 to 6). This is the slope of the line joining the two group means.
The p-value that the slope of 4 is different from 0 is p = 0.00805.

The coefficients for the linear regression specify the slope and intercept of the line that joins the two group means, as illustrated in the graph. The intercept is 2 and the slope is 4.

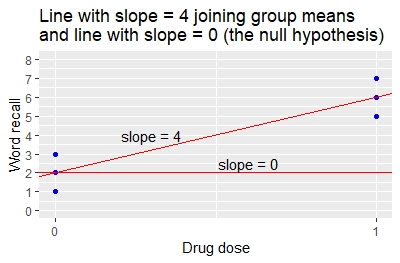
Compare the result from the linear regression to the result from the t-test.

From the t-test, the difference between the group means is 6-2=4.
From the regression, the slope is also 4 indicating that a 1-unit change in drug dose (from 0 to 1) gives a 4-unit change in mean word recall (from 2 to 6).
The t-test p-value for the difference in means, and the regression p-value for the slope, are both 0.00805. The methods give identical results.

This example shows that, for the special case of a simple linear regression where there is a single x-variable that has values 0 and 1, the t-test gives the same results as the linear regression. The relationship can also be shown algebraically.

Recognizing this relationship between the t-test and linear regression facilitates the use of multiple linear regression and multi-way analysis of variance. These alternatives to t-tests allow for the inclusion of additional explanatory variables that are associated with the response. Including such additional explanatory variables using regression or anova reduces the otherwise unexplained variance, and commonly yields greater power to detect differences than do two-sample t-tests.

Software implementations[edit]

Many spreadsheet programs and statistics packages, such as QtiPlot, LibreOffice Calc, Microsoft Excel, SAS, SPSS, Stata, DAP, gretl, R, Python, PSPP, MATLAB and Minitab, include implementations of Student’s t-test.

Language/Program	Function	Notes
Microsoft Excel pre 2010	`TTEST(array1, array2, tails, type)`	See [1]
Microsoft Excel 2010 and later	`T.TEST(array1, array2, tails, type)`	See [2]
Apple Numbers	`TTEST(sample-1-values, sample-2-values, tails, test-type)`	See [3]
LibreOffice Calc	`TTEST(Data1; Data2; Mode; Type)`	See [4]
Google Sheets	`TTEST(range1, range2, tails, type)`	See [5]
Python	`scipy.stats.ttest_ind(a, b, equal_var=True)`	See [6]
MATLAB	`ttest(data1, data2)`	See [7]
Mathematica	`TTest[{data1,data2}]`	See [8]
R	`t.test(data1, data2, var.equal=TRUE)`	See [9]
SAS	`PROC TTEST`	See [10]
Java	`tTest(sample1, sample2)`	See [11]
Julia	`EqualVarianceTTest(sample1, sample2)`	See [12]
Stata	`ttest data1 == data2`	See [13]

References[edit]

Citations[edit]

^ The Microbiome in Health and Disease. Academic Press. 2020-05-29. p. 397. ISBN 978-0-12-820001-8.
^ Szabó, István (2003). «Systeme aus einer endlichen Anzahl starrer Körper». Einführung in die Technische Mechanik. Springer Berlin Heidelberg. pp. 196–199. doi:10.1007/978-3-642-61925-0_16. ISBN 978-3-540-13293-6.
^ Schlyvitch, B. (October 1937). «Untersuchungen über den anastomotischen Kanal zwischen der Arteria coeliaca und mesenterica superior und damit in Zusammenhang stehende Fragen». Zeitschrift für Anatomie und Entwicklungsgeschichte. 107 (6): 709–737. doi:10.1007/bf02118337. ISSN 0340-2061. S2CID 27311567.
^ Helmert (1876). «Die Genauigkeit der Formel von Peters zur Berechnung des wahrscheinlichen Beobachtungsfehlers directer Beobachtungen gleicher Genauigkeit». Astronomische Nachrichten (in German). 88 (8–9): 113–131. Bibcode:1876AN…..88..113H. doi:10.1002/asna.18760880802.
^ Lüroth, J. (1876). «Vergleichung von zwei Werthen des wahrscheinlichen Fehlers». Astronomische Nachrichten (in German). 87 (14): 209–220. Bibcode:1876AN…..87..209L. doi:10.1002/asna.18760871402.
^ Pfanzagl, J. (1996). «Studies in the history of probability and statistics XLIV. A forerunner of the t-distribution». Biometrika. 83 (4): 891–898. doi:10.1093/biomet/83.4.891. MR 1766040.
^ Sheynin, Oscar (1995). «Helmert’s work in the theory of errors». Archive for History of Exact Sciences. 49 (1): 73–104. doi:10.1007/BF00374700. ISSN 0003-9519. S2CID 121241599.
^ Pearson, Karl (1895). «X. Contributions to the mathematical theory of evolution.—II. Skew variation in homogeneous material». Philosophical Transactions of the Royal Society of London A. 186: 343–414. Bibcode:1895RSPTA.186..343P. doi:10.1098/rsta.1895.0010.
^ ^a ^b Student (1908). «The Probable Error of a Mean» (PDF). Biometrika. 6 (1): 1–25. doi:10.1093/biomet/6.1.1. hdl:10338.dmlcz/143545. Retrieved 24 July 2016.
^ «T Table».
^ Wendl, Michael C. (2016). «Pseudonymous fame». Science. 351 (6280): 1406. doi:10.1126/science.351.6280.1406. PMID 27013722.
^ Walpole, Ronald E. (2006). Probability & statistics for engineers & scientists. Myers, H. Raymond. (7th ed.). New Delhi: Pearson. ISBN 81-7758-404-9. OCLC 818811849.
^ O’Connor, John J.; Robertson, Edmund F. «William Sealy Gosset». MacTutor History of Mathematics Archive. University of St Andrews.
^ Raju, T. N. (2005). «William Sealy Gosset and William A. Silverman: Two ‘Students’ of Science». Pediatrics. 116 (3): 732–5. doi:10.1542/peds.2005-1134. PMID 16140715. S2CID 32745754.
^ Dodge, Yadolah (2008). The Concise Encyclopedia of Statistics. Springer Science & Business Media. pp. 234–235. ISBN 978-0-387-31742-7.
^ Fadem, Barbara (2008). High-Yield Behavioral Science. High-Yield Series. Hagerstown, MD: Lippincott Williams & Wilkins. ISBN 9781451130300.
^ ^a ^b ^c ^d Lumley, Thomas; Diehr, Paula; Emerson, Scott; Chen, Lu (May 2002). «The Importance of the Normality Assumption in Large Public Health Data Sets». Annual Review of Public Health. 23 (1): 151–169. doi:10.1146/annurev.publhealth.23.100901.140546. ISSN 0163-7525. PMID 11910059.
^ Markowski, Carol A.; Markowski, Edward P. (1990). «Conditions for the Effectiveness of a Preliminary Test of Variance». The American Statistician. 44 (4): 322–326. doi:10.2307/2684360. JSTOR 2684360.
^ Guo, Beibei; Yuan, Ying (2017). «A comparative review of methods for comparing means using partially paired data». Statistical Methods in Medical Research. 26 (3): 1323–1340. doi:10.1177/0962280215577111. PMID 25834090. S2CID 46598415.
^ Bland, Martin (1995). An Introduction to Medical Statistics. Oxford University Press. p. 168. ISBN 978-0-19-262428-4.
^ Rice, John A. (2006). Mathematical Statistics and Data Analysis (3rd ed.). Duxbury Advanced.^{[ISBN missing]}
^ Weisstein, Eric. «Student’s t-Distribution». mathworld.wolfram.com.
^ David, H. A.; Gunnink, Jason L. (1997). «The Paired t Test Under Artificial Pairing». The American Statistician. 51 (1): 9–12. doi:10.2307/2684684. JSTOR 2684684.
^ Wang, Chang; Jia, Jinzhu (2022). «Te Test: A New Non-asymptotic T-test for Behrens-Fisher Problems». arXiv:2210.16473 [math.ST].
^ ^a ^b Sawilowsky, Shlomo S.; Blair, R. Clifford (1992). «A More Realistic Look at the Robustness and Type II Error Properties of the t Test to Departures From Population Normality». Psychological Bulletin. 111 (2): 352–360. doi:10.1037/0033-2909.111.2.352.
^ Zimmerman, Donald W. (January 1998). «Invalidation of Parametric and Nonparametric Statistical Tests by Concurrent Violation of Two Assumptions». The Journal of Experimental Education. 67 (1): 55–68. doi:10.1080/00220979809598344. ISSN 0022-0973.
^ Blair, R. Clifford; Higgins, James J. (1980). «A Comparison of the Power of Wilcoxon’s Rank-Sum Statistic to That of Student’s t Statistic Under Various Nonnormal Distributions». Journal of Educational Statistics. 5 (4): 309–335. doi:10.2307/1164905. JSTOR 1164905.
^ Fay, Michael P.; Proschan, Michael A. (2010). «Wilcoxon–Mann–Whitney or t-test? On assumptions for hypothesis tests and multiple interpretations of decision rules». Statistics Surveys. 4: 1–39. doi:10.1214/09-SS051. PMC 2857732. PMID 20414472.
^ Derrick, B; Toher, D; White, P (2017). «How to compare the means of two samples that include paired observations and independent observations: A companion to Derrick, Russ, Toher and White (2017)» (PDF). The Quantitative Methods for Psychology. 13 (2): 120–126. doi:10.20982/tqmp.13.2.p120.

Sources[edit]

O’Mahony, Michael (1986). Sensory Evaluation of Food: Statistical Methods and Procedures. CRC Press. p. 487. ISBN 0-82477337-3.
Press, William H.; Teukolsky, Saul A.; Vetterling, William T.; Flannery, Brian P. (1992). Numerical Recipes in C: The Art of Scientific Computing. Cambridge University Press. p. 616. ISBN 0-521-43108-5.

External links[edit]

Wikiversity has learning resources about t-test

«Student test». Encyclopedia of Mathematics. EMS Press. 2001 [1994].
Trochim, William M.K. «The T-Test», Research Methods Knowledge Base, conjoint.ly
Econometrics lecture (topic: hypothesis testing) on YouTube by Mark Thoma

Источник

Т-критерий Стьюдента (t-тест) простым языком

Сегодня мы говорим о t-критерии. Т-критерий наиболее популярный статистический тест в биомедицинских исследованиях. Также его называют парный Т-критерий Стьюдента, t-test, two-sample unpaired t-test. Однако, при использовании этого статистического инструмента допускается достаточно много ошибок. Сегодня в этой статье мы постараемся разобраться, как избежать ошибок применения t-критерия Стьюдента, как интерпретировать его результаты и как рассчитывать t-критерий самостоятельно. Об этом обо всем читайте далее.

При описании любого статистического критерия, будь то t-критерий Стьюдента, либо какой-либо еще, нужно вспомнить о том, как же вообще используются статистические критерии. Для того, чтобы понять, как используется любой критерий, нужно перейти к нескольким достаточно логичным для понимания этапам:

Этапы статистического вывода (statistic inference)

Первый из них – это вопрос, который мы хотим изучить с помощью статистических методов. То есть первый этап: что изучаем? И какие у нас есть предположения относительно результата? Этот этап называется этап статистических гипотез.
Второй этап – нужно определиться с тем, какие у нас есть в реальности данные для того, чтобы ответить на первый вопрос. Этот этап – тип данных.
Третий этап состоит в том, чтобы выбрать корректный для применения в данной ситуации статистический критерий.
Четвертый этап это логичный этап применения интерпретации любой формулы, какие результаты мы получили.
Пятый этап это создание, синтез выводов относительно первого, второго, третьего, четвертого, пятого этапа, то есть что же получили и что же это в реальности значит.

Предлагаю долго не ходить вокруг да около и посмотреть применение t-критерия Стьюдента на реальном примере.

Видео-версия статьи

Пример использования т-критерия Стьюдента

А пример будет достаточно простой: мне интересно, стали ли люди выше за последние 100 лет. Для этого нужно подобрать некоторые данные. Я обнаружил интересную информацию в достаточно известной статье The Guardian (Tall story’s men and women have grown taller over last century, Study Shows (The Guardian, July 2016), которая сравнивает средний возраст человека в разных странах в 1914 году и в аналогичных странах в 2014 году.

Там приведены данные практически по всем государствам. Однако, я взял лишь 5 стран для простоты вычислений: это Россия, Германия, Китай, США и ЮАР, соответственно 1914 год и 2014 год.

Общее количество наблюдений – 5 в 1914 году в группе 1914 года и общее значение также 5 в 2014 году. Будем думать опять же для простоты, что эти данные сопоставимы, и с ними можно работать.

Дальше нужно выбрать критерии – критерии, по которым мы будем давать ответ. Равны ли средние по росту в 1914 году x̅₁₉₁₄ и в 2014 году x̅₂₀₁₄. Я считаю, что нет. Поэтому моя гипотеза это то, что они не равны (x̅₁₉₁₄≠x̅₂₀₁₄). Соответственно альтернативная гипотеза моему предположению, так называемая нулевая гипотеза (нулевая гипотеза консервативна, обратная вашей, часто говорит об отсутствии статистически значимых связей/зависимостей) будет говорить о том, что они между собой на самом деле равны (x̅₁₉₁₄=x̅₂₀₁₄), то есть о том, что все эти находки случайны, и я, по сути, не прав.

Теперь нужно дать какой-то аргументированный ответ. Даем его с помощью статистического критерия. Соответственно теперь наступает самое важное: как выбрать статистический критерий? Я думаю, это будет темой отдельной статьи. Для корректности использования t-критерия Стьюдента лишь скажу, что нужно, чтобы:

Условия применения статистического критерия т-теста (критерия Стьюдента)

— данные распределялись по закону нормального распределения;

— данные были количественными;

— и это две независимые между собой выборки (независимые это значит, что в этих группах разные люди, а никак, например, до и после применения препарата у одной группы, люди должны быть разными, тогда группы являются несвязанными, либо независимыми), этот аспект стоит учитывать для выбора вида т-критерия Стьюдента, так как для парных выборок существует свой парный т-критерий (paired t-test).

В итоге Мы определились с тем, что это будет t-критерий Стьюдента.

Формула t-критерия Стьюдента достаточно простая. Она гласит о том, что в числителе у нас разница средних, в знаменателе у нас корень квадратный суммы ошибок репрезентативности по этим группам:

Ошибки репрезентативности были подробно объяснены мною в статье по доверительным интервалам. Поэтому я рекомендую вам ознакомиться с ней, чтобы лучше разобраться, что такое ошибки репрезентативности, что такое выборка, как она соотносится с генеральной совокупностью.

Для того, чтобы не тратить время, я в принципе все уже рассчитал по каждой из групп: средняя (x̅) ,стандартное отклонение (SD) и ошибка репрезентативности (m^r).

Давайте остановимся на том, что же значат эти значения:

— средняя (x̅) это среднеарифметическое по 5 наблюдениям в каждой группе;

— если совсем упрощать значение стандартного отклонения (SD), то можно сказать, что оно представляет собой обобщенную среднюю отклонения каждого значения от среднего (стандартное отклонение показывает, насколько широко значения рассеяны (разбросаны) относительно средней). И дальше мы находим нечто среднее отклонений каждого варианта в группе от среднего;

— и ошибка репрезентативности она тоже находится достаточно просто: это как раз наше отклонение от средней некоторое стандартизованное, поэтому стандартное отклонение на размер выборки (m_r=).

Итак, продолжаем. В ходе подстановки каждого значения в нашу формулу, мы находим, что t-критерий Стьюдента равен 3,78. Однако, я думаю, пока тем, кто не знаком со статистическими критериями, это мало о чем говорит.

Итак, теперь настает четвертый этап вопрос интерпретации. Ранее мы получили значение t-критерия в 3,78. Однако, что же это значит? Стоит отметить, что результаты статистических критериев и вообще их интерпретация не говорит о точном «да», либо «нет» в выводе, то есть рост отличается, либо рост не отличается. Всегда это вопрос определенной доли вероятности – доли вероятности ошибиться при констатации положительного результата (речь об ошибке первого рода (I type error, Alpha)). То есть, например, если мы скажем, что средний рост в начале ХХ и в начале XXI века отличаются с долей ошибкой меньше 5 %. Как раз эта величина в 5 % и фиксируется как достаточная для большинства биомедицинских исследований, помните, р больше, либо меньше 0,05.

Итак, как нам перейти от нашей t к р вероятности? Это сделать достаточно просто, стоит лишь воспользоваться табличными значениями t для определенных степеней свободы. Теперь вопрос: как найти эти степени свободы? Но это сделать достаточно просто. Для того, чтобы обнаружить степени свободы для наших групп, нужно лишь сложить количество наблюдений 5 и 5 в нашем случае и вычесть 2. В нашем случае степень свободы равна 8.

Итак, t=3,78, степень свободы равна 8. Переходим в табличное значение и получаем р вероятность – вероятность равна 0,005. То есть вероятность того, что мы ошибаемся при констатации факта различия роста ранее и сейчас, крайне мала – это 0,005 %, не 5 %, а 0,005 %. То есть мы можем говорить с высокой долей достоверности того, что наш рост сейчас в XXI веке и 100 лет назад отличаются.

Вот то, что касается расчета t-критерия Стьюдента и его интерпретации.

На этом наш разговор о t-критерии Стьюдента закончен. Спасибо, что ознакомились с этой статьей. Я очень надеюсь на вашу обратную связь. Пожалуйста, подписывайтесь на наш сайте, ставьте лайки, предлагайте свои темы для следующих выпусков. Спасибо большое за поддержку. С вами был Кирилл Мильчаков. Пока, до новых встреч!

Если Вам понравилась статья и оказалась полезной, Вы можете поделиться ею с коллегами и друзьями в социальных сетях:

Источник

History[edit]

Uses[edit]

Assumptions[edit]

Unpaired and paired two-sample t-tests[edit]

Independent (unpaired) samples[edit]

Paired samples[edit]

Calculations[edit]

One-sample t-test[edit]

Slope of a regression line[edit]

Independent two-sample t-test[edit]

Equal sample sizes and variance[edit]

Equal or unequal sample sizes, similar variances (1/2 < s_X₁/s_X₂ < 2)[edit]

Equal or unequal sample sizes, unequal variances (s_X₁ > 2s_X₂ or s_X₂ > 2s_X₁)[edit]

Exact method for unequal variances and sample sizes[edit]

Dependent t-test for paired samples[edit]

Worked examples[edit]

Unequal variances[edit]

Equal variances[edit]

[edit]

Alternatives to the t-test for location problems[edit]

A design which includes both paired observations and independent observations[edit]

Multivariate testing[edit]

The two-sample t-test is a special case of simple linear regression[edit]

Software implementations[edit]

See also[edit]

References[edit]

Citations[edit]

Sources[edit]

Further reading[edit]

External links[edit]

Т-критерий Стьюдента (t-тест) простым языком

Этапы статистического вывода (statistic inference)

Видео-версия статьи

Пример использования т-критерия Стьюдента

Условия применения статистического критерия т-теста (критерия Стьюдента)

History[edit]

Uses[edit]

Assumptions[edit]

Unpaired and paired two-sample t-tests[edit]

Independent (unpaired) samples[edit]

Paired samples[edit]

Calculations[edit]

One-sample t-test[edit]

Slope of a regression line[edit]

Independent two-sample t-test[edit]

Equal sample sizes and variance[edit]

Equal or unequal sample sizes, similar variances (1/2 < sX1/sX2 < 2)[edit]

Equal or unequal sample sizes, unequal variances (sX1 > 2sX2 or sX2 > 2sX1)[edit]

Exact method for unequal variances and sample sizes[edit]

Dependent t-test for paired samples[edit]

Worked examples[edit]

Unequal variances[edit]

Equal variances[edit]

[edit]

Alternatives to the t-test for location problems[edit]

A design which includes both paired observations and independent observations[edit]

Multivariate testing[edit]

The two-sample t-test is a special case of simple linear regression[edit]

Software implementations[edit]

See also[edit]

References[edit]

Citations[edit]

Sources[edit]

Further reading[edit]

External links[edit]

Т-критерий Стьюдента (t-тест) простым языком

Этапы статистического вывода (statistic inference)

Видео-версия статьи

Пример использования т-критерия Стьюдента

Условия применения статистического критерия т-теста (критерия Стьюдента)

Equal or unequal sample sizes, similar variances (1/2 < s_X₁/s_X₂ < 2)[edit]

Equal or unequal sample sizes, unequal variances (s_X₁ > 2s_X₂ or s_X₂ > 2s_X₁)[edit]