Ошибки, встроенные в систему: их роль в статистике
Время на прочтение
6 мин
Количество просмотров 14K
В прошлой статье я указал, как распространена проблема неправильного использования t-критерия в научных публикациях (и это возможно сделать только благодаря их открытости, а какой трэш творится при его использовании во всяких курсовых, отчетах, обучающих задачах и т.д. — неизвестно). Чтобы обсудить это, я рассказал об основах дисперсионного анализа и задаваемом самим исследователем уровне значимости α. Но для полного понимания всей картины статистического анализа необходимо подчеркнуть ряд важных вещей. И самая основная из них — понятие ошибки.
Ошибка и некорректное применение: в чем разница?
В любой физической системе содержится какая-либо ошибка, неточность. В самой разнообразной форме: так называемый допуск — отличие в размерах разных однотипных изделий; нелинейная характеристика — когда прибор или метод измеряют что-то по строго известному закону в определенных пределах, а дальше становятся неприменимыми; дискретность — когда мы чисто технически не можем обеспечить плавность выходной характеристики.
И в то же время существует чисто человеческая ошибка — некорректное использование устройств, приборов, математических законов. Между ошибкой, присущей системе, и ошибкой применения этой системы есть принципиальная разница. Важно различать и не путать между собой эти два понятия, называемые одним и тем же словом «ошибка». Я в данной статье предпочитаю использовать слово «ошибка» для обозначения свойства системы, а «некорректное применение» — для ошибочного ее использования.
То есть, ошибка линейки равна допуску оборудования, наносящего штрихи на ее полотно. А ошибкой в смысле некорректного применения было бы использовать ее при измерении деталей наручных часов. Ошибка безмена написана на нем и составляет что-то около 50 граммов, а неправильным использованием безмена было бы взвешивание на нем мешка в 25 кг, который растягивает пружину из области закона Гука в область пластических деформаций. Ошибка атомно-силового микроскопа происходит из его дискретности — нельзя «пощупать» его зондом предметы мельче, чем диаметром в один атом. Но способов неправильно использовать его или неправильно интерпретировать данные существует множество. И так далее.
Так, а что же за ошибка имеет место в статистических методах? А этой ошибкой как раз и является пресловутый уровень значимости α.
Ошибки первого и второго рода
Ошибкой в математическом аппарате статистики является сама ее Байесовская вероятностная сущность. В прошлой статье я уже упоминал, на чем стоят статистические методы: определение уровня значимости α как наибольшей допустимой вероятности неправомерно отвергнуть нулевую гипотезу, и самостоятельное задание исследователем этой величины перед исследователем.
Вы уже видите эту условность? На самом деле, в критериальных методах нету привычной математической строгости. Математика здесь оперирует вероятностными характеристиками.
И тут наступает еще один момент, где возможна неправильная трактовка одного слова в разном контексте. Необходимо различать само понятие вероятности и фактическую реализацию события, выражающуюся в распределении вероятности. Например, перед началом любого нашего эксперимента мы не знаем, какую именно величину мы получим в результате. Есть два возможных исхода: загадав некоторое значение результата, мы либо действительно его получим, либо не получим. Логично, что вероятность и того, и другого события равна 1/2. Но показанная в предыдущей статье Гауссова кривая показывает распределение вероятности того, что мы правильно угадаем совпадение.
Наглядно можно проиллюстрировать это примером. Пусть мы 600 раз бросаем два игральных кубика — обычный и шулерский. Получим следующие результаты:
До эксперимента для обоих кубиков выпадение любой грани будет равновероятно — 1/6. Однако после эксперимента проявляется сущность шулерского кубика, и мы можем сказать, что плотность вероятности выпадения на нем шестерки — 90%.
Другой пример, который знают химики, физики и все, кто интересуется квантовыми эффектами — атомные орбитали. Теоретически электрон может быть «размазан» в пространстве и находиться практически где угодно. Но на практике есть области, где он будет находиться в 90 и более процентах случаев. Эти области пространства, образованные поверхностью с плотностью вероятности нахождения там электрона 90%, и есть классические атомные орбитали, в виде сфер, гантелей и т.д.
Так вот, самостоятельно задавая уровень значимости, мы заведомо соглашаемся на описанную в его названии ошибку. Из-за этого ни один результат нельзя считать «стопроцентно достоверным» — всегда наши статистические выводы будут содержать некоторую вероятность сбоя.
Ошибка, формулируемая определением уровня значимости α, называется ошибкой первого рода. Ее можно определить, как «ложная тревога», или, более корректно, ложноположительный результат. В самом деле, что означают слова «ошибочно отвергнуть нулевую гипотезу»? Это значит, по ошибке принять наблюдаемые данные за значимые различия двух групп. Поставить ложный диагноз о наличии болезни, поспешить явить миру новое открытие, которого на самом деле нет — вот примеры ошибок первого рода.
Но ведь тогда должны быть и ложноотрицательные результаты? Совершенно верно, и они называются ошибками второго рода. Примеры — не поставленный вовремя диагноз или же разочарование в результате исследования, хотя на самом деле в нем есть важные данные. Ошибки второго рода обозначаются буквой, как ни странно, β. Но само это понятие не так важно для статистики, как число 1-β. Число 1-β называется мощностью критерия, и как нетрудно догадаться, оно характеризует способность критерия не упустить значимое событие.
Однако содержание в статистических методах ошибок первого и второго рода не является только лишь их ограничением. Само понятие этих ошибок может использоваться непосредственным образом в статистическом анализе. Как?
ROC-анализ
ROC-анализ (от receiver operating characteristic, рабочая характеристика приёмника) — это метод количественного определения применимости некоторого признака к бинарной классификации объектов. Говоря проще, мы можем придумать некоторый способ, как отличить больных людей от здоровых, кошек от собак, черное от белого, а затем проверить правомерность такого способа. Давайте снова обратимся к примеру.
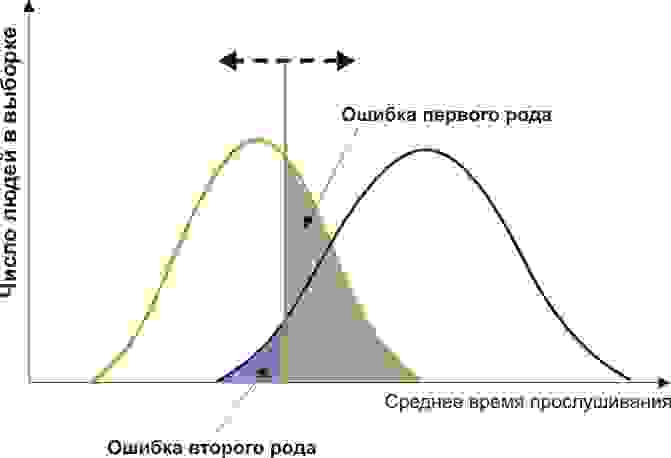
Пусть вы — подающий надежды криминалист, и разрабатываете новый способ скрытно и однозначно определять, является ли человек преступником. Вы придумали количественный признак: оценивать преступные наклонности людей по частоте прослушивания ими Михаила Круга. Но будет ли давать адекватные результаты ваш признак? Давайте разбираться.
Вам понадобится две группы людей для валидации вашего критерия: обычные граждане и преступники. Положим, действительно, среднегодовое время прослушивания ими Михаила Круга различается (см. рисунок):
Здесь мы видим, что по количественному признаку времени прослушивания наши выборки пересекаются. Кто-то слушает Круга спонтанно по радио, не совершая преступлений, а кто-то нарушает закон, слушая другую музыку или даже будучи глухим. Какие у нас есть граничные условия? ROC-анализ вводит понятия селективности (чувствительности) и специфичности. Чувствительность определяется как способность выявлять все-все интересующие нас точки (в данном примере — преступников), а специфичность — не захватывать ничего ложноположительного (не ставить под подозрение простых обывателей). Мы можем задать некоторую критическую количественную черту, отделяющую одних от других (оранжевая), в пределах от максимальной чувствительности (зеленая) до максимальной специфичности (красная).
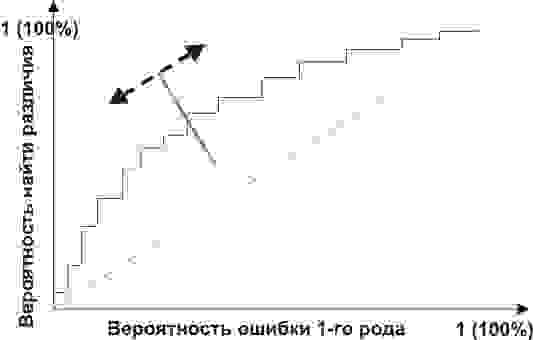
Посмотрим на следующую схему:
Смещая значение нашего признака, мы меняем соотношения ложноположительного и ложноотрицательного результатов (площади под кривыми). Точно так же мы можем дать определения Чувствительность = Полож. рез-т/(Полож. рез-т + ложноотриц. рез-т) и Специфичность = Отриц. рез-т/(Отриц. рез-т + ложноположит. рез-т).
Но главное, мы можем оценить соотношение положительных результатов к ложноположительным на всем отрезке значений нашего количественного признака, что и есть наша искомая ROC-кривая (см. рисунок):
А как нам понять из этого графика, насколько хорош наш признак? Очень просто, посчитать площадь под кривой (AUC, area under curve). Пунктирная линия (0,0; 1,1) означает полное совпадение двух выборок и совершенно бессмысленный критерий (площадь под кривой равна 0,5 от всего квадрата). А вот выпуклость ROC кривой как раз и говорит о совершенстве критерия. Если же нам удастся найти такой критерий, что выборки вообще не будут пересекаться, то площадь под кривой займет весь график. В целом же признак считается хорошим, позволяющим надежно отделить одну выборку от другой, если AUC > 0,75-0,8.
С помощью такого анализа вы можете решать самые разные задачи. Решив, что слишком много домохозяек оказались под подозрением из-за Михаила Круга, а кроме того упущены опасные рецидивисты, слушающие Ноггано, вы можете отвергнуть этот критерий и разработать другой.
Возникнув, как способ обработки радиосигналов и идентификации «свой-чужой» после атаки на Перл-Харбор (отсюда и пошло такое странное название про характеристику приемника), ROC-анализ нашел широкое применение в биомедицинской статистике для анализа, валидации, создания и характеристики панелей биомаркеров и т.д. Он гибок в использовании, если оно основано на грамотной логике. Например, вы можете разработать показания для медицинской диспансеризации пенсионеров-сердечников, применив высокоспецифичный критерий, повысив эффективность выявления болезней сердца и не перегружая врачей лишними пациентами. А во время опасной эпидемии ранее неизвестного вируса вы наоборот, можете придумать высокоселективный критерий, чтобы от вакцинации в прямом смысле не ускользнул ни один чих.
С ошибками обоих родов и их наглядностью в описании валидируемых критериев мы познакомились. Теперь же, двигаясь от этих логических основ, можно разрушить ряд ложных стереотипных описаний результатов. Некоторые неправильные формулировки захватывают наши умы, часто путаясь своими схожими словами и понятиями, а также из-за очень малого внимания, уделяемого неверной интерпретации. Об этом, пожалуй, нужно будет написать отдельно.
Статистическая погрешность — это та неопределенность в оценке истинного значения измеряемой величины, которая возникает из-за того, что несколько повторных измерений тем же самым инструментом дали различающиеся результаты. Возникает она, как правило, из-за того, что результаты измерения в микромире не фиксированы, а вероятностны. Она тесно связана с объемом статистики: обычно чем больше данных, тем меньше статистическая погрешность и тем точнее результат измерения. Среди всех типов погрешностей она, пожалуй, самая безобидная: понятно, как ее считать, и понятно, как с ней бороться.
Статистическая погрешность: чуть подробнее
Предположим, что ваш детектор может очень точно измерить какую-то величину в каждом конкретном столкновении. Это может быть энергия или импульс какой-то родившейся частицы, или дискретная величина (например, сколько мюонов родилось в событии), или вообще элементарный ответ «да» или «нет» на какой-то вопрос (например, родилась ли в этом событии хоть одна частица с импульсом больше 100 ГэВ).
Это конкретное число, полученное в одном столкновении, почти бессмысленно. Скажем, взяли вы одно событие и выяснили, что в нём хиггсовский бозон не родился. Никакой научной пользы от такого единичного факта нет. Законы микромира вероятностны, и если вы организуете абсолютно такое же столкновение протонов, то картина рождения частиц вовсе не обязана повторяться, она может оказаться совсем другой. Если бозон не родился сейчас, не родился в следующем столкновении, то это еще ничего не говорит о том, может ли он родиться вообще и как это соотносится с теоретическими предсказаниями. Для того, чтобы получить какое-то осмысленное число в экспериментах с элементарными частицами, надо повторить эксперимент много раз и набрать статистику одинаковых столкновений. Всё свое рабочее время коллайдеры именно этим и занимаются, они накапливают статистику, которую потом будут обрабатывать экспериментаторы.
В каждом конкретном столкновении результат измерения может быть разный. Наберем статистику столкновений и усредним по ней результат. Этот средний результат, конечно, тоже не фиксирован, он может меняться в зависимости от статистики, но он будет намного стабильнее, он не будет так сильно прыгать от одной статистической выборки к другой. У него тоже есть некая неопределенность (в статистическом анализе она так и называется: «неопределенность среднего»), но она обычно небольшая. Вот эта величина и называется статистической погрешностью измерения.
Итак, когда экспериментаторы предъявляют измерение какой-то величины, то они сообщают результат усреднения этой величины по всей набранной статистике столкновений и сопровождают его статистической погрешностью. Именно такие средние значения имеют физический смысл, только их может предсказывать теория.
Есть, конечно, и иной источник статистической погрешности: недостаточный контроль условий эксперимента при повторном измерении. Если в физике частиц этот источник можно попытаться устранить, по крайней мере, в принципе, то в других разделах естественных наук он выходит на первый план; например, в медицинских исследованиях каждый человек отличается от другого по большому числу параметров.
Как считать статистическую погрешность?
Существует теория расчета статистической погрешности, в которую мы, конечно, вдаваться не будем. Но есть одно очень простое правило, которое легко запомнить и которое срабатывает почти всегда. Пусть у вас есть статистическая выборка из N столкновений и в ней присутствует n событий какого-то определенного типа. Тогда в другой статистической выборке из N событий, набранной в тех же условиях, можно ожидать примерно n ± √n таких событий. Поделив это на N, мы получим среднюю вероятность встретить такое событие и погрешность среднего: n/N ± √n/N. Оценка истинного значения вероятности такого типа события примерно соответствует этому выражению.
Сразу же, впрочем, подчеркнем, что эта простая оценка начинает сильно «врать», когда количество событий очень мало. В науке обсчета маленькой статистики есть много дополнительных тонкостей.
Более серьезное (но умеренно краткое) введение в методы статистической обработки данных в применении к экспериментам на LHC см. в лекциях arXiv.1307.2487.
Именно поэтому эксперименты в физике элементарных частиц стараются оптимизировать не только по энергии, но и по светимости. Ведь чем больше светимость, тем больше столкновений будет произведено — значит, тем больше будет статистическая выборка. И уже это позволит сделать измерения более точными — даже без каких-либо улучшений в эксперименте. Примерная зависимость тут такая: если вы увеличите статистику в k раз, то относительные статистические погрешности уменьшатся примерно в √k раз.
Этот пример — некая симуляция того, как могло бы происходить измерение массы ρ-мезона свыше полувека назад, на заре адронной физики, если бы он был вначале обнаружен в процессе e+e– → π+π–. А теперь перенесемся в наше время.
Сейчас этот процесс изучен вдоль и поперек, статистика набрана огромная (миллионы событий), а значит, и масса ρ-мезона сейчас определена несравнимо точнее. На рис. 3 показано современное состояние дел в этой области масс. Если ранние эксперименты еще имели какие-то существенные погрешности, то сейчас они практически неразличимы глазом. Огромная статистика позволила не только измерить массу (примерно равна 775 МэВ с точностью в десятые доли МэВ), но и заметить очень странную форму этого пика. Такая форма получается потому, что практически в том же месте на шкале масс находится и другой мезон, ω(782), который «вмешивается» в процесс и искажает форму ρ-мезонного пика.
Другой, гораздо более реальный пример влияния статистики на процесс поиска и изучения хиггсовского бозона обсуждался в новости Анимации показывают, как в данных LHC зарождался хиггсовский сигнал.
Статистические ошибки
Использование
методов биометрии позволяет исследователю
на ограниченном по численности материале
делать заключения о проявлении признака,
его изменчивости и других параметрах
в генеральной совокупности. Но так
как выборочная совокупность — часть
генеральной и ее формируют методом
случайного отбора, то в выборку могут
попасть животные с более низкими
продуктивными качествами, или несколько
лучшие особи. В этом случае вычисленные
значения M, б, Cv и
других биометрических величин будут
отличаться от значений этих величин в
генеральной совокупности, то есть
выборка отражает генеральную совокупность
с ошибкой. Эти ошибки, связанные с
методом выборочности, называются
статистическими и устранить их нельзя.
Ошибки не будет лишь в том случае, когда
в обработку включаются все члены
генеральной совокупности. Величины
статистических ошибок зависят от
изменчивости признаков и объема выборки:
чем более изменчив признак, тем больше
ошибка, и чем больше объем выборки, тем
она меньше. Ошибки статистических
величин в биометрии принято обозначать
буквой m.
Ошибки
имеют все статистические величины.
Вычисляют их по формулам:
Все
ошибки измеряют в тех же единицах, что
и сами показатели, и записывают обычно
рядом с ними.
Статистические
ошибки указывают интервал, в котором
находится величина того или иного
статистического показателя в генеральной
совокупности. Зная среднее значение
признака (М) и его ошибку (m), можно
установить доверительные границы
средней величины в генеральной
совокупности по формуле: Мген.=Мв.
tm, где t — нормированное отклонение,
которое зависит от уровня вероятности
и объема выборки. Цифровое значение t
для каждого конкретного случая находят
с помощью специальной таблицы. Например,
нас интересует средняя частота пульса
у овец породы прекос. Для изучения этого
показателя была сформирована выборка
в количестве 50 голов и определена у
этих животных средняя частота пульса.
Оказалось, что этот показатель равен
75 ударов в минуту, изменчивость его б =
12 ударов. Ошибка средней арифметической
величины в этом случае составит:
б
12
m
= ──── = ──── = 1,7 (уд./мин).
n
50
Итоговая
запись будет иметь вид: М
m или 75
1,7, то есть частота пульса 75 ударов в
минуту — среднее значение для 50 голов.
Чтобы определить среднюю частоту пульса
в генеральной совокупности животных,
возьмем в качестве доверительной
вероятности P = 0,95. В этом случае, исходя
из таблицы, t = 2,01. Определим доверительные
границы частоты пульса в генеральной
совокупности M
tm.
75,0
+ 2,01 x 1,7 = 75,0 + 3,4 = 78,4 (уд./мин)
75,0
— 2,01 x 1,7 = 75,0 — 3,4 = 71,6 (уд./мин)
Таким
образом, средняя частота пульса для
генеральной совокупности будет в
пределах от 71,6 до 78,4 ударов в минуту.
Зная
величину статистических ошибок,
устанавливают также, правильно ли
выборочная совокупность отражает тот
или иной параметр генеральной, то есть
устанавливают критерий доверительности
выборочных величин.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
From Wikipedia, the free encyclopedia
«Systematic bias» redirects here. For the sociological and organizational phenomenon, see Systemic bias.
Observational error (or measurement error) is the difference between a measured value of a quantity and its true value.[1] In statistics, an error is not necessarily a «mistake». Variability is an inherent part of the results of measurements and of the measurement process.
Measurement errors can be divided into two components: random and systematic.[2]
Random errors are errors in measurement that lead to measurable values being inconsistent when repeated measurements of a constant attribute or quantity are taken. Systematic errors are errors that are not determined by chance but are introduced by repeatable processes inherent to the system.[3] Systematic error may also refer to an error with a non-zero mean, the effect of which is not reduced when observations are averaged.[citation needed]
Measurement errors can be summarized in terms of accuracy and precision.
Measurement error should not be confused with measurement uncertainty.
Science and experiments[edit]
When either randomness or uncertainty modeled by probability theory is attributed to such errors, they are «errors» in the sense in which that term is used in statistics; see errors and residuals in statistics.
Every time we repeat a measurement with a sensitive instrument, we obtain slightly different results. The common statistical model used is that the error has two additive parts:
- Systematic error which always occurs, with the same value, when we use the instrument in the same way and in the same case.
- Random error which may vary from observation to another.
Systematic error is sometimes called statistical bias. It may often be reduced with standardized procedures. Part of the learning process in the various sciences is learning how to use standard instruments and protocols so as to minimize systematic error.
Random error (or random variation) is due to factors that cannot or will not be controlled. One possible reason to forgo controlling for these random errors is that it may be too expensive to control them each time the experiment is conducted or the measurements are made. Other reasons may be that whatever we are trying to measure is changing in time (see dynamic models), or is fundamentally probabilistic (as is the case in quantum mechanics — see Measurement in quantum mechanics). Random error often occurs when instruments are pushed to the extremes of their operating limits. For example, it is common for digital balances to exhibit random error in their least significant digit. Three measurements of a single object might read something like 0.9111g, 0.9110g, and 0.9112g.
Characterization[edit]
Measurement errors can be divided into two components: random error and systematic error.[2]
Random error is always present in a measurement. It is caused by inherently unpredictable fluctuations in the readings of a measurement apparatus or in the experimenter’s interpretation of the instrumental reading. Random errors show up as different results for ostensibly the same repeated measurement. They can be estimated by comparing multiple measurements and reduced by averaging multiple measurements.
Systematic error is predictable and typically constant or proportional to the true value. If the cause of the systematic error can be identified, then it usually can be eliminated. Systematic errors are caused by imperfect calibration of measurement instruments or imperfect methods of observation, or interference of the environment with the measurement process, and always affect the results of an experiment in a predictable direction. Incorrect zeroing of an instrument leading to a zero error is an example of systematic error in instrumentation.
The Performance Test Standard PTC 19.1-2005 “Test Uncertainty”, published by the American Society of Mechanical Engineers (ASME), discusses systematic and random errors in considerable detail. In fact, it conceptualizes its basic uncertainty categories in these terms.
Random error can be caused by unpredictable fluctuations in the readings of a measurement apparatus, or in the experimenter’s interpretation of the instrumental reading; these fluctuations may be in part due to interference of the environment with the measurement process. The concept of random error is closely related to the concept of precision. The higher the precision of a measurement instrument, the smaller the variability (standard deviation) of the fluctuations in its readings.
Sources[edit]
Sources of systematic error[edit]
Imperfect calibration[edit]
Sources of systematic error may be imperfect calibration of measurement instruments (zero error), changes in the environment which interfere with the measurement process and sometimes imperfect methods of observation can be either zero error or percentage error. If you consider an experimenter taking a reading of the time period of a pendulum swinging past a fiducial marker: If their stop-watch or timer starts with 1 second on the clock then all of their results will be off by 1 second (zero error). If the experimenter repeats this experiment twenty times (starting at 1 second each time), then there will be a percentage error in the calculated average of their results; the final result will be slightly larger than the true period.
Distance measured by radar will be systematically overestimated if the slight slowing down of the waves in air is not accounted for. Incorrect zeroing of an instrument leading to a zero error is an example of systematic error in instrumentation.
Systematic errors may also be present in the result of an estimate based upon a mathematical model or physical law. For instance, the estimated oscillation frequency of a pendulum will be systematically in error if slight movement of the support is not accounted for.
Quantity[edit]
Systematic errors can be either constant, or related (e.g. proportional or a percentage) to the actual value of the measured quantity, or even to the value of a different quantity (the reading of a ruler can be affected by environmental temperature). When it is constant, it is simply due to incorrect zeroing of the instrument. When it is not constant, it can change its sign. For instance, if a thermometer is affected by a proportional systematic error equal to 2% of the actual temperature, and the actual temperature is 200°, 0°, or −100°, the measured temperature will be 204° (systematic error = +4°), 0° (null systematic error) or −102° (systematic error = −2°), respectively. Thus the temperature will be overestimated when it will be above zero and underestimated when it will be below zero.
Drift[edit]
Systematic errors which change during an experiment (drift) are easier to detect. Measurements indicate trends with time rather than varying randomly about a mean. Drift is evident if a measurement of a constant quantity is repeated several times and the measurements drift one way during the experiment. If the next measurement is higher than the previous measurement as may occur if an instrument becomes warmer during the experiment then the measured quantity is variable and it is possible to detect a drift by checking the zero reading during the experiment as well as at the start of the experiment (indeed, the zero reading is a measurement of a constant quantity). If the zero reading is consistently above or below zero, a systematic error is present. If this cannot be eliminated, potentially by resetting the instrument immediately before the experiment then it needs to be allowed by subtracting its (possibly time-varying) value from the readings, and by taking it into account while assessing the accuracy of the measurement.
If no pattern in a series of repeated measurements is evident, the presence of fixed systematic errors can only be found if the measurements are checked, either by measuring a known quantity or by comparing the readings with readings made using a different apparatus, known to be more accurate. For example, if you think of the timing of a pendulum using an accurate stopwatch several times you are given readings randomly distributed about the mean. Hopings systematic error is present if the stopwatch is checked against the ‘speaking clock’ of the telephone system and found to be running slow or fast. Clearly, the pendulum timings need to be corrected according to how fast or slow the stopwatch was found to be running.
Measuring instruments such as ammeters and voltmeters need to be checked periodically against known standards.
Systematic errors can also be detected by measuring already known quantities. For example, a spectrometer fitted with a diffraction grating may be checked by using it to measure the wavelength of the D-lines of the sodium electromagnetic spectrum which are at 600 nm and 589.6 nm. The measurements may be used to determine the number of lines per millimetre of the diffraction grating, which can then be used to measure the wavelength of any other spectral line.
Constant systematic errors are very difficult to deal with as their effects are only observable if they can be removed. Such errors cannot be removed by repeating measurements or averaging large numbers of results. A common method to remove systematic error is through calibration of the measurement instrument.
Sources of random error[edit]
The random or stochastic error in a measurement is the error that is random from one measurement to the next. Stochastic errors tend to be normally distributed when the stochastic error is the sum of many independent random errors because of the central limit theorem. Stochastic errors added to a regression equation account for the variation in Y that cannot be explained by the included Xs.
Surveys[edit]
The term «observational error» is also sometimes used to refer to response errors and some other types of non-sampling error.[1] In survey-type situations, these errors can be mistakes in the collection of data, including both the incorrect recording of a response and the correct recording of a respondent’s inaccurate response. These sources of non-sampling error are discussed in Salant and Dillman (1994) and Bland and Altman (1996).[4][5]
These errors can be random or systematic. Random errors are caused by unintended mistakes by respondents, interviewers and/or coders. Systematic error can occur if there is a systematic reaction of the respondents to the method used to formulate the survey question. Thus, the exact formulation of a survey question is crucial, since it affects the level of measurement error.[6] Different tools are available for the researchers to help them decide about this exact formulation of their questions, for instance estimating the quality of a question using MTMM experiments. This information about the quality can also be used in order to correct for measurement error.[7][8]
Effect on regression analysis[edit]
If the dependent variable in a regression is measured with error, regression analysis and associated hypothesis testing are unaffected, except that the R2 will be lower than it would be with perfect measurement.
However, if one or more independent variables is measured with error, then the regression coefficients and standard hypothesis tests are invalid.[9]: p. 187 This is known as attenuation bias.[10]
See also[edit]
- Bias (statistics)
- Cognitive bias
- Correction for measurement error (for Pearson correlations)
- Errors and residuals in statistics
- Error
- Replication (statistics)
- Statistical theory
- Metrology
- Regression dilution
- Test method
- Propagation of uncertainty
- Instrument error
- Measurement uncertainty
- Errors-in-variables models
- Systemic bias
References[edit]
- ^ a b Dodge, Y. (2003) The Oxford Dictionary of Statistical Terms, OUP. ISBN 978-0-19-920613-1
- ^ a b John Robert Taylor (1999). An Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements. University Science Books. p. 94, §4.1. ISBN 978-0-935702-75-0.
- ^ «Systematic error». Merriam-webster.com. Retrieved 2016-09-10.
- ^ Salant, P.; Dillman, D. A. (1994). How to conduct your survey. New York: John Wiley & Sons. ISBN 0-471-01273-4.
- ^ Bland, J. Martin; Altman, Douglas G. (1996). «Statistics Notes: Measurement Error». BMJ. 313 (7059): 744. doi:10.1136/bmj.313.7059.744. PMC 2352101. PMID 8819450.
- ^ Saris, W. E.; Gallhofer, I. N. (2014). Design, Evaluation and Analysis of Questionnaires for Survey Research (Second ed.). Hoboken: Wiley. ISBN 978-1-118-63461-5.
- ^ DeCastellarnau, A. and Saris, W. E. (2014). A simple procedure to correct for measurement errors in survey research. European Social Survey Education Net (ESS EduNet). Available at: http://essedunet.nsd.uib.no/cms/topics/measurement Archived 2019-09-15 at the Wayback Machine
- ^ Saris, W. E.; Revilla, M. (2015). «Correction for measurement errors in survey research: necessary and possible» (PDF). Social Indicators Research. 127 (3): 1005–1020. doi:10.1007/s11205-015-1002-x. hdl:10230/28341. S2CID 146550566.
- ^ Hayashi, Fumio (2000). Econometrics. Princeton University Press. ISBN 978-0-691-01018-2.
- ^ Angrist, Joshua David; Pischke, Jörn-Steffen (2015). Mastering ‘metrics : the path from cause to effect. Princeton, New Jersey. p. 221. ISBN 978-0-691-15283-7. OCLC 877846199.
The bias generated by this sort of measurement error in regressors is called attenuation bias.
Further reading[edit]
- Cochran, W. G. (1968). «Errors of Measurement in Statistics». Technometrics. 10 (4): 637–666. doi:10.2307/1267450. JSTOR 1267450.
From Wikipedia, the free encyclopedia
«Systematic bias» redirects here. For the sociological and organizational phenomenon, see Systemic bias.
Observational error (or measurement error) is the difference between a measured value of a quantity and its true value.[1] In statistics, an error is not necessarily a «mistake». Variability is an inherent part of the results of measurements and of the measurement process.
Measurement errors can be divided into two components: random and systematic.[2]
Random errors are errors in measurement that lead to measurable values being inconsistent when repeated measurements of a constant attribute or quantity are taken. Systematic errors are errors that are not determined by chance but are introduced by repeatable processes inherent to the system.[3] Systematic error may also refer to an error with a non-zero mean, the effect of which is not reduced when observations are averaged.[citation needed]
Measurement errors can be summarized in terms of accuracy and precision.
Measurement error should not be confused with measurement uncertainty.
Science and experiments[edit]
When either randomness or uncertainty modeled by probability theory is attributed to such errors, they are «errors» in the sense in which that term is used in statistics; see errors and residuals in statistics.
Every time we repeat a measurement with a sensitive instrument, we obtain slightly different results. The common statistical model used is that the error has two additive parts:
- Systematic error which always occurs, with the same value, when we use the instrument in the same way and in the same case.
- Random error which may vary from observation to another.
Systematic error is sometimes called statistical bias. It may often be reduced with standardized procedures. Part of the learning process in the various sciences is learning how to use standard instruments and protocols so as to minimize systematic error.
Random error (or random variation) is due to factors that cannot or will not be controlled. One possible reason to forgo controlling for these random errors is that it may be too expensive to control them each time the experiment is conducted or the measurements are made. Other reasons may be that whatever we are trying to measure is changing in time (see dynamic models), or is fundamentally probabilistic (as is the case in quantum mechanics — see Measurement in quantum mechanics). Random error often occurs when instruments are pushed to the extremes of their operating limits. For example, it is common for digital balances to exhibit random error in their least significant digit. Three measurements of a single object might read something like 0.9111g, 0.9110g, and 0.9112g.
Characterization[edit]
Measurement errors can be divided into two components: random error and systematic error.[2]
Random error is always present in a measurement. It is caused by inherently unpredictable fluctuations in the readings of a measurement apparatus or in the experimenter’s interpretation of the instrumental reading. Random errors show up as different results for ostensibly the same repeated measurement. They can be estimated by comparing multiple measurements and reduced by averaging multiple measurements.
Systematic error is predictable and typically constant or proportional to the true value. If the cause of the systematic error can be identified, then it usually can be eliminated. Systematic errors are caused by imperfect calibration of measurement instruments or imperfect methods of observation, or interference of the environment with the measurement process, and always affect the results of an experiment in a predictable direction. Incorrect zeroing of an instrument leading to a zero error is an example of systematic error in instrumentation.
The Performance Test Standard PTC 19.1-2005 “Test Uncertainty”, published by the American Society of Mechanical Engineers (ASME), discusses systematic and random errors in considerable detail. In fact, it conceptualizes its basic uncertainty categories in these terms.
Random error can be caused by unpredictable fluctuations in the readings of a measurement apparatus, or in the experimenter’s interpretation of the instrumental reading; these fluctuations may be in part due to interference of the environment with the measurement process. The concept of random error is closely related to the concept of precision. The higher the precision of a measurement instrument, the smaller the variability (standard deviation) of the fluctuations in its readings.
Sources[edit]
Sources of systematic error[edit]
Imperfect calibration[edit]
Sources of systematic error may be imperfect calibration of measurement instruments (zero error), changes in the environment which interfere with the measurement process and sometimes imperfect methods of observation can be either zero error or percentage error. If you consider an experimenter taking a reading of the time period of a pendulum swinging past a fiducial marker: If their stop-watch or timer starts with 1 second on the clock then all of their results will be off by 1 second (zero error). If the experimenter repeats this experiment twenty times (starting at 1 second each time), then there will be a percentage error in the calculated average of their results; the final result will be slightly larger than the true period.
Distance measured by radar will be systematically overestimated if the slight slowing down of the waves in air is not accounted for. Incorrect zeroing of an instrument leading to a zero error is an example of systematic error in instrumentation.
Systematic errors may also be present in the result of an estimate based upon a mathematical model or physical law. For instance, the estimated oscillation frequency of a pendulum will be systematically in error if slight movement of the support is not accounted for.
Quantity[edit]
Systematic errors can be either constant, or related (e.g. proportional or a percentage) to the actual value of the measured quantity, or even to the value of a different quantity (the reading of a ruler can be affected by environmental temperature). When it is constant, it is simply due to incorrect zeroing of the instrument. When it is not constant, it can change its sign. For instance, if a thermometer is affected by a proportional systematic error equal to 2% of the actual temperature, and the actual temperature is 200°, 0°, or −100°, the measured temperature will be 204° (systematic error = +4°), 0° (null systematic error) or −102° (systematic error = −2°), respectively. Thus the temperature will be overestimated when it will be above zero and underestimated when it will be below zero.
Drift[edit]
Systematic errors which change during an experiment (drift) are easier to detect. Measurements indicate trends with time rather than varying randomly about a mean. Drift is evident if a measurement of a constant quantity is repeated several times and the measurements drift one way during the experiment. If the next measurement is higher than the previous measurement as may occur if an instrument becomes warmer during the experiment then the measured quantity is variable and it is possible to detect a drift by checking the zero reading during the experiment as well as at the start of the experiment (indeed, the zero reading is a measurement of a constant quantity). If the zero reading is consistently above or below zero, a systematic error is present. If this cannot be eliminated, potentially by resetting the instrument immediately before the experiment then it needs to be allowed by subtracting its (possibly time-varying) value from the readings, and by taking it into account while assessing the accuracy of the measurement.
If no pattern in a series of repeated measurements is evident, the presence of fixed systematic errors can only be found if the measurements are checked, either by measuring a known quantity or by comparing the readings with readings made using a different apparatus, known to be more accurate. For example, if you think of the timing of a pendulum using an accurate stopwatch several times you are given readings randomly distributed about the mean. Hopings systematic error is present if the stopwatch is checked against the ‘speaking clock’ of the telephone system and found to be running slow or fast. Clearly, the pendulum timings need to be corrected according to how fast or slow the stopwatch was found to be running.
Measuring instruments such as ammeters and voltmeters need to be checked periodically against known standards.
Systematic errors can also be detected by measuring already known quantities. For example, a spectrometer fitted with a diffraction grating may be checked by using it to measure the wavelength of the D-lines of the sodium electromagnetic spectrum which are at 600 nm and 589.6 nm. The measurements may be used to determine the number of lines per millimetre of the diffraction grating, which can then be used to measure the wavelength of any other spectral line.
Constant systematic errors are very difficult to deal with as their effects are only observable if they can be removed. Such errors cannot be removed by repeating measurements or averaging large numbers of results. A common method to remove systematic error is through calibration of the measurement instrument.
Sources of random error[edit]
The random or stochastic error in a measurement is the error that is random from one measurement to the next. Stochastic errors tend to be normally distributed when the stochastic error is the sum of many independent random errors because of the central limit theorem. Stochastic errors added to a regression equation account for the variation in Y that cannot be explained by the included Xs.
Surveys[edit]
The term «observational error» is also sometimes used to refer to response errors and some other types of non-sampling error.[1] In survey-type situations, these errors can be mistakes in the collection of data, including both the incorrect recording of a response and the correct recording of a respondent’s inaccurate response. These sources of non-sampling error are discussed in Salant and Dillman (1994) and Bland and Altman (1996).[4][5]
These errors can be random or systematic. Random errors are caused by unintended mistakes by respondents, interviewers and/or coders. Systematic error can occur if there is a systematic reaction of the respondents to the method used to formulate the survey question. Thus, the exact formulation of a survey question is crucial, since it affects the level of measurement error.[6] Different tools are available for the researchers to help them decide about this exact formulation of their questions, for instance estimating the quality of a question using MTMM experiments. This information about the quality can also be used in order to correct for measurement error.[7][8]
Effect on regression analysis[edit]
If the dependent variable in a regression is measured with error, regression analysis and associated hypothesis testing are unaffected, except that the R2 will be lower than it would be with perfect measurement.
However, if one or more independent variables is measured with error, then the regression coefficients and standard hypothesis tests are invalid.[9]: p. 187 This is known as attenuation bias.[10]
See also[edit]
- Bias (statistics)
- Cognitive bias
- Correction for measurement error (for Pearson correlations)
- Errors and residuals in statistics
- Error
- Replication (statistics)
- Statistical theory
- Metrology
- Regression dilution
- Test method
- Propagation of uncertainty
- Instrument error
- Measurement uncertainty
- Errors-in-variables models
- Systemic bias
References[edit]
- ^ a b Dodge, Y. (2003) The Oxford Dictionary of Statistical Terms, OUP. ISBN 978-0-19-920613-1
- ^ a b John Robert Taylor (1999). An Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements. University Science Books. p. 94, §4.1. ISBN 978-0-935702-75-0.
- ^ «Systematic error». Merriam-webster.com. Retrieved 2016-09-10.
- ^ Salant, P.; Dillman, D. A. (1994). How to conduct your survey. New York: John Wiley & Sons. ISBN 0-471-01273-4.
- ^ Bland, J. Martin; Altman, Douglas G. (1996). «Statistics Notes: Measurement Error». BMJ. 313 (7059): 744. doi:10.1136/bmj.313.7059.744. PMC 2352101. PMID 8819450.
- ^ Saris, W. E.; Gallhofer, I. N. (2014). Design, Evaluation and Analysis of Questionnaires for Survey Research (Second ed.). Hoboken: Wiley. ISBN 978-1-118-63461-5.
- ^ DeCastellarnau, A. and Saris, W. E. (2014). A simple procedure to correct for measurement errors in survey research. European Social Survey Education Net (ESS EduNet). Available at: http://essedunet.nsd.uib.no/cms/topics/measurement Archived 2019-09-15 at the Wayback Machine
- ^ Saris, W. E.; Revilla, M. (2015). «Correction for measurement errors in survey research: necessary and possible» (PDF). Social Indicators Research. 127 (3): 1005–1020. doi:10.1007/s11205-015-1002-x. hdl:10230/28341. S2CID 146550566.
- ^ Hayashi, Fumio (2000). Econometrics. Princeton University Press. ISBN 978-0-691-01018-2.
- ^ Angrist, Joshua David; Pischke, Jörn-Steffen (2015). Mastering ‘metrics : the path from cause to effect. Princeton, New Jersey. p. 221. ISBN 978-0-691-15283-7. OCLC 877846199.
The bias generated by this sort of measurement error in regressors is called attenuation bias.
Further reading[edit]
- Cochran, W. G. (1968). «Errors of Measurement in Statistics». Technometrics. 10 (4): 637–666. doi:10.2307/1267450. JSTOR 1267450.
В статистике и оптимизации ошибки и остатки тесно связаны и легко запутанные меры отклонения наблюдаемого значения элемента статистической выборки от его «теоретического значения». ошибка (или возмущение ) наблюдаемого значения — это отклонение наблюдаемого значения от (ненаблюдаемого) истинного значения интересующей величины (например, среднего генерального значения), и остаток наблюдаемого значения представляет собой разность между наблюдаемым значением и оценочным значением представляющей интерес величины (например, выборочное среднее). Это различие наиболее важно в регрессионном анализе, где концепции иногда называют ошибками регрессии и остатками регрессии, и где они приводят к концепции студентизированных остатков.
Содержание
- 1 Введение
- 2 В одномерных распределениях
- 2.1 Замечание
- 3 Регрессии
- 4 Другие варианты использования слова «ошибка» в статистике
- 5 См. Также
- 6 Ссылки
- 7 Внешние ссылки
Введение
Предположим, есть серия наблюдений из одномерного распределения, и мы хотим оценить среднее этого распределения. (так называемая локационная модель ). В этом случае ошибки — это отклонения наблюдений от среднего по совокупности, а остатки — это отклонения наблюдений от среднего по выборке.
A статистическая ошибка (или нарушение ) — это величина, на которую наблюдение отличается от его ожидаемого значения, последнее основано на всей генеральной совокупности из которого статистическая единица была выбрана случайным образом. Например, если средний рост среди 21-летних мужчин составляет 1,75 метра, а рост одного случайно выбранного мужчины — 1,80 метра, то «ошибка» составляет 0,05 метра; если рост случайно выбранного мужчины составляет 1,70 метра, то «ошибка» составляет -0,05 метра. Ожидаемое значение, являющееся средним для всей генеральной совокупности, обычно ненаблюдаемо, и, следовательно, статистическая ошибка также не может быть обнаружена.
A невязка (или аппроксимирующее отклонение), с другой стороны, представляет собой наблюдаемую оценку ненаблюдаемой статистической ошибки. Рассмотрим предыдущий пример с ростом мужчин и предположим, что у нас есть случайная выборка из n человек. среднее значение выборки может служить хорошей оценкой среднего значения генеральной совокупности. Тогда у нас есть:
- Разница между ростом каждого человека в выборке и ненаблюдаемым средним по совокупности является статистической ошибкой, тогда как
- разница между ростом каждого человека в выборке и наблюдаемой выборкой среднее — это остаток.
Обратите внимание, что из-за определения выборочного среднего, сумма остатков в случайной выборке обязательно равна нулю, и, таким образом, остатки не обязательно независимы. Статистические ошибки, с другой стороны, независимы, и их сумма в случайной выборке почти наверняка не равна нулю.
Можно стандартизировать статистические ошибки (особенно нормального распределения ) в z-балле (или «стандартном балле») и стандартизировать остатки в t-статистика или, в более общем смысле, стьюдентизированные остатки.
в одномерном распределении
Если мы предположим нормально распределенную совокупность со средним μ и стандартным отклонением σ и независимо выбираем людей, тогда мы имеем
- X 1,…, X n ∼ N (μ, σ 2) { displaystyle X_ {1}, dots, X_ {n} sim N ( mu, sigma ^ {2}) ,}
и выборочное среднее
- X ¯ = X 1 + ⋯ + X nn { displaystyle { overline {X}} = {X_ { 1} + cdots + X_ {n} over n}}
— случайная величина, распределенная так, что:
- X ¯ ∼ N (μ, σ 2 n). { displaystyle { overline {X}} sim N left ( mu, { frac { sigma ^ {2}} {n}} right).}
Тогда статистические ошибки
- ei = X i — μ, { displaystyle e_ {i} = X_ {i} — mu, ,}
с ожидаемыми значениями нуля, тогда как остатки равны
- ri = X i — X ¯. { displaystyle r_ {i} = X_ {i} — { overline {X}}.}
Сумма квадратов статистических ошибок, деленная на σ, имеет хи -квадратное распределение с n степенями свободы :
- 1 σ 2 ∑ i = 1 nei 2 ∼ χ n 2. { displaystyle { frac {1} { sigma ^ {2}}} sum _ {i = 1} ^ {n} e_ {i} ^ {2} sim chi _ {n} ^ {2}.}
Однако это количество не наблюдается, так как среднее значение для генеральной совокупности неизвестно. Сумма квадратов остатков, с другой стороны, является наблюдаемой. Частное этой суммы по σ имеет распределение хи-квадрат только с n — 1 степенями свободы:
- 1 σ 2 ∑ i = 1 n r i 2 ∼ χ n — 1 2. { displaystyle { frac {1} { sigma ^ {2}}} sum _ {i = 1} ^ {n} r_ {i} ^ {2} sim chi _ {n-1} ^ { 2}.}
Эта разница между n и n — 1 степенями свободы приводит к поправке Бесселя для оценки выборочной дисперсии генеральной совокупности с неизвестным средним и неизвестной дисперсией. Коррекция не требуется, если известно среднее значение для генеральной совокупности.
Замечание
Примечательно, что сумма квадратов остатков и выборочного среднего могут быть показаны как независимые друг от друга, используя, например, Теорема Басу. Этот факт, а также приведенные выше нормальное распределение и распределение хи-квадрат составляют основу вычислений с использованием t-статистики :
- T = X ¯ n — μ 0 S n / n, { displaystyle T = { frac {{ overline {X}} _ {n} — mu _ {0}} {S_ {n} / { sqrt {n}}}},}
где X ¯ n — μ 0 { displaystyle { overline {X}} _ {n} — mu _ {0}}


- Var (X ¯ n) = σ 2 n { displaystyle operatorname {Var} ({ overline {X}} _ {n}) = { frac { sigma ^ {2}} {n}}}
Распределения вероятностей числителя и знаменателя по отдельности зависят от значения ненаблюдаемого стандартного отклонения генеральной совокупности σ, но σ появляется как в числителе, так и в знаменателе и отменяет. Это удачно, потому что это означает, что, хотя мы не знаем σ, мы знаем распределение вероятностей этого частного: оно имеет t-распределение Стьюдента с n — 1 степенями свободы. Таким образом, мы можем использовать это частное, чтобы найти доверительный интервал для μ. Эту t-статистику можно интерпретировать как «количество стандартных ошибок от линии регрессии».
Регрессии
В регрессионном анализе различие между ошибками и остатками является тонким и важным, и приводит к концепции стьюдентизированных остатков. Для ненаблюдаемой функции, которая связывает независимую переменную с зависимой переменной — скажем, линии — отклонения наблюдений зависимой переменной от этой функции являются ненаблюдаемыми ошибками. Если запустить регрессию на некоторых данных, то отклонения наблюдений зависимой переменной от подобранной функции являются остатками. Если линейная модель применима, диаграмма рассеяния остатков, построенная против независимой переменной, должна быть случайной около нуля без тенденции к остаткам. Если данные демонстрируют тенденцию, регрессионная модель, вероятно, неверна; например, истинная функция может быть квадратичным полиномом или полиномом более высокого порядка. Если они случайны или не имеют тенденции, но «разветвляются» — они демонстрируют явление, называемое гетероскедастичностью. Если все остатки равны или не разветвляются, они проявляют гомоскедастичность.
Однако терминологическое различие возникает в выражении среднеквадратическая ошибка (MSE). Среднеквадратичная ошибка регрессии — это число, вычисляемое из суммы квадратов вычисленных остатков, а не ненаблюдаемых ошибок. Если эту сумму квадратов разделить на n, количество наблюдений, результатом будет среднее квадратов остатков. Поскольку это смещенная оценка дисперсии ненаблюдаемых ошибок, смещение устраняется путем деления суммы квадратов остатков на df = n — p — 1 вместо n, где df — число степеней свободы (n минус количество оцениваемых параметров (без учета точки пересечения) p — 1). Это формирует объективную оценку дисперсии ненаблюдаемых ошибок и называется среднеквадратической ошибкой.
Другой метод вычисления среднего квадрата ошибки при анализе дисперсии линейной регрессии с использованием техники, подобной той, что использовалась в ANOVA (они одинаковы, потому что ANOVA — это тип регрессии), сумма квадратов остатков (иначе говоря, сумма квадратов ошибки) делится на степени свободы (где степени свободы равно n — p — 1, где p — количество параметров, оцениваемых в модели (по одному для каждой переменной в уравнении регрессии, не включая точку пересечения). Затем можно также вычислить средний квадрат модели, разделив сумму квадратов модели за вычетом степеней свободы, которые представляют собой просто количество параметров. Затем значение F можно рассчитать путем деления среднего квадрата модели на средний квадрат ошибки, и затем мы можем определить значимость (вот почему вы хотите, чтобы средние квадраты начинались с.).
Однако из-за поведения процесса регрессии распределения остатков в разных точках данных (входной переменной) могут различаться, даже если сами ошибки распределены одинаково. Конкретно, в линейной регрессии , где ошибки одинаково распределены, изменчивость остатков входных данных в середине области будет выше, чем изменчивость остатков на концах области: линейные регрессии соответствуют конечным точкам лучше среднего. Это также отражено в функциях влияния различных точек данных на коэффициенты регрессии : конечные точки имеют большее влияние.
Таким образом, чтобы сравнить остатки на разных входах, нужно скорректировать остатки на ожидаемую изменчивость остатков, что называется стьюдентизацией. Это особенно важно в случае обнаружения выбросов, когда рассматриваемый случай каким-то образом отличается от другого в наборе данных. Например, можно ожидать большой остаток в середине домена, но он будет считаться выбросом в конце домена.
Другое использование слова «ошибка» в статистике
Использование термина «ошибка», как обсуждалось в разделах выше, означает отклонение значения от гипотетического ненаблюдаемого значение. По крайней мере, два других использования также встречаются в статистике, оба относятся к наблюдаемым ошибкам прогнозирования:
Среднеквадратичная ошибка или Среднеквадратичная ошибка (MSE) и Среднеквадратичная ошибка (RMSE) относятся к величине, на которую значения, предсказанные оценщиком, отличаются от оцениваемых количеств (обычно за пределами выборки, на основе которой была оценена модель).
Сумма квадратов ошибок (SSE или SSe), обычно сокращенно SSE или SS e, относится к остаточной сумме квадратов (сумма квадратов остатков) регрессии; это сумма квадратов отклонений фактических значений от прогнозируемых значений в пределах выборки, используемой для оценки. Это также называется оценкой методом наименьших квадратов, где коэффициенты регрессии выбираются так, чтобы сумма квадратов минимально (т.е. его производная равна нулю).
Аналогично, сумма абсолютных ошибок (SAE) является суммой абсолютных значений остатков, которая минимизирована в наименьшие абсолютные отклонения подход к регрессии.
См. также
Портал математики
- Абсолютное отклонение
- Консенсус-прогнозы
- Обнаружение и исправление ошибок
- Объясненная сумма квадраты
- Инновация (обработка сигналов)
- Неподходящая сумма квадратов
- Погрешность
- Средняя абсолютная погрешность
- Погрешность наблюдения
- Распространение ошибки
- Вероятная ошибка
- Случайные и систематические ошибки
- Разбавление регрессии
- Среднеквадратичное отклонение
- Ошибка выборки
- Стандартная ошибка
- Стьюдентизированная невязка
- Ошибки типа I и типа II
Ссылки
- Кук, Р. Деннис; Вайсберг, Сэнфорд (1982). Остатки и влияние на регресс (Отредактированный ред.). Нью-Йорк: Чепмен и Холл. ISBN 041224280X. Проверено 23 февраля 2013 г.
- Кокс, Дэвид Р. ; Снелл, Э. Джойс (1968). «Общее определение остатков». Журнал Королевского статистического общества, серия B. 30(2): 248–275. JSTOR 2984505.
- Вайсберг, Сэнфорд (1985). Прикладная линейная регрессия (2-е изд.). Нью-Йорк: Вили. ISBN 9780471879572. Проверено 23 февраля 2013 г.
- , Энциклопедия математики, EMS Press, 2001 [1994]
Внешние ссылки
СМИ, связанные с ошибками и остатками на Викимедиа Commons
| Часть серии по |
| Регрессивный анализ |
|---|
 |
| Модели |
|
|
|
|
|
| Оценка |
|
|
|
|
| Фон |
|
|
В статистике и оптимизации ошибки и остатки являются двумя тесно связанными и легко путаемыми мерами отклонения наблюдаемого значения элемента статистической выборки от его «теоретического значения». В ошибка (или же беспокойство) наблюдаемого значения — это отклонение наблюдаемого значения от (ненаблюдаемого) истинный значение интересующей величины (например, среднее значение генеральной совокупности), и остаточный наблюдаемого значения — это разница между наблюдаемым значением и по оценкам значение интересующей величины (например, выборочное среднее). Это различие наиболее важно в регрессионном анализе, где концепции иногда называют ошибки регрессии и остатки регрессии и где они приводят к концепции стьюдентизированных остатков.
Вступление
Предположим, что есть серия наблюдений из одномерное распределение и мы хотим оценить иметь в виду этого распределения (так называемый модель местоположения ). В этом случае ошибки — это отклонения наблюдений от среднего по совокупности, а остатки — это отклонения наблюдений от среднего по выборке.
А статистическая ошибка (или же беспокойство) — это величина, на которую наблюдение отличается от ожидаемое значение, последнее основано на численность населения из которого статистическая единица была выбрана случайным образом. Например, если средний рост среди 21-летних мужчин составляет 1,75 метра, а рост одного случайно выбранного мужчины — 1,80 метра, то «ошибка» составляет 0,05 метра; если рост случайно выбранного мужчины составляет 1,70 метра, то «ошибка» составляет -0,05 метра. Ожидаемое значение, являющееся иметь в виду всего населения, обычно не наблюдается, и, следовательно, статистическая ошибка также не может быть обнаружена.
А остаточный (или подходящее отклонение), с другой стороны, является наблюдаемым оценивать ненаблюдаемой статистической ошибки. Рассмотрим предыдущий пример с ростом мужчин и предположим, что у нас есть случайная выборка п люди. В выборочное среднее может служить хорошей оценкой численность населения иметь в виду. Тогда у нас есть:
- Разница между ростом каждого человека в выборке и ненаблюдаемой численность населения означает это статистическая ошибка, в то время как
- Разница между ростом каждого человека в выборке и наблюдаемым образец означает это остаточный.
Обратите внимание, что из-за определения выборочного среднего, сумма остатков в случайной выборке обязательно равна нулю, и, следовательно, остатки обязательно нет независимый. Статистические ошибки, с другой стороны, независимы, и их сумма в пределах случайной выборки равна почти наверняка не ноль.
Можно стандартизировать статистические ошибки (особенно нормальное распределение ) в z-оценка (или «стандартная оценка») и стандартизируйте остатки в т-статистический, или в более общем смысле стьюдентизированные остатки.
В одномерных распределениях
Если предположить нормально распределенный совокупность со средними μ и стандартное отклонение σ, и выбираем индивидуумов независимо, то имеем
и выборочное среднее
случайная величина, распределенная таким образом, что:
В статистические ошибки тогда
с ожидал значения нуля,[1] тогда как остатки находятся
Сумма квадратов статистические ошибки, деленное на σ2, имеет распределение хи-квадрат с п степени свободы:
Однако это количество не наблюдается, так как среднее значение для населения неизвестно. Сумма квадратов остатки, с другой стороны, наблюдается. Частное этой суммы по σ2 имеет распределение хи-квадрат только с п — 1 степень свободы:
Эта разница между п и п — 1 степень свободы дает Поправка Бесселя для оценки выборочная дисперсия популяции с неизвестным средним и неизвестной дисперсией. Коррекция не требуется, если известно среднее значение для генеральной совокупности.
Примечательно, что сумма квадратов остатков и средние выборочные значения могут быть показаны как независимые друг от друга, используя, например, Теорема Басу. Этот факт, а также приведенные выше нормальное распределение и распределение хи-квадрат составляют основу расчетов, включающих t-статистика:
куда 


Распределения вероятностей числителя и знаменателя по отдельности зависят от значения ненаблюдаемого стандартного отклонения совокупности σ, но σ появляется как в числителе, так и в знаменателе и отменяется. Это удачно, потому что это означает, что даже если мы не знаемσ, мы знаем распределение вероятностей этого частного: оно имеет Распределение Стьюдента с п — 1 степень свободы. Поэтому мы можем использовать это частное, чтобы найти доверительный интервал заμ. Эту t-статистику можно интерпретировать как «количество стандартных ошибок от линии регрессии».[3]
Регрессии
В регрессивный анализ, различие между ошибки и остатки тонкий и важный, и ведет к концепции стьюдентизированные остатки. При наличии ненаблюдаемой функции, которая связывает независимую переменную с зависимой переменной — скажем, линии — отклонения наблюдений зависимой переменной от этой функции являются ненаблюдаемыми ошибками. Если запустить регрессию на некоторых данных, то отклонения наблюдений зависимой переменной от приспособленный функции — остатки. Если применима линейная модель, диаграмма рассеяния остатков, построенная против независимой переменной, должна быть случайной около нуля без тенденции к остаткам.[2] Если данные демонстрируют тенденцию, регрессионная модель, вероятно, неверна; например, истинная функция может быть квадратичным полиномом или полиномом более высокого порядка. Если они случайны или не имеют тенденции, но «разветвляются» — они демонстрируют явление, называемое гетероскедастичность. Если все остатки равны или не разветвляются, они демонстрируют гомоскедастичность.
Однако возникает терминологическая разница в выражении среднеквадратичная ошибка (MSE). Среднеквадратичная ошибка регрессии — это число, вычисляемое из суммы квадратов вычисленных остатки, а не ненаблюдаемые ошибки. Если эту сумму квадратов разделить на п, количество наблюдений, результат — это среднее квадратов остатков. Поскольку это пристрастный Для оценки дисперсии ненаблюдаемых ошибок смещение устраняется путем деления суммы квадратов остатков на df = п − п — 1 вместо п, куда df это количество степени свободы (п минус количество оцениваемых параметров (без учета точки пересечения) p — 1). Это формирует несмещенную оценку дисперсии ненаблюдаемых ошибок и называется среднеквадратической ошибкой.[4]
Другой метод вычисления среднего квадрата ошибки при анализе дисперсии линейной регрессии с использованием техники, подобной той, что использовалась в ANOVA (они такие же, потому что ANOVA — это тип регрессии), сумма квадратов остатков (иначе говоря, сумма квадратов ошибки) делится на степени свободы (где степени свободы равны п − п — 1, где п — количество параметров, оцениваемых в модели (по одному для каждой переменной в уравнении регрессии, не включая точку пересечения). Затем можно также вычислить средний квадрат модели, разделив сумму квадратов модели за вычетом степеней свободы, которые представляют собой просто количество параметров. Затем значение F можно рассчитать, разделив средний квадрат модели на средний квадрат ошибки, и затем мы можем определить значимость (вот почему вы хотите, чтобы средние квадраты начинались с).[5]
Однако из-за поведения процесса регрессии распределения остатков в разных точках данных (входной переменной) может отличаться даже если сами ошибки одинаково распределены. Конкретно в линейная регрессия где ошибки одинаково распределены, вариативность остатков входных данных в середине области будет выше чем изменчивость остатков на концах области:[6] линейные регрессии лучше подходят для конечных точек, чем средние. Это также отражено в функции влияния различных точек данных на коэффициенты регрессии: конечные точки имеют большее влияние.
Таким образом, чтобы сравнить остатки на разных входах, необходимо скорректировать остатки на ожидаемую изменчивость остатки, который называется студенчество. Это особенно важно в случае обнаружения выбросы, где рассматриваемый случай чем-то отличается от другого случая в наборе данных. Например, можно ожидать большой остаток в середине домена, но он будет считаться выбросом в конце домена.
Другое использование слова «ошибка» в статистике
Термин «ошибка», как обсуждалось в предыдущих разделах, используется в смысле отклонения значения от гипотетического ненаблюдаемого значения. По крайней мере, два других использования также встречаются в статистике, оба относятся к наблюдаемым ошибкам прогнозирования:
Средняя квадратичная ошибка или же среднеквадратичная ошибка (MSE) и Средняя квадратическая ошибка (RMSE) относятся к количеству, на которое значения, предсказанные оценщиком, отличаются от оцениваемых количеств (обычно за пределами выборки, на основе которой была оценена модель).
Сумма квадратов ошибок (SSE или же SSе), обычно сокращенно SSE или SSе, относится к остаточная сумма квадратов (сумма квадратов остатков) регрессии; это сумма квадратов отклонений фактических значений от прогнозируемых значений в пределах выборки, используемой для оценки. Это также называется оценкой наименьших квадратов, когда коэффициенты регрессии выбираются таким образом, чтобы сумма квадратов была минимальной (т. Е. Ее производная равна нулю).
Точно так же сумма абсолютных ошибок (SAE) — сумма абсолютных значений остатков, которая минимизируется в наименьшие абсолютные отклонения подход к регрессу.
Смотрите также
- Абсолютное отклонение
- Консенсус-прогнозы
- Обнаружение и исправление ошибок
- Объясненная сумма квадратов
- Инновации (обработка сигналов)
- Неподходящая сумма квадратов
- Допустимая погрешность
- Средняя абсолютная ошибка
- Ошибка наблюдения
- Распространение ошибки
- Вероятная ошибка
- Случайные и систематические ошибки
- Разбавление регрессии
- Среднеквадратичное отклонение
- Ошибка выборки
- Стандартная ошибка
- Студентизованный остаток
- Ошибки типа I и типа II
Рекомендации
- ^ Уэзерилл, Дж. Барри. (1981). Промежуточные статистические методы. Лондон: Чепмен и Холл. ISBN 0-412-16440-Х. OCLC 7779780.
- ^ а б Современное введение в вероятность и статистику: понимание, почему и как. Деккинг, Мишель, 1946-. Лондон: Спрингер. 2005 г. ISBN 978-1-85233-896-1. OCLC 262680588.CS1 maint: другие (связь)
- ^ Брюс, Питер С., 1953- (2017-05-10). Практическая статистика для специалистов по данным: 50 основных концепций. Брюс, Эндрю, 1958- (Первое изд.). Севастополь, Калифорния. ISBN 978-1-4919-5293-1. OCLC 987251007.CS1 maint: несколько имен: список авторов (связь)
- ^ Steel, Robert G.D .; Торри, Джеймс Х. (1960). Принципы и процедуры статистики с особым акцентом на биологические науки. Макгроу-Хилл. п.288.
- ^ Зельтерман, Даниэль (2010). Прикладные линейные модели с SAS ([Online-Ausg.]. Ред.). Кембридж: Издательство Кембриджского университета. ISBN 9780521761598.
- ^ «7.3: Типы выбросов в линейной регрессии». Статистика LibreTexts. 2013-11-21. Получено 2019-11-22.
- Кук, Р. Деннис; Вайсберг, Сэнфорд (1982). Остатки и влияние на регресс (Ред. Ред.). Нью-Йорк: Чепмен и Холл. ISBN 041224280X. Получено 23 февраля 2013.
- Кокс, Дэвид Р.; Снелл, Э. Джойс (1968). «Общее определение остатков». Журнал Королевского статистического общества, серия B. 30 (2): 248–275. JSTOR 2984505.
- Вайсберг, Сэнфорд (1985). Прикладная линейная регрессия (2-е изд.). Нью-Йорк: Вили. ISBN 9780471879572. Получено 23 февраля 2013.
- «Ошибки, теория», Энциклопедия математики, EMS Press, 2001 [1994]
внешняя ссылка
СМИ, связанные с Ошибки и остатки в Wikimedia Commons
СТАТИСТИЧЕСКАЯ ОШИБКА
- СТАТИСТИЧЕСКАЯ ОШИБКА
- Общий термин, используемый для обозначения любой погрешности в составлении выборки или в проведении анализа данных, которая делает невозможным выведение надежного заключения.
Толковый словарь по психологии.
2013.
Смотреть что такое «СТАТИСТИЧЕСКАЯ ОШИБКА» в других словарях:
-
ОШИБКА, СРЕДНЯЯ СТАТИСТИЧЕСКАЯ — Буквально – средняя статистическая ошибка в серии наблюдений или суждений … Толковый словарь по психологии
-
Статистическая проверка гипотез — [statistical verification of hypotheses, hypotesis testing] понятие математической статистики, « процедура обоснованного сопоставления высказанной гипотезы относительно природы или величины неизвестных статистических параметров анализируемого… … Экономико-математический словарь
-
ошибка — Большая, гибельная, глубокая, глупая, грубая, губительная, детская, досадная, жестокая, закономерная, извинительная, исправимая, коренная, кричащая, крупная, легкомысленная, маленькая, мальчишеская, мелкая, невероятная, невинная, незаметная,… … Словарь эпитетов
-
ОШИБКА ОПЫТА — статистическая величина, вычисленная на основании данных опыта и позволяющая судить о достоверности этих данных … Словарь ботанических терминов
-
Ошибка опыта — статистическая величина, вычисленная на основании данных опыта и позволяющая судить о достоверности этих данных … Толковый словарь по почвоведению
-
Статистическая значимость — В статистике величину называют статистически значимой, если мала вероятность её случайного возникновения или еще более крайних величин. Здесь под крайностью понимается степень отклонения тестовой статистики от нуль гипотезы. Разница называется… … Википедия
-
Статистическая проверка гипотез — система приёмов в математической статистике (См. Математическая статистика), предназначенных для проверки соответствия опытных данных некоторой статистической гипотезе (См. Статистическая гипотеза). Процедуры С. п. г. позволяют принимать… … Большая советская энциклопедия
-
Статистическая проверка гипотез — один из разделов математической статистики, в котором развиваются идеи и методы статистической проверки соответствия между экспериментальными данными и гипотезами о значимости коэффициентов связи, различиях средних, дисперсий и других… … Социологический справочник
-
Ошибка первого рода — Ложное срабатывание (англ. false positive, англ. false alarm) или ошибка первого рода ошибочное детектирование события, которого на самом деле не было. В информационных технологиях этот термин часто применяется к системам и средствам защиты… … Википедия
-
Систематическая ошибка тестов, обусловленная культурными факторами (cultural bias in tests) — Между разными соц. и расовыми группами наблюдаются существенные различия в средних значениях оценок по стандартизованным тестам умственных способностей, широко применяемым при приеме в школы и колледжи, наборе в вооруженные силы и найме на работу … Психологическая энциклопедия
а) Виды ошибок
В процессе исследования явлений может
возникать отклонение исчисленных
показателей от их действительной
величины, то есть могут возникать ошибки
статистического наблюдения.
По источникам происхождения ошибки
наблюдения можно подразделить на
следующие:
-
преднамеренные;
-
непреднамеренные,
которые в свою очередь делятся на:
-
случайные;
-
систематические;
-
репрезентативности
(представительности).
Преднамеренные(сознательные, злостные) получаются в
результате того, что сознательно
сообщаются неправильные данные. Например,
сокрытие фирмами прибыли от налогообложения,
искажение сведений об объеме выпускаемой
продукции, приписки и т. д.
Законом
предусматривается применение экономических
и административных мер к предприятиям
и лицам за злостные ошибки (иногда и
уголовная ответственность).
Непреднамеренные
случайныеошибки чаще связаны с
невнимательностью регистратора,
небрежностью в заполнении документов,
неточностью измерительных приборов,
ошибками в ответах опрашиваемых.
Непреднамеренные
систематическиеошибки возникают
при округлении признака в большую или
меньшую сторону, при использовании ЭВМ.
Ошибки
репрезентативности(представительности)
свойственны несплошному наблюдению,
они возникают вследствие неправильного
выбора единиц для обследования, нарушен
принцип случайного отбора, и выборочная
совокупность не полно характеризует
генеральную.
Б) Способы предотвращения ошибок статистического наблюдения
Чтобы
предупредить возникновение ошибок или
уменьшить их размеры необходимо:
-
обеспечивать
правильный подбор и подготовку кадров; -
вести широкую
разъяснительную работу, применять меры
взыскания за искажение фактов; -
проводить
систематический контроль.
Контроль может
быть: счетным и логическим.
Счетный контроль
заключается в проверке точности
арифметических расчетов.
Логический
контроль проводится путем сопоставления
полученных данных с известными признаками,
логическое осмысление, сопоставление
с данными за прошлый период.
Например, о
заработной плате работников предприятия
можно судить по отчету, по труду и по
отчету о себестоимости продукции.
Сведения о заработной плате должны быть
одинаковыми, сопоставимыми (приведите
примеры).
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
2.4. Точность статистического наблюдения
Под точностью статистического наблюдения понимают степень соответствия значения наблюдаемого показателя, вычисленного по материалам обследования, его действительной величине. Расхождение, или разница, между ними называется ошибкой статистического наблюдения.
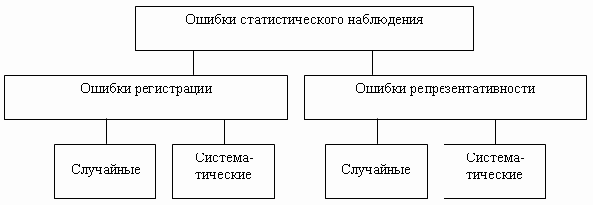
Различают две группы ошибок:
- ошибки регистрации;
- ошибки репрезентативности.
Ошибки регистрации присущи любому статистическому наблюдению, как сплошному, так и несплошному. Они делятся на случайные ошибки регистрации и систематические ошибки регистрации.
Случайными ошибками регистрации называют ошибки, возникающие вследствие действия случайных факторов. К ним можно отнести различного рода непреднамеренные описки: например, вместо возраста человека «15 лет» указано «5 лет», у Ивановой Марии Петровны в графе пол отмечен «Мужской» и т. п. Такие ошибки легко выявляются методом логического анализа, например, если человеку 8 лет, но имеется высшее образование, а в графе «Семейное положение» указано «Состоит в браке», то, естественно, следует исправить возраст. Если объем исследуемой совокупности велик или велика доля отбора при выборочном наблюдении, случайные ошибки регистрации имеют тенденцию взаимопогашаться вследствие действия закона больших чисел, поскольку ошибки, как правило, разнонаправлены и искажают статистический показатель как в большую, так и в меньшую сторону. При небольшом объеме наблюдения требуется тщательная выверка его результатов — логический анализ данных.
Систематические ошибки регистрации чаще всего имеют однонаправленные искажения: они либо увеличивают, либо уменьшают статистический показатель, и, что характерно, подобная ситуация повторяется от обследования к обследованию. Так, по результатам переписей (практически всех!) число замужних женщин превышает число женатых мужчин — мужчинам приятнее ощущать себя неженатыми, а для женщины как бы «стыдно» быть не замужем. Другой пример, когда человек округляет свой возраст — вместо 32 лет говорит 30, вместо 79-80 и т. п. (это явление широко известно и даже получило свое название — «аккумуляция возрастов»). Систематические ошибки регистрации могут возникать и из-за неточностей измерительных приборов, если сбор информации проводят путем непосредственного наблюдения.
Ошибки репрезентативности присущи только несплошному обследованию. Они также делятся на случайные и систематические ошибки.
Случайные ошибки репрезентативности возникают из-за того, что обследованию подвергается не вся совокупность в целом, а только ее часть, и, следовательно, при несплошном наблюдении они присутствуют всегда. В теории статистики разработаны специальные методы для оценки величин таких ошибок, на их основе для наблюдаемых показателей строят доверительные интервалы, т.д. эти ошибки вычисляются и находятся как бы «под контролем».
Хуже обстоит дело, если наряду со случайными ошибками имеются и ошибки систематические.
Систематические ошибки репрезентативности возникают, если при несплошном наблюдении кардинально нарушаются технологии отбора единиц из генеральной совокупности объектов, но чаще — если в ходе обследования не удается получить информацию обо всех отобранных для наблюдения единицах, например, вследствие отказа отвечать на вопросы анкеты, или если человека не удалось застать дома и т. п.
Ошибки статистического наблюдения для наглядности можно изобразить в виде схемы (рис. 2.1).
Рис.
2.1.
Виды ошибок статистического наблюдения
Для повышения точности наблюдения необходимо:
- правильно разработать формуляр статистического наблюдения: вопросы должны быть четкими, однозначными, не допускающими двойного толкования;
- иметь хорошо обученный персонал для проведения обследования;
- строго придерживаться выбранной технологии обследования (если проводится несплошное наблюдение) и помнить, что если не удается опросить какую-то конкретную единицу, отобранную для наблюдения, замена ее на другую единицу может привести к возникновению систематической ошибки репрезентативности;
- провести логический анализ данных, основанный на логических взаимосвязях показателей, после сбора всей совокупности анкет или формуляров;
- целесообразно провести и арифметический контроль данных, т.д. заново пересчитать расчетные величины, если какие-либо показатели получаются в результате определенных арифметических действий;
- предпринять определенные меры по восстановлению данных при наличии незаполненных анкет или формуляров либо при получении результатов обследования сделать поправку на неответы респондентов.
8. Практическая работа № 3. Ошибки
статистического наблюдения
В данной работе мы
рассмотрим пример решения типовой задачи на данную тему.
Статистический материал,
собранный в результате статистического наблюдения, должен быть точным, достоверным.
Поэтому первичный материал перед его обработкой подвергается предварительному
контролю, который может быть логическим и арифметическим (счетным).
Задача.
Имеются следующие исходные данные из формы № 3
«Отчет о поступлении, продаже и остатках товаров» торговой организации за
квартал (тыс. руб.):
Таблица 1
|
Номер п/п |
наименование товарных групп |
Остатки товаров на начало квартала |
Поступило товаров за квартал |
Передано в общественное питание и прочий документированный |
Продано в розницу и прочий недокументированный |
Остатки товаров на конец квартала |
|
|
А |
1 |
2 |
3 |
4 |
5 |
||
|
1 |
Мясо |
32 |
270 |
60 |
212 |
30 |
|
|
2 |
Масло животного |
20 |
95 |
5 |
900 |
20 |
|
|
3 |
Сахар |
35 |
215 |
13 |
213 |
32 |
|
|
4 |
Кондитерские изделия |
55 |
210 |
8 |
197 |
60 |
|
|
Итого |
142 |
790 |
86 |
712 |
142 |
Требуется проверить
правильность исчисления данных гр. 4 и итоговых показателей. Следует иметь в
виду, что движение товаров торговом предприятии можно представить в балансовой
форме, которая имеет вид следующего уравнения:
Остаток на начало периода + поступление за
период =
расход за период + остаток на конец
периода
гр. 1 + гр. 2 = гр. 3. + гр. 4 + гр. 5.
гр. 4 = гр. 1 + гр. 2 – гр. 3 – гр.5
При контроле можно
применить логическую и арифметическую проверки.
Начинаем проверку с
первой товарной группы – мясо. Сличаем остатки, поступление и продажу.
Наблюдаются незначительные
расхождения. Далее проверяем арифметически:
32 + 270 =60 + 212 + 30
302 = 302.
Имеется балансовое
равенство.
Проверяем (гр.4) «продано
в розницу»:
32 + 270 – 60 – 30 = 212.
Ответы увязываются логически и арифметически.
По товарной группе –
масло животное – обращает на себя внимание в гр. 4 цифра 900. Проверяем, есть
ли балансовая увязка:
20 + 95 ≠ 5 + 900 + 20.
Равенства нет.
Исходя из взаимосвязи
показателей исчисляем данные гр. 4.
20 + 95 – 5 – 20 = 90
Следовательно в 4 столбце
необходимо было записать 90, а не 900.
Теперь проверяем
балансовое равенство исходя из проведенного расчета:
20 + 95 = 5 + 90 + 20,
115 = 115.
Оно имеется. Значит,
допущена ошибка. Видимо, при заполнении отчета механически вместо цифры 90 была
записана цифра 900, т.е. подставлен лишний нуль. Вносим исправление: в гр.4,
стр. 2 вместо 900 ставим 90.
Аналогично проверяем
каждую строку отчета по товарной группе.
По товарной группе –
сахар – не получается балансовой увязки
35 + 215≠13 + 213 + 32
Проверяем расчет гр.4:
35 + 215 – 13 – 32 = 205.
В отчете записано 213,
значит, допущена арифметическая ошибка. Вносим исправления: вместо 213
записываем 205.
Проверяем исходя из
расчета –
35+215=13+205+32
250=250
По кондитерским изделиям
балансовая увязка получается
55 + 210 = 8 + 197 + 60,
265 = 265.
Ошибки нет.
Далее проверяем итоговые
показатели отчета, суммируя данные по каждой графе отдельно, и затем увязываем в
балансовое равенство.
Итоги по гр.1, 2, 3, 5
подсчитаны правильно.
По гр. 4 с учетом
внесенных исправлений получаем другое число, а именно
212 + 90 + 205 + 197=
704.
Это число и записываем вместо
712.
Теперь итоговые данные
соответствуют балансовой схеме:
142 + 790 = 86 + 704 +
142,
932 = 932.
Отчет проверен,
исправления внесены, данные можно использовать для оперативной и аналитической
работы.