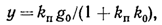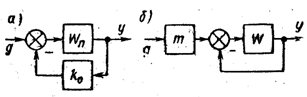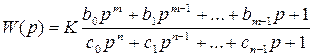Статическая ошибка сау это - TopOshibok.ru - решение и исправление самых разных ошибок

В
любой реальной CАУ
невозможно точное равенство задающего
воздействия g
и управляемой величины y.
Ошибку САУ при этом вычислим согласно
уравнению ошибки как разность этих
воздействий, т.е.:

Учитывая
историю переходных процессов, ошибку
можно представить в виде двух составляющих:
установившейся (статической) и переходной
(динамической):

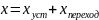
В
линейных САУ установившаяся (статическая)
ошибка определяется частным решением
её дифференциального уравнения, а
переходная (динамическая) ошибка –
решением однородного дифференциального
уравнения.

Таким
образом, установившуюся ошибку САУ в
неподвижном состоянии называют
статической, а ошибку при переходных
режимах – динамической.

Текущая
ошибка отработки переменного сигнала
называется динамической ошибкой САУ.
Динамическая ошибка системы изменяется
с течением времени. Она зависит от
структуры, параметров и характера
изменения воздействий САУ.

38 Повышение качества и синтез линейных сау

В
системе регулирования по отклонению
установившаяся [ошибка имеет три
составляющие:

(⁵—²⁴)

|
где

—
ошибка воспроизведения задающего
воздействия
—
ошибка, вызываемая действием возмущений;
—
ошибка чувствительного элемента,
измеряющего рассогласование

Как
было показано в гл. 4, установившаяся
ошибка может [быть представлена в виде
ряда (4.3). При этом коэффициенты [ошибок
воспроизведения

вычисляют
по передаточной функции

замкнутой
системы для ошибки воспроизведения

Нужно,
заметить, что в статической системе

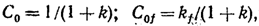
где
k
—
передаточный коэффициент разомкнутой
системна;
—
передаточный коэффициент прямой, цепи
от возмущения

до
выходной координаты у.

Следовательно,
уменьшение установившейся ошибки
постоянных значениях задающего
воздействия и возмущения достигается
увеличением передаточного коэффициента
разомкнутой системы. Однако с
увеличением статической точности в
большинстве случаев уменьшаются запасы
устойчивости I
и при значительном увеличении k
система
становится неустойчивой.

Противоречие
между статической точностью и
устойчивостью проиллюстрировано на
рис. 5.9, где сплошными линиями показаны
логарифмические частотные характеристики
разомкнутой системы с передаточной
функцией

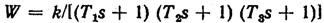
при

Если
передаточный коэффициент увеличить
до k
— 60,
то ЛАЧХ принимает положение, показанное
пунктиром. Частота среза увеличилась
и запас устойчивости по фазе уменьшился
с

до

Столь
малый запас по фазе совершенно недопустим.

При
повышении статической точности путем
увеличения передаточного коэффициента
k
разомкнутой
системы необходимы мероприятия для
обеспечения достаточного запаса
устойчивости. Они будут рассмотрены
в следующем параграфе. Возможно,
вообще говоря, создание такой структуры
системы, которая допускает неограниченное
увеличение передаточного коэффициента
k
разомкнутой
цепи 121.

Другой
путь повышения статической точности
— обеспечение астатизма. В астатической
системе младшие коэффициенты ошибки
имеют следующие значения:

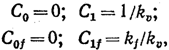
где
k₀
—
передаточный коэффициент разомкнутой
системы называемый в данном случае
добротностью системы по скорости
(или коэффициентом добротности
по скорости). Таким образом, в астатической
системе отсутствует установившаяся
ошибка от постоянного задающего
воздействия и постоянных возмущений.

Для
астатизма относительно возмущения
интегрирующее звено должно быть введено
до точки, в которой приложено возмущение
(рис. 5.10).

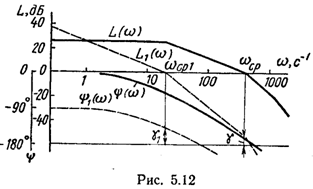
Влияние
интегрирующего звена на динамические
свойства системы

где
сплошными линиями показаны
логарифмические частотные характеристики
системы с передаточной функцией
(5.26). При введении в разомкнутую цепь
этой системы интегрирующего звена
характеристики принимают положение,
показанное пунктиром. Фазочастотная
характеристика переместилась вниз
на —90°, а амплитудно-частотная
характеристика повернулась вокруг
точки а
по
направлению часовой стрелки . В
результате запас устойчивости по фазе
уменьшился с

до
недопустимо малого значения

Система
остается устойчивой, но переходный
процесс будет сильно колебательным.
Кроме того, уменьшилась частота среза
и переходные процессы будут более
продолжительными.

Однако
в других ситуациях введение интегрирующего
звена может не только не ухудшить, а
даже улучшить динамические свойства
системы. Пусть, например, постоянные
времени системы с передаточной функцией
(5.26) имеют следующие значения: Т₁
=
= 0,05 с, Т₂
=
0,0025 с и T₃
= 0,001 с. Логарифмические частотные
характеристики разомкнутой системы
показаны

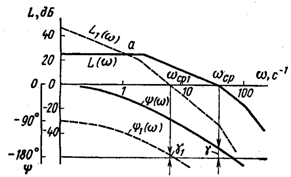
При
введении интегрирующего звена
характеристики принимают положение,
показанное пунктирными линиями. В
данном случае интегрирующее звено
уменьшило частоту среза, но запас
устойчивости по фазе увеличился с

|до

.
Хотя быстродействие системы
уменьшилось, но уменьшилась и
колебательность.

Таким
образом, при повышении статической
точности путем введения интегрирующего
звена могут оказаться необходимыми
мероприятия по сохранению запасов
устойчивости САУ.

Значительно
лучшие результаты получают при получении
астатизма с помощью изодромного звена,
т. е- звена с передаточной функцией

постоянная
времени изодрома.

Если
постоянная времени

достаточно
велика, то запас устойчивости может
быть сохранен неизменным. Уменьшение
передаточного коэффициента разомкнутой
системы должно быть скомпенсировано
увеличением коэффициента усиления
усилителя. Следует учитывать, что при
большом значении

могут
увеличиться старшие коэффициенты
ошибки.

Астатизм
САУ относительно задающего воздействия
можно обеспечить более простыми
способами: неединичной обратной
связью и масштабированием [3).

Структурная
схема системы с неединичной обратной
связью показана на рис. 5.13, а.
В
установившемся режиме регулируемая
координата связана с постоянным задающим
воздействием соотношением

(5.27)

где
k_n
—
передаточный коэффициент прямой цепи
системы.

Если
выполнить основную обратную связь
системы с коэффициентом

и
система относительно задающего
воздействия будет астатической.Структурная
схема системы масштабированием входной
(величины показана на рис. 5.13, б.
Ее
особенность — наличие

усилительного
звена с передаточным коэффициентом
m
на входе. В установившемся режиме

где
k
—
передаточный коэффициент разомкнутой
системы.

При
/л = 1 -f-
УЬ
получаем
у
= g₀
и
система является астатической
относительно задающего воздействия.

Недостаток
этих способов в том, что астатизм
обеспечивается только при сохранении
указанных соотношений между передаточными
коэффициентами. Неточное определение
передаточного коэффициента какого-либо
элемента системы и его изменение в
процессе эксплуатации ведут к появлению
статической ошибки. Астатизм,
достигнутый введением интегрирующего
или изодромного звена, сохраняется и
при изменении параметров системы.
Однако нужно иметь в виду, что введение
двух интегрирующих звеньев в систему,
состоящую из усилительных, апериодических
и колебательных звеньев, сделает ее
структурно-неустойчивой. Возможно
обеспечение астатизма и более высокого
порядка. При этом из-за введения большого
числа интегрирующих или изодромных
звеньев и мероприятий, обеспечивающих
требуемые динамические свойства,
структура САУ значительно усложняется.

Компенсация
внешнего воздействия (обеспечение
инвариантности). Рассмотренные выше
способы улучшения статических и
динамических свойств системы связаны
лишь с изменениями параметров
элементов САУ и структуры ее отдельных
участков, но при этом не затрагивают
принципа действия системы.

Помимо
принципа регулирования по отклонению
существует принцип регулирования
по внешнему воздействию. Значительный
эффект дает их одновременное использование.
В этом случае системы называются
комбинированными. Кроме замкнутого
контура они имеют дополнительную
цепь влияния внешнего воздействия —
возмущения или задающего.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

ОШИБКИ В СИСТЕМАХ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

— в общем случае это функционалы, характеризующие отклонение показателя качества работы (Ф) системы автоматического управления (САУ) от его заданного или экстремального значения Показатель качества определяется -эконом. требованиями к САУ и может представлять либо совокупность заданных (требуемых) значений регулируемых величин системы, напр., в системах автомат, регулирования (САР), либо некоторую функцию от этих величин (напр., в системах экстремального регулирования или в самонастраивающихся системах). В качестве меры отклонения обычно принимают разность , причем величины, входящие в это выражение, в общем случае векторные. О. в с. а. у. зависят от процесса управления, т. е. являются ф-цией времени Эта зависимость определяет два вида ошибок: динамические (при и установившиеся Динамические О. в

с. а. у. могут оцениваться по значениям, взятым в определенные моменты времени (напр., максимум ошибки в процессе управления), либо по интегральным критериям (напр., среднеквадратичная ошибка , где Т — период наблюдения).

О. в с. а. у. зависят прежде всего от структуры систем, а также от возмущений, действующих на объект управления, от ограниченности управляющего воздействия по величине и мощности, погрешностей в измерительных цепях и т. п. В связи с этим в линейных САУ выделяют вынужденную составляющую ошибки, определяемую действием возмущения на объект управления или задания, и свободную составляющую, определяемую начальным отклонением показателя качества работы САУ. Кроме того, рассматривают О. в с. а. у., связанные с действием случайных сигналов на объект управления и соответствующие оценки этих ошибок (например, математическое ожидание и дисперсия). В следящих САР вынужденная составляющая ошибки определяется изменением задания во времени . При этом помимо основной ошибки разности задания и регулируемой величины, называемой также ошибкой по положению, различают и ее производные по времени 1, 2-го и более высоких порядков, называемые соответственно ошибками по скорости, по ускорению и т. д. Для линейных следящих САР, если задание меняется медленно по сравнению с изменениями импульсной переходной ф-ции системы, вынужденная составляющая ошибки может быть представлена как линейная функция от задания и его производных по времени:

где — порядок той производной задания, которая имеет достаточно малую величину и изменением которой во времени можно пренебречь, коэффициенты ошибок, определяемые как

где передаточная функция системы по ошибке. Пользуясь формулами (1) и (2), можно по передаточной ф-ции систем, по ошибке и по виду зависимости определить характер изменения вынужденной составляющей ошибки. Например, в случае задания и системы с астатизмом 1-го порядка (один нулевой корень передаточной ф-ции) получают т. е. вынужденная составляющая ошибки равна нулю.

С помощью методов автоматического управления теории структура САУ может быть выбрана таким образом, чтобы минимизировать О. в с. а. у. при принятой ее оценке или минимизировать некоторый показатель, связанный с изменением ошибки во времени (напр., время переходного процесса). Путем рационального выбора структуры некоторые виды ошибок САУ могут быть сведены к нулю, напр., установившиеся ошибки в САР при интегральном регулирования законе или динамические ошибки, связанные с действием возмущений на объект управления в некоторых случаях инвариантных систем управления. См. также Астатизм -го порядка, Инвариантность систем автоматического управления.

Лит.: Современные методы проектирования систем автоматического управления. М., 1967; Ивахненко А. Г. Электроавтоматика. К., 1957 [библиогр. с. 440—442]; Воронов А. А. Основы теории автоматического управления, ч. 1. М. Л., 1965 [библиогр. с. 382—392]. Л. М. Бойчук.

Виды ошибок регулирования и методы их снижения.

Прямые показатели качества подразделяются
на показатели качества динамического
и установившегося режимов.

Показателями качества динамических
режимов определяются из графика
переходного процесса и основными из
них являются (рис.1.42):

—перерегулирование или забросσ,
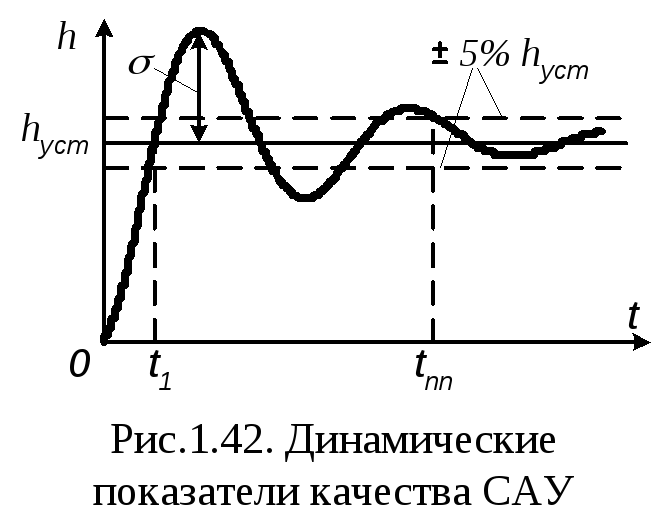
равный максимуму отклонения значения
переходного процесса относительно
установившегося значения процессаh_ycm;

— время первой установки t₁,
определяемое моментом первого пересечения
графиком переходного процесса
установившегося значенияh_ycm;

— время переходного процесса t_ПП,
определяемое момент окончательного
входа графика переходного процесса в
зону допуска, равную±5%от
установившегося значения процессаh_ycm.

Для всех названных динамических
показателей качества невозможно в общем
случае получить формулы для их расчета.
Это является существенным препятствием
для решения задач анализа и синтеза
САУ.

Показателями качества установившихся
режимов являются ошибки регулирования,
равные абсолютной величине разности
между заданным и фактическим значениями
сигналов САУ и которые в зависимости
от вида входного сигнала САУ подразделяются
на статические (ε_СТ) и
скоростные ошибки (ε_СК) и
ошибки (ε_m)
при отработке гармонического входного
сигнала.

Д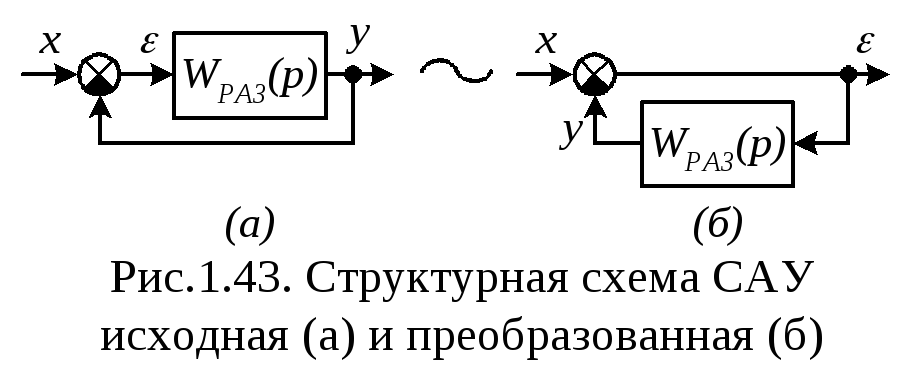ля
всех названных ошибок регулирования
можно в общем случае получить формулы
их расчета.

Из структурной схемы замкнутой САУ
(рис.1.43) следуют выражения передаточной
функции САУ W_ε(p)по ошибке и изображенияε(р)ошибки
регулирования:

Расчет ошибки ε_mотработки гармонического входного
сигналаx=X_msinωt
производится по формуле

где
— модуль комплексного числа.

Статическая (ε_СТ) и
скоростная (ε_СК) ошибки
равны установившимся значениям оригиналаи,
или в общем виде, по формуле.
Значениевычисляют через изображениеε(р)
по доказываемой в теории операционного
исчисления формуле предельного перехода,

(1.54)

Выражение передаточной функции
разомкнутой САУ в общем случае может
быть приведено к виду:

(1.55)

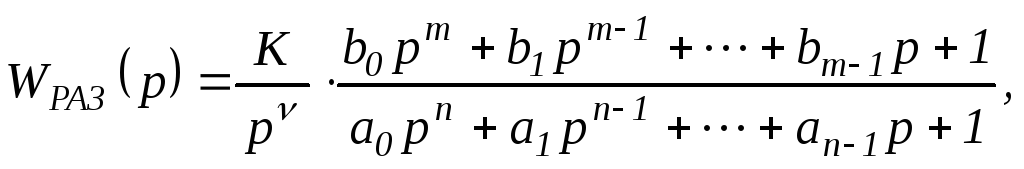
где К– общий коэффициент усиления
разомкнутой САУ:

ν— порядок астатизма САУ, причемνявляется целым неотрицательным
числом.

Для удобства вычислений по формуле
(1.54) подставим в нее выражение W_РАЗ(р)из (1.55) и выполним предельный переход:

(1.56)

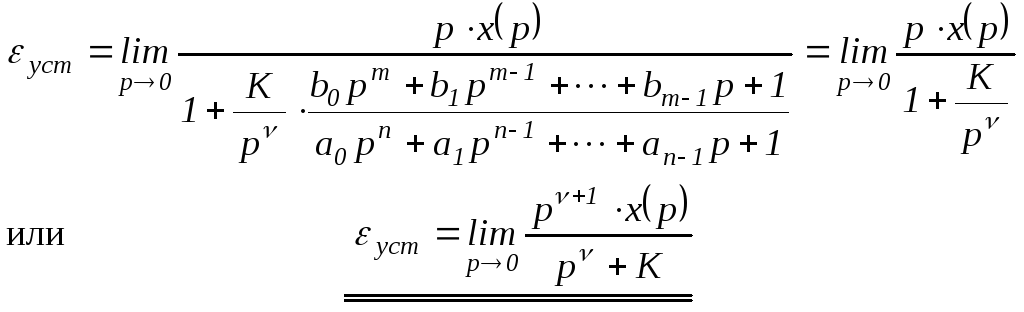
Статическая ошибка регулирования ε_СТрассчитывается при постоянном входном
сигналеx(t)=X=const,
а скоростнаяε_СК— при
входном сигналеx=Vt,
изменяющемуся во времени с постоянной
скоростьюV=const.
Далее расчеты статической (ε_СТ)
и скоростной (ε_СК) ошибок
выполним раздельно.

Расчеты статической ошибки εСт регулирования

Входной сигнал x(t)=X=constи изображением его является.
В соответствии с (1.56) статическую ошибкуε_СТследует вычислять по
формуле

(1.57)

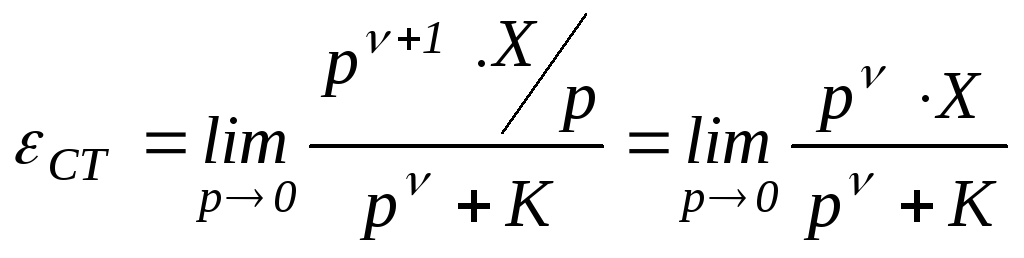
1). Пусть в (1.57) значение порядка νастатизма САУ равно нулю:ν=0. Такая
САУ называется статической. Тогда
статическая ошибкаε_СТбудет равна

В статической САУ имеется статическая
ошибка ε_СТ, которую можно
только уменьшить путем увеличения
общего коэффициента усиленияКразомкнутой САУ, но обратить в ноль ее
нельзя.

2). Пусть в (1.57) значение порядка νастатизма САУ равно 1:ν=1. Такая САУ
называется астатической 1-го порядка.
Тогда статическая ошибкаε_СТбудет равна

В астатической САУ 1-го порядка статическая
ошибка ε_СТравна нулю,
т.е САУ является абсолютно точной. Можно
проверить, что при астатизме САУ выше1, статическая ошибка регулирования
всегда будет нулевой.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Качество управления. Ошибка системы. Система автоматической стабилизации скорости вращения электродвигателя

Страницы работы

Фрагмент текста работы

6 Качество управления

Ошибка системы

Любая автоматическая система должна быть не
только устойчивой, но и достаточно точной в работе. В любой реальной системе
невозможно точное равенство задающего воздействия g
и управляемой величины y во всё время процесса управления. Возникает
ошибка системы x=g—y. Её можно представить в виде X=X_п+Х_уст.,
где X_п – переходная ошибка, а Х_уст. – это ошибка
системы по окончанию переходного процесса. Для определения X_п приходится
либо находить корни характеристического уравнения, либо использовать критерии
качества, не требующие нахождения ошибки X_п (частотный критерий качества, интегральный
критерий качества).

6.2 Ошибки САУ в установившемся режиме

Рассмотрим неподвижное состояние, когда g=const ,или f=const. Имеются 2 вида систем: статические и
астатические. Статической системой автоматического управления называется
система, переходная функция которой в разомкнутом состоянии при размыкании по
ошибке имеет вид:

В статических САУ интегрирующие звенья или отсутствуют.
или охвачены обратной связью, т.е. нет множителя p
в знаменателе.

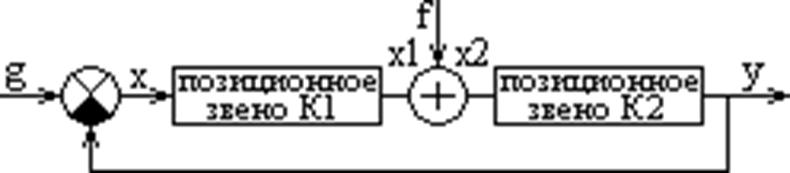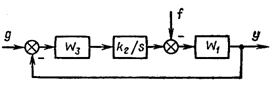
Определим ошибку Х_уст., если g=g₀, f=f₀,
тогда Х_уст.=g₀—y_уст. (а),

Но y_уст.=Х_2уст.К₂= (Х_1уст.+f₀)К₂= (Х_уст.К₁+f₀)K₂
(в).

Подставим (в) в (а): Х_уст.= g₀-К₁К₂
Х_уст.-К₂f₀. Х_уст.(1+K₁K₂)= g₀—K₂f₀.

Пусть К₁К₂=К, тогда Х_уст.=
(g₀/1+К)-( К₂f₀/1+К).

Из выражения (в) следует, что для
уменьшения ошибки от задающего воздействия g
необходимо увеличивать общий коэффициент передачи звеньев, стоящих до
возмущения (К₁) и уменьшать для стоящих после возмущения(K₂). В
статических САУ ошибку от задающего воздействия легко ликвидировать
масштабированием. Этот метод рассмотрим позднее. Исследуем ошибку от
возмущающего воздействия.

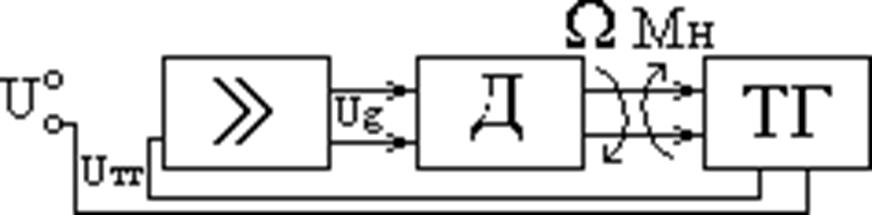
Пример: Система автоматической стабилизации скорости вращения
электродвигателя.

М_н – момент нагрузки.

При изменении М_н меняется скорость вращения
ω, что приводит к изменению U_тг (напряжения, вырабатываемого тахогенератором). При
правильном выборе знака обратной связи скорость вращения будет меняться
значительно меньше, чем при отсутствии обратной связи. Покажем, что в системе
будет установившаяся ошибка. При изменении момента нагрузки М_н
изменится и момент двигателя, потому что в установившемся режиме M_дв = М_н.
M_дв меняется при изменении ω или U_двиг., но U_двиг. (U_д) при постоянном U может измениться
лишь при изменении U_тг, т.е. U_д = U— U_тг. Поэтому при изменении М_н обязательно
меняется ω, т.е. появляется ошибка.

6.3 Оценка динамических
свойств САУ по переходной характеристике

1) Качество оценивается по перерегулированию

σ %= (y_m-y_уст_.)/ y_уст_.·100%
.

σ %= |10-50|%.

Рис 2) Быстродействие можно оценивать как время
переходного процесса от момента подачи скачка до момента t_п, начиная с
которого для всех t ≥ t_п: |y(t)- y_уст. | ≤ Δy_уст., Δy_уст.=1-5%.

6.4 Корневые оценки
динамических свойств САУ

О динамических свойствах САУ можно судить по
расположению полюсов и нулей замкнутой системы управления.

Рис 1-й вариант: имеется один вещественный полюс.

; => .

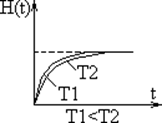
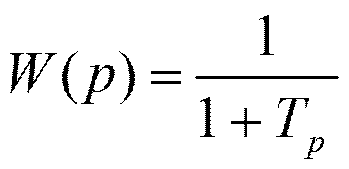
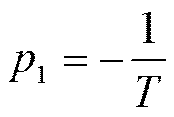
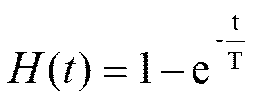
Чем меньше Т, тем быстрее растёт сигнал на выходе.

Рис При приближении полюса к мнимой оси
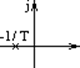
быстродействие уменьшается.

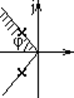
2-й вариант: два комплексно сопряжённых полюса.

Рис Рис ; .

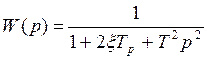
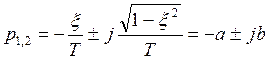
Можно показать, что. Перерегулирование зависит от
параметра —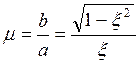
этот параметр называется колебательностью. При равном удалении полюсов
от мнимой оси σ % больше в той системе, в которой полюсы дальше отстоят от
вещественной оси. Увеличение μ приводит к возрастанию перерегулирования, чтобы
колебательность системы не превышала заданной величины, полюса должны быть
расположены внутри области, в которой tgφ=μ.

Рис Если еще имеется и отрицательный нуль
(корень числителя) – это эквивалентно действию дифференцирующего звена и
колебательность возрастает с приближением нуля к мнимой оси. Добавление
вещественного полюса уменьшает перерегулирование и увеличивает время
переходного процесса. Если имеется несколько полюсов и нулей, но они достаточно
удалены от мнимой оси, то их влиянием можно пренебречь.

Улучшение качества
правления

Способы уменьшения ошибки

Общими методами уменьшения ошибки
(повышения точности) САР являются:

1.
Увеличение
коэффициента усиления K
разомкнутой цепи

2.
Повышение порядка
астатизма r

3.
Применение
регулирования по производным

4.
Включение
масштабирующих устройств на входе или выходе

6.5.1.1 Повышение
точности систем увеличением коэффициента усиления

Метод эффективен, широко применяется, но обычно
увеличение K приводит к
уменьшению запаса устойчивости

Повышение точности
систем увеличением порядка астатизма

Астатическими называются системы, переходная функция которых в
разомкнутом виде имеет вид: 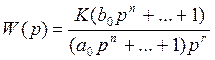. Степень r
называется порядком астатизма.

В астатической системе обязательно имеются
интегрирующие звенья.

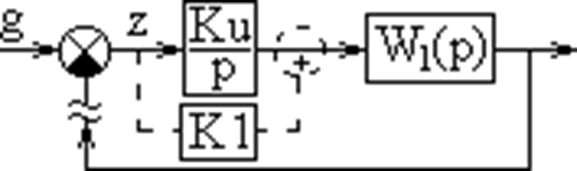
К_u/p– интегрирующее звено.

Рассмотрим установившееся состояние системы при g=g₀, f₁=f₁₀, f₂=f₂₀. После
окончания переходного процесса y=y_уст. Это может быть только если Х₂=0,
иначе интегратор вырабатывал бы возрастающий сигнал Х₃. Х₂=К₁Х_уст.+
f₁₀=0. Найдём отсюда Х_уст.=- f₁₀/ К₁.

В выражение не входит f₂ и К₂.
Ошибка астатической системы в режиме неподвижного состояния зависит лишь от
возмущающего воздействия, приложенного до интегрирующего звена. Поэтому
надо создавать системы в которых возмущение приложено после интегрирующего
звена, тогда ошибка равна нулю.

Статическую систему ,не имеющую интегрирующих звеньев,
будем называть

Информация о работе

Уважаемый посетитель!

Чтобы распечатать файл, скачайте его (в формате Word).

Ссылка на скачивание — внизу страницы.

Источник

1. Точность САУ

2. План

1 Общие положения
2 Понятие о типовых режимах САУ
3 Теорема о предельном значении оригинала и
методика определения установившихся
ошибок
4 Ошибки статических и астатических САУ в
типовых режимах
5 Ошибки САУ при произвольных входных
сигналах (коэффициенты ошибок)
6 Методы повышения точности САУ

3. 1 Общие положения

Точность является важнейшим критерием
качества систем. В настоящее время
практически все многочисленные
элементы любых технических систем
изготавливаются автоматически т.е. с
помощью САУ. Таким образом точность
САУ определяет качество продукции,
товаров, их надежность,
энергопотребление, долговечность и т.д.
и т.п.

4. 2 Понятие о типовых режимах САУ

Точность САУ принято оценивать по величине
ошибок в типовых режимах. Типовыми
называются режимы просто описываемые
математически и имеющие четкий
физический смысл. К ним относятся:
— режим покоя, когда х(t)=const;
— режим линейно-нарастающих сигналов, когда
х(t)=a*t, где а=const;
— режим гармонических входных сигналов,
когда х(t)=A*sinωt.

5.

ε
Итак, нам необходимо вычислить
установившуюся ошибку ε(t) при t→∞,
при типовых режимах и по ней можно
будет судить о точности САУ.

6. 3 Теорема о предельном значении оригинала и методика определения установившихся ошибок

Сформулируем для этого теорему о
предельном значении оригинала:
limX(t)=limX(s),
t→ ∞
s→ 0
т.е. предел оригинала при t→∞ равен
пределу изображения по Лапласу при
s→0.

7.

Передаточная функция САУ по ошибке:
( s)
1
F (s)
x( s ) 1 w p ( s )
Итак, чтобы определить установившуюся (при t→ ∞)
ошибку САУ нужно:
— Найти x(s) зная x(t)
— Определить Fε(s)
— Найти ε(s)= X(s) * Fε (s)
— Определить εуст= lim ε(s)
S→0

8. 4 Ошибки статических и астатических САУ в типовых режимах

Рассмотрим ошибки САУ в типовых режимах:
1. Ошибка САУ в покое (статическая ошибка)
X(t)=X0=const X(s)=X0
K
Пусть W p ( s )
— статическая
(T1S 1)(T2 S 1)
САУ, поскольку в знаменателе нет
множителя S, т.е. интегрирующего элемента
в системе

9.

По теореме о предельном значении аргумента
1
ст lim (t ) lim (s) (s) * F (s) (s) *
t
s 0
1 Wp ( s)
Подставляя Wp(s) в (1) получим:
X 0 (T1S 1)(T2 S 1)
X0
ст lim
s 0 (T S 1)(T S 1) K
1 K
1
2
(1)

10.

Статическая ошибка в
статической САУ в
(1+К) раз меньше
входной величины.
y(t)
X0
εст
t

11.

Пусть теперь
— астатическая САУ (есть
интегратор, т.е.
множитель S в знаменателе передаточной
функции)
K
W p ( s)
S (T1S 1)
ст
X 0 *1
X 0 S (TS 1)
lim (s) lim
lim
0
s 0
s 0 1 W ( s )
s 0 K S (TS 1)
p

12.

Таким образом,
статическая ошибка
в астатической САУ
равна 0
y(t)
X0
εст=0
t

13.

2. Второй типовой режим — движение с постоянной
скоростью (скоростная ошибка)
x(t)=at
a=cost
x( s)
a
s
Пусть:
K
W p ( s)
— статическая САУ
(T1S 1)(T2 S 1)
Тогда:
a (T1S 1)(T2 S 1)
(
t
)
lim
t a s 0 s K (T1S 1)(T2 S 1)

14.

x(t)=at
εα→∞
y(t)
α
t
tgα=a
Ошибка в статической
САУ при линейнонарастающем входном
сигнале x(t)=at
возрастает до ∞.
Т.о. статические САУ в
таком режиме не
работоспособны.

15.

Пусть теперь
K
Wp ( s)
S (TS 1)
— астатическая САУ
Тогда
S ( ST 1)
a
a
*
t a ( t ) lims 0(s) lim
s 0 s
K S (TS 1) K

16.

a
a
K
x(t)
y(t)
t
Т.о. в астатических
САУ при x(t)=at
a=const
устанавливается
ошибка в “К” раз
меньше чем “a”, т.е.
они работоспособны
в таких режимах.

17. 3. Третий режим — гармонических входных сигналов.

Пусть x(t)=xmsinωkt
xm,ωk – амплитуда и
частота “качки”.
x(s)
ε(s)
Wp(S)
y(s)

18. Определим амплитуду εm ошибки САУ в этом режиме.

Для этого найдем:
1
( s)
F ( s)
1 W p ( s ) x( s )
— ПФ САУ по ошибке
Подставим S=jωk
X ( j k )
( j k )
1 Wp ( j k )
(1)

19. Выражение (1) справедливо и для амплитуд, т.е.

m
xm
Xm
1 W p ( j k ) W p ( j k )
Откуда следует:
W p ( j k )
Ак
20 lg
xm
xm
(2)
m
Прологарифмируем (2):
L(ω)
m
ω
ω=ωk
Ак – контрольная точка
20 lg W p ( j k ) 20 lg
xm
m
(3)

20.

Из (3) следует, что САУ будет иметь амплитуду
ошибки не более допустимой εдоп, если
20 lg W p ( j k ) L( k ) 20 lg
xm
доп

21. Т.о. чтобы ошибка САУ в гармоническом режиме не превышала допустимой εдоп необходимо:

1. Определить положение контрольной точки
Ак с координатами:
xm
ω=ωк и 20 lg
доп
2. Обеспечить прохождение L(ω) выше
контрольной точки Ак

22. 5 Ошибки САУ при произвольных входных сигналах (коэффициенты ошибок)

Пусть на вход САУ действует сигнал x(t)
произвольной формы. Чтобы определить
ошибку ε(t) в этом случае найдем вначале ее
изображение.
x(s)
ε(s)
Wp(S)
y(s)

23.

( s)
Поскольку:
1
F ( s)
x( s ) 1 W p ( s )
(1)
То:
x( s )
( s)
1 Wp ( s)
(2)
Разложим далее Fε(s) по возрастающим
степеням S в ряд, тогда (2) можно записать в
виде:
C2 2 C3 3
( s ) C0 C1S S S x( s )
2!
3!
(3)

24.

При нулевых начальных условиях
S p
d
dt
и переходя в (3) к оригиналам можно записать
2
dx(t ) C2 d x(t )
(t ) C0 x(t ) C1 *
*
2
dt 2! dt
Величины С0, С1, С2 … называются
коэффициентами ошибок САУ.
(4)

25. Чтобы определить ошибку САУ при произвольной форме входного сигнала x(t) необходимо:

1. Определить передаточную функцию
САУ по ошибке Fε(s);
2. Разложить в ряд Fε(s) путем деления
ее числителя на знаменатель и найти
коэффициенты С0, С1, С2 …;
3. Подставить коэффициенты ошибок в
(4) и найти установившуюся ошибку
ε(t).

26. Пример

Найти ошибку в САУ при:
Если:
bt 2
x(t ) x0 at
2
K
W p (s)
S (T1S 1)(T2 S 1)

27. Решение:

1.Найдем
1
F (s)
1 Wp ( s)
1
S (T1S 1)(T2 S 1)
T1T2 S 3 (T1 T2 ) S 2 S
F ( s)
1 W p ( s) K S (T1S 1)(T2 S 1) T1T2 S 3 (T1 T2 ) S 2 S K

28. 2. Разложим (1) в степенной ряд путем деления числителя на знаменатель

S (T1 T2 ) S T1T2 S
2
—
—
3
1
1
S S 2 * (T1 T2 ) S 3 …
K
K
1 2
T T 3
T1 T2 S T1T2 1 2 S …
K
K
1 2
T1 T2 S …
K
K S (T1 T2 )S 2 T1T2 S 3
1 2
1 1
S * T1 T2 S
K
K K

29.

Ограничимся первыми тремя членами
ряда, т.к. входной сигнал X(t) имеет
лишь три не нулевых первых
производных.

30.

3. Итак:
1
1 2
T1T2
F ( s ) S
2 S
K
K
K
(5)
Сопоставляя (5) и (4) имеем коэффициенты
ошибок:
T1T2
1
1
С0=0
C2 2
2 (6)
C1
K
K
K

31.

4. Определим далее производные от X(t):
bt 2
x(t ) x0 at
2
dx(t )
a bt
dt
d 2 x(t )
b
dt
(7)

32.

5. Подставляя коэффициенты С0, С1, С2… и
производные (7) в (4) получим:
1
1
T1T2
(t ) * (a bt )
2 *b
K
K
K
Т.е. ошибка с течением времени будет
нарастать до ∞ из-за члена “bt”.

33. 6 Методы повышения точности САУ

Анализируя выражения для
коэффициентов ошибок отметим, что:
1. Все коэффициенты обратнопропорциональны коэффициенту К –
усиления системы;
2. Чем выше порядок астатизма “v” тем
большее количество первых
коэффициентов ошибок равны 0

34. ВНИМАНИЕ

Порядок астатизма “v” определяется числом
интегрирующих звеньев в контуре системы.
Формально “v” равно показателю степени
множителя S в знаменателе передаточной
функции wp.
N ( s)
wp v
S M ( s)

35. 1. Первый способ повышения точности САУ – увеличение К

Т.о. самым универсальным способом
повышения точности САУ являются
увеличение коэффициента К усиления
системы. При этом все коэффициенты
ошибок уменьшаются, а это означает, что
система во всех режимах работы будет иметь
меньшие ошибки. Однако этот способ
снижает запасы устойчивости системы и рано
или поздно приводит к полной потере
устойчивости. Это можно показать на
примере критерия Найквиста.

36.

Im
K2>K1
К1
К2
-1;j0
wp(jω)
Re

37. 2. Способ повышения точности САУ – путем увеличения астатизма “v”

Этот способ исключает первые коэффициенты в
ряду ошибок. Действительно:
v=0 (статическая САУ)
Все коэффициенты не
равны 0, т.е. с0≠0 с1≠0
с2≠0 …, т.е. статическая
система в любых
режимах работы, в т.ч. и
в покое будет иметь
ошибки

38.

v=1 (астатическая САУ
с астатизмом
первого порядка)
с0=0 с1≠0 с2≠0 …, т.е.
такая система не
будет иметь ошибки
в режиме покоя.
v=2 (астатическая САУ
с астатизмом
второго порядка)
с0=0 с1=0 с2≠0 с3≠0 …,
такая система не
будет иметь ошибок
не только в режиме
покоя, но и при
линейнонарастающем
сигнале

39.

К сожалению, этот способ также снижает
запасы устойчивости САУ. Действительно:
Im
v=2
Re
-1;j0
v=0
v=1
По критерию Найквиста системы при v=0, v=1
могут быть как устойчивыми так и не
устойчивыми, но при v=2 они становятся не
устойчивыми при любых коэффициентах К.

40. 3. Повышение точности САУ с использованием принципов комбинированного управления.

Принцип комбинированного управления
состоит в том, что в дополнение к принципу
обратной связи реализуется принцип
управления по возмущению. V(t)
Измеритель
x(t)
y(t)
Регулятор
Объект

41.

Здесь сочетается (комбинируются) оба
названных принципа:
— Управление по возмущению (за счет
измерения возмущения v(t) и выработки
дополнительного управляющего сигнала
компенсирующего действия возмущения);
— Управление по отклонению или принцип
обратной связи реализуется за счет главной
отрицательной обратной связи и сигнала
рассогласования и регулятора.

42.

Рассмотрим следящую систему с
комбинированным управлением и найдем
передаточную функцию обычной системы
эквивалентной по точности.
W3(S)
y(s)
x(s)
W1(s)
W2(S)
≡
Wэ(S)

43.

Для этого приравняем их передаточные функции.
wэ (s)
y(s) w1 (s)w2 (s)
w2 (s)
F (s)
w3 (s)
x(s) 1 w1 (s)w2 (s)
1 w1 (s)w2 (s) 1 wэ (s)
(1)

44.

Из (1) после некоторых преобразований можно
получить:
w1 ( s) w3 ( s)
wэ ( s) w2 ( s) *
1 w3 ( s) w2 ( s)
(2)
Как видно из последнего выражения, при:
1
w3 ( s )
w2 ( s )
wэ(s)=∞
Условие (3) называется условием полной
инвариантности.
(3)

45.

Это означает, что ошибка рассматриваемой
комбинированной следящей системы будет
равна 0 в любых режимах работы поскольку:
( s)
1
F ( s )
0
x( s ) 1 wэ ( s )

46.

Достоинство принципа комбинированного
управления в том, что он не изменяет
(не ухудшает) устойчивости и качества
переходных процессов. Однако,
реализовать точно условие полной
инвариантности практически
невозможно.

47. ПРИМЕР

Пусть:
K
w2 ( s)
S (T1S 1)(T2 S 1)
Найдем:
1
S (T1S 1)(T2 S 1) 1
T1 T2 2 T1T2 3
w3 ( s)
S
S
S
w2 ( s)
K
K
K
K

48.

Структурная схема такой комбинированной
следящей системы имеет вид:
III
II
I
T1T2
S3
K
T1 T2 2
S
K
1
S
K
x(s)
w1(s)
K
S (T1S 1)(T2 S 1)
y(s)

49.

Итак, чтобы точно реализовать условие полной
инвариантности в нашем примере необходимо:
• реализовать канал I (тахогенератор)
• реализовать канал II (это 2-ая производная от угла)
• реализовать канал III (это 3-ая производная от угла)
Точно это сделать практически нельзя. Кроме того, в
реальных САУ имеется множество нелинейностей,
которые мы не учитывали при выводе условия
полной инвариантности.
Поэтому часто используют частично-инвариантные
САУ, т.е. САУ не имеющие ошибок лишь в некоторых
режимах.

Источник

Уровень сложности
Средний

Время на прочтение
6 мин

Количество просмотров 3.5K

7.1 Общие понятия о точности процесса управления

Как отмечалось в разделе 6, интегральная оценка управления складывается из 3-х основных понятий:

устойчивость САР;
точность САР;
качество переходного процесса.

Очевидно, что главным является устойчивость САР (или запас устойчивости). Если САР не устойчива или очень мал запас устойчивости, то говорить о точности (неустойчивая САР) или о качестве переходного процесса (малые запасы устойчивости) не имеет смысла.

Если САР устойчива и запасы устойчивости достаточны по величине, то понятие точность САР является весьма важным показателем.

Точность определяют по отработке САР следующих видов воздействий:

ступенчатое внешнее воздействие (управляющее или возмущающее) часто называется постоянным внешним воздействием;
линейное внешнее воздействие т.е. линейно изменяющееся внешнее воздействие (управляющее или возмущающее);
гармоническое воздействие, т.е. ;
медленно меняющееся произвольное внешнее (управляющее или возмущающее) воздействие;
другие воздействия (параболическое, импульсное и т.д.).

Наиболее часто для оценки точности САР используются постоянное (ступенчатое) и линейное воздействия.

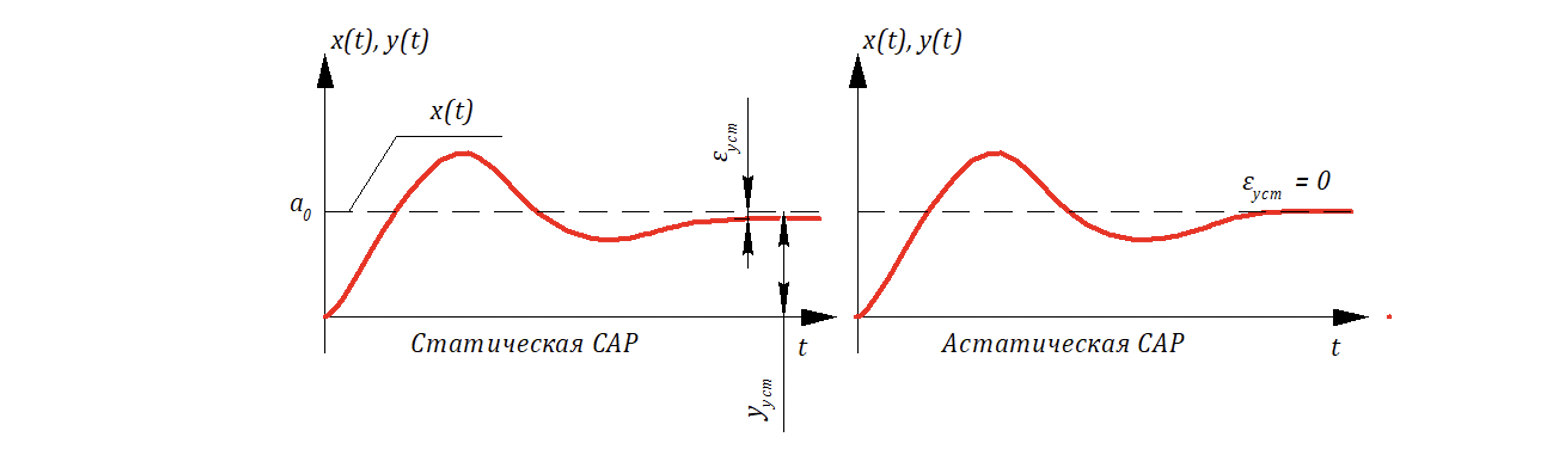
Различают статические и астатические САР:

Рисунок 7.1.1 Переходные процессы статической и астатической САР

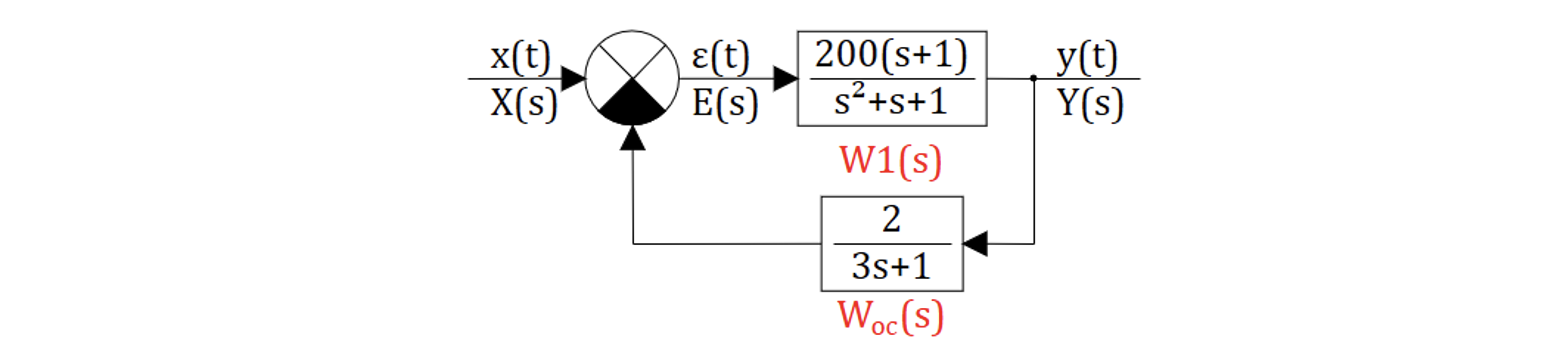
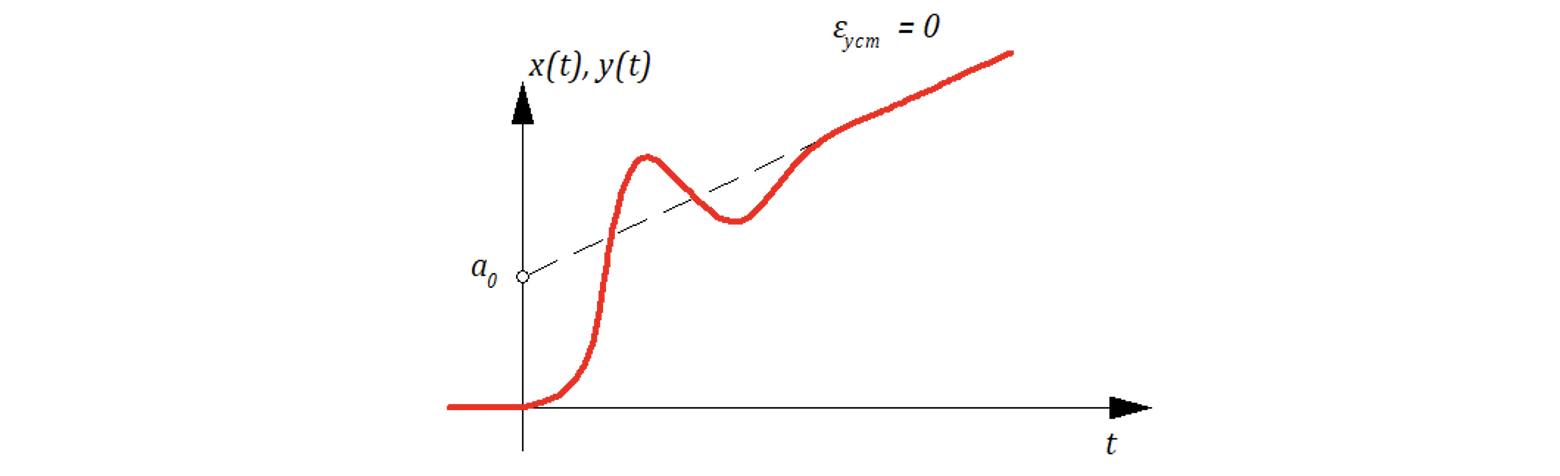
Данные графики будем относить к следующей структуре САР:

Рисунок 7.1.2 Струкутурная схема САР для анализа устойчивости

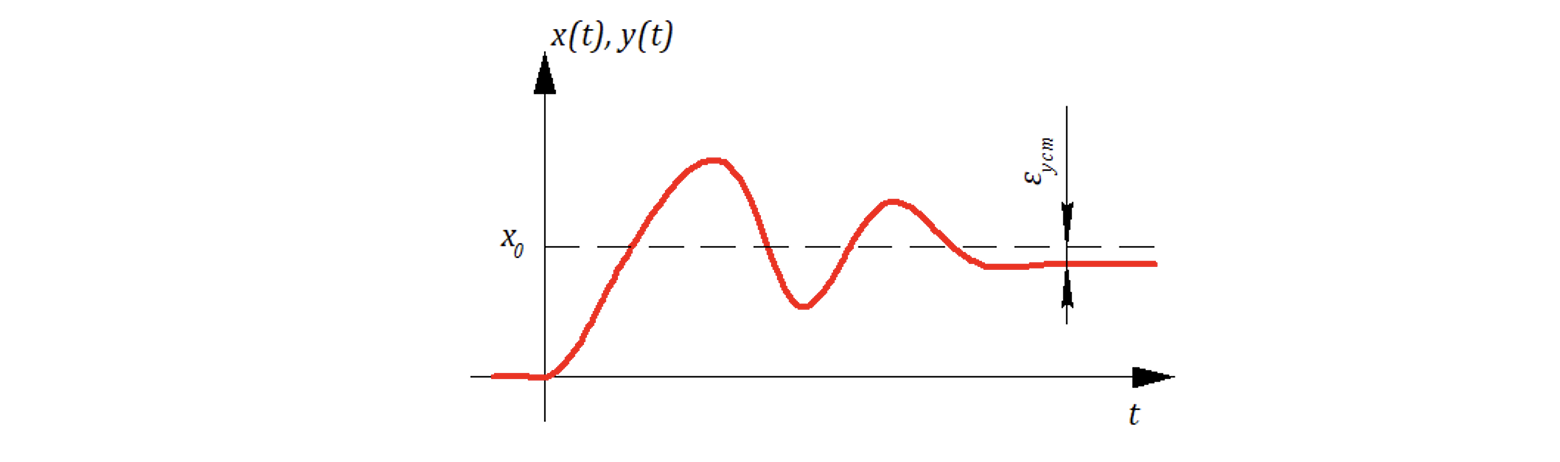
По установившейся ошибкой понимают:

$\varepsilon _{уст.}=\lim_{t\rightarrow\infty}\varepsilon(t)$

Если входное воздействие — ступенчатое, to $\varepsilon_{уст.}$ — «постоянная» ошибка.

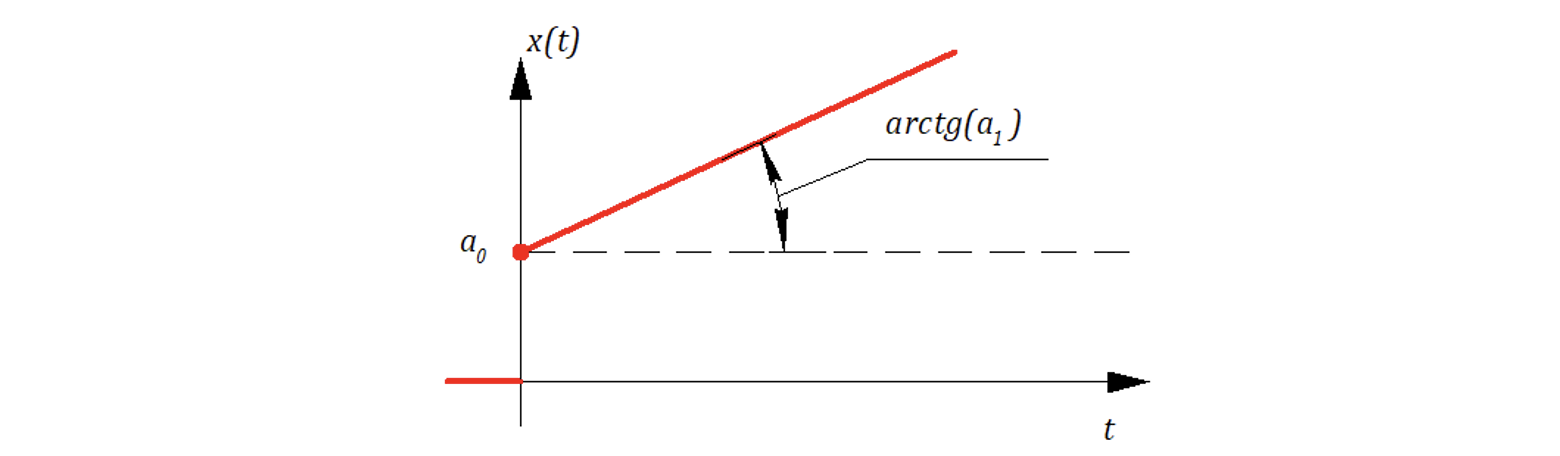
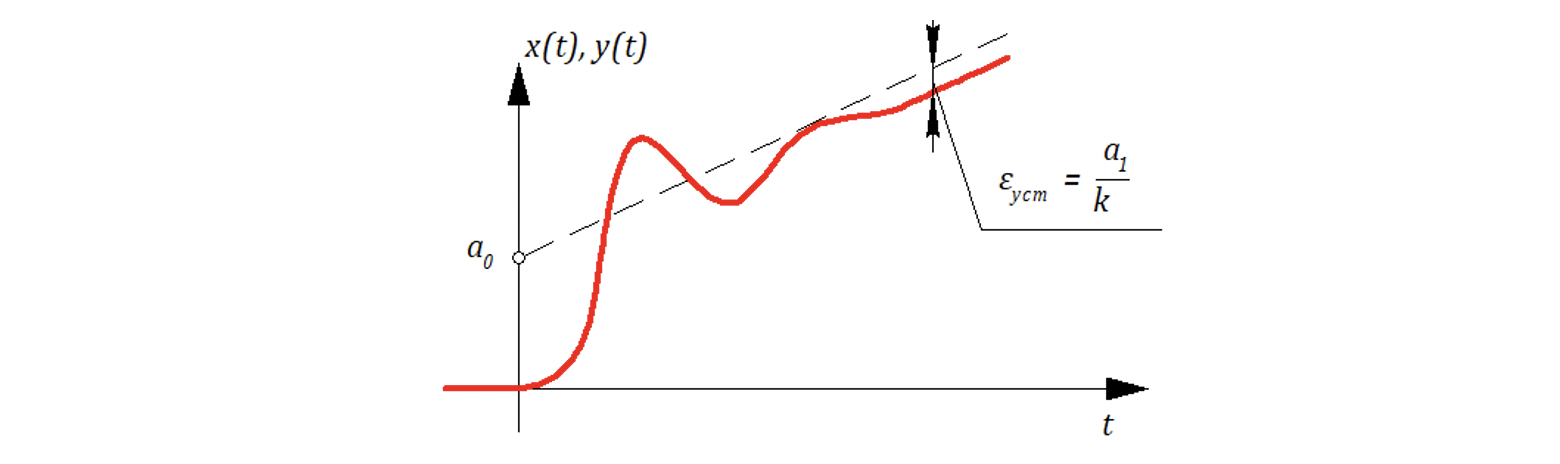
Если входное воздействие — линейное, to $\varepsilon_{уст.}$ — «скоростная» ошибка.

Различают астатизм по управляющему воздействию, а также астатизм по возмущающему воздействию, причем наличие того или иного астатизма определяется по-разному (см. следующие подразделы).

Главной задачей системы автоматического регулирования является точная и быстрая (но плавная) отработка управляющих воздействий, причем учитывая требования качества САР – точность очень важная «характеристика».

Наиболее часто точность САР оценивают по отработке управляющих воздействий. Рассмотрим последовательно различные виды управляющих (задающих) воздействий.

7.2 Точность при постоянном задающем воздействии. Постоянные ошибки

Для упрощения дальнейших преобразований будем считать, что структура САР приведена к стандартному виду (см. п.5 Передаточные функции и уравнения динамики система автоматического регулирования):

Рисунок 7.2.1 САР общего вида

Примем, что отсутствует возмущающее воздействие

Рассмотрим единичное ступенчатое воздействие $x(t)=x_0\cdot1(t);$

Считая, что замкнутая САР устойчива, найдем $\varepsilon_{уст}=\lim_{t\rightarrow\infty}\varepsilon(t)$

Примем, что свободные коэффициенты в полиномах и передаточной функции разомкнутой САР равны 1.

$W(s)=\frac{k\cdot N(s)}{L(s)}$ — передаточная функция замкнутой САР.

Используя передаточную функцию замкнутой САР (см. раздел 5) для ошибки можно записать выражение:

$\Phi_\varepsilon(s)=\frac{E(s)}{X(s)} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(7.2.1)}$

где: $\Phi(s)= \frac{k\cdot N(s)}{L(s)+k\cdot N(s)}$ — главная передаточная функция (см. раздел 5).

согласно 1-й предельной теореме (см. раздел 2)

$\lim_{t\rightarrow\infty}\varepsilon(t)= \lim_{s\rightarrow 0}s\cdot E(s) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(7.2.2)}$

Учитывая, что единичное ступенчатое воздействие в отображениях: $x(t)=x_0\cdot1(t)\rightarrow X(s)=\frac{x_0}{s}$ :

$\lim_{t\rightarrow\infty}\varepsilon(t)=\lim_{s\rightarrow0}s\cdot \Phi_\varepsilon(s)\cdot X(s)=\lim_{s\rightarrow 0}\cdot s\cdot\frac{L(s)}{L(s)+k\cdot N(s)}\cdot\frac{x_0}{s}\Rightarrow$ $\varepsilon_{уст}=\lim_{t\rightarrow\infty}\varepsilon(t)=\frac{x_0}{k+1} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(7.2.3)}$

Т.е. если полином имеет свободный член, равный единице, то САР не может точно «отработать» постоянное воздействие, т.е. она статична.

Величина $\varepsilon_{уст}=\frac{x_0}{1+k}$ — называют постоянной или статической ошибкой.

Рисунок 7.2.2 Переходной процесс после ступенчатого воздействия для статичной САР

В случае если полином не имеет свободных членов, то его можно представить как $L(s)=s\cdot L_1(s)$ где — полином который имеет свободный член равный единицы. В этом случае установившаяся погрешность:

$\varepsilon_{уст}=\lim_{s\rightarrow0}s\cdot\frac{s\cdot L_1(s)}{s\cdot L_1+k\cdot N(s)}\cdot\frac{x_0}{s}=0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(7.2.4)}$

Если $L(s)=s^{v} \cdot L_1(s)$ , где — порядок астатизьма, то при постоянном (ступенчатом) воздействии установившаяся ошибка равна нулю.

$\Rightarrow \varepsilon_{уст}=\lim_{t\rightarrow\infty}\varepsilon(t)=\left\{ \begin{align} &\frac{x_0}{k+1}, если \ \ САР - статическая \\ &0, если \ \ САР - астатическая \end{align} \right.$

Из соотношения 7.2.3 очевидно, чем выше k — коэффициент усиления, тем меньше ошибка (для статических САР). Выводы: необходимо повышать общий коэффициент усиления разомкнутой САР, для сокращения ошибки.

Однако увеличение может привести к резкому уменьшению запасов устойчивости (что ухудшит качество переходного процесса) вплоть до потери устойчивости (см. раздел 6).

Цитата:

«Необходимо отметить, что для разомкнутой САР, имеющей $W(i\cdot\omega)$ годограф похожий на рис. 6.5.5 левый вариант, устойчивость системы (замкнутой) нарушится только с увеличением общего коэффициента усиления К. (Дейстивительно при увеличении коэффициента K увеличится длинна вектора и он может охватить точку -1). «

Поэтому при проектировании САР необходимо «решать» «оптимальную» задачу, т.е. выбрать оптимальное значение , обеспечивающее удовлетворительную точность и неплохое качество переходного процесса.

В последнее время практически все САР проектируются как астатические, что легко достигается за счет использования астатических регуляторов (например ПИ-регуляторов (пропорционально-интегрирующих).

В этом случае говорить о постоянной ошибке нет смысла, т.к. $\varepsilon_{уст}=0$

Пример 1:

Определить установившуюся ошибку, если входное воздействие $x(t)=0.2\cdot1(t)$ , а структура САР имеет вид:

Рисунок 7.2.3 Структура САР для анализа

Необходимо заметить, что прямое использование формулы (7.2.3) в данном случае не проходит, т.к. статическая ошибка $\varepsilon_{уст}$ в исходной САР не соответствует статической ошибке в эквивалентной САР:

Рисунок 7.2.4 Эквивалентная струкутура

Прежде чем определять статическую ошибку $\varepsilon_{уст}$ необходимо удостовериться в том, что исходная замкнутая САР устойчива. Выполеним преобразование:

$\Rightarrow \Phi(s)=\frac{W_1(s)}{1+W_1(s)\cdot W_{oc}(s)}=\frac{200\cdot(s+1)\cdot(3\cdot s+1)}{(s+s+1)\cdot(3\cdot s+1)+400\cdot(s+1)}\Rightarrow$

Характерестический полином эквивалентной передаточной функции: $D(s)=3\cdot s^3+4\cdot s^2+404\cdot s+401$

Для определение устойчивости критерий Гурвица (см. раздел 6):

$Г =\left | \begin{matrix}4 \ \ 401 \ \ 0\\ 3 \ \ 404 \ \ 0 \\ 0 \ \ 4 \ \ 401 \end{matrix} \right |=\left\{ \begin{align} &\Delta_1=4>0;\\ &\Delta_2 =\left | \begin{matrix} 4 \ \ 401\\ 3 \ \ 404 \end{matrix} \right |=4\cdot 404-3\cdot401>0; \\ &\Delta_3 =\Delta_2\cdot 401>0; \end{align} \right.$

Все главные определители матрицы Гурвица больше нуля $\Rightarrow$ САР устойчива.

Перейдя к изображению $x(t)=0.2\cdot 1(t)\rightarrow X(s)= \frac{0.2}{s}$ Найдем выражения для отклонение в изображениях:

$E(s)=X(s)-Y_1(s)=X(s)-W_{ос}(s)\cdot Y(s)=X(s)-W_{ос}(s)\cdot W_1(s)\cdot E(s)\Rightarrow$ $E(s)=\frac{X(s)}{1+W_{oc}(s)\cdot W_1(s)}$

Подставляем значения и $W_{oc}$ , имеем:

$E(s)=\frac{0.2}{s\cdot [1+\frac{200(s+1)}{s^2+s+1}\cdot\frac{2}{3\cdot s+1}]}=\frac{0.2\cdot(s^2+s+1)\cdot(3\cdot s+1)}{s\cdot[(s^2+s+1)\cdot(3\cdot s+1)+400\cdot(s+1)]}$ $\varepsilon_{уст}=\lim_{s\rightarrow 0} s\cdot E(s) = \lim_{s\rightarrow0}s\cdot\frac{0.2\cdot(s^2+s+1)\cdot(3\cdot s+1)}{s\cdot[(s^2+s+1)\cdot(3\cdot s+1)+400\cdot(s+1)]}=\frac{0.2}{401}$ $\varepsilon_{уст}\approx5\cdot10^{-4}$

7.3 Точность при линейном воздействии. Скоростные ошибки

В данном подразделе рассмотрим САР замкнутую единичной обратной связью (если обратная связь не единична, то с помощью структурных преобразований ее можно привести к единичной, подробнее об этом смотри раздел 4 Структурные преобразования систем автоматического регулирования)

Рисунок 7.3.1 САР с единичной обратной связи

где $x(t)=a_0\cdot1(t)+a_1\cdot t$ — входное воздействие.

Рисунок 7.3.2 Линейное входное воздействие

В соответствии со своим назначением устойчивая САР обязана «отслеживать» (с какой-то степенью точности) управляющее воздействие.

Воспользуемся первой предельной теоремой:

$\varepsilon_{уст}=\lim_{t\rightarrow\infty}\varepsilon(t)=\lim_{s\rightarrow0}s\cdot E (s)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(7.3.1)}$

Рассмотрим различные варианты САР: статическую и астатическую (1-го и 2-го порядка)

Статическая САР

Передаточная функция соответствует статической САР:

$W(s)=\frac{k\cdot N(s)}{L(s)}$

где полниномы и имеют свободный член равный 1.

Отклонение в отображениях:

$E(s)=X(s)\cdot\Phi(s)$

Где — изображение входного воздействия; $\Phi_\varepsilon(s)$ — передаточная функция по возмущению:

$\Phi_\varepsilon(s)=\frac{L(s)}{(L(s)+k\cdot N(s))}$

Изображение входного воздействия $x(t)\rightarrow X(s)$ :

$X(s)=\frac{a_0}{s}+\frac{a_1}{s^2}=\frac{a_0\cdot s+a_1}{s^2}$ $\varepsilon_{уст}=\lim_{s\rightarrow 0}s\cdot E(s)=\lim_{s\rightarrow0}s\cdot\Phi_\varepsilon \cdot X(s)=\frac{L(s)}{L(s)+k\cdot N(s)}\cdot\frac{a_0\cdot s+a_1}{s^2}=\infty$ $\varepsilon_{уст}=\infty \ \ \ \ \ \ \ \ \ \ \ \mathbf{(7.3.2)}$

Вывод: Cтатическая САР не способна «отслеживать» линейное воздействие.

Астатическая САР со степенью астатизма 1

Для САР со степенью астатизма 1 полином не содержит совбодного члена равного 1, но его можно представит в виде произведения $s\cdot L_1(s)$ где — полином содержащий свободный член равный 1.

Примечание: Степень астатизма равна количеству нулевых полюсов полинома (см. раздел 5)

В этом случае установившиеся статистическая ошибка:

$\varepsilon_{уст}=\lim_{s\rightarrow 0}s\cdot E(s)=\lim_{s\rightarrow0}s\cdot\frac{s\cdot L_1(s)}{s\cdot L_1(s)+k\cdot N(s)}\cdot\frac{a_0\cdot s+a_1}{s^2}=\frac{a_1}{k}$ $\varepsilon_{уст}=\frac{a_1}{k} \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(7.3.3)}$

Вывод: Если разомкнутая САР имеет астатизм первого порядка (имеет один нулевой полюс), то установившияся ошибка для замкнутой САР $\varepsilon_{уст}={a_1}/{k}$

Рисунок 7.3.3 Реакция на линейное воздействие САР с астатизьмом 1-го порядка

Ошибка в астатической САР (1^-го порядка) называется скоростной ошибкой, а общий коэффициент часто называют коэффициентом добротности или просто добротностью.

Анализ формулы (7.3.3) показывает, что чем выше тем меньше $\varepsilon_{уст}$ . Однако необходимо помнить, что повышение может привести к потери устойчивости САР (или уменьшению запасов устойчивости с соответствующим ухудшением качества переходного процесса).(см. раздел 6).

Астатическая САР со степенью астатизма 2

Для САР со степенью астатизма 2 полином не содержит не только совбодного члена равного 1, и члена у которого степень равна 1. Такой полином можно представит в виде произведения $s^2\cdot L_1(s)$ где — полином содержащий свободный член равный 1.

В этом случае установившиеся статистическая ошибка:

$\varepsilon_{уст}=\lim_{s\rightarrow0}s\cdot\frac{s^2\cdot L(s)}{s^2\cdot L_1(s)+k\cdot N(s)}\cdot\frac{a_0\cdot s+a_1}{s^2}=0$ $\varepsilon_{уст}=0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(7.3.6)}$

Рисунок 7.3.4 Реакция на линейное воздействие системы с астатизьмом 2-го порядка

Очевидно, что если степень астатизма >2, то установившаяся статическая ошибка, тем более будет равна 0. Т.е. чем выше астатизм САР, тем лучше точность. Хотя повышение астатизма ухудшает устойчивость (запас устойчивости).

Модели из статьи можно взять здесь…

В предыдущих сериях:

1. Введение в теорию автоматического управления.2. Математическое описание систем автоматического управления 2.1 — 2.3, 2.3 — 2.8, 2.9 — 2.13.

3. Частотные характеристики звеньев и систем автоматического управления регулирования. 3.1. Амплитудно-фазовая частотная характеристика: годограф, АФЧХ, ЛАХ, ФЧХ. 3.2. Типовые звенья систем автоматического управления регулирования. Классификация типовых звеньев. Простейшие типовые звенья. 3.3. Апериодическое звено 1–го порядка инерционное звено. На примере входной камеры ядерного реактора. 3.4. Апериодическое звено 2-го порядка. 3.5. Колебательное звено. 3.6. Инерционно-дифференцирующее звено. 3.7. Форсирующее звено. 3.8. Инерционно-интегрирующее звено (интегрирующее звено с замедлением). 3.9. Изодромное звено (изодром). 3.10 Минимально-фазовые и не минимально-фазовые звенья. 3.11 Математическая модель кинетики нейтронов в «точечном» реакторе «нулевой» мощности.

4. Структурные преобразования систем автоматического регулирования.

5. Передаточные функции и уравнения динамики замкнутых систем автоматического регулирования (САР).

6. Устойчивость систем автоматического регулирования. 6.1 Понятие об устойчивости САР. Теорема Ляпунова. 6.2 Необходимые условия устойчивости линейных и линеаризованных САР. 6.3 Алгебраический критерий устойчивости Гурвица. 6.4 Частотный критерий устойчивости Михайлова. 6.5 Критерий Найквиста.

Источник

Точность систем автоматического управления

1. Точность САУ

Точность САУ оценивается в установившемся режиме по величине установившейся ошибки при типовых воздействиях. При анализе точности систем рассматривается установившийся режим, так как текущее значение ошибки резко меняется вследствие наличия переходных процессов и не может быть мерой точности.

Рассмотрим систему представленную на рис. 1.

На схеме приняты следующие обозначения: K_у(p) – передаточная функция устройства управления; K₀(p) – передаточная функция объекта управления; f – возмущающее воздействие; x – задающее воздействие; y – регулируемая величина.

Ошибка по задающему воздействию равна (t) = x(t) – y(t).

Изображение ошибки равно

(1)

Установившееся значение ошибки определяется с помощью теоремы о конечном значении функции

(2)

Ошибка по возмущению воздействию равна (t) = – y(t), т.е. равна изменению регулируемой величины под действием возмущения при отсутствии входного воздействия.

В общем случае как задающее, так и возмущающее воздействия являются сложными функциями времени. При определении ошибок пользуются типовыми воздействиями, которые с одной стороны соответствуют наиболее тяжелым режимам работы системы и, вместе с тем, достаточно просты для аналитических исследований.

Кроме того, типовые воздействия удобны для сравнительного анализа различных систем, и соответствуют наиболее часто применяемым законам изменения управляющих и возмущающих воздействий.

2. Типы ошибок

Различают следующие типы ошибок:

– статическая ошибка (ошибка по положению) – ошибка, возникающая в системе при отработке единичного воздействия;

– кинетическая ошибка (ошибка по скорости) – ошибка, возникающая в системе при отработке линейно – возрастающего воздействия;

– инерционная ошибка (ошибка по ускорению) – ошибка, возникающая в системе при отработке квадратичного воздействия.

С точки зрения ошибок, системы можно классифицировать на статические и астатические.

Передаточная функция статической системы имеет вид

(3)

Передаточная функция астатической системы имеет вид

(4)

где K*(p) – передаточная функция, не содержащая интегрирующих звеньев а s – порядок астатизма.

Рассмотрим статическую систему (s = 0). Определим выражения для соответствующих ошибок.

1. Статическая ошибка определяется следующим соотношением

(5)

2. Кинетическая ошибка определяется следующим соотношением

(6)

3. Инерционная ошибка определяется следующим соотношением

(7)

Эта система не может быть использована как синхронно – следящая, так как кинетическая ошибка стремится к бесконечности.

Пример 1. Для заданной системы (рис. 2) определить установившиеся ошибки

x y

—

Рис. 2

Решение: Определим установившиеся ошибки.

1. Статическая ошибка определяется следующим соотношением

Кинетическая ошибка определяется следующим соотношением

Инерционная ошибка определяется следующим соотношением

На графиках это можно изобразить следующим образом (рис. 3)

Рассмотрим астатическую систему первого порядка (s = 1).

Определим выражения для установившихся ошибок.

Статическая ошибка определяется следующим соотношением

(8)

Кинетическая ошибка определяется следующим соотношением

(9)

Инерционная ошибка определяется следующим соотношением

(10)

Эта система может быть использована как синхронно – следящая, так как кинетическая ошибка равна нулю.

Пример 2. Для заданной системы (рис. 4) определить ошибки

Решение: Определим выражения для ошибок.

Статическая ошибка определяется следующим соотношением

2. Кинетическая ошибка определяется следующим соотношением

Т.е. ошибка является функцией скорости изменения входного воздействия и коэффициента усиления системы.

3. Инерционная ошибка определяется следующим соотношением

Графики изменения ошибок приведены на рис. 5.

а) b) c)

Рис. 5

ассмотрим астатическую систему второго порядка (s = 2).

Определим выражения для ошибок.

1. Статическая ошибка определяется следующим соотношением

(11)

Кинетическая ошибка определяется следующим соотношением

(12)

Инерционная ошибка определяется следующим соотношением

(13)

Инерционная ошибка является функцией ускорения изменения входного воздействия и коэффициента усиления системы.

Эта система может быть использована как синхронно – следящая, так как кинетическая ошибка равна нулю.

Пример 3. Для заданной системы (рис. 6) определить установившиеся ошибки

x y

—

Рис. 6

Решение: Определим выражения для ошибок.

1. Статическая ошибка определяется следующим соотношением

Кинетическая ошибка определяется следующим соотношением

3. Инерционная ошибка определяется следующим соотношением

На графиках это можно изобразить следующим образом (рис. 7)

b) c)

Рис. 7

Для повышения точности САУ необходимо увеличивать коэффициент усиления системы и порядок астатизма, но это может привести к неустойчивости, т.е. требования по точности и устойчивости противоречивы.

Определение ошибок по виду частотных характеристик САУ

О характере ошибок можно судить по низкочастотной ветви любой частотной характеристики (АФХ, ЛАЧХ, ФЧХ), так как низкочастотная ветвь характеризует статику системы. Частотные характеристики систем с различным порядком астатизма приведены в таблице 1.

Таблица 1

	АФХ	ЛАЧХ	ФЧХ
s = 0; _c= x₀/(1+k); _к= ; _и= .	+j -1 +
s = 1; _c= 0; _к= v/k_v; _и= .	+j -1 +
s = 1; _c= 0; _к= 0; _и= /k.	+j -1 +

3. Ошибки по возмущению

Установившаяся ошибка по возмущению равна

(14)

Рассмотрим примеры

Пример 4. Для заданной системы (рис. 9) со статическим регулятором определить ошибку по возмущению.

Решение: Пусть f(p) = f₀ /p, при этом ошибка равна

При статическом регуляторе установившаяся ошибка по возмущению зависит от амплитуды воздействия и коэффициента усиления регулятора т.е. _f= f(f₀, k₁).

Пример 5. Для заданной системы (рис. 10) с астатическим регулятором, определить ошибку по возмущению.

Решение: Пусть f(p) = f₀ /p, при этом ошибка равна

При астатическом регуляторе ошибка по возмущению равна нулю.

Литература

Вероятностные методы в вычислительной технике. Под ред. А.Н. Лебедева и Е.А. Чернявского – М.: Высш. Шк., 1986. -312 с.
Зайцев Г.Ф. Теория автоматического управления и регулирования. – 2-е изд., перераб. и доп. Киев, Издательство Выща школа Головное издательство, 198
Справочник по теории автоматического управления. /Под ред. А.А. Красовского – М.: Наука, 1987. – 712 с.
Теория автоматического управления: Учебник для вузов. Ч1 / Под ред. А.А. Воронова – М.: Высш. Шк., 1986. – 367 с.
Теория автоматического управления: Учебник для вузов. Ч2 / Под ред. А.А. Воронова – М.: Высш. Шк., 1986. -504 с.
Шандров Б.В. Технические средства автоматизации: учебник для студентов высших учебных заведений. Москва, Издательский центр «Академия», 2007.

Источник

38 Повышение качества и синтез линейных сау

ОШИБКИ В СИСТЕМАХ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

Виды ошибок регулирования и методы их снижения.

Расчеты статической ошибки εСт регулирования

Качество управления. Ошибка системы. Система автоматической стабилизации скорости вращения электродвигателя

Страницы работы

Фрагмент текста работы

Способы уменьшения ошибки

6.5.1.1 Повышение точности систем увеличением коэффициента усиления

Повышение точности систем увеличением порядка астатизма

Похожие материалы

Информация о работе

1. Точность САУ

2. План

3. 1 Общие положения

4. 2 Понятие о типовых режимах САУ

5.

6. 3 Теорема о предельном значении оригинала и методика определения установившихся ошибок

7.

8. 4 Ошибки статических и астатических САУ в типовых режимах

9.

10.

11.

12.

13.

14.

15.

16.

17. 3. Третий режим — гармонических входных сигналов.

18. Определим амплитуду εm ошибки САУ в этом режиме.

19. Выражение (1) справедливо и для амплитуд, т.е.

20.

21. Т.о. чтобы ошибка САУ в гармоническом режиме не превышала допустимой εдоп необходимо:

22. 5 Ошибки САУ при произвольных входных сигналах (коэффициенты ошибок)

23.

24.

25. Чтобы определить ошибку САУ при произвольной форме входного сигнала x(t) необходимо:

26. Пример

27. Решение:

28. 2. Разложим (1) в степенной ряд путем деления числителя на знаменатель

29.

30.

31.

32.

33. 6 Методы повышения точности САУ

34. ВНИМАНИЕ

35. 1. Первый способ повышения точности САУ – увеличение К

36.

37. 2. Способ повышения точности САУ – путем увеличения астатизма “v”

38.

39.

40. 3. Повышение точности САУ с использованием принципов комбинированного управления.

41.

42.

43.

44.

45.

46.

47. ПРИМЕР

48.

49.

7.1 Общие понятия о точности процесса управления

7.2 Точность при постоянном задающем воздействии. Постоянные ошибки

7.3 Точность при линейном воздействии. Скоростные ошибки

Статическая САР

Астатическая САР со степенью астатизма 1

Астатическая САР со степенью астатизма 2

Рассмотрим астатическую систему первого порядка (s = 1).

Интересное по теме:

6.5.1.1 Повышение
точности систем увеличением коэффициента усиления

Повышение точности
систем увеличением порядка астатизма