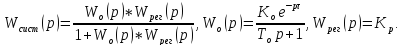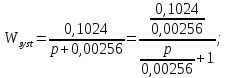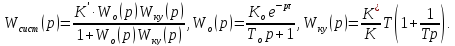Глава 8. Типовые законы регулирования. Одноконтурные САР
8.1. Основные типы автоматических регуляторов
Регулятор на основе усилительного звена называется П-регулятором (пропорциональный). Его положительной характеристикой является высокое быстродействие: при отклонении регулируемой величины от заданного значения регулятор выдает регулирующее воздействие, пропорциональное величине отклонения x, что обеспечивает быструю компенсацию возмущения. Существенным недостатком П-регулятора является наличие статической ошибки в переходном процессе АСР с П-регулятором (рис. 37). Статическая ошибка возникает потому, что у П-регулятора между регулируемой величиной x и регулирующим воздействием xр существует зависимость, однозначно определяемая коэффициентом K. Поэтому генерировать регулирующее воздействие xр для компенсации возмущения xв П-регулятор может только путем изменения регулируемой величины x, что и создает статическую ошибку.
Регулятор на основе интегрирующего звена (48) называется И‑регулятором:
Если xвых усилительного звена (П-регулятор) однозначно определяется величиной правой части уравнения, что является причиной возникновения статической погрешности в АСР с П-регулятором, то правая часть уравнения (48) интегрирующего звена (И-регулятор) определяет не величину, а скорость изменения xвых. Величина xвых будет изменяться до тех пор, пока правая часть уравнения (48) не станет равна нулю, т. е. пока регулируемая величина x при наличии возмущения xв не вернется к заданному значению. Следовательно, в АСР с И-регулятором не возникает статическая погрешность.
Однако у И-регулятора имеется свой недостаток сравнительно с П-регулятором: в случае возникновения возмущения регулирующее воздействие П-регулятора меняется быстрее, чем у И-регулятора с его конечной скоростью, что замедляет процесс компенсации возмущения и ухудшает критерии качества регулирования (рис. 40).
Рис. 40. Переходные процессы в АСР с П- и И-регуляторами
Таким образом, П-регулятор обеспечивает высокое быстродействие (что уменьшает динамическую ошибку), но не может обеспечить при наличии возмущения заданное значение регулируемой величины (статическая ошибка). И-регулятор, наоборот, не создает статическую ошибку, но вследствие относительно медленного изменения xр имеет большую динамическую ошибку.
Сравнивая характеристики П- и И-регуляторов можно сделать вывод: если включить усилительное и интегрирующие звенья параллельно, то автоматический регулятор будет лишен указанных недостатков. Такой регулятор называется ПИ-регулятором (рис. 41).
Рис. 41. Принципиальная схема АСР с ПИ-регулятором
Действительно, быстродействие ПИ-регулятора обеспечивает усилительное звено, а статическую ошибку снимает интегрирующее звено. Для управления производственными процессами чаще всего используются ПИ-регуляторы.
Кривая разгона идеального ПИ-регулятора показана на рис. 42 .
Уравнение ПИ-регулятора при нулевых начальных условиях имеет вид:

Отношение коэффициентов Kp1/Kp определяет степень влияния интегрирующей части, и его обратная величина называется временем изодрома Tи.

Время изодрома – это время, в течение которого интегрирующее звено изменяет регулирующее воздействие xр ПИ-регулятора на величину Dxр, равную предварительному изменению Dxр усилительного звена (рис. 42). Поэтому иногда время изодрома называют временем удвоения.
Рис. 42. График кривой разгона идеального ПИ-регулятора:
а – скачкообразное изменение входного воздействия x;
б – реакция (кривая разгона) ПИ-регулятора xр
Уравнение ПИ-регулятора можно записать как
откуда передаточная функция
Амплитудно-фазовая характеристика:

В том случае, если рассмотренные регуляторы не обеспечивают требуемое качество регулирования, необходимо увеличить интенсивность процесса компенсации возмущения. Этого можно достигнуть увеличением регулирующего воздействия, которое в свою очередь определяется коэффициентом усиления автоматического регулятора Kp
. Однако ниже будет показано, что увеличение коэффициента усиления регулятора в АСР приводит к тому, что в системе начинают генерироваться незатухающие колебания.
В связи с этим представляет интерес рассмотреть алгоритм, который реализует дифференцирующее звено.
Входной величиной любого регулятора является кривая разгона регулируемой величины (рис. 27), которая определяется величиной возмущения и передаточной функцией объекта регулирования (9). В свою очередь, регулирующее воздействие xp (рис. 27) определяется кривой разгона x и передаточной функцией регулятора.
На рис. 43 показана реакция дифференцирующего звена (Д‑регулятора) на входное воздействие в виде кривой разгона в соответствии с уравнением (51).
Рис. 43. Реакция дифференцирующего звена на кривую разгона
а –изменение входного воздействия x в виде кривой разгона;
б – реакция xр дифференцирующего звена
Из рис. 43,а следует, что дифференцирующее звено обеспечивает большее регулирующее воздействие в начале переходного процесса. Это означает, что дифференцирующий регулятор активно компенсирует возмущение и исключает возникновение незатухающих колебаний.
Если включить дифференцирующее звено параллельно ПИ‑регулятору (рис. 44), то получим ПИД-регулятор, обеспечивающий интенсивную компенсацию возмущений. При этом недостаток дифференцирующего звена (при Хвх = const, Хвых = 0 ) компенсируется усилительным и интегрирующим звеньями.
Рис. 44. Принципиальная схема АСР с ПИД-регулятором
На рис. 45 показана кривая разгона ПИД-регулятора.
Рис. 45. Кривая разгона ПИД-регулятора
На рис. 46 показаны переходные процессы на с различными регуляторами. ПИД-регулятор уменьшает динамическую ошибку сравнительно с ПИ-регулятором на 25–30%. Также можно объединить дифференцирующее звено с усилительным звеном и улучшить показатели П-регулятора, получив ПД-регулятор.

Все пять типов рассмотренных автоматических регуляторов имеют общую особенность своего функционирования – обеспечивают стабилизацию регулируемой величины после окончания переходного процесса.
8.2. Критерии качества регулирования
Качество процесса регулирования в АСР характеризуют следующие показатели (критерии) (рис. 16):
Рис. 16. Показатели качества регулирования:
1 – переходной процесс без статической ошибки;
2 – переходной процесс со статической ошибкой
1. Максимальное отклонение в процессе регулирования от заданного значения (динамическая ошибка) ΔХдин.
2. Статическая ошибка ΔХст — возможные отклонения от заданного значения по окончании переходного процесса при использовании некоторых типов регуляторов (подробнее такие АСР рассмотрены ниже).
3. Длительность переходного процесса Тр – период времени с момента начала отклонения регулируемого параметра от задания до возвращения его к заданному значению с определенной степенью точности регулирования ±Δ.
Например, если ±Δ=±25%, это означает, что для заданного значения температуры в 100 °С процесс регулирования будет завершен при достижении диапазона (100 ± 2,5) °С.
4. Степень затухания показывает характер затухания переходного процесса регулирования:
Для того, чтобы переходный процесс затухал за 2 ¸ 3 периода колебаний, степень затухания должна быть равна

5. Степень колебательности процесса m определяет характер колебательности процесса и равна отношению действительной части корня характеристического уравнения к коэффициенту при его мнимой части. Степень колебательности связана со степенью затухания следующим соотношением:
6. Интегральный квадратичный критерий – критерий, определяющий площадь под кривой переходного процесса, возведенной в квадрат (рис. 17):
Уменьшение интегрального критерия соответствует ускорению процесса регулирования.
Рис. 17. Интегральный квадратичный критерий качества регулирования
Однако все приведенные шесть критериев качества не определяют величину потерь производства при отклонениях регулируемой величины от оптимального значения в переходных процессах регулирования. Для определения таких потерь можно использовать экономический критерий.
7. Экономический критерий рассмотрим на примере, регулирования температуры химического реактора θ, когда степень превращения Q в реакторе определяется температурой (рис. 18а).
Разделим переходной процесс на равные интервалы времени Δt и запишем значения θ
в этих точках по графику (18, б). На графике (18, а) для этих температур определим уменьшение степени превращения вследствие отклонения от оптимального режима, а затем сделаем расчет потерь исходных продуктов для каждого интервала Δθ, суммируем эти потери для всего переходного процесса и представим потери в денежном выражении.
Рис. 18. Экономический критерий качества регулирования:
а – зависимость степени превращения Q от температуры θ;
б – переходный процесс регулирования температуры
Совместно со специалистом по технологии или по его заданию необходимо определить, какой из указанных критериев для рассматриваемой АСР является превалирующим, и задать максимально допустимую величину этого критерия, т. е. определить, какое качество регулирования должна обеспечить проектируемая АСР.
8.3. Выбор закона регулирования
При выборе регулятора следует определиться с группой регулирующих устройств – непрерывного, релейного или импульсного действия. Такой выбор ориентировочно может быть сделан по величине отношения запаздывания к постоянной времени объекта τ/Tоб:
· при отношении τ/Tоб меньше 0.2 целесообразно использовать регулятор релейного действия;
· если отношение τ/Tоб от 0.2 до 1.0, то нужно использовать регулятор непрерывного действия;
· при отношении τ/Tоб больше единицы можно использовать регулятор импульсного действия, или специальные регуляторы, например, регулятор («предиктор») Смита.
Затем необходимо определиться с типом регулятора, т.е. выбрать определенный закон регулирования: П-, И-, ПИ-, ПД- или ПИД-закон
8.4. Методы расчета одноконтурных САР
Как указывалось выше, качество автоматического регулирования определяется свойствами системы в целом, т. е. суммарными свойствами объекта и регулятора. Поскольку объект обычно является неизменяемой частью системы, то обеспечить определенные свойства системы, а следовательно и заданное качество регулирования, можно соответствующим подбором свойств автоматического регулятора, что зависит от параметров его настройки. В свою очередь, параметры настройки являются коэффициентами передачи в уравнении автоматического регулятора.
Таким образом, параметры настройки автоматического регулятора определяются свойствами объекта регулирования, т. е. величинами τоб, Тоб, Коб.
8.4.1. Расчет по «приближенным» формулам
Приближенные формулы для расчета параметров настройки автоматических регуляторов (Kр – коэффициент усиления; Tи – время изодрома; Тд – время дифференцирования) сведены в следующую таблицу:
Таблица 8.1. Формулы для приближенного расчета
параметров настройки регуляторов

Формулы сгруппированы в столбцы в зависимости от характера переходного процесса, который желательно получить, используя рассчитанный таким образом регулятор: апериодический или с перерегулированием в 20 %. В формулы входят следующие свойства объекта регулирования: Коб – коэффициент усиления; Тоб – постоянная времени; τоб – время запаздывания (полного).
Рис. 53. Кривые разгона:
1 – фактическая кривая разгона промышленного объекта;
2 – аппроксимированная (приближенная) кривая разгона
Необходимо отметить, что для пневматических регуляторов требуется определять не Kp, а диапазон дросселирования:
Рассмотрим методику более точного определения параметров настройки на примере расчета наиболее «популярного» регулятора – ПИ-регулятора.
8.4.2. Метод незатухающих колебаний
(метод Циглера-Никольса)
При использовании метода незатухающих колебаний [6], который иногда также называется по именам авторов методом Циглера-Никольса, поиск оптимальных параметров настройки осуществляется по величине критического коэффициента усиления П-регулятора и величине периода автоколебательного процесса.
Рис. 54. К поиску параметров настройки методом Циглера-Никольса
Расчет параметров настройки регуляторов проводится в два этапа.
1. На исследуемом объекте устанавливается П-регулятор и, последовательно увеличивая коэффициент усиления (уменьшая диапазон дросселирования), АСР выводится в режим незатухающих колебаний (автоколебаний на границе устойчивости). При этом фиксируется величина коэффициента усиления П-регулятора Ккрр и период незатухающих автоколебаний Т (рис. 54).
2. На втором этапе по величинам Кркр и Т определяются параметры настройки П-, ПИ- и ПИД-регуляторов:
Метод незатухающих колебаний не требует сложных вычислений, но имеет свои характерные недостатки:
· получить Кркр и Т можно только на действующем объекте, оснащенном АСР с П-регулятором;
· не все объекты химической технологии допускают режим автоколебаний;
· практически трудно уловить момент начала автоколебаний.
Данные недостатки имеют место лишь при настройке регулятора методом Циглера-Никольса непосредственно на действующем объекте. Если заменить реальный объект его математической моделью, данный метод лишается указанных недостатков, кроме того, моделирование позволяет на порядок ускорить процесс поиска параметров настройки. Но для выполнения моделирования требуется достаточно точное математическое описание объекта регулирования, а получить его удается не всегда.
8.4.3. Метод расширенных частотных характеристик
Уравнение ПИ-регулятора (65) или (66):
Передаточная функция ПИ-регулятора:

Знак «минус» указывает, что действие регулятора направлено против возмущения.
Из передаточной функции получаем амплитудно-фазовую характеристику ПИ-регулятора путем замены p на iw:

Так как по формуле Эйлера


с затуханием за три периода
Заменив iw на комплексную переменную (-mw+iw), получаем расширенную амплитудно-фазовую характеристику (РАФХ)Ю

Расширенными такие характеристики называются потому, что они как бы «расширены» по отношению к обычной АФХ (рис. 56).
Предположим, что объект регулирования имеет передаточную функцию второго порядка следующего вида:

Для дальнейшего математического моделирования АСР передаточную функцию необходимо преобразовать:

Рис. 56. АФХ объекта регулирования с самовыравниванием:
1 – обычная; 2 – расширенная
Расширенная амплитудно-фазовая характеристика объекта регулирования при замене p на (-mw+iw) будет иметь вид:



Где Rоб(m,w) -расширенная амплитудно-частотная характеристика объекта; Fоб(m,w) -расширенная фазочастотная харктеристика объекта. Величина 40w в выражении для Fоб (m,w) опеделяет угол в радианах и для пересчета в градусы неоходимо 40w умножить на 57,3
Условием нахождения замкнутой АСР на границе устойчивости является уравнение:

Аналогично, исходным уравнением для получения заданной степени колебательности m, а следовательно, определенной степени затухания y, является соотношение:
Это соотношение двух комплексных чисел возможно в том случае, если произведение модулей РАФХ равно единице, а аргументы (фазы) равны между собой, т. е.

Решая эти уравнения относительно S0 и Kp, получаем:


Обычно принимают степень колебательности m = 0,221, что соответствует степени затухания ψ=0,75 и обеспечивает затухание процесса регулирования примерно за три периода. Тогда

Уравнения для определения параметров настройки ПИ-регулятора можно преобразовать:


Подставляя в приведенные уравнения численные значения частоты w от 0 до значения, когда S0 становится отрицательной величиной, строим на плоскости параметров настройки кривую равной степени колебательности


Пример кривых равной степени колебательности в плоскости параметров настройки ПИ-регулятора показан на рис. 57. Графики процессов регулирования с различными параметрами настройки ПИ-регулятора при m = 0,221 показаны на рис. 58. Все процессы регулирования, показанные на рис. 58, реализованы ПИ-регулятором с параметрами настройки, полученными по кривой равной степени колебательности в точках 1, 2, 3, 4 (рис. 57), и все имеют m = 0,221, т. е. затухают примерно за три периода, но обладают существенно различным характером.
В связи с этим возникает задача определения оптимальных параметров настройки на кривой равной степени колебательности.
Рис. 57. Кривые равной степени колебательности
В качестве критерия оптимальности выбираем продолжительность переходного процесса – время регулирования (т. е. быстродействие АСР) и отсутствие постоянной или врéменной статической ошибки. Это исключает из рассмотрения параметры настройки в точке 4 (параметры настройки П-регулятора) и в точке 3 (врéменная статическая ошибка) (рис. 58).
Рис. 58. Графики процессов регулирования для ПИ-регулятора
с различными параметрами настройки в точках 1, 2, 3 и 4
при степени колебательности m =0,221
Быстродействие автоматического регулятора прежде всего зависит от величины регулирующего воздействия, которое для ПИ-регулятора, как следует из уравнения (65), прямо пропорционально величине коэффициента усиления Kp и обратно пропорционально времени изодрома Tи. Расчеты показывают, что если двигаться по кривой равной степени колебательности вправо, то величина регулирующего воздействия при прочих равных условиях сначала возрастает и достигает максимального значения на кривой равной степени колебательности вблизи ее вершины, когда
а затем начинает уменьшаться в связи с резким увеличением Tи (рис. 57).
Рис. 59. Выбор оптимальных параметров настройки
Таким образом, оптимальные параметры настройки ПИ-регулятора находятся в точке 2 на кривой равной степени колебательности (рис. 59).
Источник
Плютто В. П., Дубровский И. И. Элементы теории управления химико-технологическими процессами и системами. Конспект лекций: Учеб. пособие – М.: РХТУ им. Д. И. Менделеева, 2003. – 127 с.
Рис.
11. Схема САР с П-регулятором.
Передаточная
функция:
Используя
найденную выше функцию корректирующего
устройства исследуем нашу систему для
П-регулятора.
Таким
образом в качестве корректирующего
устройства будем использовать:
Найдем
Wсист
используя функции Matlab:
W1=tf([70],[909.1
1]);
temp=70*feedback(W1*0.019,[1]);
Wsyst=minreal(temp);
Построим
графики переходной функции для эталонной
функции и для синтезированного нами
объекта.
We=tf([70],[666.7
1]);
hold
on
step(We,’-‘);
step(Wsyst,
‘—‘);
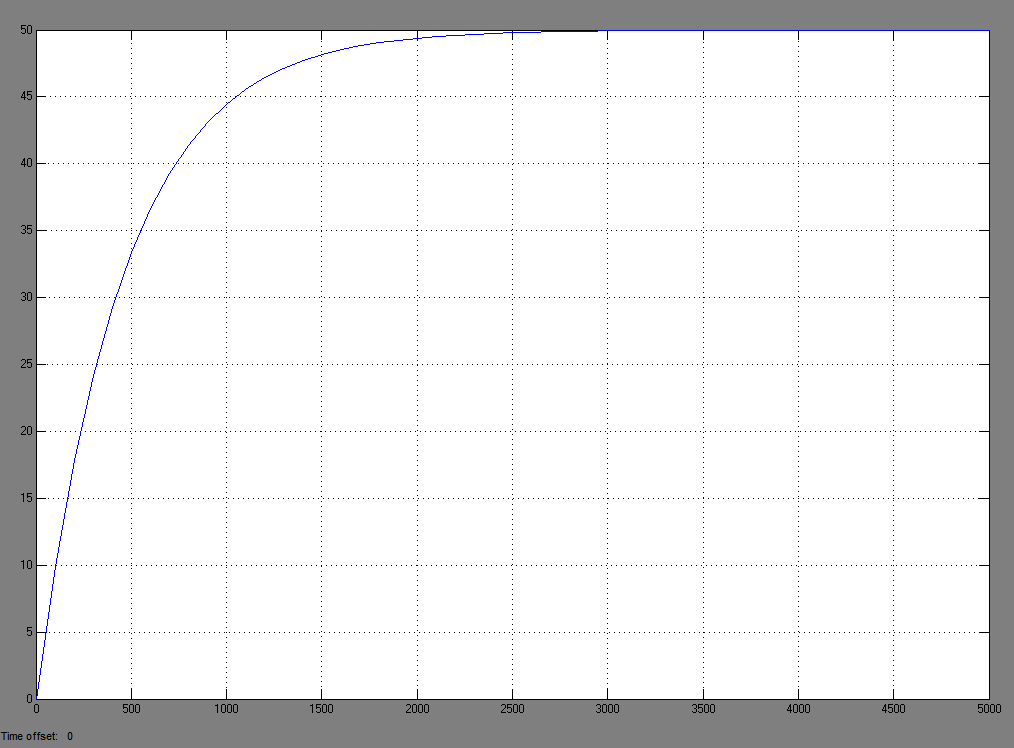
Рис.12.
График переходной функции САР с
П-регулятором и эталонного объекта.
Проведем
синтез объекта в Simulink:
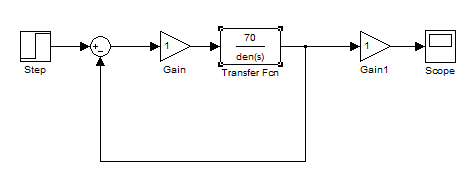
Рис.
13. Синтез САР в Simulink.
Рис.14.
График переходной функции САР с
П-регулятором полученный при моделировании
в Simulink.
Путем
несложных преобразований получим:
Отсюда
следует, что:
Модель
динамики объекта:

Вывод:
в результате проведенного синтеза САУ
мы получили объект автоматического
регулирования с пропорциональным
регулятором, ошибка полученного объекта
незначительна только при малых значениях
t.
При дальнейшем увеличении t,
статическая ошибка становится сравнимой
с величиной полученной функции.
Вывод:
были определены
параметры настройки системы автоматического
регулирования с пропорциональным (П-)
и пропорционально-интегральным (ПИ-)
регуляторами.
3.2. Система автоматического регулирования с пи-регулятором
Рис.
15. Схема САР с ПИ-регулятором.
Передаточная
функция:
Найдем
Wсист
используя функции Matlab:
Wo=tf([70],[909.1
1]);
temp=tf([0.0015],[1
0])/Wo;
Wky=minreal(temp);
temp=70*feedback(Wo*Wky,[1]);
Wsyst=minreal(temp);
Введем
задержку в 14 сек. для нашего объекта:
p=tf(‘p’);
p=exp(-p*14);
Построим
графики переходной функции для эталонной
функции и для синтезированного нами
объекта, для большей наглядности введем
задержку для синтезированного объекта.
We=tf([70],[666.7
1]);
Ws=Wsyst*p;
hold
on
step(We,’-‘);
step(Ws,
‘—‘);
Рис.16.
График переходной функции САР с
ПИ-регулятором и эталонного объекта.
Проведем
синтез этого объекта в Simulink:
Рис.
17. Синтез САР в Simulink.
Рис.18.
График переходной функции САР с
ПИ-регулятором полученный при моделировании
в Simulink.
Путем
несложных преобразований получим:
Отсюда
следует, что:

Модель
динамики объекта:

Вывод:
в результате проведенного синтеза САУ
мы получили объект автоматического
регулирования с пропорционально-интегральным
регулятором полностью идентичный
заданной нами эталонной системе.
Анализ
показателей
качества: статическая ошибка ПИ-регулятора
меньше статической ошибки П-регулятора,
следовательно, использование ПИ-регулятора
даёт более точные результаты, однако
время регулирования П-регулятора меньше
времени регулирования ПИ-регулятора.
4.Исследование устойчивости сар
Устойчивость
– это способность системы, выведенной
из состояния равновесия под влиянием
возмущающих или управляющих воздействий
с течением времени прийти в равновесное
состояние под действием своих внутренних
сил.
Автоматическая
система управления называется устойчивой,
если она за счет своих внутренних сил
возвращается в состояние установившегося
равновесия после незапланированного
возмущения. Систему считают неустойчивой,
если при сколь угодно малых отклонениях
от состояния установившегося равновесия,
она не возвращается к этому состоянию,
а непрерывно удаляется от него или
совершает около него недопустимо большие
колебания.
Устойчивость
– это свойство, которым должна обладать
любая САР.
Рис.
19. Структурная схема САР с ПИ-регулятором.
Запишем
передаточную функцию САР в разомкнутом
состоянии:

где


ПФ объекта: .
Исследуем
на устойчивость синтезированный объект,
охваченный единичной отрицательной
обратной связью.
Wo=tf([70],[909.1
1]);
Wky=tf([0.01948
2.14e-5],[1 0]);
Wz=70*feedback(Wo*Wky,[1]);
Найдем
критическую величину сдвига фазы, при
которой исследуемый объект теряет
устойчивость.
margin(Wz);
Рис.20.
Критическая величина сдвига фазы
объекта.
Найдем
критическую задержку, для нашего объекта:
Построим
АФЧХ объекта и объекта с запаздыванием
на величину τ.
p=tf(‘p’);
Wot=Wo*exp(-p*15);
Wraz=Wky*Wo;
Wrazt=Wky*Wot;
hold
on
nyquist(Wraz);
nyquist(Wrazt);
Рис.21.
АФЧХ разомкнутой системы.
Построим
АФЧХ замкнутой системы.
hold
on
Wz=feedback(Wraz,[1]);
Wzt=feedback(Wrazt,[1]);
Рис.21.
АФЧХ замкнутой
системы.
Рис.22.
АФЧХ замкнутой системы (увеличенный
фрагмент рис. 21.).
Устойчивость
системы определяем по критерию Найквиста.
Устойчивость определяется по АФЧХ
разомкнутой САР, для которой возможны
2 случая:
-
Разомкнутая
САР, устойчивая в разомкнутом состоянии,
будет устойчива и в замкнутом, если её
АФЧХ не охватывает точку (-1, j0)
при изменении ω от 0 до ∞. -
Разомкнутая
САР, неустойчивая в разомкнутом
состоянии, будет устойчива в замкнутом
состоянии, если её АФЧХ охватывается
точку (-1, j0)
при изменении ω от 0 до ∞ q
раз (где q
– число корней характеристического
уравнения разомкнутой САР).
Вывод:
САР устойчива в разомкнутом состоянии,
так как её АФЧХ не охватывает точку (-1,
j0)
при изменении ω от 0 до ∞, следовательно
по критерию Найквиста (1 случай) САР
будет устойчива и в замкнутом состоянии.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Классический ПИД-регулятор
Простейшая система автоматического регулирования с обратной связью показана на рисунке. В ней блок R называют регулятором (от слова Regulator), P — объектом регулирования (от слова Process), r — управляющим воздействием или уставкой (reference), e — сигналом рассогласования или ошибки (error), u — выходной величиной регулятора, y — регулируемой величиной.

Частный случай ПИД-регулятора — пропорциональный или П-регулятор: u(t)=K·e(t). С помощью П-регулятора можно управлять любым устойчивым объектом, однако он дает относительно медленные переходные процессы и ненулевую статическую ошибку (статическая ошибка e0 — постоянная ошибка в установившемся режиме системы; см. рис. ниже).

С увеличением пропорционального коэффициента K статическая ошибка e0 уменьшается, время нарастания переходного процесса tн уменьшается, перерегулирование σ увеличивается.
Чтобы убрать статическую ошибку в установившемся режиме, в регулятор вводят интегральный канал с коэффициентом усиления Ki, так что:
Такой регулятор называется пропорционально-интегральным или ПИ-регулятором. Интегратор выдает сигнал, пропорциональный накопленной ошибке, поэтому переходный процесс несколько замедляется.

Однако за счет интегрального канала обеспечивается нулевая ошибка e0 в установившемся состоянии при ступенчатом возмущении и ступенчатом изменении задающего сигнала-уставки.

С увеличением коэффициента интегральной составляющей ПИ-регулятора Ki время нарастания переходного процесса tн уменьшается, перерегулирование σ увеличивается, время регулирования tр увеличивается.
Для ускорения переходных процессов добавляют дифференциальный канал с коэффициентом усиления Kd:
|
|
(1.01) |
Распространена также другая модификация выражения (1.01):
|
|
(1.02) |
где t — время; K — пропорциональный коэффициент (безразмерный), Ti — постоянная интегрирования (размерность времени) и Td — постоянная дифференцирования (размерность времени) регулятора. Такой регулятор называют ПИД-регулятором.
Регуляторы этого типа очень хорошо зарекомендовали себя в практических задачах. Кроме того, иногда используются ПД-регуляторы (пропорционально-дифференциальные), у которых нет интегрального канала.
Управление по производной – это быстрый способ управления. Сигнал дифференциального канала наиболее важен при изменениях входов и исчезает в установившемся режиме. Он позволяет реагировать не на само увеличение ошибки, а на тенденцию ее изменения, и принять превентивные меры
. Главный недостаток дифференциального канала – большое влияние высокочастотных помех, например, шумов измерений.

С увеличением коэффициента дифференциальной составляющей ПИД-регулятора Kd перерегулирование σ уменьшается, время регулирования tр уменьшается.
|
При увеличении коэффициентов |
|||
|
Kp |
Ki |
Kd |
|
|
Время нарастания tн |
|
|
|
|
Пере- регулирование σ |
|
|
|
|
Время регулирования tр |
|
|
|
|
Статическая ошибка e0 |
|
|
|
|
|
Для устойчивого объекта можно выбрать коэффициенты регулятора опытным путем, выполняя эксперименты с реальным объектом. Предложено несколько методов решения этой задачи, например, правила Зиглера-Никольса (Ziegler J. G. — Nichols N. B.), Коэна-Куна (Cohen O.H. – Coon O.A.) или CHR (Chien K. L. — Hrones J. A. — Reswick J. B.).
Список используемой литературы
- Поляков К.Ю.,
Теория автоматического управления для
чайников
, Санкт-Петербург, 2008 г. - Востриков А.С., Французова Г.А.,
Теория автоматического регулирования
. 2003 г. - Глушков В.М., Амосов Н.М., Артеменко И.А. Энциклопедия кибернетики. Том 2. Киев, 1974 г.
- Теория автоматического управления: Учеб. для вузов по спец.
Автоматика и телемеханика
. В 2-х ч. Ч. I. Теория линейных систем автоматического управления / Н. А. Бабаков, А. А. Воронов, А. А. Воронова и др.; Под ред. А. А. Воронова.—2-е изд., перераб. и доп. — М.: Высш. шк., 1986. — 367 с. - Денисенко В.В.,
Энциклопедия АСУ ТП
, bookasutp.ru - Dew Toochinda,
Scilab Ninja. Control Engineering with Scilab
,Scilab Control Engineering Basics
, scilab.ninja/study-modules/scilab-control-engineering-basics/
У нас на сайте Вы можете приобрести качественные частотные преобразователи. Подробности тут
Всем привет. Рассмотрев в прошлой статье основу технологии построения веб-интерфейса, мы возьмем небольшую паузу с проектированием, и рассмотрим пару статей по ПИД–регулятору. Куда войдут основы автоматики, и на примере устройства синхронизации двигателей фрезерного станка на микроконтроллере, познакомимся с основными законами управления. А также рассчитаем основные коэффициенты законов для матмодели. В конце статьи выложен проект в Proteus на ATmega8.
Но для начала «пробежимся» по основным понятиям, что б понимать о чем мы с Вами будем далее говорить. В проекте предполагается управлять двигателем, т.е. объектом. Что в свою очередь автоматика так и называет объект управления (ОУ). У него имеется три параметра:
1. Выходная величина y.
2. Входной задающий параметр u.
3. Входное возмущающее воздействие f.
На рисунке слева представлен общий вид ОУ с его параметрами. Справа наш пример представленный в протеусе в виде двигателя с энкодером, где входным задающим параметром является постоянное напряжение и в зависимости от его величины изменяется частота вращения двигателя. Выходным параметром является показания энкодера, а именно угол поворота (число импульсов за один оборот). Третий параметр — возмущающее воздействие — это воздействие со стороны внешней среды, которое нарушает правильное функционирование объекта, т.е. трение, нагрузка и т.д.
Для исключения последнего используется второй параметр, т.е. задающий. Техническое устройство, осуществляющее автоматическое управление называется управляющим устройством (УУ). А ОУ совместно с управляющим и задающим устройствами называют систему автоматического управления (САУ). Ниже структурная схема системы.

1. Принцип разомкнутого управления – вырабатывается на основе заданного алгоритма и не контролируется другими факторами.
2. Принцип компенсации возмущений, где результат возмущения в виде корректива вносится в алгоритм управления.
3. Принцип управления по ошибке. Здесь коррективы вносятся в алгоритм управления по фактическому значению выходной величины.
Наш проект будет строится по последнему принципу управления – по ошибке. Ниже, слева структурная схема, а справа проект, где осуществляется управление по ошибке.
ЗУ — это у нас двигатель с энкодером (с левой стороны), с которого импульсы поступают в микроконтроллер. Где в свою очередь прописана матмодель ПИД-регулятора. Контроллер выступает в роли УУ. Далее ШИМ генерирует необходимый импульс и посылает его на вход второго двигателя с энкодером, который правее. (Мы с Вами уже рассматривали ШИМ-управление на AVR). Выход импульсов с которого, является выходной величиной и ошибкой в обратной связи y ос. Кнопки — это возмущающее воздействие, которыми мы произвольно добавляем импульсы ОУ. Где в свою очередь УУ должно быстро и плавно подрегулировать под угол поворота задающего устройства.
Далее САУ классифицируются по:
1. Алгоритму функционирования:
— системы стабилизации — поддержание регулируемого параметра на заданном уровне;
— программное управление – алгоритм задан в функции времени, где выходная величина изменяется во времени по заданному закону;
— следящие системы — алгоритм функционирования заранее не известен, где регулируемая величина должна воспроизводить изменение некоторой внешней величины;
— экстремальные системы — показатель качества или эффективности процесса может быть выражен в виде функции параметров системы, а сама функция имеет экстремум (максимум или минимум).
— системы оптимального управления — процесс управления ведется таким образом, что некоторая характеристика процесса была бы оптимальной;
— адаптивные системы – некоторые параметры ОУ и др. элементов системы могут изменяться.
Наш алгоритм это программное управление, где выходная величина будет результатом ПИД управления.
2. По виду дифференциальных уравнений, описываемых систему – линейные (статические характеристики всех элементов являются прямолинейными) и нелинейные (статическая характеристика является нелинейной).
3. По характеру сигналов в основных элементах — непрерывные и дискретные(в последних непрерывный входной сигнал преобразуется на выходе в последовательность импульсов).
Наш проект нелинейный и сигналы дискретные. И последнее, рассмотрим типовые законы управления, определяющие алгоритм управления в функции от ошибки управления. Под законом регулирования понимают алгоритм, в соответствии с которым управляющее устройство формирует воздействие, подаваемое на вход ОУ. Законы управления описываются передаточными функциями, которые являются одним из способов математического описания динамической системы. Вид передаточной функции управляющего устройства определяет закон управления. Различают пять основных законов управления: пропорциональный (П), интегральный (И), пропорционально –интегральный (ПИ), пропорционально-дифференциальный (ПД), пропорционально — интегрально – дифференциальный (ПИД).
Рассмотрим каждый закон в отдельности на примере устройства синхронизации. Итак, исходные данные:
Соберем пример в Proteus. Возьмем два движка с инкрементальными энкодерами, микроконтроллер, два счетчика импульсов, а также подключим осциллограф и ЖК индикатор для отображения рассогласования (ошибки). Рассмотрение датчиков угла поворота (энкодера) выходит за пределы статьи, единственное, что нам надо знать, они предназначены для преобразования угла поворота вращающегося объекта (вала) в электрические сигналы, позволяющие определить угол его поворота. Выше был представлен рисунок нашего проекта в Proteus. Ниже на рисунке пример настройки мотора с энкодером:

— минимальную массу ротора EffectiveMass= 0,01;
— нагрузка ротора Load/MaxTorque % = 1, чтобы он по инерции не крутился;
— обороты ZeroLoad RPM=20;
— количество импульсов на оборот PulsesperRevolution=24.
Как видите в протеусе отдельного энкодера нет, только с двигателем. Кратко о его подключении. Один конец двигателя на землю, на второй напряжение от -12 или +12 В. И три вывода энкодера. Мы используем один как на рисунке выше. Приведенные параметры являются настроечными параметрами от которых будет зависеть динамика привода, т.е. его поведение.
П — регулятор. Одно из простых устройств и алгоритмов управления, в обратной связи, которое формирует управляющий сигнал. Выдает выходной сигнал u (t), пропорциональный входному (ошибке регулирования) e (t), с коэффициентом пропорциональности К, который вырабатывается пропорциональной частью П-регулятора в противодейтвие отклонению реглируемой величины от данного значения, в данный момент времени.
u (t)=Kр*e (t), где Kр — коэффициент усиления регулятора.
Чем больше отклонение, тем больше выход именно по данному значению. Т.е. статическая ошибка равна отклонению регулируемой величины. Здесь присутствует вероятность, что система никогда не стабилизируется на заданном значении. Увеличение коэффициента усиления увеличивает разницу между входом и выходом, при этом уменьшается статическая ошибка. Но рост этого коэффициента может привести к автоколебаниям в системе, а дальнейшее его увеличение приведет к потере устойчивости.
Обычно на практике усилительные свойства П-регулятора характеризуют следующими величинами:
— предел пропорциональности d=1/Kр — величина, обратная Kр
— предел пропорциональности, выраженный в процентах D=d*100%=100%/Kр. Показывает, на сколько процентов от своего максимального значения должен изменится входной сигнал, чтобы выходной изменился на 100%.
Автоколеба́ния — это незатухающие колебания в диссипативной ( устойчивое состояние, возникающее в неравновесной среде при условии диссипации (рассеивания) энергии, которая поступает извне) динамической системе с нелинейной обратной связью, поддерживающиеся за счёт энергии постоянного, т. е. непериодического внешнего воздействия.
На рисунке ниже слева нормальный процесс П-регулирования, где видно, что линейность графика прямо пропорционально уменьшению ошибки. Справа, процесс автоколебаний в системе при большом коэффициенте.
П-регулятор находит свое применение в тех же процессах, где не требуется точного поддержания заданного значения, описанных ранее, то есть в контролируемом процессе будет присутствовать статическая ошибка. Возникает данная ошибка из-за того, что выходной сигнал слишком мал для оказания существенного воздействия на поддержание системы на заданном уровне. Вполне допускается, что регулятор выведет требуемое значение, но при возникновении возмущающих воздействий, регулятор не сможет вернуть заданное значение, пока рассогласование не станет достаточно велико, чтобы выходной сигнал смог оказать достаточное воздействие. Для нашего примера такой закон не подходит. Идем далее.
И-регулятор. Что значит интегральное управление? А то, что устройство вырабатывает сигнал (u (t)), пропорциональный интегралу от ошибки регулирования (e (t)). Система при таком законе астатическая, т.е.возмущение происходит на том участке системы, который находится за интегрирующим звеном. Но при этом динамические свойства системы с И-законом обычно хуже чем у системы П-управления. Ниже представлен закон И-регулятора.

Время изодрома Ти=1/K0 — величина, обратная K0. Также показывает за какое время выход регулятора изменится на 100% (регулирующий орган переместится из одного крайнего положения в другое) при скачкообразном изменении входного сигнала на 100%. Таким образом Ти характеризует быстродействие регулятора. С уменьшением T растет колебательность переходного процесса. При слишком малых значениях T система регулирования может перейти в неустойчивое состояние. Ниже на рисунке слева устойчивое состояние, справа — неустойчивое состояние.
В системе регулирования с И-регулятором обычно отсутствует статическая ошибка регулирования. Как правило И-регулятор не используется самостоятельно, а в составе ПИ- или ПИД- регуляторов.

K1 — коэффициент усиления пропорциональной части,
K0 — коэффициент усиления интегральной части
Так как ПИ-регулятор можно рассматривать как два регулятора, соединенные параллельно, то усилительные свойства ПИ-регулятора характеризуют два параметра:
1) предел пропорциональности d=1/K1 — величина, обратная K1
2) время изодрома Ти=1/K0 — величина, обратная K0 .
Динамические свойства системы с ПИ-регулятором лучше, чем с И-законом. Изодромная система в переходном режиме приближается к системе с пропорциональным управлением. А в установившемся режиме подобна системе с интегральным управлением. Чем больше коэффициент пропорциональности, тем меньше выходная мощность при одной и той же ошибке регулирования, чем больше постоянная времени интегрирования, тем медленнее накапливается интегральная составляющая. ПИ регулирование обеспечивает нулевую ошибку регулирования и нечувствительно к помехам измерительного канала. Ошибка регулирования (статическая) исключается за счет интегрального звена, которое образуется путем постоянного суммирования ε за определенный промежуток времени и формирования сигнала управления, пропорционального полученной величине.
Недостатком ПИ регулирования является медленная реакция на возмущающие воздействия. Для настройки ПИ регулятора следует сначала установить постоянную времени интегрирования равный нулю, а коэффициент пропорциональности — максимальным. Затем как при настройке пропорционального регулятора, уменьшением коэффициента пропорциональности нужно добиться появления в системе незатухающих колебаний. Близкое к оптимальному значение коэффициента пропорциональности будет в два раза больше того, при котором возникли колебания, а близкое к оптимальному значение постоянной времени интегрирования — на 20% меньше периода колебаний. Оптимальным является переходной процесс с 20% перерегулированием.
ПД-регулятор. Если нагрузка объекта изменяется часто и резко, и при этом объект имеет существенное запаздывание, то ПИ-регулятор дает неудовлетворительное качество регулирования. Тогда целесообразно в закон регулирования вводить дифференцирующую составляющую, т.е. воздействовать на регулирующий орган дополнительно по величине первой производной от изменения регулируемого параметра. Cигнал ПД-регулятора ( u (t) ) зависит от ошибки регулирования ( e (t) ) и от производной от этой ошибки (от скорости изменения ошибки).
ПД-регулятор характеризуют два параметра:
1. Предел пропорциональности d=1/K1 — величина обратная К1.
2. Постоянная времени дифференцирования (время предварения) Тд=K2. Это интервал времени между моментами достижения регулирующим органом одинакового положения при наличии дифференциальной составляющей и без нее. Параметр настройки дифференциальной составляющей. За счет дифференциальной составляющей упреждается перемещение регулирующего органа.
Дифференцирующее звено вычисляет скорость изменения ошибки, т.е. прогнозирует направление и величину изменения ошибки. Если она положительна, то ошибка растет и дифференцирующая часть вместе с пропорциональной увеличивает воздействие регулятора на объект. Если отрицательна — уменьшается воздействие на объект. Эта система регулирования имеет статическую ошибку регулирования, но быстродействие у нее выше, чем П- , И- , Пи-регуляторы. В начале переходного процесса ПД-регулятор имеет высокое усиление и, следовательно, точность, а в установившемся режиме он вырождается в П-регулятор со свойственной ему статической ошибкой. Если статическую ошибку скомпенсировать, как это делается в П-регуляторах, то возрастет ошибка в начале переходного процесса. Таким образом, ПД-регулятор по своим потребительским свойствам оказывается хуже П-регулятора, поэтому на практике он используется крайне редко. П-звено имеет положительное свойство — вносит в контур регулирования положительный фазовый сдвиг, что повышает запас устойчивости системы при малом времени предварения. Однако с увеличением этого времени растет усиление регулятора на высоких частотах, что приводит к режиму автоколебаний. Чем больше время дифференцирования, тем больше скачок в перемещении регулирующего органа.
ПИД-регулятор. Это сумма трех регуляторов П, И и Д (Пропорционально-интегрально-дифференцирующий). Выходной сигнал ПИД-регулятора ( u (t) ) зависит от ошибки регулирования ( e (t) ), от интеграла от этой ошибки и от производной от этой ошибки.
Усилительные свойства характеризуют три параметра:

2. Время изодрома Ти=1/K0.
3. Время предварения Тд=K2.
Системы регулирования с ПИД-регуляторами сочетают в себе достоинства П- , И- , и ПД- регуляторов. В таких системах отсутствует статическая ошибка и они обладают высоким быстродействием.
Ниже выложен проект в Proteus на ATmega8. Где представлена выше описанная модель ПИД — регулятора.
Синхронизация двигателей станка ( Скачали: 633 чел. )
В следующей статье рассмотрим расчет основных коэффициентов законов регулирования для нашего проекта, а именно синхронизации двигателей станка. Написание матмодели для микроконтроллера и существующие варианты. А также этапы проектирования: от замысла до платы. На этом мы сегодня и остановимся. Всем пока.
Просмотрено
20099
раз.