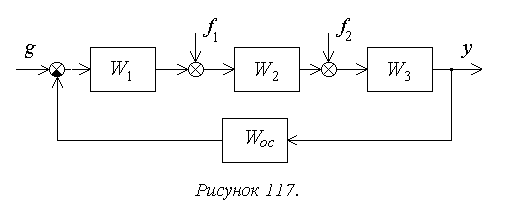
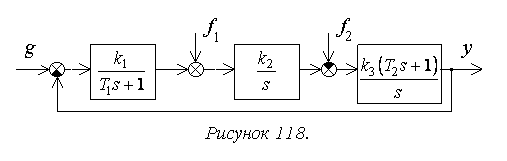
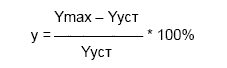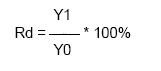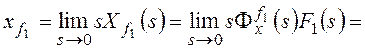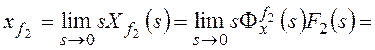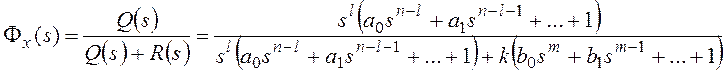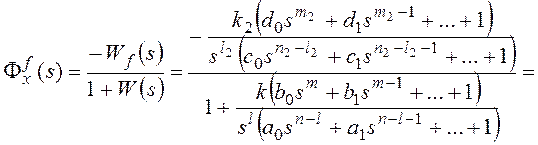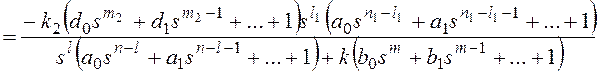К системам автоматического регулирования (САР) предъявляются требования не только
устойчивости процессов регулирования. Для работоспособности системы не менее необходимо, чтобы процесс автоматического регулирования осуществлялся при обеспечении определенных показателей качества процесса управления.
Если исследуемая САР является устойчивой, возникает вопрос о том, насколько качественно происходит регулирование в этой системе и удовлетворяет ли оно технологическим требованиям обьекта управления.На практике качество регулирования определяется визуально по графику переходной характеристики. Однако, имеются точные но более сложные математические методы, дающие конкретные числовые значения (которые не рассматриваются в данной методике).
Классификация показателей качества состоит из нескольких групп:
- прямые — определяемые непосредственно по переходной характеристике процесса,
- корневые — определяемые по корням характеристического полинома,
- частотные — по частотным характеристикам,
- интегральные — получаемые путем интегрирования функций.
Прямыми показателями качества процесса управления, определяемые непосредственно по
переходной характеристике являются:
- Установившееся значение выходной величины Yуст,
- Степень затухания ?,
- Время достижения первого максимума tmax,
- Время регулирования tp,
- Ошибка регулирования Ест (статистическая или среднеквадратическая составляющие),
- Перерегулирование у,
- Динамический коэффициент регулирования Rd,
- Показатель колебательности М.
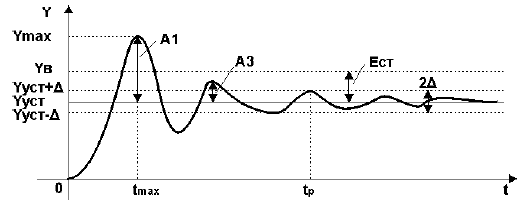
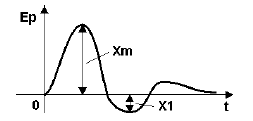
Например, переходная характеристика, снятая на объекте управления при отработке ступенчатого воздействия, имеет колебательный вид и представлена на рис.1.
Рисунок 1 — Определение показателей качества по переходной характеристике
Установившееся значение выходной величины Yуст
Установившееся значение выходной величины Yуст определяется по переходной характеристике,представленной на рис.1.
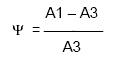
Степень затухания ?
Степень затухания ? определяется по формуле:
где А1 и А3 — соответственно 1-я и 3-я амплитуды переходной характеристики рис.1.
Время достижения первого максимума tmax
Время достижения первого максимума tmax определяется по переходной характеристике,представленной на рис.1.
Время регулирования tp
Время регулирования tp определяется согласно рис.1 следующим образом:Находится допустимое отклонение Д, например, задано Д = 5%Yуст и строится «зона» толщиной 2 Д(см. рис.1). Время tp соответствует последней точке пересечения Y(t) с данной границей. То есть время,когда колебания регулируемой величины перестают превышать 5 % от установившегося значения.
Настройки регулятора необходимо выбирать так, чтобы обеспечить минимально возможное значение общего времени регулирования, либо минимальное значение первой полуволны переходного процесса.
В непрерывных системах с типовыми регуляторами это время бывает минимальным при так называемых оптимальных апериодических переходных процессах. Дальнейшего уменьшения времени регулирования до абсолютного минимума можно достичь при использовании специальных оптимальных по быстродействию систем регулирования.
Ошибка регулирования Ест
Статическая ошибка регулирования Ест = Ув — Ууст, где Ув — входная величина (см. рис.1).В некоторых САР наблюдается ошибка, которая не исчезает даже по истечении длительногоинтервала времени — это статическая ошибка регулирования Ест. Данная ошибка не должна превышатьнекоторой наперед заданной величины. У регуляторов с интегральной составляющей ошибки в установившемся состоянии теоретическиравны нулю, но практически незначительные ошибки могут существовать из-за наличия зоннечувствительности в элементах системы.
Перерегулирование у
Величина перерегулирования у зависит от вида отрабатываемого сигнала.При отработке ступенчатого воздействия (по сигналу задания) – см. рис.1 величина перерегулирования у определяется по формуле:
где значения величин Ymax и Yуст определяются согласно рис.1.
При отработке возмущающего воздействия, величина перерегулирования у определяется изсоотношения:
где значения величин Xm и X1 определяются согласно рис. 2.
Рисунок 2 — График переходного процесса при отработке возмущения
Динамический коэффициент регулирования Rd
Динамический коэффициент регулирования Rd определяется из формулы:
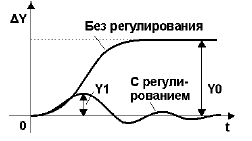
где значения величин Y1 и Y0 определяются согласно рис. 3.
Рисунок 3 — К понятию динамического коэффициента регулирования
Величина динамического коэффициента Rd характеризует степень воздействия регулятора напроцесс, т.е. степень понижения динамического отклонения в системе с регулятором и без него.
Показатель колебательности М
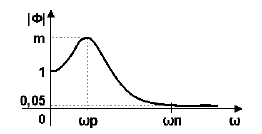
Показатель колебательности M характеризует величину максимума модуля частотной передаточной функции замкнутой системы (на частоте резонанса) и, тем самым, характеризует колебательные свойства системы. Показатель колебательности наглядно иллюстрируется на рисунке 4.
Рисунок 4 — График модуля частотной передаточной функции замкнутой системы
Условно считается, что значение М=1,5-1,6 является оптимальным для промышленных САР, т.к. вэтом случае у обеспечивается в районе от 20% до 40%. При увеличении значения M колебательность всистеме возрастает.
В некоторых случаях нормируется полоса пропускания системы щп, которая соответствует уровню усиления в замкнутой системе 0,05. Чем больше полоса пропускания, тем больше быстродействие замкнутой системы. Однако при этом повышается чувствительность системы к шумам в канале измерения и возрастает дисперсия ошибки регулирования.
Вместо введения
Системы автоматического управления (САУ) предназначены для автоматического изменения одного или нескольких параметров объекта управления с целью установления требуемого режима его работы. САУ обеспечивает поддержание постоянства заданных значений регулируемых параметров или их изменение по заданному закону либо оптимизирует определенные критерии качества управления. Например, к таким системам относятся:
- системы стабилизации,
- системы программного управления,
- следящие системы
Это достаточно широкий класс систем, которые можно найти где угодно. Но какое это отношение имеет к Unity3D и вероятно к играм в частности? В принципе прямое: в любой игре так или иначе использующей симуляцию как элемент геймплея реализуются САУ, к таким играм относятся, например, Kerbal Space Programm, Digital Combat Simulator (бывший Lock On), Strike Suit Zero и т.д. (кто знает еще примеры — пишите в комментариях). В принципе любая игра, моделирующая реальные физические процессы, в том числе и просто кинематику с динамикой движения, может реализовывать те или иные САУ — этот подход проще, естественнее, а у разработчика уже есть есть набор готовых инструментов, предоставленных всякими Вышнеградскими, Ляпуновыми, Калманами, Чебышевами и прочими Коломогоровами, поэтому можно обойтись без изобретения велосипеда, т.к. его уже изобрели, да так, что получилась отдельная наука: Теория автоматического управления. Главное тут не переусердствовать. Одна тут только проблема: рассказывают про ТАУ не везде, не всем, зачастую мало и не очень понятно.
Немножко теории
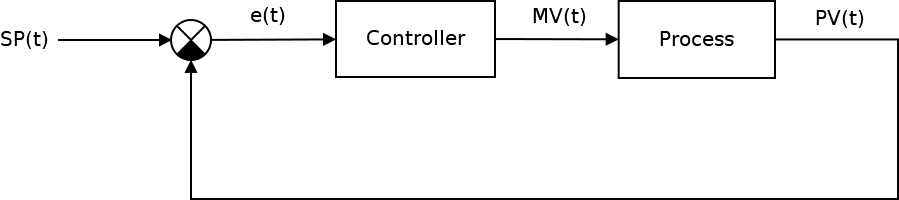
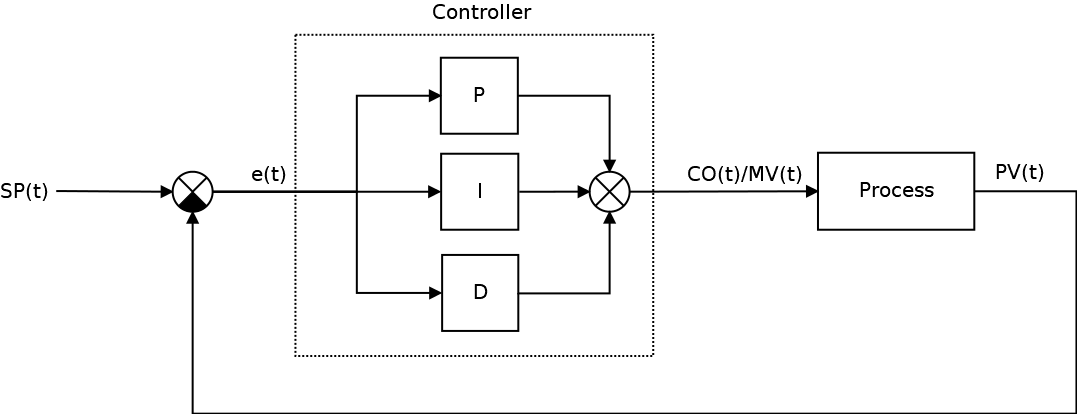
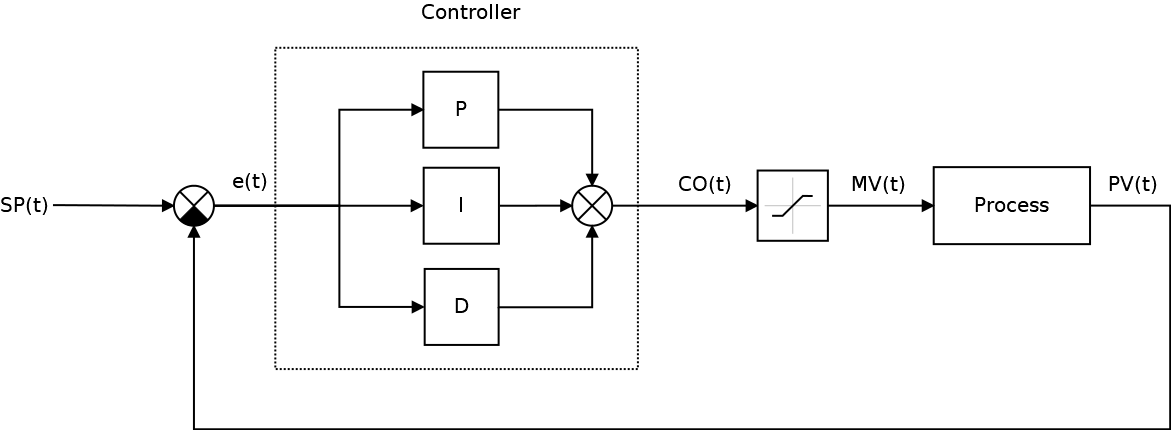
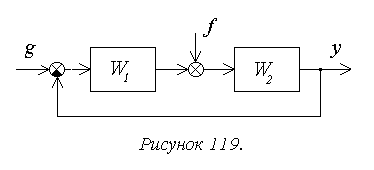
Классическая система автоматического управления представленная на следующем рисунке:
Ключевым элементом любой САУ является регулятор представляющий из себя устройство, которое следит за состоянием объекта управления и обеспечивает требуемый закон управления. Процесс управления включает в себя: вычисление ошибки управления или сигнала рассогласования e(t) как разницы между желаемой уставкой (set point или SP) и текущей величиной процесса (process value или PV), после чего регулятор вырабатывает управляющие сигналы (manipulated value или MV).
Одной из разновидностью регуляторов является пропорционально-интегрально-дифференцирующий (ПИД) регулятор, который формирует управляющий сигнал, являющийся суммой трёх слагаемых: пропорционального, интегрального и дифференциального.
Где, ошибка рассогласования, а также,
— пропорциональная,
— интегральная,
— дифференциальная составляющие (термы) закона управления, который в итоговом виде описывается следующими формулами
Пропорциональная составляющая P — отвечает за т.н. пропорциональное управление, смысл которого в том, что выходной сигнал регулятора, противодействует отклонению регулируемой величины (ошибки рассогласования или еще это называют невязкой) от заданного значения. Чем больше ошибка рассогласования, тем больше командное отклонение регулятора. Это самый простой и очевидный закон управления. Недостаток пропорционального закона управления заключается в том, что регулятор никогда не стабилизируется в заданном значении, а увеличение коэффициента пропорциональности всегда приводит к автоколебаниям. Именно поэтому в довесок к пропорциональному закону управления приходиться использовать интегральный и дифференциальный.
Интегральная составляющая I накапливает (интегрирует) ошибку регулирования, что позволяет ПИД-регулятору устранять статическую ошибку (установившуюся ошибку, остаточное рассогласование). Или другими словами: интегральное звено всегда вносит некоторое смещение и если система подвержена некоторыми постоянным ошибкам, то оно их компенсирует (за счет своего смещения). А вот если же этих ошибок нет или они пренебрежительно малы, то эффект будет обратным — интегральная составляющая сама будет вносить ошибку смещения. Именно по этой причине её не используют, например, в задачах сверхточного позиционирования. Ключевым недостатком интегрального закона управления является эффект насыщения интегратора (Integrator windup).
Дифференциальная составляющая D пропорциональна темпу изменения отклонения регулируемой величины и предназначена для противодействия отклонениям от целевого значения, которые прогнозируются в будущем. Примечательно то, что дифференциальная компонента устраняет затухающие колебания. Дифференциальное регулирование особенно эффективно для процессов, которые имеют большие запаздывания. Недостатком дифференциального закона управления является его неустойчивость к воздействую шумов (Differentiation noise).
Таким образом, в зависимости от ситуации могут применятся П-, ПД-, ПИ- и ПИД-регуляторы, но основным законом управления в основном является пропорциональный (хотя в некоторых специфических задачах и могут использоваться исключительно только звенья дифференциаторов и интеграторов).
Казалось бы, вопрос реализации ПИД-регуляторов уже давно избит и здесь на Хабре есть парочка неплохих статей на эту тему в том числе и на Unity3D, также есть неплохая статья PID Without a PhD (перевод) и цикл статей в журнале «Современные технологии автоматизации» в двух частях: первая и вторая. Также к вашим услугам статья на Википедии (наиболее полную читайте в английском варианте). А на форумах коммьюнити Unity3D нет-нет, да и всплывет PID controller как и на gamedev.stackexchange
При вопрос по реализации ПИД-регуляторов несколько глубже чем и кажется. Настолько, что юных самоделкиных, решивших, реализовать такую схему регулирования ждет немало открытий чудных, а тема актуальная. Так что надеюсь сей опус, кому-нибудь да пригодиться, поэтому приступим.
Попытка номер раз
В качестве примера попытаемся реализовать схему регулирования на примере управления поворотом в простенькой космической 2D-аркаде, по шагам, начиная с самого начала (не забыли, что это туториал?).
Почему не 3D? Потому что реализация не измениться, за исключением того, что придется воротить ПИД-регулятор для контроля тангажа, рысканья и крена. Хотя вопрос корректного применения ПИД-регулирования вместе с кватернионами действительно интересный, возможно в будущем его и освящу, но даже в NASA предпочитают углы Эйлера вместо кватернионов, так что обойдемся простенькой моделью на двухмерной плоскости.
Для начала создадим сам объект игровой объект космического корабля, который будет состоять из собственно самого объекта корабля на верхнем уровне иерархии, прикрепим к нему дочерний объект Engine (чисто спецэффектов ради). Вот как это выглядит у меня:
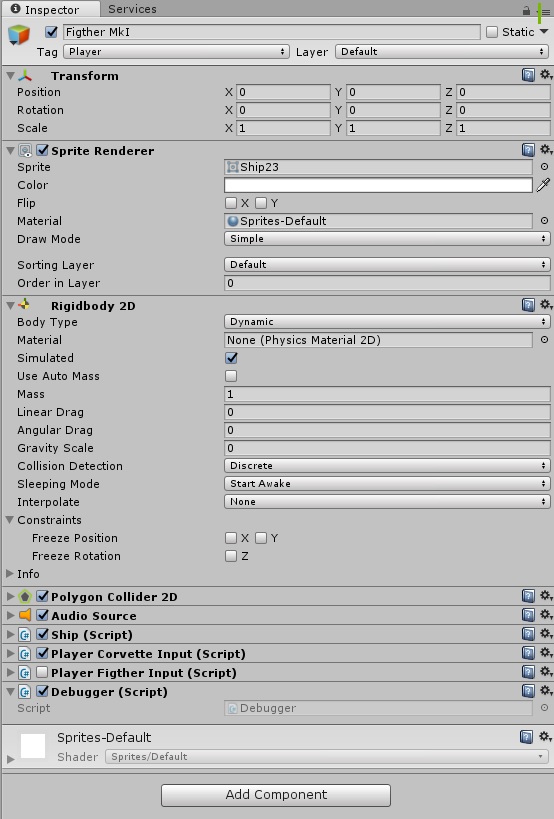
А на сам объект космического корабля накидаем в инспекторе всяческих компонент. Забегая вперед, приведу скрин того, как он будет выглядеть в конце:
Но это потом, а пока в нем еще нет никаких скриптов, только стандартный джентльменский набор: Sprite Render, RigidBody2D, Polygon Collider, Audio Source (зачем?).
Собственно физика у нас сейчас самое главное и управление будет осуществляться исключительно через неё, в противном случае, применение ПИД-регулятора потеряло бы смысл. Масса нашего космического корабля оставим также в 1 кг, а все коэффициенты трения и гравитации равны нулю — в космосе же.
Т.к. помимо самого космического корабля есть куча других, менее умных космических объектов, то сначала опишем родительский класс BaseBody, который в себе будет содержать ссылки на на наши компоненты, методы инициализации и уничтожения, а также ряд дополнительных полей и методов, например для реализации небесной механики:
BaseBody.cs
using UnityEngine;
using System.Collections;
using System.Collections.Generic;
namespace Assets.Scripts.SpaceShooter.Bodies
{
[RequireComponent(typeof(SpriteRenderer))]
[RequireComponent(typeof(AudioSource))]
[RequireComponent(typeof(Rigidbody2D))]
[RequireComponent(typeof(Collider2D))]
public class BaseBody : MonoBehaviour
{
readonly float _deafultTimeDelay = 0.05f;
[HideInInspector]
public static List<BaseBody> _bodies = new List<BaseBody>();
#region RigidBody
[HideInInspector]
public Rigidbody2D _rb2d;
[HideInInspector]
public Collider2D[] _c2d;
#endregion
#region References
[HideInInspector]
public Transform _myTransform;
[HideInInspector]
public GameObject _myObject;
/// <summary>
/// Объект, который появляется при уничтожении
/// </summary>
public GameObject _explodePrefab;
#endregion
#region Audio
public AudioSource _audioSource;
/// <summary>
/// Звуки, которые проигрываются при получении повреждения
/// </summary>
public AudioClip[] _hitSounds;
/// <summary>
/// Звуки, которые проигрываются при появлении объекта
/// </summary>
public AudioClip[] _awakeSounds;
/// <summary>
/// Звуки, которые воспроизводятся перед смертью
/// </summary>
public AudioClip[] _deadSounds;
#endregion
#region External Force Variables
/// <summary>
/// Внешние силы воздйствующие на объект
/// </summary>
[HideInInspector]
public Vector2 _ExternalForces = new Vector2();
/// <summary>
/// Текущий вектор скорости
/// </summary>
[HideInInspector]
public Vector2 _V = new Vector2();
/// <summary>
/// Текущий вектор силы гравитации
/// </summary>
[HideInInspector]
public Vector2 _G = new Vector2();
#endregion
public virtual void Awake()
{
Init();
}
public virtual void Start()
{
}
public virtual void Init()
{
_myTransform = this.transform;
_myObject = gameObject;
_rb2d = GetComponent<Rigidbody2D>();
_c2d = GetComponentsInChildren<Collider2D>();
_audioSource = GetComponent<AudioSource>();
PlayRandomSound(_awakeSounds);
BaseBody bb = GetComponent<BaseBody>();
_bodies.Add(bb);
}
/// <summary>
/// Уничтожение персонажа
/// </summary>
public virtual void Destroy()
{
_bodies.Remove(this);
for (int i = 0; i < _c2d.Length; i++)
{
_c2d[i].enabled = false;
}
float _t = PlayRandomSound(_deadSounds);
StartCoroutine(WaitAndDestroy(_t));
}
/// <summary>
/// Ждем некоторое время перед уничтожением
/// </summary>
/// <param name="waitTime">Время ожидания</param>
/// <returns></returns>
public IEnumerator WaitAndDestroy(float waitTime)
{
yield return new WaitForSeconds(waitTime);
if (_explodePrefab)
{
Instantiate(_explodePrefab, transform.position, Quaternion.identity);
}
Destroy(gameObject, _deafultTimeDelay);
}
/// <summary>
/// Проигрывание случайного звука
/// </summary>
/// <param name="audioClip">Массив звуков</param>
/// <returns>Длительность проигрываемого звука</returns>
public float PlayRandomSound(AudioClip[] audioClip)
{
float _t = 0;
if (audioClip.Length > 0)
{
int _i = UnityEngine.Random.Range(0, audioClip.Length - 1);
AudioClip _audioClip = audioClip[_i];
_t = _audioClip.length;
_audioSource.PlayOneShot(_audioClip);
}
return _t;
}
/// <summary>
/// Получение урона
/// </summary>
/// <param name="damage">Уровень урона</param>
public virtual void Damage(float damage)
{
PlayRandomSound(_hitSounds);
}
}
}Вроде описали все что надо, даже больше чем нужно (в рамках этой статьи). Теперь отнаследуем от него класс корабля Ship, который должен уметь двигаться и поворачивать:
SpaceShip.cs
using UnityEngine;
using System.Collections;
using System.Collections.Generic;
namespace Assets.Scripts.SpaceShooter.Bodies
{
public class Ship : BaseBody
{
public Vector2 _movement = new Vector2();
public Vector2 _target = new Vector2();
public float _rotation = 0f;
public void FixedUpdate()
{
float torque = ControlRotate(_rotation);
Vector2 force = ControlForce(_movement);
_rb2d.AddTorque(torque);
_rb2d.AddRelativeForce(force);
}
public float ControlRotate(Vector2 rotate)
{
float result = 0f;
return result;
}
public Vector2 ControlForce(Vector2 movement)
{
Vector2 result = new Vector2();
return result;
}
}
}Пока в нем нет ничего интересно, на текущий момент это просто класс-заглушка.
Также опишем базовый(абстрактный) класс для всех контроллеров ввода BaseInputController:
BaseInputController.cs
using UnityEngine;
using Assets.Scripts.SpaceShooter.Bodies;
namespace Assets.Scripts.SpaceShooter.InputController
{
public enum eSpriteRotation
{
Rigth = 0,
Up = -90,
Left = -180,
Down = -270
}
public abstract class BaseInputController : MonoBehaviour
{
public GameObject _agentObject;
public Ship _agentBody; // Ссылка на компонент логики корабля
public eSpriteRotation _spriteOrientation = eSpriteRotation.Up; //Это связано с нестандартной
// ориентации спрайта "вверх" вместо "вправо"
public abstract void ControlRotate(float dt);
public abstract void ControlForce(float dt);
public virtual void Start()
{
_agentObject = gameObject;
_agentBody = gameObject.GetComponent<Ship>();
}
public virtual void FixedUpdate()
{
float dt = Time.fixedDeltaTime;
ControlRotate(dt);
ControlForce(dt);
}
public virtual void Update()
{
//TO DO
}
}
}И наконец, класс контроллера игрока PlayerFigtherInput:
PlayerInput.cs
using UnityEngine;
using Assets.Scripts.SpaceShooter.Bodies;
namespace Assets.Scripts.SpaceShooter.InputController
{
public class PlayerFigtherInput : BaseInputController
{
public override void ControlRotate(float dt)
{
// Определяем позицию мыши относительно игрока
Vector3 worldPos = Input.mousePosition;
worldPos = Camera.main.ScreenToWorldPoint(worldPos);
// Сохраняем координаты указателя мыши
float dx = -this.transform.position.x + worldPos.x;
float dy = -this.transform.position.y + worldPos.y;
//Передаем направление
Vector2 target = new Vector2(dx, dy);
_agentBody._target = target;
//Вычисляем поворот в соответствии с нажатием клавиш
float targetAngle = Mathf.Atan2(dy, dx) * Mathf.Rad2Deg;
_agentBody._targetAngle = targetAngle + (float)_spriteOrientation;
}
public override void ControlForce(float dt)
{
//Передаем movement
_agentBody._movement = Input.GetAxis("Vertical") * Vector2.up
+ Input.GetAxis("Horizontal") * Vector2.right;
}
}
}Вроде бы закончили, теперь наконец можно перейти к тому, ради чего все это затевалось, т.е. ПИД-регуляторам (не забыли надеюсь?). Его реализация кажется простой до безобразия:
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace Assets.Scripts.Regulator
{
[System.Serializable] // Этот атрибут необходим для того что бы поля регулятора
// отображались в инспекторе и сериализовывались
public class SimplePID
{
public float Kp, Ki, Kd;
private float lastError;
private float P, I, D;
public SimplePID()
{
Kp = 1f;
Ki = 0;
Kd = 0.2f;
}
public SimplePID(float pFactor, float iFactor, float dFactor)
{
this.Kp = pFactor;
this.Ki = iFactor;
this.Kd = dFactor;
}
public float Update(float error, float dt)
{
P = error;
I += error * dt;
D = (error - lastError) / dt;
lastError = error;
float CO = P * Kp + I * Ki + D * Kd;
return CO;
}
}
}Значения коэффициентов по умолчанию возьмем с потолка: это будет тривиальный единичный коэффициент пропорционального закона управления Kp = 1, небольшое значение коэффициента для дифференциального закона управления Kd = 0.2, который должен устранить ожидаемые колебания и нулевое значение для Ki, которое выбрано потому, что в нашей программной модели нет никаких статичных ошибок (но вы всегда можете их внести, а потом героически побороться с помощью интегратора).
Теперь вернемся к нашему классу SpaceShip и попробуем заюзать наше творение в качестве регулятора поворота космического корабля в методе ControlRotate:
public float ControlRotate(Vector2 rotate)
{
float MV = 0f;
float dt = Time.fixedDeltaTime;
//Вычисляем ошибку
float angleError = Mathf.DeltaAngle(_myTransform.eulerAngles.z, targetAngle);
//Получаем корректирующее ускорение
MV = _angleController.Update(angleError, dt);
return MV;
}ПИД-регулятор будет осуществлять точное угловое позиционировая космического корабля только за счет крутящего момента. Все честно, физика и САУ, почти как в реальной жизни.
И без этих ваших Quaternion.Lerp
if (!_rb2d.freezeRotation)
rb2d.freezeRotation = true;
float deltaAngle = Mathf.DeltaAngle(_myTransform.eulerAngles.z, targetAngle);
float T = dt * Mathf.Abs( _rotationSpeed / deltaAngle);
// Трансформируем угол в вектор
Quaternion rot = Quaternion.Lerp(
_myTransform.rotation,
Quaternion.Euler(new Vector3(0, 0, targetAngle)),
T);
// Изменяем поворот объекта
_myTransform.rotation = rot;Получившейся исходный код Ship.cs под спойлером
using UnityEngine;
using Assets.Scripts.Regulator;
namespace Assets.Scripts.SpaceShooter.Bodies
{
public class Ship : BaseBody
{
public GameObject _flame;
public Vector2 _movement = new Vector2();
public Vector2 _target = new Vector2();
public float _targetAngle = 0f;
public float _angle = 0f;
[Header("PID")]
public SimplePID _angleController = new SimplePID();
public void FixedUpdate()
{
float torque = ControlRotate(_targetAngle);
Vector2 force = ControlForce(_movement);
_rb2d.AddTorque(torque);
_rb2d.AddRelativeForce(force);
}
public float ControlRotate(float rotate)
{
float MV = 0f;
float dt = Time.fixedDeltaTime;
_angle = _myTransform.eulerAngles.z;
//Вычисляем ошибку
float angleError = Mathf.DeltaAngle(_angle, rotate);
//Получаем корректирующее ускорение
MV = _angleController.Update(angleError, dt);
return MV;
}
public Vector2 ControlForce(Vector2 movement)
{
Vector2 MV = new Vector2();
//Кусок кода спецэффекта работающего двигателя ради
if (movement != Vector2.zero)
{
if (_flame != null)
{
_flame.SetActive(true);
}
}
else
{
if (_flame != null)
{
_flame.SetActive(false);
}
}
MV = movement;
return MV;
}
}
}
Все? Расходимся по домам?
WTF! Что происходит? Почему корабль поворачивается как-то странно? И почему он так резко отскакивает от других объектов? Неужели этот глупый ПИД-регулятор не работает?
Без паники! Давайте попробуем разобраться что происходит.
В момент получения нового значения SP, происходит резкий (ступенчатый) скачок рассогласования ошибки, которая, как мы помним, вычисляется вот так: соответственно происходит резкий скачок производной ошибки
, которую мы вычисляем в этой строчке кода:
D = (error - lastError) / dt;Можно, конечно, попробовать другие схемы дифференцирования, например, трехточечную, или пятиточечную, или… но все равно это не поможет. Ну вот не любят производные резких скачков — в таких точках функция не является дифференцируемой. Однако поэкспериментировать с разными схемами дифференцирования и интегрирования стоит, но потом и не в этой статье.
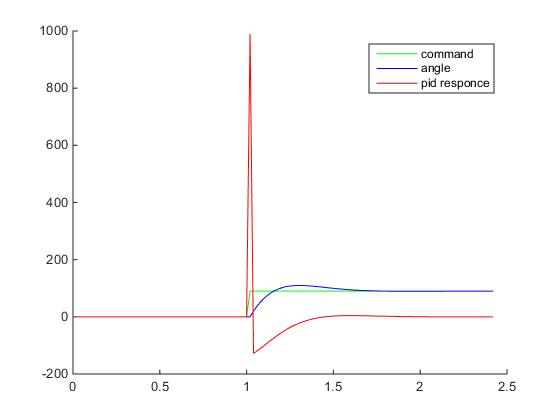
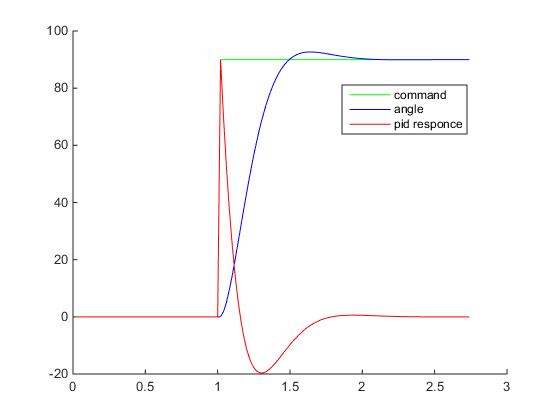
Думаю что настал момент построить графики переходного процесса: ступенчатое воздействие от S(t) = 0 в SP(t) = 90 градусов для тела массой в 1 кг, длинной плеча силы в 1 метр и шагом сетки дифференцирования 0.02 с — прям как в нашем примере на Unity3D (на самом деле не совсем, при построении этих графиков не учитывалось, что момент инерции зависит от геометрии твердого тела, поэтому переходный процесс будет немножко другой, но все же достаточно похожий для демонстрации). Все величены на грифике приведены в абсолютных значениях:
Хм, что здесь происходит? Куда улетел отклик ПИД-регулятора?
Поздравляю, мы только что столкнулись с таким явлением как «удар» (kick). Очевидно, что в момент времени, когда процесс еще PV = 0, а уставка уже SP = 90, то при численном дифференцировании получим значение производной порядка 4500, которое умножится на Kd=0.2 и сложится с пропорциональным теромом, так что на выходе мы получим значение углового ускорения 990, а это уже форменное надругательство над физической моделью Unity3D (угловые скорости будут достигать 18000 град/с… я думаю это предельное значение угловой скорости для RigidBody2D).
- Может стоит подобрать коэффициенты ручками, так чтобы скачок был не таким сильным?
- Нет! Самое лучше чего мы таким образом сможем добиться — небольшая амплитуда скачка производной, однако сам скачок как был так и останется, при этом можно докрутиться до полной неэффективности дифференциальной составляющей.
Впрочем можете поэкспериментировать.
Попытка номер два. Сатурация
Логично, что привод (в нашем случае виртуальные маневровые двигатели SpaceShip), не может отрабатывать сколько угодно большие значения которые может выдать наш безумный регулятор. Так что первое что мы сделаем — сатурируем выход регулятора:
public float ControlRotate(Vector2 rotate, float thrust)
{
float CO = 0f;
float MV = 0f;
float dt = Time.fixedDeltaTime;
//Вычисляем ошибку
float angleError = Mathf.DeltaAngle(_myTransform.eulerAngles.z, targetAngle);
//Получаем корректирующее ускорение
CO = _angleController.Update(angleError, dt);
//Сатурируем
MV = CO;
if (MV > thrust) MV = thrust;
if (MV< -thrust) MV = -thrust;
return MV;
}А очередной раз переписанный класс Ship полностью выглядит так
namespace Assets.Scripts.SpaceShooter.Bodies
{
public class Ship : BaseBody
{
public GameObject _flame;
public Vector2 _movement = new Vector2();
public Vector2 _target = new Vector2();
public float _targetAngle = 0f;
public float _angle = 0f;
public float _thrust = 1f;
[Header("PID")]
public SimplePID _angleController = new SimplePID(0.1f,0f,0.05f);
public void FixedUpdate()
{
_torque = ControlRotate(_targetAngle, _thrust);
_force = ControlForce(_movement);
_rb2d.AddTorque(_torque);
_rb2d.AddRelativeForce(_force);
}
public float ControlRotate(float targetAngle, float thrust)
{
float CO = 0f;
float MV = 0f;
float dt = Time.fixedDeltaTime;
//Вычисляем ошибку
float angleError = Mathf.DeltaAngle(_myTransform.eulerAngles.z, targetAngle);
//Получаем корректирующее ускорение
CO = _angleController.Update(angleError, dt);
//Сатурируем
MV = CO;
if (MV > thrust) MV = thrust;
if (MV< -thrust) MV = -thrust;
return MV;
}
public Vector2 ControlForce(Vector2 movement)
{
Vector2 MV = new Vector2();
if (movement != Vector2.zero)
{
if (_flame != null)
{
_flame.SetActive(true);
}
}
else
{
if (_flame != null)
{
_flame.SetActive(false);
}
}
MV = movement * _thrust;
return MV;
}
public void Update()
{
}
}
}Итоговая схема нашего САУ тогда станет уже вот такой
При этом уже становится понятно, что выход контроллера CO(t) немного не одно и тоже, что управляемая величина процесса MV(t).
Собственно с этого места можно уже добавлять новую игровую сущность — привод, через которую и будет осуществляться управление процессом, логика работы которой может быть более сложной, чем просто Mathf.Clamp(), например, можно ввести дискретизацию значений (дабы не перегружать игровую физику величинами идущими шестыми после запятой), мертвую зону (опять таки не имеет смысл перегружать физику сверхмалыми реакциями), ввести задержку в упраление и нелинейность (например, сигмоиду) привода, после чего посмотреть, что из этого получится.
Запустив игру, мы обнаружим, что космический корабль стал наконец управляемым:
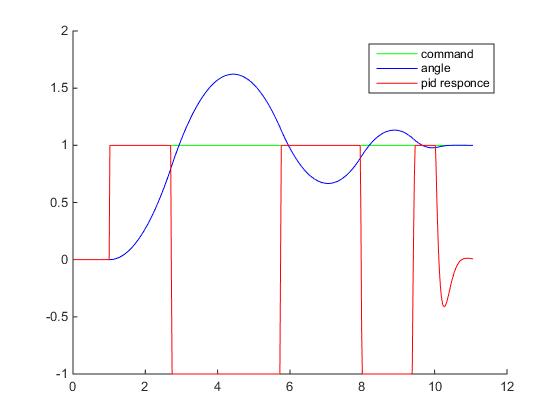
Если построить графики, то можно увидеть, что реакция контроллера стала уже вот такой:
Здесь уже используются нормированные величены, углы поделены на значение SP, а выход контроллера отнормирован относительно максимального значения на котором уже происходит сатурация.
Теперь на графике видно наличие ошибки перерегулирования (overshooting) и затухающие колебания. Уменьшая Kp и увеличивая Kd можно добиться уменьшения колебаний, но зато увеличится время реакции контроллера (скорость поворота корабля). И наоборот, увеличивая Kp и уменьшая Kd — можно добиться увеличения скорости реакции контроллера, но появятся паразитные колебания, которые при определенных (критических) значениях, перестанут быть затухающими.
Ниже приведена известна таблица влияния увеличения параметров ПИД-регулятора (как уменьшить шрифт, а то таблица безе переносов не лезет?):
А общий алгоритм ручной настройки ПИД-регулятора следующий:
- Подбираем пропорциональный коэффициенты при отключенных дифференциальных и интегральных звеньях до тех пор пока не начнутся автоколебания.
- Постепенно увеличивая дифференциальную составляющую избавляемся от автоколебаний
- Если наблюдается остаточная ошибка регулирования (смещение), то устраняем её за счет интегральной составляющей.
Каких-то общих значений параметров ПИД-регулятора нет: конкретные значения зависят исключительно от параметров процесса (его передаточной характеристики): ПИД-регулятор отлично работающий с одним объектом управления окажется неработоспособным с другим. Более того, коэффициенты при пропорциональной, интегральной и дифференциальной составляющих еще и взаимозависимы.
В общем не будем о грустном, дальше нас ждет самое интересное…
Попытка номер три. Еще раз производные
Приделав костыль в виде ограничения значений выхода контроллера мы так и не решили самую главную проблему нашего регулятора — дифференциальная составляющая плохо себя чувствует при ступенчатом изменении ошибки на входе регуляторе. На самом деле есть множество других костылей, например, в момент скачкообразного изменения SP «отключать» дифференциальную составляющую или же поставить фильтры нижних частот между SP(t) и операцией за счет которого будет происходить плавное нарастание ошибки, а можно совсем развернуться и впендюрить самый настоящий фильтр Калмана для сглаживания входных данных. В общем костылей много, и добавить наблюдателя конечно хотелось бы, но не в этот раз.
Поэтому снова вернемся к производной ошибки рассогласования и внимательно на неё посмотрим:
Ничего не заметили? Если хорошенько присмотреться, то можно обнаружить, что вообще-то SP(t), не меняется во времени (за исключением моментов ступенчатого изменения, когда регулятор получает новую команду), т.е. её производная равна нулю:
тогда
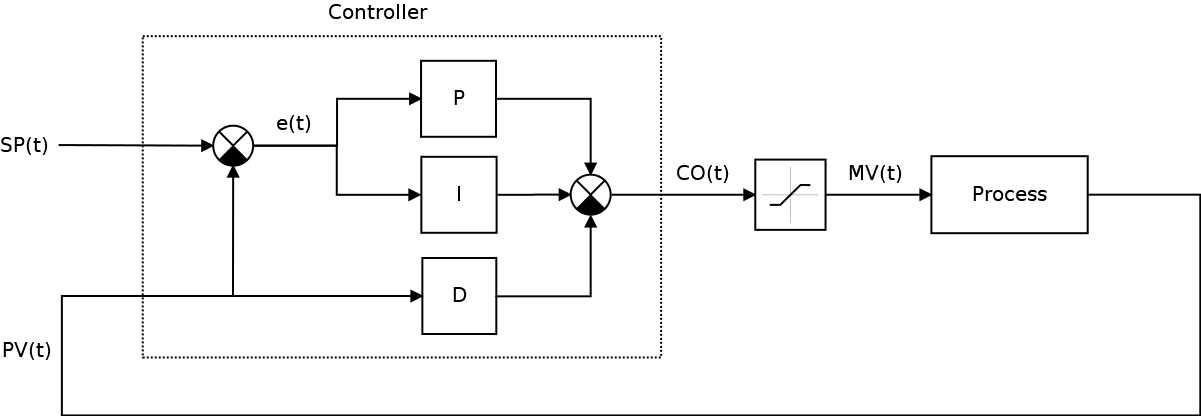
Иными словами, вместо производной ошибки, которая дифференцируема не везде мы можем использовать производную от процесса, который в мире классической механики как правило непрерывен и дифференцируем везде, а схема нашей САУ уже приобретет следующий вид:
Модифицируем код регулятора:
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace Assets.Scripts.Regulator
{
[System.Serializable]
public class SimplePID
{
public float Kp, Ki, Kd;
private float P, I, D;
private float lastPV = 0f;
public SimplePID()
{
Kp = 1f;
Ki = 0f;
Kd = 0.2f;
}
public SimplePID(float pFactor, float iFactor, float dFactor)
{
this.Kp = pFactor;
this.Ki = iFactor;
this.Kd = dFactor;
}
public float Update(float error, float PV, float dt)
{
P = error;
I += error * dt;
D = -(PV - lastPV) / dt;
lastPV = PV;
float CO = Kp * P + Ki * I + Kd * D;
return CO;
}
}
}И немного изменим метод ControlRotate:
public float ControlRotate(Vector2 rotate, float thrust)
{
float CO = 0f;
float MV = 0f;
float dt = Time.fixedDeltaTime;
//Вычисляем ошибку
float angleError = Mathf.DeltaAngle(_myTransform.eulerAngles.z, targetAngle);
//Получаем корректирующее ускорение
CO = _angleController.Update(angleError, _myTransform.eulerAngles.z, dt);
//Сатурируем
MV = CO;
if (CO > thrust) MV = thrust;
if (CO < -thrust) MV = -thrust;
return MV;
}И-и-и-и… если запустить игру, то обнаружиться, что на самом деле ничего ничего не изменилось с последней попытки, что и требовалось доказать. Однако, если убрать сатурацию, то график реакции регулятора будет выглядеть вот так:
Скачок CO(t) по прежнему присутствует, однако он уже не такой большой как был в самом начале, а самое главное — он стал предсказуемым, т.к. обеспечивается исключительно пропорциональной составляющей, и ограничен максимально возможной ошибкой рассогласования и пропорциональным коэффициентом ПИД-регулятора (а это уже намекает на то, что Kp имеет смысл выбрать все же меньше единицы, например, 1/90f), но не зависит от шага сетки дифференцирования (т.е. dt). В общем, я настоятельно рекомендую использовать именно производную процесса, а не ошибки.
Думаю теперь никого не удивит, но таким же макаром можно заменить на
, однако останавливаться на этом мы не будем, можете сами поэкспериментировать и рассказать в комментариях, что из этого получилось (самому интересно)
Попытка номер четыре. Альтернативные реализации ПИД-регулятор
Помимо описанного выше идеального представления ПИД-регулятора, на практике часто применяется стандартная форма, без коэффициентов Ki и Kd, вместо которых используются временные постоянные.
Такой подход связан с тем, что ряд методик настройки ПИД-регулятора основан на частотных характеристиках ПИД-регулятора и процесса. Собственно вся ТАУ и крутится вокруг частотных характеристик процессов, поэтому для желающих углубиться, и, внезапно, столкнувшихся с альтернативной номенклатурой, приведу пример т.н. стандартной формы ПИД-регулятора:
где, — постоянная дифференцирования, влияющая на прогнозирование состояния системы регулятором,
— постоянная интегрирования, влияющая на интервал усреднения ошибки интегральным звеном.
Основные принципы настройки ПИД-регулятора в стандартной форме аналогичны идеализированному ПИД-регулятору:
- увеличение пропорционального коэффициента увеличивает быстродействие и снижает запас устойчивости;
- с уменьшением интегральной составляющей ошибка регулирования с течением времени уменьшается быстрее;
- уменьшение постоянной интегрирования уменьшает запас устойчивости;
- увеличение дифференциальной составляющей увеличивает запас устойчивости и быстродействие
Исходный код стандартной формы, вы можете найти под спойлером
namespace Assets.Scripts.Regulator
{
[System.Serializable]
public class StandartPID
{
public float Kp, Ti, Td;
public float error, CO;
public float P, I, D;
private float lastPV = 0f;
public StandartPID()
{
Kp = 0.1f;
Ti = 10000f;
Td = 0.5f;
bias = 0f;
}
public StandartPID(float Kp, float Ti, float Td)
{
this.Kp = Kp;
this.Ti = Ti;
this.Td = Td;
}
public float Update(float error, float PV, float dt)
{
this.error = error;
P = error;
I += (1 / Ti) * error * dt;
D = -Td * (PV - lastPV) / dt;
CO = Kp * (P + I + D);
lastPV = PV;
return CO;
}
}
}В качестве значений по умолчанию, выбраны Kp = 0.01, Ti = 10000, Td = 0.5 — при таких значениях корабль поворачивается достаточно быстро и обладает некоторым запасом устойчивости.
Помимо такой формы ПИД-регулятора, часто используется т.н. реккурентная форма:
Не будем на ней останавливаться, т.к. она актуальна прежде всего для хардверных программистов, работающих с FPGA и микроконтроллерами, где такая реализация значительно удобнее и эффективнее. В нашем же случае — давайте что-нибудь сваям на Unity3D — это просто еще одна реализация ПИД-контроллера, которая ни чем не лучше других и даже менее понятная, так что еще раз дружно порадуемся как хорошо программировать в уютненьком C#, а не в жутком и страшном VHDL, например.
Вместо заключения. Куда бы еще присобачить ПИД-регулятор
Теперь попробуем немного усложнить управление корабля используя двухконтурное управление: один ПИД-регулятор, уже знакомый нам _angleController, отвечает по прежнему за угловое позиционирование, а вот второй — новый, _angularVelocityController — контролирует скорость поворота:
public float ControlRotate(float targetAngle, float thrust)
{
float CO = 0f;
float MV = 0f;
float dt = Time.fixedDeltaTime;
_angle = _myTransform.eulerAngles.z;
//Контроллер угла поворота
float angleError = Mathf.DeltaAngle(_angle, targetAngle);
float torqueCorrectionForAngle =
_angleController.Update(angleError, _angle, dt);
//Контроллер стабилизации скорости
float angularVelocityError = -_rb2d.angularVelocity;
float torqueCorrectionForAngularVelocity =
_angularVelocityController.Update(angularVelocityError, -angularVelocityError, dt);
//Суммарный выход контроллера
CO = torqueCorrectionForAngle + torqueCorrectionForAngularVelocity;
//Дискретизируем с шагом 100
CO = Mathf.Round(100f * CO) / 100f;
//Сатурируем
MV = CO;
if (CO > thrust) MV = thrust;
if (CO < -thrust) MV = -thrust;
return MV;
}Назначение второго регулятора — гашение избыточных угловых скоростей, за счет изменения крутящего момента — это сродни наличию углового трения, которое мы отключили еще при создании игрового объекта. Такая схема управления [возможно] позволит получить более стабильное поведение корабля, и даже обойтись только пропорциональными коэффициентами управления — второй регулятор будет гасить все колебания, выполняя функцию, аналогичную дифференциальной составляющей первого регулятора.
Помимо этого, добавим новый класс ввода игрока — PlayerInputCorvette, в котором повороты буду осуществляться уже за счет нажатия клавиш «вправо-влево», а целеуказание с помощью мыши мы оставим для чего-нибудь более полезного, например, для управления турелью. Заодно у нас теперь появился такой параметр как _turnRate — отвечающий за скорость/отзывчивость поворота (не понятно только куда его поместить лучше в InputCOntroller или все же Ship).
public class PlayerCorvetteInput : BaseInputController
{
public float _turnSpeed = 90f;
public override void ControlRotate()
{
// Находим указатель мыши
Vector3 worldPos = Input.mousePosition;
worldPos = Camera.main.ScreenToWorldPoint(worldPos);
// Сохраняем относительные координаты указателя мыши
float dx = -this.transform.position.x + worldPos.x;
float dy = -this.transform.position.y + worldPos.y;
//Передаем направление указателя мыши
Vector2 target = new Vector2(dx, dy);
_agentBody._target = target;
//Вычисляем поворот в соответствии с нажатием клавиш
_agentBody._rotation -= Input.GetAxis("Horizontal") * _turnSpeed * Time.deltaTime;
}
public override void ControlForce()
{
//Передаем movement
_agentBody._movement = Input.GetAxis("Vertical") * Vector2.up;
}
}Также для наглядности накидаем на коленках скрипт для отображения отладочной информации
namespace Assets.Scripts.SpaceShooter.UI
{
[RequireComponent(typeof(Ship))]
[RequireComponent(typeof(BaseInputController))]
public class Debugger : MonoBehaviour
{
Ship _ship;
BaseInputController _controller;
List<SimplePID> _pids = new List<SimplePID>();
List<string> _names = new List<string>();
Vector2 _orientation = new Vector2();
// Use this for initialization
void Start()
{
_ship = GetComponent<Ship>();
_controller = GetComponent<BaseInputController>();
_pids.Add(_ship._angleController);
_names.Add("Angle controller");
_pids.Add(_ship._angularVelocityController);
_names.Add("Angular velocity controller");
}
// Update is called once per frame
void Update()
{
DrawDebug();
}
Vector3 GetDiretion(eSpriteRotation spriteRotation)
{
switch (_controller._spriteOrientation)
{
case eSpriteRotation.Rigth:
return transform.right;
case eSpriteRotation.Up:
return transform.up;
case eSpriteRotation.Left:
return -transform.right;
case eSpriteRotation.Down:
return -transform.up;
}
return Vector3.zero;
}
void DrawDebug()
{
//Направление поворота
Vector3 vectorToTarget = transform.position
+ 5f * new Vector3(-Mathf.Sin(_ship._targetAngle * Mathf.Deg2Rad),
Mathf.Cos(_ship._targetAngle * Mathf.Deg2Rad), 0f);
// Текущее направление
Vector3 heading = transform.position + 4f * GetDiretion(_controller._spriteOrientation);
//Угловое ускорение
Vector3 torque = heading - transform.right * _ship._Torque;
Debug.DrawLine(transform.position, vectorToTarget, Color.white);
Debug.DrawLine(transform.position, heading, Color.green);
Debug.DrawLine(heading, torque, Color.red);
}
void OnGUI()
{
float x0 = 10;
float y0 = 100;
float dx = 200;
float dy = 40;
float SliderKpMax = 1;
float SliderKpMin = 0;
float SliderKiMax = .5f;
float SliderKiMin = -.5f;
float SliderKdMax = .5f;
float SliderKdMin = 0;
int i = 0;
foreach (SimplePID pid in _pids)
{
y0 += 2 * dy;
GUI.Box(new Rect(25 + x0, 5 + y0, dx, dy), "");
pid.Kp = GUI.HorizontalSlider(new Rect(25 + x0, 5 + y0, 200, 10),
pid.Kp,
SliderKpMin,
SliderKpMax);
pid.Ki = GUI.HorizontalSlider(new Rect(25 + x0, 20 + y0, 200, 10),
pid.Ki,
SliderKiMin,
SliderKiMax);
pid.Kd = GUI.HorizontalSlider(new Rect(25 + x0, 35 + y0, 200, 10),
pid.Kd,
SliderKdMin,
SliderKdMax);
GUIStyle style1 = new GUIStyle();
style1.alignment = TextAnchor.MiddleRight;
style1.fontStyle = FontStyle.Bold;
style1.normal.textColor = Color.yellow;
style1.fontSize = 9;
GUI.Label(new Rect(0 + x0, 5 + y0, 20, 10), "Kp", style1);
GUI.Label(new Rect(0 + x0, 20 + y0, 20, 10), "Ki", style1);
GUI.Label(new Rect(0 + x0, 35 + y0, 20, 10), "Kd", style1);
GUIStyle style2 = new GUIStyle();
style2.alignment = TextAnchor.MiddleLeft;
style2.fontStyle = FontStyle.Bold;
style2.normal.textColor = Color.yellow;
style2.fontSize = 9;
GUI.TextField(new Rect(235 + x0, 5 + y0, 60, 10), pid.Kp.ToString(), style2);
GUI.TextField(new Rect(235 + x0, 20 + y0, 60, 10), pid.Ki.ToString(), style2);
GUI.TextField(new Rect(235 + x0, 35 + y0, 60, 10), pid.Kd.ToString(), style2);
GUI.Label(new Rect(0 + x0, -8 + y0, 200, 10), _names[i++], style2);
}
}
}
}Класс Ship также претерпел необратимые мутации и теперь должен выглядеть вот так:
namespace Assets.Scripts.SpaceShooter.Bodies
{
public class Ship : BaseBody
{
public GameObject _flame;
public Vector2 _movement = new Vector2();
public Vector2 _target = new Vector2();
public float _targetAngle = 0f;
public float _angle = 0f;
public float _thrust = 1f;
[Header("PID")]
public SimplePID _angleController = new SimplePID(0.1f,0f,0.05f);
public SimplePID _angularVelocityController = new SimplePID(0f,0f,0f);
private float _torque = 0f;
public float _Torque
{
get
{
return _torque;
}
}
private Vector2 _force = new Vector2();
public Vector2 _Force
{
get
{
return _force;
}
}
public void FixedUpdate()
{
_torque = ControlRotate(_targetAngle, _thrust);
_force = ControlForce(_movement, _thrust);
_rb2d.AddTorque(_torque);
_rb2d.AddRelativeForce(_force);
}
public float ControlRotate(float targetAngle, float thrust)
{
float CO = 0f;
float MV = 0f;
float dt = Time.fixedDeltaTime;
_angle = _myTransform.eulerAngles.z;
//Контроллер угла поворота
float angleError = Mathf.DeltaAngle(_angle, targetAngle);
float torqueCorrectionForAngle =
_angleController.Update(angleError, _angle, dt);
//Контроллер стабилизации скорости
float angularVelocityError = -_rb2d.angularVelocity;
float torqueCorrectionForAngularVelocity =
_angularVelocityController.Update(angularVelocityError, -angularVelocityError, dt);
//Суммарный выход контроллера
CO = torqueCorrectionForAngle + torqueCorrectionForAngularVelocity;
//Дискретизируем с шагом 100
CO = Mathf.Round(100f * CO) / 100f;
//Сатурируем
MV = CO;
if (CO > thrust) MV = thrust;
if (CO < -thrust) MV = -thrust;
return MV;
}
public Vector2 ControlForce(Vector2 movement, float thrust)
{
Vector2 MV = new Vector2();
if (movement != Vector2.zero)
{
if (_flame != null)
{
_flame.SetActive(true);
}
}
else
{
if (_flame != null)
{
_flame.SetActive(false);
}
}
MV = movement * thrust;
return MV;
}
public void Update()
{
}
}
}А вот, собственно заключительное видео того, что должно получиться:
К сожалению получилось охватить не все, что хотелось бы, в частности почти не затронут вопрос настройки ПИД-регулятора и практически не освящена интегральная составляющая — фактически приведен пример только для ПД-регулятора. Собственно изначально планировалось несколько больше примеров (круиз-контроль, вращение турели и компенсация вращательного момента), но статья итак уже разбухла, да и вообще:
Немного ссылок
- Годная статья на английской вики
- PID tutorial
- ПИД-регуляторы: вопросы реализации. Часть 1
- ПИД-регуляторы: вопросы реализации. Часть 2
- PID Without a PhD
- PID Without a PhD. Перевод
- Derivative Action and PID Control
- Control System Lab: PID
- ПИД-регулятор своими руками
- Корректная реализация разностной схемы ПИД регулятора
- Программируем квадрокоптер на Arduino (часть 1)
- Виртуальный квадрокоптер на Unity + OpenCV (Часть 1)
- Поляков К.Ю. Теория автоматического управления для чайников
- PID control system analysis, design, and technology
- Aidan O’Dwyer. Handbook of PI and PID Controller Tuning Rules (3rd ed.)
- PID process control, a “Cruise Control” example
- https://www.mathworks.com/discovery/pid-control.html
- http://scilab.ninja/study-modules/scilab-control-engineering-basics/module-4-pid-control/
- https://sourceforge.net/p/octave/control/ci/default/tree/inst/optiPID.m
Еще немного ссылок на другие примеры
http://luminaryapps.com/blog/use-a-pid-loop-to-control-unity-game-objects/
http://www.habrador.com/tutorials/pid-controller/3-stabilize-quadcopter/
https://www.gamedev.net/articles/programming/math-and-physics/pid-control-of-physics-bodies-r3885/
https://ksp-kos.github.io/KOS/tutorials/pidloops.html
Расчеты статической ошибки εСт регулирования
Входной сигнал x(t)=X=constи изображением его является.
В соответствии с (1.56) статическую ошибкуεСТследует вычислять по
формуле

1). Пусть в (1.57) значение порядка νастатизма САУ равно нулю:ν=0. Такая
САУ называется статической. Тогда
статическая ошибкаεСТбудет равна
В статической САУ имеется статическая
ошибка εСТ, которую можно
только уменьшить путем увеличения
общего коэффициента усиленияКразомкнутой САУ, но обратить в ноль ее
нельзя.
2). Пусть в (1.57) значение порядка νастатизма САУ равно 1:ν=1. Такая САУ
называется астатической 1-го порядка.
Тогда статическая ошибкаεСТбудет равна
В астатической САУ 1-го порядка статическая
ошибка εСТравна нулю,
т.е САУ является абсолютно точной. Можно
проверить, что при астатизме САУ выше1, статическая ошибка регулирования
всегда будет нулевой.
Расчеты скоростной ошибки εСт регулирования
Входной сигнал x(t)=Vtи изображением его является.
В соответствии с (1.56) скоростную ошибкуεСКследует вычислять по
формуле

1). Пусть в (1.58) значение порядка νастатизма САУ равно нулю:ν=0. Такая
САУ называется статической. Тогда
скоростная ошибкаεСКбудет равна
В статической САУ скоростная ошибка
εСКбесконечно большая
и, поэтому, такая САУ неработоспособна.
2). Пусть в (1.58) значение порядка νастатизма САУ равно 1:ν=1. Такая САУ
называется астатической 1-го порядка.
Тогда скоростная ошибкаεСКбудет равна
В астатической САУ 1-го порядка имеется
скоростная ошибка εСК,
которую можно только уменьшить путем
увеличения общего коэффициента усиленияКразомкнутой САУ, но обратить в
ноль ее нельзя.
3). Пусть в (1.58) значение порядка νастатизма САУ равно 2:ν=2. Такая САУ
называется астатической 2-го порядка.
Тогда скоростная ошибкаεСКбудет равна
В астатической САУ 2-го порядка скоростная
ошибка εСКравна нулю,
т.е САУ является абсолютно точной.
Выводы по расчетам статической и скоростной ошибок регулирования:
1. Ошибки регулирования могут быть
уменьшены путем увеличения общего
коэффициента усиления Ки порядка
астатизмаνразомкнутой САУ.
2. При увеличении Кошибки регулирования
только уменьшаются. но не обращаются в
ноль.
3. При увеличении νСАУ становится
абсолютно точной — ошибка регулирования
становится нулевой.
Косвенные
показатели качества САУ и их связь с
прямыми показателями качества.
Использование ЛАЧХ для оценки качества
САУ
Невозможность получения формул для
расчета динамических показателей
качества (рис.1.42), а также требования
задач синтеза САУ, обусловило разработки
комплексных показателей качества.
Косвенные показатели качества, в
большинстве своем, являются частотными,
которые определяются из ЧХ, АЧХ, ФЧХ и
ЛАЧХ. Косвенные показатели качества
должны удовлетворять следующим
требованиям:
1. Косвенные показатели должны просто
вычисляться или определяться из частотных
характеристик разомкнутой САУ.
2. Погрешность определения значений
прямых показателей качества через
значения косвенных показателей качества
должна быть мала.
3. Косвенные показатели должны быть
приспособлены для эффективного решения
задач синтеза САУ.
4
Косвенные показатели должны давать
возможность просто анализировать
влияние параметров настроек регуляторов
САУ и характеристик любых других звеньев
САУ на прямые показатели качества.
Косвенных показателей качества или их
наборов разработано достаточно много.
Каждый косвенный показатель качества
или их набор вводятся для эффективного
решения конкретных типов задач
автоматического управления и, поэтому,
универсальных косвенных показателей
качества не существует в принципе. По
сути, косвенные показатели упрощают
анализ и синтез САУ, но прямые показатели
качества определяются через косвенные
всегда неточно.
Прежде всего рассмотрим набор косвенных
показателей качества, полученных из
построений Найквиста (см. тему 1.12):
частоту среза ωСРи запас
по фазеγ. Частота срезаωСРпросто определяется из ЛАЧХ (рис.1.41).
Запас по фазеγрассчитывается по
выражению ФЧХφ(ω) только при
одном значении частотыωСР:γ=φ(ωСР ).
Основой применения косвенных показателей
качества — частоты среза ωСРи запаса по фазеγ— являются
графические зависимости (рис.14.1) между
косвенными и прямыми показателями
качества — перерегулированиемσ,
временем первой установкиt1и временем переходного процессаtПП.
По оси ординат отложены значения
перерегулирования σ, в процентах
от установившегося значенияhycm(рис.1.42). По оси временt1иtППзаписаны
формулы, по которым рассчитываютсяt1иtППв
зависимости от частоты срезаωСР.
Если из частотных характеристик
определены значения запаса по фазеγи частоты срезаωСР, то по
графикам можно определить значения
перерегулированияσ, времени первой
установкиt1и времени переходного процессаtПП.
Например, пусть заданы значенияγ=30оиωСР=1,5 с-1.
Тогда, согласно приведенным на рис.1.44
построениям, получим:
σ=19 %,
Найденные значения σ,t1иtППне
являются точными. Этот факт, отражен на
рис.1.44 как «размытость» графиков.
По этим значениям σ,t1иtППможно
построить примерный график переходного
процесса (рис.1.45). Как принято, косвенные
показатели качества выбираются такими,
чтобы найденные с их помощью оценки
прямых показателей качества имели бы
погрешность не более 10 %. Это вполне
приемлемо в инженерной практике.
Графические зависимости между косвенными
γиωСРи прямымиσ,t1иtППпоказателями качества САУ, приведенные
на рис.1.44, можно описать в виде следующих
зависимостей пропорционального типа
Важная в практике эксплуатации САУ
задача определения влияния типовых
законов регулирования (пропорционального,
интегрального и дифференциального) на
прямые показатели качества чрезвычайно
эффективно решается с помощью введенных
косвенных показателей γиωСР.
Ч
метод синтеза следящей САУ (см. тему
1.23) основан на использовании косвенного
показателя качества – показателя
колебательностиМ. Показателем
колебательностиМназывается
величина, численно равная максимуму
нормированной АЧХ (рис.1.46). По значению
показателя колебательностиМможно
оценить величину перерегулированияσ(рис.1.47).
Значение показателя колебательности
Мможет быть найдено графически,
без вычислений АЧХ, при использовании
только годографа частотной характеристикиWраз(p)и, соответственно, ЛАЧХ разомкнутой
САУ. Именно такие построения положены
в основу расчета среднечастотного
участка желаемой ЛАЧХ при упомянутом
выше частотном синтезе следящей САУ.
Требования
САУ рулевого устройства.
привод должен обеспечивать перекладку
от -35˚ до +30˚ за 28с.
При полном ходе в течение 1 часа привод
должен обеспечить 350 перекладок.
Посты управления должны снабжаться
аксиометрами с точностью до 1º в ДП и
1,5º при α = ± 5º. При больших углах ± 2,5º
Требования к СЭЭС:
А) статические требования:
Ошибка регулирования частоты- менее 5%
Ошибка регулирования напряжения – от
-10 до +6%
Неравномерность распределения нагрузки
параллельно работающих генераторов :
не более 10% от мощности наибольшего
генератора или не более 25% от мощности
наименьшего генератора. Из двух вариантов
или выбирается меньший.
Б) динамические показатели
Заброс/провал частоты – не более 10% в
течение 5сек
Заброс/провал напряжения – не более
20% в течение 1,5сек
Требования ДАУ ГД
-
Регулятор
частоты должен быть всережимным,
допустимая регулировка частоты в
пределах от 40 до 115% -
Не
должно быть временной задержки между
перемещением рукоятки на мостике и
началом разворота лопастей и частоты
вращения дизеля -
Точность
поддержания частоты не хуже 1,5% -
Должно
быть реализовано несколько постов
управления ГД и ВРШ, а именно с разных
постов, при наборе и сбросе хода, при
реверсе, при управлении ВГ, когда он
включен в судовую сеть -
Пуск
реверсивной характеристики ГД должны
быть соизмеримы с квалифицированным
ручным управлением
-
Перечислите
типовые позиционные, интегрирующие и
дифференцирующие звенья САУ и приведите
их примеры из судовых систем автоматики.
Укажите передаточные функции и
переходные характеристики этих звеньев.
Виды типовых позиционных звеньев:
1. Безинерционное (пропорциональное)
звеноимеет передаточную функцию и
описывается алгебраическим уравнением,
соответственно, вида W(p)=k, y=kx
Примерами безинерционных звеньев служат
рычажная передача (рис.1.10а),
потенциометрический датчик перемещения
(рис.1.10б).
В этих звеньях выходной сигнал уповторяет без задержки по форме входной
сигналх.
Выражение переходного процесса y=kx
2. Апериодическое (инерционное) звено
1-го порядка имеет передаточную функцию
и описывается уравнением вида
где k, Т — коэффициент
передачи и постоянная времени звена.
Примерами этого звена служат интегрирующая
RC—цепь (рис.1.11а),
‘электродвигатель, обмотки которого
разогреваются во время работы (рис.1.11б).
Выполним вывод передаточной функции
для RC—цепи. Используя
закон Ома, получим
Переходный процесс описывается
выражением
где вместо x=1(t),
как должно быть для переходного процесса,
принято фактическое значение сигналаx, благодаря чему
рассчитывается реакция звена на скачок
произвольной величины.
График переходного процесса приведён
на рис.1.11в. Установившееся значение
yуст, равноеkx, достигается на
бесконечности:t.
Время переходного процессаtпп,
определяемое по моменту окончательного
вхождения графика в 5% зону допуска отууст, составляет3T.
Звено обладаетсамовыравниванием.
Свойство самовыравнивания состоит в
том, что звено самостоятельно без
применения дополнительного регулирования
приходит к постоянному по величине
установившемуся значению.
3
Инерционное звено 2-го порядкаимеет
передаточную функцию
Особенность звена в том, что его
характеристическое уравнение имеет
действительные корни.
Примерами этого звена служит RLC-цепь
(рис.1.13а) при большом сопротивленииRрезистора,
электропривод, приводящий во вращение
нагрузку с большим моментом инерцииJ(рис.6.4б).
Переходный процесс описывается выражением
где с1 и с2
— постоянные интегрирования.
Г
переходного процесса (рис.1.14а) имеет
точку перегиба. Время переходного
процессаtппможно определить только графически.
4. Колебательное звеноимеет
передаточную функцию
где T— период свободных
(незатухающих) колебаний;
ξ— параметр затухания,
принимающий значения0<ξ<1.
Особенность звена в том, что его
характеристическое уравнение имеет
комплексно сопряженные корни.
Примерами этого звена служит RLC-цепь
(рис.1.13а) при малом сопротивленииRрезистора,
электропривод, приводящий во вращение
нагрузку с малым моментом инерцииJ(рис.1.13б). Переходный процесс описывается
выражением
где
— резонансная частота с учётом затухания
колебаний.
График переходного процесса приведён
на рис.1.14б. Чем меньше значение параметра
ξ, тем медленнее
затухает переходный процесс. Время
переходного процесса можно определить
только графически.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Глава 8. Типовые законы регулирования. Одноконтурные САР
8.1. Основные типы автоматических регуляторов
Регулятор на основе усилительного звена называется П-регулятором (пропорциональный). Его положительной характеристикой является высокое быстродействие: при отклонении регулируемой величины от заданного значения регулятор выдает регулирующее воздействие, пропорциональное величине отклонения x, что обеспечивает быструю компенсацию возмущения. Существенным недостатком П-регулятора является наличие статической ошибки в переходном процессе АСР с П-регулятором (рис. 37). Статическая ошибка возникает потому, что у П-регулятора между регулируемой величиной x и регулирующим воздействием xр существует зависимость, однозначно определяемая коэффициентом K. Поэтому генерировать регулирующее воздействие xр для компенсации возмущения xв П-регулятор может только путем изменения регулируемой величины x, что и создает статическую ошибку.
Регулятор на основе интегрирующего звена (48) называется И‑регулятором:
Если xвых усилительного звена (П-регулятор) однозначно определяется величиной правой части уравнения, что является причиной возникновения статической погрешности в АСР с П-регулятором, то правая часть уравнения (48) интегрирующего звена (И-регулятор) определяет не величину, а скорость изменения xвых. Величина xвых будет изменяться до тех пор, пока правая часть уравнения (48) не станет равна нулю, т. е. пока регулируемая величина x при наличии возмущения xв не вернется к заданному значению. Следовательно, в АСР с И-регулятором не возникает статическая погрешность.
Однако у И-регулятора имеется свой недостаток сравнительно с П-регулятором: в случае возникновения возмущения регулирующее воздействие П-регулятора меняется быстрее, чем у И-регулятора с его конечной скоростью, что замедляет процесс компенсации возмущения и ухудшает критерии качества регулирования (рис. 40).
Рис. 40. Переходные процессы в АСР с П- и И-регуляторами
Таким образом, П-регулятор обеспечивает высокое быстродействие (что уменьшает динамическую ошибку), но не может обеспечить при наличии возмущения заданное значение регулируемой величины (статическая ошибка). И-регулятор, наоборот, не создает статическую ошибку, но вследствие относительно медленного изменения xр имеет большую динамическую ошибку.
Сравнивая характеристики П- и И-регуляторов можно сделать вывод: если включить усилительное и интегрирующие звенья параллельно, то автоматический регулятор будет лишен указанных недостатков. Такой регулятор называется ПИ-регулятором (рис. 41).
Рис. 41. Принципиальная схема АСР с ПИ-регулятором
Действительно, быстродействие ПИ-регулятора обеспечивает усилительное звено, а статическую ошибку снимает интегрирующее звено. Для управления производственными процессами чаще всего используются ПИ-регуляторы.
Кривая разгона идеального ПИ-регулятора показана на рис. 42 .
Уравнение ПИ-регулятора при нулевых начальных условиях имеет вид:

Отношение коэффициентов Kp1/Kp определяет степень влияния интегрирующей части, и его обратная величина называется временем изодрома Tи.

Время изодрома – это время, в течение которого интегрирующее звено изменяет регулирующее воздействие xр ПИ-регулятора на величину Dxр, равную предварительному изменению Dxр усилительного звена (рис. 42). Поэтому иногда время изодрома называют временем удвоения.
Рис. 42. График кривой разгона идеального ПИ-регулятора:
а – скачкообразное изменение входного воздействия x;
б – реакция (кривая разгона) ПИ-регулятора xр
Уравнение ПИ-регулятора можно записать как
откуда передаточная функция
Амплитудно-фазовая характеристика:

В том случае, если рассмотренные регуляторы не обеспечивают требуемое качество регулирования, необходимо увеличить интенсивность процесса компенсации возмущения. Этого можно достигнуть увеличением регулирующего воздействия, которое в свою очередь определяется коэффициентом усиления автоматического регулятора Kp
. Однако ниже будет показано, что увеличение коэффициента усиления регулятора в АСР приводит к тому, что в системе начинают генерироваться незатухающие колебания.
В связи с этим представляет интерес рассмотреть алгоритм, который реализует дифференцирующее звено.
Входной величиной любого регулятора является кривая разгона регулируемой величины (рис. 27), которая определяется величиной возмущения и передаточной функцией объекта регулирования (9). В свою очередь, регулирующее воздействие xp (рис. 27) определяется кривой разгона x и передаточной функцией регулятора.
На рис. 43 показана реакция дифференцирующего звена (Д‑регулятора) на входное воздействие в виде кривой разгона в соответствии с уравнением (51).
Рис. 43. Реакция дифференцирующего звена на кривую разгона
а –изменение входного воздействия x в виде кривой разгона;
б – реакция xр дифференцирующего звена
Из рис. 43,а следует, что дифференцирующее звено обеспечивает большее регулирующее воздействие в начале переходного процесса. Это означает, что дифференцирующий регулятор активно компенсирует возмущение и исключает возникновение незатухающих колебаний.
Если включить дифференцирующее звено параллельно ПИ‑регулятору (рис. 44), то получим ПИД-регулятор, обеспечивающий интенсивную компенсацию возмущений. При этом недостаток дифференцирующего звена (при Хвх = const, Хвых = 0 ) компенсируется усилительным и интегрирующим звеньями.
Рис. 44. Принципиальная схема АСР с ПИД-регулятором
На рис. 45 показана кривая разгона ПИД-регулятора.
Рис. 45. Кривая разгона ПИД-регулятора
На рис. 46 показаны переходные процессы на с различными регуляторами. ПИД-регулятор уменьшает динамическую ошибку сравнительно с ПИ-регулятором на 25–30%. Также можно объединить дифференцирующее звено с усилительным звеном и улучшить показатели П-регулятора, получив ПД-регулятор.

Все пять типов рассмотренных автоматических регуляторов имеют общую особенность своего функционирования – обеспечивают стабилизацию регулируемой величины после окончания переходного процесса.
8.2. Критерии качества регулирования
Качество процесса регулирования в АСР характеризуют следующие показатели (критерии) (рис. 16):
Рис. 16. Показатели качества регулирования:
1 – переходной процесс без статической ошибки;
2 – переходной процесс со статической ошибкой
1. Максимальное отклонение в процессе регулирования от заданного значения (динамическая ошибка) ΔХдин.
2. Статическая ошибка ΔХст — возможные отклонения от заданного значения по окончании переходного процесса при использовании некоторых типов регуляторов (подробнее такие АСР рассмотрены ниже).
3. Длительность переходного процесса Тр – период времени с момента начала отклонения регулируемого параметра от задания до возвращения его к заданному значению с определенной степенью точности регулирования ±Δ.
Например, если ±Δ=±25%, это означает, что для заданного значения температуры в 100 °С процесс регулирования будет завершен при достижении диапазона (100 ± 2,5) °С.
4. Степень затухания показывает характер затухания переходного процесса регулирования:
Для того, чтобы переходный процесс затухал за 2 ¸ 3 периода колебаний, степень затухания должна быть равна

5. Степень колебательности процесса m определяет характер колебательности процесса и равна отношению действительной части корня характеристического уравнения к коэффициенту при его мнимой части. Степень колебательности связана со степенью затухания следующим соотношением:
6. Интегральный квадратичный критерий – критерий, определяющий площадь под кривой переходного процесса, возведенной в квадрат (рис. 17):
Уменьшение интегрального критерия соответствует ускорению процесса регулирования.
Рис. 17. Интегральный квадратичный критерий качества регулирования
Однако все приведенные шесть критериев качества не определяют величину потерь производства при отклонениях регулируемой величины от оптимального значения в переходных процессах регулирования. Для определения таких потерь можно использовать экономический критерий.
7. Экономический критерий рассмотрим на примере, регулирования температуры химического реактора θ, когда степень превращения Q в реакторе определяется температурой (рис. 18а).
Разделим переходной процесс на равные интервалы времени Δt и запишем значения θ
в этих точках по графику (18, б). На графике (18, а) для этих температур определим уменьшение степени превращения вследствие отклонения от оптимального режима, а затем сделаем расчет потерь исходных продуктов для каждого интервала Δθ, суммируем эти потери для всего переходного процесса и представим потери в денежном выражении.
Рис. 18. Экономический критерий качества регулирования:
а – зависимость степени превращения Q от температуры θ;
б – переходный процесс регулирования температуры
Совместно со специалистом по технологии или по его заданию необходимо определить, какой из указанных критериев для рассматриваемой АСР является превалирующим, и задать максимально допустимую величину этого критерия, т. е. определить, какое качество регулирования должна обеспечить проектируемая АСР.
8.3. Выбор закона регулирования
При выборе регулятора следует определиться с группой регулирующих устройств – непрерывного, релейного или импульсного действия. Такой выбор ориентировочно может быть сделан по величине отношения запаздывания к постоянной времени объекта τ/Tоб:
· при отношении τ/Tоб меньше 0.2 целесообразно использовать регулятор релейного действия;
· если отношение τ/Tоб от 0.2 до 1.0, то нужно использовать регулятор непрерывного действия;
· при отношении τ/Tоб больше единицы можно использовать регулятор импульсного действия, или специальные регуляторы, например, регулятор («предиктор») Смита.
Затем необходимо определиться с типом регулятора, т.е. выбрать определенный закон регулирования: П-, И-, ПИ-, ПД- или ПИД-закон
8.4. Методы расчета одноконтурных САР
Как указывалось выше, качество автоматического регулирования определяется свойствами системы в целом, т. е. суммарными свойствами объекта и регулятора. Поскольку объект обычно является неизменяемой частью системы, то обеспечить определенные свойства системы, а следовательно и заданное качество регулирования, можно соответствующим подбором свойств автоматического регулятора, что зависит от параметров его настройки. В свою очередь, параметры настройки являются коэффициентами передачи в уравнении автоматического регулятора.
Таким образом, параметры настройки автоматического регулятора определяются свойствами объекта регулирования, т. е. величинами τоб, Тоб, Коб.
8.4.1. Расчет по «приближенным» формулам
Приближенные формулы для расчета параметров настройки автоматических регуляторов (Kр – коэффициент усиления; Tи – время изодрома; Тд – время дифференцирования) сведены в следующую таблицу:
Таблица 8.1. Формулы для приближенного расчета
параметров настройки регуляторов

Формулы сгруппированы в столбцы в зависимости от характера переходного процесса, который желательно получить, используя рассчитанный таким образом регулятор: апериодический или с перерегулированием в 20 %. В формулы входят следующие свойства объекта регулирования: Коб – коэффициент усиления; Тоб – постоянная времени; τоб – время запаздывания (полного).
Рис. 53. Кривые разгона:
1 – фактическая кривая разгона промышленного объекта;
2 – аппроксимированная (приближенная) кривая разгона
Необходимо отметить, что для пневматических регуляторов требуется определять не Kp, а диапазон дросселирования:
Рассмотрим методику более точного определения параметров настройки на примере расчета наиболее «популярного» регулятора – ПИ-регулятора.
8.4.2. Метод незатухающих колебаний
(метод Циглера-Никольса)
При использовании метода незатухающих колебаний [6], который иногда также называется по именам авторов методом Циглера-Никольса, поиск оптимальных параметров настройки осуществляется по величине критического коэффициента усиления П-регулятора и величине периода автоколебательного процесса.
Рис. 54. К поиску параметров настройки методом Циглера-Никольса
Расчет параметров настройки регуляторов проводится в два этапа.
1. На исследуемом объекте устанавливается П-регулятор и, последовательно увеличивая коэффициент усиления (уменьшая диапазон дросселирования), АСР выводится в режим незатухающих колебаний (автоколебаний на границе устойчивости). При этом фиксируется величина коэффициента усиления П-регулятора Ккрр и период незатухающих автоколебаний Т (рис. 54).
2. На втором этапе по величинам Кркр и Т определяются параметры настройки П-, ПИ- и ПИД-регуляторов:
Метод незатухающих колебаний не требует сложных вычислений, но имеет свои характерные недостатки:
· получить Кркр и Т можно только на действующем объекте, оснащенном АСР с П-регулятором;
· не все объекты химической технологии допускают режим автоколебаний;
· практически трудно уловить момент начала автоколебаний.
Данные недостатки имеют место лишь при настройке регулятора методом Циглера-Никольса непосредственно на действующем объекте. Если заменить реальный объект его математической моделью, данный метод лишается указанных недостатков, кроме того, моделирование позволяет на порядок ускорить процесс поиска параметров настройки. Но для выполнения моделирования требуется достаточно точное математическое описание объекта регулирования, а получить его удается не всегда.
8.4.3. Метод расширенных частотных характеристик
Уравнение ПИ-регулятора (65) или (66):
Передаточная функция ПИ-регулятора:

Знак «минус» указывает, что действие регулятора направлено против возмущения.
Из передаточной функции получаем амплитудно-фазовую характеристику ПИ-регулятора путем замены p на iw:

Так как по формуле Эйлера


с затуханием за три периода
Заменив iw на комплексную переменную (-mw+iw), получаем расширенную амплитудно-фазовую характеристику (РАФХ)Ю

Расширенными такие характеристики называются потому, что они как бы «расширены» по отношению к обычной АФХ (рис. 56).
Предположим, что объект регулирования имеет передаточную функцию второго порядка следующего вида:

Для дальнейшего математического моделирования АСР передаточную функцию необходимо преобразовать:

Рис. 56. АФХ объекта регулирования с самовыравниванием:
1 – обычная; 2 – расширенная
Расширенная амплитудно-фазовая характеристика объекта регулирования при замене p на (-mw+iw) будет иметь вид:



Где Rоб(m,w) -расширенная амплитудно-частотная характеристика объекта; Fоб(m,w) -расширенная фазочастотная харктеристика объекта. Величина 40w в выражении для Fоб (m,w) опеделяет угол в радианах и для пересчета в градусы неоходимо 40w умножить на 57,3
Условием нахождения замкнутой АСР на границе устойчивости является уравнение:

Аналогично, исходным уравнением для получения заданной степени колебательности m, а следовательно, определенной степени затухания y, является соотношение:
Это соотношение двух комплексных чисел возможно в том случае, если произведение модулей РАФХ равно единице, а аргументы (фазы) равны между собой, т. е.

Решая эти уравнения относительно S0 и Kp, получаем:


Обычно принимают степень колебательности m = 0,221, что соответствует степени затухания ψ=0,75 и обеспечивает затухание процесса регулирования примерно за три периода. Тогда

Уравнения для определения параметров настройки ПИ-регулятора можно преобразовать:


Подставляя в приведенные уравнения численные значения частоты w от 0 до значения, когда S0 становится отрицательной величиной, строим на плоскости параметров настройки кривую равной степени колебательности


Пример кривых равной степени колебательности в плоскости параметров настройки ПИ-регулятора показан на рис. 57. Графики процессов регулирования с различными параметрами настройки ПИ-регулятора при m = 0,221 показаны на рис. 58. Все процессы регулирования, показанные на рис. 58, реализованы ПИ-регулятором с параметрами настройки, полученными по кривой равной степени колебательности в точках 1, 2, 3, 4 (рис. 57), и все имеют m = 0,221, т. е. затухают примерно за три периода, но обладают существенно различным характером.
В связи с этим возникает задача определения оптимальных параметров настройки на кривой равной степени колебательности.
Рис. 57. Кривые равной степени колебательности
В качестве критерия оптимальности выбираем продолжительность переходного процесса – время регулирования (т. е. быстродействие АСР) и отсутствие постоянной или врéменной статической ошибки. Это исключает из рассмотрения параметры настройки в точке 4 (параметры настройки П-регулятора) и в точке 3 (врéменная статическая ошибка) (рис. 58).
Рис. 58. Графики процессов регулирования для ПИ-регулятора
с различными параметрами настройки в точках 1, 2, 3 и 4
при степени колебательности m =0,221
Быстродействие автоматического регулятора прежде всего зависит от величины регулирующего воздействия, которое для ПИ-регулятора, как следует из уравнения (65), прямо пропорционально величине коэффициента усиления Kp и обратно пропорционально времени изодрома Tи. Расчеты показывают, что если двигаться по кривой равной степени колебательности вправо, то величина регулирующего воздействия при прочих равных условиях сначала возрастает и достигает максимального значения на кривой равной степени колебательности вблизи ее вершины, когда
а затем начинает уменьшаться в связи с резким увеличением Tи (рис. 57).
Рис. 59. Выбор оптимальных параметров настройки
Таким образом, оптимальные параметры настройки ПИ-регулятора находятся в точке 2 на кривой равной степени колебательности (рис. 59).
Источник
Плютто В. П., Дубровский И. И. Элементы теории управления химико-технологическими процессами и системами. Конспект лекций: Учеб. пособие – М.: РХТУ им. Д. И. Менделеева, 2003. – 127 с.
Лекция 17. Расчет установившейся ошибки в системах управления.
Структурные признаки астатизма
Установившейся (статической) ошибкой называют
постоянное значение сигнала ошибки x(t)=g(t)-y(t),
которое она приобретает по окончании переходного процесса: , рисунок 116.
Очевидно, установившаяся ошибка зависит от законов
изменения и численных характеристик входных сигналов системы. Поэтому при ее
определении принято рассматривать так называемые типовые входные сигналы,
законы изменения которых составляют степенной ряд относительно времени.
Например, для задающего воздействия:
,
,

далее.
При наличии нескольких воздействий на линейную систему
для определения xуст используется
принцип суперпозиции – реакция линейной системы на совокупность входных
сигналов совпадает с алгебраической суммой ее реакций на каждый из сигналов в
отдельности:
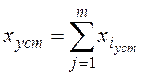
каждое слагаемое, или составляющая сигнала ошибки, определяется
для i-го входного сигнала при условии, что остальные
тождественно равны нулю. Такой подход полностью соответствует определению
передаточной функции и позволяет выполнять расчет установившейся ошибки на
основе структурной схемы системы.
Рассмотрим порядок расчета установившейся ошибки на
следующем достаточно общем примере (рисунок 117).
В соответствии с принципом суперпозиции установившаяся
ошибка будет определяться здесь в виде суммы трех составляющих .
Изображение по Лапласу ошибки от задающего воздействия
получают через передаточную функцию замкнутой системы по ошибке при известном изображении задающего
воздействия G(s):
, где
F(s) – основная передаточная функция замкнутой системы.
Для структурной схемы на рисунке 117
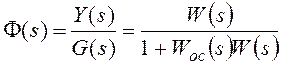
— передаточная функция
разомкнутой системы, или прямой цепи системы, для рассматриваемого примера.
Непосредственно для расчета
установившегося значения ошибки от задающего воздействия используют теорему о
конечном значении для преобразования Лапласа:
В результате:
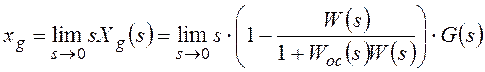
Изображение по Лапласу ошибки от возмущающего
воздействия получают через передаточную функцию замкнутой системы по ошибке от
возмущения при известном изображении возмущающего
воздействия F(s):
, где
Ff(s) –передаточная функция замкнутой системы по
возмущающему воздействию,
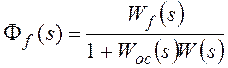
Wf(s)
– передаточная функция разомкнутой системы по возмущению (передаточная функция
участка прямой цепи системы от точки приложения возмущающего воздействия до
выхода системы).
Для структурной схемы на рисунке 8 необходимо
учитывать два возмущающих воздействия, приложенные в различные точки системы.
Для f1:
,
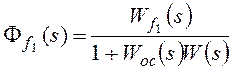
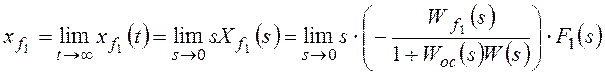
Для f2:
,
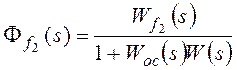
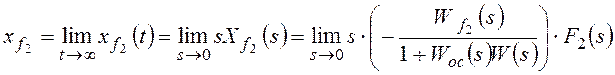
Расчет упрощается для
системы с единичной отрицательной обратной связью (рисунок 118):
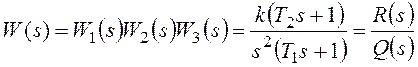
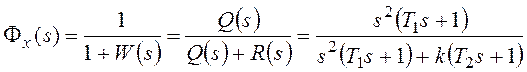
разомкнутой системы.
Найдем установившуюся ошибку
для некоторых типовых вариантов задающего воздействия.
При получим:
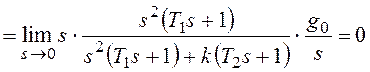
При получим:
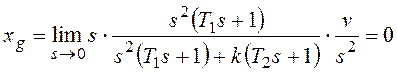
При 
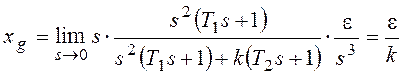
Если установившаяся ошибка
тождественно равна нулю при каком-либо типовом варианте входного сигнала,
независимо от его численных характеристик, систему называют астатической по
рассматриваемому входному сигналу.
Количество типовых вариантов
входного сигнала – членов степенного ряда, при которых установившаяся ошибка
тождественно равна нулю, определяет порядок астатизма.
Рассматриваемая система
обладает свойством астатизма второго порядка по задающему воздействию.
Рассмотрим установившуюся
ошибку от возмущения f1:
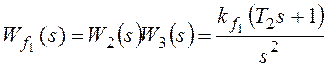
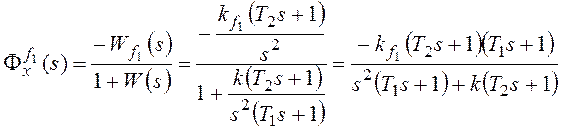
–
коэффициент передачи разомкнутой системы по возмущению f1.
При получим:
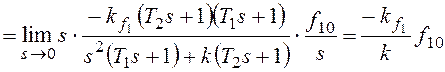
При получим:
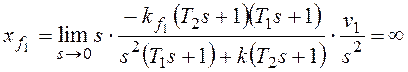
При 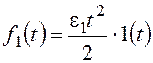
тот же результат.
Отметим, что по возмущению f1 рассматриваемая система
не является астатической. Кроме того, она не в состоянии отработать два последних
варианта входного сигнала.
Рассмотрим установившуюся
ошибку от возмущения f2:
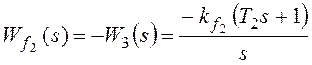
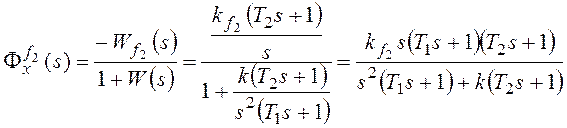
–
коэффициент передачи разомкнутой системы по возмущению f2.
При получим:
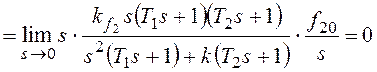
При получим:
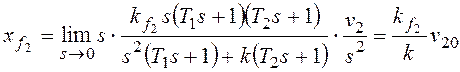
При 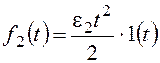
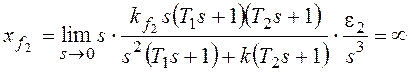
По возмущению f2 рассматриваемая система имеет
астатизм первого порядка. Она не в состоянии отработать возмущающее
воздействие, изменяющееся во времени с постоянным ускорением.
Подведем некоторые итоги:
1. Наличие и глубина
свойства астатизма зависят от точки приложения входного сигнала.
2. Постоянные времени
звеньев системы не влияют на ее точность.
3. Увеличение значения
коэффициента передачи разомкнутой системы приводит к снижению величины
установившейся ошибки.
Для систем с единичной
отрицательной обратной связью существуют достаточно простые структурные
признаки астатизма.
Рассмотрим структуру,
показанную на рисунке 119.
В общем случае передаточная
функция разомкнутой системы может быть представлена в следующей форме:
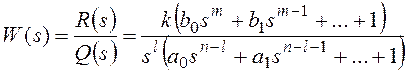
Тогда получим:
и для общего вида задающего воздействия 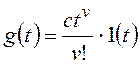
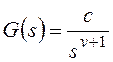
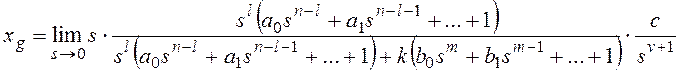
Результат нахождения этого
предела зависит от соотношения показателей степени:
— при l>v установившаяся
ошибка равна нулю независимо от остальных параметров, то есть имеет место
астатизм;
— при l=v получаем
константу;
— при l<v установившаяся
ошибка стремится к бесконечности, то есть система не в состоянии отработать
входной сигнал.
Учитывая, что минимальное
значение v нулевое,
получаем условие астатизма по задающему воздействию: l>0.
Таким образом, структурный
признак астатизма по задающему воздействию в системе с единичной отрицательной
обратной связью состоит в наличии нулевых корней в знаменателе передаточной
функции разомкнутой системы, или интегрирующих звеньев в прямой цепи системы.
Нетрудно также убедиться,
что положительное значение l совпадает
с порядком астатизма.
Для получения признака
астатизма по возмущающему воздействию представим передаточные функции на
рисунке 10 в форме:
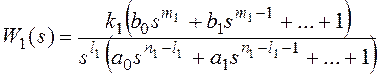
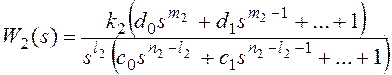
k1k2=k, m1+m2=m,
n1+n2=n,
причем и
.
Тогда получим:
и для общего вида возмущающего воздействия 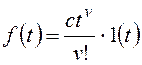
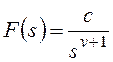
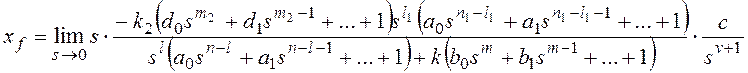
Все вышеприведенные выводы
можно повторить для показателя степени l1.
Таким образом, структурный
признак астатизма по возмущающему воздействию в системе с единичной
отрицательной обратной связью состоит в наличии нулевых корней в знаменателе
передаточной функции участка системы до точки приложения воздействия, или
интегрирующих звеньев на том же участке.
Максимальная
динамическая ошибка
– наибольшее
отклонение регулируемой переменной от
заданного значения Узад:
.
(3.1)
В
устойчивой САР максимальным является
первое отклонение. Таким образом,
показатель
характеризует динамическую точность
регулирования [14].
Время
регулирования
tp
–промежуток времени от момента нанесения
возмущающего воздействия до момента,
начиная с которого отклонение регулируемой
переменной от установившегося значения
становится и остается меньше наперед
заданного значения ].
Остаточное
отклонение (остаточная неравномерность)
—
абсолютная статическая ошибка
регулирования, определяемая как разность
между установившимся значением
регулируемой величины и ее заданным
значением:
=Ууст
– Узад.
(3.2)
Показатель
характеризует точность регулирования
в статическом режиме [5].
Во
всех системах регулирования обязательно
имеется статическая ошибка. Ее можно
уменьшать путем увеличения общего
коэффициента усиления регулятора.
Однако она все равно остается, так как
увеличение коэффициента усиления
регулятора всегда ограничено.
Причиной
статической ошибки системы регулирования
является то, что в равновесном состоянии
регулятора положение регулирующего
органа жестко связано с величиной
регулируемой величины [6].
Система
регулирования, которая по принципу
своего действия обладает статической
ошибкой, называется статической
системой, а
регулятор в этом случае называется
статическим
регулятором.
Статический регулятор осуществляет
следующий закон регулирования:
y
= kрегх,
(3.3)
где
х
– отклонение регулируемой величины, у
– регулирующее воздействие регулятора
на объект.
Система
автоматического регулирования, не
обладающая статической ошибкой,
называется астатической
системой автоматического
регулирования,
а регулятор называется астатическим
регулятором [3].
3.2. Критерии устойчивости сар
Понятие
устойчивости САР связано с способностью
системы возвращаться в состояние
равновесия после исчезновения внешних
сил, которые вывели ее из этого состояния.
Устойчивость
систем автоматического управления
является одним из важнейших условий их
работоспособности, так как устойчивость
включает в себя требование затухания
переходных процессов во времени.
Очевидно, что система с расходящимся
процессом была бы неработоспособной.
Рассмотрим
дифференциальное уравнение движения
линеаризованной системы автоматического
регулирования, записанное для регулируемой
величины у(t)
при наличии управляющего воздействия
g(t)
и при равенстве нулю возмущающих
воздействий (см. формулу (2.4)):
.(3.4)
Процесс
регулирования определяется решением
дифференциального уравнения, как сумма
двух решений – частного решения
неоднородного уравнения (3.4)
с правой частью и общего решения уравнения
(3.4)
без правой части [1].
Характеристическое
уравнение САР имеет вид:
.
(3.5)
Корни
характеристического уравнения (3.5)
определяются только видом левой части
уравнения (3.4).
Постоянные интегрирования определяются
также и видом правой части. Поэтому
быстрота затухания и форма переходного
процесса определяются как левой, так и
правой частями исходного дифференциального
уравнения. Однако поскольку в понятие
устойчивости входит только факт наличия
или отсутствия затухания переходного
процесса (независимо от быстроты
затухания и формы переходного процесса),
то устойчивость линейной системы не
зависит от вида правой части
дифференциального уравнения (3.4)
и определяется только характеристическим
уравнением (3.5)
[13].
Так
как получающаяся при решении линейного
дифференциального уравнения (3.4) формула
переходного процесса содержит составляющие
в виде экспонент от вещественных частей
корней характеристического уравнения
САР (3.5) (см. главу 2), то для того, чтобы
САР была устойчивой и переходный процесс
затухал, необходимо, чтобы вещественные
части корней были отрицательными.
Следовательно,
для устойчивости линейной САР необходимо,
чтобы все корни лежали слева от мнимой
оси, в левой полуплоскости комплексных
чисел. Если хотя бы один корень окажется
справа от мнимой оси, то система будет
неустойчивой. Система будет находиться
на границе устойчивости при наличии:
нулевого корня
();
пары чисто мнимых корней
;
бесконечного корня
().
Во всех трех случаях предполагается,
что все остальные корни имеют отрицательные
вещественные части.
Необходимым
(но не достаточным) условием устойчивости
САР является положительность всех
коэффициентов характеристического
уравнения [7]. Это означает, что система
является неустойчивой, если хотя бы
один из коэффициентов характеристического
уравнения отрицателен. Если все
коэффициенты характеристического
уравнения положительны, то требуются
дополнительные исследования САР на
устойчивость с помощью критериев
устойчивости Гурвица, Михайлова или
Найквиста [3].
В
программе «SAU»
для определения устойчивости САР
используется критерий устойчивости
Гурвица, как наиболее удобный с точки
зрения компьютерной реализации. В методе
Гурвица для характеристического
уравнения (3.5) составляется квадратная
матрица коэффициентов, содержащая n
строк и n
столбцов:

(3.6)
Критерий
устойчивости сводится к тому, что при
а0>0
должны быть больше нуля все n
определителей Гурвица, получаемых из
квадратной матрицы коэффициентов.
Определители
Гурвица составляются по следующему
правилу:
;
;
(3.7)
Последний
определитель включает в себя всю матрицу.
Но так как в последнем столбце матрицы
все элементы, кроме нижнего, равны нулю,
то последний определитель Гурвица
выражается через предпоследний следующим
образом:
.
(3.8)
Однако
в устойчивой системе предпоследний
определитель тоже должен быть
положительным. Поэтому условие
положительности последнего определителя
сводится к условию
,
т.е. к положительности свободного члена
характеристического уравнения [1].
Условия
нахождения системы на границе устойчивости
можно получить, приравнивая к нулю
последний определитель ()
при положительности всех остальных
определителей. Как следует из (3.8),
это условие распадается на два условия:
и
.
Первое
условие соответствует границе устойчивости
первого типа (апериодическая граница
устойчивости), а второе – границе
устойчивости второго типа (колебательная
граница устойчивости).
Для
уравнения второго порядка необходимым
и достаточным условием устойчивости
является положительность всех
коэффициентов характеристического
уравнения. Для уравнений более высокого
порядка необходимо исследование с
помощью составления определителей
Гурвица и проверки их на положительность.
Существенным
недостатком критерия Гурвица является
то, что для уравнений высоких порядков
в лучшем случае можно получить ответ о
том, устойчива или неустойчива система
автоматического регулирования. При
этом в случае неустойчивой системы
критерий не дает ответа на то, каким
образом надо изменять параметры системы,
чтобы сделать ее устойчивой. Это
обстоятельство привело к поискам других
критериев, которые более удобны в
инженерной практике.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Статическая ошибка — регулирование
Cтраница 1
Статическая ошибка регулирования может задаваться в абсолютной величине или в безразмерной: по отношению к номинальному значению регулируемого параметра или к диапазону шкалы вторичного прибора.
[1]
Статическая ошибка регулирования теоретически равна нулю, а практически определяется возможной точностью задания и измерения скорости.
[2]
Статическая ошибка регулирования указывает на величину остаточного отклонения параметра; она нежелательна в любом контуре регулирования.
[3]
Статическая ошибка регулирования получается тем меньше, чем больше коэффициент усиления регулятора.
[5]
Статическая ошибка регулирования системы гармонического компаундирования определяется различием воздействия поля реакции якоря по первой и высшим гармоникам. Снижение напряжения определяется воздействием продольной и поперечной составляющих тока якоря, компаундирующее же действие, то есть увеличение напряжения гармонической обмотки и соответственно тока возбуждения генератора, определяется только продольной составляющей тока якоря. Статическую ошибку регулирования возможно, по-видимому, свести к минимуму соответствующим выбором параметров xd и xq генератора.
[6]
Уменьшение статической ошибки регулирования ( ошибки в установившемся режиме) и увеличение быстродействия системы может быть достигнуто последовательным включением в контур системы автоматического регулирования ( в регулятор, осуществляющий основную обратную связь) безынерционного звена с большим коэффициентом усиления.
[8]
Для устранения статической ошибки регулирования ( остаточного отклонения регулируемой величины) напряжение небаланса, снимаемое с движка реостата Лр, подается на сетку левого триода лампы Лг, где усиливается по величине. Усиленное напряжение затем поступает на вход лампы Л3, в анодную цепь которой включена управляющая обмотка асинхронного конденсаторного двигателя Д-32. Скорость вращения двигателя пропорциональна величине сигнала небаланса. Перемещение движка сопротивления Л2 направлено в ту же сторону, что и движка реостата обратной связи RO. Частота импульсов может изменяться в пределах от 45 в минуту до 40 в час путем изменения положения движка переменного сопротивления Д4, изменяющего время разряда RC-цетш.
[9]
Для уменьшения статической ошибки регулирования иногда рекомендуется установка в приточной камере двух калориферов ( или двух рядов калориферов), соединенных последовательно по воздуху и параллельно по воде. Теплопроизводительность каждого калорифера составляет приблизительно 50 % от общей требуемой. Благодаря этому статическая ошибка выбранного регулятора может быть снижена вдвое, так как регулируется только половина нагрузки. Первый по ходу воздуха калорифер отключается двухпозиционным регулятором, датчик которого установлен на входе наружного воздуха, когда достигается температура, при которой требуется только половина нагрузки — теплопроизводительности. Для определения температуры настройки двухпозиционного регулятора требуется провести дополнительные несложные расчеты.
[10]
Говоря о статической ошибке регулирования, считают, что после каждого изменения нагрузки или после отклонения от заданного режима работы, которое вызывается другими причинами, снова устанавливается постоянная скорость вращения вала, пусть не та, что была раньше, но постоянная, и остается дальше неизменным положение всех элементов регулятора.
[11]
Что называется статической ошибкой регулирования.
[12]
При этом условии статическая ошибка регулирования может быть сведена до весьма малой величины.
[13]
Теоретически при kpoo статическая ошибка регулирования становится равной нулю.
[14]
Страницы:
1
2
3
4
5
Глава 8. Типовые законы регулирования. Одноконтурные САР
8.1. Основные типы автоматических регуляторов
Регулятор на основе усилительного звена называется П-регулятором (пропорциональный). Его положительной характеристикой является высокое быстродействие: при отклонении регулируемой величины от заданного значения регулятор выдает регулирующее воздействие, пропорциональное величине отклонения x, что обеспечивает быструю компенсацию возмущения. Существенным недостатком П-регулятора является наличие статической ошибки в переходном процессе АСР с П-регулятором (рис. 37). Статическая ошибка возникает потому, что у П-регулятора между регулируемой величиной x и регулирующим воздействием xр существует зависимость, однозначно определяемая коэффициентом K. Поэтому генерировать регулирующее воздействие xр для компенсации возмущения xв П-регулятор может только путем изменения регулируемой величины x, что и создает статическую ошибку.
Регулятор на основе интегрирующего звена (48) называется И‑регулятором:
Если xвых усилительного звена (П-регулятор) однозначно определяется величиной правой части уравнения, что является причиной возникновения статической погрешности в АСР с П-регулятором, то правая часть уравнения (48) интегрирующего звена (И-регулятор) определяет не величину, а скорость изменения xвых. Величина xвых будет изменяться до тех пор, пока правая часть уравнения (48) не станет равна нулю, т. е. пока регулируемая величина x при наличии возмущения xв не вернется к заданному значению. Следовательно, в АСР с И-регулятором не возникает статическая погрешность.
Однако у И-регулятора имеется свой недостаток сравнительно с П-регулятором: в случае возникновения возмущения регулирующее воздействие П-регулятора меняется быстрее, чем у И-регулятора с его конечной скоростью, что замедляет процесс компенсации возмущения и ухудшает критерии качества регулирования (рис. 40).
Рис. 40. Переходные процессы в АСР с П- и И-регуляторами
Таким образом, П-регулятор обеспечивает высокое быстродействие (что уменьшает динамическую ошибку), но не может обеспечить при наличии возмущения заданное значение регулируемой величины (статическая ошибка). И-регулятор, наоборот, не создает статическую ошибку, но вследствие относительно медленного изменения xр имеет большую динамическую ошибку.
Сравнивая характеристики П- и И-регуляторов можно сделать вывод: если включить усилительное и интегрирующие звенья параллельно, то автоматический регулятор будет лишен указанных недостатков. Такой регулятор называется ПИ-регулятором (рис. 41).
Рис. 41. Принципиальная схема АСР с ПИ-регулятором
Действительно, быстродействие ПИ-регулятора обеспечивает усилительное звено, а статическую ошибку снимает интегрирующее звено. Для управления производственными процессами чаще всего используются ПИ-регуляторы.
Кривая разгона идеального ПИ-регулятора показана на рис. 42 .
Уравнение ПИ-регулятора при нулевых начальных условиях имеет вид:

Отношение коэффициентов Kp1/Kp определяет степень влияния интегрирующей части, и его обратная величина называется временем изодрома Tи.

Время изодрома – это время, в течение которого интегрирующее звено изменяет регулирующее воздействие xр ПИ-регулятора на величину Dxр, равную предварительному изменению Dxр усилительного звена (рис. 42). Поэтому иногда время изодрома называют временем удвоения.
Рис. 42. График кривой разгона идеального ПИ-регулятора:
а – скачкообразное изменение входного воздействия x;
б – реакция (кривая разгона) ПИ-регулятора xр
Уравнение ПИ-регулятора можно записать как
откуда передаточная функция
Амплитудно-фазовая характеристика:

В том случае, если рассмотренные регуляторы не обеспечивают требуемое качество регулирования, необходимо увеличить интенсивность процесса компенсации возмущения. Этого можно достигнуть увеличением регулирующего воздействия, которое в свою очередь определяется коэффициентом усиления автоматического регулятора Kp
. Однако ниже будет показано, что увеличение коэффициента усиления регулятора в АСР приводит к тому, что в системе начинают генерироваться незатухающие колебания.
В связи с этим представляет интерес рассмотреть алгоритм, который реализует дифференцирующее звено.
Входной величиной любого регулятора является кривая разгона регулируемой величины (рис. 27), которая определяется величиной возмущения и передаточной функцией объекта регулирования (9). В свою очередь, регулирующее воздействие xp (рис. 27) определяется кривой разгона x и передаточной функцией регулятора.
На рис. 43 показана реакция дифференцирующего звена (Д‑регулятора) на входное воздействие в виде кривой разгона в соответствии с уравнением (51).
Рис. 43. Реакция дифференцирующего звена на кривую разгона
а –изменение входного воздействия x в виде кривой разгона;
б – реакция xр дифференцирующего звена
Из рис. 43,а следует, что дифференцирующее звено обеспечивает большее регулирующее воздействие в начале переходного процесса. Это означает, что дифференцирующий регулятор активно компенсирует возмущение и исключает возникновение незатухающих колебаний.
Если включить дифференцирующее звено параллельно ПИ‑регулятору (рис. 44), то получим ПИД-регулятор, обеспечивающий интенсивную компенсацию возмущений. При этом недостаток дифференцирующего звена (при Хвх = const, Хвых = 0 ) компенсируется усилительным и интегрирующим звеньями.
Рис. 44. Принципиальная схема АСР с ПИД-регулятором
На рис. 45 показана кривая разгона ПИД-регулятора.
Рис. 45. Кривая разгона ПИД-регулятора
На рис. 46 показаны переходные процессы на с различными регуляторами. ПИД-регулятор уменьшает динамическую ошибку сравнительно с ПИ-регулятором на 25–30%. Также можно объединить дифференцирующее звено с усилительным звеном и улучшить показатели П-регулятора, получив ПД-регулятор.

Все пять типов рассмотренных автоматических регуляторов имеют общую особенность своего функционирования – обеспечивают стабилизацию регулируемой величины после окончания переходного процесса.
8.2. Критерии качества регулирования
Качество процесса регулирования в АСР характеризуют следующие показатели (критерии) (рис. 16):
Рис. 16. Показатели качества регулирования:
1 – переходной процесс без статической ошибки;
2 – переходной процесс со статической ошибкой
1. Максимальное отклонение в процессе регулирования от заданного значения (динамическая ошибка) ΔХдин.
2. Статическая ошибка ΔХст — возможные отклонения от заданного значения по окончании переходного процесса при использовании некоторых типов регуляторов (подробнее такие АСР рассмотрены ниже).
3. Длительность переходного процесса Тр – период времени с момента начала отклонения регулируемого параметра от задания до возвращения его к заданному значению с определенной степенью точности регулирования ±Δ.
Например, если ±Δ=±25%, это означает, что для заданного значения температуры в 100 °С процесс регулирования будет завершен при достижении диапазона (100 ± 2,5) °С.
4. Степень затухания показывает характер затухания переходного процесса регулирования:
Для того, чтобы переходный процесс затухал за 2 ¸ 3 периода колебаний, степень затухания должна быть равна

5. Степень колебательности процесса m определяет характер колебательности процесса и равна отношению действительной части корня характеристического уравнения к коэффициенту при его мнимой части. Степень колебательности связана со степенью затухания следующим соотношением:
6. Интегральный квадратичный критерий – критерий, определяющий площадь под кривой переходного процесса, возведенной в квадрат (рис. 17):
Уменьшение интегрального критерия соответствует ускорению процесса регулирования.
Рис. 17. Интегральный квадратичный критерий качества регулирования
Однако все приведенные шесть критериев качества не определяют величину потерь производства при отклонениях регулируемой величины от оптимального значения в переходных процессах регулирования. Для определения таких потерь можно использовать экономический критерий.
7. Экономический критерий рассмотрим на примере, регулирования температуры химического реактора θ, когда степень превращения Q в реакторе определяется температурой (рис. 18а).
Разделим переходной процесс на равные интервалы времени Δt и запишем значения θ
в этих точках по графику (18, б). На графике (18, а) для этих температур определим уменьшение степени превращения вследствие отклонения от оптимального режима, а затем сделаем расчет потерь исходных продуктов для каждого интервала Δθ, суммируем эти потери для всего переходного процесса и представим потери в денежном выражении.
Рис. 18. Экономический критерий качества регулирования:
а – зависимость степени превращения Q от температуры θ;
б – переходный процесс регулирования температуры
Совместно со специалистом по технологии или по его заданию необходимо определить, какой из указанных критериев для рассматриваемой АСР является превалирующим, и задать максимально допустимую величину этого критерия, т. е. определить, какое качество регулирования должна обеспечить проектируемая АСР.
8.3. Выбор закона регулирования
При выборе регулятора следует определиться с группой регулирующих устройств – непрерывного, релейного или импульсного действия. Такой выбор ориентировочно может быть сделан по величине отношения запаздывания к постоянной времени объекта τ/Tоб:
· при отношении τ/Tоб меньше 0.2 целесообразно использовать регулятор релейного действия;
· если отношение τ/Tоб от 0.2 до 1.0, то нужно использовать регулятор непрерывного действия;
· при отношении τ/Tоб больше единицы можно использовать регулятор импульсного действия, или специальные регуляторы, например, регулятор («предиктор») Смита.
Затем необходимо определиться с типом регулятора, т.е. выбрать определенный закон регулирования: П-, И-, ПИ-, ПД- или ПИД-закон
8.4. Методы расчета одноконтурных САР
Как указывалось выше, качество автоматического регулирования определяется свойствами системы в целом, т. е. суммарными свойствами объекта и регулятора. Поскольку объект обычно является неизменяемой частью системы, то обеспечить определенные свойства системы, а следовательно и заданное качество регулирования, можно соответствующим подбором свойств автоматического регулятора, что зависит от параметров его настройки. В свою очередь, параметры настройки являются коэффициентами передачи в уравнении автоматического регулятора.
Таким образом, параметры настройки автоматического регулятора определяются свойствами объекта регулирования, т. е. величинами τоб, Тоб, Коб.
8.4.1. Расчет по «приближенным» формулам
Приближенные формулы для расчета параметров настройки автоматических регуляторов (Kр – коэффициент усиления; Tи – время изодрома; Тд – время дифференцирования) сведены в следующую таблицу:
Таблица 8.1. Формулы для приближенного расчета
параметров настройки регуляторов

Формулы сгруппированы в столбцы в зависимости от характера переходного процесса, который желательно получить, используя рассчитанный таким образом регулятор: апериодический или с перерегулированием в 20 %. В формулы входят следующие свойства объекта регулирования: Коб – коэффициент усиления; Тоб – постоянная времени; τоб – время запаздывания (полного).
Рис. 53. Кривые разгона:
1 – фактическая кривая разгона промышленного объекта;
2 – аппроксимированная (приближенная) кривая разгона
Необходимо отметить, что для пневматических регуляторов требуется определять не Kp, а диапазон дросселирования:
Рассмотрим методику более точного определения параметров настройки на примере расчета наиболее «популярного» регулятора – ПИ-регулятора.
8.4.2. Метод незатухающих колебаний
(метод Циглера-Никольса)
При использовании метода незатухающих колебаний [6], который иногда также называется по именам авторов методом Циглера-Никольса, поиск оптимальных параметров настройки осуществляется по величине критического коэффициента усиления П-регулятора и величине периода автоколебательного процесса.
Рис. 54. К поиску параметров настройки методом Циглера-Никольса
Расчет параметров настройки регуляторов проводится в два этапа.
1. На исследуемом объекте устанавливается П-регулятор и, последовательно увеличивая коэффициент усиления (уменьшая диапазон дросселирования), АСР выводится в режим незатухающих колебаний (автоколебаний на границе устойчивости). При этом фиксируется величина коэффициента усиления П-регулятора Ккрр и период незатухающих автоколебаний Т (рис. 54).
2. На втором этапе по величинам Кркр и Т определяются параметры настройки П-, ПИ- и ПИД-регуляторов:
Метод незатухающих колебаний не требует сложных вычислений, но имеет свои характерные недостатки:
· получить Кркр и Т можно только на действующем объекте, оснащенном АСР с П-регулятором;
· не все объекты химической технологии допускают режим автоколебаний;
· практически трудно уловить момент начала автоколебаний.
Данные недостатки имеют место лишь при настройке регулятора методом Циглера-Никольса непосредственно на действующем объекте. Если заменить реальный объект его математической моделью, данный метод лишается указанных недостатков, кроме того, моделирование позволяет на порядок ускорить процесс поиска параметров настройки. Но для выполнения моделирования требуется достаточно точное математическое описание объекта регулирования, а получить его удается не всегда.
8.4.3. Метод расширенных частотных характеристик
Уравнение ПИ-регулятора (65) или (66):
Передаточная функция ПИ-регулятора:

Знак «минус» указывает, что действие регулятора направлено против возмущения.
Из передаточной функции получаем амплитудно-фазовую характеристику ПИ-регулятора путем замены p на iw:

Так как по формуле Эйлера


с затуханием за три периода
Заменив iw на комплексную переменную (-mw+iw), получаем расширенную амплитудно-фазовую характеристику (РАФХ)Ю

Расширенными такие характеристики называются потому, что они как бы «расширены» по отношению к обычной АФХ (рис. 56).
Предположим, что объект регулирования имеет передаточную функцию второго порядка следующего вида:

Для дальнейшего математического моделирования АСР передаточную функцию необходимо преобразовать:

Рис. 56. АФХ объекта регулирования с самовыравниванием:
1 – обычная; 2 – расширенная
Расширенная амплитудно-фазовая характеристика объекта регулирования при замене p на (-mw+iw) будет иметь вид:



Где Rоб(m,w) -расширенная амплитудно-частотная характеристика объекта; Fоб(m,w) -расширенная фазочастотная харктеристика объекта. Величина 40w в выражении для Fоб (m,w) опеделяет угол в радианах и для пересчета в градусы неоходимо 40w умножить на 57,3
Условием нахождения замкнутой АСР на границе устойчивости является уравнение:

Аналогично, исходным уравнением для получения заданной степени колебательности m, а следовательно, определенной степени затухания y, является соотношение:
Это соотношение двух комплексных чисел возможно в том случае, если произведение модулей РАФХ равно единице, а аргументы (фазы) равны между собой, т. е.

Решая эти уравнения относительно S0 и Kp, получаем:


Обычно принимают степень колебательности m = 0,221, что соответствует степени затухания ψ=0,75 и обеспечивает затухание процесса регулирования примерно за три периода. Тогда

Уравнения для определения параметров настройки ПИ-регулятора можно преобразовать:


Подставляя в приведенные уравнения численные значения частоты w от 0 до значения, когда S0 становится отрицательной величиной, строим на плоскости параметров настройки кривую равной степени колебательности


Пример кривых равной степени колебательности в плоскости параметров настройки ПИ-регулятора показан на рис. 57. Графики процессов регулирования с различными параметрами настройки ПИ-регулятора при m = 0,221 показаны на рис. 58. Все процессы регулирования, показанные на рис. 58, реализованы ПИ-регулятором с параметрами настройки, полученными по кривой равной степени колебательности в точках 1, 2, 3, 4 (рис. 57), и все имеют m = 0,221, т. е. затухают примерно за три периода, но обладают существенно различным характером.
В связи с этим возникает задача определения оптимальных параметров настройки на кривой равной степени колебательности.
Рис. 57. Кривые равной степени колебательности
В качестве критерия оптимальности выбираем продолжительность переходного процесса – время регулирования (т. е. быстродействие АСР) и отсутствие постоянной или врéменной статической ошибки. Это исключает из рассмотрения параметры настройки в точке 4 (параметры настройки П-регулятора) и в точке 3 (врéменная статическая ошибка) (рис. 58).
Рис. 58. Графики процессов регулирования для ПИ-регулятора
с различными параметрами настройки в точках 1, 2, 3 и 4
при степени колебательности m =0,221
Быстродействие автоматического регулятора прежде всего зависит от величины регулирующего воздействия, которое для ПИ-регулятора, как следует из уравнения (65), прямо пропорционально величине коэффициента усиления Kp и обратно пропорционально времени изодрома Tи. Расчеты показывают, что если двигаться по кривой равной степени колебательности вправо, то величина регулирующего воздействия при прочих равных условиях сначала возрастает и достигает максимального значения на кривой равной степени колебательности вблизи ее вершины, когда
а затем начинает уменьшаться в связи с резким увеличением Tи (рис. 57).
Рис. 59. Выбор оптимальных параметров настройки
Таким образом, оптимальные параметры настройки ПИ-регулятора находятся в точке 2 на кривой равной степени колебательности (рис. 59).
Источник
Плютто В. П., Дубровский И. И. Элементы теории управления химико-технологическими процессами и системами. Конспект лекций: Учеб. пособие – М.: РХТУ им. Д. И. Менделеева, 2003. – 127 с.
К системам автоматического регулирования (САР) предъявляются требования не только
устойчивости процессов регулирования. Для работоспособности системы не менее необходимо, чтобы процесс автоматического регулирования осуществлялся при обеспечении определенных показателей качества процесса управления.
Если исследуемая САР является устойчивой, возникает вопрос о том, насколько качественно происходит регулирование в этой системе и удовлетворяет ли оно технологическим требованиям обьекта управления.На практике качество регулирования определяется визуально по графику переходной характеристики. Однако, имеются точные но более сложные математические методы, дающие конкретные числовые значения (которые не рассматриваются в данной методике).
Классификация показателей качества состоит из нескольких групп:
- прямые — определяемые непосредственно по переходной характеристике процесса,
- корневые — определяемые по корням характеристического полинома,
- частотные — по частотным характеристикам,
- интегральные — получаемые путем интегрирования функций.
Прямыми показателями качества процесса управления, определяемые непосредственно по
переходной характеристике являются:
- Установившееся значение выходной величины Yуст,
- Степень затухания ?,
- Время достижения первого максимума tmax,
- Время регулирования tp,
- Ошибка регулирования Ест (статистическая или среднеквадратическая составляющие),
- Перерегулирование у,
- Динамический коэффициент регулирования Rd,
- Показатель колебательности М.
Например, переходная характеристика, снятая на объекте управления при отработке ступенчатого воздействия, имеет колебательный вид и представлена на рис.1.
Рисунок 1 — Определение показателей качества по переходной характеристике
Установившееся значение выходной величины Yуст
Установившееся значение выходной величины Yуст определяется по переходной характеристике,представленной на рис.1.
Степень затухания ?
Степень затухания ? определяется по формуле:
где А1 и А3 — соответственно 1-я и 3-я амплитуды переходной характеристики рис.1.
Время достижения первого максимума tmax
Время достижения первого максимума tmax определяется по переходной характеристике,представленной на рис.1.
Время регулирования tp
Время регулирования tp определяется согласно рис.1 следующим образом:Находится допустимое отклонение Д, например, задано Д = 5%Yуст и строится «зона» толщиной 2 Д(см. рис.1). Время tp соответствует последней точке пересечения Y(t) с данной границей. То есть время,когда колебания регулируемой величины перестают превышать 5 % от установившегося значения.
Настройки регулятора необходимо выбирать так, чтобы обеспечить минимально возможное значение общего времени регулирования, либо минимальное значение первой полуволны переходного процесса.
В непрерывных системах с типовыми регуляторами это время бывает минимальным при так называемых оптимальных апериодических переходных процессах. Дальнейшего уменьшения времени регулирования до абсолютного минимума можно достичь при использовании специальных оптимальных по быстродействию систем регулирования.
Ошибка регулирования Ест
Статическая ошибка регулирования Ест = Ув — Ууст, где Ув — входная величина (см. рис.1).В некоторых САР наблюдается ошибка, которая не исчезает даже по истечении длительногоинтервала времени — это статическая ошибка регулирования Ест. Данная ошибка не должна превышатьнекоторой наперед заданной величины. У регуляторов с интегральной составляющей ошибки в установившемся состоянии теоретическиравны нулю, но практически незначительные ошибки могут существовать из-за наличия зоннечувствительности в элементах системы.
Перерегулирование у
Величина перерегулирования у зависит от вида отрабатываемого сигнала.При отработке ступенчатого воздействия (по сигналу задания) – см. рис.1 величина перерегулирования у определяется по формуле:
где значения величин Ymax и Yуст определяются согласно рис.1.
При отработке возмущающего воздействия, величина перерегулирования у определяется изсоотношения:
где значения величин Xm и X1 определяются согласно рис. 2.
Рисунок 2 — График переходного процесса при отработке возмущения
Динамический коэффициент регулирования Rd
Динамический коэффициент регулирования Rd определяется из формулы:
где значения величин Y1 и Y0 определяются согласно рис. 3.
Рисунок 3 — К понятию динамического коэффициента регулирования
Величина динамического коэффициента Rd характеризует степень воздействия регулятора напроцесс, т.е. степень понижения динамического отклонения в системе с регулятором и без него.
Показатель колебательности М
Показатель колебательности M характеризует величину максимума модуля частотной передаточной функции замкнутой системы (на частоте резонанса) и, тем самым, характеризует колебательные свойства системы. Показатель колебательности наглядно иллюстрируется на рисунке 4.
Рисунок 4 — График модуля частотной передаточной функции замкнутой системы
Условно считается, что значение М=1,5-1,6 является оптимальным для промышленных САР, т.к. вэтом случае у обеспечивается в районе от 20% до 40%. При увеличении значения M колебательность всистеме возрастает.
В некоторых случаях нормируется полоса пропускания системы щп, которая соответствует уровню усиления в замкнутой системе 0,05. Чем больше полоса пропускания, тем больше быстродействие замкнутой системы. Однако при этом повышается чувствительность системы к шумам в канале измерения и возрастает дисперсия ошибки регулирования.