Глава 8. Типовые законы регулирования. Одноконтурные САР
8.1. Основные типы автоматических регуляторов
Регулятор на основе усилительного звена называется П-регулятором (пропорциональный). Его положительной характеристикой является высокое быстродействие: при отклонении регулируемой величины от заданного значения регулятор выдает регулирующее воздействие, пропорциональное величине отклонения x, что обеспечивает быструю компенсацию возмущения. Существенным недостатком П-регулятора является наличие статической ошибки в переходном процессе АСР с П-регулятором (рис. 37). Статическая ошибка возникает потому, что у П-регулятора между регулируемой величиной x и регулирующим воздействием xр существует зависимость, однозначно определяемая коэффициентом K. Поэтому генерировать регулирующее воздействие xр для компенсации возмущения xв П-регулятор может только путем изменения регулируемой величины x, что и создает статическую ошибку.
Регулятор на основе интегрирующего звена (48) называется И‑регулятором:
Если xвых усилительного звена (П-регулятор) однозначно определяется величиной правой части уравнения, что является причиной возникновения статической погрешности в АСР с П-регулятором, то правая часть уравнения (48) интегрирующего звена (И-регулятор) определяет не величину, а скорость изменения xвых. Величина xвых будет изменяться до тех пор, пока правая часть уравнения (48) не станет равна нулю, т. е. пока регулируемая величина x при наличии возмущения xв не вернется к заданному значению. Следовательно, в АСР с И-регулятором не возникает статическая погрешность.
Однако у И-регулятора имеется свой недостаток сравнительно с П-регулятором: в случае возникновения возмущения регулирующее воздействие П-регулятора меняется быстрее, чем у И-регулятора с его конечной скоростью, что замедляет процесс компенсации возмущения и ухудшает критерии качества регулирования (рис. 40).
Рис. 40. Переходные процессы в АСР с П- и И-регуляторами
Таким образом, П-регулятор обеспечивает высокое быстродействие (что уменьшает динамическую ошибку), но не может обеспечить при наличии возмущения заданное значение регулируемой величины (статическая ошибка). И-регулятор, наоборот, не создает статическую ошибку, но вследствие относительно медленного изменения xр имеет большую динамическую ошибку.
Сравнивая характеристики П- и И-регуляторов можно сделать вывод: если включить усилительное и интегрирующие звенья параллельно, то автоматический регулятор будет лишен указанных недостатков. Такой регулятор называется ПИ-регулятором (рис. 41).
Рис. 41. Принципиальная схема АСР с ПИ-регулятором
Действительно, быстродействие ПИ-регулятора обеспечивает усилительное звено, а статическую ошибку снимает интегрирующее звено. Для управления производственными процессами чаще всего используются ПИ-регуляторы.
Кривая разгона идеального ПИ-регулятора показана на рис. 42 .
Уравнение ПИ-регулятора при нулевых начальных условиях имеет вид:
Отношение коэффициентов Kp1/Kp определяет степень влияния интегрирующей части, и его обратная величина называется временем изодрома Tи.
Время изодрома – это время, в течение которого интегрирующее звено изменяет регулирующее воздействие xр ПИ-регулятора на величину Dxр, равную предварительному изменению Dxр усилительного звена (рис. 42). Поэтому иногда время изодрома называют временем удвоения.
Рис. 42. График кривой разгона идеального ПИ-регулятора:
а – скачкообразное изменение входного воздействия x;
б – реакция (кривая разгона) ПИ-регулятора xр
Уравнение ПИ-регулятора можно записать как
откуда передаточная функция
Амплитудно-фазовая характеристика:
В том случае, если рассмотренные регуляторы не обеспечивают требуемое качество регулирования, необходимо увеличить интенсивность процесса компенсации возмущения. Этого можно достигнуть увеличением регулирующего воздействия, которое в свою очередь определяется коэффициентом усиления автоматического регулятора Kp
. Однако ниже будет показано, что увеличение коэффициента усиления регулятора в АСР приводит к тому, что в системе начинают генерироваться незатухающие колебания.
В связи с этим представляет интерес рассмотреть алгоритм, который реализует дифференцирующее звено.
Входной величиной любого регулятора является кривая разгона регулируемой величины (рис. 27), которая определяется величиной возмущения и передаточной функцией объекта регулирования (9). В свою очередь, регулирующее воздействие xp (рис. 27) определяется кривой разгона x и передаточной функцией регулятора.
На рис. 43 показана реакция дифференцирующего звена (Д‑регулятора) на входное воздействие в виде кривой разгона в соответствии с уравнением (51).
Рис. 43. Реакция дифференцирующего звена на кривую разгона
а –изменение входного воздействия x в виде кривой разгона;
б – реакция xр дифференцирующего звена
Из рис. 43,а следует, что дифференцирующее звено обеспечивает большее регулирующее воздействие в начале переходного процесса. Это означает, что дифференцирующий регулятор активно компенсирует возмущение и исключает возникновение незатухающих колебаний.
Если включить дифференцирующее звено параллельно ПИ‑регулятору (рис. 44), то получим ПИД-регулятор, обеспечивающий интенсивную компенсацию возмущений. При этом недостаток дифференцирующего звена (при Хвх = const, Хвых = 0 ) компенсируется усилительным и интегрирующим звеньями.
Рис. 44. Принципиальная схема АСР с ПИД-регулятором
На рис. 45 показана кривая разгона ПИД-регулятора.
Рис. 45. Кривая разгона ПИД-регулятора
На рис. 46 показаны переходные процессы на с различными регуляторами. ПИД-регулятор уменьшает динамическую ошибку сравнительно с ПИ-регулятором на 25–30%. Также можно объединить дифференцирующее звено с усилительным звеном и улучшить показатели П-регулятора, получив ПД-регулятор.
Все пять типов рассмотренных автоматических регуляторов имеют общую особенность своего функционирования – обеспечивают стабилизацию регулируемой величины после окончания переходного процесса.
8.2. Критерии качества регулирования
Качество процесса регулирования в АСР характеризуют следующие показатели (критерии) (рис. 16):
Рис. 16. Показатели качества регулирования:
1 – переходной процесс без статической ошибки;
2 – переходной процесс со статической ошибкой
1. Максимальное отклонение в процессе регулирования от заданного значения (динамическая ошибка) ΔХдин.
2. Статическая ошибка ΔХст — возможные отклонения от заданного значения по окончании переходного процесса при использовании некоторых типов регуляторов (подробнее такие АСР рассмотрены ниже).
3. Длительность переходного процесса Тр – период времени с момента начала отклонения регулируемого параметра от задания до возвращения его к заданному значению с определенной степенью точности регулирования ±Δ.
Например, если ±Δ=±25%, это означает, что для заданного значения температуры в 100 °С процесс регулирования будет завершен при достижении диапазона (100 ± 2,5) °С.
4. Степень затухания показывает характер затухания переходного процесса регулирования:
Для того, чтобы переходный процесс затухал за 2 ¸ 3 периода колебаний, степень затухания должна быть равна
5. Степень колебательности процесса m определяет характер колебательности процесса и равна отношению действительной части корня характеристического уравнения к коэффициенту при его мнимой части. Степень колебательности связана со степенью затухания следующим соотношением:
6. Интегральный квадратичный критерий – критерий, определяющий площадь под кривой переходного процесса, возведенной в квадрат (рис. 17):
Уменьшение интегрального критерия соответствует ускорению процесса регулирования.
Рис. 17. Интегральный квадратичный критерий качества регулирования
Однако все приведенные шесть критериев качества не определяют величину потерь производства при отклонениях регулируемой величины от оптимального значения в переходных процессах регулирования. Для определения таких потерь можно использовать экономический критерий.
7. Экономический критерий рассмотрим на примере, регулирования температуры химического реактора θ, когда степень превращения Q в реакторе определяется температурой (рис. 18а).
Разделим переходной процесс на равные интервалы времени Δt и запишем значения θ
в этих точках по графику (18, б). На графике (18, а) для этих температур определим уменьшение степени превращения вследствие отклонения от оптимального режима, а затем сделаем расчет потерь исходных продуктов для каждого интервала Δθ, суммируем эти потери для всего переходного процесса и представим потери в денежном выражении.
Рис. 18. Экономический критерий качества регулирования:
а – зависимость степени превращения Q от температуры θ;
б – переходный процесс регулирования температуры
Совместно со специалистом по технологии или по его заданию необходимо определить, какой из указанных критериев для рассматриваемой АСР является превалирующим, и задать максимально допустимую величину этого критерия, т. е. определить, какое качество регулирования должна обеспечить проектируемая АСР.
8.3. Выбор закона регулирования
При выборе регулятора следует определиться с группой регулирующих устройств – непрерывного, релейного или импульсного действия. Такой выбор ориентировочно может быть сделан по величине отношения запаздывания к постоянной времени объекта τ/Tоб:
· при отношении τ/Tоб меньше 0.2 целесообразно использовать регулятор релейного действия;
· если отношение τ/Tоб от 0.2 до 1.0, то нужно использовать регулятор непрерывного действия;
· при отношении τ/Tоб больше единицы можно использовать регулятор импульсного действия, или специальные регуляторы, например, регулятор («предиктор») Смита.
Затем необходимо определиться с типом регулятора, т.е. выбрать определенный закон регулирования: П-, И-, ПИ-, ПД- или ПИД-закон
8.4. Методы расчета одноконтурных САР
Как указывалось выше, качество автоматического регулирования определяется свойствами системы в целом, т. е. суммарными свойствами объекта и регулятора. Поскольку объект обычно является неизменяемой частью системы, то обеспечить определенные свойства системы, а следовательно и заданное качество регулирования, можно соответствующим подбором свойств автоматического регулятора, что зависит от параметров его настройки. В свою очередь, параметры настройки являются коэффициентами передачи в уравнении автоматического регулятора.
Таким образом, параметры настройки автоматического регулятора определяются свойствами объекта регулирования, т. е. величинами τоб, Тоб, Коб.
8.4.1. Расчет по «приближенным» формулам
Приближенные формулы для расчета параметров настройки автоматических регуляторов (Kр – коэффициент усиления; Tи – время изодрома; Тд – время дифференцирования) сведены в следующую таблицу:
Таблица 8.1. Формулы для приближенного расчета
параметров настройки регуляторов
Формулы сгруппированы в столбцы в зависимости от характера переходного процесса, который желательно получить, используя рассчитанный таким образом регулятор: апериодический или с перерегулированием в 20 %. В формулы входят следующие свойства объекта регулирования: Коб – коэффициент усиления; Тоб – постоянная времени; τоб – время запаздывания (полного).
Рис. 53. Кривые разгона:
1 – фактическая кривая разгона промышленного объекта;
2 – аппроксимированная (приближенная) кривая разгона
Необходимо отметить, что для пневматических регуляторов требуется определять не Kp, а диапазон дросселирования:
Рассмотрим методику более точного определения параметров настройки на примере расчета наиболее «популярного» регулятора – ПИ-регулятора.
8.4.2. Метод незатухающих колебаний
(метод Циглера-Никольса)
При использовании метода незатухающих колебаний [6], который иногда также называется по именам авторов методом Циглера-Никольса, поиск оптимальных параметров настройки осуществляется по величине критического коэффициента усиления П-регулятора и величине периода автоколебательного процесса.
Рис. 54. К поиску параметров настройки методом Циглера-Никольса
Расчет параметров настройки регуляторов проводится в два этапа.
1. На исследуемом объекте устанавливается П-регулятор и, последовательно увеличивая коэффициент усиления (уменьшая диапазон дросселирования), АСР выводится в режим незатухающих колебаний (автоколебаний на границе устойчивости). При этом фиксируется величина коэффициента усиления П-регулятора Ккрр и период незатухающих автоколебаний Т (рис. 54).
2. На втором этапе по величинам Кркр и Т определяются параметры настройки П-, ПИ- и ПИД-регуляторов:
Метод незатухающих колебаний не требует сложных вычислений, но имеет свои характерные недостатки:
· получить Кркр и Т можно только на действующем объекте, оснащенном АСР с П-регулятором;
· не все объекты химической технологии допускают режим автоколебаний;
· практически трудно уловить момент начала автоколебаний.
Данные недостатки имеют место лишь при настройке регулятора методом Циглера-Никольса непосредственно на действующем объекте. Если заменить реальный объект его математической моделью, данный метод лишается указанных недостатков, кроме того, моделирование позволяет на порядок ускорить процесс поиска параметров настройки. Но для выполнения моделирования требуется достаточно точное математическое описание объекта регулирования, а получить его удается не всегда.
8.4.3. Метод расширенных частотных характеристик
Уравнение ПИ-регулятора (65) или (66):
Передаточная функция ПИ-регулятора:
Знак «минус» указывает, что действие регулятора направлено против возмущения.
Из передаточной функции получаем амплитудно-фазовую характеристику ПИ-регулятора путем замены p на iw:
Так как по формуле Эйлера
с затуханием за три периода
Заменив iw на комплексную переменную (-mw+iw), получаем расширенную амплитудно-фазовую характеристику (РАФХ)Ю
Расширенными такие характеристики называются потому, что они как бы «расширены» по отношению к обычной АФХ (рис. 56).
Предположим, что объект регулирования имеет передаточную функцию второго порядка следующего вида:
Для дальнейшего математического моделирования АСР передаточную функцию необходимо преобразовать:
Рис. 56. АФХ объекта регулирования с самовыравниванием:
1 – обычная; 2 – расширенная
Расширенная амплитудно-фазовая характеристика объекта регулирования при замене p на (-mw+iw) будет иметь вид:
Где Rоб(m,w) -расширенная амплитудно-частотная характеристика объекта; Fоб(m,w) -расширенная фазочастотная харктеристика объекта. Величина 40w в выражении для Fоб (m,w) опеделяет угол в радианах и для пересчета в градусы неоходимо 40w умножить на 57,3
Условием нахождения замкнутой АСР на границе устойчивости является уравнение:
Аналогично, исходным уравнением для получения заданной степени колебательности m, а следовательно, определенной степени затухания y, является соотношение:
Это соотношение двух комплексных чисел возможно в том случае, если произведение модулей РАФХ равно единице, а аргументы (фазы) равны между собой, т. е.
Решая эти уравнения относительно S0 и Kp, получаем:
Обычно принимают степень колебательности m = 0,221, что соответствует степени затухания ψ=0,75 и обеспечивает затухание процесса регулирования примерно за три периода. Тогда
Уравнения для определения параметров настройки ПИ-регулятора можно преобразовать:
Подставляя в приведенные уравнения численные значения частоты w от 0 до значения, когда S0 становится отрицательной величиной, строим на плоскости параметров настройки кривую равной степени колебательности
Пример кривых равной степени колебательности в плоскости параметров настройки ПИ-регулятора показан на рис. 57. Графики процессов регулирования с различными параметрами настройки ПИ-регулятора при m = 0,221 показаны на рис. 58. Все процессы регулирования, показанные на рис. 58, реализованы ПИ-регулятором с параметрами настройки, полученными по кривой равной степени колебательности в точках 1, 2, 3, 4 (рис. 57), и все имеют m = 0,221, т. е. затухают примерно за три периода, но обладают существенно различным характером.
В связи с этим возникает задача определения оптимальных параметров настройки на кривой равной степени колебательности.
Рис. 57. Кривые равной степени колебательности
В качестве критерия оптимальности выбираем продолжительность переходного процесса – время регулирования (т. е. быстродействие АСР) и отсутствие постоянной или врéменной статической ошибки. Это исключает из рассмотрения параметры настройки в точке 4 (параметры настройки П-регулятора) и в точке 3 (врéменная статическая ошибка) (рис. 58).
Рис. 58. Графики процессов регулирования для ПИ-регулятора
с различными параметрами настройки в точках 1, 2, 3 и 4
при степени колебательности m =0,221
Быстродействие автоматического регулятора прежде всего зависит от величины регулирующего воздействия, которое для ПИ-регулятора, как следует из уравнения (65), прямо пропорционально величине коэффициента усиления Kp и обратно пропорционально времени изодрома Tи. Расчеты показывают, что если двигаться по кривой равной степени колебательности вправо, то величина регулирующего воздействия при прочих равных условиях сначала возрастает и достигает максимального значения на кривой равной степени колебательности вблизи ее вершины, когда
а затем начинает уменьшаться в связи с резким увеличением Tи (рис. 57).
Рис. 59. Выбор оптимальных параметров настройки
Таким образом, оптимальные параметры настройки ПИ-регулятора находятся в точке 2 на кривой равной степени колебательности (рис. 59).
Источник
Плютто В. П., Дубровский И. И. Элементы теории управления химико-технологическими процессами и системами. Конспект лекций: Учеб. пособие – М.: РХТУ им. Д. И. Менделеева, 2003. – 127 с.
ПИ-регулятор
(изодромный
регулятор)
;
на
низких частотах преобладает интегрирующий
эффект (отсутствует статическая ошибка),а
на высоких частотах – эффект от
(качество переходного процесса лучше,
чем при И-законе регулирования).
– закон
регулирования.
-
– отсутствие
регулятора; -
–
П-регулятор; -
–
ПИ-регулятор.
Достоинства:
-
Простота
реализации; -
Существенно
улучшает точность регулирования в
статике:
• Установившаяся
ошибка при постоянном входном воздействии
равна нулю;
• Эта ошибка
нечувствительна к изменениям параметров
объекта.
Недостатки:
повышается астатизм системы на единицу
и, как следствие, снижение запасов
устойчивости, увеличивается колебательность
переходного процесса, увеличивается
.
Реализация
ПИ-регулятора
ПИД-регулятор
На
низких частотах преобладает интегрирующий
эффект, а на высоких – дифференцирующий.
.
– закон
регулирования.
Статическая система
при установке ПИД-регулятора становится
астатической (статическая ошибка равна
нулю), однако в динамике астатизм
снимается за счет действия дифференцирующей
составляющей, т. е. качество переходного
процесса улучшается.
Достоинства:
-
Высокая
статическая точность; -
Высокое
быстродействие; -
Большой
запас устойчивости.
Недостатки:
-
Применимы
для систем, описываемых
дифференциальными
уравнениями невысокого
порядка,
когда объект имеет один или два полюса,
или
может быть аппроксимирован моделью
второго
порядка.
-
Требования
к качеству управления низкие.
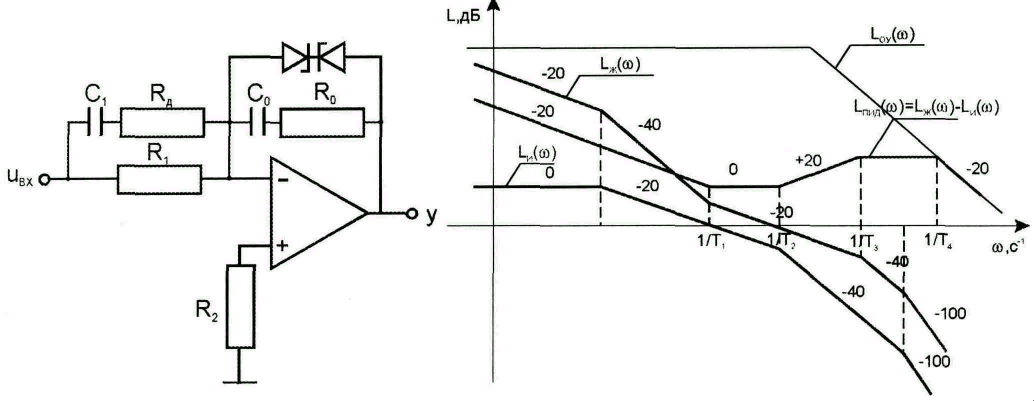
Реализация ПИД-регулятора
где
,
,
,
,
причем
.
По
ЛАЧХ операционного усилителя определяем
.
Тогда передаточная функция реального
регулятора имеет вид
.
В
системах чаще всего применяется
ПИД-регулятор.
Расчёт систем
комбинированного управления
Комбинированное
– такое управление в автоматической
системе, когда наряду с замкнутым
контуром регулирования по отклонению
используется внешнее компенсирующее
устройство по задающим или возмущающим
воздействиям.
Принцип инвариантности
– принцип компенсации динамической и
статической ошибок независимо от формы
входного воздействия по каналу управления
или компенсации возмущающего воздействия.
-
Расчет
компенсирующих устройств по каналу
возмущения
Пусть
структурная схема исходной системы
преобразована к виду, изображенному на
рис.1.
Перенесем
на вход системы точку приложения
возмущения (рис. 2).
Запишем
уравнение для выходной координаты:
.
Влияние
на выходную функцию со стороны возмущения
f
будет отсутствовать, если выполняется
условие абсолютной
инвариантности
системы к возмущающему воздействию:
—
условие полной компенсации возмущения.
Внешние
регуляторы используются для получения
инвариантности по каналу возмущения с
точностью до .
Пример.
Пусть объект и регулятор ведут себя как
апериодические звенья. Наибольшая
постоянная времени, как правило,
принадлежит объекту.
Тогда
,
,
,
,
.
Графики
на рис. 3.
1/Тp
Компенсирующая цепь должна обладать
дифференцирующими свойствами, причем
активными дифференцирующими свойствами
на высоких частотах (так как характеристика
отчасти располагается выше оси частот).
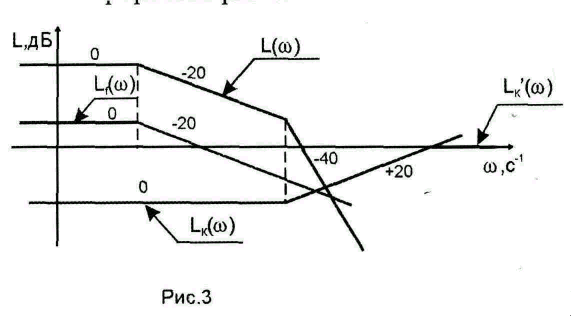
1/Т0
Достижение абсолютной инвариантности
невозможно, однако эффект компенсации
может быть значительным даже при простой
компенсирующей цепи, обеспечивающей
реализацию
в ограниченном диапазоне частот (
на рис. 3).
Технически
трудно и не всегда возможно измерить
возмущение, поэтому при проектировании
систем часто используют косвенные
методы измерения возмущающих воздействий.
2.
Расчет
систем с компенсацией динамической
ошибки по каналу управления
y1
y1+u-y
Для этой системы,
структурная схема которой изображена
на рис. 4, справедливы следующие
соотношения:
;
=
– передаточная функция по сигналу
ошибки.
Можем
добиться условия полной компенсации
ошибки, если выбрать компенсирующую
цепь с параметрами:
(1) 
– условие абсолютной инвариантности
системы к ошибке по каналу управления.
Передаточная
функция системы с компенсирующей цепью
.
В
этом случае
,
.
Следящие
системы реализуются астатическими.
Рассмотрим пример для таких систем
(рис.5).
В области высоких
частот дифференцирование второго
порядка в компенсирующей цепи приводит
к насыщению усилителей и размыканию
цепи при высоком уровне помех. Поэтому
осуществляется приближенная реализация,
которая дает ощутимый эффект регулирования.
Астатические
системы характеризуются
добротностью
– передаточный
коэффициент
k
определяется при =1
и =k.
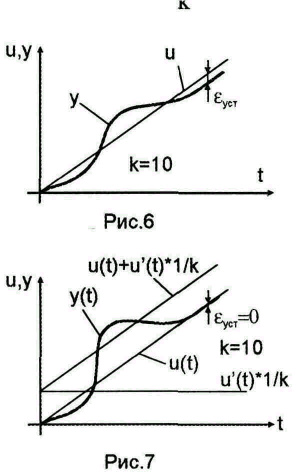
Если
k=10,
то ошибка в 10%, так как
,
система низкого качества (рис.6).
Введем
компенсирующую цепь с передаточной
функцией
.
Такой цепью может служить тахогенератор,
если
вход
механический. Реализация системы с
малой добротностью
проста.
Пусть
,
из условия (1) получим
.
Тогда,
имея систему с астатизмом 1-го порядка,
получим систему с
астатизмом
второго порядка (рис.7).
Всегда
Y
отстает от управляющего сигнала; введя
,
уменьшаем ошибку. Компенсирующая цепь
не влияет на устойчивость.
Как
правило, компенсирующее звено должно
обладать дифференцирующими свойствами
и реализовываться с использованием
активных элементов. Точное выполнение
условия абсолютной инвариантности
невозможно в виду технической
нецелесообразности получения производной
выше второго порядка (в контур регулирования
вводится высокий уровень помех, возрастает
сложность компенсирующего устройства)
и инерционности реальных технических
устройств. Количество апериодических
звеньев в компенсирующем устройстве
проектируют равным числу элементарных
дифференцирующих звеньев. Постоянные
времени апериодических звеньев
рассчитывают по условию работы звеньев
в существенной области частот, т.е.
,
.
Соседние файлы в папке Lekcii
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Классический ПИД-регулятор
Простейшая система автоматического регулирования с обратной связью показана на рисунке. В ней блок R называют регулятором (от слова Regulator), P — объектом регулирования (от слова Process), r — управляющим воздействием или уставкой (reference), e — сигналом рассогласования или ошибки (error), u — выходной величиной регулятора, y — регулируемой величиной.
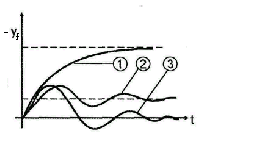
Частный случай ПИД-регулятора — пропорциональный или П-регулятор: u(t)=K·e(t). С помощью П-регулятора можно управлять любым устойчивым объектом, однако он дает относительно медленные переходные процессы и ненулевую статическую ошибку (статическая ошибка e0 — постоянная ошибка в установившемся режиме системы; см. рис. ниже).
С увеличением пропорционального коэффициента K статическая ошибка e0 уменьшается, время нарастания переходного процесса tн уменьшается, перерегулирование σ увеличивается.
Чтобы убрать статическую ошибку в установившемся режиме, в регулятор вводят интегральный канал с коэффициентом усиления Ki, так что:
Такой регулятор называется пропорционально-интегральным или ПИ-регулятором. Интегратор выдает сигнал, пропорциональный накопленной ошибке, поэтому переходный процесс несколько замедляется.
Однако за счет интегрального канала обеспечивается нулевая ошибка e0 в установившемся состоянии при ступенчатом возмущении и ступенчатом изменении задающего сигнала-уставки.
С увеличением коэффициента интегральной составляющей ПИ-регулятора Ki время нарастания переходного процесса tн уменьшается, перерегулирование σ увеличивается, время регулирования tр увеличивается.
Для ускорения переходных процессов добавляют дифференциальный канал с коэффициентом усиления Kd:
|
|
(1.01) |
Распространена также другая модификация выражения (1.01):
|
|
(1.02) |
где t — время; K — пропорциональный коэффициент (безразмерный), Ti — постоянная интегрирования (размерность времени) и Td — постоянная дифференцирования (размерность времени) регулятора. Такой регулятор называют ПИД-регулятором.
Регуляторы этого типа очень хорошо зарекомендовали себя в практических задачах. Кроме того, иногда используются ПД-регуляторы (пропорционально-дифференциальные), у которых нет интегрального канала.
Управление по производной – это быстрый способ управления. Сигнал дифференциального канала наиболее важен при изменениях входов и исчезает в установившемся режиме. Он позволяет реагировать не на само увеличение ошибки, а на тенденцию ее изменения, и принять превентивные меры
. Главный недостаток дифференциального канала – большое влияние высокочастотных помех, например, шумов измерений.
С увеличением коэффициента дифференциальной составляющей ПИД-регулятора Kd перерегулирование σ уменьшается, время регулирования tр уменьшается.
|
При увеличении коэффициентов |
|||
|
Kp |
Ki |
Kd |
|
|
Время нарастания tн |
|
|
|
|
Пере- регулирование σ |
|
|
|
|
Время регулирования tр |
|
|
|
|
Статическая ошибка e0 |
|
|
|
|
|
Для устойчивого объекта можно выбрать коэффициенты регулятора опытным путем, выполняя эксперименты с реальным объектом. Предложено несколько методов решения этой задачи, например, правила Зиглера-Никольса (Ziegler J. G. — Nichols N. B.), Коэна-Куна (Cohen O.H. – Coon O.A.) или CHR (Chien K. L. — Hrones J. A. — Reswick J. B.).
Список используемой литературы
- Поляков К.Ю.,
Теория автоматического управления для
чайников
, Санкт-Петербург, 2008 г. - Востриков А.С., Французова Г.А.,
Теория автоматического регулирования
. 2003 г. - Глушков В.М., Амосов Н.М., Артеменко И.А. Энциклопедия кибернетики. Том 2. Киев, 1974 г.
- Теория автоматического управления: Учеб. для вузов по спец.
Автоматика и телемеханика
. В 2-х ч. Ч. I. Теория линейных систем автоматического управления / Н. А. Бабаков, А. А. Воронов, А. А. Воронова и др.; Под ред. А. А. Воронова.—2-е изд., перераб. и доп. — М.: Высш. шк., 1986. — 367 с. - Денисенко В.В.,
Энциклопедия АСУ ТП
, bookasutp.ru - Dew Toochinda,
Scilab Ninja. Control Engineering with Scilab
,Scilab Control Engineering Basics
, scilab.ninja/study-modules/scilab-control-engineering-basics/
У нас на сайте Вы можете приобрести качественные частотные преобразователи. Подробности тут
Продолжение разработки проекта контроллера модуля Пельтье, начатой в уроке 36. Узнаем, что такое ПИД регулятор.
Предыдущий урок Список уроков Следующий урок
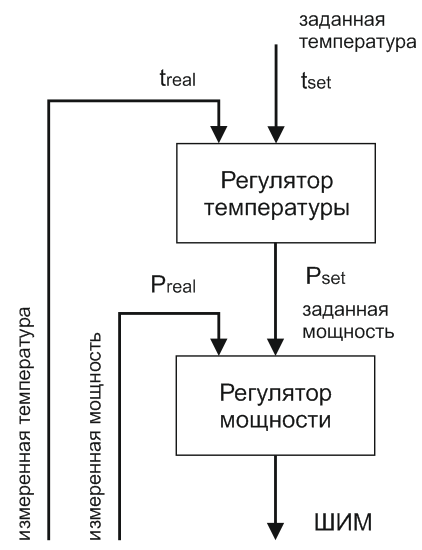
Основная задача контроллера холодильника – поддержание в камере заданной температуры. Делать это будет регулятор температуры за счет изменения электрической мощности на модуле Пельтье.
В предыдущем уроке мы разработали регулятор мощности. Связь регуляторов мощности и температуры выглядит так.
- Регулятор температуры получает измеренную температуру, сравнивает ее с заданной температурой и вычисляет значение заданной мощности для регулятора мощности.
- Регулятор мощности формирует ШИМ, соответствующий заданной мощности.
Регулятор мощности мы построили по интегральному закону регулирования. Для стабилизации температуры будем использовать более сложный алгоритм управления – пропорционально-интегрально-дифференцирующий (ПИД) регулятор.
ПИД регулятор.
В предыдущем уроке я подробно рассказал об интегральном регуляторе. Подчеркнул его достоинства и недостатки.
Регулятор, работающий по такому принципу, обладает высокой точностью. Остальные критерии качества регулирования – быстродействие и устойчивость — у него не на высоте.
Для того чтобы добиться высоких показателей для всех критериев необходимо использовать регулятор, объединяющий в себе разные законы регулирования.
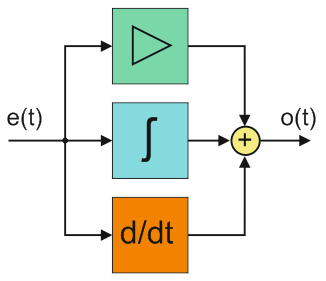
Именно таким устройством является пропорционально-интегрально-дифференцирующий (ПИД) регулятор. Он формирует выходной сигнал, являющийся суммой трех составляющих с разными передаточными характеристиками. Благодаря этому ПИД регулятор обеспечивает высокое качество регулирования и позволяет оптимизировать управление по отдельным критериям.
В формировании выходного сигнала ПИД регулятора участвуют:
- Пропорциональная составляющая – значение пропорционально ошибке рассогласования (разности заданного и реального значений регулируемого параметра).
- Интегрирующая составляющая – интеграл ошибки рассогласования.
- Дифференцирующая составляющая – производная ошибки рассогласования.
Математическая форма записи закона ПИД регулятора имеет вид:
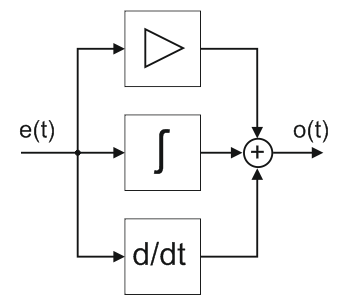
o(t) = P + I + D = Kp e(t) + Ki ∫e(t)dt + Kd de(t)/dt
- o(t) – выходной сигнал;
- P – пропорциональная составляющая;
- I – интегрирующая составляющая;
- D – дифференцирующая составляющая;
- Kp, Ki, Kd – коэффициенты пропорционального, интегрирующего, дифференцирующего звеньев;
- e(t) – ошибка рассогласования.
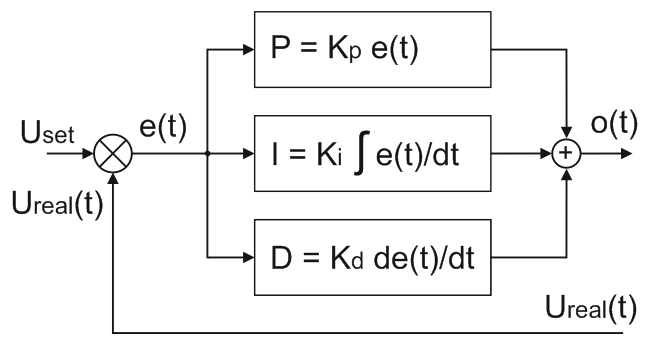
В схематичном виде ПИД регулятор можно представить так.
Структурная схема ПИД регулятора напряжения U выглядит так.
- Измеренное напряжение Ureal(t) вычитается из заданного Uset.
- Полученная ошибка рассогласования e(t) поступает на пропорциональное, интегрирующее и дифференцирующее звенья.
- В результате суммы составляющих получается управляющее воздействие o(t), которое подается на регулирующий элемент.
При программной реализации ПИД регулятора вычисления выходного сигнала происходят через равные промежутки времени. Т.е. регулятор является дискретным по времени. Поэтому, далее я буду употреблять выражения: предыдущее состояние сигнала, предыдущее значение и т.п. Речь идет о состоянии системы в предыдущей точке временной дискретизации.
Составляющие ПИД регулятора.
Еще раз. Выходной сигнал ПИД регулятора это сумма трех составляющих:
- пропорциональной;
- интегрирующей;
- дифференцирующей.
Пропорциональная составляющая.
P(t) = Kp * e(t)
Не имеет памяти, т.е. значение выходного сигнала не зависит от предыдущего состояния системы. Просто ошибка рассогласования, умноженная на коэффициент, передается на выход. Выходной сигнал компенсирует отклонение регулируемого параметра. Сигнал тем больше, чем больше ошибка рассогласования. При ошибке равной 0, сигнал на выходе тоже равен 0.
Пропорциональная составляющая не способна компенсировать ошибку полностью. Это видно из формулы. Выходной сигнал в Kp раз больше ошибки. Если ошибка рассогласования равна 0, то и выходной сигнал регулятора равен 0. А тогда и компенсировать нечем.
Поэтому в пропорциональных регуляторах всегда существует так называемая статическая ошибка. Уменьшить ее можно за счет увеличения коэффициента Kp, но это может привести к снижению устойчивости системы и даже к автоколебаниям.
К недостаткам пропорциональных регуляторов следует отнести:
- наличие статической ошибки регулирования;
- невысокая устойчивость при увеличении коэффициента.
Есть весомое преимущество:
- Высокая скорость регулирования. Реакция пропорционального регулятора на ошибку рассогласования ограничена только временем дискретизации системы.
Регуляторы, работающие только по пропорциональному закону, применяют редко.
Главная задача пропорциональной составляющей в ПИД регуляторе – повысить быстродействие.
Интегрирующая составляющая.
I(t) = Ki ∫e(t)dt
Пропорциональна интегралу ошибки рассогласования. С учетом временной дискретности регулятора можно написать так:
I(t) = I(t-1) + Ki * e(t)
- I(t-1) – значение I в предыдущей точке временной дискретизации.
Ошибка рассогласования умножается на коэффициент и прибавляется к предыдущему значению интегрирующего звена. Т.е. выходной сигнал все время накапливается и со временем увеличивает свое воздействие на объект. Таким образом, ошибка рассогласования полностью компенсируется даже при малых значениях ошибки и коэффициента Ki. В установившемся состоянии выходной сигнал регулятора полностью обеспечивается интегрирующей составляющей.
К недостаткам интегрального регулятора следует отнести:
- низкое быстродействие;
- посредственная устойчивость.
Достоинство:
- Способность полностью компенсировать ошибку рассогласования при любом коэффициенте усиления.
На практике часто используют интегрирующие регуляторы (только интегрирующая составляющая) и пропорционально-интегрирующие (интегрирующая и пропорциональная составляющие).
Главная задача интегрирующего звена в ПИД регуляторе – компенсация статической ошибки, обеспечение высокой точности регулирования.
Дифференцирующая составляющая.
D(t) = Kd de(t)/dt
Пропорциональна скорости изменения ошибки рассогласования. Своеобразный показатель ускорения ошибки рассогласования. Дифференцирующая составляющая предсказывает отклонения регулируемого параметра в будущем и противодействует этому отклонению. Как правило, она компенсирует запаздывания воздействия регулятора на объект и повышает устойчивость системы.
С учетом временной дискретности регулятора дифференцирующую составляющую можно вычислить так:
D(t) = Kd * ( e(t) — e(t-1) )
Она показывает, насколько изменилось значение ошибки рассогласования за одну временную единицу дискретности регулятора.
Регуляторов, состоящих из единственного дифференцирующего звена, не бывает.
Главная задача дифференцирующего звена в ПИД регуляторе – повышение устойчивости.
Настройка ПИД регулятора.
Качество регулирования ПИД регуляторов в значительной мере зависит от того, насколько оптимально выбраны коэффициенты. Коэффициенты ПИД регулятора определяются на практике в системе с реальным объектом путем подбора. Существуют разные методики настройки. Я расскажу только об общих принципах.
О качестве регулирования судят по переходной характеристике регулятора. Т.е. по графику изменения регулируемого параметра во времени.
К традиционным пунктам последовательности настройки ПИД регулятора я бы добавил, что, прежде всего, надо определиться какие критерии качества регулирования предпочтительнее.
В предыдущем уроке при разработке регулятора мощности нас в первую очередь интересовали точность и устойчивость. А быстродействие мы даже искусственно снизили. Какие-то регуляторы работают в условиях значительных помех и им важнее устойчивость, от других требуется высокое быстродействие даже в ущерб точности. Критерии оптимизации могут быть разными. В общем случае ПИД регуляторы настраивают для обеспечения всех критериев качества регулирования на высоком уровне.
Составляющие ПИД регулятора настраиваются отдельно.
- Отключается интегрирующее и дифференцирующее звенья и выбирается коэффициент пропорционального звена. Если регулятор пропорционально-интегрирующий (отсутствует дифференцирующее звено), то добиваются полного отсутствия колебаний на переходной характеристике. При настройке регулятора на высокое быстродействие колебания могут остаться. Их попытается скомпенсировать дифференцирующее звено.
- Подключается дифференцирующее звено. Его коэффициентом стремятся убрать колебания параметра регулирования. Если не удается, то уменьшают пропорциональный коэффициент.
- За счет интегрирующего звена убирают остаточную ошибку рассогласования.
Настройка ПИД регулятора носит итерационный характер. Т.е. пункты подбора коэффициентов могут многократно повторяться до тех пор, пока не будет достигнут приемлемый результат.
Благодаря высоким характеристикам и универсальности ПИД регуляторы широко применяются в системах автоматизации производства.
В следующем уроке будем разрабатывать ПИД регулятор температуры.
Предыдущий урок Список уроков Следующий урок
Автор публикации
272
Комментарии: 1919Публикации: 197Регистрация: 13-12-2015
Настройка ПИД-регулятора
В данной статье приведены основные принципы и правила настройки коэффициентов ПИД-регулятора сточки зрения практического применения. Теоретические основы можно прочитать вот в этой статье.
Для простоты изложения рассмотрим настройку регулятора на примере. Допустим, необходимо поддерживать температуру в помещении с помощью обогревателя, управляемого регулятором. Для измерения текущей температуры используем термопару.
Задача настройки
Настройка регулятора производится с одной единственной целью: подобрать его коэффициенты для данной задачи таким образом, чтобы регулятор поддерживал величину физического параметра на заданном уровне. В нашем примере физическая величина — это температура.
Допустим текущая температура в помещении 10 °С, а мы хотим, чтобы было 25°С. Мы включаем регулятор и он начинает управлять мощностью обогревателя таким образом, чтобы температура достигла требуемого уровня. Посмотрим как это может выглядеть.
На данном рисунке красным цветом показана идеальная кривая изменения температуры в помещении при работе регулятора. Физическая величина плавно, без скачков, но в тоже время достаточно быстро подходит к заданному значению. Оптимальное время, за которое температура может достигнуть заданной отметки, определить довольно сложно. Оно зависит от многих параметров: размеров комнаты, мощности обогревателя и др. В теории это время можно рассчитать, но на практике чаще всего это определяется экспериментально.
Чёрным цветом показан график изменения температуры в том случае, если коэффициенты подобраны совсем плохо. Система теряет устойчивость. Регулятор при этом идёт «в разнос» и температура «уходит» от заданного значения.
Рассмотрим более благоприятные случаи.
На этом рисунке показаны графики, далёкие от идеального. В первом случае наблюдается сильное перерегулирование: температура слишком долго «скачет» относительно уставки, прежде чем достичь её. Во втором случае регулирование происходит плавно, но слишком медленно.
А вот и приемлемые кривые:
Данные кривые тоже не идеальны, но могут быть сочтены за удовлетворительные.
В процессе настройки регулятора, пользователю необходимо стремиться получить кривую, близкую к идеальной. Однако, в реальных условиях сделать это не так-то просто — приходится долго и мучительно подбирать коэффициенты. Поэтому зачастую останавливаются на «приемлемой» кривой регулирования. Например, в нашем примере нас могли бы устроить коэффициенты регулятора, при которых заданная температура достигалась бы за 15-20 минут с максимальным перерегулированием (максимальными «скачками» температуры) 2 °С. А вот время достижение уставки более часа и максимальные «скачки» температуры 5 °С — нас бы не устроили.
Далее поговорим о том, как подобрать коэффициенты для достижения оптимального регулирования. Рекомендуется настраивать коэффициенты в том же порядке, в котором это описано.
Настраиваем пропорциональный коэффициент
Выставляем дифференциальный и интегральный коэффициенты в ноль, тем самым убирая соответствующие составляющие. Пропорциональный коэффициент выставляем в 1.
Далее нужно задать значение уставки температуры отличное от текущей и посмотреть, как регулятор будет менять мощность обогревателя, чтобы достичь заданного значения. Характер изменения можно отследить «визуально», если у вас получится мысленно представить этот график. Либо можно регистрировать в таблицу измеренное значение температуры каждые 5-10 секунд и по полученным значением построить график. Затем нужно проанализировать полученную зависимость в соответствии с рисунком:
При большом перерегулировании, необходимо уменьшать пропорциональный коэффициент, а если регулятор долго достигает уставки — увеличивать. Так убавляя-прибавляя коэффициент необходимо получить график регулирования как можно ближе к идеальному. Поскольку достичь идеала удастся вряд ли, лучше оставить небольшое перерегулирование (его можно будет скорректировать другими коэффициентами), чем длительное нарастание графика.
Настраиваем дифференциальный коэффициент
Постепенно увеличивая дифференциальную составляющую, необходимо добиться уменьшения или полного исчезновения «скачков» графика (перерегулирования) перед выходом на уставку. При этом кривая должна стать еще больше похожа на идеальную. Если слишком сильно завысить дифференциальный коэффициент, температура при выходе на уставку будет расти не плавно, а скачками (как показано на рисунке).
При появлении таких скачков необходимо прекратить увеличение дифференциального коэффициента.
Настраиваем интегральный коэффициент
При настройке двух предыдущих коэффициентов можно получить практически идеальную кривую регулирования или близкую к ней кривую, удовлетворяющую условиям задачи. Однако, как правило возникает так называемая «статическая ошибка». При этом в нашем примере температура стабилизируется не на заданном значении 25 °С, а на несколько меньшем значении. Дело в том, что если температура станет равной уставке (то есть разность текущей и заданной температур станет равна 0), то пропорциональная и дифференциальная составляющая будут равны нулю (см. функцию преобразования ПИД-регулятора). При этом мощность регулятора тоже станет равна 0 и он начнёт остывать.
Для того чтобы исключить этот эффект, используют интегральную составляющую. Её необходимо постепенно увеличивать до исчезновение статической ошибки. Однако, чрезмерное её увеличение тоже может привести к возникновению скачков температуры.
Заключение
Настройка ПИД-регулятора довольно сложный и трудоёмкий процесс. На практике достаточно тяжело достичь оптимального регулирования и зачастую в этом нет необходимости. Чаще всего достаточно добиться такого вида переходного процесса, который устроит пользователя в условиях текущей задачи.