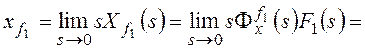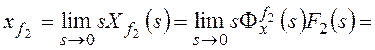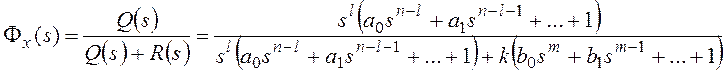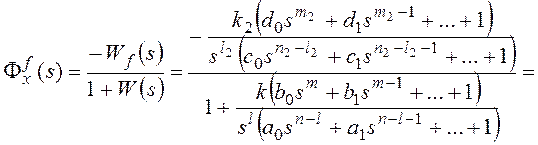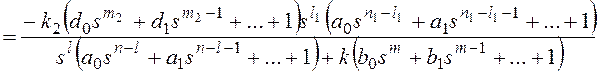Точность системы автоматического управления Статическая ошибка системы
В системах
автоматического управления часто
приходится решать задачу стабилизации
управляемой величины. Точность поддержания
требуемого значения управляемой величины
в такой системе можно оценить как разницу
между заданным значением управляемой
величины и её установившимся значением
в системе после окончания переходного
процесса:
.
Эта величина
получила название статической ошибки
системы. При вычислении статической
ошибки предполагается, что система
находится в статике и все сигналы в ней
имеют постоянные величины. Статическая
ошибка используется для оценки точности
установления в системе заданной
постоянной выходной величины после
окончания переходного процесса.
Используя
передаточную функцию замкнутой системы
по ошибке, для изображения ошибки в
системе можно записать
,
гдепередаточная
функция замкнутой системы по ошибке,изображение
задающего воздействия.
Для статики,
когда все сигналы в системе неизменны,
выражение для ошибки можно перенести
в область оригиналов
.
Поскольку
,
гдеW(p)
– передаточная функция разомкнутой
системы, то статическую ошибку системы
можно вычислить, зная передаточную
функцию разомкнутой системы:
,
где.
Вместо
абсолютного значения статической ошибки
часто используют относительную
статическую ошибку
.
Если система
статическая (т.е. не содержит интегрирующих
звеньев), то передаточную функцию
разомкнутой системы можно представить
в следующем нормированном виде:
,
гдеK– коэффициент
усиления системы,A*(p),B*(p)
– нормированные полиномыA(p)
иB(p).
При этоми
.
Тогдаи статическая ошибка в статической
системе
.
Статическая
ошибка в статической системе уменьшается
с увеличением коэффициента усиления
системы. Статическая система всегда
будет иметь некоторую ошибку. Физический
смысл такой ошибки заключается в
необходимости некоторого рассогласования
между задающей и выходной величинами
системы для получения сигнала управления.
Если в системе
управления имеются интегрирующие
звенья, то система будет астатической.
Для астатической системы первого порядка
(содержащей одно интегрирующее звено)
передаточная функция разомкнутой
системы
и передаточная функция замкнутой системы
по ошибке
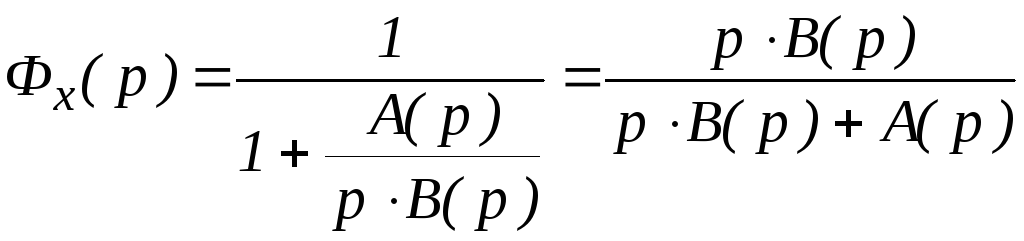
В этом случае всегда
и, следовательно, статическая ошибка
астатической системы будет равна нулю.
Таким образом, статическая ошибка в
астатической системе в принципе
отсутствует, что обуславливает более
высокую точность астатических систем,
по сравнению со статическими системами.
В астатической системе автоматического
управления установившееся значение
управляемой величины равно заданному
значению этой величины.
Вынужденная ошибка системы
Процесс в
системе складывается из свободного
процесса и вынужденного процесса:
.
Для
устойчивой системы свободный процесс
по истечении времениtпзатухает и в системе устанавливается
вынужденный процесс
Точность
поддержания заданного значения
управляемой величины в вынужденном
режиме характеризуется вынужденной
ошибкой системы
.
Вынужденная
ошибка хорошо характеризует работу
системы автоматического управления в
том случае, когда изменения управляющего
воздействия происходят существенно
медленнее собственных переходных
процессов в системе и последними можно
пренебречь.
Рассмотрим
вычисление вынужденной ошибки системы
автоматического управления. Изображение
для вынужденной ошибки
.
В общем случае
является дробно-рациональной функцией
отpи ее можно разложить
в ряд Тейлора по степенямрвблизи, тогда
и
выражение для вынужденной ошибки системы
примет вид
где
постоянные
коэффициенты.
Для полученного
изображения вынужденной ошибки на
основе свойств преобразования Лапласа
легко находится выражение для оригинала
ошибки
где
,
,
…коэффициенты
ошибок, полученные выше (C0– коэффициент статической ошибки,C1
– коэффициент скоростной ошибки и
т. д.).
Коэффициенты
ошибки могут быть также получены делением
числителя передаточной функции на ее
знаменатель. Полученное выражение для
вынужденной ошибки позволяет оценить
точность системы автоматического
управления в установившемся режиме.
Вынужденная ошибка, например, хорошо
характеризует точность работы следящих
систем автоматического управления.
Соседние файлы в папке ТАУ
- #
- #
- #
Уровень сложности
Средний
Время на прочтение
6 мин
Количество просмотров 3.5K
7.1 Общие понятия о точности процесса управления
Как отмечалось в разделе 6, интегральная оценка управления складывается из 3-х основных понятий:
-
устойчивость САР;
-
точность САР;
-
качество переходного процесса.
Очевидно, что главным является устойчивость САР (или запас устойчивости). Если САР не устойчива или очень мал запас устойчивости, то говорить о точности (неустойчивая САР) или о качестве переходного процесса (малые запасы устойчивости) не имеет смысла.
Если САР устойчива и запасы устойчивости достаточны по величине, то понятие точность САР является весьма важным показателем.
Точность определяют по отработке САР следующих видов воздействий:
-
ступенчатое внешнее воздействие (управляющее или возмущающее) часто называется постоянным внешним воздействием;
-
линейное внешнее воздействие т.е. линейно изменяющееся внешнее воздействие (управляющее или возмущающее);
-
гармоническое воздействие, т.е. ;
-
медленно меняющееся произвольное внешнее (управляющее или возмущающее) воздействие;
-
другие воздействия (параболическое, импульсное и т.д.).
Наиболее часто для оценки точности САР используются постоянное (ступенчатое) и линейное воздействия.
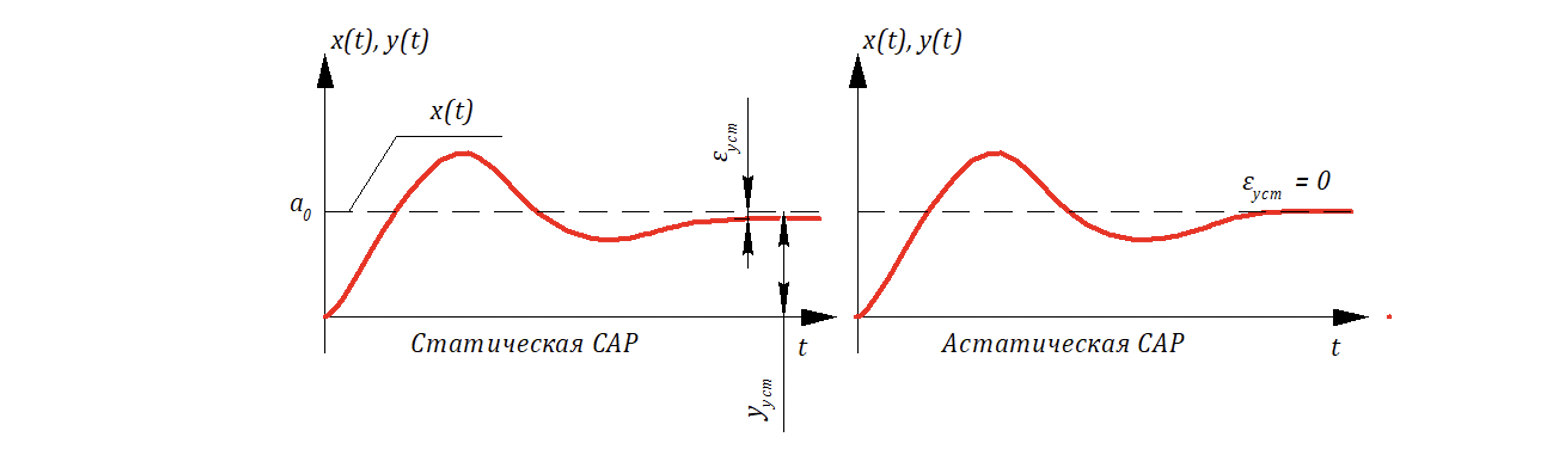
Различают статические и астатические САР:
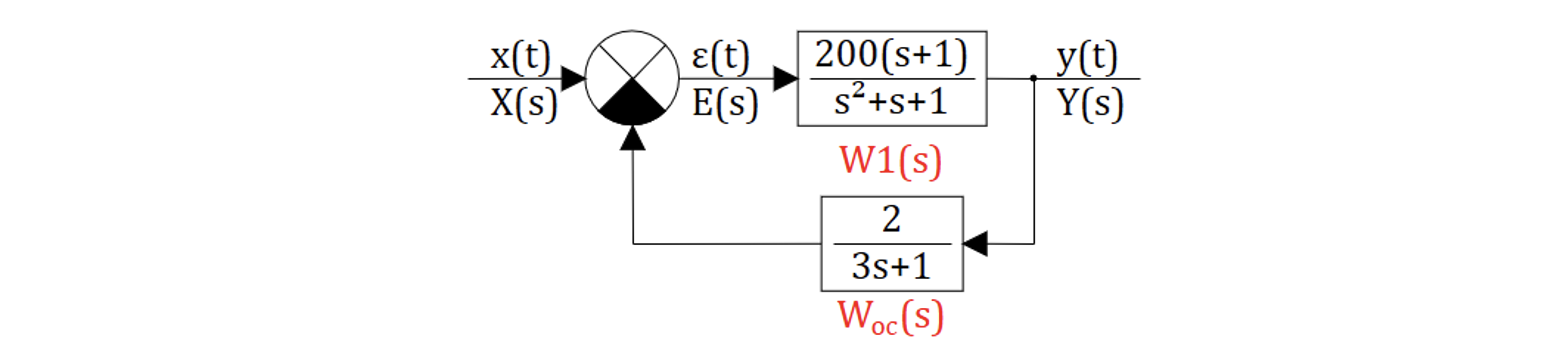
Данные графики будем относить к следующей структуре САР:
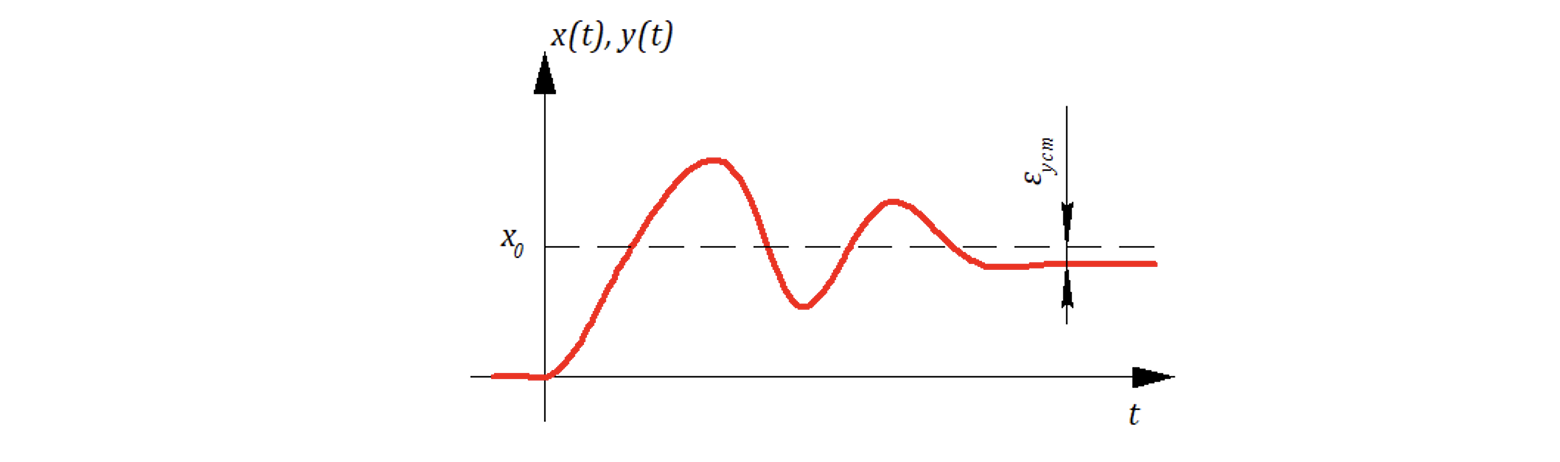
По установившейся ошибкой понимают:
Если входное воздействие — ступенчатое, to
— «постоянная» ошибка.
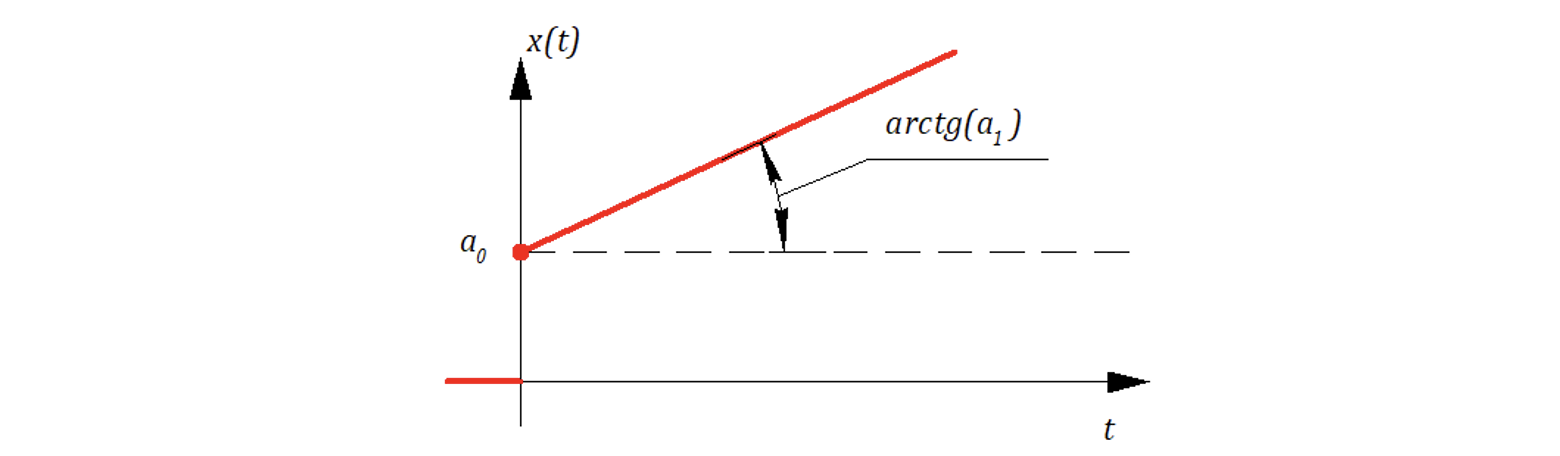
Если входное воздействие — линейное, to
— «скоростная» ошибка.
Различают астатизм по управляющему воздействию, а также астатизм по возмущающему воздействию, причем наличие того или иного астатизма определяется по-разному (см. следующие подразделы).
Главной задачей системы автоматического регулирования является точная и быстрая (но плавная) отработка управляющих воздействий, причем учитывая требования качества САР – точность очень важная «характеристика».
Наиболее часто точность САР оценивают по отработке управляющих воздействий. Рассмотрим последовательно различные виды управляющих (задающих) воздействий.
7.2 Точность при постоянном задающем воздействии. Постоянные ошибки
Для упрощения дальнейших преобразований будем считать, что структура САР приведена к стандартному виду (см. п.5 Передаточные функции и уравнения динамики система автоматического регулирования):
Примем, что отсутствует возмущающее воздействие
Рассмотрим единичное ступенчатое воздействие
Считая, что замкнутая САР устойчива, найдем
Примем, что свободные коэффициенты в полиномах и
передаточной функции разомкнутой САР равны 1.
— передаточная функция замкнутой САР.
Используя передаточную функцию замкнутой САР (см. раздел 5) для ошибки можно записать выражение:
где: — главная передаточная функция (см. раздел 5).
согласно 1-й предельной теореме (см. раздел 2)
Учитывая, что единичное ступенчатое воздействие в отображениях: :
Т.е. если полином имеет свободный член, равный единице, то САР не может точно «отработать» постоянное воздействие, т.е. она статична.
Величина — называют постоянной или статической ошибкой.
В случае если полином не имеет свободных членов, то его можно представить как
где
— полином который имеет свободный член равный единицы. В этом случае установившаяся погрешность:
Если , где
— порядок астатизьма, то при постоянном (ступенчатом) воздействии установившаяся ошибка равна нулю.
Из соотношения 7.2.3 очевидно, чем выше k — коэффициент усиления, тем меньше ошибка (для статических САР). Выводы: необходимо повышать общий коэффициент усиления разомкнутой САР, для сокращения ошибки.
Однако увеличение может привести к резкому уменьшению запасов устойчивости (что ухудшит качество переходного процесса) вплоть до потери устойчивости (см. раздел 6).
Цитата:
«Необходимо отметить, что для разомкнутой САР, имеющей
годограф похожий на рис. 6.5.5 левый вариант, устойчивость системы (замкнутой) нарушится только с увеличением общего коэффициента усиления К. (Дейстивительно при увеличении коэффициента K увеличится длинна вектора и он может охватить точку -1). «
Поэтому при проектировании САР необходимо «решать» «оптимальную» задачу, т.е. выбрать оптимальное значение , обеспечивающее удовлетворительную точность и неплохое качество переходного процесса.
В последнее время практически все САР проектируются как астатические, что легко достигается за счет использования астатических регуляторов (например ПИ-регуляторов (пропорционально-интегрирующих).
В этом случае говорить о постоянной ошибке нет смысла, т.к.
Пример 1:
Определить установившуюся ошибку, если входное воздействие , а структура САР имеет вид:
Необходимо заметить, что прямое использование формулы (7.2.3) в данном случае не проходит, т.к. статическая ошибка в исходной САР не соответствует статической ошибке в эквивалентной САР:
Прежде чем определять статическую ошибку необходимо удостовериться в том, что исходная замкнутая САР устойчива. Выполеним преобразование:
Характерестический полином эквивалентной передаточной функции:
Для определение устойчивости критерий Гурвица (см. раздел 6):
Все главные определители матрицы Гурвица больше нуля САР устойчива.
Перейдя к изображению Найдем выражения для отклонение в изображениях:
Подставляем значения и
, имеем:
7.3 Точность при линейном воздействии. Скоростные ошибки
В данном подразделе рассмотрим САР замкнутую единичной обратной связью (если обратная связь не единична, то с помощью структурных преобразований ее можно привести к единичной, подробнее об этом смотри раздел 4 Структурные преобразования систем автоматического регулирования)
где — входное воздействие.
В соответствии со своим назначением устойчивая САР обязана «отслеживать» (с какой-то степенью точности) управляющее воздействие.
Воспользуемся первой предельной теоремой:
Рассмотрим различные варианты САР: статическую и астатическую (1-го и 2-го порядка)
Статическая САР
Передаточная функция соответствует статической САР:
где полниномы и
имеют свободный член равный 1.
Отклонение в отображениях:
Где — изображение входного воздействия;
— передаточная функция по возмущению:
Изображение входного воздействия :
Вывод: Cтатическая САР не способна «отслеживать» линейное воздействие.
Астатическая САР со степенью астатизма 1
Для САР со степенью астатизма 1 полином не содержит совбодного члена равного 1, но его можно представит в виде произведения
где
— полином содержащий свободный член равный 1.
Примечание: Степень астатизма равна количеству нулевых полюсов полинома (см. раздел 5)
В этом случае установившиеся статистическая ошибка:
Вывод: Если разомкнутая САР имеет астатизм первого порядка (имеет один нулевой полюс), то установившияся ошибка для замкнутой САР
Ошибка в астатической САР (1-го порядка) называется скоростной ошибкой, а общий коэффициент часто называют коэффициентом добротности или просто добротностью.
Анализ формулы (7.3.3) показывает, что чем выше тем меньше
. Однако необходимо помнить, что повышение
может привести к потери устойчивости САР (или уменьшению запасов устойчивости с соответствующим ухудшением качества переходного процесса).(см. раздел 6).
Астатическая САР со степенью астатизма 2
Для САР со степенью астатизма 2 полином не содержит не только совбодного члена равного 1, и члена у которого степень
равна 1. Такой полином можно представит в виде произведения
где
— полином содержащий свободный член равный 1.
В этом случае установившиеся статистическая ошибка:
Очевидно, что если степень астатизма >2, то установившаяся статическая ошибка, тем более будет равна 0. Т.е. чем выше астатизм САР, тем лучше точность. Хотя повышение астатизма ухудшает устойчивость (запас устойчивости).
Модели из статьи можно взять здесь…
В предыдущих сериях:
1. Введение в теорию автоматического управления.2. Математическое описание систем автоматического управления 2.1 — 2.3, 2.3 — 2.8, 2.9 — 2.13.
3. Частотные характеристики звеньев и систем автоматического управления регулирования. 3.1. Амплитудно-фазовая частотная характеристика: годограф, АФЧХ, ЛАХ, ФЧХ. 3.2. Типовые звенья систем автоматического управления регулирования. Классификация типовых звеньев. Простейшие типовые звенья. 3.3. Апериодическое звено 1–го порядка инерционное звено. На примере входной камеры ядерного реактора. 3.4. Апериодическое звено 2-го порядка. 3.5. Колебательное звено. 3.6. Инерционно-дифференцирующее звено. 3.7. Форсирующее звено. 3.8. Инерционно-интегрирующее звено (интегрирующее звено с замедлением). 3.9. Изодромное звено (изодром). 3.10 Минимально-фазовые и не минимально-фазовые звенья. 3.11 Математическая модель кинетики нейтронов в «точечном» реакторе «нулевой» мощности.
4. Структурные преобразования систем автоматического регулирования.
5. Передаточные функции и уравнения динамики замкнутых систем автоматического регулирования (САР).
6. Устойчивость систем автоматического регулирования. 6.1 Понятие об устойчивости САР. Теорема Ляпунова. 6.2 Необходимые условия устойчивости линейных и линеаризованных САР. 6.3 Алгебраический критерий устойчивости Гурвица. 6.4 Частотный критерий устойчивости Михайлова. 6.5 Критерий Найквиста.
Точность системы автоматического управления Статическая ошибка системы
В системах
автоматического управления часто
приходится решать задачу стабилизации
управляемой величины. Точность поддержания
требуемого значения управляемой величины
в такой системе можно оценить как разницу
между заданным значением управляемой
величины и её установившимся значением
в системе после окончания переходного
процесса:
.
Эта величина
получила название статической ошибки
системы. При вычислении статической
ошибки предполагается, что система
находится в статике и все сигналы в ней
имеют постоянные величины. Статическая
ошибка используется для оценки точности
установления в системе заданной
постоянной выходной величины после
окончания переходного процесса.
Используя
передаточную функцию замкнутой системы
по ошибке, для изображения ошибки в
системе можно записать
,
гдепередаточная
функция замкнутой системы по ошибке,изображение
задающего воздействия.
Для статики,
когда все сигналы в системе неизменны,
выражение для ошибки можно перенести
в область оригиналов
.
Поскольку
,
гдеW(p)
– передаточная функция разомкнутой
системы, то статическую ошибку системы
можно вычислить, зная передаточную
функцию разомкнутой системы:
,
где.
Вместо
абсолютного значения статической ошибки
часто используют относительную
статическую ошибку
.
Если система
статическая (т.е. не содержит интегрирующих
звеньев), то передаточную функцию
разомкнутой системы можно представить
в следующем нормированном виде:
,
гдеK– коэффициент
усиления системы,A*(p),B*(p)
– нормированные полиномыA(p)
иB(p).
При этоми
.
Тогдаи статическая ошибка в статической
системе
.
Статическая
ошибка в статической системе уменьшается
с увеличением коэффициента усиления
системы. Статическая система всегда
будет иметь некоторую ошибку. Физический
смысл такой ошибки заключается в
необходимости некоторого рассогласования
между задающей и выходной величинами
системы для получения сигнала управления.
Если в системе
управления имеются интегрирующие
звенья, то система будет астатической.
Для астатической системы первого порядка
(содержащей одно интегрирующее звено)
передаточная функция разомкнутой
системы
и передаточная функция замкнутой системы
по ошибке
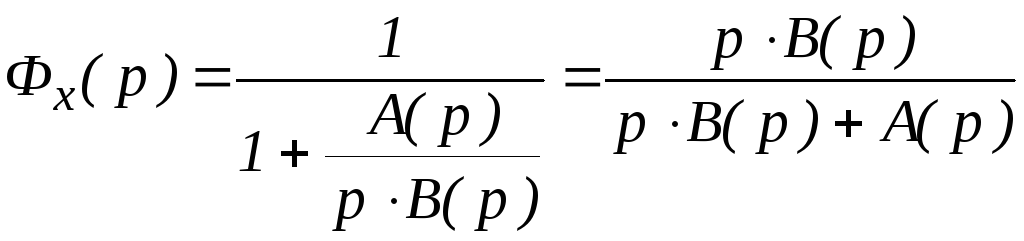
В этом случае всегда
и, следовательно, статическая ошибка
астатической системы будет равна нулю.
Таким образом, статическая ошибка в
астатической системе в принципе
отсутствует, что обуславливает более
высокую точность астатических систем,
по сравнению со статическими системами.
В астатической системе автоматического
управления установившееся значение
управляемой величины равно заданному
значению этой величины.
Вынужденная ошибка системы
Процесс в
системе складывается из свободного
процесса и вынужденного процесса:
.
Для
устойчивой системы свободный процесс
по истечении времениtпзатухает и в системе устанавливается
вынужденный процесс
Точность
поддержания заданного значения
управляемой величины в вынужденном
режиме характеризуется вынужденной
ошибкой системы
.
Вынужденная
ошибка хорошо характеризует работу
системы автоматического управления в
том случае, когда изменения управляющего
воздействия происходят существенно
медленнее собственных переходных
процессов в системе и последними можно
пренебречь.
Рассмотрим
вычисление вынужденной ошибки системы
автоматического управления. Изображение
для вынужденной ошибки
.
В общем случае
является дробно-рациональной функцией
отpи ее можно разложить
в ряд Тейлора по степенямрвблизи, тогда
и
выражение для вынужденной ошибки системы
примет вид
где
постоянные
коэффициенты.
Для полученного
изображения вынужденной ошибки на
основе свойств преобразования Лапласа
легко находится выражение для оригинала
ошибки
где
,
,
…коэффициенты
ошибок, полученные выше (C0– коэффициент статической ошибки,C1
– коэффициент скоростной ошибки и
т. д.).
Коэффициенты
ошибки могут быть также получены делением
числителя передаточной функции на ее
знаменатель. Полученное выражение для
вынужденной ошибки позволяет оценить
точность системы автоматического
управления в установившемся режиме.
Вынужденная ошибка, например, хорошо
характеризует точность работы следящих
систем автоматического управления.
Соседние файлы в папке ТАУ
- #
- #
- #
Статическая ошибка — регулирование
Cтраница 2
И-регулятор не имеет статической ошибки регулирования, поскольку выход регулятора будет расти при любом малом значении рассогласования. Таким образом, в отличие от системы с П — регулятором системы с И-регулятором не имеют статической ошибки, но динамическая ошибка в этих системах большая. Это объясняется тем, что в начальный момент И-регулятор еще не успевает из-за своих инерционных свойств выработать значительный выходной сигнал.
[16]
И-регулятор не имеет статической ошибки регулирования, поскольку выход регулятора будет расти при любом малом значении рассогласования. Таким образом, в отличие от системы с П — регулято-ром системы с И-регулятором не имеют статической ошибки, но динамическая ошибка в этих системах большая. Это объясняется тем, что в начальный момент И-регулятор еще не успевает из-за своих инерционных свойств выработать значительный выходной сигнал.
[18]
И-регулятор не имеет статической ошибки регулирования, поскольку выход регулятора будет расти при любом малом значении рассогласования. Таким образом, в отличие от системы с П — регулятором системы с И-регулятором не имеют статической ошибки, но динамическая ошибка в этих системах большая.
[20]
Этот коэффициент равен отношению статической ошибки регулирования к установившемуся отклонению того же параметра в случае отсутствия регулятора.
[21]
Изменение скорости б называется статической ошибкой регулирования скорости.
[22]
Почему в статической АСР возникает статическая ошибка регулирования.
[23]
Для пропорционального закона регулирования характерна статическая ошибка регулирования Д, связанная с принципом регулирования — изменением положения регулирующего органа только при отклонении регулируемого параметра от заданной величины.
[25]
ВЫХо и, следовательно, статическая ошибка регулирования бст равна нулю.
[27]
Из этого выражения следует, что статическая ошибка регулирования увеличивается при росте отклонения регулируемой величины при работе без регулятора и уменьшается с ростом коэффициента усилителя разомкнутой системы.
[29]
САР на регулируемом объекте допускается наличие статической ошибки регулирования.
[30]
Страницы:
1
2
3
4
5
Глава 8. Типовые законы регулирования. Одноконтурные САР
8.1. Основные типы автоматических регуляторов
Регулятор на основе усилительного звена называется П-регулятором (пропорциональный). Его положительной характеристикой является высокое быстродействие: при отклонении регулируемой величины от заданного значения регулятор выдает регулирующее воздействие, пропорциональное величине отклонения x, что обеспечивает быструю компенсацию возмущения. Существенным недостатком П-регулятора является наличие статической ошибки в переходном процессе АСР с П-регулятором (рис. 37). Статическая ошибка возникает потому, что у П-регулятора между регулируемой величиной x и регулирующим воздействием xр существует зависимость, однозначно определяемая коэффициентом K. Поэтому генерировать регулирующее воздействие xр для компенсации возмущения xв П-регулятор может только путем изменения регулируемой величины x, что и создает статическую ошибку.
Регулятор на основе интегрирующего звена (48) называется И‑регулятором:
Если xвых усилительного звена (П-регулятор) однозначно определяется величиной правой части уравнения, что является причиной возникновения статической погрешности в АСР с П-регулятором, то правая часть уравнения (48) интегрирующего звена (И-регулятор) определяет не величину, а скорость изменения xвых. Величина xвых будет изменяться до тех пор, пока правая часть уравнения (48) не станет равна нулю, т. е. пока регулируемая величина x при наличии возмущения xв не вернется к заданному значению. Следовательно, в АСР с И-регулятором не возникает статическая погрешность.
Однако у И-регулятора имеется свой недостаток сравнительно с П-регулятором: в случае возникновения возмущения регулирующее воздействие П-регулятора меняется быстрее, чем у И-регулятора с его конечной скоростью, что замедляет процесс компенсации возмущения и ухудшает критерии качества регулирования (рис. 40).
Рис. 40. Переходные процессы в АСР с П- и И-регуляторами
Таким образом, П-регулятор обеспечивает высокое быстродействие (что уменьшает динамическую ошибку), но не может обеспечить при наличии возмущения заданное значение регулируемой величины (статическая ошибка). И-регулятор, наоборот, не создает статическую ошибку, но вследствие относительно медленного изменения xр имеет большую динамическую ошибку.
Сравнивая характеристики П- и И-регуляторов можно сделать вывод: если включить усилительное и интегрирующие звенья параллельно, то автоматический регулятор будет лишен указанных недостатков. Такой регулятор называется ПИ-регулятором (рис. 41).
Рис. 41. Принципиальная схема АСР с ПИ-регулятором
Действительно, быстродействие ПИ-регулятора обеспечивает усилительное звено, а статическую ошибку снимает интегрирующее звено. Для управления производственными процессами чаще всего используются ПИ-регуляторы.
Кривая разгона идеального ПИ-регулятора показана на рис. 42 .
Уравнение ПИ-регулятора при нулевых начальных условиях имеет вид:

Отношение коэффициентов Kp1/Kp определяет степень влияния интегрирующей части, и его обратная величина называется временем изодрома Tи.

Время изодрома – это время, в течение которого интегрирующее звено изменяет регулирующее воздействие xр ПИ-регулятора на величину Dxр, равную предварительному изменению Dxр усилительного звена (рис. 42). Поэтому иногда время изодрома называют временем удвоения.
Рис. 42. График кривой разгона идеального ПИ-регулятора:
а – скачкообразное изменение входного воздействия x;
б – реакция (кривая разгона) ПИ-регулятора xр
Уравнение ПИ-регулятора можно записать как
откуда передаточная функция
Амплитудно-фазовая характеристика:

В том случае, если рассмотренные регуляторы не обеспечивают требуемое качество регулирования, необходимо увеличить интенсивность процесса компенсации возмущения. Этого можно достигнуть увеличением регулирующего воздействия, которое в свою очередь определяется коэффициентом усиления автоматического регулятора Kp
. Однако ниже будет показано, что увеличение коэффициента усиления регулятора в АСР приводит к тому, что в системе начинают генерироваться незатухающие колебания.
В связи с этим представляет интерес рассмотреть алгоритм, который реализует дифференцирующее звено.
Входной величиной любого регулятора является кривая разгона регулируемой величины (рис. 27), которая определяется величиной возмущения и передаточной функцией объекта регулирования (9). В свою очередь, регулирующее воздействие xp (рис. 27) определяется кривой разгона x и передаточной функцией регулятора.
На рис. 43 показана реакция дифференцирующего звена (Д‑регулятора) на входное воздействие в виде кривой разгона в соответствии с уравнением (51).
Рис. 43. Реакция дифференцирующего звена на кривую разгона
а –изменение входного воздействия x в виде кривой разгона;
б – реакция xр дифференцирующего звена
Из рис. 43,а следует, что дифференцирующее звено обеспечивает большее регулирующее воздействие в начале переходного процесса. Это означает, что дифференцирующий регулятор активно компенсирует возмущение и исключает возникновение незатухающих колебаний.
Если включить дифференцирующее звено параллельно ПИ‑регулятору (рис. 44), то получим ПИД-регулятор, обеспечивающий интенсивную компенсацию возмущений. При этом недостаток дифференцирующего звена (при Хвх = const, Хвых = 0 ) компенсируется усилительным и интегрирующим звеньями.
Рис. 44. Принципиальная схема АСР с ПИД-регулятором
На рис. 45 показана кривая разгона ПИД-регулятора.
Рис. 45. Кривая разгона ПИД-регулятора
На рис. 46 показаны переходные процессы на с различными регуляторами. ПИД-регулятор уменьшает динамическую ошибку сравнительно с ПИ-регулятором на 25–30%. Также можно объединить дифференцирующее звено с усилительным звеном и улучшить показатели П-регулятора, получив ПД-регулятор.

Все пять типов рассмотренных автоматических регуляторов имеют общую особенность своего функционирования – обеспечивают стабилизацию регулируемой величины после окончания переходного процесса.
8.2. Критерии качества регулирования
Качество процесса регулирования в АСР характеризуют следующие показатели (критерии) (рис. 16):
Рис. 16. Показатели качества регулирования:
1 – переходной процесс без статической ошибки;
2 – переходной процесс со статической ошибкой
1. Максимальное отклонение в процессе регулирования от заданного значения (динамическая ошибка) ΔХдин.
2. Статическая ошибка ΔХст — возможные отклонения от заданного значения по окончании переходного процесса при использовании некоторых типов регуляторов (подробнее такие АСР рассмотрены ниже).
3. Длительность переходного процесса Тр – период времени с момента начала отклонения регулируемого параметра от задания до возвращения его к заданному значению с определенной степенью точности регулирования ±Δ.
Например, если ±Δ=±25%, это означает, что для заданного значения температуры в 100 °С процесс регулирования будет завершен при достижении диапазона (100 ± 2,5) °С.
4. Степень затухания показывает характер затухания переходного процесса регулирования:
Для того, чтобы переходный процесс затухал за 2 ¸ 3 периода колебаний, степень затухания должна быть равна

5. Степень колебательности процесса m определяет характер колебательности процесса и равна отношению действительной части корня характеристического уравнения к коэффициенту при его мнимой части. Степень колебательности связана со степенью затухания следующим соотношением:
6. Интегральный квадратичный критерий – критерий, определяющий площадь под кривой переходного процесса, возведенной в квадрат (рис. 17):
Уменьшение интегрального критерия соответствует ускорению процесса регулирования.
Рис. 17. Интегральный квадратичный критерий качества регулирования
Однако все приведенные шесть критериев качества не определяют величину потерь производства при отклонениях регулируемой величины от оптимального значения в переходных процессах регулирования. Для определения таких потерь можно использовать экономический критерий.
7. Экономический критерий рассмотрим на примере, регулирования температуры химического реактора θ, когда степень превращения Q в реакторе определяется температурой (рис. 18а).
Разделим переходной процесс на равные интервалы времени Δt и запишем значения θ
в этих точках по графику (18, б). На графике (18, а) для этих температур определим уменьшение степени превращения вследствие отклонения от оптимального режима, а затем сделаем расчет потерь исходных продуктов для каждого интервала Δθ, суммируем эти потери для всего переходного процесса и представим потери в денежном выражении.
Рис. 18. Экономический критерий качества регулирования:
а – зависимость степени превращения Q от температуры θ;
б – переходный процесс регулирования температуры
Совместно со специалистом по технологии или по его заданию необходимо определить, какой из указанных критериев для рассматриваемой АСР является превалирующим, и задать максимально допустимую величину этого критерия, т. е. определить, какое качество регулирования должна обеспечить проектируемая АСР.
8.3. Выбор закона регулирования
При выборе регулятора следует определиться с группой регулирующих устройств – непрерывного, релейного или импульсного действия. Такой выбор ориентировочно может быть сделан по величине отношения запаздывания к постоянной времени объекта τ/Tоб:
· при отношении τ/Tоб меньше 0.2 целесообразно использовать регулятор релейного действия;
· если отношение τ/Tоб от 0.2 до 1.0, то нужно использовать регулятор непрерывного действия;
· при отношении τ/Tоб больше единицы можно использовать регулятор импульсного действия, или специальные регуляторы, например, регулятор («предиктор») Смита.
Затем необходимо определиться с типом регулятора, т.е. выбрать определенный закон регулирования: П-, И-, ПИ-, ПД- или ПИД-закон
8.4. Методы расчета одноконтурных САР
Как указывалось выше, качество автоматического регулирования определяется свойствами системы в целом, т. е. суммарными свойствами объекта и регулятора. Поскольку объект обычно является неизменяемой частью системы, то обеспечить определенные свойства системы, а следовательно и заданное качество регулирования, можно соответствующим подбором свойств автоматического регулятора, что зависит от параметров его настройки. В свою очередь, параметры настройки являются коэффициентами передачи в уравнении автоматического регулятора.
Таким образом, параметры настройки автоматического регулятора определяются свойствами объекта регулирования, т. е. величинами τоб, Тоб, Коб.
8.4.1. Расчет по «приближенным» формулам
Приближенные формулы для расчета параметров настройки автоматических регуляторов (Kр – коэффициент усиления; Tи – время изодрома; Тд – время дифференцирования) сведены в следующую таблицу:
Таблица 8.1. Формулы для приближенного расчета
параметров настройки регуляторов

Формулы сгруппированы в столбцы в зависимости от характера переходного процесса, который желательно получить, используя рассчитанный таким образом регулятор: апериодический или с перерегулированием в 20 %. В формулы входят следующие свойства объекта регулирования: Коб – коэффициент усиления; Тоб – постоянная времени; τоб – время запаздывания (полного).
Рис. 53. Кривые разгона:
1 – фактическая кривая разгона промышленного объекта;
2 – аппроксимированная (приближенная) кривая разгона
Необходимо отметить, что для пневматических регуляторов требуется определять не Kp, а диапазон дросселирования:
Рассмотрим методику более точного определения параметров настройки на примере расчета наиболее «популярного» регулятора – ПИ-регулятора.
8.4.2. Метод незатухающих колебаний
(метод Циглера-Никольса)
При использовании метода незатухающих колебаний [6], который иногда также называется по именам авторов методом Циглера-Никольса, поиск оптимальных параметров настройки осуществляется по величине критического коэффициента усиления П-регулятора и величине периода автоколебательного процесса.
Рис. 54. К поиску параметров настройки методом Циглера-Никольса
Расчет параметров настройки регуляторов проводится в два этапа.
1. На исследуемом объекте устанавливается П-регулятор и, последовательно увеличивая коэффициент усиления (уменьшая диапазон дросселирования), АСР выводится в режим незатухающих колебаний (автоколебаний на границе устойчивости). При этом фиксируется величина коэффициента усиления П-регулятора Ккрр и период незатухающих автоколебаний Т (рис. 54).
2. На втором этапе по величинам Кркр и Т определяются параметры настройки П-, ПИ- и ПИД-регуляторов:
Метод незатухающих колебаний не требует сложных вычислений, но имеет свои характерные недостатки:
· получить Кркр и Т можно только на действующем объекте, оснащенном АСР с П-регулятором;
· не все объекты химической технологии допускают режим автоколебаний;
· практически трудно уловить момент начала автоколебаний.
Данные недостатки имеют место лишь при настройке регулятора методом Циглера-Никольса непосредственно на действующем объекте. Если заменить реальный объект его математической моделью, данный метод лишается указанных недостатков, кроме того, моделирование позволяет на порядок ускорить процесс поиска параметров настройки. Но для выполнения моделирования требуется достаточно точное математическое описание объекта регулирования, а получить его удается не всегда.
8.4.3. Метод расширенных частотных характеристик
Уравнение ПИ-регулятора (65) или (66):
Передаточная функция ПИ-регулятора:

Знак «минус» указывает, что действие регулятора направлено против возмущения.
Из передаточной функции получаем амплитудно-фазовую характеристику ПИ-регулятора путем замены p на iw:

Так как по формуле Эйлера


с затуханием за три периода
Заменив iw на комплексную переменную (-mw+iw), получаем расширенную амплитудно-фазовую характеристику (РАФХ)Ю

Расширенными такие характеристики называются потому, что они как бы «расширены» по отношению к обычной АФХ (рис. 56).
Предположим, что объект регулирования имеет передаточную функцию второго порядка следующего вида:

Для дальнейшего математического моделирования АСР передаточную функцию необходимо преобразовать:

Рис. 56. АФХ объекта регулирования с самовыравниванием:
1 – обычная; 2 – расширенная
Расширенная амплитудно-фазовая характеристика объекта регулирования при замене p на (-mw+iw) будет иметь вид:



Где Rоб(m,w) -расширенная амплитудно-частотная характеристика объекта; Fоб(m,w) -расширенная фазочастотная харктеристика объекта. Величина 40w в выражении для Fоб (m,w) опеделяет угол в радианах и для пересчета в градусы неоходимо 40w умножить на 57,3
Условием нахождения замкнутой АСР на границе устойчивости является уравнение:

Аналогично, исходным уравнением для получения заданной степени колебательности m, а следовательно, определенной степени затухания y, является соотношение:
Это соотношение двух комплексных чисел возможно в том случае, если произведение модулей РАФХ равно единице, а аргументы (фазы) равны между собой, т. е.

Решая эти уравнения относительно S0 и Kp, получаем:


Обычно принимают степень колебательности m = 0,221, что соответствует степени затухания ψ=0,75 и обеспечивает затухание процесса регулирования примерно за три периода. Тогда

Уравнения для определения параметров настройки ПИ-регулятора можно преобразовать:


Подставляя в приведенные уравнения численные значения частоты w от 0 до значения, когда S0 становится отрицательной величиной, строим на плоскости параметров настройки кривую равной степени колебательности


Пример кривых равной степени колебательности в плоскости параметров настройки ПИ-регулятора показан на рис. 57. Графики процессов регулирования с различными параметрами настройки ПИ-регулятора при m = 0,221 показаны на рис. 58. Все процессы регулирования, показанные на рис. 58, реализованы ПИ-регулятором с параметрами настройки, полученными по кривой равной степени колебательности в точках 1, 2, 3, 4 (рис. 57), и все имеют m = 0,221, т. е. затухают примерно за три периода, но обладают существенно различным характером.
В связи с этим возникает задача определения оптимальных параметров настройки на кривой равной степени колебательности.
Рис. 57. Кривые равной степени колебательности
В качестве критерия оптимальности выбираем продолжительность переходного процесса – время регулирования (т. е. быстродействие АСР) и отсутствие постоянной или врéменной статической ошибки. Это исключает из рассмотрения параметры настройки в точке 4 (параметры настройки П-регулятора) и в точке 3 (врéменная статическая ошибка) (рис. 58).
Рис. 58. Графики процессов регулирования для ПИ-регулятора
с различными параметрами настройки в точках 1, 2, 3 и 4
при степени колебательности m =0,221
Быстродействие автоматического регулятора прежде всего зависит от величины регулирующего воздействия, которое для ПИ-регулятора, как следует из уравнения (65), прямо пропорционально величине коэффициента усиления Kp и обратно пропорционально времени изодрома Tи. Расчеты показывают, что если двигаться по кривой равной степени колебательности вправо, то величина регулирующего воздействия при прочих равных условиях сначала возрастает и достигает максимального значения на кривой равной степени колебательности вблизи ее вершины, когда
а затем начинает уменьшаться в связи с резким увеличением Tи (рис. 57).
Рис. 59. Выбор оптимальных параметров настройки
Таким образом, оптимальные параметры настройки ПИ-регулятора находятся в точке 2 на кривой равной степени колебательности (рис. 59).
Источник
Плютто В. П., Дубровский И. И. Элементы теории управления химико-технологическими процессами и системами. Конспект лекций: Учеб. пособие – М.: РХТУ им. Д. И. Менделеева, 2003. – 127 с.
Лекция 17. Расчет установившейся ошибки в системах управления.
Структурные признаки астатизма
Установившейся (статической) ошибкой называют
постоянное значение сигнала ошибки x(t)=g(t)-y(t),
которое она приобретает по окончании переходного процесса: , рисунок 116.
Очевидно, установившаяся ошибка зависит от законов
изменения и численных характеристик входных сигналов системы. Поэтому при ее
определении принято рассматривать так называемые типовые входные сигналы,
законы изменения которых составляют степенной ряд относительно времени.
Например, для задающего воздействия:
,
,

далее.
При наличии нескольких воздействий на линейную систему
для определения xуст используется
принцип суперпозиции – реакция линейной системы на совокупность входных
сигналов совпадает с алгебраической суммой ее реакций на каждый из сигналов в
отдельности:
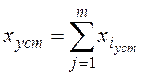
каждое слагаемое, или составляющая сигнала ошибки, определяется
для i-го входного сигнала при условии, что остальные
тождественно равны нулю. Такой подход полностью соответствует определению
передаточной функции и позволяет выполнять расчет установившейся ошибки на
основе структурной схемы системы.
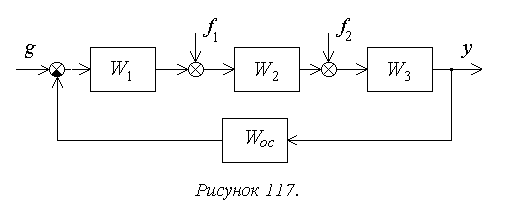
Рассмотрим порядок расчета установившейся ошибки на
следующем достаточно общем примере (рисунок 117).
В соответствии с принципом суперпозиции установившаяся
ошибка будет определяться здесь в виде суммы трех составляющих .
Изображение по Лапласу ошибки от задающего воздействия
получают через передаточную функцию замкнутой системы по ошибке при известном изображении задающего
воздействия G(s):
, где
F(s) – основная передаточная функция замкнутой системы.
Для структурной схемы на рисунке 117
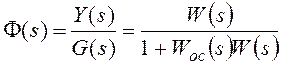
— передаточная функция
разомкнутой системы, или прямой цепи системы, для рассматриваемого примера.
Непосредственно для расчета
установившегося значения ошибки от задающего воздействия используют теорему о
конечном значении для преобразования Лапласа:
В результате:
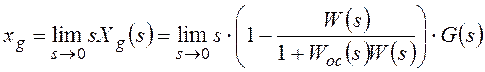
Изображение по Лапласу ошибки от возмущающего
воздействия получают через передаточную функцию замкнутой системы по ошибке от
возмущения при известном изображении возмущающего
воздействия F(s):
, где
Ff(s) –передаточная функция замкнутой системы по
возмущающему воздействию,
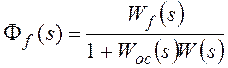
Wf(s)
– передаточная функция разомкнутой системы по возмущению (передаточная функция
участка прямой цепи системы от точки приложения возмущающего воздействия до
выхода системы).
Для структурной схемы на рисунке 8 необходимо
учитывать два возмущающих воздействия, приложенные в различные точки системы.
Для f1:
,
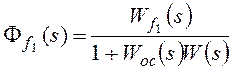
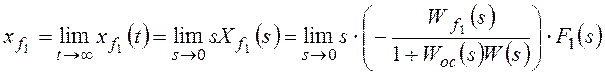
Для f2:
,
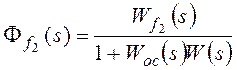
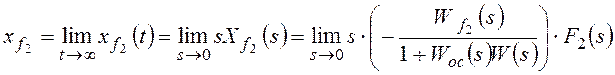
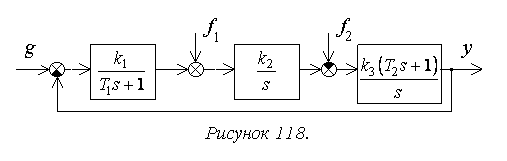
Расчет упрощается для
системы с единичной отрицательной обратной связью (рисунок 118):
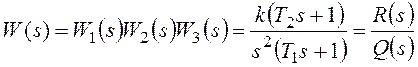
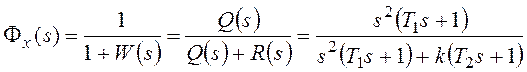
разомкнутой системы.
Найдем установившуюся ошибку
для некоторых типовых вариантов задающего воздействия.
При получим:
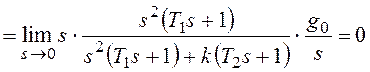
При получим:
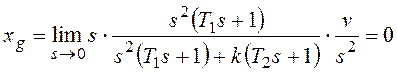
При 
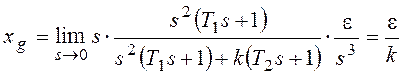
Если установившаяся ошибка
тождественно равна нулю при каком-либо типовом варианте входного сигнала,
независимо от его численных характеристик, систему называют астатической по
рассматриваемому входному сигналу.
Количество типовых вариантов
входного сигнала – членов степенного ряда, при которых установившаяся ошибка
тождественно равна нулю, определяет порядок астатизма.
Рассматриваемая система
обладает свойством астатизма второго порядка по задающему воздействию.
Рассмотрим установившуюся
ошибку от возмущения f1:
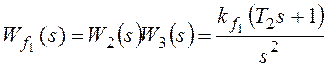
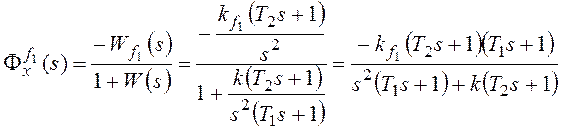
–
коэффициент передачи разомкнутой системы по возмущению f1.
При получим:
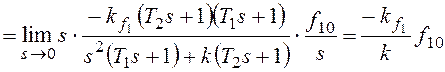
При получим:
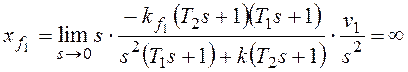
При 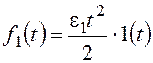
тот же результат.
Отметим, что по возмущению f1 рассматриваемая система
не является астатической. Кроме того, она не в состоянии отработать два последних
варианта входного сигнала.
Рассмотрим установившуюся
ошибку от возмущения f2:
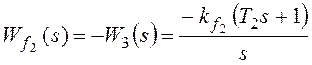
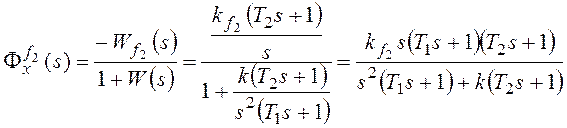
–
коэффициент передачи разомкнутой системы по возмущению f2.
При получим:
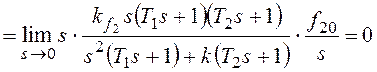
При получим:
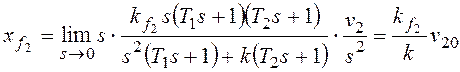
При 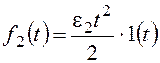
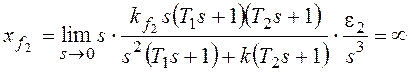
По возмущению f2 рассматриваемая система имеет
астатизм первого порядка. Она не в состоянии отработать возмущающее
воздействие, изменяющееся во времени с постоянным ускорением.
Подведем некоторые итоги:
1. Наличие и глубина
свойства астатизма зависят от точки приложения входного сигнала.
2. Постоянные времени
звеньев системы не влияют на ее точность.
3. Увеличение значения
коэффициента передачи разомкнутой системы приводит к снижению величины
установившейся ошибки.
Для систем с единичной
отрицательной обратной связью существуют достаточно простые структурные
признаки астатизма.
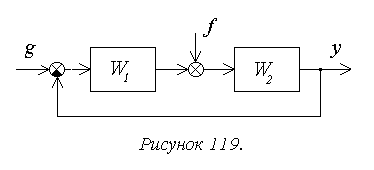
Рассмотрим структуру,
показанную на рисунке 119.
В общем случае передаточная
функция разомкнутой системы может быть представлена в следующей форме:
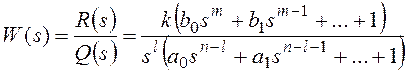
Тогда получим:
и для общего вида задающего воздействия 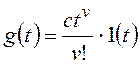
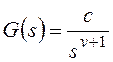
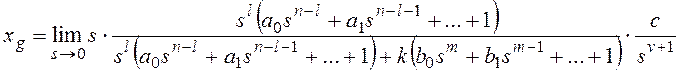
Результат нахождения этого
предела зависит от соотношения показателей степени:
— при l>v установившаяся
ошибка равна нулю независимо от остальных параметров, то есть имеет место
астатизм;
— при l=v получаем
константу;
— при l<v установившаяся
ошибка стремится к бесконечности, то есть система не в состоянии отработать
входной сигнал.
Учитывая, что минимальное
значение v нулевое,
получаем условие астатизма по задающему воздействию: l>0.
Таким образом, структурный
признак астатизма по задающему воздействию в системе с единичной отрицательной
обратной связью состоит в наличии нулевых корней в знаменателе передаточной
функции разомкнутой системы, или интегрирующих звеньев в прямой цепи системы.
Нетрудно также убедиться,
что положительное значение l совпадает
с порядком астатизма.
Для получения признака
астатизма по возмущающему воздействию представим передаточные функции на
рисунке 10 в форме:
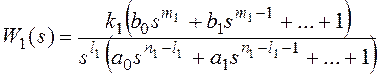
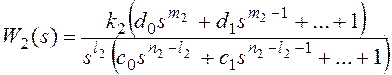
k1k2=k, m1+m2=m,
n1+n2=n,
причем и
.
Тогда получим:
и для общего вида возмущающего воздействия 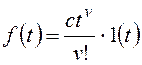
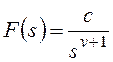
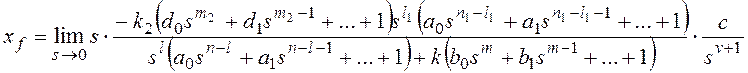
Все вышеприведенные выводы
можно повторить для показателя степени l1.
Таким образом, структурный
признак астатизма по возмущающему воздействию в системе с единичной
отрицательной обратной связью состоит в наличии нулевых корней в знаменателе
передаточной функции участка системы до точки приложения воздействия, или
интегрирующих звеньев на том же участке.
Точность систем управления является
важнейшим показателем их качества. Чем выше точность, тем выше качество
системы. Однако предъявление повышенных требований к точности вызывает
неоправданное удорожание системы, усложняет ее конструкцию. Недостаточная
точность может привести к несоответствию характеристик системы условиям
функционирования и необходимости ее повторной разработки. Поэтому на этапе
проектирования системы должно быть проведено тщательное обоснование требуемых
показателей точности.
В этом разделе рассматриваются методы
определения ошибок, возникающих при работе систем управления с детерминированными
входными воздействиями. Вначале анализируются ошибки систем в переходном
режиме. Затем особое внимание уделено простым способам расчета ошибок систем в
установившемся режиме. Будет показано, что все системы управления можно разделить
по величине установившихся ошибок на системы без памяти, так называемые статические
системы, и системы, обладающие памятью, – астатические
системы управления.
Типовые
входные воздействия
Для оценки качества работы систем
управления рассматривают их поведение при некоторых типовых воздействиях.
Обычно такими воздействиями служат следующие три основные вида функций:
а) ступенчатое воздействие: g(t) = , g(p) = ;
б) линейное воздействие: g(t) = t , t > 0
; ;
в) квадратичное воздействие:
/2 , t > 0 ;
g(p) = .
В
некоторых случаях рассматривают обобщенное полиномиальное воздействие:
Ступенчатое воздействие является одним
из простейших, но именно с его помощью определяется ряд важных свойств систем
управления, связанных с видом переходного процесса. Линейное и квадратичное
воздействия часто бывают связаны с задачами слежения за координатами
движущегося объекта. Тогда линейное воздействие соответствует движению объекта
с постоянной скоростью; квадратичное — движению объекта с постоянным ускорением.
Переходные процессы при типовых
воздействиях можно построить следующим образом. Пусть задана передаточная
функция замкнутой системы управления W(p). Тогда
x(p)
= W(p) g(p),
где g(p) – изображение соответствующего воздействия.
Например, если , то и для g(t) = g0
получим .
С помощью вычетов или по таблицам
находим обратное преобразование Лапласа и получаем вид переходного процесса x(t)
для заданного входного воздействия:
где Res
x(p)
– вычет функции x(p)
в точке a.
Обычно реакция системы на ступенчатое
воздействие имеет вид, показанный на рис. 21,а или рис. 21,б.
Переходный процесс,
как правило, характеризуют двумя параметрами – длительностью переходного
процесса (временем установления) и величиной перерегулирования.
Под временем установления tу
понимают временной интервал, по истечении которого отклонение |x(t) — xуст
| выходного процесса от установившегося значения xуст не
превышает определенную величину, например, 0,1gо. Время
установления является важным параметром САУ, позволяющим оценить ее быстродействие.
Величину tу можно оценить приближенно по амплитудно-частотной
характеристике системы. При заданной частоте среза . Для оценки качества системы
используется также величина перерегулирования, определяемая соотношением .
В зависимости от
характера собственных колебаний системы переходный процесс в ней может быть
колебательным, как это показано на рис. 21, б, или плавным гладким, называемым
апериодическим (рис. 21,а). Если корни характеристического уравнения системы
действительны, то переходный процесс в ней апериодический. В случае
комплексных корней характеристического уравнения собственные колебания
устойчивой системы управления являются затухающими гармоническими и переходный
процесс в системе имеет колебательный характер.
При малом запасе устойчивости САУ ее
собственные колебания затухают медленно, и перерегулирование в переходном режиме
получается значительным. Как следствие, величина перерегулирования может
служить мерой запаса устойчивости системы. Для многих систем запас
устойчивости считается достаточным, если величина перерегулирования .
Установившийся
режим
При проектировании систем управления
часто требуется оценить ошибку слежения в установившемся режиме . В зависимости от
вида воздействия и свойств системы эта ошибка может быть нулевой, постоянной
или бесконечно большой величиной.
Очень важно, что величина
установившейся ошибки может быть легко найдена с помощью теоремы о предельном
значении оригинала: .
При использовании этой теоремы нужно
выразить величину ошибки e (p) через g(p). Для этого рассмотрим
структурную схему замкнутой системы управления (рис. 22).
Очевидно, e (p) = g(p) — x(p)
= g(p) — H(p)e(p). Отсюда или e (p) = He(p)g(p)
, где He(p) = называется передаточной функцией
системы управления от входного воздействия g(p) к ошибке слежения e(p).
Таким образом, величину установившейся ошибки можно найти с помощью следующего
соотношения:
,
где He(p) = 1/(1+H(p));
g(p) — изображение типового входного воздействия.
Пример 1.
Рассмотрим
систему управления, в составе которой нет интеграторов, например,
.
Найдем величину установившейся
ошибки при ступенчатом входном воздействии g(t) = g0, t ³ 0.
В этом случае

Предположим теперь, что входное
воздействие изменяется линейно t или .
Тогда . Соответствующие входные воздействия и
переходные процессы можно представить графиками на рис. 23,а и б.
Пример 2.
Рассмотрим
теперь систему, содержащую один интегратор. Типичным примером может быть
система сервопривода (рис. 6) с .
Для ступенчатого воздействия g(t) = g0
или g(p) = получим

При линейном входном воздействии

Такие процессы можно проиллюстрировать
соответствующими кривыми на рис.24, а и б.
Пример 3.
Рассмотрим систему с двумя интеграторами. Пусть, например, . При ступенчатом
воздействии 
При линейном 
Наконец, если входное воздействие
квадратичное g(t) = at2/2 (g(p) = a/p3),
то

Таким образом, в системе с двумя
интеграторами может осуществляться слежение за квадратичным входным
воздействием при конечной величине установившейся ошибки. Например, можно
следить за координатами объекта, движущегося с постоянным ускорением.
Статические
и астатические системы управления
Анализ рассмотренных примеров
показывает, что системы управления, содержащие интегрирующие звенья, выгодно
отличаются от систем без интеграторов. По этому признаку все системы делятся на
статические
системы, не содержащие интегрирующих звеньев, и астатические
системы, которые содержат интеграторы. Системы с одним интегратором называются
системами с астатизмом первого порядка
. Системы с двумя интеграторами –
системами с астатизмом второго порядка
и т.д.
Для статических систем даже при
неизменяющемся воздействии g(t) = g0 установившаяся ошибка имеет
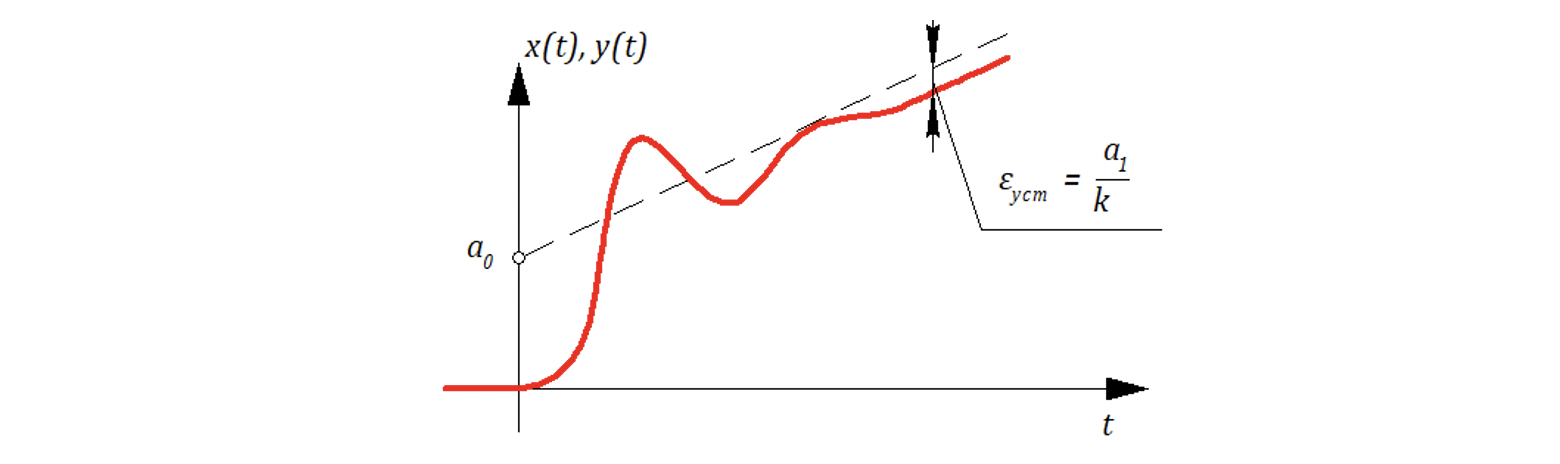
конечную величину g(t) = g0 . В системах с астатизмом первого
порядка при ступенчатом воздействии установившаяся ошибка равна нулю, но при линейно
изменяющемся воздействии . Наконец, в системах с астатизмом
второго порядка ненулевая установившаяся ошибка появляется только при
квадратичных входных воздействиях g(t) = at2 /2 и
составляет величину eуст =
a/k.
Какие же физические причины лежат в
основе таких свойств астатических систем управления?
Рассмотрим систему управления с
астатизмом второго порядка (рис. 25)
Пусть входной сигнал системы управления
изменяется линейно: t. Как было
установлено, в такой системе установившаяся ошибка равна нулю, т.е. e
(t) =0. Каким же образом система работает при нулевом сигнале ошибки? Если x(t)
= t , то на
входе второго интегратора должен быть сигнал . Действительно, при нулевом
рассогласовании e (t) =0 в системе с интеграторами
возможно существование ненулевого выходного сигнала первого интегратора . Первый интегратор
после окончания переходного процесса «запоминает» скорость изменения входного
воздействия и в дальнейшем работа системы управления осуществляется по
«памяти». Таким образом, физическим объяснением такого значительного различия
статических и астатических систем является наличие памяти у астатических систем
управления.
Итак, существуют простые возможности
определения важнейшего показателя систем управления – величины их динамических
ошибок. Детальный анализ переходных процессов в системах управления обычно
выполняют с помощью моделирования на ПЭВМ. Вместе с тем величины
установившихся ошибок легко находятся аналитически. При этом астатические
системы управления, т.е. системы с интеграторами, имеют существенно лучшие
показатели качества по сравнению со статическими системами.
Оценивают по величинам статической и динамической ошибок. По этим характеристикам автоматические системы бывают статические и астатические.
Статическая ошибка
— это разность величин регулируемого параметра в исходном и конечном (после окончания регулирования) состояниях равновесия системы.
Рисунок 6.17 — График регулирования астатической (а) и статической (б) САУ.
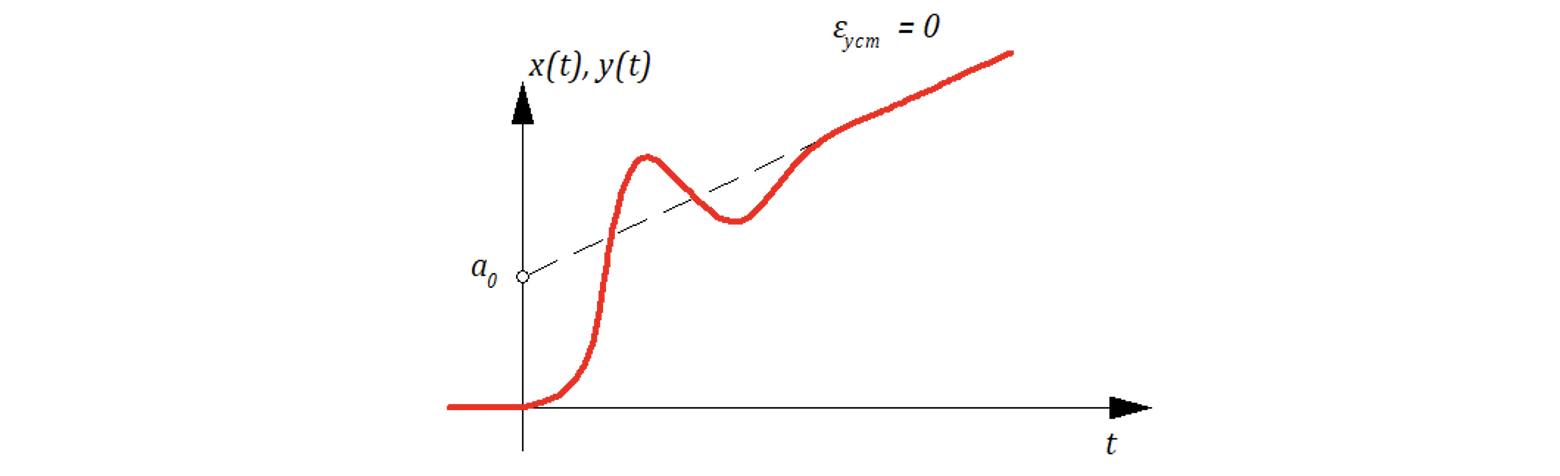
В астатической
системе статическая ошибка равна нулю, т.е. система после процесса регулирования возвращается в исходное состояние равновесия. В астатических САУ конечное и исходное равновесие совпадает с заданием. Поэтому в этих САУ динамическая ошибка равна максимальному отклонению параметра в процессе регулирования (рис. 6.17а).
В статической
системе в установившемся состоянии — через достаточно долгое время после начала регулирования τ, всегда имеется статическая ошибка регулирования (рис.6.17б).
Динамическая ошибка
— это максимальное в процессе регулирования отклонение регулируемого параметра от конечного состояния равновесия
Δ дин = (Y вых ма x — Y вых ном).
Время регулирования
— это отрезок времени Δτ
с момента нанесения на замкнутую САУ возмущающего воздействия, по истечении которого отличие регулируемого параметра от конечного состояния равновесия становится равным и меньше ± 5% от заданной величины. Если заданная величина равна нулю, то ± 5% берут от величины динамической ошибки.
Перерегулирование
— это динамическая ошибка, отнесённая к номинальной величине регулируемого параметра в процентах.
Перерегулирование вычисляют по формуле:
σ = (Y вых ма x — Y вых ном)100%/Y вых ном.
Степень затухания
— это показатель качества, который характеризует, насколько процентов уменьшается амплитуда колебаний выходного сигнала системы за один период колебаний. Степень затухания Ψ
определяется по формуле:
ψ = (Δ дин — Δ 3) 100% / Δ дин
,
где: Δ з — амплитуда колебаний третьего периода. Если Δ з = 0, то Ψ
= 100%.
Обобщённый показатель качества
. Для определения величины этого показателя вычисляют интеграл (площадь подынтегральной фигуры) изменения в процессе регулирования выходного сигнала системы за период времени регулирования:
t рег
J = ∫ (Δ) 2 dt.
Δ — амплитуду колебаний берут в квадрате, чтобы просуммировать как положительные, так и отрицательные отклонения выходного сигнала. Естественно, чем меньше динамическая, статическая ошибки и время регулирования, тем меньше величина интеграла J и выше качество работы САУ.
Оптимальные процессы регулирования.
На практике часто требования к качеству работы проектируемой САУ задаются не в виде величины отдельных показателей качества, а в виде требования реализации одного из трёх оптимальных процессов регулирования.
Первый из них — апериодический
процесс регулирования показан на рис. 6.18а.
Регулируемый параметр после отклонения плавно возвращается к заданной величине. В этом процессе по сравнению с двумя последующими будет минимально время регулирования, но максимальна динамическая ошибка.
Второй — процесс регулирования с 20% перерегулированием условно дан на рис. 6.18б. В этом процессе по сравнению с апериодическим меньше динамическая ошибка, но больше время регулирования. Для этого процесса перерегулирование не должно превышать 20%.
Третий- процесс регулирования с минимальным интегральным показателем качества (рис. 6.18в). В этом процессе регулирования интегральный показатель качества сведён к минимуму, а из трёх рассмотренных оптимальных процессов регулирования будет минимальная динамическая ошибка, но время регулирования — максимальное.
Выбор оптимального процесса из трёх определяется видом технологического процесса объекта управления. Иногда кратковременная большая динамическая ошибка может быть очень опасна. Например, при управлении давлением пара в котле. Для такого объекта апериодический процесс не самый лучший. В некоторых случаях большое время перерегулирования может быть опасным для проведения операции — например, при выпечке хлеба, значительное повышение температуры в печи не может быть длительным.
Автоматические системы регулирования принято подразделять на статические и астатические в зависимости от того имеют ли они или не имеют отклонение или ошибку в установившемся состоянии при воздействиях, удовлетворяющих определенным условиям. Система регулирования называется статической по отношению к возмущающему воздействию, если при воздействии, стремящемся с течением времени к некоторому установившемуся постоянному значению, отклонение регулируемой величины так же стремится к постоянному значению, зависящему от величины воздействия. Система регулирования называется астатической по отношению к возмущающему воздействию, если при воздействии, стремящемся с течением времени к некоторому установившемуся постоянному значению, отклонение регулируемой величины стремится к нулю вне зависимости от величины воздействия.
Рис. 1.9 Переходные процессы в статических (1) и астатических (2) АСР.
В статической системе регулирования статическая характеристика всегда изображается наклонной линией (Рис.1.10,а).
Рис. 1.10 Статические характеристики статической и астатической АСР.
Система регулирования называется статической по отношению к управляющему воздействию, если при воздействии, стремящемуся с течением времени к некоторому установившемуся постоянному значению, ошибка так же стремится к постоянному значению, зависящему от величины воздействия. Система регулирования называется астатической по отношению к управляющему воздействию, если при воздействии, стремящемуся с течением времени к некоторому установившемуся постоянному значению, ошибка стремится к нулю вне зависимости от величины воздействия. Для астатических систем регулирования статическая характеристика всегда изображается прямой, параллельной оси абсцисс (Рис. 1.10,б). Следует подчеркнуть, что одна и та же система регулирования может быть астатической по отношению, например, какому-либо возмущающему воздействию и статической по отношению к управляющему воздействию и наоборот. Таковой, в частности, является автоматическая система регулирования давления свежего пара при выходе из котла.
Определение:
. САУ называется статической
, если при воздействии, стремящемся с течением времени к некоторому установившемуся значению, ошибка также стремится к постоянному значению, зависящему от величины воздействия. САУ называется астатической
, если при воздействии, стремящемся с течением времени к некоторому установившемуся значению, ошибка стремится к нулю независимо от величины воздействия.
2.2. СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ СИСТЕМ УПРАВЛЕНИЯ .
Математические модели систем управления включают два вида описания состояния: статическое и динамическое.
Виды статических характеристик.
Режим работы систем, в котором управляемая и все промежуточные величины не изменяются во времени, называется статическим (установившимся) и описывается уравнениями зависимости выходного состояния объекта управления от постоянных (независимых от времени) значений управляющих воздействий u и любых других дестабилизирующих факторов f. Уравнения этой зависимости вида y = F(u,f) называются уравнениями статики систем. Соответствующие им графики называются статическими характеристиками.
Рис. 2.2.1. Статическая характеристика САУ.
Статическая характеристика звена с одним входом u может быть представлена кривой y = F(u). Если звено имеет второй вход по возмущению f, то статическая характеристика задается семейством кривых y = F(u) при различных значениях f, или y = F(f) при различных u (рис. 2.2.1).
Примером функционального звена системы регулирования уровня воды в баке может быть обычный рычаг с поплавком. Уравнение статики для него имеет вид y = K u. Функцией звена является усиление (или ослабление) входного сигнала в K раз. Коэффициент K = y/u, равный отношению выходной величины к входной, называется коэффициентом усиления звена
. Если входная и выходная величины имеют разную природу, его называют коэффициентом передачи
. Звенья с линейными статическими характеристиками называются линейными
. Статические характеристики реальных звеньев систем, как правило, нелинейные. Для них характерна зависимость коэффициента передачи от величины входного сигнала: K=Dy/Du ≠ const, которая может быть выражена какой-либо математической зависимостью, задаваться таблично или графически. Если все звенья системы линейные, то система имеет линейную статическую характеристику. Если хотя бы одно звено нелинейное, то система нелинейная
.
Рис. 2.2.2.
Статическое и астатическое регулирование.
Если на управляемый процесс действует возмущение (дестабилизирующий фактор) f, то значение имеет статическая характеристика системы в форме y = F(f) при y 0 = const. Возможны два характерных вида этих характеристик (рис. 2.2.2). В соответствии с тем, какая из двух характеристик свойственна данной системе, различают статическое и астатическое регулирование
.
Рассмотрим систему регулирования уровня воды в баке. Возмущающим фактором системы является поток Q воды из бака. Пусть при Q = 0 имеем y = y 0 , сигнал рассогласования по заданному уровню воды e = 0. Звено управления Р системы (регулятор) настраивается так, чтобы вода при этом в бак не поступала. При Q ≠ 0, уровень воды понижается (e ≠ 0), поплавок опускается и открывает заслонку, в бак начинает поступать вода. Новое состояние равновесия достигается при равенстве входящего и выходящего потоков воды. Следовательно, при Q ≠ 0 заслонка должна быть обязательно открыта, что возможно только при каком-то новом уровне воды y 1 , при котором e = К (y 0 -y 1) ≠ 0. Причем, чем больше Q, тем при больших значениях e устанавливается новое равновесное состояние. Статическая характеристика системы имеет характерный наклон (рис. 2.2.2б).
Статические регуляторы
работают при обязательном отклонении e регулируемой величины y от требуемого значения у 0 . Это отклонение тем больше, чем больше возмущение f, и называется статической ошибкой регулятора
. Чем больше коэффициент передачи К регулятора, тем на большую величину будет открываться заслонка при одних и тех же значениях e, обеспечивая большую величину потока Q, при этом статическая характеристика системы пойдет более полого. Поэтому для уменьшения статической ошибки надо увеличивать коэффициент передачи регулятора. Этот параметр регулирования получил название статизма
d и равен тангенсу угла a наклона статической характеристики, построенной в относительных единицах:
d = tg(a) = (Dy/y н) / (Df/f н),
где y н, f н — точка номинального режима системы. При достаточно больших значениях К имеем d » 1/K.
Астатический регулятор
применяется, если статическая ошибка регулирования недопустима и регулируемая величина должна поддерживать постоянное требуемое значение независимо от величины возмущающего фактора. Статическая характеристика астатической системы не имеет наклона. Для того чтобы получить астатическое регулирование, необходимо в регулятор включить астатическое звено. Астатическое звено отличается тем, что каждому значению входной величины может соответствовать множество значений выходной величины. Так, для регулирования уровня воды в астатическом режиме может быть применен импульсный двигатель. Если уровень воды понизится, то появившееся значение e > 0 включит импульсный двигатель и он начнет открывать заслонку до тех пор, пока значение e не станет равным нулю (по определенному порогу). При поднятии уровня воды значение e сменит знак, и запустит двигатель в противоположную сторону, опуская заслонку.
Астатические регуляторы не имеют статической ошибки, но они инерционны, сложны конструктивно и более дороги.
Обеспечение требуемой статической точности регулирования является первой основной задачей при расчете элементов системы управления.
Статическая система
— это такая система автоматического регулирования, в которой ошибка регулирования стремится к постоянному значению при входном воздействии, стремящемся к некоторому постоянному значению. Иными словами статическая система не может обеспечить постоянства управляемого параметра при переменной нагрузке.
Зависимость между значением управляемого параметра и величиной внешнего воздействия (нагрузкой) на объект управления. По виду зависимости между значением управляемого параметра и нагрузкой системы делят на статические и динамические. Зависимость динамической ошибки (q) от времени (t) для систем в установившемся режиме имеет вид q(t) = x(t) — y(t), где x(t) — сигнал управления, y(t) — выходная характеристика.
При установившихся значениях сигнала управления и выходной характеристики ошибка системы q(уст) = x(уст) — y(уст). В зависимости от значения q(уст) и определяют тип системы.
Точность
регулирования
Точность в установившемся
режиме
Качество работы любой системы
регулирования в конечном счете
определяется величиной ошибки, равной
разности
между требуемым (заданным)
и действительным (фактическим)
значениями регулируемой величины. В
следящих системах, в частности,
совпадает с командой
.
Величина мгновенного значения ошибки
в течение всего времени работы системы
позволяет наиболее полно судить о
свойствах системы регулирования. Ошибки
регулирования можно разделить на
статические и динамические, т.е.
соответствующие установившемуся
(статическому) и переходному (динамическому)
режимам. В данном разделе речь пойдет
об ошибке установившегося режима.
Теорема о конечном значении
оригинала
Для определения величины ошибки
в установившемся режиме можно
воспользоваться теоремой о конечном
значении оригинала:
Согласно этой теореме установившемуся
режиму ()
по Лапласу соответствует
,
а по Фурье — круговая частота
.
П
2.8.1.
Оценим величину ошибок
от управляющего и возмущающих воздействий,
приложенных в различных точках схемы
рис.2.8.1. На схеме
— передаточная функция регулятора;
— передаточная функция объекта;
—
возмущение, приложенное к объекту;
—
возмущение, приложенное к регулятору.
Любому чувствительному элементу
присущи свои ошибки. Ошибку чувствительного
элемента можно рассматривать как
некоторое возмущающее воздействие,
которое отнесем к
.
Воспользовавшись принципом суперпозиции
(наложения), изображение реакции найдем
как сумму реакций на все входные сигналы.
В результате для изображения ошибки
получим
Здесь
— изображение ошибки от команды;
Изображение ошибки от помехи
на входе регулятора;
Изображение ошибки от помехи
на входе объекта.
Передаточные функции для ошибок
равны

;
Таким образом, общая ошибка
является суммой составляющих ошибки
от команды и помех. При этом в случае
статического регулятора и объекта с
коэффициентами усиления
,
и постоянных входных воздействиях
,
и
по теореме о конечном значении оригинала
(2.8.1) получим
– статическая ошибка от входного
сигнала;
— статическая ошибка от погрешности
чувствительного элемента (или возмущения
на входе регулятора);
— статическая ошибка от возмущающего
воздействия на входе объекта регулирования
(выходе регулятора).
Чтобы ошибка от команды была
маленькой, надо взять
.
В этом случае
;

То есть помеха на входе системы переходит
в ошибку (с противоположным знаком),
помеха на входе объекта уменьшается в
раз. Очевидно, что
нельзя уменьшить за счет выбора
коэффициента усиления (методами теории
автоматического регулирования). Для
уменьшения ошибки надо уменьшить
величину возмущающего воздействия.
Ошибку
можно уменьшить за счет увеличения
коэффициента усиления регулятора, т.е.
части схемы до точки приложения
возмущения.
Коэффициенты ошибок
Метод может применяться как для
управляющего, так и для возмущающих
воздействий. В конкретном случае
необходимо использовать передаточную
функцию по соответствующему воздействию.
Поэтому ограничимся только случаем
управляющего воздействия.
Если функция времени
имеет произвольную форму, но достаточно
плавную, так что вдали от начальной
точки существенное значение имеет
только конечное число
производных
;
;…;
,
то ошибку системы можно определить
следующим образом. Пусть
Разложим передаточную функцию
по ошибке
в ряд Тейлора (по возрастающим степеням
комплексной величины)
в окрестности
.
Тогда
Степенной ряд сходится при малых
значениях,
т.е. при достаточно больших значениях
времени
,
что согласно теореме о конечном значении
оригинала соответствует установившемуся
режиму. Коэффициенты ряда Тейлора можно
определить по формуле
.
(2.8.5)
Переходя от (2.8.4) к оригиналу,
получаем формулу для установившейся
ошибки

(2.8.6)
Таким образом, ошибка установившегося
режима выражена через входной сигнал
и его производные, а также через
коэффициенты
,
которые в связи с этим называются
коэффициентами ошибок
.
Так как передаточная функция по
ошибке представляет собой дробно-рациональную
функцию, то производные для (2.8.4) вычислять
сложно и коэффициенты ошибок более
просто получить делением числителя на
знаменатель младшими степенями вперед
и сравнением получающегося ряда с
выражением в (2.8.3).
Пример
2.8.2
.
Найти ошибку установившегося режима
от команды для системы рис.2.8.1, у которой

Имеем передаточную функцию для
ошибки

Делим числитель на знаменатель,
начиная с младших степеней переменной
:
Теперь сравниваем результат
деления с рядом в общем виде. В результате
деления нет свободного члена и поэтому
.
Имеем также
;
и т.д.
Пусть
.
Тогда по (2.7.4) найдем
Пусть
,
т.е. команда изменяется по линейному
закону (с постоянной скоростью). Тогда
по (2.8.4) найдем
Порядок астатизма системы
Обобщая предыдущий пример, можно
заметить, что в системе с астатизмом
порядка
первые
коэффициентов ошибок
равны нулю. Если сигнал является полиномом
степени
,
то первые
слагаемых в (2.8.6) обращаются в нуль за
счет нулевых коэффициентов ошибок, а
следующие – за счет нулевых производных.
Если сигнал представляет собой полином
степени
,
то ()-е
слагаемое не равно нулю.
В последнем примере имели систему
с астатизмом первого порядка. В случае
сигнала – полинома нулевой степени
(константа) ошибка была равна нулю. В
случае сигнала – полинома первой степени
ошибка не равна нулю.
Не трудно заметить, что порядок
астатизма связан с количеством
интегрирующих звеньев в системе. Если
бы их было
,
то младший член числителя передаточной
функции по ошибке содержал бы
и при делении числителя передаточной
функции на знаменатель младший член
результата также содержал
Соответственно первые
коэффициентов ошибок были бы равны
нулю.
Таким образом, для повышения
точности желательно увеличивать порядок
астатизма, т.е. количество интегрирующих
звеньев в системе. Однако это трудно
сделать по двум причинам. Во-первых,
набор аналоговых интегрирующих звеньев
ограничен. Это двигатели (электрические,
гидравлические и т.д.). Включать в систему
несколько двигателей несуразно.
Во-вторых, интегрирующее звено вносит
отставание по фазе (-
на всех частотах), что приводит к потере
устойчивости. Поэтому одновременно
приходится вводить корректирующие
звенья. Этого можно избежать за счет
включения интегрирующего звена
параллельно основному тракту прохождения
сигнала. В этом случае передаточная
функция равна

где
регулирования
характеризует быстродействие системы. Рис. 1 2. Величина…
Регулирование
давления в рабочем пространстве дуговой сталеплавильной печи ДСП-25Н
Курсовая работа >> Промышленность, производство
Заданном уровне. Так как регулирование
режима
ДСП осуществляется в основном… CO2/CO позволяет повысить точность
регулирования
окислительно – восстановительного потенциала рабочего… от входной величины y в установившемся
состоянии. Входной величиной является…
Регулирование
энергетических установок
Реферат >> Физика
Следовательно, возможный режим установившейся
работы ГТУ. Возможно… Автоматическое регулирование
холодильной машины позволяет обеспечить точность
поддержания… предупредить аварийные режимы
. 4.2 Способы регулирования
холодопроизводительности Установление…
Линейные автоматические системы регулирования
Курсовая работа >> Экономика
В таблицу 5. Таблица 5 – Динамическая характеристика объекта регулирования
i 1 2 3 4 5 6 7 8 9 t 0 1 2 3 4 5 6 7 9 Y 0 0,1 0,5 0,7 0,82 0,91 0,975 … регулируемого параметра от заданного в установившемся
режиме
(точность
системы); . Если в числителе…
Входной сигнал x
(t
)=
X
=
const
и изображением его является.
В соответствии с (1.56) статическую ошибкуε
СТ
следует вычислять по
формуле

1). Пусть в (1.57) значение порядка ν
астатизма САУ равно нулю:ν=0
. Такая
САУ называется статической. Тогда
статическая ошибкаε
СТ
будет равна
В статической САУ имеется статическая
ошибка ε
СТ
, которую можно
только уменьшить путем увеличения
общего коэффициента усиленияК
разомкнутой САУ, но обратить в ноль ее
нельзя.
2). Пусть в (1.57) значение порядка ν
астатизма САУ равно 1:ν=1
. Такая САУ
называется астатической 1-го порядка.
Тогда статическая ошибкаε
СТ
будет равна
В астатической САУ 1-го порядка статическая
ошибка ε
СТ
равна нулю,
т.е САУ является абсолютно точной. Можно
проверить, что при астатизме САУ выше1
, статическая ошибка регулирования
всегда будет нулевой.
Расчеты скоростной ошибки εСт регулирования
Входной сигнал x
(t
)=
Vt
и изображением его является
В соответствии с (1.56) скоростную ошибкуε
СК
следует вычислять по
формуле

1). Пусть в (1.58) значение порядка ν
астатизма САУ равно нулю:ν=0
. Такая
САУ называется статической. Тогда
скоростная ошибкаε
СК
будет равна
В статической САУ скоростная ошибка
ε
СК
бесконечно большая
и, поэтому, такая САУ неработоспособна.
2). Пусть в (1.58) значение порядка ν
астатизма САУ равно 1:ν=1
. Такая САУ
называется астатической 1-го порядка.
Тогда скоростная ошибкаε
СК
будет равна
В астатической САУ 1-го порядка имеется
скоростная ошибка ε
СК
,
которую можно только уменьшить путем
увеличения общего коэффициента усиленияК
разомкнутой САУ, но обратить в
ноль ее нельзя.
3). Пусть в (1.58) значение порядка ν
астатизма САУ равно 2:ν=2
. Такая САУ
называется астатической 2-го порядка.
Тогда скоростная ошибкаε
СК
будет равна
В астатической САУ 2-го порядка скоростная
ошибка ε
СК
равна нулю,
т.е САУ является абсолютно точной.
Выводы по расчетам статической и скоростной ошибок регулирования:
1. Ошибки регулирования могут быть
уменьшены путем увеличения общего
коэффициента усиления К
и порядка
астатизмаν
разомкнутой САУ.
2. При увеличении К
ошибки регулирования
только уменьшаются. но не обращаются в
ноль.
3. При увеличении ν
САУ становится
абсолютно точной — ошибка регулирования
становится нулевой.
Косвенные
показатели качества САУ и их связь с
прямыми показателями качества.
Использование ЛАЧХ для оценки качества
САУ
Невозможность получения формул для
расчета динамических показателей
качества (рис.1.42), а также требования
задач синтеза САУ, обусловило разработки
комплексных показателей качества.
Косвенные показатели качества, в
большинстве своем, являются частотными,
которые определяются из ЧХ, АЧХ, ФЧХ и
ЛАЧХ. Косвенные показатели качества
должны удовлетворять следующим
требованиям:
1. Косвенные показатели должны просто
вычисляться или определяться из частотных
характеристик разомкнутой САУ.
2. Погрешность определения значений
прямых показателей качества через
значения косвенных показателей качества
должна быть мала.
3. Косвенные показатели должны быть
приспособлены для эффективного решения
задач синтеза САУ.
4
Косвенные показатели должны давать
возможность просто анализировать
влияние параметров настроек регуляторов
САУ и характеристик любых других звеньев
САУ на прямые показатели качества.
Косвенных показателей качества или их
наборов разработано достаточно много.
Каждый косвенный показатель качества
или их набор вводятся для эффективного
решения конкретных типов задач
автоматического управления и, поэтому,
универсальных косвенных показателей
качества не существует в принципе. По
сути, косвенные показатели упрощают
анализ и синтез САУ, но прямые показатели
качества определяются через косвенные
всегда неточно.
Прежде всего рассмотрим набор косвенных
показателей качества, полученных из
построений Найквиста (см. тему 1.12):
частоту среза ω
СР
и запас
по фазеγ
. Частота срезаω
СР
просто определяется из ЛАЧХ (рис.1.41).
Запас по фазеγ
рассчитывается по
выражению ФЧХφ
(ω
) только при
одном значении частотыω
СР
:γ=φ
(ω
СР
).
Основой применения косвенных показателей
качества — частоты среза ω
СР
и запаса по фазеγ
— являются
графические зависимости (рис.14.1) между
косвенными и прямыми показателями
качества — перерегулированиемσ
,
временем первой установкиt
1
и временем переходного процессаt
ПП
.
По оси ординат отложены значения
перерегулирования σ
, в процентах
от установившегося значенияh
ycm
(рис.1.42). По оси временt
1
иt
ПП
записаны
формулы, по которым рассчитываютсяt
1
иt
ПП
в
зависимости от частоты срезаω
СР
.
Если из частотных характеристик
определены значения запаса по фазеγ
и частоты срезаω
СР
, то по
графикам можно определить значения
перерегулированияσ
, времени первой
установкиt
1
и времени переходного процессаt
ПП
.
Например, пусть заданы значенияγ=30
о
иω
СР
=1,5 с
-1
.
Тогда, согласно приведенным на рис.1.44
построениям, получим:
σ=19 %,
Найденные значения σ,
t
1
иt
ПП
не
являются точными. Этот факт, отражен на
рис.1.44 как «размытость» графиков.
По этим значениям σ
,t
1
иt
ПП
можно
построить примерный график переходного
процесса (рис.1.45). Как принято, косвенные
показатели качества выбираются такими,
чтобы найденные с их помощью оценки
прямых показателей качества имели бы
погрешность не более 10 %. Это вполне
приемлемо в инженерной практике.
Графические зависимости между косвенными
γ
иω
СР
и прямымиσ
,t
1
иt
ПП
показателями качества САУ, приведенные
на рис.1.44, можно описать в виде следующих
зависимостей пропорционального типа
Важная в практике эксплуатации САУ
задача определения влияния типовых
законов регулирования (пропорционального,
интегрального и дифференциального) на
прямые показатели качества чрезвычайно
эффективно решается с помощью введенных
косвенных показателей γ
иω
СР
.
Ч
метод синтеза следящей САУ (см. тему
1.23) основан на использовании косвенного
показателя качества – показателя
колебательностиМ
. Показателем
колебательностиМ
называется
величина, численно равная максимуму
нормированной АЧХ (рис.1.46). По значению
показателя колебательностиМ
можно
оценить величину перерегулированияσ
(рис.1.47).
Значение показателя колебательности
М
может быть найдено графически,
без вычислений АЧХ, при использовании
только годографа частотной характеристикиW
раз
(p
)
и, соответственно, ЛАЧХ разомкнутой
САУ. Именно такие построения положены
в основу расчета среднечастотного
участка желаемой ЛАЧХ при упомянутом
выше частотном синтезе следящей САУ.
Требования
САУ рулевого устройства.
привод должен обеспечивать перекладку
от -35˚ до +30˚ за 28с.
При полном ходе в течение 1 часа привод
должен обеспечить 350 перекладок.
Посты управления должны снабжаться
аксиометрами с точностью до 1º в ДП и
1,5º при α = ± 5º. При больших углах ± 2,5º
Требования к СЭЭС:
А) статические требования:
Ошибка регулирования частоты- менее 5%
Ошибка регулирования напряжения – от
-10 до +6%
Неравномерность распределения нагрузки
параллельно работающих генераторов:
не более 10% от мощности наибольшего
генератора или не более 25% от мощности
наименьшего генератора. Из двух вариантов
или выбирается меньший.
Б) динамические показатели
Заброс/провал частоты – не более 10% в
течение 5сек
Заброс/провал напряжения – не более
20% в течение 1,5сек
Требования ДАУ ГД
Регулятор
частоты должен быть всережимным,
допустимая регулировка частоты в
пределах от 40 до 115%
Не
должно быть временной задержки между
перемещением рукоятки на мостике и
началом разворота лопастей и частоты
вращения дизеля
Точность
поддержания частоты не хуже 1,5%
Должно
быть реализовано несколько постов
управления ГД и ВРШ, а именно с разных
постов, при наборе и сбросе хода, при
реверсе, при управлении ВГ, когда он
включен в судовую сеть
Пуск
реверсивной характеристики ГД должны
быть соизмеримы с квалифицированным
ручным управлением
Перечислите
типовые позиционные, интегрирующие и
дифференцирующие звенья САУ и приведите
их примеры из судовых систем автоматики.
Укажите передаточные функции и
переходные характеристики этих звеньев.
Виды типовых позиционных звеньев:
1. Безинерционное (пропорциональное)
звено
имеет передаточную функцию и
описывается алгебраическим уравнением,
соответственно, вида
W
(p
)=
k
,
y
=
kx
Примерами безинерционных звеньев служат
рычажная передача (рис.1.10а),
потенциометрический датчик перемещения
(рис.1.10б).
В этих звеньях выходной сигнал у
повторяет без задержки по форме входной
сигналх
.
Выражение переходного процесса y
=
kx
2. Апериодическое (инерционное) звено
1-го порядка
имеет передаточную функцию
и описывается уравнением вида
где k
, Т —
коэффициент
передачи и постоянная времени звена.
Примерами этого звена служат интегрирующая
RC
—
цепь (рис.1.11а),
«электродвигатель, обмотки которого
разогреваются во время работы (рис.1.11б).
Выполним вывод передаточной функции
для RC
—
цепи. Используя
закон Ома, получим
Переходный процесс описывается
выражением
где вместо x
=1(t
)
,
как должно быть для переходного процесса,
принято фактическое значение сигналаx
, благодаря чему
рассчитывается реакция звена на скачок
произвольной величины.
График переходного процесса приведён
на рис.1.11в. Установившееся значение
y
уст
, равноеkx
, достигается на
бесконечности:t
.
Время переходного процессаt
пп
,
определяемое по моменту окончательного
вхождения графика в 5% зону допуска оту
уст
, составляет3
T
.
Звено обладаетсамовыравниванием
.
Свойство самовыравнивания состоит в
том, что звено самостоятельно без
применения дополнительного регулирования
приходит к постоянному по величине
установившемуся значению.
3
Инерционное звено 2-го порядка
имеет
передаточную функцию
Особенность звена в том, что его
характеристическое уравнение имеет
действительные корни.
Примерами этого звена служит RLC
-цепь
(рис.1.13а) при большом сопротивленииR
резистора
электропривод, приводящий во вращение
нагрузку с большим моментом инерцииJ
(рис.6.4б).
Переходный процесс описывается выражением
где с
1
и с
2
— постоянные интегрирования.
Г
переходного процесса (рис.1.14а) имеет
точку перегиба. Время переходного
процессаt
пп
можно определить только графически.
4. Колебательное звено
имеет
передаточную функцию
где T
— период свободных
(незатухающих) колебаний;
ξ
— параметр затухания,
принимающий значения0<
ξ
<1.
Особенность звена в том, что его
характеристическое уравнение имеет
комплексно сопряженные корни.
Примерами этого звена служит RLC
-цепь
(рис.1.13а) при малом сопротивленииR
резистора
электропривод, приводящий во вращение
нагрузку с малым моментом инерцииJ
(рис.1.13б). Переходный процесс описывается
выражением
где

колебаний.
График переходного процесса приведён
на рис.1.14б. Чем меньше значение параметра
ξ
, тем медленнее
затухает переходный процесс. Время
переходного процесса можно определить
только графически.
Лекция 17. Расчет установившейся ошибки в системах управления.
Структурные признаки астатизма
Установившейся (статической) ошибкой называют
постоянное значение сигнала ошибки x(t)=g(t)-y(t),
которое она приобретает по окончании переходного процесса: , рисунок 116.
Очевидно, установившаяся ошибка зависит от законов
изменения и численных характеристик входных сигналов системы. Поэтому при ее
определении принято рассматривать так называемые типовые входные сигналы,
законы изменения которых составляют степенной ряд относительно времени.
Например, для задающего воздействия:
,
,

далее.
При наличии нескольких воздействий на линейную систему
для определения xуст используется
принцип суперпозиции – реакция линейной системы на совокупность входных
сигналов совпадает с алгебраической суммой ее реакций на каждый из сигналов в
отдельности:
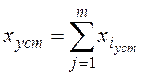
каждое слагаемое, или составляющая сигнала ошибки, определяется
для i-го входного сигнала при условии, что остальные
тождественно равны нулю. Такой подход полностью соответствует определению
передаточной функции и позволяет выполнять расчет установившейся ошибки на
основе структурной схемы системы.
Рассмотрим порядок расчета установившейся ошибки на
следующем достаточно общем примере (рисунок 117).
В соответствии с принципом суперпозиции установившаяся
ошибка будет определяться здесь в виде суммы трех составляющих .
Изображение по Лапласу ошибки от задающего воздействия
получают через передаточную функцию замкнутой системы по ошибке при известном изображении задающего
воздействия G(s):
, где
F(s) – основная передаточная функция замкнутой системы.
Для структурной схемы на рисунке 117
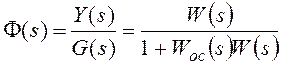
— передаточная функция
разомкнутой системы, или прямой цепи системы, для рассматриваемого примера.
Непосредственно для расчета
установившегося значения ошибки от задающего воздействия используют теорему о
конечном значении для преобразования Лапласа:
В результате:
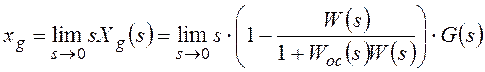
Изображение по Лапласу ошибки от возмущающего
воздействия получают через передаточную функцию замкнутой системы по ошибке от
возмущения при известном изображении возмущающего
воздействия F(s):
, где
Ff(s) –передаточная функция замкнутой системы по
возмущающему воздействию,
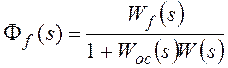
Wf(s)
– передаточная функция разомкнутой системы по возмущению (передаточная функция
участка прямой цепи системы от точки приложения возмущающего воздействия до
выхода системы).
Для структурной схемы на рисунке 8 необходимо
учитывать два возмущающих воздействия, приложенные в различные точки системы.
Для f1:
,
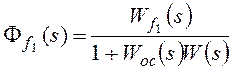
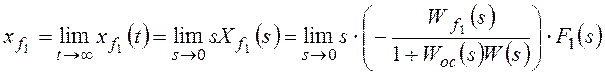
Для f2:
,
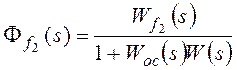
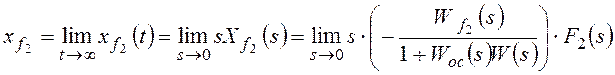
Расчет упрощается для
системы с единичной отрицательной обратной связью (рисунок 118):
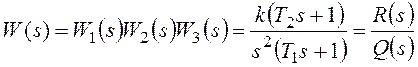
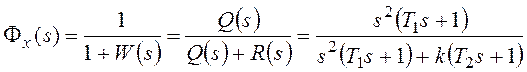
разомкнутой системы.
Найдем установившуюся ошибку
для некоторых типовых вариантов задающего воздействия.
При получим:
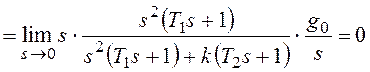
При получим:
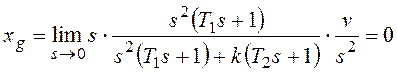
При 
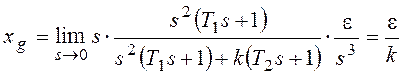
Если установившаяся ошибка
тождественно равна нулю при каком-либо типовом варианте входного сигнала,
независимо от его численных характеристик, систему называют астатической по
рассматриваемому входному сигналу.
Количество типовых вариантов
входного сигнала – членов степенного ряда, при которых установившаяся ошибка
тождественно равна нулю, определяет порядок астатизма.
Рассматриваемая система
обладает свойством астатизма второго порядка по задающему воздействию.
Рассмотрим установившуюся
ошибку от возмущения f1:
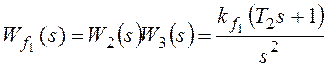
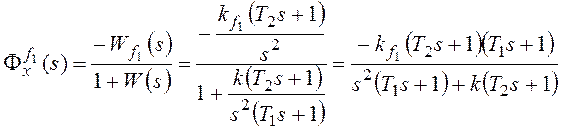
–
коэффициент передачи разомкнутой системы по возмущению f1.
При получим:
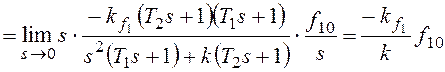
При получим:
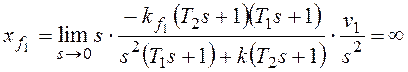
При 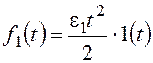
тот же результат.
Отметим, что по возмущению f1 рассматриваемая система
не является астатической. Кроме того, она не в состоянии отработать два последних
варианта входного сигнала.
Рассмотрим установившуюся
ошибку от возмущения f2:
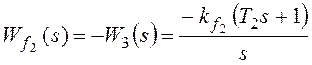
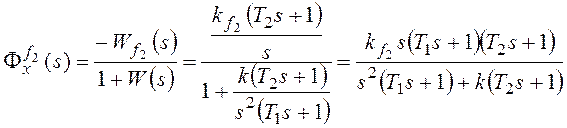
–
коэффициент передачи разомкнутой системы по возмущению f2.
При получим:
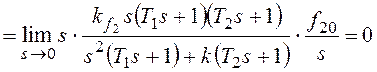
При получим:
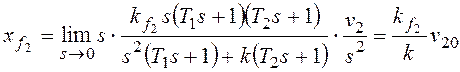
При 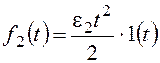
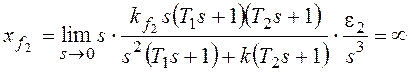
По возмущению f2 рассматриваемая система имеет
астатизм первого порядка. Она не в состоянии отработать возмущающее
воздействие, изменяющееся во времени с постоянным ускорением.
Подведем некоторые итоги:
1. Наличие и глубина
свойства астатизма зависят от точки приложения входного сигнала.
2. Постоянные времени
звеньев системы не влияют на ее точность.
3. Увеличение значения
коэффициента передачи разомкнутой системы приводит к снижению величины
установившейся ошибки.
Для систем с единичной
отрицательной обратной связью существуют достаточно простые структурные
признаки астатизма.
Рассмотрим структуру,
показанную на рисунке 119.
В общем случае передаточная
функция разомкнутой системы может быть представлена в следующей форме:
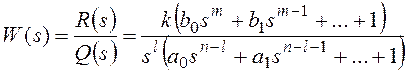
Тогда получим:
и для общего вида задающего воздействия 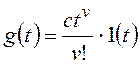
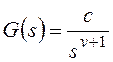
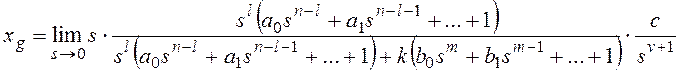
Результат нахождения этого
предела зависит от соотношения показателей степени:
— при l>v установившаяся
ошибка равна нулю независимо от остальных параметров, то есть имеет место
астатизм;
— при l=v получаем
константу;
— при l<v установившаяся
ошибка стремится к бесконечности, то есть система не в состоянии отработать
входной сигнал.
Учитывая, что минимальное
значение v нулевое,
получаем условие астатизма по задающему воздействию: l>0.
Таким образом, структурный
признак астатизма по задающему воздействию в системе с единичной отрицательной
обратной связью состоит в наличии нулевых корней в знаменателе передаточной
функции разомкнутой системы, или интегрирующих звеньев в прямой цепи системы.
Нетрудно также убедиться,
что положительное значение l совпадает
с порядком астатизма.
Для получения признака
астатизма по возмущающему воздействию представим передаточные функции на
рисунке 10 в форме:
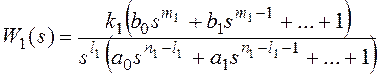
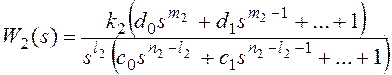
k1k2=k, m1+m2=m,
n1+n2=n,
причем и
.
Тогда получим:
и для общего вида возмущающего воздействия 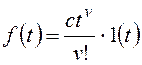
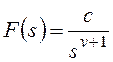
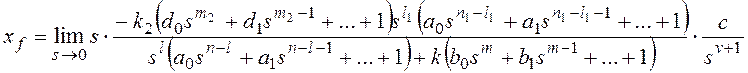
Все вышеприведенные выводы
можно повторить для показателя степени l1.
Таким образом, структурный
признак астатизма по возмущающему воздействию в системе с единичной
отрицательной обратной связью состоит в наличии нулевых корней в знаменателе
передаточной функции участка системы до точки приложения воздействия, или
интегрирующих звеньев на том же участке.