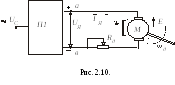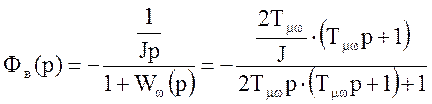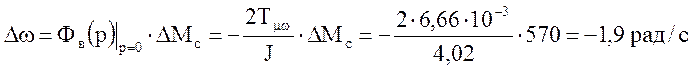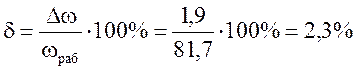Многие
производственные механизмы, например,
механизмы подачи и главного движения
металлорежущих станков, механизмы
подъемно-транспортных установок и др.
требуют регулирования скорости
исполнительных органов. Для таких
механизмов используются регулируемые
электроприводы.
Важнейшими
показателями качества для регулируемого
электропривода являются диапазон
регулирования скорости и падение
скорости от нагрузки.
Под
диапазоном
регулирования скорости
понимают отношение верхней (наибольшей)
скорости
к нижней
(наименьшей скорости. Под верхней и
нижней скоростями обычно понимают
задаваемые значения угловых скоростей
на холостом ходу (см. рис. 2.8)
.
(2.8)
Например,
если электропривод имеет верхнюю
скорость
=1000об/мин
иD
=1000, то нижняя скорость
обмин.
Падение
скорости под нагрузкой
(см. рис.2.8) определяют обычно при
номинальном значении нагрузки (момента).
Величинуназывают такжеабсолютной
статической ошибкой от нагрузки.
Для оценки качества работы электропривода
удобнее использовать значение
относительной
статической ошибки от нагрузки.
Относительная
ошибка определяется обычно в процентах
по выражению
,
где
— заданное значение угловой скорости
или частоты вращения.
Значение
абсолютной ошибки
на верхней и нижней характеристиках,
как правило, одно и то же. При этом
относительная ошибка на верхней скорости
,
(2.9)
а
на нижней
(2.10)
Используя
выражения (2.9) и (2.10), найдем отношение
.
Тогда,
с учетом выражения (2.9) для диапазона
регулирования, получим
.
(2.11)
Таким
образом, относительная
статическая ошибка от нагрузки на нижней
скорости в D
раз больше, чем на верхней.
Производственные
механизмы, как правило, требуют поддержания
скорости с заданной точностью во
всем диапазоне
регулирования. Отсюда следует, что при
проектировании электропривода нужно
прежде всего обеспечить требуемую
точность стабилизации на
нижней скорости.
2. 2. Механические характеристики и способы регулирования скорости двигателей постоянного тока (дпт) независимого возбуждения (нв)
2.2.1. Электромеханические и механические характеристики дпт нв
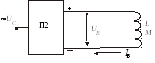
Схема
подключения ДПТ НВ приведена на рис.
2.9. Напряжение Uя
на якорь двигателя М
с электромагнитным возбуждением подается
от подключенного к сети переменного
тока преобразователя (выпрямителя) П1.
Рис.2.9
(предполагается,
что он нерегулируемый). Обмотка возбуждения
LM
двигателя может быть подключена к
другому преобразователю П2
или к точкам а,
в первого
преобразователя. При наличии сети
постоянного тока якорь и обмотка
возбуждения так же получают питание от
одного источника.
Для
подключения машины с возбуждением от
постоянных магнитов (см. рис. 2.10) достаточно
одного преобразователя. В цепь якоря
при питании его от неуправляемого
преобразователя обычно включается
добавочное сопротивление Rд
(его
назначение поясняется ниже).
В
двигательном режиме электрическая
энергия потребляется машиной из сети
и преобразуется в механическую энергию.
Направление
тока якоря Iя
и ЭДС Е
рис.2.9, 2.10 показано для двигательного
режима.
Напряжение
Uя
(В), приложенное к якорю, в установившемся
режиме уравновешивается ЭДС Е
(В),
наведенной в якоре (ее называют также
противоЭДС), и падением напряжения в
якорной цепи
Uя
= Е + Iя(Rя+Rд),
(2.12)
где Rя
– сопротивление якорной цепи двигателя,
Ом, включающее сопротивления обмотки
якоря, щеточного контакта, дополнительных
полюсов и компенсационной обмотки; Rд
– добавочное сопротивление.
ЭДС машины
определяется соотношением
Е= сФд,
(2.13)
здесь
конструктивный коэффициент
с
= рN/
2а,
р
– число
пар полюсов;
N
– число активных проводников обмотки
якоря;
а
– число пар параллельных ветвей обмотки
якоря;
Ф
– магнитный поток, Вб, создаваемый
обмоткой возбуждения или постоянными
магнитами.
Подставляя
выражение (2.13) для Е
в уравнение (2.12) и решая его относительно
д,
получим:
д
=
.
(2.14)
Это
уравнение устанавливает связь между
частотой вращения и током якоря д
= f(Iя)
и называется электромеханической
характеристикой двигателя.
Электромагнитный
момент двигателя (Нм),
определяется током якоря и магнитным
потоком:
М = сФIя.
(2.15)
Момент
на валу двигателя меньше электромагнитного
на значение, определяемое потерями в
стали и механическими потерями. Для
инженерных расчетов этими потерями
можно пренебречь, и принять, что момент
на валу равен электромагнитному моменту.
Тогда, определив из (2.15) ток якоря и
подставив его в соотношение (2.14), получим
уравнение механической
характеристики двигателя:
д
=
.
(2.16)
Полученные
выражения (2.14), (2.16) для характеристик
двигателя представляют собой уравнение
прямой. Они справедливы, если пренебречь
реакцией якоря.
В
уравнениях (2.14), (2.16) первое слагаемое
представляет собой угловую
скорость идеального холостого хода
(при этом ток якоря и момент равны 0)
0
=
.
(2.17)
Второй
член в этих уравнениях характеризует
статическое
падение угловой скорости
от нагрузки
или
(2.18)
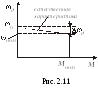
На
рис. 2.11 падение скорости показано для
номинального
значения момента Mном
(тока
Iном).
При неизменном магнитном потоке момент
и ток якоря, как следует из соотношения
(2.15) пропорциональны. Поэтому механическая
и электромеханическая характеристики
двигателя (см. рис. 2.11) отличаются только
масштабом по оси ординат. Характеристика,
полученная при номинальном значении
напряжения на якоре Uном,
номинальном магнитном потоке Фном
и отсутствие внешних резисторов в
якорной цепи, называется естественной.
Жесткость естественной характеристики
определяется только сопротивлением
якорной цепи двигателя:
или
.
(2.19)
Снижение
скорости д
под нагрузкой объясняется следующим.
При увеличении момента сопротивления
механизма угловая скорость начинает
снижаться. В результате уменьшается
ЭДС Е
согласно (2.13). Ток якоря при этом, как
следует из (2.12) увеличивается. Соответственно
возрастает момент двигателя (см. уравнение
(2.15)). Этот процесс продолжается до тех
пор, пока момент двигателя не сравняется
с моментом сопротивления. После достижения
равенства М=Мс
наступит новый установившийся режим с
меньшей угловой скоростью д.
При
инженерных расчетах коэффициенты,
входящие в уравнения характеристик
двигателя, могут быть определены через
номинальные параметры двигателя,
приводимые в каталогах. При номинальном
магнитном потоке
(2.20)
Здесь
коэффициент Кд
— коэффициент
передачи двигателя, его размерность
.
С использованием этого понятия уравнения
(2.14), (2.16) могут быть переписаны в виде:
(2.21)
(2.22)
В
этих уравнениях, как и в (2.14, 2.16), первый
член представляет собой угловую скорость
идеального холостого хода, а второй –
падение скорости от нагрузки:
,
(2.23)
или
(2.24)
Пример.
Известны номинальные данные двигателя:
Рассчитать
естественную характеристику двигателя.
Находим
номинальную угловую скорость
Коэффициент
передачи двигателя по (2.9)
.
Угловая
скорость на холостом ходу при номинальном
напряжении с учетом (2.23)
Полученных
результатов ()
достаточно для построения характеристики
(см. рис. 2.11). Для проверки находим по
(2.13) падение угловой скорости при
номинальном токе
а так же
вычислим
по очевидному соотношению
Совпадение
результатов подтверждает правильность
вычислений.
Для
построения механической характеристики
необходимо дополнительно рассчитать
с учетом (2.2) номинальный момент двигателя
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вместо введения
Системы автоматического управления (САУ) предназначены для автоматического изменения одного или нескольких параметров объекта управления с целью установления требуемого режима его работы. САУ обеспечивает поддержание постоянства заданных значений регулируемых параметров или их изменение по заданному закону либо оптимизирует определенные критерии качества управления. Например, к таким системам относятся:
- системы стабилизации,
- системы программного управления,
- следящие системы
Это достаточно широкий класс систем, которые можно найти где угодно. Но какое это отношение имеет к Unity3D и вероятно к играм в частности? В принципе прямое: в любой игре так или иначе использующей симуляцию как элемент геймплея реализуются САУ, к таким играм относятся, например, Kerbal Space Programm, Digital Combat Simulator (бывший Lock On), Strike Suit Zero и т.д. (кто знает еще примеры — пишите в комментариях). В принципе любая игра, моделирующая реальные физические процессы, в том числе и просто кинематику с динамикой движения, может реализовывать те или иные САУ — этот подход проще, естественнее, а у разработчика уже есть есть набор готовых инструментов, предоставленных всякими Вышнеградскими, Ляпуновыми, Калманами, Чебышевами и прочими Коломогоровами, поэтому можно обойтись без изобретения велосипеда, т.к. его уже изобрели, да так, что получилась отдельная наука: Теория автоматического управления. Главное тут не переусердствовать. Одна тут только проблема: рассказывают про ТАУ не везде, не всем, зачастую мало и не очень понятно.
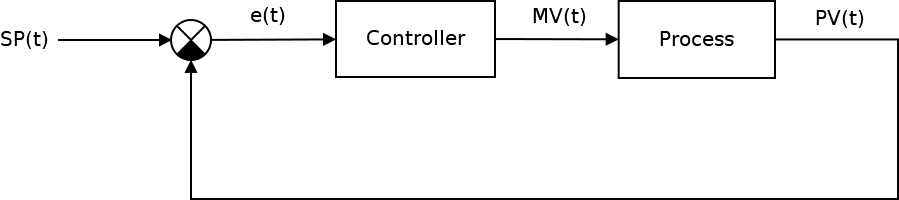
Немножко теории
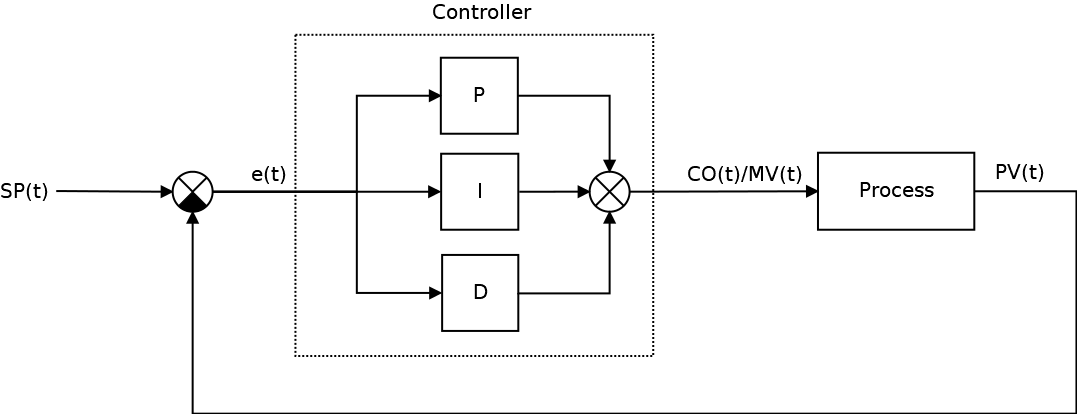
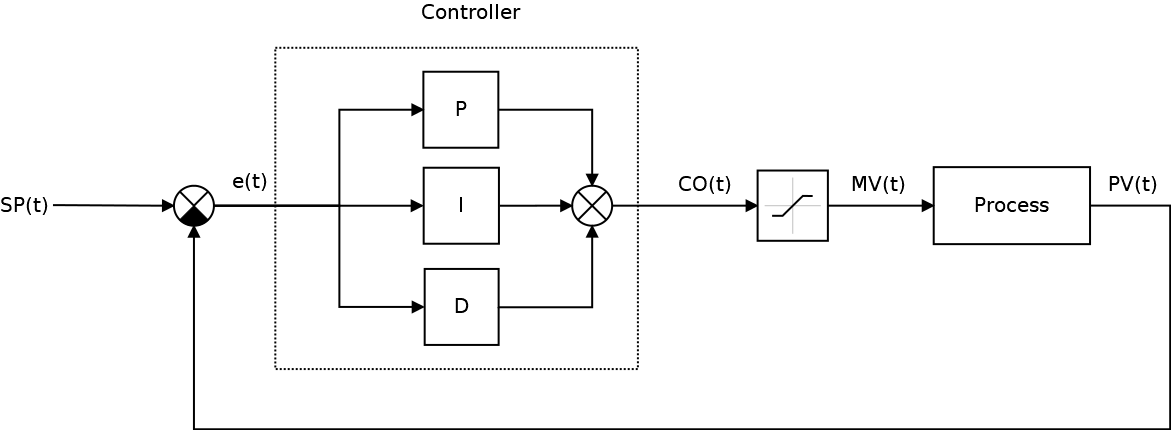
Классическая система автоматического управления представленная на следующем рисунке:
Ключевым элементом любой САУ является регулятор представляющий из себя устройство, которое следит за состоянием объекта управления и обеспечивает требуемый закон управления. Процесс управления включает в себя: вычисление ошибки управления или сигнала рассогласования e(t) как разницы между желаемой уставкой (set point или SP) и текущей величиной процесса (process value или PV), после чего регулятор вырабатывает управляющие сигналы (manipulated value или MV).
Одной из разновидностью регуляторов является пропорционально-интегрально-дифференцирующий (ПИД) регулятор, который формирует управляющий сигнал, являющийся суммой трёх слагаемых: пропорционального, интегрального и дифференциального.
Где, ошибка рассогласования, а также,
— пропорциональная,
— интегральная,
— дифференциальная составляющие (термы) закона управления, который в итоговом виде описывается следующими формулами
Пропорциональная составляющая P — отвечает за т.н. пропорциональное управление, смысл которого в том, что выходной сигнал регулятора, противодействует отклонению регулируемой величины (ошибки рассогласования или еще это называют невязкой) от заданного значения. Чем больше ошибка рассогласования, тем больше командное отклонение регулятора. Это самый простой и очевидный закон управления. Недостаток пропорционального закона управления заключается в том, что регулятор никогда не стабилизируется в заданном значении, а увеличение коэффициента пропорциональности всегда приводит к автоколебаниям. Именно поэтому в довесок к пропорциональному закону управления приходиться использовать интегральный и дифференциальный.
Интегральная составляющая I накапливает (интегрирует) ошибку регулирования, что позволяет ПИД-регулятору устранять статическую ошибку (установившуюся ошибку, остаточное рассогласование). Или другими словами: интегральное звено всегда вносит некоторое смещение и если система подвержена некоторыми постоянным ошибкам, то оно их компенсирует (за счет своего смещения). А вот если же этих ошибок нет или они пренебрежительно малы, то эффект будет обратным — интегральная составляющая сама будет вносить ошибку смещения. Именно по этой причине её не используют, например, в задачах сверхточного позиционирования. Ключевым недостатком интегрального закона управления является эффект насыщения интегратора (Integrator windup).
Дифференциальная составляющая D пропорциональна темпу изменения отклонения регулируемой величины и предназначена для противодействия отклонениям от целевого значения, которые прогнозируются в будущем. Примечательно то, что дифференциальная компонента устраняет затухающие колебания. Дифференциальное регулирование особенно эффективно для процессов, которые имеют большие запаздывания. Недостатком дифференциального закона управления является его неустойчивость к воздействую шумов (Differentiation noise).
Таким образом, в зависимости от ситуации могут применятся П-, ПД-, ПИ- и ПИД-регуляторы, но основным законом управления в основном является пропорциональный (хотя в некоторых специфических задачах и могут использоваться исключительно только звенья дифференциаторов и интеграторов).
Казалось бы, вопрос реализации ПИД-регуляторов уже давно избит и здесь на Хабре есть парочка неплохих статей на эту тему в том числе и на Unity3D, также есть неплохая статья PID Without a PhD (перевод) и цикл статей в журнале «Современные технологии автоматизации» в двух частях: первая и вторая. Также к вашим услугам статья на Википедии (наиболее полную читайте в английском варианте). А на форумах коммьюнити Unity3D нет-нет, да и всплывет PID controller как и на gamedev.stackexchange
При вопрос по реализации ПИД-регуляторов несколько глубже чем и кажется. Настолько, что юных самоделкиных, решивших, реализовать такую схему регулирования ждет немало открытий чудных, а тема актуальная. Так что надеюсь сей опус, кому-нибудь да пригодиться, поэтому приступим.
Попытка номер раз
В качестве примера попытаемся реализовать схему регулирования на примере управления поворотом в простенькой космической 2D-аркаде, по шагам, начиная с самого начала (не забыли, что это туториал?).
Почему не 3D? Потому что реализация не измениться, за исключением того, что придется воротить ПИД-регулятор для контроля тангажа, рысканья и крена. Хотя вопрос корректного применения ПИД-регулирования вместе с кватернионами действительно интересный, возможно в будущем его и освящу, но даже в NASA предпочитают углы Эйлера вместо кватернионов, так что обойдемся простенькой моделью на двухмерной плоскости.
Для начала создадим сам объект игровой объект космического корабля, который будет состоять из собственно самого объекта корабля на верхнем уровне иерархии, прикрепим к нему дочерний объект Engine (чисто спецэффектов ради). Вот как это выглядит у меня:
А на сам объект космического корабля накидаем в инспекторе всяческих компонент. Забегая вперед, приведу скрин того, как он будет выглядеть в конце:
Но это потом, а пока в нем еще нет никаких скриптов, только стандартный джентльменский набор: Sprite Render, RigidBody2D, Polygon Collider, Audio Source (зачем?).
Собственно физика у нас сейчас самое главное и управление будет осуществляться исключительно через неё, в противном случае, применение ПИД-регулятора потеряло бы смысл. Масса нашего космического корабля оставим также в 1 кг, а все коэффициенты трения и гравитации равны нулю — в космосе же.
Т.к. помимо самого космического корабля есть куча других, менее умных космических объектов, то сначала опишем родительский класс BaseBody, который в себе будет содержать ссылки на на наши компоненты, методы инициализации и уничтожения, а также ряд дополнительных полей и методов, например для реализации небесной механики:
BaseBody.cs
using UnityEngine;
using System.Collections;
using System.Collections.Generic;
namespace Assets.Scripts.SpaceShooter.Bodies
{
[RequireComponent(typeof(SpriteRenderer))]
[RequireComponent(typeof(AudioSource))]
[RequireComponent(typeof(Rigidbody2D))]
[RequireComponent(typeof(Collider2D))]
public class BaseBody : MonoBehaviour
{
readonly float _deafultTimeDelay = 0.05f;
[HideInInspector]
public static List<BaseBody> _bodies = new List<BaseBody>();
#region RigidBody
[HideInInspector]
public Rigidbody2D _rb2d;
[HideInInspector]
public Collider2D[] _c2d;
#endregion
#region References
[HideInInspector]
public Transform _myTransform;
[HideInInspector]
public GameObject _myObject;
/// <summary>
/// Объект, который появляется при уничтожении
/// </summary>
public GameObject _explodePrefab;
#endregion
#region Audio
public AudioSource _audioSource;
/// <summary>
/// Звуки, которые проигрываются при получении повреждения
/// </summary>
public AudioClip[] _hitSounds;
/// <summary>
/// Звуки, которые проигрываются при появлении объекта
/// </summary>
public AudioClip[] _awakeSounds;
/// <summary>
/// Звуки, которые воспроизводятся перед смертью
/// </summary>
public AudioClip[] _deadSounds;
#endregion
#region External Force Variables
/// <summary>
/// Внешние силы воздйствующие на объект
/// </summary>
[HideInInspector]
public Vector2 _ExternalForces = new Vector2();
/// <summary>
/// Текущий вектор скорости
/// </summary>
[HideInInspector]
public Vector2 _V = new Vector2();
/// <summary>
/// Текущий вектор силы гравитации
/// </summary>
[HideInInspector]
public Vector2 _G = new Vector2();
#endregion
public virtual void Awake()
{
Init();
}
public virtual void Start()
{
}
public virtual void Init()
{
_myTransform = this.transform;
_myObject = gameObject;
_rb2d = GetComponent<Rigidbody2D>();
_c2d = GetComponentsInChildren<Collider2D>();
_audioSource = GetComponent<AudioSource>();
PlayRandomSound(_awakeSounds);
BaseBody bb = GetComponent<BaseBody>();
_bodies.Add(bb);
}
/// <summary>
/// Уничтожение персонажа
/// </summary>
public virtual void Destroy()
{
_bodies.Remove(this);
for (int i = 0; i < _c2d.Length; i++)
{
_c2d[i].enabled = false;
}
float _t = PlayRandomSound(_deadSounds);
StartCoroutine(WaitAndDestroy(_t));
}
/// <summary>
/// Ждем некоторое время перед уничтожением
/// </summary>
/// <param name="waitTime">Время ожидания</param>
/// <returns></returns>
public IEnumerator WaitAndDestroy(float waitTime)
{
yield return new WaitForSeconds(waitTime);
if (_explodePrefab)
{
Instantiate(_explodePrefab, transform.position, Quaternion.identity);
}
Destroy(gameObject, _deafultTimeDelay);
}
/// <summary>
/// Проигрывание случайного звука
/// </summary>
/// <param name="audioClip">Массив звуков</param>
/// <returns>Длительность проигрываемого звука</returns>
public float PlayRandomSound(AudioClip[] audioClip)
{
float _t = 0;
if (audioClip.Length > 0)
{
int _i = UnityEngine.Random.Range(0, audioClip.Length - 1);
AudioClip _audioClip = audioClip[_i];
_t = _audioClip.length;
_audioSource.PlayOneShot(_audioClip);
}
return _t;
}
/// <summary>
/// Получение урона
/// </summary>
/// <param name="damage">Уровень урона</param>
public virtual void Damage(float damage)
{
PlayRandomSound(_hitSounds);
}
}
}Вроде описали все что надо, даже больше чем нужно (в рамках этой статьи). Теперь отнаследуем от него класс корабля Ship, который должен уметь двигаться и поворачивать:
SpaceShip.cs
using UnityEngine;
using System.Collections;
using System.Collections.Generic;
namespace Assets.Scripts.SpaceShooter.Bodies
{
public class Ship : BaseBody
{
public Vector2 _movement = new Vector2();
public Vector2 _target = new Vector2();
public float _rotation = 0f;
public void FixedUpdate()
{
float torque = ControlRotate(_rotation);
Vector2 force = ControlForce(_movement);
_rb2d.AddTorque(torque);
_rb2d.AddRelativeForce(force);
}
public float ControlRotate(Vector2 rotate)
{
float result = 0f;
return result;
}
public Vector2 ControlForce(Vector2 movement)
{
Vector2 result = new Vector2();
return result;
}
}
}Пока в нем нет ничего интересно, на текущий момент это просто класс-заглушка.
Также опишем базовый(абстрактный) класс для всех контроллеров ввода BaseInputController:
BaseInputController.cs
using UnityEngine;
using Assets.Scripts.SpaceShooter.Bodies;
namespace Assets.Scripts.SpaceShooter.InputController
{
public enum eSpriteRotation
{
Rigth = 0,
Up = -90,
Left = -180,
Down = -270
}
public abstract class BaseInputController : MonoBehaviour
{
public GameObject _agentObject;
public Ship _agentBody; // Ссылка на компонент логики корабля
public eSpriteRotation _spriteOrientation = eSpriteRotation.Up; //Это связано с нестандартной
// ориентации спрайта "вверх" вместо "вправо"
public abstract void ControlRotate(float dt);
public abstract void ControlForce(float dt);
public virtual void Start()
{
_agentObject = gameObject;
_agentBody = gameObject.GetComponent<Ship>();
}
public virtual void FixedUpdate()
{
float dt = Time.fixedDeltaTime;
ControlRotate(dt);
ControlForce(dt);
}
public virtual void Update()
{
//TO DO
}
}
}И наконец, класс контроллера игрока PlayerFigtherInput:
PlayerInput.cs
using UnityEngine;
using Assets.Scripts.SpaceShooter.Bodies;
namespace Assets.Scripts.SpaceShooter.InputController
{
public class PlayerFigtherInput : BaseInputController
{
public override void ControlRotate(float dt)
{
// Определяем позицию мыши относительно игрока
Vector3 worldPos = Input.mousePosition;
worldPos = Camera.main.ScreenToWorldPoint(worldPos);
// Сохраняем координаты указателя мыши
float dx = -this.transform.position.x + worldPos.x;
float dy = -this.transform.position.y + worldPos.y;
//Передаем направление
Vector2 target = new Vector2(dx, dy);
_agentBody._target = target;
//Вычисляем поворот в соответствии с нажатием клавиш
float targetAngle = Mathf.Atan2(dy, dx) * Mathf.Rad2Deg;
_agentBody._targetAngle = targetAngle + (float)_spriteOrientation;
}
public override void ControlForce(float dt)
{
//Передаем movement
_agentBody._movement = Input.GetAxis("Vertical") * Vector2.up
+ Input.GetAxis("Horizontal") * Vector2.right;
}
}
}Вроде бы закончили, теперь наконец можно перейти к тому, ради чего все это затевалось, т.е. ПИД-регуляторам (не забыли надеюсь?). Его реализация кажется простой до безобразия:
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace Assets.Scripts.Regulator
{
[System.Serializable] // Этот атрибут необходим для того что бы поля регулятора
// отображались в инспекторе и сериализовывались
public class SimplePID
{
public float Kp, Ki, Kd;
private float lastError;
private float P, I, D;
public SimplePID()
{
Kp = 1f;
Ki = 0;
Kd = 0.2f;
}
public SimplePID(float pFactor, float iFactor, float dFactor)
{
this.Kp = pFactor;
this.Ki = iFactor;
this.Kd = dFactor;
}
public float Update(float error, float dt)
{
P = error;
I += error * dt;
D = (error - lastError) / dt;
lastError = error;
float CO = P * Kp + I * Ki + D * Kd;
return CO;
}
}
}Значения коэффициентов по умолчанию возьмем с потолка: это будет тривиальный единичный коэффициент пропорционального закона управления Kp = 1, небольшое значение коэффициента для дифференциального закона управления Kd = 0.2, который должен устранить ожидаемые колебания и нулевое значение для Ki, которое выбрано потому, что в нашей программной модели нет никаких статичных ошибок (но вы всегда можете их внести, а потом героически побороться с помощью интегратора).
Теперь вернемся к нашему классу SpaceShip и попробуем заюзать наше творение в качестве регулятора поворота космического корабля в методе ControlRotate:
public float ControlRotate(Vector2 rotate)
{
float MV = 0f;
float dt = Time.fixedDeltaTime;
//Вычисляем ошибку
float angleError = Mathf.DeltaAngle(_myTransform.eulerAngles.z, targetAngle);
//Получаем корректирующее ускорение
MV = _angleController.Update(angleError, dt);
return MV;
}ПИД-регулятор будет осуществлять точное угловое позиционировая космического корабля только за счет крутящего момента. Все честно, физика и САУ, почти как в реальной жизни.
И без этих ваших Quaternion.Lerp
if (!_rb2d.freezeRotation)
rb2d.freezeRotation = true;
float deltaAngle = Mathf.DeltaAngle(_myTransform.eulerAngles.z, targetAngle);
float T = dt * Mathf.Abs( _rotationSpeed / deltaAngle);
// Трансформируем угол в вектор
Quaternion rot = Quaternion.Lerp(
_myTransform.rotation,
Quaternion.Euler(new Vector3(0, 0, targetAngle)),
T);
// Изменяем поворот объекта
_myTransform.rotation = rot;Получившейся исходный код Ship.cs под спойлером
using UnityEngine;
using Assets.Scripts.Regulator;
namespace Assets.Scripts.SpaceShooter.Bodies
{
public class Ship : BaseBody
{
public GameObject _flame;
public Vector2 _movement = new Vector2();
public Vector2 _target = new Vector2();
public float _targetAngle = 0f;
public float _angle = 0f;
[Header("PID")]
public SimplePID _angleController = new SimplePID();
public void FixedUpdate()
{
float torque = ControlRotate(_targetAngle);
Vector2 force = ControlForce(_movement);
_rb2d.AddTorque(torque);
_rb2d.AddRelativeForce(force);
}
public float ControlRotate(float rotate)
{
float MV = 0f;
float dt = Time.fixedDeltaTime;
_angle = _myTransform.eulerAngles.z;
//Вычисляем ошибку
float angleError = Mathf.DeltaAngle(_angle, rotate);
//Получаем корректирующее ускорение
MV = _angleController.Update(angleError, dt);
return MV;
}
public Vector2 ControlForce(Vector2 movement)
{
Vector2 MV = new Vector2();
//Кусок кода спецэффекта работающего двигателя ради
if (movement != Vector2.zero)
{
if (_flame != null)
{
_flame.SetActive(true);
}
}
else
{
if (_flame != null)
{
_flame.SetActive(false);
}
}
MV = movement;
return MV;
}
}
}
Все? Расходимся по домам?
WTF! Что происходит? Почему корабль поворачивается как-то странно? И почему он так резко отскакивает от других объектов? Неужели этот глупый ПИД-регулятор не работает?
Без паники! Давайте попробуем разобраться что происходит.
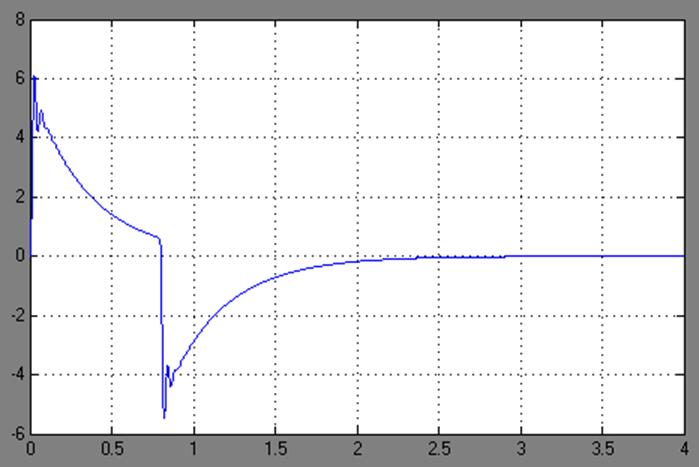
В момент получения нового значения SP, происходит резкий (ступенчатый) скачок рассогласования ошибки, которая, как мы помним, вычисляется вот так: соответственно происходит резкий скачок производной ошибки
, которую мы вычисляем в этой строчке кода:
D = (error - lastError) / dt;Можно, конечно, попробовать другие схемы дифференцирования, например, трехточечную, или пятиточечную, или… но все равно это не поможет. Ну вот не любят производные резких скачков — в таких точках функция не является дифференцируемой. Однако поэкспериментировать с разными схемами дифференцирования и интегрирования стоит, но потом и не в этой статье.
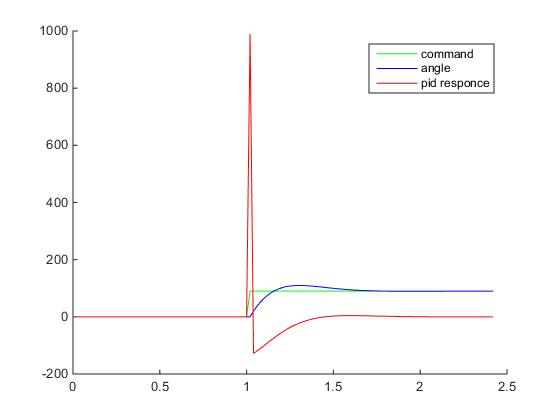
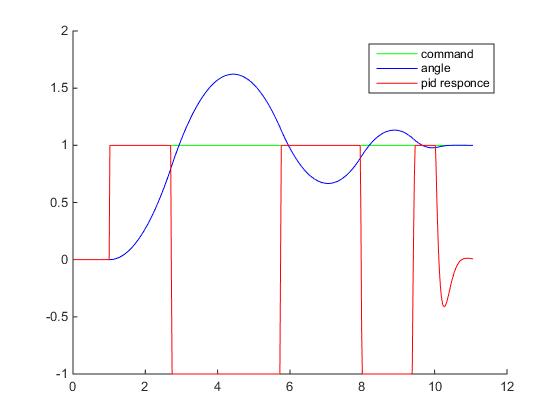
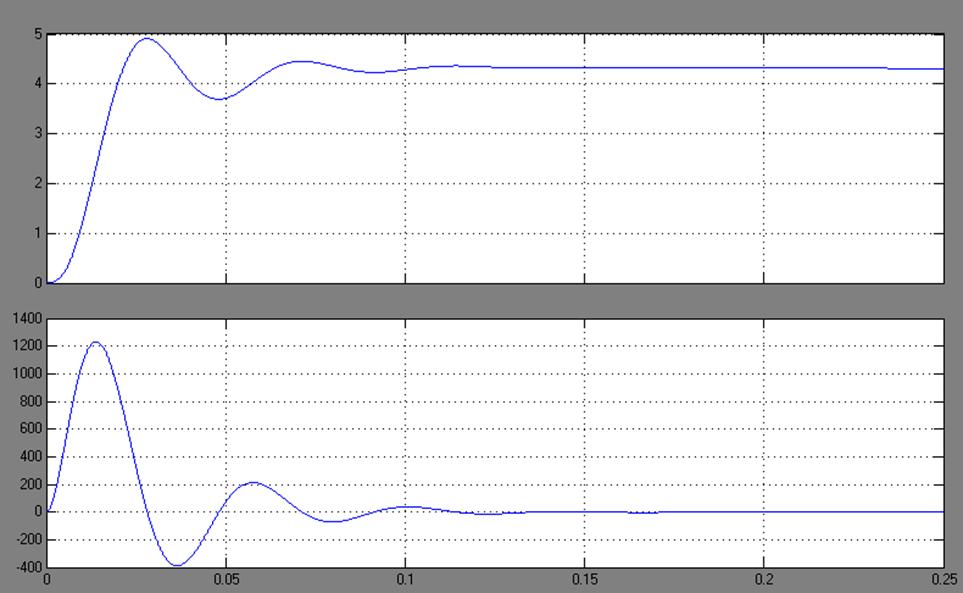
Думаю что настал момент построить графики переходного процесса: ступенчатое воздействие от S(t) = 0 в SP(t) = 90 градусов для тела массой в 1 кг, длинной плеча силы в 1 метр и шагом сетки дифференцирования 0.02 с — прям как в нашем примере на Unity3D (на самом деле не совсем, при построении этих графиков не учитывалось, что момент инерции зависит от геометрии твердого тела, поэтому переходный процесс будет немножко другой, но все же достаточно похожий для демонстрации). Все величены на грифике приведены в абсолютных значениях:
Хм, что здесь происходит? Куда улетел отклик ПИД-регулятора?
Поздравляю, мы только что столкнулись с таким явлением как «удар» (kick). Очевидно, что в момент времени, когда процесс еще PV = 0, а уставка уже SP = 90, то при численном дифференцировании получим значение производной порядка 4500, которое умножится на Kd=0.2 и сложится с пропорциональным теромом, так что на выходе мы получим значение углового ускорения 990, а это уже форменное надругательство над физической моделью Unity3D (угловые скорости будут достигать 18000 град/с… я думаю это предельное значение угловой скорости для RigidBody2D).
- Может стоит подобрать коэффициенты ручками, так чтобы скачок был не таким сильным?
- Нет! Самое лучше чего мы таким образом сможем добиться — небольшая амплитуда скачка производной, однако сам скачок как был так и останется, при этом можно докрутиться до полной неэффективности дифференциальной составляющей.
Впрочем можете поэкспериментировать.
Попытка номер два. Сатурация
Логично, что привод (в нашем случае виртуальные маневровые двигатели SpaceShip), не может отрабатывать сколько угодно большие значения которые может выдать наш безумный регулятор. Так что первое что мы сделаем — сатурируем выход регулятора:
public float ControlRotate(Vector2 rotate, float thrust)
{
float CO = 0f;
float MV = 0f;
float dt = Time.fixedDeltaTime;
//Вычисляем ошибку
float angleError = Mathf.DeltaAngle(_myTransform.eulerAngles.z, targetAngle);
//Получаем корректирующее ускорение
CO = _angleController.Update(angleError, dt);
//Сатурируем
MV = CO;
if (MV > thrust) MV = thrust;
if (MV< -thrust) MV = -thrust;
return MV;
}А очередной раз переписанный класс Ship полностью выглядит так
namespace Assets.Scripts.SpaceShooter.Bodies
{
public class Ship : BaseBody
{
public GameObject _flame;
public Vector2 _movement = new Vector2();
public Vector2 _target = new Vector2();
public float _targetAngle = 0f;
public float _angle = 0f;
public float _thrust = 1f;
[Header("PID")]
public SimplePID _angleController = new SimplePID(0.1f,0f,0.05f);
public void FixedUpdate()
{
_torque = ControlRotate(_targetAngle, _thrust);
_force = ControlForce(_movement);
_rb2d.AddTorque(_torque);
_rb2d.AddRelativeForce(_force);
}
public float ControlRotate(float targetAngle, float thrust)
{
float CO = 0f;
float MV = 0f;
float dt = Time.fixedDeltaTime;
//Вычисляем ошибку
float angleError = Mathf.DeltaAngle(_myTransform.eulerAngles.z, targetAngle);
//Получаем корректирующее ускорение
CO = _angleController.Update(angleError, dt);
//Сатурируем
MV = CO;
if (MV > thrust) MV = thrust;
if (MV< -thrust) MV = -thrust;
return MV;
}
public Vector2 ControlForce(Vector2 movement)
{
Vector2 MV = new Vector2();
if (movement != Vector2.zero)
{
if (_flame != null)
{
_flame.SetActive(true);
}
}
else
{
if (_flame != null)
{
_flame.SetActive(false);
}
}
MV = movement * _thrust;
return MV;
}
public void Update()
{
}
}
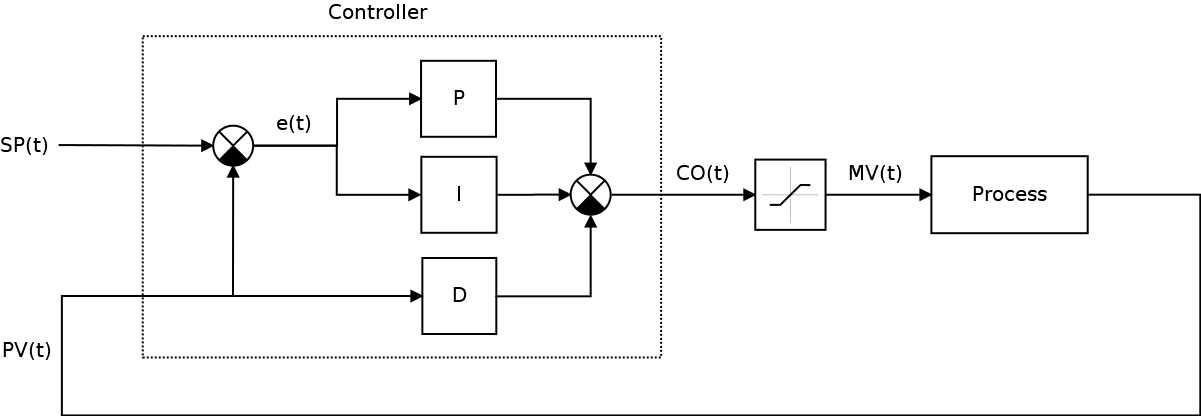
}Итоговая схема нашего САУ тогда станет уже вот такой
При этом уже становится понятно, что выход контроллера CO(t) немного не одно и тоже, что управляемая величина процесса MV(t).
Собственно с этого места можно уже добавлять новую игровую сущность — привод, через которую и будет осуществляться управление процессом, логика работы которой может быть более сложной, чем просто Mathf.Clamp(), например, можно ввести дискретизацию значений (дабы не перегружать игровую физику величинами идущими шестыми после запятой), мертвую зону (опять таки не имеет смысл перегружать физику сверхмалыми реакциями), ввести задержку в упраление и нелинейность (например, сигмоиду) привода, после чего посмотреть, что из этого получится.
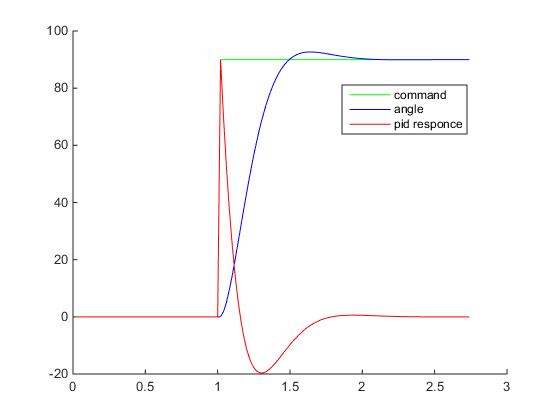
Запустив игру, мы обнаружим, что космический корабль стал наконец управляемым:
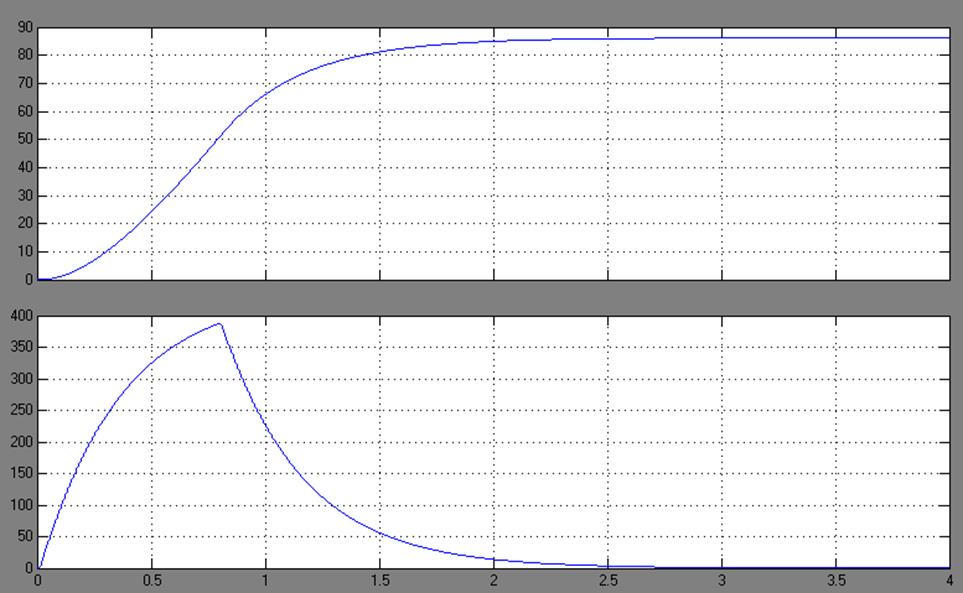
Если построить графики, то можно увидеть, что реакция контроллера стала уже вот такой:
Здесь уже используются нормированные величены, углы поделены на значение SP, а выход контроллера отнормирован относительно максимального значения на котором уже происходит сатурация.
Теперь на графике видно наличие ошибки перерегулирования (overshooting) и затухающие колебания. Уменьшая Kp и увеличивая Kd можно добиться уменьшения колебаний, но зато увеличится время реакции контроллера (скорость поворота корабля). И наоборот, увеличивая Kp и уменьшая Kd — можно добиться увеличения скорости реакции контроллера, но появятся паразитные колебания, которые при определенных (критических) значениях, перестанут быть затухающими.
Ниже приведена известна таблица влияния увеличения параметров ПИД-регулятора (как уменьшить шрифт, а то таблица безе переносов не лезет?):
А общий алгоритм ручной настройки ПИД-регулятора следующий:
- Подбираем пропорциональный коэффициенты при отключенных дифференциальных и интегральных звеньях до тех пор пока не начнутся автоколебания.
- Постепенно увеличивая дифференциальную составляющую избавляемся от автоколебаний
- Если наблюдается остаточная ошибка регулирования (смещение), то устраняем её за счет интегральной составляющей.
Каких-то общих значений параметров ПИД-регулятора нет: конкретные значения зависят исключительно от параметров процесса (его передаточной характеристики): ПИД-регулятор отлично работающий с одним объектом управления окажется неработоспособным с другим. Более того, коэффициенты при пропорциональной, интегральной и дифференциальной составляющих еще и взаимозависимы.
В общем не будем о грустном, дальше нас ждет самое интересное…
Попытка номер три. Еще раз производные
Приделав костыль в виде ограничения значений выхода контроллера мы так и не решили самую главную проблему нашего регулятора — дифференциальная составляющая плохо себя чувствует при ступенчатом изменении ошибки на входе регуляторе. На самом деле есть множество других костылей, например, в момент скачкообразного изменения SP «отключать» дифференциальную составляющую или же поставить фильтры нижних частот между SP(t) и операцией за счет которого будет происходить плавное нарастание ошибки, а можно совсем развернуться и впендюрить самый настоящий фильтр Калмана для сглаживания входных данных. В общем костылей много, и добавить наблюдателя конечно хотелось бы, но не в этот раз.
Поэтому снова вернемся к производной ошибки рассогласования и внимательно на неё посмотрим:
Ничего не заметили? Если хорошенько присмотреться, то можно обнаружить, что вообще-то SP(t), не меняется во времени (за исключением моментов ступенчатого изменения, когда регулятор получает новую команду), т.е. её производная равна нулю:
тогда
Иными словами, вместо производной ошибки, которая дифференцируема не везде мы можем использовать производную от процесса, который в мире классической механики как правило непрерывен и дифференцируем везде, а схема нашей САУ уже приобретет следующий вид:
Модифицируем код регулятора:
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace Assets.Scripts.Regulator
{
[System.Serializable]
public class SimplePID
{
public float Kp, Ki, Kd;
private float P, I, D;
private float lastPV = 0f;
public SimplePID()
{
Kp = 1f;
Ki = 0f;
Kd = 0.2f;
}
public SimplePID(float pFactor, float iFactor, float dFactor)
{
this.Kp = pFactor;
this.Ki = iFactor;
this.Kd = dFactor;
}
public float Update(float error, float PV, float dt)
{
P = error;
I += error * dt;
D = -(PV - lastPV) / dt;
lastPV = PV;
float CO = Kp * P + Ki * I + Kd * D;
return CO;
}
}
}И немного изменим метод ControlRotate:
public float ControlRotate(Vector2 rotate, float thrust)
{
float CO = 0f;
float MV = 0f;
float dt = Time.fixedDeltaTime;
//Вычисляем ошибку
float angleError = Mathf.DeltaAngle(_myTransform.eulerAngles.z, targetAngle);
//Получаем корректирующее ускорение
CO = _angleController.Update(angleError, _myTransform.eulerAngles.z, dt);
//Сатурируем
MV = CO;
if (CO > thrust) MV = thrust;
if (CO < -thrust) MV = -thrust;
return MV;
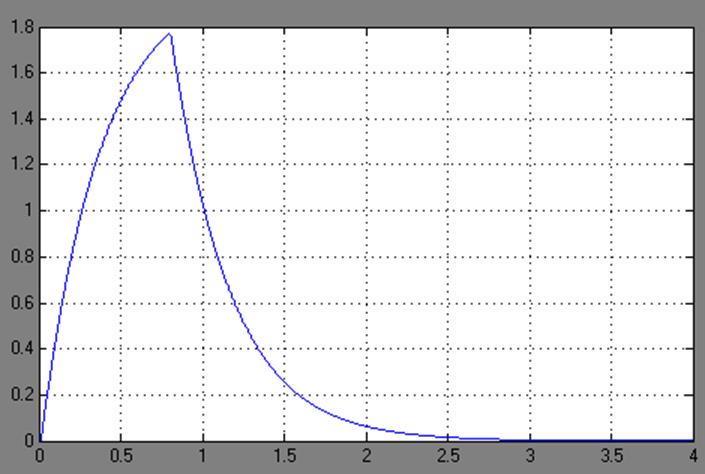
}И-и-и-и… если запустить игру, то обнаружиться, что на самом деле ничего ничего не изменилось с последней попытки, что и требовалось доказать. Однако, если убрать сатурацию, то график реакции регулятора будет выглядеть вот так:
Скачок CO(t) по прежнему присутствует, однако он уже не такой большой как был в самом начале, а самое главное — он стал предсказуемым, т.к. обеспечивается исключительно пропорциональной составляющей, и ограничен максимально возможной ошибкой рассогласования и пропорциональным коэффициентом ПИД-регулятора (а это уже намекает на то, что Kp имеет смысл выбрать все же меньше единицы, например, 1/90f), но не зависит от шага сетки дифференцирования (т.е. dt). В общем, я настоятельно рекомендую использовать именно производную процесса, а не ошибки.
Думаю теперь никого не удивит, но таким же макаром можно заменить на
, однако останавливаться на этом мы не будем, можете сами поэкспериментировать и рассказать в комментариях, что из этого получилось (самому интересно)
Попытка номер четыре. Альтернативные реализации ПИД-регулятор
Помимо описанного выше идеального представления ПИД-регулятора, на практике часто применяется стандартная форма, без коэффициентов Ki и Kd, вместо которых используются временные постоянные.
Такой подход связан с тем, что ряд методик настройки ПИД-регулятора основан на частотных характеристиках ПИД-регулятора и процесса. Собственно вся ТАУ и крутится вокруг частотных характеристик процессов, поэтому для желающих углубиться, и, внезапно, столкнувшихся с альтернативной номенклатурой, приведу пример т.н. стандартной формы ПИД-регулятора:
где, — постоянная дифференцирования, влияющая на прогнозирование состояния системы регулятором,
— постоянная интегрирования, влияющая на интервал усреднения ошибки интегральным звеном.
Основные принципы настройки ПИД-регулятора в стандартной форме аналогичны идеализированному ПИД-регулятору:
- увеличение пропорционального коэффициента увеличивает быстродействие и снижает запас устойчивости;
- с уменьшением интегральной составляющей ошибка регулирования с течением времени уменьшается быстрее;
- уменьшение постоянной интегрирования уменьшает запас устойчивости;
- увеличение дифференциальной составляющей увеличивает запас устойчивости и быстродействие
Исходный код стандартной формы, вы можете найти под спойлером
namespace Assets.Scripts.Regulator
{
[System.Serializable]
public class StandartPID
{
public float Kp, Ti, Td;
public float error, CO;
public float P, I, D;
private float lastPV = 0f;
public StandartPID()
{
Kp = 0.1f;
Ti = 10000f;
Td = 0.5f;
bias = 0f;
}
public StandartPID(float Kp, float Ti, float Td)
{
this.Kp = Kp;
this.Ti = Ti;
this.Td = Td;
}
public float Update(float error, float PV, float dt)
{
this.error = error;
P = error;
I += (1 / Ti) * error * dt;
D = -Td * (PV - lastPV) / dt;
CO = Kp * (P + I + D);
lastPV = PV;
return CO;
}
}
}В качестве значений по умолчанию, выбраны Kp = 0.01, Ti = 10000, Td = 0.5 — при таких значениях корабль поворачивается достаточно быстро и обладает некоторым запасом устойчивости.
Помимо такой формы ПИД-регулятора, часто используется т.н. реккурентная форма:
Не будем на ней останавливаться, т.к. она актуальна прежде всего для хардверных программистов, работающих с FPGA и микроконтроллерами, где такая реализация значительно удобнее и эффективнее. В нашем же случае — давайте что-нибудь сваям на Unity3D — это просто еще одна реализация ПИД-контроллера, которая ни чем не лучше других и даже менее понятная, так что еще раз дружно порадуемся как хорошо программировать в уютненьком C#, а не в жутком и страшном VHDL, например.
Вместо заключения. Куда бы еще присобачить ПИД-регулятор
Теперь попробуем немного усложнить управление корабля используя двухконтурное управление: один ПИД-регулятор, уже знакомый нам _angleController, отвечает по прежнему за угловое позиционирование, а вот второй — новый, _angularVelocityController — контролирует скорость поворота:
public float ControlRotate(float targetAngle, float thrust)
{
float CO = 0f;
float MV = 0f;
float dt = Time.fixedDeltaTime;
_angle = _myTransform.eulerAngles.z;
//Контроллер угла поворота
float angleError = Mathf.DeltaAngle(_angle, targetAngle);
float torqueCorrectionForAngle =
_angleController.Update(angleError, _angle, dt);
//Контроллер стабилизации скорости
float angularVelocityError = -_rb2d.angularVelocity;
float torqueCorrectionForAngularVelocity =
_angularVelocityController.Update(angularVelocityError, -angularVelocityError, dt);
//Суммарный выход контроллера
CO = torqueCorrectionForAngle + torqueCorrectionForAngularVelocity;
//Дискретизируем с шагом 100
CO = Mathf.Round(100f * CO) / 100f;
//Сатурируем
MV = CO;
if (CO > thrust) MV = thrust;
if (CO < -thrust) MV = -thrust;
return MV;
}Назначение второго регулятора — гашение избыточных угловых скоростей, за счет изменения крутящего момента — это сродни наличию углового трения, которое мы отключили еще при создании игрового объекта. Такая схема управления [возможно] позволит получить более стабильное поведение корабля, и даже обойтись только пропорциональными коэффициентами управления — второй регулятор будет гасить все колебания, выполняя функцию, аналогичную дифференциальной составляющей первого регулятора.
Помимо этого, добавим новый класс ввода игрока — PlayerInputCorvette, в котором повороты буду осуществляться уже за счет нажатия клавиш «вправо-влево», а целеуказание с помощью мыши мы оставим для чего-нибудь более полезного, например, для управления турелью. Заодно у нас теперь появился такой параметр как _turnRate — отвечающий за скорость/отзывчивость поворота (не понятно только куда его поместить лучше в InputCOntroller или все же Ship).
public class PlayerCorvetteInput : BaseInputController
{
public float _turnSpeed = 90f;
public override void ControlRotate()
{
// Находим указатель мыши
Vector3 worldPos = Input.mousePosition;
worldPos = Camera.main.ScreenToWorldPoint(worldPos);
// Сохраняем относительные координаты указателя мыши
float dx = -this.transform.position.x + worldPos.x;
float dy = -this.transform.position.y + worldPos.y;
//Передаем направление указателя мыши
Vector2 target = new Vector2(dx, dy);
_agentBody._target = target;
//Вычисляем поворот в соответствии с нажатием клавиш
_agentBody._rotation -= Input.GetAxis("Horizontal") * _turnSpeed * Time.deltaTime;
}
public override void ControlForce()
{
//Передаем movement
_agentBody._movement = Input.GetAxis("Vertical") * Vector2.up;
}
}Также для наглядности накидаем на коленках скрипт для отображения отладочной информации
namespace Assets.Scripts.SpaceShooter.UI
{
[RequireComponent(typeof(Ship))]
[RequireComponent(typeof(BaseInputController))]
public class Debugger : MonoBehaviour
{
Ship _ship;
BaseInputController _controller;
List<SimplePID> _pids = new List<SimplePID>();
List<string> _names = new List<string>();
Vector2 _orientation = new Vector2();
// Use this for initialization
void Start()
{
_ship = GetComponent<Ship>();
_controller = GetComponent<BaseInputController>();
_pids.Add(_ship._angleController);
_names.Add("Angle controller");
_pids.Add(_ship._angularVelocityController);
_names.Add("Angular velocity controller");
}
// Update is called once per frame
void Update()
{
DrawDebug();
}
Vector3 GetDiretion(eSpriteRotation spriteRotation)
{
switch (_controller._spriteOrientation)
{
case eSpriteRotation.Rigth:
return transform.right;
case eSpriteRotation.Up:
return transform.up;
case eSpriteRotation.Left:
return -transform.right;
case eSpriteRotation.Down:
return -transform.up;
}
return Vector3.zero;
}
void DrawDebug()
{
//Направление поворота
Vector3 vectorToTarget = transform.position
+ 5f * new Vector3(-Mathf.Sin(_ship._targetAngle * Mathf.Deg2Rad),
Mathf.Cos(_ship._targetAngle * Mathf.Deg2Rad), 0f);
// Текущее направление
Vector3 heading = transform.position + 4f * GetDiretion(_controller._spriteOrientation);
//Угловое ускорение
Vector3 torque = heading - transform.right * _ship._Torque;
Debug.DrawLine(transform.position, vectorToTarget, Color.white);
Debug.DrawLine(transform.position, heading, Color.green);
Debug.DrawLine(heading, torque, Color.red);
}
void OnGUI()
{
float x0 = 10;
float y0 = 100;
float dx = 200;
float dy = 40;
float SliderKpMax = 1;
float SliderKpMin = 0;
float SliderKiMax = .5f;
float SliderKiMin = -.5f;
float SliderKdMax = .5f;
float SliderKdMin = 0;
int i = 0;
foreach (SimplePID pid in _pids)
{
y0 += 2 * dy;
GUI.Box(new Rect(25 + x0, 5 + y0, dx, dy), "");
pid.Kp = GUI.HorizontalSlider(new Rect(25 + x0, 5 + y0, 200, 10),
pid.Kp,
SliderKpMin,
SliderKpMax);
pid.Ki = GUI.HorizontalSlider(new Rect(25 + x0, 20 + y0, 200, 10),
pid.Ki,
SliderKiMin,
SliderKiMax);
pid.Kd = GUI.HorizontalSlider(new Rect(25 + x0, 35 + y0, 200, 10),
pid.Kd,
SliderKdMin,
SliderKdMax);
GUIStyle style1 = new GUIStyle();
style1.alignment = TextAnchor.MiddleRight;
style1.fontStyle = FontStyle.Bold;
style1.normal.textColor = Color.yellow;
style1.fontSize = 9;
GUI.Label(new Rect(0 + x0, 5 + y0, 20, 10), "Kp", style1);
GUI.Label(new Rect(0 + x0, 20 + y0, 20, 10), "Ki", style1);
GUI.Label(new Rect(0 + x0, 35 + y0, 20, 10), "Kd", style1);
GUIStyle style2 = new GUIStyle();
style2.alignment = TextAnchor.MiddleLeft;
style2.fontStyle = FontStyle.Bold;
style2.normal.textColor = Color.yellow;
style2.fontSize = 9;
GUI.TextField(new Rect(235 + x0, 5 + y0, 60, 10), pid.Kp.ToString(), style2);
GUI.TextField(new Rect(235 + x0, 20 + y0, 60, 10), pid.Ki.ToString(), style2);
GUI.TextField(new Rect(235 + x0, 35 + y0, 60, 10), pid.Kd.ToString(), style2);
GUI.Label(new Rect(0 + x0, -8 + y0, 200, 10), _names[i++], style2);
}
}
}
}Класс Ship также претерпел необратимые мутации и теперь должен выглядеть вот так:
namespace Assets.Scripts.SpaceShooter.Bodies
{
public class Ship : BaseBody
{
public GameObject _flame;
public Vector2 _movement = new Vector2();
public Vector2 _target = new Vector2();
public float _targetAngle = 0f;
public float _angle = 0f;
public float _thrust = 1f;
[Header("PID")]
public SimplePID _angleController = new SimplePID(0.1f,0f,0.05f);
public SimplePID _angularVelocityController = new SimplePID(0f,0f,0f);
private float _torque = 0f;
public float _Torque
{
get
{
return _torque;
}
}
private Vector2 _force = new Vector2();
public Vector2 _Force
{
get
{
return _force;
}
}
public void FixedUpdate()
{
_torque = ControlRotate(_targetAngle, _thrust);
_force = ControlForce(_movement, _thrust);
_rb2d.AddTorque(_torque);
_rb2d.AddRelativeForce(_force);
}
public float ControlRotate(float targetAngle, float thrust)
{
float CO = 0f;
float MV = 0f;
float dt = Time.fixedDeltaTime;
_angle = _myTransform.eulerAngles.z;
//Контроллер угла поворота
float angleError = Mathf.DeltaAngle(_angle, targetAngle);
float torqueCorrectionForAngle =
_angleController.Update(angleError, _angle, dt);
//Контроллер стабилизации скорости
float angularVelocityError = -_rb2d.angularVelocity;
float torqueCorrectionForAngularVelocity =
_angularVelocityController.Update(angularVelocityError, -angularVelocityError, dt);
//Суммарный выход контроллера
CO = torqueCorrectionForAngle + torqueCorrectionForAngularVelocity;
//Дискретизируем с шагом 100
CO = Mathf.Round(100f * CO) / 100f;
//Сатурируем
MV = CO;
if (CO > thrust) MV = thrust;
if (CO < -thrust) MV = -thrust;
return MV;
}
public Vector2 ControlForce(Vector2 movement, float thrust)
{
Vector2 MV = new Vector2();
if (movement != Vector2.zero)
{
if (_flame != null)
{
_flame.SetActive(true);
}
}
else
{
if (_flame != null)
{
_flame.SetActive(false);
}
}
MV = movement * thrust;
return MV;
}
public void Update()
{
}
}
}А вот, собственно заключительное видео того, что должно получиться:
К сожалению получилось охватить не все, что хотелось бы, в частности почти не затронут вопрос настройки ПИД-регулятора и практически не освящена интегральная составляющая — фактически приведен пример только для ПД-регулятора. Собственно изначально планировалось несколько больше примеров (круиз-контроль, вращение турели и компенсация вращательного момента), но статья итак уже разбухла, да и вообще:
Немного ссылок
- Годная статья на английской вики
- PID tutorial
- ПИД-регуляторы: вопросы реализации. Часть 1
- ПИД-регуляторы: вопросы реализации. Часть 2
- PID Without a PhD
- PID Without a PhD. Перевод
- Derivative Action and PID Control
- Control System Lab: PID
- ПИД-регулятор своими руками
- Корректная реализация разностной схемы ПИД регулятора
- Программируем квадрокоптер на Arduino (часть 1)
- Виртуальный квадрокоптер на Unity + OpenCV (Часть 1)
- Поляков К.Ю. Теория автоматического управления для чайников
- PID control system analysis, design, and technology
- Aidan O’Dwyer. Handbook of PI and PID Controller Tuning Rules (3rd ed.)
- PID process control, a “Cruise Control” example
- https://www.mathworks.com/discovery/pid-control.html
- http://scilab.ninja/study-modules/scilab-control-engineering-basics/module-4-pid-control/
- https://sourceforge.net/p/octave/control/ci/default/tree/inst/optiPID.m
Еще немного ссылок на другие примеры
http://luminaryapps.com/blog/use-a-pid-loop-to-control-unity-game-objects/
http://www.habrador.com/tutorials/pid-controller/3-stabilize-quadcopter/
https://www.gamedev.net/articles/programming/math-and-physics/pid-control-of-physics-bodies-r3885/
https://ksp-kos.github.io/KOS/tutorials/pidloops.html
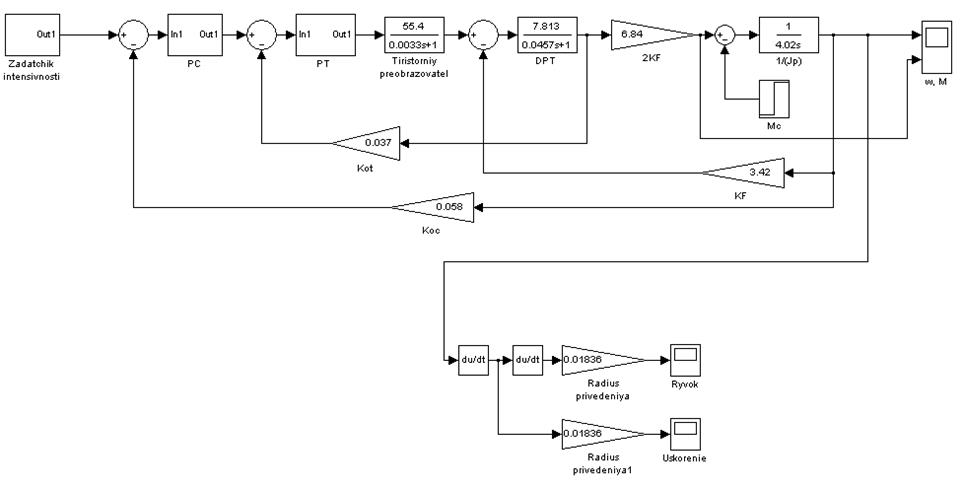
2.3. Автоматическое управление угловой скоростью и током якоря дпт нв в замкнутых системах электропривода
2.3.1. Регулирование угловой скорости в системе УП-ДПТ НВ с отрицательной обратной связью по скорости и отсечкой по току якоря
Как отмечалось в разделе выше, для обеспечения большего диапазона регулирования скорости целесообразно осуществляет регулирование wд изменением напряжения на якоре. В простейшей схеме (см. рис. 2.16) диапазон регулирования wд ограничен падением скорости под нагрузкой. Этот недостаток устраняется использованием замкнутых систем с отрицательной обратной связью по угловой скорости. Функциональная схема такой системы приведена на рис. 2.23. Она содержит двигатель М, выходной величиной которого является угловая скорость wд; управляемый преобразователь УП, создающий регулирующее воздействие Uя на двигатель; усилитель У, на входе которого сравниваются
 |
напряжение Uзд и напряжение обратной связи Uос. Напряжение Uзд создается задатчиком скорости (ЗС).
В качестве задатчика обратной связи используется тахогенератор BR, напряжение на выходе которого Uос пропорционально wд.
На выходе узла сравнение сигналов (на схеме узел показан в виде окружности) формируется напряжение ошибки

Как известно из теории автоматического управления, в замкнутой системе обеспечивается стабилизация регулируемой переменной – в данном случае wд.
Рекомендуемые материалы
Напомним, как протекает этот процесс. Если, например, под действием нагрузки wд начинает снижаться, то уменьшается Uос, а напряжение Ud, в соответствии с выражением (2.30), начинает увеличиваться. При этом возрастает напряжение на выходе усилителя Uу и якоре двигателя Uя. В результате угловая скорость стремится к заданному значению. Несложно убедиться, что в случае возрастания wд, действие обратной связи приведет к снижению Uя, и угловая скорость вновь будет стремиться к заданной.
 |
Таким образом в замкнутой системе удается получить механические характеристики близкие к абсолютно жестким (см. рис. 2.24 участок характеристики для 
Упрощенная принципиальная схема рассматриваемой системы приведена на рис. 2.25. Датчиком скорости в схеме является тахогенератор BR – машина постоянного тока с возбуждением от постоянных магнитов, вал которой механически соединен с валом двигателя М. Машина BR работает в режиме генератора, и ее ЭДС – напряжение обратной связи Uос, в соответствии с уравнением (2.13), пропорционально wд.
Сравнение электрических сигналов в современных схемах осуществляется на входе операционного усилителя DА. На его инвертирующий вход через резистор R1 подается напряжение задания Uзд, снимаемое с потенциометра RP (задатчика скорости), а через R2 напряжение Uос.
На входе усилителя происходит сравнение (вычитание) этих сигналов в соответствии с (2.30), а напряжение на выходе усилителя

где Ку – коэффициент усиления усилителя.
В цепь обратной связи операционного усилителя включен резистор R3, определяющий значение Ку.
Рассмотренные узлы и элементы схемы обеспечивают ее работу в режиме стабилизации скорости. Однако для нормальной работы электропривода этого недостаточно. Действительно, если произойдет, например, поломка механизма, порождающая возрастание момента статического сопротивления, то соответственно, будут нарастать ток якоря и момент двигателя. Недопустимое нарастание тока якоря возникает также при пуске двигателя и других переходных режимах.
Для исключения подобных ситуаций схема должна быть дополнена узлом ограничения тока якоря. Один из возможных вариантов реализации этого узла показан на рис. 2.25 (его также называют узлом токовой отсечки). Он включает датчик тока якоря – шунт RS, включенный в якорную цепь и стабилитроны VD1, VD2. Сигнал Uост с шунта RS может поступать на вход операционного усилителя через VD1, VD2 и резистор R4.
 |
Рассмотрим работу схемы.
При проектировании схемы задаются значением тока отсечки Iотс . С учетом допустимой кратковременной перегрузки двигателя его обычно принимают Iотс=(2…2,5)Iном. Напряжение стабилизации стабилитронов выбирают

Тогда при токе якоря 



Если же ток якоря превысит ток отсечки 


Схема переходит в режим стабилизации тока якоря (2-ой участок на рис. 2.24). При возрастании тока Iя увеличивается напряжение Uост, а сигнал ошибки Ud уменьшается. Это ведет к снижению напряжения на выходе усилителя Uу, уменьшается также Uя и wд. В итоге двигатель останавливается.
В реверсивном электроприводе полярность напряжения на шунте изменяется, поэтому необходимо использовать 2 стабилитрона, включенных встречно.
Как следует из изложенного, в схеме для ограничения тока якоря используется отрицательная обратная связь по току якоря. В отличие от обратной связи по скорости, связь по току задержанная – она вступает в действие только тогда, когда ток якоря превышает ток отсечки.
Узел токовой отсечки обеспечивает ограничение тока якоря также в переходных режимах. Например, при пуске двигателя в начальный момент сигнал тахогенератора Uос = 0, а сигнал ошибки Ud, как следует из (2.31), значительно превышает установившееся значение. Поэтому напряжения Uу и Uя начинают интенсивно нарастать.
Поскольку wд и ЭДС двигателя пока малы, ток якоря резко возрастает, и вступает в действие токовая отсечка. Следовательно, разгон двигателя идет при ограниченном значении тока (на рис. 2.24 процесс изменения Iя при пуске условно показан стрелками).
По мере разгона двигателя wд , ЭДС двигателя и сигнал обратной связи по скорости Uос возрастают, а сигнал Ud уменьшается. При подходе к заданной скорости ток якоря начинает спадать, и система переходит в режим стабилизации заданного значения скорости (например, wв на рис. 2.24).
Таким образом, задержанная отрицательная обратная связь в электроприводе обеспечивает ограничение тока (момента) двигателя в переходных режимах и в ситуациях, связанных с недопустимым возрастанием момента сопротивления производственного механизма.
2.3.2. Уравнение статики системы УП-ДПТ НВ
с отрицательной обратной связью по угловой скорости
Важнейшим показателем качества работы электропривода в установившихся режимах является значение статической ошибки в поддержании скорости. Статическая ошибка возникает из-за изменения нагрузки, отклонений сетевого напряжения, дрейфа нуля усилителя и других возмущений. Наибольший «вклад» в величину статической ошибки, во многих случаях, вносит изменение нагрузки. Как показано выше, использование отрицательной обратной связи по скорости позволяет уменьшить статическую ошибку. Получим количественные соотношения для оценки значения статической ошибки Dwд, вызванной изменением нагрузки, и выясним за счет чего можно обеспечить требуемую точность поддержания угловой скорости.
Для анализа статической точности систем, как известно из теории автоматического управления, целесообразно использовать алгоритмическую (структурную) схему системы. Алгоритмическая схема системы с отрицательной обратной связью по угловой скорости показана на рис. 2.26.
 |
Свойства отдельных звеньев отражены на ней соответствующими коэффициентами передачи: Ку – усилителя, Куп – управляемого преобразователя, Кд – двигателя, КBR – тахогенератора. Падение напряжения в якорной цепи двигателя и управляемого преобразователя при номинальном токе Iном учтено помехой нагрузки

где Rя, Rуп – сопротивление якорной цепи двигателя и выходное сопротивление УП.
Запишем уравнение для разомкнутой системы (размыкание системы по цепи обратной связи условно показано на рис. 2.26 волнистыми линиями). На основе принципа суперпозиции сигнал на выходе системы можно представить в виде двух составляющих. Одна из них зависит от Uзд, а вторая от hн:

Первая составляющая представляет собой угловую скорость 

Сравнивая выражения (2.23) и (2.12), легко заметить, что они отличаются только учетом 
Уравнение для замкнутой системы записывается из аналогичных соображений, необходимо только учесть, что в замкнутой системе на вход поступает сигнал ошибки 
 |

Напряжение обратной связи, как следует из алгоритмической схемы, можно определить через выходной сигнал системы
тогда

Подставив последнее выражение для 

Первый член в этом выражении, так же, как в (2.33), это угловая скорость двигателя 


С учетом этого понятия и выражения (2.37) для статической ошибки разомкнутой системы статическую ошибку замкнутой системы можно представить в виде

Аналогичное соотношение несложно получить и для относительных статических ошибок

Из уравнений (2.38), (2.39) следует, что абсолютная и относительная статические ошибки от нагрузки в замкнутой системе уменьшаются в (1+Кр) раз по сравнению с разомкнутой.
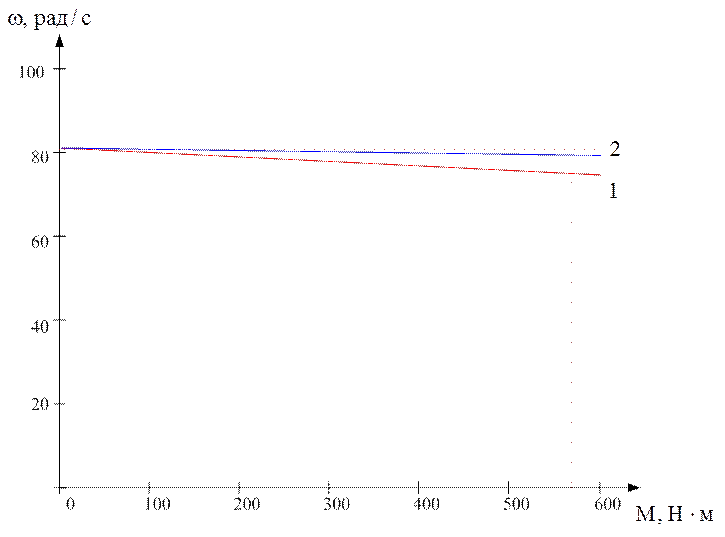
Очевидно, что для уменьшения статических ошибок 




В современных приводах, выполненных в виде замкнутых систем с интегральными регуляторами, удается на нижней скорости обеспечить относительную ошибку не более 10…15% при D=1000…10000.
Если, например, имеется электропривод с диапазоном регулирования D = 10000 и наибольшей (верхней) частотой вращения nВ = 1000об/мин, соответственно, 
При этом, чтобы относительная ошибка не превышала 10%, абсолютное падение скорости должно быть не больше
Dnн = 10%×nН = 0,01об/мин;

Отсюда видно насколько жесткие требования обеспечиваются в современных широкорегулируемых электроприводах.
2.3.3. Регулирование угловой скорости в системе УП-ДПТ НВ
с отрицательной обратной связью по напряжению
 |
Упрощенная принципиальная схема рассматриваемой системы показана на рис. 2.28 (узел токовой отсечки на схеме не показан, он может быть выполнен так же, как в схеме по рис. 2.25).
Рис. 2.28
Схема отличается от рассмотренной выше с обратной связью по скорости (см. рис. 2.25) только тем, что в ней сигнал обратной связи снимается с потенциометра RP2 и пропорционален напряжению на якоре Uя. Конструктивно система несколько проще предыдущей за счет отсутствия тахогенератора. Регулирование скорости здесь так же осуществляется изменением напряжения на якоре.
На входе системы (см. также рис. 2.29) сравниваются сигнал задания Uзд и сигнал обратной связи по напряжению на якоре Uосн. Сигнал ошибки

Регулируемой переменной в схеме является напряжение на якоре Uя. Процесс стабилизации Uя протекает следующим образом. Если, например, нагрузка на двигателе возрастает, то ток якоря увеличивается и возрастает падение напряжения в преобразователе. Это ведет к снижению напряжения на выходе УП, поступающего на якорь двигателя,

где Еуп – ЭДС преобразователя;
Rуп – выходное сопротивление преобразователя.
 |
Соответственно, снижается сигнал обратной связи Uосн, а сигнал ошибки Ud (см. уравнение (2.40)) увеличивается. Что, в свою очередь, приводит к возрастанию напряжения на выходе усилителя и напряжения Uя. Обратите внимание, что в схеме стабилизируется не скорость двигателя 
К этому же выводу можно прийти и анализируя алгоритмическую схему системы, показанную на рис. 2.29. На этой схеме, в отличие от рис. 2.26, отдельно показаны помеха нагрузки преобразователя 


Произведение коэффициентов КуКупКос=Крн – представляет собой коэффициент усиления разомкнутой системы со связью по напряжению. Первый член в уравнении (2.41) – угловая скорость двигателя на холостом ходу; второй – падение скорости от нагрузки преобразователя; третий – падение скорости от нагрузки двигателя.
Очевидно, что выбрав Крн®

В связи с этим в системе с отрицательной обратной связью по напряжению не удается обеспечить высокую точность стабилизации скорости. Такие системы применяются при нежестких требованиях к допустимой статической ошибке и небольшом диапазоне регулирования (D =5…10).
2.3.4 Регуляторы в системах ЭП
Как уже отмечалось, современные АЭП выполняются в виде замкнутых систем автоматического управления. При этом возникает задача обеспечения устойчивости замкнутой системы и требуемых показателей качества регулирования. Эти задачи решаются введением в систему операционных усилителей, охваченных определенными видами обратных связей. Такие усилители в системах автоматического регулирования принято называть регуляторами. Кроме того, на входе усилителя удобно осуществлять операцию сравнивания электрических сигналов. Схема суммирующего усилителя приведена на рис. 2.30. На инвертирующий вход (на схеме помечен окружностью) DА усилителя подается: через резистор R1 – сигнал задания Uзд; через резистор R2 – сигнал отрицательной обратной связи Uос (например, сигнал обратной связи по скорости двигателя). Известно, что динамические свойства операционного усилителя, охваченного обратной связью, приближенно можно описать передаточной функцией

где 
Для рассматриваемой схемы 

Напряжение на выходе усилителя
Uвых = UздKу – UосKу = (Uзд – Uос)Kу.
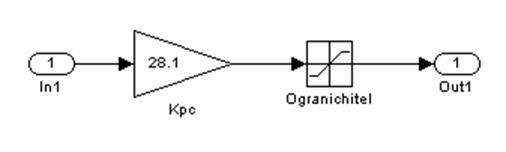
Последнему выражению соответствует алгоритмическая схема, представленная на рис. 2.31. Из нее следует, что рассматриваемая схема обеспечивает сравнение (вычитание) напряжений и усиление сигнала ошибки Uδ=Uзд – Uос. Приведенную схему (см. рис. 2.30) называют пропорциональным регулятором, или сокращенно П-регулятором.
 |
 |
Для уменьшения статистической ошибки, как отмечалось выше, необходимо вводить в систему интегрирующее звено. Схема интегрального регулятора (И-регулятора) приведена на рис. 2.32 (для простоты считаем здесь и далее R1=R2). На основании выражения (2.42) несложно получить передаточную функцию регулятора

где Ти – постоянная времени интегрирующего преобразования.
Передаточная функция соответствует интегрирующему (астатическому) звену.
При скачкообразном изменении сигнала Ud напряжение Uвых линейно нарастает (см. рис. 2.33). Учитывая свойства И-регулятора «накапливать» входной сигнал, можно дать следующие пояснение особенностям работы астатической системы. Если в системе появляется сигнал ошибки, то напряжение на выходе регулятора начинает изменяться и, соответственно, изменяется воздействие на двигатель. Этот процесс продолжается до тех пор, пока сигнал ошибки не будет сведен к нулю, т.е. пока не будет достигнуто равенство
Uос = Uзд.

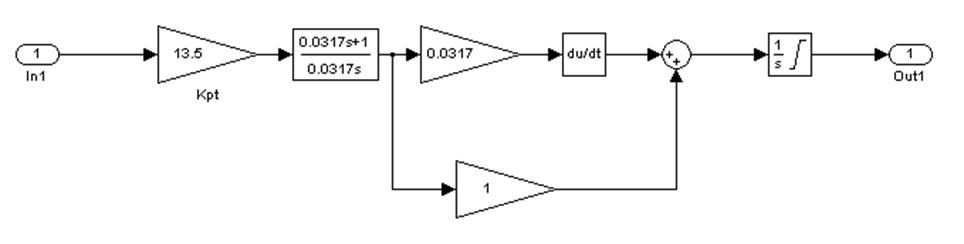
Алгоритмическая схема регулятора приведена на рис. 2.34. И-регулятор обеспечивает сравнение сигналов Uзд и Uос, а его выходное напряжение пропорционально интегралу от сигнала ошибки.
 |
 |
 |
Схема пропорционально-интегрального регулятора (ПИ-регулятора) приведена на рис. 2.35. В цепь обратной связи операционного усилителя последовательно включены резистор R3 и емкость С. На основании выражения (2.42) несложно найти передаточную функцию регулятора

где T =R3×C, Tи = R2×С – соответственно, постоянные времени дифференцирующего и интегрирующего преобразования.
 |

Передаточную функцию (2.43) можно
исать и в другом виде. Деля почленн
Выражение (2.43) можно записать и в другом виде, деля почленно числитель на знаменатель, получим

где K=T/Tи – коэффициент усиления пропорциональной части регулятора. Как следует из последнего выражения, передаточную функцию можно представить в виде суммы пропорциональной части (П) и интегральной (И) части. Отсюда название регулятора. Реакция ПИ-регулятора на скачкообразное изменение сигнала (Uзд — Uoc) приведена на рис. 2.36. Сравнивая рис. 2.34 и рис. 2.36, можно отметить, что ПИ-регулятор в первый момент времени более «энергично» воздействует на управляемый преобразователь и, соответственно, двигатель. Благодаря этому, в принципе, быстродействие системы может быть улучшено.
Схема пропорционально-интегрально-дифференциального регулятора (ПИД-регулятора) приведена на рис. 2.37. По сравнению с предыдущей схемой здесь добавлены емкости С2 и С3, включенные параллельно резисторам R1, R2. Иногда емкость включают только параллельно R2. Тогда для сигнала обратной связи схема имеет свойства ПИД- регулятора, а для сигнала задания – свойства ПИ- регулятора.
Используя выражение (2.42), передаточную функцию рассматриваемого регулятора можно записать в виде

где постоянные времени дифференцирования Т1, Т2 и интегрирования Ти определяются соотношениями:
Т1 = R3×C1; T2 = R2×C3; Tи = R2×C1.
Раскрыв скобки в числителе (2.44) и деля почленно числитель на знаменатель, получим передаточную функцию ПИД- регулятора в виде

где K = (T1 + T2)/Tи; T = T1×T2/Tи.
Как следует из последнего выражения, передаточная функция может быть представлена в виде суммы трех слагаемых: первое слагаемое – пропорциональное звено, второе – интегральное, третье – дифференциальное. Это определило название регулятора.
Реакция ПИД-регулятора на скачок сигнала (Uзд – Uос) приведена на рис. 2.38. Можно отметить, что в начальный момент времени при появлении сигнала рассогласования ПИД-регулятор обеспечивает ещё более «энергичное» воздействие, чем ПИ- регулятор (см. рис. 2.36)
Отметим, что описанное влияние различных регуляторов на динамические свойства системы ЭП поясняет лишь качественный характер процессов. Вопрос о выборе того или иного тока регулятора и его параметров, как известно из курса теории автоматического управления, решается при синтезе корректирующих звеньев.
2.3.5 Регулирование угловой скорости в системе генератор-двигатель (Г-Д) с обратной связью по скорости и токовой отсечкой
Упрощенная схема системы Г-Д приведена на рис. 2.39. Она содержит двигатель постоянного тока независимого возбуждения М; генератор постоянного тока G, от которого получает питание якорь двигателя; усилитель мощности УМ, к выходу которого подключена обмотка возбуждение OBG генератора; регулятор, выполненный на операционном усилителя DА; задатчик частоты вращения RP; тахогенератор BR; датчик тока якоря – шунт Rh; стабилитроны VD1, VD2. Генератор G приводится в движение приводным (гонным) двигателем (на схеме не показан). На промышленных предприятиях, где имеется сеть переменного тока, в качестве гонного двигателя используется асинхронный короткозамкнутый двигатель. В автономных установках, например, на удаленных буровых установках, судах речного, морского, железнодорожного транспорта и т.п., в качестве приводного двигателя может служить двигатель внутреннего сгорания, паровая или газовая турбина и т.п.
Регулирование угловой скорости двигателя в схеме осуществляется изменением напряжения Uя на якоре двигателя M. Изменение Uя осуществляется за счет регулирование напряжения Uв на обмотке возбуждения генератора. Для согласования между напряжением и мощностью на выходе регулятора с потребной мощностью и напряжением питания обмотки OBG служит усилитель мощности, например, транзисторный усилитель.
Стабилизация скорости двигателя достигается за счет отрицательной обратной связи по скорости. Так, если под действием возмущений wд начинает снижаться, то уменьшается сигнал обратной связи по скорости Uocw, а сигнал ошибки
Ud = Uзд – Uocw
увеличивается. При этом повышается напряжение на выходе регулятора, на выходе УМ и на якоре двигателя. В результате wд стремиться к заданному значению. Точность стабилизации wд, как показано выше, определяется коэффициентом усиления разомкнутой системы. При использовании регулятора, содержащего интегральную составляющую (например, ПИД-регулятор, как на рис. 2.39), удается получить достаточно высокую точность стабилизации (см. первый участок характеристики на рис. 2.40).
Для ограничения тока якоря служит узел токовой отсечки. Один из возможных вариантов его реализации (см. рис. 2.39) включает шунт Rh и стабилитроны VD1, VD2. Этот узел работает также, как описано в п. 2.3.1. Пока ток якоря Iя меньше тока отсечки Iотс, стабилитроны имеют большее сопротивление и не оказывают влияние на работу схемы. Если ток Iя превышает Iотс сопротивление стабилитрона резко снижается и на выход регулятора через резистор R4 начинает поступать дополнительный сигнал (Uост – Uz). При этом сигнал ошибки
Ud = Uзд – Uocw – (Uост – Uz).
 |
По мере увеличения тока якоря Iя растет напряжение Uост. Как следствие, снижается Ud, Uв, Uя, wд. В результате достигается ограничение тока якоря (второй участок характеристик на рис. 2.40)
К достоинствам схемы можно отнести простоту реверса двигателя и реализации рекуперативного торможения. Реверс осуществляется изменением полярности напряжения на задатчике RP, что в конечном счете ведет к изменению полярности напряжения на якоре двигателя. Генераторное торможение с отдачей энергии в сеть возможно, если в качестве гонного двигателя генератора используется электродвигатель, например, асинхронный. Поясним это. Предположим, что машина работает на характеристике 1 (рис. 2.41) в т.а. Чтобы снизить скорость, напряжение на датчике RP снижают, и после переходного процесса машина должна перейти на характеристику 2 в т.b.
Процесс перехода на новую характеристику протекает так. В первый момент времени wд, вследствие механической инерционности привода, остается неизменной (на рис. процесс перехода условно показан стрелками). Напряжение генератора уменьшается и становиться меньше противоЭДС двигателя. Ток в якорной цепи меняет знак.
Рис. 2.41
Машина M теперь работает генератором, а машина G – двигателем и заставляет гонный двигатель вращаться со скоростью выше скорости идеального холостого хода. Последний переходит в режим генератора и отдает электрическую энергию в сеть переменного тока. Если ток якоря превышает по модулю Iост, то в переходном процессе вступает в действие токовая отсечка, и процесс перехода на новую характеристику, от т. с до т. d, идет при токе Iя = |Iотс|. Далее под действием момента сопротивления Мc механизма wд продолжает снижаться до нового установившегося режима в т. b.
Система Г-Д имеет очевидные недостатки. Прежде всего, это большая установленная мощность электрических машин: мощность генератора и гонного двигателя должны быть не меньше мощности двигателя. Т.е. общая установленная мощность электрических машин равна или превышает мощность двигателя в 3 раза. Кроме того, наличие дополнительных вращающихся машин приводит к снижению надежности, значительным затратам на профилактику и ремонт. Значительная инерционность генератора затрудняет достижение высоких динамических характеристик системы.
В связи с этим в настоящее время система Г-Д используется в основном в автономных устройствах, а в промышленных установках, получающих питание от электрических сетей, такая система почти не применяется.
2.3.6. Регулирование угловой скорости в системе управляемый выпрямитель – двигатель постоянного тока независимого возбуждения
(УВ — ДПТ)
В настоящее время в различных областях техники наиболее широко применяются регулируемые электроприводы с ДПТ с управляемыми вентильными (тиристорными) выпрямителями (УВ).
Такие приводы выпускаются промышленностью в виде блочных изделий – комплектных тиристорных электроприводов. В однозонных приводах выход УВ подключается к якорю двигателя и регулирование скорости осуществляется за счет изменения напряжения на якоре ДПТ. В двухзонных ЭП используется два УВ, один работает на якорь, а второй – на обмотку возбуждения, и регулирование угловой скорости осуществляется как изменением напряжения на якоре, так и за счет изменения потока возбуждения (напряжения на обмотке возбуждения).
Остановимся на особенностях регулирования напряжения на якоре и обмотке возбуждения ДПТ НВ с помощью УВ.
Основными приборами, применяемыми в управляемых выпрямителях, являются полупроводниковые вентили — диоды и тиристоры. Общим свойством этих приборов является то, что они могут находиться в двух состояниях — открытом и закрытом. В открытом состоянии прямое падение напряжения на вентилях в 102-103 раз меньше, чем напряжения, выделяемые на других элементах схемы (например, среднее значение прямого падения напряжения на тиристоре меньше 1 В). Ток, протекающий через вентили в закрытом состоянии, в 103-104 раз меньше тока в открытом состоянии. Все это позволяет при анализе электромагнитных процессов считать полупроводниковые вентили идеальными ключами и пренебрегать их прямыми падениями напряжения и обратными токами.
Полупроводниковый диод находится в открытом состоянии при прямом напряжении на его аноде (положительном относительно катода) и в закрытом — при отрицательном.

2.3.6.1. Однофазный однополупериодный УВ. Фазовый способ регулирования выпрямленного напряжения
Принцип работы УВ поясним на примере простейшей однофазной однополупериодной схемы УВ (рис. 2.42), работающей на активную R нагрузку. В этой схеме VS — тиристор, СИФУ — система импульсно-фазового управления. Тиристор служит для выпрямления и регулирования выпрямленного напряжения на нагрузке. СИФУ предназначена для управления моментом отпирания тиристора.
Фазовый способ регулирования основан на управлении моментом отпирания тиристоров, включенных последовательно между источником переменного


Диаграммы, поясняющие работу схемы, приведены на рис. 2.43, а. На первой диаграмме приведена зависимость сетевого напряжения uс от угла u (здесь и далее u = wt, рад; w=2pfc — угловая частота, рад/сек; fс — частота сетевого напряжения, Гц; t — время, с). Напряжение uс изменяется по синусоидальному закону с периодом 2p:
uc = Um sin u,
где Um — амплитудное значение сетевого напряжения (
На второй диаграмме приведены управляющие импульсы uу прямоугольной формы. Амплитуда и длительность импульсов выбирается исходя из условия надежного отпирания тиристора. Импульсы формируются СИФУ при положительном напряжении на аноде тиристора (относительно катода) и сдвинуты относительно сетевого напряжения на угол регулирования a (угол запаздывания). Величина угла регулирования зависит от входного сигнала uвх СИФУ.
На третьей и четвертой диаграммах приведены зависимости мгновенных значений напряжения на нагрузке — ud(u) и тока нагрузки — i(u).
Рассмотрим работу схемы на отдельных интервалах.
Интервал 0£u<a. На этом интервале тиристор закрыт, ток тиристора i(u) и напряжение на нагрузке ud(u) практически равны нулю.
При u=a на управляющий электрод тиристора подается управляющий импульс uу и тиристор открывается. При этом ток анода тиристора i практически мгновенно возрастает и оказывается больше тока выключения, поэтому после окончания управляющего импульса тиристор удерживается в открытом состоянии.
Интервал a£u<p. На этом интервале тиристор открыт, напряжение на нагрузке практически равно сетевому напряжению — ud(u)» uс(u), а ток нагрузки — i(u)=ud /Rн.
Интервал p£u£2p+a. На этом интервале тиристор закрыт, а состояние схемы будет таким же, как и на интервале 0£u<a.
На интервалах 2p£u£4p, 4p£u£6p, …, 2ip£u£2(i+1)p, где i=0,1,2,…, работа схемы идентична работе на интервале 0£u£2p.

 |
Мгновенное значение напряжения на нагрузке ud(a) равно сетевому напряжению uс(a) на интервалах, когда тиристор открыт, и равно нулю на интервалах, когда тиристор закрыт. При работе преобразователя на обмотку возбуждения или якорь ДПТ в качестве выходной переменной УВ рассматривают среднее (за период) значение выпрямленного напряжения Uср (постоянную составляющую выпрямленного напряжения). Геометрически Uср можно определить следующим образом. Построим прямоугольник шириной 2p, площадь которого равна площади фигуры, ограниченной кривой мгновенного напряжения на нагрузке ud и осью абцисс. Высота полученного прямоугольника будет равна среднему значению напряжения на нагрузке. Очевидно, что значение Uср зависит от угла регулирования a. Величина среднего значения напряжения на нагрузке находится из выражения
где 
Полученное выражение описывает зависимость среднего значения напряжения на нагрузке от угла регулирования a — Uср(a) и представляет собой регулировочную характеристику. Из выражения видно, что при изменении угла a в пределах 0£a£p среднее значение напряжения на нагрузке Uср(a) изменяется в пределах 
При активной нагрузке выходное напряжение УВ равно падению напряжения на сопротивлении нагрузки: u(u)=Ri(u). Поэтому среднее значение тока и среднее значение напряжения связаны соотношением
2.3.6.2. Однофазная схема УВ с нулевым диодом
Рассмотрим особенности работы УВ на обмотку возбуждения ДПТ НВ.
Характерной особенностью обмоток возбуждения двигателей постоянного тока является большая (относительно якоря) индуктивность, небольшая потребляемая мощность и небольшой требуемый диапазон изменения тока возбуждения. Мощност
Описываемая схема предназначена для регулирования тока возбуждения двигателя постоянного тока и, следовательно, для регулирования скорости его вращения вверх от номинальной скорости.
На рис. 2.44 приведена упрощенная принципиальная электрическая схема однофазного однополупериодного нереверсивного управляемого выпрямителя с нулевым диодом.
Схема содержит силовой трансформатор Т, тиристор VS, систему импульсно-фазового управления СИФУ, нулевой диод VD и обмотку возбуждения LM.
Трансформатор Т служит для получения на вторичной обмотке требуемого действующего значения переменного напряжения, определяющего максимальное значение напряжения на обмотке возбуждения LM, а также для гальванической развязки между сетью и остальной частью схемы. Тиристор VS служит для выпрямления и регулирования среднего (за период) значения выпрямленного напряжения на обмотке возбуждения LM. СИФУ управляет работой тиристора VS. Нулевой диод VD предназначен для устранения отрицательных выбросов напряжения на обмотке возбуждения LM, что позволяет увеличить среднее значение выпрямленного напряжения и тока.
В этой схеме нагрузка (обмотка возбуждения) носит активно-
Рассмотрим работу схемы на отдельных интервалах (рис. 2.45).
Интервал 0£u<a. В исходном состоянии (u=0) тиристор закрыт. Тогда на интервале 0£u<a тиристор остается в закрытом состоянии, ток анода iVS(u) тиристора равен нулю, а обмотка возбуждения оказывается отключенной от вторичной обмотки трансформатора. Но ток, протекающий через обмотку возбуждения, не равен нулю. За счет энергии, накопленной индуктивностью обмотки возбуждения LM на предыдущем интервале (u<0), ток обмотки возбуждения iLM(u) протекает в направлении, указанном на схеме, через диод VD. Благодаря току диод удерживается в открытом состоянии. При этом напряжение uLM(u) на обмотке возбуждения LM определяется прямым падением напряжения uVD(u)=0 на диоде VD, а ток iLM(u) обмотки возбуждения уменьшается во времени по экспоненциальной зависимости.
 |
Интервал a£u<p. При u=a на управляющий электрод тиристора с СИФУ подается управляющий импульс, тиристор открывается, а напряжение на обмотке возбуждения ud возрастает скачком от нуля до значения u2(a). После снятия управляющего импульса тиристор удерживается в открытом состоянии, т.к. ток анода оказывается больше тока выключения. Под действием напряжения u2 диод VD закрывается и не оказывает влияния на работу схемы.

При p£u напряжение u2, прикладываемое к обмотке возбуждени
Интервал p<u£2p+a. На данном интервале тиристор VS закрыт, а диод VD удерживается в открытом состоянии. Напряжение ud(u) на обмотке возбуждения LM равно прямому падению напряжения uVD на диоде VD, т.е. практически равно нулю. Напряжение uVS(u) на аноде тиристора равно напряжению u2(u) на вторичной обмотке трансформатора Т. Ток iVS(u) через закрытый тиристор VS равен нулю, а ток iLM(u) обмотки возбуждения LM под действием энергии, накопленной ее индуктивностью на интервале a£u£p, протекает через диод и уменьшается по экспоненциальной зависимости.
На последующих интервалах 2p+a£u£3p, 4p+a£u£5p и т.д. работа управляемого выпрямителя совпадает с описанной ранее работой на интервале a£u£p, а на интервалах 3p£u£4p+a, 5p£u£6p+a и т.д. — с работой на интервале p£u£2p+a.
Как видно из рис. 2.45, напряжение ud(u) на обмотке возбуждения LM имеет вид однополярных почти прямоугольных импульсов, частота которых равна частоте питающей сети. Величина напряжения ud(u) при открытом тиристоре VS равна напряжению u2(u) на вторичной обмотке трансформатора и равна нулю при закрытом тиристоре. Среднее за период (2p) значение напряжения Ud (постоянная составляющая напряжения) на обмотке возбуждения LM пропорционально площади, ограниченной кривой напряжения и осью абцисс, и, следовательно, зависит от угла регулирования a. Например, Uср(a) максимально при a=0 и равно нулю при a=p. Таким образом, изменение напряжения Uвх на входе СИФУ приводит к изменению угла регулирования a и, следовательно, к изменению среднего за период напряжения Uср на обмотке возбуждения LM.
Из рассмотренного не сложно заметить, что с точки зрения функционального назначения в управляемом выпрямителе можно выделить два блока (рис. 2.46): СИФУ и блок вентилей (БВ). В рассмотренных схемах БВ состоит из одного тиристора, в более сложных схемах тиристоров несколько.
На функциональной схеме СИФУ показывают в виде прямоугольника. На вход СИФУ поступает напряжение Uвх постоянного тока, что условно показано в верхней части блока. Выходной сигнал СИФУ представляет собой последовательность управляющих импульсов. Причем эти импульсы сдвигаются по фазе в зависимости от Uвх (это условно показано в нижней части блока СИФУ). Для БВ входным сигналом являются импульсы СИФУ, а в качестве выходного сигнала в системах электропривода рассматривают среднее значение выпрямленного напряжения Uср.
 |
Следует обратить внимание на следующее. Как установлено выше, с увеличением угла регулирования a значение Uср снижается. Такая, обратная зависимость Uср(a) весьма неудобна при управлении. В связи с этим СИФУ выполняют так, чтобы ее характеристика «вход – выход» обеспечивала обратную зависимость a( Uвх): при возрастании Uвх угол a уменьшается. В результате для УВ в целом удается получить прямую связь между входным и выходным сигналами. Действительно, при возрастании входного сигнала Uвх УВ угол a будет уменьшаться, а выходной сигнал Uср — увеличиваться.
2.3.6.3 Однофазная двухполупериодная схема УВ с нулевым выводом
Схема однофазного двухполупериодного тиристорного выпрямителя приведена на рис. 2.47. Нагрузкой на рис. 2.47 а является обмотка возбуждения LM ДТП.
схеме используется трансформатор Т со средней точкой. Вторичные обмотки трансформатора Т включены так, что их напряжения U21, U22 сдвинуты на 180° (находится в противофазе). На управляющие электроды тиристоров VS1, VS2 подаются импульсы, сдвинутые друг относительно друга на 180°.
На рис. 2.48 показаны диаграммы, соответствующие работе схемы на обмотку возбуждения (рис. 2.47 а) с углом a=30°. На первой диаграмме показаны напряжения U21, U22; на второй – управляющие импульсы; на третьей – напряжение на нагрузке.
Работа схемы во многом аналогична предыдущей, поэтому опишем ее более кратко. На интервале 0<v<a ток в обмотке возбуждения поддерживается, как и в предыдущей схеме за счет энергии, накопленной в индуктивности на предыдущем интервале.
 |
Рис. 2.48
При v=a на управляющий электрод тиристора VS1 от СИФУ (на схеме не показана) подается управляющий импульс, тиристор открывается, напряжение на обмотке возбуждения возрастает скачком до значения U21(a). Ток в обмотке возбуждения начинает возрастать во времени и протекает от верхней вторичной обмотки трансформатора через VS1 и LM. В индуктивности обмотки возбуждения запасается энергия.
На интервале p/2<v<p напряжение на нагрузке, равное U21, начинает снижаться. При этом снижается и ток в обмотке возбуждения, а ЭДС самоиндукция меняет свой знак и действует согласно с напряжение U21.
На интервале p<v<p+a знак U21 изменится, однако тиристор VS1 остается в открытом состоянии за счет ЭДС самоиндукции, и цепь протекания тока останется прежней.
При v=p+a подается управляющий импульс на управляющий электрод тиристора VS2. В этот момент потенциал анода тиристора VS2 выше потенциала катода и VS2 открывается. Напряжение на обмотке возбуждения скачком возрастает да значения U22(p+a). При этом к катоду тиристора VS1 прикладывается положительный потенциал и он закрывается. Ток начинает протекать от нижней по схеме обмотки трансформатора через VS2 и LM. Далее процессы в схеме повторяются.
Обратим внимание, что кривая напряжения на обмотке возбуждения имеет как участки, расположенные выше оси абсцисс (+), так и участки, расположенные ниже этой оси (-). При a=30° площадь «положительных» участков больше площади «отрицательных» и, следовательно, среднее значение выпрямляемого напряжения Uср больше нуля. Очевидно также, что если установить a=0, то “отрицательные” участки будут отсутствовать, и Uср будет максимальным. Если же угол управления a увеличится, то площадь «отрицательных» участков будет возрастать, а Uср снижаться. При угле управления a=90° (см. диаграммы на рис. 2.49) площадь «отрицательных» участков становиться равной площади «положительных», а Uср=0.
Продолжая рассуждения, можно заметить, что при a>90° «отрицательные» площадки станут больше «положительных», и, соответственно, среднее значение выпрямленного напряжения поменяет свой знак – станет меньше нуля.
В рассматриваемой схеме такой режим возможен только гипотетически. Действительно, при отрицательном значении Uср среднее значение тока также должно стать отрицательным. Иными словами направление протекания тока должно изменится, а это невозможно в силу односторонней проводимости вентилей.
Рассмотрим работу схемы на якорь двигателя (рис. 2.47, в). Обмотка якоря двигателя так же, как обмотка возбуждения, имеет индуктивность. Поэтому процессы в схеме во много аналогичны рассмотренным для рис. 2.47 а. Основное отличие заключается в том, что при работе ДПТ создает противо ЭДС, направленную встречно выпрямленному напряжению. Если при работе на обмотку возбуждения среднее значение тока в ней определяется выражением

где RLM – сопротивление обмотки возбуждения, то при работе на якорь двигателя среднее значение тока определяется с учетом противо ЭДС

где Rя – сопротивление якорной цепи. При работе на якорь ДПТ и регулировании угла a так же, как в предыдущих схемах, будет изменяться среднее значение напряжение на выходе УВ и, соответственно, изменяться угловая скорость двигателя. Следует иметь в виду, что угловая скорость будет определяться именно средним значением выпрямленного напряжение, т. к. в силу инерционности двигатель практически не реагирует на мгновенные изменения напряжения на выходе УВ.
При углах a<90° энергия поступает из сети переменного тока к якорю и машина работает в двигательном режиме – преобразует электрическую энергию в механическую.
Такой режим работы УВ называют выпрямительным.
Если в рассматриваемой схеме увеличивать угол a от 0 до 90°, то Еср будет меняться от наибольшей до 0, соответственно, и угловая скорость двигателя будет изменяться от наибольшей до нуля.
Если попытаться установить a>90°, то напряжение Uср должно изменить свой знак и, соответственно, должно поменяться направление протекание тока Iя. Как уже отмечалось, ток через тиристоры в обратном направлении протекать не может, следовательно, в рассматриваемом случае работа с a>90° также невозможна.
Рассмотрим другую ситуацию. Предположим, что электропривод работает на грузоподъемный механизм. Пусть происходит подъем груза. Машина М при этом работает в двигательном режиме, УВ – в выпрямительном режиме.
 |
Предположим далее, что груз нужно опустить. Для этого устанавливают угол a>90°. Знак среднего значения напряжения Uср по сравнению с выпрямительным режимом поменяется на противоположный. Под действием момента, создаваемого грузом двигатель начнет вращаться в противоположную сторону. Его противо ЭДС поменяет свой знак. Если по абсолютному значению |E|>|Uср|, то направление
Рис. 2.49
протекания тока останется прежним, а его значение будет определяться выражением

Таким образом в рассматриваемой ситуации машина за счет момента, создаваемого грузом работает в генераторном режиме, а электрическая энергия передается от якоря в цепь переменного тока. Говорят, что управляемый выпрямитель работает при этом в инверторном режиме.
Разумеется в автоматизированном ЭП переход УВ в инверторный режим обеспечивается автоматически за счет работы соответствующих блоков системы. Приведенные здесь рассуждение лишь поясняют возможность работы УВ с a>90°, т.е. работы в инверторном режиме.
2.3.6.4 Трехфазные схемы УВ

Силовая часть трехфазной нулевой схемы УВП приведена на рис. 2.50.
Трехфазный трансформатор TV1 служит для согласования напряжения на якоре двигателя с сетевым напряжением, а также для гальванической развязки цепи якоря электродвигателя с сетью. Схема содержит тиристоры VS1, VS2, VS3. Вторичные ЭДС различных фаз трансформатора, поступающие на тиристоры, сдвинуты на 120°. Соответственно, и управляющие импульсы, подаваемые на управляющие электроды тиристоров с выхода СИФУ, сдвинуты на 120°. При работе схемы в режиме непрерывного тока ток в каждом из тиристоров протекает в течение 1/3 периода, т.е. в течение 1/3 периода якорь двигателя через один из тиристоров подключается к синусоидальной переменной ЭДС соответствующей фазы. За период изменения напряжения в сети переменного тока якоря двигатель поочередно подключается к трем различным фазам. Регулируя с помощью СИФУ угол a, можно, так же, как в однофазной схеме, изменять среднее значение напряжения на якоре двигателя.
Силовая часть трехфазной мостовой схемы УВ приведена на рис. 2.51. она содержит 6 тиристоров VS1 – VS6. Особенностью этой схемы является то, что управляющие импульсы, подаваемые на тиристоры VS4 – VS6, сдвинуты на 180° по отношению к импульсам на тиристорах VS1 – VS3. Для того, чтобы обеспечить протекание тока в нагрузке, нужно открыть два тиристора одновременно – один в анодной и один в катодной группе вентилей. Одновременность открытия тиристоров анодной и катодной групп обеспечивается тем, что через 60° после основного управляющего импульса на каждый из тиристоров подается дополнительный управляющий импульс.
При работе схемы в режиме непрерывного тока каждый из тиристоров проводит ток в течение 1/3 периода, а напряжение на нагрузке удобно рассматривать как результат взаимодействия двух последовательно включенных нулевых схем выпрямления. Регулирование среднего значения напряжения на якоре двигателя, как и в предыдущих схемах, осуществляется изменением угла управления a.
Как показано выше, напряжение на выходе УВ имеет форму импульсов. Причем пульсации напряжения и, как следует, пульсации тока якоря наиболее значительны в однофазных схемах и существенно снижаются в трехфазных схемах, особенно мостовых. Обычно однофазные схемы УВ применяются при мощности нагрузки до единиц киловатт. Трехфазная нулевая схема в основном используется в диапазоне мощности от единицы до нескольких десятков киловатт. При большой мощности в основном применяется трехфазная мостовая схема.
Необходимо учитывать, что УВП, как потребитель энергии, забирают из сети несинусоидальный ток и, следовательно, является источниками тока высших гармоник.
Высшие гармонические составляющие кривой тока искажают форму напряжения в сети и неблагоприятно влияют на работу конденсаторных установок, синхронных машин и самих УВ. Важнейшим энергетическим показателем электроприемников является коэффициент мощности, характеризующий сдвиг по фазе тока в цепи. В тиристорных преобразователях кривая тока отстает от кривой напряжения, причем, с увеличением угла a фазовый сдвиг увеличивается. Иными словами, УВ потребляет из сети не только активную, но и реактивную мощность. Причем последняя увеличивается при возрастании угла a. Эти обстоятельства требуют принятия специальных мер по повышению коэффициента мощности.
2.3.6.5 Реверсивные электроприводы с УВ
Изменить направления вращения ДПТ НВ (осуществить реверс двигателя) можно за счет изменения полярности напряжения или на обмотке возбуждения, или на якоре двигателя. Первый способ, несмотря на его кажущуюся привлекательность – малую мощность в цепи возбуждения, используется редко. Это связано с тем, что при изменении полярности напряжения на обмотке возбуждения ток в ней снижается до нуля, а затем меняет свой знак. При этом момент двигателя, пропорциональный магнитному потоку обмотки возбуждения, также снижается, достигает нулевого значения, а затем меняет свой знак. Снижение момента затягивает процесс реверса.


В реверсивных приводах при снижении скорости и реверсе двигателя реализуется инверторный режим работы выпрямителя. Поясним это.
Предположим, что в исходном состоянии работает комплект «В» и частоту вращения двигателя необходимо уменьшить. Для этого уменьшают величину задающего сигнала в системе ЭП. В результате напряжение на выходе комплекта «В» начинает резко снижаться и, соответственно, уменьшается ток Iя. В некоторый момент он становиться равным нулю. После этого система управления УВ выдает команду на включение вентилей комплекта «Н». Причем комплект «Н» переводится в инверторный режим (полярность на его выходе для инверторного режима показана в окружностях). При этом ток якоря меняет знак и протекает из цепи постоянного тока в цепь переменного тока. Величина ЭДС комплекта «Н» устанавливается такой, чтоб, ток якоря

не превышал допустимого тока двигателя (тока отсечки). Так организуется режим генераторного торможения двигателя с отдачей энергии в сеть переменного тока (сравните с аналогичным режимом в системе Г-Д).
Следует подчеркнуть, что включение комплекта «Н» в выпрямительном режиме в рассматриваемой ситуации недопустимо. Действительно при таком включении ЭДС двигателя будет действовать согласно с напряжением УВ, и ток якоря
будет недопустимо большим.
При работе же комплекта «Н» в инверторном режиме напряжение на выходе УВ ограничивает ток якоря.
При подходе двигателя к заданной пониженной скорости ток якоря уменьшается, комплект «Н» отключается и вновь вступает в работу комплект «В».
Аналогично протекает процесс реверса двигателя. Только в этом случае, комплект «Н» остается постоянно включенным, угол a постепенно изменяется в сторону уменьшения. При a<90о комплект Н переходит в выпрямительный режим, полярность напряжения на якоре двигателя меняется, и двигатель начинает вращаться в противоположную сторону.
Управление комплектами «В» и «Н» осуществляется автоматически соответствующими блоками тиристорного привода.
2.3.6.6 Системы подчиненного регулирования тока якоря и угловой скорости ДПТ НВ
В рассмотренных выше схемах (см. рис. 2.25, рис. 2.28, рис. 2.39) замкнутых систем ЭП для обеспечения требуемых характеристик используется отрицательная обратная связь по скорости двигателя. Токовая отсечка организуется с помощью дополнительного узла. Причем сигналы с датчика скорости и датчика тока якоря поступают на один усилитель (регулятор). Такой принцип построения системы, как правило, не позволяет получить максимально достижимого быстродействия системы. Кроме того, схема регулятора оказывается в большинстве случаев достаточно сложной (не типовой), что вызывает дополнительные проблемы при наладке системы.
Современные АЭП выполняются в виде систем подчиненного регулирования (СПР) координат. Функциональная схема однозонной системы подчиненного регулирования тока якоря и угловой скорости ДПТ НВ приведена на рис. 2.53. В системе обеспечивается регулирование угловой скорости двигателя за счет изменения напряжения Uя на якоре. Это напряжение регулируется с помощью управляемого выпрямителя, содержащего СИФУ и блок вентилей (БВ).
Система содержит два замкнутых контура: внутренний токовый и внешний скоростной. Внутренний контур включает СИФУ, БВ, датчик тока якоря (шунт Rh) и регулятор тока РТ. Внешний контур охватывает элементы внутреннего и дополнительно содержит якорь двигателя М, датчик скорости (тахогенератор BR) и регулятор скорости.
Поясним работу схемы.
Начнем с внутреннего контура. Он выполнен в виде замкнутой системы с отрицательной обратной связью по току якоря. Входным (задающим) сигналом для этого контура является выходное напряжение Uрс регулятора скорости. На входе РТ осуществляется сравнение (вычитание) сигналов Uрт и сигнала Uост обратной связи по току якоря. Сигнал ошибки на входе РТ
Ud2 = Uрт – Uост.
При постоянном значении Uрс внутренний контур работает в режиме стабилизации тока якоря.
Если, например, ток якоря начинает снижаться, то сигнал Uост также уменьшается, а сигнал ошибки Ud2 увеличивается. При этом увеличивается напряжение на выходе РТ и, как следствие, возрастает напряжение на якоре двигателя – ток якоря начинает возрастать, стремясь к заданному значению.
Рассмотрим работу внешнего, скоростного контура. Сигнал на входе РС определяется соотношением
Ud1 = Uзд – Uocw.
Если wд по каким-либо причинам снижается, то напряжение Uocw тахогенератора так же уменьшается, а сигнал ошибки Ud1 увеличивается. Это приводит к возрастанию напряжения Uрс на выходе РС, т.е. на вход токового контура начинает поступать больший сигнал задания. За счет работы внутреннего контура ток якоря увеличивается и, соответственно, wд растет, стремясь к заданному значению.
Из приведенных рассуждений несложно заметить, что в этой схеме задача регулирования тока якоря подчинена задаче регулирования wд. Отсюда название систем – подчиненного регулирования.
Аналогично протекают процессы при управлении скоростью. Так, чтобы увеличить wд увеличивают напряжение задания Uзд. При этом Ud1 и Uрт увеличиваются, внутренний контур обеспечивает возрастание тока якоря, и двигатель разгоняется до заданного значения скорости.
Упрощенная принципиальная схема СПР тока якоря и угловой скорости ДПТ НВ для нереверсивного ЭП приведена на рис. 2.54.
Регулятор тока в схеме выполнен на операционном усилителе DA2 в виде ПИ-регулятора. Использование ПИ-регулятора позволяет получить максимальное быстродействие токового контура. На вход РТ через резисторы R4 и R5 поступает сигнал с выхода РС – UPC и с выхода датчика тока (шунт Rh) – Uост.
 |
Регулятор скорости выполнен на операционном усилителе DA1 в виде ПИ-регулятора. Использование ПИ-регулятора в скоростном контуре придает астатизм системе (см. п. 2.3.2). В астатической системе при использовании идеального регулятора статическая ошибка в поддержании скорости сводится к нулю. На вход РС через R1 поступает сигнал Uзд с датчика скорости (потенциометр RP1) и через R2 – сигнал отрицательной обратной связи Uocw по скорости, снимаемый с тахогенератора. Для настройки значения тока отсечки в схеме предусмотрен потенциометр RP2. Максимальное значение напряжения на выходе РС определяется насыщением усилителя. На вход РТ подается часть выходного напряжения РС, снимаемого с делителя RP2. Перемещая движок RP2, например, вниз можно уменьшать максимальное значение сигнала Uрс. Этот сигнал является задающим для внутреннего токового контура. А его максимальное значение определяет максимальный ток якоря – ток отсечки.
2.3.6.7 Достоинства и недостатки электроприводов с управляемыми выпрямителями
Отметим основные особенности приводов, выполненных по схеме УВ – ДПТ НВ:
1) тиристорный преобразователь имеет очень малую инерционность, что позволяет обеспечить высокое быстродействие электропривода;
2) электропривод имеет высокую надежность, достаточно прост в обслуживании;
3) тиристорный электропривод имеет высокий КПД (более 95%);
4) малые габариты и масса, блочная компоновка привода позволяют сократить требуемые производственные площади, уменьшить капитальные затраты на установку.
Вместе с этой лекцией читают «18 Переломы».
В то же время, тиристорным электроприводам свойственны следующие недостатки:
1) значительные пульсации тока на выходе УВ увеличивают нагрев двигателя и ухудшают его коммутацию;
2) при глубоком регулировании скорости тиристорный электропривод имеет низкий коэффициент мощности;
3) перегрузочная способность тиристорного преобразователя ниже, чем генераторного;
4) при работе тиристорного привода искажается форма кривой напряжения в сети переменного тока и возникают помехи в сети, действующие как на другие электроприемники, так и на сам тиристорный привод;
5) в системе Г-Д преобразовательной установке свойственна естественная рекуперация энергии в сеть в генераторных режимах работы двигателя, в тиристорных преобразователях для обеспечения рекуперации необходимо применение специальных схем, в частности, с двумя комплектами вентилей, что повышает сложность и стоимость электропривода.
Тогда
величина статической ошибки составит:
Относительная
статическая ошибка:
Сравнивая
относительную статическую ошибку с требованиями, предъявляемыми к электроприводу,
можно заключить, что синтез произведен верно и требуемая жесткость
характеристик обеспечена.
Построим статические характеристики разомкнутой и
замкнутой системы электропривода:
Рис.7. Статические
характеристики:
1 – разомкнутой
системы; 2 – замкнутой системы.
7. Анализ динамики электропривода
Анализ
динамики системы автоматического управления электроприводом пассажирского лифта
заключается в построении переходных процессов и определении по ним основных
динамических показателей системы (перерегулирование, время переходного
процесса).
Расчет переходных процессов произведем в программе Matlab
в приложении Simulink.
Рис.8. Фрагмент программы Matlab: структурная
схема системы автоматического управления электроприводом пассажирского лифта.
Рис.9. Фрагмент программы Matlab: регулятор
скорости,
синтезированный на технический оптимум.
Рис.10. Фрагмент программы Matlab: регулятор
тока,
синтезированный на технический оптимум.
Рис.11. Фрагмент программы Matlab: задатчик
интенсивности
с апериодическим звеном для ограничения рывка.
Построим
переходные процессы момента двигателя М(t) и угловой
скорости ω(t). Построение переходных процессов «в малом»
выполняется для определения качества переходных процессов, поэтому выполним его
без задатчика интенсивности и ограничения рывка.
Рис.12. Фрагмент
программы Matlab: переходные процессы при Uз = 0,25 В.
При
синтезе регулятора скорости на технический оптимум быстродействие контура
скорости равно:
tрег = 8,4·Тμω = 8,4 · 6,66·10-3 =
56 мс
Анализируя
переходной процесс, видно, что быстродействие контура:
tрег = 150 мс
Анализ переходных процессов «в большом» выполним с
задатчиком интенсивности и апериодическим звеном для ограничения рывка.
Рис.13. Фрагмент
программы Matlab: переходные процессы при Uз = 5 В.
Как
видно из переходных процессов, время переходного процесса составляет tрег = 3 с. Такое время переходного процесса
обеспечивается тем, что задатчиком интенсивности ограничивается ускорение
лифта, а апериодическим звеном ограничивается рывок. Графики изменения
ускорения и рывка представлены на рис.14 и рис.15.
Рис.14. График
изменения ускорения во времени.
Рис.15. График
изменения рывка во времени.
8. Синтез и расчет узлов ограничений и защит.
При
синтезе системы автоматического управления за основу берем схему электропривода
КТЭ. В качестве системы защит возьмём узел защиты данного электропривода.
Система
защит и сигнализации осуществляет следующие виды защит:
1) Защита от внутренних коротких замыканий при выходе
из строя тиристоров осуществляется путем блокировки управляющих импульсов по
сигналу срабатывания герконовых датчиков на стороне переменного тока и
отключения автоматических выключателей.
2) Защита при превышении мгновенного значения тока
осуществляется с помощью электронной токовой защиты совместно с автоматическим
выключателем. Электронная токовая защита обеспечивает достаточное
быстродействие, сдвигая импульсы управления силовых тиристоров в инверсную
область с последующим их блокированием. Сигналы токовой защиты поступают с герконовых
и полупроводникового датчиков. Настройку уставки герконовых датчиков
необходимо производить сначала на стороне постоянного тока, а затем переменного
тока при рабочем напряжении главных цепей и отключенном датчике тока S402A
(А22).
3)
Защита при аномальных режимах в сети собственных нужд реализована на ячейке
ключей № 501В. При аномомальных режимах в сети собственных нужд, например таких
как снижение напряжения собственных нужд более чем на 15% от номинального,
обрыве фазы, сигнал с выхода ячейки № 501В поступает на вход ячейки памяти №
617, где происходит формирование общего аварийного сигнала, воздействующего на
откключение привода КТЭ.
4)
Защита при опрокидывании и прорыве инвертора.
5)
Защита при появлении уравнительных токов.
6)
Защита при неисправности источника стабилизированного напряжения
7)
Защита при аварийной перегрузке тиристоров по среднеквадратичному току. Для
данной защиты используется сигнал с датчика тока S402A.
Защита собрана на ячейке защиты от перегруза № 314. При достижении током КТЭ
значения 1,5·Iн с
выдержкой времени происходит аварийное отключение КТЭ по каналу
среднеквадратичной токовой перегрузки тиристоров.

Защита при превышении или при снижении ниже допустимого уровня тока возбуждения
электродвигателя. Она собрана на пороговых устройствах №501В, №311. Уставки
срабатывания защит регулируются переменными резисторами R24, R32
ячеек №501В и №311 соответственно, таким образом, чтобы срабатывание защиты
происходило при превышении тока возбуждения выше 1,25·Iн и при снижении тока возбуждения ниже 0,7·Iн.