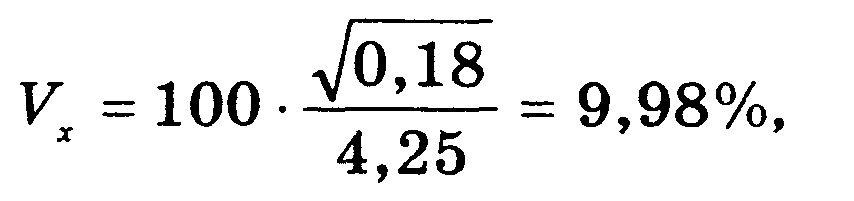Стандартные ошибки выборочных оценок параметров - Решение и исправление самых разных ошибок на TopOshibok.ru

From Wikipedia, the free encyclopedia

For a value that is sampled with an unbiased normally distributed error, the above depicts the proportion of samples that would fall between 0, 1, 2, and 3 standard deviations above and below the actual value.

The standard error (SE)^[1] of a statistic (usually an estimate of a parameter) is the standard deviation of its sampling distribution^[2] or an estimate of that standard deviation. If the statistic is the sample mean, it is called the standard error of the mean (SEM).^[1]

The sampling distribution of a mean is generated by repeated sampling from the same population and recording of the sample means obtained. This forms a distribution of different means, and this distribution has its own mean and variance. Mathematically, the variance of the sampling mean distribution obtained is equal to the variance of the population divided by the sample size. This is because as the sample size increases, sample means cluster more closely around the population mean.

Therefore, the relationship between the standard error of the mean and the standard deviation is such that, for a given sample size, the standard error of the mean equals the standard deviation divided by the square root of the sample size.^[1] In other words, the standard error of the mean is a measure of the dispersion of sample means around the population mean.

In regression analysis, the term «standard error» refers either to the square root of the reduced chi-squared statistic or the standard error for a particular regression coefficient (as used in, say, confidence intervals).

Standard error of the sample mean[edit]

Exact value[edit]

Suppose a statistically independent sample of observations $x_{1},x_{2},\ldots ,x_{n}$ is taken from a statistical population with a standard deviation of $\sigma$ . The mean value calculated from the sample, ${\bar {x}}$ , will have an associated standard error on the mean, ${\sigma }_{\bar {x}}$ , given by:^[1]

${\sigma }_{\bar {x}}={\frac {\sigma }{\sqrt {n}}}.$

Practically this tells us that when trying to estimate the value of a population mean, due to the factor $1/{\sqrt {n}}$ , reducing the error on the estimate by a factor of two requires acquiring four times as many observations in the sample; reducing it by a factor of ten requires a hundred times as many observations.

Estimate[edit]

The standard deviation $\sigma$ of the population being sampled is seldom known. Therefore, the standard error of the mean is usually estimated by replacing $\sigma$ with the sample standard deviation $\sigma _{x}$ instead:

${\sigma }_{\bar {x}}\ \approx {\frac {\sigma _{x}}{\sqrt {n}}}.$

As this is only an estimator for the true «standard error», it is common to see other notations here such as:

${\widehat {\sigma }}_{\bar {x}}:={\frac {\sigma _{x}}{\sqrt {n}}}\qquad {\text{ or }}\qquad {s}_{\bar {x}}\ :={\frac {s}{\sqrt {n}}}.$

A common source of confusion occurs when failing to distinguish clearly between:

Accuracy of the estimator[edit]

When the sample size is small, using the standard deviation of the sample instead of the true standard deviation of the population will tend to systematically underestimate the population standard deviation, and therefore also the standard error. With n = 2, the underestimate is about 25%, but for n = 6, the underestimate is only 5%. Gurland and Tripathi (1971) provide a correction and equation for this effect.^[3] Sokal and Rohlf (1981) give an equation of the correction factor for small samples of n < 20.^[4] See unbiased estimation of standard deviation for further discussion.

Derivation[edit]

The standard error on the mean may be derived from the variance of a sum of independent random variables,^[5] given the definition of variance and some simple properties thereof. If $x_{1},x_{2},\ldots ,x_{n}$ is a sample of independent observations from a population with mean ${\bar {x}}$ and standard deviation $\sigma$ , then we can define the total

$T=(x_{1}+x_{2}+\cdots +x_{n})$

which due to the Bienaymé formula, will have variance

$\operatorname {Var} (T)={\big (}\operatorname {Var} (x_{1})+\operatorname {Var} (x_{2})+\cdots +\operatorname {Var} (x_{n}){\big )}=n\sigma ^{2}.$

where we’ve approximated the standard deviations, i.e., the uncertainties, of the measurements themselves with the best value for the standard deviation of the population. The mean of these measurements ${\bar {x}}$ is simply given by

${\bar {x}}=T/n.$

The variance of the mean is then

$\operatorname {Var} ({\bar {x}})=\operatorname {Var} \left({\frac {T}{n}}\right)={\frac {1}{n^{2}}}\operatorname {Var} (T)={\frac {1}{n^{2}}}n\sigma ^{2}={\frac {\sigma ^{2}}{n}}.$

The standard error is, by definition, the standard deviation of ${\bar {x}}$ which is simply the square root of the variance:

$\sigma _{\bar {x}}={\sqrt {\frac {\sigma ^{2}}{n}}}={\frac {\sigma }{\sqrt {n}}}.$

For correlated random variables the sample variance needs to be computed according to the Markov chain central limit theorem.

Independent and identically distributed random variables with random sample size[edit]

There are cases when a sample is taken without knowing, in advance, how many observations will be acceptable according to some criterion. In such cases, the sample size is a random variable whose variation adds to the variation of such that,

$\operatorname {Var} (T)=\operatorname {E} (N)\operatorname {Var} (X)+\operatorname {Var} (N){\big (}\operatorname {E} (X){\big )}^{2}$

^[6]
which follows from the law of total variance.

If has a Poisson distribution, then $\operatorname {E} (N)=\operatorname {Var} (N)$ with estimator $n=N$ . Hence the estimator of $\operatorname {Var} (T)$ becomes $nS_{X}^{2}+n{\bar {X}}^{2}$ , leading the following formula for standard error:

$\operatorname {Standard~Error} ({\bar {X}})={\sqrt {\frac {S_{X}^{2}+{\bar {X}}^{2}}{n}}}$

(since the standard deviation is the square root of the variance).

Student approximation when σ value is unknown[edit]

In many practical applications, the true value of σ is unknown. As a result, we need to use a distribution that takes into account that spread of possible σ’s.
When the true underlying distribution is known to be Gaussian, although with unknown σ, then the resulting estimated distribution follows the Student t-distribution. The standard error is the standard deviation of the Student t-distribution. T-distributions are slightly different from Gaussian, and vary depending on the size of the sample. Small samples are somewhat more likely to underestimate the population standard deviation and have a mean that differs from the true population mean, and the Student t-distribution accounts for the probability of these events with somewhat heavier tails compared to a Gaussian. To estimate the standard error of a Student t-distribution it is sufficient to use the sample standard deviation «s» instead of σ, and we could use this value to calculate confidence intervals.

Note: The Student’s probability distribution is approximated well by the Gaussian distribution when the sample size is over 100. For such samples one can use the latter distribution, which is much simpler.

Assumptions and usage[edit]

An example of how $\operatorname {SE}$ is used is to make confidence intervals of the unknown population mean. If the sampling distribution is normally distributed, the sample mean, the standard error, and the quantiles of the normal distribution can be used to calculate confidence intervals for the true population mean. The following expressions can be used to calculate the upper and lower 95% confidence limits, where ${\bar {x}}$ is equal to the sample mean, $\operatorname {SE}$ is equal to the standard error for the sample mean, and 1.96 is the approximate value of the 97.5 percentile point of the normal distribution:

In particular, the standard error of a sample statistic (such as sample mean) is the actual or estimated standard deviation of the sample mean in the process by which it was generated. In other words, it is the actual or estimated standard deviation of the sampling distribution of the sample statistic. The notation for standard error can be any one of SE, SEM (for standard error of measurement or mean), or S_E.

Standard errors provide simple measures of uncertainty in a value and are often used because:

in many cases, if the standard error of several individual quantities is known then the standard error of some function of the quantities can be easily calculated;
when the probability distribution of the value is known, it can be used to calculate an exact confidence interval;
when the probability distribution is unknown, Chebyshev’s or the Vysochanskiï–Petunin inequalities can be used to calculate a conservative confidence interval; and
as the sample size tends to infinity the central limit theorem guarantees that the sampling distribution of the mean is asymptotically normal.

Standard error of mean versus standard deviation[edit]

In scientific and technical literature, experimental data are often summarized either using the mean and standard deviation of the sample data or the mean with the standard error. This often leads to confusion about their interchangeability. However, the mean and standard deviation are descriptive statistics, whereas the standard error of the mean is descriptive of the random sampling process. The standard deviation of the sample data is a description of the variation in measurements, while the standard error of the mean is a probabilistic statement about how the sample size will provide a better bound on estimates of the population mean, in light of the central limit theorem.^[7]

Put simply, the standard error of the sample mean is an estimate of how far the sample mean is likely to be from the population mean, whereas the standard deviation of the sample is the degree to which individuals within the sample differ from the sample mean.^[8] If the population standard deviation is finite, the standard error of the mean of the sample will tend to zero with increasing sample size, because the estimate of the population mean will improve, while the standard deviation of the sample will tend to approximate the population standard deviation as the sample size increases.

Extensions[edit]

Finite population correction (FPC)[edit]

The formula given above for the standard error assumes that the population is infinite. Nonetheless, it is often used for finite populations when people are interested in measuring the process that created the existing finite population (this is called an analytic study). Though the above formula is not exactly correct when the population is finite, the difference between the finite- and infinite-population versions will be small when sampling fraction is small (e.g. a small proportion of a finite population is studied). In this case people often do not correct for the finite population, essentially treating it as an «approximately infinite» population.

If one is interested in measuring an existing finite population that will not change over time, then it is necessary to adjust for the population size (called an enumerative study). When the sampling fraction (often termed f) is large (approximately at 5% or more) in an enumerative study, the estimate of the standard error must be corrected by multiplying by a »finite population correction» (a.k.a.: FPC):^[9]
^[10]

$\operatorname {FPC} ={\sqrt {\frac {N-n}{N-1}}}$

which, for large N:

$\operatorname {FPC} \approx {\sqrt {1-{\frac {n}{N}}}}={\sqrt {1-f}}$

to account for the added precision gained by sampling close to a larger percentage of the population. The effect of the FPC is that the error becomes zero when the sample size n is equal to the population size N.

This happens in survey methodology when sampling without replacement. If sampling with replacement, then FPC does not come into play.

Correction for correlation in the sample[edit]

Expected error in the mean of A for a sample of n data points with sample bias coefficient ρ. The unbiased standard error plots as the ρ = 0 diagonal line with log-log slope −1⁄2.

If values of the measured quantity A are not statistically independent but have been obtained from known locations in parameter space x, an unbiased estimate of the true standard error of the mean (actually a correction on the standard deviation part) may be obtained by multiplying the calculated standard error of the sample by the factor f:

$f={\sqrt {\frac {1+\rho }{1-\rho }}},$

where the sample bias coefficient ρ is the widely used Prais–Winsten estimate of the autocorrelation-coefficient (a quantity between −1 and +1) for all sample point pairs. This approximate formula is for moderate to large sample sizes; the reference gives the exact formulas for any sample size, and can be applied to heavily autocorrelated time series like Wall Street stock quotes. Moreover, this formula works for positive and negative ρ alike.^[11] See also unbiased estimation of standard deviation for more discussion.

References[edit]

^ ^a ^b ^c ^d Altman, Douglas G; Bland, J Martin (2005-10-15). «Standard deviations and standard errors». BMJ: British Medical Journal. 331 (7521): 903. doi:10.1136/bmj.331.7521.903. ISSN 0959-8138. PMC 1255808. PMID 16223828.
^ Everitt, B. S. (2003). The Cambridge Dictionary of Statistics. Cambridge University Press. ISBN 978-0-521-81099-9.
^ Gurland, J; Tripathi RC (1971). «A simple approximation for unbiased estimation of the standard deviation». American Statistician. 25 (4): 30–32. doi:10.2307/2682923. JSTOR 2682923.
^ Sokal; Rohlf (1981). Biometry: Principles and Practice of Statistics in Biological Research (2nd ed.). p. 53. ISBN 978-0-7167-1254-1.
^ Hutchinson, T. P. (1993). Essentials of Statistical Methods, in 41 pages. Adelaide: Rumsby. ISBN 978-0-646-12621-0.
^ Cornell, J R; Benjamin, C A (1970). Probability, Statistics, and Decisions for Civil Engineers. NY: McGraw-Hill. pp. 178–179. ISBN 0486796094.
^ Barde, M. (2012). «What to use to express the variability of data: Standard deviation or standard error of mean?». Perspect. Clin. Res. 3 (3): 113–116. doi:10.4103/2229-3485.100662. PMC 3487226. PMID 23125963.
^ Wassertheil-Smoller, Sylvia (1995). Biostatistics and Epidemiology : A Primer for Health Professionals (Second ed.). New York: Springer. pp. 40–43. ISBN 0-387-94388-9.
^ Isserlis, L. (1918). «On the value of a mean as calculated from a sample». Journal of the Royal Statistical Society. 81 (1): 75–81. doi:10.2307/2340569. JSTOR 2340569. (Equation 1)
^ Bondy, Warren; Zlot, William (1976). «The Standard Error of the Mean and the Difference Between Means for Finite Populations». The American Statistician. 30 (2): 96–97. doi:10.1080/00031305.1976.10479149. JSTOR 2683803. (Equation 2)
^ Bence, James R. (1995). «Analysis of Short Time Series: Correcting for Autocorrelation». Ecology. 76 (2): 628–639. doi:10.2307/1941218. JSTOR 1941218.

Источник

Выборочный
метод —
это система научных принципов случайного
отбора определенной части совокупности,
которая представляла бы всю совокупность
и характеристики которой служили бы
надежной основой статистического
вывода.

Совокупность,
из которой отбираются элементы для
обследования, называют генеральной,
а совокупность, которую непосредственно
обследуют, — выборочной.
Статистические характеристики выборочной
совокупности рассматриваются как оценки
соответствующих характеристик генеральной
совокупности. Поскольку выборочная
совокупность неточно воспроизводит
структуру генеральной, то выборочные
оценки также не совпадают с характеристиками
генеральной совокупности. Различия
между ними называют ошибками
репрезентативности.
По причинам появления эти ошибки делятся
на систематические
(тенденционные) и случайные.
Систематические
ошибки
появляются, если при формировании
выборочной совокупности нарушен принцип
случайности отбора (преднамеренный
отбор элементов, несовершенная основа
выборки и т. п.). Случайные
ошибки
— это следствие случайности отбора
элементов совокупности для обследования.

При
организации выборочного обследования
важно предупредить появление
систематических ошибок. Избежать
случайных ошибок невозможно, однако на
основе теории выборочного метода можно
определить их размер и по возможности
регулировать.

В
практике выборочных наблюдений используют
два типа выборочных оценок — точечные
и интервальные. Точечная
оценка
— это значение параметра по данным
выборки: выборочная средняя

или выборочная доля р. Интервальная
оценка
— это интервал значений параметра,
рассчитанный по данным выборки для
определенной вероятности, т. е.
доверительный интервал. Границы его
определяются на основе точечной оценки
и предельной ошибки выборки 
= t:

для
средней

для
доли

где

— средняя, или стандартная ошибка
выборки; t — квантиль распределения
вероятностей (доверительное число);

и d₀
— средняя и доля в генеральной
совокупности.

Стандартная
ошибка выборки

является средним квадратическим
отклонением выборочных оценок от
значений параметра, генеральной
совокупности:

при
повторном отборе

при
бесповторном

где
²
— выборочная дисперсия; n
и N — соответственно объем выборочной
и генеральной совокупностей.

При
практическом использовании данных
формул следует учитывать, что:

1)
дисперсия альтернативного признака
рассчитывается как произведение долей
²
= р(1 — р) = pq;

2)
в больших по объему совокупностях (30 и
более единиц) поправка

не вносит существенных изменений в
расчеты, а поэтому учитывается только
в малочисленных (малых) выборках;

3)
корректирующий множитель для бесповторной
выборки
при
малых величинах

приближается к 1, поэтому при 1—5%-й
выборке расчет 
проводится по формуле для повторной
выборки.

Предельная
ошибка выборки

= t
— это максимально возможная ошибка для
принятой вероятности F(x). Доверительное
число t
показывает, как соотносятся предельная
и стандартная ошибки. Так, t = 1 для
вероятности 0,683; t = 2 для вероятности
0,954; t = 3 для вероятности 0,997.

Таким
образом, используют следующие формулы
предельной ошибки выборки:

	повторная выборка	бесповторная выборка
для средней
для доли

Как
видно из формул, размер предельной
ошибки зависит от вариации признака
²,
объема выборки n
и ее доли в генеральной совокупности
,
а также принятого уровня вероятности,
которому соответствует квантиль t.

При
малых выборках (n
< 30) квантиль t определяют по распределению
вероятностей Стьюдента. В прил. 2 приведены
значения t для F(x) = 0,95 и числа степеней
свободы k= n
— 1.

Пример.
По данным анализа плавки легированной
стали (10 проб), содержание никеля
составляет в среднем 4,25% при ²
= 0,18. Предельная ошибка выборки с
вероятностью F(x) = 0,95, для которой

(9) = 2,26:

Доверительные
границы: 4,25 ± 0,32, т.е. с вероятностью 0,95
можно утверждать, что содержание никеля
в легированной стали не меньше 3,93 и не
больше 4,57%.

При
сравнении точности выборочных оценок
используют относительную ошибку выборки
V_,
которая показывает, на сколько процентов
выборочная оценка отклоняется от
параметра генеральной совокупности:

В
нашем примере 
= 0,14, а

Относительную
ошибку выборки можно рассчитывать на
основе коэффициента вариации признака
V_х:

для
повторной выборки

для
бесповторной выборки.

Так,
коэффициент вариации содержания никеля
в легированной стали составит

следовательно,

Аналогично
рассчитывают относительную ошибку
выборки для доли:

В
практике выборочных обследований
используют разные способы формирования
выборочных совокупностей, в частности:
простой случайный, механический,
типический (районированный), серийный.

Простой
случайный отбор
проводится путем жеребьевки или на
основе таблиц случайных чисел. Это
классический способ формирования
выборочной совокупности, и именно на
нем основывается теория выборочного
метода.

При
механическом отборе
основой выборки является упорядоченная
численность элементов генеральной
совокупности. Отбор элементов
осуществляется через одинаковые
интервалы, шаг интервала зависит от
доли выборки. Так, при
=
0,05 шаг интервала составляет

= 20. Ошибка механической выборки
вычисляется по формуле бесповторной
выборки. Для
моментных наблюдений,
фиксирующих состояние непрерывного
процесса на определенные моменты
времени, используют формулу ошибки
повторной выборки.

Типический
(районированный) отбор
предусматривает предварительную
структуризацию генеральной совокупности
и независимый отбор элементов в каждой
составной части. Объем типической
выборки — это сумма частных
выборок
n_j,
т. е.

, где m — число составных частей (групп,
типических районов и т. п.).

При
вычислении ошибки типической выборки
используют среднюю из групповых дисперсий

Как
правило,
,
следовательно, ошибка типической выборки
меньше, чем механической или простой
случайной. Чаще всего используют отбор,
пропорциональный численности составляющих
совокупности, т. е. доля выборки для всех
составляющих одинакова.

При
серийном
отборе
основа выборки состоит из серий элементов
совокупности, связанных территориально
(районы, поселки), организационно (фирмы,
акционерные общества) и т. п. Серии
отбираются по схеме механической или
простой случайной выборки, обследованию
подлежат все элементы серии. При
вычислении ошибки выборки учитывается
межсерийная вариация:

где
s — число серий,

— средняя k-й серии.

Проектируя
выборочные наблюдения, определяют
минимально достаточный объем выборки,
при котором выборочные оценки представляли
бы основные свойства генеральной
совокупности:

для
повторного отбора

для
бесповторного

Для
определения объема выборки n
используют оценки дисперсий ²
аналогичных или пробных обследований.
Если такие обследования отсутствуют,
можно воспользоваться соотношением
,
а для доли взять наибольшее значение
дисперсии ²
= 0,25.

Пример.
Изучается отношение сельского населения
региона к праву купли-продажи земли. По
результатам аналогичных обследований
в других регионах, 40% опрошенных
поддерживают это право. При каком объеме
выборки предельная ошибка (с вероятностью
0,954) не превысит 5%?

Опираясь
на результаты аналогичных обследований,
определим 2
= pq = 0,4 • 0,6 = 0,24. Тогда минимальный
достаточный объем выборки составит

Если
в основу расчета л положить относительную
ошибку выборки V_
= tV_
формулы соответственно модифицируются:

для
средней

для
доли

Статистическая
гипотеза
— это определенное предположение
относительно свойств генеральной
совокупности, которое можно проверить
по данным выборочного наблюдения.
Гипотеза, которую необходимо проверить,
формулируется как отсутствие различий
между параметром генеральной совокупности
G и заданной величиной а (нулевая
гипотеза).
Содержание ее записывают так: Н₀
:G = а. Каждой нулевой гипотезе
противопоставляют альтернативную Н_а.
В зависимости от значимости отклонений
она формулируется как Н_а
: G > а; Н_а
: G < а или Н₀
: G 
а.

Если
выборочные данные противоречат гипотезе
Н₀
она отклоняется, если согласовываются
с ней — Н₀не отклоняется.
Проверка гипотез непременно связана с
риском принятия ошибочного решения:
риск I рода — отклонение верной нулевой
гипотезы, риск II рода — принятие Н₀
когда в действительности верна
альтернативная.

Правило,
по которому гипотеза Н₀
отклоняется или не отклоняется, называют
статистическим критерием. Математической
основой любого критерия является
статистическая характеристика Z, закон
распределения которой известен (например,
характеристика t-распределения
Стьюдента).

Вероятность
риска отклонить верную гипотезу называют
уровнем значимости а, а значение
статистической характеристики для
вероятности 1 — а — критическим значением
Z_1-а.
В приложении приведены критические
значения наиболее распространенных
статистических критериев. Если выборочное
значение Z > Z^_1-а,
гипотеза Н₀
отклоняется, при Z < Z_1-а
не отклоняется.

В
случае проверки справедливости Н₀
: G = а против Н₀
: G 
а используют двусторонний критерий, а
критическое значение Z определяется
для а/2 , т. е.

Пример/
На курсах восточных языков используют
две методики обучения — новую и
традиционную. Для сравнения эффективности
новой методики проведено тестирование
двух групп китайского языка по 100-балльной
системе. Восемь слушателей, обучавшихся
по новой методике, получили

средний
бал

= 84 при дисперсии

= 32; 10 слушателей, обучавшихся по
традиционной методике, за такой же тест
имели средний балл

= 76 при дисперсии

= 24. Разность между средними двух групп
составляет (
—
)
= 84 — 76 = 8 баллов. Необходимо проверить,
случайны ли эти различия, или они
обусловлены большей эффективностью
новой методики. Нулевая гипотеза
формулируется, исходя из предположения,
что отклонение средних случайно, т.е.
Н₀:

=
.
Альтернативная гипотеза предусматривает,
что новая методика эффективнее, т. е. Н_a
:

>
.
При таком формулировании H_a
проводится односторонняя проверка
нулевой гипотезы. Статистической
характеристикой проверки H₀
является нормированное отклонение
средних

подчиненное
распределению вероятностей Стьюдента
с числом степеней, свободы k = n₁
+ n₂
— 2.

В
нашем примере k = 8 + 10 — 2 = 16; оценка средней
из групповых дисперсий составляет:

Критическое
значение одностороннего t-критерия при
а = 0,05 и k = 16 составляет t_0,95
(16) = 1,75, что меньше фактического (t = 3,03).
Следовательно, нулевая гипотеза Н₀
:

=

отклоняется. С вероятностью 0,95 можно
утверждать, что новая методика изучения
восточных языков эффективнее.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Загрузить PDF

Стандартной ошибкой называется величина, которая характеризует стандартное (среднеквадратическое) отклонение выборочного среднего. Другими словами, эту величину можно использовать для оценки точности выборочного среднего. Множество областей применения стандартной ошибки по умолчанию предполагают нормальное распределение. Если вам нужно рассчитать стандартную ошибку, перейдите к шагу 1.

1

Запомните определение среднеквадратического отклонения. Среднеквадратическое отклонение выборки – это мера рассеянности значения. Среднеквадратическое отклонение выборки обычно обозначается буквой s. Математическая формула среднеквадратического отклонения приведена выше.
2

Узнайте, что такое истинное среднее значение. Истинное среднее является средним группы чисел, включающим все числа всей группы – другими словами, это среднее всей группы чисел, а не выборки.
3

Научитесь рассчитывать среднеарифметическое значение. Среднеаримфетическое означает попросту среднее: сумму значений собранных данных, разделенную на количество значений этих данных.
4

Узнайте, что такое выборочное среднее. Когда среднеарифметическое значение основано на серии наблюдений, полученных в результате выборок из статистической совокупности, оно называется “выборочным средним”. Это среднее выборки чисел, которое описывает среднее значение лишь части чисел из всей группы. Его обозначают как:
5

Усвойте понятие нормального распределения. Нормальные распределения, которые используются чаще других распределений, являются симметричными, с единичным максимумом в центре – на среднем значении данных. Форма кривой подобна очертаниям колокола, при этом график равномерно опускается по обе стороны от среднего. Пятьдесят процентов распределения лежит слева от среднего, а другие пятьдесят процентов – справа от него. Рассеянность значений нормального распределения описывается стандартным отклонением.
6

Запомните основную формулу. Формула для вычисления стандартной ошибки приведена выше.

Реклама

1
Рассчитайте выборочное среднее. Чтобы найти стандартную ошибку, сначала нужно определить среднеквадратическое отклонение (поскольку среднеквадратическое отклонение s входит в формулу для вычисления стандартной ошибки). Начните с нахождения средних значений. Выборочное среднее выражается как среднее арифметическое измерений x1, x2, . . . , xn. Его рассчитывают по формуле, приведенной выше.
- Допустим, например, что вам нужно рассчитать стандартную ошибку выборочного среднего результатов измерения массы пяти монет, указанных в таблице:
  Вы сможете рассчитать выборочное среднее, подставив значения массы в формулу:
2
Вычтите выборочное среднее из каждого измерения и возведите полученное значение в квадрат. Как только вы получите выборочное среднее, вы можете расширить вашу таблицу, вычтя его из каждого измерения и возведя результат в квадрат.
- Для нашего примера расширенная таблица будет иметь следующий вид:
3
Найдите суммарное отклонение ваших измерений от выборочного среднего. Общее отклонение – это сумма возведенных в квадрат разностей от выборочного среднего. Чтобы определить его, сложите ваши новые значения.
- В нашем примере нужно будет выполнить следующий расчет:
  Это уравнение дает сумму квадратов отклонений измерений от выборочного среднего.
4
Рассчитайте среднеквадратическое отклонение ваших измерений от выборочного среднего. Как только вы будете знать суммарное отклонение, вы сможете найти среднее отклонение, разделив ответ на n -1. Обратите внимание, что n равно числу измерений.
- В нашем примере было сделано 5 измерений, следовательно n – 1 будет равно 4. Расчет нужно вести следующим образом:
5
Найдите среднеквадратичное отклонение. Сейчас у вас есть все необходимые значения для того, чтобы воспользоваться формулой для нахождения среднеквадратичного отклонения s.
- В нашем примере вы будете рассчитывать среднеквадратичное отклонение следующим образом:
  Следовательно, среднеквадратичное отклонение равно 0,0071624.
Реклама

1
Чтобы вычислить стандартную ошибку, воспользуйтесь базовой формулой со среднеквадратическим отклонением.
- В нашем примере вы сможете рассчитать стандартную ошибку следующим образом:
  Таким образом в нашем примере стандартная ошибка (среднеквадратическое отклонение выборочного среднего) составляет 0,0032031 грамма.

Советы

Стандартную ошибку и среднеквадратическое отклонение часто путают. Обратите внимание, что стандартная ошибка описывает среднеквадратическое отклонение выборочного распределения статистических данных, а не распределения отдельных значений
В научных журналах понятия стандартной ошибки и среднеквадратического отклонения несколько размыты. Для объединения двух величин используется знак ±.

Об этой статье

Эту страницу просматривали 48 054 раза.

Была ли эта статья полезной?

Провести анализ этих данных, используя один из статистических ППП, на основе описательной статистики.

1. Рассчитать для всех трех переменных среднюю арифметическую, моду, медиану, стандартное отклонение, верхний и нижний квартили, асимметрию, эксцесс и коэффициент вариации.

2.На основе рассчитанных статистик провести сравнительный анализ средних оценок удовлетворенности и их стандартных отклонений по каждой из приведенных позиций.

3.Прокомментировать значения коэффициентов вариации.

4.Прокомментировать в сравнительном анализе значения квартилей.

5.Прокомментировать в сравнительном анализе значения асимметрий.

6.Прокомментировать в сравнительном анализе значения эксцессов.

7.Прокомментировать различия в средних арифметических и медианах внутри каждой из позиции и соотнести это со значениями асимметрии.

8.Построить для каждой переменной полигон, гистограмму (частот и относительных частот, накопленных частот), а также ящичковые диаграммы. Прокомментировать их вид с точки зрения анализа ответов..

9.Провести сравнительный анализ информации для каждого предприятия.


	Пример 2. Имеются данные о средних сроках (в днях) оборота наличных денежных
средств для 39 фирм:	13,9	11,1	9,5	19,6	8,5		29,8	6,2 5,9 40,9 4 10,3	31,8
65,2	38,2	10,8		13,7	18,8	8,1	16,7	26,1	28,2	11,1	17,2	10,3	38,8	54,11	12,2
18	37	14,4	19,7	10,2	68,1	6,7	9,5	10,3	3,8		11,65	16,8.
	Проанализировать эту информацию, рассчитав для нее описательные статистики и
построив гистограмму и »ящик-с-усами».
	Известно,		что	распределения с	более	длинным правым	хвостом	путем

логарифмирования можно преобразовать в приближенно симметричные. Проверить это на данном примере.

Пример 3. Любой статистический ППП поставляется с набором учебных файлов. Проанализируйте, например, в ППП Statgraphics Plus в файле Cardata с помощью описательной статистики переменные “price” и “ mpg”.

Исследователь имеет дело, как правило, с выборкой и по выборочным данным пытается сделать выводы о свойствах генеральной совокупности. Характеристики генеральной совокупности будем называть параметрами. Параметры, как правило, нам неизвестны, и мы можем лишь приближенно оценивать их на основе выборочных данных. Тем самым мы получаем оценки параметров генеральной совокупности. Отметим, что оценка будет давать верное представление о параметре, если она получена из генеральной совокупности на основе случайной выборки. Выборка называется случайной, если для каждого элемента совокупности вероятность попасть в эту выборку известна и одинакова. Только случайная выборка может представлять генеральную совокупность, и только на ее основе можно получить “хорошие” оценки. Как известно, “хорошая” оценка должна удовлетворять следующим четырем критериям: состоятельности, несмещенности, эффективности и достаточности. Напомним два из них.

Оценка называется эффективной, если она обладает наименьшей дисперсией, и несмещенной, если ее математическое ожидание совпадает со значением параметра.

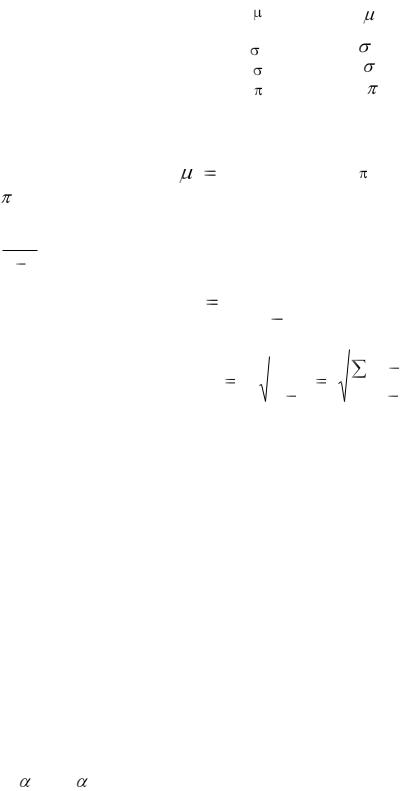
Введем обозначения, которым будем придерживаться в дальнейшем:

Характеристика	Параметр	Оценка	Выборочное
				значение
Средняя		ˆ
		х
Дисперсия	2	ˆ	2		2
	S

Станд. отклонение		ˆ
		S
Доля			ˆ
			р

Оценивание некоторого отдельного параметра дает точечную оценку. Известно, что «хорошей» оценкой средней арифметической генеральной совокупности является

выборочная средняя, т. е. ˆ
х ; аналогично для :

ˆ = р. Но выборочная дисперсия дает смещенную (заниженную) оценку генеральной дисперсии. Чтобы убрать эффект смещенности, вводят поправочный коэффициент

n 1 , тогда несмещенной оценкой генеральной дисперсии является исправленная

выборочная дисперсия: σˆ2

и,

соответственно, несмещенной оценкой

стандартного отклонения является

σˆ

x)2

Следует отметить, что в литературе можно встретить обозначение S и для исправленного выборочного стандартного отклонения.

До сих пор речь шла о точечных оценках параметров генеральной совокупности. Как известно, оценка – это приближенное значение параметра генеральной совокупности. О мере точности и надежности точечной оценки судить сложно, поскольку значение оценки вычисляется на основе случайной выборки и является случайным. Единственное, что можно здесь утверждать, так это то, что в соответствии с критерием состоятельности уверенность в точности точечной оценки увеличивается по мере увеличения объема выборки.

Когда речь идет о точечной оценке, нелегко продемонстрировать влияние объема выборки на точность оценки, однако это влияние очевидно при вычислении интервальной оценки. Заметим, что, переходя от точечных оценок к интервальным, мы тем самым переходим от описательной статистики к аналитической статистике или статистике вывода.

Интервальной оценкой параметра генеральной совокупности называют интервал, который с заданной вероятностью накрывает истинное значение параметра. Интервальную оценку называют доверительным интервалом, а связанную с ним и указанную выше вероятность – доверительной вероятностью. Интервальная оценка обладает такими свойствами, как точность и надежность. Точность интервальной оценки определяется величиной интервала, а надежность – степенью доверия, равной (1- ), где — вероятность того, что доверительный интервал не содержит параметр.

Интервальное оценивание связано с понятием стандартной ошибки оцениваемого параметра, которая, в свою очередь, связана с выборочным распределением. Если, например, осуществить несколько независимых случайных выборок из одной и той же генеральной совокупности и для каждой из них рассчитать выборочную среднюю, то

полученные выборочные средние можно представить как элементы отдельной выборки и их распределение называется выборочным распределением.

Известно, что если исходная совокупность имеет параметры	и , то выборочное
распределение выборочных средних при достаточно больших объемах выборки (n	30)
может быть аппроксимировано нормальным распределением,	независимо от	вида

исходного распределения, с параметрами и x = / n . x называется стандартной ошибкой выборки или просто стандартной ошибкой и характеризует меру вариации выборочных средних вокруг генеральной средней. Как видно из определения, стандартная ошибка уменьшается при увеличении объема выборки.

Оценка стандартной ошибки рассчитывается по формуле

S			S	,	(2.1)

x
	n	1

если генеральная совокупность бесконечна, и по формуле

S			N	n	S	,	(2.2)


x	N	1
				n 1

если генеральная совокупность конечна (объема N).

Рассмотрим доверительный интервал для средней арифметической генеральной совокупности. Известно, что он симметричен относительно точечной оценки параметра и рассчитывается из соотношений:

z / 2 S

или

x t / 2

в зависимости от того, какое распределение используется при его определении:

нормальное или Стьюдента.

Здесь:

z /2— значения z–статистики, справа и слева от которых находятся площади под

кривой нормального распределения, равные

/2 (определяются по таблице значений

стандартизованного нормального распределения при фиксированной вероятности

);

t /2 — значения статистики Стьюдента, справа и слева от которых находятся

площади под кривой распределения Стьюдента, равные

/2 (определяются по таблице

значений распределения Стьюдента при фиксированной

вероятности

чиcле

степеней свободы

= n-1);

sх – оценка стандартной ошибки выборки.

Отметим, что z-статистика используется при определении доверительного интервала в случае, если известно, что исследуемая совокупность имеет нормальный закон распределения и объем выборки достаточно велик, в противном случае используется статистика Стьюдента. Известно, что статистика Стьюдента может использоваться и в том случае, когда выполняются условия применимости z- статистики, поэтому в дальнейшем будем использовать t-статистику, если это не будет противоречить условиям решаемой задачи.

Во многих случаях появляется необходимость найти интервальную оценку для

разности средних двух совокупностей, т.е. для 1 — 2, по выборочным средним х1 и

х2 . Приведем эту оценку:

x1 x2

t /2

. S

x 2

здесь S

— стандартная ошибка разности средних.

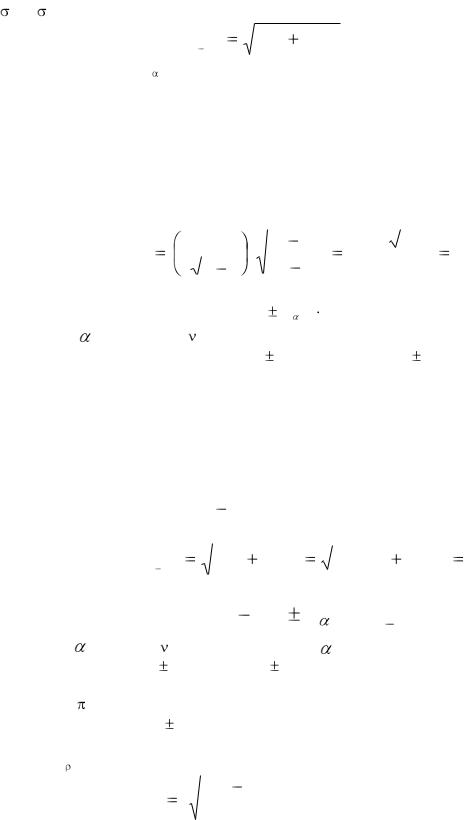
Стандартная ошибка разности средних и число степеней свободы для статистики Стьюдента определяются по-разному, в зависимости от того, равны или не равны объемы выборок и равны или нет дисперсии совокупностей. Например, приближенная формула для определения значения стандартной ошибки разности двух средних, основанная на допущениях о большом объеме двух выборок и их независимом отборе из двух генеральных совокупностей, характеризующихся одинаковой дисперсией (т.е.

12 = 22) имеет вид:

S				S		2	S	2	,
x		x	x		x

	1	2		1			2
а число степеней для t /2 равно n1 + n2	–2.

Рассмотрим решение задачи на принятие решения, в котором оказывается полезной интервальная оценка средней генеральной совокупности. Пусть составлена случайная выборка из 37 рабочих фирмы, в которой работает 785 человек. Причем средняя месячная зарплата для рабочих, попавших в выборку, равна 1100 руб. со стандартным отклонением 105 руб.

Используя 95 % — е доверительные пределы, вычислить среднюю месячную зарплату рабочих фирмы и общие расходы фирмы на зарплату.

Стандартную ошибку для средней в этом случае вычислим по формуле (2.2):

105

748

17,1.

Доверительные пределы равны:

x t

/ 2

При

= 0,05 и

= 36

tα/2 = 2,03 ( из таблицы t-распределения). Тогда

доверительный интервал равен:

1 100

2,03 · 17,1 = 1 100 34,7 или

(1 065,3 ;

1 134,7) (руб.).

Умножив на численность рабочих фирмы, получим оценку общих расходов фирмы на зарплату: от 836 260,5 до 890 739,5 (руб.).

Предположим теперь, что нам необходимо оценить наиболее вероятную разницу в средней зарплате для двух фирм, если во второй фирме для выборки из 30 рабочих средняя зарплата равна 1 000 руб. при стандартной ошибке средней в 20 руб.

Точечная оценка разности равна:

x2 = 1 100 – 1 000 = 100 (руб.).

Вычислим стандартную ошибку разности средних:

(17,1)2

(20)2 26,3.

Тогда интервальная оценка равна:

x 2

t /2 S

При

= 0,05 и

= n1 + n2 –2 = 65

t /2 = 2. Тогда имеем

100

2 . 26,3 = 100

52,6

или (47,4

; 152,6) (руб.).

Доверительный интервал для доли генеральной совокупности (относительной

величины)	определяется из соотношения:
	p	Zα/2 Sp ,	(2.3)
где р –	выборочная доля,
S —	оценка стандартной ошибки доли.

Известно, что Sρ			ρ (1	ρ)	.
		n

Для определения доверительного интервала при этом используется аппроксимация биноминального распределения нормальным, поэтому использовать статистику

Стьюдента здесь нельзя.
Как известно, такая аппроксимация возможна	при достаточно больших объемах
выборки (n	50) и при выполнении условий np 5	и n(1 — p) 5.
Аналогично определяется доверительный интервал (интервальная оценка) для
разности долей двух генеральных совокупностей (	1 — 2):
			p1 – p2	Z	/2		. S p1–p2 ,	(2.4)

где Sp	p			Sp	2	Sp		2	— одна из формул для вычисления стандартной ошибки
1		2	1			2

разности долей (в предположениях, аналогичных предыдущим).

Рассмотрим пример. Пусть фирмой при маркетинговом исследовании был организован опрос жителей одного из районов города относительно предпочтения товаров этой фирмы. Из 200 случайно отобранных жителей района 120 высказались в пользу товаров этой фирмы. Найти интервальную оценку доли жителей района, предпочитающих товары этой фирмы.

Точечная оценка доли: p = 120/200 = 0,6. Интервальную оценку вычислим по соотношению (2.3):

	Sp		0,6 (1	0,6)	0,035.

	200

Z /2 при	= 0,05 определим по таблице: Z0,025 = 1,96.	Тогда имеем:
	0,6 1,96 · 0,035	или	0,53	0,67.

Итак, в данном районе города товары этой фирмы предпочитают от 53 % до 67 % жителей.

Предположим, что в другом районе города в случайной выборке из 150 человек 55 % опрошенных предпочитают товары этой фирмы со стандартной ошибкой доли, равной 0,04. Тогда интервальная оценка разности долей жителей двух районов города определится из соотношения (2.4).

				2	2
Sp	p		Sp	Sp	0,0352	0,042 0,053.
1		2	1		2
Получим: 0,6 – 0,55	1,96	0,053	или -0,054	0,154.

Как известно, если доверительный интервал для разности двух величин содержит нуль, то эти величины различаются незначимо. Для нашего примера это означает, что в обоих исследуемых районах предпочтения для товаров этой фирмы примерно одинаковы.

2.1. Определение объема выборки, обеспечивающего заданную точность расчетов

Как уже отмечалось, интервальная оценка устанавливает прямую зависимость точности оценки от объема выборки. Запишем доверительный интервал для средней арифметической генеральной совокупности в виде:

		S
x t	/2		.


n	1

Выражение, прибавляемое и вычитаемое из выборочной средней, задает размах доверительного интервала и определяет, тем самым, точность интервальной оценки. При фиксированном стандартном отклонении точность оценки изменяется при

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Download Article

After collecting data, oftentimes the first thing you need to do is analyze it. This usually entails finding the mean, the standard deviation, and the standard error of the data. This article will show you how it’s done.

Cheat Sheets

1
Obtain a set of numbers you wish to analyze. This information is referred to as a sample.
- For example, a test was given to a class of 5 students, and the test results are 12, 55, 74, 79 and 90.

1
Calculate the mean. Add up all the numbers and divide by the population size:^[1]
- Mean (μ) = ΣX/N, where Σ is the summation (addition) sign, x_i is each individual number, and N is the population size.
- In the case above, the mean μ is simply (12+55+74+79+90)/5 = 62.

1
Calculate the standard deviation. This represents the spread of the population.
Standard deviation = σ = sq rt [(Σ((X-μ)^2))/(N)].^[2]
- For the example given, the standard deviation is sqrt[((12-62)^2 + (55-62)^2 + (74-62)^2 + (79-62)^2 + (90-62)^2)/(5)] = 27.4. (Note that if this was the sample standard deviation, you would divide by n-1, the sample size minus 1.)

1
Calculate the standard error (of the mean). This represents how well the sample mean approximates the population mean. The larger the sample, the smaller the standard error, and the closer the sample mean approximates the population mean. Do this by dividing the standard deviation by the square root of N, the sample size.^[3]
Standard error = σ/sqrt(n)^[4]
- So for the example above, if this were a sampling of 5 students from a class of 50 and the 50 students had a standard deviation of 17 (σ = 21), the standard error = 17/sqrt(5) = 7.6.

Add New Question

Question

How do you find the mean given number of observations?

To find the mean, add all the numbers together and divide by how many numbers there are. e.g to find the mean of 1,7,8,4,2: 1+7+8+4+2 = 22/5 = 4.4.
Question

The standard error is calculated as 0.2 and the standard deviation of a sample is 5kg. Can it be said to be smaller or larger than the standard deviation?

The standard error (SE) must be smaller than the standard deviation (SD), because the SE is calculating by dividing the SD by something — i.e. making it smaller.
Question

How can I find out the standard deviation of 50 samples?

The results of all your figures (number plus number plus number etc.) divided by quantity of samples 50 =SD.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Video

Calculations of the mean, standard deviation, and standard error are most useful for analysis of normally distributed data. One standard deviation about the central tendency covers approximately 68 percent of the data, 2 standard deviation 95 percent of the data, and 3 standard deviation 99.7 percent of the data. The standard error gets smaller (narrower spread) as the sample size increases.

Thanks for submitting a tip for review!

Check your math carefully. It is very easy to make mistakes or enter numbers incorrectly.

References

About This Article

Article SummaryX

The mean is simply the average of a set of numbers. You can work it out by adding up all the numbers and dividing the total by the amount of numbers. For example, if you wanted to find the average test score of 3 students who scored 74, 79, and 90, you’d add the 3 numbers together to get 243, then divide it by 3 to get 81. The standard error represents how well the sample mean approximates the population mean. All you need to do is divide the standard deviation by the square root of the sample size. For instance, if you were sampling 5 students from a class of 50 and the 50 students had a standard deviation of 17, you’d divide 17 by the square root of 5 to get 7.6. For more tips, including how to calculate the standard deviation, read on!

Did this summary help you?

Thanks to all authors for creating a page that has been read 995,281 times.

Did this article help you?

Download Article

Cheat Sheets

1
Obtain a set of numbers you wish to analyze. This information is referred to as a sample.
- For example, a test was given to a class of 5 students, and the test results are 12, 55, 74, 79 and 90.

1
Calculate the mean. Add up all the numbers and divide by the population size:^[1]
- Mean (μ) = ΣX/N, where Σ is the summation (addition) sign, x_i is each individual number, and N is the population size.
- In the case above, the mean μ is simply (12+55+74+79+90)/5 = 62.

1
Calculate the standard deviation. This represents the spread of the population.
Standard deviation = σ = sq rt [(Σ((X-μ)^2))/(N)].^[2]
- For the example given, the standard deviation is sqrt[((12-62)^2 + (55-62)^2 + (74-62)^2 + (79-62)^2 + (90-62)^2)/(5)] = 27.4. (Note that if this was the sample standard deviation, you would divide by n-1, the sample size minus 1.)

1
Calculate the standard error (of the mean). This represents how well the sample mean approximates the population mean. The larger the sample, the smaller the standard error, and the closer the sample mean approximates the population mean. Do this by dividing the standard deviation by the square root of N, the sample size.^[3]
Standard error = σ/sqrt(n)^[4]
- So for the example above, if this were a sampling of 5 students from a class of 50 and the 50 students had a standard deviation of 17 (σ = 21), the standard error = 17/sqrt(5) = 7.6.

Add New Question

Question

How do you find the mean given number of observations?

To find the mean, add all the numbers together and divide by how many numbers there are. e.g to find the mean of 1,7,8,4,2: 1+7+8+4+2 = 22/5 = 4.4.
Question

The standard error is calculated as 0.2 and the standard deviation of a sample is 5kg. Can it be said to be smaller or larger than the standard deviation?

The standard error (SE) must be smaller than the standard deviation (SD), because the SE is calculating by dividing the SD by something — i.e. making it smaller.
Question

How can I find out the standard deviation of 50 samples?

The results of all your figures (number plus number plus number etc.) divided by quantity of samples 50 =SD.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Video

Calculations of the mean, standard deviation, and standard error are most useful for analysis of normally distributed data. One standard deviation about the central tendency covers approximately 68 percent of the data, 2 standard deviation 95 percent of the data, and 3 standard deviation 99.7 percent of the data. The standard error gets smaller (narrower spread) as the sample size increases.

Thanks for submitting a tip for review!

Check your math carefully. It is very easy to make mistakes or enter numbers incorrectly.

References

About This Article

Article SummaryX

Did this summary help you?

Thanks to all authors for creating a page that has been read 995,281 times.

Did this article help you?

Стандартное отклонение и стандартная ошибка: в чем разница?

17 авг. 2022 г.
читать 2 мин

В статистике студенты часто путают два термина: стандартное отклонение и стандартная ошибка .

Стандартное отклонение измеряет, насколько разбросаны значения в наборе данных.

Стандартная ошибка — это стандартное отклонение среднего значения в повторных выборках из совокупности.

Давайте рассмотрим пример, чтобы ясно проиллюстрировать эту идею.

Пример: стандартное отклонение против стандартной ошибки

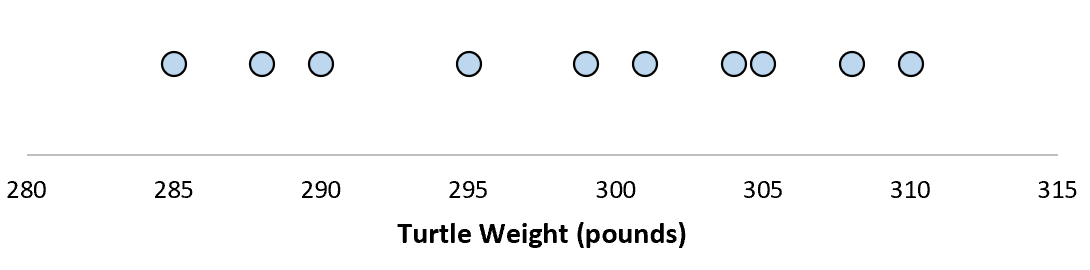
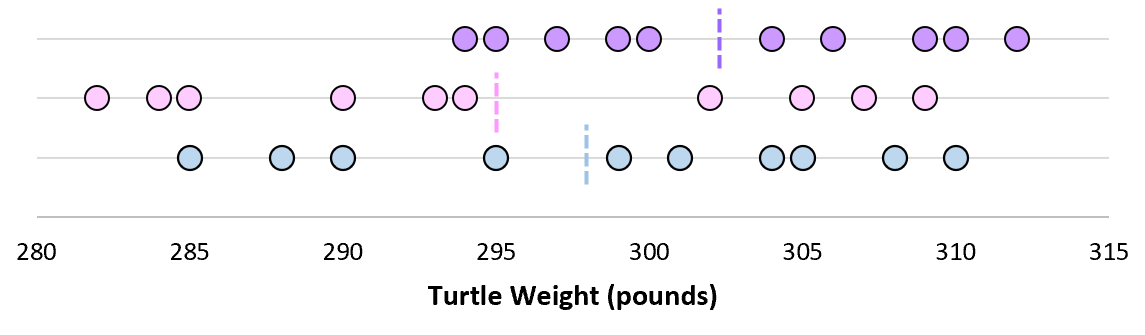
Предположим, мы измеряем вес 10 разных черепах.

Для этой выборки из 10 черепах мы можем вычислить среднее значение выборки и стандартное отклонение выборки:

Предположим, что стандартное отклонение оказалось равным 8,68. Это дает нам представление о том, насколько распределен вес этих черепах.

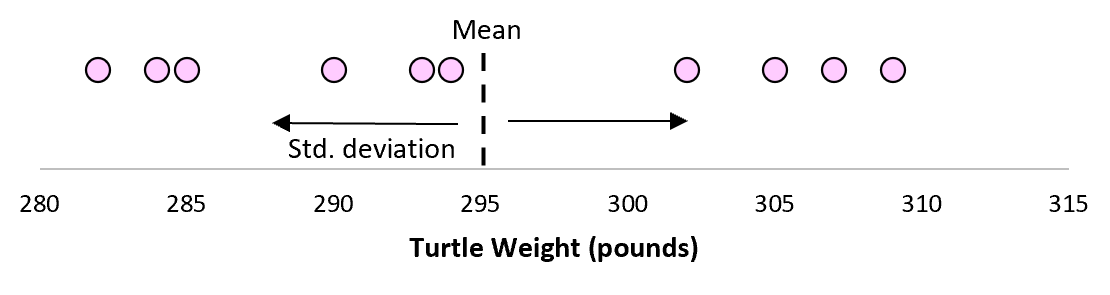
Но предположим, что мы собираем еще одну простую случайную выборку из 10 черепах и также проводим их измерения. Более чем вероятно, что эта выборка из 10 черепах будет иметь немного другое среднее значение и стандартное отклонение, даже если они взяты из одной и той же популяции:

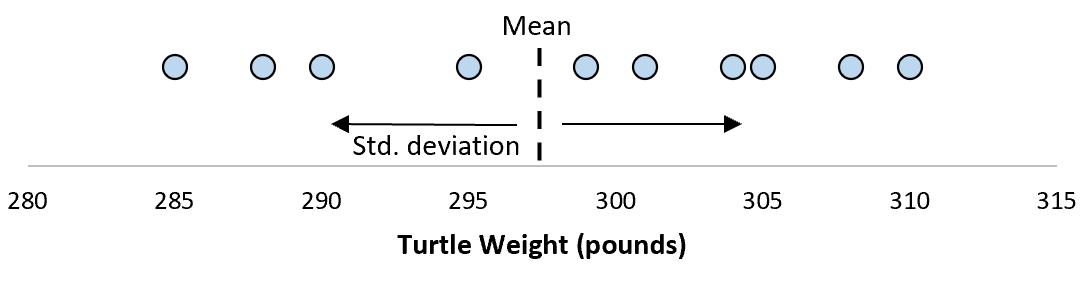
Теперь, если мы представим, что мы берем повторные выборки из одной и той же совокупности и записываем выборочное среднее и выборочное стандартное отклонение для каждой выборки:

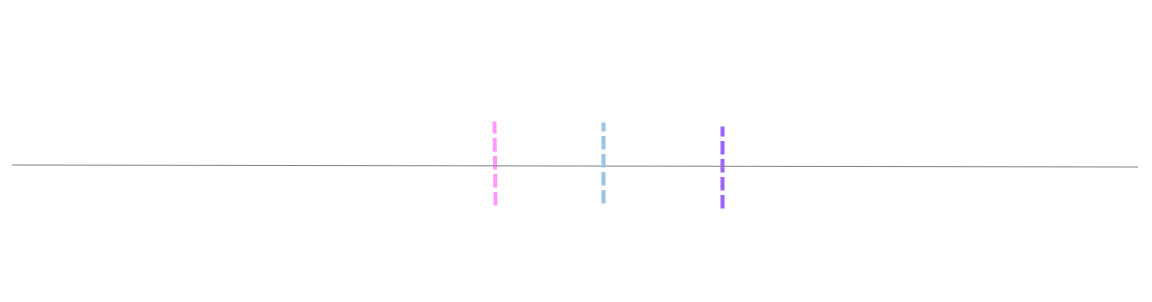
Теперь представьте, что мы наносим каждое среднее значение выборки на одну и ту же строку:

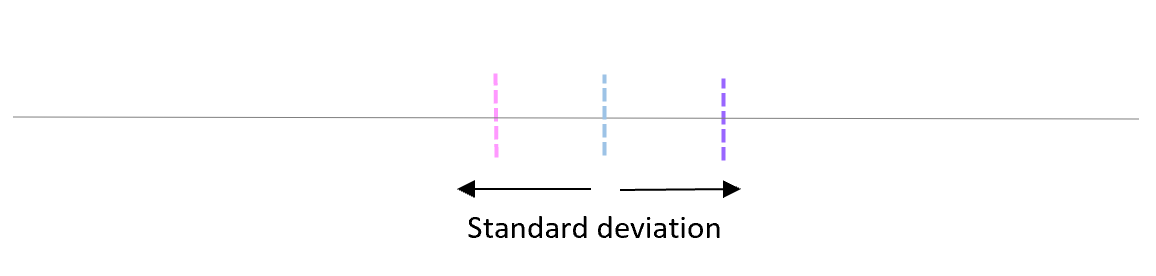
Стандартное отклонение этих средних значений известно как стандартная ошибка.

Формула для фактического расчета стандартной ошибки:

Стандартная ошибка = s/ √n

куда:

s: стандартное отклонение выборки
n: размер выборки

Какой смысл использовать стандартную ошибку?

Когда мы вычисляем среднее значение данной выборки, нас на самом деле интересует не среднее значение этой конкретной выборки, а скорее среднее значение большей совокупности, из которой взята выборка.

Однако мы используем выборки, потому что для них гораздо проще собирать данные, чем для всего населения. И, конечно же, среднее значение выборки будет варьироваться от выборки к выборке, поэтому мы используем стандартную ошибку среднего значения как способ измерить, насколько точна наша оценка среднего значения.

Вы заметите из формулы для расчета стандартной ошибки, что по мере увеличения размера выборки (n) стандартная ошибка уменьшается:

Стандартная ошибка = s/ √n

Это должно иметь смысл, поскольку большие размеры выборки уменьшают изменчивость и увеличивают вероятность того, что среднее значение нашей выборки ближе к фактическому среднему значению генеральной совокупности.

Когда использовать стандартное отклонение против стандартной ошибки

Если мы просто заинтересованы в измерении того, насколько разбросаны значения в наборе данных, мы можем использовать стандартное отклонение .

Однако, если мы заинтересованы в количественной оценке неопределенности оценки среднего значения, мы можем использовать стандартную ошибку среднего значения .

В зависимости от вашего конкретного сценария и того, чего вы пытаетесь достичь, вы можете использовать либо стандартное отклонение, либо стандартную ошибку.

Источник

Загрузить PDF

1

Запомните определение среднеквадратического отклонения. Среднеквадратическое отклонение выборки – это мера рассеянности значения. Среднеквадратическое отклонение выборки обычно обозначается буквой s. Математическая формула среднеквадратического отклонения приведена выше.
2

Узнайте, что такое истинное среднее значение. Истинное среднее является средним группы чисел, включающим все числа всей группы – другими словами, это среднее всей группы чисел, а не выборки.
3

Научитесь рассчитывать среднеарифметическое значение. Среднеаримфетическое означает попросту среднее: сумму значений собранных данных, разделенную на количество значений этих данных.
4

Узнайте, что такое выборочное среднее. Когда среднеарифметическое значение основано на серии наблюдений, полученных в результате выборок из статистической совокупности, оно называется “выборочным средним”. Это среднее выборки чисел, которое описывает среднее значение лишь части чисел из всей группы. Его обозначают как:
5

Усвойте понятие нормального распределения. Нормальные распределения, которые используются чаще других распределений, являются симметричными, с единичным максимумом в центре – на среднем значении данных. Форма кривой подобна очертаниям колокола, при этом график равномерно опускается по обе стороны от среднего. Пятьдесят процентов распределения лежит слева от среднего, а другие пятьдесят процентов – справа от него. Рассеянность значений нормального распределения описывается стандартным отклонением.
6

Запомните основную формулу. Формула для вычисления стандартной ошибки приведена выше.

Реклама

1
Рассчитайте выборочное среднее. Чтобы найти стандартную ошибку, сначала нужно определить среднеквадратическое отклонение (поскольку среднеквадратическое отклонение s входит в формулу для вычисления стандартной ошибки). Начните с нахождения средних значений. Выборочное среднее выражается как среднее арифметическое измерений x1, x2, . . . , xn. Его рассчитывают по формуле, приведенной выше.
- Допустим, например, что вам нужно рассчитать стандартную ошибку выборочного среднего результатов измерения массы пяти монет, указанных в таблице:
  Вы сможете рассчитать выборочное среднее, подставив значения массы в формулу:
2
Вычтите выборочное среднее из каждого измерения и возведите полученное значение в квадрат. Как только вы получите выборочное среднее, вы можете расширить вашу таблицу, вычтя его из каждого измерения и возведя результат в квадрат.
- Для нашего примера расширенная таблица будет иметь следующий вид:
3
Найдите суммарное отклонение ваших измерений от выборочного среднего. Общее отклонение – это сумма возведенных в квадрат разностей от выборочного среднего. Чтобы определить его, сложите ваши новые значения.
- В нашем примере нужно будет выполнить следующий расчет:
  Это уравнение дает сумму квадратов отклонений измерений от выборочного среднего.
4
Рассчитайте среднеквадратическое отклонение ваших измерений от выборочного среднего. Как только вы будете знать суммарное отклонение, вы сможете найти среднее отклонение, разделив ответ на n -1. Обратите внимание, что n равно числу измерений.
- В нашем примере было сделано 5 измерений, следовательно n – 1 будет равно 4. Расчет нужно вести следующим образом:
5
Найдите среднеквадратичное отклонение. Сейчас у вас есть все необходимые значения для того, чтобы воспользоваться формулой для нахождения среднеквадратичного отклонения s.
- В нашем примере вы будете рассчитывать среднеквадратичное отклонение следующим образом:
  Следовательно, среднеквадратичное отклонение равно 0,0071624.
Реклама

1
Чтобы вычислить стандартную ошибку, воспользуйтесь базовой формулой со среднеквадратическим отклонением.
- В нашем примере вы сможете рассчитать стандартную ошибку следующим образом:
  Таким образом в нашем примере стандартная ошибка (среднеквадратическое отклонение выборочного среднего) составляет 0,0032031 грамма.

Советы

Стандартную ошибку и среднеквадратическое отклонение часто путают. Обратите внимание, что стандартная ошибка описывает среднеквадратическое отклонение выборочного распределения статистических данных, а не распределения отдельных значений
В научных журналах понятия стандартной ошибки и среднеквадратического отклонения несколько размыты. Для объединения двух величин используется знак ±.

Об этой статье

Эту страницу просматривали 50 283 раза.

Была ли эта статья полезной?

Источник

Один из первых шагов при планировании количественного маркетингового исследования – определение объема выборки.

Калькулятор для расчета достаточного объема выборки
Калькулятор ошибки выборки для доли признака
Калькулятор ошибки выборки для среднего значения
Калькулятор значимости различий долей
Калькулятор значимости различий средних

1. Формула (даже две)

Бытует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с размером генеральной совокупности. Например, при опросах организаций (B2B).

Если речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная.

На рис.1. пример выборки 15000 человек (!) при опросе в муниципальном районе. Возможно, от численности населения взяли 10%?
Размер выборки никогда не рассчитывается как процент от генеральной совокупности!

Рис.1. Размер выборки 15000 человек, как реальный пример некомпетентности (или хуже).

В таких случаях для расчета объема выборки используется следующая формула:

где

n – объем выборки,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует,
∆ – предельная ошибка выборки.

Доверительный уровень – это вероятность того, что реальная доля лежит в границах полученного доверительного интервала: выборочная доля (p) ± ошибка выборки (Δ). Доверительный уровень устанавливает сам исследователь в соответствии со своими требованиями к надежности полученных результатов. Чаще всего применяются доверительные уровни, равные 0,95 или 0,99. В маркетинговых исследованиях, как правило, выбирается доверительный уровень, равный 0,95. При этом уровне коэффициент Z равен 1,96.

Значения p и q чаще всего неизвестны до проведения исследования и принимаются за 0,5. При этом значении размер ошибки выборки максимален.

Допустимая предельная ошибка выборки выбирается исследователем в зависимости от целей исследования. Считается, что для принятия бизнес-решений ошибка выборки должна быть не больше 4%. Этому значению соответствует объем выборки 500-600 респондентов. Для важных стратегических решений целесообразно минимизировать ошибку выборки.

Рассмотрим кривую зависимости ошибки выборки от ее объема (Рис.2).

Рис.2. Зависимость ошибки выборки от ее объема при 95% доверительном уровне

Как видно из диаграммы, с ростом объема выборки значение ошибки уменьшается все медленнее. Так, при объеме выборки 1500 человек предельная ошибка выборки составит ±2,5%, а при объеме 2000 человек – ±2,2%. То есть, при определенном объеме выборки дальнейшее его увеличение не дает значительного выигрыша в ее точности.

ШПАРГАЛКА (скопируйте ссылку или текст)

Подходы к решению проблемы:

Случай 1. Генеральная совокупность значительно больше выборки:

Случай 2. Генеральная совокупность сопоставима с объемом выборки: (см. раздел исследований B2B)

где
n – объем выборки,

N – объем генеральной совокупности,

Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,

p – доля респондентов с наличием исследуемого признака,

q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует, (значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования)

∆ – предельная ошибка выборки.

Например,

рассчитаем ошибку выборки объемом 1000 человек при 95% доверительном уровне, если генеральная совокупность значительно больше объема выборки:

Ошибка выборки = 1,96 * КОРЕНЬ(0,5*0,5/1000) = 0,031 = ±3,1%

При расчете объема выборки следует также учитывать стоимость проведения исследования. Например, при цене за 1 анкету 200 рублей стоимость опроса 1000 человек составит 200 000 рублей, а опрос 1500 человек будет стоить 300 000 рублей. Увеличение затрат в полтора раза сократит ошибку выборки всего на 0,6%, что обычно неоправданно экономически.

2. Причины «раздувать» выборку

Анализ полученных данных обычно включает в себя и анализ подвыборок, объемы которых меньше основной выборки. Поэтому ошибка для выводов по подвыборкам больше, чем ошибка по выборке в целом. Если планируется анализ подгрупп / сегментов, объем выборки должен быть увеличен (в разумных пределах).

Рис.3 демонстрирует данную ситуацию. Если для исследования авиапассажиров используется выборка численностью 500 человек, то для выводов по выборке в целом ошибка составляет 4,4%, что вполне приемлемо для принятия бизнес-решений. Но при делении выборки на подгруппы в зависимости от цели поездки, выводы по каждой подгруппе уже недостаточно точны. Если мы захотим узнать какие-либо количественные характеристики группы пассажиров, совершающих бизнес-поездку и покупавших билет самостоятельно, ошибка полученных показателей будет достаточно велика. Даже увеличение выборки до 2000 человек не обеспечит приемлемой точности выводов по этой подвыборке.

Рис.3. Проектирование объема выборки с учетом необходимости анализа подвыборок

Другой пример – анализ подгрупп потребителей услуг торгово-развлекательного центра (Рис.4).

Рис.4. Потенциальный спрос на услуги торгово-развлекательного центра

При объеме выборки в 1000 человек выводы по каждой отдельной услуге (например, социально-демографический профиль, частота пользования, средний чек и др.) будут недостаточно точными для использования в бизнес планировании. Особенно это касается наименее популярных услуг (Таблица 1).

Таблица 1. Ошибка по подвыборкам потенциальных потребителей услуг торгово-развлекательного центра при выборке 1000 чел.

Чтобы ошибка в самой малочисленной подвыборке «Ночной клуб» составила меньше 5%, объем выборки исследования должен составлять около 4000 человек. Но это будет означать 4-кратное удорожание проекта. В таких случаях возможно компромиссное решение:

увеличение выборки до 1800 человек, что даст достаточную точность для 6 самых популярных видов услуг (от кинотеатра до парка аттракционов);
добор 200-300 пользователей менее популярных услуг с опросом по укороченной анкете (см. Таблицу 2).

Таблица 2. Разница в ошибке выборки по подвыборкам при разных объемах выборки.

При обсуждении с исследовательским агентством точности результатов планируемого исследования рекомендуется принимать во внимание бюджет, требования к точности результатов в целом по выборке и в разрезе подгрупп. Если бюджет не позволяет получить информацию с приемлемой ошибкой, лучше пока отложить проект (или поторговаться).

КАЛЬКУЛЯТОРЫ ДЛЯ РАСЧЕТА СТАТИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ И ОПРЕДЕЛЕНИЯ ЗНАЧИМОСТИ РАЗЛИЧИЙ:

КАЛЬКУЛЯТОР ДЛЯ РАСЧЕТА
ДОСТАТОЧНОГО ОБЪЁМА ВЫБОРКИ

Доверительный уровень:

Ошибка выборки (?):
%

Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)

РЕЗУЛЬТАТ

Один из важных вопросов, на которые нужно ответить при планировании исследования, — это оптимальный объем выборки. Слишком маленькая выборка не сможет обеспечить приемлемую точность результатов опроса, а слишком большая приведет к лишним расходам.

Онлайн-калькулятор объема выборки поможет рассчитать оптимальный размер выборки, исходя из максимально приемлемого для исследователя размера ошибки выборки.

Все дальнейшие формулы и расчеты относятся только к простой случайной выборке!
Формулы для других типов выборки отличаются.

Объем выборки рассчитывается по следующим формулам

1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)

2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:

Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.

N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели соков и нектаров, постоянно проживающие в Москве и Московской области). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).

p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.

q = 1 — p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален. В данном калькуляторе значения p и q по умолчанию равны 0,5.

Δ– предельная ошибка выборки (для доли признака), приемлемая для исследователя. Считается, что для принятия бизнес-решений ошибка выборки не должна превышать 4%.

n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании.

ПРИМЕР РАСЧЕТА ОБЪЕМА ВЫБОРКИ:

Допустим, мы хотим рассчитать объем выборки, предельная ошибка которой составит 4%. Мы принимаем доверительный уровень, равный 95%. Генеральная совокупность значительно больше выборки. Тогда объем выборки составит:

n = 1,96 * 1,96 * 0,5 * 0,5 / (0,04 * 0,04) = 600,25 ≈ 600 человек

Таким образом, если мы хотим получить результаты с предельной ошибкой 4%, нам нужно опросить 600 человек.

КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА

Доверительный уровень:

Объём выборки (n):

Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)

Доля признака (p):
%

РЕЗУЛЬТАТ

Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).

Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.

Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.

Ошибка выборки для доли признака рассчитывается по следующим формулам.

1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)

2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:

N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели шоколада, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).

n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.

Δ– предельная ошибка выборки.

Таким образом, зная объем выборки исследования, мы можем заранее оценить показатель ее ошибки.
А получив значение p, мы можем рассчитать доверительный интервал для доли признака: (p — ∆; p + ∆)

ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА:

Например, в ходе исследования были опрошены 1000 человек (n=1000). 20% из них заинтересовались новым продуктом (p=0,2). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):

∆ = 1,96 * КОРЕНЬ (0,2*0,8/1000) = 0,0248 = ±2,48%

Рассчитаем доверительный интервал:

(p — ∆; p + ∆) = (20% — 2,48%; 20% + 2,48%) = (17,52%; 22,48%)

Таким образом, с вероятностью 95% мы можем быть уверены, что реальная доля заинтересованных в новом продукте (среди всей генеральной совокупности) находится в пределах полученного диапазона (17,52%; 22,48%).

Если бы мы выбрали доверительный уровень, равный 99%, то для тех же значений p и n ошибка выборки была бы больше, а доверительный интервал – шире. Это логично, поскольку, если мы хотим быть более уверены в том, что наш доверительный интервал «накроет» реальное значение признака, то интервал должен быть более широким.

КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ

Доверительный уровень:

Объём выборки (n):

Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)

Среднее значение (x̄):

Стандартное отклонение (s):

РЕЗУЛЬТАТ

Ошибка выборки для среднего значения рассчитывается по следующим формулам.

1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)

2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:

N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели мороженого, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).

s — выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:

где, x ̅ – среднее арифметическое показателя, x_i– значение i-го показателя, n – объем выборки

Δ– предельная ошибка выборки.

Зная среднее значение показателя x ̅ и ошибку ∆, мы можем рассчитать доверительный интервал для среднего значения:(x ̅ — ∆; x ̅ + ∆)

ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ:

Например, в ходе исследования были опрошены 1000 человек (n=1000). Каждого из них попросили указать их примерную среднюю сумму покупки (средний чек) в известной сети магазинов. Среднее арифметическое всех ответов составило 500 руб. (x ̅=500), а стандартное отклонение составило 120 руб. (s=120). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):

∆ = 1,96 * 120 / КОРЕНЬ (1000) = 7,44

Рассчитаем доверительный интервал:

(x ̅ — ∆; x ̅ + ∆) = (500 – 7,44; 500 + 7,44) = (492,56; 507,44)

Таким образом, с вероятностью 95% мы можем быть уверены, что значение среднего чека по всей генеральной совокупности находится в границах полученного диапазона: от 492,56 руб. до 507,44 руб.

КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ ДОЛЕЙ

Доверительный уровень:

	Измерение 1	Измерение 2
Доля признака (p):	%	%
Объём выборки (n):

РЕЗУЛЬТАТ

Если в прошлогоднем исследовании вашу марку вспомнили 10% респондентов, а в исследовании текущего года – 15%, не спешите открывать шампанское, пока не воспользуетесь нашим онлайн-калькулятором для оценки статистической значимости различий.

Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.

Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.

В приведенном здесь калькуляторе используется двухвыборочный z-тест для долей. Для его применения должны соблюдаться следующие условия:

Обе выборки – простые случайные
Выборки независимы (между значениями двух выборок нет закономерной связи)
Генеральные совокупности значительно больше выборок
Произведения n*p и n*(1-p), где n=размер выборки а p=доля признака, – не меньше 5.

В калькуляторе используются следующие вводные данные:

Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.

Доля признака (p) – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.

Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.

Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.

КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ СРЕДНИХ

Доверительный уровень:

	Измерение 1	Измерение 2
Среднее значение (x̄):
Стандартное отклонение (s):
Объём выборки (n):

РЕЗУЛЬТАТ

Допустим, выборочный опрос посетителей двух разных ТРЦ показал, что средний чек в одном из них равен 1000 рублей, а в другом – 1200 рублей. Следует ли отсюда вывод, что суммы среднего чека в двух этих ТРЦ действительно отличаются?

В приведенном здесь калькуляторе используется двухвыборочный z-тест для средних значений. Для его применения должны соблюдаться следующие условия:

Обе выборки – простые случайные
Выборки независимы (между значениями двух выборок нет закономерной связи)
Генеральные совокупности значительно больше выборок
Распределения значений в выборках близки к нормальному распределению.

В калькуляторе используются следующие вводные данные:

Среднее значение ( ̅x) – среднее арифметическое показателя.

Стандартное отклонение (s) – выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:

где, x ̅ – среднее арифметическое показателя, x_i– значение i-го показателя, n – объем выборки

Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.

Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.

Вы можете подписаться на уведомления о новых материалах СканМаркет

Источник

Standard error of the sample mean[edit]

Exact value[edit]

Estimate[edit]

Accuracy of the estimator[edit]

Derivation[edit]

Independent and identically distributed random variables with random sample size[edit]

Student approximation when σ value is unknown[edit]

Assumptions and usage[edit]

Standard error of mean versus standard deviation[edit]

Extensions[edit]

Finite population correction (FPC)[edit]

Correction for correlation in the sample[edit]

See also[edit]

References[edit]

Советы

Об этой статье

Была ли эта статья полезной?

Оценка стандартной ошибки рассчитывается по формуле

Cheat Sheets

Video

References

About This Article

Did this article help you?

Cheat Sheets

Video

References

About This Article

Did this article help you?

Стандартное отклонение и стандартная ошибка: в чем разница?

Пример: стандартное отклонение против стандартной ошибки

Какой смысл использовать стандартную ошибку?

Когда использовать стандартное отклонение против стандартной ошибки

Советы

Об этой статье

Была ли эта статья полезной?

КАЛЬКУЛЯТОРЫ ДЛЯ РАСЧЕТА СТАТИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ И ОПРЕДЕЛЕНИЯ ЗНАЧИМОСТИ РАЗЛИЧИЙ: