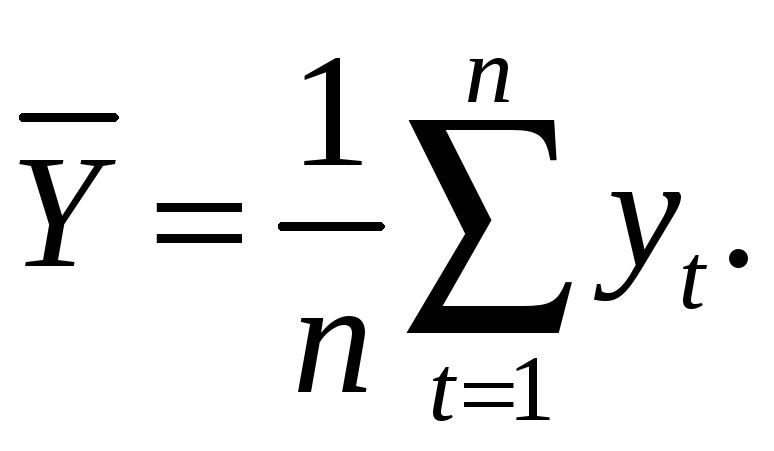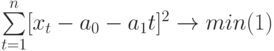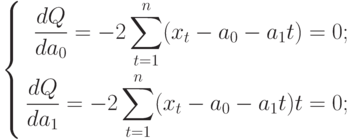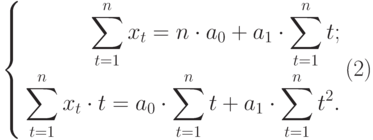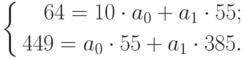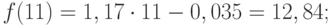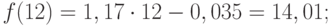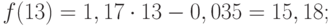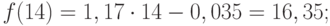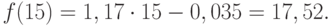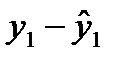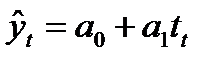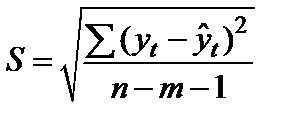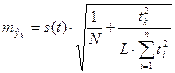Все методы
прогнозирования базируются на информации
об объекте прогнозирования и его прошлом
развитии. Прогноз, получающийся в
результате применения методов
прогнозирования, определяет ожидаемые
варианты экономического развития. При
этом предполагается, что основные
факторы и тенденции прошлого периода
сохранятся на период прогноза или что
можно обосновать и учесть направление
их изменений в рассматриваемой
перспективе. Такую гипотезу выдвигают
исходя из инерционности развития
социально-экономических явлений и
процессов. Инерционность проявляется
во взаимосвязях, т. e.
сохраняются зависимости, корреляции
прогнозируемой переменной от совокупности
факторных признаков, темпы и направление
развития, вариация показателей на
протяжении длительного периода времени.
Инерционность развития экономики
связана с длительно действующими
факторами (структура основных фондов,
их возраст и эффективность, степень
устойчивости технологических взаимосвязей
отраслей производства и др.).
Для того чтобы
в прогнозе содержалось не только
правильное качественное предсказание,
но и наиболее вероятное количественное
значение прогнозируемого признака,
необходимо, чтобы прогностическая
модель допускала малую ошибку прогноза.
Ошибка прогноза будет тем меньше, чем
меньше срок упреждения и чем длиннее
прошлый период, на информации из которого
построена прогностическая модель, т.
e.
чем длиннее база прогноза. Нет общих
правил определения допустимого срока
упреждения при заданной точности
прогноза, и наоборот: нельзя указать
точность прогноза в зависимости от
срока упреждения. В большинстве случаев
срок упреждения не должен превышать
третьей части длины базы прогноза.
Например, для прогноза на 5 лет желательно,
чтобы база прогноза (ряд динамики)
содержала не менее 15 уровней. В каждом
конкретном случае соотношение длины
базы прогноза и срока упреждения
необходимо обосновывать, используя
имеющуюся информацию.
При прогнозировании
нужно взвешивать все существующие
методы, чтобы воспользоваться тем из
них, который наиболее полно отвечает
данным обстоятельствам. Прежде всего,
следует рассмотреть метод, в котором
исследуемый динамический ряд
экстраполируется. При этом тренд,
краткосрочную осцилляцию, сезонный
эффект объединяют сложением или
умножением, в зависимости от обстоятельств,
с тем чтобы сформировать прогноз. Затем
исследуют ошибки прогноза, т. e.
вычисляют стандартную ошибку оценки
или доверительный интервал оценки,
выражая на языке вероятностей степень
уверенности в том, что оценка лежит в
заданной области. Все эти действия
основываются на том, что исследуемая
выборка извлечена случайным образом
из генеральной совокупности. При
прогнозировании, осуществляя разложение
(на тренд, краткосрочную осцилляцию,
сезонную и случайную компоненты), строят
модель. Ошибки прогноза проявляются и
вследствие ошибок спецификации этой
модели.
Наиболее точный
способ оценивания надежности метода
прогноза состоит в исследовании его
“работы” за какой-либо период. По ряду
рассчитанных ошибок можно сформировать
хорошую эмпирическую оценку ошибки,
которая, вероятно, встретится в будущем.
Однако такой метод оценки надежности
требует большего труда. Разумным
компромиссом оказывается вычисление
ошибок для прошлых моментов времени на
основе текущих значений. Это может
привести к недооценке истинных ошибок,
но, по крайней мере, будет получено
некоторое представление об ошибках в
будущем.
Число единиц
времени, на которое делается прогноз,
называется горизонтом
прогнозирования.
Рассмотрим
теперь наиболее распространенные методы
прогнозирования экономических явлений
и процессов, называемые адаптивными,
так как при получении новой информации
о динамических рядах производится
корректировка параметров моделирования,
т. e.
их адаптация к новым непрерывно
изменяющимся условиям.
9.1. Прогнозирование
с использованием показателей средних
характеристик ряда динамики.
Одним из наиболее распространенных
методов краткосрочного прогнозирования
социально-экономических явлений и
процессов является экстраполяция, т.
e.
распространение прошлых и настоящих
закономерностей, связей, соотношений
на будущее. Наиболее простым методом
экстраполяции одномерных рядов динамики
является использование средних
характеристик: среднего
уровня, среднего абсолютного прироста
и среднего темпа роста.
При использовании
среднего уровня ряда динамики в
прогнозировании социально-экономических
явлений прогнозируемый уровень
принимается равным среднему значению
уровней ряда в прошлом:
,
Прогноз вычисляется
на
моментов времени вперед (период
упреждения), т. e.
до момента
(горизонт прогнозирования). Получается
прогностическая точечная оценка,
которая, вообще говоря, не совпадает с
фактическими данными. Поэтому для
средней указывается доверительный
интервал прогноза
,
где
табличное
значение
-критерия
Стьюдента с
= n
— 1 степенями свободы и уровнем доверия
;
средняя
квадратичная ошибка средней:

Применение
доверительного интервала для
прогнозирования увеличивает степень
надежности прогноза, но, тем не менее,
прогнозируемый показатель равен среднему
уровню. Чтобы учесть вариацию показателя
вокруг средней в прошлом и будущем, для
прогностической величины вычисляют
доверительный интервал:
(9.1)
так как общая
дисперсия, связанная с колебаемостью
выборочной средней и варьированием
уровней ряда вокруг средней, будет равна

где

Если общая
тенденция развития динамического ряда
является линейной или выполняется
неравенство:
где
— остаточная дисперсия, не объясненная
экстраполяцией по среднему абсолютному
приросту;
—
общий прирост показателя от начального
уровня до конечного, то выполняется
экстраполяция по среднему абсолютному
приросту. Прогнозное значение уровня
определяют по формуле:
где
— уровень ряда динамики, принятый за
базу экстраполяции;
— средний абсолютный прирост;
— период упреждения.
Если развитие
ряда динамики списывается геометрической
прогрессией или показательной кривой,
то экстраполяция выполняется по среднему
темпу роста. Прогнозируемый уровень
ряда определяется по следующей формуле:
где
— средний темп роста;
—
уровень ряда динамики, принятый за базу
экстраполяции.
В качестве
базового уровня для экстраполяции
берется последний уровень ряда
,
так как будущее развитие начинается
именно с этого уровня. В некоторых
случаях в качестве базового уровня
лучше брать расчетный уровень,
соответствующий тренду, описывающему
динамический ряд. Для этого определяют
экспоненциальную кривую и на ее основе
находят базовый уровень. Для выбора
базового уровня можно прибегнуть к
усреднению нескольких последних уровней,
т. e.
вычислить экспоненциальную или
геометрическую среднюю нескольких
последних уровней.
Отметим, что
если уровни ряда динамики непрерывно
возрастают за рассматриваемый период,
то средний темп роста вычисляют по
формуле
где
— число цепных темпов роста;
— произведение уровней динамического
ряда;
— цепной темп роста;
— сумма порядковых номеров уровней
динамического ряда;
— начальный уровень ряда.
Если же уровни
ряда динамики в одни годы растут, а в
другие снижаются, то для вычисления
среднего темпа роста можно воспользоваться
следующей формулой:
Доверительный
интервал прогноза по среднему темпу
роста может быть построен в случае,
когда средний темп роста определяется
по экспоненциальной функции.
Указанные
способы экстраполяции тренда динамического
ряда являются весьма приближенными.
Пример 9.1.
Выпуск цемента за период с 1975 по 1990 г.
характеризуется динамическим рядом,
представленным в табл. 9.1.
Проиллюстрируем
построение прогнозов с использованием
средних характеристик данного ряда
динамики: среднего уровня, среднего
абсолютного прироста и среднего темпа
роста.
При экстраполяции
на основе среднего уровня ряда используется
принцип, при котором прогнозируемый
уровень принимается равным среднему
значению уровней в прошлом:
Таблица 9.1
-
Год, t
Производство цемента, млн.т..
Год, t
Производство цемента, млн.т
1975
122
1983
128
1976
124
1984
130
1977
127
1985
131
1978
127
1986
145
1979
123
1987
137
1980
125
1988
139
1981
127
1989
140
1982
124
1990
142
Доверительный
интервал прогноза для средней вычислим
по формуле (9.1):

Табличное
значение t-статистики
Стьюдента
с
= n
— 1 = 15 степенями свободы при уровне
доверия
= 0,05 равно
=
2,13. Среднее квадратичное отклонение,
связанное с выборочной средней и
варьированием уровней ряда вокруг
средней, равно:
Подставив
найденные значения в формулу (9.1), полущим
доверительный интервал (116,1639; 143,9561),
который с доверительной вероятностью
0,95 включает прогнозируемое значение
производства цемента равно:
млн.т.
Считая,
что общая тенденция производства цемента
является линейной, прогноз производства
цемента на 1991г. вычислим по среднему
абсолютному приросту:
За базу экстраполяции примем среднее
арифметическое трех последних уровней
исходного динамического ряда:
Средний
абсолютный прирост
Тогда прогнозное
значение уровня на 1991г.
(млн.т.)
Экстраполяция по
среднему темпу роста осуществляется
по формуле
где
За базу экстраполяции
примем среднее арифметическое трех
последних уровней, т. e.
140,3.
В этом случае прогнозируемый уровень
ряда равен:
(млн.т.)
Доверительные
интервалы прогноза по среднему абсолютному
приросту и среднему темпу роста могут
быть получены в том случае, когда общая
тенденция развития является линейной
или когда средний темп роста определяется
с помощью статистического оценивания
параметров экспоненциальной кривой.
9.2. Прогнозирование
динамики социально-экономических
явлений по трендовым моделям.
Прогнозирование с помощью трендов —
также один из простейших и распространенных
методов статистического прогнозирования.
Суть этого метода заключается во
временной экстраполяции. При этом
предполагается, что:
— период, для
которого построен тренд, достаточен
для выявления тенденции;
— анализируемый
процесс устойчив и обладает инерционностью;
— не ожидается
сильных внешних воздействий на изучаемый
процесс, которые могут серьезно повлиять
на тенденцию развития.
При соблюдении
этих условий экстраполяция осуществляется
путем подстановки в уравнение тренда
значения независимой переменной
,
соответствующей периоду упреждения
(прогноза). Получается точечная оценка
прогнозируемого показателя (в конкретном
году, квартале, месяце, дне) по уравнению,
описывающему тенденцию. Полученный
прогноз является средней оценкой для
прогнозируемого интервала времени, так
как тренд характеризует некоторый
средний уровень на каждый момент времени.
Отдельные наблюдения, как правило,
отклоняются от него в прошлом. Естественно
ожидать, что подобные отклонения будут
происходить и в будущем. Поэтому
определяется область, в которой с
определенной вероятностью следует
ожидать прогнозируемое значение, т. e.
вычисляется доверительный интервал:
,
(9.2)
где
— точечный прогноз на момент
+
;
— табличное значение
-критерия
Стьюдента с
степенями свободы при уровне доверия
;
— число параметров тренда;
— средняя квадратичная ошибка тренда:

В основу расчета
доверительного интервала прогноза
положен показатель, определяющий
колеблемость ряда заданных значений
признака. Чем выше эта колеблемость тем
менее определено положение тренда и
тем уже должен быть интервал для вариантов
прогноза при одном и том же уровне
доверия. В качестве такого показателя
ряда наблюдаемых значений признака
обычно рассматривается среднее
квадратичное отклонение фактических
наблюдений от расчетных, полученных
при выравнивании динамического ряда,
т. e.
средняя квадратичная ошибка тренда.
Доверительный
интервал (9.1) учитывает неопределенность,
связанную с положением тренда. Но он
должен учитывать также и возможность
отклонения от тренда, т. e.
среднюю квадратичную ошибку прогноза
.
Тогда доверительный интервал прогноза
будет иметь вид
.
(9.3)
Стандартная
ошибка прогноза, когда тренд описывается
прямой
,
вычисляется по формуле:
и доверительный
интервал (9.2) примет вид
(9.4)
где
— среднее квадратичное отклонение
фактических уровней динамического ряда
от расчетных, называемая стандартной
ошибкой тренда; К — величина, зависящая
только от длины динамического ряда и
периода упреждения
;
табличное значение
— критерия Стьюдента с
= n-2
степенями свободы при уровне доверия
.
С увеличением
значения К уменьшаются, а с увеличением
— увеличиваются. Поэтому достаточно
надежный прогноз получается при
относительно большом числе наблюдений
(для линейного тренда n
= 6, для параболического второй степени
n
= 13, для кубического n
= 23), когда период упреждения не очень
большой. При одном и том же
с ростом
доверительный интервал прогноза
увеличивается. Кроме того, доверительный
интервал прогноза при одной и той же
величине средней квадратичной ошибки
будет тем шире, чем выше степень
полинома, характеризующего тренд.
Доверительные
интервалы для линейного тренда,
изображены на рис. 9.1.
Рис.
9.1
Проиллюстрируем
нахождение прогноза по уравнению тренда
и построение доверительного интервала
на примере.
Пример
9.2. Рассмотрим
динамический ряд, характеризующий
производительность труда с февраля
1988г. по апрель 1989г. (см. пример 3.7). Для
данного ряда наилучшей функцией,
характеризующей тренд, была признана
прямая
,
поэтому прогностическая модель имеет
вид:
.
Прогнозирование
с помощью этой модели осуществляется
весьма просто: необходимо вместо
в уравнение подставить нужное значение
и найти прогноз. Так, для прогнозирования
производительности труда в апреле
1989г. нужно подставить
=
15, вследствие чего
Если прогноз
необходимо сделать в году
,
a
период упреждения равен
,
то в прогностическую модель подставляется
значение
,
где n
= 14 соответствует марту 1989г. Доверительные
интервалы найдем, используя выражение
(9.3). Необходимые для этого значения
можно определить из соответствующей
таблицы (см. [19,прил. 7]). Результаты
вычислений сведены в табл. 9.2.
Таблица 9.2
-
Месяц
и год, t
Факти-
ческий
уровень
Выравнен-
ное значе-
ние и про-
гноз
90% доверительный
интервал
нижняя
граница
верхняя
граница
02.1988
20
22,72
2,72
—
—
—
03.1988
24
24,63
0,63
—
—
—
04.1988
28
26,54
1,46
—
—
—
05.1988
30
28,45
1,55
—
—
—
06.1988
31
30,36
0,64
—
—
—
07.1988
33
32,27
0,73
—
—
—
08.1988
34
34,18
0,18
—
—
—
09.1988
37
36,09
0,91
—
—
—
10.1988
38
38,00
0,0
—
—
—
11.1988
40
39,91
0,09
—
—
—
12.1988
41
41,82
0,82
—
—
—
01.1989
43
43,73
0,73
—
—
—
02.1989
45
45,64
0,64
—
—
—
03.1989
48
47,55
0,45
—
—
—
04.1989
—
49,46
1,15
2,0462
47,11
51,81
05.1989
—
51,37
1,15
2,1000
48,95
53,78
06.1989
—
53,28
1,15
2,1590
50,80
55,76
Среднее
квадратичное отклонение равно 1,15. Из
таблицы видим, что доверительные
интервалы оказались достаточно широкими
— свыше 9% прогнозируемого уровня.
Этот пример
показывает, что экстраполяция по тренду
— достаточно грубая операция, основывающаяся
на целом ряде допущений.
9.3.
Построение доверительных интервалов
для полиномиальных трендов.
При построении доверительных интервалов
прогнозов будет предполагать, что ошибки
прогнозов связаны только с ошибками в
оценках параметров прогностических
моделей.
Предположим,
что тренд описывается прямой, квадратичной
и кубической параболами. Для построения
доверительных интервалов прогнозов,
определяемых линейным и параболическим
трендами, определяем стандартные ошибки
прогноза по формулам:
— для линейного
тренда
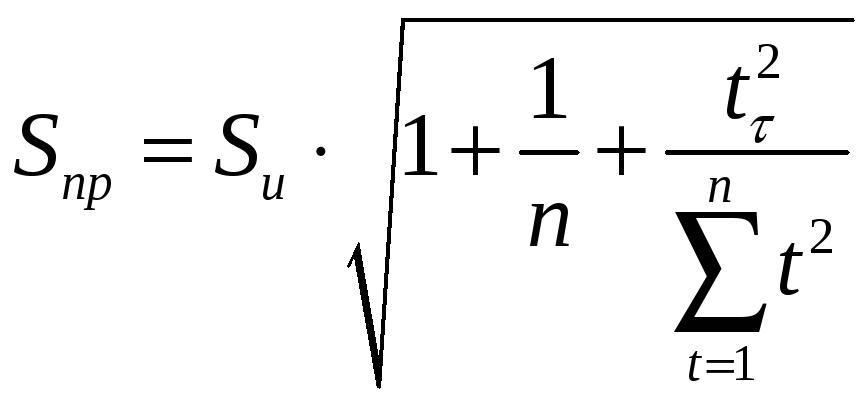
— для тренда,
определяемого параболой второго порядка,

— для тренда,
определяемого параболой третьего
порядка,

Сопоставляя
подкоренные выражения стандартных
ошибок, видим, что при одном и том же
значении
доверительный интервал прогноза тем
шире, чем выше степень полинома,
характеризующего тренд. Это объясняется
тем, что дисперсия уравнения тренда
определяется как взвешенная сумма
дисперсий соответствующих параметров
уравнений. Хотя средняя квадратичная
ошибка тренда является не единственной
характеристикой, определяющей ширину
доверительного интервала, однако она
оказывает преобладающее влияние на эту
величину.
9.4.
Построение доверительных интервалов
для трендов, приводимых к линейному.
Процедура построения доверительных
интервалов полностью переносится и на
случаи, когда уравнение кривой может
быть после некоторых преобразований
сведено к линейному тренду. Оценивание
параметров преобразованных уравнений,
как было указано ранее, осуществляется
методом наименьших квадратов.
В
практике криволинейного выравнивания
широко распространены два вида
преобразований: логарифмирование и
обратное преобразование
.
При этом возможно преобразование как
зависимой переменной
,
так и независимой
или одновременно той и другой.
Рассмотрим
процедуру построения доверительного
интервала прогноза для модифицированной
экспоненты
Прологарифмировав
уравнение, получим линейную функцию от
:
.
Пусть
асимптота
задана, т.е.
,
и не содержит ошибки. Обозначим
.
Тогда доверительный интервал прогноза
для модифицированной экспоненты будет
определяться как доверительный интервал
(9.3) для прямой, т.е.
,
где
среднее квадратичное отклонение от
тренда
.
Зная границы доверительного интервала
для
,
легко определить доверительные границы
прогноза для
:
.
(9.5)
Так
как экспоненциальная кривая
логарифмированием преобразуется к виду
,
то доверительный интервал прогноза
имеет вид
.
(9.6)
В доверительных
интервалах (9.4) и (9.5)

Пример
9.3.
В табл. 9.3 дан динамический ряд,
характеризующий объем продаж.
Таблица
9.3
-
Год
Объем продаж
,
млн.р.Год
Объем продаж
,
млн.р.1971
288
1981
765
1972
308
1982
823
1973
345
1983
877
1974
382
1984
915
1975
436
1985
974
1976
535
1986
1035
1977
562
1987
1128
1978
603
1988
1232
1979
650
1989
1274
1980
681
1990
1318
Для
выбора функции тренда применим метод
характеристик. Построив графики
скользящих средних приростов и их
характеристик, сделаем вывод о том, что
тренд описывается показательной функцией
.
Прологарифмировав уравнение, получим
прямую
,
оценку параметров которой осуществим
методом наименьших квадратов. Итак,
наилучшей функцией, характеризующей
объем продаж, является функция
.
Для
построения доверительного интервала
прогноза вычислим прежде всего среднее
квадратичное отклонение:
.
Используя
формулу (9.5), строим доверительные
интервалы прогноза для периода упреждения:
Значения
коэффициента
будут равны соответственно:

,
Значение
квантиля
,
взятое из таблицы распределения Стьюдента
при заданном уровне значимости
и
степенях свободны, равно
.
Вычислим для
значения
:
Тогда
доверительные интервалы, для
,
будут иметь вид:
Прогноз
для
составит
соответственно:
Вычисленные
значения прогноза принадлежат
соответствующим доверительным интервалам.
Отметим еще раз,
что процедура разработки прогноза с
использованием аналитического
выравнивания тренда состоит из
предварительного выбора одной или
нескольких кривых, которые наилучшим
образом соответствуют характеру
изменения ряда динамики, оценки параметров
выбранных кривых, проверки их адекватности
прогнозируемому процессу, окончательного
выбора кривой роста и вычисления
точечного и интервального прогнозов.
9.5.
Прогнозирование методом экспоненциального
сглаживания.
Вначале введем понятие экспоненциальной
средней.
При вычислении скользящих средних –
простой и взвешенной – всем уровням
динамического ряда присваивались
одинаковые веса. Вес отдельного наблюдения
указывает на часть вклада его значения
в значение средней. В случае простой
скользящей средней эта часть равна
для наблюдений, входящих в среднюю, и
нулю для наблюдений, отсутствующих в
ней. При этом недавние данные имеют тот
же вес, что и данные, относящиеся к
далекому прошлому (старые). Однако
понятно, что недавние данные имеют более
важное значение и должны иметь больший
вес. Поэтому предлагается процедура
усреднения с разными весами. При этом
система весов образует ряд, в котором
веса убывают во времени по экспоненциальному
закону:
,
.
Сумма этого ряда
стремится к единице при неограниченном
увеличении числа слагаемых.
Используя
экспоненциально взвешенные веса,
экспоненциально взвешенную среднюю
первого порядка будем вычислять по
формуле
, (9.7)
которую можно
преобразовать к виду:
(9.8)
На основе этого
уравнения строятся другие модели
экспоненциального сглаживания.
Иногда при
построении моделей прибегают к вычислению
экспоненциально взвешенных средних
более высоких порядков, т.е. средних,
получаемых путем многократного
экспоненциального сглаживания. Такая
средняя вычисляется по формуле:
(9.9)
Из этой формулы
легко получаются выражения:
Экспоненциально
взвешенная средняя имеет ряд преимуществ
перед традиционной скользящей средней.
1.
Для вычисления экспоненциально взвешенной
средней
используется предыдущая экспоненциально
взвешенная средняя
и последнее значение уровня
.
2. Для построения
прогноза по экспоненциально взвешенной
средней необходимо задать начальную
оценку прогноза. При поступлении новых
данных прогнозирование можно продолжать
незамедлительно, т.е. нет необходимости
заново строить процедуру вычисления
прогноза.
3. В экспоненциально
взвешенной средней значения весов
убывают со временем, т.е. нет такой точки,
на которой веса обрываются.
Метод
экспоненциально взвешенной средней
разработан для анализа динамических
рядов, состоящих из большего числа
наблюдений. Поэтому, если динамические
ряды слишком короткие (
уровней) и в случае, когда темпы роста
и прироста велики, метод не “успевает”
отразить все изменения. Метод тем точнее,
чем больше число наблюдений (уровней
динамического ряда).
Рассмотрим
теперь, как применяется метод
экспоненциально взвешенной средней
при прогнозировании экономических
показателей.
Предположим,
что динамический ряд представлен в виде
,
где
— тренд;
— случайная компонента. Если на изучаемом
интервале времени коэффициенты
уравнения, описывающего тренд, остаются
неизменными, то для построения модели
прогноза можно использовать метод
наименьших квадратов. Однако в течение
анализируемого периода коэффициенты
уравнения тренда изменяются во времени.
И так как динамические ряды, характеризующие
экономические процессы, содержат
небольшое число уровней, применение
метода наименьших квадратов для оценки
параметров модели прогноза может
привести к существенным ошибкам. Поэтому
применяется метод
экспоненциально взвешенной средней,
в котором новым данным придаются большие
веса, чем старым.
Пусть
тренд определяется линейной функцией
.
Как показал Р.Г. Браун, оценки коэффициентов
и
выражаются через экспоненциально
взвешенные средние по формулам:
.
Прогноз для
случая, когда тренд характеризуется
линейной функцией, вычисляется по
формуле
.
(9.10)
Чтобы
воспользоваться формулой (9.9) для
прогнозирования, нужно определить
значения параметров
и
,
которые выражаются через экспоненциально
взвешенные средние. А из формул (9.7) и
(9.8) следует, что для вычисления
и
необходимо задать начальные значения
и
или в общем случае
,
которые будем называть в дальнейшем
начальными условиями.
Начальные
условия либо задают исходя из экономических
соображений (например, из величины
лага), либо вычисляют по формулам:
В
качестве значений коэффициентов
и
нужно брать коэффициенты уравнения
тренда, полученные методом наименьших
квадратов, т.е. найденные при решении
системы
Затем вычисляются
экспоненциально взвешенные средние
первого и второго порядков:
,
,
…
,
,
…
Ошибка прогноза
при использовании доверительного
интервала (9.3) определяется по формуле

где
– средняя квадратичная ошибка,
характеризующая отклонения от линейного
тренда:

При
использовании прогностической модели
(9.10) одной из основных проблем является
выбор оптимального значения параметра
сглаживания
,
где
.
От численного значения
зависит, насколько быстро будет
уменьшаться вес предшествующих
наблюдений, т.е. насколько быстро будет
уменьшаться степень их влияния на
сглаженный уровень. Это значит, что
чувствительность экспоненциально
взвешенной средней в целях повышения
адекватности прогностической модели
может быть в любой момент изменена путем
изменения значений
.
Чем больше
,
тем выше чувствительность средней. Чем
меньше значение
,
тем устойчивее становится экспоненциально
взвешенная средняя. Если подходящими
оказываются более высокие значения
,
это указывает на нарушение условий
стационарности и означает, что
экспоненциально взвешенная средняя
становится неприемлемой для прогнозирования.
Значения
при условии равенства среднего значения
степени старения данных можно выбирать,
используя формулу
или
.
Значения
,
используемые в области экономического
прогнозирования, находятся в пределах
от 0,05 до 0,3. Длина усреднения в скользящем
среднем с точки зрения чувствительности
прогноза может быть найдена в соответствии
с
из таблицы
-
0,05
0,1
0,2
0,3
39
19
9
6
Достоинство
метода экспоненциально взвешенной
средней по сравнению с другими методами
состоит в его точности, которая
увеличивается с увеличением числа
уровней динамического ряда. Но остается
нерешенной проблема выбора оптимального
значения параметра сглаживания
и начальных условий. Точность прогноза
по этому методу падает с увеличением
горизонта прогнозирования.
Пример
9.4.
Рассмотрим динамический ряд, характеризующий
производство цемента (таблица 9.4).
.
Таблица
9.4
-
Год
Производство цемента
,
млн. т.
Год
Производство
цемента
,
млн. т.
Год
Производство цемента
,
млн. т
1975
122
1981
127
1987
137
1976
124
1982
124
1988
139
1977
127
1983
128
1989
140
1978
127
1984
130
1990
142
1979
123
1985
131
20811980
125
1986
135
Для
построения тренда
описывающего динамический ряд, начало
координат было перенесено в середину
ряда. Тогда система нормальных уравнений
для оценки параметров тренда упрощается:
Решая
ее, находим:
.
Уравнение тренда имеет вид:
.
Для
прогноза выпуска цемента на 1991 г.
воспользуемся формулой (9.10). Оценки
коэффициентов
и
найдем из выражений:
которые
содержат экспоненциально взвешенные
средние
и
и
параметр
. Параметр сглаживания
положим равным 0,15, так как для
рекомендуется брать
в нашем примере
.
Вычисление
и
осуществим по рекуррентной формуле
(9.9), предварительно определив начальные
условия
и
,
,
где,
и
— коэффициенты уравнения тренда. Тогда:
,
Затем
вычисляем
и
,
и
осуществляем прогноз на 1976 г. Далее по
рекуррентной формуле (9.9) вычисляем
новые
и
:
,
,
и по
ним находим
и
которые используем для прогноза
производства цемента на 1977 г., и т.д. В
таблице 9.5 приведены:
— экспоненциально
взвешенные средние, вычисленные по
формуле (9.9);
-соответствующие
коэффициенты
и
;
— результаты
прогноза и отклонения фактических
уровней от прогнозируемых в случае
ретроспективного прогноза;
— указан прогноз
производства цемента на 1991 г.
Таблица
9.5
|
Год |
Производст-во цемента, млн. т |
|
|
|
|
Прогноз |
Отклонение
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1976 |
124 |
125,82 |
123,36 |
128,28 |
0,43 |
128,71 |
-4,71 |
|
1977 |
127 |
125,60 |
123,70 |
127,50 |
0,34 |
127,84 |
-0,84 |
|
1978 |
127 |
125,81 |
124,02 |
127,60 |
0,32 |
127,95 |
-0,92 |
|
1979 |
123 |
125,39 |
124,23 |
126,55 |
0,20 |
126,75 |
-3,75 |
|
1980 |
125 |
125,33 |
124,39 |
126,27 |
0,17 |
126,44 |
-1,44 |
|
1981 |
127 |
125,58 |
124,57 |
126,59 |
0,18 |
126,77 |
0,23 |
|
1982 |
124 |
125,39 |
124,69 |
125,99 |
0,11 |
126,10 |
-2,10 |
|
1983 |
128 |
125,74 |
124,85 |
126,63 |
0,16 |
126,69 |
1,31 |
|
1984 |
130 |
126,38 |
125,08 |
127,68 |
0,23 |
127,91 |
2,09 |
|
1985 |
131 |
127,07 |
125,38 |
128,76 |
0,30 |
129,06 |
1,94 |
|
1986 |
135 |
128,26 |
125,81 |
130,71 |
0,43 |
131,14 |
3,86 |
|
1987 |
137 |
129,57 |
126,37 |
132,77 |
0,56 |
133,33 |
3,67 |
|
1988 |
139 |
130,98 |
127,06 |
134,90 |
0,69 |
135,59 |
3,41 |
|
1989 |
140 |
132,33 |
127,85 |
136,81 |
0,79 |
137,60 |
2,40 |
|
1990 |
142 |
133,78 |
128,74 |
138,82 |
0,89 |
139,71 |
2,99 |
|
1991 |
— |
135,01 |
129,68 |
140,34 |
0,94 |
141,28 |
— |
Для
прогноза производства цемента на 1991 г.
использовались следующие значения
экспоненциально взвешенных средних:
,
и оценки коэффициентов модели
,
.
Ошибку прогноза вычислим по формуле
где
средняя квадратичная ошибка
Тогда
доверительный интервал прогноза
определяется в виде (9.3), где
— квантиль распределения Стьюдента при
уровне доверия
и числе степеней свободы
,
равный
.
Подставив значения
и
,
получим доверительный интервал прогноза
.
9.6.
Прогнозирование методом гармонических
весов.
Автор метода
гармонических весов
польский статистик З. Хевиг предложил
проводить экстраполяцию по скользящему
тренду. При этом отдельные точки ломаной
линии взвешиваются с помощью гармонических
весов, что позволяет более поздним
уровням динамического ряда придавать
больший вес.
Рассмотрим
временной ряд
,
математическая модель которого имеет
вид
,
где
—
неслучайная функция времени (тренд);
— стационарная случайная компонента.
Если
нет достаточно достоверной априорной
информации о закономерностях изменения
изучаемого экономического явления, то
простая экстраполяция по тренду может
привести к существенным ошибкам. Поэтому
условно можно предположить, что некоторым
приближением фактического тренда
— является ломаная линия, каждое звено
которой сглаживает заданное число
уровней динамического ряда
.
Таким образом, ломаную линию можно
представить как скользящий тренд.
Проводя экстраполяцию по скользящему
тренду и взвешивая при этом отдельные
точки ломаной линии, с тем чтобы более
поздним наблюдениям придать больший
вес, получаем прогноз. Доверительный
интервал для прогнозируемых показателей
строится с использованием неравенства
Чебышева.
Для
применения метода гармонических весов
ряд динамики разбивается на интервалы,
каждый из которых содержит 3 – 5 уровней.
Число интервалов
меньше
.
Для каждого интервала определяется
линейный тренд
Причем
для
для
для
.
Оценивание
параметров скользящего тренда
осуществляется методом наименьших
квадратов. Вычислив оценки параметров
и
,
получим
уравнение.
Вычислим далее значение
в
точках
,
где
.
Для каждого уравнения
получим число значений функции
,
равное числу уровней, содержащихся в
интервале скольжения. Образуем множества
,
значений функции —
,
для которых
.
Эти функции обозначим
,
а число таких функций —
.
Вычислим средние функций, содержащихся
в построенных множествах:
(9.11)
Соединив
точки
отрезками прямой, получим тренд
исследуемого динамического ряда в виде
ломаной линии.
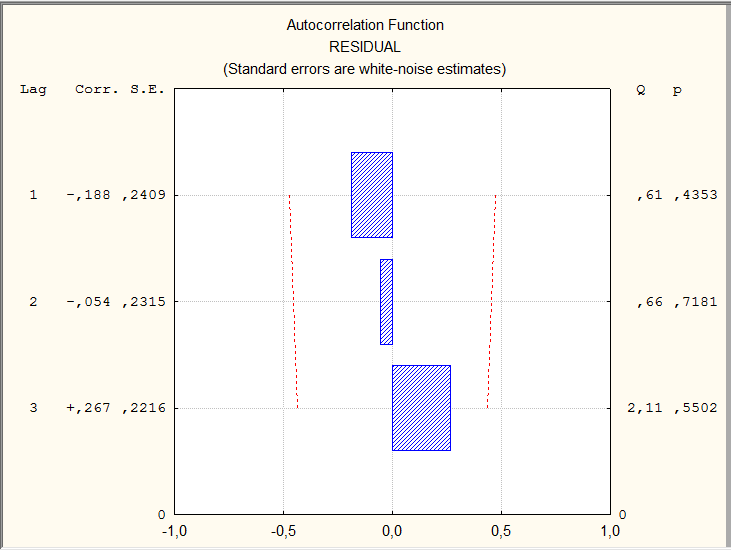
Затем
проверим гипотезу о том, что отклонения
от скользящего тренда имеют случайный
характер. Для проверки гипотезы
,
состоящий в том, что отклонения от
скользящего тренда образуют стационарный
процесс, строится автокорреляционная
функция, которая представляет собой
множество коэффициентов корреляции
между динамическим рядом, состоящим из
отклонений
,
и этим же рядом, сдвинутым относительно
первоначального положения на
моментов
времени. Нормированная автокорреляционная
функция отклонений вычисляется по
формуле
(9.12)
где
Величину
называют сдвигом.
Сдвиг, которому соответствует наибольший
коэффициент автокорреляции, называют
временным
лагом.
График нормированной автокорреляционной
функции называют коррелограммой.
Для
построения коррелограммы на оси абсцисс
откладывают значения
,
а на оси ординат — значения коэффициентов
автокорреляции
.
Затем точки с координатами
соединяют
отрезками прямой. В результате получают
ломаную линию, которая и называется
коррелограммой.
При
вычислении коэффициентов автокорреляции
с ростом
число коррелируемых пар уменьшается,
а известно, что при небольшом числе
наблюдений существенными оказываются
лишь большие коэффициенты. Поэтому
наибольшее значение
должно быть таким, чтобы число пар
наблюдений оказалось достаточным для
вычисления коэффициентов автокорреляции
.
На практике ориентируются на правило,
из которого следует, что
.
Значения
автокорреляционной функции образуют
ряд
,
,
…,
(верхний индекс означает число наблюдений,
для которого вычисляется автокорреляционная
функция). Затем исключают из динамического
ряда первый или последний уровень и
вычисляют значения автокорреляционной
функции
,
,
…,
.
Продолжая указанный процесс, исключают
уровней динамического ряда и вычисляют
значения
автокорреляционных
функций. Таким образом, получают
групп
коэффициентов автокорреляции, в каждой
из которых будет
коэффициентов. Отклонения от скользящего
тренда образуют стационарный в широком
смысле процесс, если коэффициенты
автокорреляции, входящие в одну и ту же
группу, однородны.
Проверка
на однородность коэффициентов
автокорреляции
производится следующим образом. Для
каждого
,
входящего в
– ю группу, вычисляют
критерий:
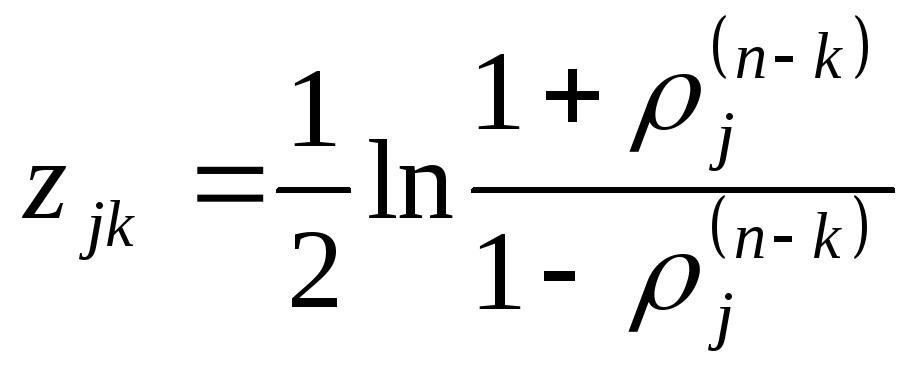
.
Затем
для этой группы находят среднюю
и вычисляют величину
,
(9.13)
которая
распределена по закону
—
квадрат с
степенями свободы. Тогда, сравнивая
вычисленное значение величины (9.13) с
табличным, при
с вероятностью
принимаем гипотезу об однородности
рассматриваемой группы коэффициентов
автокорреляции. Аналогичную проверку
однородности проводим для всех групп
коэффициентов автокорреляции. Если
гипотеза об однородности принимается
для всех групп, то делаем вывод о том,
что отклонения от скользящего тренда
образуют стационарный в широком смысле
случайный процесс. Кроме того, если
значения автокорреляционной функции,
вычисленные для ряда отклонений от
скользящего тренда, уменьшаются, это
значит, что более поздняя информация
сильнее отражается на прогнозируемой
величине, чем более ранняя.
Установив, что
отклонения образуют стационарный
процесс, вычисляем приросты, равные
разностям средних значений скользящих
трендов:
.
Средняя приростов
вычисляется по формуле
,
где
гармонические коэффициенты, удовлетворяющие
следующим условиям:
,
.
(9.14)
Гармонические
коэффициенты
определяем так, чтобы более поздним
наблюдениям придавались большие веса.
Для этого полагаем
,
где
,
т.е.
.
Следовательно,
и гармонические коэффициенты
удовлетворяют условиям (9.14).
Предположим,
что приросты
являются значениями случайной величины
с математическим ожиданием
и дисперсией
.
Тогда
их оценками будут средняя приростов
и статистическая дисперсия

Применив неравенство Чебышева, можно
записать:
,
где
заданное положительное число;
. Так как значения
коррелированны между собой, то
в неравенстве Чебышева является величиной
переменной, вычисляемой по формуле
.
Прогнозирование
методом гармонических весов производится
путем прибавления к последнему значению
ряда динамики
среднего прироста
,
т.е.
.
Доверительный интервал прогноза имеет
вид:
.
Пример
9.5.
Рассмотрим динамический ряд, характеризующий
производство цемента (см. таблицу 9.5).
Этот динамический ряд не имеет
скачкообразных изменений и достаточно
хорошо описывается линейным трендом.
Поэтому для дисконтирования уровней
ряда динамики с целью определения
прогноза производства цемента в 1991 г.
применим метод гармонических весов.
Построим вначале скользящий тренд. Для
этого разобьем исходный ряд динамики
на интервалы, каждый из которых содержит
5 уровней. Для каждого интервала скольжения
строим методом наименьших квадратов
линейный тренд
.
Так, первый интервал скольжения состоит
из уровней 122, 124, 127, 127, 123, то система
нормальных уравнений для оценки
параметров, имеет вид
откуда
находим
,
.
Следовательно, линейный тренд для
первого интервала скольжения выражается
уравнением
Аналогично
определяем параметры уравнений для
всех
интервалов скольжения:
С
помощью построенных уравнений определим
значения
скользящего тренда по формуле (9.11).
При
имеем
При
имеем
два значения функций, для которых:
,
,
откуда
Аналогично
находим все остальные значения
:
Проверим
теперь гипотезу о том, что отклонения
от скользящего тренда имеют случайный
характер. Для этого вычислим нормированную
автокорреляционную функцию (9.12) для
…
Значения автокорреляционной функции
для
равны:
Значения
автокорреляционной функции для
после исключения первого отклонения
будут равны:
Пусть
,
тогда:
Отметим,
что для
значения коэффициентов автокорреляции
можно подвергать сомнению. Но для
подтверждения убывания коэффициентов
автокорреляции вычисление проводилось
до значения
.
И тогда, с уверенностью, можно утверждать,
что значения автокорреляционной функции
постоянно затухают. Проверим однородность
коэффициентов автокорреляции. Для этого
вычислим
критерий:
и
по формуле (9.13). Значения
для трех групп коэффициентов автокорреляции
равны:
Вычисленные
значения меньше табличного
следовательно, с вероятностью
можно
утверждать, что отклонения от тренда
образуют стационарный в широком смысле
случайный процесс.
Затем
вычисляем приросты по формуле
:
и
гармонические веса
:
Гармонические
коэффициенты вычисляем по формуле
Все эти коэффициенты
положительны, их сумма равна единице.
Найдем средний
прирост:
Тогда прогноз
производства цемента на 1991 г. равен:
Для
построения доверительного интервала
вычислим среднее квадратичное отклонение:

Найдем
функцию
Так
как
,
то
.
Произведение
.
Пусть
,
тогда вероятность того, что прогноз
производства цемента выйдет за пределы
доверительного интервала, не превосходит
0,04, что следует из неравенства Чебышева
так
как
.
Доверительный интервал имеет вид:
.
Еще раз
подчеркнем, что метод гармонических
весов применяется, когда в ряду динамики
отсутствуют сезонные и циклические
колебания. Следовательно, мы спрогнозировали
только значение детерминированной
компоненты динамического ряда.
9.7.
Особенности прогнозирования сезонных
колебаний.
В прогностической модели сезонность
учитывается, как правило, посредством
декомпозиции прогностических методов.
При этом предполагается, что характеристики
движения ряда могут быть выделены,
изучены и оценены изолированно друг от
друга. Окончательный же прогноз будет
осуществляться сведением прогнозов
различных элементов в один.
При
прогнозировании сезонного ряда
необходимо определить, как изменение
значения переменной в данный момент
(на данный месяц) связано с изменением
значения этой переменной, отстоящей на
сезонный цикл (чаще всего, равный одному
году). А так как каждый момент времени
принадлежит одному циклу, задача
заключается в установлении формы
сезонной зависимости. Для решения
сформулированной задачи период наблюдения
должен быть не менее четырех лет. Сезонные
колебания численно описываются индексами
сезонности. Они, по определению,
представляют собой отношение текущего
значения к среднему значению этого
показателя, соответствующему моментам
времени, лежащим внутри цикла. При
прогнозировании сезонных рядов необходимо
помнить последние L
индексов сезонности (L
= 12 для календарных месяцев, L
= 4 для кварталов). Сумма индексов
сезонности должна быть равна 12 (или 4
для поквартальных данных). В противном
случае их выправляют. Это необходимое
условие (средняя индексов равна единице)
для несмещенности прогнозов. Многие
методы декомпозиции предполагают в
какой-либо форме наличие линейного
тренда, вследствие чего при построении
прогноза учитывают связанный с этим
линейный рост. Сезонный анализ данных
без выделения и оценивания линейного
тренда привел бы к смещению индексов
сезонности, т.е. к заметному отличию
суммы этих индексов за год от 12.
Рассмотрим различные
прогностические модели.
Сезонно-декомпозиционная
прогностическая модель
Холта — Винтера основана на применении
метода экспоненциально взвешенной
средней. Указанная модель предполагает
оценку стационарно-линейного и сезонного
факторов. Оценка стационарного фактора,
т.е. оценка среднемесячного значения
показателя, независимо от времени года
проводится по формуле
,
где
предыдущее значение экспоненциально
взвешенной средней. При этом предполагается,
что динамический ряд фактических данных
очищен от сезонности делением его на
сезонный индекс, соответствующий моменту
времени
,
т.е. сдвинутому на
единиц времени назад.
Оценка линейного
роста вычисляется на основе модели
роста Холта
,
где
прошлый показатель роста. А оценка
сезонной компоненты, т.е. адаптация
индекса сезонности, предполагает
вычисление индекса сезонности (отношение
значения текущего уровня к среднестационарному
значению) и определение экспоненциально
взвешенной средней его текущего значения
.
При
изолированной оценке трех компонент
динамического ряда, определяющих
движение процесса, прогноз на
моментов времени вперед
строится следующим образом. Суммируются
оценки линейного роста
и стационарного фактора
,
и результат с учетом сезонности
домножается на соответствующее значение
индекса сезонности
:
(9.15)
Тамара
установил, что в большинстве практических
ситуаций значения
и
равны соответственно 0,2; 0,2; 0,5. Винтер
также получил близкие значения этих
коэффициентов (0,2; 0,2; 0,6 соответственно),
приводящие к наименьшей стандартной
ошибке прогноза.
Модель
Холта — Винтера в практике прогнозирования
сезонных временных рядов встречается
чаще всего. Ее прогностическая точность
не уступает точности других, более
сложных, моделей поведения сезонно
изменяющихся временных рядов (средняя
абсолютная процентная ошибка по этой
модели в большинстве случаев меньше
%
).
Прогнозирование
сезонных колебаний можно осуществлять
также посредством формулы
где
прогнозируемое значение уровня
динамического ряда;
—
средний индекс сезонности
-го
квартала;
—
уравнение тренда;
— случайная
компонента.
При прогнозировании
сезонных колебаний используются средние
индексы по расположению, которые
вычисляются следующим образом. В
ранжированном ряду показателей
сезонности для каждого квартала
отбрасываются наибольшие и наименьшие
значения. Затем вычисляется средняя
арифметическая из центральных значений
показателей сезонности. Если число
индексов четное, то для вычисления
средней берут 4 или 6 центральных точек,
если же нечетное, — то 3 или 5. Такая средняя
по расположению не подвержена влиянию
крайних значений.
Если динамический
ряд можно представить в виде ряда Фурье
и предположить,
что в будущем периоде сохранится эта
же амплитуда колебаний, то можно
попытаться оценить значение исследуемого
показателя на перспективу. Однако при
вычислении значений функции следует
исходить из значений предполагаемого
тренда, а не от среднего уровня. При
этом трудно оценить погрешность. Поэтому
вычисленную ошибку аппроксимации
переносят в будущем и строят доверительные
интервалы. Среднюю ошибку аппроксимации
вычисляют для фактических данных с
учетом тренда. Прогностическая
модель записывается в виде

где
—
тренд динамического ряда.
Для того чтобы
построенные амплитуды лучше соответствовали
амплитудам будущего периода, нужно
брать небольшой период, предшествующий
предсказываемому.
Пример
9.6.
Рассмотрим данные примера 7.6
и воспользуемся прогностической моделью
для
вычисления прогноза объема ежеквартальной
продажи на 1991 г. Значения индексов
возьмем из табл.
7.6,
будем
рассчитывать по уравнению тренда
.
Случайную компоненту оценим с помощью
доверительного интервала
,
где
— квантиль распределения Стьюдента,
определяемый из таблицы в зависимости
от доверительной вероятности
и числа степеней свободы
— определяется из ретроспективного
прогноза.
Прогностические
модели для расчета объема ежеквартальных
продаж для I
– IV
кварталов имеют соответственно следующий
вид:
(9.16)
Вначале
рассчитаем ретроспективный прогноз и
средние квадратичные отклонения прогноза
от фактических данных, т.е.
:

.
Из
таблицы критических значений
найдем
для числа степеней свободы
и уровня доверия
.
Тогда доверительные оценки значений
объема продаж в I-IV
кварталах равны соответственно:
Осуществим
прогноз объема продаж на 1991 г., используя
прогностические модели (9.16), и укажем
доверительные интервалы (табл. 9.6).
Таблица
9.6
-
Квартал
Прогноз
Доверительный интервал
I
25,13 (
=37)
(24,05; 26,21)
II
26,11 (
=39)
(25,29; 26,93)
III
18,87 (
=41)
(18,28; 19,46)
IV
25,57 (
=42)
(24,53; 26,61)
Как
видим, общая тенденция изменения объема
продаж, установившаяся в изучаемом
периоде, сохранится и на прогнозируемый
период. Заметим, что при ретроспективном
и перспективном прогнозировании мы
использовали такое же изменение времени,
как в примере
7.6.
Рассмотрим
теперь процедуру разработки прогноза
с помощью сезонно-декомпозиционной
прогностической модели Холта-Винтера
(9.15), в которой
— экспоненциально взвешенное среднее
значение поквартального объема продаж:
;
оценка линейного роста:
;
предыдущий показатель роста, вычисляемый
как средний абсолютный прирост
экспоненциально взвешенная средняя
текущего значения коэффициента сезонности
.
Формулу (9.15)
применим для каждого квартала. Сначала
определим прогноз объема продаж на
первый квартал. Рассчитаем начальные
условия:
где
,
взяты из уравнения тренда
а
.
Вычисление
и
осуществим по рекуррентной формуле
(9.9).
Результаты промежуточных расчетов
приведены в табл. 9.7.
Таким
образом, в табл. 9.7 мы определим
,
и оно равно 22,8. Значение
— это предыдущий показатель линейного
роста, а
находим
из табл. 7.6.
Таблица
9.7
|
Год |
Объем продаж в I |
|
|
|
|
|
|
|
|
1983 |
18,6 |
19,792 |
19,991 |
19,593 |
-0,050 |
19,5 |
-0,9 |
0,81 |
|
1984 |
21,8 |
19,554 |
19,904 |
19,204 |
-0,087 |
19,8 |
2,0 |
4,00 |
|
1985 |
23,4 |
20,332 |
19,990 |
20,674 |
0,085 |
20,8 |
2,6 |
6,76 |
|
1986 |
22,6 |
20,786 |
20,149 |
21,423 |
0,159 |
21,6 |
1,0 |
1,00 |
|
1987 |
21,9 |
21,009 |
20,121 |
21,897 |
0,222 |
22,1 |
0,8 |
0,64 |
|
1988 |
21,8 |
21,167 |
20,330 |
22,004 |
0,209 |
22,2 |
-0,4 |
0,16 |
|
1989 |
23,1 |
21,554 |
20,575 |
22,533 |
0,245 |
22,8 |
0,3 |
0,09 |
|
1990 |
24,6 |
22,163 |
20,893 |
23,433 |
0,317 |
23,8 |
0,8 |
0,64 |
Тогда:
,
,
.
Применив
формулу (9.15), получим прогноз объема
продаж на первый квартал 1991 г.:
.
Так как
сезонно-декомпозиционная модель Холта
— Винтера основана на применении метода
экспоненциально взвешенной средней,
ошибку прогноза можно вычислить по
формуле
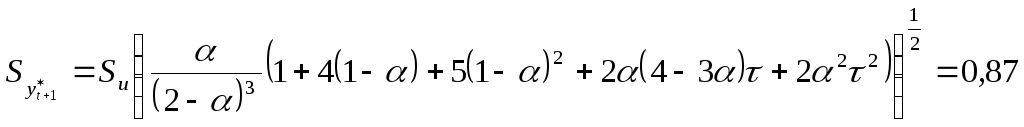
где

Тогда доверительный интервал прогноза
будет иметь вид
Аналогично
проводится процедура вычисления прогноза
объема продаж на второй квартал 1991 г.
Так как уравнение тренда для всех
кварталов одно и то же, начальные условия
также будут одни и те же, т.е.
Используя
результаты промежуточных вычислений,
находим:
,
Тогда прогноз
объема продаж на второй квартал 1991 г.
.
Доверительный
интервал прогноза имеет вид
Для вычисления
прогноза объема продаж на третий квартал
1991 г. найдем:
,
Прогноз объема
продаж
,
a
его доверительный интервал имеет вид
Вычислим прогноз
объема продаж на четвертый квартал 1991
г. Так как
,
то
.
Доверительный
интервал прогноза имеет вид
Значения
прогноза объема продаж, полученные
методом Холта — Винтера, выше, чем
значения, полученные по формуле
но общая тенденция изменения объема
продаж сохраняется и на прогнозируемый
период.
Пример
9.7.
Используя данные о надое молока по
совхозу “Старо Борисов” Борисовского
района Минской области (табл. 9.8), построим
прогноз валового надоя по кварталам на
1991 г.
Таблица
9.8
-
Год
Квартал
Валовой надои молока
,
ц1988
I
1
419,2
II
2
533,6
III
3
511,1
IV
4
398,8
1989
I
5
454,1
II
6
555,9
III
7
612,2
IV
8
459,3
1990
I
9
518,2
II
10
598,7
III
11
624,2
IV
12
554,0
Так
как очевидно, что исследуемый динамический
ряд имеет сезонную компоненту, которая
по определению имеет точную периодичность,
ее (сезонную компоненту) можно представить
суммой гармоник с регулярными частотами
и длинами волн в 12; 6; 4; 3; 2, 4 и 2 месяца.
Поэтому для построения модели сезонной
волны можно применять гармонический
анализ. Наиболее удобным для гармонического
анализа является период с двенадцатью
наблюдениями, так как гармонический
анализ основывается на исследовании
колебаний вокруг среднего уровня.
Наибольшее количество гармоник, которое
можно рассчитать для этого ряда, равно
6. Найдем коэффициенты
,
ряда Фурье
по формулам:
где
. Получим модель сезонной волны в виде
(9.17)
Части общей
дисперсии, учитываемые гармониками,
составляют:
— первая — 27,7 %;
-вторая — 5,9; -третья — 55,3; -четвертая — 2,5;
-пятая — 8,3; —шестая — 0,3 %. Таким образом,
шестью гармониками учитывается 100 %
общей дисперсии. В табл. 9.9 приводятся
расчетные значения по модели (9.17) и их
отклонения от фактических.
Таблица 9.9
-
Год
Квартал
t
Фактические значения
Расчетные значения для шести гармоник
для шести гармоник
Отклонения фактических данных от
расчетных для шести гармоник1988
I
1
419,2
448,5
0,07
-29,3
II
2
533,6
543,7
0,019
-10,1
III
3
511,1
471,34
0,078
39,8
IV
4
398,6
372,1
0,067
26,5
1989
I
5
454,1
473,7
0,043
-19,6
II
6
555,9
496,8
0,116
59,1
III
7
612,2
604,4
0,013
7,8
IV
8
459,3
458,0
0,003
1,3
1990
I
9
518,2
495,2
0,044
23,0
II
10
598,7
595,8
0,005
2,9
III
11
624,2
530,1
0,151
94,5
IV
12
554,0
537,4
0,03
16,6
0,639
Средняя ошибка
аппроксимации
или
5,3%.
Если
предположить, что в будущем сохранится
эта же амплитуда колебаний, можно
попытаться оценить значение исследуемого
показателя на перспективу. При этом
следует исходить не из среднего уровня,
а из значений тренда. Следовательно,
для прогнозирования валового надоя
молока построим тренд исследуемого
динамического ряда. В качестве тренда
возьмем функцию
.
Параметры
и
оценим, решив систему
откуда
=
438,532 и
= 12,522. Таким образом, уравнение тренда
имеет вид
Тогда прогностическая модель запишется
так:
Прогноз ожидаемого
валового надоя молока в совхозе будет
следующим:
— первый квартал
-529,959 ц; — второй — 650,450; — третий — 607,437;
-четвертый — 475 281 ц.
При таком
прогнозе трудно оценить погрешность.
Можно перенести рассчитанную ошибку
аппроксимации в перспективный анализ
и тем самым оценить погрешность прогноза.
Description
Standard Error, for a specified period, measures how far prices have deviated from a Linear Regression Line for the same period. The higher the Standard Error the farther prices have deviated from a Linear Regression Line for the same period. The lower the Standard Error, the closer the prices are to the Linear Regression Line. If all the closing prices equaled the corresponding values of the Linear Regression Line, Standard Error would be zero.
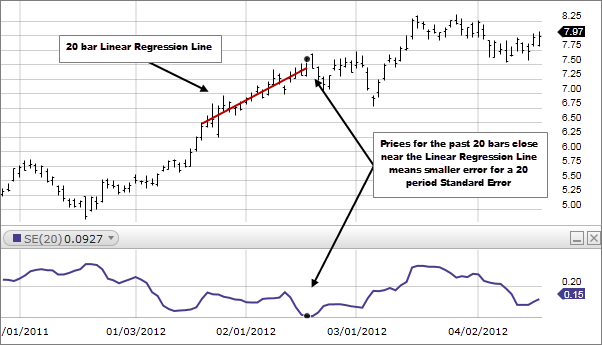
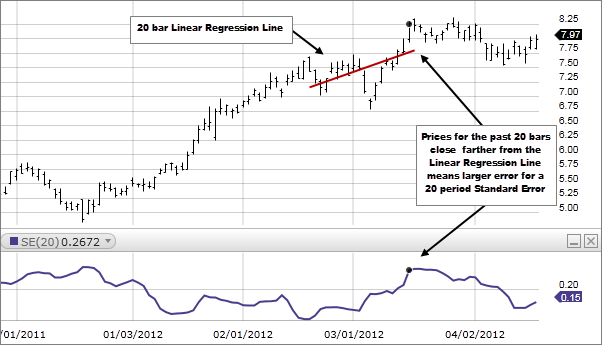
How this indicator works
- The larger the error, the less reliable the trend, as prices are dispersed away from the Linear Regression Line.
- The smaller the error, the more reliable the trend, as prices are congregating around the Linear Regression line.
Calculation
Standard Error is a fairly complex statistical calculation. It uses the least square fit method to fit a trend line to the data by minimizing the distance between the price and the Linear Regression trend line. This is used to find an estimate of the next period’s price. The Standard Error indicator returns the statistical difference between the estimate and the actual price.
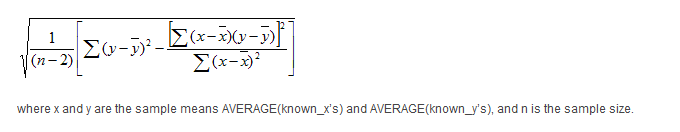
Когда мы подгоняем регрессионную модель к набору данных, нас часто интересует, насколько хорошо регрессионная модель «подходит» к набору данных. Две метрики, обычно используемые для измерения согласия, включают R -квадрат (R2) и стандартную ошибку регрессии , часто обозначаемую как S.
В этом руководстве объясняется, как интерпретировать стандартную ошибку регрессии (S), а также почему она может предоставить более полезную информацию, чем R 2 .
Стандартная ошибка по сравнению с R-квадратом в регрессии
Предположим, у нас есть простой набор данных, который показывает, сколько часов 12 студентов занимались в день в течение месяца, предшествующего важному экзамену, а также их баллы за экзамен:
Если мы подгоним простую модель линейной регрессии к этому набору данных в Excel, мы получим следующий результат:
R-квадрат — это доля дисперсии переменной отклика, которая может быть объяснена предикторной переменной. При этом 65,76% дисперсии экзаменационных баллов можно объяснить количеством часов, потраченных на учебу.
Стандартная ошибка регрессии — это среднее расстояние, на которое наблюдаемые значения отклоняются от линии регрессии. В этом случае наблюдаемые значения отклоняются от линии регрессии в среднем на 4,89 единицы.
Если мы нанесем фактические точки данных вместе с линией регрессии, мы сможем увидеть это более четко:
Обратите внимание, что некоторые наблюдения попадают очень близко к линии регрессии, в то время как другие не так близки. Но в среднем наблюдаемые значения отклоняются от линии регрессии на 4,19 единицы .
Стандартная ошибка регрессии особенно полезна, поскольку ее можно использовать для оценки точности прогнозов. Примерно 95% наблюдений должны находиться в пределах +/- двух стандартных ошибок регрессии, что является быстрым приближением к 95% интервалу прогнозирования.
Если мы заинтересованы в прогнозировании с использованием модели регрессии, стандартная ошибка регрессии может быть более полезной метрикой, чем R-квадрат, потому что она дает нам представление о том, насколько точными будут наши прогнозы в единицах измерения.
Чтобы проиллюстрировать, почему стандартная ошибка регрессии может быть более полезной метрикой для оценки «соответствия» модели, рассмотрим другой пример набора данных, который показывает, сколько часов 12 студентов занимались в день в течение месяца, предшествующего важному экзамену, а также их экзаменационная оценка:
Обратите внимание, что это точно такой же набор данных, как и раньше, за исключением того, что все значения s сокращены вдвое.Таким образом, студенты из этого набора данных учились ровно в два раза дольше, чем студенты из предыдущего набора данных, и получили ровно половину экзаменационного балла.
Если мы подгоним простую модель линейной регрессии к этому набору данных в Excel, мы получим следующий результат:
Обратите внимание, что R-квадрат 65,76% точно такой же, как и в предыдущем примере.
Однако стандартная ошибка регрессии составляет 2,095 , что ровно вдвое меньше стандартной ошибки регрессии в предыдущем примере.
Если мы нанесем фактические точки данных вместе с линией регрессии, мы сможем увидеть это более четко:
Обратите внимание на то, что наблюдения располагаются гораздо плотнее вокруг линии регрессии. В среднем наблюдаемые значения отклоняются от линии регрессии на 2,095 единицы .
Таким образом, несмотря на то, что обе модели регрессии имеют R-квадрат 65,76% , мы знаем, что вторая модель будет давать более точные прогнозы, поскольку она имеет более низкую стандартную ошибку регрессии.
Преимущества использования стандартной ошибки
Стандартную ошибку регрессии (S) часто бывает полезнее знать, чем R-квадрат модели, потому что она дает нам фактические единицы измерения. Если мы заинтересованы в использовании регрессионной модели для получения прогнозов, S может очень легко сказать нам, достаточно ли точна модель для прогнозирования.
Например, предположим, что мы хотим создать 95-процентный интервал прогнозирования, в котором мы можем прогнозировать результаты экзаменов с точностью до 6 баллов от фактической оценки.
Наша первая модель имеет R-квадрат 65,76%, но это ничего не говорит нам о том, насколько точным будет наш интервал прогнозирования. К счастью, мы также знаем, что у первой модели показатель S равен 4,19. Это означает, что 95-процентный интервал прогнозирования будет иметь ширину примерно 2*4,19 = +/- 8,38 единиц, что слишком велико для нашего интервала прогнозирования.
Наша вторая модель также имеет R-квадрат 65,76%, но опять же это ничего не говорит нам о том, насколько точным будет наш интервал прогнозирования. Однако мы знаем, что вторая модель имеет S 2,095. Это означает, что 95-процентный интервал прогнозирования будет иметь ширину примерно 2*2,095= +/- 4,19 единиц, что меньше 6 и, следовательно, будет достаточно точным для использования для создания интервалов прогнозирования.
Дальнейшее чтение
Введение в простую линейную регрессию
Что такое хорошее значение R-квадрата?
Анализ временных рядов
Составляющие временного ряда
При анализе временного ряда выделяют три составляющие: тренд, сезонность и шум. Тренд — это общая тенденция, сезонность, как следует из названия — влияния периодичности (день недели, время года и т.д.) и, наконец, шум — это случайные факторы.
Что бы понять отличие этих трёх величин, смоделируем функцию расстояния от земли до луны. Известно, что в среднем луна каждый год отдаляется на 4 см — это тренд, в течение дня луна совершает оборот вокруг земли и расстояние колеблется от
405400 км — это сезонность. Шум — это «случайные» факторы, например, влияние других планет. Если мы изобразим сумму этих трёх графиков, то мы получим временной ряд — функцию, показывающую изменение расстояния от земли до луны во времени.
Тренд. Методы сглаживания
Методы сглаживания необходимы для удаления шума из временного ряда. Существуют различные способы сглаживания, основные — это метод скользящей средней и метод экспоненциального сглаживания.
Метод скользящей средней
Идея метода скользящего среднего заключается в смещении точки графика на среднее значение некоторого интервала. В качестве интервала берут нечётное количество участков, например, три — предыдущий, текущий и следующий периоды, находится среднее и принимается в качестве сглаженного значения:
У данного метода есть проблема: случайное высокое или низкое значение сильно влияют на скользящую линию. В качестве решения были введены веса. Для распределение веса используют оконные функции, основные оконные функции — это окно Дирихле (прямоугольная функция), В-сплайны, полиномы, синусоидальные и косинусоидальные:
Минусы использования скользящей средней — это сложность вычислений и некорректные данные на концах графика.
| Исходные данные | Скользящая средняя | Взвешенная скользящая средняя (синусоидальное окно, n=5) | Взвешенная скользящая средняя (окно Ганна, n=5) |
| 800 | 858 | 283 | 0 |
| 915 | 869 | 482 | 400 |
| 892 | 985 | 528 | 458 |
| 1334 | 1069 | 621 | 446 |
| 1136 | 1067 | 692 | 667 |
| 905 | 1171 | 680 | 568 |
| 1310 | 1111 | 659 | 453 |
| 1094 | 1159 | 681 | 655 |
| 1328 | 1221 | 740 | 547 |
| 1151 | 1236 | 729 | 664 |
| 1370 | 1462 | 765 | 576 |
| 1999 | 1495 | 899 | 685 |
| 1460 | 1950 | 1000 | 1000 |
| 2971 | 1878 | 1244 | 730 |
| 1080 | 2260 | 1192 | 1486 |
| 3530 | 2495 | 1419 | 540 |
| 2400 | 2148 | 1498 | 1765 |
| 1582 | 2857 | 1504 | 1200 |
| 3914 | 2602 | 1512 | 791 |
| 2510 | 2669 | 2269 | 1957 |
| Таблица 1. Сглаживание методом скользящей средней |
Как видно из графика, увеличение n выдаёт более плавную функцию, таким образом нивелируя более мелкие колебания во временном ряду. Обратите внимание, что при сглаживании не имеет значения, совпадает график среднего с графиком данных или нет, целью является построение правильной формы.
Метод экспоненциального сглаживания
Метод экспоненциального сглаживания получил своё название потому, что в сглаженной функции экспоненциально убывает влияние предыдущего периода с неким коэффициентом чувствительности α. Сглаженное значение находится как разница между предыдущим действительным значением и рассчитанным значением:
Коэффициент чувствительности, α, выбирается между 0 и 1, в качестве базиса используют значение 0,3. Если есть достаточная выборка, то коэффициент подбирается путём оптимизации.
| Исходные данные | Экспоненциальное сглаживание, α=0,1 | Экспоненциальное сглаживание, α=0,6 |
| 800 | 800 | 800 |
| 915 | -640 | 160 |
| 892 | 668 | 485 |
| 1334 | -512 | 341 |
| 1136 | 594 | 664 |
| 905 | -421 | 416 |
| 1310 | 469 | 377 |
| 1094 | -291 | 635 |
| 1328 | 371 | 402 |
| 1151 | -201 | 636 |
| 1370 | 296 | 436 |
| 1999 | -129 | 648 |
| 1460 | 316 | 940 |
| 2971 | -138 | 500 |
| 1080 | 421 | 1583 |
| 3530 | -271 | 15 |
| 2400 | 597 | 2112 |
| 1582 | -297 | 595 |
| 3914 | 426 | 711 |
| 2510 | 8 | 2064 |
| Таблица 2. Экспоненциальное сглаживание |
Методы прогнозирования
Методы прогнозирования основываются на выявлении тенденции во временном ряду и последующем использовании найденного значения для предсказания будущих значений. В методах прогнозирования выделяют тренд и сезонность, в общем случае, все типы сезонности могут быть найдены последовательными итерациями. Например, при анализе данных за год, можно выделить сезонность времени года, а в оставшемся тренде найти сезонность по дням недели и так далее.
Двойное экспоненциальное сглаживание
Двойное экспоненциальное сглаживание выдаёт сглаженное значение уровня и тенденции.
Внимание! Может возникнуть путаница, метод Хольт-Винтерса отличается терминами: тренд, сезонность и шум соответственно называются уровень, тренд и сезонность.
Smooth — сглаживание, сглаженный уровень на период τ, sτ, зависит от значения уровня на текущий период (Dτ), тренда за предыдущий период (tτ-1) и рассчитанного сглаженного значения на предыдущий период (sτ-1):
sτ = αDτ + (1 — α)(sτ-1 + tτ-1)
Trend — тенденция, тренд на период τ, tτ, зависит от рассчитанного сглаженного значения за предыдущий и текущий периоды (sτ и sτ-1) и от предыдущей тенденции:
tτ = β(sτ-sτ-1) + (1-β)tτ-1
Рассчитанные по данным формулам уровень и тренд могут быть использованы в прогнозировании:
D’τ+h = sτ + h·tτ
При расчёте, значения s и t для первого периода назначают s1 = D1 и t=0
Метод Хольт-Винтерса
Метод Хольт-Винтерса включает в себя сезонную составляющую, т.е. периодичность. Существуют две разновидности метода — мультипликативный и аддитивный. В отличие от двойного экспоненциального сглаживания, метод Хольт-Винтерса изучает также влияние периодичности.
Общая идея нахождения значений сглаженного уровня, тренда и периодичности заключается в следующем: сглаженный уровень (s — smooth, иногда используют l — level) — это базовый уровень значений, тренд (t — trend) — это показатель скорости роста, разница между сглаженными значениями текущего и предыдущего периода. Для изучения периодичности (p — period), мы разбиваем данные на периоды размером k и выделяем влияние каждого элемента (1,2. k) периода на сглаженный уровень.
Для более точных расчётов вводится показатель обратной связи.
В общем понимании, обратная связь — это влияние предыдущих значений на новые: например, когда Вы начинаете говорить, Вы регулируете громкость своего голоса в зависимости от того, что слышат Ваши уши — это и есть обратная связь.
Для начала расчётов, значения s, t и k, в самом простом виде, могут быть выбраны как sτ = Dτ, t = 0, p = 0.
Для прогнозирования используется следующая формула:
Мультипликативный метод Хольт-Винтерса
Мультипликативный метод отличается от аддитивного тем, что параметры, влияющие на периодичность и сглаженный уровень рассчитываются отношением:
Для прогнозирования используется следующая формула:
Метод Хольт-Винтерса в excel
Таблица для скачивания в форматах ods и xls.
Качество прогнозирования
Проверка качества прогнозирования возможна в случае наличия достаточной выборки и является важной проверкой на достоверность прогноза, для проверки и оптимизации значений α, β и γ необходимо построить прогноз на существующие данные, например, если у нас в наличии данные за пять лет и мы хотим предсказать следующий год, то необходимо построить модель на первых четырёх годах, проверить и оптимизировать коэффициенты для минимизации ошибки между прогнозом и данными на 5й год. После оптимизации модель может быть перестроена с учётом последнего периода для повышения точности, далее следует построение прогноза.
Методы оптимизации будут описаны в отдельной статье, ниже представлен пример прогнозирования методом Хольт Винтерса.
Анализ временных рядов, тренд ряда динамики, точечная оценка прогноза
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Анализ временных рядов
Временной ряд (или ряд динамики) – это упорядоченная по времени последовательность значений некоторой произвольной переменной величины. Тем самым, временной ряд существенным образом отличается от простой выборки данных. Каждое отдельное значение данной переменной называется отсчётом (уровнем элементов) временного ряда.
Временные ряды состоят из двух элементов:
- периода времени, за который или по состоянию на который приводятся числовые значения;
- числовых значений того или иного показателя, называемых уровнями ряда.
Временные ряды классифицируются по следующим признакам:
- по форме представления уровней: ряды абсолютных показателей, относительных показателей, средних величин;
- по количеству показателей, когда определяются уровни в каждый момент времени: одномерные и многомерные временные ряды;
- по характеру временного параметра: моментные и интервальные временные ряды. В моментных временных рядах уровни характеризуют значения показателя по состоянию на определенные моменты времени. В интервальных рядах уровни характеризуют значение показателя за определенные периоды времени. Важная особенность интервальных временных рядов абсолютных величин заключается в возможности суммирования их уровней. Отдельные же уровни моментного ряда абсолютных величин содержат элементы повторного счета. Это делает бессмысленным суммирование уровней моментных рядов;
- по расстоянию между датами и интервалами времени выделяют равноотстоящие – когда даты регистрации или окончания периодов следуют друг за другом с равными интервалами и неполные (неравноотстоящие) – когда принцип равных интервалов не соблюдается;
- по наличию пропущенных значений: полные и неполные временные ряды. Временные ряды бывают детерминированными и случайными: первые получают на основе значений некоторой неслучайной функции (ряд последовательных данных о количестве дней в месяцах); вторые есть результат реализации некоторой случайной величины;
- в зависимости от наличия основной тенденции выделяют стационарные ряды – в которых среднее значение и дисперсия постоянны и нестационарные – содержащие основную тенденцию развития.
Временные ряды, как правило, возникают в результате измерения некоторого показателя. Это могут быть как показатели (характеристики) технических систем, так и показатели природных, социальных, экономических и других систем (например, погодные данные). Типичным примером временного ряда можно назвать биржевой курс, при анализе которого пытаются определить основное направление развития (тенденцию или тренда).
Анализ временных рядов – совокупность математико-статистических методов анализа, предназначенных для выявления структуры временных рядов и для их прогнозирования. Сюда относятся, в частности, методы регрессионного анализа. Выявление структуры временного ряда необходимо для того, чтобы построить математическую модель того явления, которое является источником анализируемого временного ряда. Прогноз будущих значений временного ряда используется для эффективного принятия решений.
Прогноз, характеристики и параметры прогнозирования
Прогноз (от греч. 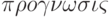
Прогнозирование, разработка прогноза; в узком значении – специальное научное исследование конкретных перспектив развития какого-либо процесса.
- по срокам: краткосрочные, среднесрочные, долгосрочные;
- по масштабу: личные, на уровне предприятия (организации), местные, региональные, отраслевые, мировые (глобальные).
К основным методам прогнозирования относятся:
- статистические методы;
- экспертные оценки (метод Дельфи);
- моделирование.
Прогноз – обоснованное суждение о возможном состоянии объекта в будущем или альтернативных путях и сроках достижения этих состояний. Прогнозирование – процесс разработки прогноза. Этап прогнозирования – часть процесса разработки прогнозов, характеризующаяся своими задачами, методами и результатами. Деление на этапы связано со спецификой построения систематизированного описания объекта прогнозирования, сбора данных, с построением модели, верификацией прогноза.
Прием прогнозирования – одна или несколько математических или логических операций, направленных на получение конкретного результата в процессе разработки прогноза. В качестве приема могут выступать сглаживание динамического ряда, определение компетентности эксперта, вычисление средневзвешенного значения оценок экспертов и т. д.
Модель прогнозирования – модель объекта прогнозирования, исследование которой позволяет получить информацию о возможных состояниях объекта прогнозирования в будущем и (или) путях и сроках их осуществления.
Метод прогнозирования – способ исследования объекта прогнозирования, направленный на разработку прогноза. Методы прогнозирования являются основанием для методик прогнозирования.
Методика прогнозирования – совокупность специальных правил и приемов (одного или нескольких методов) разработки прогнозов.
Прогнозирующая система – система методов и средств их реализации, функционирующая в соответствии с основными принципами прогнозирования. Средствами реализации являются экспертная группа, совокупность программ и т. д. Прогнозирующие системы могут быть автоматизированными и неавтоматизированными.
Прогнозный вариант – один из прогнозов, составляющих группу возможных прогнозов.
Объект прогнозирования – процесс, система, или явление, о состоянии которого даётся прогноз.
Характеристика объекта прогнозирования – качественное или количественное отражение какого-либо свойства объекта прогнозирования.
Переменная объекта прогнозирования – количественная характеристика объекта прогнозирования, которая является или принимается за изменяемую в течение периода основания и (или) периода упреждения прогноза.
Период основания прогноза – промежуток времени, за который используют информацию для разработки прогноза. Этот промежуток времени называют также периодом предыстории.
Период упреждения прогноза – промежуток времени, на который разрабатывается прогноз.
Прогнозный горизонт – максимально возможный период упреждения прогноза заданной точности.
Точность прогноза – оценка доверительного интервала прогноза для заданной вероятности его осуществления.
Достоверность прогноза – оценка вероятности осуществления прогноза для заданного доверительного интервала.
Ошибка прогноза – апостериорная величина отклонения прогноза от действительного состояния объекта.
Источник ошибки прогноза – фактор, способный привести к появлению ошибки прогноза. Различают источники регулярных и нерегулярных ошибок.
Верификация прогноза – оценка достоверности и точности или обоснованности прогноза.
Статистические методы прогнозирования – научная и учебная дисциплина, к основным задачам которой относятся разработка, изучение и применение современных математико-статистических методов прогнозирования на основе объективных данных; развитие теории и практики вероятностно-статистического моделирования экспертных методов прогнозирования; методов прогнозирования в условиях риска и комбинированных методов прогнозирования с использованием совместно экономико-математических и эконометрических (как математико-статистических, так и экспертных) моделей. Научной базой статистических методов прогнозирования является прикладная статистика и теория принятия решений.
Простейшие методы восстановления используемых для прогнозирования зависимостей исходят из заданного временного ряда, т. е. функции, определённой в конечном числе точек на оси времени. Временной ряд при этом часто рассматривается в рамках той или иной вероятностной модели, вводятся другие факторы (независимые переменные), помимо времени, например, объем денежной массы. Временной ряд может быть многомерным. Основные решаемые задачи – интерполяция и экстраполяция. Метод наименьших квадратов в простейшем случае (линейная функция от одного фактора) был разработан К. Гауссом в 1794–1795 гг. Могут оказаться полезными предварительные преобразования переменных, например, логарифмирование. Наиболее часто используется метод наименьших квадратов при нескольких факторах.
Оценивание точности прогноза (в частности, с помощью доверительных интервалов) – необходимая часть процедуры прогнозирования. Обычно используют вероятностно-статистические модели восстановления зависимости, например, строят наилучший прогноз по методу максимального правдоподобия. Разработаны параметрические (обычно на основе модели нормальных ошибок) и непараметрические оценки точности прогноза и доверительные границы для него (на основе Центральной Предельной Теоремы теории вероятностей). Применяются также эвристические приемы, не основанные на вероятностно-статистической теории: метод скользящих средних, метод экспоненциального сглаживания.
Многомерная регрессия, в том числе с использованием непараметрических оценок плотности распределения – основной на настоящий момент статистический аппарат прогнозирования. Нереалистическое предположение о нормальности погрешностей измерений и отклонений от линии (поверхности) регрессии использовать не обязательно; однако для отказа от предположения нормальности необходимо опереться на иной математический аппарат, основанный на многомерной Центральной Предельной Теореме теории вероятностей, технологии линеаризации и наследования сходимости. Он позволяет проводить точечное и интервальное оценивание параметров, проверять значимость их отличия от 0 в непараметрической постановке, строить доверительные границы для прогноза.
Уравнение тренда временного ряда
Рассматривая временной ряд как множество результатов наблюдений изучаемого процесса, проводимых последовательно во времени, в качестве основных целей исследования временных рядов можно выделить: выявление и анализ характерного изменения параметра у, оценка возможного изменения параметра в будущем (прогноз).
Значения временного ряда можно представить в виде: 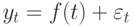

Неслучайная функция f (t) называется трендом. Тренд отражает характерное изменение (тенденцию) yt за некоторый промежуток времени. На практике в качестве тренда выбирают несколько возможных теоретических или эмпирических моделей. Могут быть выбраны, например, линейная, параболическая, логарифмическая, показательная функции. Для выявления типа модели на координатную плоскость наносят точки с координатами ( t, yt ) и по характеру расположения точек делают вывод о виде уравнения тренда. Для получения уравнения тренда применяют различные методы: сглаживание с помощью скользящей средней, метод наименьших квадратов и другие.
Уравнение тренда линейного вида будем искать в виде yt=f(t ), где f (t) = a0+a1(t ).
Пример 1. Имеется временной ряд:
| ti | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| xti | 2 | 1 | 4 | 4 | 6 | 8 | 7 | 9 | 12 | 11 |
Построим график xti во времени. Добавим на графике линию тренда исходных значений ряда. При этом, щелкнув правой кнопкой мыши по линии тренда, можно вызвать контекстное меню «Формат линии тренда», а в нем поставить флажок «показывать уравнение на диаграмме», тогда на диаграмме высветится уравнение линии тренда, вычисленное встроенными возможностями Excel .
Чтобы определить уравнение тренда, необходимо найти значения коэффициентов а0 и а1. Эти коэффициенты следует определять, исходя из условия минимального отклонения значений функции f (t) в точках ti от значений исходного временного ряда в тех же точках ti . Это условие можно записать в виде (на основе метода наименьших квадратов):
где n – количество значений временного ряда.
Для того, чтобы найти значения а0 и а1, необходимо иметь систему из двух уравнений. Эти уравнения можно получить, используя условие равенства нулю производной функции в точках её экстремума. В нашем случае эта функция имеет вид 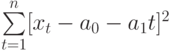
Полученная система может быть преобразована (математически) в систему так называемых нормальных уравнений. При этом уравнения примут вид:
Теперь необходимо решить преобразованную систему уравнений относительно а0 и а1. Однако предварительно следует составить и заполнить вспомогательную таблицу:
| t | t 2 | хt | хtt |
|---|---|---|---|
| 1 | 1 | 2 | 2 |
| 2 | 4 | 1 | 2 |
| 3 | 9 | 4 | 12 |
| 4 | 16 | 4 | 16 |
| 5 | 25 | 6 | 30 |
| 6 | 36 | 8 | 48 |
| 7 | 49 | 7 | 49 |
| 8 | 64 | 9 | 72 |
| 9 | 81 | 12 | 108 |
| 10 | 100 | 11 | 110 |
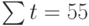 |
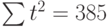 |
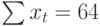 |
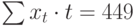 |
Подставив значения n = 10 в систему уравнений (2), получим
Решив систему уравнений относительно а0 и а1, получим а0 = -0,035, а1 = 1,17. Тогда функция тренда заданного временного ряда f (t) имеет вид:
f (t) = -0,035 + 1,17t.
Изобразим полученную функцию на графике.
Временной ряд приведен в таблице. Используя средства MS Excel :
- построить график временного ряда;
- добавить линию тренда и ее уравнение;
- найти уравнение тренда методом наименьших квадратов, сравнить уравнения (выше на графике и полученное);
- построить график временного ряда и полученной функции тренда в одной системе координат.
1. Реализация аспирина по аптеке (у.е.) за последние 7 недель приведена в таблице:
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| хti | 3,2 | 3,3 | 2,9 | 2,2 | 1,6 | 1,5 | 1,2 |
2. Динамика потребления молочных продуктов (у.е.) по району за последние 7 месяцев:
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| хti | 30 | 29 | 27 | 24 | 25 | 24 | 23 |
3. Динамика числа работников, занятых в одной из торговых сетей города за последние 8 лет приведена в таблице:
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 280 | 361 | 384 | 452 | 433 | 401 | 512 | 497 |
4. Динамика потребления сульфаниламидных препаратов в клинике по годам (тыс. упаковок):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 14 | 21 | 29 | 33 | 38 | 44 | 46 | 50 |
5. Динамика продаж однокомнатных квартир в городе за последние 8 лет (тыс. ед.):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| уt | 39 | 40 | 36 | 34 | 36 | 37 | 33 | 35 |
6. Динамика потребления антибиотиков в клинике (тыс. упаковок):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 10 | 17 | 18 | 13 | 17 | 21 | 25 | 29 |
7. Динамика производства хлебобулочных изделий на хлебозаводе (тонн):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 510 | 502 | 564 | 680 | 523 | 642 | 728 | 665 |
8. Динамика потребления противовирусных препаратов по аптечной сети в начале эпидемии гриппа (тыс. единиц):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 36 | 42 | 34 | 38 | 12 | 32 | 26 | 20 |
9. Динамика потребления противовирусных препаратов по аптечной сети в конце эпидемии гриппа (тыс. единиц):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 46 | 52 | 44 | 48 | 32 | 42 | 36 | 30 |
10. Динамика потребления витаминов по аптечной сети в весенний период (с марта по апрель) в разные годы (у.е.):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 0,9 | 1,7 | 1,5 | 1,7 | 1,5 | 2,1 | 2,5 | 3,6 |
Пример 2. Используя данные примера 1, приведенного выше, вычислить точечный прогноз исходного временного ряда на 5 шагов вперед.
Исходя из условия задачи, необходимо определить точечную оценку прогноза для t = 11, 12, 13, 14, 15, где t в данном случае – шаг упреждения.
Рассмотрим решение этой задачи средствами Microsoft Excel . При решении данной задачи следует так же, как и в примере 1, ввести исходные данные. Выделив данные, построить точечный график, щелкнув правой кнопкой мыши по ряду данных, вызвать контекстное меню и выбрать «Добавить линию тренда».
Щелкнув правой кнопкой мыши по линии тренда, вызвать контекстное меню, выбрать «Формат линии тренда», в окне Параметры линии тренда указать прогноз на 5 периодов и поставить флажок в окошке «Показывать уравнение на диаграмме (рис. 14.3 рис. 14.3.). В версии Excel ранее 2007 окно диалога представлено на рисунке 14.4 рис. 14.4.
Итоговый график представлен на рисунке 14.5 рис. 14.5.
Значения прогноза для 11, 12, 13, 14 и 15 уровней получим, используя функцию ПРЕДСКАЗ( ). Данная функция позволяет получить значения прогноза линейного тренда. Вычисленные значения: 12,87, 14,04, 15,22, 16,39, 17,57.
Значения точечного прогноза для исходного временного ряда на 5 шагов вперед можно вычислить и с помощью уравнения функции тренда f(t ), найденного по методу наименьших квадратов. Для этого в полученное для f (t) выражение необходимо подставить значения t = 11, 12, 13, 14, 15. В результате получим (эти значения следует рассчитать, сформировав формулу в табличном процессоре MS Excel ):
Сравнивая результаты точечных прогнозных оценок, полученных разными способами, выявляем, что данные отличаются незначительно, таким образом, в любом из способов расчета присутствует определенная погрешность (ошибка) прогноза (
Используя значения временного ряда Задания 1 согласно вашего варианта, вычислить точечный прогноз на 4 шага вперед. Продлить линию тренда на 4 прогнозных значения, вывести уравнение тренда, определить эти значения с помощью функции ПРЕДСКАЗ() или ТЕНДЕНЦИЯ(), а также по выражению функции тренда f(t ), полученному по методу наименьших квадратов в Задании 1. Сравнить полученные результаты.
Компоненты временного ряда
ТЕМА 5. МЕТОДЫ АНАЛИЗА ВРЕМЕННЫХ РЯДОВ
Лекция 9. Компоненты временного ряда. Модели тренда. Индексы сезонности.
Основная цель анализа временных рядов – прогнозирование будущего состояния объекта (процесса), получение базовой информации для принятия управленческих решений. Для реализации прогноза необходима модель, адекватно описывающая поведение ряда. Выбор конкретной модели определяется характером изменения уровней ряда, присутствием тех или иных компонент.
Компоненты временного ряда
Уровни рядов динамики формируются под влиянием множества факторов. Одни из них действуют стабильно на протяжении длительного периода времени и формируют основную тенденцию временного ряда, которая называется трендом.
Ряд факторов влияют на уровни ряда с определенной периодичностью, циклически (экономические циклы, циклы солнечной активности и т.п.). Для обнаружения и анализа влияния циклических факторов необходимы достаточно длинные временные ряды.
Повторяющиеся колебания уровней внутри года – результат влияния сезонных факторов.
Влияние случайных факторов на уровни ряда происходит без какой-либо периодичности, и, следовательно, не поддается измерению.
Исходя из вышесказанного, уровень временного ряда может быть представлен как функция четырех компонент:
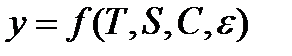
где T – трендовая компонента; S – сезонная компонента; C – циклическая компонента; 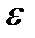
Чем сильнее влияние не трендовых компонент, тем сложнее выявить и описать основную тенденцию ряда, а именно это является центральной задачей при построении моделей временных рядов.
Сгладить влияние на уровни ряда не трендовых компонент позволяет процедура выравнивания временных рядов. Суть этой процедурысостоит в замене фактических уровней изучаемого ряда теоретическими. Теоретические уровни –это уровни, в той или иной мере очищенные от влиянияне трендовых компонент и полученные врезультате определенных расчетов, преобразований исходного ряда.
В арсенале статистикидва приема выравнивания временных рядов: механическое выравнивание и аналитическое.
Механическое выравнивание может быть осуществлено:
« Методом укрупнения интервалов. Данный метод предполагает объединение временных периодов и расчет по ним либо суммарных значений показателей, либо средних величин. Например, если ряд был представлен данными по месяцам, то выравнивание будет заключаться в объединении уровней и представлении ряда данными по кварталам. Укрупнение временных интервалов приведет к снижению степени колеблемости уровней и к более отчетливому проявлению тенденции.
« Метод скользящей средней.Данный метод предполагает расчет среднего уровня за определенный временной интервал (например, 3-5 лет), и дальнейшее скольжение интервала по временному ряду (напомним, что в средних величинах происходит взаимопогашение влияния случайных факторов). Полученные средние (выровненные) значения уровней относятся к середине интервала, по которому рассчитываются средние. Так, если период скольжения три года, первая средняя величина будет рассчитана:


Если период скольжения – четная величина, то применяют метод центрирования. Этот прием выражается в подсчете средней арифметической величины из значений, полученных по двум шагам скольжения.
Увеличение периода скольжения позволяет более отчетливо проявиться основной тенденции, однако результатом является существенно укороченный временной ряд, что неблагоприятно может сказаться на качестве трендовой модели.
Аналитическое выравнивание позволяет не только выявить основную тенденцию ряда, но и получить аналитическую форму тренда в виде уравнения.
Уравнение (модель) тренда – это парное уравнение регрессии, в качестве фактора в котором выступает время (t).Переменная «t» задается простой последовательностью чисел от 1 до n. В общем виде уравнение может быть записано:
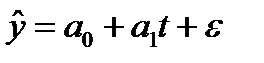
где 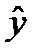

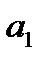
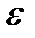
Расчет параметров трендовой модели осуществляется с использованием метода наименьших квадратов (о котором говорилось в теме регрессионного анализа).
Центральной проблемой построения трендовой модели является выбор типа уравнения тренда, наилучшим образом описывающего основную тенденцию изучаемого ряда. Для решения этой задачи могут быть использованы:
· графическое представление временного ряда;
· метод конечных разностей;
· формализованный подход, т.е. метод критериев.
При графическом представлении временных рядов по оси абсцисс откладываются периоды или моменты времени, по оси ординат – значения уровней ряда. Расположение эмпирической линии тренда на графике позволяет выдвинуть гипотезу о типе уравнения тренда.
Метод конечных разностей основан на свойствах математических функций и анализе показателей изменения уровней временных рядов. Так, если примерно постоянными являются первые разности (абсолютные приросты), для описания тренда можно воспользоваться полиномом первой степени (линейной функцией). Если примерно постоянны вторые разности (показатели ускорения), то следует использовать полином второй степени и т.д.
В настоящее время выбор функции, для описания тренда, как правило, формализован, т.е. осуществляется с использованием статистических критериев на базе пакетов прикладных программ. Аналитик одновременно строит несколько уравнений тренда, а затем, исходя из значений определенных критериев, выбирает одно, дающее лучшую аппроксимацию.
В качестве критериев выбора модели тренда могут быть использованы следующие характеристики:
1. Минимальная сумма квадратов отклонений теоретических значений уровней ряда (полученных на основе уравнения тренда) от фактических:
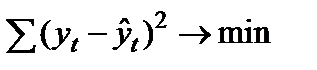
где yt– фактическое значение уровня ряда периода t; 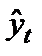
2. Минимальная величина остаточной дисперсии ( 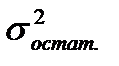

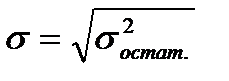
3. Минимальное значение средней ошибки аппроксимации:
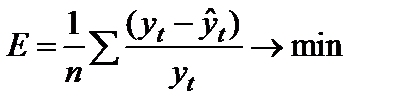
4. Максимальное значение F-критерия Фишера, оценивающего значимость уравнения в целом (см. тему регрессионного анализа): 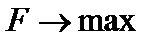
5. Максимальное значение коэффициента детерминации, характеризующего долю объясненной дисперсии в общей дисперсии результативного признака: 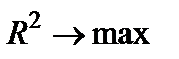
Продолжая анализировать динамику показателя обеспеченности жильем, построим три уравнения тренда, используя линейную функцию, параболу второго порядка и экспоненту. Результаты расчетов, выполненных в пакете STATISTICA, представлены в таблицах 9.1, 9.2, 9.3 (структура и анализ таблиц трендовых моделей аналогичны таблицам парных уравнений регрессии.См. соответствующую лекцию.).
Таблица 9.1 — Линейный тренд временного ряда показателей общей площади жилых помещений, приходящейся в среднем на одного жителя, м.кв./чел.
Графа «В» таблицы содержит значения параметров уравнения, t- статистика позволяет оценить статистическую значимость параметров модели. В верхней части таблицы приведены значения коэффициента корреляции (R), коэффициента детерминации (R?= 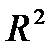
Уравнение может быть записано: y = 18,82 + 0,34 t.
Таблица 9.2 — Параболический тренд временного ряда показателей общей жилой площади, приходящейся в среднем на одного жителя, м.кв./чел.
Расчет характеристик, содержащихся в таблицах 9.2 и 9.3, выполнен в процедуре нелинейного оценивания программыSTATISTICA, в этих таблицах значения параметров уравнения находятся в графе Estimate, в двух последних графах дополнительно приводятся значения границ доверительных интервалов для генеральных параметров.
Таблица 9.3 — Экспоненциальный тренд временного ряда показателей общей жилой площади, приходящейся в среднем на одного жителя, м.кв./чел.
Для анализа результатов расчетов и выбора модели тренда построим сводную таблицу 9.4.
Таблица 9.4 — Оценка статистической значимости параметров и уравнений тренда
| Уравнение тренда | 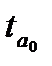 |
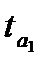 |
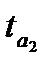 |
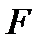 |
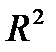 |
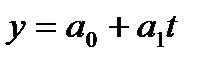 |
333,66 | 51,88 | — | 2692,0 | 0,995 |
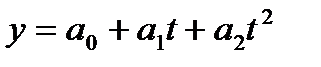 |
199,58 | 12,78 | 0,88 | 2691,96 | 0,995 |
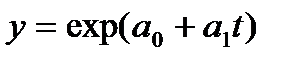 |
887,97 | 43,40 | — | 1550,0 | 0,994 |
Параметры линейной и экспоненциальной моделей статистически значимы, поскольку расчетное значение t — статистики для каждого параметра больше табличного значения t — статистики с учетом принятого уровня значимости и соответствующего числа степеней свободы ( 

В уравнении полинома второго порядка параметр 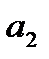


Выбор между двумя статистически значимыми уравнениями осуществляется на основе значений коэффициентов детерминации, характеризующих долю объясненной дисперсии в общей дисперсии зависимой переменной. Предпочтение следует отдать линейной модели, которой соответствует большее значение коэффициента детерминации ( 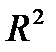
Уравнение тренда может бытьпризнано моделью, пригодной для прогнозирования, если оно отвечает следующим требованиям:
· уравнение в целом статистически значимо (оценка по F-критерию);
· все параметры уравнения статистически значимы (оценка по t-статистике);
· в остатках уравнения отсутствует автокорреляция.
Процедуры оценки статистической значимости уравнения в целом и его параметров подробно рассмотрены в разделе КРА. Остановимся на оценке автокорреляции в остатках модели.
Остатки– это разность между фактическими значениями уровней временного ряда и выровненными (теоретическими) значениями, полученными по уравнению тренда.
Фактические уровни: Теоретические
(выровненные) уровни: Остатки:
y1 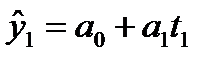
y2
y3 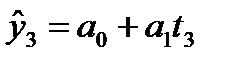

…… ………………………. ……………..
yt
Рисунок 9.1 — Определение величины остатков модели временного ряда
Автокорреляция остатков – это зависимость остатков периода t от остатков предшествующих периодов (t-i). Если построенное уравнение обеспечивает удовлетворительную аппроксимацию, то отклонения от тренда (остатки) должны носить случайный характер и в их последовательности не должно быть корреляции.
Исследование автокорреляции остатков трендовой модели имеет особое значение, если ставится задача прогнозирования поведения временного ряда. Дело в том, что наличие автокорреляции свидетельствует о наличии тенденции в остатках, т.е. о сохранении в них части полезной информации. Поскольку основная задача построения трендовой модели – как можно более полно описать основную тенденцию изучаемого ряда – сохранение тенденции в остатках, говорит о том, что модель не может быть признана пригодной для получения прогнозаудовлетворительногокачества.
Оценка автокорреляции в остатках может быть проведена на основе коэффициентов автокорреляции, либо с использованием специального критерия — критерияДарбина-Уотсона.
Если остатки периода t обозначить 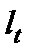
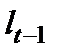
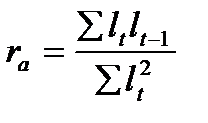
Коэффициент автокорреляции изменяется в пределах: 
По достаточно большим временным рядам могут быть рассчитаны коэффициенты автокорреляции разных порядков, т.е. коэффициенты, оценивающие зависимость не только между остатками соседних периодов, но между остатками, разделенными двумя, тремя и большим числом временных интервалов. Интервал, разделяющий зависимые остатки, называют лагом. Величина лага определяет порядок коэффициента автокорреляции. Последовательность коэффициентов автокорреляции разного порядка называется автокорреляционной функцией, которая характеризует зависимость величины коэффициентов автокорреляции от величины лага.
В таблице 9.5 приведены фактические (ObservedValue), теоретические (PredictedValue), т.е. рассчитанные по линейной модели, значения показателя обеспеченности жильем и величины остатков (Residual), равные разности значений двух первых столбцов.
Таблица 9.5 — Фактические, теоретические уровни и остатки линейного тренда временного ряда показателей общей жилой площади, приходящейся в среднем на одного жителя, м.кв./чел.
Для оценки автокорреляции остатков рассчитаем коэффициенты автокорреляции. Поскольку анализируемый временной ряд содержит всего 14 уровней, то рассчитаем коэффициенты лишь трех порядков: первого, который покажет степень корреляционной зависимости между смежными значениями остатков; второго, т.е. будет дана оценка зависимости между остатками, разделенными двумя годами; третьего порядка — оценка корреляционной связи между остатками с интервалом в три года.
Автокорреляционная функция остатков линейной модели и ее графическое отображение представлены на рисунке 9.2.
Рисунок 9.2 — Автокорреляционная функция остатков линейной модели временного ряда показателей общей жилой площади, приходящейся в среднем на одного жителя, м.кв./чел.
Графическое отображение коэффициентов автокорреляции (прямоугольники) сопровождается числовыми значениями этих характеристик (графа Corr.): коэффициент автокорреляции первого порядка 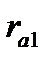
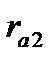
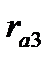

где: 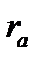
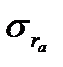
В результате расчетов получены следующие величины t — статистики: 

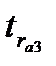

Рассмотрим еще один метод оценки автокорреляции в остатках — критерий Дарбина-Уотсона (D-W). Используя введенные ранее обозначения (см. 9.5), критерий может быть рассчитан следующим образом:

Между критерием Дарбина-Уотсона и коэффициентом автокорреляции существует следующее соотношение: 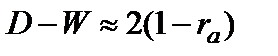
Исходя из этого соотношения, очевидно, что если:
Таким образом, значение критерия может изменяться в пределах:
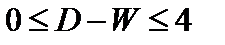
Близость D-W к 0 и к 4 означает присутствие автокорреляции в остатках, к 2 – ее отсутствие.
КритерийДарбина-Уотсона табулирован. По таблицам, исходя из числа уровней динамического ряда и числа факторов в уравнении тренда, находят границы значения критерия: 
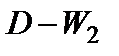
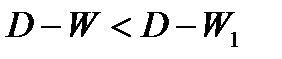
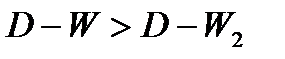
Если 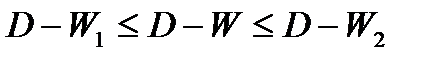
Оценивая остатки линейной модели рассматриваемого примера, в программе STATISTICA было получено значение критерия Дарбина-Уотсона=1,91. Табличные значения верхней и нижней границ критерия (см. приложение . )следующие: 
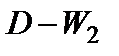
Таким образом, весь комплекс требований, необходимых для признания модели тренда пригодной для прогнозирования, выполнен: уравнение тренда статистически значимо, параметры статистически значимы, в остатках модели отсутствует автокорреляция.
Регрессионную модель тренда, отвечающую всем формальным требованиям, можно использовать для оценки величины переменной y в последующие периоды времени t. Чтобы получить, так называемый, точечный прогноз при заданном значении t, вычисляется значение построенной функции регрессии в точке t.
В рассматриваемом примере исходный временной ряд включал 14 уровней (данные с 2000 по 2013 годы), следовательно, точечный прогноз может быть выполнен на 15-й период(на 2014 год) и дальнейшие периоды. Подставляя в уравнение значение t=15 (y=18,82 + 0,34*15), получаем, что прогнозируемое среднее значение показателя обеспеченности жильем в России в 2014 году составит 23,92 м.кв./чел.
Однако следует помнить, что уравнение тренда описывает лишь общую тенденцию изменения показателя. Фактическая реализация событий отличается от прогнозируемой. Совпадение фактических и прогнозных значений маловероятно. Уравнение тренда всегда содержит ошибку, которую принято оценивать среднеквадратической (стандартной) ошибкой тренда:
где 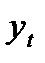
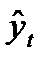
Как видим, средняя ошибка тренда – это корень квадратный из остаточной дисперсии, которая оценивает степень колеблемости уровней временного ряда ( 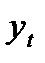
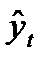
С учетом ошибки тренда может быть рассчитан доверительный интервал прогноза:
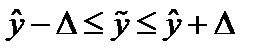
где 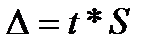
При выполнении расчетов с использованием специализированных компьютерных программ, величина ошибки определяется в одной процедуре с расчетом значений параметров уравнения. В таблице 9.1 представлено значение стандартной ошибка линейного тренда (St.Errorofesimate): S=0,0999. Величина коэффициента доверия, исходя из уровня значимости 0,05 и числа степеней свободы 12 (14-1-1), равна 2,179 (см. прил. Табл. Стьюд.), тогда


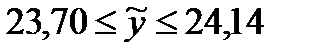
Прогнозирование на основе временных рядов называют экстраполяцией — продлением в будущее тенденции, сложившейся в прошлом. Следовательно, доверять результатам прогнозирования можно при условии, что факторы, повлиявшие на формирование тенденции в прошлом, неизменно будут действовать и в будущем. Еще один практический совет, выработанный статистикой: период упреждения, т.е. период на который делается прогноз, не должен превышать 1/3 длины ряда, на основе которого построена модель.
источники:
http://intuit.ru/studies/courses/3659/901/lecture/32720
http://poisk-ru.ru/s43356t9.html
Прогнозирование на основе тренда
Методика статистического прогноза по тренду и колеблемости основана на их экстраполяции, т.е. на предположении, что параметры тренда и колеблемости сохраняться до прогнозируемого периода. Такая экстраполяция справедлива, если система развивается эволюционно в достаточно стабильных условиях. Обычно рекомендуют, чтобы сроки прогноза не превышали 1/3 длительности базы расчета тренда. Методика прогнозирования по тренду с учетом колеблемости следующая:
1. Строится уравнение тренда (по методу наименьших квадратов или скользящего среднего) и вычисляются среднее квадратическое отклонение уровней ряда от тренда s(t). Прежде всего вычисляется точечный прогноз – значение уровня тренда в прогнозируемом периоде. Однако, параметры тренда, полученные по ограниченному числу уровней ряда, — это лишь выборочные средние оценки. Если взять базу для расчета тренда несколько иную (добавить 2 года в начале или в конце), то получим иные параметры. Следовательно, прогноз будет иной. Поэтому точечный прогноз имеет вероятностную форму и вычисляется средняя ошибка прогноза. Средняя ошибка прогноза линейного тренда на год с номером tk вычисляется по формулам:
а) для однократного выравнивания
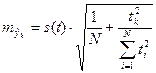
tk — номер года прогноза
N – количество уровней (количество наблюдений)
б) для скользящего среднего при L-сдвигах базы и ее длине n
Для получения достаточно надежных границ прогноза (скажем, с вероятностью 0,9 того, что ошибка будет не более указанной), следует среднюю ошибку умножить на величину t-критерия Стьюдента при указанной вероятности (или значимости 1-0,9 = 0,1) и при числе степеней свободы =N-p, где р – количество параметров в уравнении тренда.
Получают предельную ошибку с данной вероятностью
Тогда прогноз с учетом предельной ошибки будет равен
Анализ временных рядов, тренд ряда динамики, точечная оценка прогноза
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Анализ временных рядов
Временной ряд (или ряд динамики) – это упорядоченная по времени последовательность значений некоторой произвольной переменной величины. Тем самым, временной ряд существенным образом отличается от простой выборки данных. Каждое отдельное значение данной переменной называется отсчётом (уровнем элементов) временного ряда.
Временные ряды состоят из двух элементов:
- периода времени, за который или по состоянию на который приводятся числовые значения;
- числовых значений того или иного показателя, называемых уровнями ряда.
Временные ряды классифицируются по следующим признакам:
- по форме представления уровней: ряды абсолютных показателей, относительных показателей, средних величин;
- по количеству показателей, когда определяются уровни в каждый момент времени: одномерные и многомерные временные ряды;
- по характеру временного параметра: моментные и интервальные временные ряды. В моментных временных рядах уровни характеризуют значения показателя по состоянию на определенные моменты времени. В интервальных рядах уровни характеризуют значение показателя за определенные периоды времени. Важная особенность интервальных временных рядов абсолютных величин заключается в возможности суммирования их уровней. Отдельные же уровни моментного ряда абсолютных величин содержат элементы повторного счета. Это делает бессмысленным суммирование уровней моментных рядов;
- по расстоянию между датами и интервалами времени выделяют равноотстоящие – когда даты регистрации или окончания периодов следуют друг за другом с равными интервалами и неполные (неравноотстоящие) – когда принцип равных интервалов не соблюдается;
- по наличию пропущенных значений: полные и неполные временные ряды. Временные ряды бывают детерминированными и случайными: первые получают на основе значений некоторой неслучайной функции (ряд последовательных данных о количестве дней в месяцах); вторые есть результат реализации некоторой случайной величины;
- в зависимости от наличия основной тенденции выделяют стационарные ряды – в которых среднее значение и дисперсия постоянны и нестационарные – содержащие основную тенденцию развития.
Временные ряды, как правило, возникают в результате измерения некоторого показателя. Это могут быть как показатели (характеристики) технических систем, так и показатели природных, социальных, экономических и других систем (например, погодные данные). Типичным примером временного ряда можно назвать биржевой курс, при анализе которого пытаются определить основное направление развития (тенденцию или тренда).
Анализ временных рядов – совокупность математико-статистических методов анализа, предназначенных для выявления структуры временных рядов и для их прогнозирования. Сюда относятся, в частности, методы регрессионного анализа. Выявление структуры временного ряда необходимо для того, чтобы построить математическую модель того явления, которое является источником анализируемого временного ряда. Прогноз будущих значений временного ряда используется для эффективного принятия решений.
Прогноз, характеристики и параметры прогнозирования
Прогноз (от греч. 
Прогнозирование, разработка прогноза; в узком значении – специальное научное исследование конкретных перспектив развития какого-либо процесса.
- по срокам: краткосрочные, среднесрочные, долгосрочные;
- по масштабу: личные, на уровне предприятия (организации), местные, региональные, отраслевые, мировые (глобальные).
К основным методам прогнозирования относятся:
- статистические методы;
- экспертные оценки (метод Дельфи);
- моделирование.
Прогноз – обоснованное суждение о возможном состоянии объекта в будущем или альтернативных путях и сроках достижения этих состояний. Прогнозирование – процесс разработки прогноза. Этап прогнозирования – часть процесса разработки прогнозов, характеризующаяся своими задачами, методами и результатами. Деление на этапы связано со спецификой построения систематизированного описания объекта прогнозирования, сбора данных, с построением модели, верификацией прогноза.
Прием прогнозирования – одна или несколько математических или логических операций, направленных на получение конкретного результата в процессе разработки прогноза. В качестве приема могут выступать сглаживание динамического ряда, определение компетентности эксперта, вычисление средневзвешенного значения оценок экспертов и т. д.
Модель прогнозирования – модель объекта прогнозирования, исследование которой позволяет получить информацию о возможных состояниях объекта прогнозирования в будущем и (или) путях и сроках их осуществления.
Метод прогнозирования – способ исследования объекта прогнозирования, направленный на разработку прогноза. Методы прогнозирования являются основанием для методик прогнозирования.
Методика прогнозирования – совокупность специальных правил и приемов (одного или нескольких методов) разработки прогнозов.
Прогнозирующая система – система методов и средств их реализации, функционирующая в соответствии с основными принципами прогнозирования. Средствами реализации являются экспертная группа, совокупность программ и т. д. Прогнозирующие системы могут быть автоматизированными и неавтоматизированными.
Прогнозный вариант – один из прогнозов, составляющих группу возможных прогнозов.
Объект прогнозирования – процесс, система, или явление, о состоянии которого даётся прогноз.
Характеристика объекта прогнозирования – качественное или количественное отражение какого-либо свойства объекта прогнозирования.
Переменная объекта прогнозирования – количественная характеристика объекта прогнозирования, которая является или принимается за изменяемую в течение периода основания и (или) периода упреждения прогноза.
Период основания прогноза – промежуток времени, за который используют информацию для разработки прогноза. Этот промежуток времени называют также периодом предыстории.
Период упреждения прогноза – промежуток времени, на который разрабатывается прогноз.
Прогнозный горизонт – максимально возможный период упреждения прогноза заданной точности.
Точность прогноза – оценка доверительного интервала прогноза для заданной вероятности его осуществления.
Достоверность прогноза – оценка вероятности осуществления прогноза для заданного доверительного интервала.
Ошибка прогноза – апостериорная величина отклонения прогноза от действительного состояния объекта.
Источник ошибки прогноза – фактор, способный привести к появлению ошибки прогноза. Различают источники регулярных и нерегулярных ошибок.
Верификация прогноза – оценка достоверности и точности или обоснованности прогноза.
Статистические методы прогнозирования – научная и учебная дисциплина, к основным задачам которой относятся разработка, изучение и применение современных математико-статистических методов прогнозирования на основе объективных данных; развитие теории и практики вероятностно-статистического моделирования экспертных методов прогнозирования; методов прогнозирования в условиях риска и комбинированных методов прогнозирования с использованием совместно экономико-математических и эконометрических (как математико-статистических, так и экспертных) моделей. Научной базой статистических методов прогнозирования является прикладная статистика и теория принятия решений.
Простейшие методы восстановления используемых для прогнозирования зависимостей исходят из заданного временного ряда, т. е. функции, определённой в конечном числе точек на оси времени. Временной ряд при этом часто рассматривается в рамках той или иной вероятностной модели, вводятся другие факторы (независимые переменные), помимо времени, например, объем денежной массы. Временной ряд может быть многомерным. Основные решаемые задачи – интерполяция и экстраполяция. Метод наименьших квадратов в простейшем случае (линейная функция от одного фактора) был разработан К. Гауссом в 1794–1795 гг. Могут оказаться полезными предварительные преобразования переменных, например, логарифмирование. Наиболее часто используется метод наименьших квадратов при нескольких факторах.
Оценивание точности прогноза (в частности, с помощью доверительных интервалов) – необходимая часть процедуры прогнозирования. Обычно используют вероятностно-статистические модели восстановления зависимости, например, строят наилучший прогноз по методу максимального правдоподобия. Разработаны параметрические (обычно на основе модели нормальных ошибок) и непараметрические оценки точности прогноза и доверительные границы для него (на основе Центральной Предельной Теоремы теории вероятностей). Применяются также эвристические приемы, не основанные на вероятностно-статистической теории: метод скользящих средних, метод экспоненциального сглаживания.
Многомерная регрессия, в том числе с использованием непараметрических оценок плотности распределения – основной на настоящий момент статистический аппарат прогнозирования. Нереалистическое предположение о нормальности погрешностей измерений и отклонений от линии (поверхности) регрессии использовать не обязательно; однако для отказа от предположения нормальности необходимо опереться на иной математический аппарат, основанный на многомерной Центральной Предельной Теореме теории вероятностей, технологии линеаризации и наследования сходимости. Он позволяет проводить точечное и интервальное оценивание параметров, проверять значимость их отличия от 0 в непараметрической постановке, строить доверительные границы для прогноза.
Уравнение тренда временного ряда
Рассматривая временной ряд как множество результатов наблюдений изучаемого процесса, проводимых последовательно во времени, в качестве основных целей исследования временных рядов можно выделить: выявление и анализ характерного изменения параметра у, оценка возможного изменения параметра в будущем (прогноз).
Значения временного ряда можно представить в виде: 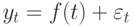

Неслучайная функция f (t) называется трендом. Тренд отражает характерное изменение (тенденцию) yt за некоторый промежуток времени. На практике в качестве тренда выбирают несколько возможных теоретических или эмпирических моделей. Могут быть выбраны, например, линейная, параболическая, логарифмическая, показательная функции. Для выявления типа модели на координатную плоскость наносят точки с координатами ( t, yt ) и по характеру расположения точек делают вывод о виде уравнения тренда. Для получения уравнения тренда применяют различные методы: сглаживание с помощью скользящей средней, метод наименьших квадратов и другие.
Уравнение тренда линейного вида будем искать в виде yt=f(t ), где f (t) = a0+a1(t ).
Пример 1. Имеется временной ряд:
| ti | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| xti | 2 | 1 | 4 | 4 | 6 | 8 | 7 | 9 | 12 | 11 |
Построим график xti во времени. Добавим на графике линию тренда исходных значений ряда. При этом, щелкнув правой кнопкой мыши по линии тренда, можно вызвать контекстное меню «Формат линии тренда», а в нем поставить флажок «показывать уравнение на диаграмме», тогда на диаграмме высветится уравнение линии тренда, вычисленное встроенными возможностями Excel .
Чтобы определить уравнение тренда, необходимо найти значения коэффициентов а0 и а1. Эти коэффициенты следует определять, исходя из условия минимального отклонения значений функции f (t) в точках ti от значений исходного временного ряда в тех же точках ti . Это условие можно записать в виде (на основе метода наименьших квадратов):
где n – количество значений временного ряда.
Для того, чтобы найти значения а0 и а1, необходимо иметь систему из двух уравнений. Эти уравнения можно получить, используя условие равенства нулю производной функции в точках её экстремума. В нашем случае эта функция имеет вид 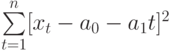
Полученная система может быть преобразована (математически) в систему так называемых нормальных уравнений. При этом уравнения примут вид:
Теперь необходимо решить преобразованную систему уравнений относительно а0 и а1. Однако предварительно следует составить и заполнить вспомогательную таблицу:
| t | t 2 | хt | хtt |
|---|---|---|---|
| 1 | 1 | 2 | 2 |
| 2 | 4 | 1 | 2 |
| 3 | 9 | 4 | 12 |
| 4 | 16 | 4 | 16 |
| 5 | 25 | 6 | 30 |
| 6 | 36 | 8 | 48 |
| 7 | 49 | 7 | 49 |
| 8 | 64 | 9 | 72 |
| 9 | 81 | 12 | 108 |
| 10 | 100 | 11 | 110 |
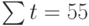 |
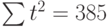 |
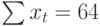 |
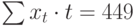 |
Подставив значения n = 10 в систему уравнений (2), получим
Решив систему уравнений относительно а0 и а1, получим а0 = -0,035, а1 = 1,17. Тогда функция тренда заданного временного ряда f (t) имеет вид:
f (t) = -0,035 + 1,17t.
Изобразим полученную функцию на графике.
Временной ряд приведен в таблице. Используя средства MS Excel :
- построить график временного ряда;
- добавить линию тренда и ее уравнение;
- найти уравнение тренда методом наименьших квадратов, сравнить уравнения (выше на графике и полученное);
- построить график временного ряда и полученной функции тренда в одной системе координат.
1. Реализация аспирина по аптеке (у.е.) за последние 7 недель приведена в таблице:
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| хti | 3,2 | 3,3 | 2,9 | 2,2 | 1,6 | 1,5 | 1,2 |
2. Динамика потребления молочных продуктов (у.е.) по району за последние 7 месяцев:
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| хti | 30 | 29 | 27 | 24 | 25 | 24 | 23 |
3. Динамика числа работников, занятых в одной из торговых сетей города за последние 8 лет приведена в таблице:
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 280 | 361 | 384 | 452 | 433 | 401 | 512 | 497 |
4. Динамика потребления сульфаниламидных препаратов в клинике по годам (тыс. упаковок):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 14 | 21 | 29 | 33 | 38 | 44 | 46 | 50 |
5. Динамика продаж однокомнатных квартир в городе за последние 8 лет (тыс. ед.):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| уt | 39 | 40 | 36 | 34 | 36 | 37 | 33 | 35 |
6. Динамика потребления антибиотиков в клинике (тыс. упаковок):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 10 | 17 | 18 | 13 | 17 | 21 | 25 | 29 |
7. Динамика производства хлебобулочных изделий на хлебозаводе (тонн):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 510 | 502 | 564 | 680 | 523 | 642 | 728 | 665 |
8. Динамика потребления противовирусных препаратов по аптечной сети в начале эпидемии гриппа (тыс. единиц):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 36 | 42 | 34 | 38 | 12 | 32 | 26 | 20 |
9. Динамика потребления противовирусных препаратов по аптечной сети в конце эпидемии гриппа (тыс. единиц):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 46 | 52 | 44 | 48 | 32 | 42 | 36 | 30 |
10. Динамика потребления витаминов по аптечной сети в весенний период (с марта по апрель) в разные годы (у.е.):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 0,9 | 1,7 | 1,5 | 1,7 | 1,5 | 2,1 | 2,5 | 3,6 |
Пример 2. Используя данные примера 1, приведенного выше, вычислить точечный прогноз исходного временного ряда на 5 шагов вперед.
Исходя из условия задачи, необходимо определить точечную оценку прогноза для t = 11, 12, 13, 14, 15, где t в данном случае – шаг упреждения.
Рассмотрим решение этой задачи средствами Microsoft Excel . При решении данной задачи следует так же, как и в примере 1, ввести исходные данные. Выделив данные, построить точечный график, щелкнув правой кнопкой мыши по ряду данных, вызвать контекстное меню и выбрать «Добавить линию тренда».
Щелкнув правой кнопкой мыши по линии тренда, вызвать контекстное меню, выбрать «Формат линии тренда», в окне Параметры линии тренда указать прогноз на 5 периодов и поставить флажок в окошке «Показывать уравнение на диаграмме (рис. 14.3 рис. 14.3.). В версии Excel ранее 2007 окно диалога представлено на рисунке 14.4 рис. 14.4.
Итоговый график представлен на рисунке 14.5 рис. 14.5.
Значения прогноза для 11, 12, 13, 14 и 15 уровней получим, используя функцию ПРЕДСКАЗ( ). Данная функция позволяет получить значения прогноза линейного тренда. Вычисленные значения: 12,87, 14,04, 15,22, 16,39, 17,57.
Значения точечного прогноза для исходного временного ряда на 5 шагов вперед можно вычислить и с помощью уравнения функции тренда f(t ), найденного по методу наименьших квадратов. Для этого в полученное для f (t) выражение необходимо подставить значения t = 11, 12, 13, 14, 15. В результате получим (эти значения следует рассчитать, сформировав формулу в табличном процессоре MS Excel ):
Сравнивая результаты точечных прогнозных оценок, полученных разными способами, выявляем, что данные отличаются незначительно, таким образом, в любом из способов расчета присутствует определенная погрешность (ошибка) прогноза (
Используя значения временного ряда Задания 1 согласно вашего варианта, вычислить точечный прогноз на 4 шага вперед. Продлить линию тренда на 4 прогнозных значения, вывести уравнение тренда, определить эти значения с помощью функции ПРЕДСКАЗ() или ТЕНДЕНЦИЯ(), а также по выражению функции тренда f(t ), полученному по методу наименьших квадратов в Задании 1. Сравнить полученные результаты.
Лабораторная работа №6. Анализ динамических рядов
Лабораторная работа №6. Анализ динамических рядов
При исследовании многих природных и производственных процессов возникает задача анализа в динамике событий и их последовательностей, которые не поддаются методам стандартного математического анализа, поскольку зависят от случайных факторов. Основными задачами в таких исследованиях являются детальное изучение этих процессов, выделение их существенных характеристик, которое может привести к возможности прогнозирования развития этих процессов в будущем. Также представляет интерес выделение внутренних закономерностей, которым подчинено развитие этих процессов.
Временной ряд (динамический ряд, ряд динамики) – это последовательно измеренные через некоторые промежутки времени данные о значении какого-либо параметра исследуемого процесса (или нескольких параметров, в этом случае говорят о многомерном временном ряде).
Временной ряд состоит из двух элементов:
— периода времени, за который или по состоянию на который приводятся числовые значения;
— числовых значений показателя, называемых уровнями ряда.
Временные ряды бывают детерминированными (получены на основе значений некоторой неслучайной функции, например, ряд последовательных данных о количестве дней в месяцах) и случайными (результат реализации некоторой случайной величины).
Классификация временных рядов проводится по следующим признакам.
• По характеру показателя, для которого определяются уровни:
— детерминированные ряды, которые получены на основе значений некоторой неслучайной функции, например, ряд последовательных данных о количестве дней в месяцах;
— случайные ряды, представляющие собой реализацию некоторой случайной величины.
• По форме представления уровней:
— ряды абсолютных величин;
— ряды средних величин.
• По характеру временного показателя:
— моментные ряды, в которых уровни характеризуют значение показателя по состоянию на определенные моменты времени;
— интервальные ряды, уровни которых характеризуют значение показателя за определенные периоды времени. Важная особенность интервальных временных рядов абсолютных величин заключается в возможности суммирования их уровней.
• По расстоянию между датами и интервалами времени:
— полные или равноотстоящие ряды, если даты регистрации или окончания периодов следуют друг за другом с равными интервалами;
— неполные или неравноотстоящие ряды, если принцип равных интервалов не соблюдается или имеются пропущенные значения.
При изучении рядов динамики обычно решают следующие задачи:
1. Вычислить числовые и функциональные характеристики ряда (описательные методы).
2. Определить, имеется ли некоторая неслучайная, закономерная компонента, описывающая тенденцию (тренд) процесса.
3. Определить, нет ли регулярных, колебательных “сезонных” компонент, которые связаны с периодическими естественными колебаниями параметров случайного процесса.
4. Выделить и описать основные колебания случайного процесса вокруг тренда, в случае необходимости удалить влияние второстепенных факторов.
5. Дать прогноз развития случайной процесса на ближайшее будущее и указать степень уверенности в этом прогнозе.
Следует иметь в виду, что при изучении рядов динамики необходимо соблюдение ряда условий:
• Статистические данные должны быть сопоставимы по территории, кругу охватываемых объектов, единицам измерения, времени регистрации, ценам, методологии расчета. Сопоставимость по территории означает, что данные по странам и регионам, границы которых изменились, должны быть пересчитаны в старых пределах. Сопоставимость по кругу охватываемых объектов означает сравнение совокупностей с равным числом элементов. Сопоставимость обеспечивается так называемым смыканием рядов динамики. При этом абсолютные уровни могут заменяться относительными, иногда делают пересчет в условные абсолютные уровни и т. п.
• Числовые уровни рядов динамики должны быть упорядоченными во времени. Не допускается анализ рядов с пропусками отдельных уровней (неполных динамических рядов), если же такие пропуски неизбежны, то их восполняют условными расчетными значениями.
• Временные ряды применяются только для краткосрочного прогнозирования (чаще всего на 1 период вперед).
• Для анализа и прогноза необходима достоверная информация о развитии исследуемого явления минимум за пять периодов.
Числовые характеристики динамических рядов
• Интенсивность изменений уровней ряда во времени характеризуют аналитические показатели. Различают базисные (изменение относительно начального уровня ряда) и цепные (изменение относительно предыдущего уровня) показатели:
Табл.6.1. Аналитические показатели ряда динамики
Абсолютный прирост Di
Коэффициент роста Кр
Коэффициент прироста Кпр
Темп прироста Тпр
Абсолютное значение одного процента прироста А
• Ряд динамики в целом характеризуют средние показатели:
Средний уровень ряда:
— для полного интервального ряда абсолютных величин:

— для полного интервального ряда относительных и средних величин средний уровень должен определяться с учетом информации, связанной с осредняемым:


— для моментного динамического ряда:

в частности, для полного моментного ряда:

Средний абсолютный прирост:

Средний коэффициент (темп) роста:

Средний коэффициент (темп) прироста:


Пример 6.1. Имеются данные о числе пожаров (тыс. случаев) в России в 1974-1988 гг. Вычислить характеристики динамического ряда.
Решение. Прежде всего классифицируем данный динамический ряд: это полный интервальный ряд абсолютных величин.
Перенесем данные в Еxcel, расположив их в два столбца. Добавим также столбец «№ периода», начиная с 0.
Для аналитических показателей подготовим две таблицы – для базисных и цепных показателей, по периодам начиная с 1, и вычислим соответствующие показатели в таблице по формулам в таблице 6.1, результат будет выглядеть так:
Вычислим теперь средние показатели.
Поскольку мы имеем дело с полным интервальным рядом абсолютных величин, средний уровень ряда вычисляем по самой простой формуле среднего арифметического уровней, используя функцию СРЗНАЧ:
Средний абсолютный прирост также вычислить просто:
Для вычисления среднего коэффициента роста воспользуемся функцией ПРОИЗВЕД, а для извлечения корня применим возведение в степень 1/n:
Анализ тренда динамического ряда
Перейдем теперь к задачам собственно анализа временного ряда и прогнозирования.
В общем виде временной ряд представляют, в зависимости от задачи, в виде аддитивной (6.1) или мультипликативной (6.2) модели, на основании которой дается прогноз:


где 

В детерминированную составляющую могут входить три элемента:
— эволюционная составляющая — характеризует основную тенденцию развития исследуемого объекта (тренд)
— сезонная составляющая — показывает колебания показателя в течение года.
— циклическая составляющая — формируется под воздействием долговременных циклических факторов
Стохастическая составляющая формируется под воздействием большого числа случайных факторов, не отражаемых в прогнозной модели.
Выделение тренда может быть произведено тремя методами:
1. Укрупнение интервалов. Ряд динамики разделяют на некоторое достаточно большое число равных интервалов. Если средние уровни по интервалам не позволяют увидеть тенденцию развития явления, переходят к расчету уровней за большие промежутки времени, увеличивая длину каждого интервала (одновременно уменьшается количество интервалов).
2. Метод скользящей средней. В этом методе исходные уровни ряда заменяются средними величинами, которые получают из данного уровня и нескольких симметрично его окружающих. Целое число уровней, по которым рассчитывается среднее значение, называют интервалом (окном) сглаживания. Интервал может быть нечетным (3, 5, 7 и т. д. точек) или четным (2, 4, 6 и т. д. точек).
При нечетном сглаживании полученное среднее арифметическое значение закрепляют за серединой расчетного интервала.
При четном сглаживании:
— определяют нецентрированные скользящие средние по четному числу уровней,
— вычисляют центрированные скользящие средние как смежные парные средние нецентрированных скользящих средних и относят их к соответствующим периодам или моментам времени.
3. Аналитическое выравнивание. Под этим понимают построение уравнения регрессии

Вид уравнения регрессии выбирают так, чтобы оно давало содержательное объяснение изучаемого процесса; основываясь на характере изменения цепных темпов роста, чаще всего выбирают линейную, параболическую, экспоненциальную зависимость или линеаризуемые функции (полулогарифмическую, степенную, гиперболы). Следует помнить, что для достаточной надежности уравнения тренда, как правило, на каждый параметр должно иметься 6-7 моментов или интервалов. Но анализ длинных рядов динамики не всегда возможен, поскольку основная тенденция ряда могла изменяться из-за каких-то внешних причин. Поэтому предпочтение отдается функциям с малым числом параметров
Методы выравнивания можно комбинировать, например, построив уравнение регрессии по уровням, сглаженным методом скользящей средней. Обычно это делают для выявления сезонности, выбирая окно сглаживания равным периоду предполагаемой сезонности (например, год для выявления внутригодичной сезонности).
При аналитическом выравнивании обычно данные временные моменты (например, годы) заменяют на условные моменты времени (например, 1,2,… или 0,1,2…). Кроме того, для простоты вычислений часто условные моменты выбирают так, чтобы их сумма была равна 0 (например, -5,-4,-3,-2,-1,0,1,2,3,4,5)
В Excel аналитическое выделение тренда осуществляется теми же методами, что и построение уравнения регрессии в корреляционно-регрессионном анализе.
Выбор наилучшего уравнения тренда осуществляется по следующим критериям:
• Чем больше значение коэффициента детерминации R2, тем точнее уравнение тренда описывает вариацию уровней динамического ряда. Влияние случайного фактора оценивается как (1-R2)
• Чем больше величина F-критерия, тем предпочтительнее данное уравнение тренда. Если значение F-критерия меньше критического, то уравнение не пригодно для описания тренда и прогнозирования
• Существует (и реализовано в различных статистических пакетах) множество методик анализа остатков 
Один из способов визуальной проверки качества уравнения регрессии заключается в анализе графиков остатков.
Другой способ предоставляет критерий Дарбина-Уотсона DW, позволяющий оценить автокорреляцию остатков:

При заданном уровне значимости, числе уровней динамического ряда и числе параметров при t в уравнении тренда находят табличные критические значения критерия.
Если ral>0 , то при DW DW2 нет автокорреляции остатков, уравнение можно использовать.
источники:
http://intuit.ru/studies/courses/22487/901/lecture/32720
http://pandia.ru/text/80/138/1023.php