Стандартная ошибка точечного прогноза это - Решение и исправление самых разных ошибок на TopOshibok.ru

Точечный прогноз
заключается в получении прогнозного
значения уp,
которое определяется путем подстановки
в уравнение регрессии соответствующего
(прогнозного) значения xp:

уp = a + b* xp

Интервальный
прогноз
заключается в построении доверительного
интервала прогноза, т. е. нижней и верхней
границ уpmin,
уpmax интервала,
содержащего точную величину для
прогнозного значения yp
(ypmin < yp <
ypmin) с заданной
вероятностью.

При построении
доверительного интервала прогноза
используется стандартная
ошибка прогноза:

,
где

Строится доверительный
интервал прогноза:

Множественный регрессионный анализ

(слайд
1)
Множественная регрессия применяется
в ситуациях, когда из множества факторов,
влияющих на результативный признак,
нельзя выделить один доминирующий
фактор и необходимо учитывать влияние
нескольких факторов. Например, объем
выпуска продукции определяется величиной
основных и оборотных средств, численностью
персонала, уровнем менеджмента и т. д.,
уровень спроса зависит не только от
цены, но и от имеющихся у населения
денежных средств.

Основная цель
множественной регрессии – построить
модель с несколькими факторами и
определить при этом влияние каждого
фактора в отдельности, а также их
совместное воздействие на изучаемый
показатель.

Таким образом,
множественная регрессия – это уравнение
связи с несколькими независимыми
переменными:

(слайд
2)
Построение уравнения множественной
регрессии

1. Постановка задачи

По имеющимся данным
n наблюдений
(табл. 3.1) за совместным изменением p+1
параметра y
и xj и
((yi,xj,i);
j=1,
2, …, p;
i=1,
2, …, n)
необходимо определить аналитическую
зависимость ŷ
= f(x1,x2,…,xp),
наилучшим образом описывающую данные
наблюдений.

Таблица 3.1

Данные наблюдений

	y	х1	х2	…	хр
1	y1	x11	х21	…	xp1
2	y2	х12	х22	…	xp2
…	…	…	…	…	…
n	yn	х1n	x2n	…	xpn

Каждая строка
таблицы представляет собой результат
одного наблюдения. Наблюдения различаются
условиями их проведения.

Вопрос о том, какую
зависимость следует считать наилучшей,
решается на основе какого-либо критерия.
В качестве такого критерия обычно
используется минимум суммы квадратов
отклонений расчетных значений
результативного показателя ŷi
от наблюдаемых
значений yi:

2. Спецификация модели

(слайд
3)
Спецификация модели включает в себя
решение двух задач:

– отбор факторов,
подлежащих включению в модель;

– выбор формы
уравнения регрессии.

2.1. Отбор факторов при построении множественной регрессии

Включение в
уравнение множественной регрессии того
или иного набора факторов связано прежде
всего с представлениями исследователя
о природе взаимосвязи моделируемого
показателя с другими экономическими
явлениями.

К факторам,
включаемым в модель, предъявляются
следующие требования:

1. Факторы должны
быть количественно измеримы.
Включение фактора в модель должно
приводить к существенному увеличению
доли объясненной части в общей вариации
зависимой переменной. Поскольку данная
величина характеризуется коэффициентом
детерминации,
включение нового фактора в модель должно
приводить к заметному изменению
коэффициента. Если этого не происходит,
то включаемый в анализ фактор не улучшает
модель и является лишним.

Например, если для
регрессии, включающей 5 факторов,
коэффициент детерминации составил
0,85, и включение шестого фактора дало
коэффициент детерминации 0,86, то вряд
ли целесообразно дополнять модель этим
фактором.

Если необходимо
включить в модель качественный фактор,
не имеющий количественной оценки, то
нужно придать ему количественную
определенность. В этом случае в модель
включается соответствующая ему
«фиктивная»
переменная,
имеющая конечное количество формально
численных значений, соответствующих
градациям качественного фактора (балл,
ранг).

Например, если
нужно учесть влияние уровня образования
(на размер заработной платы), то в
уравнение регрессии можно включить
переменную, принимающую значения: 0 –
при начальном образовании, 1 – при
среднем, 2 – при высшем.

Несмотря на то,
что теоретически регрессионная модель
позволяет учесть любое количество
факторов, на практике в этом нет
необходимости, т.к. неоправданное их
увеличение приводит к затруднениям в
интерпретации модели и снижению
достоверности результатов.

2. Факторы не
должны быть взаимно коррелированы
и, тем более, находиться в точной
функциональной связи. Наличие высокой
степени коррелированности между
факторами может привести к неустойчивости
и ненадежности оценок коэффициентов
регрессии, а также к невозможности
выделить изолированное влияние факторов
на результативный показатель. В результате
параметры регрессии оказываются
неинтерпретируемыми.

Пример.
Рассмотрим регрессию себестоимости
единицы продукции (у)
от заработной платы работника (х)
и производительности труда в час (z).

Коэффициент
регрессии при переменной z
показывает, что с ростом производительности
труда на 1 ед-цу в час себестоимость
единицы продукции снижается в среднем
на 10 руб. при постоянном уровне оплаты
труда.

А параметр при х
нельзя интерпретировать как снижение
себестоимости единицы продукции за
счет роста заработной платы. Отрицательное
значение коэффициента регрессии в
данном случае обусловлено высокой
корреляцией между х
и z
(0,95).

(слайд
4)
Считается, что две переменные явно
коллинеарны,
т.е. находятся между собой в линейной
зависимости, если коэффициент
интеркорреляции
(корреляции между двумя объясняющими
переменными) ≥ 0,7. Если факторы явно
коллинеарны, то они дублируют друг друга
и один из них рекомендуется исключить
из уравнения. Предпочтение при этом
отдается не тому фактору, который более
тесно связан с результатом, а тому,
который при достаточно тесной связи с
результатом имеет наименьшую тесноту
связи с другими факторами.

В этом требовании
проявляется специфика множественной
регрессии как метода исследования
комплексного воздействия факторов в
условиях их независимости друг от друга.

Наряду с парной
коллинеарностью может иметь место
линейная зависимость между более чем
двумя переменными – мультиколлинеарность,
т.е. совокупное воздействие факторов
друг на друга.

Наличие
мультиколлинеарности факторов может
означать, что некоторые факторы всегда
будут действовать в унисон. В результате
вариация в исходных данных перестанет
быть полностью независимой, что не
позволит оценить воздействие каждого
фактора в отдельности. Чем сильнее
мультиколлинеарность факторов, тем
менее надежна оценка распределения
суммы объясненной вариации по отдельным
факторам с помощью МНК.

(слайд
5) Включение
в модель мультиколлинеарных факторов
нежелательно по следующим причинам:

затрудняется
интерпретация параметров множественной
регрессии; параметры линейной регрессии
теряют экономический смысл;
оценки параметров
не надежны, имеют большие стандартные
ошибки и меняются с изменением количества
наблюдений (не только по величине, но
и по знаку), что делает модель непригодной
для анализа и прогнозирования.

(слайд
6) Для
оценки мультиколлинеарности используется
определитель
матрицы парных коэффициентов
интеркорреляции:

(!)
Если факторы не коррелируют между собой,
то матрица коэффициентов интеркорреляции
является единичной, поскольку в этом
случае все недиагональные элементы
равны 0. Например, для уравнения с тремя
переменными
матрица коэффициентов интеркорреляции
имела бы определитель, равный 1, посколькуи.

(слайд
7)

(!)
Если между факторами существует полная
линейная зависимость
и все коэффициенты корреляции равны 1,
то определитель такой матрицы равен 0
(Если
две строки матрицы совпадают, то её
определитель равен нулю).

Чем ближе к 0
определитель матрицы коэффициентов
интеркорреляции, тем сильнее
мультиколлинеарность и ненадежнее
результаты множественной регрессии.

Чем ближе к 1
определитель
матрицы коэффициентов интеркорреляции,
тем меньше мультиколлинеарность
факторов.

(слайд

Способы
преодоления мультиколлинеарности
факторов:

1)
исключение из модели одного или нескольких
факторов;

2)
переход к совмещенным уравнениям
регрессии, т.е. к уравнениям, которые
отражают не только влияние факторов,
но и их взаимодействие. Например, если
,
то можно построить следующее совмещенное
уравнение:;

3)
переход к уравнениям приведенной формы
(в уравнение регрессии подставляется
рассматриваемый фактор, выраженный из
другого уравнения).

(слайд
9)
2.2. Выбор формы уравнения регрессии

Различают следующие
виды уравнений
множественной регрессии:

линейные,
нелинейные,
сводящиеся к линейным,
нелинейные, не
сводящиеся к линейным (внутренне
нелинейные).

В первых двух
случаях для оценки параметров модели
применяются методы классического
линейного регрессионного анализа. В
случае внутренне нелинейных уравнений
для оценки параметров применяются
методы нелинейной оптимизации.

Основное требование,
предъявляемое к уравнениям регрессии,
заключается в наличии наглядной
экономической интерпретации модели и
ее параметров. Исходя из этих соображений,
наиболее часто используются линейная
и степенная зависимости.

Линейная
множественная регрессия имеет вид:

Параметры bi
при факторах хi
называются коэффициентами
«чистой» регрессии.
Они показывают, на сколько единиц в
среднем изменится результативный
признак за счет изменения соответствующего
фактора на единицу при неизмененном
значении других факторов, закрепленных
на среднем уровне.

(слайд
10)
Например, зависимость спроса на товар
(Qd) от цены (P) и дохода (I) характеризуется
следующим уравнением:

Qd = 2,5 — 0,12P + 0,23 I.

Коэффициенты
данного уравнения говорят о том, что
при увеличении цены на единицу, спрос
уменьшится в среднем на 0,12 единиц, а при
увеличении дохода на единицу, спрос
возрастет в среднем 0,23 единицы.

Параметр а
не всегда может быть содержательно
проинтерпретирован.

Степенная
множественная регрессия имеет вид:

Параметры bj
(степени факторов хi)
являются коэффициентами эластичности.
Они показывают, на сколько % в среднем
изменится результативный признак за
счет изменения соответствующего фактора
на 1% при неизмененном значении остальных
факторов.

Наиболее широкое
применение этот вид уравнения регрессии
получил в производственных функциях,
а также при исследовании спроса и
потребления.

Например, зависимость
выпуска продукции Y от затрат капитала
K и труда L:
говорит
о том, что увеличение затрат капитала
K на 1% при неизменных затратах труда
вызывает увеличение выпуска продукции
Y на 0,23%. Увеличение затрат труда L на 1%
при неизменных затратах капитала K
вызывает увеличение выпуска продукции
Y на 0,81 %.

Возможны и другие
линеаризуемые функции для построения
уравнения множественной регрессии:

экспонента

;
гипербола

.

Чем сложнее функция,
тем менее интерпретируемы ее параметры.
Кроме того, необходимо помнить о
соотношении между количеством наблюдений
и количеством факторов в модели. Так,
для анализа трехфакторной модели должно
быть проведено не менее 21 наблюдения.

(слайд
11) 3.
Оценка параметров модели

Параметры уравнения
множественной регрессии оцениваются,
как и в парной регрессии, методом
наименьших квадратов,
согласно которому следует выбирать
такие значения
параметров а
и bi,
при которых сумма квадратов отклонений
фактических значений результативного
признака yi
от теоретических
значений ŷ
минимальна,
т. е.:

Если
,
тогдаS
является функцией неизвестных параметров
a,
bi:

Чтобы найти минимум
функции, нужно найти частные производные
по каждому из параметров и приравнять
их к 0:

Отсюда получаем
систему уравнений:

(слайд
12) Ее
решение может быть осуществлено методом
определителей:

где ∆
– определитель системы;

∆a,
∆b1,
∆bp
– частные определители (∆j).

–определитель
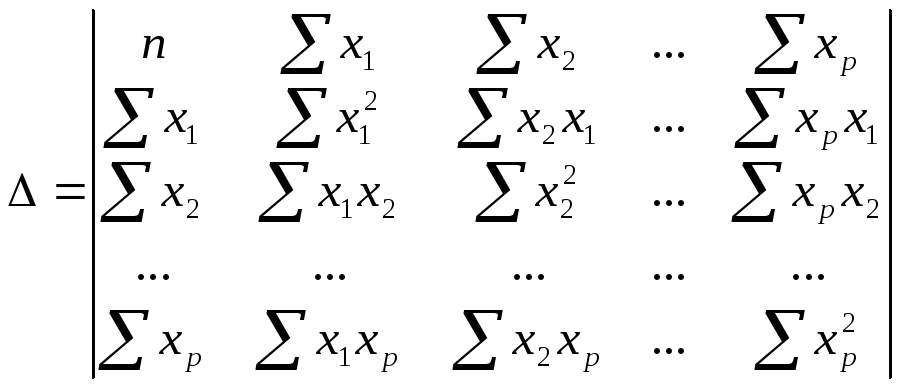
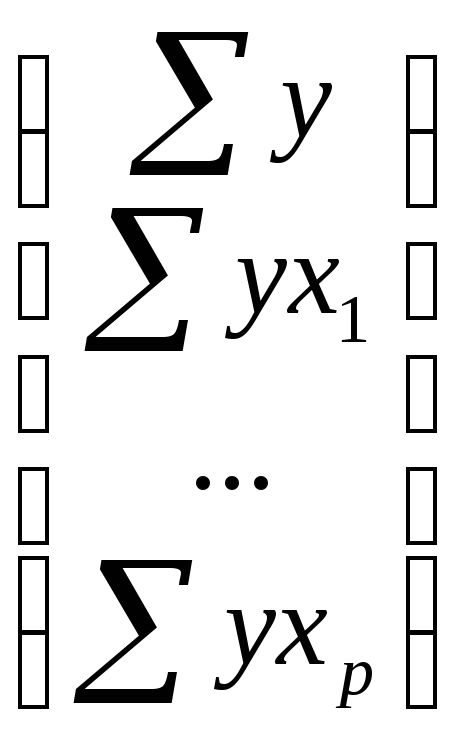
системы,

∆j
– частные
определители, которые получаются из
основного определителя путем замены
j-го столбца на столбец свободных членов
.

При использовании
данного метода возможно возникновение
следующих ситуаций:

1) если основной
определитель системы Δ равен
нулю и все определители Δj
также равны
нулю, то данная система имеет бесконечное
множество решений;

2) если основной
определитель системы Δ равен
нулю и хотя бы один из определителей Δj
также равен
нулю, то система решений не имеет.

(слайд
13) Помимо
классического МНК для определения
неизвестных параметров линейной модели
множественной регрессии используется
метод оценки параметров через
β-коэффициенты
– стандартизованные коэффициенты
регрессии.

Построение
модели множественной регрессии в
стандартизированном, или нормированном,
масштабе
означает, что все переменные, включенные
в модель регрессии, стандартизируются
с помощью специальных формул.

Уравнение
регрессии
в стандартизованном масштабе:

где
,— стандартизованные переменные;

— стандартизованные
коэффициенты регрессии.

Т.е. посредством
процесса стандартизации точкой отсчета
для каждой нормированной переменной
устанавливается ее среднее значение
по выборочной совокупности. При этом в
качестве единицы измерения
стандартизированной переменной
принимается ее среднеквадратическое
отклонение σ.

β-коэффициенты
показывают,
на сколько сигм (средних квадратических
отклонений) изменится в среднем результат
за счет изменения соответствующего
фактора xi
на одну сигму при неизменном среднем
уровне других факторов.

Стандартизованные
коэффициенты регрессии βi
сравнимы
между собой, что позволяет ранжировать
факторы по силе их воздействия на
результат. Большее относительное влияние
на изменение результативной переменной
y оказывает
тот фактор, которому соответствует
большее по модулю значение коэффициента
βi.
В этом основное
достоинство стандартизованных
коэффициентов регрессии,
в отличие от коэффициентов «чистой»
регрессии, которые не сравнимы между
собой.

(слайд
14)
Связь коэффициентов «чистой» регрессии
bi
с коэффициентами βi
описывается соотношением:

,
или

Параметр a
определяется как
.

Коэффициенты
β определяются при помощи
МНК
из следующей системы уравнений
методом определителей:

Для оценки параметров
нелинейных
уравнений множественной регрессии
предварительно осуществляется
преобразование последних в линейную
форму (с помощью замены переменных) и
МНК применяется для нахождения параметров
линейного уравнения множественной
регрессии в преобразованных переменных.
В случае внутренне
нелинейных
зависимостей для оценки параметров
приходится применять методы нелинейной
оптимизации.

(слайд
1) 4.
Проверка качества уравнения регрессии

Практическая
значимость уравнения множественной
регрессии оценивается с помощью
показателя множественной корреляции
и его квадрата – коэффициента детерминации.

Показатель
множественной корреляции
характеризует тесноту связи рассматриваемого
набора факторов с исследуемым признаком,
т.е. оценивает тесноту совместного
влияния факторов на результат.

Независимо от
формы связи показатель
множественной корреляции
рассчитывается по формуле:

Коэффициент
множественной корреляции принимает
значения в диапазоне 0 ≤ R
≤ 1. Чем ближе
он к 1, тем теснее связь результативного
признака со всем набором исследуемых
факторов.

При линейной
зависимости признаков формулу индекса
множественной корреляции можно записать
в виде:

где
—
стандартизованные коэффициенты
регрессии,

—
парные коэффициенты корреляции результата
с каждым фактором.

Данная формула
получила название линейного
коэффициента множественной корреляции,
или совокупного
коэффициента корреляции.

Индекс детерминации
для нелинейных по оцениваемым параметрам
функций принято называть «квази-».Для его
определения по функциям, использующим
логарифмические преобразования
(степенная, экспонента), необходимо
сначала найти теоретические значения
ln
y,
затем трансформировать их через
антилогарифмы (антилогарифм ln
y
= y)
и далее определить индекс детерминации
как «квази-»
по формуле:

Величина «квази-»
не будет совпадать с совокупным
коэффициентом корреляции, который может
быть рассчитан для линейного в логарифмах
уравнения множественной регрессии,
потому что в последнем раскладывается
на факторную и остаточную суммы квадратов
не,
а.

(слайд
2)
Использование коэффициента множественной
детерминации

для оценки качества модели обладает
тем недостатком, что включение в модель
нового фактора (даже несущественного)
автоматически увеличивает величину.
Поэтому при большом количестве факторов
предпочтительней использовать так
называемый скорректированный
(улучшенный) коэффициент множественной
детерминации

,
определяемый соотношением:

где n
– число наблюдений,

m
– число параметров при переменных х
(чем больше величина m,
тем сильнее различия между к-том множ.
детерминации

и скорректированным к-том
).

При заданном объеме
наблюдений и при прочих равных условиях
с увеличением числа независимых
переменных (параметров) скорректированный
к-т множ. детерминации убывает. Его
величина может стать и отрицательной
при слабых связях результата с факторами.
При небольшом числе наблюдений
нескорректированная величина к-та
имеет
тенденцию переоценивать долю вариации
результативного признака, связанную с
влиянием факторов, включенных в
регрессионную модель. Чем
больше объем совокупности, по которой
исчислена регрессия, тем меньше
различаются
и
.

Отметим, что низкое
значение коэффициента множественной
корреляции и коэффициента множественной
детерминации может быть обусловлено
следующими причинами:

– в регрессионную
модель не включены существенные факторы;

– неверно выбрана
форма аналитической зависимости, не
отражающая реальные соотношения между
переменными, включенными в модель.

(слайд
3)
Значимость уравнения множественной
регрессии в целом оценивается с помощью
F—
критерия Фишера:

Выдвигаемая
«нулевая» гипотеза H0 о статистической
незначимости уравнения регрессии
отвергается при выполнении условия F
> Fкрит,
где Fкрит
определяется по таблицам F-критерия
Фишера по двум степеням свободы k1
= m,
k2=
n-m—1
и заданному уровню значимости α.

Значимость одного
и того же фактора может быть различной
в зависимости от последовательности
введения его в модель.

(слайд
4) Мерой
для оценки включения фактора в модель
служит частный
F-критерий
(оценивает статистическую значимость
присутствия каждого из факторов в
уравнении):

где
—
коэффициент множ. детерминации для
модели с полным

набором
факторов;

—
тот же показатель, но без включения в
модель фактора х1;

n
– число наблюдений;

m
– число параметров при переменных х.

Если фактическое
значение F
превышает табличное, то дополнительное
включение в модель фактора xi
статистически оправдано и коэффициент
чистой регрессии bi
при факторе xi
статистически значим.

Если же фактическое
значение F
меньше табличного, то нецелесообразно
включать в модель дополнительный фактор,
поскольку он не увеличивает существенно
долю объясненной вариации результата,
а коэффициент регрессии при данном
факторе статистически не значим.

(слайд
5) Частный
F-критерий
оценивает значимость коэффициентов
чистой регрессии. Зная величину
,
можно определить и t-критерий
Стьюдента:

или

где m_bi
– средняя квадратическая ошибка
коэффициента регрессии b_i,
она может быть определена по формуле:

Величина
стандартной ошибки совместно с
t-распределением Стьюдента при n-m-1
степенях свободы применяется для
проверки значимости коэффициента
регрессии и для расчета его доверительного
интервала.

Соседние файлы в папке Эконометрика

Источник

1. Модель простой линейной регрессии

LOGO

2. Основные понятия

ОСНОВНЫЕ ПОНЯТИЯ

3. Определение модели

Простая линейная регрессия — это модель,
описывающая зависимость величины y от одной
переменной x в виде y a bx
a, b — коэффициенты
— случайная величина
Терминология
x — объясняющая переменная или
существенный фактор или регрессор
a, b — параметры регрессии
— случайный фактор
y — результирующий показатель или отклик

4. Спецификация модели

Система уравнений y1 a bx1 1 ,
y a bx ,
2
2
2
yn a bxn n ,
− описание моделью выборочных данных
(x1; y1),(x2 ; y2 ),…,(xn ; yn )
1, 2 , , n − сериальные ошибки

5. Теоретическое уравнение модели

Сериальная ошибка
— это разность между имеющимся значением
зависимой переменной и соответствующим ему
значением, предсказанным по уравнению модели
Теоретическое уравнение модели
― такое уравнение, у которого на имеющейся
выборке каждая из сериальных ошибок
принимает наименьшее значение
Обозначение y a bx

6.

Выборка
y
P4
P1
P2
x1
x2
P3
x3
x4 x
6

7.

Теоретическое уравнение
y
P4 ε4
ε1
Q4
P1
Q1
x1
ε2 Q2
P2
x2
ε3 Q 3
P3
x3
x4 x
6

8. Теоретические ограничения

У каждой сериальной ошибки математическое
ожидание равно нулю
Дисперсии всех сериальных ошибок одинаковы
(гомоскедастичность возмущений)
Сериальные ошибки не коррелируют между собой
(отсутствие автокорреляции возмущений)
Объем выборки больше двух
Выборочные значения существенного фактора не
случайны
Элементы выборки не расположены на одной
вертикальной прямой

9. Теоретические ограничения

Нормальная регрессия
Параметрическая или нормальная или
гауссовская регрессия −
все сериальные ошибки имеют нормальное
распределение
Общий случай
Сериальные ошибки − одинаково
распределенные независимые случайные
величины

10. Метод наименьших квадратов

Задача о поиске теоретического уравнения не
разрешима
2
n
Найти a и b такие, что yi a bxi min
i 1
Оценки aˆ и b по методу наименьших квадратов
Формулы для вычисления
n
b
( xk x )( yk y )
k 1
n
2
(
x
x
)
k
k 1
,
aˆ y bx ,

11. Эмпирическое уравнение модели

Эмпирическое уравнение модели −
такое уравнение, у которого на имеющейся
выборке сумма квадратов сериальных ошибок
принимает наименьшее значение
Обозначение y aˆ bx

12. Выровненные значения и остатки

Выровненное значение − значение зависимой
переменной, предсказанное с помощью
эмпирического уравнения модели
Обозначение: выровненное значение с номером i: yˆ i
Остаток − это разность между имеющимся
значением зависимой переменной и
соответствующим ему значением, предсказанным
по эмпирическому уравнению
Обозначение: остаток с номером i: ei
Вычисление: ei yi yˆi

13. Пример

Зависимость расходов на транспорт от дохода
(США, 1946-2002 годы)
Transp – совокупные расходы на транспорт в США
за год (в миллиардах долларов в ценах 2000 года)
DPI – совокупный личный располагаемый доход в
США за год (в миллиардах долларов в ценах 2000
года)

14. Пример

Transportation
350
300
250
200
150
100
50
0
0,0
1 000,0
2 000,0
3 000,0
4 000,0
5 000,0
6 000,0
7 000,0
8 000,0

15. Пример

Зависимость расходов на транспорт от дохода
(США, 1946-2002 годы)
Коэффициенты
Y-пересечение 3,878780296
DPI
0,037518081
Уравнение модели Transp 3,8788 0,0375DPI
Transp –расходы на транспорт
DPI –личный располагаемый доход

16. Интрерпретация уравнения модели

Зависимость расходов на транспорт от дохода
(США, 1946-2002 годы)
Transp 3,8788 0,0375DPI
Коэффициент при DPI:
если доход увеличивается на 1 млрд. долларов, то
расходы на транспорт возрастают на 37,5 млн.
долларов
Свободный член:
формально показывает, что нулевом доходе расходы
на транспорт будут равны 3,8788 млрд. долларов

17. Интрерпретация уравнения модели

Коэффициент при объясняющей переменной:
показывает, на сколько единиц примерно
изменяется зависимая переменная при увеличении
независимой переменной на единицу
Свободный член равен величине зависимой
переменной при нулевом значении существенного
фактора

18. Теорема о сумме квадратов

ТЕОРЕМА О СУММЕ
КВАДРАТОВ

19. Суммы квадратов

Остатки: e1 y1 yˆ1, e2 y2 yˆ 2 , , en yn yˆ n
Любой анализ качества модели − это анализ
остатков
Полная сумма квадратов (total sum of squares):
n
TSS ( yk y ) 2
k 1
Регрессионная сумма квадратов (regression sum of
n
squares):
RSS ( yˆ k y ) 2
k 1
Сумма квадратов ошибок (error sum of squares)
n
2
ˆ
ESS ( yk yk )
k 1

20. Теорема о сумме квадратов

Если в модели простой регрессии выполняются
все теоретические предположения, то верно
равенство:
TSS RSS ESS

21. Пример

Зависимость расходов на транспорт от дохода
(США, 1946-2002 годы)
Дисперсионный анализ
Регрессия
Остаток
Итого
Сумма RSS
df
1
55
56
Сумма TSS
SS
284507,5155
5135,225939
289642,7414
Сумма ESS

22. Значимость модели

Модель является значимой, если в теоретическом
уравнении модели коэффициент при
существенном факторе не равен нулю

23. Проверка значимости модели

Тест Фишера
Проверка
при
Основная гипотеза – модель незначимая
заданном
уровне
Альтернативная – модель значимая
значимости
α
Наблюдаемое значение:
n 2 RSS
F
ESS
Критическое значение: квантиль уровня 1– α
распределения Фишера с 1 и n – 2 степенями свободы
Выводы: если наблюдаемое больше критического, то
модель значимая (с возможной 100α%-й ошибкой)
если наблюдаемое меньше критического, то гипотеза о
незначимости модели не отвергается

24. Пример

Зависимость расходов на транспорт от дохода
(США, 1946-2002 годы) Проверка при
Наблюдаемое
значение
F
Значимость F
3047,171349 7,45928E-50
уровне
значимости
4,016195493
Критическое
значение
p-значение
меньше 0,05
Модель значимая
(с возможной 5%-й ошибкой)
α = 0,05

25. Коэффициент детерминации

Коэффициент детерминации:
RSS
ESS
2
R
R 1
TSS
TSS
Выводы о качестве модели
Коэффициент меньше примерно 0,2:
модель плохо описывает имеющиеся данные
Коэффициент больше примерно 0,7: модель
линейной регрессии дает хорошее описание
Коэффициент от 0,2 до 0,7: нельзя сделать вывод
о качестве модели
2

26. Пример

Зависимость расходов на транспорт от дохода
(США, 1946-2002 годы)
Множественный R
R-квадрат
Нормированный R-квадрат
Стандартная ошибка
Наблюдения
0,991095597
0,982270483
0,981948128
9,662698606
57
Модель
качественная

27. Стандартные ошибки

СТАНДАРТНЫЕ ОШИБКИ

28. Стандартная ошибка модели

Стандартная ошибка модели
– несмещенная оценка среднего квадратического
отклонения сериальных ошибок
Формула вычисления:
1
s
ESS
n 2
n – объем выборки
ESS – сумма квадратов сериальных ошибок

29. Пример

Зависимость расходов на транспорт от дохода
(США, 1946-2002 годы)
Регрессионная статистика
Множественный R
0,991095597
R-квадрат
0,982270483
Нормированный R-квадрат 0,981948128
Стандартная ошибка
9,662698606
Наблюдения
57
Стандартная
ошибка модели

30. Стандартные ошибки параметров

Стандартная ошибка параметра a
– несмещенная оценка среднего квадратического
отклонения случайной величины â
Формула вычисления:
1
x2
sa s
n
n
2
(
x
x
)
k
k 1
s – стандартная ошибка модели
n – объем выборки

31. Стандартные ошибки параметров

Стандартная ошибка параметра b
– несмещенная оценка среднего квадратического
отклонения случайной величины bˆ
Формула вычисления:
1
sb s n
2
(
x
x
)
k
k 1
s – стандартная ошибка модели

32. Пример

Зависимость расходов на транспорт от дохода
(США, 1946-2002 годы)
Y-пересечение
DPI
Коэффициенты
Стандартная ошибка
3,878780296
2,716479676
0,037518081
0,000679661
Стандартная ошибка
свободного члена
Стандартная ошибка
параметра при DPI

33. Интервальные оценки

Интервальная оценка параметра:
показывает с вероятностью 1– α , в каком
интервале содержится истинное значение
параметра
Вероятность 1– α — надежность
Интервал обычно вычисляется с помощью
точечной оценки параметра

34. Интервальные оценки

Интервальная оценка свободного члена:
нижняя граница интервала aˆ t1 , n 2 sa
верхняя граница интервала aˆ t1 , n 2 sa
aˆ – точечная оценка свободного члена
sa – стандартная ошибка свободного члена
t1 ,n 2 – двусторонняя квантиль уровня 1– α
распределения Стьюдента с n – 2 степенями свободы

35. Интервальные оценки

Интервальная оценка углового коэффициента:
нижняя граница интервала bˆ t1 , n 2 sb
верхняя граница интервала bˆ t1 , n 2 sb
bˆ – точечная оценка углового коэффициента
sb – стандартная ошибка углового коэффициента
t1 ,n 2 – двусторонняя квантиль уровня 1– α
распределения Стьюдента с n – 2 степенями свободы

36. Пример

Зависимость расходов на транспорт от дохода
(США, 1946-2002 годы)
Интервальная оценка
свободного члена
Коэффициенты
Y-пересечение
3,878780296
DPI
0,037518081
Нижние 95%
-1,565166628
Верхние 95%
9,32272722
0,03615601
0,038880151
Интервальная оценка
параметра DPI

37. Значимость параметров модели

ЗНАЧИМОСТЬ ПАРАМЕТРОВ
МОДЕЛИ

38. Определения

Параметр при существенном факторе x
называется значимым, если его истинное
значение не равно нулю
Значимость параметра при x означает: модель
учитывает влияние данного фактора на зависимую
переменную
Параметр при существенном факторе x
называется статистически незначимым, если
его значимость не установлена
Статистическая незначимость параметра при x
означает: возможно, модель не учитывает
влияние
данного фактора на зависимую
переменную

39. Значимость модели и параметров

В модели простой линейной регрессии значимость
параметра при существенном факторе равносильна
значимости модели!

40. Проверка значимости параметра

Тест Стьюдента
Основная гипотеза – параметр b незначимый Проверка
при
Альтернативная – параметр b значимый
заданном
ˆ
уровне
b
Наблюдаемое значение:
значимости
tˆ
α
sb
Критическое значение: квантиль уровня 1– α
распределения Стьюдента с n – 2 степенями свободы
Выводы: если наблюдаемое больше критического, то
параметр значимый (с возможной 100α%-й ошибкой)
если наблюдаемое меньше критического, то гипотеза
о незначимости параметра не отвергается
(статистическая незначимость параметра)

41. Пример

Зависимость расходов на транспорт от дохода
Проверка при
(США, 1946-2002 годы) уровне
значимости
α = 0,05
Y-пересечение
DPI
Коэффициенты
3,878780296
0,037518081
4,051748692
Наблюдаемое
значение
t-статистика
1,42787017
P-Значение
0,158983049
55,20118974
7,45928E-50
2,004044783
Критическое
значение
Параметр при DPI значимый
(с возможной 5%-й ошибкой)
p-значение
меньше 0,05

42. Прогнозирование

ПРОГНОЗИРОВАНИЕ

43. Виды прогнозирования

Безусловное прогнозирование (предсказание):
значение существенного фактора, соответствующее
прогнозируемому значению, известно
Условное прогнозирование:
значение существенного фактора, соответствующее
прогнозируемому значению, не известно

44. Точечный прогноз

Точечный прогноз:
значение зависимой переменной, вычисленное с
помощью эмпирического уравнения модели
ˆ
Вычисление: yˆ 0 aˆ bx
0
x0 – значение соответствующего существенного
фактора

45. Стандартная ошибка

Стандартная ошибка точечного прогноза:
несмещенная оценка стандартного отклонения
случайной величины aˆ a bˆ b x0
Вычисление:
1
2
( x0 x )
s0 s 1 n
n
2
( xk x )
k 1
s – стандартная ошибка точечного прогноза
x0 – значение соответствующего существенного
фактора

46. Интервальный прогноз

Интервальная прогноз:
показывает с вероятностью 1– α , в каком
интервале содержится истинное значение
зависимой переменной
Вероятность 1– α — надежность

47. Интервальный прогноз

Вычисление:
нижняя граница интервала yˆ0 t1 , n 2 s0
верхняя граница интервала yˆ0 t1 , n 2 s0
yˆ 0 – точечный прогноз
s0 – стандартная ошибка прогноза
t1 ,n 2 – двусторонняя квантиль уровня 1– α
распределения Стьюдента с n – 2 степенями свободы

48. Пример

Зависимость расходов на транспорт от дохода
(США, 1946-2002 годы)
x0 ( 2003 год)
7787,4
Точечный прогноз y0
296,0471
Стандартная ошибка прогноза
10,16842
Интервальный прогноз
Нижняя 95% граница
Нижняя 95% граница
275,669122
316,4250403

49. Нелинейная регрессия

НЕЛИНЕЙНАЯ РЕГРЕССИЯ

50. Нелинейные модели

Два вида регрессий:
нелинейные относительно объясняющих
переменных, но линейные по оцениваемым
параметрам
Все после замены становятся линейными
y a b ln x
y a b/ x
y a bx cx 2
нелинейные по оцениваемым параметрам
y ea bx
y axb
Некоторые сводятся к линейным
после логарифмирования

51. Пример

Эрнст Энгель (1821-1896)
Кривые Энгеля
немецкий экономист и статистик
показывает зависимость между объёмом
потребления товаров или услуг и доходом
потребителя при неизменных ценах и предпочтениях
E1 — кривая для нормальных товаров
E2 — кривая для предметов роскоши
E3 — кривая для низкокачественных товаров

52. Основные нелинейные модели

Гиперболическая
y a b/ x
Параболическая
y a bx cx 2
Экспоненциальная y ea bx
Степенная
y axb
После
замены
становятся
линейными
ln y a bx
ln y ln a b ln x
Полулогарифмическая
регрессия
Логарифмическая
регрессия

53. Выбор лучшей модели

ВЫБОР ЛУЧШЕЙ МОДЕЛИ

54. Оценка качества модели

Инструменты
Точечная диаграмма (расположение точек вдоль
линии тренда)
Статистика Фишера (значимость модели по тесту
Фишера)
Коэффициент детерминации (оценка качества
модели по его величине)
Средняя относительная погрешность (оценка
качества модели по её величине)
100% n yi yˆi
ср
n i 1 yi

55. Оценка качества модели

Характеристики подходящей модели
На диаграмме точки расположены, в основном,
вдоль линии тренда
Могут использоваться модели с
меньшим коэффициентом
Модель значимая
Коэффициент детерминации не меньше заданного
уровня (обычно 0,65-0,7)
Средняя относительная погрешность не меньше
заданного уровня (обычно 10% — 25%)
Могут использоваться модели с
большей погрешностью

56. Пример

Зависимость расходов на транспорт от дохода
(США, 1946-2002 годы)
Transportation
350
300
Точки
расположены
вдоль
линейного
тренда
250
200
150
100
50
0
0,0
1 000,0 2 000,0 3 000,0 4 000,0 5 000,0 6 000,0 7 000,0 8 000,0

57. Пример

Зависимость расходов на транспорт от дохода
(США, 1946-2002 годы)
Модель
значимая
Статистика Фишера
F
Значимость F
3047,171349 7,45928E-50
Коэффициент детерминации
R-квадрат 0,982270483
Модель хорошо описывает выборочные данные
Средняя относительная погрешность
Средняя относительная
5,26%
погрешность
Модель подходящая

58. Выбор модели

Два этапа
Первый этап: выбор подходящих моделей
Обычно используются: линейная, гиперболическая,
параболическая, экспоненциальная, степенная
модели
Для моделей с зависимой переменной, отличной от
исходной, предсказанные значения, остатки,
коэффициенты детерминации и среднюю
относительную погрешность необходимо вычислять
отдельно!

59. Выбор модели

Два этапа
Второй этап: выбор лучшей модели
Для сравнения подходящих моделей используются
такие же инструменты, как на первом этапе

60. Пример

Зависимость расходов на транспорт от дохода
(США, 1946-2002 годы)
Transportation
400
y = 44,966e0,0003x
R² = 0,9736
350
y = 2E-06×2 + 0,0226x + 26,452
R² = 0,9897
300
250
y = 0,0375x + 3,8788
R² = 0,9823
y = 0,0897×0,8975
R² = 0,9824
200
150
100
Все модели
подходящие
50
0
0,0
1 000,0
2 000,0
3 000,0
4 000,0
5 000,0
6 000,0
7 000,0
8 000,0

61. Пример

Зависимость расходов на транспорт от дохода
(США, 1946-2002 годы)
Основные характеристики
Линейная Параболическая Экспоненциальная Степенная
Коэффициент
детерминации
Средняя
относительная
погрешность
Значимость
параметра при DPI
0,9823
0,9897
0,9736
0,9824
5,26%
3,52%
7,01%
5,32%
да
да (при DPI и DPI2)
да
да

Источник

Имея
прямую регрессии, необходимо оценить
насколько сильно точки исходных данных
отклоняются от прямой регрессии. Можно
выполнить оценку разброса, аналогичную
стандартному отклонению выборки. Этот
показатель, называемый стандартной
ошибкой оценки, демонстрирует величину
отклонения точек исходных данных от
прямой регрессии в направлении оси Y.
Стандартная ошибка оценки ()
вычисляется по следующей формуле.

Стандартная
ошибка оценки измеряет степень отличия
реальных значений Y от оцененной величины.
Для сравнительно больших выборок следует
ожидать, что около 67% разностей по модулю
не будет превышать

и около 95% модулей разностей будет не
больше 2.

Стандартная
ошибка оценки подобна стандартному
отклонению. Ее можно использовать для
оценки стандартного отклонения
совокупности. Фактически

оценивает стандартное отклонение

слагаемого ошибки

в статистической модели простой линейной
регрессии. Другими словами,

оценивает общее стандартное отклонение

нормального распределения значений Y,
имеющих математические ожидания

для каждого X.

Малая
стандартная ошибка оценки, полученная
при регрессионном анализе, свидетельствует,
что все точки данных находятся очень
близко к прямой регрессии. Если стандартная
ошибка оценки велика, точки данных могут
значительно удаляться от прямой.

2.3 Прогнозирование величины y

Регрессионную
прямую можно использовать для оценки
величины переменной Y
при данных значениях переменной X. Чтобы
получить точечный прогноз, или предсказание
для данного значения X, просто вычисляется
значение найденной функции регрессии
в точке X.

Конечно
реальные значения величины Y,
соответствующие рассматриваемым
значениям величины X, к сожалению, не
лежат в точности на регрессионной
прямой. Фактически они разбросаны
относительно прямой в соответствии с
величиной
.
Более того, выборочная регрессионная
прямая является оценкой регрессионной
прямой генеральной совокупности,
основанной на выборке из определенных
пар данных. Другая случайная выборка
даст иную выборочную прямую регрессии;
это аналогично ситуации, когда различные
выборки из одной и той же генеральной
совокупности дают различные значения
выборочного среднего.

Есть
два источника неопределенности в
точечном прогнозе, использующем уравнение
регрессии.

Неопределенность,
обусловленная отклонением точек данных
от выборочной прямой регрессии.
Неопределенность,
обусловленная отклонением выборочной
прямой регрессии от регрессионной
прямой генеральной совокупности.

Интервальный
прогноз значений переменной Y
можно построить так, что при этом будут
учтены оба источника неопределенности.

Стандартная
ошибка прогноза

дает меру вариативности предсказанного
значения Y
около истинной величины Y
для данного значения X.
Стандартная ошибка прогноза равна:

Стандартная
ошибка прогноза зависит от значения X,
для которого прогнозируется величина
Y.

минимально, когда
,
поскольку тогда числитель в третьем
слагаемом под корнем в уравнении будет
0. При прочих неизменных величинах
большему отличию соответствует большее
значение стандартной ошибки прогноза.

Если
статистическая модель простой линейной
регрессии соответствует действительности,
границы интервала прогноза величины Y
равны:

где

— квантиль распределения Стьюдента с
n-2 степенями свободы ().
Если выборка велика (),
этот квантиль можно заменить соответствующим
квантилем нормального распределения.
Например, для большой выборки 95%-ный
интервал прогноза задается следующими
значениями:

Завершим
раздел обзором предположений, положенных
в основу статистической модели линейной
регрессии.

Для
заданного значения X генеральная
совокупность значений Y имеет нормальное
распределение относительно регрессионной
прямой совокупности. На практике
приемлемые результаты получаются
и
тогда, когда значения Y имеют
нормальное распределение лишь
приблизительно.
Разброс
генеральной совокупности точек данных
относительно регрессионной прямой
совокупности остается постоянным всюду
вдоль этой прямой. Иными словами, при
возрастании значений X в точках данных
дисперсия генеральной совокупности
не увеличивается и не уменьшается.
Нарушение этого предположения называется
гетероскедастичностью.
Слагаемые
ошибок

независимы между собой. Это предположение
определяет случайность выборки точек
Х-Y.
Если точки данных X-Y
записывались в течение некоторого
времени, данное предположение часто
нарушается. Вместо независимых данных,
такие последовательные наблюдения
будут давать серийно коррелированные
значения.
В
генеральной совокупности существует
линейная зависимость между X и Y.
По аналогии с простой линейной регрессией
может рассматриваться и нелинейная
зависимость между X и У. Некоторые такие
случаи будут обсуждаться ниже.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Ошибка прогнозирования: виды, формулы, примеры

Ошибка прогнозирования — это такая величина, которая показывает, как сильно прогнозное значение отклонилось от фактического. Она используется для расчета точности прогнозирования, что в свою очередь помогает нам оценивать как точно и корректно мы сформировали прогноз. В данной статье я расскажу про основные процентные «ошибки прогнозирования» с кратким описанием и формулой для расчета. А в конце статьи я приведу общий пример расчётов в Excel. Напомню, что в своих расчетах я в основном использую ошибку WAPE или MAD-Mean Ratio, о которой подробно я рассказал в статье про точность прогнозирования, здесь она также будет упомянута.

В каждой формуле буквой Ф обозначено фактическое значение, а буквой П — прогнозное. Каждая ошибка прогнозирования (кроме последней!), может использоваться для нахождения общей точности прогнозирования некоторого списка позиций, по типу того, что изображен ниже (либо для любого другого подобной детализации):

Алгоритм для нахождения любой из ошибок прогнозирования для такого списка примерно одинаковый: сначала находим ошибку прогнозирования по одной позиции, а затем рассчитываем общую. Итак, основные ошибки прогнозирования!

MPE — Mean Percent Error

MPE — средняя процентная ошибка прогнозирования. Основная проблема данной ошибки заключается в том, что в нестабильном числовом ряду с большими выбросами любое незначительное колебание факта или прогноза может значительно поменять показатель ошибки и, как следствие, точности прогнозирования. Помимо этого, ошибка является несимметричной: одинаковые отклонения в плюс и в минус по-разному влияют на показатель ошибки.

Для каждой позиции рассчитывается ошибка прогноза (из факта вычитается прогноз) — Error
Для каждой позиции рассчитывается процентная ошибка прогноза (ошибка прогноза делится на фактический показатель) — Percent Error
Находится среднее арифметическое всех процентных ошибок прогноза (процентные ошибки суммируются и делятся на количество) — Mean Percent Error

MAPE — Mean Absolute Percent Error

MAPE — средняя абсолютная процентная ошибка прогнозирования. Основная проблема данной ошибки такая же, как и у MPE — нестабильность.

Для каждой позиции рассчитывается абсолютная ошибка прогноза (прогноз вычитается из факта по модулю) — Absolute Error
Для каждой позиции рассчитывается абсолютная процентная ошибка прогноза (абсолютная ошибка прогноза делится на фактический показатель) — Absolute Percent Error
Находится среднее арифметическое всех абсолютных процентных ошибок прогноза (абсолютные процентные ошибки суммируются и делятся на количество) — Mean Absolute Percent Error

Вместо среднего арифметического всех абсолютных процентных ошибок прогноза можно использовать медиану числового ряда (MdAPE — Median Absolute Percent Error), она наиболее устойчива к выбросам.

WMAPE / MAD-Mean Ratio / WAPE — Weighted Absolute Percent Error

WAPE — взвешенная абсолютная процентная ошибка прогнозирования. Одна из «лучших ошибок» для расчета точности прогнозирования. Часто называется как MAD-Mean Ratio, то есть отношение MAD (Mean Absolute Deviation — среднее абсолютное отклонение/ошибка) к Mean (среднее арифметическое). После упрощения дроби получается искомая формула WAPE, которая очень проста в понимании:

Для каждой позиции рассчитывается абсолютная ошибка прогноза (прогноз вычитается из факта, по модулю) — Absolute Error
Находится сумма всех фактов по всем позициям (общий фактический объем)
Сумма всех абсолютных ошибок делится на сумму всех фактов — WAPE

Данная ошибка прогнозирования является симметричной и наименее чувствительна к искажениям числового ряда.

Рекомендуется к использованию при расчете точности прогнозирования. Более подробно читать здесь.

RMSE (as %) / nRMSE — Root Mean Square Error

RMSE — среднеквадратичная ошибка прогнозирования. Примерно такая же проблема, как и в MPE и MAPE: так как каждое отклонение возводится в квадрат, любое небольшое отклонение может значительно повлиять на показатель ошибки. Стоит отметить, что существует также ошибка MSE, из которой RMSE как раз и получается путем извлечения корня. Но так как MSE дает расчетные единицы измерения в квадрате, то использовать данную ошибку будет немного неправильно.

Для каждой позиции рассчитывается квадрат отклонений (разница между фактом и прогнозом, возведенная в квадрат) — Square Error
Затем рассчитывается среднее арифметическое (сумма квадратов отклонений, деленное на количество) — MSE — Mean Square Error
Извлекаем корень из полученного результат — RMSE
Для перевода в процентную или в «нормализованную» среднеквадратичную ошибку необходимо:
1. Разделить на разницу между максимальным и минимальным значением показателей
2. Разделить на разницу между третьим и первым квартилем значений показателей
3. Разделить на среднее арифметическое значений показателей (наиболее часто встречающийся вариант)

MASE — Mean Absolute Scaled Error

MASE — средняя абсолютная масштабированная ошибка прогнозирования. Согласно Википедии, является очень хорошим вариантом для расчета точности, так как сама ошибка не зависит от масштабов данных и является симметричной: то есть положительные и отрицательные отклонения от факта рассматриваются в равной степени.

Важно! Если предыдущие ошибки прогнозирования мы могли использовать для нахождения точности прогнозирования некого списка номенклатур, где каждой из которых соответствует фактическое и прогнозное значение (как было в примере в начале статьи), то данная ошибка для этого не предназначена: MASE используется для расчета точности прогнозирования одной единственной позиции, основываясь на предыдущих показателях факта и прогноза, и чем больше этих показателей, тем более точно мы сможем рассчитать показатель точности. Вероятно, из-за этого ошибка не получила широкого распространения.

Здесь данная формула представлена исключительно для ознакомления и не рекомендуется к использованию.

Суть формулы заключается в нахождении среднего арифметического всех масштабированных ошибок, что при упрощении даст нам следующую конечную формулу:

Также, хочу отметить, что существует ошибка RMMSE (Root Mean Square Scaled Error — Среднеквадратичная масштабированная ошибка), которая примерно похожа на MASE, с теми же преимуществами и недостатками.

Это основные ошибки прогнозирования, которые могут использоваться для расчета точности прогнозирования. Но не все! Их очень много и, возможно, чуть позже я добавлю еще немного информации о некоторых из них. А примеры расчетов уже описанных ошибок прогнозирования будут выложены через некоторое время, пока что я подготавливаю пример, ожидайте.

Об авторе

HeinzBr

Автор статей и создатель сайта SHTEM.RU

В зависимости от контекста термин «прогнозирование» в эконометрике может трактоваться по-разному. Применительно к данным временных рядов речь обычно идет о прогнозировании будущего значения зависимой переменной, например, курса рубля или ВВП. Когда же речь идет о пространственных выборках, под прогнозированием понимают предсказание значения зависимой переменной для заданных значений объясняющих переменных. Например, предсказание цены квартиры с заданной жилой площадью.

Формально задачу построения прогноза можно представить следующим образом. Имеется модель, для которой выполнены все предпосылки КЛМПР:

begin{equation*} y_i=beta _1+beta _2x_i+varepsilon _i end{equation*}

Представим, что мы уже воспользовались МНК и получили оцененную на основе n наблюдений линию регрессии:

begin{equation*} widehat y_i=widehat {beta }_1+widehat {beta }_2x_i end{equation*}

Теперь пусть у нас есть известное (n+1)-ое наблюдение регрессора (x_{n+1}), но неизвестно соответствующее значение зависимой переменной (y_{n+1}) и нужно построить его прогноз. Естественной идеей будет подставить известное значение в оцененную регрессию:

begin{equation*} widehat y_{n+1}=widehat {beta }_1+widehat {beta }_2x_{n+1} end{equation*}

Оказывается, что это хорошая мысль: такой прогноз будет несмещенным и эффективным (то есть будет характеризоваться минимальной ожидаемой квадратичной ошибкой прогноза).

Докажем несмещенность этого прогноза.

Вычислим математическое ожидание фактического значения (y_{n+1}) и нашего прогноза (widehat y_{n+1}). Если прогноз несмещенный, то эти математические ожидания будут совпадать.

Воспользуемся тем, что, как мы доказали выше, (widehat {beta }_1) и (widehat {beta }_2) — несмещенные оценки коэффициентов (beta _1) и (beta _2):

begin{equation*} Eleft(widehat y_{n+1}right)=Eleft(widehat {beta }_1+widehat {beta }_2x_{n+1}right)=Eleft(widehat {beta }_1right)+Eleft(widehat {beta }_2right)x_{n+1}=beta _1+beta _2x_{n+1} end{equation*}

Кроме того:

begin{equation*} Eleft(y_{n+1}right)=Eleft(beta _1+beta _2x_{n+1}+varepsilon _{n+1}right)=end{equation*}

begin{equation*} =beta _1+beta _2x_{n+1}+Eleft(varepsilon _{n+1}right)=beta _1+beta _2x_{n+1} end{equation*}

Следовательно, (Eleft(y_{n+1}right)=Eleft(widehat y_{n+1}right)).

Кроме самого прогноза нас интересует его точность. Чтобы её оценить, целесообразно вычислить математические ожидания квадрата ошибки прогноза:

begin{equation*} Eleft(widehat y_{n+1}-y_{n+1}right)^2=Eleft(widehat {beta }_1+widehat {beta }_2x_{n+1}-beta _1-beta _2x_{n+1}-varepsilon _{n+1}right)^2= end{equation*}

begin{equation*} =Eleft(left(widehat {beta }_1-beta _1right)+left(widehat {beta }_2-beta _2right)x_{n+1}-varepsilon _{n+1}right)^2= end{equation*}

begin{equation*} =Eleft(widehat {beta }_1-beta _1right)^2+x_{n+1}^2Eleft(widehat {beta }_2-beta _2right)^2+Eleft(varepsilon _{n+1}right)^2+ end{equation*}

begin{equation*} +2x_{n+1}Eleft(left(widehat {beta }_1-beta _1right)left(widehat {beta }_2-beta _2right)right)-2Eleft(left(widehat {beta }_1-beta _1right)varepsilon _{n+1}right)-end{equation*}

begin{equation*}-2x_{n+1}Eleft(left(widehat {beta }_2-beta _2right)varepsilon _{n+1}right)= end{equation*}

begin{equation*} mathit{var}left(widehat {beta }_1right)+x_{n+1}^2mathit{var}left(widehat {beta }_2right)+sigma ^2+2x_{n+1}mathit{cov}left(widehat {beta }_1,widehat {beta }_2right)-0-0= end{equation*}

begin{equation*} frac{frac{sigma ^2} n{ast}sum x_i^2}{sum left(x_i-overline xright)^2}+x_{n+1}^2frac{sigma ^2}{Sigma left(x_i-overline xright)^2}+sigma ^2-2x_{n+1}frac{overline x{ast}sigma ^2}{Sigma left(x_i-overline xright)^2}= end{equation*}

begin{equation*} =sigma ^2{ast}left(1+frac 1 n+frac{left(x_{n+1}-overline xright)^2}{sum left(x_i-overline xright)^2}right)end{equation*}

Здесь в предпоследнем равенстве мы воспользовались формулами для (mathit{var}left(widehat {beta }_1right)), (mathit{var}left(widehat {beta }_2right)) и (mathit{cov}left(widehat {beta }_1,widehat {beta }_2right)), представленными выше.

Дисперсия ошибки прогноза (sigma ^2), неизвестная нам в реальности, может быть заменена несмещенной оценкой (S^2.) Если проделать эту замену, а затем извлечь из полученного результата корень, то получим стандартную ошибку прогноза:

begin{equation*} delta =sqrt{s^2{ast}left(1+frac 1 n+frac{left(x_{n+1}-overline xright)^2}{sum left(x_i-overline xright)^2}right)}end{equation*}

Эту стандартную ошибку прогноза можно использовать для построения доверительного интервала прогноза.

95-процентный доверительный интервал для прогноза — это такой интервал, который накрывает истинное прогнозное значение зависимой переменной с вероятностью 95%. Он имеет вид:

begin{equation*} left(widehat y_{n+1}-delta {ast}t_{n-2}^{alpha },widehat y_{n+1}+delta {ast}t_{n-2}^{alpha }right.) end{equation*}

Обратите внимание, что величина стандартной ошибки прогноза зависит от соотношения (x_{n+1}) и (overline x). Если (x_{n+1}=overline x), то последняя дробь в этой большой формуле окажется равной нулю, и стандартная ошибка прогноза будет минимальной. Чем сильнее (x_{n+1}) отличается от (overline x), тем больше будет эта дробь. Таким образом, чем меньше наблюдение, для которого вы строите прогноз, похоже на вашу исходную выборку, тем менее точным этот прогноз окажется.

Пример 2.6. Построение прогноза

Рассматривается классическая линейная модель парной регрессии (y_i=beta _1+beta _2{ast}x_i+varepsilon _i.) Имеется следующая информация о 10 наблюдениях анализируемых переменных:

begin{equation*} sum _{i=1}^{10}x_i=20,sum _{i=1}^{10}x_i^2=50,sum _{i=1}^{10}y_i=8,sum _{i=1}^{10}y_i^2=26, end{equation*}

begin{equation*} sum _{i=1}^{10}x_i{ast}y_i=10 end{equation*}

Для одиннадцатого наблюдения дано (x_{11}=5). Предполагая, что это наблюдение удовлетворяет исходной модели, вычислите наилучший линейный несмещенный прогноз (y_{11}) и оцените его точность, построив для него 95-процентный доверительный интервал.

Решение:

begin{equation*} widehat {beta _2}=frac{overline{mathit{xy}}-overline x{ast}overline y}{overline{x^2}-overline x^2}=-0,6 end{equation*}

begin{equation*} widehat {beta _1}=overline y-widehat {beta _2}{ast}overline x=2 end{equation*}

Прогноз (widehat y_{11}=widehat {beta _1}+widehat {beta _2}{ast}x_{11}=2-0,6{ast}5=-1).

Сумма квадратов остатков равна:

begin{equation*} sum _{i=1}^{10}e_i^2=sum _{i=1}^{10}e_i{ast}left(y_i-widehat {beta _1}-widehat {beta _2}{ast}x_iright)= end{equation*}

begin{equation*} sum _{i=1}^{10}e_iy_i-widehat {beta _1}sum _{i=1}^{10}e_i-widehat {beta _2}sum _{i=1}^{10}e_ix_i=sum _{i=1}^{10}e_iy_i-widehat {beta _1}{ast}0-widehat {beta _2}{ast}0 end{equation*}

Последнее равенство верно в силу свойств остатков регрессии. Таким образом:

begin{equation*} sum _{i=1}^{10}e_i^2=sum _{i=1}^{10}e_iy_i=sum _{i=1}^{10}left(y_i-widehat {beta _1}-widehat {beta _2}{ast}x_iright)y_i= end{equation*}

begin{equation*} sum _{i=1}^{10}y_i^2-widehat {beta _1}sum _{i=1}^{10}y_i-widehat {beta _2}{ast}sum _{i=1}^{10}x_iy_i=26-2{ast}8+0,6{ast}10=16 end{equation*}

begin{equation*} delta =sqrt{s^2{ast}left(1+frac 1 n+frac{left(x_{11}-overline xright)^2}{sum left(x_i-overline xright)^2}right)}=end{equation*}

begin{equation*}=sqrt{frac{sum e_i^2}{n-2}{ast}left(1+frac 1 n+frac{left(x_{11}-overline xright)^2}{sum left(x_i-overline xright)^2}right)}= end{equation*}

begin{equation*} =sqrt{frac{16}{10-2}{ast}left(1+frac 1{10}+frac{left(5-2right)^2}{10}right)}=2 end{equation*}

Теперь можно посчитать доверительный интервал прогноза:

begin{equation*} left(widehat y_{11}-delta {ast}t_8,widehat y_{11}+delta {ast}t_8right) end{equation*}

begin{equation*} left(-1-2{ast}2,306,-1+2{ast}2,306right) end{equation*}

begin{equation*} left(-5,612,3,612right) end{equation*}

Заметим, что в этом примере точность прогноза не слишком высока, что объясняется маленьким количеством наблюдений и тем, что (x_{11}) довольно далек от среднего по выборке значения переменной (x).

Для получения более точного прогноза лучше, конечно, использовать больше данных.

Ответ: (widehat y_{11}=-1,) доверительный интервал: (left(-5,612,3,612right))

Что такое стандартная ошибка оценки? (Определение и пример)

17 авг. 2022 г.
читать 3 мин

Стандартная ошибка оценки — это способ измерения точности прогнозов, сделанных регрессионной моделью.

Часто обозначаемый σ est , он рассчитывается как:

σ est = √ Σ(y – ŷ) 2 /n

куда:

y: наблюдаемое значение
ŷ: Прогнозируемое значение
n: общее количество наблюдений

Стандартная ошибка оценки дает нам представление о том, насколько хорошо регрессионная модель соответствует набору данных. Особенно:

Чем меньше значение, тем лучше соответствие.
Чем больше значение, тем хуже соответствие.

Для регрессионной модели с небольшой стандартной ошибкой оценки точки данных будут плотно сгруппированы вокруг предполагаемой линии регрессии:

И наоборот, для регрессионной модели с большой стандартной ошибкой оценки точки данных будут более свободно разбросаны по линии регрессии:

В следующем примере показано, как рассчитать и интерпретировать стандартную ошибку оценки для регрессионной модели в Excel.

Пример: стандартная ошибка оценки в Excel

Используйте следующие шаги, чтобы вычислить стандартную ошибку оценки для регрессионной модели в Excel.

Шаг 1: введите данные

Сначала введите значения для набора данных:

Шаг 2: выполните линейную регрессию

Затем щелкните вкладку « Данные » на верхней ленте. Затем выберите параметр « Анализ данных» в группе « Анализ ».

Если вы не видите эту опцию, вам нужно сначала загрузить пакет инструментов анализа .

В появившемся новом окне нажмите « Регрессия », а затем нажмите « ОК ».

В появившемся новом окне заполните следующую информацию:

Как только вы нажмете OK , появится вывод регрессии:

Мы можем использовать коэффициенты из таблицы регрессии для построения оценочного уравнения регрессии:

ŷ = 13,367 + 1,693 (х)

И мы видим, что стандартная ошибка оценки для этой регрессионной модели оказывается равной 6,006.Проще говоря, это говорит нам о том, что средняя точка данных отклоняется от линии регрессии на 6,006 единицы.

Мы можем использовать оценочное уравнение регрессии и стандартную ошибку оценки, чтобы построить 95% доверительный интервал для прогнозируемого значения определенной точки данных.

Например, предположим, что x равно 10. Используя оценочное уравнение регрессии, мы можем предсказать, что y будет равно:

ŷ = 13,367 + 1,693 * (10) = 30,297

И мы можем получить 95% доверительный интервал для этой оценки, используя следующую формулу:

95% ДИ = [ŷ – 1,96*σ расч ., ŷ + 1,96*σ расч .]

Для нашего примера доверительный интервал 95% будет рассчитываться как:

95% ДИ = [ŷ – 1,96*σ расч ., ŷ + 1,96*σ расч .]
95% ДИ = [30,297 – 1,96*6,006, 30,297 + 1,96*6,006]
95% ДИ = [18,525, 42,069]

Дополнительные ресурсы

Как выполнить простую линейную регрессию в Excel
Как выполнить множественную линейную регрессию в Excel
Как создать остаточный график в Excel

When we fit a regression model to a dataset, we’re often interested in how well the regression model “fits” the dataset. Two metrics commonly used to measure goodness-of-fit include R-squared (R²) and the standard error of the regression, often denoted S.

This tutorial explains how to interpret the standard error of the regression (S) as well as why it may provide more useful information than R².

Standard Error vs. R-Squared in Regression

Suppose we have a simple dataset that shows how many hours 12 students studied per day for a month leading up to an important exam along with their exam score:

If we fit a simple linear regression model to this dataset in Excel, we receive the following output:

R-squared is the proportion of the variance in the response variable that can be explained by the predictor variable. In this case, 65.76% of the variance in the exam scores can be explained by the number of hours spent studying.

The standard error of the regression is the average distance that the observed values fall from the regression line. In this case, the observed values fall an average of 4.89 units from the regression line.

If we plot the actual data points along with the regression line, we can see this more clearly:

Notice that some observations fall very close to the regression line, while others are not quite as close. But on average, the observed values fall 4.19 units from the regression line.

The standard error of the regression is particularly useful because it can be used to assess the precision of predictions. Roughly 95% of the observation should fall within +/- two standard error of the regression, which is a quick approximation of a 95% prediction interval.

If we’re interested in making predictions using the regression model, the standard error of the regression can be a more useful metric to know than R-squared because it gives us an idea of how precise our predictions will be in terms of units.

To illustrate why the standard error of the regression can be a more useful metric in assessing the “fit” of a model, consider another example dataset that shows how many hours 12 students studied per day for a month leading up to an important exam along with their exam score:

Notice that this is the exact same dataset as before, except all of the values are cut in half. Thus, the students in this dataset studied for exactly half as long as the students in the previous dataset and received exactly half the exam score.

If we fit a simple linear regression model to this dataset in Excel, we receive the following output:

Notice that the R-squared of 65.76% is the exact same as the previous example.

However, the standard error of the regression is 2.095, which is exactly half as large as the standard error of the regression in the previous example.

If we plot the actual data points along with the regression line, we can see this more clearly:

Notice how the observations are packed much more closely around the regression line. On average, the observed values fall 2.095 units from the regression line.

So, even though both regression models have an R-squared of 65.76%, we know that the second model would provide more precise predictions because it has a lower standard error of the regression.

The Advantages of Using the Standard Error

The standard error of the regression (S) is often more useful to know than the R-squared of the model because it provides us with actual units. If we’re interested in using a regression model to produce predictions, S can tell us very easily if a model is precise enough to use for prediction.

For example, suppose we want to produce a 95% prediction interval in which we can predict exam scores within 6 points of the actual score.

Our first model has an R-squared of 65.76%, but this doesn’t tell us anything about how precise our prediction interval will be. Luckily we also know that the first model has an S of 4.19. This means a 95% prediction interval would be roughly 2*4.19 = +/- 8.38 units wide, which is too wide for our prediction interval.

Our second model also has an R-squared of 65.76%, but again this doesn’t tell us anything about how precise our prediction interval will be. However, we know that the second model has an S of 2.095. This means a 95% prediction interval would be roughly 2*2.095= +/- 4.19 units wide, which is less than 6 and thus sufficiently precise to use for producing prediction intervals.

Further Reading

Introduction to Simple Linear Regression
What is a Good R-squared Value?