Стандартная ошибка среднего простыми словами

Стандартное отклонение и стандартная ошибка: в чем разница?

  • Редакция Кодкампа


читать 2 мин

В статистике студенты часто путают два термина: стандартное отклонение и стандартная ошибка .

Стандартное отклонение измеряет, насколько разбросаны значения в наборе данных.

Стандартная ошибка — это стандартное отклонение среднего значения в повторных выборках из совокупности.

Давайте рассмотрим пример, чтобы ясно проиллюстрировать эту идею.

Пример: стандартное отклонение против стандартной ошибки

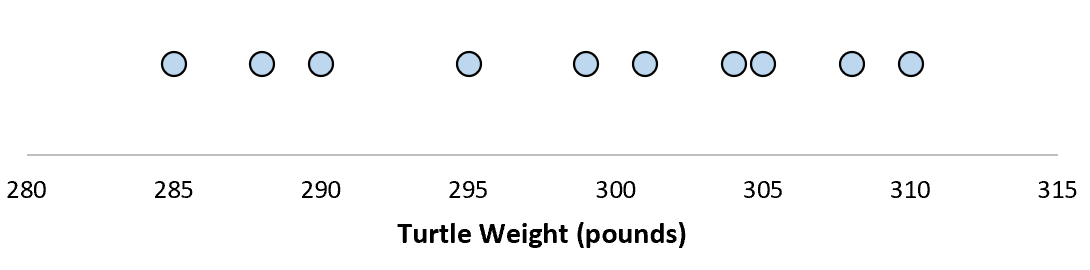
Предположим, мы измеряем вес 10 разных черепах.

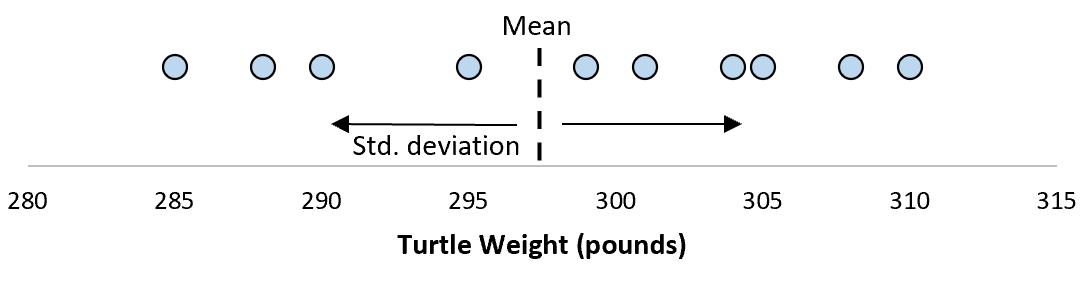
Для этой выборки из 10 черепах мы можем вычислить среднее значение выборки и стандартное отклонение выборки:

Предположим, что стандартное отклонение оказалось равным 8,68. Это дает нам представление о том, насколько распределен вес этих черепах.

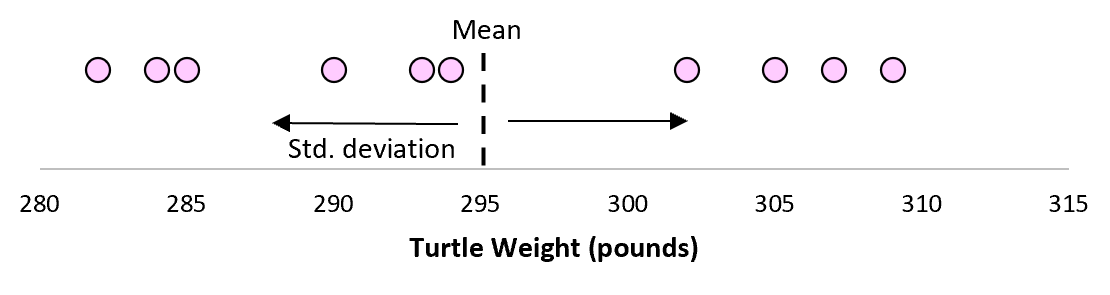
Но предположим, что мы собираем еще одну простую случайную выборку из 10 черепах и также проводим их измерения. Более чем вероятно, что эта выборка из 10 черепах будет иметь немного другое среднее значение и стандартное отклонение, даже если они взяты из одной и той же популяции:

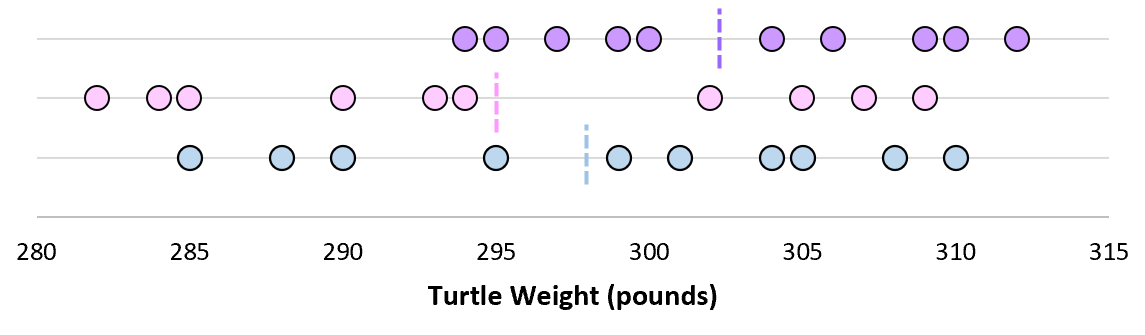
Теперь, если мы представим, что мы берем повторные выборки из одной и той же совокупности и записываем выборочное среднее и выборочное стандартное отклонение для каждой выборки:

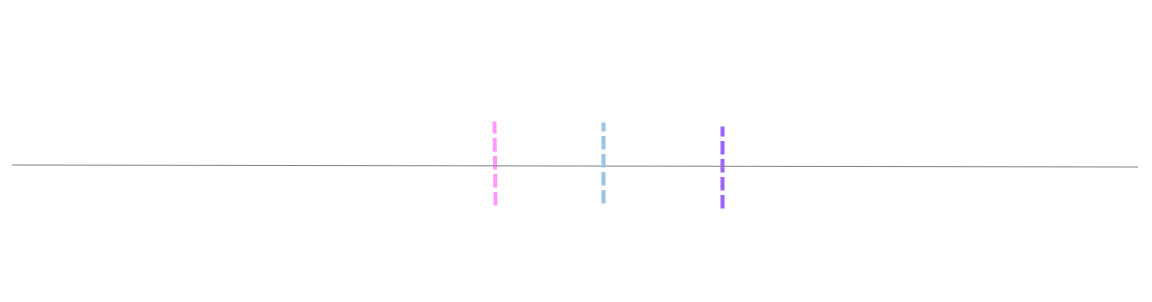
Теперь представьте, что мы наносим каждое среднее значение выборки на одну и ту же строку:

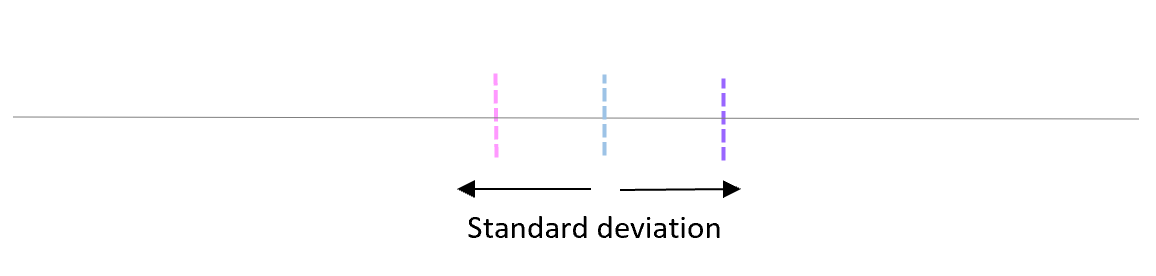
Стандартное отклонение этих средних значений известно как стандартная ошибка.

Формула для фактического расчета стандартной ошибки:

Стандартная ошибка = s/ √n

куда:

  • s: стандартное отклонение выборки
  • n: размер выборки

Какой смысл использовать стандартную ошибку?

Когда мы вычисляем среднее значение данной выборки, нас на самом деле интересует не среднее значение этой конкретной выборки, а скорее среднее значение большей совокупности, из которой взята выборка.

Однако мы используем выборки, потому что для них гораздо проще собирать данные, чем для всего населения. И, конечно же, среднее значение выборки будет варьироваться от выборки к выборке, поэтому мы используем стандартную ошибку среднего значения как способ измерить, насколько точна наша оценка среднего значения.

Вы заметите из формулы для расчета стандартной ошибки, что по мере увеличения размера выборки (n) стандартная ошибка уменьшается:

Стандартная ошибка = s/ √n

Это должно иметь смысл, поскольку большие размеры выборки уменьшают изменчивость и увеличивают вероятность того, что среднее значение нашей выборки ближе к фактическому среднему значению генеральной совокупности.

Когда использовать стандартное отклонение против стандартной ошибки

Если мы просто заинтересованы в измерении того, насколько разбросаны значения в наборе данных, мы можем использовать стандартное отклонение .

Однако, если мы заинтересованы в количественной оценке неопределенности оценки среднего значения, мы можем использовать стандартную ошибку среднего значения .

В зависимости от вашего конкретного сценария и того, чего вы пытаетесь достичь, вы можете использовать либо стандартное отклонение, либо стандартную ошибку.

Источник

Стандартное отклонение и стандартная ошибка: в чем разница?

  • Редакция Кодкампа

17 авг. 2022 г.
читать 2 мин

В статистике студенты часто путают два термина: стандартное отклонение и стандартная ошибка .

Стандартное отклонение измеряет, насколько разбросаны значения в наборе данных.

Стандартная ошибка — это стандартное отклонение среднего значения в повторных выборках из совокупности.

Давайте рассмотрим пример, чтобы ясно проиллюстрировать эту идею.

Пример: стандартное отклонение против стандартной ошибки

Предположим, мы измеряем вес 10 разных черепах.

Для этой выборки из 10 черепах мы можем вычислить среднее значение выборки и стандартное отклонение выборки:

Предположим, что стандартное отклонение оказалось равным 8,68. Это дает нам представление о том, насколько распределен вес этих черепах.

Но предположим, что мы собираем еще одну простую случайную выборку из 10 черепах и также проводим их измерения. Более чем вероятно, что эта выборка из 10 черепах будет иметь немного другое среднее значение и стандартное отклонение, даже если они взяты из одной и той же популяции:

Теперь, если мы представим, что мы берем повторные выборки из одной и той же совокупности и записываем выборочное среднее и выборочное стандартное отклонение для каждой выборки:

Теперь представьте, что мы наносим каждое среднее значение выборки на одну и ту же строку:

Стандартное отклонение этих средних значений известно как стандартная ошибка.

Формула для фактического расчета стандартной ошибки:

Стандартная ошибка = s/ √n

куда:

  • s: стандартное отклонение выборки
  • n: размер выборки

Какой смысл использовать стандартную ошибку?

Когда мы вычисляем среднее значение данной выборки, нас на самом деле интересует не среднее значение этой конкретной выборки, а скорее среднее значение большей совокупности, из которой взята выборка.

Однако мы используем выборки, потому что для них гораздо проще собирать данные, чем для всего населения. И, конечно же, среднее значение выборки будет варьироваться от выборки к выборке, поэтому мы используем стандартную ошибку среднего значения как способ измерить, насколько точна наша оценка среднего значения.

Вы заметите из формулы для расчета стандартной ошибки, что по мере увеличения размера выборки (n) стандартная ошибка уменьшается:

Стандартная ошибка = s/ √n

Это должно иметь смысл, поскольку большие размеры выборки уменьшают изменчивость и увеличивают вероятность того, что среднее значение нашей выборки ближе к фактическому среднему значению генеральной совокупности.

Когда использовать стандартное отклонение против стандартной ошибки

Если мы просто заинтересованы в измерении того, насколько разбросаны значения в наборе данных, мы можем использовать стандартное отклонение .

Однако, если мы заинтересованы в количественной оценке неопределенности оценки среднего значения, мы можем использовать стандартную ошибку среднего значения .

В зависимости от вашего конкретного сценария и того, чего вы пытаетесь достичь, вы можете использовать либо стандартное отклонение, либо стандартную ошибку.


Загрузить PDF


Загрузить PDF

Стандартной ошибкой называется величина, которая характеризует стандартное (среднеквадратическое) отклонение выборочного среднего. Другими словами, эту величину можно использовать для оценки точности выборочного среднего. Множество областей применения стандартной ошибки по умолчанию предполагают нормальное распределение. Если вам нужно рассчитать стандартную ошибку, перейдите к шагу 1.

  1. Изображение с названием Calculate Standard Error Step 1

    1

    Запомните определение среднеквадратического отклонения. Среднеквадратическое отклонение выборки – это мера рассеянности значения. Среднеквадратическое отклонение выборки обычно обозначается буквой s. Математическая формула среднеквадратического отклонения приведена выше.

  2. Изображение с названием Calculate Standard Error Step 2

    2

    Узнайте, что такое истинное среднее значение. Истинное среднее является средним группы чисел, включающим все числа всей группы – другими словами, это среднее всей группы чисел, а не выборки.

  3. Изображение с названием Calculate Standard Error Step 3

    3

    Научитесь рассчитывать среднеарифметическое значение. Среднеаримфетическое означает попросту среднее: сумму значений собранных данных, разделенную на количество значений этих данных.

  4. Изображение с названием Calculate Standard Error Step 4

    4

    Узнайте, что такое выборочное среднее. Когда среднеарифметическое значение основано на серии наблюдений, полученных в результате выборок из статистической совокупности, оно называется “выборочным средним”. Это среднее выборки чисел, которое описывает среднее значение лишь части чисел из всей группы. Его обозначают как:

  5. Изображение с названием Calculate Standard Error Step 5

    5

    Усвойте понятие нормального распределения. Нормальные распределения, которые используются чаще других распределений, являются симметричными, с единичным максимумом в центре – на среднем значении данных. Форма кривой подобна очертаниям колокола, при этом график равномерно опускается по обе стороны от среднего. Пятьдесят процентов распределения лежит слева от среднего, а другие пятьдесят процентов – справа от него. Рассеянность значений нормального распределения описывается стандартным отклонением.

  6. Изображение с названием Calculate Standard Error Step 6

    6

    Запомните основную формулу. Формула для вычисления стандартной ошибки приведена выше.

    Реклама

  1. Изображение с названием Calculate Standard Error Step 7

    1

    Рассчитайте выборочное среднее. Чтобы найти стандартную ошибку, сначала нужно определить среднеквадратическое отклонение (поскольку среднеквадратическое отклонение s входит в формулу для вычисления стандартной ошибки). Начните с нахождения средних значений. Выборочное среднее выражается как среднее арифметическое измерений x1, x2, . . . , xn. Его рассчитывают по формуле, приведенной выше.

    • Допустим, например, что вам нужно рассчитать стандартную ошибку выборочного среднего результатов измерения массы пяти монет, указанных в таблице:
      Вы сможете рассчитать выборочное среднее, подставив значения массы в формулу:

  2. Изображение с названием Calculate Standard Error Step 8

    2

    Вычтите выборочное среднее из каждого измерения и возведите полученное значение в квадрат. Как только вы получите выборочное среднее, вы можете расширить вашу таблицу, вычтя его из каждого измерения и возведя результат в квадрат.

    • Для нашего примера расширенная таблица будет иметь следующий вид:

  3. Изображение с названием Calculate Standard Error Step 9

    3

    Найдите суммарное отклонение ваших измерений от выборочного среднего. Общее отклонение – это сумма возведенных в квадрат разностей от выборочного среднего. Чтобы определить его, сложите ваши новые значения.

    • В нашем примере нужно будет выполнить следующий расчет:
      Это уравнение дает сумму квадратов отклонений измерений от выборочного среднего.

  4. Изображение с названием Calculate Standard Error Step 10

    4

    Рассчитайте среднеквадратическое отклонение ваших измерений от выборочного среднего. Как только вы будете знать суммарное отклонение, вы сможете найти среднее отклонение, разделив ответ на n -1. Обратите внимание, что n равно числу измерений.

    • В нашем примере было сделано 5 измерений, следовательно n – 1 будет равно 4. Расчет нужно вести следующим образом:

  5. Изображение с названием Calculate Standard Error Step 11

    5

    Найдите среднеквадратичное отклонение. Сейчас у вас есть все необходимые значения для того, чтобы воспользоваться формулой для нахождения среднеквадратичного отклонения s.

    • В нашем примере вы будете рассчитывать среднеквадратичное отклонение следующим образом:
      Следовательно, среднеквадратичное отклонение равно 0,0071624.

    Реклама

  1. Изображение с названием Calculate Standard Error Step 12

    1

    Чтобы вычислить стандартную ошибку, воспользуйтесь базовой формулой со среднеквадратическим отклонением.

    • В нашем примере вы сможете рассчитать стандартную ошибку следующим образом:
      Таким образом в нашем примере стандартная ошибка (среднеквадратическое отклонение выборочного среднего) составляет 0,0032031 грамма.

Советы

  • Стандартную ошибку и среднеквадратическое отклонение часто путают. Обратите внимание, что стандартная ошибка описывает среднеквадратическое отклонение выборочного распределения статистических данных, а не распределения отдельных значений
  • В научных журналах понятия стандартной ошибки и среднеквадратического отклонения несколько размыты. Для объединения двух величин используется знак ±.

Реклама

Об этой статье

Эту страницу просматривали 48 054 раза.

Была ли эта статья полезной?

Среднее арифметическое, как известно, используется для получения обобщающей характеристики некоторого набора данных. Если данные более-менее однородны и в них нет аномальных наблюдений (выбросов), то среднее хорошо обобщает данные, сведя к минимуму влияние случайных факторов (они взаимопогашаются при сложении).

Когда анализируемые данные представляют собой выборку (которая состоит из случайных значений), то среднее арифметическое часто (но не всегда) выступает в роли приближенной оценки математического ожидания. Почему приближенной? Потому что среднее арифметическое – это величина, которая зависит от набора случайных чисел, и, следовательно, сама является случайной величиной. При повторных экспериментах (даже в одних и тех же условиях) средние будут отличаться друг от друга.

Для того, чтобы на основе статистического анализа данных делать корректные выводы, необходимо оценить возможный разброс полученного результата. Для этого рассчитываются различные показатели вариации. Но то исходные данные. И как мы только что установили, среднее арифметическое также обладает разбросом, который необходимо оценить и учитывать в дальнейшем (в выводах, в выборе метода анализа и т.д.).

Интуитивно понятно, что разброс средней должен быть как-то связан с разбросом исходных данных. Основной характеристикой разброса средней выступает та же дисперсия.

Дисперсия выборочных данных – это средний квадрат отклонения от средней, и рассчитать ее по исходным данным не составляет труда, например, в Excel предусмотрены специальные функции. Однако, как же рассчитать дисперсию средней, если в распоряжении есть только одна выборка и одно среднее арифметическое?

Расчет дисперсии и стандартной ошибки средней арифметической

Чтобы получить дисперсию средней арифметической нет необходимости проводить множество экспериментов, достаточно иметь только одну выборку. Это легко доказать. Для начала вспомним, что средняя арифметическая (простая) рассчитывается по формуле:

формула средней арифметической

где xi – значения переменной,
n – количество значений.

Теперь учтем два свойства дисперсии, согласно которым, 1) — постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат и 2) — дисперсия суммы независимых случайных величин равняется сумме соответствующих дисперсий. Предполагается, что каждое случайное значение xi обладает одинаковым разбросом, поэтому несложно вывести формулу дисперсии средней арифметической:

Формула дисперсии средней арифметической

Используя более привычные обозначения, формулу записывают как:

Дисперсия средней арифметической

где σ2 – это дисперсия, случайной величины, причем генеральная.

На практике же, генеральная дисперсия известна далеко не всегда, точнее совсем редко, поэтому в качестве оной используют выборочную дисперсию:

Дисперсия средней арифметической по выборке

Стандартное отклонение средней арифметической называется стандартной ошибкой средней и рассчитывается, как квадратный корень из дисперсии.

Формула стандартной ошибки средней при использовании генеральной дисперсии

Стандартная ошибка средней

Формула стандартной ошибки средней при использовании выборочной дисперсии

Стандартная ошибка средней по выборке

Последняя формула на практике используется чаще всего, т.к. генеральная дисперсия обычно не известна. Чтобы не вводить новые обозначения, стандартную ошибку средней обычно записывают в виде соотношения стандартного отклонения выборки и корня объема выборки.

Назначение и свойство стандартной ошибки средней арифметической

Стандартная ошибка средней много, где используется. И очень полезно понимать ее свойства. Посмотрим еще раз на формулу стандартной ошибки средней:

Стандартная ошибка выборочной средней

Числитель – это стандартное отклонение выборки и здесь все понятно. Чем больше разброс данных, тем больше стандартная ошибка средней – прямо пропорциональная зависимость.

Посмотрим на знаменатель. Здесь находится квадратный корень из объема выборки. Соответственно, чем больше объем выборки, тем меньше стандартная ошибка средней. Для наглядности изобразим на одной диаграмме график нормально распределенной переменной со средней равной 10, сигмой – 3, и второй график – распределение средней арифметической этой же переменной, полученной по 16-ти наблюдениям (которое также будет нормальным).

Зависимость стандартной ошибки средней от объем выборки

Судя по формуле, разброс стандартной ошибки средней должен быть в 4 раза (корень из 16) меньше, чем разброс исходных данных, что и видно на рисунке выше. Чем больше наблюдений, тем меньше разброс средней.

Казалось бы, что для получения наиболее точной средней достаточно использовать максимально большую выборку и тогда стандартная ошибка средней будет стремиться к нулю, а сама средняя, соответственно, к математическому ожиданию. Однако квадратный корень объема выборки в знаменателе говорит о том, что связь между точностью выборочной средней и размером выборки не является линейной. Например, увеличение выборки с 20-ти до 50-ти наблюдений, то есть на 30 значений или в 2,5 раза, уменьшает стандартную ошибку средней только на 36%, а со 100-а до 130-ти наблюдений (на те же 30 значений), снижает разброс данных лишь на 12%.

Лучше всего изобразить эту мысль в виде графика зависимости стандартной ошибки средней от размера выборки. Пусть стандартное отклонение равно 10 (на форму графика это не влияет).

Распределение исходных данных и средней

Видно, что примерно после 50-ти значений, уменьшение стандартной ошибки средней резко замедляется, после 100-а – наклон постепенно становится почти нулевым.

Таким образом, при достижении некоторого размера выборки ее дальнейшее увеличение уже почти не сказывается на точности средней. Этот факт имеет далеко идущие последствия. Например, при проведении выборочного обследования населения (опроса) чрезмерное увеличение выборки ведет к неоправданным затратам, т.к. точность почти не меняется. Именно поэтому количество опрошенных редко превышает 1,5 тысячи человек. Точность при таком размере выборки часто является достаточной, а дальнейшее увеличение выборки – нецелесообразным.

Подведем итог. Расчет дисперсии и стандартной ошибки средней имеет довольно простую формулу и обладает полезным свойством, связанным с тем, что относительно хорошая точность средней достигается уже при 100 наблюдениях (в этом случае стандартная ошибка средней становится в 10 раз меньше, чем стандартное отклонение выборки). Больше, конечно, лучше, но бесконечно увеличивать объем выборки не имеет практического смысла. Хотя, все зависит от поставленных задач и цены ошибки. В некоторых опросах участие принимают десятки тысяч людей.

Дисперсия и стандартная ошибка средней имеют большое практическое значение. Они используются в проверке гипотез и расчете доверительных интервалов.

Поделиться в социальных сетях:

Значение слова «СТАНДАРТНАЯ ОШИБКА» найдено в 13 источниках

СТАНДАРТНАЯ ОШИБКА

СТАНДАРТНАЯ ОШИБКА

(standard error) Показатель надежности расчетного параметра. Стандартная ошибка – это стандартное отклонение оценок, которые будут получены при многократной случайной выборке данного размера из одной и той же совокупности. Стандартная ошибка – это убывающая функция объема выборки: чем меньше стандартная ошибка, тем более достоверной является оценка.

Экономика. Толковый словарь. — М.: «ИНФРА-М», Издательство «Весь Мир»..2000.

величина, характеризующая случайную ошибку выборки стандартное отклонение выборочного распределения статистики; обозначается SE (standard error). Может вычисляться для любых выборочных статистик; используется при построении соответствующих доверительных интервалов и статистической проверке гипотез .
Наиболее часто используется С.О. среднего арифметического . Она вычисляется по формуле SE = s / Vn, где s стандартное отклонение переменной, n объем выборки. Чем меньше стандартное отклонение s и больше объем выборки n, тем меньше С.О. С.О. среднего арифметического применяется при построении доверительного интервала для математического ожидания , интервального оценивания случайной ошибки выборки , нахождения объема репрезентативной выборки при заданных доверительной вероятности и предельно допустимой ошибке выборки.
О.В. Терещенко

показатель отклонения полученного коэффициента регрессии от предполагаемого значения реального (но неизвестного) коэффициента для массива. В (t-тесте стандартная ошибка определенного коэффициента делится на этот коэффициент, показывая t-значение. t-таблица, численная таблица, состоящая из значений f-отношения и частоты их появления в (-распределении, чье среднее значение равняется нулю, t-тест: тест статистической значимости полученных коэффициентов регрессии. Если коэффициент проходит этот тест, то исследователь может быть вполне уверен в том, что значение коэффициента для массива не равняется нулю;

Стандартное отклонение распределения теоретической выборки. Оно обеспечивает оценку вариативности, которая может ожидаться в фактических выборках из основной теоретической популяции и, таким образом, и в популяционном параметре. См. стандартная ошибка среднего, которая является оценкой стандартной ошибки, наиболее часто используемой для оценки репрезентативности выборки.

Стандартное
отклонение статистики, в
частности, выборочного распределения оценки. Как правило, употребляется в
выражениях типа «стандартная ошибка среднего» (которая равна стандартному
отклонению, деленному на корень квадратный из объема выборки).

• kvadratická chyba

• směrodatná odchylka

• standardní odchylka

• střední chyba

1) mean-square error

2) standard error

. см. ВЫБОРКИ ОШИБКА.
Antinazi.Энциклопедия социологии,2009

Что такое Стандартная ошибка?

Стандартная ошибка (SE) статистики – это приблизительное стандартное отклонение статистической выборки. Стандартная ошибка – это статистический термин, который измеряет точность, с которой выборочное распределение представляет генеральную совокупность с помощью стандартного отклонения. В статистике выборочное среднее отклоняется от фактического среднего для генеральной совокупности; это отклонение представляет собой стандартную ошибку среднего.

Ключевые моменты

  • Стандартная ошибка – это приблизительное стандартное отклонение статистической выборки.
  • Стандартная ошибка может включать вариацию между вычисленным средним для генеральной совокупности и тем, которое считается известным или принимаемым как точное.
  • Чем больше точек данных участвует в расчетах среднего, тем меньше стандартная ошибка.

Понимание стандартной ошибки

Термин «стандартная ошибка» используется для обозначения стандартного отклонения различных статистических данных выборки, таких как среднее или медианное значение. Например, «стандартная ошибка среднего» относится к стандартному отклонению распределения выборочных средних, взятых из генеральной совокупности. Чем меньше стандартная ошибка, тем более репрезентативной будет выборка для генеральной совокупности.

Связь между стандартной ошибкой и стандартным отклонением такова, что для данного размера выборки стандартная ошибка равна стандартному отклонению, деленному на квадратный корень из размера выборки. Стандартная ошибка также обратно пропорциональна размеру выборки; Чем больше размер выборки, тем меньше стандартная ошибка, поскольку статистика приближается к фактическому значению.

Стандартная ошибка считается частью выводимой статистики. Он представляет собой стандартное отклонение среднего значения в наборе данных. Это служит мерой вариации случайных величин, обеспечивая измерение спреда. Чем меньше разброс, тем точнее набор данных.

Краткая справка

Стандартная ошибка и стандартное отклонение – это меры изменчивости, в то время как меры центральной тенденции включают среднее значение, медианное значение и т. Д.

Требования к стандартной ошибке 

Когда производится выборка из генеральной совокупности , обычно рассчитывается среднее или среднее значение. Стандартная ошибка может включать разброс между вычисленным средним для генеральной совокупности и тем, которое считается известным или принимаемым как точное. Это помогает компенсировать любые случайные неточности, связанные со сбором пробы.

В случаях, когда собирается несколько образцов, среднее значение каждой выборки может незначительно отличаться от других, создавая разброс между переменными. Этот разброс чаще всего измеряется как стандартная ошибка, учитывающая различия между средними значениями в наборах данных.

Чем больше точек данных участвует в расчетах среднего, тем меньше стандартная ошибка. Когда стандартная ошибка мала, данные считаются более репрезентативными для истинного среднего значения. В случаях, когда стандартная ошибка велика, данные могут иметь некоторые заметные отклонения.

Стандартное отклонение – это представление разброса каждой точки данных. Стандартное отклонение используется для определения достоверности данных на основе количества точек данных, отображаемых на каждом уровне стандартного отклонения. Стандартные ошибки больше служат способом определения точности образца или точности нескольких образцов путем анализа отклонения в пределах средних.

Имея
прямую регрессии, необходимо оценить
насколько сильно точки исходных данных
отклоняются от прямой регрессии. Можно
выполнить оценку разброса, аналогичную
стандартному отклонению выборки. Этот
показатель, называемый стандартной
ошибкой оценки, демонстрирует величину
отклонения точек исходных данных от
прямой регрессии в направлении оси Y.
Стандартная ошибка оценки ()
вычисляется по следующей формуле.

Стандартная
ошибка оценки измеряет степень отличия
реальных значений Y от оцененной величины.
Для сравнительно больших выборок следует
ожидать, что около 67% разностей по модулю
не будет превышать

и около 95% модулей разностей будет не
больше 2.

Стандартная
ошибка оценки подобна стандартному
отклонению. Ее можно использовать для
оценки стандартного отклонения
совокупности. Фактически

оценивает стандартное отклонение

слагаемого ошибки

в статистической модели простой линейной
регрессии. Другими словами,

оценивает общее стандартное отклонение

нормального распределения значений Y,
имеющих математические ожидания

для каждого X.

Малая
стандартная ошибка оценки, полученная
при регрессионном анализе, свидетельствует,
что все точки данных находятся очень
близко к прямой регрессии. Если стандартная
ошибка оценки велика, точки данных могут
значительно удаляться от прямой.

2.3 Прогнозирование величины y

Регрессионную
прямую можно использовать для оценки
величины переменной Y
при данных значениях переменной X. Чтобы
получить точечный прогноз, или предсказание
для данного значения X, просто вычисляется
значение найденной функции регрессии
в точке X.

Конечно
реальные значения величины Y,
соответствующие рассматриваемым
значениям величины X, к сожалению, не
лежат в точности на регрессионной
прямой. Фактически они разбросаны
относительно прямой в соответствии с
величиной
.
Более того, выборочная регрессионная
прямая является оценкой регрессионной
прямой генеральной совокупности,
основанной на выборке из определенных
пар данных. Другая случайная выборка
даст иную выборочную прямую регрессии;
это аналогично ситуации, когда различные
выборки из одной и той же генеральной
совокупности дают различные значения
выборочного среднего.

Есть
два источника неопределенности в
точечном прогнозе, использующем уравнение
регрессии.

  1. Неопределенность,
    обусловленная отклонением точек данных
    от выборочной прямой регрессии.

  2. Неопределенность,
    обусловленная отклонением выборочной
    прямой регрессии от регрессионной
    прямой генеральной совокупности.

Интервальный
прогноз значений переменной Y
можно построить так, что при этом будут
учтены оба источника неопределенности.

Стандартная
ошибка прогноза

дает меру вариативности предсказанного
значения Y
около истинной величины Y
для данного значения X.
Стандартная ошибка прогноза равна:

Стандартная
ошибка прогноза зависит от значения X,
для которого прогнозируется величина
Y.

минимально, когда
,
поскольку тогда числитель в третьем
слагаемом под корнем в уравнении будет
0. При прочих неизменных величинах
большему отличию соответствует большее
значение стандартной ошибки прогноза.

Если
статистическая модель простой линейной
регрессии соответствует действительности,
границы интервала прогноза величины Y
равны:

где

— квантиль распределения Стьюдента с
n-2 степенями свободы ().
Если выборка велика (),
этот квантиль можно заменить соответствующим
квантилем нормального распределения.
Например, для большой выборки 95%-ный
интервал прогноза задается следующими
значениями:

Завершим
раздел обзором предположений, положенных
в основу статистической модели линейной
регрессии.

  1. Для
    заданного значения X генеральная
    совокупность значений Y имеет нормальное
    распределение относительно регрессионной
    прямой совокупности. На практике
    приемлемые результаты получаются
    и
    тогда, когда значения Y имеют
    нормальное распределение лишь
    приблизительно.

  2. Разброс
    генеральной совокупности точек данных
    относительно регрессионной прямой
    совокупности остается постоянным всюду
    вдоль этой прямой. Иными словами, при
    возрастании значений X в точках данных
    дисперсия генеральной совокупности
    не увеличивается и не уменьшается.
    Нарушение этого предположения называется
    гетероскедастичностью.

  3. Слагаемые
    ошибок

    независимы между собой. Это предположение
    определяет случайность выборки точек
    Х-Y.
    Если точки данных X-Y
    записывались в течение некоторого
    времени, данное предположение часто
    нарушается. Вместо независимых данных,
    такие последовательные наблюдения
    будут давать серийно коррелированные
    значения.

  4. В
    генеральной совокупности существует
    линейная зависимость между X и Y.
    По аналогии с простой линейной регрессией
    может рассматриваться и нелинейная
    зависимость между X и У. Некоторые такие
    случаи будут обсуждаться ниже.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #

Для значения, которое выбирается с несмещенной ошибкой с нормальным распределением, приведенное выше показывает долю выборок, которая будет находиться между 0, 1, 2 и 3 стандартными отклонениями выше и ниже фактического значения.

Стандартная ошибка ( SE ) из статистики (обычно подсчет параметра ) является стандартным отклонением ее выборочного распределения или оценка этого стандартного отклонения. Если статистика является выборочным средним, это называется стандартной ошибкой среднего ( SEM ).

Распределение выборки из среднего генерируется путем повторного отбора образцов из того же населения и записи средств, полученных образцов. Это формирует распределение различных средних, и это распределение имеет собственное среднее значение и дисперсию . Математически дисперсия полученного распределения выборки равна дисперсии генеральной совокупности, деленной на размер выборки. Это связано с тем, что по мере увеличения размера выборки средние значения выборки сгруппируются более близко к среднему значению генеральной совокупности.

Следовательно, соотношение между стандартной ошибкой среднего и стандартным отклонением таково, что для данного размера выборки стандартная ошибка среднего равна стандартному отклонению, деленному на квадратный корень из размера выборки. Другими словами, стандартная ошибка среднего — это мера разброса выборочных средних вокруг среднего по генеральной совокупности.

В регрессионном анализе термин «стандартная ошибка» относится либо к квадратному корню из приведенной статистики хи-квадрат, либо к стандартной ошибке для конкретного коэффициента регрессии (который используется, например, в доверительных интервалах ).

Стандартная ошибка среднего

Точное значение

Если статистически независимые выборки наблюдений берется из статистической совокупности с стандартным отклонением от, то среднее значение, рассчитанное из образца будет иметь ассоциированную стандартную ошибку среднего значения на заданном с помощью:
п{ Displaystyle x_ {1}, x_ {2}, ldots, x_ {n}}сигма { bar {x}} { displaystyle { sigma} _ { bar {x}}}

{ displaystyle { sigma} _ { bar {x}} = { frac { sigma} { sqrt {n}}}}.

На практике это говорит нам о том, что при попытке оценить значение среднего по совокупности из-за фактора уменьшение ошибки оценки в два раза требует получения в четыре раза большего количества наблюдений в выборке; уменьшение его в десять раз требует в сто раз больше наблюдений.
1 / { sqrt {n}}

Оценивать

Стандартное отклонение отобранной совокупности известно редко. Таким образом, стандартная ошибка среднего обычно оцениваются путем замены с стандартным отклонением выборки вместо:
сигма сигма sigma _ {x}

{ displaystyle { sigma} _ { bar {x}} приблизительно { frac { sigma _ {x}} { sqrt {n}}}}.

Поскольку это только оценка истинной «стандартной ошибки», здесь часто встречаются другие обозначения, такие как:

{ displaystyle { widehat { sigma}} _ { bar {x}} = { frac { sigma _ {x}} { sqrt {n}}}}  или поочередно .  { displaystyle {s} _ { bar {x}} = { frac {s} { sqrt {n}}}}

Общим источником путаницы возникает при отсутствии четко различать между стандартным отклонением населения ( ), стандартное отклонение выборки ( ), стандартное отклонение среднего само по себе (, который является стандартная ошибка), а оценка из стандартное отклонение среднего ( которое является наиболее часто вычисляемой величиной и также часто в просторечии называется стандартной ошибкой ).
сигма sigma _ {x}{ displaystyle sigma _ { bar {x}}}{ displaystyle { widehat { sigma}} _ { bar {x}}}

Точность оценщика

Когда размер выборки невелик, использование стандартного отклонения выборки вместо истинного стандартного отклонения генеральной совокупности будет иметь тенденцию к систематическому занижению стандартного отклонения генеральной совокупности, а, следовательно, и стандартной ошибки. При n = 2 занижение составляет около 25%, но для n = 6 занижение составляет всего 5%. Гурланд и Трипати (1971) предлагают поправку и уравнение для этого эффекта. Сокал и Рольф (1981) приводят уравнение поправочного коэффициента для малых выборок n <20. См. Несмещенную оценку стандартного отклонения для дальнейшего обсуждения.

Вывод

Стандартная ошибка среднего может быть получена из дисперсии суммы независимых случайных величин с учетом определения дисперсии и некоторых ее простых свойств . Если это независимые наблюдения от совокупности со средним значением и стандартным отклонением, то мы можем определить общую
{ Displaystyle x_ {1}, x_ {2}, ldots, x_ {n}}п{ bar {x}}сигма

{ Displaystyle T = (x_ {1} + x_ {2} + cdots + x_ {n})}

которые по формуле Биенайме будут иметь дисперсию

{ displaystyle operatorname {Var} (T) = { big (} operatorname {Var} (x_ {1}) + operatorname {Var} (x_ {2}) + cdots + operatorname {Var} ( x_ {n}) { big)} = n sigma ^ {2}.}

Среднее значение этих измерений просто дается выражением
{ bar {x}}

{ displaystyle { bar {x}} = Т / п}.

Тогда дисперсия среднего составляет

{ displaystyle operatorname {Var} ({ bar {x}}) = operatorname {Var} left ({ frac {T} {n}} right) = { frac {1} {n ^ { 2}}} operatorname {Var} (T) = { frac {1} {n ^ {2}}} n sigma ^ {2} = { frac { sigma ^ {2}} {n}} .}

Стандартная ошибка — это, по определению, стандартное отклонение, которое представляет собой квадратный корень из дисперсии:
{ bar {x}}

{ displaystyle sigma _ { bar {x}} = { sqrt { frac { sigma ^ {2}} {n}}} = { frac { sigma} { sqrt {n}}}}.

Для коррелированных случайных величин дисперсия выборки должна быть вычислена в соответствии с центральной предельной теоремой Маркова .

Независимые и одинаково распределенные случайные величины со случайным размером выборки

Бывают случаи, когда образец берут, не зная заранее, сколько наблюдений будет приемлемым по какому-либо критерию. В таких случаях размер выборки является случайной величиной, вариация которой добавляется к вариации, так что,
NИкс

{ Displaystyle OperatorName {Var} (T) = OperatorName {E} (N) OperatorName {Var} (X) + Operatorname {Var} (N) { big (} Operatorname {E} (X) { big)} ^ {2}}

Если имеет распределение Пуассона, то с оценкой . Следовательно, оценка становится, приводя к следующей формуле для стандартной ошибки:
N{ Displaystyle OperatorName {E} (N) = OperatorName {Var} (N)}{ displaystyle N = n}{ displaystyle operatorname {Var} (T)}{ displaystyle nS_ {X} ^ {2} + n { bar {X}} ^ {2}}

{ displaystyle operatorname {Standard ~ Error} ({ bar {X}}) = { sqrt { frac {S_ {X} ^ {2} + { bar {X}} ^ {2}} {n }}}}

(поскольку стандартное отклонение — это квадратный корень из дисперсии)

Приближение Стьюдента при неизвестном значении σ

Во многих практических приложениях истинное значение σ неизвестно. В результате нам нужно использовать распределение, которое учитывает этот разброс возможных σ . Когда известно, что истинное базовое распределение является гауссовым, хотя и с неизвестным σ, тогда полученное оцененное распределение следует t-распределению Стьюдента. Стандартная ошибка — это стандартное отклонение t-распределения Стьюдента. Т-распределения немного отличаются от гауссовых и меняются в зависимости от размера выборки. Небольшие выборки с большей вероятностью недооценивают стандартное отклонение совокупности и имеют среднее значение, которое отличается от истинного среднего значения совокупности, а t-распределение Стьюдента учитывает вероятность этих событий с несколько более тяжелыми хвостами по сравнению с гауссовым. Для оценки стандартной ошибки t-распределения Стьюдента достаточно использовать выборочное стандартное отклонение «s» вместо σ, и мы могли бы использовать это значение для вычисления доверительных интервалов.

Примечание. Распределение вероятностей Стьюдента хорошо аппроксимируется распределением Гаусса, когда размер выборки превышает 100. Для таких выборок можно использовать последнее распределение, которое намного проще.

Предположения и использование

Пример того, как это используется, — это сделать доверительные интервалы для неизвестного среднего значения генеральной совокупности. Если распределение выборки имеет нормальное распределение, среднее значение выборки, стандартная ошибка и квантили нормального распределения могут использоваться для расчета доверительных интервалов для истинного среднего значения генеральной совокупности. Следующие выражения могут быть использованы для расчета верхнего и нижнего 95% доверительных интервалов, где равно среднему значению выборки, равно стандартной ошибке для среднего значения выборки, а 1,96 является приблизительным значением точки процентиля 97,5 нормального распространение :
{ displaystyle operatorname {SE}}{ bar {x}}{ displaystyle operatorname {SE}}

Верхний предел 95% и{ displaystyle = { bar {x}} + ( operatorname {SE} times 1,96),}
Нижний предел 95% { displaystyle = { bar {x}} - ( operatorname {SE} times 1.96).}

В частности, стандартная ошибка выборочной статистики (например, выборочное среднее ) — это фактическое или расчетное стандартное отклонение выборочного среднего в процессе, в котором оно было создано. Другими словами, это фактическое или оценочное стандартное отклонение выборочного распределения статистической выборки. Обозначение для стандартной ошибки может быть любым из SE, SEM (для стандартной ошибки измерения или среднего ), или S E .

Стандартные ошибки обеспечивают простые меры неопределенности значения и часто используются, потому что:

  • во многих случаях, если известна стандартная ошибка нескольких отдельных величин, то стандартную ошибку некоторой функции величин можно легко вычислить;
  • когда распределение вероятностей значения известно, его можно использовать для вычисления точного доверительного интервала ;
  • когда распределение вероятностей неизвестно, для расчета консервативного доверительного интервала можно использовать неравенства Чебышева или Высочанского – Петунина ; а также
  • поскольку размер выборки стремится к бесконечности, центральная предельная теорема гарантирует, что выборочное распределение среднего является асимптотически нормальным .

Стандартная ошибка среднего значения по сравнению со стандартным отклонением

В научно-технической литературе экспериментальные данные часто обобщаются либо с использованием среднего значения и стандартного отклонения выборочных данных, либо среднего значения со стандартной ошибкой. Это часто приводит к путанице в отношении их взаимозаменяемости. Однако среднее значение и стандартное отклонение являются описательной статистикой, тогда как стандартная ошибка среднего описывает процесс случайной выборки. Стандартное отклонение данных выборки — это описание вариации в измерениях, в то время как стандартная ошибка среднего — это вероятностное утверждение о том, как размер выборки обеспечит лучшую границу оценок среднего для генеральной совокупности в свете центрального предела. теорема.

Проще говоря, стандартная ошибка выборочного среднего — это оценка того, насколько далеко среднее значение выборки может быть от среднего значения по совокупности, тогда как стандартное отклонение выборки — это степень, в которой отдельные лица в выборке отличаются от выборочного среднего. Если стандартное отклонение генеральной совокупности конечно, стандартная ошибка среднего значения выборки будет стремиться к нулю с увеличением размера выборки, потому что оценка генерального среднего будет улучшаться, в то время как стандартное отклонение выборки будет иметь тенденцию приближаться к стандарту генеральной совокупности. отклонение по мере увеличения размера выборки.

Расширения

Поправка на конечную популяцию (FPC)

Приведенная выше формула для стандартной ошибки предполагает, что размер выборки намного меньше, чем размер генеральной совокупности, так что совокупность может считаться фактически бесконечной по размеру. Обычно это имеет место даже в случае конечных популяций, потому что большую часть времени люди в первую очередь заинтересованы в управлении процессами, которые создали существующую конечную популяцию; это называется аналитическим исследованием вслед за У. Эдвардсом Демингом . Если люди заинтересованы в управлении существующей конечной совокупностью, которая не будет меняться с течением времени, то необходимо сделать поправку на размер популяции; это называется перечислительным исследованием .

Когда доля выборки (часто называемая f ) велика (примерно 5% или более) в переписном исследовании, оценка стандартной ошибки должна быть скорректирована путем умножения на «поправку на конечную совокупность» (также известную как fpc ):

{ displaystyle operatorname {FPC} = { sqrt { frac {Nn} {N-1}}}}

что для больших N :

{ displaystyle operatorname {FPC} приблизительно { sqrt {1 - { frac {n} {N}}}} = { sqrt {1-f}}}

чтобы учесть дополнительную точность, полученную за счет выборки, близкой к большему проценту населения. Эффект FPC является то, что ошибка становится равной нулю, когда размер выборки п равен размеру популяции N .

Это происходит в методологии обследования при выборке без замены . Если выборка с заменой, то FPC не играет роли.

Поправка на корреляцию в выборке

Ожидаемая ошибка среднего значения A для выборки из n точек данных с коэффициентом смещения выборки  ρ . Несмещенная стандартная ошибка строится как  диагональная линия ρ = 0 с логарифмическим наклоном −½.

Если значения измеренной величины A не являются статистически независимыми, но были получены из известных мест в пространстве параметров  x, несмещенная оценка истинной стандартной ошибки среднего (фактически поправка на часть стандартного отклонения) может быть получена путем умножения рассчитанная стандартная ошибка выборки по коэффициенту  f :

f = { sqrt { frac {1+ rho} {1- rho}}},

где коэффициент смещения выборки ρ представляет собой широко используемую оценку Прайса – Винстена коэффициента автокорреляции (величина от -1 до +1) для всех пар точек выборки. Эта приблизительная формула предназначена для выборки среднего и большого размера; Справочник дает точные формулы для любого размера выборки и может применяться к сильно автокоррелированным временным рядам, таким как котировки акций Уолл-стрит. Более того, эта формула работает как для положительного, так и для отрицательного значения ρ. См. Также объективную оценку стандартного отклонения для более подробного обсуждения.

Смотрите также

  • Иллюстрация центральной предельной теоремы
  • Допустимая погрешность
  • Вероятная ошибка
  • Стандартная ошибка средневзвешенного значения
  • Среднее значение выборки и ковариация выборки
  • Стандартная ошибка медианы
  • Дисперсия

использованная литература

Источник

Standard Error of the Mean vs. Standard Deviation: An Overview


Standard deviation (SD) measures the amount of variability, or dispersion, from the individual data values to the mean. SD is a frequently-cited statistic in many applications from math and statistics to finance and investing.

Standard error of the mean (SEM) measures how far the sample mean (average) of the data is likely to be from the true population mean. The SEM is always smaller than the SD.

Standard deviation and standard error are both used in statistical studies, including those in finance, medicine, biology, engineering, and psychology. In these studies, the SD and the estimated SEM are used to present the characteristics of sample data and explain statistical analysis results.

However, even some researchers occasionally confuse the SD and the SEM. Such researchers should remember that the calculations for SD and SEM include different statistical inferences, each of them with its own meaning. SD is the dispersion of individual data values. In other words, SD indicates how accurately the mean represents sample data.

However, the meaning of SEM includes statistical inference based on the sampling distribution. SEM is the SD of the theoretical distribution of the sample means (the sampling distribution).

Key Takeaways

  • Standard deviation (SD) measures the dispersion of a dataset relative to its mean.
  • SD is used frequently in statistics, and in finance is often used as a proxy for the volatility or riskiness of an investment.
  • The standard error of the mean (SEM) measures how much discrepancy is likely in a sample’s mean compared with the population mean.
  • The SEM takes the SD and divides it by the square root of the sample size.
  • The SEM will always be smaller than the SD.

Standard error estimates the likely accuracy of a number based on the sample size.

Standard error of the mean, or SEM, indicates the size of the likely discrepancy compared to that of the larger population.

Calculating SD and SEM

standard deviation 

σ

=

∑

i

=

1

n

(

x

i

−

x

ˉ

)

2

n

−

1

variance

=

σ

2

standard error 

(

σ

x

ˉ

)

=

σ

n

where:

x

ˉ

=

the sample’s mean

n

=

the sample size

\begin{aligned} &\text{standard deviation } \sigma = \sqrt{ \frac{ \sum_{i=1}^n{\left(x_i — \bar{x}\right)^2} }{n-1} } \\ &\text{variance} = {\sigma ^2 } \\ &\text{standard error }\left( \sigma_{\bar x} \right) = \frac{{\sigma }}{\sqrt{n}} \\ &\textbf{where:}\\ &\bar{x}=\text{the sample’s mean}\\ &n=\text{the sample size}\\ \end{aligned}

​standard deviation σ=n−1∑i=1n​(xi​−xˉ)2​​variance=σ2standard error (σxˉ​)=n​σ​where:xˉ=the sample’s meann=the sample size​

Standard Deviation

The formula for the SD requires a few steps:

  1. First, take the square of the difference between each data point and the sample mean, finding the sum of those values.
  2. Next, divide that sum by the sample size minus one, which is the variance.
  3. Finally, take the square root of the variance to get the SD.

Standard Error of the Mean

SEM is calculated simply by taking the standard deviation and dividing it by the square root of the sample size.

Standard error gives the accuracy of a sample mean by measuring the sample-to-sample variability of the sample means. The SEM describes how precise the mean of the sample is as an estimate of the true mean of the population.

As the size of the sample data grows larger, the SEM decreases vs. the SD. As the sample size increases, the sample mean estimates the true mean of the population with greater precision.

Increasing the sample size does not make the SD necessarily larger or smaller; it just becomes a more accurate estimate of the population SD.

A sampling distribution is a probability distribution of a sample statistic taken from a greater population. Researchers typically use sample data to estimate the population data, and the sampling distribution explains how the sample mean will vary from sample to sample. The standard error of the mean is the standard deviation of the sampling distribution of the mean.

Standard Error and Standard Deviation in Finance

In finance, the SEM daily return of an asset measures the accuracy of the sample mean as an estimate of the long-run (persistent) mean daily return of the asset.

On the other hand, the SD of the return measures deviations of individual returns from the mean. Thus, SD is a measure of volatility and can be used as a risk measure for an investment.

Assets with greater day-to-day price movements have a higher SD than assets with lesser day-to-day movements. Assuming a normal distribution, around 68% of daily price changes are within one SD of the mean, with around 95% of daily price changes within two SDs of the mean.

How Are Standard Deviation and Standard Error of the Mean Different?

Standard deviation measures the variability from specific data points to the mean. Standard error of the mean measures the precision of the sample mean to the population mean that it is meant to estimate.

Is the Standard Error Equal to the Standard Deviation?

No, the standard deviation (SD) will always be larger than the standard error (SE). This is because the standard error divides the standard deviation by the square root of the sample size.

If the sample size is one, they will be the same, but a sample size of one is rarely useful.

How Can You Compute the SE From the SD?

If you have the standard error (SE) and want to compute the standard deviation (SD) from it, simply multiply it by the square root of the sample size.

Why Do We Use Standard Error Instead of Standard Deviation?

What Is the Empirical Rule, and How Does It Relate to Standard Deviation?

A normal distribution is also known as a standard bell curve, since it looks like a bell in graph form. According to the empirical rule, or the 68-95-99.7 rule, 68% of all data observed under a normal distribution will fall within one standard deviation of the mean. Similarly, 95% falls within two standard deviations and 99.7% within three.

The Bottom Line

Investors and analysts measure standard deviation as a way to estimate the potential volatility of a stock or other investment. It helps determine the level of risk to the investor that is involved. When reading an analyst’s report, the level of riskiness of an investment may be labeled «standard deviation.»

Standard error of the mean is an indication of the likely accuracy of a number. The larger the sample size, the more accurate the number should be.

Источник

Стандартное отклонение (SD), измеряет количество изменчивости или дисперсии, из отдельных значений данных, к среднему значению, в то время как стандартная ошибка среднего (SEM) мер, как далеко образец среднее (среднее) данных, вероятно, будет от истинного среднего значения населения. SEM всегда меньше SD.

Ключевые выводы

  • Стандартное отклонение (SD) измеряет разброс набора данных относительно его среднего значения.
  • Стандартная ошибка среднего (SEM) измеряет, насколько вероятно расхождение между средним значением выборки по сравнению со средним значением генеральной совокупности.
  • SEM берет SD и делит его на квадратный корень из размера выборки.

SEM против SD

Стандартное отклонение и стандартная ошибка используются во всех типах статистических исследований, включая исследования в области финансов, медицины, биологии, инженерии, психологии и т. Д. В этих исследованиях стандартное отклонение (SD) и расчетная стандартная ошибка среднего (SEM) ) используются для представления характеристик данных выборки и объяснения результатов статистического анализа. Однако некоторые исследователи иногда путают SD и SEM. Таким исследователям следует помнить, что расчеты SD и SEM включают разные статистические выводы, каждый из которых имеет свое значение. SD — это разброс отдельных значений данных.

Другими словами, SD указывает, насколько точно среднее значение представляет данные выборки. Однако значение SEM включает статистический вывод, основанный на распределении выборки. SEM — это стандартное отклонение теоретического распределения выборочных средних (выборочное распределение).

Расчет стандартного отклонения

Формула SD требует нескольких шагов:

  1. Во-первых, возьмите квадрат разницы между каждой точкой данных и средним значением выборки, найдя сумму этих значений.
  2. Затем разделите эту сумму на размер выборки минус один, который представляет собой дисперсию.
  3. Наконец, извлеките квадратный корень из дисперсии, чтобы получить стандартное отклонение.

Стандартная ошибка среднего

SEM рассчитывается путем деления стандартного отклонения на квадратный корень из размера выборки.

Стандартная ошибка дает точность выборочного среднего путем измерения изменчивости выборочного среднего от образца к образцу. SEM описывает, насколько точное среднее значение выборки является оценкой истинного среднего значения совокупности. По мере увеличения размера выборки данных SEM уменьшается по сравнению с SD; следовательно, по мере увеличения размера выборки среднее значение выборки оценивает истинное среднее значение генеральной совокупности с большей точностью. Напротив, увеличение размера выборки не обязательно делает SD больше или меньше, это просто становится более точной оценкой SD населения.

Стандартная ошибка и стандартное отклонение в финансах

В финансах стандартная ошибка средней дневной доходности актива измеряет точность выборочного среднего как оценки долгосрочной (постоянной) средней дневной доходности актива.

С другой стороны, стандартное отклонение доходности измеряет отклонения индивидуальных доходов от среднего значения. Таким образом, SD является мерой волатильности и может использоваться в качестве меры риска для инвестиций. Активы с более высокими ежедневными движениями цен имеют более высокое SD, чем активы с меньшими ежедневными движениями. Предполагая нормальное распределение, около 68% дневных изменений цен находятся в пределах одного стандартного отклонения от среднего, при этом около 95% дневных изменений цен находятся в пределах двух стандартных значений среднего.

From Wikipedia, the free encyclopedia

For a value that is sampled with an unbiased normally distributed error, the above depicts the proportion of samples that would fall between 0, 1, 2, and 3 standard deviations above and below the actual value.

The standard error (SE)[1] of a statistic (usually an estimate of a parameter) is the standard deviation of its sampling distribution[2] or an estimate of that standard deviation. If the statistic is the sample mean, it is called the standard error of the mean (SEM).[1]

The sampling distribution of a mean is generated by repeated sampling from the same population and recording of the sample means obtained. This forms a distribution of different means, and this distribution has its own mean and variance. Mathematically, the variance of the sampling mean distribution obtained is equal to the variance of the population divided by the sample size. This is because as the sample size increases, sample means cluster more closely around the population mean.

Therefore, the relationship between the standard error of the mean and the standard deviation is such that, for a given sample size, the standard error of the mean equals the standard deviation divided by the square root of the sample size.[1] In other words, the standard error of the mean is a measure of the dispersion of sample means around the population mean.

In regression analysis, the term «standard error» refers either to the square root of the reduced chi-squared statistic or the standard error for a particular regression coefficient (as used in, say, confidence intervals).

Standard error of the sample mean[edit]

Exact value[edit]

Suppose a statistically independent sample of n observations {displaystyle x_{1},x_{2},ldots ,x_{n}} is taken from a statistical population with a standard deviation of sigma . The mean value calculated from the sample, {bar {x}}, will have an associated standard error on the mean, {displaystyle {sigma }_{bar {x}}}, given by:[1]

{displaystyle {sigma }_{bar {x}} ={frac {sigma }{sqrt {n}}}}.

Practically this tells us that when trying to estimate the value of a population mean, due to the factor 1/{sqrt {n}}, reducing the error on the estimate by a factor of two requires acquiring four times as many observations in the sample; reducing it by a factor of ten requires a hundred times as many observations.

Estimate[edit]

The standard deviation sigma of the population being sampled is seldom known. Therefore, the standard error of the mean is usually estimated by replacing sigma with the sample standard deviation sigma _{x} instead:

{displaystyle {sigma }_{bar {x}} approx {frac {sigma _{x}}{sqrt {n}}}}.

As this is only an estimator for the true «standard error», it is common to see other notations here such as:

{displaystyle {widehat {sigma }}_{bar {x}}approx {frac {sigma _{x}}{sqrt {n}}}}   or alternately   {displaystyle {s}_{bar {x}} approx {frac {s}{sqrt {n}}}}.

A common source of confusion occurs when failing to distinguish clearly between:

Accuracy of the estimator[edit]

When the sample size is small, using the standard deviation of the sample instead of the true standard deviation of the population will tend to systematically underestimate the population standard deviation, and therefore also the standard error. With n = 2, the underestimate is about 25%, but for n = 6, the underestimate is only 5%. Gurland and Tripathi (1971) provide a correction and equation for this effect.[3] Sokal and Rohlf (1981) give an equation of the correction factor for small samples of n < 20.[4] See unbiased estimation of standard deviation for further discussion.

Derivation[edit]

The standard error on the mean may be derived from the variance of a sum of independent random variables,[5] given the definition of variance and some simple properties thereof. If {displaystyle x_{1},x_{2},ldots ,x_{n}} are n independent samples from a population with mean {bar {x}} and standard deviation sigma , then we can define the total

{displaystyle T=(x_{1}+x_{2}+cdots +x_{n})}

which due to the Bienaymé formula, will have variance

{displaystyle operatorname {Var} (T)approx {big (}operatorname {Var} (x_{1})+operatorname {Var} (x_{2})+cdots +operatorname {Var} (x_{n}){big )}=nsigma ^{2}.}

where we’ve approximated the standard deviations, i.e., the uncertainties, of the measurements themselves with the best value for the standard deviation of the population. The mean of these measurements {bar {x}} is simply given by

{displaystyle {bar {x}}=T/n}.

The variance of the mean is then

{displaystyle operatorname {Var} ({bar {x}})=operatorname {Var} left({frac {T}{n}}right)={frac {1}{n^{2}}}operatorname {Var} (T)={frac {1}{n^{2}}}nsigma ^{2}={frac {sigma ^{2}}{n}}.}

The standard error is, by definition, the standard deviation of {bar {x}} which is simply the square root of the variance:

{displaystyle sigma _{bar {x}}={sqrt {frac {sigma ^{2}}{n}}}={frac {sigma }{sqrt {n}}}}.

For correlated random variables the sample variance needs to be computed according to the Markov chain central limit theorem.

Independent and identically distributed random variables with random sample size[edit]

There are cases when a sample is taken without knowing, in advance, how many observations will be acceptable according to some criterion. In such cases, the sample size N is a random variable whose variation adds to the variation of X such that,

{displaystyle operatorname {Var} (T)=operatorname {E} (N)operatorname {Var} (X)+operatorname {Var} (N){big (}operatorname {E} (X){big )}^{2}}[6]

If N has a Poisson distribution, then {displaystyle operatorname {E} (N)=operatorname {Var} (N)} with estimator {displaystyle N=n}. Hence the estimator of {displaystyle operatorname {Var} (T)} becomes {displaystyle nS_{X}^{2}+n{bar {X}}^{2}}, leading the following formula for standard error:

{displaystyle operatorname {Standard~Error} ({bar {X}})={sqrt {frac {S_{X}^{2}+{bar {X}}^{2}}{n}}}}

(since the standard deviation is the square root of the variance)

Student approximation when σ value is unknown[edit]

In many practical applications, the true value of σ is unknown. As a result, we need to use a distribution that takes into account that spread of possible σ’s.
When the true underlying distribution is known to be Gaussian, although with unknown σ, then the resulting estimated distribution follows the Student t-distribution. The standard error is the standard deviation of the Student t-distribution. T-distributions are slightly different from Gaussian, and vary depending on the size of the sample. Small samples are somewhat more likely to underestimate the population standard deviation and have a mean that differs from the true population mean, and the Student t-distribution accounts for the probability of these events with somewhat heavier tails compared to a Gaussian. To estimate the standard error of a Student t-distribution it is sufficient to use the sample standard deviation «s» instead of σ, and we could use this value to calculate confidence intervals.

Note: The Student’s probability distribution is approximated well by the Gaussian distribution when the sample size is over 100. For such samples one can use the latter distribution, which is much simpler.

Assumptions and usage[edit]

An example of how {displaystyle operatorname {SE} } is used is to make confidence intervals of the unknown population mean. If the sampling distribution is normally distributed, the sample mean, the standard error, and the quantiles of the normal distribution can be used to calculate confidence intervals for the true population mean. The following expressions can be used to calculate the upper and lower 95% confidence limits, where {bar {x}} is equal to the sample mean, {displaystyle operatorname {SE} } is equal to the standard error for the sample mean, and 1.96 is the approximate value of the 97.5 percentile point of the normal distribution:

Upper 95% limit {displaystyle ={bar {x}}+(operatorname {SE} times 1.96),} and
Lower 95% limit {displaystyle ={bar {x}}-(operatorname {SE} times 1.96).}

In particular, the standard error of a sample statistic (such as sample mean) is the actual or estimated standard deviation of the sample mean in the process by which it was generated. In other words, it is the actual or estimated standard deviation of the sampling distribution of the sample statistic. The notation for standard error can be any one of SE, SEM (for standard error of measurement or mean), or SE.

Standard errors provide simple measures of uncertainty in a value and are often used because:

  • in many cases, if the standard error of several individual quantities is known then the standard error of some function of the quantities can be easily calculated;
  • when the probability distribution of the value is known, it can be used to calculate an exact confidence interval;
  • when the probability distribution is unknown, Chebyshev’s or the Vysochanskiï–Petunin inequalities can be used to calculate a conservative confidence interval; and
  • as the sample size tends to infinity the central limit theorem guarantees that the sampling distribution of the mean is asymptotically normal.

Standard error of mean versus standard deviation[edit]

In scientific and technical literature, experimental data are often summarized either using the mean and standard deviation of the sample data or the mean with the standard error. This often leads to confusion about their interchangeability. However, the mean and standard deviation are descriptive statistics, whereas the standard error of the mean is descriptive of the random sampling process. The standard deviation of the sample data is a description of the variation in measurements, while the standard error of the mean is a probabilistic statement about how the sample size will provide a better bound on estimates of the population mean, in light of the central limit theorem.[7]

Put simply, the standard error of the sample mean is an estimate of how far the sample mean is likely to be from the population mean, whereas the standard deviation of the sample is the degree to which individuals within the sample differ from the sample mean.[8] If the population standard deviation is finite, the standard error of the mean of the sample will tend to zero with increasing sample size, because the estimate of the population mean will improve, while the standard deviation of the sample will tend to approximate the population standard deviation as the sample size increases.

Extensions[edit]

Finite population correction (FPC)[edit]

The formula given above for the standard error assumes that the population is infinite. Nonetheless, it is often used for finite populations when people are interested in measuring the process that created the existing finite population (this is called an analytic study). Though the above formula is not exactly correct when the population is finite, the difference between the finite- and infinite-population versions will be small when sampling fraction is small (e.g. a small proportion of a finite population is studied). In this case people often do not correct for the finite population, essentially treating it as an «approximately infinite» population.

If one is interested in measuring an existing finite population that will not change over time, then it is necessary to adjust for the population size (called an enumerative study). When the sampling fraction (often termed f) is large (approximately at 5% or more) in an enumerative study, the estimate of the standard error must be corrected by multiplying by a »finite population correction» (a.k.a.: FPC):[9]
[10]

{displaystyle operatorname {FPC} ={sqrt {frac {N-n}{N-1}}}}

which, for large N:

{displaystyle operatorname {FPC} approx {sqrt {1-{frac {n}{N}}}}={sqrt {1-f}}}

to account for the added precision gained by sampling close to a larger percentage of the population. The effect of the FPC is that the error becomes zero when the sample size n is equal to the population size N.

This happens in survey methodology when sampling without replacement. If sampling with replacement, then FPC does not come into play.

Correction for correlation in the sample[edit]

Expected error in the mean of A for a sample of n data points with sample bias coefficient ρ. The unbiased standard error plots as the ρ = 0 diagonal line with log-log slope −½.

If values of the measured quantity A are not statistically independent but have been obtained from known locations in parameter space x, an unbiased estimate of the true standard error of the mean (actually a correction on the standard deviation part) may be obtained by multiplying the calculated standard error of the sample by the factor f:

f={sqrt {frac {1+rho }{1-rho }}},

where the sample bias coefficient ρ is the widely used Prais–Winsten estimate of the autocorrelation-coefficient (a quantity between −1 and +1) for all sample point pairs. This approximate formula is for moderate to large sample sizes; the reference gives the exact formulas for any sample size, and can be applied to heavily autocorrelated time series like Wall Street stock quotes. Moreover, this formula works for positive and negative ρ alike.[11] See also unbiased estimation of standard deviation for more discussion.

See also[edit]

  • Illustration of the central limit theorem
  • Margin of error
  • Probable error
  • Standard error of the weighted mean
  • Sample mean and sample covariance
  • Standard error of the median
  • Variance
  • Variance of the mean and predicted responses

References[edit]

  1. ^ a b c d Altman, Douglas G; Bland, J Martin (2005-10-15). «Standard deviations and standard errors». BMJ: British Medical Journal. 331 (7521): 903. doi:10.1136/bmj.331.7521.903. ISSN 0959-8138. PMC 1255808. PMID 16223828.
  2. ^ Everitt, B. S. (2003). The Cambridge Dictionary of Statistics. CUP. ISBN 978-0-521-81099-9.
  3. ^ Gurland, J; Tripathi RC (1971). «A simple approximation for unbiased estimation of the standard deviation». American Statistician. 25 (4): 30–32. doi:10.2307/2682923. JSTOR 2682923.
  4. ^ Sokal; Rohlf (1981). Biometry: Principles and Practice of Statistics in Biological Research (2nd ed.). p. 53. ISBN 978-0-7167-1254-1.
  5. ^ Hutchinson, T. P. (1993). Essentials of Statistical Methods, in 41 pages. Adelaide: Rumsby. ISBN 978-0-646-12621-0.
  6. ^ Cornell, J R, and Benjamin, C A, Probability, Statistics, and Decisions for Civil Engineers, McGraw-Hill, NY, 1970, ISBN 0486796094, pp. 178–9.
  7. ^ Barde, M. (2012). «What to use to express the variability of data: Standard deviation or standard error of mean?». Perspect. Clin. Res. 3 (3): 113–116. doi:10.4103/2229-3485.100662. PMC 3487226. PMID 23125963.
  8. ^ Wassertheil-Smoller, Sylvia (1995). Biostatistics and Epidemiology : A Primer for Health Professionals (Second ed.). New York: Springer. pp. 40–43. ISBN 0-387-94388-9.
  9. ^ Isserlis, L. (1918). «On the value of a mean as calculated from a sample». Journal of the Royal Statistical Society. 81 (1): 75–81. doi:10.2307/2340569. JSTOR 2340569. (Equation 1)
  10. ^ Bondy, Warren; Zlot, William (1976). «The Standard Error of the Mean and the Difference Between Means for Finite Populations». The American Statistician. 30 (2): 96–97. doi:10.1080/00031305.1976.10479149. JSTOR 2683803. (Equation 2)
  11. ^ Bence, James R. (1995). «Analysis of Short Time Series: Correcting for Autocorrelation». Ecology. 76 (2): 628–639. doi:10.2307/1941218. JSTOR 1941218.

Стандартное отклонение и стандартная ошибка: в чем разница?

  • Редакция Кодкампа

17 авг. 2022 г.
читать 2 мин

В статистике студенты часто путают два термина: стандартное отклонение и стандартная ошибка .

Стандартное отклонение измеряет, насколько разбросаны значения в наборе данных.

Стандартная ошибка — это стандартное отклонение среднего значения в повторных выборках из совокупности.

Давайте рассмотрим пример, чтобы ясно проиллюстрировать эту идею.

Пример: стандартное отклонение против стандартной ошибки

Предположим, мы измеряем вес 10 разных черепах.

Для этой выборки из 10 черепах мы можем вычислить среднее значение выборки и стандартное отклонение выборки:

Предположим, что стандартное отклонение оказалось равным 8,68. Это дает нам представление о том, насколько распределен вес этих черепах.

Но предположим, что мы собираем еще одну простую случайную выборку из 10 черепах и также проводим их измерения. Более чем вероятно, что эта выборка из 10 черепах будет иметь немного другое среднее значение и стандартное отклонение, даже если они взяты из одной и той же популяции:

Теперь, если мы представим, что мы берем повторные выборки из одной и той же совокупности и записываем выборочное среднее и выборочное стандартное отклонение для каждой выборки:

Теперь представьте, что мы наносим каждое среднее значение выборки на одну и ту же строку:

Стандартное отклонение этих средних значений известно как стандартная ошибка.

Формула для фактического расчета стандартной ошибки:

Стандартная ошибка = s/ √n

куда:

  • s: стандартное отклонение выборки
  • n: размер выборки

Какой смысл использовать стандартную ошибку?

Когда мы вычисляем среднее значение данной выборки, нас на самом деле интересует не среднее значение этой конкретной выборки, а скорее среднее значение большей совокупности, из которой взята выборка.

Однако мы используем выборки, потому что для них гораздо проще собирать данные, чем для всего населения. И, конечно же, среднее значение выборки будет варьироваться от выборки к выборке, поэтому мы используем стандартную ошибку среднего значения как способ измерить, насколько точна наша оценка среднего значения.

Вы заметите из формулы для расчета стандартной ошибки, что по мере увеличения размера выборки (n) стандартная ошибка уменьшается:

Стандартная ошибка = s/ √n

Это должно иметь смысл, поскольку большие размеры выборки уменьшают изменчивость и увеличивают вероятность того, что среднее значение нашей выборки ближе к фактическому среднему значению генеральной совокупности.

Когда использовать стандартное отклонение против стандартной ошибки

Если мы просто заинтересованы в измерении того, насколько разбросаны значения в наборе данных, мы можем использовать стандартное отклонение .

Однако, если мы заинтересованы в количественной оценке неопределенности оценки среднего значения, мы можем использовать стандартную ошибку среднего значения .

В зависимости от вашего конкретного сценария и того, чего вы пытаетесь достичь, вы можете использовать либо стандартное отклонение, либо стандартную ошибку.

What Is the Standard Error?

The standard error (SE) of a statistic is the approximate standard deviation of a statistical sample population.

The standard error is a statistical term that measures the accuracy with which a sample distribution represents a population by using standard deviation. In statistics, a sample mean deviates from the actual mean of a population; this deviation is the standard error of the mean.

Key Takeaways

  • The standard error (SE) is the approximate standard deviation of a statistical sample population.
  • The standard error describes the variation between the calculated mean of the population and one which is considered known, or accepted as accurate.
  • The more data points involved in the calculations of the mean, the smaller the standard error tends to be.

Standard Error

Understanding Standard Error

The term «standard error» is used to refer to the standard deviation of various sample statistics, such as the mean or median. For example, the «standard error of the mean» refers to the standard deviation of the distribution of sample means taken from a population. The smaller the standard error, the more representative the sample will be of the overall population.

The relationship between the standard error and the standard deviation is such that, for a given sample size, the standard error equals the standard deviation divided by the square root of the sample size. The standard error is also inversely proportional to the sample size; the larger the sample size, the smaller the standard error because the statistic will approach the actual value.

The standard error is considered part of inferential statistics. It represents the standard deviation of the mean within a dataset. This serves as a measure of variation for random variables, providing a measurement for the spread. The smaller the spread, the more accurate the dataset.

Standard error and standard deviation are measures of variability, while central tendency measures include mean, median, etc.

Formula and Calculation of Standard Error

The standard error of an estimate can be calculated as the standard deviation divided by the square root of the sample size:

SE = σ / √n

where

  • σ = the population standard deviation
  • √n = the square root of the sample size

If the population standard deviation is not known, you can substitute the sample standard deviation, s, in the numerator to approximate the standard error.

Requirements for Standard Error 

When a population is sampled, the mean, or average, is generally calculated. The standard error can include the variation between the calculated mean of the population and one which is considered known, or accepted as accurate. This helps compensate for any incidental inaccuracies related to the gathering of the sample.

In cases where multiple samples are collected, the mean of each sample may vary slightly from the others, creating a spread among the variables. This spread is most often measured as the standard error, accounting for the differences between the means across the datasets.

The more data points involved in the calculations of the mean, the smaller the standard error tends to be. When the standard error is small, the data is said to be more representative of the true mean. In cases where the standard error is large, the data may have some notable irregularities.

The standard deviation is a representation of the spread of each of the data points. The standard deviation is used to help determine the validity of the data based on the number of data points displayed at each level of standard deviation. Standard errors function more as a way to determine the accuracy of the sample or the accuracy of multiple samples by analyzing deviation within the means.

Standard Error vs. Standard Deviation

The standard error normalizes the standard deviation relative to the sample size used in an analysis. Standard deviation measures the amount of variance or dispersion of the data spread around the mean. The standard error can be thought of as the dispersion of the sample mean estimations around the true population mean. As the sample size becomes larger, the standard error will become smaller, indicating that the estimated sample mean value better approximates the population mean.

Example of Standard Error

Say that an analyst has looked at a random sample of 50 companies in the S&P 500 to understand the association between a stock’s P/E ratio and subsequent 12-month performance in the market. Assume that the resulting estimate is -0.20, indicating that for every 1.0 point in the P/E ratio, stocks return 0.2% poorer relative performance. In the sample of 50, the standard deviation was found to be 1.0.

The standard error is thus:

SE = 1.0/√50 = 1/7.07 = 0.141

Therefore, we would report the estimate as -0.20% ± 0.14, giving us a confidence interval of (-0.34 — -0.06). The true mean value of the association of the P/E on returns of the S&P 500 would therefore fall within that range with a high degree of probability.

Say now that we increase the sample of stocks to 100 and find that the estimate changes slightly from -0.20 to -0.25, and the standard deviation falls to 0.90. The new standard error would thus be:

SE = 0.90/√100 = 0.90/10 = 0.09.

The resulting confidence interval becomes -0.25 ± 0.09 = (-0.34 — -0.16), which is a tighter range of values.

What Is Meant by Standard Error?

Standard error is intuitively the standard deviation of the sampling distribution. In other words, it depicts how much disparity there is likely to be in a point estimate obtained from a sample relative to the true population mean.

What Is a Good Standard Error?

Standard error measures the amount of discrepancy that can be expected in a sample estimate compared to the true value in the population. Therefore, the smaller the standard error the better. In fact, a standard error of zero (or close to it) would indicate that the estimated value is exactly the true value.

How Do You Find the Standard Error?

The standard error takes the standard deviation and divides it by the square root of the sample size. Many statistical software packages automatically compute standard errors.

The Bottom Line

The standard error (SE) measures the dispersion of estimated values obtained from a sample around the true value to be found in the population. Statistical analysis and inference often involves drawing samples and running statistical tests to determine associations and correlations between variables. The standard error thus tells us with what degree of confidence we can expect the estimated value to approximate the population value.


Загрузить PDF


Загрузить PDF

Стандартной ошибкой называется величина, которая характеризует стандартное (среднеквадратическое) отклонение выборочного среднего. Другими словами, эту величину можно использовать для оценки точности выборочного среднего. Множество областей применения стандартной ошибки по умолчанию предполагают нормальное распределение. Если вам нужно рассчитать стандартную ошибку, перейдите к шагу 1.

  1. Изображение с названием Calculate Standard Error Step 1

    1

    Запомните определение среднеквадратического отклонения. Среднеквадратическое отклонение выборки – это мера рассеянности значения. Среднеквадратическое отклонение выборки обычно обозначается буквой s. Математическая формула среднеквадратического отклонения приведена выше.

  2. Изображение с названием Calculate Standard Error Step 2

    2

    Узнайте, что такое истинное среднее значение. Истинное среднее является средним группы чисел, включающим все числа всей группы – другими словами, это среднее всей группы чисел, а не выборки.

  3. Изображение с названием Calculate Standard Error Step 3

    3

    Научитесь рассчитывать среднеарифметическое значение. Среднеаримфетическое означает попросту среднее: сумму значений собранных данных, разделенную на количество значений этих данных.

  4. Изображение с названием Calculate Standard Error Step 4

    4

    Узнайте, что такое выборочное среднее. Когда среднеарифметическое значение основано на серии наблюдений, полученных в результате выборок из статистической совокупности, оно называется “выборочным средним”. Это среднее выборки чисел, которое описывает среднее значение лишь части чисел из всей группы. Его обозначают как:

  5. Изображение с названием Calculate Standard Error Step 5

    5

    Усвойте понятие нормального распределения. Нормальные распределения, которые используются чаще других распределений, являются симметричными, с единичным максимумом в центре – на среднем значении данных. Форма кривой подобна очертаниям колокола, при этом график равномерно опускается по обе стороны от среднего. Пятьдесят процентов распределения лежит слева от среднего, а другие пятьдесят процентов – справа от него. Рассеянность значений нормального распределения описывается стандартным отклонением.

  6. Изображение с названием Calculate Standard Error Step 6

    6

    Запомните основную формулу. Формула для вычисления стандартной ошибки приведена выше.

    Реклама

  1. Изображение с названием Calculate Standard Error Step 7

    1

    Рассчитайте выборочное среднее. Чтобы найти стандартную ошибку, сначала нужно определить среднеквадратическое отклонение (поскольку среднеквадратическое отклонение s входит в формулу для вычисления стандартной ошибки). Начните с нахождения средних значений. Выборочное среднее выражается как среднее арифметическое измерений x1, x2, . . . , xn. Его рассчитывают по формуле, приведенной выше.

    • Допустим, например, что вам нужно рассчитать стандартную ошибку выборочного среднего результатов измерения массы пяти монет, указанных в таблице:
      Вы сможете рассчитать выборочное среднее, подставив значения массы в формулу:

  2. Изображение с названием Calculate Standard Error Step 8

    2

    Вычтите выборочное среднее из каждого измерения и возведите полученное значение в квадрат. Как только вы получите выборочное среднее, вы можете расширить вашу таблицу, вычтя его из каждого измерения и возведя результат в квадрат.

    • Для нашего примера расширенная таблица будет иметь следующий вид:

  3. Изображение с названием Calculate Standard Error Step 9

    3

    Найдите суммарное отклонение ваших измерений от выборочного среднего. Общее отклонение – это сумма возведенных в квадрат разностей от выборочного среднего. Чтобы определить его, сложите ваши новые значения.

    • В нашем примере нужно будет выполнить следующий расчет:
      Это уравнение дает сумму квадратов отклонений измерений от выборочного среднего.

  4. Изображение с названием Calculate Standard Error Step 10

    4

    Рассчитайте среднеквадратическое отклонение ваших измерений от выборочного среднего. Как только вы будете знать суммарное отклонение, вы сможете найти среднее отклонение, разделив ответ на n -1. Обратите внимание, что n равно числу измерений.

    • В нашем примере было сделано 5 измерений, следовательно n – 1 будет равно 4. Расчет нужно вести следующим образом:

  5. Изображение с названием Calculate Standard Error Step 11

    5

    Найдите среднеквадратичное отклонение. Сейчас у вас есть все необходимые значения для того, чтобы воспользоваться формулой для нахождения среднеквадратичного отклонения s.

    • В нашем примере вы будете рассчитывать среднеквадратичное отклонение следующим образом:
      Следовательно, среднеквадратичное отклонение равно 0,0071624.

    Реклама

  1. Изображение с названием Calculate Standard Error Step 12

    1

    Чтобы вычислить стандартную ошибку, воспользуйтесь базовой формулой со среднеквадратическим отклонением.

    • В нашем примере вы сможете рассчитать стандартную ошибку следующим образом:
      Таким образом в нашем примере стандартная ошибка (среднеквадратическое отклонение выборочного среднего) составляет 0,0032031 грамма.

Советы

  • Стандартную ошибку и среднеквадратическое отклонение часто путают. Обратите внимание, что стандартная ошибка описывает среднеквадратическое отклонение выборочного распределения статистических данных, а не распределения отдельных значений
  • В научных журналах понятия стандартной ошибки и среднеквадратического отклонения несколько размыты. Для объединения двух величин используется знак ±.

Реклама

Об этой статье

Эту страницу просматривали 48 972 раза.

Была ли эта статья полезной?

Источник

Стандартное отклонение (SD), измеряет количество изменчивости или дисперсии, из отдельных значений данных, к среднему значению, в то время как стандартная ошибка среднего (SEM) мер, как далеко образец среднее (среднее) данных, вероятно, будет от истинного среднего значения населения. SEM всегда меньше SD.

Ключевые выводы

  • Стандартное отклонение (SD) измеряет разброс набора данных относительно его среднего значения.
  • Стандартная ошибка среднего (SEM) измеряет, насколько вероятно расхождение между средним значением выборки по сравнению со средним значением генеральной совокупности.
  • SEM берет SD и делит его на квадратный корень из размера выборки.

SEM против SD

Стандартное отклонение и стандартная ошибка используются во всех типах статистических исследований, включая исследования в области финансов, медицины, биологии, инженерии, психологии и т. Д. В этих исследованиях стандартное отклонение (SD) и расчетная стандартная ошибка среднего (SEM) ) используются для представления характеристик данных выборки и объяснения результатов статистического анализа. Однако некоторые исследователи иногда путают SD и SEM. Таким исследователям следует помнить, что расчеты SD и SEM включают разные статистические выводы, каждый из которых имеет свое значение. SD — это разброс отдельных значений данных.

Другими словами, SD указывает, насколько точно среднее значение представляет данные выборки. Однако значение SEM включает статистический вывод, основанный на распределении выборки. SEM — это стандартное отклонение теоретического распределения выборочных средних (выборочное распределение).

Расчет стандартного отклонения

Формула SD требует нескольких шагов:

  1. Во-первых, возьмите квадрат разницы между каждой точкой данных и средним значением выборки, найдя сумму этих значений.
  2. Затем разделите эту сумму на размер выборки минус один, который представляет собой дисперсию.
  3. Наконец, извлеките квадратный корень из дисперсии, чтобы получить стандартное отклонение.

Стандартная ошибка среднего

SEM рассчитывается путем деления стандартного отклонения на квадратный корень из размера выборки.

Стандартная ошибка дает точность выборочного среднего путем измерения изменчивости выборочного среднего от образца к образцу. SEM описывает, насколько точное среднее значение выборки является оценкой истинного среднего значения совокупности. По мере увеличения размера выборки данных SEM уменьшается по сравнению с SD; следовательно, по мере увеличения размера выборки среднее значение выборки оценивает истинное среднее значение генеральной совокупности с большей точностью. Напротив, увеличение размера выборки не обязательно делает SD больше или меньше, это просто становится более точной оценкой SD населения.

Стандартная ошибка и стандартное отклонение в финансах

В финансах стандартная ошибка средней дневной доходности актива измеряет точность выборочного среднего как оценки долгосрочной (постоянной) средней дневной доходности актива.

С другой стороны, стандартное отклонение доходности измеряет отклонения индивидуальных доходов от среднего значения. Таким образом, SD является мерой волатильности и может использоваться в качестве меры риска для инвестиций. Активы с более высокими ежедневными движениями цен имеют более высокое SD, чем активы с меньшими ежедневными движениями. Предполагая нормальное распределение, около 68% дневных изменений цен находятся в пределах одного стандартного отклонения от среднего, при этом около 95% дневных изменений цен находятся в пределах двух стандартных значений среднего.

Источник

Понравилась статья? Поделить с друзьями:
  • Стандартная ошибка модели значения
  • Стандартная ошибка среднего пример
  • Стандартная ошибка разности выборочных средних
  • Стандартная ошибка для коэффициента корреляции
  • Стандартная ошибка среднего показывает