Стандартная ошибка среднего показывает - Решение и исправление самых разных ошибок на TopOshibok.ru

From Wikipedia, the free encyclopedia

For a value that is sampled with an unbiased normally distributed error, the above depicts the proportion of samples that would fall between 0, 1, 2, and 3 standard deviations above and below the actual value.

The standard error (SE)^[1] of a statistic (usually an estimate of a parameter) is the standard deviation of its sampling distribution^[2] or an estimate of that standard deviation. If the statistic is the sample mean, it is called the standard error of the mean (SEM).^[1]

The sampling distribution of a mean is generated by repeated sampling from the same population and recording of the sample means obtained. This forms a distribution of different means, and this distribution has its own mean and variance. Mathematically, the variance of the sampling mean distribution obtained is equal to the variance of the population divided by the sample size. This is because as the sample size increases, sample means cluster more closely around the population mean.

Therefore, the relationship between the standard error of the mean and the standard deviation is such that, for a given sample size, the standard error of the mean equals the standard deviation divided by the square root of the sample size.^[1] In other words, the standard error of the mean is a measure of the dispersion of sample means around the population mean.

In regression analysis, the term «standard error» refers either to the square root of the reduced chi-squared statistic or the standard error for a particular regression coefficient (as used in, say, confidence intervals).

Standard error of the sample mean[edit]

Exact value[edit]

Suppose a statistically independent sample of observations $x_{1},x_{2},\ldots ,x_{n}$ is taken from a statistical population with a standard deviation of $\sigma$ . The mean value calculated from the sample, ${\bar {x}}$ , will have an associated standard error on the mean, ${\sigma }_{\bar {x}}$ , given by:^[1]

${\sigma }_{\bar {x}}={\frac {\sigma }{\sqrt {n}}}.$

Practically this tells us that when trying to estimate the value of a population mean, due to the factor $1/{\sqrt {n}}$ , reducing the error on the estimate by a factor of two requires acquiring four times as many observations in the sample; reducing it by a factor of ten requires a hundred times as many observations.

Estimate[edit]

The standard deviation $\sigma$ of the population being sampled is seldom known. Therefore, the standard error of the mean is usually estimated by replacing $\sigma$ with the sample standard deviation $\sigma _{x}$ instead:

${\sigma }_{\bar {x}}\ \approx {\frac {\sigma _{x}}{\sqrt {n}}}.$

As this is only an estimator for the true «standard error», it is common to see other notations here such as:

${\widehat {\sigma }}_{\bar {x}}:={\frac {\sigma _{x}}{\sqrt {n}}}\qquad {\text{ or }}\qquad {s}_{\bar {x}}\ :={\frac {s}{\sqrt {n}}}.$

A common source of confusion occurs when failing to distinguish clearly between:

Accuracy of the estimator[edit]

When the sample size is small, using the standard deviation of the sample instead of the true standard deviation of the population will tend to systematically underestimate the population standard deviation, and therefore also the standard error. With n = 2, the underestimate is about 25%, but for n = 6, the underestimate is only 5%. Gurland and Tripathi (1971) provide a correction and equation for this effect.^[3] Sokal and Rohlf (1981) give an equation of the correction factor for small samples of n < 20.^[4] See unbiased estimation of standard deviation for further discussion.

Derivation[edit]

The standard error on the mean may be derived from the variance of a sum of independent random variables,^[5] given the definition of variance and some simple properties thereof. If $x_{1},x_{2},\ldots ,x_{n}$ is a sample of independent observations from a population with mean ${\bar {x}}$ and standard deviation $\sigma$ , then we can define the total

$T=(x_{1}+x_{2}+\cdots +x_{n})$

which due to the Bienaymé formula, will have variance

$\operatorname {Var} (T)={\big (}\operatorname {Var} (x_{1})+\operatorname {Var} (x_{2})+\cdots +\operatorname {Var} (x_{n}){\big )}=n\sigma ^{2}.$

where we’ve approximated the standard deviations, i.e., the uncertainties, of the measurements themselves with the best value for the standard deviation of the population. The mean of these measurements ${\bar {x}}$ is simply given by

${\bar {x}}=T/n.$

The variance of the mean is then

$\operatorname {Var} ({\bar {x}})=\operatorname {Var} \left({\frac {T}{n}}\right)={\frac {1}{n^{2}}}\operatorname {Var} (T)={\frac {1}{n^{2}}}n\sigma ^{2}={\frac {\sigma ^{2}}{n}}.$

The standard error is, by definition, the standard deviation of ${\bar {x}}$ which is simply the square root of the variance:

$\sigma _{\bar {x}}={\sqrt {\frac {\sigma ^{2}}{n}}}={\frac {\sigma }{\sqrt {n}}}.$

For correlated random variables the sample variance needs to be computed according to the Markov chain central limit theorem.

Independent and identically distributed random variables with random sample size[edit]

There are cases when a sample is taken without knowing, in advance, how many observations will be acceptable according to some criterion. In such cases, the sample size is a random variable whose variation adds to the variation of such that,

$\operatorname {Var} (T)=\operatorname {E} (N)\operatorname {Var} (X)+\operatorname {Var} (N){\big (}\operatorname {E} (X){\big )}^{2}$

^[6]
which follows from the law of total variance.

If has a Poisson distribution, then $\operatorname {E} (N)=\operatorname {Var} (N)$ with estimator $n=N$ . Hence the estimator of $\operatorname {Var} (T)$ becomes $nS_{X}^{2}+n{\bar {X}}^{2}$ , leading the following formula for standard error:

$\operatorname {Standard~Error} ({\bar {X}})={\sqrt {\frac {S_{X}^{2}+{\bar {X}}^{2}}{n}}}$

(since the standard deviation is the square root of the variance).

Student approximation when σ value is unknown[edit]

In many practical applications, the true value of σ is unknown. As a result, we need to use a distribution that takes into account that spread of possible σ’s.
When the true underlying distribution is known to be Gaussian, although with unknown σ, then the resulting estimated distribution follows the Student t-distribution. The standard error is the standard deviation of the Student t-distribution. T-distributions are slightly different from Gaussian, and vary depending on the size of the sample. Small samples are somewhat more likely to underestimate the population standard deviation and have a mean that differs from the true population mean, and the Student t-distribution accounts for the probability of these events with somewhat heavier tails compared to a Gaussian. To estimate the standard error of a Student t-distribution it is sufficient to use the sample standard deviation «s» instead of σ, and we could use this value to calculate confidence intervals.

Note: The Student’s probability distribution is approximated well by the Gaussian distribution when the sample size is over 100. For such samples one can use the latter distribution, which is much simpler.

Assumptions and usage[edit]

An example of how $\operatorname {SE}$ is used is to make confidence intervals of the unknown population mean. If the sampling distribution is normally distributed, the sample mean, the standard error, and the quantiles of the normal distribution can be used to calculate confidence intervals for the true population mean. The following expressions can be used to calculate the upper and lower 95% confidence limits, where ${\bar {x}}$ is equal to the sample mean, $\operatorname {SE}$ is equal to the standard error for the sample mean, and 1.96 is the approximate value of the 97.5 percentile point of the normal distribution:

In particular, the standard error of a sample statistic (such as sample mean) is the actual or estimated standard deviation of the sample mean in the process by which it was generated. In other words, it is the actual or estimated standard deviation of the sampling distribution of the sample statistic. The notation for standard error can be any one of SE, SEM (for standard error of measurement or mean), or S_E.

Standard errors provide simple measures of uncertainty in a value and are often used because:

in many cases, if the standard error of several individual quantities is known then the standard error of some function of the quantities can be easily calculated;
when the probability distribution of the value is known, it can be used to calculate an exact confidence interval;
when the probability distribution is unknown, Chebyshev’s or the Vysochanskiï–Petunin inequalities can be used to calculate a conservative confidence interval; and
as the sample size tends to infinity the central limit theorem guarantees that the sampling distribution of the mean is asymptotically normal.

Standard error of mean versus standard deviation[edit]

In scientific and technical literature, experimental data are often summarized either using the mean and standard deviation of the sample data or the mean with the standard error. This often leads to confusion about their interchangeability. However, the mean and standard deviation are descriptive statistics, whereas the standard error of the mean is descriptive of the random sampling process. The standard deviation of the sample data is a description of the variation in measurements, while the standard error of the mean is a probabilistic statement about how the sample size will provide a better bound on estimates of the population mean, in light of the central limit theorem.^[7]

Put simply, the standard error of the sample mean is an estimate of how far the sample mean is likely to be from the population mean, whereas the standard deviation of the sample is the degree to which individuals within the sample differ from the sample mean.^[8] If the population standard deviation is finite, the standard error of the mean of the sample will tend to zero with increasing sample size, because the estimate of the population mean will improve, while the standard deviation of the sample will tend to approximate the population standard deviation as the sample size increases.

Extensions[edit]

Finite population correction (FPC)[edit]

The formula given above for the standard error assumes that the population is infinite. Nonetheless, it is often used for finite populations when people are interested in measuring the process that created the existing finite population (this is called an analytic study). Though the above formula is not exactly correct when the population is finite, the difference between the finite- and infinite-population versions will be small when sampling fraction is small (e.g. a small proportion of a finite population is studied). In this case people often do not correct for the finite population, essentially treating it as an «approximately infinite» population.

If one is interested in measuring an existing finite population that will not change over time, then it is necessary to adjust for the population size (called an enumerative study). When the sampling fraction (often termed f) is large (approximately at 5% or more) in an enumerative study, the estimate of the standard error must be corrected by multiplying by a »finite population correction» (a.k.a.: FPC):^[9]
^[10]

$\operatorname {FPC} ={\sqrt {\frac {N-n}{N-1}}}$

which, for large N:

$\operatorname {FPC} \approx {\sqrt {1-{\frac {n}{N}}}}={\sqrt {1-f}}$

to account for the added precision gained by sampling close to a larger percentage of the population. The effect of the FPC is that the error becomes zero when the sample size n is equal to the population size N.

This happens in survey methodology when sampling without replacement. If sampling with replacement, then FPC does not come into play.

Correction for correlation in the sample[edit]

Expected error in the mean of A for a sample of n data points with sample bias coefficient ρ. The unbiased standard error plots as the ρ = 0 diagonal line with log-log slope −1⁄2.

If values of the measured quantity A are not statistically independent but have been obtained from known locations in parameter space x, an unbiased estimate of the true standard error of the mean (actually a correction on the standard deviation part) may be obtained by multiplying the calculated standard error of the sample by the factor f:

$f={\sqrt {\frac {1+\rho }{1-\rho }}},$

where the sample bias coefficient ρ is the widely used Prais–Winsten estimate of the autocorrelation-coefficient (a quantity between −1 and +1) for all sample point pairs. This approximate formula is for moderate to large sample sizes; the reference gives the exact formulas for any sample size, and can be applied to heavily autocorrelated time series like Wall Street stock quotes. Moreover, this formula works for positive and negative ρ alike.^[11] See also unbiased estimation of standard deviation for more discussion.

References[edit]

^ ^a ^b ^c ^d Altman, Douglas G; Bland, J Martin (2005-10-15). «Standard deviations and standard errors». BMJ: British Medical Journal. 331 (7521): 903. doi:10.1136/bmj.331.7521.903. ISSN 0959-8138. PMC 1255808. PMID 16223828.
^ Everitt, B. S. (2003). The Cambridge Dictionary of Statistics. Cambridge University Press. ISBN 978-0-521-81099-9.
^ Gurland, J; Tripathi RC (1971). «A simple approximation for unbiased estimation of the standard deviation». American Statistician. 25 (4): 30–32. doi:10.2307/2682923. JSTOR 2682923.
^ Sokal; Rohlf (1981). Biometry: Principles and Practice of Statistics in Biological Research (2nd ed.). p. 53. ISBN 978-0-7167-1254-1.
^ Hutchinson, T. P. (1993). Essentials of Statistical Methods, in 41 pages. Adelaide: Rumsby. ISBN 978-0-646-12621-0.
^ Cornell, J R; Benjamin, C A (1970). Probability, Statistics, and Decisions for Civil Engineers. NY: McGraw-Hill. pp. 178–179. ISBN 0486796094.
^ Barde, M. (2012). «What to use to express the variability of data: Standard deviation or standard error of mean?». Perspect. Clin. Res. 3 (3): 113–116. doi:10.4103/2229-3485.100662. PMC 3487226. PMID 23125963.
^ Wassertheil-Smoller, Sylvia (1995). Biostatistics and Epidemiology : A Primer for Health Professionals (Second ed.). New York: Springer. pp. 40–43. ISBN 0-387-94388-9.
^ Isserlis, L. (1918). «On the value of a mean as calculated from a sample». Journal of the Royal Statistical Society. 81 (1): 75–81. doi:10.2307/2340569. JSTOR 2340569. (Equation 1)
^ Bondy, Warren; Zlot, William (1976). «The Standard Error of the Mean and the Difference Between Means for Finite Populations». The American Statistician. 30 (2): 96–97. doi:10.1080/00031305.1976.10479149. JSTOR 2683803. (Equation 2)
^ Bence, James R. (1995). «Analysis of Short Time Series: Correcting for Autocorrelation». Ecology. 76 (2): 628–639. doi:10.2307/1941218. JSTOR 1941218.

Источник

Представление результатов исследования

В научных публикациях важно представление результатов исследования. Очень часто окончательный результат приводится в следующем виде: M±m, где M – среднее арифметическое, m –ошибка среднего арифметического. Например, 163,7±0,9 см.

Прежде чем разбираться в правилах представления результатов исследования, давайте точно усвоим, что же такое ошибка среднего арифметического.

Ошибка среднего арифметического

Среднее арифметическое, вычисленное на основе выборочных данных (выборочное среднее), как правило, не совпадает с генеральным средним (средним арифметическим генеральной совокупности). Экспериментально проверить это утверждение невозможно, потому что нам неизвестно генеральное среднее. Но если из одной и той же генеральной совокупности брать повторные выборки и вычислять среднее арифметическое, то окажется, что для разных выборок среднее арифметическое будет разным.

Чтобы оценить, насколько выборочное среднее арифметическое отличается от генерального среднего, вычисляется ошибка среднего арифметического или ошибка репрезентативности.

Ошибка среднего арифметического обозначается как m или

Ошибка среднего арифметического рассчитывается по формуле:

где: S — стандартное отклонение, n – объем выборки; Например, если стандартное отклонение равно S=5 см, объем выборки n=36 человек, то ошибка среднего арифметического равна: m=5/6 = 0,833.

Ошибка среднего арифметического показывает, какая ошибка в среднем допускается, если использовать вместо генерального среднего выборочное среднее.

Так как при небольшом объеме выборки истинное значение генерального среднего не может быть определено сколь угодно точно, поэтому при вычислении выборочного среднего арифметического нет смысла оставлять большое число значащих цифр.

Правила записи результатов исследования

В записи ошибки среднего арифметического оставляем две значащие цифры, если первые цифры в ошибке «1» или «2».
В остальных случаях в записи ошибки среднего арифметического оставляем одну значащую цифру.
В записи среднего арифметического положение последней значащей цифры должно соответствовать положению первой значащей цифры в записи ошибки среднего арифметического.

Представление результатов научных исследований

В своей статье «Осторожно, статистика!», опубликованной в 1989 году В.М. Зациорский указал, какие числовые характеристики должны быть представлены в публикации, чтобы она имела научную ценность. Он писал, что исследователь «…должен назвать: 1) среднюю величину (или другой так называемый показатель положения); 2) среднее квадратическое отклонение (или другой показатель рассеяния) и 3) число испытуемых. Без них его публикация научной ценности иметь не будет “с. 52

В научных публикациях в области физической культуры и спорта очень часто окончательный результат приводится в виде: (М±m) (табл.1).

Таблица 1 — Изменение механических свойств латеральной широкой мышцы бедра под воздействием физической нагрузки (n=34)

	Эффективный модуль упругости (Е), кПа	Эффективный модуль вязкости (V), Па с
Этап эксперимента	Рассл.	Напряж.	Рассл.	Напряж.
До ФН	7,0±0,3	17,1±1,4	29,7±1,7	46±4
После ФН	7,7±0,3	18,7±1,4	30,9±2,0	53±6

Литература

Высшая математика и математическая статистика: учебное пособие для вузов / Под общ. ред. Г. И. Попова. – М. Физическая культура, 2007.– 368 с.
Гласс Дж., Стэнли Дж. Статистические методы в педагогике и психологии. М.: Прогресс. 1976.- 495 с.
Зациорский В.М. Осторожно — статистика! // Теория и практика физической культуры, 1989.- №2.
Катранов А.Г. Компьютерная обработка данных экспериментальных исследований: Учебное пособие/ А. Г. Катранов, А. В. Самсонова; СПб ГУФК им. П.Ф. Лесгафта. – СПб.: изд-во СПб ГУФК им. П.Ф. Лесгафта, 2005. – 131 с.
Основы математической статистики: Учебное пособие для ин-тов физ. культ / Под ред. В.С. Иванова.– М.: Физкультура и спорт, 1990. 176 с.

Источник

Стандартное отклонение и стандартная ошибка: в чем разница?

17 авг. 2022 г.
читать 2 мин

В статистике студенты часто путают два термина: стандартное отклонение и стандартная ошибка .

Стандартное отклонение измеряет, насколько разбросаны значения в наборе данных.

Стандартная ошибка — это стандартное отклонение среднего значения в повторных выборках из совокупности.

Давайте рассмотрим пример, чтобы ясно проиллюстрировать эту идею.

Пример: стандартное отклонение против стандартной ошибки

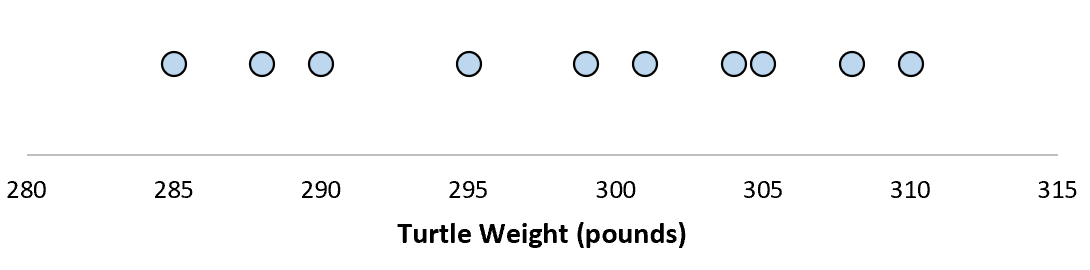
Предположим, мы измеряем вес 10 разных черепах.

Для этой выборки из 10 черепах мы можем вычислить среднее значение выборки и стандартное отклонение выборки:

Предположим, что стандартное отклонение оказалось равным 8,68. Это дает нам представление о том, насколько распределен вес этих черепах.

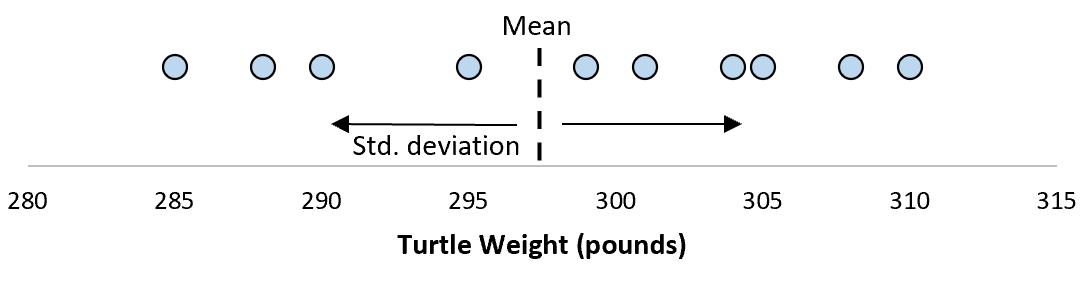
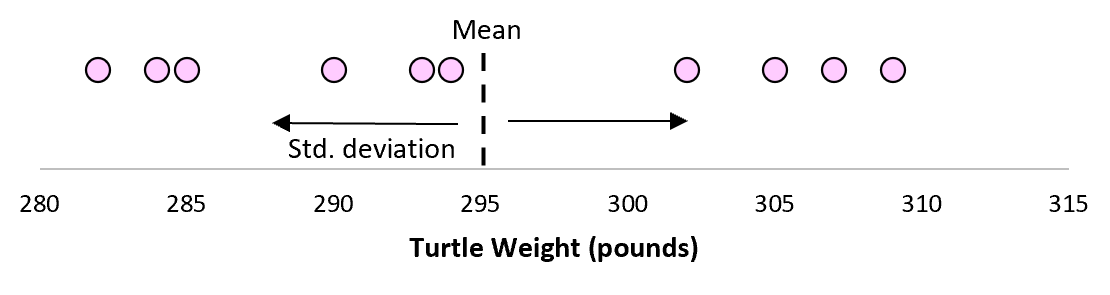
Но предположим, что мы собираем еще одну простую случайную выборку из 10 черепах и также проводим их измерения. Более чем вероятно, что эта выборка из 10 черепах будет иметь немного другое среднее значение и стандартное отклонение, даже если они взяты из одной и той же популяции:

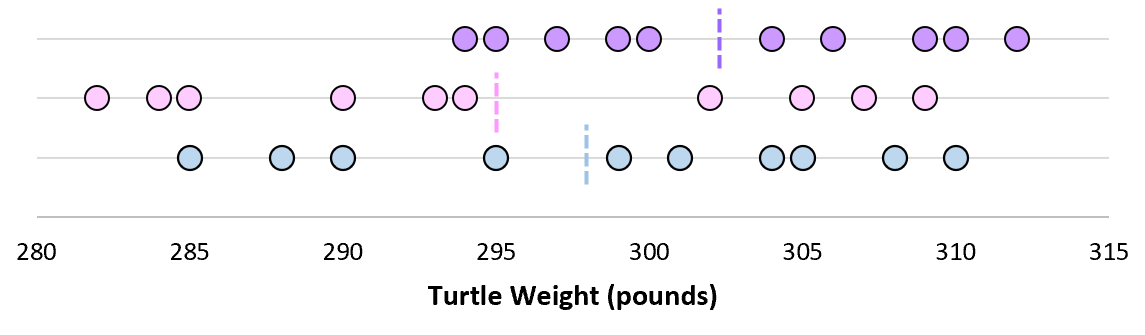
Теперь, если мы представим, что мы берем повторные выборки из одной и той же совокупности и записываем выборочное среднее и выборочное стандартное отклонение для каждой выборки:

Теперь представьте, что мы наносим каждое среднее значение выборки на одну и ту же строку:

Стандартное отклонение этих средних значений известно как стандартная ошибка.

Формула для фактического расчета стандартной ошибки:

Стандартная ошибка = s/ √n

куда:

s: стандартное отклонение выборки
n: размер выборки

Какой смысл использовать стандартную ошибку?

Когда мы вычисляем среднее значение данной выборки, нас на самом деле интересует не среднее значение этой конкретной выборки, а скорее среднее значение большей совокупности, из которой взята выборка.

Однако мы используем выборки, потому что для них гораздо проще собирать данные, чем для всего населения. И, конечно же, среднее значение выборки будет варьироваться от выборки к выборке, поэтому мы используем стандартную ошибку среднего значения как способ измерить, насколько точна наша оценка среднего значения.

Вы заметите из формулы для расчета стандартной ошибки, что по мере увеличения размера выборки (n) стандартная ошибка уменьшается:

Стандартная ошибка = s/ √n

Это должно иметь смысл, поскольку большие размеры выборки уменьшают изменчивость и увеличивают вероятность того, что среднее значение нашей выборки ближе к фактическому среднему значению генеральной совокупности.

Когда использовать стандартное отклонение против стандартной ошибки

Если мы просто заинтересованы в измерении того, насколько разбросаны значения в наборе данных, мы можем использовать стандартное отклонение .

Однако, если мы заинтересованы в количественной оценке неопределенности оценки среднего значения, мы можем использовать стандартную ошибку среднего значения .

В зависимости от вашего конкретного сценария и того, чего вы пытаетесь достичь, вы можете использовать либо стандартное отклонение, либо стандартную ошибку.

Источник

Стандартная ошибка

Стандартная ошибка — это стандартное отклонение выборочного распределения статистики. Этот термин также может использоваться для оценки (хорошего предположения) этого стандартного отклонения, взятого из выборки всей группы.

Среднее значение некоторой части группы (называемой выборкой) является обычным способом оценки среднего значения для всей группы. Часто бывает слишком сложно или стоит слишком много денег, чтобы измерить всю группу. Но если измерить другую выборку, то ее среднее значение будет немного отличаться от первой выборки. Стандартная ошибка среднего — это способ узнать, насколько близка средняя по выборке к средней по всей группе. Это способ узнать, насколько вы можете быть уверены в среднем значении по выборке.

В реальных измерениях истинное значение стандартного отклонения среднего для всей группы обычно неизвестно. Поэтому термин стандартная ошибка часто используется для обозначения близкого к истинному значению для всей группы. Чем больше измерений в выборке, тем ближе к истинному значению для всей группы.

Для значения, отобранного с несмещенной нормально распределенной ошибкой, выше показана доля выборок, которые будут находиться в пределах 0, 1, 2 и 3 стандартных отклонений выше и ниже фактического значения.

Как найти стандартную ошибку среднего значения

Один из способов найти стандартную ошибку среднего — это множество выборок. Сначала находят среднее значение для каждой выборки. Затем находят среднее и стандартное отклонение этих средних по выборкам. Стандартное отклонение для всех средних по выборке и есть стандартная ошибка среднего. Это может быть большой объем работы. Иногда иметь большое количество образцов слишком сложно или стоит слишком много денег.

Другой способ найти стандартную ошибку среднего — использовать уравнение, для которого нужна только одна выборка. Стандартная ошибка среднего обычно оценивается по стандартному отклонению для выборки из всей группы (стандартное отклонение выборки), деленному на квадратный корень из размера выборки.

S E x ¯ = s n {\displaystyle SE_{\bar {x}}\ ={\frac {s}{\sqrt {n}}}} $SE_{\bar {x}}\ ={\frac {s}{\sqrt {n}}}$

где

s — стандартное отклонение выборки (т.е. выборочная оценка стандартного отклонения популяции), и

n — количество измерений в выборке.

Насколько большой должна быть выборка, чтобы оценка стандартной ошибки среднего была близка к фактической стандартной ошибке среднего для всей группы? В выборке должно быть не менее шести измерений. Тогда стандартная ошибка среднего для выборки будет находиться в пределах 5% от стандартной ошибки среднего, если бы измерялась вся группа.

Исправления для некоторых случаев

Существует еще одно уравнение, которое можно использовать, если количество измерений составляет 5% или более от всей группы:

Существуют специальные уравнения, которые необходимо использовать, если образец имеет менее 20 измерений.

Иногда выборка поступает из одного места, хотя вся группа может быть рассредоточена. Кроме того, иногда выборка может быть сделана за короткий промежуток времени, когда вся группа охватывает более длительный период. В этом случае числа в выборке не являются независимыми. Тогда используются специальные уравнения, чтобы попытаться исправить это.

Полезность

Практический результат: Можно быть более уверенным в среднем значении, если провести больше измерений в выборке. Тогда стандартная ошибка среднего значения будет меньше, поскольку стандартное отклонение делится на большее число. Однако, чтобы сделать неопределенность (стандартную ошибку среднего) среднего значения в два раза меньше, размер выборки (n) должен быть в четыре раза больше. Это происходит потому, что стандартное отклонение делится на квадратный корень из размера выборки. Чтобы сделать неопределенность на одну десятую больше, размер выборки (n) должен быть в сто раз больше!

Стандартные ошибки легко вычисляются и часто используются, потому что:

Если известна стандартная ошибка нескольких отдельных величин, то во многих случаях можно легко рассчитать стандартную ошибку некоторой функции этих величин;
Если вероятностное распределение значения известно, его можно использовать для расчета хорошего приближения к точному доверительному интервалу; и
Если распределение вероятности неизвестно, для оценки доверительного интервала можно использовать другие уравнения
Когда размер выборки становится очень большим, принцип центральной предельной теоремы показывает, что числа в выборке очень похожи на числа во всей группе (они имеют нормальное распределение).

Относительная стандартная ошибка

Относительная стандартная ошибка (RSE) — это стандартная ошибка, деленная на среднее значение. Это число меньше единицы. Умножение его на 100% дает его в процентах от среднего значения. Это помогает показать, является ли неопределенность важной или нет. Например, рассмотрим два исследования доходов домохозяйств, в результате которых среднее значение по выборке составляет $50 000. Если стандартная ошибка одного опроса составляет $10 000, а другого — $5 000, то относительные стандартные ошибки равны 20% и 10% соответственно. Опрос с меньшей относительной стандартной ошибкой лучше, потому что он имеет более точное измерение (неопределенность меньше).

На самом деле, люди, которым необходимо знать средние значения, часто решают, насколько мала должна быть неопределенность, прежде чем они решат использовать информацию. Например, Национальный центр статистики здравоохранения США не сообщает среднее значение, если относительная стандартная ошибка превышает 30%. NCHS также требует не менее 30 наблюдений для того, чтобы оценка была представлена в отчете. ^[]

Пример

Например, в воде Мексиканского залива водится много красной рыбы. Чтобы узнать, сколько в среднем весит красноперка длиной 42 см, невозможно измерить всех красноперок длиной 42 см. Вместо этого можно измерить некоторых из них. Рыба, которую измеряют, называется образцом. В таблице показан вес двух образцов красноперки длиной 42 см. Средний (средний) вес первого образца составляет 0,741 кг. Средний (средний) вес второго образца — 0,735 кг, что немного отличается от первого образца. Каждое из этих средних значений немного отличается от среднего значения, которое было бы получено при измерении каждой красной рыбы длиной 42 см (что в любом случае невозможно).

Неопределенность среднего значения можно использовать для того, чтобы узнать, насколько близки средние значения выборок к среднему значению, которое было бы получено в результате измерения всей группы. Неопределенность среднего оценивается как стандартное отклонение для выборки, деленное на квадратный корень из числа выборок минус один. Из таблицы видно, что неопределенности в средних для двух выборок очень близки друг к другу. Кроме того, относительная неопределенность — это неопределенность среднего значения, деленная на среднее значение, умноженное на 100%. Относительная неопределенность в данном примере составляет 2,38% и 2,50% для двух образцов.

Зная неопределенность среднего, можно узнать, насколько близко выборочное среднее к среднему, которое было бы получено в результате измерения всей группы. Среднее по всей группе находится между а) средним по выборке плюс неопределенность в среднем и б) средним по выборке минус неопределенность в среднем. В данном примере средний вес всей красноперки длиной 42 см в Мексиканском заливе, как ожидается, составит 0,723-0,759 кг по первой выборке и 0,717-0,753 по второй выборке.

Пример красной рыбы (также известной как красный барабан, Sciaenops ocellatus), используемой в примере.

Вопросы и ответы

В: Что такое стандартная ошибка?

О: Стандартная ошибка — это стандартное отклонение выборочного распределения статистики.

В: Можно ли использовать термин стандартная ошибка для оценки стандартного отклонения?

О: Да, термин стандартная ошибка может быть использован для оценки (хорошего предположения) этого стандартного отклонения, взятого из выборки всей группы.

В: Как можно оценить среднее значение для всей группы?

О: Среднее значение некоторой части группы (называемой выборкой) — это обычный способ оценки среднего значения для всей группы.

В: Почему трудно измерить всю группу?

О: Часто бывает слишком трудно или слишком дорого измерить всю группу.

В: Что такое стандартная ошибка среднего, и что она определяет?

О: Стандартная ошибка среднего — это способ узнать, насколько близко среднее значение выборки к среднему значению всей группы. Это способ узнать, насколько можно быть уверенным в среднем значении по выборке.

В: Известно ли обычно истинное значение стандартного отклонения среднего при реальных измерениях?

О: Нет, истинное значение стандартного отклонения среднего для всей группы обычно не известно в реальных измерениях.

В: Как количество измерений в выборке влияет на точность оценки?

О: Чем больше измерений в выборке, тем ближе предположение будет к истинному значению для всей группы.

Источник

Что такое Стандартная формула ошибки?

Стандартная ошибка — это ошибка, которая возникает в распределении выборки при выполнении статистического анализа. Это вариант стандартного отклонения, так как оба понятия соответствуют мерам спреда. Высокая стандартная ошибка соответствует более высокому разбросу данных для взятой выборки. Вычисление формулы стандартной ошибки выполняется для выборки. В то же время стандартное отклонение определяет генеральную совокупность.

Оглавление

Что такое Стандартная формула ошибки?
- Объяснение
- Пример формулы стандартной ошибки
- Калькулятор стандартной ошибки
- Актуальность и использование
- Стандартная формула ошибки в Excel
- Рекомендуемые статьи

Следовательно, стандартная ошибка среднего значения будет выражаться и определяться в соответствии с соотношением, описанным следующим образом:

σ͞x = σ/√n

Стандартная формула ошибки

Здесь,

Стандартная ошибка, выраженная как σ͞x.
Стандартное отклонение совокупности выражается как σ.
Количество переменных в выборке, выраженное как n.

В статистическом анализе среднее значение, медиана и мода являются центральной тенденцией. Центральная тенденция Центральная тенденция — это статистическая мера, которая отображает центральную точку всего распределения данных, и вы можете найти ее с помощью 3 различных мер, т. е. среднего, медианы и моды.Подробнее меры. Стандартное отклонение, дисперсия и стандартная ошибка среднего классифицируются как меры изменчивости. Стандартная ошибка среднего для выборочных данных напрямую связана со стандартным отклонением большей совокупности и обратно пропорциональна или связана с квадратным корнем. число. Чтобы использовать эту функцию, введите термин =SQRT и нажмите клавишу табуляции, которая вызовет функцию SQRT. Более того, эта функция принимает один аргумент из нескольких переменных, используемых для создания выборки. Следовательно, если размер выборки Размер выборкиФормула размера выборки отображает соответствующий диапазон генеральной совокупности, в которой проводится эксперимент или опрос. Он измеряется с использованием размера генеральной совокупности, критического значения нормального распределения при требуемом доверительном уровне, доли выборки и предела погрешности. Если больше, то может быть равная вероятность того, что стандартная ошибка также будет большой.

Объяснение

Можно объяснить формулу для стандартной ошибки среднего, используя следующие шаги:

Определите и организуйте выборку и определите количество переменных.
Затем среднее значение выборки соответствует количеству переменных, присутствующих в выборке.
Затем определите стандартное отклонение выборки.
Затем определите квадратный корень из числа переменных, включенных в выборку.
Теперь разделите стандартное отклонение, вычисленное на шаге 3, на полученное значение на шаге 4, чтобы получить стандартную ошибку.

Пример формулы стандартной ошибки

Ниже приведены примеры формул для расчета стандартной ошибки.

.free_excel_div{фон:#d9d9d9;размер шрифта:16px;радиус границы:7px;позиция:относительная;margin:30px;padding:25px 25px 25px 45px}.free_excel_div:before{content:””;фон:url(центр центр без повтора #207245;ширина:70px;высота:70px;позиция:абсолютная;верх:50%;margin-top:-35px;слева:-35px;граница:5px сплошная #fff;граница-радиус:50%} Вы можете скачать этот шаблон стандартной формулы ошибки Excel здесь – Стандартная формула ошибки Шаблон Excel

Пример №1

Возьмем в качестве примера акции ABC. В течение 30 лет акции приносили средний долларовый доход в размере 45 долларов. Кроме того, было замечено, что акции приносят прибыль со стандартным отклонением в 2 доллара. Помогите инвестору рассчитать общую стандартную ошибку средней доходности, предлагаемой акцией ABC.

Решение:

Стандартное отклонение (σ) = $2
Количество лет (n) = 30
Средняя доходность в долларах = 45 долларов.

Расчет стандартной ошибки выглядит следующим образом:

Стандартная формула ошибки — пример 1.2

σ͞x = σ/√n
= 2 доллара США/√30
= 2 доллара США / 5,4773

Стандартная ошибка,

Стандартная формула ошибки — пример 1.3

σx = 0,3651 доллара США

Таким образом, инвестиция предлагает инвестору стандартную долларовую ошибку в среднем 0,36515 доллара при удерживании позиции ABC в течение 30 лет. Однако, если бы акции сохранялись для более высокого инвестиционного горизонта, то стандартная ошибка среднего значения в долларах значительно уменьшилась бы.

Пример #2

Возьмем в качестве примера инвестора, который получил следующую доходность акций XYZ:

Год инвестиций Предлагаемая доходность120%225%35%410%

Помогите инвестору рассчитать общую стандартную ошибку средней доходности акций XYZ.

Решение:

Сначала определите среднее значение доходности, как показано ниже: –

Стандартная формула ошибки — пример 2.2

͞X = (x1+x2+x3+x4)/количество лет
= (20+25+5+10)/4
=15%

Теперь определите стандартное отклонение доходности, как показано ниже: –

Стандартная формула ошибки — пример 2.3

σ = √ ((x1-͞X)2 + (x2-͞X)2 + (x3-͞X)2 + (x4-͞X)2) / √ (количество лет -1)
= √ ((20-15) 2 + (25-15) 2 + (5-15) 2 + (10-15) 2) / √ (4-1)
= (√ (5) 2 + (10) 2 + (-10) 2 + (-5) 2 ) / √ (3)
= (√25+100+100+25)/ √ (3)
=√250/√3
=√83,3333
“=” 9,1287%

Теперь вычисление стандартной ошибки выглядит следующим образом:

Стандартная формула ошибки — пример 2.4

σ͞x = σ/√n
= 9,128709/√4
= 9,128709/2

Стандартная ошибка,

Стандартная формула ошибки — пример 2.5

σx = 4,56%

Таким образом, инвестиции предлагают инвестору стандартную ошибку в долларах в среднем 4,56% при удержании позиции XYZ в течение 4 лет.

Калькулятор стандартной ошибки

Вы можете использовать следующий калькулятор.

.cal-tbl td{ верхняя граница: 0 !важно; }.cal-tbl tr{ высота строки: 0.5em; } Только экран @media и (минимальная ширина устройства: 320 пикселей) и (максимальная ширина устройства: 480 пикселей) { .cal-tbl tr{ line-height: 1em !important; } } σnСтандартная формула ошибки

Формула стандартной ошибки =σ =√n 0 = 0√0

Актуальность и использование

Стандартная ошибка имеет тенденцию быть высокой, если размер выборки для анализа мал. Следовательно, выборка всегда берется из большей совокупности, которая включает больший размер переменных. Это всегда помогает статистику определить достоверность среднего значения выборки относительно среднего значения генеральной совокупности.

Большая стандартная ошибка говорит статистику, что выборка неоднородна в отношении среднего значения генеральной совокупности. Относительно населения наблюдается большой разброс в выборке. Точно так же небольшая стандартная ошибка говорит статистику, что выборка однородна относительно среднего значения генеральной совокупности. Отсутствуют или незначительные различия в выборке относительно населения.

Не следует смешивать его со стандартным отклонением. Вместо этого следует рассчитать стандартное отклонение для всей совокупности. Стандартная ошибкаСтандартная ошибкаСтандартная ошибка (SE) — это метрика, которая измеряет точность выборочного распределения, обозначающего совокупность, с использованием стандартного отклонения. Другими словами, это мера дисперсии среднего значения выборки, связанная со средним значением генеральной совокупности, а не стандартное отклонение. С другой стороны, оно определяется для среднего значения выборки.

Стандартная формула ошибки в Excel

Теперь давайте возьмем пример Excel, чтобы проиллюстрировать концепцию стандартной формулы ошибки в шаблоне Excel ниже. Предположим, администрация школы хочет определить стандартную ошибку среднего значения роста футболистов.

Выборка состоит из следующих значений: –

Пример 3.1

Помогите администрации оценить стандартную ошибку среднего значения.

Шаг 1: Определите среднее значение, как показано ниже: –

Пример 3.2

Шаг 2: Определите стандартное отклонение, как показано ниже: –

Пример 3.3

Шаг 3: Определите стандартную ошибку среднего значения, как показано ниже: –

Пример 3.4

Следовательно, стандартная ошибка среднего значения для футболистов составляет 1,846 дюйма. Руководство должно заметить, что оно значительно велико. Таким образом, выборочные данные, взятые для анализа, неоднородны и имеют большую дисперсию.

Руководству следует либо исключить более мелких игроков, либо добавить игроков значительно выше, чтобы сбалансировать средний рост футбольной команды, заменив их людьми с меньшим ростом по сравнению с их сверстниками.

Standard error of the sample mean[edit]

Exact value[edit]

Estimate[edit]

Accuracy of the estimator[edit]

Derivation[edit]

Independent and identically distributed random variables with random sample size[edit]

Student approximation when σ value is unknown[edit]

Assumptions and usage[edit]

Standard error of mean versus standard deviation[edit]

Extensions[edit]

Finite population correction (FPC)[edit]

Correction for correlation in the sample[edit]

See also[edit]

References[edit]

Представление результатов исследования

Ошибка среднего арифметического

Правила записи результатов исследования

Представление результатов научных исследований

Литература

Стандартное отклонение и стандартная ошибка: в чем разница?

Пример: стандартное отклонение против стандартной ошибки

Какой смысл использовать стандартную ошибку?

Когда использовать стандартное отклонение против стандартной ошибки

Стандартная ошибка

Как найти стандартную ошибку среднего значения

Исправления для некоторых случаев

Полезность

Относительная стандартная ошибка

Пример

Вопросы и ответы

В: Что такое стандартная ошибка?

В: Можно ли использовать термин стандартная ошибка для оценки стандартного отклонения?

В: Как можно оценить среднее значение для всей группы?

В: Почему трудно измерить всю группу?

В: Что такое стандартная ошибка среднего, и что она определяет?

В: Известно ли обычно истинное значение стандартного отклонения среднего при реальных измерениях?

В: Как количество измерений в выборке влияет на точность оценки?

Что такое Стандартная формула ошибки?

Объяснение

Пример формулы стандартной ошибки

Калькулятор стандартной ошибки

Актуальность и использование

Стандартная формула ошибки в Excel

Рекомендуемые статьи