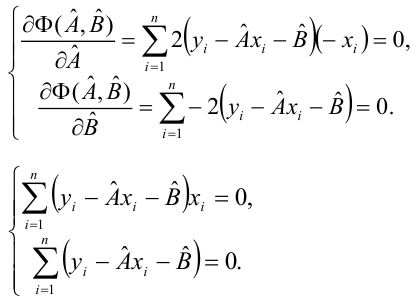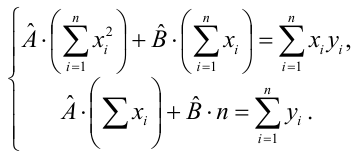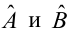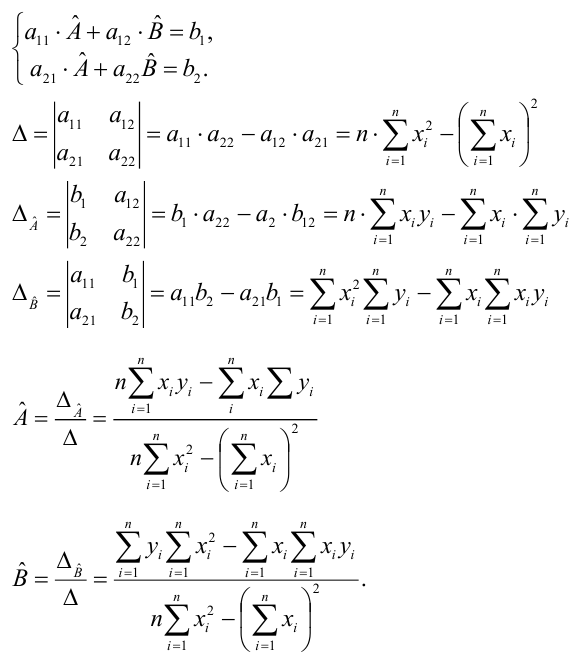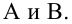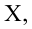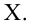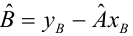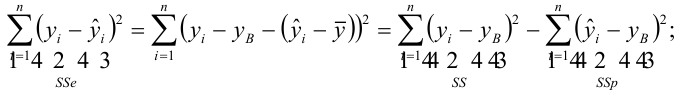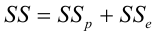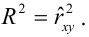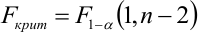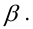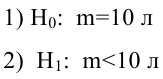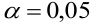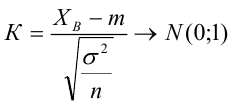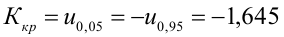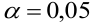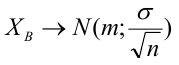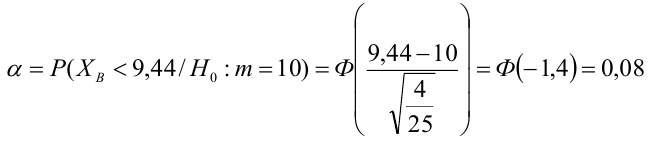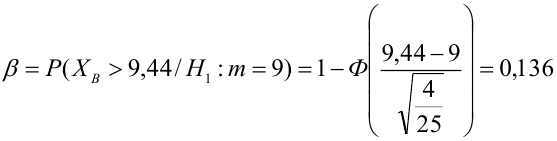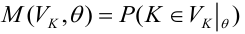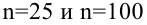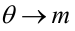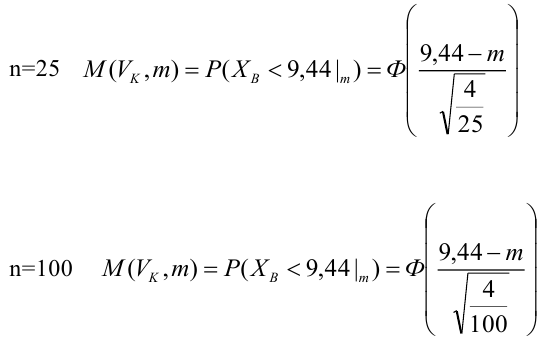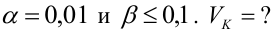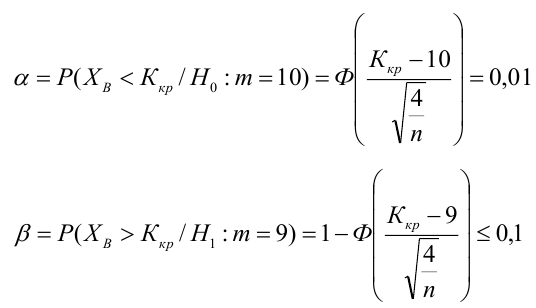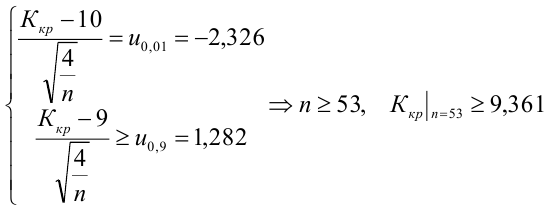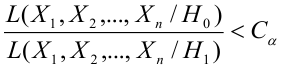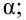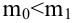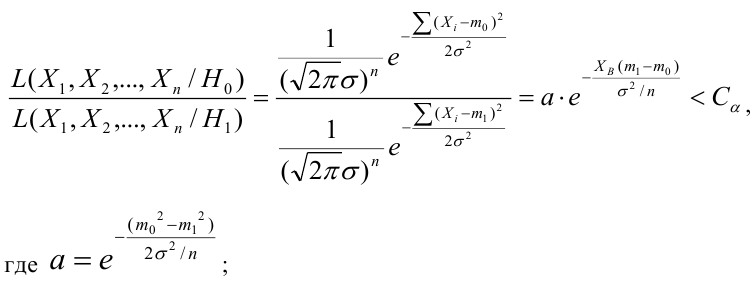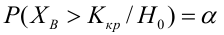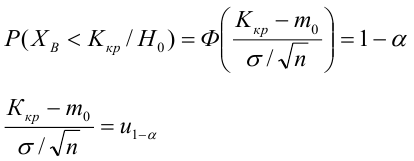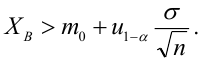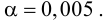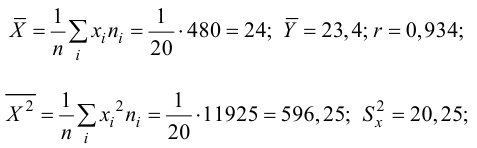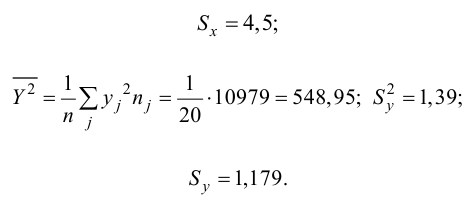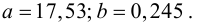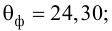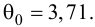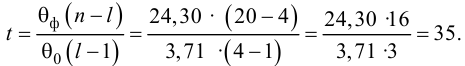На
основании уравнения (3.20) можно показать,
что b
будет несмещенной оценкой
,
если выполняется 4-е условие Гаусса —
Маркова:
(3.21)
так
как
— константа. Если мы примем сильную форму
4-го условия Гаусса — Маркова и предположим,
что х — неслучайная величина, мы можем
также считать Var(x)
известной константой и, таким образом,
(3.22)
Далее,
если х — неслучайная величина, то
M{Cov(x,u)}
= 0 и, следовательно, M{b}
=
Таким
образом,
— несмещенная оценка
Можно получить тот же результат со
слабой формой 4-го условия Гаусса —
Маркова (которая допускает, что переменная
х имеет случайную ошибку, но предполагает,
что она распределена независимо от u
).
За
исключением того случая, когда случайные
факторы в n
наблюдениях в точности «гасят»
друг друга, что может произойти лишь
при случайном совпадении, b
будет отличаться от
в каждом конкретном эксперименте. Не
будет систематической ошибки, завышающей
или занижающей оценку. То же самое
справедливо и для коэффициента а.
Используем
уравнение (2.15):
(3.23)
Следовательно,
(3.24)
Поскольку
у определяется уравнением (3.1),
(3.25)
так
как M{u}=0,
если выполнено 1-е условие Гаусса —
Маркова. Следовательно
(3.26)
Подставив
это выражение в (3.24) и воспользовавшись
тем, что
получим:
(3.27)
Таким
образом, а
— это несмещенная оценка а при условии
выполнения 1-го и 4-го условий Гаусса —
Маркова. Безусловно, для любой конкретной
выборки фактор случайности приведет к
расхождению оценки и истинного значения.
Рассмотрим
теперь теоретические дисперсии оценок
а и Ь. Они задаются следующими выражениями
(доказательства для эквивалентных
выражений можно найти в работе Дж. Томаса
[Thomas,
1983, section
833]):
(3.28)
Из
уравнения 3.28 можно сделать три очевидных
заключения. Во-первых, дисперсии а
и b
прямо пропорциональны дисперсии
остаточного члена
.
Чем
больше фактор случайности, тем хуже
будут оценки при прочих равных условиях.
Это уже было проиллюстрировано в
экспериментах по методу Монте-Карло.
Оценки в серии II
были гораздо более неточными, чем в
серии I,
и это произошло потому, что в каждой
выборке мы удвоили случайный член.
Удвоив u,
мы удвоили его стандартное отклонение
и, следовательно, удвоили стандартные
отклонения a
и b.
Во вторых, чем больше число наблюдений,
тем меньше дисперсионных оценок. Это
также имеет определенный смысл. Чем
большей информацией вы располагаете,
тем более точными, вероятно, будут ваши
оценки. В третьих, чем больше дисперсия
,
тем меньше будет дисперсия коэффициентов
регрессии. В чем причина этого? Напомним,
что (I)
коэффициенты регрессии вычисляются на
основании предположения, что наблюдаемые
изменения
происходят вследствие изменений
,
но (2) в действительности они лишь отчасти
вызваны изменениями
,
а отчасти вариациями u.
Чем меньше дисперсия
,
тем больше, вероятно, будет относительное
влияние фактора случайности при
определении отклонений
и тем более вероятно, что регрессионный
анализ может оказаться неверным. В
действительности, как видно из уравнения
(3.28), важное значение имеет не абсолютная,
а относительная величина
и Var(x).
На
практике мы не можем вычислить
теоретические дисперсии
или
,
так как
неизвестно, однако мы можем получить
оценку
на основе остатков. Очевидно, что разброс
остатков относительно линии регрессии
будет отражать неизвестный разброс u
относительно линии
,
хотя в общем остаток и случайный член
в любом данном наблюдении не равны друг
другу. Следовательно, выборочная
дисперсия остатков Var(е),
которую мы можем измерить, сможет быть
использована для оценки
,
которую мы получить не можем.
Прежде
чем пойти дальше, задайте себе следующий
вопрос: какая прямая будет ближе к
точкам, представляющим собой выборку
наблюдений по
и
,
истинная прямая
или линия регрессии
?
Ответ будет таков: линия регрессии,
потому что по определению она строится
таким образом, чтобы свести к минимуму
сумму квадратов расстояний между ней
и значениями наблюдений. Следовательно,
разброс остатков у нее меньше, чем
разброс значений u,
и Var(e)
имеет тенденцию занижать оценку
.
Действительно, можно показать, что
математическое ожидание Var(e),
если имеется всего одна независимая
переменная, равно
.
Однако отсюда следует, что если определить
как
,
(3.29)
То
будет представлять собой несмещенную
оценку
.
Таким
образом, несмещенной оценкой параметра
регрессии
является оценка
.
(3.30)
Теперь
вспомним следующие определения:
стандартное
отклонение случайной величины
– корень квадратный из теоретической
дисперсии случайной величины; среднее
ожидаемое расстояние между наблюдениями
этой случайной величины и ее математическим
ожиданием,
стандартная
ошибка случайной величины
– оценка стандартного отклонения
случайной величины, полученная по данным
выборки.
Используя
уравнения (3.28) и (3.29), можно получить
оценки теоретических дисперсий для a
и b
и после извлечения квадратного корня
– оценки их стандартных отклонений.
Вместо слишком громоздкого термина
«оценка стандартного отклонения функции
плотности вероятости» коэффицинта
регрессии будем использовать термин
«стандартная ошибка» коэффициента
регрессии, которую в дальнейшем мы будем
обозначать в виде сокрашения «с.о.».
Таким образом, для парного регрессионного
анализа мы имеем:
и
(3.31)
Если
воспользоваться компьютерной программой
оценивания регрессии, то стандартные
ошибки будут подсчитаны автоматически
одновременно с оценками a
и b.
Подводя
итог сказанному о точности коэффициентов
регрессии, акценктируем внимание на
следующих выводах.
1.
Оценка a
для параметра
имеет нормальное распределение с
математическим ожиданием a
и стандартным отклонением
,
оценка b
для параметра
имеет
нормальное распределение с математическим
ожиданием b
и стандартным отклонением
.
2.
Для улучшения точности оценок по МНК
можно увеличивать количество наблюдений
в выборке n,
увеличивать диапазон наблюдений Var(x)
или уменьшать
,
(например, увеличивать точность
измерений).
3.
Стандартная ошибка оценки a
считается по формуле
а
стандартная ошибка оценки b
считается по формуле
.
В компьютерных программах именно эти
числа приводятся в круглых скобках под
значениями оценок.
Полученные
соотношения проиллюстрируем экспериментами
по методу Монте-Карло, описанными ранее.
В серии I
u
определялось на основе случайных чисел,
взятых из генеральной совокупности с
нулевым средним и единичной дисперсией
а x
представлял собой набор чисел от 1 до
20. Можно легко вычислить Var(x),
которая равна 33,25.
Следовательно,
(3.32)
.
(3.33)
Таким
образом, истинное стандартное отклонение
для b
равно
.
Какие же результаты получены вместо
этого компьютером в 10 экспериментах
серии I?
Он должен был вычислить стандартную
ошибку, используя уравнение (3.31).
Результаты этих расчетов для 10
экспериментов представлены в табл. 3.5.
Таблица 3.5
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
22.03.2016179.71 Кб71а1.doc
- #
- #
- #
- #
- #
- #
- #
Когда мы подгоняем регрессионную модель к набору данных, нас часто интересует, насколько хорошо регрессионная модель «подходит» к набору данных. Две метрики, обычно используемые для измерения согласия, включают R -квадрат (R2) и стандартную ошибку регрессии , часто обозначаемую как S.
В этом руководстве объясняется, как интерпретировать стандартную ошибку регрессии (S), а также почему она может предоставить более полезную информацию, чем R 2 .
Стандартная ошибка по сравнению с R-квадратом в регрессии
Предположим, у нас есть простой набор данных, который показывает, сколько часов 12 студентов занимались в день в течение месяца, предшествующего важному экзамену, а также их баллы за экзамен:
Если мы подгоним простую модель линейной регрессии к этому набору данных в Excel, мы получим следующий результат:
R-квадрат — это доля дисперсии переменной отклика, которая может быть объяснена предикторной переменной. При этом 65,76% дисперсии экзаменационных баллов можно объяснить количеством часов, потраченных на учебу.
Стандартная ошибка регрессии — это среднее расстояние, на которое наблюдаемые значения отклоняются от линии регрессии. В этом случае наблюдаемые значения отклоняются от линии регрессии в среднем на 4,89 единицы.
Если мы нанесем фактические точки данных вместе с линией регрессии, мы сможем увидеть это более четко:
Обратите внимание, что некоторые наблюдения попадают очень близко к линии регрессии, в то время как другие не так близки. Но в среднем наблюдаемые значения отклоняются от линии регрессии на 4,19 единицы .
Стандартная ошибка регрессии особенно полезна, поскольку ее можно использовать для оценки точности прогнозов. Примерно 95% наблюдений должны находиться в пределах +/- двух стандартных ошибок регрессии, что является быстрым приближением к 95% интервалу прогнозирования.
Если мы заинтересованы в прогнозировании с использованием модели регрессии, стандартная ошибка регрессии может быть более полезной метрикой, чем R-квадрат, потому что она дает нам представление о том, насколько точными будут наши прогнозы в единицах измерения.
Чтобы проиллюстрировать, почему стандартная ошибка регрессии может быть более полезной метрикой для оценки «соответствия» модели, рассмотрим другой пример набора данных, который показывает, сколько часов 12 студентов занимались в день в течение месяца, предшествующего важному экзамену, а также их экзаменационная оценка:
Обратите внимание, что это точно такой же набор данных, как и раньше, за исключением того, что все значения s сокращены вдвое.Таким образом, студенты из этого набора данных учились ровно в два раза дольше, чем студенты из предыдущего набора данных, и получили ровно половину экзаменационного балла.
Если мы подгоним простую модель линейной регрессии к этому набору данных в Excel, мы получим следующий результат:
Обратите внимание, что R-квадрат 65,76% точно такой же, как и в предыдущем примере.
Однако стандартная ошибка регрессии составляет 2,095 , что ровно вдвое меньше стандартной ошибки регрессии в предыдущем примере.
Если мы нанесем фактические точки данных вместе с линией регрессии, мы сможем увидеть это более четко:
Обратите внимание на то, что наблюдения располагаются гораздо плотнее вокруг линии регрессии. В среднем наблюдаемые значения отклоняются от линии регрессии на 2,095 единицы .
Таким образом, несмотря на то, что обе модели регрессии имеют R-квадрат 65,76% , мы знаем, что вторая модель будет давать более точные прогнозы, поскольку она имеет более низкую стандартную ошибку регрессии.
Преимущества использования стандартной ошибки
Стандартную ошибку регрессии (S) часто бывает полезнее знать, чем R-квадрат модели, потому что она дает нам фактические единицы измерения. Если мы заинтересованы в использовании регрессионной модели для получения прогнозов, S может очень легко сказать нам, достаточно ли точна модель для прогнозирования.
Например, предположим, что мы хотим создать 95-процентный интервал прогнозирования, в котором мы можем прогнозировать результаты экзаменов с точностью до 6 баллов от фактической оценки.
Наша первая модель имеет R-квадрат 65,76%, но это ничего не говорит нам о том, насколько точным будет наш интервал прогнозирования. К счастью, мы также знаем, что у первой модели показатель S равен 4,19. Это означает, что 95-процентный интервал прогнозирования будет иметь ширину примерно 2*4,19 = +/- 8,38 единиц, что слишком велико для нашего интервала прогнозирования.
Наша вторая модель также имеет R-квадрат 65,76%, но опять же это ничего не говорит нам о том, насколько точным будет наш интервал прогнозирования. Однако мы знаем, что вторая модель имеет S 2,095. Это означает, что 95-процентный интервал прогнозирования будет иметь ширину примерно 2*2,095= +/- 4,19 единиц, что меньше 6 и, следовательно, будет достаточно точным для использования для создания интервалов прогнозирования.
Дальнейшее чтение
Введение в простую линейную регрессию
Что такое хорошее значение R-квадрата?
В статистике регрессия — это метод, который можно использовать для анализа взаимосвязи между переменными-предикторами и переменной-откликом.
Когда вы используете программное обеспечение (например, R, SAS, SPSS и т. д.) для выполнения регрессионного анализа, вы получите в качестве выходных данных таблицу регрессии, в которой суммируются результаты регрессии. Важно уметь читать эту таблицу, чтобы понимать результаты регрессионного анализа.
В этом руководстве рассматривается пример регрессионного анализа и дается подробное объяснение того, как читать и интерпретировать выходные данные таблицы регрессии.
Пример регрессии
Предположим, у нас есть следующий набор данных, который показывает общее количество часов обучения, общее количество сданных подготовительных экзаменов и итоговый балл за экзамен, полученный для 12 разных студентов:
Чтобы проанализировать взаимосвязь между учебными часами и сданными подготовительными экзаменами и окончательным экзаменационным баллом, который получает студент, мы запускаем множественную линейную регрессию, используя отработанные часы и подготовительные экзамены, взятые в качестве переменных-предикторов, и итоговый экзаменационный балл в качестве переменной ответа.
Мы получаем следующий вывод:
Проверка соответствия модели
В первом разделе показано несколько различных чисел, которые измеряют соответствие регрессионной модели, т. е. насколько хорошо регрессионная модель способна «соответствовать» набору данных.
Вот как интерпретировать каждое из чисел в этом разделе:
Несколько R
Это коэффициент корреляции.Он измеряет силу линейной зависимости между переменными-предикторами и переменной отклика. R, кратный 1, указывает на идеальную линейную зависимость, тогда как R, кратный 0, указывает на отсутствие какой-либо линейной зависимости. Кратный R — это квадратный корень из R-квадрата (см. ниже).
В этом примере множитель R равен 0,72855 , что указывает на довольно сильную линейную зависимость между предикторами часов обучения и подготовительных экзаменов и итоговой оценкой экзаменационной переменной ответа.
R-квадрат
Его часто записывают как r 2 , а также называют коэффициентом детерминации.Это доля дисперсии переменной отклика, которая может быть объяснена предикторной переменной.
Значение для R-квадрата может варьироваться от 0 до 1. Значение 0 указывает, что переменная отклика вообще не может быть объяснена предикторной переменной. Значение 1 указывает, что переменная отклика может быть полностью объяснена без ошибок с помощью переменной-предиктора.
В этом примере R-квадрат равен 0,5307 , что указывает на то, что 53,07% дисперсии итоговых экзаменационных баллов можно объяснить количеством часов обучения и количеством сданных подготовительных экзаменов.
Связанный: Что такое хорошее значение R-квадрата?
Скорректированный R-квадрат
Это модифицированная версия R-квадрата, которая была скорректирована с учетом количества предикторов в модели. Он всегда ниже R-квадрата. Скорректированный R-квадрат может быть полезен для сравнения соответствия различных моделей регрессии друг другу.
В этом примере скорректированный R-квадрат равен 0,4265.
Стандартная ошибка регрессии
Стандартная ошибка регрессии — это среднее расстояние, на которое наблюдаемые значения отклоняются от линии регрессии. В этом примере наблюдаемые значения отклоняются от линии регрессии в среднем на 7,3267 единиц.
Связанный: Понимание стандартной ошибки регрессии
Наблюдения
Это просто количество наблюдений в нашем наборе данных. В этом примере общее количество наблюдений равно 12 .
Тестирование общей значимости регрессионной модели
В следующем разделе показаны степени свободы, сумма квадратов, средние квадраты, F-статистика и общая значимость регрессионной модели.
Вот как интерпретировать каждое из чисел в этом разделе:
Степени свободы регрессии
Это число равно: количеству коэффициентов регрессии — 1. В этом примере у нас есть член пересечения и две переменные-предикторы, поэтому у нас всего три коэффициента регрессии, что означает, что степени свободы регрессии равны 3 — 1 = 2 .
Всего степеней свободы
Это число равно: количество наблюдений – 1. В данном примере у нас 12 наблюдений, поэтому общее количество степеней свободы 12 – 1 = 11 .
Остаточные степени свободы
Это число равно: общая df – регрессионная df.В этом примере остаточные степени свободы 11 – 2 = 9 .
Средние квадраты
Средние квадраты регрессии рассчитываются как регрессия SS / регрессия df.В этом примере регрессия MS = 546,53308/2 = 273,2665 .
Остаточные средние квадраты вычисляются как остаточный SS / остаточный df.В этом примере остаточная MS = 483,1335/9 = 53,68151 .
F Статистика
Статистика f рассчитывается как регрессия MS/остаточная MS. Эта статистика показывает, обеспечивает ли регрессионная модель лучшее соответствие данным, чем модель, которая не содержит независимых переменных.
По сути, он проверяет, полезна ли регрессионная модель в целом. Как правило, если ни одна из переменных-предикторов в модели не является статистически значимой, общая F-статистика также не является статистически значимой.
В этом примере статистика F равна 273,2665/53,68151 = 5,09 .
Значение F (P-значение)
Последнее значение в таблице — это p-значение, связанное со статистикой F. Чтобы увидеть, значима ли общая модель регрессии, вы можете сравнить p-значение с уровнем значимости; распространенные варианты: 0,01, 0,05 и 0,10.
Если p-значение меньше уровня значимости, имеется достаточно доказательств, чтобы сделать вывод о том, что регрессионная модель лучше соответствует данным, чем модель без переменных-предикторов. Этот вывод хорош, потому что он означает, что переменные-предикторы в модели действительно улучшают соответствие модели.
В этом примере p-значение равно 0,033 , что меньше обычного уровня значимости 0,05. Это указывает на то, что регрессионная модель в целом статистически значима, т. е. модель лучше соответствует данным, чем модель без переменных-предикторов.
Тестирование общей значимости регрессионной модели
В последнем разделе показаны оценки коэффициентов, стандартная ошибка оценок, t-stat, p-значения и доверительные интервалы для каждого термина в регрессионной модели.
Вот как интерпретировать каждое из чисел в этом разделе:
Коэффициенты
Коэффициенты дают нам числа, необходимые для записи оценочного уравнения регрессии:
у шляпа знак равно б 0 + б 1 Икс 1 + б 2 Икс 2 .
В этом примере расчетное уравнение регрессии имеет вид:
итоговый балл за экзамен = 66,99 + 1,299 (часы обучения) + 1,117 (подготовительные экзамены)
Каждый отдельный коэффициент интерпретируется как среднее увеличение переменной отклика на каждую единицу увеличения данной переменной-предиктора при условии, что все остальные переменные-предикторы остаются постоянными. Например, для каждого дополнительного часа обучения среднее ожидаемое увеличение итогового экзаменационного балла составляет 1,299 балла при условии, что количество сданных подготовительных экзаменов остается постоянным.
Перехват интерпретируется как ожидаемый средний итоговый балл за экзамен для студента, который учится ноль часов и не сдает подготовительных экзаменов. В этом примере ожидается, что учащийся наберет 66,99 балла, если он будет заниматься ноль часов и не сдавать подготовительных экзаменов. Однако будьте осторожны при интерпретации перехвата выходных данных регрессии, потому что это не всегда имеет смысл.
Например, в некоторых случаях точка пересечения может оказаться отрицательным числом, что часто не имеет очевидной интерпретации. Это не означает, что модель неверна, это просто означает, что перехват сам по себе не должен интерпретироваться как означающий что-либо.
Стандартная ошибка, t-статистика и p-значения
Стандартная ошибка — это мера неопределенности оценки коэффициента для каждой переменной.
t-stat — это просто коэффициент, деленный на стандартную ошибку. Например, t-stat для часов обучения составляет 1,299 / 0,417 = 3,117.
В следующем столбце показано значение p, связанное с t-stat. Это число говорит нам, является ли данная переменная отклика значимой в модели. В этом примере мы видим, что значение p для часов обучения равно 0,012, а значение p для подготовительных экзаменов равно 0,304. Это указывает на то, что количество учебных часов является важным предиктором итогового экзаменационного балла, а количество подготовительных экзаменов — нет.
Доверительный интервал для оценок коэффициентов
В последних двух столбцах таблицы представлены нижняя и верхняя границы 95% доверительного интервала для оценок коэффициентов.
Например, оценка коэффициента для часов обучения составляет 1,299, но вокруг этой оценки есть некоторая неопределенность. Мы никогда не можем знать наверняка, является ли это точным коэффициентом. Таким образом, 95-процентный доверительный интервал дает нам диапазон вероятных значений истинного коэффициента.
В этом случае 95% доверительный интервал для часов обучения составляет (0,356, 2,24). Обратите внимание, что этот доверительный интервал не содержит числа «0», что означает, что мы вполне уверены, что истинное значение коэффициента часов обучения не равно нулю, т. е. является положительным числом.
Напротив, 95% доверительный интервал для Prep Exams составляет (-1,201, 3,436). Обратите внимание, что этот доверительный интервал действительно содержит число «0», что означает, что истинное значение коэффициента подготовительных экзаменов может быть равно нулю, т. е. несущественно для прогнозирования результатов итоговых экзаменов.
Дополнительные ресурсы
Понимание нулевой гипотезы для линейной регрессии
Понимание F-теста общей значимости в регрессии
Как сообщить о результатах регрессии
На
основании уравнения (3.20) можно показать,
что b
будет несмещенной оценкой
,
если выполняется 4-е условие Гаусса —
Маркова:
(3.21)
так
как
— константа. Если мы примем сильную форму
4-го условия Гаусса — Маркова и предположим,
что х — неслучайная величина, мы можем
также считать Var(x)
известной константой и, таким образом,
(3.22)
Далее,
если х — неслучайная величина, то
M{Cov(x,u)}
= 0 и, следовательно, M{b}
=
Таким
образом,
— несмещенная оценка
Можно получить тот же результат со
слабой формой 4-го условия Гаусса —
Маркова (которая допускает, что переменная
х имеет случайную ошибку, но предполагает,
что она распределена независимо от u
).
За
исключением того случая, когда случайные
факторы в n
наблюдениях в точности «гасят»
друг друга, что может произойти лишь
при случайном совпадении, b
будет отличаться от
в каждом конкретном эксперименте. Не
будет систематической ошибки, завышающей
или занижающей оценку. То же самое
справедливо и для коэффициента а.
Используем
уравнение (2.15):
(3.23)
Следовательно,
(3.24)
Поскольку
у определяется уравнением (3.1),
(3.25)
так
как M{u}=0,
если выполнено 1-е условие Гаусса —
Маркова. Следовательно
(3.26)
Подставив
это выражение в (3.24) и воспользовавшись
тем, что
получим:
(3.27)
Таким
образом, а
— это несмещенная оценка а при условии
выполнения 1-го и 4-го условий Гаусса —
Маркова. Безусловно, для любой конкретной
выборки фактор случайности приведет к
расхождению оценки и истинного значения.
Рассмотрим
теперь теоретические дисперсии оценок
а и Ь. Они задаются следующими выражениями
(доказательства для эквивалентных
выражений можно найти в работе Дж. Томаса
[Thomas,
1983, section
833]):
(3.28)
Из
уравнения 3.28 можно сделать три очевидных
заключения. Во-первых, дисперсии а
и b
прямо пропорциональны дисперсии
остаточного члена
.
Чем
больше фактор случайности, тем хуже
будут оценки при прочих равных условиях.
Это уже было проиллюстрировано в
экспериментах по методу Монте-Карло.
Оценки в серии II
были гораздо более неточными, чем в
серии I,
и это произошло потому, что в каждой
выборке мы удвоили случайный член.
Удвоив u,
мы удвоили его стандартное отклонение
и, следовательно, удвоили стандартные
отклонения a
и b.
Во вторых, чем больше число наблюдений,
тем меньше дисперсионных оценок. Это
также имеет определенный смысл. Чем
большей информацией вы располагаете,
тем более точными, вероятно, будут ваши
оценки. В третьих, чем больше дисперсия
,
тем меньше будет дисперсия коэффициентов
регрессии. В чем причина этого? Напомним,
что (I)
коэффициенты регрессии вычисляются на
основании предположения, что наблюдаемые
изменения
происходят вследствие изменений
,
но (2) в действительности они лишь отчасти
вызваны изменениями
,
а отчасти вариациями u.
Чем меньше дисперсия
,
тем больше, вероятно, будет относительное
влияние фактора случайности при
определении отклонений
и тем более вероятно, что регрессионный
анализ может оказаться неверным. В
действительности, как видно из уравнения
(3.28), важное значение имеет не абсолютная,
а относительная величина
и Var(x).
На
практике мы не можем вычислить
теоретические дисперсии
или
,
так как
неизвестно, однако мы можем получить
оценку
на основе остатков. Очевидно, что разброс
остатков относительно линии регрессии
будет отражать неизвестный разброс u
относительно линии
,
хотя в общем остаток и случайный член
в любом данном наблюдении не равны друг
другу. Следовательно, выборочная
дисперсия остатков Var(е),
которую мы можем измерить, сможет быть
использована для оценки
,
которую мы получить не можем.
Прежде
чем пойти дальше, задайте себе следующий
вопрос: какая прямая будет ближе к
точкам, представляющим собой выборку
наблюдений по
и
,
истинная прямая
или линия регрессии
?
Ответ будет таков: линия регрессии,
потому что по определению она строится
таким образом, чтобы свести к минимуму
сумму квадратов расстояний между ней
и значениями наблюдений. Следовательно,
разброс остатков у нее меньше, чем
разброс значений u,
и Var(e)
имеет тенденцию занижать оценку
.
Действительно, можно показать, что
математическое ожидание Var(e),
если имеется всего одна независимая
переменная, равно
.
Однако отсюда следует, что если определить
как
,
(3.29)
То
будет представлять собой несмещенную
оценку
.
Таким
образом, несмещенной оценкой параметра
регрессии
является оценка
.
(3.30)
Теперь
вспомним следующие определения:
стандартное
отклонение случайной величины
– корень квадратный из теоретической
дисперсии случайной величины; среднее
ожидаемое расстояние между наблюдениями
этой случайной величины и ее математическим
ожиданием,
стандартная
ошибка случайной величины
– оценка стандартного отклонения
случайной величины, полученная по данным
выборки.
Используя
уравнения (3.28) и (3.29), можно получить
оценки теоретических дисперсий для a
и b
и после извлечения квадратного корня
– оценки их стандартных отклонений.
Вместо слишком громоздкого термина
«оценка стандартного отклонения функции
плотности вероятости» коэффицинта
регрессии будем использовать термин
«стандартная ошибка» коэффициента
регрессии, которую в дальнейшем мы будем
обозначать в виде сокрашения «с.о.».
Таким образом, для парного регрессионного
анализа мы имеем:
и
(3.31)
Если
воспользоваться компьютерной программой
оценивания регрессии, то стандартные
ошибки будут подсчитаны автоматически
одновременно с оценками a
и b.
Подводя
итог сказанному о точности коэффициентов
регрессии, акценктируем внимание на
следующих выводах.
1.
Оценка a
для параметра
имеет нормальное распределение с
математическим ожиданием a
и стандартным отклонением
,
оценка b
для параметра
имеет
нормальное распределение с математическим
ожиданием b
и стандартным отклонением
.
2.
Для улучшения точности оценок по МНК
можно увеличивать количество наблюдений
в выборке n,
увеличивать диапазон наблюдений Var(x)
или уменьшать
,
(например, увеличивать точность
измерений).
3.
Стандартная ошибка оценки a
считается по формуле
а
стандартная ошибка оценки b
считается по формуле
.
В компьютерных программах именно эти
числа приводятся в круглых скобках под
значениями оценок.
Полученные
соотношения проиллюстрируем экспериментами
по методу Монте-Карло, описанными ранее.
В серии I
u
определялось на основе случайных чисел,
взятых из генеральной совокупности с
нулевым средним и единичной дисперсией
а x
представлял собой набор чисел от 1 до
20. Можно легко вычислить Var(x),
которая равна 33,25.
Следовательно,
(3.32)
.
(3.33)
Таким
образом, истинное стандартное отклонение
для b
равно
.
Какие же результаты получены вместо
этого компьютером в 10 экспериментах
серии I?
Он должен был вычислить стандартную
ошибку, используя уравнение (3.31).
Результаты этих расчетов для 10
экспериментов представлены в табл. 3.5.
Таблица 3.5
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
22.03.2016179.71 Кб71а1.doc
- #
- #
- #
- #
- #
- #
- #
This article is to tell you the whole interpretation of the regression summary table. There are many statistical softwares that are used for regression analysis like Matlab, Minitab, spss, R etc. but this article uses python. The Interpretation is the same for other tools as well. This article needs the basics of statistics including basic knowledge of regression, degrees of freedom, standard deviation, Residual Sum Of Squares(RSS), ESS, t statistics etc.
In regression there are two types of variables i.e. dependent variable (also called explained variable) and independent variable (explanatory variable).
The regression line used here is,
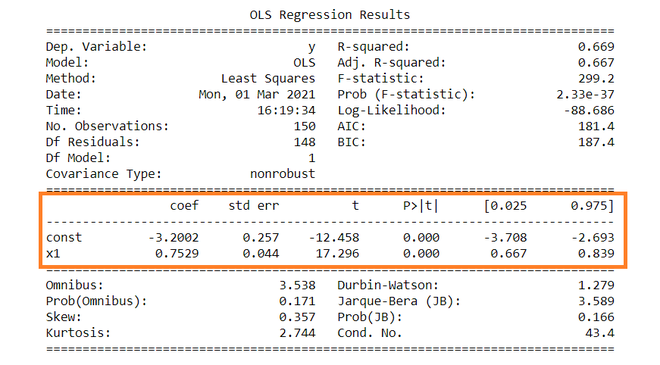
The summary table of the regression is given below.
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.669
Model: OLS Adj. R-squared: 0.667
Method: Least Squares F-statistic: 299.2
Date: Mon, 01 Mar 2021 Prob (F-statistic): 2.33e-37
Time: 16:19:34 Log-Likelihood: -88.686
No. Observations: 150 AIC: 181.4
Df Residuals: 148 BIC: 187.4
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const -3.2002 0.257 -12.458 0.000 -3.708 -2.693
x1 0.7529 0.044 17.296 0.000 0.667 0.839
==============================================================================
Omnibus: 3.538 Durbin-Watson: 1.279
Prob(Omnibus): 0.171 Jarque-Bera (JB): 3.589
Skew: 0.357 Prob(JB): 0.166
Kurtosis: 2.744 Cond. No. 43.4
==============================================================================
Dependent variable: Dependent variable is one that is going to depend on other variables. In this regression analysis Y is our dependent variable because we want to analyse the effect of X on Y.
Model: The method of Ordinary Least Squares(OLS) is most widely used model due to its efficiency. This model gives best approximate of true population regression line. The principle of OLS is to minimize the square of errors ( ∑ei2 ).
Number of observations: The number of observation is the size of our sample, i.e. N = 150.
Degree of freedom(df) of residuals:
Degree of freedom is the number of independent observations on the basis of which the sum of squares is calculated.
D.f Residuals = 150 – (1+1) = 148
Degree of freedom(D.f) is calculated as,
Degrees of freedom, D . f = N – K
Where, N = sample size(no. of observations) and K = number of variables + 1
Df of model:
Df of model = K – 1 = 2 – 1 = 1 ,
Where, K = number of variables + 1
Constant term: The constant terms is the intercept of the regression line. From regression line (eq…1) the intercept is -3.002. In regression we omits some independent variables that do not have much impact on the dependent variable, the intercept tells the average value of these omitted variables and noise present in model.
Coefficient term: The coefficient term tells the change in Y for a unit change in X i.e if X rises by 1 unit then Y rises by 0.7529. If you are familiar with derivatives then you can relate it as the rate of change of Y with respect to X .
Standard error of parameters: Standard error is also called the standard deviation. Standard error shows the sampling variability of these parameters. Standard error is calculated by as –
Standard error of intercept term (b1):
Standard error of coefficient term(b2):
Here, σ2 is the Standard error of regression (SER) . And σ2 is equal to RSS( Residual Sum Of Square i.e ∑ei2 ).
t – statistics:
In theory, we assume that error term follows the normal distribution and because of this the parameters b1 and b2 also have normal distributions with variance calculated in above section.
That is ,
- b1 ∼ N(B1, σb12)
- b2 ∼ N(B2 , σb22)
Here B1 and B2 are true means of b1 and b2.
t – statistics are calculated by assuming following hypothesis –
- H0 : B2 = 0 ( variable X has no influence on Y)
- Ha : B2 ≠ 0 (X has significant impact on Y)
Calculations for t – statistics :
t = ( b1 – B1 ) / s.e (b1)
From summary table , b1 = -3.2002 and se(b1) = 0.257, So,
t = (-3.2002 – 0) / 0.257 = -12.458
Similarly, b2 = 0.7529 , se(b2) = 0.044
t = (0.7529 – 0) / 0.044 = 17.296
p – values:
In theory, we read that p-value is the probability of obtaining the t statistics at least as contradictory to H0 as calculated from assuming that the null hypothesis is true. In the summary table, we can see that P-value for both parameters is equal to 0. This is not exactly 0, but since we have very larger statistics (-12.458 and 17.296) p-value will be approximately 0.
If you know about significance levels then you can see that we can reject the null hypothesis at almost every significance level.
Confidence intervals:
There are many approaches to test the hypothesis, including the p-value approach mentioned above. The confidence interval approach is one of them. 5% is the standard significance level (∝) at which C.I’s are made.
C.I for B1 is ( b1 – t∝/2 s.e(b1) , b1 + t∝/2 s.e(b1) )
Since ∝ = 5 %, b1 = -3.2002, s.e(b1) =0.257 , from t table , t0.025,148 = 1.655,
After putting values the C.I for B1 is approx. ( -3.708 , -2.693 ). Same can be done for b2 as well.
While calculating p values we rejected the null hypothesis we can see same in C.I as well. Since 0 does not lie in any of the intervals so we will reject the null hypothesis.
R – squared value:
R2 is the coefficient of determination that tells us that how much percentage variation independent variable can be explained by independent variable. Here, 66.9 % variation in Y can be explained by X. The maximum possible value of R2 can be 1, means the larger the R2 value better the regression.
F – statistic:
F test tells the goodness of fit of a regression. The test is similar to the t-test or other tests we do for the hypothesis. The F – statistic is calculated as below –
Inserting the values of R2, n and k, F = (0.669/1) / (0.331/148) = 229.12.
You can calculate the probability of F >229.1 for 1 and 148 df, which comes to approx. 0. From this, we again reject the null hypothesis stated above.
The remaining terms are not often used. Terms like Skewness and Kurtosis tells about the distribution of data. Skewness and kurtosis for the normal distribution are 0 and 3 respectively. Jarque-Bera test is used for checking whether an error has normal distribution or not.
Ниворожкина Л.И. Основы статистики с элементами теории вероятностей для экономистов: Руководство для решения задач — файл n1.doc
приобрести
Ниворожкина Л.И. Основы статистики с элементами теории вероятностей для экономистов: Руководство для решения задач
скачать (17128 kb.)
Доступные файлы (1):
- Смотрите также:
- Рушайло М.Ф. Элементы теории вероятностей и математической статистики (Документ)
- Рушайло М.Ф. Элементы теории вероятностей и математической статистики (Документ)
- Кремер Н.Ш. Теория вероятностей и математическая статистика (Документ)
- Мордкович А.Г., Семенов П.В. События. Вероятности. Статистическая обработка данных: Дополнительные параграфы к курсу алгебры 7-9 кл. общеобразовательных учреждений (Документ)
- Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике (Документ)
- Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике (Документ)
- Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике (Документ)
- Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике (Документ)
- Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике (Документ)
- Кремер Н.Ш. Теория вероятностей и математическая статистика (Документ)
- Коваленко И.Н., Гнеденко Б.В. Теория вероятностей (Документ)
- Кафедра «Электроснабжение» В. Б. Козловская, В. В. Сталович математические задачи энергетики (Документ)
n1.doc
Хотя метод наименьших квадратов дает нам линию регрессии, которая обеспечивает минимум вариации, регрессионное уравнение не является идеальным в смысле предсказания, поскольку не все значения зависимого признака Y удовлетворяют уравнению регрессии. Нам необходима статистическая мера вариации фактических значений Y от предсказанных значений Y. Эта мера в то же время является средней вариацией каждого значения относительно среднего значения Y. Мера вариации относительно линии регрессии называется стандартной ошибкой оценки.
Колеблемость фактических значений признака Y относительно линии регрессии показана на рис. 9.3.
Из диаграммы видно, что хотя теоретическая линия регрессии проходит относительно близко от фактических значений Y, часть этих точек лежит выше или ниже линии регрессии. При этом
Стандартная ошибка оценки определяется как
где уi — фактические значения Y;
yx — предсказанные значения Y для заданного х.
Для вычисления более удобна следующая формула:
Нам уже известны
Тогда
Итак, для нашего примера: Syx = 0,497. Эта стандартная ошибка характеризует меру вариации фактических данных относительно линии регрессии. Интерпретация этой меры аналогична интерпретации среднего квадратического отклонения. Если среднее квадратическое отклонение — это мера вариации относительно средней, то стандартная ошибка — это оценка меры вариации относительно линии регрессии. Однако стандартная ошибка оценки может быть использована для выводов о значении yx и выяснения, является ли статистически значимой взаимосвязь между двумя переменными.
9.11. Измерение вариации по уравнению регрессии
Для проверки того, насколько хорошо независимая переменная предсказывает зависимую переменную в нашей модели, необходим расчет ряда мер вариации. Первая из них — общая (полная) сумма квадратов отклонений результативного признака от средней — есть мера вариации значений Y относительно их среднего Y . В регрессионном анализе общая сумма квадратов может быть разложена на объясняемую вариацию или сумму квадратов отклонений за счет регрессии и необъясняемую вариацию или остаточную сумму квадратов отклонений (рис. 9.4).
Сумма квадратов отклонений вследствие регрессии это — сумма квадратов разностей между y
(средним значением Y) и yx (значением Y, предсказанным по уравнению регрессии). Сумма квадратов отклонений, не объясняемая регрессией (остаточная сумма квадратов), — это сумма квадратов разностей y и yx . Эти меры вариации могут быть представлены следующим образом (табл. 9.8):
Таблица 9.8
| Общая сумма квадратов
(ST) |
= | Сумма квадратов за счет регрессии
(SR) |
+ | Остаточная сумма квадратов
(SE) |
Легко увидеть, что остаточная сумма квадратов (y-yx)2 — это выражение, стоящее под знаком корня в формуле (9.25) (стандартной ошибки оценки). Тем не менее в процессе вычислений стандартной ошибки мы всегда вначале вычисляем сумму квадратов ошибки.
Остаточная сумма квадратов может быть представлена следующим образом:
Объясняемая сумма квадратов выразится так:
В самом деле
51,3605 = 46,9145 + 4,4460.
Из этого соотношения определяется коэффициент детерминации:
Отсюда коэффициент детерминации — доля вариации Y, которая объясняется независимыми переменными в регрессионной модели. Для нашего примера rг= 46,9145/51,3605 = 0,913.
Следовательно, 91,3% вариации еженедельной выручки магазинов могут быть объяснены числом покупателей, варьирующим от магазина к магазину. Только 8,7% вариации можно объяснить иными факторами, не включенными в уравнение регрессии.
В случае парной регрессии коэффициент детерминации равен квадратному корню из квадрата коэффициента линейной корреляции Пирсона
В простой линейной регрессии г имеет тот же знак, что и b1, Если b1 > 0, то r > 0; если b1 < 0, то r < 0, если b1 = 0, то r = 0.
В нашем примере r2 = 0,913 и b1 > 0, коэффициент корреляции r = 0,956. Близость коэффициента корреляции к 1 свидетельствует о тесной положительной связи между выручкой магазина от продажи пива и числом посетителей.
Мы интерпретировали коэффициент корреляции в терминах регрессии, однако корреляция и регрессия — две различные техники. Корреляция устанавливает силу связи между признаками, а регрессия — форму этой связи. В ряде случаев для анализа достаточно найти меру связи между признаками, без использования одного из них в качестве факторного признака для другого.
9.12. Доверительные интервалы для оценки неизвестного генерального значения yген(yх) и индивидуального значения yi
Поскольку в основном для построения регрессионных моделей используются данные выборок, то зачастую интерпретация взаимоотношений между переменными в генеральной совокупности базируется на выборочных результатах.
Как было сказано выше, регрессионное уравнение используется для прогноза значений Y по заданному значению X. В нашем примере показано, что при 600 посетителях магазина сумма выручки могла бы быть 7,661 у. е. Однако это значение — только точечная оценка истинного среднего значения. Мы знаем, что для оценки истинного значения генерального параметра возможна интервальная оценка.
Доверительный интервал для оценки неизвестного генерального значения yген(yх) имеет вид
где
Здесь yx — предсказанное значение Y
(yx==b0+b1yi);
Syx — стандартная ошибка оценки;
п — объем выборки;
хi — заданное значение X.
Легко видеть, что длина доверительного интервала зависит от нескольких факторов. Для заданного уровня значимости увеличение вариации вокруг линии регрессии, измеряемой стандартной ошибкой оценки, увеличивает длину интервала. Увеличение объема выборки уменьшит длину интервала. Более того, ширина интервала также варьирует с различными значениями X. Когда оценивается yx по значениям X, близким к x, то интервал тем уже, чем меньше абсолютное отклонение хi от x (рис. 9.5).
Когда оценка осуществляется по значениям X, удаленным от среднего x, то длина интервала возрастает.
Рассчитаем 95%-й доверительный интервал для среднего значения выручки во всех магазинах с числом посетителей, равным 600. По данным нашего примера уравнение регрессии имеет вид
yx = 2,423 + 0,00873x:
и для xi = 600 получим yi; =7,661, а также
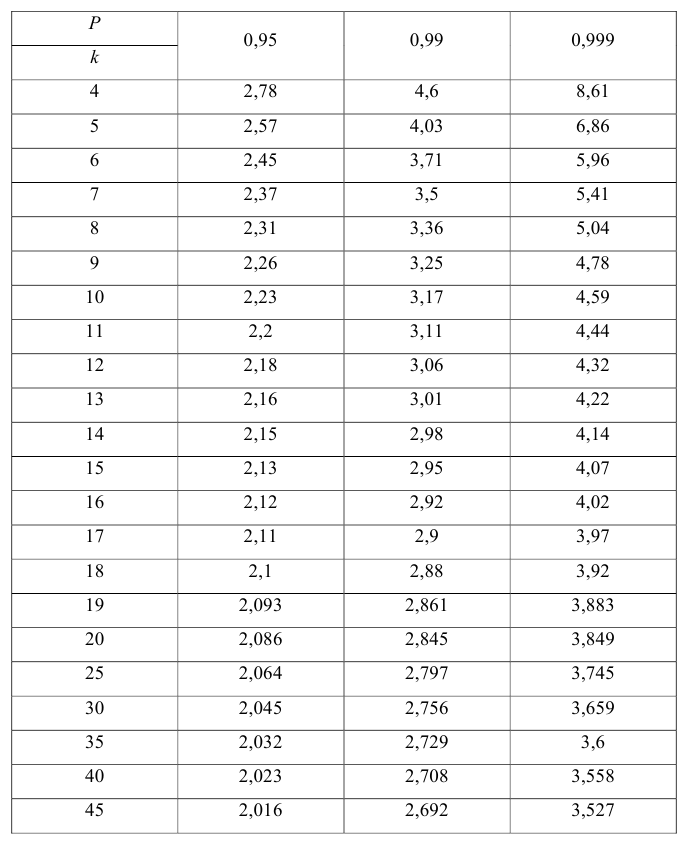
По таблице Стьюдента (приложение 5)
t18 = 2,10.
Отсюда, используя формулы (9.31) и (9.32), рассчитаем границы искомого доверительного интервала для yx
Итак, 7,369 yx 7,953.
Следовательно, наша оценка состоит в том, что средняя дневная выручка находится между 7,369 и 7,953 у. е. для всех магазинов с 600 посетителями.
Для построения доверительного интервала для индивидуальных значений Yx, лежащих на линии регрессии, используется доверительный интервал регрессии вида
где hi yi, , Syx ,п и хi — определяются, как и в формулах (9.31) и (9.32).
Определим 95% -и доверительный интервал для оценки дневных продаж отдельного магазина с 600 посетителями
В результате вычислений получим
Итак, 6,577 yi 8,745.
Следовательно, с 95%-й уверенностью можно утверждать, что ежедневная выручка отдельного магазина, который посетили 600 покупателей, находится в пределах от 6,577 до 8,745 у. е. Длина этого интервала больше чем длина интервала, полученного ранее для оценки среднего значения Y.
9.10. Стандартная ошибка оценки уравнения регрессии
Содержание:
Регрессионный анализ:
Регрессионным анализом называется раздел математической статистики, объединяющий практические методы исследования корреляционной зависимости между случайными величинами по результатам наблюдений над ними. Сюда включаются методы выбора модели изучаемой зависимости и оценки ее параметров, методы проверки статистических гипотез о зависимости.
Пусть между случайными величинами X и Y существует линейная корреляционная зависимость. Это означает, что математическое ожидание Y линейно зависит от значений случайной величины X. График этой зависимости (линия регрессии Y на X) имеет уравнение
Линейная модель пригодна в качестве первого приближения и в случае нелинейной корреляции, если рассматривать небольшие интервалы возможных значений случайных величин.
Пусть параметры линии регрессии 
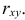
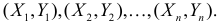
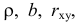
Неизвестная нам линия регрессии 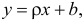

Такие значения 
Решения этой системы уравнений дают оценки называемые оценками по методу наименьших квадратов.
и
Известно, что оценки по методу наименьших квадратов являются несмещенными и, более того, среди всех несмещенных оценок обладают наименьшей дисперсией. Для оценки коэффициента корреляции можно воспользоваться тем, что 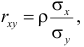
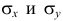
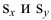
По методу наименьших квадратов можно находить оценки параметров линии регрессии и при нелинейной корреляции. Например, для линии регрессии вида 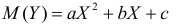
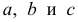
Пример:
По данным наблюдений двух случайных величин найти коэффициент корреляции и уравнение линии регрессии Y на X
Решение. Вычислим величины, необходимые для использования формул (3.7.1)–(3.7.3):
По формулам (3.7.1) и (3.7.2) получим
Итак, оценка линии регрессии имеет вид 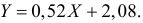
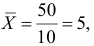
Аналогично, 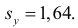
Ответ.
Пример:
Получена выборка значений величин X и Y
Для представления зависимости между величинами предполагается использовать модель 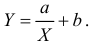
Решение. Рассмотрим сначала задачу оценки параметров этой модели в общем виде. Линия 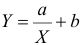
Необходимые условия экстремума приводят к системе из двух уравнений:
Откуда
Решения системы уравнений (3.7.4) и (3.7.5) и будут оценками по методу наименьших квадратов для параметров
На основе опытных данных вычисляем:
В итоге получаем систему уравнений (?????) и (?????) в виде
Эта система имеет решения
Ответ.
Если наблюдений много, то результаты их обычно группируют и представляют в виде корреляционной таблицы.
В этой таблице 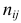
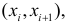
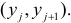
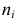
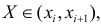
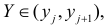
Если величины дискретны, то вместо интервалов указывают отдельные значения этих величин. Для непрерывных случайных величин представителем каждого интервала считают его середину и полагают, что 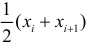
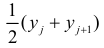
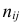
При больших значениях X и Y можно для упрощения вычислений перенести начало координат и изменить масштаб по каждой из осей, а после завершения вычислений вернуться к старому масштабу.
Пример:
Проделано 80 наблюдений случайных величин X и Y. Результаты наблюдений представлены в виде таблицы. Найти линию регрессии Y на X. Оценить коэффициент корреляции.
Решение. Представителем каждого интервала будем считать его середину. Перенесем начало координат и изменим масштаб по каждой оси так, чтобы значения X и Y были удобны для вычислений. Для этого перейдем к новым переменным 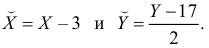
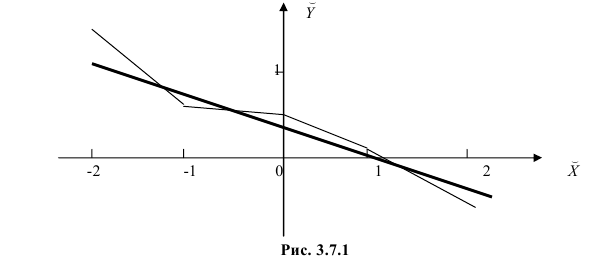
Чтобы иметь представление о виде линии регрессии, вычислим средние значения 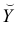
Нанесем эти значения на координатную плоскость, соединив для наглядности их отрезками прямой (рис. 3.7.1).
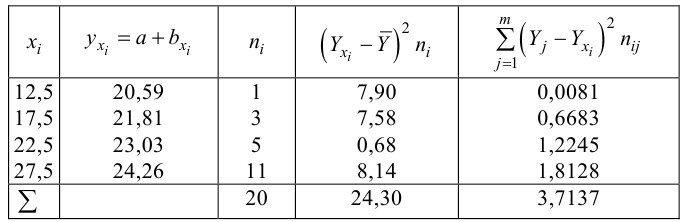
По виду полученной ломанной линии можно предположить, что линия регрессии Y на X является прямой. Оценим ее параметры. Для этого сначала вычислим с учетом группировки данных в таблице все величины, необходимые для использования формул (3.31–3.33):
Тогда
В новом масштабе оценка линии регрессии имеет вид 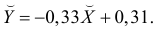
Для оценки 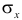
Подобным же образом можно оценить 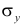
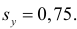
Вернемся к старому масштабу:
Коэффициент корреляции пересчитывать не нужно, так как это величина безразмерная и от масштаба не зависит.
Ответ.
Пусть некоторые физические величины X и Y связаны неизвестной нам функциональной зависимостью 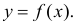
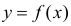
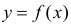
Регрессионный анализ
Основные положения регрессионного анализа:
Основная задача регрессионного анализа — изучение зависимости между результативным признаком Y и наблюдавшимся признаком X, оценка функции регрессий.
Предпосылки регрессионного анализа:
- Y — независимые случайные величины, имеющие постоянную дисперсию;
- X— величины наблюдаемого признака (величины не случайные);
- условное математическое ожидание
можно представить в виде
Выражение (2.1), как уже упоминалось в п. 1.2, называется функцией регрессии (или модельным уравнением регрессии) Y на X. Оценке в этом выражении подлежат параметры 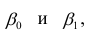
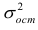
Остаточной дисперсией называется та часть рассеивания результативного признака, которую нельзя объяснить действием наблюдаемого признака; Остаточная дисперсия может служить для оценки точности подбора вида функции регрессии (модельного уравнения регрессии), полноты набора признаков, включенных в анализ. Оценки параметров функции регрессии находят, используя метод наименьших квадратов.
В данном вопросе рассмотрен линейный регрессионный анализ. Линейным он называется потому, что изучаем лишь те виды зависимостей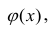
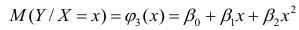
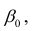
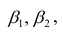
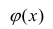
Важное место в линейном регрессионном анализе занимает так называемая «нормальная регрессия». Она имеет место, если сделать предположения относительно закона распределения случайной величины Y. Предпосылки «нормальной регрессии»:
- Y — независимые случайные величины, имеющие постоянную дисперсию и распределенные по нормальному закону;
- X— величины наблюдаемого признака (величины не случайные);
- условное математическое ожидание
можно представить в виде (2.1).
В этом случае оценки коэффициентов регрессии — несмещённые с минимальной дисперсией и нормальным законом распределения. Из этого положения следует что при «нормальной регрессии» имеется возможность оценить значимость оценок коэффициентов регрессии, а также построить доверительный интервал для коэффициентов регрессии и условного математического ожидания M(YX=x).
Линейная регрессия
Рассмотрим простейший случай регрессионного анализа — модель вида (2.1), когда зависимость 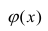
по переменным. Оценки параметров модели (2.1) 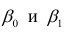
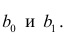
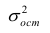
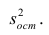
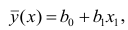
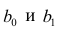
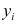
Составим систему нормальных уравнений: первое уравнение
откуда
второе уравнение
откуда
Итак,
Оценки, полученные по способу наименьших квадратов, обладают минимальной дисперсией в классе линейных оценок. Решая систему (2.2) относительно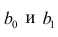
Остаётся получить оценку параметра 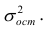
где т — количество наблюдений.
Еслит велико, то для упрощения расчётов наблюдавшиеся данные принята группировать, т.е. строить корреляционную таблицу. Пример построения такой таблицы приведен в п. 1.5. Формулы для нахождения коэффициентов регрессии по сгруппированным данным те же, что и для расчёта по несгруппированным данным, но суммы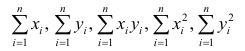
где 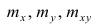
Нелинейная регрессия
Рассмотрим случай, когда зависимость нелинейна по переменным х, например модель вида
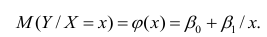
На рис. 2.1 изображено поле корреляции. Очевидно, что зависимость между Y и X нелинейная и её графическим изображением является не прямая, а кривая. Оценкой выражения (2.6) является уравнение регрессии
где 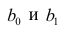
Принцип нахождения коэффициентов тот же — метод наименьших квадратов, т.е.
или
Дифференцируя последнее равенство по 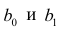
В общем случае нелинейной зависимости между переменными Y и X связь может выражаться многочленом k-й степени от x:
Коэффициенты регрессии определяют по принципу наименьших квадратов. Система нормальных уравнений имеет вид
Вычислив коэффициенты системы, её можно решить любым известным способом.
Оценка значимости коэффициентов регрессии. Интервальная оценка коэффициентов регрессии
Проверить значимость оценок коэффициентов регрессии — значит установить, достаточна ли величина оценки для статистически обоснованного вывода о том, что коэффициент регрессии отличен от нуля. Для этого проверяют гипотезу о равенстве нулю коэффициента регрессии, соблюдая предпосылки «нормальной регрессии». В этом случае вычисляемая для проверки нулевой гипотезы 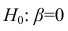
имеет распределение Стьюдента с к= n-2 степенями свободы (b — оценка коэффициента регрессии, 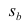
коэффициента регрессии, иначе стандартная ошибка оценки). По уровню значимости а и числу степеней свободы к находят по таблицам распределения Стьюдента (см. табл. 1 приложений) критическое значение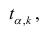
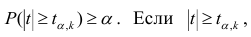
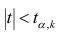
Оценки среднеквадратического отклонения коэффициентов регрессии вычисляют по следующим формулам:
где 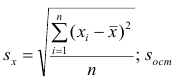
формуле (2.5).
Доверительный интервал для значимых параметров строят по обычной схеме. Из условия
где а — уровень значимости, находим
Интервальная оценка для условного математического ожидания
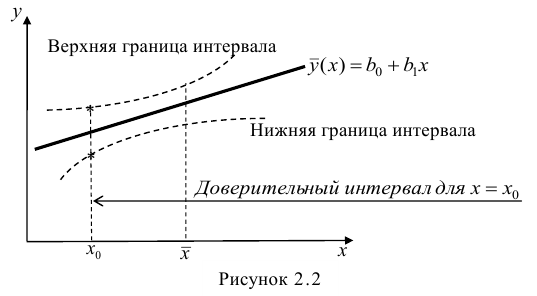
Линия регрессии характеризует изменение условного математического ожидания результативного признака от вариации остальных признаков.
Точечной оценкой условного математического ожидания 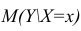
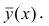
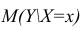
построить доверительный интервал в точке
Известно, что 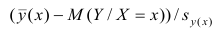
Стьюдента с k=n—2 степенями свободы. Найдя оценку среднеквадратического отклонения для условного среднего, можно построить доверительный интервал для условного математического ожидания
Оценку дисперсии условного среднего вычисляют по формуле
или для интервального ряда
Доверительный интервал находят из условия
где а — уровень значимости. Отсюда
Доверительный интервал для условного математического ожидания можно изобразить графически (рис, 2.2).
Из рис. 2.2 видно, что в точке 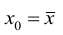
Проверка значимости уравнения регрессии
Оценить значимость уравнения регрессии — значит установить, соответствует ли математическая, модель, выражающая зависимость между Y и X, экспериментальным данным. Для оценки значимости в предпосылках «нормальной регрессии» проверяют гипотезу 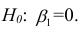
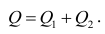
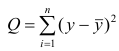
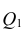
X) и 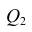
Для проверки нулевой гипотезы вычисляют статистику 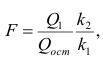
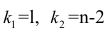
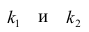
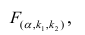
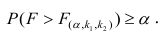
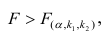
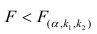
Многомерный регрессионный анализ
В случае, если изменения результативного признака определяются действием совокупности других признаков, имеет место многомерный регрессионный анализ. Пусть результативный признак У, а независимые признаки 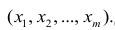
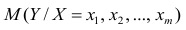
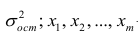
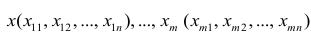
Оценке подлежат параметры 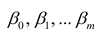
Заменив параметры их оценками, запишем уравнение регрессии
Коэффициенты в этом выражении находят методом наименьших квадратов.
Исходными данными для вычисления коэффициентов 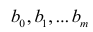

Как и в двумерном случае, составляют систему нормальных уравнений
которую можно решить любым способом, известным из линейной алгебры. Рассмотрим один из них — способ обратной матрицы. Предварительно преобразуем систему уравнений. Выразим из первого уравнения значение 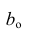
Подставим в остальные уравнения системы вместо 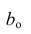
Пусть С — матрица коэффициентов при неизвестных параметрах 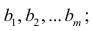
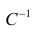
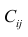
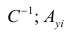
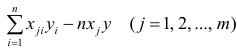
запишем окончательные выражения для параметров:
Оценкой остаточной дисперсии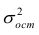
где 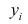
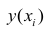
Если выборка получена из нормально распределенной генеральной совокупности, то, аналогично изложенному в п. 2.4, можно проверить значимость оценок коэффициентов регрессии, только в данном случае статистику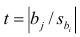
где 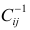
го столбца;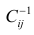
При заданном уровне значимости а и числе степеней свободы к=n— m—1 по табл. 1 приложений находят критическое значение 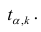
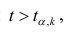
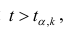
Для значимых коэффициентов регрессии целесообразно построить доверительные интервалы по формуле (2.10). Для оценки значимости уравнения регрессии следует проверить нулевую гипотезу о том, что все коэффициенты регрессии (кроме свободного члена) равны нулю: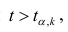
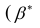
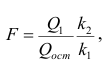
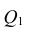
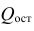
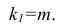
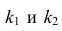
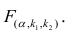
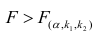
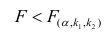
Факторный анализ
Основные положения. В последнее время всё более широкое распространение находит один из новых разделов многомерного статистического анализа — факторный анализ. Первоначально этот метод
разрабатывался для объяснения многообразия корреляций между исходными параметрами. Действительно, результатом корреляционного анализа является матрица коэффициентов корреляций. При малом числе параметров можно произвести визуальный анализ этой матрицы. С ростом числа параметра (10 и более) визуальный анализ не даёт положительных результатов. Оказалось, что всё многообразие корреляционных связей можно объяснить действием нескольких обобщённых факторов, являющихся функциями исследуемых параметров, причём сами обобщённые факторы при этом могут быть и неизвестны, однако их можно выразить через исследуемые параметры.
Один из основоположников факторного анализа Л. Терстоун приводит такой пример: несколько сотен мальчиков выполняют 20 разнообразных гимнастических упражнений. Каждое упражнение оценивают баллами. Можно рассчитать матрицу корреляций между 20 упражнениями. Это большая матрица размером 20><20. Изучая такую матрицу, трудно уловить закономерность связей между упражнениями. Нельзя ли объяснить скрытую в таблице закономерность действием каких-либо обобщённых факторов, которые в результате эксперимента непосредственно, не оценивались? Оказалось, что обо всех коэффициентах корреляции можно судить по трём обобщённым факторам, которые и определяют успех выполнения всех 20 гимнастических упражнений: чувство равновесия, усилие правого плеча, быстрота движения тела.
Дальнейшие разработки факторного анализа доказали, что этот метод может быть с успехом применён в задачах группировки и классификации объектов. Факторный анализ позволяет группировать объекты со сходными сочетаниями признаков и группировать признаки с общим характером изменения от объекта к объекту. Действительно, выделенные обобщённые факторы можно использовать как критерии при классификации мальчиков по способностям к отдельным группам гимнастических упражнений.
Методы факторного анализа находят применение в психологии и экономике, социологии и экономической географии. Факторы, выраженные через исходные параметры, как правило, легко интерпретировать как некоторые существенные внутренние характеристики объектов.
Факторный анализ может быть использован и как самостоятельный метод исследования, и вместе с другими методами многомерного анализа, например в сочетании с регрессионным анализом. В этом случае для набора зависимых переменных наводят обобщённые факторы, которые потом входят в регрессионный анализ в качестве переменных. Такой подход позволяет сократить число переменных в регрессионном анализе, устранить коррелированность переменных, уменьшить влияние ошибок и в случае ортогональности выделенных факторов значительно упростить оценку значимости переменных.
Представление, информации в факторном анализе
Для проведения факторного анализа информация должна быть представлена в виде двумерной таблицы чисел размерностью 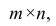
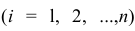
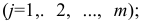
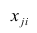
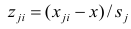
Основная модель факторного анализа. Основная модель факторного анализа имеет вид
где 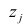
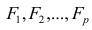
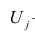
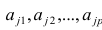
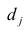
Модель предполагает, что каждый из j признаков, входящих в исследуемый набор и заданных в стандартной форме, может быть представлен в виде линейной комбинации небольшого числа общих факторов 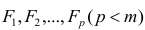
Термин «общий фактор» подчёркивает, что каждый такой фактор имеет существенное значение для анализа всех признаков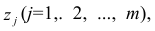
Термин «характерный фактор» показывает, что он относится только к данному j-му признаку. Это специфика признака, которая не может быть, выражена через факторы
Факторные нагрузки 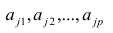
Для j-го признака и i-го объекта модель (2.19) можно записать в. виде
где 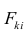
Дисперсию признака 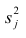
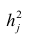
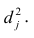
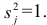
Если общие и характерные факторы не коррелируют между собой, то дисперсию j-го признака можно представить в виде
где 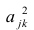
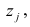
Полный вклад k-го фактора в суммарную дисперсию признаков
Вклад общих факторов в суммарную дисперсию
Факторное отображение
Используя модель (2.19), запишем выражения для каждого из параметров:
Коэффициенты системы (2,21) — факторные нагрузки — можно представить в виде матрицы, каждая строка которой соответствует параметру, а столбец — фактору.
Факторный анализ позволяет получить не только матрицу отображений, но и коэффициенты корреляции между параметрами и
факторами, что является важной характеристикой качества факторной модели. Таблица таких коэффициентов корреляции называется факторной структурой или просто структурой.
Коэффициенты отображения можно выразить через выборочные парные коэффициенты корреляции. На этом основаны методы вычисления факторного отображения.
Рассмотрим связь между элементами структуры и коэффициентами отображения. Для этого, учитывая выражение (2.19) и определение выборочного коэффициента корреляции, умножим уравнения системы (2.21) на соответствующие факторы, произведём суммирование по всем n наблюдениям и, разделив на n, получим следующую систему уравнений:
где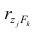
м фактором;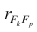
Если предположить, что общие факторы между собой, не коррелированы, то уравнения (2.22) можно записать в виде
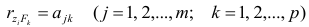
элементам структуры.
Введём понятие, остаточного коэффициента корреляции и остаточной корреляционной матрицы. Исходной информацией для построения факторной модели (2.19) служит матрица выборочных парных коэффициентов корреляции. Используя построенную факторную модель, можно снова вычислить коэффициенты корреляции между признаками и сравнись их с исходными Коэффициентами корреляции. Разница между ними и есть остаточный коэффициент корреляции.
В случае независимости факторов имеют место совсем простые выражения для вычисляемых коэффициентов корреляции между параметрами: для их вычисления достаточно взять сумму произведений коэффициентов отображения, соответствующих наблюдавшимся признакам:
где 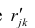
и к-м признаком. Остаточный коэффициент корреляции
Матрица остаточных коэффициентов корреляции называется остаточной матрицей или матрицей остатков
где 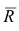
Результаты факторного анализа удобно представить в виде табл. 2.10.
Здесь суммы квадратов нагрузок по строкам — общности параметров, а суммы квадратов нагрузок по столбцам — вклады факторов в суммарную дисперсию параметров. Имеет место соотношение
Определение факторных нагрузок
Матрицу факторных нагрузок можно получить различными способами. В настоящее время наибольшее распространение получил метод главных факторов. Этот метод основан на принципе последовательных приближений и позволяет достичь любой точности. Метод главных факторов предполагает использование ЭВМ. Существуют хорошие алгоритмы и программы, реализующие все вычислительные процедуры.
Введём понятие редуцированной корреляционной матрицы или просто редуцированной матрицы. Редуцированной называется матрица выборочных коэффициентов корреляции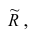
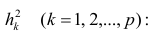
Редуцированная и полная матрицы связаны соотношением
где D — матрица характерностей.
Общности, как правило, неизвестны, и нахождение их в факторном анализе представляет серьезную проблему. Вначале определяют (хотя бы приближённо) число общих факторов, совокупность, которых может с достаточной точностью аппроксимировать все взаимосвязи выборочной корреляционной матрицы. Доказано, что число общих факторов (общностей) равно рангу редуцированной матрицы, а при известном ранге можно по выборочной корреляционной матрице найти оценки общностей. Числа общих факторов можно определить априори, исходя из физической природы эксперимента. Затем рассчитывают матрицу факторных нагрузок. Такая матрица, рассчитанная методом главных факторов, обладает одним интересным свойством: сумма произведений каждой пары её столбцов равна нулю, т.е. факторы попарно ортогональны.
Сама процедура нахождения факторных нагрузок, т.е. матрицы А, состоит из нескольких шагов и заключается в следующем: на первом шаге ищут коэффициенты факторных нагрузок при первом факторе так, чтобы сумма вкладов данного фактора в суммарную общность была максимальной:
Максимум 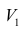
где 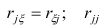
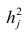
Затем рассчитывают матрицу коэффициентов корреляции с учётом только первого фактора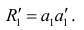
На втором шаге определяют коэффициенты нагрузок при втором факторе так, чтобы сумма вкладов второго фактора в остаточную общность (т.е. полную общность без учёта той части, которая приходится на долю первого фактора) была максимальной. Сумма квадратов нагрузок при втором факторе
Максимум 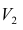
где 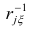
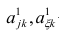
Факторный анализ учитывает суммарную общность. Исходная суммарная общность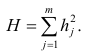
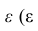
Адекватность факторной модели оценивается по матрице остатков (если величины её коэффициентов малы, то модель считают адекватной).
Такова последовательность шагов для нахождения факторных нагрузок. Для нахождения максимума функции (2.24) при условии (2.25) используют метод множителей Лагранжа, который приводит к системе т уравнений относительно m неизвестных
Метод главных компонент
Разновидностью метода главных факторов является метод главных компонент или компонентный анализ, который реализует модель вида
где m — количество параметров (признаков).
Каждый из наблюдаемых, параметров линейно зависит от m не коррелированных между собой новых компонент (факторов) 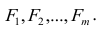
Если для дальнейшего анализа оставить все найденные т компонент, то тем самым будет использована вся информация, заложенная в корреляционной матрице. Однако это неудобно и нецелесообразно. На практике обычно оставляют небольшое число компонент, причём количество их определяется долей суммарной дисперсии, учитываемой этими компонентами. Существуют различные критерии для оценки числа оставляемых компонент; чаще всего используют следующий простой критерий: оставляют столько компонент, чтобы суммарная дисперсия, учитываемая ими, составляла заранее установленное число процентов. Первая из компонент должна учитывать максимум суммарной дисперсии параметров; вторая — не коррелировать с первой и учитывать максимум оставшейся дисперсии и так до тех пор, пока вся дисперсия не будет учтена. Сумма учтённых всеми компонентами дисперсий равна сумме дисперсий исходных параметров. Математический аппарат компонентного анализа полностью совпадает с аппаратом метода главных факторов. Отличие только в исходной матрице корреляций.
Компонента (или фактор) через исходные переменные выражается следующим образом:
где 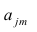
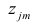
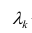
компонент.
Для иллюстрации возможностей факторного анализа покажем, как, используя метод главных компонент, можно сократить размерность пространства независимых переменных, перейдя от взаимно коррелированных параметров к независимым факторам, число которых р
Следует особо остановиться на интерпретации результатов, т.е. на смысловой стороне факторного анализа. Собственно факторный анализ состоит из двух важных этапов; аппроксимации корреляционной матрицы и интерпретации результатов. Аппроксимировать корреляционную матрицу, т.е. объяснить корреляцию между параметрами действием каких-либо общих для них факторов, и выделить сильно коррелирующие группы параметров достаточно просто: из корреляционной матрицы одним из методов
факторного анализа непосредственно получают матрицу нагрузок — факторное решение, которое называют прямым факторным решением. Однако часто это решение не удовлетворяет исследователей. Они хотят интерпретировать фактор как скрытый, но существенный параметр, поведение которого определяет поведение некоторой своей группы наблюдаемых параметров, в то время как, поведение других параметров определяется поведением других факторов. Для этого у каждого параметра должна быть наибольшая по модулю факторная нагрузка с одним общим фактором. Прямое решение следует преобразовать, что равносильно повороту осей общих факторов. Такие преобразования называют вращениями, в итоге получают косвенное факторное решение, которое и является результатом факторного анализа.
Приложения
Значение t — распределения Стьюдента
Понятие о регрессионном анализе. Линейная выборочная регрессия. Метод наименьших квадратов (МНК)
Основные задачи регрессионного анализа:
- Вычисление выборочных коэффициентов регрессии
- Проверка значимости коэффициентов регрессии
- Проверка адекватности модели
- Выбор лучшей регрессии
- Вычисление стандартных ошибок, анализ остатков
Построение простой регрессии по экспериментальным данным.
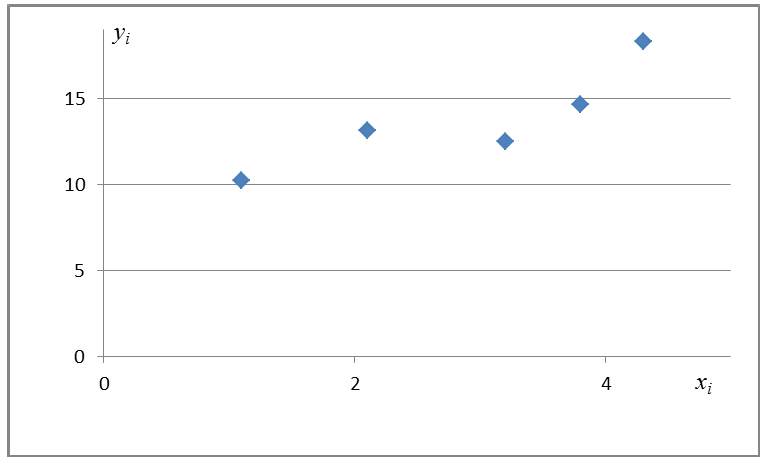
Предположим, что случайные величины 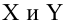
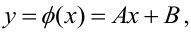
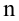
Диаграмма рассеяния (разброса, рассеивания)
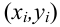
Выборочное уравнение прямой линии регрессии 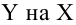
Задача: подобрать 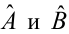
Для того, что бы провести прямую 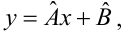
чтобы
Постулаты регрессионного анализа, которые должны выполняться при использовании МНК.
подчинены нормальному закону распределения.
- Дисперсия
постоянна и не зависит от номера измерения.
- Результаты наблюдений
в разных точках независимы.
- Входные переменные
независимы, неслучайны и измеряются без ошибок.
Введем функцию ошибок 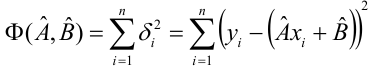
Решив систему, получим искомые значения
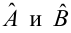
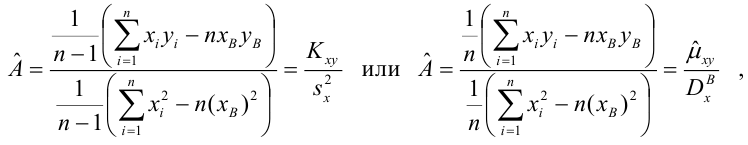
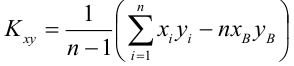
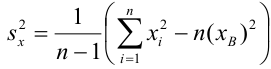
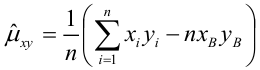
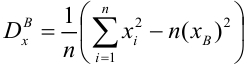
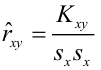
Коэффициент детерминации
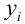
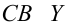
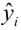
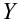
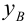
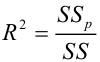
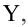
Коэффициент детерминации принимает значения от 0 до 1. Чем ближе значение коэффициента к 1, тем сильнее зависимость. При оценке регрессионных моделей это используется для доказательства адекватности модели (качества регрессии). Для приемлемых моделей предполагается, что коэффициент детерминации должен быть хотя бы не меньше 0,5 (в этом случае коэффициент множественной корреляции превышает по модулю 0,7). Модели с коэффициентом детерминации выше 0,8 можно признать достаточно хорошими (коэффициент корреляции превышает 0,9). Подтверждение адекватности модели проводится на основе дисперсионного анализа путем проверки гипотезы о значимости коэффициента детерминации.
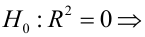
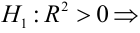
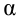
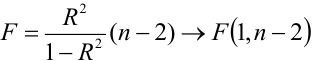
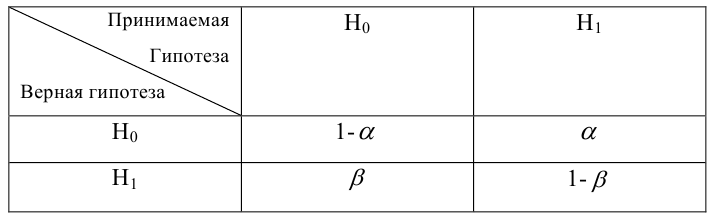
Критическая область — правосторонняя;
Если 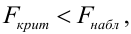
Мощность статистического критерия. Функция мощности
Определение. Мощностью критерия 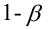
Задача: построить критическую область таким образом, чтобы мощность критерия была максимальной.
Определение. Наилучшей критической областью (НКО) называют критическую область, которая обеспечивает минимальную ошибку второго рода
Пример:
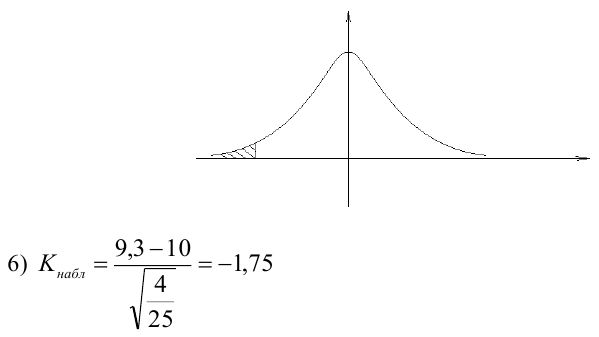
По паспортным данным автомобиля расход топлива на 100 километров составляет 10 литров. В результате измерения конструкции двигателя ожидается, что расход топлива уменьшится. Для проверки были проведены испытания 25 автомобилей с модернизированным двигателем; выборочная средняя расхода топлива по результатам испытаний составила 9,3 литра. Предполагая, что выборка получена из нормально распределенной генеральной совокупности с математическим ожиданием 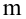
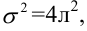
3) Уровень значимости
4) Статистический критерий
5) Критическая область — левосторонняя
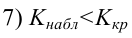
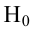
Пример:
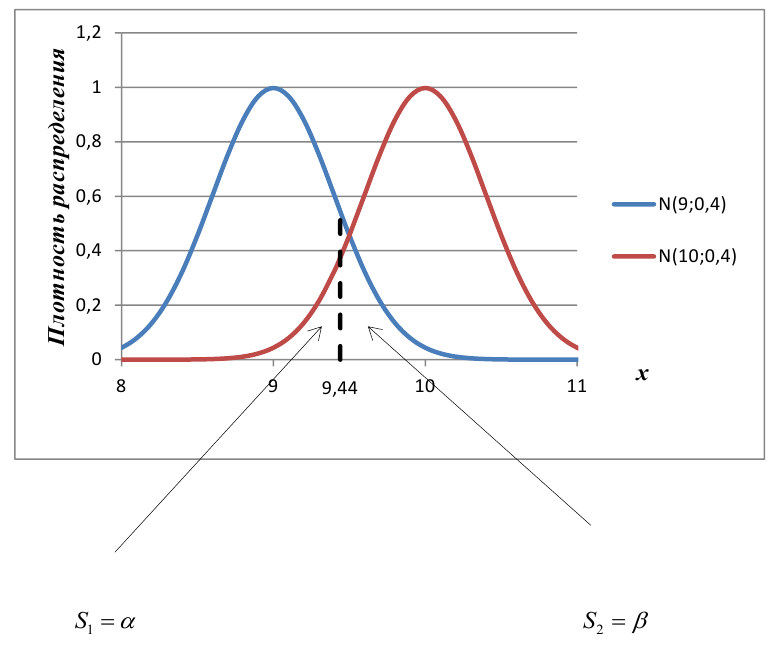
В условиях примера 1 предположим, что наряду с 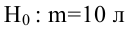
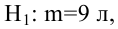
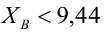
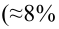
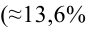
Определение. Пусть проверяется 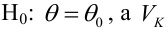
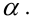
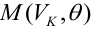
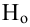
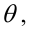
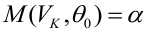
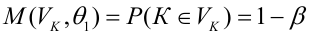
Пример:
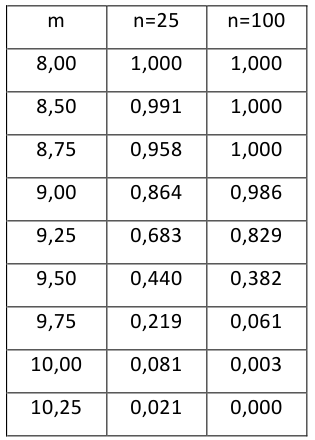
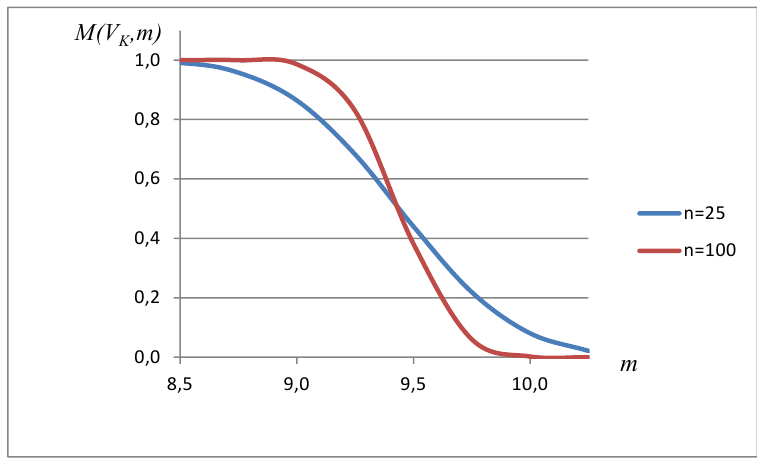
Построить график функции мощности из примера 2 для

Пример:
Какой минимальный объем выборки следует взять в условии примера 2 для того, чтобы обеспечить
Лемма Неймана-Пирсона.
При проверке простой гипотезы 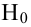
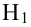
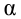
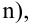
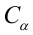
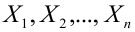
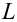
Пример:
Случайная величина 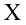
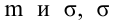
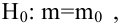
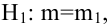
Решение:
Ошибка первого рода:
НКО:
Пример:
Для зависимости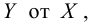
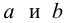
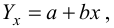
Решение. Воспользуемся предыдущими результатами
Согласно формуле (24), уравнение регрессии будет иметь вид 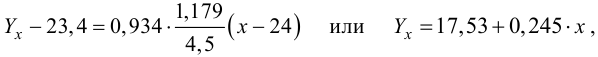
Для выяснения значимости уравнения регрессии вычислим суммы 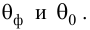
Из (27) и (28) по данным таблицы получим
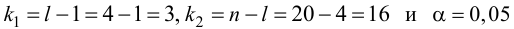
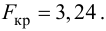
Вычислим статистику
Так как 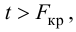
- Корреляционный анализ
- Статистические решающие функции
- Случайные процессы
- Выборочный метод
- Проверка гипотезы о равенстве вероятностей
- Доверительный интервал для математического ожидания
- Доверительный интервал для дисперсии
- Проверка статистических гипотез

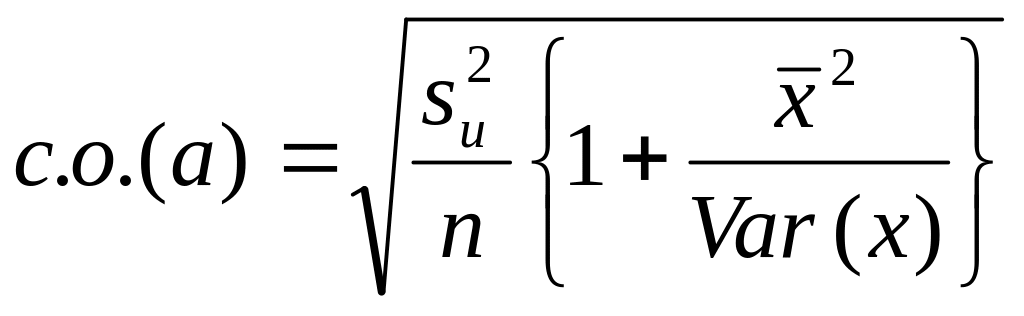
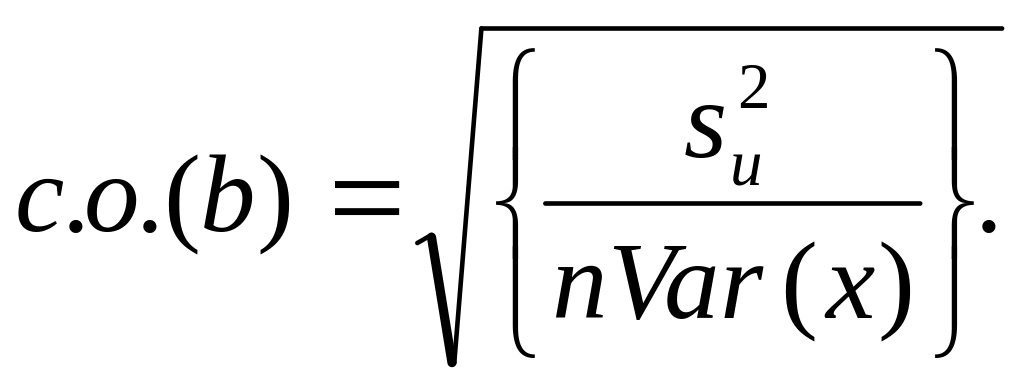

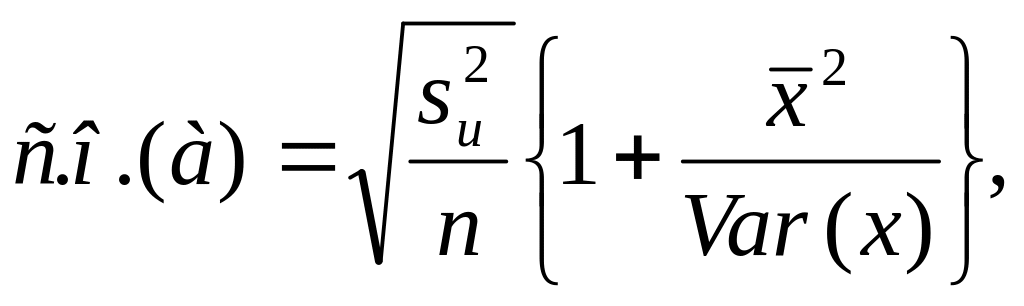











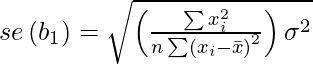

















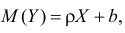
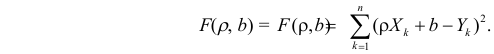
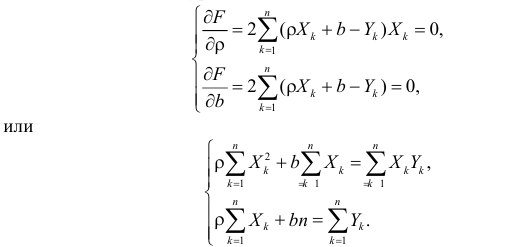
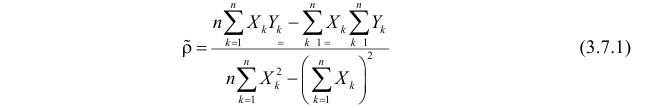
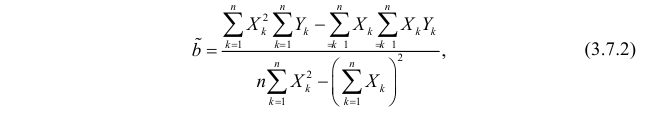
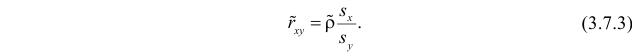
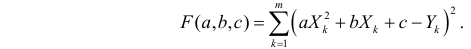

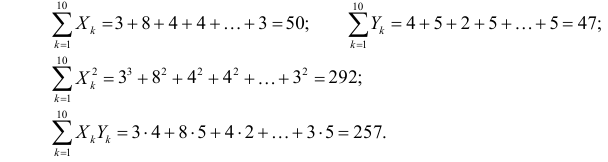
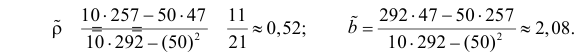
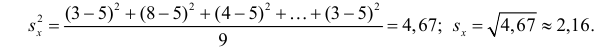
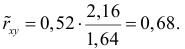
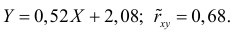

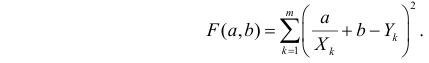
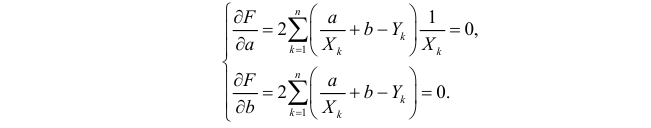
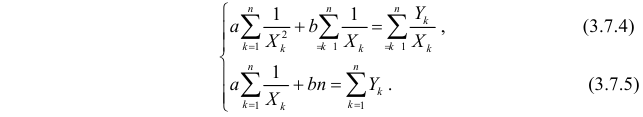
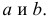
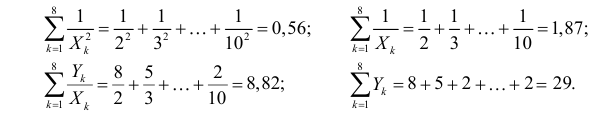
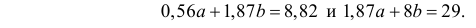
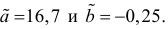
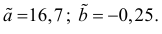




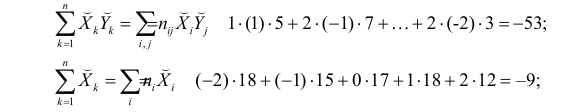
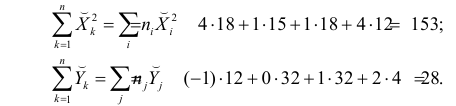
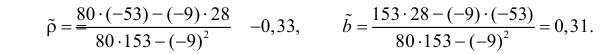
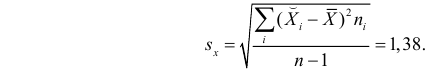
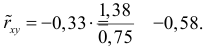
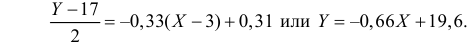
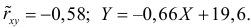
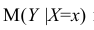 можно представить в виде
можно представить в виде 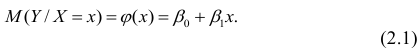
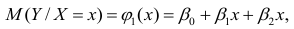
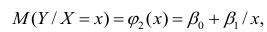
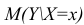 можно представить в виде (2.1).
можно представить в виде (2.1).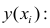
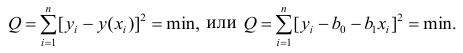
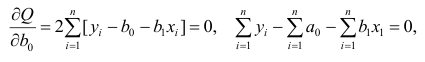
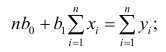
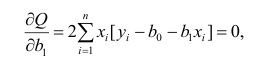
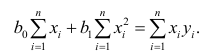
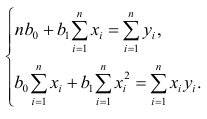
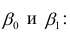
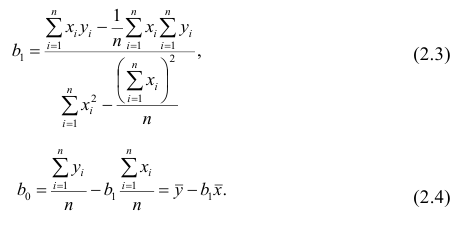
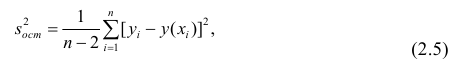
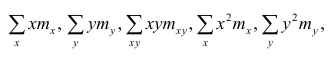
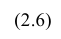
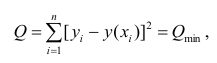
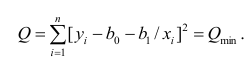
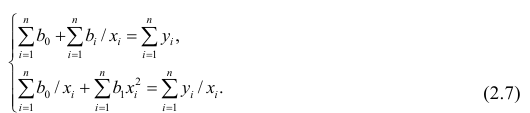
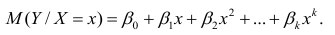
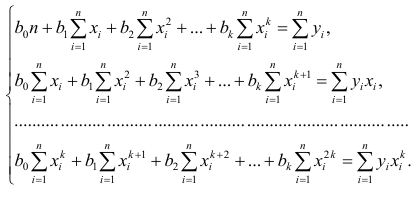

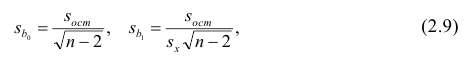
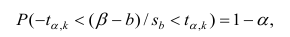

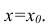
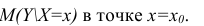
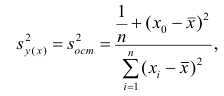
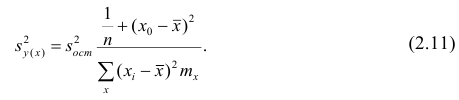
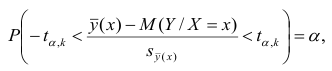
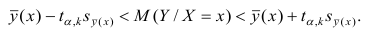
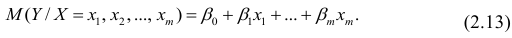
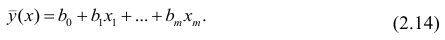
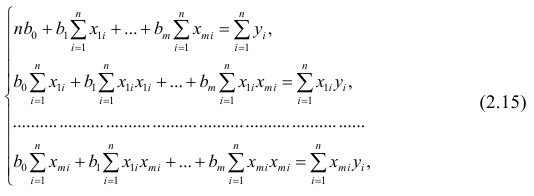
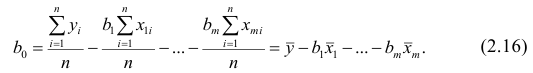
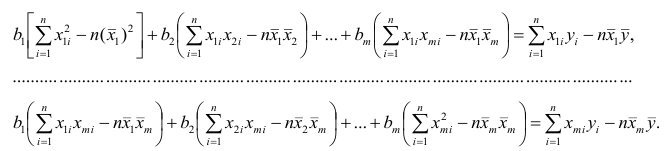
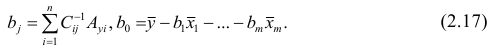
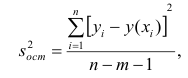
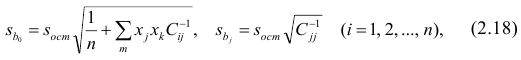
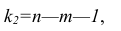
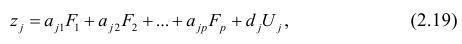
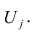
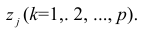
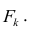
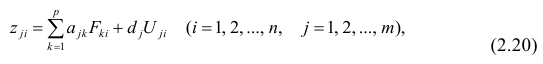
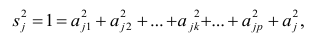
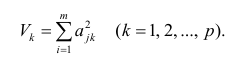
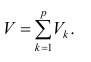
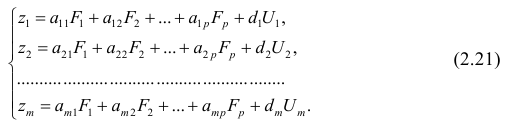
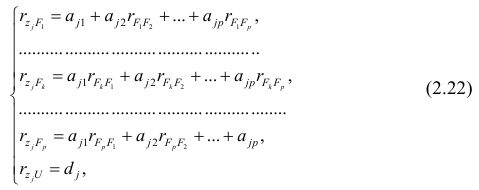
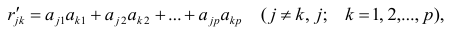
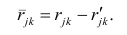

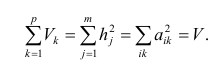
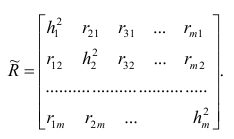


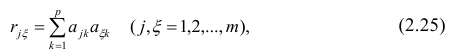

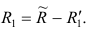

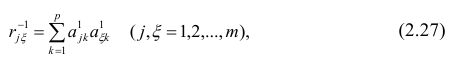
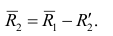
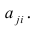
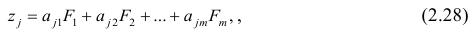
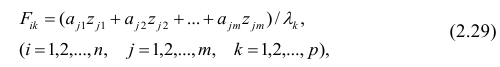
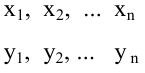
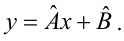
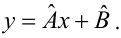
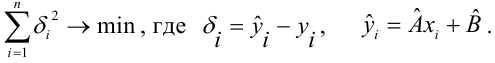
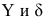 подчинены нормальному закону распределения.
подчинены нормальному закону распределения.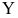 постоянна и не зависит от номера измерения.
постоянна и не зависит от номера измерения.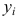 в разных точках независимы.
в разных точках независимы.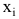 независимы, неслучайны и измеряются без ошибок.
независимы, неслучайны и измеряются без ошибок.