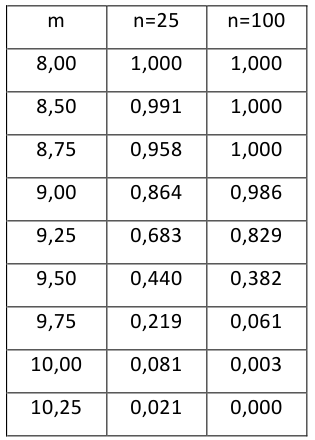
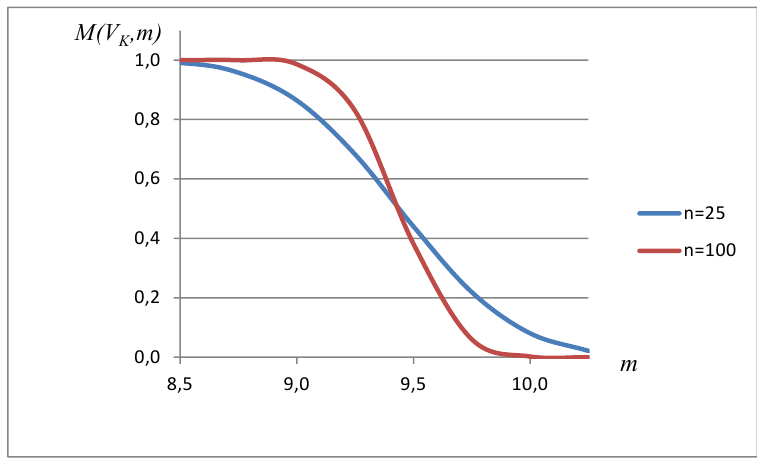
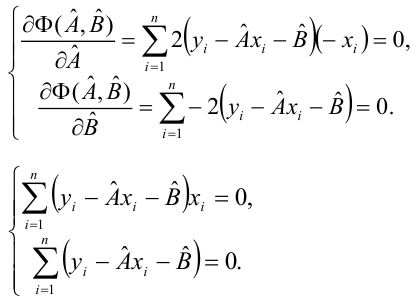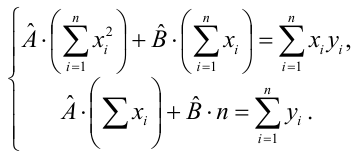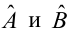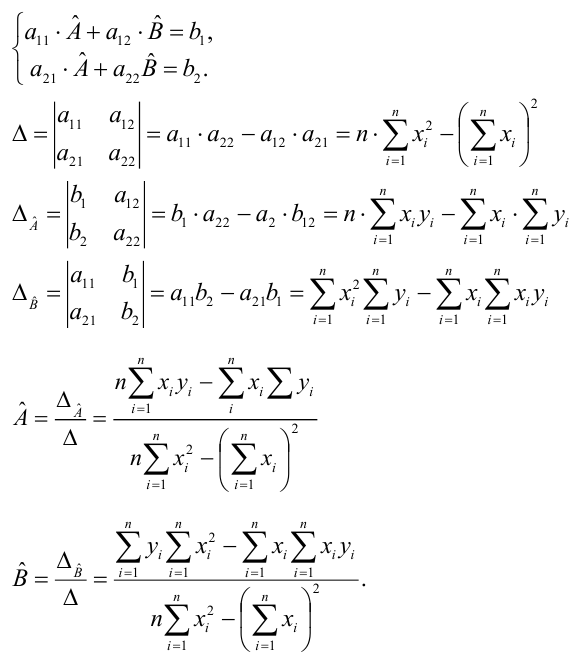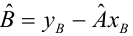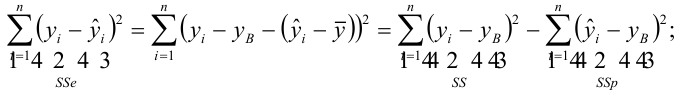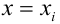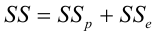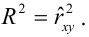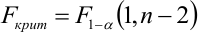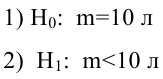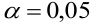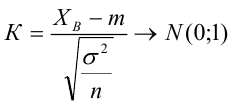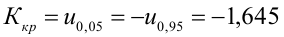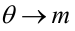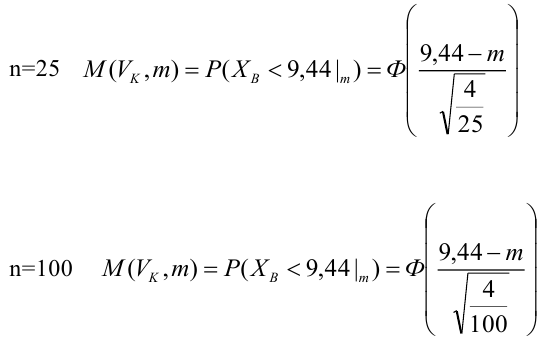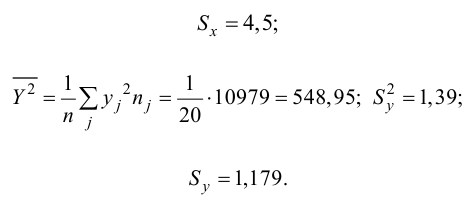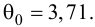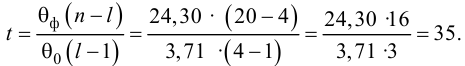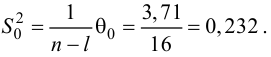Когда мы подгоняем регрессионную модель к набору данных, нас часто интересует, насколько хорошо регрессионная модель «подходит» к набору данных. Две метрики, обычно используемые для измерения согласия, включают R -квадрат (R2) и стандартную ошибку регрессии , часто обозначаемую как S.
В этом руководстве объясняется, как интерпретировать стандартную ошибку регрессии (S), а также почему она может предоставить более полезную информацию, чем R 2 .
Стандартная ошибка по сравнению с R-квадратом в регрессии
Предположим, у нас есть простой набор данных, который показывает, сколько часов 12 студентов занимались в день в течение месяца, предшествующего важному экзамену, а также их баллы за экзамен:
Если мы подгоним простую модель линейной регрессии к этому набору данных в Excel, мы получим следующий результат:
R-квадрат — это доля дисперсии переменной отклика, которая может быть объяснена предикторной переменной. При этом 65,76% дисперсии экзаменационных баллов можно объяснить количеством часов, потраченных на учебу.
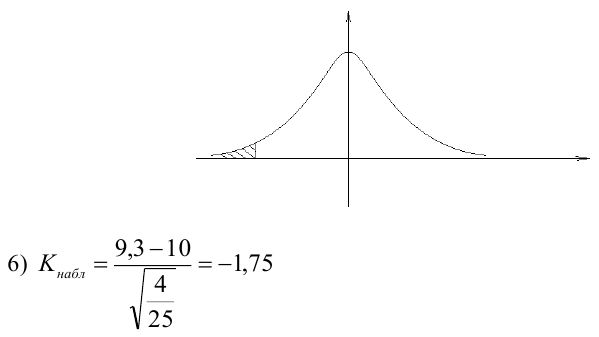
Стандартная ошибка регрессии — это среднее расстояние, на которое наблюдаемые значения отклоняются от линии регрессии. В этом случае наблюдаемые значения отклоняются от линии регрессии в среднем на 4,89 единицы.
Если мы нанесем фактические точки данных вместе с линией регрессии, мы сможем увидеть это более четко:
Обратите внимание, что некоторые наблюдения попадают очень близко к линии регрессии, в то время как другие не так близки. Но в среднем наблюдаемые значения отклоняются от линии регрессии на 4,19 единицы .
Стандартная ошибка регрессии особенно полезна, поскольку ее можно использовать для оценки точности прогнозов. Примерно 95% наблюдений должны находиться в пределах +/- двух стандартных ошибок регрессии, что является быстрым приближением к 95% интервалу прогнозирования.
Если мы заинтересованы в прогнозировании с использованием модели регрессии, стандартная ошибка регрессии может быть более полезной метрикой, чем R-квадрат, потому что она дает нам представление о том, насколько точными будут наши прогнозы в единицах измерения.
Чтобы проиллюстрировать, почему стандартная ошибка регрессии может быть более полезной метрикой для оценки «соответствия» модели, рассмотрим другой пример набора данных, который показывает, сколько часов 12 студентов занимались в день в течение месяца, предшествующего важному экзамену, а также их экзаменационная оценка:
Обратите внимание, что это точно такой же набор данных, как и раньше, за исключением того, что все значения s сокращены вдвое.Таким образом, студенты из этого набора данных учились ровно в два раза дольше, чем студенты из предыдущего набора данных, и получили ровно половину экзаменационного балла.
Если мы подгоним простую модель линейной регрессии к этому набору данных в Excel, мы получим следующий результат:
Обратите внимание, что R-квадрат 65,76% точно такой же, как и в предыдущем примере.
Однако стандартная ошибка регрессии составляет 2,095 , что ровно вдвое меньше стандартной ошибки регрессии в предыдущем примере.
Если мы нанесем фактические точки данных вместе с линией регрессии, мы сможем увидеть это более четко:
Обратите внимание на то, что наблюдения располагаются гораздо плотнее вокруг линии регрессии. В среднем наблюдаемые значения отклоняются от линии регрессии на 2,095 единицы .
Таким образом, несмотря на то, что обе модели регрессии имеют R-квадрат 65,76% , мы знаем, что вторая модель будет давать более точные прогнозы, поскольку она имеет более низкую стандартную ошибку регрессии.
Преимущества использования стандартной ошибки
Стандартную ошибку регрессии (S) часто бывает полезнее знать, чем R-квадрат модели, потому что она дает нам фактические единицы измерения. Если мы заинтересованы в использовании регрессионной модели для получения прогнозов, S может очень легко сказать нам, достаточно ли точна модель для прогнозирования.
Например, предположим, что мы хотим создать 95-процентный интервал прогнозирования, в котором мы можем прогнозировать результаты экзаменов с точностью до 6 баллов от фактической оценки.
Наша первая модель имеет R-квадрат 65,76%, но это ничего не говорит нам о том, насколько точным будет наш интервал прогнозирования. К счастью, мы также знаем, что у первой модели показатель S равен 4,19. Это означает, что 95-процентный интервал прогнозирования будет иметь ширину примерно 2*4,19 = +/- 8,38 единиц, что слишком велико для нашего интервала прогнозирования.
Наша вторая модель также имеет R-квадрат 65,76%, но опять же это ничего не говорит нам о том, насколько точным будет наш интервал прогнозирования. Однако мы знаем, что вторая модель имеет S 2,095. Это означает, что 95-процентный интервал прогнозирования будет иметь ширину примерно 2*2,095= +/- 4,19 единиц, что меньше 6 и, следовательно, будет достаточно точным для использования для создания интервалов прогнозирования.
Дальнейшее чтение
Введение в простую линейную регрессию
Что такое хорошее значение R-квадрата?
Проверка адекватности регрессионной модели и значимости показателей тесноты корреляционной связи
Информация, содержащаяся в эмпирических данных, извлекается с большей полнотой, чем полученная традиционными методами описательной статистики, и, что самое важное, может быть представлена с разных точек зрения. Тем самым перед исследователем открывается обширная область для теоретических выводов, формирования новых представлений и гипотез.
Особое внимание необходимо обратить на интерпретацию и оценку параметров уравнения. Параметры уравнения регрессии следует проверить на их значимость.
Для того чтобы получить оценку значимости коэффициентов регрессии при линейной зависимости у от х, и х2, используют t-кри- терий Стьюдента.
Значимость коэффициентов линейного уравнения регрессии а0 и ах оценивается с помощью ^-критерия Стьюдента (п /табл с уровнем значимости 0,05 и числом степеней свободы (п-т- 1).
Уравнение признают окончательным и применяют в качестве модели изучаемого показателя для последующего анализа в том случае, если в данном уравнении все коэффициенты регрессии значимы.
Показатели множественной регрессии и корреляции могут оказаться подверженными действию случайных факторов, поэтому только после проверки адекватности уравнения оно может быть пригодно.
Прежде всего, следует установить, соответствуют ли полученные данные тем гипотетическим представлениям, которые сложились в результате анализа, и показывают ли они причинно-следственные связи, которые ожидались. Для оценки адекватности модели можно вычислить отклонение теоретических данных от эмпирических, остаточную дисперсию, а также ошибку аппроксимации, которая определяется по формуле:
1) для однофакторной регрессионной модели:
2) для многофакторной регрессионной модели:
Общая оценка адекватности уравнения может быть получена с помощью дисперсионного F-критерия Фишера, на основании которого проводят проверку значимости регрессии:
1) для однофакторной регрессионной модели:
где т — число параметров в уравнении регрессии; п — число единиц наблюдения;
2) для многофакторной регрессионной модели:
Распределение Фишера [Рональд Фишер (1890—1968) — английский ученый] — двухпараметрическое распределение неотрицательной случайной величины, являющейся в частном случае, при т= 1, квадратом случайной величины, распределенной по Стьюденту. Для распределения Фишера имеются таблицы критических значений, зависящих от чисел степеней свободы т и п- т — I, при различных уровнях значимости.
Считается, что влияние факторного признака статистически существенно, для принятого уровня значимости 0,05 или 0,01, если Fp (расчетное) > FT (табличное), то влияние факторного признака считается существенным и данное уравнение регрессии будет статистически значимым.
FT зависит от трех параметров:
- 1) определяет достоверность выводов (называется уровнем значимости). Для социологических и экономических задач FT — 0,05 — определяет вероятность отвергнуть правильную гипотезу в 5 случаях из 100;
- 2) определяется количеством значений факторного признака
- (т-1);
- 3) определяется объемом выборки, уменьшенным на количество значений факторного признака (п — т).
FT определяется по таблице критических значений критерия Фишера.
Вернемся к примеру 10.1.
Проведем оценку адекватности регрессионной модели:
выражающей зависимость между производительностью труда и выполнением плана реализации, с помощью F-критерия Фишера:
Эмпирическое значение Fбольше табличного, следовательно, уравнение регрессии можно признать адекватным.
Оценим значимость параметров уравнения регрессии с помощью /-критерия Стьюдента:
Табличное значение /-критерия с уровнем значимости 0,05 и числом степеней свободы (п — 2) равно 2,307. Так как /эмп > /табл, то параметры уравнения регрессии признаются значимыми.
Значимость коэффициента корреляции оценим с помощью /-критерия Стьюдента по формуле
Эмпирическое значение / больше табличного, следовательно, коэффициент корреляции можно признать значимым.
Вычислим ошибку аппроксимации по формуле
На основании данных расчетов можно сделать заключение, что построенная регрессионная модель зависимости производительности труда от выполнения плана реализации может быть использована для анализа и прогноза.
Итак, в общем виде многообразие видов регрессионных моделей порождается формой связи изучаемых признаков (линейной или нелинейной) и представлениями о распределении остатков (ошибки, шума) модели. Кроме того, модели более высокого уровня включают не одно, а систему регрессионных уравнений. Поиск решений для множества моделей приводит исследователя к задаче преобразования этих моделей и получения форм с хорошо известными и реализуемыми алгоритмами оценивания, как, например, в описанном выше случае с нелинейными моделями. Реформирование моделей производится при помощи трансформационных изменений переменных (отклика предикторов) или введением особых ограничений на признаковые или параметрические значения.
Благодаря своей разработанности и гибкости метод регрессионного анализа в настоящее время широко распространен в аналитической практике. Он становится также неотъемлемой частью или обычным логическим дополнением многих методов многомерной статистики в факторном, дискриминантном анализе, методе канонических корреляций, многомерном шкалировании, кластерном анализе и т. д.
Дальнейшее развитие теории регрессионного анализа, прежде всего, видится в разработке новых нелинейных форм, позволяющих с высокой степенью адекватности описывать реальные процессы, расклассификации многочисленных регрессионных моделей и методов их решения, ориентированной на конкретные группы исследовательских задач, определении перспектив использования регрессионного анализа в сочетании с другими методами статистического анализа.
Пример 10.3. По территории регионов имеются следующие данные:
Прожиточный min в день одного трудоспособного, руб.
Среднедневная заработная плата, руб.
Простая линейная регрессия в EXCEL
history 26 января 2019 г.
- Группы статей
- Статистический анализ
Регрессия позволяет прогнозировать зависимую переменную на основании значений фактора. В MS EXCEL имеется множество функций, которые возвращают не только наклон и сдвиг линии регрессии, характеризующей линейную взаимосвязь между факторами, но и регрессионную статистику. Здесь рассмотрим простую линейную регрессию, т.е. прогнозирование на основе одного фактора.
Disclaimer : Данную статью не стоит рассматривать, как пересказ главы из учебника по статистике. Статья не обладает ни полнотой, ни строгостью изложения положений статистической науки. Эта статья – о применении MS EXCEL для целей Регрессионного анализа. Теоретические отступления приведены лишь из соображения логики изложения. Использование данной статьи для изучения Регрессии – плохая идея.
Статья про Регрессионный анализ получилась большая, поэтому ниже для удобства приведены ее разделы:
Примечание : Если прогнозирование переменной осуществляется на основе нескольких факторов, то имеет место множественная регрессия .
Чтобы разобраться, чем может помочь MS EXCEL при проведении регрессионного анализа, напомним вкратце теорию, введем термины и обозначения, которые могут отличаться в зависимости от различных источников.
Примечание : Для тех, кому некогда, незачем или просто не хочется разбираться в теоретических выкладках предлагается сразу перейти к вычислительной части — оценке неизвестных параметров линейной модели .
Немного теории и основные понятия
Пусть у нас есть массив данных, представляющий собой значения двух переменных Х и Y. Причем значения переменной Х мы можем произвольно задавать (контролировать) и использовать эту переменную для предсказания значений зависимой переменной Y. Таким образом, случайной величиной является только переменная Y.
Примером такой задачи может быть производственный процесс изготовления некого волокна, причем прочность этого волокна (Y) зависит только от рабочей температуры процесса в реакторе (Х), которая задается оператором.
Построим диаграмму рассеяния (см. файл примера лист Линейный ), созданию которой посвящена отдельная статья . Вообще, построение диаграммы рассеяния для целей регрессионного анализа де-факто является стандартом.
СОВЕТ : Подробнее о построении различных типов диаграмм см. статьи Основы построения диаграмм и Основные типы диаграмм .
Приведенная выше диаграмма рассеяния свидетельствует о возможной линейной взаимосвязи между Y от Х: очевидно, что точки данных в основном располагаются вдоль прямой линии.
Примечание : Наличие даже такой очевидной линейной взаимосвязи не может являться доказательством о наличии причинной взаимосвязи переменных. Наличие причинной взаимосвязи не может быть доказано на основании только анализа имеющихся измерений, а должно быть обосновано с помощью других исследований, например теоретических выкладок.
Примечание : Как известно, уравнение прямой линии имеет вид Y = m * X + k , где коэффициент m отвечает за наклон линии ( slope ), k – за сдвиг линии по вертикали ( intercept ), k равно значению Y при Х=0.
Предположим, что мы можем зафиксировать переменную Х ( рабочую температуру процесса ) при некотором значении Х i и произвести несколько наблюдений переменной Y ( прочность нити ). Очевидно, что при одном и том же значении Хi мы получим различные значения Y. Это обусловлено влиянием других факторов на Y. Например, локальные колебания давления в реакторе, концентрации раствора, наличие ошибок измерения и др. Предполагается, что воздействие этих факторов имеет случайную природу и для каждого измерения имеются одинаковые условия проведения эксперимента (т.е. другие факторы не изменяются).
Полученные значения Y, при заданном Хi, будут колебаться вокруг некого значения . При увеличении количества измерений, среднее этих измерений, будет стремиться к математическому ожиданию случайной величины Y (при Х i ) равному μy(i)=Е(Y i ).
Подобные рассуждения можно привести для любого значения Хi.
Чтобы двинуться дальше, воспользуемся материалом из раздела Проверка статистических гипотез . В статье о проверке гипотезы о среднем значении генеральной совокупности в качестве нулевой гипотезы предполагалось равенство неизвестного значения μ заданному μ0.
В нашем случае простой линейной регрессии в качестве нулевой гипотезы предположим, что между переменными μy(i) и Хi существует линейная взаимосвязь μ y(i) =α* Х i +β. Уравнение μ y(i) =α* Х i +β можно переписать в обобщенном виде (для всех Х и μ y ) как μ y =α* Х +β.
Для наглядности проведем прямую линию соединяющую все μy(i).
Данная линия называется регрессионной линией генеральной совокупности (population regression line), параметры которой ( наклон a и сдвиг β ) нам не известны (по аналогии с гипотезой о среднем значении генеральной совокупности , где нам было неизвестно истинное значение μ).
Теперь сделаем переход от нашего предположения, что μy=a* Х + β , к предсказанию значения случайной переменной Y в зависимости от значения контролируемой переменной Х. Для этого уравнение связи двух переменных запишем в виде Y=a*X+β+ε, где ε — случайная ошибка, которая отражает суммарный эффект влияния других факторов на Y (эти «другие» факторы не участвуют в нашей модели). Напомним, что т.к. переменная Х фиксирована, то ошибка ε определяется только свойствами переменной Y.
Уравнение Y=a*X+b+ε называют линейной регрессионной моделью . Часто Х еще называют независимой переменной (еще предиктором и регрессором , английский термин predictor , regressor ), а Y – зависимой (или объясняемой , response variable ). Так как регрессор у нас один, то такая модель называется простой линейной регрессионной моделью ( simple linear regression model ). α часто называют коэффициентом регрессии.
Предположения линейной регрессионной модели перечислены в следующем разделе.
Предположения линейной регрессионной модели
Чтобы модель линейной регрессии Yi=a*Xi+β+ε i была адекватной — требуется:
- Ошибки ε i должны быть независимыми переменными;
- При каждом значении Xi ошибки ε i должны быть иметь нормальное распределение (также предполагается равенство нулю математического ожидания, т.е. Е[ε i ]=0);
- При каждом значении Xi ошибки ε i должны иметь равные дисперсии (обозначим ее σ 2 ).
Примечание : Последнее условие называется гомоскедастичность — стабильность, гомогенность дисперсии случайной ошибки e. Т.е. дисперсия ошибки σ 2 не должна зависеть от значения Xi.
Используя предположение о равенстве математического ожидания Е[ε i ]=0 покажем, что μy(i)=Е[Yi]:
Е[Yi]= Е[a*Xi+β+ε i ]= Е[a*Xi+β]+ Е[ε i ]= a*Xi+β= μy(i), т.к. a, Xi и β постоянные значения.
Дисперсия случайной переменной Y равна дисперсии ошибки ε, т.е. VAR(Y)= VAR(ε)=σ 2 . Это является следствием, что все значения переменной Х являются const, а VAR(ε)=VAR(ε i ).
Задачи регрессионного анализа
Для проверки гипотезы о линейной взаимосвязи переменной Y от X делают выборку из генеральной совокупности (этой совокупности соответствует регрессионная линия генеральной совокупности , т.е. μy=a* Х +β). Выборка будет состоять из n точек, т.е. из n пар значений .
На основании этой выборки мы можем вычислить оценки наклона a и сдвига β, которые обозначим соответственно a и b . Также часто используются обозначения â и b̂.
Далее, используя эти оценки, мы также можем проверить гипотезу: имеется ли линейная связь между X и Y статистически значимой?
Первая задача регрессионного анализа – оценка неизвестных параметров ( estimation of the unknown parameters ). Подробнее см. раздел Оценки неизвестных параметров модели .
Вторая задача регрессионного анализа – Проверка адекватности модели ( model adequacy checking ).
Примечание : Оценки параметров модели обычно вычисляются методом наименьших квадратов (МНК), которому посвящена отдельная статья .
Оценка неизвестных параметров линейной модели (используя функции MS EXCEL)
Неизвестные параметры простой линейной регрессионной модели Y=a*X+β+ε оценим с помощью метода наименьших квадратов (в статье про МНК подробно описано этот метод ).
Для вычисления параметров линейной модели методом МНК получены следующие выражения:
Таким образом, мы получим уравнение прямой линии Y= a *X+ b , которая наилучшим образом аппроксимирует имеющиеся данные.
Примечание : В статье про метод наименьших квадратов рассмотрены случаи аппроксимации линейной и квадратичной функцией , а также степенной , логарифмической и экспоненциальной функцией .
Оценку параметров в MS EXCEL можно выполнить различными способами:
Сначала рассмотрим функции НАКЛОН() , ОТРЕЗОК() и ЛИНЕЙН() .
Пусть значения Х и Y находятся соответственно в диапазонах C 23: C 83 и B 23: B 83 (см. файл примера внизу статьи).
Примечание : Значения двух переменных Х и Y можно сгенерировать, задав тренд и величину случайного разброса (см. статью Генерация данных для линейной регрессии в MS EXCEL ).
В MS EXCEL наклон прямой линии а ( оценку коэффициента регрессии ), можно найти по методу МНК с помощью функции НАКЛОН() , а сдвиг b ( оценку постоянного члена или константы регрессии ), с помощью функции ОТРЕЗОК() . В английской версии это функции SLOPE и INTERCEPT соответственно.
Аналогичный результат можно получить с помощью функции ЛИНЕЙН() , английская версия LINEST (см. статью об этой функции ).
Формула =ЛИНЕЙН(C23:C83;B23:B83) вернет наклон а . А формула = ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);2) — сдвиг b . Здесь требуются пояснения.
Функция ЛИНЕЙН() имеет 4 аргумента и возвращает целый массив значений:
ЛИНЕЙН(известные_значения_y; [известные_значения_x]; [конст]; [статистика])
Если 4-й аргумент статистика имеет значение ЛОЖЬ или опущен, то функция ЛИНЕЙН() возвращает только оценки параметров модели: a и b .
Примечание : Остальные значения, возвращаемые функцией ЛИНЕЙН() , нам потребуются при вычислении стандартных ошибок и для проверки значимости регрессии . В этом случае аргумент статистика должен иметь значение ИСТИНА.
Чтобы вывести сразу обе оценки:
- в одной строке необходимо выделить 2 ячейки,
- ввести формулу в Строке формул
- нажать CTRL+SHIFT+ENTER (см. статью про формулы массива ).
Если в Строке формул выделить формулу = ЛИНЕЙН(C23:C83;B23:B83) и нажать клавишу F9 , то мы увидим что-то типа <3,01279389265416;154,240057900613>. Это как раз значения a и b . Как видно, оба значения разделены точкой с запятой «;», что свидетельствует, что функция вернула значения «в нескольких ячейках одной строки».
Если требуется вывести параметры линии не в одной строке, а одном столбце (ячейки друг под другом), то используйте формулу = ТРАНСП(ЛИНЕЙН(C23:C83;B23:B83)) . При этом выделять нужно 2 ячейки в одном столбце. Если теперь выделить новую формулу и нажать клавишу F9, то мы увидим что 2 значения разделены двоеточием «:», что означает, что значения выведены в столбец (функция ТРАНСП() транспонировала строку в столбец ).
Чтобы разобраться в этом подробнее необходимо ознакомиться с формулами массива .
Чтобы не связываться с вводом формул массива , можно использовать функцию ИНДЕКС() . Формула = ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);1) или просто ЛИНЕЙН(C23:C83;B23:B83) вернет параметр, отвечающий за наклон линии, т.е. а . Формула =ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);2) вернет параметр b .
Оценка неизвестных параметров линейной модели (через статистики выборок)
Наклон линии, т.е. коэффициент а , можно также вычислить через коэффициент корреляции и стандартные отклонения выборок :
= КОРРЕЛ(B23:B83;C23:C83) *(СТАНДОТКЛОН.В(C23:C83)/ СТАНДОТКЛОН.В(B23:B83))
Вышеуказанная формула математически эквивалентна отношению ковариации выборок Х и Y и дисперсии выборки Х:
И, наконец, запишем еще одну формулу для нахождения сдвига b . Воспользуемся тем фактом, что линия регрессии проходит через точку средних значений переменных Х и Y.
Вычислив средние значения и подставив в формулу ранее найденный наклон а , получим сдвиг b .
Оценка неизвестных параметров линейной модели (матричная форма)
Также параметры линии регрессии можно найти в матричной форме (см. файл примера лист Матричная форма ).
В формуле символом β обозначен столбец с искомыми параметрами модели: β0 (сдвиг b ), β1 (наклон a ).
Матрица Х равна:
Матрица Х называется регрессионной матрицей или матрицей плана . Она состоит из 2-х столбцов и n строк, где n – количество точек данных. Первый столбец — столбец единиц, второй – значения переменной Х.
Матрица Х T – это транспонированная матрица Х . Она состоит соответственно из n столбцов и 2-х строк.
В формуле символом Y обозначен столбец значений переменной Y.
Чтобы перемножить матрицы используйте функцию МУМНОЖ() . Чтобы найти обратную матрицу используйте функцию МОБР() .
Пусть дан массив значений переменных Х и Y (n=10, т.е.10 точек).
Слева от него достроим столбец с 1 для матрицы Х.
и введя ее как формулу массива в 2 ячейки, получим оценку параметров модели.
Красота применения матричной формы полностью раскрывается в случае множественной регрессии .
Построение линии регрессии
Для отображения линии регрессии построим сначала диаграмму рассеяния , на которой отобразим все точки (см. начало статьи ).
Для построения прямой линии используйте вычисленные выше оценки параметров модели a и b (т.е. вычислите у по формуле y = a * x + b ) или функцию ТЕНДЕНЦИЯ() .
Формула = ТЕНДЕНЦИЯ($C$23:$C$83;$B$23:$B$83;B23) возвращает расчетные (прогнозные) значения ŷi для заданного значения Хi из столбца В2 .
Примечание : Линию регрессии можно также построить с помощью функции ПРЕДСКАЗ() . Эта функция возвращает прогнозные значения ŷi, но, в отличие от функции ТЕНДЕНЦИЯ() работает только в случае одного регрессора. Функция ТЕНДЕНЦИЯ() может быть использована и в случае множественной регрессии (в этом случае 3-й аргумент функции должен быть ссылкой на диапазон, содержащий все значения Хi для выбранного наблюдения i).
Как видно из диаграммы выше линия тренда и линия регрессии не обязательно совпадают: отклонения точек от линии тренда случайны, а МНК лишь подбирает линию наиболее точно аппроксимирующую случайные точки данных.
Линию регрессии можно построить и с помощью встроенных средств диаграммы, т.е. с помощью инструмента Линия тренда. Для этого выделите диаграмму, в меню выберите вкладку Макет , в группе Анализ нажмите Линия тренда , затем Линейное приближение. В диалоговом окне установите галочку Показывать уравнение на диаграмме (подробнее см. в статье про МНК ).
Построенная таким образом линия, разумеется, должна совпасть с ранее построенной нами линией регрессии, а параметры уравнения a и b должны совпасть с параметрами уравнения отображенными на диаграмме.
Примечание: Для того, чтобы вычисленные параметры уравнения a и b совпадали с параметрами уравнения на диаграмме, необходимо, чтобы тип у диаграммы был Точечная, а не График , т.к. тип диаграммы График не использует значения Х, а вместо значений Х используется последовательность 1; 2; 3; . Именно эти значения и берутся при расчете параметров линии тренда . Убедиться в этом можно если построить диаграмму График (см. файл примера ), а значения Хнач и Хшаг установить равным 1. Только в этом случае параметры уравнения на диаграмме совпадут с a и b .
Коэффициент детерминации R 2
Коэффициент детерминации R 2 показывает насколько полезна построенная нами линейная регрессионная модель .
Предположим, что у нас есть n значений переменной Y и мы хотим предсказать значение yi, но без использования значений переменной Х (т.е. без построения регрессионной модели ). Очевидно, что лучшей оценкой для yi будет среднее значение ȳ. Соответственно, ошибка предсказания будет равна (yi — ȳ).
Примечание : Далее будет использована терминология и обозначения дисперсионного анализа .
После построения регрессионной модели для предсказания значения yi мы будем использовать значение ŷi=a*xi+b. Ошибка предсказания теперь будет равна (yi — ŷi).
Теперь с помощью диаграммы сравним ошибки предсказания полученные без построения модели и с помощью модели.
Очевидно, что используя регрессионную модель мы уменьшили первоначальную (полную) ошибку (yi — ȳ) на значение (ŷi — ȳ) до величины (yi — ŷi).
(yi — ŷi) – это оставшаяся, необъясненная ошибка.
Очевидно, что все три ошибки связаны выражением:
(yi — ȳ)= (ŷi — ȳ) + (yi — ŷi)
Можно показать, что в общем виде справедливо следующее выражение:
или в других, общепринятых в зарубежной литературе, обозначениях:
Total Sum of Squares = Regression Sum of Squares + Error Sum of Squares
Примечание : SS — Sum of Squares — Сумма Квадратов.
Как видно из формулы величины SST, SSR, SSE имеют размерность дисперсии (вариации) и соответственно описывают разброс (изменчивость): Общую изменчивость (Total variation), Изменчивость объясненную моделью (Explained variation) и Необъясненную изменчивость (Unexplained variation).
По определению коэффициент детерминации R 2 равен:
R 2 = Изменчивость объясненная моделью / Общая изменчивость.
Этот показатель равен квадрату коэффициента корреляции и в MS EXCEL его можно вычислить с помощью функции КВПИРСОН() или ЛИНЕЙН() :
R 2 принимает значения от 0 до 1 (1 соответствует идеальной линейной зависимости Y от Х). Однако, на практике малые значения R2 вовсе не обязательно указывают, что переменную Х нельзя использовать для прогнозирования переменной Y. Малые значения R2 могут указывать на нелинейность связи или на то, что поведение переменной Y объясняется не только Х, но и другими факторами.
Стандартная ошибка регрессии
Стандартная ошибка регрессии ( Standard Error of a regression ) показывает насколько велика ошибка предсказания значений переменной Y на основании значений Х. Отдельные значения Yi мы можем предсказывать лишь с точностью +/- несколько значений (обычно 2-3, в зависимости от формы распределения ошибки ε).
Теперь вспомним уравнение линейной регрессионной модели Y=a*X+β+ε. Ошибка ε имеет случайную природу, т.е. является случайной величиной и поэтому имеет свою функцию распределения со средним значением μ и дисперсией σ 2 .
Оценив значение дисперсии σ 2 и вычислив из нее квадратный корень – получим Стандартную ошибку регрессии. Чем точки наблюдений на диаграмме рассеяния ближе находятся к прямой линии, тем меньше Стандартная ошибка.
Примечание : Вспомним , что при построении модели предполагается, что среднее значение ошибки ε равно 0, т.е. E[ε]=0.
Оценим дисперсию σ 2 . Помимо вычисления Стандартной ошибки регрессии эта оценка нам потребуется в дальнейшем еще и при построении доверительных интервалов для оценки параметров регрессии a и b .
Для оценки дисперсии ошибки ε используем остатки регрессии — разности между имеющимися значениями yi и значениями, предсказанными регрессионной моделью ŷ. Чем лучше регрессионная модель согласуется с данными (точки располагается близко к прямой линии), тем меньше величина остатков.
Для оценки дисперсии σ 2 используют следующую формулу:
где SSE – сумма квадратов значений ошибок модели ε i =yi — ŷi ( Sum of Squared Errors ).
SSE часто обозначают и как SSres – сумма квадратов остатков ( Sum of Squared residuals ).
Оценка дисперсии s 2 также имеет общепринятое обозначение MSE (Mean Square of Errors), т.е. среднее квадратов ошибок или MSRES (Mean Square of Residuals), т.е. среднее квадратов остатков . Хотя правильнее говорить сумме квадратов остатков, т.к. ошибка чаще ассоциируется с ошибкой модели ε, которая является непрерывной случайной величиной. Но, здесь мы будем использовать термины SSE и MSE, предполагая, что речь идет об остатках.
Примечание : Напомним, что когда мы использовали МНК для нахождения параметров модели, то критерием оптимизации была минимизация именно SSE (SSres). Это выражение представляет собой сумму квадратов расстояний между наблюденными значениями yi и предсказанными моделью значениями ŷi, которые лежат на линии регрессии.
Математическое ожидание случайной величины MSE равно дисперсии ошибки ε, т.е. σ 2 .
Чтобы понять почему SSE выбрана в качестве основы для оценки дисперсии ошибки ε, вспомним, что σ 2 является также дисперсией случайной величины Y (относительно среднего значения μy, при заданном значении Хi). А т.к. оценкой μy является значение ŷi = a * Хi + b (значение уравнения регрессии при Х= Хi), то логично использовать именно SSE в качестве основы для оценки дисперсии σ 2 . Затем SSE усредняется на количество точек данных n за вычетом числа 2. Величина n-2 – это количество степеней свободы ( df – degrees of freedom ), т.е. число параметров системы, которые могут изменяться независимо (вспомним, что у нас в этом примере есть n независимых наблюдений переменной Y). В случае простой линейной регрессии число степеней свободы равно n-2, т.к. при построении линии регрессии было оценено 2 параметра модели (на это было «потрачено» 2 степени свободы ).
Итак, как сказано было выше, квадратный корень из s 2 имеет специальное название Стандартная ошибка регрессии ( Standard Error of a regression ) и обозначается SEy. SEy показывает насколько велика ошибка предсказания. Отдельные значения Y мы можем предсказывать с точностью +/- несколько значений SEy (см. этот раздел ). Если ошибки предсказания ε имеют нормальное распределение , то примерно 2/3 всех предсказанных значений будут на расстоянии не больше SEy от линии регрессии . SEy имеет размерность переменной Y и откладывается по вертикали. Часто на диаграмме рассеяния строят границы предсказания соответствующие +/- 2 SEy (т.е. 95% точек данных будут располагаться в пределах этих границ).
В MS EXCEL стандартную ошибку SEy можно вычислить непосредственно по формуле:
= КОРЕНЬ(СУММКВРАЗН(C23:C83; ТЕНДЕНЦИЯ(C23:C83;B23:B83;B23:B83)) /( СЧЁТ(B23:B83) -2))
или с помощью функции ЛИНЕЙН() :
Примечание : Подробнее о функции ЛИНЕЙН() см. эту статью .
Стандартные ошибки и доверительные интервалы для наклона и сдвига
В разделе Оценка неизвестных параметров линейной модели мы получили точечные оценки наклона а и сдвига b . Так как эти оценки получены на основе случайных величин (значений переменных Х и Y), то эти оценки сами являются случайными величинами и соответственно имеют функцию распределения со средним значением и дисперсией . Но, чтобы перейти от точечных оценок к интервальным , необходимо вычислить соответствующие стандартные ошибки (т.е. стандартные отклонения ).
Стандартная ошибка коэффициента регрессии a вычисляется на основании стандартной ошибки регрессии по следующей формуле:
где Sx – стандартное отклонение величины х, вычисляемое по формуле:
где Sey – стандартная ошибка регрессии, т.е. ошибка предсказания значения переменой Y ( см. выше ).
В MS EXCEL стандартную ошибку коэффициента регрессии Se можно вычислить впрямую по вышеуказанной формуле:
= КОРЕНЬ(СУММКВРАЗН(C23:C83; ТЕНДЕНЦИЯ(C23:C83;B23:B83;B23:B83)) /( СЧЁТ(B23:B83) -2))/ СТАНДОТКЛОН.В(B23:B83) /КОРЕНЬ(СЧЁТ(B23:B83) -1)
или с помощью функции ЛИНЕЙН() :
Формулы приведены в файле примера на листе Линейный в разделе Регрессионная статистика .
Примечание : Подробнее о функции ЛИНЕЙН() см. эту статью .
При построении двухстороннего доверительного интервала для коэффициента регрессии его границы определяются следующим образом:
где — квантиль распределения Стьюдента с n-2 степенями свободы. Величина а с «крышкой» является другим обозначением наклона а .
Например для уровня значимости альфа=0,05, можно вычислить с помощью формулы =СТЬЮДЕНТ.ОБР.2Х(0,05;n-2)
Вышеуказанная формула следует из того факта, что если ошибки регрессии распределены нормально и независимо, то выборочное распределение случайной величины
является t-распределением Стьюдента с n-2 степенью свободы (то же справедливо и для наклона b ).
Примечание : Подробнее о построении доверительных интервалов в MS EXCEL можно прочитать в этой статье Доверительные интервалы в MS EXCEL .
В результате получим, что найденный доверительный интервал с вероятностью 95% (1-0,05) накроет истинное значение коэффициента регрессии. Здесь мы считаем, что коэффициент регрессии a имеет распределение Стьюдента с n-2 степенями свободы (n – количество наблюдений, т.е. пар Х и Y).
Примечание : Подробнее о построении доверительных интервалов с использованием t-распределения см. статью про построение доверительных интервалов для среднего .
Стандартная ошибка сдвига b вычисляется по следующей формуле:
В MS EXCEL стандартную ошибку сдвига Seb можно вычислить с помощью функции ЛИНЕЙН() :
При построении двухстороннего доверительного интервала для сдвига его границы определяются аналогичным образом как для наклона : b +/- t*Seb.
Проверка значимости взаимосвязи переменных
Когда мы строим модель Y=αX+β+ε мы предполагаем, что между Y и X существует линейная взаимосвязь. Однако, как это иногда бывает в статистике, можно вычислять параметры связи даже тогда, когда в действительности она не существует, и обусловлена лишь случайностью.
Единственный вариант, когда Y не зависит X (в рамках модели Y=αX+β+ε), возможен, когда коэффициент регрессии a равен 0.
Чтобы убедиться, что вычисленная нами оценка наклона прямой линии не обусловлена лишь случайностью (не случайно отлична от 0), используют проверку гипотез . В качестве нулевой гипотезы Н 0 принимают, что связи нет, т.е. a=0. В качестве альтернативной гипотезы Н 1 принимают, что a <>0.
Ниже на рисунках показаны 2 ситуации, когда нулевую гипотезу Н 0 не удается отвергнуть.
На левой картинке отсутствует любая зависимость между переменными, на правой – связь между ними нелинейная, но при этом коэффициент линейной корреляции равен 0.
Ниже — 2 ситуации, когда нулевая гипотеза Н 0 отвергается.
На левой картинке очевидна линейная зависимость, на правой — зависимость нелинейная, но коэффициент корреляции не равен 0 (метод МНК вычисляет показатели наклона и сдвига просто на основании значений выборки).
Для проверки гипотезы нам потребуется:
- Установить уровень значимости , пусть альфа=0,05;
- Рассчитать с помощью функции ЛИНЕЙН() стандартное отклонение Se для коэффициента регрессии (см. предыдущий раздел );
- Рассчитать число степеней свободы: DF=n-2 или по формуле = ИНДЕКС(ЛИНЕЙН(C24:C84;B24:B84;;ИСТИНА);4;2)
- Вычислить значение тестовой статистики t 0 =a/S e , которая имеет распределение Стьюдента с числом степеней свободы DF=n-2;
- Сравнить значение тестовой статистики |t0| с пороговым значением t альфа ,n-2. Если значение тестовой статистики больше порогового значения, то нулевая гипотеза отвергается ( наклон не может быть объяснен лишь случайностью при заданном уровне альфа) либо
- вычислить p-значение и сравнить его с уровнем значимости .
В файле примера приведен пример проверки гипотезы:
Изменяя наклон тренда k (ячейка В8 ) можно убедиться, что при малых углах тренда (например, 0,05) тест часто показывает, что связь между переменными случайна. При больших углах (k>1), тест практически всегда подтверждает значимость линейной связи между переменными.
Примечание : Проверка значимости взаимосвязи эквивалентна проверке статистической значимости коэффициента корреляции . В файле примера показана эквивалентность обоих подходов. Также проверку значимости можно провести с помощью процедуры F-тест .
Доверительные интервалы для нового наблюдения Y и среднего значения
Вычислив параметры простой линейной регрессионной модели Y=aX+β+ε мы получили точечную оценку значения нового наблюдения Y при заданном значении Хi, а именно: Ŷ= a * Хi + b
Ŷ также является точечной оценкой для среднего значения Yi при заданном Хi. Но, при построении доверительных интервалов используются различные стандартные ошибки .
Стандартная ошибка нового наблюдения Y при заданном Хi учитывает 2 источника неопределенности:
- неопределенность связанную со случайностью оценок параметров модели a и b ;
- случайность ошибки модели ε.
Учет этих неопределенностей приводит к стандартной ошибке S(Y|Xi), которая рассчитывается с учетом известного значения Xi.
где SS xx – сумма квадратов отклонений от среднего значений переменной Х:
В MS EXCEL 2010 нет функции, которая бы рассчитывала эту стандартную ошибку , поэтому ее необходимо рассчитывать по вышеуказанным формулам.
Доверительный интервал или Интервал предсказания для нового наблюдения (Prediction Interval for a New Observation) построим по схеме показанной в разделе Проверка значимости взаимосвязи переменных (см. файл примера лист Интервалы ). Т.к. границы интервала зависят от значения Хi (точнее от расстояния Хi до среднего значения Х ср ), то интервал будет постепенно расширяться при удалении от Х ср .
Границы доверительного интервала для нового наблюдения рассчитываются по формуле:
Аналогичным образом построим доверительный интервал для среднего значения Y при заданном Хi (Confidence Interval for the Mean of Y). В этом случае доверительный интервал будет уже, т.к. средние значения имеют меньшую изменчивость по сравнению с отдельными наблюдениями ( средние значения, в рамках нашей линейной модели Y=aX+β+ε, не включают ошибку ε).
Стандартная ошибка S(Yср|Xi) вычисляется по практически аналогичным формулам как и стандартная ошибка для нового наблюдения:
Как видно из формул, стандартная ошибка S(Yср|Xi) меньше стандартной ошибки S(Y|Xi) для индивидуального значения .
Границы доверительного интервала для среднего значения рассчитываются по формуле:
Проверка адекватности линейной регрессионной модели
Модель адекватна, когда все предположения, лежащие в ее основе, выполнены (см. раздел Предположения линейной регрессионной модели ).
Проверка адекватности модели в основном основана на исследовании остатков модели (model residuals), т.е. значений ei=yi – ŷi для каждого Хi. В рамках простой линейной модели n остатков имеют только n-2 связанных с ними степеней свободы . Следовательно, хотя, остатки не являются независимыми величинами, но при достаточно большом n это не оказывает какого-либо влияния на проверку адекватности модели.
Чтобы проверить предположение о нормальности распределения ошибок строят график проверки на нормальность (Normal probability Plot).
В файле примера на листе Адекватность построен график проверки на нормальность . В случае нормального распределения значения остатков должны быть близки к прямой линии.
Так как значения переменной Y мы генерировали с помощью тренда , вокруг которого значения имели нормальный разброс, то ожидать сюрпризов не приходится – значения остатков располагаются вблизи прямой.
Также при проверке модели на адекватность часто строят график зависимости остатков от предсказанных значений Y. Если точки не демонстрируют характерных, так называемых «паттернов» (шаблонов) типа вор о нок или другого неравномерного распределения, в зависимости от значений Y, то у нас нет очевидных доказательств неадекватности модели.
В нашем случае точки располагаются примерно равномерно.
Часто при проверке адекватности модели вместо остатков используют нормированные остатки. Как показано в разделе Стандартная ошибка регрессии оценкой стандартного отклонения ошибок является величина SEy равная квадратному корню из величины MSE. Поэтому логично нормирование остатков проводить именно на эту величину.
SEy можно вычислить с помощью функции ЛИНЕЙН() :
Иногда нормирование остатков производится на величину стандартного отклонения остатков (это мы увидим в статье об инструменте Регрессия , доступного в надстройке MS EXCEL Пакет анализа ), т.е. по формуле:
Вышеуказанное равенство приблизительное, т.к. среднее значение остатков близко, но не обязательно точно равно 0.
Что такое регрессионный анализ?
Регрессионный анализ — это набор статистических методов оценки отношений между переменными. Его можно использовать для оценки степени взаимосвязи между переменными и для моделирования будущей зависимости. По сути, регрессионные методы показывают, как по изменениям «независимых переменных» можно зафиксировать изменение «зависимой переменной».
Зависимую переменную в бизнесе называют предиктором (характеристика, за изменением которой наблюдают). Это может быть уровень продаж, риски, ценообразование, производительность и так далее. Независимые переменные — те, которые могут объяснять поведение выше приведенных факторов (время года, покупательная способность населения, место продаж и многое другое).Регрессионный анализ включает несколько моделей. Наиболее распространенные из них: линейная, мультилинейная (или множественная линейная) и нелинейная.
Как видно из названий, модели отличаются типом зависимости переменных: линейная описывается линейной функцией; мультилинейная также представляет линейную функцию, но в нее входит больше параметров (независимых переменных); нелинейная модель — та, в которой экспериментальные данные характеризуются функцией, являющейся нелинейной (показательной, логарифмической, тригонометрической и так далее).
Чаще всего используются простые линейные и мультилинейные модели.
Регрессионный анализ предлагает множество приложений в различных дисциплинах, включая финансы.
Рассмотрим поподробнее принципы построения и адаптации результатов метода.
Линейный регрессионный анализ основан на шести фундаментальных предположениях:
- Переменные показывают линейную зависимость;
- Независимая переменная не случайна;
- Значение невязки (ошибки) равно нулю;
- Значение невязки постоянно для всех наблюдений;
- Значение невязки не коррелирует по всем наблюдениям;
- Остаточные значения подчиняются нормальному распределению.
Простая линейная модель выражается с помощью следующего уравнения:
Основы линейной регрессии
Что такое регрессия?
Разместим точки на двумерном графике рассеяния и скажем, что мы имеем линейное соотношение, если данные аппроксимируются прямой линией.
Если мы полагаем, что y зависит от x, причём изменения в y вызываются именно изменениями в x, мы можем определить линию регрессии (регрессия y на x), которая лучше всего описывает прямолинейное соотношение между этими двумя переменными.
Статистическое использование слова «регрессия» исходит из явления, известного как регрессия к среднему, приписываемого сэру Френсису Гальтону (1889).
Он показал, что, хотя высокие отцы имеют тенденцию иметь высоких сыновей, средний рост сыновей меньше, чем у их высоких отцов. Средний рост сыновей «регрессировал» и «двигался вспять» к среднему росту всех отцов в популяции. Таким образом, в среднем высокие отцы имеют более низких (но всё-таки высоких) сыновей, а низкие отцы имеют сыновей более высоких (но всё-таки довольно низких).
Линия регрессии
Математическое уравнение, которое оценивает линию простой (парной) линейной регрессии:
x называется независимой переменной или предиктором.
Y – зависимая переменная или переменная отклика. Это значение, которое мы ожидаем для y (в среднем), если мы знаем величину x, т.е. это «предсказанное значение y»
- a – свободный член (пересечение) линии оценки; это значение Y, когда x=0 (Рис.1).
- b – угловой коэффициент или градиент оценённой линии; она представляет собой величину, на которую Y увеличивается в среднем, если мы увеличиваем x на одну единицу.
- a и b называют коэффициентами регрессии оценённой линии, хотя этот термин часто используют только для b.
Парную линейную регрессию можно расширить, включив в нее более одной независимой переменной; в этом случае она известна как множественная регрессия.
Рис.1. Линия линейной регрессии, показывающая пересечение a и угловой коэффициент b (величину возрастания Y при увеличении x на одну единицу)
Метод наименьших квадратов
Мы выполняем регрессионный анализ, используя выборку наблюдений, где a и b – выборочные оценки истинных (генеральных) параметров, α и β , которые определяют линию линейной регрессии в популяции (генеральной совокупности).
Наиболее простым методом определения коэффициентов a и b является метод наименьших квадратов (МНК).
Подгонка оценивается, рассматривая остатки (вертикальное расстояние каждой точки от линии, например, остаток = наблюдаемому y – предсказанный y, Рис. 2).
Линию лучшей подгонки выбирают так, чтобы сумма квадратов остатков была минимальной.
Рис. 2. Линия линейной регрессии с изображенными остатками (вертикальные пунктирные линии) для каждой точки.
Предположения линейной регрессии
Итак, для каждой наблюдаемой величины остаток равен разнице
и соответствующего предсказанного
Каждый остаток может быть положительным или отрицательным.
Можно использовать остатки для проверки следующих предположений, лежащих в основе линейной регрессии:
- Остатки нормально распределены с нулевым средним значением;
Если допущения линейности, нормальности и/или постоянной дисперсии сомнительны, мы можем преобразовать или
и рассчитать новую линию регрессии, для которой эти допущения удовлетворяются (например, использовать логарифмическое преобразование или др.).
Аномальные значения (выбросы) и точки влияния
«Влиятельное» наблюдение, если оно опущено, изменяет одну или больше оценок параметров модели (т.е. угловой коэффициент или свободный член).
Выброс (наблюдение, которое противоречит большинству значений в наборе данных) может быть «влиятельным» наблюдением и может хорошо обнаруживаться визуально, при осмотре двумерной диаграммы рассеяния или графика остатков.
И для выбросов, и для «влиятельных» наблюдений (точек) используют модели, как с их включением, так и без них, обращают внимание на изменение оценки (коэффициентов регрессии).
При проведении анализа не стоит отбрасывать выбросы или точки влияния автоматически, поскольку простое игнорирование может повлиять на полученные результаты. Всегда изучайте причины появления этих выбросов и анализируйте их.
Гипотеза линейной регрессии
При построении линейной регрессии проверяется нулевая гипотеза о том, что генеральный угловой коэффициент линии регрессии β равен нулю.
Если угловой коэффициент линии равен нулю, между и
нет линейного соотношения: изменение
не влияет на
Для тестирования нулевой гипотезы о том, что истинный угловой коэффициент равен нулю можно воспользоваться следующим алгоритмом:
Вычислить статистику критерия, равную отношению , которая подчиняется
распределению с
степенями свободы, где
стандартная ошибка коэффициента
,
— оценка дисперсии остатков.
Обычно если достигнутый уровень значимости нулевая гипотеза отклоняется.
Можно рассчитать 95% доверительный интервал для генерального углового коэффициента :
где процентная точка
распределения со степенями свободы
что дает вероятность двустороннего критерия
Это тот интервал, который содержит генеральный угловой коэффициент с вероятностью 95%.
Для больших выборок, скажем, мы можем аппроксимировать
значением 1,96 (то есть статистика критерия будет стремиться к нормальному распределению)
Оценка качества линейной регрессии: коэффициент детерминации R 2
Из-за линейного соотношения и
мы ожидаем, что
изменяется, по мере того как изменяется
, и называем это вариацией, которая обусловлена или объясняется регрессией. Остаточная вариация должна быть как можно меньше.
Если это так, то большая часть вариации будет объясняться регрессией, а точки будут лежать близко к линии регрессии, т.е. линия хорошо соответствует данным.
Долю общей дисперсии , которая объясняется регрессией называют коэффициентом детерминации, обычно выражают через процентное соотношение и обозначают R 2 (в парной линейной регрессии это величина r 2 , квадрат коэффициента корреляции), позволяет субъективно оценить качество уравнения регрессии.
Разность представляет собой процент дисперсии который нельзя объяснить регрессией.
Нет формального теста для оценки мы вынуждены положиться на субъективное суждение, чтобы определить качество подгонки линии регрессии.
Применение линии регрессии для прогноза
Можно применять регрессионную линию для прогнозирования значения по значению
в пределе наблюдаемого диапазона (никогда не экстраполируйте вне этих пределов).
Мы предсказываем среднюю величину для наблюдаемых, которые имеют определенное значение
путем подстановки этого значения
в уравнение линии регрессии.
Итак, если прогнозируем
как
Используем эту предсказанную величину и ее стандартную ошибку, чтобы оценить доверительный интервал для истинной средней величины
в популяции.
Повторение этой процедуры для различных величин позволяет построить доверительные границы для этой линии. Это полоса или область, которая содержит истинную линию, например, с 95% доверительной вероятностью.
Подобным образом можно рассчитать более широкую область, внутри которой, как мы ожидаем, лежит наибольшее число (обычно 95%) наблюдений.
Простые регрессионные планы
Простые регрессионные планы содержат один непрерывный предиктор. Если существует 3 наблюдения со значениями предиктора P , например, 7, 4 и 9, а план включает эффект первого порядка P , то матрица плана X будет иметь вид
а регрессионное уравнение с использованием P для X1 выглядит как
Если простой регрессионный план содержит эффект высшего порядка для P , например квадратичный эффект, то значения в столбце X1 в матрице плана будут возведены во вторую степень:
а уравнение примет вид
Y = b 0 + b 1 P 2
Сигма -ограниченные и сверхпараметризованные методы кодирования не применяются по отношению к простым регрессионным планам и другим планам, содержащим только непрерывные предикторы (поскольку, просто не существует категориальных предикторов). Независимо от выбранного метода кодирования, значения непрерывных переменных увеличиваются в соответствующей степени и используются как значения для переменных X . При этом перекодировка не выполняется. Кроме того, при описании регрессионных планов можно опустить рассмотрение матрицы плана X , а работать только с регрессионным уравнением.
Пример: простой регрессионный анализ
Этот пример использует данные, представленные в таблице:
Рис. 3. Таблица исходных данных.
Данные составлены на основе сравнения переписей 1960 и 1970 в произвольно выбранных 30 округах. Названия округов представлены в виде имен наблюдений. Информация относительно каждой переменной представлена ниже:
Рис. 4. Таблица спецификаций переменных.
Задача исследования
Для этого примера будут анализироваться корреляция уровня бедности и степень, которая предсказывает процент семей, которые находятся за чертой бедности. Следовательно мы будем трактовать переменную 3 ( Pt_Poor ) как зависимую переменную.
Можно выдвинуть гипотезу: изменение численности населения и процент семей, которые находятся за чертой бедности, связаны между собой. Кажется разумным ожидать, что бедность ведет к оттоку населения, следовательно, здесь будет отрицательная корреляция между процентом людей за чертой бедности и изменением численности населения. Следовательно мы будем трактовать переменную 1 ( Pop_Chng ) как переменную-предиктор.
Просмотр результатов
Коэффициенты регрессии
Рис. 5. Коэффициенты регрессии Pt_Poor на Pop_Chng.
На пересечении строки Pop_Chng и столбца Парам. не стандартизованный коэффициент для регрессии Pt_Poor на Pop_Chng равен -0.40374 . Это означает, что для каждого уменьшения численности населения на единицу, имеется увеличение уровня бедности на .40374. Верхний и нижний (по умолчанию) 95% доверительные пределы для этого не стандартизованного коэффициента не включают ноль, так что коэффициент регрессии значим на уровне p . Обратите внимание на не стандартизованный коэффициент, который также является коэффициентом корреляции Пирсона для простых регрессионных планов, равен -.65, который означает, что для каждого уменьшения стандартного отклонения численности населения происходит увеличение стандартного отклонения уровня бедности на .65.
Распределение переменных
Коэффициенты корреляции могут стать существенно завышены или занижены, если в данных присутствуют большие выбросы. Изучим распределение зависимой переменной Pt_Poor по округам. Для этого построим гистограмму переменной Pt_Poor .
Рис. 6. Гистограмма переменной Pt_Poor.
Как вы можете заметить, распределение этой переменной заметно отличается от нормального распределения. Тем не менее, хотя даже два округа (два правых столбца) имеют высокий процент семей, которые находятся за чертой бедности, чем ожидалось в случае нормального распределения, кажется, что они находятся «внутри диапазона.»
Рис. 7. Гистограмма переменной Pt_Poor.
Это суждение в некоторой степени субъективно. Эмпирическое правило гласит, что выбросы необходимо учитывать, если наблюдение (или наблюдения) не попадают в интервал (среднее ± 3 умноженное на стандартное отклонение). В этом случае стоит повторить анализ с выбросами и без, чтобы убедиться, что они не оказывают серьезного эффекта на корреляцию между членами совокупности.
Диаграмма рассеяния
Если одна из гипотез априори о взаимосвязи между заданными переменными, то ее полезно проверить на графике соответствующей диаграммы рассеяния.
Рис. 8. Диаграмма рассеяния.
Диаграмма рассеяния показывает явную отрицательную корреляцию ( -.65 ) между двумя переменными. На ней также показан 95% доверительный интервал для линии регрессии, т.е., с 95% вероятностью линия регрессии проходит между двумя пунктирными кривыми.
Критерии значимости
Рис. 9. Таблица, содержащая критерии значимости.
Критерий для коэффициента регрессии Pop_Chng подтверждает, что Pop_Chng сильно связано с Pt_Poor , p .
На этом примере было показано, как проанализировать простой регрессионный план. Была также представлена интерпретация не стандартизованных и стандартизованных коэффициентов регрессии. Обсуждена важность изучения распределения откликов зависимой переменной, продемонстрирована техника определения направления и силы взаимосвязи между предиктором и зависимой переменной.
источники:
http://excel2.ru/articles/prostaya-lineynaya-regressiya-v-ms-excel
http://vc.ru/u/425321-sf-education/224225-chto-takoe-regressionnyy-analiz
http://statistica.ru/theory/osnovy-lineynoy-regressii/
Основы линейной регрессии
Что такое регрессия?
Линия регрессии
Метод наименьших квадратов
Предположения линейной регрессии
Аномальные значения (выбросы) и точки влияния
Гипотеза линейной регрессии
Оценка качества линейной регрессии: коэффициент детерминации R2
Применение линии регрессии для прогноза
Простые регрессионные планы
Пример: простой регрессионный анализ
Рассмотрим две непрерывные переменные x=(x1, x2, .., xn), y=(y1, y2, …, yn).
Разместим точки на двумерном графике рассеяния и скажем, что мы имеем линейное соотношение, если данные аппроксимируются прямой линией.
Если мы полагаем, что y зависит от x, причём изменения в y вызываются именно изменениями в x, мы можем определить линию регрессии (регрессия y на x), которая лучше всего описывает прямолинейное соотношение между этими двумя переменными.
Статистическое использование слова «регрессия» исходит из явления, известного как регрессия к среднему, приписываемого сэру Френсису Гальтону (1889).
Он показал, что, хотя высокие отцы имеют тенденцию иметь высоких сыновей, средний рост сыновей меньше, чем у их высоких отцов. Средний рост сыновей «регрессировал» и «двигался вспять» к среднему росту всех отцов в популяции. Таким образом, в среднем высокие отцы имеют более низких (но всё-таки высоких) сыновей, а низкие отцы имеют сыновей более высоких (но всё-таки довольно низких).
Линия регрессии
Математическое уравнение, которое оценивает линию простой (парной) линейной регрессии:
Y=a+bx.
x называется независимой переменной или предиктором.
Y – зависимая переменная или переменная отклика. Это значение, которое мы ожидаем для y (в среднем), если мы знаем величину x, т.е. это «предсказанное значение y»
- a – свободный член (пересечение) линии оценки; это значение Y, когда x=0 (Рис.1).
- b – угловой коэффициент или градиент оценённой линии; она представляет собой величину, на которую Y увеличивается в среднем, если мы увеличиваем x на одну единицу.
- a и b называют коэффициентами регрессии оценённой линии, хотя этот термин часто используют только для b.
Парную линейную регрессию можно расширить, включив в нее более одной независимой переменной; в этом случае она известна как множественная регрессия.
Рис.1. Линия линейной регрессии, показывающая пересечение a и угловой коэффициент b (величину возрастания Y при увеличении x на одну единицу)
Метод наименьших квадратов
Мы выполняем регрессионный анализ, используя выборку наблюдений, где a и b – выборочные оценки истинных (генеральных) параметров, α и β , которые определяют линию линейной регрессии в популяции (генеральной совокупности).
Наиболее простым методом определения коэффициентов a и b является метод наименьших квадратов (МНК).
Подгонка оценивается, рассматривая остатки (вертикальное расстояние каждой точки от линии, например, остаток = наблюдаемому y – предсказанный y, Рис. 2).
Линию лучшей подгонки выбирают так, чтобы сумма квадратов остатков была минимальной.
Рис. 2. Линия линейной регрессии с изображенными остатками (вертикальные пунктирные линии) для каждой точки.
Предположения линейной регрессии
Предположения линейной регрессии
Итак, для каждой наблюдаемой величины остаток равен разнице
и соответствующего предсказанного
Каждый остаток может быть положительным или отрицательным.
Можно использовать остатки для проверки следующих предположений, лежащих в основе линейной регрессии:
- Остатки нормально распределены с нулевым средним значением;
Если допущения линейности, нормальности и/или постоянной дисперсии сомнительны, мы можем преобразовать или
и рассчитать новую линию регрессии, для которой эти допущения удовлетворяются (например, использовать логарифмическое преобразование или др.).
Аномальные значения (выбросы) и точки влияния
«Влиятельное» наблюдение, если оно опущено, изменяет одну или больше оценок параметров модели (т.е. угловой коэффициент или свободный член).
Выброс (наблюдение, которое противоречит большинству значений в наборе данных) может быть «влиятельным» наблюдением и может хорошо обнаруживаться визуально, при осмотре двумерной диаграммы рассеяния или графика остатков.
И для выбросов, и для «влиятельных» наблюдений (точек) используют модели, как с их включением, так и без них, обращают внимание на изменение оценки (коэффициентов регрессии).
При проведении анализа не стоит отбрасывать выбросы или точки влияния автоматически, поскольку простое игнорирование может повлиять на полученные результаты. Всегда изучайте причины появления этих выбросов и анализируйте их.
Гипотеза линейной регрессии
Гипотеза линейной регрессии
При построении линейной регрессии проверяется нулевая гипотеза о том, что генеральный угловой коэффициент линии регрессии β равен нулю.
Если угловой коэффициент линии равен нулю, между и
нет линейного соотношения: изменение
не влияет на
Для тестирования нулевой гипотезы о том, что истинный угловой коэффициент равен нулю можно воспользоваться следующим алгоритмом:
Вычислить статистику критерия, равную отношению , которая подчиняется
распределению с
степенями свободы, где
стандартная ошибка коэффициента
,
— оценка дисперсии остатков.
Обычно если достигнутый уровень значимости нулевая гипотеза отклоняется.
Можно рассчитать 95% доверительный интервал для генерального углового коэффициента :
где процентная точка
распределения со степенями свободы
что дает вероятность двустороннего критерия
Это тот интервал, который содержит генеральный угловой коэффициент с вероятностью 95%.
Для больших выборок, скажем, мы можем аппроксимировать
значением 1,96 (то есть статистика критерия будет стремиться к нормальному распределению)
Оценка качества линейной регрессии: коэффициент детерминации R2
Из-за линейного соотношения и
мы ожидаем, что
изменяется, по мере того как изменяется
, и называем это вариацией, которая обусловлена или объясняется регрессией. Остаточная вариация должна быть как можно меньше.
Если это так, то большая часть вариации будет объясняться регрессией, а точки будут лежать близко к линии регрессии, т.е. линия хорошо соответствует данным.
Долю общей дисперсии , которая объясняется регрессией называют коэффициентом детерминации, обычно выражают через процентное соотношение и обозначают R2 (в парной линейной регрессии это величина r2, квадрат коэффициента корреляции), позволяет субъективно оценить качество уравнения регрессии.
Разность представляет собой процент дисперсии который нельзя объяснить регрессией.
Нет формального теста для оценки мы вынуждены положиться на субъективное суждение, чтобы определить качество подгонки линии регрессии.
Применение линии регрессии для прогноза
Можно применять регрессионную линию для прогнозирования значения по значению
в пределе наблюдаемого диапазона (никогда не экстраполируйте вне этих пределов).
Мы предсказываем среднюю величину для наблюдаемых, которые имеют определенное значение
путем подстановки этого значения
в уравнение линии регрессии.
Итак, если прогнозируем
как
Используем эту предсказанную величину и ее стандартную ошибку, чтобы оценить доверительный интервал для истинной средней величины
в популяции.
Повторение этой процедуры для различных величин позволяет построить доверительные границы для этой линии. Это полоса или область, которая содержит истинную линию, например, с 95% доверительной вероятностью.
Подобным образом можно рассчитать более широкую область, внутри которой, как мы ожидаем, лежит наибольшее число (обычно 95%) наблюдений.
Простые регрессионные планы
Простые регрессионные планы содержат один непрерывный предиктор. Если существует 3 наблюдения со значениями предиктора P, например, 7, 4 и 9, а план включает эффект первого порядка P, то матрица плана X будет иметь вид
а регрессионное уравнение с использованием P для X1 выглядит как
Y = b0 + b1P
Если простой регрессионный план содержит эффект высшего порядка для P, например квадратичный эффект, то значения в столбце X1 в матрице плана будут возведены во вторую степень:
а уравнение примет вид
Y = b0 + b1P2
Сигма-ограниченные и сверхпараметризованные методы кодирования не применяются по отношению к простым регрессионным планам и другим планам, содержащим только непрерывные предикторы (поскольку, просто не существует категориальных предикторов). Независимо от выбранного метода кодирования, значения непрерывных переменных увеличиваются в соответствующей степени и используются как значения для переменных X. При этом перекодировка не выполняется. Кроме того, при описании регрессионных планов можно опустить рассмотрение матрицы плана X, а работать только с регрессионным уравнением.
Пример: простой регрессионный анализ
Этот пример использует данные, представленные в таблице:

Рис. 3. Таблица исходных данных.
Данные составлены на основе сравнения переписей 1960 и 1970 в произвольно выбранных 30 округах. Названия округов представлены в виде имен наблюдений. Информация относительно каждой переменной представлена ниже:

Рис. 4. Таблица спецификаций переменных.
Задача исследования
Для этого примера будут анализироваться корреляция уровня бедности и степень, которая предсказывает процент семей, которые находятся за чертой бедности. Следовательно мы будем трактовать переменную 3 (Pt_Poor) как зависимую переменную.
Можно выдвинуть гипотезу: изменение численности населения и процент семей, которые находятся за чертой бедности, связаны между собой. Кажется разумным ожидать, что бедность ведет к оттоку населения, следовательно, здесь будет отрицательная корреляция между процентом людей за чертой бедности и изменением численности населения. Следовательно мы будем трактовать переменную 1 (Pop_Chng) как переменную-предиктор.
Просмотр результатов
Коэффициенты регрессии

Рис. 5. Коэффициенты регрессии Pt_Poor на Pop_Chng.
На пересечении строки Pop_Chng и столбца Парам. не стандартизованный коэффициент для регрессии Pt_Poor на Pop_Chng равен -0.40374. Это означает, что для каждого уменьшения численности населения на единицу, имеется увеличение уровня бедности на .40374. Верхний и нижний (по умолчанию) 95% доверительные пределы для этого не стандартизованного коэффициента не включают ноль, так что коэффициент регрессии значим на уровне p<.05. Обратите внимание на не стандартизованный коэффициент, который также является коэффициентом корреляции Пирсона для простых регрессионных планов, равен -.65, который означает, что для каждого уменьшения стандартного отклонения численности населения происходит увеличение стандартного отклонения уровня бедности на .65.
Распределение переменных
Коэффициенты корреляции могут стать существенно завышены или занижены, если в данных присутствуют большие выбросы. Изучим распределение зависимой переменной Pt_Poor по округам. Для этого построим гистограмму переменной Pt_Poor.

Рис. 6. Гистограмма переменной Pt_Poor.
Как вы можете заметить, распределение этой переменной заметно отличается от нормального распределения. Тем не менее, хотя даже два округа (два правых столбца) имеют высокий процент семей, которые находятся за чертой бедности, чем ожидалось в случае нормального распределения, кажется, что они находятся «внутри диапазона.»

Рис. 7. Гистограмма переменной Pt_Poor.
Это суждение в некоторой степени субъективно. Эмпирическое правило гласит, что выбросы необходимо учитывать, если наблюдение (или наблюдения) не попадают в интервал (среднее ± 3 умноженное на стандартное отклонение). В этом случае стоит повторить анализ с выбросами и без, чтобы убедиться, что они не оказывают серьезного эффекта на корреляцию между членами совокупности.
Диаграмма рассеяния
Если одна из гипотез априори о взаимосвязи между заданными переменными, то ее полезно проверить на графике соответствующей диаграммы рассеяния.

Рис. 8. Диаграмма рассеяния.
Диаграмма рассеяния показывает явную отрицательную корреляцию (-.65) между двумя переменными. На ней также показан 95% доверительный интервал для линии регрессии, т.е., с 95% вероятностью линия регрессии проходит между двумя пунктирными кривыми.
Критерии значимости

Рис. 9. Таблица, содержащая критерии значимости.
Критерий для коэффициента регрессии Pop_Chng подтверждает, что Pop_Chng сильно связано с Pt_Poor, p<.001.
Итог
На этом примере было показано, как проанализировать простой регрессионный план. Была также представлена интерпретация не стандартизованных и стандартизованных коэффициентов регрессии. Обсуждена важность изучения распределения откликов зависимой переменной, продемонстрирована техника определения направления и силы взаимосвязи между предиктором и зависимой переменной.
Связанные определения:
Линейная регрессия
Матрица плана
Общая линейная модель
Регрессия
В начало
Содержание портала
АКТУАЛЬНОСТЬ ТЕМЫ
Общие положения
Про регрессионный анализ вообще, и его применение в DataScience написано очень много. Есть множество учебников, монографий, справочников и статей по прикладной статистике, огромное количество информации в интернете, примеров расчетов. Можно найти множество кейсов, реализованных с использованием средств Python. Казалось бы — что тут еще можно добавить?
Однако, как всегда, есть нюансы:
1. Регрессионный анализ — это прежде всего процесс, набор действий исследователя по определенному алгоритму: «подготовка исходных данных — построение модели — анализ модели — прогнозирование с помощью модели». Это ключевая особенность. Не представляет особой сложности сформировать DataFrame исходных данных и построить модель, запустить процедуру из библиотеки statsmodels. Однако подготовка исходных данных и последующий анализ модели требуют гораздо больших затрат человеко-часов специалиста и строк программного кода, чем, собственно, построение модели. На этих этапах часто приходится возвращаться назад, корректировать модель или исходные данные. Этому, к сожалению, во многих источниках, не удаляется достойного внимания, а иногда — и совсем не уделяется внимания, что приводит к превратному представлению о регрессионном анализе.
2. Далеко не во всех источниках уделяется должное внимание интерпретации промежуточных и финальных результатов. Специалист должен уметь интерпретировать каждую цифру, полученную в ходе работы над моделью.
3. Далеко не все процедуры на этапах подготовки исходных данных или анализа модели в источниках разобраны подробно. Например, про проверку значимости коэффициента детерминации найти информацию не представляет труда, а вот про проверку адекватности модели, построение доверительных интервалов регрессии или про специфические процедуры (например, тест Уайта на гетероскедастичность) информации гораздо меньше.
4. Своеобразная сложность может возникнуть с проверкой статистических гипотез: для отечественной литературы по прикладной статистике больше характерно проверять гипотезы путем сравнения расчетного значения критерия с табличным, а в иностранных источниках чаще определяется расчетный уровень значимости и сравнивается с заданным (чаще всего 0.05 = 1-0.95). В разных источниках информации реализованы разные подходы. Инструменты python (прежде всего библиотеки scipy и statsmodels) также в основном оперируют с расчетным уровнем значимости.
5. Ну и, наконец, нельзя не отметить, что техническая документация библиотеки statsmodels составлена, на мой взгляд, далеко не идеально: информация излагается путано, изобилует повторами и пропусками, описание классов, функций и свойств выполнено фрагментарно и количество примеров расчетов — явно недостаточно.
Поэтому я решил написать ряд обзоров по регрессионному анализу средствами Python, в которых акцент будет сделан на практических примерах, алгоритме действий исследователя, интерпретации всех полученных результатов, конкретных методических рекомендациях. Буду стараться по возможности избегать теории (хотя совсем без нее получится) — все-таки предполагается, что специалист DataScience должен знать теорию вероятностей и математическую статистику, хотя бы в рамках курса высшей математики для технического или экономического вуза.
В данном статье остановимся на самои простом, классическом, стереотипном случае — простой линейной регрессии (simple linear regression), или как ее еще принято называть — парной линейной регрессионной модели (ПЛРМ) — в ситуации, когда исследователя не подстерегают никакие подводные камни и каверзы — исходные данные подчиняются нормальному закону, в выборке отсутствуют аномальные значения, отсутствует ложная корреляция. Более сложные случаи рассмотрим в дальнейшем.
Для построение регрессионной модели будем пользоваться библиотекой statsmodels.
В данной статье мы рассмотрим по возможности полный набор статистических процедур. Некоторые из них (например, дескриптивная статистика или дисперсионный анализ регрессионной модели) могут показаться избыточными. Все так, но эти процедуры улучшают наше представление о процессе и об исходных данных, поэтому в разбор я их включил, а каждый исследователь сам вправе для себя определить, потребуются ему эти процедуры или нет.
Краткий обзор источников
Источников информации по корреляционному и регрессионному анализу огромное количество, в них можно просто утонуть. Поэтому позволю себе просто порекомендовать ряд источников, на мой взгляд, наиболее полезных:
-
Кобзарь А.И. Прикладная математическая статистика. Для инженеров и научных работников. — М.: ФИЗМАТЛИТ, 2006. — 816 с.
-
Львовский Е.Н. Статистические методы построения эмпирических формул. — М.: Высшая школа, 1988. — 239 с.
-
Фёрстер Э., Рёнц Б. Методы корреляционного и регрессионного анализа / пер с нем. — М.: Финансы и статистика, 1983. — 302 с.
-
Афифи А., Эйзен С. Статистический анализ. Подход с использованием ЭВМ / пер с англ. — М.: Мир, 1982. — 488 с.
-
Дрейпер Н., Смит Г. Прикладной регрессионный анализ. Книга 1 / пер.с англ. — М.: Финансы и статистика, 1986. — 366 с.
-
Айвазян С.А. и др. Прикладная статистика: Исследование зависимостей. — М.: Финансы и статистика, 1985. — 487 с.
-
Прикладная статистика. Основы эконометрики: В 2 т. 2-е изд., испр. — Т.2: Айвазян С.А. Основы эконометрики. — М.: ЮНИТИ-ДАНА, 2001. — 432 с.
-
Магнус Я.Р. и др. Эконометрика. Начальный курс — М.: Дело, 2004. — 576 с.
-
Носко В.П. Эконометрика. Книга 1. — М.: Издательский дом «Дело» РАНХиГС, 2011. — 672 с.
-
Брюс П. Практическая статистика для специалистов Data Science / пер. с англ. — СПб.: БХВ-Петербург, 2018. — 304 с.
-
Уатт Дж. и др. Машинное обучение: основы, алгоритмы и практика применения / пер. с англ. — СПб.: БХВ-Петербург, 2022. — 640 с.
Прежде всего следует упомянуть справочник Кобзаря А.И. [1] — это безусловно выдающийся труд. Ничего подобного даже близко не издавалось. Всем рекомендую иметь под рукой.
Есть очень хорошее практическое пособие [2] — для начинающих и практиков.>
Добротная работа немецких авторов [3]. Все разобрано подробно, обстоятельно, с примерами — очень хорошая книга. Примеры приведены из области экономики.
Еще одна добротная работа — [4], с примерами медико-биологического характера.
Работа [5] считается одним из наиболее полных изложений прикладного регрессионного анализа.
Более сложные работы — [6] (классика жанра), [7], [8], [9] — выдержаны на достаточно высоком математическом уровне, примеры из экономической области.
Свежие работы [10] (с примерами на языке R) и [11] (с примерами на python).
Cтатьи
Статей про регрессионный анализ в DataScience очень много, обращаю внимание на некоторые весьма полезные из них.
Серия статей «Python, корреляция и регрессия», охватывающая весь процесс регрессионного анализа:
-
первичная обработка данных, визуализация и корреляционный анализ;
-
регрессия;
-
теория матриц в регрессионном анализе, проверка адекватности, мультиколлинеарность;
-
прогнозирование с помощью регрессионных моделей.
Очень хороший обзор «Интерпретация summary из statsmodels для линейной регрессии». В этой статье даны очень полезные ссылки:
-
Statistical Models
-
Interpreting Linear Regression Through statsmodels .summary()
Статья «Регрессионные модели в Python».
Основные предпосылки (гипотезы) регрессионного анализа
Очень кратко — об этом написано тысячи страниц в учебниках — но все же вспомним некоторые основы теории.
Проверка исходных предпосылок является очень важным моментом при статистическом анализе регрессионной модели. Если мы рассматриваем классическую линейную регрессионную модель вида:
то основными предпосылками при использовании обычного метода наименьших квадратов (МНК) для оценки ее параметров являются:
-
Среднее значение (математическое ожидание) случайной составляющей равно нулю:
-
Дисперсия случайной составляющей является постоянной:
В случае нарушения данного условия мы сталкиваемся с явлением гетероскедастичности.
-
Значения случайной составляющей статистически независимы (некоррелированы) между собой:
В случае нарушения данного условия мы сталкиваемся с явлением автокорреляции.
-
Условие существования обратной матрицы
что эквивалентно одному из двух следующих условий:
то есть число наблюдений должно превышать число параметров.
-
Значения случайной составляющей некоррелированы со значениями независимых переменных:
-
Случайная составляющая имеет нормальный закон распределения (с математическим ожиданием равным нулю — следует из условия 1):
Более подробно — см.: [3, с.90], [4, с.147], [5, с.122], [6, с.208], [7, с.49], [8, с.68], [9, с.88].
Кроме гетероскедастичности и автокорреляции возможно возникновение и других статистических аномалий — мультиколлинеарности, ложной корреляции и т.д.
Доказано, что оценки параметров, полученные с помощью МНК, обладают наилучшими свойствами (несмещенность, состоятельность, эффективность) при соблюдении ряда условий:
-
выполнение приведенных выше исходных предпосылок регрессионного анализа;
-
число наблюдений на одну независимую переменную должно быть не менее 5-6;
-
должны отсутствовать аномальные значения (выбросы).
Кроме обычного МНК существуют и другие его разновидности (взвешенный МНК, обобщенный МНК), которые применяются при наличии статистических аномалий. Кроме МНК применяются и другие методы оценки параметров моделей. В этом обзоре мы эти вопросы рассматривать не будем.
Алгоритм проведения регрессионного анализа
Алгоритм действий исследователя при построении регрессионной модели (полевые работы мы, по понятным причинам, не рассматриваем — считаем, что исходные данные уже получены):
-
Подготовительный этап — постановка целей и задач исследования.
-
Первичная обработка исходных данных — об этом много написано в учебниках и пособиях по DataScience, сюда могут относится:
-
выявление нерелевантных признаков (признаков, которые не несут полезной информации), нетипичных данных (выбросов), неинформативных признаков (имеющих большое количество одинаковых значений) и работа с ними (удаление/преобразование);
-
выделение категориальных признаков;
-
работа с пропущенными значениями;
-
преобразование признаков-дат в формат datetime и т.д.
-
Визуализация исходных данных — предварительный графический анализ.
-
Дескриптивная (описательная) статистика — расчет выборочных характеристик и предварительные выводы о свойствах исходных данных.
-
Исследование закона распределения исходных данных и, при необходимости, преобразование исходных данных к нормальному закону распределения.
-
Выявление статистически аномальных значений (выбросов), принятие решения об их исключении.
Этапы 4, 5 и 6 могут быть при необходимости объединены.
-
Корреляционный анализ — исследование корреляционных связей между исходными данными; это разведка перед проведением регрессионного анализа.
-
Построение регрессионной модели:
-
выбор моделей;
-
выбор методов;
-
оценка параметров модели.
-
Статистический анализ регрессионной модели:
-
оценка ошибок аппроксимации (error metrics);
-
анализ остатков (проверка нормальности распределения остатков и гипотезы о равенстве нулю среднего значения остатков);
-
проверка адекватности модели;
-
проверка значимости коэффициента детерминации;
-
проверка значимости коэффициентов регрессии;
-
проверка мультиколлинеарности (для множественных регрессионных моделей; вообще мультиколлинеарные переменные выявляются еще на стадии корреляционного анализа);
-
проверка автокорреляции;
-
проверка гетероскедастичности.
Этапы 8 и 9 могут быть при необходимости повторяться несколько раз.
-
Сравнительный анализ нескольких регрессионных моделей, выбор наилучшей (при необходимости).
-
Прогнозирование с помощью регрессионной модели и оценка качества прогноза.
-
Выводы и рекомендации.
Само собой, этот алгоритм не есть истина в последней инстанции — в зависимости от особенностей исходных данных и вида модели могут возникать дополнительные задачи.
Применение пользовательских функций
Далее в обзоре мной будут использованы несколько пользовательских функций для решения разнообразных задач. Все эти функции созданы для облегчения работы и уменьшения размера программного кода. Данные функции загружается из пользовательского модуля my_module__stat.py, который доступен в моем репозитории на GitHub. Лично мне так удобнее работать, хотя каждый исследователь сам формирует себе инструменты по душе — особенно в части визуализации. Желающие могут пользоваться этими функциями, либо создать свои.
Итак, вот перечень данных функций:
-
graph_scatterplot_sns — функция позволяет построить точечную диаграмму средствами seaborn и сохранить график в виде png-файла;
-
graph_hist_boxplot_probplot_XY_sns — функция позволяет визуализировать исходные данные для простой линейной регрессии путем одновременного построения гистограммы, коробчатой диаграммы и вероятностного графика (для переменных X и Y) средствами seaborn и сохранить график в виде png-файла; имеется возможность выбирать, какие графики строить (h — hist, b — boxplot, p — probplot);
-
descriptive_characteristics — функция возвращает в виде DataFrame набор статистических характеристики выборки, их ошибок и доверительных интервалов;
-
detecting_outliers_mad_test — функция выполняет проверку наличия аномальных значений (выбросов) по критерию наибольшего абсолютного отклонения (более подробно — см.[1, с.547]);
-
norm_distr_check — проверка нормальности распределения исходных данных с использованием набора из нескольких статистических тестов;
-
corr_coef_check — функция выполняет расчет коэффициента линейной корреляции Пирсона, проверку его значимости и расчет доверительных интервалов; об этой функции я писал в своей статье.
-
graph_regression_plot_sns — — функция позволяет построить график регрессионной модели.
Ряд пользовательских функций мы создаем в процессе данного обзора (они тоже включены в пользовательский модуль my_module__stat.py):
-
regression_error_metrics — расчет ошибок аппроксимации регрессионной модели;
-
ANOVA_table_regression_model — вывод таблицы дисперсионного анализа регрессионной модели;
-
regression_model_adequacy_check — проверка адекватности регрессионной модели по критерию Фишера;
-
determination_coef_check — проверка значимости коэффициента детерминации по критерию Фишера;
-
regression_coef_check — проверка значимости коэффициентов регрессии по критеирю Стьюдента;
-
Goldfeld_Quandt_test, Breush_Pagan_test, White_test — проверка гетероскедастичности с использование тестов Голдфелда-Квандта, Бриша-Пэгана и Уайта соответственно;
-
regression_pair_predict — функция для прогнозирования с помощью парной регрессионной модели: рассчитывает прогнозируемое значение переменной Y по заданной модели, а также доверительные интервалы среднего и индивидуального значения для полученного прогнозируемого значения Y;
-
graph_regression_pair_predict_plot_sns — прогнозирование: построение графика регрессионной модели (с доверительными интервалами) и вывод расчетной таблицы с данными для заданной области значений X.
ПОСТАНОВКА ЗАДАЧИ
В качестве примера рассмотрим практическую задачу из области экспертизы промышленной безопасности — калибровку ультразвукового прибора для определения прочности бетона.
Итак, суть задачи: при обследовании несущих конструкций зданий и сооружений эксперт определяет прочность бетона с использованием ультразвукового прибора «ПУЛЬСАР-2.1», для которого необходимо предварительно построить градуировочную зависимость. Заключается это в следующем — производятся замеры с фиксацией следующих показателей:
-
X — показания ультразвукового прибора «ПУЛЬСАР-2.1» (м/с)
-
Y — результаты замера прочности бетона (методом отрыва со скалыванием) склерометром ИПС-МГ4.03.
Предполагается, что между показателями X и Y имеется линейная регрессионная зависимость, которая позволит прогнозировать прочность бетона на основании измерений, проведенных прибором «ПУЛЬСАР-2.1».
Были выполнены замеры фактической прочности бетона конструкций для бетонов одного вида с одним типом крупного заполнителя, с единой технологией производства. Для построения были выбраны 14 участков (не менее 12), включая участки, в которых значение косвенного показателя максимальное, минимальное и имеет промежуточные значения.
Настройка заголовков отчета:
# Общий заголовок проекта
Task_Project = 'Калибровка ультразвукового прибора "ПУЛЬСАР-2.1" nдля определения прочности бетона'
# Заголовок, фиксирующий момент времени
AsOfTheDate = ""
# Заголовок раздела проекта
Task_Theme = ""
# Общий заголовок проекта для графиков
Title_String = f"{Task_Project}n{AsOfTheDate}"
# Наименования переменных
Variable_Name_X = "Скорость УЗК (м/с)"
Variable_Name_Y = "Прочность бетона (МПа)"
# Константы
INCH = 25.4 # мм/дюйм
DecPlace = 5 # number of decimal places - число знаков после запятой
# Доверительная вероятность и уровень значимости:
p_level = 0.95
a_level = 1 - p_level Подключение модулей и библиотек:
# Стандартные модули и библиотеки
import os # загрузка модуля для работы с операционной системой
import sys
import platform
print('{:<35}{:^0}'.format("Текущая версия Python: ", platform.python_version()), 'n')
import math
from math import * # подключаем все содержимое модуля math, используем без псевдонимов
import numpy as np
#print ("Текущая версия модуля numpy: ", np.__version__)
print('{:<35}{:^0}'.format("Текущая версия модуля numpy: ", np.__version__))
from numpy import nan
import scipy as sci
print('{:<35}{:^0}'.format("Текущая версия модуля scipy: ", sci.__version__))
import scipy.stats as sps
import pandas as pd
print('{:<35}{:^0}'.format("Текущая версия модуля pandas: ", pd.__version__))
import matplotlib as mpl
print('{:<35}{:^0}'.format("Текущая версия модуля matplotlib: ", mpl.__version__))
import matplotlib.pyplot as plt
import seaborn as sns
print('{:<35}{:^0}'.format("Текущая версия модуля seaborn: ", sns.__version__))
import statsmodels.api as sm
import statsmodels.formula.api as smf
import statsmodels.graphics.api as smg
import statsmodels.stats.api as sms
from statsmodels.compat import lzip
print('{:<35}{:^0}'.format("Текущая версия модуля statsmodels: ", sm.__version__))
import statistics as stat # module 'statistics' has no attribute '__version__'
import sympy as sym
print('{:<35}{:^0}'.format("Текущая версия модуля sympy: ", sym.__version__))
# Настройки numpy
np.set_printoptions(precision = 4, floatmode='fixed')
# Настройки Pandas
pd.set_option('display.max_colwidth', None) # текст в ячейке отражался полностью вне зависимости от длины
pd.set_option('display.float_format', lambda x: '%.4f' % x)
# Настройки seaborn
sns.set_style("darkgrid")
sns.set_context(context='paper', font_scale=1, rc=None) # 'paper', 'notebook', 'talk', 'poster', None
# Настройки Mathplotlib
f_size = 8 # пользовательская переменная для задания базового размера шрифта
plt.rcParams['figure.titlesize'] = f_size + 12 # шрифт заголовка
plt.rcParams['axes.titlesize'] = f_size + 10 # шрифт заголовка
plt.rcParams['axes.labelsize'] = f_size + 6 # шрифт подписей осей
plt.rcParams['xtick.labelsize'] = f_size + 4 # шрифт подписей меток
plt.rcParams['ytick.labelsize'] = f_size + 4
plt.rcParams['legend.fontsize'] = f_size + 6 # шрифт легенды
# Пользовательские модули и библиотеки
Text1 = os.getcwd() # вывод пути к текущему каталогу
#print(f"Текущий каталог: {Text1}")
sys.path.insert(1, "D:REPOSITORYMyModulePython")
from my_module__stat import *ФОРМИРОВАНИЕ ИСХОДНЫХ ДАННЫХ
Показания ультразвукового прибора «ПУЛЬСАР-2.1» (м/с):
X = np.array([
4416, 4211, 4113, 4110, 4122,
4427, 4535, 4311, 4511, 4475,
3980, 4490, 4007, 4426
])Результаты замера прочности бетона (методом отрыва со скалыванием) прибором ИПС-МГ4.03:
Y = np.array([
34.2, 35.1, 31.5, 30.8, 30.0,
34.0, 35.4, 35.8, 38.0, 37.7,
30.0, 37.8, 31.0, 35.2
])Запишем данные в DataFrame:
calibrarion_df = pd.DataFrame({
'X': X,
'Y': Y})
display(calibrarion_df)
calibrarion_df.info()Сохраняем данные в csv-файл:
calibrarion_df.to_csv(
path_or_buf='data/calibrarion_df.csv',
mode='w+',
sep=';')Cоздаем копию исходной таблицы для работы:
dataset_df = calibrarion_df.copy()ВИЗУАЛИЗАЦИЯ ДАННЫХ
Границы значений переменных (при построении графиков):
(Xmin_graph, Xmax_graph) = (3800, 4800)
(Ymin_graph, Ymax_graph) = (25, 45)# Пользовательская функция
graph_scatterplot_sns(
X, Y,
Xmin=Xmin_graph, Xmax=Xmax_graph,
Ymin=Ymin_graph, Ymax=Ymax_graph,
color='orange',
title_figure=Task_Project,
x_label=Variable_Name_X,
y_label=Variable_Name_Y,
s=100,
file_name='graph/scatterplot_XY_sns.png')Существует универсальный набор графиков — гистограмма, коробчатая диаграмма, вероятностный график — которые позволяют исследователю сделать предварительные выводы о свойствах исходных данных.
Так как объем выборки невелик (n=14), строить гистограммы распределения переменных X и Y не имеет смысла, поэтому ограничимся построением коробчатых диаграмм и вероятностных графиков:
# Пользовательская функция
graph_hist_boxplot_probplot_XY_sns(
data_X=X, data_Y=Y,
data_X_min=Xmin_graph, data_X_max=Xmax_graph,
data_Y_min=Ymin_graph, data_Y_max=Ymax_graph,
graph_inclusion='bp', # выбираем для построения виды графиков: b - boxplot, p - probplot)
data_X_label=Variable_Name_X,
data_Y_label=Variable_Name_Y,
title_figure=Task_Project,
file_name='graph/hist_boxplot_probplot_XY_sns.png') Для сравнения характера распределений переменных X и Y возможно также построить совмещенную коробчатую диаграмму по стандартизованным данным:
# стандартизуем исходные данные
standardize_df = lambda X: ((X - np.mean(X))/np.std(X))
dataset_df_standardize = dataset_df.copy()
dataset_df_standardize = dataset_df_standardize.apply(standardize_df)
display(dataset_df_standardize)
# построим график
fig, axes = plt.subplots(figsize=(210/INCH, 297/INCH/2))
axes.set_title("Распределение стандартизованных переменных X и Y", fontsize = 16)
sns.boxplot(
data=dataset_df_standardize,
orient='h',
width=0.5,
ax=axes)
plt.show()Графический анализ позволяет сделать следующие выводы:
-
Отсутствие выбросов на коробчатых диаграммах свидетельствует об однородности распределения переменных.
-
Смещение медианы вправо на коробчатых диаграммах свидетельствует о левосторонней асимметрии распределения.
ДЕСКРИПТИВНАЯ (ОПИСАТЕЛЬНАЯ СТАТИСТИКА)
Собственно говоря, данный этап требуется проводить далеко не всегда, однако с помощью статистических характеристик выборки мы тоже можем сделать полезные выводы.
Описательная статистика исходных данных средствами библиотеки Pandas — самый простой вариант:
dataset_df.describe()Описательная статистика исходных данных средствами библиотеки statsmodels — более развернутый вариант, с большим количеством показателей:
from statsmodels.stats.descriptivestats import Description
result = Description(
dataset_df,
stats=["nobs", "missing", "mean", "std_err", "ci", "ci", "std", "iqr", "mad", "coef_var", "range", "max", "min", "skew", "kurtosis", "mode",
"median", "percentiles", "distinct", "top", "freq"],
alpha=a_level,
use_t=True)
display(result.summary())Описательная статистика исходных данных с помощью пользовательской функции descriptive_characteristics:
# Пользовательская функция
descriptive_characteristics(X)Выводы:
-
Сравнение показателей среднего арифметического (mean) и медианы (median) свидетельствует о левосторонней асимметрии (т.к.mean < median).
-
Значение коэффициента вариации CV = 0.0445 и доверительный интервал для него 0.0336 ≤ CV ≤ 0.0657 свидетельствует об однородности исходных данных (т.к. CV ≤ 0.33).
-
Значение показателя асимметрии skew (As) = -0.3101 свидетельствует об умеренной левосторонней асимметрии распределении (т.к. |As| ≤ 0.5, As < 0).
-
Значение показателя эксцесса kurtosis (Es) = -1.4551 свидетельствует о плосковершинном распределении (platykurtic distribution) (т.к. Es < 0).
# Пользовательская функция
descriptive_characteristics(Y)Выводы:
-
Сравнение показателей среднего арифметического (mean) и медианы (median) свидетельствует о левосторонней асимметрии (т.к.mean < median).
-
Значение коэффициента вариации CV = 0.0822 и доверительный интервал для него 0.06202 ≤ CV ≤ 0.1217 свидетельствует об однородности исходных данных (т.к. CV ≤ 0.33).
-
Значение показателя асимметрии skew (As) = -0.1109 свидетельствует о приблизительно симметричном распределении (т.к. |As| ≤ 0.25).
-
Значение показателя эксцесса kurtosis (Es) = -1.3526 свидетельствует о плосковершинном распределении (platykurtic distribution) (т.к. Es < 0).
ПРОВЕРКА НОРМАЛЬНОСТИ РАСПРЕДЕЛЕНИЯ
Для проверки нормальности распределения использована пользовательская функция norm_distr_check, которая объединяет в себе набор стандартных статистических тестов проверки нормальности. Все тесты относятся к стандартному инструментарию Pyton (библиотека scipy, модуль stats), за исключением теста Эппса-Палли (Epps-Pulley test); о том, как реализовать этот тест средствами Pyton я писал в своей статье https://habr.com/ru/post/685582/.
Примечание: для использования функции norm_distr_check в каталог с ipynb-файлом необходимо поместить папку table c файлом Tep_table.csv, который содержит табличные значения статистики критерия Эппса-Палли.
# пользовательская функция
norm_distr_check(X)# Пользовательская функция
norm_distr_check (Y)Вывод: большинство статистических тестов позволяют принять гипотезу о нормальности распределения переменных X и Y.
ПРОВЕРКА АНОМАЛЬНЫХ ЗНАЧЕНИЙ (ВЫБРОСОВ)
Статистическую проверку аномальных значений (выбросов) не стоит путать с проверкой выбросов, которая проводится на этапе первичной обработки результатов наблюдений. Последняя проводится с целью отсеять явные ошибочные данные (например, в результате неправильно поставленной запятой величина показателя может увеличиться/уменьшиться на порядок); здесь же мы говорим о статистической проверке данных, которые уже прошли этап первичной обработки.
Имеется довольно много критериев для проверки аномальных значений (подробнее см.[1]); вообще данная процедура довольно неоднозначная:
-
критерии зависят от вида распределения;
-
мало данных о сравнительной мощности этих критериев;
-
даже в случае принятии гипотезы о нормальном распределении в выборке могут быть обнаружены аномальные значения и пр.
Кроме существует дилемма: если какие-то значения в выборке признаны выбросами — стоит или не стоит исследователю исключать их? Ведь каждое значение несет в себе информацию, причем иногда весьма ценную, а сильно отклоняющиеся от основного массива данные (которые не являются выбросами в смысле первичной обработки, но являются статистическим значимыми аномальными значениями) могут кардинально изменить статистический вывод.
В общем, о задаче выявления аномальных значений (выбросов) можно написать отдельно, а пока, в данном разборе, ограничимся проверкой аномальных значений по критерию наибольшего максимального отклонения (см.[1, с.547]) с помощью пользовательской функции detecting_outliers_mad_test. Данные функция возвращает DataFrame, которые включает список аномальных значений со следующими признаками:
-
value — проверяемое значение из выборки;
-
mad_calc и mad_table — расчетное и табличное значение статистики критерия;
-
outlier_conclusion — вывод (выброс или нет).
Обращаю внимание, что критерий наибольшего максимального отклонения можно использовать только для нормально распределенных данных.
# пользовательская функция
print("Проверка наличия выбросов переменной X:n")
result = detecting_outliers_mad_test(X)
mask = (result['outlier_conclusion'] == 'outlier')
display(result[mask])# пользовательская функция
print("Проверка наличия выбросов переменной Y:n")
result = detecting_outliers_mad_test(Y)
mask = (result['outlier_conclusion'] == 'outlier')
display(result[mask])Вывод: в случае обеих переменных X и Y список пуст, следовательно, аномальных значений (выбросов) не выявлено.
КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
Корреляционный анализ — это разведка перед построением регрессионной модели.
Выполним расчет коэффициента линейной корреляции Пирсона, проверку его значимости и построение доверительных интервалов с помощью пользовательской функции corr_coef_check (про эту функцию более подробно написано в моей статье https://habr.com/ru/post/683442/):
# пользовательская функция
display(corr_coef_check(X, Y, scale='Evans'))Выводы:
-
Значение коэффициента корреляции coef_value = 0.8900 свидетельствует о весьма сильной корреляционной связи (по шкале Эванса).
-
Коэффициент корреляции значим по критерию Стьюдента: t_calc ≥ t_table, a_calc ≤ a_level.
-
Доверительный интервал для коэффициента корреляции: 0.6621 ≤ coef_value ≤ 0.9625.
РЕГРЕССИОННЫЙ АНАЛИЗ
Предварительная визуализация
python позволяет выполнить предварительную визуализацию, например, с помощью функции jointplot библиотеки seaborn:
fig = plt.figure(figsize=(297/INCH, 210/INCH))
axes = sns.jointplot(
x=X, y=Y,
kind='reg',
ci=95)
plt.show()Построение модели
Выполним оценку параметров и анализ простой линейной регрессии (simple linear regression), используя библиотеку statsmodels (https://www.statsmodels.org/) и входящий в нее модуль линейной регрессии Linear Regression (https://www.statsmodels.org/stable/regression.html).
Данный модуль включает в себя классы, реализующие различные методы оценки параметров моделей линейной регрессии, в том числе:
-
класс OLS (https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.OLS.html#statsmodels.regression.linear_model.OLS) — Ordinary Least Squares (обычный метод наименьших квадратов).
-
класс WLS (https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.WLS.html#statsmodels.regression.linear_model.WLS) — Weighted Least Squares (метод взвешенных наименьших квадратов) (https://en.wikipedia.org/wiki/Weighted_least_squares), применяется, если имеет место гетероскедастичность данных (https://ru.wikipedia.org/wiki/Гетероскедастичность).
-
класс GLS (https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.GLS.html#statsmodels.regression.linear_model.GLS) — Generalized Least Squares (обобщенный метод наименьших квадратов) (https://en.wikipedia.org/wiki/Generalized_least_squares), применяется, если существует определенная степень корреляции между остатками в модели регрессии.
-
класс GLSAR (https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.GLSAR.html#statsmodels.regression.linear_model.GLSAR) — Generalized Least Squares with AR covariance structure (обобщенный метод наименьших квадратов, ковариационная структура с автокорреляцией — экспериментальный метод)
-
класс RecurciveLS (https://www.statsmodels.org/stable/examples/notebooks/generated/recursive_ls.html) — Recursive least squares (рекурсивный метод наименьших квадратов) (https://en.wikipedia.org/wiki/Recursive_least_squares_filter)
-
классы RollingOLS (https://www.statsmodels.org/stable/generated/statsmodels.regression.rolling.RollingOLS.html#statsmodels.regression.rolling.RollingOLS) и RollingWLS (https://www.statsmodels.org/stable/generated/statsmodels.regression.rolling.RollingWLS.html#statsmodels.regression.rolling.RollingWLS) — скользящая регрессия (https://www.statsmodels.org/stable/examples/notebooks/generated/rolling_ls.html, https://help.fsight.ru/ru/mergedProjects/lib/01_regression_models/rolling_regression.htm)
и т.д.
Так как исходные данные подчиняются нормальному закону распределения и аномальные значения (выбросы) отсутствуют, воспользуемся для оценки параметров обычным методом наименьших квадратов (класс OLS):
model_linear_ols = smf.ols(formula='Y ~ X', data=dataset_df)
result_linear_ols = model_linear_ols.fit()
print(result_linear_ols.summary())Альтернативная форма выдачи результатов:
print(result_linear_ols.summary2())Результаты построения модели мы получаем как класс statsmodels.regression.linear_model.RegressionResults (https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.RegressionResults.html#statsmodels.regression.linear_model.RegressionResults).
Экспресс-выводы, которые мы можем сразу сделать из результатов построения модели:
-
Коэффициенты регрессии модели Y = b0 + b1∙X:
-
Intercept = b0 = -21.3741
-
b1 = 0.0129
-
-
Коэффициент детерминации R-squared = 0.776, его скорректированная оценка Adj. R-squared = 0.757 — это означает, что регрессионная модуль объясняет 75.75% вариации переменной Y.
-
Проверка значимости коэффициента детерминации:
-
расчетное значение статистики критерия Фишера: F-statistic = 41.61
-
расчетный уровень значимости Prob (F-statistic) = 3.16e-05
-
так как значение Prob (F-statistic) < 0.05, то нулевая гипотеза R-squared = 0 НЕ ПРИНИМАЕТСЯ, т.е. коэффициент детерминации ЗНАЧИМ
-
-
Проверка значимости коэффициентов регрессии:
-
расчетный уровень значимости P>|t| не превышает 0.05 — это означает, что оба коэффициента регрессии значимы
-
об этом же свидетельствует то, что доверительный интервал для обоих коэффициентов регрессии ([0.025; 0.975]) не включает в себя точку 0
Также в таблице результатов содержится прочая информация по коэффициентам регрессии: стандартная ошибка Std.Err. расчетное значение статистики критерия Стьюдента t для проверки гипотезы о значимости.
-
-
Анализ остатков модели:
-
Тест Omnibus — про этот тест подробно написано в https://en.wikipedia.org/wiki/Omnibus_test, https://medium.com/swlh/interpreting-linear-regression-through-statsmodels-summary-4796d359035a, http://work.thaslwanter.at/Stats/html/statsModels.html.
Расчетное значение статистики критерия Omnibus = 3.466 — по сути расчетное значение F-критерия (см. https://en.wikipedia.org/wiki/Omnibus_test).
Prob(Omnibus) = 0.177 — показывает вероятность нормального распределения остатков (значение 1 указывает на совершенно нормальное распределение).
Учитывая, что в дальнейшем мы проверим нормальность распределения остатков по совокупности различных тестов, в том числе с достаточно высокой мощностью, и все тесты позволят принять гипотезу о нормальном распределении — в данном случае к тесту Omnibus возникают вопросы. С этим тестом нужно разбираться отдельно.
-
Skew = 0.014 и Kurtosis = 1.587 — показатели асимметрии и эксцесса остатков свидетельствуют, что распределение остатков практически симметричное, островершинное.
-
проверка нормальности распределения остатков по критерию Харке-Бера: расчетное значение статистики критерия Jarque-Bera (JB) = 1.164 и расчетный уровень значимости Prob(JB) = 0.559. К данным результатам также возникают вопросы, особенно, если учесть, что критерий Харке-Бера является асимптотическим, расчетное значение имеет распределение хи-квадрат, поэтому данный критерий рекомендуют применять только для больших выборок (см. https://en.wikipedia.org/wiki/Jarque–Bera_test). Проверку нормальности распределения остатков модели лучше проводить с использованием набора стандартных статистических тестов python (см. далее).
-
-
Проверка автокорреляции по критерию Дарбина-Уотсона: Durbin-Watson = 1.443.
Мы не будем здесь разбирать данный критерий, так как явление автокорреляции больше характерно для данных, выражаемых в виде временных рядов. Однако, для грубой оценки считается, что при расчетном значении статистики криетрия Дарбина=Уотсона а интервале [1; 2] автокорреляция отсутствует (см.https://en.wikipedia.org/wiki/Durbin–Watson_statistic).
Более подробно про критерий Дарбина-Уотсона — см. [1, с.659].
Прочая информация, которую можно извлечь из результатов построения модели:
-
Covariance Type — тип ковариации, подробнее см. https://habr.com/ru/post/681218/, https://towardsdatascience.com/simple-explanation-of-statsmodel-linear-regression-model-summary-35961919868b#:~:text=Covariance type is typically nonrobust,with respect to each other.
-
Scale — масштабный коэффициент для ковариационной матрицы (https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.RegressionResults.scale.html#statsmodels.regression.linear_model.RegressionResults.scale), равен величине Mean squared error (MSE) (cреднеквадратической ошибке), об подробнее см. далее, в разделе про ошибки аппроксимации моделей.
-
Показатели сравнения качества различных моделей:
-
Log-Likelihood — логарифмическая функция правдоподобия, подробнее см. https://en.wikipedia.org/wiki/Likelihood_function#Log-likelihood, https://habr.com/ru/post/433804/
-
AIC — информационный критерий Акаике (Akaike information criterion), подробнее см. https://en.wikipedia.org/wiki/Akaike_information_criterion
-
BIC — информационный критерий Байеса (Bayesian information criterion), подробнее см. https://en.wikipedia.org/wiki/Bayesian_information_criterion
В данной статье мы эти показатели рассматривать не будем, так как задача выбора одной модели из нескольких перед нами не стоит.
-
-
Число обусловленности Cond. No = 96792 используется для проверки мультиколлинеарности (считается, что мультиколлинеарность есть, если значение Cond. No > 30) (см. http://work.thaslwanter.at/Stats/html/statsModels.html). В нашем случае парной регрессионной модели о мультиколлинеарности речь не идет.
Далее будем извлекать данные из стандартного набора выдачи результатов и анализировать их более подробно. Последующие этапы вовсе не обязательно проводить в полном объеме при решении задач, но здесь мы рассмотрим их подробно.
Параметры и уравнение регрессионной модели
Извлечем параметры полученной модели — как свойство params модели:
print('Параметры модели: n', result_linear_ols.params, type(result_linear_ols.params))Имея параметры модели, можем формализовать уравнение модели Y = b0 + b1*X:
b0 = result_linear_ols.params['Intercept']
b1 = result_linear_ols.params['X']
Y_calc = lambda x: b0 + b1*xГрафик регрессионной модели
Для построения графиков регрессионных моделей можно воспользоваться стандартными возможностями библиотек statsmodels, seaborn, либо создать пользовательскую функцию — на усмотрение исследователя:
1. Построение графиков регрессионных моделей с использованием библиотеки statsmodels
С помощью функции statsmodels.graphics.plot_fit (https://www.statsmodels.org/stable/generated/statsmodels.graphics.regressionplots.plot_fit.html#statsmodels.graphics.regressionplots.plot_fit) — отображается график Y and Fitted vs.X (фактические и расчетные значения Y с доверительным интервалом для каждого значения Y):
fig, ax = plt.subplots(figsize=(297/INCH, 210/INCH))
fig = sm.graphics.plot_fit(
result_linear_ols, 'X',
vlines=True, # это параметр отвечает за отображение доверительных интервалов для Y
ax=ax)
ax.set_ylabel(Variable_Name_Y)
ax.set_xlabel(Variable_Name_X)
ax.set_title(Task_Project)
plt.show()С помощью функции statsmodels.graphics.plot_regress_exog (https://www.statsmodels.org/stable/generated/statsmodels.graphics.regressionplots.plot_regress_exog.html#statsmodels.graphics.regressionplots.plot_regress_exog) — отображается область 2х2, которая содержит:
-
предыдущий график Y and Fitted vs.X;
-
график остатков Residuals versus X;
-
график Partial regression plot — график частичной регрессии, пытается показать эффект добавления другой переменной в модель, которая уже имеет одну или несколько независимых переменных (более подробно см. https://en.wikipedia.org/wiki/Partial_regression_plot);
-
график CCPR Plot (Component-Component plus Residual Plot) — еще один способ оценить влияние одной независимой переменной на переменную отклика, принимая во внимание влияние других независимых переменных (более подробно — см. https://towardsdatascience.com/calculating-price-elasticity-of-demand-statistical-modeling-with-python-6adb2fa7824d, https://www.kirenz.com/post/2021-11-14-linear-regression-diagnostics-in-python/linear-regression-diagnostics-in-python/).
fig = plt.figure(figsize=(297/INCH, 210/INCH))
sm.graphics.plot_regress_exog(result_linear_ols, 'X', fig=fig)
plt.show()2. Построение графиков регрессионных моделей с использованием библиотеки seaborn
Воспользуемся модулем regplot библиотеки seaborn (https://seaborn.pydata.org/generated/seaborn.regplot.html). Данный модуль позволяет визуализировать различные виды регрессии:
-
линейную
-
полиномиальную
-
логистическую
-
взвешенную локальную регрессию (LOWESS — Locally Weighted Scatterplot Smoothing) (см. http://www.machinelearning.ru/wiki/index.php?title=Алгоритм_LOWESS, https://www.statsmodels.org/stable/generated/statsmodels.nonparametric.smoothers_lowess.lowess.html)
Более подробно про модуль regplot можно прочитать в статье: https://pyprog.pro/sns/sns_8_regression_models.html.
Есть более совершенный модуль lmplot (https://seaborn.pydata.org/generated/seaborn.lmplot.html), который объединяет в себе regplot и FacetGrid, но мы его здесь рассматривать не будем.
# создание рисунка (Figure) и области рисования (Axes)
fig = plt.figure(figsize=(297/INCH, 420/INCH/1.5))
ax1 = plt.subplot(2,1,1)
ax2 = plt.subplot(2,1,2)
# заголовок рисунка (Figure)
title_figure = Task_Project
fig.suptitle(title_figure, fontsize = 18)
# заголовок области рисования (Axes)
title_axes_1 = 'Линейная регрессионная модель'
ax1.set_title(title_axes_1, fontsize = 16)
# график регрессионной модели
order_mod = 1 # порядок модели
#label_legend_regr_model = 'фактические данные'
sns.regplot(
#data=dataset_df,
x=X, y=Y,
#x_estimator=np.mean,
order=order_mod,
logistic=False,
lowess=False,
robust=False,
logx=False,
ci=95,
scatter_kws={'s': 30, 'color': 'red'},
line_kws={'color': 'blue'},
#label=label_legend_regr_model,
ax=ax1)
ax1.set_ylabel(Variable_Name_Y)
ax1.legend()
# график остатков
title_axes_2 = 'График остатков'
ax2.set_title(title_axes_2, fontsize = 16)
sns.residplot(
#data=dataset_df,
x=X, y=Y,
order=order_mod,
lowess=False,
robust=False,
scatter_kws={'s': 30, 'color': 'darkorange'},
ax=ax2)
ax2.set_xlabel(Variable_Name_X)
plt.show()3. Построение графиков регрессионных моделей с помощью пользовательской функции
# Пользовательская функция
graph_regression_plot_sns(
X, Y,
regression_model=Y_calc,
Xmin=Xmin_graph, Xmax=Xmax_graph,
Ymin=Ymin_graph, Ymax=Ymax_graph,
title_figure=Task_Project,
x_label=Variable_Name_X,
y_label=Variable_Name_Y,
label_legend_regr_model=f'линейная регрессия Y = {b0:.3f} + {b1:.4f}*X',
s=80,
file_name='graph/regression_plot_lin.png')Статистический анализ регрессионной модели
1. Расчет ошибки аппроксимации (Error Metrics)
Ошибки аппроксимации (Error Metrics) позволяют получить общее представление о качестве модели, а также позволяют сравнивать между собой различные модели.
Создадим пользовательскую функцию, которая рассчитывает основные ошибки аппроксимации для заданной модели:
-
Mean squared error (MSE) или Mean squared deviation (MSD) — среднеквадратическая ошибка (https://en.wikipedia.org/wiki/Mean_squared_error):
-
Root mean square error (RMSE) или Root mean square deviation (RMSD) — квадратный корень из MSE (https://en.wikipedia.org/wiki/Root-mean-square_deviation):
-
Mean absolute error (MAE) — средняя абсолютная ошибка (https://en.wikipedia.org/wiki/Mean_absolute_error):
-
Mean squared prediction error (MSPE) — среднеквадратическая ошибка прогноза (среднеквадратическая ошибка в процентах) (https://en.wikipedia.org/wiki/Mean_squared_prediction_error):
-
Mean absolute percentage error (MAPE) — средняя абсолютная ошибка в процентах (https://en.wikipedia.org/wiki/Mean_absolute_percentage_error):
Про выбор метрики см. также https://machinelearningmastery.ru/how-to-select-the-right-evaluation-metric-for-machine-learning-models-part-2-regression-metrics-d4a1a9ba3d74/.
# Пользовательская функция
def regression_error_metrics(model, model_name=''):
model_fit = model.fit()
Ycalc = model_fit.predict()
n_fit = model_fit.nobs
Y = model.endog
MSE = (1/n_fit) * np.sum((Y-Ycalc)**2)
RMSE = sqrt(MSE)
MAE = (1/n_fit) * np.sum(abs(Y-Ycalc))
MSPE = (1/n_fit) * np.sum(((Y-Ycalc)/Y)**2)
MAPE = (1/n_fit) * np.sum(abs((Y-Ycalc)/Y))
model_error_metrics = {
'MSE': MSE,
'RMSE': RMSE,
'MAE': MAE,
'MSPE': MSPE,
'MAPE': MAPE}
result = pd.DataFrame({
'MSE': MSE,
'RMSE': RMSE,
'MAE': MAE,
'MSPE': "{:.3%}".format(MSPE),
'MAPE': "{:.3%}".format(MAPE)},
index=[model_name])
return model_error_metrics, result
(model_error_metrics, result) = regression_error_metrics(model_linear_ols, model_name='linear_ols')
display(result)В литературе по прикладной статистике нет единого мнения о допустимом размере относительных ошибок аппроксимации: в одних источниках допустимой считается ошибка 5-7%, в других она может быть увеличена до 8-10%, и даже до 15%.
Вывод: модель хорошо аппроксимирует фактические данные (относительная ошибка аппроксимации MAPE = 3.405% < 10%).
2. Дисперсионный анализ регрессионной модели (ДАРМ)
ДАРМ не входит в стандартную форму выдачи результатов Regression Results, однако я решил написать здесь о нем по двум причинам:
-
Именно анализ дисперсии регрессионной модели, разложение этой дисперсии на составляющие дает фундаментальное представление о сути регрессии, а термины, используемые при ДАРМ, применяются на последующих этапах анализа.
-
С терминами ДАРМ в литературе по прикладной статистике имеется некоторая путаница, в разных источниках они могут именоваться по-разному (см., например, [8, с.52]), поэтому, чтобы двигаться дальше, необходимо определиться с понятиями.
При ДАРМ общую вариацию результативного признака (Y) принято разделять на две составляющие — вариация, обусловленная регрессией и вариация, обусловленная отклонениями от регрессии (остаток), при этом в разных источниках эти термины могут именоваться и обозначаться по-разному, например:
-
Вариация, обусловленная регрессией — может называться Explained sum of squares (ESS), Sum of Squared Regression (SSR) (https://en.wikipedia.org/wiki/Explained_sum_of_squares, https://towardsdatascience.com/anova-for-regression-fdb49cf5d684), Sum of squared deviations (SSD).
-
Вариация, обусловленная отклонениями от регрессии (остаток) — может называться Residual sum of squares (RSS), Sum of squared residuals (SSR), Squared estimate of errors, Sum of Squared Error (SSE) (https://en.wikipedia.org/wiki/Residual_sum_of_squares, https://towardsdatascience.com/anova-for-regression-fdb49cf5d684); в отчественной практике также применяется термин остаточная дисперсия.
-
Общая (полная) вариация — может называться Total sum of squares (TSS), Sum of Squared Total (SST) (https://en.wikipedia.org/wiki/Partition_of_sums_of_squares, https://towardsdatascience.com/anova-for-regression-fdb49cf5d684).
Как видим, путаница знатная:
-
в разных источниках под SSR могут подразумеваться различные показатели;
-
легко перепутать показатели ESS и SSE;
-
в библиотеке statsmodel также есть смешение терминов: для показателя Explained sum of squares используется свойство ess, а для показателя Sum of squared (whitened) residuals — свойство ssr.
Мы будем пользоваться системой обозначений, принятой в большинстве источников — SSR (Sum of Squared Regression), SSE (Sum of Squared Error), SST (Sum of Squared Total). Стандартная таблица ДАРМ в этом случае имеет вид:
Примечания:
-
Здесь приведена таблица ДАРМ для множественной линейной регрессионной модели (МЛРМ), в нашем случае при ПЛРМ мы имеем частный случай p=1.
-
Показатели Fcalc-ad и Fcalc-det — расчетные значения статистики критерия Фишера при проверке адекватности модели и значимости коэффициента детерминации (об этом — см.далее).
Более подробно про дисперсионный анализ регрессионной модели — см.[4, глава 3].
Класс statsmodels.regression.linear_model.RegressionResults позволяет нам получить данные для ANOVA (см. https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.RegressionResults.html#statsmodels.regression.linear_model.RegressionResults) как свойства класса:
-
Сумма квадратов, обусловленная регрессией / SSR (Sum of Squared Regression) — свойство ess.
-
Сумма квадратов, обусловленная отклонением от регрессии / SSE (Sum of Squared Error) — свойство ssr.
-
Общая (полная) сумма квадратов / SST (Sum of Squared Total) — свойство centered_tss.
-
Кол-во наблюдений / Number of observations — свойство nobs.
-
Число степеней свободы модели / Model degrees of freedom — равно числу переменных модели (за исключением константы, если она присутствует — свойство df_model.
-
Среднеквадратичная ошибка модели / Mean squared error the model — сумма квадратов, объясненная регрессией, деленная на число степеней свободы регрессии — свойство mse_model.
-
Среднеквадратичная ошибка остатков / Mean squared error of the residuals — сумма квадратов остатков, деленная на остаточные степени свободы — свойство mse_resid.
-
Общая среднеквадратичная ошибка / Total mean squared error — общая сумма квадратов, деленная на количество наблюдений — свойство mse_total.
Также имеется модуль statsmodels.stats.anova.anova_lm, который позволяет получить результаты ДАРМ (нескольких типов — 1, 2, 3):
# тип 1
print('The type of Anova test: 1')
display(sm.stats.anova_lm(result_linear_ols, typ=1))
# тип 2
print('The type of Anova test: 2')
display(sm.stats.anova_lm(result_linear_ols, typ=2))
# тип 3
print('The type of Anova test: 3')
display(sm.stats.anova_lm(result_linear_ols, typ=3))На мой взгляд, форма таблица результатов statsmodels.stats.anova.anova_lm не вполне удобна, поэтому сформируем ее самостоятельно, для чего создадим пользовательскую функцию ANOVA_table_regression_model:
# Пользовательская функция
def ANOVA_table_regression_model(model_fit):
n = int(model_fit.nobs)
p = int(model_fit.df_model)
SSR = model_fit.ess
SSE = model_fit.ssr
SST = model_fit.centered_tss
result = pd.DataFrame({
'sources_of_variation': ('regression (SSR)', 'deviation from regression (SSE)', 'total (SST)'),
'sum_of_squares': (SSR, SSE, SST),
'degrees_of_freedom': (p, n-p-1, n-1)})
result['squared_error'] = result['sum_of_squares'] / result['degrees_of_freedom']
R2 = 1 - result.loc[1, 'sum_of_squares'] / result.loc[2, 'sum_of_squares']
F_calc_adequacy = result.loc[2, 'squared_error'] / result.loc[1, 'squared_error']
F_calc_determ_check = result.loc[0, 'squared_error'] / result.loc[1, 'squared_error']
result['F-ratio'] = (F_calc_determ_check, F_calc_adequacy, '')
return result
result = ANOVA_table_regression_model(result_linear_ols)
display(result)
print(f"R2 = 1 - SSE/SST = {1 - result.loc[1, 'sum_of_squares'] / result.loc[2, 'sum_of_squares']}")
print(f"F_calc_adequacy = MST / MSE = {result.loc[2, 'squared_error'] / result.loc[1, 'squared_error']}")
print(f"F_calc_determ_check = MSR / MSE = {result.loc[0, 'squared_error'] / result.loc[1, 'squared_error']}")ДАРМ позволяет визуализировать вариацию:
fig, axes = plt.subplots(figsize=(210/INCH, 297/INCH/1.5))
axes.pie(
(result.loc[0, 'sum_of_squares'], result.loc[1, 'sum_of_squares']),
labels=(result.loc[0, 'sources_of_variation'], result.loc[1, 'sources_of_variation']),
autopct='%.1f%%',
startangle=60)
plt.show()На основании данных ДАРМ мы рассчитали ряд показателей (R2, Fcalc-ad и Fcalc-det), которые будут использоваться в дальнейшем.
3. Анализ остатков (проверка нормальности распределения остатков и гипотезы о равенстве нулю среднего значения остатков)
Проверка нормальности распределения остатков — один их важнейших этапов анализа регрессионной модели. Требование нормальности распределения остатков не требуется для отыскания параметров модели, но необходимо в дальнейшем для проверки статистических гипотез с использованием критериев Фишера и Стьюдента (проверка адекватности модели, значимости коэффициента детерминации, значимости коэффициентов регрессии) и построения доверительных интервалов [5, с.122].
Остатки регрессионной модели:
print('Остатки регрессионной модели:n', result_linear_ols.resid, type(result_linear_ols.resid))
res_Y = np.array(result_linear_ols.resid)statsmodels может выдавать различные преобразованные виды остатков (см. https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.RegressionResults.resid_pearson.html, https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.RegressionResults.wresid.html).
График остатков:
# Пользовательская функция
graph_scatterplot_sns(
X, res_Y,
Xmin=Xmin_graph, Xmax=Xmax_graph,
Ymin=-3.0, Ymax=3.0,
color='red',
#title_figure=Task_Project,
title_axes='Остатки линейной регрессионной модели', title_axes_fontsize=18,
x_label=Variable_Name_X,
y_label='ΔY = Y - Ycalc',
s=75,
file_name='graph/residuals_plot_sns.png')Проверка нормальности распределения остатков:
# Пользовательская функция
graph_hist_boxplot_probplot_sns(
data=res_Y,
data_min=-2.5, data_max=2.5,
graph_inclusion='bp',
data_label='ΔY = Y - Ycalc',
#title_figure=Task_Project,
title_axes='Остатки линейной регрессионной модели', title_axes_fontsize=16,
file_name='graph/residuals_hist_boxplot_probplot_sns.png') norm_distr_check(res_Y)Вывод: большинство статистических тестов позволяют принять гипотезу о нормальности распределения остатков.
Проверка гипотезы о равенстве нулю среднего значения остатков — так как остатки имеют нормальное распределение, воспользуемся критерием Стьюдента (функция scipy.stats.ttest_1samp, https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.ttest_ind.html):
sps.ttest_1samp(res_Y, popmean=0)Вывод: так как расчетный уровень значимости превышает заданный (0.05), то нулевая гипотеза о равенстве нулю остатков ПРИНИМАЕТСЯ.
4. Проверка адекватности модели
Суть проверки адекватности регрессионной модели заключается в сравнении полной дисперсии MST и остаточной дисперсии MSE — проверяется гипотеза о равенстве этих дисперсий по критерию Фишера. Если дисперсии различаются значимо, то модель считается адекватной. Более подробно про проверку адекватности регрессионной — см.[1, с.658], [2, с.49], [4, с.154].
Для проверки адекватности регрессионной модели создадим пользовательскую функцию regression_model_adequacy_check:
def regression_model_adequacy_check(
model_fit,
p_level: float=0.95,
model_name=''):
n = int(model_fit.nobs)
p = int(model_fit.df_model) # Число степеней свободы регрессии, равно числу переменных модели (за исключением константы, если она присутствует)
SST = model_fit.centered_tss # SST (Sum of Squared Total)
dfT = n-1
MST = SST / dfT
SSE = model_fit.ssr # SSE (Sum of Squared Error)
dfE = n - p - 1
MSE = SSE / dfE
F_calc = MST / MSE
F_table = sci.stats.f.ppf(p_level, dfT, dfE, loc=0, scale=1)
a_calc = 1 - sci.stats.f.cdf(F_calc, dfT, dfE, loc=0, scale=1)
conclusion_model_adequacy_check = 'adequacy' if F_calc >= F_table else 'adequacy'
# формируем результат
result = pd.DataFrame({
'SST': (SST),
'SSE': (SSE),
'dfT': (dfT),
'dfE': (dfE),
'MST': (MST),
'MSE': (MSE),
'p_level': (p_level),
'a_level': (a_level),
'F_calc': (F_calc),
'F_table': (F_table),
'F_calc >= F_table': (F_calc >= F_table),
'a_calc': (a_calc),
'a_calc <= a_level': (a_calc <= a_level),
'adequacy_check': (conclusion_model_adequacy_check),
},
index=[model_name]
)
return result
regression_model_adequacy_check(result_linear_ols, p_level=0.95, model_name='linear_ols')Вывод: модель является АДЕКВАТНОЙ.
5. Коэффициент детерминации и проверка его значимости
Различают несколько видов коэффициента детерминации:
-
Собственно обычный коэффициент детерминации:
Его значение может быть получено как свойство rsquared модели.
-
Скорректированный (adjusted) коэффициент детерминации — используется для того, чтобы была возможность сравнивать модели с разным числом признаков так, чтобы число регрессоров (признаков) не влияло на статистику R2, при его расчете используются несмещённые оценки дисперсий:
Его значение может быть получено как свойство rsquared_adj модели.
-
Обобщённый (extended) коэффициент детерминации — используется для сравнения моделей регрессии со свободным членом и без него, а также для сравнения между собой регрессий, построенных с помощью различных методов: МНК, обобщённого метода наименьших квадратов (ОМНК), условного метода наименьших квадратов (УМНК), обобщённо-условного метода наименьших квадратов (ОУМНК). В данном разборе ПЛРМ рассматривать этот коэффициент мы не будем.
Более подробно с теорией вопроса можно ознакомиться, например: http://www.machinelearning.ru/wiki/index.php?title=Коэффициент_детерминации), а также в [7].
Значения коэффициента детерминации и скорректированного коэффициента детерминации, извлеченные с помощью свойств rsquared и rsquared_adj модели.
print('R2 =', result_linear_ols.rsquared)
print('R2_adj =', result_linear_ols.rsquared_adj)Значимость коэффициента детерминации можно проверить по критерию Фишера [3, с.201-203; 8, с.83].
Расчетное значение статистики критерия Фишера может быть получено с помощью свойства fvalue модели:
print(f"result_linear_ols.fvalue = {result_linear_ols.fvalue}")Расчетный уровень значимости при проверке гипотезы по критерию Фишера может быть получено с помощью свойства f_pvalue модели:
print(f"result_linear_ols.f_pvalue = {result_linear_ols.f_pvalue}")Можно рассчитать уровень значимости самостоятельно (так сказать, для лучшего понимания и общей демонстрации возможностей) — для этого воспользуемся библиотекой scipy, модулем распределения Фишера scipy.stats.f, свойством cdf (функция распределения):
df1 = int(result_linear_ols.df_model)
df2 = int(result_linear_ols.nobs - result_linear_ols.df_model - 1)
F_calc = result_linear_ols.fvalue
a_calc = 1 - sci.stats.f.cdf(F_calc, df1, df2, loc=0, scale=1)
print(a_calc)Как видим, результаты совпадают.
Табличное значение статистики критерия Фишера получить с помощью Regression Results нельзя. Рассчитаем его самостоятельно — для этого воспользуемся библиотекой scipy, модулем распределения Стьюдента scipy.stats.f, свойством ppf (процентные точки):
F_table = sci.stats.f.ppf(p_level, df1, df2, loc=0, scale=1)
print(F_table)Для удобства создадим пользовательскую функцию determination_coef_check для проверки значимости коэффициента детерминации, которая объединяет все вышеперечисленные расчеты:
# Пользовательская функция
def determination_coef_check(
model_fit,
p_level: float=0.95):
a_level = 1 - p_level
R2 = model_fit.rsquared
R2_adj = model_fit.rsquared_adj
n = model_fit.nobs # объем выборки
p = model_fit.df_model # Model degrees of freedom. The number of regressors p. Does not include the constant if one is present.
F_calc = R2 / (1 - R2) * (n-p-1)/p
df1 = int(p)
df2 = int(n-p-1)
F_table = sci.stats.f.ppf(p_level, df1, df2, loc=0, scale=1)
a_calc = 1 - sci.stats.f.cdf(F_calc, df1, df2, loc=0, scale=1)
conclusion_determ_coef_sign = 'significance' if F_calc >= F_table else 'not significance'
# формируем результат
result = pd.DataFrame({
'notation': ('R2'),
'coef_value (R)': (sqrt(R2)),
'coef_value_squared (R2)': (R2),
'p_level': (p_level),
'a_level': (a_level),
'F_calc': (F_calc),
'df1': (df1),
'df2': (df2),
'F_table': (F_table),
'F_calc >= F_table': (F_calc >= F_table),
'a_calc': (a_calc),
'a_calc <= a_level': (a_calc <= a_level),
'significance_check': (conclusion_determ_coef_sign),
'conf_int_low': (''),
'conf_int_high': ('')
},
index=['Coef. of determination'])
return result
determination_coef_check(
result_linear_ols,
p_level=0.95)Вывод: коэффициент детерминации ЗНАЧИМ.
6. Коэффициенты регрессии и проверка их значимости
Ранее мы уже извлекли коэффициенты регрессии как параметры модели b0 и b1 (как свойство params модели). Также можно получить их значения, как свойство bse модели:
print(b0, b1)
print(result_linear_ols.bse, type(result_linear_ols.bse))Значимость коэффициентов регрессии можно проверить по критерию Стьюдента [3, с.203-212; 8, с.78].
Расчетные значения статистики критерия Стьюдента могут быть получены с помощью свойства tvalues модели:
print(f"result_linear_ols.tvalues = n{result_linear_ols.tvalues}")Расчетные значения уровня значимости при проверке гипотезы по критерию Стьюдента могут быть получены с помощью свойства pvalues модели:
print(f"result_linear_ols.pvalues = n{result_linear_ols.pvalues}")Доверительные интервалы для коэффициентов регрессии могут быть получены с помощью свойства conf_int модели:
print(result_linear_ols.conf_int(), 'n')Можно рассчитать уровень значимости самостоятельно (как ранее для критерия Фишера — для лучшего понимания и общей демонстрации возможностей) — для этого воспользуемся библиотекой scipy, модулем распределения Стьюдента scipy.stats.t, свойством cdf (функция распределения):
t_calc = result_linear_ols.tvalues
df = int(result_linear_ols.nobs - result_linear_ols.df_model - 1)
a_calc = 2*(1-sci.stats.t.cdf(abs(t_calc), df, loc=0, scale=1))
print(a_calc)Как видим, результаты совпадают.
Табличные значения статистики критерия Стьюдента получить с помощью Regression Results нельзя. Рассчитаем их самостоятельно — для этого воспользуемся библиотекой scipy, модулем распределения Стьюдента scipy.stats.t, свойством ppf (процентные точки):
t_table = sci.stats.t.ppf((1 + p_level)/2 , df)
print(t_table)Для удобства создадим пользовательскую функцию regression_coef_check для проверки значимости коэффициентов регрессии, которая объединяет все вышеперечисленные расчеты:
def regression_coef_check(
model_fit,
notation_coef: list='',
p_level: float=0.95):
a_level = 1 - p_level
# параметры модели (коэффициенты регрессии)
model_params = model_fit.params
# стандартные ошибки коэффициентов регрессии
model_bse = model_fit.bse
# проверка гипотезы о значимости регрессии
t_calc = abs(model_params) / model_bse
n = model_fit.nobs # объем выборки
p = model_fit.df_model # Model degrees of freedom. The number of regressors p. Does not include the constant if one is present.
df = int(n - p - 1)
t_table = sci.stats.t.ppf((1 + p_level)/2 , df)
a_calc = 2*(1-sci.stats.t.cdf(t_calc, df, loc=0, scale=1))
conclusion_ = ['significance' if elem else 'not significance' for elem in (t_calc >= t_table).values]
# доверительный интервал коэффициента регрессии
conf_int_low = model_params - t_table*model_bse
conf_int_high = model_params + t_table*model_bse
# формируем результат
result = pd.DataFrame({
'notation': (notation_coef),
'coef_value': (model_params),
'std_err': (model_bse),
'p_level': (p_level),
'a_level': (a_level),
't_calc': (t_calc),
'df': (df),
't_table': (t_table),
't_calc >= t_table': (t_calc >= t_table),
'a_calc': (a_calc),
'a_calc <= a_level': (a_calc <= a_level),
'significance_check': (conclusion_),
'conf_int_low': (conf_int_low),
'conf_int_high': (conf_int_high),
})
return result
regression_coef_check(
result_linear_ols,
notation_coef=['b0', 'b1'],
p_level=0.95)Вывод: коэффициенты регрессии b0 и b1 ЗНАЧИМЫ.
7. Проверка гетероскедастичности
Для проверка гетероскедастичности statsmodels предлагает нам следующие инструменты:
-
тест Голдфелда-Квандта (https://www.statsmodels.org/stable/generated/statsmodels.stats.diagnostic.het_goldfeldquandt.html#statsmodels.stats.diagnostic.het_goldfeldquandt) — теорию см. [8, с.178], также https://ru.wikipedia.org/wiki/Тест_Голдфелда_—_Куандта.
-
тест Бриша-Пэгана (Breush-Pagan test) (https://www.statsmodels.org/stable/generated/statsmodels.stats.diagnostic.het_breuschpagan.html#statsmodels.stats.diagnostic.het_breuschpagan) — теорию см.[8, с.179], также https://en.wikipedia.org/wiki/Breusch–Pagan_test.
-
тест Уайта (White test) (https://www.statsmodels.org/stable/generated/statsmodels.stats.diagnostic.het_white.html#statsmodels.stats.diagnostic.het_white) — теорию см.[8, с.177], а также https://ru.wikipedia.org/wiki/Тест_Уайта.
Тест Голдфелда-Квандта (Goldfeld–Quandt test)
# тест Голдфелда-Квандта (Goldfeld–Quandt test)
test = sms.het_goldfeldquandt(result_linear_ols.resid, result_linear_ols.model.exog)
test_result = lzip(['F_calc', 'p_calc'], test) # распаковка результатов теста
# расчетное значение статистики F-критерия
F_calc_tuple = test_result[0]
F_calc = F_calc_tuple[1]
print(f"Расчетное значение статистики F-критерия: F_calc = {round(F_calc, DecPlace)}")
# расчетный уровень значимости
p_calc_tuple = test_result[1]
p_calc = p_calc_tuple[1]
print(f"Расчетное значение доверительной вероятности: p_calc = {round(p_calc, DecPlace)}")
#a_calc = 1 - p_value
#print(f"Расчетное значение уровня значимости: a_calc = 1 - p_value = {round(a_calc, DecPlace)}")
# вывод
if p_calc < a_level:
conclusion_GQ_test = f"Так как p_calc = {round(p_calc, DecPlace)} < a_level = {round(a_level, DecPlace)}" +
", то дисперсии в подвыборках отличаются значимо, т.е. гипотеза о наличии гетероскедастичности ПРИНИМАЕТСЯ"
else:
conclusion_GQ_test = f"Так как p_calc = {round(p_calc, DecPlace)} >= a_level = {round(a_level, DecPlace)}" +
", то дисперсии в подвыборках отличаются незначимо, т.е. гипотеза о наличии гетероскедастичности ОТВЕРГАЕТСЯ"
print(conclusion_GQ_test)Для удобства создадим пользовательскую функцию Goldfeld_Quandt_test:
def Goldfeld_Quandt_test(
model_fit,
p_level: float=0.95,
model_name=''):
a_level = 1 - p_level
# реализация теста
test = sms.het_goldfeldquandt(model_fit.resid, model_fit.model.exog)
test_result = lzip(['F_statistic', 'p_calc'], test) # распаковка результатов теста
# расчетное значение статистики F-критерия
F_calc_tuple = test_result[0]
F_statistic = F_calc_tuple[1]
# расчетный уровень значимости
p_calc_tuple = test_result[1]
p_calc = p_calc_tuple[1]
# вывод
conclusion_test = 'heteroscedasticity' if p_calc < a_level else 'not heteroscedasticity'
result = pd.DataFrame({
'test': ('Goldfeld–Quandt test'),
'p_level': (p_level),
'a_level': (a_level),
'F_statistic': (F_statistic),
'p_calc': (p_calc),
'p_calc < a_level': (p_calc < a_level),
'heteroscedasticity_check': (conclusion_test)
},
index=[model_name])
return result
Goldfeld_Quandt_test(result_linear_ols, p_level=0.95, model_name='linear_ols')Тест Бриша-Пэгана (Breush-Pagan test)
# тест Бриша-Пэгана (Breush-Pagan test)
name = ["Lagrange multiplier statistic", "p-value", "f-value", "f p-value"]
test = sms.het_breuschpagan(result_linear_ols.resid, result_linear_ols.model.exog)
lzip(name, test)Для удобства создадим пользовательскую функцию Breush_Pagan_test:
def Breush_Pagan_test(
model_fit,
p_level: float=0.95,
model_name=''):
a_level = 1 - p_level
# реализация теста
test = sms.het_breuschpagan(model_fit.resid, model_fit.model.exog)
name = ['Lagrange_multiplier_statistic', 'p_calc_LM', 'F_statistic', 'p_calc']
test_result = lzip(name, test) # распаковка результатов теста
# расчетное значение статистики теста множителей Лагранжа
LM_calc_tuple = test_result[0]
Lagrange_multiplier_statistic = LM_calc_tuple[1]
# расчетный уровень значимости статистики теста множителей Лагранжа
p_calc_LM_tuple = test_result[1]
p_calc_LM = p_calc_LM_tuple[1]
# расчетное значение F-статистики гипотезы о том, что дисперсия ошибки не зависит от x
F_calc_tuple = test_result[2]
F_statistic = F_calc_tuple[1]
# расчетный уровень значимости F-статистики
p_calc_tuple = test_result[3]
p_calc = p_calc_tuple[1]
# вывод
conclusion_test = 'heteroscedasticity' if p_calc < a_level else 'not heteroscedasticity'
# вывод
conclusion_test = 'heteroscedasticity' if p_calc < a_level else 'not heteroscedasticity'
result = pd.DataFrame({
'test': ('Breush-Pagan test'),
'p_level': (p_level),
'a_level': (a_level),
'Lagrange_multiplier_statistic': (Lagrange_multiplier_statistic),
'p_calc_LM': (p_calc_LM),
'p_calc_LM < a_level': (p_calc_LM < a_level),
'F_statistic': (F_statistic),
'p_calc': (p_calc),
'p_calc < a_level': (p_calc < a_level),
'heteroscedasticity_check': (conclusion_test)
},
index=[model_name])
return result
Breush_Pagan_test(result_linear_ols, p_level=0.95, model_name='linear_ols')Тест Уайта (White test)
# тест Уайта (White test)
name = ["Lagrange multiplier statistic", "p-value", "f-value", "f p-value"]
test = sms.het_white(result_linear_ols.resid, result_linear_ols.model.exog)
lzip(name, test)Для удобства создадим пользовательскую функцию White_test:
def White_test(
model_fit,
p_level: float=0.95,
model_name=''):
a_level = 1 - p_level
# реализация теста
test = sms.het_white(model_fit.resid, model_fit.model.exog)
name = ['Lagrange_multiplier_statistic', 'p_calc_LM', 'F_statistic', 'p_calc']
test_result = lzip(name, test) # распаковка результатов теста
# расчетное значение статистики теста множителей Лагранжа
LM_calc_tuple = test_result[0]
Lagrange_multiplier_statistic = LM_calc_tuple[1]
# расчетный уровень значимости статистики теста множителей Лагранжа
p_calc_LM_tuple = test_result[1]
p_calc_LM = p_calc_LM_tuple[1]
# расчетное значение F-статистики гипотезы о том, что дисперсия ошибки не зависит от x
F_calc_tuple = test_result[2]
F_statistic = F_calc_tuple[1]
# расчетный уровень значимости F-статистики
p_calc_tuple = test_result[3]
p_calc = p_calc_tuple[1]
# вывод
conclusion_test = 'heteroscedasticity' if p_calc < a_level else 'not heteroscedasticity'
# вывод
conclusion_test = 'heteroscedasticity' if p_calc < a_level else 'not heteroscedasticity'
result = pd.DataFrame({
'test': ('White test'),
'p_level': (p_level),
'a_level': (a_level),
'Lagrange_multiplier_statistic': (Lagrange_multiplier_statistic),
'p_calc_LM': (p_calc_LM),
'p_calc_LM < a_level': (p_calc_LM < a_level),
'F_statistic': (F_statistic),
'p_calc': (p_calc),
'p_calc < a_level': (p_calc < a_level),
'heteroscedasticity_check': (conclusion_test)
},
index=[model_name])
return result
White_test(result_linear_ols, p_level=0.95, model_name='linear_ols')Объединим результаты всех тестов гетероскедастичность в один DataFrame:
Goldfeld_Quandt_test_df = Goldfeld_Quandt_test(result_linear_ols, p_level=0.95, model_name='linear_ols')
Breush_Pagan_test_df = Breush_Pagan_test(result_linear_ols, p_level=0.95, model_name='linear_ols')
White_test_df = White_test(result_linear_ols, p_level=0.95, model_name='linear_ols')
heteroscedasticity_tests_df = pd.concat([Breush_Pagan_test_df, White_test_df, Goldfeld_Quandt_test_df])
display(heteroscedasticity_tests_df)Выводы
Итак, мы провели статистический анализ регрессионной модели и установили:
-
исходные данные имеют нормальное распределение;
-
между переменными имеется весьма сильная корреляционная связь;
-
регрессионная модель хорошо аппроксимирует фактические данные;
-
остатки модели имеют нормальное распределение;
-
регрессионная модель адекватна по критерию Фишера;
-
коэффициент детерминации значим по критеию Фишера;
-
коэффициенты регрессии значимы по критерию Стьюдента;
-
гетероскедастичность отсутствует.
Применительно к рассматриваемой задаче выполнять проверку автокорреляции не имеет особого смысла из-за особенностей исходных данных (результаты замеров прочности бетона на разных участках здания).
Про статистический анализ регрессионных моделей с помощью statsmodels— см. еще https://www.statsmodels.org/stable/examples/notebooks/generated/regression_diagnostics.html.
Доверительные интервалы регрессионной модели
Для регрессионных моделей определяют доверительные интервалы двух видов [3, с.184-192; 4, с.172; 8, с.205-209]:
-
Доверительный интервал средних значений переменной Y.
-
Доверительный интервал индивидуальных значений переменной Y.
При этом размер доверительного интервала для индивидуальных значений больше, чем для средних значений.
Доверительные интервалы регрессионных моделей (ДИРМ) могут быть найдены разными способами:
-
непосредственно путем расчетов по формулам (см., например, https://habr.com/ru/post/558158/);
-
с использованием инструментария библиотеки statsmodels (см., например, https://www.stackfinder.ru/questions/17559408/confidence-and-prediction-intervals-with-statsmodels).
Разбререм более подробно способ с использованием библиотеки statsmodels. Прежде всего, с помощью свойства summary_table класса statsmodels.stats.outliers_influence.OLSInfluence (https://www.statsmodels.org/stable/generated/statsmodels.stats.outliers_influence.OLSInfluence.html?highlight=olsinfluence) мы можем получить таблицу данных, содержащую необходимую нам информацию:
-
Dep Var Population — фактические значения переменной Y;
-
Predicted Value — предсказанные значения переменной Y по по регрессионной модели;
-
Std Error Mean Predict — среднеквадратическая ошибка предсказанного среднего;
-
Mean ci 95% low и Mean ci 95% upp — границы доверительного интервала средних значений переменной Y;
-
Predict ci 95% low и Predict ci 95% upp — границы доверительного интервала индивидуальных значений переменной Y;
-
Residual — остатки регрессионной модели;
-
Std Error Residual — среднеквадратическая ошибка остатков;
-
Student Residual — стьюдентизированные остатки (подробнее см. http://statistica.ru/glossary/general/studentizirovannie-ostatki/);
-
Cook’s D — Расстояние Кука (Cook’s distance) — оценивает эффект от удаления одного (рассматриваемого) наблюдения; наблюдение считается выбросом, если Di > 4/n (более подробно — см.https://translated.turbopages.org/proxy_u/en-ru.ru.f584ceb5-63296427-aded8f31-74722d776562/https/en.wikipedia.org/wiki/Cook’s_distance, http://www.machinelearning.ru/wiki/index.php?title=Расстояние_Кука).
from statsmodels.stats.outliers_influence import summary_table
st, data, ss2 = summary_table(result_linear_ols, alpha=0.05)
print(st, 'n', type(st))В нашем случае критическое значение расстояния Кука равно:
print(f'D_crit = 4/n = {4/result_linear_ols.nobs}')то есть выбросов, смещающих оценки коэффициентов регрессии, не наблюдается.
Мы получили данные как класс statsmodels.iolib.table.SimpleTable. Свойство data преобразует данные в список. Далее для удобства работы преобразуем данные в DataFrame:
st_data_df = pd.DataFrame(st.data)Будем использовать данный DataFrame в дальнейшем, несколько преобразуем его:
-
изменим наименование столбцов (с цифр на названия показателей из таблицы summary_table)
-
удалим строки с текстовыми значениями
-
изменим индекс
-
добавим новый столбец — значения переменной X
-
отсортируем по возрастанию значений переменной X (это необходимо, чтобы графики границ доверительных интервалов выглядели как линии)
st_df = st_data_df.copy()
# изменим наименования столбцов
str = st_df.iloc[0,0:] + ' ' + st_df.iloc[1,0:]
st_df = st_df.rename(str, axis='columns')
# удалим строки 0, 1
st_df = st_df.drop([0,1])
# изменим индекс
st_df = st_df.set_index(np.arange(0, result_linear_ols.nobs))
# добавим новый столбец - значения переменной X
st_df.insert(1, 'X', X)
# отсортируем по возрастанию значений переменной X
st_df = st_df.sort_values(by='X')
display(st_df)С помощью полученных данных мы можем построить график регрессионной модели с доверительными интервалами:
# создание рисунка (Figure) и области рисования (Axes)
fig, axes = plt.subplots(figsize=(297/INCH, 210/INCH))
# заголовок рисунка (Figure)
title_figure = Task_Project
fig.suptitle(title_figure, fontsize = 16)
# заголовок области рисования (Axes)
title_axes = 'Линейная регрессионная модель'
axes.set_title(title_axes, fontsize = 14)
# фактические данные
sns.scatterplot(
x=st_df['X'], y=st_df['Dep Var Population'],
label='фактические данные',
s=50,
color='red',
ax=axes)
# график регрессионной модели
label_legend_regr_model=f'линейная регрессия Y = {b0:.3f} + {b1:.4f}*X'
sns.lineplot(
x=st_df['X'], y=st_df['Predicted Value'],
label=label_legend_regr_model,
color='blue',
ax=axes)
# доверительный интервал средних значений переменной Y
Mean_ci_low = st_df['Mean ci 95% low']
plt.plot(
st_df['X'], Mean_ci_low,
color='magenta', linestyle='--', linewidth=1,
label='доверительный интервал средних значений Y')
Mean_ci_upp = st_df['Mean ci 95% upp']
plt.plot(
st_df['X'], Mean_ci_upp,
color='magenta', linestyle='--', linewidth=1)
# доверительный интервал индивидуальных значений переменной Y
Predict_ci_low = st_df['Predict ci 95% low']
plt.plot(
st_df['X'], Predict_ci_low,
color='orange', linestyle='-.', linewidth=2,
label='доверительный интервал индивидуальных значений Y')
Predict_ci_upp = st_df['Predict ci 95% upp']
plt.plot(
st_df['X'], Predict_ci_upp,
color='orange', linestyle='-.', linewidth=2)
axes.set_xlabel(Variable_Name_X)
axes.set_ylabel(Variable_Name_Y)
axes.legend(prop={'size': 12})
plt.show()Однако, мы получили данные о границах доверительных интервалов регрессионной модели только в пределах области фактических значений переменной X. Как быть, если мы хотим распространить прогноз за пределы этой области?
Прогнозирование
Под прогнозированием мы в данном случае будем понимать определение значений переменной Y и доверительных интервалов для ее средних и индивидуальных значений при заданном X. По сути, нам предстоит построить аналог рассмотренной выше таблицы summary_table, только с другими значениями X, причем эти значения могут выходить за пределы тех значений, которые использовались нами для построения регрессии.
Методика расчета доверительных интервалов регрессионных моделей разобрана в статье «Python, корреляция и регрессия: часть 4» (https://habr.com/ru/post/558158/), всем рекомендую ознакомиться.
Найти прогнозные значения Y не представляет труда, так как ранее мы уже формализовали модель в виде лямбда-функции, а вот для построения доверительных интервалов придется выполнить расчеты по формулам. Для этого создадим пользовательскую функцию regression_pair_predict, которая в случае парной регрессии (pair regression) для заданного значения X возвращает:
-
прогнозируемое по регрессионной модели значение y_calc
-
доверительный интервал [y_calc_mean_ci_low, y_calc_mean_ci_upp] средних значений переменной Y
-
доверительный интервал [y_calc_predict_ci_low, y_calc_predict_ci_upp] индивидуальных значений переменной Y
Алгоритм расчета доверительных интервалов для множественной регрессии (multiple regression) отличается и в данном обзоре не рассматривается (рассмотрим в дальнейшем).
Про прогнозирование с помощью регрессионных моделей — см.также:
-
https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.RegressionResults.predict.html?highlight=predict#statsmodels.regression.linear_model.RegressionResults.predict
-
How to Make Predictions Using Regression Model in Statsmodels
-
https://www.statsmodels.org/stable/examples/notebooks/generated/predict.html
def regression_pair_predict(
x_in,
model_fit,
regression_model,
p_level: float=0.95):
a_level = 1 - p_level
X = pd.DataFrame(model_fit.model.exog)[1].values # найти лучшее решение
Y = model_fit.model.endog
# вспомогательные величины
n = int(result_linear_ols.nobs)
SSE = model_fit.ssr # SSE (Sum of Squared Error)
dfE = n - p - 1
MSE = SSE / dfE # остаточная дисперсия
Xmean = np.mean(X)
SST_X = np.sum([(X[i] - Xmean)**2 for i in range(0, n)])
t_table = sci.stats.t.ppf((1 + p_level)/2 , dfE)
S2_y_calc_mean = MSE * (1/n + (x_in - Xmean)**2 / SST_X)
S2_y_calc_predict = MSE * (1 + 1/n + (x_in - Xmean)**2 / SST_X)
# прогнозируемое значение переменной Y
y_calc=regression_model(x_in)
# доверительный интервал средних значений переменной Y
y_calc_mean_ci_low = y_calc - t_table*sqrt(S2_y_calc_mean)
y_calc_mean_ci_upp = y_calc + t_table*sqrt(S2_y_calc_mean)
# доверительный интервал индивидуальных значений переменной Y
y_calc_predict_ci_low = y_calc - t_table*sqrt(S2_y_calc_predict)
y_calc_predict_ci_upp = y_calc + t_table*sqrt(S2_y_calc_predict)
result = y_calc, y_calc_mean_ci_low, y_calc_mean_ci_upp, y_calc_predict_ci_low, y_calc_predict_ci_upp
return resultСравним результаты расчета доверительных интервалов разными способами — с использованием функции regression_pair_predict и средствами statsmodels, для этого сформируем DaraFrame с новыми данными:
regression_pair_predict_df = pd.DataFrame(
[regression_pair_predict(elem, result_linear_ols, regression_model=Y_calc) for elem in st_df['X'].values],
columns=['y_calc', 'y_calc_mean_ci_low', 'y_calc_mean_ci_upp', 'y_calc_predict_ci_low', 'y_calc_predict_ci_upp'])
regression_pair_predict_df.insert(0, 'X', st_df['X'].values)
display(regression_pair_predict_df)Видим, что результаты расчетов идентичны, следовательно мы можем использовать функцию regression_pair_predict для прогнозирования.
def graph_regression_pair_predict_plot_sns(
model_fit,
regression_model_in,
Xmin=None, Xmax=None, Nx=10,
Ymin_graph=None, Ymax_graph=None,
title_figure=None, title_figure_fontsize=18,
title_axes=None, title_axes_fontsize=16,
x_label=None,
y_label=None,
label_fontsize=14, tick_fontsize=12,
label_legend_regr_model='', label_legend_fontsize=12,
s=50, linewidth_regr_model=2,
graph_size=(297/INCH, 210/INCH),
result_output=True,
file_name=None):
# фактические данные
X = pd.DataFrame(model_fit.model.exog)[1].values # найти лучшее решение
Y = model_fit.model.endog
X = np.array(X)
Y = np.array(Y)
# границы
if not(Xmin) and not(Xmax):
Xmin=min(X)
Xmax=max(X)
Xmin_graph=min(X)*0.99
Xmax_graph=max(X)*1.01
else:
Xmin_graph=Xmin
Xmax_graph=Xmax
if not(Ymin_graph) and not(Ymax_graph):
Ymin_graph=min(Y)*0.99
Ymax_graph=max(Y)*1.01
# формируем DataFrame данных
Xcalc = np.linspace(Xmin, Xmax, num=Nx)
Ycalc = regression_model_in(Xcalc)
result_df = pd.DataFrame(
[regression_pair_predict(elem, model_fit, regression_model=regression_model_in) for elem in Xcalc],
columns=['y_calc', 'y_calc_mean_ci_low', 'y_calc_mean_ci_upp', 'y_calc_predict_ci_low', 'y_calc_predict_ci_upp'])
result_df.insert(0, 'x_calc', Xcalc)
# заголовки графика
fig, axes = plt.subplots(figsize=graph_size)
fig.suptitle(title_figure, fontsize = title_figure_fontsize)
axes.set_title(title_axes, fontsize = title_axes_fontsize)
# фактические данные
sns.scatterplot(
x=X, y=Y,
label='фактические данные',
s=s,
color='red',
ax=axes)
# график регрессионной модели
sns.lineplot(
x=Xcalc, y=Ycalc,
color='blue',
linewidth=linewidth_regr_model,
legend=True,
label=label_legend_regr_model,
ax=axes)
# доверительный интервал средних значений переменной Y
Mean_ci_low = result_df['y_calc_mean_ci_low']
plt.plot(
result_df['x_calc'], Mean_ci_low,
color='magenta', linestyle='--', linewidth=1,
label='доверительный интервал средних значений Y')
Mean_ci_upp = result_df['y_calc_mean_ci_upp']
plt.plot(
result_df['x_calc'], Mean_ci_upp,
color='magenta', linestyle='--', linewidth=1)
# доверительный интервал индивидуальных значений переменной Y
Predict_ci_low = result_df['y_calc_predict_ci_low']
plt.plot(
result_df['x_calc'], Predict_ci_low,
color='orange', linestyle='-.', linewidth=2,
label='доверительный интервал индивидуальных значений Y')
Predict_ci_upp = result_df['y_calc_predict_ci_upp']
plt.plot(
result_df['x_calc'], Predict_ci_upp,
color='orange', linestyle='-.', linewidth=2)
axes.set_xlim(Xmin_graph, Xmax_graph)
axes.set_ylim(Ymin_graph, Ymax_graph)
axes.set_xlabel(x_label, fontsize = label_fontsize)
axes.set_ylabel(y_label, fontsize = label_fontsize)
axes.tick_params(labelsize = tick_fontsize)
#axes.tick_params(labelsize = tick_fontsize)
axes.legend(prop={'size': label_legend_fontsize})
plt.show()
if file_name:
fig.savefig(file_name, orientation = "portrait", dpi = 300)
if result_output:
return result_df
else:
return
graph_regression_pair_predict_plot_sns(
model_fit=result_linear_ols,
regression_model_in=Y_calc,
Xmin=Xmin_graph-300, Xmax=Xmax_graph+200, Nx=25,
Ymin_graph=Ymin_graph-5, Ymax_graph=Ymax_graph+5,
title_figure=Task_Project, title_figure_fontsize=16,
title_axes='Линейная регрессионная модель', title_axes_fontsize=14,
x_label=Variable_Name_X,
y_label=Variable_Name_Y,
label_legend_regr_model=f'линейная регрессия Y = {b0:.3f} + {b1:.4f}*X',
s=50,
result_output=True,
file_name='graph/regression_plot_lin.png')Выводы и рекомендации
Исследована зависимость показаний ультразвукового прибора «ПУЛЬСАР-2.1» (X) и результатов замера прочности бетона (методом отрыва со скалыванием) склерометром ИПС-МГ4.03 (Y).
Между переменными имеется весьма сильная линейная корреляционная связь. Получена регрессионная модель:
Y = b0 + b1∙X = -21.3741 + 0.0129∙X
Модель хорошо аппроксимирует фактические данные, является адекватной, значимой и может использоваться для предсказания прочности бетона.
Также построен график прогноза с доверительными интервалами.
ИТОГИ
Итак, мы рассмотрели все этапы регрессионного анализа в случае простой линейной регрессии (simple linear regression) с использованием библиотеки statsmodels на конкретном практическом примере; подробно остановились на статистическом анализа модели с проверкой гипотез; также предложен ряд пользовательских функций, облегчающих работу исследователя и уменьшающих размер программного кода.
Конечно, мы разобрали далеко не все вопросы анализа регрессионных моделей и возможности библиотеки statsmodels применительно к simple linear regression, в частности статистики влияния (Influence Statistics), инструмент Leverage, анализ стьюдентизированных остатков и пр. — это темы для отдельных обзоров.
Исходный код находится в моем репозитории на GitHub.
Надеюсь, данный обзор поможет специалистам DataScience в работе.
На
основании уравнения (3.20) можно показать,
что b
будет несмещенной оценкой
,
если выполняется 4-е условие Гаусса —
Маркова:
(3.21)
так
как
— константа. Если мы примем сильную форму
4-го условия Гаусса — Маркова и предположим,
что х — неслучайная величина, мы можем
также считать Var(x)
известной константой и, таким образом,
(3.22)
Далее,
если х — неслучайная величина, то
M{Cov(x,u)}
= 0 и, следовательно, M{b}
=
Таким
образом,
— несмещенная оценка
Можно получить тот же результат со
слабой формой 4-го условия Гаусса —
Маркова (которая допускает, что переменная
х имеет случайную ошибку, но предполагает,
что она распределена независимо от u
).
За
исключением того случая, когда случайные
факторы в n
наблюдениях в точности «гасят»
друг друга, что может произойти лишь
при случайном совпадении, b
будет отличаться от
в каждом конкретном эксперименте. Не
будет систематической ошибки, завышающей
или занижающей оценку. То же самое
справедливо и для коэффициента а.
Используем
уравнение (2.15):
(3.23)
Следовательно,
(3.24)
Поскольку
у определяется уравнением (3.1),
(3.25)
так
как M{u}=0,
если выполнено 1-е условие Гаусса —
Маркова. Следовательно
(3.26)
Подставив
это выражение в (3.24) и воспользовавшись
тем, что
получим:
(3.27)
Таким
образом, а
— это несмещенная оценка а при условии
выполнения 1-го и 4-го условий Гаусса —
Маркова. Безусловно, для любой конкретной
выборки фактор случайности приведет к
расхождению оценки и истинного значения.
Рассмотрим
теперь теоретические дисперсии оценок
а и Ь. Они задаются следующими выражениями
(доказательства для эквивалентных
выражений можно найти в работе Дж. Томаса
[Thomas,
1983, section
833]):
(3.28)
Из
уравнения 3.28 можно сделать три очевидных
заключения. Во-первых, дисперсии а
и b
прямо пропорциональны дисперсии
остаточного члена
.
Чем
больше фактор случайности, тем хуже
будут оценки при прочих равных условиях.
Это уже было проиллюстрировано в
экспериментах по методу Монте-Карло.
Оценки в серии II
были гораздо более неточными, чем в
серии I,
и это произошло потому, что в каждой
выборке мы удвоили случайный член.
Удвоив u,
мы удвоили его стандартное отклонение
и, следовательно, удвоили стандартные
отклонения a
и b.
Во вторых, чем больше число наблюдений,
тем меньше дисперсионных оценок. Это
также имеет определенный смысл. Чем
большей информацией вы располагаете,
тем более точными, вероятно, будут ваши
оценки. В третьих, чем больше дисперсия
,
тем меньше будет дисперсия коэффициентов
регрессии. В чем причина этого? Напомним,
что (I)
коэффициенты регрессии вычисляются на
основании предположения, что наблюдаемые
изменения
происходят вследствие изменений
,
но (2) в действительности они лишь отчасти
вызваны изменениями
,
а отчасти вариациями u.
Чем меньше дисперсия
,
тем больше, вероятно, будет относительное
влияние фактора случайности при
определении отклонений
и тем более вероятно, что регрессионный
анализ может оказаться неверным. В
действительности, как видно из уравнения
(3.28), важное значение имеет не абсолютная,
а относительная величина
и Var(x).
На
практике мы не можем вычислить
теоретические дисперсии
или
,
так как
неизвестно, однако мы можем получить
оценку
на основе остатков. Очевидно, что разброс
остатков относительно линии регрессии
будет отражать неизвестный разброс u
относительно линии
,
хотя в общем остаток и случайный член
в любом данном наблюдении не равны друг
другу. Следовательно, выборочная
дисперсия остатков Var(е),
которую мы можем измерить, сможет быть
использована для оценки
,
которую мы получить не можем.
Прежде
чем пойти дальше, задайте себе следующий
вопрос: какая прямая будет ближе к
точкам, представляющим собой выборку
наблюдений по
и
,
истинная прямая
или линия регрессии
?
Ответ будет таков: линия регрессии,
потому что по определению она строится
таким образом, чтобы свести к минимуму
сумму квадратов расстояний между ней
и значениями наблюдений. Следовательно,
разброс остатков у нее меньше, чем
разброс значений u,
и Var(e)
имеет тенденцию занижать оценку
.
Действительно, можно показать, что
математическое ожидание Var(e),
если имеется всего одна независимая
переменная, равно
.
Однако отсюда следует, что если определить
как
,
(3.29)
То
будет представлять собой несмещенную
оценку
.
Таким
образом, несмещенной оценкой параметра
регрессии
является оценка
.
(3.30)
Теперь
вспомним следующие определения:
стандартное
отклонение случайной величины
– корень квадратный из теоретической
дисперсии случайной величины; среднее
ожидаемое расстояние между наблюдениями
этой случайной величины и ее математическим
ожиданием,
стандартная
ошибка случайной величины
– оценка стандартного отклонения
случайной величины, полученная по данным
выборки.
Используя
уравнения (3.28) и (3.29), можно получить
оценки теоретических дисперсий для a
и b
и после извлечения квадратного корня
– оценки их стандартных отклонений.
Вместо слишком громоздкого термина
«оценка стандартного отклонения функции
плотности вероятости» коэффицинта
регрессии будем использовать термин
«стандартная ошибка» коэффициента
регрессии, которую в дальнейшем мы будем
обозначать в виде сокрашения «с.о.».
Таким образом, для парного регрессионного
анализа мы имеем:
и
(3.31)
Если
воспользоваться компьютерной программой
оценивания регрессии, то стандартные
ошибки будут подсчитаны автоматически
одновременно с оценками a
и b.
Подводя
итог сказанному о точности коэффициентов
регрессии, акценктируем внимание на
следующих выводах.
1.
Оценка a
для параметра
имеет нормальное распределение с
математическим ожиданием a
и стандартным отклонением
,
оценка b
для параметра
имеет
нормальное распределение с математическим
ожиданием b
и стандартным отклонением
.
2.
Для улучшения точности оценок по МНК
можно увеличивать количество наблюдений
в выборке n,
увеличивать диапазон наблюдений Var(x)
или уменьшать
,
(например, увеличивать точность
измерений).
3.
Стандартная ошибка оценки a
считается по формуле
а
стандартная ошибка оценки b
считается по формуле
.
В компьютерных программах именно эти
числа приводятся в круглых скобках под
значениями оценок.
Полученные
соотношения проиллюстрируем экспериментами
по методу Монте-Карло, описанными ранее.
В серии I
u
определялось на основе случайных чисел,
взятых из генеральной совокупности с
нулевым средним и единичной дисперсией
а x
представлял собой набор чисел от 1 до
20. Можно легко вычислить Var(x),
которая равна 33,25.
Следовательно,
(3.32)
.
(3.33)
Таким
образом, истинное стандартное отклонение
для b
равно
.
Какие же результаты получены вместо
этого компьютером в 10 экспериментах
серии I?
Он должен был вычислить стандартную
ошибку, используя уравнение (3.31).
Результаты этих расчетов для 10
экспериментов представлены в табл. 3.5.
Таблица 3.5
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
22.03.2016179.71 Кб71а1.doc
- #
- #
- #
- #
- #
- #
- #
Ниворожкина Л.И. Основы статистики с элементами теории вероятностей для экономистов: Руководство для решения задач — файл n1.doc
приобрести
Ниворожкина Л.И. Основы статистики с элементами теории вероятностей для экономистов: Руководство для решения задач
скачать (17128 kb.)
Доступные файлы (1):
- Смотрите также:
- Рушайло М.Ф. Элементы теории вероятностей и математической статистики (Документ)
- Рушайло М.Ф. Элементы теории вероятностей и математической статистики (Документ)
- Кремер Н.Ш. Теория вероятностей и математическая статистика (Документ)
- Мордкович А.Г., Семенов П.В. События. Вероятности. Статистическая обработка данных: Дополнительные параграфы к курсу алгебры 7-9 кл. общеобразовательных учреждений (Документ)
- Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике (Документ)
- Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике (Документ)
- Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике (Документ)
- Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике (Документ)
- Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике (Документ)
- Кремер Н.Ш. Теория вероятностей и математическая статистика (Документ)
- Коваленко И.Н., Гнеденко Б.В. Теория вероятностей (Документ)
- Кафедра «Электроснабжение» В. Б. Козловская, В. В. Сталович математические задачи энергетики (Документ)
n1.doc
Хотя метод наименьших квадратов дает нам линию регрессии, которая обеспечивает минимум вариации, регрессионное уравнение не является идеальным в смысле предсказания, поскольку не все значения зависимого признака Y удовлетворяют уравнению регрессии. Нам необходима статистическая мера вариации фактических значений Y от предсказанных значений Y. Эта мера в то же время является средней вариацией каждого значения относительно среднего значения Y. Мера вариации относительно линии регрессии называется стандартной ошибкой оценки.
Колеблемость фактических значений признака Y относительно линии регрессии показана на рис. 9.3.
Из диаграммы видно, что хотя теоретическая линия регрессии проходит относительно близко от фактических значений Y, часть этих точек лежит выше или ниже линии регрессии. При этом
Стандартная ошибка оценки определяется как
где уi — фактические значения Y;
yx — предсказанные значения Y для заданного х.
Для вычисления более удобна следующая формула:
Нам уже известны
Тогда
Итак, для нашего примера: Syx = 0,497. Эта стандартная ошибка характеризует меру вариации фактических данных относительно линии регрессии. Интерпретация этой меры аналогична интерпретации среднего квадратического отклонения. Если среднее квадратическое отклонение — это мера вариации относительно средней, то стандартная ошибка — это оценка меры вариации относительно линии регрессии. Однако стандартная ошибка оценки может быть использована для выводов о значении yx и выяснения, является ли статистически значимой взаимосвязь между двумя переменными.
9.11. Измерение вариации по уравнению регрессии
Для проверки того, насколько хорошо независимая переменная предсказывает зависимую переменную в нашей модели, необходим расчет ряда мер вариации. Первая из них — общая (полная) сумма квадратов отклонений результативного признака от средней — есть мера вариации значений Y относительно их среднего Y . В регрессионном анализе общая сумма квадратов может быть разложена на объясняемую вариацию или сумму квадратов отклонений за счет регрессии и необъясняемую вариацию или остаточную сумму квадратов отклонений (рис. 9.4).
Сумма квадратов отклонений вследствие регрессии это — сумма квадратов разностей между y
(средним значением Y) и yx (значением Y, предсказанным по уравнению регрессии). Сумма квадратов отклонений, не объясняемая регрессией (остаточная сумма квадратов), — это сумма квадратов разностей y и yx . Эти меры вариации могут быть представлены следующим образом (табл. 9.8):
Таблица 9.8
| Общая сумма квадратов
(ST) |
= | Сумма квадратов за счет регрессии
(SR) |
+ | Остаточная сумма квадратов
(SE) |
Легко увидеть, что остаточная сумма квадратов (y-yx)2 — это выражение, стоящее под знаком корня в формуле (9.25) (стандартной ошибки оценки). Тем не менее в процессе вычислений стандартной ошибки мы всегда вначале вычисляем сумму квадратов ошибки.
Остаточная сумма квадратов может быть представлена следующим образом:
Объясняемая сумма квадратов выразится так:
В самом деле
51,3605 = 46,9145 + 4,4460.
Из этого соотношения определяется коэффициент детерминации:
Отсюда коэффициент детерминации — доля вариации Y, которая объясняется независимыми переменными в регрессионной модели. Для нашего примера rг= 46,9145/51,3605 = 0,913.
Следовательно, 91,3% вариации еженедельной выручки магазинов могут быть объяснены числом покупателей, варьирующим от магазина к магазину. Только 8,7% вариации можно объяснить иными факторами, не включенными в уравнение регрессии.
В случае парной регрессии коэффициент детерминации равен квадратному корню из квадрата коэффициента линейной корреляции Пирсона
В простой линейной регрессии г имеет тот же знак, что и b1, Если b1 > 0, то r > 0; если b1 < 0, то r < 0, если b1 = 0, то r = 0.
В нашем примере r2 = 0,913 и b1 > 0, коэффициент корреляции r = 0,956. Близость коэффициента корреляции к 1 свидетельствует о тесной положительной связи между выручкой магазина от продажи пива и числом посетителей.
Мы интерпретировали коэффициент корреляции в терминах регрессии, однако корреляция и регрессия — две различные техники. Корреляция устанавливает силу связи между признаками, а регрессия — форму этой связи. В ряде случаев для анализа достаточно найти меру связи между признаками, без использования одного из них в качестве факторного признака для другого.
9.12. Доверительные интервалы для оценки неизвестного генерального значения yген(yх) и индивидуального значения yi
Поскольку в основном для построения регрессионных моделей используются данные выборок, то зачастую интерпретация взаимоотношений между переменными в генеральной совокупности базируется на выборочных результатах.
Как было сказано выше, регрессионное уравнение используется для прогноза значений Y по заданному значению X. В нашем примере показано, что при 600 посетителях магазина сумма выручки могла бы быть 7,661 у. е. Однако это значение — только точечная оценка истинного среднего значения. Мы знаем, что для оценки истинного значения генерального параметра возможна интервальная оценка.
Доверительный интервал для оценки неизвестного генерального значения yген(yх) имеет вид
где
Здесь yx — предсказанное значение Y
(yx==b0+b1yi);
Syx — стандартная ошибка оценки;
п — объем выборки;
хi — заданное значение X.
Легко видеть, что длина доверительного интервала зависит от нескольких факторов. Для заданного уровня значимости увеличение вариации вокруг линии регрессии, измеряемой стандартной ошибкой оценки, увеличивает длину интервала. Увеличение объема выборки уменьшит длину интервала. Более того, ширина интервала также варьирует с различными значениями X. Когда оценивается yx по значениям X, близким к x, то интервал тем уже, чем меньше абсолютное отклонение хi от x (рис. 9.5).
Когда оценка осуществляется по значениям X, удаленным от среднего x, то длина интервала возрастает.
Рассчитаем 95%-й доверительный интервал для среднего значения выручки во всех магазинах с числом посетителей, равным 600. По данным нашего примера уравнение регрессии имеет вид
yx = 2,423 + 0,00873x:
и для xi = 600 получим yi; =7,661, а также
По таблице Стьюдента (приложение 5)
t18 = 2,10.
Отсюда, используя формулы (9.31) и (9.32), рассчитаем границы искомого доверительного интервала для yx
Итак, 7,369 yx 7,953.
Следовательно, наша оценка состоит в том, что средняя дневная выручка находится между 7,369 и 7,953 у. е. для всех магазинов с 600 посетителями.
Для построения доверительного интервала для индивидуальных значений Yx, лежащих на линии регрессии, используется доверительный интервал регрессии вида
где hi yi, , Syx ,п и хi — определяются, как и в формулах (9.31) и (9.32).
Определим 95% -и доверительный интервал для оценки дневных продаж отдельного магазина с 600 посетителями
В результате вычислений получим
Итак, 6,577 yi 8,745.
Следовательно, с 95%-й уверенностью можно утверждать, что ежедневная выручка отдельного магазина, который посетили 600 покупателей, находится в пределах от 6,577 до 8,745 у. е. Длина этого интервала больше чем длина интервала, полученного ранее для оценки среднего значения Y.
9.10. Стандартная ошибка оценки уравнения регрессии
Содержание:
Регрессионный анализ:
Регрессионным анализом называется раздел математической статистики, объединяющий практические методы исследования корреляционной зависимости между случайными величинами по результатам наблюдений над ними. Сюда включаются методы выбора модели изучаемой зависимости и оценки ее параметров, методы проверки статистических гипотез о зависимости.
Пусть между случайными величинами X и Y существует линейная корреляционная зависимость. Это означает, что математическое ожидание Y линейно зависит от значений случайной величины X. График этой зависимости (линия регрессии Y на X) имеет уравнение
Линейная модель пригодна в качестве первого приближения и в случае нелинейной корреляции, если рассматривать небольшие интервалы возможных значений случайных величин.
Пусть параметры линии регрессии 
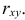
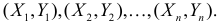
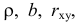
Неизвестная нам линия регрессии 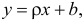

Такие значения 
Решения этой системы уравнений дают оценки называемые оценками по методу наименьших квадратов.
и
Известно, что оценки по методу наименьших квадратов являются несмещенными и, более того, среди всех несмещенных оценок обладают наименьшей дисперсией. Для оценки коэффициента корреляции можно воспользоваться тем, что 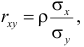
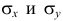
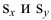
По методу наименьших квадратов можно находить оценки параметров линии регрессии и при нелинейной корреляции. Например, для линии регрессии вида 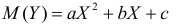
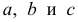
Пример:
По данным наблюдений двух случайных величин найти коэффициент корреляции и уравнение линии регрессии Y на X
Решение. Вычислим величины, необходимые для использования формул (3.7.1)–(3.7.3):
По формулам (3.7.1) и (3.7.2) получим
Итак, оценка линии регрессии имеет вид 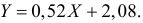
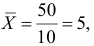
Аналогично, 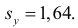
Ответ.
Пример:
Получена выборка значений величин X и Y
Для представления зависимости между величинами предполагается использовать модель 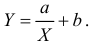
Решение. Рассмотрим сначала задачу оценки параметров этой модели в общем виде. Линия 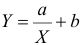
Необходимые условия экстремума приводят к системе из двух уравнений:
Откуда
Решения системы уравнений (3.7.4) и (3.7.5) и будут оценками по методу наименьших квадратов для параметров
На основе опытных данных вычисляем:
В итоге получаем систему уравнений (?????) и (?????) в виде
Эта система имеет решения
Ответ.
Если наблюдений много, то результаты их обычно группируют и представляют в виде корреляционной таблицы.
В этой таблице 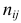
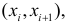
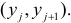
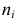
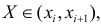
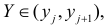
Если величины дискретны, то вместо интервалов указывают отдельные значения этих величин. Для непрерывных случайных величин представителем каждого интервала считают его середину и полагают, что 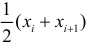
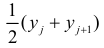
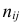
При больших значениях X и Y можно для упрощения вычислений перенести начало координат и изменить масштаб по каждой из осей, а после завершения вычислений вернуться к старому масштабу.
Пример:
Проделано 80 наблюдений случайных величин X и Y. Результаты наблюдений представлены в виде таблицы. Найти линию регрессии Y на X. Оценить коэффициент корреляции.
Решение. Представителем каждого интервала будем считать его середину. Перенесем начало координат и изменим масштаб по каждой оси так, чтобы значения X и Y были удобны для вычислений. Для этого перейдем к новым переменным 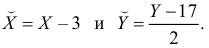
Чтобы иметь представление о виде линии регрессии, вычислим средние значения 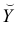
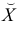
Нанесем эти значения на координатную плоскость, соединив для наглядности их отрезками прямой (рис. 3.7.1).
По виду полученной ломанной линии можно предположить, что линия регрессии Y на X является прямой. Оценим ее параметры. Для этого сначала вычислим с учетом группировки данных в таблице все величины, необходимые для использования формул (3.31–3.33):
Тогда
В новом масштабе оценка линии регрессии имеет вид 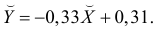
Для оценки 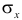
Подобным же образом можно оценить 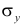
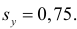
Вернемся к старому масштабу:
Коэффициент корреляции пересчитывать не нужно, так как это величина безразмерная и от масштаба не зависит.
Ответ.
Пусть некоторые физические величины X и Y связаны неизвестной нам функциональной зависимостью 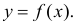
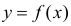
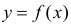
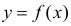
Регрессионный анализ
Основные положения регрессионного анализа:
Основная задача регрессионного анализа — изучение зависимости между результативным признаком Y и наблюдавшимся признаком X, оценка функции регрессий.
Предпосылки регрессионного анализа:
- Y — независимые случайные величины, имеющие постоянную дисперсию;
- X— величины наблюдаемого признака (величины не случайные);
- условное математическое ожидание
можно представить в виде
Выражение (2.1), как уже упоминалось в п. 1.2, называется функцией регрессии (или модельным уравнением регрессии) Y на X. Оценке в этом выражении подлежат параметры 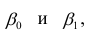
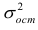
Остаточной дисперсией называется та часть рассеивания результативного признака, которую нельзя объяснить действием наблюдаемого признака; Остаточная дисперсия может служить для оценки точности подбора вида функции регрессии (модельного уравнения регрессии), полноты набора признаков, включенных в анализ. Оценки параметров функции регрессии находят, используя метод наименьших квадратов.
В данном вопросе рассмотрен линейный регрессионный анализ. Линейным он называется потому, что изучаем лишь те виды зависимостей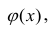
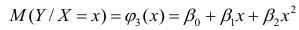
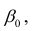
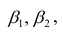
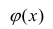
Важное место в линейном регрессионном анализе занимает так называемая «нормальная регрессия». Она имеет место, если сделать предположения относительно закона распределения случайной величины Y. Предпосылки «нормальной регрессии»:
- Y — независимые случайные величины, имеющие постоянную дисперсию и распределенные по нормальному закону;
- X— величины наблюдаемого признака (величины не случайные);
- условное математическое ожидание
можно представить в виде (2.1).
В этом случае оценки коэффициентов регрессии — несмещённые с минимальной дисперсией и нормальным законом распределения. Из этого положения следует что при «нормальной регрессии» имеется возможность оценить значимость оценок коэффициентов регрессии, а также построить доверительный интервал для коэффициентов регрессии и условного математического ожидания M(YX=x).
Линейная регрессия
Рассмотрим простейший случай регрессионного анализа — модель вида (2.1), когда зависимость 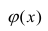
по переменным. Оценки параметров модели (2.1) 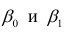
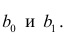
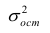
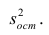
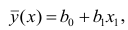
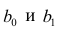
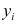
Составим систему нормальных уравнений: первое уравнение
откуда
второе уравнение
откуда
Итак,
Оценки, полученные по способу наименьших квадратов, обладают минимальной дисперсией в классе линейных оценок. Решая систему (2.2) относительно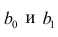
Остаётся получить оценку параметра 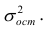
где т — количество наблюдений.
Еслит велико, то для упрощения расчётов наблюдавшиеся данные принята группировать, т.е. строить корреляционную таблицу. Пример построения такой таблицы приведен в п. 1.5. Формулы для нахождения коэффициентов регрессии по сгруппированным данным те же, что и для расчёта по несгруппированным данным, но суммы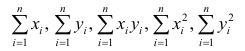
где 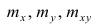
Нелинейная регрессия
Рассмотрим случай, когда зависимость нелинейна по переменным х, например модель вида
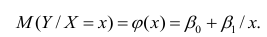
На рис. 2.1 изображено поле корреляции. Очевидно, что зависимость между Y и X нелинейная и её графическим изображением является не прямая, а кривая. Оценкой выражения (2.6) является уравнение регрессии
где 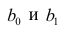
Принцип нахождения коэффициентов тот же — метод наименьших квадратов, т.е.
или
Дифференцируя последнее равенство по 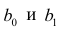
В общем случае нелинейной зависимости между переменными Y и X связь может выражаться многочленом k-й степени от x:
Коэффициенты регрессии определяют по принципу наименьших квадратов. Система нормальных уравнений имеет вид
Вычислив коэффициенты системы, её можно решить любым известным способом.
Оценка значимости коэффициентов регрессии. Интервальная оценка коэффициентов регрессии
Проверить значимость оценок коэффициентов регрессии — значит установить, достаточна ли величина оценки для статистически обоснованного вывода о том, что коэффициент регрессии отличен от нуля. Для этого проверяют гипотезу о равенстве нулю коэффициента регрессии, соблюдая предпосылки «нормальной регрессии». В этом случае вычисляемая для проверки нулевой гипотезы 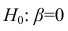
имеет распределение Стьюдента с к= n-2 степенями свободы (b — оценка коэффициента регрессии, 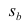
коэффициента регрессии, иначе стандартная ошибка оценки). По уровню значимости а и числу степеней свободы к находят по таблицам распределения Стьюдента (см. табл. 1 приложений) критическое значение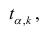
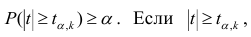
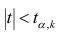
Оценки среднеквадратического отклонения коэффициентов регрессии вычисляют по следующим формулам:
где 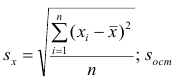
формуле (2.5).
Доверительный интервал для значимых параметров строят по обычной схеме. Из условия
где а — уровень значимости, находим
Интервальная оценка для условного математического ожидания
Линия регрессии характеризует изменение условного математического ожидания результативного признака от вариации остальных признаков.
Точечной оценкой условного математического ожидания 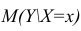
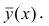
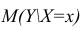
построить доверительный интервал в точке
Известно, что 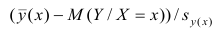
Стьюдента с k=n—2 степенями свободы. Найдя оценку среднеквадратического отклонения для условного среднего, можно построить доверительный интервал для условного математического ожидания
Оценку дисперсии условного среднего вычисляют по формуле
или для интервального ряда
Доверительный интервал находят из условия
где а — уровень значимости. Отсюда
Доверительный интервал для условного математического ожидания можно изобразить графически (рис, 2.2).
Из рис. 2.2 видно, что в точке 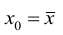
Проверка значимости уравнения регрессии
Оценить значимость уравнения регрессии — значит установить, соответствует ли математическая, модель, выражающая зависимость между Y и X, экспериментальным данным. Для оценки значимости в предпосылках «нормальной регрессии» проверяют гипотезу 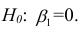
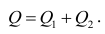
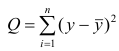
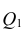
X) и 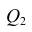
Для проверки нулевой гипотезы вычисляют статистику 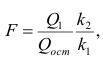
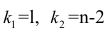
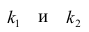
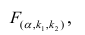
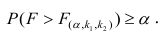
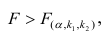
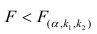
Многомерный регрессионный анализ
В случае, если изменения результативного признака определяются действием совокупности других признаков, имеет место многомерный регрессионный анализ. Пусть результативный признак У, а независимые признаки 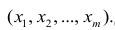
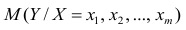
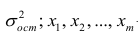
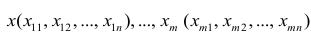
Оценке подлежат параметры 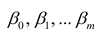
Заменив параметры их оценками, запишем уравнение регрессии
Коэффициенты в этом выражении находят методом наименьших квадратов.
Исходными данными для вычисления коэффициентов 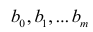

Как и в двумерном случае, составляют систему нормальных уравнений
которую можно решить любым способом, известным из линейной алгебры. Рассмотрим один из них — способ обратной матрицы. Предварительно преобразуем систему уравнений. Выразим из первого уравнения значение 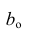
Подставим в остальные уравнения системы вместо 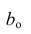
Пусть С — матрица коэффициентов при неизвестных параметрах 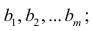
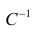
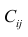
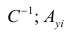
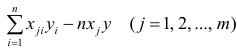
запишем окончательные выражения для параметров:
Оценкой остаточной дисперсии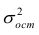
где 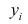
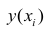
Если выборка получена из нормально распределенной генеральной совокупности, то, аналогично изложенному в п. 2.4, можно проверить значимость оценок коэффициентов регрессии, только в данном случае статистику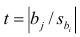
где 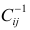
го столбца;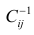
При заданном уровне значимости а и числе степеней свободы к=n— m—1 по табл. 1 приложений находят критическое значение 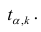
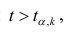
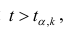
Для значимых коэффициентов регрессии целесообразно построить доверительные интервалы по формуле (2.10). Для оценки значимости уравнения регрессии следует проверить нулевую гипотезу о том, что все коэффициенты регрессии (кроме свободного члена) равны нулю: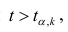
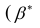
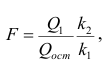
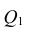
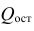
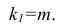
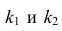
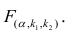
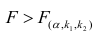
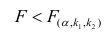
Факторный анализ
Основные положения. В последнее время всё более широкое распространение находит один из новых разделов многомерного статистического анализа — факторный анализ. Первоначально этот метод
разрабатывался для объяснения многообразия корреляций между исходными параметрами. Действительно, результатом корреляционного анализа является матрица коэффициентов корреляций. При малом числе параметров можно произвести визуальный анализ этой матрицы. С ростом числа параметра (10 и более) визуальный анализ не даёт положительных результатов. Оказалось, что всё многообразие корреляционных связей можно объяснить действием нескольких обобщённых факторов, являющихся функциями исследуемых параметров, причём сами обобщённые факторы при этом могут быть и неизвестны, однако их можно выразить через исследуемые параметры.
Один из основоположников факторного анализа Л. Терстоун приводит такой пример: несколько сотен мальчиков выполняют 20 разнообразных гимнастических упражнений. Каждое упражнение оценивают баллами. Можно рассчитать матрицу корреляций между 20 упражнениями. Это большая матрица размером 20><20. Изучая такую матрицу, трудно уловить закономерность связей между упражнениями. Нельзя ли объяснить скрытую в таблице закономерность действием каких-либо обобщённых факторов, которые в результате эксперимента непосредственно, не оценивались? Оказалось, что обо всех коэффициентах корреляции можно судить по трём обобщённым факторам, которые и определяют успех выполнения всех 20 гимнастических упражнений: чувство равновесия, усилие правого плеча, быстрота движения тела.
Дальнейшие разработки факторного анализа доказали, что этот метод может быть с успехом применён в задачах группировки и классификации объектов. Факторный анализ позволяет группировать объекты со сходными сочетаниями признаков и группировать признаки с общим характером изменения от объекта к объекту. Действительно, выделенные обобщённые факторы можно использовать как критерии при классификации мальчиков по способностям к отдельным группам гимнастических упражнений.
Методы факторного анализа находят применение в психологии и экономике, социологии и экономической географии. Факторы, выраженные через исходные параметры, как правило, легко интерпретировать как некоторые существенные внутренние характеристики объектов.
Факторный анализ может быть использован и как самостоятельный метод исследования, и вместе с другими методами многомерного анализа, например в сочетании с регрессионным анализом. В этом случае для набора зависимых переменных наводят обобщённые факторы, которые потом входят в регрессионный анализ в качестве переменных. Такой подход позволяет сократить число переменных в регрессионном анализе, устранить коррелированность переменных, уменьшить влияние ошибок и в случае ортогональности выделенных факторов значительно упростить оценку значимости переменных.
Представление, информации в факторном анализе
Для проведения факторного анализа информация должна быть представлена в виде двумерной таблицы чисел размерностью 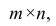
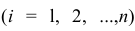
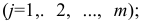
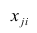
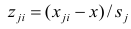
Основная модель факторного анализа. Основная модель факторного анализа имеет вид
где 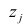
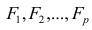
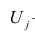
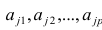
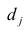
Модель предполагает, что каждый из j признаков, входящих в исследуемый набор и заданных в стандартной форме, может быть представлен в виде линейной комбинации небольшого числа общих факторов 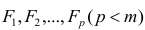
Термин «общий фактор» подчёркивает, что каждый такой фактор имеет существенное значение для анализа всех признаков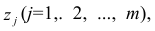
Термин «характерный фактор» показывает, что он относится только к данному j-му признаку. Это специфика признака, которая не может быть, выражена через факторы
Факторные нагрузки 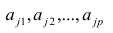
Для j-го признака и i-го объекта модель (2.19) можно записать в. виде
где 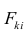
Дисперсию признака 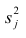
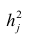
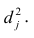
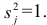
Если общие и характерные факторы не коррелируют между собой, то дисперсию j-го признака можно представить в виде
где 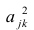
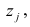
Полный вклад k-го фактора в суммарную дисперсию признаков
Вклад общих факторов в суммарную дисперсию
Факторное отображение
Используя модель (2.19), запишем выражения для каждого из параметров:
Коэффициенты системы (2,21) — факторные нагрузки — можно представить в виде матрицы, каждая строка которой соответствует параметру, а столбец — фактору.
Факторный анализ позволяет получить не только матрицу отображений, но и коэффициенты корреляции между параметрами и
факторами, что является важной характеристикой качества факторной модели. Таблица таких коэффициентов корреляции называется факторной структурой или просто структурой.
Коэффициенты отображения можно выразить через выборочные парные коэффициенты корреляции. На этом основаны методы вычисления факторного отображения.
Рассмотрим связь между элементами структуры и коэффициентами отображения. Для этого, учитывая выражение (2.19) и определение выборочного коэффициента корреляции, умножим уравнения системы (2.21) на соответствующие факторы, произведём суммирование по всем n наблюдениям и, разделив на n, получим следующую систему уравнений:
где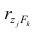
м фактором;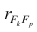
Если предположить, что общие факторы между собой, не коррелированы, то уравнения (2.22) можно записать в виде
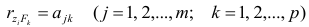
элементам структуры.
Введём понятие, остаточного коэффициента корреляции и остаточной корреляционной матрицы. Исходной информацией для построения факторной модели (2.19) служит матрица выборочных парных коэффициентов корреляции. Используя построенную факторную модель, можно снова вычислить коэффициенты корреляции между признаками и сравнись их с исходными Коэффициентами корреляции. Разница между ними и есть остаточный коэффициент корреляции.
В случае независимости факторов имеют место совсем простые выражения для вычисляемых коэффициентов корреляции между параметрами: для их вычисления достаточно взять сумму произведений коэффициентов отображения, соответствующих наблюдавшимся признакам:
где 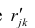
и к-м признаком. Остаточный коэффициент корреляции
Матрица остаточных коэффициентов корреляции называется остаточной матрицей или матрицей остатков
где 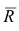
Результаты факторного анализа удобно представить в виде табл. 2.10.
Здесь суммы квадратов нагрузок по строкам — общности параметров, а суммы квадратов нагрузок по столбцам — вклады факторов в суммарную дисперсию параметров. Имеет место соотношение
Определение факторных нагрузок
Матрицу факторных нагрузок можно получить различными способами. В настоящее время наибольшее распространение получил метод главных факторов. Этот метод основан на принципе последовательных приближений и позволяет достичь любой точности. Метод главных факторов предполагает использование ЭВМ. Существуют хорошие алгоритмы и программы, реализующие все вычислительные процедуры.
Введём понятие редуцированной корреляционной матрицы или просто редуцированной матрицы. Редуцированной называется матрица выборочных коэффициентов корреляции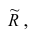
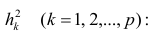
Редуцированная и полная матрицы связаны соотношением
где D — матрица характерностей.
Общности, как правило, неизвестны, и нахождение их в факторном анализе представляет серьезную проблему. Вначале определяют (хотя бы приближённо) число общих факторов, совокупность, которых может с достаточной точностью аппроксимировать все взаимосвязи выборочной корреляционной матрицы. Доказано, что число общих факторов (общностей) равно рангу редуцированной матрицы, а при известном ранге можно по выборочной корреляционной матрице найти оценки общностей. Числа общих факторов можно определить априори, исходя из физической природы эксперимента. Затем рассчитывают матрицу факторных нагрузок. Такая матрица, рассчитанная методом главных факторов, обладает одним интересным свойством: сумма произведений каждой пары её столбцов равна нулю, т.е. факторы попарно ортогональны.
Сама процедура нахождения факторных нагрузок, т.е. матрицы А, состоит из нескольких шагов и заключается в следующем: на первом шаге ищут коэффициенты факторных нагрузок при первом факторе так, чтобы сумма вкладов данного фактора в суммарную общность была максимальной:
Максимум 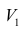
где 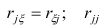
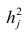
Затем рассчитывают матрицу коэффициентов корреляции с учётом только первого фактора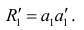
На втором шаге определяют коэффициенты нагрузок при втором факторе так, чтобы сумма вкладов второго фактора в остаточную общность (т.е. полную общность без учёта той части, которая приходится на долю первого фактора) была максимальной. Сумма квадратов нагрузок при втором факторе
Максимум 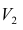
где 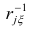
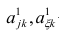
Факторный анализ учитывает суммарную общность. Исходная суммарная общность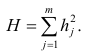
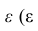
Адекватность факторной модели оценивается по матрице остатков (если величины её коэффициентов малы, то модель считают адекватной).
Такова последовательность шагов для нахождения факторных нагрузок. Для нахождения максимума функции (2.24) при условии (2.25) используют метод множителей Лагранжа, который приводит к системе т уравнений относительно m неизвестных
Метод главных компонент
Разновидностью метода главных факторов является метод главных компонент или компонентный анализ, который реализует модель вида
где m — количество параметров (признаков).
Каждый из наблюдаемых, параметров линейно зависит от m не коррелированных между собой новых компонент (факторов) 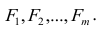
Если для дальнейшего анализа оставить все найденные т компонент, то тем самым будет использована вся информация, заложенная в корреляционной матрице. Однако это неудобно и нецелесообразно. На практике обычно оставляют небольшое число компонент, причём количество их определяется долей суммарной дисперсии, учитываемой этими компонентами. Существуют различные критерии для оценки числа оставляемых компонент; чаще всего используют следующий простой критерий: оставляют столько компонент, чтобы суммарная дисперсия, учитываемая ими, составляла заранее установленное число процентов. Первая из компонент должна учитывать максимум суммарной дисперсии параметров; вторая — не коррелировать с первой и учитывать максимум оставшейся дисперсии и так до тех пор, пока вся дисперсия не будет учтена. Сумма учтённых всеми компонентами дисперсий равна сумме дисперсий исходных параметров. Математический аппарат компонентного анализа полностью совпадает с аппаратом метода главных факторов. Отличие только в исходной матрице корреляций.
Компонента (или фактор) через исходные переменные выражается следующим образом:
где 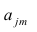
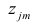
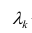
компонент.
Для иллюстрации возможностей факторного анализа покажем, как, используя метод главных компонент, можно сократить размерность пространства независимых переменных, перейдя от взаимно коррелированных параметров к независимым факторам, число которых р
Следует особо остановиться на интерпретации результатов, т.е. на смысловой стороне факторного анализа. Собственно факторный анализ состоит из двух важных этапов; аппроксимации корреляционной матрицы и интерпретации результатов. Аппроксимировать корреляционную матрицу, т.е. объяснить корреляцию между параметрами действием каких-либо общих для них факторов, и выделить сильно коррелирующие группы параметров достаточно просто: из корреляционной матрицы одним из методов
факторного анализа непосредственно получают матрицу нагрузок — факторное решение, которое называют прямым факторным решением. Однако часто это решение не удовлетворяет исследователей. Они хотят интерпретировать фактор как скрытый, но существенный параметр, поведение которого определяет поведение некоторой своей группы наблюдаемых параметров, в то время как, поведение других параметров определяется поведением других факторов. Для этого у каждого параметра должна быть наибольшая по модулю факторная нагрузка с одним общим фактором. Прямое решение следует преобразовать, что равносильно повороту осей общих факторов. Такие преобразования называют вращениями, в итоге получают косвенное факторное решение, которое и является результатом факторного анализа.
Приложения
Значение t — распределения Стьюдента
Понятие о регрессионном анализе. Линейная выборочная регрессия. Метод наименьших квадратов (МНК)
Основные задачи регрессионного анализа:
- Вычисление выборочных коэффициентов регрессии
- Проверка значимости коэффициентов регрессии
- Проверка адекватности модели
- Выбор лучшей регрессии
- Вычисление стандартных ошибок, анализ остатков
Построение простой регрессии по экспериментальным данным.
Предположим, что случайные величины 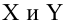
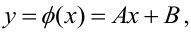
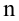
Диаграмма рассеяния (разброса, рассеивания)
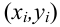
Выборочное уравнение прямой линии регрессии 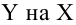
Задача: подобрать 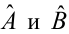
Для того, что бы провести прямую 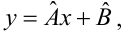
чтобы
Постулаты регрессионного анализа, которые должны выполняться при использовании МНК.
подчинены нормальному закону распределения.
- Дисперсия
постоянна и не зависит от номера измерения.
- Результаты наблюдений
в разных точках независимы.
- Входные переменные
независимы, неслучайны и измеряются без ошибок.
Введем функцию ошибок 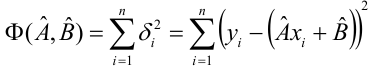
Решив систему, получим искомые значения
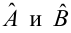
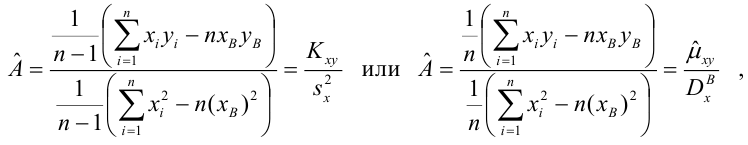
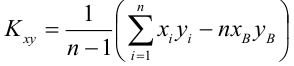
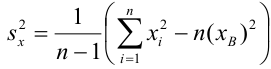
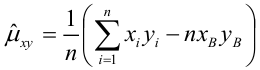
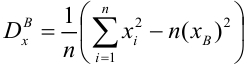
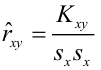
Коэффициент детерминации
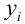
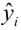
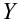
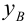
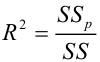
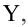
Коэффициент детерминации принимает значения от 0 до 1. Чем ближе значение коэффициента к 1, тем сильнее зависимость. При оценке регрессионных моделей это используется для доказательства адекватности модели (качества регрессии). Для приемлемых моделей предполагается, что коэффициент детерминации должен быть хотя бы не меньше 0,5 (в этом случае коэффициент множественной корреляции превышает по модулю 0,7). Модели с коэффициентом детерминации выше 0,8 можно признать достаточно хорошими (коэффициент корреляции превышает 0,9). Подтверждение адекватности модели проводится на основе дисперсионного анализа путем проверки гипотезы о значимости коэффициента детерминации.
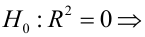
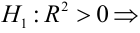
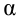
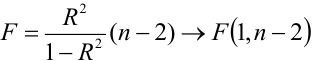
Критическая область — правосторонняя;
Если 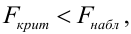
Мощность статистического критерия. Функция мощности
Определение. Мощностью критерия 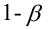
Задача: построить критическую область таким образом, чтобы мощность критерия была максимальной.
Определение. Наилучшей критической областью (НКО) называют критическую область, которая обеспечивает минимальную ошибку второго рода
Пример:
По паспортным данным автомобиля расход топлива на 100 километров составляет 10 литров. В результате измерения конструкции двигателя ожидается, что расход топлива уменьшится. Для проверки были проведены испытания 25 автомобилей с модернизированным двигателем; выборочная средняя расхода топлива по результатам испытаний составила 9,3 литра. Предполагая, что выборка получена из нормально распределенной генеральной совокупности с математическим ожиданием 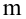
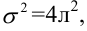
3) Уровень значимости
4) Статистический критерий
5) Критическая область — левосторонняя
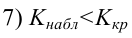
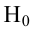
Пример:
В условиях примера 1 предположим, что наряду с 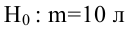
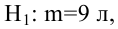
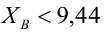
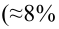
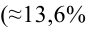
Определение. Пусть проверяется 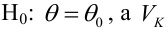
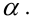
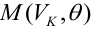
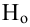
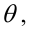
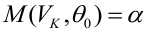
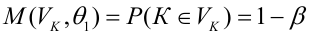
Пример:
Построить график функции мощности из примера 2 для

Пример:
Какой минимальный объем выборки следует взять в условии примера 2 для того, чтобы обеспечить
Лемма Неймана-Пирсона.
При проверке простой гипотезы 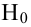
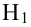
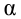
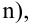
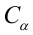
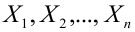
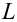
Пример:
Случайная величина 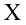
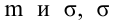
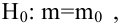
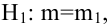
Решение:
Ошибка первого рода:
НКО:
Пример:
Для зависимости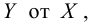
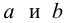
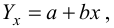
Решение. Воспользуемся предыдущими результатами
Согласно формуле (24), уравнение регрессии будет иметь вид 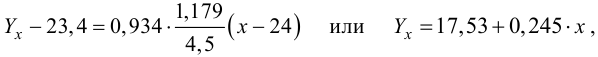
Для выяснения значимости уравнения регрессии вычислим суммы 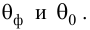
Из (27) и (28) по данным таблицы получим
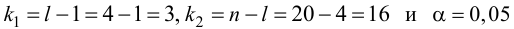
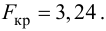
Вычислим статистику
Так как 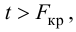
- Корреляционный анализ
- Статистические решающие функции
- Случайные процессы
- Выборочный метод
- Проверка гипотезы о равенстве вероятностей
- Доверительный интервал для математического ожидания
- Доверительный интервал для дисперсии
- Проверка статистических гипотез
















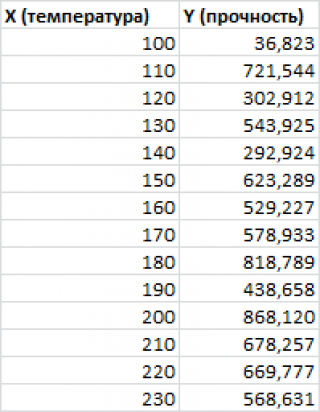
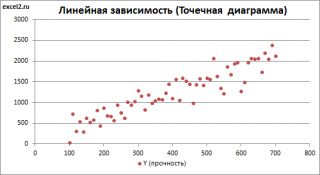
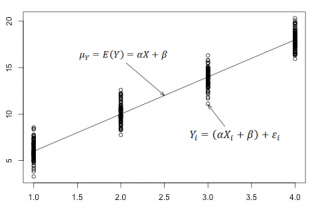
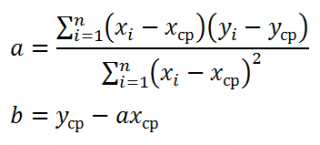
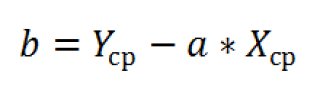
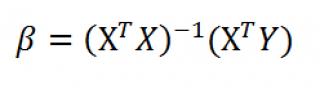
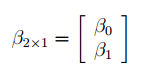
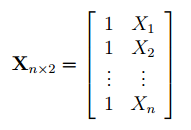
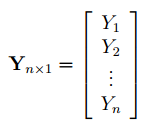
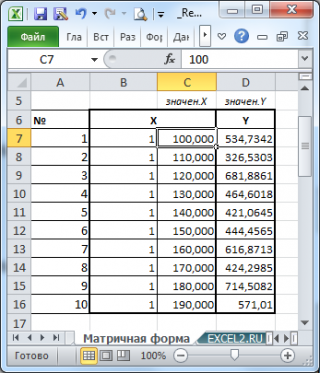
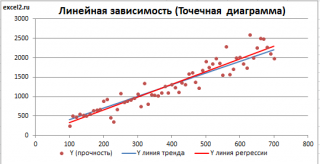
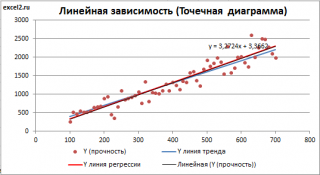
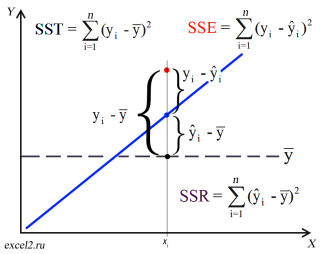
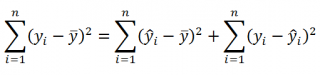
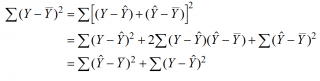
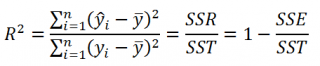
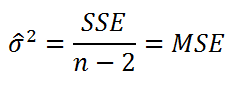
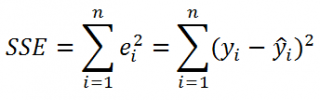
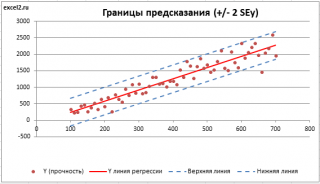
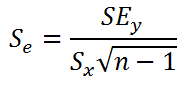
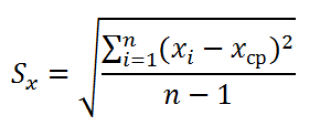
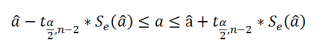
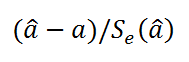
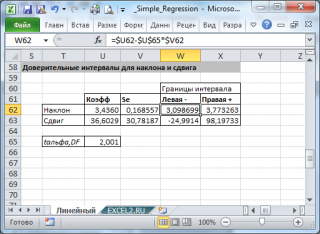
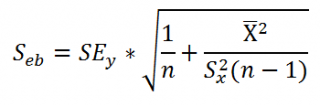
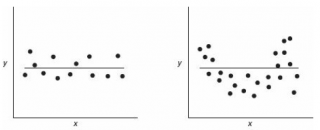
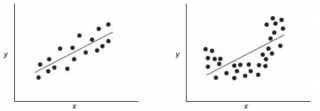
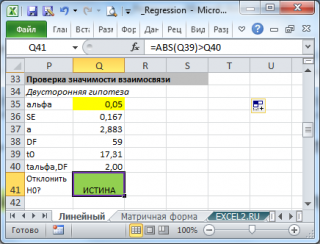
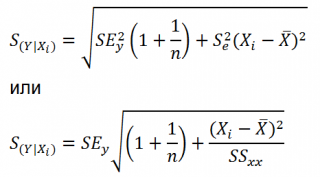
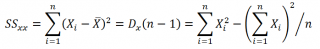
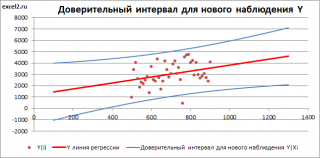
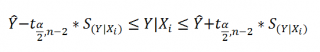
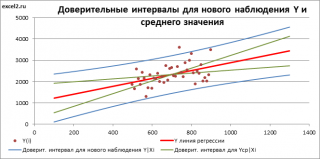
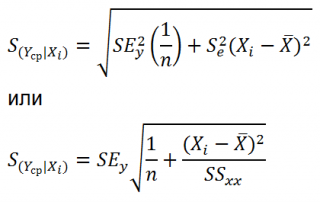
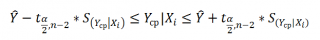
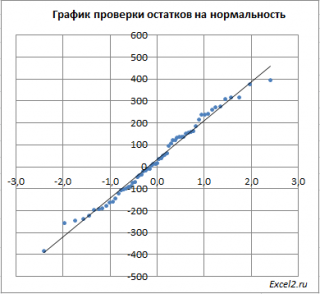
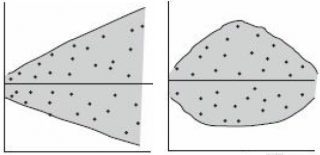
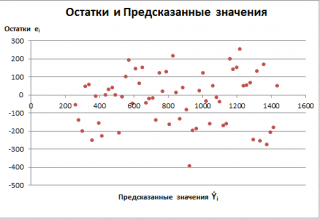
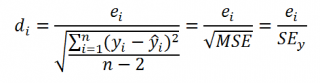



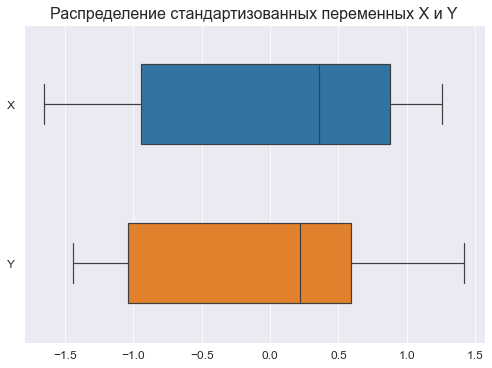

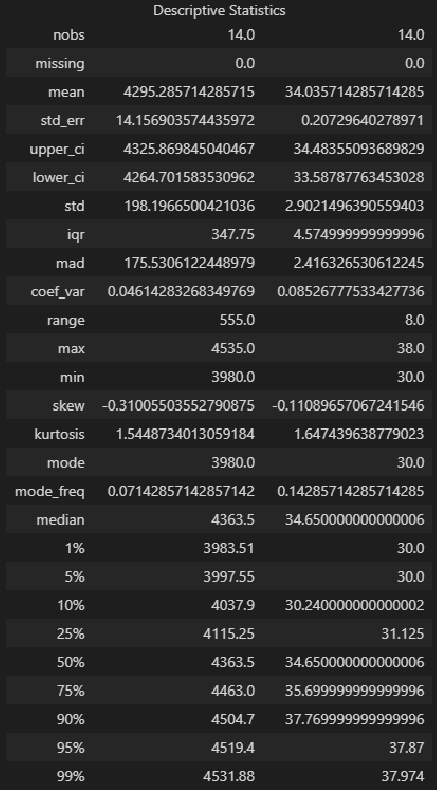
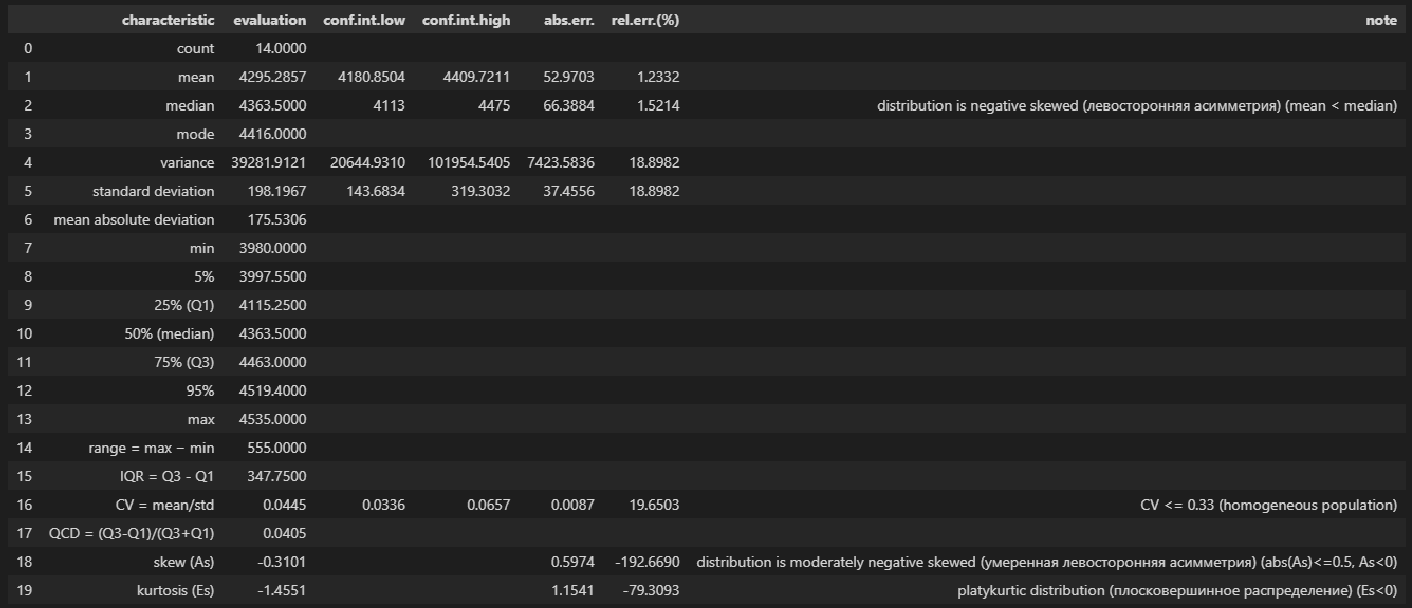
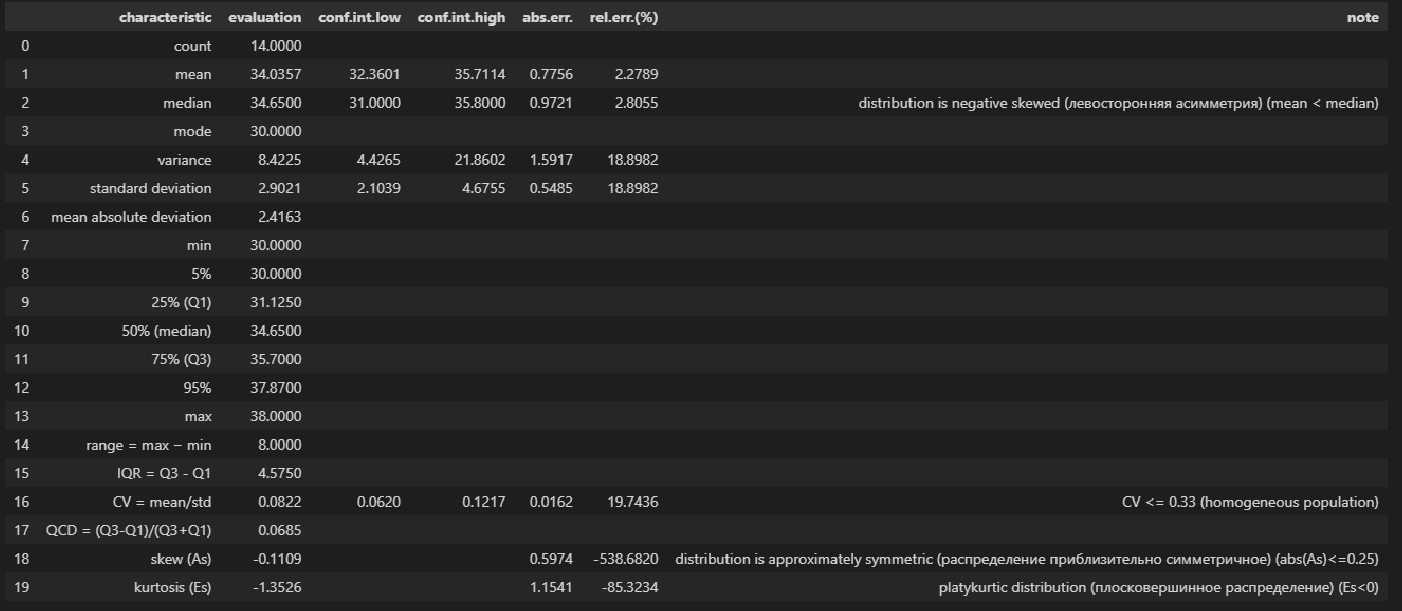

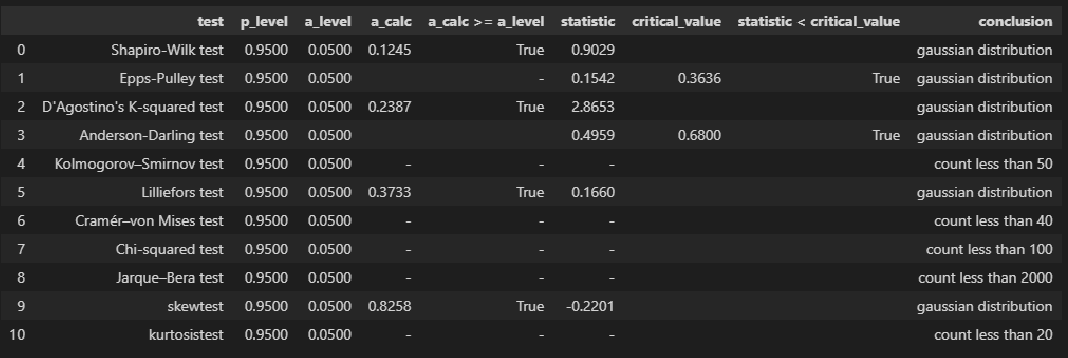

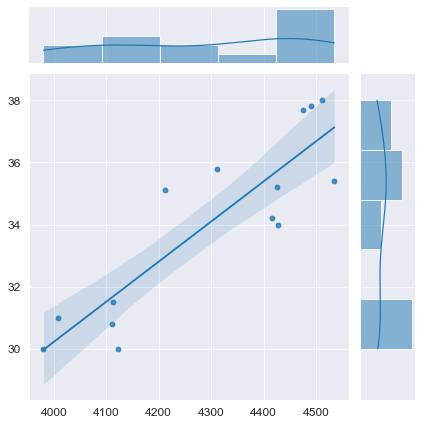
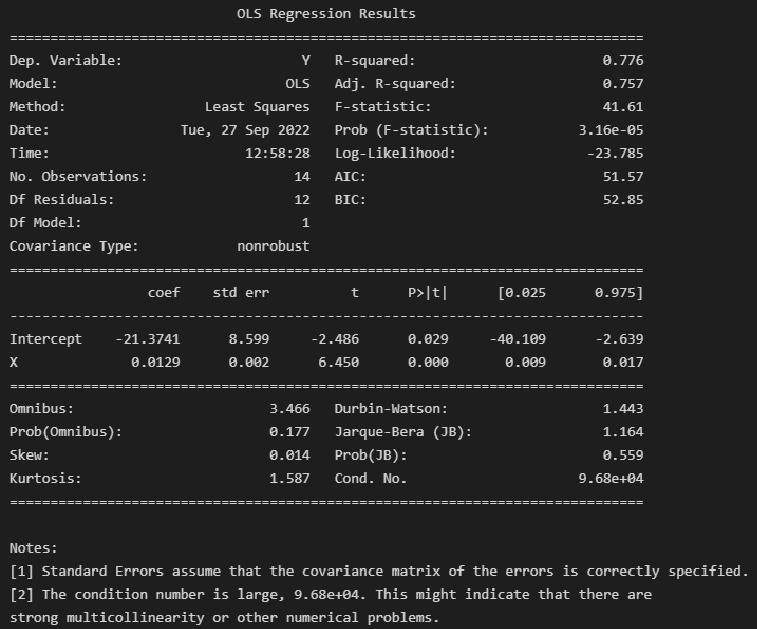
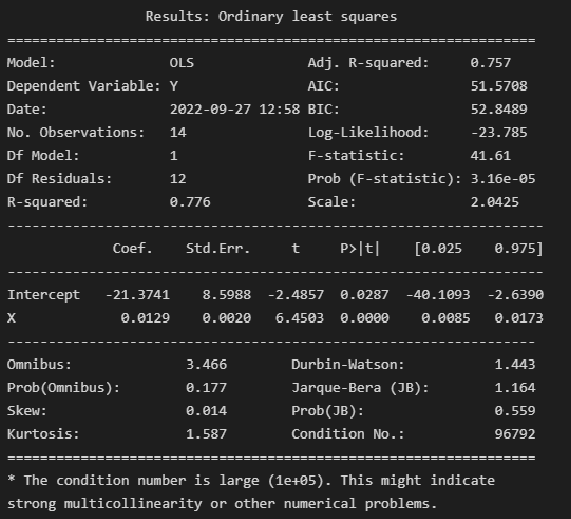
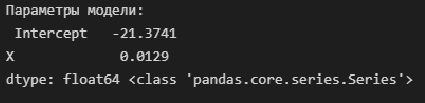
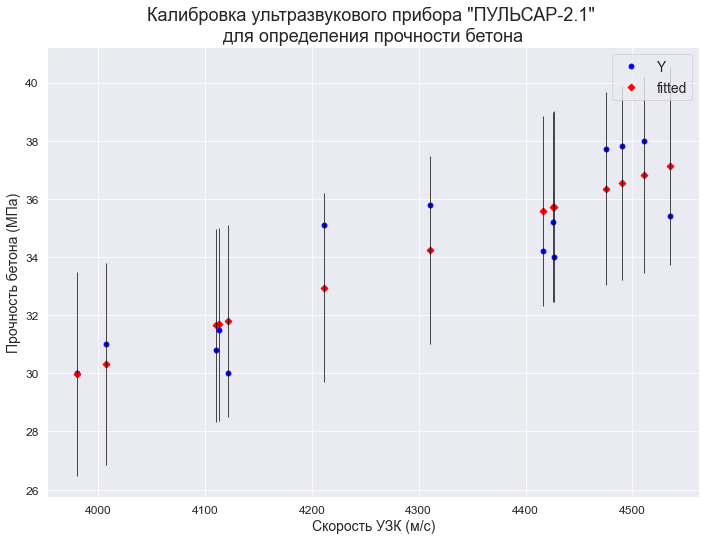

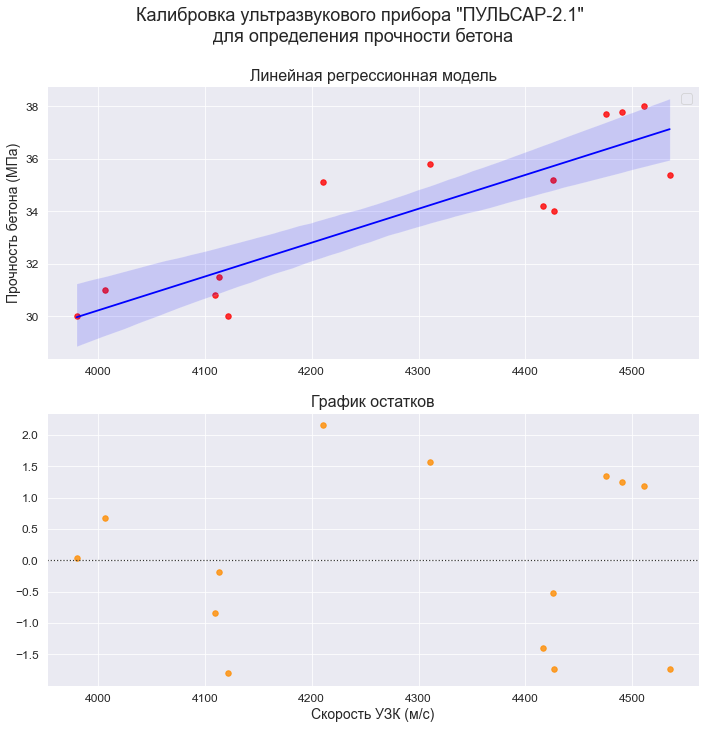
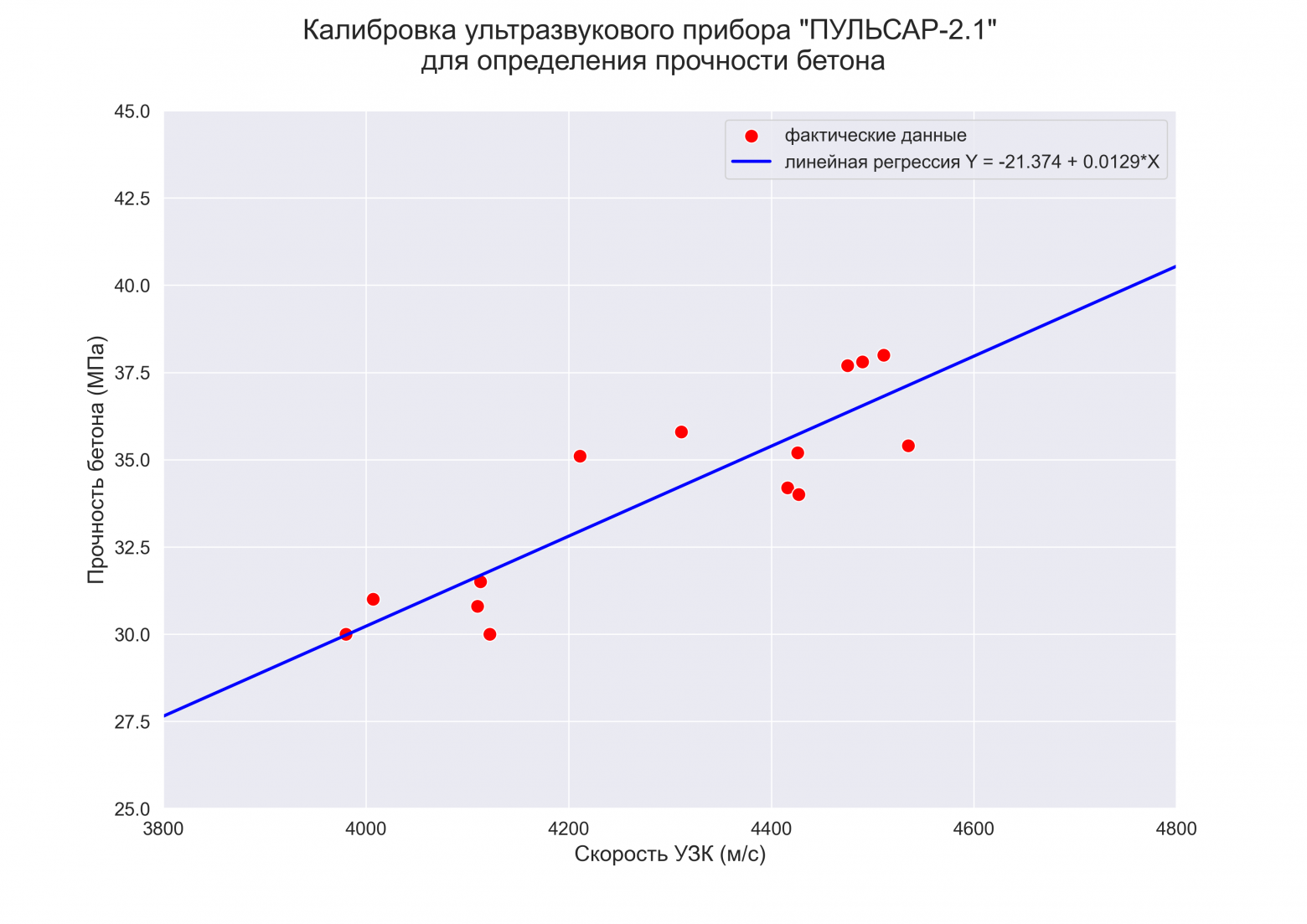


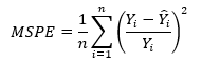



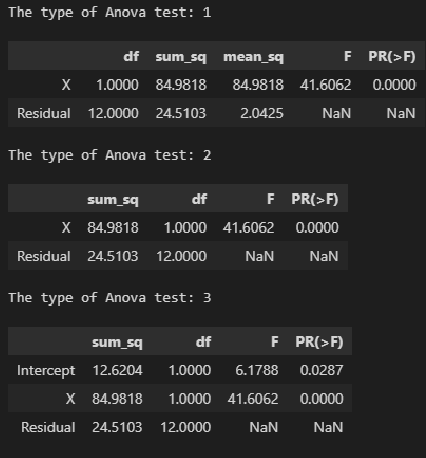
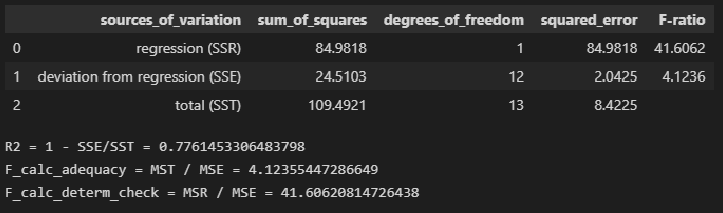
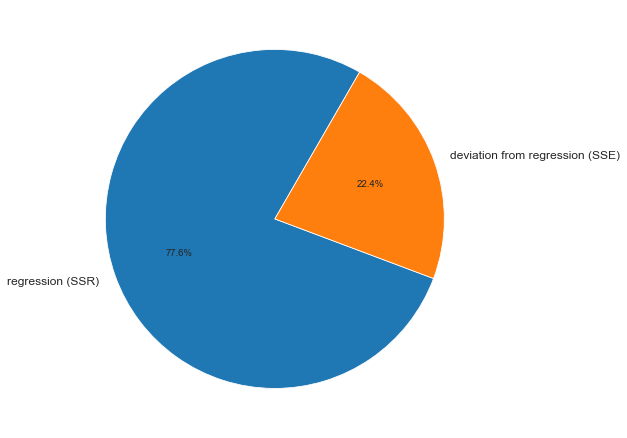


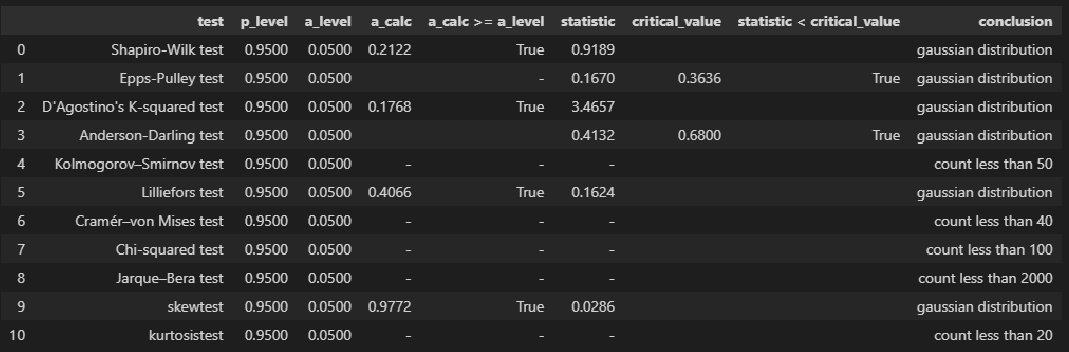











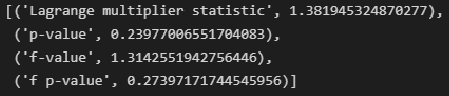










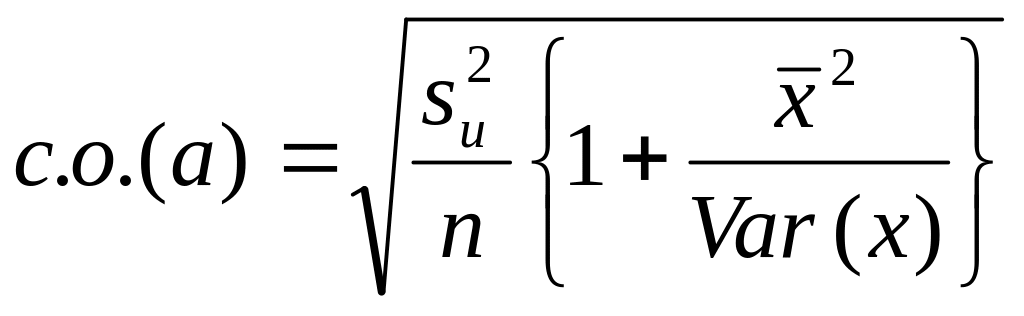
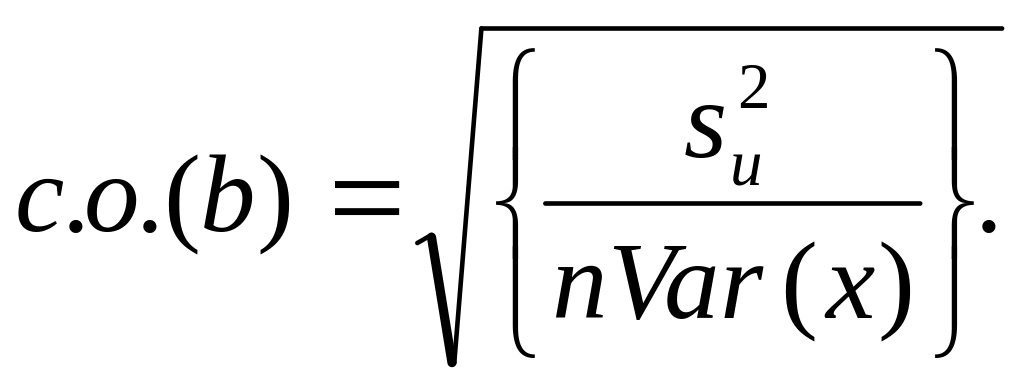

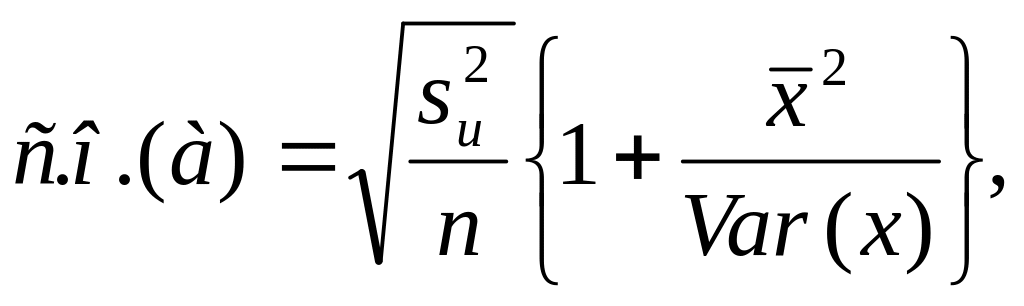
















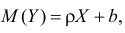
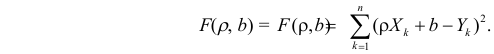
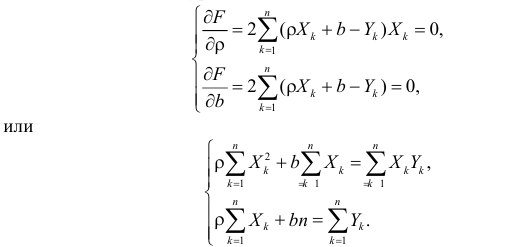
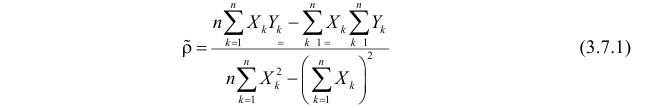
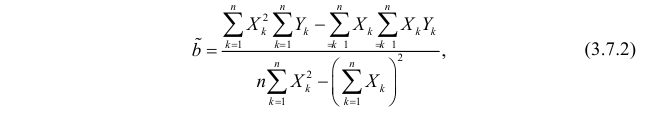
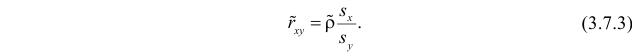
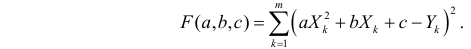

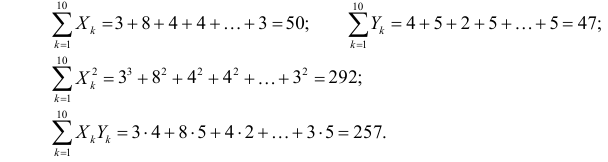
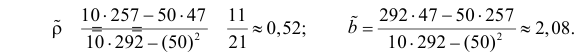
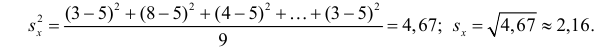
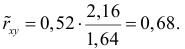
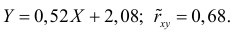

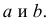
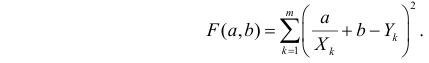
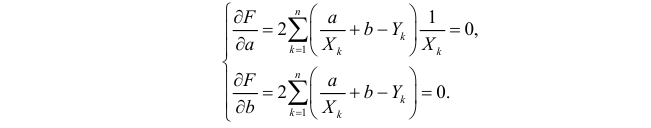
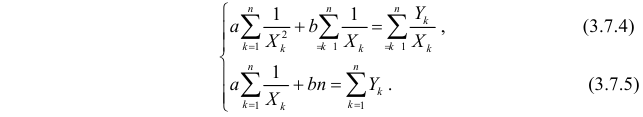
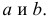
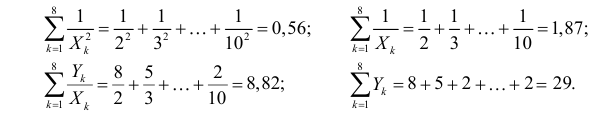
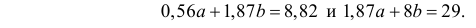
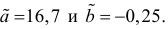
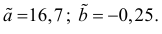

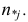



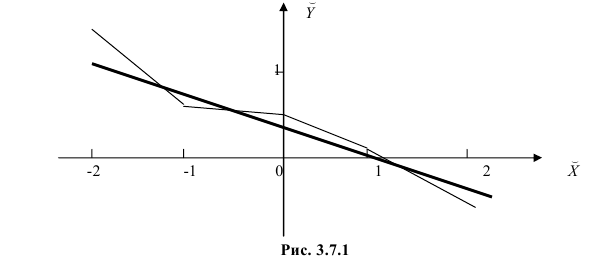
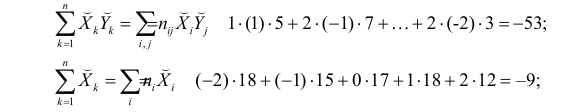
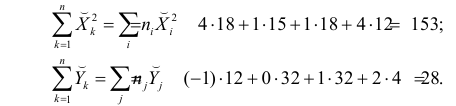
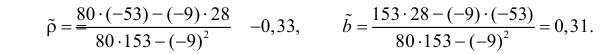
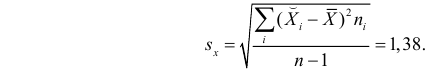
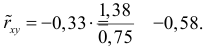
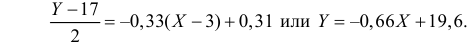
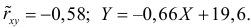
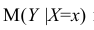 можно представить в виде
можно представить в виде 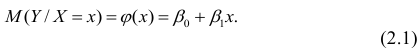
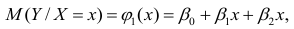
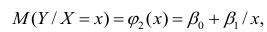
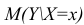 можно представить в виде (2.1).
можно представить в виде (2.1).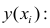
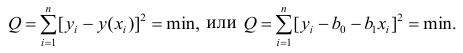
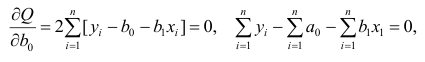
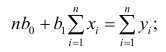
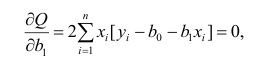
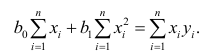
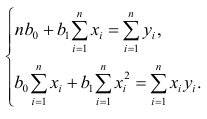
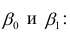
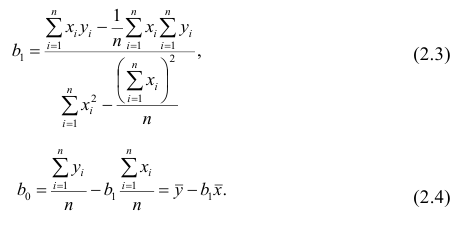
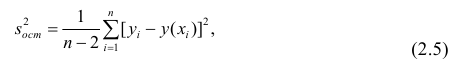
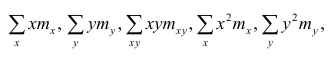
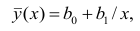
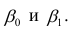
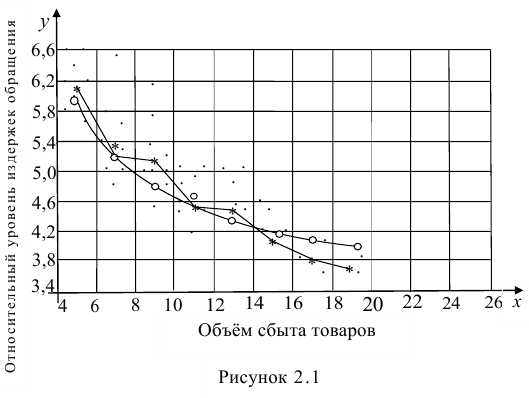
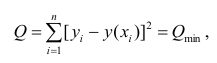
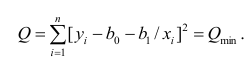
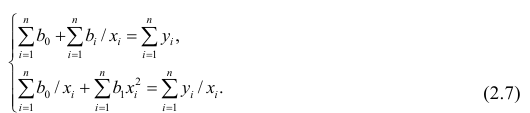
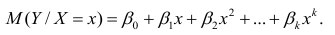
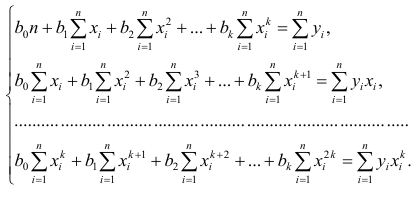

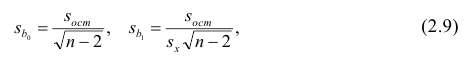
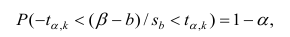

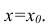
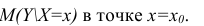
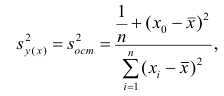
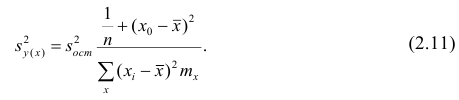
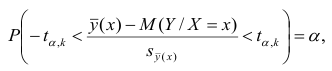
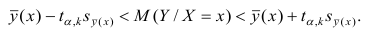
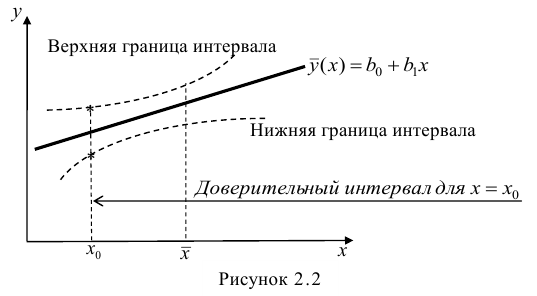
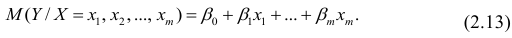
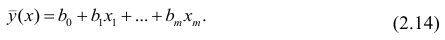
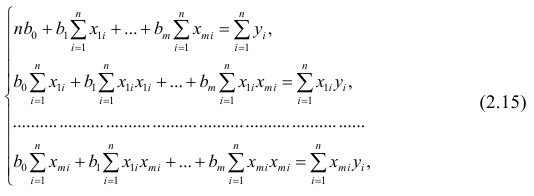
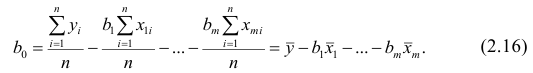
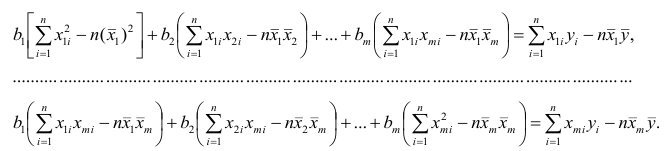
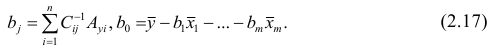
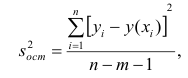
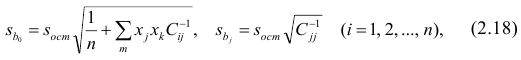
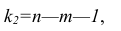
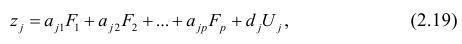
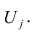
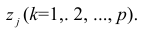
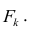
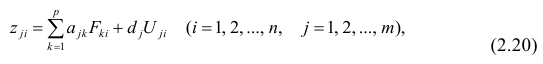
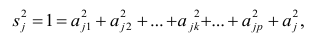
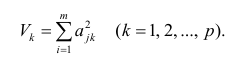
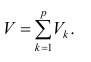
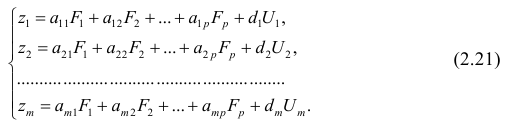
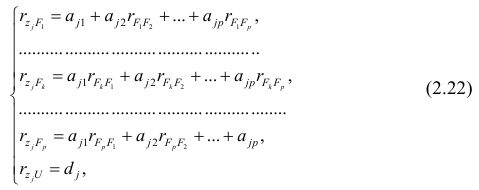
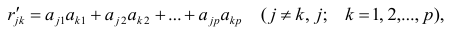
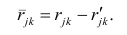
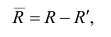

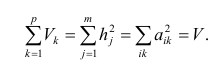
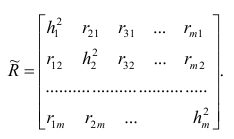


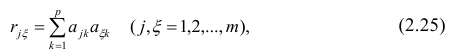

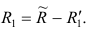

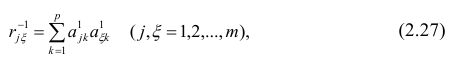
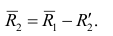
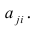
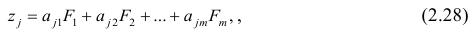
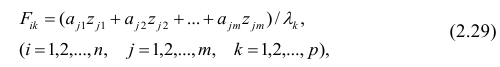
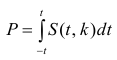
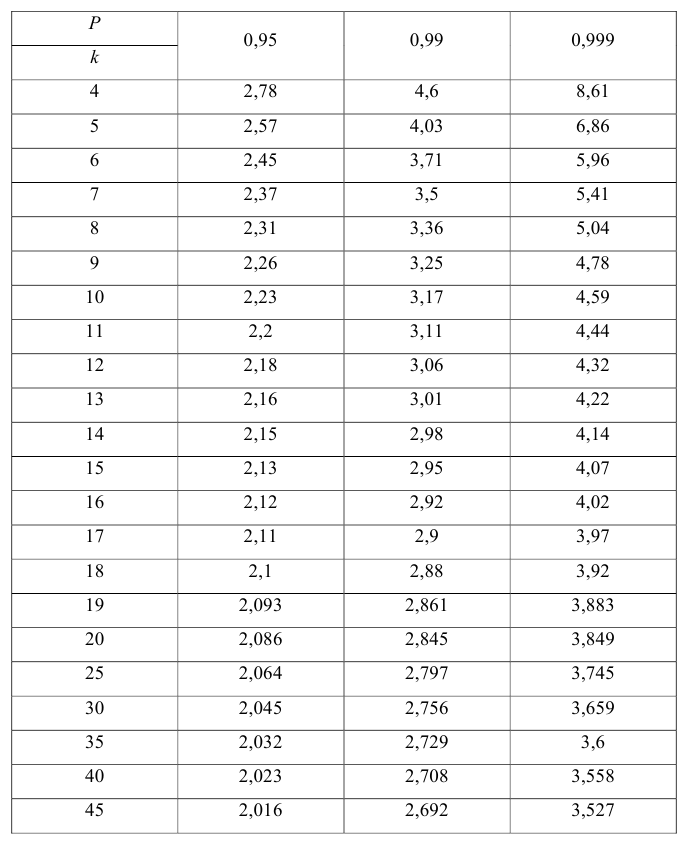
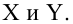
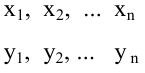
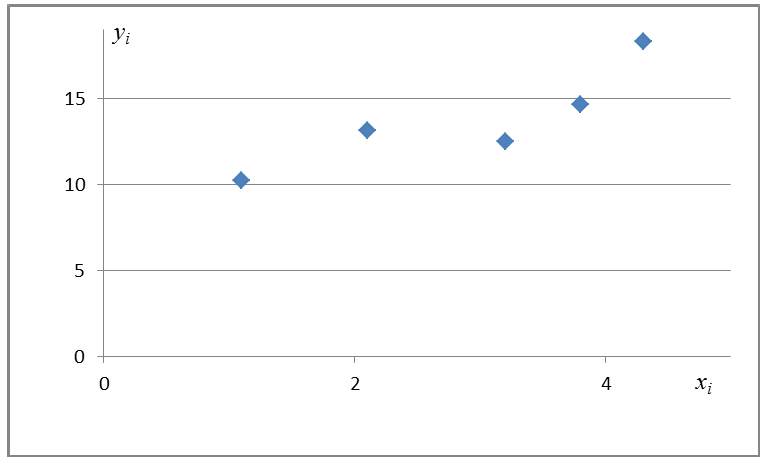
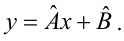
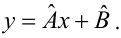
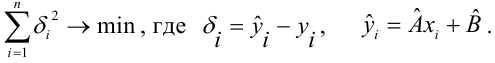
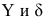 подчинены нормальному закону распределения.
подчинены нормальному закону распределения.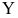 постоянна и не зависит от номера измерения.
постоянна и не зависит от номера измерения.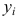 в разных точках независимы.
в разных точках независимы.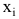 независимы, неслучайны и измеряются без ошибок.
независимы, неслучайны и измеряются без ошибок.