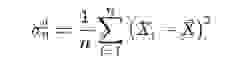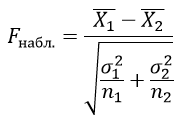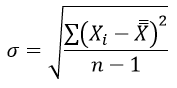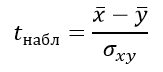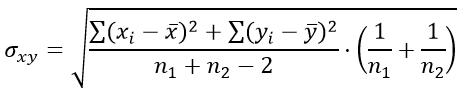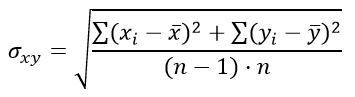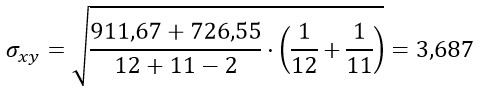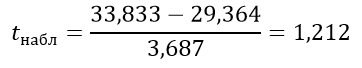Как погрешность превращается в грех
Время на прочтение
7 мин
Количество просмотров 29K
Одна городская легенда гласит, что создатель сахарных пакетиков-палочек повесился, узнав, что потребители не разламывают их пополам над чашкой, а аккуратно отрывают кончик. Это, разумеется, не так, но если следовать такой логике, то один британский любитель пива «Гиннесс» по имени Уильям Госсет должен был не просто повеситься, но и своим вращением в гробу уже пробурить Землю до самого центра. А все потому, что его знаковое изобретение, опубликованное под псевдонимом Стьюдент, уже десятки лет используют катастрофически неправильно.
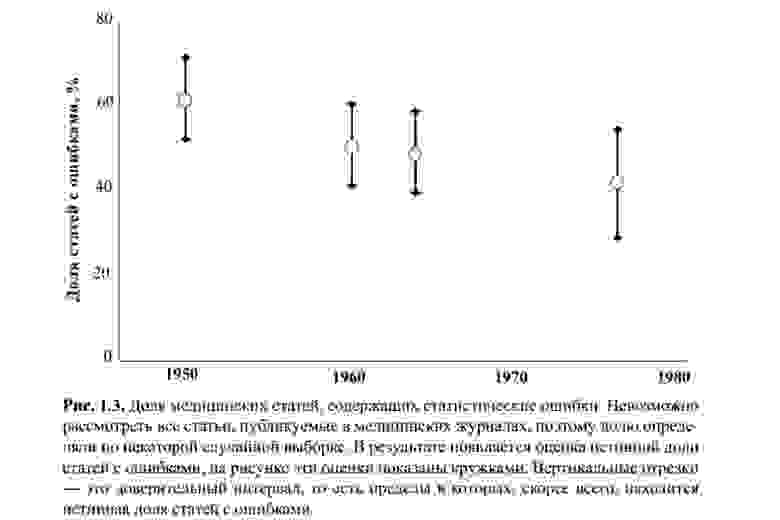
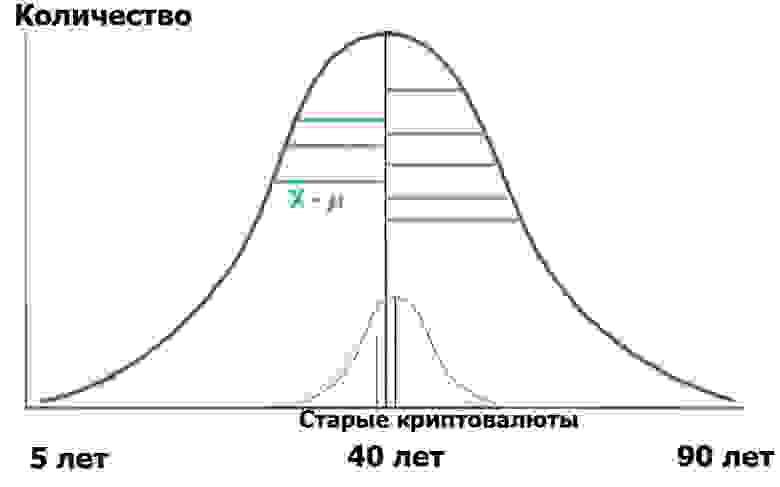
Рисунок выше приведен из книги С. Гланц. Медико-биологическая статистика. Пер. с англ. — М., Практика, 1998. — 459 с. Мне неизвестно, проверял ли кто-нибудь на статистические ошибки расчеты для этой диаграммы. Однако и ряд современных статей по теме, и мой собственный опыт говорят о том, что t-критерий Стьюдента остается самым известным, и оттого — самым популярным в применении, по поводу и без.
Причиной этому является поверхностное образование (строгие преподаватели учат, что надо «проверять статистику», иначе уууууу!), простота использования (таблицы и онлайн-калькуляторы доступны во множестве) и банальное нежелание вникать в то, что «и так работает». Большинство людей, хоть раз применявших этот критерий в своей курсовой или даже научной работе, скажут что-то вроде: «ну вот, мы сравнивали 5 злых школьников и 7 школьников-геймеров по уровню агрессии, у нас значение по таблице выходит близко к р=0,05 и это значит, что игры — зло. Ну да, не точно, а с вероятностью 95%». Сколько логических и методологических ошибок они уже сделали?
Основы
На чем основан t-критерий Стьюдента? Логика берется из теоремы Байеса, математическая основа — из распределения Гаусса, методология базируется на дисперсионном анализе:
где параметр μ — математическое ожидание (среднее значение) распределения, а параметр σ — среднеквадратическое отклонение (σ ² — дисперсия) распределения.
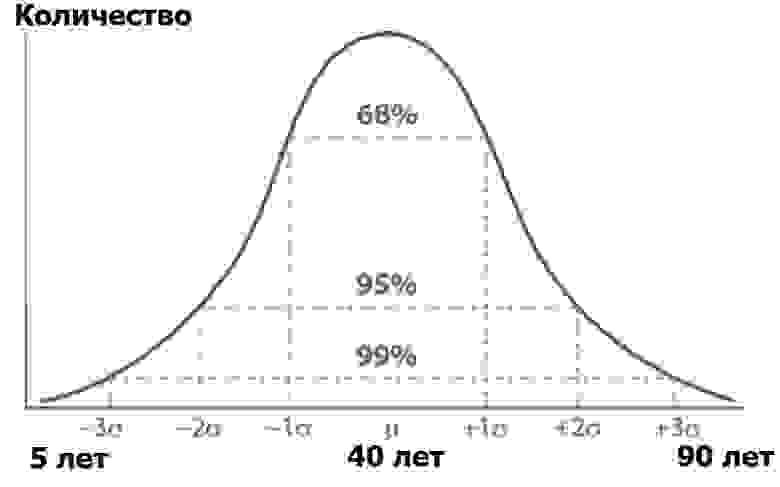
Что такое дисперсионный анализ? Представим себе аудиторию Хабра, сортированную по числу людей каждого из определенных возрастов. Количество людей по возрасту, скорее всего, будет подчиняться нормальному распределению — согласно функции Гаусса:
Нормальное распределение имеет интересное свойство — почти все его значения лежат в пределе трех стандартных отклонений от среднего значения. А что такое стандартное отклонение? Это корень из дисперсии. Дисперсия, в свою очередь — это сумма квадратов разности всех членов генеральной совокупности и среднего значения, деленная на число этих членов:
То есть, каждое значение вычли из среднего, возвели в квадрат, чтобы убить минусы, и затем взяли среднее, просто просуммировав и поделив на число этих значений. Получилась мера средней разбросанности значений относительно среднего — дисперсия.
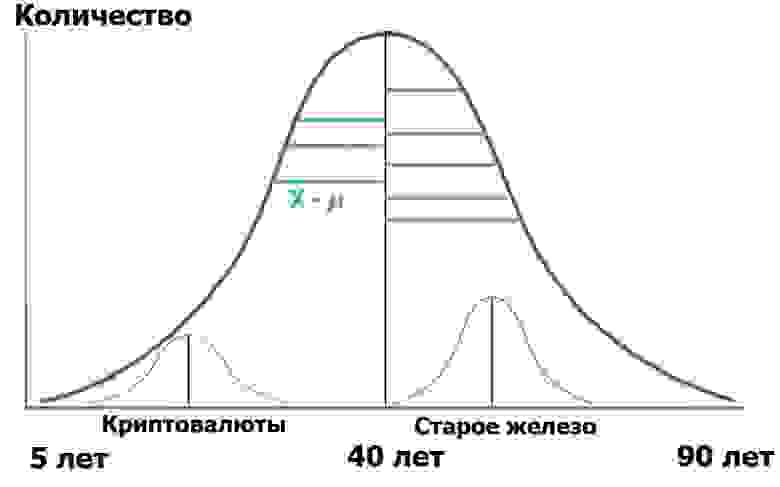
Представим, что мы отобрали в этой генеральной совокупности две выборки: читателей хаба «Криптовалюты» и читателей хаба «Старое железо». Мы распределим их по возрасту — у каждой из тем есть свое поколение фанатов. Делая случайную выборку, мы всегда получаем распределения, близкие к нормальным. Вот и сейчас у нас получились маленькие распределньица внутри нашей генеральной совокупности:
Для наглядности я показал зеленые отрезки — расстояния от точек распределения до среднего значения. Если длины этих зеленых отрезков возвести в квадрат, просуммировать и усреднить — это и будет дисперсия.
А теперь — внимание. Мы можем охарактеризовать генеральную совокупность через эти две маленькие выборки. С одной стороны, дисперсии выборок характеризуют дисперсию всей генеральной совокупности. С другой стороны, средние значения самих выборок — это тоже числа, для которых можно вычислить дисперсию! Итак: у нас есть среднее от дисперсий выборок и дисперсия средних значений выборок.
Тогда мы можем провести дисперсионный анализ, грубо представив его в виде логической формулы:
F= (дисперсия совокупности по средним значениям выборок) / (дисперсия совокупности по дисперсиям выборок)
Что нам даст вышеозначенная формула? Очень просто. В статистике все начинается с «нулевой гипотезы», которую можно сформулировать как «нам показалось», «все совпадения случайны» — по смыслу, и «не существует связи между двумя наблюдаемыми событиями» — если строго. Так вот, в нашем случае, нулевой гипотезой будет отсутствие значимых различий между возрастным распределением наших пользователей в двух хабах. В случае нулевой гипотезы наша диаграмма будет выглядеть как-то так:
Это означает, что и дисперсии выборок, и их средние значения очень близки или равны между собой, а потому, говоря очень общо, наш критерий
F= (дисперсия совокупности по средним значениям выборок)/ (дисперсия совокупности по дисперсиям выборок) = 1
А вот если дисперсии выборок равны, но возраста хабраюзеров действительно сильно отличаются, то числитель (дисперсия средних значений) будет большим, и F будет намного больше единицы. Тогда и диаграмма будет выглядеть скорее как на предыдущем рисунке. А что нам это даст? Ничего, если не обратить внимание на формулировку: нулевой гипотезой будет отсутствие значимых различий.
А вот значимость… ее мы задаем сами. Она обозначается как α и имеет следующий смысл: уровень значимости есть максимальная приемлемая вероятность ошибочно отвергнуть нулевую гипотезу. Иными словами, мы будем рассматривать наше событие как достоверное отличие одной группы от другой, только если вероятность Р нашей ошибки меньше α. Это и есть пресловутое р<0,05, потому как обычно в медико-биологических исследованиях уровень значимости задают в 5%.
Ну а дальше — все просто. В зависимости от α существуют критические значения F, начиная с которых мы отвергаем нулевую гипотезу. Они и выпускаются в виде таблиц, которыми мы так привыкли пользоваться. Это — что касается дисперсионного анализа. А что со Стьюдентом?
Так говорил Студент
А критерий Стьюдента — это просто частный случай дисперсионного анализа. Я опять не буду перегружать вас формулами, которые легко гуглятся, а передам суть:
t= (разность средних значений выборок) / (стандартная ошибка разности выборочных средних)
Так вот, все это длинное объяснение нужно было, чтобы очень грубо и бегло, но наглядно показать, на чем основан t-критерий. И соответственно, из каких его неотъемлемых свойств напрямую вытекают ограничения его использования, на которых так часто ошибаются даже профессиональные ученые.
Свойство первое: нормальность распределения.
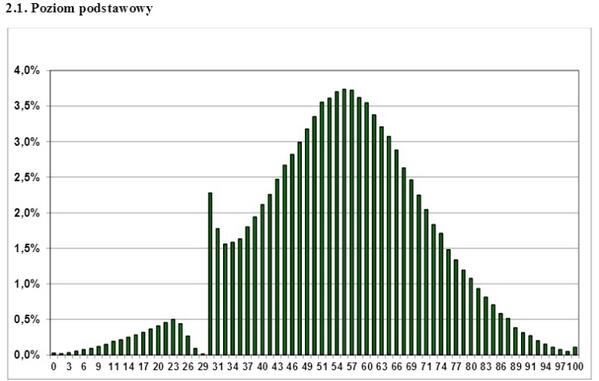
Это — пару лет как гуляющий по Интернету график распределения баллов сдачи польского государственного экзамена. Какой можно из него сделать вывод? Что этот экзамен не сдают только совсем отбитые гопники? Что преподаватели «дотягивают» учеников? Нет, только один — к распределению, отличному от нормального, нельзя применять параметрические критерии анализа, вроде Стьюдента. Если у вас однобокий, зубчатый, волнистый, дискретный график распределения — забудьте про t-критерий, его использовать нельзя. Тем не менее, это иногда успешно игнорируется даже серьезными научными работами.
Что же делать в таком случае? Использовать так называемые непараметрические критерии анализа. В них реализуется другой подход, а именно ранжирование данных, то есть уход от значений каждой из точек к присвоенному ей рангу. Эти критерии менее точны, чем параметрические, но по крайней мере их использование корректно, в отличие от ничем не оправданного использования параметрического критерия на ненормальной совокупности. Из таких критериев наиболее известен U-критерий Манна-Уитни, причем зачастую его используют как критерий «для малой выборки». Да, он позволяет иметь дело с выборками до 5 точек, но это, как уже должно быть понятно, не основное его назначение.
Свойство второе: вы же помните формулу? Значения F-критерия менялись при отличии (увеличенной дисперсии) средних значений выборок. А вот знаменатель, то есть, сами дисперсии, меняться не должны. Поэтому еще одним критерием применимости должно быть равенство дисперсий. О том, что эта проверка соблюдается еще реже, говорится например, тут: Ошибки статистического анализа биомедицинских данных. Леонов В.П. Международный журнал медицинской практики, 2007, вып. 2, стр.19-35.
Свойство третье: сравнение двух выборок. t-критерий очень любят использовать для сравнения более, чем двух групп. Делается это, как правило, следующим образом: попарно сравниваются отличия группы А от В, В от С и А от С. Затем на основании этого делается некий вывод, что является абсолютно некорректным. В этом случае возникает эффект множественных сравнений.
Получив достаточно высокое значение t в каком либо из трех сравнений исследователи сообщают что «P < 0,05». Но на самом же деле вероятность ошибки значительно превышает 5%.
Почему?
Разбираемся: допустим, в исследовании был принят уровень значимости 5%. Значит, максимальная приемлемая вероятность ошибочно отвергнуть нулевую гипотезу при сравнении групп А и В — 5%. Казалось бы, все правильно? Но ведь точно такая же ошибка произойдет в случае сравнения групп В и С, и при сравнении групп А и С тоже. Следовательно, вероятность ошибиться в целом при такого рода оценке составит не 5%, а значительно больше. В общем случае эта вероятность равна
P′ =1 − (1- 0,05 )^k
где k — число сравнений.
Тогда в нашем исследовании вероятность ошибиться при отвергании нулевой гипотезы составляет примерно 15%. При сравнении четырех групп число пар и соответственно возможных попарных сравнений равно 6. Поэтому при уровне значимости в каждом из сравнений 0,05
вероятность ошибочно обнаружить различие хотя бы в одном равна уже не 0,05, а 0,31.
Такую ошибку все же несложно устранить. Один из способов — это введение поправки Бонферрони. Неравенство Бонферрони указывает нам, что если k раз применить критерии
с уровнем значимости α, то вероятность хотя бы в одном случае найти различие там, где его нет не превышает произведения k на α. Отсюда:
α′ < αk,
где α′ — вероятность хотя бы один раз ошибочно выявить различия. Тогда наша проблема решается очень просто: нужно разделить наш уровень значимости на поправку Бонферрони — то есть, на кратность сравнений. Для трех сравнений нам необходимо взять из таблиц t-критерия значения, соответствующие α = 0,05/3 = 0,0167. Повторюсь — очень просто, но эту поправку нельзя игнорировать. Да, кстати, увлекаться этой поправкой тоже не стоит, уже после деления на 8 значения t-критерия излишне устрожаются.
Далее идут «мелочи», которые очень часто вообще не замечают. Я сознательно не привожу тут формул, чтобы не снижать читаемость текста, но следует помнить, что расчеты t-критерия варьируются для следующих случаев:
-
Различный размер двух выборок (вообще, нужно помнить, что в общем случае мы сравниваем две группы по формуле для двухвыборочного критерия);
-
Наличие зависимых выборок. Это — случаи, когда измеряют данные у одного больного в различные интервалы времени, данные у группы животных до и после эксперимента, и т. д.
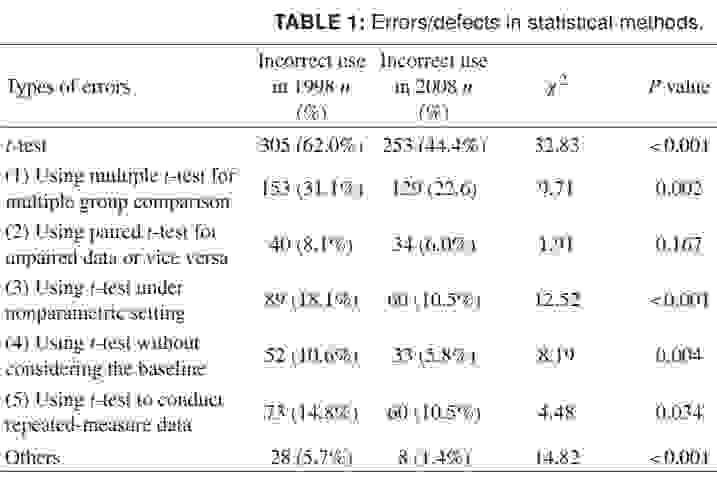
Напоследок, чтобы вы представили весь масштаб происходящего, я привожу более свежие данные по неправильному использованию t-критерия. Цифры приведены для 1998 и 2008 года для ряда китайских научных журналов, и говорят сами за себя. Очень хочется, чтобы это оказалось в большей степени небрежностью оформления, чем недостверными научными данными:
Источник: Misuse of Statistical Methods in 10 Leading Chinese Medical Journals in 1998 and 2008. Shunquan Wu et al, The Scientific World Journal, 2011, 11, 2106–2114
Помните, низкая значимость результатов — еще не такая печальная вещь, как ложный результат. Нельзя доводить до научного греха — ложных выводов — искажением данных неправильно примененной статистикой.
Про логическую интерпретацию, в том числе неправильную, статистических данных, я, пожалуй, расскажу отдельно.
Считайте правильно.
Стандартная ошибка разности средних Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Стандартное отклонение образца X: 2.8 —> Конверсия не требуется
Размер образца X: 14 —> Конверсия не требуется
Стандартное отклонение образца Y: 3.2 —> Конверсия не требуется
Размер образца Y: 16 —> Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
1.09544511501033 —> Конверсия не требуется
7 Ошибки Калькуляторы
Стандартная ошибка разности средних формула
Стандартная ошибка разности средних = sqrt(((Стандартное отклонение образца X^2)/Размер образца X)+((Стандартное отклонение образца Y^2)/Размер образца Y))
σμ1-μ2 = sqrt(((σX^2)/NX)+((σY^2)/NY))
Что такое стандартная ошибка и ее важность?
В статистике и анализе данных большое значение имеет стандартная ошибка. Термин «стандартная ошибка» используется для обозначения стандартного отклонения различных выборочных статистических данных, таких как среднее значение или медиана. Например, «стандартная ошибка среднего» относится к стандартному отклонению распределения выборочных средних, взятых из совокупности. Чем меньше стандартная ошибка, тем более репрезентативной будет выборка для генеральной совокупности. Соотношение между стандартной ошибкой и стандартным отклонением таково, что для данного размера выборки стандартная ошибка равна стандартному отклонению, деленному на квадратный корень размера выборки. Стандартная ошибка также обратно пропорциональна размеру выборки; чем больше размер выборки, тем меньше стандартная ошибка, потому что статистика будет приближаться к фактическому значению.
Стандартная ошибка
До сих пор не
объяснялось, как было вычислено
стандартное отклонение этого
гипотетического выборочного
распределения. Вот эта формула:
SmА—mБ
называется
стандартной
ошибкой разности между средними.
Использование
термина стандартная
ошибка вместо
стандартного
отклонения показывает,
что мы вывели стандартное отклонение,
а не пришли к нему через (невозможные)
бесконечные вычисления. Заметьте, что
здесь используется S,
а не σ̅.
Это потому,
что популяционный параметр σ̅МА—МБ
оценивается
на основе выборочных статистик.
Для вычисления в
формулу просто подставляют величины
S2A и
S2Б,
полученные
нами в предыдущих статистических
приложениях. Так,
Вы можете видеть,
что формула применима также и в том
случае, когда NA
и NБ
различны,
т. е. когда число испытуемых (или проб в
интраиндивидуальном эксперименте)
различно для двух условий.
Определение величины t
Следующий шаг
состоит в том, чтобы найти, на сколько
единиц стандартной ошибки отстоит
полученная нами разность МА—Мб
от нуля,
представляющего 263среднюю
нуль-гипотезы. Поскольку полученная
нами разность равнялась +23, а стандартная
ошибка МА—Мб
=6,10, то
очевидно, что наша разность находится
на расстоянии 3,77 единицы стандартной
ошибки выше нуля. Единицы стандартной
ошибки называют t-едини-цами.
Выражение
полученной разности в единицах стандартной
ошибки называют нахождением
величины t
для данной разности. Это
может быть выражено следующей
формулой:
Подставляя значения
из нашего эксперимента по измерению
времени реакции, мы имеем
Заметьте, что нуль
в числителе при числовых операциях
можно опустить. Он служит для того, чтобы
напомнить нам, что мы проверяем
нуль-гипотезу:
М̅А—М̅б
= 0.
Отвержение или неотвержение нуль-гипотезы
Теперь мы готовы
(наконец!) описать, как были получены
диаграммы на рис. 6.1, показывающие
величину
|
|
|
Рис. |
264Разности между средними, необходимую для отвержения нуль-гипотезы. Давайте перерисуем выборочное распределение разностей.
Вы найдете в
Статистической таблице 2 в
конце
данного приложения величину t,
достаточную
для отвержения нуль-гипотезы. Она
дана и для альфа-уровня 0,05, и для
альфа-уровня 0,01. Эти критические
величины зависят
от величины N
для каждого
условия, или, иначе, от числа степеней
свободы, N—1,
для каждого среднего. (Если вы имеете
данное среднее, скажем, 179 мс для 17
испытуемых, эта величина могла
бы быть
получена путем свободного
приписывания любых
величин 16 испытуемым. Однако затем вам
придется
приписать
семнадцатому испытуемому совершенно
определенную величину, чтобы получить
заданное среднее.) Таким образом,
поскольку было 17 испытуемых для каждого
условия, имели место 16+16 = 32 степени
свободы (или df).
В таблице нет
значений именно для 32df
(но величина
для 30df
вполне
годится, так как разница между величинами
t
для 30 и 35df
очень мала.
Чтобы отвергнуть нуль-гипотезу для
0,05 альфа-уровня, требуется t,
равное 2,04,
для альфа-уровня 0,01—t,
равное 2,75.
Величина t,
равная в
нашем эксперименте 3,77, показывает,
что полученная разность +23 попадает в
область
отвержения, даже
если использовать альфа-уровень 0,01.
Вероятности
показаны так же, как на рис. 6.1 (в). Исходя
из этого, наше статистическое решение
будет заключаться в отвержении
нуль-гипотезы.
Распределение,
представленное в величинах t,
является
выборочным распределением t.
Точная форма
t-распределения
будет разной в зависимости от числа
степеней свободы в эксперименте. Вот
почему вы должны находить критические
величины, чтобы определить, является
ли полученное вами различие значимым.
Соседние файлы в папке Готтсданкер
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Критерий Стьюдента применяется для проверки равенства средних значений двух выборок, сравнение количественных значений только двух выборок с нормальным распределением случайной величины.
Критерий Стьюдента определяется по формуле:
$\bar{X_1}$ – выборочные средние значения первой выборки;
$\bar{X_2}$ – выборочные средние значения второй выборки;
n1 – объем первой выборки;
n2 – объем второй выборки;
σ1 и σ2 – среднее квадратическое отклонение в соответствующих выборках и находятся из формулы:
Число степеней свободы определяется по формуле:
k=n1+n2−2
Fкр(α, k) определяется по таблице
При Fнабл<Fкр нулевая гипотеза принимается.
Формула критерия Стьюдента для несвязанных независимых выборок:
Формула для определения стандартной ошибки разности средних арифметических σxy:
Число степеней свободы определяется выражением:
k=n1+n2–2
При n1=n2 число степеней свободы находится по формуле:
k=2n-2
а стандартная ошибка разности средних арифметических σxy задаётся выражением:
Пример
Даны две выборки.
В первой выборки продажа товара со скидкой, а во второй без скидки.
| № п/п | X | Y |
| 1 | 25 | 19 |
| 2 | 34 | 31 |
| 3 | 23 | 17 |
| 4 | 35 | 24 |
| 5 | 33 | 28 |
| 6 | 25 | 31 |
| 7 | 45 | 39 |
| 8 | 41 | 32 |
| 9 | 27 | 38 |
| 10 | 54 | 43 |
| 11 | 32 | 21 |
| 12 | 32 |
По критерию Стьюдента определить зависит ли спрос на товар от скидок на него при p=0.99?
Решение
В соответствии с таблицей n1=12, n2=11
Вычислим дисперсии D(X), D(Y)
| № п/п | X | Y | D(X) | D(Y) |
| 1 | 25 | 19 | 78,028 | 107,4 |
| 2 | 34 | 31 | 0,0278 | 2,6777 |
| 3 | 23 | 17 | 117,36 | 152,86 |
| 4 | 35 | 24 | 1,3611 | 28,769 |
| 5 | 33 | 28 | 0,6944 | 1,8595 |
| 6 | 25 | 31 | 78,028 | 2,6777 |
| 7 | 45 | 39 | 124,69 | 92,86 |
| 8 | 41 | 32 | 51,361 | 6,9504 |
| 9 | 27 | 38 | 46,694 | 74,587 |
| 10 | 54 | 43 | 406,69 | 185,95 |
| 11 | 32 | 21 | 3,3611 | 69,95 |
| 12 | 32 | 3,3611 | ||
| Сумма | 406 | 323 | 911,67 | 726,55 |
| Среднее | 33,833 | 29,364 |
Подставим значения в формулу стандартной ошибки разности средних арифметических σxy:
Вычисляем критерий Стьюдента:
Число степеней свободы равно:
k=12+11–2=21
По таблице Стьюдента находим критическое значение:
tкрит=2,8310
Отсюда tкрит> tнабл, следовательно, зависит.
19864
Критерий Стьюдента применяется для проверки равенства средних значений двух выборок, сравнение количественных значений только двух выборок с нормальным распределением случайной величины.
Критерий Стьюдента определяется по формуле:
$bar{X_1}$ – выборочные средние значения первой выборки;
$bar{X_2}$ – выборочные средние значения второй выборки;
n1 – объем первой выборки;
n2 – объем второй выборки;
σ1 и σ2 – среднее квадратическое отклонение в соответствующих выборках и находятся из формулы:
Число степеней свободы определяется по формуле:
k=n1+n2−2
Fкр(α, k) определяется по таблице
При Fнабл<Fкр нулевая гипотеза принимается.
Формула критерия Стьюдента для несвязанных независимых выборок:
Формула для определения стандартной ошибки разности средних арифметических σxy:
Число степеней свободы определяется выражением:
k=n1+n2–2
При n1=n2 число степеней свободы находится по формуле:
k=2n-2
а стандартная ошибка разности средних арифметических σxy задаётся выражением:
Пример
Даны две выборки.
В первой выборки продажа товара со скидкой, а во второй без скидки.
| № п/п | X | Y |
| 1 | 25 | 19 |
| 2 | 34 | 31 |
| 3 | 23 | 17 |
| 4 | 35 | 24 |
| 5 | 33 | 28 |
| 6 | 25 | 31 |
| 7 | 45 | 39 |
| 8 | 41 | 32 |
| 9 | 27 | 38 |
| 10 | 54 | 43 |
| 11 | 32 | 21 |
| 12 | 32 |
По критерию Стьюдента определить зависит ли спрос на товар от скидок на него при p=0.99?
Решение
В соответствии с таблицей n1=12, n2=11
Вычислим дисперсии D(X), D(Y)
| № п/п | X | Y | D(X) | D(Y) |
| 1 | 25 | 19 | 78,028 | 107,4 |
| 2 | 34 | 31 | 0,0278 | 2,6777 |
| 3 | 23 | 17 | 117,36 | 152,86 |
| 4 | 35 | 24 | 1,3611 | 28,769 |
| 5 | 33 | 28 | 0,6944 | 1,8595 |
| 6 | 25 | 31 | 78,028 | 2,6777 |
| 7 | 45 | 39 | 124,69 | 92,86 |
| 8 | 41 | 32 | 51,361 | 6,9504 |
| 9 | 27 | 38 | 46,694 | 74,587 |
| 10 | 54 | 43 | 406,69 | 185,95 |
| 11 | 32 | 21 | 3,3611 | 69,95 |
| 12 | 32 | 3,3611 | ||
| Сумма | 406 | 323 | 911,67 | 726,55 |
| Среднее | 33,833 | 29,364 |
Подставим значения в формулу стандартной ошибки разности средних арифметических σxy:
Вычисляем критерий Стьюдента:
Число степеней свободы равно:
k=12+11–2=21
По таблице Стьюдента находим критическое значение:
tкрит=2,8310
Отсюда tкрит> tнабл, следовательно, зависит.
19000
Критерий Стьюдента применяется для проверки равенства средних значений двух выборок, сравнение количественных значений только двух выборок с нормальным распределением случайной величины.
Критерий Стьюдента определяется по формуле:
$bar{X_1}$ – выборочные средние значения первой выборки;
$bar{X_2}$ – выборочные средние значения второй выборки;
n1 – объем первой выборки;
n2 – объем второй выборки;
σ1 и σ2 – среднее квадратическое отклонение в соответствующих выборках и находятся из формулы:
Число степеней свободы определяется по формуле:
k=n1+n2−2
Fкр(α, k) определяется по таблице
При Fнабл<Fкр нулевая гипотеза принимается.
Формула критерия Стьюдента для несвязанных независимых выборок:
Формула для определения стандартной ошибки разности средних арифметических σxy:
Число степеней свободы определяется выражением:
k=n1+n2–2
При n1=n2 число степеней свободы находится по формуле:
k=2n-2
а стандартная ошибка разности средних арифметических σxy задаётся выражением:
Пример
Даны две выборки.
В первой выборки продажа товара со скидкой, а во второй без скидки.
| № п/п | X | Y |
| 1 | 25 | 19 |
| 2 | 34 | 31 |
| 3 | 23 | 17 |
| 4 | 35 | 24 |
| 5 | 33 | 28 |
| 6 | 25 | 31 |
| 7 | 45 | 39 |
| 8 | 41 | 32 |
| 9 | 27 | 38 |
| 10 | 54 | 43 |
| 11 | 32 | 21 |
| 12 | 32 |
По критерию Стьюдента определить зависит ли спрос на товар от скидок на него при p=0.99?
Решение
В соответствии с таблицей n1=12, n2=11
Вычислим дисперсии D(X), D(Y)
| № п/п | X | Y | D(X) | D(Y) |
| 1 | 25 | 19 | 78,028 | 107,4 |
| 2 | 34 | 31 | 0,0278 | 2,6777 |
| 3 | 23 | 17 | 117,36 | 152,86 |
| 4 | 35 | 24 | 1,3611 | 28,769 |
| 5 | 33 | 28 | 0,6944 | 1,8595 |
| 6 | 25 | 31 | 78,028 | 2,6777 |
| 7 | 45 | 39 | 124,69 | 92,86 |
| 8 | 41 | 32 | 51,361 | 6,9504 |
| 9 | 27 | 38 | 46,694 | 74,587 |
| 10 | 54 | 43 | 406,69 | 185,95 |
| 11 | 32 | 21 | 3,3611 | 69,95 |
| 12 | 32 | 3,3611 | ||
| Сумма | 406 | 323 | 911,67 | 726,55 |
| Среднее | 33,833 | 29,364 |
Подставим значения в формулу стандартной ошибки разности средних арифметических σxy:
Вычисляем критерий Стьюдента:
Число степеней свободы равно:
k=12+11–2=21
По таблице Стьюдента находим критическое значение:
tкрит=2,8310
Отсюда tкрит> tнабл, следовательно, зависит.
18953
Условное обозначение средней ошибки среднего арифметического — т. Следует помнить, что под «ошибкой» в статистике понимается не ошибка исследования, а мера представительства данной величины, т. е. мера, которой средняя арифметическая величина, полученная на выборочной совокупности (в нашем примере — на 125 детях), отличается от истинной средней арифметической величины, которая была бы получена на генеральной совокупности (в нашем примере это были бы все дети аналогичного возраста, уровня подготовленности и т. д.). Например, в приведенном ранее примере определялась точность попадания малым мячом в цель у 125 детей и была получена средняя арифметическая величина примерно равная 5,6 см. Теперь надо установить, в какой мере эта величина будет характерна, если взять для исследования 200, 300, 500 и больше аналогичных детей. Ответ на этот вопрос и даст вычисление средней ошибки среднего арифметического, которое производится по формуле:
Для приведенного примера величина средней ошибки среднего арифметического будет равна:
Следовательно, M±m = 5,6±0,38. Это означает, что полученная средняя арифметическая величина (M = 5,6) может иметь в других аналогичных исследованиях значения от 5,22 (5,6 — 0,38 = 5,22) до 5,98 (5,6+0,38 = 5,98).
4. Вычисление средней ошибки разности
Условное обозначение средней ошибки разности — t. Таким образом, установлены основные статистические параметры, характеризующие количественную сторону эффективности одной из методик обучения метанию малых мячей в цель. Но в приведенном примере речь шла о сравнительном эксперименте, в котором сопоставлялись две методики обучения. Предположим, что вычисленные параметры характеризуют методику «А». Тогда для методики «Б» также необходимо вычислить аналогичные статистические параметры. Допустим, они будут равны:
МБ 4,7; σБ ± 3,67 mБ ± 0,33
Теперь есть числовые характеристики двух разных методик обучения. Необходимо установить, насколько эти характеристики достоверно различны, т. е. установить статистически реальную значимость разницы между ними. Условно принято считать, что если разница равна трем своим ошибкам или больше, то она является достоверной:
В приведенном примере:
0,9<1,5
Следовательно, найденные количественные характеристики двух методик обучения не имеют достоверных различий и объясняются не закономерными, а случайными факторами. Поэтому можно сделать следующий педагогический вывод: обе методики обучения равноценны по своей эффективности; новая методика расширяет существующие способы решения данной педагогической задачи.
Подобное вычисление средней ошибки разности применяется в тех случаях, когда имеются количественно значительные показатели п (т. е. при большом числе вариант). Если же в распоряжении экспериментатора имеется небольшое число наблюдений (менее 20), то целесообразно вычислять среднюю ошибку разности по формулам:
где С — число степеней свободы вариаций от 1 до ∞, которые равны числу наблюдений без единицы (С = п — 1).
В виде примера можно привести исследование, в котором оценивалась разница в величине становой динамометрии боксеров двух весовых категорий (А. Г. Жданова, 1961). Были получены следующие исходные данные: тяжелый вес — п1 = 12 человек, легкий вес — п2 = 15человек.
М1 = 139,2 кг M2 = 135,0 кг
σ1 = ± 4,2 кг σ2 = ±4,0 кг
m1 = ± 1,23 кг m2 = ± 1,69 кг
Если подставить эти значения в формулы, то получится:
Далее достоверность различия определяют по таблице вероятностей P/t/≥/t1/ по распределению Стьюдента (t — критерий Стьюдента).
В данной таблице столбец t является нормированным отклонением и содержит числа, которые показывают, во сколько раз разница больше средней ошибки. По вычисленным показателям t и С в таблице определяется число Р, которое показывает вероятность разницы между М1 и М2. Чем больше Р, тем менее существенна разница, тем меньше достоверность различий.
В приведенном примере при значении t 2,0 и С = 25 число Р будет равняться 0,0455 (в таблице оно расположено на пересечении строки, соответствующей t 2,0, и столбца, соответствующего С = ∞). Это свидетельствует о том, что реальная разница весьма вероятна.
В тех случаях, когда расчеты показывают отсутствие достоверности различия, преждевременно считать, что между изучаемыми явлениями вообще не может быть различия. Можно лишь утверждать, что нет различия при данных условиях исследования. При увеличении объема выборки достоверность в различии может появиться. Это положение является главным доказательством важности правильного определения необходимого числа исследований до начала эксперимента.
СПИСОК ЛИТЕРАТУРЫ
-
Масальгин Н.А. Математико-статистические методы в спорте. М., ФиС, 1974.
-
Методика и техника статистической обработки первичной социологической информации. Отв. ред. Г.В. Осипов. М., «Наука», 1968.
-
Начинская С.В. Основы спортивной статистики. — К.: Вища шк., 1987. — 189 с.
-
Толоконцев Н.А. Вычисление среднего квадратичного отклонения по размаху. Сравнение с общепринятым методом. Тезисы докладов третьего совещания по применению математических методов в биологии. ЛГУ, 1961, стр. 83 — 85.
-
Фаламеев А.И., Выдрин В.М. Научно-исследовательская работа в тяжелой атлетике. ГДОИФК им. П. Ф. Лесгафта, 1974.
Оценка разности двух показателей
При оценке
существенности разности двух показателей
вначале находят разность
двух показателей
α
по формуле:
После этого
вычисляют среднюю
ошибку разности Sα
и
коэффициент доверительности tα
по формулам:
,
Пример:
Из 125 студентов у 43 (pЭГ
= 34,40%) выявлен высокий уровень личностной
тревожности в экспериментальной группе
(ЭГ). В контрольной группе (КГ) из 125
студентов – высокий уровень личностной
тревожности у 59 (pКГ
= 47,20%). Необходимо определить, имеются
ли существенные различия между
показателями экспериментальной (pЭГ)
и контрольной (pКГ)
групп.
В нашем примере α
= 12,80, Sα
= 6,16, tα
= 2,08. Разность показателей α
превышает
свою ошибку Sα
более, чем в 2 раза (tα
= 2,08).
По таблице Стьюдента
находим, что эмпирическое значение tα
(2,08) превышает табличное для вероятности
ошибки P
= 0,05 (5%). Значение коэффициента Стьюдента
зависит не только от вероятности P
, но и от объема выборки. Число
степеней свободы n‘
при оценке
одного показателя равняется n
– 1, при
оценке достоверности разности двух
показателей n‘
= n1
+ n2
– 2. Так как
эмпирическое значение tα
(2,08) превышает табличное для вероятности
ошибки P
= 0,05 (5%), следовательно, имеются существенные
различия в показателях высоких уровней
личностной тревожности среди студентов
экспериментальной и контрольной групп.
Таблица 2 – Значения
критерия t
(по Стьюденту)
|
Число степеней |
Вероятность |
|||
|
0,05 = 5% |
0,02 = 2% |
0,01 = 1% |
0,001 = 0,1% |
|
|
30 |
2,042 |
2,457 |
2,750 |
3,64 |
|
∞ |
1,957 |
2,326 |
2,575 |
3,29 |
Определение средней ошибки показателей равных или близких к нулю или 100%
Величина средней
ошибки рассчитывается по формуле:
где
Sp
– величина
средней ошибки;
t
– доверительный
коэффициент;
n
– число
наблюдений (объем выборки).
Пример:
По данным минутной пробы Н.И Моисеевой
– В.М. Сысуева у всех 35 студентов
зарегистрирован средний уровень
способности к адаптации и ориентации
во времени (p
= 100%). Значит ли это, что в данной группе
отсутствуют студенты, имеющие высокие
или низкие способности к адаптации?
Принимаем
доверительный коэффициент t
= 2, что соответствует вероятности ошибки
меньше 5% (0,05), тогда средняя ошибка
показателя Sp
= 10,3%.
Следовательно,
при последующих испытаниях число лиц,
имеющих средние способности к адаптации
и ориентации во времени, может быть p
= 100% –
10,3% = 89,7%.
Если необходимо
увеличить надежность вывода, можно
принять t
= 3.
Критерий х2
Часто возникает
задача сравнения частных (например,
процентных) распределений
данных. В этом случае можно воспользоваться
статистикой, именуемой х2-критерий:
где
Pk
–
частоты
результатов наблюдений до эксперимента;
Vk
–
частоты результатов наблюдений после
эксперимента;
S
–
общее
число групп, на которые разделились
результаты наблюдений.
Полученное
расчетным путем значение х2
сопоставляется
с табличным и в случае его превышения
или равенства делается вывод о значимости
различий с определенной вероятностью
допустимой
ошибки.
Таблица 3 – Граничные
(критические)
значения х2-критерия
|
Число |
Вероятность |
||
|
0,05 |
0,01 |
0,001 |
|
|
1 |
3,84 |
6,64 |
10,83 |
|
2 |
5,99 |
9,21 |
13,82 |
|
3 |
7,81 |
11,34 |
16,27 |
|
4 |
9,49 |
13,23 |
18,46 |
|
5 |
11,07 |
15,09 |
20,52 |
|
6 |
12,59 |
16,81 |
22,46 |
|
7 |
14,07 |
18,48 |
24,32 |
|
8 |
15,51 |
20,09 |
26,12 |
|
9 |
16,92 |
21,67 |
27,88 |
|
10 |
18,31 |
23,21 |
29,59 |
Например,
из 100 испытуемых до
начала эксперимента 30 человек показали
результаты
ниже средних, 50 –
средние
и 20 –
выше средних.
После проведения формирующего эксперимента
результаты
распределились следующим образом: 20
человек
показали результаты ниже среднего, 40 –
средние и 40
–
выше среднего уровня.
Можно ли, опираясь
на эти данные, утверждать, что формирующий
эксперимент, направленный на увеличение
показателей (например, уровней самооценки)
удался?
Для
ответа на данный вопрос воспользуемся
формулой.
В данном примере переменная Pk
принимает
значение
30 %, 50 %, 20 %, a
Vk
–
20
%, 40 %, 40 %. Подставив
эти значения в формулу, получим
Воспользуемся
теперь таблицей «Граничные
(критические)
значения х2-критерия»,
где для заданного числа степеней
свободы (S–1=3–1=2)
можно определить степень
значимости различий показателей до и
после эксперимента. Полученное нами
значение 25,33 больше соответствующего
табличного значения
(13,82) при вероятности допустимой ошибки
меньше
0,1 % (0,001). Следовательно, эксперимент
удался, и мы можем
это утверждать, допуская ошибку, не
превышающую
0,1 %.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Стандартная ошибка разности средних Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Стандартное отклонение образца X: 2.8 —> Конверсия не требуется
Размер образца X: 14 —> Конверсия не требуется
Стандартное отклонение образца Y: 3.2 —> Конверсия не требуется
Размер образца Y: 16 —> Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
1.09544511501033 —> Конверсия не требуется
7 Ошибки Калькуляторы
Стандартная ошибка разности средних формула
Стандартная ошибка разности средних = sqrt(((Стандартное отклонение образца X^2)/Размер образца X)+((Стандартное отклонение образца Y^2)/Размер образца Y))
σμ1-μ2 = sqrt(((σX^2)/NX)+((σY^2)/NY))
Что такое стандартная ошибка и ее важность?
В статистике и анализе данных большое значение имеет стандартная ошибка. Термин «стандартная ошибка» используется для обозначения стандартного отклонения различных выборочных статистических данных, таких как среднее значение или медиана. Например, «стандартная ошибка среднего» относится к стандартному отклонению распределения выборочных средних, взятых из совокупности. Чем меньше стандартная ошибка, тем более репрезентативной будет выборка для генеральной совокупности. Соотношение между стандартной ошибкой и стандартным отклонением таково, что для данного размера выборки стандартная ошибка равна стандартному отклонению, деленному на квадратный корень размера выборки. Стандартная ошибка также обратно пропорциональна размеру выборки; чем больше размер выборки, тем меньше стандартная ошибка, потому что статистика будет приближаться к фактическому значению.