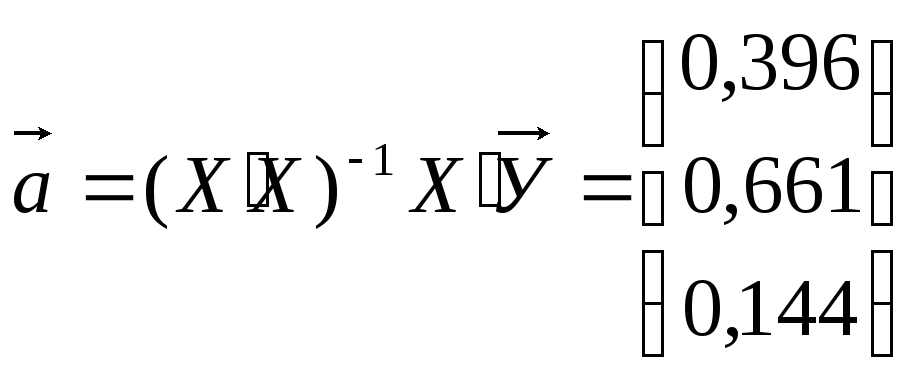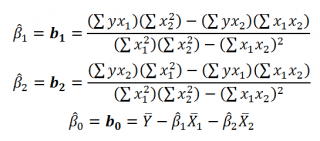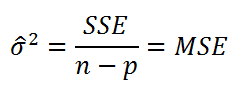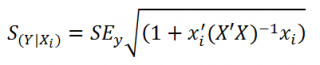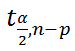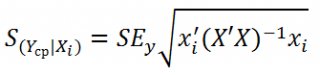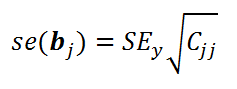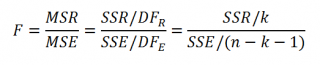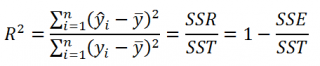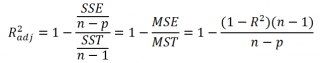Вопросы:
-
Оценка параметров линейной модели
множественной регрессии. -
Оценка качества множественной линейной
регрессии. -
Анализ и прогнозирование на основе
многофакторных моделей.
Множественная регрессия является
обобщением парной регрессии. Она
используется для описания зависимости
между объясняемой (зависимой) переменой
У и объясняющими (независимыми) переменными
Х1,Х2,…,Хk.
Множественная регрессия может быть как
линейная, так и нелинейная, но наибольшее
распространение в экономике получила
линейная множественная регрессия.
1.
Теоретическая линейная модель
множественной регрессии имеет вид:
(1)
соответствующую выборочную регрессию
обозначим:
(2)
Как и в парной регрессии случайный член
ε должен удовлетворять основным
предположениям регрессионного анализа.
Тогда с помощью МНК получают наилучшие
несмещенные и эффективные оценки
параметров теоретической регрессии.
Кроме того переменные Х1,Х2,…,Хkдолжны быть некоррелированы (линейно
независимы) друг с другом. Для того,
чтобы записать формулы для оценки
коэффициентов регрессии (2), полученные
на основе МНК, введем следующие
обозначения:
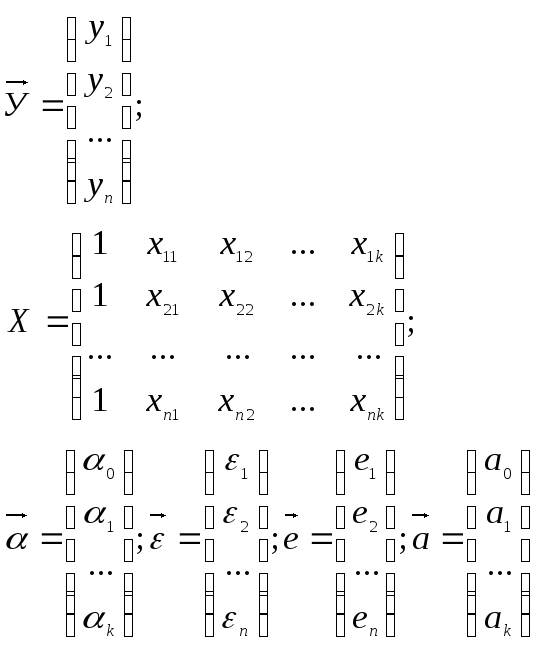
Тогда можно записать в векторно-матричной
форме теоретическую модель:
и выборочную регрессию
.
МНК приводит к следующей формуле для
оценки вектора
коэффициентов выборочной регрессии:
(3)
Для оценки коэффициентов множественной
линейной регрессии с двумя независимыми
переменными
,
можно решить систему уравнений:

Как и в парной линейной регрессии для
множественной регрессии рассчитывается
стандартная ошибка регрессии S:
(5)
и стандартные ошибки коэффициентов
регрессии:
(6)
значимость коэффициентов проверяется
с помощью t-критерия.
(7)
имеющего распространение Стьюдента с
числом степеней свободы v=n-k-1.
2.
Для оценки качества регрессии используется
коэффициент (индекс) детерминации:
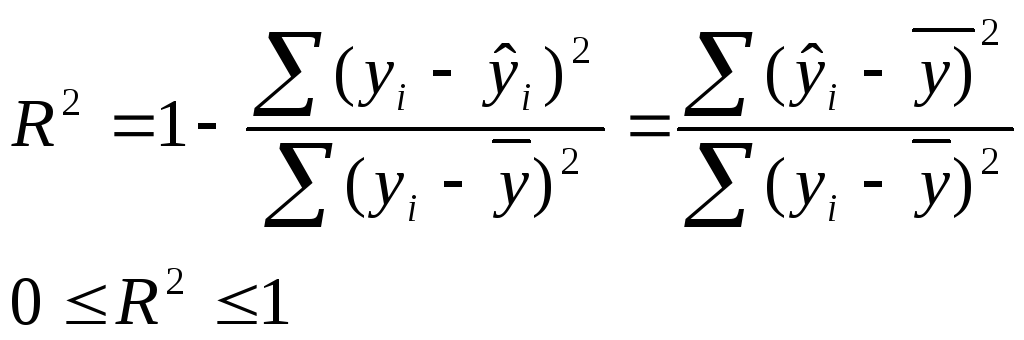
чем ближе
к
1, тем выше качество регрессии.
Для проверки значимости коэффициента
детерминации используется критерий
Фишера или F- статистика.
(9)
с v1 =k,v2=n-k-1
степенями свободы.
В многофакторной регрессии добавление
дополнительных объясняющих переменных
увеличивает коэффициент детерминации.
Для компенсации такого увеличения
вводится скорректированный (или
нормированный) коэффициент детерминации:
(10)
Если увеличение доли объясняемой
регрессии при добавлении новой переменной
мало, то
может
уменьшиться. Значит, добавлять новую
переменную нецелесообразно.
Пример 4:
Пусть рассматривается зависимость
прибыли предприятия от затрат на новое
оборудование и технику и от затрат на
повышение квалификации работников.
Собраны статистические данные по 6
однотипным предприятиям. Данные в млн.
ден. ед. приводятся в таблице 1.
Таблица 1
|
Номер |
Прибыль i-го |
Затраты на |
Затраты на |
|
1 2 3 4 5 6 |
2 3 5 6 8 8 |
3 3 5 7 9 10 |
1 4 5 6 8 11 |
Построить двухфакторную линейную
регрессию
и оценить ее значимость. Введем
обозначения:
Транспонируем матрицу Х:
Обращение этой матрицы:
таким образом зависимость прибыли от
затрат на новое оборудование и технику
и от затрат на повышение квалификации
работников можно описать следующей
регрессией:
Используя формулу (5), где k=2
рассчитаем стандартную ошибку регрессииS=0,636.
Стандартные ошибки коэффициентов
регрессии рассчитаем, используя формулу
(6):
Аналогично:
Проверим значимость коэффициентов
регрессии а1, а2. посчитаемtрасч.
Выберем уровень значимости
,
число степеней свободы
значит коэффициент а1значим.
Оценим значимость коэффициента а2:
Коэффициент а2незначим.
Рассчитаем коэффициент детерминации
по формуле (7)
.
Прибыль предприятия на 96% зависит от
затрат на новое оборудование и технику
и повышение квалификации на 4% от прочих
и случайных факторов. Проверим значимость
коэффициента детерминации. РассчитаемFрасч.:
т.о. коэффициент детерминации значим,
уравнение регрессии значимо.
3.
Большое значение в анализе на основе
многофакторной регрессии имеет сравнение
влияния факторов на зависимый показатель
у. Коэффициенты регрессии для этой цели
не используется, из-за различий единиц
измерения и различной степени колеблемости.
От этих недостатков свободные коэффициенты
эластичности:
(11)
Эластичность показывает, на сколько
процентов в среднем изменяется зависимый
показатель у при изменении переменной
на 1% при условии неизменности значений
остальных переменных. Чем больше,
тем больше влияние соответствующей
переменной. Как и в парной регрессии
для множественной регрессии различают
точечный прогноз и интервальный прогноз.
Точечный прогноз (число) получают при
подстановке прогнозных значений
независимых переменных в уравнение
множественной регрессии. Обозначим
через:
(12)
вектор прогнозных значений независимых
переменных, тогда точечный прогноз
(13)
или
(14)
Стандартная ошибка предсказания в
случае множественной регрессии
определяется следующим образом:
(15)
Выберем уровень значимости α по таблице
распределения Стьюдента. Для уровня
значимости α и числа степеней свободы
ν = n-k-1 найдемtкр. Тогда истинное
значение урс вероятностью 1- α
попадает в интервал:
(16)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
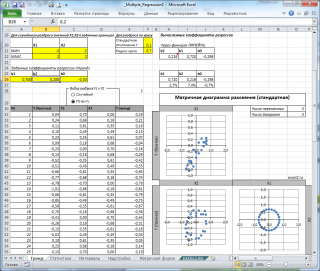
Рассмотрим использование
MS
EXCEL
для прогнозирования переменной
Y
на основании нескольких переменных Х, т.е. множественную регрессию.
Перед прочтением этой статьи рекомендуется освежить в памяти
простую линейную регрессию
– прогнозирование на основе значений только одного фактора.
Disclaimer
: Данную статью не стоит рассматривать, как пересказ главы из учебника по статистике. Статья не обладает ни полнотой, ни строгостью изложения положений статистической науки. Эта статья – о применении MS EXCEL для целей
Множественного регрессионного анализа.
Теоретические отступления приведены лишь из соображения логики изложения. Использование данной статьи для изучения
Регрессии
– плохая идея.
Статья про
Множественный регрессионный анализ
получилась большая, поэтому ниже для удобства приведены ее разделы:
- Оценка неизвестных параметров
- Диаграмма рассеяния
-
Вычисление прогнозных значений Y
(отдельное наблюдение и среднее значение) и построение доверительных интервалов
- Стандартные ошибки и доверительные интервалы для коэффициентов регрессии
- Проверка гипотез
- Генерация данных для множественной регрессии с помощью заданного тренда
- Коэффициент детерминации
Прогнозирование единственной переменной Y на основании значений 2-х или более переменных Х называется
множественной регрессией
.
Множественная линейная регрессионная модель
(Multiple Linear Regression Model)
имеет вид Y=β
0
+β
1
*X
1
+β
2
*X
2
+…+β
k
*X
k
+ε. В этом случае переменная Y зависит от k поясняющих переменных Х, т.е.
регрессоров
. ε —
случайная ошибка
. Модель является линейной относительно неизвестных параметров β.
Оценка неизвестных параметров
В этой статье рассмотрим модель с 2-мя регрессорами. Сначала введем необходимые обозначения и понятия множественной регрессии.
Для описания зависимости Y от 2-х переменных
линейная модель
имеет вид:
Y=β
0
+β
1
*X
1
+β
2
*X
2
+ε.
Параметры этой модели β
i
нам неизвестны, но их можно оценить, используя случайную выборку (измеренные значения переменной Y от заданных Х). Оценки параметров модели (β
0
, β
1
, β
2
) обычно вычисляются
методом наименьших квадратов (МНК)
, который минимизирует сумму квадратов ошибок прогнозирования (критерий минимизации в англоязычной литературе обозначают как SSE – Sum of Squared Errors).
Соответствующие оценки параметров будем обозначать как
b
0
,
b
1
и
b
2
.
Ошибка ε имеет случайную природу и имеет свою функцию распределения со
средним значением
=0 и
дисперсией σ
2
.
Оценки
b
1
и
b
2
называются
коэффициентами регрессии
, они определяют влияние соответствующей переменной X, когда все остальные независимые переменные остаются
неизменными
.
Сдвиг (intercept)
или
постоянный
член
b
0
, определяет прогнозируемое значение Y, когда все поясняющие переменные Х равны 0 (часто
сдвиг
не имеет физического смысла в рамках модели и обусловлен лишь математическими вычислениями
МНК
).
Вычислив оценки, полученные методом
МНК,
позволяют прогнозировать значения переменной Y:
Y=
b
0
+
b
1
*X
1
+
b
2
*X
2
Примечание
: Для случая 2-х регрессоров, все спрогнозированные значения переменной Y будут лежать в плоскости (в
плоскости регрессии
).
В качестве примера рассмотрим технологический процесс изготовления нити:
Инженер, на основе имеющегося опыта, предположил, что
прочность нити
Y зависит от
концентрации исходного раствора
(Х
1
) и
температуры реакции
(Х
2
), и соответствует модели линейной регрессии. Для нахождения комбинации переменных Х, при которых Y принимает максимальное значение, необходимо определить коэффициенты регрессии, сделав выборку.
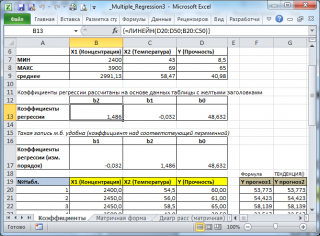
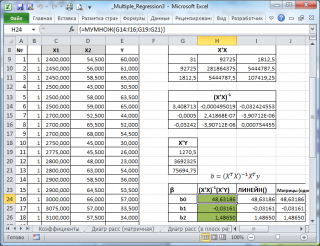
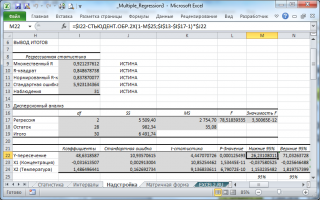
В MS EXCEL
коэффициенты множественной регрессии
удобнее всего вычислить с помощью функции
ЛИНЕЙН()
. Это сделано в
файле примера на листе Коэффициенты
. Чтобы вычислить оценки:
-
выделите 3 ячейки в одной строке (т.к. мы рассматриваем случай 2-х регрессоров, то будут вычислены 2
коэффициента регрессии
+
величина сдвига
= 3 значения, для вывода которых понадобится 3 ячейки). Пусть это будет диапазон
С8:Е8
; -
в
Строке формул
введите =
ЛИНЕЙН(D20:D50;B20:C50)
. Предполагается, что в столбце
В
содержатся прогнозируемые значения Y (в нашей модели это Прочность нити), в столбцах
С
и
D
содержатся значения контролируемых параметров Х (Х1 – Концентрация в столбце С и Х2 – Температура в столбце D). -
нажмите
CTRL
+
SHIFT
+
ENTER
(т.к. этоформула массива
).
В левой ячейке будет рассчитано значение
коэффициента регрессии
b
2
для переменной Х2, в средней ячейке — значение
коэффициента регрессии
b
1
для переменной Х1, в правой –
сдвиг
. Обратите внимание, что порядок вывода
коэффициентов
регрессии
обратный по отношению к расположению столбцов с данными соответствующих переменных Х (вычисленный коэффициент
b
2
располагается
левее
по отношению к
b
1
, тогда как значения переменной Х2 располагаются
правее
значений переменной Х1). Это может привести к путанице, поэтому лучше разместить коэффициенты над соответствующими столбцами с данными, как это сделано в строке 17
файла примера
.
Примечание
: В принципе без функции
ЛИНЕЙН()
можно обойтись, записав альтернативные формулы. Для этого в
файле примера на листе Коэффициенты
в столбцах
I
:
K
вычислены отклонения значений переменных Х
1i
, Х
2i
, Y
i
от их средних значений
, т.е.:
Далее коэффициенты регрессии рассчитываются по следующим формулам (эти формулы справедливы только при прогнозировании по 2-м независимым переменным Х):
При прогнозировании по 3-м и более независимым переменным Х формулы для вычисления
коэффициентов регрессии
значительно усложняются, поэтому следует использовать матричный подход.
В
файле примера на листе Матричная форма
выполнены расчеты
коэффициентов регрессии
с помощью матричного подхода.
Расчет можно произвести как пошагово, так и одной
формулой массива
:
=МУМНОЖ(МОБР(МУМНОЖ(ТРАНСП(B9:D33);(B9:D33)));МУМНОЖ(ТРАНСП(B9:D33);(E9:E33)))
Коэффициенты регрессии
(вектор
b
)
в этом случае вычисляются по формуле
b
=(X
T
X)
-1
(X
T
Y) или в другом виде записи
b
=(X
’
X)
-1
(X
’
Y)
Под Х подразумевается матрица, состоящая из столбцов значений переменной Х с дополнительным столбцом единиц, а под Y – вектор-столбец значений Y.
Символ
Т
или ‘ – это
транспонирование матрицы
, а обозначение
-1
говорит о
вычислении обратной матрицы
.
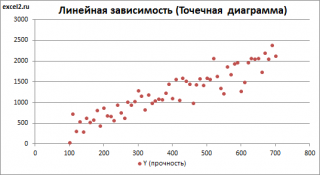
Диаграмма рассеяния
В случае
простой линейной регрессии
(один регрессор, т.е. одна переменная Х) для визуализации связи между прогнозируемым значением Y и переменной Х строят
диаграмму рассеяния
(двумерную).
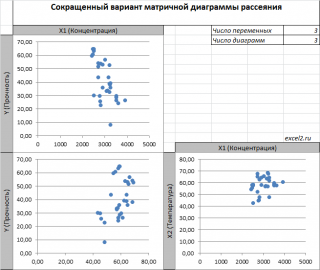
В случае
множественной
линейной регрессии
двумерную диаграмму рассеяния можно построить только для анализа влияния каждого отдельного регрессора на Y (при этом остальные Х не меняются), т.е. так называемую Матричную диаграмму рассеивания (См.
файл примера лист Диагр расс (матричная)
).
К сожалению, такую диаграмму трудно интерпретировать.
Более того, матричная диаграмма может вводить в заблуждение (см.
Introduction
to
linear
regression
analysis
/
D
.
C
.
Montgomery
,
E
.
A
.
Peck
,
G
.
G
.
Vining
, раздел 3.2.5
), демонстрируя наличие или отсутствие линейной взаимосвязи между отдельным регрессором X
i
и Y.
Для случая с 2-мя регрессорами можно предложить альтернативный вид матричной
диаграммы рассеяния
. В стандартной диаграмме рассеяния строятся проекции на координатные плоскости Х1;Х2, Y;X1 и Y;X2. Однако, если взглянуть на точки относительно
плоскости регрессии
, то картину, на мой взгляд, будет проще интерпретировать.
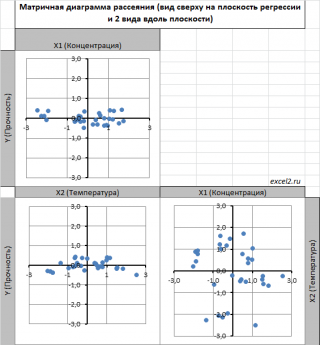
Сравним две матричные диаграммы рассеяния (см.
файл примера на листе «Диагр расс (в плоск регрессии)»
, построенные для одних и тех же наблюдений. Первая – стандартная,
вторая представляет собой вид сверху на плоскость регрессии и 2 вида вдоль плоскости.
На второй диаграмме становится очевидно, что разброс точек относительно плоскости регрессии совсем не большой и поэтому, скорее всего, построенная модель является полезной, а выбранные 2 переменные Х позволяют прогнозировать Y (конечно, для подтверждения этой гипотезы нужно
провести процедуру F-теста
).
Несколько слов о построении альтернативной матричной диаграммы рассеяния:
-
Перед построением необходимо нормировать значения наблюдений (для каждой переменной вычесть
среднее
и разделить на
стандартное отклонение
). В этом случае практически все точки на диаграммах будут находится в диапазоне +/-3 (по аналогии со
стандартным нормальным распределением
, 99% значений которого лежат в пределах +/-3 сигма). В этом случае, на диаграмме можно фиксировать мин/макс значений осей, чтобы EXCEL автоматически не модифицировал масштаб осей при изменении данных (это не всегда удобно);
-
Теперь координаты точек необходимо рассчитать в системе отсчета относительно плоскости регрессии (в которой плоскость Оху’ совпадает с плоскостью регрессии). Для этого необходимо найти
матрицу вращения
, например, через вращение приводящее к совмещению нормали к плоскости регрессии и вектора оси Z (0;0;1);
-
Новые координаты позволяют построить альтернативную матричную диаграмму. Кроме того, для удобства можно вращать систему координат вокруг новой оси Z, чтобы нагляднее представить себе распределение точек относительно плоскости регрессии (для этого использована Полоса прокрутки в ячейках
Q
31:
S
31
).
Вычисление прогнозных значений Y (отдельное наблюдение и среднее значение) и построение доверительных интервалов
После того, как нами были найдены тем или иным способом коэффициенты регрессии можно приступать к вычислению прогнозных значений Y на основе заданных значений переменных Х.
Уравнение прогнозирования или уравнение регрессии в случае 2-х независимых переменных (регрессоров) записывается в виде:
Y=
b
0
+
b
1
*
Х
1
+
b
2
*
Х
2
Примечание:
В MS EXCEL
прогнозное значение Y для заданных Х
1
и Х
2
можно также предсказать с помощью функции
ТЕНДЕНЦИЯ()
. При этом 2-й аргумент будет ссылкой на столбцы, содержащие все значения переменных Х
1
и Х
2
, а 3-й аргумент функции должен быть ссылкой на диапазон ячеек, содержащий 2 значения Х (Х
1i
и Х
2i
) для выбранного наблюдения i (см.
файл примера, лист Коэффициенты, столбец G
). Функция
ПРЕДСКАЗ()
, использованная нами в простой регрессии, не работает в случае
множественной регрессии
.
Найдя прогнозное значение Y, мы, таким образом, вычислим его точечную оценку. Понятно, что фактическое значение Y, полученное при наблюдении, будет, скорее всего, отличаться от этой оценки. Чтобы ответить на вопрос о том, на сколько хорошо мы можем предсказывать новые значения Y, нам потребуется построить
доверительный интервал
этой оценки, т.е. диапазон в котором с определенной заданной вероятностью, скажем 95%, мы ожидаем новое значение Y.
Доверительные интервалы
построим при фиксированном Х для:
- нового наблюдения Y;
- среднего значения Y (интервал будет уже, чем для отдельного нового наблюдения)
Как и в случае
простой линейной регрессии
, для построения
доверительных интервалов
нам потребуется сначала вычислить
стандартную ошибку модели
(standard error of the model)
, которая приблизительно показывает насколько велика ошибка предсказания значений переменной Y на основании значений переменных Х.
Для вычисления
стандартной ошибки
оценивают
дисперсию
ошибки ε, т.е. сигма^2
(ее часто обозначают как
MS
Е либо
MSres
)
. Затем, вычислив из полученной оценки квадратный корень, получим
Стандартную ошибку регрессии (часто обозначают как
SEy
или
sey
).
где SSE – сумма квадратов значений ошибок модели ei=yi — ŷi (
Sum of Squared Errors
). MSE означает Mean Square of Errors (среднее квадратов ошибок, точнее остатков).
Величина n-p – это количество
степеней свободы
(
df
–
degrees
of
freedom
), т.е. число параметров системы, которые могут изменяться независимо (вспомним, что у нас в этом примере есть n независимых наблюдений переменной Y, р – количество оцениваемых параметров модели). В случае
простой множественной регрессии
с 2-мя регрессорами
число степеней свободы
равно n-3, т.к. при построении
плоскости регрессии
было оценено 3 параметра модели
b
(т.е. на это было «потрачено» 3
степени свободы
).
В MS EXCEL
стандартную ошибку
SEy можно вычислить формулы (см.
файл примера, лист Статистика
):
=
ИНДЕКС(ЛИНЕЙН($E$13:$E$43;$C$13:$D$43;;ИСТИНА);3;2)
Стандартная ошибка
нового наблюдения Y при заданных значениях Х (вектор Хi) вычисляется по формуле:
x
i
— вектор-столбец со значениями переменных Х (с дополнительной 1) для заданного наблюдения i.
Соответствующий доверительный интервал вычисляется по формуле:
где α (альфа) –
уровень значимости
(обычно принимают равным 0,05=5%)
р – количество оцениваемых параметров модели (в нашем случае = 3)
n-p – число степеней свободы
–
квантиль
распределения Стьюдента
(задает количество
стандартных ошибок
, в +/- диапазоне которых вероятность обнаружить новое наблюдение равно 1-альфа). Т.е. если
квантиль
равен 2, то диапазон шириной +/- 2
стандартных ошибок
относительно прогнозного значения Y будет с вероятностью 95% содержать новое наблюдение Y (для каждого заданного Хi). В MS EXCEL вычисления квантиля производят по формуле =
СТЬЮДЕНТ.ОБР.2Х(0,05;n-p)
, подробнее см.
в статье про распределение Стьюдента
.
– прогнозное значение Yi вычисляемое по формуле Yi=
b
0+
b
1*
Х1i+
b
2*
Х2i (точечная оценка).
Стандартная ошибка
среднего значения Y при заданных значениях Х (вектор Хi) будет меньше, чем стандартная ошибка отдельного наблюдения. Вычисления производятся по формуле:
x
i
— вектор-столбец со значениями переменных Х (с дополнительной 1) для заданного наблюдения i.
Соответствующий
доверительный интервал
вычисляется по формуле:
Прогнозное значение Yi (точечная оценка) используется тоже, что и для отдельного наблюдения.
Стандартные ошибки и доверительные интервалы для коэффициентов регрессии
В разделе
Оценка неизвестных параметров
мы получили точечные оценки
коэффициентов регрессии
. Так как эти оценки получены на основе случайных величин (значений переменных Х и Y), то эти оценки сами являются случайными величинами и соответственно имеют функцию распределения со
средним значением
и
дисперсией
. Но, чтобы перейти от
точечных оценок
к
интервальным
, необходимо вычислить соответствующие
стандартные ошибки
(т.е.
стандартные отклонения
)
коэффициентов регрессии
.
Стандартная ошибка коэффициента регрессии
b
j
(обозначается
se
(
b
j
)
) вычисляется на основании
стандартной ошибки
по следующей формуле:
где C
jj
является диагональным элементом матрицы (X
’
X)
-1
. Для коэффициента сдвига
b
0
индекс j=1 (верхний левый элемент), для
b
1
индекс j=2,
b
2
индекс j=3 (нижний правый элемент).
SEy –
стандартная ошибка регрессии
(см.
выше
).
В MS EXCEL
стандартные ошибки коэффициентов регрессии
можно вычислить с помощью функции
ЛИНЕЙН()
:
=
ИНДЕКС(ЛИНЕЙН($E$13:$E$43;$C$13:$D$43;;ИСТИНА);2;j)
Примечание
: Подробнее о функции
ЛИНЕЙН()
см. статью
Функция MS EXCEL ЛИНЕЙН()
.
Применяя матричный подход
стандартные ошибки
можно вычислить и через обычные формулы (точнее через
формулу массива
, см.
файл примера лист Статистика
):
=
КОРЕНЬ(СУММКВРАЗН(E13:E43;F13:F43) /(n-p)) *КОРЕНЬ (ИНДЕКС (МОБР (МУМНОЖ(ТРАНСП(B13:D43);(B13:D43)));j;j))
При построении
двухстороннего доверительного интервала
для
коэффициента регрессии
его границы определяются следующим образом:
b
j
+/- t*Se(
b
j
)
где t – это
t-значение
, которое можно вычислить с помощью формулы =
СТЬЮДЕНТ.ОБР.2Х(0,05;n-p)
для
уровня значимости
0,05.
В результате получим, что найденный
доверительный интервал
с вероятностью 95% (1-0,05) накроет истинное значение
коэффициента регрессии
b
j
.
Здесь мы считаем, что
коэффициент регрессии
b
j
имеет
распределение Стьюдента
с n-p
степенями свободы
(n – количество наблюдений, т.е. пар Х и Y).
Проверка гипотез
Когда мы строим модель, мы предполагаем, что между Y и переменными X существует линейная взаимосвязь. Однако, как это иногда бывает в статистике, можно вычислять параметры связи даже тогда, когда в действительности она не существует, и обусловлена лишь случайностью.
Единственный вариант, когда Y не зависит X, возможен, когда все
коэффициенты регрессии
β
равны 0.
Чтобы убедиться, что вычисленная нами оценка
коэффициентов регрессии
не обусловлена лишь случайностью (они не случайно отличны от 0), используют
проверку гипотез
. В качестве
нулевой гипотезы
Н
0
принимают, что линейной связи нет, т.е. ВСЕ β=0. В качестве альтернативной гипотезы
Н
1
принимают, что ХОТЯ БЫ ОДИН коэффициент β <>0.
Процедура проверки значимости множественной регрессии, приведенная ниже, является обобщением
дисперсионного анализа
, использованного нами в случае
простой линейной регрессии (F-тест)
.
Если нулевая гипотеза справедлива, то
тестовая
F
-статистика
имеет
F-распределение
со степенями свободы
k
и
n
—
k
-1
, т.е. F
k, n-k-1
:
Проверку значимости регрессии можно также осуществить через вычисление
p
-значения
. В этом случае вычисляют вероятность того, что случайная величина F примет значение F
0
(это и есть
p-значение
), затем сравнивают p-значение с заданным
уровнем значимости α (альфа)
. Если
p-значение
больше уровня значимости
,
то нулевую гипотезу нет оснований отклонить, и регрессия незначима.
В MS EXCEL значение F
0
можно вычислить на основании значений выборки по вышеуказанной формуле или с помощью функции
ЛИНЕЙН()
:
=
ИНДЕКС(ЛИНЕЙН(E13:E43; C13:D43;;ИСТИНА);4;1)
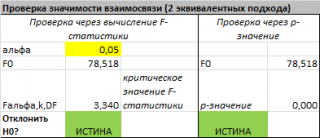
В MS EXCEL для проверки гипотезы через
p
-значение
используйте формулу =F.РАСП.ПХ(F
0
;k;n-k-1)<
альфа
Если формула вернет ИСТИНА, то регрессия значима. Если формула вернет ЛОЖЬ, то у нас нет оснований отклонить нулевую гипотезу, т.е. «скорее всего» все коэффициенты регрессии равны 0 (см.
файл примера лист Статистика
, где показано эквивалентность обоих подходов проверки значимости регрессии).
В MS EXCEL критическое значение для заданного
уровня значимости
F
1-альфа, k, n-k-1
можно вычислить по формуле =
F.ОБР(1- альфа;k;n-k-1)
или =
F.ОБР.ПХ(альфа;k; n-k-1)
. Другими словами требуется вычислить
верхний альфа-
квантиль
F
-распределения
с соответствующими
степенями свободы
.
Таким образом, при значении статистики F
0
> F
1-альфа, k, n-k-1
мы имеем основание для отклонения нулевой гипотезы.
В программах статистики результаты процедуры
F
-теста
выводят с помощью стандартной таблицы
дисперсионного анализа
. В
файле примера такая таблица приведена на листе Надстройка
, которая построена на основе результатов, возвращаемых инструментом
Регрессия надстройки Пакета анализа MS EXCEL
.
Генерация данных для множественной регрессии с помощью заданного тренда
Иногда, бывает удобно сгенерировать значения наблюдений, имея заданный тренд.
Для решения этой задачи нам потребуется:
- задать значения регрессоров в нужном диапазоне (значения переменных Х);
-
задать коэффициенты регрессии (
b
); -
задать тренд (вычислить значения Y=
b
0
+
b
1
*
Х
1
+
b
2
*
Х
2
); - задать величину разброса Y вокруг тренда (варианты: случайный разброс в заданных границах или заданная фигура, например, круг)
Все вычисления выполнены в
файле примера, лист Тренд
для случая 2-х регрессоров. Там же построены
диаграммы рассеяния
.
Коэффициент детерминации
Коэффициент детерминации
R
2
показывает насколько полезна построенная нами
линейная регрессионная модель
.
По определению
коэффициент детерминации
R
2
равен:
R
2
=
Изменчивость объясненная моделью (
SSR
) / Общая изменчивость (
SST
).
Этот показатель можно вычислить с помощью функции
ЛИНЕЙН()
:
=
ИНДЕКС(ЛИНЕЙН(E13:E43;C13:D43;;ИСТИНА);3)
При добавлении в модель новой объясняющей переменной Х,
коэффициент детерминации
будет всегда расти. Поэтому, рост
коэффициента детерминации
не может служить основанием для вывода о том, что новая модель (с дополнительным регрессором) лучше прежней.
Более подходящей статистикой, которая лишена указанного недостатка, является
нормированный
коэффициент детерминации
(Adjusted R-squared):
где p – число независимых
регрессоров
(вычисления см.
файл примера лист Статистика
).
When doing least squares estimation (assuming a normal random component) the regression parameter estimates are normally distributed with mean equal to the true regression parameter and covariance matrix $\Sigma = s^2\cdot(X^TX)^{-1}$ where $s^2$ is the residual variance and $X^TX$ is the design matrix. $X^T$ is the transpose of $X$ and $X$ is defined by the model equation $Y=X\beta+\epsilon$ with $\beta$ the regression parameters and $\epsilon$ is the error term. The estimated standard deviation of a beta parameter is gotten by taking the corresponding term in $(X^TX)^{-1}$ multiplying it by the sample estimate of the residual variance and then taking the square root. This is not a very simple calculation but any software package will compute it for you and provide it in the output.
Example
On page 134 of Draper and Smith (referenced in my comment), they provide the following data for fitting by least squares a model $Y = \beta_0 + \beta_1 X + \varepsilon$ where $\varepsilon \sim N(0, \mathbb{I}\sigma^2)$.
X Y XY
0 -2 0
2 0 0
2 2 4
5 1 5
5 3 15
9 1 9
9 0 0
9 0 0
9 1 9
10 -1 -10
--- -- ---
Sum 60 5 32
Sum of Squares 482 21 528
Looks like an example where the slope should be close to 0.
$$X^t = \pmatrix{
1 &1 &1 &1 &1 &1 &1 &1 &1 &1 \\
0 &2 &2 &5 &5 &9 &9 &9 &9 &10
}.$$
So
$$X^t X = \pmatrix{n &\sum X_i \\ \sum X_i &\sum X_i^2} = \pmatrix{10 &60 \\60 &482}$$
and
$$\eqalign{
(X^t X)^{-1}
&= \pmatrix{
\frac{\sum X_i^2}{n \sum (X_i — \bar{X})^2} &\frac{-\bar{X}}{\sum (X_i-\bar{X})^2} \\
\frac{-\bar{X}}{\sum (X_i-\bar{X})^2} &\frac{1}{\sum (X_i-\bar{X})^2}
} \\
&= \pmatrix{\frac{482}{10(122)} &-\frac{6}{122} \\ -\frac{6}{122} &\frac{1}{122}} \\
&= \pmatrix{0.395 &-0.049 \\ -0.049 &0.008}
}$$
where $\bar{X} = \sum X_i/n = 60/10 = 6$.
Estimate for $β = (X^TX)^{-1} X^TY$ = ( b0 ) =(Yb-b1 Xb)
b1 Sxy/Sxx
b1 = 1/61 = 0.0163 and b0 = 0.5- 0.0163(6) = 0.402
From $(X^TX)^{-1}$ above Sb1 =Se (0.008) and Sb0=Se(0.395) where Se is the estimated standard deviation for the error term. Se =√2.3085.
Sorry that the equations didn’t carry subscripting and superscripting when I cut and pasted them. The table didn’t reproduce well either because the spaces got ignored. The first string of 3 numbers correspond to the first values of X Y and XY and the same for the followinf strings of three. After Sum comes the sums for X Y and XY respectively and then the sum of squares for X Y and XY respectively. The 2×2 matrices got messed up too. The values after the brackets should be in brackets underneath the numbers to the left.
Когда мы хотим понять взаимосвязь между одной переменной-предиктором и переменной-ответом, мы часто используем простую линейную регрессию .
Однако, если мы хотим понять взаимосвязь между несколькими переменными-предикторами и переменной ответа, мы можем вместо этого использовать множественную линейную регрессию .
Если у нас есть p переменных-предикторов, то модель множественной линейной регрессии принимает форму:
Y = β 0 + β 1 X 1 + β 2 X 2 + … + β p X p + ε
куда:
- Y : переменная ответа
- X j : j -я предикторная переменная
- β j : среднее влияние на Y увеличения X j на одну единицу при неизменности всех остальных предикторов.
- ε : Член ошибки
Значения β 0 , β 1 , B 2 , … , β p выбираются методом наименьших квадратов , который минимизирует сумму квадратов невязок (RSS):
RSS = Σ(y i – ŷ i ) 2
куда:
- Σ : греческий символ, означающий сумму
- y i : Фактическое значение отклика для i -го наблюдения
- ŷ i : прогнозируемое значение отклика на основе модели множественной линейной регрессии.
Метод, используемый для нахождения этих оценок коэффициентов, основан на матричной алгебре, и мы не будем здесь подробно останавливаться на нем. К счастью, любой статистический софт может рассчитать эти коэффициенты за вас.
Как интерпретировать вывод множественной линейной регрессии
Предположим, мы подогнали модель множественной линейной регрессии, используя предикторные переменные: количество часов обучения и количество сданных подготовительных экзаменов, а также переменную ответа на экзамене .
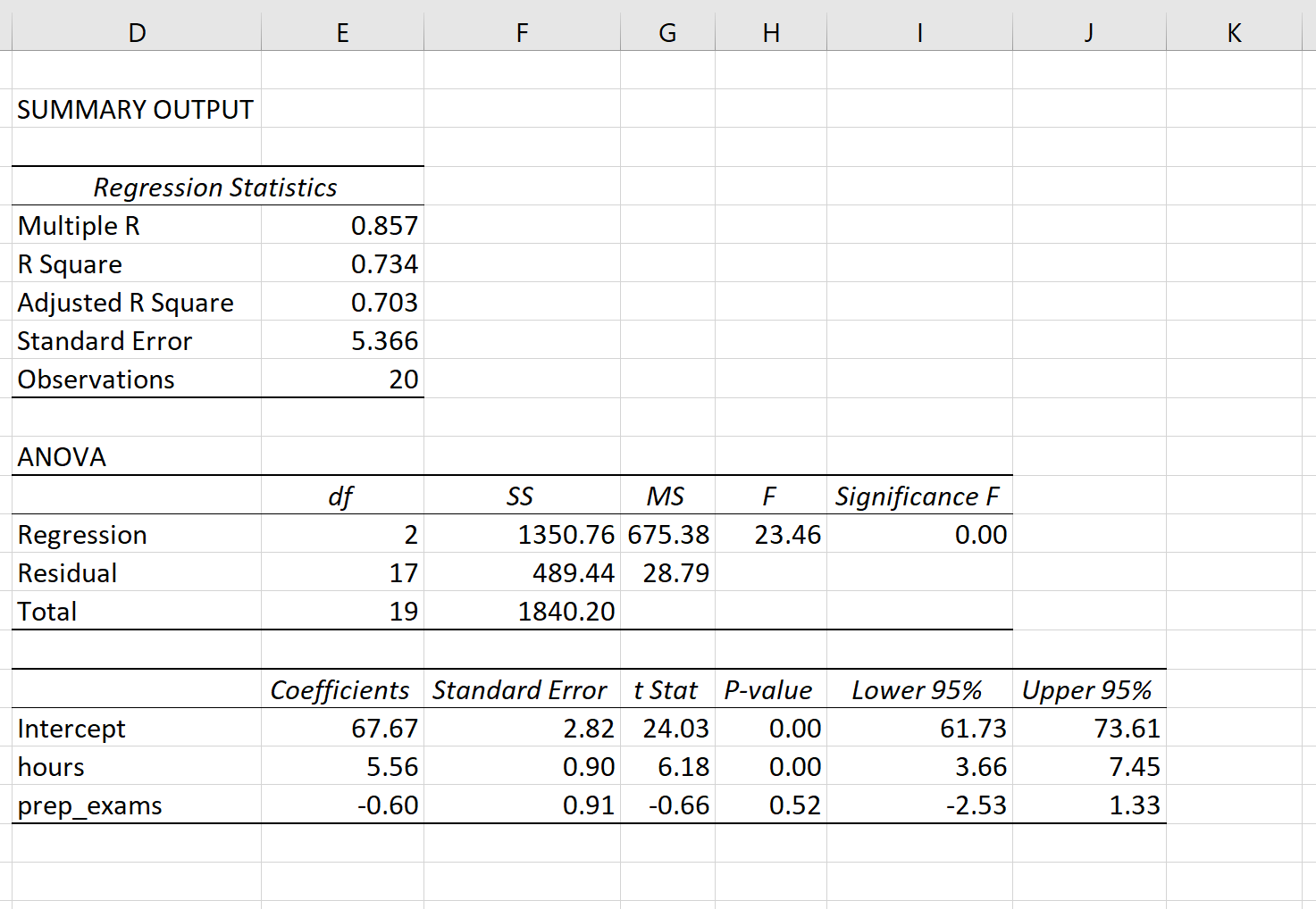
На следующем снимке экрана показано, как могут выглядеть выходные данные множественной линейной регрессии для этой модели:
Примечание. На приведенном ниже снимке экрана показаны выходные данные множественной линейной регрессии для Excel , но числа, показанные в выходных данных, являются типичными для выходных данных регрессии, которые вы увидите с помощью любого статистического программного обеспечения.
Из выходных данных модели коэффициенты позволяют нам сформировать предполагаемую модель множественной линейной регрессии:
Экзаменационный балл = 67,67 + 5,56*(часы) – 0,60*(подготовительные экзамены)
Способ интерпретации коэффициентов следующий:
- Каждое дополнительное увеличение количества часов обучения на одну единицу связано со средним увеличением экзаменационного балла на 5,56 балла, при условии, что подготовительные экзамены остаются постоянными.
- Каждое дополнительное увеличение количества сданных подготовительных экзаменов на одну единицу связано со средним снижением экзаменационного балла на 0,60 балла при условии, что количество учебных часов остается постоянным.
Мы также можем использовать эту модель, чтобы найти ожидаемый результат экзамена, который студент получит на основе общего количества часов обучения и сданных подготовительных экзаменов. Например, студент, который занимается 4 часа и сдает 1 подготовительный экзамен, должен получить на экзамене 89,31 балла:
Экзаменационный балл = 67,67 + 5,56*(4) -0,60*(1) = 89,31
Вот как интерпретировать остальную часть вывода модели:
- R-квадрат: известен как коэффициент детерминации. Это доля дисперсии переменной отклика, которая может быть объяснена объясняющими переменными. В этом примере 73,4% вариаций в экзаменационных баллах можно объяснить количеством часов обучения и количеством сданных подготовительных экзаменов.
- Стандартная ошибка: это среднее расстояние, на которое наблюдаемые значения отклоняются от линии регрессии. В этом примере наблюдаемые значения отклоняются от линии регрессии в среднем на 5,366 единицы.
- F: это общая статистика F для регрессионной модели, рассчитанная как MS регрессии / остаточная MS.
- Значимость F: это значение p, связанное с общей статистикой F. Он говорит нам, является ли регрессионная модель в целом статистически значимой. Другими словами, он говорит нам, имеют ли объединенные две объясняющие переменные статистически значимую связь с переменной отклика. В этом случае p-значение меньше 0,05, что указывает на то, что объясняющие переменные количество часов обучения и количество сданных подготовительных экзаменов в совокупности имеют статистически значимую связь с экзаменационным баллом.
- Коэффициент P-значения. Отдельные p-значения говорят нам, является ли каждая независимая переменная статистически значимой. Мы можем видеть, что изученные часы статистически значимы (p = 0,00), в то время как пройденные подготовительные экзамены (p = 0,52) не являются статистически значимыми при α = 0,05. Поскольку сданные подготовительные экзамены не являются статистически значимыми, мы можем принять решение удалить их из модели.
Как оценить соответствие модели множественной линейной регрессии
Есть два числа, которые обычно используются для оценки того, насколько хорошо модель множественной линейной регрессии «соответствует» набору данных:
1. R-квадрат: это доля дисперсии переменной отклика , которая может быть объяснена переменными-предикторами.
Значение для R-квадрата может варьироваться от 0 до 1. Значение 0 указывает, что переменная отклика вообще не может быть объяснена предикторной переменной. Значение 1 указывает, что переменная отклика может быть полностью объяснена без ошибок с помощью переменной-предиктора.
Чем выше R-квадрат модели, тем лучше модель может соответствовать данным.
2. Стандартная ошибка: это среднее расстояние, на которое наблюдаемые значения отклоняются от линии регрессии. Чем меньше стандартная ошибка, тем лучше модель соответствует данным.
Если мы заинтересованы в прогнозировании с использованием модели регрессии, стандартная ошибка регрессии может быть более полезной метрикой, чем R-квадрат, потому что она дает нам представление о том, насколько точными будут наши прогнозы в единицах измерения.
Для полного объяснения плюсов и минусов использования R-квадрата и стандартной ошибки для оценки соответствия модели ознакомьтесь со следующими статьями:
- Что такое хорошее значение R-квадрата?
- Понимание стандартной ошибки регрессионной модели
Предположения множественной линейной регрессии
Существует четыре ключевых предположения, которые множественная линейная регрессия делает в отношении данных:
1. Линейная зависимость. Существует линейная зависимость между независимой переменной x и зависимой переменной y.
2. Независимость: Остатки независимы. В частности, нет корреляции между последовательными остатками в данных временных рядов.
3. Гомоскедастичность: остатки имеют постоянную дисперсию на каждом уровне x.
4. Нормальность: остатки модели нормально распределены.
Для полного объяснения того, как проверить эти предположения, ознакомьтесь с этой статьей .
Множественная линейная регрессия с использованием программного обеспечения
В следующих руководствах представлены пошаговые примеры выполнения множественной линейной регрессии с использованием различных статистических программ:
Как выполнить множественную линейную регрессию в R
Как выполнить множественную линейную регрессию в Python
Как выполнить множественную линейную регрессию в Excel
Как выполнить множественную линейную регрессию в SPSS
Как выполнить множественную линейную регрессию в Stata
Как выполнить линейную регрессию в Google Sheets
ЭКОНОМЕТРИКА
Конспект лекций для магистрантов
Содержание
Раздел 1. Основы регрессионного анализа ………………………………………………………………3
1.1. Предмет и цель исследований эконометрики. Основные понятия ………………….3
1.1.1. Сущность и история возникновения эконометрики …………………………………3
1.1.2. Основные понятия эконометрики …………………………………………………………..3
1.1.3. Парная линейная регрессия …………………………………………………………………….5
1.2. Оценка параметров парной линейной регрессии. Метод наименьших
квадратов (МНК). ……………………………………………………………………………………………………….6
1.2.1. МНК для парной линейной регрессии …………………………………………………….6
1.2.2. Условия Гаусса-Маркова (предпосылки МНК) ……………………………………….7
1.2.3. Статистика Дарбина-Уотсона (DW) ………………………………………………………..8
1.2.4. Коэффициенты корреляции и детерминации …………………………………………..9
1.3.
Оценка
существенности
уравнения
регрессии
и
его
параметров.
Прогнозирование в линейной регрессии …………………………………………………………………….10
1.3.1. Оценка значимости по критериям Фишера и Стьюдента ……………………….10
1.3.2. Прогнозирование в линейной регрессии ……………………………………………….14
1.3.3. Ошибки аппроксимации ……………………………………………………………………….15
Раздел 2. Множественная регрессия ……………………………………………………………………..15
2.1. Отбор факторов и выбор формы уравнения множественной регрессии ………..15
2.1.1. Требования к отбору факторов ……………………………………………………………..15
2.1.2. Фиктивные переменные ……………………………………………………………………….18
2.1.3. Ошибки спецификации …………………………………………………………………………20
2.2. Традиционный метод наименьших квадратов для множественной регрессии.
Частная и множественная корреляция ……………………………………………………………………….21
2.2.1. МНК для множественной регрессии ……………………………………………………..21
2.2.2. Частные уравнения, частная корреляция ……………………………………………….22
2.2.3. Коэффициенты множественной корреляции и детерминации ………………..24
2.2.4. Оценка значимости уравнения множественной регрессии ……………………..26
Раздел 3. Нелинейная регрессия ……………………………………………………………………………29
1
3.1. Линеаризация нелинейной регрессии ………………………………………………………….29
3.1.1. Виды нелинейной регрессии …………………………………………………………………29
3.1.2. Линеаризация……………………………………………………………………………………….30
3.1.3. Критерий Чоу……………………………………………………………………………………….31
3.1.4. Метод наименьших квадратов для нелинейных регрессионных моделей .32
3.1.5. Корреляция для нелинейной регрессии. Коэффициенты эластичности …..34
3.1.6. Оценка существенности нелинейной регрессии …………………………………….36
2
Раздел 1. Основы регрессионного анализа
1.1. Предмет и цель исследований эконометрики. Основные понятия
1.1.1. Сущность и история возникновения эконометрики
Эконометрика – это отрасль экономической науки, целью которой является
количественное описание экономических отношений. Таким образом, эконометрика
дополняет имеющуюся теорию, используя реальные данные для проверки и уточнения
постулируемых отношений. Если априорно выведен какой-то экономический закон, то с
помощью эконометрических методов его можно эмпирически проанализировать и
доказать.
Эконометрика возникла на стыке трех дисциплин: экономической теории, методов
математического анализа и математической статистики.
Задача эконометрики состоит в том, чтобы с помощью статистики найти выражения
тех закономерностей, которые экономическая теория и математическая экономика
определяют в общем. В эконометрике оперируют конкретными экономическими данными
и количественно описывают конкретные взаимосвязи, т.е. коэффициенты, представленные
в общем виде в этих взаимосвязях, заменяют конкретными численными значениями.
Если обратиться к истории, то можно увидеть, что от зарождения до выделения в
самостоятельную область знания эконометрика прошла длинный путь. Одним из первых
количественных законов стал закон Кинга (Г.Кинг, 1648-1712), в котором выяснялись
закономерности спроса на основе соотношений между урожаем зерновых и ценами на
зерно. Впервые парную корреляцию начали применять на рубеже XIX и XX веков
(Дж.Юл, 1895, 1896; Г.Хукер, 1901) при изучении показателей благосостояния.
Первой
книгой,
которую
можно
назвать
эконометрической,
была
книга
американского ученого Г.Мура «Законы заработной платы: эссе по статистической
экономике» (1911). В конце 1930 года в США было создано первое международное
эконометрическое общество. С 1933 года начал издаваться журнал «Econometrica». В 1941
году появился первый учебник по эконометрике, автором которого был Я.Тинберген.
1.1.2. Основные понятия эконометрики
Эконометрическая модель, как правило; основана на теоретическом предположении
о круге взаимосвязанных переменных и характере связи между ними. При стремлении к
«наилучшему» описанию связей приоритет отдается качественному анализу. В связи с
этим можно выделить следующие этапы эконометрического исследования:
1) постановка задачи;
2) получение данных, анализ их качества;
3
3) разработка теоретической модели, спецификация модели;
4) оценка параметров;
5) апробация и интерпретация результатов;
6) сопровождение модели.
Основной базой данных для эконометрических исследований служат данные
официальной статистики либо бухгалтерского учета. Таким образом, проблемы
экономического измерения — это проблемы статистики и учета. Используя экономическую
теорию, можно определить связь между признаками и показателями, а применяя
статистику и учет, можно ответить на вопросы, связанные с конкретными значениями
экономических показателей.
При моделировании экономических процессов используются два типа данных:
1) пространственные;
2) временные.
Пространственными данными является набор сведений по разным объектам,
взятым за один и тот же период или момент времени (статическая взаимосвязь).
Примерами таких данных могут служить набор сведений по разным фирмам (объем
производства, численнocть работников, размер основных производственных фондов,
доход за определенный период и т.д.), данные об объеме, ценах потребления некоторого
товара по потребителям.
Временными данными является набор сведений, характеризующих один и тот же
объект, но в разные периоды или моменты времени (динамическая взаимосвязь).
Примером таких данных могут служить ежемесячные или ежеквартальные данные о
средней заработной плате, индексе потребительских цен, объеме выпуска либо
ежедневном курсе доллара или евро на бирже. Отличительная особенность временных
данных заключается в том, что они естественным образом упорядочены по времени,
кроме того, наблюдения в близкие моменты времени могут быть зависимы.
Набор сведений представляет собой множество признаков, характеризующих объект
исследования. Признаки являются взаимосвязанными, причем в этой взаимосвязи они
могут выступать в одной из двух ролей:
1) в качестве результативного признака (аналог зависимой переменной у в
математике);
2) факторного признака, значения которого определяют значения признакарезультата (аналог независимой переменной x в математике).
В эконометрической модели результативный признак называют объясняемой
переменной, а факторный признак — объясняющей переменной.
4
Переменные, участвующие в эконометрической модели любого типа, разделяются на
следующие виды:
• экзогенные или независимые (x), значения которых задаются извне, т.е. автономно,
в определенной степени они являются управляемыми (планируемыми);
• эндогенные или зависимые (у), значения которых определяются внутри модели,
или взаимозависимые;
• лаговые — экзогенные или эндогенные переменные эконометрической модели,
датированные предыдущими моментами времени и находящиеся в уравнении с текущими
переменными. Так, yt — .текущая эндогенная переменная, a yt-1 , yt-2 — лаговые эндогенные
переменные;
• предопределенные переменные. К ним относятся текущие (xt) и лаговые
экзогенные·переменные (xt , xt-1), а также лаговые эндогенные переменные (yt-1 , yt-2.).
1.1.3. Парная линейная регрессия
Регрессионный анализ — это один из наиболее распространенных инструментов
эконометрического анализа, который позволяет оценить связи между зависимой
(объясняемой) и независимыми (объясняющими) переменными. Зависимую переменную
иногда
называют
результативным
признаком,
а
объясняющие
переменные
предикторами, регрессорами или факторами.
Обозначим
зависимую
(объясняемую)
переменную
как
y,
а
независимые
(объясняющие) переменные как x1, x2, …….. , xk . Если k = 1 и есть только одна
независимая переменная x1 (которую обозначим x ), то регрессия называется простой или
парной. Если k = 2, 3, ….., то регрессия называется множественной.
Определение вида модели, исходя из соответствующей теории связи между
переменными, называется спецификацией модели. При изучении зависимости между
двумя переменными достаточно наглядным является графический метод. Он основан на
поле корреляции. Полем корреляции называется графическое изображение взаимосвязи
между двумя переменными на координатной плоскости. Если пары переменных (xi, yi),
(i=1,…,n) изображать в виде точек на плоскости, то можно получить представление о
функциональной зависимости между ними.
Начнем с построения простейшей модели парной регрессии
y = a + bx + ε ,
(1.1)
где y – зависимая переменная, состоящая из двух слагаемых: 1) неслучайной
составляющей yx = a + bx (x – независимая переменная, a и b – постоянные числа –
параметры уравнения); 2) и случайной составляющей ε.
Существование отклонений от прямой регрессии, т.е. случайных составляющих ε,
объясняется рядом причин, например:
5
1. Ошибки измерения.
2. Невключение объясняющих переменных.
3. Неправильный выбор вида зависимости в уравнении.
4. Отражение уравнением регрессии связи между агрегированными переменными.
1.2. Оценка параметров парной линейной регрессии. Метод наименьших квадратов
(МНК).
1.2.1. МНК для парной линейной регрессии
Для оценки параметров a, b обычно применяют метод наименьших квадратов
(МНК). Существуют и другие методы оценки параметров, например, метод моментов,
метод наименьших модулей, метод максимального правдоподобия. Рассмотрим метод
наименьших квадратов.
Если имеется n наблюдений, уравнение (1.1) можно представить в следующем виде:
yi = a + bxi + εi ,
i = 1, 2, 3, … , n.
Случайное отклонение ε можно рассматривать как последовательность n случайных
величин εi , i = 1, 2, 3, … , n.
Метод наименьших квадратов позволяет получить такие оценки параметров a и b,
при которых сумма квадратов отклонений фактических значений признака yi от расчетных
(теоретических) yxi является минимальной:
(1.2)
Необходимым условием существования минимума функции двух переменных Q(a,b)
(1.2) является равенство нулю ее частных производных по неизвестным параметрам a и b:
(1.3)
После преобразований получаем систему уравнений:
(1.4)
Система уравнений (1.4) представляет собой систему нормальных уравнений МНК.
Разделив оба уравнения системы (1.4) на n, получим:
Отсюда находим a и b:
6
В этих уравнениях
и
— это средние значения переменных x и y.
Коэффициент b при x называется коэффициентом регрессии. Если переменную x
изменить на единицу, т.е. взять за x величину x+1, то новое значение yx(x+1) будет равно
yx(x)+b. Следовательно, коэффициент регрессии показывает среднее изменение результата
y при изменении фактора x на единицу.
Коэффициент a – свободный член уравнения регрессии — указывает на значение
результативного признака при нулевом значении фактора. Это важный индикатор для
выбора вида уравнения регрессии. Например, если в результате вычислений коэффициент
a оказался отрицательным, а экономический смысл задачи диктует положительность или
равенство нулю показателя a , значит, выбор вида уравнения был неудачен.
1.2.2. Условия Гаусса-Маркова (предпосылки МНК)
Свойства
оценок
коэффициентов
регрессии,
а
следовательно,
и
качество
построенной регрессии существенно зависят от свойств случайного отклонения ε.
Доказано, что для получения по МНК наилучших результатов необходимо, чтобы
выполнялся ряд предпосылок относительно случайного отклонения:
1. Математическое ожидание случайного отклонения εi равно нулю:
М(εi) = 0, i = 1, 2, … , n.
2. Дисперсии случайных отклонений εi для всех наблюдений равны:
D(εi) = D(εj) = σ2=const, i, j = 1, 2, … , n.
Выполнимость данной предпосылки называется гомоскедастичностью
(постоянством дисперсий отклонений).
Невыполнимость данной предпосылки называется гетероскедастичностью
(непостоянством дисперсий отклонений).
3. Случайные отклонения εi при разных наблюдениях являются независимы друг от
друга, т.е. корреляционный момент, или ковариация, между εi и εj при i≠j равна 0:
cov(εi,εj) = 0 для i≠j, i, j = 1, 2, … , n.
Выполнимость данной предпосылки означает отсутствие автокорреляции.
Невыполнимость данной предпосылки говорит о наличии автокорреляции
случайных отклонений.
4. Случайное отклонение εi должно быть независимо от объясняющих переменных:
cov(εi,xi) = 0, i = 1, 2, … , n.
5. Модель является линейной относительно параметров.
Теорема Гаусса-Маркова.
Если предпосылки 1-5 выполнены, то оценки, полученные по МНК, обладают
следующими свойствами:
7
1.
Оценки являются несмещенными, т.е. математическое ожидание оценки
параметра равно самому параметру. Это вытекает из условия, что М(εi)=0, и говорит об
отсутствии систематической ошибки в определении положения линии регрессии.
2.
Оценки состоятельны, т.к. дисперсия оценок параметров при возрастании числа
наблюдений n стремится к нулю. Другими словами, при увеличении объема выборки
надежность оценок увеличивается.
3.
Оценки эффективны, т.е. они имеют наименьшую дисперсию по сравнению с
любыми другими оценками данных параметров, линейными относительно величин yi.
Такие оценки называются наилучшими линейными несмещенными оценками.
1.2.3. Статистика Дарбина-Уотсона (DW)
Выполнимость
предпосылки
Гаусса-Маркова
о
независимости
случайных
отклонений между собой при разных наблюдениях (cov(εi,εj) = 0 – отсутствие
автокорреляции) проверяют с помощью статистики Дарбина-Уотсона DW.
При этом обычно проверяется некоррелированность не любых случайных
отклонений, а только соседних. Соседними обычно считаются соседние во времени (при
рассмотрении временных рядов) или по возрастанию объясняющей переменной x (в
случае пространственной выборки) значения εi. Для этих величин несложно рассчитать
коэффициент корреляции, называемый
коэффициентом автокорреляции первого
порядка:
На практике для анализа коррелированности отклонений вместо коэффициента
корреляции используют тесно с ним связанную статистику Дарбина-Уотсона DW,
рассчитываемую по формуле:
Здесь сделано допущение, что при больших n выполняется соотношение:
2
Тогда
Нетрудно
заметить,
что
если
,
то
(положительная
автокорреляция) и W=0.
Если
, то
(отрицательная автокорреляция) и DW=4.
Во всех других случаях 0
4-dl , то присутствует отрицательная автокорреляция отклонений.
Если du 0, тогда 0≤ rxy ≤1. Чем ближе
значение коэффициента корреляции по модулю |rxy | к единице, тем теснее связь между
признаками в линейной форме. Однако, если абсолютная величина коэффициента
корреляции близка к нулю, то это означает, что между рассматриваемыми признаками
отсутствует линейная связь. При другом виде уравнения регрессии связь может оказаться
достаточно тесной.
Для оценки качества подбора линейного уравнения регрессии находят также квадрат
коэффициента корреляции, называемый коэффициентом детерминации R2 = (rxy)2 . Он
отражает долю вариации результативного признака, объясненную с помощью уравнения
регрессии, или, иными словами, долю дисперсии результата, объясненную регрессией, в
общей дисперсии y:
Следовательно, величина (1-R2) характеризует долю вариации, или долю дисперсии
результата у, вызванную влиянием всех остальных, не учтенных в модели факторов.
Значения коэффициента детерминации могут изменяться от нуля до единицы (0 ≤ R2 ≤ 1).
Например, R2=0,94 означает, что уравнением регрессии объясняется 94% дисперсии
результативного признака, а прочими, не учтенными в модели факторами — 6%. Чем ближе
коэффициент детерминации к единице, тем меньше роль других факторов и линейное
уравнение регрессии описывает лучше исходные данные.
1.3. Оценка существенности уравнения регрессии и его параметров.
Прогнозирование в линейной регрессии
1.3.1. Оценка значимости по критериям Фишера и Стьюдента
После выбора уравнения линейной регрессии и оценки его параметров проводится
оценка статистической значимости как уравнения в целом, так и отдельных его
параметров.
Оценка значимости уравнения регрессии в целом осуществляется с помощью
критерия Фишера, который называют также F-критерием. При этом выдвигается нулевая
10
гипотеза (Н0): коэффициент регрессии равен нулю (b = 0), следовательно, фактор х не
оказывает влияния на результат у и линия регрессии параллельна оси абсцисс.
Перед тем как приступить к расчету критерия Фишера, проведем анализ дисперсии.
Общую сумму квадратов отклонений у от
можно разложить на сумму квадратов
отклонений, объясненную регрессией и сумму квадратов отклонений, не объясненную
регрессией:
где Σ(y —
)2 — общая сумма квадратов отклонений значений результата от среднего по
выборке; Σ(yx —
)2 — сумма квадратов отклонений, объясненная регрессией; Σ(y — ух)2 —
сумма квадратов отклонений, не объясненная регрессией, или остаточная сумма квадратов
отклонений.
Общая сумма квадратов отклонений результативного признака у от среднего
значения
определяется влиянием различных причин. Условно всю совокупность причин
можно разделить на две группы: изучаемый фактор х и прочие, случайные и не
включаемые в модель факторы. Если фактор х не оказывает влияния на результат, то
линия регрессии на графике параллельна оси абсцисс и
= yх. Тогда вся дисперсия
результативного признака обусловлена воздействием прочих факторов и общая сумма
квадратов отклонений совпадает с остаточной:
Σ(y — )2 = Σ(y — ух)2,
Если же прочие факторы не влияют на результат, то у связан с х функционально и
остаточная сумма квадратов равна нулю. В этом случае сумма квадратов отклонений,
объясненная регрессией, совпадает с общей суммой квадратов:
Σ(y — )2 = Σ(yx — )2
Поскольку не все точки поля корреляции лежат на линии регрессии, то всегда имеет
место их разброс, обусловленный как влиянием фактора х, (регрессией у по х), так и
действием прочих причин (необъясненная вариация). Пригодность линии регрессии для
прогноза зависит от того, какая часть общей вариации признака у приходится на
объясненную вариацию. Очевидно, что если сумма квадратов отклонений, обусловленная
регрессией, будет больше остаточной суммы квадратов, то уравнение регрессии
статистически значимо и фактор х оказывает существенное воздействие на результат у.
Это равносильно тому, что коэффициент детерминации R2 будет приближаться к единице.
Любая сумма квадратов отклонений связана с числом степеней свободы df, т.е. с
числом свободы независимого варьирования признака.
11
Для общей суммы квадратов Σ(y — )2 требуется (п-1) независимых отклонений, ибо в
совокупности из п единиц после расчета среднего уровня свободно варьируют лишь (п-1)
число отклонений.
При заданном наборе переменных у и х расчетное значение ух является в линейной
регрессии функцией только одного параметра — коэффициента регрессии b. Таким
образом, факторная сумма квадратов отклонений имеет число степеней свободы, равное
единице. Число степеней свободы остаточной суммы квадратов при линейной регрессии
составляет (п-2).
Существует равенство между числами степеней свободы общей, факторной и
остаточной сумм квадратов. Запишем два равенства:
Σ(y — )2 = Σ(yx — )2 + Σ(y — ух)2,
n – 1 = 1 + (n – 2)
Разделив каждую сумму квадратов на соответствующее ей число степеней свободы,
получим дисперсии на одну степень свободы:
Так как эти дисперсии рассчитаны на одну степень свободы, их можно сравнивать
между собой. Критерий Фишера позволяет проверить нулевую гипотезу Н0 о том, что
факторная и остаточная дисперсии на одну степень свободы равны между собой
(Dфакт=Dост). Критерий Фишера рассчитывается по следующей формуле:
Если гипотеза Н0 подтверждается, то факторная и остаточная дисперсии одинаковы,
и уравнение регрессии незначимо. Чтобы отвергнуть нулевую гипотезу и подтвердить
значимость уравнения регрессии в целом, факторная дисперсия на одну степень свободы
должна превышать остаточную дисперсию на одну степень свободы в несколько раз.
Существуют специальные таблицы критических значений Фишера при различных
уровнях надежности и степенях свободы. В них содержатся максимальные значения
отношений дисперсий, при которых нулевая гипотеза подтверждается. Значение критерия
Фишера для конкретного случая сравнивается с табличным, и на основе этого гипотеза Н0
принимается или отвергается.
Если Fфакт > Fтабл , тогда гипотеза Н0 отклоняется и делается вывод, что связь между
у и х существенна и уравнение регрессии статистически значимо. Если Fфакт ≤ Fтабл ,
12
тогда гипотеза Н0 принимается и делается вывод, что уравнение регрессии статистически
незначимо, так как существует риск (при заданном уровне надежности) сделать
неправильный вывод о наличии связи между х и у.
Между критерием Фишера и коэффициентом детерминации существует связь,
которая выражается следующей формулой для парной линейной регрессии:
В линейной регрессии часто оценивается не только значимость уравнения регрессии
в целом, но и значимость его отдельных параметров, а также коэффициента корреляции.
Для того чтобы осуществить такую оценку, необходимо для всех параметров
рассчитывать стандартные ошибки (та , тb , тr):
Теперь нужно рассчитать критерии Стьюдента ta, tb, tr·. Для параметров а, b и
коэффициента корреляции r критерий Стьюдента определяет соотношение между самим
параметром и его ошибкой:
Фактические значения критерия Стьюдента сравниваются с табличными при
определенном уровне надежности α и числе степеней свободы df= (п-2). По результатам
этого сравнения принимаются или отвергаются нулевые гипотезы о несущественности
параметров или коэффициента корреляции. Если фактическое значение критерия
Стьюдента по модулю больше табличного, тогда гипотеза о несущественности
отвергается. Подтверждение существенности коэффициента регрессии равнозначно
подтверждению существенности уравнения регрессии в целом.
В парной линейной регрессии между критерием Фишера, критериями Стьюдента
коэффициентов регрессии и корреляции существует связь.
F = tb2 = tr2
13
На основании полученной связи можно сделать вывод, что статистическая
незначимость коэффициента регрессии или коэффициента корреляции влечет за собой
незначимость уравнения регрессии в целом, либо, наоборот, незначимость уравнения
регрессии подразумевает несущественность указанных коэффициентов.
На основе стандартных ошибок параметров и табличных значений критерия
Стьюдента можно рассчитать доверительные интервалы:
γa = a ± Δa
γb = b ± Δb
где Δa = tтабл·та — предельная ошибка параметра а; Δb = tтабл·тb — предельная ошибка
коэффициента регрессии b.
Поскольку коэффициент регрессии имеет четкую экономическую интерпретацию, то
доверительные границы интервала для него не должны содержать противоречивых
результатов. Например, такая запись, как -5≤ b ≤ 10, указывает, что истинное значение
коэффициента регрессии одновременно содержит положительные и отрицательные
величины и даже нуль, а этого не может быть. Следовательно, связь между данными
нельзя выразить такой моделью (в частности, парной линейной регрессией), должна
подбираться другая модель.
1.3.2. Прогнозирование в линейной регрессии
После построения уравнения регрессии, и проверки его значимости можно
применять это уравнение для прогнозирования. Однако при этом существуют свои
особенности.
Используя уравнение регрессии, можно получить предсказываемое значение
результата ( yр ) с помощью точечного прогноза при заданном значении фактора хр, т.е.
надо просто подставить в уравнение уx = а + bх соответствующее значение х. Однако
точечный прогноз не дает требуемых представлений, поэтому дополнительно строится его
интервальная оценка, а для этого осуществляться определение стандартной ошибки
предсказываемого значения тур .
Доверительный интервал для прогнозируемого значения рассчитывается следующим
образом:
,
где
— предельная ошибка прогноза.
При прогнозировании на основе уравнения регрессии следует помнить, что величина
прогноза зависит не только от стандартной ошибки индивидуального значения у, но и от
14
точности прогноза фактора х. Его величина может задаваться на основе исследования
других моделей в зависимости от конкретной ситуации, а также по результатам анализа
динамики данного фактора.
1.3.3. Ошибки аппроксимации
Практически всегда фактические значения результативного признака отличаются от
теоретических, рассчитанных по уравнению регрессии. Чем меньше это отличие, тем
ближе будут теоретические значения подходить к эмпирическим, следовательно, тем
лучше подобрано уравнение регрессии. Величина отклонений фактических значений от
расчетных результативного признака (у — yх) по каждому наблюдению представляет собой
абсолютную ошибку аппроксимации. Число ошибок соответствует размеру совокупности.
В отдельных случаях ошибка аппроксимации может оказаться равной нулю (когда в
одном наблюдении фактическое и теоретическое значения результата совпадают).
Отклонения (у- yх) несравнимы между собой за исключением величины, равной нулю.
Для сравнения отклонений относительно фактических значений используются их
величины, выраженные в процентах. Поскольку (у — yх) может быть как положительной,
так отрицательной величиной, то ошибки аппроксимации для каждого наблюдения
принято определять в процентах по модулю
Эти ошибки уже поддаются сравнению, но они оценивают каждое наблюдение в
отдельности. Такую ошибку принято называть относительной ошибкой аппроксимации.
Чтобы оценить качество модели в целом, можно определить среднюю ошибку
аппроксимации, представляющую собой среднее арифметическое относительных ошибок
аппроксимации по всем наблюдениям, включаемым в модель:
Модель считается подобранной достаточно хорошо, если средняя ошибка
аппроксимации не превышает 8-10%.
Раздел 2. Множественная регрессия
2.1. Отбор факторов и выбор формы уравнения множественной регрессии
2.1.1. Требования к отбору факторов
Несмотря на то, что парная линейная регрессия легко интерпретируется, в
действительности она встречается очень редко, поэтому более широкое применение
получила множественная регрессия. Парная регрессия может дать хороший результат
15
при моделировании, если влиянием других факторов, воздействующих на объект
исследования, можно пренебречь. Но поведение отдельных экономических переменных
контролировать нельзя, т.е. равенство всех прочих условий для оценки влияния одного
исследуемого фактора обеспечить не удается. В этом случае следует попытаться выявить
влияние других факторов, введя их в модель. Естественным продолжением парной
линейной регрессии является множественная линейная регрессионная модель с р
переменными:
y = a +b1x1 + b2x2 + … + bpxp + ε
Каждый фактор xi представляет собой набор из п наблюдений по одному и тому же
признаку. Коэффициенты bi — это частные производные у по факторам xi:
при условии, что все остальные факторы постоянны.
Главная цель множественного регрессионного анализа заключается в построении
модели с большим числом факторов и определении при этом влияния каждого из них в
отдельности, а также их совокупности на моделируемый показатель.
Модель линейной множественной регрессии, для которой выполняются условия
Гаусса — Маркова, называется нормальной линейной множественной регрессией.
Приступая к построению множественной регрессии, исследователь в самом начале
сталкивается с проблемами отбора факторов, которые будут учитываться в регрессионном
уравнении, и выбором его вида. При отборе факторов существуют определенные правила,
выполнение которых необходимо, иначе оценки параметров уравнения и оно само будут
недостоверными и не отразят истинную связь результативного признака с факторными.
Факторы должны отвечать следующим требованиям:
1. Факторы должны быть количественно измеряемы. Если модель необходимо
включить качественный фактор, не имеющий количественной меры, то ему нужно
придать количественную определенность (например, в модели урожайности качество
почвы задается в виде баллов; в модели стоимости объектов недвижимости учитывается
место ее нахождения: районы могут быть проранжированы), наличию или отсутствию
какого-либо признака также должно придаваться числовое значение (например, мужчина 0, женщина — 1).
2. Каждый фактор должен быть достаточно тесно связан с результатом (т.е.
коэффициент парной линейной корреляции между каждым включаемым в модель
фактором и результатом должен отличаться от нуля, причем на достаточно большую
величину, что требуется для подтверждения наличия связи).
16
3. Факторы не должны быть тесно связаны между собой и тем более находиться в
строгой функциональной связи (не должны коррелировать друг с другом).
Если между факторами существует высокая корреляция, то нельзя определить
непосредственно влияние каждого из них на результативный показатель, и параметры
уравнения регрессии оказываются неинтерпретируемыми.
Отбор факторов для включения в модель обычно осуществляется в два этапа: на
первом подбираются факторы в зависимости от экономической сущности проблемы (т.е.
набор факторов определяется непосредственно самим исследователем), а на втором на
основе матрицы парных коэффициентов корреляции устанавливается теснота связи для
параметров регрессии.
Считается, что две переменные явно коллинеарны, т.е. линейно зависимы друг от
друга, если rxixj≥0,7. Если факторы явно коллинеарны, то они дублируют друг друга, и
один из них рекомендуется исключать из регрессии. Особенность исключения фактора
состоит в том, что предпочтение отдается не более тесно связанному с результатом, а
тому, который при достаточно тесной связи с результатом имеет наименьшую тесноту
связи с другими факторами, включаемыми в модель. В требовании проявляется специфика
множественной регрессии как метода исследования совокупного воздействия факторов в
условиях их независимости друг от друга.
Однако матрица парных коэффициентов корреляции позволяет проследить лишь
явную связь между факторами (попарно). Намного сложнее установить так называемую
мультuколлuнеарность факторов, когда более чем два из них связаны между собой
нестрогой линейной зависимостью. В связи с этим наибольшие трудности встречаются,
когда необходимо выявить совокупное воздействие нескольких факторов друг на друга.
Если при исследовании модели приходится сталкиваться с мультиколлинеарностью, то
это означает, что некоторые из включаемых в модель факторов всегда будут действовать
вместе.
На практике о наличии мультиколлинеарности судят по определителю матрицы
парной межфакторной корреляции.
Предположим, что модель имеет следующий вид:
y = a +b1x1 + b2x2 + b3x3 + ε.
Построим для нее матрицу парной межфакторной корреляции и найдем ее
определитель:
rх1х1
rх1х2
rх1х3
Det ІRІ = rх2х1
rх2х2
rх2х3
rх3х1
rх3х2
rх3х3
17
Если факторы вообще не коррелируют между собой, то определитель данной
матрицы равняется единице, так как в этом случае:
rх1х1 = rх2х2 = rх3х3 = 1;
rхiхj = rхjхi ;
rх1х2 = rх1х3 = rх2х3 = 0,
и матрица единична, поскольку все недиагональные элементы равны нулю:
1 0 0
Det ІRІ = 0 1 0
= 1.
0 0 1
Если же наоборот, между факторами существует полная линейная зависимость и все
коэффициенты корреляции равны единице, то определитель такой матрицы равен нулю:
1 1 1
Det ІRІ = 1 1 1
= 0.
1 1 1
Можно сделать вывод, что чем ближе к нулю определитель матрицы межфакторной
корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты
множественной регрессии. И наоборот, чем ближе к единице определитель матрицы
межфакторной корреляции, тем меньше мультиколлинеарность факторов.
При наличии явной мультиколлинеарности в модель следует включать не все
факторы, а только те, которые в меньшей степени влияют на мультиколлинеарность (при
условии, что качество модели снижается при этом незначительно). В наибольшей степени
«ответственным» за мультиколлинеарность будет тот признак, который теснее связан с
другими факторами модели (имеет более высокие по модулю значения коэффициентов
парной линейной корреляции).
При отборе факторов также рекомендуется соблюдать следующее правило: число
включаемых в модель факторов должно быть в шесть-семь раз меньше объема
совокупности, по которой строится регрессия.
2.1.2. Фиктивные переменные
До сих пор в качестве факторов рассматривались экономические переменные,
принимающие количественные значения в некотором интервале. Вместе с тем может
оказаться необходимым включить в модель фактор, имеющий два или более качественных
уровней. Это могут быть разного рода атрибутивные признаки, такие, например, как
профессия, пол, образование, климатические условия, принадлежность к определенному
региону. Чтобы ввести такие переменные в регрессионную модель, им должны быть
присвоены те или иные цифровые значения, т.е. качественные переменные должны быть
преобразованы в количественные. Такого вида сконструированные переменные в
18
эконометрике
принято
называть
фиктивными
переменными.
Преобразование
качественных переменных в количественные соответствует первому требованию по
отбору факторов для множественной регрессии.
Предположим, что определено уравнение для потребления кофе:
где
— количество потребляемого кофе;
– цена;
фиктивная переменная
Теоретические значения размера потребления кофе для мужчин будут получены из
уравнения
Для женщин соответствующие значения получим из уравнения
Сопоставив эти результаты, видим, что различия в уровне потребления мужчин и
женщин состоят в различии свободных членов данных уравнений: a – для женщин и a+b –
для мужчин.
В рассмотренном примере качественный фактор имел только два альтернативных
значения (мужчина и женщина), которым и соответствовали обозначения 1 и 0. Если же
число градаций качественного признака-фактора превышает два, то в модель вводится
несколько фиктивных переменных, число которых должно быть меньше числа
качественных градаций.
Общее правило звучит так: если качественная переменная имеет k альтернативных
значений, то при моделировании используются (k-1) фиктивных переменных.
Коэффициенты при фиктивных переменных называются дифференциальными
коэффициентами свободного члена.
Мы рассмотрели модели с фиктивными переменными, в которых последние
выступают факторами. Может возникнуть необходимость построить модель, в которой
бинарный признак играет роль результата. Подобного вида модели применяются,
например, при обработке данных социологических опросов. В качестве зависимой
переменной y рассматриваются ответы на вопросы, данные в альтернативной форме: «да»
или «нет». Поэтому зависимая переменная имеет два значения: 1, когда имеет место ответ
«да», и 0 – во всех остальных случаях. Модель такой зависимой переменной имеет вид:
Такая модель называется вероятностной линейной моделью.
19
2.1.3. Ошибки спецификации
Одним из базовых предположений построения качественной модели является
правильная спецификация уравнения регрессии. Правильная спецификация уравнения
регрессии означает, что оно в целом верно отражает соотношение между экономическими
показателями, участвующими в модели. Это является необходимой предпосылкой
дальнейшего качественного оценивания.
Неправильный
выбор
функциональной
формы
или
набора
объясняющих
переменных называется ошибками спецификации. Рассмотрим основные типы ошибок
спецификации.
1. Отбрасывание значимой переменной.
Например, y = a + b1·x1 + ε вместо
y = a + b1·x1 + b2·x2 + ε .
Исследователь по каким-то причинам (недостаток информации, поверхностное
знание о предмете исследования и т.п.) считает, что на переменную y реально
воздействует лишь переменная x1. При этом он не рассматривает в качестве объясняющей
переменную x2, совершая ошибку отбрасывания существенной переменной. Последствия
данной ошибки достаточно серьезны. Оценки, полученные с помощью МНК по такому
уравнению являются смещенными и несостоятельными даже при бесконечно большом
числе испытаний. Следовательно, возможные интервальные оценки и результаты
проверки соответствующих гипотез будут ненадежны.
2. Добавление незначимой переменной.
В
некоторых
случаях
в
уравнение
регрессии
включают
слишком
много
объясняющих переменных, причем не всегда обоснованно.
Например, y = a + b1·x1 + b2·x2 + ε вместо y = a + b1·x1 + ε .
Исследователь подменяет простую модель более сложной, добавляя при этом не
оказывающую реального воздействия на у объясняющую переменную x2. В этом случае
совершается ошибка добавления несущественной переменной.
Последствия данной ошибки будут не столь серьезными, как в предыдущем случае.
Оценки параметров регрессии остаются для такой модели, как правило, несмещенными и
состоятельными. Однако их точность уменьшится, увеличиваю при этом стандартные
ошибки, т.е. оценки становятся неэффективными, что отразится на их устойчивости.
3. Выбор неправильной функциональной формы.
Например, ln y = a + b1·x1 + b2·x2 + ε или y = a + b1·ln x1 + b2·ln x2 + ε вместо
y=
a + b1·x1 + b2·x2 + ε
Любое эмпирическое уравнение регрессии с теми же переменными, но имеющее
другой функциональный вид, приводит к искажению истинной зависимости. Последствия
данной ошибки будут весьма серьезными. Обычно такая ошибка приводит либо к
20
получению смещенных оценок, либо к ухудшению статистических свойств оценок
коэффициентов регрессии и других показателей качества уравнения.
2.2. Традиционный метод наименьших квадратов для множественной регрессии.
Частная и множественная корреляция
2.2.1. МНК для множественной регрессии
Параметры уравнения множественной регрессии оцениваются, как и в парной
регрессии, с помощью метода наименьших квадратов. При его применении должна
минимизироваться остаточная сумма квадратов отклонений фактических величин от
тeopeтических. Для уравнения множественной регрессии y = a +b1x1 + b2x2 + … + bpxp + ε
это выглядит следующим образом:
Q = Σ (y- yx)2 = Σ (y – (a +b1x1 + b2x2 + … + bpxp ))2→min
В данном случае неизвестными являются параметры регрессии а, b1, b2, … , bр.
Чтобы их найти, продифференцируем остаточную сумму квадратов отклонений по этим
переменным и приравниваем их к нулю. В итоге строится система нормальных уравнений,
решение которой и позволяет получить оценки параметров регрессии:
Σу = пa +b1Σx1 + b2Σx2 + … + bpΣxp
Σуx1 = aΣx1 +b1Σx12 + b2Σx2x1 + … + bpΣxpx1
………………………………………………………
Σуxp = aΣxp +b1Σx1xp + b2Σx2xp + … + bpΣxp2
Эта система может быть решена с помощью метода определителей:
a = Δa/Δ , b1 = Δ b1/Δ , b2 = Δb2/Δ , … , bp = Δbp/Δ
Здесь определитель системы
n
Σx1
Σx2
Σx1
Σx12
Σx2x1 …
Σxpx1
Σx1x2
Σx22
…
Σxpx2
…
…
…
…
…
Σxp
Σx1xp
Σx2xp …
Σxp2
Δ = Σx2
Σxp
…
,
а частичные определители Δa, Δ b1 , Δb2 , … , Δbp получаются в результате замены
соответствующего столбца матрицы определителя системы данными из ее левой части,
например:
Σу
Σx1
Σx2
Σуx1
Σx12
Σx2x1 …
Σxpx1
Σx1x2
Σx22
…
Σxpx2
…
…
…
…
Σx1xp
Σx2xp …
Σxp2
Δa = Σyx2
…
Σyxp
…
Σxp
21
2.2.2. Частные уравнения, частная корреляция
Уравнение множественной линейной регрессии характеризует весь исследуемый
процесс в целом. На его основе могут быть построены частные уравнения регрессии,
которые связывают результативный признак с соответствующим фактором хi при
закреплении других, учитываемых в уравнении множественной регрессии на среднем
уровне:
yx1 x2,x3,…,xp = a +b1x1 + b2x2 + b3x3+ … + bpxp
yx2 x1,x3,…,xp = a +b1x1 + b2x2 + b3x3+ … + bpxp
……………………………………………………
yxp x1,x2,…,xp-1 = a +b1x1 + b2x2 + b3x3+ … + bpxp
Частные уравнения регрессии характеризуют влияние только определенного фактора
на результат, так как другие закреплены на неизменном среднем уровне. На основе
частных уравнений регрессии можно найти частные коэффициенты эластичности. Они
показывают, на сколько процентов в среднем изменится результат при изменении
соответствующего фактора на 1% при постоянных значениях всех остальных факторов.
Эти коэффициенты рассчитываются по следующей формуле:
rде bi — коэффициент «чистой» регрессии для фактора xi в уравнении множественной
регрессии; yxi
x1,x2,…,xi-1,xi+1,…,xp
— частное уравнение регрессии для фактора xi , для
множественной линейной регрессии оно принимает следующий вид:
a +b1x1 + b2x2 + … +bi-1xi-1+ bixi + bi+1xi+1…+ … + bpxp
Частные коэффициенты эластичности рассчитываются для каждого наблюдения и
характеризуют влияние фактора именно на его результат. Кроме того, могут быть
найдены и средние коэффициенты эластичности, которые будут характеризовать
влияние каждого фактора на результат в среднем по совокупности:
где xi — среднее арифметическое по ряду наблюдений фактора xi; yxi,x1,x2,…,xi-1,xi+1,…,xp среднее по частному уравнению регрессии для фактора xi во множественной линейной
регрессии оно принимает вид:
a +b1x1 + b2x2 + … + bpxp
Коэффициенты эластичности можно использовать при отборе факторов для
множественной регрессии. В данном случае сравниваются либо средние по совокупности
22
коэффициенты эластичности, либо коэффициенты эластичности для конкретного
наблюдения, если надо установить силу влияния каждого фактора при этом наблюдении.
Во множественном регрессионном анализе возникает проблема определения
тесноты связи между двумя признаками в «чистом» виде, т.е. при устранении воздействия
других факторов. Это можно сделать только для учтенных в модели факторов.
Показателем «чистого» влияния фактора на результат является частный коэффициент
корреляции.
Рассмотрим пример двухфакторной модели ух = a + b1x1 + b2x2 . Коэффициенты
частной корреляции, показывающие в «чистом» виде тесноту связи фактора и результата,
для двухфакторной модели рассчитываются через коэффициенты детерминации по
следующим формулам:
Эти коэффициенты являются частными коэффициентами корреляции первого
порядка, так как они фиксируют тecноту связи фактора и результата при постоянном
воздействии одного фактора.
Для расчета коэффициентов частной корреляции могут быть использованы парные
коэффициенты
корреляции.
Для
двухфакторной
модели
коэффициенты
частной
корреляции первого порядка вычисляются следующим образом:
При дополнительном включении в модель фактора xi частный коэффициент
корреляции рассчитывается по формуле:
где R2yx1x2…xi…xp , R2yx1x2…xi-1 xi+1…xp – множественный коэффициент детерминации для модели
множественной регрессии соответственно со всем количеством факторов и с р-1, где в
модель не введен фактор xi.
Значения частных коэффициентов корреляции, рассчитанные таким способом,
изменяются от нуля до единицы. Соответственно, чем ближе частный коэффициент
23
корреляции к единице, тем теснее связь между определенным фактором xi и результатом у
при неизменном уровне всех других факторов, включенных в уравнение регрессии.
Порядок частного коэффициента корреляции определяется количеством факторов,
влияние которых исключается: (р-1).
Коэффициенты частной корреляции более высоких порядков так же, как и для
двухфакторной модели, можно рассчитывать, используя частные коэффициенты
корреляции более низких порядков:
Такие
формулы
расчета
коэффициентов
частной
корреляции
называются
рекуррентными, коэффициенты частной корреляции, рассчитанные по ним, изменяют
свое значение от -1 до 1. Чем ближе по модулю коэффициент частной корреляции к
единице, тем теснее связь фактора и результата при устранении влияния прочих факторов,
включенных в модель.
Частные коэффициенты корреляции используются не только для ранжирования
факторов по степени влияния на результат, но и для их отбора. При низких значениях
коэффициентов нет смысла вводить в модель дополнительные факторы и тем самым лишь
усложнять ее.
2.2.3. Коэффициенты множественной корреляции и детерминации
Общее качество уравнения множественной регрессии оценивается с помощью
коэффициента множественной корреляции и его квадрата – коэффициента множественной
детерминации.
По аналогии с парной регрессией коэффициент множественной детерминации
можно определить как долю дисперсии результата, объясненную вариацией включенных в
модель факторов, в его общей дисперсии:
Значения коэффициента множественной детерминации изменяются от нуля до
единицы (0≤R2yx1x2…xp≤1). Чем ближе этот коэффициент к единице, тем больше уравнение
регрессии объясняет поведение результата.
Коэффициент
множественной
корреляции
характеризует
тесноту
связи
рассматриваемого набора факторов с исследуемым признаком или, иными словами,
оценивает тесноту связи совместного влияния факторов на результат.
24
Коэффициент множественной корреляции может быть найден как корень
квадратный из коэффициента множественной детерминации:
Значения коэффициентов множественной корреляции изменяются от нуля до
единицы (0≤Ryx1x2…xp≤1). Чем ближе коэффициент единице, тем теснее связь между
результатом и всеми факторами в совокупности и уравнение регрессии лучше описывает
фактические данные. Если множественный коэффициент корреляции Ryx1x2…xp близок к
нулю, то уравнение регрессии плохо описывает фактические данные, и факторы
оказывают слабое влияние на результат.
Значение коэффициента множественной корреляции больше или равно величине
максимального коэффициента парной корреляции:
Ry x1x2…xp ≥ І ry xi (max) І ,
где i = 1,р.
Если в уравнении регрессии учитывается какой-либо фактор, оказывающий
наиболее сильное воздействие на результативный признак, то частный коэффициент
корреляции будет достаточно близок к коэффициенту множественной корреляции, но ни в
коем случае не больше него.
Иногда для расчета коэффициента множественной корреляции используется еще
одна формула (она применима только для линейной множественной регрессии):
где DetІR+І, DetІRІ — определители матриц соответственно парных коэффициентов
корреляции и межфакторной корреляции.
Эти определители будут иметь следующий вид для уравнения линейной
множественной регрессии с р числом факторов:
Det ІR+І =
1
ryx1
ryx2
…
ryxp
ryx1
1
rx1x2
…
rx1xp
ryx2
rx1x2
1
…
rx2xp
…
…
…
…
…
ryxp
rx1xp
rx2xp
…
1
,
т.е. матрица включает все парные коэффициенты корреляции для уравнения регрессии;
Det ІRІ =
1
rx1x2
…
rx1xp
rx1x2
1
…
rx2xp
…
…
…
…
rx1xp
rx2xp
…
,
1
25
т.е.
данная
матрица
получается
из
предыдущей
матрицы
путем
исключения
коэффициентов парной корреляции факторов с результатом (вычеркиваются первая
строка и первый столбец).
Для того, чтобы не допустить возможного преувеличения тесноты связи, обычно
применяется скорректированный коэффициент множественной корреляции. Он
содержит поправку на число степеней свободы. Ocтaточная сумма квадратов отклонений
делится на число степеней свободы остаточной вариации (п — т — 1), а общая сумма
квадратов отклонений — на число степеней свободы в целом по совокупности (п — 1).
Формула
скорректированного
коэффициента
множественной
корреляции
имеет
следующий вид:
где т — число параметров при переменных х (в линейной зависимости оно будет равно
числу включаемых в модель факторов = p); п — число наблюдений.
, R2 – коэффициент множественной детерминации, то
Так как
скорректированный коэффициент множественной корреляции
а скорректированный коэффициент множественной детерминации
Добавление в модель новых объясняющих переменных осуществляется до тех пор,
пока растет скорректированный коэффициент детерминации.
2.2.4. Оценка значимости уравнения множественной регрессии
Построение эмпирического уравнения регрессии является начальным этапом
эконометрического анализа. Первое же построенное по выборке уравнение регрессии
очень редко является удовлетворительным по тем или иным характеристикам. Поэтому
следующей важнейшей задачей эконометрического анализа является проверка качества
уравнения регрессии. В эконометрике принята устоявшаяся схема такой проверки.
Итак,
проверка
статистического
качества
оцененного
уравнения
регрессии
проводится по следующим направлениям:
проверка значимости уравнения регрессии;
проверка статистической значимости коэффициентов уравнения регрессии;
26
проверка свойств данных, выполнимость которых предполагалась при
оценивании уравнения (проверка выполнимости предпосылок МНК).
Проверка значимости уравнения множественной регрессии, так же как и парной
регрессии, осуществляется с помощью критерия Фишера. В данном случае (в отличие от
парной регрессии) выдвигается нулевая гипотеза Н0 о том, что все коэффициенты
регрессии равны нулю (b1=0, b2=0, … , bm=0). Критерий Фишера определяется по
следующей формуле:
где Dфакт — факторная дисперсия, объясненная регрессией, на одну степень свободы; Dост остаточная дисперсия на одну степень свободы; R2 — коэффициент множественной
детерминации; т — число параметров при факторах х в уравнении регрессии (в парной
линейной регрессии т = 1); п — число наблюдений.
Полученное значение F-критерия сравнивается с табличным при определенном
уровне значимости. Если его фактическое значение больше табличного, тогда гипотеза Но
о незначимости уравнения регрессии отвергается, и принимается альтернативная гипотеза
о его статистической значимости.
С помощью критерия Фишера можно оценить значимость не только уравнения
регрессии в целом, но и значимость дополнительного включения в модель каждого
фактора. Такая оценка необходима для того, чтобы не загружать модель факторами, не
оказывающими существенного влияния на результат. Кроме того, поскольку модель
состоит из несколько факторов, то они могут вводиться в нее в различной
последовательности, а так как между факторами существует корреляция, значимость
включения в модель одного и того же фактора может различаться в зависимости от
последовательности введения в нее факторов.
Для
оценки
значимости
включения
дополнительного
фактора
в
модель
рассчитывается частный критерий Фишера Fxi. Он построен на сравнении прироста
факторной дисперсии, обусловленного включением в модель дополнительного фактора, с
остаточной дисперсией на одну степень свободы по регрессии в целом. Следовательно,
формула расчета частного F-критерия для фактора будет иметь следующий вид:
где R2yx1x2…xi…xp — коэффициент множественной детерминации для модели с полным
набором п факторов; R2yx1x2…x i-1
x i+1…xp
— коэффициент множественной детерминации для
модели, не включающей фактор xi; п — число наблюдений; т — число параметров при
факторах x в уравнении регрессии.
27
Фактическое значение частного критерия Фишера сравнивается с табличным при
уровне значимости 0,05 или 0,1 и соответствующих числах степеней свободы. Если
фактическое значение Fxi превышает Fтабл , то дополнительное включение фактора xi в
модель статистически оправдано, и коэффициент «чистой» регрессии bi при факторе xi
статистически значим. Если же Fxi меньше Fтабл , то дополнительное включение в модель
фактора существенно не увеличивает долю объясненной вариации результата у, и,
следовательно, его включение в модель не имеет смысла, коэффициент регрессии при
данном факторе в этом случае статистически незначим.
С помощью частного критерия Фишера можно проверить значимость всех
коэффициентов регрессии в предположении, что каждый соответствующий фактор xi
вводится в уравнение множественной регрессии последним, а все остальные факторы
были уже включены в модель раньше.
Оценка значимости коэффициентов «чистой» регрессии bi по критерию Стьюдента
t может быть проведена и без расчета частных F-критериев. В этом случае, как и при
парной регрессии, для каждого фактора применяется формула
tbi = bi / mbi ,
где bi — коэффициент «чистой» регрессии при факторе xi ; mbi — стандартная ошибка
коэффициента регрессии bi .
Для множественной линейной регрессии стандартная ошибка коэффициента
регрессии рассчитывается по следующей формуле:
где σy , σxi — среднее квадратическое отклонение соответственно для результата у и xi ;
R2yx1x2…xi…xp — коэффициент множественной детерминации для множественной регрессии с
набором из р факторов; R2xi x1x2…x i-1
x i+1…xp
— коэффициент детерминации для зависимости
фактора xi с остальными факторами множественной регрессии.
Полученные значения t-критериев сравниваются с табличными, и на основе этого
сравнения принимается или отвергается гипотеза о значимости каждого коэффициента
регрессии в отдельности.
28
Раздел 3. Нелинейная регрессия
3.1. Линеаризация нелинейной регрессии
3.1.1. Виды нелинейной регрессии
Во многих случаях при проведении регрессионного анализа применение линейной
модели к изучаемым данным может оказаться неэффективным. В этом случае для
исследования
зависимости
между
результативной
и
факторными
переменными
применяют нелинейные функции.
Различают два основных класса нелинейных моделей:
1) нелинейные модели относительно факторных переменных, но линейные по
оцениваемым параметрам;
2) нелинейные модели по оцениваемым параметрам.
Рассмотрим подробнее первый класс нелинейных моделей. К таким моделям
относятся полиномиальные функции различных порядков (начиная со второго) и
гиперболическая функция.
Общий вид полиномиальной функции п-го порядка или п-й степени можно
представить в виде следующей формулы:
yi = β0 + β1xi + β2x2i + … +βnxni + εi
Наиболее часто из полиномиальных функций используется полином второго
порядка, или параболическая функция:
yi = β0 + β1xi + β2x2i + εi
Регрессионные модели, нелинейные по переменным, отличаются тем, что зависимая
переменная yi линейно связана с оцениваемыми параметрами β0 , … , βn.
Полиномы высоких степеней (более четвертой) использовать при изучении
социально-экономических
связей
между
переменными
не
рекомендуется.
Это
ограничение основано на том, что такие полиномы имеют больше изгибов и отразить
реальную зависимость результативного признака от факторных переменных практически
не способны.
Гиперболическая функция вида
yi = β0 + β1 / xi + εi
также отражает линейную связь между зависимой переменной yi и параметрами β0 и β1, но
является нелинейной по факторной переменной xi . Данная гиперболическая функция равносторонняя.
29
3.1.2. Линеаризация
Для того, чтобы оценить неизвестные параметры β0 , … , βn нелинейной
регрессионной модели, необходимо привести ее к линейному виду. Суть линеаризации
нелинейных по независимым переменным регрессионных моделей заключается в замене
нелинейных факторных переменных на линейные. В общем случае полиномиальной
регрессии процесс замены нелинейных переменных функции п-го порядка выглядит
следующим образом: x = с1, ; х2 = c2 ; xЗ = с3; … ; xп = cп.
Тогда уравнение множественной нелинейной регрессии можно записать в виде
линейного множественного регрессионного уравнения
yi = β0 + β1xi + β2x2i + … +βnxni + εi
=>
=>
yi = β0 + β1c1i + β2c2i + … +βncni + εi
Гиперболическую функцию также можно привести к линейному виду с помощью
замены нелинейной факторной переменной на линейную. Пусть 1/х = с . Тогда исходное
уравнение гиперболической функции можно записать в преобразованном виде:
yi = β0 + β1 / xi + εi
=>
yi = β0 + β1сi + εi
Таким образом, и полиномиальную функцию любой степени, и гиперболоид можно
свести к модели линейной регрессии, что позволяет применять к преобразованной модели
традиционные методы нахождения неизвестных параметров уравнения регрессии
(например, классический МНК) и стандартные методы проверки различных гипотез.
Ко второму классу нелинейных моделей относятся регрессионные модели, в
которых результативная переменная yi нелинейно связана с параметрами уравнения β0 ,…,
βn . К такому типу регрессионных моделей относятся:
1) степенная функция
yi = β0 · x i β1 · εi
2) показательная функция
yi = β0 · β1xi · εi
3) логарифмическая парабола
yi = β0 · β1xi · β2xi · εi2
4) экспоненциальная функция
yi = e β0+β1xi · εi
5) обратная функция
и другие.
Нелинейные по параметрам регрессионные модели в свою очередь делятся на
модели подлежащие линеаризации (внутренне линейные функции) и неподлежащие
30
линеаризации (внутренне нелинейные функции). Примером моделей, которые можно
свести к линейной форме, является показательная функция вида yi = β0 · β1xi · εi , где
случайная ошибка εi мультипликативно связана с факторным признаком xi . Данная
модель нелинейна по параметру β1. Для ее линеаризации вначале осуществим процесс
логарифмирования:
ln yi = ln β0 + xi ·ln β1 + ln εi
Затем воспользуемся методом замен. Пусть ln yi = Yi; ln β0 = А; ln β1 =В; ln εi =Еi.
Тогда преобразованная показательная функция имеет следующий вид:
Yi = А + В xi + Еi .
Следовательно, показательная функция yi = β0 · β1xi · εi
является внутренне
линейной, и оценки ее параметров могут быть найдены с помощью традиционного метода
наименьших квадратов.
Если же взять показательную функцию, включающую случайную ошибку εi
аддитивно, т.е. yi = β0 · β1xi+ εi , то данную модель уже невозможно привести к линейному
виду с помощью логарифмирования. Она является внутренне нелинейной.
Пусть задана степенная функция вида yi = β0 · x i β1 · εi . Прологарифмируем обе части
уравнения:
ln yi = ln β0 + β1·ln xi + ln εi
Теперь воспользуемся методом замен: ln yi = Yi; ln β0 = А; ln xi =Xi; ln εi = Еi .
Тогда преобразованная степенная функция имеет следующий вид:
Yi = А + β1 Xi + Еi .
Степенная функция также является внутренне линейной и ее оценки можно найти с
помощью традиционного метода наименьших квадратов. Но если взять степенную
функцию; виде уравнения yi = β0 · x i β1+ εi , где случайная ошибка аддитивно связана с
факторной переменной, то модель становится внутренне нелинейной.
3.1.3. Критерий Чоу
Одним из нетрадиционных методов линеаризации нелинейных регрессионных
моделей является разбиение всего множества наблюдений на несколько частей, каждую из
которых можно аппроксимировать линейной зависимостью. Может оказаться так, что
линейные регрессии для подвыборок окажутся более эффективными, чем общая
нелинейная модель регрессии. Проверка такого утверждения осуществляется с помощью
теста или критерия Чоу.
Пусть общая выборка имеет объем n. Через S обозначим сумму квадратов
отклонений
для общей нелинейной регрессии. Разобьем общую выборку на две
подвыборки объемами n1 и n2 соответственно (n1 + n2 = n) и построим для каждой из
31
подвыборок частные линейные уравнения регрессии. Через S1 и S2 обозначим суммы
квадратов отклонений для каждой из подвыборок.
Для определения значимости частных регрессионных моделей используется
критерий Фишера. В этом случае выдвигается основная гипотеза о том, что качество
общей регрессионной модели лучше качества частных регрессионных моделей, или
подвыборок. Альтернативная гипотеза утверждает, что регрессионный анализ отдельных
самостоятельных частей выборки дает результат лучше, чем регрессионный анализ
выборки в целом. Наблюдаемое значение F-критерия определяется по формуле
где S — S1 — S2 — величина, характеризующая улучшение качества модели регрессии после
разделения ее на подвыборки; m — количество факторных переменных; п — объем общей
выборочной совокупности.
Критическое значение F-критерия определяется по таблице распределения Фишера в
зависимости от уровня значимости α и двух степеней свободы: k1 = m + 1 и k2 = п — 2т — 2.
Если наблюдаемое значение F-критерия больше критического (F > Fтабл), то основная
гипотеза отклоняется, и качество частных регрессионных моделей превосходит качество
общей модели регрессии. Если наблюдаемое значение F- критерия меньше критического
(F < Fтабл), то основная гипотеза принимается, и аппроксимировать отдельные
подвыборки линейной зависимостью не имеет смысла.
3.1.4. Метод наименьших квадратов для нелинейных регрессионных моделей
Метод наименьших квадратов можно применять к нелинейным регрессионным
моделям только в том случае, если возможна их линеаризация, т.е. они нелинейны по
факторным переменным или нелинейны по параметрам, но внутренне линейны.
Рассмотрим применение МНК для определения неизвестных параметров уравнения
параболической зависимости следующего вида:
yi = β0 + β1xi + β2x2i + εi
Данный полином второго порядка (или второй степени) является нелинейным по
факторным переменным xi . Для нахождения неизвестных параметров уравнения
регрессии β0 , β1 , β2 необходимо минимизировать с помощью МНК функцию Q:
n
n
2
Q = Σ (yi — yx i ) = Σ (yi — β0 — β1xi — β2x2i )2 → min
i=1
i=1
Процесс минимизации функции сводится к вычислению частных производных этой
функции по каждому из оцениваемых параметров. Составим систему уравнений для
данной функции Q, не пользуясь при этом методом замен:
32
дQ = -2 Σ (yi — β0 — β1xi — β2x2i ) = 0
дβ0
дQ = -2 Σ (yi — β0 — β1xi — β2x2i ) xi = 0
дβ1
дQ = -2 Σ (yi — β0 — β1xi — β2x2i ) x2i = 0
дβ2
После элементарных преобразований данной системы уравнений получим
nβ0 + β1 Σ xi + β2 Σ x2i = Σ yi
β0 Σ xi + β1 Σ x2i + β2 Σ x3i = Σ xi yi
β0 Σ x2i + β1 Σ x3i + β2 Σ x4i = Σ x2i yi
Данная система является системой нормальных уравнений относительно параметров
β0, β1 , β2 для параболической зависимости yi = β0 + β1xi + β2x2i + εi . Эта система является
квадратной, т.е. количество уравнений равняется количеству неизвестных переменных.
Коэффициенты β0 , β1 , β2 можно найти с помощью метода Гаусса, если свести систему
нормальных уравнений к линейному виду с помощью метода замен.
В общем случае полинома п-й степени
yi = β0 + β1xi + β2x2i + … +βnxni + εi .
Для нахождения неизвестных коэффициентов уравнения регрессии с помощью МНК
необходимо минимизировать функцию Q следующего вида:
n
n
2
Q = Σ (yi — yx i ) = Σ (yi — β0 — β1xi — β2x2i — … — βnxni)2 → min
i=1
i=1
Тогда систему нормальных уравнений можно записать таким образом:
Σ yi =β0 n + β1 Σ xi + β2 Σ x2i + … + βn Σ xni
Σ yi xi = β0 Σ xi + β1 Σ x2i + β2 Σ x3i + … + βn Σ xn+1i
………………………………………………………………
Σ yi xn-1i = β0 Σ xn-1i + β1 Σ xni + β2 Σ xn+1i + … + βn Σ x2n-1i
Σ yi xni = β0 Σ xni + β1 Σ xn+1i + β2 Σ xn+2i + … + βn Σ x2ni
Решением данной системы будут являться оценки коэффициентов регрессионной
зависимости, выраженной полиномом п-го порядка.
Метод Гаусса применяется в большинстве случаев для решения систем линейных
уравнений, когда число неизвестных параметров не совпадает с количеством уравнений.
Однако его используют и для решения квадратных систем линейных уравнений.
Основная идея решения системы линейных уравнений методом Гаусса заключается
в том, что исходную систему из т линейных уравнений с п неизвестными переменными
необходимо преобразовать к треугольному виду. Для этого в одном из уравнений системы
33
оставляют все неизвестные переменные. В другом сокращают одну из неизвестных
переменных для того, чтобы их число стало (п — 1). В следующем уравнении убирают две
неизвестные переменные, чтобы их число уже было (п — 2). В конце данного процесса
система примет треугольный вид: первое уравнение содержит все, а последнее — только (п
— т) неизвестных, которые называются базисными. Остальные переменные называются
свободными. Дальнейшее решение сводится к выражению свободных неизвестных
переменных через базисные и получению общего решения системы линейных уравнений.
Для осуществления базисного решения системы линейных уравнений свободные
переменные приравнивают к нулю.
3.1.5. Корреляция для нелинейной регрессии. Коэффициенты эластичности
Качество нелинейной регрессионной модели можно определить с помощью
нелинейного показателя корреляции, который называется индексом корреляции для
нелинейных форм связи R.
R можно вычислить на основе теоремы о разложении сумм квадратов. Сумма
квадратов разностей между значениями результативной переменной и ее средним
значением по выборке может быть представлена следующим образом:
,
где
— общая сумма квадратов (TSS – Total Sum Square);
—
сумма квадратов объясненной регрессии (RSS – Regression Sum Square);
—
сумма квадратов остатков (ESS – Error Sum Square).
На основании данной теоремы
Индекс корреляции для нелинейных форм связи изменяется в пределах [0; 1] . Чем
ближе его значение к единице, тем сильнее взаимосвязь между изучаемыми переменными.
Если возвести индекс корреляции в квадрат, то полученная величина будет
называться индексом детерминации для нелинейных форм связи:
Индекс детерминации для нелинейных форм связи по характеристикам аналогичен
обычному множественному коэффициенту детерминации. Индекс R2 показывает, на
сколько процентов построенная модель регрессии объясняет разброс значений зависимой
переменной относительно среднего значения, т.е. какая доля общей дисперсии
результативного признака объясняется вариацией факторных модельных признаков.
Индекс детерминации можно назвать количественной характеристикой объясненной
34
построенным уравнением регрессии дисперсии результативного признака. Чем больше
значение данного показателя, тем лучше уравнение регрессии описывает выявленную
взаимосвязь.
Кроме
рассмотренных
показателей,
для
изучения
зависимости
между
результативной переменной и факторными признаками используются различные
коэффициенты эластичности, которые позволяют оценить тесноту связи между
переменными х и у.
Общий коэффициент эластичности показывает, на сколько процентов изменится
результативный показатель у при изменении величины факторного признака на 1%.
Формула расчета общего коэффициента эластичности имеет вид
где
— первая производная результативной переменной по факторному признаку.
Средний
коэффициент
факторного признака
где
эластичности
вычисляется
для
среднего
значения
по приведенной выше формуле:
— значение функции при среднем значении факторного признака.
Средний
коэффициент
эластичности
характеризует
процентное
изменение
результативного признака у относительно своего среднего значения при изменении
факторного признака на 1% относительного . Такие коэффициенты рассчитываются по
индивидуальным формулам для каждой разновидности функции.
Например, для показательной функции вида
средний коэффициент
эластичности определяется как:
Основное достоинство степенной функции вида
заключается в том, что
средний коэффициент эластичности равен коэффициенту регрессии:
Помимо средних коэффициентов эластичности могут быть также рассчитаны
точечные коэффициенты эластичности. Общая формула их расчета
т.е. эластичность зависит от конкретного заданного значения факторного признака х1.
35
Точечный коэффициент эластичности характеризует процентное изменение
результативной переменной у относительно уровня функции у(х1) при изменении
факторного признака на 1% относительно заданного уровня х1.
Например,
для
параболической
функции
точечный
коэффициент эластичности находится следующим образом:
Знаменателем данного показателя является значение параболической функции в
точке x1.
3.1.6. Оценка существенности нелинейной регрессии
Если нелинейное по факторным переменным уравнение регрессии с помощью
метода замен можно свести к парному линейному уравнению регрессии, то на это
уравнение будут распространяться все методы проверки гипотез для парной линейной
зависимости.
Проверка гипотезы о значимости нелинейной регрессионной модели в целом
осуществляется через F-критерий. Выдвигается основная гипотеза Но о незначимости
коэффициента детерминации для нелинейных форм связи, т.е. о незначимости
полученного уравнения регрессии:
Но :R2= 0.
Альтернативной является обратная гипотеза Н1 о значимости построенного
уравнения регрессии:
Н1 :R2 ≠ 0.
Наблюдаемое значение F-критерия вычисляется по формуле
Fнабл = R2(п — l)
(1-R2)(l-1) ,
где п — объем выборочной совокупности; l — число оцениваемых параметров по
выборочной совокупности.
Критическое значение рассматриваемого критерия Fкрит вычисляется по таблице
распределения Фишера в зависимости от уровня значимости α и числа степеней свободы
k1 = l-1 и k2 = п-l. Если наблюдаемое значение F-критерия больше критического Fнабл >
Fкрит , то основная гипотеза отклоняется, следовательно уравнение нелинейной регрессии
является значимым. Если наблюдаемое значение F-критерия меньше критического (Fнабл <
Fкрит), то основная гипотеза принимается, и уравнение нелинейной регрессии признается
незначимым.
Если
существует
возможность
выбора
между
линейной
и
нелинейной
регрессионными моделями при изучении конкретной зависимости между переменными,
36
то предпочтение всегда отдается более простой линейной форме связи. Проверить
предположение о вероятной линейной зависимости между изучаемыми переменными
можно с помощью линейного коэффициента детерминации r2 и индекса детерминации для
нелинейных форм связи R2.
Выдвигается основная гипотеза Но о линейной зависимости между переменными.
Альтернативной является гипотеза о их нелинейной связи. Проверка этих гипотез
осуществляется с помощью t-критерия Стьюдента. Наблюдаемое значение t-критерия
где
— величина ошибки разности (R2 — r2), вычисляемая по формуле
Критическое значение рассматриваемого критерия tкрит определяется по таблице
распределения Стьюдента в зависимости от уровня значимости α и числа степеней
свободы (п – l – 1), где l — число оцениваемых параметров βi в регрессионной модели. Если
наблюдаемое значение t-критерия больше критического (tнабл > tкрит ), то основная
гипотеза отклоняется и между изучаемыми переменными существует нелинейная
взаимосвязь. Если наблюдаемое значение t-критерия меньше критического (tнабл < tкрит), то
зависимость
между
переменными
может
регрессионным уравнением.
37
быть
аппроксимирована
линейным