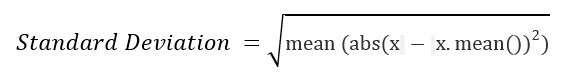Стандартная ошибка numpy

Is it gonna rain today? Should I take my umbrella to the office or not? To know the answer to such questions we will just take out our phone and check the weather forecast. How is this done? There are computer models which use statistics to compare weather conditions from the past with the current conditions to predict future weather conditions. From studying the amount of fluoride that is safe in our toothpaste to predicting the future stock rates, everything requires statistics. Data is everything in statistics. Calculating the range, median, and mode of the data set is all a part of descriptive statistics.

Data representation, manipulation, and visualization are key components in statistics. You can read about it  here.

The next important step is analyzing the data, which can be done using both descriptive and inferential statistics. Both descriptive and inferential statistics are used to analyze results and draw conclusions in most of the research studies conducted on groups of people.

Through this article, we will learn descriptive statistics using python.

Introduction

Descriptive statistics describe the basic and important features of data. Descriptive statistics help simplify and summarize large amounts of data in a sensible manner. For instance, consider the Cumulative Grade Point Index (CGPI), which is used to describe the general performance of a student across a wide range of course experiences.

Descriptive statistics involve evaluating measures of center(centrality measures) and measures of dispersion(spread).

Centrality measures

Centrality measures give us an estimate of the center of a distribution. It gives us a sense of a typical value we would expect to see. The three major measures of center include the mean, median, and mode.

1. Mean means…

   …the average of the given values. To compute mean, sum all the values and divide the sum by the number of values.

   (displaystyleoverline{x}=frac{1}{n}sum_{i=1}^n x_i)

   Consider a class of 7 students. Suppose they appear for midterm exams and score the following marks out of 20:

   Name	Subject 1	Subject 2	Subject 3	Subject 4	Total Marks
   Student 1	10	8	15	11.5	44.5
   Student 2	14	9	7.5	11	41.5
   Student 3	11	17	11.5	9	48.5
   Student 4	7	14.5	10	12	43.5
   Student 5	9.5	12	10.5	14	46
   Student 6	15	18	7	12	52
   Student 7	19	15.5	11	7.5	53

   

   Mean with python

   There are various libraries in python such as pandas, numpy, statistics (Python version 3.4) that support mean calculation.

   numpy.mean(a, axis=None, dtype=None)

   a: array containing numbers whose mean is required
   axis: axis or axes along which the means are computed, default is to compute the mean of the flattened array
   dtype: type of data to be used in calculations

   >>> import numpy as np
   >>> A = np.array([[10,14,11,7,9.5,15,19],[8,9,17,14.5,12,18,15.5],
       [15,7.5,11.5,10,10.5,7,11],[11.5,11,9,12,14,12,7.5]])
   >>> B = A.T
   >>> print B
   [[ 10. 8. 15. 11.5]
    [ 14. 9. 7.5 11. ]
    [ 11. 17. 11.5 9. ]
    [ 7. 14.5 10. 12. ]
    [ 9.5 12. 10.5 14. ]
    [ 15. 18. 7. 12. ]
    [ 19. 15.5 11. 7.5]]
   >>> print(np.mean(B))
   11.75
   >>> print(np.mean(B,axis=0))
   [ 12.21428571 13.42857143 10.35714286 11. ]
   >>> print(np.mean(A,axis=1))
   [ 11.125 10.375 12.125 10.875 11.5 13. 13.25 ]
   
   

   In the above code, axis=0 calculates the mean along every column and axis=1 calculates it along every row of the array.

   Why mean?

   Now that we have learned how to calculate mean manually as well as by using python, let’s understand its importance. Mean represents the typical value that acts as a yardstick for all observations. For instance, in our example above, average marks of the class will help the teacher to judge the performance of an individual relative to others.

2. Median is…

   …the value where the upper half of the data lies above it and lower half lies below it. In other words, it is the middle value of a data set.

   To calculate the median, arrange the data points in the increasing order and the middle value is the median. It is easy to find out the middle value if there is an odd number of data points, say, we want to find the median for marks of all students for Subject 1. When marks are arranged in the increasing order, we get {7,9.5,10,11,14,15,19}. Clearly, the middle value is 11; therefore, the median is 11.

   If Student 7 did not write the exam, we will have marks as {7,9.5,10,11,14,15}. This time there is no clear middle value. Then, take the mean of the third and fourth values, which is (10+11)/2=10.5, so the median in this case is 10.5.

   

   Median with python

   Median can be calculated using numpy, pandas and statistics(version 3.4) libraries in python.

   numpy.median(a, axis=None, out=None)

   a: array containing numbers whose median is required
   axis: axis or axes along which the median is computed, default is to compute the median of the flattened array
   out: alternative output array to place the result, must have the same shape and buffer length as the expected output.

   >>> import numpy as np
   >>> A=np.array([[10,14,11,7,9.5,15,19],[8,9,17,14.5,12,18,15.5],
     [15,7.5,11.5,10,10.5,7,11],[11.5,11,9,12,14,12,7.5]])
   >>> B=A.T
   >>> a=np.median(B, axis=0)
   >>> b=np.median(B, axis=1)
   >>> print(a,b)
   [ 11. 14.5 10.5 11.5] [ 10.75 10. 11.25 11. 11.25 13.5 13.25]
   

   Median wins over mean when…

   The median is a better choice when the indicator can be affected by some outliers. Looking at the picture below, we can see that Student 9 and Student 10 scored much more than the rest and their scores were included in the calculation of mean, making it less representative of the typical observation. On the other hand, median is the middle value which is not affected by these outliers. It gives us a better estimate of the typical score. However, this means that presence of Student 9’s and Student 10’s relatively higher scores are hidden.

   

   Mean wins over median when…

   The mean is a better choice when there are no extreme values that can affect it. It is a better summary because the information from every observation is included rather than median, which is just the middle value.

   

   We can also derive the sum of all the observations, for example, the total marks scored by all students, when the number of observations is provided.

3. Mode is…

   …the value that occurs the most number of times in our data set. Suppose there are 15 students appearing for an exam and following is the result:

   

   When the mode is not unique, we say that the data set is bimodal, while a data set with more than two modes is multimodal.

   Mode with python

   Similar to the mean and the median, we can calculate mode using numpy(scipy), pandas, and statistics.

   scipy.stats.mstats.mode(a, axis=0)

   a: array containing numbers whose mode is required
   axis: axis or axes along which the mode is computed, default is to compute the mode of the flattened array

   It returns (mode: array of modal values, count: array of counts for each mode).

   >>> import numpy as np
   >>> from scipy import stats
   >>> A=np.array([[10,14,11,7,9.5,15,19],[8,9,17,14.5,12,18,15.5],
     [15,7.5,11.5,10,10.5,7,11],[11.5,11,9,12,14,12,7.5]])
   >>> B=A.T
   >>> a=stats.mode(B,axis=0)
   >>> b=stats.mode(B,axis=1)
   >>> print(a)
   ModeResult(mode=array([[ 7., 8., 7., 12.]]), count=array([[1, 1, 1, 2]]))
   >>> print(b)
   ModeResult(mode=array([[ 8. ],
     [ 7.5],
     [ 9. ],
     [ 7. ],
     [ 9.5],
     [ 7. ],
     [ 7.5]]), count=array([[1],
     [1],
     [1],
     [1],
     [1],
     [1],
     [1]]))
   
   

   Why mode?

   Mode also makes sense when we do not have a numeric-valued data set which is required in case of the mean and the median. For instance, if a company wants to figure out the most common place their employees belong to, then the mode will be a city (which can’t be done in the case of mean and median).

   Why not mode?

   Mode is not useful when our distribution is flat; i.e., the frequencies of all groups are similar, for example, in midterm exam for Subject 1 case, the distribution is flat as there is no particular number which is appearing more than once. In such cases, the mode does not provide any useful information. Also, at times mode can appear at the tail of the distribution which is not necessarily at or near the center of a distribution.

Measures of dispersion

Measures of dispersion are values that describe how the data varies. It gives us a sense of how much the data tends to diverge from the typical value, while central measures give us an idea about the typical value of the distribution.

1. Range is…

   …one of the simplest dispersion measures. It is the difference between the maximum and minimum values in the distribution. For instance:

   

   Range with python

   We use numpy.ptp() function to calculate range in python. There are other functions to calculate minimum and maximum such as numpy.amin() and numpy.amax(). ‘ptp’ stands for ‘peak to peak’.

   numpy.ptp(a, axis=None, out=None)

   a: array containing numbers whose range is required
   axis: axis or axes along which the range is computed, default is to compute the range of the flattened array. It returns a new array with the result.

   >>> import numpy as np
   >>> A=np.array([[10,14,11,7,9.5,15,19],[8,9,17,14.5,12,18,15.5],
       [15,7.5,11.5,10,10.5,7,11],[11.5,11,9,12,14,12,7.5]])
   >>> B=A.T
   >>> a=np.ptp(B, axis=0)
   >>> b=np.ptp(B,axis=1)
   >>> print(a)
   [ 12. 10. 8. 6.5]
   >>> print(b)
   [ 7. 6.5 8. 7.5 4.5 11. 11.5]

   Why range?

   The range gives a quick sense of the spread of the distribution to those who require only a rough indication of the data.

   Why not range?

   There are some disadvantages of using the range as a measure of spread. One being it does not give any information of the data in between maximum and minimum. There can be two data sets with the same range, but the values(hence the distribution) may differ significantly as shown below.

   

   Also, the range is very sensitive to extreme values as it is the difference between the maximum and minimum values.

   

   The distribution above has range 18, but it can be clearly seen that the data is clustered around 8 to 12, suggesting a range of 4. This does not give a good indication of the observations in the data set.

2. Percentile is…

   …a measure which indicates the value below which a given percentage of points in a dataset fall. For instance, the 35th percentile((P_{35})) is the score below which 35% of the data points may be found. We can observe that median represents the 50th percentile. Similarly, we can have 0th percentile representing the minimum and 100th percentile representing the maximum of all data points.

   There are various methods of calculation of quartiles and percentiles, but we will stick to the one below. To calculate (k^{th}) percentile((P_{k})) for a data set of (N) observations which is arranged in increasing order, go through the following steps:

   • Step 1: Calculate (displaystyle i=frac{k}{100}times N)
   • Step 2: If (i) is a whole number, then count the observations in the data set from left to right till we reach the (i^{th}) data point. The (k^{th}) percentile, in this case, is equal to the average of the value of (i^{th}) data point and the value of the data point that follows it.
   • Step 3: If (i) is not a whole number, then round it up to the nearest integer and count the observations in the data set from left to right till we reach the (i^{th}) data point. The (k^{th}) percentile now is just equal to the value corresponding this data point.

   Suppose we want to calculate (P_{27}) for the marks of students in Subject 2. Let us first arrange the data in increasing order which results in the following dataset {8,9,12,14.5,15.5,17,18}.

   Following the steps above,
   Step 1: (displaystyle i=frac{27}{100}times 7 = 1.89)
   Step 2: Not applicable here as 1.89 is not a whole number, so let us move to step 3
   Step 3: Rounding up 1.89 gives 2, hence 27th percentile is the value of second observation, i.e., 9
   Therefore, 9 is (27^{th}) percentile which means that 27% of the students have scored below 9.

   Quartiles are…

   …the three points that split the data set into four equal parts such that each group consists of one-fourth of the data. We also call 25th percentile the first quartile((Q_1)), 50th percentile the second quartile((Q_2)), and 75th percentile the third quartile((Q_3)).

   Percentiles and quartiles with python

   numpy.percentile(a, q, axis=None,iterpolation=’linear’)

   a: array containing numbers whose range is required
   q: percentile to compute(must be between 0 and 100)
   axis: axis or axes along which the range is computed, default is to compute the range of the flattened array
   interpolation: it can take the values as ‘linear’, ‘lower’, ‘higher’, ‘midpoint’or ‘nearest’. This parameter specifies the method which is to be used when the desired quartile lies between two data points, say i and j.

   • linear: returns i + (j-i)*fraction, fraction here is the fractional part of the index surrounded by i and j
   • lower: returns i
   • higher: returns j
   • midpoint: returns (i+j)/2
   • nearest: returns the nearest point whether i or j

   numpy.percentile() agrees with the manual calculation of percentiles (as shown above) only when interpolation is set as ‘lower’.

   >>> import numpy as np
   >>> A=np.array([[10,14,11,7,9.5,15,19],[8,9,17,14.5,12,18,15.5],
     [15,7.5,11.5,10,10.5,7,11],[11.5,11,9,12,14,12,7.5]])
   >>> B=A.T
   >>> a=np.percentile(B,27,axis=0, interpolation='lower')
   >>> b=np.percentile(B,25,axis=1, interpolation='lower')
   >>> c=np.percentile(B,75,axis=0, interpolation='lower')
   >>> d=np.percentile(B,50,axis=0, interpolation='lower')
   >>> print(a)
   [ 9.5  9.   7.5  9. ] 
   >>> print(b)
   [ 8.   7.5  9.   7.   9.5  7.   7.5]
   >>> print(c)
   [ 14.   15.5  11.   12. ]
   >>> print(d)
   [ 11.   14.5  10.5  11.5]

   Why percentiles?

   Percentile gives the relative position of a particular value within the dataset. If we are interested in relative positions, then mean and standard deviations does not make sense. In the case of exam scores, we do not know if it might have been a difficult exam and 7 points out of 20 was an amazing score. In this case, personal scores in itself are meaningless, but the percentile would reflect everything. For example, GRE and GMAT scores are all in terms of percentiles.

   Another good property of percentiles is that it has a universal interpretation; i.e., it does not depend on whether we are looking at exam scores or the height of the players across a few basketball teams. 55th percentile would always mean that 55 % would always be found below the value and other 45% would be above it. It helps in comparing the data sets which have different means and deviations.

3. Interquartile Range(IQR) is…

   …the difference between the third quartile and the first quartile.

   (IQR=Q_3-Q_1)

   Interquartile range with python

   scipy.stats.iqr(a, axis=0, interpolation=’linear’)

   >>> import numpy as np
   >>> from scipy.stats import iqr
   >>> A=np.array([[10,14,11,7,9.5,15,19],[8,9,17,14.5,12,18,15.5]
     [15,7.5,11.5,10,10.5,7,11],[11.5,11,9,12,14,12,7.5]])
   >>> B=A.T
   >>> a=iqr(B, axis=0 , rng=(25, 75), interpolation='lower')
   >>> b=iqr(B, axis=1 , rng=(25, 75), interpolation='lower')
   >>> print(a,b)
   [ 4.5  6.5  3.5  3. ] [ 3.5  3.5  2.5  5.   2.5  8.   8. ]

   Why IQR?

   The interquartile range is a better option than range because it is not affected by outliers. It removes the outliers by just focusing on the distance within the middle 50% of the data.
4. Variance is…

   …the average of the squared differences from the mean. For a dataset, (X={a_1,a_2,ldots,a_n) with the mean as (overline{x}), variance is

   (displaystyle Var(X)=frac{1}{n}sum_{i=1}^n(a_i-overline{x})^2)

   Variance with Python

   Variance can be calculated in python using different libraries like numpy, pandas, and statistics.

   numpy.var(a, axis=None, dtype=None, ddof=0)

   Parameters are the same as numpy.mean except

   ddof : int, optional(ddof stands for delta degrees of freedom. It is the divisor used in the calculation, which is N – ddof, where N is the number of elements. The default value of ddof is 0)

   >>> import numpy as np
   >>> A=np.array([[10,14,11,7,9.5,15,19],[8,9,17,14.5,12,18,15.5],
     [15,7.5,11.5,10,10.5,7,11],[11.5,11,9,12,14,12,7.5]])
   >>> B=A.T
   >>> a = np.var(B,axis=0)
   >>> b = np.var(B,axis=1)
   >>> print(a)
   [ 13.98979592  12.8877551    6.12244898   3.92857143]
   >>> print(b)
   [  6.546875   5.921875   8.796875   7.546875   2.875     16.5       19.0625  ]
   

   Why variance?

   It is an important measure in descriptive statistics because it allows us to measure the spread of a data set around its mean. The observations may or may not be meaningful if observations in data sets are highly spread.

5. Standard deviation is…

   …the square root of variance.

   Standard deviation with Python

   It can be calculated in python using different libraries like numpy, pandas, and statistics.

   numpy.std(a, axis=None, dtype=None, ddof=0)

   Parameters are the same as numpy.var().

   >>> import numpy as np
   >>> A=np.array([[10,14,11,7,9.5,15,19],[8,9,17,14.5,12,18,15.5],
     [15,7.5,11.5,10,10.5,7,11],[11.5,11,9,12,14,12,7.5]])
   >>> B=A.T
   >>> a = np.std(B,axis=0)
   >>> b = np.std(B,axis=1)
   >>> print(a)
   [ 3.74029356  3.58995196  2.4743583   1.98206242]
   >>> print(b)
   [ 2.55868619  2.43349029  2.96595263  2.74715762  1.6955825   4.0620192  4.3660623 ]
   

   Variance versus standard deviation

   The only similarity between variance and standard deviation is that they are both non-negative. The most important difference is that standard deviation is on the same scale as the values in the data set. Therefore, it is expressed in the same units, whereas variance is scaled larger. So it is not expressed in the same units as the values.

6. Skewness refers to…

   … whether the distribution has a longer tail on one side or the other or has left-right symmetry. There have been different skewness coefficients proposed over the years. The most common way to calculate is by taking the mean of the cubes of differences of each point from the mean and then dividing it by the cube of the standard deviation. This gives a coefficient that is independent of the units of the observations.

   It can be positive(representing right skewed distribution), negative(representing left skewed distribution), or zero(representing unskewed distribution).

   Skewness with python

   scipy.stats.skew(a, axis=0)

   >>> import numpy as np
   >>> import scipy
   >>> A=np.array([[10,14,11,7,9.5,15,19],[8,9,17,14.5,12,18,15.5],
       [15,7.5,11.5,10,10.5,7,11],[11.5,11,9,12,14,12,7.5]])
   >>> B=A.T
   >>> a=scipy.stats.skew(B,axis=0)
   >>> print(a)
   [ 0.45143419 -0.30426514  0.38321624 -0.39903339]
   
   

7. Kurtosis quantifies…

   …whether the shape of a distribution mat

   Kurtosis with python

   scipy.stats.kurtosis(a, axis=0, fisher=True)

   The parameters remain the same except fisher

   fisher: if True then Fisher’s definition is used and if False, Pearson’s definition is used. Default is True

   >>> import numpy as np
   >>> import scipy
   >>> A=np.array([[10,14,11,7,9.5,15,19],[8,9,17,14.5,12,18,15.5],[15,7.5,11.5,10,10.5,7,11],
       [11.5,11,9,12,14,12,7.5]])
   >>> B=A.T
   >>> a=scipy.stats.kurtosis(B,axis=0,fisher=False) #Pearson Kurtosis 
   >>> b=scipy.stats.kurtosis(B,axis=1) #Fisher's Kurtosis
   >>> print(a,b)
   [ 2.19732518  1.6138826   2.516175    2.30595041] [-1.11918934 -1.25539366 
   -0.86157952 -1.24277613 -1.30245747 -1.22038567 -1.46061811]

   Why skewness and kurtosis?

   Skewness and kurtosis are used to describe some aspects of the symmetry and shape of the distribution of the observations in a data set.

Limitations of descriptive statistics

Descriptive statistics measures are limited in the way that we can only make the summary about the people or objects that are actually measured. The data cannot be used to generalize to other people or objects. For example, if we have recorded the marks of the students for the past few years and would want to predict the marks for next exam, we cannot do that only relying on descriptive statistics; inferential statistics would help. Descriptive statistics can often be difficult when we are dealing with a large dataset.

Next, we will learn about inferential statistics that can help gain insights into the population from which the data was collected.