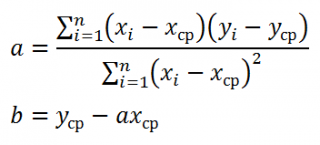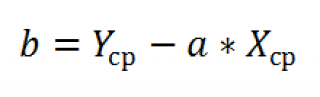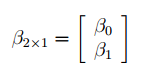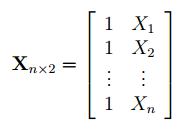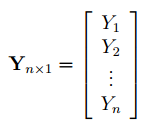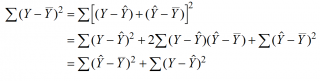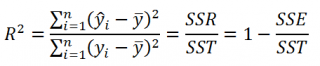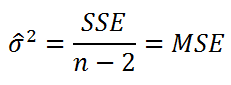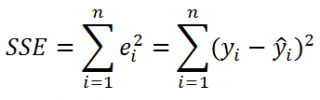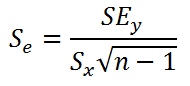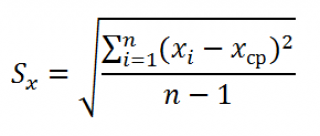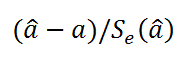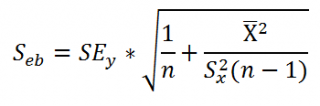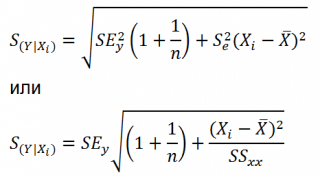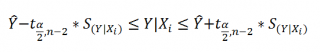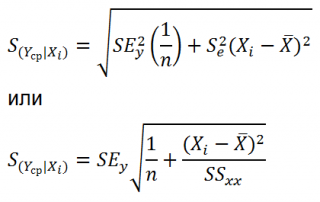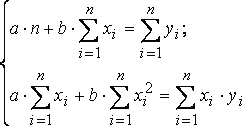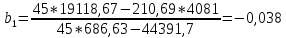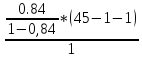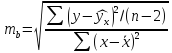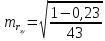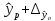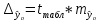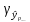Стандартная ошибка линейной регрессии формула


Регрессия позволяет прогнозировать зависимую переменную на основании значений фактора. В

MS

EXCEL

имеется множество функций, которые возвращают не только наклон и сдвиг линии регрессии, характеризующей линейную взаимосвязь между факторами, но и регрессионную статистику. Здесь рассмотрим простую линейную регрессию, т.е. прогнозирование на основе одного фактора.


Disclaimer

: Данную статью не стоит рассматривать, как пересказ главы из учебника по статистике. Статья не обладает ни полнотой, ни строгостью изложения положений статистической науки. Эта статья – о применении MS EXCEL для целей

Регрессионного анализа.

Теоретические отступления приведены лишь из соображения логики изложения. Использование данной статьи для изучения

Регрессии

– плохая идея.

Статья про

Регрессионный анализ

получилась большая, поэтому ниже для удобства приведены ее разделы:

  • Немного теории и основные понятия
  • Предположения линейной регрессионной модели
  • Задачи регрессионного анализа
  • Оценка неизвестных параметров линейной модели (используя функции MS EXCEL)
  • Оценка неизвестных параметров линейной модели (через статистики выборок)
  • Оценка неизвестных параметров линейной модели (матричная форма)
  • Построение линии регрессии
  • Коэффициент детерминации
  • Стандартная ошибка регрессии
  • Стандартные ошибки и доверительные интервалы для наклона и сдвига
  • Проверка значимости взаимосвязи переменных
  • Доверительные интервалы для нового наблюдения Y и среднего значения
  • Проверка адекватности линейной регрессионной модели


Примечание

: Если прогнозирование переменной осуществляется на основе нескольких факторов, то имеет место

множественная регрессия

.

Чтобы разобраться, чем может помочь MS EXCEL при проведении регрессионного анализа, напомним вкратце теорию, введем термины и обозначения, которые могут отличаться в зависимости от различных источников.


Примечание

: Для тех, кому некогда, незачем или просто не хочется разбираться в теоретических выкладках предлагается сразу перейти к вычислительной части —

оценке неизвестных параметров линейной модели

.

Немного теории и основные понятия

Пусть у нас есть массив данных, представляющий собой значения двух переменных Х и Y. Причем значения переменной Х мы можем произвольно задавать (контролировать) и использовать эту переменную для предсказания значений зависимой переменной Y. Таким образом, случайной величиной является только переменная Y.

Примером такой задачи может быть производственный процесс изготовления некого волокна, причем

прочность этого волокна

(Y) зависит только от

рабочей температуры процесса

в реакторе (Х), которая задается оператором.

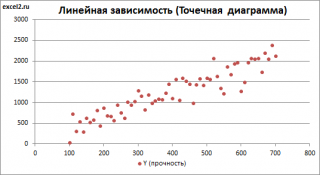
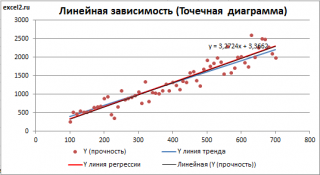
Построим

диаграмму рассеяния

(см.

файл примера лист Линейный

), созданию которой

посвящена отдельная статья

. Вообще, построение

диаграммы рассеяния

для целей

регрессионного анализа

де-факто является стандартом.


СОВЕТ

: Подробнее о построении различных типов диаграмм см. статьи

Основы построения диаграмм

и

Основные типы диаграмм

.

Приведенная выше

диаграмма рассеяния

свидетельствует о возможной

линейной взаимосвязи

между Y от Х: очевидно, что точки данных в основном располагаются вдоль прямой линии.


Примечание

: Наличие даже такой очевидной

линейной взаимосвязи

не может являться доказательством о наличии причинной взаимосвязи переменных. Наличие

причинной

взаимосвязи не может быть доказано на основании только анализа имеющихся измерений, а должно быть обосновано с помощью других исследований, например теоретических выкладок.


Примечание

: Как известно, уравнение прямой линии имеет вид

Y

=

m

*

X

+

k

, где коэффициент

m

отвечает за наклон линии (

slope

),

k

– за сдвиг линии по вертикали (

intercept

),

k

равно значению Y при Х=0.

Предположим, что мы можем зафиксировать переменную Х (

рабочую температуру процесса

) при некотором значении Х

i

и произвести несколько наблюдений переменной Y (

прочность нити

). Очевидно, что при одном и том же значении Хi мы получим различные значения Y. Это обусловлено влиянием других факторов на Y. Например, локальные колебания давления в реакторе, концентрации раствора, наличие ошибок измерения и др. Предполагается, что воздействие этих факторов имеет случайную природу и для каждого измерения имеются одинаковые условия проведения эксперимента (т.е. другие факторы не изменяются).

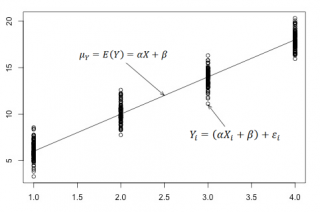
Полученные значения Y, при заданном Хi, будут колебаться вокруг некого

значения

. При увеличении количества измерений, среднее этих измерений, будет стремиться к

математическому ожиданию

случайной величины Y (при Х

i

) равному μy(i)=Е(Y

i

).

Подобные рассуждения можно привести для любого значения Хi.

Чтобы двинуться дальше, воспользуемся материалом из раздела

Проверка статистических гипотез

. В статье о

проверке гипотезы о среднем значении генеральной совокупности

в качестве

нулевой

гипотезы

предполагалось равенство неизвестного значения μ заданному μ0.

В нашем случае

простой линейной регрессии

в качестве

нулевой

гипотезы

предположим, что между переменными μy(i) и Хi существует линейная взаимосвязь μ

y(i)

=α* Х

i

+β. Уравнение μ

y(i)

=α* Х

i

+β можно переписать в обобщенном виде (для всех Х и μ

y

) как μ

y

=α* Х +β.

Для наглядности проведем прямую линию соединяющую все μy(i).

Данная линия называется

регрессионной линией генеральной совокупности

(population regression line), параметры которой (

наклон

a и

сдвиг β

) нам не известны (по аналогии с

гипотезой о среднем значении генеральной совокупности

, где нам было неизвестно истинное значение μ).

Теперь сделаем переход от нашего предположения, что μy=a* Х +

β

, к предсказанию значения случайной переменной Y в зависимости от значения контролируемой переменной Х. Для этого уравнение связи двух переменных запишем в виде Y=a*X+β+ε, где ε — случайная ошибка, которая отражает суммарный эффект влияния других факторов на Y (эти «другие» факторы не участвуют в нашей модели). Напомним, что т.к. переменная Х фиксирована, то ошибка ε определяется только свойствами переменной Y.

Уравнение Y=a*X+b+ε называют

линейной регрессионной моделью

. Часто Х еще называют

независимой переменной

(еще

предиктором

и

регрессором

, английский термин

predictor

,

regressor

), а Y –

зависимой

(или

объясняемой

,

response

variable

). Так как

регрессор

у нас один, то такая модель называется

простой линейной регрессионной моделью

(

simple

linear

regression

model

). α часто называют

коэффициентом регрессии.

Предположения линейной регрессионной модели перечислены в следующем разделе.

Предположения линейной регрессионной модели

Чтобы модель линейной регрессии Yi=a*Xi+β+ε

i

была адекватной — требуется:

  • Ошибки ε

    i

    должны быть независимыми переменными;
  • При каждом значении Xi ошибки ε

    i

    должны быть иметь нормальное распределение (также предполагается равенство нулю математического ожидания, т.е. Е[ε

    i

    ]=0);
  • При каждом значении Xi ошибки ε

    i

    должны иметь равные дисперсии (обозначим ее σ

    2

    ).


Примечание

: Последнее условие называется

гомоскедастичность

— стабильность, гомогенность дисперсии случайной ошибки e. Т.е.

дисперсия

ошибки σ

2

не должна зависеть от значения Xi.

Используя предположение о равенстве математического ожидания Е[ε

i

]=0 покажем, что μy(i)=Е[Yi]:

Е[Yi]= Е[a*Xi+β+ε

i

]= Е[a*Xi+β]+ Е[ε

i

]= a*Xi+β= μy(i), т.к. a, Xi и β постоянные значения.


Дисперсия

случайной переменной Y равна

дисперсии

ошибки ε, т.е. VAR(Y)= VAR(ε)=σ

2

. Это является следствием, что все значения переменной Х являются const, а VAR(ε)=VAR(ε

i

).

Задачи регрессионного анализа

Для проверки гипотезы о линейной взаимосвязи переменной Y от X делают выборку из генеральной совокупности (этой совокупности соответствует

регрессионная линия генеральной совокупности

, т.е.  μy=a* Х +β). Выборка будет состоять из n точек, т.е. из n пар значений {X;Y}.

На основании этой выборки мы можем вычислить оценки наклона a и сдвига β, которые обозначим соответственно

a

и

b

. Также часто используются обозначения â и b̂.

Далее, используя эти оценки, мы также можем проверить гипотезу: имеется ли линейная связь между X и Y статистически значимой?

Таким образом:


Первая задача

регрессионного анализа

– оценка неизвестных параметров (

estimation

of

the

unknown

parameters

). Подробнее см. раздел

Оценки неизвестных параметров модели

.


Вторая задача

регрессионного анализа

–

Проверка адекватности модели

(

model

adequacy

checking

).


Примечание

: Оценки параметров модели обычно вычисляются

методом наименьших квадратов

(МНК),

которому посвящена отдельная статья

.

Оценка неизвестных параметров линейной модели (используя функции MS EXCEL)

Неизвестные параметры

простой линейной регрессионной модели

Y=a*X+β+ε оценим с помощью

метода наименьших квадратов

(в

статье про МНК подробно описано этот метод

).

Для вычисления параметров линейной модели методом МНК получены следующие выражения:

Таким образом, мы получим уравнение прямой линии Y=

a

*X+

b

, которая наилучшим образом аппроксимирует имеющиеся данные.


Примечание

: В статье про

метод наименьших квадратов

рассмотрены случаи аппроксимации

линейной

и

квадратичной функцией

, а также

степенной

,

логарифмической

и

экспоненциальной функцией

.

Оценку параметров в MS EXCEL можно выполнить различными способами:

  • с помощью функций

    НАКЛОН()

    и

    ОТРЕЗОК()

    ;
  • с помощью функции

    ЛИНЕЙН()

    ; см. статью

    Функция MS EXCEL ЛИНЕЙН()

  • формулами через статистики выборок

    ;

  • в матричной форме

    ;

  • с помощью

    инструмента Регрессия надстройки Пакет Анализа

    .

Сначала рассмотрим функции

НАКЛОН()

,

ОТРЕЗОК()

и

ЛИНЕЙН()

.

Пусть значения Х и Y находятся соответственно в диапазонах

C

23:

C

83

и

B

23:

B

83

(см.

файл примера

внизу статьи).


Примечание

: Значения двух переменных Х и Y можно сгенерировать, задав тренд и величину случайного разброса (см. статью

Генерация данных для линейной регрессии в MS EXCEL

).

В MS EXCEL наклон прямой линии

а

(

оценку

коэффициента регрессии

), можно найти по

методу МНК

с помощью функции

НАКЛОН()

, а сдвиг

b

(

оценку

постоянного члена

или

константы регрессии

), с помощью функции

ОТРЕЗОК()

. В английской версии это функции SLOPE и INTERCEPT соответственно.

Аналогичный результат можно получить с помощью функции

ЛИНЕЙН()

, английская версия LINEST (см.

статью об этой функции

).

Формула

=ЛИНЕЙН(C23:C83;B23:B83)

вернет наклон

а

. А формула =

ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);2)

— сдвиг

b

. Здесь требуются пояснения.

Функция

ЛИНЕЙН()

имеет 4 аргумента и возвращает целый массив значений:

ЛИНЕЙН(известные_значения_y; [известные_значения_x]; [конст]; [статистика])

Если 4-й аргумент

статистика

имеет значение ЛОЖЬ или опущен, то функция

ЛИНЕЙН()

возвращает только оценки параметров модели:

a

и

b

.


Примечание

: Остальные значения, возвращаемые функцией

ЛИНЕЙН()

, нам потребуются при вычислении

стандартных ошибок

и для

проверки значимости регрессии

. В этом случае аргумент

статистика

должен иметь значение ИСТИНА.

Чтобы вывести сразу обе оценки:

  • в одной строке необходимо выделить 2 ячейки,
  • ввести формулу в

    Строке формул

  • нажать

    CTRL

    +

    SHIFT

    +

    ENTER

    (см. статью про

    формулы массива

    ).

Если в

Строке формул

выделить формулу =

ЛИНЕЙН(C23:C83;B23:B83)

и нажать

клавишу F9

, то мы увидим что-то типа {3,01279389265416;154,240057900613}. Это как раз значения

a

и

b

. Как видно, оба значения разделены точкой с запятой «;», что свидетельствует, что функция вернула значения «в нескольких ячейках одной строки».

Если требуется вывести параметры линии не в одной строке, а одном столбце (ячейки друг под другом), то используйте формулу =

ТРАНСП(ЛИНЕЙН(C23:C83;B23:B83))

. При этом выделять нужно 2 ячейки в одном столбце. Если теперь выделить новую формулу и нажать клавишу F9, то мы увидим что 2 значения разделены двоеточием «:», что означает, что значения выведены в столбец (функция

ТРАНСП()

транспонировала строку в столбец

).

Чтобы разобраться в этом подробнее необходимо ознакомиться с

формулами массива

.

Чтобы не связываться с вводом

формул массива

, можно

использовать функцию ИНДЕКС()

. Формула =

ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);1)

или просто

ЛИНЕЙН(C23:C83;B23:B83)

вернет параметр, отвечающий за наклон линии, т.е.

а

. Формула

=ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);2)

вернет параметр

b

.

Оценка неизвестных параметров линейной модели (через статистики выборок)

Наклон линии, т.е. коэффициент

а

, можно также вычислить через

коэффициент корреляции

и

стандартные отклонения выборок

:

=

КОРРЕЛ(B23:B83;C23:C83) *(СТАНДОТКЛОН.В(C23:C83)/ СТАНДОТКЛОН.В(B23:B83))

Вышеуказанная формула математически эквивалентна отношению

ковариации

выборок Х и Y и

дисперсии

выборки Х:

=

КОВАРИАЦИЯ.В(B23:B83;C23:C83)/ДИСП.В(B23:B83)

И, наконец, запишем еще одну формулу для нахождения сдвига

b

. Воспользуемся тем фактом, что

линия регрессии

проходит через точку

средних значений

переменных Х и Y.

Вычислив

средние значения

и подставив в формулу ранее найденный наклон

а

, получим сдвиг

b

.

Оценка неизвестных параметров линейной модели (матричная форма)

Также параметры

линии регрессии

можно найти в матричной форме (см.

файл примера лист Матричная форма

).

В формуле символом β обозначен столбец с искомыми параметрами модели: β0 (сдвиг

b

), β1 (наклон

a

).

Матрица Х равна:

Матрица

Х

называется

регрессионной матрицей

или

матрицей плана

. Она состоит из 2-х столбцов и n строк, где n – количество точек данных. Первый столбец — столбец единиц, второй – значения переменной Х.

Матрица

Х

T

– это

транспонированная матрица

Х

. Она состоит соответственно из n столбцов и 2-х строк.

В формуле символом

Y

обозначен столбец значений переменной Y.

Чтобы

перемножить матрицы

используйте функцию

МУМНОЖ()

. Чтобы

найти обратную матрицу

используйте функцию

МОБР()

.

Пусть дан массив значений переменных Х и Y (n=10, т.е.10 точек).

Слева от него достроим столбец с 1 для матрицы Х.

Записав формулу

=

МУМНОЖ(МОБР(МУМНОЖ(ТРАНСП(B7:C16);(B7:C16))); МУМНОЖ(ТРАНСП(B7:C16);(D7:D16)))

и введя ее как

формулу массива

в 2 ячейки, получим оценку параметров модели.

Красота применения матричной формы полностью раскрывается в случае

множественной регрессии

.

Построение линии регрессии

Для отображения

линии регрессии

построим сначала

диаграмму рассеяния

, на которой отобразим все точки (см.

начало статьи

).

Для построения прямой линии используйте вычисленные выше оценки параметров модели

a

и

b

(т.е. вычислите

у

по формуле

y

=

a

*

x

+

b

) или функцию

ТЕНДЕНЦИЯ()

.

Формула =

ТЕНДЕНЦИЯ($C$23:$C$83;$B$23:$B$83;B23)

возвращает расчетные (прогнозные) значения ŷi для заданного значения Хi из столбца

В2

.


Примечание

:

Линию регрессии

можно также построить с помощью функции

ПРЕДСКАЗ()

. Эта функция возвращает прогнозные значения ŷi, но, в отличие от функции

ТЕНДЕНЦИЯ()

работает только в случае одного регрессора. Функция

ТЕНДЕНЦИЯ()

может быть использована и в случае

множественной регрессии

(в этом случае 3-й аргумент функции должен быть ссылкой на диапазон, содержащий все значения Хi для выбранного наблюдения i).

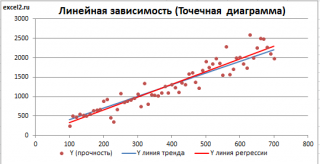
Как видно из диаграммы выше

линия тренда

и

линия регрессии

не обязательно совпадают: отклонения точек от

линии тренда

случайны, а МНК лишь подбирает линию наиболее точно аппроксимирующую случайные точки данных.


Линию регрессии

можно построить и с помощью встроенных средств диаграммы, т.е. с помощью инструмента

Линия тренда.

Для этого выделите диаграмму, в меню выберите

вкладку Макет

, в

группе Анализ

нажмите

Линия тренда

, затем

Линейное приближение.

В диалоговом окне установите галочку

Показывать уравнение на диаграмме

(подробнее см. в

статье про МНК

).

Построенная таким образом линия, разумеется, должна совпасть с ранее построенной нами

линией регрессии,

а параметры уравнения

a

и

b

должны совпасть с параметрами уравнения отображенными на диаграмме.


Примечание:

Для того, чтобы вычисленные параметры уравнения

a

и

b

совпадали с параметрами уравнения на диаграмме, необходимо, чтобы тип у диаграммы был

Точечная, а не График

, т.к. тип диаграммы

График

не использует значения Х, а вместо значений Х используется последовательность 1; 2; 3; … Именно эти значения и берутся при расчете параметров

линии тренда

. Убедиться в этом можно если построить диаграмму

График

(см.

файл примера

), а значения

Хнач

и

Хшаг

установить равным 1. Только в этом случае параметры уравнения на диаграмме совпадут с

a

и

b

.

Коэффициент детерминации R

2


Коэффициент детерминации

R

2

показывает насколько полезна построенная нами

линейная регрессионная модель

.

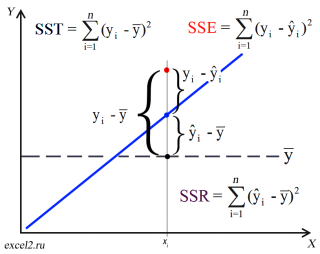
Предположим, что у нас есть n значений переменной Y и мы хотим предсказать значение yi, но без использования значений переменной Х (т.е. без построения

регрессионной модели

). Очевидно, что лучшей оценкой для yi будет

среднее значение

ȳ. Соответственно, ошибка предсказания будет равна (yi — ȳ).


Примечание

: Далее будет использована терминология и обозначения

дисперсионного анализа

.

После построения

регрессионной модели

для предсказания значения yi мы будем использовать значение ŷi=a*xi+b. Ошибка предсказания теперь будет равна (yi — ŷi).

Теперь с помощью диаграммы сравним ошибки предсказания полученные без построения модели и с помощью модели.

Очевидно, что используя

регрессионную модель

мы уменьшили первоначальную (полную) ошибку (yi — ȳ)  на значение (ŷi — ȳ)  до величины (yi — ŷi).

(yi — ŷi) – это оставшаяся, необъясненная ошибка.

Очевидно, что все три ошибки связаны выражением:

(yi — ȳ)= (ŷi — ȳ) + (yi — ŷi)

Можно показать, что в общем виде справедливо следующее выражение:

Доказательство:

или в других, общепринятых в зарубежной литературе, обозначениях:


SST

=

SSR

+

SSE

Что означает:


Total Sum of Squares

=

Regression Sum of Squares

+

Error Sum of Squares


Примечание

: SS — Sum of Squares — Сумма Квадратов.

Как видно из формулы величины SST, SSR, SSE имеют размерность

дисперсии

(вариации) и соответственно описывают разброс (изменчивость):

Общую изменчивость

(Total variation),

Изменчивость объясненную моделью

(Explained variation) и

Необъясненную изменчивость

(Unexplained variation).

По определению

коэффициент детерминации

R

2

равен:

R

2

=

Изменчивость объясненная моделью / Общая изменчивость.

Этот показатель равен квадрату

коэффициента корреляции

и в MS EXCEL его можно вычислить с помощью функции

КВПИРСОН()

или

ЛИНЕЙН()

:

=

ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83;;ИСТИНА);3)

R

2

принимает значения от 0 до 1 (1 соответствует идеальной линейной зависимости Y от Х). Однако, на практике малые значения R2 вовсе не обязательно указывают, что переменную Х нельзя использовать для прогнозирования переменной Y. Малые значения R2 могут указывать на нелинейность связи или на то, что поведение переменной Y объясняется не только Х, но и другими факторами.

Стандартная ошибка регрессии


Стандартная ошибка регрессии

(

Standard Error of a regression

) показывает насколько велика ошибка предсказания значений переменной Y на основании значений Х. Отдельные значения Yi мы можем предсказывать лишь с точностью +/- несколько значений (обычно 2-3, в зависимости от формы распределения ошибки ε).

Теперь вспомним уравнение

линейной регрессионной модели

Y=a*X+β+ε. Ошибка ε имеет случайную природу, т.е. является случайной величиной и поэтому имеет свою функцию распределения со

средним значением

μ и

дисперсией

σ

2

.

Оценив значение

дисперсии

σ

2

и вычислив из нее квадратный корень – получим

Стандартную ошибку регрессии.

Чем точки наблюдений на диаграмме

рассеяния

ближе находятся к прямой линии, тем меньше

Стандартная ошибка.


Примечание

:

Вспомним

, что при построении модели предполагается, что

среднее значение

ошибки ε равно 0, т.е. E[ε]=0.

Оценим

дисперсию σ

2

. Помимо вычисления

Стандартной ошибки регрессии

эта оценка нам потребуется в дальнейшем еще и при построении

доверительных интервалов

для оценки параметров регрессии

a

и

b

.

Для оценки

дисперсии

ошибки ε используем

остатки регрессии

— разности между имеющимися значениями

yi

и значениями, предсказанными регрессионной моделью ŷ. Чем лучше регрессионная модель согласуется с данными (точки располагается близко к прямой линии), тем меньше величина остатков.

Для оценки

дисперсии σ

2

используют следующую формулу:

где SSE – сумма квадратов значений ошибок модели ε

i

=yi — ŷi (

Sum of Squared Errors

).

SSE часто обозначают и как SSres – сумма квадратов остатков (

Sum

of

Squared

residuals

).

Оценка

дисперсии

s

2

также имеет общепринятое обозначение MSE (Mean Square of Errors), т.е. среднее квадратов

ошибок

или MSRES (Mean Square of Residuals), т.е. среднее квадратов

остатков

. Хотя правильнее говорить сумме квадратов остатков, т.к. ошибка чаще ассоциируется с ошибкой модели ε, которая является непрерывной случайной величиной. Но, здесь мы будем использовать термины SSE и MSE, предполагая, что речь идет об остатках.


Примечание

: Напомним, что когда

мы использовали МНК

для нахождения параметров модели, то критерием оптимизации была минимизация именно SSE (SSres). Это выражение представляет собой сумму квадратов расстояний между наблюденными значениями yi и предсказанными моделью значениями ŷi, которые лежат на

линии регрессии.

Математическое ожидание

случайной величины MSE равно

дисперсии ошибки

ε, т.е.

σ

2

.

Чтобы понять почему SSE выбрана в качестве основы для оценки

дисперсии

ошибки ε, вспомним, что

σ

2

является также

дисперсией

случайной величины Y (относительно

среднего значения

μy, при заданном значении Хi). А т.к. оценкой μy является значение ŷi =

a

* Хi +

b

(значение

уравнения регрессии

при Х= Хi), то логично использовать именно SSE в качестве основы для оценки

дисперсии

σ

2

. Затем SSE усредняется на количество точек данных n за вычетом числа 2. Величина n-2 – это количество

степеней свободы

(

df

–

degrees

of

freedom

), т.е. число параметров системы, которые могут изменяться независимо (вспомним, что у нас в этом примере есть n независимых наблюдений переменной Y). В случае

простой линейной регрессии

число степеней свободы

равно n-2, т.к. при построении

линии регрессии

было оценено 2 параметра модели (на это было «потрачено» 2

степени свободы

).

Итак, как сказано было выше, квадратный корень из s

2

имеет специальное название

Стандартная ошибка регрессии

(

Standard Error of a regression

) и обозначается SEy. SEy показывает насколько велика ошибка предсказания. Отдельные значения Y мы можем предсказывать с точностью +/- несколько значений SEy (см.

этот раздел

). Если ошибки предсказания ε имеют

нормальное распределение

, то примерно 2/3 всех предсказанных значений будут на расстоянии не больше SEy от

линии регрессии

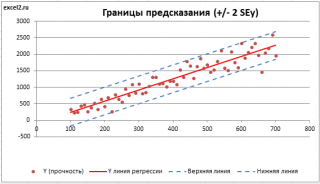
. SEy имеет размерность переменной Y и откладывается по вертикали. Часто на

диаграмме рассеяния

строят

границы предсказания

соответствующие +/- 2 SEy (т.е. 95% точек данных будут располагаться в пределах этих границ).

В MS EXCEL

стандартную ошибку

SEy можно вычислить непосредственно по формуле:

=

КОРЕНЬ(СУММКВРАЗН(C23:C83; ТЕНДЕНЦИЯ(C23:C83;B23:B83;B23:B83)) /( СЧЁТ(B23:B83) -2))

или с помощью функции

ЛИНЕЙН()

:

=

ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83;;ИСТИНА);3;2)


Примечание

: Подробнее о функции

ЛИНЕЙН()

см.

эту статью

.

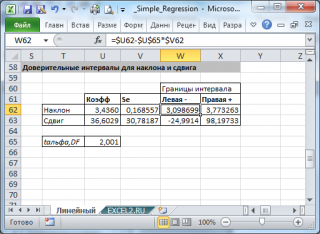
Стандартные ошибки и доверительные интервалы для наклона и сдвига

В разделе

Оценка неизвестных параметров линейной модели

мы получили точечные оценки наклона

а

и сдвига

b

. Так как эти оценки получены на основе случайных величин (значений переменных Х и Y), то эти оценки сами являются случайными величинами и соответственно имеют функцию распределения со

средним значением

и

дисперсией

. Но, чтобы перейти от

точечных оценок

к

интервальным

, необходимо вычислить соответствующие

стандартные ошибки

(т.е.

стандартные отклонения

).


Стандартная ошибка коэффициента регрессии

a

вычисляется на основании

стандартной ошибки регрессии

по следующей формуле:

где Sx – стандартное отклонение величины х, вычисляемое по формуле:

где Sey –

стандартная ошибка регрессии,

т.е. ошибка предсказания значения переменой Y

(

см. выше

).

В MS EXCEL

стандартную ошибку коэффициента регрессии

Se можно вычислить впрямую по вышеуказанной формуле:

=

КОРЕНЬ(СУММКВРАЗН(C23:C83; ТЕНДЕНЦИЯ(C23:C83;B23:B83;B23:B83)) /( СЧЁТ(B23:B83) -2))/  СТАНДОТКЛОН.В(B23:B83) /КОРЕНЬ(СЧЁТ(B23:B83) -1)

или с помощью функции

ЛИНЕЙН()

:

=

ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83;;ИСТИНА);2;1)

Формулы приведены в

файле примера на листе Линейный

в разделе

Регрессионная статистика

.


Примечание

: Подробнее о функции

ЛИНЕЙН()

см.

эту статью

.

При построении

двухстороннего доверительного интервала

для

коэффициента регрессии

его границы определяются следующим образом:

где  —

квантиль распределения Стьюдента

с n-2 степенями свободы. Величина

а

с «крышкой» является другим обозначением

наклона

а

.

Например для

уровня значимости

альфа=0,05, можно вычислить с помощью формулы

=СТЬЮДЕНТ.ОБР.2Х(0,05;n-2)

Вышеуказанная формула следует из того факта, что если ошибки регрессии распределены нормально и независимо, то выборочное распределение случайной величины

является

t-распределением Стьюдента

с n-2 степенью свободы (то же справедливо и для наклона

b

).


Примечание

: Подробнее о построении

доверительных интервалов

в MS EXCEL можно прочитать в этой статье

Доверительные интервалы в MS EXCEL

.

В результате получим, что найденный

доверительный интервал

с вероятностью 95% (1-0,05) накроет истинное значение

коэффициента регрессии.

Здесь мы считаем, что

коэффициент регрессии

a

имеет

распределение Стьюдента

с n-2

степенями свободы

(n – количество наблюдений, т.е. пар Х и Y).


Примечание

: Подробнее о построении

доверительных интервалов

с использованием t-распределения см. статью про построение

доверительных интервалов

для среднего

.


Стандартная ошибка сдвига

b

вычисляется по следующей формуле:

В MS EXCEL

стандартную ошибку сдвига

Seb можно вычислить с помощью функции

ЛИНЕЙН()

:

=

ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83;;ИСТИНА);2;2)

При построении

двухстороннего доверительного интервала

для

сдвига

его границы определяются аналогичным образом как для

наклона

:

b

+/- t*Seb.

Проверка значимости взаимосвязи переменных

Когда мы строим модель Y=αX+β+ε мы предполагаем, что между Y и X существует линейная взаимосвязь. Однако, как это иногда бывает в статистике, можно вычислять параметры связи даже тогда, когда в действительности она не существует, и обусловлена лишь случайностью.

Единственный вариант, когда Y не зависит X (в рамках модели Y=αX+β+ε), возможен, когда

коэффициент регрессии

a

равен 0.

Чтобы убедиться, что вычисленная нами оценка

наклона

прямой линии не обусловлена лишь случайностью (не случайно отлична от 0), используют

проверку гипотез

. В качестве

нулевой гипотезы

Н

0

принимают, что связи нет, т.е. a=0. В качестве альтернативной гипотезы

Н

1

принимают, что a <>0.

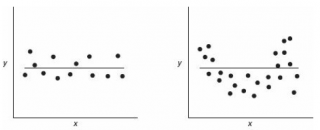
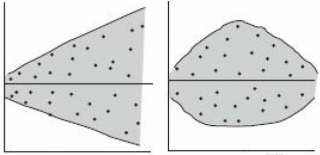
Ниже на рисунках показаны 2 ситуации, когда

нулевую гипотезу

Н

0

не удается отвергнуть.

На левой картинке отсутствует любая зависимость между переменными, на правой – связь между ними нелинейная, но при этом

коэффициент линейной корреляции

равен 0.

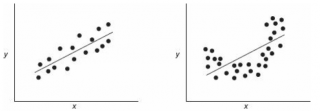
Ниже — 2 ситуации, когда

нулевая гипотеза

Н

0

отвергается.

На левой картинке очевидна линейная зависимость, на правой — зависимость нелинейная, но коэффициент корреляции не равен 0 (метод МНК вычисляет показатели наклона и сдвига просто на основании значений выборки).

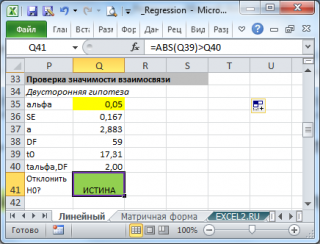
Для проверки гипотезы нам потребуется:

  • Установить

    уровень значимости

    , пусть альфа=0,05;

  • Рассчитать с помощью функции

    ЛИНЕЙН()

    стандартное отклонение

    Se для

    коэффициента регрессии

    (см.

    предыдущий раздел

    );

  • Рассчитать число степеней свободы: DF=n-2 или по формуле =

    ИНДЕКС(ЛИНЕЙН(C24:C84;B24:B84;;ИСТИНА);4;2)
  • Вычислить значение тестовой статистики t

    0

    =a/S

    e

    , которая имеет

    распределение Стьюдента

    с

    числом степеней свободы

    DF=n-2;

  • Сравнить значение

    тестовой статистики

    |t0| с пороговым значением t

    альфа

    ,n-2. Если значение

    тестовой статистики

    больше порогового значения, то

    нулевая гипотеза

    отвергается (

    наклон

    не может быть объяснен лишь случайностью при заданном уровне альфа) либо
  • вычислить

    p-значение

    и сравнить его с

    уровнем значимости

    .

В

файле примера

приведен пример проверки гипотезы:

Изменяя

наклон

тренда k (ячейка

В8

) можно убедиться, что при малых углах тренда (например, 0,05) тест часто показывает, что связь между переменными случайна. При больших углах (k>1), тест практически всегда подтверждает значимость линейной связи между переменными.


Примечание

: Проверка значимости взаимосвязи эквивалентна

проверке статистической значимости коэффициента корреляции

. В

файле примера

показана эквивалентность обоих подходов. Также проверку значимости можно провести с помощью

процедуры F-тест

.

Доверительные интервалы для нового наблюдения Y и среднего значения

Вычислив параметры

простой линейной регрессионной модели

Y=aX+β+ε мы получили точечную оценку значения нового наблюдения Y при заданном значении Хi, а именно: Ŷ=

a

* Хi +

b

Ŷ также является точечной оценкой для

среднего значения

Yi при заданном Хi. Но, при построении

доверительных интервалов

используются различные

стандартные ошибки

.


Стандартная ошибка

нового наблюдения Y при заданном Хi учитывает 2 источника неопределенности:

  • неопределенность связанную со случайностью оценок параметров модели

    a

    и

    b

    ;
  • случайность ошибки модели ε.

Учет этих неопределенностей приводит к

стандартной ошибке

S(Y|Xi), которая рассчитывается с учетом известного значения Xi.

где SS

xx

– сумма квадратов отклонений от

среднего

значений переменной Х:


Примечание

: Se –

стандартная ошибка коэффициента регрессии

(

наклона

а

).

В

MS EXCEL 2010

нет функции, которая бы рассчитывала эту

стандартную ошибку

, поэтому ее необходимо рассчитывать по вышеуказанным формулам.


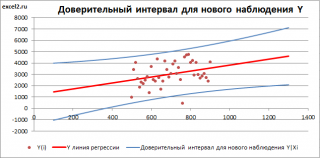
Доверительный интервал

или

Интервал предсказания для нового наблюдения

(Prediction Interval for a New Observation) построим по схеме показанной в разделе

Проверка значимости взаимосвязи переменных

(см.

файл примера лист Интервалы

). Т.к. границы интервала зависят от значения Хi (точнее от расстояния Хi до среднего значения Х

ср

), то интервал будет постепенно расширяться при удалении от Х

ср

.

Границы

доверительного интервала

для

нового наблюдения

рассчитываются по формуле:

Аналогичным образом построим

доверительный интервал

для

среднего значения

Y при заданном Хi (Confidence Interval for the Mean of Y). В этом случае

доверительный интервал

будет уже, т.к.

средние значения

имеют меньшую изменчивость по сравнению с отдельными наблюдениями (

средние значения,

в рамках нашей линейной модели Y=aX+β+ε, не включают ошибку ε).


Стандартная ошибка

S(Yср|Xi) вычисляется по практически аналогичным формулам как и

стандартная ошибка

для нового наблюдения:

Как видно из формул,

стандартная ошибка

S(Yср|Xi) меньше

стандартной ошибки

S(Y|Xi) для индивидуального значения

.

Границы

доверительного интервала

для

среднего значения

рассчитываются по формуле:

Проверка адекватности линейной регрессионной модели

Модель адекватна, когда все предположения, лежащие в ее основе, выполнены (см. раздел

Предположения линейной регрессионной модели

).

Проверка адекватности модели в основном основана на исследовании остатков модели (model residuals), т.е. значений ei=yi – ŷi для каждого Хi. В рамках

простой линейной модели

n остатков имеют только n-2 связанных с ними

степеней свободы

. Следовательно, хотя, остатки не являются независимыми величинами, но при достаточно большом n это не оказывает какого-либо влияния на проверку адекватности модели.

Чтобы проверить предположение о

нормальности распределения

ошибок строят

график проверки на нормальность

(Normal probability Plot).

В

файле примера на листе Адекватность

построен

график проверки на нормальность

. В случае

нормального распределения

значения остатков должны быть близки к прямой линии.

Так как значения переменной Y мы

генерировали с помощью тренда

, вокруг которого значения имели нормальный разброс, то ожидать сюрпризов не приходится – значения остатков располагаются вблизи прямой.

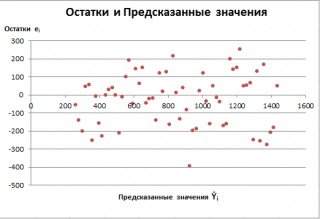
Также при проверке модели на адекватность часто строят график зависимости остатков от предсказанных значений Y. Если точки не демонстрируют характерных, так называемых «паттернов» (шаблонов) типа вор

о

нок или другого неравномерного распределения, в зависимости от значений Y, то у нас нет очевидных доказательств неадекватности модели.

В нашем случае точки располагаются примерно равномерно.

Часто при проверке адекватности модели вместо остатков используют нормированные остатки. Как показано в разделе

Стандартная ошибка регрессии

оценкой

стандартного отклонения ошибок

является величина SEy равная квадратному корню из величины MSE. Поэтому логично нормирование остатков проводить именно на эту величину.

SEy можно вычислить с помощью функции

ЛИНЕЙН()

:

=

ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83;;ИСТИНА);3;2)

Иногда нормирование остатков производится на величину

стандартного отклонения

остатков (это мы увидим в статье об инструменте

Регрессия

, доступного в

надстройке MS EXCEL Пакет анализа

), т.е. по формуле:

Вышеуказанное равенство приблизительное, т.к. среднее значение остатков близко, но не обязательно точно равно 0.

Источник

  1. Линейное уравнение регрессии

Формула
линейного уравнения регрессии (1)


(1)

Где,

x,y
– переменные,

a,b
– параметры.

Система
нормальных уравнений (2) в общем виде:


(2)

Где,

x,y
– то же что и в формуле (1),

a,b
– то же что и в формуле (1),

n
— количество наблюдений в совокупности.

Система
нормальных уравнений с вычисленными
коэффициентами:

Решение
системы:

Построенное
линейное уравнение регрессии:

Рис.
1 График линейного уравнения регрессии

  1. Показательное
    уравнение регрессии

Показательное
уравнение регрессии имеет следующий
вид:


(3),

где,

,

,

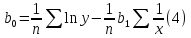
где,

x,y
– то же что и в формуле (1),

a,b
– то же что и в формуле (1),

n
– то же что и в формуле (2).

Найдем
b0

и b1:

,

.

Полечим
показательное уравнение регрессии:

  1. Логарифмическое
    уравнение регрессии

Логарифмическое
уравнение регрессии определяется по
формуле:


(6)

Где,

x,y
– то же что и в формуле (1),

b
– то же что и в формуле (1),

,


(8),

Где,

x,y
– то же что и в формуле (1),

b
– то же что и в формуле (1),

n
– то же что и в формуле (2).

Найдем
b0

и b1:

Получим
логарифмическое уравнение регрессии:

Рис.
1 График логарифмического уравнения
регрессии

  1. Индекс парной корреляции для уравнений регрессии

Индекс
парной корреляции исчисляется по
следующей формуле:


(9)

Где,

y
– то же что и в формуле (1),


– значение
у из исследуемого уравнения,


—
среднее значение y.

Для
оценки качества построенной модели
регрессии можно использовать индекс
детерминации или среднюю ошибку
аппроксимации. Чем выше показатель
детерминации или чем ниже ошибка
аппроксимации, чем лучше модель описывает
исходные данные.

Средняя
ошибка аппроксимации – среднее
относительное отклонение расчетных
значений от фактических, рассчитывается
по формуле


(10)

Где,

n
– то же что и в формуле (2),

y
– то же что и в фотрмуле (1).

Индекс
парной корреляции для линейного уравнения
регрессии:

=
0,92

Средняя
ошибка аппроксимации для линейного
уравнения регрессии:

=6%

Индекс
парной корреляции для логарифмического
уравнения регрессии:

=0,95

Средняя
ошибка аппроксимации для логарифмического
уравнения регрессии:

=6%

Построенные
уравнения считаются удовлетворительными,
так как
.
Коэффициент
детерминации достаточно высокий, а это
значит, что модель точно описывает
исходные данные.

  1. Поверка значимости уравнения регрессии и отдельных коэффициентов линейного уравнения

Оценка
статистической значимости уравнения
регрессии в целом осуществляется с
помощью F-критерия
Фишера.

Величина
Fфакт
определяется
по формуле:


(11)

Где,


—
индекс детерминации,

n
– то же что и в формуле (2),

m
– число параметров при переменных.

Таким
образом, для

  • линейного
    уравнения регрессии:

Fфакт
=

=2,26

Fкрит
=4,08, при α =0,05

Fтабл>Fфакт
, гипотеза H0
не отклоняется и признается статистическая
незначимость, ненадежность уравнения
регрессии.

  • логарифмического
    уравнения регрессии:

=3,87

Fкрит
=4,08, при α =0,05

Fтабл>Fфакт
, гипотеза H0
не отклоняется и признается статистическая
незначимость, ненадежность уравнения
регрессии.

Для
оценки статистической значимости
коэффициентов линейной регрессии
применяется t-критерий
Стьюдента:

Величины
tb,факт
и
ta,
факт определяются
по формулам:


(12)


(13)


(14)

Где,

a,b
– то же что и в формуле (1),

rxy

— коэффициент корреляции,

mb,
ma,
mrxy
– стандартные ошибки.

Таким
образом, для

  • линейного
    уравнения регрессии:


=0,45


=0,66


=0,46

  • логарифмического
    уравнения регрессии:


=1,93


=3,03


=0,4

Стандартные
ошибки параметров линейной регрессии
и коэффициента корреляции определяются
по формулам:


(15)


(16)

(17)

Где,
y
– то же что и в формуле (1),


– то
же что и в формуле (9),


—
то же что и в формуле (9),

rxy

— то же что и в формуле (14),

x
– то же что и в формуле (1)

Таким
образом, для

  • линейного
    уравнения регрессии:


=
0,8


=86,3


=
0,13

  • логарифмического
    уравнения регрессии:


=
0,14


=18,69


=
0,14

  1. Построение
    интервального прогноза для значения
    x
    =
    xmax
    по
    уравнению линейной регрессии

При
построении доверительного интервала
прогноза используется стандартная
ошибка индивидуального значения прогноза
,
которая рассчитывается по формуле:


(18)

Где,


(19),

Где,

x,y
– то же что и в формуле (1),

n
– то же что и в формуле (2),

m
– то же что и в формуле (15)

Затем
строится доверительный интервал
прогноза, т.е. определяются нижняя

и верхняя
границы
интервала прогноза:


=
(20)


=
(21),

Где,


(22),

Где,


—
максимально возможное значение критерия
под влиянием случайных факторов при
данной степени свободы k=n-2
и уровне значимости α.

—
стандартная ошибка прогноза

Таким
образом, для

  • линейного
    уравнения регрессии:


=
35,74


==57.73


==67,03

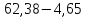
  • логарифмического
    уравнения регрессии:

=7,74


=7,19


==321,2


==323,06

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Когда мы подгоняем регрессионную модель к набору данных, нас часто интересует, насколько хорошо регрессионная модель «подходит» к набору данных. Две метрики, обычно используемые для измерения согласия, включают R -квадрат (R2) и стандартную ошибку регрессии , часто обозначаемую как S.

В этом руководстве объясняется, как интерпретировать стандартную ошибку регрессии (S), а также почему она может предоставить более полезную информацию, чем R 2 .

Стандартная ошибка по сравнению с R-квадратом в регрессии

Предположим, у нас есть простой набор данных, который показывает, сколько часов 12 студентов занимались в день в течение месяца, предшествующего важному экзамену, а также их баллы за экзамен:

Пример интерпретации стандартной ошибки регрессии

Если мы подгоним простую модель линейной регрессии к этому набору данных в Excel, мы получим следующий результат:

Вывод регрессии в Excel

R-квадрат — это доля дисперсии переменной отклика, которая может быть объяснена предикторной переменной. При этом 65,76% дисперсии экзаменационных баллов можно объяснить количеством часов, потраченных на учебу.

Стандартная ошибка регрессии — это среднее расстояние, на которое наблюдаемые значения отклоняются от линии регрессии. В этом случае наблюдаемые значения отклоняются от линии регрессии в среднем на 4,89 единицы.

Если мы нанесем фактические точки данных вместе с линией регрессии, мы сможем увидеть это более четко:

Обратите внимание, что некоторые наблюдения попадают очень близко к линии регрессии, в то время как другие не так близки. Но в среднем наблюдаемые значения отклоняются от линии регрессии на 4,19 единицы .

Стандартная ошибка регрессии особенно полезна, поскольку ее можно использовать для оценки точности прогнозов. Примерно 95% наблюдений должны находиться в пределах +/- двух стандартных ошибок регрессии, что является быстрым приближением к 95% интервалу прогнозирования.

Если мы заинтересованы в прогнозировании с использованием модели регрессии, стандартная ошибка регрессии может быть более полезной метрикой, чем R-квадрат, потому что она дает нам представление о том, насколько точными будут наши прогнозы в единицах измерения.

Чтобы проиллюстрировать, почему стандартная ошибка регрессии может быть более полезной метрикой для оценки «соответствия» модели, рассмотрим другой пример набора данных, который показывает, сколько часов 12 студентов занимались в день в течение месяца, предшествующего важному экзамену, а также их экзаменационная оценка:

Обратите внимание, что это точно такой же набор данных, как и раньше, за исключением того, что все значения s сокращены вдвое.Таким образом, студенты из этого набора данных учились ровно в два раза дольше, чем студенты из предыдущего набора данных, и получили ровно половину экзаменационного балла.

Если мы подгоним простую модель линейной регрессии к этому набору данных в Excel, мы получим следующий результат:

Вывод регрессии из простой линейной модели в Excel

Обратите внимание, что R-квадрат 65,76% точно такой же, как и в предыдущем примере.

Однако стандартная ошибка регрессии составляет 2,095 , что ровно вдвое меньше стандартной ошибки регрессии в предыдущем примере.

Если мы нанесем фактические точки данных вместе с линией регрессии, мы сможем увидеть это более четко:

Диаграмма рассеяния для простой линейной регрессии

Обратите внимание на то, что наблюдения располагаются гораздо плотнее вокруг линии регрессии. В среднем наблюдаемые значения отклоняются от линии регрессии на 2,095 единицы .

Таким образом, несмотря на то, что обе модели регрессии имеют R-квадрат 65,76% , мы знаем, что вторая модель будет давать более точные прогнозы, поскольку она имеет более низкую стандартную ошибку регрессии.

Преимущества использования стандартной ошибки

Стандартную ошибку регрессии (S) часто бывает полезнее знать, чем R-квадрат модели, потому что она дает нам фактические единицы измерения. Если мы заинтересованы в использовании регрессионной модели для получения прогнозов, S может очень легко сказать нам, достаточно ли точна модель для прогнозирования.

Например, предположим, что мы хотим создать 95-процентный интервал прогнозирования, в котором мы можем прогнозировать результаты экзаменов с точностью до 6 баллов от фактической оценки.

Наша первая модель имеет R-квадрат 65,76%, но это ничего не говорит нам о том, насколько точным будет наш интервал прогнозирования. К счастью, мы также знаем, что у первой модели показатель S равен 4,19. Это означает, что 95-процентный интервал прогнозирования будет иметь ширину примерно 2*4,19 = +/- 8,38 единиц, что слишком велико для нашего интервала прогнозирования.

Наша вторая модель также имеет R-квадрат 65,76%, но опять же это ничего не говорит нам о том, насколько точным будет наш интервал прогнозирования. Однако мы знаем, что вторая модель имеет S 2,095. Это означает, что 95-процентный интервал прогнозирования будет иметь ширину примерно 2*2,095= +/- 4,19 единиц, что меньше 6 и, следовательно, будет достаточно точным для использования для создания интервалов прогнозирования.

Дальнейшее чтение

Введение в простую линейную регрессию
Что такое хорошее значение R-квадрата?

Источник

Основы линейной регрессии

Время на прочтение
13 мин

Количество просмотров 135K

Здравствуй, Хабр!

Цель этой статьи — рассказать о линейной регрессии, а именно собрать и показать формулировки и интерпретации задачи регрессии с точки зрения математического анализа, статистики, линейной алгебры и теории вероятностей. Хотя в учебниках эта тема изложена строго и исчерпывающе, ещё одна научно-популярная статья не помешает.

! Осторожно, трафик! В статье присутствует заметное число изображений для иллюстраций, часть в формате gif.

Содержание

  • Введение
  • Метод наименьших квадратов
    • Математический анализ
    • Статистика
    • Теория вероятностей
  • Мультилинейная регрессия
    • Линейная алгебра
  • Произвольный базис
  • Заключительные замечания
    • Проблема выбора размерности
    • Численные методы
  • Реклама и заключение

Введение

Есть три сходных между собой понятия, три сестры: интерполяция, аппроксимация и регрессия.
У них общая цель: из семейства функций выбрать ту, которая обладает определенным свойством.


Интерполяция — способ выбрать из семейства функций ту, которая проходит через заданные точки. Часто функцию затем используют для вычисления в промежуточных точках. Например, мы вручную задаем цвет нескольким точкам и хотим чтобы цвета остальных точек образовали плавные переходы между заданными. Или задаем ключевые кадры анимации и хотим плавные переходы между ними. Классические примеры: интерполяция полиномами Лагранжа, сплайн-интерполяция, многомерная интерполяция (билинейная, трилинейная, методом ближайшего соседа и т.д). Есть также родственное понятие экстраполяции — предсказание поведения функции вне интервала. Например, предсказание курса доллара на основании предыдущих колебаний — экстраполяция.

Аппроксимация — способ выбрать из семейства «простых» функций приближение для «сложной» функции на отрезке, при этом ошибка не должна превышать определенного предела. Аппроксимацию используют, когда нужно получить функцию, похожую на данную, но более удобную для вычислений и манипуляций (дифференцирования, интегрирования и т.п). При оптимизации критических участков кода часто используют аппроксимацию: если значение функции вычисляется много раз в секунду и не нужна абсолютная точность, то можно обойтись более простым аппроксимантом с меньшей «ценой» вычисления. Классические примеры включают ряд Тейлора на отрезке, аппроксимацию ортогональными многочленами, аппроксимацию Паде, аппроксимацию синуса Бхаскара и т.п.

Регрессия — способ выбрать из семейства функций ту, которая минимизирует функцию потерь. Последняя характеризует насколько сильно пробная функция отклоняется от значений в заданных точках. Если точки получены в эксперименте, они неизбежно содержат ошибку измерений, шум, поэтому разумнее требовать, чтобы функция передавала общую тенденцию, а не точно проходила через все точки. В каком-то смысле регрессия — это «интерполирующая аппроксимация»: мы хотим провести кривую как можно ближе к точкам и при этом сохранить ее максимально простой чтобы уловить общую тенденцию. За баланс между этими противоречивыми желаниями как-раз отвечает функция потерь (в английской литературе «loss function» или «cost function»).

В этой статье мы рассмотрим линейную регрессию. Это означает, что семейство функций, из которых мы выбираем, представляет собой линейную комбинацию наперед заданных базисных функций ${f_i}$

$ f = \sum_i w_i f_i. $

Цель регрессии — найти коэффициенты этой линейной комбинации, и тем самым определить регрессионную функцию $f$ (которую также называют моделью). Отмечу, что линейную регрессию называют линейной именно из-за линейной комбинации базисных функций — это не связано с самыми базисными функциями (они могут быть линейными или нет).

Регрессия с нами уже давно: впервые метод опубликовал Лежандр в 1805 году, хотя Гаусс пришел к нему раньше и успешно использовал для предсказания орбиты «кометы» (на самом деле карликовой планеты) Цереры. Существует множество вариантов и обобщений линейной регрессии: LAD, метод наименьших квадратов, Ridge регрессия, Lasso регрессия, ElasticNet и многие другие.

Метод наименьших квадратов

Начнём с простейшего двумерного случая. Пусть нам даны точки на плоскости $\{(x_1,y_1),\cdots,(x_N,y_N)\}$ и мы ищем такую аффинную функцию

$ f(x) = a + b \cdot x, $

чтобы ее график ближе всего находился к точкам. Таким образом, наш базис состоит из константной функции и линейной $(1, x)$.

Как видно из иллюстрации, расстояние от точки до прямой можно понимать по-разному, например геометрически — это длина перпендикуляра. Однако в контексте нашей задачи нам нужно функциональное расстояние, а не геометрическое. Нас интересует разница между экспериментальным значением и предсказанием модели для каждого $x_i,$ поэтому измерять нужно вдоль оси $y$.

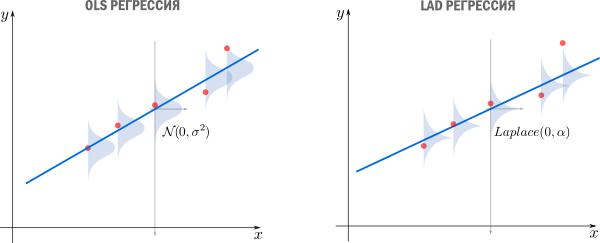
Первое, что приходит в голову, в качестве функции потерь попробовать выражение, зависящее от абсолютных значений разниц $|f(x_i) - y_i|$. Простейший вариант — сумма модулей отклонений $\sum_i |f(x_i) - y_i|$ приводит к Least Absolute Distance (LAD) регрессии.

Впрочем, более популярная функция потерь — сумма квадратов отклонений регрессанта от модели. В англоязычной литературе она носит название Sum of Squared Errors (SSE)

$ \text{SSE}(a,b)=\text{SS}_{res[iduals]}=\sum_{i=1}^N{\text{отклонение}_i}^2=\sum_{i=1}^N(y_i-f(x_i))^2=\sum_{i=1}^N(y_i-a-b\cdot x_i)^2, $

Метод наименьших квадратов (по англ. OLS) — линейная регрессия c $\text{SSE}(a,b)$ в качестве функции потерь.

Такой выбор прежде всего удобен: производная квадратичной функции — линейная функция, а линейные уравнения легко решаются. Впрочем, далее я укажу и другие соображения в пользу $\text{SSE}(a,b)$.

Математический анализ

Простейший способ найти $\text{argmin}_{a,b} \, \text{SSE}(a,b)$ — вычислить частные производные по $ a $ и $ b $, приравнять их нулю и решить систему линейных уравнений

$ \begin{aligned} \frac{\partial}{\partial a}\text{SSE}(a,b)&=-2\sum_{i=1}^N(y_i-a-bx_i), \\ \frac{\partial}{\partial b}\text{SSE}(a,b)&=-2\sum_{i=1}^N(y_i-a-bx_i)x_i. \end{aligned} $

Значения параметров, минимизирующие функцию потерь, удовлетворяют уравнениям

$ \begin{aligned} 0 &= -2\sum_{i=1}^N(y_i-\hat{a}-\hat{b}x_i), \\ 0 &= -2\sum_{i=1}^N(y_i-\hat{a}-\hat{b}x_i)x_i, \end{aligned} $

которые легко решить

$ \begin{aligned} \hat{a}&=\frac{\sum_i y_i}{N}-\hat{b}\frac{\sum_i x_i}{N},\\ \hat{b}&=\frac{\frac{\sum_i x_i y_i}{N}-\frac{\sum_i x_i\sum_i y_i}{N^2}}{\frac{\sum_i x_i^2}{N}-\left(\frac{\sum_i x_i^2}{N}\right)^2}. \end{aligned} $

Мы получили громоздкие и неструктурированные выражения. Сейчас мы их облагородим и вдохнем в них смысл.

Статистика

Полученные формулы можно компактно записать с помощью статистических эстиматоров: среднего $\langle{\cdot}\rangle$, вариации $\sigma_{\cdot}$ (стандартного отклонения), ковариации $\sigma({\cdot},{\cdot})$ и корреляции $\rho({\cdot},{\cdot})$

$ \begin{aligned} \hat{a}&=\langle{y}\rangle-\hat{b}\langle{x}\rangle, \\ \hat{b}&=\frac{\langle{xy}\rangle-\langle{x}\rangle\langle{y}\rangle}{\langle{x^2}\rangle-\langle{x}\rangle^2}. \end{aligned} $

Перепишем $\hat{b}$ как

$ \hat{b} = \frac{\sigma(x,y)}{\sigma_x^2}, $

где $\sigma_x$ это нескорректированное (смещенное) стандартное выборочное отклонение, а $\sigma(x,y)$ — ковариация. Теперь вспомним, что коэффициент корреляции (коэффициент корреляции Пирсона)

$ \rho(x,y)=\frac{\sigma(x,y)}{\sigma_x \sigma_y} $

и запишем

$ \hat{b}=\rho(x,y)\frac{\sigma_y}{\sigma_x}. $

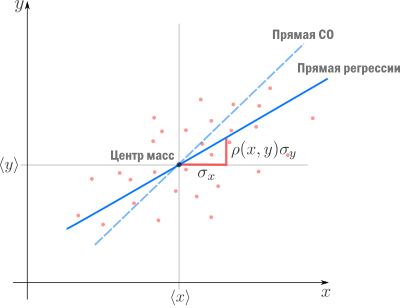
Теперь мы можем оценить все изящество дескриптивной статистики, записав уравнение регрессионной прямой так

$ \boxed{y-\langle {y} \rangle = \rho(x,y)\frac{\sigma_y}{\sigma_x}(x-\langle {x} \rangle)}. $

Во-первых, это уравнение сразу указывает на два свойства регрессионной прямой:

Во-вторых, теперь становится понятно, почему метод регрессии называется именно так. В единицах стандартного отклонения $y$ отклоняется от своего среднего значения меньше чем $x$, потому что $|\rho(x,y)|\leq1$. Это называется регрессией(от лат. regressus — «возвращение») по отношению к среднему. Это явление было описано сэром Фрэнсисом Гальтоном в конце XIX века в его статье «Регрессия к посредственности при наследовании роста». В статье показано, что черты (такие как рост), сильно отклоняющиеся от средних, редко передаются по наследству. Характеристики потомства как бы стремятся к среднему — на детях гениев природа отдыхает.

Возведя коэффициент корреляции в квадрат, получим коэффициент детерминации $R = \rho^2$. Квадрат этой статистической меры показывает насколько хорошо регрессионная модель описывает данные. $R^2$, равный $1$, означает что функция идеально ложится на все точки — данные идеально скоррелированны. Можно доказать, что $R^2$ показывает какая доля вариативности в данных объясняется лучшей из линейных моделей. Чтобы понять, что это значит, введем определения

$ \begin{aligned} \text{Var}_{data} &= \frac{1}{N}\sum_i (y_i-\langle y \rangle)^2, \\ \text{Var}_{res} &= \frac{1}{N} \sum_i (y_i-\text{модель}(x_i))^2, \\ \text{Var}_{reg} &= \frac{1}{N} \sum_i (\text{модель}(x_i)-\langle y \rangle)^2. \end{aligned} $

$\text{Var}_{data}$ — вариация исходных данных (вариация точек $y_i$).

$\text{Var}_{res}$ — вариация остатков, то есть вариация отклонений от регрессионной модели — от $y_i$ нужно отнять предсказание модели и найти вариацию.

$\text{Var}_{reg}$ — вариация регрессии, то есть вариация предсказаний регрессионной модели в точках $x_i$ (обратите внимание, что среднее предсказаний модели совпадает с $\langle y \rangle$).

Дело в том, что вариация исходных данных разлагается в сумму двух других вариаций: вариации случайного шума (остатков) и вариации, которая объясняется моделью (регрессии)

$ \boxed{{\color{red}{\text{Var}_{data}}} ={\color{green}{\text{Var}_{res}}}+ {\color{blue}{\text{Var}_{reg}}}.} $

или

$ \sigma^2_{data} =\sigma^2_{res}+ \sigma^2_{reg}. $

Как видим, стандартные отклонения образуют прямоугольный треугольник.

Мы стремимся избавиться от вариативности, связанной с шумом и оставить лишь вариативность, которая объясняется моделью, — хотим отделить зерна от плевел. О том, насколько это удалось лучшей из линейных моделей, свидетельствует $R^2$, равный единице минус доля вариации ошибок в суммарной вариации

$ R^2=\frac{\text{Var}_{data}-\text{Var}_{res}}{\text{Var}_{data}}=1-\frac{\color{green}{\text{Var}_{res}}}{\color{red}{\text{Var}_{data}}} $

или доле объясненной вариации (доля вариации регрессии в полной вариации)

$ R^2=\frac{\color{blue}{\text{Var}_{reg}}}{\color{red}{\text{Var}_{data}}}. $

$R$ равен косинусу угла в прямоугольном треугольнике $(\sigma_{data}, \sigma_{reg}, \sigma_{res})$. Кстати, иногда вводят долю необъясненной вариации $FUV=1-R^2$ и она равна квадрату синуса в этом треугольнике. Если коэффициент детерминации мал, возможно мы выбрали неудачные базисные функции, линейная регрессия неприменима вовсе и т.п.

Теория вероятностей

Ранее мы пришли к функции потерь $\text{SSE}(a,b)$ из соображений удобства, но к ней же можно прийти с помощью теории вероятностей и метода максимального правдоподобия (ММП). Напомню вкратце его суть. Предположим, у нас есть $N$ независимых одинаково распределенных случайных величин (в нашем случае — результатов измерений). Мы знаем вид функции распределения (напр. нормальное распределение), но хотим определить параметры, которые в нее входят (например $\mu$ и $\sigma$). Для этого нужно вычислить вероятность получить $N$ датапоинтов в предположении постоянных, но пока неизвестных параметров. Благодаря независимости измерений, мы получим произведение вероятностей реализации каждого измерения. Если мыслить полученную величину как функцию параметров (функция правдоподобия) и найти её максимум, мы получим оценку параметров. Зачастую вместо функции правдоподобия используют ее логарифм — дифференцировать его проще, а результат — тот же.

Вернемся к задаче простой регрессии. Допустим, что значения $x$ нам известны точно, а в измерении $y$ присутствует случайный шум (свойство слабой экзогенности). Более того, положим, что все отклонения от прямой (свойство линейности) вызваны шумом с постоянным распределением (постоянство распределения). Тогда

$ y = a + bx + \epsilon, $

где $\epsilon$ — нормально распределенная случайная величина

$ \epsilon \sim \mathcal{N}(0,\,\sigma^{2}), \qquad p(\epsilon) = \frac{1}{\sqrt{2 \pi \sigma^2}} e^{-\frac{\epsilon^2}{2\sigma^2}}. $

Исходя из предположений выше, запишем функцию правдоподобия

$ \begin{aligned} L(a,b|\mathbf{y})&=P(\mathbf{y}|a,b)=\prod_i P(y_i|a,b)=\prod_i p(y_i-a-bx|a,b)=\\ &= \prod_i \frac{1}{\sqrt{2 \pi \sigma^2}} e^{-\frac{(y_i-a-bx)^2}{2\sigma^2}}= \frac{1}{\sqrt{2 \pi \sigma^2}}e^{-\frac{\sum_i (y_i-a-bx)^2}{2 \sigma^2}}=\\ &= \frac{1}{\sqrt{2 \pi \sigma^2}}e^{-\frac{\text{SSE}(a,b)}{2 \sigma^2}} \end{aligned} $

и ее логарифм

$ l(a,b|\mathbf{y})=\log{L(a,b|\mathbf{y})}=-\text{SSE}(a,b)+const. $

Таким образом, максимум правдоподобия достигается при минимуме $\text{SSE}$

$ (\hat{a},\hat{b})=\text{argmax}_{a,b} \, l(a,b|\mathbf{y}) = \text{argmin}_{a,b} \, \text{SSE}(a,b), $

что дает основание принять ее в качестве функции потерь. Кстати, если

$ \begin{aligned} \epsilon \sim \text{Laplace}(0, \alpha), \qquad p_{L}(\epsilon; \mu, \alpha) =\frac{\alpha}{2}e^{-\alpha |\epsilon-\mu|} \end{aligned} $

мы получим функцию потерь LAD регрессии

$ E_{LAD}(a,b)=\sum_i |y_i-a-bx_i|, $

которую мы упоминали ранее.

Подход, который мы использовали в этом разделе — один из возможных. Можно прийти к такому же результату, используя более общие свойства. В частности, свойство постоянства распределения можно ослабить, заменив на свойства независимости, постоянства вариации (гомоскедастичность) и отсутствия мультиколлинеарности. Также вместо ММП эстимации можно воспользоваться другими методами, например линейной MMSE эстимацией.

Мультилинейная регрессия

До сих пор мы рассматривали задачу регрессии для одного скалярного признака $x$, однако обычно регрессор — это $n$-мерный вектор $\mathbf{x}$. Другими словами, для каждого измерения мы регистрируем $n$ фич, объединяя их в вектор. В этом случае логично принять модель с $n+1$ независимыми базисными функциями векторного аргумента — $n$ степеней свободы соответствуют $n$ фичам и еще одна — регрессанту $y$. Простейший выбор — линейные базисные функции $(1, x_1, \cdots, x_n)$. При $n = 1$ получим уже знакомый нам базис $(1, x)$.

Итак, мы хотим найти такой вектор (набор коэффициентов) $\mathbf{w}$, что

$ \sum_{j=0}^n w_j x_j^{(i)}= \mathbf{w}^{\top}\mathbf{x}^{(i)} \simeq y_i, \qquad \qquad \qquad \qquad i=1\dots N. $

Знак «$\simeq$» означает, что мы ищем решение, которое минимизирует сумму квадратов ошибок

$ \hat{\mathbf{w}}=\text{argmin}_\mathbf{w} \, \sum_{i=1}^N \left({y_i - \mathbf{w}^{\top}\mathbf{x}^{(i)}}\right)^2 $

Последнее уравнение можно переписать более удобным образом. Для этого расположим $\mathbf{x}^{(i)}$ в строках матрицы (матрицы информации)

$ X= \begin{pmatrix} - & \mathbf{x}^{(1)\top} & - \\ \cdots & \cdots & \cdots\\ - & \mathbf{x}^{(N)\top} & - \end{pmatrix} = \begin{pmatrix} | & | & & | \\ \mathbf{x}_0 & \mathbf{x}_1 & \cdots & \mathbf{x}_n \\ | & | & & | \end{pmatrix} = \begin{pmatrix} 1 & x^{(1)}_{1} & \cdots & x^{(1)}_{n} \\ \cdots & \cdots & \cdots & \cdots\\ 1 & x^{(N)}_{1} & \cdots & x^{(N)}_{n} \end{pmatrix}. $

Тогда столбцы матрицы $\mathbf{x}_{i}$ отвечают измерениям $i$-ой фичи. Здесь важно не запутаться: $N$ — количество измерений, $n$ — количество признаков (фич), которые мы регистрируем. Систему можно записать как

$ X \, \mathbf{w} \simeq \mathbf{y}. $

Квадрат нормы разности векторов в правой и левой частях уравнения образует функцию потерь

$ \text{SSE}(\mathbf{w}) = {\|\mathbf{y}-X \mathbf{w}\|}^2, \qquad \qquad \mathbf{w} \in \mathbb{R}^{n+1}; \, \mathbf{y} \in \mathbb{R}^{N}, $

которую мы намерены минимизировать

$ \begin{aligned} \hat{\mathbf{w}}&=\text{argmin}_\mathbf{w} \, \text{SSE}(\mathbf{w}) = \text{argmin}_\mathbf{w} \, (\mathbf{y}-X \mathbf{w})^{\top}(\mathbf{y}-X \mathbf{w})=\\ &= \text{argmin}_\mathbf{w} \,(\mathbf{y}^{\top}\mathbf{y}-2\mathbf{w}^{\top}X^{\top}\mathbf{y}+\mathbf{w}^{\top}X^{\top}X\mathbf{w}). \end{aligned} $

Продифференцируем финальное выражение по $\mathbf{w}$ (если забыли как это делается — загляните в Matrix cookbook)

$ \frac{\partial \, \text{SSE}(\mathbf{w})}{\partial \mathbf{w}}=-2 X^{\top}\mathbf{y}+2 X^{\top}X\mathbf{w}, $

приравняем производную к $\mathbf{0}$ и получим т.н. нормальные уравнения

$ X^{\top}X \, \hat{\mathbf{w}}=X^{\top}\mathbf{y}. $

Если столбцы матрицы информации $X$ линейно независимы (нет идеально скоррелированных фич), то матрица $X^{\top}X$ имеет обратную (доказательство можно посмотреть, например, в видео академии Хана). Тогда можно записать

$ \boxed{\hat{\mathbf{w}} = (X^{\top}X)^{-1}X^{\top}\mathbf{y}=X^{+}\mathbf{y}}, $

где

$ X^{+}=(X^{\top}X)^{-1}X^{\top} $

псевдообратная к $X$. Понятие псевдообратной матрицы введено в 1903 году Фредгольмом, она сыграла важную роль в работах Мура и Пенроуза.

Напомню, что обратить $X^{\top}X$ и найти $X^{+}$ можно только если столбцы $X$ линейно независимы. Впрочем, если столбцы $X$ близки к линейной зависимости, вычисление $(X^{\top}X)^{-1}$ уже становится численно нестабильным. Степень линейной зависимости признаков в $X$ или, как говорят, мультиколлинеарности матрицы $X^{\top}X$, можно измерить числом обусловленности — отношением максимального собственного значения к минимальному. Чем оно больше, тем ближе $X^{\top}X$ к вырожденной и неустойчивее вычисление псевдообратной.

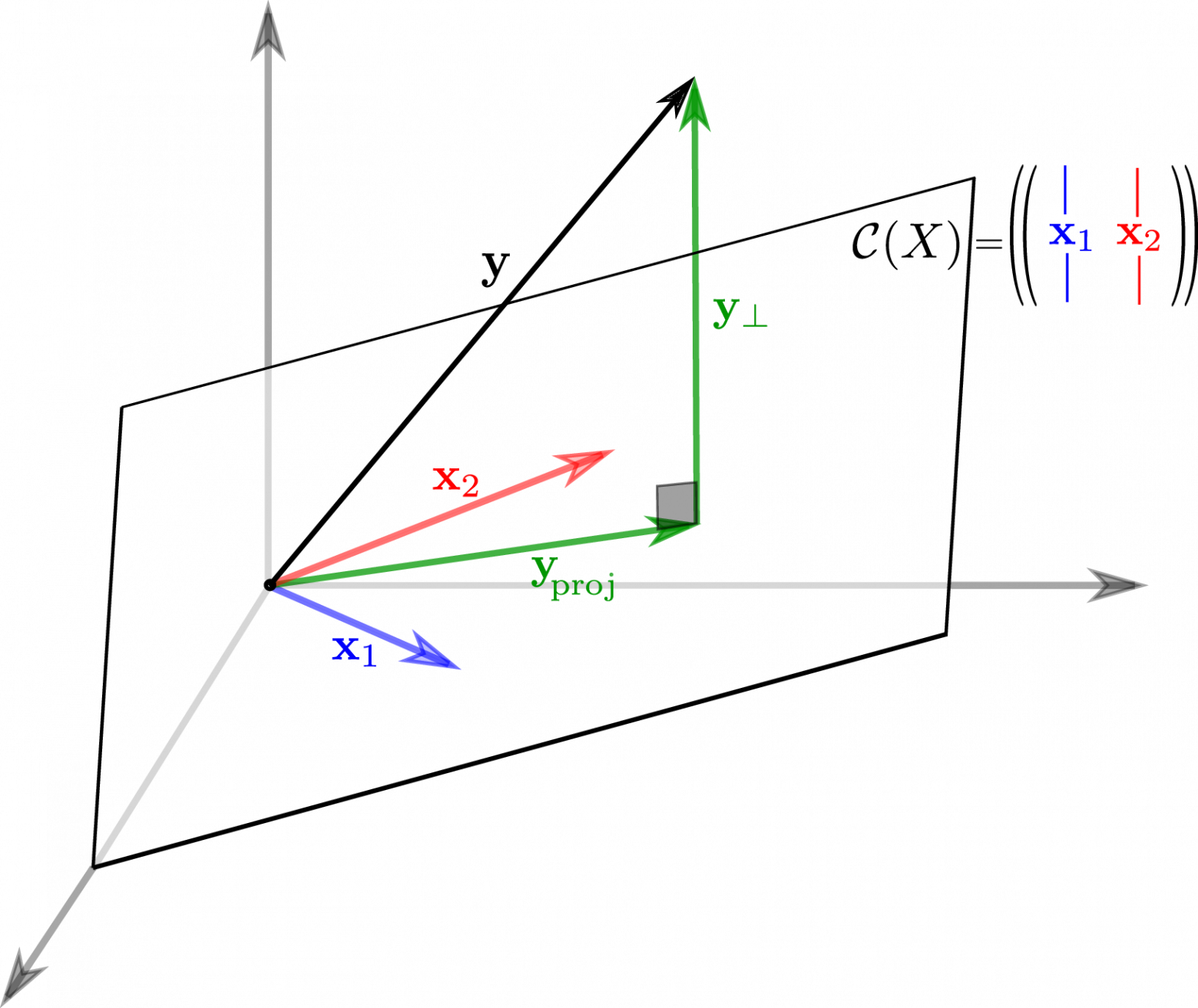
Линейная алгебра

К решению задачи мультилинейной регрессии можно прийти довольно естественно и с помощью линейной алгебры и геометрии, ведь даже то, что в функции потерь фигурирует норма вектора ошибок уже намекает, что у задачи есть геометрическая сторона. Мы видели, что попытка найти линейную модель, описывающую экспериментальные точки, приводит к уравнению

$ X \, \mathbf{w} \simeq \mathbf{y}. $

Если количество переменных равно количеству неизвестных и уравнения линейно независимы, то система имеет единственное решение. Однако, если число измерений превосходит число признаков, то есть уравнений больше чем неизвестных — система становится несовместной, переопределенной. В этом случае лучшее, что мы можем сделать — выбрать вектор $\mathbf{w}$, образ которого $X\mathbf{w}$ ближе остальных к $\mathbf{y}$. Напомню, что множество образов или колоночное пространство $\mathcal{C}(X)$ — это линейная комбинация вектор-столбцов матрицы $X$

$ \begin{pmatrix} | & | & & | \\ \mathbf{x}_0 & \mathbf{x}_1 & \cdots & \mathbf{x}_n \\ | & | & & | \end{pmatrix} \mathbf{w} = w_0 \mathbf{x}_0 + w_1 \mathbf{x}_1 + \cdots w_n \mathbf{x}_n . $

$\mathcal{C}(X)$ — $n+1$-мерное линейное подпространство (мы считаем фичи линейно независимыми), линейная оболочка вектор-столбцов $X$. Итак, если $\mathbf{y}$ принадлежит $\mathcal{C}(X)$, то мы можем найти решение, если нет — будем искать, так сказать, лучшее из нерешений.

Если в дополнение к векторам $\mathcal{C}(X)$ мы рассмотрим все вектора им перпендикулярные, то получим еще одно подпространство и сможем любой вектор из $\mathbb{R}^{N}$ разложить на две компоненты, каждая из которых живет в своем подпространстве. Второе, перпендикулярное пространство, можно характеризовать следующим образом (нам это понадобится в дальнейшем). Пускай $\mathbf{v} \in \mathbb{R}^{N}$, тогда

$ X^\top \mathbf{v} = \begin{pmatrix} - & \mathbf{x}_0^{\top} & - \\ \cdots & \cdots & \cdots\\ - & \mathbf{x}_n^{\top} & - \end{pmatrix} \mathbf{v} = \begin{pmatrix} \mathbf{x}_0^{\top} \cdot \mathbf{v} \\ \cdots \\ \mathbf{x}_n^{\top} \cdot \mathbf{v} \\ \end{pmatrix} $

равен нулю в том и только в том случае, если $\mathbf{v}$ перпендикулярен всем $\mathbf{x}_i$, а значит и целому $\mathcal{C}(X)$. Таким образом, мы нашли два перпендикулярных линейных подпространства, линейные комбинации векторов из которых полностью, без дыр, «покрывают» все $\mathbb{R}^N$. Иногда это обозначают c помощью символа ортогональной прямой суммы

где $\text{ker}(X^{\top})=\{\mathbf{v}|X^{\top}\mathbf{v}=\mathbf{0}\}$. В каждое из подпространств можно попасть с помощью соответствующего оператора проекции, но об этом ниже.

Теперь представим $\mathbf{y}$ в виде разложения

$ \mathbf{y} = \mathbf{y}_{\text{proj}} + \mathbf{y}_{\perp}, \qquad \mathbf{y}_{\text{proj}} \in \mathcal{C}(X), \qquad \mathbf{y}_{\perp} \in \text{ker}(X^{\top}). $

Если мы ищем решение $\hat{\mathbf{w}}$, то естественно потребовать, чтобы $|| \mathbf{y} - X\mathbf{w} ||$ была минимальна, ведь это длина вектора-остатка. Учитывая перпендикулярность подпространств и теорему Пифагора

$ \text{argmin}_\mathbf{w} || \mathbf{y} - X\mathbf{w} || = \text{argmin}_\mathbf{w} || \mathbf{y}_{\perp} + \mathbf{y}_{\text{proj}} - X\mathbf{w} || = \text{argmin}_\mathbf{w} \sqrt{|| \mathbf{y}_{\perp} ||^2 + || \mathbf{y}_{\text{proj}} - X\mathbf{w} ||^2}, $

но поскольку, выбрав подходящий $\mathbf{w}$, я могу получить любой вектор колоночного пространства, то задача сводится к

$ X\hat{\mathbf{w}} = \mathbf{y}_{\text{proj}}, $

а $\mathbf{y}_{\perp}$ останется в качестве неустранимой ошибки. Любой другой выбор $\hat{\mathbf{w}}$ сделает ошибку только больше.

Если теперь вспомнить, что $X^{\top} \mathbf{y}_{\perp} = \mathbf{0}$, то легко видеть

$ X^\top X \mathbf{w} = X^{\top} \mathbf{y}_{\text{proj}} = X^{\top} \mathbf{y}_{\text{proj}} + X^{\top} \mathbf{y}_{\perp} = X^{\top} \mathbf{y}, $

что очень удобно, так как $\mathbf{y}_{\text{proj}}$ у нас нет, а вот $\mathbf{y}$ — есть. Вспомним из предыдущего параграфа, что $X^{\top} X$ имеет обратную при условии линейной независимости признаков и запишем решение

$ \mathbf{w} = (X^\top X)^{-1} X^\top \mathbf{y} = X^{+} \mathbf{y}, $

где $X^{+}$ уже знакомая нам псевдообратная матрица. Если нам интересна проекция $\mathbf{y}_{\text{proj}}$, то можно записать

$ \mathbf{y}_{\text{proj}} = X \mathbf{w} = X X^{+} \mathbf{y} = \text{Proj}_X \mathbf{y}, $

где $\text{Proj}_X$ — оператор проекции на колоночное пространство.

Выясним геометрический смысл коэффициента детерминации.

Заметьте, что фиолетовый вектор $\bar{y} \cdot \boldsymbol{1}=\bar{y} \cdot (1,1,\dots,1)^{\top}$ пропорционален первому столбцу матрицы информации $X$, который состоит из одних единиц согласно нашему выбору базисных функций. В RGB треугольнике

$ {\color{red}{\mathbf{y}-\hat{y} \cdot \boldsymbol{1}}}={\color{green}{\mathbf{y}-\bar{\mathbf{y}}}}+{\color{blue}{\hat{\mathbf{y}}-\bar{y} \cdot \boldsymbol{1}}}. $

Так как этот треугольник прямоугольный, то по теореме Пифагора

$ {\color{red}{\|\mathbf{y}-\hat{y} \cdot \boldsymbol{1}\|^2}}={\color{green}{\|\mathbf{y}-\bar{\mathbf{y}}\|^2}}+{\color{blue}{\|\hat{\mathbf{y}}-\bar{y} \cdot \boldsymbol{1}\|^2}}. $

Это геометрическая интерпретация уже известного нам факта, что

$ {\color{red}{\text{Var}_{data}}} = {\color{green}{\text{Var}_{res}}}+{\color{blue}{\text{Var}_{reg}}}. $

Мы знаем, что

$ R^2=\frac{\color{blue}{\text{Var}_{reg}}}{\color{red}{\text{Var}_{data}}}, $

а значит

$ R=\cos{\theta}. $

Красиво, не правда ли?

Произвольный базис

Как мы знаем, регрессия выполняется на базисных функциях $f_i$ и её результатом есть модель

$ f = \sum_i w_i f_i, $

но до сих пор мы использовали простейшие $f_i$, которые просто ретранслировали изначальные признаки без изменений, ну разве что дополняли их постоянной фичей $f_0(\mathbf{x}) = 1$. Как можно было заметить, на самом деле ни вид $f_i$, ни их количество ничем не ограничены — главное, чтобы функции в базисе были линейно независимы. Обычно, выбор делается исходя из предположений о природе процесса, который мы моделируем. Если у нас есть основания полагать, что точки $\{(x_1,y_1),\cdots,(x_N,y_N)\}$ ложатся на параболу, а не на прямую, то стоит выбрать базис $(1, x, x^2)$. Количество базисных функций может быть как меньшим, так и большим, чем количество изначальных фич.

Если мы определились с базисом, то дальше действуем следующим образом. Мы формируем матрицу информации

$ \Phi = \begin{pmatrix} - & \boldsymbol{f}^{(1)\top} & - \\ \cdots & \cdots & \cdots\\ - & \boldsymbol{f}^{(N)\top} & - \end{pmatrix} = \begin{pmatrix} {f}_{0}\left(\mathbf{x}^{(1)}\right) & {f}_{1}\left(\mathbf{x}^{(1)}\right) & \cdots & {f}_{n}\left(\mathbf{x}^{(1)}\right) \\ \cdots & \cdots & \cdots & \cdots\\ {f}_{0}\left(\mathbf{x}^{(N)}\right) & {f}_{1}\left(\mathbf{x}^{(N)}\right) & \cdots & {f}_{n}\left(\mathbf{x}^{(N)}\right) \end{pmatrix}, $

записываем функцию потерь

$ E(\mathbf{w})={\|{\boldsymbol{\epsilon}}(\mathbf{w})\|}^2={\|\mathbf{y}-\Phi \, \mathbf{w}\|}^2 $

и находим её минимум, например с помощью псевдообратной матрицы

$ \hat{\mathbf{w}} = \text{argmin}_\mathbf{w} \,E(\mathbf{w}) = (\Phi^{\top}\Phi)^{-1}\Phi^{\top}\mathbf{y}=\Phi^{+}\mathbf{y} $

или другим методом.

Заключительные замечания

Проблема выбора размерности

На практике часто приходится самостоятельно строить модель явления, то есть определяться сколько и каких нужно взять базисных функций. Первый порыв «набрать побольше» может сыграть злую шутку: модель окажется слишком чувствительной к шумам в данных (переобучение). С другой стороны, если излишне ограничить модель, она будет слишком грубой (недообучение).

Есть два способа выйти из ситуации. Первый: последовательно наращивать количество базисных функций, проверять качество регрессии и вовремя остановиться. Или же второй: выбрать функцию потерь, которая определит число степеней свободы автоматически. В качестве критерия успешности регрессии можно использовать коэффициент детерминации, о котором уже упоминалось выше, однако, проблема в том, что $R^2$ монотонно растет с ростом размерности базиса. Поэтому вводят скорректированный коэффициент

$ \bar{R}^2=1-(1-R^2)\left[\frac{N-1}{N-(n+1)}\right], $

где $N$ — размер выборки, $n$ — количество независимых переменных. Следя за $\bar{R}^2$, мы можем вовремя остановиться и перестать добавлять дополнительные степени свободы.

Вторая группа подходов — регуляризации, самые известные из которых Ridge($L_2$/гребневая/Тихоновская регуляризация), Lasso($L_1$ регуляризация) и Elastic Net(Ridge+Lasso). Главная идея этих методов: модифицировать функцию потерь дополнительными слагаемыми, которые не позволят вектору коэффициентов $\mathbf{w}$ неограниченно расти и тем самым воспрепятствуют переобучению

$ \begin{aligned} E_{\text{Ridge}}(\mathbf{w})&=\text{SSE}(\mathbf{w})+\alpha \sum_i |w_i|^2 = \text{SSE}(\mathbf{w})+\alpha \| \mathbf{w}\|_{L_2}^2,\\ E_{\text{Lasso}}(\mathbf{w})&=\text{SSE}(\mathbf{w})+\beta \sum_i |w_i| =\text{SSE}(\mathbf{w})+\beta \| \mathbf{w}\|_{L_1},\\ E_{\text{EN}}(\mathbf{w})&=\text{SSE}(\mathbf{w})+\alpha \| \mathbf{w}\|_{L_2}^2+\beta \| \mathbf{w}\|_{L_1}, \\ \end{aligned} $

где $\alpha$ и $\beta$ — параметры, которые регулируют «силу» регуляризации. Это обширная тема с красивой геометрией, которая заслуживает отдельного рассмотрения. Упомяну кстати, что для случая двух переменных при помощи вероятностной интерпретации можно получить Ridge и Lasso регрессии, удачно выбрав априорное распределения для коэффициента $b$

$ y = a + bx + \epsilon,\qquad \epsilon \sim \mathcal{N}(0,\,\sigma^{2}),\qquad \left\{\begin{aligned} &b \sim \mathcal{N}(0,\,\tau^{2})&\leftarrow\text{Ridge},\\ &b \sim \text{Laplace} (0,\,\alpha)&\leftarrow\text{Lasso}. \end{aligned}\right. $

Численные методы

Скажу пару слов, как минимизировать функцию потерь на практике. SSE — это обычная квадратичная функция, которая параметризируется входными данными, так что принципиально ее можно минимизировать методом скорейшего спуска или другими методами оптимизации. Разумеется, лучшие результаты показывают алгоритмы, которые учитывают вид функции SSE, например метод стохастического градиентного спуска. Реализация Lasso регрессии в scikit-learn использует метод координатного спуска.

Также можно решить нормальные уравнения с помощью численных методов линейной алгебры. Эффективный метод, который используется в scikit-learn для МНК — нахождение псевдообратной матрицы с помощью сингулярного разложения. Поля этой статьи слишком узки, чтобы касаться этой темы, за подробностями советую обратиться к курсу лекций К.В.Воронцова.

Реклама и заключение

Эта статья — сокращенный пересказ одной из глав курса по классическому машинному обучению в Киевском академическом университете (преемник Киевского отделения Московского физико-технического института, КО МФТИ). Автор статьи помогал в создании этого курса. Технически курс выполнен на платформе Google Colab, что позволяет совмещать формулы, форматированные LaTeX, исполняемый код Python и интерактивные демонстрации на Python+JavaScript, так что студенты могут работать с материалами курса и запускать код с любого компьютера, на котором есть браузер. На главной странице собраны ссылки на конспекты, «рабочие тетради» для практик и дополнительные ресурсы. В основу курса положены следующие принципы:

  • все материалы должны быть доступны студентам с первой пары;
  • лекция нужны для понимания, а не для конспектирования (конспекты уже готовы, нет смысла их писать, если не хочется);
  • конспект — больше чем лекция (материала в конспектах больше, чем было озвучено на лекции, фактически конспекты представляют собой полноценный учебник);
  • наглядность и интерактивность (иллюстрации, фото, демки, гифки, код, видео с youtube).

Если хотите посмотреть на результат — загляните на страничку курса на GitHub.

Надеюсь вам было интересно, спасибо за внимание.

Источник

Понравилась статья? Поделить с друзьями:
  • Стандартная ошибка excel это
  • Стандартная ошибка для доли
  • Стандартная ошибка прогнозирования формула
  • Стандартная ошибка среднего может обозначаться символами
  • Стандартная квадратичная ошибка