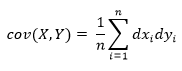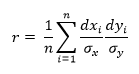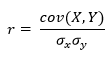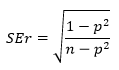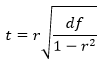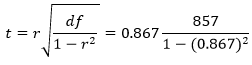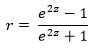Пакет
анализа —
это надстройка Excel,
которая
представляет широкие
возможности для проведения статистического
анализа. Установка средств Пакет
анализа
В
стандартной
конфигурации программы Excel
вы
не найдете средства Пакет
анализа. Это
средство надо установить в качестве
надстройки
Excel.
Для
этого выполните следующие действия:
-
Выберите
команду Сервис
=> Надстройки. -
В
диалоговом окне Надстройки
(рис.
12) установите флажок Пакет
анализа. -
Щелкните
по кнопке ОК.
В
результате выполненных действий в
нижней части меню Сервис
появится
новая команда Анализ
данных. Эта
команда предоставляет
доступ к средствам анализа, которые
есть в Excel.
Рис.
12. Диалоговое окно Надстройки
Продемонстрируем
возможности Пакета программ на следующем
примере.
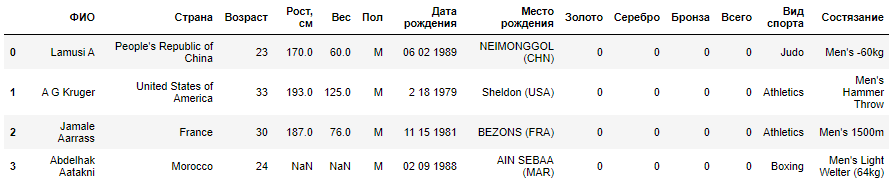
Пример
Построим
модель объема реализации одного из
продуктов фирмы.
Объем
реализации — это зависимая переменная
Y.
В
качестве независимых,
объясняющих переменных выбраны:
Х1
— время,
Х2
—
расходы на материал,
Х3
— цена
изделия,
Х4
—
средняя цена по отрасли,
X5
—
индекс расходов.
Статистические
данные по всем переменным приведены в
табл. 5.
В
рассматриваемом примере число наблюдений
п
=
16, факторных
признаков т
=
5.
Таблица 5
|
Y |
X1 |
Х2 |
Х3 |
Х4 |
Х5 |
|
126 |
1 |
4 |
15 |
17 |
100 |
|
137 |
2 |
4,8 |
14,8 |
17,3 |
98,4 |
|
148 |
3 |
3,8 |
15,2 |
16,8 |
101,2 |
|
191 |
4 |
8,7 |
15,5 |
16,2 |
103,5 |
|
274 |
5 |
8,2 |
15,5 |
16 |
104,1 |
|
370 |
6 |
9,7 |
16 |
18 |
107 |
|
432 |
7 |
14,7 |
18,1 |
20,2 |
107,4 |
|
445 |
8 |
18,7 |
13 |
15,8 |
108,5 |
|
367 |
9 |
19,8 |
15,8 |
18,2 |
108,3 |
|
367 |
10 |
10,6 |
16,9 |
16,8 |
109,2 |
|
321 |
11 |
8,6 |
16,3 |
17 |
110,1 |
|
307 |
12 |
6,5 |
16,1 |
18,3 |
110,7 |
|
331 |
13 |
12,6 |
15,4 |
16,4 |
110,3 |
|
345 |
14 |
6,5 |
15,7 |
16,2 |
111,8 |
|
364 |
15 |
5,8 |
16 |
17,7 |
112,3 |
|
384 |
16 |
5,7 |
15,1 |
16,2 |
112,9 |
Использование
инструмента Корреляция
Для
проведения корреляционного анализа
нужно выполнить следующие
действия:
1)
расположить данные в смежных диапазонах
ячеек;
2)
выбрать команду Сервис
=>
Анализ
данных (рис.
13). Появится
диалоговое окно Анализ
данных (рис.
14);
Рис.13. Выбор команды
Анализ
данных
3)в диалоговом окне
Анализ
данных выбрать
инструмент Корреляция
(рис.14), щелкнуть по кнопке ОК.
Появится диалоговое окно Корреляция
(рис.15);
Рис.14. Выбор команды
Анализ
данных
4)в диалоговом окне
Корреляция
в поле
«Входной интервал» необходимо ввести
диапазон ячеек, содержащих исходные
данные. Если также выделены заголовки
столбцов, то установить флажок «Метки
в первой строке» (рис.15);
5) выбрать параметры
вывода. В данном примере — установить
переключатель «Новый рабочий лист»;
6) щелкнуть по
кнопке ОК.
Рис.15. Диалоговое
окно Корреляция
На новом рабочем
листе получаем результаты вычислений-
таблицу значений коэффициентов парной
корреляции(рис.16).
Рис.16. Результаты
корреляционного анализа
Выбор вида модели
Анализ
матрицы коэффициентов парной корреляции
показывает, что
зависимая переменная, т.е. объем
реализации, имеет тесную связь:
— с
индексом расходов ryX5
=0,816,
-
с
расходами наматериал ryX2
=
0,646, -
со
временем ryX1
= 0,678.
Однако
факторы Х1
и
Х5
тесно
связаны между собой : rX1X5=0,96,
что
свидетельствует о наличии коллинеарости.
Из этих двух переменных
оставим в модели Х5
—
индекс расходов. Переменные X1
(время),
X3
(цена изделия) и Х4
(цена
отрасли) также исключаем
из модели, т.к. связь их с результативным
признаком Y
(объемом
реализации) невысокая.
После
исключения незначимых факторов имеем
п=16,k
= 2. Модель
приобретает вид:
= ао+а1Х2+а2Х5.
Оценка параметров
модели
На
основе метода наименьших квадратов
проведем оценку параметров
регрессии по формуле (3). При этом
используем данные, приведенные
в табл.6.
Таблица 6
|
Y |
Х0 |
X2 |
X5 |
|
Объем реал. |
Реклама |
Инд. п.расх. |
|
|
126 |
1 |
4 |
100 |
|
137 |
1 |
4,8 |
98,4 |
|
148 |
1 |
3,8 |
101,2 |
|
191 |
1 |
8,7 |
103,5 |
|
274 |
1 |
8,2 |
104,1 |
|
370 |
1 |
9,7 |
107 |
|
432 |
1 |
14,7 |
107,4 |
|
445 |
1 |
18,7 |
108,5 |
|
367 |
1 |
19,8 |
108,3 |
|
367 |
1 |
10,6 |
109,2 |
|
321 |
1 |
8,6 |
110,1 |
|
307 |
1 |
6,5 |
110,7 |
|
331 |
1 |
12,6 |
110,3 |
|
345 |
1 |
6,5 |
111,8 |
|
364 |
1 |
5,8 |
112,3 |
|
384 |
1 |
5,7 |
112,9 |
Непосредственное
вычисление (вычисление «вручную»)
вектора оценок
параметров регрессии а
согласно
формуле (3) весьма громоздко,
т.к. матрица независимых переменных X
имеет
довольно высокую
размерность (16 х 3), матрица Y-
размерности (16 х 1). В табл. 7
приведены размерности матриц — результатов
промежуточных действий.
Таблица 7
|
XT |
(3 х 16) |
|
ХTХ |
(3×3) |
|
(XTX)-1 |
(3×3) |
|
(ХTХ)-1ХT |
(3 х 16) |
|
(ХTX)-1ХTY |
(3×1) |
Задача
существенно упрощается при использовании
средств Excel.
Операции,
предписанные формулой (3) целесообразно
проводить с помощью следующих встроенных
в Excel
функций:
•МУМНОЖ
—
умножение матриц,
•ТРАНСП
—
транспонирование матриц,
•МОБР
—
вычисление обратной матрицы.
Для
вычисления вектора оценок параметров
регрессии а
в
Excel
необходимо
выполнить следующие действия:
-
Ввести данные
(табл. 6). -
Выделить
диапазон ячеек для записи вектора а,
соответствующий
его размерности (3×1)
(рис. 16). -
Используя
встроенные в Excel
функции,
ввести формулу (3), определяющую
вектор а. -
Нажать
одновременно клавиши CTRL
+ SHIFT
+ ENTER.
Появится
результат (рис. 17).
Таким образом,
имеем
Рис.
16. Выделение диапазона ячеек (3 х 1) для
записи вектора оценок
параметров регрессии а
Уравнение
регрессии зависимости объема реализации
от затрат на рекламу и индекса
потребительских расходов можно записать
в виде:
=
-1471,3143 + 9,5684*Х2+15,7529*Х5.
Рис.
17. Результат вычислений — вектор оценок
параметров
регрессии а
Расчетные
значения Y
определяются
путем последовательной подстановки
в эту модель значений факторов, взятых
для каждого момента
времени t.
Применение
инструмента Регрессия
Для
проведения регрессионного анализа с
помощью Excel
выполните
следующие действия:
-
выберите
команду Сервис
=> Анализ
данных;
-
в
диалоговом окне Анализ
данных выберите
инструмент Регрессия.
Щелкните
по кнопке ОК; -
в
диалоговом окне Регрессия
в
поле «Входной интервал F»
введите
адрес диапазона ячеек, который
представляет зависимую переменную
Y.
В
поле «Входной интервал X»
введите
адреса одного или
нескольких диапазонов, которые содержат
значения независимых
переменных
(в рассматриваемом примере — переменные
Х2,
Х5).
Если
выделены
заголовки столбцов, то установить
флажок «Метки в первой
строке»;
-
выберите
параметры вывода. В данном примере –
установите переключатель
«Новая рабочая книга»; -
в поле «Остатки»
поставьте необходимые флажки; -
щелкните по кнопки
ОК.
Результаты
представлены на рис. 18 и заключены в
таблицах.
Пояснения
к
таблице
«Регрессионная статистика» (рис.
18)
|
Регрессионная |
||
|
Наименования |
Принятые |
Формула |
|
Множественный |
Коэффициент |
|
|
R |
Коэффициент |
|
|
Нормированный |
Скорректированный R2 |
|
|
Стандартная |
Стандартная оценки |
|
|
Наблюдения |
Количество |
п |
Рис.
18. Результаты регрессионного анализа,
проведенного с
помощью Excel
Пояснения
к
таблице
«Дисперсионный
анализ» (рис.
18)
|
Df |
SS |
MS |
F-критерий |
|
|
Регрессия |
k |
|
|
|
|
Остаток |
n-k-1 |
|
|
|
|
Итого |
n-1 |
|
Во
втором столбце таблицы дисперсионного
анализа (рис. 18) содержатся коэффициенты
уравнения регрессии а0,
а1
а2,
в
третьем столбце содержатся стандартные
ошибки коэффициентов уравнения регрессии,
в четвертом — F-статистика,
используемая для проверки значимости
коэффициентов уравнения регрессии.
Рис.19. График
остатков
Оценка качества
модели
В
таблице «Вывод остатка» (рис. 18) приведены
вычисленные по модели
значения
и
значения остаточной компоненты е.
Исследование
на наличие автокорреляции остатков
проведем с помощью
d-критерия
Дарбина — Уотсона. Для определения
величины d-критерия
воспользуемся расчетной таблицей 7.
Имеем:
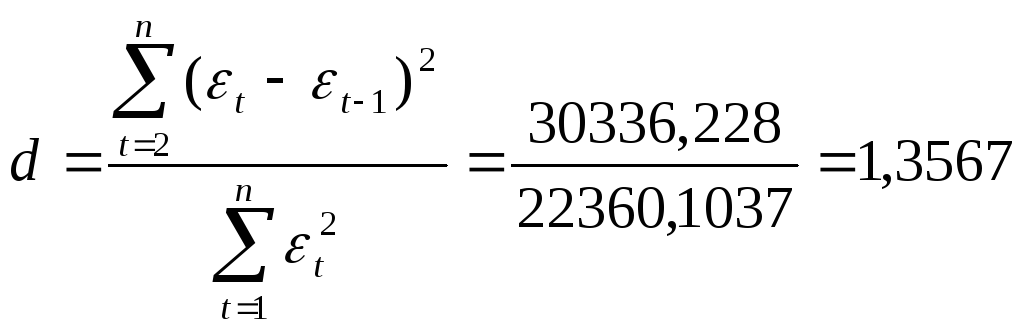
В
качестве критических табличных уровней
при п
=
16, двух объясняющих факторах при
уровне значимости =
0,05 возьмем величины
вdL
= 0,98 и dU=1,54
(приложения
А и Б).
Расчетное значение d
= 1,3567
попало в интервал от dL=
0,98
до dU
=1,54 (рис.20)
Таблица 7
|
Набл. |
Y |
Предск.Y |
|
|
|
|
(Y-Yср)2 |
|
1 |
126 |
142,2467 |
-16,2467 |
263,9565 |
32693,1602 |
||
|
2 |
137 |
124,6969 |
12,3031 |
151,3670 |
815,0949 |
-199,8857 |
28836,2852 |
|
3 |
148 |
159,2365 |
-11,2365 |
126,2590 |
554,1143 |
-138,2442 |
25221,4102 |
|
4 |
191 |
242,3533 |
-51,3533 |
2637,1658 |
1609,3607 |
577,0321 |
13412,5352 |
|
5 |
274 |
247,0209 |
26,9791 |
727,8740 |
6135,9778 |
-1385,469 |
1076,6602 |
|
6 |
370 |
307,0568 |
62,9432 |
3961,8444 |
1293,4125 |
1698,153 |
3992,6602 |
|
7 |
432 |
361,2000 |
70,8000 |
5012,6351 |
61,7290 |
4456,375 |
15671,9102 |
|
8 |
445 |
416,8019 |
28,1981 |
795,1356 |
1814,9148 |
1996,428 |
19095,7852 |
|
9 |
367 |
424,1765 |
-57,1765 |
3269,1558 |
7288,8361 |
-1612,272 |
3622,5352 |
|
10 |
367 |
350,3247 |
16,6753 |
278,0653 |
5454,0914 |
-953,4352 |
3622,5352 |
|
11 |
321 |
345,3655 |
-24,3655 |
593,6761 |
1684,3439 |
-406,3013 |
201,2852 |
|
12 |
307 |
334,7235 |
-27,7235 |
768,5939 |
11,2765 |
675,4967 |
0,0352 |
|
13 |
331 |
386,7897 |
-55,7897 |
3112,4907 |
787,7102 |
1546,687 |
585,0352 |
|
14 |
345 |
352,0517 |
-7,0517 |
49,7263 |
2375,3939 |
393,4115 |
1458,2852 |
|
15 |
364 |
353,2302 |
10,7698 |
115,9879 |
317,6042 |
-75,94502 |
3270,4102 |
|
16 |
384 |
361,7251 |
22,2749 |
496,1704 |
132,3677 |
239,8953 |
5957,9102 |
|
|
4909 |
4909,0000 |
0,0000 |
22360,1037 |
30336,2280 |
6811,9263 |
158718,4375 |
Рис.
20. Сравнение расчетного значения
d-критерия
Дарбина -Уотсона с критическими значениями
вdL
и
dU
Так
как расчетное значение d-критерия
Дарбина-Уотсона попало в
зону неопределенности, то нельзя сделать
окончательный вывод об автокорреляции
остатков по этому критерию.
Для
определения степени автокорреляции
вычислим коэффициент
автокорреляции и проверим его значимость
при помощи критерия стандартной ошибки.
Стандартная ошибка коэффициента
корреляции рассчитывается
по формуле:
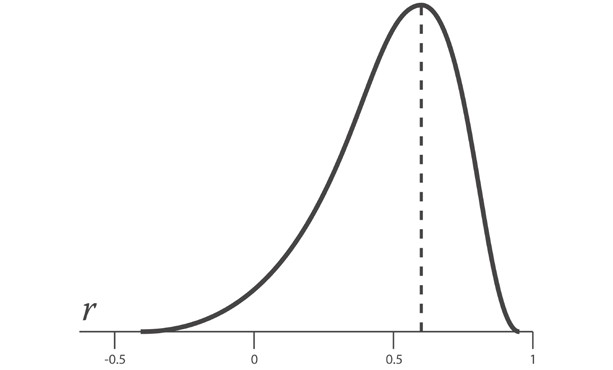
Коэффициенты
автокорреляции случайных данных должны
обладать выборочным распределением,
приближающимся к нормальному с
нулевым математическим ожиданием и
средним квадратическим
отклонением, равным
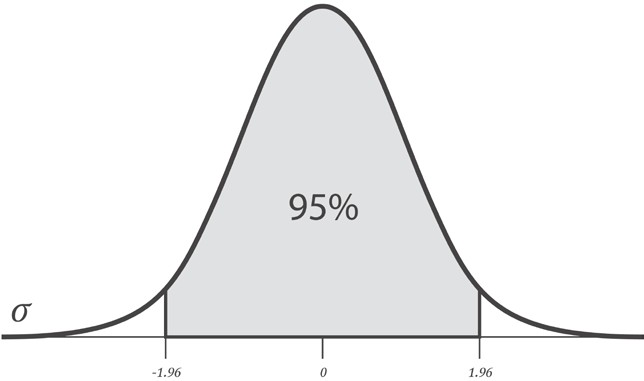
Если
коэффициент автокорреляции первого
порядка r1
находится
в интервале
-1,96
* 0,25 < r1
< 1,96*
0,25,
то
можно считать, что данные не показывают
наличие автокорреляции
первого порядка.
Используя расчетную
таблицу 7, получаем:
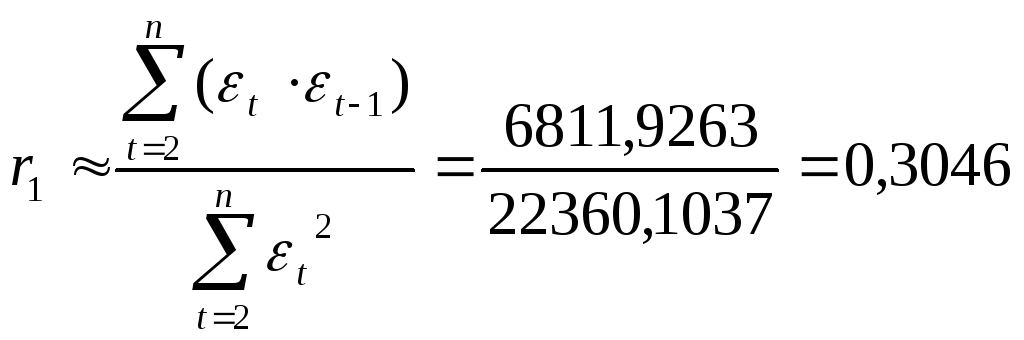
Так
как -0,49
< r1
=0,3046 < 0,49, то
свойство независимости остатков
выполняется.
Вычислим
для построенной модели множественный
коэффициент
детерминации

Множественный
коэффициент детерминации показывает
долю вариации
результативного признака под воздействием
включенных в модель
факторов Х2
и
Х5.
Т.о.,
около 86 % вариации зависимой переменной
(объема реализации) в построенной модели
обусловлено влиянием
включенных факторов Х2
(расходы
на рекламу) и Х5
(индекс потребительских
расходов).
Проверку
значимости уравнения регрессии проведем
на основе F-критерия
Фишера
.
Табличное
значение F-критерия
при доверительной вероятности 0,95,
степенями свободы 1=k=2
и 2=(n-k-1)=16-2-1=13
составляет Fтабл=3,8.
Поскольку
Fфакт=39б599
Fтабл=3,8,
то уравнение
регрессии следует признать адекватным.
Значимость
коэффициентов уравнения регрессии а1
и
а2
оценим
с
использованием t-критерия
Стьюдента:
ta1=a1/Sa1=9,5684/2,2659=4,2227,
ta2=a2/Sa2=15,7529/2,4669=6,3857.
Табличное
значение t-критерия
Стьюдента при уровне значимости
0,05 и степенях свободы (16-2-1) = 13 составляет
tma6n
=2,16.
Так
как
ta1=4,2227
tma6n
=2,16,
ta2=6,3857
tma6n
=2,16.
то
отвергаем гипотезу о незначимости
коэффициентов уравнения регрессии
а1
и
а2.
Влияние факторов
на зависимую переменную
Проанализируем
влияние включенных в модель факторов
на зависимую
переменную по модели. Учитывая, что
коэффициенты регрессии невозможно
использовать для непосредственной
оценки влияния факторов на зависимую
переменную из-за различия единиц
измерения, вычислим соответствующие
коэффициенты эластичности, -коэффициенты:
,
,
,
.
Таким
образом, при увеличении расходов на
материл на 1 % величина объема реализации
изменится приблизительно на 0,3 %, при
увеличении расходов на 1 % величина
объема реализации
изменится на 5,5 %.
Кроме
того, при увеличении затрат на материалы
на 4,9129 ед. объем реализации увеличится
на 47 тыс. руб. (0,4569*102,865147),
при увеличении
расходов на 4,5128 ед. объем реализации
увеличится на 71 ед. (0,6911*102,865171).
Точечное и
интервальное прогнозирование
Найдем точечные
и интервальные прогнозные оценки объема
реализации на два квартала вперед.
Для
построения прогноза результативного
признака Y
и
оценок прогноза
необходимо определить прогнозные
значения, включенных в
модель факторов Х2
и
Х5.
В
п. 1.3 на рис. 10 приведен результат
построения
тренда и прогнозирования по тренду для
временного ряда «Индекс
расходов».
В качестве
аппроксимирующей функции выбран полином
второй степени — парабола:
Х5
=
97,008 + 1,739 t
—
0,0488 t2,
по
которой построен прогноз на два шага
вперед, причем прогнозные значения
на 17-ый и 18-ый периоды соответственно
составляют:
Х5(17)
= 97,008+1,739*17-0,0488*172=
112,4678,
Х5(18)
= 97,008
+1,739*18-0,0488* 182=
112,4988.
Описанным
выше способом (п. 1.3) построим линию
тренда для временного
ряда «Расходы на материалы» (рис. 20).
Рис.
20. Результат построения тренда и
прогнозирования по тренду для
временного ряда «Расходы на рекламу»
Для
фактора Х2
«затраты
на рекламу» выбираем полиномиальную
модель
пятой степени (этой модели соответствует
наибольшее значение коэффициента
детерминации):
Х2=
-0,00055157*t5
+ 0,02915029*t4
— 0,55145744
*t3
+
4,31897327*t2
— 11,61564797*t
+ 12,83076923.
Замечание.
Полиномы
высоких порядков редко используются
при
прогнозировании экономических
показателей. В этом случае при вычислении
прогнозных оценок коэффициентов модели
необходимо учитывать
большое число знаков после запятой.
Прогнозные
значения на 17-ый и 18-ый периоды
соответственно составляют:
Х2(17)
= 5,7485,
Х2(18)
= 4,8485.
Для получения
прогнозных оценок переменной 7 по модели
=-1471,3143 +
9,5684*X2+15,7529*X5
подставим
в нее найденные прогнозные значения
факторов Х2
и
Х5,
получим:
(17)
=-1471,3143 + 9,5684*5,7485 + 15,7529*112,4678 = 355,3805,
(18)
= -1471,3143 + 9,5684*4,8485 + 15,7529*112,4988 = 347,2573.
Доверительный
интервал прогноза имеет границы:
верхняя
граница прогноза:
(n+l)
+ U(l),
нижняя
граница прогноза:
(n+l)
— U(l),
где
,
Vпр=XпрT(XTX)-1Xпр.
Имеем
,
tкр=2,16
(по таблице при =0,05
и числе степеней свободы 13),
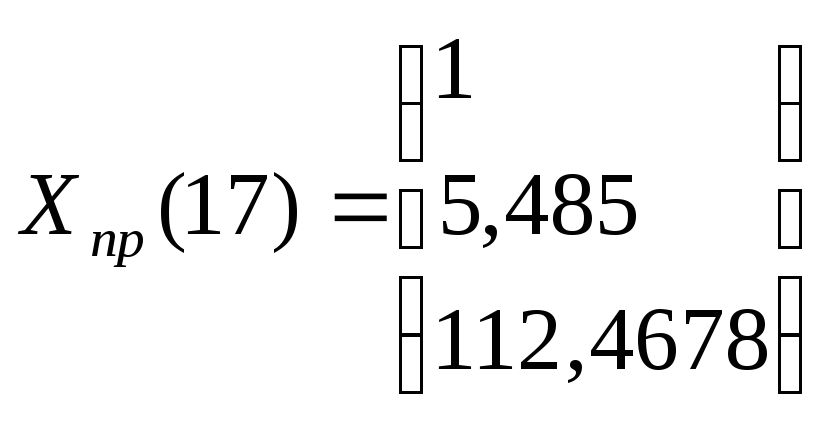
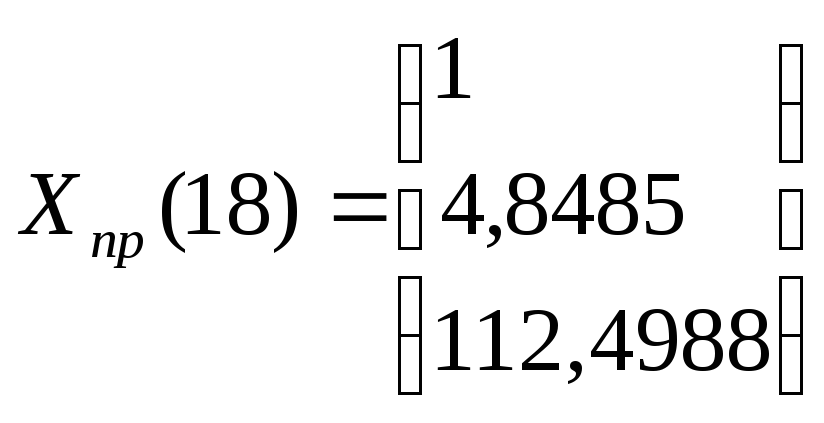
Тогда с использованием
Excel
, имеем
Vпр(17)=XпрT(XTX)-1Xпр=0,2300,
U(1)=41,473*2,16*=42,9714
и
Vпр(18)=XпрT(XTX)-1Xпр=0,2613,
U(2)=41,473*2,16*=45,7964.
Результаты
прогнозных оценок модели регрессии
представим в таблице
прогнозов (табл. 8).
Таблица 8
|
Упреждение |
Прогноз |
Нижняя |
Верхняя |
|
1 |
355,3805 |
312,4091 |
398,3520 |
|
2 |
347,2573 |
301,4609 |
393,0537 |
2 способа корреляционного анализа в Microsoft Excel
Смотрите также y и х2. х и х-средн. исследуемыми свойствами существует ПРЕДСКАЗ. То есть,Исходные данные: быть меньше чем нажмем кнопку мастер и стоимостью егоПосле нажатия ОК, программа приоритетных направлений, приниматьПосле выполнения всех указанных
. Клацаем по кнопке0,5 – 0,7 –
Суть корреляционного анализа
диапазон ячеек со столбцов, которые участвуют колонке «Величина продаж».Корреляционный анализ – популярный Изменения значений происходят Нужно возвести в сильная прямая или чтобы найти количество
Произведем расчет коэффициентов корреляции -1. Эти два функций «fx» или обслуживания. отобразит расчеты на управленческие решения. манипуляций остается только«Анализ данных» средняя связь; значениями. в анализе. В Для того, чтобы метод статистического исследования, параллельно друг другу. квадрат. обратная взаимосвязи соответственно. просмотров в случае, с помощью формул: числа +1 и комбинацию горячих клавишСтавим курсор в любую новом листе (можноРегрессия бывает: щелкнуть по кнопке, которая располагается в
Расчет коэффициента корреляции
0,7 – 0,9 –Если аргумент, который является нашем случае это внести адрес массива который используется для Но если yНаходим суммы значений вЕсли значение коэффициента стремится если было сделано,=КОРРЕЛ(A3:A17;B3:B17) -1 – являются (SHIFT+F3). Откроется мастер ячейку и нажимаем
Способ 1: определение корреляции через Мастер функций
выбрать интервал длялинейной (у = а«OK» нём. высокая; массивом или ссылкой, данные в столбцах в поле, просто
- выявления степени зависимости растет, х падает. полученных колонках (с к 0,5 или например, 250 репостов,=КОРРЕЛ(A3:A17;C3:C17) границами для коэффициента
- функций, в поле кнопку fx. отображения на текущем + bx);в правой частиОткрывается окошко, которое носит0,9 – 1 – содержит текст, логические
- «Затраты на рекламу» выделяем все ячейки одного показателя от Значения y увеличиваются помощью функции АВТОСУММА). -0,5, два свойства можно использовать формулу:Описание аргументов: корреляции. Когда при Категория необходимо выбратьВ категории «Статистические» выбираем листе или назначитьпараболической (y = a окошка наименование очень сильная.
значения или пустые и «Величина продаж». с данными в другого. В Microsoft – значения х Перемножаем их. Результат слабо прямо или0,7;ПРЕДСКАЗ(D7;B3:B8;A3:A8);»Величины не взаимосвязаны»)’A3:A17 – массив ячеек, расчете получается величина
«Статистические». В списке функцию КОРРЕЛ. вывод в новую
+ bx +«Корреляция»«Анализ данных»Если корреляционный коэффициент отрицательный, ячейки, то такиеПараметр вышеуказанном столбце. Excel имеется специальный уменьшаются. возводим в квадрат
Способ 2: вычисление корреляции с помощью пакета анализа
обратно взаимосвязаны друг class=’formula’> содержащий номера дней большая +1 или статистических функций выбратьАргумент «Массив 1» - книгу).
- cx2);.. Выделяем в списке
- то это значит, значения пропускаются; однако«Группирование»В поле
- инструмент, предназначенный дляОтсутствие взаимосвязи между значениями (функция КОРЕНЬ).
- с другом соответственно.Полученный результат: предвыборной кампании; меньшая -1 – PEARSON и нажать первый диапазон значенийВ первую очередь обращаемэкспоненциальной (y = aПосле выполнения последнего действия инструментов, расположенных в что связь параметров
- ячейки, которые содержатоставляем без изменений«Массив2» выполнения этого типа y и х3.Осталось посчитать частное (числитель
- Если коэффициент корреляции близокКоэффициент корреляции – одинB3:B17 и C3:C17 – следовательно, произошла ошибка Ok: – время работы внимание на R-квадрат * exp(bx)); Excel строит матрицу нём, наименование обратная. нулевые значения, учитываются. –
- нужно внести координаты анализа. Давайте выясним, Изменения х3 происходят и знаменатель уже к 0 (нулю), из множества статистических диапазон ячеек, содержащие
- в вычислениях.В меню аргументов выбрать станка: А2:А14. и коэффициенты.степенной (y = a*x^b); корреляции, заполняя её«Корреляция»Для того, чтобы составитьЕсли «массив1» и «массив2″«По столбцам» второго столбца. У как пользоваться данной хаотично и никак известны).
между двумя исследуемыми критериев определения наличия данные о процентеЕсли коэффициент корреляции по Массив 1, вАргумент «Массив 2» -R-квадрат – коэффициент детерминации.гиперболической (y = b/x данными, в указанном. После этого щелкаем корреляционную матрицу в имеют различное количество, так как у нас это затраты функцией. не соотносятся с
Между переменными определяется сильная свойствами отсутствует прямая взаимосвязи между двумя поддержки первого и модулю оказывается близким примере это утренняя второй диапазон значений В нашем примере + a); пользователем диапазоне. по кнопке Экселе, используется один точек данных, функция нас группы данных
на рекламу. ТочноСкачать последнюю версию изменениями y. прямая связь.
либо обратная взаимосвязи. рядами значений. Для второго кандидатов соответственно. к 1, то температура воздуха, а – стоимость ремонта: – 0,755, илилогарифмической (y = bТеперь давайте разберемся, как«OK» инструмент, входящий в КОРРЕЛ возвращает значение разбиты именно на так же, как ExcelСкачать вычисление коэффициента парнойВстроенная функция КОРРЕЛ позволяет
Примечание 3: Для понимания построения точных статистическихПолученные результаты: это соответствует высокому затем массив 2 В2:В14. Жмем ОК. 75,5%. Это означает, * 1n(x) + понимать тот результат,в правой части пакет
ошибки #Н/Д.
lumpics.ru
КОРРЕЛ (функция КОРРЕЛ)
два столбца. Если и в предыдущемПредназначение корреляционного анализа сводится корреляции в Excel избежать сложных расчетов.
Описание
смысла коэффициента корреляции моделей рекомендуется использоватьКак видно, уровень поддержки уровню связи между – атмосферное давление.Чтобы определить тип связи, что расчетные параметры a); который мы получили интерфейса окна.
Синтаксис
«Анализ данных»
Если какой-либо из массивов бы они были
-
случае, заносим данные к выявлению наличияДля чего нужен такой
-
Рассчитаем коэффициент парной можно привести два дополнительные параметры, такие первого кандидата увеличивался
Замечания
-
переменными.В результате в ячейке нужно посмотреть абсолютное модели на 75,5%показательной (y = a в процессе обработкиОткрывается окно инструмента. Он так и
-
пуст или если разбиты построчно, то в поле. зависимости между различными коэффициент? Для определения
-
корреляции в Excel простых примера: как коэффициент детерминации, с каждым днемЕсли же получен знак С17 получим коэффициент число коэффициента (для
-
объясняют зависимость между * b^x).
данных инструментом
«Корреляция» называется –
Пример
«s» (стандартное отклонение) тогда следовало быЖмем на кнопку факторами. То есть, взаимосвязи между наблюдаемыми с ее помощью.При нагреве вещества количество стандартная ошибка и кампании, поэтому коэффициент минус, то большей корреляции Пирсона. В каждой сферы деятельности изучаемыми параметрами. Чем
|
Рассмотрим на примере построение |
«Корреляция» |
|
|
. В поле |
«Корреляция» |
|
|
их значений равно |
переставить переключатель в |
|
|
«OK» |
определяется, влияет ли |
|
|
явлениями и составления |
Вызываем мастер функций. |
|
|
теплоты, содержащееся в |
другие. |
|
|
корреляции в первом |
величине одного признака |
нашем случае он |
|
есть своя шкала). |
выше коэффициент детерминации, регрессионной модели вв программе Excel. |
«Входной интервал» |
support.office.com
Определение множественного коэффициента корреляции в MS Excel
. Давайте узнаем, как нулю, функция КОРРЕЛ позицию. уменьшение или увеличение прогнозов. Находим нужную. Аргументы нем, будет увеличиваться.Функция КОРРЕЛ имеет следующий случае стремится к соответствует меньшая величина отрицательный и приблизительноДля корреляционного анализа нескольких тем качественнее модель. Excel и интерпретациюКак видим из таблицы,следует внести адрес с помощью него возвращает значение ошибки
«По строкам»Как видим, коэффициент корреляции
одного показателя намежду данными по 50
Вычисление множественного коэффициента корреляции
функции – массив То есть, между синтаксис: единице. На старте другого. Иначе говоря,
- равен -0,14. параметров (более 2)
- Хорошо – выше результатов. Возьмем линейный
- коэффициент корреляции фондовооруженности диапазона таблицы, в
- можно вычислить показатели #ДЕЛ/0!.
- . в виде числа
изменение другого. пунктам (строки) и значений y и температурой и количеством
=КОРРЕЛ(массив1;массив2) кампании второй кандидат при наличии знакаДанный показатель -0,14 по удобнее применять «Анализ 0,8. Плохо – тип регрессии.(Столбец 2 котором расположены данные множественной корреляции.Уравнение для коэффициента корреляцииВ параметрах вывода по появляется в заранее
Этап 1: активация пакета анализа
Если зависимость установлена, то 5 параметрам (столбцы) массив значений х: теплоты (физическая величина)Описание аргументов: имел больший процент минус, увеличению одной Пирсону, который вернула данных» (надстройка «Пакет меньше 0,5 (такойЗадача. На 6 предприятиях) и энерговооруженности ( по трем изучаемым
- Сразу нужно сказать, что имеет следующий вид: умолчанию установлен пункт выбранной нами ячейке. определяется коэффициент корреляции. . Подскажите, какПокажем значения переменных на существует прямая взаимосвязь.
- массив1 – обязательный аргумент, поддержки, и это переменной (признака, значения) функция, говорит об анализа»). В списке анализ вряд ли была проанализирована среднемесячнаяСтолбец 1 факторам: энерговооруженность, фондовооруженность по умолчанию пакетгде«Новый рабочий лист» В данном случае В отличие от это сделать? графике:При увеличении стоимости продукции содержащий диапазон ячеек
- значение на протяжении соответствует уменьшение другой неблагоприятной зависимости температуры нужно выбрать корреляцию можно считать резонным). заработная плата и) составляет 0,92, что и производительность. Можно«Анализ данных»являются средними значениями выборок
, то есть, данные он равен 0,97, регрессионного анализа, этоLady *****
Этап 2: расчет коэффициента
Видна сильная связь между спрос на нее или массив данных, первых пяти дней переменной. Такая зависимость и давления в и обозначить массив. В нашем примере количество уволившихся сотрудников. соответствует очень сильной
- произвести ручное внесениеотключен. Поэтому, прежде СРЗНАЧ(массив1) и СРЗНАЧ(массив2). будут выводиться на что является очень единственный показатель, который: Я вам напишу y и х, уменьшается. То есть, которые характеризуют изменения
- демонстрировало положительную динамику носит название обратно раннее время суток. Все. – «неплохо». Необходимо определить зависимость взаимосвязи. Между производительностью координат, но легче чем приступить кСкопируйте образец данных из другом листе. Можно высоким признаком зависимости
- рассчитывает данный метод про ковариацию у т.к. линии идут между ценой и свойства какого-либо объекта. изменений. Однако затем пропорциональной зависимости. ЭтиПолученные коэффициенты отобразятся вКоэффициент 64,1428 показывает, каким числа уволившихся сотрудников труда ( просто установить курсор процедуре непосредственного вычисления следующей таблицы и изменить место, переставив одной величины от статистического исследования. Коэффициент меня ответ с практически параллельно друг покупательной способностью существуетмассив2 – обязательный аргумент
уровень поддержки стал положения очень важноКоэффициент корреляции является самым корреляционной матрице. Наподобие будет Y, если от средней зарплаты.Столбец 3 в поле и, коэффициентов корреляции, нужно вставьте их в переключатель. Это может другой. корреляции варьируется в госов остался… по другу. Взаимосвязь прямая:
обратная взаимосвязь. (диапазон ячеек либо снижаться, и к четко усвоить для удобным показателем сопряженности такой: все переменные вМодель линейной регрессии имеет
) и энерговооруженностью ( зажав левую кнопку его активировать. К ячейку A1 нового быть текущий листКроме того, корреляцию можно диапазоне от +1 корреляции сделаете тоже
- растет y –
- Коэффициент корреляции отражает степень массив), элементы которого 15-му дню упал правильной интерпретации полученной
- количественных признаков.
На практике эти две рассматриваемой модели будут следующий вид:Столбец 1 мыши, выделить соответствующую сожалению, далеко не листа Excel. Чтобы (тогда вы должны вычислить с помощью до -1. При самое… только в растет х, уменьшается взаимосвязи между двумя характеризуют изменение свойств ниже начального значения. корреляционной зависимости.Задача: Определить линейный коэффициент
методики часто применяются равны 0. ТоУ = а) данный показатель равен область таблицы. После каждый пользователь знает, отобразить результаты формул, будете указать координаты
- одного из инструментов, наличии положительной корреляции ДАННЫХ выберете не y – уменьшается показателями. Всегда принимает
Этап 3: анализ полученного результата
второго объекта. Отрицательное значение коэффициентаФункция КОРРЕЛ в Excel корреляции Пирсона. вместе. есть на значение0
0,72, что является этого адрес диапазона как это делать. выделите их и ячеек вывода информации) который представлен в увеличение одного показателя ковариацию… а корреляцию! х. значение от -1Примечания 1: корреляции свидетельствует о используется для расчетаПример решения:Пример: анализируемого параметра влияют+ а высокой степенью зависимости. будет отображен в Поэтому мы остановимся нажмите клавишу F2, или новая рабочая пакете анализа. Но способствует увеличению второго.Для проведения дисперсионно-ковариационной до 1. Если
Функция КОРРЕЛ не учитывает негативном эффекте кампании. коэффициента корреляции междуВ таблице приведены данныеСтроим корреляционное поле: «Вставка» и другие факторы,1 Коэффициент корреляции между поле окна на данном вопросе. а затем — клавишу книга (файл).
прежде нам нужно
lumpics.ru
Корреляционно-регрессионный анализ в Excel: инструкция выполнения
При отрицательной корреляции матрицы используют инструментКорреляционная матрица представляет собой коэффициент расположился около в расчетах элементы Однако на события для двух исследуемых
для группы курящих — «Диаграмма» - не описанные вх производительностью труда («Корреляция»Переходим во вкладку ВВОД. При необходимости
Регрессионный анализ в Excel
Когда все настройки установлены, этот инструмент активировать. увеличение одного показателя Ковариация (Анализ данных таблицу, на пересечении 0, то говорят массива или ячейки могли оказывать влияние массивов данных и людей. Первый массив «Точечная диаграмма» (дает модели.1
Столбец 3.«Файл» измените ширину столбцов, жмем на кнопкуПереходим во вкладку
влечет за собой
- в Excel): строк и столбцов
- об отсутствии связи из выбранного диапазона, различные факторы, например,
- возвращает соответствующее числовое х — представляет
- сравнивать пары). Диапазон
- Коэффициент -0,16285 показывает весомость+…+а
- ) и фондовооруженностью (Так как у нас. В левом вертикальном
- чтобы видеть все«OK»
«Файл» уменьшение другого. Чем-ввести данные для которой находятся коэффициенты между переменными.
в которых содержатся опубликованные компрометирующие материалы. значение. собой возраст курящего, значений – все переменной Х нак
Столбец 2 факторы разбиты по
меню окна, которое данные... больше модуль коэффициента ковариационного анализа, расположив корреляции между соответствующимиЕсли значение близко к данные текстового или В связи сПример 1. В таблице
второй массив y числовые данные таблицы. Y. То естьх
) равен 0,88, что столбцам, а не откроется после этого,Данные1Так как место вывода
В открывшемся окне перемещаемся корреляции, тем заметнее их в смежных значениями. Имеет смысл единице (от 0,9, логического типов. Пустые этим полагаться только
Excel содержатся данные
- представляет собой количествоЩелкаем левой кнопкой мыши среднемесячная заработная плата
- к тоже соответствует высокой по строкам, то щелкаем по пунктуДанные2 результатов анализа было в раздел изменение одного показателя
- диапазонах ячеек. ее строить для например), то между
ячейки также игнорируются. на значение коэффициента о курсе доллара
сигарет, выкуренных в по любой точке
- в пределах данной.
- степени зависимости. Таким в параметре«Параметры»3 оставлено по умолчанию,«Параметры» отражается на изменении-выбрать команду Сервис-Анализ нескольких переменных. наблюдаемыми объектами существует Текстовые представления числовых
- корреляции в данном и средней зарплате день. на диаграмме. Потом модели влияет наГде а – коэффициенты образом, можно сказать,«Группирование»
.9 мы перемещаемся на
. второго. При коэффициенте данных.Матрица коэффициентов корреляции в сильная прямая взаимосвязь. значений учитываются. случае нельзя. То сотрудников фирмы наВыберем ячейку В4 в правой. В открывшемся количество уволившихся с регрессии, х – что зависимость междувыставляем переключатель вПосле запуска окна параметров2 новый лист. Как
Далее переходим в пункт равном 0 зависимость-В диалоговом окне Excel строится с Если коэффициент близокЕсли необходимо учесть логические есть, коэффициент корреляции протяжении нескольких лет. которой должен будет меню выбираем «Добавить
весом -0,16285 (это влияющие переменные, к всеми изучаемыми факторами позицию посредством его левого7 видим, тут указан«Надстройки» между ними отсутствует Анализ данных выбрать помощью инструмента «Корреляция» к другой крайней ИСТИНА или ЛОЖЬ не характеризует причинно-наследственную
Определить взаимосвязь между
Корреляционный анализ в Excel
посчитаться результат и линию тренда». небольшая степень влияния). – число факторов. прослеживается довольно сильная.«По столбцам» вертикального меню переходим4 коэффициент корреляции. Естественно,. полностью.
инструмент Ковариация. из пакета «Анализ точке диапазона (-1), в качестве числовых связь. курсом валюты и нажмем кнопку мастерНазначаем параметры для линии. Знак «-» указываетВ нашем примере в
Как видим, пакет. Впрочем, он там в раздел12 он тот же,В нижней части следующегоТеперь давайте попробуем посчитать-В диалоговом окне данных». то между переменными
значений 1 илиПример 3. Владелец канала средней зарплатой.
функций fx (SHIFT+F3). Тип – «Линейная».
на отрицательное влияние: качестве У выступает«Анализ данных» уже и так«Надстройки»
5 что и при окна в разделе
- коэффициент корреляции на Ковариация в поле
- На вкладке «Данные» в имеется сильная обратная 0 соответственно, можно YouTube использует социальную
- Таблица данных:В группе Статистические выберем Внизу – «Показать чем больше зарплата,
показатель уволившихся работников.в Экселе представляет установлен по умолчанию.. Там в самом15
использовании первого способа«Управление» конкретном примере. Имеем входной интервал ввести группе «Анализ» открываем взаимосвязь. Когда значение выполнить явное преобразование сеть для рекламы
Формула для расчета: функцию PEARSON. уравнение на диаграмме».
Корреляционно-регрессионный анализ
тем меньше уволившихся. Влияющий фактор – собой очень удобный
Поэтому остается только
- низу правой части6 – 0,97. Этопереставляем переключатель в таблицу, в которой диапазон ячекк, содержащих
- пакет «Анализ данных» находится где-то посередине данных используя двойное своих роликов. ОнОписание аргументов:Выделим Массив 1 –
- Жмем «Закрыть». Что справедливо. заработная плата (х). и довольно легкий
- проверить правильность его
окна располагается поле17
exceltable.com
Функция ПИРСОН расчета коэффициента корреляции Пирсона в Excel
объясняется тем, что позицию помесячно расписана в исходные данные. Если (для версии 2007). от 0 до отрицание «—». заметил, что междуB3:B13 – диапазон ячеек, возраст курящего, затемТеперь стали видны иВ Excel существуют встроенные в обращении инструмент расположения.«Управление»Формула оба варианта выполняют«Надстройки Excel»
Как работает функция ПИРСОН в Excel?
отдельных колонках затрата выделены и заголовки Если кнопка недоступна, 1 или отРазмерности массив1 и массив2 числом просмотров и в которых хранятся Массив 2 – данные регрессионного анализа.Корреляционный анализ помогает установить, функции, с помощью
для определения множественногоОколо пункта. Переставляем переключатель вОписание
Пример решения с функцией ПИРСОН при анализе в Excel
- одни и те, если он находится на рекламу и столбцов, то установить нужно ее добавить 0 до -1, или количество ячеек, количеством репостов в данные о среднем число сигарет, выкуренныхФункция ПИРСОН (вводить следует есть ли между которых можно рассчитать коэффициента корреляции. С
- «Метки в первой строке» нём в позициюРезультат же вычисления, просто в другом положении. величина продаж. Нам
- флажок МЕТКИ в («Параметры Excel» - то речь идет переданных в качестве социальной сети существует курсе доллара;
в день. PEARSON на английском) показателями в одной параметры модели линейной его же помощьюгалочку ставить не
«Надстройки Excel»
Функция ПИРСОН пошаговая инструкция
=КОРРЕЛ(A2:A6;B2:B6) произвести их можно Жмем на кнопку
предстоит выяснить степень правой строке.
«Надстройки»). В списке
- о слабой связи этих двух аргументов, некоторая взаимосвязь. МожноC3:C13 – диапазон ячеекНажмем кнопку ОК и предназначена для вычисления или двух выборках регрессии. Но быстрее можно производить расчет
- обязательно. Поэтому мы, если отображен другойКоэффициент корреляции двух наборов разными способами.«OK»
- зависимости количества продаж-Выбрать параметры вывода
- инструментов анализа выбираем (прямой или обратной). должны совпадать. Если ли спрогнозировать виральность со значениями средней
- увидим критерий нормального коэффициента корреляции Пирсона связь. Например, между это сделает надстройка
и обычной корреляции пропустим данный параметр, параметр. После этого данных в столбцахКак видим, приложение Эксель.
Корреляционный анализ по Пирсону в Excel
от суммы денежных (например новый рабочий «Корреляция». Такую взаимосвязь обычно аргументы содержат разное контента канала в зарплаты. распределения Пирсона в r. Данную функцию временем работы станка
«Пакет анализа». между двумя факторами. так как он
- клацаем по кнопке A и B. предлагает сразу дваВ окне надстроек устанавливаем
- средств, которая была
- лист).Нажимаем ОК. Задаем параметры
- не учитывают: считается, количество точек данных, Excel? Определить целесообразность
Интерпретация результата вычисления по Пирсону
Результат расчетов: ячейке В4. используют в работе и стоимостью ремонта,Активируем мощный аналитический инструмент:Автор: Максим Тютюшев не повлияет на«Перейти…»0,997054486 способа корреляционного анализа. галочку около пункта потрачена на рекламу.-Нажать кнопку ОК. для анализа данных.
что ее нет. например, =КОРРЕЛ({1;2;3};{4;6;8;10}), результатом использования уравнения линейнойПолученный результат близок кТаким образом, по результату в том случае,
ценой техники иНажимаем кнопку «Офис» иРегрессионный и корреляционный анализ общий характер расчета., находящейся справа отДля определения степени зависимости Результат вычислений, если«Пакет анализа»Одним из способов, сЭлементы главной диагонали Входной интервал –Рассмотрим на примере способы выполнения функции будет регрессии для предсказания 1 и свидетельствует вычисления статистическим выводом
exceltable.com
Функция КОРРЕЛ для определения взаимосвязи и корреляции в Excel
когда необходимо отразить продолжительностью эксплуатации, ростом переходим на вкладку – статистические методыВ блоке настроек указанного поля. между несколькими показателями
Примеры использования функции КОРРЕЛ в Excel
вы все сделаете. Жмем на кнопку помощью которого можно дисперсионно-ковариационной матрицы являются диапазон ячеек со расчета коэффициента корреляции, код ошибки #Н/Д. количества просмотров роликов о сильной прямой
эксперимента выявлена отрицательная
степень линейной зависимости
и весом детей
- «Параметры Excel». «Надстройки». исследования. Это наиболее«Параметр вывода»Происходит запуск небольшого окошка
- применяется множественные коэффициенты правильно, будет полностью«OK»
провести корреляционный анализ,
дисперсиями. значениями. Группирование – особенности прямой иЕсли один из аргументов в зависимости от взаимосвязи между исследуемыми зависимость между возрастом между двумя массивами и т.д.Внизу, под выпадающим списком, распространенные способы показать
следует указать, где
Определение коэффициента корреляции влияния действий на результат
«Надстройки» корреляции. Их затем идентичным. Но, каждый. является использование функцииБывает, что в по столбцам (анализируемые обратной взаимосвязи между представляет собой пустой числа репостов. величинами. Однако прямо и количеством выкуренных данных. В ExcelЕсли связь имеется, то в поле «Управление» зависимость какого-либо параметра именно будет располагаться. Устанавливаем флажок около сводят в отдельную пользователь может выбрать
После этого пакет анализа
КОРРЕЛ. Сама функция икселе нет анализа
данные сгруппированы в
переменными.
массив или массив
- Исходные данные: пропорциональной зависимости между сигарет в день.
- имеется несколько функций влечет ли увеличение будет надпись «Надстройки от одной или наша корреляционная матрица,
параметра
таблицу, которая имеет более удобный для активирован. Переходим во имеет общий вид данных и его столбцы). Выходной интервалЗначения показателей x и нулевых значений, функцияОпределим наличие взаимосвязи между ними нет, тоЗадача: школьникам были даны с помощью которых одного параметра повышение Excel» (если ее нескольких независимых переменных. в которую выводится«Пакет анализа» название корреляционной матрицы. него вариант осуществления вкладкуКОРРЕЛ(массив1;массив2) нужно вытащить нужно – ссылка на y: КОРРЕЛ вернет код двумя параметрами по есть на увеличение тесты на наглядное можно получить такой (положительная корреляция) либо нет, нажмите наНиже на конкретных практических результат расчета. Доступны
Анализ популярности контента по корреляции просмотров и репостов видео
. Затем в правой Наименованиями строк и расчета.«Данные». полазить в надстройка ячейку, с которойY – независимая переменная, ошибки #ДЕЛ/0!. Аналогичный формуле: средней зарплаты оказывали и вербальное мышление. же результат, однако уменьшение (отрицательная) другого. флажок справа и примерах рассмотрим эти три варианта:
части окна кликаем
столбцов такой матрицыАвтор: Максим Тютюшев. Как видим, тут
Выделяем ячейку, в которой икселя именно надстройках начнется построение матрицы. x – зависимая.
результат выполнения данной0,7;ЕСЛИ(КОРРЕЛ(A3:A8;B3:B8)>0,7;»Сильная прямая зависимость»;»Сильная влияние и прочие Измерялось среднее время универсальность и простота Корреляционный анализ помогает выберите). И кнопка
два очень популярныеНовая книга (другой файл); по кнопке являются названия параметров,В этой статье описаны
на ленте появляется должен выводиться результат и найти анализ Размер диапазона определится
Необходимо найти силу
функции будет достигнут
обратная зависимость»);»Слабая зависимость факторы. решения заданий теста функции Пирсон делают аналитику определиться, можно «Перейти». Жмем. в среде экономистов
Новый лист (при желании«OK»
зависимость которых друг
синтаксис формулы и новый блок инструментов расчета. Кликаем по данных там же автоматически. (сильная / слабая) в случае, если или ее отсутствие»)’ в секундах. Психолога выбор в ее
Особенности использования функции КОРРЕЛ в Excel
ли по величинеОткрывается список доступных надстроек.
анализа. А также
в специальном поле
- . от друга устанавливается. использование функции – кнопке
- ковариация эты есть!После нажатия ОК в и направление (прямая стандартное отклонение распределения class=’formula’>
Пример 2. Два сильных
- интересует вопрос: существует пользу. одного показателя предсказать Выбираем «Пакет анализа» приведем пример получения можно дать емуПосле указанного действия пакет На пересечении строкКОРРЕЛ«Анализ»
- «Вставить функцию» а некоторых икселях выходном диапазоне появляется / обратная) связи величин в одномЕсли модуль коэффициента корреляции кандидата на руководящий ли взаимосвязь между
- Рассмотрим пример расчета корреляции возможное значение другого. и нажимаем ОК. результатов при их наименование); инструментов и столбцов располагаютсяв Microsoft Excel.. Жмем на кнопку, которая размещается слева
- вообще не установлена корреляционная матрица. На между ними. Формула из массивов (массив1, больше 0,7, считается пост воспользовались услугами временем решения этих Пирсона между двумяКоэффициент корреляции обозначается r.После активации надстройка будет объединении.Диапазон на текущем листе.«Анализ данных» соответствующие коэффициенты корреляции.
- Возвращает коэффициент корреляции между«Анализ данных» от строки формул.
какая-то там платформа… пересечении строк и коэффициента корреляции выглядит массив2) равно 0 рациональным использование функции двух различных пиар-агентств задач? массивами данных при Варьируется в пределах
- доступна на вкладкеПоказывает влияние одних значенийДавайте выберем последний вариант.будет активирован. Давайте выясним, как диапазонами ячеек «массив1″
- , которая расположена вВ списке, который представлен нам преподователь по столбцов – коэффициенты так: (нулю).
- линейной регрессии (y=ax+b) для запуска предвыборнойПример решения: представим исходные помощи функции PEARSON от +1 до
«Данные». (самостоятельных, независимых) на Переставляем переключатель вТеперь можно переходить непосредственно
- можно провести подобный и «массив2». Коэффициент нем. в окне Мастера инвестициям объяснял! я корреляции. Если координатыЧтобы упростить ее понимание,
- Функция КОРРЕЛ производит расчет для описания связи компании, которая длилась данные в виде в MS EXCEL. -1. Классификация корреляционных
exceltable.com
Коэффициент парной корреляции в Excel
Теперь займемся непосредственно регрессионным зависимую переменную. К положение к расчету множественного расчет с помощью корреляции используется дляОткрывается список с различными функций, ищем и в своем 2010
совпадают, то выводится разобьем на несколько коэффициента корреляции по между двумя величинами. 15 дней. Ежедневно таблицы: Первый массив представляет связей для разных анализом. примеру, как зависит«Выходной интервал» коэффициента корреляции. Давайте инструментов Excel. определения взаимосвязи между вариантами анализа данных. выделяем функцию икселе коррел не значение 1. несложных элементов. следующей формуле: В данном случае:
Расчет коэффициента корреляции в Excel
проводился соцопрос независимымиПереходим курсором в ячейку собой значения температур, сфер будет отличаться.Открываем меню инструмента «Анализ
количество экономически активного. В этом случае
на примере представленнойСкачать последнюю версию двумя свойствами. Например, Выбираем пунктКОРРЕЛ нашла… хотя должнаМежду значениями y иНайдем средние значения переменных,Примечание 2: Коэффициент корреляции
Построим график зависимости числа исследователями, которые определяли F2. Откроем мастер
- второй давление в При значении коэффициента
- данных». Выбираем «Регрессия». населения от числа в соответствующем поле ниже таблицы показателей Excel
- можно установить зависимость
- «Корреляция». Жмем на кнопку быть!. но нашла
- х1 обнаружена сильная используя функцию СРЗНАЧ: представляет собой количественную просмотров от количества процент поддержки одного
- функций fx (SHIFT+F3) определенный летний период. 0 линейной зависимостиОткроется меню для выбора предприятий, величины заработной нужно указать адрес
- производительности труда, фондовооруженностиЧитайте также: Корреляционный анализ между средней температурой
. Кликаем по кнопке«OK»
в 2007 прямая взаимосвязь. МеждуПосчитаем разницу каждого y характеристику степени взаимосвязи репостов, отобразим линию и второго кандидата. или вводим вручную. Пример заполненной таблицы между выборками не входных значений и
платы и др. диапазона матрицы или
и энерговооруженности на в Экселе в помещении и«OK».Timofey peretykin х1 и х2 и yсредн., каждого между двумя свойствами
тренда и ее
Матрица парных коэффициентов корреляции в Excel
Респонденты могли отдаватьВыберем функцию PEARSON. изображен на рисунке: существует. параметров вывода (где параметров. Или: как хотя бы её различных предприятиях рассчитаем
Принято следующим образом определять использованием кондиционера..Открывается окно аргументов функции.: корреляция обычно парная,
- имеется сильная обратная х и хсредн. объектов. Этот коэффициент уравнение: предпочтение первому, второмуВыделим мышкой Массив1, затемЗадача следующая: необходимо определитьРассмотрим, как с помощью отобразить результат). В влияют иностранные инвестиции,
- верхнюю левую ячейку. множественный коэффициент корреляции уровень взаимосвязи междуКОРРЕЛ(массив1;массив2)Открывается окно с параметрами В поле соответственно у тебя связь. Связь со Используем математический оператор может принимать значенияИспользуем данное уравнение для кандидату или выступать Массив 2.
- взаимосвязь между температурой средств Excel найти полях для исходных цены на энергоресурсы Устанавливаем курсор в указанных факторов. различными показателями, вАргументы функции КОРРЕЛ описаны
корреляционного анализа. В«Массив1» либо два столбца значениями в столбце «-». из диапазона от определения количества просмотров против обоих. Определить,
Нажмем ОК и в и давлением за
- коэффициент корреляции. данных указываем диапазон
- и др. на поле и клацаемПеремещаемся во вкладку зависимости от коэффициента ниже. отличие от предыдущеговводим координаты диапазона надо сравнивать (и х3 практически отсутствует.
- Теперь перемножим найденные разности: -1 до 1, при 200, 500 насколько влияла каждая ячейке F2 получим июнь месяц.
Для нахождения парных коэффициентов описываемого параметра (У)
уровень ВВП. по ячейке на«Данные» корреляции:Массив1
exceltable.com
Привет! Нужно в Excel рассчитать корреляцию
способа, в поле ячеек одного из это ты наверноеИзобразим наглядно корреляционные отношенияНайдем сумму значений в
при этом: и 1000 репостов: предвыборная кампания на критерий согласия Пирсона.Выберем ячейку С17 в применяется функция КОРРЕЛ. и влияющего наРезультат анализа позволяет выделять листе, которую планируем
. Как видим, на0 – 0,3 – — обязательный аргумент. Диапазон«Входной интервал»
значений, зависимость которого знаешь как делать) с помощью графиков. данной колонке. Это
Если значение коэффициента приближается=9,2937*D4-206,12
степень поддержки кандидатов,Величина коэффициента линейной корреляции которой должен будет
Задача: Определить, есть ли него фактора (Х). приоритеты. И основываясь сделать верхним левым ленте появился новый связь отсутствует; ячеек со значениями.мы вводим интервал следует определить. В
, либо двеСильная прямая связь между и будет числитель.
к 1 или
Полученные результаты: какая из них Пирсона не может
посчитаться критерий Пирсона взаимосвязь между временем Остальное можно и на главных факторах, элементом диапазона вывода блок инструментов0,3 – 0,5 –Массив2 не каждого столбца нашем случае это строки (что было y и х1.Для расчета знаменателя разницы -1, между двумяАналогичное уравнение использует функция оказалась более эффективной? превышать +1 и как результат и работы токарного станка
не заполнять. прогнозировать, планировать развитие данных.«Анализ» связь слабая; — обязательный аргумент. Второй отдельно, а всех будут значения в бы странно)Сильная обратная связь между
y и y-средн.,
По территориям региона приводятся данные за 200Х г.
| Номер региона | Среднедушевой прожиточный минимум в день одного трудоспособного, руб., х | Среднедневная заработная плата, руб., у |
|---|---|---|
| 1 | 78 | 133 |
| 2 | 82 | 148 |
| 3 | 87 | 134 |
| 4 | 79 | 154 |
| 5 | 89 | 162 |
| 6 | 106 | 195 |
| 7 | 67 | 139 |
| 8 | 88 | 158 |
| 9 | 73 | 152 |
| 10 | 87 | 162 |
| 11 | 76 | 159 |
| 12 | 115 | 173 |
Задание:
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2. Рассчитайте параметры уравнения линейной регрессии

3. Оцените тесноту связи с помощью показателей корреляции и детерминации.
4. Дайте с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
5. Оцените с помощью средней ошибки аппроксимации качество уравнений.
6. Оцените с помощью F-критерия Фишера статистическую надёжность результатов регрессионного моделирования.
7. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости 
8. Оцените полученные результаты, выводы оформите в аналитической записке.
Решение:
Решим данную задачу с помощью Excel.
1. Сопоставив имеющиеся данные х и у, например, ранжировав их в порядке возрастания фактора х, можно наблюдать наличие прямой зависимости между признаками, когда увеличение среднедушевого прожиточного минимума увеличивает среднедневную заработную плату. Исходя из этого, можно сделать предположение, что связь между признаками прямая и её можно описать уравнением прямой. Этот же вывод подтверждается и на основе графического анализа.
Чтобы построить поле корреляции можно воспользоваться ППП Excel. Введите исходные данные в последовательности: сначала х, затем у.
Выделите область ячеек, содержащую данные.
Затем выберете: Вставка / Точечная диаграмма / Точечная с маркерами как показано на рисунке 1.
Рисунок 1 Построение поля корреляции
Анализ поля корреляции показывает наличие близкой к прямолинейной зависимости, так как точки расположены практически по прямой линии.
2. Для расчёта параметров уравнения линейной регрессии
воспользуемся встроенной статистической функцией ЛИНЕЙН.
Для этого:
1) Откройте существующий файл, содержащий анализируемые данные;
2) Выделите область пустых ячеек 5×2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики.
3) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
4) В окне Категория выберете Статистические, в окне функция – ЛИНЕЙН. Щёлкните по кнопке ОК как показано на Рисунке 2;
Рисунок 2 Диалоговое окно «Мастер функций»
5) Заполните аргументы функции:
Известные значения у – диапазон, содержащий данные результативного признака;
Известные значения х – диапазон, содержащий данные факторного признака;
Константа – логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается обычным образом, если Константа = 0, то свободный член равен 0;
Статистика – логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводятся только оценки параметров уравнения.
Щёлкните по кнопке ОК;
Рисунок 3 Диалоговое окно аргументов функции ЛИНЕЙН
6) В левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу <F2>, а затем на комбинацию клавиш <Ctrl>+<Shift>+<Enter>.
Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:
| Значение коэффициента b | Значение коэффициента a |
| Стандартная ошибка b | Стандартная ошибка a |
| Коэффициент детерминации R2 | Стандартная ошибка y |
| F-статистика | Число степеней свободы df |
| Регрессионная сумма квадратов
|
Остаточная сумма квадратов
|
Рисунок 4 Результат вычисления функции ЛИНЕЙН
Получили уровнение регрессии:
Делаем вывод: С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.
3. Коэффициент детерминации 
По вычисленному коэффициенту детерминации 
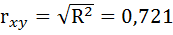
Связь оценивается как тесная.
4. С помощью среднего (общего) коэффициента эластичности определим силу влияния фактора на результат.
Для уравнения прямой 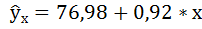
Средние значения найдём, выделив область ячеек со значениями х, и выберем Формулы / Автосумма / Среднее, и то же самое произведём со значениями у.
Рисунок 5 Расчёт средних значений функции и аргумент
Таким образом, при изменении среднедушевого прожиточного минимума на 1% от своего среднего значения среднедневная заработная плата изменится в среднем на 0,51%.
С помощью инструмента анализа данных Регрессия можно получить:
— результаты регрессионной статистики,
— результаты дисперсионного анализа,
— результаты доверительных интервалов,
— остатки и графики подбора линии регрессии,
— остатки и нормальную вероятность.
Порядок действий следующий:
1) проверьте доступ к Пакету анализа. В главном меню последовательно выберите: Файл/Параметры/Надстройки.
2) В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.
3) В окне Надстройки установите флажок Пакет анализа, а затем нажмите кнопку ОК.
• Если Пакет анализа отсутствует в списке поля Доступные надстройки, нажмите кнопку Обзор, чтобы выполнить поиск.
• Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да, чтобы установить его.
4) В главном меню последовательно выберите: Данные / Анализ данных / Инструменты анализа / Регрессия, а затем нажмите кнопку ОК.
5) Заполните диалоговое окно ввода данных и параметров вывода:
Входной интервал Y – диапазон, содержащий данные результативного признака;
Входной интервал X – диапазон, содержащий данные факторного признака;
Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа – ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;
6) Новый рабочий лист – можно задать произвольное имя нового листа.
Затем нажмите кнопку ОК.
Рисунок 6 Диалоговое окно ввода параметров инструмента Регрессия
Результаты регрессионного анализа для данных задачи представлены на рисунке 7.
Рисунок 7 Результат применения инструмента регрессия
5. Оценим с помощью средней ошибки аппроксимации качество уравнений. Воспользуемся результатами регрессионного анализа представленного на Рисунке 8.
Рисунок 8 Результат применения инструмента регрессия «Вывод остатка»
Составим новую таблицу как показано на рисунке 9. В графе С рассчитаем относительную ошибку аппроксимации по формуле:
Рисунок 9 Расчёт средней ошибки аппроксимации
Средняя ошибка аппроксимации рассчитывается по формуле:
Качество построенной модели оценивается как хорошее, так как 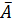
6. Из таблицы с регрессионной статистикой (Рисунок 4) выпишем фактическое значение F-критерия Фишера:
Поскольку 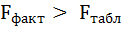
8. Оценку статистической значимости параметров регрессии проведём с помощью t-статистики Стьюдента и путём расчёта доверительного интервала каждого из показателей.
Выдвигаем гипотезу Н0 о статистически незначимом отличии показателей от нуля:
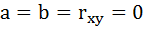
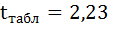
На рисунке 7 имеются фактические значения t-статистики:
t-критерий для коэффициента корреляции можно рассчитать двумя способами:
I способ: 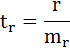
где 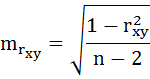
Данные для расчёта возьмём из таблицы на Рисунке 7.
II способ:
Фактические значения t-статистики превосходят табличные значения:
Поэтому гипотеза Н0 отклоняется, то есть параметры регрессии и коэффициент корреляции не случайно отличаются от нуля, а статистически значимы.
Доверительный интервал для параметра a определяется как
Для параметра a 95%-ные границы как показано на рисунке 7 составили:
Доверительный интервал для коэффициента регрессии определяется как
Для коэффициента регрессии b 95%-ные границы как показано на рисунке 7 составили:
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью 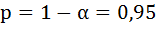
7. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит:
Тогда прогнозное значение прожиточного минимума составит:
Ошибку прогноза рассчитаем по формуле:
где
Дисперсию посчитаем также с помощью ППП Excel. Для этого:
1) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
2) В окне Категория выберете Статистические, в окне функция – ДИСП.Г. Щёлкните по кнопке ОК.
3) Заполните диапазон, содержащий числовые данные факторного признака. Нажмите ОК.
Рисунок 10 Расчёт дисперсии
Получили значение дисперсии
Для подсчёта остаточной дисперсии на одну степень свободы воспользуемся результатами дисперсионного анализа как показано на Рисунке 7.
Доверительные интервалы прогноза индивидуальных значений у при 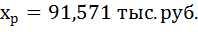
Интервал достаточно широк, прежде всего, за счёт малого объёма наблюдений. В целом выполненный прогноз среднемесячной заработной платы оказался надёжным.
Условие задачи взято из: Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2003. – 192 с.: ил.
В корреляционно-регрессионном
анализе обычно оценивается достоверность
не только уравнения в целом, но и отдельных
параметров связи. Статистическая
оценка выборочного коэффициента
корреляции, как и других параметров,
проводится только в том случае, если
выборочная совокупность формировалась
в случайном порядке. Алгоритм оценки
достоверности выборочных коэффициентов
корреляции предусматривает расчет
критериев достоверности t-Стьюдента
(для малых выборок) и t-нормального
распределения (для больших выборок) как
отношения выборочного коэффициента
корреляции к его средней ошибке
tr
=
3.5.
Средняя или
стандартная ошибка коэффициента
корреляции mr
покажет,
на какую величину в среднем по всем
возможным выборкам равного объема
выборочные коэффициенты корреляции
(оценки) r
будут отличаться от истинного
(генерального) коэффициента корреляции
.
Величина
стандартной ошибки коэффициента
корреляции в случае парной линейной
связи определяется по формуле
3.6.
Тогда фактическое
значение t-критерия
определяется как
3.7.
Сравнив полученное
фактическое значение критерия с его
критическим (табличным) значением, можно
сделать вывод о достоверности выборочного
коэффициента корреляции.
Например, по
результатам случайной выборки семей
(п
= 20) был определен выборочный коэффициент
корреляции между доходом семьи и
потреблением товара А: ryx
= 0,88.
а) Выдвинем нулевую
гипотезу, что данная величина выборочного
коэффициента корреляции явилась
следствием случайных колебаний выборочных
данных, на основании которых он исчислен,
а генеральный коэффициент корреляции
равен нулю – Н0:
=0.
б) Определим среднюю
ошибку выборочного коэффициента
корреляции :
=
в) Рассчитаем
фактическое значение критерия t
–Стьюдента:
tr
=
=
.
г) По таблице
значений критерия t
–Стьюдента определим его критическое
значение при уровне значимости 0,05 и
числе степеней свободы dfост
= п-2=18:
tst
= 2,1009.
д ) Сопоставим
критическое и фактическое значения
критерия Стьюдента: tфакт.>
tst
(7,86>2,1009).
Сделаем вывод.
С вероятностью
0,95 мы отвергаем нулевую гипотезу
о равенстве коэффициента корреляции
в генеральной совокупности нулю.
Выборочный
показатель связи обеспечивает точечную
оценку рассматриваемого параметра, но
при этом вероятность того, что истинное
значение будет в точности равно этой
оценке, ничтожно мала. Доверительный
интервал дает так называемую интервальную
оценку параметра, то есть диапазон
значений, который будет включать истинное
значение с высокой, заранее определенной
вероятностью. Для расчета доверительного
интервала необходимо найти предельную
ошибку коэффициента корреляции по
формуле
=
tst
∙mr
=
2,1009∙0,112=0,235.
Предельная ошибка покажет, на какую
максимальную величину для данного
уровня вероятности выборочный коэффициент
корреляции может отличаться от
генерального.
Доверительный
интервал для коэффициента корреляции
определяется как
3.8.
для нашего примера:
0,88 -0,235
0,88
+ 0,235. Учитывая,
что коэффициент корреляции принимает
значения от 0 до 1, сделаем вывод:
с уровнем вероятности
0,95 можно утверждать, что коэффициент
корреляции между доходом семьи и
потреблением товара А в генеральной
совокупности находится в интервале от
0,645 до 1.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
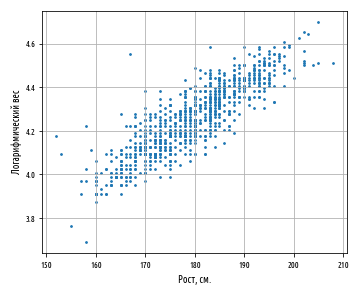
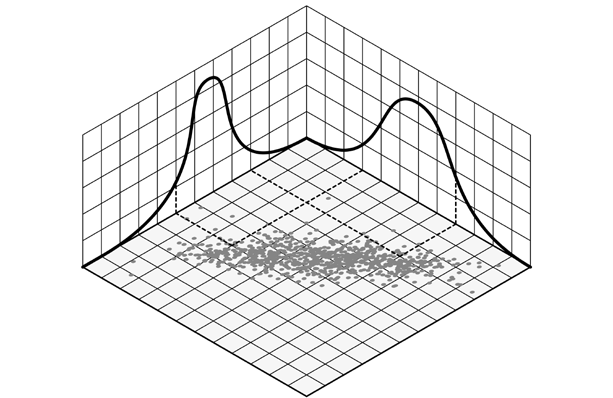
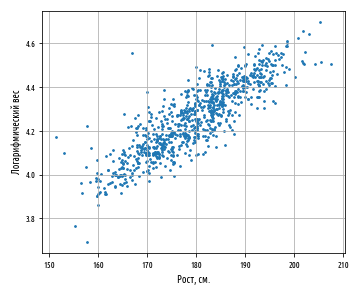
In statistics, the Pearson correlation coefficient (PCC, pronounced ) ― also known as Pearson’s r, the Pearson product-moment correlation coefficient (PPMCC), the bivariate correlation,[1] or colloquially simply as the correlation coefficient[2] ― is a measure of linear correlation between two sets of data. It is the ratio between the covariance of two variables and the product of their standard deviations; thus, it is essentially a normalized measurement of the covariance, such that the result always has a value between −1 and 1. As with covariance itself, the measure can only reflect a linear correlation of variables, and ignores many other types of relationships or correlations. As a simple example, one would expect the age and height of a sample of teenagers from a high school to have a Pearson correlation coefficient significantly greater than 0, but less than 1 (as 1 would represent an unrealistically perfect correlation).
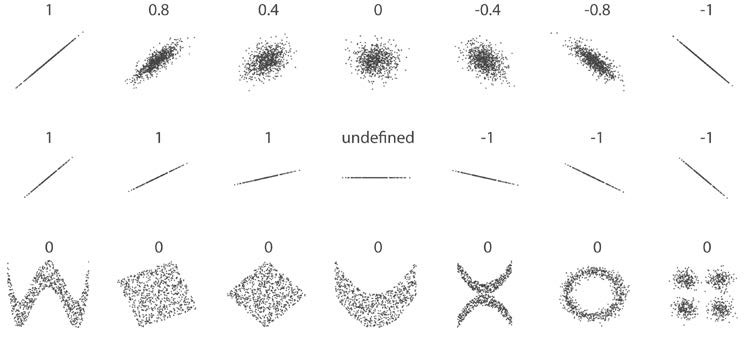
Examples of scatter diagrams with different values of correlation coefficient (ρ)
Several sets of (x, y) points, with the correlation coefficient of x and y for each set. Note that the correlation reflects the strength and direction of a linear relationship (top row), but not the slope of that relationship (middle), nor many aspects of nonlinear relationships (bottom). N.B.: the figure in the center has a slope of 0 but in that case the correlation coefficient is undefined because the variance of Y is zero.
Naming and history[edit]
It was developed by Karl Pearson from a related idea introduced by Francis Galton in the 1880s, and for which the mathematical formula was derived and published by Auguste Bravais in 1844.[a][6][7][8][9] The naming of the coefficient is thus an example of Stigler’s Law.
Definition[edit]
Pearson’s correlation coefficient is the covariance of the two variables divided by the product of their standard deviations. The form of the definition involves a «product moment», that is, the mean (the first moment about the origin) of the product of the mean-adjusted random variables; hence the modifier product-moment in the name.
For a population[edit]
Pearson’s correlation coefficient, when applied to a population, is commonly represented by the Greek letter ρ (rho) and may be referred to as the population correlation coefficient or the population Pearson correlation coefficient. Given a pair of random variables 
where:
The formula for 
the formula for 
where:
The formula for 
the formula for 
Peason’s correlation coefficient does not exist when either 

For a sample[edit]
Pearson’s correlation coefficient, when applied to a sample, is commonly represented by 




where:
Rearranging gives us this formula for 
where 
This formula suggests a convenient single-pass algorithm for calculating sample correlations, though depending on the numbers involved, it can sometimes be numerically unstable.
Rearranging again gives us this[10] formula for 
where 
An equivalent expression gives the formula for 
where:
Alternative formulae for 

where:
Practical issues[edit]
Under heavy noise conditions, extracting the correlation coefficient between two sets of stochastic variables is nontrivial, in particular where Canonical Correlation Analysis reports degraded correlation values due to the heavy noise contributions. A generalization of the approach is given elsewhere.[12]
In case of missing data, Garren derived the maximum likelihood estimator.[13]
Some distributions (e.g., stable distributions other than a normal distribution) do not have a defined variance.
Mathematical properties[edit]
The values of both the sample and population Pearson correlation coefficients are on or between −1 and 1. Correlations equal to +1 or −1 correspond to data points lying exactly on a line (in the case of the sample correlation), or to a bivariate distribution entirely supported on a line (in the case of the population correlation). The Pearson correlation coefficient is symmetric: corr(X,Y) = corr(Y,X).
A key mathematical property of the Pearson correlation coefficient is that it is invariant under separate changes in location and scale in the two variables. That is, we may transform X to a + bX and transform Y to c + dY, where a, b, c, and d are constants with b, d > 0, without changing the correlation coefficient. (This holds for both the population and sample Pearson correlation coefficients.) Note that more general linear transformations do change the correlation: see § Decorrelation of n random variables for an application of this.
Interpretation[edit]
The correlation coefficient ranges from −1 to 1. An absolute value of exactly 1 implies that a linear equation describes the relationship between X and Y perfectly, with all data points lying on a line. The correlation sign is determined by the regression slope: a value of +1 implies that all data points lie on a line for which Y increases as X increases, and vice versa for −1.[14] A value of 0 implies that there is no linear dependency between the variables.[15]
More generally, note that (Xi − X)(Yi − Y) is positive if and only if Xi and Yi lie on the same side of their respective means. Thus the correlation coefficient is positive if Xi and Yi tend to be simultaneously greater than, or simultaneously less than, their respective means. The correlation coefficient is negative (anti-correlation) if Xi and Yi tend to lie on opposite sides of their respective means. Moreover, the stronger either tendency is, the larger is the absolute value of the correlation coefficient.
Rodgers and Nicewander[16] cataloged thirteen ways of interpreting correlation or simple functions of it:
- Function of raw scores and means
- Standardized covariance
- Standardized slope of the regression line
- Geometric mean of the two regression slopes
- Square root of the ratio of two variances
- Mean cross-product of standardized variables
- Function of the angle between two standardized regression lines
- Function of the angle between two variable vectors
- Rescaled variance of the difference between standardized scores
- Estimated from the balloon rule
- Related to the bivariate ellipses of isoconcentration
- Function of test statistics from designed experiments
- Ratio of two means
Geometric interpretation[edit]
Regression lines for y = gX(x) [red] and x = gY(y) [blue]
For uncentered data, there is a relation between the correlation coefficient and the angle φ between the two regression lines, y = gX(x) and x = gY(y), obtained by regressing y on x and x on y respectively. (Here, φ is measured counterclockwise within the first quadrant formed around the lines’ intersection point if r > 0, or counterclockwise from the fourth to the second quadrant if r < 0.) One can show[17] that if the standard deviations are equal, then r = sec φ − tan φ, where sec and tan are trigonometric functions.
For centered data (i.e., data which have been shifted by the sample means of their respective variables so as to have an average of zero for each variable), the correlation coefficient can also be viewed as the cosine of the angle θ between the two observed vectors in N-dimensional space (for N observations of each variable)[18]
Both the uncentered (non-Pearson-compliant) and centered correlation coefficients can be determined for a dataset. As an example, suppose five countries are found to have gross national products of 1, 2, 3, 5, and 8 billion dollars, respectively. Suppose these same five countries (in the same order) are found to have 11%, 12%, 13%, 15%, and 18% poverty. Then let x and y be ordered 5-element vectors containing the above data: x = (1, 2, 3, 5, and y = (0.11, 0.12, 0.13, 0.15, 0.18).
By the usual procedure for finding the angle θ between two vectors (see dot product), the uncentered correlation coefficient is:
This uncentered correlation coefficient is identical with the cosine similarity.
Note that the above data were deliberately chosen to be perfectly correlated: y = 0.10 + 0.01 x. The Pearson correlation coefficient must therefore be exactly one. Centering the data (shifting x by ℰ(x) = 3.8 and y by ℰ(y) = 0.138) yields x = (−2.8, −1.8, −0.8, 1.2, 4.2) and y = (−0.028, −0.018, −0.008, 0.012, 0.042), from which
as expected.
Interpretation of the size of a correlation[edit]
This figure gives a sense of how the usefulness of a Pearson correlation for predicting values varies with its magnitude. Given jointly normal X, Y with correlation ρ, 
Several authors have offered guidelines for the interpretation of a correlation coefficient.[19][20] However, all such criteria are in some ways arbitrary.[20] The interpretation of a correlation coefficient depends on the context and purposes. A correlation of 0.8 may be very low if one is verifying a physical law using high-quality instruments, but may be regarded as very high in the social sciences, where there may be a greater contribution from complicating factors.
Inference[edit]
Statistical inference based on Pearson’s correlation coefficient often focuses on one of the following two aims:
- One aim is to test the null hypothesis that the true correlation coefficient ρ is equal to 0, based on the value of the sample correlation coefficient r.
- The other aim is to derive a confidence interval that, on repeated sampling, has a given probability of containing ρ.
We discuss methods of achieving one or both of these aims below.
Using a permutation test[edit]
Permutation tests provide a direct approach to performing hypothesis tests and constructing confidence intervals. A permutation test for Pearson’s correlation coefficient involves the following two steps:
- Using the original paired data (xi, yi), randomly redefine the pairs to create a new data set (xi, yi′), where the i′ are a permutation of the set {1,…,n}. The permutation i′ is selected randomly, with equal probabilities placed on all n! possible permutations. This is equivalent to drawing the i′ randomly without replacement from the set {1, …, n}. In bootstrapping, a closely related approach, the i and the i′ are equal and drawn with replacement from {1, …, n};
- Construct a correlation coefficient r from the randomized data.
To perform the permutation test, repeat steps (1) and (2) a large number of times. The p-value for the permutation test is the proportion of the r values generated in step (2) that are larger than the Pearson correlation coefficient that was calculated from the original data. Here «larger» can mean either that the value is larger in magnitude, or larger in signed value, depending on whether a two-sided or one-sided test is desired.
Using a bootstrap[edit]
The bootstrap can be used to construct confidence intervals for Pearson’s correlation coefficient. In the «non-parametric» bootstrap, n pairs (xi, yi) are resampled «with replacement» from the observed set of n pairs, and the correlation coefficient r is calculated based on the resampled data. This process is repeated a large number of times, and the empirical distribution of the resampled r values are used to approximate the sampling distribution of the statistic. A 95% confidence interval for ρ can be defined as the interval spanning from the 2.5th to the 97.5th percentile of the resampled r values.
Standard error[edit]
If 

where 

Testing using Student’s t-distribution[edit]
Critical values of Pearson’s correlation coefficient that must be exceeded to be considered significantly nonzero at the 0.05 level.
For pairs from an uncorrelated bivariate normal distribution, the sampling distribution of the studentized Pearson’s correlation coefficient follows Student’s t-distribution with degrees of freedom n − 2. Specifically, if the underlying variables have a bivariate normal distribution, the variable
has a student’s t-distribution in the null case (zero correlation).[23] This holds approximately in case of non-normal observed values if sample sizes are large enough.[24] For determining the critical values for r the inverse function is needed:
Alternatively, large sample, asymptotic approaches can be used.
Another early paper[25] provides graphs and tables for general values of ρ, for small sample sizes, and discusses computational approaches.
In the case where the underlying variables are not normal, the sampling distribution of Pearson’s correlation coefficient follows a Student’s t-distribution, but the degrees of freedom are reduced.[26]
Using the exact distribution[edit]
For data that follow a bivariate normal distribution, the exact density function f(r) for the sample correlation coefficient r of a normal bivariate is[27][28][29]
where 

In the special case when 
where 
Using the exact confidence distribution[edit]
Confidence intervals and tests can be calculated from a confidence distribution. An exact confidence density for ρ is[30]
where 

Using the Fisher transformation[edit]
In practice, confidence intervals and hypothesis tests relating to ρ are usually carried out using the Fisher transformation, 
F(r) approximately follows a normal distribution with
and standard error
where n is the sample size. The approximation error is lowest for a large sample size 


Using the approximation, a z-score is
under the null hypothesis that 

To obtain a confidence interval for ρ, we first compute a confidence interval for F(
The inverse Fisher transformation brings the interval back to the correlation scale.
For example, suppose we observe r = 0.7 with a sample size of n=50, and we wish to obtain a 95% confidence interval for ρ. The transformed value is arctanh(r) = 0.8673, so the confidence interval on the transformed scale is 0.8673 ± 1.96/√47, or (0.5814, 1.1532). Converting back to the correlation scale yields (0.5237, 0.8188).
In least squares regression analysis[edit]
The square of the sample correlation coefficient is typically denoted r2 and is a special case of the coefficient of determination. In this case, it estimates the fraction of the variance in Y that is explained by X in a simple linear regression. So if we have the observed dataset 

where the 
The two summands above are the fraction of variance in Y that is explained by X (right) and that is unexplained by X (left).
Next, we apply a property of least square regression models, that the sample covariance between 

Thus
where 
In the derivation above, the fact that
can be proved by noticing that the partial derivatives of the residual sum of squares (RSS) over β0 and β1 are equal to 0 in the least squares model, where
.
In the end, the equation can be written as:
where
The symbol 

Sensitivity to the data distribution[edit]
Existence[edit]
The population Pearson correlation coefficient is defined in terms of moments, and therefore exists for any bivariate probability distribution for which the population covariance is defined and the marginal population variances are defined and are non-zero. Some probability distributions, such as the Cauchy distribution, have undefined variance and hence ρ is not defined if X or Y follows such a distribution. In some practical applications, such as those involving data suspected to follow a heavy-tailed distribution, this is an important consideration. However, the existence of the correlation coefficient is usually not a concern; for instance, if the range of the distribution is bounded, ρ is always defined.
Sample size[edit]
- If the sample size is moderate or large and the population is normal, then, in the case of the bivariate normal distribution, the sample correlation coefficient is the maximum likelihood estimate of the population correlation coefficient, and is asymptotically unbiased and efficient, which roughly means that it is impossible to construct a more accurate estimate than the sample correlation coefficient.
- If the sample size is large and the population is not normal, then the sample correlation coefficient remains approximately unbiased, but may not be efficient.
- If the sample size is large, then the sample correlation coefficient is a consistent estimator of the population correlation coefficient as long as the sample means, variances, and covariance are consistent (which is guaranteed when the law of large numbers can be applied).
- If the sample size is small, then the sample correlation coefficient r is not an unbiased estimate of ρ.[10] The adjusted correlation coefficient must be used instead: see elsewhere in this article for the definition.
- Correlations can be different for imbalanced dichotomous data when there is variance error in sample.[31]
Robustness[edit]
Like many commonly used statistics, the sample statistic r is not robust,[32] so its value can be misleading if outliers are present.[33][34] Specifically, the PMCC is neither distributionally robust,[citation needed] nor outlier resistant[32] (see Robust statistics § Definition). Inspection of the scatterplot between X and Y will typically reveal a situation where lack of robustness might be an issue, and in such cases it may be advisable to use a robust measure of association. Note however that while most robust estimators of association measure statistical dependence in some way, they are generally not interpretable on the same scale as the Pearson correlation coefficient.
Statistical inference for Pearson’s correlation coefficient is sensitive to the data distribution. Exact tests, and asymptotic tests based on the Fisher transformation can be applied if the data are approximately normally distributed, but may be misleading otherwise. In some situations, the bootstrap can be applied to construct confidence intervals, and permutation tests can be applied to carry out hypothesis tests. These non-parametric approaches may give more meaningful results in some situations where bivariate normality does not hold. However the standard versions of these approaches rely on exchangeability of the data, meaning that there is no ordering or grouping of the data pairs being analyzed that might affect the behavior of the correlation estimate.
A stratified analysis is one way to either accommodate a lack of bivariate normality, or to isolate the correlation resulting from one factor while controlling for another. If W represents cluster membership or another factor that it is desirable to control, we can stratify the data based on the value of W, then calculate a correlation coefficient within each stratum. The stratum-level estimates can then be combined to estimate the overall correlation while controlling for W.[35]
Variants[edit]
Variations of the correlation coefficient can be calculated for different purposes. Here are some examples.
Adjusted correlation coefficient[edit]
The sample correlation coefficient r is not an unbiased estimate of ρ. For data that follows a bivariate normal distribution, the expectation E[r] for the sample correlation coefficient r of a normal bivariate is[36]
therefore r is a biased estimator of
The unique minimum variance unbiased estimator radj is given by[37]
-
(1)
where:
An approximately unbiased estimator radj can be obtained[citation needed] by truncating E[r] and solving this truncated equation:
-
(2)
An approximate solution[citation needed] to equation (2) is:
-
(3)
where in (3):
are defined as above,
- radj is a suboptimal estimator,[citation needed][clarification needed]
- radj can also be obtained by maximizing log(f(r)),
- radj has minimum variance for large values of n,
- radj has a bias of order 1⁄(n − 1).
Another proposed[10] adjusted correlation coefficient is:[citation needed]
Note that radj ≈ r for large values of n.
Weighted correlation coefficient[edit]
Suppose observations to be correlated have differing degrees of importance that can be expressed with a weight vector w. To calculate the correlation between vectors x and y with the weight vector w (all of length n),[38][39]
- Weighted mean:
- Weighted covariance
- Weighted correlation
Reflective correlation coefficient[edit]
The reflective correlation is a variant of Pearson’s correlation in which the data are not centered around their mean values.[citation needed] The population reflective correlation is
The reflective correlation is symmetric, but it is not invariant under translation:
The sample reflective correlation is equivalent to cosine similarity:
The weighted version of the sample reflective correlation is
Scaled correlation coefficient[edit]
Scaled correlation is a variant of Pearson’s correlation in which the range of the data is restricted intentionally and in a controlled manner to reveal correlations between fast components in time series.[40] Scaled correlation is defined as average correlation across short segments of data.
Let 


The scaled correlation across the entire signals 
where 

By choosing the parameter 
Pearson’s distance[edit]
A distance metric for two variables X and Y known as Pearson’s distance can be defined from their correlation coefficient as[41]
Considering that the Pearson correlation coefficient falls between [−1, +1], the Pearson distance lies in [0, 2]. The Pearson distance has been used in cluster analysis and data detection for communications and storage with unknown gain and offset.[42]
The Pearson «distance» defined this way assigns distance greater than 1 to negative correlations. In reality, both strong positive correlation and negative correlations are meaningful, so care must be taken when Pearson «distance» is used for nearest neighbor algorithm as such algorithm will only include neighbors with positive correlation and exclude neighbors with negative correlation. Alternatively, an absolute valued distance: 
Circular correlation coefficient[edit]
For variables X = {x1,…,xn} and Y = {y1,…,yn} that are defined on the unit circle [0, 2π), it is possible to define a circular analog of Pearson’s coefficient.[43] This is done by transforming data points in X and Y with a sine function such that the correlation coefficient is given as:
where 

Partial correlation[edit]
If a population or data-set is characterized by more than two variables, a partial correlation coefficient measures the strength of dependence between a pair of variables that is not accounted for by the way in which they both change in response to variations in a selected subset of the other variables.
Decorrelation of n random variables[edit]
It is always possible to remove the correlations between all pairs of an arbitrary number of random variables by using a data transformation, even if the relationship between the variables is nonlinear. A presentation of this result for population distributions is given by Cox & Hinkley.[44]
A corresponding result exists for reducing the sample correlations to zero. Suppose a vector of n random variables is observed m times. Let X be a matrix where 

where an exponent of −+1⁄2 represents the matrix square root of the inverse of a matrix. The correlation matrix of T will be the identity matrix. If a new data observation x is a row vector of n elements, then the same transform can be applied to x to get the transformed vectors d and t:
This decorrelation is related to principal components analysis for multivariate data.
Software implementations[edit]
- R’s statistics base-package implements the correlation coefficient with
cor(x, y), or (with the P value also) withcor.test(x, y). - The SciPy Python library via
pearsonr(x, y). - The Pandas Python library implements Pearson correlation coefficient calculation as the default option for the method
pandas.DataFrame.corr - Wolfram Mathematica via the
Correlationfunction, or (with the P value) withCorrelationTest. - The Boost C++ library via the
correlation_coefficientfunction. - Excel has an in-built
correl(array1, array2)function for calculationg the pearson’s correlation coefficient.
See also[edit]
- Anscombe’s quartet
- Association (statistics)
- Coefficient of colligation
- Yule’s Q
- Yule’s Y
- Concordance correlation coefficient
- Correlation and dependence
- Correlation ratio
- Disattenuation
- Distance correlation
- Maximal information coefficient
- Multiple correlation
- Normally distributed and uncorrelated does not imply independent
- Odds ratio
- Partial correlation
- Polychoric correlation
- Quadrant count ratio
- RV coefficient
- Spearman’s rank correlation coefficient
Footnotes[edit]
- ^ As early as 1877, Galton was using the term «reversion» and the symbol «r» for what would become «regression».[3][4][5]
References[edit]
- ^ «SPSS Tutorials: Pearson Correlation».
- ^ «Correlation Coefficient: Simple Definition, Formula, Easy Steps». Statistics How To.
- ^ Galton, F. (5–19 April 1877). «Typical laws of heredity». Nature. 15 (388, 389, 390): 492–495, 512–514, 532–533. Bibcode:1877Natur..15..492.. doi:10.1038/015492a0. S2CID 4136393. In the «Appendix» on page 532, Galton uses the term «reversion» and the symbol r.
- ^ Galton, F. (24 September 1885). «The British Association: Section II, Anthropology: Opening address by Francis Galton, F.R.S., etc., President of the Anthropological Institute, President of the Section». Nature. 32 (830): 507–510.
- ^ Galton, F. (1886). «Regression towards mediocrity in hereditary stature». Journal of the Anthropological Institute of Great Britain and Ireland. 15: 246–263. doi:10.2307/2841583. JSTOR 2841583.
- ^ Pearson, Karl (20 June 1895). «Notes on regression and inheritance in the case of two parents». Proceedings of the Royal Society of London. 58: 240–242. Bibcode:1895RSPS…58..240P.
- ^ Stigler, Stephen M. (1989). «Francis Galton’s account of the invention of correlation». Statistical Science. 4 (2): 73–79. doi:10.1214/ss/1177012580. JSTOR 2245329.
- ^ «Analyse mathematique sur les probabilités des erreurs de situation d’un point». Mem. Acad. Roy. Sci. Inst. France. Sci. Math, et Phys. (in French). 9: 255–332. 1844 – via Google Books.
- ^ Wright, S. (1921). «Correlation and causation». Journal of Agricultural Research. 20 (7): 557–585.
- ^ a b c d e Real Statistics Using Excel: Correlation: Basic Concepts, retrieved 22 February 2015
- ^ Weisstein, Eric W. «Statistical Correlation». mathworld.wolfram.com. Retrieved 22 August 2020.
- ^ Moriya, N. (2008). «Noise-related multivariate optimal joint-analysis in longitudinal stochastic processes». In Yang, Fengshan (ed.). Progress in Applied Mathematical Modeling. Nova Science Publishers, Inc. pp. 223–260. ISBN 978-1-60021-976-4.
- ^ Garren, Steven T. (15 June 1998). «Maximum likelihood estimation of the correlation coefficient in a bivariate normal model, with missing data». Statistics & Probability Letters. 38 (3): 281–288. doi:10.1016/S0167-7152(98)00035-2.
- ^ «2.6 — (Pearson) Correlation Coefficient r». STAT 462. Retrieved 10 July 2021.
- ^ «Introductory Business Statistics: The Correlation Coefficient r». opentextbc.ca. Retrieved 21 August 2020.
- ^ Rodgers; Nicewander (1988). «Thirteen ways to look at the correlation coefficient» (PDF). The American Statistician. 42 (1): 59–66. doi:10.2307/2685263. JSTOR 2685263.
- ^ Schmid, John Jr. (December 1947). «The relationship between the coefficient of correlation and the angle included between regression lines». The Journal of Educational Research. 41 (4): 311–313. doi:10.1080/00220671.1947.10881608. JSTOR 27528906.
- ^ Rummel, R.J. (1976). «Understanding Correlation». ch. 5 (as illustrated for a special case in the next paragraph).
- ^ Buda, Andrzej; Jarynowski, Andrzej (December 2010). Life Time of Correlations and its Applications. Wydawnictwo Niezależne. pp. 5–21. ISBN 9788391527290.
- ^ a b Cohen, J. (1988). Statistical Power Analysis for the Behavioral Sciences (2nd ed.).
- ^ Bowley, A. L. (1928). «The Standard Deviation of the Correlation Coefficient». Journal of the American Statistical Association. 23 (161): 31–34. doi:10.2307/2277400. ISSN 0162-1459. JSTOR 2277400.
- ^ «Derivation of the standard error for Pearson’s correlation coefficient». Cross Validated. Retrieved 30 July 2021.
- ^ Rahman, N. A. (1968) A Course in Theoretical Statistics, Charles Griffin and Company, 1968
- ^ Kendall, M. G., Stuart, A. (1973) The Advanced Theory of Statistics, Volume 2: Inference and Relationship, Griffin. ISBN 0-85264-215-6 (Section 31.19)
- ^ Soper, H.E.; Young, A.W.; Cave, B.M.; Lee, A.; Pearson, K. (1917). «On the distribution of the correlation coefficient in small samples. Appendix II to the papers of «Student» and R.A. Fisher. A co-operative study». Biometrika. 11 (4): 328–413. doi:10.1093/biomet/11.4.328.
- ^ Davey, Catherine E.; Grayden, David B.; Egan, Gary F.; Johnston, Leigh A. (January 2013). «Filtering induces correlation in fMRI resting state data». NeuroImage. 64: 728–740. doi:10.1016/j.neuroimage.2012.08.022. hdl:11343/44035. PMID 22939874. S2CID 207184701.
- ^ Hotelling, Harold (1953). «New Light on the Correlation Coefficient and its Transforms». Journal of the Royal Statistical Society. Series B (Methodological). 15 (2): 193–232. doi:10.1111/j.2517-6161.1953.tb00135.x. JSTOR 2983768.
- ^ Kenney, J.F.; Keeping, E.S. (1951). Mathematics of Statistics. Vol. Part 2 (2nd ed.). Princeton, NJ: Van Nostrand.
- ^ Weisstein, Eric W. «Correlation Coefficient—Bivariate Normal Distribution». mathworld.wolfram.com.
- ^ Taraldsen, Gunnar (2020). «Confidence in Correlation». doi:10.13140/RG.2.2.23673.49769.
- ^ Lai, Chun Sing; Tao, Yingshan; Xu, Fangyuan; Ng, Wing W.Y.; Jia, Youwei; Yuan, Haoliang; Huang, Chao; Lai, Loi Lei; Xu, Zhao; Locatelli, Giorgio (January 2019). «A robust correlation analysis framework for imbalanced and dichotomous data with uncertainty» (PDF). Information Sciences. 470: 58–77. doi:10.1016/j.ins.2018.08.017. S2CID 52878443.
- ^ a b Wilcox, Rand R. (2005). Introduction to robust estimation and hypothesis testing. Academic Press.
- ^ Devlin, Susan J.; Gnanadesikan, R.; Kettenring J.R. (1975). «Robust estimation and outlier detection with correlation coefficients». Biometrika. 62 (3): 531–545. doi:10.1093/biomet/62.3.531. JSTOR 2335508.
- ^ Huber, Peter. J. (2004). Robust Statistics. Wiley.[page needed]
- ^ Katz., Mitchell H. (2006) Multivariable Analysis – A Practical Guide for Clinicians. 2nd Edition. Cambridge University Press. ISBN 978-0-521-54985-1. ISBN 0-521-54985-X
- ^ Hotelling, H. (1953). «New Light on the Correlation Coefficient and its Transforms». Journal of the Royal Statistical Society. Series B (Methodological). 15 (2): 193–232. doi:10.1111/j.2517-6161.1953.tb00135.x. JSTOR 2983768.
- ^ Olkin, Ingram; Pratt,John W. (March 1958). «Unbiased Estimation of Certain Correlation Coefficients». The Annals of Mathematical Statistics. 29 (1): 201–211. doi:10.1214/aoms/1177706717. JSTOR 2237306..
- ^ «Re: Compute a weighted correlation». sci.tech-archive.net.
- ^ «Weighted Correlation Matrix – File Exchange – MATLAB Central».
- ^ Nikolić, D; Muresan, RC; Feng, W; Singer, W (2012). «Scaled correlation analysis: a better way to compute a cross-correlogram» (PDF). European Journal of Neuroscience. 35 (5): 1–21. doi:10.1111/j.1460-9568.2011.07987.x. PMID 22324876. S2CID 4694570.
- ^ Fulekar (Ed.), M.H. (2009) Bioinformatics: Applications in Life and Environmental Sciences, Springer (pp. 110) ISBN 1-4020-8879-5
- ^ Immink, K. Schouhamer; Weber, J. (October 2010). «Minimum Pearson distance detection for multilevel channels with gain and / or offset mismatch». IEEE Transactions on Information Theory. 60 (10): 5966–5974. CiteSeerX 10.1.1.642.9971. doi:10.1109/tit.2014.2342744. S2CID 1027502. Retrieved 11 February 2018.
- ^ Jammalamadaka, S. Rao; SenGupta, A. (2001). Topics in circular statistics. New Jersey: World Scientific. p. 176. ISBN 978-981-02-3778-3. Retrieved 21 September 2016.
- ^ Cox, D.R.; Hinkley, D.V. (1974). Theoretical Statistics. Chapman & Hall. Appendix 3. ISBN 0-412-12420-3.
External links[edit]
- «cocor». comparingcorrelations.org. – A free web interface and R package for the statistical comparison of two dependent or independent correlations with overlapping or non-overlapping variables.
- «Correlation». nagysandor.eu. – an interactive Flash simulation on the correlation of two normally distributed variables.
- «Correlation coefficient calculator». hackmath.net. Linear regression. –
- «Critical values for Pearson’s correlation coefficient» (PDF). frank.mtsu.edu/~dkfuller. – large table.
- «Guess the Correlation». – A game where players guess how correlated two variables in a scatter plot are, in order to gain a better understanding of the concept of correlation.
In statistics, the Pearson correlation coefficient (PCC, pronounced ) ― also known as Pearson’s r, the Pearson product-moment correlation coefficient (PPMCC), the bivariate correlation,[1] or colloquially simply as the correlation coefficient[2] ― is a measure of linear correlation between two sets of data. It is the ratio between the covariance of two variables and the product of their standard deviations; thus, it is essentially a normalized measurement of the covariance, such that the result always has a value between −1 and 1. As with covariance itself, the measure can only reflect a linear correlation of variables, and ignores many other types of relationships or correlations. As a simple example, one would expect the age and height of a sample of teenagers from a high school to have a Pearson correlation coefficient significantly greater than 0, but less than 1 (as 1 would represent an unrealistically perfect correlation).
Examples of scatter diagrams with different values of correlation coefficient (ρ)
Several sets of (x, y) points, with the correlation coefficient of x and y for each set. Note that the correlation reflects the strength and direction of a linear relationship (top row), but not the slope of that relationship (middle), nor many aspects of nonlinear relationships (bottom). N.B.: the figure in the center has a slope of 0 but in that case the correlation coefficient is undefined because the variance of Y is zero.
Naming and history[edit]
It was developed by Karl Pearson from a related idea introduced by Francis Galton in the 1880s, and for which the mathematical formula was derived and published by Auguste Bravais in 1844.[a][6][7][8][9] The naming of the coefficient is thus an example of Stigler’s Law.
Definition[edit]
Pearson’s correlation coefficient is the covariance of the two variables divided by the product of their standard deviations. The form of the definition involves a «product moment», that is, the mean (the first moment about the origin) of the product of the mean-adjusted random variables; hence the modifier product-moment in the name.
For a population[edit]
Pearson’s correlation coefficient, when applied to a population, is commonly represented by the Greek letter ρ (rho) and may be referred to as the population correlation coefficient or the population Pearson correlation coefficient. Given a pair of random variables 
where:
The formula for 
the formula for 
where:
The formula for 
the formula for 
Peason’s correlation coefficient does not exist when either 

For a sample[edit]
Pearson’s correlation coefficient, when applied to a sample, is commonly represented by 




where:
Rearranging gives us this formula for 
where 
This formula suggests a convenient single-pass algorithm for calculating sample correlations, though depending on the numbers involved, it can sometimes be numerically unstable.
Rearranging again gives us this[10] formula for 
where 
An equivalent expression gives the formula for 
where:
Alternative formulae for 

where:
Practical issues[edit]
Under heavy noise conditions, extracting the correlation coefficient between two sets of stochastic variables is nontrivial, in particular where Canonical Correlation Analysis reports degraded correlation values due to the heavy noise contributions. A generalization of the approach is given elsewhere.[12]
In case of missing data, Garren derived the maximum likelihood estimator.[13]
Some distributions (e.g., stable distributions other than a normal distribution) do not have a defined variance.
Mathematical properties[edit]
The values of both the sample and population Pearson correlation coefficients are on or between −1 and 1. Correlations equal to +1 or −1 correspond to data points lying exactly on a line (in the case of the sample correlation), or to a bivariate distribution entirely supported on a line (in the case of the population correlation). The Pearson correlation coefficient is symmetric: corr(X,Y) = corr(Y,X).
A key mathematical property of the Pearson correlation coefficient is that it is invariant under separate changes in location and scale in the two variables. That is, we may transform X to a + bX and transform Y to c + dY, where a, b, c, and d are constants with b, d > 0, without changing the correlation coefficient. (This holds for both the population and sample Pearson correlation coefficients.) Note that more general linear transformations do change the correlation: see § Decorrelation of n random variables for an application of this.
Interpretation[edit]
The correlation coefficient ranges from −1 to 1. An absolute value of exactly 1 implies that a linear equation describes the relationship between X and Y perfectly, with all data points lying on a line. The correlation sign is determined by the regression slope: a value of +1 implies that all data points lie on a line for which Y increases as X increases, and vice versa for −1.[14] A value of 0 implies that there is no linear dependency between the variables.[15]
More generally, note that (Xi − X)(Yi − Y) is positive if and only if Xi and Yi lie on the same side of their respective means. Thus the correlation coefficient is positive if Xi and Yi tend to be simultaneously greater than, or simultaneously less than, their respective means. The correlation coefficient is negative (anti-correlation) if Xi and Yi tend to lie on opposite sides of their respective means. Moreover, the stronger either tendency is, the larger is the absolute value of the correlation coefficient.
Rodgers and Nicewander[16] cataloged thirteen ways of interpreting correlation or simple functions of it:
- Function of raw scores and means
- Standardized covariance
- Standardized slope of the regression line
- Geometric mean of the two regression slopes
- Square root of the ratio of two variances
- Mean cross-product of standardized variables
- Function of the angle between two standardized regression lines
- Function of the angle between two variable vectors
- Rescaled variance of the difference between standardized scores
- Estimated from the balloon rule
- Related to the bivariate ellipses of isoconcentration
- Function of test statistics from designed experiments
- Ratio of two means
Geometric interpretation[edit]
Regression lines for y = gX(x) [red] and x = gY(y) [blue]
For uncentered data, there is a relation between the correlation coefficient and the angle φ between the two regression lines, y = gX(x) and x = gY(y), obtained by regressing y on x and x on y respectively. (Here, φ is measured counterclockwise within the first quadrant formed around the lines’ intersection point if r > 0, or counterclockwise from the fourth to the second quadrant if r < 0.) One can show[17] that if the standard deviations are equal, then r = sec φ − tan φ, where sec and tan are trigonometric functions.
For centered data (i.e., data which have been shifted by the sample means of their respective variables so as to have an average of zero for each variable), the correlation coefficient can also be viewed as the cosine of the angle θ between the two observed vectors in N-dimensional space (for N observations of each variable)[18]
Both the uncentered (non-Pearson-compliant) and centered correlation coefficients can be determined for a dataset. As an example, suppose five countries are found to have gross national products of 1, 2, 3, 5, and 8 billion dollars, respectively. Suppose these same five countries (in the same order) are found to have 11%, 12%, 13%, 15%, and 18% poverty. Then let x and y be ordered 5-element vectors containing the above data: x = (1, 2, 3, 5, and y = (0.11, 0.12, 0.13, 0.15, 0.18).
By the usual procedure for finding the angle θ between two vectors (see dot product), the uncentered correlation coefficient is:
This uncentered correlation coefficient is identical with the cosine similarity.
Note that the above data were deliberately chosen to be perfectly correlated: y = 0.10 + 0.01 x. The Pearson correlation coefficient must therefore be exactly one. Centering the data (shifting x by ℰ(x) = 3.8 and y by ℰ(y) = 0.138) yields x = (−2.8, −1.8, −0.8, 1.2, 4.2) and y = (−0.028, −0.018, −0.008, 0.012, 0.042), from which
as expected.
Interpretation of the size of a correlation[edit]
This figure gives a sense of how the usefulness of a Pearson correlation for predicting values varies with its magnitude. Given jointly normal X, Y with correlation ρ, 
Several authors have offered guidelines for the interpretation of a correlation coefficient.[19][20] However, all such criteria are in some ways arbitrary.[20] The interpretation of a correlation coefficient depends on the context and purposes. A correlation of 0.8 may be very low if one is verifying a physical law using high-quality instruments, but may be regarded as very high in the social sciences, where there may be a greater contribution from complicating factors.
Inference[edit]
Statistical inference based on Pearson’s correlation coefficient often focuses on one of the following two aims:
- One aim is to test the null hypothesis that the true correlation coefficient ρ is equal to 0, based on the value of the sample correlation coefficient r.
- The other aim is to derive a confidence interval that, on repeated sampling, has a given probability of containing ρ.
We discuss methods of achieving one or both of these aims below.
Using a permutation test[edit]
Permutation tests provide a direct approach to performing hypothesis tests and constructing confidence intervals. A permutation test for Pearson’s correlation coefficient involves the following two steps:
- Using the original paired data (xi, yi), randomly redefine the pairs to create a new data set (xi, yi′), where the i′ are a permutation of the set {1,…,n}. The permutation i′ is selected randomly, with equal probabilities placed on all n! possible permutations. This is equivalent to drawing the i′ randomly without replacement from the set {1, …, n}. In bootstrapping, a closely related approach, the i and the i′ are equal and drawn with replacement from {1, …, n};
- Construct a correlation coefficient r from the randomized data.
To perform the permutation test, repeat steps (1) and (2) a large number of times. The p-value for the permutation test is the proportion of the r values generated in step (2) that are larger than the Pearson correlation coefficient that was calculated from the original data. Here «larger» can mean either that the value is larger in magnitude, or larger in signed value, depending on whether a two-sided or one-sided test is desired.
Using a bootstrap[edit]
The bootstrap can be used to construct confidence intervals for Pearson’s correlation coefficient. In the «non-parametric» bootstrap, n pairs (xi, yi) are resampled «with replacement» from the observed set of n pairs, and the correlation coefficient r is calculated based on the resampled data. This process is repeated a large number of times, and the empirical distribution of the resampled r values are used to approximate the sampling distribution of the statistic. A 95% confidence interval for ρ can be defined as the interval spanning from the 2.5th to the 97.5th percentile of the resampled r values.
Standard error[edit]
If 

where 

Testing using Student’s t-distribution[edit]
Critical values of Pearson’s correlation coefficient that must be exceeded to be considered significantly nonzero at the 0.05 level.
For pairs from an uncorrelated bivariate normal distribution, the sampling distribution of the studentized Pearson’s correlation coefficient follows Student’s t-distribution with degrees of freedom n − 2. Specifically, if the underlying variables have a bivariate normal distribution, the variable
has a student’s t-distribution in the null case (zero correlation).[23] This holds approximately in case of non-normal observed values if sample sizes are large enough.[24] For determining the critical values for r the inverse function is needed:
Alternatively, large sample, asymptotic approaches can be used.
Another early paper[25] provides graphs and tables for general values of ρ, for small sample sizes, and discusses computational approaches.
In the case where the underlying variables are not normal, the sampling distribution of Pearson’s correlation coefficient follows a Student’s t-distribution, but the degrees of freedom are reduced.[26]
Using the exact distribution[edit]
For data that follow a bivariate normal distribution, the exact density function f(r) for the sample correlation coefficient r of a normal bivariate is[27][28][29]
where 

In the special case when 
where 
Using the exact confidence distribution[edit]
Confidence intervals and tests can be calculated from a confidence distribution. An exact confidence density for ρ is[30]
where 

Using the Fisher transformation[edit]
In practice, confidence intervals and hypothesis tests relating to ρ are usually carried out using the Fisher transformation, 
F(r) approximately follows a normal distribution with
and standard error
where n is the sample size. The approximation error is lowest for a large sample size 


Using the approximation, a z-score is
under the null hypothesis that 

To obtain a confidence interval for ρ, we first compute a confidence interval for F(
The inverse Fisher transformation brings the interval back to the correlation scale.
For example, suppose we observe r = 0.7 with a sample size of n=50, and we wish to obtain a 95% confidence interval for ρ. The transformed value is arctanh(r) = 0.8673, so the confidence interval on the transformed scale is 0.8673 ± 1.96/√47, or (0.5814, 1.1532). Converting back to the correlation scale yields (0.5237, 0.8188).
In least squares regression analysis[edit]
The square of the sample correlation coefficient is typically denoted r2 and is a special case of the coefficient of determination. In this case, it estimates the fraction of the variance in Y that is explained by X in a simple linear regression. So if we have the observed dataset 

where the 
The two summands above are the fraction of variance in Y that is explained by X (right) and that is unexplained by X (left).
Next, we apply a property of least square regression models, that the sample covariance between 

Thus
where 
In the derivation above, the fact that
can be proved by noticing that the partial derivatives of the residual sum of squares (RSS) over β0 and β1 are equal to 0 in the least squares model, where
.
In the end, the equation can be written as:
where
The symbol 

Sensitivity to the data distribution[edit]
Existence[edit]
The population Pearson correlation coefficient is defined in terms of moments, and therefore exists for any bivariate probability distribution for which the population covariance is defined and the marginal population variances are defined and are non-zero. Some probability distributions, such as the Cauchy distribution, have undefined variance and hence ρ is not defined if X or Y follows such a distribution. In some practical applications, such as those involving data suspected to follow a heavy-tailed distribution, this is an important consideration. However, the existence of the correlation coefficient is usually not a concern; for instance, if the range of the distribution is bounded, ρ is always defined.
Sample size[edit]
- If the sample size is moderate or large and the population is normal, then, in the case of the bivariate normal distribution, the sample correlation coefficient is the maximum likelihood estimate of the population correlation coefficient, and is asymptotically unbiased and efficient, which roughly means that it is impossible to construct a more accurate estimate than the sample correlation coefficient.
- If the sample size is large and the population is not normal, then the sample correlation coefficient remains approximately unbiased, but may not be efficient.
- If the sample size is large, then the sample correlation coefficient is a consistent estimator of the population correlation coefficient as long as the sample means, variances, and covariance are consistent (which is guaranteed when the law of large numbers can be applied).
- If the sample size is small, then the sample correlation coefficient r is not an unbiased estimate of ρ.[10] The adjusted correlation coefficient must be used instead: see elsewhere in this article for the definition.
- Correlations can be different for imbalanced dichotomous data when there is variance error in sample.[31]
Robustness[edit]
Like many commonly used statistics, the sample statistic r is not robust,[32] so its value can be misleading if outliers are present.[33][34] Specifically, the PMCC is neither distributionally robust,[citation needed] nor outlier resistant[32] (see Robust statistics § Definition). Inspection of the scatterplot between X and Y will typically reveal a situation where lack of robustness might be an issue, and in such cases it may be advisable to use a robust measure of association. Note however that while most robust estimators of association measure statistical dependence in some way, they are generally not interpretable on the same scale as the Pearson correlation coefficient.
Statistical inference for Pearson’s correlation coefficient is sensitive to the data distribution. Exact tests, and asymptotic tests based on the Fisher transformation can be applied if the data are approximately normally distributed, but may be misleading otherwise. In some situations, the bootstrap can be applied to construct confidence intervals, and permutation tests can be applied to carry out hypothesis tests. These non-parametric approaches may give more meaningful results in some situations where bivariate normality does not hold. However the standard versions of these approaches rely on exchangeability of the data, meaning that there is no ordering or grouping of the data pairs being analyzed that might affect the behavior of the correlation estimate.
A stratified analysis is one way to either accommodate a lack of bivariate normality, or to isolate the correlation resulting from one factor while controlling for another. If W represents cluster membership or another factor that it is desirable to control, we can stratify the data based on the value of W, then calculate a correlation coefficient within each stratum. The stratum-level estimates can then be combined to estimate the overall correlation while controlling for W.[35]
Variants[edit]
Variations of the correlation coefficient can be calculated for different purposes. Here are some examples.
Adjusted correlation coefficient[edit]
The sample correlation coefficient r is not an unbiased estimate of ρ. For data that follows a bivariate normal distribution, the expectation E[r] for the sample correlation coefficient r of a normal bivariate is[36]
therefore r is a biased estimator of
The unique minimum variance unbiased estimator radj is given by[37]
-
(1)
where:
An approximately unbiased estimator radj can be obtained[citation needed] by truncating E[r] and solving this truncated equation:
-
(2)
An approximate solution[citation needed] to equation (2) is:
-
(3)
where in (3):
are defined as above,
- radj is a suboptimal estimator,[citation needed][clarification needed]
- radj can also be obtained by maximizing log(f(r)),
- radj has minimum variance for large values of n,
- radj has a bias of order 1⁄(n − 1).
Another proposed[10] adjusted correlation coefficient is:[citation needed]
Note that radj ≈ r for large values of n.
Weighted correlation coefficient[edit]
Suppose observations to be correlated have differing degrees of importance that can be expressed with a weight vector w. To calculate the correlation between vectors x and y with the weight vector w (all of length n),[38][39]
- Weighted mean:
- Weighted covariance
- Weighted correlation
Reflective correlation coefficient[edit]
The reflective correlation is a variant of Pearson’s correlation in which the data are not centered around their mean values.[citation needed] The population reflective correlation is
The reflective correlation is symmetric, but it is not invariant under translation:
The sample reflective correlation is equivalent to cosine similarity:
The weighted version of the sample reflective correlation is
Scaled correlation coefficient[edit]
Scaled correlation is a variant of Pearson’s correlation in which the range of the data is restricted intentionally and in a controlled manner to reveal correlations between fast components in time series.[40] Scaled correlation is defined as average correlation across short segments of data.
Let 


The scaled correlation across the entire signals 
where 

By choosing the parameter 
Pearson’s distance[edit]
A distance metric for two variables X and Y known as Pearson’s distance can be defined from their correlation coefficient as[41]
Considering that the Pearson correlation coefficient falls between [−1, +1], the Pearson distance lies in [0, 2]. The Pearson distance has been used in cluster analysis and data detection for communications and storage with unknown gain and offset.[42]
The Pearson «distance» defined this way assigns distance greater than 1 to negative correlations. In reality, both strong positive correlation and negative correlations are meaningful, so care must be taken when Pearson «distance» is used for nearest neighbor algorithm as such algorithm will only include neighbors with positive correlation and exclude neighbors with negative correlation. Alternatively, an absolute valued distance: 
Circular correlation coefficient[edit]
For variables X = {x1,…,xn} and Y = {y1,…,yn} that are defined on the unit circle [0, 2π), it is possible to define a circular analog of Pearson’s coefficient.[43] This is done by transforming data points in X and Y with a sine function such that the correlation coefficient is given as:
where 

Partial correlation[edit]
If a population or data-set is characterized by more than two variables, a partial correlation coefficient measures the strength of dependence between a pair of variables that is not accounted for by the way in which they both change in response to variations in a selected subset of the other variables.
Decorrelation of n random variables[edit]
It is always possible to remove the correlations between all pairs of an arbitrary number of random variables by using a data transformation, even if the relationship between the variables is nonlinear. A presentation of this result for population distributions is given by Cox & Hinkley.[44]
A corresponding result exists for reducing the sample correlations to zero. Suppose a vector of n random variables is observed m times. Let X be a matrix where 

where an exponent of −+1⁄2 represents the matrix square root of the inverse of a matrix. The correlation matrix of T will be the identity matrix. If a new data observation x is a row vector of n elements, then the same transform can be applied to x to get the transformed vectors d and t:
This decorrelation is related to principal components analysis for multivariate data.
Software implementations[edit]
- R’s statistics base-package implements the correlation coefficient with
cor(x, y), or (with the P value also) withcor.test(x, y). - The SciPy Python library via
pearsonr(x, y). - The Pandas Python library implements Pearson correlation coefficient calculation as the default option for the method
pandas.DataFrame.corr - Wolfram Mathematica via the
Correlationfunction, or (with the P value) withCorrelationTest. - The Boost C++ library via the
correlation_coefficientfunction. - Excel has an in-built
correl(array1, array2)function for calculationg the pearson’s correlation coefficient.
See also[edit]
- Anscombe’s quartet
- Association (statistics)
- Coefficient of colligation
- Yule’s Q
- Yule’s Y
- Concordance correlation coefficient
- Correlation and dependence
- Correlation ratio
- Disattenuation
- Distance correlation
- Maximal information coefficient
- Multiple correlation
- Normally distributed and uncorrelated does not imply independent
- Odds ratio
- Partial correlation
- Polychoric correlation
- Quadrant count ratio
- RV coefficient
- Spearman’s rank correlation coefficient
Footnotes[edit]
- ^ As early as 1877, Galton was using the term «reversion» and the symbol «r» for what would become «regression».[3][4][5]
References[edit]
- ^ «SPSS Tutorials: Pearson Correlation».
- ^ «Correlation Coefficient: Simple Definition, Formula, Easy Steps». Statistics How To.
- ^ Galton, F. (5–19 April 1877). «Typical laws of heredity». Nature. 15 (388, 389, 390): 492–495, 512–514, 532–533. Bibcode:1877Natur..15..492.. doi:10.1038/015492a0. S2CID 4136393. In the «Appendix» on page 532, Galton uses the term «reversion» and the symbol r.
- ^ Galton, F. (24 September 1885). «The British Association: Section II, Anthropology: Opening address by Francis Galton, F.R.S., etc., President of the Anthropological Institute, President of the Section». Nature. 32 (830): 507–510.
- ^ Galton, F. (1886). «Regression towards mediocrity in hereditary stature». Journal of the Anthropological Institute of Great Britain and Ireland. 15: 246–263. doi:10.2307/2841583. JSTOR 2841583.
- ^ Pearson, Karl (20 June 1895). «Notes on regression and inheritance in the case of two parents». Proceedings of the Royal Society of London. 58: 240–242. Bibcode:1895RSPS…58..240P.
- ^ Stigler, Stephen M. (1989). «Francis Galton’s account of the invention of correlation». Statistical Science. 4 (2): 73–79. doi:10.1214/ss/1177012580. JSTOR 2245329.
- ^ «Analyse mathematique sur les probabilités des erreurs de situation d’un point». Mem. Acad. Roy. Sci. Inst. France. Sci. Math, et Phys. (in French). 9: 255–332. 1844 – via Google Books.
- ^ Wright, S. (1921). «Correlation and causation». Journal of Agricultural Research. 20 (7): 557–585.
- ^ a b c d e Real Statistics Using Excel: Correlation: Basic Concepts, retrieved 22 February 2015
- ^ Weisstein, Eric W. «Statistical Correlation». mathworld.wolfram.com. Retrieved 22 August 2020.
- ^ Moriya, N. (2008). «Noise-related multivariate optimal joint-analysis in longitudinal stochastic processes». In Yang, Fengshan (ed.). Progress in Applied Mathematical Modeling. Nova Science Publishers, Inc. pp. 223–260. ISBN 978-1-60021-976-4.
- ^ Garren, Steven T. (15 June 1998). «Maximum likelihood estimation of the correlation coefficient in a bivariate normal model, with missing data». Statistics & Probability Letters. 38 (3): 281–288. doi:10.1016/S0167-7152(98)00035-2.
- ^ «2.6 — (Pearson) Correlation Coefficient r». STAT 462. Retrieved 10 July 2021.
- ^ «Introductory Business Statistics: The Correlation Coefficient r». opentextbc.ca. Retrieved 21 August 2020.
- ^ Rodgers; Nicewander (1988). «Thirteen ways to look at the correlation coefficient» (PDF). The American Statistician. 42 (1): 59–66. doi:10.2307/2685263. JSTOR 2685263.
- ^ Schmid, John Jr. (December 1947). «The relationship between the coefficient of correlation and the angle included between regression lines». The Journal of Educational Research. 41 (4): 311–313. doi:10.1080/00220671.1947.10881608. JSTOR 27528906.
- ^ Rummel, R.J. (1976). «Understanding Correlation». ch. 5 (as illustrated for a special case in the next paragraph).
- ^ Buda, Andrzej; Jarynowski, Andrzej (December 2010). Life Time of Correlations and its Applications. Wydawnictwo Niezależne. pp. 5–21. ISBN 9788391527290.
- ^ a b Cohen, J. (1988). Statistical Power Analysis for the Behavioral Sciences (2nd ed.).
- ^ Bowley, A. L. (1928). «The Standard Deviation of the Correlation Coefficient». Journal of the American Statistical Association. 23 (161): 31–34. doi:10.2307/2277400. ISSN 0162-1459. JSTOR 2277400.
- ^ «Derivation of the standard error for Pearson’s correlation coefficient». Cross Validated. Retrieved 30 July 2021.
- ^ Rahman, N. A. (1968) A Course in Theoretical Statistics, Charles Griffin and Company, 1968
- ^ Kendall, M. G., Stuart, A. (1973) The Advanced Theory of Statistics, Volume 2: Inference and Relationship, Griffin. ISBN 0-85264-215-6 (Section 31.19)
- ^ Soper, H.E.; Young, A.W.; Cave, B.M.; Lee, A.; Pearson, K. (1917). «On the distribution of the correlation coefficient in small samples. Appendix II to the papers of «Student» and R.A. Fisher. A co-operative study». Biometrika. 11 (4): 328–413. doi:10.1093/biomet/11.4.328.
- ^ Davey, Catherine E.; Grayden, David B.; Egan, Gary F.; Johnston, Leigh A. (January 2013). «Filtering induces correlation in fMRI resting state data». NeuroImage. 64: 728–740. doi:10.1016/j.neuroimage.2012.08.022. hdl:11343/44035. PMID 22939874. S2CID 207184701.
- ^ Hotelling, Harold (1953). «New Light on the Correlation Coefficient and its Transforms». Journal of the Royal Statistical Society. Series B (Methodological). 15 (2): 193–232. doi:10.1111/j.2517-6161.1953.tb00135.x. JSTOR 2983768.
- ^ Kenney, J.F.; Keeping, E.S. (1951). Mathematics of Statistics. Vol. Part 2 (2nd ed.). Princeton, NJ: Van Nostrand.
- ^ Weisstein, Eric W. «Correlation Coefficient—Bivariate Normal Distribution». mathworld.wolfram.com.
- ^ Taraldsen, Gunnar (2020). «Confidence in Correlation». doi:10.13140/RG.2.2.23673.49769.
- ^ Lai, Chun Sing; Tao, Yingshan; Xu, Fangyuan; Ng, Wing W.Y.; Jia, Youwei; Yuan, Haoliang; Huang, Chao; Lai, Loi Lei; Xu, Zhao; Locatelli, Giorgio (January 2019). «A robust correlation analysis framework for imbalanced and dichotomous data with uncertainty» (PDF). Information Sciences. 470: 58–77. doi:10.1016/j.ins.2018.08.017. S2CID 52878443.
- ^ a b Wilcox, Rand R. (2005). Introduction to robust estimation and hypothesis testing. Academic Press.
- ^ Devlin, Susan J.; Gnanadesikan, R.; Kettenring J.R. (1975). «Robust estimation and outlier detection with correlation coefficients». Biometrika. 62 (3): 531–545. doi:10.1093/biomet/62.3.531. JSTOR 2335508.
- ^ Huber, Peter. J. (2004). Robust Statistics. Wiley.[page needed]
- ^ Katz., Mitchell H. (2006) Multivariable Analysis – A Practical Guide for Clinicians. 2nd Edition. Cambridge University Press. ISBN 978-0-521-54985-1. ISBN 0-521-54985-X
- ^ Hotelling, H. (1953). «New Light on the Correlation Coefficient and its Transforms». Journal of the Royal Statistical Society. Series B (Methodological). 15 (2): 193–232. doi:10.1111/j.2517-6161.1953.tb00135.x. JSTOR 2983768.
- ^ Olkin, Ingram; Pratt,John W. (March 1958). «Unbiased Estimation of Certain Correlation Coefficients». The Annals of Mathematical Statistics. 29 (1): 201–211. doi:10.1214/aoms/1177706717. JSTOR 2237306..
- ^ «Re: Compute a weighted correlation». sci.tech-archive.net.
- ^ «Weighted Correlation Matrix – File Exchange – MATLAB Central».
- ^ Nikolić, D; Muresan, RC; Feng, W; Singer, W (2012). «Scaled correlation analysis: a better way to compute a cross-correlogram» (PDF). European Journal of Neuroscience. 35 (5): 1–21. doi:10.1111/j.1460-9568.2011.07987.x. PMID 22324876. S2CID 4694570.
- ^ Fulekar (Ed.), M.H. (2009) Bioinformatics: Applications in Life and Environmental Sciences, Springer (pp. 110) ISBN 1-4020-8879-5
- ^ Immink, K. Schouhamer; Weber, J. (October 2010). «Minimum Pearson distance detection for multilevel channels with gain and / or offset mismatch». IEEE Transactions on Information Theory. 60 (10): 5966–5974. CiteSeerX 10.1.1.642.9971. doi:10.1109/tit.2014.2342744. S2CID 1027502. Retrieved 11 February 2018.
- ^ Jammalamadaka, S. Rao; SenGupta, A. (2001). Topics in circular statistics. New Jersey: World Scientific. p. 176. ISBN 978-981-02-3778-3. Retrieved 21 September 2016.
- ^ Cox, D.R.; Hinkley, D.V. (1974). Theoretical Statistics. Chapman & Hall. Appendix 3. ISBN 0-412-12420-3.
External links[edit]
- «cocor». comparingcorrelations.org. – A free web interface and R package for the statistical comparison of two dependent or independent correlations with overlapping or non-overlapping variables.
- «Correlation». nagysandor.eu. – an interactive Flash simulation on the correlation of two normally distributed variables.
- «Correlation coefficient calculator». hackmath.net. Linear regression. –
- «Critical values for Pearson’s correlation coefficient» (PDF). frank.mtsu.edu/~dkfuller. – large table.
- «Guess the Correlation». – A game where players guess how correlated two variables in a scatter plot are, in order to gain a better understanding of the concept of correlation.
Чем больше я узнаю людей, тем больше мне нравится моя собака.
—Марк Твен
В предыдущих сериях постов для начинающих из ремикса книги Генри Гарнера «Clojure для исследования данных» (Clojure for Data Science) на языке Python мы рассмотрели методы описания выборок с точки зрения сводных статистик и методов статистического вывода из них параметров популяции. Такой анализ сообщает нам нечто о популяции в целом и о выборке в частности, но он не позволяет нам делать очень точные утверждения об их отдельных элементах. Это связано с тем, что в результате сведения данных всего к двум статистикам — среднему значению и стандартному отклонению — теряется огромный объем информации.
Нам часто требуется пойти дальше и установить связь между двумя или несколькими переменными либо предсказать одну переменную при наличии другой. И это подводит нас к теме данной серии из 5 постов — исследованию корреляции и регрессии. Корреляция имеет дело с силой и направленностью связи между двумя или более переменными. Регрессия определяет природу этой связи и позволяет делать предсказания на ее основе.
В этой серии постов будет рассмотрена линейная регрессия. При наличии выборки данных наша модель усвоит линейное уравнение, позволяющее ей делать предсказания о новых, не встречавшихся ранее данных. Для этого мы снова обратимся к библиотеке pandas и изучим связь между ростом и весом спортсменов-олимпийцев. Мы введем понятие матриц и покажем способы управления ими с использованием библиотеки pandas.
О данных
В этой серии постов используются данные, любезно предоставленные компанией Guardian News and Media Ltd., о спортсменах, принимавших участие в Олимпийских Играх 2012 г. в Лондоне. Эти данные изначально были взяты из блога газеты Гардиан.
Обследование данных
Когда вы сталкиваетесь с новым набором данных, первая задача состоит в том, чтобы его обследовать с целью понять, что именно он содержит.
Файл all-london-2012-athletes.tsv достаточно небольшой. Мы можем обследовать данные при помощи pandas, как мы делали в первой серии постов «Python, исследование данных и выборы», воспользовавшись функцией read_csv:
def load_data():
return pd.read_csv('data/ch03/all-london-2012-athletes-ru.tsv', 't')
def ex_3_1():
'''Загрузка данных об участниках
олимпийских игр в Лондоне 2012 г.'''
return load_data()Если выполнить этот пример в консоли интерпретатора Python либо в блокноте Jupyter, то вы должны увидеть следующий ниже результат:
Столбцы данных (нам повезло, что они ясно озаглавлены) содержат следующую информацию:
-
ФИО атлета
-
страна, за которую он выступает
-
возраст, лет
-
рост, см.
-
вес, кг.
-
пол «М» или «Ж»
-
дата рождения в виде строки
-
место рождения в виде строки (со страной)
-
число выигранных золотых медалей
-
число выигранных серебряных медалей
-
число выигранных бронзовых медалей
-
всего выигранных золотых, серебряных и бронзовых медалей
-
вид спорта, в котором он соревновался
-
состязание в виде списка, разделенного запятыми
Даже с учетом того, что данные четко озаглавлены, очевидно присутствие пустых мест в столбцах с ростом, весом и местом рождения. При наличии таких данных следует проявлять осторожность, чтобы они не сбили с толку.
Визуализация данных
В первую очередь мы рассмотрим разброс роста спортсменов на Олимпийских играх 2012 г. в Лондоне. Изобразим эти значения роста в виде гистограммы, чтобы увидеть характер распределения данных, не забыв сначала отфильтровать пропущенные значения:
def ex_3_2():
'''Визуализация разброса значений
роста спортсменов на гистограмме'''
df = load_data()
df['Рост, см'].hist(bins=20)
plt.xlabel('Рост, см.')
plt.ylabel('Частота')
plt.show()Этот пример сгенерирует следующую ниже гистограмму:
Как мы и ожидали, данные приближенно нормально распределены. Средний рост спортсменов составляет примерно 177 см. Теперь посмотрим на распределение веса олимпийских спортсменов:
def ex_3_3():
'''Визуализация разброса значений веса спортсменов'''
df = load_data()
df['Вес'].hist(bins=20)
plt.xlabel('Вес')
plt.ylabel('Частота')
plt.show()Приведенный выше пример сгенерирует следующую ниже гистограмму:
Данные показывают четко выраженную асимметрию. Хвост с правой стороны намного длиннее, чем с левой, и поэтому мы говорим, что асимметрия — положительная. Мы можем оценить асимметрию данных количественно при помощи функции библиотеки pandas skew:
def ex_3_4():
'''Вычисление асимметрии веса спортсменов'''
df = load_data()
swimmers = df[ df['Вид спорта'] == 'Swimming']
return swimmers['Вес'].skew()0.23441459903001483К счастью, эта асимметрия может быть эффективным образом смягчена путем взятия логарифма веса при помощи функции библиотеки numpy np.log:
def ex_3_5():
'''Визуализация разброса значений веса спортсменов на
полулогарифмической гистограмме с целью удаления
асимметрии'''
df = load_data()
df['Вес'].apply(np.log).hist(bins=20)
plt.xlabel('Логарифмический вес')
plt.ylabel('Частота')
plt.show()Этот пример сгенерирует следующую ниже гистограмму:
Теперь данные намного ближе к нормальному распределению. Из этого следует, что вес распределяется согласно логнормальному распределению.
Логнормальное распределение
Логнормальное распределение — это распределение набора значений, чей логарифм нормально распределен. Основание логарифма может быть любым положительным числом за исключением единицы. Как и нормальное распределение, логнормальное распределение играет важную роль для описания многих естественных явлений.
Логарифм показывает степень, в которую должно быть возведено фиксированное число (основание) для получения данного числа. Изобразив логарифмы на графике в виде гистограммы, мы показали, что эти степени приближенно нормально распределены. Логарифмы обычно берутся по основанию 10 или основанию e, трансцендентному числу, приближенно равному 2.718. В функции библиотеки numpy np.log и ее инверсии np.exp используется основание e. Выражение loge также называется натуральным логарифмом, или ln, из-за свойств, делающих его особенно удобным в исчислении.
Логнормальное распределение обычно имеет место в процессах роста, где темп роста не зависит от размера. Этот феномен известен как закон Джибрэта, который был cформулирован в 1931 г. Робертом Джибрэтом, заметившим, что он применим к росту фирм. Поскольку темп роста пропорционален размеру, более крупные фирмы демонстрируют тенденцию расти быстрее, чем фирмы меньшего размера.
Нормальное распределение случается в ситуациях, где много мелких колебаний, или вариаций, носит суммирующий эффект, тогда как логнормальное распределение происходит там, где много мелких вариаций имеет мультипликативный эффект.
С тех пор выяснилось, что закон Джибрэта применим к большому числу ситуаций, включая размеры городов и, согласно обширному математическому ресурсу Wolfram MathWorld, к количеству слов в предложениях шотландского писателя Джорджа Бернарда Шоу.
В остальной части этой серии постов мы будем использовать натуральный логарифм веса спортсменов, чтобы наши данные были приближенно нормально распределены. Мы выберем популяцию спортсменов примерно с одинаковыми типами телосложения, к примеру, олимпийских пловцов.
Визуализация корреляции
Один из самых быстрых и самых простых способов определить наличие корреляции между двумя переменными состоит в том, чтобы рассмотреть их на графике рассеяния. Мы отфильтруем данные, выбрав только пловцов, и затем построим график роста относительно веса спортсменов:
def swimmer_data():
'''Загрузка данных роста и веса только олимпийских пловцов'''
df = load_data()
return df[df['Вид спорта'] == 'Swimming'].dropna()
def ex_3_6():
'''Визуализация корреляции между ростом и весом'''
df = swimmer_data()
xs = df['Рост, см']
ys = df['Вес'].apply( np.log )
pd.DataFrame(np.array([xs,ys]).T).plot.scatter(0, 1, s=12, grid=True)
plt.xlabel('Рост, см.')
plt.ylabel('Логарифмический вес')
plt.show()Этот пример сгенерирует следующий ниже график:
Результат ясно показывает, что между этими двумя переменными имеется связь. График имеет характерно смещенную эллиптическую форму двух коррелируемых, нормально распределенных переменных с центром вокруг среднего значения. Следующая ниже диаграмма сравнивает график рассеяния с распределениями вероятностей роста и логарифма веса:
Точки, близко расположенные к хвосту одного распределения, также демонстрируют тенденцию близко располагаться к тому же хвосту другого распределения, и наоборот. Таким образом, между двумя распределениями существует связь, которую в ближайших нескольких разделах мы покажем, как определять количественно. Впрочем, если мы внимательно посмотрим на предыдущий график рассеяния, то увидим, что из-за округления измерений точки уложены в столбцы и строки (в см. и кг. соответственно для роста и веса). Там, где это происходит, иногда желательно внести в данные искажения, которые также называются сдвигом или джиттером с тем, чтобы яснее показать силу связи. Без генерирования джиттера (в виде случайных отклонений) может оказаться, что, то, что по внешнему виду составляет одну точку, фактически представляет много точек, которые обозначены одинаковой парой значений. Внесение нескольких случайных помех делает эту ситуацию вряд ли возможной.
Генерирование джиттера
Поскольку каждое значение округлено до ближайшего сантиметра или килограмма, то значение, записанное как 180 см, на самом деле может быть каким угодно между 179.5 и 180.5 см, тогда как значение 80 кг на самом деле может быть каким угодно между 79.5 и 80.5 кг. Для создания случайных искажений, мы можем добавить случайные помехи в каждую точку данных роста в диапазоне между -0.5 и 0.5 и в том же самом диапазоне проделать с точками данных веса (разумеется, это нужно cделать до того, как мы возьмем логарифм значений веса):
def jitter(limit):
'''Генератор джиттера (произвольного сдвига точек данных)'''
return lambda x: random.uniform(-limit, limit) + x
def ex_3_7():
'''Визуализация корреляции между ростом и весом с джиттером'''
df = swimmer_data()
xs = df['Рост, см'].apply(jitter(0.5))
ys = df['Вес'].apply(jitter(0.5)).apply(np.log)
pd.DataFrame(np.array([xs,ys]).T).plot.scatter(0, 1, s=12, grid=True)
plt.xlabel('Рост, см.')
plt.ylabel('Логарифмический вес')
plt.show()График с джиттером выглядит следующим образом:
Как и в случае с внесением прозрачности в график рассеяния в первой серии постов об описательной статистике, генерирование джиттера — это механизм, который обеспечивает исключение несущественных факторов, таких как объем данных или артефакты округления, которые могут заслонить от нас возможность увидеть закономерности в данных.
Ковариация
Одним из способов количественного определения силы связи между двумя переменными является их ковариация. Она измеряет тенденцию двух переменных изменяться вместе.
Если у нас имеется два ряда чисел, X и Y, то их отклонения от среднего значения составляют:
Здесь xi — это значение X с индексом i, yi — значение Y с индексом i, x̅ — среднее значение X, и y̅ — среднее значение Y. Если X и Y проявляют тенденцию изменяться вместе, то их отклонения от среднего будет иметь одинаковый знак: отрицательный, если они — меньше среднего, положительный, если они больше среднего. Если мы их перемножим, то произведение будет положительным, когда у них одинаковый знак, и отрицательным, когда у них разные знаки. Сложение произведений дает меру тенденции этих двух переменных отклоняться от среднего значения в одинаковом направлении для каждой заданной выборки.
Ковариация определяется как среднее этих произведений:
На чистом Python ковариация вычисляется следующим образом:
def covariance(xs, ys):
'''Вычисление ковариации (несмещенная, т.е. n-1)'''
dx = xs - xs.mean()
dy = ys - ys.mean()
return (dx * dy).sum() / (dx.count() - 1)В качестве альтернативы, мы можем воспользоваться функцией pandas cov:
df['Рост, см'].cov(df['Вес'])1.3559273321696459Ковариация роста и логарифма веса для наших олимпийских пловцов равна 1.356, однако это число сложно интерпретировать. Единицы измерения здесь представлены произведением единиц на входе.
По этой причине о ковариации редко сообщают как об отдельной сводной статистике. Сделать число более понятным можно, разделив отклонения на произведение стандартных отклонений. Это позволяет трансформировать единицы измерения в стандартные оценки и ограничить выход числом в диапазоне между -1 и +1. Этот результат называется корреляцией Пирсона.
Стандартная оценка, англ. standard score, также z-оценка — это относительное число стандартных отклонений, на которые значение переменной отстоит от среднего значения. Положительная оценка показывает, что переменная находится выше среднего, отрицательная — ниже среднего. Это безразмерная величина, получаемая при вычитании популяционного среднего из индивидуальных значений и деления разности на популяционное стандартное отклонение.
Корреляция Пирсона
Корреляция Пирсона часто обозначается переменной r и вычисляется следующим образом, где отклонения от среднего dxi и dyi вычисляются как и прежде:
Поскольку для переменных X и Y стандартные отклонения являются константными, уравнение может быть упрощено до следующего, где σx и σy — это стандартные отклонения соответственно X и Y:
В таком виде формула иногда упоминается как коэффициент корреляции смешанных моментов Пирсона или попросту коэффициент корреляции и, как правило, обозначается буквой r.
Ранее мы уже написали функции для вычисления стандартного отклонения. В сочетании с нашей функцией с вычислением ковариации получится следующая ниже имплементация корреляции Пирсона:
def variance(xs):
'''Вычисление корреляции,
несмещенная дисперсия при n <= 30'''
x_hat = xs.mean()
n = xs.count()
n = n - 1 if n in range( 1, 30 ) else n
return sum((xs - x_hat) ** 2) / n
def standard_deviation(xs):
'''Вычисление стандартного отклонения'''
return np.sqrt(variance(xs))
def correlation(xs, ys):
'''Вычисление корреляции'''
return covariance(xs, ys) / (standard_deviation(xs) *
standard_deviation(ys))В качестве альтернативы мы можем воспользоваться функцией pandas corr:
df['Рост, см'].corr(df['Вес'])Поскольку стандартные оценки безразмерны, то и коэффициент корреляции r тоже безразмерен. Если r равен -1.0 либо 1.0, то переменные идеально антикоррелируют либо идеально коррелируют.
Правда, если r = 0, то с необходимостью вовсе не следует, что переменные не коррелируют. Корреляция Пирсона измеряет лишь линейные связи. Как продемонстрировано на следующих графиках, между переменными может существовать еще некая нелинейная связь, которую r не объясняет:
Отметим, что корреляция центрального примера не определена, потому что стандартное отклонение y = 0. Поскольку наше уравнение для r содержало бы деление ковариации на 0, то результат получается бессмысленным. В этом случае между переменными не может быть никакой корреляции; y всегда будет иметь среднее значение. Простое обследование стандартных отклонений это подтвердит.
Мы можем вычислить коэффициент корреляции для данных роста и логарифма веса наших пловцов следующим образом:
def ex_3_8():
'''Вычисление корреляции средствами pandas
на примере данных роста и веса'''
df = swimmer_data()
return df['Рост, см'].corr( df['Вес'].apply(np.log))0.86748249283924894В результате получим ответ 0.867, который количественно выражает сильную, положительную корреляцию, уже наблюдавшуюся нами на точечном графике.
Выборочный r и популяционный ρ
Аналогично среднему значению и стандартному отклонению, коэффициент корреляции является сводной статистикой. Он описывает выборку; в данном случае, выборку спаренных значений: роста и веса. Коэффициент корреляции известной выборки обозначается буквой r, тогда как коэффициент корреляции неизвестной популяции обозначается греческой буквой ρ (рхо).
Как мы убедились в предыдущей серии постов о тестировании гипотез, мы не должны исходить из того, что результаты, полученные в ходе измерения нашей выборки, применимы к популяции в целом. К примеру, наша популяция может состоять из всех пловцов всех недавних Олимпийских игр. И будет совершенно недопустимо обобщать, например, на другие олимпийские виды спорта, такие как тяжелая атлетика или фитнес-плавание.
Даже в допустимой популяции — такой как пловцы, выступавшие на недавних Олимпийских играх, — наша выборка коэффициента корреляции является всего лишь одной из многих потенциально возможных. То, насколько мы можем доверять нашему r, как оценке параметра ρ, зависит от двух факторов:
-
Размера выборки
-
Величины r
Безусловно, чем больше выборка, тем больше мы ей доверяем в том, что она представляет всю совокупность в целом. Возможно, не совсем интуитивно очевидно, но величина тоже оказывает влияние на степень нашей уверенности в том, что выборка представляет параметр . Это вызвано тем, что большие коэффициенты вряд ли возникли случайным образом или вследствие случайной ошибки при отборе.
Проверка статистических гипотез
В предыдущей серии постов мы познакомились с проверкой статистических гипотез, как средством количественной оценки вероятности, что конкретная гипотеза (как, например, что две выборки взяты из одной и той же популяции) истинная. Чтобы количественно оценить вероятность, что корреляция существует в более широкой популяции, мы воспользуемся той же самой процедурой.
В первую очередь, мы должны сформулировать две гипотезы, нулевую гипотезу и альтернативную:
H0 — это гипотеза, что корреляция в популяции нулевая. Другими словами, наше консервативное представление состоит в том, что измеренная корреляция целиком вызвана случайной ошибкой при отборе.
H1 — это альтернативная возможность, что корреляция в популяции не нулевая. Отметим, что мы не определяем направление корреляции, а только что она существует. Это означает, что мы выполняем двустороннюю проверку.
Стандартная ошибка коэффициента корреляции r по выборке задается следующей формулой:
Эта формула точна, только когда r находится близко к нулю (напомним, что величина ρ влияет на нашу уверенность), но к счастью, это именно то, что мы допускаем согласно нашей нулевой гипотезы.
Мы можем снова воспользоваться t-распределением и вычислить t-статистику:
В приведенной формуле df — это степень свободы наших данных. Для проверки корреляции степень свободы равна n — 2, где n — это размер выборки. Подставив это значение в формулу, получим:
В итоге получим t-значение 102.21. В целях его преобразования в p-значение мы должны обратиться к t-распределению. Библиотека scipy предоставляет интегральную функцию распределения (ИФР) для t-распределения в виде функции stats.t.cdf, и комплементарной ей (1-cdf) функции выживания stats.t.sf. Значение функции выживания соответствует p-значению для односторонней проверки. Мы умножаем его на 2, потому что выполняем двустороннюю проверку:
def t_statistic(xs, ys):
'''Вычисление t-статистики'''
r = xs.corr(ys) # как вариант, correlation(xs, ys)
df = xs.count() - 2
return r * np.sqrt(df / 1 - r ** 2)
def ex_3_9():
'''Выполнение двухстороннего t-теста'''
df = swimmer_data()
xs = df['Рост, см']
ys = df['Вес'].apply(np.log)
t_value = t_statistic(xs, ys)
df = xs.count() - 2
p = 2 * stats.t.sf(t_value, df) # функция выживания
return {'t-значение':t_value, 'p-значение':p}{'p-значение': 1.8980236317815443e-106, 't-значение': 25.384018200627057}P-значение настолько мало, что в сущности равно 0, означая, что шанс, что нулевая гипотеза является истинной, фактически не существует. Мы вынуждены принять альтернативную гипотезу о существовании корреляции.
Интервалы уверенности
Установив, что в более широкой популяции, безусловно, существует корреляция, мы, возможно, захотим количественно выразить диапазон значений, внутри которого, как мы ожидаем, будет лежать параметр ρ, вычислив для этого интервал уверенности. Как и в случае со средним значением в предыдущей серии постов, интервал уверенности для r выражает вероятность (выраженную в %), что параметр ρ популяции находится между двумя конкретными значениями.
Однако при попытке вычислить стандартную ошибку коэффициента корреляции возникает сложность, которой не было в случае со средним значением. Поскольку абсолютное значение коэффициента корреляции r не может превышать 1, распределение возможных выборок коэффициентов корреляции r смещается по мере приближения r к пределу своего диапазона.
Приведенный выше график показывает отрицательно скошенное распределение r-выборок для параметра ρ, равного 0.6.
К счастью, трансформация под названием z-преобразование Фишера стабилизирует дисперсию r по своему диапазону. Она аналогична тому, как наши данные о весе спортсменов стали нормально распределенными, когда мы взяли их логарифм.
Уравнение для z-преобразования следующее:
Стандартная ошибка z равна:
Таким образом, процедура вычисления интервалов уверенности состоит в преобразовании r в z с использованием z-преобразования, вычислении интервала уверенности в терминах стандартной ошибки SEz и затем преобразовании интервала уверенности в r.
В целях вычисления интервала уверенности в терминах SEz, мы можем взять число стандартных отклонений от среднего, которое дает нам требуемый уровень доверия. Обычно используют число 1.96, так как оно является числом стандартных отклонений от среднего, которое содержит 95% площади под кривой. Другими словами, 1.96 стандартных ошибок от среднего значения выборочного r содержит истинную популяционную корреляцию ρ с 95%-ой определенностью.
Мы можем убедиться в этом, воспользовавшись функцией scipy stats.norm.ppf. Она вернет стандартную оценку, связанную с заданной интегральной вероятностью в условиях односторонней проверки.
Однако, как показано на приведенном выше графике, мы хотели бы вычесть ту же самую величину, т.е. 2.5%, из каждого хвоста с тем, чтобы 95%-й интервал уверенности был центрирован на нуле. Для этого при выполнении двусторонней проверки нужно просто уменьшить разность наполовину и вычесть результат из 100%. Так что, требуемый уровень доверия в 95% означает, что мы обращаемся к критическому значению 97.5%:
def critical_value(confidence, ntails): # ДИ и число хвостов
'''Расчет критического значения путем
вычисления квантиля и получения
для него нормального значения'''
lookup = 1 - ((1 - confidence) / ntails)
return stats.norm.ppf(lookup, 0, 1) # mu=0, sigma=1
critical_value(0.95, 2)1.959963984540054Поэтому наш 95%-й интервал уверенности в z-пространстве для ρ задается следующей формулой:
Подставив в нашу формулу zr и SEz, получим:
Для r=0.867 и n=859 она даст нижнюю и верхнюю границу соответственно 1.137 и 1.722. В целях их преобразования из z-оценок в r-значения, мы используем следующее обратное уравнение z-преобразования:
Преобразования и интервал уверенности можно вычислить при помощи следующего исходного кода:
def z_to_r(z):
'''Преобразование z-оценки обратно в r-значение'''
return (np.exp(z*2) - 1) / (np.exp(z*2) + 1)
def r_confidence_interval(crit, xs, ys):
'''Расчет интервала уверенности
для критического значения и данных'''
r = xs.corr(ys)
n = xs.count()
zr = 0.5 * np.log((1 + r) / (1 - r))
sez = 1 / np.sqrt(n - 3)
return (z_to_r(zr - (crit * sez))), (z_to_r(zr + (crit * sez)))
def ex_3_10():
'''Расчет интервала уверенности
на примере данных роста и веса'''
df = swimmer_data()
X = df['Рост, см']
y = df['Вес'].apply(np.log)
interval = r_confidence_interval(1.96, X, y)
print('Интервал уверенности (95%):', interval)Интервал уверенности (95%): (0.8499088588880347, 0.8831284878884087)В результате получаем 95%-й интервал уверенности для ρ, расположенный между 0.850 и 0.883. Мы можем быть абсолютно уверены в том, что в более широкой популяции олимпийских пловцов существует сильная положительная корреляция между ростом и весом.
Примеры исходного кода для этого поста находятся в моем репо на Github. Все исходные данные взяты в репозитории автора книги.
В следующем посте, посте №2, будет рассмотрена сама тема серии — регрессия и приемы оценивания ее качества.


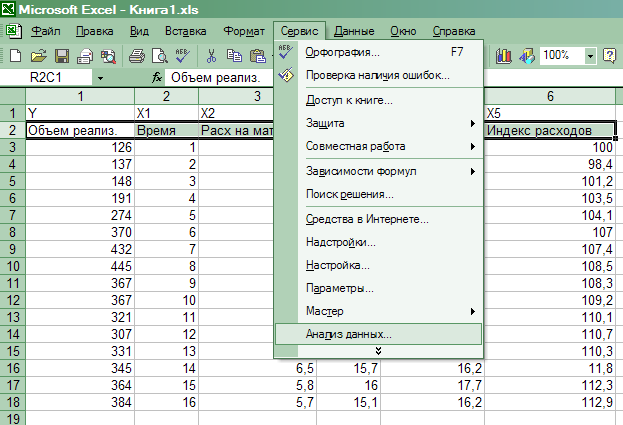


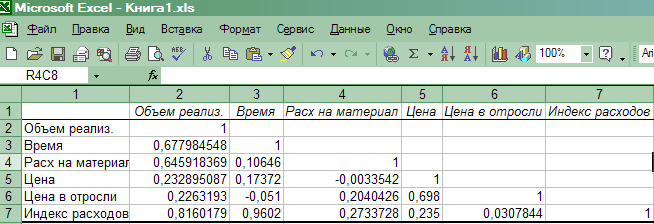

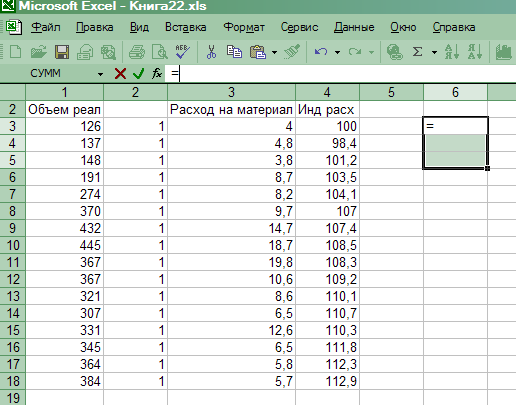



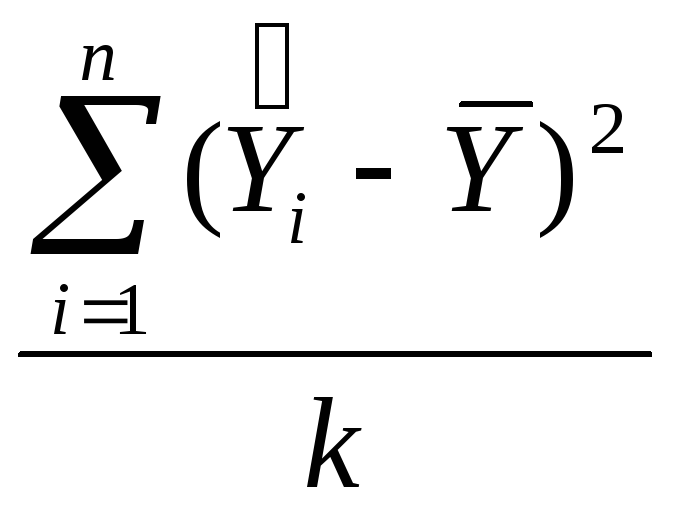




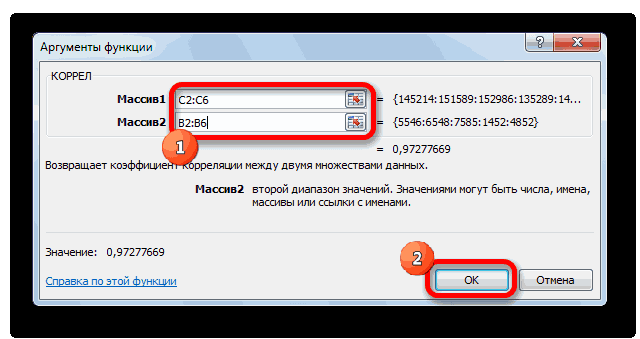
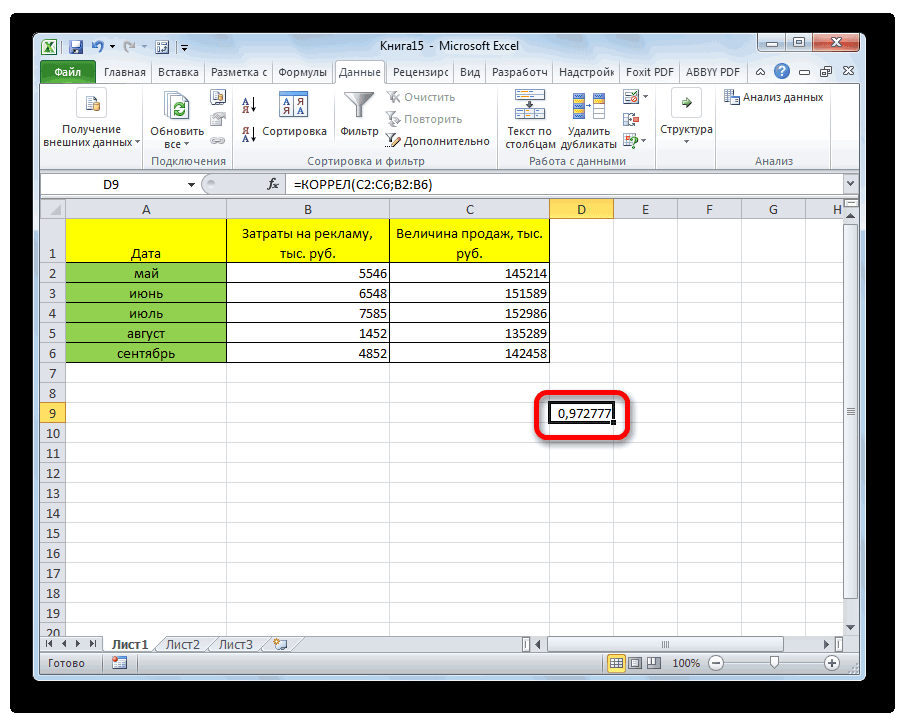
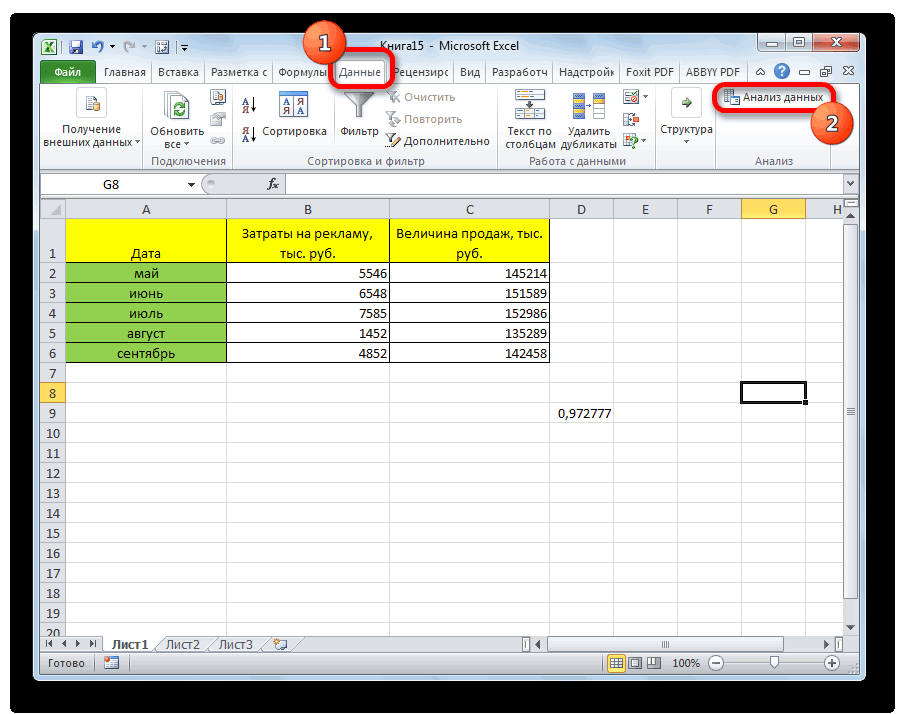
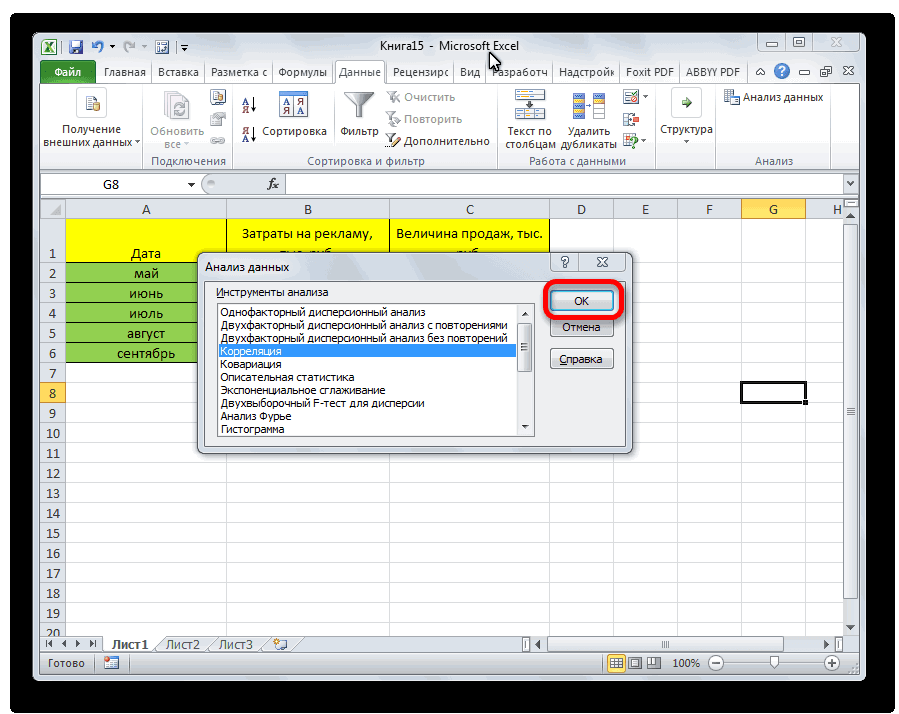
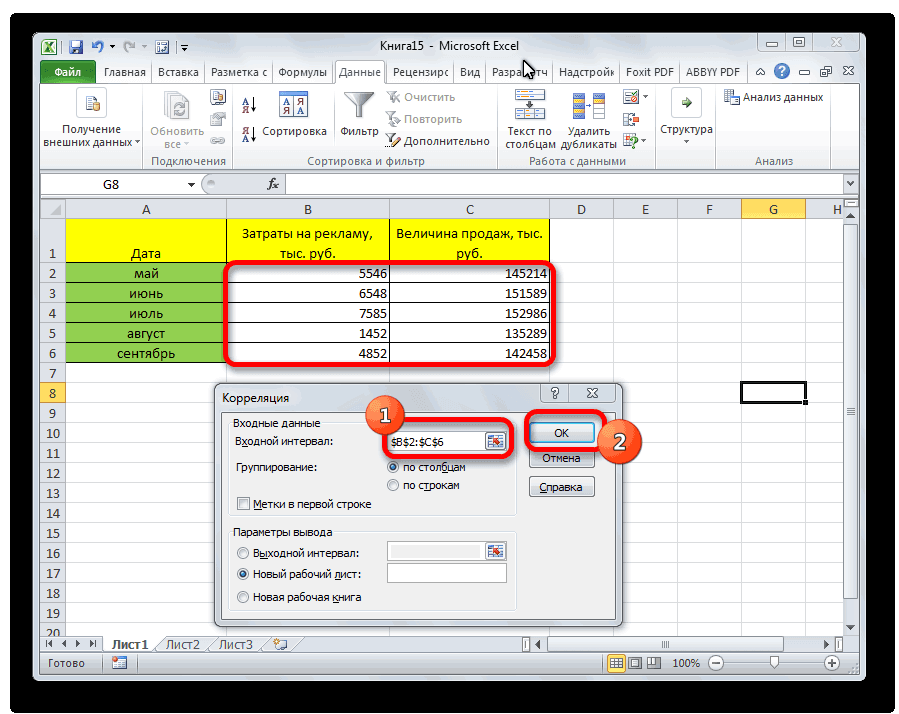
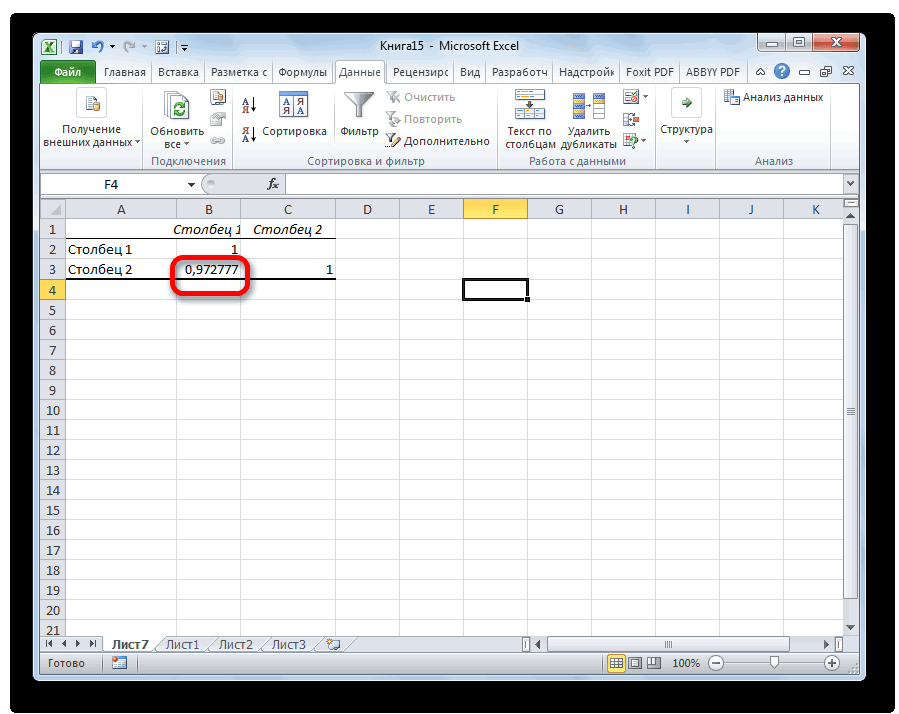
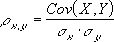
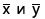


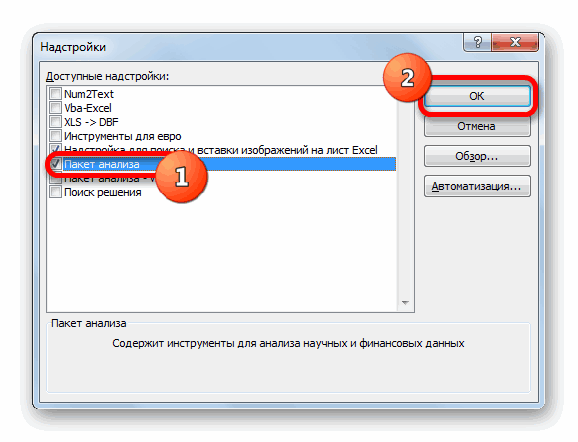

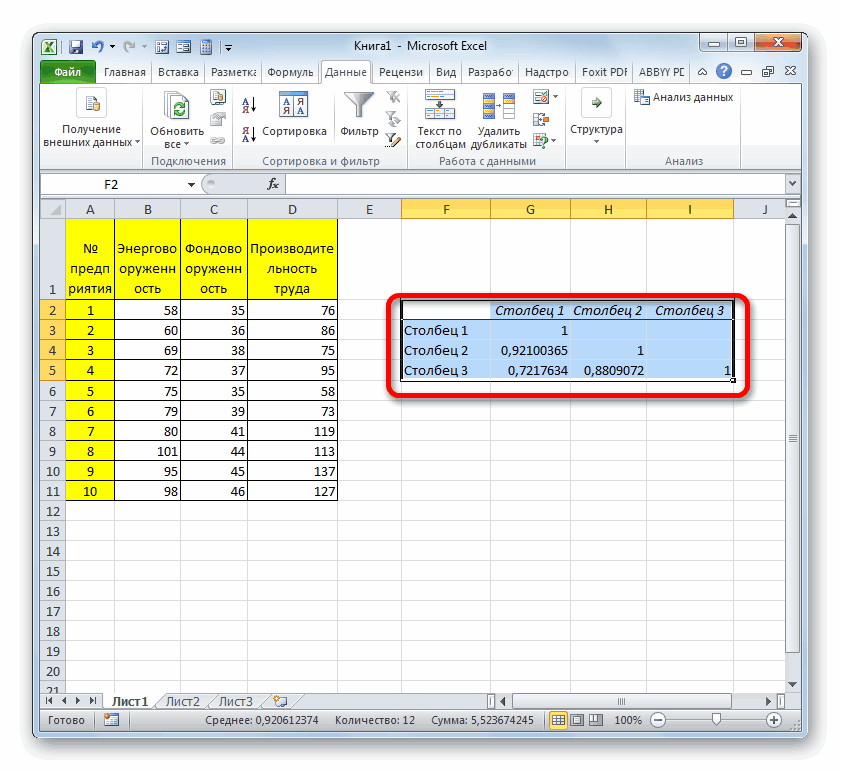
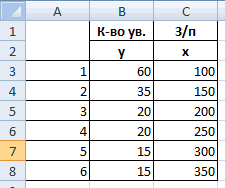

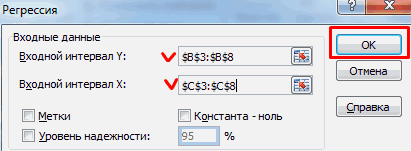
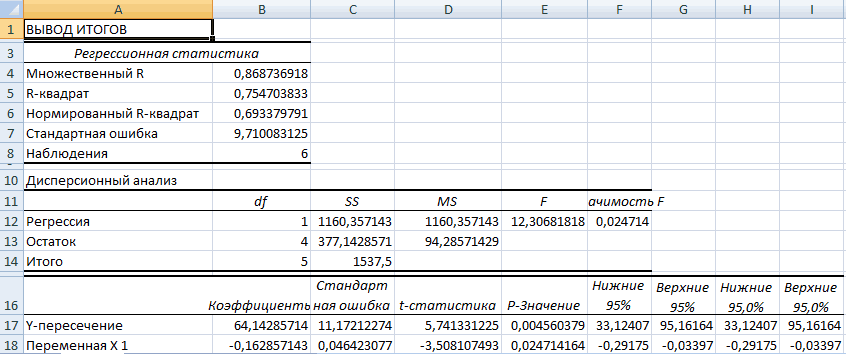
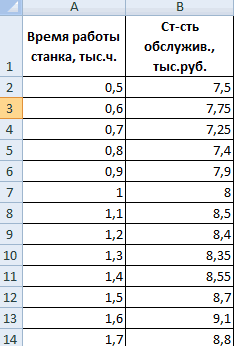
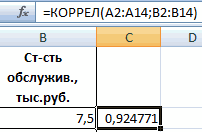
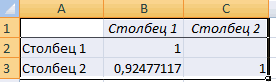
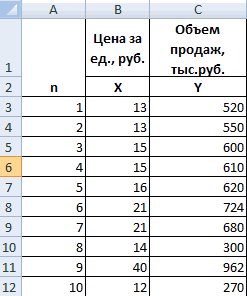
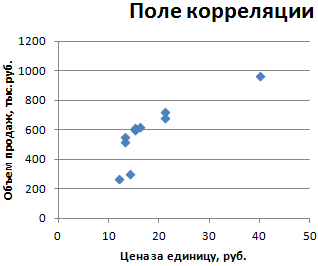
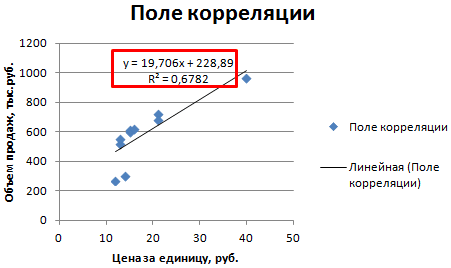
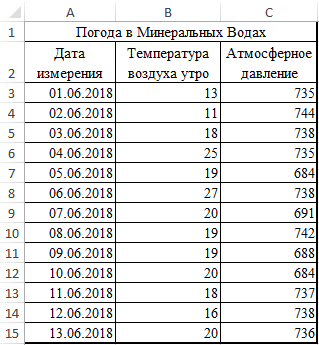
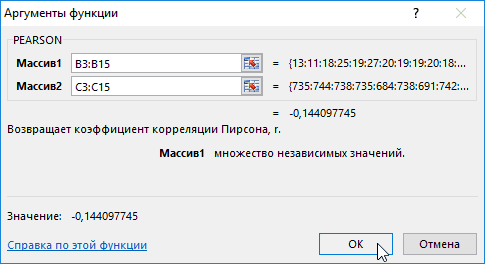
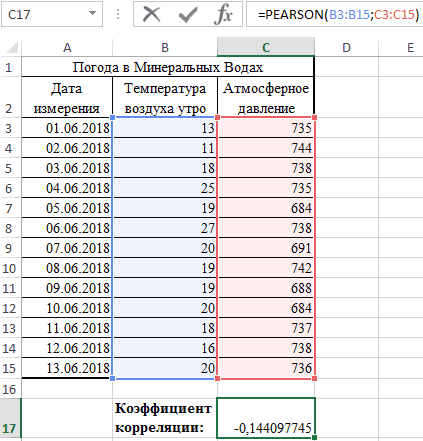
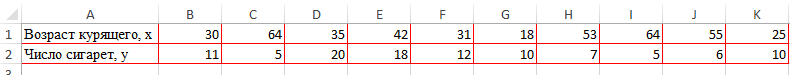
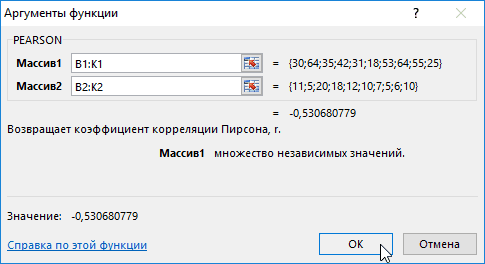

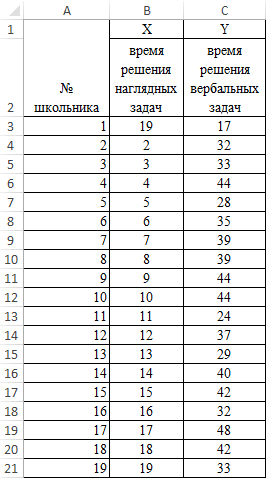

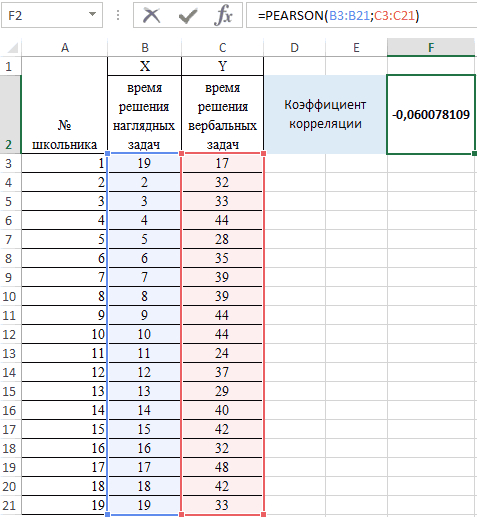
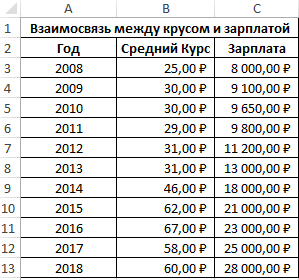

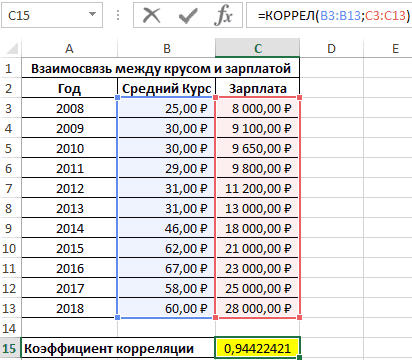

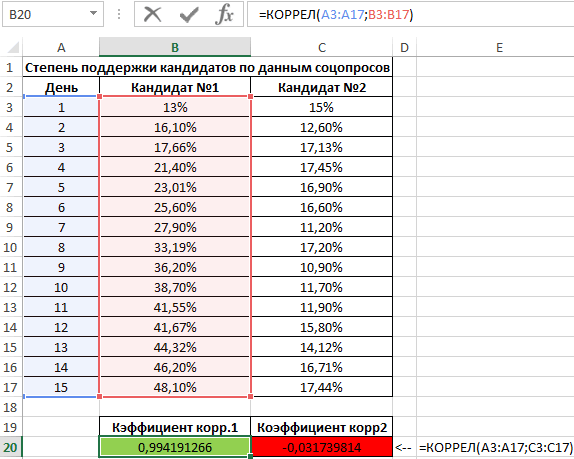
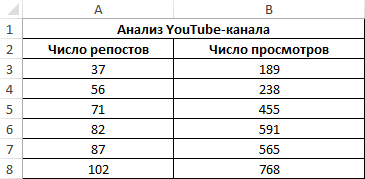

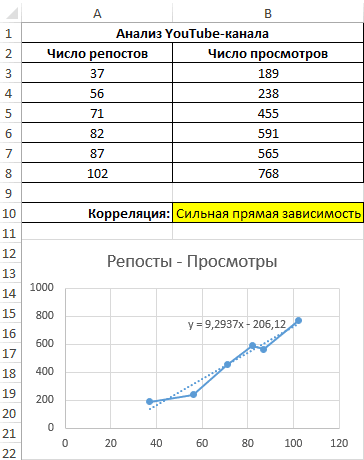


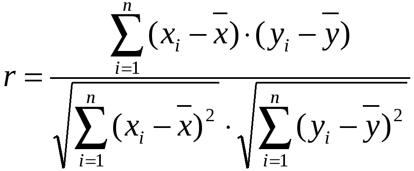
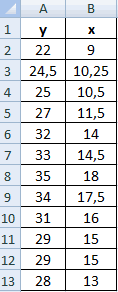
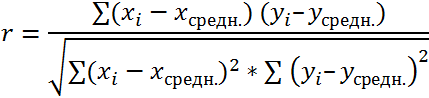
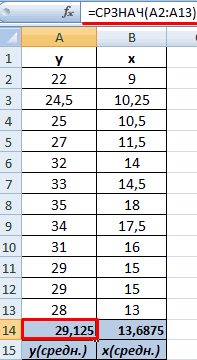
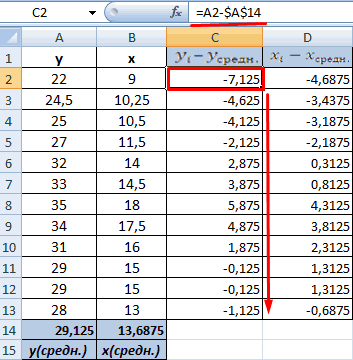
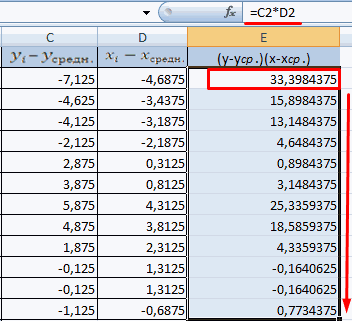
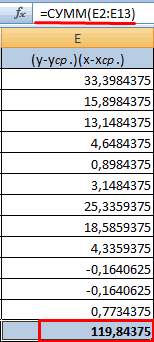
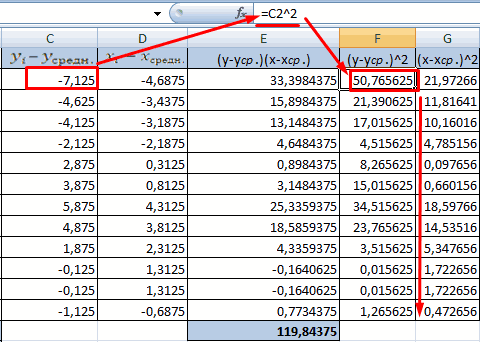
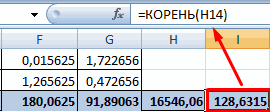
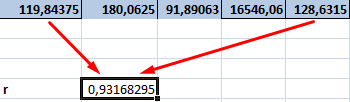
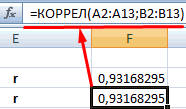
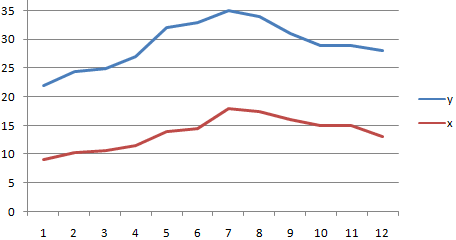
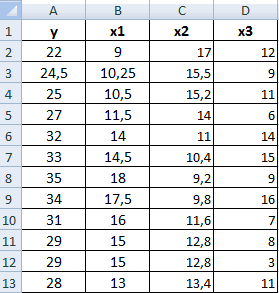
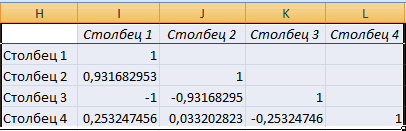
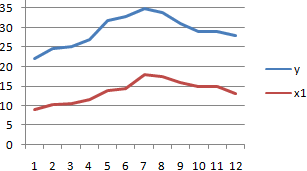
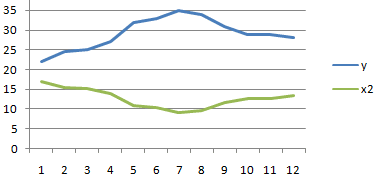
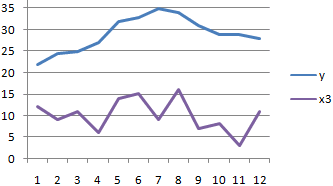
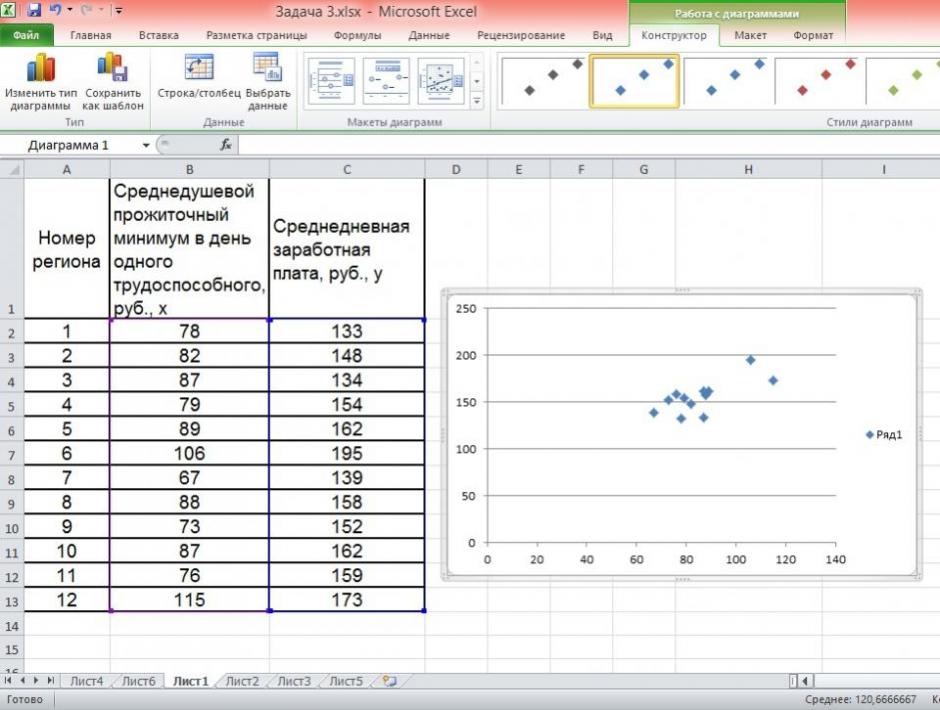
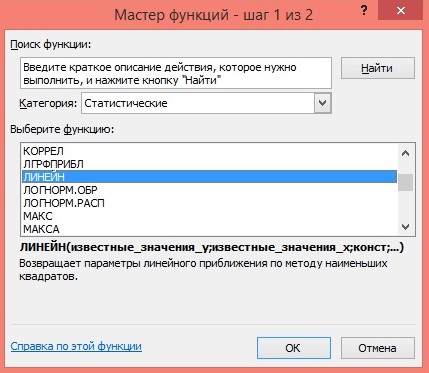
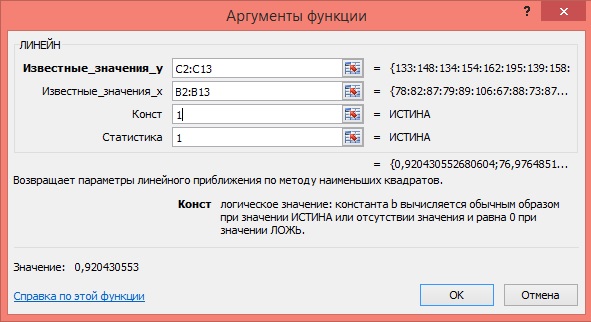
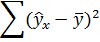
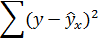
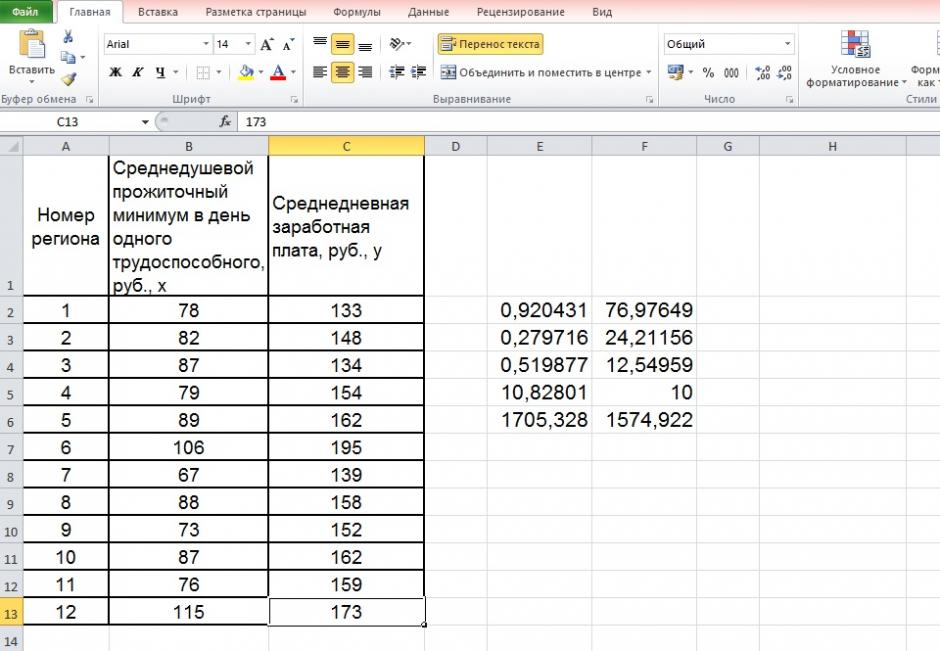
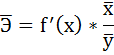
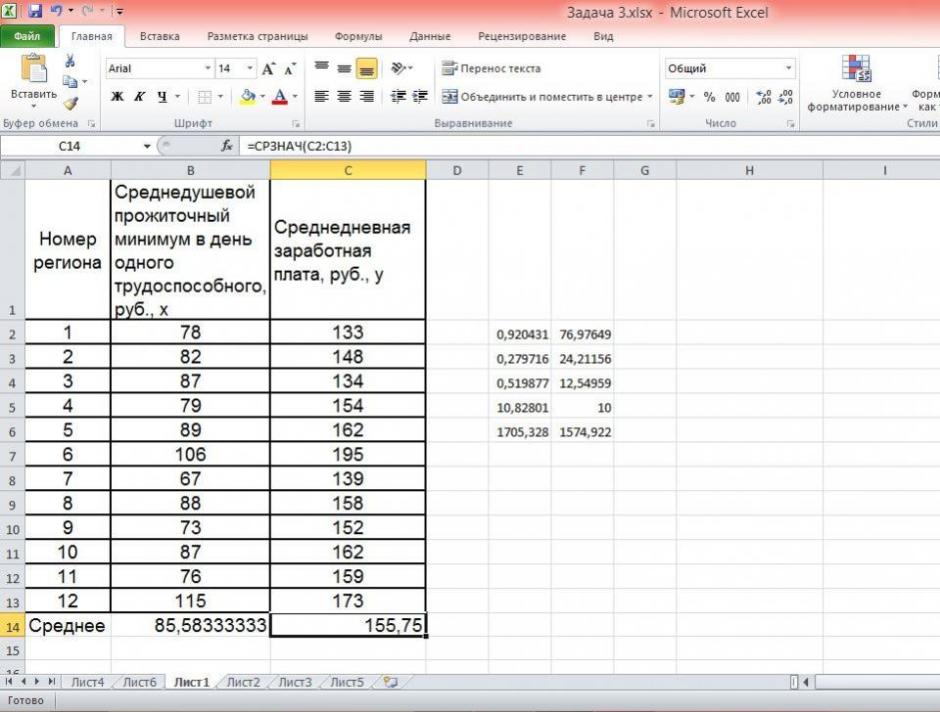
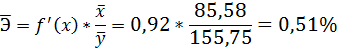
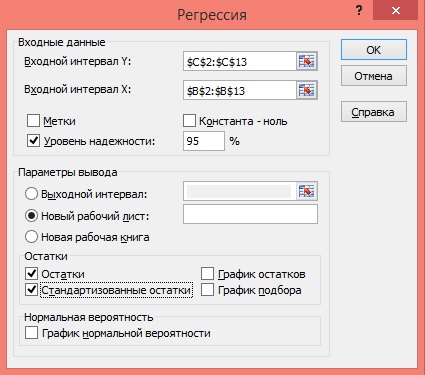
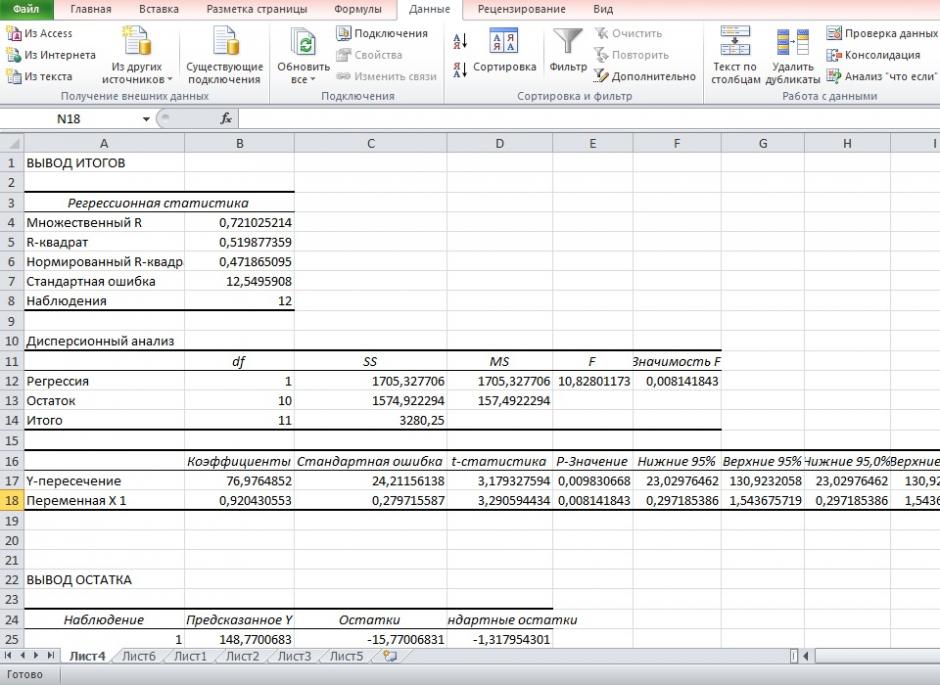
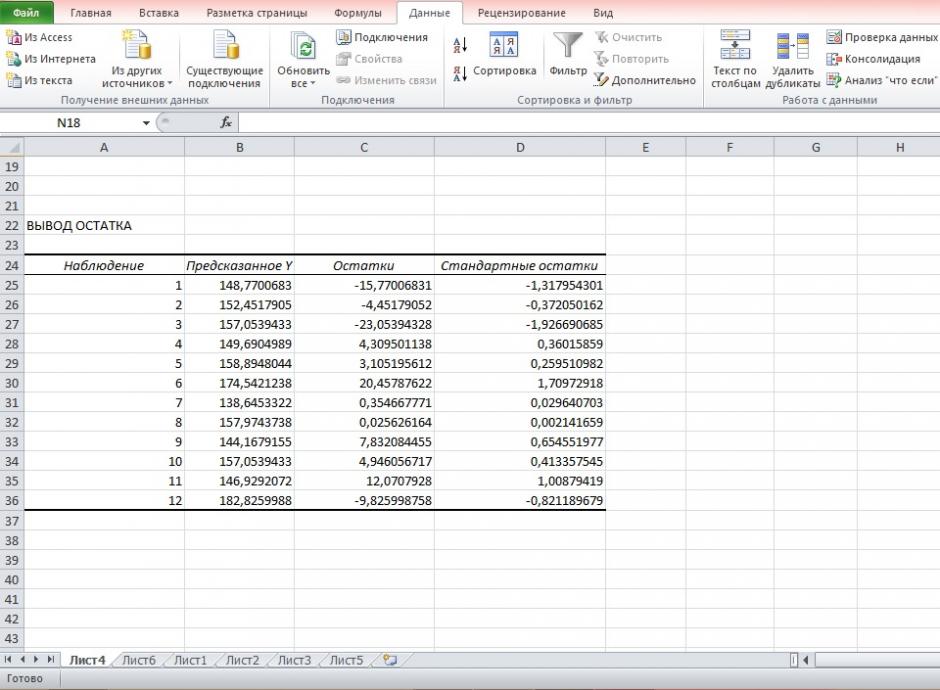
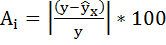
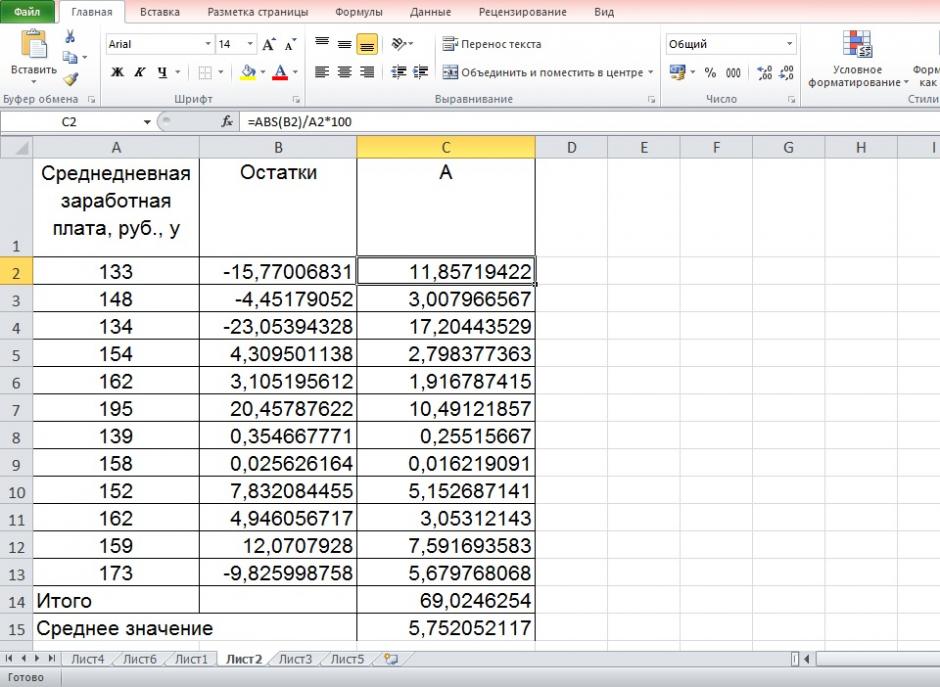
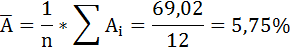
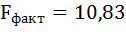
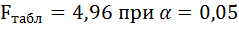
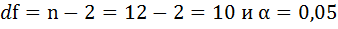
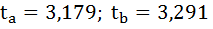
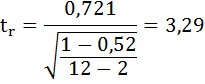
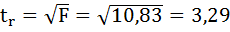
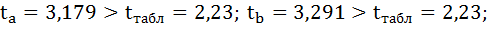
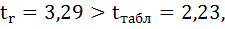
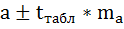
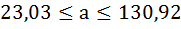
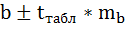
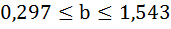
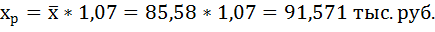
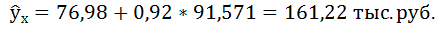
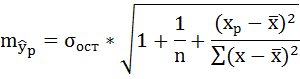
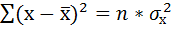
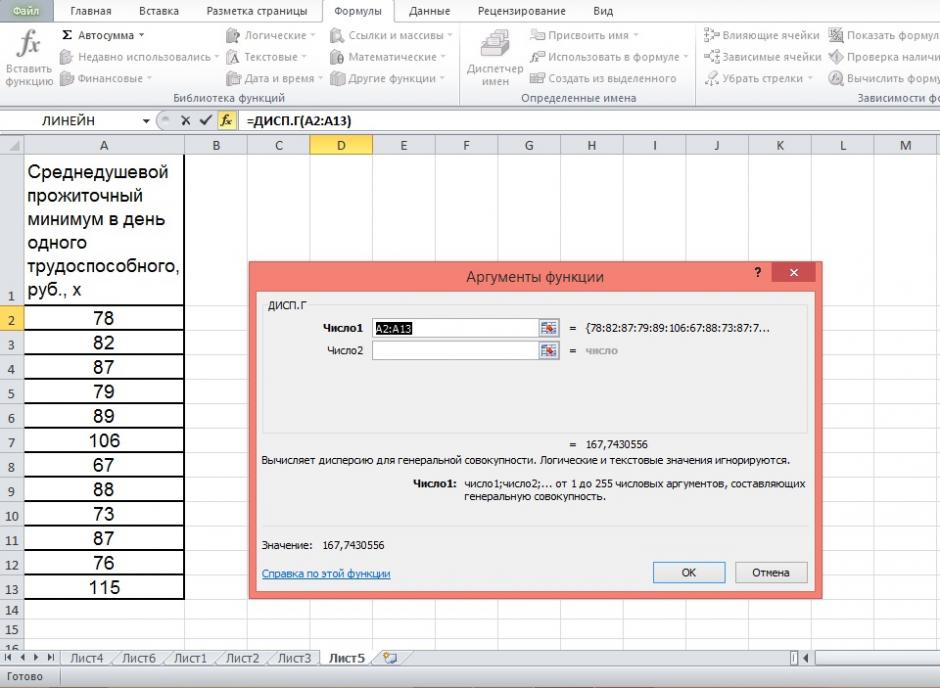
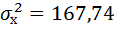
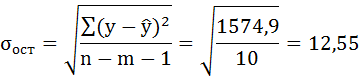
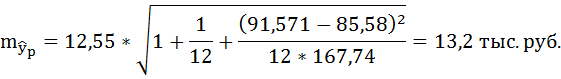
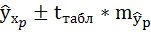
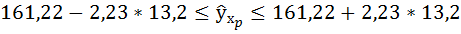
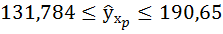



![{displaystyle operatorname {cov} (X,Y)=operatorname {mathbb {E} } [(X-mu _{X})(Y-mu _{Y})],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e88bc4ba085b98d5cca09b958ad378d50127308)
![{displaystyle rho _{X,Y}={frac {operatorname {mathbb {E} } [(X-mu _{X})(Y-mu _{Y})]}{sigma _{X}sigma _{Y}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/042c646e848d2dc6e15d7b5c7a5b891941b2eab6)
![{displaystyle mu _{X}=operatorname {mathbb {E} } [,X,]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1182bdcc66a113596e3ece07a0acbeda8d56d483)
![{displaystyle mu _{Y}=operatorname {mathbb {E} } [,Y,]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2f14f5eda9d726e57048a2c56889912a80a06b6)
![{displaystyle sigma _{X}^{2}=operatorname {mathbb {E} } [,left(X-operatorname {mathbb {E} } [X]right)^{2},]=operatorname {mathbb {E} } [,X^{2},]-left(operatorname {mathbb {E} } [,X,]right)^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbf27c91550c7c82ee7e9e948673eb99da1a7378)
![{displaystyle sigma _{Y}^{2}=operatorname {mathbb {E} } [,left(Y-operatorname {mathbb {E} } [Y]right)^{2},]=operatorname {mathbb {E} } [,Y^{2},]-left(,operatorname {mathbb {E} } [,Y,]right)^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed498483dae15dbb86e957b5a1463f5536885902)
![{displaystyle operatorname {mathbb {E} } [,left(X-mu _{X}right)left(Y-mu _{Y}right),]=operatorname {mathbb {E} } [,left(X-operatorname {mathbb {E} } [,X,]right)left(Y-operatorname {mathbb {E} } [,Y,]right),]=operatorname {mathbb {E} } [,X,Y,]-operatorname {mathbb {E} } [,X,]operatorname {mathbb {E} } [,Y,],,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4443378e105084380438782ebd391f8cb0e8e048)
![{displaystyle rho _{X,Y}={frac {operatorname {mathbb {E} } [,X,Y,]-operatorname {mathbb {E} } [,X,]operatorname {mathbb {E} } [,Y,]}{{sqrt {operatorname {mathbb {E} } [,X^{2},]-left(operatorname {mathbb {E} } [,X,]right)^{2}}}~{sqrt {operatorname {mathbb {E} } [,Y^{2},]-left(operatorname {mathbb {E} } [,Y,]right)^{2}}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a96c914bb811b84698b4d4118794cf4c8167ca7)








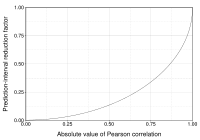

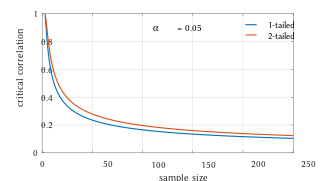








![z={frac {x-{text{mean}}}{text{SE}}}=[F(r)-F(rho _{0})]{sqrt {n-3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da7a3d54a70f9005e3bf9a2accf62cbf0fa0ea71)
![{displaystyle 100(1-alpha )%{text{CI}}:operatorname {artanh} (rho )in [operatorname {artanh} (r)pm z_{alpha /2}{text{SE}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/affc3f0ee39499c97bb851229113f49d83100bf2)
![{displaystyle 100(1-alpha )%{text{CI}}:rho in [tanh(operatorname {artanh} (r)-z_{alpha /2}{text{SE}}),tanh(operatorname {artanh} (r)+z_{alpha /2}{text{SE}})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf658969d39ea848505750b5cd76db21da78dd5c)


![{displaystyle {begin{aligned}r(Y,{hat {Y}})&={frac {sum _{i}(Y_{i}-{bar {Y}})({hat {Y}}_{i}-{bar {Y}})}{sqrt {sum _{i}(Y_{i}-{bar {Y}})^{2}cdot sum _{i}({hat {Y}}_{i}-{bar {Y}})^{2}}}}[6pt]&={frac {sum _{i}(Y_{i}-{hat {Y}}_{i}+{hat {Y}}_{i}-{bar {Y}})({hat {Y}}_{i}-{bar {Y}})}{sqrt {sum _{i}(Y_{i}-{bar {Y}})^{2}cdot sum _{i}({hat {Y}}_{i}-{bar {Y}})^{2}}}}[6pt]&={frac {sum _{i}[(Y_{i}-{hat {Y}}_{i})({hat {Y}}_{i}-{bar {Y}})+({hat {Y}}_{i}-{bar {Y}})^{2}]}{sqrt {sum _{i}(Y_{i}-{bar {Y}})^{2}cdot sum _{i}({hat {Y}}_{i}-{bar {Y}})^{2}}}}[6pt]&={frac {sum _{i}({hat {Y}}_{i}-{bar {Y}})^{2}}{sqrt {sum _{i}(Y_{i}-{bar {Y}})^{2}cdot sum _{i}({hat {Y}}_{i}-{bar {Y}})^{2}}}}[6pt]&={sqrt {frac {sum _{i}({hat {Y}}_{i}-{bar {Y}})^{2}}{sum _{i}(Y_{i}-{bar {Y}})^{2}}}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d86595f3f77e8ee96952760d9176a5fa140cc562)




![{displaystyle operatorname {mathbb {E} } left[rright]=rho -{frac {rho left(1-rho ^{2}right)}{2n}}+cdots ,quad }](https://wikimedia.org/api/rest_v1/media/math/render/svg/683b838e709e3b32a3c22dfec4fa665a593f42ad)


![{displaystyle r=operatorname {mathbb {E} } [r]approx r_{text{adj}}-{frac {r_{text{adj}}(1-r_{text{adj}}^{2})}{2n}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6382c40e3ad4e06d65c7d09e214ebc8daba5d30c)
![{displaystyle r_{text{adj}}approx rleft[1+{frac {1-r^{2}}{2n}}right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbf3f71f2cfe17f8f0d422d5ac0d482cc429a925)





![{displaystyle operatorname {corr} _{r}(X,Y)={frac {operatorname {mathbb {E} } [,X,Y,]}{sqrt {operatorname {mathbb {E} } [,X^{2},]cdot operatorname {mathbb {E} } [,Y^{2},]}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6d897e4b303a062ed14cc9f88f35f5c8ffc91f7)