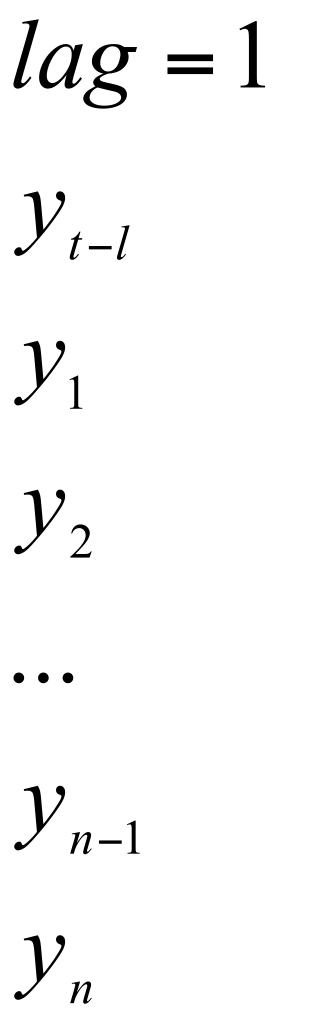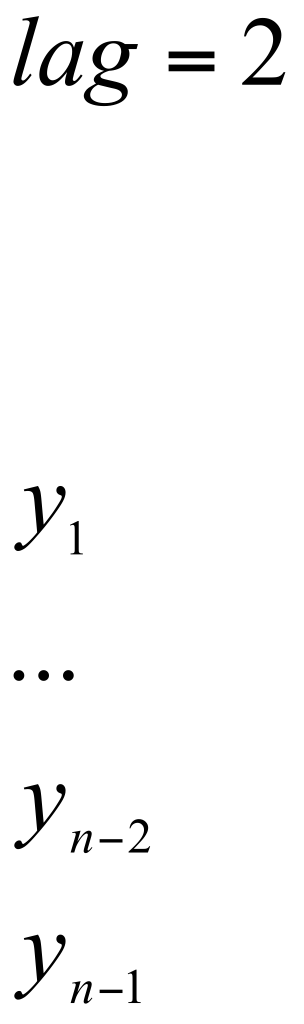Стандартная ошибка автокорреляции - Решение и исправление самых разных ошибок на TopOshibok.ru

— Стандартная ошибка (ср.Кв. Отклонение)

— фактическое
уравнение уровней ряда.

— число уровней.

— число уровней
ряда.

Величина
t
зависит от принятой доверительной
вероятности и в соответствии с этим
уравнением и числом степеней свободы
берется из таблицы Т-Стьюдента, поскольку
длина изучаемых динамических радов как
правило не велика, что соответствует
понятию малой выборки.

Наличие
в формуле предельной ошибки величины
t
позволяет
указать вероятность попадания прогноза
в рассчитанный доверительный интервал.

При
увеличении периода упреждения точность
прогноза снижается, поэтому максимальный
период на который имеет смысл прогнозировать
не должен превышать 1/3 длины ряда, по
которой построено уравнение тренда.

Часто
для расчета доверительных границ
используют поправочный коэффициент
Q,,
умножая на него предыдущую ошибку
тренда. Коэффициент учитывает как длину
изучаемого временного ряда, так и период
упреждения. Для разных видов тренда
рассчитывается свой коэффициент:

n
– длина динамического ряда.

l
– период упреждения

40. Автокорреляция уровней рядов динамики.

Автокорреляция
в РД – это зависимость последующих
уровней временного ряда от предшествующих.
Или зависимость исходного ряда от этого
ряда, но смещенного на определенный
временной интервал, называемый лагом.

Автокорреляция
уровней рядов оценивается………….,
который рассчитывается аналогично
коэффициенту парной корреляции.

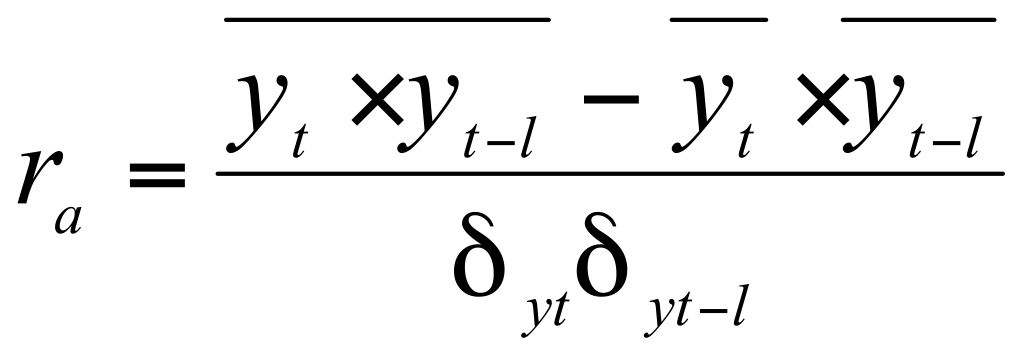
Если
изучаемый ДР имеет достаточную длину,
т.е.

,
а

,
то формула коэффициента корреляции
м.б. записана:

Оценка
статистической значимости коэффициента
автокорреляции осуществляется на основе
t
– статистики, которая рассчитывается
как отношение самого показателя

к
стандартной ошибке.

рассчитывается
по модулю. При расчете t
– статистики берется по модулю от 0 до
1.

Расчет
коэффициента автокорреляции во всех
пакетах прикладных программ t
– статистики сопровождается расчетом
стандартной ошибки, поэтому вычисление
t
– статистики вызывает затруднения.

Фактическое
значение t
– статистики сравнивается с табличным,
если фактическое значение

табличному, то значение коэффициента
статистически значимо, что подтверждает
наличие автокорреляции.

Величина
временного лага на которой производится
смещение исходного ряда определяет
порядок коэффициента автокорреляции,
т.е. если временной лаг равен 1, говорят
о коэффициенте автокорреляции первого
прядка.

Если
лаг равен 2, то рассчитывается коэффициент
второго порядка.

При
увеличении лага уменьшается число
коррелируемых пар и поэтому снижается
достоверность рассчитываемых показателей.
Величина лага не должна превышать
занчения n/4.

При
наличие достаточно длинных временных
рядов м.б. подсчитаны коэффициенты
автокорреляции высоких рядов.
последовательность значений коэффициентов
автокорреляции называется автокорреляционной
функцией, на основе которой можно судить
о наличие тенденции в изучаемом ряду,
а также о внутренней структуре изучаемого
процесса (в частности о наличие или
отсутствии периодических колебаний и
о величине периода).

Автокорреляционная
функция и коррелограмма свидетельствует
о наличие колеблемости уровней изучаемого
ДР с периодом колебаний равным 4-м
временным интервалам, что соответствует
максимальным значениям коэффициентов
автокорреляции.

Самое
высокое значение коэффициента корреляции
12 пар, вероятно, следует считать не
совсем надежным, однако его значения
приводятся для иллюстрации периода
имеющихся периода колебаний в изучаемом
ряду.

Если
во временном ряду отсутствуют периодические
колебания, то корреляционная функция
имеет затухающий характер, поскольку
значения коэффициента автокорреляции
высоких порядков приближается к 0.

Значение
коэффициента автокорреляции первого
порядка близкое к 1 говорит о наличие в
изучаемом ряду ярко выраженной тенденции.

Если
подтверждается наличие автокорреляции
в уровнях рядов, то. м.б. построена
автокорреляционная модель в которой в
качестве признака-результата будет
выступать исходный ряд, а в качестве
признака-фактора — смещенный. период
смещения определяется максимальным
значением коэффициента автокорреляции.

41.

42.
Анализ сезонности в рядах динамики

Сезонность
– это устойчиво – повторяющиеся
(закономерные) колебания значений
признака внутри года.

Динамика
продаж автомобилей Ford Motor Company

Год

Квартал

V
продаж, млн. $

Скользящая
средняя V
продаж

Отношение
к скользящей средней (3/4)

V
продаж с поправкой на сезонные
колебания, млн. $

Объем
продаж по уравнению тренда

1994

1995

1996

1997

1998

1999

2000

17115

19883

17205

17898

20636

22903

19370

21498

22686

22264

20107

23511

26070

28375

24926

27766

28601

29861

24437

27597

28297

31762

26459

31505

30037

32805

28196

31897

—

18453

19277

19931

20652

21358

21909

22297

22640

23315

24127

25118

26252

27101

27603

27727

27645

27568

27786

28276

29017

29723

30071

30419

30685

—

0,93

0,92

1,04

1,11

0,91

0,98

1,02

1,12

0,86

0,97

1,04

1,08

0,92

1,01

1,03

1,08

0,86

0,99

1,00

1,1

0,89

1,05

0,99

1,07

—

16806

18169

19126

18106

20263

20981

21532

21748

22276

23144

22352

23785

25599

25994

27708

28089

28084

27355

27165

27918

27786

29097

29413

31872

29494

30052

31343

32268

18038

18574

19109

19645

20180

20716

21252

21787

22323

22858

23394

23930

24465

25001

25537

26072

26608

27143

27679

28215

28750

29286

29821

30357

30893

31428

31969

32500

При
изучении динамических рядов, содержащих
сезонную компоненту возникает задача
выделить и описать основную тенденцию
ряда, осуществить прогноз этой основной
тенденции и затем скорректировать его
с учетом сезонной волны. Наличие сезонных
колебаний по внутригодичным данным
невелирует основную тенденцию ряда.
Для более четкого ее проявления, проводят
выравнивание фактических данных методом
скользящей средней.

Поскольку
данные таблицы представлены по кварталам
период скольжения должен охватывать 4
временных периода. Однако, чтобы не
применять метод центрирования можно
взять период скольжения равный 5 и
использовать при этом формулу средней
хронологической, чтобы вес первого
квартала соответствовал весу других
кварталов.

Это
выровненное значение скользящей средней
по третьему кварталу.

В
четвертой графе таблицы – выровненный
динамический ряд, в котором устраняется
эффект сезонности. Для расчета индексов
сезонности необходимо рассчитать
отношение полученной скользящей средней
по каждому периоду времени. Это отношение
покажет во сколько раз больше или меньше
фактическое значение уровня ряда по
сравнению с выровненным.

На
основе рассчитанных показателей получают
значение индексов сезонности, которые
также рассчитываются на основе формулы
средней арифметической простой.

Индекс
сезонности

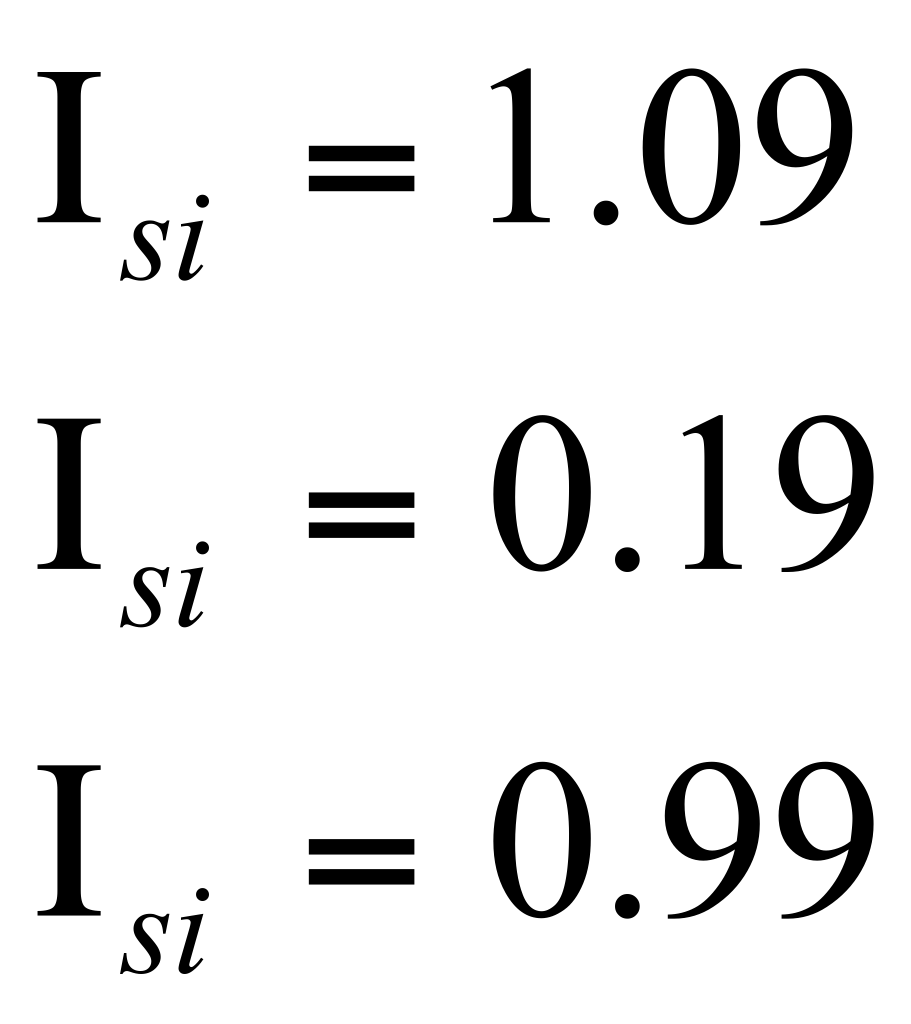
Индекс
сезонности для второго квартала равный
1,09 означает, что во втором квартале
можно ожидать рост объема продаж на 9%,
в то время как в третьем квартале следует
ожидать снижения объема продаж на 11%

Графическое
представление индексов сезонности
носит название «Графика сезонной волны»

График
сезонной волны наглядно демонстрирует,
что объемы продаж компании достигают
пика во втором квартале и минимума в
третьем квартале, после чего объем
продаж снова растет вплоть до 2-го
квартала следующего года.

Зная
величину индексов сезонности можно
определить объемы продаж с поправкой
на сезонность, т. е. разделив фактические
объемы продаж на соответствующие
индексы сезонности. Следует заметить,
что эти величины могут быть рассчитаны
и для этих периодов времени для которых
не были определены скользящие сред
ние,
т. е. это 1,3 кварталы 1994 и 3,4 кварталы
2000.

В
шестой графе таблицы мы получаем данные
объемов продаж, определенные с учетом
влияния сезонных колебаний, именно на
основе этих данных в дальнейшем строиться
– трендовая модель, описывающая основную
тенденцию объемов продаж за 7 лет.

Полученное
уравнение тренда имеет следующий вид:

Y=17502+535,612t

Величина
параметры при факторе t
показывает что в среднем ежеквартально
объем продаж увеличивается на 535 млн. $
без учета сезонности.

На
основе этого уравнения тренда можно
рассчитать прогноз и затем скорректировать
его с учетом сезонного факторы.

Прогноз

Год

квартал

Прогноз
без учета сезонной волны

Прогноз
с учетом сезонной волны

2001

33035

33571

34106

34642

33643

36648

30682

34244

Прогноз
без учета сезонной волны получаем на
основе уравнения тренда, подставляя
порядковый номер квартала на который
осуществляется прогноз.

Y=
13502+535,612*29

Y=
17502+535,612*30 и т. д.

Прогноз
с учетом сезонной волны получают путем
умножения данных на соответствующий
индекс сезонности.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Автокорреляция и частичная автокорреляция

Что такое автокорреляция и частичная автокорреляция?

Autocorrelation — линейная зависимость переменной с собой в две точки времени. Для стационарных процессов автокорреляция между любыми двумя наблюдениями зависит только от временной задержки h между ними. Задайте Cov (_yt, _yt–h) = _γh. Автокорреляция h Лаг— определяется

Знаменатель γ 0 является задержкой 0 ковариацией, то есть безусловным отклонением процесса.

Корреляция между двумя переменными может быть результатом взаимной линейной зависимости от других переменных (путаница). Partial autocorrelation является автокорреляцией между _yt и _yt–h после удаления любой линейной зависимости от y 1, _y 2,…, _{y t–h} + 1. Частичная лаг- h автокорреляция обозначенаϕh,h.

Теоретические ACF и PACF

Автокорреляционная функция (ACF) для временных рядов _yt, t = 1,…, N, является последовательностьюρh,
h = 1, 2…, N – 1. Частичная автокорреляционная функция (PACF) является последовательностью ϕh,h,
h = 1, 2…, N – 1.

Теоретические ACF и PACF для условных средних моделей AR, MA и ARMA известны и отличаются для каждой модели. Эти различия между моделями важно иметь в виду, когда вы выбираете модели.

Условная средняя модель	Поведение ACF	Поведение PACF
AR (p)	Хвосты отрываются постепенно	Обрезает после p лагов
MA (q)	Обрезает после q лагов	Хвосты отрываются постепенно
ARMA (p, q)	Хвосты отрываются постепенно	Хвосты отрываются постепенно

Выборка ACF и PACF

Автокорреляция выборки и частичная автокорреляция выборки являются статистическими данными, которые оценивают теоретическую автокорреляцию и частичную автокорреляцию. Используя эти качественные инструменты выбора модели, можно сравнить выборку ACF и PACF ваших данных с известными теоретическими автокорреляционными функциями [1].

Для наблюдаемого ряда y 1, _y 2,..._, yT, обозначите среднее значение выборкиy¯. Образец автокорреляции h лаг- дается

Стандартная ошибка для проверки значимости одной лаг- h автокорреляции ,ρ^h, приблизительно

Когда вы используете autocorr чтобы построить график выборочной автокорреляционной функции (также известной как коррелограмма), приблизительно 95% доверительных интервалов рисуются в ±2SEρ по умолчанию. Необязательные входные параметры позволяют вам изменить вычисление доверительных границ.

Выборка лаг- h частичная автокорреляция является оцененным коэффициентом лаг- h в модели AR, содержащей h лагов,ϕ^h,h. Стандартная ошибка для проверки значимости одной лаг- h частичной автокорреляции приблизительно 1/N. Когда вы используете parcorr чтобы построить график выборки функции частичной автокорреляции, приблизительно 95% доверия интервалов рисуются в ±2/N по умолчанию. Необязательные входные параметры позволяют вам изменить вычисление доверительных границ.

Вычислите выборку ACF и PACF в MATLAB

В этом примере показано, как вычислить и построить график выборки ACF и PACF временных рядов с помощью функций Econometrics Toolbox™ autocorr и parcorr, и приложение Econometric Modeler.

Сгенерируйте синтетические временные ряды

Симулируйте процесс MA (2) yt путем фильтрации ряда 1000 стандартных Гауссовых отклонений εt через разностное уравнение

yt=εt-εt-1+εt-2.

rng('default') % For reproducibility
e = randn(1000,1);
y = filter([1 -1 1],1,e);

Построение и вычисление ACF

Постройте график выборки ACF yt путем передачи моделируемых временных рядов в autocorr.

Автокорреляция образца лагов, больше 2, незначительна.

Вычислите выборку ACF путем вызова autocorr снова. Возвращает первый выходной аргумент.

acf(j) является образцом автокорреляции yt при задержке j – 1.

Построение и вычисление PACF

Постройте график выборки PACF yt путем передачи моделируемых временных рядов в parcorr.

С увеличением задержки выборки PACF постепенно уменьшается.

Вычислите выборку PACF путем вызова parcorr снова. Возвращает первый выходной аргумент.

pacf = 21×1

    1.0000
   -0.6697
   -0.1541
    0.2929
    0.3421
    0.0314
   -0.1483
   -0.2290
   -0.0394
    0.1419
      ⋮

pacf(j) является выборкой частичной автокорреляции yt при задержке j – 1.

The выборки ACF и PACF предполагают, что yt является процессом МА (2).

Использование Econometric Modeler

Откройте приложение Econometric Modeler путем ввода econometricModeler в командной строке.

Загрузите моделируемые временные ряды y.

На вкладке Econometric Modeler, в разделе Import, выберите Import > Import From Workspace.
В диалоговом окне «Импорт данных», в окне «Импорт?» столбец установите флажок для y переменная.
Нажмите кнопку Импорт.

Переменная y1 появляется в Диспетчере данных, а график временных рядов появляется в окне рисунка временных рядов (y1).

Отобразите выборку ACF, нажав ACF на вкладке Графики.

Постройте график выборки PACF, нажав PACF на вкладке Графики. Поместите график PACF под график ACF путем перетаскивания вкладки PACF (y1) в нижнюю половину документа.

Ссылки

[1] Box, George E. P., Gwilym M. Jenkins, and Gregory C. Reinsel. Анализ временных рядов: прогнозирование и управление. 3-й эд. Englewood Cliffs, Нью-Джерси: Prentice Hall, 1994.

См. также

Приложения

Econometric Modeler

Функции

autocorr | parcorr

Похожие темы

Обнаружение последовательной корреляции с помощью приложения Econometric Modeler
Обнаружение автокорреляции
Обнаружение эффектов ARCH с помощью приложения Econometric Modeler
Обнаружение эффектов ARCH
Выбор модели Бокса-Дженкинса
Q-тест Ljung-Box
Авторегрессионная модель
Модель скользящего среднего значения
Авторегрессионная модель скользящего среднего значения

Источник

7.7. что можно сделать в отношении автокорреляции?

Возможно, вам удастся устранить автокорреляцию путем определения ответственного за нее фактора или факторов и соответствующего расширения уравнения регрессии. Когда такое возможно, это может оказаться наилучшим решением. Пример приводится в упражнении 10.4.

В других случаях процедура, которую следует принять, будет зависеть от характера зависимости между значениями случайного члена. В литературе наибольшее внимание уделяется так называемой авторегрессионной схеме первого порядка (7.21), так как она интуитивно правдоподобна, но для того, чтобы было целесообразным ее использование в более сложных моделях, оснований обычно не хватает. Вместе с тем если наблюдения проводятся ежеквартально или ежемесячно, могут оказаться более подходящими другие модели, но мы не будем их здесь рассматривать.

Если бы уравнение (7.21) было правильной спецификацией для измерения величины случайного члена, то вы могли бы полностью устранить автокорреляцию, если бы знали величину р. Это будет продемонстрировано на примере уравнения регрессии, включающего только одну объясняющую переменную, однако при большем их числе действует тот же принцип.

Предположим, что истинная модель задается выражением (7.20), так что наблюдения / и / — 1 формируются как

у, = а + рх, + и,; (7.23)

j,_i=« + P*/-i+«W (7-24)

Теперь вычтем из обеих частей уравнения (7.23) умноженное на р соотношение (7.24) и получим:

y,-W,-i = а(1-р) + Р(х,-рх,_,) + w,-pw,_,. (7.25)

Обозначим у{ = yt -pj>,_i, х, = х, pxt_{ и qt = 1-р. Тогда формулу (7.25) можно переписать как

у, = aqt + рх, + щ put_{. (7.26)

Вместе с тем из уравнения (7.21) имеем к, — put_{ = є,. Таким образом, формула (7.26) принимает вид:

у, =agt +рх; +£,. (7.27)

Мы предположили, что р известно. Тогда можно вычислить величины у/, Зс; и qt (последняя одинакова для всех наблюдений) для наблюдений, включающих от 2 до Г исходных данных. Если теперь оценить регрессию между yt, xt и qt (заметим, что в уравнение не должна включаться постоянная), то будут получены оценки а и р, не связанные с проблемой автокорреляции, поскольку, согласно предположению, значения є не зависят друг от друга.

Остается, однако, небольшая проблема. Если в выборке нет данных, предшествующих первому наблюдению, то мы не сможем вычислить уі и хх и потеряем первое наблюдение. Число степеней свободы уменьшается на единицу, и это вызовет потерю эффективности, которая может в небольших выборках перевесить повышение эффективности от устранения автокорреляции.

Эту проблему, к счастью, можно довольно легко обойти, пользуясь так называемой поправкой Прайса—Уинстена (Prais, Winsten, 1954). Случайный член є, согласно определению, не зависит от значения и в любом предшествующем наблюдении. В частности, все величины є2, …,егне зависят от и{. Следовательно, если при устранении автокорреляции все другие наблюдения преобразуются, то не требуется преобразовывать первое наблюдение. Можно сохранить его,

включив в новую схему, полагая, что у{ = у{, qx = 1, хх = хх.

Мы можем таким способом спасти первое наблюдение, но здесь есть небольшая проблема, которую требуется решить. Если р велико, то первое наблюдение будет оказывать непропорционально большое воздействие на оценки, исчисленные по уравнению регрессии. Чтобы нейтрализовать этот эффект, уменьшим вес данного наблюдения умножением его на величину yj р2, полагая

У = ^1-р2У], хх = yjl-p2xl и <7] = Vі ~Р2Причина выбора такого столь необычного веса объясняется в приложении 7.4.

Конечно, на практике величина р неизвестна, его оценка получается одновременно с оценками аир. Имеется несколько стандартных способов такого оценивания, и, вероятно, один или нескольких таких способов могут быть реализованы в имеющемся у вас регрессионном пакете.

Метод Кокрана—Оркатта представляет собой итеративный процесс, включающий следующие этапы.

Оценивается регрессия (7,20) с исходными непреобразованными данными.

Вычисляются остатки.

Оценивается регрессионная зависимость et от соответствующая формуле (7.21), и коэффициент при et_{ представляет собой оценку р.

С этой оценкой р уравнение (7.20) преобразуется в (7.27), оценивание которого позволяет получись пересмотренные оценки аир.

Повторно вычисляются остатки, и процесс возвращается к этапу 3.

Чередование этапов пересмотра оценок а и р и оценки р продолжается до тех пор, пока не будет получена требуемая точность сходимости, т. е. до тех пор, пока оценки на последнем и предпоследнем циклах не совпадут с заданной степенью точности.

Метод Хилдрета—Лу, также широко применяемый в регрессионных пакетах, основан на тех же самых принципах, но использует другой алгоритм вычислений. Здесь регрессия (7.27) оценивается для каждого значения р из определенного диапазона с заданным шагом внутри его. (Например, исследователь может задать диапазон от р = -1,00 до р = 1,00 с шагом 0,01.) Значение, которое дает минимальную стандартную ошибку для преобразованного уравнения, принимается в качестве оценки р, а коэффициенты регрессии определяются при оценивании уравнения (7.27) с использованием этого значения.

Когда статистика Дарбина—Уотсона указывает на очень тесную положительную автокорреляцию, можно применить упрощенную процедуру, заключающуюся в предположении, что р= 1. Тогда уравнение (7.25) принимает вид:

у, у,-х = Р (х, х,_х) + «,-«,-,. (7.28)

Другими словами, оценивается регрессионная зависимость разности значений у в последовательных наблюдениях от разности значений х. Она известна как уравнение регрессии первых разностей и часто записывается в виде:

Ау,= рАхг + u-ur_v (7.29)

Так как фактическое (неизвестное) значение р, вероятно, будет меньшим единицы, эта процедура, по-видимому, компенсирует автокорреляцию с некоторым избытком. Можно показать, что теоретическая корреляция между последовательными значениями (ut — ut_x) равна —(1 — р)/2. Чем ближе р к единице, тем эта корреляция меньше и, следовательно, тем более вероятно улучшение результатов.

Примеры использования метода первых разностей можно найти в литературе до конца 1970-х гг., но в современных исследованиях он обычно не применяется. До относительно недавнего времени привлекала присущая ему простота вычислений, но теперь, когда итеративные процессы благодаря разработке более мощных и быстродействующих компьютеров связаны с меньшими затратами времени и стали менее дорогостоящими, этот метод считается устаревшим.

Таблица 7.4
Метод	Доход		Цена
Эластичность	со.	Эластичность	со.	р	со.	d	R2
МНК	0,637	0,026	-0,476	0,121	—	—	0,63	0,987
СО— PW	0,651	0,034	-0,578	0,130	0,67	0,16	1.74	0,999

В табл. 7.4 представлены результаты построения логарифмических регрессий между расходами на питание (у), личным доходом (х) и ценой (р) с использованием данных для США (1959—1983 гг.), приведенных в табл. Б.1 и Б.2; применялись обычный метод наименьших квадратов и метод Кокрана—Оркатта с поправкой Прайса—Уинстена (СО—PW). Так как регрессии являются логарифмическими, коэффициенты при у и р следует интерпретировать как показатели эластичности.

Для регрессии по МНК J-статистика указывает на положительную автокорреляцию, статистически значимую при уровне значимости в 1\% и выше; эта гипотеза подтверждается значимостью оценки р в регрессии Кокрана—Оркатта. Приведем пример ситуации, в которой часто возникает недоразумение. Напомним, что стандартная ошибка представляет собой оценку стандартного отклонения рассматриваемого коэффициента (это анализируется в разделах 3.1 и 3.5). Предположим, что мы оценили регрессию и статистика Дарбина—Уотсона (d) указывает на тесную положительную автокорреляцию. Предположим также, что рассчитанная стандартная ошибка данного коэффициента составляет 0,40. По причине автокорреляции стандартная ошибка представляет собой смещенную оценку истинного стандартного отклонения. Последнее могло быть значительно выше, например 0,90. При оценивании регрессии с использованием СО—PW или другого подобного метода истинное стандартное отклонение с повышением эффективности должно снизиться. Для определенности предположим, что оно снижается с 0,90 до 0,70. Стандартная ошибка в этой регрессии должна представлять собой приблизительно несмещенную оценку стандартного отклонения. Предположим, что она составляет 0,68. Часто бывает так, что студент делает вывод о том, что регрессия СО—PW менее эффективна, чем первоначальная, потому что рассчитанная стандартная ошибка возросла с 0,40 до 0,68, Это, конечно, неверно, поскольку оценка 0,40 неверна, и сравнение не имеет смысла. Такая ситуация отражена в табл. 7.5.

Таблица 7.5
	Пер вона чальная	Регрессия
	регрессия	CO-PW
Стандартное отклонение (истинное)	0,90	0,70
Стандартная ошибка (рассчитанная)	0,40	0,68

В рассматриваемом случае представляется, что стандартные ошибки эластичности спроса по доходу и цене в регрессии по обычному МНК ниже, чем в регрессии по СО—PW; может показаться, что МНК более эффективен. Однако по указанным выше причинам это, вероятно, является не более чем иллюзией. Этот вопрос более подробно рассматривается в приложении 7.1, где дается также общая сравнительная оценка МНК и СО—PW.

Упражнения

7.8. Ваш регрессионный пакет, скорее всего, включает один или несколько методов, применяемых в случае автокорреляции. Используйте такой метод для оценивания измененного варианта функции спроса, если статистика Дарбина—Уотсона в упражнении 7.6 указала на наличие автокорреляции. Сравните пересмотренные оценки коэффициентов и стандартные ошибки с предшествующими и дайте соответствующие комментарии.

7.9. Студент (назовем его А) получил 30 наблюдений по двум переменным (у и х). Ему сообщили, что у линейно зависит от х и от случайного члена и:

у, = а + рх, + и„

и ему поручено получить оценку р. Истинное значение Р, не известное студенту, составляет 5. Студент предпринимает следующее:

Использовав обычный метод наименьших квадратов, он получает оценку Р, равную 4,64. Стандартная ошибка составляет 1,30; статистика Дарбина—Уотсона (d) равна 0,70.

Затем студент получает информацию о том, что случайный член подвергается воздействию автокорреляции первого порядка, определяемой выражением:

и, = 0,70^_, + е„

1. Объясните, почему студенты, должно быть, не удовлетворены результатами эксперимента 1.

где є, удовлетворяет обычным условиям Гаусса—Маркова и нормально распределено. Студент определяет, что Yt = yt — 0,70д>,_! и Xt = х — 0,70х,_, оценивает регрессию между Yt и Хп получая оценку 5,14 для Р со стандартной ошибкой 0,75 и’статистику Дарбина—Уотсона 1,91. Девять других студентов (В, С, J) выполняют такие же эксперименты с наблюдениями величины у, полученными по такой же модели и при тех же значениях х, но с другими случайными числами для є,. Результаты приводятся в таблице.

Объясните, почему студенты провели эксперимент 2, когда стал известен характер автокорреляции.

Сравните результаты экспериментов. (Сначала посмотрите на коэффициенты и затем — на стандартные ошибки.)

Источник