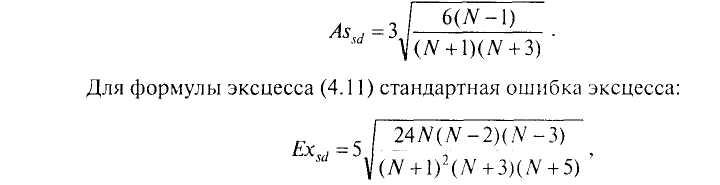Стандартная ошибка асимметрии и эксцесса

1. Асимметрия и эксцесс распределения случайной величины.

090309-matmetody.txt

Характеристики ассиметрии.

Основная мера ассиметрии — это коэффициент
ассиметрии. То есть, степерь отклонения
графика распределения частот от
симметричного вида относительно среднего
значения. Обозначается буквой A с индексом
s и считается по формуле (рис 8). Коэффициент
ассиметрии изменяется от минус
бесконечности до плюс бесконечности.
Ассиметрия бывает левосторонняя
(положительная), когда коэффициент
больше нуля — As>0 и правосторонняя
(отрицательная) — As<0. При левосторонней
ассиметрии чаще встречаются значения
ниже среднего арифметического. При
правой, соответственно чаще всего
встречаются значения, превосходящие
среднее арифметическое. Для симметричных
распределений коэффициент ассиметрии
равен нулю, а мода, медиана и среднее
арифметическое значение совпадают
между собой.

Характеристики эксцесса.

Характеризует его коэффициент
эксцесса (или островершинности) —
рассчитывается по формуле.

Островершинное распределение
характеризуется положительным эксцессом,
плосковершинное — отрицательным,
средневершинное имеет нулевой эксцесс.

с. 52 (59)

Для
проверки нормальности используются
различные процедуры, позво­ляющие
выяснить, отличается ли от нормального
выборочное распределение измеренной
переменной. Необходимость такого
сопоставления возникает, когда
мы сомневаемся в том, в какой шкале
представлен признак — в поряд­ковой
или метрической. А сомнения такие
возникают очень часто, так как заранее
нам, как правило, не известно, в какой
шкале удастся измерить изу­чаемое
свойство (исключая, конечно, случаи явно
номинативного измерения).

Важность
определения того, в какой шкале измерен
признак, трудно пе­реоценить,
по крайней мере, по двум причинам. От
этого зависит, во-первых,
полнота
учета исходной эмпирической информации
(в частности, об инди­видуальных
различиях), во-вторых,
доступность
многих методов анализа дан­ных.
Если исследователь принимает решение
об измерении в порядковой шкале,
то неизбежное последующее ранжирование
ведет к потере части ис­ходной
информации о различиях между испытуемыми,
изучаемыми группа­ми,
о взаимосвязях между признаками и т. д.
Кроме того, метрические дан­ные
позволяют использовать значительно
более широкий набор методов анализа
и, как следствие, сделать выводы
исследования более глубокими и
содержательными.

Наиболее
весомым аргументом в пользу того, что
признак измерен в мет­рической
шкале, является соответствие выборочного
распределения нормаль­ному.
Это является следствием закона нормального
распределения. Если
вы­борочное
распределение не отличается от
нормального, то это значит, что измеряемое
свойство удалось отразить в метрической
шкале (обычно
— интер­вальной).

Существует
множество различных способов проверки
нормальности, из которых
мы кратко опишем лишь некоторые,
предполагая, что эти проверки читатель
будет производить при помощи компьютерных
программ.

Графический
способ (Q—Q
Plots,
Р-Р Plots).
Строят
либо квантильные гра­фики,
либо графики накопленных частот.

Критерии
асимметрии и эксцесса. Эти
критерии определяют допустимую степень
отклонения эмпирических значений
асимметрии и эксцесса от нуле­вых
значений, соответствующих нормальному
распределению. Допустимая степень
отклонения — та, которая позволяет
считать, что эти статистики су­щественно
не отличаются от нормальных параметров.
Величина допустимых отклонений
определяется так называемыми стандартными
ошибками асим­метрии
и эксцесса. Для формулы асимметрии
(4.10) стандартная ошибка оп­ределяются
по формуле:

где
N
— объем
выборки.

Выборочные
значения асимметрии и эксцесса
значительно отличаются от нуля,
если не превышают значения своих
стандартных ошибок. Это можно считать
признаком соответствия выборочного
распределения нормальному закону.
Следует отметить, что компьютерные
программы вычисляют показа­тели
асимметрии, эксцесса и соответствующие
им стандартные ошибки по другим, более
сложным формулам.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

The standard errors are valid for normal distributions, but not for other distributions. To see why, you can run the following code (which uses the spssSkewKurtosis function shown above) to estimate the true confidence level of the interval obtained by taking the kurtosis estimate plus or minus 1.96 standard errors:

set.seed(12345)
Nsim = 10000
Correct = numeric(Nsim)
b1.ols = numeric(Nsim)
b1.alt = numeric(Nsim)
for (i in 1:Nsim) {
 Data = rnorm(1000)  
 Kurt = spssSkewKurtosis(Data)[2,1]
 seKurt =  spssSkewKurtosis(Data)[2,2]
  LowerLimit = Kurt -1.96*seKurt
  UpperLimit = Kurt +1.96*seKurt
  Correct[i] = LowerLimit <= 0 & 0 <= UpperLimit  
 }

TrueConfLevel = mean(Correct)
TrueConfLevel

This gives you 0.9496, acceptably close to the expected 95%, so the standard errors work as expected when the data come from a normal distribution. But if you change Data = rnorm(1000) to Data = runif(1000), then you are assuming that the data come from a uniform distribution, whose theoretical (excess) kurtosis is -1.2. Making the corresponding change from Correct[i] = LowerLimit <= 0 & 0 <= UpperLimit to Correct[i] = LowerLimit <= -1.2 & -1.2 <= UpperLimit gives the result 1.0, meaning that the 95% intervals were always correct, rather than correct for 95% of the samples. Hence, the standard error seems to be overestimated (too large) for the (light-tailed) uniform distribution.

If you change Data = rnorm(1000) to Data = rexp(1000), then you are assuming that the data come from an exponential distribution, whose theoretical (excess) kurtosis is 6.0. Making the corresponding change from Correct[i] = LowerLimit <= 0 & 0 <= UpperLimit to Correct[i] = LowerLimit <= 6.0 & 6.0 <= UpperLimit gives the result 0.1007, meaning that the 95% intervals were correct only for 10.07% of the samples, rather than correct for 95% of the samples. Hence, the standard error seems to be underestimated (too small) for the (heavy-tailed) exponential distribution.

Those standard errors are grossly incorrect for non-normal distributions, as the simulation above shows. Thus, the only use of those standard errors is to compare the estimated kurtosis with the expected theoretical normal value (0.0); e.g., using a test of hypothesis. They cannot be used to construct a confidence interval for the true kurtosis.