Среднюю абсолютную ошибку mae

«Хорошая» аналитическая модель должна удовлетворять двум, зачастую противоречивым, требованиям — как можно лучше соответствовать данным и при этом быть удобной для интерпретации пользователем. Действительно, повышение соответствия модели данным как правило связано с её усложнением (в случае регрессии — увеличением числа входных переменных модели). А чем сложнее модель, тем ниже её интерпретируемость.

Поэтому при выборе между простой и сложной моделью последняя должна значимо увеличивать соответствие модели данным чтобы оправдать рост сложности и соответствующее снижение интерпретируемости. Если это условие не выполняется, то следует выбрать более простую модель.

Таким образом, чтобы оценить, насколько повышение сложности модели значимо увеличивает её точность, необходимо использовать аппарат оценки качества регрессионных моделей. Он включает в себя следующие меры:

• Среднеквадратичная ошибка (MSE).
• Корень из среднеквадратичной ошибки (RMSE).
• Среднеквадратичная ошибка в процентах (MSPE).
• Средняя абсолютная ошибка (MAE).
• Средняя абсолютная ошибка в процентах (MAPE).
• Cимметричная средняя абсолютная процентная ошибка (SMAPE).
• Средняя абсолютная масштабированная ошибка (MASE)
• Средняя относительная ошибка (MRE).
• Среднеквадратичная логарифмическая ошибка (RMSLE).
• Коэффициент детерминации R-квадрат.
• Скорректированный коэффициент детеминации.

Прежде чем перейти к изучению метрик качества, введём некоторые базовые понятия, которые нам в этом помогут. Для этого рассмотрим рисунок.

Наклонная прямая представляет собой линию регрессии с переменной, на которой расположены точки, соответствующие предсказанным значениям выходной переменной \widehat{y} (кружки синего цвета). Оранжевые кружки представляют фактические (наблюдаемые) значения y . Расстояния между ними и линией регрессии — это ошибка предсказания модели y-\widehat{y} (невязка, остатки). Именно с её использованием вычисляются все приведённые в статье меры качества.

Горизонтальная линия представляет собой модель простого среднего, где коэффициент при независимой переменной x равен нулю, и остаётся только свободный член b, который становится равным среднему арифметическому фактических значений выходной переменной, т.е. b=\overline{y}. Очевидно, что такая модель для любого значения входной переменной будет выдавать одно и то же значение выходной — \overline{y}.

В линейной регрессии такая модель рассматривается как «бесполезная», хуже которой работает только «случайный угадыватель». Однако, она используется для оценки, насколько дисперсия фактических значений y относительно линии среднего, больше, чем относительно линии регрессии с переменной, т.е. насколько модель с переменной лучше «бесполезной».

MSE

Среднеквадратичная ошибка (Mean Squared Error) применяется в случаях, когда требуется подчеркнуть большие ошибки и выбрать модель, которая дает меньше именно больших ошибок. Большие значения ошибок становятся заметнее за счет квадратичной зависимости.

Действительно, допустим модель допустила на двух примерах ошибки 5 и 10. В абсолютном выражении они отличаются в два раза, но если их возвести в квадрат, получив 25 и 100 соответственно, то отличие будет уже в четыре раза. Таким образом модель, которая обеспечивает меньшее значение MSE допускает меньше именно больших ошибок.

MSE рассчитывается по формуле:

MSE=\frac{1}{n}\sum\limits_{i=1}^{n}(y_{i}-\widehat{y}_{i})^{2},

где n — количество наблюдений по которым строится модель и количество прогнозов, y_{i} — фактические значение зависимой переменной для i-го наблюдения, \widehat{y}_{i} — значение зависимой переменной, предсказанное моделью.

Таким образом, можно сделать вывод, что MSE настроена на отражение влияния именно больших ошибок на качество модели.

Недостатком использования MSE является то, что если на одном или нескольких неудачных примерах, возможно, содержащих аномальные значения будет допущена значительная ошибка, то возведение в квадрат приведёт к ложному выводу, что вся модель работает плохо. С другой стороны, если модель даст небольшие ошибки на большом числе примеров, то может возникнуть обратный эффект — недооценка слабости модели.

RMSE

Корень из среднеквадратичной ошибки (Root Mean Squared Error) вычисляется просто как квадратный корень из MSE:

RMSE=\sqrt{\frac{1}{n}\sum\limits_{i=1}^{n}(y_{i}-\widehat{y_{i}})^{2}}

MSE и RMSE могут минимизироваться с помощью одного и того же функционала, поскольку квадратный корень является неубывающей функцией. Например, если у нас есть два набора результатов работы модели, A и B, и MSE для A больше, чем MSE для B, то мы можем быть уверены, что RMSE для A больше RMSE для B. Справедливо и обратное: если MSE(A)<MSE(B), то и RMSE(A)<RMSE(B).

Следовательно, сравнение моделей с помощью RMSE даст такой же результат, что и для MSE. Однако с MSE работать несколько проще, поэтому она более популярна у аналитиков. Кроме этого, имеется небольшая разница между этими двумя ошибками при оптимизации с использованием градиента:

\frac{\partial RMSE}{\partial \widehat{y}_{i}}=\frac{1}{2\sqrt{MSE}}\frac{\partial MSE}{\partial \widehat{y}_{i}}

Это означает, что перемещение по градиенту MSE эквивалентно перемещению по градиенту RMSE, но с другой скоростью, и скорость зависит от самой оценки MSE. Таким образом, хотя RMSE и MSE близки с точки зрения оценки моделей, они не являются взаимозаменяемыми при использовании градиента для оптимизации.

Влияние каждой ошибки на RMSE пропорционально величине квадрата ошибки. Поэтому большие ошибки оказывают непропорционально большое влияние на RMSE. Следовательно, RMSE можно считать чувствительной к аномальным значениям.

MSPE

Среднеквадратичная ошибка в процентах (Mean Squared Percentage Error) представляет собой относительную ошибку, где разность между наблюдаемым и фактическим значениями делится на наблюдаемое значение и выражается в процентах:

MSPE=\frac{100}{n}\sum\limits_{i=1}^{n}\left ( \frac{y_{i}-\widehat{y}_{i}}{y_{i}} \right )^{2}

Проблемой при использовании MSPE является то, что, если наблюдаемое значение выходной переменной равно 0, значение ошибки становится неопределённым.

MSPE можно рассматривать как взвешенную версию MSE, где вес обратно пропорционален квадрату наблюдаемого значения. Таким образом, при возрастании наблюдаемых значений ошибка имеет тенденцию уменьшаться.

MAE

Cредняя абсолютная ошибка (Mean Absolute Error) вычисляется следующим образом:

MAE=\frac{1}{n}\sum\limits_{i=1}^{n}\left | y_{i}-\widehat{y}_{i} \right |

Т.е. MAE рассчитывается как среднее абсолютных разностей между наблюдаемым и предсказанным значениями. В отличие от MSE и RMSE она является линейной оценкой, а это значит, что все ошибки в среднем взвешены одинаково. Например, разница между 0 и 10 будет вдвое больше разницы между 0 и 5. Для MSE и RMSE, как отмечено выше, это не так.

Поэтому MAE широко используется, например, в финансовой сфере, где ошибка в 10 долларов должна интерпретироваться как в два раза худшая, чем ошибка в 5 долларов.

MAPE

Средняя абсолютная процентная ошибка (Mean Absolute Percentage Error) вычисляется следующим образом:

MAPE=\frac{100}{n}\sum\limits_{i=1}^{n}\frac{\left | y_{i}-\widehat{y_{i}} \right |}{\left | y_{i} \right |}

Эта ошибка не имеет размерности и очень проста в интерпретации. Её можно выражать как в долях, так и в процентах. Если получилось, например, что MAPE=11.4, то это говорит о том, что ошибка составила 11.4% от фактического значения.

SMAPE

Cимметричная средняя абсолютная процентная ошибка (Symmetric Mean Absolute Percentage Error) — это мера точности, основанная на процентных (или относительных) ошибках. Обычно определяется следующим образом:

SMAPE=\frac{100}{n}\sum\limits_{i=1}^{n}\frac{\left | y_{i}-\widehat{y_{i}} \right |}{(\left | y_{i} \right |+\left | \widehat{y}_{i} \right |)/2}

Т.е. абсолютная разность между наблюдаемым и предсказанным значениями делится на полусумму их модулей. В отличие от обычной MAPE, симметричная имеет ограничение на диапазон значений. В приведённой формуле он составляет от 0 до 200%. Однако, поскольку диапазон от 0 до 100% гораздо удобнее интерпретировать, часто используют формулу, где отсутствует деление знаменателя на 2.

Одной из возможных проблем SMAPE является неполная симметрия, поскольку в разных диапазонах ошибка вычисляется неодинаково. Это иллюстрируется следующим примером: если y_{i}=100 и \widehat{y}_{i}=110, то SMAPE=4.76, а если y_{i}=100 и \widehat{y}_{i}=90, то SMAPE=5.26.

Ограничение SMAPE заключается в том, что, если наблюдаемое или предсказанное значение равно 0, ошибка резко возрастет до верхнего предела (200% или 100%).

MASE

Средняя абсолютная масштабированная ошибка (Mean absolute scaled error) — это показатель, который позволяет сравнивать две модели. Если поместить MAE для новой модели в числитель, а MAE для исходной модели в знаменатель, то полученное отношение и будет равно MASE. Если значение MASE меньше 1, то новая модель работает лучше, если MASE равно 1, то модели работают одинаково, а если значение MASE больше 1, то исходная модель работает лучше, чем новая модель. Формула для расчета MASE имеет вид:

MASE=\frac{MAE_{i}}{MAE_{j}}

MASE симметрична и устойчива к выбросам.

MRE

Средняя относительная ошибка (Mean Relative Error) вычисляется по формуле:

MRE=\frac{1}{n}\sum\limits_{i=1}^{n}\frac{\left | y_{i}-\widehat{y}_{i}\right |}{\left | y_{i} \right |}

Несложно увидеть, что данная мера показывает величину абсолютной ошибки относительно фактического значения выходной переменной (поэтому иногда эту ошибку называют также средней относительной абсолютной ошибкой, MRAE). Действительно, если значение абсолютной ошибки, скажем, равно 10, то сложно сказать много это или мало. Например, относительно значения выходной переменной, равного 20, это составляет 50%, что достаточно много. Однако относительно значения выходной переменной, равного 100, это будет уже 10%, что является вполне нормальным результатом.

Очевидно, что при вычислении MRE нельзя применять наблюдения, в которых y_{i}=0.

Таким образом, MRE позволяет более адекватно оценить величину ошибки, чем абсолютные ошибки. Кроме этого она является безразмерной величиной, что упрощает интерпретацию.

RMSLE

Среднеквадратичная логарифмическая ошибка (Root Mean Squared Logarithmic Error) представляет собой RMSE, вычисленную в логарифмическом масштабе:

RMSLE=\sqrt{\frac{1}{n}\sum\limits_{i=1}^{n}(log(\widehat{y}_{i}+1)-log{(y_{i}+1}))^{2}}

Константы, равные 1, добавляемые в скобках, необходимы чтобы не допустить обращения в 0 выражения под логарифмом, поскольку логарифм нуля не существует.

Известно, что логарифмирование приводит к сжатию исходного диапазона изменения значений переменной. Поэтому применение RMSLE целесообразно, если предсказанное и фактическое значения выходной переменной различаются на порядок и больше.

R-квадрат

Перечисленные выше ошибки не так просто интерпретировать. Действительно, просто зная значение средней абсолютной ошибки, скажем, равное 10, мы сразу не можем сказать хорошая это ошибка или плохая, и что нужно сделать чтобы улучшить модель.

В этой связи представляет интерес использование для оценки качества регрессионной модели не значения ошибок, а величину показывающую, насколько данная модель работает лучше, чем модель, в которой присутствует только константа, а входные переменные отсутствуют или коэффициенты регрессии при них равны нулю.

Именно такой мерой и является коэффициент детерминации (Coefficient of determination), который показывает долю дисперсии зависимой переменной, объяснённой с помощью регрессионной модели. Наиболее общей формулой для вычисления коэффициента детерминации является следующая:

R^{2}=1-\frac{\sum\limits_{i=1}^{n}(\widehat{y}_{i}-y_{i})^{2}}{\sum\limits_{i=1}^{n}({\overline{y}}_{i}-y_{i})^{2}}

Практически, в числителе данного выражения стоит среднеквадратическая ошибка оцениваемой модели, а в знаменателе — модели, в которой присутствует только константа.

Главным преимуществом коэффициента детерминации перед мерами, основанными на ошибках, является его инвариантность к масштабу данных. Кроме того, он всегда изменяется в диапазоне от −∞ до 1. При этом значения близкие к 1 указывают на высокую степень соответствия модели данным. Очевидно, что это имеет место, когда отношение в формуле стремится к 0, т.е. ошибка модели с переменными намного меньше ошибки модели с константой. R^{2}=0 показывает, что между независимой и зависимой переменными модели имеет место функциональная зависимость.

Когда значение коэффициента близко к 0 (т.е. ошибка модели с переменными примерно равна ошибке модели только с константой), это указывает на низкое соответствие модели данным, когда модель с переменными работает не лучше модели с константой.

Кроме этого, бывают ситуации, когда коэффициент R^{2} принимает отрицательные значения (обычно небольшие). Это произойдёт, если ошибка модели среднего становится меньше ошибки модели с переменной. В этом случае оказывается, что добавление в модель с константой некоторой переменной только ухудшает её (т.е. регрессионная модель с переменной работает хуже, чем предсказание с помощью простой средней).

На практике используют следующую шкалу оценок. Модель, для которой R^{2}>0.5, является удовлетворительной. Если R^{2}>0.8, то модель рассматривается как очень хорошая. Значения, меньшие 0.5 говорят о том, что модель плохая.

Скорректированный R-квадрат

Основной проблемой при использовании коэффициента детерминации является то, что он увеличивается (или, по крайней мере, не уменьшается) при добавлении в модель новых переменных, даже если эти переменные никак не связаны с зависимой переменной.

В связи с этим возникают две проблемы. Первая заключается в том, что не все переменные, добавляемые в модель, могут значимо увеличивать её точность, но при этом всегда увеличивают её сложность. Вторая проблема — с помощью коэффициента детерминации нельзя сравнивать модели с разным числом переменных. Чтобы преодолеть эти проблемы используют альтернативные показатели, одним из которых является скорректированный коэффициент детерминации (Adjasted coefficient of determinftion).

Скорректированный коэффициент детерминации даёт возможность сравнивать модели с разным числом переменных так, чтобы их число не влияло на статистику R^{2}, и накладывает штраф за дополнительно включённые в модель переменные. Вычисляется по формуле:

R_{adj}^{2}=1-\frac{\sum\limits_{i=1}^{n}(\widehat{y}_{i}-y_{i})^{2}/(n-k)}{\sum\limits_{i=1}^{n}({\overline{y}}_{i}-y_{i})^{2}/(n-1)}

где n — число наблюдений, на основе которых строится модель, k — количество переменных в модели.

Скорректированный коэффициент детерминации всегда меньше единицы, но теоретически может принимать значения и меньше нуля только при очень малом значении обычного коэффициента детерминации и большом количестве переменных модели.

Сравнение метрик

Резюмируем преимущества и недостатки каждой приведённой метрики в следующей таблице:

Мера	Сильные стороны	Слабые стороны
MSE	Позволяет подчеркнуть большие отклонения, простота вычисления.	Имеет тенденцию занижать качество модели, чувствительна к выбросам. Сложность интерпретации из-за квадратичной зависимости.
RMSE	Простота интерпретации, поскольку измеряется в тех же единицах, что и целевая переменная.	Имеет тенденцию занижать качество модели, чувствительна к выбросам.
MSPE	Нечувствительна к выбросам. Хорошо интерпретируема, поскольку имеет линейный характер.	Поскольку вклад всех ошибок отдельных наблюдений взвешивается одинаково, не позволяет подчёркивать большие и малые ошибки.
MAPE	Является безразмерной величиной, поэтому её интерпретация не зависит от предметной области.	Нельзя использовать для наблюдений, в которых значения выходной переменной равны нулю.
SMAPE	Позволяет корректно работать с предсказанными значениями независимо от того больше они фактического, или меньше.	Приближение к нулю фактического или предсказанного значения приводит к резкому росту ошибки, поскольку в знаменателе присутствует как фактическое, так и предсказанное значения.
MASE	Не зависит от масштаба данных, является симметричной: положительные и отрицательные отклонения от фактического значения учитываются одинаково. Устойчива к выбросам. Позволяет сравнивать модели.	Сложность интерпретации.
MRE	Позволяет оценить величину ошибки относительно значения целевой переменной.	Неприменима для наблюдений с нулевым значением выходной переменной.
RMSLE	Логарифмирование позволяет сделать величину ошибки более устойчивой, когда разность между фактическим и предсказанным значениями различается на порядок и выше	Может быть затруднена интерпретация из-за нелинейности.
R-квадрат	Универсальность, простота интерпретации.	Возрастает даже при включении в модель бесполезных переменных. Плохо работает когда входные переменные зависимы.
R-квадрат скорр.	Корректно отражает вклад каждой переменной в модель.	Плохо работает, когда входные переменные зависимы.

В данной статье рассмотрены наиболее популярные меры качества регрессионных моделей, которые часто используются в различных аналитических приложениях. Эти меры имеют свои особенности применения, знание которых позволит обоснованно выбирать и корректно применять их на практике.

Однако в литературе можно встретить и другие меры качества моделей регрессии, которые предлагаются различными авторами для решения конкретных задач анализа данных.

Другие материалы по теме:

Отбор переменных в моделях линейной регрессии

Репрезентативность выборочных данных

Логистическая регрессия и ROC-анализ — математический аппарат

Время на прочтение
4 мин

Количество просмотров 5.7K

Функции потерь Python являются важной частью моделей машинного обучения. Эти функции показывают, насколько сильно предсказанный моделью результат отличается от фактического.

Существует несколько способов вычислить эту разницу. В этом материале мы рассмотрим некоторые из наиболее распространенных функций потерь.

Ниже будут рассмотрены следующие четыре функции потерь.

• Среднеквадратическая ошибка

• Среднеквадратическая ошибка

• Средняя абсолютная ошибка

• Кросс-энтропийные потери

Из этих четырех функций потерь первые три применяются к модели классификации.

1. Среднеквадратическая ошибка (MSE)

Среднеквадратичная ошибка (MSE) рассчитывается как среднее значение квадратов разностей между прогнозируемыми и фактически наблюдаемыми значениями. Математически это можно выразить следующим образом:

Реализация MSE на языке Python выглядит следующим образом:

import numpy as np # импортируем библиотеку numpy
def mean_squared_error(act, pred): # функция 

   diff = pred - act # находим разницу между прогнозируемыми и наблюдаемыми значениями
   differences_squared = diff ** 2 # возводим в квадрат (чтобы избавиться от отрицательных значений)
   mean_diff = differences_squared.mean() # находим среднее значение
   
   return mean_diff

act = np.array([1.1,2,1.7]) # создаем список актуальных значений
pred = np.array([1,1.7,1.5]) # список прогнозируемых значений

print(mean_squared_error(act,pred)) 

Выход :

0.04666666666666667

Вы также можете использовать mean_squared_error из sklearn для расчета MSE. Вот как работает функция:

from sklearn.metrics import mean_squared_error
act = np.array([1.1,2,1.7])
pred = np.array([1,1.7,1.5])
mean_squared_error(act, pred)

Выход :

0.04666666666666667

2. Корень среднеквадратической ошибки (RMSE)

Итак, ранее, для того, чтобы найти действительную ошибку среди между прогнозируемыми и фактически наблюдаемыми значениями (там могли быть положительные и отрицательные значения), мы возводили их в квадрат (для того чтобы отрицательные значения участвовали в расчетах в полной мере). Это была среднеквадратичная ошибка (MSE).

Корень среднеквадратической ошибки (RMSE) мы используем для того чтобы избавиться от квадратной степени, в которую мы ранее возвели действительную ошибку среди между прогнозируемыми и фактически наблюдаемыми значениями. Математически мы можем представить это следующим образом:

Реализация Python для RMSE выглядит следующим образом:

import numpy as np
def root_mean_squared_error(act, pred):

   diff = pred - act # находим разницу между прогнозируемыми и наблюдаемыми значениями
   differences_squared = diff ** 2 # возводим в квадрат
   mean_diff = differences_squared.mean() # находим среднее значение
   rmse_val = np.sqrt(mean_diff) # извлекаем квадратный корень
   return rmse_val

act = np.array([1.1,2,1.7])
pred = np.array([1,1.7,1.5])

print(root_mean_squared_error(act,pred))

Выход :

0.21602468994692867

Вы также можете использовать mean_squared_error из sklearn для расчета RMSE. Давайте посмотрим, как реализовать RMSE, используя ту же функцию:

from sklearn.metrics import mean_squared_error
act = np.array([1.1,2,1.7])
pred = np.array([1,1.7,1.5])
mean_squared_error(act, pred, squared = False) #Если установлено значение False, функция возвращает значение RMSE.

Выход :

0.21602468994692867

Если для параметра squared установлено значение True, функция возвращает значение MSE. Если установлено значение False, функция возвращает значение RMSE.

3. Средняя абсолютная ошибка (MAE)

Средняя абсолютная ошибка (MAE) рассчитывается как среднее значение абсолютной разницы между прогнозами и фактическими наблюдениями. Математически мы можем представить это следующим образом:

Реализация Python для MAE выглядит следующим образом:

import numpy as np 
def mean_absolute_error(act, pred): #
    diff = pred - act # находим разницу между прогнозируемыми и наблюдаемыми значениями
    abs_diff = np.absolute(diff) # находим абсолютную разность между прогнозами и фактическими наблюдениями.
    mean_diff = abs_diff.mean() # находим среднее значение
    return mean_diff

act = np.array([1.1,2,1.7])
pred = np.array([1,1.7,1.5])
mean_absolute_error(act,pred)

Выход :

0.20000000000000004

Вы также можете использовать mean_absolute_error из sklearn для расчета MAE.

from sklearn.metrics import mean_absolute_error
act = np.array([1.1,2,1.7])
pred = np.array([1,1.7,1.5])
mean_absolute_error(act, pred)

Выход :

0.20000000000000004

4. Функция потерь перекрестной энтропии в Python

Функция потерь перекрестной энтропии также известна как отрицательная логарифмическая вероятность. Это чаще всего используется для задач классификации. Проблема классификации — это проблема, в которой вы классифицируете пример как принадлежащий к одному из более чем двух классов.

Давайте посмотрим, как вычислить ошибку в случае проблемы бинарной классификации.

Давайте рассмотрим проблему классификации, когда модель пытается провести классификацию между собакой и кошкой.

Код Python для поиска ошибки приведен ниже.

from sklearn.metrics import log_loss
log_loss(["Dog", "Cat", "Cat", "Dog"],[[.1, .9], [.9, .1], [.8, .2], [.35, .65]])

Выход :

0.21616187468057912

Мы используем метод log_loss из sklearn.

Первый аргумент в вызове функции — это список правильных меток классов для каждого входа. Второй аргумент — это список вероятностей, предсказанных моделью.

Вероятности представлены в следующем формате:

[P(dog), P(cat)]

Заключение

Это руководство было посвящено функциям потерь в Python. Мы рассмотрели различные функции потерь как для задач регрессии, так и для задач классификации. Надеюсь, вам понравился материал, ведь все было достаточно легко и понятно!

Кстати, для тех, кто хотел бы пойти дальше в изучении функций потерь, мы предлагаем разобрать одну вот такую — это очень интересная функция потерь Triplet Loss в Python (функцию тройных потерь), которую для вас любезно подготовил автор.

From Wikipedia, the free encyclopedia

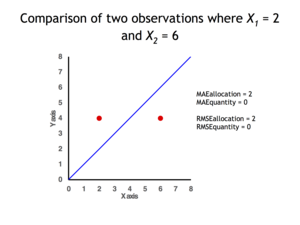
In statistics, mean absolute error (MAE) is a measure of errors between paired observations expressing the same phenomenon. Examples of Y versus X include comparisons of predicted versus observed, subsequent time versus initial time, and one technique of measurement versus an alternative technique of measurement. MAE is calculated as the sum of absolute errors divided by the sample size:^[1]

It is thus an arithmetic average of the absolute errors , where is the prediction and the true value. Alternative formulations may include relative frequencies as weight factors. The mean absolute error uses the same scale as the data being measured. This is known as a scale-dependent accuracy measure and therefore cannot be used to make comparisons between predicted values that use different scales.^[2] The mean absolute error is a common measure of forecast error in time series analysis,^[3] sometimes used in confusion with the more standard definition of mean absolute deviation. The same confusion exists more generally.

Quantity disagreement and allocation disagreement[edit]

In remote sensing the MAE is sometimes expressed as the sum of two components: quantity disagreement and allocation disagreement. Quantity disagreement is the absolute value of the mean error:^[4]

Allocation disagreement is MAE minus quantity disagreement.

It is also possible to identify the types of difference by looking at an plot. Quantity difference exists when the average of the X values does not equal the average of the Y values. Allocation difference exists if and only if points reside on both sides of the identity line.^[4][5]

[edit]

The mean absolute error is one of a number of ways of comparing forecasts with their eventual outcomes. Well-established alternatives are the mean absolute scaled error (MASE) and the mean squared error. These all summarize performance in ways that disregard the direction of over- or under- prediction; a measure that does place emphasis on this is the mean signed difference.

Where a prediction model is to be fitted using a selected performance measure, in the sense that the least squares approach is related to the mean squared error, the equivalent for mean absolute error is least absolute deviations.

MAE is not identical to root-mean square error (RMSE), although some researchers report and interpret it that way. The MAE is conceptually simpler and also easier to interpret than RMSE: it is simply the average absolute vertical or horizontal distance between each point in a scatter plot and the Y=X line. In other words, MAE is the average absolute difference between X and Y. Furthermore, each error contributes to MAE in proportion to the absolute value of the error. This is in contrast to RMSE which involves squaring the differences, so that a few large differences will increase the RMSE to a greater degree than the MAE.^[4]

Optimality property[edit]

The mean absolute error of a real variable c with respect to the random variable X is

Provided that the probability distribution of X is such that the above expectation exists, then m is a median of X if and only if m is a minimizer of the mean absolute error with respect to X.^[6] In particular, m is a sample median if and only if m minimizes the arithmetic mean of the absolute deviations.^[7]

More generally, a median is defined as a minimum of

as discussed at Multivariate median (and specifically at Spatial median).
This optimization-based definition of the median is useful in statistical data-analysis, for example, in k-medians clustering.

Proof of optimality[edit]

Statement: The classifier minimising is .

Proof:

The Loss functions for classification is

Differentiating with respect to a gives

This means

Hence,

See also[edit]

• Least absolute deviations
• Mean absolute percentage error
• Mean percentage error
• Symmetric mean absolute percentage error

References[edit]

  Перевод

  Ссылка на автора

Каждая модель машинного обучения пытается решить проблему с другой целью, используя свой набор данных, и, следовательно, важно понять контекст, прежде чем выбрать метрику. Обычно ответы на следующий вопрос помогают нам выбрать подходящий показатель:

• Тип задачи: регрессия? Классификация?
• Бизнес цель?
• Каково распределение целевой переменной?

Ну, в этом посте я буду обсуждать полезность каждой метрики ошибки в зависимости от цели и проблемы, которую мы пытаемся решить. Часть 1 фокусируется только на показателях оценки регрессии.

Метрики регрессии

• Средняя квадратическая ошибка (MSE)
• Среднеквадратическая ошибка (RMSE)
• Средняя абсолютная ошибка (MAE)
• R в квадрате (R²)
• Скорректированный R квадрат (R²)
• Среднеквадратичная ошибка в процентах (MSPE)
• Средняя абсолютная ошибка в процентах (MAPE)
• Среднеквадратичная логарифмическая ошибка (RMSLE)

Средняя квадратическая ошибка (MSE)

Это, пожалуй, самый простой и распространенный показатель для оценки регрессии, но, вероятно, наименее полезный. Определяется уравнением

гдеyᵢфактический ожидаемый результат иŷᵢэто прогноз модели.

MSE в основном измеряет среднеквадратичную ошибку наших прогнозов. Для каждой точки вычисляется квадратная разница между прогнозами и целью, а затем усредняются эти значения.

Чем выше это значение, тем хуже модель. Он никогда не бывает отрицательным, поскольку мы возводим в квадрат отдельные ошибки прогнозирования, прежде чем их суммировать, но для идеальной модели это будет ноль.

Преимущество:Полезно, если у нас есть неожиданные значения, о которых мы должны заботиться. Очень высокое или низкое значение, на которое мы должны обратить внимание.

Недостаток:Если мы сделаем один очень плохой прогноз, возведение в квадрат сделает ошибку еще хуже, и это может исказить метрику в сторону переоценки плохости модели. Это особенно проблематичное поведение, если у нас есть зашумленные данные (то есть данные, которые по какой-либо причине не совсем надежны) — даже в «идеальной» модели может быть высокий MSE в этой ситуации, поэтому становится трудно судить, насколько хорошо модель выполняет. С другой стороны, если все ошибки малы или, скорее, меньше 1, то ощущается противоположный эффект: мы можем недооценивать недостатки модели.

Обратите внимание, чтоесли мы хотим иметь постоянный прогноз, лучшим будетсреднее значение целевых значений.Его можно найти, установив производную нашей полной ошибки по этой константе в ноль, и найти ее из этого уравнения.

Среднеквадратическая ошибка (RMSE)

RMSE — это просто квадратный корень из MSE. Квадратный корень введен, чтобы масштаб ошибок был таким же, как масштаб целей.

Теперь очень важно понять, в каком смысле RMSE похож на MSE, и в чем разница.

Во-первых, они похожи с точки зрения их минимизаторов, каждый минимизатор MSE также является минимизатором для RMSE и наоборот, поскольку квадратный корень является неубывающей функцией. Например, если у нас есть два набора предсказаний, A и B, и скажем, что MSE для A больше, чем MSE для B, то мы можем быть уверены, что RMSE для A больше RMSE для B. И это также работает в противоположном направлении. ,

Что это значит для нас?

Это означает, что, если целевым показателем является RMSE, мы все равно можем сравнивать наши модели, используя MSE, поскольку MSE упорядочит модели так же, как RMSE. Таким образом, мы можем оптимизировать MSE вместо RMSE.

На самом деле, с MSE работать немного проще, поэтому все используют MSE вместо RMSE. Также есть небольшая разница между этими двумя моделями на основе градиента.

Это означает, что путешествие по градиенту MSE эквивалентно путешествию по градиенту RMSE, но с другой скоростью потока, и скорость потока зависит от самой оценки MSE.

Таким образом, хотя RMSE и MSE действительно схожи с точки зрения оценки моделей, они не могут быть сразу взаимозаменяемыми для методов на основе градиента. Возможно, нам нужно будет настроить некоторые параметры, такие как скорость обучения.

Средняя абсолютная ошибка (MAE)

В MAE ошибка рассчитывается как среднее абсолютных разностей между целевыми значениями и прогнозами. MAE — это линейная оценка, которая означает, чтовсе индивидуальные различия взвешены одинаковов среднем. Например, разница между 10 и 0 будет вдвое больше разницы между 5 и 0. Однако то же самое не верно для RMSE. Математически он рассчитывается по следующей формуле:

Что важно в этой метрике, так это то, что онанаказывает огромные ошибки, которые не так плохо, как MSE.Таким образом, он не так чувствителен к выбросам, как среднеквадратическая ошибка.

MAE широко используется в финансах, где ошибка в 10 долларов обычно в два раза хуже, чем ошибка в 5 долларов. С другой стороны, метрика MSE считает, что ошибка в 10 долларов в четыре раза хуже, чем ошибка в 5 долларов. MAE легче обосновать, чем RMSE.

Еще одна важная вещь в MAE — это его градиенты относительно прогнозов. Gradiend — это пошаговая функция, которая принимает -1, когда Y_hat меньше цели, и +1, когда она больше.

Теперь градиент не определен, когда предсказание является совершенным, потому что, когда Y_hat равен Y, мы не можем оценить градиент. Это не определено.

Таким образом, формально, MAE не дифференцируемо, но на самом деле, как часто ваши прогнозы точно измеряют цель. Даже если они это сделают, мы можем написать простое условие IF и вернуть ноль, если это так, и через градиент в противном случае. Также известно, что вторая производная везде нулевая и не определена в нулевой точке.

Обратите внимание, чтоесли мы хотим иметь постоянный прогноз, лучшим будетсрединное значение целевых значений.Его можно найти, установив производную нашей полной ошибки по этой константе в ноль, и найти ее из этого уравнения.

R в квадрате (R²)

А что если я скажу вам, что MSE для моих моделей предсказаний составляет 32? Должен ли я улучшить свою модель или она достаточно хороша? Или что, если мой MSE был 0,4? На самом деле, трудно понять, хороша наша модель или нет, посмотрев на абсолютные значения MSE или RMSE. Мы, вероятно, захотим измерить, как Во многом наша модель лучше, чем постоянная базовая линия.

Коэффициент детерминации, или R² (иногда читаемый как R-два), является еще одним показателем, который мы можем использовать для оценки модели, и он тесно связан с MSE, но имеет преимущество в том, чтобезмасштабное— не имеет значения, являются ли выходные значения очень большими или очень маленькими,R² всегда будет между -∞ и 1.

Когда R² отрицательно, это означает, что модель хуже, чем предсказание среднего значения.

MSE модели рассчитывается, как указано выше, в то время как MSE базовой линии определяется как:

гдеYс чертой означает среднее из наблюдаемогоyᵢ.

Чтобы сделать это более ясным, этот базовый MSE можно рассматривать как MSE, чтопростейшиймодель получит. Простейшей возможной моделью было бывсегдапредсказать среднее по всем выборкам. Значение, близкое к 1, указывает на модель с ошибкой, близкой к нулю, а значение, близкое к нулю, указывает на модель, очень близкую к базовой линии.

В заключение, R² — это соотношение между тем, насколько хороша наша модель, и тем, насколько хороша модель наивного среднего.

Распространенное заблуждение:Многие статьи в Интернете утверждают, что диапазон R² лежит между 0 и 1, что на самом деле не соответствует действительности. Максимальное значение R² равно 1, но минимальное может быть минус бесконечность.

Например, рассмотрим действительно дрянную модель, предсказывающую крайне отрицательное значение для всех наблюдений, даже если y_actual положительно. В этом случае R² будет меньше 0. Это крайне маловероятный сценарий, но возможность все еще существует.

MAE против MSE

Я заявил, что MAE более устойчив (менее чувствителен к выбросам), чем MSE, но это не значит, что всегда лучше использовать MAE. Следующие вопросы помогут вам решить:

Взять домой сообщение

В этой статье мы обсудили несколько важных метрик регрессии. Сначала мы обсудили среднеквадратичную ошибку и поняли, что наилучшей константой для нее является среднее целевое значение. Среднеквадратичная ошибка и R² очень похожи на MSE с точки зрения оптимизации. Затем мы обсудили среднюю абсолютную ошибку и когда люди предпочитают использовать MAE вместо MSE.

Спасибо за чтение, и я с нетерпением жду, чтобы услышать ваши вопросы Наслаждайтесь!

P.SСледите за моей следующей статьей, которая изучает другие более продвинутые метрики регрессии. Если вы хотите больше узнать о мире машинного обучения, вы также можете подписаться на меня в Instagram, напишите мне напрямую или найди меня на linkedin, Я хотел бы услышать от вас.

Ресурсы:
[1] https://dmitryulyanov.github.io/about

•