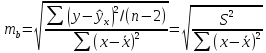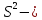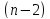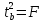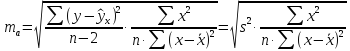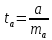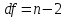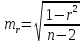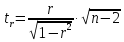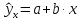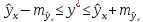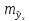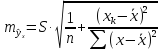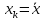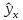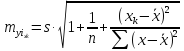Средняя стандартная ошибка прогноза формула - Решение и исправление самых разных ошибок на TopOshibok.ru

Вариант 1

Задание 1. Модель парной линейной регрессии.

Имеются данные о размере среднемесячных доходов в разных группах семей

Номер группы	Среднедушевой денежный доход в месяц, руб., X	Доля оплаты труда в структуре доходов семьи, %, Y
1	79,8	64,2
2	152,1	66,1
3	199,3	69,0
4	240,8	70,6
5	282,4	72,4
6	301,8	74,3
7	385,3	76,0
8	457,8	77,1
9	577,4	78,4

Задания:

1. Рассчитать линейный коэффициент парной корреляции, оценить его статистическую значимость и построить для него доверительный интервал с уровнем значимости a =0,05. Сделать выводы

2. Построить линейное уравнение парной регрессии Y на X и оценить статистическую значимость параметров регрессии. Сделать рисунок.

3. Оценить качество уравнения регрессии при помощи коэффициента детерминации. Сделать выводы. Проверить качество уравнения регрессии при помощи F-критерия Фишера.

4. Выполнить прогноз доли оплаты труда структуре доходов семьи Y при прогнозном значении среднедушевого денежного дохода X, составляющем 111% от среднего уровня. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал для уровня значимости a =0,05. Сделать выводы.

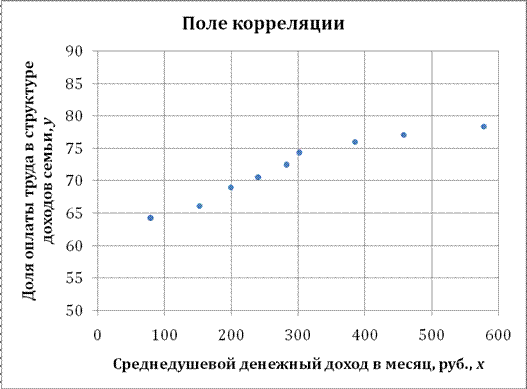
Решение: Построим поле корреляции зависимости доли оплаты труда в структуре доходов семьи от среднедушевого денежного дохода в месяц.

Точки на построенном графике размещаются вблизи кривой, напоминающей по форме Прямую, поэтому можно предположить, что между указанными величинами существует Линейная зависимость вида .

Для расчета линейного коэффициента парной корреляции и параметров линейной регрессии составим вспомогательную таблицу.

№ п/п	X	Y	X×Y	X2	Y2
1	79,8	64,2	5123,16	6368,04	4121,64
2	152,1	66,1	10053,81	23134,41	4369,21
3	199,3	69,0	13751,70	39720,49	4761,00
4	240,8	70,6	17000,48	57984,64	4984,36
5	282,4	72,4	20445,76	79749,76	5241,76
6	301,8	74,3	22423,74	91083,24	5520,49
7	385,3	76,0	29282,80	148456,09	5776,00
8	457,8	77,1	35296,38	209580,84	5944,41
9	577,4	78,4	45268,16	333390,76	6146,56
S	2676,7	648,1	198645,99	989468,27	46865,43
Среднее	297,41	72,01	22071,78	109940,92	5207,27

Вычислим коэффициент корреляции. Используем следующую формулу:

= 0,9568.

Можно сказать, что между рассматриваемыми признаками существует Прямая тесная Корреляционная связь.

Среднюю ошибку коэффициента корреляции определим по формуле:

= 0,032.

Найдем табличное значение TТабл по таблице распределения Стьюдента для
a = 0,05 и числе степеней свободы K = N – M – 1 = 9 – 1 – 1 = 7.

TТабл(0,05; 7) = 2,36.

Запишем доверительный интервал для коэффициента корреляции.

Доверительный интервал не включает число 0, поэтому при заданном уровне значимости коэффициент корреляции является статистически значимым.

Вычислим параметры уравнения регрессии.

= 0,03.

= 72,01 – 0,03×297,41 = 63,09.

Получим следующее уравнение: .

Для проверки статистической значимости (существенности) линейного коэффициента парной корреляции рассчитаем T-критерий Стьюдента по формуле:

= 23,04.

Фактическое значение по абсолютной величине больше табличного, что свидетельствует о значимости линейного коэффициента корреляции и существенности связи между рассматриваемыми признаками.

Проверим значимость оценок теоретических коэффициентов регрессии с помощью t-статистики Стьюдента и сделаем соответствующие выводы о значимости этих оценок.

Для определения статистической значимости коэффициентов A и B найдем T-статистики Стьюдента:

Рассчитаем по полученному уравнению теоретические значения. Составим вспомогательную таблицу.

№ п/п	X	Y
1	79,8	64,2	65,48	1,6384	47354,1
2	152,1	66,1	67,65	2,4025	21115,0
3	199,3	69,0	69,07	0,0049	9625,6
4	240,8	70,6	70,31	0,0841	3204,7
5	282,4	72,4	71,56	0,7056	225,3
6	301,8	74,3	72,14	4,6656	19,3
7	385,3	76,0	74,65	1,8225	7724,7
8	457,8	77,1	76,82	0,0784	25725,0
9	577,4	78,4	80,41	4,0401	78394,4
S	2676,7	648,1	648,09	15,4421	193388,1

Вычислим стандартные ошибки коэффициентов уравнения.

= 1,2.

= 0,003.

Вычислим T-статистики.

Сравнение расчетных и табличных величин критерия Стьюдента показывает, что и , т. е. оценки A и B теоретических коэффициентов регрессии статистически значимы.

Сделаем рисунок.

Рассчитаем коэффициент детерминации: = 0,95682= 0,915 = 91,5%.

Таким образом, вариация результата Y на 91,5% объясняется вариацией фактора X.

Оценку значимости уравнения регрессии проведем с помощью F-критерия Фишера:

= 75,81.

Найдем табличное значение Fтабл по таблице критических точек Фишера для
a = 0,05; K1 = M = 1 (число факторов), K2 = N – M – 1 = 9 – 1 – 1 = 7.

Fтабл(0,05; 1; 7) = 5,59.

Поскольку F > FТабл, уравнение регрессии с вероятностью 0,95 в целом Является статистически значимым.

Выполним прогноз доли оплаты труда структуре доходов семьи y при прогнозном значении среднедушевого денежного дохода x, составляющем 111% от среднего уровня.

XP = 297,41 × 1,11 = 330,1.

Вычислим прогнозное значение Yp с помощью уравнения регрессии.

» 73%.

Доверительный интервал прогноза имеет вид

(УP – Tкр×My, УP + Tкр×My),

Где , M = 2 – число параметров уравнения.

= 1,695 » 1,7.

Запишем доверительный интервал прогноза:

Данный прогноз является надежным, поскольку доверительный интервал не включает число 0, точность прогноза составляет 4.

Задание 2. Модель парной нелинейной регрессии.

По территориям Центрального района известны данные за 1995 г.

Район	Прожиточный минимум в среднем на одного пенсионера в месяц, тыс. руб., X	Средний размер назначенных ежемесячных пенсий, тыс. руб., Y
Брянская обл.	178	240
Владимирская обл.	202	226
Ивановская обл.	197	221
Калужская обл.	201	226
Костромская обл.	189	220
Орловская обл.	166	232
Рязанская обл.	199	215
Смоленская обл.	180	220
Тверская обл.	181	222
Тульская обл.	186	231
Ярославская обл.	250	229

Задания:

1. Построить поле корреляции и сформулируйте гипотезу о форме связи. Рассчитать параметры уравнений полулогарифмической () и степенной () парной регрессии. Сделать рисунки.

2. Дать с помощью среднего коэффициента эластичности сравнительную оценку силы связи фактора с результатом для каждой модели. Сделать выводы. Оценить качество уравнений регрессии с помощью средней ошибки аппроксимации и коэффициента детерминации. Сделать выводы.

3. По значениям рассчитанных характеристик выбрать лучшее уравнение регрессии. Дать экономический смысл коэффициентов выбранного уравнения регрессии

4. Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости a =0,05. Сделать выводы.

Решение: Решение: Для предварительного определения вида связи между указанными признаками построим поле корреляции. Для этого построим в системе координат точки, у которых первая координата X, а вторая – Y.

Получим следующий рисунок.

По внешнему виду диаграммы рассеяния трудно предположить, какая зависимость существует между указанными показателями.

Построение полулогарифмической модели регрессии.

Уравнение логарифмической кривой: .

Обозначим:

Получим линейное уравнение регрессии:

Y = A + B×X.

Произведем линеаризацию модели путем замены . В результате получим линейное уравнение .

Рассчитаем его параметры, используя данные таблицы.

№ п/п	X	Y	X = ln(X)	Xy	X2	Y2				Ai
1	178	240	5,1818	1243,63	26,85	57600	226,40	206,314	184,904	6,006
2	202	226	5,3083	1199,67	28,18	51076	225,17	0,132	0,694	0,370
3	197	221	5,2832	1167,59	27,91	48841	225,41	21,496	19,464	1,957
4	201	226	5,3033	1198,55	28,13	51076	225,22	0,132	0,615	0,348
5	189	220	5,2417	1153,18	27,48	48400	225,82	31,769	33,833	2,576
6	166	232	5,1120	1185,98	26,13	53824	227,08	40,496	24,172	2,165
7	199	215	5,2933	1138,06	28,02	46225	225,31	113,132	106,362	4,577
8	180	220	5,1930	1142,45	26,97	48400	226,29	31,769	39,601	2,781
9	181	222	5,1985	1154,07	27,02	49284	226,24	13,223	17,968	1,874
10	186	231	5,2257	1207,15	27,31	53361	225,97	28,769	25,273	2,225
11	250	229	5,5215	1264,41	30,49	52441	223,09	11,314	34,980	2,651
Итого	2129	2482	57,862	13054,74	304,48	560528	2482,00	498,545	487,867	27,530
Среднее	193,5	225,6	5,260	1186,79	27,68	50957,091	225,636	45,322	44,352	2,503

= -9,76.

= 225,6 – (-9,76)×5,26 = 276,99.

Уравнение модели имеет вид:

Определим индекс корреляции

Используя данные таблицы, получим:

Рассчитаем коэффициент детерминации: = 0,14642= 0,021 = 2,1%.

Вариация результата Y всего на 2,1% объясняется вариацией фактора X.

Сделаем рисунок.

Рассчитаем средний коэффициент эластичности по формуле:

= -0,04%.

Коэффициент эластичности показывает, что при среднем росте признака X на 1% признак Y снижается на 0,04%.

Вычислим среднюю ошибку аппроксимации. Используя данные расчетной таблицы, получаем:

= 2,5%.

Построение степенной модели парной регрессии.

Уравнение степенной модели имеет вид: .

Для построения этой модели необходимо произвести линеаризацию переменных. Для этого произведем логарифмирование обеих частей уравнения:

Произведем линеаризацию модели путем замены и . В результате получим линейное уравнение .

Рассчитаем его параметры, используя данные таблицы.

№ п/п	X	Y	X = ln(X)	Y = ln(Y)	XY	X2	Y2					Ai
1	178	240	5,1818	5,4806	28,3995	26,851	30,037	226,3	206,3	188,391	241,661	6,07
2	202	226	5,3083	5,4205	28,7737	28,178	29,382	225,1	0,132	0,835	71,479	0,406
3	197	221	5,2832	5,3982	28,5196	27,912	29,140	225,3	21,496	18,671	11,934	1,918
4	201	226	5,3033	5,4205	28,7467	28,125	29,382	225,1	0,132	0,753	55,570	0,385
5	189	220	5,2417	5,3936	28,2720	27,476	29,091	225,7	31,769	32,607	20,661	2,530
6	166	232	5,1120	5,4467	27,8437	26,132	29,667	226,9	40,496	25,675	758,752	2,233
7	199	215	5,2933	5,3706	28,4284	28,019	28,844	225,2	113,132	104,576	29,752	4,540
8	180	220	5,1930	5,3936	28,0089	26,967	29,091	226,2	31,769	38,059	183,479	2,728
9	181	222	5,1985	5,4027	28,0858	27,024	29,189	226,1	13,223	16,950	157,388	1,821
10	186	231	5,2257	5,4424	28,4407	27,308	29,620	225,9	28,769	26,413	56,934	2,275
11	250	229	5,5215	5,4337	30,0021	30,487	29,525	223,1	11,314	34,846	3187,116	2,646
Итого	2129	2482	57,862	59,603	313,521	304,479	322,969	2480,927	498,545	487,777	4774,727	27,548
Среднее	193,5	225,6	5,260	5,418	28,502	27,680	29,361	225,539	45,322	44,343	434,066	2,504

С учетом введенных обозначений уравнение примет вид: Y = A + BX – линейное уравнение регрессии. Рассчитаем его параметры, используя данные таблицы.

= -0,042.

= 5,418 – 0,959×5,26 = 5,637.

Перейдем к исходным переменным X и Y, выполнив потенцирование данного уравнения.

A = eA = e5,637 = 280,76

Получим уравнение степенной модели регрессии: .

Определим индекс корреляции

Используя данные таблицы, получим:

Рассчитаем коэффициент детерминации: = 0,1472= 0,021 = 2,1%.

Вариация результата Y всего на 2,1% объясняется вариацией фактора X.

Сделаем рисунок.

Для степенной модели средний коэффициент эластичности равен коэффициенту B.

= -0,042%.

Коэффициент эластичности показывает, что при среднем росте признака X на 1% признак Y снижается на 0,042%.

Вычислим среднюю ошибку аппроксимации. Используя данные расчетной таблицы, получаем:

= 2,5%.

Сводная таблица вычислений

Параметры	Модель
Полулогарифмическая	Степенная
Уравнение связи
Индекс корреляции	0,1464	0,147
Коэффициент детерминации	0,021	0,021
Средняя ошибка аппроксимации, %	2,5	2,5

Для выявления формы связи между указанными признаками были построены полулогарифмическая и степенная модели регрессии. Анализ показателей корреляции, а также оценка качества моделей с использованием средней ошибки аппроксимации позволил предположить, что из перечисленных моделей более адекватной является степенная модель, поскольку для нее индекс корреляции принимает наибольшее значение R = 0,147, свидетельствующий о том, что между рассматриваемыми признаками наблюдается Слабая корреляционная связь.

Рассчитаем прогнозное значение результата по степенной модели регрессии, если прогнозируется увеличение значения фактора на 10% от среднего уровня.

Прогнозное значение составит:

= 193,5 × 1,1 = 212,9 тыс. р., тогда прогнозное значение Y составит:

= 224,6 тыс. р.

Определим доверительный интервал прогноза для уровня значимости a = 0,05.

Вычислим Среднюю стандартную ошибку прогноза По следующей формуле:

, где

Получаем: = 7,55.

Найдем предельную ошибку прогноза , где для доверительной вероятности 0,95 значение T составляет 1,96.

= 14,8.

Запишем доверительный интервал прогноза.

= 224,6 – 14,8 = 209,8 тыс. р.

= 224,6 + 14,8 = 239,4 тыс. р.

Таким образом, с вероятностью 0,95 можно утверждать, что прогнозное значение среднего размера назначенных ежемесячных пенсий будет находиться в пределах от 209,8 тыс. р. до 239,4 тыс. р.

Задание 3. Моделирование временных рядов

Имеются поквартальные данные по розничному товарообороту России в 1995-1999 гг.

Номер квартала	Товарооборот % к предыдущему периоду	Номер квартала	Товарооборот % к предыдущему периоду
1	100	11	98,8
2	93,9	12	101,9
3	96,5	13	113,1
4	101,8	14	98,4
5	107,8	15	97,3
6	96,3	16	112,1
7	95,7	17	97,6
8	98,2	18	93,7
9	104	19	114,3
10	99	20	108,4

Задания:

1. Построить график данного временного ряда. Охарактеризовать структуру этого ряда.

2. Рассчитать сезонную компоненты временного ряда и построить его Мультипликативную Модель.

3. Рассчитать трендовую компоненту временного ряда и построить его график

4. Оценить качество модели через показатели средней абсолютной ошибки и среднего относительного отклонения.

Решение: Пронумеруем указанные месяцы от 1 до 24 и построим график временного ряда.

Полученный график показывает, что а данном временном ряду присутствуют сезонные колебания.

Построим мультипликативную модель временного ряда.

Эта модель предполагает, что каждый уровень временного ряда может быть представлен как произведение трендовой (T), сезонной (S) и случайной (E) компонент.

Построение мультипликативной моделей сведем к расчету значений T, S и E для каждого уровня ряда.

Процесс построения модели включает в себя следующие шаги.

1) Выравнивание исходного ряда методом скользящей средней.

2) Расчет значений сезонной компоненты S.

3) Устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных T×E.

4) Аналитическое выравнивание уровней T×E и расчет значений T с использованием полученного уравнения тренда.

5) Расчет полученных по модели значений T×E.

6) Расчет абсолютных и/или относительных ошибок.

Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Для этого:

1.1. Просуммируем уровни ряда последовательно за каждые четыре месяца со сдвигом на один момент времени и определим условные годовые уровни объема продаж (гр. 3 табл. 2.1).

1.2. Разделив полученные суммы на 4, найдем скользящие средние (гр. 4 табл. 2.1). Полученные таким образом выровненные значения уже не содержат сезонной компоненты.

1.3. Приведем эти значения в соответствие с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних – центрированные скользящие средние (гр. 5 табл. 2.1).

Таблица 2.1

№ месяца, T	Товарооборот, Yi	Итого за четыре месяца	Скользящая средняя за четыре месяца	Центрированная скользящая средняя	Оценка сезонной компоненты
1	2	3	4	5	6
1	100,0	–	–	–	–
2	93,9	392	98	–	–
3	96,5	400	100	99	0,975
4	101,8	402	100,5	100,25	1,015
5	107,8	402	100,5	100,5	1,073
6	96,3	398	99,5	100	0,963
7	95,7	394	98,5	99	0,967
8	98,2	397	99,25	98,875	0,993
9	104,0	400	100	99,625	1,044
10	99,0	404	101	100,5	0,985
11	98,8	413	103,25	102,125	0,967
12	101,9	412	103	103,125	0,988
13	113,1	411	102,75	102,875	1,099
14	98,4	309	77,25	90	1,093
15	97,3	196	49	63,125	1,541
16	112,1	303	75,75	62,375	1,797
17	97,6	418	104,5	90,125	1,083
18	93,7	414	103,5	104	0,901
19	114,3	–	–	–	–
20	108,4	–	–	–	–

Шаг 2. Найдем оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользящие средние (гр. 6 табл. 2.1). Эти оценки используются для расчета сезонной компоненты S (табл. 2.2). Для этого найдем средние за каждый месяц оценки сезонной компоненты Si. Так же как и в аддитивной модели считается, что сезонные воздействия за период взаимопогашаются. В мультипликативной модели это выражается в том, что сумма значений сезонной компоненты по всем месяцам должна быть равна числу периодов в цикле. В нашем случае число периодов одного цикла равно 4.

Таблица 2.2

Показатели	Год	№ квартала, I
I	II	III	IV
	1	–	–	0,975	1,015
	2	1,073	0,963	0,967	0,993
	3	1,044	0,985	0,967	0,988
	4	1,099	1,093	1,541	1,797
	5	1,083	0,901	–	–
Всего за I-й квартал		4,299	3,942	4,45	4,793
Средняя оценка сезонной компоненты для I-го квартала,		0,860	0,788	0,890	0,959
Скорректированная сезонная компонента,		0,984	0,901	1,018	1,097

Имеем: 0,860 + 0,788 + 0,890 + 0,959 = 3,497.

Определяем корректирующий коэффициент: K = 4 : 3,497 = 1,144.

Скорректированные значения сезонной компоненты получаются при умножении ее средней оценки на корректирующий коэффициент K.

Проверяем условие: равенство 4 суммы значений сезонной компоненты:

0,984 + 0,901 + 1,018 + 1,097 = 4.

Шаг 3. Разделим каждый уровень исходного ряда на соответствующие значения сезонной компоненты. В результате получим величины (гр. 4 табл. 2.3), которые содержат только тенденцию и случайную компоненту.

Таблица 2.3

T	Yt	St		T	T×S
1	2	3	4	5	6	7
1	100,0	0,984	101,6	100,02	98,42	1,016
2	93,9	0,901	104,2	100,19	90,27	1,040
3	96,5	1,018	94,8	100,36	102,17	0,945
4	101,8	1,097	92,8	100,53	110,28	0,923
5	107,8	0,984	109,6	100,7	99,09	1,088
6	96,3	0,901	106,9	100,87	90,88	1,060
7	95,7	1,018	94,0	101,04	102,86	0,930
8	98,2	1,097	89,5	101,21	111,03	0,884
9	104,0	0,984	105,7	101,38	99,76	1,043
10	99,0	0,901	109,9	101,55	91,50	1,082
11	98,8	1,018	97,1	101,72	103,55	0,954
12	101,9	1,097	92,9	101,89	111,77	0,912
13	113,1	0,984	114,9	102,06	100,43	1,126
14	98,4	0,901	109,2	102,23	92,11	1,068
15	97,3	1,018	95,6	102,4	104,24	0,933
16	112,1	1,097	102,2	102,57	112,52	0,996
17	97,6	0,984	99,2	102,74	101,10	0,965
18	93,7	0,901	104,0	102,91	92,72	1,011
19	114,3	1,018	112,3	103,08	104,94	1,089
20	108,4	1,097	98,8	103,25	113,27	0,957
Среднее	101,4					1,0011

Шаг 4. Определим компоненту T в мультипликативной модели. Для этого рассчитаем параметры линейного тренда, используя уровни T×E. Составим вспомогательную таблицу.

Таблица 2.4

	T		T2
	1	2	3	4	5	6	7
	1	101,6	1	101,6	2,5	1,58	2,0
	2	104,2	4	208,4	13,2	3,87	56,3
	3	94,8	9	284,4	32,1	5,88	24,0
	4	92,8	16	371,2	71,9	8,33	0,2
	5	109,6	25	548	75,9	8,08	41,0
	6	106,9	36	641,4	29,4	5,63	26,0
	7	94,0	49	658	51,3	7,48	32,5
	8	89,5	64	716	164,6	13,07	10,2
	9	105,7	81	951,3	18,0	4,08	6,8
	10	109,9	100	1099	56,3	7,58	5,8
	11	97,1	121	1068,1	22,6	4,81	6,8
	12	92,9	144	1114,8	97,4	9,69	0,3
	13	114,9	169	1493,7	160,5	11,20	136,9
	14	109,2	196	1528,8	39,6	6,39	9,0
	15	95,6	225	1434	48,2	7,13	16,8
	20	102,2	400	2044	0,2	0,37	114,5
	21	99,2	441	2083,2	12,3	3,59	14,4
	22	104,0	484	2288	1,0	1,05	59,3
	23	112,3	529	2582,9	87,6	8,19	166,4
	24	98,8	576	2371,2	23,7	4,49	49,0
Сумма	230	2035,2	3670	23588	1008,3	122,49	778,2
Среднее	11,5	101,8	183,5	1179,4	50,4	6,12	38,91

Вычислим параметры уравнения тренда.

= 0,17.

= 99,85.

В результате получим уравнение тренда:

T = 99,85 + 0,17×T.

Подставляя в это уравнение значения T = 1,2,…,16, найдем уровни T для каждого момента времени (гр. 5 табл. 2.3).

Шаг 5. Найдем уровни ряда, умножив значения T на соответствующие значения сезонной компоненты (гр. 6 табл. 2.3). На одном графике откладываем фактические значения уровней временного ряда и теоретические, полученные по мультипликативной модели.

Расчет ошибки в мультипликативной модели произведем по формуле:

Средняя абсолютная ошибка составила 1,0011 (см. гр. 7 табл. 2.3).

Рассчитаем сумму квадратов абсолютных ошибок .

Используя 5-й столбец таблицы 2.4, получим:

= 7,099.

Рассчитаем среднюю относительную ошибку: .

Используя 6-й столбец таблицы 2.4, получим, что средняя относительная ошибка составила 6,12%, т. е. построенная модель достаточно точно описывает динамику данного явления.

< Предыдущая		Следующая >

Источник

Ошибка прогнозирования: виды, формулы, примеры

Ошибка прогнозирования — это такая величина, которая показывает, как сильно прогнозное значение отклонилось от фактического. Она используется для расчета точности прогнозирования, что в свою очередь помогает нам оценивать как точно и корректно мы сформировали прогноз. В данной статье я расскажу про основные процентные «ошибки прогнозирования» с кратким описанием и формулой для расчета. А в конце статьи я приведу общий пример расчётов в Excel. Напомню, что в своих расчетах я в основном использую ошибку WAPE или MAD-Mean Ratio, о которой подробно я рассказал в статье про точность прогнозирования, здесь она также будет упомянута.

В каждой формуле буквой Ф обозначено фактическое значение, а буквой П — прогнозное. Каждая ошибка прогнозирования (кроме последней!), может использоваться для нахождения общей точности прогнозирования некоторого списка позиций, по типу того, что изображен ниже (либо для любого другого подобной детализации):

Алгоритм для нахождения любой из ошибок прогнозирования для такого списка примерно одинаковый: сначала находим ошибку прогнозирования по одной позиции, а затем рассчитываем общую. Итак, основные ошибки прогнозирования!

MPE — Mean Percent Error

MPE — средняя процентная ошибка прогнозирования. Основная проблема данной ошибки заключается в том, что в нестабильном числовом ряду с большими выбросами любое незначительное колебание факта или прогноза может значительно поменять показатель ошибки и, как следствие, точности прогнозирования. Помимо этого, ошибка является несимметричной: одинаковые отклонения в плюс и в минус по-разному влияют на показатель ошибки.

Для каждой позиции рассчитывается ошибка прогноза (из факта вычитается прогноз) — Error
Для каждой позиции рассчитывается процентная ошибка прогноза (ошибка прогноза делится на фактический показатель) — Percent Error
Находится среднее арифметическое всех процентных ошибок прогноза (процентные ошибки суммируются и делятся на количество) — Mean Percent Error

MAPE — Mean Absolute Percent Error

MAPE — средняя абсолютная процентная ошибка прогнозирования. Основная проблема данной ошибки такая же, как и у MPE — нестабильность.

Для каждой позиции рассчитывается абсолютная ошибка прогноза (прогноз вычитается из факта по модулю) — Absolute Error
Для каждой позиции рассчитывается абсолютная процентная ошибка прогноза (абсолютная ошибка прогноза делится на фактический показатель) — Absolute Percent Error
Находится среднее арифметическое всех абсолютных процентных ошибок прогноза (абсолютные процентные ошибки суммируются и делятся на количество) — Mean Absolute Percent Error

Вместо среднего арифметического всех абсолютных процентных ошибок прогноза можно использовать медиану числового ряда (MdAPE — Median Absolute Percent Error), она наиболее устойчива к выбросам.

WMAPE / MAD-Mean Ratio / WAPE — Weighted Absolute Percent Error

WAPE — взвешенная абсолютная процентная ошибка прогнозирования. Одна из «лучших ошибок» для расчета точности прогнозирования. Часто называется как MAD-Mean Ratio, то есть отношение MAD (Mean Absolute Deviation — среднее абсолютное отклонение/ошибка) к Mean (среднее арифметическое). После упрощения дроби получается искомая формула WAPE, которая очень проста в понимании:

Для каждой позиции рассчитывается абсолютная ошибка прогноза (прогноз вычитается из факта, по модулю) — Absolute Error
Находится сумма всех фактов по всем позициям (общий фактический объем)
Сумма всех абсолютных ошибок делится на сумму всех фактов — WAPE

Данная ошибка прогнозирования является симметричной и наименее чувствительна к искажениям числового ряда.

Рекомендуется к использованию при расчете точности прогнозирования. Более подробно читать здесь.

RMSE (as %) / nRMSE — Root Mean Square Error

RMSE — среднеквадратичная ошибка прогнозирования. Примерно такая же проблема, как и в MPE и MAPE: так как каждое отклонение возводится в квадрат, любое небольшое отклонение может значительно повлиять на показатель ошибки. Стоит отметить, что существует также ошибка MSE, из которой RMSE как раз и получается путем извлечения корня. Но так как MSE дает расчетные единицы измерения в квадрате, то использовать данную ошибку будет немного неправильно.

Для каждой позиции рассчитывается квадрат отклонений (разница между фактом и прогнозом, возведенная в квадрат) — Square Error
Затем рассчитывается среднее арифметическое (сумма квадратов отклонений, деленное на количество) — MSE — Mean Square Error
Извлекаем корень из полученного результат — RMSE
Для перевода в процентную или в «нормализованную» среднеквадратичную ошибку необходимо:
1. Разделить на разницу между максимальным и минимальным значением показателей
2. Разделить на разницу между третьим и первым квартилем значений показателей
3. Разделить на среднее арифметическое значений показателей (наиболее часто встречающийся вариант)

MASE — Mean Absolute Scaled Error

MASE — средняя абсолютная масштабированная ошибка прогнозирования. Согласно Википедии, является очень хорошим вариантом для расчета точности, так как сама ошибка не зависит от масштабов данных и является симметричной: то есть положительные и отрицательные отклонения от факта рассматриваются в равной степени.

Важно! Если предыдущие ошибки прогнозирования мы могли использовать для нахождения точности прогнозирования некого списка номенклатур, где каждой из которых соответствует фактическое и прогнозное значение (как было в примере в начале статьи), то данная ошибка для этого не предназначена: MASE используется для расчета точности прогнозирования одной единственной позиции, основываясь на предыдущих показателях факта и прогноза, и чем больше этих показателей, тем более точно мы сможем рассчитать показатель точности. Вероятно, из-за этого ошибка не получила широкого распространения.

Здесь данная формула представлена исключительно для ознакомления и не рекомендуется к использованию.

Суть формулы заключается в нахождении среднего арифметического всех масштабированных ошибок, что при упрощении даст нам следующую конечную формулу:

Также, хочу отметить, что существует ошибка RMMSE (Root Mean Square Scaled Error — Среднеквадратичная масштабированная ошибка), которая примерно похожа на MASE, с теми же преимуществами и недостатками.

Это основные ошибки прогнозирования, которые могут использоваться для расчета точности прогнозирования. Но не все! Их очень много и, возможно, чуть позже я добавлю еще немного информации о некоторых из них. А примеры расчетов уже описанных ошибок прогнозирования будут выложены через некоторое время, пока что я подготавливаю пример, ожидайте.

Об авторе

HeinzBr

Автор статей и создатель сайта SHTEM.RU

Источник

В
линейной регрессии обычно оценивается
значимость не только уравнения в целом,
но и отдельных его параметров. С этой
целью по каждому из параметров определяется
его стандартная ошибка: т_b
и
т_а.

Стандартная
ошибка коэффициента регрессии параметра
bрассчитывается
по формуле:

Где

остаточная дисперсия на одну степень
свободы.

Отношение
коэффициента регрессии к его стандартной
ошибке дает t-статистику,
которая подчиняется статистике Стьюдента
при

степенях
свободы. Эта статистика применяется
для проверки статистической значимости
коэффициента регрессии и для расчета
его доверительных интервалов.

Для
оценки значимости коэффициента регрессии
его величину сравнивают с его стандартной
ошибкой, т.е. определяют фактическое
значение t-критерия
Стьюдента:
,
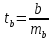
которое затем сравнивают с табличным
значением при определенном уровне
значимостиα
и
числе степеней свободы
.

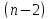
Справедливо
равенство

Доверительный
интервал для коэффициента регрессии
определяется как
.

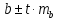
Стандартная
ошибка параметра а
определяется
по формуле

Процедура
оценивания значимости данного параметра
не отличается от рассмотренной выше
для коэффициента регрессии: вычисляется
t-критерий:

Его
величина сравнивается с табличным
значением при

степенях свободы.

Значимость
линейного коэффициента корреляции
проверяется на основе величины ошибки
коэффициента корреляции m_r:

Фактическое
значение t-критерия
Стьюдента определяется как

Данная
формула свидетельствует, что в парной
линейной регрессии
,
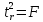
ибо как уже указывалось,
.
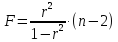
Кроме того,,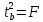
следовательно,.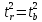

Таким
образом, проверка гипотез о значимости
коэффициентов регрессии и корреляции
равносильна проверке гипотезы о
значимости линейного уравнения регрессии.

Рассмотренную
формулу оценки коэффициента корреляции
рекомендуется применять при большом
числе наблюдений, а также если r
не близко к +1 или –1.

2.3 Интервальный прогноз на основе линейного уравнения регрессии

В
прогнозных расчетах по уравнению
регрессии определяется предсказываемое
y_р
значение
как точечный прогноз
_х
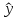
при
х_р
= х_k
т.
е. путем подстановки в линейное уравнение
регрессии

соответствующего
значения х.
Однако
точечный прогноз явно нереален, поэтому
он дополняется расчетом стандартной
ошибки
_х,
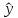
т.
е.
,
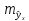
и
соответственно мы получаем интервальную
оценку прогнозного значения у*:

Считая,
что прогнозное значение фактора х_р
= х_k
получим
следующую формулу расчета стандартной
ошибки предсказываемого по линии
регрессии значения, т. е.

имеет выражение:

Рассмотренная
формула стандартной ошибки предсказываемого
среднего значения у
при
заданном значении х_k
характеризует
ошибку положения линии регрессии.
Величина стандартной ошибки
достигает
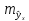
минимума при
и
возрастает по мере того, как «удаляется»
от
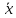
в любом направлении. Иными словами, чем
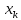
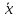
больше разность междуи,
тем больше ошибка,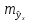
с
которой предсказывается среднее значение
у
для
заданного значения
.
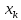
Можно ожидать наилучшие результаты
прогноза, если признак-фактор х находится
в центре области наблюдений х, и нельзя
ожидать хороших результатов прогноза
при удалении.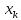
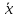
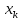
от. Если же значение.
оказывается за пределами наблюдаемых
значенийх,
используемых при построении линейной
регрессии, то результаты прогноза
ухудшаются в зависимости от того,
насколько
.
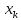
отклоняется от области наблюдаемых
значений факторах.

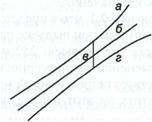
На
графике, приведенном на рис. 1, доверительные
границы для

представляют
собой гиперболы, расположенные по обе
стороны от линии регрессии. Рис. 1
показывает, как изменяются пределы в
зависимости от изменения
.:
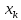
две гиперболы по обе стороны от линии
регрессии определяют 95 %-ные доверительные
интервалы для среднего значенияу
при
заданном значении х.

Однако
фактические значения у
варьируют
около среднего значения
.
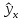
Индивидуальные
значения у
могут
отклоняться от

на
величину случайной ошибки ε, дисперсия
которой оценивается как остаточная
дисперсия на одну степень свободы
.
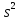
Поэтому ошибка предсказываемого
индивидуального значенияу
должна включать не только стандартную
ошибку
,
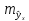
но и случайную ошибкуs.

Рис.
1. Доверительный интервал линии регрессии:

а
— верхняя
доверительная граница; б
— линия
регрессии;

в
— доверительный
интервал для

при
;

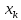
г
— нижняя
доверительная граница.

Средняя
ошибка прогнозируемого индивидуального
значения у
составит:

При
прогнозировании на основе уравнения
регрессии следует помнить, что величина
прогноза зависит не только от стандартной
ошибки индивидуального значения у,
но
и от точности прогноза значения фактора
х.
Его
величина может задаваться на основе
анализа других моделей исходя из
конкретной ситуации, а также анализа
динамики данного фактора.

Рассмотренная
формула средней ошибки индивидуального
значения признака у
может
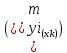
быть использована также для оценки
существенности различия предсказываемого
значения и некоторого гипотетического
значения.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Эконометрика

Вариант 1

Задание 1. Модель парной линейной регрессии.

Имеются данные о размере среднемесячных доходов в разных группах семей

Номер группы	Среднедушевой денежный доход в месяц, руб., X	Доля оплаты труда в структуре доходов семьи, %, Y
1	79,8	64,2
2	152,1	66,1
3	199,3	69,0
4	240,8	70,6
5	282,4	72,4
6	301,8	74,3
7	385,3	76,0
8	457,8	77,1
9	577,4	78,4

Задания:

№ п/п	X	Y	X×Y	X2	Y2
1	79,8	64,2	5123,16	6368,04	4121,64
2	152,1	66,1	10053,81	23134,41	4369,21
3	199,3	69,0	13751,70	39720,49	4761,00
4	240,8	70,6	17000,48	57984,64	4984,36
5	282,4	72,4	20445,76	79749,76	5241,76
6	301,8	74,3	22423,74	91083,24	5520,49
7	385,3	76,0	29282,80	148456,09	5776,00
8	457,8	77,1	35296,38	209580,84	5944,41
9	577,4	78,4	45268,16	333390,76	6146,56
S	2676,7	648,1	198645,99	989468,27	46865,43
Среднее	297,41	72,01	22071,78	109940,92	5207,27

Вычислим коэффициент корреляции. Используем следующую формулу:

= 0,9568.

Можно сказать, что между рассматриваемыми признаками существует Прямая тесная Корреляционная связь.

Среднюю ошибку коэффициента корреляции определим по формуле:

= 0,032.

TТабл(0,05; 7) = 2,36.

Запишем доверительный интервал для коэффициента корреляции.

Вычислим параметры уравнения регрессии.

= 0,03.

= 72,01 – 0,03×297,41 = 63,09.

Получим следующее уравнение: .

= 23,04.

Для определения статистической значимости коэффициентов A и B найдем T-статистики Стьюдента:

Рассчитаем по полученному уравнению теоретические значения. Составим вспомогательную таблицу.

№ п/п	X	Y
1	79,8	64,2	65,48	1,6384	47354,1
2	152,1	66,1	67,65	2,4025	21115,0
3	199,3	69,0	69,07	0,0049	9625,6
4	240,8	70,6	70,31	0,0841	3204,7
5	282,4	72,4	71,56	0,7056	225,3
6	301,8	74,3	72,14	4,6656	19,3
7	385,3	76,0	74,65	1,8225	7724,7
8	457,8	77,1	76,82	0,0784	25725,0
9	577,4	78,4	80,41	4,0401	78394,4
S	2676,7	648,1	648,09	15,4421	193388,1

Вычислим стандартные ошибки коэффициентов уравнения.

= 1,2.

= 0,003.

Вычислим T-статистики.

Сделаем рисунок.

Рассчитаем коэффициент детерминации: = 0,95682= 0,915 = 91,5%.

Таким образом, вариация результата Y на 91,5% объясняется вариацией фактора X.

Оценку значимости уравнения регрессии проведем с помощью F-критерия Фишера:

= 75,81.

Fтабл(0,05; 1; 7) = 5,59.

Поскольку F > FТабл, уравнение регрессии с вероятностью 0,95 в целом Является статистически значимым.

XP = 297,41 × 1,11 = 330,1.

Вычислим прогнозное значение Yp с помощью уравнения регрессии.

» 73%.

Доверительный интервал прогноза имеет вид

(УP – Tкр×My, УP + Tкр×My),

Где , M = 2 – число параметров уравнения.

= 1,695 » 1,7.

Запишем доверительный интервал прогноза:

Задание 2. Модель парной нелинейной регрессии.

По территориям Центрального района известны данные за 1995 г.

Район	Прожиточный минимум в среднем на одного пенсионера в месяц, тыс. руб., X	Средний размер назначенных ежемесячных пенсий, тыс. руб., Y
Брянская обл.	178	240
Владимирская обл.	202	226
Ивановская обл.	197	221
Калужская обл.	201	226
Костромская обл.	189	220
Орловская обл.	166	232
Рязанская обл.	199	215
Смоленская обл.	180	220
Тверская обл.	181	222
Тульская обл.	186	231
Ярославская обл.	250	229

Задания:

Получим следующий рисунок.

Построение полулогарифмической модели регрессии.

Уравнение логарифмической кривой: .

Обозначим:

Получим линейное уравнение регрессии:

Y = A + B×X.

Произведем линеаризацию модели путем замены . В результате получим линейное уравнение .

Рассчитаем его параметры, используя данные таблицы.

№ п/п	X	Y	X = ln(X)	Xy	X2	Y2				Ai
1	178	240	5,1818	1243,63	26,85	57600	226,40	206,314	184,904	6,006
2	202	226	5,3083	1199,67	28,18	51076	225,17	0,132	0,694	0,370
3	197	221	5,2832	1167,59	27,91	48841	225,41	21,496	19,464	1,957
4	201	226	5,3033	1198,55	28,13	51076	225,22	0,132	0,615	0,348
5	189	220	5,2417	1153,18	27,48	48400	225,82	31,769	33,833	2,576
6	166	232	5,1120	1185,98	26,13	53824	227,08	40,496	24,172	2,165
7	199	215	5,2933	1138,06	28,02	46225	225,31	113,132	106,362	4,577
8	180	220	5,1930	1142,45	26,97	48400	226,29	31,769	39,601	2,781
9	181	222	5,1985	1154,07	27,02	49284	226,24	13,223	17,968	1,874
10	186	231	5,2257	1207,15	27,31	53361	225,97	28,769	25,273	2,225
11	250	229	5,5215	1264,41	30,49	52441	223,09	11,314	34,980	2,651
Итого	2129	2482	57,862	13054,74	304,48	560528	2482,00	498,545	487,867	27,530
Среднее	193,5	225,6	5,260	1186,79	27,68	50957,091	225,636	45,322	44,352	2,503

= -9,76.

= 225,6 – (-9,76)×5,26 = 276,99.

Уравнение модели имеет вид:

Определим индекс корреляции

Используя данные таблицы, получим:

Рассчитаем коэффициент детерминации: = 0,14642= 0,021 = 2,1%.

Вариация результата Y всего на 2,1% объясняется вариацией фактора X.

Сделаем рисунок.

Рассчитаем средний коэффициент эластичности по формуле:

= -0,04%.

Коэффициент эластичности показывает, что при среднем росте признака X на 1% признак Y снижается на 0,04%.

Вычислим среднюю ошибку аппроксимации. Используя данные расчетной таблицы, получаем:

= 2,5%.

Построение степенной модели парной регрессии.

Уравнение степенной модели имеет вид: .

Произведем линеаризацию модели путем замены и . В результате получим линейное уравнение .

Рассчитаем его параметры, используя данные таблицы.

№ п/п	X	Y	X = ln(X)	Y = ln(Y)	XY	X2	Y2					Ai
1	178	240	5,1818	5,4806	28,3995	26,851	30,037	226,3	206,3	188,391	241,661	6,07
2	202	226	5,3083	5,4205	28,7737	28,178	29,382	225,1	0,132	0,835	71,479	0,406
3	197	221	5,2832	5,3982	28,5196	27,912	29,140	225,3	21,496	18,671	11,934	1,918
4	201	226	5,3033	5,4205	28,7467	28,125	29,382	225,1	0,132	0,753	55,570	0,385
5	189	220	5,2417	5,3936	28,2720	27,476	29,091	225,7	31,769	32,607	20,661	2,530
6	166	232	5,1120	5,4467	27,8437	26,132	29,667	226,9	40,496	25,675	758,752	2,233
7	199	215	5,2933	5,3706	28,4284	28,019	28,844	225,2	113,132	104,576	29,752	4,540
8	180	220	5,1930	5,3936	28,0089	26,967	29,091	226,2	31,769	38,059	183,479	2,728
9	181	222	5,1985	5,4027	28,0858	27,024	29,189	226,1	13,223	16,950	157,388	1,821
10	186	231	5,2257	5,4424	28,4407	27,308	29,620	225,9	28,769	26,413	56,934	2,275
11	250	229	5,5215	5,4337	30,0021	30,487	29,525	223,1	11,314	34,846	3187,116	2,646
Итого	2129	2482	57,862	59,603	313,521	304,479	322,969	2480,927	498,545	487,777	4774,727	27,548
Среднее	193,5	225,6	5,260	5,418	28,502	27,680	29,361	225,539	45,322	44,343	434,066	2,504

= -0,042.

= 5,418 – 0,959×5,26 = 5,637.

Перейдем к исходным переменным X и Y, выполнив потенцирование данного уравнения.

A = eA = e5,637 = 280,76

Получим уравнение степенной модели регрессии: .

Определим индекс корреляции

Используя данные таблицы, получим:

Рассчитаем коэффициент детерминации: = 0,1472= 0,021 = 2,1%.

Вариация результата Y всего на 2,1% объясняется вариацией фактора X.

Сделаем рисунок.

Для степенной модели средний коэффициент эластичности равен коэффициенту B.

= -0,042%.

Коэффициент эластичности показывает, что при среднем росте признака X на 1% признак Y снижается на 0,042%.

Вычислим среднюю ошибку аппроксимации. Используя данные расчетной таблицы, получаем:

= 2,5%.

Сводная таблица вычислений

Параметры	Модель
Полулогарифмическая	Степенная
Уравнение связи
Индекс корреляции	0,1464	0,147
Коэффициент детерминации	0,021	0,021
Средняя ошибка аппроксимации, %	2,5	2,5

Прогнозное значение составит:

= 193,5 × 1,1 = 212,9 тыс. р., тогда прогнозное значение Y составит:

= 224,6 тыс. р.

Определим доверительный интервал прогноза для уровня значимости a = 0,05.

Вычислим Среднюю стандартную ошибку прогноза По следующей формуле:

, где

Получаем: = 7,55.

Найдем предельную ошибку прогноза , где для доверительной вероятности 0,95 значение T составляет 1,96.

= 14,8.

Запишем доверительный интервал прогноза.

= 224,6 – 14,8 = 209,8 тыс. р.

= 224,6 + 14,8 = 239,4 тыс. р.

Задание 3. Моделирование временных рядов

Имеются поквартальные данные по розничному товарообороту России в 1995-1999 гг.

Номер квартала	Товарооборот % к предыдущему периоду	Номер квартала	Товарооборот % к предыдущему периоду
1	100	11	98,8
2	93,9	12	101,9
3	96,5	13	113,1
4	101,8	14	98,4
5	107,8	15	97,3
6	96,3	16	112,1
7	95,7	17	97,6
8	98,2	18	93,7
9	104	19	114,3
10	99	20	108,4

Задания:

1. Построить график данного временного ряда. Охарактеризовать структуру этого ряда.

2. Рассчитать сезонную компоненты временного ряда и построить его Мультипликативную Модель.

3. Рассчитать трендовую компоненту временного ряда и построить его график

4. Оценить качество модели через показатели средней абсолютной ошибки и среднего относительного отклонения.

Решение: Пронумеруем указанные месяцы от 1 до 24 и построим график временного ряда.

Полученный график показывает, что а данном временном ряду присутствуют сезонные колебания.

Построим мультипликативную модель временного ряда.

Построение мультипликативной моделей сведем к расчету значений T, S и E для каждого уровня ряда.

Процесс построения модели включает в себя следующие шаги.

1) Выравнивание исходного ряда методом скользящей средней.

2) Расчет значений сезонной компоненты S.

3) Устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных T×E.

4) Аналитическое выравнивание уровней T×E и расчет значений T с использованием полученного уравнения тренда.

5) Расчет полученных по модели значений T×E.

6) Расчет абсолютных и/или относительных ошибок.

Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Для этого:

Таблица 2.1

№ месяца, T	Товарооборот, Yi	Итого за четыре месяца	Скользящая средняя за четыре месяца	Центрированная скользящая средняя	Оценка сезонной компоненты
1	2	3	4	5	6
1	100,0	–	–	–	–
2	93,9	392	98	–	–
3	96,5	400	100	99	0,975
4	101,8	402	100,5	100,25	1,015
5	107,8	402	100,5	100,5	1,073
6	96,3	398	99,5	100	0,963
7	95,7	394	98,5	99	0,967
8	98,2	397	99,25	98,875	0,993
9	104,0	400	100	99,625	1,044
10	99,0	404	101	100,5	0,985
11	98,8	413	103,25	102,125	0,967
12	101,9	412	103	103,125	0,988
13	113,1	411	102,75	102,875	1,099
14	98,4	309	77,25	90	1,093
15	97,3	196	49	63,125	1,541
16	112,1	303	75,75	62,375	1,797
17	97,6	418	104,5	90,125	1,083
18	93,7	414	103,5	104	0,901
19	114,3	–	–	–	–
20	108,4	–	–	–	–

Таблица 2.2

Показатели	Год	№ квартала, I
I	II	III	IV
	1	–	–	0,975	1,015
	2	1,073	0,963	0,967	0,993
	3	1,044	0,985	0,967	0,988
	4	1,099	1,093	1,541	1,797
	5	1,083	0,901	–	–
Всего за I-й квартал		4,299	3,942	4,45	4,793
Средняя оценка сезонной компоненты для I-го квартала,		0,860	0,788	0,890	0,959
Скорректированная сезонная компонента,		0,984	0,901	1,018	1,097

Имеем: 0,860 + 0,788 + 0,890 + 0,959 = 3,497.

Определяем корректирующий коэффициент: K = 4 : 3,497 = 1,144.

Проверяем условие: равенство 4 суммы значений сезонной компоненты:

0,984 + 0,901 + 1,018 + 1,097 = 4.

Таблица 2.3

T	Yt	St		T	T×S
1	2	3	4	5	6	7
1	100,0	0,984	101,6	100,02	98,42	1,016
2	93,9	0,901	104,2	100,19	90,27	1,040
3	96,5	1,018	94,8	100,36	102,17	0,945
4	101,8	1,097	92,8	100,53	110,28	0,923
5	107,8	0,984	109,6	100,7	99,09	1,088
6	96,3	0,901	106,9	100,87	90,88	1,060
7	95,7	1,018	94,0	101,04	102,86	0,930
8	98,2	1,097	89,5	101,21	111,03	0,884
9	104,0	0,984	105,7	101,38	99,76	1,043
10	99,0	0,901	109,9	101,55	91,50	1,082
11	98,8	1,018	97,1	101,72	103,55	0,954
12	101,9	1,097	92,9	101,89	111,77	0,912
13	113,1	0,984	114,9	102,06	100,43	1,126
14	98,4	0,901	109,2	102,23	92,11	1,068
15	97,3	1,018	95,6	102,4	104,24	0,933
16	112,1	1,097	102,2	102,57	112,52	0,996
17	97,6	0,984	99,2	102,74	101,10	0,965
18	93,7	0,901	104,0	102,91	92,72	1,011
19	114,3	1,018	112,3	103,08	104,94	1,089
20	108,4	1,097	98,8	103,25	113,27	0,957
Среднее	101,4					1,0011

Таблица 2.4

	T		T2
	1	2	3	4	5	6	7
	1	101,6	1	101,6	2,5	1,58	2,0
	2	104,2	4	208,4	13,2	3,87	56,3
	3	94,8	9	284,4	32,1	5,88	24,0
	4	92,8	16	371,2	71,9	8,33	0,2
	5	109,6	25	548	75,9	8,08	41,0
	6	106,9	36	641,4	29,4	5,63	26,0
	7	94,0	49	658	51,3	7,48	32,5
	8	89,5	64	716	164,6	13,07	10,2
	9	105,7	81	951,3	18,0	4,08	6,8
	10	109,9	100	1099	56,3	7,58	5,8
	11	97,1	121	1068,1	22,6	4,81	6,8
	12	92,9	144	1114,8	97,4	9,69	0,3
	13	114,9	169	1493,7	160,5	11,20	136,9
	14	109,2	196	1528,8	39,6	6,39	9,0
	15	95,6	225	1434	48,2	7,13	16,8
	20	102,2	400	2044	0,2	0,37	114,5
	21	99,2	441	2083,2	12,3	3,59	14,4
	22	104,0	484	2288	1,0	1,05	59,3
	23	112,3	529	2582,9	87,6	8,19	166,4
	24	98,8	576	2371,2	23,7	4,49	49,0
Сумма	230	2035,2	3670	23588	1008,3	122,49	778,2
Среднее	11,5	101,8	183,5	1179,4	50,4	6,12	38,91

Вычислим параметры уравнения тренда.

= 0,17.

= 99,85.

В результате получим уравнение тренда:

T = 99,85 + 0,17×T.

Подставляя в это уравнение значения T = 1,2,…,16, найдем уровни T для каждого момента времени (гр. 5 табл. 2.3).

Расчет ошибки в мультипликативной модели произведем по формуле:

Средняя абсолютная ошибка составила 1,0011 (см. гр. 7 табл. 2.3).

Рассчитаем сумму квадратов абсолютных ошибок .

Используя 5-й столбец таблицы 2.4, получим:

= 7,099.

Рассчитаем среднюю относительную ошибку: .

< Предыдущая		Следующая >

Источник

Оценка ошибки прогнозирования временного ряда

Работая с научными публикациями, сталкиваюсь с различными показателями ошибок прогнозирования временных рядов. Среди всех встречающихся оценок ошибки прогнозирования стоит отметить две, которые в настоящее время, являются самыми популярными: MAE и MAPE.
Пусть ошибка есть разность:
,
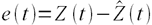
где Z(t) – фактическое значение временного ряда, а – прогнозное.
Тогда формулы для оценок ошибки прогнозирования временных рядов для N отчетов можно записать в следующем виде.

MAPE – средняя абсолютная ошибка в процентах

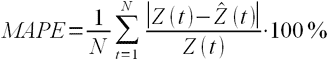
Данная оценка применяется для временных рядов, фактические значения которых значительно больше 1. Например, оценки ошибки прогнозирования энергопотребления почти во всех статьях приводятся как значения MAPE.

Если же фактические значения временного ряда близки к 0, то в знаменателе окажется очень маленькое число, что сделает значение MAPE близким к бесконечности – это не совсем корректно. Например, фактическая цена РСВ = 0.01 руб/МВт.ч, a прогнозная = 10 руб/МВт.ч, тогда MAPE = (0.01 – 10)/0.01 = 999%, хотя в действительности мы не так уж сильно ошиблись, всего на 10 руб/МВт.ч. Для рядов, содержащих значения близкие к нулю, применяют следующую оценку ошибки прогноза.

MAE – средняя абсолютная ошибка

Для оценки ошибки прогнозирования цен РСВ и индикатора БР корректнее использовать MAE.

После того, как получены значения для MAPE и/или MAE, то в работах обычно пишут: «Прогнозирование временного ряда энергопотребления с часовым разрешение проводилось на интервале с 01.01.2001 до 31.12.2001 (общее количество отсчетов N ~ 8500). Для данного прогноза значение MAPE = 1.5%». При этом, просматривая статьи, можно сложить общее впечатление об ошибки прогнозирования энергопотребления, для которого MAPE обычно колеблется от 1 до 5%; или ошибки прогнозирования цен на электроэнергию, для которого MAPE колеблется от 5 до 15% в зависимости от периода и рынка. Получив значение MAPE для собственного прогноза, вы можете оценить, насколько здорово у вас получается прогнозировать.

Кроме указанных иногда используют другие оценки ошибки, менее популярные, но также применимые. Подробнее об этих оценках ошибки прогноза читайте указанные статьи в Википедии.

MSE – среднеквадратичная ошибка

RMSE – квадратный корень из среднеквадратичной ошибки

ME – средняя ошибка

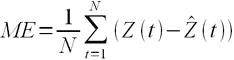
SD – стандартное отклонение

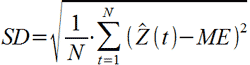
, где ME – есть средняя ошибка, определенная по формуле выше.

Связь точности и ошибки прогнозирования

Точность прогнозирования есть понятие прямо противоположное ошибке прогнозирования. Если ошибка прогнозирования велика, то точность мала и наоборот, если ошибка прогнозирования мала, то точность велика. По сути дела оценка ошибки прогноза MAPE есть обратная величина для точности прогнозирования — зависимость здесь простая.

Точность прогноза в % = 100% – MAPE

Величину точности оценивать не принято, говоря о прогнозировании всегда оценивают, то есть определяют значение именно ошибки прогноза, то есть величину MAPE и/или MAE. Однако нужно понимать, что если MAPE = 5%, то точность прогнозирования = 95%. Говоря о высокой точности, мы всегда говорим о низкой ошибки прогноза и в этой области недопонимания быть не должно. Вы практически не найдете материалов о прогнозировании, в которых приведены оценки именно точности прогноза, хотя с точки зрения здравого маркетинга корректней говорить именно о высокой точности. В рекламных статьях всегда будет написано о высокой точности.

При этом величина MAPE является количественной оценкой именно ошибки, и эта величина нам ясно говорит и о точности прогнозирования, исходя из приведенной выше простой формулы. Таким образом, оценивая ошибку, мы всегда оцениваем точность прогнозирования.

Источник