Средняя процентная ошибка mpe

Из данной статьи вы узнаете:

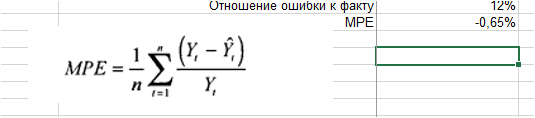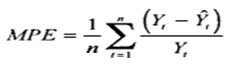
• Для чего нужна средняя процентная ошибка;
• Как она рассчитывается.

+ сможете скачать пример расчета в Excel.

MPE (mean percentage error) — средняя процентная ошибка прогноза.

MPE – средняя процентная ошибка прогноза используется в случаях, когда надо определить модель прогноза дает последовательно завышенные прогнозы или последовательно заниженные прогнозы.

Если значение больше нуля, то прогнозы последовательно занижены, т.е. в среднем меньше факта.

Если ошибка меньше нуля, то прогнозы последовательно завышены, т.е. модель делает прогноз в среднем выше факта.

Как рассчитать среднюю процентную ошибку?

1. Рассчитываем ошибку для каждого значения модели;
2. Делим на фактические данные ошибку в каждый момент времени.

Рассчитываем среднее по пункту 2, и получает среднюю процентную ошибку — MPE:

Рассчитаем на примере прогноза объема продаж:

Скачайте файл с примером расчета ошибки MPE в Excel.

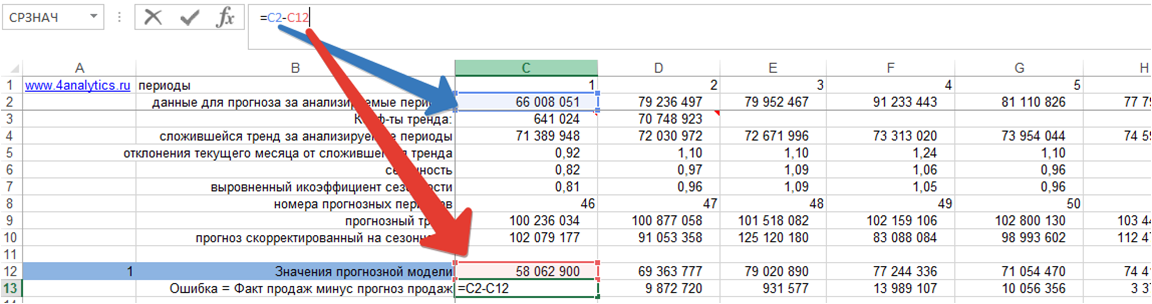
1. Ошибка = фактические продаж минус значения прогнозной модели для каждого момента времени:

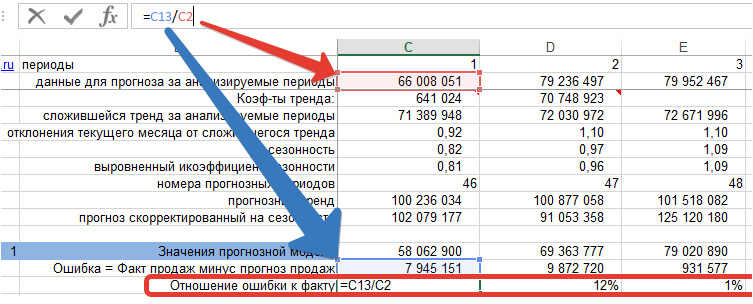
2. Делим ошибку на фактические продажи для каждого периода времени:

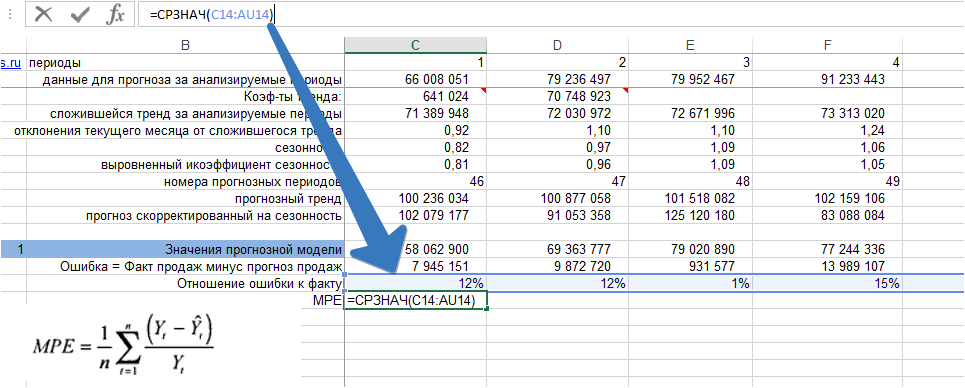
3. Рассчитываем среднее значение % ошибки — MPE:

Мы видим, что средняя процентная ошибка у нас получилась -0,65% — это говорит о том, что модель прогноза в среднем дает завышенные прогноза на 0,65%:

Скачайте файл с примером расчета ошибки MPE в Excel.

Из данной статьи вы узнали, для чего использовать среднюю процентную ошибку прогноза — MPE и как ее рассчитать в Excel.

Если у вас остались вопросы, пожалуйста, задавайте в комментариях, буду рад помочь!

Статья полезная? Поделитесь с друзьями

In statistics, the mean percentage error (MPE) is the computed average of percentage errors by which forecasts of a model differ from actual values of the quantity being forecast.

The formula for the mean percentage error is:

where a_t is the actual value of the quantity being forecast, f_t is the forecast, and n is the number of different times for which the variable is forecast.

Because actual rather than absolute values of the forecast errors are used in the formula, positive and negative forecast errors can offset each other; as a result, the formula can be used as a measure of the bias in the forecasts.

A disadvantage of this measure is that it is undefined whenever a single actual value is zero.

See also[edit]

• Percentage error
• Mean absolute percentage error
• Mean squared error
• Mean squared prediction error
• Minimum mean-square error
• Squared deviations
• Peak signal-to-noise ratio
• Root mean square deviation
• Errors and residuals in statistics

References[edit]

• Khan, Aman U.; Hildreth, W. Bartley (2003). Case studies in public budgeting and financial management. New York, N.Y: Marcel Dekker. ISBN 0-8247-0888-1.
• Waller, Derek J. (2003). Operations Management: A Supply Chain Approach. Cengage Learning Business Press. ISBN 1-86152-803-5.

Оценка точности прогноза

Для
оценки точности прогноза рассчитывают
3 показателя:

1. Среднее
   абсолютное отклонение (MAD
   – mean
   absolute
   derivation)
   

,

где
— фактическое
значение,

—
прогноз.

Среднее
абсолютное отклонение показывает, на
какое количество единиц (например,
количество пользователей, тыс.руб. и
т.п.) в среднем отклонялся в большую или
меньшую сторону наш прогноз. Позволяет
определить ошибку в конкретных единицах

1. Среднеквадратическая
   ошибка (MSE
   — mean
   square
   error)
   является одной из определяющих, т.к.
   позволяет усиливать наиболее значимые
   ошибки.

Характеризует
вариабельность отклонений в течении
рассматриваемого периода.

1. Средняя
   процентная ошибка
   (MPE
   – mean
   percentage
   error)
   позволяет оценить возможное смещение
   прогноза, является ли прогноз
   переоценивающим или недооценивающим.

,

=
S
+ T

В
случае несмещенного прогноза средняя
процентная ошибка близка 0.

Если
MPE
<0,
то это значит, что прогноз завышен или,
иначе говоря, он является переоценивающим

В
противном случае (MPE
>0),
то прогноз является недооценивающим.

Применение
мультипликативных моделей обусловлено
тем, что в некоторых временных рядах
значение сезонной компоненты представляет
собой определенную долю трендового
значения.

Выбор уровня детализации объектов прогнозирования

Один
из наиболее сложных вопросов в области
прогнозирования заключается в выборе
объекта исследования и уровня детализации.
При этом необходимо определить будут
ли прогнозироваться обобщающие
показатели, характеризующие финансовый
результат организации или необходимо
составлять прогнозы факторных переменных.

Безусловно,
детальное прогнозирование – это
достаточно трудоемкая задача, но без
этого невозможно построить точный
прогноз. Декомпозиция позволяет лучше
учесть влияние факторов внешней среды
и достаточно быстро пересчитывать
прогноз при изменении ситуации.

Встает
вопрос:

надо
ли строить прогноз по всем продуктам и
по всем клиентам или нет?

Для
ответа на этот вопрос может быть
использовано правило Парето.

Итальянский экономист и социолог Вильфредо Парето в 1897 году сформулировал эмпирический принцип (т.е. основанный на опыте), получивший название правило Парето. Парето изучал закономерности накопления и распределения материальных благ. Рассчитывая налоги для маленького города Палермо (Италия) установил, что у 20%-ти населения г.Палермо сосредоточено 80% денежных средств этого города.

Позже
эту зависимость подтвердили и для других
случайных цифр. И она получила название
Правила Парето или правила 20/80.

Было
установлено, что:

• 20%
  клиентов приносят компании 80% дохода,

• 20%
  компаний обеспечивают 80% налоговых
  поступлений в бюджет,

• на
  20% банков в России приходится 80% совокупных
  банковских активов.

• 20%
  времени менеджеры тратят на выполнение
  80%-ти общего объема работы,

• 20%
  продуктов приносят компании 80% доходов.

Как
только появляется массив данных,
включающий более 300 случайных измерений,
то они пытаются преломиться именно в
это соотношение.

В общем случае правило Парето формулируется так: 20% причин отвечают за 80% следствий.

Соответственно,
чтобы построить достаточно точный
прогноз, мы должны уделить особое
внимание лишь небольшой части товаров
(20%),а остальные 80% товаров можно
прогнозировать общим массивом без
декомпозиции и на точность прогноза
это серьезно не повлияет.

Для
выбора уровня детализации могут быть
использованы метод АВС и XYZ-анализа.

Метод
АВС-анализа основан на делении определенной
совокупности объектов по удельному
весу каждой группы, определяемому по
тому или иному выбранному показателю.
АВС-анализ основан на принципе Парето,
который означает, что 20% усилий дают 80%
результата, а остальные 80% усилий — лишь
20% результата.

Число
групп при проведении АВС-анализа может
быть любым, но наибольшее распространение
получило деление рассматриваемой
совокупности на три группы: А, В и С
(75:20:5), чем и обусловлено название метода
(ABC-Analysis).

Группа
А
включает незначительное число объектов
с высоким уровнем удельного веса по
выбранному показателю,
группа В
— среднее число объектов со средним
уровнем удельного веса по выбранному
показателю, группа
С
— большое число объектов с незначительной
величиной удельного веса по выбранному
показателю.

Экономический
смысл применения АВС-анализа в прогнозных
исследованиях сводится к сокращению
трудоемкости. Необходимо наиболее
тщательным образом прогнозировать
товары и услуги, относящиеся к группе
А. Таким образом может быть достигнут
максимальный эффект при минимальных
затратах.

Алгоритм
проведения АВС-анализа может быть
представлен в виде следующего алгоритма:

1. Определение
   цели анализа

2. Определение
   объектов анализа

3. Определение
   параметра для дифференциации объектов

4. Сортировка
   объектов анализа в порядке убывания
   значения параметра.

5. Деление
   на группы А, В и С.

Для
определения принадлежности выбранного
объекта к группе необходимо:

• определить
  долю каждого объекта,

• рассчитать
  кумулятивную долю,

• присвоить
  значения групп выбранным объектам.

1. Интерпретация
   результатов

Для
выделения групп объектов (А, В, С) могут
быть использованы различные подходы,
наиболее распространенными же являются
эмпирический подход и метод касательных.

Эмпирический
подход
заключается в разделении объектов на
группы на основе усредненных результатов
ранее проведенных исследований, наиболее
распространенным является разделение
на группы, представленные в таблице

Таблица
— Разбиение объектов анализа на группы

Наименование группы	Характеристика диапазона
Группа А	включает примерно 15% объектов, которые определяют 75% результата.
Группа В	35% объектов, которые обеспечивают до 20% результата
Группа С	около 50% объектов, которые обеспечивают 5% результата

Для
разбиения на группы также может быть
использован метод
касательных,
предложенный Лукинским В.С. Предполагает
выполнение следующие последовательности
действий:

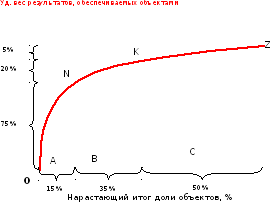
Этап
1 — На основе данных таблицы отсортированной
по убыванию построим кумулятивную
кривую.

Этап
2 – Соединим начало и окончание графика
прямой ОZ.

Этап
3 – Проведем касательную к кривой АВС,
параллельную прямой ОZ.

Точка
касания N
разделит группы А и В.

Этап
4 — Теперь соединим точки N
и Z
и проведем касательную к кривой
АВС-анализа, параллельную NZ.
Точка касания K
разделяет группы В и С.

Преимущество
метода в его гибкости, простоте и
наглядности. Недостатком можно назвать
сложность его автоматизации.

Рисунок
– Графическая иллюстрация метода
касательных

Одновременно
с АВС используется XYZ-анализ.

Основная
идея XYZ-анализа
состоит в группировании объектов по
стабильности спроса, оцениваемого
коэффициентом вариации. Коэффициент
вариации рассчитывается по формуле:

,

В
качестве параметра как правила выступает
объем продаж. Результатом XYZ
–анализа является группировка товаров
по трем категориям, исходя из стабильности
их поведения:

• категория
  Х
  – это группа товаров, характеризующиеся
  стабильной величиной потребления и
  высокой степенью прогнозирования.
  Коэффициент
  вариации не превышает 10%;

• категория
  Y
  включает объекты с колебанием продаж
  от 10 до 25%;

• к
  категории
  Z
  относятся объекты с нерегулярным
  спросом, значение коэффициента вариации
  по которым превышает 25%.

Объединение
результатов АВС и XYZ-анализа
позволяет сформировать эффективные
решения для каждой типовой группы. Для
прогнозирования спроса на товары групп
АХ, ВХ и СХ рекомендуется использовать
количественные методы. Группы АY,
BY,
CY
характеризуются нерегулярным спросом,
что обуславливает необходимость
использования комбинированных методик
прогнозирования, основанных на сочетании
математических подходов и
интуитивно-логического анализа,
прогнозирование объектов категорий
AZ,
BZ,
CZ
целесообразно применять экспертный
подход.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Ошибка прогнозирования: виды, формулы, примеры

Ошибка прогнозирования — это такая величина, которая показывает, как сильно прогнозное значение отклонилось от фактического. Она используется для расчета точности прогнозирования, что в свою очередь помогает нам оценивать как точно и корректно мы сформировали прогноз. В данной статье я расскажу про основные процентные «ошибки прогнозирования» с кратким описанием и формулой для расчета. А в конце статьи я приведу общий пример расчётов в Excel. Напомню, что в своих расчетах я в основном использую ошибку WAPE или MAD-Mean Ratio, о которой подробно я рассказал в статье про точность прогнозирования, здесь она также будет упомянута.

В каждой формуле буквой Ф обозначено фактическое значение, а буквой П — прогнозное. Каждая ошибка прогнозирования (кроме последней!), может использоваться для нахождения общей точности прогнозирования некоторого списка позиций, по типу того, что изображен ниже (либо для любого другого подобной детализации):

Алгоритм для нахождения любой из ошибок прогнозирования для такого списка примерно одинаковый: сначала находим ошибку прогнозирования по одной позиции, а затем рассчитываем общую. Итак, основные ошибки прогнозирования!

---

MPE — Mean Percent Error

MPE — средняя процентная ошибка прогнозирования. Основная проблема данной ошибки заключается в том, что в нестабильном числовом ряду с большими выбросами любое незначительное колебание факта или прогноза может значительно поменять показатель ошибки и, как следствие, точности прогнозирования. Помимо этого, ошибка является несимметричной: одинаковые отклонения в плюс и в минус по-разному влияют на показатель ошибки.

1. Для каждой позиции рассчитывается ошибка прогноза (из факта вычитается прогноз) — Error
2. Для каждой позиции рассчитывается процентная ошибка прогноза (ошибка прогноза делится на фактический показатель) — Percent Error
3. Находится среднее арифметическое всех процентных ошибок прогноза (процентные ошибки суммируются и делятся на количество) — Mean Percent Error

---

MAPE — Mean Absolute Percent Error

MAPE — средняя абсолютная процентная ошибка прогнозирования. Основная проблема данной ошибки такая же, как и у MPE — нестабильность.

1. Для каждой позиции рассчитывается абсолютная ошибка прогноза (прогноз вычитается из факта по модулю) — Absolute Error
2. Для каждой позиции рассчитывается абсолютная процентная ошибка прогноза (абсолютная ошибка прогноза делится на фактический показатель) — Absolute Percent Error
3. Находится среднее арифметическое всех абсолютных процентных ошибок прогноза (абсолютные процентные ошибки суммируются и делятся на количество) — Mean Absolute Percent Error

Вместо среднего арифметического всех абсолютных процентных ошибок прогноза можно использовать медиану числового ряда (MdAPE — Median Absolute Percent Error), она наиболее устойчива к выбросам.

---

WMAPE / MAD-Mean Ratio / WAPE — Weighted Absolute Percent Error

WAPE — взвешенная абсолютная процентная ошибка прогнозирования. Одна из «лучших ошибок» для расчета точности прогнозирования. Часто называется как MAD-Mean Ratio, то есть отношение MAD (Mean Absolute Deviation — среднее абсолютное отклонение/ошибка) к Mean (среднее арифметическое). После упрощения дроби получается искомая формула WAPE, которая очень проста в понимании:

1. Для каждой позиции рассчитывается абсолютная ошибка прогноза (прогноз вычитается из факта, по модулю) — Absolute Error
2. Находится сумма всех фактов по всем позициям  (общий фактический объем)
3. Сумма всех абсолютных ошибок делится на сумму всех фактов — WAPE

Данная ошибка прогнозирования является симметричной и наименее чувствительна к искажениям числового ряда.

Рекомендуется к использованию при расчете точности прогнозирования. Более подробно читать здесь.

---

RMSE (as %) / nRMSE — Root Mean Square Error

RMSE — среднеквадратичная ошибка прогнозирования. Примерно такая же проблема, как и в MPE и MAPE: так как каждое отклонение возводится в квадрат, любое небольшое отклонение может значительно повлиять на показатель ошибки. Стоит отметить, что существует также ошибка MSE, из которой RMSE как раз и получается путем извлечения корня. Но так как MSE дает расчетные единицы измерения в квадрате, то использовать данную ошибку будет немного неправильно.

1. Для каждой позиции рассчитывается квадрат отклонений (разница между фактом и прогнозом, возведенная в квадрат) — Square Error
2. Затем рассчитывается среднее арифметическое (сумма квадратов отклонений, деленное на количество) — MSE — Mean Square Error
3. Извлекаем корень из полученного результат — RMSE
4. Для перевода в процентную или в «нормализованную» среднеквадратичную ошибку необходимо:
   1. Разделить на разницу между максимальным и минимальным значением показателей
   2. Разделить на разницу между третьим и первым квартилем значений показателей
   3. Разделить на среднее арифметическое значений показателей (наиболее часто встречающийся вариант)

---

MASE — Mean Absolute Scaled Error

MASE — средняя абсолютная масштабированная ошибка прогнозирования. Согласно Википедии, является очень хорошим вариантом для расчета точности, так как сама ошибка не зависит от масштабов данных и является симметричной: то есть положительные и отрицательные отклонения от факта рассматриваются в равной степени.

Важно! Если предыдущие ошибки прогнозирования мы могли использовать для нахождения точности прогнозирования некого списка номенклатур, где каждой из которых соответствует фактическое и прогнозное значение (как было в примере в начале статьи), то данная ошибка для этого не предназначена: MASE используется для расчета точности прогнозирования одной единственной позиции, основываясь на предыдущих показателях факта и прогноза, и чем больше этих показателей, тем более точно мы сможем рассчитать показатель точности. Вероятно, из-за этого ошибка не получила широкого распространения.

Здесь данная формула представлена исключительно для ознакомления и не рекомендуется к использованию.

Суть формулы заключается в нахождении среднего арифметического всех масштабированных ошибок, что при упрощении даст нам следующую конечную формулу:

Также, хочу отметить, что существует ошибка RMMSE (Root Mean Square Scaled Error — Среднеквадратичная масштабированная ошибка), которая примерно похожа на MASE, с теми же преимуществами и недостатками.

---

Это основные ошибки прогнозирования, которые могут использоваться для расчета точности прогнозирования. Но не все! Их очень много и, возможно, чуть позже я добавлю еще немного информации о некоторых из них. А примеры расчетов уже описанных ошибок прогнозирования будут выложены через некоторое время, пока что я подготавливаю пример, ожидайте.

Об авторе

HeinzBr

Автор статей и создатель сайта SHTEM.RU

Рассмотрим часто используемые показатели производительности.
Введем следующие обозначения:
$y_{t}$ — представляет фактическое значение в момент времени t.
$f_{t}$ — представляет собой прогнозируемое значение (расчетное значение) в момент времени t
$e_{t}=y_{t}-f_{t}$ — представляет собой ошибку прогноза (остаточную) в момент времени t
n — количество наблюдений

Средняя ошибка прогноза (mean forecast error — MFE)

$$MFE=\frac{1}{n} \sum_{1}^{n}e_{t}$$


— среднее значение всех ошибок прогноза, величина и знак показывает смещение прогноза относительно фактических значений, если равно нулю, смещения нет
Зависит от масштаба измерений и преобразования данных. 
Не наказывает экстремальные значения ошибок.

Средняя абсолютная ошибка прогноза ( mean absolute error — MAE)

$$MAE=\frac{1}{n}\sum_{1}^{n}\left | e_{t} \right |$$


среднее значение всех ошибок прогноза по абсолютной величине, показывает на величину общей погрешности
Желательны небольшие значения MAE.
Зависит от масштаба измерений и преобразования данных.

Не наказывает экстремальные значения ошибок.


Средняя процентная ошибка (mean percentage error  — MPE)


$$MPE=\frac{1}{n} \sum_{1}^{n}\left ( \frac{e_{t}}{y_{t}} \right )*100$$


средний процент ошибок, величина и знак показывает смещение прогноза относительно фактических значений в процентах

Желательно, чтобы MPE был близок к нулю.


Средняя абсолютная процентная ошибка (mean absolute percentage error — MAPE)


$$MAPE=\frac{1}{n} \sum_{1}^{n}\left | \frac{e_{t}}{y_{t}} \right |*100$$


средняя абсолютная ошибка в процентах без знака ошибки.
Зависит от преобразование данных, но не от масштаба измерений

Не наказывает экстремальные значения ошибок.


Среднеквадратичная ошибка (mean squared error — MSE)


$$MSE=\frac{1}{n}\sum_{1}^{n}e_{t}^{2}$$


средняя квадратичная ошибка, подчеркивает большие ошибки за счет возведения каждой ошибки в квадрат.

Зависит от масштаба измерений и преобразования данных.

Сумма квадратов ошибок (sum of squared estimate of errors — SSE)

$$SSE=\sum_{1}^{n}e_{t}^{2}$$

сумма квадратов ошибок прогноза.

Свойства такие же, как и у MSE.



Среднеквадратичная ошибка со знаком (signed mean squared error — SMSE)


$$SMSE=\frac{1}{n} \sum_{1}^{n}\left ( \frac{e_{t}}{\left | e_{t} \right |} \right )*e_{t}^{2}$$




тоже, что и MSE только с учетом знака.




U-статистика Тейла


$$U=\frac{\sqrt{\frac{1}{n}\sum_{1}^{n}e_{t}^{2}}}{\sqrt{\frac{1}{n}\sum_{1}^{n}f_{t}^{2}}+\sqrt{\frac{1}{n}\sum_{1}^{n}y_{t}^{2}}}$$



Диапазоны 0 ≤ U ≤ 1
U = 0 означает идеальный прогноз.
Зависит от масштаба измерений и преобразования данных.
Индекс Тейла показывает степень схожести временных рядов  и чем ближе он к нулю, тем ближе сравниваемые ряды.

Корень среднеквадратичной ошибки (root mean squared error — RMSE)


$$RMSE=\sqrt{MSE}=\sqrt{\frac{1}{n}\sum_{1}^{n}e_{t}^{2}}$$



Такие же свойства как MSE


Нормированная среднеквадратичная ошибка (normalized mean square error—NMSE)


$$NMSE=\frac{MSE}{\sigma ^{2}}=\frac{1}{\sigma ^{2}n}\sum_{1}^{n}e_{t}^{2}$$




Сбалансированный ошибка , характеризующая точность прогноза.
Чем меньше, тем лучше.



Проверим эти метрики на примере смоделированных прогнозов. Для этого берем датафрейм с месячными показателями посещаемости магазина одежды за пять лет с января 2015 по декабрь 2019 годы.


head(df)


# A tibble: 6 x 3
   year month visit
  <dbl> <dbl> <dbl>
1  2015     1 14328
2  2015     2  6974
3  2015     3 10174
4  2015     4  8994
5  2015     5 10715

6  2015     6  9381


str(df)


Classes ‘tbl_df’, ‘tbl’ and ‘data.frame’: 60 obs. of  3 variables:
 $ year : num  2015 2015 2015 2015 2015 …
 $ month: num  1 2 3 4 5 6 7 8 9 10 …

 $ visit: num  14328 6974 10174 8994 10715 


С имитируем три три прогноза с помощью трех последовательностей мультипликативной случайной составляющей, представляющей собой случайную величину с нормальным распределением с показателями 𝛔=0.95 и sd=0.05 (прогноз с занижением),𝛔=1.05 и sd=0.05 (прогноз с завышением),𝛔=1.0 и sd=0.05 (идеальный прогноз)


df$visit_n <- df$visit*rnorm(60,0.95,0.05)
df$visit_p <- df$visit*rnorm(60,1.05,0.05)
df$visit_z <- df$visit*rnorm(60,1.00,0.05)



round(colSums(df[,c(3:6)]),0)


  visit      visit_n    visit_p visit_z 

 592714  563092  626292  594431 


Как видим, суммарное количество посетителей по полученным временным рядам получилось, как и было задумано. Сделаем из полученного датафрейма объект класса ts и выведем его график.


ts_month <- ts(data = df_month[,c(3:6)],
                start = c(2015, 1),
                frequency = 12)


autoplot(ts_month)

 Можно переходить к расчету ошибок прогноза.


mfe <- df %>%
  summarise(mfe_n = mean(visit_n-visit),
            mfe_p = mean(visit_p-visit),
            mfe_z = mean(visit_z-visit))


mae <- df %>%
  summarise(mae_n = mean(abs(visit_n-visit)),
            mae_p = mean(abs(visit_p-visit)),
            mae_z = mean(abs(visit_z-visit)))


mpe <- df %>%
  summarise(mpe_n = mean((visit_n-visit)/visit*100),
            mpe_p = mean((visit_p-visit)/visit*100),
            mpe_z = mean((visit_z-visit)/visit*100))


mape <- df %>%
  summarise(mape_n = mean(abs(visit_n-visit)/visit*100),
            mape_p = mean(abs(visit_p-visit)/visit*100),
            mape_z = mean(abs(visit_z-visit)/visit*100))
mse <- df %>%
  summarise(mse_n = mean((visit_n-visit)^2),
            mse_p = mean((visit_p-visit)^2),
            mse_z = mean((visit_z-visit)^2))


sse <- df %>%
  summarise(sse_n = sum((visit_n-visit)^2),
            sse_p = sum((visit_p-visit)^2),
            sse_z = sum((visit_z-visit)^2))


smse <- df %>%
  summarise(smse_n = mean(sign(visit_n-visit)*(visit_n-visit)^2),
            smse_p = mean(sign(visit_p-visit)*(visit_p-visit)^2),
            smse_z = mean(sign(visit_z-visit)*(visit_z-visit)^2))


ut <- df %>%
  summarise(ut_n = sqrt(mean((visit_n-visit)^2))/(sqrt(mean(visit_n^2))+sqrt(mean(visit^2))),
            ut_p = sqrt(mean((visit_p-visit)^2))/(sqrt(mean(visit_p^2))+sqrt(mean(visit^2))),
            ut_z = sqrt(mean((visit_z-visit)^2))/(sqrt(mean(visit_z^2))+sqrt(mean(visit^2))))


rmse <- df %>%
  summarise(rmse_n = sqrt(mean((visit_n-visit)^2)),
            rmse_p = sqrt(mean((visit_p-visit)^2)),
            rmse_z = sqrt(mean((visit_z-visit)^2)))


nmse <- df %>%
  summarise(nmse_n = mean((visit_n-visit)^2)/var(visit_n),
            nmse_p = mean((visit_p-visit)^2)/var(visit_p),
            nmse_z = mean((visit_z-visit)^2)/var(visit_z))

round(df_err,2)


      mfe       mae         mpe    mape      mse            sse            smse          ut      rmse       nmse
n -493.876  538.623   -5.19   5.627   462593.4   27755605   -454568.44   0.034   680.142   0.102
p  660.635  700.996    6.38   6.840   760386.2   45623174    746613.43    0.042   872.001   0.128
z  -24.242   394.060    0.02   3.943   274906.5   16494390    -68096.34     0.026   524.315   0.068




Оценим величину разброса значений оценок через коэффициент вариации


round(sapply(df_err, function(x){sd(x)/mean(x)}),2)


  mfe   mae   mpe   mape   mse   sse   smse    ut     rmse  nmse 

12.22  0.28   14.35   0.27     0.49   0.49   8.21    0.23   0.25    0.30 


Как видно, наименьшую вариацию показывает  u-статистика, напомним, что чем ближе она к нулю, тем точнее прогноз. На практике удобнее использовать MAPE как выражение ошибки в процентах без знака. Однако может быть интересно и MPE — ошибка в процентах со знаком, чтобы понимать величину и сторону смещения прогноза.