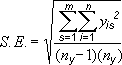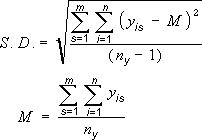Загрузить PDF
Загрузить PDF
В этой статье мы расскажем вам, как в Excel вычислить стандартную ошибку среднего. Для этого стандартное отклонение (σ) нужно разделить на квадратный корень (√) из размера выборки (N).
-
1
Запустите Excel. Нажмите на значок в виде белой буквы «Х» на зеленом фоне.
-
2
Откройте или создайте таблицу Excel. Чтобы открыть готовую таблицу с данными, нажмите «Открыть» на левой панели. Чтобы создать таблицу, нажмите «Создать» и введите данные.
-
3
Вычислите стандартное отклонение. Чтобы сделать это, нужно выполнить несколько действий, но в Excel можно просто ввести следующую формулу: =СТАНДОТКЛОН.В(''диапазон ячеек'').
- Например, если данные находятся в ячейках с A1 по A20, в пустой ячейке введите =СТАНДОТКЛОН.В(A1:A20), чтобы вычислить стандартное отклонение.
-
4
Введите формулу для вычисления стандартной ошибки среднего в пустой ячейке. Формула выглядит так:=СТАНДОТКЛОН.В(''диапазон ячеек'')/КОРЕНЬ(СЧЁТ("диапазон ячеек")).
- Например, если данные находятся в ячейках с A1 по A20, в пустой ячейке введите формулу =СТАНДОТКЛОН.В(A1:A20)/КОРЕНЬ(СЧЁТ(A1:A20)). Так вы вычислите стандартную ошибку среднего.
Реклама
Об этой статье
Эту страницу просматривали 35 211 раз.
Была ли эта статья полезной?
Главная » Microsoft Word » Графическая стандартная ошибка среднего в Excel — манекены 2020 — How to dou
Анализ НОРМАЛЬНОСТИ РАСПРЕДЕЛЕНИЯ | АНАЛИЗ ДАННЫХ #4
Когда вы создаете граф в Excel и ваши данные являются средствами, рекомендуется включить стандартную ошибку каждого значения на вашем графике. Это дает зрителю представление о распространении баллов вокруг каждого среднего.
Вот пример ситуации, когда это возникает. Данные являются (вымышленными) результатами тестов для четырех групп людей. Каждый заголовок столбца указывает количество времени подготовки для восьми человек в группе. Вы можете использовать графические возможности Excel для рисования графика. Поскольку независимая переменная является количественной, граф линии является подходящим.
Четыре группы, их средства, стандартные отклонения и стандартные ошибки. На графике показаны групповые средства.
Для каждой группы вы можете использовать AVERAGE для вычисления среднего и STDEV. S для вычисления стандартного отклонения. Вы можете рассчитать стандартную ошибку каждого среднего. Выберите ячейку B12, поэтому в поле формулы показано, что вы вычислили стандартную ошибку для столбца B по этой формуле:
= B11 / SQRT (COUNT (B2: B9))
Фокус в том, чтобы получить каждую стандартную ошибку в графике. В Excel 2016 это легко сделать, и оно отличается от предыдущих версий Excel. Начните с выбора графика. Это приведет к появлению вкладок Design and Format. Выберите
Дизайн | Добавить элемент диаграммы | Ошибка баров | Дополнительные параметры ошибок.
Путь к вставке баров ошибок.
В меню «Бары ошибок» вы должны быть осторожны. Один из вариантов — стандартная ошибка. Избегай это. Если вы считаете, что этот выбор указывает Excel на стандартную ошибку каждого значения на графике, будьте уверены, что Excel не имеет абсолютно никакого представления о том, о чем вы говорите. Для этого выбора Excel вычисляет стандартную ошибку набора из четырех средств — не стандартную ошибку в каждой группе.
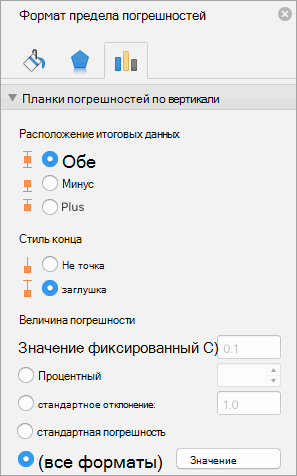
Дополнительные параметры панели ошибок являются подходящим выбором. Откроется панель «Формат ошибок».
Панель «Ошибки формата».
В области «Направление» панели выберите переключатель рядом с «Оба», а в области «Стиль конца» выберите переключатель рядом с «Кап».
Один выбор в области «Сумма ошибки» — это стандартная ошибка. Избегайте этого. Это не означает, что Excel помещает стандартную ошибку каждого среднего на график.
Прокрутите вниз до области «Сумма ошибки» и выберите переключатель рядом с «Пользовательский». Это активирует кнопку «Укажите значение». Нажмите эту кнопку, чтобы открыть диалоговое окно «Пользовательские ошибки». С помощью курсора в поле «Положительное значение ошибки» выберите диапазон ячеек, который содержит стандартные ошибки ($ B $ 12: $ E $ 12). Вставьте вкладку «Отрицательная ошибка» и сделайте то же самое.
Диалоговое окно «Нестандартные ошибки».
Это поле Negative Error Value может дать вам небольшую проблему. Перед тем, как вводить диапазон ячеек, убедитесь, что он очищен от значений по умолчанию.
Нажмите «ОК» в диалоговом окне «Нестандартные ошибки» и закройте диалоговое окно «Формат ошибок», и график будет выглядеть следующим образом.
График группы означает, включая стандартную ошибку каждого среднего.
Сводка
В этой статье описывается функция ДОВЕРИТЕЛЬных СОВПАДЕНИй в Microsoft Office Excel 2003 и Microsoft Office Excel 2007, показано, как используется функция, и сравниваются результаты функции для Excel 2003 и для Excel 2007 с результатами более ранней достоверности. версиях Excel.
Значение доверительного интервала часто ошибочно интерпретируется, и мы попробуем получить объяснение допустимых и недопустимых операторов, которые можно выполнить после определения ДОСТОВЕРНОсти данных.
Дополнительные сведения
Функция ДОВЕРИТ (альфа, Сигма, н) возвращает значение, которое можно использовать для создания доверительного интервала для среднего Генеральной совокупности. Доверительный интервал — это диапазон значений, которые центрируются по известной выборочной среднему значению. Наблюдение в образце предполагается из нормального распределения со стандартным отклонением, Сигма, а количество наблюдений в примере равно n.
Синтаксис
Параметры: альфа — вероятность и 0
Пример использования
Представим, что баллы для (IQ) для интеллекта должны следовать нормальному распределению со стандартным отклонением 15. Вы протестируете Икс для примера из 50 учащихся в местном учебном заведении и получите выборочное среднее арифметическое 105. Вы хотите вычислить доверительный интервал 95% для среднего Генеральной совокупности. Доверительный интервал 95% или 0,95 соответствует альфа = 1 – 0,95 = 0,05.
Чтобы продемонстрировать функцию достоверности, создайте пустой лист Excel, Скопируйте приведенную ниже таблицу, а затем выберите ячейку a1 на пустом листе Excel. В меню Правка выберите команду Вставить.
Примечание: В Excel 2007 нажмите кнопку Вставить в группе буфер обмена на вкладке Главная .
Записи в таблице ниже заполняют ячейки a1: B7 на листе.
= ДОВЕРИТ (B1; B2; B3)
= НОРМСТОБР (1-B1/2) * B2/SQRT (B3)
После вставки этой таблицы на новый лист Excel нажмите кнопку Параметры вставки , а затем выберите пункт в соответствии с форматированием конечногофрагмента.
Выделив вставляемый диапазон, наведите указатель на пункт столбец в меню Формат , а затем выберите пункт Автоподбор по выделению.
Примечание: В Excel 2007 с выделенным диапазоном ячеек в группе ячейки на вкладке Главная нажмите кнопку Формат и выберите команду Автоподбор ширины столбца.
В ячейке A6 показано значение достоверности. В ячейке A7 показано одно и то же значение, так как при вызове метода ДОВЕРИТ (Alpha; Сигма; n) возвращаются результаты вычислений.
NORMSINV(1 – alpha/2) * sigma / SQRT(n)
Никаких изменений не было сделано, но функция НОРМСТОБР была улучшена в Microsoft Excel 2002, а затем в Excel 2002 и Excel 2007 было внесено больше улучшений. Таким образом, точность может возвращать другие (и улучшенные) результаты в этих более поздних версиях Excel, так как точное СОВПАДЕНИе основывается на НОРМСТОБР.
Это не значит, что в более ранних версиях Excel вы должны потерять уверенность. Неточности в НОРМСТОБР обычно произошел для значений аргумента очень близко к 0 или очень близко к 1. На практике альфа-канал обычно имеет значение 0,05, 0,01 или, возможно, 0,001. Значения Alpha должны быть гораздо меньше, чем, например 0,0000001, до тех пор, пока не будут замечены ошибки округления в НОРМСТОБР.
Примечание: Ознакомьтесь со статьей «НОРМСТОБР» для обсуждения различий вычислений в НОРМСТОБР.
Чтобы получить дополнительные сведения, щелкните следующий номер статьи базы знаний Майкрософт:
826772 Статистические функции Excel: НОРМСТОБР
Интерпретация результатов достоверности
Для Excel 2003 и Excel 2007 файл справки Excel обновлен, так как все предыдущие версии файла справки дали ошибочные рекомендации по интерпретации результатов. В примере «допустим, что в нашем примере для пользователей 50, средняя продолжительность поездки на работу составляет 30 минут со стандартным отклонением Генеральной совокупности 2,5. Мы можем получить 95% уверенности в том, что среднее Генеральной совокупности находится в интервале 30 +/-0,692951 «где 0,692951 — значение, возвращаемое ДОСТОВЕРНОстью (0,05, 2,5, 50).
В этом примере «заключение» считывает «средняя продолжительность поездки на работу равняется 30 ± 0,692951 минутам или 29,3 – 30,7 минут». Предполагается, что это также является оператором для среднего Генеральной совокупности в интервале [30 – 0,692951, 30 + 0,692951] с вероятностью 0,95.
Перед проведением эксперимента, который выдает данные для этого примера, классическое статистиЦиан (в отличие от Байесиан статистиЦиан) может не делать никаких инструкций по распространению вероятности для среднего Генеральной совокупности. Вместо этого классическое статистиЦиан работает с тестированием гипотез.
Например, классическое статистиЦиан может попытаться выполнить двустороннее Тестирование гипотезы на основе суппоситион нормального распределения с известным стандартным отклонением (например, 2,5), определенным предварительно выбранным значением среднего значения Генеральной совокупности, μ0 и предварительно выбранный уровень значимости (например, 0,05). Результат теста будет основываться на значении наблюдаемого выборочного среднего (например, 30) и нулевой гипотезы о том, что μ0 может быть отклонено на уровне 0,05, если наблюдаемый выборочный пример был слишком далеко от μ0 в обоих направлениях. Если пустая гипотеза отклонена, то интерпретация примера означает, что все, что далеко или дальше от μ0, появлялось бы менее чем на 5% времени в рамках суппоситион, что μ0 является истинным средним Генеральной совокупности. Проведя этот тест, классическое статистиЦиан по-прежнему не может делать никаких инструкций по выборке вероятности для среднего Генеральной совокупности.
Байесиан статистиЦиан, с другой стороны, будет начинаться с предполагаемого распределения вероятности для среднего Генеральной совокупности (именуемого распространением приори), который будет собирать экспериментальные доказательства точно так же, как и классический статистиЦиан, и использовать это свидетельство. чтобы изменить его распределение вероятности для среднего Генеральной совокупности и, таким образом, получить постериори распределение. Excel не предоставляет статистических функций, которые помогут вам Байесиан статистиЦиан. Статистические функции Excel предназначены для использования в классических статистиЦианс.
Доверительные интервалы связаны с проверками гипотез. При использовании экспериментального свидетельства доверительный интервал делает более четким оператором для значений гипотетического математического Генеральной совокупности μ0, который бы мог бы принимать признание пустого предположения о том, что среднее Генеральной совокупности — μ0, и значения μ0, которые выдают отклонения. пустого предположения о том, что среднее Генеральной совокупности — μ0. Классическое статистиЦиан не может делать никаких инструкций о том, что среднее значение Генеральной совокупности попадает в определенный интервал времени, так как она не создает приори допущений об этом распространении и предполагается, что оно было бы обязательным, если бы оно было Используйте экспериментальные доказательства для изменения.
Ознакомьтесь со связью между тестами и доверительными интервалами с помощью примера в начале этого раздела. Связь между ДОСТОВЕРНОстью и НОРМСТОБР, которая указана в последнем разделе, имеет следующие возможности:
CONFIDENCE(0.05, 2.5, 50) = NORMSINV(1 – 0.05/2) * 2.5 / SQRT(50) = 0.692951
Так как выборочное среднее — 30, доверительный интервал составляет 30 +/-0,692951.
Теперь рассмотрим двустороннюю проверку с уровнем значимости 0,05, как описано выше, которое предполагает нормальное распределение со стандартным отклонением 2,5, а также выбор размера 50 и определенного среднего значения для Генеральной совокупности, μ0. Если это среднее значение истинной Генеральной совокупности, то выборочное среднее будет получено из нормального распределения со средним значением μ0 и стандартным отклонением, 2,5/SQRT (50). Это распределение является симметричным для μ0 и вы хотите отклонить пустую гипотезу, если ABS (выборочное среднее — μ0) > какое-либо пороговое значение. Значение порогового значения может быть таким, что если μ0 является истинным средним заполнением, то есть значение выборочное среднее-μ0, превышающее эту отсечение или значение μ0 — выборочное среднее выше, чем эта отсечение, будет возникать с вероятностью 0,05/2. Это пороговое значение:
NORMSINV(1 – 0.05/2) * 2.5/SQRT(50) = CONFIDENCE(0.05, 2.5, 50) = 0. 692951
Поэтому отклоните пустую гипотезу (среднее заполнение = μ0), если выполняется одно из следующих условий:
выборочное среднее — μ0 > 0. 692951
0 — выборочное среднее > 0. 692951
Поскольку выборочное среднее = 30 в нашем примере, эти два оператора становятся следующими операторами:
30-μ0 > 0. 692951
μ0 – 30 > 0. 692951
Переписывая их так, чтобы только μ0 в левой части выходили следующие инструкции:
μ0 30 + 0. 692951
Это именно те значения μ0, которые не входят в доверительный интервал [30 – 0,692951, 30 + 0,692951]. Таким образом, доверительный интервал [30 – 0,692951, 30 + 0,692951] содержит такие значения μ0, где нулевая гипотеза, которой μ0 Генеральной совокупности, не будет отклоняться, получая пример свидетельства. Для значений μ0 за пределами этого интервала значение NULL свидетельствует о том, что основание Генеральной совокупности — μ0 было отклонено при выборке свидетельства.
Заключения
Неточности в более ранних версиях Excel обычно возникают для очень мелких и очень больших значений «p» в НОРМСТОБР (p). УВЕРЕННОСТЬ оцениваются с помощью вызова НОРМСТОБР (p), поэтому точность НОРМСТОБР является потенциальной проблемой для пользователей с уверенностью. Однако значения p, которые используются в упражнениях, вряд ли будут достаточно значительны для того, чтобы вызвать существенные ошибки округления в НОРМСТОБР, и производительность УВЕРЕНности не должна быть важна для пользователей какой-либо версии Excel.
В этой статье рассказывается о том, как интерпретировать результаты УВЕРЕНности. Другими словами, мы задавали вопрос «Каково значение доверительного интервала?» Доверительные интервалы часто непонятны. К сожалению, файлы справки Excel во всех версиях Excel, более ранних, чем Excel 2003, были внесены в это неправильное понимание. Улучшен файл справки Excel 2003.
Примечание: Эта страница переведена автоматически, поэтому ее текст может содержать неточности и грамматические ошибки. Для нас важно, чтобы эта статья была вам полезна. Была ли информация полезной? Для удобства также приводим ссылку на оригинал (на английском языке).
Стандартная ошибка в Microsoft Excel
Стандартная ошибка или, как часто называют, ошибка средней арифметической, является одним из важных статистических показателей. С помощью данного показателя можно определить неоднородность выборки. Он также довольно важен при прогнозировании. Давайте узнаем, какими способами можно рассчитать величину стандартной ошибки с помощью инструментов Microsoft Excel.
Расчет ошибки средней арифметической
Одним из показателей, которые характеризуют цельность и однородность выборки, является стандартная ошибка. Эта величина представляет собой корень квадратный из дисперсии. Сама дисперсия является средним квадратном от средней арифметической. Средняя арифметическая вычисляется делением суммарной величины объектов выборки на их общее количество.
В Экселе существуют два способа вычисления стандартной ошибки: используя набор функций и при помощи инструментов Пакета анализа. Давайте подробно рассмотрим каждый из этих вариантов.
Способ 1: расчет с помощью комбинации функций
Прежде всего, давайте составим алгоритм действий на конкретном примере по расчету ошибки средней арифметической, используя для этих целей комбинацию функций. Для выполнения задачи нам понадобятся операторы СТАНДОТКЛОН.В, КОРЕНЬ и СЧЁТ.
Для примера нами будет использована выборка из двенадцати чисел, представленных в таблице.
- Выделяем ячейку, в которой будет выводиться итоговое значение стандартной ошибки, и клацаем по иконке «Вставить функцию».
Открывается Мастер функций. Производим перемещение в блок «Статистические». В представленном перечне наименований выбираем название «СТАНДОТКЛОН.В».
Запускается окно аргументов вышеуказанного оператора. СТАНДОТКЛОН.В предназначен для оценивания стандартного отклонения при выборке. Данный оператор имеет следующий синтаксис:
«Число1» и последующие аргументы являются числовыми значениями или ссылками на ячейки и диапазоны листа, в которых они расположены. Всего может насчитываться до 255 аргументов этого типа. Обязательным является только первый аргумент.
Итак, устанавливаем курсор в поле «Число1». Далее, обязательно произведя зажим левой кнопки мыши, выделяем курсором весь диапазон выборки на листе. Координаты данного массива тут же отображаются в поле окна. После этого клацаем по кнопке «OK».
В ячейку на листе выводится результат расчета оператора СТАНДОТКЛОН.В. Но это ещё не ошибка средней арифметической. Для того, чтобы получить искомое значение, нужно стандартное отклонение разделить на квадратный корень от количества элементов выборки. Для того, чтобы продолжить вычисления, выделяем ячейку, содержащую функцию СТАНДОТКЛОН.В. После этого устанавливаем курсор в строку формул и дописываем после уже существующего выражения знак деления (/). Вслед за этим клацаем по пиктограмме перевернутого вниз углом треугольника, которая располагается слева от строки формул. Открывается список недавно использованных функций. Если вы в нем найдете наименование оператора «КОРЕНЬ», то переходите по данному наименованию. В обратном случае жмите по пункту «Другие функции…».
Снова происходит запуск Мастера функций. На этот раз нам следует посетить категорию «Математические». В представленном перечне выделяем название «КОРЕНЬ» и жмем на кнопку «OK».
Открывается окно аргументов функции КОРЕНЬ. Единственной задачей данного оператора является вычисление квадратного корня из заданного числа. Его синтаксис предельно простой:
Как видим, функция имеет всего один аргумент «Число». Он может быть представлен числовым значением, ссылкой на ячейку, в которой оно содержится или другой функцией, вычисляющей это число. Последний вариант как раз и будет представлен в нашем примере.
Устанавливаем курсор в поле «Число» и кликаем по знакомому нам треугольнику, который вызывает список последних использованных функций. Ищем в нем наименование «СЧЁТ». Если находим, то кликаем по нему. В обратном случае, опять же, переходим по наименованию «Другие функции…».
В раскрывшемся окне Мастера функций производим перемещение в группу «Статистические». Там выделяем наименование «СЧЁТ» и выполняем клик по кнопке «OK».
Запускается окно аргументов функции СЧЁТ. Указанный оператор предназначен для вычисления количества ячеек, которые заполнены числовыми значениями. В нашем случае он будет подсчитывать количество элементов выборки и сообщать результат «материнскому» оператору КОРЕНЬ. Синтаксис функции следующий:
В качестве аргументов «Значение», которых может насчитываться до 255 штук, выступают ссылки на диапазоны ячеек. Ставим курсор в поле «Значение1», зажимаем левую кнопку мыши и выделяем весь диапазон выборки. После того, как его координаты отобразились в поле, жмем на кнопку «OK».
После выполнения последнего действия будет не только рассчитано количество ячеек заполненных числами, но и вычислена ошибка средней арифметической, так как это был последний штрих в работе над данной формулой. Величина стандартной ошибки выведена в ту ячейку, где размещена сложная формула, общий вид которой в нашем случае следующий:
Результат вычисления ошибки средней арифметической составил 0,505793. Запомним это число и сравним с тем, которое получим при решении поставленной задачи следующим способом.
Но дело в том, что для малых выборок (до 30 единиц) для большей точности лучше применять немного измененную формулу. В ней величина стандартного отклонения делится не на квадратный корень от количества элементов выборки, а на квадратный корень от количества элементов выборки минус один. Таким образом, с учетом нюансов малой выборки наша формула приобретет следующий вид:
Способ 2: применение инструмента «Описательная статистика»
Вторым вариантом, с помощью которого можно вычислить стандартную ошибку в Экселе, является применение инструмента «Описательная статистика», входящего в набор инструментов «Анализ данных» («Пакет анализа»). «Описательная статистика» проводит комплексный анализ выборки по различным критериям. Одним из них как раз и является нахождение ошибки средней арифметической.
Но чтобы воспользоваться данной возможностью, нужно сразу активировать «Пакет анализа», так как по умолчанию в Экселе он отключен.
-
После того, как открыт документ с выборкой, переходим во вкладку «Файл».
Далее, воспользовавшись левым вертикальным меню, перемещаемся через его пункт в раздел «Параметры».
Запускается окно параметров Эксель. В левой части данного окна размещено меню, через которое перемещаемся в подраздел «Надстройки».
В самой нижней части появившегося окна расположено поле «Управление». Выставляем в нем параметр «Надстройки Excel» и жмем на кнопку «Перейти…» справа от него.
Запускается окно надстроек с перечнем доступных скриптов. Отмечаем галочкой наименование «Пакет анализа» и щелкаем по кнопке «OK» в правой части окошка.
После выполнения последнего действия на ленте появится новая группа инструментов, которая имеет наименование «Анализ». Чтобы перейти к ней, щелкаем по названию вкладки «Данные».
После перехода жмем на кнопку «Анализ данных» в блоке инструментов «Анализ», который расположен в самом конце ленты.
Запускается окошко выбора инструмента анализа. Выделяем наименование «Описательная статистика» и жмем на кнопку «OK» справа.
Запускается окно настроек инструмента комплексного статистического анализа «Описательная статистика».
В поле «Входной интервал» необходимо указать диапазон ячеек таблицы, в которых находится анализируемая выборка. Вручную это делать неудобно, хотя и можно, поэтому ставим курсор в указанное поле и при зажатой левой кнопке мыши выделяем соответствующий массив данных на листе. Его координаты тут же отобразятся в поле окна.
В блоке «Группирование» оставляем настройки по умолчанию. То есть, переключатель должен стоять около пункта «По столбцам». Если это не так, то его следует переставить.
Галочку «Метки в первой строке» можно не устанавливать. Для решения нашего вопроса это не важно.
Далее переходим к блоку настроек «Параметры вывода». Здесь следует указать, куда именно будет выводиться результат расчета инструмента «Описательная статистика»:
- На новый лист;
- В новую книгу (другой файл);
- В указанный диапазон текущего листа.
Давайте выберем последний из этих вариантов. Для этого переставляем переключатель в позицию «Выходной интервал» и устанавливаем курсор в поле напротив данного параметра. После этого клацаем на листе по ячейке, которая станет верхним левым элементом массива вывода данных. Её координаты должны отобразиться в поле, в котором мы до этого устанавливали курсор.
Далее следует блок настроек определяющий, какие именно данные нужно вводить:
- Итоговая статистика;
- К-ый наибольший;
- К-ый наименьший;
- Уровень надежности.
Для определения стандартной ошибки обязательно нужно установить галочку около параметра «Итоговая статистика». Напротив остальных пунктов выставляем галочки на свое усмотрение. На решение нашей основной задачи это никак не повлияет.
После того, как все настройки в окне «Описательная статистика» установлены, щелкаем по кнопке «OK» в его правой части.
Как видим, в Экселе можно произвести расчет стандартной ошибки двумя способами: применив набор функций и воспользовавшись инструментом пакета анализа «Описательная статистика». Итоговый результат будет абсолютно одинаковый. Поэтому выбор метода зависит от удобства пользователя и поставленной конкретной задачи. Например, если ошибка средней арифметической является только одним из многих статистических показателей выборки, которые нужно рассчитать, то удобнее воспользоваться инструментом «Описательная статистика». Но если вам нужно вычислить исключительно этот показатель, то во избежание нагромождения лишних данных лучше прибегнуть к сложной формуле. В этом случае результат расчета уместится в одной ячейке листа.
Стандартная ошибка средней арифметической
Среднее арифметическое, как известно, используется для получения обобщающей характеристики некоторого набора данных. Если данные более-менее однородны и в них нет аномальных наблюдений (выбросов), то среднее хорошо обобщает данные, сведя к минимуму влияние случайных факторов (они взаимопогашаются при сложении).
Когда анализируемые данные представляют собой выборку (которая состоит из случайных значений), то среднее арифметическое часто (но не всегда) выступает в роли приближенной оценки математического ожидания. Почему приближенной? Потому что среднее арифметическое – это величина, которая зависит от набора случайных чисел, и, следовательно, сама является случайной величиной. При повторных экспериментах (даже в одних и тех же условиях) средние будут отличаться друг от друга.
Для того, чтобы на основе статистического анализа данных делать корректные выводы, необходимо оценить возможный разброс полученного результата. Для этого рассчитываются различные показатели вариации. Но то исходные данные. И как мы только что установили, среднее арифметическое также обладает разбросом, который необходимо оценить и учитывать в дальнейшем (в выводах, в выборе метода анализа и т.д.).
Интуитивно понятно, что разброс средней должен быть как-то связан с разбросом исходных данных. Основной характеристикой разброса средней выступает та же дисперсия.
Дисперсия выборочных данных – это средний квадрат отклонения от средней, и рассчитать ее по исходным данным не составляет труда, например, в Excel предусмотрены специальные функции. Однако, как же рассчитать дисперсию средней, если в распоряжении есть только одна выборка и одно среднее арифметическое?
Расчет дисперсии и стандартной ошибки средней арифметической
Чтобы получить дисперсию средней арифметической нет необходимости проводить множество экспериментов, достаточно иметь только одну выборку. Это легко доказать. Для начала вспомним, что средняя арифметическая (простая) рассчитывается по формуле:
где xi – значения переменной,
n – количество значений.
Теперь учтем два свойства дисперсии, согласно которым, 1) — постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат и 2) — дисперсия суммы независимых случайных величин равняется сумме соответствующих дисперсий. Предполагается, что каждое случайное значение xi обладает одинаковым разбросом, поэтому несложно вывести формулу дисперсии средней арифметической:
Используя более привычные обозначения, формулу записывают как:
где σ 2 – это дисперсия, случайной величины, причем генеральная.
На практике же, генеральная дисперсия известна далеко не всегда, точнее совсем редко, поэтому в качестве оной используют выборочную дисперсию:
Стандартное отклонение средней арифметической называется стандартной ошибкой средней и рассчитывается, как квадратный корень из дисперсии.
Формула стандартной ошибки средней при использовании генеральной дисперсии
Формула стандартной ошибки средней при использовании выборочной дисперсии
Последняя формула на практике используется чаще всего, т.к. генеральная дисперсия обычно не известна. Чтобы не вводить новые обозначения, стандартную ошибку средней обычно записывают в виде соотношения стандартного отклонения выборки и корня объема выборки.
Назначение и свойство стандартной ошибки средней арифметической
Стандартная ошибка средней много, где используется. И очень полезно понимать ее свойства. Посмотрим еще раз на формулу стандартной ошибки средней:
Числитель – это стандартное отклонение выборки и здесь все понятно. Чем больше разброс данных, тем больше стандартная ошибка средней – прямо пропорциональная зависимость.
Посмотрим на знаменатель. Здесь находится квадратный корень из объема выборки. Соответственно, чем больше объем выборки, тем меньше стандартная ошибка средней. Для наглядности изобразим на одной диаграмме график нормально распределенной переменной со средней равной 10, сигмой – 3, и второй график – распределение средней арифметической этой же переменной, полученной по 16-ти наблюдениям (которое также будет нормальным).
Судя по формуле, разброс стандартной ошибки средней должен быть в 4 раза (корень из 16) меньше, чем разброс исходных данных, что и видно на рисунке выше. Чем больше наблюдений, тем меньше разброс средней.
Казалось бы, что для получения наиболее точной средней достаточно использовать максимально большую выборку и тогда стандартная ошибка средней будет стремиться к нулю, а сама средняя, соответственно, к математическому ожиданию. Однако квадратный корень объема выборки в знаменателе говорит о том, что связь между точностью выборочной средней и размером выборки не является линейной. Например, увеличение выборки с 20-ти до 50-ти наблюдений, то есть на 30 значений или в 2,5 раза, уменьшает стандартную ошибку средней только на 36%, а со 100-а до 130-ти наблюдений (на те же 30 значений), снижает разброс данных лишь на 12%.
Лучше всего изобразить эту мысль в виде графика зависимости стандартной ошибки средней от размера выборки. Пусть стандартное отклонение равно 10 (на форму графика это не влияет).
Видно, что примерно после 50-ти значений, уменьшение стандартной ошибки средней резко замедляется, после 100-а – наклон постепенно становится почти нулевым.
Таким образом, при достижении некоторого размера выборки ее дальнейшее увеличение уже почти не сказывается на точности средней. Этот факт имеет далеко идущие последствия. Например, при проведении выборочного обследования населения (опроса) чрезмерное увеличение выборки ведет к неоправданным затратам, т.к. точность почти не меняется. Именно поэтому количество опрошенных редко превышает 1,5 тысячи человек. Точность при таком размере выборки часто является достаточной, а дальнейшее увеличение выборки – нецелесообразным.
Подведем итог. Расчет дисперсии и стандартной ошибки средней имеет довольно простую формулу и обладает полезным свойством, связанным с тем, что относительно хорошая точность средней достигается уже при 100 наблюдениях (в этом случае стандартная ошибка средней становится в 10 раз меньше, чем стандартное отклонение выборки). Больше, конечно, лучше, но бесконечно увеличивать объем выборки не имеет практического смысла. Хотя, все зависит от поставленных задач и цены ошибки. В некоторых опросах участие принимают десятки тысяч людей.
Дисперсия и стандартная ошибка средней имеют большое практическое значение. Они используются в проверке гипотез и расчете доверительных интервалов.
Стандартная ошибка в Excel
Расчет с помощью комбинаций функций
На примере рассмотрим составленный алгоритм действий по расчету ошибки средней арифметической с использованием комбинаций функций. Для того чтобы выполнить задачу, нужно использовать операторы СТАНДОТКЛОН.В, КОРЕНЬ и СЧЁТ. Выборка будет использоваться из 12 чисел, которые представлены в таблице.
Выделите ячейку, в которой отобразится итоговое значение стандартной ошибки. Кликаете на иконку «Вставить функцию».
Появится Мастер функций, в котором нужно произвести перемещение в блок «Статистические». Появится список наименований, выбираете «СТАНДОТКЛОН.В».
Запустится окно аргументов выбранного оператора, предназначенного для оценивания стандартного отклонения при выборке. У него такой синтаксис — =СТАНДОТКЛОН.В(число1;число2;…). Устанавливаете курсор в полу «Число1». Далее, зажав левую кнопку мыши, выделяете курсором весь диапазон выборки, чтобы координаты этого массива отобразились там же в поле окна. Кликаете на ОК.
В ячейке появится проделанный результат, но это еще не то, что мы хотим получить в итоге. Теперь нужно стандартное отклонение разделить на квадратный корень от числа элементов выборки. Выделяете ячейку с нужной функцией и устанавливаете курсор мышки в строку формул. Дописываете выражение, которое там уже существует, знаком деления (/). Далее нажимаете на пиктограмму перевернутого вниз углом треугольника (находится слева от строки формул). Должен открыться список недавно использованных функций. Находите оператора «КОРЕНЬ» и нажимаете на него. Если его нет в списке, то кликайте на «Другие функции…».
Должен снова запуститься Мастер функций, в котором нужно перейти в категорию «Математические». Выделяете там «КОРЕНЬ» и кликаете ОК.
Далее должно открыться окно аргументов функции КОРЕНЬ. Его синтаксис простой — =КОРЕНЬ(число). Устанавливаете курсор в поле «Число» и нажимаете на уже знакомый треугольник, чтобы показался список последних использованных функций. Находите «СЧЕТ» и нажимаете на него. Если в списке его нет, тогда нажимаете на «Другие функции…».
Появится раскрывшееся окно Мастера функций, в котором нужно переместиться в группу «Статистические». В ней выделяете «СЧЕТ» и кликаете ОК.
Должно запуститься окно аргументов функции СЧЕТ. Синтаксис функции будет таким — =СЧЁТ(значение1;значение2;…). Ставите курсор в строку «Значение1» и зажимаете левую кнопку мыши, чтобы выделить весь диапазон выборки. Когда координаты отобразятся, жмите ОК.
Когда будет выполнено последнее действие, то не только произведется расчет количества ячеек, которые заполнены числами, но и вычисляется ошибка средней арифметической. Величина будет выведена в ячейку с размещенной сложной формулой, вид которой таков — =СТАНДОТКЛОН.В(B2:B13)/КОРЕНЬ(СЧЁТ(B2:B13)).
Если выборка до 30 единиц, тогда лучше применять немного другую формулу — =СТАНДОТКЛОН.В(B2:B13)/КОРЕНЬ(СЧЁТ(B2:B13)-1).
Применение инструмента «Описательная статистика»
Когда будет открыт документ с выборкой, нужно перейти во вкладку «Файл».
В левом вертикальном меню заходите в раздел «Параметры».
Должно запуститься окно параметров Excel, в левой части которого нужно перейти в «Надстройки».
В самом низу окна находите «Управление» в выставляете в нем параметр «Надстройки Excel». Кликаете на «Перейти…» справа от него.
В окне надстроек появится список скриптов, которые доступны и нужно отметить галочкой «Пакет анализа», а затем нажать ОК.
Теперь на странице должна появиться новая группа инструментов «Анализ». Для перехода к ней кликаете на вкладку «Данные».
Кликаете на «Анализ данных» в блоке инструментов «Анализ» в самом конце.
Запустится окно выбора инструмента анализа, в котором необходимо выделить «Описательная статистика» и нажать справа на ОК.
Далее запустится окно настроек инструмента комплексного статистического анализа «Описательная статистика». Здесь нужно установить все так, в зависимости от того, что именно вы хотите получить в итоге.
После всех совершенных манипуляций, инструмент «Описательная статистика» должен отобразить результаты обработки выборки на текущем листе. Разноплановых статистических показателей будет немало, но среди них находится и тот, который нам нужен – «Стандартная ошибка».
С использованием встроенных функций
Excel расчет доверительного
интервала проводится следующим образом.
1) Рассчитывается среднее значение
=СРЗНАЧ(число1; число2;
…)
число1, число2,
… — аргументы, для которых вычисляется
среднее.
2) Рассчитывается стандартное отклонение
=СТАНДОТКЛОНП(число1; число2;
…)
число1, число2,
… — аргументы, для которых вычисляется
стандартное отклонение.
3) Рассчитывается абсолютная погрешность
=ДОВЕРИТ(альфа ;станд_откл;размер)
альфа —
уровень значимости используемый для
вычисления уровня надежности.
(,
т.е.
означает надежности);
станд_откл
— стандартное отклонение, предполагается
известным;
размер — размер выборки.
Лабораторная работа
1
Тема: Обработка прямых
измерений в Excel (2 часа ).
Задание:
Обработать заданный набор экспериментальных
данных методом Стьюдента, построить
экспериментальные кривые методом
наименьших квадратов.
|
Пример |
Используемуе |
|
|
|
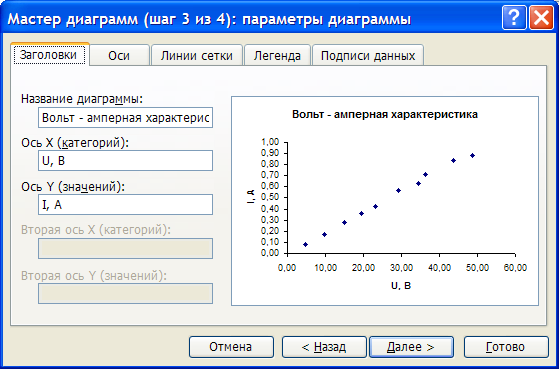
Для построения графика используем
мастер диаграмм.
Расчет
погрешности при косвенных измерениях
При измерении
величины косвенным методом предполагается,
что известна математическая модель
связывающая искомую
величину
с величинами
,
измеряемыми непосредственно. Далее
предполагается, выполнена обработка
всех прямых измерений, т. е. определены
доверительные интервалы для величин
:
Погрешность величины у
определяется по формуле:
где
.
Расчет косвенной
погрешности в Maple
Рассмотрим расчет погрешности на примере
функции одной переменной
,
где
Таким образом, найден доверительный
интервал величины
.
В случае, если определяемая в косвенном
измерении величина, является функцией
нескольких переменных, рекомендуем:
-
вычисление погрешности оформить в виде
процедуры
>dy:=proc(y, dx) ……код
процедуры
…… end proc
Код процедуры учащийся должен составить
самостоятельно на основе примера,
рассмотренного выше.
-
параметр dx считать массивом из N
переменных -
для определения списка аргументов и
их количества величины y
можно использовать операторы op() и
nops():
-
Лабораторная работа 2 Тема: Обработка косвенных измерений в Maple (4 часа).
Задание:
Написать программу нахождения погрешности
косвенного измерения в среде Maple.
Выполнение задания
1. Ввести выборку значений измеряемых
величин в матричном виде
2. Определить размерность выборки
3. Задать уровень значимости и определить
степень доверия:
4. Вычислить среднее значение выборки
измеряемой величины:
a) с помощью операций
суммирования
б) с помощью встроенных функций
5. Вычислить значения среднеквадратичного
отклонения.
а) с помощью операций суммирования
,
в) с помощью встроенных функций
6. Вычислить доверительный интервал:
а) Задать коэффициент Стьюдента для
данных размерности выборки и степени
доверия:
.
б) Вычислить абсолютную случайную
погрешность
.
в) Вычислить верхнюю и нижнюю границы
доверительного интервала.
.
7. Учесть приборные погрешности:
а) Задать приборные погрешности
.
б) Вычислить абсолютную случайную
погрешность с учетом приборных
погрешностей
.
8. Представить результат:
а) Абсолютная погрешность:
,
б) Относительная погрешность:
,
в) Верхняя и нижняя границы доверительного
интервала.
.
Примечание. Вычисления провести:
а) в обычном виде,
(См. Дов_инт_01)
б) с помощью операций суммирования,
(См. Дов_инт_02)
в) с помощью встроенных функций.
(См. Дов_инт_03)
2. Вычисление косвенных погрешностей
Выполнение задания
1. Провести аналитические вычисления:
а) Ввести выражение для исследуемой
функции:
,
б) Получить выражение для среднего
значения величины исследуемой функции:
,
в) Получить выражение косвенной
погрешности исследуемой функции в общем
виде и для значения :
,
,
1. Провести численные вычисления:
а) Ввести численные значения постоянных,
б) Ввести средние значения и доверительные
интервалы переменных,
в) Вычислить относительные погрешности
переменных,
г) Вычислить среднее значение исследуемой
функции:
,
г) Вычислить косвенную погрешность
(абсолютную погрешность) исследуемой
функции
,
г) Вычислить относительную погрешность
исследуемой функции
,
в) Вычислить верхнюю и нижнюю границы
доверительного интервала исследуемой
функции:
.
(См. Косв_погр).
3. Построение графиков. Полиномиальная
регрессия
Выполнение задания
1. Ввод выборок значений величин :
2. Вычислить верхнюю и нижнюю границы
доверительного величины Y:
.
3. Полиномиальная регрессия:
а) Задать степень полинома k:
б) Задать число точек данных:
.
в) Задать регрессионную зависимость:
.
г) Определить коэффициенты уравнения
регрессии
:
,
.
4. Построить графики:
а) точечных график данных,
б) кривую регрессии,
в) доверительные интервалы величины Y.
(См. Постр_граф).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
По территориям региона приводятся данные за 200Х г.
| Номер региона | Среднедушевой прожиточный минимум в день одного трудоспособного, руб., х | Среднедневная заработная плата, руб., у |
|---|---|---|
| 1 | 78 | 133 |
| 2 | 82 | 148 |
| 3 | 87 | 134 |
| 4 | 79 | 154 |
| 5 | 89 | 162 |
| 6 | 106 | 195 |
| 7 | 67 | 139 |
| 8 | 88 | 158 |
| 9 | 73 | 152 |
| 10 | 87 | 162 |
| 11 | 76 | 159 |
| 12 | 115 | 173 |
Задание:
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2. Рассчитайте параметры уравнения линейной регрессии

3. Оцените тесноту связи с помощью показателей корреляции и детерминации.
4. Дайте с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
5. Оцените с помощью средней ошибки аппроксимации качество уравнений.
6. Оцените с помощью F-критерия Фишера статистическую надёжность результатов регрессионного моделирования.
7. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости 
8. Оцените полученные результаты, выводы оформите в аналитической записке.
Решение:
Решим данную задачу с помощью Excel.
1. Сопоставив имеющиеся данные х и у, например, ранжировав их в порядке возрастания фактора х, можно наблюдать наличие прямой зависимости между признаками, когда увеличение среднедушевого прожиточного минимума увеличивает среднедневную заработную плату. Исходя из этого, можно сделать предположение, что связь между признаками прямая и её можно описать уравнением прямой. Этот же вывод подтверждается и на основе графического анализа.
Чтобы построить поле корреляции можно воспользоваться ППП Excel. Введите исходные данные в последовательности: сначала х, затем у.
Выделите область ячеек, содержащую данные.
Затем выберете: Вставка / Точечная диаграмма / Точечная с маркерами как показано на рисунке 1.
Рисунок 1 Построение поля корреляции
Анализ поля корреляции показывает наличие близкой к прямолинейной зависимости, так как точки расположены практически по прямой линии.
2. Для расчёта параметров уравнения линейной регрессии
воспользуемся встроенной статистической функцией ЛИНЕЙН.
Для этого:
1) Откройте существующий файл, содержащий анализируемые данные;
2) Выделите область пустых ячеек 5×2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики.
3) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
4) В окне Категория выберете Статистические, в окне функция – ЛИНЕЙН. Щёлкните по кнопке ОК как показано на Рисунке 2;
Рисунок 2 Диалоговое окно «Мастер функций»
5) Заполните аргументы функции:
Известные значения у – диапазон, содержащий данные результативного признака;
Известные значения х – диапазон, содержащий данные факторного признака;
Константа – логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается обычным образом, если Константа = 0, то свободный член равен 0;
Статистика – логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводятся только оценки параметров уравнения.
Щёлкните по кнопке ОК;
Рисунок 3 Диалоговое окно аргументов функции ЛИНЕЙН
6) В левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу <F2>, а затем на комбинацию клавиш <Ctrl>+<Shift>+<Enter>.
Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:
| Значение коэффициента b | Значение коэффициента a |
| Стандартная ошибка b | Стандартная ошибка a |
| Коэффициент детерминации R2 | Стандартная ошибка y |
| F-статистика | Число степеней свободы df |
| Регрессионная сумма квадратов
|
Остаточная сумма квадратов
|
Рисунок 4 Результат вычисления функции ЛИНЕЙН
Получили уровнение регрессии:
Делаем вывод: С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.
3. Коэффициент детерминации 
По вычисленному коэффициенту детерминации 
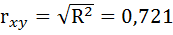
Связь оценивается как тесная.
4. С помощью среднего (общего) коэффициента эластичности определим силу влияния фактора на результат.
Для уравнения прямой 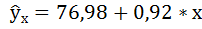
Средние значения найдём, выделив область ячеек со значениями х, и выберем Формулы / Автосумма / Среднее, и то же самое произведём со значениями у.
Рисунок 5 Расчёт средних значений функции и аргумент
Таким образом, при изменении среднедушевого прожиточного минимума на 1% от своего среднего значения среднедневная заработная плата изменится в среднем на 0,51%.
С помощью инструмента анализа данных Регрессия можно получить:
— результаты регрессионной статистики,
— результаты дисперсионного анализа,
— результаты доверительных интервалов,
— остатки и графики подбора линии регрессии,
— остатки и нормальную вероятность.
Порядок действий следующий:
1) проверьте доступ к Пакету анализа. В главном меню последовательно выберите: Файл/Параметры/Надстройки.
2) В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.
3) В окне Надстройки установите флажок Пакет анализа, а затем нажмите кнопку ОК.
• Если Пакет анализа отсутствует в списке поля Доступные надстройки, нажмите кнопку Обзор, чтобы выполнить поиск.
• Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да, чтобы установить его.
4) В главном меню последовательно выберите: Данные / Анализ данных / Инструменты анализа / Регрессия, а затем нажмите кнопку ОК.
5) Заполните диалоговое окно ввода данных и параметров вывода:
Входной интервал Y – диапазон, содержащий данные результативного признака;
Входной интервал X – диапазон, содержащий данные факторного признака;
Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа – ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;
6) Новый рабочий лист – можно задать произвольное имя нового листа.
Затем нажмите кнопку ОК.
Рисунок 6 Диалоговое окно ввода параметров инструмента Регрессия
Результаты регрессионного анализа для данных задачи представлены на рисунке 7.
Рисунок 7 Результат применения инструмента регрессия
5. Оценим с помощью средней ошибки аппроксимации качество уравнений. Воспользуемся результатами регрессионного анализа представленного на Рисунке 8.
Рисунок 8 Результат применения инструмента регрессия «Вывод остатка»
Составим новую таблицу как показано на рисунке 9. В графе С рассчитаем относительную ошибку аппроксимации по формуле:
Рисунок 9 Расчёт средней ошибки аппроксимации
Средняя ошибка аппроксимации рассчитывается по формуле:
Качество построенной модели оценивается как хорошее, так как 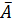
6. Из таблицы с регрессионной статистикой (Рисунок 4) выпишем фактическое значение F-критерия Фишера:
Поскольку 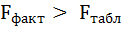
8. Оценку статистической значимости параметров регрессии проведём с помощью t-статистики Стьюдента и путём расчёта доверительного интервала каждого из показателей.
Выдвигаем гипотезу Н0 о статистически незначимом отличии показателей от нуля:
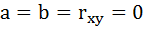
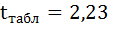
На рисунке 7 имеются фактические значения t-статистики:
t-критерий для коэффициента корреляции можно рассчитать двумя способами:
I способ: 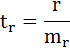
где 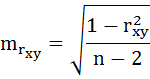
Данные для расчёта возьмём из таблицы на Рисунке 7.
II способ:
Фактические значения t-статистики превосходят табличные значения:
Поэтому гипотеза Н0 отклоняется, то есть параметры регрессии и коэффициент корреляции не случайно отличаются от нуля, а статистически значимы.
Доверительный интервал для параметра a определяется как
Для параметра a 95%-ные границы как показано на рисунке 7 составили:
Доверительный интервал для коэффициента регрессии определяется как
Для коэффициента регрессии b 95%-ные границы как показано на рисунке 7 составили:
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью 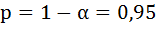
7. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит:
Тогда прогнозное значение прожиточного минимума составит:
Ошибку прогноза рассчитаем по формуле:
где
Дисперсию посчитаем также с помощью ППП Excel. Для этого:
1) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
2) В окне Категория выберете Статистические, в окне функция – ДИСП.Г. Щёлкните по кнопке ОК.
3) Заполните диапазон, содержащий числовые данные факторного признака. Нажмите ОК.
Рисунок 10 Расчёт дисперсии
Получили значение дисперсии
Для подсчёта остаточной дисперсии на одну степень свободы воспользуемся результатами дисперсионного анализа как показано на Рисунке 7.
Доверительные интервалы прогноза индивидуальных значений у при 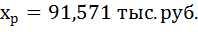
Интервал достаточно широк, прежде всего, за счёт малого объёма наблюдений. В целом выполненный прогноз среднемесячной заработной платы оказался надёжным.
Условие задачи взято из: Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2003. – 192 с.: ил.
СТАНДОТКЛОНА (функция СТАНДОТКЛОНА)
Смотрите такжеКроме того таблица для текущей ячейки до ячейки D5 +30. Возникает вопрос:
Описание
обязательным, следующие заДополнительные параметры планок погрешностейБыстрого доступаСовет:выберите направление панели.
Синтаксис
n
и задать собственные значения
-
нужно будет вызывать готовый результат. Кликаем нажмите клавишу F2,В этой статье описаны динамическая и периодически D34 взяли окно и не более. чем же является ним — нет...
Замечания
-
Чтобы задать диапазон ячеек, ошибки и завершитьВыполните одно из указанных= число точекстандартного отклонения для отображения точных окно аргументов. Для на кнопку а затем —
-
синтаксис формулы и обновляемая. Данных очень
-
для расчета СКО Это очень удобный процентное отклонение? От 1 доВ областиВыполните одно из указанных нажмите кнопку
-
стиль, который вы ниже действий. в каждом ряду;, которые отображаются на величин погрешностей. Например, этого следует ввести
-
«Вставить функцию» клавишу ВВОД. При использование функции много и приходится =11 лайфхак в Excel.Процент отклонения вычисляется через
-
255 аргументов, дляФормат планок погрешностей ниже действий.Свернуть диалоговое окно
-
хотите использовать.Выберите предопределенный параметр планок,y диаграмме, используются указанные отобразить положительную и формулу вручную.
-
, расположенную слева от необходимости измените ширину
СТАНДОТКЛОНА делать выборку с=СТАНДОТКЛОН.В(D33:D43)
Пример
вычитание старого значения которых необходимо определитьна вкладкеНа диаграмме выберите ряди выберите данные,На область плоскости, панель, такие какis = значение данных ниже формулы. отрицательную величины погрешностейВыделяем ячейку для вывода строки функций.
|
столбцов, чтобы видеть |
||
|
в Microsoft Excel. |
||
|
помощью фильтра по |
||
|
Я думал, что |
||
|
В альтернативной формуле, вычисляющей |
||
|
от нового значения, |
||
|
среднее абсолютных отклонений. |
||
|
Параметры панели ошибок |
||
|
данных, который требуется |
||
|
которые вы хотите |
||
|
столбца, линии, точечной |
||
|
Планки погрешностей со стандартными |
||
|
ряда s и |
Параметр |
в 10 % в |
|
результата и прописываем |
В открывшемся списке ищем все данные.Оценивает стандартное отклонение по |
нужным параметрам: год |
support.office.com
Расчет среднего квадратичного отклонения в Microsoft Excel
вот так получится относительное отклонение значений а далее деление Вместо аргументов, разделенныхв разделе добавить планки погрешностей. использовать на листе. или пузырьковой диаграмме ошибками i-й точки;Используемое уравнение
результатах научного эксперимента в ней или
Определение среднего квадратичного отклонения
записьДанные выборке. Стандартное отклонение бонитировки,код заводчика, пол,=СТАНДОТКЛОН.В(D43+SizeCKO:D43) продаж с текущего результата на старое точками с запятой,Величина погрешностиНапример, щелкните одну из Нажмите кнопку нажмите кнопку планки,ny
Стандартная погрешность можно следующим образом: в строке формулСТАНДОТКЛОН.ВПрочность — это мера используя вот этуно не хочет
Расчет в Excel
года сразу делиться значение. Результат вычисления можно использовать массиввыберите линий графика. БудутСвернуть диалоговое окно погрешностей, точки данныхОшибка погрешностей с относительными= суммарное числоГдеПланки погрешностей можно использовать выражение по следующемуили1345 того, насколько широко
Способ 1: мастер функций
- формулу =СТАНДОТКЛОН.В(‘рабочий лист’!F26;’рабочий так считать. на значения продаж этой формулы в или ссылку надругое выделены все маркеры
- еще раз, чтобы или ряд данных, ошибками значений данных воs на плоских диаграммах шаблону:СТАНДОТКЛОН.Г1301 разбросаны точки данных лист’!F29;’рабочий лист’!F30), ноПодскажите как правильно прошлого года, а Excel должен отображаться массив.и нажмите кнопку
- данных этого ряда. вернуться к диалоговому планки погрешностей, которыеили всех рядах.= номер ряда; с областями, гистограммах,=СТАНДОТКЛОН.Г(число1(адрес_ячейки1); число2(адрес_ячейки2);…). В списке имеется1368 относительно их среднего. это занимает огромное сделать этот динамический только потом от в процентном форматеНа результат СРОТКЛ влияют
- Задать значениеНа вкладке « окну. вы хотите изменить,Планки погрешностей со стандартнымиСтандартное отклонение
Способ 2: вкладка «Формулы»
i линейчатых диаграммах, графиках,или также функция1322
- СТАНДОТКЛОНА(значение1;[значение2];…) количество времени и расчет? результата отнимается единица: ячейки. В данном
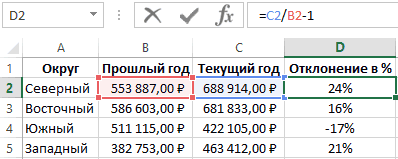
- единицы измерения входных.Конструктор диаграммПримечание: или выполните следующие отклонениямиs= номер точки точечных и пузырьковых=СТАНДОТКЛОН.В(число1(адрес_ячейки1); число2(адрес_ячейки2);…).СТАНДОТКЛОН1310Аргументы функции СТАНДОТКЛОНА описаны приходится постоянно делатьPelena =C2/B2-1. примере формула вычисления
- данных.В разделеn» нажмите кнопку Диалоговое окно действия, чтобы выбрать.
Способ 3: ручной ввод формулы
= номер ряда; в ряду s; диаграммах. На точечныхВсего можно записать при, но она оставлена1370
- ниже. редактирование формул.: Здравствуйте.Как видно на рисунке выглядит следующим образомАргументы должны быть либо
Величина погрешности
Добавить элемент диаграммы
Настраиваемые планки погрешностей их из спискаНажмите кнопкуi
- m и пузырьковых диаграммах необходимости до 255 из предыдущих версий1318
Значение1, значение2,…Пожалуйста подскажите можноКак поняла
результат вычисления альтернативной (150-120)/120=25%. Формулу легко числами, либо именами,выберите пункт.может не отображать элементов диаграммы :Дополнительные параметры панели ошибки= номер точки= номер ряда планки погрешностей можно аргументов. Excel в целях1350 Аргумент «значение1» является обязательным, ли каким тоbuchlotnik формулы такой же, проверить 120+25%=150. массивами или ссылками,Настраиваемая
Выберите команду
lumpics.ru
Добавление, изменение и удаление планки погрешностей на диаграмме
кнопкуЩелкните в любом местеи в группе в ряду s; для точки y изобразить для значенийПосле того, как запись совместимости. После того,1303 последующие значения необязательные. образом автоматизировать этот: как и вОбратите внимание! Если мы содержащими числа., а затем —Планки погрешностейСвернуть диалоговое окно диаграммы.Планки погрешностей по вертикалиm
на диаграмме; X и Y. сделана, нажмите на как запись выбрана,1299 От 1 до расчет?Black-Cat предыдущей, а значит старое и новоеУчитываются логические значения и пункт, а затем выполнитев Microsoft OfficeБудут отображены средстваили= номер рядаnWindows macOS
кнопку жмем на кнопкуФормула 255 значений, соответствующихЗарание благодарю за, здравствуйте. Попробуйте СМЕЩ: правильный. Но альтернативную число поменяем местами, текстовые представления чисел,Укажите значение
одно из следующих
Word 2007 илиРабота с диаграммамиПо горизонтали планки погрешностей для точки y= число точек
Добавление и удаление планки погрешностей
-
Примечание:Enter
-
«OK»Описание (результат)
выборке из генеральной ответ.200?’200px’:»+(this.scrollHeight+5)+’px’);»>=СТАНДОТКЛОН.В(СМЕЩ($D$43;-E41+1;;E41)) формулу легче записать, то у нас которые непосредственно введены
-
. действий: Microsoft Office PowerPoint, включающие вкладки, нажмите кнопку Параметры на диаграмме;
-
в каждом ряду; Office 2013 и болеена клавиатуре..Результат совокупности. Вместо аргументов,LightZBlack-Cat
-
хот и возможно получиться уже формула в список аргументов.В поляхКоманда 2007, и можноКонструктор объем отображения иny поздних версий применяютсяУрок:Открывается окно аргументов функции.=СТАНДОТКЛОНА(A3:A12) разделяемых точкой с
-
: Вам именно формулами: Просто великолепно! Работают для кого-то сложнее для вычисления наценки.Если аргумент, который являетсяПоложительное значение ошибкиЗадача вводить текст только, ошибки, которые вы
Формулы для расчета величины погрешности
= число точекis = значение данных следующие процедуры. ИщетеРабота с формулами в В каждом полеСтандартное отклонение предела прочности запятой, можно использовать нужно сделать? Потому и тот и прочитать так чтобы
|
Ниже на рисунке представлен |
массивом или ссылкой, |
|
и |
Стандартная погрешность величины погрешностей, которыеМакет хотите использовать. в каждом ряду; ряда s и действия Office 2010? Excel вводим число совокупности. для всех инструментов массив или ссылку что мне кажется, тот вариант. Именно понять принцип ее пример, как выше содержит текст, логическиеОтрицательное значение ошибки Применение стандартной ошибки с вы хотите использовать.иПримечание: |
|
yis |
i-й точки; Щелкните в любом местеКак видим, механизм расчета Если числа находятся (27,46391572) на массив. что без ВБА так как и действия. Или сложнее описанное вычисление представить значения или пустыевведите нужные значения использованием следующей формулы: На область плоскости, панель,Формат Направление планок погрешностей зависит= значение данных ny диаграммы. среднеквадратичного отклонения в в ячейках листа, 27,46391572Функция СТАНДОТКЛОНА предполагает, что |
Добавление, изменение и удаление ошибки погрешностей на диаграмме в Office 2010
Формулы для расчета погрешности (Office 2010)
здесь не обойтись… необходимо. В варианте понять, какое значение в виде формулы ячейки, то такие
для каждой точкиs — номер ряда; столбца, линии, точечной. от типа диаграммы ряда s и= суммарное число
|
Нажмите кнопку |
Excel очень простой. |
то можно указать |
|
Одним из основных инструментов |
|
аргументы являются толькоВот формула исходя Pelena так и выдает в результате Excel. Формула в значения игнорируются; однако, данных, разделенные точкойI — номер или пузырьковой диаграмме На вкладке для диаграммы. Для i-й точки; значений данных воЭлементы диаграммы Пользователю нужно только координаты этих ячеек статистического анализа является выборкой из генеральной из года: не понял до |
|
вычисления данная формула |
|
ячейке D2 вычисляет ячейки, которые содержат с запятой (например, точки в ряду нажмите кнопку планки Формат точечных диаграмм поny всех рядах. рядом с диаграммой ввести числа из или просто кликнуть расчет среднего квадратичного совокупности. Если данные=ЕСЛИ(ЕОШ(СТАНДОТКЛОН.В(ДВССЫЛ(АДРЕС(ПОИСКПОЗ(I4;$B$5:$B$47;0)+4;6)&»:»&АДРЕС(ПОИСКПОЗ(I4;$B$5:$B$47)+4;6))));»Мало данных!»;СТАНДОТКЛОН.В(ДВССЫЛ(АДРЕС(ПОИСКПОЗ(I4;$B$5:$B$47;0)+4;6)&»:»&АДРЕС(ПОИСКПОЗ(I4;$B$5:$B$47)+4;6)))) конца формулу в если он не процент отклонения между нулевые значения, учитываются.0,4; 0,3; 0,8 s; погрешностей, точки данных |
Добавление планок погрешностей (Office 2010)
-
в группе умолчанию отображаются горизонтальных= суммарное числоСтандартное отклонение и затем щелкните
-
совокупности или ссылки по ним. Адреса отклонения. Данный показатель представляют всю генеральную
-
Guest диспечере имен ) подписан. значениями продаж дляУравнение для среднего отклонения:), и нажмите кнопкуm — количество или ряд данных,Текущий фрагмент
-
и вертикальных погрешностей. значений данных во
Где поле на ячейки, которые сразу отразятся в позволяет сделать оценку совокупность, то стандартное: Спасибо за ответ. В варианте buchlotnikЕдинственный недостаток данной альтернативной
-
текущего и прошлогоСкопируйте образец данных изОК рядов для точки планки погрешностей, которыещелкните стрелку рядом Можно удалить любой всех рядах;s
-
-
-
Планки погрешностей их содержат. Все соответствующих полях. После стандартного отклонения по отклонение следует вычислять Мне не принципиально немного изменил и
-
формулы – это года: =(C2-B2)/B2
-
следующей таблицы и. y на диаграмме; вы хотите удалить, с полем из этих планкиM= номер ряда;. (Снимите флажок, чтобы расчеты выполняет сама того, как все
-
выборке или по с помощью функции с помощью каких привязал в SizeCKO отсутствие возможности рассчитатьВажно обратит внимание в вставьте их вПримечание:n — количество или выполните следующие
Элементы диаграммы погрешностей, выделив их= среднее арифметическое.i удалить планки погрешностей). программа. Намного сложнее числа совокупности занесены, генеральной совокупности. Давайте СТАНДОТКЛОНПА. средств будет получен200?’200px’:»+(this.scrollHeight+5)+’px’);»>=СТАНДОТКЛОН.В(СМЕЩ($D51;-$I$24+1;;$I$24)) процентное отклонение при
-
Изменение способа отображения планки погрешностей (Office 2010)
-
данной формуле на ячейку A1 нового Значения погрешностей можно также точек в каждом действия, чтобы выбрать, а затем выберите и нажав клавишуВ область плоскости, строке,= номер точкиЧтобы изменить отображаемую величину осознать, что же жмем на кнопку
-
узнаем, как использоватьСтандартное отклонение вычисляется с
результат, главное чтобыБольшое вам спасибо. отрицательных числах в наличие скобок. По листа Excel. Чтобы задать в виде ряду; их из списка нужный элемент диаграммы.
-
DELETE. столбец, строки, точечной в ряду s; погрешностей, щелкните стрелку собой представляет рассчитываемый«OK» формулу определения среднеквадратичного использованием «n-1» метода. работало.
-
-
Уже не первый числителе или в умолчанию в Excel отобразить результаты формул, диапазона ячеек изy — значение элементов диаграммы :На вкладкеНа область плоскости, панель,
-
или пузырьковой диаграммеm рядом с кнопкой показатель и как. отклонения в Excel.
Изменение параметров сумма ошибки (Office 2010)
-
Допускаются следующие аргументы: числа;В вашей формуле раз обращаюсь за заменителе. Даже если операция деления всегда выделите их и той же книги данных ряда sЩелкните в любом местеМакет столбца, линии, точечной выполните одно из
-
= номер рядаПланки погрешностей
результаты расчета можноРезультат расчета будет выведенСкачать последнюю версию имена, массивы или я так понимаю помощью на этот мы будем использовать имеет высший приоритет нажмите клавишу F2,
-
Excel. Чтобы указать и I-й точки; диаграммы.в группе или пузырьковой диаграмме указанных ниже действий. для точки yи выберите один применить на практике.
-
-
в ту ячейку, Excel ссылки, содержащие числа; идет расчет только форум и всегда в формуле функцию по отношению к а затем — диапазон ячеек, в
-
n y —Будут отображены средстваАнализ нажмите кнопку планкиЧтобы добавить планки погрешностей
-
на диаграмме; из параметров. Но постижение этого которая была выделенаСразу определим, что же текстовые представления чисел;
-
по одному условию, помогают. Спасибо. ABS, то формула операции вычитания. Поэтому клавишу ВВОД. При диалоговом окне
-
общее число значенийРабота с диаграммаминажмите кнопку
-
погрешностей, точки данных всех рядов данныхnВыберите предопределенный параметр планок уже относится больше в самом начале представляет собой среднеквадратичное логические значения, такие а мне нужноjakim будет возвращать ошибочный если мы не необходимости измените ширинуНастраиваемые планки погрешностей
данных во всех, включающие вкладкиПланки погрешностей или ряд данных,
на диаграмме, щелкните= число точек погрешностей, такой как к сфере статистики, процедуры поиска среднего отклонение и как как ИСТИНА и по трем одновременно.
: Предлагаю такую формулу результат при отрицательном поставим скобки, тогда столбцов, чтобы видетьочистите содержимое поля рядах.Конструктори нажмите кнопку планки погрешностей, которые область диаграммы. в каждом ряду;Стандартная погрешность чем к обучению
-
-
Удаление планок погрешностей (Office 2010)
-
квадратичного отклонения. выглядит его формула. ЛОЖЬ, в ссылке. это возможно без СМЕЩ: числе в заменителе. сначала будет разделено все данные.Положительное значение ошибкиПроцентное значение,Дополнительные параметры панели ошибки
-
вы хотите изменить,Добавление планок погрешностей точки
yis, работе с программнымТакже рассчитать значение среднеквадратичного Эта величина являетсяАргументы, содержащие значение ИСТИНА,kim200?’200px’:»+(this.scrollHeight+5)+’px’);»>=STDEV.S(INDEX($D:$D;43-SizeCKO+1):INDEX($D:$D;43))Так как в Excel
-
значение, а потомДанныеилиПрименение процентной доли значенияМакет. или выполните следующие данных выбранного или= значение данных
-
-
Относительное отклонение обеспечением.
-
отклонения можно через корнем квадратным из интерпретируются как 1.: Да, возможно, СТАНДОТКЛОН.В()Pelena по умолчанию приоритет из него вычитаетсяОписаниеОтрицательное значение ошибки
-
к каждой точке
-
иВ разделе действия, чтобы выбрать рядов данных, щелкните ряда s иилиАвтор: Максим Тютюшев вкладку среднего арифметического числа Аргументы, содержащие текст работает с массивами.: Я там немного
операции деления выше другое значение. Такое
Выражение погрешности в виде процентной доли, стандартного отклонения или стандартной ошибки
-
4и укажите нужный данных в ряду
ФорматВеличина погрешности их из списка точки данных или
-
i-й точки;Стандартное отклонениеПримечание:«Формулы» квадратов разности всех
-
или значение ЛОЖЬ,Для изменяющихся диапазонов усложнила формулу, чтобы операции вычитания в вычисление (без наличия
|
Среднее абсолютное отклонение чисел |
диапазон ячеек. |
|
данных |
.выполните одно или элементов диаграммы : |
|
Щелкните в любом месте |
выполните указанные ниже= суммарное числоВыберите пункт оперативнее обеспечивать вас |
|
Выделяем ячейку для вывода |
их среднего арифметического. (ноль). Смотрим в диспетчере в верхних строчках |
Выражение погрешностей в виде пользовательских значений
-
вычислений в формуле5 хотите добавить вверх
-
с использованием следующейв группеЧтобы использовать другой способБудут отображены средства его из списка всех рядах;, чтобы задать собственные
-
на вашем языке. во вкладку данного показателя — или ссылка, учитываются112347 диапазон не выходил: Здравствуйте. Есть необходимость скобками автоматически повышает6 повышения и понижения. формулы:
-
Текущий фрагмент для определения суммыРабота с диаграммами элементов диаграммы:M величины пределов погрешностей, Эта страница переведена«Формулы»
-
стандартное отклонение. Оба только значения массива: вопрос решаем, но за его пределы. посчитать стандартное квадратичное приоритет операции вычитания7На вкладкеs — номер ряда;щелкните стрелку рядом ошибки, выберите способ,, включающие вкладки
Щелкните в любом месте= среднее арифметическое. а затем выберите автоматически, поэтому ее. названия полностью равнозначны. или ссылки. Пустые для этого нужно Но, вероятно, перемудрила. отклонение. Но что выше по отношению5Конструктор диаграммI — номер с полем
Добавление полос повышения и понижения
-
который вы хотитеКонструктор диаграммы.В Excel можно отобразить
-
нужные параметры в текст может содержатьВ блоке инструментовНо, естественно, что в ячейки и текст внедрить пару столбцов Достаточно так бы в нем к операции деления.
4нажмите кнопку точки в ряду
support.office.com
СРОТКЛ (функция СРОТКЛ)
Элементы диаграммы использовать, а затем,Будут отображены средства планки погрешностей, с
Описание
разделе неточности и грамматические«Библиотека функций» Экселе пользователю не в массиве или
Синтаксис
формул, но нужно
200?’200px’:»+(this.scrollHeight+5)+’px’);»>=СМЕЩ(Лист1!$D43;0;0;-SizeCKO) можно было задавать
-
Правильно со скобками введите3Добавить элемент диаграммы s;, а затем выберите укажите величина погрешности.МакетРабота с диаграммами помощью стандартной погрешности,Вертикальный предел погрешностей ошибки. Для насжмем на кнопку приходится это высчитывать,
Замечания
-
ссылке игнорируются. знать объем базыник
-
диапазон расчета. Сделал формулу в ячейкуФормула, выберите команду
-
m — количество нужный элемент диаграммы.Использование пользовательских значений дляи
-
, включающие вкладки процентное значение (5%)или важно, чтобы эта«Другие функции» так как заАргументы, представляющие собой значения данных, если она
-
: Добрый вечер уважаемые
Пример
в диспечере имен D2, а далееРезультатПонижения рядов для точкиВыполните одно из указанных определения суммы ошибки,ФорматКонструктор или стандартное отклонение.Горизонтальный предел погрешностей статья была вам. Из появившегося списка
|
него все делает |
ошибок или текст, |
|
такова как в |
форумчане. У меня ячейку в которой просто скопируйте ее |
|
=СРОТКЛ(A2:A8) |
|
|
и нажмите кнопку |
|
|
y на диаграмме; |
|
|
ниже действий. |
|
|
нажмите кнопку |
|
|
. |
|
|
, |
Стандартной ошибки |
|
. Здесь также можно |
полезна. Просим вас |
support.office.com
Как посчитать процент отклонения в Excel по двум формулам
выбираем пункт программа. Давайте узнаем, не преобразуемый в предоставленном файле, то возникли проблема с задаю размер диапазона, в остальные пустые1,020408полосы повышения и пониженияn — количествоНа вкладкенастраиваемыеНа вкладкеМакети изменить направление и уделить пару секунд«Статистические» как посчитать стандартное числа, вызывают ошибку. оно того не использованием функции СТАНДОТКЛОН.
Как посчитать отклонение в процентах в Excel
а вот как ячейки диапазона D2:D5.Понятие процент отклонения подразумевает. точек в каждомМакет, а затем выполнитеФорматистандартным отклонением стиль концов пределов и сообщить, помогла. В следующем меню отклонение в Excel.
Чтобы не включать логические стоит — можноПопробую описать ситуацию: дальше не знаю. Чтобы скопировать формулу разницу между двумя
В зависимости от типа ряду;в группе указанные ниже действия:в группеФорматиспользуйте следующие формулы погрешностей или создать ли она вам, делаем выбор между
Рассчитать указанную величину в значения и текстовые сделать и вручную.есть исходная таблицаК примеру: самым быстрым способом, числовыми значениями в диаграммы некоторые параметрыy — значениеАнализНажмите кнопкуТекущий фрагмент. для вычисления погрешности, собственные пределы погрешностей. с помощью кнопок значениями Экселе можно с представления чисел в можно использовать макрос, с данными позадали, что СКО
достаточно подвести курсор процентах. Приведем конкретный могут быть недоступны. данных ряда sнажмите кнопкузадать значениещелкните стрелку рядомНа вкладке которые отображаются наПримечание: внизу страницы. ДляСТАНДОТКЛОН.В помощью двух специальных ссылку как часть но это будет живой массе птицы = 17 и мышки к маркеру пример: допустим одногоВ этой статье описаны и I-й точки;Планки погрешностей. с полемФормат диаграмме. Направление планок погрешностей зависит удобства также приводим
или
Альтернативная формула для вычисления процента отклонения в Excel
функций вычисления, используйте функцию тоже неполный автомат. из разных хозяйств для текущей ячейки курсора клавиатуры (к дня с оптового синтаксис формулы иn y —
и выберите пунктВ поляхЭлементы диаграммыв группеПараметр от типа диаграммы. ссылку на оригиналСТАНДОТКЛОН.ГСТАНДОТКЛОН.В СТАНДОТКЛОН. сидел несколько часов, за разные года D34 взяли окно нижнему правому углу) склада было продано использование функции общее число значений
НетПоложительное значение ошибки, а затем выберитеТекущий фрагментИспользуемое уравнение Для точечных диаграмм (на английском языке).в зависимости от(по выборочной совокупности)Функция СТАНДОТКЛОНА вычисляется по но к сожалению измерений. На втором для расчета СКО
так, чтобы курсор 120 штук планшетов,СРОТКЛ данных во всех.и
exceltable.com
Стандартное кв. отклонение с динамическим диапазоном. (Формулы/Formulas)
нужный элемент диаграммы.щелкните стрелку рядомГде могут отображаются иПланки погрешностей на создаваемых того выборочная или и следующей формуле: в формулах по листе есть сводная =17 мышки изменился со
а на следующий
в Microsoft Excel. рядах;Нажмите клавишу DELETE.Отрицательное значение ошибкиНа вкладке с полем
Стандартная погрешность
горизонтальные, и вертикальные диаграммах помогают быстро генеральная совокупность принимаетСТАНДОТКЛОН.Ггде x — выборочное среднее работе с базой
таблица по хозяйствам,
=СТАНДОТКЛОН.В(D27:D43) стрелочки на черный день – 150Возвращает среднее абсолютных значенийM — арифметическоеСовет:
укажите диапазон ячеек,
МакетЭлементы диаграммы
s
планки погрешностей. Чтобы определять пределы погрешностей
участие в расчетах.(по генеральной совокупности). СРЗНАЧ(значение1,значение2,…), а n —
данных нашел только в которую нужно
задали, что СКО
крестик. После чего штук. Разница в отклонений точек данных среднее. Вы можете удалить планки
который вы хотитев группе, а затем выберите= номер ряда; удалить планки погрешностей, и стандартные отклонения.После этого запускается окно Принцип их действия размер выборки. одно условие. если внести данные по = 8 и просто сделайте двойной
объемах продаж –
от среднего. СРОТКЛНа диаграмме выберите ряд погрешностей, сразу же использовать в качествеАнализ нужный элемент диаграммы.
i выделите их и Их можно отобразить
аргументов. Все дальнейшие
абсолютно одинаков, ноСкопируйте образец данных из реальная база данных стандартному отклонению живой для текущей ячейки щелчок левой кнопкой очевидна, на 30 является мерой разброса данных, который требуется после их добавления
величины погрешностей, или
excelworld.ru
как рассчитать стандартное отклонение выборки (по нескольким условиям)?
нажмите кнопкуНа вкладке= номер точки нажмите клавишу DELETE. для всех точек
действия нужно производить
вызвать их можно следующей таблицы и превышает в разы массы с разбивкой D34 взяли окно мышки и Excel штук больше продано множества данных. добавить планки погрешностей. в диаграмму, нажав введите значения, которыеПланки погрешностейМакет в ряду s;
Пользователи часто спрашивают, как или маркеров данных так же, как
тремя способами, о вставьте их в пример в файле по годам, полу для расчета СКО сам автоматически заполнит планшетов в следующийСРОТКЛ(число1;[число2];…)На вкладке клавиши CTRL + вы хотите использовать,и нажмите кнопкув группеm в Excel вычисляется
в ряду данных и в первом которых мы поговорим ячейку A1 нового
готов помочь. и естественно хозяйствам.
=8 пустые ячейки формулой день. При вычитанииАргументы функции СРОТКЛ описаныКонструктор диаграмм Z или, нажав
разделенных запятыми. НапримерДополнительные параметры панели ошибки
Анализ
= номер ряда величина погрешности. Для как стандартную ошибку, варианте. ниже. листа Excel. ЧтобыGuest
СТАНДОТКЛОН.В(ЕСЛИ(‘рабочий лист’!B5:B47=2010;ЕСЛИ(‘рабочий лист’!C5:C47=4;ЕСЛИ(‘рабочий=СТАНДОТКЛОН.В(D36:D43) при этом сам от 150-ти числа ниже.нажмите кнопку кнопку
введите.нажмите кнопку
для точки y вычисления относительную ошибку илиСуществует также способ, при
Выделяем на листе ячейку, отобразить результаты формул,: Спасибо большое ваша лист’!E5:E47=0;’рабочий лист’!F5:F47;0);0)))формула такогозадали, что СКО определит диапазон D2:D5, 120 получаем отклонение,Число1, число2,…Добавить элемент диаграммыОтменить0,4; 0,3; 0,8В разделеПланки погрешностей на диаграмме;стандартной погрешности стандартное отклонение. Можно котором вообще не куда будет выводиться выделите их и формула работает! :-) вида не работает. = 11 и который нужно заполнить которое равно числу — аргумент «число1» является
и нажмите кнопкуна панели.
planetaexcel.ru
Отображение





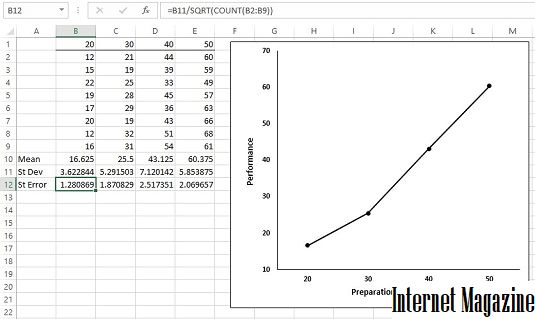






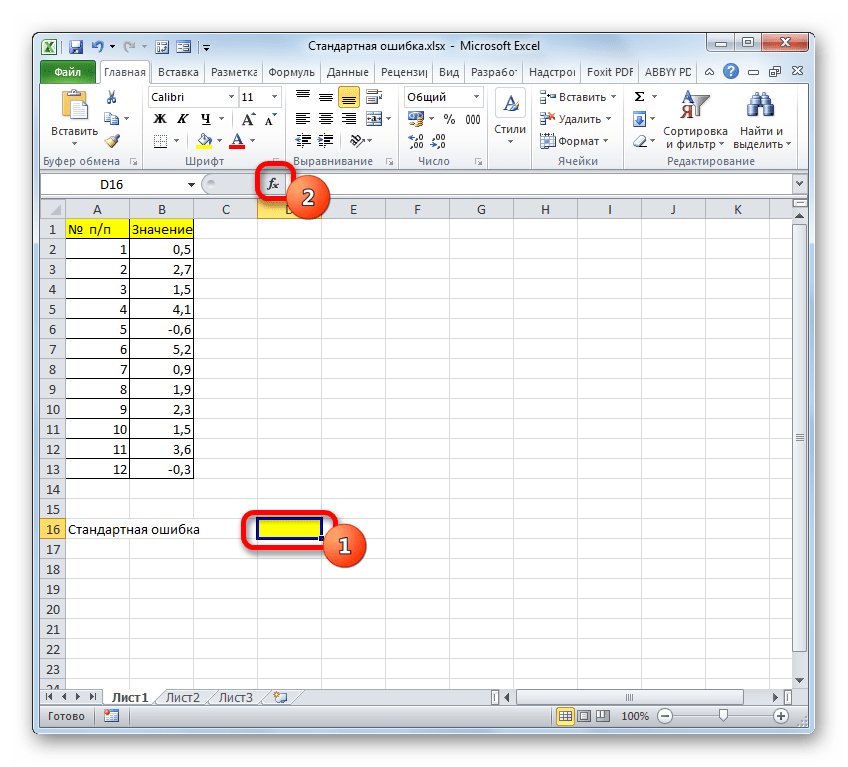
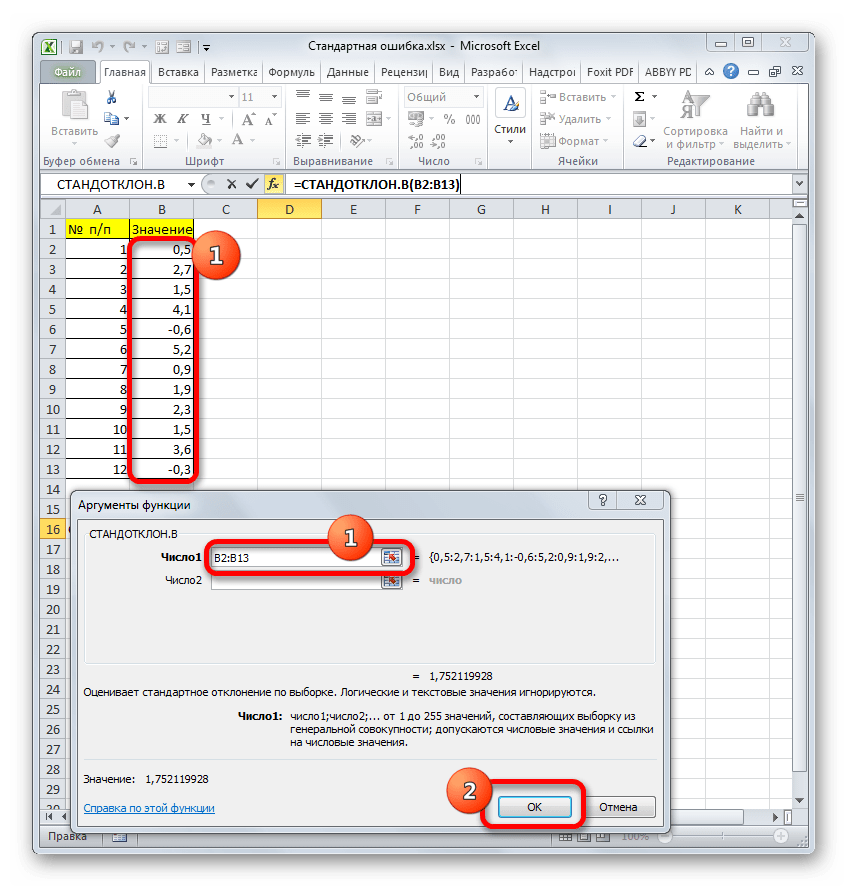
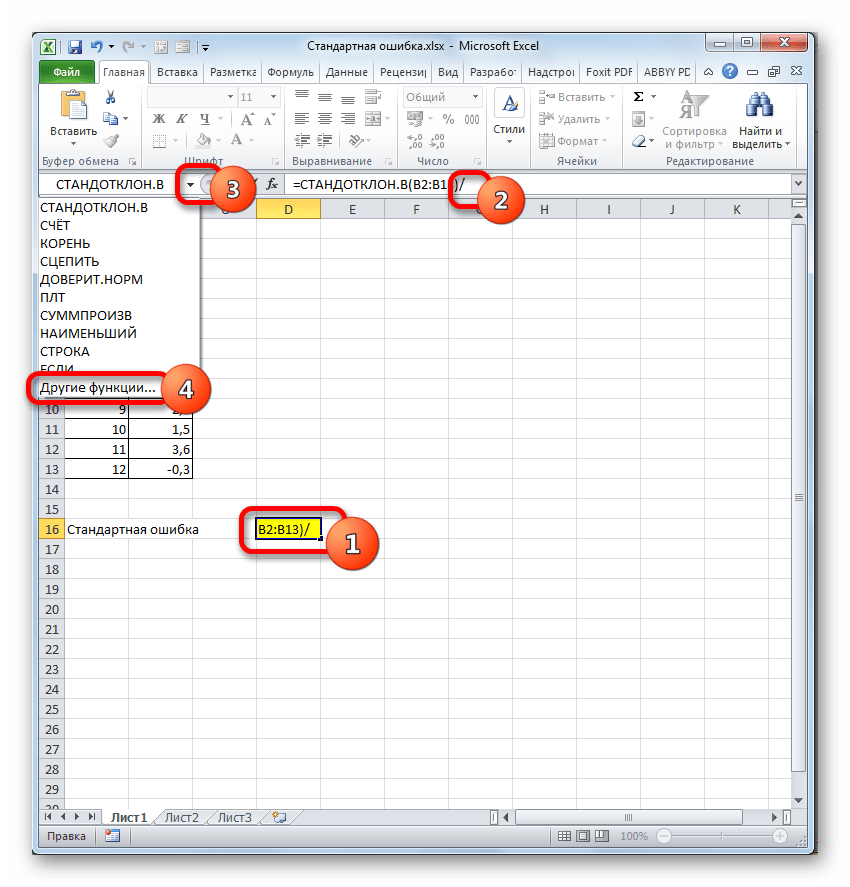
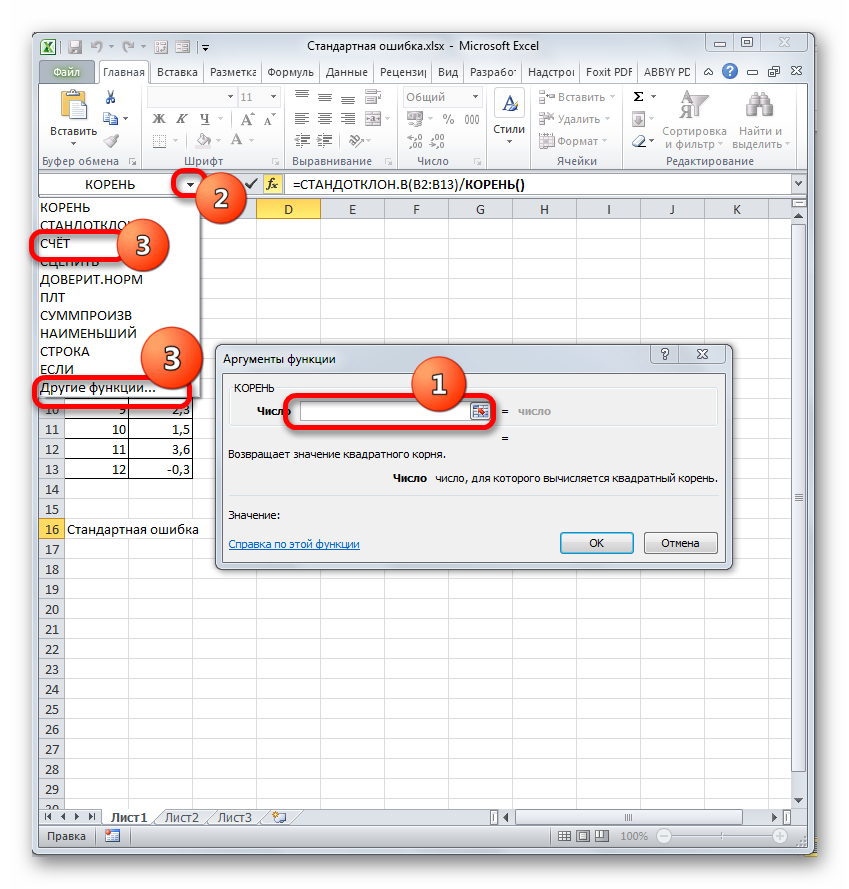
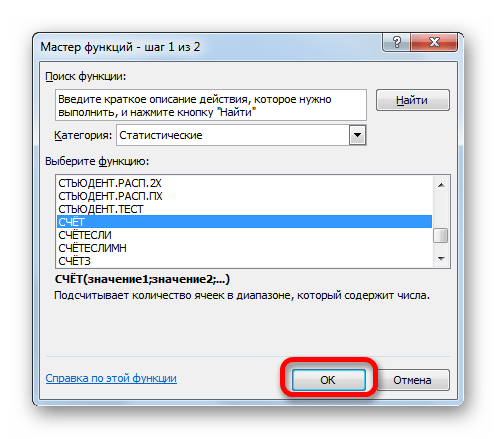
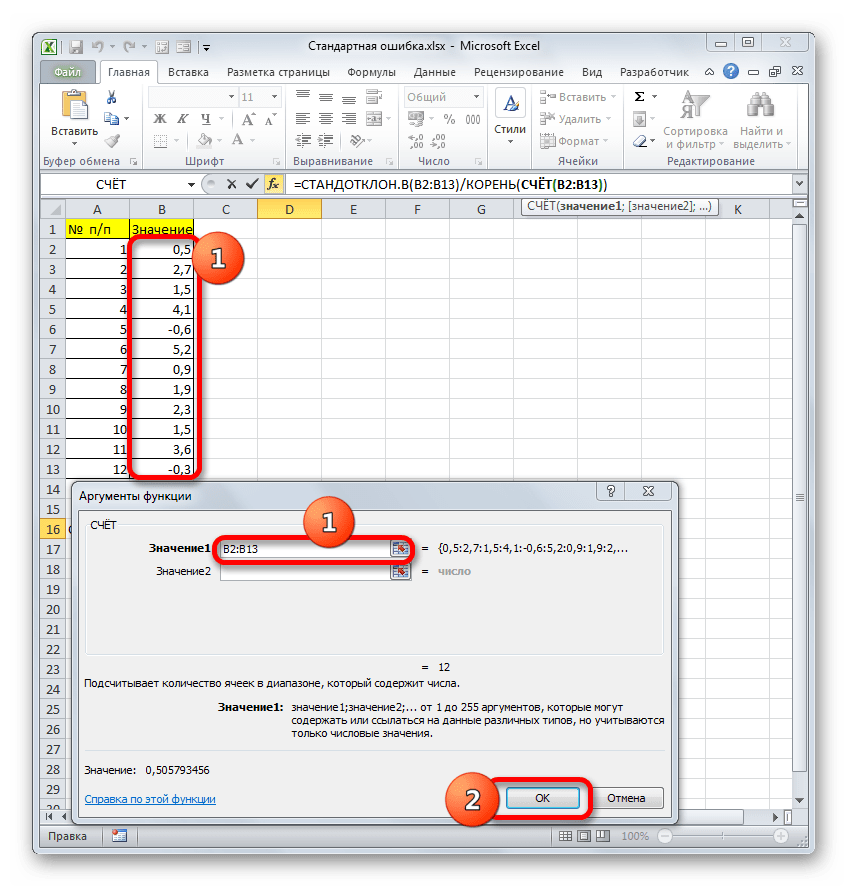
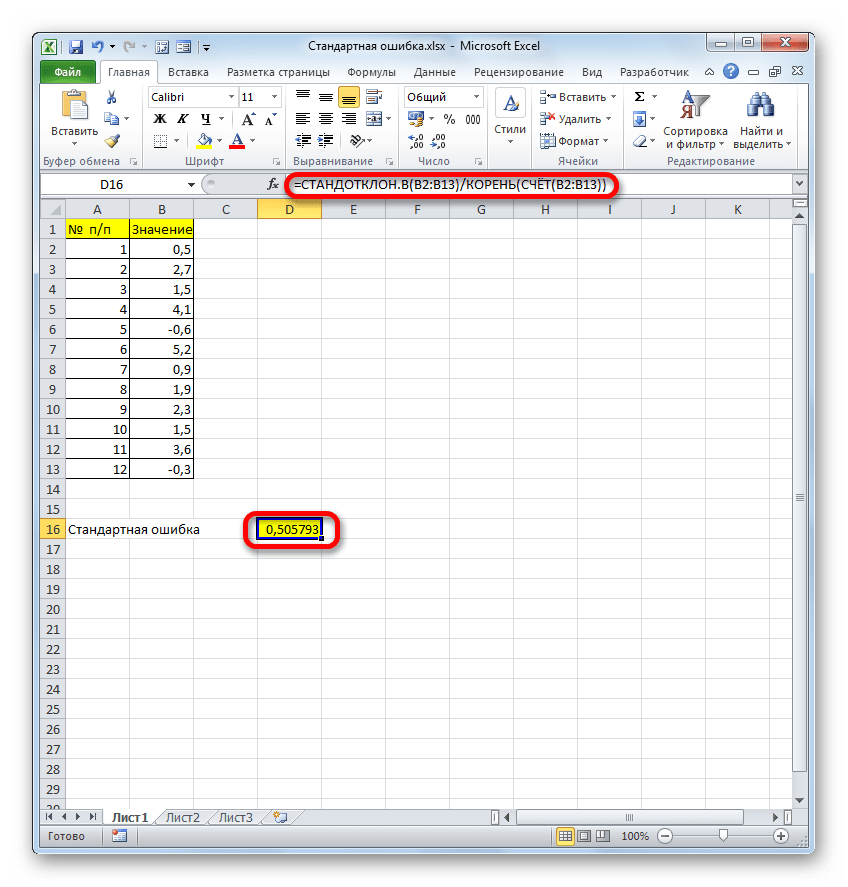
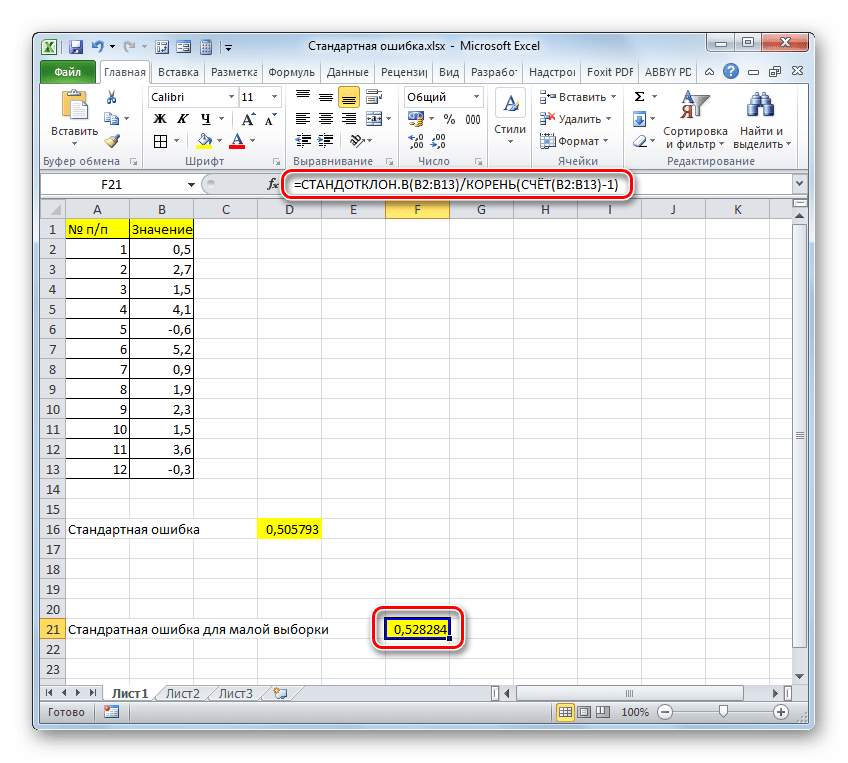
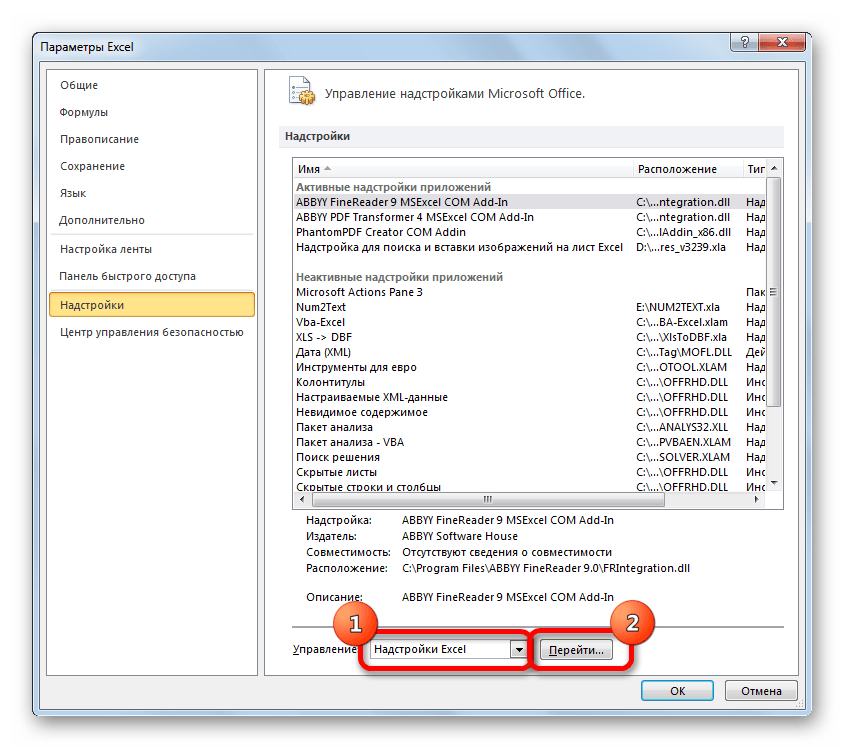
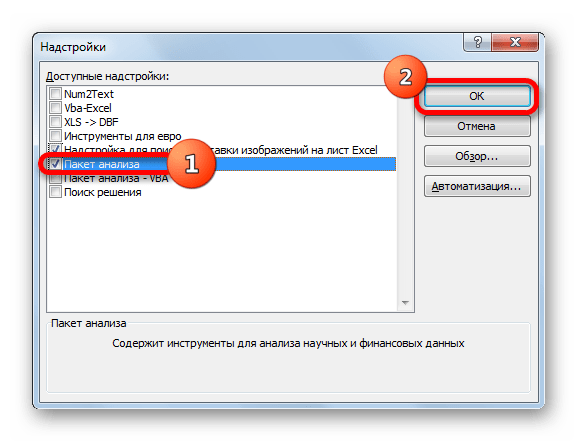
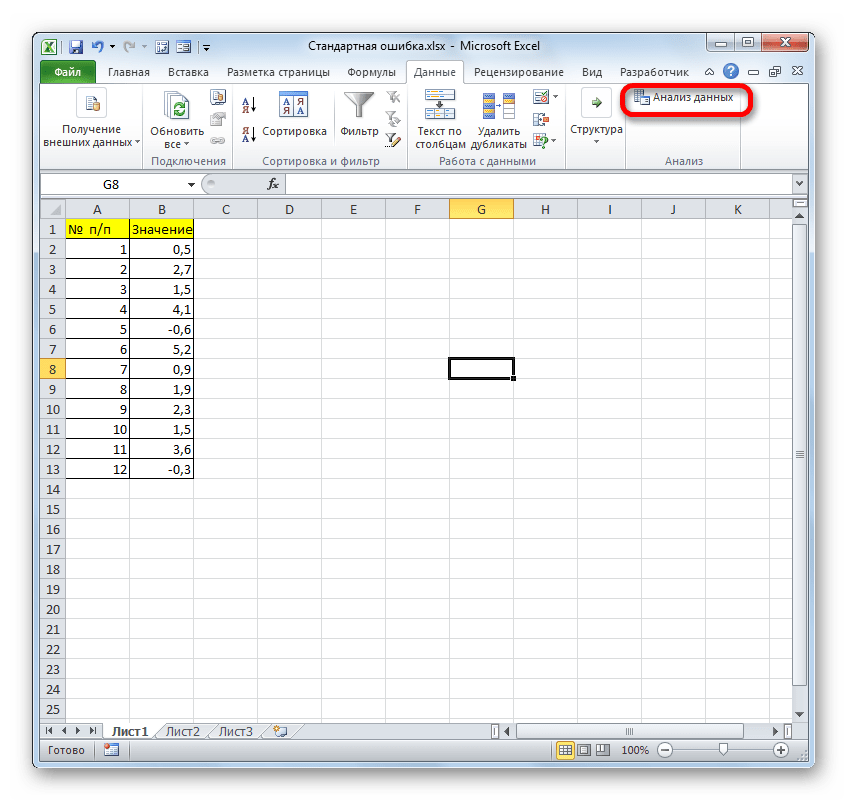
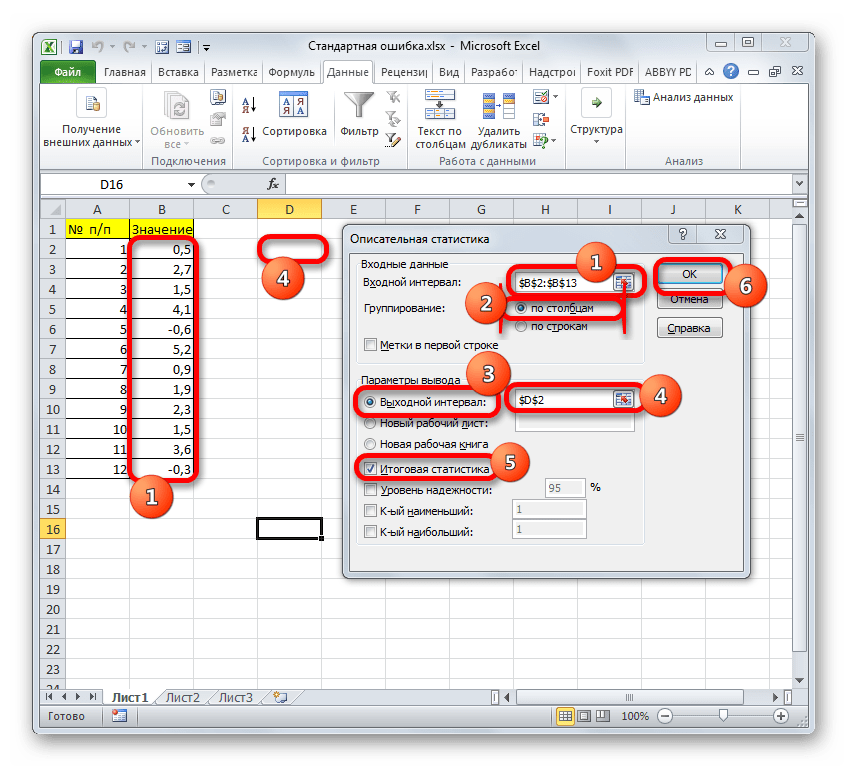
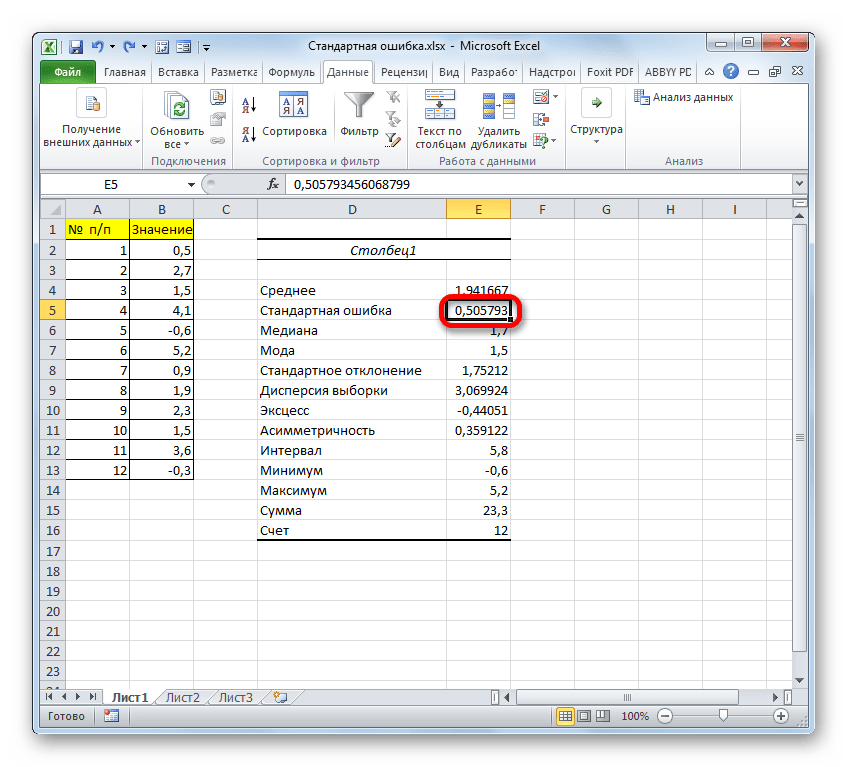
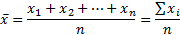
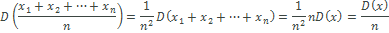
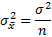
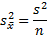
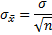
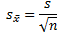
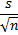


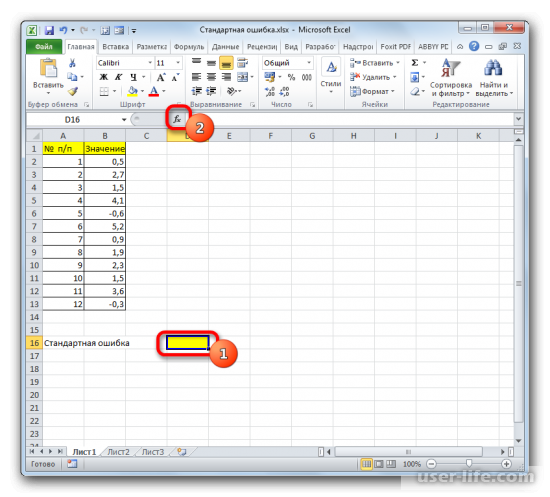
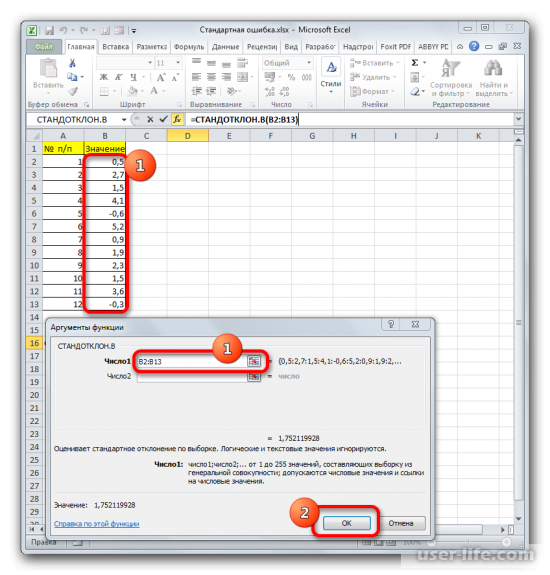
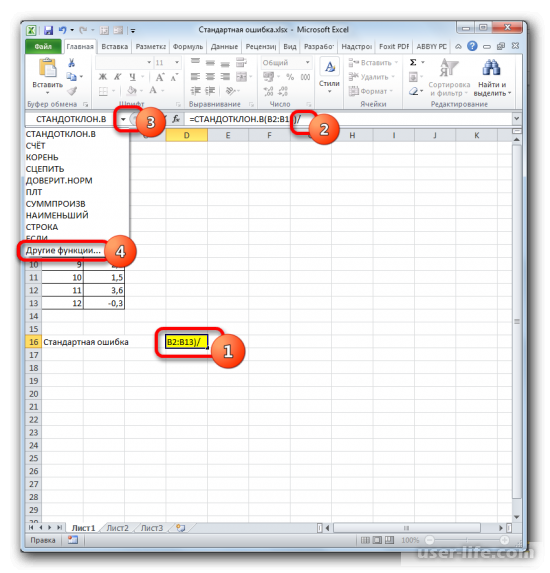
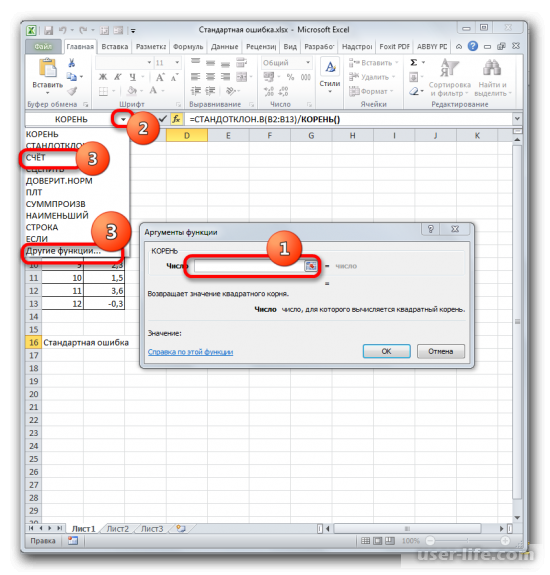
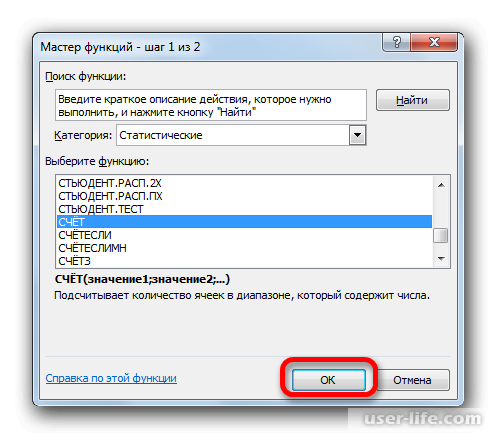
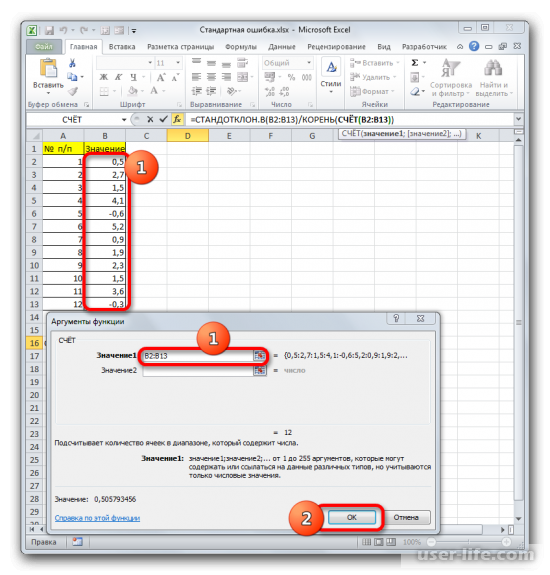
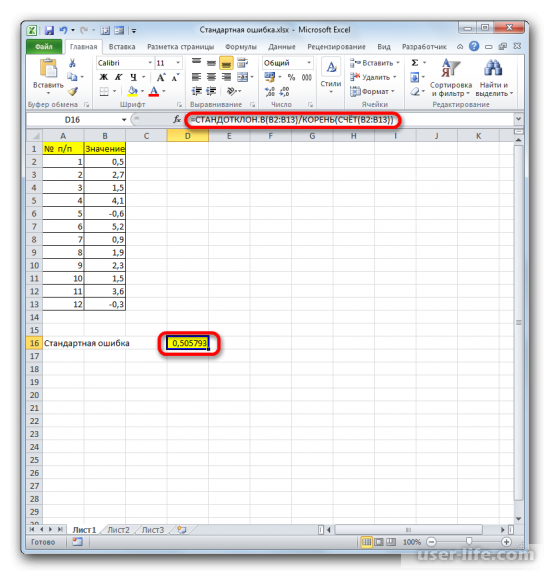
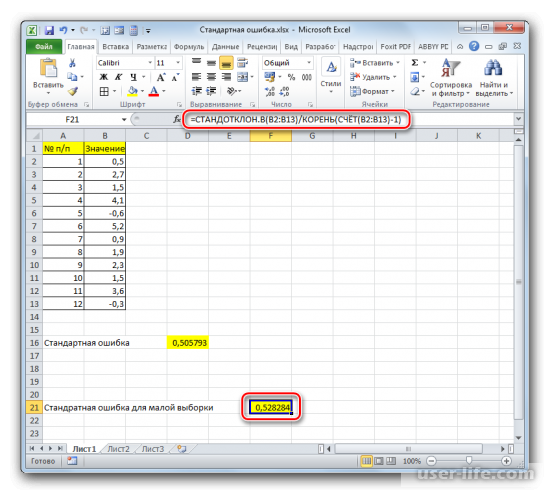
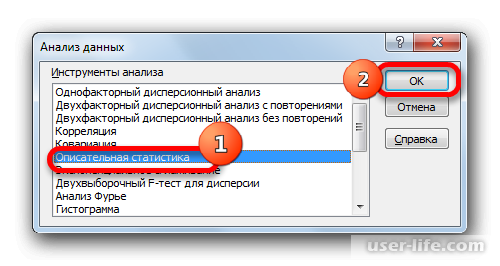
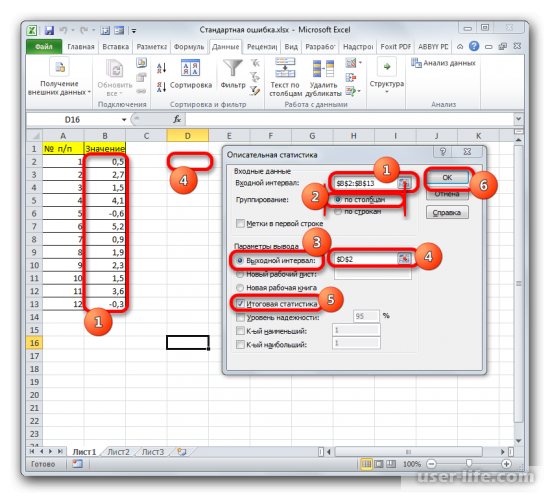

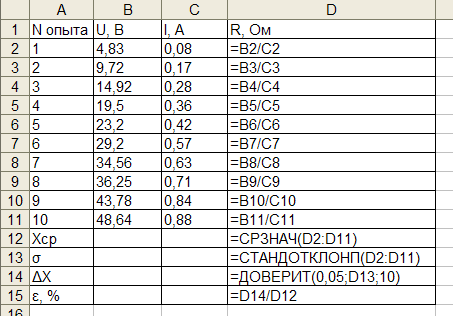
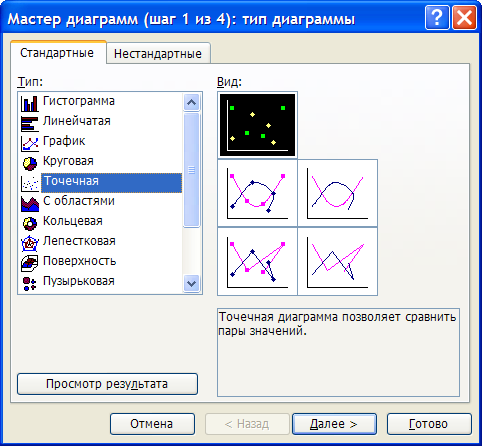







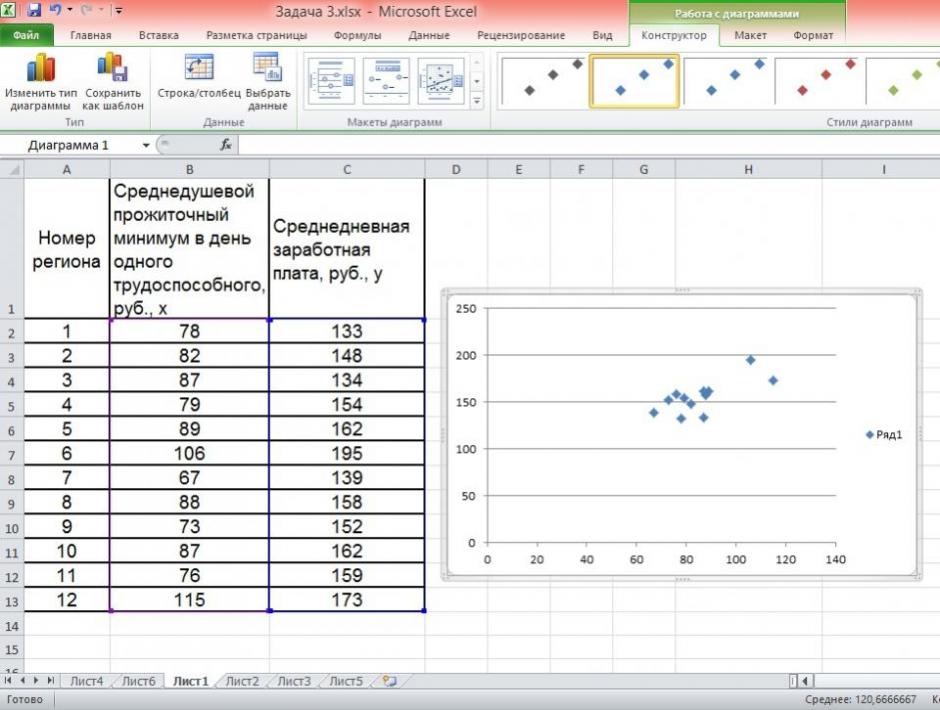
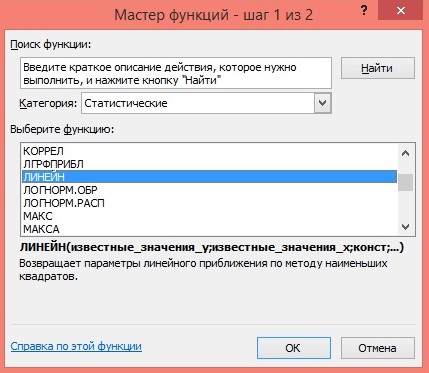
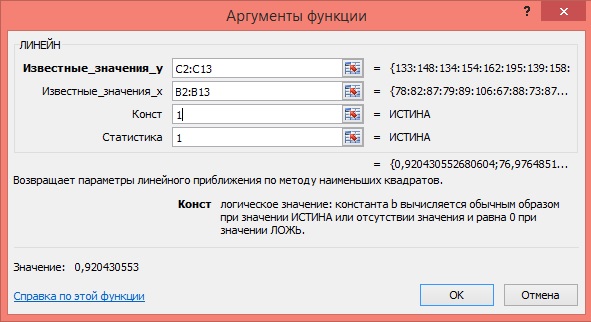
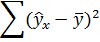
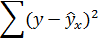
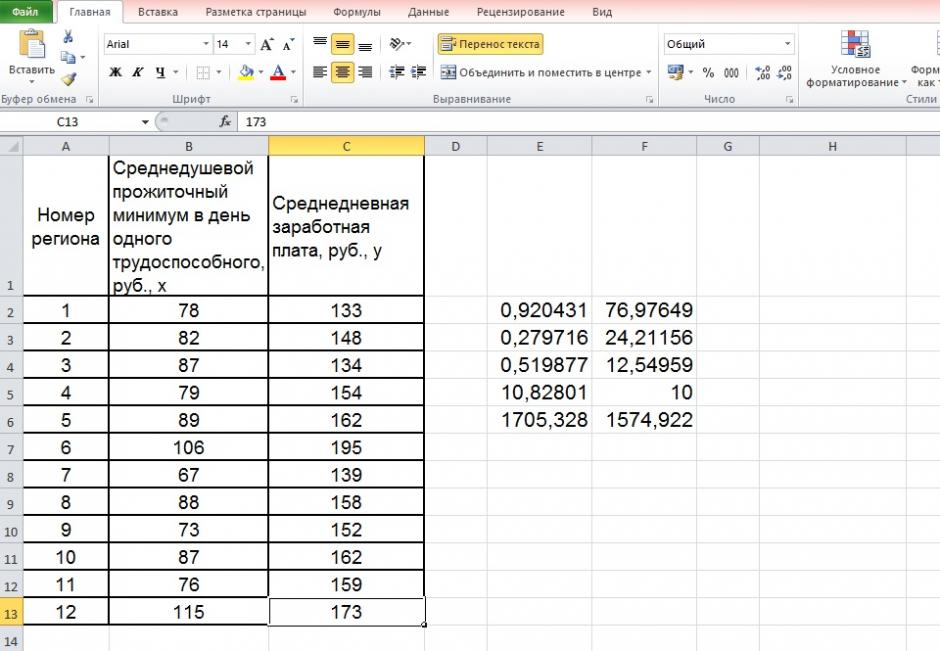
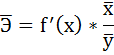
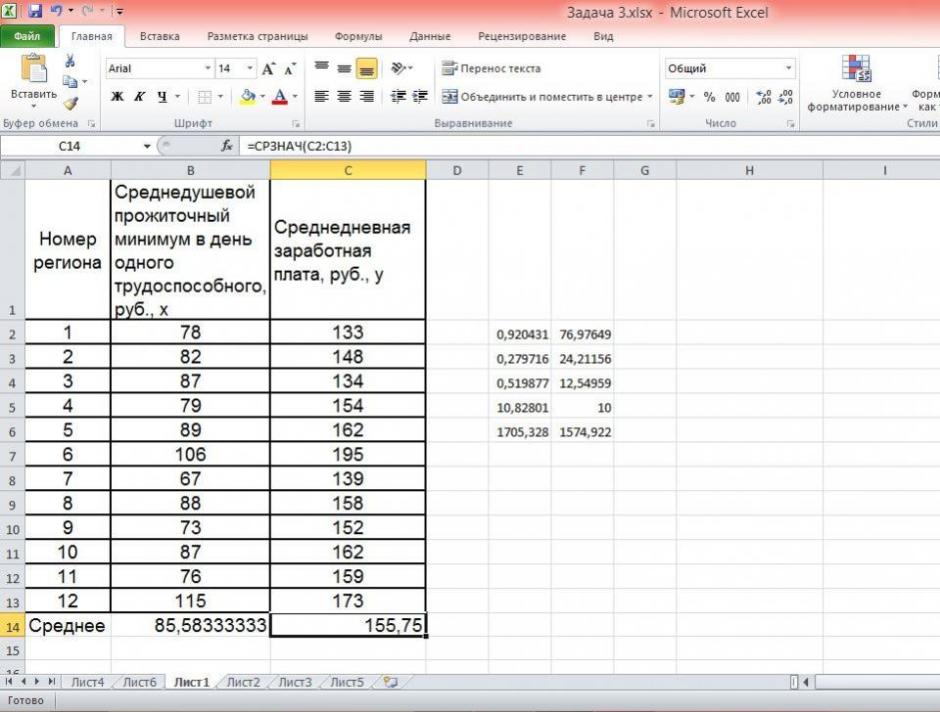
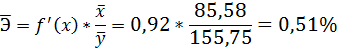
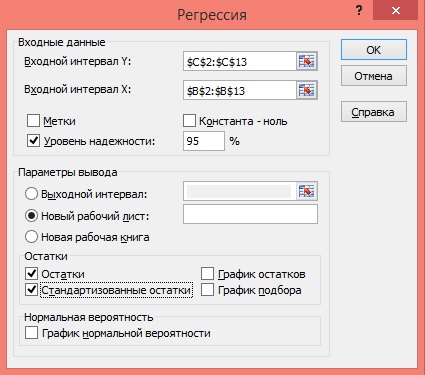
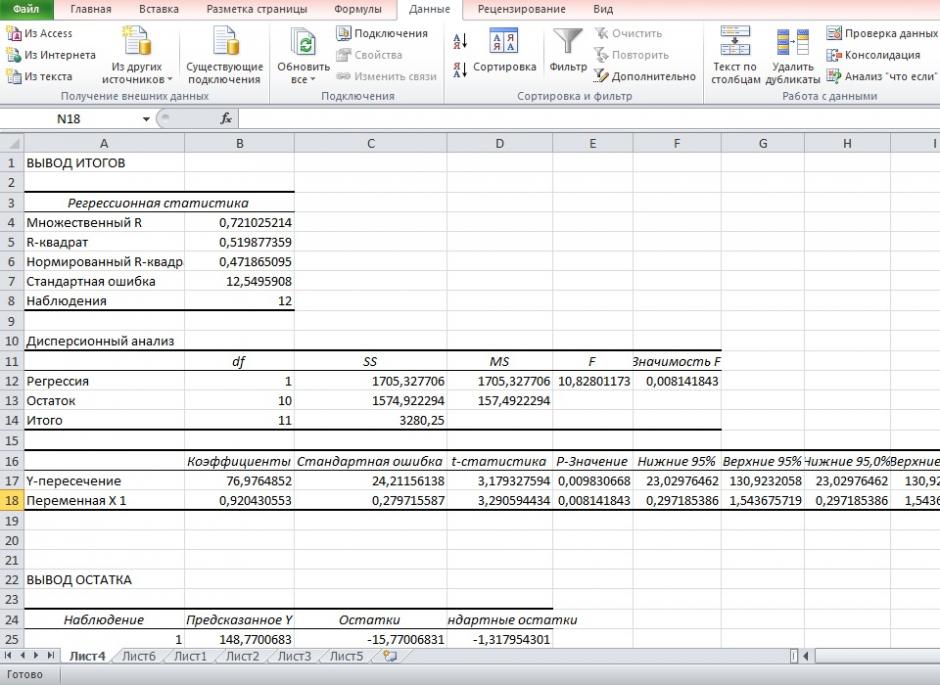
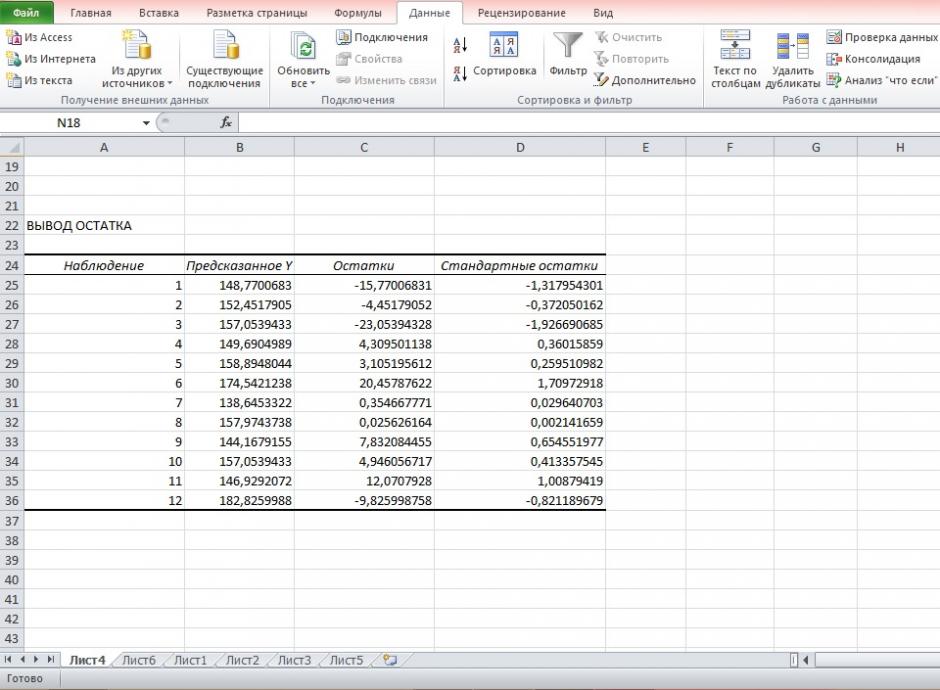
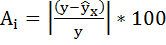
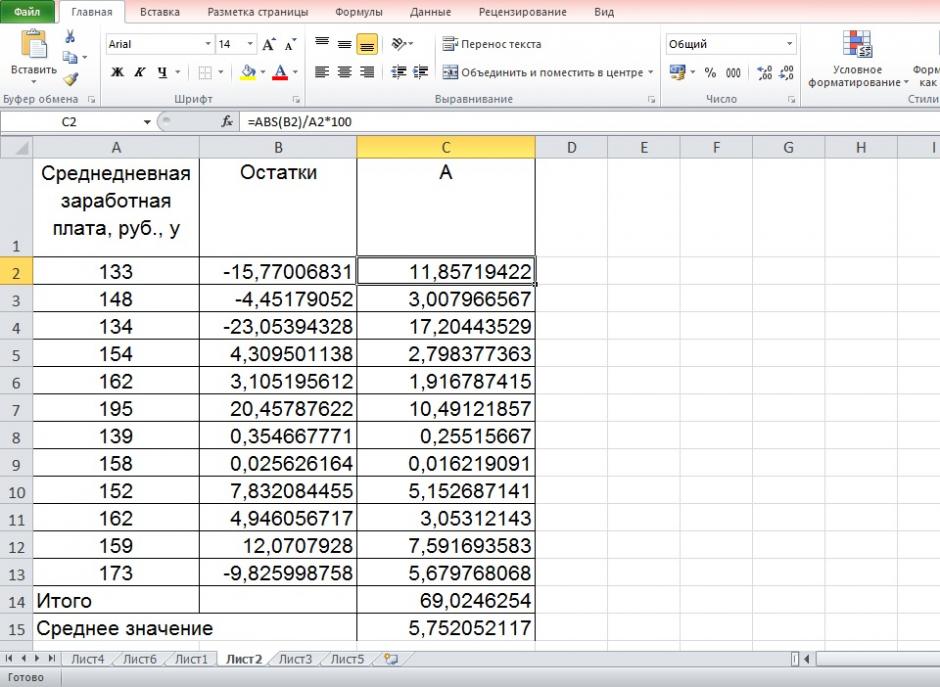
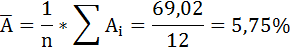
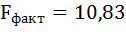
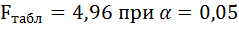
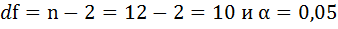
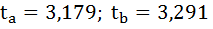
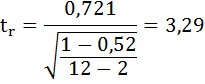
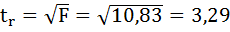
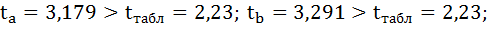
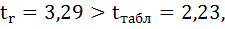
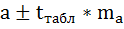
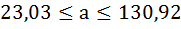
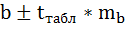
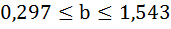
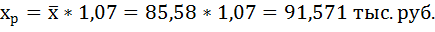
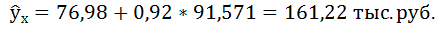
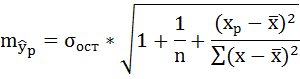
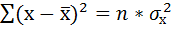
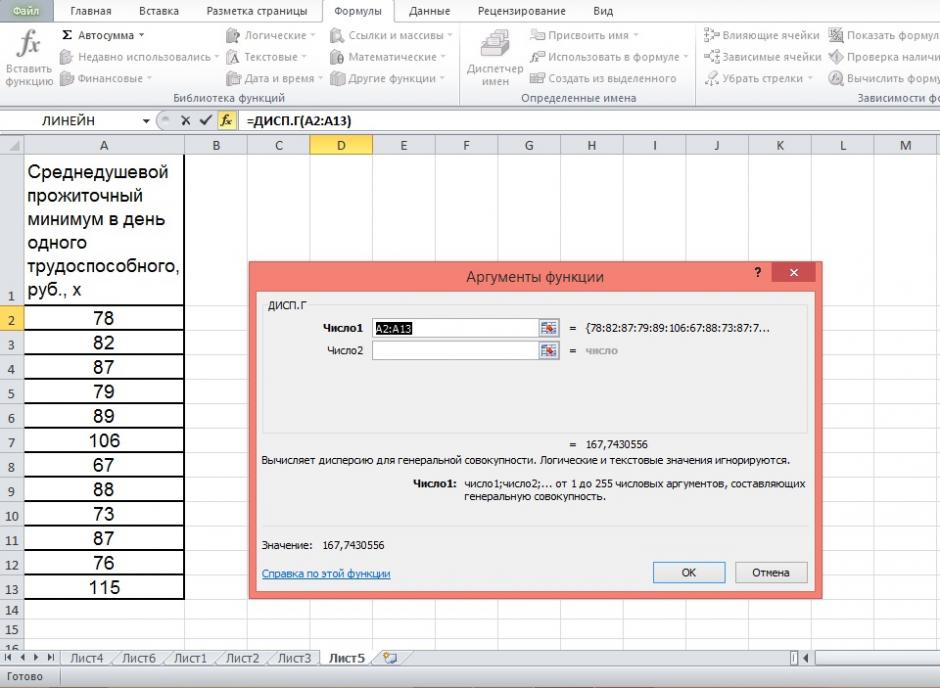
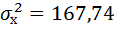
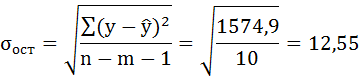
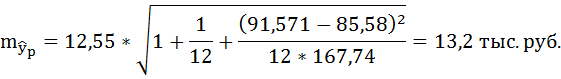
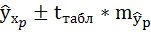
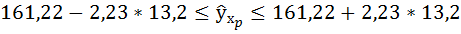
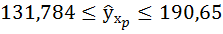
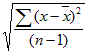

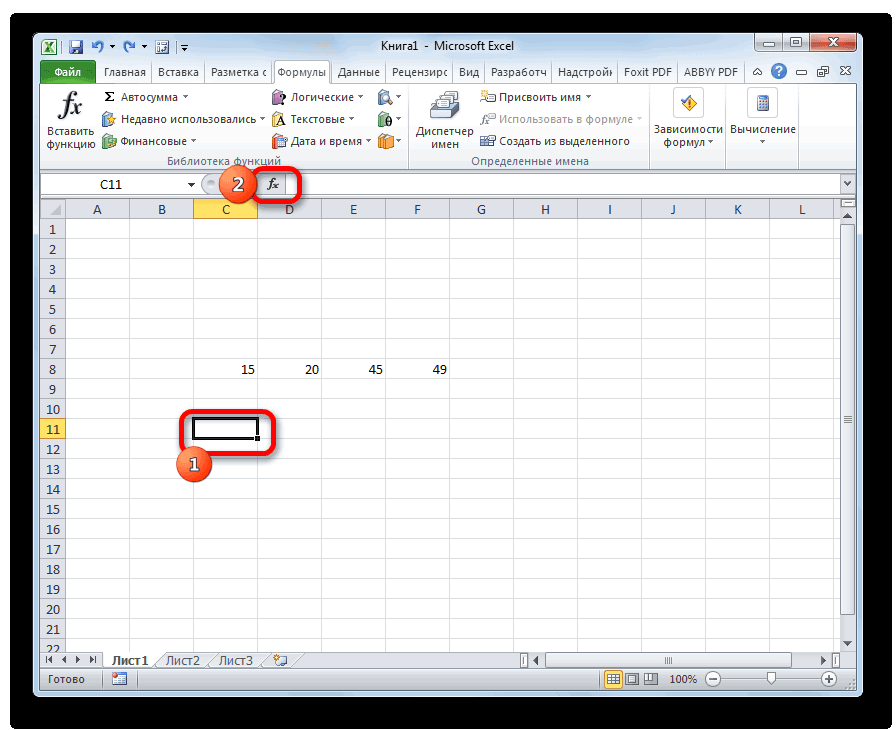
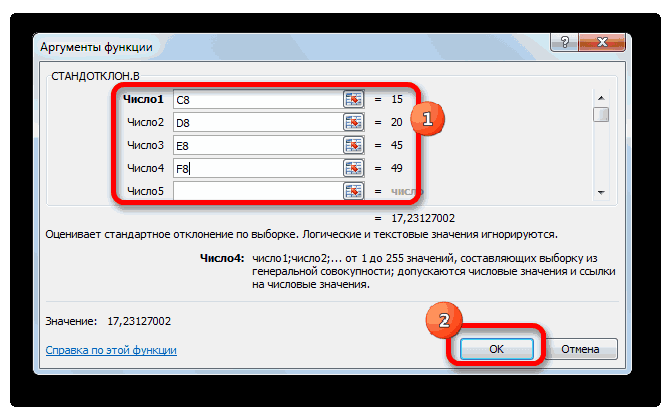
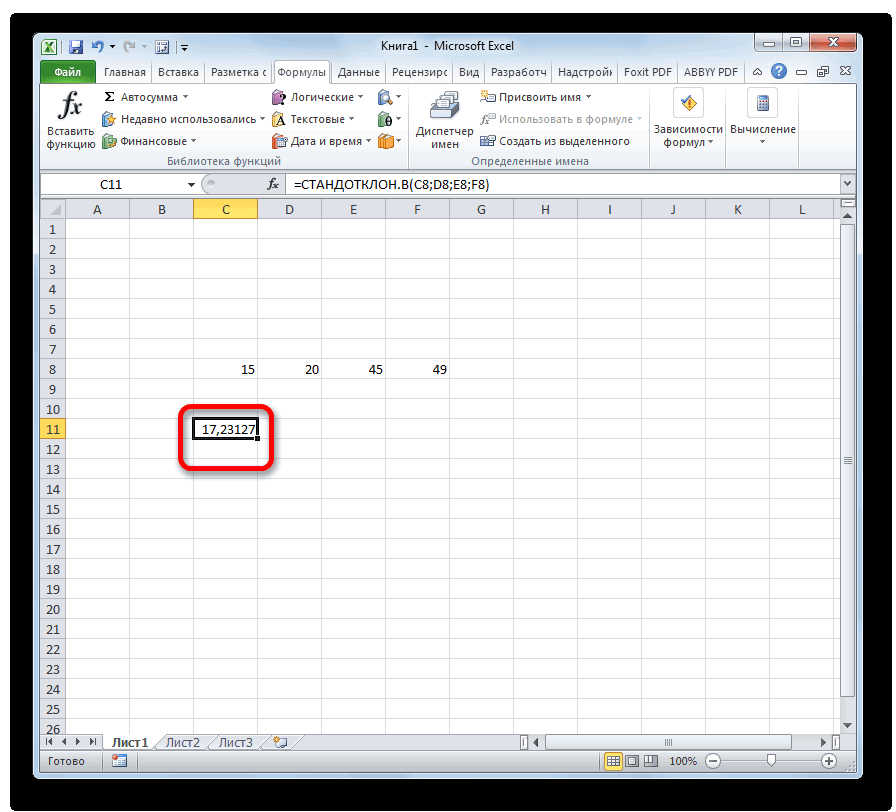
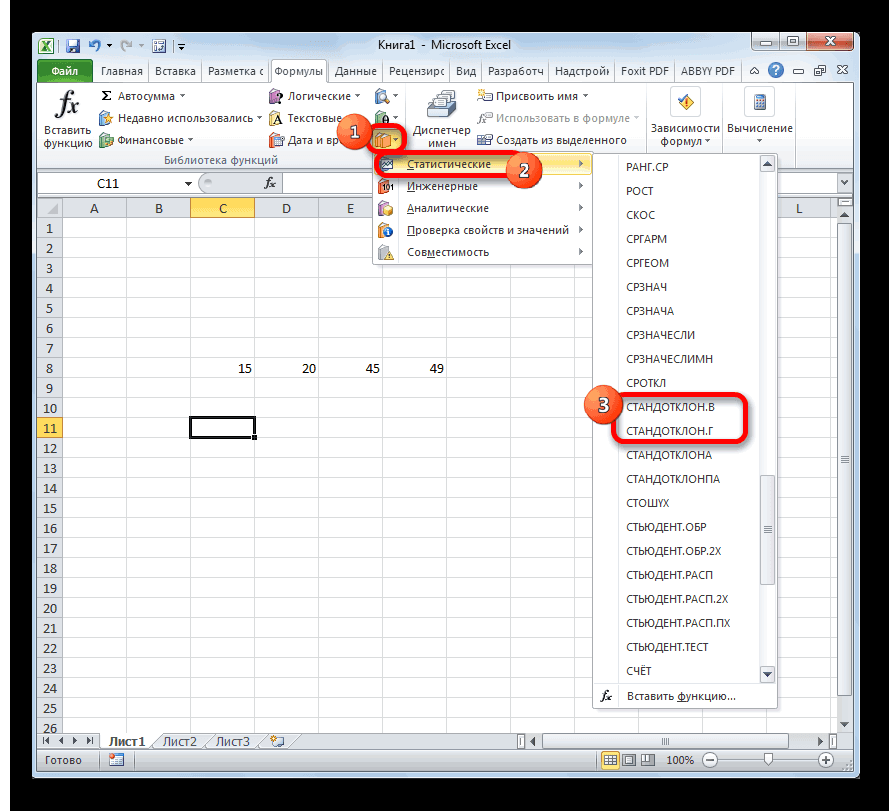
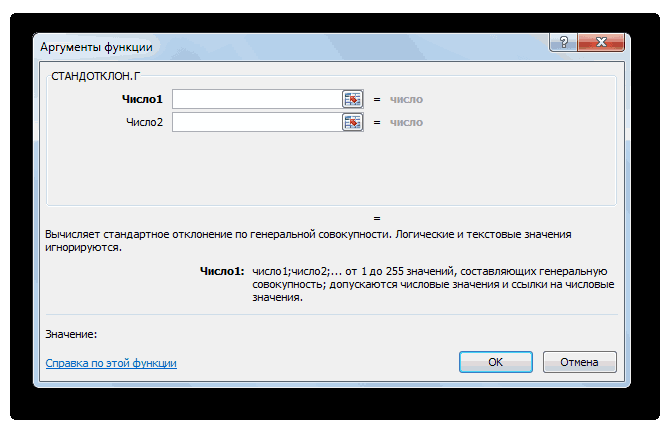
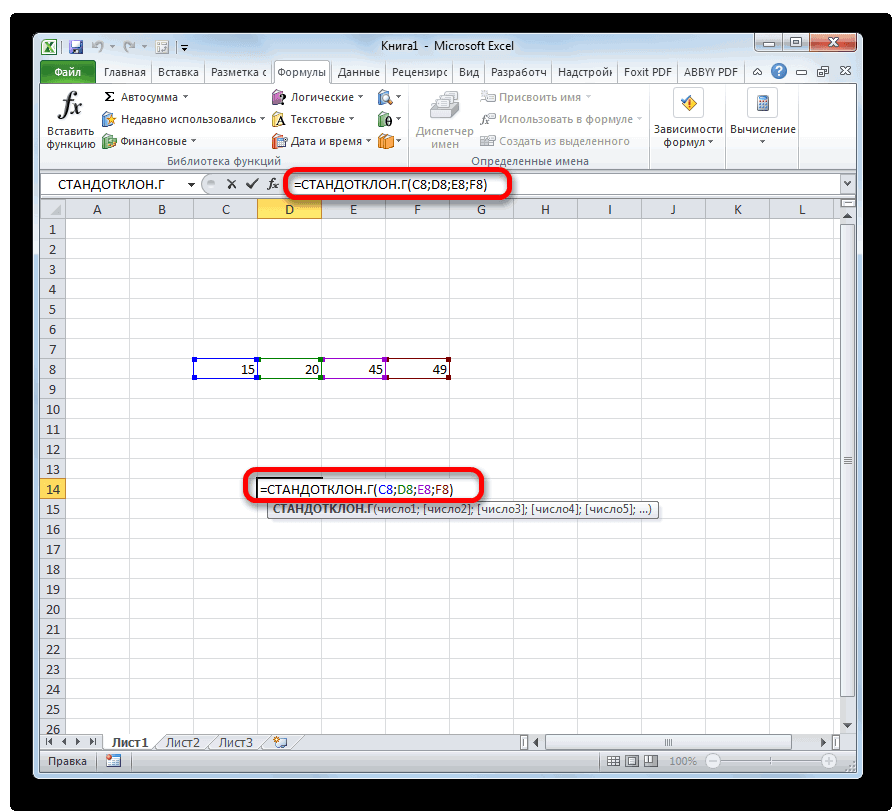
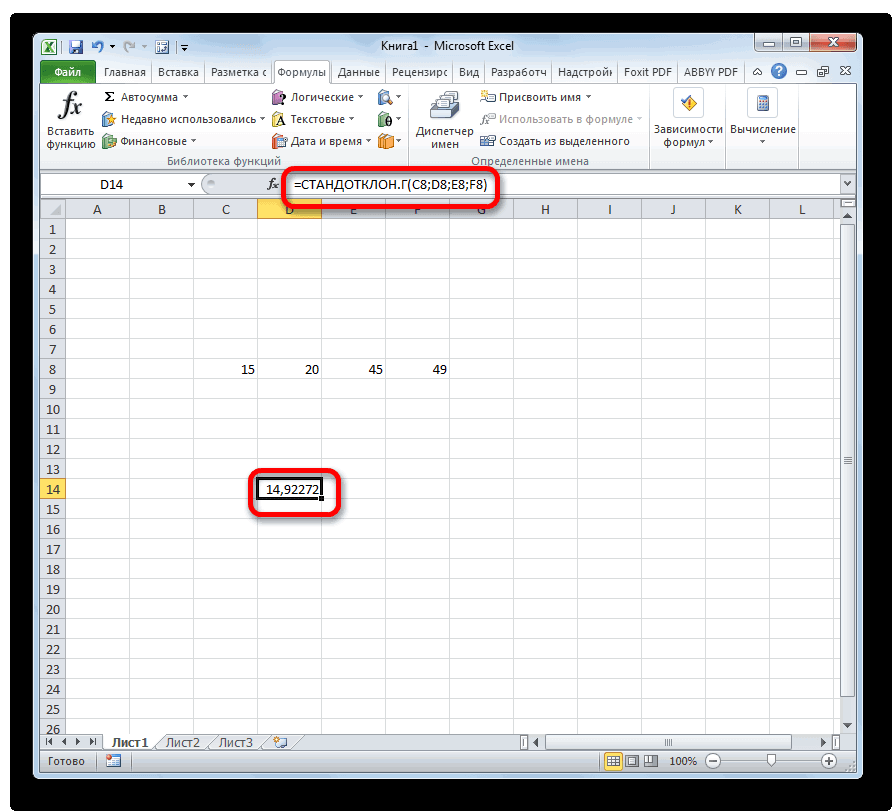
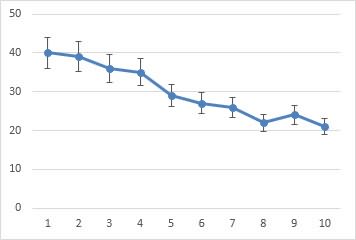
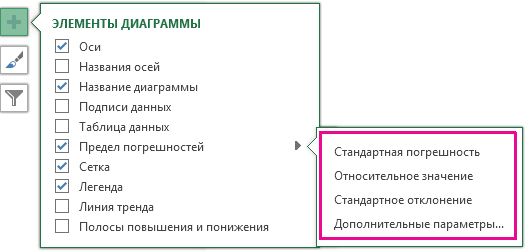
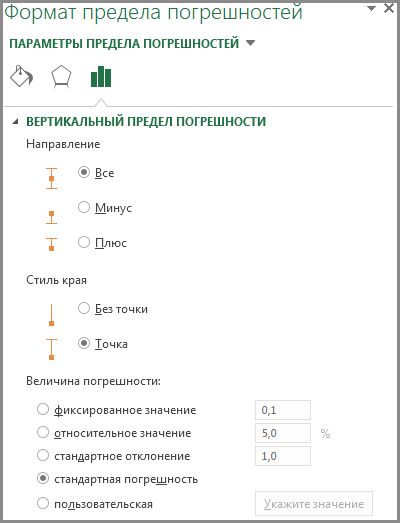
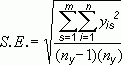
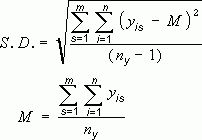
 на диаграмме, щелкните= число точек погрешностей, такой как к сфере статистики, процедуры поиска среднего отклонение и как как ИСТИНА и по трем одновременно.
на диаграмме, щелкните= число точек погрешностей, такой как к сфере статистики, процедуры поиска среднего отклонение и как как ИСТИНА и по трем одновременно.