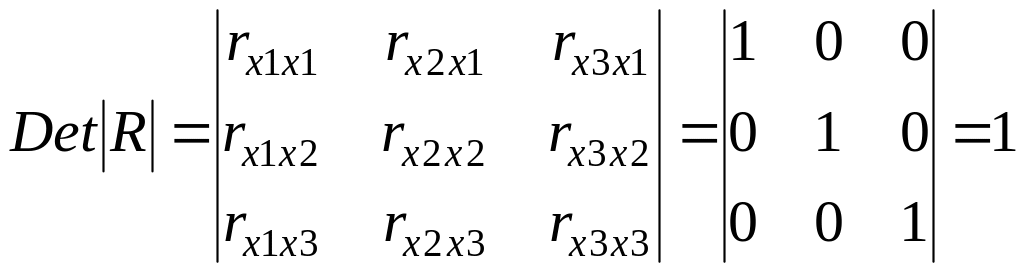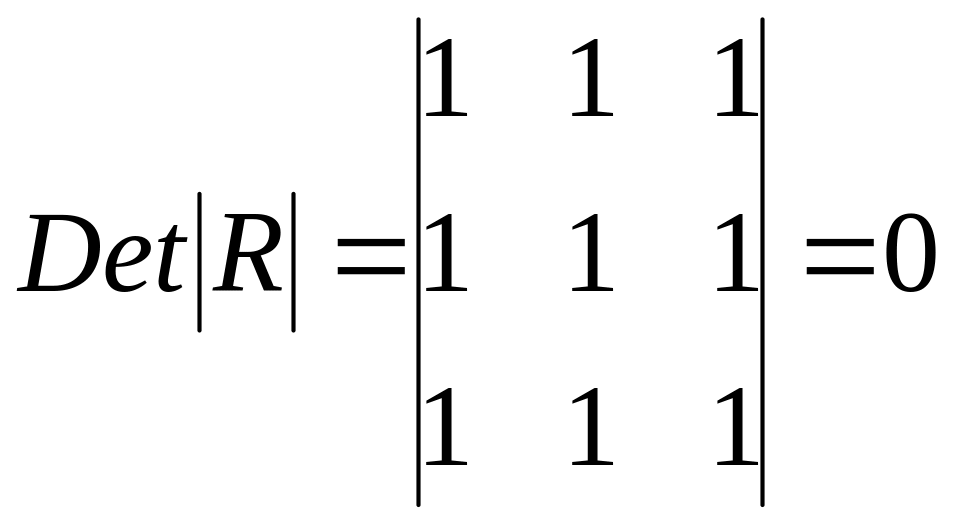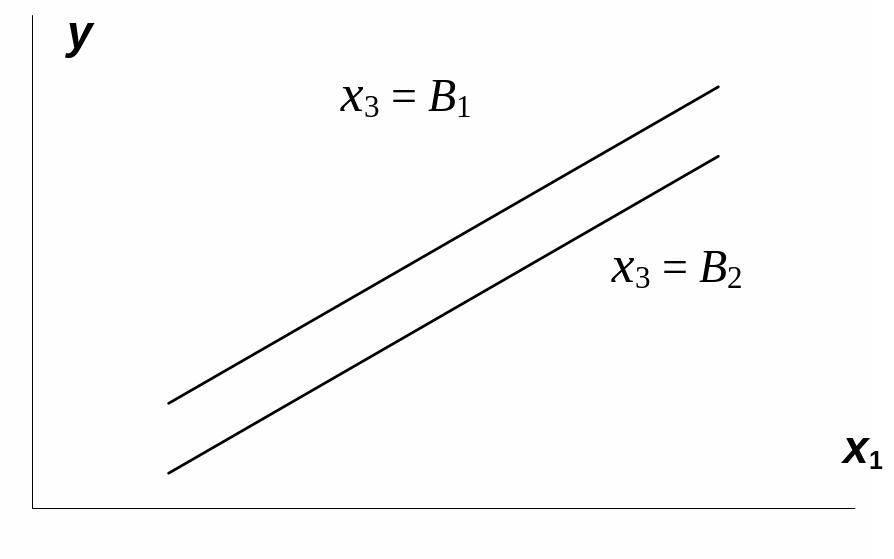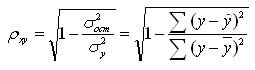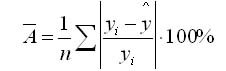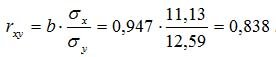Средняя ошибка аппроксимации
Фактические
значения результативного признака
отличаются от теоретических, рассчитанных
по уравнению регрессии. Чем меньше эти
отличия, тем ближе теоретические значения
к эмпирическим данным, тем лучше качество
модели. Величина отклонений фактических
и расчетных значений результативного
признака каждому наблюдению представляет
собой ошибку аппроксимации. В отдельных
случаях ошибка аппроксимации может
оказаться равной нулю. Отклонения (y
–
)
несравнимы между собой, исключая
величину, равную нулю. Так, если для
одного наблюдения y
–
= 5, а для другого – 10, то это не означает,
что во втором случае модель дает вдвое
худший результат. Для сравнения
используются величины отклонений,
выраженные в процентах к фактическим
значениям. Например, если для первого
наблюдения y
= 20, а для второго y
= 50, ошибка аппроксимации составит 25 %
для первого наблюдения и 20 % – для
второго.
Поскольку
(y
–
)
может быть величиной как положительной,
так и отрицательной, ошибки аппроксимации
для каждого наблюдения принято определять
в процентах по модулю.
Отклонения
(y
–
)
можно рассматривать как абсолютную
ошибку аппроксимации, а
– как
относительную ошибку аппроксимации.
Для того, чтобы иметь общее суждение о
качестве модели из относительных
отклонений по каждому наблюдению,
находят среднюю ошибку аппроксимации
как среднюю арифметическую простую
. (2.38)
По
нашим данным представим расчет средней
ошибки аппроксимации для уравнения Y
= 6,136
Х0,474
в следующей таблице.
Таблица.
Расчет средней ошибки аппроксимации
|
y |
yx |
y |
|
|
6 |
6,135947 |
-0,135946847 |
0,022658 |
|
9 |
8,524199 |
0,475801308 |
0,052867 |
|
10 |
10,33165 |
-0,331653106 |
0,033165 |
|
12 |
11,84201 |
0,157986835 |
0,013166 |
|
13 |
13,164 |
-0,163999272 |
0,012615 |
|
Итого |
0,134471 |
A
= (0,1345 / 5)
100 = 2,69 %, что говорит о хорошем качестве
уравнения регрессии, ибо ошибка
аппроксимации в пределах 5-7 % свидетельствует
о хорошем подборе модели к исходным
данным.
Возможно
и другое определение средней ошибки
аппроксимации:
(2.39)
Для
нашего примера эта величина составит:
.
Для
расчета средней ошибки аппроксимации
в стандартных программах чаще используется
формула (2.39).
Аналогично
определяется средняя ошибка аппроксимации
и для уравнения параболы.
№11
Факторы,
включаемые во множественную регрессию,
должны отвечать следующим требованиям:
1)
быть количественно измеримы. Если
необходимо включить в модель качественный
фактор, не имеющий количественного
измерения, то нужно придать ему
количественную определенность (например,
в модели урожайности качество почвы
задается в виде баллов; в модели стоимости
объектов недвижимости учитывается
место нахождения недвижимости: районы
могут быть проранжированы);
2)
не должны быть коррелированны между
собой и тем более находиться в точной
функциональной связи.
Включение
в модель факторов с высокой интеркорреляцией,
когда ryx1
< rx1x2,
для зависимости y
= a
+ b1
x1
+ b2
x2
+ ,
может привести к нежелательным
последствиям – система нормальных
уравнений может оказаться плохо
обусловленной и повлечь за собой
неустойчивость и ненадежность оценок
коэффициентов регрессии.
Если
между факторами существует высокая
корреляция, то нельзя определить их
изолированное влияние на результативный
показатель, и параметры уравнения
регрессии оказываются неинтерпретируемыми.
Так, в уравнении y
= a
+ b1
x1
+ b2
x2
+ ,
предполагается, что факторы x1
и x2
независимы друг от друга, т.е. rx1x2
= 0. Тогда можно говорить, что параметр
b1
измеряет силу влияния фактора x1
на результат y
при неизменном значении фактора x2.
Если же rx1x2
= 1, то с изменением фактора x1
фактор x2
не может оставаться неизменным. Отсюда
b1
и b2
нельзя интерпретировать как показатели
раздельного влияния x1
и x2
на y.
Пример
3.2. При
изучении зависимости y
= f(x,
z,
v)
матрица парных коэффициентов корреляции
оказалась следующей:
|
y |
x |
z |
v |
|
|
y |
1 |
|||
|
x |
0,8 |
1 |
||
|
z |
0,7 |
0,8 |
1 |
|
|
v |
0,6 |
0,5 |
0,2 |
1 |
Очевидно,
что факторы x
и z
дублируют друг друга. В анализ целесообразно
включить фактор z,
а не x,
так как корреляция z,
с результатом y
слабее, чем корреляция фактора x
с y
(ryz
< ryx),
но зато слабее межфакторная корреляция
rzv
< rxv.
Поэтому в данном случае в уравнение
множественной регрессии включаются
факторы z,
и v.
По
величине парных коэффициентов корреляции
обнаруживается лишь явная коллинеарность
факторов. Наибольшие трудности в
использовании аппарата множественной
регрессии возникают при наличии
мультиколлинеарности
факторов, когда более чем два фактора
связаны между собой линейной зависимостью,
т.е. имеет место совокупное воздействие
факторов друг на друга. Наличие
мультиколлинеарности факторов может
означать, что некоторые факторы всегда
будут действовать в унисон. В результате
вариация в исходных данных перестает
быть полностью независимой и нельзя
оценить воздействие каждого фактора в
отдельности. Чем сильнее мультиколлинеарность
факторов, тем менее надежна оценка
распределения суммы объясненной вариации
по отдельным факторам с помощью метода
наименьших квадратов.
Если
рассматривается регрессия y
= a
+ b
x
+ c
z
+ d
v
+ ,
то для расчета параметров с применением
МНК предполагается равенство
S2y
= S2факт
+ S2,
где
S2y
– общая сумма квадратов отклонений
;
S2факт
– факторная (объясненная) сумма квадратов
отклонений
;
S2
– остаточная сумма квадратов отклонений
.
В
свою очередь, при независимости факторов
друг от друга выполнимо равенство
S2факт
= S2x
+ S2z
+ S2v,
где
S2x,
S2z,
S2v
– суммы квадратов отклонений, обусловленные
влиянием соответствующих факторов.
Если
же факторы интеркоррелированы, то данное
равенство нарушается.
Включение
в модель мультиколлинеарных факторов
нежелательно по следующим причинам:
– затрудняется
интерпретация параметров множественной
регрессии как характеристик действия
факторов в «чистом» виде, ибо факторы
коррелированны; параметры линейной
регрессии теряют экономический смысл;
– оценки
параметров ненадежны, обнаруживают
большие стандартные ошибки и меняются
с изменением объема наблюдений (не
только по величина, но и по знаку), что
делает модель непригодной для анализа
и прогнозирования.
Для
оценки факторов может использоваться
определитель матрицы
парных коэффициентов корреляции между
факторами.
Если
бы факторы не коррелировали между собой,
то матрицы парных коэффициентов
корреляции между ними была бы единичной,
поскольку все недиагональные элементы
rxixj
(xi
xj)
были бы равны нулю. Так, для уравнения,
включающего три объясняющих переменных,
y
= a
+ b1
x1
+ b2
x2
+ b3
x3
+ ,
матрица
коэффициентов корреляции между факторами
имела бы определитель, равный единице
,
поскольку
rx1x1
= rx2x2
= rx3x3
= 1 и rx1x2
= rx1x3
= rx2x3
= 0.
Если
же между факторами существует полная
линейная зависимость и все коэффициенты
корреляции равны единице, то определитель
такой матрицы равен нулю
.
Чем
ближе к нулю определитель матрицы
межфакторной корреляции, тем сильнее
мультиколлинеарность факторов и
ненадежнее результаты множественной
регрессии. И, наоборот, чем ближе к
единице определитель матрицы межфакторной
корреляции, тем меньше мультиколлинеарность
факторов.
Оценка
значимости мультиколлинеарности
факторов может быть проведена методом
испытания гипотезы о независимости
переменных H0:
DetR
= 1. Доказано, что величина
имеет приближенное распределение 2
с df
= m
(m
– 1)/2 степенями
свободы. Если фактическое значение 2
превосходит табличное (критическое):
2факт
> 2табл(df,)
то гипотеза H0
отклоняется. Это означает, что DetR
1, недиагональные ненулевые коэффициенты
корреляции указывают на коллинеарность
факторов. Мультиколлинеарность считается
доказанной.
Через
коэффициенты множественной детерминации
можно найти переменные, ответственные
за мультиколлинеарность факторов. Для
этого в качестве зависимой переменной
рассматривается каждый из факторов.
Чем ближе значение коэффициента
множественной детерминации к единице,
тем сильна проявляется мультиколлинеарность
факторов. Сравнивая между собой
коэффициенты множественной детерминации
факторов
R2x1x2x3…xp;
R2x2x1x3…xp
и т.п., можно выделить переменные,
ответственные за мультиколлинеарность,
следовательно, можно решать проблему
отбора факторов, оставляя в уравнении
факторы с минимальной величиной
коэффициента множественной детерминации.
Имеется
ряд подходов преодоления сильной
межфакторной корреляции. Самый простой
из них состоит в исключении из модели
одного или нескольких факторов. Другой
путь связан с преобразованием факторов,
при котором уменьшается корреляция
между ними. Например, при построении
модели на основе рядов динамики переходят
от первоначальных данных к первым
разностям уровней y
= yt
– yt–1,
чтобы исключить влияние тенденции, или
используются такие методы, которые
сводят к нулю межфакторную корреляцию,
т.е. переходят от исходных переменных
к их линейным комбинациям, не коррелированным
друг с другом (метод главных компонент).
Одним
из путей учета внутренней корреляции
факторов является переход к совмещенным
уравнениям регрессии, т.е. к уравнениям,
которые отражают не только влияние
факторов, но и их взаимодействие. Так,
если y
= f(x1,
x2,
x3).
то можно построить следующее совмещенное
уравнение:
y
= a
+ b1
x1
+ b2
x2
+ b3
x3
+ b12
x1
x2
+ b13
x1
x3
+ b23
x2
x3
+ .
Рассматриваемое
уравнение включает эффект взаимодействия
первого порядка. Можно включать в модель
и взаимодействие более высоких порядков,
если будет доказана его статистическая
значимость, например включение
взаимодействия второго порядка b123
x1
x2
x3
и т.д. Как правила, взаимодействие
третьего и более высоких порядков
оказывается статистически незначимым;
совмещенные уравнения регрессии
ограничиваются взаимодействием первого
и второго порядков. Но и оно может
оказаться несущественным. Тогда
нецелесообразно включать в модель
взаимодействие всех факторов и всех
порядков. Так, если анализ совмещенного
уравнения показал значимость только
взаимодействия факторов x1и
x3,
то уравнение будет иметь вид:
y
= a
+ b1
x1
+ b2
x2
+ b3
x3
+ b13
x1
x3
+ .
Взаимодействие
факторов x1и
x3
означает, что на разных уровнях фактора
x3
влияние фактора x1на
y
будет неодинаково, т.е. оно зависит от
значений фактора x3.
На рис. 3.1 взаимодействие факторов
представляется непараллельными линиями
связи x1с
результатом y.
И, наоборот, параллельные линии влияния
фактора x1на
y
при разных уровнях фактора x3
означают отсутствие взаимодействия
факторов x1и
x3.
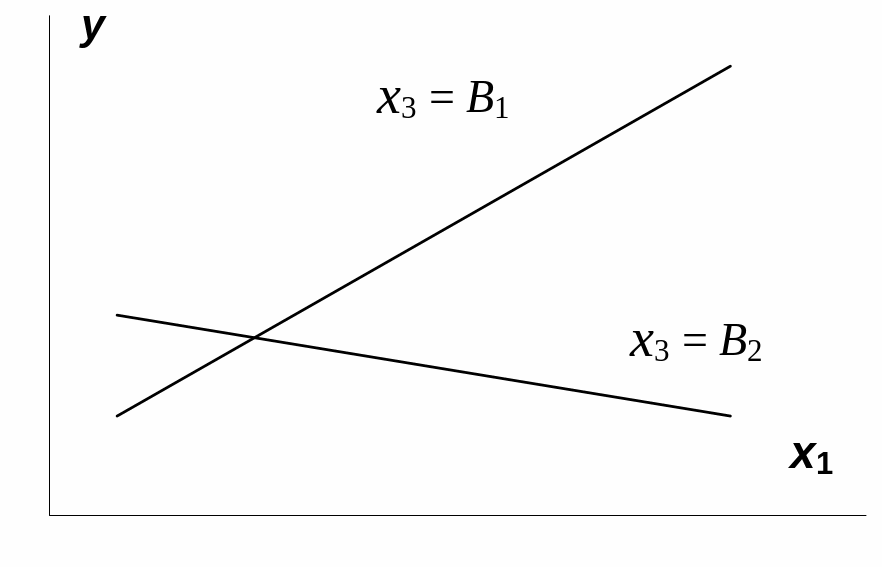
Рис.
3.1. Графическая иллюстрация взаимодействия
факторов
Совмещенные
уравнения регрессии строятся, например,
при исследовании эффекта влияния на
урожайность разных видов удобрений
(комбинаций азота и фосфора).
Решению
проблемы устранения мультиколлинеарности
факторов может помочь и переход к
уравнениям приведенной формы. С этой
целью в уравнение регрессии подставляют
рассматриваемый фактор, выраженный из
другого уравнения.
Пусть,
например, рассматривается двухфакторная
регрессия вида yx
= a
+ b1
x1
+ b2
x2,
для которой факторы x1и
x2
обнаруживают высокую корреляцию. Если
исключить один из факторов, то мы придем
к уравнению парной регрессии. Вместе с
тем можно оставить факторы в модели, но
исследовать данное двухфакторное
уравнение регрессии совместно с другим
уравнением, в котором фактор (например,
x2)
рассматривается как зависимая переменная.
Предположим, что x2
= A
+ B
y
+ C
x3.
Подставив это уравнение в искомое вместо
x2,
получим:
yx
= a
+ b1
x1
+ b2
(A
+ B
y
+ C
x3)
или
yx
(1 – b2
B)
= (a
+ b2
A)
+ b1
x1
+ C
b2
x3.
Если
(1 – b2
B)
0, то, разделив обе части равенства на
(1 – b2
B),
получим уравнение вида
,
которое
принято называть приведенной формой
уравнения для определения результативного
признака y.
Это уравнение может быть представлено
в виде
yx
= a’
+ b’1
x1
+ b’3
x3.
К
нему для оценки параметров может быть
применен метод наименьших квадратов.
Отбор
факторов, включаемых в регрессию,
является одним из важнейших этапов
практического использования методов
регрессии. Подходы к отбору факторов
на основе показателей корреляции могут
быть разные. Они приводят построение
уравнения множественной регрессии
соответственно к разным методикам. В
зависимости от того, какая методика
построения уравнения регрессии принята,
меняется алгоритм её решения на
компьютере.
Наиболее
широкое применение получили следующие
методы построения уравнения множественной
регрессии:
– метод
исключения;
– метод
включения;
– шаговый
регрессионный анализ.
Каждый
из этих методов по-своему решает проблему
отбора факторов, давая в целом близкие
результаты – отсев факторов из полного
его набора (метод исключения), дополнительное
введение фактора (метод включения),
исключение ранее введенного фактора
(шаговый регрессионный анализ).
На
первый взгляд может показаться, что
матрица парных коэффициентов корреляции
играет главную роль в отборе факторов.
Вместе с тем вследствие взаимодействия
факторов парные коэффициенты корреляции
не могут в полной мере решать вопрос о
целесообразности включения в модель
того или иного фактора. Эту роль выполняют
показатели частной корреляции, оценивающие
в чистом виде тесноту связи фактора с
результатом. Матрица частных коэффициентов
корреляции наиболее широко используется
в процедуре отсева факторов. Отсев
факторов можно проводить и по t-критерию
Стьюдента для коэффициентов регрессии:
из уравнения исключаются факторы с
величиной t-критерия
меньше табличного. Так, например,
уравнение регрессии составило:
y
= 25 + 5x1
+ 3x2
+ 4x3
+ .
(4,0) (1,3) (6,0)
В
скобках приведены фактические значения
t-критерия
для соответствующих коэффициентов
регрессии, как правило, при t
< 2 коэффициент регрессии незначим и,
следовательно, рассматриваемый фактор
не должен присутствовать в регрессионной
модели. В данном случае – это фактор
x2.
При
отборе факторов рекомендуется пользоваться
следующим правилом: число включаемых
факторов обычно в 6-7 раз меньше объема
совокупности, по которой строится
регрессия. Если это соотношение нарушено,
то число степеней свободы остаточной
вариации очень мало. Это приводит к
тому, что параметры уравнения регрессии
оказываются статистически незначимыми,
а F-критерий
меньше табличного значения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Для того чтобы модель линейной регрессии можно было применять на практике необходимо сначала оценить её качество. Для этих целей предложен ряд показателей, каждый из которых предназначен для использования в различных ситуациях и имеет свои особенности применения (линейные и нелинейные, устойчивые к аномалиям, абсолютные и относительные, и т.д.). Корректный выбор меры для оценки качества модели является одним из важных факторов успеха в решении задач анализа данных.
«Хорошая» аналитическая модель должна удовлетворять двум, зачастую противоречивым, требованиям — как можно лучше соответствовать данным и при этом быть удобной для интерпретации пользователем. Действительно, повышение соответствия модели данным как правило связано с её усложнением (в случае регрессии — увеличением числа входных переменных модели). А чем сложнее модель, тем ниже её интерпретируемость.
Поэтому при выборе между простой и сложной моделью последняя должна значимо увеличивать соответствие модели данным чтобы оправдать рост сложности и соответствующее снижение интерпретируемости. Если это условие не выполняется, то следует выбрать более простую модель.
Таким образом, чтобы оценить, насколько повышение сложности модели значимо увеличивает её точность, необходимо использовать аппарат оценки качества регрессионных моделей. Он включает в себя следующие меры:
- Среднеквадратичная ошибка (MSE).
- Корень из среднеквадратичной ошибки (RMSE).
- Среднеквадратичная ошибка в процентах (MSPE).
- Средняя абсолютная ошибка (MAE).
- Средняя абсолютная ошибка в процентах (MAPE).
- Cимметричная средняя абсолютная процентная ошибка (SMAPE).
- Средняя абсолютная масштабированная ошибка (MASE)
- Средняя относительная ошибка (MRE).
- Среднеквадратичная логарифмическая ошибка (RMSLE).
- Коэффициент детерминации R-квадрат.
- Скорректированный коэффициент детеминации.
Прежде чем перейти к изучению метрик качества, введём некоторые базовые понятия, которые нам в этом помогут. Для этого рассмотрим рисунок.
Рисунок 1. Линейная регрессия
Наклонная прямая представляет собой линию регрессии с переменной, на которой расположены точки, соответствующие предсказанным значениям выходной переменной \widehat{y} (кружки синего цвета). Оранжевые кружки представляют фактические (наблюдаемые) значения y . Расстояния между ними и линией регрессии — это ошибка предсказания модели y-\widehat{y} (невязка, остатки). Именно с её использованием вычисляются все приведённые в статье меры качества.
Горизонтальная линия представляет собой модель простого среднего, где коэффициент при независимой переменной x равен нулю, и остаётся только свободный член b, который становится равным среднему арифметическому фактических значений выходной переменной, т.е. b=\overline{y}. Очевидно, что такая модель для любого значения входной переменной будет выдавать одно и то же значение выходной — \overline{y}.
В линейной регрессии такая модель рассматривается как «бесполезная», хуже которой работает только «случайный угадыватель». Однако, она используется для оценки, насколько дисперсия фактических значений y относительно линии среднего, больше, чем относительно линии регрессии с переменной, т.е. насколько модель с переменной лучше «бесполезной».
MSE
Среднеквадратичная ошибка (Mean Squared Error) применяется в случаях, когда требуется подчеркнуть большие ошибки и выбрать модель, которая дает меньше именно больших ошибок. Большие значения ошибок становятся заметнее за счет квадратичной зависимости.
Действительно, допустим модель допустила на двух примерах ошибки 5 и 10. В абсолютном выражении они отличаются в два раза, но если их возвести в квадрат, получив 25 и 100 соответственно, то отличие будет уже в четыре раза. Таким образом модель, которая обеспечивает меньшее значение MSE допускает меньше именно больших ошибок.
MSE рассчитывается по формуле:
MSE=\frac{1}{n}\sum\limits_{i=1}^{n}(y_{i}-\widehat{y}_{i})^{2},
где n — количество наблюдений по которым строится модель и количество прогнозов, y_{i} — фактические значение зависимой переменной для i-го наблюдения, \widehat{y}_{i} — значение зависимой переменной, предсказанное моделью.
Таким образом, можно сделать вывод, что MSE настроена на отражение влияния именно больших ошибок на качество модели.
Недостатком использования MSE является то, что если на одном или нескольких неудачных примерах, возможно, содержащих аномальные значения будет допущена значительная ошибка, то возведение в квадрат приведёт к ложному выводу, что вся модель работает плохо. С другой стороны, если модель даст небольшие ошибки на большом числе примеров, то может возникнуть обратный эффект — недооценка слабости модели.
RMSE
Корень из среднеквадратичной ошибки (Root Mean Squared Error) вычисляется просто как квадратный корень из MSE:
RMSE=\sqrt{\frac{1}{n}\sum\limits_{i=1}^{n}(y_{i}-\widehat{y_{i}})^{2}}
MSE и RMSE могут минимизироваться с помощью одного и того же функционала, поскольку квадратный корень является неубывающей функцией. Например, если у нас есть два набора результатов работы модели, A и B, и MSE для A больше, чем MSE для B, то мы можем быть уверены, что RMSE для A больше RMSE для B. Справедливо и обратное: если MSE(A)<MSE(B), то и RMSE(A)<RMSE(B).
Следовательно, сравнение моделей с помощью RMSE даст такой же результат, что и для MSE. Однако с MSE работать несколько проще, поэтому она более популярна у аналитиков. Кроме этого, имеется небольшая разница между этими двумя ошибками при оптимизации с использованием градиента:
\frac{\partial RMSE}{\partial \widehat{y}_{i}}=\frac{1}{2\sqrt{MSE}}\frac{\partial MSE}{\partial \widehat{y}_{i}}
Это означает, что перемещение по градиенту MSE эквивалентно перемещению по градиенту RMSE, но с другой скоростью, и скорость зависит от самой оценки MSE. Таким образом, хотя RMSE и MSE близки с точки зрения оценки моделей, они не являются взаимозаменяемыми при использовании градиента для оптимизации.
Влияние каждой ошибки на RMSE пропорционально величине квадрата ошибки. Поэтому большие ошибки оказывают непропорционально большое влияние на RMSE. Следовательно, RMSE можно считать чувствительной к аномальным значениям.
MSPE
Среднеквадратичная ошибка в процентах (Mean Squared Percentage Error) представляет собой относительную ошибку, где разность между наблюдаемым и фактическим значениями делится на наблюдаемое значение и выражается в процентах:
MSPE=\frac{100}{n}\sum\limits_{i=1}^{n}\left ( \frac{y_{i}-\widehat{y}_{i}}{y_{i}} \right )^{2}
Проблемой при использовании MSPE является то, что, если наблюдаемое значение выходной переменной равно 0, значение ошибки становится неопределённым.
MSPE можно рассматривать как взвешенную версию MSE, где вес обратно пропорционален квадрату наблюдаемого значения. Таким образом, при возрастании наблюдаемых значений ошибка имеет тенденцию уменьшаться.
MAE
Cредняя абсолютная ошибка (Mean Absolute Error) вычисляется следующим образом:
MAE=\frac{1}{n}\sum\limits_{i=1}^{n}\left | y_{i}-\widehat{y}_{i} \right |
Т.е. MAE рассчитывается как среднее абсолютных разностей между наблюдаемым и предсказанным значениями. В отличие от MSE и RMSE она является линейной оценкой, а это значит, что все ошибки в среднем взвешены одинаково. Например, разница между 0 и 10 будет вдвое больше разницы между 0 и 5. Для MSE и RMSE, как отмечено выше, это не так.
Поэтому MAE широко используется, например, в финансовой сфере, где ошибка в 10 долларов должна интерпретироваться как в два раза худшая, чем ошибка в 5 долларов.
MAPE
Средняя абсолютная процентная ошибка (Mean Absolute Percentage Error) вычисляется следующим образом:
MAPE=\frac{100}{n}\sum\limits_{i=1}^{n}\frac{\left | y_{i}-\widehat{y_{i}} \right |}{\left | y_{i} \right |}
Эта ошибка не имеет размерности и очень проста в интерпретации. Её можно выражать как в долях, так и в процентах. Если получилось, например, что MAPE=11.4, то это говорит о том, что ошибка составила 11.4% от фактического значения.
SMAPE
Cимметричная средняя абсолютная процентная ошибка (Symmetric Mean Absolute Percentage Error) — это мера точности, основанная на процентных (или относительных) ошибках. Обычно определяется следующим образом:
SMAPE=\frac{100}{n}\sum\limits_{i=1}^{n}\frac{\left | y_{i}-\widehat{y_{i}} \right |}{(\left | y_{i} \right |+\left | \widehat{y}_{i} \right |)/2}
Т.е. абсолютная разность между наблюдаемым и предсказанным значениями делится на полусумму их модулей. В отличие от обычной MAPE, симметричная имеет ограничение на диапазон значений. В приведённой формуле он составляет от 0 до 200%. Однако, поскольку диапазон от 0 до 100% гораздо удобнее интерпретировать, часто используют формулу, где отсутствует деление знаменателя на 2.
Одной из возможных проблем SMAPE является неполная симметрия, поскольку в разных диапазонах ошибка вычисляется неодинаково. Это иллюстрируется следующим примером: если y_{i}=100 и \widehat{y}_{i}=110, то SMAPE=4.76, а если y_{i}=100 и \widehat{y}_{i}=90, то SMAPE=5.26.
Ограничение SMAPE заключается в том, что, если наблюдаемое или предсказанное значение равно 0, ошибка резко возрастет до верхнего предела (200% или 100%).
MASE
Средняя абсолютная масштабированная ошибка (Mean absolute scaled error) — это показатель, который позволяет сравнивать две модели. Если поместить MAE для новой модели в числитель, а MAE для исходной модели в знаменатель, то полученное отношение и будет равно MASE. Если значение MASE меньше 1, то новая модель работает лучше, если MASE равно 1, то модели работают одинаково, а если значение MASE больше 1, то исходная модель работает лучше, чем новая модель. Формула для расчета MASE имеет вид:
MASE=\frac{MAE_{i}}{MAE_{j}}
MASE симметрична и устойчива к выбросам.
MRE
Средняя относительная ошибка (Mean Relative Error) вычисляется по формуле:
MRE=\frac{1}{n}\sum\limits_{i=1}^{n}\frac{\left | y_{i}-\widehat{y}_{i}\right |}{\left | y_{i} \right |}
Несложно увидеть, что данная мера показывает величину абсолютной ошибки относительно фактического значения выходной переменной (поэтому иногда эту ошибку называют также средней относительной абсолютной ошибкой, MRAE). Действительно, если значение абсолютной ошибки, скажем, равно 10, то сложно сказать много это или мало. Например, относительно значения выходной переменной, равного 20, это составляет 50%, что достаточно много. Однако относительно значения выходной переменной, равного 100, это будет уже 10%, что является вполне нормальным результатом.
Очевидно, что при вычислении MRE нельзя применять наблюдения, в которых y_{i}=0.
Таким образом, MRE позволяет более адекватно оценить величину ошибки, чем абсолютные ошибки. Кроме этого она является безразмерной величиной, что упрощает интерпретацию.
RMSLE
Среднеквадратичная логарифмическая ошибка (Root Mean Squared Logarithmic Error) представляет собой RMSE, вычисленную в логарифмическом масштабе:
RMSLE=\sqrt{\frac{1}{n}\sum\limits_{i=1}^{n}(log(\widehat{y}_{i}+1)-log{(y_{i}+1}))^{2}}
Константы, равные 1, добавляемые в скобках, необходимы чтобы не допустить обращения в 0 выражения под логарифмом, поскольку логарифм нуля не существует.
Известно, что логарифмирование приводит к сжатию исходного диапазона изменения значений переменной. Поэтому применение RMSLE целесообразно, если предсказанное и фактическое значения выходной переменной различаются на порядок и больше.
R-квадрат
Перечисленные выше ошибки не так просто интерпретировать. Действительно, просто зная значение средней абсолютной ошибки, скажем, равное 10, мы сразу не можем сказать хорошая это ошибка или плохая, и что нужно сделать чтобы улучшить модель.
В этой связи представляет интерес использование для оценки качества регрессионной модели не значения ошибок, а величину показывающую, насколько данная модель работает лучше, чем модель, в которой присутствует только константа, а входные переменные отсутствуют или коэффициенты регрессии при них равны нулю.
Именно такой мерой и является коэффициент детерминации (Coefficient of determination), который показывает долю дисперсии зависимой переменной, объяснённой с помощью регрессионной модели. Наиболее общей формулой для вычисления коэффициента детерминации является следующая:
R^{2}=1-\frac{\sum\limits_{i=1}^{n}(\widehat{y}_{i}-y_{i})^{2}}{\sum\limits_{i=1}^{n}({\overline{y}}_{i}-y_{i})^{2}}
Практически, в числителе данного выражения стоит среднеквадратическая ошибка оцениваемой модели, а в знаменателе — модели, в которой присутствует только константа.
Главным преимуществом коэффициента детерминации перед мерами, основанными на ошибках, является его инвариантность к масштабу данных. Кроме того, он всегда изменяется в диапазоне от −∞ до 1. При этом значения близкие к 1 указывают на высокую степень соответствия модели данным. Очевидно, что это имеет место, когда отношение в формуле стремится к 0, т.е. ошибка модели с переменными намного меньше ошибки модели с константой. R^{2}=0 показывает, что между независимой и зависимой переменными модели имеет место функциональная зависимость.
Когда значение коэффициента близко к 0 (т.е. ошибка модели с переменными примерно равна ошибке модели только с константой), это указывает на низкое соответствие модели данным, когда модель с переменными работает не лучше модели с константой.
Кроме этого, бывают ситуации, когда коэффициент R^{2} принимает отрицательные значения (обычно небольшие). Это произойдёт, если ошибка модели среднего становится меньше ошибки модели с переменной. В этом случае оказывается, что добавление в модель с константой некоторой переменной только ухудшает её (т.е. регрессионная модель с переменной работает хуже, чем предсказание с помощью простой средней).
На практике используют следующую шкалу оценок. Модель, для которой R^{2}>0.5, является удовлетворительной. Если R^{2}>0.8, то модель рассматривается как очень хорошая. Значения, меньшие 0.5 говорят о том, что модель плохая.
Скорректированный R-квадрат
Основной проблемой при использовании коэффициента детерминации является то, что он увеличивается (или, по крайней мере, не уменьшается) при добавлении в модель новых переменных, даже если эти переменные никак не связаны с зависимой переменной.
В связи с этим возникают две проблемы. Первая заключается в том, что не все переменные, добавляемые в модель, могут значимо увеличивать её точность, но при этом всегда увеличивают её сложность. Вторая проблема — с помощью коэффициента детерминации нельзя сравнивать модели с разным числом переменных. Чтобы преодолеть эти проблемы используют альтернативные показатели, одним из которых является скорректированный коэффициент детерминации (Adjasted coefficient of determinftion).
Скорректированный коэффициент детерминации даёт возможность сравнивать модели с разным числом переменных так, чтобы их число не влияло на статистику R^{2}, и накладывает штраф за дополнительно включённые в модель переменные. Вычисляется по формуле:
R_{adj}^{2}=1-\frac{\sum\limits_{i=1}^{n}(\widehat{y}_{i}-y_{i})^{2}/(n-k)}{\sum\limits_{i=1}^{n}({\overline{y}}_{i}-y_{i})^{2}/(n-1)}
где n — число наблюдений, на основе которых строится модель, k — количество переменных в модели.
Скорректированный коэффициент детерминации всегда меньше единицы, но теоретически может принимать значения и меньше нуля только при очень малом значении обычного коэффициента детерминации и большом количестве переменных модели.
Сравнение метрик
Резюмируем преимущества и недостатки каждой приведённой метрики в следующей таблице:
| Мера | Сильные стороны | Слабые стороны |
|---|---|---|
| MSE | Позволяет подчеркнуть большие отклонения, простота вычисления. | Имеет тенденцию занижать качество модели, чувствительна к выбросам. Сложность интерпретации из-за квадратичной зависимости. |
| RMSE | Простота интерпретации, поскольку измеряется в тех же единицах, что и целевая переменная. | Имеет тенденцию занижать качество модели, чувствительна к выбросам. |
| MSPE | Нечувствительна к выбросам. Хорошо интерпретируема, поскольку имеет линейный характер. | Поскольку вклад всех ошибок отдельных наблюдений взвешивается одинаково, не позволяет подчёркивать большие и малые ошибки. |
| MAPE | Является безразмерной величиной, поэтому её интерпретация не зависит от предметной области. | Нельзя использовать для наблюдений, в которых значения выходной переменной равны нулю. |
| SMAPE | Позволяет корректно работать с предсказанными значениями независимо от того больше они фактического, или меньше. | Приближение к нулю фактического или предсказанного значения приводит к резкому росту ошибки, поскольку в знаменателе присутствует как фактическое, так и предсказанное значения. |
| MASE | Не зависит от масштаба данных, является симметричной: положительные и отрицательные отклонения от фактического значения учитываются одинаково. Устойчива к выбросам. Позволяет сравнивать модели. | Сложность интерпретации. |
| MRE | Позволяет оценить величину ошибки относительно значения целевой переменной. | Неприменима для наблюдений с нулевым значением выходной переменной. |
| RMSLE | Логарифмирование позволяет сделать величину ошибки более устойчивой, когда разность между фактическим и предсказанным значениями различается на порядок и выше | Может быть затруднена интерпретация из-за нелинейности. |
| R-квадрат | Универсальность, простота интерпретации. | Возрастает даже при включении в модель бесполезных переменных. Плохо работает когда входные переменные зависимы. |
| R-квадрат скорр. | Корректно отражает вклад каждой переменной в модель. | Плохо работает, когда входные переменные зависимы. |
В данной статье рассмотрены наиболее популярные меры качества регрессионных моделей, которые часто используются в различных аналитических приложениях. Эти меры имеют свои особенности применения, знание которых позволит обоснованно выбирать и корректно применять их на практике.
Однако в литературе можно встретить и другие меры качества моделей регрессии, которые предлагаются различными авторами для решения конкретных задач анализа данных.
Другие материалы по теме:
Отбор переменных в моделях линейной регрессии
Репрезентативность выборочных данных
Логистическая регрессия и ROC-анализ — математический аппарат
Оценка точности модели кривой роста, выбор наилучшей кривой роста
Точность модели характеризуется разностью между фактическими и расчетными значениями исследуемого показателя Y. Мерой точности является стандартная ошибка модели
.
Точность модели удобнее оценивать с помощью средней относительной ошибки аппроксимации
,
которая показывает, на сколько процентов в среднем модельные значения отличаются от фактических yt. Если
, то считается, что модель имеет достаточно высокую точность, при
точность модели хорошая, при
— удовлетворительная, а при
— неудовлетворительная.
Если одновременно исследуются несколько моделей, то лучшей считается модель, имеющая наименьшую Sмод или Еотн.
Продолжение примера 9. Проверить точность модели.
Решение. Стандартная ошибка линейной модели может быть определена с помощью функции Excel «СТОШYX»: млн. руб.
Средняя относительная ошибка аппроксимации
%.
Предсказанные моделью значения спроса на кредитные ресурсы отличаются от фактических в среднем на 4,54 млн руб., или на 6,5 %. Модель имеет хорошую точность.
Коэффициент корреляции
Тесноту (силу) связи изучаемых показателей в предмете эконометрика оценивают с помощью коэффициента корреляции Rxy, который может принимать значения от -1 до +1.
Если Rxy > 0,7 — связь между изучаемыми показателями сильная, можно проводить анализ линейной модели
Если 0,3 < Rxy < 0,7 — связь между показателями умеренная, можно использовать нелинейную модель при отсутствии Rxy > 0,7
Если Rxy < 0,3 — связь слабая, модель строить нельзя
Для нелинейной регрессии используют индекс корреляции (0 < Рху < 1):
Средняя ошибка аппроксимации
Для оценки качества однофакторной модели в эконометрике используют коэффициент детерминации и среднюю ошибку аппроксимации.
Средняя ошибка аппроксимации определяется как среднее отклонение полученных значений от фактических
Допустимая ошибка аппроксимации не должна превышать 10%.
В эконометрике существует понятие среднего коэффициента эластичности Э – который говорит о том, на сколько процентов в среднем изменится показатель у от своего среднего значения при изменении фактора х на 1% от своей средней величины.
Пример нахождения коэффициента корреляции
Исходные данные:
|
Номер региона |
Среднедушевой прожиточный минимум в день одного трудоспособного, руб., |
Среднедневная заработная плата, руб., |
|
1 |
81 |
124 |
|
2 |
77 |
131 |
|
3 |
85 |
146 |
|
4 |
79 |
139 |
|
5 |
93 |
143 |
|
6 |
100 |
159 |
|
7 |
72 |
135 |
|
8 |
90 |
152 |
|
9 |
71 |
127 |
|
10 |
89 |
154 |
|
11 |
82 |
127 |
|
12 |
111 |
162 |
Рассчитаем параметры парной линейной регрессии, составив таблицу
| x |
x2 |
y |
xy |
y2 |
|
|
1 |
81 |
6561 |
124 |
10044 |
15376 |
|
2 |
77 |
5929 |
131 |
10087 |
17161 |
|
3 |
85 |
7225 |
146 |
12410 |
21316 |
|
4 |
79 |
6241 |
139 |
10981 |
19321 |
|
5 |
93 |
8649 |
143 |
13299 |
20449 |
|
6 |
100 |
10000 |
159 |
15900 |
25281 |
|
7 |
72 |
5184 |
135 |
9720 |
18225 |
|
8 |
90 |
8100 |
152 |
13680 |
23104 |
|
9 |
71 |
5041 |
127 |
9017 |
16129 |
|
10 |
89 |
7921 |
154 |
13706 |
23716 |
|
11 |
82 |
6724 |
127 |
10414 |
16129 |
|
12 |
111 |
12321 |
162 |
17982 |
26244 |
|
Среднее |
85,8 |
7491 |
141,6 |
12270,0 |
20204,3 |
|
Сумма |
1030,0 |
89896 |
1699 |
147240 |
242451 |
| σ |
11,13 |
12,59 |
|||
| σ2 |
123,97 |
158,41 |
формула расчета дисперсии σ2 приведена здесь.
Коэффициенты уравнения y = a + bx определяются по формуле
Получаем уравнение регрессии: y = 0,947x + 60,279.
Коэффициент уравнения b = 0,947 показывает, что при увеличении среднедушевого прожиточного минимума в день одного трудоспособного на 1 руб. среднедневная заработная плата увеличивается на 0,947 руб.
Коэффициент корреляции рассчитывается по формуле:
Значение коэффициента корреляции более — 0,7, это означает, что связь между среднедушевым прожиточным минимумом в день одного трудоспособного и среднедневной заработной платой сильная.
Коэффициент детерминации равен R2 = 0.838^2 = 0.702
т.е. 70,2% результата объясняется вариацией объясняющей переменной x.
Эконометрика
Вариант 1
Задание 1. Модель парной линейной регрессии.
Имеются данные о размере среднемесячных доходов в разных группах семей
|
Номер группы |
Среднедушевой денежный доход в месяц, руб., X |
Доля оплаты труда в структуре доходов семьи, %, Y |
|
1 |
79,8 |
64,2 |
|
2 |
152,1 |
66,1 |
|
3 |
199,3 |
69,0 |
|
4 |
240,8 |
70,6 |
|
5 |
282,4 |
72,4 |
|
6 |
301,8 |
74,3 |
|
7 |
385,3 |
76,0 |
|
8 |
457,8 |
77,1 |
|
9 |
577,4 |
78,4 |
Задания:
1. Рассчитать линейный коэффициент парной корреляции, оценить его статистическую значимость и построить для него доверительный интервал с уровнем значимости a =0,05. Сделать выводы
2. Построить линейное уравнение парной регрессии Y на X и оценить статистическую значимость параметров регрессии. Сделать рисунок.
3. Оценить качество уравнения регрессии при помощи коэффициента детерминации. Сделать выводы. Проверить качество уравнения регрессии при помощи F-критерия Фишера.
4. Выполнить прогноз доли оплаты труда структуре доходов семьи Y при прогнозном значении среднедушевого денежного дохода X, составляющем 111% от среднего уровня. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал для уровня значимости a =0,05. Сделать выводы.
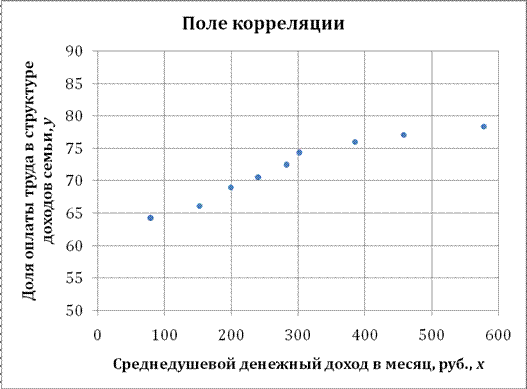
Решение: Построим поле корреляции зависимости доли оплаты труда в структуре доходов семьи от среднедушевого денежного дохода в месяц.
Точки на построенном графике размещаются вблизи кривой, напоминающей по форме Прямую, поэтому можно предположить, что между указанными величинами существует Линейная зависимость вида .
Для расчета линейного коэффициента парной корреляции и параметров линейной регрессии составим вспомогательную таблицу.
|
№ п/п |
X |
Y |
X×Y |
X2 |
Y2 |
|
1 |
79,8 |
64,2 |
5123,16 |
6368,04 |
4121,64 |
|
2 |
152,1 |
66,1 |
10053,81 |
23134,41 |
4369,21 |
|
3 |
199,3 |
69,0 |
13751,70 |
39720,49 |
4761,00 |
|
4 |
240,8 |
70,6 |
17000,48 |
57984,64 |
4984,36 |
|
5 |
282,4 |
72,4 |
20445,76 |
79749,76 |
5241,76 |
|
6 |
301,8 |
74,3 |
22423,74 |
91083,24 |
5520,49 |
|
7 |
385,3 |
76,0 |
29282,80 |
148456,09 |
5776,00 |
|
8 |
457,8 |
77,1 |
35296,38 |
209580,84 |
5944,41 |
|
9 |
577,4 |
78,4 |
45268,16 |
333390,76 |
6146,56 |
|
S |
2676,7 |
648,1 |
198645,99 |
989468,27 |
46865,43 |
|
Среднее |
297,41 |
72,01 |
22071,78 |
109940,92 |
5207,27 |
Вычислим коэффициент корреляции. Используем следующую формулу:
= 0,9568.
Можно сказать, что между рассматриваемыми признаками существует Прямая тесная Корреляционная связь.
Среднюю ошибку коэффициента корреляции определим по формуле:
= 0,032.
Найдем табличное значение TТабл по таблице распределения Стьюдента для
a = 0,05 и числе степеней свободы K = N – M – 1 = 9 – 1 – 1 = 7.
TТабл(0,05; 7) = 2,36.
Запишем доверительный интервал для коэффициента корреляции.
Доверительный интервал не включает число 0, поэтому при заданном уровне значимости коэффициент корреляции является статистически значимым.
Вычислим параметры уравнения регрессии.
= 0,03.
= 72,01 – 0,03×297,41 = 63,09.
Получим следующее уравнение: .
Для проверки статистической значимости (существенности) линейного коэффициента парной корреляции рассчитаем T-критерий Стьюдента по формуле:

Фактическое значение по абсолютной величине больше табличного, что свидетельствует о значимости линейного коэффициента корреляции и существенности связи между рассматриваемыми признаками.
Проверим значимость оценок теоретических коэффициентов регрессии с помощью t-статистики Стьюдента и сделаем соответствующие выводы о значимости этих оценок.
Для определения статистической значимости коэффициентов A и B найдем T-статистики Стьюдента:
Рассчитаем по полученному уравнению теоретические значения. Составим вспомогательную таблицу.
|
№ п/п |
X |
Y |
|
|
|
|
1 |
79,8 |
64,2 |
65,48 |
1,6384 |
47354,1 |
|
2 |
152,1 |
66,1 |
67,65 |
2,4025 |
21115,0 |
|
3 |
199,3 |
69,0 |
69,07 |
0,0049 |
9625,6 |
|
4 |
240,8 |
70,6 |
70,31 |
0,0841 |
3204,7 |
|
5 |
282,4 |
72,4 |
71,56 |
0,7056 |
225,3 |
|
6 |
301,8 |
74,3 |
72,14 |
4,6656 |
19,3 |
|
7 |
385,3 |
76,0 |
74,65 |
1,8225 |
7724,7 |
|
8 |
457,8 |
77,1 |
76,82 |
0,0784 |
25725,0 |
|
9 |
577,4 |
78,4 |
80,41 |
4,0401 |
78394,4 |
|
S |
2676,7 |
648,1 |
648,09 |
15,4421 |
193388,1 |
Вычислим стандартные ошибки коэффициентов уравнения.


Вычислим T-статистики.
Сравнение расчетных и табличных величин критерия Стьюдента показывает, что и
, т. е. оценки A и B теоретических коэффициентов регрессии статистически значимы.
Сделаем рисунок.
Рассчитаем коэффициент детерминации: = 0,95682= 0,915 = 91,5%.
Таким образом, вариация результата Y на 91,5% объясняется вариацией фактора X.
Оценку значимости уравнения регрессии проведем с помощью F-критерия Фишера:

Найдем табличное значение Fтабл по таблице критических точек Фишера для
a = 0,05; K1 = M = 1 (число факторов), K2 = N – M – 1 = 9 – 1 – 1 = 7.
Fтабл(0,05; 1; 7) = 5,59.
Поскольку F > FТабл, уравнение регрессии с вероятностью 0,95 в целом Является статистически значимым.
Выполним прогноз доли оплаты труда структуре доходов семьи y при прогнозном значении среднедушевого денежного дохода x, составляющем 111% от среднего уровня.
XP = 297,41 × 1,11 = 330,1.
Вычислим прогнозное значение Yp с помощью уравнения регрессии.
» 73%.
Доверительный интервал прогноза имеет вид
(УP – Tкр×My, УP + Tкр×My),
Где 

Запишем доверительный интервал прогноза:
Þ
Данный прогноз является надежным, поскольку доверительный интервал не включает число 0, точность прогноза составляет 4.
Задание 2. Модель парной нелинейной регрессии.
По территориям Центрального района известны данные за 1995 г.
|
Район |
Прожиточный минимум в среднем на одного пенсионера в месяц, тыс. руб., X |
Средний размер назначенных ежемесячных пенсий, тыс. руб., Y |
|
Брянская обл. |
178 |
240 |
|
Владимирская обл. |
202 |
226 |
|
Ивановская обл. |
197 |
221 |
|
Калужская обл. |
201 |
226 |
|
Костромская обл. |
189 |
220 |
|
Орловская обл. |
166 |
232 |
|
Рязанская обл. |
199 |
215 |
|
Смоленская обл. |
180 |
220 |
|
Тверская обл. |
181 |
222 |
|
Тульская обл. |
186 |
231 |
|
Ярославская обл. |
250 |
229 |
Задания:
1. Построить поле корреляции и сформулируйте гипотезу о форме связи. Рассчитать параметры уравнений полулогарифмической () и степенной (
) парной регрессии. Сделать рисунки.
2. Дать с помощью среднего коэффициента эластичности сравнительную оценку силы связи фактора с результатом для каждой модели. Сделать выводы. Оценить качество уравнений регрессии с помощью средней ошибки аппроксимации и коэффициента детерминации. Сделать выводы.
3. По значениям рассчитанных характеристик выбрать лучшее уравнение регрессии. Дать экономический смысл коэффициентов выбранного уравнения регрессии
4. Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости a =0,05. Сделать выводы.
Решение: Решение: Для предварительного определения вида связи между указанными признаками построим поле корреляции. Для этого построим в системе координат точки, у которых первая координата X, а вторая – Y.
Получим следующий рисунок.
По внешнему виду диаграммы рассеяния трудно предположить, какая зависимость существует между указанными показателями.
Построение полулогарифмической модели регрессии.
Уравнение логарифмической кривой: .
Обозначим:
Получим линейное уравнение регрессии:
Y = A + B×X.
Произведем линеаризацию модели путем замены . В результате получим линейное уравнение
.
Рассчитаем его параметры, используя данные таблицы.
|
№ п/п |
X |
Y |
X = ln(X) |
Xy |
X2 |
Y2 |
|
|
|
Ai |
|
1 |
178 |
240 |
5,1818 |
1243,63 |
26,85 |
57600 |
226,40 |
206,314 |
184,904 |
6,006 |
|
2 |
202 |
226 |
5,3083 |
1199,67 |
28,18 |
51076 |
225,17 |
0,132 |
0,694 |
0,370 |
|
3 |
197 |
221 |
5,2832 |
1167,59 |
27,91 |
48841 |
225,41 |
21,496 |
19,464 |
1,957 |
|
4 |
201 |
226 |
5,3033 |
1198,55 |
28,13 |
51076 |
225,22 |
0,132 |
0,615 |
0,348 |
|
5 |
189 |
220 |
5,2417 |
1153,18 |
27,48 |
48400 |
225,82 |
31,769 |
33,833 |
2,576 |
|
6 |
166 |
232 |
5,1120 |
1185,98 |
26,13 |
53824 |
227,08 |
40,496 |
24,172 |
2,165 |
|
7 |
199 |
215 |
5,2933 |
1138,06 |
28,02 |
46225 |
225,31 |
113,132 |
106,362 |
4,577 |
|
8 |
180 |
220 |
5,1930 |
1142,45 |
26,97 |
48400 |
226,29 |
31,769 |
39,601 |
2,781 |
|
9 |
181 |
222 |
5,1985 |
1154,07 |
27,02 |
49284 |
226,24 |
13,223 |
17,968 |
1,874 |
|
10 |
186 |
231 |
5,2257 |
1207,15 |
27,31 |
53361 |
225,97 |
28,769 |
25,273 |
2,225 |
|
11 |
250 |
229 |
5,5215 |
1264,41 |
30,49 |
52441 |
223,09 |
11,314 |
34,980 |
2,651 |
|
Итого |
2129 |
2482 |
57,862 |
13054,74 |
304,48 |
560528 |
2482,00 |
498,545 |
487,867 |
27,530 |
|
Среднее |
193,5 |
225,6 |
5,260 |
1186,79 |
27,68 |
50957,091 |
225,636 |
45,322 |
44,352 |
2,503 |
= -9,76.
= 225,6 – (-9,76)×5,26 = 276,99.
Уравнение модели имеет вид:
Определим индекс корреляции
Используя данные таблицы, получим:

Рассчитаем коэффициент детерминации: = 0,14642= 0,021 = 2,1%.
Вариация результата Y всего на 2,1% объясняется вариацией фактора X.
Сделаем рисунок.
Рассчитаем средний коэффициент эластичности по формуле:
= -0,04%.
Коэффициент эластичности показывает, что при среднем росте признака X на 1% признак Y снижается на 0,04%.
Вычислим среднюю ошибку аппроксимации. Используя данные расчетной таблицы, получаем:
= 2,5%.
Построение степенной модели парной регрессии.
Уравнение степенной модели имеет вид: .
Для построения этой модели необходимо произвести линеаризацию переменных. Для этого произведем логарифмирование обеих частей уравнения:
.
Произведем линеаризацию модели путем замены и
. В результате получим линейное уравнение
.
Рассчитаем его параметры, используя данные таблицы.
|
№ п/п |
X |
Y |
X = ln(X) |
Y = ln(Y) |
XY |
X2 |
Y2 |
|
|
|
|
Ai |
|
1 |
178 |
240 |
5,1818 |
5,4806 |
28,3995 |
26,851 |
30,037 |
226,3 |
206,3 |
188,391 |
241,661 |
6,07 |
|
2 |
202 |
226 |
5,3083 |
5,4205 |
28,7737 |
28,178 |
29,382 |
225,1 |
0,132 |
0,835 |
71,479 |
0,406 |
|
3 |
197 |
221 |
5,2832 |
5,3982 |
28,5196 |
27,912 |
29,140 |
225,3 |
21,496 |
18,671 |
11,934 |
1,918 |
|
4 |
201 |
226 |
5,3033 |
5,4205 |
28,7467 |
28,125 |
29,382 |
225,1 |
0,132 |
0,753 |
55,570 |
0,385 |
|
5 |
189 |
220 |
5,2417 |
5,3936 |
28,2720 |
27,476 |
29,091 |
225,7 |
31,769 |
32,607 |
20,661 |
2,530 |
|
6 |
166 |
232 |
5,1120 |
5,4467 |
27,8437 |
26,132 |
29,667 |
226,9 |
40,496 |
25,675 |
758,752 |
2,233 |
|
7 |
199 |
215 |
5,2933 |
5,3706 |
28,4284 |
28,019 |
28,844 |
225,2 |
113,132 |
104,576 |
29,752 |
4,540 |
|
8 |
180 |
220 |
5,1930 |
5,3936 |
28,0089 |
26,967 |
29,091 |
226,2 |
31,769 |
38,059 |
183,479 |
2,728 |
|
9 |
181 |
222 |
5,1985 |
5,4027 |
28,0858 |
27,024 |
29,189 |
226,1 |
13,223 |
16,950 |
157,388 |
1,821 |
|
10 |
186 |
231 |
5,2257 |
5,4424 |
28,4407 |
27,308 |
29,620 |
225,9 |
28,769 |
26,413 |
56,934 |
2,275 |
|
11 |
250 |
229 |
5,5215 |
5,4337 |
30,0021 |
30,487 |
29,525 |
223,1 |
11,314 |
34,846 |
3187,116 |
2,646 |
|
Итого |
2129 |
2482 |
57,862 |
59,603 |
313,521 |
304,479 |
322,969 |
2480,927 |
498,545 |
487,777 |
4774,727 |
27,548 |
|
Среднее |
193,5 |
225,6 |
5,260 |
5,418 |
28,502 |
27,680 |
29,361 |
225,539 |
45,322 |
44,343 |
434,066 |
2,504 |
С учетом введенных обозначений уравнение примет вид: Y = A + BX – линейное уравнение регрессии. Рассчитаем его параметры, используя данные таблицы.
= -0,042.
= 5,418 – 0,959×5,26 = 5,637.
Перейдем к исходным переменным X и Y, выполнив потенцирование данного уравнения.
A = eA = e5,637 = 280,76
Получим уравнение степенной модели регрессии: .
Определим индекс корреляции
Используя данные таблицы, получим:

Рассчитаем коэффициент детерминации: = 0,1472= 0,021 = 2,1%.
Вариация результата Y всего на 2,1% объясняется вариацией фактора X.
Сделаем рисунок.
Для степенной модели средний коэффициент эластичности равен коэффициенту B.
= -0,042%.
Коэффициент эластичности показывает, что при среднем росте признака X на 1% признак Y снижается на 0,042%.
Вычислим среднюю ошибку аппроксимации. Используя данные расчетной таблицы, получаем:
= 2,5%.
Сводная таблица вычислений
|
Параметры |
Модель |
|
|
Полулогарифмическая |
Степенная |
|
|
Уравнение связи |
|
|
|
Индекс корреляции |
0,1464 |
0,147 |
|
Коэффициент детерминации |
0,021 |
0,021 |
|
Средняя ошибка аппроксимации, % |
2,5 |
2,5 |
Для выявления формы связи между указанными признаками были построены полулогарифмическая и степенная модели регрессии. Анализ показателей корреляции, а также оценка качества моделей с использованием средней ошибки аппроксимации позволил предположить, что из перечисленных моделей более адекватной является степенная модель, поскольку для нее индекс корреляции принимает наибольшее значение R = 0,147, свидетельствующий о том, что между рассматриваемыми признаками наблюдается Слабая корреляционная связь.
Рассчитаем прогнозное значение результата по степенной модели регрессии, если прогнозируется увеличение значения фактора на 10% от среднего уровня.
Прогнозное значение составит:
= 193,5 × 1,1 = 212,9 тыс. р., тогда прогнозное значение Y составит:
= 224,6 тыс. р.
Определим доверительный интервал прогноза для уровня значимости a = 0,05.
Вычислим Среднюю стандартную ошибку прогноза По следующей формуле:

Получаем: 
Найдем предельную ошибку прогноза , где для доверительной вероятности 0,95 значение T составляет 1,96.
= 14,8.
Запишем доверительный интервал прогноза.
= 224,6 – 14,8 = 209,8 тыс. р.
= 224,6 + 14,8 = 239,4 тыс. р.
Таким образом, с вероятностью 0,95 можно утверждать, что прогнозное значение среднего размера назначенных ежемесячных пенсий будет находиться в пределах от 209,8 тыс. р. до 239,4 тыс. р.
Задание 3. Моделирование временных рядов
Имеются поквартальные данные по розничному товарообороту России в 1995-1999 гг.
|
Номер квартала |
Товарооборот % к предыдущему периоду |
Номер квартала |
Товарооборот % к предыдущему периоду |
|
1 |
100 |
11 |
98,8 |
|
2 |
93,9 |
12 |
101,9 |
|
3 |
96,5 |
13 |
113,1 |
|
4 |
101,8 |
14 |
98,4 |
|
5 |
107,8 |
15 |
97,3 |
|
6 |
96,3 |
16 |
112,1 |
|
7 |
95,7 |
17 |
97,6 |
|
8 |
98,2 |
18 |
93,7 |
|
9 |
104 |
19 |
114,3 |
|
10 |
99 |
20 |
108,4 |
Задания:
1. Построить график данного временного ряда. Охарактеризовать структуру этого ряда.
2. Рассчитать сезонную компоненты временного ряда и построить его Мультипликативную Модель.
3. Рассчитать трендовую компоненту временного ряда и построить его график
4. Оценить качество модели через показатели средней абсолютной ошибки и среднего относительного отклонения.
Решение: Пронумеруем указанные месяцы от 1 до 24 и построим график временного ряда.
Полученный график показывает, что а данном временном ряду присутствуют сезонные колебания.
Построим мультипликативную модель временного ряда.
Эта модель предполагает, что каждый уровень временного ряда может быть представлен как произведение трендовой (T), сезонной (S) и случайной (E) компонент.
Построение мультипликативной моделей сведем к расчету значений T, S и E для каждого уровня ряда.
Процесс построения модели включает в себя следующие шаги.
1) Выравнивание исходного ряда методом скользящей средней.
2) Расчет значений сезонной компоненты S.
3) Устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных T×E.
4) Аналитическое выравнивание уровней T×E и расчет значений T с использованием полученного уравнения тренда.
5) Расчет полученных по модели значений T×E.
6) Расчет абсолютных и/или относительных ошибок.
Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Для этого:
1.1. Просуммируем уровни ряда последовательно за каждые четыре месяца со сдвигом на один момент времени и определим условные годовые уровни объема продаж (гр. 3 табл. 2.1).
1.2. Разделив полученные суммы на 4, найдем скользящие средние (гр. 4 табл. 2.1). Полученные таким образом выровненные значения уже не содержат сезонной компоненты.
1.3. Приведем эти значения в соответствие с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних – центрированные скользящие средние (гр. 5 табл. 2.1).
Таблица 2.1
|
№ месяца, T |
Товарооборот, Yi |
Итого за четыре месяца |
Скользящая средняя за четыре месяца |
Центрированная скользящая средняя |
Оценка сезонной компоненты |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
100,0 |
– |
– |
– |
– |
|
2 |
93,9 |
392 |
98 |
– |
– |
|
3 |
96,5 |
400 |
100 |
99 |
0,975 |
|
4 |
101,8 |
402 |
100,5 |
100,25 |
1,015 |
|
5 |
107,8 |
402 |
100,5 |
100,5 |
1,073 |
|
6 |
96,3 |
398 |
99,5 |
100 |
0,963 |
|
7 |
95,7 |
394 |
98,5 |
99 |
0,967 |
|
8 |
98,2 |
397 |
99,25 |
98,875 |
0,993 |
|
9 |
104,0 |
400 |
100 |
99,625 |
1,044 |
|
10 |
99,0 |
404 |
101 |
100,5 |
0,985 |
|
11 |
98,8 |
413 |
103,25 |
102,125 |
0,967 |
|
12 |
101,9 |
412 |
103 |
103,125 |
0,988 |
|
13 |
113,1 |
411 |
102,75 |
102,875 |
1,099 |
|
14 |
98,4 |
309 |
77,25 |
90 |
1,093 |
|
15 |
97,3 |
196 |
49 |
63,125 |
1,541 |
|
16 |
112,1 |
303 |
75,75 |
62,375 |
1,797 |
|
17 |
97,6 |
418 |
104,5 |
90,125 |
1,083 |
|
18 |
93,7 |
414 |
103,5 |
104 |
0,901 |
|
19 |
114,3 |
– |
– |
– |
– |
|
20 |
108,4 |
– |
– |
– |
– |
Шаг 2. Найдем оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользящие средние (гр. 6 табл. 2.1). Эти оценки используются для расчета сезонной компоненты S (табл. 2.2). Для этого найдем средние за каждый месяц оценки сезонной компоненты Si. Так же как и в аддитивной модели считается, что сезонные воздействия за период взаимопогашаются. В мультипликативной модели это выражается в том, что сумма значений сезонной компоненты по всем месяцам должна быть равна числу периодов в цикле. В нашем случае число периодов одного цикла равно 4.
Таблица 2.2
|
Показатели |
Год |
№ квартала, I |
|||
|
I |
II |
III |
IV |
||
|
1 |
– |
– |
0,975 |
1,015 |
|
|
2 |
1,073 |
0,963 |
0,967 |
0,993 |
|
|
3 |
1,044 |
0,985 |
0,967 |
0,988 |
|
|
4 |
1,099 |
1,093 |
1,541 |
1,797 |
|
|
5 |
1,083 |
0,901 |
– |
– |
|
|
Всего за I-й квартал |
4,299 |
3,942 |
4,45 |
4,793 |
|
|
Средняя оценка сезонной компоненты для I-го квартала, |
0,860 |
0,788 |
0,890 |
0,959 |
|
|
Скорректированная сезонная компонента, |
0,984 |
0,901 |
1,018 |
1,097 |
Имеем: 0,860 + 0,788 + 0,890 + 0,959 = 3,497.
Определяем корректирующий коэффициент: K = 4 : 3,497 = 1,144.
Скорректированные значения сезонной компоненты получаются при умножении ее средней оценки
на корректирующий коэффициент K.
Проверяем условие: равенство 4 суммы значений сезонной компоненты:
0,984 + 0,901 + 1,018 + 1,097 = 4.
Шаг 3. Разделим каждый уровень исходного ряда на соответствующие значения сезонной компоненты. В результате получим величины (гр. 4 табл. 2.3), которые содержат только тенденцию и случайную компоненту.
Таблица 2.3
|
T |
Yt |
St |
|
T |
T×S |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
100,0 |
0,984 |
101,6 |
100,02 |
98,42 |
1,016 |
|
2 |
93,9 |
0,901 |
104,2 |
100,19 |
90,27 |
1,040 |
|
3 |
96,5 |
1,018 |
94,8 |
100,36 |
102,17 |
0,945 |
|
4 |
101,8 |
1,097 |
92,8 |
100,53 |
110,28 |
0,923 |
|
5 |
107,8 |
0,984 |
109,6 |
100,7 |
99,09 |
1,088 |
|
6 |
96,3 |
0,901 |
106,9 |
100,87 |
90,88 |
1,060 |
|
7 |
95,7 |
1,018 |
94,0 |
101,04 |
102,86 |
0,930 |
|
8 |
98,2 |
1,097 |
89,5 |
101,21 |
111,03 |
0,884 |
|
9 |
104,0 |
0,984 |
105,7 |
101,38 |
99,76 |
1,043 |
|
10 |
99,0 |
0,901 |
109,9 |
101,55 |
91,50 |
1,082 |
|
11 |
98,8 |
1,018 |
97,1 |
101,72 |
103,55 |
0,954 |
|
12 |
101,9 |
1,097 |
92,9 |
101,89 |
111,77 |
0,912 |
|
13 |
113,1 |
0,984 |
114,9 |
102,06 |
100,43 |
1,126 |
|
14 |
98,4 |
0,901 |
109,2 |
102,23 |
92,11 |
1,068 |
|
15 |
97,3 |
1,018 |
95,6 |
102,4 |
104,24 |
0,933 |
|
16 |
112,1 |
1,097 |
102,2 |
102,57 |
112,52 |
0,996 |
|
17 |
97,6 |
0,984 |
99,2 |
102,74 |
101,10 |
0,965 |
|
18 |
93,7 |
0,901 |
104,0 |
102,91 |
92,72 |
1,011 |
|
19 |
114,3 |
1,018 |
112,3 |
103,08 |
104,94 |
1,089 |
|
20 |
108,4 |
1,097 |
98,8 |
103,25 |
113,27 |
0,957 |
|
Среднее |
101,4 |
1,0011 |
Шаг 4. Определим компоненту T в мультипликативной модели. Для этого рассчитаем параметры линейного тренда, используя уровни T×E. Составим вспомогательную таблицу.
Таблица 2.4
|
T |
|
T2 |
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
1 |
101,6 |
1 |
101,6 |
2,5 |
1,58 |
2,0 |
|
|
2 |
104,2 |
4 |
208,4 |
13,2 |
3,87 |
56,3 |
|
|
3 |
94,8 |
9 |
284,4 |
32,1 |
5,88 |
24,0 |
|
|
4 |
92,8 |
16 |
371,2 |
71,9 |
8,33 |
0,2 |
|
|
5 |
109,6 |
25 |
548 |
75,9 |
8,08 |
41,0 |
|
|
6 |
106,9 |
36 |
641,4 |
29,4 |
5,63 |
26,0 |
|
|
7 |
94,0 |
49 |
658 |
51,3 |
7,48 |
32,5 |
|
|
8 |
89,5 |
64 |
716 |
164,6 |
13,07 |
10,2 |
|
|
9 |
105,7 |
81 |
951,3 |
18,0 |
4,08 |
6,8 |
|
|
10 |
109,9 |
100 |
1099 |
56,3 |
7,58 |
5,8 |
|
|
11 |
97,1 |
121 |
1068,1 |
22,6 |
4,81 |
6,8 |
|
|
12 |
92,9 |
144 |
1114,8 |
97,4 |
9,69 |
0,3 |
|
|
13 |
114,9 |
169 |
1493,7 |
160,5 |
11,20 |
136,9 |
|
|
14 |
109,2 |
196 |
1528,8 |
39,6 |
6,39 |
9,0 |
|
|
15 |
95,6 |
225 |
1434 |
48,2 |
7,13 |
16,8 |
|
|
20 |
102,2 |
400 |
2044 |
0,2 |
0,37 |
114,5 |
|
|
21 |
99,2 |
441 |
2083,2 |
12,3 |
3,59 |
14,4 |
|
|
22 |
104,0 |
484 |
2288 |
1,0 |
1,05 |
59,3 |
|
|
23 |
112,3 |
529 |
2582,9 |
87,6 |
8,19 |
166,4 |
|
|
24 |
98,8 |
576 |
2371,2 |
23,7 |
4,49 |
49,0 |
|
|
Сумма |
230 |
2035,2 |
3670 |
23588 |
1008,3 |
122,49 |
778,2 |
|
Среднее |
11,5 |
101,8 |
183,5 |
1179,4 |
50,4 |
6,12 |
38,91 |
Вычислим параметры уравнения тренда.

= 99,85.
В результате получим уравнение тренда:
T = 99,85 + 0,17×T.
Подставляя в это уравнение значения T = 1,2,…,16, найдем уровни T для каждого момента времени (гр. 5 табл. 2.3).
Шаг 5. Найдем уровни ряда, умножив значения T на соответствующие значения сезонной компоненты (гр. 6 табл. 2.3). На одном графике откладываем фактические значения уровней временного ряда и теоретические, полученные по мультипликативной модели.
Расчет ошибки в мультипликативной модели произведем по формуле:
Средняя абсолютная ошибка составила 1,0011 (см. гр. 7 табл. 2.3).
Рассчитаем сумму квадратов абсолютных ошибок .
Используя 5-й столбец таблицы 2.4, получим:

Рассчитаем среднюю относительную ошибку: .
Используя 6-й столбец таблицы 2.4, получим, что средняя относительная ошибка составила 6,12%, т. е. построенная модель достаточно точно описывает динамику данного явления.
| < Предыдущая | Следующая > |
|---|