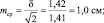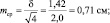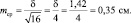Средняя и предельная ошибки выборки
Средняя ошибка выборкивсегда
присутствует в выборочных исследованиях
и появляется вследствие того, что
обследуются не все единицы статистической
совокупности, а лишь ее часть.
Средняя ошибка выборки превращается в
предельную ошибкуΔ
при умножении ее на коэффициент
доверияt, который задается
предварительно, исходя из требуемой
точности наблюдения. Предельная ошибка
позволяет судить об «истинном» размере
параметра в генеральной совокупности
с определенной степенью вероятности
|
|
При типическом и серийном
отборе, при расчете ошибки выборки
вместо общей дисперсии (σ2)
следует использовать
среднюю из внутригрупповых дисперсий
и межгрупповую дисперсию,
где—
частная дисперсия i группы,объем i группы
Формулы предельной ошибки случайной
выборки при определении средней
Для повторного отбора
|
|
где |
Для бесповторного отбора
|
|
Формулы предельной ошибки случайной
выборки при определении доли
Для повторного отбора
|
|
где |
Для бесповторного отбора
|
|
где |
Формулы численности случайной
выборки при определении средней величины
|
Для повторного |
Для |
|
|
|
Формулы численности случайной выборки при определении доли изучаемого признака
|
Для повторного |
Для |
|
|
|
Предельная разница между генеральной
и выборочной средней соответствует
величине предельной ошибки
|
для средней |
для доли: |
|
|
|
Значения вероятности и соответственно
tнаходятся по таблицам
распределения:
-
Лапласа
-
Стьюдента (в случае малой выборки)
Формулы случайной выборки подходят и
для механической выборки.
При необходимости округления, при
случайной выборке – округление в большую
сторону, при механической – в меньшую.
Малая выборка
Если численность выборочной совокупности
не более 30 единиц, то средняя ошибка
малой выборки при определении средней
величины рассчитывается по формуле:
|
при определении доли |
|
|
|
|
Для расчета ошибки малой выборки
применяется уточненная формула дисперсии
|
|
где n-1 — |
Типы задач выборочного наблюдения
-
определение ошибки выборки,
-
определение численности выборочной
совокупности n
, -
определение вероятности того, что
выборочная средняя (или доля) отклонится
от генеральной не более, чем на заданную
величину t=Δ/μ, -
оценка случайности расхождений
показателей выборочных наблюдений, -
перенос выборочных характеристик на
генеральную совокупность.
Проверка гипотез о средней и доле
Оценка случайности расхождений
показателей выборочных наблюдений
|
|
|
-
Если при n>30 коэффициент t<3, то делается
вывод о случайности расхождений. -
Если n≤ 30 , то полученное
значение t сравнивают с табличным,
определяемым по таблице распределения
Стьюдента -
Если
,
расхождение считается существенным. -
Если
,
расхождение считается случайным.
Методы переноса выборочных данных на
генеральную совокупность
-
метод взвешивания;
-
метод перевзвешивания;
-
метод заполнения случайным подбором
в классах замещения.
11.2. Оценка результатов выборочного наблюдения
11.2.1. Средняя и предельная ошибки выборки. Построение доверительных границ для средней и доли
Средняя ошибка выборки показывает, насколько отклоняется в среднем параметр выборочной совокупности от соответствующего параметра генеральной. Если рассчитать среднюю из ошибок всех возможных выборок определенного вида заданного объема (n), извлеченных из одной и той же генеральной совокупности, то получим их обобщающую характеристику — среднюю ошибку выборки (
В теории выборочного наблюдения выведены формулы для определения 
Например, если применяется повторная собственно случайная выборка, то 


При бесповторном собственно случайном отборе в формулы вносится поправка (1 — n/N):


Вероятность получения именно такой величины ошибки всегда равна 0,683. На практике же предпочитают получать данные с большей вероятностью, но это приводит к возрастанию величины ошибки выборки.
Предельная ошибка выборки (

Если ошибку выборки увеличить в два раза (t = 2), то получим гораздо большую вероятность того, что она не превысит определенного предела (в нашем случае — двойной средней ошибки) — 0,954. Если взять t = 3, то доверительная вероятность составит 0,997 — практически достоверность.
Уровень предельной ошибки выборки зависит от следующих факторов:
- степени вариации единиц генеральной совокупности;
- объема выборки;
- выбранных схем отбора (бесповторный отбор дает меньшую величину ошибки);
- уровня доверительной вероятности.
Если объем выборки больше 30, то значение t определяется по таблице нормального распределения, если меньше — по таблице распределения Стьюдента.
Приведем некоторые значения коэффициента доверия из таблицы нормального распределения.
| Значение доверительной вероятности P | 0,683 | 0,954 | 0,997 |
|---|---|---|---|
| Значение коэффициента доверия t | 1,0 | 2,0 | 3,0 |
Доверительный интервал для среднего значения признака и для доли в генеральной совокупности устанавливается следующим образом:
Итак, определение границ генеральной средней и доли состоит из следующих этапов:
Ошибки выборки при различных видах отбора
- Собственно случайная и механическая выборка. Средняя ошибка собственно случайной и механической выборки находятся по формулам, представленным в табл. 11.3.
 |
|
где |
Пример 11.2. Для изучения уровня фондоотдачи было проведено выборочное обследование 90 предприятий из 225 методом случайной повторной выборки, в результате которого получены данные, представленные в таблице.
| Уровень фондоотдачи, руб. | До 1,4 | 1,4-1,6 | 1,6-1,8 | 1,8-2,0 | 2,0-2,2 | 2,2 и выше | Итого |
|---|---|---|---|---|---|---|---|
| Количество предприятий | 13 | 15 | 17 | 15 | 16 | 14 | 90 |
В рассматриваемом примере имеем 40%-ную выборку (90 : 225 = 0,4, или 40%). Определим ее предельную ошибку и границы для среднего значения признака в генеральной совокупности по шагам алгоритма:
- По результатам выборочного обследования рассчитаем среднее значение и дисперсию в выборочной совокупности:
| Результаты наблюдения | Расчетные значения | |||
|---|---|---|---|---|
| уровень фондоотдачи, руб., xi | количество предприятий, fi | середина интервала, xi\xb4 | xi\xb4fi | xi\xb42fi |
| До 1,4 | 13 | 1,3 | 16,9 | 21,97 |
| 1,4-1,6 | 15 | 1,5 | 22,5 | 33,75 |
| 1,6-1,8 | 17 | 1,7 | 28,9 | 49,13 |
| 1,8-2,0 | 15 | 1,9 | 28,5 | 54,15 |
| 2,0-2,2 | 16 | 2,1 | 33,6 | 70,56 |
| 2,2 и выше | 14 | 2,3 | 32,2 | 74,06 |
| Итого | 90 | — | 162,6 | 303,62 |
Выборочная средняя
Выборочная дисперсия изучаемого признака
- Определяем среднюю ошибку повторной случайной выборки
- Зададим вероятность, на уровне которой будем говорить о величине предельной ошибки выборки. Чаще всего она принимается равной 0,999; 0,997; 0,954.
Для наших данных определим предельную ошибку выборки, например, с вероятностью 0,954. По таблице значений вероятности функции нормального распределения (см. выдержку из нее, приведенную в Приложении 1) находим величину коэффициента доверия t, соответствующего вероятности 0,954. При вероятности 0,954 коэффициент t равен 2.
- Предельная ошибка выборки с вероятностью 0,954 равна
- Найдем доверительные границы для среднего значения уровня фондоотдачи в генеральной совокупности
Таким образом, в 954 случаях из 1000 среднее значение фондоотдачи будет не выше 1,88 руб. и не ниже 1,74 руб.
Выше была использована повторная схема случайного отбора. Посмотрим, изменятся ли результаты обследования, если предположить, что отбор осуществлялся по схеме бесповторного отбора. В этом случае расчет средней ошибки проводится по формуле
Тогда при вероятности равной 0,954 величина предельной ошибки выборки составит:
Доверительные границы для среднего значения признака при бесповторном случайном отборе будут иметь следующие значения:
Сравнив результаты двух схем отбора, можно сделать вывод о том, что применение бесповторной случайной выборки дает более точные результаты по сравнению с применением повторного отбора при одной и той же доверительной вероятности. При этом, чем больше объем выборки, тем существеннее сужаются границы значений средней при переходе от одной схемы отбора к другой.
По данным примера определим, в каких границах находится доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., в генеральной совокупности:
- рассчитаем выборочную долю.
Количество предприятий в выборке с уровнем фондоотдачи, не превышающим значения 2,0 руб., составляет 60 единиц. Тогда
m = 60, n = 90, w = m/n = 60 : 90 = 0,667;
- рассчитаем дисперсию доли в выборочной совокупности

- средняя ошибка выборки при использовании повторной схемы отбора составит
Если предположить, что была использована бесповторная схема отбора, то средняя ошибка выборки с учетом поправки на конечность совокупности составит
- зададим доверительную вероятность и определим предельную ошибку выборки.
При значении вероятности Р = 0,997 по таблице нормального распределения получаем значение для коэффициента доверия t = 3 (см. выдержку из нее, приведенную в Приложении 1):
- установим границы для генеральной доли с вероятностью 0,997:
Таким образом, с вероятностью 0,997 можно утверждать, что в генеральной совокупности доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., не меньше, чем 54,7%, и не больше 78,7%.
- Типическая выборка. При типической выборке генеральная совокупность объектов разбита на k групп, тогда
N1 + N2 + … + Ni + … + Nk = N.
Объем извлекаемых из каждой типической группы единиц зависит от принятого способа отбора; их общее количество образует необходимый объем выборки
n1 + n2 + … + ni + … + nk = n.
Существуют следующие два способа организации отбора внутри типической группы: пропорциональной объему типических групп и пропорциональной степени колеблемости значений признака у единиц наблюдения в группах. Рассмотрим первый из них, как наиболее часто используемый.
Отбор, пропорциональный объему типических групп, предполагает, что в каждой из них будет отобрано следующее число единиц совокупности:
n = ni · Ni/N
где ni — количество извлекаемых единиц для выборки из i-й типической группы;
n — общий объем выборки;
Ni — количество единиц генеральной совокупности, составивших i-ю типическую группу;
N — общее количество единиц генеральной совокупности.
Отбор единиц внутри групп происходит в виде случайной или механической выборки.
Формулы для оценивания средней ошибки выборки для среднего и доли представлены в табл. 11.6.

|
Здесь 
Пример 11.3. В одном из московских вузов проведено выборочное обследование студентов с целью определения показателя средней посещаемости вузовской библиотеки одним студентом за семестр. Для этого была использована 5%-ная бесповторная типическая выборка, типические группы которой соответствуют номеру курса. При отборе, пропорциональном объему типических групп, получены следующие данные:
| Номер курса | Всего студентов, чел., Ni | Обследовано в результате выборочного наблюдения, чел., ni | Среднее число посещений библиотеки одним студентом за семестр, xi | Внутригрупповая выборочная дисперсия, 
|
|---|---|---|---|---|
| 1 | 650 | 33 | 11 | 6 |
| 2 | 610 | 31 | 8 | 15 |
| 3 | 580 | 29 | 5 | 18 |
| 4 | 360 | 18 | 6 | 24 |
| 5 | 350 | 17 | 10 | 12 |
| Итого | 2 550 | 128 | 8 | — |
Число студентов, которое необходимо обследовать на каждом курсе, рассчитаем следующим образом:
- общий объем выборочной совокупности:
n = 2550/130*5 =128 (чел.);
- количество единиц, отобранных из каждой типической группы:
аналогично для других групп:
n2 = 31 (чел.);
n3 = 29 (чел.);
n4 = 18 (чел.);
n5 = 17 (чел.).
Проведем необходимые расчеты.
- Выборочная средняя, исходя из значений средних типических групп, составит:
- Средняя из внутригрупповых дисперсий
- Средняя ошибка выборки:
С вероятностью 0,954 находим предельную ошибку выборки:
- Доверительные границы для среднего значения признака в генеральной совокупности:
Таким образом, с вероятностью 0,954 можно утверждать, что один студент за семестр посещает вузовскую библиотеку в среднем от семи до девяти раз.
- Малая выборка. В связи с небольшим объемом выборочной совокупности те формулы для определения ошибок выборки, которые использовались нами ранее при «больших» выборках, становятся неподходящими и требуют корректировки.
Среднюю ошибку малой выборки определяют по формуле
Предельная ошибка малой выборки:
Распределение значений выборочных средних всегда имеет нормальный закон распределения (или приближается к нему) при п > 100, независимо от характера распределения генеральной совокупности. Однако в случае малых выборок действует иной закон распределения — распределение Стьюдента. В этом случае коэффициент доверия находится по таблице t-распределения Стьюдента в зависимости от величины доверительной вероятности Р и объема выборки п. В Приложении 1 приводится фрагмент таблицы t-распределения Стьюдента, представленной в виде зависимости доверительной вероятности от объема выборки и коэффициента доверия t.
Пример 11.4. Предположим, что выборочное обследование восьми студентов академии показало, что на подготовку к контрольной работе по статистике они затратили следующее количество часов: 8,5; 8,0; 7,8; 9,0; 7,2; 6,2; 8,4; 6,6.
Оценим выборочные средние затраты времени и построим доверительный интервал для среднего значения признака в генеральной совокупности, приняв доверительную вероятность равной 0,95.
- Среднее значение признака в выборке равно
- Значение среднего квадратического отклонения составляет
- Средняя ошибка выборки:
- Значение коэффициента доверия t = 2,365 для п = 8 и Р = 0,95 .
- Предельная ошибка выборки:
- Доверительный интервал для среднего значения признака в генеральной совокупности:
То есть с вероятностью 0,95 можно утверждать, что затраты времени студента на подготовку к контрольной работе находятся в пределах от 6,9 до 8,5 ч.
11.2.2. Определение численности выборочной совокупности
Перед непосредственным проведением выборочного наблюдения всегда решается вопрос, сколько единиц исследуемой совокупности необходимо отобрать для обследования. Формулы для определения численности выборки выводят из формул предельных ошибок выборки в соответствии со следующими исходными положениями (табл. 11.7):
- вид предполагаемой выборки;
- способ отбора (повторный или бесповторный);
- выбор оцениваемого параметра (среднего значения признака или доли).
Кроме того, следует заранее определиться со значением доверительной вероятности, устраивающей потребителя информации, и с размером допустимой предельной ошибки выборки.
 |
Примечание: при использовании приведенных в таблице формул рекомендуется получаемую численность выборки округлять в большую сторону для обеспечения некоторого запаса в точности.
Пример 11.5. Рассчитаем, сколько из 507 промышленных предприятий следует проверить налоговой инспекции, чтобы с вероятностью 0,997 определить долю предприятий с нарушениями в уплате налогов. По данным прошлого аналогичного обследования величина среднего квадратического отклонения составила 0,15; размер ошибки выборки предполагается получить не выше, чем 0,05.
При использовании повторного случайного отбора следует проверить
При бесповторном случайном отборе потребуется проверить
Как видим, использование бесповторного отбора позволяет проводить обследование гораздо меньшего числа объектов.
Пример 11.6. Планируется провести обследование заработной платы на предприятиях отрасли методом случайного бесповторного отбора. Какова должна быть численность выборочной совокупности, если на момент обследования в отрасли число занятых составляло 100 000 чел.? Предельная ошибка выборки не должна превышать 100 руб. с вероятностью 0,954. По результатам предыдущих обследований заработной платы в отрасли известно, что среднее квадратическое отклонение составляет 500 руб.
Следовательно, для решения поставленной задачи необходимо включить в выборку не менее 100 человек.
2.1. Стандартное отклонение среднего выборочного значения (ошибка среднего) и доверительный интервал
Результаты измерений обычно показывают с так называемой «средней статистической ошибкой средней величины» и для нашего случая (см. табл. 1.1) это будет запись: «высота сеянцев в опыте составила 5,0 ± 0,28 см». Словосочетание «средняя статистическая ошибка» обычно сокращают до названия «ошибка среднего» или просто «ошибка», обозначают буквой m и определяют по очень простой формуле. Для итогов упомянутой таблицы, где расчеты по 25 высотам дали значение δ = 1,42 см, эта ошибка составит:
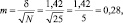
|
где δ – |
стандартное отклонение; |
|
N – |
число наблюдений или объем выборки, шт. |
Если объем выборки взять 100 шт., то ошибка снизится в 2 раза: 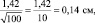
Рассмотрим эту «среднюю статистическую ошибку» (далее просто ошибка) подробно, так как именно в ней скрыто понимание того, что называют статистическим мышлением. Интуитивно мы понимаем, что малая выборка дает большую ошибку, т.е. неточное определение среднего значения. Последний термин настолько привычен, что мы даже не задумываемся о том, что его правильное и полное название «среднее выборочное значение», т.е. среднее, определяемое в некоторой выборке. И выборки могут быть очень разные по численности. Начнем с самых малых. Например, что произойдет с ошибкой, если объем выборки сократить до 2 измерений? Такие выборки бывают, например, в почвенных исследованиях, когда каждое измерение достается дорогой ценой. Для этого вернемся к рис. 1.1. На нем стандартное отклонение ±δ, которое отражает разброс значений вокруг среднего в левую и правую сторону в виде холма, наблюдается при объеме выборки 1 шт. В этом случае ошибка среднего выборочного значения будет равна стандартному отклонению: m = δ = 1,42. С увеличением N ошибка уменьшается:
при объеме выборки N = 2 ошибка будет
при объеме выборки N = 4 ошибка будет
при объеме выборки N = 16 ошибка будет
Важно понять, что ряд распределения частот этих выборочных средних будет постепенно как бы съеживаться и приближаться к центру, где находится так называемое «генеральное» среднее. Поясним, что в математике генеральное среднее значение называется математическим ожиданием и его обозначают буквой «М». Например, это может быть средняя высота, рассчитанная по всем измеренным в теплице сеянцам, или среднее число семян в 1 шишке у дерева после подсчета семян во всех собранных с дерева шишках (50, 100, 500 и т.д., т.е. весьма небольшая генеральная совокупность). Распределение частот значений выборочных средних, которых может быть множество, будет иметь форму такого же холма, как и распределение единичных значений на рис. 1.1. При этом, если выборка будет из 1 шт., то холм будет в точности таким же, но при выборках из 2 шт. его форма съежится в 
в 
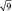
Для этих сокращающихся рядов распределения выборочных средних можно рассчитать свое, особое стандартное отклонение. Вероятно, чтобы не путать его со СТАНДОТКЛ, его стали называть по-другому, т.е. «средней статистической ошибкой средней величины». Чем больше по объему выборки, тем короче ряд распределения средних значений этих выборок с его «хвостами» в левую и правую сторону, и тем меньше величина этого особого стандартного отклонения. Закон распределения частот выборочных средних точно такой же, и имеет те же свойства: в пределах ±2m находится 95 % всех значений выборочных средних, в пределах ±3m – 99,5 %, а в пределах ±4m находится 100 % всех значений xср. Форма этого распределения меняется от пологой при малых выборках до очень крутой, вплоть до «схлопывания» в центре при выборках большого объема, когда ошибка среднего стремится к нулю.
Здесь следует пояснить, что, на наш взгляд, словосочетание «средняя статистическая ошибка средней величины», сокращаемое до «ошибки среднего значения» или просто до «ошибки», вводит нас в некоторое заблуждение, так как мы привыкли со школы, что ошибки надобно исправлять. Более правильным, вместо слов «ошибка среднего значения», будет использование слов «стандартное отклонение выборочных средних значений от генерального среднего». Не случайно математики выбрали для обозначения величины этого отклонения букву «m», а для обозначения генерального среднего (математического ожидания) – букву «М». Слова для объяснения этих сложных явлений могут быть разными, но и у математиков, и у биологов есть единодушие в понимании статистического смысла, лежащего за этими буквенными символами. Вообще, лучше было бы ввести некий иной термин вместо слов «ошибка» или «отклонение», так как они изначально имеют в нашем сознании иной смысл; на наш взгляд, более всего подходит слово «скачок» (чем сильнее отскакивает выборочное среднее от генерального среднего, тем реже оно встречается). Но так уж получилось, что не нашлось нейтрального (иностранного) слова, и слово «ошибка» традиционно используют, и мы также будем его использовать; важно понимать его иной, чем в обыденном употреблении, математический и статистический смысл.
Для самого точного определения средней высоты сеянцев нужно измерять все растения в питомнике, и тогда мы получим «генеральное среднее значение». Но так не делают, а измеряют несколько сотен растений в разных местах и этого бывает достаточно для определения среднего выборочного значения с приемлемой точностью. В нашем примере при 100 растениях ошибка его определения составит 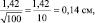
Вообще, точность опыта не самоцель; гораздо важнее сократить численность (объем) выборки до минимума. Представим себе, что средняя высота сеянцев xср = 5,0 см, а ее ±δ = 1,42 см, рассмотренные выше, получены при измерении 1000 растений потомства сосны, например, из Кунгура. Поделив ±δ на корень из 1000 получаем ошибку опыта m = ±0,045 см. Далее получаем точность опыта
Р = m/xср×100 = 0,045/5,0×100 = 0,9 %.
Точность получилась очень высокой. Но в питомнике есть потомства и из других мест и такой уровень точности совершенно не нужен, так как нужно узнать еще высоты сеянцев, например, из Очера, Осы, Добрянки и других районов. Если выборку из 1 тыс. растений снижать, то будет увеличиваться ошибка в определении средней высоты. И нужно найти приемлемую величину такой ошибки, которая позволит нам, тем не менее, уверенно утверждать, что это потомство растет быстрее, либо медленнее других. Причем происхождений может быть несколько сотен и минимизация выборок крайне важна, так как масштабы работ ограничены физическими возможностями бригады селекционеров. Следовательно, надо сокращать объем выборки. Как это сделать правильно?
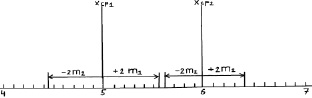
Рассмотрим два потомства. Первое – это упомянутые сеянцы происхождением из Кунгура (хср1), второе – сеянцы из Кизела с хср2 = 6,0 см и δ2 = ± 1,0 см (превышение высоты на 20 %). Надо это превышение доказать. При выборках из 100 растений ранее определенная ошибка m1 была равна 0,14 см, вторая ошибка m2 после расчетов по формуле (2.1) составит 0,1 см. По закону нормального распределения 99,5 % всех возможных значений этих средних хср1 и хср2 будут в пределах «плюс-минус три ошибки», что можно показать графически (рис. 2.1) или в виде формул:
хср1 ± 3m1 = 5,0 ± 3×0,14 = 5,0 ± 0,4 см
и
хср2 ± 3m2 = 6,0 ± 3×0,1 = 6,0 ± 0,3 см.
Возможные теоретические значения средних в генеральной совокупности не перекрывают друг друга, значит, различие достоверно. А если сократить выборки до 50 сеянцев? Тогда 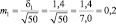
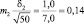
хср1 ± 3m1 = 5,0 ± 3×0,20 = 5,0 ± 0,6 см;
хср2 ± 3m2 = 6,0 ± 3×0,14 = 6,0 ± 0,3 см.
Рис. 2.1. Средние значения по выборкам из 100 растений и их тройные ошибки (пределы возможных значений выборочных средних в 99,5 % случаев)
Снова вынесем эти пределы на график (рис. 2.2).
Рис. 2.2. Средние значения при N = 50 растений и их тройные ошибки
Как видим, пределы сблизились и если еще сократить выборки, то они перекроются. Можно ли далее снижать объем выборки?
Можно, но здесь вступает в силу так называемое условие безошибочного прогноза. Мы это условие задали на уровне 99,5 % и для этого взяли ±3m для распределения ошибок. Но можно взять уровень пониже, с пределами ±2δ (уровень 95 %) и даже с пределами ±1,7δ (уровень 90 %).
При выборках из 25 штук сеянцев, получаем две ошибки: 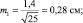
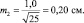
хср1 ± 2m1 = 5,0 ± 2×0,28 = 5,0 ± 0,56 см;
хср2 ± 2m2 = 6,0 ± 2×0,20 = 6,0 ± 0,40 см.
Выносим эти пределы опять на график (рис. 2.3).
Рис. 2.3. Средние значения при N = 25 растений и их двойные ошибки (пределы возможных значений средних в 95 % случаев)
Как видим, просвет все еще есть, и поэтому между возможными значениями средних высот сеянцев в других выборках из происхождений Кунгур и Кизел различия будут опять доказаны. Но уровень доказательства понизился до 95 %, и для 5 % оставшихся случаев нет гарантии, что различия будут иметь место при выборке из 25 растений. Их может и не быть, но эту вероятность в 5 % мы допускаем.
1.1. Ошибки
выборочного наблюдения
Средняя
ошибка выборки показывает, как генеральная средняя отклоняется в среднем от выборочной средней в ту или другую сторону. Формула
расчета средней ошибки выборки определяется видом исследуемого признака единиц
совокупности (количественный или альтернативный) и
способом отбора (бесповторный или повторный).
·
Если отбор повторный, а признак количественный
средняя ошибка выборки определяется по формуле
, где
— дисперсия признака в выборочной совокупности
n- число единиц
в выборке
·
Если отбор бесповторный, а признак
количественный

число единиц в генеральной совокупности
·
Если отбор повторный, а признак альтернативный

доля
·
Если отбор бесповторный, а признак
альтернативный
Предельная ошибка выборки— показывающая с определенной степенью вероятности
отклонения средней от выборочной средней.
Предельная ошибка выборки
, где параметр t зависит
от вероятности
Некоторые значения параметра t приведены
в таблице:
|
Вероятность, p |
0.95 |
0.954 |
0.9876 |
0.9907 |
0.9973 |
0.9999 |
|
Параметр t |
1.96 |
2.0 |
2.5 |
2.6 |
3.0 |
4.0 |
·
Если отбор повторный, а признак количественный
средняя ошибка выборки определяется по формуле
, где
— дисперсия признака в выборочной совокупности
n- число единиц
в выборке
·
Если отбор бесповторный, а признак
количественный

число единиц в генеральной совокупности
·
Если отбор повторный, а признак альтернативный

доля
·
Если отбор бесповторный, а признак
альтернативный
Доверительный интервал для генеральной средней
Доверительный интервал для
генеральной доли
Пример расчета доверительного
интервала:
При выборочном обследовании 5% продукции по методу случайного
бесповторного отбора получены данные о содержании сахара в образцах:
|
Сахарность, % |
Число |
|
16-17 17-18 18-19 19-20 20-21 |
10 158 154 50 28 |
|
На основании этих данных вычислите:
1. Средний процент сахаристости.
2. Дисперсию и среднее квадратическое
отклонение.
3. С вероятностью 0.954 возможные пределы среднего значения
сахаристости продукции для всей партии.
4. С вероятностью 0.997 возможный процент продукции высшего
сорта по всей партии, если известно, что из 400 проб, попавших в выборку , 80
ед. отнесены к продукции высшего сорта.
Решение.
1.
Средний процент сахаристости найдем по формуле средней взвешенной
, где xi–
середина i-го интервала
=18,32 %
2.
Дисперсия
=336,49
D(X)=336.49–
18.322=0.8676
Среднее квадратическое отклонение
=0,93%
5. Предельная ошибка для
среднего процента сахаристости
для вероятности 0,954 параметр t=2.0
Доверительный интервал для среднего значения процента
сахаристости
С вероятностью 0,954 можно утверждать, что в генеральной
совокупности средний процент сахаристости лежит в пределах от 18,23% до 18,41%.
5. Доля продукции высшего сорта в выборочной совокупности
Предельная ошибка для
доли продукции высшего сорта
для вероятности 0,997 параметр t=3.0
Доверительный интервал для доли продукции высшего сорта
С вероятностью 0,997 можно утверждать, что в генеральной
совокупности доля продукции высшего сорта лежит в пределах от 14,0% до 26,0%.
Тема 8. Выборочный метод
8.1. Сущность выборочного наблюдения, причины и практика его применения
Выборочное обследование – наиболее распространенный вид несплошного наблюдения в практике отечественной и зарубежной статистики. Сущность этого вида наблюдения состоит в том, что характеристика всей совокупности единиц дается по некоторой их части, отобранной научно обоснованным методом. В основе отбора единиц в выборку лежит принцип случайности, который обеспечивает равную возможность попадания в отобранную часть любой из единиц всей генеральной совокупности. Именно принцип случайности, заложенный в основу выборочного метода, и обеспечивает объективность результатов наблюдения, позволяет установить границы возможных ошибок и получить достоверные данные для характеристики всей совокупности.
Если отбор единиц произведен строго случайно, выборочная совокупность будет представительной или репрезентативной.
Выборочное наблюдение является наиболее совершенным и научно обоснованным методом несплошного наблюдения. При выборочном методе численность и доля единиц, которая будет обследоваться, известна до начала наблюдения, этим оно отличается от анкетного. В отличие от способа основного массива и монографического описания при проведении выборки неизвестно какие единицы совокупности будут подвергнуты обследованию. Выборочный метод, таким образом, в отличие от названных, исключает тенденциозность отбора и в большей степени обеспечивает представительство всех видов, групп, составляющих изучаемую совокупность.
Выборочный метод широко применяется в социально-экономических исследованиях, т.к. обладает рядом достоинств. Во-первых, он дает большую экономию средств и требует меньше времени для проведения наблюдения. То есть, выборочное наблюдение более экономичное, а результаты его носят более оперативный характер, чем при сплошном наблюдении. Во-вторых, при выборочном наблюдении при значительном сокращении объема работы обследование можно провести по более широкой программе, т.е. изучить явление более глубоко и детально. В-третьих, поскольку объем работы сокращается, то при выборке допускается меньше ошибок регистрации, и часто получают более точные результаты, чем при сплошном наблюдении.
Выборочный метод иногда является единственно возможным методом изучения явления, т.к. применение сплошного обследования может привести к физическому уничтожению всех единиц наблюдения. Например, при контроле качества некоторых видов продукции в промышленности, проверке семян на всхожесть в сельском хозяйстве и т.д.
Применение выборочного метода вызывается необходимостью контроля данных сплошного наблюдения. Например, контрольные проверки размеров посевных площадей и численности скота в личных хозяйствах населения.
Использование этого метода является целесообразным при изучении расходов населения, времени работы оборудования, рабочего времени и т.д.
Часто выборочный метод применяется в сочетании со сплошным наблюдением, например, при переписях населения.
8.2. Ошибки репрезентативности и теоретические основы их определения
В статистике принято называть совокупность отобранных единиц выборочной совокупностью (n), а совокупность единиц, из которых производится отбор – генеральной совокупностью (N). Генеральная и выборочная совокупности характеризуются такими показателями как средний размер признака, дисперсия, доля.
Рекомендуемые материалы
Задача выборочного наблюдения – дать верное представление о показателях всей генеральной совокупности на основе данных их некоторой части, попавшей в выборку.
Естественно, что когда изучают не всю, а только часть совокупности, результаты расчетов показателей выборочной и генеральной совокупности не совпадают. Эти отклонения выборочной средней и выборочной доли от доли и средней в генеральной совокупности называются ошибками выборки, или ошибками репрезентативности. Ошибки репрезентативности – это специфические ошибки, присущие только выборке и появляются они вследствие расхождения структуры выборочной и генеральной совокупности.
Как уже отмечалось, при выборочном наблюдении имеют место и ошибки регистрации, но они незначительны.
Основной организационный принцип выборочного наблюдения состоит в том, чтобы не допустить тенденциозного подбора выборочной совокупности, т.е. обеспечить строгое соблюдение принципа случайности отбора единиц в выборку. На результаты выборочного наблюдения можно полагаться именно благодаря тому, что отбор носит случайный характер. Это и позволяет максимально сократить возможные пределы отклонений выборочных результатов от показателей, вычисленных по всей генеральной совокупности.
Обобщенное действие механизма случайности в математике представляет закон больших чисел. Теория выборочного метода, основывается на доказательствах теорем русских математиков П.Л. Чебышева и А.М. Ляпунова. Из сущности закона больших чисел вытекает:
1) хотя каждая выборочная средняя и доля являются случайной величиной, однако средняя арифметическая из всех выборочных средних равняется генеральной средней;
2) каждый из возможных результатов выборочного наблюдения имеет свою вероятность появления, которая зависит от доли индивидуальных значений в генеральной совокупности. Чем больше доля индивидуальных показателей в генеральной совокупности, тем выше вероятность этих значений попасть в выборку;
3) каждая выборочная средняя отличается от генеральной средней. Разница между выборочной и генеральной средними представляет собой ошибку репрезентативности (выборки). Последняя измеряется средним квадратом отклонений всех возможных значений выборочных средних от генеральной средней, т.е. дисперсией.
В математической статистике доказывается, что между дисперсией выборочных средних и генеральной дисперсией существует определенное соотношение.
Дисперсия выборочных средних равна отношению генеральной дисперсии к численности выборочной совокупности.
Корень квадратный из этого отношения представляет собой стандартную (среднюю) ошибку репрезентативности (выборки):

Эта величина средней ошибки играет огромную роль в теории выборочного метода. Знание ее позволяет определять размер конкретных выборок и сказать какая выборка будет лучше еще до самой работы по выборочному обследованию.
Если выборочное обследование проводится с целью определения доли единиц, обладающих изучаемым признаком, то используются те же формулы расчетов, но в этом случае средняя и дисперсия заменяются аналогичными показателями альтернативного признака. Отсюда средняя ошибка выборки равна:

где 
Из приведенной формулы видно, что величина средней ошибки выборки зависит от вариации признака в генеральной совокупности, которая характеризуется дисперсией, и объема выборочной совокупности. Чем сильнее колеблется изучаемый признак у единиц генеральной совокупности, тем больше дисперсия, а отсюда и больше ошибка выборки, и, наоборот, чем больше объем выборочной совокупности, тем меньше ошибка выборки.
При организации выборки величина колеблемости признака в генеральной совокупности (N) неизвестна. В математической статистике доказано, что соотношение между дисперсиями генеральной и выборочной совокупностей выражается формулой:

Поскольку величина 

4) при достаточно большом объеме выборки распределение средних вокруг генеральной средней подчинено закону нормального распределения. Это означает, что отклонение от генеральной средней расположено в ту или другую сторону симметрично. Если взять одно среднее квадратическое отклонение в ту или другую сторону, то тем самым будет принято во внимание 68,3% всех выборочных средних, т.е. выборочная средняя не отклонится в ту или другую сторону на одну сигму. Если взять два средних квадратических отклонения, то во внимание будет принято 95,4% всех выборочных средних, если взять три средних квадратических отклонения – 99,7% средних. Зная среднюю ошибку выборки и вероятности с какой уверенностью хотят гарантировать результаты выборочного наблюдения можно установить пределы ошибок.

где 

Коэффициент доверия выражает число средних ошибок, которые нужно взять, чтобы получить заданную вероятность. Так при вероятности 0,683 


При выборочном наблюдении утверждения носят ориентировочный характер и выборочные показатели выражаются в интервале от и до.
Границы этих интервалов называются доверительными пределами. Нижний доверительный предел равен выборочной средней (доли) минус ошибка выборки.
8.3. Способы отбора и виды выборочного наблюдения
Репрезентативность выборки зависит не только от объема выборочной совокупности, но и от того как она образована, от характера отбора.
В генеральной совокупности могут отбираться отдельные единицы совокупности или же их группы.
В зависимости от того что является единицей отбора, последний делится на два вида: индивидуальный и групповой.
При индивидуальном отборе единицей отбора является непосредственно единица наблюдения. Например, проверка качества продукции непосредственно на рабочем месте. Контролер проверяет не каждую изготовленную деталь, а отбирает часть деталей из всей партии, которые подвергает проверке.
Групповой отбор заключается в том, что для наблюдения отбираются не только единицы совокупности, а их группы или серии. Примером могут служить контрольные проверки веса продукции, если она реализуется в упаковке (чай, макаронные изделия, сахар-рафинад и т.д.). Для контроля отбираются ящики, в отобранных ящиках взвешивается каждая пачка.
В некоторых случаях групповой отбор производится в сочетании с индивидуальным. Такой отбор называется комбинированным и связан со ступенчатостью. Здесь выборочная совокупность формируется не сразу, а проходит несколько стадий, ступеней, поэтому он еще называется многоступенчатым. Наиболее простым его случаем является двухступенчатый отбор, когда на первой ступени отбираются группы, на второй – отдельные единицы из отобранных групп.
Например, для контроля за соблюдением весовых стандартов пачек чая, сахара сначала отбираются ящики, в которых упакованы пачки, а из этих ящиков отбираются отдельные пачки.
Средняя ошибка выборки при двухступенчатом отборе исчисляется по формуле:
где 


Иногда сплошное наблюдение проводится в комбинации с выборочным. Например, переписи населения. Все население обследуется по основной программе, а 25% его обследуется по расширенной программе. Сплошное наблюдение может комбинироваться и с несколькими выборочными обследованиями, различающимися детализацией программ и числом обследуемых единиц.
Точность результатов и размеры ошибок выборочного наблюдения во многом зависят и от способа отбора единиц выборочной совокупности.
В зависимости от цели изучения и характера исходных данных, для обеспечения наибольшей репрезентативности выборки применяются следующие виды и способы отбора единиц совокупности для наблюдения:
а) собственно-случайная выборка,
б) механическая,
в) типическая (районированная),
г) серийно-гнездовая.
Собственно-случайная выборка.
При собственно-случайной выборке из генеральной совокупности отбираются для наблюдения отдельные единицы в случайном порядке. Для этого используются таблицы случайных чисел или жеребьевка.
Собственно-случайная выборка может проводиться по способу повторного и бесповторного отбора.
При повторном отборе отобранная единица после регистрации ее данных возвращается в генеральную совокупность и таким образом может попасть в выборку вторично и даже несколько раз. При бесповторном отборе каждая единица участвует в выборке только один раз.
Случайный отбор дает хорошие результаты в условиях, когда между единицами исследуемой совокупности нет резких различий.
При проведении собственно-случайной выборки нужно иметь исчерпывающий перечень всех единиц генеральной совокупности. Может оказаться, что пока организуется жеребьевка, единицы совокупности снова возникнут или ликвидируются. А при изучении качества продукции в течение дня вообще не имеется исчерпывающего перечня единиц. Неудобство этого способа отбора еще состоит и в том, что для жеребьевки на каждую единицу генеральной совокупности изготавливаются карточки (фишки) для жеребьевки.
Среднюю ошибку выборки для средней определяют в зависимости от способа отбора по разным формулам.
При повторном отборе:

При бесповторном отборе:

Аналогично вычисляют среднюю ошибку выборки для доли признака.
При повторном отборе:

При бесповторном отборе:

Бесповторный отбор обеспечивает большую репрезентативность выборки, чем повторный.
Собственно-случайная выборка применяется при контроле качества продукции, качества уборочных работ в сельском хозяйстве, при изучении оплаты пассажирами проезда в общественном транспорте и т.д.
Механическая выборка.
Механическая выборка представляет собой последовательный отбор единиц через равные интервалы в порядке определенного расположения их в генеральной совокупности или каком-нибудь перечне. Интервалы отбора определяются в соответствие с долей выборочной совокупности. Если, например, десятипроцентная выборка, то отбирается каждая десятая единица, если пятипроцентная – каждая двадцатая единица и т.д.
Расположение единиц генеральной совокупности в списке может быть двояким – упорядоченным или неупорядоченным относительно изучаемого признака. Так, списки рабочих могут быть составлены в алфавитном порядке по первым буквам фамилий; поскольку первые буквы фамилий рабочих не связаны с выполнением норм выработки, такое расположение является неупорядоченным относительно изучаемого признака. Если рабочих в списки записать по возрастанию или убыванию процента выполнения норм, расположение будет упорядоченным. Способ расположения единиц генеральной совокупности влияет на порядок их отбора в выборочную совокупность. В случае неупорядоченного расположения единиц из первых десяти рабочих можно взять любого (первого, второго, десятого) и затем последовательно брать одного через 10 человек. Если расположение упорядоченное, в выборочную совокупность следует отбирать рабочих, стоящих посредине каждого десятка; в противном случае может образоваться систематическая ошибка выборки. В самом деле, если рабочие в списках расположены по нисходящему проценту выполнения норм, то первые номера в каждом десятке будут всегда лучше по изучаемому признаку, а последние номера – худшими. Следовательно, отобрав в выборку первые номера, статистик завысит выборочный показатель выполнения норм, отобрав последние номера – занизит. Поэтому следует брать из каждого десятка пятые или шестые номера.
Механический отбор из упорядоченной (ранжированной) совокупности иногда называют систематическим отбором.
Механический отбор можно применять и не прибегая к спискам, а используя тот естественный порядок, в котором фактически расположены единицы генеральной совокупности, если только этот порядок не приведет к тенденциозным ошибкам.
Механическая выборка всегда бывает бесповторной и ошибки определяются по формулам собственно-случайной выборки.
Применяется механическая выборка при контроле за результатами сплошного наблюдения, при изучении потерь рабочего времени и т.д.
Например, из общего числа пенсионных вкладов банка была проведена 5%-ная механическая выборка. Результаты выборки следующие:
Таблица 8.1
|
Размер пенсионного вклада, тыс р. |
Число вкладов |
|
до 20 |
25 |
|
20-40 |
37 |
|
40-60 |
70 |
|
60-80 |
50 |
|
80 и выше |
18 |
|
Итого |
200 |
Определить: 1) с вероятностью 0,683 пределы среднего размера пенсионного вклада во всей генеральной совокупности; 2) с вероятностью 0,954 пределы доли вкладов, размер которых превышает 80 тыс. р.
Решение:
1. Предельная ошибка выборки на средний размер пенсионного вклада при механической выборке определяется по формуле:

Вероятности 0,683 соответствует коэффициент доверия (t), равный 1.
Вычислим среднюю и дисперсию по выборочной совокупности.


Вывод: с вероятностью 0,683 можно утверждать, что средний размер пенсионного вклада у всех вкладчиков банка будет находиться в пределах:

2. Предельная ошибка доли:

При вероятности 0,954 t=2.
W – доля вкладов, размер которых превышает 80 тыс. р.


Вывод: с вероятностью 0,954 можно утверждать, что доля вкладов, размер которых составляет 80 тыс. р. и выше во всей генеральной совокупности будет находиться в следующих доверительных пределах:

Типическая выборка.
Типический (районированный) отбор применяют в том случае, если изучаемая совокупность неоднородна.
При этом отборе генеральная совокупность предварительно расчленяется на типы (районы) из которых отбираются единицы либо посредством жеребьевки, либо механическим способом.
Типы (районы) могут быть образованы искусственно или использованы те, которые сложились естественно.
Количество единиц, отбираемых из каждого типа (района), как правило, берется пропорционально численности типов в генеральной совокупности. Однако в принципе наиболее точный результат дает типический отбор, учитывающий вариацию признака в отдельных частях (типах, районах) генеральной совокупности. Для достижения этого численность частей выборочной совокупности, имеющих большую вариацию, несколько увеличивается.
Случайная ошибка при типическом отборе меньше, чем при собственно-случайном и механическом отборах, так как типический отбор дает более репрезентативную выборку, лучше обеспечивает возможность сохранить в выборке то соотношение между типами (районами), которое имеется в генеральной совокупности.
Предельная ошибка при пропорциональной типической выборке исчисляется по нижеследующим формулам.
При повторном отборе:


При бесповторном отборе:


Пропорциональная типическая выборка широко применяется в социологических, бюджетных обследованиях, при изучении урожайности по типам хозяйств.
Например, для исчисления среднего размера депозита в банке была проведена 2% – типическая выборка. Распределение депозитов по срокам хранения и их статистические характеристики в выборке представлены в табл. 8.2.
Таблица 8.2
|
Срок хранения депозита |
Число депозитов |
Средний размер депозита, тыс. р. |
Дисперсия |
|
3 месяца |
500 |
40 |
340 |
|
6 месяцев |
300 |
65 |
580 |
|
1 год |
200 |
100 |
260 |
Вычислим средний размер депозита:
С вероятностью 0,954 установить предельную ошибку выборки на средний размер депозита.
Вычислим среднюю групповую дисперсию:
Средняя ошибка выборки составит:
Предельная ошибка выборки при вероятности 0,954 составит:
Таким образом, средний размер депозита в генеральной совокупности будет находиться в пределах от 58,26 до 60,74 тыс. р.
Серийная (гнездовая) выборка.
Весьма часто в практике выборочного наблюдения применяется гнездовой или серийный отбор. При гнездовой или серийной выборке отбор производится не единицами, а целыми гнездами, сериями единиц совокупности, в пределах которых обследуются все единицы полностью. Например, 200 рабочих из 2000 можно отобрать целыми бригадами; отбор бригад может быть осуществлен посредством жеребьевки или механически. В отобранных бригадах общей численностью 200 человек должны быть обследованы все рабочие сплошь.
Серии (гнезда) состоят из единиц, связанных между собой или территориально, или организационно, или, наконец, во времени. Отбор серий может производится в порядке повторного и бесповторного отбора. Серии могут быть равновеликими и неравновеликими. На практике чаще применяется серийный отбор с равными сериями.
Серийный отбор значительно проще в организационном отношении и дешевле других способов. Однако получающаяся в процессе этого отбора ошибки выборки в подавляющем большинстве случаев больше, чем при любом другом способе отбора.
Средняя ошибка выборки при отборе равновеликими сериями будет выражаться формулами:
при повторном отборе: 
при бесповторном отборе: 
где 

Приведем пример. Выборочное наблюдение урожайности зерновых культур по области проводилось при помощи отбора районов. По каждому отобранному району находилась средняя урожайность, которая оказалась следующей: I район – 14 ц с 1 га, II район – 15 ц с 1 га, III район – 14,5 ц с 1 га, IV район – 15,5 ц с 1 га, V район – 16 ц с 1 га. С вероятностью 0,997 оценить урожайность зерновых во всей области. В области 25 районов.
Найдем сначала общую среднюю:
затем межгрупповую дисперсию:
Средняя ошибка серийного бесповторного отбора:
Найдем предельную ошибку выборки:
Следовательно, с вероятностью 0,997 можно ожидать, что средняя урожайность зерновых в этой области заключается в пределах:
8.5. Определение необходимой численности выборки
Ошибки выборочного наблюдения и доверительные пределы генеральной средней (генеральной доли) определяются после того, как получены данные, характеризующие каждую единицу выборочной совокупности. А поэтому при проведении выборки первоначально необходимо определить сколько единиц или какая часть генеральной совокупности должна быть подвергнута наблюдению. Это важный момент в проведении выборочного наблюдения. Важность его в том, что излишняя численность выборочной совокупности вызывает необоснованное завышение затрат времени, труда, материальных и денежных средств, а недостаточная – дает результаты с большей погрешностью. Объем выборки должен быть оптимальным.
Факторами, определяющими численность выборки, являются:
1. Показатели вариации данного признака. Здесь обнаруживается прямая зависимость, т.е. чем больше показатель вариации, тем больше объем выборки.
2. Размер вероятности. Зависимость также прямая. Чем выше вероятность, тем выше коэффициент доверия, а, следовательно, и численность выборки. Величина вероятности зависит от того какое явление изучается. Естественно, что при контроле качества продовольственной продукции величина вероятности выше, чем непродовольственной продукции.
3. Размер возможной допустимой ошибки (
4. Способ отбора единиц для обследования. При прочих равных условиях для бесповторной выборки требуется меньшая численность выборки, чем при повторном отборе.
Основной трудностью, возникающей при установлении необходимой численности выборки, является определение среднеквадратического отклонения, которое характеризует вариацию признака. Значение этого показателя отсутствует как для генеральной, так и выборочной совокупности, поскольку задача определения необходимой численности выборки возникает тогда, когда еще выборка не проведена. Поэтому на практике используют несколько методов приближенного расчета среднеквадратического отклонения. Рассмотрим некоторые из них.
1. Вместо среднеквадратического отклонения данного отчетного периода берут значение данного показателя в базисном периоде. Этот прием применяется в тех случаях, когда мы в отчетном периоде, по сравнению с базисным, не ожидаем резкого изменения в исследуемых признаках.
2. Расчет среднеквадратического отклонения может быть основан на той связи, которая существует между показателями средней арифметической и коэффициентом вариации. Практика показывает, что во всех более или менее однородных совокупностях коэффициент вариации колеблется в пределах от 25-35%. Иначе говоря, коэффициент вариации обычно приблизительно равен 

3. Следующий прием опирается на величину размаха вариации. Разность между максимальным и минимальным значениями признака равна приблизительно шести средним квадратическим отклонениям. Разделив размах колебаний на шесть, мы получим приближенное значение среднего квадратического отклонения. Этот прием можно использовать, т.к. максимальное и минимальное значение изучаемого признака известны до проведения наблюдения.
При установлении колеблемости доли, как и средней, в первую очередь надо попытаться найти ориентировочные данные о величине W. Если таких данных нет, то берется максимальная величина произведения W на (1-W). Эта величина равна 0,25.
Необходимую численность выборочной совокупности определяют на основе алгебраического преобразования формулы предельной ошибки выборки для разных видов и способов отбора.
Для собственно-случайной повторной выборки:

Чтобы найти численность выборки, нужно освободиться от радикала. Это достигается возведением левой и правой частей уравнения в квадрат.

отсюда численность выборки: 
Объем выборочной совокупности прямо пропорционален квадрату коэффициента доверия и дисперсии и обратно пропорционален квадрату предельной ошибки выборки.
При бесповторном собственно-случайном и механическом отборе численность выборки будет равна:

Для доли признака численность выборки будет определяться по формулам:


Аналогичным преобразованием предельной ошибки определяется численность выборочной совокупности при типической и серийной выборке.
Допустим, что для установления средней дневной выработки рабочих предприятия проводится собственно-случайная бесповторная выборка. Сколько рабочих должно быть обследовано, чтобы получить результат с точностью 0,3 р. с вероятностью 0,954. Общая численность рабочих завода 5000 человек. По данным прошлогоднего обследования среднее квадратическое отклонение выработки составляет 1,6 р.

Следовательно, должно быть обследовано 112 рабочих, чтобы выполнить поставленные перед наблюдением требования.
8.6. Способы распространения данных выборочного наблюдения
Конечной целью выборочного наблюдения является характеристика генеральной совокупности на основе данных, полученных по выборочной совокупности. Существуют два способа распространения данных выборочного наблюдения на генеральную совокупность – способ прямого пересчета и способ поправочных коэффициентов.
Способ прямого перерасчета заключается в том, что выборочная средняя или доля умножаются на численность генеральной совокупности и получается соответствующий объемный показатель. Так, в статистике сельского хозяйства выход шерсти от овец, находящихся в личном пользовании, определяется путем умножения полученных по выборке данных о среднем настриге шерсти с одной овцы на всю численность овец, находящихся в личной собственности. Например, согласно выборке, в области годовой настриг шерсти с одной овцы составляет 3 кг (с ошибкой выборки 


Второй пример. в 3%-ной выборке численностью 150 светильников 6 светильников оказались бракованными (ошибка выборки 

Вместе с этой лекцией читают «22 Сатурн».
Данный способ применяется тогда, когда известна численность единиц в генеральной совокупности.
Способ поправочных коэффициентом используется при проведении контрольных выборочных наблюдений для проверки и уточнения данных сплошного наблюдения. Он заключается в том, что по одним и тем же объектам сопоставляют данные сплошного и контрольного выборочного наблюдения. В результате такого сопоставления исчисляют поправочные коэффициенты, которые применяют для внесения поправок в данные сплошных наблюдений. Поправочные коэффициенты исчисляют, например, на основе данных контрольных выборочных обследований скота, находящегося в личной собственности населения сельской местности, при контроле за качеством деталей непосредственно на рабочем месте и т.д.
Например, по данным сплошного наблюдения численность крупного рогатого скота в личном подсобном хозяйстве граждан составляет 1 0000 голов.
Для контрольной проверки отобрано 1 000 семей, в хозяйствах которых сплошным наблюдением определена численность поголовья скота 1000 голов. В результате контрольного обхода в этих хозяйствах установлена численность крупного рогатого скота 1 050 голов.
Отсюда поправочный коэффициент составляет 1 050:1 000=1,05.
Общее поголовье скота в личном подсобном хозяйстве граждан равно 

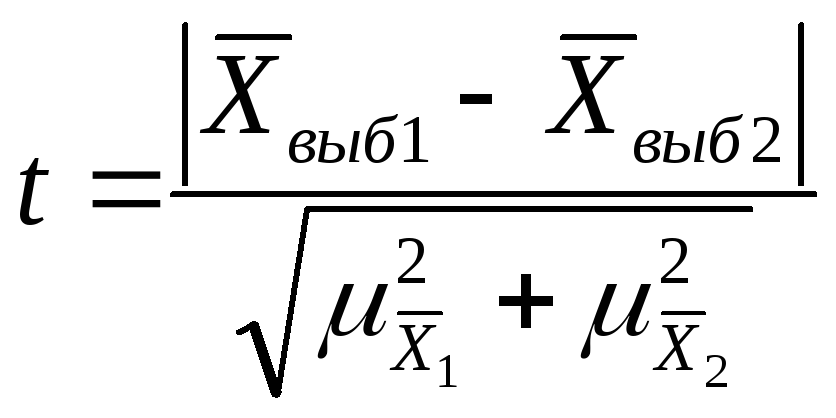
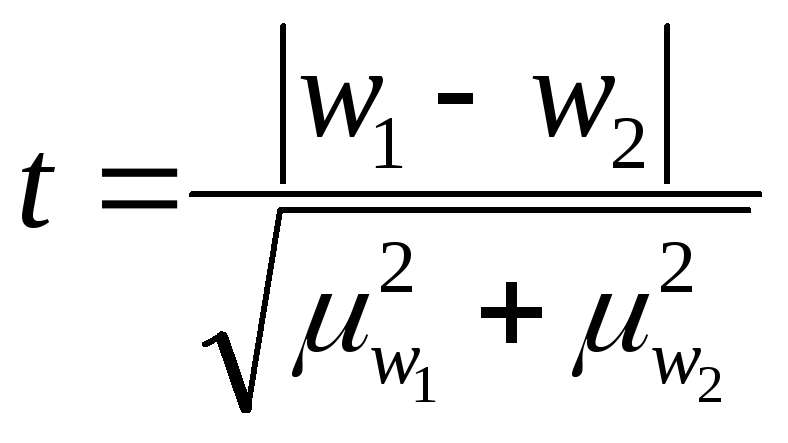













 ) при использовании типического отбора, пропорционального объему типических групп
) при использовании типического отбора, пропорционального объему типических групп