Повторный и бесповторный отбор.
Ошибка выборки
Краткая теория
На основании выборочных данных дается оценка статистических
показателей по всей (генеральной) совокупности. Подобное возможно, если выборка
основывается на принципах случайности отбора и репрезентативности
(представительности) выборочных данных. Каждая единица генеральной совокупности
должна иметь равную возможность (вероятность) попасть в выборку.
При формировании выборочной совокупности используются следующие
способы отбора: а) собственно-случайный отбор; б) механическая выборка; в)
типический (районированный) отбор; г) многоступенчатая (комбинированная)
выборка; д) моментно-выборочное наблюдение.
Выборка может осуществляться по схеме повторного и бесповторного
отбора.
В первом случае единицы совокупности, попавшие в выборку, снова
возвращаются в генеральную, а во втором случае – единицы совокупности, попавшие
в выборку, в генеральную совокупность уже не возвращаются.
Выборка может осуществляться отдельными единицами или сериями
(гнездами).
Собственно-случайная выборка
Отбор в этом случае производится либо по жребию, либо по таблицам
случайных чисел.
На основании приемов классической выборки решаются следующие
задачи:
а) определяются границы среднего значения показателя по генеральной
совокупности;
б) определяются границы доли признака по генеральной совокупности.
Предельная ошибка средней при собственно-случайном отборе
исчисляется по формулам:
а) при повторном отборе:
б) при бесповторном отборе:
где
– численность выборочной совокупности;
– численность генеральной совокупности;
– дисперсия признака;
– критерий кратности ошибки: при
;
при
;
при
.
Значения
определяются
по таблице функции Лапласа.
Границы (пределы) среднего значения признака по генеральной
совокупности определяются следующим неравенством:
где
– среднее значение признака по выборочной
совокупности.
Предельная ошибка доли при собственно-случайном отборе определяется
по формулам:
а) при повторном отборе:
при бесповторном отборе:
где
– доля единиц совокупности с заданным
значением признака в обзей численности выборки,
– дисперсия доли признака.
Границы (пределы) доли признака по всей (генеральной) совокупности
определяются неравенством:
где
– доля признака по генеральной совокупности.
Типическая (районированная) выборка
Особенность этого вида
выборки заключается в том, что предварительно генеральная совокупность по
признаку типизации разбивается на частные группы (типы, районы), а затем в
пределах этих групп производится выборка.
Предельная ошибка средней
при типическом бесповторном отборе определяется по формуле:
где
– средняя из внутригрупповых дисперсий
по каждой типичной группе.
При пропорциональном отборе из групп генеральной совокупности
средняя из внутригрупповых дисперсий определяется по формуле:
где
– численности единиц совокупности групп по выборке.
Границы (пределы) средней по генеральной совокупности на основании
данных типической выборки определяются по тому же неравенству, что при
собственно-случайной выборке. Только предварительно необходимо вычислить общую
выборочную среднюю
из частных выборочных средних
.
Для случая пропорционального отбора это определяется по формуле:
При непропорциональном отборе средняя из внутригрупповых дисперсий вычисляется по
формуле:
где
– численность единиц групп по генеральной
совокупности.
Общая выборочная средняя в этом случае определяется по формуле:
Предельная ошибка доли
признака при типическом бесповторном отборе определяется формулой:
Средняя дисперсия доли
признака из групповых дисперсий доли
при
типической пропорциональной выборке вычисляется по формуле:
Средняя доля признака по
выборке из показателей групповых долей рассчитывается формуле:
Средняя дисперсия доли при
непропорциональном типическом отборе определяется следующим образом:
а средняя доля признака:
Формулы ошибок выборки при типическом повторном отборе будут те же,
то и для случая бесповторного отбора. Отличие заключается только в том, что в
них будет отсутствовать по корнем сомножитель
.
Серийная выборка
Серийная ошибка выборки
может применяться в двух вариантах:
а) объем серий различный
б) все серии имеют
одинаковое число единиц (равновеликие серии).
Наиболее распространенной
в практике статистических исследований является серийная выборка с
равновеликими сериями. Генеральная совокупность делится на одинаковые по объему
группы-серии
и
производится отбор не единиц совокупности, а серий
. Группы (серии) для обследования отбирают в
случайном порядке или путем механической выборки как повторным, так и
бесповторными способами. Внутри каждой отобранной серии осуществляется сплошное
наблюдение. Предельные ошибки выборки
при
серийном отборе исчисляются по формулам:
а) при повторном отборе
б) при бесповторном отборе
где
– число
серий в генеральной совокупности;
– число
отобранных серий;
– межсерийная дисперсия, исчисляемая для случая равновеликих
серий по формуле:
где
–
среднее значение признака в каждой из отобранных серий;
– межсерийная
средняя, исчисляемая для случая равновеликих серий по формуле:
Определение численности выборочной совокупности
При проектировании
выборочного наблюдения важно наряду с организационными вопросами решить одну из
основных постановочных задач: какова должна быть необходимая численность
выборки с тем, чтобы с заданной степенью точности (вероятности) заранее
установленная ошибка выборки не была бы превзойдена.
Примеры решения задач
Задача 1
На основании результатов проведенного на заводе 5%
выборочного наблюдения (отбор случайный, бесповторный) получен следующий ряд
распределения рабочих по заработной плате:
| Группы рабочих по размеру заработной платы, тыс.р. | до 200 | 200-240 | 240-280 | 280-320 | 320 и выше | Итого |
| Число рабочих | 33 | 35 | 47 | 45 | 40 | 200 |
На основании приведенных данных определите:
1) с вероятностью 0,954 (t=2) возможные пределы, в которых
ожидается средняя заработная плата рабочего в целом по заводу (по генеральной
совокупности);
2) с вероятностью 0,997 (t=3) предельную ошибку и границы доли
рабочих с заработной платой от 320 тыс.руб. и выше.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Вычислим среднюю з/п: Для этого просуммируем произведения середин
интервалов и соответствующих частот, и полученную сумму разделим на сумму
частот.
2) Выборочная дисперсия:
Найдем доверительный интервал для средней. Предельная ошибка выборочной
средней считается по формуле:
где
—
аргумент функции Лапласа.
Искомые возможные пределы, в которых ожидается средняя заработная плата
рабочего в целом по заводу:
Найдем доверительный интервал для выборочной доли. Предельная ошибка
выборочной доли считается по формуле:
Доля рабочих с з/п от 320 тыс.р.:
Искомые границы доли рабочих с заработной платой от 320 тыс.руб. и выше:
Задача 2
В
городе 23560 семей. В порядке механической выборки предполагается определить
количество семей в городе с числом детей трое и более. Какова должна быть
численность выборки, чтобы с вероятностью 0,954 ошибка выборки не превышала
0,02 человека. На основе предыдущих обследований известно, что дисперсия равна
0,3.
Решение
Численность
выборки можно найти по формуле:
В нашем случае:
Вывод к задаче
Таким образом численность
выборки должна составить 2661 чел.
Задача 3
С
целью определения средней месячной заработной платы персонала фирмы было
проведено 25%-ное выборочное обследование с отбором
единиц пропорционально численности типических групп. Для отбора сотрудников
внутри каждого филиала использовался механический отбор. Результаты
обследования представлены в следующей таблице:
| Номер филиала |
Средняя месячная заработная плата, руб. |
Среднее квадратическое отклонение, руб. |
Число сотрудников, чел. |
| 1 | 870 | 40 | 30 |
| 2 | 1040 | 160 | 80 |
| 3 | 1260 | 190 | 140 |
| 4 | 1530 | 215 | 190 |
С
вероятностью 0,954 определите пределы средней месячной заработной платы всех
сотрудников гостиниц.
Решение
Предельная
ошибка выборочной средней:
Средняя
из внутригрупповых дисперсий:
Получаем:
Средняя
месячная заработная плата по всей совокупности филиалов:
Искомые
пределы средней месячной заработной платы:
Вывод к задаче
Таким
образом с вероятностью 0,954 средняя месячная заработная плата всех сотрудников
гостиниц находится в пределах от 1294,3 руб. до 1325,7 руб.
Собственно-случайная
выборка
состоит в том, что выборочная совокупность
образуется в результате случайного
(непреднамеренного) отбора отдельных
единиц из генеральной совокупности.
При этом количество отобранных в
выборочную совокупность единиц обычно
определяется исходя из принятой доли
выборки.
Доля выборки есть
отношение числа единиц выборочной
совокупности n к численности единиц
генеральной совокупности N, т.е..
Так, при 5%-ной
выборке из партии товара в 2 000 ед.
численность выборки n составляет 100 ед.
(5*2000:100), а при 20%-ной выборке она составит
400 ед. (20*2000:100) и т.д.
Механическая
выборка
состоит в том, что отбор единиц в
выборочную совокупность производится
из генеральной совокупности, разбитой
на равные интервалы (группы). При этом
размер интервала в генеральной
совокупности равен обратной величине
доли выборки.
Так, при 2%-ной
выборке отбирается каждая 50-я единица
(1:0,02), при 5%-ной выборке — каждая 20-я
единица (1:0,05) и т.д.
Таким образом, в
соответствии с принятой долей отбора,
генеральная совокупность как бы
механически разбивается на равновеликие
группы. Из каждой группы в выборку
отбирается лишь одна единица.
Важной особенностью
механической выборки является то, что
формирование выборочной совокупности
можно осуществить, не прибегая к
составлению списков. На практике часто
используют тот порядок, в котором
фактически размещаются единицы
генеральной совокупности. Например,
последовательность выхода готовых
изделий с конвейера или поточной линии,
порядок размещения единиц партии товара
при хранении, транспортировке, реализации
и т.д.
21. Средняя и предельная ошибки выборки при типическом и серийном способах отбора.
Типическая
выборка. При
типической выборке генеральная
совокупность вначале расчленяется на
однородные типические группы. Затем из
каждой типической группы собственно-случайной
или механической выборкой производится
индивидуальный отбор единиц в выборочную
совокупность.
Типическая выборка
обычно применяется при изучении сложных
статистических совокупностей. Например,
при выборочном обследовании
производительности труда работников
торговли, состоящих из отдельных групп
по квалификации.
Важной особенностью
типической выборки является то, что она
дает более точные результаты по сравнению
с другими способами отбора единиц в
выборочную совокупность.
Для определения
средней ошибки типической выборки
используются формулы:
повторный отбор
,
бесповторный отбор
,
Дисперсия определяется
по следующим формулам:
,
Серийная выборка.
При серийной выборке генеральную
совокупность делят на одинаковые по
объему группы — серии. В выборочную
совокупность отбираются серии. Внутри
серий производится сплошное наблюдение
единиц, попавших в серию.
При бесповторном
отборе серий средняя ошибка выборочной
серии определяется по формуле:
,
где
— межсерийная дисперсия средних;
R — число серий в
генеральной совокупности;
r — число отобранных
серий.
В статистике
различают одноступенчатые и многоступенчатые
способы отбора единиц в выборочную
совокупность.
При одноступенчатой
выборке каждая отобранная единица сразу
же подвергается изучению по заданному
признаку. Так обстоит дело при
собственно-случайной и серийной выборке.
При многоступенчатой
выборке производят подбор из генеральной
совокупности отдельных групп, а из групп
выбираются отдельные единицы. Так
производится типическая выборка с
механическим способом отбора единиц в
выборочную совокупность.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание курса лекций “Статистика”
Выборочное наблюдение как источник статистической информации в изучении социально-экономических явлений и процессов
Статистическая методология исследования массовых явлений различает, как известно, два способа наблюдения в зависимости от полноты охвата объекта: сплошное и несплошное. Разновидностью несплошного наблюдения является выборочное, которое в условиях рыночных отношений в России находит все более широкое применение. Переход статистики РФ на международные стандарты системы национального счетоводства требует более широкого применения выборки для получения и анализа показателей СНС не только в промышленности, но и в других секторах экономики.
Под выборочным наблюдением понимается несплошное наблюдение, при котором статистическому обследованию (наблюдению) подвергаются единицы изучаемой совокупности, отобранные случайным способом. Выборочное наблюдение ставит перед собой задачу ‑ по обследуемой части дать характеристику всей совокупности единиц при условии соблюдения всех правил и принципов проведения статистического наблюдения и научно организованной работы по отбору единиц.
К выборочному наблюдению статистика прибегает по различным причинам. На современном этапе появилось множество субъектов хозяйственной деятельности, которые характерны для рыночной экономики. Речь идет об акционерных обществах, малых и совместных предприятиях, фермерских хозяйствах и т.д. Сплошное обследование этих статистических совокупностей, состоящих из десятков и сотен тысяч единиц, потребовало бы огромных материальных, финансовых и иных затрат. Использование же выборочного обследования позволяет значительно сэкономить силы и средства, что имеет немаловажное значение.
Наряду с экономией ресурсов одной из причин превращения выборочного наблюдения в важнейший источник статистической информации является возможность значительно ускорить получение необходимых данных. Ведь при обследовании, скажем, 10% единиц совокупности будет затрачено гораздо меньше времени, а результаты могут быть представлены быстрее, и будут более актуальными. Фактор времени важен для статистического исследования особенно в условиях изменяющейся социально-экономической ситуации.
Реализация выборочного метода базируется на понятиях генеральной и выборочной совокупностей.
Генеральной совокупностью называется вся исходная изучаемая статистическая совокупность, из которой на основе отбора единиц или групп единиц формируется совокупность выборочная. Поэтому генеральную совокупность также называют основой выборки.
Отбор единиц в выборочную совокупность может быть повторным или бесповторным.
При повторном отборе попавшая в выборку единица подвергается обследованию, т.е. регистрации значений ее признаков, возвращается в генеральную совокупность и наравне с другими единицами участвует в дальнейшей процедуре отбора. Таким образом, некоторые единицы могут попадать в выборку дважды, трижды или даже большее число раз. И при изучении выборочной совокупности они будут рассматриваться как отдельные независимые наблюдения.
Отметим, что число единиц генеральной совокупности, участвующих в отборе, при таком подходе остается постоянным. Поэтому вероятность попадания в выборку для всех единиц совокупности на протяжении всего процесса отбора также не меняется.
На практике методология повторного отбора обычно используется в тех случаях, когда объем генеральной совокупности не известен и теоретически возможно повторение единиц с уже встречавшимися значениями всех регистрируемых признаков.
Например, при проведении маркетинговых исследований мы не можем сколько-нибудь точно оценить, какое число потребителей предпочитают стиральный порошок конкретной торговой марки, сколько покупателей предпочитают делать покупки именно в данном супермаркете и т.д. Поэтому возможно повторение совершенно идентичных единиц как по причине практически неограниченных объемов совокупности, так и вследствие возможной повторной регистрации. Предположим, при проведении обследования один и тот же покупатель может дважды прийти в магазин и дважды подвергнуться обследованию.
При выборочном контроле качества продукции объем генеральной совокупности также часто не определен, так как процесс производства может осуществляться постоянно, каждый день дополняя генеральную совокупность новыми единицами-изделиями. Поэтому в выборочную совокупность могут попасть два и более изделий с абсолютно одинаковыми характеристиками. Следовательно, и в этом случае при обработке результатов выборки необходимо ориентироваться на методологию, используемую при повторном отборе.
При бесповоротном отборе попавшая в выборку единица подвергается обследованию и в дальнейшей процедуре отбора не участвует. Такой отбор целесообразен и практически возможен в тех случаях, когда объем генеральной совокупности четко определен. Получаемые при этом результаты, как правило, являются более точными по сравнению с результатами, основанными на повторной выборке.
Как уже отмечалось выше, выборочное наблюдение всегда связано с определенными ошибками получаемых характеристик. Эти ошибки называются ошибками репрезентативности (представительности).
Ошибки репрезентативности обусловлены тем обстоятельством, что выборочная совокупность не может по всем параметрам в точности воспроизвести совокупность генеральную. Получаемые расхождения или ошибки репрезентативности позволяют заключить, в какой степени попавшие в выборку единицы могут представлять всю генеральную совокупность. При этом следует различать систематические и случайные ошибки репрезентативности.
Систематические ошибки репрезентативности связаны с нарушением принципов формирования выборочной совокупности. Например, вследствие каких-либо причин, связанных с организацией отбора, в выборку попали единицы, характеризующиеся несколько большими или, наоборот, несколько меньшими по сравнению с другими единицами значениями наблюдаемых признаков. В этом случае и рассчитанные выборочные характеристики будут завышенными или заниженными.
Случайные ошибки репрезентативности обусловлены действием случайных факторов, не содержащих каких-либо элементов системности в направлении воздействия на рассчитываемые выборочные характеристики. Но даже при строгом соблюдении всех принципов формирования выборочной совокупности выборочные и генеральные характеристики будут несколько различаться. Получаемые случайные ошибки могут быть статистически оценены и учтены при распространении результатов выборочного наблюдения на всю генеральную совокупность. Оценка ошибок выборочного наблюдения основана на теоремах теории вероятностей.
При дальнейшем рассмотрении теории и методов выборочного наблюдения используются следующие общепринятые условные обозначения:
N ‑ объем (число единиц) генеральной совокупности;
n ‑ объем (число единиц) выборочной совокупности;
‑ генеральная средняя, т.е. среднее значение изучаемого признака по генеральной совокупности (средняя прибыль, средняя величина активов, средняя численность работников предприятия и т.п.);
‑ выборочная средняя,
т.е. среднее значение изучаемого признака по выборочной совокупности;
М ‑ численность единиц генеральной совокупности, обладающих определенным вариантом или вариантами изучаемого признака (численность городского населения, численность сельского населения, количество бракованных изделий, число нерентабельных предприятий и т.п.);
р ‑ генеральная доля, т.е. доля единиц, обладающих определенным вариантом или вариантами изучаемого признака, во всей генеральной совокупности (доля городского населения в общей численности населения, доля бракованной продукции в общем выпуске, доля нерентабельных предприятий в общей численности предприятий и т.п.); определяетcя как
m ‑ численность единиц выборочной совокупности, обладающих определенным вариантом или вариантами изучаемого признака;
w ‑ выборочная доля, т.е. доля единиц, обладающих определенным вариантом или вариантами изучаемого признака, в выборочной совокупности,
определяется как ;
‑ средняя ошибка выборки;
‑ предельная ошибка выборки;
‑ коэффициент доверия, определяемый в зависимости от уровня вероятности.
Ошибка выборки или отклонение выборочной средней от средней генеральной находится в прямой зависимости от дисперсии изучаемого признака в генеральной совокупности, и в обратной зависимости ‑ от объема выборки.
Таким образом среднюю ошибку выборки можно представить как
(10.1)
При проведении выборочного наблюдения дисперсия изучаемого признака в генеральной совокупности, как правило, не известна. В то же время, между генеральной дисперсией и средней из всех возможных выборочных дисперсий существует следующее соотношение:
(10.2)
В связи с тем, что на практике в большинстве случаев из генеральной совокупности в определенный момент времени производится только одна выборка, дисперсия изучаемого признака по этой выборке и используется при расчете ошибки.
Учитывая, что при достаточно большом объеме выборки отношение 
(10.3)
Где ‑ дисперсия изучаемого признака по выборочной совокупности.
При определении возможных границ значений характеристик генеральной совокупности рассчитывается предельная ошибка выборки, которая зависит от величины ее средней ошибки и уровня вероятности, с которым гарантируется, что генеральная средняя не выйдет за указанные границы.
Согласно теореме А.М. Ляпунова, вероятность той или иной величины предельной ошибки, при достаточно большом объеме выборочной совокупности, подчиняется нормальному закону распределения и может быть определена на основе интеграла Лапласа.
Значения интеграла Лапласа при различных величинах t табулированы и представлены в статистических справочниках.
При обобщении результатов выборочного наблюдения наиболее часто используются следующие уровни вероятности и соответствующие им значения t:
Таблица 10.1 ‑ !!!Некоторые значения t
| Вероятность, рi. | 0,683 | 0,866 | 0,954 | 0,988 | 0,997 | 0,999 |
| Значение t | 1,0 | 1,5 | 2,0 | 2,5 | 3,0 | 3,5 |
Например, если при расчете предельной ошибки выборки мы используем значение t=2, то с вероятностью 0,954 можно утверждать, что расхождение между выборочной средней и генеральной средней не превысит двукратной величины средней ошибки выборки.
Теоретической основой для определения границ генеральной доли, т.е. доли единиц, обладающих тем или иным вариантом признака, является теорема Вернули. Согласно данной теореме вероятность получения сколь угодно малого расхождения между выборочной долей и генеральной долей при достаточно большом объеме выборки будет стремиться к единице. С учетом того, что вероятность расхождения между выборочной и генеральной долями подчиняется нормальному закону распределения, эта вероятность также определяется по функции F(t) при заданном значении t.
Процесс подготовки и проведения выборочного наблюдения включает ряд последовательных этапов:
- Определение цели обследования.
- Установление границ генеральной совокупности.
- Составление программы наблюдения и программы разработки данных
- Определение вида выборки, процента отбора и метода отбора
- Отбор и регистрация наблюдаемых признаков у отобранных единиц.
- Насчет выборочных характеристик и их ошибок.
- Распространение полученных результатов на генеральную совокупность.
В зависимости от состава и структуры генеральной совокупности выбирается вид выборки или способ отбора.
К наиболее распространенным на практике видам относятся:
- собственно-случайная (простая случайная) выборка;
- механическая (систематическая) выборка;
- типическая (стратифицированная, расслоенная) выборка;
- серийная (гнездовая) выборка.
Отбор единиц из генеральной совокупности может быть комбинированным, многоступенчатым и многофазным.
Комбинированный отбор предполагает объединение нескольких видов выборки. Так, например, можно комбинировать типическую и серийную, серийную и собственно-случайную выборки. Ошибка такой выборки определяется ступенчатостью отбора.
Многоступенчатым называется отбор, при котором из генеральной совокупности сначала извлекаются укрупненные группы, потом ‑ более мелкие и так до тех пор, пока не будут отобраны те единицы, которые подвергаются обследованию.
Многофазная выборка, в отличие от многоступенчатой, предполагает сохранение одной и той же единицы отбора на всех этапах его проведения; при этом отобранные на каждой стадии единицы подвергаются обследованию, каждый раз – по более расширенной программе.
Собственно-случайная (простая случайная) выборка заключается в отборе единиц из генеральной совокупности наугад или наудачу без каких-либо элементов системности.
Однако прежде чем производить собственно-случайный отбор, необходимо убедиться, что все без исключения единицы генеральной совокупности имеют абсолютно равные шансы попадания в выборку, в списках или перечне отсутствуют пропуски, игнорирования отдельных единиц и т.п. Следует также установить четкие границы генеральной совокупности таким образом, чтобы включение или не включение в нее отдельных единиц не вызывало сомнений. Так, например, при обследовании студентов необходимо указать, будут ли приниматься во внимание лица, находящиеся в академическом отпуске, студенты негосударственных вузов, военных училищ и т.п.; при обследовании торговых предприятий важно определиться, включит ли генеральная совокупность торговые павильоны, коммерческие палатки и прочие подобные объекты.
Технически собственно-случайный отбор проводят методом жеребьевки или по таблице случайных чисел.
Расчет ошибок позволяет решить одну из главных проблем организации выборочного наблюдения – оценить репрезентативность (представительность) выборочной совокупности.
Различают среднюю и предельную ошибки выборки. Эти два вида связаны следующим соотношением:
(10.4)
Величина средней ошибки выборки рассчитывается дифференцированно в зависимости от способа отбора и процедуры выборки.
Так, при собственно-случайном повторном отборе средняя ошибка определяется по формуле:
(10.5)
а при расчете средней ошибки собственно-случайной бесповторной выборки:
(10.6)
Расчет средней и предельной ошибок выборки позволяет определить возможные пределы, в которых будут находиться характеристики генеральной совокупности.
Например, для выборочной средней такие пределы устанавливаются на основе следующих соотношений:
(10.7)
где и
‑ генеральная и выборочная средняя соответственно;
‑ предельная ошибка выборочной средней.
Пример.
При проверке веса импортируемого груза на таможне методом случайной повторной выборки было отобрано 200 изделий. В результате был установлен средний вес изделия 30 г. при среднем квадратическом отклонении 4 г. С вероятностью 0,997 определите пределы, в которых находится средний вес изделия в генеральной совокупности.
Решение. Рассчитаем сначала предельную ошибку выборки. Так как при р = 0,997, t = 3, она равна:
Определим пределы генеральной средней:

Вывод: Следовательно, с вероятностью 0,997 можно утверждать, что средний вес изделий в генеральной совокупности находится в пределах от 29,16 г. до 30,84 г.
Пример 2.
В городе проживает 250 тыс. семей. Для определения среднего числа детей в семье была организована 2%-ная случайная бесповторная выборка семей. По ее результатам было получено следующее распределение семей по числу детей:
Таблица 10.2 ‑ Распределение семей по числу детей в городе N
| Число детей в семье | 0 | 1 | 2 | 3 | 4 | 5 |
| Количество
семей |
1000 | 2000 | 1200 | 400 | 200 | 200 |
С вероятностью 0,954 определите пределы, в которых будет находиться среднее число детей в генеральной совокупности.
Решение. В начале на основе имеющегося распределения семей определим выборочные среднюю и дисперсию:
Таблица 10.3 ‑ Вспомогательная таблица для расчета среднего числа детей
|
Число детей в семье, х; |
Количество семей, f | ||||
|
0 1 2 3 4 5 |
1000 2000 1200 400 200 200 |
0
2000 2400 1200 800 1000 |
-1,5
-0,5 0,5 1,5 2,5 3,5 |
2,25
0,25 0,25 2,25 6,25 12,25 |
2250 500 300 900 1250 2450 |
|
Итого |
5000 | 7400 | – | – | 7650 |
Вычислим теперь предельную ошибку выборки (с учетом того, что при р = 0,954 t = 2).
Следовательно, пределы генеральной средней:
Таким образом, с вероятностью 0,954 можно утверждать, что среднее число детей в семьях города практически не отличается от 1,5, т.е. в среднем на каждые две семьи приходится три ребенка.
Наряду с определением ошибок выборки и пределов для генеральной средней эти же показатели могут быть определены для доли признака.
В этом случае особенности расчета связаны с определением дисперсии доли, которая вычисляется так:
(10.8)
где ‑ доля единиц, обладающих данным признаком в выборочной совокупности, определяемая как отношение количества соответствующих единиц к объему выборки.
Тогда, например, при собственно-случайном повторном отборе для определения предельной ошибки выборки используется следующая формула:
(10.9)
Соответственно, при бесповторном отборе:
(10.10)
Пределы доли признака в генеральной совокупности p выглядят следующим образом:
(10.11)
Рассмотрим пример.
С целью определения средней фактической продолжительности рабочего дня в государственном учреждении с численностью служащих 480 человек, в январе 2009 г. было проведена 25%-ная случайная бесповторная выборка. По результатам наблюдения оказалось, что у 10% обследованных потери времени достигали более 45 мин. в день. С вероятностью 0,683 установите пределы, в которых находится генеральная доля служащих с потерями рабочего времени более 45 мин. в день.
Решение. Определим объем выборочной совокупности:
n= 480 х 0,25 = 120 чел.
Выборочная доля w равна по условию 10%.
Учитывая, что при р = 0,683 t=1, вычислим предельную ошибку выборочной доли:
Пределы доли признака в генеральной совокупности:
Таким образом, с вероятностью 0,683 можно утверждать, что доля работников учреждения с потерями рабочего времени более 45 мин. в день находится в пределах от 7,6% до 12,4%.
Мы рассмотрели определение границ генеральной средней и генеральной доли по результатам уже проведенного выборочного наблюдения, при известном объеме выборки или проценте отбора. На этапе же проектирования выборочного наблюдения именно объем выборочной совокупности и требует определения.
Для определения необходимого объема собственно-случайной повторной выборки применяют следующую формулу:
(10.12)
Полученный на основе использования данной формулы результат всегда округляется в большую сторону. Например, если мы получили, что необходимый объем выборки составляет 493,1 единицы, то обследовав 493 единицы мы не достигнем требуемой точности. Поэтому, для достижения желаемого результата обследованием должны быть охвачены 494 единицы.
С другой стороны, рассчитанное значение необходимого объема выборки свободно может быть увеличено в большую сторону на несколько единиц. Если мы располагаем необходимыми ресурсами, если по причинам организационного порядка (компактность расположения единиц, фиксированная нагрузка на каждого регистратора и т.п.) мы вполне можем охватить больший объем, то включение в выборочную совокупность 500 или, например, 550 единиц только уменьшит значения полученных случайной и предельной ошибок.
При определении необходимого объема выборки для определения границ генеральной доли задача оценки вариации решается значительно проще. Если дисперсия изучаемого альтернативного признака неизвестна, то можно использовать ее максимальное возможное значение:
Например, предприятию связи с вероятностью 0,954 необходимо определить удельный вес телефонный разговоров продолжительностью менее 1 минуты с предельной ошибкой 2%. Сколько разговоров нужно обследовать в порядке собственно-случайного повторного отбора для решения этой задачи?
Для получения ответа на поставленный вопрос воспользуемся формулой (10.12) и будем ориентироваться на максимальную возможную дисперсию доли телефонных разговоров такой продолжительности. Расчет приводит к следующему результату:
Таким образом, обследованием должны быть охвачены не менее 2500 разговоров на предмет их продолжительности.
Необходимый объем собственно-случайной бесповторной выборки может быть определен по следующей формуле:
(10.13)
Укажем на одну особенность формулы (10.13). При проведении вычислений объем генеральной совокупности должен быть выражен только в единицах, а не в тысячах или в миллионах единиц.
Например, подставив в данную формулу общую численность населения региона, выраженную в тысячах человек, мы не получим правильное значение необходимой численности выборки, также выраженное в тысячах человек, как это иногда бывает в других расчетах. Результат вычислений будет неверен.
Механическая выборка может быть применена в тех случаях, когда генеральная совокупность каким-либо образом упорядочена, т.е. имеется определенная последовательность в расположении единиц (табельные номера работников, списки избирателей, телефонные номера респондентов, номера домов и квартир и т.п.). Для проведения отбора желательно, чтобы все единицы также имели порядковые номера от 1 до N.
Для проведения механической выборки устанавливается пропорция отбора, которая определяется соотнесением объемов выборочной и генеральной совокупностей.
Так, если из совокупности в 500000 единиц предполагается отобрать 10000 единиц, то пропорция отбора составит
Отбор единиц осуществляется в соответствии с установленной пропорцией через равные интервалы.
Например, при пропорции 1:50 (2%-ная выборка) отбирается каждая 50-я единица, при пропорции 1:20 (5%-ная выборка) – каждая 20-я единица и т.д.
Интервал отбора также можно определить как частное от деления 100% на установленный процент отбора.
Так, например при 2%-ном отборе интервал составит 50 (100%:2%), при 4%-ном отборе ‑ 25 (100%:4%). В тех случаях, когда результат деления получается дробным, сформировать выборку механическим способом при строгом соблюдении процента отбора не представляется возможным.
Например, по этой причине нельзя сформировать 3%-ную или 6%-ную выборки.
Генеральную совокупность при механическом отборе можно ранжировать или упорядочить по величине изучаемого или коррелирующего с ним признака, что позволит повысить репрезентативность выборки. Однако в этом случае возрастает опасность систематической ошибки, связанной с занижением значений изучаемого признака (если из каждого интервала регистрируется первое значение) или его завышением (если из каждого интервала регистрируется последнее значение). Поэтому целесообразно из каждого интервала отбирать центральную или одну из двух центральных единиц.
Например, при 5%-ной выборке интервал отбора составит 20 единиц, тогда отбор целесообразно начинать с 10-й или с 11-й единицы. В первом случае в выборку попадут 10, 30, 50, 70 и с таким же интервалом последующие единицы; во втором случае – единицы с номерами 11,31,51,71 и т.д.
При механической выборке также может появиться опасность систематической ошибки, обусловленной случайным совпадением выбранного интервала и циклических закономерностей в расположении единиц генеральной совокупности. Так, при переписи населения 1989 г. в ходе 25%-го выборочного обследования семей имела место опасность попадания в выборку квартир только одного типа (например, только однокомнатных или только трехкомнатных), так как на лестничных площадках многих типовых домов располагаются именно по 4 квартиры. Чтобы избежать систематической ошибки, в каждом новом подъезде счетчик менял начало отбора.
Для определения средней ошибки механической выборки, а также необходимой ее численности, используются соответствующие формулы, применяемые при собственно-случайном бесповторном отборе(10.6 и 10.13). При этом, определив необходимую численность выборки и сопоставив ее с объемом генеральной совокупности, как правило, приходится производить соответствующее округление для получения целочисленного интервала отбора.
Например, в области зарегистрировано 12000 фермерских хозяйств. Определим, сколько из них нужно отобрать в порядке механического отбора для определения средней площади сельхозугодий с ошибкой ± 2 га. (Р=0,997). По результатам ранее проведенного обследования известно, что среднее квадратическое отклонение площади сельхозугодий составляет 8 га. Произведем расчет, воспользовавшись формулой (10.13).
С учетом полученного необходимого объема выборки (143 фермерских хозяйства) определим интервал отбора: 12000:143=83,9.
Определенный таким способом интервал всегда округляется в меньшую сторону, так как при округлении в большую сторону произведенная выборка не достигнет рассчитанного по формуле необходимого объема.
Следовательно, в нашем примере, из общего списка фермерских хозяйств необходимо отобрать для обследования каждое 83-е хозяйство. При этом процент отбора составит 1,2% (100% : 83).
Типический отбор целесообразно использовать в тех случаях, когда все единицы генеральной совокупности объединены в несколько крупных типических групп.. Такие группы также называют стартами или слоями, в связи с чем типический отбор также называют стратифицированным или расслоенным. При обследованиях населения в качестве типических групп могут быть выбраны области, районы, социальные, возрастные или образовательные группы, при обследовании предприятий – отрасли или подотрасли, формы собственности и т.п.
Рассматривать генеральную совокупность в разрезе нескольких крупных групп единиц имеет смысл только в том случае, если средние значения изучаемых признаков по группам существенно различаются. Например, с большой уверенностью можно предположить, что доходы населения крупного города будут в среднем выше доходов населения, проживающего в сельской местности; численность работников промышленного предприятия в среднем будет выше численности работников торгового или сельскохозяйственного предприятия; средний возраст студентов будет значительно меньше среднего возраста занятого населения и, тем более, пенсионеров. В то же время, нет никакого смысла при выделении типических групп ориентироваться на признак, не связанный или очень слабо связанный с изучаемым.
Отбор единиц в выборочную совокупность из каждой типической группы осуществляется собственно-случайным или механическим способом. Поскольку в выборочную совокупность в той или иной пропорции обязательно попадают представители всех групп, типизация генеральной совокупности позволяет исключить влияние межгрупповой дисперсии на среднюю ошибку выборки. В то же время, в выделенных типических группах обследуются далеко не все единицы, а только включенные в выборку. Следовательно, на величине полученной ошибки будет сказываться различие между единицами внутри этих групп, т.е. внутригрупповая вариация. Поэтому, ошибка типической выборки будет определяться величиной не общей дисперсии, а только ее части – средней из внутригрупповых дисперсий.
При типической выборке, пропорциональной объему типических групп, число единиц, подлежащих отбору из каждой группы, определяется следующим образом:
(10.14)
Где Ni – объем i-ой группы. а ni ‑ объем выборки из i-ой группы.
Пример. Предположим, общая численность населения области составляет 1,5 млн. чел., в том числе городское – 900 тыс. чел. и сельское – 600 тыс. чел. Если в ходе выборочного наблюдения планируется обследовать 100 тыс. жителей, то эта численность должна быть поделена пропорционально объему типических групп следующим образом:
Средняя ошибка типической выборки определяется по формулам:
(10.15)

где – средняя из внутригрупповых дисперсий.
При выборке, пропорциональной дифференциации признака, число наблюдений по каждой группе рассчитывается по формуле:
(10.17)
Где ‑ среднее отклонение признака в i-ой группе.
Cредняя ошибка такого отбора определяется следующим образом:
(10.18)
(10.19)
Отбор, пропорциональный дифференциации признака, дает лучшие результаты, однако на практике его применение затруднено вследствие трудности получения сведений о вариации до проведения выборочного наблюдения.
Таблица 10.4 ‑ Результаты обследования рабочих предприятия
| Цех | Всего рабочих, человек | Обследовано, человек | Число дней временной нетрудоспособности за год | |
| средняя | дисперсия | |||
| I
II III |
1000
1400 800 |
100
140 80 |
18
12 15 |
49
25 16 |
Рассмотрим оба варианта типической выборки на условном примере. Предположим, 10% бесповторный типический отбор рабочих предприятия, пропорциональный размерам цехов, проведенный с целью оценки потерь из-за временной нетрудоспособности, привел к следующим результатам (табл. 10.4)
Рассчитаем среднюю из внутригрупповых дисперсий:
Определим среднюю и предельную ошибки выборки (с вероятностью 0,954):
Рассчитаем выборочную среднюю:
С вероятностью 0,954 можно сделать вывод, что среднее число дней временной нетрудоспособности одного рабочего в целом по предприятию находится в пределах:
Воспользуемся полученными внутригрупповыми дисперсиями для проведения отбора пропорционального дифференциации признака. Определим необходимый объем выборки по каждому цеху:
С учетом полученных значений рассчитаем среднюю ошибку выборки:
В данном случае средняя, а следовательно, и предельная ошибки будут несколько меньше, что отразится и на границах генеральной средней.
Серийный отбор. Данный способ отбора удобен в тех случаях, когда единицы совокупности объединены в небольшие группы или серии. В качестве таких серий могут рассматриваться упаковки с определенным количеством готовой продукции, партии товара, студенческие группы, бригады и другие объединения. Сущность серийной выборки заключается в собственно-случайном или механическом отборе серий, внутри которых производится сплошное обследование единиц.
Поскольку внутри групп (серий) обследуются все без исключения единицы, средняя ошибка серийной выборки (при отборе равновеликих серий) зависит от величины только межгрупповой (межсерийной) дисперсии и определяется по следующим формулам:
(10.20)
(10.21)
Где r ‑ число отобранных серий; R ‑ общее число серий.
Межгрупповую дисперсию вычисляют следующим образом:

где ‑ средняя i-й серии;
‑ общая средняя по всей выборочной совокупности.
Пример.
В области, состоящей из 20 районов, проводилось выборочное обследование урожайности на основе отбора серий (районов). Выборочные средние по районам составили соответственно 14,5 ц/га; 16 ц/га; 15,5 ц/га; 15 ц/га и 14 ц/га. С вероятностью 0,954 определите пределы урожайности во всей области.
Решение. Рассчитаем общую среднюю:
Межгрупповая (межсерийная) дисперсия равна:
Определим теперь предельную ошибку серийной бесповторной выборки (t = 2 при р = 0,954):
Вывод: Следовательно, урожайность будет с вероятностью 0,954 находиться в пределах:
Определение необходимого объема выборки
При проектировании выборочного наблюдения возникает вопрос о необходимой численности выборки. Эта численность может быть определена на базе допустимой ошибки при выборочном наблюдении, исходя из вероятности, на основе которой можно гарантировать величину устанавливаемой ошибки, и, наконец, на базе способа отбора.
Формулы необходимого объема выборки для различных способов формирования выборочной совокупности могут быть выведены из соответствующих соотношений, используемых при расчете предельных ошибок выборки. Приведем наиболее часто применяемые на практике выражения необходимого объема выборки:
– собственно-случайная и механическая выборка:
(10.23)
(10.24)
– типическая выборка:
(10.25)
(10.26)
– серийная выборка:
(10.27)
(10.28)
При этом в зависимости от целей исследования дисперсии и ошибки выборки могут быть рассчитаны для средней величины или доли признака.
Рассмотрим примеры определения необходимого объема выборки при различных способах формирования выборочной совокупности.
Пример.
В 100 туристических агентствах города предполагается провести обследование среднемесячного количества реализованных путевок методом механического отбора. Какова должна быть численность выборки, чтобы с вероятностью 0,683 ошибка не превышала 3 путевок, если по данным пробного обследования дисперсия составляет 225.
Решение. Рассчитаем необходимый объем выборки:
Пример.
С целью определения доли сотрудников коммерческих банков области в возрасте старше 40 лет предполагается организовать типическую выборку пропорциональную численности сотрудников мужского и женского пола с механическим отбором внутри групп. Общее число сотрудников банков составляет 12 тыс. чел., в том числе 7 тыс. мужчин и 5 тыс. женщин.
На основании предыдущих обследований известно, что средняя из внутригрупповых дисперсий составляет 1600. Определите необходимый объем выборки при вероятности 0,997 и ошибке 5%.
Решение. Рассчитаем общую численность типической выборки:
Вычислим теперь объем отдельных типических групп:
Вывод: Таким образом, необходимый объем выборочной совокупности сотрудников банков составляет 550 чел., в т.ч. 319 мужчин и 231 женщина.
Пример.
В акционерном обществе 200 бригад рабочих. Планируется проведение выборочного обследования с целью определения удельного веса рабочих, имеющих профессиональные заболевания. Известно, что межсерийная дисперсия доли равна 225. С вероятностью 0,954 рассчитайте необходимое количество бригад для обследования рабочих, если ошибка выборки не должна превышать 5%.
Решение. Необходимое количество бригад рассчитаем на основе формулы объема серийной бесповторной выборки:
Содержание курса лекций “Статистика”
Контрольные задания
Самостоятельно проведите выборочное наблюдение и произведите соответствующие расчеты.
Общее понятие о выборочном методе. Множество всех единиц совокупности, обладающих определенным признаком и подлежащих изучению, носит в статистике название генеральной совокупности.
На практике по тем или иным причинам не всегда возможно или же нецелесообразно рассматривать всю генеральную совокупность. Тогда ограничиваются изучением лишь некоторой части ее, конечной целью которого является распространение полученных результатов на всю генеральную совокупность, т. е. применяют выборочный метод.
Для этого из генеральной совокупности особым образом отбирается часть элементов, так называемая выборка, и результаты обработки выборочных данных (например, средние арифметические значения) обобщаются на всю совокупность.
Теоретической основой выборочного метода является закон больших чисел. В силу этого закона при ограниченном рассеивании признака в генеральной совокупности и достаточно большой выборке с вероятностью, близкой к полной достоверности, выборочная средняя может быть сколь угодно близка к генеральной средней. Закон этот, включающий в себя группу теорем, доказан строго математически. Таким образом, средняя арифметическая, рассчитанная по выборке, может с достаточным основанием рассматриваться как показатель, характеризующий генеральную совокупность в целом.
Разумеется, не всякая выборка может быть основой для характеристики всей совокупности, к которой она принадлежит. Таким свойством обладают лишь репрезентативные (представительные) выборки, т. е. выборки, которые правильно отражают свойства генеральной совокупности. Существуют способы, позволяющие гарантировать достаточную репрезентативность выборки. Как доказано в ряде теорем математической статистики, таким способом при условии достаточно большой выборки является метод случайного отбора элементов генеральной совокупности, такого отбора, когда каждый элемент генеральной совокупности имеет равный с другими элементами шанс попасть в выборку. Выборки, полученные таким способом, называются случайными выборками. Случайность выборки является, таким образом, существенным условием применения выборочного метода
Области применения выборочного метода в исторических исследованиях. Сфера приложения этого метода в изучении истории обширна. Во-первых, историки могут применять выборочный метод при проведении всякого рода обследований с целью изучения различных явлений и процессов современности. Правда, сейчас такими исследованиями больше занимаются социологи, чем историки, хотя именно историки могут проводить конкретно-социологические обследования, опираясь на исторические данные, и добиваться наибольшего эффекта таких исследований.
Во-вторых, историки нередко имеют дело с сохранившимися данными ранее проведенных собственно выборочных обследований. Такие обследования стали все более широко применяться с конца XIX в. Так, при проведении ряда сплошных обследований и переписей выборочно собирались и собираются сведения по более широкой программе. Многие данные собирались только выборочно. Наиболее интересными среди них для историков являются описания разного рода хозяйственных комплексов (крестьянских хозяйств, промышленных предприятий, колхозов, совхозов и т. д.), а также бюджетные и другого рода обследования различных слоев населения.
В-третьих, в распоряжении историков имеется значительное число разнообразных первичных сплошных массовых данных, полная обработка которых весьма затруднительна даже при применении современной вычислительной техники. При изучении их может быть применен выборочный метод. Такие материалы имеются по всем периодам истории, но особенно много их по истории XIX—XX вв.
Наконец, историкам очень часто приходится иметь дело с частичными данными, так называемыми естественными выборками. При обработке этих данных также может быть применен выборочный метод. Характер естественных выборок бывает различным. Прежде всего они могут представлять собой сохранившийся остаток некогда существовавшей более или менее полной совокупности данных. Так, многие актовые материалы, документы текущего делопроизводства и отчетности представляют остатки в прошлом обширных и систематических массивов данных. Далее, при систематическом сборе тех или иных сведений отдельные показатели могли учитываться лишь частично (именно частично, а не выборочно). Так, при составлении «Экономических примечаний» к Генеральному межеванию второй половины XVIII в., которое охватило большую часть территории страны, ряд показателей (количество населения, площадь земельных угодий и др.) учитывался повсеместно, а некоторые важные данные (о величине барских запашек, размерах оброка) были собраны в силу целого ряда причин лишь частично. Многие сведения вообще собирались только частично. Это прежде всего относится к тем из них, которые не являлись нормативными и сбором которых занимались различные местные органы, научные и общественные организации и отдельные лица.
Итак, области выборочного метода в исторических исследованиях весьма обширны, а задачи, которые следует при этом решать, различны.
Так, при организации выборочного обследования и формировании выборки из имеющихся сплошных данных исследователь располагает определенной свободой маневра для обеспечения репрезентативности выборок. При этом он может опираться на хорошо разработанную в математической статистике теорию, методику и технику получения таких выборок.
При оперировании же данными ранее проведенных выборочных обследований следует проверить, в какой мере они были выполнены в соответствии с требованиями, предъявляемыми к выборочному методу. Для этого надо знать, как было проведено это обследование. Чаще всего это вполне можно сделать.
И совсем иное дело — естественные выборки данных, с которыми очень часто имеет дело историк. Прежде всего необходимо доказать их репрезентативность. Без этого экстраполяция показателей выборок на всю изучаемую совокупность будет необоснованной. Поскольку пока еще нет достаточно надежных методов математической проверки репрезентативности естественных выборок, то решающую роль здесь играет выяснение истории их возникновения и содержательный анализ имеющихся данных.
Виды выборочного изучения. В зависимости от того, как осуществляется отбор элементов совокупности в выборку, различают несколько видов выборочного обследования. Отбор может быть случайным, механическим, типическим и серийным.
Случайным является такой отбор, при котором все элементы генеральной совокупности имеют равную возможность быть отобранными. Другими словами, для каждого элемента генеральной совокупности обеспечена равная вероятность попасть в выборку.
Требование случайности отбора достигается на практике с помощью жребия или таблицы случайных чисел.
При отборе способом жеребьевки все элементы генеральной совокупности предварительно нумеруются и номера их наносятся на карточки. После тщательной перетасовки из пачки любым способом (подряд или в любом другом порядке) выбирается нужное число карточек, соответствующее объему выборки. При этом можно либо откладывать отобранные карточки в сторону (тем самым осуществляется так называемый бесповторный отбор), либо, вытащив карточку, записать ее номер и возвратить в пачку, тем самым давая ей возможность появиться в выборке еще раз (повторный отбор). При повторном отборе всякий раз после возвращения карточки пачка должна быть тщательно перетасована.
Способ жеребьевки применяется в тех случаях, когда число элементов всей изучаемой совокупности невелико. При большом объеме генеральной совокупности осуществление случайного отбора методом жеребьевки становится сложным. Более надежным и менее трудоемким в случае большого объема обрабатываемых данных является метод использования таблицы случайных чисел.
Таблиц случайных чисел существует несколько, одна из них приведена в приложении (табл. 9). Способ отбора с помощью таблицы случайных чисел рассмотрим на примере.
Пример 1. Пусть совокупность состоит из 900 элементов, а намеченный объем выборки равен 20 единицам.
Из таблицы случайных чисел (см. табл. 9 приложения) отбираем числа, не превосходящие 900, до тех пор, пока не наберем нужных 20 чисел. Получаем:
146 867 505 139 653 480 426 765 478 807 47 220 522 221 835 368 275 424 703
Выписанные числа будем считать порядковыми номерами тех элементов генеральной совокупности, которые попали в выборку.
Для очень больших совокупностей отбор с помощью таблицы случайных чисел становится трудно осуществимым, так как сложно перенумеровать всю совокупность. Здесь лучше применить механический отбор.
Механический отбор производится следующим образом. Если формируется 10%-ная выборка, т. е. из каждых десяти элементов должен быть отобран один, то вся совокупность условно разбивается на равные части по 10 элементов. Затем из первой десятки выбирается случайным образом элемент. Например, жеребьевка указала девятый номер. Отбор остальных элементов выборки полностью определяется указанной пропорцией отбора N номером первого отобранного элемента. В рассматриваемом случае выборка будет состоять из элементов 9, 19, 29 и т. д.
Механическим отбором следует пользоваться осторожно, так как существует реальная опасность возникновения так называемых систематических ошибок (см. § 2). Поэтому прежде чем делать механическую выборку, необходимо проанализировать изучаемую совокупность. Если ее элементы расположены случайным образом, то выборка, полученная механическим способом, будет случайной. Однако нередко элементы исходной совокупности бывают частично или даже полностью упорядочены. Весьма нежелательным для механического отбора является порядок элементов, имеющий правильную повторяемость, период которой может совпасть с периодом механической выборки.
Нередко элементы совокупности бывают упорядочены по величине изучаемого признака в убывающем или возрастающем порядке и не имеют периодичности. Механический отбор из такой совокупности приобретает характер направленного отбора, так как отдельные части совокупности оказываются представленными в выборке пропорционально их численности во всей совокупности, т. е. отбор направлен на то, чтобы сделать выборку представительной.
Механический отбор, как никакой другой, широко использовался в русской и советской статистике.
Большую ценность представляют обследования земских статистиков, которые наряду со сплошным подворным обследованием крестьянских хозяйств по сокращенной «похозяйственней карточке» изучали по расширенной программе определенную часть хозяйств, отобранных механическим способом.
Механический отбор использовался советскими статистиками для учета посевных площадей, численности скота, размеров урожая и многого другого накануне сплошной коллективизации, когда в сельском хозяйстве насчитывалось 25 млн. мелких крестьянских хозяйств (так называемый 10%-ный весенний опрос крестьянских хозяйств и 5%-ный осенний опрос).
Другим видом направленного отбора является типический отбор. Следует отличать типический отбор от отбора типичных объектов. Отбор типичных объектов применялся в земской статистике, а также при бюджетных обследованиях. При этом отбор «типичных селений» или «типичных хозяйств» производился по некоторым экономическим признакам, например по размерам землевладения на двор, по роду занятий жителей и т. п. Отбор такого рода не может быть основой для применения выборочного метода, так как здесь не выполнено основное его требование — случайность отбора.
При собственно типическом отборе в выборочном методе совокупность разбивается на группы, однородные в качественном отношении, а затем уже внутри каждой группы производится случайный отбор. Типический отбор организовать сложнее, чем собственно случайный, так как необходимы определенные знания о составе и свойствах генеральной совокупности, но зато он дает более точные результаты.
При серийном отборе вся совокупность разбивается на группы (серии). Затем путем случайного или механического отбора выделяют определенную часть этих серий и производят их сплошную обработку. По сути дела, серийный отбор представляет собой случайный или механический отбор, осуществленный для укрупненных элементов исходной совокупности.
В теоретическом плане серийная выборка является самой несовершенной из рассмотренных. Для обработки материала она, как правило, не используется, но представляет определенные удобства при организации обследования, особенно в изучении сельского хозяйства. Например, ежегодные выборочные обследования крестьянских хозяйств в годы, предшествовавшие коллективизации, проводились способом серийного отбора. Историку полезно знать о серийной выборке, поскольку он может встретиться с результатами таких обследований.
Кроме описанных выше классических способов отбора в практике выборочного метода используются и другие способы. Рассмотрим два из них.
Изучаемая совокупность может иметь многоступенчатую структуру, она может состоять из единиц первой ступени, которые, в свою очередь, состоят из единиц второй ступени, и т. д. Например, губернии включают в себя уезды, уезды можно рассматривать как совокупность волостей, волости состоят из сел, а села — из дворов.
К таким совокупностям можно применять многоступенчатый отбор, т. е. последовательно осуществлять отбор на каждой ступени. Так, из совокупности губерний механическим, типическим или случайным способом можно отобрать уезды (первая ступень), затем одним из указанных способов выбрать волости (вторая ступень), далее провести отбор сел (третья ступень) и, наконец, дворов (четвертая ступень).
Примером двухступенчатого механического отбора может служить давно практикуемый отбор бюджетов рабочих. На первой ступени механически выбираются предприятия, на второй — рабочие, бюджет которых обследуется.
Изменчивость признаков исследуемых объектов может быть различной. Например, обеспеченность крестьянских хозяйств собственной рабочей силой колеблется меньше, чем, скажем, размеры их посевов. В связи с этим меньшая по объему выборка по обеспеченности рабочей силой будет столь же представительной, как и большая по числу элементов выборка данных о размерах посевов. В этом случае из выборки, по которой определяются размеры посевов, можно сделать под выборку, достаточно репрезентативную для определения обеспеченности рабочей силой, осуществив тем самым двухфазный отбор. В общем случае можно добавить и следующие фазы, т. е. из полученной подвыборки сделать еще подвыборку и т. д. Этот же способ отбора применяется в тех случаях, когда цели исследования требуют различной точности при исчислении разных показателей.
Потребность в многофазном отборе возникла при выборочной обработке материалов профессиональной переписи 1918 года. Как показали исследования, для выявления доли рабочих Ярославской губернии, уходящих на полевые работы, требовалась выборка одного объема, тогда как для изучения общей связи рабочих с землей можно было ограничиться выборкой меньшего объема. Разные объемы выборок потребовались и при изучении групп рабочих различных отраслей промышленности Ярославской губернии. Так, предварительные расчеты показали, что для достаточно надежных выводов по группе рабочих полиграфической промышленности требовалась, по крайней мере, 5%-ная выборка, а для исследования рабочих текстильной, пищевой, металлообрабатывающей и машиностроительной промышленности достаточной оказалась 1%-ная выборка (См.: Соколов А. К. Методика выборочной обработки первичных материалов профессиональной переписи 1918 г.— История СССР, 1971, № 4.).
Изложенные выше способы формирования выборок не исчерпывают собой всех типов отбора, применяемых на практике (Наиболее полное описание видов отбора дано в кн.: Пейте Ф. Выборочный метод в переписях и обследованиях. М., 1965.).
Стандартные ошибки выборок
Как уже отмечалось, выборочный метод позволяет результаты выборочной обработки материалов переносить на всю генеральную совокупность. При этом, естественно, имеет место некоторая ошибка, и эффективность выборочного метода заключается в том, что он позволяет оценить эту ошибку.
Ошибки, возникающие при использовании выборочных данных для суждения о всей совокупности, показывают, насколько хорошо характеристики выборки представляют соответствующие характеристики генеральной совокупности, и называются поэтому ошибками представительности (репрезентативности). Различают ошибки представительности двоякого рода: систематические и случайные.
Систематические ошибки возникают в том случае, если не выполнены условия случайности отбора.
Систематическая ошибка может возникнуть и в случае, когда формально отбор произведен случайным образом, но исходная совокупность не является полной и представительной для решения поставленной задачи.
В теории выборочного метода не рассматриваются систематические ошибки, но исследователь должен помнить о возможности их появления и принять меры, обеспечивающие их исключение. С помощью выборочного метода определяются величины ошибок второго рода, т. е. величины случайных ошибок.
Случайные ошибки выборок возникают за счет того, что для анализа всей совокупности используется только часть ее.
Хотя выборочный метод и позволяет обоснованно судить о средней арифметической некоторого количественного признака генеральной совокупности по средней арифметической, исчисленной по выборке, это, однако, не означает, что выборочная средняя совпадает с генеральной средней. Она, как правило, в той или иной степени от нее отличается.
Величина ошибки выборки представляет собой разность между генеральной и выборочной средними. Ошибки выборки различны для каждой конкретной выборки и в принципе могут быть обобщенно охарактеризованы с помощью средней из всех таких отдельных ошибок.
В математической статистике получены формулы, которые позволяют приближенно вычислить среднюю ошибку выборки, основываясь на данных только той выборки, которая имеется в распоряжении исследователя. Вычисление средней ошибки выборки зависит от способа отбора элементов из совокупности в выборку.
Средняя ошибка выборки при собственно случайном повторном методе отбора определяется формулой
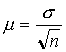
где о — оценка среднего квдаратического отклонения в генеральной совокупности по выборке; n — число элементов в выборке (ее объем) (На практике величину а заменяют на среднее квадратическое отклонение выборки по формуле (4.7), но пользоваться этой формулой можно лишь при достаточно большом объеме выборки(n>30). Методы расчета средней ошибки для малых выборок изложены в § 4 этой главы.).
Как видим, средняя ошибка выборки (ее называют иногда стандартной ошибкой выборки) существенно зависит от среднего квадратического отклонения отдельных значений признака от выборочной средней: чем больше среднее квадратическое отклонение, т. е. чем больше разброс значений признака, тем, при прочих равных условиях, больше средняя ошибка выборки. Объем выборки воздействует на среднюю ошибку выборки в обратном направлении: чем больше численность выборки, тем меньше средняя ошибка выборки, что вполне объяснимо, так как большая выборка лучше представляет всю совокупность.
Средняя ошибка выборки при случайном бесповторном отборе находится по формуле

где N — объем генеральной совокупности.
Формула (5.2) отличается от формулы (5.1) только множителем— 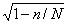
Рассмотрим расчет средней (стандартной) ошибки выборки на конкретных примерах.
Пример 2. Из 2689 уставных грамот Тамбовской губернии необходимо сделать случайную 10%-ную выборку бесповторным способом и определить средние размеры дореформенного и пореформенного наделов на душу и соответствующие им средние ошибки выборки (Занесенные на специальные бланки материалы уставных грамот были любезно предоставлены авторам Б. Г. Литваком. Комплекс этих материалов, включающих данные о размерах дореформенного и пореформенного наделов, о форме эксплуатации, о величине высшего душевого надела и некоторые другие, возник в связи с отменой крепостного права и определял поземельные отношения крестьян и помещиков.).
Формирование выборки осуществим с помощью таблицы случайных чисел (табл. 9 приложения). Воспользуемся следующим способом, позволяющим рациональнее использовать таблицу случайных чисел. Из чисел от 3001 до 6000 будем вычитать 3000, а из чисел от 6001 до 9000 будем вычитать 6000. Из полученных чисел будем, как указывалось, отбирать те, которые не превосходят 2689. Так, первое число таблицы 5489 дает нам 2489, второе — 3522 дает 522 и т. д. В итоге получаем номера единиц совокупности, попавших в выборку.
Для дальнейшей работы полезно полученные числа расположить в возрастающем порядке. Во-первых, это облегчит отбор уставных грамот с соответствующими порядковыми номерами, во-вторых, выявит повторения, от которых нам нужно избавиться, так как выборка делается бесповторным способом. Исключение повторяющихся чисел приводит к тому, что количество отобранных чисел уменьшается. Обращаясь снова к таблице случайных чисел, доводим объем выборки до нужного размера.
Отобрав соответствующие уставные грамоты (их оказалось 264), переходим к расчету средних арифметических и соответствующих им средних ошибок выборки (В этом примере и во всех остальных примерах этой главы, базирующихся на материалах уставных грамот, мы из-за недостатка места не будем давать исходные данные, служащие для расчета выборочных характеристик, и ограничимся приведением результатов проделанных на их основе вычислений.).
Средний дореформенный надел на душу оказался равным 3,16 дес. (суммируем все наделы на душу и делим на число слагаемых — количество грамот):
Средний пореформенный надел на душу равен 2,71 дес. ( 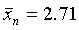
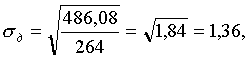
Пользуясь полученными результатами и учитывая, что N =2689, имеем
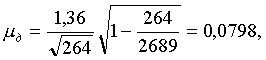
Поставленная задача полностью решена.
Пример 3. Из тех же 2689 уставных грамот Тамбовской губернии необходимо сделать случайную 10%-ную выборку повторным способом, определить средний размер дореформенного надела на душу по выборке и среднюю ошибку выборки
Техника подготовительной работы та же, что и в предыдущем примере, только повторно попавшие в выборку грамоты не исключаются. Результаты расчетов среднего размера дореформенного надела и среднего квадратического отклонения выборки по сформированной указанным способом выборке следующие:
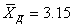
Для расчета средней ошибки выборки воспользуемся формулой (5.1):
Итак, средняя ошибка выборки при повторном способе отбора оказалась большей (0,0846), чем при бесповторном (0,0798). Но разница между ними небольшая, так как отношение n к N невелико.
Средняя ошибка выборки при механическом способе отбора вычисляется по формуле случайной бесповторной выборки (5.2) или в случае, когда множителем 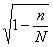
Пример 4. Генеральная совокупность та же, что и в предыдущих примерах Необходимо сделать 10%-ную механическую выборку, вычислить средний надел земли на душу до реформы и определить среднюю ошибку выборки.
Случайным образом отбираем в выборку одну уставную грамоту из первых десяти. По жребию выпало число 10. Следовательно, в выборку попадут грамоты с порядковыми номерами 10, 20, 30 и т. д.
Для этой выборки, включающей 263 элемента, средний размер дореформенного надела на душу (xд) равен 2,97 дес., а среднее квадратическое отклонение выборочных данных ?=1,48. Воспользовавшись формулой (5.2), определяем среднюю ошибку выборки:
Как правило, средняя ошибка выборки при механическом отборе оказывается меньше средней ошибки выборки при собственно случайном отборе.
Средняя ошибка выборки при типическом отборе определяется следующими формулами:
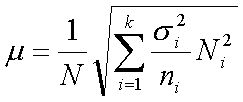
для повторной выборки и
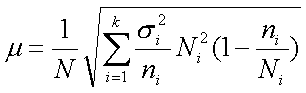
для бесповторной выборки, где N — объем генеральной совокупности; Ni—объем i-й типической группы; ni—объем выборки из i-й типической группы; ?i— среднее квадратическое отклонение i-й типической группы; k — число типических групп.
Средняя арифметическая типической выборки рассчитывается по формуле
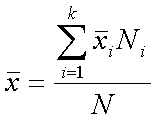
где 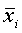
Для того чтобы сделать типическую выборку, нужно прежде всего решить вопрос о том, каковы должны быть объемы выборки по каждой из выделенных типических групп. В зависимости от исследовательских задач и характера изучаемой совокупности, можно воспользоваться одним из следующих приемов.
Самый простой способ определения объема выборки из каждой типической группы, состоит в том, что объем всей намеченной выборки п делят на число типических групп k, т. е.
ni=n/k (5,6)
Второй, наиболее широко применяемый способ заключается в том, что объемы выборок из групп устанавливаются пропорционально объемам соответствующих типических групп, т. е.
В итоге для расчетов получается такая формула:
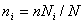
где ni — объем выборки из i-й типической группы; n — общий объем выборки из генеральной совокупности; Ni — объем i-й типической группы; N — объем генеральной совокупности.
Третий способ состоит в том, что число элементов в выборке для каждой типической группы определяется пропорционально средним квадратическим отклонениям соответствующих типических групп (?i), т. е. при определении ni руководствуются следующим соотношением:

Такой прием часто дает ощутимый выигрыш в точности. Сложность его использования состоит в том, что необходимо предварительно знать средние квадратические отклонения признака в типических группах, из которых будет извлекаться выборка. Для этого используются результаты расчетов по аналогичным данным либо делают пробные выборки из каждой группы и их средние квадратические отклонения кладут в основу расчета. Формула для расчета ni будет такой:
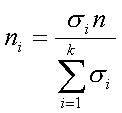
где ?i, — среднее квадратическое отклонение i-й группы; 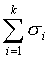
Наконец, четвертый способ образования типической выборки учитывает и размеры типических групп (Ni) и колеблемость признака в этих группах (?i); при формировании выборки исходят из того, что
Формула для расчета ni, четвертым способом такова:
где Ni — объем i-й типической группы; ?i — среднее квадратическое отклонение i-й группы; n—общий объем выборки из генеральной совокупности; k— число типических групп.
Из указанных четырех способов определения численности выборок из типических групп самым простым, но и самым несовершенным является первый. Несложен для расчетов второй способ. Его целесообразно применять в тех случаях, когда типические группы резко отличаются по объему. Если типические группы имеют примерно одинаковый объем, то лучше формировать выборки с учетом рассеивания признака, т. е. третьим способом. Если, наконец, объемы типических групп различны и заметно отличны их средние квадратические отклонения, то наилучшие результаты достигаются при применении четвертого способа.
Рассмотрим теперь на примерах методику вычисления средних арифметических типических выборок и возникающих при этом стандартных ошибок.
Случайный отбор элементов из типических групп может проводиться двумя способами. Если типические группы в исходных данных разделены и каждая имеет собственную нумерацию, то случайный отбор элементов до нужного объема производится из каждой группы отдельно. Если же элементы типических групп расположены в генеральной совокупности вперемешку, как в нашем случае, то отбор осуществляется из всей совокупности, при этом следят, чтобы объемы отдельных групп не были превышены. Случайные числа, соответствующие элементам тех групп, объемы выборок по которым достигнуты, отбрасываются.
Пример 5. Из совокупности уставных грамот Тамбовской губернии сделать 10%-ную типическую выборку с учетом численности групп. Вычислить средний пореформенный надел на душу и среднюю ошибку выборки.
При знакомстве с уставными грамотами обращает на себя внимание тот факт, что надел земли на душу после реформы тяготеет к высшему душевному наделу. Естественно предположить, что типические группы, образованные с учетом размера высшего душевого надела, будут более однородными, чем вся совокупность в целом.
Разобьем всю совокупность на три группы. К первой группе отнесем селения с размером высшего душевого надела, равным 3,00 дес., ко второй — 3,25 дес., к третьей — 3,50 дес. Объемы групп будут равны соответственно 1717, 445 и 525 (Две грамоты мы не учитываем, так как в одной из них указан высший размер душевого надела, равный 2,0 дес., в другой—2,75 дес., в результате чего общий объем совокупности составил N1+N2+N3=2687 грамот.).
Получены следующие результаты расчетов средних характеристик по каждой из трех групп выборки:
для первой группы (высший душевой надел—3,00 дес.)
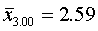
для второй типической группы (высший душевой надел — 3,25 дес.)
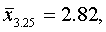
для третьей типической группы (высший душевой надел — 3,50 дес.)
Пользуясь соответствующими формулами табл. 2, имеем окончательно:
Средняя ошибка выборки, полученная таким способом, оказалась несколько меньше средней ошибки выборки, полученной при случайном отборе. В данном случае различие типических групп невелико. При больших различиях групп выигрыш в точности, даваемый типическим отбором, бывает более существенным.
Пример 6. Определить объемы выборок каждой типической группы так, чтобы они оказались пропорциональными средним квадратическим отклонениям соответствующих групп. Совокупность и общий объем выборки те же, что и в предыдущем примере.
Воспользуемся промежуточными результатами примера 5:
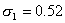
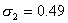
Тогда по формуле (5.8) объемы выборок типических групп будут такими:
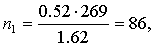
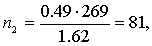
т. е. из первой типической группы (высший размер душевого надела равен 3,00 дес.) следует отобрать 86 грамот, из второй типической группы (высший размер душевого надела — 3,25 дес.) — 81 грамоту, из третьей типической группы (высший размер душевого надела — 3,50 дес.) — 102 грамоты.
Пример 7. Генеральная совокупность и критерий, по которому происходит деление на типические группы, те же, что и в предыдущих двух примерах. Сделать типическую 10%-ную выборку, отбирая количество элементов в типических группах пропорционально численности этих групп и средним квадратическим отклонениям.
Рассчитать средний пореформенный надел на душу и среднюю ошибку выборки.
По формуле (5.9) численность выборок из типических групп будет следующей:
Аналогично рассчитываются n2 и n3: n2=41, n3=60.
Следовательно, из первой типической группы нужно взять 168 грамот, из второй — 41 грамоту, из третьей — 60. Отобрав требуемое количество грамот (техника отбора была изложена выше), переходим к вычислению интересующих нас характеристик.
Результаты расчета средних по группам следующие:
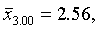
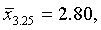
Соответствующие им средние квадратические отклонения равны:
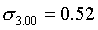
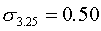
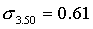
Средний по всей выборке пореформенный надел на душу равен (по формуле (5.5)):
Для расчета средней ошибки выборки воспользуемся соответствующей формулой из сводной табл. 2:
Средняя ошибка выборки получилась меньше, чем при случайном методе отбора, но несколько больше соответствующей характеристики, полученной для типической выборки, образованной пропорционально численности типических групп. Последнее произошло, надо полагать, потому, что типические группы по размеру высшего душевого надела отличаются, в основном, по численности и значительно меньше—по разбросу признака.
Сведем воедино итоги рассмотренных примеров, чтобы еще раз сравнить полученные результаты (см. табл. 1).
В целом приведенные примеры подтверждают установленные в статистике общие положения. Важнейшим для применения выборочного метода в исторических исследованиях является то, что наиболее точные результаты дает типический отбор. Стандартная ошибка средней при этом методе отбора получается меньшей, чем при случайном и механическом отборе (сравним процентные отношения ошибок к средним арифметическим). При этом следует иметь в виду, что размеры наделов крестьян являются признаком, рассеивание которого является небольшим. При большей неоднородности изучаемых совокупностей данных преимущества типического отбора будут еще очевиднее. Что касается собственно случайного и механического отбора, то они в общем дают близкие результаты. Надо лишь всегда проверять, насколько механический отбор является близким к случайному. Принципиальных различий между бесповторным и повторным случайным отбором нет.
Для удобства пользования формулы выборочного метода, применяемые для вычисления выборочных средних арифметических и их стандартных ошибок при разных видах отбора, сведены в табл. 2. В эту таблицу не вошли формулы для расчета средних ошибок выборок при многоступенчатом способе отбора (Эти сведения можно найти в кн.: Йейтс Ф. Выборочный метод в переписях и обследованиях.). Что касается многофазного отбора, то он равносилен взятию выборок различных объемов для разных признаков и ничего нового в вычислительные процедуры не вносит.
Таблица 2. Формулы выборочного метода для средней арифметической при различных видах отбора.
|
Выборочная средняя |
Объем выборки из типических групп |
Средняя ошибка выборки ? |
||
|
при повторном отборе |
при повторном отборе |
|||
|
Собственно случайный отбор и механический отбор (При механическом отборе применяется формула бесповторной выборки, за исключением тех случаев, когда множителем |
|
|
|
|
|
Типический отбор: |
|
|
|
|
|
Эти формулы являются одновременно и общим для всех случаев типического отбора |
||||
|
в) при объемах выборки, пропорциональных объемам типических групп |
|
|
|
|
|
г) при объемах выборки, пропорциональных объемам типических групп и их средним квадратическим отклонениям |
|
|
|
Таблица 3.Формулы выборочного метода для доли признака при различных видах отбора.
|
Выборочная средняя |
Объем выборки из типических групп |
Средняя ошибка выборки ? |
||
|
при повторном отборе |
При повторном отборе |
|||
|
Собственно случайный отбор и механический отбор (При механическом отборе применяется формула бесповторной выборки, за исключением тех случаев, когда множителем |
|
|
|
|
|
Типический отбор: |
|
|
|
|
|
Эти формулы являются одновременно и общим для всех случаев типического отбора |
||||
|
в) при объемах выборки, пропорциональных объемам типических групп |
|
|
|
|
|
г) при объемах выборки, пропорциональных объемам типических групп и их средним квадратическим отклонениям |
|
|
|
|
Средняя ошибка выборки для доли признака. Выборочный метод позволяет оценить не только среднюю арифметическую генеральной совокупности, но и долю некоторого (качественного или количественного) признака во всей совокупности.
Доля признака во всей совокупности (q) вычисляется как отношение числа элементов, обладающих этим признаком (No), к числу элементов всей совокупности (N), т. е. q=Nо/N.
Отметим, что рассмотренная выше теория и методика применения выборочного метода для расчета средней может быть применена и для расчета доли без каких-либо принципиальных изменений.
Сводка всех формул выборочного метода для доли признака дана в табл. 3.
Пример 8. На основе 10%-ной случайной бесповторной выборки из совокупности уставных грамот Тамбовской губернии вычислить доли селений с системой эксплуатации крестьян; а) оброчной, б) барщинной и в) смешанной, а также соответствующие им средние ошибки выборки
Из 264 грамот, составивших 10%-ную случайную бесповторную выборку, грамот, описывающих селения с оброчной, барщинной и смешанной системами эксплуатации, оказалось соответственно 51, 197 и 16 Тогда выборочная доля селений с оброчной системой эксплуатации равна 
Воспользовавшись формулой для собственно случайной бесповторной выборки из табл. 3, рассчитаем средние ошибки выборки для доли:
?б=0,03; ?ом=0,01
Точность и надежность выборочного метода: предельные ошибки. Определение объема выборки
Предельная ошибка выборки и доверительный интервал. Средняя ошибка выборки дает некоторое представление об ошибке репрезентативности, т. е. об ошибке, с которой выборочная средняя представляет действительное значение генеральной средней. Именно она показывает, какова будет ошибка в среднем, если из одной и той же генеральной совокупности сделать много выборок одинакового объема. Однако в каждой конкретной выборке ошибка может существенно отличаться от средней ошибки, т. е. нет гарантии, что ошибка, которая действительно была допущена в конкретном выборочном исследовании,
не превышает средней ошибки.
Поэтому гораздо полезнее было бы знать те границы, в которых «практически наверняка» находится действительная ошибка, допущенная в данной конкретной выборке. Эти границы (пределы) указываются предельной ошибкой выборки (обозначим ее Δ). Предельная ошибка выборки показывает тот предел,
которого практически наверняка не превосходит действительная ошибка. Иначе говоря, предельная ошибка Δ показывает действительно допущенную ошибку с избытком, с превышением (возможно, очень значительным) и тем самым гарантирует, что действительная ошибка не превосходит Δ.
Предельная ошибка Δ вычисляется на основе знания средней ошибки μ по формуле
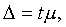
где t — величина, вычисляемая по специальной таблице. Обратим внимание на то, что в определении предельной ошибки постоянно употреблялись слова «практически наверняка». Необходимо пояснить смысл понятия «практическая уверенность».
Установленный предел Δ для ошибки выборки лишь указывает, что если из генеральной совокупности сделать много выборок, то для подавляющего большинства из них ошибка выборки не превысит вычисленного нами предела Δ. При этом, правда, могут быть все-таки и такие выборки, у которых ошибка выборки больше Δ, и не исключено, что конкретная выборка входит в их число. Однако можно точно измерить степень уверенности в том, что ошибка конкретной выборки не превысит Δ. Для этого нужно указать долю выборок, у которых ошибка выборки не превосходит Δ. Обозначим эту долю выборок через Р, где 
Значением Р фактически измеряется надежность результатов выборочного исследования: для значений Р, достаточно близких к единице, практически исключается возможность того, что генеральная средняя будет отличаться от вычисленной выборочной средней больше чем на Δ. Со своей стороны Δ указывает точность, гарантируемую заданным уровнем надежности Р. Таким образом, предельная ошибка выборки позволяет одновременно и взаимосвязано указать точность и надежность результатов выборочного исследования.
В математической статистике доказано, что распределение выборочных средних при достаточно больших n подчиняется нормальному закону (см. § 3, гл. 4) со средним значением, равным генеральной средней 
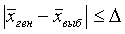
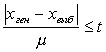
Эта же таблица позволяет решать и обратную задачу: по заданной вероятности Р найти величину предельной ошибки Δ, которая соответствует Р, другими словами, найти точность, соответствующую данному уровню надежности. Какова, например, предельная ошибка, соответствующая надежности 0,9545? По табл. 1 приложения найдем значение t, соответствующее вероятности Ф(t)= 0,9545. Оказывается, t=2. С вероятностью 0,9545 отклонение выборочной средней от генеральной по модулю не превосходит Δ=2μ, т. е. не выше двукратной средней ошибки выборки.
Разумеется, всегда желательно обеспечить большую надежность результатов, поэтому надо стараться выбрать Р возможно ближе к 1. Однако необходимо учитывать, что с возрастанием надежности увеличивается и t, а значит, и предельная ошибка Δ=tμ, т. е. падает точность результатов, что может оказаться по тем или иным соображениям недопустимым. Поэтому на практике приходится довольствоваться некоторым компромиссом между противоречивыми требованиями максимальной надежности и максимальной точности. Если такого компромисса достичь не удается и надежность и точность неудовлетворительны, следует сделать вывод, что объем выборки недостаточен и необходимо произвести новую выборку большего объема или же дополнить старую.
Знание предельной ошибки выборки позволяет указать и пределы для генеральной средней. Действительно, поскольку выборочная средняя 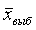
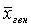
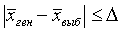
или, иначе,
(5.11)
Таким образом, с помощью вычисления выборочной средней и предельной ошибки выборки можно указать интервал, в котором практически наверняка находится генеральная средняя (так называемый доверительный интервал). При этом всегда указывается надежность Р этого результата (то значение Р, которое использовалось в вычислении Δ).
Пример 9. Вычислить предельные ошибки выборки по результатам примера 2 § 1 и определить пределы для генеральной средней.
Выборочная средняя для дореформенного надела равна 3,16, средняя ошибка выборки—0,0798.
Пусть Р=0,9545. Этому значению Р по табл. 1 приложения соответствует t=2. Пользуясь формулой (5.10), имеем Δ=2*0,0798=0,1596=0,16, т. е. предельная ошибка выборки равна приблизительно 0.16.
Переходим к определению пределов. Чтобы вычислить нижний предел, нужно из выборочной средней вычесть предельную ошибку выборки:
3,16—0,16=3,00.
Верхний предел получаем, прибавив к выборочной средней предельную ошибку:
3,16+0.16=3,32.
Тогда имеем следующие пределы для генеральной средней 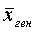
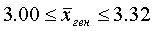
Результаты можно интерпретировать так: с надежностью (вероятностью) 0,95 генеральная средняя будет не меньше 3,00 дес. и не больше 3,32 дес. Или, другими словами, если выборки повторять много раз, то в 95 случаях из 100 получим, что выборочная средняя будет отстоять от генеральной средней не далее, чем на величину вычисленной нами предельной ошибки, равной 0,16 дес.
Возьмем теперь Р= 0,9876=0,99. Тогда t=2,5,.
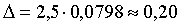
и генеральная средняя заключена в следующих пределах:
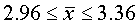
Пределы для генеральной средней расширились, но зато увеличилась степень доверия к результатам: уже примерно в 99 случаях из 100 мы не ошибаемся, указывая эти границы для средней.
Как правило, в исторических исследованиях рассмотренный в примере уровень надежности (Р=0,95; P=0,99) оказывается достаточным.
Порядок вычисления предельной ошибки выборки для доли признака ничем не отличается от вычисления предельной ошибки для средней арифметической.
Определение объема выборки. Вопрос об определении объема выборки является в выборочном методе исходным, ибо всякая выборка имеет заданный объем.
Заметим сразу, что зачастую исследователь лишен возможности решать вопрос об объеме выборки либо в силу ограниченности имеющихся в его распоряжении данных (естественные выборки), либо в силу тех или иных технических причин.
В тех же случаях, когда постановка вопроса об определении объема выборки возможна, его решение производится в следующем порядке.
Прежде всего производится пробная выборка произвольного объема. При этом можно пойти по одному из двух различных путей. Во-первых, можно попытаться сразу угадать нужный объем выборки, основываясь на каких-либо соображениях разумности объема выборки (например, можно попробовать 10%- или 20%-ную выборку). В случае если объем этой выборки окажется недостаточным, можно будет впоследствии дополнить эту выборку до нужного объема.
При втором подходе пробная выборка берется совсем небольшой (как правило, 1% и менее от объема генеральной совокупности). При этом практически следует руководствоваться некоторым компромиссом между требованием достаточной репрезентативности выборки и желанием уменьшить объем предварительных расчетов. На основе этой пробной выборки по приведенной ниже формуле (5.12) определяется необходимый объем окончательной выборки. Далее уже можно делать выборку заданного объема и проводить по ней выборочное исследование.
Анализ пробной выборки начинается с вычисления выборочной средней 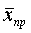
Например, если 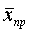
Δ=10*5/100==0,5.
Далее, зададимся уровнем надежности результатов. Выберем, например, Р=0,95.
Заметим, что стремясь к большей точности и надежности результатов, не следует излишествовать в этом направлении, так как может оказаться, что для достижения поставленных требований придется брать выборку объемом во всю совокупность. При этом теряет смысл само применение выборочного метода. Как правило, такие повышенные требования к результатам не оправдываются целями исследования и без ущерба для дела можно остановиться на более умеренных ограничениях. В том же случае, когда высокие требования вытекают из целей исследования и вычисленный объем выборки оказывается порядка объема всей совокупности, следует сделать вывод о том, что в данном случае применение выборочного метода нецелесообразно.
Рассчитав характеристики пробной выборки, переходят к оценке результатов этой выборки. Если используется первый путь исследования (относительно большой пробной выборки), то задав предельную ошибку Δ, следует сравнить ее с предельной ошибкой, вычисленной по пробной выборке Δпр (при одном и том же значении Р). Если окажется, что Δпр<=Δ то пробной выборки вообще достаточно, она может рассматриваться в качестве основной и ее результаты служат результатами всего выборочного исследования. Если же Δпр> Δ, что нередко имеет место при втором пути исследования, то определяют необходимый объем выборки по следующей формуле:
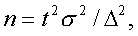
(5.12)
где σ2 — дисперсия признака, вычисленная по пробной выборке; Δ— заданная точность результатов выборочного исследования (заданная предельная ошибка выборки); t — величина, которая находится по табл. 1 приложения исходя из заданной надежности Р результатов выборочного исследования.
Заметим, что если пробная выборка мала (n<30), то для определения t используется табл. 2 приложения. В ней при определении t учитывается также объем пробной выборки (для нахождения табличного значения t берется объем пробной выборки, предварительно уменьшенный на единицу). Кроме того, в том случае и вычисляется так, как указано в § 4 этой главы.
Отметим, что приведенная формула дает общий объем выборки приближенно. Поэтому желательно если есть возможность, еще несколько увеличить объем выборки по сравнению с вычисленным.
Сделав окончательную выборку найденного объема, следует обязательно проверить, совпадает ли ее предельная ошибка с заданной, т. е. удовлетворяются ли заданные требования к точности и надежности результатов. В том редком случае, когда окажется, что действительная предельная ошибка существенно больше заданной (это может произойти из-за нерепрезентативности пробной выборки), придется еще раз повторить процедуру определения объема выборки уже на основе полученных более полных и точных данных.
Приведем также формулу для нахождения необходимого объема выборки при определении доли признака:
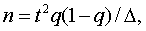
где t и Δ имеют тот же смысл, что и в предыдущей формуле,a q — доля признака в пробной выборке.
Рассмотрим пример, поясняющий основные моменты решения задачи об определении объема выборки.
Пример 10. Воспользовавшись данными по предприятиям европейской России за 1879 г. (См.: Указатель фабрик и заводов европейской России/Сост. П. А. Орлов. Спб., 1881, вып. 1. В «Указателе» содержатся сведения по фабрикам и заводам со стоимостью производимой продукции свыше 2 тыс. руб. (всего около 12000 предприятий).), определить объемы выборок, необходимые для расчетов средней стоимости произведенной продукции в расчете на одного рабочего на предприятиях: а) с паровыми двигателями, б) без паровых двигателей.
Сделаем сначала пробную 1%-ную выборку (случайным бесповторным способом) (Из-за недостатка места выборочные данные не приведены). Отметим, что среди предприятий, попавших в выборку (128 предприятий), 87 составляют предприятия без паровых двигателей и 41 —с паровыми двигателями.
Пользуясь выборочными данными, вычисляем по каждому типу предприятий среднюю стоимость произведенной на одного рабочего продукции 
Для предприятий без паровых двигателей получаем соответственно 
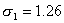
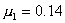
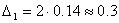
Для предприятий с паровыми двигателями получим 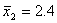
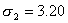
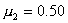
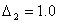
для предприятий без паровых двигателей
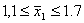
для предприятий с паровыми двигателями
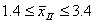
При сопоставлении полученных результатов напрашиваются следующие выводы: средняя стоимость продукции на одного рабочего на предприятиях без паровых двигателей и на предприятиях с паровыми двигателями различна, причем на предприятиях с паровыми двигателями она заметно выше. Однако, строго говоря, такой вывод пока еще неправомерен и может рассматриваться лишь как гипотеза. Дело в том, что доверительные интервалы для генеральных средних по предприятиям без паровых двигателей (1,1; 1,7) и по предприятиям с паровыми двигателями (1,4; 3,4) пересекаются, так что средние генеральные вполне могут совпадать или даже находиться в соотношении, противоположном высказанной гипотезе.
Нетрудно заметить, что указанная неопределенность результатов получается главным образом в силу того, что предельная ошибка выборки по предприятиям с паровыми двигателями Δ2 слишком велика. В самом деле, различие между выборочными средними по двум типам предприятий составляет
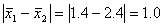
Поэтому, чтобы попытаться подтвердить и обосновать высказанную выше гипотезу, достаточно, чтобы предельные ошибки выборок для обеих групп предприятий (Δ1, Δ2) не превышали половины этой разности, т. е. 0,5, тогда доверительные интервалы не будут пересекаться.
Отметим, что предельная ошибка выборки по предприятиям без паровых двигателей Δ=0.3 вполне удовлетворительна. Чтобы обеспечить предельную ошибку выборки, равную 0,5, для другой группы предприятий, рассчитаем необходимый объем выборки из совокупности предприятий с паровыми двигателями. Выбирая t по табл. 1 приложения, соответствующие значению Р= 0,9545, и пользуясь формулой (5.12), получим
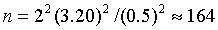
Дополнив теперь выборку из группы предприятий с паровыми двигателями до рассчитанного объема, получим новые значения средней, среднего квадратического отклонения, средней и предельной ошибок выборки:
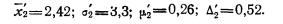
Сравним интервалы для генеральных средних. Для предприятий без паровых двигателей используем результат пробной выборки (которая оказалась для этой группы предприятий и окончательной):
А для предприятий с паровыми двигателями имеем после увеличения объема выборки
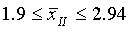
Как видим, теперь доверительные интервалы действительно не пересекаются и высказанная выше гипотеза о том, что средняя стоимость продукции на одного рабочего существенно больше для предприятий с паровыми двигателями, получает убедительное и надежное подтверждение. Другими словами, данные, использованные в примере 10, свидетельствуют о том, что внедрение машин повышало производительность труда.
Интересно отметить, что для достижения нужной точности и надежности результатов из совокупности предприятий с паровыми двигателями нам пришлось сделать примерно в два раза большую выборку, чем из группы предприятий без паровых двигателей. Это объясняется тем, что для предприятий с паровыми двигателями существенно больше разброс изучаемого признака, что вполне естественно для прогрессивной технологии, применяемой на этих предприятиях.
В заключение отметим еще один поучительный факт, с которым мы столкнулись в рассмотренном примере. По предприятиям с паровыми двигателями первоначальный объем выборки составлял 41 единицу, при этом обеспечивалась точность, определяемая предельной ошибкой выборки, равная единице (Δ2=1). Такая точность, как оказалось, была недостаточной, потребовалась в два раза большая точность—Δ2`=0.5. Это привело к тому, что объем новой выборки составил 164 единицы, что в четыре раза больше первоначального.
Следовательно, необходимый объем выборки растет пропорционально квадрату требуемой точности, что следует прямо из формулы (5.12). А так как квадраты чисел при возрастании самих чисел возрастают очень быстро, то повышенные требования к точности могут привести к неумеренному росту объема выборки. Поэтому важно, чтобы требования к точности выборочного исследования всегда диктовались целями и содержанием исследования. В рассмотренном примере такой целью было обоснование содержательной научной гипотезы.
§ 4. Малые выборки
Рассмотренные выше приемы расчета ошибок выборки основаны на доказанном в математике факте нормальности распределения выборочных средних. Однако этот факт имеет место только при достаточно большом объеме выборки n. Если пользоваться изложенными приемами при п меньшем 20, могут возникнуть грубые ошибки.
Выборки, объем которых меньше 20—30 единиц совокупности, будем называть малыми (Четкой границы между большой и малой выборками в общем случае указать невозможно. Выборка, сделанная из совокупности с небольшим разбросом признака, может считаться большой, тогда как выборка такого же объема, произведенная из более разнородной совокупности, окажется малой. Вопрос о том, к какой категории отнести выборку, решается в каждом конкретном случае). Для расчета ошибок таких выборок используется несколько иной математический аппарат.
Средняя ошибка малой выборки вычисляется по формуле
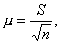
где S — оценка среднего квадратического отклонения в генеральной совокупности по малой выборке. Она равна:
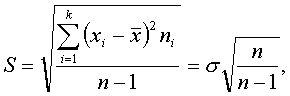
где σ вычисляется по формуле (4.7); n — объем выборки;k — число вариант, т. е. S несколько отличается от оценки среднего квадратического отклонения в генеральной совокупности по большой выборке, см. (5.1).
Пример 11. В табл. 4 приведены данные о размерах оброка в конце XVIII в. (в руб. серебром на муж. душу). Первая выборка состоит из 16 уездов нечерноземной полосы, вторая выборка—из 16 уездов черноземной полосы. Перед нами две «естественные выборки», которые можно рассматривать как случайные, т. е. репрезентативные Требуется рассчитать выборочные средние и средние ошибки выборок.
Вычисляем последовательно средние арифметические, средние квадратические отклонения малых выборок, и, наконец, стандартные ошибки выборок Получаем:
для нечерноземной полосы
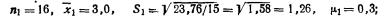
для черноземной полосы
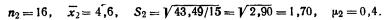
Заметим, что в пределах интересующей нас точности вычислений поправка на малую выборку не изменила величины стандартной ошибки. Заметное различие появляется при вычислении предельной ошибки выборки.
Предельная ошибка малой выборки вычисляется по формуле
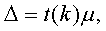
где t рассчитывают исходя из так называемого закона распределения Стьюдента с k степенями свободы (в отличие от больших выборок, где t вычисляется на основе нормального закона распределения).
Связь между t и вероятностью (уровнем надежности) Р в распределении Стьюдента сложнее, чем в нормальном распределении и опосредствуется через объем выборки. При возрастании объема выборки распределение Стьюдента приближается к нормальному, практически с ним совпадая при достаточно больших n.
При вычислении предельной ошибки малой выборки значение t(k) определяется по таблице распределения Стьюдента с k степенями свободы (табл. 2 приложения), с учетом заданного уровня надежности Р и объема выборки (для подстановки в таблицу фактический объем выборки надо предварительно уменьшить на единицу: k=n—1).
Пример 12. Используя данные предыдущего примера, найти предельные ошибки выборки для средних размеров оброка с уровнем надежности P=0,9 и Р=0,95 и определить границы для генеральной средней.
Обращаясь к табл. 2 приложения и учитывая, что при объеме выборки, равном 16, k, используемое для нахождения табличного значения t, равно 16—1=15, а заданный уровень надежности—0,9, находим t (15) =1,75.
Тогда предельная ошибка выборки для среднего размера оброка нечерноземной полосы по формуле (5.16) будет равна
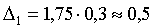
Следовательно, границы генеральной средней таковы:
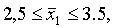
т. е. с вероятностью 0,9 средний размер оброка в нечерноземной полосе не выйдет за указанные границы.
Предельная ошибка второй выборки (для размеров оброка в черноземной полосе) и границы генеральной средней находятся аналогично. Имеем:
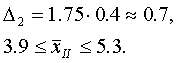
Чтобы получить более достоверные результаты, возьмем большую вероятность (уровень надежности). Пусть Р=0,95, тогда из табл. 2 приложения найдем t (15)=2,13, и для нечерноземной полосы
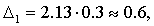
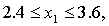
для черноземной полосы
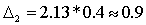
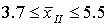
Итак, в конце XVIII в. средний размер оброка в черноземной полосе выше, чем средний размер оброка в нечерноземной полосе. Важно, что границы, в которых заключены средние, не пересекаются. Это свидетельствует о том, что различие размеров оброка в двух районах имело не случайный, а закономерный характер.
Для более строгих выводов о существенности различия между двумя выборочными средними есть специальные методы, изложенные в гл. 9 (§2 — критерии для средних, § 3 — критерии для дисперсий). Так, если имеются две выборочные средние 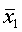
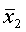
Отметим, что в тех же разделах гл. 9 рассмотрены аналогичные критерии для больших выборок, которые вместо распределения Стьюдента используют нормальное распределение, поскольку при возрастании объема выборки распределение Стьюдента стремится к нормальному.
В заключение скажем несколько слов о больших и малых выборках. Различать большие и малые выборки необходимо, но точной границы между ними установить нельзя. Важно иметь в виду, что к большим выборкам можно применять аппарат теории малых выборок, тогда как обратное приводит к значительным ошибкам. В сомнительных случаях для получения надежных результатов рекомендуется пользоваться аппаратом малых выборок.
В больших выборках средние теснее группируются около генеральной средней, что позволяет получать более точные и надежные результаты, тогда как в малых выборках приходится довольствоваться более широкими границами для средних или меньшей достоверностью результатов. Тем не менее теория малых выборок нашла в практике широкое распространение и применяется даже в тех случаях, когда во власти исследователя сделать выборку большой (См., например: Дружинин Н. К. Выборочный метод и его применение в социально-экономических исследованиях М., 1970, с. 77.).
Историку обычно не приходится выбирать между формированием большой или же малой выборки, поскольку он часто имеет дело с естественными малыми «выборками, число которых он не может изменить, т. е. он стоит перед альтернативой: либо воспользоваться данными малой выборки для анализа исследуемых явлений, либо отказаться от такого анализа. Обработка этих выборок методами математической статистики позволяет в ряде случаев (когда само использование выборочного метода возможно) обоснованно решить вопрос о правомерности или неправомерности тех или иных выводов и заключений на основе имеющихся материалов. И в том и в другом случае исследование приобретает более объективный и глубокий характер, нежели при традиционных методах.
Для того чтобы применить выборочный метод к естественным выборкам, необходимо доказать тем или иным способом случайность образования имеющейся выборки. В проверке случайности выборки ведущая роль принадлежит традиционным методам содержательного источниковедческого анализа. Отсутствие преднамеренности в порядке сбора и хранения тех сведений, след от которых остался в виде естественной выборки, свидетельствует о случайности последней. Математические методы позволяют дополнить этот анализ (см. гл. 9).
И наконец, последнее замечание. В этой главе мы ограничились оценкой средней арифметической генеральной совокупности с помощью характеристик, вычисленных по выборке. Но выборочный метод позволяет решать и более сложные вопросы анализа совокупностей. В частности, по выборке можно судить о наличии или об отсутствии связи между признаками, о форме связи. К процедурам выборочного метода мы будем обращаться при необходимости в соответствующих главах.
11.2. Оценка результатов выборочного наблюдения
11.2.1. Средняя и предельная ошибки выборки. Построение доверительных границ для средней и доли
Средняя ошибка выборки показывает, насколько отклоняется в среднем параметр выборочной совокупности от соответствующего параметра генеральной. Если рассчитать среднюю из ошибок всех возможных выборок определенного вида заданного объема (n), извлеченных из одной и той же генеральной совокупности, то получим их обобщающую характеристику — среднюю ошибку выборки (
В теории выборочного наблюдения выведены формулы для определения 
Например, если применяется повторная собственно случайная выборка, то 


При бесповторном собственно случайном отборе в формулы вносится поправка (1 — n/N):


Вероятность получения именно такой величины ошибки всегда равна 0,683. На практике же предпочитают получать данные с большей вероятностью, но это приводит к возрастанию величины ошибки выборки.
Предельная ошибка выборки (

Если ошибку выборки увеличить в два раза (t = 2), то получим гораздо большую вероятность того, что она не превысит определенного предела (в нашем случае — двойной средней ошибки) — 0,954. Если взять t = 3, то доверительная вероятность составит 0,997 — практически достоверность.
Уровень предельной ошибки выборки зависит от следующих факторов:
- степени вариации единиц генеральной совокупности;
- объема выборки;
- выбранных схем отбора (бесповторный отбор дает меньшую величину ошибки);
- уровня доверительной вероятности.
Если объем выборки больше 30, то значение t определяется по таблице нормального распределения, если меньше — по таблице распределения Стьюдента.
Приведем некоторые значения коэффициента доверия из таблицы нормального распределения.
| Значение доверительной вероятности P | 0,683 | 0,954 | 0,997 |
|---|---|---|---|
| Значение коэффициента доверия t | 1,0 | 2,0 | 3,0 |
Доверительный интервал для среднего значения признака и для доли в генеральной совокупности устанавливается следующим образом:
Итак, определение границ генеральной средней и доли состоит из следующих этапов:
Ошибки выборки при различных видах отбора
- Собственно случайная и механическая выборка. Средняя ошибка собственно случайной и механической выборки находятся по формулам, представленным в табл. 11.3.
 |
|
где |
Пример 11.2. Для изучения уровня фондоотдачи было проведено выборочное обследование 90 предприятий из 225 методом случайной повторной выборки, в результате которого получены данные, представленные в таблице.
| Уровень фондоотдачи, руб. | До 1,4 | 1,4-1,6 | 1,6-1,8 | 1,8-2,0 | 2,0-2,2 | 2,2 и выше | Итого |
|---|---|---|---|---|---|---|---|
| Количество предприятий | 13 | 15 | 17 | 15 | 16 | 14 | 90 |
В рассматриваемом примере имеем 40%-ную выборку (90 : 225 = 0,4, или 40%). Определим ее предельную ошибку и границы для среднего значения признака в генеральной совокупности по шагам алгоритма:
- По результатам выборочного обследования рассчитаем среднее значение и дисперсию в выборочной совокупности:
| Результаты наблюдения | Расчетные значения | |||
|---|---|---|---|---|
| уровень фондоотдачи, руб., xi | количество предприятий, fi | середина интервала, xi\xb4 | xi\xb4fi | xi\xb42fi |
| До 1,4 | 13 | 1,3 | 16,9 | 21,97 |
| 1,4-1,6 | 15 | 1,5 | 22,5 | 33,75 |
| 1,6-1,8 | 17 | 1,7 | 28,9 | 49,13 |
| 1,8-2,0 | 15 | 1,9 | 28,5 | 54,15 |
| 2,0-2,2 | 16 | 2,1 | 33,6 | 70,56 |
| 2,2 и выше | 14 | 2,3 | 32,2 | 74,06 |
| Итого | 90 | — | 162,6 | 303,62 |
Выборочная средняя
Выборочная дисперсия изучаемого признака
- Определяем среднюю ошибку повторной случайной выборки
- Зададим вероятность, на уровне которой будем говорить о величине предельной ошибки выборки. Чаще всего она принимается равной 0,999; 0,997; 0,954.
Для наших данных определим предельную ошибку выборки, например, с вероятностью 0,954. По таблице значений вероятности функции нормального распределения (см. выдержку из нее, приведенную в Приложении 1) находим величину коэффициента доверия t, соответствующего вероятности 0,954. При вероятности 0,954 коэффициент t равен 2.
- Предельная ошибка выборки с вероятностью 0,954 равна
- Найдем доверительные границы для среднего значения уровня фондоотдачи в генеральной совокупности
Таким образом, в 954 случаях из 1000 среднее значение фондоотдачи будет не выше 1,88 руб. и не ниже 1,74 руб.
Выше была использована повторная схема случайного отбора. Посмотрим, изменятся ли результаты обследования, если предположить, что отбор осуществлялся по схеме бесповторного отбора. В этом случае расчет средней ошибки проводится по формуле
Тогда при вероятности равной 0,954 величина предельной ошибки выборки составит:
Доверительные границы для среднего значения признака при бесповторном случайном отборе будут иметь следующие значения:
Сравнив результаты двух схем отбора, можно сделать вывод о том, что применение бесповторной случайной выборки дает более точные результаты по сравнению с применением повторного отбора при одной и той же доверительной вероятности. При этом, чем больше объем выборки, тем существеннее сужаются границы значений средней при переходе от одной схемы отбора к другой.
По данным примера определим, в каких границах находится доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., в генеральной совокупности:
- рассчитаем выборочную долю.
Количество предприятий в выборке с уровнем фондоотдачи, не превышающим значения 2,0 руб., составляет 60 единиц. Тогда
m = 60, n = 90, w = m/n = 60 : 90 = 0,667;
- рассчитаем дисперсию доли в выборочной совокупности

- средняя ошибка выборки при использовании повторной схемы отбора составит
Если предположить, что была использована бесповторная схема отбора, то средняя ошибка выборки с учетом поправки на конечность совокупности составит
- зададим доверительную вероятность и определим предельную ошибку выборки.
При значении вероятности Р = 0,997 по таблице нормального распределения получаем значение для коэффициента доверия t = 3 (см. выдержку из нее, приведенную в Приложении 1):
- установим границы для генеральной доли с вероятностью 0,997:
Таким образом, с вероятностью 0,997 можно утверждать, что в генеральной совокупности доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., не меньше, чем 54,7%, и не больше 78,7%.
- Типическая выборка. При типической выборке генеральная совокупность объектов разбита на k групп, тогда
N1 + N2 + … + Ni + … + Nk = N.
Объем извлекаемых из каждой типической группы единиц зависит от принятого способа отбора; их общее количество образует необходимый объем выборки
n1 + n2 + … + ni + … + nk = n.
Существуют следующие два способа организации отбора внутри типической группы: пропорциональной объему типических групп и пропорциональной степени колеблемости значений признака у единиц наблюдения в группах. Рассмотрим первый из них, как наиболее часто используемый.
Отбор, пропорциональный объему типических групп, предполагает, что в каждой из них будет отобрано следующее число единиц совокупности:
n = ni · Ni/N
где ni — количество извлекаемых единиц для выборки из i-й типической группы;
n — общий объем выборки;
Ni — количество единиц генеральной совокупности, составивших i-ю типическую группу;
N — общее количество единиц генеральной совокупности.
Отбор единиц внутри групп происходит в виде случайной или механической выборки.
Формулы для оценивания средней ошибки выборки для среднего и доли представлены в табл. 11.6.

|
Здесь 
Пример 11.3. В одном из московских вузов проведено выборочное обследование студентов с целью определения показателя средней посещаемости вузовской библиотеки одним студентом за семестр. Для этого была использована 5%-ная бесповторная типическая выборка, типические группы которой соответствуют номеру курса. При отборе, пропорциональном объему типических групп, получены следующие данные:
| Номер курса | Всего студентов, чел., Ni | Обследовано в результате выборочного наблюдения, чел., ni | Среднее число посещений библиотеки одним студентом за семестр, xi | Внутригрупповая выборочная дисперсия, 
|
|---|---|---|---|---|
| 1 | 650 | 33 | 11 | 6 |
| 2 | 610 | 31 | 8 | 15 |
| 3 | 580 | 29 | 5 | 18 |
| 4 | 360 | 18 | 6 | 24 |
| 5 | 350 | 17 | 10 | 12 |
| Итого | 2 550 | 128 | 8 | — |
Число студентов, которое необходимо обследовать на каждом курсе, рассчитаем следующим образом:
- общий объем выборочной совокупности:
n = 2550/130*5 =128 (чел.);
- количество единиц, отобранных из каждой типической группы:
аналогично для других групп:
n2 = 31 (чел.);
n3 = 29 (чел.);
n4 = 18 (чел.);
n5 = 17 (чел.).
Проведем необходимые расчеты.
- Выборочная средняя, исходя из значений средних типических групп, составит:
- Средняя из внутригрупповых дисперсий
- Средняя ошибка выборки:
С вероятностью 0,954 находим предельную ошибку выборки:
- Доверительные границы для среднего значения признака в генеральной совокупности:
Таким образом, с вероятностью 0,954 можно утверждать, что один студент за семестр посещает вузовскую библиотеку в среднем от семи до девяти раз.
- Малая выборка. В связи с небольшим объемом выборочной совокупности те формулы для определения ошибок выборки, которые использовались нами ранее при «больших» выборках, становятся неподходящими и требуют корректировки.
Среднюю ошибку малой выборки определяют по формуле
Предельная ошибка малой выборки:
Распределение значений выборочных средних всегда имеет нормальный закон распределения (или приближается к нему) при п > 100, независимо от характера распределения генеральной совокупности. Однако в случае малых выборок действует иной закон распределения — распределение Стьюдента. В этом случае коэффициент доверия находится по таблице t-распределения Стьюдента в зависимости от величины доверительной вероятности Р и объема выборки п. В Приложении 1 приводится фрагмент таблицы t-распределения Стьюдента, представленной в виде зависимости доверительной вероятности от объема выборки и коэффициента доверия t.
Пример 11.4. Предположим, что выборочное обследование восьми студентов академии показало, что на подготовку к контрольной работе по статистике они затратили следующее количество часов: 8,5; 8,0; 7,8; 9,0; 7,2; 6,2; 8,4; 6,6.
Оценим выборочные средние затраты времени и построим доверительный интервал для среднего значения признака в генеральной совокупности, приняв доверительную вероятность равной 0,95.
- Среднее значение признака в выборке равно
- Значение среднего квадратического отклонения составляет
- Средняя ошибка выборки:
- Значение коэффициента доверия t = 2,365 для п = 8 и Р = 0,95 .
- Предельная ошибка выборки:
- Доверительный интервал для среднего значения признака в генеральной совокупности:
То есть с вероятностью 0,95 можно утверждать, что затраты времени студента на подготовку к контрольной работе находятся в пределах от 6,9 до 8,5 ч.
11.2.2. Определение численности выборочной совокупности
Перед непосредственным проведением выборочного наблюдения всегда решается вопрос, сколько единиц исследуемой совокупности необходимо отобрать для обследования. Формулы для определения численности выборки выводят из формул предельных ошибок выборки в соответствии со следующими исходными положениями (табл. 11.7):
- вид предполагаемой выборки;
- способ отбора (повторный или бесповторный);
- выбор оцениваемого параметра (среднего значения признака или доли).
Кроме того, следует заранее определиться со значением доверительной вероятности, устраивающей потребителя информации, и с размером допустимой предельной ошибки выборки.
 |
Примечание: при использовании приведенных в таблице формул рекомендуется получаемую численность выборки округлять в большую сторону для обеспечения некоторого запаса в точности.
Пример 11.5. Рассчитаем, сколько из 507 промышленных предприятий следует проверить налоговой инспекции, чтобы с вероятностью 0,997 определить долю предприятий с нарушениями в уплате налогов. По данным прошлого аналогичного обследования величина среднего квадратического отклонения составила 0,15; размер ошибки выборки предполагается получить не выше, чем 0,05.
При использовании повторного случайного отбора следует проверить
При бесповторном случайном отборе потребуется проверить
Как видим, использование бесповторного отбора позволяет проводить обследование гораздо меньшего числа объектов.
Пример 11.6. Планируется провести обследование заработной платы на предприятиях отрасли методом случайного бесповторного отбора. Какова должна быть численность выборочной совокупности, если на момент обследования в отрасли число занятых составляло 100 000 чел.? Предельная ошибка выборки не должна превышать 100 руб. с вероятностью 0,954. По результатам предыдущих обследований заработной платы в отрасли известно, что среднее квадратическое отклонение составляет 500 руб.
Следовательно, для решения поставленной задачи необходимо включить в выборку не менее 100 человек.
























































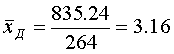
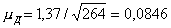
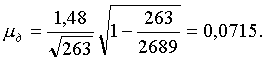
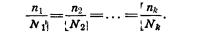
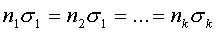
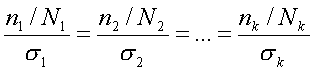
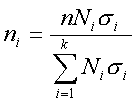
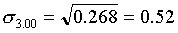
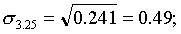
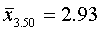
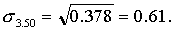
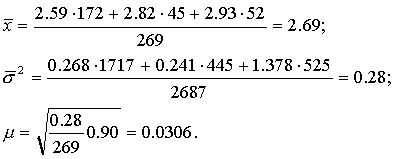
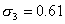
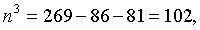
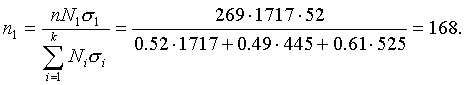
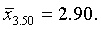
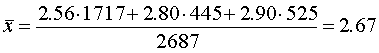
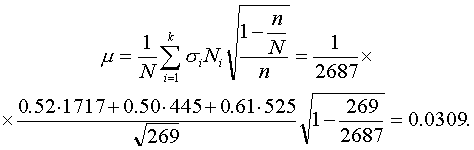
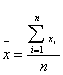
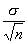
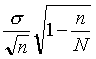
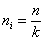
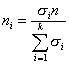
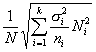
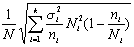
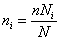
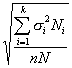
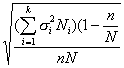
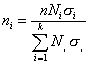
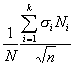
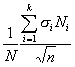
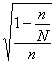
 можно пренебречь.
можно пренебречь.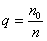
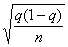
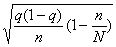
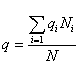
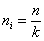
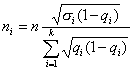
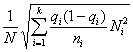
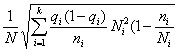
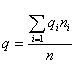
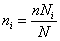
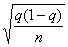
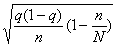
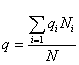
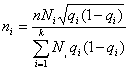
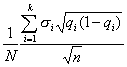
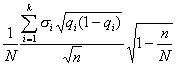
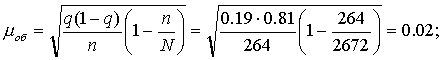
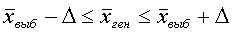














 ) при использовании типического отбора, пропорционального объему типических групп
) при использовании типического отбора, пропорционального объему типических групп














