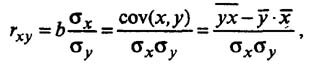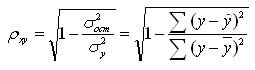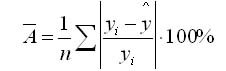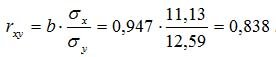Средняя ошибка аппроксимации позволяет судить о - Решение и исправление самых разных ошибок на TopOshibok.ru

2.6.1
Коэффициент детерминации.
Для оценки качества построенной модели
регрессии можно использовать коэффициент
детерминации
.
Коэффициент детерминации может быть
вычислен по формуле:

С другой стороны,
для парной линейной регрессии верно
равенство:

При
близости значения коэффициента
детерминации к 1 говорят, что уравнение
регрессии статистически значимо и
фактор
оказывает сильное воздействие на
результирующий признак.

При анализе модели
парной линейной регрессии по значению
коэффициента детерминации можно сделать
следующие предварительные выводы о
качестве модели:

Если
,
то будем считать, что использование
регрессионной модели для аппроксимации
зависимости между переменнымиистатистически необоснованно.
Если
,
то использование регрессионной модели
возможно, но после оценивания параметров
модель подлежит дальнейшему многостороннему
статистическому анализу.
Если
,
то будем. считать, что у нас есть основания
для использования регрессионной модели
при анализе поведения переменной.

2.6.2 Средняя ошибка аппроксимации.

Другой
показатель качества построенной модели
–– среднее относительное отклонение
расчетных значений от фактических или
средняя
ошибка аппроксимации:

Построенное
уравнение регрессии считается
удовлетворительным, если значение
не превышает 10% – 12% .

3. Пример.

По
21 региону страны изучается зависимость
розничной продажи телевизоров ()
от среднедушевого денежного дохода в
месяц ().

Номер региона	Среднедушевой денежный доход в месяц, тыс. руб.,	Объем розничной продажи телевизоров, тыс. шт.,
1	2	28
2	2,4	21,3
3	2,1	21
4	2,6	23,3
5	1,7	15,8
6	2,5	21,9
7	2,4	20
8	2,6	22
9	2,8	23,9
10	2,6	26
11	2,6	24,6
12	2,5	21
13	2,9	27
14	2,6	21
15	2,2	24
16	2,6	24
17	3,3	31,9
18	3,9	33
19	4	35,4
20	3,7	34
21	3,4	31

Необходимо
найти зависимость, наилучшим образом
отражающую связь между переменными
и
.

Рассмотрим вопрос
применения модели линейной регрессии
в этой задаче.

Построим
поле корреляции, т.е. нанесем исходные
данные на координатную плоскость. Для
этого воспользуемся, например,
возможностями MS
Excel
2003.

Подготовим таблицу
исходных данных.

Нанесем на
координатную плоскость исходные данные:

Характер
расположения точек на графике дает нам
основание предположить, что искомая
функция регрессии линейная:
.
Для оценки коэффициентов уравнения
регрессии необходимо составить и решить
систему нормальных уравнений ( ).

По исходным данным
рассчитываем необходимые суммы:

Номер региона
1	2	28	56	4	784
2	2,4	21,3	51,12	5,76	453,69
3	2,1	21	44,1	4,41	441
4	2,6	23,3	60,58	6,76	542,89
5	1,7	15,8	26,86	2,89	249,64
6	2,5	21,9	54,75	6,25	479,61
7	2,4	20	48	5,76	400
8	2,6	22	57,2	6,76	484
9	2,8	23,9	66,92	7,84	571,21
10	2,6	26	67,6	6,76	676
11	2,6	24,6	63,96	6,76	605,16
12	2,5	21	52,5	6,25	441
13	2,9	27	78,3	8,41	729
14	2,6	21	54,6	6,76	441
15	2,2	24	52,8	4,84	576
16	2,6	24	62,4	6,76	576
17	3,3	31,9	105,27	10,89	1017,61
18	3,9	33	128,7	15,21	1089
19	4	35,4	141,6	16	1253,16
20	3,7	34	125,8	13,69	1156
21	3,4	31	105,4	11,56	961
Сумма	57,4	530,1	1504,46	164,32	13926,97

Составляем систему
уравнений:

Имеем систему
линейных алгебраических уравнений,
которая может быть решена, например, по
формулам Крамера. Для этого вычислим
следующие определители:

Тогда, согласно
теореме Крамера,

Получаем уравнение
регрессии:

Величина
коэффициента регрессии
означает, что увеличение среднедушевого
месячного дохода на 1 тыс. руб. приведет
к увеличение объема розничной продажи
в среднем на 7 540 телевизоров. Коэффициентв данном случае не имеет содержательной
интерпретации.

Оценим тесноту
линейной связи между переменными и
качество построенной модели в целом.

Для оценки тесноты
линейной зависимости рассчитаем
коэффициент детерминации. Для этого
необходимо провести ряд дополнительных
вычислений.

Прежде
всего, найдем выборочное
среднее
по формуле:

Для рассматриваемого
примера имеем:

Теперь произведем
расчет остальных вспомогательных
величин:

Номер региона
1	2	28	19,76	8,24	67,89	2,76	7,60
2	2,4	21,3	22,75	-1,45	2,11	-3,94	15,55
3	2,1	21	20,51	0,49	0,24	-4,24	18,00
4	2,6	23,3	24,25	-0,95	0,90	-1,94	3,77
5	1,7	15,8	17,52	-1,72	2,95	-9,44	89,17
6	2,5	21,9	23,50	-1,60	2,56	-3,34	11,17
7	2,4	20	22,75	-2,75	7,57	-5,24	27,49
8	2,6	22	24,25	-2,25	5,04	-3,24	10,52
9	2,8	23,9	25,74	-1,84	3,39	-1,34	1,80
10	2,6	26	24,25	1,75	3,08	0,76	0,57
11	2,6	24,6	24,25	0,35	0,13	-0,64	0,41
12	2,5	21	23,50	-2,50	6,24	-4,24	18,00
13	2,9	27	26,49	0,51	0,26	1,76	3,09
14	2,6	21	24,25	-3,25	10,54	-4,24	18,00
15	2,2	24	21,26	2,74	7,53	-1,24	1,54
16	2,6	24	24,25	-0,25	0,06	-1,24	1,54
17	3,3	31,9	29,48	2,42	5,86	6,66	44,32
18	3,9	33	33,96	-0,96	0,93	7,76	60,17
19	4	35,4	34,71	0,69	0,47	10,16	103,17
20	3,7	34	32,47	1,53	2,34	8,76	76,69
21	3,4	31	30,23	0,77	0,60	5,76	33,14
Сумма	57,4	530,1			130,68		545,73

Здесь
столбец «»
– это значения,рассчитанные с помощью построенного
уравнения регрессии, столбцы «»
и– это столбцы, так называемых, «остатков»:
разностей между исходными значениями,и рассчитанными с помощью уравнения
регрессии,
а также их квадратов, а в последних двух
столбцах – разности между исходными
значениями,
выборочным средним,
а также их квадраты.

Для
вычисления коэффициента детерминации
воспользуемся формулой ( ):

Значение
коэффициента детерминации позволяет
сделать предварительный вывод о том,
что у нас имеются основания использовать
модель линейной регрессии в данной
задаче, поскольку
.

Построим
линию регрессии на корреляционном поле,
для чего добавим на координатной
плоскости точки, соответствующие
уравнению регрессии ().

Нанесем
теперь уравнение регрессии на диаграмму,
используя специальные средства Excel.
Для этого необходимо выделить правой
кнопкой мыши исходные точки и выбрать
опцию Добавить
линию тренда.

В
открывшемся меню Параметры
линии тренда
выбрать Линейную
аппроксимацию.
Далее поставить флажок напротив полей
Показывать
уравнение на диаграмме
и Поместить
на диаграмму величину достоверности
аппроксимации .

Нажав
на ОК, получаем еще одну прямую на
диаграмме, которая совпадает с построенными
ранее точками линии регрессии:

Сплошная
черная линия на диаграмме – это линия
регрессии, рассчитанная средствами
Excel.
Линия регрессии, построенная нами ранее,
совпала с данной линией регрессии.
Нетрудно убедиться, что уравнение
регрессии и коэффициент детерминации
тоже совпадают с полученными ранее
вручную.

Найдем
теперь среднюю ошибку аппроксимации
для оценки погрешности модели. Для этого
нам потребуется вычислить еще ряд
промежуточных величин:

Номер региона
1	2	28	19,76	8,24	0,29
2	2,4	21,3	22,75	-1,45	0,07
3	2,1	21	20,51	0,49	0,02
4	2,6	23,3	24,25	-0,95	0,04
5	1,7	15,8	17,52	-1,72	0,11
6	2,5	21,9	23,50	-1,60	0,07
7	2,4	20	22,75	-2,75	0,14
8	2,6	22	24,25	-2,25	0,10
9	2,8	23,9	25,74	-1,84	0,08
10	2,6	26	24,25	1,75	0,07
11	2,6	24,6	24,25	0,35	0,01
12	2,5	21	23,50	-2,50	0,12
13	2,9	27	26,49	0,51	0,02
14	2,6	21	24,25	-3,25	0,15
15	2,2	24	21,26	2,74	0,11
16	2,6	24	24,25	-0,25	0,01
17	3,3	31,9	29,48	2,42	0,08
18	3,9	33	33,96	-0,97	0,03
19	4	35,4	34,71	0,69	0,02
20	3,7	34	32,47	1,53	0,05
21	3,4	31	30,23	0,77	0,02

Здесь
столбец «»
– это значения,рассчитанные с помощью построенного
уравнения регрессии, столбец «»
– это столбец так называемых «остатков»:
разностей между исходными значениями,
и рассчитанными с помощью уравнения
регрессии,и, наконец, последний столбец «»
– это вспомогательный столбец для
вычисления элементов суммы по формуле
( ). Просуммируем теперь элементы
последнего столбца и разделим полученную
сумму на 21 – общее количество исходных
данных:

Переведем это
число в проценты и запишем окончательное
выражение для средней ошибки аппроксимации:

Итак,
средняя ошибка аппроксимации оказалась
около 8%, что говорит о небольшой
погрешности построенной модели. Данную
модель, с учетом неплохих характеристик
ее качества, вполне можно использовать
для прогноза – одной из основных целей
эконометрического анализа. Предположим,
что среднедушевой месячный доход в
одном из регионов составит 4,1 тыс. руб.
Оценим, каков будет уровень продаж
телевизоров в этом регионе согласно
построенной модели? Для этого необходимо
выбранное значение фактора
подставить в уравнение регрессии (
):

(тыс.
руб.),

т.е. при таком
уровне дохода, розничная продажа
телевизоров составит, в среднем, 35 480
телевизоров.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Коэффициент корреляции

Тесноту (силу) связи изучаемых показателей в предмете эконометрика оценивают с помощью коэффициента корреляции Rxy, который может принимать значения от -1 до +1.

Если Rxy > 0,7 — связь между изучаемыми показателями сильная, можно проводить анализ линейной модели

Если 0,3 < Rxy < 0,7 — связь между показателями умеренная, можно использовать нелинейную модель при отсутствии Rxy > 0,7

Если Rxy < 0,3 — связь слабая, модель строить нельзя

Для нелинейной регрессии используют индекс корреляции (0 < Рху < 1):

Средняя ошибка аппроксимации

Для оценки качества однофакторной модели в эконометрике используют коэффициент детерминации и среднюю ошибку аппроксимации.

Средняя ошибка аппроксимации определяется как среднее отклонение полученных значений от фактических

Допустимая ошибка аппроксимации не должна превышать 10%.

В эконометрике существует понятие среднего коэффициента эластичности Э – который говорит о том, на сколько процентов в среднем изменится показатель у от своего среднего значения при изменении фактора х на 1% от своей средней величины.

Пример нахождения коэффициента корреляции

Исходные данные:

Номер региона	Среднедушевой прожиточный минимум в день одного трудоспособного, руб.,	Среднедневная заработная плата, руб.,
1	81	124
2	77	131
3	85	146
4	79	139
5	93	143
6	100	159
7	72	135
8	90	152
9	71	127
10	89	154
11	82	127
12	111	162

Рассчитаем параметры парной линейной регрессии, составив таблицу

	x	x²	y	xy	y²
1	81	6561	124	10044	15376
2	77	5929	131	10087	17161
3	85	7225	146	12410	21316
4	79	6241	139	10981	19321
5	93	8649	143	13299	20449
6	100	10000	159	15900	25281
7	72	5184	135	9720	18225
8	90	8100	152	13680	23104
9	71	5041	127	9017	16129
10	89	7921	154	13706	23716
11	82	6724	127	10414	16129
12	111	12321	162	17982	26244
Среднее	85,8	7491	141,6	12270,0	20204,3
Сумма	1030,0	89896	1699	147240	242451
σ	11,13		12,59
σ2	123,97		158,41

формула расчета дисперсии σ2 приведена здесь.

Коэффициенты уравнения y = a + bx определяются по формуле

Получаем уравнение регрессии: y = 0,947x + 60,279.

Коэффициент уравнения b = 0,947 показывает, что при увеличении среднедушевого прожиточного минимума в день одного трудоспособного на 1 руб. среднедневная заработная плата увеличивается на 0,947 руб.
Коэффициент корреляции рассчитывается по формуле:

Значение коэффициента корреляции более — 0,7, это означает, что связь между среднедушевым прожиточным минимумом в день одного трудоспособного и среднедневной заработной платой сильная.

Коэффициент детерминации равен R2 = 0.838^2 = 0.702
т.е. 70,2% результата объясняется вариацией объясняющей переменной x.

Источник

После выполнения указанных действий проводится проверка на адекватность и надежность модели в целом по всем участвующим в переборе уравнениям регрессии. Для этого применяют такие показатели, как коэффициенты множественной корреляции, средняя ошибка аппроксимации и -критерий. Оценка моделей по совокупности этих характеристик позволяет установить наиболее оптимальную форму связи. [c.18]

Оценка этой формы связи по коэффициенту множественной корреляции и средней ошибке аппроксимации показывает, что адекватность данной модели не подтверждается. Действительно, хотя значение коэффициента достаточно высокое (0,92), средняя ошибка аппроксимации составляет более 10% (I = 14,5%). Поэтому данная форма должна быть исключена из перебора известных уравнений регрессии. [c.29]

Анализ полученной формы связи по той же причине, что и в первом случае, позволяет сделать вывод о непригодности и этой модели. Коэффициент множественной корреляции хотя и имеет более высокое значение, чем в линейной зависимости (0,93), но по величине средней ошибки аппроксимации (б = 12,4%) это уравнение регрессии подлежит исключению из дальнейшего перебора. [c.29]

Последняя модель себестоимости добычи нефти, как показывает оценка ее по известным критериям, удовлетворяет условиям адекватности. Коэффициент множественной корреляции R составляет 0,98, что свидетельствует о том, что колеблемость исследуемого показателя более чем на 96 % определяется факторами, включенными в эту модель. При оценке по f-критерию (t R = 30,5) можно утверждать, что с вероятностью 0,99 факторы, включенные в модель, имеют существенную связь с исследуемым показателем (t a n = 2,58). Средняя ошибка аппроксимации составляет всего лишь 2,9 %, а F-критерий, характеризующий уровень остаточной дисперсии, превышает критическое (табличное) значение в четыре раза. К этому следует добавить, что полученная модель себестоимости добычи нефти представляет собой достаточно простую форму связи, легко решается и поддается экономической интерпретации. [c.30]

Оценка полученной модели по статистическим характеристикам показывает, что колеблемость затрат исследуемой подсистемы на 85 % обусловлена колеблемостью факторов, включенных в модель, коэффициент множественной корреляции высокий (/ = 0,92) и существенный (f = = 39,8), модель является адекватной, средняя ошибка аппроксимации (ё = 5,7%) меньше 10%. [c.39]

Статистический анализ показывает, что уравнение значимо Рф = 5,054 при /»табл = 3,01, корреляционное отношение равно 0,9959, ее»стандартная ошибка равна 0,0015. Среднее квадратическое отклонение расчетной себестоимости от фактической равно 0,018. Средняя ошибка аппроксимации 1,1%. [c.90]

Средняя ошибка аппроксимации [c.94]

Средняя ошибка аппроксимации……,……. [c.95]

В случаях, когда трудно обосновать форму зависимости, решение задачи можно провести по разным моделям и сравнить полученные результаты. Адекватность разных моделей фактическим зависимостям проверяется по критерию Фишера, показателю средней ошибки аппроксимации и величине множественного коэффициента детерминации, о которых речь пойдет несколько позже (см. 7.4). [c.144]

Эти сведения вводятся в ПЭВМ и рассчитываются матрицы парных и частных коэффициентов корреляции, уравнение множественной регрессии, а также показатели, с помощью которых оценивается надежность коэффициентов корреляции и уравнения связи критерий Стьюдента, критерий Фишера, средняя ошибка аппроксимации, множественные коэффициенты корреляции и детерминации. [c.145]

Для того чтобы убедиться в надежности уравнения связи и правомерности его использования для практической цели, необходимо дать статистическую оценку надежности показателей связи. Для этого используются критерий Фишера (F-отношение), средняя ошибка аппроксимации ( ), коэффициенты множественной корреляции (/ ) и детерминации (D). [c.151]

Для статистической оценки точности уравнения связи используется также средняя ошибка аппроксимации [c.152]

Чем меньше теоретическая линия регрессии (рассчитанная по уравнению) отклоняется от фактической (эмпиричной), тем меньше средняя ошибка аппроксимации. В нашем примере она составляет 0,0364, или 3,64 %. Учитывая, что в экономических расчетах допускается погрешность 5-8 %, можно сделать вывод, что исследуемое уравнение связи довольно точно описывает изучаемые зависимости. [c.152]

После построения уравнения регрессии необходимо сделать проверку его значимости с помощью специальных критериев установить, не является ли полученная зависимость, выраженная уравнением регрессии, случайной, т.е. можно ли ее использовать в прогнозных целях и для факторного анализа. В статистике разработаны методики строгой проверки значимости коэффициентов регрессии с помощью дисперсионного анализа и расчета специальных критериев (например, F-критерия). Нестрогая проверка может быть выполнена путем расчета среднего относительного линейного отклонения (ё), называемого средней ошибкой аппроксимации [c.123]

Модель считается адекватной, т.е. пригодной для практического использования, если средняя ошибка аппроксимации не превосходит 15%. [c.123]

Оценку качества построенной модели даст коэффициент (индекс) детерминации, а также средняя ошибка аппроксимации. [c.6]

Средняя ошибка аппроксимации — среднее отклонение расчетных значений от фактических [c.6]

Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата ух. По ним рассчитаем показатели тесноты связи — индекс корреляции рху и среднюю ошибку аппроксимации 7, [c.13]

Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации. [c.16]

Это означает, что 52% вариации заработной латы (у) объясняется вариацией фактора х — среднедушевого прожиточного минимума. Качество модели определяет средняя ошибка аппроксимации [c.18]

Оцените с помощью средней ошибки аппроксимации качество уравнений. [c.38]

Оцените качество уравнений с помощью средней ошибки аппроксимации. [c.42]

Оцените качество уравнения через среднюю ошибку аппроксимации. [c.92]

Оцените качество каждого тренда через среднюю ошибку аппроксимации, линейный коэффициент автокорреляции отклонений. [c.166]

СРЕДНЯЯ ОШИБКА АППРОКСИМАЦИИ [c.87]

Представим расчет средней ошибки аппроксимации для уравнения ух = 9,876 + 5,129 hue в табл. 2.7. А = — 7,3 = 1,2%, что [c.88]

Расчет средней ошибки аппроксимации [c.88]

В стандартных программах чаще используется первая формула для расчета Средней ошибки аппроксимации. [c.88]

В чем смысл средней ошибки аппроксимации и как она определяется [c.89]

Средняя ошибка аппроксимации [c.10]

Модели парной регрессии. Парная линейная регрессия. Методы оценки коэффициентов регрессии. Метод наименьших квадратов (МНК). Свойства оценок МНК. Оценка статистической значимости коэффициентов регрессии. Элементы корреляционного анализа. Измерители тесноты связи (коэффициенты ковариации, корреляции и детерминации). Оценка значимости коэффициента корреляции. Дисперсионный анализ результатов регрессии. Оценка статистической значимости уравнения регрессии. Анализ ряда остатков условия Гаусса-Маркова. Нелинейные модели регрессии и их линеаризация. Выбор функции регрессии тесты Бокса-Кокса. Корреляция в случае нелинейной регрессии. Средняя ошибка аппроксимации. [c.3]

Выбор вида модели основан на логическом анализе изучаемых показателей, сравнении статистических характеристик (средняя ошибка аппроксимации, критерий Фишера, коэффициенты множественной корреляции и детерминации), рассчитанных для различных функций по одним и тем же первичным данным. [c.31]

Проверка приведенной в формуле (154) себестоимости по фактическим данным 103 СМУ показала, что средняя ошибка аппроксимации, определяющая степень соответствия расчетных значений фактическим, составила всего 1,5%, что вполне допустимо. [c.227]

Исчисляемый коэффициент детерминации получился равным 0,869. Это говорит о том, что размер заработной платы водителей на 86,9% зависит от Р и Л ри на 13,1% — от неучтенных в модели факторов. Средняя ошибка аппроксимации составила всего лишь 0,17%. Модель была получена на основе конкретных показателей ряда автотранспортных предприятий Владимирского транспортного управления, поэтому она может -быть использована в практической работе только на этих предприятиях. Предлагаемая же методика может быть использована в любом транспортном управлении, министерстве при планировании и анализе себестоимости автомобильных перевозок и установлении нормативов по заработной плате водителей за время работы на линии. [c.36]

Источник