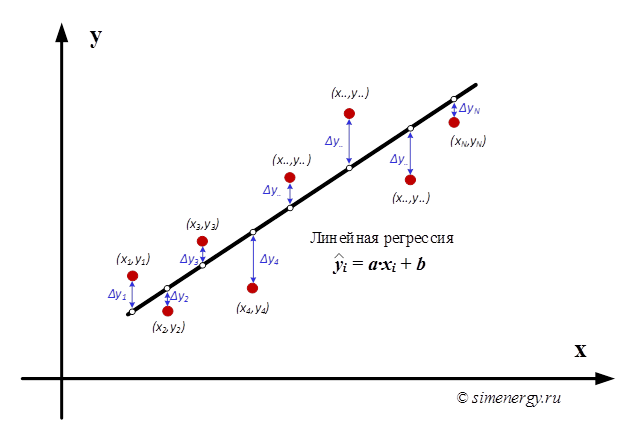
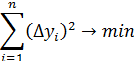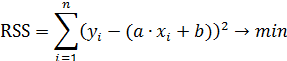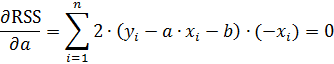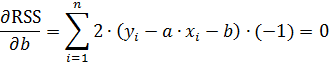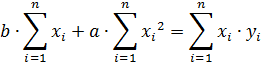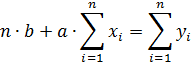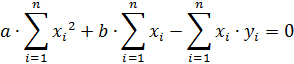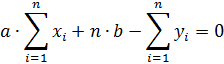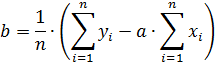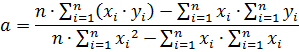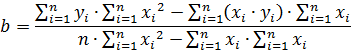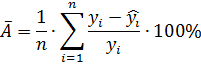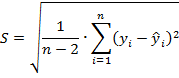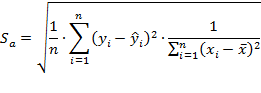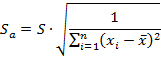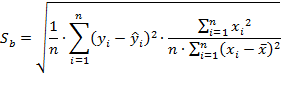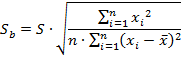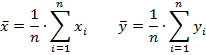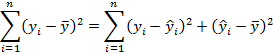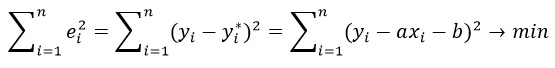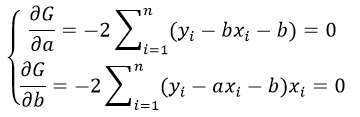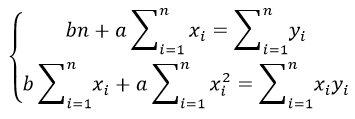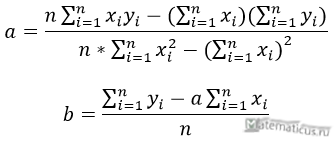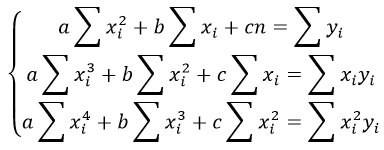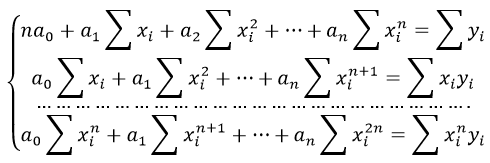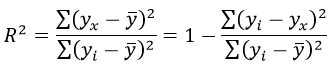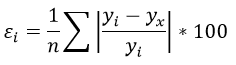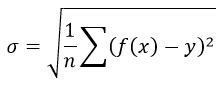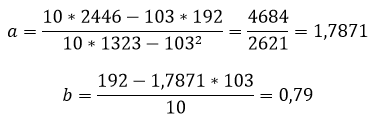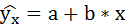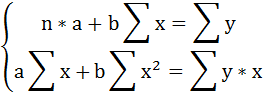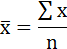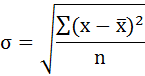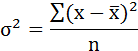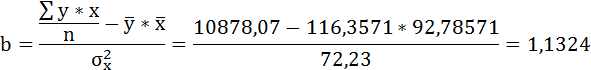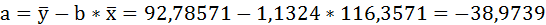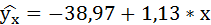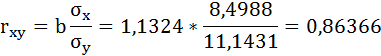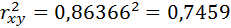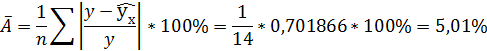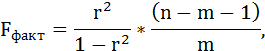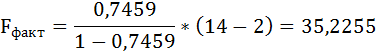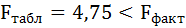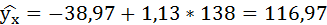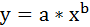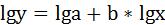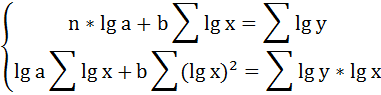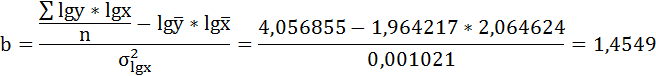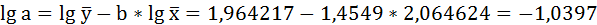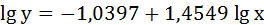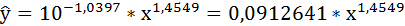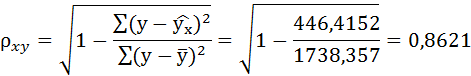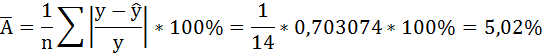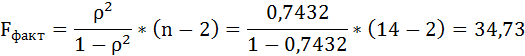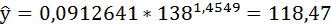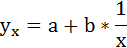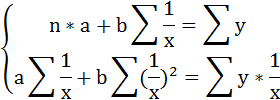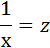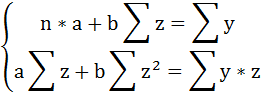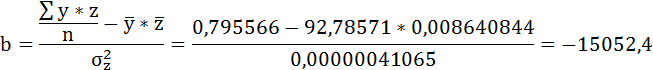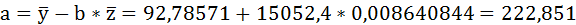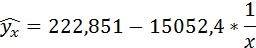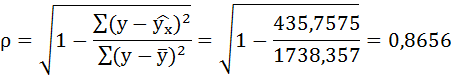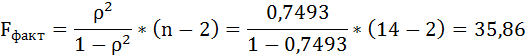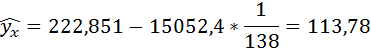Аппроксимация метод приближения, при котором некоторые величины (или объекты) выражаются через другие, более простые величины (или объекты). Таким образом, аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к более простым математическим моделям, которые более удобны к изучению.
В качестве исходных данных задан массив экспериментально полученных значений двух измеряемых величин: y1, y2, y3, … yn и x1, x2, x3, … xn , которые связаны некоторой функциональной зависимостью y=f(x), вид которой заранее не известен. Каждая пара совместно измеренных значений (xi, yi) определяет положение некоторой точки. Величины xi и yi не свободны от погрешностей, поэтому определяемые ими точки не лежат точно на какой-то кривой, а образуют некоторое облако с нечеткими границами. Необходимо определить регрессионную кривую y=f(x), проходящую через данную область точек.
Линейная регрессия (англ. Linear regression) — модель зависимости одной переменной y от другой или нескольких других переменных x (факторов, регрессоров, независимых переменных) с линейной функцией зависимости:
где переменные «a» и «b» – параметры зависимости y=f(x).
Рис.1. Линейная регрессия
Выбор параметров «a» и «b» должен быть выполнен таким образом, чтобы искомая теоретическая кривая y=f(x) наилучшим образом проходила через заданную область точек. Существуют различные критерии выбора наилучшего соответствия экспериментальных точек и регрессионной кривой. Одним из наиболее общих способов отыскания оценок истинных значений искомых параметров является разработанный Лежандром и Гауссом метод наименьших квадратов (МНК).
Примечание: Метод получения оценок параметров оптимальной прямой с помощью минимизации суммы квадратов отклонений называется Методом Наименьших Квадратов (сокращенно МНК) или Ordinary Least Squares (сокращенно OLS), а полученные оценки параметров называются МНК- или OLS-оценками.
Суть метода наименьших квадратов заключается в том, чтобы подобрать такие значения коэффициентов, при которых сумма квадратов отклонений измеренных в эксперименте значений (xi, yi) от искомой кривой y=f(x) была бы минимальна.
Обозначим функцию, которую требуется минимизировать через переменную RSS (Resudiual Sum of Squares) – остаточная сумма квадратов отклонений.
Сумма квадратов отклонений является функцией двух независимых переменных: «a» и «b». Для нахождения минимума суммы квадратов отклонений функции необходимо приравнять к нулю ее частные производные по «a» и «b».
Преобразуем полученную систему выражений
Перепишем систему уравнений в следующем виде
Из последнего выражения определяем параметр «b»
Далее подставляем полученное выражение в первое уравнение. Решая полученную систему уравнение, определим неизвестные параметры «a» и «b» (коэффициенты регрессионной кривой)
С учетом найденных коэффициентов «a» и «b» строится регрессионная кривая по следующему выражению:
где переменная — значения регрессионной кривой.
После того, как найдено уравнение линейной регрессии, проводится оценка, как уравнения в целом, так и отдельных его параметров.
П.1. Средняя ошибка аппроксимации
Общей характеристикой качества построенной регрессии (не только парной и линейной, но и любой другой) является средняя ошибка аппроксимации, которая показывает среднее отклонение расчетных значений от фактических. Средняя ошибка аппроксимации рассчитывается по формуле:
где переменная — значения регрессионной кривой
, переменная
– значения из массива исходных данных, а переменная 𝑛 — количество измерений.
Значение средней ошибки аппроксимации до 15% свидетельствует о хорошо подобранной модели уравнения.
П.2. Стандартная ошибка регрессии
Стандартная ошибка регрессии (Standard Error) — это среднее расстояние, на которое наблюдаемые значения отклоняются от линии регрессии.
Стандартная ошибка регрессии определяется как корень квадратный из остаточной дисперсии
где переменная — значения регрессионной кривой
, переменная
– значения из массива исходных данных, а переменная 𝑛 — количество измерений.
В знаменателе формулы используется выражение , которое соответствует количеству степеней свободы: N-k-1, где N-число точек, k-число переменных в регрессионном уравнении (например, для линейной модели y=a*x+b переменная k равна 1).
Значение стандартной ошибки позволяет увидеть степень отклонения значений, полученных с помощью регрессии, от фактически наблюдаемых, и таким образом оценить точность соответствующей модели.
Значение стандартной ошибки измеряет степень отличия реальных значений Y от уравнения линейной регрессии. Малая стандартная ошибка оценки, полученная при регрессионном анализе, свидетельствует, что все точки данных находятся очень близко к прямой регрессии. Если стандартная ошибка оценки велика, точки данных могут значительно удаляться от прямой.
П.3. Интервальные оценки параметров уравнения регрессии
Помимо определения качества уравнения регрессии в целом, также проводится оценка отдельных его параметров, а именно интервальные оценки параметров уравнения регрессии (Standard Error Coefficients).
Уравнение регрессии (y=ax+b) содержит коэффициенты «a» и «b», которые определяются теоретически по исходным данным. В результате полученное уравнение с определённой точностью описывает изменение экспериментальных данных. Поскольку уравнение регрессии может быть использовано при анализе и прогнозировании необходимо для данных коэффициентов уметь определять доверительные интервалы, в границах которых с определенной вероятностью находятся действительные значения параметров.
П.1. Доверительный интервал для коэффициента регрессии «a» определяется следующим соотношением
где переменная — стандартная ошибка оценки коэффициента регрессии «a»
Стандартная ошибка определяется по следующему выражению:
где переменная определяется из таблицы критических точек распределения Стьюдента в зависимости от уровня ошибки
, а
— среднее значение параметра.
П.2. Доверительный интервал для коэффициента регрессии «b» определяется следующим соотношением
где переменная – стандартная ошибка оценки свободного члена уравнения регрессии (коэффициента регрессии «b»)
Стандартная ошибка определяется по следующему выражению:
где переменная определяется из таблицы критических точек распределения Стьюдента в зависимости от уровня ошибки
, а
— среднее значение параметра.
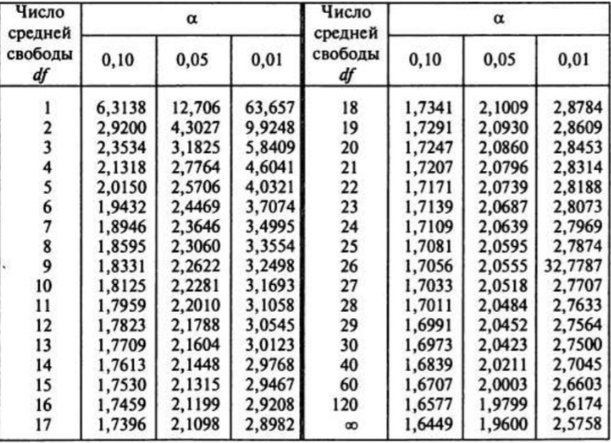
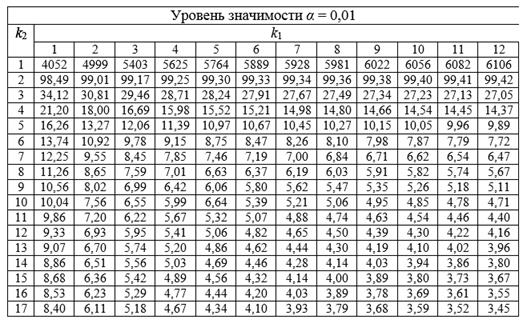
Переменная определяется из таблицы критических точек распределения Стьюдента. Для этого в качестве исходных данных выбирается уровень ошибки (0,10 или 0,05 или 0,01 или другие значения в расширенной таблице), а далее выбирается значение переменной
в зависимости от количества степеней свободы: N-k-1, где N-число точек, k-число переменных в регрессионном уравнении (например, для линейной модели y=a*x+b переменная k равна 1).
Рис.2. Таблица критических точек распределения Стьюдента в зависимости от уровня ошибки
Другой способ проверки статистической значимости параметров регрессии непосредственно не связан с построением доверительных интервалов. Проверка гипотезы осуществляется с помощью критерия Стьюдента (t-критерий Стьюдента). На основе полученных значений параметров регрессионной кривой, а также рассчитанных стандартных ошибок оценки коэффициента регрессии определяются эмпирические значения t-статистик:
где переменные «a» и «b» — значение параметра, а переменные и
— стандартная ошибка оценки коэффициента регрессии.
Далее полученные значения сравниваются со значениями , которые берутся из таблицы критических точек распределения Стьюдента при выбранной доверительной вероятности (как правило, 0.95) и числе степеней свободы: N-k-1, где N-число точек, k-число переменных в регрессионном уравнении (например, для линейной модели y=a*x+b переменная k равна 1). Если расчетное значение превышает по абсолютной величине табличное значение, то соответствующий коэффициент является статистически значимым с заданной доверительной вероятностью.
П.4. Линейный коэффициент корреляции Пирсона
Коэффициент корреляции Пирсона характеризует существование линейной зависимости между двумя случайными величинами. Для случайных величин X и Y выборочный коэффициент корреляции определяется по формуле:
Параметры и
— стандартные отклонения, соответствующие случайным величинам X и Y, а cov(X,Y) – коэффициент ковариации переменных X и Y.
где 𝑥𝑖, 𝑦𝑖 – элементы выборки, n – размер выборки, а — среднее значение параметров.
Используя формулы средних перепишем выражение для определения линейного коэффициента корреляции Пирсона.
Все значения коэффициента корреляции находятся в интервале от -1 до +1. Близость к нулю абсолютного значения обычно означает слабую линейную взаимосвязь между переменными. В случае если абсолютное значение
близко к единице, то это говорит о сильной линейной взаимосвязи между ними. Коэффициент корреляции отражает тесноту именно линейной связи между переменными, т.е. близость его к нулю свидетельствует об отсутствии именно линейной зависимости. Однако при этом переменные могут иметь связь другого вида: нелинейную.
Также формула для определения коэффициента корреляции Пирсона может быть использована для анализа двух других случайных величин: значений из массива исходных данных и значений регрессионной кривой .
П.5. Коэффициент детерминации
Следующим критерием оценки качества точности уравнения регрессии является коэффициент детерминации (Coefficient of determination). Коэффициент детерминации определяется как отношение объясненной ошибки (SSR) к общей ошибки (SST).
Коэффициент детерминации представляет собой квадрат корреляционного отношения.
Коэффициент детерминации является удобной оценкой степени связи между регрессивной линией и фактическими данными. Коэффициент детерминации показывает, какая доля общей вариации исследуемого показателя определяется (детерминируется) совокупным влиянием функции регрессии (т. е. выбранными нами объясняющими показателями).
Данное выражение переписывают в другом виде в случае линейной регрессии, т.к. в случае линейной регрессии с константой справедливо следующее соотношение:
В результате для линейной регрессии с константой коэффициент детерминации определяется следующим образом:
где 𝑦𝑖 – элементы выборки, n – размер выборки, — среднее значение параметров, а
– значения функции линейной регрессии .
Примечание: Еще раз обращаем Ваше внимание, что данная запись справедлива только для модели с константой, в общем случае необходимо использовать предыдущую формулу.
Коэффициент детерминации измеряет долю изменчивости Y, которую можно объяснить с помощью информации об изменчивости (разнице значений) независимой переменной X. Коэффициент детерминации изменяется в диапазоне от −∞ до 1.
Если коэффициент детерминации равен 1, это соответствует идеальной модели, когда все точки наблюдений лежат точно на линии регрессии, т.е. сумма квадратов их отклонений равна 0.
Если коэффициент детерминации равен 0, это означает, что связь между переменными регрессионной модели отсутствует, и вместо нее для оценки значения выходной переменной можно использовать простое среднее ее наблюдаемых значений.
Так же следует обратить внимание, что в случае линейной регрессии коэффициент корреляции значений из массива исходных данных и значений регрессионной кривой равен квадратному корню из коэффициента детерминации
:
П.6. Критерий Фишера (F-тест)
Критерий Фишера (F-критерий Фишера) — статистический критерий для оценки значимости различия дисперсий двух случайных выборок, который позволяет оценивать значимость линейных регрессионных моделей. В частности, он используется для проверки целесообразности включения или исключения независимых переменных (признаков) в регрессионную модель.
Критерий Фишера позволяет подтвердить или опровергнуть нулевую гипотезу с помощью сравнения дисперсии двух независимых выборок. Нулевая гипотеза — принимаемое по умолчанию предположение о том, что не существует связи между двумя наблюдаемыми событиями.
Для определения статистической значимости в начале рассчитывается значение F-критерия Фишера. Фактическое значение статистики Фишера равно отношению удельных (рассчитанных на одну степень свободы) факторной и остаточной дисперсий:
где n – объём выборки, m – число параметров «Х» в уравнении регрессии.
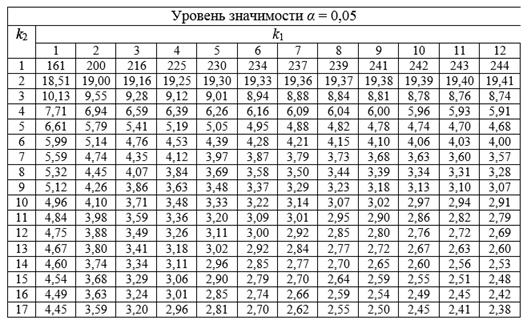
Затем значение F-критерия Фишера сравнивают с критическим (или табличным) значением. При этом табличное значение определяется на основе числа наблюдений, степеней свободы и заданного уровня значимости следующим образом: Fтабл (a; k1; k2), где k1 = m, где m – это количество факторов в построенной регрессионной модели (число степеней свободы большей дисперсии), а k2 = n – m – 1, где n – число наблюдений (число степеней свободы меньшей дисперсии).
Рис.3. Таблица критических точек распределения Фишера-Снедекора при допустимом уровне значимости a=0.01
Рис.4. Таблица критических точек распределения Фишера-Снедекора при допустимом уровне значимости a=0.05
В частности, для линейной регрессии (частный F-критерий) переменные k1 = 1, k2 = n – 2 (n – число наблюдений).
Вычисленное значение F – отношения признается достоверным, если оно больше табличного. Следовательно, полученное значение не случайно, оно сформировалось под влиянием существенных факторов, то есть подтверждается статистическая значимость всего уравнения и показателя тесноты связи.
П.1. В случае если значение критерия Фишера больше критического
, то принимается нулевая гипотеза и делается вывод об отсутствии статистически значимых различий частоты исхода в зависимости от наличия фактора риска.
П.2. В случае если значение критерия Фишера меньше критического
, то принимается альтернативная гипотеза и делается вывод о наличии статистически значимых различий частоты исхода в зависимости от воздействия фактора риска. Соответственно уравнение регрессии считается статистически незначимым и тем самым признается ненадежность уравнения регрессии.
Интерпретация частного F — критерия Фишера следующая: в том случае, когда рассчитанная величина частного Fxi превышает критическое значение, то дополнительное включение фактора xi в регрессионную модель статистически оправданно и коэффициент регрессии bi при соответствующем факторе xi статистически значим. Но если рассчитанная величина Fxi меньше табличного, то дополнительное включение в модель фактора xi не оправдано, т.к. данный фактор, как и коэффициент регрессии при нём является статистически незначимым.
П.7.Использование нелинейных функций.
Аппроксимация опытных данных также может быть выполнена нелинейными функциями. При этом отдельные нелинейные функции могут быть приведены к линейным функциям путем замены переменных. Соответственно, для этих нелинейных функций, могут использоваться методы для анализа линейной функции. Рассмотрим данные нелинейные функций и методику преобразования данных функций к линейному виду.
П.7.1. Задана исходная нелинейная функция #1 (Степенная функция)
Преобразуем функцию с линейному виду с помощью логарифмирования. В результате получим функцию в следующем виде:
Далее делаем замену переменных и получаем линейную функцию вида:
где переменная , переменная
, коэффициент
и коэффициент
Методика расчета коэффициентов для нелинейной функции #1 следующая:
а) Выполняется расчет коэффициентов и
для линеаризованной функции в соответствии с выше представленной методикой. В качестве исходных данных берутся следующие переменные:
и
б) Выполняется расчет коэффициентов a и b для выбранной нелинейной функции из ранее найденных коэффициентов и
:
в) С учетом найденных коэффициентов «a» и «b» строится нелинейная функция:
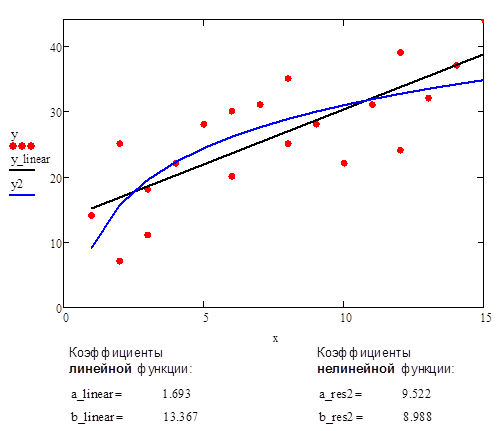
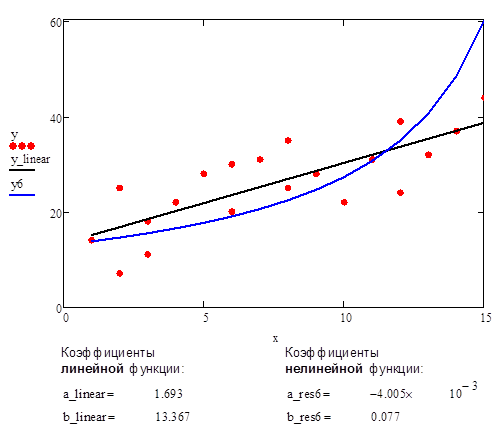
В качестве сравнительного примера приведен график аппроксимации данных с помощью прямой линии и нелинейной функции #1.
Рис.5. Аппроксимации данных с помощью прямой линии и нелинейной функции #1 (Степенная функция)
П.7.2. Исходная нелинейная функция #2 (логарифмическая функция)
Делаем замену переменных и получаем линейную функцию вида:
где переменная , переменная
, коэффициент
и коэффициент
Методика расчета коэффициентов для нелинейной функции #2 следующая:
а) Выполняется расчет коэффициентов и
для линеаризованной функции в соответствии с выше представленной методикой. В качестве исходных данных берутся следующие переменные:
и
б) Выполняется расчет коэффициентов a и b для выбранной нелинейной функции из ранее найденных коэффициентов и
:
в) С учетом найденных коэффициентов «a» и «b» строится нелинейная функция:
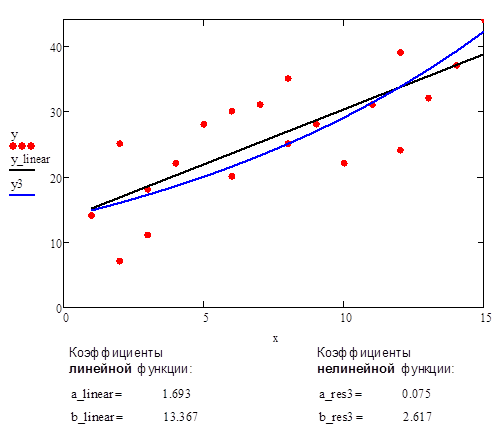
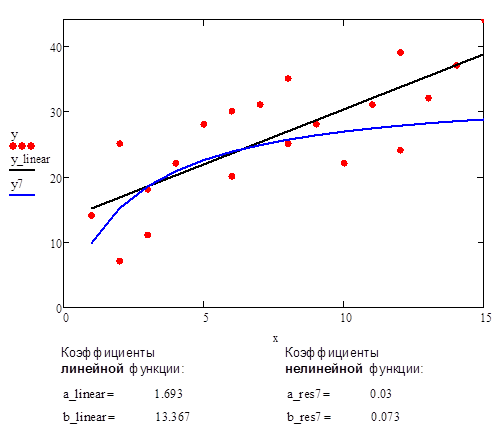
В качестве сравнительного примера приведен график аппроксимации данных с помощью прямой линии и нелинейной функции #2.
Рис.6. Аппроксимации данных с помощью прямой линии и нелинейной функции #2 (логарифмическая функция)
П.7.3. Исходная нелинейная функция #3 (экспоненциальная функция)
Преобразуемая функция с помощью логарифмирования к следующему виду:
Далее делаем замену переменных и получаем линейную функцию вида:
где переменная , переменная
, коэффициент
и коэффициент
Методика расчета коэффициентов для нелинейной функции #3 следующая:
а) Выполняется расчет коэффициентов и
для линеаризованной функции в соответствии с выше представленной методикой. В качестве исходных данных берутся следующие переменные:
и
б) Выполняется расчет коэффициентов a и b для выбранной нелинейной функции из ранее найденных коэффициентов и
:
в) С учетом найденных коэффициентов «a» и «b» строится нелинейная функция:
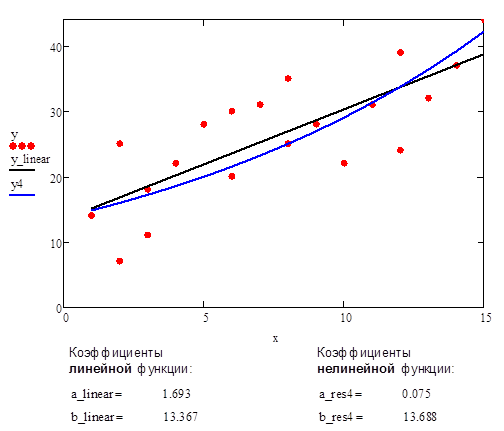
В качестве сравнительного примера приведен график аппроксимации данных с помощью прямой линии и нелинейной функции #3.
Рис.7. Аппроксимации данных с помощью прямой линии и нелинейной функции #3 (экспоненциальная функция)
П.7.4. Исходная нелинейная функция #4 (экспоненциальная функция)
Преобразуемая функция с помощью логарифмирования к следующему виду:
Далее делаем замену переменных и получаем линейную функцию вида:
где переменная , переменная
, коэффициент
и коэффициент
Методика расчета коэффициентов для нелинейной функции #4 следующая:
а) Выполняется расчет коэффициентов и
для линеаризованной функции в соответствии с выше представленной методикой. В качестве исходных данных берутся следующие переменные:
и
б) Выполняется расчет коэффициентов a и b для выбранной нелинейной функции из ранее найденных коэффициентов и
:
в) С учетом найденных коэффициентов «a» и «b» строится нелинейная функция:
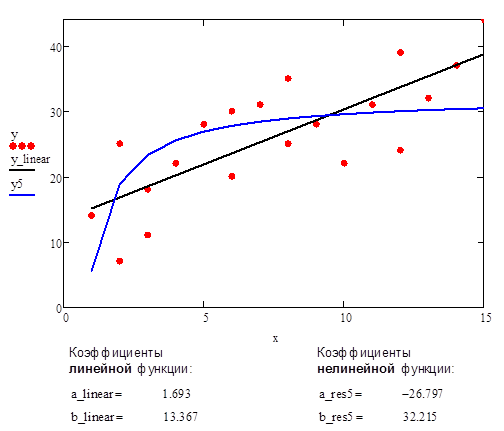
В качестве сравнительного примера приведен график аппроксимации данных с помощью прямой линии и нелинейной функции #4.
Рис.8. Аппроксимации данных с помощью прямой линии и нелинейной функции #4 (экспоненциальная функция)
П.7.5. Исходная нелинейная функция #5 (гиперболическая функция, гипербола)
Делаем замену переменных и получаем линейную функцию вида:
где переменная , переменная
, коэффициент
и коэффициент
Методика расчета коэффициентов для нелинейной функции #5 следующая:
а) Выполняется расчет коэффициентов и
для линеаризованной функции в соответствии с выше представленной методикой. В качестве исходных данных берутся следующие переменные:
и
б) Выполняется расчет коэффициентов a и b для выбранной нелинейной функции из ранее найденных коэффициентов и
:
в) С учетом найденных коэффициентов «a» и «b» строится нелинейная функция:
В качестве сравнительного примера приведен график аппроксимации данных с помощью прямой линии и нелинейной функции #5.
Рис.9. Аппроксимация данных с помощью прямой линии и нелинейной функции #5 (гиперболическая функция, гипербола)
П.7.6. Исходная нелинейная функция #6 (дробно-линейная функция)
Преобразуемая функция к следующему виду:
Далее делаем замену переменных и получаем линейную функцию вида:
где переменная , переменная
, коэффициент
и коэффициент
Методика расчета коэффициентов для нелинейной функции #6 следующая:
а) Выполняется расчет коэффициентов и
для линеаризованной функции в соответствии с выше представленной методикой. В качестве исходных данных берутся следующие переменные:
и
б) Выполняется расчет коэффициентов a и b для выбранной нелинейной функции из ранее найденных коэффициентов и
:
в) С учетом найденных коэффициентов «a» и «b» строится нелинейная функция:
В качестве сравнительного примера приведен график аппроксимации данных с помощью прямой линии и нелинейной функции #6.
Рис.10. Аппроксимация данных с помощью прямой линии и нелинейной функции #6 (дробно-линейная функция)
П.7.7. Исходная нелинейная функция #7 (Дробно-линейная функция)
Преобразуемая функция к следующему виду:
Далее делаем замену переменных и получаем линейную функцию вида:
где переменная , переменная
, коэффициент
и коэффициент
Методика расчета коэффициентов для нелинейной функции #7 следующая:
а) Выполняется расчет коэффициентов и
для линеаризованной функции в соответствии с выше представленной методикой. В качестве исходных данных берутся следующие переменные:
и
б) Выполняется расчет коэффициентов a и b для выбранной нелинейной функции из ранее найденных коэффициентов и
:
в) С учетом найденных коэффициентов «a» и «b» строится нелинейная функция:
В качестве сравнительного примера приведен график аппроксимации данных с помощью прямой линии и нелинейной функции #7.
Рис.11. Аппроксимация данных с помощью прямой линии и нелинейной функции #7 (дробно-линейная функция)
Выбор аппроксимирующей функции является важной задачей, так как от выбранной функции в существенной мере зависят количественные характеристики и качественные свойства описания объекта.
2.6.1
Коэффициент детерминации.
Для оценки качества построенной модели
регрессии можно использовать коэффициент
детерминации
.
Коэффициент детерминации может быть
вычислен по формуле:

С другой стороны,
для парной линейной регрессии верно
равенство:
.
При
близости значения коэффициента
детерминации к 1 говорят, что уравнение
регрессии статистически значимо и
фактор
оказывает сильное воздействие на
результирующий признак.
При анализе модели
парной линейной регрессии по значению
коэффициента детерминации можно сделать
следующие предварительные выводы о
качестве модели:
-
Если
,
то будем считать, что использование
регрессионной модели для аппроксимации
зависимости между переменнымии
статистически необоснованно.
-
Если
,
то использование регрессионной модели
возможно, но после оценивания параметров
модель подлежит дальнейшему многостороннему
статистическому анализу. -
Если
,
то будем. считать, что у нас есть основания
для использования регрессионной модели
при анализе поведения переменной.
2.6.2 Средняя ошибка аппроксимации.
Другой
показатель качества построенной модели
–– среднее относительное отклонение
расчетных значений от фактических или
средняя
ошибка аппроксимации:
.
Построенное
уравнение регрессии считается
удовлетворительным, если значение
не превышает 10% – 12% .
3. Пример.
По
21 региону страны изучается зависимость
розничной продажи телевизоров ()
от среднедушевого денежного дохода в
месяц ().
|
Номер региона |
Среднедушевой |
Объем |
|
1 |
2 |
28 |
|
2 |
2,4 |
21,3 |
|
3 |
2,1 |
21 |
|
4 |
2,6 |
23,3 |
|
5 |
1,7 |
15,8 |
|
6 |
2,5 |
21,9 |
|
7 |
2,4 |
20 |
|
8 |
2,6 |
22 |
|
9 |
2,8 |
23,9 |
|
10 |
2,6 |
26 |
|
11 |
2,6 |
24,6 |
|
12 |
2,5 |
21 |
|
13 |
2,9 |
27 |
|
14 |
2,6 |
21 |
|
15 |
2,2 |
24 |
|
16 |
2,6 |
24 |
|
17 |
3,3 |
31,9 |
|
18 |
3,9 |
33 |
|
19 |
4 |
35,4 |
|
20 |
3,7 |
34 |
|
21 |
3,4 |
31 |
Необходимо
найти зависимость, наилучшим образом
отражающую связь между переменными
и
.
Рассмотрим вопрос
применения модели линейной регрессии
в этой задаче.
Построим
поле корреляции, т.е. нанесем исходные
данные на координатную плоскость. Для
этого воспользуемся, например,
возможностями MS
Excel
2003.
Подготовим таблицу
исходных данных.
Нанесем на
координатную плоскость исходные данные:
Характер
расположения точек на графике дает нам
основание предположить, что искомая
функция регрессии линейная:
.
Для оценки коэффициентов уравнения
регрессии необходимо составить и решить
систему нормальных уравнений ( ).
По исходным данным
рассчитываем необходимые суммы:
|
Номер региона |
|
|
|
|
|
|
1 |
2 |
28 |
56 |
4 |
784 |
|
2 |
2,4 |
21,3 |
51,12 |
5,76 |
453,69 |
|
3 |
2,1 |
21 |
44,1 |
4,41 |
441 |
|
4 |
2,6 |
23,3 |
60,58 |
6,76 |
542,89 |
|
5 |
1,7 |
15,8 |
26,86 |
2,89 |
249,64 |
|
6 |
2,5 |
21,9 |
54,75 |
6,25 |
479,61 |
|
7 |
2,4 |
20 |
48 |
5,76 |
400 |
|
8 |
2,6 |
22 |
57,2 |
6,76 |
484 |
|
9 |
2,8 |
23,9 |
66,92 |
7,84 |
571,21 |
|
10 |
2,6 |
26 |
67,6 |
6,76 |
676 |
|
11 |
2,6 |
24,6 |
63,96 |
6,76 |
605,16 |
|
12 |
2,5 |
21 |
52,5 |
6,25 |
441 |
|
13 |
2,9 |
27 |
78,3 |
8,41 |
729 |
|
14 |
2,6 |
21 |
54,6 |
6,76 |
441 |
|
15 |
2,2 |
24 |
52,8 |
4,84 |
576 |
|
16 |
2,6 |
24 |
62,4 |
6,76 |
576 |
|
17 |
3,3 |
31,9 |
105,27 |
10,89 |
1017,61 |
|
18 |
3,9 |
33 |
128,7 |
15,21 |
1089 |
|
19 |
4 |
35,4 |
141,6 |
16 |
1253,16 |
|
20 |
3,7 |
34 |
125,8 |
13,69 |
1156 |
|
21 |
3,4 |
31 |
105,4 |
11,56 |
961 |
|
Сумма |
57,4 |
530,1 |
1504,46 |
164,32 |
13926,97 |
Составляем систему
уравнений:
Имеем систему
линейных алгебраических уравнений,
которая может быть решена, например, по
формулам Крамера. Для этого вычислим
следующие определители:
Тогда, согласно
теореме Крамера,
Получаем уравнение
регрессии:
Величина
коэффициента регрессии
означает, что увеличение среднедушевого
месячного дохода на 1 тыс. руб. приведет
к увеличение объема розничной продажи
в среднем на 7 540 телевизоров. Коэффициентв данном случае не имеет содержательной
интерпретации.
Оценим тесноту
линейной связи между переменными и
качество построенной модели в целом.
Для оценки тесноты
линейной зависимости рассчитаем
коэффициент детерминации. Для этого
необходимо провести ряд дополнительных
вычислений.
Прежде
всего, найдем выборочное
среднее
по формуле:
.
Для рассматриваемого
примера имеем:
Теперь произведем
расчет остальных вспомогательных
величин:
|
Номер региона |
|
|
|
|
|
|
|
|
1 |
2 |
28 |
19,76 |
8,24 |
67,89 |
2,76 |
7,60 |
|
2 |
2,4 |
21,3 |
22,75 |
-1,45 |
2,11 |
-3,94 |
15,55 |
|
3 |
2,1 |
21 |
20,51 |
0,49 |
0,24 |
-4,24 |
18,00 |
|
4 |
2,6 |
23,3 |
24,25 |
-0,95 |
0,90 |
-1,94 |
3,77 |
|
5 |
1,7 |
15,8 |
17,52 |
-1,72 |
2,95 |
-9,44 |
89,17 |
|
6 |
2,5 |
21,9 |
23,50 |
-1,60 |
2,56 |
-3,34 |
11,17 |
|
7 |
2,4 |
20 |
22,75 |
-2,75 |
7,57 |
-5,24 |
27,49 |
|
8 |
2,6 |
22 |
24,25 |
-2,25 |
5,04 |
-3,24 |
10,52 |
|
9 |
2,8 |
23,9 |
25,74 |
-1,84 |
3,39 |
-1,34 |
1,80 |
|
10 |
2,6 |
26 |
24,25 |
1,75 |
3,08 |
0,76 |
0,57 |
|
11 |
2,6 |
24,6 |
24,25 |
0,35 |
0,13 |
-0,64 |
0,41 |
|
12 |
2,5 |
21 |
23,50 |
-2,50 |
6,24 |
-4,24 |
18,00 |
|
13 |
2,9 |
27 |
26,49 |
0,51 |
0,26 |
1,76 |
3,09 |
|
14 |
2,6 |
21 |
24,25 |
-3,25 |
10,54 |
-4,24 |
18,00 |
|
15 |
2,2 |
24 |
21,26 |
2,74 |
7,53 |
-1,24 |
1,54 |
|
16 |
2,6 |
24 |
24,25 |
-0,25 |
0,06 |
-1,24 |
1,54 |
|
17 |
3,3 |
31,9 |
29,48 |
2,42 |
5,86 |
6,66 |
44,32 |
|
18 |
3,9 |
33 |
33,96 |
-0,96 |
0,93 |
7,76 |
60,17 |
|
19 |
4 |
35,4 |
34,71 |
0,69 |
0,47 |
10,16 |
103,17 |
|
20 |
3,7 |
34 |
32,47 |
1,53 |
2,34 |
8,76 |
76,69 |
|
21 |
3,4 |
31 |
30,23 |
0,77 |
0,60 |
5,76 |
33,14 |
|
Сумма |
57,4 |
530,1 |
130,68 |
545,73 |
Здесь
столбец «»
– это значения,
рассчитанные с помощью построенного
уравнения регрессии, столбцы «»
и– это столбцы, так называемых, «остатков»:
разностей между исходными значениями,
и рассчитанными с помощью уравнения
регрессии,
а также их квадратов, а в последних двух
столбцах – разности между исходными
значениями,
выборочным средним,
а также их квадраты.
Для
вычисления коэффициента детерминации
воспользуемся формулой ( ):
Значение
коэффициента детерминации позволяет
сделать предварительный вывод о том,
что у нас имеются основания использовать
модель линейной регрессии в данной
задаче, поскольку
.
Построим
линию регрессии на корреляционном поле,
для чего добавим на координатной
плоскости точки, соответствующие
уравнению регрессии ().
Нанесем
теперь уравнение регрессии на диаграмму,
используя специальные средства Excel.
Для этого необходимо выделить правой
кнопкой мыши исходные точки и выбрать
опцию Добавить
линию тренда.
В
открывшемся меню Параметры
линии тренда
выбрать Линейную
аппроксимацию.
Далее поставить флажок напротив полей
Показывать
уравнение на диаграмме
и Поместить
на диаграмму величину достоверности
аппроксимации .
Нажав
на ОК, получаем еще одну прямую на
диаграмме, которая совпадает с построенными
ранее точками линии регрессии:
Сплошная
черная линия на диаграмме – это линия
регрессии, рассчитанная средствами
Excel.
Линия регрессии, построенная нами ранее,
совпала с данной линией регрессии.
Нетрудно убедиться, что уравнение
регрессии и коэффициент детерминации
тоже совпадают с полученными ранее
вручную.
Найдем
теперь среднюю ошибку аппроксимации
для оценки погрешности модели. Для этого
нам потребуется вычислить еще ряд
промежуточных величин:
|
Номер региона |
|
|
|
|
|
|
1 |
2 |
28 |
19,76 |
8,24 |
0,29 |
|
2 |
2,4 |
21,3 |
22,75 |
-1,45 |
0,07 |
|
3 |
2,1 |
21 |
20,51 |
0,49 |
0,02 |
|
4 |
2,6 |
23,3 |
24,25 |
-0,95 |
0,04 |
|
5 |
1,7 |
15,8 |
17,52 |
-1,72 |
0,11 |
|
6 |
2,5 |
21,9 |
23,50 |
-1,60 |
0,07 |
|
7 |
2,4 |
20 |
22,75 |
-2,75 |
0,14 |
|
8 |
2,6 |
22 |
24,25 |
-2,25 |
0,10 |
|
9 |
2,8 |
23,9 |
25,74 |
-1,84 |
0,08 |
|
10 |
2,6 |
26 |
24,25 |
1,75 |
0,07 |
|
11 |
2,6 |
24,6 |
24,25 |
0,35 |
0,01 |
|
12 |
2,5 |
21 |
23,50 |
-2,50 |
0,12 |
|
13 |
2,9 |
27 |
26,49 |
0,51 |
0,02 |
|
14 |
2,6 |
21 |
24,25 |
-3,25 |
0,15 |
|
15 |
2,2 |
24 |
21,26 |
2,74 |
0,11 |
|
16 |
2,6 |
24 |
24,25 |
-0,25 |
0,01 |
|
17 |
3,3 |
31,9 |
29,48 |
2,42 |
0,08 |
|
18 |
3,9 |
33 |
33,96 |
-0,97 |
0,03 |
|
19 |
4 |
35,4 |
34,71 |
0,69 |
0,02 |
|
20 |
3,7 |
34 |
32,47 |
1,53 |
0,05 |
|
21 |
3,4 |
31 |
30,23 |
0,77 |
0,02 |
Здесь
столбец «»
– это значения,
рассчитанные с помощью построенного
уравнения регрессии, столбец «»
– это столбец так называемых «остатков»:
разностей между исходными значениями,
и рассчитанными с помощью уравнения
регрессии,
и, наконец, последний столбец «
»
– это вспомогательный столбец для
вычисления элементов суммы по формуле
( ). Просуммируем теперь элементы
последнего столбца и разделим полученную
сумму на 21 – общее количество исходных
данных:
.
Переведем это
число в проценты и запишем окончательное
выражение для средней ошибки аппроксимации:
.
Итак,
средняя ошибка аппроксимации оказалась
около 8%, что говорит о небольшой
погрешности построенной модели. Данную
модель, с учетом неплохих характеристик
ее качества, вполне можно использовать
для прогноза – одной из основных целей
эконометрического анализа. Предположим,
что среднедушевой месячный доход в
одном из регионов составит 4,1 тыс. руб.
Оценим, каков будет уровень продаж
телевизоров в этом регионе согласно
построенной модели? Для этого необходимо
выбранное значение фактора
подставить в уравнение регрессии (
):
(тыс.
руб.),
т.е. при таком
уровне дохода, розничная продажа
телевизоров составит, в среднем, 35 480
телевизоров.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Парная линейная регрессия и метод наименьших квадратов (МНК)
Краткая теория
Простейшей системой
корреляционной связи является линейная связь между двумя признаками — парная
линейная корреляция. Практическое значение ее в том, что есть системы, в
которых среди всех факторов, влияющих на результативный признак, выделяется
один важнейший фактор, который в основном определяет вариацию результативного
признака. Измерение парных корреляций составляет необходимый этап в изучении
сложных, многофакторных связей. Есть такие системы связей, при изучении которых
следует предпочесть парную корреляцию. Внимание к линейным связям объясняется
ограниченной вариацией переменных и тем, что в большинстве случаев нелинейные
формы связей для выполнения расчетов преобразуются в линейную форму.
Уравнение парной линейной
корреляционной связи называется уравнением парной регрессии и имеет вид:
где
–
среднее значение результативного признака
при
определенном значении факторного признака
;
– свободный
член уравнения;
– коэффициент
регрессии, измеряющий среднее отношение отклонения результативного признака от
его средней величины к отклонению факторного признака от его средней величины
на одну единицу его измерения – вариация
, приходящаяся на единицу вариации
.
Параметры уравнения
находят
методом наименьших квадратов (метод решения систем уравнений, при котором в
качестве решения принимается точка минимума суммы квадратов отклонений), то
есть в основу этого метода положено требование минимальности сумм квадратов
отклонений эмпирических данных
от
выровненных
:
Для нахождения минимума
данной функции приравняем к нулю ее частные производные.
В результате получим
систему двух линейных уравнений, которая называется системой нормальных
уравнений:
Решая эту систему в общем
виде, получим:
Параметры уравнения парной
линейной регрессии иногда удобно исчислять по следующим формулам, дающим тот же
результат:
или
Если
коэффициент линейной корреляции
уже
рассчитан, то легко может быть найден коэффициент
парной
регрессии:
где
,
– стандартные
отклонения.
Примеры решения задач
Задача 1
Имеются следующие данные о
цене на нефть
(ден.
ед.) и индексе акций нефтяных компаний
(усл.
ед.).
| Цена на нефть (ден. ед.) | 17,28 | 17,05 | 18,30 | 18,80 | 19,20 | 18,50 |
| Индекс акций (усл. ед.) | 537 | 534 | 550 | 555 | 560 | 552 |
- Построить
корреляционное поле. - Предполагая, что между
переменными x и y существует линейная зависимость, найти уравнение линейной
регрессии - Оценить тесноту связи.
Решение
Построим корреляционное
поле, для этого отметим в системе координат
6 точек, соответствующих данным парам значений этих признаков.
Корреляционное поле и линия регрессии
Расположение точек на
рисунке показывает, что зависимость между компонентами
и
двумерной дискретной случайной величины может
выражаться линейным уравнением регрессии
.
Составим
расчетную таблицу:
Расчетная вспомогательная таблица
|
|
|
|
|
|
|
| 1 | 17,28 | 537 | 298,5984 | 288369 | 9279,36 |
| 2 | 17,05 | 534 | 290,7025 | 285156 | 9104,7 |
| 3 | 18,3 | 550 | 334,89 | 302500 | 10065 |
| 4 | 18,8 | 555 | 353,44 | 308025 | 10434 |
| 5 | 19,2 | 560 | 368,64 | 313600 | 10752 |
| 6 | 18,5 | 552 | 342,25 | 304704 | 10212 |
| Сумма | 109,13 | 3288 | 1988,521 | 1802354 | 59847,06 |
Коэффициенты
уравнения регрессии
можно найти методом наименьших квадратов,
решив систему нормальных уравнений:
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Подставляя
в систему уравнений числовые значения, получаем:
Решая
систему уравнений, получаем:
Уравнение
парной линейной регрессии:
Коэффициент линейной корреляции
вычислим по формуле:
Вывод
Таким
образом уравнение линейной регрессии, устанавливающее зависимость между ценой
на нефть и индексом акций имеет вид
— с увеличением цены на нефть на 1 ден.ед.
цена акций увеличивается на 12,078 ед. Коэффициент корреляции очень близок к
единице — между исследуемыми величинами существует очень тесная связь.
Задача 2
По
территории региона приводятся данные за 2011 г.
Требуется:
-
Построить линейное уравнение парной регрессии
от
.
Рассчитать линейный коэффициент парной корреляции и среднюю ошибку
аппроксимации.
Оценить статистическую значимость параметров регрессии и корреляции с помощью
–критерия Фишера и
–критерия Стьюдента.
Выполнить прогноз заработной платы
при прогнозном значении среднедушевого
прожиточного минимума
, составляющем
107% от среднего уровня.
Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный
интервал.
На одном графике построить исходные данные и теоретическую прямую.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Уравнение линейной парной регрессии
1)
Для расчета параметров уравнения линейной регрессии строим расчетную таблицу:
Получено
уравнение линейной регрессии
Вывод
С
увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная
заработная плата возрастает в среднем на 1.012 руб.
Коэффициент линейной корреляции
2)
Теснота линейной связи оценивается с помощью
коэффициента корреляции
:
Коэффициент
детерминации:
Вывод
Это
означает, что 69.2% вариации заработной платы
объясняется вариацией фактора
–среднедушевого прожиточного минимума.
Средняя ошибка аппроксимации
Качество
модели можно оценить с помощью средней ошибки аппроксимации:
Вывод
Качество
построенной модели оценивается как хорошее, так как средняя ошибка
аппроксимации не превышает 8-10%.
F-критерий
3)
Рассчитаем
– критерий.
По таблице F-распределения Фишера-Снедекора, при уровне значимости α=0,05 и числе степеней свободы k1=1 и k2=12-2=10, критическое значение:
Вывод
– гипотеза о статистической незначимости
уравнения регрессии отклоняется.
Статистическая значимость параметров регрессии
Оценку
статистической значимости параметров регрессии проведем с помощью
t–статистики Стьюдента
и путем расчета
доверительного интервала каждого из показателей.
Выдвигаем
гипотезу
о статистически незначимом отличии показателей
от нуля:
для числа степеней свободы
и
составит 2,23
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Определим
случайные ошибки
Тогда:
Фактическое значение превосходит
табличное значение t–статистики.
Нулевая
гипотеза отклоняется – то есть
не случайно отличается от нуля, а
статистически значимо.
Фактическое значение превосходит
табличное значение t–статистики. Нулевая
гипотеза отклоняется – то есть
не случайно отличается от нуля, а
статистически значимо.
Фактическое значение превосходит
табличное значение t–статистики. Нулевая
гипотеза отклоняется – то есть
не случайно отличается от нуля, а
статистически значимо.
Рассчитаем
доверительные интервалы для параметров регрессии
и
. Для этого
определим предельную ошибку для каждого показателя:
Доверительные
интервалы:
или
или
Точечный прогноз
4)
Полученные оценки уравнения регрессии позволяют использовать его для прогноза.
Если прогнозное значение прожиточного минимума составит
руб., тогда прогнозное значение среднедневной
заработной платы составит:
Интервальный прогноз
5)
Ошибка прогноза составит:
Предельная
ошибка прогноза, которая в 95% случаев не будет превышена, составит:
Доверительный
интервал прогноза:
6) Построим исходные данные
и теоретическую прямую:
Корреляционное поле и прямая уравнения регрессии
Метод наименьших квадратов (МНК) заключается в том, что сумма квадратов отклонений значений y от полученного уравнения регрессии — минимальное. Уравнение линейной регрессии имеет вид
y=ax+b
a, b – коэффициенты линейного уравнения регрессии;
x – независимая переменная;
y – зависимая переменная.
Нахождения коэффициентов уравнения линейной регрессии через метод наименьших квадратов:
частные производные функции приравниваем к нулю
отсюда получаем систему линейных уравнений
Формулы определения коэффициентов уравнения линейной регрессии:
Также запишем уравнение регрессии для квадратной нелинейной функции:
Система линейных уравнений регрессии полинома n-ого порядка:
Формула коэффициента детерминации R2:
Формула средней ошибки аппроксимации для уравнения линейной регрессии (оценка качества модели):
Чем меньше ε, тем лучше. Рекомендованный показатель ε<10%
Формула среднеквадратической погрешности:
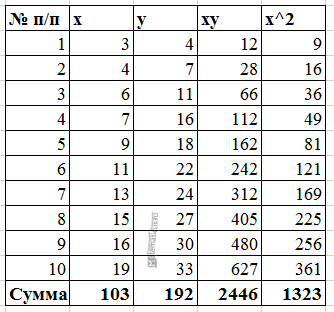
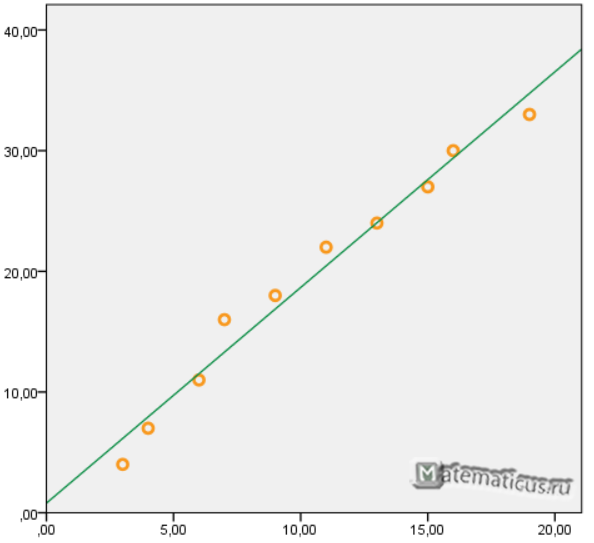
Для примера, проведём расчет для получения линейного уравнения регрессии аппроксимации функции, заданной в табличном виде:
| x | y |
| 3 | 4 |
| 4 | 7 |
| 6 | 11 |
| 7 | 16 |
| 9 | 18 |
| 11 | 22 |
| 13 | 24 |
| 15 | 27 |
| 16 | 30 |
| 19 | 33 |
Решение
Расчеты значений суммы, произведения x и у приведены в таблицы.
Расчет коэффициентов линейной регрессии:
при этом средняя ошибка аппроксимации равна:
ε=11,168%
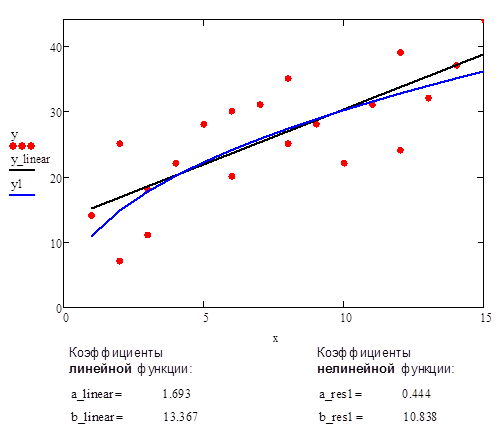
Получаем уравнение линейной регрессии с помощью метода наименьших квадратов:
y=1,7871x+0,79
График функции линейной зависимости y=1,7871x+0,79 и табличные значения, в виде точек
Коэффициент корреляции равен 0,988
Коэффициента детерминации равен 0,976
17630
Имеются следующие данные разных стран об индексе розничных цен на продукты питания (х) и об индексе промышленного производства (у).
| Индекс розничных цен на продукты питания (х) | Индекс промышленного производства (у) | |
|---|---|---|
| 1 | 100 | 70 |
| 2 | 105 | 79 |
| 3 | 108 | 85 |
| 4 | 113 | 84 |
| 5 | 118 | 85 |
| 6 | 118 | 85 |
| 7 | 110 | 96 |
| 8 | 115 | 99 |
| 9 | 119 | 100 |
| 10 | 118 | 98 |
| 11 | 120 | 99 |
| 12 | 124 | 102 |
| 13 | 129 | 105 |
| 14 | 132 | 112 |
Требуется:
1. Для характеристики зависимости у от х рассчитать параметры следующих функций:
А) линейной;
Б) степенной;
В) равносторонней гиперболы.
2. Для каждой модели рассчитать показатели: тесноты связи и среднюю ошибку аппроксимации.
3. Оценить статистическую значимость параметров регрессии и корреляции.
4. Выполнить прогноз значения индекса промышленного производства у при прогнозном значении индекса розничных цен на продукты питания х=138.
Решение:
1. Для расчёта параметров линейной регрессии
Решаем систему нормальных уравнений относительно a и b:
Построим таблицу расчётных данных, как показано в таблице 1.
Таблица 1 Расчетные данные для оценки линейной регрессии
| № п/п | х | у | ху | x2 | y2 |  |
 |
|---|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 7000 | 10000 | 4900 | 74,26340 | 0,060906 |
| 2 | 105 | 79 | 8295 | 11025 | 6241 | 79,92527 | 0,011712 |
| 3 | 108 | 85 | 9180 | 11664 | 7225 | 83,32238 | 0,019737 |
| 4 | 113 | 84 | 9492 | 12769 | 7056 | 88,98425 | 0,059336 |
| 5 | 118 | 85 | 10030 | 13924 | 7225 | 94,64611 | 0,113484 |
| 6 | 118 | 85 | 10030 | 13924 | 7225 | 94,64611 | 0,113484 |
| 7 | 110 | 96 | 10560 | 12100 | 9216 | 85,58713 | 0,108467 |
| 8 | 115 | 99 | 11385 | 13225 | 9801 | 91,24900 | 0,078293 |
| 9 | 119 | 100 | 11900 | 14161 | 10000 | 95,77849 | 0,042215 |
| 10 | 118 | 98 | 11564 | 13924 | 9604 | 94,64611 | 0,034223 |
| 11 | 120 | 99 | 11880 | 14400 | 9801 | 96,91086 | 0,021102 |
| 12 | 124 | 102 | 12648 | 15376 | 10404 | 101,4404 | 0,005487 |
| 13 | 129 | 105 | 13545 | 16641 | 11025 | 107,1022 | 0,020021 |
| 14 | 132 | 112 | 14784 | 17424 | 12544 | 110,4993 | 0,013399 |
| Итого: | 1629 | 1299 | 152293 | 190557 | 122267 | 1299,001 | 0,701866 |
| Среднее значение: | 116,3571 | 92,78571 | 10878,07 | 13611,21 | 8733,357 | х | х |
 |
8,4988 | 11,1431 | х | х | х | х | х |
 |
72,23 | 124,17 | х | х | х | х | х |
Среднее значение определим по формуле:
Cреднее квадратическое отклонение рассчитаем по формуле:
и занесём полученный результат в таблицу 1.
Возведя в квадрат полученное значение получим дисперсию:
Параметры уравнения можно определить также и по формулам:
Таким образом, уравнение регрессии:
Следовательно, с увеличением индекса розничных цен на продукты питания на 1, индекс промышленного производства увеличивается в среднем на 1,13.
Рассчитаем линейный коэффициент парной корреляции:
Связь прямая, достаточно тесная.
Определим коэффициент детерминации:
Вариация результата на 74,59% объясняется вариацией фактора х.
Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчётные) значения 
Так как
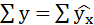
следовательно, параметры уравнения определены правильно.
Рассчитаем среднюю ошибку аппроксимации – среднее отклонение расчётных значений от фактических:
В среднем расчётные значения отклоняются от фактических на 5,01%.
Оценку качества уравнения регрессии проведём с помощью F-теста.
F-тест состоит в проверке гипотезы Н0 о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fфакт и критического (табличного) Fтабл значений F-критерия Фишера.
Fфакт определяется по формуле:
где n – число единиц совокупности;
m – число параметров при переменных х.
Таким образом, Н0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.
Полученные оценки уравнения регрессии позволяют использовать его для прогноза.
Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:
2. Степенная регрессия имеет вид:
Для определения параметров производят логарифмирование степенной функции:
Для определения параметров логарифмической функции строят систему нормальных уравнений по способу наименьших квадратов:
Построим таблицу расчётных данных, как показано в таблице 2.
Таблица 2 Расчетные данные для оценки степенной регрессии
| №п/п | х | у | lg x | lg y | lg x*lg y | (lg x)2 | (lg y)2 |
|---|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 2,000000 | 1,845098 | 3,690196 | 4,000000 | 3,404387 |
| 2 | 105 | 79 | 2,021189 | 1,897627 | 3,835464 | 4,085206 | 3,600989 |
| 3 | 108 | 85 | 2,033424 | 1,929419 | 3,923326 | 4,134812 | 3,722657 |
| 4 | 113 | 84 | 2,053078 | 1,924279 | 3,950696 | 4,215131 | 3,702851 |
| 5 | 118 | 85 | 2,071882 | 1,929419 | 3,997528 | 4,292695 | 3,722657 |
| 6 | 118 | 85 | 2,071882 | 1,929419 | 3,997528 | 4,292695 | 3,722657 |
| 7 | 110 | 96 | 2,041393 | 1,982271 | 4,046594 | 4,167284 | 3,929399 |
| 8 | 115 | 99 | 2,060698 | 1,995635 | 4,112401 | 4,246476 | 3,982560 |
| 9 | 119 | 100 | 2,075547 | 2,000000 | 4,151094 | 4,307895 | 4,000000 |
| 10 | 118 | 98 | 2,071882 | 1,991226 | 4,125585 | 4,292695 | 3,964981 |
| 11 | 120 | 99 | 2,079181 | 1,995635 | 4,149287 | 4,322995 | 3,982560 |
| 12 | 124 | 102 | 2,093422 | 2,008600 | 4,204847 | 4,382414 | 4,034475 |
| 13 | 129 | 105 | 2,110590 | 2,021189 | 4,265901 | 4,454589 | 4,085206 |
| 14 | 132 | 112 | 2,120574 | 2,049218 | 4,345518 | 4,496834 | 4,199295 |
| Итого | 1629 | 1299 | 28,90474 | 27,49904 | 56,79597 | 59,69172 | 54,05467 |
| Среднее значение | 116,3571 | 92,78571 | 2,064624 | 1,964217 | 4,056855 | 4,263694 | 3,861048 |
 |
8,4988 | 11,1431 | 0,031945 | 0,053853 | х | х | х |
 |
72,23 | 124,17 | 0,001021 | 0,0029 | х | х | х |
Продолжение таблицы 2 Расчетные данные для оценки степенной регрессии
| №п/п | х | у |  |
 |
 |
 |
|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 74,16448 | 17,34292 | 0,059493 | 519,1886 |
| 2 | 105 | 79 | 79,62057 | 0,385112 | 0,007855 | 190,0458 |
| 3 | 108 | 85 | 82,95180 | 4,195133 | 0,024096 | 60,61728 |
| 4 | 113 | 84 | 88,59768 | 21,13866 | 0,054734 | 77,1887 |
| 5 | 118 | 85 | 94,35840 | 87,57961 | 0,110099 | 60,61728 |
| 6 | 118 | 85 | 94,35840 | 87,57961 | 0,110099 | 60,61728 |
| 7 | 110 | 96 | 85,19619 | 116,7223 | 0,11254 | 10,33166 |
| 8 | 115 | 99 | 90,88834 | 65,79901 | 0,081936 | 38,6174 |
| 9 | 119 | 100 | 95,52408 | 20,03384 | 0,044759 | 52,04598 |
| 10 | 118 | 98 | 94,35840 | 13,26127 | 0,037159 | 27,18882 |
| 11 | 120 | 99 | 96,69423 | 5,316563 | 0,023291 | 38,6174 |
| 12 | 124 | 102 | 101,4191 | 0,337467 | 0,005695 | 84,90314 |
| 13 | 129 | 105 | 107,4232 | 5,872099 | 0,023078 | 149,1889 |
| 14 | 132 | 112 | 111,0772 | 0,85163 | 0,00824 | 369,1889 |
| Итого | 1629 | 1299 | 1296,632 | 446,4152 | 0,703074 | 1738,357 |
| Среднее значение | 116,3571 | 92,78571 | х | х | х | х |
 |
8,4988 | 11,1431 | х | х | х | х |
 |
72,23 | 124,17 | х | х | х | х |
Решая систему нормальных уравнений, определяем параметры логарифмической функции.
Получим линейное уравнение:
Выполнив его потенцирование, получим:
Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата 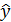
Связь достаточно тесная.
В среднем расчётные значения отклоняются от фактических на 5,02%.
Таким образом, Н0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.
Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:
3. Уравнение равносторонней гиперболы
Для определения параметров этого уравнения используется система нормальных уравнений:
Произведем замену переменных
и получим следующую систему нормальных уравнений:
Решая систему нормальных уравнений, определяем параметры гиперболы.
Составим таблицу расчётных данных, как показано в таблице 3.
Таблица 3 Расчетные данные для оценки гиперболической зависимости
| №п/п | х | у | z | yz | 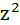 |
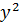 |
|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 0,010000000 | 0,700000 | 0,0001000 | 4900 |
| 2 | 105 | 79 | 0,009523810 | 0,752381 | 0,0000907 | 6241 |
| 3 | 108 | 85 | 0,009259259 | 0,787037 | 0,0000857 | 7225 |
| 4 | 113 | 84 | 0,008849558 | 0,743363 | 0,0000783 | 7056 |
| 5 | 118 | 85 | 0,008474576 | 0,720339 | 0,0000718 | 7225 |
| 6 | 118 | 85 | 0,008474576 | 0,720339 | 0,0000718 | 7225 |
| 7 | 110 | 96 | 0,009090909 | 0,872727 | 0,0000826 | 9216 |
| 8 | 115 | 99 | 0,008695652 | 0,860870 | 0,0000756 | 9801 |
| 9 | 119 | 100 | 0,008403361 | 0,840336 | 0,0000706 | 10000 |
| 10 | 118 | 98 | 0,008474576 | 0,830508 | 0,0000718 | 9604 |
| 11 | 120 | 99 | 0,008333333 | 0,825000 | 0,0000694 | 9801 |
| 12 | 124 | 102 | 0,008064516 | 0,822581 | 0,0000650 | 10404 |
| 13 | 129 | 105 | 0,007751938 | 0,813953 | 0,0000601 | 11025 |
| 14 | 132 | 112 | 0,007575758 | 0,848485 | 0,0000574 | 12544 |
| Итого: | 1629 | 1299 | 0,120971823 | 11,13792 | 0,0010510 | 122267 |
| Среднее значение: | 116,3571 | 92,78571 | 0,008640844 | 0,795566 | 0,0000751 | 8733,357 |
 |
8,4988 | 11,1431 | 0,000640820 | х | х | х |
 |
72,23 | 124,17 | 0,000000411 | х | х | х |
Продолжение таблицы 3 Расчетные данные для оценки гиперболической зависимости
| №п/п | х | у |  |
 |
 |
 |
|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 72,3262 | 0,033231 | 5,411206 | 519,1886 |
| 2 | 105 | 79 | 79,49405 | 0,006254 | 0,244083 | 190,0458 |
| 3 | 108 | 85 | 83,47619 | 0,017927 | 2,322012 | 60,61728 |
| 4 | 113 | 84 | 89,64321 | 0,067181 | 31,84585 | 77,1887 |
| 5 | 118 | 85 | 95,28761 | 0,121031 | 105,8349 | 60,61728 |
| 6 | 118 | 85 | 95,28761 | 0,121031 | 105,8349 | 60,61728 |
| 7 | 110 | 96 | 86,01027 | 0,10406 | 99,79465 | 10,33166 |
| 8 | 115 | 99 | 91,95987 | 0,071112 | 49,56344 | 38,6174 |
| 9 | 119 | 100 | 96,35957 | 0,036404 | 13,25272 | 52,04598 |
| 10 | 118 | 98 | 95,28761 | 0,027677 | 7,357059 | 27,18882 |
| 11 | 120 | 99 | 97,41367 | 0,016024 | 2,516453 | 38,6174 |
| 12 | 124 | 102 | 101,46 | 0,005294 | 0,291565 | 84,90314 |
| 13 | 129 | 105 | 106,1651 | 0,011096 | 1,357478 | 149,1889 |
| 14 | 132 | 112 | 108,8171 | 0,028419 | 10,1311 | 369,1889 |
| Итого: | 1629 | 1299 | 1298,988 | 0,666742 | 435,7575 | 1738,357 |
| Среднее значение: | 116,3571 | 92,78571 | х | х | х | х |
 |
8,4988 | 11,1431 | х | х | х | х |
 |
72,23 | 124,17 | х | х | х | х |
Значения параметров регрессии a и b составили:
Получено уравнение:
Индекс корреляции:
Связь достаточно тесная.
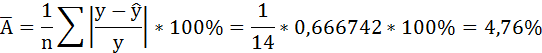
В среднем расчётные значения отклоняются от фактических на 4,76%.
Таким образом, Н0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.
Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:
По уравнению равносторонней гиперболы получена наибольшая оценка тесноты связи по сравнению с линейной и степенной регрессиями. Средняя ошибка аппроксимации остаётся на допустимом уровне.