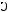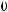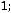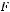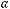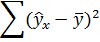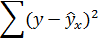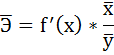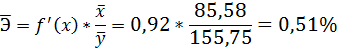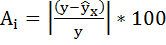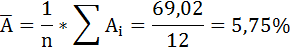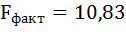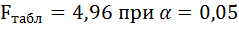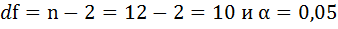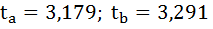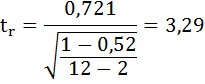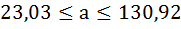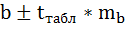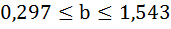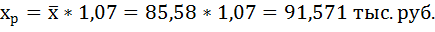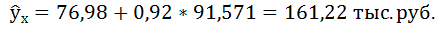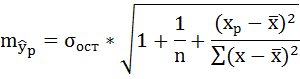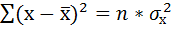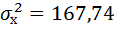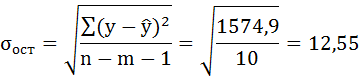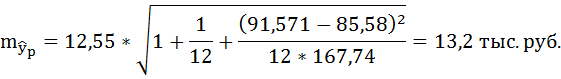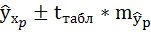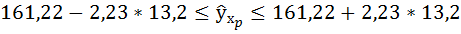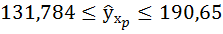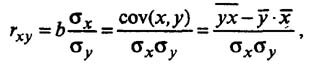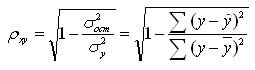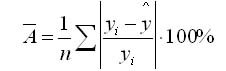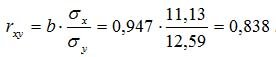В пустые столбцы (последние два) необходимо вставить из основной таблицы теоретически рассчитанные по уравнению регрессии значения переменной YY, и значения переменной x. В результате получим таблицу, изображенную на рис. 2.24.
Закроем эту таблицу. В результате на диаграмме рассеяния появится новый график (рис. 2.25)
|
Рис. 2.24. Редактирование данных графика |
Рис. 2.25. Вид диаграммы рассеяния |
|
с добавленной линией регрессии |
Щелкнув правой кнопкой мыши на какой-либо точке нового графика, и выбрав в выпадающем меню команду Свойства графика, можем отредактировать его вид (рис. 2.26): изменить тип, размер и цвет меток и линий, включить легенду и др.
Рис. 2.26. Окно редактирования вида графика
9.Постройте доверительную область для линии регрессии.
Для построения доверительной области линии регрессии введем в исходную таблицу дополнительно три столбца: для вычисления ошибки регрессии Sp, нижней доверительной границы y_low и верхней доверительной границы y_hight.
На рис. 2.27 приводится пример определения переменной Sp – ошибки среднего предсказанного значения:
44
Среднее значение переменной x и ее дисперсия взяты из таблицы описательных статистик (п.2). Стандартная ошибка регрессии выдается в таблице итогов регрессии Se=2,29497.
Рис. 2.27. Расчет ошибки для линии регрессии
Нижняя и верхняя границы среднего предсказанного значения (доверительные границы регрессии) опре-
|
деляются по формулам |
и |
. В результате получим таблицу, пока- |
||
|
занную на рис. 2.28 (без последнего столбца). |
Рис. 2.28. Вид таблицы с добавленными столбцами – доверительными границами линии регрессии
Для построения доверительных границ на диаграмме рассеяния, воспользуемся тем же алгоритмом, что и для добавления линии регрессии (рис.2.22 -2.26). Результат показан на рис. 2.29.
45
Рис. 2.29. Диаграмма рассеяния с линией регрессии
иее доверительным интервалом
10.Оцените качество построенной модели через среднюю относительную ошибку аппроксимации. Определите среднеквадратическую ошибку модели.
Для расчета относительной ошибки аппроксимации и среднеквадратической ошибки добавим новые переменные в исходную таблицу – МАРЕ (рис. 2.30) и MSE. Они вычисляются по формулам:
Результаты определения новой переменной МАРЕ, приводятся на рис. 2.28 (последний столбец).
Рис. 2.30. Определение переменной для расчета относительной ошибки аппроксимации
46
Аналогично определим и переменную MSE. Обратим внимание, что в формулах мы вводим только выражение стоящее под знаком суммы.
Остается вычислить среднее значение по столбцам. Для этого щелкнем правой кнопкой мыши на названиях столбцов и в выпадающем меню выполним последовательно команды Блоковые статистики→По столбцу → Среднее (рис.2.31).
Рис. 2.31. Меню расчета блоковых статистик
В результате появится дополнительная строка, в которой вычислены среднее значение по столбцам, т.е. искомые характеристики – средняя относительная ошибка аппроксимации MAPE и средняя квадратическая ошибка MSE. Получили МАРЕ = 2,99% (рис. 2.32). Эта величина меньше 10%, следовательно, точность модели высокая. MSE=3,7621. Эти характеристики будут использоваться для сравнения с нелинейной моделью регрессии. Чем меньше эти обе ошибки, тем точнее считается построенная модель.
Рис. 2.32. Таблица данных с вычисленными ошибками MAPE и MSE
11. Определите средний коэффициент эластичности.
Средний коэффициент эластичности переменной y по переменной x можно вычислить, зная коэффициент b1 и средние значения переменных x и y:
Cредний коэффициент эластичности 
показывает, что при увеличении среднемесячной заработной платы (x) на 1% доля расходов на питание (y) уменьшится (знак «минус») на 0,59%.
12. Дайте экономическую интерпретацию построенной модели.
47
Уравнение регрессии является достаточно точным. Относительная ошибка аппроксимации составляет всего 3% (МАРЕ=2, 99%). Коэффициент b1= -5,51987 показывает, что при увеличении x – среднемесячной заработной платы на одну тысячу доля расходов на питание — переменная y – в среднем уменьшается на 5,5%. Построенное уравнение регрессии на 89% объясняет поведение зависимой переменной y (показатель R2=0,8876). Средний ко-
эффициент эластичности 
говорит о том, что увеличение средней заработной платы на 1% приведет к уменьшению доли расходов на питание на 0,59%. В целом модель адекватна исходным данным и может применяться для прогноза.
************************ Нелинейная модель парной регрессии ************************
13. Рассчитайте параметры одной из функций регрессии в соответствии с выдвинутой гипотезой (п.2).
Нами было выдвинуто предположение, о том, что нелинейная регрессия может иметь форму степенной, экспоненциальной или гиперболической функции. Рассмотрим для примера степенную модель:
Эту модель можно линеаризовать, прологарифмировав обе части равенства:
.
|
Введем обозначения |
Тогда последнее уравнение примет линейный |
вид:
Организуем новую таблицу для расчетов параметров степенной модели. Для этого выполним команду Файл →Создать или щелкнем на кнопке, изображающей чистый бланк на панели инструментов Стандартная (первая кнопка).
В появившемся диалоговом окне укажем, что создаем таблицу, содержащую 11 переменных и 7 наблюдений. Скопируем из имеющейся таблицы данных значения переменных x и y, рассчитаем в следующих двух столбцах преобразованные переменные 
. В программе Statistica натуральный логарифм вычисляется с помощью встроенной функции Log( ).
Рис. 2.33 Таблица данных для построения нелинейной модели регрессии
В результате получим таблицу, изображенную на рис. 2.33. Если таблица создалась в отдельно расположенном окне, то для удобства работы ее лучше поместить в нашу рабочую книгу. Для этого щелкнем в окне таблицы на ее названии (сделаем окно с таблицей активным) и на панели инструментов Стандартная нажмем кнопку Добавить в рабочую книгу. В раскрывшемся списке выберем имя нашей рабочей книги.
6. Определите параметры уравнения нелинейной регрессии и дайте интерпретацию коэффициентов регрессии.
Определим параметры b0 и b1 линеаризованного уравнения регрессии, используя модуль Множественная регрессия. Для этого выполним команду Анализ → Множественная регрессия. Нажав на кнопку Переменные в стартовом окне модуля, попадем в окно выбора переменных для анализа (рис. 2.14), в котором в качестве зависимой переменной укажем W, а в качестве независимой – Z. Подтвердим ввод переменных в этом окне, и, вернувшись в стартовое окно модуля Множественная регрессия, подтвердим определение модели.
Откроется окно результатов множественной регрессии, подобное изображенному на рис. 2.15.
При нажатии кнопки Итоговая таблица регрессии Ststistica выдает две таблицы с результатами анализа: Итоговые статистики — таблицу, в которой отражены основные показатели из информационного окна; таблицу Итоги регрессии для зависимой переменной: W — значения и характеристики коэффициентов регрессии (рис. 2.34).
48
Рис. 2.34. Итоги регрессии.
Запишем линеаризованное уравнение регрессии, подставив вычисленные коэффициенты:
Коэффициент детерминации R2=0,8876. Это означает, что почти 89% вариации результативного признака W объясняется вариацией признака Z.
Для записи степенной формы уравнения регрессии необходимо вернуться к исходным переменным и параметрам:
Уравнение регрессии примет вид:
Интерпретация коэффициента b1: в степенной модели данный коэффициент является средним коэффициентом эластичности. Он показывает, что при увеличении средней заработной платы на 1% доля расходов на питание уменьшится на 0,57% (вывод формул – см. ниже).
Введем в нашу таблицу дополнительные столбцы – для рассчитанного по уравнению регрессии значения W и значения переменной у. Назовем соответствующие переменные W_t и y_t.
Значения переменной W_t мы можем вычислить по формуле 
Другой способ — скопировать из столбца Предск. значение таблицы Остатки и предсказанные. Для вывода этой таблицы необходимо выполнить следующее: в окне Результаты множественной регрессии перейти на вкладку Остатки/ предсказанные/ наблюдаемые значения, выбрать кнопку Анализ остатков, и в появив-
шемся одноименное окне нажать на кнопку Остатки и предсказанные. Обратите внимание, что последние четыре строки (итоговые статистики) предсказанных значений переменной W копировать не надо (рис. 2.35).
Рис. 2.35. Таблица Предсказанные значения и остатки для степенной модели
49
Значения переменной y_t вычисляются по формуле
Кроме этого для дальнейших расчетов нам понадобится определить ошибку степенной модели и сумму квадратов ошибок. Для этого добавим в нашу таблицу две новые переменные: E1 – для вычисления ошибки модели, и E12 – для вычисления квадрата ошибки.
Результат вставки значений W_t и расчета значений y_t, E1 и E12 представлены на рис. 2.36.
Рис. 2.36. Таблица данных с новыми переменными
7.С вероятностью 0,95 оцените статистическую значимость уравнения регрессии в целом и каждого параметра.
а) Проверим значимость уравнения регрессии в целом.
Проверяемая гипотеза: H0: R2=0; альтернативная гипотеза: H1: R2≠0 . Для линеаризованной модели
коэффициент детерминации 
статистически значим при уровне надежности 0,95%. Это следует из того, что рассчитанное по нашим данным значение F-статистики 
. Нулевая гипотеза отклоняется.
Здесь возникает проблема, описанная в Замечании п. 2.3 (Парная нелинейная регрессия): коэффициент детерминации вычислен для переменных 
, а не для исходных переменных y и x. Для степенной модели необходимо рассчитать индекс детерминации:
Для нахождения средней квадратической ошибки MSE по столбцу Е2 необходимо вычислить блоковую статистику – сумму (рис. 2.36) и поделить вычисленное значение на число наблюдений. В результате получим MSE=2,32355 Дисперсия переменной 
известна (см. Описательные статистики — п.2 задания, рис. 2.7) 
. Тогда индекс детерминации равен
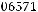
Оценка статистической значимости индекса детерминации осуществляется так же, как и оценка значимости коэффициента детерминации — с помощью F-критерия Фишера с заменой 
на 
:
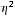
Для нашего примера n=7, p=1 (число факторов), тогда k1=1; k2=7-1-1=7-2=5. Вычисленное значение F- критерия больше 
. Значит гипотеза 
отклоняется. Уравнение в целом значимо.
50
б) Для проверки значимости коэффициентов уравнения регрессии используется t-статистика Стьюдента. Выборочные значения этой статистики для каждого коэффициента представлены в таблице (рис. 2.34) в столбце t(5):
Так как оба значения по модулю больше tкр=t(0,95; n-p-1)=t(0,95; 5)= 2,0128, то оба коэффициента признаются статистически значимыми (отличными от нуля).
8.Отобразите на поле корреляций теоретически рассчитанную линию регрессии.
Для построения поля корреляций выполним команду Графика→ Диаграммы рассеяния. Дальнейшие действия те же, что и в инструкции по выполнению заданий п.3 и п.8 линейной модели регрессии. В результате получим график, изображенный на рис.2.38 (средняя кривая).
9.Постройте доверительную область для линии регрессии.
Для построения доверительной области линии регрессии так же, как и в случае линейной модели, введем в
таблицу три новые переменные: для вычисления ошибки регрессии Sp, нижней доверительной границы y_low и верхней доверительной границы y_hight. Обратите внимание, что стандартная ошибка модели вычисляется по формуле:
Дальнейший алгоритм – такой же, как и для линейной модели регрессии. Расчеты этих переменных приведены на рис. 2.37. Кривая линии регрессии и границы доверительной области изображены на рис. 2.38.
Рис. 2.37. Таблица с вычислением доверительных границ для линии регрессии.
10.Оцените качество построенной модели через среднюю относительную ошибку аппроксимации. Определите среднеквадратическую ошибку модели.
Для вычисления средней ошибки аппроксимации введем в таблицу дополнительный столбец, назовем его MAPE1. Переменную определим так же, как и в случае линейной модели. Вычислив блоковую статистику – среднее по столбцу, получим значение искомой характеристики MAPE1=2,021( рис. 2.33).
Средняя квадратическая ошибка вычислена уже в задании п.7 для степенной модели: MSE=2,32297
11. Определите средний коэффициент эластичности.
Коэффициент эластичности (вообще, а не средний) вычисляется по формуле:
Он же и будет средним коэффициентом эластичности.
51
Рис. 2.38. Диаграмма рассеяния с добавленной линией регрессии
идоверительными границами
12.Дайте экономическую интерпретацию построенной модели.
Уравнение степенной линии регрессии имеет вид:
Параметр b1= — 0,57523 в степенной модели является коэффициентом эластичности, он показывает, что при увеличении средней заработной платы на 1% доля расходов на питание уменьшится на 0,57%.
Показатели качества построенного уравнения регрессии достаточно хорошие. Найденный нами индекс детерминации 
говорит о том, что 94% вариации результативного показателя y объясняется уравнением регрессии.
Средняя относительная ошибка MAPE1=2,021%, что меньше 10% — значит, точность модели – высокая. Средняя квадратическая ошибка MSE=2,32297 – также небольшая величина.
*************************** Конец исследования нелинейной модели регрессии ***********************
***************************************************************************************************
14 Выберете лучшую из моделей (п.5 или п.13), выбор обоснуйте.
Так как обе модели (и линейная, и степенная) являются достаточно точными, то возникают вопросы: какую из моделей лучше использовать, и так ли необходима нелинейная модель.
Выпишем основные характеристики построенных моделей:
|
Модель |
Коэффициент(индекс) |
Средняя |
Средняя |
Результат |
|
детерминации |
квадратическая ошибка |
относительная ошибка |
сравнения |
|
|
R2 ( ) |
MSE |
MAPE, % |
||
|
Линейная |
0,8876 |
3,672 |
2,985 |
|
|
Степенная |
0,9405 |
2,323 |
2,021 |
Лучшая по всем |
|
показателям |
||||
Для ответа на второй вопрос проверим гипотезу о равенстве коэффициента детерминации линейной модели
|
индексу детерминации степенной модели: |
. Для этого в соответствии с алгоритмом, изложенным в п. |
||
|
2.3 — Парная нелинейная регрессия, вычислим ошибку разности |
и t— статистику: |
||
52
Вычисленное с помощью вероятностного калькулятора критическое значение tкр=t(0,95; n)=t(0,95; 7)= 2,36468 больше 
. Значит, гипотеза 
принимается. По качеству модели практически не отличаются. Следовательно, не имеет смысла усложнять модель и можно остановить свой выбор на линейной модели регрессии.
15С вероятностью 0,95 постройте доверительный интервал ожидаемого значения результативного признака в предположении, что значение признака-фактора увеличится на 5% относительно своего среднего уровня.
Определим значение переменной xp, для которого необходимо предсказать по линейной модели значение зависимой переменной
Вернемся в стартовое окно модуля Множественная регрессия, выберем для анализа зависимую переменную y и независимую переменную x.
В окне результатов множественной регрессии перейдем на вкладку Остатки/ предсказанные/наблюдаемые значения. Установим уровень значимости 
, и нажмем кнопку Предсказать зависимую переменную (рис.
2.39).
Рис.2.39. Выбор параметров для прогноза по линейной модели
Впоявившемся диалоговом окне укажем значение зависимой переменной 
и нажмем кнопку ОК (рис. 2.40).
Врезультате появится таблица, в которой представлено предсказанное по линейному уравнению регрессии значение зависимой переменной 
, а также нижняя и верхняя границы доверительного 95%-ого
интервала (рис. 2.41).
53
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
08.08.2019238.08 Кб0па.doc
- #
- #
- #
- #
- #
- #
-
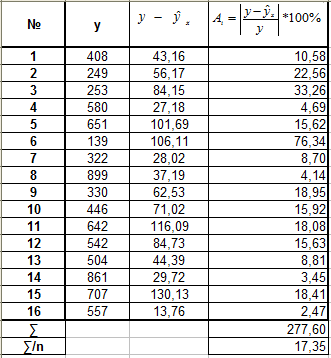
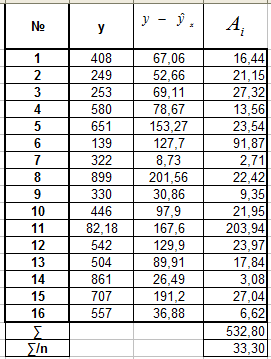
Оценим качество уравнений с помощью средней ошибки аппроксимации
Средняя ошибка аппроксимации — среднее
отклонение расчетных (теоретических)
значений зависимой переменной y
от фактических (эмпирических) значений
Допустимый предел значений
не
более 10-12 %.
А. Для линейной регрессии Б. Для
степенной регрессии
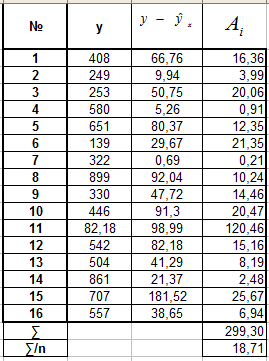
В. Для экспоненциальной регрессии
Г. Для полулогарифмической регрессии
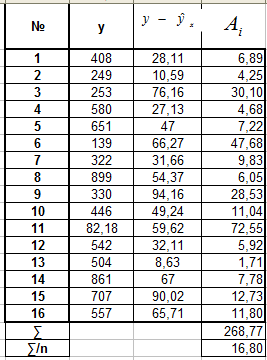
Е. Для гиперболической регрессии
Вывод: для каждой из построенных
моделей ошибка аппроксимации превышает
допустимые пределы, что говорит о плохом
качестве моделей регрессии.
Наименьшей (хотя и недопустимой) она
является для уравнения полулогарифмической
регрессии
.
-
Оценим статистическую надежность результатов регрессионного моделирования с помощью f-критерия Фишера.
Н0 — гипотеза о статистической
незначимости показателя детерминации
R²
(Fфакт = 0) и уравнения
регрессии.
n – общее число наблюдений
(n=16); m –
число параметров при переменной x
(m=1)/
По таблице значений F-критерия
Фишера при условии значимости
= 0,05 и число степеней свободы k1
= m = 1, k2
= n – m
– 1 = 16-1-1= 14 находим Fкр
— максимально возможное значение
критерия под влиянием случайных факторов
при данных степенях свободы и уровне
значимости : Fкр
= 4,60.
А. Для линейной регрессии
(
)
Так как
то гипотеза Н0 отвергается,
т.е. R²
статистически значим, как и уравнение
линейной регрессии.
Б. Для степенной регрессии
(
)
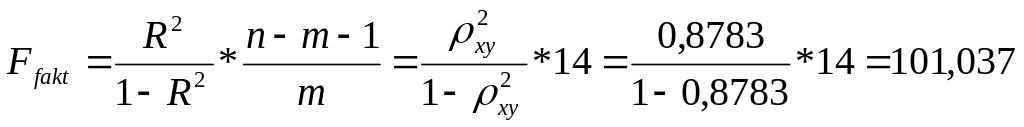
Так как
то гипотеза Н0 отвергается,
т.е. R²
статистически значим, как и уравнение
степенной регрессии.
В. Для экспоненциальной регрессии
(
)
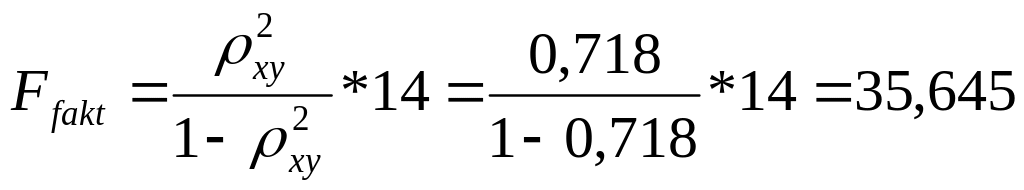
Так как
то гипотеза Н0 отвергается,
т.е. R²
статистически значим, как и уравнение
полулогарифмической регрессии.
Д. Для гиперболической регрессии
(
)
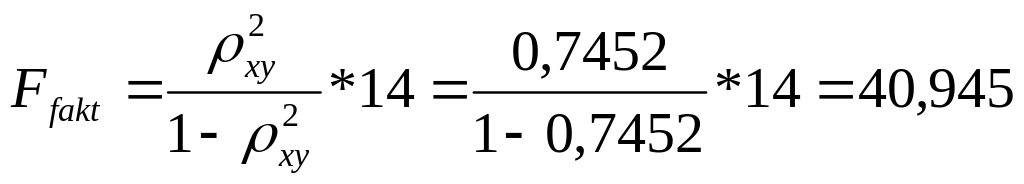
Так как
то гипотеза Н0 отвергается,
т.е. R²
статистически значим, как и уравнение
гиперболической регрессии.
Вывод: F-критерия
Фишера показывает, во сколько раз
уравнение регрессии предсказывает
результаты наблюдений лучше, чем прямая
.
Статистически значимыми являются
уравнения линейной, степенной,
экспоненциальной, гиперболической
регрессии, из них всех лучше предсказывает
результаты наблюдений уравнение
степенной регрессии (
)
-
По значениям характеристик, рассчитанных в пп. 4,6,7 выберем лучшее уравнение регрессии и дадим его обоснование.
П.4. Наибольшее значение коэффициента
эластичности имеет уравнение
степенной регрессии (
.
П.6. Наименьшую ошибку аппроксимации
(хотя и не допустимую) имеет уравнение
полулогарифмической регрессии
.
Уравнение степенной регрессии
отличается на небольшую величину:
П.7. Согласно F-критерию
Фишера лучше всех предсказывает
результаты наблюдений уравнение
степенной регрессии (
)
Вывод: Лучше всех описывает данные
наблюдений (зависимость между средней
заработанной платой и выплатами
социального характера x
и потребительскими расходами на душу
населения y) уравнение
степенной регрессии
Качество модели плохое, так как
>10%,
возможно из-за небольшого числа наблюдений
(n=16).
-
По линейному уравнению регрессии
рассчитаем прогнозное значение
результата (y), если
прогнозное значение фактора (x)
увеличивается на 7% от его среднего
уровня:
Уравнение линейной регрессии y=a
+ b*x (
).
n – общее число
наблюдений (n=16); m
– число параметров при переменной x
(m=1);
tкр
= 2,1448
Прогнозное значение фактора (x):
xпр =
тыс.
руб.;
xпр —
= 44,25 – 885 = -840,75; (xпр —
= (-840,75)² = 706860,5625.
Прогнозное значение фактора (y):
yпр = a
+ b* xпр =
160,48 + 0,39*44,25 = 177,74 тыс. руб.
Стандартная ошибка прогноза:
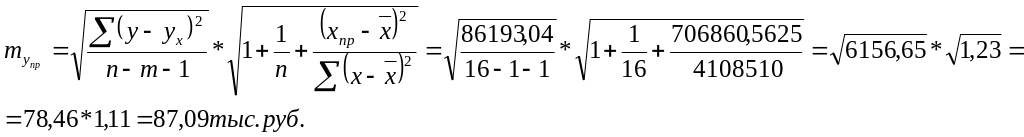
Предельная ошибка прогноза, которая
в 95% случаев не будет превышена, составит:
Доверительный интервал прогноза для
уровня значимости
=0,05:
(min
max
или
(
=
(177,74 – 186,79; 177,74 + 186,79) = (-9,05; 364,53)
11
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
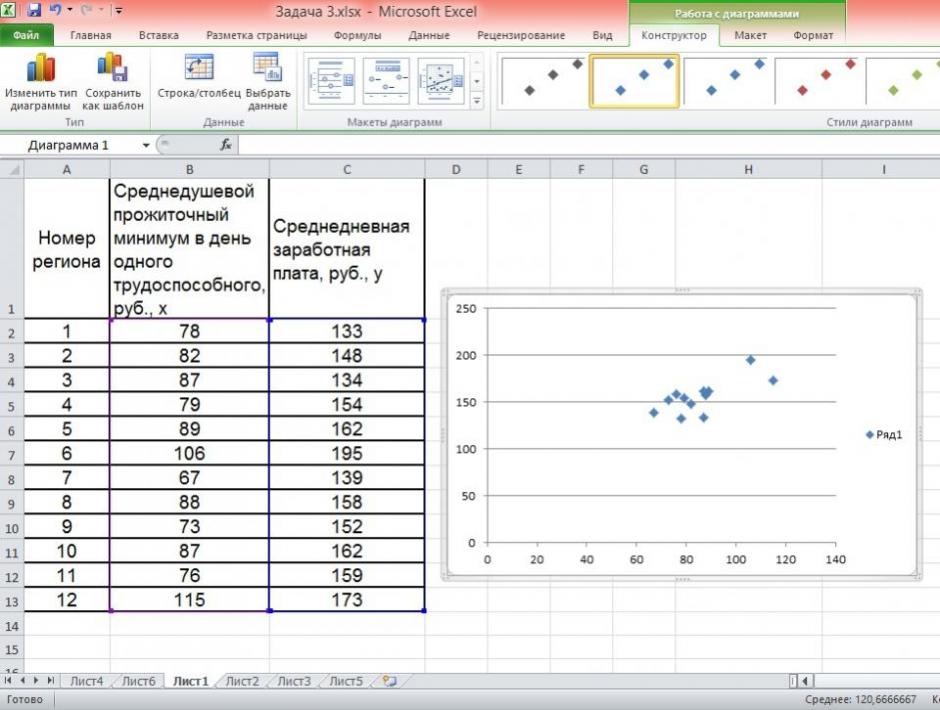
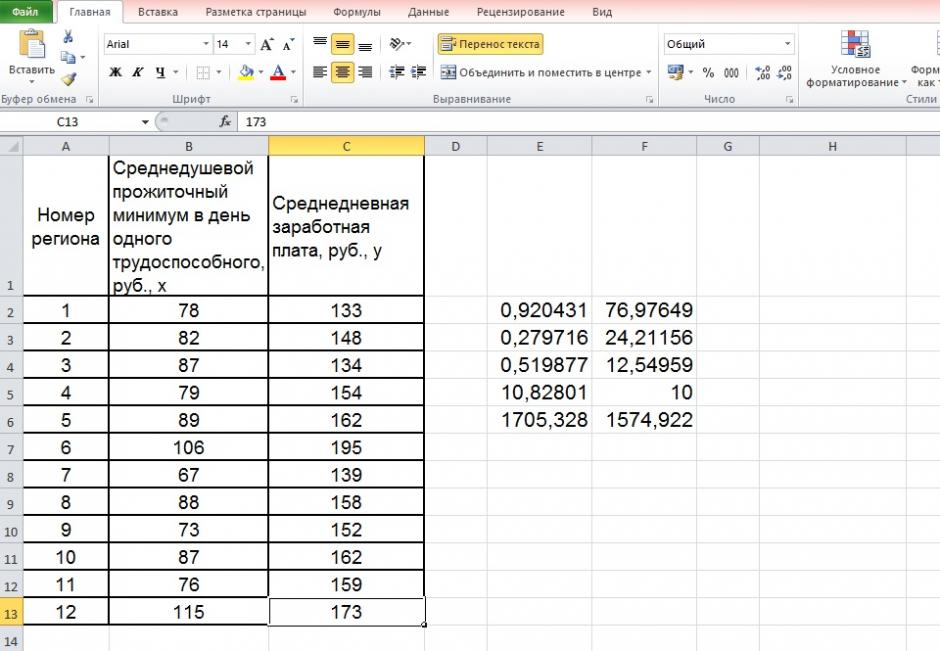
По территориям региона приводятся данные за 200Х г.
| Номер региона | Среднедушевой прожиточный минимум в день одного трудоспособного, руб., х | Среднедневная заработная плата, руб., у |
|---|---|---|
| 1 | 78 | 133 |
| 2 | 82 | 148 |
| 3 | 87 | 134 |
| 4 | 79 | 154 |
| 5 | 89 | 162 |
| 6 | 106 | 195 |
| 7 | 67 | 139 |
| 8 | 88 | 158 |
| 9 | 73 | 152 |
| 10 | 87 | 162 |
| 11 | 76 | 159 |
| 12 | 115 | 173 |
Задание:
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2. Рассчитайте параметры уравнения линейной регрессии
.
3. Оцените тесноту связи с помощью показателей корреляции и детерминации.
4. Дайте с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
5. Оцените с помощью средней ошибки аппроксимации качество уравнений.
6. Оцените с помощью F-критерия Фишера статистическую надёжность результатов регрессионного моделирования.
7. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости 
.
8. Оцените полученные результаты, выводы оформите в аналитической записке.
Решение:
Решим данную задачу с помощью Excel.
1. Сопоставив имеющиеся данные х и у, например, ранжировав их в порядке возрастания фактора х, можно наблюдать наличие прямой зависимости между признаками, когда увеличение среднедушевого прожиточного минимума увеличивает среднедневную заработную плату. Исходя из этого, можно сделать предположение, что связь между признаками прямая и её можно описать уравнением прямой. Этот же вывод подтверждается и на основе графического анализа.
Чтобы построить поле корреляции можно воспользоваться ППП Excel. Введите исходные данные в последовательности: сначала х, затем у.
Выделите область ячеек, содержащую данные.
Затем выберете: Вставка / Точечная диаграмма / Точечная с маркерами как показано на рисунке 1.
Рисунок 1 Построение поля корреляции
Анализ поля корреляции показывает наличие близкой к прямолинейной зависимости, так как точки расположены практически по прямой линии.
2. Для расчёта параметров уравнения линейной регрессии
воспользуемся встроенной статистической функцией ЛИНЕЙН.
Для этого:
1) Откройте существующий файл, содержащий анализируемые данные;
2) Выделите область пустых ячеек 5×2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики.
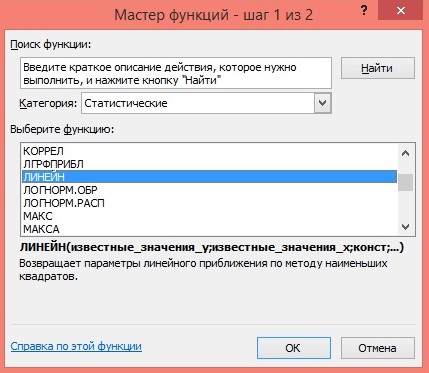
3) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
4) В окне Категория выберете Статистические, в окне функция – ЛИНЕЙН. Щёлкните по кнопке ОК как показано на Рисунке 2;
Рисунок 2 Диалоговое окно «Мастер функций»
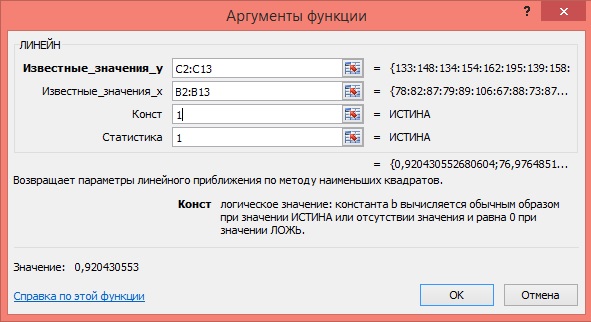
5) Заполните аргументы функции:
Известные значения у – диапазон, содержащий данные результативного признака;
Известные значения х – диапазон, содержащий данные факторного признака;
Константа – логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается обычным образом, если Константа = 0, то свободный член равен 0;
Статистика – логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводятся только оценки параметров уравнения.
Щёлкните по кнопке ОК;
Рисунок 3 Диалоговое окно аргументов функции ЛИНЕЙН
6) В левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу <F2>, а затем на комбинацию клавиш <Ctrl>+<Shift>+<Enter>.
Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:
| Значение коэффициента b | Значение коэффициента a |
| Стандартная ошибка b | Стандартная ошибка a |
| Коэффициент детерминации R2 | Стандартная ошибка y |
| F-статистика | Число степеней свободы df |
| Регрессионная сумма квадратов
|
Остаточная сумма квадратов
|
Рисунок 4 Результат вычисления функции ЛИНЕЙН
Получили уровнение регрессии:
Делаем вывод: С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.
3. Коэффициент детерминации 
означает, что 52% вариации заработной платы (у) объясняется вариацией фактора х – среднедушевого прожиточного минимума, а 48% — действием других факторов, не включённых в модель.
По вычисленному коэффициенту детерминации можно рассчитать коэффициент корреляции: 
.
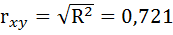
Связь оценивается как тесная.
4. С помощью среднего (общего) коэффициента эластичности определим силу влияния фактора на результат.
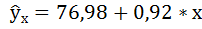
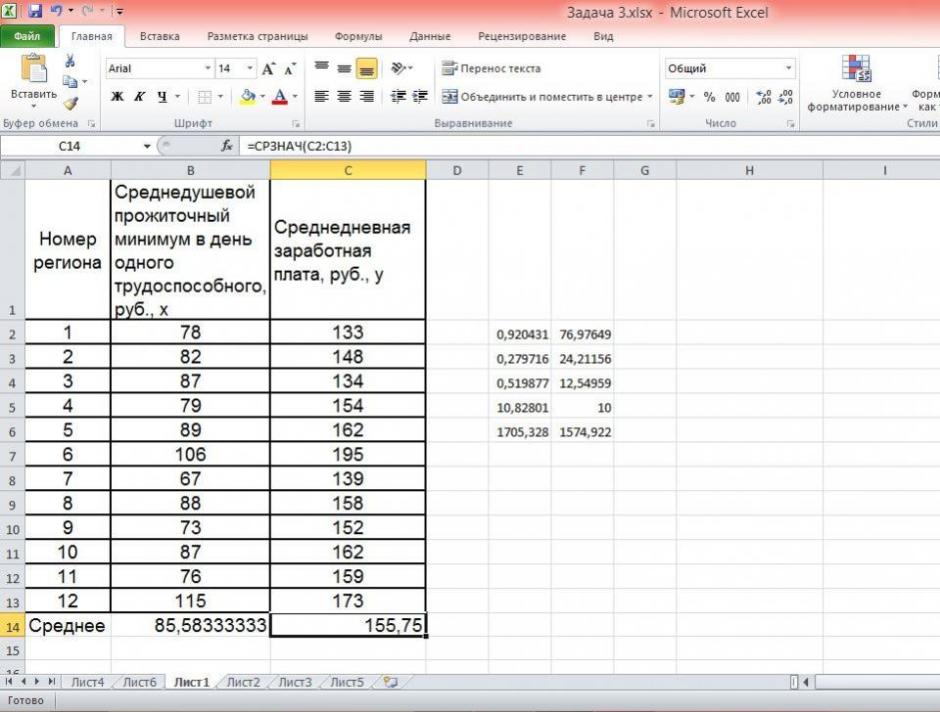
Для уравнения прямой средний (общий) коэффициент эластичности определим по формуле:
Средние значения найдём, выделив область ячеек со значениями х, и выберем Формулы / Автосумма / Среднее, и то же самое произведём со значениями у.
Рисунок 5 Расчёт средних значений функции и аргумент
Таким образом, при изменении среднедушевого прожиточного минимума на 1% от своего среднего значения среднедневная заработная плата изменится в среднем на 0,51%.
С помощью инструмента анализа данных Регрессия можно получить:
— результаты регрессионной статистики,
— результаты дисперсионного анализа,
— результаты доверительных интервалов,
— остатки и графики подбора линии регрессии,
— остатки и нормальную вероятность.
Порядок действий следующий:
1) проверьте доступ к Пакету анализа. В главном меню последовательно выберите: Файл/Параметры/Надстройки.
2) В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.
3) В окне Надстройки установите флажок Пакет анализа, а затем нажмите кнопку ОК.
• Если Пакет анализа отсутствует в списке поля Доступные надстройки, нажмите кнопку Обзор, чтобы выполнить поиск.
• Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да, чтобы установить его.
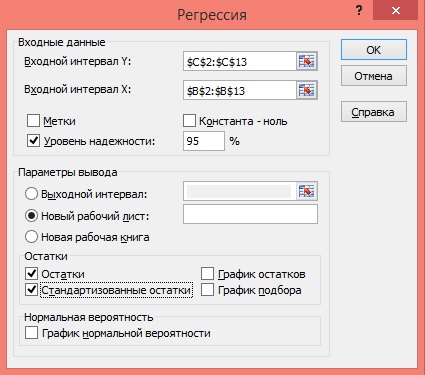
4) В главном меню последовательно выберите: Данные / Анализ данных / Инструменты анализа / Регрессия, а затем нажмите кнопку ОК.
5) Заполните диалоговое окно ввода данных и параметров вывода:
Входной интервал Y – диапазон, содержащий данные результативного признака;
Входной интервал X – диапазон, содержащий данные факторного признака;
Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа – ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;
6) Новый рабочий лист – можно задать произвольное имя нового листа.
Затем нажмите кнопку ОК.
Рисунок 6 Диалоговое окно ввода параметров инструмента Регрессия
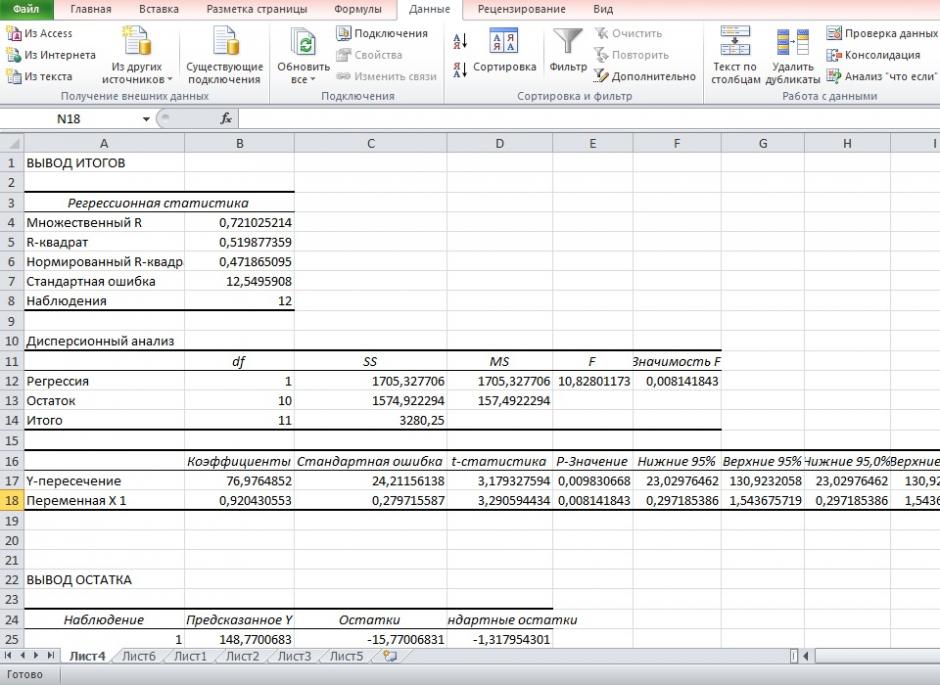
Результаты регрессионного анализа для данных задачи представлены на рисунке 7.
Рисунок 7 Результат применения инструмента регрессия
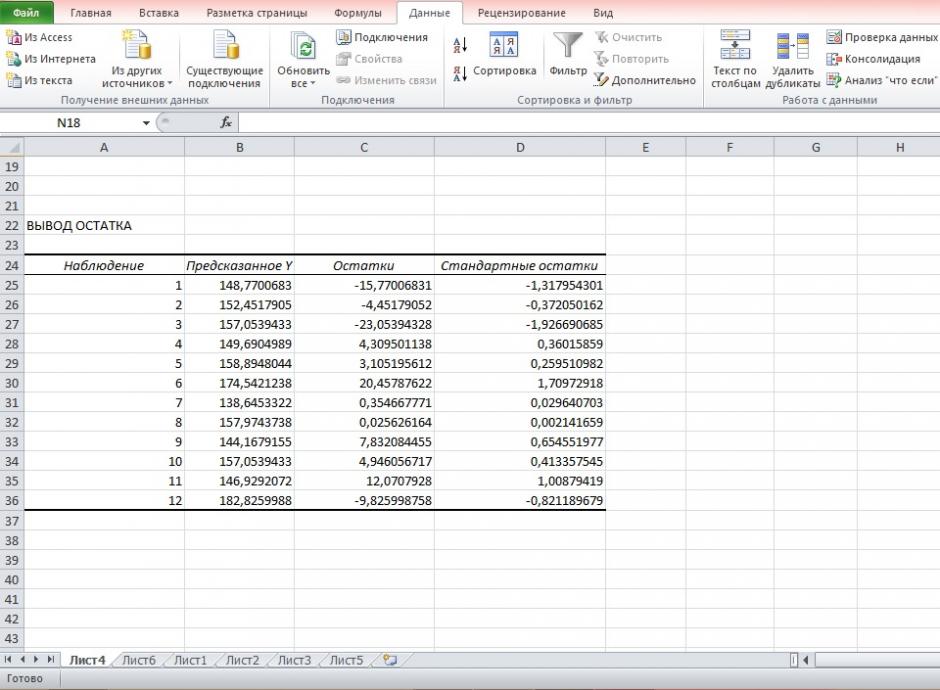
5. Оценим с помощью средней ошибки аппроксимации качество уравнений. Воспользуемся результатами регрессионного анализа представленного на Рисунке 8.
Рисунок 8 Результат применения инструмента регрессия «Вывод остатка»
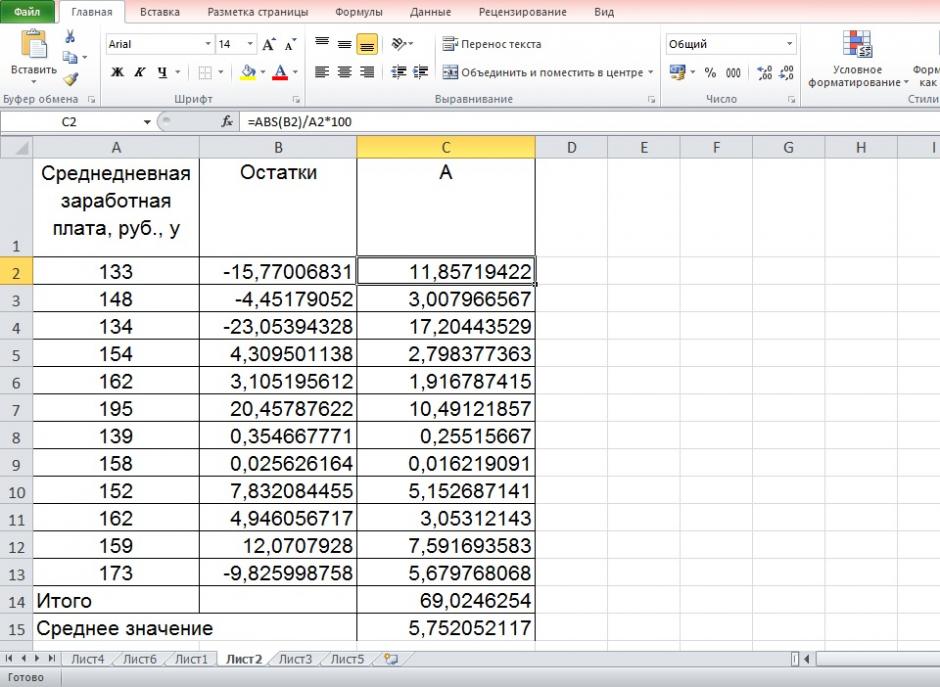
Составим новую таблицу как показано на рисунке 9. В графе С рассчитаем относительную ошибку аппроксимации по формуле:
Рисунок 9 Расчёт средней ошибки аппроксимации
Средняя ошибка аппроксимации рассчитывается по формуле:
Качество построенной модели оценивается как хорошее, так как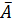 
не превышает 8 – 10%.
6. Из таблицы с регрессионной статистикой (Рисунок 4) выпишем фактическое значение F-критерия Фишера: 
Поскольку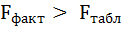 
при 5%-ном уровне значимости, то можно сделать вывод о значимости уравнения регрессии (связь доказана).
8. Оценку статистической значимости параметров регрессии проведём с помощью t-статистики Стьюдента и путём расчёта доверительного интервала каждого из показателей.
Выдвигаем гипотезу Н0 о статистически незначимом отличии показателей от нуля:
.
для числа степеней свободы 
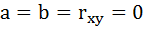
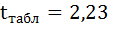
На рисунке 7 имеются фактические значения t-статистики:
t-критерий для коэффициента корреляции можно рассчитать двумя способами:
I способ: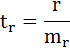 
где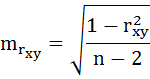 
– случайная ошибка коэффициента корреляции.
Данные для расчёта возьмём из таблицы на Рисунке 7.
II способ: 
Фактические значения t-статистики превосходят табличные значения:
Поэтому гипотеза Н0 отклоняется, то есть параметры регрессии и коэффициент корреляции не случайно отличаются от нуля, а статистически значимы.
Доверительный интервал для параметра a определяется как
Для параметра a 95%-ные границы как показано на рисунке 7 составили:
Доверительный интервал для коэффициента регрессии определяется как
Для коэффициента регрессии b 95%-ные границы как показано на рисунке 7 составили:
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью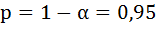 
параметры a и b, находясь в указанных границах, не принимают нулевых значений, т.е. не являются статистически незначимыми и существенно отличны от нуля.
7. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит:
Тогда прогнозное значение прожиточного минимума составит:
Ошибку прогноза рассчитаем по формуле:
где 
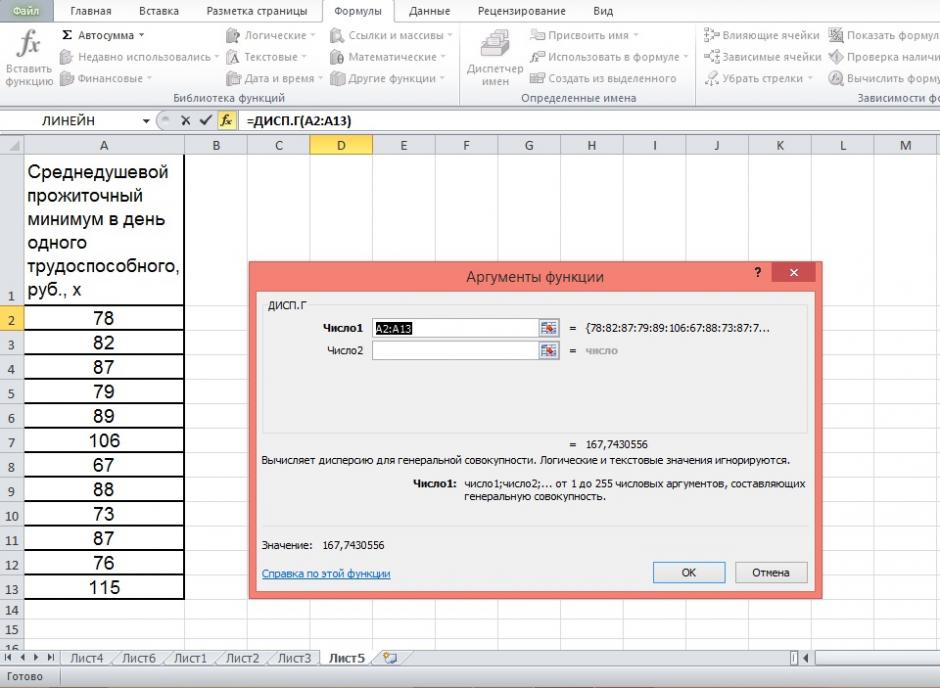
Дисперсию посчитаем также с помощью ППП Excel. Для этого:
1) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
2) В окне Категория выберете Статистические, в окне функция – ДИСП.Г. Щёлкните по кнопке ОК.
3) Заполните диапазон, содержащий числовые данные факторного признака. Нажмите ОК.
Рисунок 10 Расчёт дисперсии
Получили значение дисперсии 
Для подсчёта остаточной дисперсии на одну степень свободы воспользуемся результатами дисперсионного анализа как показано на Рисунке 7.
Доверительные интервалы прогноза индивидуальных значений у при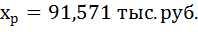 
с вероятностью 0,95 определяются выражением:
Интервал достаточно широк, прежде всего, за счёт малого объёма наблюдений. В целом выполненный прогноз среднемесячной заработной платы оказался надёжным.
Условие задачи взято из: Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2003. – 192 с.: ил.
Коэффициент корреляции
Тесноту (силу) связи изучаемых показателей в предмете эконометрика оценивают с помощью коэффициента корреляции Rxy, который может принимать значения от -1 до +1.
Если Rxy > 0,7 — связь между изучаемыми показателями сильная, можно проводить анализ линейной модели
Если 0,3 < Rxy < 0,7 — связь между показателями умеренная, можно использовать нелинейную модель при отсутствии Rxy > 0,7
Если Rxy < 0,3 — связь слабая, модель строить нельзя
Для нелинейной регрессии используют индекс корреляции (0 < Рху < 1):
Средняя ошибка аппроксимации
Для оценки качества однофакторной модели в эконометрике используют коэффициент детерминации и среднюю ошибку аппроксимации.
Средняя ошибка аппроксимации определяется как среднее отклонение полученных значений от фактических
Допустимая ошибка аппроксимации не должна превышать 10%.
В эконометрике существует понятие среднего коэффициента эластичности Э – который говорит о том, на сколько процентов в среднем изменится показатель у от своего среднего значения при изменении фактора х на 1% от своей средней величины.
Пример нахождения коэффициента корреляции
Исходные данные:
|
Номер региона |
Среднедушевой прожиточный минимум в день одного трудоспособного, руб., |
Среднедневная заработная плата, руб., |
|
1 |
81 |
124 |
|
2 |
77 |
131 |
|
3 |
85 |
146 |
|
4 |
79 |
139 |
|
5 |
93 |
143 |
|
6 |
100 |
159 |
|
7 |
72 |
135 |
|
8 |
90 |
152 |
|
9 |
71 |
127 |
|
10 |
89 |
154 |
|
11 |
82 |
127 |
|
12 |
111 |
162 |
Рассчитаем параметры парной линейной регрессии, составив таблицу
| x |
x2 |
y |
xy |
y2 |
|
|
1 |
81 |
6561 |
124 |
10044 |
15376 |
|
2 |
77 |
5929 |
131 |
10087 |
17161 |
|
3 |
85 |
7225 |
146 |
12410 |
21316 |
|
4 |
79 |
6241 |
139 |
10981 |
19321 |
|
5 |
93 |
8649 |
143 |
13299 |
20449 |
|
6 |
100 |
10000 |
159 |
15900 |
25281 |
|
7 |
72 |
5184 |
135 |
9720 |
18225 |
|
8 |
90 |
8100 |
152 |
13680 |
23104 |
|
9 |
71 |
5041 |
127 |
9017 |
16129 |
|
10 |
89 |
7921 |
154 |
13706 |
23716 |
|
11 |
82 |
6724 |
127 |
10414 |
16129 |
|
12 |
111 |
12321 |
162 |
17982 |
26244 |
|
Среднее |
85,8 |
7491 |
141,6 |
12270,0 |
20204,3 |
|
Сумма |
1030,0 |
89896 |
1699 |
147240 |
242451 |
| σ |
11,13 |
12,59 |
|||
| σ2 |
123,97 |
158,41 |
формула расчета дисперсии σ2 приведена здесь.
Коэффициенты уравнения y = a + bx определяются по формуле
Получаем уравнение регрессии: y = 0,947x + 60,279.
Коэффициент уравнения b = 0,947 показывает, что при увеличении среднедушевого прожиточного минимума в день одного трудоспособного на 1 руб. среднедневная заработная плата увеличивается на 0,947 руб.
Коэффициент корреляции рассчитывается по формуле:
Значение коэффициента корреляции более — 0,7, это означает, что связь между среднедушевым прожиточным минимумом в день одного трудоспособного и среднедневной заработной платой сильная.
Коэффициент детерминации равен R2 = 0.838^2 = 0.702
т.е. 70,2% результата объясняется вариацией объясняющей переменной x.