Средняя квадратическая ошибка прогноза формула

  • Редакция Кодкампа


читать 2 мин

Регрессионный анализ — это метод, который мы можем использовать для понимания взаимосвязи между одной или несколькими переменными-предикторами и переменной отклика .

Один из способов оценить, насколько хорошо регрессионная модель соответствует набору данных, — вычислить среднеквадратичную ошибку , которая представляет собой показатель, указывающий нам среднее расстояние между прогнозируемыми значениями из модели и фактическими значениями в наборе данных.

Чем ниже RMSE, тем лучше данная модель может «соответствовать» набору данных.

Формула для нахождения среднеквадратичной ошибки, часто обозначаемая аббревиатурой RMSE , выглядит следующим образом:

СКО = √ Σ(P i – O i ) 2 / n

куда:

  • Σ — причудливый символ, означающий «сумма».
  • P i — прогнозируемое значение для i -го наблюдения в наборе данных.
  • O i — наблюдаемое значение для i -го наблюдения в наборе данных.
  • n — размер выборки

В следующем примере показано, как интерпретировать RMSE для данной модели регрессии.

Пример: как интерпретировать RMSE для регрессионной модели

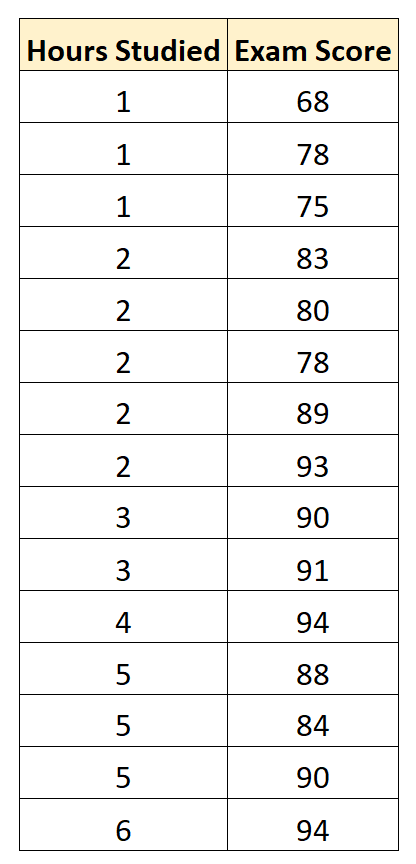
Предположим, мы хотим построить регрессионную модель, которая использует «учебные часы» для прогнозирования «экзаменационного балла» студентов на конкретном вступительном экзамене в колледж.

Мы собираем следующие данные для 15 студентов:

Затем мы используем статистическое программное обеспечение (например, Excel, SPSS, R, Python) и т. д., чтобы найти следующую подогнанную модель регрессии:

Экзаменационный балл = 75,95 + 3,08 * (часы обучения)

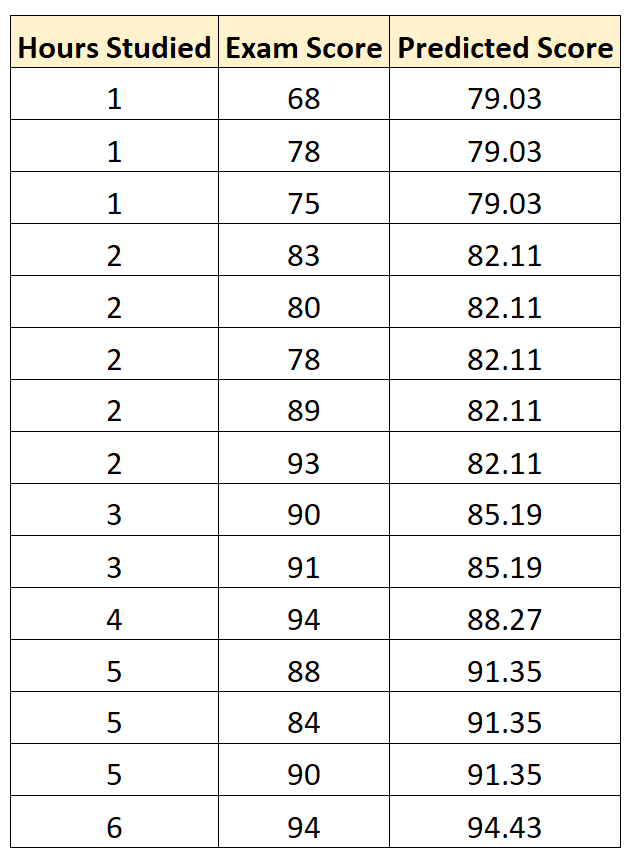
Затем мы можем использовать это уравнение, чтобы предсказать экзаменационную оценку каждого студента, исходя из того, сколько часов они учились:

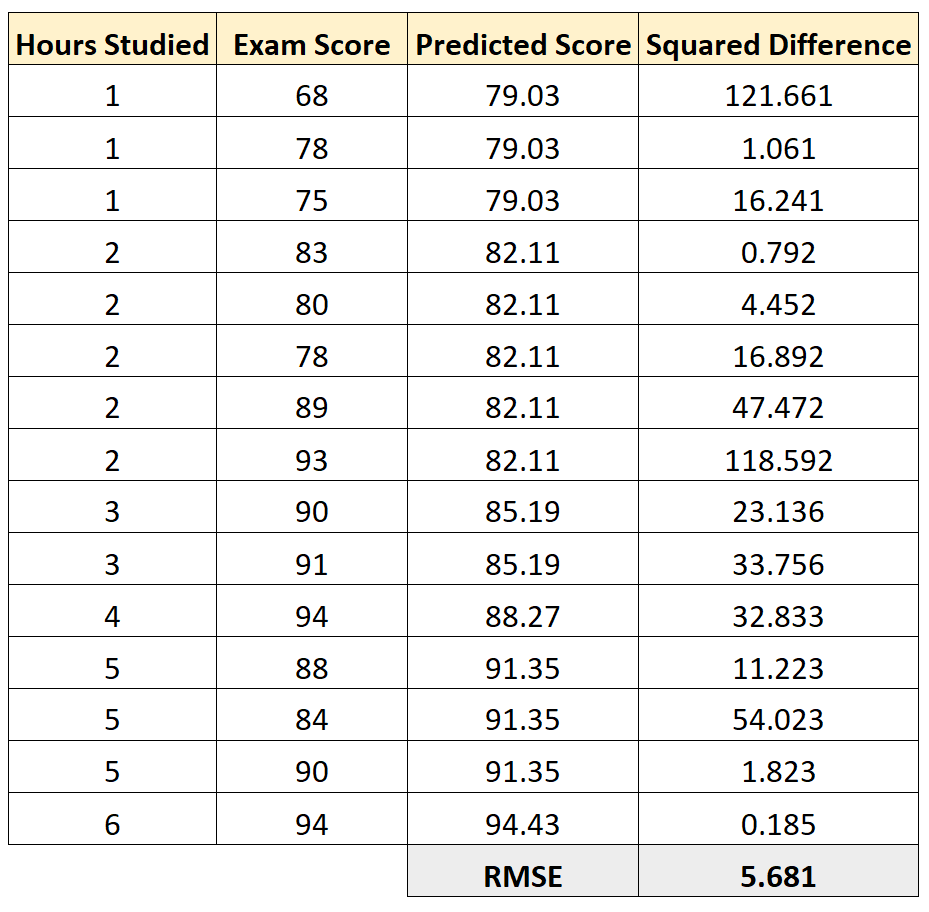
Затем мы можем вычислить квадрат разницы между каждой прогнозируемой оценкой экзамена и фактической оценкой экзамена. Затем мы можем извлечь квадратный корень из среднего значения этих разностей:

RMSE для этой регрессионной модели оказывается равным 5,681 .

Напомним, что остатки регрессионной модели представляют собой разницу между наблюдаемыми значениями данных и значениями, предсказанными моделью.

Остаток = (P i – O i )

куда

  • P i — прогнозируемое значение для i -го наблюдения в наборе данных.
  • O i — наблюдаемое значение для i -го наблюдения в наборе данных.

И помните, что RMSE регрессионной модели рассчитывается как:

СКО = √ Σ(P i – O i ) 2 / n

Это означает, что RMSE представляет собой квадратный корень из дисперсии остатков.

Это значение полезно знать, поскольку оно дает нам представление о среднем расстоянии между наблюдаемыми значениями данных и прогнозируемыми значениями данных.

Это отличается от R-квадрата модели, который сообщает нам долю дисперсии переменной отклика, которая может быть объяснена предикторной переменной (переменными) в модели.

Сравнение значений RMSE из разных моделей

RMSE особенно полезен для сравнения соответствия различных моделей регрессии.

Например, предположим, что мы хотим построить регрессионную модель, чтобы предсказать результаты экзаменов студентов, и мы хотим найти наилучшую возможную модель среди нескольких потенциальных моделей.

Предположим, мы подгоняем три разные модели регрессии и находим соответствующие им значения RMSE:

  • RMSE модели 1: 14,5
  • RMSE модели 2: 16,7
  • RMSE модели 3: 9,8

Модель 3 имеет самый низкий RMSE, что говорит нам о том, что она способна лучше всего соответствовать набору данных из трех потенциальных моделей.

Дополнительные ресурсы

Калькулятор среднеквадратичной ошибки
Как рассчитать RMSE в Excel
Как рассчитать RMSE в R
Как рассчитать RMSE в Python

Источник

Среднеквадратичная ошибка (Mean Squared Error) – Среднее арифметическое (Mean) квадратов разностей между предсказанными и реальными значениями Модели (Model) Машинного обучения (ML):

MSE как среднее дистанций между предсказаниями и реальными наблюдениями

Рассчитывается с помощью формулы, которая будет пояснена в примере ниже:

$$MSE = \frac{1}{n} × \sum_{i=1}^n (y_i — \widetilde{y}_i)^2$$
$$MSE\space{}{–}\space{Среднеквадратическая}\space{ошибка,}$$
$$n\space{}{–}\space{количество}\space{наблюдений,}$$
$$y_i\space{}{–}\space{фактическая}\space{координата}\space{наблюдения,}$$
$$\widetilde{y}_i\space{}{–}\space{предсказанная}\space{координата}\space{наблюдения,}$$

MSE практически никогда не равен нулю, и происходит это из-за элемента случайности в данных или неучитывания Оценочной функцией (Estimator) всех факторов, которые могли бы улучшить предсказательную способность.

Пример. Исследуем линейную регрессию, изображенную на графике выше, и установим величину среднеквадратической Ошибки (Error). Фактические координаты точек-Наблюдений (Observation) выглядят следующим образом:

Мы имеем дело с Линейной регрессией (Linear Regression), потому уравнение, предсказывающее положение записей, можно представить с помощью формулы:

$$y = M * x + b$$
$$y\space{–}\space{значение}\space{координаты}\space{оси}\space{y,}$$
$$M\space{–}\space{уклон}\space{прямой}$$
$$x\space{–}\space{значение}\space{координаты}\space{оси}\space{x,}$$
$$b\space{–}\space{смещение}\space{прямой}\space{относительно}\space{начала}\space{координат}$$

Параметры M и b уравнения нам, к счастью, известны в данном обучающем примере, и потому уравнение выглядит следующим образом:

$$y = 0,5252 * x + 17,306$$

Зная координаты реальных записей и уравнение линейной регрессии, мы можем восстановить полные координаты предсказанных наблюдений, обозначенных серыми точками на графике выше. Простой подстановкой значения координаты x в уравнение мы рассчитаем значение координаты ỹ:

Рассчитаем квадрат разницы между Y и Ỹ:

Сумма таких квадратов равна 4 445. Осталось только разделить это число на количество наблюдений (9):

$$MSE = \frac{1}{9} × 4445 = 493$$

Само по себе число в такой ситуации становится показательным, когда Дата-сайентист (Data Scientist) предпринимает попытки улучшить предсказательную способность модели и сравнивает MSE каждой итерации, выбирая такое уравнение, что сгенерирует наименьшую погрешность в предсказаниях.

MSE и Scikit-learn

Среднеквадратическую ошибку можно вычислить с помощью SkLearn. Для начала импортируем функцию:

import sklearn
from sklearn.metrics import mean_squared_error

Инициализируем крошечные списки, содержащие реальные и предсказанные координаты y:

y_true = [5, 41, 70, 77, 134, 68, 138, 101, 131]
y_pred = [23, 35, 55, 90, 93, 103, 118, 121, 129]

Инициируем функцию mean_squared_error(), которая рассчитает MSE тем же способом, что и формула выше: 

mean_squared_error(y_true, y_pred)

Интересно, что конечный результат на 3 отличается от расчетов с помощью Apple Numbers:

496.0

Ноутбук, не требующий дополнительной настройки на момент написания статьи, можно скачать здесь.

Автор оригинальной статьи: @mmoshikoo

Фото: @tobyelliott

Источник

From Wikipedia, the free encyclopedia

In statistics the mean squared prediction error (MSPE), also known as mean squared error of the predictions, of a smoothing, curve fitting, or regression procedure is the expected value of the squared prediction errors (PE), the square difference between the fitted values implied by the predictive function \widehat {g} and the values of the (unobservable) true value g. It is an inverse measure of the explanatory power of {\displaystyle {\widehat {g}},} and can be used in the process of cross-validation of an estimated model.
Knowledge of g would be required in order to calculate the MSPE exactly; in practice, MSPE is estimated.[1]

Formulation[edit]

If the smoothing or fitting procedure has projection matrix (i.e., hat matrix) L, which maps the observed values vector y to predicted values vector {\displaystyle {\hat {y}}=Ly,} then PE and MSPE are formulated as:

{\displaystyle \operatorname {PE_{i}} =g(x_{i})-{\widehat {g}}(x_{i}),}
{\displaystyle \operatorname {MSPE} =\operatorname {E} \left[\operatorname {PE} _{i}^{2}\right]=\sum _{i=1}^{n}\operatorname {PE} _{i}^{2}/n.}

The MSPE can be decomposed into two terms: the squared bias (mean error) of the fitted values and the variance of the fitted values:

{\displaystyle \operatorname {MSPE} =\operatorname {ME} ^{2}+\operatorname {VAR} ,}
{\displaystyle \operatorname {ME} =\operatorname {E} \left[{\widehat {g}}(x_{i})-g(x_{i})\right]}
{\displaystyle \operatorname {VAR} =\operatorname {E} \left[\left({\widehat {g}}(x_{i})-\operatorname {E} \left[{g}(x_{i})\right]\right)^{2}\right].}

The quantity SSPE=nMSPE is called sum squared prediction error.
The root mean squared prediction error is the square root of MSPE: RMSPE=√MSPE.

Computation of MSPE over out-of-sample data[edit]

The mean squared prediction error can be computed exactly in two contexts. First, with a data sample of length n, the data analyst may run the regression over only q of the data points (with q < n), holding back the other n – q data points with the specific purpose of using them to compute the estimated model’s MSPE out of sample (i.e., not using data that were used in the model estimation process). Since the regression process is tailored to the q in-sample points, normally the in-sample MSPE will be smaller than the out-of-sample one computed over the n – q held-back points. If the increase in the MSPE out of sample compared to in sample is relatively slight, that results in the model being viewed favorably. And if two models are to be compared, the one with the lower MSPE over the n – q out-of-sample data points is viewed more favorably, regardless of the models’ relative in-sample performances. The out-of-sample MSPE in this context is exact for the out-of-sample data points that it was computed over, but is merely an estimate of the model’s MSPE for the mostly unobserved population from which the data were drawn.

Second, as time goes on more data may become available to the data analyst, and then the MSPE can be computed over these new data.

Estimation of MSPE over the population[edit]

When the model has been estimated over all available data with none held back, the MSPE of the model over the entire population of mostly unobserved data can be estimated as follows.

For the model y_{i}=g(x_{i})+\sigma \varepsilon _{i} where \varepsilon _{i}\sim {\mathcal {N}}(0,1), one may write

{\displaystyle n\cdot \operatorname {MSPE} (L)=g^{\text{T}}(I-L)^{\text{T}}(I-L)g+\sigma ^{2}\operatorname {tr} \left[L^{\text{T}}L\right].}

Using in-sample data values, the first term on the right side is equivalent to

{\displaystyle \sum _{i=1}^{n}\left(\operatorname {E} \left[g(x_{i})-{\widehat {g}}(x_{i})\right]\right)^{2}=\operatorname {E} \left[\sum _{i=1}^{n}\left(y_{i}-{\widehat {g}}(x_{i})\right)^{2}\right]-\sigma ^{2}\operatorname {tr} \left[\left(I-L\right)^{T}\left(I-L\right)\right].}

Thus,

{\displaystyle n\cdot \operatorname {MSPE} (L)=\operatorname {E} \left[\sum _{i=1}^{n}\left(y_{i}-{\widehat {g}}(x_{i})\right)^{2}\right]-\sigma ^{2}\left(n-\operatorname {tr} \left[L\right]\right).}

If \sigma ^{2} is known or well-estimated by \widehat {\sigma }^{2}, it becomes possible to estimate MSPE by

{\displaystyle n\cdot \operatorname {\widehat {MSPE}} (L)=\sum _{i=1}^{n}\left(y_{i}-{\widehat {g}}(x_{i})\right)^{2}-{\widehat {\sigma }}^{2}\left(n-\operatorname {tr} \left[L\right]\right).}

Colin Mallows advocated this method in the construction of his model selection statistic Cp, which is a normalized version of the estimated MSPE:

{\displaystyle C_{p}={\frac {\sum _{i=1}^{n}\left(y_{i}-{\widehat {g}}(x_{i})\right)^{2}}{{\widehat {\sigma }}^{2}}}-n+2p.}

where p the number of estimated parameters p and \widehat {\sigma }^{2} is computed from the version of the model that includes all possible regressors.
That concludes this proof.

See also[edit]

  • Akaike information criterion
  • Bias-variance tradeoff
  • Mean squared error
  • Errors and residuals in statistics
  • Law of total variance
  • Mallows’s Cp
  • Model selection

References[edit]

  1. ^ Pindyck, Robert S.; Rubinfeld, Daniel L. (1991). «Forecasting with Time-Series Models». Econometric Models & Economic Forecasts (3rd ed.). New York: McGraw-Hill. pp. 516–535. ISBN 0-07-050098-3.
Источник

Важным этапом прогнозирования
социально-экономических явлений
является оценка точности и надежности
прогнозов.

Эмпирической мерой точности прогноза,
служит величина его ошибки, которая
определяется как разность между
прогнозными ()
и фактическими (уt)
значениями исследуемого показателя.
Данный подход возможен только в двух
случаях:

а) период упреждения известен, уже
закончился и исследователь располагает
необходимыми фактическими значениями
прогнозируемого показателя;

б) строится ретроспективный прогноз,
то есть рассчитываются прогнозные
значения показателя для периода времени
за который уже имеются фактические
значения. Это делается с целью проверки
разработанной методики прогнозирования.

В данном случае вся имеющаяся информация
делится на две части в соотношении 2/3
к 1/3. Одна часть информации (первые 2/3
от исходного временного ряда) служит
для оценивания параметров модели
прогноза. Вторая часть информации
(последняя 1/3 части исходного ряда)
служит для реализации оценок прогноза.

Полученные, таким образом, ретроспективно
ошибки прогноза в некоторой степени
характеризуют точность предлагаемой
и реализуемой методики прогнозирования.
Однако величина ошибки ретроспективного
прогноза не может в полной мере и
окончательно характеризовать используемый
метод прогнозирования, так как она
рассчитана только для 2/3 имеющихся
данных, а не по всему временному ряду.

В случае если, ретроспективное
прогнозирование осуществлять по связным
и многомерным динамическим рядам, то
точность прогноза, соответственно,
будет зависеть от точности определения
значений факторных признаков, включенных
в многофакторную динамическую модель,
на всем периоде упреждения. При этом,
возможны следующие подходы к
прогнозированию по связным временным
рядам: можно использовать как фактические,
так и прогнозные значения признаков.

Все показатели оценки точности
статистических прогнозов условно можно
разделить на три группы:

  • аналитические;

  • сравнительные;

  • качественные.

Аналитические показатели точности
прогноза позволяют количественно
определить величину ошибки прогноза.
К ним относятся следующие показатели
точности прогноза:

Абсолютная ошибка прогноза (D*)
определяется как разность между
эмпирическим и прогнозным значениями
признака и вычисляется по формуле:

, (16.1)

где уt– фактическое
значение признака;

—
прогнозное значение признака.

Относительная ошибка прогноза (d*отн)
может быть определена как отношение
абсолютной ошибки прогноза (D*):

  • к
    фактическому значению признака (уt):



(16.2)

— к прогнозному
значению признака ()



(16.3)

Абсолютная и относительная ошибки
прогноза являются оценкой проверки
точности единичного прогноза, что
снижает их значимость в оценке точности
всей прогнозной модели, так как на
изучаемое социально-экономическое
явление подвержено влиянию различных
факторов внешнего и внутреннего
свойства. Единично удовлетворительный
прогноз может быть получен и на базе
реализации слабо обусловленной и
недостаточно адекватной прогнозной
модели и наоборот – можно получить
большую ошибку прогноза по достаточно
хорошо аппроксимирующей модели.

Поэтому на практике иногда определяют
не ошибку прогноза, а некоторый
коэффициент качества прогноза (Кк),
который показывает соотношение между
числом совпавших (с) и общим числом
совпавших (с) и несовпавших (н) прогнозов
и определяется по формуле:

(16.4)

Значение Кк= 1 означает, что имеет
место полное совпадение значений
прогнозных и фактических значений и
модель на 100% описывает изучаемое
явление. Данный показатель оценивает
удовлетворительный вес совпавших
прогнозных значений в целом по временному
ряду и изменяющегося в пределах от 0 до
1.

Следовательно, оценку точности получаемых
прогнозных моделей целесообразно
проводить по совокупности сопоставлений
прогнозных и фактических значений
изучаемых признаков.

Средним показателем точности прогноза
является средняя абсолютная ошибка
прогноза (),
которая определяется как средняя
арифметическая простая из абсолютных
ошибок прогноза по формуле вида:

, (16.5)

де n– длина временного
ряда.

Средняя абсолютная ошибка прогноза
показывает обобщенную характеристику
степени отклонения фактических и
прогнозных значений признака и имеет
ту же размерность, что и размерность
изучаемого признака.

Для оценки точности прогноза используется
средняя квадратическая ошибка прогноза,
определяемая по формуле:

(16.6)

Размерность средней квадратической
ошибки прогноза также соответствует
размерности изучаемого признака. Между
средней абсолютной и средней квадратической
ошибками прогноза существует следующее
примерное соотношение:

(16.7)

Недостатками средней абсолютной и
средней квадратической ошибками
прогноза является их существенная
зависимость от масштаба измерения
уровней изучаемых социально-экономических
явлений.

Поэтому на практике в качестве
характеристики точности прогноза
определяют среднюю ошибку аппроксимации,
которая выражается в процентах
относительно фактических значений
признака, и определяется по формуле
вида:

(16.8)

Данный показатель является относительным
показателем точности прогноза и не
отражает размерность изучаемых
признаков, выражается в процентах и на
практике используется для сравнения
точности прогнозов полученных как по
различным моделям, так и по различным
объектам. Интерпретация оценки точности
прогноза на основе данного показателя
представлена в следующей таблице:

,%

Интерпретация
точности

< 10

10 – 20

20 – 50

> 50

Высокая

Хорошая

Удовлетворительная

Не удовлетворительная

В качестве сравнительного показателя
точности прогноза используется
коэффициент корреляции между прогнозными
и фактическими значениями признака,
который определяется по формуле:

, (16.9)

где
—
средний уровень ряда динамики прогнозных
оценок.

Используя данный коэффициент в оценке
точности прогноза следует помнить, что
коэффициент парной корреляции в силу
своей сущности отражает линейное
соотношение коррелируемых величин и
характеризует лишь взаимосвязь между
временным рядом фактических значений
и рядом прогнозных значений признаков.
И даже если коэффициент корреляции R= 1, то это еще не предполагает полного
совпадения фактических и прогнозных
оценок, а свидетельствует лишь о наличии
линейной зависимости между временными
рядами прогнозных и фактических значений
признака.

Одним из показателей оценки точности
статистических прогнозов является
коэффициент несоответствия (КН), который
был предложен Г. Тейлом и может
рассчитываться в различных модификациях:

  1. Коэффициент несоответствия (КН1),
    определяемый как отношение средней
    квадратической ошибки к квадрату
    фактических значений признака:

(16.10)

КН = о, если
,
то есть полное совпадение фактических
и прогнозных значений признака.

КН = 1, если при прогнозировании получают
среднюю квадратическую ошибку адекватную
по величине ошибке, полученной одним
из простейших методов экстраполяции
неизменности абсолютных цепных
приростов.

КН > 1, когда прогноз дает худшие
результаты, чем предположение о
неизменности исследуемого явления.
Верхней границы коэффициент несоответствия
не имеет.

2.Коэффициент несоответствия КН2определяется как отношение средней
квадратической ошибки прогноза к сумме
квадратов

отклонений
фактических значений признака от
среднего уровня исходного временного
ряда за весь рассматриваемый период:

, (16.11)

где — средний уровень исходного ряда
динамики.

Если КН > 1, то прогноз на уровне среднего
значения признака дал бы лучший
результат, чем имеющийся прогноз.

3.Коэффициент несоответствия (КН3),
определяемый как отношение средней
квадратической ошибке прогноза к сумме
квадратов отклонений фактических
значений признака от теоретических,
выравненных по уравнению тренда:

, (16.12)

где — теоретические уровни временного ряда,
полученные по

модели тренда.

Если КН > 1, то прогноз методом
экстраполяции тренда дает хороший
результат.

Источник

Ошибка прогнозирования: виды, формулы, примеры

Ошибка прогнозирования — это такая величина, которая показывает, как сильно прогнозное значение отклонилось от фактического. Она используется для расчета точности прогнозирования, что в свою очередь помогает нам оценивать как точно и корректно мы сформировали прогноз. В данной статье я расскажу про основные процентные «ошибки прогнозирования» с кратким описанием и формулой для расчета. А в конце статьи я приведу общий пример расчётов в Excel. Напомню, что в своих расчетах я в основном использую ошибку WAPE или MAD-Mean Ratio, о которой подробно я рассказал в статье про точность прогнозирования, здесь она также будет упомянута.

В каждой формуле буквой Ф обозначено фактическое значение, а буквой П — прогнозное. Каждая ошибка прогнозирования (кроме последней!), может использоваться для нахождения общей точности прогнозирования некоторого списка позиций, по типу того, что изображен ниже (либо для любого другого подобной детализации):

Алгоритм для нахождения любой из ошибок прогнозирования для такого списка примерно одинаковый: сначала находим ошибку прогнозирования по одной позиции, а затем рассчитываем общую. Итак, основные ошибки прогнозирования!

MPE — Mean Percent Error

MPE — средняя процентная ошибка прогнозирования. Основная проблема данной ошибки заключается в том, что в нестабильном числовом ряду с большими выбросами любое незначительное колебание факта или прогноза может значительно поменять показатель ошибки и, как следствие, точности прогнозирования. Помимо этого, ошибка является несимметричной: одинаковые отклонения в плюс и в минус по-разному влияют на показатель ошибки.

Ошибка прогнозирования MPE

  1. Для каждой позиции рассчитывается ошибка прогноза (из факта вычитается прогноз) — Error
  2. Для каждой позиции рассчитывается процентная ошибка прогноза (ошибка прогноза делится на фактический показатель) — Percent Error
  3. Находится среднее арифметическое всех процентных ошибок прогноза (процентные ошибки суммируются и делятся на количество) — Mean Percent Error
MAPE — Mean Absolute Percent Error

MAPE — средняя абсолютная процентная ошибка прогнозирования. Основная проблема данной ошибки такая же, как и у MPE — нестабильность.

Ошибка прогнозирования MAPE

  1. Для каждой позиции рассчитывается абсолютная ошибка прогноза (прогноз вычитается из факта по модулю) — Absolute Error
  2. Для каждой позиции рассчитывается абсолютная процентная ошибка прогноза (абсолютная ошибка прогноза делится на фактический показатель) — Absolute Percent Error
  3. Находится среднее арифметическое всех абсолютных процентных ошибок прогноза (абсолютные процентные ошибки суммируются и делятся на количество) — Mean Absolute Percent Error

Вместо среднего арифметического всех абсолютных процентных ошибок прогноза можно использовать медиану числового ряда (MdAPE — Median Absolute Percent Error), она наиболее устойчива к выбросам.

WMAPE / MAD-Mean Ratio / WAPE — Weighted Absolute Percent Error

WAPE — взвешенная абсолютная процентная ошибка прогнозирования. Одна из «лучших ошибок» для расчета точности прогнозирования. Часто называется как MAD-Mean Ratio, то есть отношение MAD (Mean Absolute Deviation — среднее абсолютное отклонение/ошибка) к Mean (среднее арифметическое). После упрощения дроби получается искомая формула WAPE, которая очень проста в понимании:

Ошибка прогнозирования WAPE MAD-Mean Ratio

  1. Для каждой позиции рассчитывается абсолютная ошибка прогноза (прогноз вычитается из факта, по модулю) — Absolute Error
  2. Находится сумма всех фактов по всем позициям  (общий фактический объем)
  3. Сумма всех абсолютных ошибок делится на сумму всех фактов — WAPE

Данная ошибка прогнозирования является симметричной и наименее чувствительна к искажениям числового ряда.

Рекомендуется к использованию при расчете точности прогнозирования. Более подробно читать здесь.

RMSE (as %) / nRMSE — Root Mean Square Error

RMSE — среднеквадратичная ошибка прогнозирования. Примерно такая же проблема, как и в MPE и MAPE: так как каждое отклонение возводится в квадрат, любое небольшое отклонение может значительно повлиять на показатель ошибки. Стоит отметить, что существует также ошибка MSE, из которой RMSE как раз и получается путем извлечения корня. Но так как MSE дает расчетные единицы измерения в квадрате, то использовать данную ошибку будет немного неправильно.

Ошибка прогнозирования RMSE

  1. Для каждой позиции рассчитывается квадрат отклонений (разница между фактом и прогнозом, возведенная в квадрат) — Square Error
  2. Затем рассчитывается среднее арифметическое (сумма квадратов отклонений, деленное на количество) — MSE — Mean Square Error
  3. Извлекаем корень из полученного результат — RMSE
  4. Для перевода в процентную или в «нормализованную» среднеквадратичную ошибку необходимо:
    1. Разделить на разницу между максимальным и минимальным значением показателей
    2. Разделить на разницу между третьим и первым квартилем значений показателей
    3. Разделить на среднее арифметическое значений показателей (наиболее часто встречающийся вариант)
MASE — Mean Absolute Scaled Error

MASE — средняя абсолютная масштабированная ошибка прогнозирования. Согласно Википедии, является очень хорошим вариантом для расчета точности, так как сама ошибка не зависит от масштабов данных и является симметричной: то есть положительные и отрицательные отклонения от факта рассматриваются в равной степени.

Важно! Если предыдущие ошибки прогнозирования мы могли использовать для нахождения точности прогнозирования некого списка номенклатур, где каждой из которых соответствует фактическое и прогнозное значение (как было в примере в начале статьи), то данная ошибка для этого не предназначена: MASE используется для расчета точности прогнозирования одной единственной позиции, основываясь на предыдущих показателях факта и прогноза, и чем больше этих показателей, тем более точно мы сможем рассчитать показатель точности. Вероятно, из-за этого ошибка не получила широкого распространения.

Здесь данная формула представлена исключительно для ознакомления и не рекомендуется к использованию.

Суть формулы заключается в нахождении среднего арифметического всех масштабированных ошибок, что при упрощении даст нам следующую конечную формулу:

Ошибка прогнозирования MASE

Также, хочу отметить, что существует ошибка RMMSE (Root Mean Square Scaled Error — Среднеквадратичная масштабированная ошибка), которая примерно похожа на MASE, с теми же преимуществами и недостатками.

Это основные ошибки прогнозирования, которые могут использоваться для расчета точности прогнозирования. Но не все! Их очень много и, возможно, чуть позже я добавлю еще немного информации о некоторых из них. А примеры расчетов уже описанных ошибок прогнозирования будут выложены через некоторое время, пока что я подготавливаю пример, ожидайте.

Об авторе

HeinzBr

Автор статей и создатель сайта SHTEM.RU

Источник

Понравилась статья? Поделить с друзьями:
  • Средняя квадратическая ошибка положения конечной точки хода
  • Средняя квадратическая ошибка единицы веса
  • Средняя квадратичная ошибка среднего арифметического значения
  • Средняя квадратическая ошибка показывает
  • Средняя квадратическая ошибка выборки формула