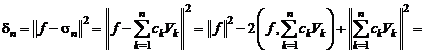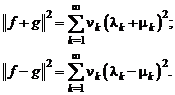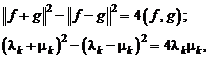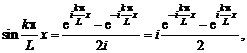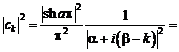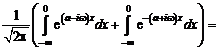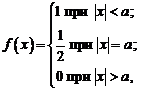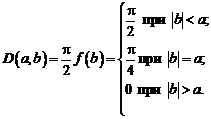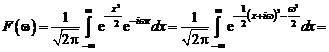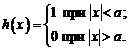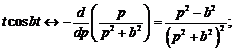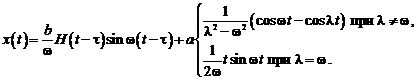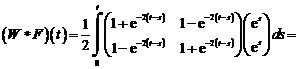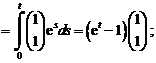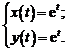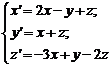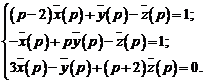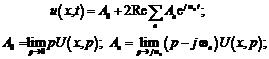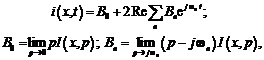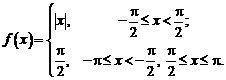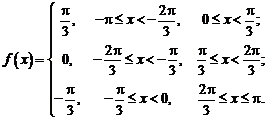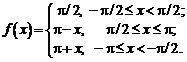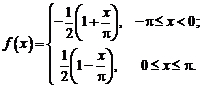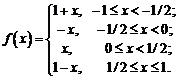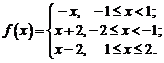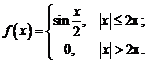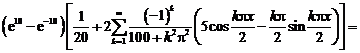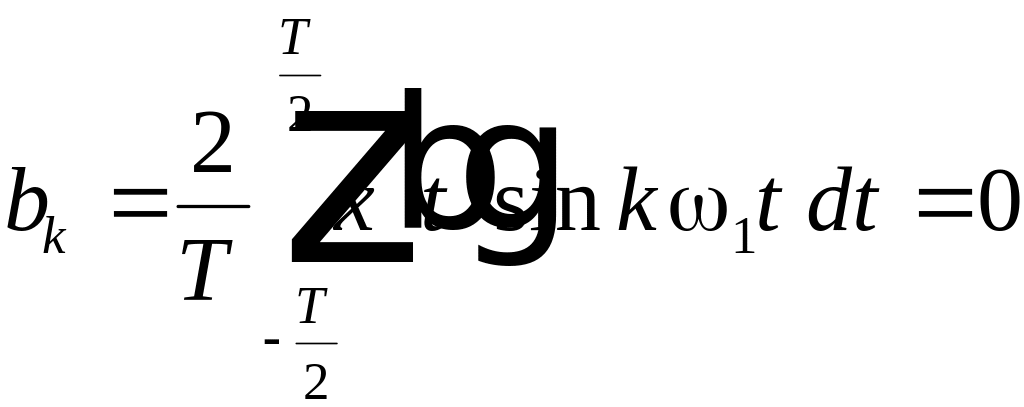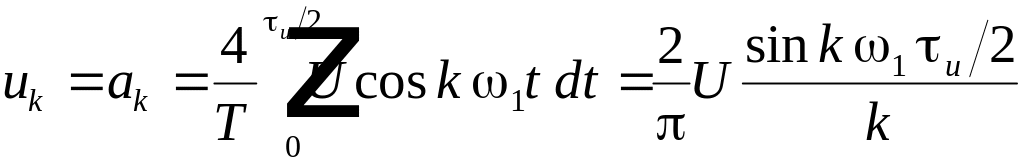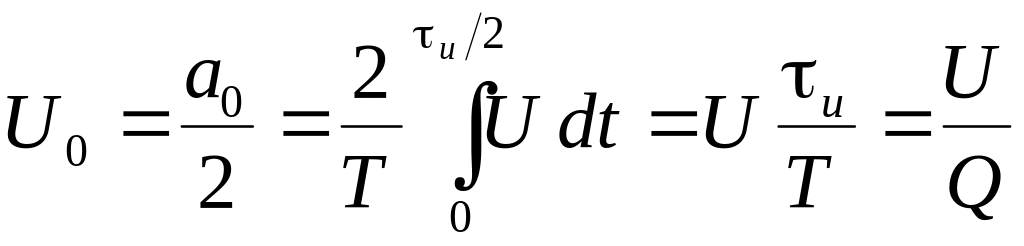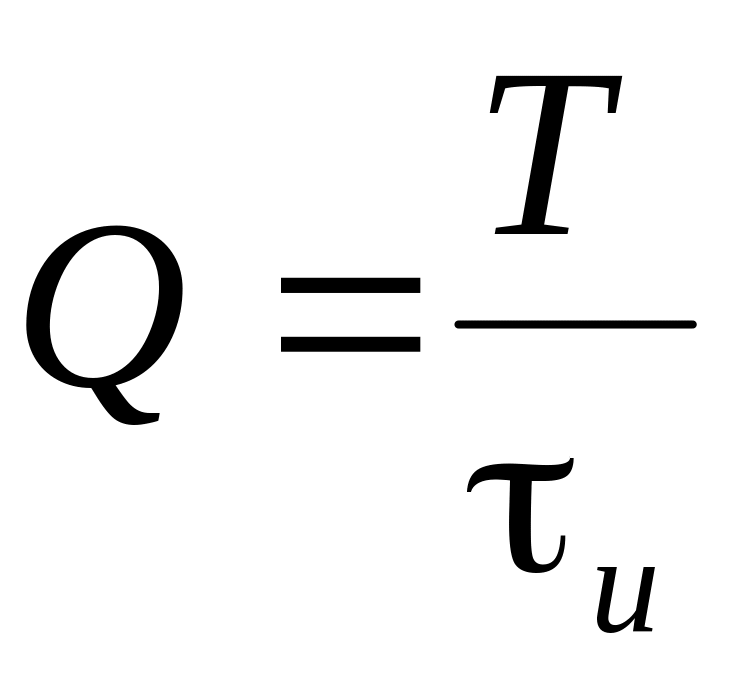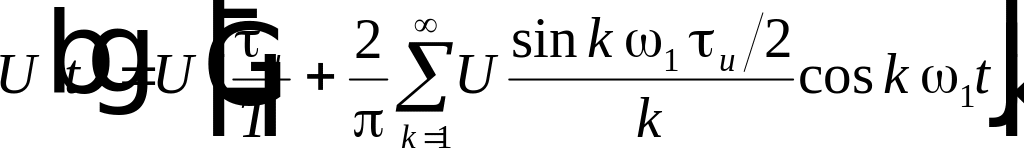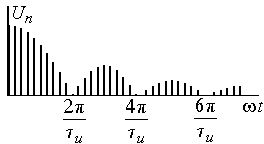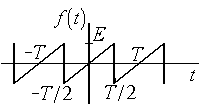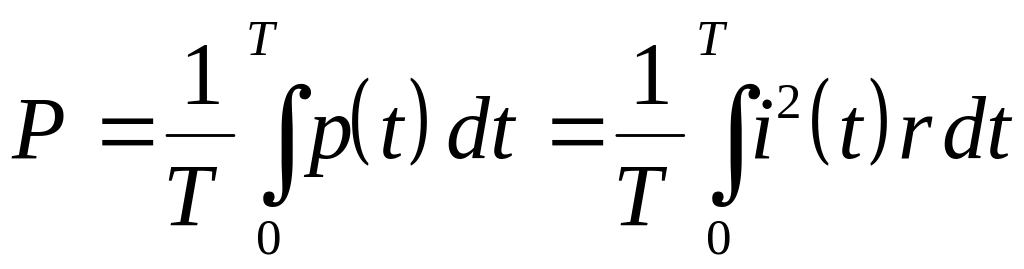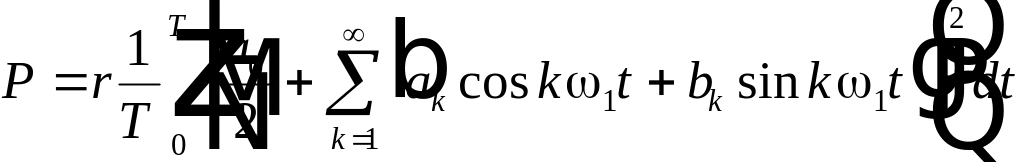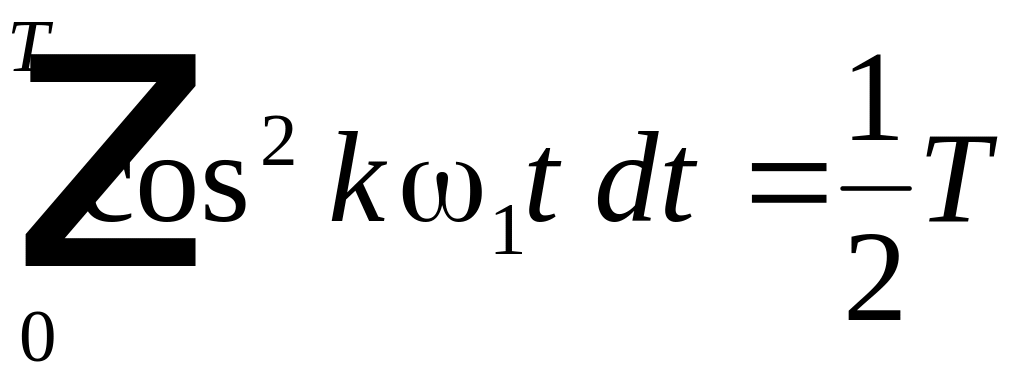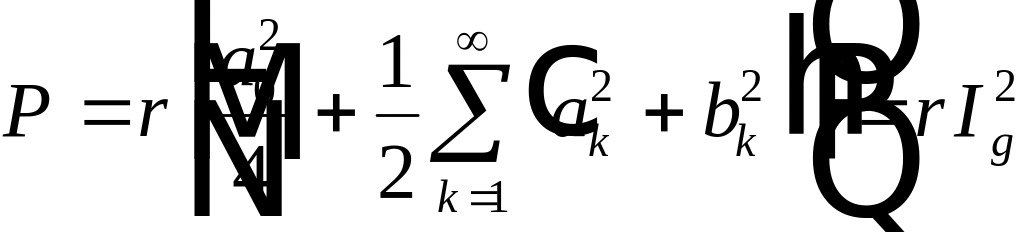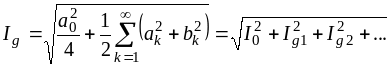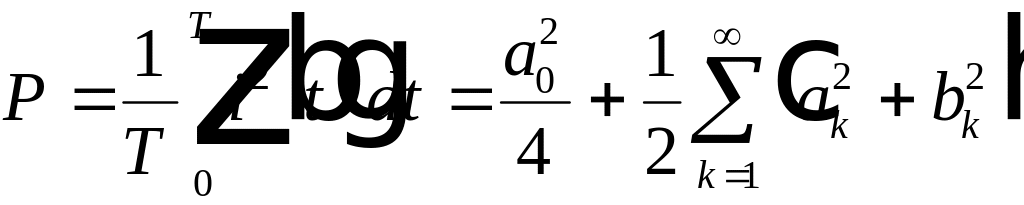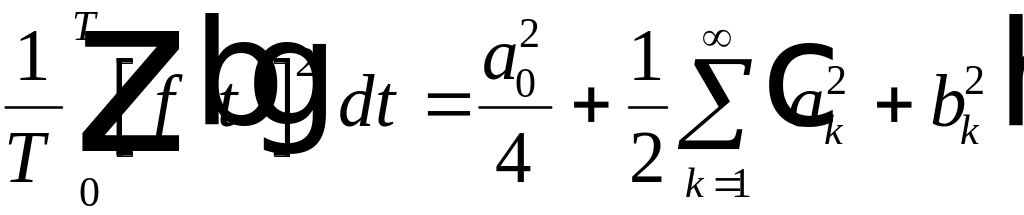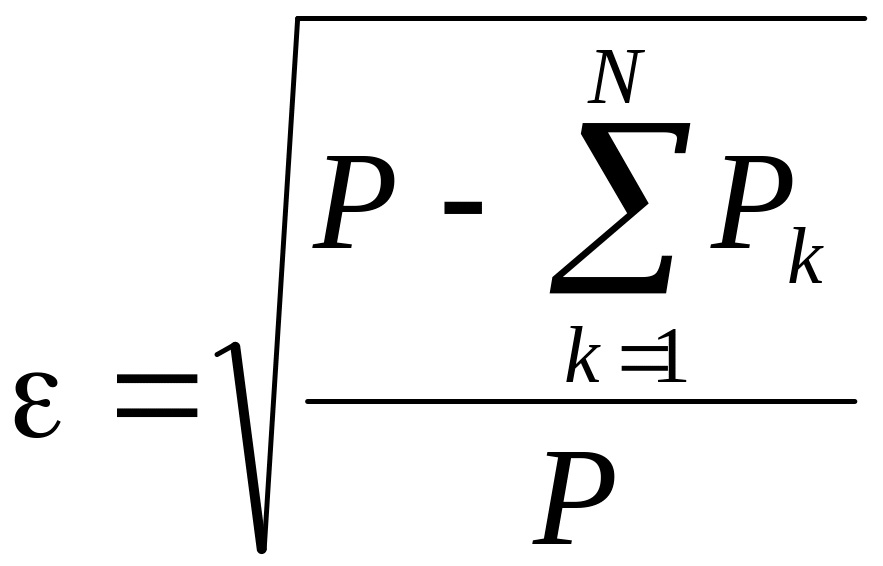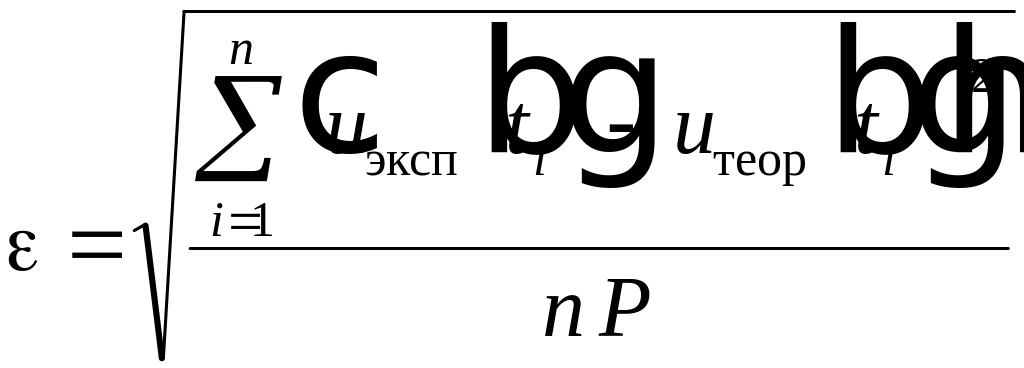Сходимость ряда Фурье в смысле среднего квадратичного
8 разделов
от теории до практики
1 пример
Примеры решения задач
видео
Примеры решения задач
-
Унитарное пространство.
Начать изучение
-
Нормированные пространства.
Начать изучение
-
Сходимость. Полные пространства. Гильбертовы пространства.
Начать изучение
-
Пополнение унитарного пространства.
Начать изучение
-
Ряды Фурье по ортогональным системам.
Начать изучение
-
Минимальное свойство коэффициентов Фурье. Неравенство Бесселя.
Начать изучение
-
Полнота системы элементов {ei} в унитарном пространстве. Полнота тригонометрической системы в L2(-π, π).
Начать изучение
-
Эквивалентность полноты и замкнутости ортогональной системы в гильбертовом пространстве.
Начать изучение
Унитарное пространство.
При дальнейшем изложении удобно будет пользоваться геометрическим языком. Из курса линейной алгебры известны определения комплексного линейного и унитарного пространства. Напомним, что в линейном пространстве определены операции сложения элементов (векторов) и умножения элементов на комплексные числа, причем эти операции удовлетворяют следующим аксиомам.
Аксиомы линейного пространства \(E\):
- \(x+y=y+x\) для любых \(x, y \in E\);
- \(x+(y+x)=(x+y)+z\) для любых \(x, y, z \in E\);
- существует элемент \(0 \in E\) такой, что для любого \(x \in E\) справедливо равенство \(x+0=x\);
- для любого \(x \in E\) существует элемент \(-x \in E\) такой, что \(x+(-x)=0\);
- для любого \(x \in E\) и для любых \(\lambda, \mu \in \mathbb{C}\) справедливо равенство \(\lambda(\mu x)=(\lambda\mu)x\);
- \((\lambda+\mu)x=\lambda x+\mu x\) для любых \(x \in E\), \(\lambda, \mu \in \mathbb{C}\);
- \(\lambda(x+y)=\lambda x+\lambda y\) для любых \(x, y \in E\), \(\lambda \in \mathbb{C}\);
- \(1 \cdot x=x\) для любого \(x \in E\).
Греческими буквами обозначались комплексные числа, латинскими — элементы линейного пространства \(E\).
Определение.
Унитарным называется комплексное линейное пространство \(E\), для каждой пары элементов которого определено комплексное число \((x, y)\) — их скалярное произведение.
Аксиомы скалярного произведения:
- \((x, y)=\overline{(y, x)}\) для любых \(x, y \in E\);
- \((x+y, z)=(x, z)+(y, z)\) для любых \(x, y, z \in E\);
- \((\lambda x, y)=\lambda(x, y)\) для любых \(x, y \in E\), \(\lambda \in \mathbb{C}\);
- \((x, x) \geq 0\) для любого \(x \in E\), причем \((x, x)=0\) тогда и только тогда, когда \(x=0\).
Здесь через \(\overline{\gamma}\) обозначается число, комплексно сопряженное комплексному числу \(\gamma\).
Неотрицательное число \(\left\|x\right\|=\sqrt{(x, x)}\) называется нормой элемента \(x\). Из аксиом унитарного пространства выводятся следующие свойства.
Свойство 1.
\(\left\|x\right\|=0\) эквивалентно \(x=0\).
Свойство 2.
\((x, \lambda y)=\overline{\lambda}(x, y)\).
Доказательство.
\(\circ\) \((x, \lambda y)=\overline{(\lambda y, x)}=\overline{\lambda(y, x)}=\overline{\lambda}\overline{(y, x)}=\overline{\lambda}(x, y)\). \(\bullet\)
Свойство 3.
Для любых \(x, y \in E\) справедливо неравенство Коши—Буняковского
$$
|(x, y)| \leq \left\|x\right\| \cdot \left\|y\right\|.\label{ref1}
$$
Доказательство.
\(\circ\) Так как для любых \(x, y \in E\) и \(\lambda \in \mathbb{C}\) справедливо неравенство \((x+\lambda y, x+\lambda y) \geq 0\), то, пользуясь свойствами скалярного произведения, получаем
$$
0 \leq (x, x)+\lambda(y, x)+\overline{\lambda}(x, y)+\lambda\overline{\lambda}(y, y).\label{ref2}
$$
Если \(\left\|y\right\|=0\), то \(y=0\) и неравенство Коши-Буняковского становится тривиальным. Пусть \(\left\|y\right\| \neq 0\). Положим в \eqref{ref2} \(\lambda=-\dfrac{(x, y)}{\left\|y\right\|^{2}}\). Получаем
$$
0 \leq \left\|x\right\|^{2}-\dfrac{(x, y)}{\left\|y\right\|^{2}}(y, x)-\dfrac{\overline{(x, y)}}{\left\|y\right\|^{2}}(x, y)+\dfrac{(x, y)\overline{(x, y)}}{\left\|y\right\|^{4}}\left\|y\right\|^{2},\nonumber
$$
откуда сразу следует неравенство Коши-Буняковского. \(\bullet\)
Свойство 4.
Для любых \(x, y \in E\) справедливо неравенство для нормы
$$
\left\|x+y\right\| \leq \left\|x\right\|+\left\|y\right\|.\nonumber
$$
Доказательство.
\(\circ\) Неравенство для нормы следует из неравенства Коши-Буняковского. В самом деле,
$$
\left\|x+y\right\|^{2}=(x+y, x+y)=(x, x)+(y, x)+(x, y)+(y, y) \leq
$$
$$
\leq \left\|x\right\|^{2}+2\left\|x\right\|\ \left\|y\right\|+\left\|y\right\|^{2}=(\left\|x\right\|+\left\|y\right\|)^{2}.\ \bullet\nonumber
$$
Свойство 5.
Положительная однородность нормы: \(\left\|\lambda x\right\|=|\lambda| \cdot \left\|x\right\|\).
Доказательство.
\(\circ\) \(\left\|\lambda x\right\|^{2}=(\lambda x, \lambda x)=\lambda\overline{\lambda}(x, x)=|\lambda|^{2}\left\|x\right\|^{2}\). \(\bullet\)
Из курса линейной алгебры известно унитарное пространство \(E^{n}\), элементами которого являются упорядоченные наборы \(n\) комплексных чисел
$$
\gamma=(\gamma_{1}, \ldots, \gamma_{n}),\ \gamma_{i} \in \mathbb{C},\ i=\overline{1, n}\nonumber
$$
Естественным образом определяется в \(E^{n}\) сложение элементов (векторов) и умножение их на комплексные числа. Скалярное произведение двух векторов \(\gamma=(\gamma_{1}, \ldots, \gamma_{n})\) и \(\delta=(\delta_{1}, \ldots, \delta_{n})\) есть комплексное число, определенное формулой
$$
(\gamma, \delta)=\gamma_{1}\overline{\delta}_{1}+\ldots+\gamma_{n}\overline{\delta}_{n}.
$$
По аналогии с вещественным пространством \(L_{2}^{C}(a, b)\), введем комплексное пространство \(L_{2}^{C}(a, b)\), элементами которого являются комплекснозначные функции, для каждой из которых найдется такое разбиение отрезка \([a, b]\) точками \(\{x_{i}\}\), \(i=\overline{0, n}\), что на любом из интервалов \((x_{i-1}, x_{i})\) функция непрерывна, а интеграл от квадрата ее модуля по отрезку \([a, b]\) сходится как несобственный.
Лемма 1.
Множество \(L_{2}^{C}(a, b)\) является линейным пространством с естественными операциями сложения и умножения на комплексные числа.
Доказательство.
\(\circ\) Пусть функции \(f, \varphi \in L_{2}^{C}(a, b)\). Из неравенства
$$
|f+\varphi|^{2}=(f+\varphi)(\overline{f}+\overline{\varphi})=f\overline{f}+f\overline{\varphi}+\overline{f}\varphi+\varphi\overline{\varphi} \leq\\ \leq |f|^{2}+|\varphi|^{2}+2|f| \cdot |\varphi| \leq 2|f|^{2}+2|\varphi|^{2}\nonumber
$$
и признака сравнения для несобственных интегралов следует, что несобственный интеграл \(\displaystyle\int\limits_{a}^{b}|f+\varphi|^{2}dx\) сходится и, следовательно, \(f+\varphi \in L_{2}^{C}(a, b)\).
Если \(f \in L_{2}^{C}(a, b)\), то и \(\alpha f \in L_{2}^{C}(a, b)\) для любого \(\alpha \in \mathbb{C}\). Проверка всех аксиом линейного пространства тривиальна. \(\bullet\)
Договоримся не различать две функции \(f\) и \(\varphi\) из пространства \(L_{2}^{C}(a, b)\), если их значения не совпадают лишь в конечном числе точек.
Лемма 2.
Линейное пространство \(L_{2}^{C}(a, b)\) будет унитарным, если определить скалярное произведение функций \(f, \varphi \in L_{2}^{C}(a, b)\) при помощи следующей формулы:
$$
(f, \varphi)=\int\limits_{a}^{b} f(x)\overline{\varphi(x)}\ dx.\label{ref3}
$$
Доказательство.
\(\circ\) Так как \(|f\overline{\varphi}| \leq \displaystyle\frac{1}{2}|f|^{2}+\frac{1}{2}|\varphi|^{2}\), то по признаку сравнения несобственный интеграл \eqref{ref3} сходится. Первые три аксиомы скалярного произведения проверяются без труда. Проверим выполнение аксиомы 4).
Пусть \((f, f)=\displaystyle\int\limits_{a}^{b}|f|^{2}dx\). Так как \(f \in L_{2}^{C}(a, b)\), то найдется такое разбиение отрезка \([a, b]\) точками \(\{x_{i}\}\), \(i=\overline{0, n}\), что на каждом из интервалов \((x_{i-1}, x_{i})\) функция \(f(x)\) непрерывна. Так как \((x_{i-1}, x_{i}) \subset [a, b]\), то
$$
\int\limits_{x_{i-1}}^{x_{i}} |f(x)|^{2}\ dx=0,\ i=\overline{1, n}.\nonumber
$$
Из этого равенства следует, что \(f(x)=0\) на любом интервале \((x_{i-1}, x_{i})\), \(i=\overline{1, n}\). Следовательно, функция \(f(x)\) отлична от нуля лишь в конечном числе точек. Согласно договоренности такая функция отождествляется с функцией, тождественно равной нулю на \([a, b]\). \(\bullet\)
Нормированные пространства.
В нормированных пространствах определены длины векторов, но нет скалярного произведения. Более точно, комплексное или вещественное линейное пространство \(E\) называется нормированным, если каждому элементу \(x\) поставлено в соответствие неотрицательное число \(\left\|x\right\|\) (норма элемента \(x\)), причем удовлетворяются следующие аксиомы нормы:
- \(\left\|\lambda x\right\|=|\lambda| \cdot \left\|x\right\|\) для любого , \(x \in E\) и любого \(\lambda \in \mathbb{C}\);
- \(\left\|x+y\right\| \leq \left\|x\right\|+\left\|y\right\|\) для любых \(x, y \in E\);
- \(\left\|x\right\|=0\) в том и только том случае, когда \(x=0\).
Если \(E\) есть унитарное пространство, то число \(\left\|x\right\|=\sqrt{(x, x)}\) удовлетворяет всем аксиомам нормы, и поэтому каждое унитарное пространство будет и нормированным пространством.
Множество непрерывных функций на отрезке \([a, b]\) станет нормированным пространством \(C[a, b]\), если определить норму функции следующим образом:
$$
\left\| f \right\|=\max_{a \leq x \leq b} |f(x)|.\label{ref4}
$$
Все аксиомы нормы проверяются без труда.
Заметим еще, что любое нормированное пространство есть частный случай метрического пространства, если ввести метрику следующим образом:
$$
\rho(x, y)=\left\|x-y\right\|.\label{ref5}
$$
Из аксиом нормы тогда следует, что для расстояния \eqref{ref5} выполняются все аксиомы метрики:
- \(\rho(x, y)=\rho(y, x)\);
- \(\rho(x, y)+\rho(y, z) \geq \rho(x, z)\);
- \(\rho(x, y)=0 \Leftrightarrow x=y\).
Поскольку нормированные и унитарные пространства есть частные случаи метрических пространств, то на них переносятся все метрические понятия, например понятие предела последовательности.
Сходимость. Полные пространства. Гильбертовы пространства.
Определение.
Последовательность точек \(\{x_{n}\}\) унитарного пространства \(E\) сходится к точке \(x \in E\), если
$$
\lim_{n \rightarrow \infty} \left\|x_{n}-x\right\|=0.\label{ref6}
$$
Запись \(\displaystyle\lim_{n \rightarrow \infty} x_{n}=x\) означает, что выполнено равенство \eqref{ref6}.
Запишем основные свойства пределов (часть из них представлена без доказательств).
Свойство 1.
Если \(\displaystyle\lim_{n \rightarrow \infty} x_{n}=x\) и \(\displaystyle\lim_{n \rightarrow \infty} y_{n}=y\), то
$$
\lim_{n \rightarrow \infty} (x_{n}+y_{n})=\lim_{n \rightarrow \infty} x_{n}+\lim_{n \rightarrow \infty} y_{n}=x+y.\nonumber
$$
Свойство 2.
Если \(\alpha_{n} \in \boldsymbol{R}\), \(x_{n} \in E\) и \(\displaystyle\lim_{n \rightarrow \infty} x_{n}=x\), \(\displaystyle\lim_{n \rightarrow \infty} \alpha_{n}=\alpha\), то
$$
\lim_{n \rightarrow \infty} \alpha_{n}x_{n}=\alpha x.\nonumber
$$
Свойство 3.
Сходящаяся последовательность ограничена, то есть если существует \(\displaystyle\lim_{n \rightarrow \infty} x_{n}=x\), то найдется число \(C > 0\) такое, что для всех \(n \in \mathbb{N}\) выполнено неравенство \(\left\|x_{n}\right\| \leq C\).
Свойство 4.
Скалярное произведение непрерывно, то есть если \(\displaystyle\lim_{n \rightarrow \infty} x_{n}=x\) и \(\displaystyle\lim_{n \rightarrow \infty} y_{n}=y\), то
$$
\lim_{n \rightarrow \infty} (x_{n}, y_{n})=(x, y).\nonumber
$$
Доказательство.
\(\circ\) Пусть \(\displaystyle\lim_{n \rightarrow \infty} x_{n}=x\) и \(\displaystyle\lim_{n \rightarrow \infty} y_{n}=y\). Так как сходящаяся последовательность ограничена, то существует такое число \(C\), что \(\left\|y_{n}\right\| \leq C\) для всех \(n \in N\). Воспользовавшись неравенством Коши-Буняковского, получаем, что
$$
|(x_{n}, y_{n})-(x, y)|=|(x_{n}-x, y_{n})+(x, y_{n}-y)| \leq \\ \leq \left\|y_{n}\right\| \cdot \left\|x_{n}-x\right\|+\left\|x\right\| \cdot \left\|y_{n}-y\right\| \leq C\left\|x_{n}-x\right\|+\left\|x\right\| \cdot \left\|y_{n}-y\right\| \rightarrow 0
$$
при \(n \rightarrow \infty\). Следовательно, \(\displaystyle\lim_{n \rightarrow \infty} (x_{n}, y_{n})=(x, y)\). \(\bullet\)
Замечание.
Сходимость в пространстве \(L_{2}^{C}\) называют сходимостью в смысле среднего квадратичного.
Будем говорить, что последовательность точек \(x_{n}\) унитарного (или нормированного) пространства \(E\) фундаментальна, если для любого \(\varepsilon > 0\) найдется номер \(N\) такой, что для всех \(n, m \geq N\) выполнено неравенство \(\left\|x_{n}-x_{m}\right\| < \varepsilon\).
Введенное понятие фундаментальной последовательности точек унитарного пространства находится в полном соответствии с введенным ранее понятием фундаментальной последовательности точек метрического пространства. Достаточно вспомнить формулу \(\rho(x, y)=\left\|x-y\right\|\), задающую метрику в унитарном пространстве. Если последовательность сходится, то она фундаментальна. В произвольном унитарном пространстве фундаментальная последовательность может не сходиться.
Говорят, что унитарное (нормированное, метрическое) пространство полное, если любая фундаментальная последовательность его точек сходится к точке этого пространства.
Полное нормированное пространство называется банаховым, полное унитарное бесконечномерное пространство называется гильбертовым.
Нетрудно видеть, что каждое конечномерное унитарное пространство будет полным (критерий Коши сходимости в пространстве \(\boldsymbol{R}^{n}\)).
Покажем, что существуют неполные бесконечномерные унитарные пространства.
Пример.
Пространство \(L_{2}^{C}(0, 1)\) неполное.
Решение.
\(\circ\) Для доказательства рассмотрим счетное множество точек
$$
1, \frac{1}{2}, \frac{1}{2^{2}}, \ldots, \frac{1}{2^{n}}, \ldots\nonumber
$$
Построим следующую функцию (рис. 70.1):
$$
f(x)=\left\{
\begin{array}{ll}
1, & \displaystyle\frac{1}{2^{2n+1}} \leq x \leq \frac{1}{2^{2n}},\ n=0, 1, \ldots,\\
\\
0, & \displaystyle\frac{1}{2^{2n}} \leq x \leq \frac{1}{2^{2n-1}},\ n=1, 2, \ldots
\end{array} \right.\nonumber
$$
Очевидно, что \(f \notin L_{2}^{C}(0, 1)\), так как множество ее точек разрыва счетно. Построим последовательность
$$
f_{n}(x)=\left\{
\begin{array}{ll}
f(x), & \displaystyle\frac{1}{2^{n}} \leq x < 1,\\
\\
0, & \displaystyle 0 < x \leq \frac{1}{2^{n}}.
\end{array} \right.\nonumber
$$
Покажем, что последовательность \(f_{n}\) фундаментальна в пространстве \(L_{2}^{C}(0, 1)\). Так как на отрезке \([1/2^{n}, 1]\) функции \(f_{n+p}\) и \(f_{n}\) совпадают, то
$$
\left\|f_{n+p}-f_{n}\right\|^{2}=\int\limits_{0}^{1} |f_{n+p}(x)-f_{n}(x)|^{2}\ dx=\int\limits_{0}^{1/2^{n}} |f_{n+p}(x)-f_{n}(x)|^{2}\ dx \leq\\\leq \frac{1}{2^{n}} \max|f_{n+p}(x)-f_{n}(x)| \leq \frac{1}{2^{n}} < \varepsilon\ \mbox{при}\ n > N(\varepsilon).\nonumber
$$
Последовательность \(\{f_{n}\}\) фундаментальна. Покажем, что она не может быть сходящейся. Если \(\varphi \in L_{2}^{C}(0, 1)\) и \(\left\|f_{n}-\varphi\right\|^{2} \rightarrow 0\) то для всех \(m \in N\) выполнено условие
$$
\int\limits_{1/2^{m+1}}^{1/2^{m}} |f_{n}-\varphi|^{2}\ dx \rightarrow 0\ \mbox{при}\ n \rightarrow \infty.\nonumber
$$
Если \(n > m\), то \(f_{n}=f\) при \(x \in \displaystyle\left(\frac{1}{2^{m+1}}, \frac{1}{2^{m}}\right)\). Поэтому
$$
\int\limits_{1/2^{m+1}}^{1/2^{m}} |f_{n}-\varphi|^{2}\ dx=0,\ m=0, 1, \ldots\label{ref7}
$$
Так как функция \(\varphi(x)\) имеет конечное число точек разрыва, то при достаточно большом \(m\) на интервале \(\displaystyle\left(\frac{1}{2^{m+1}}, \frac{1}{2^{m}}\right)\) у функции \(\varphi(x)\) точек разрыва не будет, функция \(f(x)\) непрерывна на этом же интервале. Поэтому из \eqref{ref7} следует, что
$$
f(x)=\varphi(x)\ \mbox{при}\ x \in \left(\frac{1}{2^{m+1}}, \frac{1}{2^{m}}\right),\ m=M+1, \ldots\nonumber
$$
Но тогда функция \(\varphi\), как и функция \(f\), должна иметь счетное множество точек разрыва и, следовательно, не может принадлежать пространству \(L_{2}^{C}(a, b)\). Итак, пространство \(L_{2}^{C}(a, b)\) неполное. \(\bullet\)
Пополнение унитарного пространства.
Определение.
Два унитарных пространства называются изоморфными, если можно установить такое взаимно однозначное отображение \(F\) пространства \(E_{1}\) на пространство \(E_{2}\), что для любых \(x, y \in E\) и любого \(\alpha \in \mathbb{C}\) выполнены равенства
$$
F(x+y)=F(x)+F(y),\quad F(\alpha x)=\alpha F(x),\quad (Fx, Fy)=(x, y).\nonumber
$$
Подмножество \(L\) унитарного пространства \(E\), само являющееся унитарным пространством с тем же скалярным произведением, называется подпространством пространства \(E\).
Пусть \(A\) и \(B\) — подмножества унитарного (или нормированного) пространства \(E\). Говорят, что \(B\) плотно в \(A\), если для любого \(\varepsilon > 0\) и любого \(x \in A\) найдется \(y \in B\) такой, что \(\left\|x-y\right\| < \varepsilon\).
Лемма 3.
Если \(A, B, C \subset E\) и \(C\) плотно в \(B\), а \(B\) плотно в \(A\), то \(C\) плотно в \(A\).
Доказательство.
\(\circ\) Пусть \(\varepsilon > 0\) и \(x \in A\). Так как \(B\) плотно в \(A\), то найдется \(y \in B\) такой, что \(\left\|x-y\right\| < \varepsilon/2\). Так как \(C\) плотно в \(B\), то найдется \(z \in \mathbb{C}\) такой, что \(\left\|y-z\right\| < \varepsilon/2\). Тогда
$$
\left\|x-z\right\| \leq \left\|x-y\right\|+\left\|y-z\right\| < \frac{\varepsilon}{2}+\frac{\varepsilon}{2}=\varepsilon.\nonumber
$$
Следовательно, \(C\) плотно в \(A\). \(\bullet\)
Лемма 4.
Подпространство функций, непрерывных на отрезке \([a, b]\) и принимающих на концах этого отрезка равные значения, плотно в \(L_{2}^{C}(a, b)\).
Доказательство.
\(\circ\) Обозначим для краткости через \(B\) подпространство кусочно непрерывных на \([a, b]\) функций, а через \(C\) — подпространство непрерывных функций, принимающих на концах отрезка \([a, b]\) одинаковые значения. Договоримся, что будем доопределять нулем функции вне отрезка \([a, b]\).
Покажем, что \(B\) плотно в \(L_{2}^{C}(a, b)\). Возьмем произвольную функцию \(f \in L_{2}^{C}(a, b)\) и любое \(\varepsilon > 0\). Тогда существует такое разбиение \(x_{0}=a < x_{1} < \ldots < x_{n}=b\), что на каждом из интервалов \((x_{i-1}, x_{i})\) функция \(f(x)\) непрерывна, а интеграл \(\int\limits_{a}^{b}|f|^{2}dx\) сходится как несобственный. Найдется такое \(\delta > 0\), что
$$
\sum_{i=0}^{n} \int\limits_{x_{i}-\delta}^{x_{i}+\delta}|f|^{2}dx < \varepsilon,\quad (x_{i}-\delta, x_{i}+\delta) \cap (x_{j}-\delta, x_{j}+\delta)=\varnothing,\ i \neq j.\nonumber
$$
Возьмем функцию
$$
\varphi_{n}(x)=\left\{
\begin{array}{ll}
0, & x \in \displaystyle\bigcup_{i=0}^{n}(x_{i}-\delta, x_{i}+\delta),\\
f(x) & \mbox{в остальных точках}.
\end{array} \right.\nonumber
$$
Очевидно, что \(\varphi(x)\) кусочно непрерывна и
$$
\left\|f-\varphi\right\|^{2}=\sum_{i=0}^{n} \int\limits_{x_{i}-\delta}^{x_{i}+\delta}|f|^{2}dx < \varepsilon.
$$
Итак, \(B\) плотно в \(L_{2}^{C}(a, b)\). Покажем, что \(C\) плотно в \(B\). Пусть \(\varphi \in B\) и \(\tilde{x}_{0}=a < \tilde{x}_{1} < \ldots < \tilde{x}_{n}=b\) — ее точки разрыва первого рода. Построим непрерывную функцию \(\psi(x)\), обращающуюся в нуль во всех точках \(\tilde{x}_{i}\), (рис. 70.2):
$$
\psi_{n}(x)=\left\{
\begin{array}{ll}
\displaystyle\frac{\tilde{x}_{i}-x}{\varepsilon} \varphi(\tilde{x}_{i}-\varepsilon), & \tilde{x}_{i}-\varepsilon \leq x \leq \tilde{x}_{i},\\
\displaystyle\frac{x-\tilde{x}_{i}}{\varepsilon} \varphi(\tilde{x}_{i}+\varepsilon), & \tilde{x}_{i} \displaystyle\leq x \leq \tilde{x}_{i}+\varepsilon,\ i=\overline{0, m},\\
\varphi(x), & \mbox{в остальных точках}
\end{array} \right.\nonumber
$$
где \(\varepsilon < \displaystyle\frac{1}{4} \max_{i=\overline{0, m}} \bigtriangleup \tilde{x}_{i}\), \(\bigtriangleup \tilde{x}_{i}=\tilde{x}_{i}-\tilde{x}_{i-1}\).
Функция \(\psi(x)\) непрерывна на отрезке \([a, b]\) и
$$
|\psi(x)| \leq M=\max_{a \leq x \leq b} |\varphi(x)|.\nonumber
$$
В самом деле, так как функция \(\psi(x)\) линейна на отрезках \([\tilde{x}_{i}-\varepsilon, \tilde{x}_{i}]\) и \([\tilde{x}_{i}, \tilde{x}_{i}+\varepsilon]\) и \(\psi(\tilde{x}_{i})=0\), то
$$
\max_{\tilde{x}_{i}-\varepsilon \leq x \leq \tilde{x}_{i}} |\psi(x)|=|\psi(\tilde{x}_{i}-\varepsilon)|=|\varphi(\tilde{x}_{i}-\varepsilon)| \leq M,\nonumber
$$
$$
\max_{\tilde{x}_{i} \leq x \leq \tilde{x}_{i}+\varepsilon} |\psi(x)|=|\psi(\tilde{x}_{i}+\varepsilon)|=|\varphi(\tilde{x}_{i}+\varepsilon)| \leq M,\nonumber
$$
Вне отрезков \([\tilde{x}_{i}-\varepsilon, \tilde{x}_{i}]\) и \([\tilde{x}_{i}, \tilde{x}_{i}+\varepsilon]\) функция совпадает с \(\varphi(x)\) и ее значения по модулю не превосходят \(M\).
Оценивая среднеквадратичное отклонение функции \(\varphi(x)\) от функции \(\psi(x)\), получаем
$$
\left\|\varphi(x)-\psi(x)\right\|^{2}=\sum_{i=1}^{n} \int\limits_{\tilde{x}_{i}-\varepsilon}^{\tilde{x}_{i}+\varepsilon}|\varphi(x)-\psi(x)|^{2}dx \leq 8Mn\varepsilon.\nonumber
$$
Отсюда следует, что \(C\) плотно в \(B\). Итак, \(C\) плотно в \(B\), а \(B\) плотно в \(L_{2}^{C}(a, b)\). В силу леммы 3 \(C\) плотно в \(L_{2}^{C}(a, b)\). \(\bullet\)
Пополнением унитарного пространства \(E\) называется полное унитарное пространство \(\tilde{E}\), содержащее плотное в \(\tilde{E}\) подпространство \(L\), изоморфное \(E\).
Теорема 1.
Для любого унитарного пространства существует пополнение, единственное с точностью до изоморфизма.
Доказательство.
Данная теорема приводится без доказательства.
Пополнение пространства \(L_{2}^{C}(a, b)\) называется пространством \(L_{2}(a, b)\). Можно показать, что \(L_{2}^{C}(a, b)\) изоморфно гильбертову пространству функций, интегрируемых с квадратом по Лебегу.
Ряды Фурье по ортогональным системам.
Пусть \(H\) бесконечномерное унитарное пространство. Систему элементов \(\{e_{i}\}_{i=1, \ldots} \in H\) будем называть линейно независимой, если при любом \(n\) элементы \(e_{1}, e_{2}, \ldots, e_{n}\) линейно независимы. Если любой элемент \(x \in H\) можно представить в виде суммы сходящегося ряда
$$
x=\lim_{m \rightarrow \infty} \sum_{n=1}^{m} x_{n}e_{n}=\sum_{n=1}^{\infty}x_{n}e_{n},\label{ref8}
$$
то линейно независимая система \(\{e_{i}\}\) называется базисом в \(H\). Система \(\{e_{i}\}\) называется ортогональной, если \((e_{i}, e_{j})=0\) при \(i \neq j\), и ортонормированной, если \((e_{i}, e_{j})=\delta_{ij}\), где \(\delta_{ij}\) — символ Кронекера, то есть \(\delta_{ij}=0\) при \(i \neq j\) и \(\delta_{ii}=1\). Если, кроме того, \(\{e_{i}\}\) есть базис, то будем говорить об ортогональных и ортонормированных базисах.
Если \(\{e_{i}\}\) — ортогональный базис, то все коэффициенты \(x_{n}\) ряда \eqref{ref8} могут быть выражены через \(x\). Так как элементы \(e_{i}\) ортогональны, то при \(k \leq n\) имеем
$$
\left(\sum_{i=1}^{n} x_{i}e_{i}, e_{k}\right)=x_{k}(e_{k}, e_{k}).\label{ref9}
$$
Так как \(x=\displaystyle\lim_{n \rightarrow \infty} \sum_{i=1}^{n} x_{i}e_{i}\), а скалярное произведение непрерывно, то, переходя в \eqref{ref9} к пределу при \(n \rightarrow \infty\), получаем
$$
x_{k}=\dfrac{(x, e_{k})}{\left\|e_{k}\right\|^{2}},\ k \in N.\label{ref10}
$$
Если базис ортонормированный, то \(\left\|e_{k}\right\|=1\) и \(x_{k}=(x, e_{k})\). Числа \(x_{k}\) называются коэффициентами Фурье элемента \(x\) по ортогональной системе \(\{e_{i}\}\).
Если теперь отказаться от требования, чтобы ортогональная система \(\{e_{i}\}\) была базисом в \(H\), то коэффициенты Фурье элемента \(x\) все равно можно вычислять по формуле \eqref{ref10}. Выражение \(\displaystyle\sum_{k=1}^{\infty}x_{k}e_{k}\) где \(x_{k}\) — коэффициенты Фурье элемента \(x\), будем называть рядом Фурье элемента \(x\) по ортогональной системе \(\{e_{i}\}\). Так как, вообще говоря, ряд может и не сходиться, то будем писать
$$
x \sim \sum_{k=1}^{\infty}x_{k}e_{k},\quad x_{k}=\dfrac{(x, e_{k})}{\left\|e_{k}\right\|^{2}}.\nonumber
$$
Минимальное свойство коэффициентов Фурье. Неравенство Бесселя.
Теорема 2.
Пусть \(\{e_{i}\}\) — ортонормированная система элементов унитарного пространства \(E\), \(x\) — произвольный элемент пространства \(E\), \(n \in N\). Тогда из всех линейных комбинаций \(\displaystyle\sum_{i=1}^{n}\alpha_{i}e_{i}\), где \(\alpha_{i} \in \mathbb{C}\), \(i=\overline{1, n}\), наилучшим образом приближает элемент \(x\) но норме пространства \(E\) \(n\)-я частичная сумма ряда Фурье элемента \(x\) по ортонормированной системе \(\{e_{i}\}\), то есть
$$
\min_{\alpha_{1}, \ldots, \alpha_{n} \in \mathbb{C}} \left\|x-\sum_{i=1}^{n}\alpha_{i}e_{i}\right\|=\left\|x-\sum_{i=1}^{n}(x, e_{i})e_{i}\right\|.\nonumber
$$
Доказательство.
\(\circ\) Обозначим \(\sigma_{n}=\displaystyle\left\|x-\sum_{i=1}^{n}\alpha_{i}e_{i}\right\|^{2}\). Так как \(\left\|x\right\|^{2}=(x, x)\), то
$$
0 \leq \sigma_{n}=\left(x-\sum_{i=1}^{n}\alpha_{i}e_{i}, x-\sum_{i=1}^{n}\alpha_{i}e_{i}\right)=(x, x)-\sum_{i=1}^{n}\alpha_{i}(e_{i}, x) -\\- \sum_{i=1}^{n}\overline{\alpha}_{i}(e_{i}, x)+\sum_{i=1}^{n}\alpha_{i}\overline{\alpha}_{i}=(x, x)-\sum_{i=1}^{n}\alpha_{i}\overline{x}_{i}-\sum_{i=1}^{n}\overline{\alpha}_{i}x_{i}+\sum_{i=1}^{n}\alpha_{i}\overline{\alpha}_{i} =\\= \left\|x\right\|^{2}-\sum_{i=1}^{n}|x_{i}|^{2}+\sum_{i=1}^{n}(\alpha_{i}-x_{i})(\overline{\alpha}_{i}-\overline{x}_{i}).\nonumber
$$
Следовательно, $$ 0 \leq \sigma_{n}=\left\|x\right\|^{2}-\sum_{i=1}^{n}|x_{i}|^{2}+\sum_{i=1}^{n}|\alpha_{i}-x_{i}|^{2}.\label{ref11}
$$
Из равенства \eqref{ref11} следует, что минимум \(\sigma_{n}\) достигается при \(\alpha_{i}=x_{i}\), причем
$$
0 \leq \min_{\alpha_{1} \in \mathbb{C}, i=\overline{1, n}} \sigma_{n}=\left|\|x-\sum_{i=1}^{n}x_{i}e_{i}\right|\|^{2}=\left\|x\right\|^{2}-\sum_{i=1}^{n}|x_{i}|^{2},\ x_{i}=(x, e_{i}).\ \bullet\label{ref12}
$$
Следствие.
Для коэффициентов Фурье элемента \(x\) по ортонормированной системе \(\{e_{i}\}\) справедливо неравенство Бесселя
$$
\sum_{i=1}^{\infty}|x_{i}|^{2} \leq \left\|x\right\|^{2}.\label{ref13}
$$
\(\circ\) Из \eqref{ref12} следует, что \(\sum_{i=1}^{n}|x_{i}|^{2} \leq \left\|x\right\|^{2}\). Переходя к пределу при \(n \rightarrow \infty\), получаем неравенство Бесселя. \(\bullet\)
Полнота системы элементов {ei} в унитарном пространстве. Полнота тригонометрической системы в L2(-π, π).
Система элементов \(\{e_{i}\}\) называется полной в унитарном (нормированном) пространстве \(E\), если любой элемент \(x \in E\) может с любой степенью точности быть приближен по норме конечной линейной комбинацией \(\displaystyle\sum_{i=1}^{n}\alpha_{i}e_{i}\) то есть для любого \(\varepsilon > 0\) найдется линейная комбинация \(\displaystyle\sum_{i=1}^{n}\alpha_{i}e_{i}\) такая, что
$$
\left\|x-\sum_{i=1}^{n}\alpha_{i}e_{i}\right\| < \varepsilon.\label{ref14}
$$
Теорема 3.
Если \(\{e_{i}\}\) — ортонормированная система в унитарном пространстве \(H\), то следующие условия эквивалентны:
- система \(\{e_{i}\}\) полна в \(H\);
- для любого \(x \in H\) справедливо равенство Парсеваля
$$
\left\|x\right\|^{2}=\sum_{i=1}^{\infty}|x_{i}|^{2},\ x_{i}=(x, e_{i});\label{ref15}
$$ - для любого \(x \in H\) выполнено равенство
$$
x=\sum_{i=1}^{\infty}x_{i}e_{i}.\label{ref16}
$$
Доказательство.
\(\circ\) Докажем, что 1)\(\Rightarrow\)2). Пусть ортонормированная система \(\{e_{i}\}\) полна в \(H\). Тогда для любого \(\varepsilon > 0\) найдется линейная комбинация \(\displaystyle\sum_{i=1}^{n}\alpha_{i}e_{i}\) такая, что справедливо неравенство \eqref{ref14}.
В силу минимального свойства коэффициентов Фурье
$$
0 \leq \left\|x-\sum_{i=1}^{n}\alpha_{i}e_{i}\right\|^{2}=\left\|x\right\|^{2}-\sum_{i=1}^{n}|x_{i}|^{2} \leq \left\|x-\sum_{i=1}^{n}\alpha_{i}e_{i}\right\|^{2} < \varepsilon^{2}.
$$
Используя это неравенство и неравенство \eqref{ref13}, получаем
$$
0 \leq \left\|x\right\|^{2}-\sum_{i=1}^{\infty}|x_{i}|^{2} \leq \left\|x\right\|^{2}-\sum_{i=1}^{n}|x_{i}|^{2} < \varepsilon^{2}.\nonumber
$$
В силу произвольности \(\varepsilon\) должно быть справедливо равенство Парсеваля \eqref{ref15}.
Докажем, что 2)\(\Rightarrow\)3). Пусть справедливо равенство Парсеваля \eqref{ref15}. Тогда
$$
\left\|x-\sum_{i=1}^{n}x_{i}e_{i}\right\|^{2}=\left\|x\right\|^{2}-\sum_{i=1}^{n}|x_{i}|^{2} \rightarrow 0\ \mbox{при}\ n \rightarrow \infty,
$$
то есть справедливо равенство \eqref{ref16}.
Утверждение 3)\(\Rightarrow\)1) очевидно. \(\bullet\)
Лемма 5.
Пусть подпространство \(L\) плотно в унитарном пространстве \(H\), а система \(\{e_{i}\}\) полна в \(L\). Тогда система элементов \(\{e_{i}\}\) полна в \(H\).
Доказательство.
\(\circ\) Пусть \(x\) — произвольный элемент пространства \(H\). Так как \(L\) плотно в \(H\), то для любого \(\varepsilon > 0\) найдется элемент \(y \in L\) такой, что \(\displaystyle\left\|x-y\right\| < \frac{\varepsilon}{2}\) Так как система \(\{e_{i}\}\) полна в \(L\), то найдется линейная комбинация \(\displaystyle\sum_{i=1}^{n}\alpha_{i}e_{i}\) такая, что
$$
\left\|y-\sum_{i=1}^{n}\alpha_{i}e_{i}\right\| < \frac{\varepsilon}{2}.\nonumber
$$
Тогда
$$
\left\|x-\sum_{i=1}^{n}\alpha_{i}e_{i}\right\| \leq \left\|x-y\right\|+\left\|y-\sum_{i=1}^{n}\alpha_{i}e_{i}\right\| < \frac{\varepsilon}{2}+\frac{\varepsilon}{2}=\varepsilon.\nonumber
$$
Поэтому \(\{e_{i}\}\) — полная система в пространстве \(H\). \(\bullet\)
Теорема 4.
Тригонометрическая система полна в \(L_{2}(-\pi, \pi)\).
Доказательство.
\(\circ\) Пространство \(L_{2}(-\pi, \pi)\) есть пополнение \(L_{2}^{C}(-\pi, \pi)\). Поэтому \(L_{2}^{C}(-\pi, \pi)\) плотно в \(L_{2}(-\pi, \pi)\). Пространство непрерывных функций, принимающих одинаковые значения в точках \(\pi\) и \(-\pi\), в силу леммы 4 плотно в \(L_{2}^{C}(-\pi, \pi)\), а следовательно, и в \(L_{2}(-\pi, \pi)\).
Осталось, в силу леммы 5, показать, что тригонометрическая система полна в подпространстве \(L\) непрерывных на \([-\pi, \pi]\) функций, принимающих одинаковые значения в точках \(\pi\) и \(-\pi\). Каждую такую функцию можно в силу теоремы Вейерштрасса равномерно приблизить тригонометрическим многочленом \(T(x)\), то есть
$$
\max_{-\pi \leq x \leq \pi} |f(x)-T(x)| < \varepsilon,\nonumber
$$
где \(T(x)=\displaystyle\frac{A_{0}}{2}+\sum_{n=1}^{n} A_{n} \cos nx+B_{n} \sin nx\).
Но тогда \(f(x)\) можно приблизить с любой степенью точности тригонометрическим многочленом и по норме пространства \(L_{2}(-\pi, \pi)\) (в смысле среднего квадратичного), так как
$$
\left\|f-T\right\|=\left(\int\limits_{-\pi}^{\pi}|f-T|^{2}dx\right)^{1/2} \leq \varepsilon \sqrt{2\pi}.\nonumber
$$
Итак, тригонометрическая система полна в \(L_{2}(-\pi, \pi)\). \(\bullet\)
Следствие.
Из теорем 3 и 4 следует, что для любой функции \(f \in L_{2}^{C}[-\pi, \pi]\), в частности, для любой непрерывной или кусочно непрерывной функции, выполнено равенство Парсеваля
$$
\frac{|a_{0}|^{2}}{2}+\sum_{n=1}^{\infty} |a_{n}|^{2}+|b_{n}|^{2}=\frac{1}{\pi}\int\limits_{-\pi}^{\pi}|f(x)|^{2} dx\nonumber
$$
и ряд Фурье такой функции сходится в смысле среднего квадратичного к функции \(f(x)\), то есть
$$
\lim_{n \rightarrow \infty} \int\limits_{-\pi}^{\pi} \left|f(x)-\frac{a_{0}}{2}-\sum_{k=1}^{n} (a_{k} \cos kx+b_{k} \sin kx)\right|^{2}dx=0.\nonumber
$$
Эквивалентность полноты и замкнутости ортогональной системы в гильбертовом пространстве.
Теорема 5.
Пусть \(H\) — гильбертово пространство и \(\{e_{i}\}\) — ортонормированная система элементов. Для того чтобы ряд
$$
\sum_{i=1}^{\infty}\alpha_{i}e_{i}\nonumber
$$
сходился, необходимо и достаточно, чтобы сходился числовой ряд
$$
\sum_{i=1}^{\infty}|\alpha_{i}|^{2}.\nonumber
$$
Доказательство.
\(\circ\) Необходимость следует из неравенства Бесселя. Если \(x=\displaystyle\sum_{i=1}^{\infty}\alpha_{i}e_{i}\), то \(\alpha_{i}=\displaystyle\lim_{n \rightarrow \infty} \left(\sum_{k=1}^{n}\alpha_{k}e_{k}, e_{i}\right)=(x, e_{i})\) и \(\displaystyle\sum_{i=1}^{\infty}|\alpha_{i}|^{2} \leq \left\|x\right\|^{2}\).
Достаточность. Пусть числовой ряд \(\displaystyle\sum_{i=1}^{\infty}|\alpha_{i}|^{2}\) сходится. Тогда для любого \(\varepsilon > 0\) найдется такой номер \(N\), что для всех \(n, m > N\) выполнено неравенство
$$
\sum_{k=n}^{m}|\alpha_{i}|^{2} < \varepsilon.\nonumber
$$
Последовательность частичных сумм ряда \(\displaystyle\sum_{i=1}^{\infty}\alpha_{i}e_{i}\) будет фундаментальной, так как при любых \(n, m > N\) выполнено условие
$$
\left\|s_{n}-s_{m}\right\|^{2}=\left\|\sum_{i=n}^{m}\alpha_{i}e_{i}\right\|^{2}=\sum_{i=n}^{m}|\alpha_{i}|^{2} < \varepsilon,\nonumber
$$
где \(s_{n}=\alpha_{1}e_{1}+\ldots+\alpha_{n}e_{n}\).
Но в полном пространстве любая фундаментальная последовательность сходится. Следовательно, последовательность частичных сумм \(s_{n}\) сходится, то есть ряд \(\displaystyle\sum_{i=1}^{\infty}\alpha_{i}e_{i}\) сходится. \(\bullet\)
Следствие.
Если \(\{e_{i}\}\) — ортонормированная система в гильбертовом пространстве \(H\), то для любого \(x \in H\) ряд Фурье по ортонормированной системе \(\{e_{i}\}\) сходится и элемент \(x\) представим в виде
$$
x=\sum_{i=1}^{\infty}x_{i}e_{i}+y,\ \mbox{где}\ x_{i}=(x, e_{i}),\ (y, e_{i})=0,\ i \in N.\label{ref17}
$$
\(\circ\) Пусть \(\displaystyle\sum_{i=1}^{\infty}x_{i}e_{i}\) есть ряд Фурье элемента \(x\). В силу неравенства Бесселя числовой ряд \(\displaystyle\sum_{i=1}^{\infty}|x_{i}|^{2}\) сходится. Из теоремы 5 тогда следует, что ряд \(\displaystyle\sum_{i=1}^{\infty}x_{i}e_{i}\) будет сходящимся.
Пусть
$$
y=x-\sum_{i=1}^{\infty}x_{i}e_{i}=\lim_{n \rightarrow \infty} \left(x-\sum_{i=1}^{n}x_{i}e_{i}\right).\nonumber
$$
В силу ортогональности системы \(\{e_{i}\}\) и непрерывности скалярного произведения справедливо равенство
$$
(y, e_{i})=\lim_{n \rightarrow \infty} \left(x-\sum_{i=1}^{n}x_{i}e_{i}, e_{i}\right)=(x, e_{i})-x_{i}=0,\ i \in N.\ \bullet\nonumber
$$
Ортогональная система \(\{e_{i}\}\) называется замкнутой в унитарном пространстве \(H\), если для любого \(x \in H\) из \((x, e_{i})=0\), \(i=1, 2, \ldots\), следует \(x=0\).
Теорема 6.
Для того чтобы ортонормированная система была полной в унитарном пространстве, необходимо, а в случае полного пространства и достаточно, чтобы она была замкнутой.
Доказательство.
\(\circ\) Необходимость. Пусть \(\{e_{i}\}\) — полная система в унитарном пространстве \(H\). Если для элемента \(x \in H\) справедливы равенства \((x, e_{i})=0\), \(i \in N\), то, применяя равенство Парсеваля, получаем
$$
\left\|x\right\|^{2}=\sum_{i=1}^{\infty}|x_{i}e_{i}|^{2}=0,\nonumber
$$
то есть \(x=0\).
Достаточность. Пусть \(H\) — полное пространство. Тогда каждый элемент \(x \in H\) можно представить в виде \eqref{ref17}. Так как система \(\{e_{i}\}\) замкнута, то из равенств \((y, e_{i})=0\), \(i \in N\), следует, что \(y=0\). Таким образом, любой элемент \(x\) есть сумма своего ряда Фурье по ортонормированной системе \(\{e_{i}\}\). Следовательно, система \(\{e_{i}\}\) полна в \(H\). \(\bullet\)
8 Обобщенные ряды Фурье
8.1 Сигнальное пространство
 |
Мы уже видели, что каждая реализация измерительного сигнала x(t) является результатом чьего-то выбора (рис. 8.1) из некоторого конечного или бесконечного множества сигналов 
Одним из наиболее плодотворных путей построения ансамблей сигналов считается использование методов функционального анализа – раздела математики, который обобщает наши интуитивные представления о геометрической структуре пространства.
Пусть 
Говорят, что множество сигналов наделено определенной структурой, если имеется возможность выражать одни элементы множества через другие, например, с помощью соотношения 
Множество М сигналов образует вещественное линейное сигнальное пространство, если для сигналов, входящих в это множество, выполняются следующие условия:
— если сигнал 
— если 

Рекомендуемые материалы
— если, 

— множество М содержит нулевой сигнал 

Совокупность сигналов 
выполняется только в том случае, когда все 
Линейное сигнальное пространство L называется нормированным, если в нем можно ввести норму – число, которое характеризует «длину» или «величину» сигнала. Норму для сигнала x(t) будем обозначать, как 
1. норма неотрицательна, то есть всегда 
2. для любого α справедливо равенство 
3. если 

Чаще всего в качестве нормы будем использовать следующее выражение:
Это – энергетическая норма, поскольку выражение под корнем определяет энергию сигнала.
Линейное сигнальное пространство будем называть метрическим, если каждой паре сигналов 


1. 
2. 
3. 
Обычно метрика определяется как норма разности сигналов:

Тогда и норму сигнала можно определить как расстояние между этим сигналом и нулевым сигналом:

Линейное сигнальное пространство, если на нем введена норма и метрика, называется гильбертовым пространством, если на его элементах может быть определено скалярное произведение

которое равно взаимной энергии сигналов. При этом должно выполняться условие Коши – Буняковского:



хотя понятие угла между сигналами не имеет наглядной геометрической интерпретации.
Пример
Сигнал x(t) – отрезок синусоиды, нормированный к единице (рис. 80):

Найти амплитуду В прямоугольного импульса такой же протяженности, при которой расстояние между этими двумя сигналами будет минимальным.
Для решения задачи запишем выражение для метрики как расстояния между синусоидальным сигналом и прямоугольным импульсом:
Квадрат метрики, да и сама метрика, обратится в минимум при равенстве нулю производной:
откуда следует
8.2 Ортогональные сигналы и обобщенные ряды Фурье
Два сигнала 

Пусть задан некоторый ансамбль сигналов 






Система базисных функций называется ортонормированной, если все эти функции ортогональны, а их мощности равны единице. Очевидно, что любую систему ортогональных базисных функций можно сделать ортонормированной, если все эти функции поделить на корни квадратные из их мощности.
Произвольный сигнал конечной длительности 

Такое представление сигнала называется обобщенным рядом Фурье в данной системе ортогональных базисных функций.
Набор коэффициентов 



Для определения j-го спектрального коэффициента 

Отсюда следует, что спектральные коэффициенты 


При представлении сигнала в системе ортогональных базисных функций всегда приходится ограничиваться некоторым конечным числом N членов ряда. Получаемый при этом сигнал
называется аппроксимирующим рядом. Погрешность аппроксимации
характеризуется дисперсией погрешности, равной

Представление сигнала в виде обобщенного ряда Фурье по системе ортогональных базисных функций замечательно тем, что по мере увеличения числа N аппроксимирующего ряда погрешность аппроксимации всегда только уменьшается. При 


Для обобщенного ряда Фурье справедливо равенство Парсеваля:
Это еще раз подчеркивает математическое равноправие двух форм представления сигнала: сигнала в виде функции времени 

Таким образом, обобщенный ряд Фурье для сигнала 




Если ряд Фурье ограничен конечным числом N членов ряда, то равенство Парсеваля нарушается и средняя квадратическая погрешность (стандартное отклонение погрешности) приближения сигнала 


По итогам рассмотренных положений можно сделать следующие выводы.
1. Обобщенный ряд Фурье позволяет представить любую реализацию случайного сигнала из данной реализации как сумму произведений детерминированных функций времени на систему соответствующим образом выбранных спектральных коэффициентов.
2. На множестве реализаций случайного сигнала спектральные коэффициенты являются случайными величинами. Система случайных спектральных коэффициентов как система случайных величин описывается
o вектором математических ожиданий спектральных коэффициентов,
o вектором дисперсий спектральных коэффициентов,
o матрицей моментов взаимной корреляции спектральных коэффициентов.
3. Множество сигналов 

4. Спектральные коэффициенты могут служить информативными параметрами сигнала.
5. Система ортогональных базисных функций определяет каноническое разложение случайного сигнала, если спектральные коэффициенты для данного ансамбля являются случайными некоррелированными величинами.
Определенный интерес имеет рассмотрение двух следующих вопросов:
— выбрать, исходя из некоторых свойств ансамбля реализаций случайного сигнала, систему ортогональных базисных функций таким образом, чтобы совокупность спектральных коэффициентов была не коррелированной,
— отыскать такую систему ортогональных базисных функций, в которой последовательность спектральных коэффициентов наиболее быстро убывает с ростом индекса спектрального коэффициента.
8.3 Системы ортогональных базисных функций
В сигнальном пространстве можно построить различные системы ортогональных базисных функций. Однако спектральному анализу сигналов в различных системах функций соответствует различная интерпретация результатов и различная техническая реализация средств информационно – измерительной техники. Поэтому имеет смысл рассмотреть и сравнить друг с другом различные системы ортогональных базисных функций.
8.3.1 Система тригонометрических базисных функций
Система тригонометрических базисных функций имеет следующий вид:
Построенная таким образом система функций является ортонормированной на интервале 
8.3.2 Система полиномов Лежандра
Полиномы Лежандра порядка n вычисляются как производные:
Полиномы Лежандра порядков с 0-го до 6-го выражаются следующими формулами:
Полиномы не совпадающих друг с другом порядков попарно ортогональны и имеют мощность

поэтому соответствующие ортонормированные полиномы Лежандра принимают следующий вид:
На рис. 8.4 представлены графики первых семи полиномов Лежандра после их деления на корень квадратный из мощности, то есть после ортонормирования, включая и полином нулевого порядка. Они отличаются от полиномов Чебышева только тем, что их максимумы увеличиваются к концам диапазона, в остальном они ведут себя похожим образом.
Полиномы Лежандра замечательны тем, что среди всех других полиномов данной степени с одинаковым старшим членом они имеют наименьшее среднее квадратическое отклонение от нуля.
 |
Если измерительный сигнал 

Наоборот, сам сигнал перед разложением в ряд по полиномам Лежандра можно привести к интервалу –1<τ<+1 с помощью подстановки

Поэтому спектральные коэффициенты разложения сигнала 
Пример
Сигнал 

После замены переменных 

Таким образом, спектр сигнала имеет вид:
На рис. 8.5 представлен сам исходный сигнал 


разности представлена на рис. 8.6.
Из графика на рис. 8.6 видно, что погрешность только на концах диапазона немного превышает сотую долю амплитуды сигнала. Для сравнения на рис. 8.7 представлены графики того же самого сигнала 
 |
8.3.3 Системы базисных функций Уолша



Здесь sign(x) – функция знака, принимающая значения +1 или –1 в зависимости от знака аргумента.
При построении функции Радемахера порядка k интервал ее определения 0 – 1 разбивается на 
Система функций Радемахера является ортонормированной, но она не полна, поскольку можно обнаружить функции, например 
Система Уолша – Пэли отличается тем, что получаемые в ней спектры широкого класса непрерывных сигналов сходятся быстрее всего, то есть спектральные коэффициенты убывают наиболее быстро с ростом номера коэффициента. В системе Уолша – Пэли каждая базисная функция Уолша с номером i равна произведению функций Радемахера с номерами, совпадающими с номерами двоичных разрядов в двоичном представлении числа i, содержащих единицу. Если n – разрядное двоичное представление числа i имеет вид:

где k – номер разряда, начиная с младшего, то функция Уолша с номером i должна быть записана в виде:

Так, например, шестая функция Уолша (6 = LL0) определяется как


На рис 8.10 представлены графики функций Уолша – Пэли до шестого порядка включительно.
Ряд Фурье – Уолша для сигнала 



Ограничиваясь конечным числом членов разложения в ряд, мы получаем приближенное выражение для исходного сигнала.
Пример
В лекции «8 Качество говядины и факторы, на нее влияющие» также много полезной информации.
Найти спектр Уолша и аппроксимирующий ряд из семи членов разложения в ряд Фурье – Уолша сигнала 

Расчет спектра Уолша:
Спектр Уолша для данного сигнала имеет вид:

Аппроксимирующий ряд из первых семи членов, включая нулевой, составляет:



Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:
Скачиваний:
30
Добавлен:
27.03.2015
Размер:
214.53 Кб
Скачать
Задача
№2
Дана
Т – периодическая функция f(t)
-
Обосновать
возможность разложения f(t)
в ряд Фурье, установить вид сходимости
ряда Фурье к f(t).
Данная
функция f(t)
удовлетворяет условиям теоремы Дирихле:
Теорема
Дирихле: Если Т — периодическая функция
f(t)
удовлетворяет условиям Дирихле на каком
либо замкнутом интервале длиной Т:
-
Непрерывна
или имеет конечное число точек разрыва
первого рода -
Монотонна
либо имеет конечное число максимумов
и минимумов
Ряд
Фурье сходиться на всей оси t
и сумма ряда Фурье равно f(t)
во всех точках непрерывности этой
функции в точке t0
разрыва первого рода функции f(t)
сумма ряда Фурье равна
данная функция f(t)
удовлетворяет условиям сходимости в
среднем.
Признак
Ляпунова: Если Т – периодическая функция
f(t)
удовлетворяет условиям для
кусочно-непрерывна и интегрируема с
квадратом, то ряд Фурье сходиться
среднеквадратично к f(t).
-
Построить
график суммы ряда Фурье.
-
Представить
заданную функцию тригонометрическим
рядом Фурье, предварительно:
б)
вычислить коэффициенты ряда Фурье.
Коэффициенты
ряда Фурье
Тригонометрическое
разложение ф-ии в ряд Фурье
-
Построить
амплитудный и фазовый спектры функции.
-
Определить
число гармоник разложения функции в
ряд Фурье, содержащих в сумме не менее
90% энергии.
Чтобы
определить число гармоник, содержащих
в сумме не менее 90% энергии, сначала
рассчитаем энергию вносимую каждой
гармоникой в отдельности по следующей
формуле:
Вклад
гармоник в энергию
-
Вычислить
среднеквадратичную ошибку между
исходной функцией f(t)
и частичной суммой Фурье для t,
принадлежащих промежутку задания.
Среднеквадратичную
ошибку можно вычислить по следующей
формуле:
-
Построить
графики заданной функции и частичной
суммы ряда Фурье для значений t,
принадлежащих промежутку задания
f(t),
взяв число гармоник, определённых в
пункте №5.
-
Построить
график квадрата отклонений функции и
частичной суммы ряда для t
из промежутка задания f(t).
Задача
№3
Для функции, заданной на
конечном интервале, построить
периодическое продолжение заданным
образом. [0,2] (чётное)
-
Обосновать
возможность разложения f(t)
в ряд Фурье, установить вид сходимости
ряда Фурье к f(t).
Данная
функция f(t)
удовлетворяет условиям теоремы Дирихле:
Теорема
Дирихле: Если Т — периодическая функция
f(t)
удовлетворяет условиям Дирихле на
каком либо замкнутом интервале длиной
Т:
-
Непрерывна
или имеет конечное число точек разрыва
первого рода -
Монотонна
либо имеет конечное число максимумов
и минимумов
Ряд
Фурье сходиться на всей оси t
и сумма ряда Фурье равно f(t)
во всех точках непрерывности этой
функции в точке t0
разрыва первого рода функции f(t)
сумма ряда Фурье равна
данная функция f(t)
удовлетворяет условиям сходимости в
среднем.
Теорема
Вейерштрасса: если Т – периодическая
функция f(x)
на каком-либо замкнутом интервале.
Например [-T/2,T/2]
удовлетворяет условиям: непрерывности
и f(-T/2)=f(T/2),
то тригонометрический ряд Фурье
сходиться к f(x)
равномерно.
-
Построить
график суммы ряда Фурье.
-
Представить
заданную функцию тригонометрическим
рядом Фурье, предварительно:
б)
вычислить коэффициенты ряда Фурье
Коэффициенты
ряда Фурье
Тригонометрическое
разложение ф-ии в ряд Фурье
-
Построить
амплитудный и фазовый спектры функции.
-
Определить
число гармоник разложения функции в
ряд Фурье, содержащих в сумме не менее
90% энергии.
Вклад
гармоник в энергию
-
Вычислить
среднеквадратичную ошибку между
исходной функцией f(t)
и частичной суммой Фурье для t,
принадлежащих промежутку задания.
Среднеквадратичная
ошибка
-
Построить
графики заданной функции и частичной
суммы ряда Фурье для значений t,
принадлежащих промежутку задания
f(t),
взяв число гармоник, определённых в
пункте №5.
-
Построить
график квадрата отклонений функции и
частичной суммы ряда для t
из промежутка задания f(t).
Соседние файлы в папке Ргз фурье
- #
27.03.2015125.17 Кб263R_F_6V.xmcd
- #
27.03.2015121.41 Кб243R_F_7V.xmcd
- #
27.03.2015121 Кб243R_F_8V.xmcd
- #
27.03.2015118.29 Кб253R_F_9V.xmcd
- #
27.03.2015219.65 Кб294.doc
- #
27.03.2015214.53 Кб305.doc
- #
27.03.2015220.16 Кб286.doc
- #
27.03.2015216.06 Кб317.doc
- #
27.03.2015216.58 Кб298.doc
- #
27.03.2015212.99 Кб289.doc
- #
-
Унитарное пространство.
Начать изучение
-
Нормированные пространства.
Начать изучение
-
Сходимость. Полные пространства. Гильбертовы пространства.
Начать изучение
-
Пополнение унитарного пространства.
Начать изучение
-
Ряды Фурье по ортогональным системам.
Начать изучение
-
Минимальное свойство коэффициентов Фурье. Неравенство Бесселя.
Начать изучение
-
Полнота системы элементов {ei} в унитарном пространстве. Полнота тригонометрической системы в L2(-π, π).
Начать изучение
-
Эквивалентность полноты и замкнутости ортогональной системы в гильбертовом пространстве.
Начать изучение
Унитарное пространство.
При дальнейшем изложении удобно будет пользоваться геометрическим языком. Из курса линейной алгебры известны определения комплексного линейного и унитарного пространства. Напомним, что в линейном пространстве определены операции сложения элементов (векторов) и умножения элементов на комплексные числа, причем эти операции удовлетворяют следующим аксиомам.
Аксиомы линейного пространства (E):
- (x+y=y+x) для любых (x, y in E);
- (x+(y+x)=(x+y)+z) для любых (x, y, z in E);
- существует элемент (0 in E) такой, что для любого (x in E) справедливо равенство (x+0=x);
- для любого (x in E) существует элемент (-x in E) такой, что (x+(-x)=0);
- для любого (x in E) и для любых (lambda, mu in mathbb{C}) справедливо равенство (lambda(mu x)=(lambdamu)x);
- ((lambda+mu)x=lambda x+mu x) для любых (x in E), (lambda, mu in mathbb{C});
- (lambda(x+y)=lambda x+lambda y) для любых (x, y in E), (lambda in mathbb{C});
- (1 cdot x=x) для любого (x in E).
Греческими буквами обозначались комплексные числа, латинскими — элементы линейного пространства (E).
Определение.
Унитарным называется комплексное линейное пространство (E), для каждой пары элементов которого определено комплексное число ((x, y)) — их скалярное произведение.
Аксиомы скалярного произведения:
- ((x, y)=overline{(y, x)}) для любых (x, y in E);
- ((x+y, z)=(x, z)+(y, z)) для любых (x, y, z in E);
- ((lambda x, y)=lambda(x, y)) для любых (x, y in E), (lambda in mathbb{C});
- ((x, x) geq 0) для любого (x in E), причем ((x, x)=0) тогда и только тогда, когда (x=0).
Здесь через (overline{gamma}) обозначается число, комплексно сопряженное комплексному числу (gamma).
Неотрицательное число (left|xright|=sqrt{(x, x)}) называется нормой элемента (x). Из аксиом унитарного пространства выводятся следующие свойства.
Свойство 1.
(left|xright|=0) эквивалентно (x=0).
Свойство 2.
((x, lambda y)=overline{lambda}(x, y)).
Доказательство.
(circ) ((x, lambda y)=overline{(lambda y, x)}=overline{lambda(y, x)}=overline{lambda}overline{(y, x)}=overline{lambda}(x, y)). (bullet)
Свойство 3.
Для любых (x, y in E) справедливо неравенство Коши—Буняковского
$$
|(x, y)| leq left|xright| cdot left|yright|.label{ref1}
$$
Доказательство.
(circ) Так как для любых (x, y in E) и (lambda in mathbb{C}) справедливо неравенство ((x+lambda y, x+lambda y) geq 0), то, пользуясь свойствами скалярного произведения, получаем
$$
0 leq (x, x)+lambda(y, x)+overline{lambda}(x, y)+lambdaoverline{lambda}(y, y).label{ref2}
$$
Если (left|yright|=0), то (y=0) и неравенство Коши-Буняковского становится тривиальным. Пусть (left|yright| neq 0). Положим в eqref{ref2} (lambda=-dfrac{(x, y)}{left|yright|^{2}}). Получаем
$$
0 leq left|xright|^{2}-dfrac{(x, y)}{left|yright|^{2}}(y, x)-dfrac{overline{(x, y)}}{left|yright|^{2}}(x, y)+dfrac{(x, y)overline{(x, y)}}{left|yright|^{4}}left|yright|^{2},nonumber
$$
откуда сразу следует неравенство Коши-Буняковского. (bullet)
Свойство 4.
Для любых (x, y in E) справедливо неравенство для нормы
$$
left|x+yright| leq left|xright|+left|yright|.nonumber
$$
Доказательство.
(circ) Неравенство для нормы следует из неравенства Коши-Буняковского. В самом деле,
$$
left|x+yright|^{2}=(x+y, x+y)=(x, x)+(y, x)+(x, y)+(y, y) leq
$$
$$
leq left|xright|^{2}+2left|xright| left|yright|+left|yright|^{2}=(left|xright|+left|yright|)^{2}. bulletnonumber
$$
Свойство 5.
Положительная однородность нормы: (left|lambda xright|=|lambda| cdot left|xright|).
Доказательство.
(circ) (left|lambda xright|^{2}=(lambda x, lambda x)=lambdaoverline{lambda}(x, x)=|lambda|^{2}left|xright|^{2}). (bullet)
Из курса линейной алгебры известно унитарное пространство (E^{n}), элементами которого являются упорядоченные наборы (n) комплексных чисел
$$
gamma=(gamma_{1}, ldots, gamma_{n}), gamma_{i} in mathbb{C}, i=overline{1, n}nonumber
$$
Естественным образом определяется в (E^{n}) сложение элементов (векторов) и умножение их на комплексные числа. Скалярное произведение двух векторов (gamma=(gamma_{1}, ldots, gamma_{n})) и (delta=(delta_{1}, ldots, delta_{n})) есть комплексное число, определенное формулой
$$
(gamma, delta)=gamma_{1}overline{delta}_{1}+ldots+gamma_{n}overline{delta}_{n}.
$$
По аналогии с вещественным пространством (L_{2}^{C}(a, b)), введем комплексное пространство (L_{2}^{C}(a, b)), элементами которого являются комплекснозначные функции, для каждой из которых найдется такое разбиение отрезка ([a, b]) точками ({x_{i}}), (i=overline{0, n}), что на любом из интервалов ((x_{i-1}, x_{i})) функция непрерывна, а интеграл от квадрата ее модуля по отрезку ([a, b]) сходится как несобственный.
Лемма 1.
Множество (L_{2}^{C}(a, b)) является линейным пространством с естественными операциями сложения и умножения на комплексные числа.
Доказательство.
(circ) Пусть функции (f, varphi in L_{2}^{C}(a, b)). Из неравенства
$$
|f+varphi|^{2}=(f+varphi)(overline{f}+overline{varphi})=foverline{f}+foverline{varphi}+overline{f}varphi+varphioverline{varphi} leq\ leq |f|^{2}+|varphi|^{2}+2|f| cdot |varphi| leq 2|f|^{2}+2|varphi|^{2}nonumber
$$
и признака сравнения для несобственных интегралов следует, что несобственный интеграл (displaystyleintlimits_{a}^{b}|f+varphi|^{2}dx) сходится и, следовательно, (f+varphi in L_{2}^{C}(a, b)).
Если (f in L_{2}^{C}(a, b)), то и (alpha f in L_{2}^{C}(a, b)) для любого (alpha in mathbb{C}). Проверка всех аксиом линейного пространства тривиальна. (bullet)
Договоримся не различать две функции (f) и (varphi) из пространства (L_{2}^{C}(a, b)), если их значения не совпадают лишь в конечном числе точек.
Лемма 2.
Линейное пространство (L_{2}^{C}(a, b)) будет унитарным, если определить скалярное произведение функций (f, varphi in L_{2}^{C}(a, b)) при помощи следующей формулы:
$$
(f, varphi)=intlimits_{a}^{b} f(x)overline{varphi(x)} dx.label{ref3}
$$
Доказательство.
(circ) Так как (|foverline{varphi}| leq displaystylefrac{1}{2}|f|^{2}+frac{1}{2}|varphi|^{2}), то по признаку сравнения несобственный интеграл eqref{ref3} сходится. Первые три аксиомы скалярного произведения проверяются без труда. Проверим выполнение аксиомы 4).
Пусть ((f, f)=displaystyleintlimits_{a}^{b}|f|^{2}dx). Так как (f in L_{2}^{C}(a, b)), то найдется такое разбиение отрезка ([a, b]) точками ({x_{i}}), (i=overline{0, n}), что на каждом из интервалов ((x_{i-1}, x_{i})) функция (f(x)) непрерывна. Так как ((x_{i-1}, x_{i}) subset [a, b]), то
$$
intlimits_{x_{i-1}}^{x_{i}} |f(x)|^{2} dx=0, i=overline{1, n}.nonumber
$$
Из этого равенства следует, что (f(x)=0) на любом интервале ((x_{i-1}, x_{i})), (i=overline{1, n}). Следовательно, функция (f(x)) отлична от нуля лишь в конечном числе точек. Согласно договоренности такая функция отождествляется с функцией, тождественно равной нулю на ([a, b]). (bullet)
Нормированные пространства.
В нормированных пространствах определены длины векторов, но нет скалярного произведения. Более точно, комплексное или вещественное линейное пространство (E) называется нормированным, если каждому элементу (x) поставлено в соответствие неотрицательное число (left|xright|) (норма элемента (x)), причем удовлетворяются следующие аксиомы нормы:
- (left|lambda xright|=|lambda| cdot left|xright|) для любого , (x in E) и любого (lambda in mathbb{C});
- (left|x+yright| leq left|xright|+left|yright|) для любых (x, y in E);
- (left|xright|=0) в том и только том случае, когда (x=0).
Если (E) есть унитарное пространство, то число (left|xright|=sqrt{(x, x)}) удовлетворяет всем аксиомам нормы, и поэтому каждое унитарное пространство будет и нормированным пространством.
Множество непрерывных функций на отрезке ([a, b]) станет нормированным пространством (C[a, b]), если определить норму функции следующим образом:
$$
left| f right|=max_{a leq x leq b} |f(x)|.label{ref4}
$$
Все аксиомы нормы проверяются без труда.
Заметим еще, что любое нормированное пространство есть частный случай метрического пространства, если ввести метрику следующим образом:
$$
rho(x, y)=left|x-yright|.label{ref5}
$$
Из аксиом нормы тогда следует, что для расстояния eqref{ref5} выполняются все аксиомы метрики:
- (rho(x, y)=rho(y, x));
- (rho(x, y)+rho(y, z) geq rho(x, z));
- (rho(x, y)=0 Leftrightarrow x=y).
Поскольку нормированные и унитарные пространства есть частные случаи метрических пространств, то на них переносятся все метрические понятия, например понятие предела последовательности.
Сходимость. Полные пространства. Гильбертовы пространства.
Определение.
Последовательность точек ({x_{n}}) унитарного пространства (E) сходится к точке (x in E), если
$$
lim_{n rightarrow infty} left|x_{n}-xright|=0.label{ref6}
$$
Запись (displaystylelim_{n rightarrow infty} x_{n}=x) означает, что выполнено равенство eqref{ref6}.
Запишем основные свойства пределов (часть из них представлена без доказательств).
Свойство 1.
Если (displaystylelim_{n rightarrow infty} x_{n}=x) и (displaystylelim_{n rightarrow infty} y_{n}=y), то
$$
lim_{n rightarrow infty} (x_{n}+y_{n})=lim_{n rightarrow infty} x_{n}+lim_{n rightarrow infty} y_{n}=x+y.nonumber
$$
Свойство 2.
Если (alpha_{n} in boldsymbol{R}), (x_{n} in E) и (displaystylelim_{n rightarrow infty} x_{n}=x), (displaystylelim_{n rightarrow infty} alpha_{n}=alpha), то
$$
lim_{n rightarrow infty} alpha_{n}x_{n}=alpha x.nonumber
$$
Свойство 3.
Сходящаяся последовательность ограничена, то есть если существует (displaystylelim_{n rightarrow infty} x_{n}=x), то найдется число (C > 0) такое, что для всех (n in mathbb{N}) выполнено неравенство (left|x_{n}right| leq C).
Свойство 4.
Скалярное произведение непрерывно, то есть если (displaystylelim_{n rightarrow infty} x_{n}=x) и (displaystylelim_{n rightarrow infty} y_{n}=y), то
$$
lim_{n rightarrow infty} (x_{n}, y_{n})=(x, y).nonumber
$$
Доказательство.
(circ) Пусть (displaystylelim_{n rightarrow infty} x_{n}=x) и (displaystylelim_{n rightarrow infty} y_{n}=y). Так как сходящаяся последовательность ограничена, то существует такое число (C), что (left|y_{n}right| leq C) для всех (n in N). Воспользовавшись неравенством Коши-Буняковского, получаем, что
$$
|(x_{n}, y_{n})-(x, y)|=|(x_{n}-x, y_{n})+(x, y_{n}-y)| leq \ leq left|y_{n}right| cdot left|x_{n}-xright|+left|xright| cdot left|y_{n}-yright| leq Cleft|x_{n}-xright|+left|xright| cdot left|y_{n}-yright| rightarrow 0
$$
при (n rightarrow infty). Следовательно, (displaystylelim_{n rightarrow infty} (x_{n}, y_{n})=(x, y)). (bullet)
Замечание.
Сходимость в пространстве (L_{2}^{C}) называют сходимостью в смысле среднего квадратичного.
Будем говорить, что последовательность точек (x_{n}) унитарного (или нормированного) пространства (E) фундаментальна, если для любого (varepsilon > 0) найдется номер (N) такой, что для всех (n, m geq N) выполнено неравенство (left|x_{n}-x_{m}right| < varepsilon).
Введенное понятие фундаментальной последовательности точек унитарного пространства находится в полном соответствии с введенным ранее понятием фундаментальной последовательности точек метрического пространства. Достаточно вспомнить формулу (rho(x, y)=left|x-yright|), задающую метрику в унитарном пространстве. Если последовательность сходится, то она фундаментальна. В произвольном унитарном пространстве фундаментальная последовательность может не сходиться.
Говорят, что унитарное (нормированное, метрическое) пространство полное, если любая фундаментальная последовательность его точек сходится к точке этого пространства.
Полное нормированное пространство называется банаховым, полное унитарное бесконечномерное пространство называется гильбертовым.
Нетрудно видеть, что каждое конечномерное унитарное пространство будет полным (критерий Коши сходимости в пространстве (boldsymbol{R}^{n})).
Покажем, что существуют неполные бесконечномерные унитарные пространства.
Пример.
Пространство (L_{2}^{C}(0, 1)) неполное.
Решение.
(circ) Для доказательства рассмотрим счетное множество точек
$$
1, frac{1}{2}, frac{1}{2^{2}}, ldots, frac{1}{2^{n}}, ldotsnonumber
$$
Построим следующую функцию (рис. 70.1):
$$
f(x)=left{
begin{array}{ll}
1, & displaystylefrac{1}{2^{2n+1}} leq x leq frac{1}{2^{2n}}, n=0, 1, ldots,\
\
0, & displaystylefrac{1}{2^{2n}} leq x leq frac{1}{2^{2n-1}}, n=1, 2, ldots
end{array} right.nonumber
$$
Очевидно, что (f notin L_{2}^{C}(0, 1)), так как множество ее точек разрыва счетно. Построим последовательность
$$
f_{n}(x)=left{
begin{array}{ll}
f(x), & displaystylefrac{1}{2^{n}} leq x < 1,\
\
0, & displaystyle 0 < x leq frac{1}{2^{n}}.
end{array} right.nonumber
$$
Покажем, что последовательность (f_{n}) фундаментальна в пространстве (L_{2}^{C}(0, 1)). Так как на отрезке ([1/2^{n}, 1]) функции (f_{n+p}) и (f_{n}) совпадают, то
$$
left|f_{n+p}-f_{n}right|^{2}=intlimits_{0}^{1} |f_{n+p}(x)-f_{n}(x)|^{2} dx=intlimits_{0}^{1/2^{n}} |f_{n+p}(x)-f_{n}(x)|^{2} dx leq\leq frac{1}{2^{n}} max|f_{n+p}(x)-f_{n}(x)| leq frac{1}{2^{n}} < varepsilon mbox{при} n > N(varepsilon).nonumber
$$
Последовательность ({f_{n}}) фундаментальна. Покажем, что она не может быть сходящейся. Если (varphi in L_{2}^{C}(0, 1)) и (left|f_{n}-varphiright|^{2} rightarrow 0) то для всех (m in N) выполнено условие
$$
intlimits_{1/2^{m+1}}^{1/2^{m}} |f_{n}-varphi|^{2} dx rightarrow 0 mbox{при} n rightarrow infty.nonumber
$$
Если (n > m), то (f_{n}=f) при (x in displaystyleleft(frac{1}{2^{m+1}}, frac{1}{2^{m}}right)). Поэтому
$$
intlimits_{1/2^{m+1}}^{1/2^{m}} |f_{n}-varphi|^{2} dx=0, m=0, 1, ldotslabel{ref7}
$$
Так как функция (varphi(x)) имеет конечное число точек разрыва, то при достаточно большом (m) на интервале (displaystyleleft(frac{1}{2^{m+1}}, frac{1}{2^{m}}right)) у функции (varphi(x)) точек разрыва не будет, функция (f(x)) непрерывна на этом же интервале. Поэтому из eqref{ref7} следует, что
$$
f(x)=varphi(x) mbox{при} x in left(frac{1}{2^{m+1}}, frac{1}{2^{m}}right), m=M+1, ldotsnonumber
$$
Но тогда функция (varphi), как и функция (f), должна иметь счетное множество точек разрыва и, следовательно, не может принадлежать пространству (L_{2}^{C}(a, b)). Итак, пространство (L_{2}^{C}(a, b)) неполное. (bullet)
Пополнение унитарного пространства.
Определение.
Два унитарных пространства называются изоморфными, если можно установить такое взаимно однозначное отображение (F) пространства (E_{1}) на пространство (E_{2}), что для любых (x, y in E) и любого (alpha in mathbb{C}) выполнены равенства
$$
F(x+y)=F(x)+F(y),quad F(alpha x)=alpha F(x),quad (Fx, Fy)=(x, y).nonumber
$$
Подмножество (L) унитарного пространства (E), само являющееся унитарным пространством с тем же скалярным произведением, называется подпространством пространства (E).
Пусть (A) и (B) — подмножества унитарного (или нормированного) пространства (E). Говорят, что (B) плотно в (A), если для любого (varepsilon > 0) и любого (x in A) найдется (y in B) такой, что (left|x-yright| < varepsilon).
Лемма 3.
Если (A, B, C subset E) и (C) плотно в (B), а (B) плотно в (A), то (C) плотно в (A).
Доказательство.
(circ) Пусть (varepsilon > 0) и (x in A). Так как (B) плотно в (A), то найдется (y in B) такой, что (left|x-yright| < varepsilon/2). Так как (C) плотно в (B), то найдется (z in mathbb{C}) такой, что (left|y-zright| < varepsilon/2). Тогда
$$
left|x-zright| leq left|x-yright|+left|y-zright| < frac{varepsilon}{2}+frac{varepsilon}{2}=varepsilon.nonumber
$$
Следовательно, (C) плотно в (A). (bullet)
Лемма 4.
Подпространство функций, непрерывных на отрезке ([a, b]) и принимающих на концах этого отрезка равные значения, плотно в (L_{2}^{C}(a, b)).
Доказательство.
(circ) Обозначим для краткости через (B) подпространство кусочно непрерывных на ([a, b]) функций, а через (C) — подпространство непрерывных функций, принимающих на концах отрезка ([a, b]) одинаковые значения. Договоримся, что будем доопределять нулем функции вне отрезка ([a, b]).
Покажем, что (B) плотно в (L_{2}^{C}(a, b)). Возьмем произвольную функцию (f in L_{2}^{C}(a, b)) и любое (varepsilon > 0). Тогда существует такое разбиение (x_{0}=a < x_{1} < ldots < x_{n}=b), что на каждом из интервалов ((x_{i-1}, x_{i})) функция (f(x)) непрерывна, а интеграл (intlimits_{a}^{b}|f|^{2}dx) сходится как несобственный. Найдется такое (delta > 0), что
$$
sum_{i=0}^{n} intlimits_{x_{i}-delta}^{x_{i}+delta}|f|^{2}dx < varepsilon,quad (x_{i}-delta, x_{i}+delta) cap (x_{j}-delta, x_{j}+delta)=varnothing, i neq j.nonumber
$$
Возьмем функцию
$$
varphi_{n}(x)=left{
begin{array}{ll}
0, & x in displaystylebigcup_{i=0}^{n}(x_{i}-delta, x_{i}+delta),\
f(x) & mbox{в остальных точках}.
end{array} right.nonumber
$$
Очевидно, что (varphi(x)) кусочно непрерывна и
$$
left|f-varphiright|^{2}=sum_{i=0}^{n} intlimits_{x_{i}-delta}^{x_{i}+delta}|f|^{2}dx < varepsilon.
$$
Итак, (B) плотно в (L_{2}^{C}(a, b)). Покажем, что (C) плотно в (B). Пусть (varphi in B) и (tilde{x}_{0}=a < tilde{x}_{1} < ldots < tilde{x}_{n}=b) — ее точки разрыва первого рода. Построим непрерывную функцию (psi(x)), обращающуюся в нуль во всех точках (tilde{x}_{i}), (рис. 70.2):
$$
psi_{n}(x)=left{
begin{array}{ll}
displaystylefrac{tilde{x}_{i}-x}{varepsilon} varphi(tilde{x}_{i}-varepsilon), & tilde{x}_{i}-varepsilon leq x leq tilde{x}_{i},\
displaystylefrac{x-tilde{x}_{i}}{varepsilon} varphi(tilde{x}_{i}+varepsilon), & tilde{x}_{i} displaystyleleq x leq tilde{x}_{i}+varepsilon, i=overline{0, m},\
varphi(x), & mbox{в остальных точках}
end{array} right.nonumber
$$
где (varepsilon < displaystylefrac{1}{4} max_{i=overline{0, m}} bigtriangleup tilde{x}_{i}), (bigtriangleup tilde{x}_{i}=tilde{x}_{i}-tilde{x}_{i-1}).
Функция (psi(x)) непрерывна на отрезке ([a, b]) и
$$
|psi(x)| leq M=max_{a leq x leq b} |varphi(x)|.nonumber
$$
В самом деле, так как функция (psi(x)) линейна на отрезках ([tilde{x}_{i}-varepsilon, tilde{x}_{i}]) и ([tilde{x}_{i}, tilde{x}_{i}+varepsilon]) и (psi(tilde{x}_{i})=0), то
$$
max_{tilde{x}_{i}-varepsilon leq x leq tilde{x}_{i}} |psi(x)|=|psi(tilde{x}_{i}-varepsilon)|=|varphi(tilde{x}_{i}-varepsilon)| leq M,nonumber
$$
$$
max_{tilde{x}_{i} leq x leq tilde{x}_{i}+varepsilon} |psi(x)|=|psi(tilde{x}_{i}+varepsilon)|=|varphi(tilde{x}_{i}+varepsilon)| leq M,nonumber
$$
Вне отрезков ([tilde{x}_{i}-varepsilon, tilde{x}_{i}]) и ([tilde{x}_{i}, tilde{x}_{i}+varepsilon]) функция совпадает с (varphi(x)) и ее значения по модулю не превосходят (M).
Оценивая среднеквадратичное отклонение функции (varphi(x)) от функции (psi(x)), получаем
$$
left|varphi(x)-psi(x)right|^{2}=sum_{i=1}^{n} intlimits_{tilde{x}_{i}-varepsilon}^{tilde{x}_{i}+varepsilon}|varphi(x)-psi(x)|^{2}dx leq 8Mnvarepsilon.nonumber
$$
Отсюда следует, что (C) плотно в (B). Итак, (C) плотно в (B), а (B) плотно в (L_{2}^{C}(a, b)). В силу леммы 3 (C) плотно в (L_{2}^{C}(a, b)). (bullet)
Пополнением унитарного пространства (E) называется полное унитарное пространство (tilde{E}), содержащее плотное в (tilde{E}) подпространство (L), изоморфное (E).
Теорема 1.
Для любого унитарного пространства существует пополнение, единственное с точностью до изоморфизма.
Доказательство.
Данная теорема приводится без доказательства.
Пополнение пространства (L_{2}^{C}(a, b)) называется пространством (L_{2}(a, b)). Можно показать, что (L_{2}^{C}(a, b)) изоморфно гильбертову пространству функций, интегрируемых с квадратом по Лебегу.
Ряды Фурье по ортогональным системам.
Пусть (H) бесконечномерное унитарное пространство. Систему элементов ({e_{i}}_{i=1, ldots} in H) будем называть линейно независимой, если при любом (n) элементы (e_{1}, e_{2}, ldots, e_{n}) линейно независимы. Если любой элемент (x in H) можно представить в виде суммы сходящегося ряда
$$
x=lim_{m rightarrow infty} sum_{n=1}^{m} x_{n}e_{n}=sum_{n=1}^{infty}x_{n}e_{n},label{ref8}
$$
то линейно независимая система ({e_{i}}) называется базисом в (H). Система ({e_{i}}) называется ортогональной, если ((e_{i}, e_{j})=0) при (i neq j), и ортонормированной, если ((e_{i}, e_{j})=delta_{ij}), где (delta_{ij}) — символ Кронекера, то есть (delta_{ij}=0) при (i neq j) и (delta_{ii}=1). Если, кроме того, ({e_{i}}) есть базис, то будем говорить об ортогональных и ортонормированных базисах.
Если ({e_{i}}) — ортогональный базис, то все коэффициенты (x_{n}) ряда eqref{ref8} могут быть выражены через (x). Так как элементы (e_{i}) ортогональны, то при (k leq n) имеем
$$
left(sum_{i=1}^{n} x_{i}e_{i}, e_{k}right)=x_{k}(e_{k}, e_{k}).label{ref9}
$$
Так как (x=displaystylelim_{n rightarrow infty} sum_{i=1}^{n} x_{i}e_{i}), а скалярное произведение непрерывно, то, переходя в eqref{ref9} к пределу при (n rightarrow infty), получаем
$$
x_{k}=dfrac{(x, e_{k})}{left|e_{k}right|^{2}}, k in N.label{ref10}
$$
Если базис ортонормированный, то (left|e_{k}right|=1) и (x_{k}=(x, e_{k})). Числа (x_{k}) называются коэффициентами Фурье элемента (x) по ортогональной системе ({e_{i}}).
Если теперь отказаться от требования, чтобы ортогональная система ({e_{i}}) была базисом в (H), то коэффициенты Фурье элемента (x) все равно можно вычислять по формуле eqref{ref10}. Выражение (displaystylesum_{k=1}^{infty}x_{k}e_{k}) где (x_{k}) — коэффициенты Фурье элемента (x), будем называть рядом Фурье элемента (x) по ортогональной системе ({e_{i}}). Так как, вообще говоря, ряд может и не сходиться, то будем писать
$$
x sim sum_{k=1}^{infty}x_{k}e_{k},quad x_{k}=dfrac{(x, e_{k})}{left|e_{k}right|^{2}}.nonumber
$$
Минимальное свойство коэффициентов Фурье. Неравенство Бесселя.
Теорема 2.
Пусть ({e_{i}}) — ортонормированная система элементов унитарного пространства (E), (x) — произвольный элемент пространства (E), (n in N). Тогда из всех линейных комбинаций (displaystylesum_{i=1}^{n}alpha_{i}e_{i}), где (alpha_{i} in mathbb{C}), (i=overline{1, n}), наилучшим образом приближает элемент (x) но норме пространства (E) (n)-я частичная сумма ряда Фурье элемента (x) по ортонормированной системе ({e_{i}}), то есть
$$
min_{alpha_{1}, ldots, alpha_{n} in mathbb{C}} left|x-sum_{i=1}^{n}alpha_{i}e_{i}right|=left|x-sum_{i=1}^{n}(x, e_{i})e_{i}right|.nonumber
$$
Доказательство.
(circ) Обозначим (sigma_{n}=displaystyleleft|x-sum_{i=1}^{n}alpha_{i}e_{i}right|^{2}). Так как (left|xright|^{2}=(x, x)), то
$$
0 leq sigma_{n}=left(x-sum_{i=1}^{n}alpha_{i}e_{i}, x-sum_{i=1}^{n}alpha_{i}e_{i}right)=(x, x)-sum_{i=1}^{n}alpha_{i}(e_{i}, x) -\- sum_{i=1}^{n}overline{alpha}_{i}(e_{i}, x)+sum_{i=1}^{n}alpha_{i}overline{alpha}_{i}=(x, x)-sum_{i=1}^{n}alpha_{i}overline{x}_{i}-sum_{i=1}^{n}overline{alpha}_{i}x_{i}+sum_{i=1}^{n}alpha_{i}overline{alpha}_{i} =\= left|xright|^{2}-sum_{i=1}^{n}|x_{i}|^{2}+sum_{i=1}^{n}(alpha_{i}-x_{i})(overline{alpha}_{i}-overline{x}_{i}).nonumber
$$
Следовательно, $$ 0 leq sigma_{n}=left|xright|^{2}-sum_{i=1}^{n}|x_{i}|^{2}+sum_{i=1}^{n}|alpha_{i}-x_{i}|^{2}.label{ref11}
$$
Из равенства eqref{ref11} следует, что минимум (sigma_{n}) достигается при (alpha_{i}=x_{i}), причем
$$
0 leq min_{alpha_{1} in mathbb{C}, i=overline{1, n}} sigma_{n}=left||x-sum_{i=1}^{n}x_{i}e_{i}right||^{2}=left|xright|^{2}-sum_{i=1}^{n}|x_{i}|^{2}, x_{i}=(x, e_{i}). bulletlabel{ref12}
$$
Следствие.
Для коэффициентов Фурье элемента (x) по ортонормированной системе ({e_{i}}) справедливо неравенство Бесселя
$$
sum_{i=1}^{infty}|x_{i}|^{2} leq left|xright|^{2}.label{ref13}
$$
(circ) Из eqref{ref12} следует, что (sum_{i=1}^{n}|x_{i}|^{2} leq left|xright|^{2}). Переходя к пределу при (n rightarrow infty), получаем неравенство Бесселя. (bullet)
Полнота системы элементов {ei} в унитарном пространстве. Полнота тригонометрической системы в L2(-π, π).
Система элементов ({e_{i}}) называется полной в унитарном (нормированном) пространстве (E), если любой элемент (x in E) может с любой степенью точности быть приближен по норме конечной линейной комбинацией (displaystylesum_{i=1}^{n}alpha_{i}e_{i}) то есть для любого (varepsilon > 0) найдется линейная комбинация (displaystylesum_{i=1}^{n}alpha_{i}e_{i}) такая, что
$$
left|x-sum_{i=1}^{n}alpha_{i}e_{i}right| < varepsilon.label{ref14}
$$
Теорема 3.
Если ({e_{i}}) — ортонормированная система в унитарном пространстве (H), то следующие условия эквивалентны:
- система ({e_{i}}) полна в (H);
- для любого (x in H) справедливо равенство Парсеваля
$$
left|xright|^{2}=sum_{i=1}^{infty}|x_{i}|^{2}, x_{i}=(x, e_{i});label{ref15}
$$ - для любого (x in H) выполнено равенство
$$
x=sum_{i=1}^{infty}x_{i}e_{i}.label{ref16}
$$
Доказательство.
(circ) Докажем, что 1)(Rightarrow)2). Пусть ортонормированная система ({e_{i}}) полна в (H). Тогда для любого (varepsilon > 0) найдется линейная комбинация (displaystylesum_{i=1}^{n}alpha_{i}e_{i}) такая, что справедливо неравенство eqref{ref14}.
В силу минимального свойства коэффициентов Фурье
$$
0 leq left|x-sum_{i=1}^{n}alpha_{i}e_{i}right|^{2}=left|xright|^{2}-sum_{i=1}^{n}|x_{i}|^{2} leq left|x-sum_{i=1}^{n}alpha_{i}e_{i}right|^{2} < varepsilon^{2}.
$$
Используя это неравенство и неравенство eqref{ref13}, получаем
$$
0 leq left|xright|^{2}-sum_{i=1}^{infty}|x_{i}|^{2} leq left|xright|^{2}-sum_{i=1}^{n}|x_{i}|^{2} < varepsilon^{2}.nonumber
$$
В силу произвольности (varepsilon) должно быть справедливо равенство Парсеваля eqref{ref15}.
Докажем, что 2)(Rightarrow)3). Пусть справедливо равенство Парсеваля eqref{ref15}. Тогда
$$
left|x-sum_{i=1}^{n}x_{i}e_{i}right|^{2}=left|xright|^{2}-sum_{i=1}^{n}|x_{i}|^{2} rightarrow 0 mbox{при} n rightarrow infty,
$$
то есть справедливо равенство eqref{ref16}.
Утверждение 3)(Rightarrow)1) очевидно. (bullet)
Лемма 5.
Пусть подпространство (L) плотно в унитарном пространстве (H), а система ({e_{i}}) полна в (L). Тогда система элементов ({e_{i}}) полна в (H).
Доказательство.
(circ) Пусть (x) — произвольный элемент пространства (H). Так как (L) плотно в (H), то для любого (varepsilon > 0) найдется элемент (y in L) такой, что (displaystyleleft|x-yright| < frac{varepsilon}{2}) Так как система ({e_{i}}) полна в (L), то найдется линейная комбинация (displaystylesum_{i=1}^{n}alpha_{i}e_{i}) такая, что
$$
left|y-sum_{i=1}^{n}alpha_{i}e_{i}right| < frac{varepsilon}{2}.nonumber
$$
Тогда
$$
left|x-sum_{i=1}^{n}alpha_{i}e_{i}right| leq left|x-yright|+left|y-sum_{i=1}^{n}alpha_{i}e_{i}right| < frac{varepsilon}{2}+frac{varepsilon}{2}=varepsilon.nonumber
$$
Поэтому ({e_{i}}) — полная система в пространстве (H). (bullet)
Теорема 4.
Тригонометрическая система полна в (L_{2}(-pi, pi)).
Доказательство.
(circ) Пространство (L_{2}(-pi, pi)) есть пополнение (L_{2}^{C}(-pi, pi)). Поэтому (L_{2}^{C}(-pi, pi)) плотно в (L_{2}(-pi, pi)). Пространство непрерывных функций, принимающих одинаковые значения в точках (pi) и (-pi), в силу леммы 4 плотно в (L_{2}^{C}(-pi, pi)), а следовательно, и в (L_{2}(-pi, pi)).
Осталось, в силу леммы 5, показать, что тригонометрическая система полна в подпространстве (L) непрерывных на ([-pi, pi]) функций, принимающих одинаковые значения в точках (pi) и (-pi). Каждую такую функцию можно в силу теоремы Вейерштрасса равномерно приблизить тригонометрическим многочленом (T(x)), то есть
$$
max_{-pi leq x leq pi} |f(x)-T(x)| < varepsilon,nonumber
$$
где (T(x)=displaystylefrac{A_{0}}{2}+sum_{n=1}^{n} A_{n} cos nx+B_{n} sin nx).
Но тогда (f(x)) можно приблизить с любой степенью точности тригонометрическим многочленом и по норме пространства (L_{2}(-pi, pi)) (в смысле среднего квадратичного), так как
$$
left|f-Tright|=left(intlimits_{-pi}^{pi}|f-T|^{2}dxright)^{1/2} leq varepsilon sqrt{2pi}.nonumber
$$
Итак, тригонометрическая система полна в (L_{2}(-pi, pi)). (bullet)
Следствие.
Из теорем 3 и 4 следует, что для любой функции (f in L_{2}^{C}[-pi, pi]), в частности, для любой непрерывной или кусочно непрерывной функции, выполнено равенство Парсеваля
$$
frac{|a_{0}|^{2}}{2}+sum_{n=1}^{infty} |a_{n}|^{2}+|b_{n}|^{2}=frac{1}{pi}intlimits_{-pi}^{pi}|f(x)|^{2} dxnonumber
$$
и ряд Фурье такой функции сходится в смысле среднего квадратичного к функции (f(x)), то есть
$$
lim_{n rightarrow infty} intlimits_{-pi}^{pi} left|f(x)-frac{a_{0}}{2}-sum_{k=1}^{n} (a_{k} cos kx+b_{k} sin kx)right|^{2}dx=0.nonumber
$$
Эквивалентность полноты и замкнутости ортогональной системы в гильбертовом пространстве.
Теорема 5.
Пусть (H) — гильбертово пространство и ({e_{i}}) — ортонормированная система элементов. Для того чтобы ряд
$$
sum_{i=1}^{infty}alpha_{i}e_{i}nonumber
$$
сходился, необходимо и достаточно, чтобы сходился числовой ряд
$$
sum_{i=1}^{infty}|alpha_{i}|^{2}.nonumber
$$
Доказательство.
(circ) Необходимость следует из неравенства Бесселя. Если (x=displaystylesum_{i=1}^{infty}alpha_{i}e_{i}), то (alpha_{i}=displaystylelim_{n rightarrow infty} left(sum_{k=1}^{n}alpha_{k}e_{k}, e_{i}right)=(x, e_{i})) и (displaystylesum_{i=1}^{infty}|alpha_{i}|^{2} leq left|xright|^{2}).
Достаточность. Пусть числовой ряд (displaystylesum_{i=1}^{infty}|alpha_{i}|^{2}) сходится. Тогда для любого (varepsilon > 0) найдется такой номер (N), что для всех (n, m > N) выполнено неравенство
$$
sum_{k=n}^{m}|alpha_{i}|^{2} < varepsilon.nonumber
$$
Последовательность частичных сумм ряда (displaystylesum_{i=1}^{infty}alpha_{i}e_{i}) будет фундаментальной, так как при любых (n, m > N) выполнено условие
$$
left|s_{n}-s_{m}right|^{2}=left|sum_{i=n}^{m}alpha_{i}e_{i}right|^{2}=sum_{i=n}^{m}|alpha_{i}|^{2} < varepsilon,nonumber
$$
где (s_{n}=alpha_{1}e_{1}+ldots+alpha_{n}e_{n}).
Но в полном пространстве любая фундаментальная последовательность сходится. Следовательно, последовательность частичных сумм (s_{n}) сходится, то есть ряд (displaystylesum_{i=1}^{infty}alpha_{i}e_{i}) сходится. (bullet)
Следствие.
Если ({e_{i}}) — ортонормированная система в гильбертовом пространстве (H), то для любого (x in H) ряд Фурье по ортонормированной системе ({e_{i}}) сходится и элемент (x) представим в виде
$$
x=sum_{i=1}^{infty}x_{i}e_{i}+y, mbox{где} x_{i}=(x, e_{i}), (y, e_{i})=0, i in N.label{ref17}
$$
(circ) Пусть (displaystylesum_{i=1}^{infty}x_{i}e_{i}) есть ряд Фурье элемента (x). В силу неравенства Бесселя числовой ряд (displaystylesum_{i=1}^{infty}|x_{i}|^{2}) сходится. Из теоремы 5 тогда следует, что ряд (displaystylesum_{i=1}^{infty}x_{i}e_{i}) будет сходящимся.
Пусть
$$
y=x-sum_{i=1}^{infty}x_{i}e_{i}=lim_{n rightarrow infty} left(x-sum_{i=1}^{n}x_{i}e_{i}right).nonumber
$$
В силу ортогональности системы ({e_{i}}) и непрерывности скалярного произведения справедливо равенство
$$
(y, e_{i})=lim_{n rightarrow infty} left(x-sum_{i=1}^{n}x_{i}e_{i}, e_{i}right)=(x, e_{i})-x_{i}=0, i in N. bulletnonumber
$$
Ортогональная система ({e_{i}}) называется замкнутой в унитарном пространстве (H), если для любого (x in H) из ((x, e_{i})=0), (i=1, 2, ldots), следует (x=0).
Теорема 6.
Для того чтобы ортонормированная система была полной в унитарном пространстве, необходимо, а в случае полного пространства и достаточно, чтобы она была замкнутой.
Доказательство.
(circ) Необходимость. Пусть ({e_{i}}) — полная система в унитарном пространстве (H). Если для элемента (x in H) справедливы равенства ((x, e_{i})=0), (i in N), то, применяя равенство Парсеваля, получаем
$$
left|xright|^{2}=sum_{i=1}^{infty}|x_{i}e_{i}|^{2}=0,nonumber
$$
то есть (x=0).
Достаточность. Пусть (H) — полное пространство. Тогда каждый элемент (x in H) можно представить в виде eqref{ref17}. Так как система ({e_{i}}) замкнута, то из равенств ((y, e_{i})=0), (i in N), следует, что (y=0). Таким образом, любой элемент (x) есть сумма своего ряда Фурье по ортонормированной системе ({e_{i}}). Следовательно, система ({e_{i}}) полна в (H). (bullet)
Ряды Фурье. Интеграл Фурье. Операционное исчисление
Федеральное агентство по
образованию
Государственное
образовательное учреждение высшего профессионального образования
Санкт-Петербургский государственный горный институт им. Г.В.Плеханова
(технический университет)
А.П. Господариков, Г.А. Колтон,
С.А. Хачатрян
Ряды Фурье. Интеграл Фурье. Операционное
исчисление
Учебно-методическое пособие
САНКТ-ПЕТЕРБУРГ
2005
УДК 512 + 517.2 (075.80)
ББК 22.161.5
Г723
Учебно-методическое пособие дает возможность
получить практические навыки анализа функций с помощью разложения в ряд Фурье
или представления интегралом Фурье и предназначено для самостоятельной работы
студентов дневной и заочной форм обучения специальностей.
В пособии рассмотрены основные вопросы
операционного исчисления и широкий класс технических задач с применением основ
операционного исчисления.
Научный
редактор проф. А.П. Господариков
Рецензенты:
кафедра высшей математики № 1 Санкт-Петербургского государственного
электротехнического университета; доктор физ.-мат. наук В.М. Чистяков
(Санкт-Петербургский государственный политехнический университет).
Господариков
А.П.
Г723. Ряды
Фурье. Интеграл Фурье. Операционное исчисление: Учебно-методическое пособие /
А.П. Господариков, Г.А. Колтон, С.А. Хачатрян;
Санкт-Петербургский государственный горный институт (технический университет).
СПб, 2005. 102 с.
ISBN
5-94211-104-9
УДК 512 +
517.2 (075.80)
ББК
22.161.5
Введение
Из теории
Фурье известно, что при некотором воздействии на физические, технические и
другие системы, его результат повторяет форму начального входного сигнала,
отличаясь только масштабным коэффициентом. Понятно, что на такие сигналы (их
называют собственными) система реагирует наиболее простым образом. Если
произвольный входной сигнал есть линейная комбинация собственных сигналов, а система
линейна, то реакция системы на этот произвольный сигнал есть сумма реакций на
собственные сигналы. И поэтому полную информацию о системе можно получить по
«кирпичикам» – откликам системы на собственные входные сигналы. Так поступают,
например, в электротехнике, когда вводят частотную характеристику системы
(передаточную функцию). Для наиболее простых линейных, инвариантных во времени
систем (например, описываемых обыкновенными дифференциальными уравнениями с
постоянными коэффициентами) в некоторых случаях собственными функциями являются
гармоники вида . Таким
образом можно получить и результат произвольного воздействия на систему, если
последний будет представлен в виде линейной комбинации гармоник (в общем
случае, в виде ряда Фурье или интеграла Фурье). Вот одна из причин, по которой
в теории и приложениях возникает потребность применения понятия
тригонометрического ряда (ряда Фурье) или интеграла Фурье.
Глава 1. Ряды Фурье
§ 1.
Векторные пространства
Здесь
приведены краткие сведения из векторной алгебры, необходимые для лучшего
понимания основных положений теории рядов Фурье.
Рассмотрим
множество W геометрических векторов (векторное пространство), для которого
обычным образом введены понятие равенства векторов, линейные операции (сложение
и вычитание векторов, умножение вектора на число) и операции скалярного
умножения векторов.
Введем в
пространстве W ортогональный базис, состоящий из трех попарно ортогональных
векторов ,
и
. Произвольный вектор
является линейной комбинацией векторов базиса:
. (1.1)
Коэффициенты li (i = 1, 2, 3),
называемые координатами вектора относительно базиса
, могут быть определены следующим образом.
Скалярное произведение вектора и одного из векторов базиса
.
В силу
ортогональности базиса скалярные произведения при
, следовательно, в правой части последнего
равенства отлично от нуля лишь одно слагаемое, соответствующее , поэтому
, откуда
, (1.2)
где .
Если векторы и
заданы своими координатами
и
, то их скалярное произведение
.
Так как при скалярное произведение
, то в двойной сумме отличны
от нуля лишь слагаемые с равными индексами, поэтому
. (1.3)
В частности
при из (1.3) следует
. (1.4)
§ 2.
Скалярное произведение и норма функций
Обозначим
символом множество
функций, кусочно-непрерывных на промежутке [a, b], т.е.
функций, имеющих на промежутке [a, b] конечное число точек
разрыва первого рода и непрерывных во всех остальных точках этого промежутка.
Скалярным
произведением функций называется
число
.
Свойства
скалярного произведения функций полностью совпадают со свойствами скалярного
произведения векторов:
1. .
2. .
3. .
4. ;
.
Таким
образом, скалярное произведение линейно зависит от своих компонентов. Это
свойство называется билинейностью скалярного произведения.
Функции называются
ортогональными на
[a, b], если .
Нормой
функции на промежутке
[a, b] называется неотрицательное число , квадрат которого равен скалярному
произведению функции на
себя:
.
Свойства
нормы функции во многом совпадают со свойствами модуля вектора:
1. .
2. Если
функция непрерывна на
[a, b] и ,
то . Так как
, то при
,
откуда . Дифференцируя последнее
соотно- шение по и
применяя теорему Барроу, получим и, сле-довательно,
.
3. теорема
косинусов
.
.
Следствие. Если , то
(теорема Пифагора).
4. Обобщенная
теорема Пифагора. Если функции (k = = 1, 2, …, n) попарно
ортогональны на промежутке , то
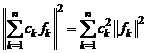
Используя
свойство билинейности скалярного произведения, получим
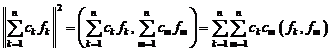
В силу
ортогональности функций скалярные
произведения при
, поэтому
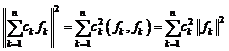
5. неравенство
Коши – Буняковского ,
или, что то же самое,
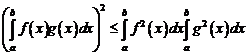
При любых
вещественных
.
Таким
образом, квадратный трехчлен в левой части последнего неравенства сохраняет
знак на всей вещественной оси, следовательно, его дискриминант .
Упражнение 1.
Доказать свойства скалярного произведения функций 1-3.
Упражнение 2.
Показать справедливость следующих утверждений:
а) функция ортогональна функциям
и
на промежутке
при любых целых k и m;
б) при любых
целых k и m функции и
ортогональны на промежутке
;
в) функции и
, а также
и
при
ортогональны на промежутках
и
;
г) функции и
не ортогональны на промежутке
.
Упражнение 3.
Используя свойство нормы 5, доказать неравенство треугольника
.
§ 3.
Ортогональные системы функций. Коэффициенты Фурье. Ряд Фурье
Счетное
множество непрерывных на промежутке функций
образуют на этом промежутке ортогональную
систему, если
1. , 2.
при
.
Пусть – ортогональная система
функций на промежутке и
. По аналогии с (1.2)
образуем величины
, (3.1)
где .
Числа называются коэффициентами
Фурье функции относительно
ортогональной системы .
Ряд
(3.2)
называется
рядом Фурье для функции .
В отличие от
того, что имеет место в векторной алгебре [см. (1.1)], здесь нельзя утверждать
ни того, что суммой ряда Фурье (3.2) является заданная функция , ни даже того, что ряд (3.2) вообще
сходится. Тем не менее, частичные суммы ряда (3.2), называемые полиномами
Фурье, играют важную роль в задаче аппроксимации функции линейными комбинациями функций
.
Термином
аппроксимация будем обозначать замену заданной функции другой, близкой к
, функцией
, более простой или более удобной для исследования.
При этом, естественно, возникает вопрос о величине погрешности, связанной с
такой заменой. Погрешность аппроксимации обычно оценивается с помощью среднего
квадратического отклонения
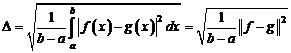
или более
простой величины
.
Ясно, что чем
меньше величина δ, тем ближе располагаются друг к другу графики функций и
, тем лучше функция
аппроксимирует функцию
.
Определим,
при каком наборе коэффициентов линейная комбинация
первых п
функций ортогональной системы наилучшим образом аппроксимирует функцию
, или, иначе говоря, при
каких величина
принимает наименьшее значение.
Преобразуем
выражение для dп, используя последовательно теорему косинусов, свойство
билинейности скалярного произведения, обобщенную теорему Пифагора и формулу (3.1)
для коэффициентов Фурье:
.
Применив
тождество , получим
Из последнего
выражения сразу следует, что принимает наименьшее значение
, (3.3)
при
Таким
образом, именно частичная сумма ряда Фурье является наилучшей аппроксимацией
функции по сравнению с
другими линейными комбинациями функций
Упражнение.
Показать, что, во-первых, система функций ортогональна на промежутке
, и, во-вторых, системы функций
и
ортогональны на промежутке
.
Указание. Воспользоваться
свойствами скалярного произведения функций.
§ 4.
Сходимость в среднем. Равенства Парсеваля
Из формулы (3.3)
с учетом того, что величина по определению не отрицательна, следует
. (4.1)
Левая часть
неравенства (4.1) представляет собой частичную сумму положительного числового
ряда
. (4.2)
Положительный
ряд с ограниченными в совокупности частичными суммами сходится, следовательно,
сходится и ряд (4.2). Переходя в (4.1) к пределу при , получим неравенство Бесселя
. (4.3)
Возвращаясь к
формуле (3.3), заметим, что с увеличением п величина уменьшается, оставаясь
неотрицательной. Следовательно, монотонно убывающая неотрицательная
последовательность сходится.
из (3.3) получим ее предел
. (4.4)
Если , где
– частичная сумма ряда Фурье (3.2),
то говорят, что ряд (3.2) сходится в среднем к функции . В этом случае из (4.4) следует
(4.5)
Соотношение (4.5)
называется равенством Парсеваля. Это аналог формулы (1.4) для квадрата модуля
вектора.
Замечание. Из сходимости ряда в
среднем, вообще говоря, не следует его сходимость в обычном смысле слова.
Если
равенство Парсеваля выполняется для всех функций из множества , или, что то же самое, для любой
функции из ряд Фурье
сходится в среднем к этой функции, то ортогональная система называется замкнутой, а соотношение (4.5)
– уравнением замкнутости. Замкнутыми системами, например, являются системы
функций из упражнения в § 3. Доказательство этого факта выходит за рамки
настоящего пособия.
Свойства
замкнутых систем следующие:
1. Если
непрерывная функция ортогональна
всем функциям замкнутой системы, то она тождественно равна нулю. Действительно,
в этом случае все коэффициенты Фурье равны нулю. Из (4.5) следует, что , и тогда (см. § 2, свойство
нормы 2)
Таким
образом, к замкнутой системе функций нельзя присоединить никакой новой функции,
отличной от тождественного нуля, которая была бы ортогональна ко всем . Это свойство замкнутой
системы функций называют ее полнотой.
Следствие. Если две непрерывные
функции и
имеют одни и те же
коэффициенты Фурье, то они тождественно совпадают. Доказательство этого
утверждения следует найти самостоятельно.
2. Пусть и
– коэффициенты Фурье функций
и
относительно замкнутой ортогональной системы
. Тогда
(4.6)
где, как и
ранее,
Соотношение
(4.6) называется обобщенным равенством Парсеваля. Это аналог формулы (1.3) для
скалярного произведения векторов.
Так как для
функций коэффициенты
Фурье, очевидно, равны ,
в силу замкнутости системы из (4.5) следует
Вычитая
почленно эти равенства и используя тождества
получим
равенство (4.6).
3. Если – замкнутая ортогональная
система функций, то
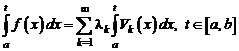
т.е. интеграл
от функции можно
получить почленным интегрированием ее ряда Фурье. Для доказательства достаточно
применить формулу (4.6) к функциям и
и учесть, что
в этом случае . Тогда
Отметим, что
справедливость формулы (4.7) установлена даже без предположения о сходимости
ряда Фурье.
Упражнение.
Доказать, что если ряд Фурье сходится равномерно на промежутке [а, b] к функции , то он сходится в среднем к этой
функции.
§ 5.
Тригонометрический ряд Фурье на промежутке [–L, L]
Система
функций
(5.1)
ортогональна
на промежутке [–L, L] (см. упражнение в § 3).
Показать, что
следует самостоятельно.
Каждой
функции ,
кусочно-непрерывной на промежутке [–L, L], сопоставим ее ряд
Фурье:
. (5.2)
Коэффициенты
Фурье , в соответствии
с (3.1), определятся формулами
(5.3)
Ряд (5.2)
называется тригонометрическим рядом Фурье.
Как
отмечалось в § 4, система функций (5.1) является замкнутой. Поэтому для любой
кусочно-непрерывной функции ее ряд Фурье (5.2) сходится в среднем к этой
функции. Равенство Парсеваля (4.5) в принятых теперь обозначениях примет вид
. (5.4)
Левая часть
последнего равенства, как легко видеть, представляет собой удвоенное среднее
значение квадрата функции на промежутке [–L, L].
Частичные
суммы
тригонометрического
ряда (5.2) называются тригонометрическими полиномами Фурье. Из формулы (3.3)
следует, что средняя квадратическая погрешность, возникающая при замене функции
ее тригонометрическим
полиномом Фурье,
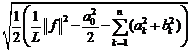
§ 6.
Сходимость тригонометрического ряда Фурье. Теорема Дирихле
Функция называется
кусочно-монотонной на промежутке , если этот промежуток можно разделить на
конечное число частей, на каждой из которых функция монотонна.
Если функция
кусочно-непрерывна и кусочно-монотонна на промежутке , то говорят, что на этом промежутке она удовлетворяет
условиям Дирихле. Для таких функций справедлива принимаемая нами без
доказательства следующая теорема.
Теорема
Дирихле.
Если функция удовлетворяет
условиям Дирихле на промежутке [–L, L], то ее ряд Фурье (5.2)
сходится во всех точках этого промежутка. При этом во внутренних точках
промежутка сумма ряда Фурье , если в точке х функция непрерывна; в
точках разрыва ; на концах
промежутка , где
– односторонние пределы в
точке а.
Если
доопределить (или переопределить) функцию , полагая
в точках разрыва и f (–L)
= = на концах
промежутка, то в соответствии с теоремой Дирихле
, (6.1)
где
коэффициенты по-прежнему
определяются формулами (5.3).
Соотношение
(6.1) обычно называется разложением функции в тригонометрический ряд Фурье. Члены ряда
(6.1)
(6.2)
называются
гармониками. Введем в рассмотрение величины и
, связанные с коэффициентами Фурье
и
соотношениями
и
. Тогда гармоника (6.2) запишется в виде
, где
– амплитуда гармоники;
– ее частота;
– начальная фаза. Множество
частот образует
дискретный частотный спектр функции на промежутке [–L, L]. Формула (6.1) примет
вид
, (6.3)
т.е. функция,
удовлетворяющая условиям Дирихле, представляет собой результат сложения
бесконечного числа гармоник. При этом амплитуды и начальные фазы слагаемых
гармоник зависят от разлагаемой функции, а частотный спектр одинаков для всех
функций, заданных на одном и том же промежутке.
Из равенства
Парсеваля (5.4) следует
, (6.4)
где .
Таким
образом, сумма квадратов амплитуд гармоник равна удвоенному среднему значению
квадрата функции на
промежутке [–L, L]. Соотношение (6.4) часто
называют энергетическим равенством.
В силу
периодичности гармоник из сходимости ряда (6.3) на промежутке [–L, L] следует его сходимость
всюду, т.е. на всей числовой оси. Суммой этого ряда, очевидно, будет 2L-периодическая
функция , которая на
промежутке [–L, L] совпадает с заданной
функцией . Функция
, определенная указанным
образом, называется периодическим продолжением.
Теорема Дирихле (другая формулировка). Если функция удовлетворяет условиям
Дирихле на промежутке [–L, L], то тригонометрический
ряд Фурье (6.1) сходится всюду к ее периодическому продолжению.
Замечание. Если функция , заданная для всех
, является 2L-периодической,
то ее периодическое продолжение совпадает с самой функцией, и, следовательно,
ряд Фурье (6.1) представляет функцию на всей числовой оси. В этом случае можно
получить другие, иногда более
удобные по сравнению с (5.3), формулы для коэффициентов Фурье:
, (6.5)
где с
– любое число.
Вместо того,
чтобы устанавливать справедливость формул (6.5), докажем более общее
утверждение: если функция имеет период Т, то интеграл
не зависит от а.
Действительно,
Выполнив в
среднем интеграле замену переменной и воспользовавшись периодичностью
подынтегральной функции, получим
Последний
интеграл не зависит от а, что, собственно, и требовалось доказать.
Таким
образом, интегралы в (6.5) не зависят от с. Полагая в этих формулах , убеждаемся в
тождественности выражений (5.3) и (6.5).
Если функция не является периодической,
то в формулах (6.5) в подынтегральные выражения вместо функции должно входить ее периодическое
продолжение .
Упражнение.
Доказать, что гармоники (6.2) являются периодическими функциями с периодом 2L,
т.е.
.
§ 7. Разложение
в тригонометрические ряды четных и нечетных функций
Функция , область определения
которой симметрична
относительно начала координат, называется четной (нечетной), если . Тогда
или [
]. Так, например, функции
и
нечетны, а
и
четны. Легко видеть, что произведение двух
четных или двух нечетных функций – четная функция, а произведение четной и нечетной
функций – нечетная функция.
Предлагаем
доказать самостоятельно следующие свойства определенного интеграла:
а) если
функция четна, то
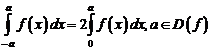
б) если
функция нечетна, то
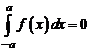
Указание. Представить интеграл в виде суммы интегралов:
и в первом из них выполнить
замену .
Пусть четная
функция удовлетворяет
условиям Дирихле на промежутке [–L, L]. Произведение будет нечетной функцией, и,
поэтому, в силу (7.2)
.
Таким
образом, ряд Фурье четной функции содержит только косинусы:
. (7.3)
Так как – четная функция, то
вследствие (7.1)
. (7.4)
Подобным же
образом получим, что ряд Фурье нечетной функции содержит только синусы:
(7.5)
где
. (7.6)
§ 8. Ряд
Фурье для функции, заданной на промежутке [0, L]
Пусть функция
удовлетворяет на
промежутке [0, L] условиям Дирихле. Построим четное продолжение
данной функции на промежуток [–L, 0], полагая для
. Полученную четную функцию разложим в
тригонометрический ряд Фурье (7.3), содержащий только косинусы:
. (8.1)
Коэффициенты
разложения можно вычислять по формулам (7.4), в которые входят только значения
первоначально заданной функции:
. (8.2)
Аналогично,
если функцию продолжить
на промежуток [–L, 0] нечетным образом, полагая для
, и разложить полученную функцию в ряд Фурье на
промежутке [–L, L], то в этом разложении
будут содержаться только синусы:
(8.3)
где
. (8.4)
На промежутке
[0,
L]
ряды (8.1) и (8.3) представляют одну и ту же функцию , но вне этого промежутка эти ряды ведут себя
по-разному. Так на промежутке [–L, 0] ряд (8.1) сходится к
четному, а ряд (8.3) к нечетному продолжению функции .
Функции
; (8.5)
, (8.6)
участвующие в
разложениях (8.1) и (8.3), образуют ортогональные системы на промежутке [0, L]. Кроме того, как
нетрудно проверить, .
Поэтому величины и
, определяемые формулами
(8.2) и (8.4), представляют собой коэффициенты Фурье функции относительно ортогональных систем
(8.5) и (8.6) соответственно, и, следовательно, ряды (8.1) и (8.3) являются рядами
Фурье на промежутке [0, L] для этой функции.
Замечание. Если функцию , заданную на [0, L], продолжить произвольным
образом на промежуток [0, L], например, просто
положив для
, то ее разложение в тригонометрический
ряд будет содержать и синусы, и косинусы:
. (8.7)
На промежутке
[0,
L]
этот ряд будет представлять заданную функцию, но, в отличие от рядов (8.1) и
(8.3), ряд (8.7), вообще говоря, не является рядом Фурье для функции на указанном промежутке,
так как система функций
,
участвующая в
разложении (8.7), не ортогональна на [0, L] (см § 2, упражнение 2, д).
§ 9. Ряды
Фурье для комплексных функций
Рассмотрим
элементы теории рядов Фурье для комплексных функций, т.е. функций вида , где i – мнимая единица,
– вещественные
функции вещественного аргумента. Обозначим символом множество комплексных кусочно-непрерывных
функций, определенных на промежутке .
Скалярным
произведением функций назовем
комплексное число
,
где – функция, комплексно сопряженная
с функцией .свойства
скалярного произведения комплексных функций следующие:
1.
2. билинейность
,
.
Доказать
свойства 1 и 2 предлагаем самостоятельно.
Как и ранее,
функции f и g будем называть ортогональными, если их скалярное
произведение равно нулю.
Определение
нормы функции оставим прежним, так что
.
Свойства
нормы, претерпевшие изменения при переходе от вещественных функций к
комплексным, следующие:
1. теорема
косинусов.
или в более
общем виде
. (9.1)
2. Обобщенная
теорема Пифагора. Если , то
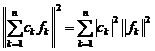
Доказать
свойства 1 и 2 следует самостоятельно.
3. Неравенство
Коши – Буняковского. Если функции и
непрерывны, то
.
В самом деле,
если , то
на
, и доказываемое неравенство выполняется. Пусть
. Число
очевидно, не отрицательно. С другой
стороны, по формуле (9.1), где и
, имеем
.
Таким
образом, , а так как
, то
, что и требовалось доказать.
Пусть теперь
система комплексных функций
(9.2)
ортогональна
на промежутке .
Сопоставим функции ее
ряд Фурье
(9.3)
где
коэффициенты Фурье
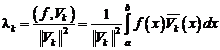
Введем
обозначения: –
частичная сумма ряда Фурье; – произвольная линейная комбинация функций
где
.
Тогда, так
же, как для вещественных функций (см. § 3), выполняется неравенство
(9.4)
где , причем равенство имеет
место тогда и только тогда, когда , т.е. среди всех функций
функция
дает наилучшее среднеквадратическое приближение
к функции .
Сходимость
ряда в среднем и замкнутость системы функций определяются точно так же, как в §
3:
а) если для
некоторой функции выполняется
равенство Парсеваля
, (9.5)
то ряд (9.3)
сходится в среднем к ,
т.е. ;
б) ортогональная
система функций (9.2) называется замкнутой на промежутке , если равенство Парсеваля
выполняется для каждой функции из .
Введем в
рассмотрение систему комплексных функций
. (9.6)
Свойства
системы функции (9.6) следующие:
1. .
2. Функции являются 2L-периодичными:
.
3. Система
функций (9.6) ортогональна на промежутке [–L, L]. Действительно, при
.
Здесь
использована формула .
4. .
Ряд Фурье для
функции по системе
функций (9.6) имеет вид
, (9.7)
где
коэффициенты Фурье
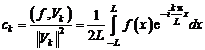
Система
функций (9.6) замкнута на [–L, L] (принимаем без
доказательства), поэтому для нее справедливы следующие утверждения:
а) ряд (9.7)
сходится в среднем к ,
б) для любой
функции из выполняется
равенство Парсеваля ,
в) среднеквадратическая
погрешность, возникающая при замене функции частичной суммой
ее ряда Фурье,
.
Теорема
Дирихле.
Если вещественная и мнимая части функции удовлетворяют на промежутке [–L, L] условиям Дирихле, то
функция является
суммой своего ряда Фурье:
. (9.9)
При этом
предполагается, что действуют прежние соглашения относительно значений функции
в точках разрыва и на концах промежутка (см. § 3).
Упражнение 1.
Доказать справедливость формулы (9.4). Доказать, что из (9.4) следует
неравенство Бесселя .
Упражнение 2.
Доказать справедливость утверждений 1, 2 и 4.
§ 10. Комплексная
форма тригонометрического ряда Фурье
Пусть
вещественная функция удовлетворяет
условиям Дирихле на промежутке [–L, L]. Запишем ее разложение в
тригонометрический ряд Фурье:
, (10.1)
где
. (10.2)
Если в (10.1)
выразить и
через показательную функцию
от мнимого аргумента:
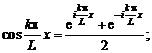
то получим
ряд
, (10.3)
где в силу
(10.2)
;
;
=
Последние три
формулы можно объединить:
. (10.4)
Ряд (10.3) с
коэффициентами (10.4) называется тригонометрическим рядом Фурье в комплексной
форме.
Пример 1. Разложить функцию , где
– комплексное число, в ряд Фурье на
промежутке .
Решение. Найдем коэффициенты
Фурье:
.
Поскольку , то
,
=.
Искомое
разложение будет иметь вид
, (10.5)
где учтено,
что
.
Применяя к
ряду (10.5) равенство Парсеваля
, (10.6)
можно найти
сумму еще одного числового ряда. Действительно, в нашем случае
;
.
Тогда из
(10.6) следует
.
Упражнение 1.
Доказать, что
;
.
Указание. Положить в (10.5) х
= 0 и х = p.
Упражнение 2.
Доказать, что при
;
.
Глава 2. Интеграл
Фурье
§ 11.
Сходимость интеграла Фурье
Пусть функция
определена на всей
числовой оси. Считая, что на произвольном конечном промежутке [–L, L] заданная функция
удовлетворяет условиям Дирихле, представим ее тригонометрическим рядом Фурье в
комплексной форме:
, (11.1)
где
– частота k-й
гармоники;
.
Введя в
(11.1) выражения (11.2), получим
. (11.3)
При величина
. Правая часть формулы (11.3)
аналогична интегральной сумме для функции по переменной w в промежутке
. Поэтому можно ожидать, что
после перехода в (11.3) к пределу при вместо ряда получим интеграл
. (11.4)
Формула
(11.4) называется интегральной формулой Фурье, а ее правая часть – интегралом
Фурье.
Рассуждения,
с помощью которых получена формула (11.4), не являются строгими и имеют лишь
наводящий характер. Условия, при которых справедлива интегральная формула
Фурье, устанавливает теорема, принимаемая нами без доказательства.
Теорема. Пусть функция , во-первых, абсолютно интегрируема
на промежутке , т.е.
интеграл сходится, и,
во-вторых, удовлетворяет условиям Дирихле на каждом конечном промежутке (–L,
L). Тогда интеграл Фурье сходится (в смысле главного значения) всюду к , т.е. равенство (11.4) выполняется
при всех х из промежутка . Здесь, по-прежнему, предполагается, что в
точке разрыва значение функции равно полусумме ее односторонних пределов в этой
точке.
§ 12.
Преобразование Фурье
Интегральную
формулу Фурье (11.4) преобразуем следующим образом. Положим
. (12.1)
Если функция непрерывна и абсолютно
интегрируема на всей оси, то функция непрерывна на промежутке
. Действительно, так как
, то
, (12.2)
и, поскольку
интеграл справа сходится, то сходится интеграл слева. следовательно, интеграл в
(12.1) сходится абсолютно. Равенство (12.2) выполняется одновременно для всех , поэтому интеграл (12.1)
сходится равномерно относительно w. Отсюда и следует, что
функция непрерывна
(точно так же, как из равномерной сходимости ряда, составленного из непрерывных
функций, следует непрерывность его суммы).
Из (11.4)
получим
. (12.3)
Комплексная
функция , определяемая
формулой (12.1), называется преобразованием Фурье или Фурье-образом функции . В свою очередь, формула
(12.3) определяет как
обратное преобразование Фурье, или прообраз функции . Равенство (12.3) при заданной функции
можно рассматривать, как интегральное
уравнение относительно функции , решение которого дается формулой (12.1). И,
наоборот, решение интегрального уравнения (12.1) относительно функции при заданной
дает формула (12.3).
В формуле
(12.3) выражение задает,
условно говоря, пакет комплексных гармоник с частотами, непрерывно
распределенными на промежутке и суммарной комплексной амплитудой
. Функция
называется спектральной плотностью. Формулу
(12.2), записанную в виде
,
можно
трактовать, как разложение функции в сумму пакетов гармоник, частоты которых
образуют сплошной спектр, распределенный на промежутке .
Равенства
Парсеваля.
Пусть и
– Фурье-образы вещественных функций
и
соответственно. Тогда
; (12.4)
, (12.5)
т.е.
скалярные произведения и нормы функций являются инвариантами преобразования
Фурье. Докажем это утверждение. по определению скалярного произведения имеем 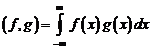
ее выражением (12.3) через
Фурье-образ , получим
.
В силу (12.1)
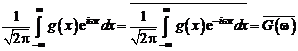
Поэтому 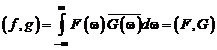
Формула (12.5) получается из (12.4) при .
Косинус- и
синус-преобразования Фурье. Если вещественная функция четна, то ее Фурье-образ, который здесь будем
обозначать , также
является вещественной четной функцией. Действительно,
.
Последний
интеграл, вследствие нечетности подынтегральной функции, обращается в нуль.
Таким образом,
. (12.6)
Здесь
использовано свойство (7.1) четных функций.
Из (12.6)
следует, что функция вещественна
и четным образом зависит от w, так как w входит в (12.6) только
через косинус.
Формула
(12.3) обратного преобразования Фурье в этом случае дает
=.
Так как и
– соответственно четная и нечетная функции
переменной w, то
. (12.7)
Формулы
(12.6) и (12.7) определяют косинус-преобразование Фурье.
Аналогично,
если вещественная функция нечетна, то ее преобразование Фурье
, где
– вещественная нечетная функция от w. При этом
; (12.8)
. (12.9)
Равенства
(12.8), (12.9) задают синус-преобразование Фурье.
Заметим, что
в формулы (12.6) и (12.8) входят значения функции только для
. Поэтому косинус- и синус-преобразования Фурье
можно применять и к функции, определенной на полубесконечном промежутке . В этом случае при
интегралы в формулах (12.7)
и (12.9) сходятся к заданной функции, а при к ее четному и нечетному продолжениям
соответственно.
Покажем, как
с помощью преобразования Фурье вычисляются некоторые несобственные «неберущиеся»
интегралы.
Пример 1. Вычислить интеграл
Лапласа .
Решение. Найдем Фурье-образ
функции где
:
.
С помощью
формулы обратного преобразования Фурье
получим
или
.
Здесь первое
слагаемое представляет собой удвоенный интеграл Лапласа, а второе равно нулю
вследствие нечетности подынтегральной функции. Поэтому
.
Пример 2. Вычислить разрывной
множитель Дирихле 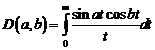
если .
Решение. Применив
косинус-преобразование Фурье к четной функции
получим
;
.
Таким
образом,
В частности
интеграл Дирихле
.
Пример 3. Вычислить интеграл
Эйлера-Пуассона .
Решение. Сначала вычислим
интеграл , применив к
функции , где
, преобразование Фурье и
введя замену
=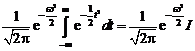
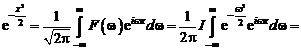
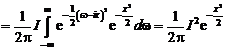
Отсюда , и, следовательно, с
заменой можно записать
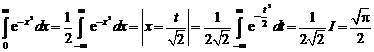
Упражнение 1.
Используя равенство Парсеваля, вычислить интегралы
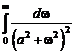
.
Упражнение 2.
Доказать, что
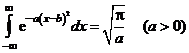
используя
равенство Парсеваля.
§ 13.
Основные сведения из теории преобразования Фурье
Тот факт, что
функция является
Фурье-образом функции ,
будем обозначать в дальнейшем одним из следующих способов: .
Свойства
преобразования Фурье:
1. Теорема
линейности.
, где
. Это свойство сразу следует из
определения (12.1) и линейности операции интегрирования.
2. Теорема
подобия. , где
. Обозначив
, получим
3. Теорема
смещения. , где
. Введя замену
, получим
.
Следствие.
, (13.1)
где . Действительно,
.
4. Теорема
о свертке. Напомним, что сверткой абсолютно интегрируемых функций и
называется функция
.
Фурье-образ
свертки функций f и g равен произведению их Фурье-образов,
умноженному на :
.
Так как по
определению
,
то, выполнив
во внутреннем интеграле замену , получим
=
==
,
что и
требовалось доказать.
5. Теорема
об образе производной. Пусть функция и ее производная
абсолютно интегрируемы на промежутке
. По формуле Ньютона –
Лейбница
.
Так как
производная интегрируема
на всей оси, интеграл в правой части последнего равенства имеет конечный предел
при . Следовательно,
существует конечный предел
. При этом
, ибо в противном случае функция
была бы неинтегрируемой на
промежутке . Точно
также доказывается, что .
Введем в
рассмотрение Фурье-образ производной
.
Выполнив
интегрирование по частям, получим
.
Так как
внеинтегральный член равен нулю, то
.
Таким
образом, операции дифференцирования функции соответствует операция умножения ее
Фурье-образа на множитель . Аналогично, если функция
имеет абсолютно интегрируемые
производные до n-го порядка включительно, то
,
.
Следствия. 1. Обыкновенное
линейное дифференциальное уравнение с постоянными коэффициентами
преобразованием Фурье переводится в линейное алгебраическое уравнение.
2. Линейное
уравнение в частных производных с постоянными коэффициентами и с двумя
независимыми переменными преобразованием Фурье по одной из переменных
переводится в обыкновенное линейное дифференциальное уравнение.
Пример 1. Доказать, что
, (13.2)
где .
Решение. Положим
Тогда
Таким
образом,
,
и по теореме
о свертке
.
Пример 2. Найти решение уравнения
(13.3)
при , удовлетворяющее
начальному условию
. (13.4)
Замечание. Уравнение (13.3)
называется уравнением теплопроводности. Уравнениями такого вида описываются
одномерные процессы диффузии, переноса тепла и т.п.
Решение. Применим к уравнению
(13.3) преобразование Фурье. Для этого, умножив обе части уравнения на , проинтегрируем его по х
от до
. Тогда
или
, (13.5)
где – Фурье-образ функции
.
Здесь
использовалась формула для Фурье-образа производной второго порядка:
.
Равенство
(13.5) – это обыкновенное линейное дифференциальное уравнение первого порядка
относительно функции переменной
t, где w – параметр.
Переходя к
Фурье-образам в равенстве (13.4), получим начальное условие для уравнения (13.5):
. (13.6)
Решением
задачи Коши (13.5), (13.6) является функция
.
С помощью
(12.3) находим – прообраз
функции :
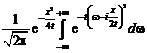
Последний
интеграл в (13.7) равен .
Поэтому
.
По теореме о
свертке
,
или
. (13.8)
Решение
уравнения теплопроводности, записанное в виде (13.8), называется интегралом
Пуассона.
Пример 3. Найти решение волнового
уравнения
, (13.9)
удовлетворяющее
начальным условиям
. (13.10)
Замечание. Задача Коши
(13.9),(13.10) является математической моделью одномерных волновых процессов в
сплошных безграничных средах. Поле возмущений в среде, выведенной из равновесного
состояния, описывается функцией , физический смысл которой определяется
спецификой рассматриваемой задачи. В задаче о малых поперечных колебаниях
струны – это отклонение
струны от ее равновесного положения, функции j(х) и задают соответственно форму
струны и распределение скоростей ее точек в начальный момент времени. Константа
, где
и r – натяжение и плотность
струны в положении равновесия. В задачах акустики – скорость возмущенного движения в точке
в момент времени
;
– скорость звука в невозмущенной среде и т.д.
Решение. Преобразуя по Фурье
уравнение (13.9) и начальные условия (13.10), получим задачу Коши для
обыкновенного дифференциального уравнения второго порядка:
где w – параметр.
Решение
задачи имеет вид
Используя
(13.1) и (13.2), получим формулу Эйлера – Даламбера
(13.11)
Для выяснения
физического смысла полученного решения преобразуем формулу (13.11). Положим
.
Тогда
. (13.12)
При возмущение
сохраняет постоянное значение
, если переменные
и
связаны зависимостью:
. Иными словами, возмущенное состояние
переносится в положительном
направлении оси абсцисс со скоростью . Поэтому говорят, что функция
определяет бегущую волну,
перемещающуюся вправо со скоростью а. Аналогично, функция задает волну, распространяющуюся
влево с той же скоростью а. Таким образом, выяснен физический смысл
постоянной величины а в уравнении (13.9): а – это скорость
распространения возмущений в среде.
Из формулы
(13.12) следует, что возмущение в точке х в момент времени есть результат сложения волн
и
, вышедших в момент времени
из точек с координатами
и
соответственно.
Итак, при
весьма общих предположениях установлено следующее:
1. Произвольную
функцию можно
представить в виде «суммы» гармоник; если задана на конечном интервале (или
периодическая), то эта сумма представляет собой ряд Фурье; если задана на всей числовой оси (но
непериодическая), то эта сумма – интеграл Фурье. С точки зрения приложений, это
означает, что самые разнообразные физические зависимости, скажем, давления, тока,
напряжения и т.д. от времени можно представить в виде линейной суперпозиции
гармонических колебаний.
2. В
представлении формулы в
виде ряда или интеграла Фурье естественно возникает ее спектр, который
однозначно определяется по функции и который, в свою очередь, однозначно
определяет саму функцию .
3. Результаты
спектрального анализа, т.е. процесса нахождения спектра той или иной
зависимости, используются при исследовании линейных систем, так как в этом
случае достаточно изучить поведение системы при воздействии на нее
гармонических колебаний, а затем просуммировать результаты этих воздействий с
учетом спектра рассматриваемого (уже произвольного) воздействия.
Упражнение.
Доказать, что, если на всей оси функция y(х)
дифференцируема, а j(х) – дважды дифференцируема, то функция (13.11)
действительно удовлетворяет уравнению (13.9) и начальным условиям (13.10).
Глава 3. Операционное
исчисление
§ 14. Преобразование
Лапласа
Понятие
оригинала.
Кусочно-непрерывная функция называется оригиналом, если выполняются
следующие условия:
1) для всех отрицательных t;
2) при
растет не быстрее экспоненты, т.е. существуют
такие постоянные M > 0 и c > 0, что для всех t.
Число с
называется показателем роста . очевидно, что для ограниченных оригиналов
показатель роста можно считать равным нулю.
Простейшим
оригиналом является единичная функция Хевисайда
Если функция удовлетворяет условию 2 и
не удовлетворяет 1, то произведение будет удовлетворять и условию 1, т.е. будет
оригиналом. Для упрощения записи будем, как правило, множитель H (t) опускать,
считая, что все рассматриваемые в этой главе функции равны нулю при
отрицательных значениях t.
Легко видеть,
что оригиналами являются такие функции, как и т.п.
Можно
доказать, что сумма, разность и произведение оригиналов являются оригиналами и
что оригиналом является функция при
(доказательства следует найти самостоятельно).
Замечание. Из этих утверждений
следует, что многочлены произвольной степени , а также функции вида
являются оригиналами.
Интеграл
Лапласа.
Интегралом Лапласа для оригинала f(t) называется несобственный
интеграл вида
, (14.1)
где – комплексный параметр.
Теорема. Интеграл Лапласа
абсолютно сходится в полуплоскости Пс: , где с – показатель роста f
(t). В самом деле, по определению оригинала имеем . Таким образом, интеграл
(14.1) мажорируется сходящимся интегралом , и, следовательно, сходится абсолютно в Пс.
Замечание. При доказательстве
теоремы получено используемое в дальнейшем неравенство:
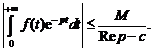
Преобразование
Лапласа.
Интеграл Лапласа
(14.3)
представляет
собой функцию параметра p, определенную в полуплоскости Пс:. Функция
называется Лаплас-образом
(изображением по Лапласу) оригинала . Тот факт, что
есть Лаплас-образ
, обозначается
или
.
Соотношение
(14.3), устанавливающее связь между оригиналом и его Лаплас-образом, называется
преобразованием Лапласа.
Свойства
преобразования Лапласа следующие:
1. Теорема
линейности. При любых постоянных и
.
Это
утверждение вытекает из определения (14.3) и свойств интегралов.
2. Имеет
место , что
непосредственно следует из неравенства (14.2).
3. Теорема
подобия. Для любого
.
Действительно,
полагая , получим
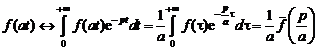
4. теорема
смещения. Для любого а . Действительно,
.
5. теорема
запаздывания. Для любого
. По определению преобразования Лапласа имеем
.
Здесь учтено,
что при
. Выполнив в последнем интеграле
замену , получим
.
Обратное
преобразование Лапласа. Установим связь между преобразованиями Лапласа и Фурье. Так
как при оригинал
, то
где
– показатель роста
.
Интеграл в
правой части последней формулы есть интеграл Фурье для . Таким образом, Лаплас-образ функции
является Фурье-образом
функции . Из формулы
обратного преобразования Фурье получим, что в точках непрерывности
.
Отсюда
(14.4)
Если в точке t
функция терпит разрыв,
то значение интеграла в (14.4) равно полусумме односторонних пределов в этой точке.
Формула
(14.4) определяет обратное преобразование Лапласа, с помощью которого оригинал
однозначно восстанавливается по своему изображению с точностью до значений в
точках разрыва.
§ 15.
Изображения простейших функций
Единичная
функция Хевисайда. Имеем:
Так как при , то
.
Для функции
Хевисайда с запаздывающим аргументом по теореме запаздывания получим
Экспонента.
По
теореме смещения
Гиперболические
и тригонометрические функции. В силу линейности преобразования Лапласа имеем
;
;
;
.
Степенная
функция с натуральным показателем. Положим , где
. Тогда при
.
При , поэтому
Отсюда
.
Так как , то
Упражнение 1.
Найти, используя теорему смещения, Лаплас-образы оригиналов
Периодические
функции. Если
оригинал является
Т-периодической функцией, то его изображение по Лапласу
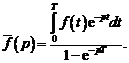
Действительно,
в этом случае
.
Выполнив
замену , в силу
периодичности будем
иметь
.
Ряд в правой
части последнего равенства представляет собой сумму бесконечной геометрической
прогрессии со знаменателем Так как при
, то ряд сходится, и его сумма равна
, откуда и следует
доказываемое утверждение.
Пример. Найти Лаплас-образ
оригинала с периодом Т
= 1).
Решение. Имеем
Следовательно,
в силу (15.1)
.
Ступенчатые
(кусочно-постоянные) функции. Ступенчатая функция , где
, а числа
образуют возрастающую последовательность,
может быть представлена в виде
,
,
где
Тогда
Упражнение 2.
Найти изображение кусочно-постоянной функции
Импульсные
функции.
Импульсной функцией будем называть функцию вида
где – функция, определенная для
всех
Используя
функцию Хевисайда с запаздывающим аргументом, можем записать
.
Введем
функции , где
. Тогда
, и по теореме запаздывания
.
Пример. Найти Лаплас-образ
импульсной функции
Решение. Так как
;
;
,
то
.
Дельта-функция
Дирака.
Рассмотрим семейство ступенчатых импульсных функций
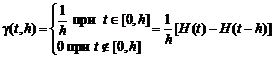
и семейство
их изображений по Лапласу
. (15.3)
При семейство функций
расходится, так как
Введем
условную функцию –
дельта-функцию Дирака, которую будем считать пределом семейства (15.2): . Таким образом,
дельта-функция равна нулю всюду, кроме точки , где она равна
.
Изображением
дельта-функции условимся считать предел семейства (15.3) при :
.
Далее по
определению положим
;
.
Можно
доказать (и это следует сделать самостоятельно) справедливость следующих
утверждений:
(15.4)
(15.5)
(15.6)
Выражения
(15.5) и (15.6) корректны только при условии непрерывности функции f(t).
Замечание 1. Из утверждения (15.6)
следует, что
что полностью
соответствует теореме запаздывания.
Замечание 2. В силу (15.4) имеем
.
Таким
образом, дельта-функцию формально можно рассматривать как производную единичной
функции Хевисайда.
В прикладных
дисциплинах дельта-функции широко используются для моделирования ударных сил,
сосредоточенных нагрузок и тому подобных явлений.
§ 16. Основные теоремы операционного исчисления
Свертка
оригиналов. Сверткой оригиналов и
называется функция
.
Функции f (t)
и g(t) называются компонентами свертки.
Найдем для
примера свертку произвольного оригинала и единичной функции
Имеем
. Так как
при
то
. (16.1)
Доказать, что
свертка оригиналов – оригинал и что свертка коммутативна, т.е. , следует самостоятельно.
Теорема 1. Если и
, то
.
Действительно,
по определению (14.3) имеем
,
где D
– треугольная область, задаваемая системой неравенств
Изменив
порядок интегрирования в двойном интеграле, получим
.
Введем вместо
t новую переменную . Тогда
,
что и
требовалось доказать.
Пример 1. Найти оригинал , если его Лаплас-образ
.
Решение. Представим данный
Лаплас-образ в виде произведения двух изображений, для которых известны
оригиналы:
.
Так как
,
то по теореме
1 имеем
.
Упражнение 1.
Доказать, что свертка линейна по каждой компоненте:
,
где а и
b – постоянные.
Упражнение 2.
Найти свертку функций и
.
Интегрирование
и дифференцирование оригиналов. Для интегрирования и дифференцирования
оригиналов справедливы следующие теоремы.
Теорема 2. Если то
.
Для
доказательства используем формулу (16.1) и теорему 1. Тогда
.
Теорема 3. Если и
– оригиналы и
, то
В самом деле,
исходя из формулы Ньютона – Лейбница, в силу (16.1) будем иметь
.
Тогда по
теореме 1
.
Отсюда , что и требовалось
доказать.
Применив
формулу (16.2) дважды, получим
и т.д. В
частности, если , то
, т.е. в этом случае
дифференцирование оригинала сводится к умножению его изображения на p.
Дифференцирование
и интегрирование изображений. Без доказательства примем следующие свойства
преобразования Лапласа:
1. Если – оригинал с показателем
роста , то его изображение
имеет в области
производные любых порядков.
2. При том же
условии пределы, производные и интегралы от в области
можно находить, выполняя соответствующие
операции под знаком интеграла (14.3).
Теорема 4.
Если , то
, т.е. дифференцирование изображения
сводится к умножению оригинала на . Действительно, дифференцируя (14.3) по
параметру p, получим
.
Справа стоит
интеграл Лапласа для функции , следовательно,
,
что и
требовалось доказать.
Применив
несколько раз теорему 4, получим
.
Теорема 5. Если – оригиналы и
, то
,
т.е.
интегрирование изображения в указанных пределах сводится к делению оригинала на
. Так как в силу (14.3)
имеем , то
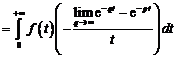
Поскольку при
и
, то
.
Рассмотрим
функции
.
По теореме 4
имеем
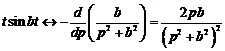
Так как , то по теореме 5
.
Точно так же
получим
.
Применяя
теорему 2, найдем изображение интегрального синуса
.
Следствия из
теорем 1-5 приведем с доказательствами.
Следствие 1. Если сходится
интеграл
, (16.3)
то
. (16.4)
Из сходимости
интеграла (16.3) следует, что изображение непрерывно в замкнутой области
. Переходя к пределу в (14.3) при
, приходим к требуемому
результату.
Следствие 2. Если сходится
интеграл 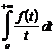
.
Так как , то в силу (14.4)
.
Для справедливо равенство
.
Следствие 3. Если – оригиналы, то
. Действительно, по теореме 3
. (16.5)
С другой
стороны, (см. § 14).
Переходя к пределу в (16.5) при , получим требуемый результат.
Следствие 4. Если – оригиналы и существует конечный
предел , то
. (16.6)
Исходим из
равенства
. (16.7)
В силу (14.4)
и теоремы 3
. (16.8)
Из (16.7) и
(16.8) получаем (16.6).
Формула
(16.6) позволяет исследовать поведение оригиналов при , имея в своем распоряжении только их
изображения.
Упражнение.
Вычислить несобственный интеграл , где
.
§ 17. Формула
разложения Хевисайда
Пусть
изображение функции представляет собой дробно-рациональную функцию.
Теорема. Пусть, где
и
– дифференцируемые функции. Введем
как полюсы функции
, т.е. корни (нули) ее
знаменателя. Тогда, если
, получим формулу Хевисайда:
. (17.1)
Доказательство
проведем для случая, когда и
– многочлены степеней т и п
соответственно, при этом т < п. Тогда – правильная рациональная
дробь. Представим в
виде суммы простейших дробей:
. (17.2)
Отсюда Коэффициенты
найдем из тождества (17.2),
переписав его в виде
,
где
.
Умножим обе
части последнего равенства на и перейдем к пределу при
. Учитывая, что
и
, получим
,
откуда и
следует (17.1). Теорема доказана.
Замечание 1. Если коэффициенты
многочленов и
вещественны, то комплексные
корни многочлена попарно
сопряжены. Следовательно, в формуле (17.1) комплексно сопряженными величинами
будут слагаемые, соответствующие комплексно сопряженным корням многочлена , и формула Хевисайда примет
вид
, (17.3)
где первая
сумма распространена на все вещественные корни многочлена , вторая – на все его комплексные
корни с положительными мнимыми частями.
Замечание 2. Каждый член формулы
(17.1) представляет собой записанное в комплексной форме колебание , где
. Таким образом, вещественным корням
() соответствуют
апериодические колебания, комплексным корням с отрицательными вещественными
частями – затухающие
колебания, чисто мнимым корням – незатухающие гармонические колебания.
Если
знаменатель не имеет
корней с положительными вещественными частями , то при достаточно больших значениях
получим установившийся
режим:
, (17.4)
где
;
– чисто мнимые корни
многочлена с
положительными мнимыми частями.
Колебания,
соответствующие корням с отрицательными вещественными частями, экспоненциально
затухают при и поэтому
не входят в установившийся режим.
Пример 1. Найти оригинал
изображения
.
Решение. Имеем . Выпишем корни многочлена
:
.
По формуле
(17.1)
.
Здесь ,
, так как числа
– корни уравнения
. Следовательно,
.
Пример 2. Найти оригинал
изображения
,
где а > 0; .
Решение. Здесь функция , помимо очевидного корня
, имеет бесконечно много
корней, являющихся нулями функции . Решая уравнение
, получим
, откуда
.
Таким
образом, корни знаменателя имеют вид
и
, где
Далее запишем
;
;
По формуле
(17.3) находим оригинал
§ 18.
Операторный метод решения дифференциальных уравнений
Дифференциальные
уравнения. Рассмотрим задачу Коши для линейного дифференциального уравнения
(18.1)
(здесь ) с начальными условиями
. (18.2)
Переходя в
(18.1) к изображениям, в силу линейности преобразования Лапласа будем иметь
. (18.3)
Изображения
производных, используя теорему 3 § 16 и начальные условия (18.2), запишем в
виде
. (18.4)
Подставив
(18.4) в (18.3), после несложных преобразований получим операторное уравнение
, (18.5)
где (характеристический
многочлен);
.
Из уравнения
(18.5) найдем операторное решение
. (18.6)
Решением
задачи Коши (18.1), (18.2) является оригинал операторного решения (18.6):
Для задачи
Коши в принятых
обозначениях можно записать
;
;
.
Операторное
уравнение имеет вид
.
разложим
операторное решение на простейшие дроби:
.
С помощью
формул, полученных в § 15, получим оригиналы:
.
Таким
образом, решение задачи Коши будет иметь вид
.
Пример 1. Решить задачу Коши для
дифференциального уравнения с начальными условиями
, где
.
Решение. Запишем операторное
уравнение
.
Его решение
имеет вид
.
Используя
теорему 2 § 16, последовательно найдем:
.
Пример 2. Решить задачу Коши для
дифференциального уравнения с нулевыми начальными условиями, где
– ступенчатая импульсная
функция.
Решение. Запишем операторное
уравнение
и его решение
.
Из теоремы 2
§ 16 следует
;
в
соответствии с теоремой запаздывания (§ 15)
.
Окончательно,
.
Пример 3. На точку массой т,
прикрепленную к пружине жесткостью с и находящуюся на гладкой горизонтальной
плоскости, действует периодически меняющаяся сила . В момент времени t точка подверглась удару,
несущему импульс .
Пренебрегая сопротивлением, найти закон движения точки, если в начальный момент
времени она покоилась в начале координат.
Решение. Уравнение движения
запишем в виде
,
где – упругая сила;
– функция Дирака. Решим
операторное уравнение
,
где . При
.
Если (случай резонанса), то
.
По теореме
запаздывания
.
Окончательно,
Интеграл
(формула) Дюамеля. Рассмотрим задачу Коши для уравнения (18.1) при начальных условиях
. Операторное решение в этом случае
имеет вид
.
Пусть весовая
функция – оригинал для
. тогда по теореме 1 § 16
получим
. (18.7)
Соотношение
(18.7) называется интегралом (формулой) Дюамеля.
Замечание. При ненулевых начальных
условиях формула Дюамеля непосредственно неприменима. В этом случае необходимо
предварительно преобразовать исходную задачу к задаче с однородными (нулевыми)
начальными условиями. Для этого введем новую функцию , полагая
(18.8)
где – начальные значения
искомого решения .
Как легко
видеть, , и следовательно,
.
Таким
образом, функция –
решение уравнения (18.1) с правой частью , полученной в результате подстановки (18.8) в
(18.1), при нулевых начальных данных.
Используя
(18.7), найдем и
.
Пример 4. С помощью интеграла
Дюамеля найти решение задачи Коши
с начальными
условиями .
Решение. Начальные данные
ненулевые. Полагаем, в соответствии с (18.8), . Тогда
, и для определения
получим уравнение
с однородными начальными условиями.
Для
рассматриваемой задачи характеристический многочлен , весовая функция
. По формуле Дюамеля
.
Окончательно,
.
Системы
линейных дифференциальных уравнений с постоянными коэффициентами. Задача Коши для системы
линейных дифференциальных уравнений в матричной записи имеет вид
, (18.9)
где – вектор искомых функций;
– вектор правых частей;
– матрица коэффициентов;
– вектор начальных данных.
Переходя в
(18.9) к изображениям, получим операторную систему
, (18.10)
где – Лаплас-образы векторов
искомых функций и правых частей соответственно.
Из (18.10)
находим операторное решение
, (18.11)
где ; Е – единичная
матрица.
Оригинал операторного решения
(18.11) является решением
исходной задачи Коши (18.9).
Обозначим весовую матрицу, т.е. матрицу-оригинал
для , где
Тогда из (18.11) в
соответствии с теоремой 1 § 16 будем иметь
. (18.12)
При нулевых
начальных условиях
. (18.13)
Соотношение
(18.13) представляет собой матричный аналог интеграла Дюамеля.
Пример 5. Найти решение задачи
Коши
с начальными
условиями .
Решение. Запишем систему и начальные
условия в матричной форме:
,
где . Тогда
;
.
Окончательно,
по формуле (18.12) получим
или
Замечание. Формулы (18.12) и
(18.13) имеют большое теоретическое значение, поскольку позволяют исследовать
поведение решения системы дифференциальных уравнений в зависимости от начальных
данных и правых частей. Однако для практического применения эти формулы мало
пригодны, так как зачастую требуют проведения громоздких выкладок, связанных с
вычислением обратных матриц, матричных сверток и т.п. Поэтому на практике
обычно применяют операторный метод, не переходя к матричной записи системы
уравнений, а при решении операторной системы используют конкретные особенности
исследуемой задачи.
Пример 6. Решить задачу Коши:
с начальными
условиями .
Решение. Перейдем в данной
системе к изображениям. С учетом начальных условий будем иметь
Запишем
решение операторной системы
.
Тогда
.
§ 19.
Приложения
Электрические
цепи.
Основными элементами электрических цепей являются сопротивления, индуктивности
и емкости (конденсаторы). Каждый из этих элементов называются двухполюсником,
поскольку он обладает двумя контактами (полюсами), которые соединяются с полюсами
других элементов цепи. Электрическое состояние двухполюсника в каждый момент
времени определяется
двумя величинами: силой тока (током) , проходящего через двухполюсник, и падением
напряжения (напряжением) на
его полюсах. Для каждого двухполюсника функции и
связаны некоторым соотношением, представляющим
собой физический закон, управляющий работой двухполюсника.
Для
сопротивления имеет место закон Ома
,
где – сопротивление
двухполюсника.
Для
индуктивности справедливо соотношение
,
где – индуктивность
двухполюсника.
Для
конденсатора выполняется соотношение
,
где С
– емкость конденсатора; –
начальный заряд на его обкладках.
В дальнейшем
будем считать, что в начальный момент времени цепь была свободна от токов и зарядов, что
соответствует задачам включения.
Если ввести
операторный ток и
операторное напряжение как
изображения функций и
соответственно, то
вышеприведенные уравнения, управляющие работой двухполюсников, перейдут в следующие:
.
Последние
соотношения могут быть записаны в виде операторного закона Ома
,
где
операторное сопротивление (импеданс) в случае активного сопротивления, индуктивности
и емкости принято в виде соответственно . Величину, обратную
,
называют операторной проводимостью
(адмитансом) двухполюсника.
При
последовательном соединении двух двухполюсников с операторными сопротивлениями и
имеем
;
и
, откуда
, и следовательно, импеданс цепи
. Аналогично, при параллельном
соединении двух элементов с адмитансами и
получим
,
,
, откуда
, и следовательно, адмитанс цепи
.
Таким
образом, в задачах включения операторные сопротивления и проводимости цепей
рассчитываются по обычным правилам соединения активных сопротивлений. Например,
если цепь состоит из последовательно соединенных сопротивления , индуктивности
и емкости
, шунтированной сопротивлением
, то ее импеданс
.
Если
электрическая цепь с адмитансом включена на эдс
, то операторный ток в ней определяется
соотношением ,
.
Как правило,
операторная проводимость цепи представляет собой рациональную дробь, полюсы
(корни знаменателя) которой расположены в левой полуплоскости , что, как следует из теоремы
Хевисайда, гарантирует устойчивость системы, т.е. исключает возможность
возникновения в такой системе незатухающих свободных колебаний.
Если эдс является ограниченной
функцией времени, то полюсы функции имеют неотрицательные вещественные части, и
следовательно (см. замечание 2 к теореме Хевисайда), по истечении достаточно
длительного промежутка времени в системе устанавливается стационарный режим,
при котором ток
,
где ;
– чисто мнимые полюсы функции
с положительными мнимыми частями;
– мнимая единица. Здесь,
как и ранее, предполагаем, что функция не имеет кратных полюсов.
Представим
эдс тригонометрическим рядом Фурье . Тогда
;
;
,
следовательно,
.
Положим
,
где – амплитуда гармоники с
частотой , bk – ее начальная фаза;
; g
. Тогда
. (19.1)
Функции и
называются амплитудно-частотной (АЧХ) и
фазочастотной характеристиками (ФЧХ) системы.
Будем
трактовать функции и
, как входной и выходной
сигналы соответственно. Из формулы (19.1) следует, что, если на вход системы
поступает сигнал с частотой w, амплитудой а и начальной фазой b, то по завершении
переходных процессов на выходе формируется сигнал той же частоты w с амплитудой и с фазой, сдвинутой
относительно фазы входного сигнала на величину. Таким образом, амплитудно-частотная и
фазочастотная характеристики представляют собой соответственно коэффициент усиления
(ослабления) и сдвиг фазы сигнала при его прохождении через систему. То
значение w, при котором АЧХ достигает максимума, называется резонансной
частотой системы.
Пример. Колебательный контур
состоит из последовательно соединенных активного сопротивления , индуктивности
и емкости C. Найти
резонансную частоту.
Решение. Импеданс контура, его адмитанс
. Амплитудно-частотная и
фазочастотная характеристики соответственно
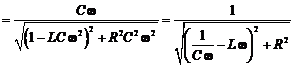
. (19.2)
Из формулы
(19.2) следует, что АЧХ достигает наибольшего значения, если .
Таким
образом, колебательный контур резонирует на частоту , наибольший коэффициент усиления сигнала
равен , сдвиг фазы на
резонансной частоте равен нулю.
Расчет
длинных электрических линий. Обозначим – удельные сопротивление, индуктивность и
емкость провода соответственно; – коэффициент утечки тока;
и
– ток и напряжение в точке с координатой х
в момент времени .
Тогда для участка линии между точками х и по известным законам физики будем иметь
;
. (19.3)
Разделив
уравнения (19.3) на Dх и перейдя к пределу при Dх ® 0, получим систему
уравнений в частных производных (телеграфную систему) для определения функций и
:
;
. (19.4)
Для
завершения постановки задачи систему (19.4) необходимо дополнить начальными и
краевыми условиями. В задаче включения начальные условия имеют вид
. (19.5)
Далее примем,
что правый конец провода заземлен, а на левом его конце поддерживается заданное
напряжение . Тогда
краевые условия запишутся в виде
, (19.6)
где – длина линии.
Применяя к
системе (19.4) преобразование Лапласа по переменной с учетом начальных условий (19.5), получим
операторную систему
, (19.7)
где и
– изображения напряжения и тока соответственно.
Краевые условия (19.6) перейдут в
, (19.8)
где .
Применяя
снова преобразование Лапласа, на этот раз по переменной х, вместо (19.7)
запишем алгебраическую систему
;
, (19.9)
где ;
;
;
– параметр преобразования Лапласа по
переменной х.
В дальнейшем,
чтобы избежать громоздких выкладок, ограничимся исследованием установившегося
режима в линии без искажений, т.е. линии, параметры которой удовлетворяют
условию .
Решение
системы (19.9) для линии без искажений имеет вид
,
где .
Возвратимся к
оригиналам:
;
. (19.10)
С помощью
второго из краевых условий (19.8) найдем
. (19.11)
Из (19.10) и
(19.11) следует, что
;
. (19.12)
При отыскании
функций и
будем использовать теорему
разложения Хевисайда, для чего необходимо найти полюсы изображений (19.12).
Нули гиперболического синуса определяются из уравнения , откуда
и
,
Следовательно, нули функции
– это числа
, расположенные в левой
полуплоскости .
Поэтому, если –
ограниченная функция, то, как следует из (19.12), напряжение и ток в
установившемся режиме соответственно
где – чисто мнимые полюсы
функции с
положительными мнимыми частями.
В частности,
если , то
, и следовательно, в
установившемся режиме
;
.
Примеры
для самостоятельного решения
Задание 1. Разложить в ряд Фурье
функции, заданные на интервале [–p, p]:
1. 2.
3.. 4.
.
5. 6.
7.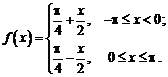
9.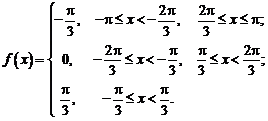
10.
11. 12.
13. 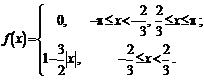

15. 16.
17. 18.
19. 20.
21.
22.
23.
24.
25. 26.
27. 28.
29.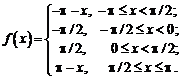
31.
Задание 2. Разложить в ряд Фурье
функции, заданные на интервале :
1. 2.
3. 4.
5. 6.
7. 8.
9.
10.
11.
12.
13.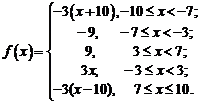
15.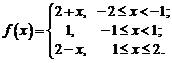
17. 18.
19. 20.
21. 22.
23. 24.
25. 26.
29 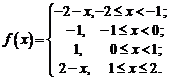
=
Указание. Для решения примера 15
воспользоваться формулами [6]
Задание 3. Представить интегралом
Фурье следующие функции:
1. 2.
3. 4.
5. 6.
7. 8.
9. 10.
11. 12.
13.. 14.
. 15.
.
16.. 17.
. 18.
.
Указание. При решении следует
воспользоваться формулами
;
;
;
;
;
.
Задание 4. Найти
косинус-преобразование Фурье следующих функций:
1. 2.
. 3.
.
4.. 5.
.
Задание 5. Найти
синус-преобразование Фурье следующих функций:
1. 2.
3. 4.
.
5. . 6.
. 7.
.
Ответы
Задание 1
1. . 2.
.
3. . 4.
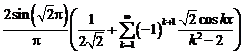
5. . 6.
.
7. .
8. .
9. .
10. .
11. .
12. 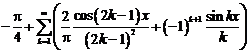
13. 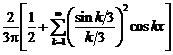
.
15. . 16.
.
17. . 18.
.
19. 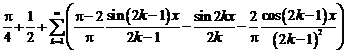
20. 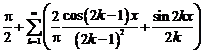
21. 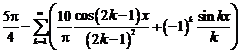
22. .
23. .
24. . 25.
.
26.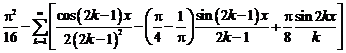
27. 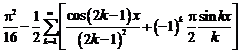
28. 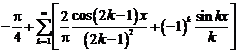
29. 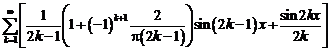
30. .
31. .
Задание 2
.
2. 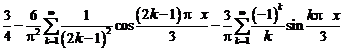
3. 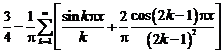
4. 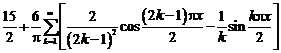
5. . 6.
. 7.
.
8.
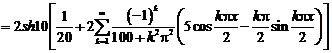
9. 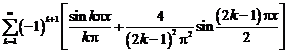
10. . 11.
.
12. 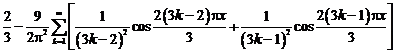
13. 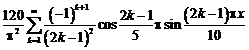
14. .
15. .
16. 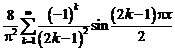
18. . 19.
.
20. .
21. 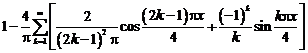
22. . 23.
.
24. . 25.
.
26. .
27. 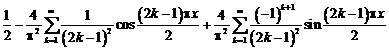
28. 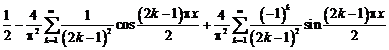
29. 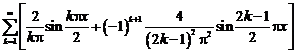
30. .
Задание 3
1. .
2. .
3. .
4. .
5. .
6. . 7.
.
8. . 9.
. 10.
.
11. 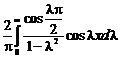
. 13.
.
14. . 15.
. 16.
.
17. . 18.
.
Задание 4
1. . 2.
.
3. . 4.
. 5.
.
Задание 5
1. . 2.
.
3. . 4.
.
Рекомендательный библиографический список
Основной:
1. Демидович Б.П.
Сборник задач и упражнений по математическому анализу. М.: Наука, 1972.
2. Пискунов Н.С.
Дифференциальное и интегральное исчисления. Часть II. М.: Наука, 1985.
3. Шипачев В.С.
Высшая математика. М.: Высшая школа, 1998.
Дополнительный:
4. Данко П.В.
Высшая математика в упражнениях и задачах / П.В.Данко, А.Г.Попов,
Г.Н.Кожевникова. М.: Высшая школа, 1997. т.2.
5. Минорский В.П.
Сборник задач по высшей математике. М.: Наука, 1987.
6. Прудников А.П.
Интегралы и ряды / А.П. Прудников, Ю.А. Брычков, О.И. Маричев. М.: Наука, 1981.
Оглавление
Введение
Глава 1. Ряды Фурье
§ 1. Векторные
пространства
§ 2. Скалярное
произведение и норма функций
§ 3. Ортогональные
системы функций. Коэффициенты Фурье. Ряд Фурье
§ 4. Сходимость в
среднем. Равенства Парсеваля
§ 5. Тригонометрический
ряд Фурье на промежутке [–L, L]
§ 6. Сходимость
тригонометрического ряда Фурье. Теорема Дирихле
§ 7. Разложение в
тригонометрические ряды четных и нечетных функций
§ 8. Ряд Фурье для
функции, заданной на промежутке [0, L]
§ 9. Ряды Фурье для
комплексных функций
§ 10. Комплексная форма
тригонометрического ряда Фурье
Глава 2. Интеграл Фурье
§ 11. Сходимость
интеграла Фурье
§ 12. Преобразование
Фурье
§ 13. Основные сведения
из теории преобразования Фурье
Глава 3. Операционное
исчисление
§ 14. Преобразование
Лапласа
§ 15. Изображения
простейших функций
§ 16. Основные теоремы
операционного исчисления
§ 17. Формула разложения
Хевисайда
§ 18. Операторный метод
решения дифференциальных уравнений
§ 19. Приложения
Примеры для
самостоятельного решения
Ответы
Рекомендательный
библиографический список
Цель
работы. Изучить возможности синтеза
сигналов с помощью ряда Фурье по
ортогональной системе тригонометрических
функций. Синтезировать периодические
сигналы различной формы и исследовать
влияние числа ортогональных составляющих
на погрешность аппроксимации.
4.1. Разложение сигналов в обобщенный ряд фурье
4.1.1. Спектры простейших периодических функций
Если
функция
четная (симметричная относительно оси
ординат), т.е.
,
то в этом случае
;
(4.1)
.
(4.2)
Разложение
функции будет следующим
. (4.3)
Аналогично
для нечетной функции можно найти, что
. (4.4)
На
рис. 4.1 показана последовательность
прямоугольных импульсов которую можно
рассматривать как четную функцию.
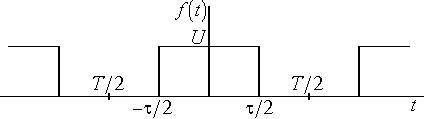
Рис.
4.1. Последовательность прямоугольных
импульсов
По
формуле (4.1) находим амплитуду
-й
гармоники:
. (4.5)
Постоянная
составляющая будет равна
;
. (4.6)
где
–
скважность импульсов. Разложение функции
запишется в виде:
. (4.7)
Графически
амплитудный и фазовый спектры прямоугольных
импульсов показаны на рис. 4.2.
Расстояния
между отдельными спектральными
составляющими обратно пропорциональны
периоду следования импульсов —
,
а положение нулей кратно
.
а) б)
Рис.
4.2. Амплитудный и фазовый спектры
прямоугольных импульсов
Можно
показать, что для импульсов, представленных
на рис. 4.3, разложения в ряд Фуре будут
иметь следующий вид:
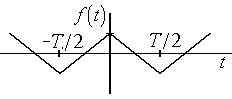
а) б)
Рис.
4.3. Пилообразное колебание и треугольные
импульсы
для
периодического пилообразного колебания
(рис 4.3,а);
; (4.8)
для
периодической последовательности
треугольных импульсов (рис.4.3,б):
. (4.9)
4.1.2. Мощность и действующее значение периодического сигнала
Пусть
несинусоидальный периодический ток
течет через активное сопротивление
.
Средняя за период мощность будет равна
. (4.10)
здесь
мгновенная мощность. Представим функцию
в виде ряда Фурье (4.6), тогда
.
Возводя
в квадрат и интегрируя каждое из слагаемых
можно убедиться, что только интегралы
вида:
, 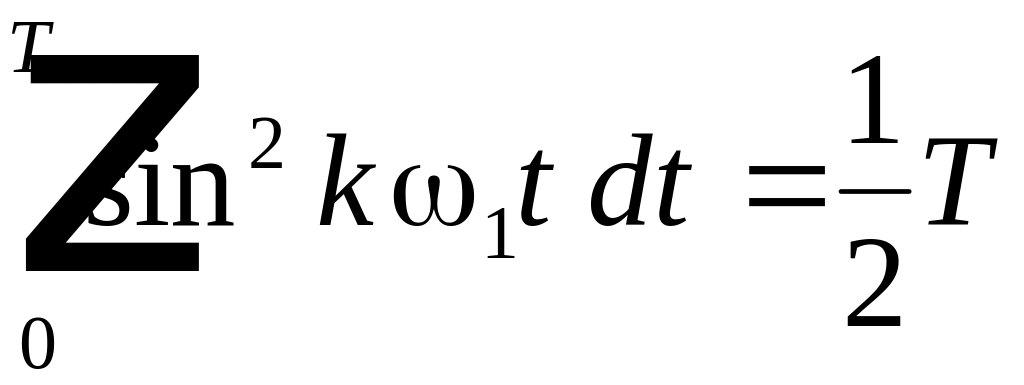
имеют
значения, не равные 0. Все остальные
интегралы равны нулю Поэтому после
интегрирования получим
,
где
. (4.11)
;
;
. (4.12)
Величины
,
,
,
,
… называют действующими значениями
тока. Аналогично вычисляются и
действующие значения напряжения. Если
сопротивление
Ом, то мощность равна
. (4.13)
Последнее
выражение справедливо для любой
периодической функции, т.е.
. (4.14)
В
таком виде последнее соотношение носит
название равенства Парсеваля.
4.1.3. Среднеквадратическая погрешность аппроксимации
Представим
приближенно функцию
разложением в усеченный ряд по
ортонормированным базисным функциям
(см. п. 2.1)
(4.15)
и
определим коэффициенты
так, чтобы минимизировать среднеквадратическую
погрешность:
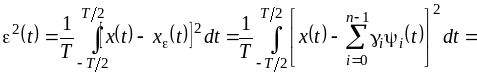
.
С
учетом (2.4) можно записать
. (4.16)
Погрешность
принимает минимальное значение, если
,
т.е. если коэффициенты разложения в
усеченном представлении (4.15) являются
коэффициентами обобщенного ряда Фурье.
Исходя из (4.16) можно записать
или
. (4.17)
Неравенство
(4.17) называют неравенством Бесселя.
С ростом
величина среднеквадратической погрешности
уменьшается. Если при
среднеквадратическая погрешность
стремится к нулю, то систему базисных
функций
называют полной. Эта система функций
является также замкнутой, т.к. для
любой функции
неравенство (4.17) переходит при
в равенство.
Точность
аппроксимации периодических сигналов
зависит от числа членов ряда при конечном
числе членов ряда. Относительную
среднеквадратическую погрешность
аппроксимации периодической функции
конечным числом членов ряда Фурье можно
определить по формуле :
. (4.18)
где
— средняя мощность сигнала;
— средняя мощность
-й
ортогональной составляющей сигнала.
Экспериментальное
значение погрешности аппроксимации
может быть найдено следующим образом.
Пусть имеется
экспериментально полученных точек
сигнала. Известен также теоретический
вид зависимости. Тогда погрешность
аппроксимации может быть вычислена
следующим образом
, (4.19)
где
— теоретическое значение отсчета сигнала
в момент времени
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Остаточный член ряда Фурье. Погрешности приближения функций. Численное дифференцирование
Страницы работы
Содержание работы
12.Остаточный член ряда Фурье.
Для функции f(x) Î L2[a,b]
обобщенный ряд Фурье сходится к ней в среднеквадратичном смысле и методическая
погрешность аппроксимации может быть определена выражением (1.48)
Представим
 |
Имея ввиду, что функции gr(x), rÎ[0,l] ортогональны, а коэфиценты Фурье вычисляются по
соотношению (1.51) получим
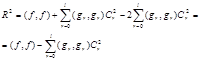 |
oткуда
(1.54)
а если gr(x), rÎ[0,l] ортонормированные, то
(1.55)
Если на приближаемую функцию
наложить дополнительные ограничения, то обобщенный ряд Фурье может сходиться к ней
и в равномерном смысле. Например, необходимым и достаточным условием
равномерной сходимости обобщенного ряда Фурье по полиномам Лежандра или
Чебышева к f(x) на [a,b]. Независимо от типа сходимости, иногда оказывается
необходимо оценить погрешность аппроксимации на [a,b] в
виде максимального отклонения ряда Фурье от приближаемой f(x), что
можно осущесвить дав оценку остаточного члена ряда Фурье
(1.56)
Однако в общнм случае
аппроксимации таких оценок не существует. В частности, же, например, для (l+1) раз
дифферинцируемых функций f(x), xÎ[a,b]
(1.57)
где a(x) –
значение частичной суммы ряда Фурье на [a,b].Если
более конкретизировать
задачу аппроксимации, положив
в качестве базисных функций ряда Фурье полиномы Чебышева, то
(1.58)
Оценка остаточного члена ряда
Фурье для непрерывной, преиодической, периода 2p функции f(x)
(1.59)
где K – некоторая
константа, определение которой, вообще говоря, проблематично, l
— максимальное значение скорости изменения f(x) на
интервале аппроксимации. Оценки (1.57) ¸(1.59) являются
неконструктивными, поскольку содержат в себе параметры, определение которых
практически невозможны или вызывают существенные трудности. Представляется
целесообразным в случае неоходимости оценку остаточного члена (1.56) давать по
некоторой модели аппроксимируемой функции, которая принадлежит к тому же
классу, что и f(x), но в то же время является наиболее неблагоприятной в
отношении точности аппроксимации. Учитывая наиболее вероятную с практической
точки зрения априорную информацию об аппроксимируемой функции, за такую модель
может быть принята функция вида
(1.60)
где fmin и
fmax – минимальное и максимальное значение f(x) на [a,b], WМ –
максимальное значение круговой частоты спектра аппроксимируемой функции, если
таковая информация может быть получена, или
WМ = VМ / AМ
где VМ – максимальная скорость изменения f(x) на [a,b]. При
аппроксимации модели (1.60) обобщенными рядами Фурье по полиномам Лежандра и
Чебышева первого рода были получены экспериментальные номограммы
которые позволили дать оценки остаточных членов в
следующем аналитическом виде
(1.61)
где K≈0,212(5,3125 + l) для полиномов
Лежандра и Kl =4
для полиномов Чебышевва. Следует отметить, что модельная оценка (1.61)
совпадает с оценкой (1.58), если модели положить AМ = 1,
a
имея в виду, что
13.Погрншности приближения функций.
Результирующая погрешноси
приближения функции f(x), xÎ[a,b] в виде некоторой F(x), xÎ[a,b]
вобщем случае складывается составляющих .
1. Методическая погрешность
используемого способа приближения, возникающая из-за отбрасывания остаточного
члена при опрнделении F(x). Данная погрешность уменьшается с увеличением числа
слагаемых в F(x), и в ряде случаев её удаётся оценить.
2. Погрешность приближенных
вычислений ЭВМ, которые, в свою очередь, можно подразделить на две группы:
Методическая погрешность,
возникающая в результате использования численных методовпри реализации
алгоритмов вычислений требуемых параметров. Данная погрешность имеет место,
например, при исппользовании квадратурных формул численного интегрирования для
определения коэфициентов Фурье. Эта погрешность может быть уменьшена за счет
использования более точного вычислительного алгоритма и оценена в виде
методической погрешности данного алгоритма.
Вычислительная погрешность,
порождаемая конечностью разрядной сетки памяти ЭВМ и зависящая (при выбранном
алгоритме) от возможностей используемой вычислительной техники.
3. Погрешность от неточного
задания исходных данных, которая носит случайный характер и может быть оценена
вероятностными характеристиками. На пример, при аппроксимации некоторой
функции f*(x)=f(x)+ sf(x), где
sf(x) –
погрешности, искажающие истинную f(x) и
характеризуемые математическим ожиданием М{sf(x)}=0
и дисперсией D{sf(x)}=s2, увеличение числа учитываемых членов ряда Фурье
приводит к тому, что математическое ожидание случайной погрешности определения
коэффициентов Фурье остаётся нулевым, а вот дисперсия возрастает.
Анализируя поведение
приведённых погрешностей в зависимости от числа слагаемых в приближающей F(x),
можно сделать вывод, что увеличение количества учитываемых членов в F(x)
приводит к тому, чтометодическая погрешность приближения уменьшается, в то
время как все остальные, связанные, как правило, свычислением коэфициентов
приближающей функции, возрастает. Таким образом, существует некое оптимальное
значение числа учитываемых членов функции F(x),
превышение которого приведёт к увеличению результирующей погрешности, поскольку
скорость нарастания вычислительной погрешности становится больше, чем скорость
уменьшения методической.
Похожие материалы
- Аппроксимация кубическим сплайном (моделирование сплайн-интерполяции)
- Вычисление корней многочлена p(x) = x6 + 5×5 – 7×4 + 3×3 – 6×2 + x +12 различными методами. Решение обыкновенных дифференциальных уравнений
- Использование методов вычислительной математики для решения задач с использованием доступных средств компьютерной поддержки
Информация о работе
Тип:
Ответы на экзаменационные билеты
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание — внизу страницы.
Цель
работы. Изучить возможности синтеза
сигналов с помощью ряда Фурье по
ортогональной системе тригонометрических
функций. Синтезировать периодические
сигналы различной формы и исследовать
влияние числа ортогональных составляющих
на погрешность аппроксимации.
4.1. Разложение сигналов в обобщенный ряд фурье
4.1.1. Спектры простейших периодических функций
Если
функция
четная (симметричная относительно оси
ординат), т.е.
,
то в этом случае
;
(4.1)
.
(4.2)
Разложение
функции будет следующим
. (4.3)
Аналогично
для нечетной функции можно найти, что
. (4.4)
На
рис. 4.1 показана последовательность
прямоугольных импульсов которую можно
рассматривать как четную функцию.
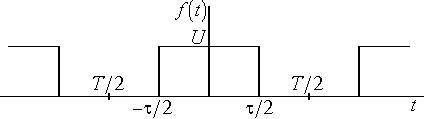
Рис.
4.1. Последовательность прямоугольных
импульсов
По
формуле (4.1) находим амплитуду
-й
гармоники:
. (4.5)
Постоянная
составляющая будет равна
;
. (4.6)
где
–
скважность импульсов. Разложение функции
запишется в виде:
. (4.7)
Графически
амплитудный и фазовый спектры прямоугольных
импульсов показаны на рис. 4.2.
Расстояния
между отдельными спектральными
составляющими обратно пропорциональны
периоду следования импульсов —
,
а положение нулей кратно
.

а) б)
Рис.
4.2. Амплитудный и фазовый спектры
прямоугольных импульсов
Можно
показать, что для импульсов, представленных
на рис. 4.3, разложения в ряд Фуре будут
иметь следующий вид:
а) б)
Рис.
4.3. Пилообразное колебание и треугольные
импульсы
для
периодического пилообразного колебания
(рис 4.3,а);
; (4.8)
для
периодической последовательности
треугольных импульсов (рис.4.3,б):
. (4.9)
4.1.2. Мощность и действующее значение периодического сигнала
Пусть
несинусоидальный периодический ток
течет через активное сопротивление
.
Средняя за период мощность будет равна
. (4.10)
здесь
мгновенная мощность. Представим функцию
в виде ряда Фурье (4.6), тогда
.
Возводя
в квадрат и интегрируя каждое из слагаемых
можно убедиться, что только интегралы
вида:
, 
имеют
значения, не равные 0. Все остальные
интегралы равны нулю Поэтому после
интегрирования получим
,
где
. (4.11)
;
;
. (4.12)
Величины
,
,
,
,
… называют действующими значениями
тока. Аналогично вычисляются и
действующие значения напряжения. Если
сопротивление
Ом, то мощность равна
. (4.13)
Последнее
выражение справедливо для любой
периодической функции, т.е.
. (4.14)
В
таком виде последнее соотношение носит
название равенства Парсеваля.
4.1.3. Среднеквадратическая погрешность аппроксимации
Представим
приближенно функцию
разложением в усеченный ряд по
ортонормированным базисным функциям
(см. п. 2.1)
(4.15)
и
определим коэффициенты
так, чтобы минимизировать среднеквадратическую
погрешность:
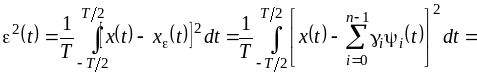
.
С
учетом (2.4) можно записать
. (4.16)
Погрешность
принимает минимальное значение, если
,
т.е. если коэффициенты разложения в
усеченном представлении (4.15) являются
коэффициентами обобщенного ряда Фурье.
Исходя из (4.16) можно записать
или
. (4.17)
Неравенство
(4.17) называют неравенством Бесселя.
С ростом
величина среднеквадратической погрешности
уменьшается. Если при
среднеквадратическая погрешность
стремится к нулю, то систему базисных
функций
называют полной. Эта система функций
является также замкнутой, т.к. для
любой функции
неравенство (4.17) переходит при
в равенство.
Точность
аппроксимации периодических сигналов
зависит от числа членов ряда при конечном
числе членов ряда. Относительную
среднеквадратическую погрешность
аппроксимации периодической функции
конечным числом членов ряда Фурье можно
определить по формуле :
. (4.18)
где
— средняя мощность сигнала;
— средняя мощность
-й
ортогональной составляющей сигнала.
Экспериментальное
значение погрешности аппроксимации
может быть найдено следующим образом.
Пусть имеется
экспериментально полученных точек
сигнала. Известен также теоретический
вид зависимости. Тогда погрешность
аппроксимации может быть вычислена
следующим образом
, (4.19)
где
— теоретическое значение отсчета сигнала
в момент времени
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Исследование влияния числа учитываемых членов ряда Фурье на точность аппроксимации
Страницы работы
Содержание работы
НГТУ
Расчетно-графическое задание
по вычислительной математике
Аппроксимация функций
Выполнил: Преподаватель:
студент Чикильдин
Г.П
группы
АП019
Малыгин Иван
Вариант №9
Новосибирск, 2002 г.
I. Цель:
Исследовать влияние числа учитываемых членов ряда Фурье на точность
аппроксимации. Определить погрешность аппроксимации.
Постановка задачи: На интервале [a,b] произвести
аппроксимацию функций f(t), заданной шагом ,
обобщённым рядом Фурье по системе ортогональных (ортонормированных) на [a,b] c весом
базисных функций
Данные:
Функция:
Интервал:
Шаг: 0,05
II. Теоретические
сведения
Система
линейно независимых функций называется
ортогональной на с весом
,
если 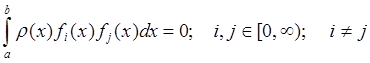
— нормирующая функция. Она неотрицательна
на и интегрируема на
с
положительным результатом.
Если для
ортогональной системы выполняется условие
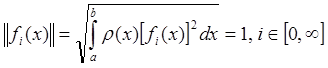
ортонормированной.
Пусть на задана система линейно независимых функций
и некоторая последовательность констант
Ряд вида
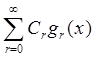
функциональным рядом. Если этот ряд сходится, то его сумму обозначают как .
Если
система функций будет ортогональна или
ортонормированна, то получаемый функциональный ряд будет называться рядом
Фурье.
Коэффициенты
, коэффициенты Фурье, в таком случает будут
определяться так:
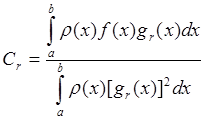

Произвольную
кусочно-непрерывную функцию на [a;b]
приближённо можно представить в виде обобщённого ряда Фурье с конечным числом
членов
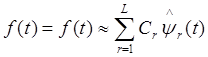
где ,
– система
ортогональных на [a;b] базисных функций, а
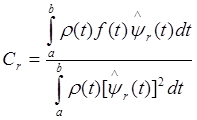
Таким
образом, чтобы решить задачу аппроксимации функции f(t) на
[a;b], необходимо при заданном базисе ,
,
, вычислить коэффициенты Фурье
согласно (*) и восстановить оценку
, аппроксимируемой функции f(t) по
(**).
Полиномы
Лежандра, ортогональные на с весом
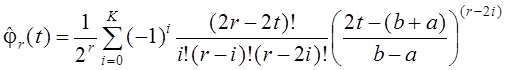
К – целая часть
Нормирующий множитель полиномов Лежандра
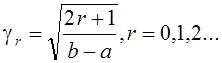
III. Листинг
program main
real f(113),t(113),ro(113),fi(7,113),f1(113),c(7),ff(113)
real a,b,dt,e(113),em,es,ep,emo,eso,epo,ff1(113)
real ff3(113),ff5(113),e1(113),e3(113),e5(113)
integer i,kon,l
open
(1,file=’data’)
write
(1,*)’Студент:Малыгин Иван’
write
(1,*)’Группа: АП-019′
write
(1,*)’Вариант №9′
write
(1,*)’Исходные данные:a=0,6;b=2,05;dt=0,025;’
write
(1,*)’аппророксимируемая функция:5+2,5*SIN(0,5*t);’
write
(1,*)’базисные функции Лежандра.’
a=0.8
b=6.4
dt=0.05
kon=(b-a)/dt+1
do 1 i=1,kon
c Вычисление реализации
аппроксимируемой
c функции f(t) на
заданном [a,b] при фиксированном dt
t(i)=0.8+0.05*(i-1)
f(i)=5+2.5*sin(0.5*t(i))
1 continue
open
(4,FILE=’graph3′)
do 2 l=1,7
c Вычисление базисных
функций полинома Лежанжра
call
n1yplg(a,b,kon,dt,l,ro,fi)
c Вычисление
коэффициентов Фурье
call
n1ykf(kon,dt,l,f,f1,fi,ro,c)
c Реализация оценки
аппроксимируемой функции f~(t)
call
n1ywst(kon,l,c,fi,ff)
c Вычисление
погрешности аппроксимации
call
n1yeee(f,ff,kon,e,em,es,ep,emo,eso,epo)
if(l.gt.2) write
(4,*)l,emo,eso
write (1,10)l
write (1,11)
write (1,16)
write (1,12)
do 4 i=1,l
write (1,13)i,c(i)
4 continue
write (1,14) l-2,l
do 3 i=1,kon
if
((l.eq.4).or.(l.eq.6)) go to 7
if (l.eq.3)
ff1(i)=ff(i)
if (l.eq.3) e1(i)=e(i)
if (l.eq.5)
ff3(i)=ff(i)
if (l.eq.5) e3(i)=e(i)
if (l.eq.7) ff5(i)=ff(i)
if (l.eq.7) e5(i)=ff(i)
7 write (1,15)
t(i),f(i),ff(i),e(i)
3 continue
2 continue
close(4)
write
(1,11)
write (1,17)
write (1,19)
c Вывод
в файл graph1 значений функции и аппроксимирующих
с полиномов
open(2,FILE=’graph1′)
do 8 i=1,kon
write (2,23)t(i),f(i),ff1(i),ff3(i),ff5(i)
8
continue
open(5,FILE=’graph4′)
c Вывод
зависимости погрешности аппроксимирующих полиномов от
с аргумента
do 9 i=1,kon
write (5,*)t(i),e1(i),e3(i),e5(i)
9 continue
open
(3,FILE=’graph2′)
c Вывод в файл graph2 реализации базисных фунций и
весовой
c функции
do 5 i=1,kon
write
(1,18)t(i),(fi(j,i),j=1,5)
write
(3,23)t(i),(fi(j,i),j=1,5),ro(i)
5 continue
close (3)
write (1,11)
write (1,20)
write (1,21)
do 6 i=1,kon
write
(1,22)t(i),ro(i)
6 continue
close (1)
close(2)
10 format (‘Количество
учитываемых членов ряда Фурье:’,I1)
11 format (1x/’__________________________________________’)
12 format
(‘Коэффициенты Фурье:’)
13 format
(‘c(‘,I1,’)=’,f6.4)
14 format (1x/’Табл.’,1x,I1/8x,’Результаты
расчетов при l=’,I1/3x, * ‘T’,9x,’F’,10x,’~F’,10x,’E’)
15 format
(F8.5,3x,F8.5,3x,F8.5,3x,F8.5,3x,F9.5)
16 format (1x)
17 format (1x/’Табл. 6’/11x,*’Реализации первых
пяти базисных функций’)
18 format
(F6.4,1x,F8.5,1x,F8.5,1x,F8.5,1x,F8.5,1x,F8.5)
19 format
(3x,’T’,6x,’^T1′,6x,’^T2′,6x,’^T3′,6x,’^Т4′,6x,’^T5′)
20 format (1x/’Табл.
7’/’Реализация весовой функции’)
21 format
(6x,’T’,8x,’Po’)
22 format
(1x,F8.5,1x,F8.5)
23 format
(F6.2,1x,6(F11.8,1x))
end
IV. Результаты.
Приведены
графики функций ,
,
,
, а
также графики базисных функций и графики
относительной и абсолютной погрешностей (EMO и ESO). Т.к.
весовая функция , она на графики не выводится. Поскольку у полиномов
при l>3достаточно
высокая степень приближения, также приведены графики зависимости погрешности от
t.
V. Заключение
1.
Погрешности аппроксимации падают с
увеличением числа L учитываемых членов ряда Фурье, но если при малых L это
падение очень заметно, то при увеличении L оно начинает
уменьшаться, что связано с возрастанием числа вычислительных операций и,
следственно, накоплением вычислительной погрешности.
2.
Ряды Фурье приближают функцию
лучше в среднеквадратическом смысле, а не в равномерном, что видно из последнего
графика: есо на порядок меньше, чем емо.
VI. Список литературы
Оглавление
Цель. Постановка задачи. 2
Теоретическая часть 2-3
Листинг 3-5
Результаты. Графики. 5-7
Заключение. 8
Список литературы. 8
Похожие материалы
- Ортогональные и нормированные системы
- Решение алгебраических уравнении и систем. Уточнение корней. Решение систем линейных алгебраических уравнений
- Изучение методики приближенного представления функций в виде интерполяционного полинома
Информация о работе
Тип:
Расчетно-графические работы