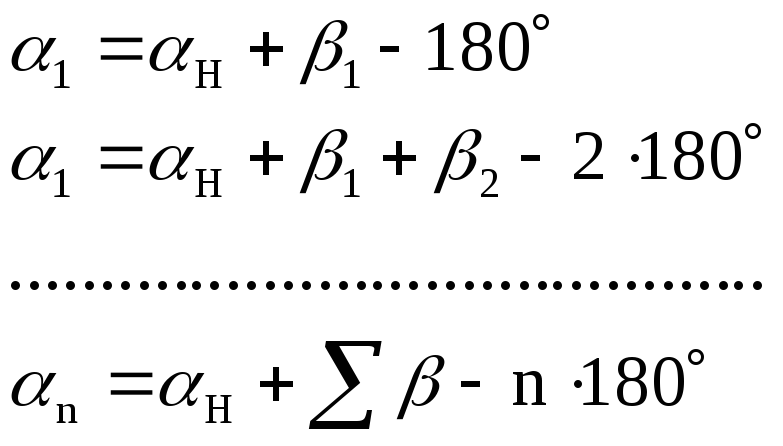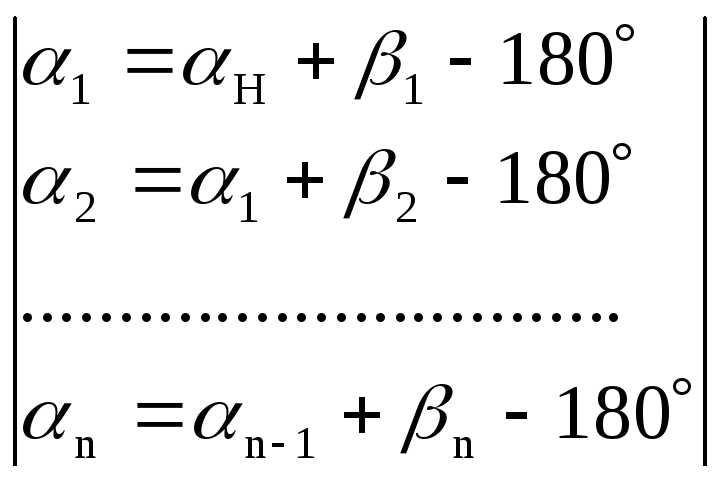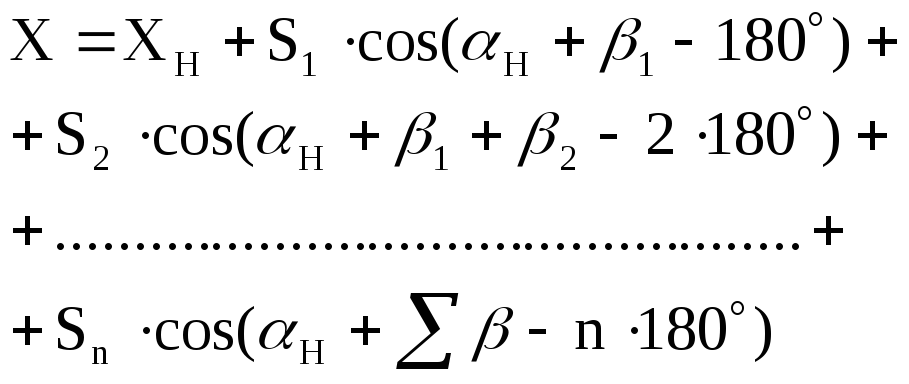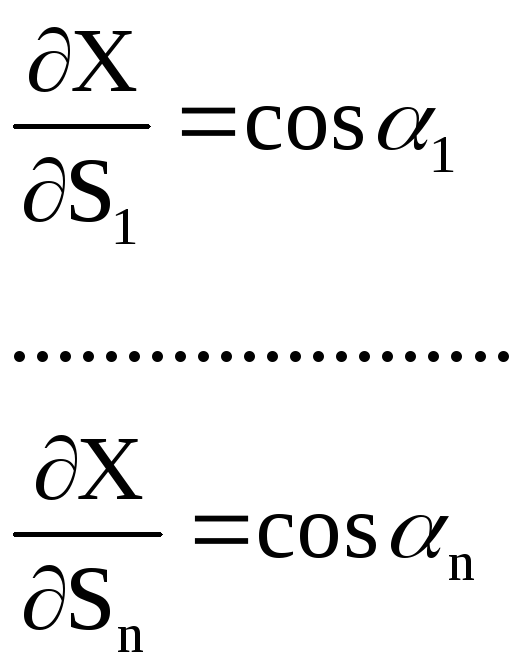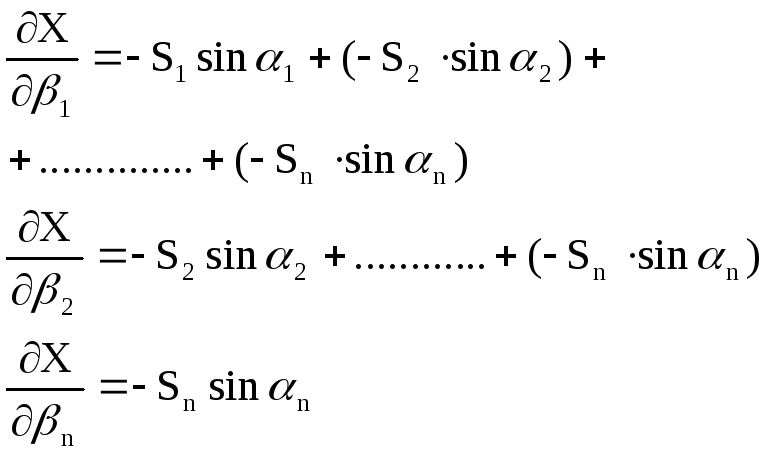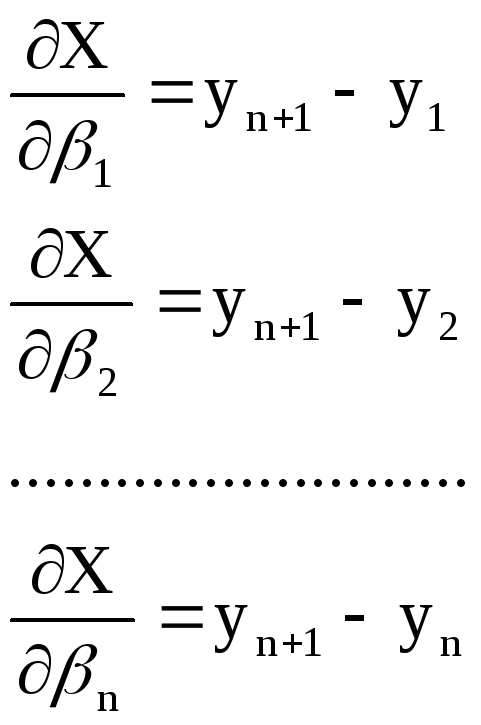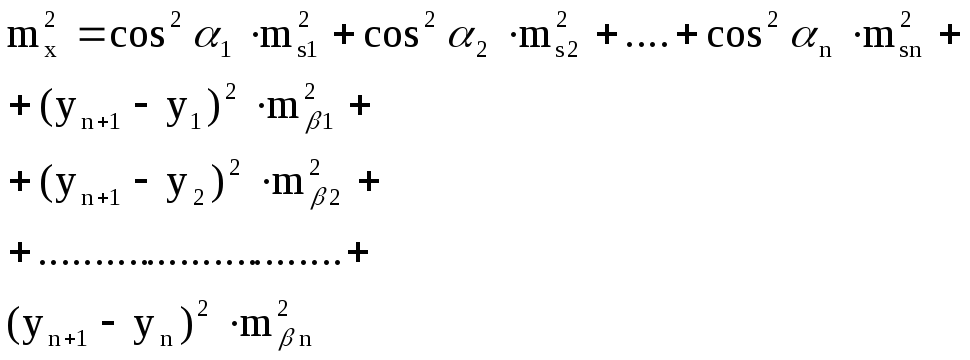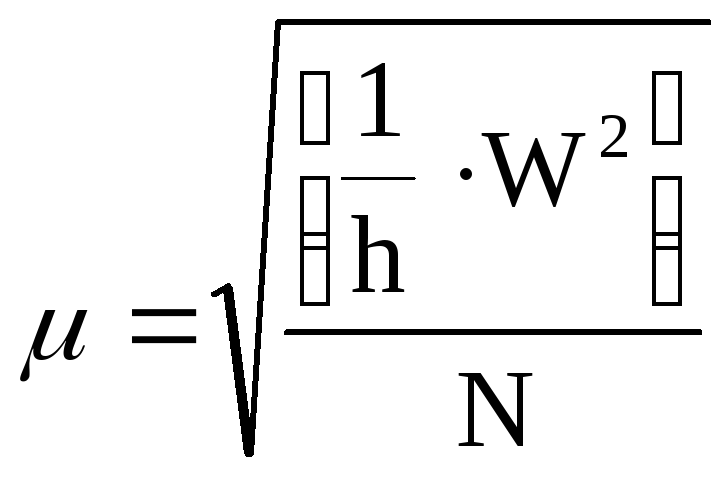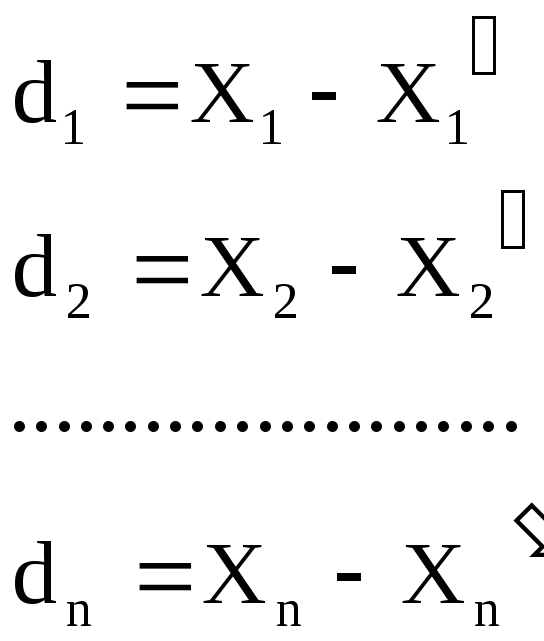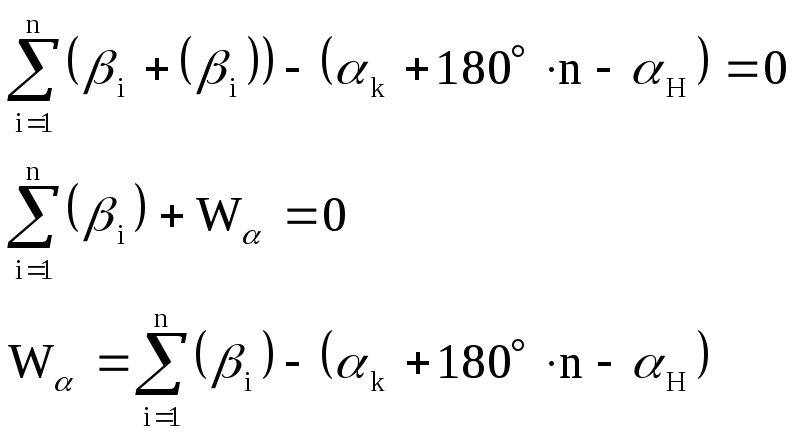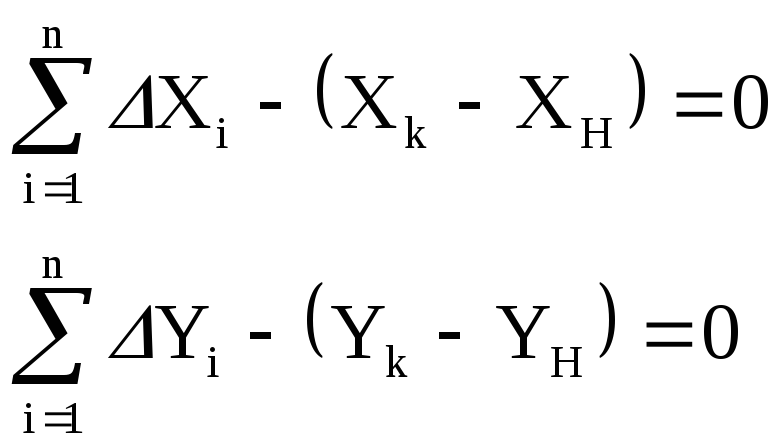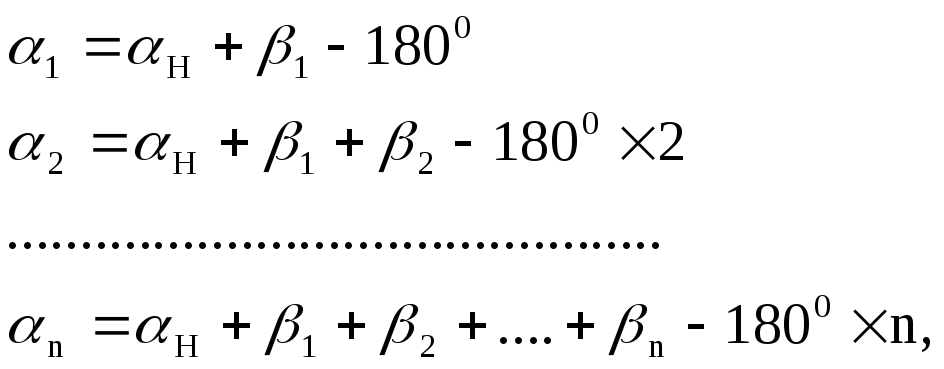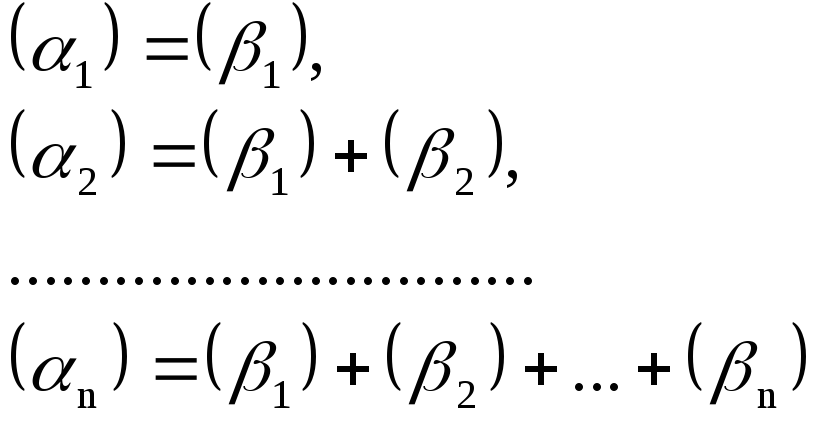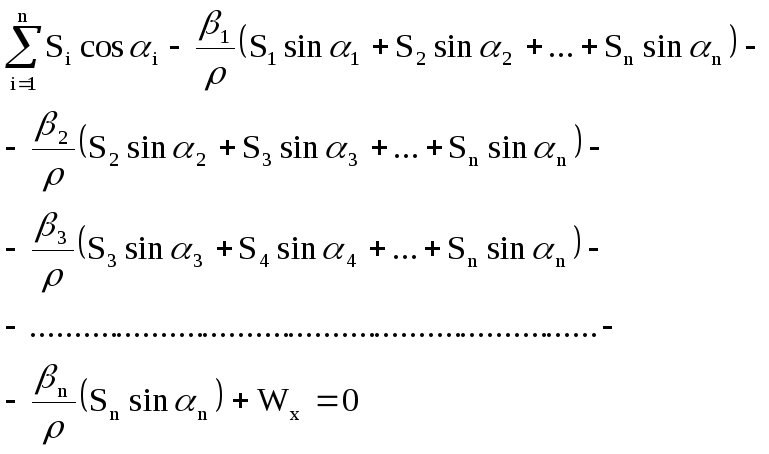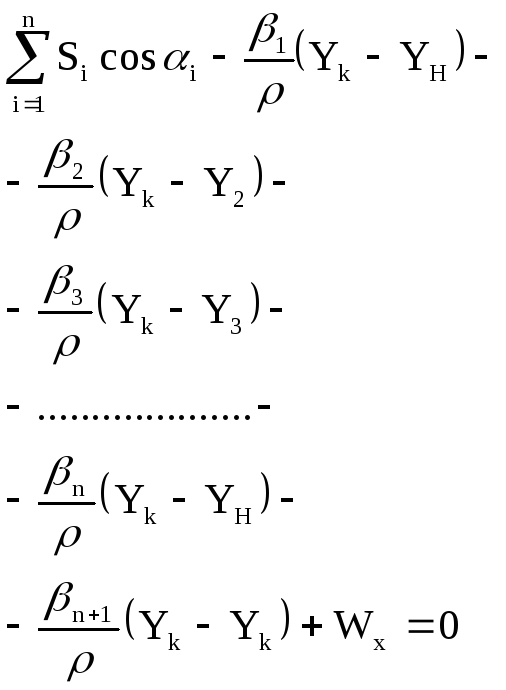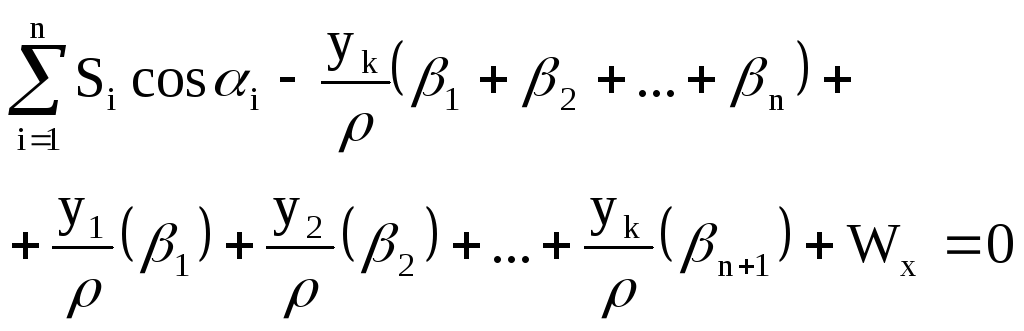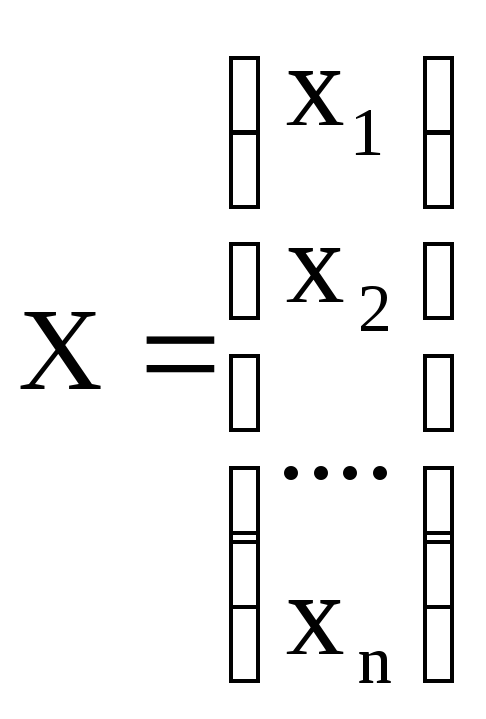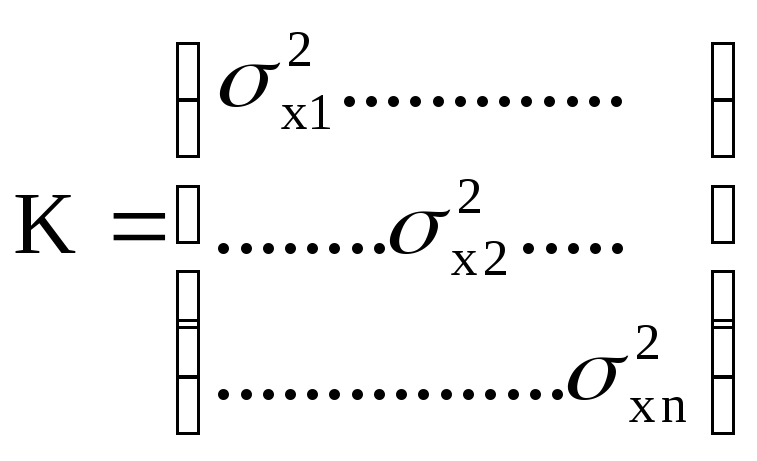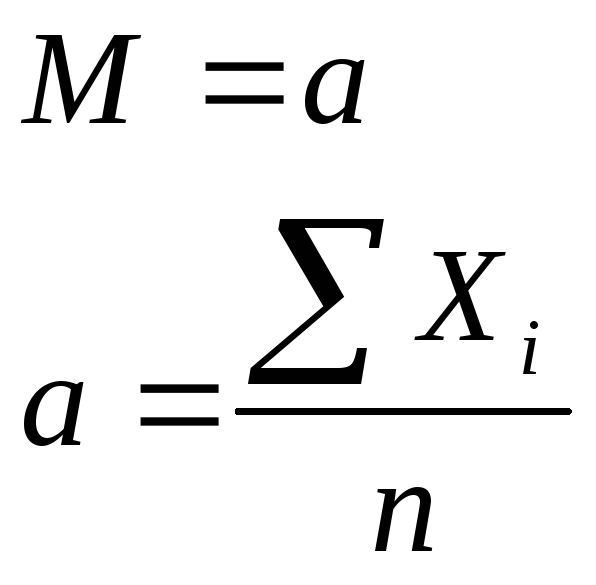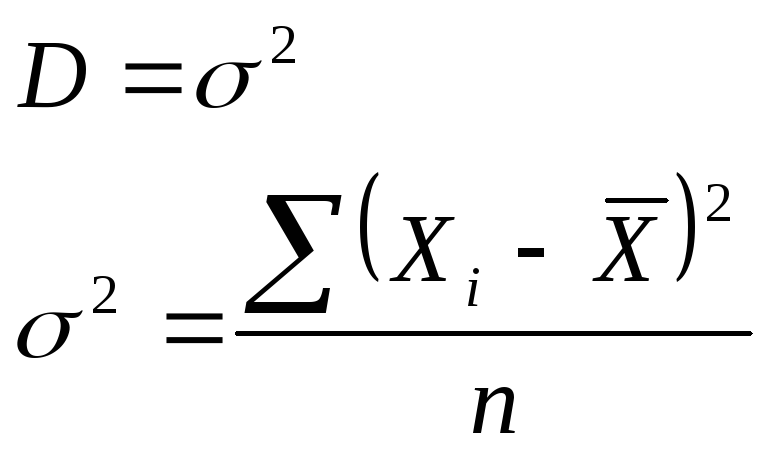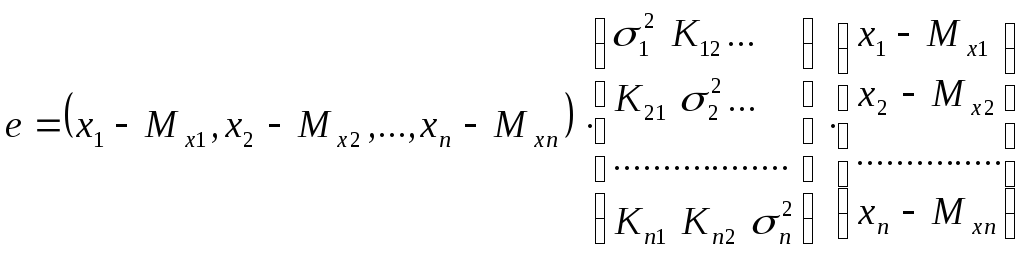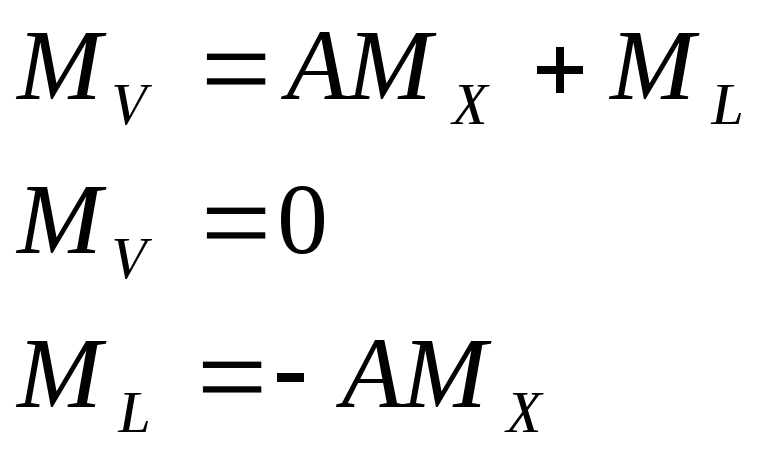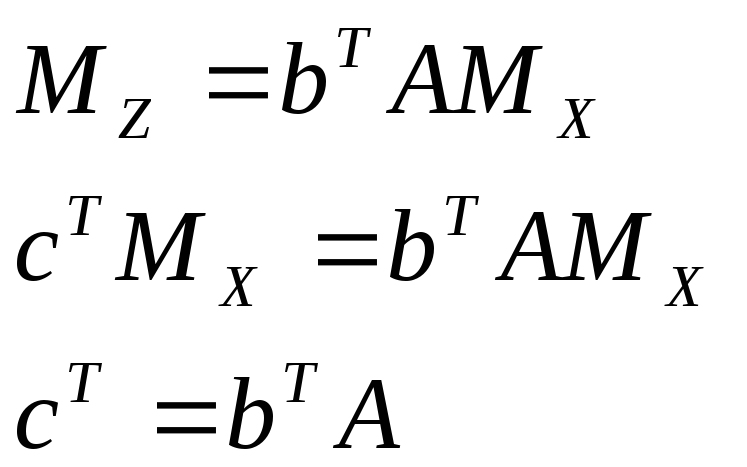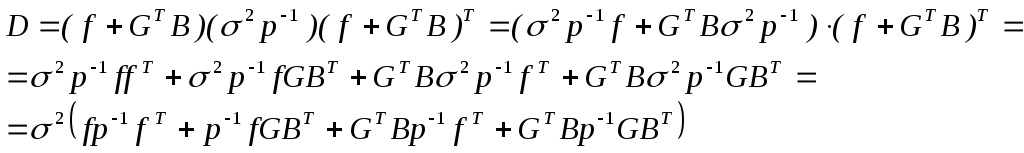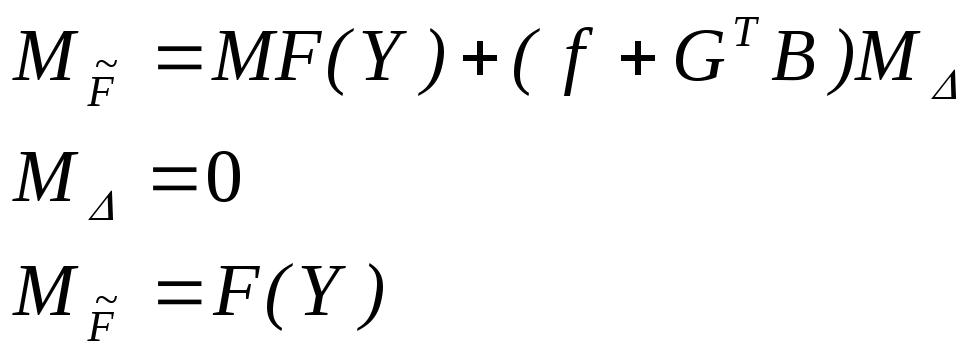Средняя квадратическая ошибка положения конечной точки хода - Решение и исправление самых разных ошибок на TopOshibok.ru

Беспалый Н.П., Ахонина Л.И.

Геодезия часть 2 Учебное пособие для студентов геодезических специальностей вузов Донецк 1999

7.4 Средняя квадратическая ошибка положения конечной точки полигонометрии

Ход вытянутый (углы не исправлены за невязку).

Ранее были получены формулы для вычисления компонентов , (7.20) и (7.28)

;

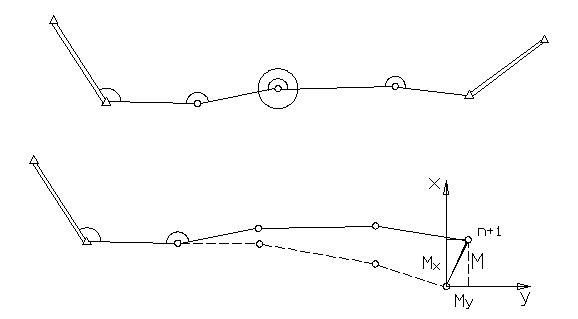
По этим величинам можно найти среднюю квадратическую ошибку самого вектора М (рис.7.4) по формуле:

(7.29)

а подставив значение из (7.20) и (7.28) получим:

(7.30)

Эта величина называется средней квадратической ошибкой положения конечной точки хода полигонометрии.

Как видно из (7.30), ошибка последнего угла _n₊₁ не оказывает влияния на величину поперечной невязки, т.е. ход считается как бы висячим. Это и понятно, т. к. углы за угловую невязку не исправлялись.

На практике углы, как правило, исправляются за угловую невязку путем ее распределения поровну на все углы. В этом случае поперечная невязка будет другая, поэтому будет другая формула для вычисления средней квадратической ошибки положения конечной точки хода полигонометрии. Эта формула приводится в конце этого параграфа.

. Ход изогнутый (углы не исправлены за угловую невязку).

В ходе полигонометрии произвольной формы возникают невязки _x, _y, _S, вычисляемые по формулам (7.17), (7.18).

Если в одном и том же ходе измерить все углы и линии «k» раз, то можно найти «k» значений невязок _x, _y, _S, т.е.

Сложив почленно все равенства и разделив левую и правую части на «k», получим:

Каждый член этого равенства является соответствующим средним квадратическим значением. Поэтому равенство можно переписать

(7.31)

Для установления зависимости между М и ошибками измерения длин линий m_S и углов m_ возьмем без вывода координатные условные уравнения для одиночного хода полигонометрии. (Вывод этих формул будет рассмотрен при изучении уравнивания полигонометрии).

(7.32)

_i — дирекционный угол линии,

V_S, V_-поправка в измеренные длины и углы,

, — разности координат конечной и каждой из точек хода,

_x, _y — невязки в приращениях координат, которые являются истинными ошибками в координатах конечного пункта полигонометрии.

Перенеся невязки _x, _y в правую часть будем иметь

(7.33)

Так как поправка и ошибка различаются между собой только знаком, то можно записать:

, , (7.34)

где dS_i и d_i – ошибки измерения длин линий и углов.

С учетом этого предыдущее выражение (7.33) можно переписать:

(7.35)

Отсюда по правилам теории ошибок вычисляем средние квадратические ошибки:

(7.36)

Подставляем эти значения в формулу (7.31), получим среднюю квадратическую ошибку положения конечной точки хода полигонометрии:

но так как , то

(7.37)

Обозначим

(7.38)

Как видно из рисунка 7.6 D_n₊₁_,i есть расстояние между последней и i‑той точкой хода.

Рисунок 7.6 – Схема для определения средней квадратической ошибки положения конечной точки висячего полигонометрического хода

С учетом (7.38) формулу (7.37) перепишем

(7.39)

По этой формуле вычисляется средняя квадратическая ошибка положения конечной точки висячего изогнутого полигонометрического хода. По этой же формуле можно вычислить среднюю квадратическую ошибку положения любой точки висячего полигонометрического хода При этом под n подразумевается число линий от начальной точки до определяемой.

Как видно из формулы (7.39) величина М зависит не только от ошибок измерения длин и углов, но и от степени изогнутости хода и количества углов поворота в нем. Величина тем меньше, чем больше вытянут ход и чем меньше в нем углов поворота.

Полученная формула не учитывает ошибок исходных данных. В этом случае ошибка в положении конечной точки хода будет и невязкой этого хода. В действительности исходные координаты и дирекционные углы сами содержат ошибки, поэтому между невязкой и ошибкой положения точки будет некоторая разница. В этом случае для учета ошибок полевых измерений и ошибок исходных данных пользуются формулой:

(7.40)

Источник

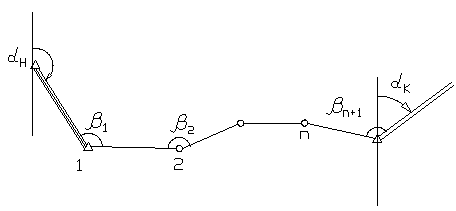
Выразим α через
β:

5.Оценка точности угловых измерений по невязкам полигонах

по
сумме углов:

;

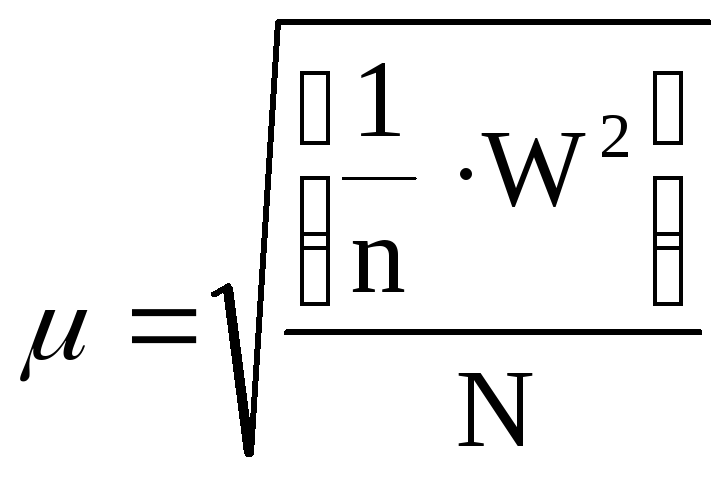
где
N–
число невязок.

сумме
превышений:

где
L–
длина хода, км.

по
разностям двойных измерений:

6. Условные уравнения в полигонометрическом ходе

1)условное уравнение
дирекционных углов:

условные
уравнения координат:

Выразим
эти условные уравнения через поправки.
Для этого первое из них запишем в виде

(1)

Выводы для второго
уравнения аналогичны, поэтому они не
приводятся.

Разлагая
условное уравнение координат в ряд
Тейлора по поправкам, получим:

,
(2)

где

(3) Поправки
в дирекционные углы выразим через
поправки в измеренные углы. Поскольку

то

Подставляем эти
значения в условные уравнения (2):

Многомерный статистический анализ

Среднее
значение и корреляционная матрица
вектора

Если задана функция:

то

Нормальное
распределение

одномерное
распределение. Математическое ожидание(М)
и дисперсия(D)

Одномерное
распределение – это такое распределение,
где исследуется один признак.

Функция нормального
распределения:

где
–
стандарт;

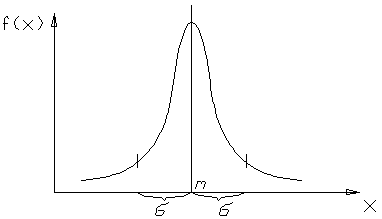
Свойства
функции: 1)всякая кривая достигает точки
максимума в точке X=m;

2)функция
непрерывна и приближается к оси Х;

3)симметрична
относительно прямой, параллельной f(х),
максимальная ордината –
;

2.Многомерное
нормальное распределение

Многомерное
нормальное распределение – распределение,
характеризующееся вектором случайных
величин, заданным математическим
ожиданием этого вектора и корреляционной
матрицей.

; ;

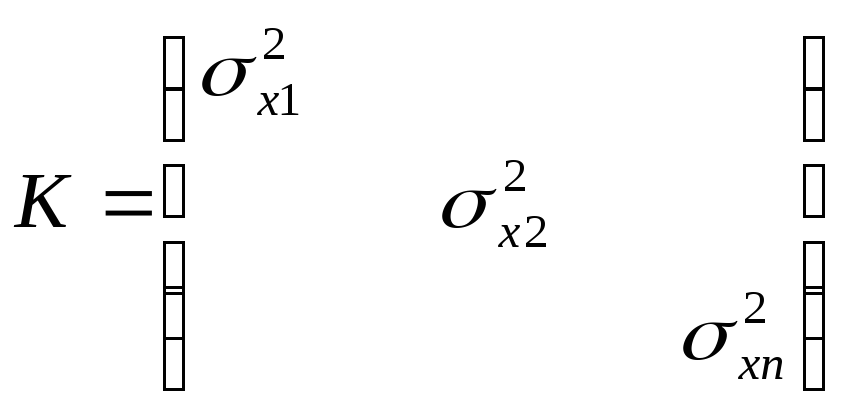
V–
отклонение вектора, от его математического
ожидания (Х_n-М_х_n)

Метод наименьших
квадратов

1.Параметрический
способ уравнивания

Одну
и ту же функцию можно выразить как через
вектор параметров (Х), так и через вектор
измерений (L)

Задача
уравнивания сводиться к получению
достаточной, несмещенной и эффективной
оценке функции Z.

А) для получения
несмещенной оценки запишем математическое
ожидание:

Составляем систему
уравнений поправок:

(1)

Это и есть условие
несмещенности.

В)
чтобы оценка была эффективной, дисперсия
функции Z
должна быть минимальной.

Найдем минимум
функционала Лагранжа:

где Λ– вектор
неопределенного множителя Лагранжа.

Найдем производную
по вектору b и приравняем ее к нулю:

(2)

Вектор
множителя Λ – неизвестен.

Подставляем (2) в
(1):

(3)

Далее, (3) подставляем
в (2):

При
таком значении b получается достаточная,
несмещенная и эффективная оценка функции
Z.

Частный
случай:

если

где
Е– единичная матрица,то

Коррелатный способ уравнивания

После уравнивания
геодезической сети, любая функция
уравненных величин, должна определяться
однозначно при любом порядке ее
вычисления.

Получаемые
после уравнивания оценки любых функций
уравненных результатов измерений должны
быть достаточными, несмещенными и
эффективными.

Введем обозначения:

F(y)–
функция результатов измерений;

у – вектор
результатов измерений;

у=Y+Δ,

где
Y–
вектор истинных значений измеренных
величин;

Δ – вектор истинных
ошибок.

Линеаризированный
вид функции:

С
тем, чтобы оценка была достаточной,
необходимо ее выводить с учетом всех
измерений в геодезической сети

где
W
– вектор свободных членов;

G
– матрица, которую следует определить.

2)
Для достижения эффективности оценки
следует найти такую матрицу G,
при которой достигается минимальная
дисперсия

F(Y)–
безошибочна, так как Y–
истинное значение

где
В – матрица коэффициентов условных
уравнений

Вид
оцениваемой функции:

а
ее дисперсия

где

–
корреляционная матрица ошибок.

где
–
поправка.

3)Полученное
значение будет несмещенным, если ошибки
измерений случайны:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Установление формы хода

Форму хода устанавливаю по критериям вытянутости. В вытянутом ходе выполняются соотношения:

(1)

(2)

(3)

где — уклонение направления сторон хода от направления замыкающей , r — расстояние от вершины хода до замыкающей.

Для проверки выполнения соотношений (1) — (3) в запроектированном ходе провожу замыкающую хода, от нее в обе стороны откладываю (в масштабе карты) расстояния r и провожу линии, параллельные замыкающей (рис. 1). Если ни одна из вершин не выходит за пределы полученной полосы, следовательно, условие выполнено (в моем случае ни одна из вершин не выходит за пределы полученной полосы).

_пред км,

Величину измеряю на схеме, сравниваю с предельным значением (2) и получаю:

15?

В моем ходе все соотношения выполняются, значит, я имею вытянутый ход.

Определение предельной погрешности планового положения точки в слабом месте хода до и после его уравнивания

Средняя квадратическая погрешность положения пункта в слабом месте хода m (после уравнивания — это середина хода) примерно в 2 раза меньше средней квадратической погрешности конечной точки хода до его уравнивания М

m = 0,5 M (4)

Предельная погрешность средней вершины хода равна 2m (согласно служебным допускам) или с учетом (4) представляется как:

=2m=M (5)

следовательно, для определения необходимо получить М. Средняя квадратическая погрешность положения конечной точки хода М определяется выражением:

=2M или M</2 (6)

где , — предельная линейная невязка хода — находится из равенства

(7)

где 1/Т — предельная относительная погрешность хода, 1/Т = 10 000. Вычисления произвожу с помощью формулы:

(8)

где , и — соответственно средние квадратические погрешности измерения сторон и углов, n — число сторон в ходе.

м²

Далее находим М:

По формулам (6) и (7) определяется допустимое значение погрешности

M<[S]/T

И получаем:

0,067 < 0,187

Применяя принцип равных влияний, т.е. равенство влияний погрешностей угловых и линейных измерений на конечный результат, исходя из формулы (8), получаю:

(9)

Подставив свои значения получаю:

м²

Из формул (6) и (7) следует, что

М</2=[S]/2T (10)

Подставляем:

0,067<0,093

Величина [] при измерении длин линий в полигонометрическом ходе с примерно равными сторонами хода может быть заменена выражением .

Заменив выражением , получаю, что

m_s = 0,023906 м

Далее нахожу средне квадратическую погрешность положения пункта в слабом месте хода m:

; = 0,5?0,067=0,0336

В ходе вычислений получила m=0,0336.

Расчет точности линейных измерений

Измерение линий производила светодальномером «Блеск» СТ5, который является основным топографическим светодальномером, выпускаемым отечественной промышленностью. Он предназначен для измерения расстояний до 5 км со средней квадратической погрешностью измерения расстояний одним приемом

, (11)

где D- измеренное расстояние.

Перед началом работы необходимо провести внешний осмотр прибора и выполнить его поверки. При внешнем осмотре следует убедиться в отсутствии механических повреждений, сохранности ампул уровней и деталей, крепления органов управления, плавности их действия и четкости фиксации; четкости изображения штрихов сетки и штрихов шкал; работоспособности всех узлов, а также термометров, барометров и других приборов.

Поверки светодальномера СТ5:

1. Напряжение аккумуляторных батарей должно быть достаточным.

2. Контрольный отсчет на табло должен соответствовать его паспортному значению.

3. Индикаторы табло должны функционировать нормально.

4. Схема измерения температуры кварцевого генератора должна функционировать нормально.

5. Визирная ось зрительной трубы должна быть параллельна направлению модулированного излучения.

Кроме перечисленных поверок, светодальномер подвергла метрологической аттестации, в результате которой определила: отклонение частоты кварцевого генератора от номинального значения, величину изменения контрольного отсчета при изменении напряжения питания, циклическую ошибку, среднюю квадратическую погрешность измерения расстояния одним приемом.

Порядок измерения линий светодальномером СТ5:

1. В начальной точке линии установили на штативах приемопередатчик, а на конечной точке — отражатель, приводим их в рабочее положение над центрами пунктов (центрируем и нивелируем) и взаимно ориентируют.

2. Включаем и прогреваем приемопередатчик.

3. Проверяем напряжение источника питания и выполняем другие контролирующие действия в соответствии с техническими требованиями инструкции по эксплуатации прибора.

4. Светодальномер наводим по максимуму сигнала, одновременно устанавливая ручкой СИГНАЛ уровень сигнала в середине рабочей зоны.

5. Берем три отсчета измеряемого расстояния в режиме ТОЧНО и записываем их в журнал. По окончании измерений переключатель ТОЧНО-КОНТРОЛЬ-ГРУБО переводим в положение КОНТРОЛЬ и по табло берем отсчет для определения поправочного коэффициента.

Наклонное расстояние между пунктами вычисляют по формуле:

, (12)

где D_ok — среднее арифметическое значение отсчетов в режиме ТОЧНО;

K_n — поправочный коэффициент, учитывающий изменение показателя атмосферы; K_f — поправочный коэффициент, учитывающий температурное изменение частоты кварцевого генератора; — поправка за циклическую погрешность.

Значение коэффициента определяли по номограмме, приведенной в паспорте дальномера, используя измеренные значения температуры воздуха и атмосферного давления. Значение коэффициентов K_f и определила по соответствующим графикам в паспорте светодальномера.

Горизонтальное проложение S измеряемой линии вычисляем по формуле:

, (13)

где-угол наклона визирной оси прибора.

Если известно превышение h между начальной и конечной точками линии, то:

(14)

где