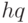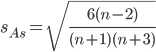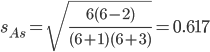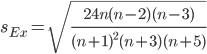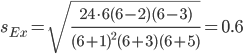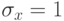Средняя квадратическая ошибка коэффициента эксцесса - Решение и исправление самых разных ошибок на TopOshibok.ru

58. Коэффициенты асимметрии и эксцесса.

Центральные
моменты распределения

Для дальнейшего изучения характера
вариации используются средние значения
разных степеней отклонений отдельных
величин признака от его средней
арифметической величины. Эти показатели
получили название центральных
моментов распределения порядка,
соответствующего степени, в которую
возводятся отклонения,
или просто моментов.

Показатели формы распределения

Асимметрия – Коэффициент
асимметрии

характеризует асимметричность
(«скошенность») распределения признака
в совокупности
Эксцесс – Показатель эксцесса

представляет собой отклонение вершины
эмпирического распределения вверх или
вниз («крутость») от вершины кривой
нормального распределения

Асимметрия распределения

При
=0
распределение считается нормальным.
При

> 0 правосторонняя асимметрия.
При
<0
левосторонняя асимметрия.
Если асимметрия более 0,5, то независимо
от знака она считается значительной
Если асимметрия меньше 0,25, то она
считается незначительной

Асимметрия
распределения рассчитанная по формулам
К.Пирсона:

является
приблизительной

Расчет
асимметрии распределения при помощи
нормированного момента третьего
порядка дает наиболее точный результат

т.е.

— нормированный
момент третьего порядка

Показатель Пирсона зависит от степени
асимметричности в средней части ряда
распределения, а показатель асимметрии,
основанный на моменте третьего порядка,
— от крайних значений признака.

Оценка существенности асимметрии

Для оценки существенности асимметрии
вычисляют показатель средней квадратической
ошибки коэффициента асимметрии

Если отношение

имеет значение больше 2, то это
свидетельствует о существенном характере
асимметрии

Эксцесс распределения

Показатель эксцесса

представляет собой отклонение вершины
эмпирического распределения вверх или
вниз («крутость») от вершины кривой
нормального распределения, НО! График
распределения может выглядеть сколь
угодно крутым в зависимости от силы
вариации признака: чем слабее вариация,
тем круче кривая распределения при
данном масштабе. Не говоря уже о том,
что, изменяя масштабы по оси абсцисс и
по оси ординат, любое распределение
можно искусствен но сделать «крутым»
и «пологим». Чтобы показать, в чем состоит
эксцесс распределения, и правильно его
интерпретировать, нужно сравнить ряды
с одинаковой силой вариации (одной и
той же величиной σ) и разными показателями
эксцесса. Чтобы не смешать эксцесс с
асимметрией, все сравниваемые ряды
должны быть симметричными. Такое
сравнение изображено на рис.

Поскольку эксцесс нормального
распределения равен 3, показатель
эксцесса вычисляется по формуле

или

где

— нормированный момент четвертого
порядка

При
>0
– высоковершинный эксцесс распределения
При
<0
– низковершинный эксцесс распределение
При

=0 – нормальное распределение

Оценка существенности эксцесса

Для оценки существенности эксцесса
вычисляют показатель его средней
квадратической ошибки

Если отношение

имеет значение больше 3, то это
свидетельствует о существенном характере
эксцесса

Источник

58. Коэффициенты асимметрии и эксцесса.

Центральные
моменты распределения

Показатели формы распределения

Асимметрия – Коэффициент
асимметрии

характеризует асимметричность
(«скошенность») распределения признака
в совокупности
Эксцесс – Показатель эксцесса

представляет собой отклонение вершины
эмпирического распределения вверх или
вниз («крутость») от вершины кривой
нормального распределения

Асимметрия распределения

При
=0
распределение считается нормальным.
При

> 0 правосторонняя асимметрия.
При
<0
левосторонняя асимметрия.
Если асимметрия более 0,5, то независимо
от знака она считается значительной
Если асимметрия меньше 0,25, то она
считается незначительной

Асимметрия
распределения рассчитанная по формулам
К.Пирсона:

является
приблизительной

т.е.

— нормированный
момент третьего порядка

Оценка существенности асимметрии

Если отношение

имеет значение больше 2, то это
свидетельствует о существенном характере
асимметрии

Эксцесс распределения

Поскольку эксцесс нормального
распределения равен 3, показатель
эксцесса вычисляется по формуле

или

где

— нормированный момент четвертого
порядка

При
>0
– высоковершинный эксцесс распределения
При
<0
– низковершинный эксцесс распределение
При

=0 – нормальное распределение

Оценка существенности эксцесса

Для оценки существенности эксцесса
вычисляют показатель его средней
квадратической ошибки

Если отношение

имеет значение больше 3, то это
свидетельствует о существенном характере
эксцесса

Подборка по базе: Теория менеджмента практическая работа.docx, Практическая работа Шуклина Д.и..doc, Практическая работа №2 (ИТ в проф.деятельности)_Бояркина ЕВ .doc, Практическая работа АКТ.docx, Курсовая Работа Попова М.С. НГДСз-21-3.doc, Курсовая работа студентки ДОУА-21о Глуховой Эвелины _СОВЕТСКИЙ С, Курсовая работа Евдокимова Ю.Д ССП 224-1210.docx, Лабораторная работа 7.docx, Практ. работа 6 по ОС (1).pdf, Практ. работа ГК 5 класс..docx

2. Структурные показатели.

Степень асимметрии.

Симметричным является распределение, в котором частоты любых двух вариантов, равностоящих в обе стороны от центра распределения, равны между собой.

Наиболее точным и распространенным показателем асимметрии является моментный коэффициент асимметрии.

As = M₃/s³

где M₃ — центральный момент третьего порядка.

s — среднеквадратическое отклонение.

M₃ = 1008417642929.4/45 = 22409280953.99

Положительная величина указывает на наличие правосторонней асимметрии

Оценка существенности показателя асимметрии дается с помощью средней квадратической ошибки коэффициента асимметрии:

Если выполняется соотношение |As|/s_As < 3, то асимметрия несущественная, ее наличие объясняется влиянием различных случайных обстоятельств. Если имеет место соотношение |As|/s_As > 3, то асимметрия существенная и распределение признака в генеральной совокупности не является симметричным.

Расчет центральных моментов проводим в аналитической таблице:

Таблица 7- Расчет центральных моментов

Группы	Середина интервала, x_центр	Кол-во, f_i	(x — x_ср)³*f_i	(x — x_ср)⁴*f_i
10470 — 13325	11897,5	2	-591260259007,48	3.9387787587509E+15
13325 — 16180	14752,5	12	-661935683552,08	2.5197685020505E+15
16180 — 19035	17607,5	12	-10342745055,34	9842845710927,800
19035 — 21890	20462,5	11	75846797074,87	1.4436173709968E+14
21890 — 24745	23317,5	4	430947710649,96	2.0505928565123E+15
24745 — 27600	26172,5	4	1765161822819,40	1.3438765344411E+16
Итого		45	1008417642929,40	2.2102110044535E+16

В анализируемом ряду распределения наблюдается несущественная асимметрия (0.422/0.617 = 0.68<3)

Применяются также структурные показатели (коэффициенты) асимметрии, характеризующие асимметрию только в центральной части распределения, т.е. основной массы единиц, и независящие от крайних значений признака. Рассчитаем структурный коэффициент асимметрии Пирсона:

Для симметричных распределений рассчитывается показатель эксцесса (островершинности). Эксцесс представляет собой выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения.

Чаще всего эксцесс оценивается с помощью показателя:

Для распределений более островершинных (вытянутых), чем нормальное, показатель эксцесса положительный (Ex > 0), для более плосковершинных (сплюснутых) — отрицательный (Ex < 0), т.к. для нормального распределения M₄/s⁴ = 3.

M₄ = 2.2102110044535E+16/45 = 4.9115800098966E+14

Число 3 вычитается из отношения μ⁴/ σ⁴ потому, что для нормального закона распределения μ⁴/ σ⁴ = 3. Таким образом, для нормального распределения эксцесс равен нулю. Островершинные кривые обладают положительным эксцессом, кривые более плосковершинные — отрицательным эксцессом.

Ex < 0 — плосковершинное распределение

Чтобы оценить существенность эксцесса рассчитывают статистику Ex/s_Ex

где s_Ex — средняя квадратическая ошибка коэффициента эксцесса.

Если отношение Ex/s_Ex > 3, то отклонение от нормального распределения считается существенным.

Поскольку s_Ex < 3, то отклонение от нормального распределения считается не существенным.

Показатели вариации.

Абсолютные показатели вариации.

Размах вариации — разность между максимальным и минимальным значениями признака первичного ряда.

R = x_max — x_min = 27600 — 10470 = 17130 руб.

Среднее линейное отклонение — вычисляют для того, чтобы учесть различия всех единиц исследуемой совокупности.

Каждое значение ряда отличается от другого в среднем на 3129.93

Дисперсия — характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего).

Несмещенная оценка дисперсии — состоятельная оценка дисперсии (исправленная дисперсия).

Среднее квадратическое отклонение.

Каждое значение ряда отличается от среднего значения 18559.17 в среднем на 3758.782

Оценка среднеквадратического отклонения.

Относительные показатели вариации.

К относительным показателям вариации относят: коэффициент осцилляции, линейный коэффициент вариации, относительное линейное отклонение.

Коэффициент вариации — мера относительного разброса значений совокупности: показывает, какую долю среднего значения этой величины составляет ее средний разброс.

Поскольку v ≤ 30%, то совокупность однородна, а вариация слабая. Полученным результатам можно доверять.

Линейный коэффициент вариации или Относительное линейное отклонение — характеризует долю усредненного значения признака абсолютных отклонений от средней величины.

Коэффициент осцилляции — отражает относительную колеблемость крайних значений признака вокруг средней.

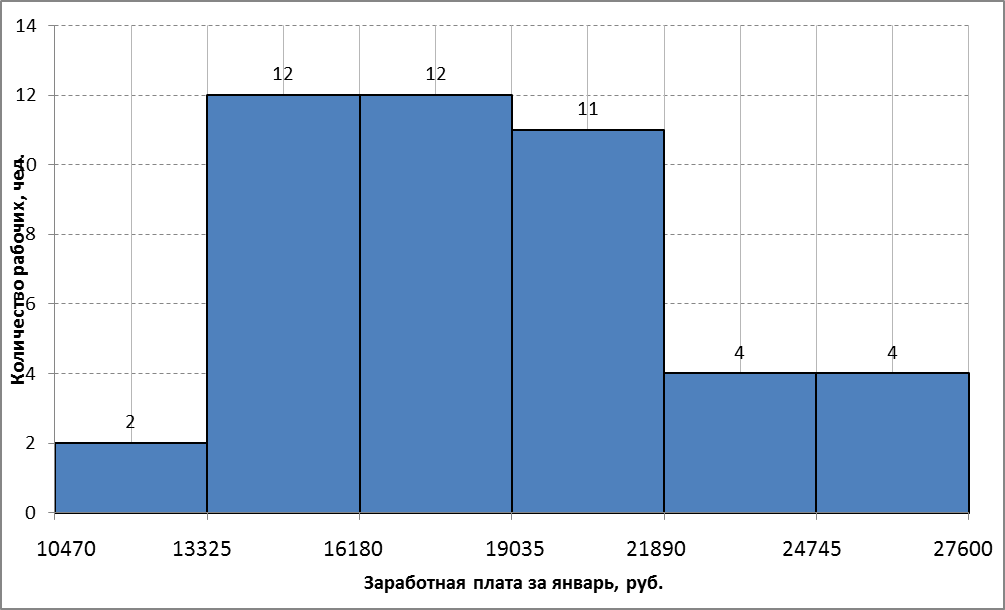
Рисунок 3- Гисторгамма распределения рабочих строительного треста по заработной плате за январь

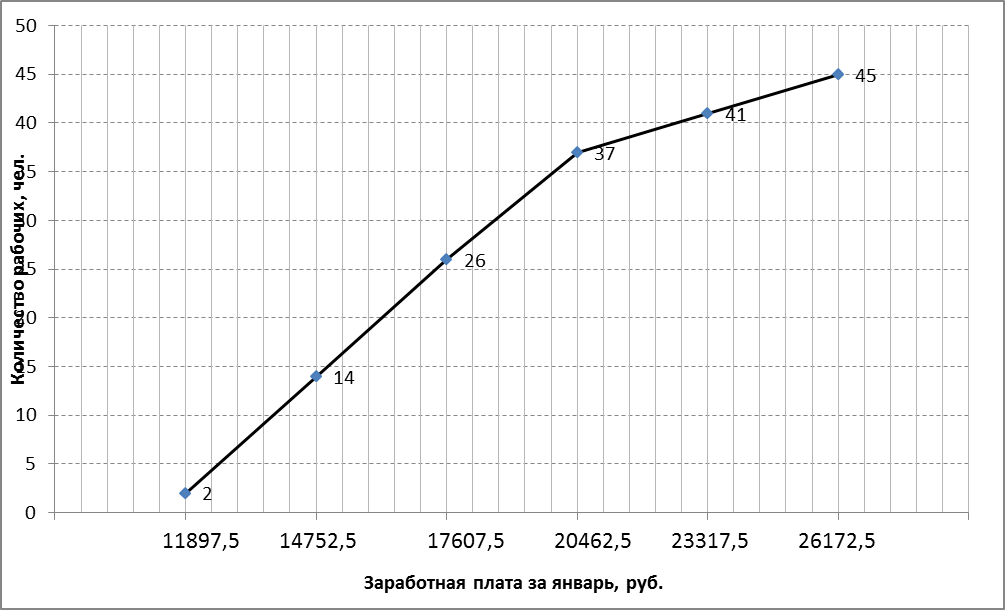
Рисунок 4- Кумулята распределения рабочих строительного треста по заработной плате

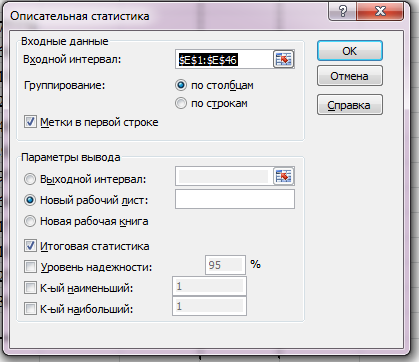
Ручные расчеты дополним данными, полученными с помощью надстройки «Описательная статистика» пакета Microsoft Excel (Файл – параметры — надстройки – анализ данных – описательная статистика).

Рисунок 4 — Параметры инструмента Ecxel анализ данных «Описательная статистика»

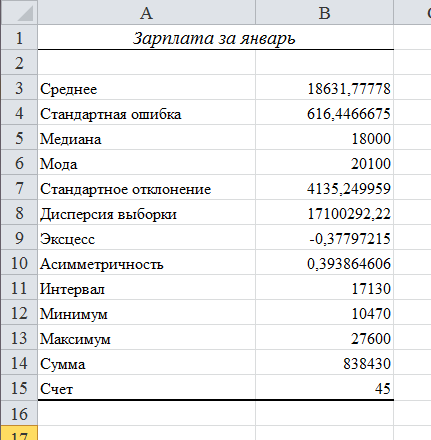
Рисунок 5 — Результаты расчета инструмента Ecxel анализ данных «Описательная статистика»

Составим сравнительную таблицу

Таблица 4- Сравнительние расчетных параметров

Наименование параметра	Ecxel «Описательная статистика»	Расчетные данные	Отклонение
Среднее	18631,77778	18559,17	-72,6078
Стандартная ошибка	616,4466675	–
Медиана	18000	18202,29	202,29
Мода	20100	16180	-3920
Стандартное отклонение	4135,249959	3758,782	-376,468
Дисперсия выборки	17100292,22	14128443	-2971849
Эксцесс	-0,37797215	-0,54	-0,16203
Асимметричность	0,393864606	0,63	0,236135
Интервал	17130	17130	0
Минимум	10470	10470	0
Максимум	27600	27600	0
Сумма	838430	838430	0
Счет	45	45	0

Некоторые параметры отличаются, так как программа рассчитывает не по группированному вариационному ряду данным, а по первичному дискретному ряду.

Выводы:

Для данного дискретного ряда характерны следующие показатели. Средняя заработная плата за январь составила 18559,17 руб. Наиболее часто встречающееся значение ряда – 16180 руб. 50% единиц совокупности имеют заработную плату меньше по величине 18202.29 руб.

В анализируемом ряду распределения наблюдается несущественная правосторонняя асимметрия (0.271/0.612 = 0.44<3).

Среднее значение примерно равно моде и медиане, что свидетельствует о нормальном распределении выборки.

Значения As и Ex мало отличаются от нуля. Поэтому можно предположить близость данной выборки к нормальному распределению.

Источник

При обработке числовых массивов результатов эксперимента, как случайных величин, на практике применяют следующие выборочные оценки
[
24
]
:

математическое ожидание

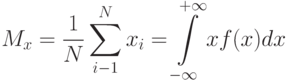$M_x=\frac 1 N \sum\limits_{i-1}^N x_i=\int\limits_{-\infty}^{+\infty} xf(x)dx$

(
1.1)

дисперсия

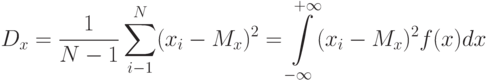$D_x=\frac 1 {N-1}\sum\limits_{i-1}^N (x_i-M_x)^2=\int\limits_{-\infty}^{+\infty}(x_i-M_x)^2 f(x)dx$

(
1.2)

коэффициент асимметрии

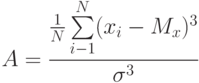$A=\frac {\frac 1 N \sum\limits_{i-1}^N(x_i-M_x)^3} {\sigma^3}$

(
1.3)

коэффициент эксцесса

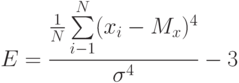$E=\frac {\frac 1 N \sum\limits_{i-1}^N(x_i-M_x)^4} {\sigma^4}-3$

(
1.4)

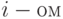
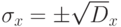
где x_i значение результата в i-ом опыте; — число результатов в массиве; $\sigma_x= \pm\sqrt D_x$ — среднеквадратичное отклонение.

Производная оценка от величины математического ожидания и дисперсии является коэффициент вариации, определяемый в процентах по формуле:

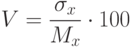$V=\frac {\sigma_x} {M_x} \cdot 100$

(
1.5)

Дисперсия, среднее квадратичное отклонение и коэффициент вариации являются количественными характеристиками, оценки рассеивания значений результатов эксперимента как случайной величины и применяются при изучении различных действий со случайным исходом. Коэффициент асимметрии и коэффициент эксцесса являются характеристиками высшего порядка. Первый характеризует «скошенность распределения», а второй – степень его «островершинности»

Вычисленные по экспериментально наблюдаемым случайным величинам и случайным функциям статистические характеристики несут информацию не обо всей генеральной совокупности, которая в общем случае бесконечна, а лишь о некоторой ее части — выборке, элементы которой измерены с определенными ошибками. В связи с этим в результате эксперимента получают лишь некоторые оценки параметров генеральной совокупности.

Следовательно, и любая выборочная оценка — это случайная величина, точность определения которой и возможные при этом ошибки необходимо контролировать. Следует также иметь в виду, что вычисленные моменты распределения являются точечными оценками выборочных величин, так как каждый из них оценивает параметры генеральной совокупности с помощью единственного числа. Они позволяют судить о значении вычисленной статистической характеристики в данной точке и ничего не говорят о возможных пределах варьирования самой оценки.

К вычисляемым в результате эксперимента оценкам случайных величин предъявляются три основных требования: состоятельности, несмещенности и эффективности. Полагают, что оценка состоятельна, если с ростом объема выборки она стремится по вероятности к истинному значению, несмещена, если ее математическое ожидание стремится к истинному значению, и эффективна, когда оценка обладает наименьшим рассеянием по сравнению с любыми другими оценками. Из двух оценок эффективнее та, которая обладает меньшей дисперсией, т. е. значения которой рассеиваются в более узком интервале.

На уровень рассеивания оценок значительное влияние оказывают ошибки, имеющие место при эксперименте.

При выборочном наблюдении встречаются ошибки трех видов: грубые, систематические и случайные.

Грубые ошибки, отличающиеся большим отклонением от центра группирования выборки, отсеиваются на этапе первичного анализа материалов.

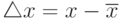
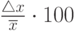
Точность измерений любой физической величины характеризуется, абсолютной $\triangle x=x-\overline x$ и относительной $\frac {\triangle x} {\overline x} \cdot 100$ ошибками (здесь $\overline x$ -истинное значение), которые, в свою очередь, состоят из суммы систематических $\delta$ и случайных $\varepsilon$ ошибок

Систематические ошибки $\delta$ постоянны при определении каждого члена выборки и зависят от технического уровня измерительной аппаратуры и техники эксперимента. Эти ошибки можно свести к минимуму периодической тарировкой приборов с помощью более совершенных и повышением точности метода определения исследуемых переменных. Случайные ошибки обусловлены влиянием большого количества факторов. Их появление неодинаково и случайно от измерения к измерению и не может быть предварительно учтено из-за их зависимости от изменения условий измерений и изменчивости самих измеряемых величин. Однако при достаточно большом количестве экспериментов суммарное значение случайных ошибок, изменяющихся примерно одинаково в положительную и отрицательную сторону, приближается к нулю. Случайные ошибки в подавляющем большинстве подчиняются нормальному закону распределения с математическим ожиданием, равным «0».

В практике исследований систематические и случайные ошибки близки друг к другу и совместно определяют ошибку измерений. При оценке точности измерений рекомендуется учитывать суммарную ошибку

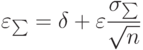$\varepsilon_{\sum}=\delta+\varepsilon \frac {\sigma_{\sum}} {\sqrt n}$

(
1.6)

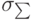
где $\sigma_{\sum}$ — среднеквадратическое отклонение случайной величины при числе измерений n.

Для величин, определяемых косвенно — методом расчета по другим измеренным случайным величинам, оценка погрешностей осуществляется вычислением статистических оценок по соответствующим функциональным зависимостям.

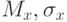
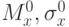
Выборочные характеристики $M_x, \sigma_x$ определяемые на основе ограниченного числа наблюдений, могут приближаться к истинным значениям характеристик генеральной совокупности $M_x^0, \sigma_x^0$ лишь с определенной точностью:

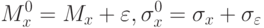$M_x^0=M_x+\varepsilon,\sigma_x^0=\sigma_x+\sigma_{\varepsilon}$

(
1.7)

Точность выборочного наблюдения (эксперимента) может задаваться в единицах измерения исследуемой величины, в единицах выборочного значения 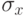$\sigma_x$ и в процентах исследуемой величины или характеристики.

Систематическая ошибка, будучи постоянной, при этом может не учитываться.

Вероятность того, что истинное значение характеристик генеральной совокупности находится в отмеченных пределах, равна

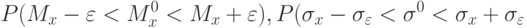$P(M_x-\varepsilon<M^0_x<M_x+\varepsilon), P(\sigma_x-\sigma_{\varepsilon}<\sigma^0<\sigma _x+\sigma_{\varepsilon}}$

(
1.8)

и называется надежностью данной оценки .

Так как математическое ожидание любой выборки само является случайной величиной, то полезно установить такой интервал, в котором с заданной степенью достоверности будет заключено значение оцениваемого параметра.

Интервал 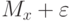$M_x+\varepsilon$ , в который в общем случае может быть произвольным , называется доверительными границами, а соответствующая вероятность — доверительной вероятностью или, как часто говорят, надежностью. Доверительную вероятность для удобства обозначают как

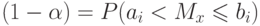$(1-\alpha)=P(a_i<M_x \leqslant b_i)$

(
1.9)

Соответственно есть вероятность ошибки, которая на кривой распределения изображается в виде двух половинок a/2 .

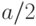
Вероятность ошибки характеризует долю риска в оценке истинного значения оцениваемой величины и часто называется уровнем значимости. Для удобства величину доверительного интервала устанавливают в долях среднеквадратического отклонения $\pm z \sigma_{\sum}$ . Тогда доверительную вероятность определяют, как площадь, ограниченную кривой нормального распределения на интервале $\pm z \sigma_{\sum}$ . Используя формулу стандартного нормального распределения (9)

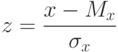$z=\frac {x-M_x} {\sigma_x}$

(
1.10)

при M_x=0 и $\sigma_x=1$

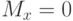
доверительную вероятность, согласно (8), записывают в таком виде:

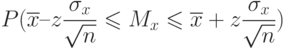$P( \overline x – z \frac {\sigma_x} {\sqrt n} \leqslant M_x \leqslant \overline x + z \frac {\sigma_x} {\sqrt n})$

(
1.11)

, где $\overline x$ — оценка среднего значения генеральной совокупности

доверительный интервал для дисперсии

$[ \frac {n\sigma_x^2} {x^2 \alpha/2} \leqslant D_x \leqslant \frac {n\sigma_x^2} {x^21- \alpha/2}]$

(
1.12)

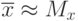
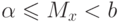
Определяют доверительный интервал в такой последовательности: вычисляют параметр выборки $\overline x \approx M_x$ , выбирают доверительную вероятность, $(1-\alpha)$ определяют соответствующее выбранному значению $(1-\alpha)$ число из таблицы табулированных значений стандартного нормального распределения; вычисляют доверительный интервал $\alpha \leqslant M_x < b$ .

С увеличением количества замеров достоверность эксперимента возрастает, а доверительный интервал уменьшается. Таблица используется в том случае, когда о дисперсии исследуемой величины нельзя составить определенного мнения. Если же на основании априорных сведений или предварительных опытов (среднее квадратичное отклонение), известно, то по формуле случайной выборочной ошибки, равной половине длины доверительного интервала

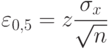$\varepsilon_{0,5}=z \frac {\sigma_x} {\sqrt n}$

(
1.13)

определяют необходимое число замеров, гарантирующее требуемую надежность

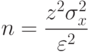$n=\frac {z^2 \sigma_x^2} {\varepsilon^2}$

(
1.14)

Точность и надежность оценки выборочных характеристик не следует смешивать с точностью исследования, которую часто вычисляют по такой формуле:

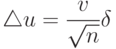$\triangle u= \frac v {\sqrt n} \delta$

(
1.15)

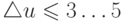
где — коэффициент вариации выборочного наблюдения, % (в случае оценки точности для сельскохозяйственных машин и процессов считается достаточным, если $\triangle u \leqslant 3…5$ %.

Кроме установления доверительных интервалов, задачи оценки случайных величин включают анализ законов распределения изучаемых величин, проверку принадлежности двух выборок к одной генеральной совокупности, сравнение средних дисперсий для различных выборок и др.

Рабочим инструментом статистического анализа при решении отмеченных задач оценки являются статистические гипотезы . Статистическими гипотезами именуются суждения, применяемые при различных видах анализа, касающихся, по существу, выяснения свойств некоторой генеральной совокупности случайных величин. Гипотеза в статистике трактуется как предположение о распределении случайных величин.

Гипотеза, отклонения от которой приписываются данному случаю, называется нулевой и обозначается . Альтернативная или противоположная гипотеза называется конкурирующей и обозначается H_0 . Гипотезы проверяют при помощи специально подобранной случайной величины, распределение которой известно или может быть установлено при малом объеме выборки.

Источник