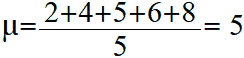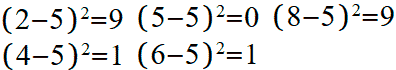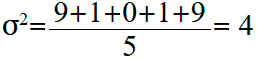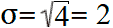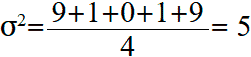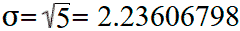Средняя квадратическая ошибка калькулятор - Решение и исправление самых разных ошибок на TopOshibok.ru

Среднее квадратичное отклонение двух, трех, четырех и более чисел. Оно же стандартное отклонение, среднеквадратическое отклонение, среднеквадратичное отклонение, средняя квадратическая, стандартный разброс — показатель рассеивания значений случайной величины относительно её математического ожидания в теории вероятностей и статистике.

Как правило перечисленные термины равны квадратному корню дисперсии.

Пример вычисления стандартного отклонения по следующим формулам:
Вычислим среднюю оценку ученика: 2; 4; 5; 6; 8.

Cредняя оценка будет равна:

Вычисляем квадраты отклонений оценок от их средней оценки:

Вычислим среднее арифметическое (дисперсию) этих значений:

Стандартное отклонение равно квадратному корню дисперсии:

Эта формула справедлива только если эти пять значений и являются генеральной совокупностью. Если бы эти данные были случайной выборкой из какой-то большой совокупности (например, оценки пяти случайно выбранных учеников большого города), то в знаменателе формулы для вычисления дисперсии вместо n = 5 нужно было бы поставить n − 1 = 4:

Тогда стандартное отклонение будет равняться:

Этот результат называется стандартным отклонением на основании несмещённой оценки дисперсии. Деление на n − 1 вместо n даёт неискажённую оценку дисперсии для больших генеральных совокупностей.

Пожалуйста напишите с чем связна такая низкая оценка:

Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Смотрите также

Источник

Калькулятор среднеквадратичной ошибки

17 авг. 2022 г.
читать 2 мин

@import url(‘https://fonts.googleapis.com/css?family=Droid+Serif|Raleway’);

h1 { text-align: center; font-size: 50px; margin-bottom: 0px; font-family: ‘Raleway’, serif; }

p { color: black; text-align: center; margin-bottom: 15px; margin-top: 15px; font-family: ‘Raleway’, sans-serif; }

words {

padding-left: 30px; color: black; font-family: Raleway; max-width: 550px; margin: 25px auto; line-height: 1.75; }

words_summary {

padding-left: 70px; color: black; font-family: Raleway; max-width: 550px; margin: 25px auto; line-height: 1.75; }

words_text {

color: black; font-family: Raleway; max-width: 550px; margin: 25px auto; line-height: 1.75; }

words_text_area {

display:inline-block; color: black; font-family: Raleway; max-width: 550px; margin: 25px auto; line-height: 1.75; padding-left: 100px; }

calcTitle {

text-align: center; font-size: 20px; margin-bottom: 0px; font-family: ‘Raleway’, serif; }

hr_top {

width: 30%; margin-bottom: 0px; border: none; height: 2px; color: black; background-color: black; }

hr_bottom {

width: 30%; margin-top: 15px; border: none; height: 2px; color: black; background-color: black; }

words label, input {

display: inline-block; vertical-align: baseline; width: 350px; }

#button { border: 1px solid; border-radius: 10px; margin-top: 20px;

cursor: pointer; outline: none; background-color: white; color: black; font-family: ‘Work Sans’, sans-serif; border: 1px solid grey; /* Green */ }

#button:hover { background-color: #f6f6f6; border: 1px solid black; }

#words_table { color: black; font-family: Raleway; max-width: 350px; margin: 25px auto; line-height: 1.75; }

summary_table {

color: black; font-family: Raleway; max-width: 550px; margin: 25px auto; line-height: 1.75; padding-left: 20px; }

.label_radio { text-align: center; }

td, tr, th { border: 1px solid black; } table { border-collapse: collapse; } td, th { min-width: 50px; height: 21px; } .label_radio { text-align: center; }

text_area_input {

padding-left: 35%; float: left; }

svg:not(:root) { overflow: visible; }

Среднеквадратическая ошибка (RMSE) — это метрика, которая говорит нам, насколько в среднем наши прогнозируемые значения отличаются от наших наблюдаемых значений в регрессионном анализе. Он рассчитывается как:

СКО = √[ Σ(P i – O i ) 2 / n ]

куда:

Σ — причудливый символ, означающий «сумма».
P i — прогнозируемое значение для i -го наблюдения
O i — наблюдаемое значение для i -го наблюдения
n — размер выборки

Чтобы найти RMSE для регрессии, просто введите список наблюдаемых значений и прогнозируемых значений в два поля ниже, затем нажмите кнопку «Рассчитать»:

Наблюдаемые значения:

34, 37, 44, 47, 48, 48, 46, 43, 32, 27, 26, 24 Прогнозируемые значения:

37, 40, 46, 44, 46, 50, 45, 44, 34, 30, 22, 23 СКО = 2,43242

function calc() {

var obs = document.getElementById(‘input_data_obs’).value.split(‘,’).map(Number);

var pred = document.getElementById(‘input_data_pred’).value.split(‘,’).map(Number);

//check that both lists are equal length if (obs.length — pred.length == 0) { document.getElementById(‘error_msg’).innerHTML = »; //calculate RMSE let error = 0 for (let i = 0; i < obs.length; i++) { error += Math.pow((pred[i] — obs[i]), 2) }

var RMSE = Math.sqrt(error / obs.length); document.getElementById(‘RMSE’).innerHTML = RMSE.toFixed(5); }

else { document.getElementById(‘RMSE’).innerHTML = »; document.getElementById(‘error_msg’).innerHTML = ‘The two lists must be of equal length.’; }

} //end calc function

Источник

Инструкции:

Введите образец данных ниже, и этот калькулятор предоставит пошаговый расчет среднеквадратичного отклонения, используя форму ниже;

Калькулятор среднеквадратичного отклонения

Подробнее о

Среднеквадратичное отклонение

чтобы вы могли лучше понять результаты, предоставляемые этим калькулятором. Для выборки данных среднеквадратичное отклонение, которое вычисляется как среднее квадратов отклонений от среднего, соответствует мере отклонения, связанной с набором данных. Математически мы получаем, что среднеквадратичное отклонение вычисляется по следующей формуле:

\[ \text{Mean Square Deviation Calculator} = \displaystyle \sum_{i=1}^n \left(\bar x — x_i\right)^2 \]

Аналогичным показателем, который вы хотели бы рассмотреть, чтобы дополнить результаты, полученные со среднеквадратичным отклонением, является

среднее абсолютное отклонение

Если вместо этого вам нужна сводка всей описательной статистики для данных выборки, включая меры центральной тенденции и отклонения, пожалуйста, ознакомьтесь с нашими пошаговыми инструкциями.

калькулятор описательной статистики

Источник

\bold{\mathrm{Basic}}

\bold{\alpha\beta\gamma}

\bold{\mathrm{AB\Gamma}}

\bold{\sin\cos}

\bold{\ge\div\rightarrow}

\bold{\overline{x}\space\mathbb{C}\forall}

\bold{\sum\space\int\space\product}

\bold{\begin{pmatrix}\square&\square\\\square&\square\end{pmatrix}}

\bold{H_{2}O}

\square^{2}

x^{\square}

\sqrt{\square}

\nthroot[\msquare]{\square}

\frac{\msquare}{\msquare}

\log_{\msquare}

\pi

\theta

\infty

\int

\frac{d}{dx}

\ge	\le	\cdot	\div	x^{\circ}	(\square)	\|\square\|	(f\:\circ\:g)	f(x)	\ln	e^{\square}
\left(\square\right)^{‘}	\frac{\partial}{\partial x}	\int_{\msquare}^{\msquare}	\lim	\sum	\sin	\cos	\tan	\cot	\csc	\sec

\alpha	\beta	\gamma	\delta	\zeta	\eta	\theta	\iota	\kappa	\lambda	\mu
\nu	\xi	\pi	\rho	\sigma	\tau	\upsilon	\phi	\chi	\psi	\omega

A	B	\Gamma	\Delta	E	Z	H	\Theta	K	\Lambda	M
N	\Xi	\Pi	P	\Sigma	T	\Upsilon	\Phi	X	\Psi	\Omega

\sin	\cos	\tan	\cot	\sec	\csc	\sinh	\cosh	\tanh	\coth	\sech
\arcsin	\arccos	\arctan	\arccot	\arcsec	\arccsc	\arcsinh	\arccosh	\arctanh	\arccoth	\arcsech

\begin{cases}\square\\\square\end{cases}	\begin{cases}\square\\\square\\\square\end{cases}	=	\ne	\div	\cdot	\times	<	>	\le	\ge
(\square)	[\square]	▭\:\longdivision{▭}	\times \twostack{▭}{▭}	+ \twostack{▭}{▭}	— \twostack{▭}{▭}	\square!	x^{\circ}	\rightarrow	\lfloor\square\rfloor	\lceil\square\rceil

\overline{\square}	\vec{\square}	\in	\forall	\notin	\exist	\mathbb{R}	\mathbb{C}	\mathbb{N}	\mathbb{Z}	\emptyset
\vee	\wedge	\neg	\oplus	\cap	\cup	\square^{c}	\subset	\subsete	\superset	\supersete

\int	\int\int	\int\int\int	\int_{\square}^{\square}	\int_{\square}^{\square}\int_{\square}^{\square}	\int_{\square}^{\square}\int_{\square}^{\square}\int_{\square}^{\square}	\sum	\prod
\lim	\lim _{x\to \infty }	\lim _{x\to 0+}	\lim _{x\to 0-}	\frac{d}{dx}	\frac{d^2}{dx^2}	\left(\square\right)^{‘}	\left(\square\right)^{»}	\frac{\partial}{\partial x}

(2\times2)	(2\times3)	(3\times3)	(3\times2)	(4\times2)	(4\times3)	(4\times4)	(3\times4)	(2\times4)	(5\times5)
(1\times2)	(1\times3)	(1\times4)	(1\times5)	(1\times6)	(2\times1)	(3\times1)	(4\times1)	(5\times1)	(6\times1)	(7\times1)

\mathrm{Радианы}	\mathrm{Степени}	\square!	(	)	%	\mathrm{очистить}
\arcsin	\sin	\sqrt{\square}	7	8	9	\div
\arccos	\cos	\ln	4	5	6	\times
\arctan	\tan	\log	1	2	3	—
\pi	e	x^{\square}	0	.	\bold{=}	+

Подпишитесь, чтобы подтвердить свой ответ

Войдите, чтобы сохранять заметки

Войти

Показать Этапы

Номер Строки

Примеры

стандартное\:отклонение\:1,\:2,\:3,\:4,\:5,\:6
стандартное\:отклонение\:\left\{0.42,\:0.52,\:0.58,\:0.62\right\}
стандартное\:отклонение\:-4,\:5,\:6,\:9
стандартное\:отклонение\:\left\{90,\:94,\:53,\:68,\:79,\:84,\:87,\:72,\:70,\:69,\:65,\:89,\:85\right\}
стандартное\:отклонение\:\frac{31}{100},\:\frac{23}{105},\:\frac{31}{205},\:\frac{54}{205}
стандартное\:отклонение\:\:\left\{1,\:7,\:-3,\:4,\:9\right\}
Показать больше

Описание

Шаг за шагом найти среднеквадратичное отклонение набора данных

standard-deviation-calculator

standard deviation

Блог-сообщения, имеющие отношение к Symbolab

Lies, Damned Lies, and Statistics

Statistics is about analyzing data, for instance the mean is commonly used to measure the “central tendency” of…

Введите Задачу

Сохранить в блокнот!

Войти

Источник

Среднеквадратическое отклонение

\begin{align}
& \sigma=\sqrt{\frac{1}{n}\sum_{i=1}^N (x_i-\bar{x})^2} \\
\end{align}

Стандартное отклонение

\begin{align}
& s=\sqrt{\frac{n}{n-1}\sigma^2}=\sqrt{\frac{1}{n-1}\sum_{i=1}^N (x_i-\bar{x})^2} \\
\end{align}

\begin{align}
& где\ \sigma^2-дисперсия;\ x_i-i-ый\ элемент\ выборки;\ n-объем\ выборки; \bar{x}-среднее\ арифметическое\ выборки. \\
\end{align}

Калькулятор вычислит среднеквадратическое отклонение, а также стандартное отклонение и среднее арифметическое. Для вычисления укажите количество чисел, добавьте числа и нажмите рассчитать.

количество чисел

Источник