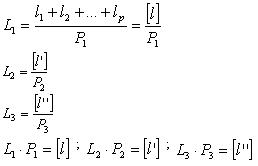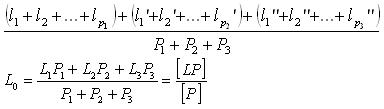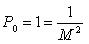Средняя квадратическая ошибка единицы веса

Дан ряд результатов
неравноточных измерений

x₁
, x₂
, . . . , x_n
;

m₁
, m₂
, . . . , m_n
.

Cоответственно

(2.22)

Как видим из
равенств (2.22) , всегда найдется такое
соотношение, когда
,
т.е. коэффициент С есть не что иное,
как средняя квадратическая ошибка
измерения, вес которой равен единице и
которая в отличие от остальных средних
квадратических ошибок обозначается
и называется ошибкой единицы веса.

Тогда

(2.23)

Следовательно,

(2.24)

В соответствии с
(2.24) можно записать

(2.25)

или

(2.26)

т.е.
cредняя квадратическая ошибка любого
результата измерения равна ошибке
единицы веса, деленной на корень
квадратный из веса соответствующего
результата.

2.4. Вычисление весов функций

2.4.1. Вес
функции независимых величин

Определим вес
функции

(2.27)

При этом известны
веса аргументов p₁
, p₂
, . . . , p_n.
В случае независимых величин имеем

(2.28)

Разделим обе части
равенства (2.28) на ²

так как
то окончательно имеем

(2.29)

2.4.2. Вес функции
неравноточных слагаемых

Дана функция вида

F
= x₁
+ x₂
+ . . . + x_n
, (2.30)

где x_i
— результаты
неравноточных измерений с соответствующими
весами: p₁,
p₂
, . . . , p_n
.

Требуется определить
вес функции F
. Cогласно
(2.29) будем иметь

(2.31)

Обратный вес
суммы неравноточных слагаемых равен
сумме обратных весов.

2.4.3. Вес суммы
равноточных слагаемых

Дана функция вида
(2.30), в которой x_i
являются результатами равноточных
измерений, т.е. p₁
= p₂
= . . . = p_n
= p. Тогда
вес такой функции определится из
равенства (2.31)

(2.32)

Откуда

(2.33)

Вес суммы
равноточных слагаемых в n раз меньше
веса одного измерения.

2.4.4. Вес простой
арифметической средины

Поскольку простая
арифметическая средина вычисляется
согласно формуле

(2.34)

ее средняя
квадратическая ошибка будет равна

,

откуда

Переходя к весам,
получим

или

(2.35)

Вес простой
арифметической средины в n раз больше
веса одного измерения.

2.4.5. Вес и
средняя квадратическая ошибка

общей
арифметической средины

Представив общую
арифметическую средину в виде линейной
функции

,
(2.36)

cогласно равенства
(2.29) получим

или

откуда

(2.37)

Вес общей
арифметической средины равен сумме
весов результатов измерений.

Средняя квадратическая ошибка
M
среднего весового согласно формуле
(2.26) вычислится

(2.38)

или

(2.39)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Средняя квадратичная погрешность единицы веса

15. Средняя квадратичная погрешность единицы веса

При оценке точности неравноточных измерений в качестве единицы меры дисперсий принимают дисперсию измерения, вес которого равен единице. Так как значение среднего квадратического отклонения неизвестно, то его заменяют средней квадратической погрешностью , соответствующей измерению с весом, равным единице, имея при этом в виду, что получена по большому числу измерений и ради краткости ее называют средней квадратичной погрешностью единицы веса.

Если дисперсия изменения с весом р равна а с весом единица то по свойству весов:

(82)

откуда

(83)

или

(84)

Сопоставив равенства (67) и (82), находим, что

(85)

Найдем выражение средней квадратичной погрешности единицы веса через погрешности 1=2=…=n измерений 1=2=…=n, которым соответствуют веса 1=2=…=n

Величины равноточны, их веса равны единице и они имеют погрешности

На основании этого по определению (29) можно написать

или

(86)

В целях контроля правильности вычисления иногда применяют приближенное равенство

(87)

Постоянно действующие пункты ФАГС в основном создаются на базе действующих пунктов спутниковых (космических) наблюдений, астрономических обсерваторий, пунктов службы вращения Земли, радиоинтерферометрических комплексов со сверхдальними базами «Квазар», программы «Дельта» и др. На пунктах ФАГС предусматривают две программы наблюдений: постоянные наблюдения спутниковых систем ГЛОНАСС и GPS (включая и международные программы) и наблюдения других специализированных спутников и космических объектов согласно межведомственным программам построения ФАГС.

Следует заметить, что спутниковые технологии не всегда можно использовать при решении традиционных геодезических задач, например, недостаточна относительная точность определений на коротких расстояниях, ограничено использование GPS-методов в точной инженерной геодезии, процесс привязки ориентирных пунктов, легко решаемый в традиционной технологии, становится довольно сложным и дорогим, особенно в закрытой местности, в спутниковой технологии, так как объем спутниковых определений в этом случае возрастает более чем в два раза.

3. Погрешности геодезических измерений (теория и решение задач)

3.1 Геодезическое измерение, результат измерения, методы и условия измерений. Равноточные и неравноточные измерения

Измерением называется процесс сравнения некоторой физической величины с другой одноименной величиной, принятой за единицу меры.

Единица меры – значение физической величины, принятой для количественной оценки величины того же рода.

Результат измерений – это число, равное отношению измеряемой величины единицы меры.

Различают следующие виды геодезических измерений:

1. Линейные, в результате, которых получают наклонные иррациональные расстояния между заданными точками. Для этой цели применяют ленты, рулетки, проволоки, оптические свето- и радиодальномеры.

2. Угловые, определяющие величины горизонтальных углов. Для выполнения таких измерений применяют теодолит, буссоли, эклиметры.

3. Высотные, в результате, которых получают разности высот отдельных точек. Для этой цели применяют нивелиры, теодолиты-тахеометры, барометры.

Различают два метода геодезических измерений: непосредственные и посредственные (косвенные).

Непосредственные – измерения, при которых определяемые величины получают в результате непосредственного сравнения с единицей измерения.

Косвенные – измерения, при которых определяемые величины получаются как функции других непосредственно измеренных величин.

Процесс измерения включает:

• Объект – свойства которого, например, размер характеризуют результат измерения.

• Техническое средство – получать результат в заданных единицах.

• Метод измерений – обусловлен теорией практических действий и приёмов технических средств.

• Исполнитель измерений – регистрирующее устройство

• Внешняя среда, в которой происходит процесс измерений.

Измерения различают равноточные и неравноточные. Равноточные – это результаты измерений однородных величин, выполняемые с помощью приборов одного класса, одним и тем же методом, одним исполнителем при одних и тех же условиях. Если хотя бы один из элементов, составляющий совокупность, меняется, то результат измерений неравноточный.

3.2 Классификация погрешностей геодезических измерений. Средняя квадратическая погрешность. Формы Гаусса и Бесселя для её вычисления

Геодезические измерения, выполняемые даже в очень хороших условиях, сопровождаются погрешностями, т.е. отклонение результата измерений L от истинного значения Х нумеруемой величины:

∆ = L-X

Истинное – такое значение измеряемой величины, которое идеальным образом отражало бы количественные свойства объекта. Недостижимое условие – истинное значение – понятие гипотетическое. Это величина, к которой можно приближаться бесконечно близко, оно не достижимо.

Точность измерений – степень приближения его результата к истинному значению. Чем ниже погрешность, тем выше точность.

Абсолютная погрешность выражается разностью значения, полученного в результате измерения и истинного измерения величины. Например, истинное значение l = 100 м, однако, при измерении этой же линии получен результат 100,05 м, тогда абсолютная погрешность:

E = X_изм – X

E = 100,05 – 100 = 0,05 (м)

Чтобы получить значение достаточно произвести одно измерение. Его называют необходимым, но чаще одним измерением не ограничиваются, а повторяют не менее двух раз. Измерения, которые делают сверх необходимого, называют избыточными (добавочными), они являются весьма важным средством контроля результата измерения.

Абсолютная погрешность не даёт представления о точности полученного результата. Например, погрешность в 0,06 м может быть получена при измерении l = 100 м или l = 1000 м. Поэтому вычисляют относительную погрешность:

C = E_ср / X

C = 0,06 / 100 = 1/1667, т.е на 1667 м измеряемой l допущена погрешность в 1 метр.

Относительная погрешность – отношение абсолютной погрешности к истинному или измеренному значению. Выражают дробью. По инструкции линия местности должна быть измерена не грубее 1/1000.

Погрешности, происходящие от отдельных факторов, называются элементарными. Погрешность обобщенная – это сумма элементарных.

Возникают:

• грубые (Q),

• систематические (O),

• случайные (∆).

Грубые погрешности измерений возникают в результате грубых промахов, просчётов исполнителя, его невнимательности, незамеченных неисправностях технических средств. Грубые погрешности совершенно недопустимы и должны быть полностью исключены из результатов измерений путем проведения повторных, дополнительных измерений.

Систематические погрешности измерений – постоянная составляющая, связанная с дефектами: зрение, неисправность технических средств, температура. Систематические погрешности могут быть как одностороннего действия, так и переменного (периодические погрешности). Их стремятся по возможности учесть или исключить из результатов измерений при организации и проведении работ.

Случайные погрешности измерений неизбежно сопутствуют всем измерениям. Погрешности случайные исключить нельзя, но можно ослабить их влияние на искомый результат за счет проведения дополнительных измерений. Это самые коварные погрешности, сопутствующие всем измерениям. Могут быть разные как по величине, так и по знаку.

E = Q + O +∆

Если грубые и систематические погрешности могут быть изучены и исключены из результата измерений, то случайные могут быть учтены на основе глубокого измерения. Изучение на основе теории вероятностей.

На практике сложность заключается в том, что измерения проводятся какое-то ограниченное количество раз и поэтому для оценки точности измерений используют приближённую оценку среднего квадратического отклонения, которую называют среднеквадратической погрешностью (СКП).

Гауссом была предложена формула среднеквадратической погрешности:

∆²_ср = (∆²₁ + ∆²₂ +… +∆²_n) / n,

∆² = m² = (∆²₁ + ∆²₂ +… +∆²_n) / n,

∆ = m,

∆_ср = m = √(∑∆²_i / n)

Формула применяется, когда погрешности вычислены по истинным значениям.

Формула Бесселя:

m = √(∑V²_i / (n-1))

Средняя квадратическая погрешность арифметической середины в n раз меньше средней квадратической погрешности отдельного измерения

М=m/n

При оценке в качестве единицы меры точности используют среднеквадратическую погрешность с весом равным единице. Её называют средней квадратической погрешностью единицы веса.

µ² = P×m² – µ = m√P, m = µ / √P, т.е. средняя квадратическая погрешность любого результата измерения равна погрешности измерения с весом 1 (µ) и делённая на корень квадратный из веса этого результата (P).

При достаточно большом числе измерений можно записать ∑m²P=∑∆²P (так как ∆ = m):

µ = √(∑(∆²×P)/n), т.е. средняя квадратическая погрешность измерения с весом, равным 1 равна корню квадратному из дроби в числителе которого сумма произведений квадратов абсолютных погрешностей неравноточных измерений на их веса, а в знаменателе – число неравноточных измерений.

Средняя квадратическая погрешность общей арифметической середины по формуле:

M₀ = µ / √∑P

Подставив вместо µ её значение получим :

M₀ = √(∑∆²×P/n) / (√∑P) = √[(∑∆²×P) / n×(∑P)]

M₀ = √[ (∆₁²P₁ + ∆₂²P₂ +… + ∆_n²P_n) / n×(P₁ + P₂ + … + P_n) ] – формула Гаусса, средняя квадратическая погрешность общей арифметической середины равна корню квадратному из дроби, в числителе которой сумма произведений квадратов погрешностей неравноточных измерений на их веса, а знаменатель – произведение количества измерений на сумму их весов.

µ = √ [∑( V²×P ) / (n-1)] Это формула Бесселя для вычисления средней арифметической погрешности с измерением веса, равным 1 для ряда неравноточных измерений по их вероятнейшим погрешностям. Она справедлива для большого ряда измерений, а для ограниченного (часто на практике) содержит погрешности: m_µ = µ / [2×(n-1)] – это надёжность оценки µ.

Контрольная задача 1

Для исследования теодолита им был многократно измерен один и тот же угол. Результаты оказались следующими: 39˚17.4′; 39˚16.8′; 39˚16.6′; 39˚16.2′; 39˚15.5′; 39˚15.8′; 39˚16.3′; 39˚16.2′. Тот же угол был измерен высокоточным угломерным прибором, что дало результат 39˚16’42». Приняв это значение за точное, вычислить среднюю квадратическую погрешность, определить надёжность СКП, найти предельную погрешность.

Решение:

№ измерения	Результаты измерений, l	Погрешности ∆ = l-X	∆2
1	39˚17.4′	+0.7′	0.49
2	16.8	+0.1	0.01
3	16.6	-0.1	0.01
4	16.2	-0.5	0.25
5	15.5	-1.2	1.44
6	15.8	-0.9	0.81
7	16.3	-0.4	0.16
8	16.2	-0.5	0.25
Сумма			3.42

39˚16’42» = 39˚16.7′

Средняя квадратическая погрешность: m = √([∆²]/n),

m = √(3.42/8) = 0.65′.

Оценка надёжности СКП: m_m = m / √2n,

m_m = 0.65 / √16=0.1625≈0.16′.

Предельная погрешность: ∆_пр = 3×m,

∆_пр = 3×0.65′ = 1.96′

Контрольная задача 2

Дана совокупность невязок треугольников триангуляции объёмом 50 единиц. Считая невязки истинными погрешностями, вычислить среднюю квадратическую погрешность и произвести надёжность СКП, вычислить предельную погрешность. На данной совокупности проверить свойство случайных погрешностей:

Lim[∆] / n =0, для чего вычислить W = [W] / n.

N	W	N	W	N	W	N	W	N	W
1	+1,02	11	-1,72	21	-0,90	31	+2,80	41	-0,44
2	+0,41	12	+1,29	22	+1,22	32	-0,81	42	-0,28
3	+0,02	13	-1,81	23	-1,84	33	+1,04	43	-0,75
4	-1,88	14	-0,08	24	-0,44	34	+0,42	44	-0,80
5	-1,44	15	-0,50	25	+0,18	35	+0,68	45	-0,95
6	-0,25	16	-1,89	26	-0,08	36	+0,55	46	-0,58
7	+0,12	17	+0,72	27	-1,11	37	+0,22	47	+1,60
8	+0,22	18	+0,24	28	+2,51	38	+1,67	48	+1,85
9	-1,05	19	-0,13	29	-1,16	39	+0,11	49	+2,22
10	+0,56	20	+0,59	30	+1,65	40	+2,08	50	-2,59

Решение: